Καθυστέρηση στατικών πυλών CMOS
|
|
|
- Τάνις Κωνσταντόπουλος
- 9 χρόνια πριν
- Προβολές:
Transcript
1 Καθυστέρηση στατικών πυλών CMOS Πρόχειρες σημειώσεις Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Άνοιξη 2008 Παρόλο που οι εξισώσεις των ρευμάτων των MOS τρανζίστορ μας δίνουν πολύ ακριβείς εκτιμήσεις της καθυστέρησης μιας πύλης, η χρήση τους απαιτεί πολλές φορές μεγάλη ανάλυση η οποία δυσκολεύει τους υπολογισμούς και δεν επιτρέπει στο σχεδιαστή να έχει μια γρήγορη εκτίμηση της ταχύτητας λειτουργίας του κυκλώματος. Μόλις πολύ πρόσφατα έχουν αναπτυχθεί μέθοδοι οι οποίες επιτρέπουν τη αποτελεσματική εκτίμηση της καθυστέρησης μιας πύλης χρησιμοποιώντας μόνο μερικές τιμές των ρευμάτων που διαρρέεουν τα τρανζίστορ, χωρίς να απαιτείται η πλήρης ανάλυση των κυματομορφών των εισόδων και των εξόδων.η παρουσίαση των μεθόδων αυτών απαιτεί βαθύτερη γνώση της λειτουργίας των τρανζίστορ και ξεφεύγει από τα όρια του μαθήματος. Στην ενότητα αυτή θα περιγράψουμε πρακτικούς τρόπους εκτίμησης της καθυστέρηση των λογικών πυλών οι οποίοι αν και δεν είναι αρκετά ακριβείς, είναι ιδιαιτέρως χρήσιμοι για τη γρήγορη εκτίμηση της καθυστέρησης. Ουσιαστικά αυτό που κάνουμε είναι να μοντελοποιούμε κάθε τρανζίστορ τη στιγμή που άγει, κατά τη φάση υπολογισμού της πύλης, σαν μία αντίσταση η οποία εμφανίζεται μεταξύ του source και του drain. Επίσης, εμφανίζουμε και κάποιες από τις παρασιτικές χωρητικότητες του τρανζίστορ οι οποίες επηρεάζουν αρνητικά την καθυστέρηση των πυλών. Αρχικά ορίζουμε το NMOS τρανζίστορ με το έλαχιστο δυνατό μέγεθος (έστω μεγέθους 1) νά έχει αντίσταση R. Η αντίσταση R παίρνει στις περισσότερες των περιπτώσεων τιμές μεταξύ 10 και 13ΚΩ μm. Για την απλούστευση της ανάλυσης μας θεωρούμε πως όλα τα τρανζίστορ έχουν το ίδιο μήκος καναλιού L. Το μόνο μέγεθος που επιτρέπουμε να μεταβληθεί είναι το πλάτος του W του κάθε τρανζίστορ. Η αντίσταση του κάθε τρανζίστορ είναι αντιστρόφως ανάλογη του πλάτους του. 1
2 Έτσι το ΝΜΟS τρανζίστορ με μέγεθος 2 έμφανίζει αντίσταση ίση με R/2. Επίσης όπως μάθαμε η κινητικότητα των φορτισμένων σωματιδίων στα PMOS τρανζίστορ είναι μικρότερη από αυτή των NMOS τρανζίστορ. Έτσι τα PMOS τρανζίστορ εμφανίζουν μεγαλύτερη αντίσταση. Ο λόγος της κινητικότητας μεταξύ των NMOS και PMOS τρανζίστορ πέρνει τιμές μεταξύ 2 και 3. Επομένως, προκύπτει πως ένα PMOS τρανζίστορ μεγέθους 1 έχει αντίσταση 2R 3R. Στη συνέχεια, θεωρούμε πως η αντίσταση ενός PMOS τρανζίστορ είναι διπλάσια από αύτη του NMOS του ίδιου πλάτους. Επομένως, για να έχουν τα PMOS τρανζίστορ την ίδια αντίσταση με τα NMOS τρανζίστορ πρέπει να είναι διπλάσια σε μέγεθος. Κάθε τρανζίστορ εμφανίζει και μια χωρητικότητα μεταξύ όλων των ζευγών των ακροδεκτών του. Για την ανάλυση που κάνουμε αρκούν τρείς βασικές χωρητικότητες. Η μία εμφανίζεται στην πύλη του τρανζίστορ ενώ οι άλλες δύο αφορούν τις χωρητικότητες του source και του drain. Για ένα τρανζίστορ με μέγεθος 1 οι τιμές των χωρητικοτήτων είναι C g στo gate και C p στo source και στο drain αντίστοιχα. Συνήθως οι τιμές του C g και του C p είναι σχετικά κοντινές και κυμαίνονται μεταξύ 1.5 και 2 ff/μm. Στην πράξη οι τιμές της αντίστασης και της χωρητικότητας εξαρτώνται από την τιμή της τάσης τροφοδοσίας. Έτσι στην περίπτωση που η ανάλυση μας περιλαμβάνει διαφορετικές τάσεις τροφοδοσίας πρέπει να μεταβάλλουμε ανάλογα και τις τιμές των R, C g και C p που θα χρησιμοποιήσουμε. Αρχικά θα δείξουμε πως μοντελοποιούμε την καθυστέρηση του απλού αντιστροφέα. Παρατηρούμε πως το PMOS τρανζίστορ του αντιστροφέα έχει διπλάσιο μέγεθος από το αντίστοιχο NMOS τρανζίστορ. Αυτό συμβαίνει ώστε τόσο το μονοπατι από το Vdd στην έξοδο όσο και από την έξοδο στο Vdd να έχουν την ίδια αντίσταση. Η καθυστέρηση διάδοσης (υπολογισμού) του αντιστροφέα, όπως και κάθε πύλης, ορίζεται ως ο χρόνος που περνάει από τη στιγμή που η είσοδος βρίσκεται στην τιμή Vdd/2 έως τη στιγμή που η έξοδος είναι στην τιμή Vdd/2. Αυτό ισχύει και για τις δύο μεταβάσεις της εισόδου (Από 0 σε Vdd και από Vdd σε 0). 2
3 Θεωρούμε πως ο αντιστροφέας οδηγεί f αντιστροφείς του ίδιου μεγέθους. H συνολική χωρητικότητα που εμφανίζεται στην πύλη του αντιστροφέα είναι ίση με WCg + 2WCg. Επομένως, εφόσον η έξοδος του αντιστροφέα οδηγεί άλλους f αντιστροφείς τότε η χωρητικότητα φορτίου που εμφανίζεται στην έξοδο του είναι ίση με 3WC g f. Αντίστοιχα εξαιτίας των παρασιτικών χωρητικοτήτων που εμφανίζει η καταβώθρα των δύο τρανζίστορ εμφανίζεται στην έξοδο μια πρόσθετη χωρητικότητα ίση με WC p + 2WC p. Σημειώνουμε πως οι χωρητικότητες της πηγής των δύο τρανζίστορ δε συνεισφέρουν στην καθυστέρηση διάδοσης της πύλης εφόσον τα άκρα τους βρίσκονται σε σταθερό δυναμικό ανεξάρτητα της εισόδου και της εξόδου. Έχοντας υπολογίσει τη συνεισφορά των επόμενων σταδίων (f αντιστροφείς) και των παρασιτικών χωρητικοτήτων του ίδιου του αντιστροφέα στην έξοδο της πύλης μπορούμε να αναλύσουμε χωριστά την καθυστέρηση ανόδου και καθόδου της έξόδου του αντιστροφέα. 3
4 Η αντίσταση του NMOS τρανζίστορ είναι ίση με R/W ενώ αντίστοιχα η αντίσταση του PMOS τρανζίστορ είναι ίση με 2R/2W = R/W. Οι χωρητικότητες στην έξοδο της πύλης πρέπει να φορτιστούν (στην περίπτωση που η είσοδος κάνει μετάβαση από το λογικό 1 στο 0) είτε να εκφορτιστούν (όταν η είσοδος μεταβαίνει από το λογικό 0 στο 1) μέσω της αντίστασης του τρανζίστορ στην κάθε περίπτωση. Η χωρητικότητα στην είσοδο του αντιστροφέα (ακροδέκτης της πύλης του κάθε τρανζίστορ) δεν επηρεάζει την καθυστέρηση γιατί ούτε φορτίζεται ούτε αποφορτίζεται κατά τη διάρκεια της μετάβασης. Φυσικά, συμμετέχει στην καθυστέρηση του προηγούμενου σταδίου. Για τον υπολογισμό της καθυστέρησης θα χρησιμοποιήσουμε το μοντέλο του Elmore. Σύμφωνα με το μοντέλο αυτό για κάθε κόμβο υπολογίζω μια μερική καθυστέρηση η οποία είναι ίση με το άθροισμα όλων των αντιστάσεων μεταξύ του Vdd ή του Gnd (αρχή του μονοπατιού) πολλαπλασιασμένων με τη χωτητικότητα του κόμβου αυτού. Έτσι η συνολική καθυστέρηση είναι το άθροισμα όλων των μερικών καθυστέρησεων όλων των κόμβων που παρεμβάλονται μεταξύ της αρχής και του τέλους. Για παράδειγμα η καθυστέρηση από το In στο B και στο C φαίνονται στο σχήμα. Έτσι για την καθυστέρηση ανόδου (rise delay) του κυκλώματος έχουμε D rise = R/W (3WC p + 3fWC g ) = 3RC p + 3fC g To ίδιο ισχύει και για την καθυστέρηση καθόδου D fall. Η καθυστέρηση ανόδου και καθόδου του αντιστροφέα αποτελείται από δύο μέρη. Το πρώτο 3 R C p περιγράφει τη συνεισφορά του ίδιου του αντιστροφέα στην καθυστέρηση μέσω των παρασιτικών χωρητικοτήτων. Αντίστοιχα, το δεύτερο 3fC g αφορά στις πύλες (ή καλώδια) των επόμενων σταδίων που έχει να οδηγήσει η έξοδος του αντιστροφέα όταν αυτός συμμετέχει σε ένα μεγαλύτερο κύκλωμα. Παρατηρείστε ότι αν και τα τρανζίστορ του αντιστροφέα είναι W φορές μεγαλύτερα από το ελάχιστο δυνατό μέγεθος αυτό δεν εμφανίζεται στη σχέση της καθυστέρησης. Η καθυστέρηση είναι συνάρτηση μόνο της χωρητικότητας των πυλών του επόμενου σταδίου που οδηγεί ο αντιστροφέας και των παρασιτικών χωρητικοτήτων του. Για παράδειγμα η συνεισφορά των παρασιτικών χωρητικοτήτων είναι σταθερή και ίση με 3RC p ανεξάρτητα από το μέγεθος του αντιστροφέα (Στην πραγματικότητα οι τιμές αυτές μεταβάλλονται σε ένα βαθμό από το μέγεθος του αντιστροφέα. Η μεταβολή αυτή επηρεάζει ελάχιστα την ανάλυση στην πράξη όπου χρησιμοποιούμε λογικά μεγέθη πυλών.) 4
5 Στο δεύτερο παράδειγμα θα αναλύσουμε την καθυστέρηση μιας πύλης NOR. Στην περίπτωση αυτή θεωρούμε ότι η πύλη ΝΟR oδηγεί 4 αντιστροφείς με μέγεθος τρανζίστορ (4W (PMOS) / 2W (NMOS)) και μια σταθερή χωρητικότητα Cw μέσω της οποίας μοντελοποιούμε τη συνεισφορά ενός καλωδίου που ενώνει την έξοδο της πύλης NOR με τους αντιστροφείς. Στο σχήμα εμφανίζονται και όλες οι χωρητικότητες των τρανζιστορ της πύλης NOR. Παρατηρείστε πως για τον ενδιάμεσο κόμβο μεταξύ των δύο PMOS σε σειρά η παρασιτική χωρητικότητα (drain του ενός τρανζίστορ και source του άλλου) υπολογίζεται μόνο μια φορά και είναι ίση με 4WCp. Αντίστοιχα όλες οι υπόλοιπες παρασιτικές χωρητικότητες αθροίζονται στην έξοδο. Τα NMOS τρανζίστορ της πύλης NOR έχουν μέγεθος W και είναι τοποθετημένα παράλληλα στην έξοδο. Για να έχουμε μια μετάβαση της εξόδου από το λογικό 1 στο 0 αρκεί μία από τις 2 εισόδους να μεταβεί στο λογικό 1. Στην περίπτωση αυτή η έξοδος θα εκφορτιστεί μέσω μιας αντίστασης R/ W. Όταν και οι δύο είσοδοι μεταβούν στο 1 τότε και τα δύο NMOS τρανζίστορ θα άγουν οδηγώντας 5
6 στην ταχύτερη εκφόρτιση της εξόδου αφού θα προσφέρουν διπλάσιο ρεύμα (ή ισοδύναμα η έξοδος εκφορτίζεται μέσω μιας αντίστασης (R/W) // (R/W) = R/2W). Διαπιστώνουμε με αυτόν τον τρόπο ότι η καθυστέρηση διάδοσης των πυλών με περισσότερες από μία εισόδους η εξαρτάται από τις τιμές των σημάτων της εισόδου. Στη γενική περίιπτωση εμείς αναζητούμε τη χειρότερη δυνατή καθυστέρηση η οποία προκύπτει όταν μόνο το ένα από τα δύο παράλληλα τρανζίστορ άγει. Τότε ο χρόνος καθόδου που προκύπτει είναι ίσος με D fall = R/W (6WC p + 4 x 6WC g + C w ) = 6RC p + 24RC g + RC w /W Αντίθετα για να φορτιστεί η έξοδος απαιτείται και τα δύο PMOS τρανζίστορ να άγουν. Τότε η έξοδος εκφορτίζεται μέσω δύο αντιστάσεων 2R/4W, φορτίζοντας πρώτα και τη χωρητικότητα του ενδιάμεσου κόμβου. Drise = 2R/4W x 4WCp + (2R/4W + 2R/4W) x (6WC p + 4 x 6WC g + C w ) = 8RCp + 24RCg + RCw/W 6
7 Αν τα 2 PMOS τρανζίστορ είχαν μέγεθος 2W το καθένα, τότε, εφόσον είναι σε σειρά, η συνολική αντίσταση που θα εμφάνιζαν θα ήταν ίση με 2R/2W + 2R/2W = 2R/W η οποία είναι διπλάσια από τη ζητούμενη R/W. Για το λόγο αυτό τα τρανζίστορ έχουv μέγεθος 4W ώστε να μειώσουν τη συνολική αντίσταση τους στο μισό. Σε περίπτωση που θέλουμε να κάνουμε μία από τις μεταβάσεις (είτε άνοδος είτε κάθοδος) πιο γρήγορη από την άλλη μπορούμε αυθαίρετα να επιλέξουμε το λόγο μεταξύ των NMOS και των PMOS τρανζίστορ. Εξαιτίας του ενδιάμεσου κόμβου παρόλου που το δίκτυο ανόδου και καθόδου έχει την ίδια αντίσταση η καθυστέρηση ανόδου είναι χειρότερη. Σε γενικές γραμμές κατα το σχεδιασμό των πυλών προσπαθούμε να εξασφαλίσουμε ίσους χρόνους ανόδου και καθόδου. Έτσι για παράδειγμα, ο μικρότερος αντιστροφέας που μπορούμε να δημιουργήσουμε θα έχει μέγεθος 1 για το NMOS τρανζίστορ και 2 για το PMOS. Αντίστοιχα προκύπτουν τα ελάχιστα μεγέθη για διάφορα είδη πυλών όπως φαίνεται στο σχήμα. Βλέπουμε ότι η μικρότερη NAND πύλη που μπορούμε να έχουμε έχει μέγεθος 2 για τα PMOS τρανζίστορ. Έτσι η αντίσταση που θα εμφανιστεί στο μονοπάτι από το Vdd στο Gnd θα είναι 2R/2 = R που είναι και η ελάχιστη δυνατή. Αντίθετα, τα ΝMOS τρανζίστορ για να έχουν και αυτά αντίσταση R πρέπει να έχουν μέγεθος 2 εφόσον βρίσκονται συνδεδεμένα σε σειρά. Έτσι R/2 + R/2 = R. Έχοντας ορίσει τα ελάχιστα μεγέθη των πυλών με ίσους χρόνους ανόδου και καθόδου λέμε ότι μια πύλη έχει μέγεθος k όταν τα μεγέθη όλων των τρανζίστορ της μικρότερης δυνατής εκδοχής της πολλαπλασιάζονται επί k. 7
ΑΣΚΗΣΗ 7. ΘΕΜΑ 1ο MINORITY A B C. C out
 ΑΣΚΗΣΗ 7 ΘΕΜΑ 1ο MINORITY A B C C out S S C out C OUT = MAJ(A,B,C) = Majority(A,B,C) = 1 when at least 2 (majority) of A, B, and C are equal to 1. Opposite Minority MAJ(A,B,C) = AB + BC + AC (PMOS and
ΑΣΚΗΣΗ 7 ΘΕΜΑ 1ο MINORITY A B C C out S S C out C OUT = MAJ(A,B,C) = Majority(A,B,C) = 1 when at least 2 (majority) of A, B, and C are equal to 1. Opposite Minority MAJ(A,B,C) = AB + BC + AC (PMOS and
4/10/2008. Στατικές πύλες CMOS και πύλες με τρανζίστορ διέλευσης. Πραγματικά τρανζίστορ. Ψηφιακή λειτουργία. Κανόνες ψηφιακής λειτουργίας
 2 η διάλεξη 25 Σεπτεμβρίου Πραγματικά τρανζίστορ Στατικές πύλες CMOS και πύλες με τρανζίστορ διέλευσης Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Η τάση στο gate του τρανζίστορ
2 η διάλεξη 25 Σεπτεμβρίου Πραγματικά τρανζίστορ Στατικές πύλες CMOS και πύλες με τρανζίστορ διέλευσης Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Η τάση στο gate του τρανζίστορ
Εργαστηριακή άσκηση. Θεωρητικός και πρακτικός υπολογισμός καθυστερήσεων σε αναστροφείς CMOS VLSI
 Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ. Δρ. Δ. Λαμπάκης (9 η σειρά διαφανειών)
 ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (9 η σειρά διαφανειών) Διεργασίες Μικροηλεκτρονικής Τεχνολογίας, Οξείδωση, Διάχυση, Φωτολιθογραφία, Επιμετάλλωση, Εμφύτευση, Περιγραφή CMOS
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (9 η σειρά διαφανειών) Διεργασίες Μικροηλεκτρονικής Τεχνολογίας, Οξείδωση, Διάχυση, Φωτολιθογραφία, Επιμετάλλωση, Εμφύτευση, Περιγραφή CMOS
Μικροηλεκτρονική - VLSI
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 6.1: Συνδυαστική Λογική - Βασικές Πύλες Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 6.1: Συνδυαστική Λογική - Βασικές Πύλες Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών
Υ52 Σχεδίαση Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων. Δεληγιαννίδης Σταύρος Φυσικός, MsC in Microelectronic Design
 Υ52 Σχεδίαση Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων Δεληγιαννίδης Σταύρος Φυσικός, MsC in Microelectronic Design TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής Τ.Ε.
Υ52 Σχεδίαση Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων Δεληγιαννίδης Σταύρος Φυσικός, MsC in Microelectronic Design TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής Τ.Ε.
Καθυστέρηση αντιστροφέα και λογικών πυλών CMOS. Εισαγωγή στην Ηλεκτρονική
 Καθυστέρηση αντιστροφέα και λογικών πυλών MOS Εισαγωγή στην Ηλεκτρονική Ορισµοί καθυστέρησης λογικών πυλών MOS Καθυστερήσεις διάδοσης (propagaion delays) εισόδουεξόδου: Καθυστέρηση ανόδου ph : η διαφορά
Καθυστέρηση αντιστροφέα και λογικών πυλών MOS Εισαγωγή στην Ηλεκτρονική Ορισµοί καθυστέρησης λογικών πυλών MOS Καθυστερήσεις διάδοσης (propagaion delays) εισόδουεξόδου: Καθυστέρηση ανόδου ph : η διαφορά
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I
 Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I 2 η Εργαστηριακή Άσκηση Μελέτη των Παρασιτικών Χωρητικοτήτων και της Καθυστέρησης στα Κυκλώματα CMOS Άδειες Χρήσης Το παρόν υλικό διατίθεται με τους όρους της
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I 2 η Εργαστηριακή Άσκηση Μελέτη των Παρασιτικών Χωρητικοτήτων και της Καθυστέρησης στα Κυκλώματα CMOS Άδειες Χρήσης Το παρόν υλικό διατίθεται με τους όρους της
HY121-Ηλεκτρονικά Κυκλώματα
 HY121-Ηλεκτρονικά Κυκλώματα Συνοπτική παρουσίαση της δομής και λειτουργίας του MOS τρανζίστορ Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Η δομή του τρανζίστορ Όπως ξέρετε υπάρχουν
HY121-Ηλεκτρονικά Κυκλώματα Συνοπτική παρουσίαση της δομής και λειτουργίας του MOS τρανζίστορ Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Η δομή του τρανζίστορ Όπως ξέρετε υπάρχουν
Εργαστηριακή άσκηση. Θεωρητικός και πρακτικός υπολογισμός καθυστερήσεων σε λογικά δίκτυα πολλών σταδίων
 Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
Υ52 Σχεδίαση Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων 6: Ταχύτητα Κατανάλωση Ανοχή στον Θόρυβο
 Υ52 Σχεδίαση Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων 6: Ταχύτητα Κατανάλωση Ανοχή στον Θόρυβο Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Εισαγωγή
Υ52 Σχεδίαση Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων 6: Ταχύτητα Κατανάλωση Ανοχή στον Θόρυβο Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Εισαγωγή
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΜΙΚΡΟΗΛΕΚΤΡΟΝΙΚΗ - VLSI Ενότητα: Συνδιαστικά κυκλώματα, βασικές στατικές λογικές πύλες, σύνθετες και δυναμικές πύλες Κυριάκης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΜΙΚΡΟΗΛΕΚΤΡΟΝΙΚΗ - VLSI Ενότητα: Συνδιαστικά κυκλώματα, βασικές στατικές λογικές πύλες, σύνθετες και δυναμικές πύλες Κυριάκης
7 η διάλεξη Ακολουθιακά Κυκλώματα
 7 η διάλεξη Ακολουθιακά Κυκλώματα 1 2 3 4 5 6 7 Παραπάνω βλέπουμε ακολουθιακό κύκλωμα σχεδιασμένο με μανταλωτές διαφορετικής φάσης. Παρατηρούμε ότι συνδυαστική λογική μπορεί να προστεθεί μεταξύ και των
7 η διάλεξη Ακολουθιακά Κυκλώματα 1 2 3 4 5 6 7 Παραπάνω βλέπουμε ακολουθιακό κύκλωμα σχεδιασμένο με μανταλωτές διαφορετικής φάσης. Παρατηρούμε ότι συνδυαστική λογική μπορεί να προστεθεί μεταξύ και των
ΑΣΚΗΣΗ 2 η N-MOS ΚΑΙ P-MOS TRANSISTOR ΩΣ ΔΙΑΚΟΠΤΗΣ
 ΑΣΚΗΣΗ 2 η N-MOS ΚΑΙ P-MOS TRANSISTOR ΩΣ ΔΙΑΚΟΠΤΗΣ ΘΕΩΡΙΑ 1. Εργαλεία εξομοίωσης, SPICE, αρχεία περιγραφής κυκλωμάτων (netlist) (Παρ. 3.4, σελ 152-155) 2. To transistor ως διακόπτης, πύλη διέλευσης. (Παρ
ΑΣΚΗΣΗ 2 η N-MOS ΚΑΙ P-MOS TRANSISTOR ΩΣ ΔΙΑΚΟΠΤΗΣ ΘΕΩΡΙΑ 1. Εργαλεία εξομοίωσης, SPICE, αρχεία περιγραφής κυκλωμάτων (netlist) (Παρ. 3.4, σελ 152-155) 2. To transistor ως διακόπτης, πύλη διέλευσης. (Παρ
Αποκωδικοποιητές Μνημών
 Αποκωδικοποιητές Μνημών Φθινόπωρο 2008 Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Γ. Δημητρακόπουλος ΗΥ422 1 Η χρήση των αποκωδικοποιητών Η δομή της μνήμης (για λόγους πυκνότητας)
Αποκωδικοποιητές Μνημών Φθινόπωρο 2008 Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Γ. Δημητρακόπουλος ΗΥ422 1 Η χρήση των αποκωδικοποιητών Η δομή της μνήμης (για λόγους πυκνότητας)
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I
 Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα
4 η διάλεξη Καθυστέρηση Διασυνδέσεων Μοντέλο Elmore
 1 4 η διάλεξη Καθυστέρηση Διασυνδέσεων Μοντέλο Elmore 2 3 Εξετάζοντας αναλυτικά την φυσική υπόσταση μιας διασύνδεσης φαίνεται ότι διασύνδεει έναν αποστολέα του σήματος με έναν δέκτη μέσω επιμέρους τμημάτων
1 4 η διάλεξη Καθυστέρηση Διασυνδέσεων Μοντέλο Elmore 2 3 Εξετάζοντας αναλυτικά την φυσική υπόσταση μιας διασύνδεσης φαίνεται ότι διασύνδεει έναν αποστολέα του σήματος με έναν δέκτη μέσω επιμέρους τμημάτων
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I
 Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης
ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ
 ΣΧΕΔΙΑΣΗ ΨΗΦΙΑΚΩΝ ΟΛΟΚΛΗΡΩΜΕΝΩΝ ΚΥΚΛΩΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΑΣΚΗΣΗ 1η: ΜΕΛΕΤΗ ΤΟΥ MOSFET Σκοπός της άσκησης Στην άσκηση αυτή θα μελετήσουμε το τρανζίστορ τύπου MOSFET και τη λειτουργία
ΣΧΕΔΙΑΣΗ ΨΗΦΙΑΚΩΝ ΟΛΟΚΛΗΡΩΜΕΝΩΝ ΚΥΚΛΩΜΑΤΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΑΣΚΗΣΗ 1η: ΜΕΛΕΤΗ ΤΟΥ MOSFET Σκοπός της άσκησης Στην άσκηση αυτή θα μελετήσουμε το τρανζίστορ τύπου MOSFET και τη λειτουργία
Μνήμες RAM. Διάλεξη 12
 Μνήμες RAM Διάλεξη 12 Δομή της διάλεξης Εισαγωγή Κύτταρα Στατικής Μνήμης Κύτταρα Δυναμικής Μνήμης Αισθητήριοι Ενισχυτές Αποκωδικοποιητές Διευθύνσεων Ασκήσεις 2 Μνήμες RAM Εισαγωγή 3 Μνήμες RAM RAM: μνήμη
Μνήμες RAM Διάλεξη 12 Δομή της διάλεξης Εισαγωγή Κύτταρα Στατικής Μνήμης Κύτταρα Δυναμικής Μνήμης Αισθητήριοι Ενισχυτές Αποκωδικοποιητές Διευθύνσεων Ασκήσεις 2 Μνήμες RAM Εισαγωγή 3 Μνήμες RAM RAM: μνήμη
Κεφάλαιο 4 ο. Γ. Τσιατούχας. VLSI Systems and Computer Architecture Lab. Λογικός Φόρτος 2
 ΚΥΚΛΩΜΑΤΑ VLSI Πανεπιστήμιο Ιωαννίνων Λογικός Φόρτος Κεφάλαιο 4 ο Τμήμα Μηχανικών Η/Υ και Πληροφορικής Γ. Τσιατούχας ΚΥΚΛΩΜΑΤΑ VLSI Διάρθρωση. Μοντέλο γραμμικής καθυστέρησης. Λογικός και ηλεκτρικός φόρτος
ΚΥΚΛΩΜΑΤΑ VLSI Πανεπιστήμιο Ιωαννίνων Λογικός Φόρτος Κεφάλαιο 4 ο Τμήμα Μηχανικών Η/Υ και Πληροφορικής Γ. Τσιατούχας ΚΥΚΛΩΜΑΤΑ VLSI Διάρθρωση. Μοντέλο γραμμικής καθυστέρησης. Λογικός και ηλεκτρικός φόρτος
Φυσική σχεδίαση ολοκληρωμένων κυκλωμάτων
 Φυσική σχεδίαση ολοκληρωμένων κυκλωμάτων Βασικές έννοιες και τεχνικές Γιώργος Δημητρακόπουλος Δημοκριτειο Πανεπιστήμιο Θράκης Φθινόπωρο 2013 Ψηφιακά ολοκληρωμένα κυκλώματα 1 Τι χρειαζόμαστε για να φτιάξουμε
Φυσική σχεδίαση ολοκληρωμένων κυκλωμάτων Βασικές έννοιες και τεχνικές Γιώργος Δημητρακόπουλος Δημοκριτειο Πανεπιστήμιο Θράκης Φθινόπωρο 2013 Ψηφιακά ολοκληρωμένα κυκλώματα 1 Τι χρειαζόμαστε για να φτιάξουμε
 Φόρτιση πυκνωτή μέσω αντίστασης Εάν αρχικά, η τάση στο άκρο του πυκνωτή είναι 0, τότε V DD V(t) για την τάση σε χρόνο t, V(t) θα έχουμε V t ( t ) (1 e ) V DD Αποφόρτιση πυκνωτή Εάν αρχικά, η τάση στο άκρο
Φόρτιση πυκνωτή μέσω αντίστασης Εάν αρχικά, η τάση στο άκρο του πυκνωτή είναι 0, τότε V DD V(t) για την τάση σε χρόνο t, V(t) θα έχουμε V t ( t ) (1 e ) V DD Αποφόρτιση πυκνωτή Εάν αρχικά, η τάση στο άκρο
Ισοδύναμα Κυκλώματα και Μετασχηματισμοί
 Πανεπιστήμιο Κρήτης Τμήμα Επιστήμης Υπολογιστών ΗΥ-121: Ηλεκτρονικά Κυκλώματα Γιώργος Δημητρακόπουλος Άνοιξη 2008 Ισοδύναμα Κυκλώματα και Μετασχηματισμοί Ισοδύναμα Κυκλώματα Thevenin-Norton Θεωρούμε ένα
Πανεπιστήμιο Κρήτης Τμήμα Επιστήμης Υπολογιστών ΗΥ-121: Ηλεκτρονικά Κυκλώματα Γιώργος Δημητρακόπουλος Άνοιξη 2008 Ισοδύναμα Κυκλώματα και Μετασχηματισμοί Ισοδύναμα Κυκλώματα Thevenin-Norton Θεωρούμε ένα
Βασικές CMOS Λογικές οικογένειες (CMOS και Domino)
 Βασικές CMOS Λογικές οικογένειες (CMOS και Domino) CMOS Κάθε λογική πύλη αποτελείται από δύο τμήματα p-mos δικτύωμα, τοποθετείται μεταξύ τροφοδοσίας και εξόδου. Όταν είναι ενεργό φορτίζει την έξοδο στην
Βασικές CMOS Λογικές οικογένειες (CMOS και Domino) CMOS Κάθε λογική πύλη αποτελείται από δύο τμήματα p-mos δικτύωμα, τοποθετείται μεταξύ τροφοδοσίας και εξόδου. Όταν είναι ενεργό φορτίζει την έξοδο στην
Ανάλυση Ηλεκτρικών Κυκλωμάτων με Αντιστάσεις
 Πανεπιστήμιο Κρήτης Τμήμα Επιστήμης Υπολογιστών ΗΥ-2: Ηλεκτρονικά Κυκλώματα Γιώργος Δημητρακόπουλος Άνοιξη 2008 Ανάλυση Ηλεκτρικών Κυκλωμάτων με Αντιστάσεις H ανάλυση ενός κυκλώματος με αντιστάσεις στη
Πανεπιστήμιο Κρήτης Τμήμα Επιστήμης Υπολογιστών ΗΥ-2: Ηλεκτρονικά Κυκλώματα Γιώργος Δημητρακόπουλος Άνοιξη 2008 Ανάλυση Ηλεκτρικών Κυκλωμάτων με Αντιστάσεις H ανάλυση ενός κυκλώματος με αντιστάσεις στη
Φυσική για Μηχανικούς
 Εικόνα: Επισκευή μιας πλακέτας κυκλωμάτων ενός υπολογιστή. Χρησιμοποιούμε καθημερινά αντικείμενα που περιέχουν ηλεκτρικά κυκλώματα, συμπεριλαμβανομένων και κάποιων με πολύ μικρότερες πλακέτες από την εικονιζόμενη.
Εικόνα: Επισκευή μιας πλακέτας κυκλωμάτων ενός υπολογιστή. Χρησιμοποιούμε καθημερινά αντικείμενα που περιέχουν ηλεκτρικά κυκλώματα, συμπεριλαμβανομένων και κάποιων με πολύ μικρότερες πλακέτες από την εικονιζόμενη.
ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΗΣ
 ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΗΣ ΔΙΟΔΟΣ (Μάθημα 4 ο 5 ο 6 ο 7 ο ) 1/12 4 o εργαστήριο Ιδανική δίοδος n Συμβολισμός της διόδου n 2/12 4 o εργαστήριο Στατική χαρακτηριστική διόδου Άνοδος (+) Κάθοδος () Αν στην ιδανική
ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΟΝΙΚΗΣ ΔΙΟΔΟΣ (Μάθημα 4 ο 5 ο 6 ο 7 ο ) 1/12 4 o εργαστήριο Ιδανική δίοδος n Συμβολισμός της διόδου n 2/12 4 o εργαστήριο Στατική χαρακτηριστική διόδου Άνοδος (+) Κάθοδος () Αν στην ιδανική
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I 4 η Εργαστηριακή Άσκηση
 Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I 4 η Εργαστηριακή Άσκηση Σχεδιασμός Πολύπλοκων Κυκλωμάτων CMOS και Μελέτη της Καθυστέρησης Εξόδου (Critical Path Delay) Άδειες Χρήσης Το παρόν υλικό διατίθεται
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I 4 η Εργαστηριακή Άσκηση Σχεδιασμός Πολύπλοκων Κυκλωμάτων CMOS και Μελέτη της Καθυστέρησης Εξόδου (Critical Path Delay) Άδειες Χρήσης Το παρόν υλικό διατίθεται
ΑΣΚΗΣΗ 3 η Ο ΑΝΤΙΣΤΡΟΦΕΑΣ CMOS
 ΑΣΚΗΣΗ 3 η Ο ΑΝΤΙΣΤΡΟΦΕΑΣ CMOS ΘΕΩΡΙΑ Οι ασκήσεις 3 και 4 αφορούν τον αντιστροφέα CMOS, ο οποίος είναι η απλούστερη αλ α ταυτόχρονα και σημαντικότερη πύλη για την κατανόηση της λειτουργίας των Ολοκληρωμένων
ΑΣΚΗΣΗ 3 η Ο ΑΝΤΙΣΤΡΟΦΕΑΣ CMOS ΘΕΩΡΙΑ Οι ασκήσεις 3 και 4 αφορούν τον αντιστροφέα CMOS, ο οποίος είναι η απλούστερη αλ α ταυτόχρονα και σημαντικότερη πύλη για την κατανόηση της λειτουργίας των Ολοκληρωμένων
Πολυσύνθετες πύλες. Διάλεξη 11
 Πολυσύνθετες πύλες NMOS και CMOS Διάλεξη 11 Δομή της διάλεξης Εισαγωγή ΗσύνθετηλογικήNMOS ΗσύνθετηλογικήCMOS Η πύλη μετάδοσης CMOS Ασκήσεις 2 Πολυσύνθετες πύλες NMOS και CMOS Εισαγωγή 3 Εισαγωγή Στη λογική
Πολυσύνθετες πύλες NMOS και CMOS Διάλεξη 11 Δομή της διάλεξης Εισαγωγή ΗσύνθετηλογικήNMOS ΗσύνθετηλογικήCMOS Η πύλη μετάδοσης CMOS Ασκήσεις 2 Πολυσύνθετες πύλες NMOS και CMOS Εισαγωγή 3 Εισαγωγή Στη λογική
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ. Δρ. Δ. Λαμπάκης (10 η σειρά διαφανειών)
 ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (10 η σειρά διαφανειών) Σχεδιασμός και Προσομοίωση Βασικών Κυκλωμάτων Τεχνολογίας CMOS Με βάση το εργαλείο σχεδιασμού Microwind Σκοπός: η
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (10 η σειρά διαφανειών) Σχεδιασμός και Προσομοίωση Βασικών Κυκλωμάτων Τεχνολογίας CMOS Με βάση το εργαλείο σχεδιασμού Microwind Σκοπός: η
«Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο
 ΤΕΙ Δυτικής Ελλάδας Τμήμα Μηχανικών Πληροφορικής ΤΕ Εργαστήριο Σχεδίασης Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων «Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο 2016-2017 Διάλεξη 2 η :
ΤΕΙ Δυτικής Ελλάδας Τμήμα Μηχανικών Πληροφορικής ΤΕ Εργαστήριο Σχεδίασης Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων «Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο 2016-2017 Διάλεξη 2 η :
10o ΕΡΓΑΣΤΗΡΙΟ Στοιχεία Χωροθεσίας (Layout) CMOS
 10o ΕΡΓΑΣΤΗΡΙΟ Στοιχεία Χωροθεσίας (Layout) CMOS Εισαγωγή Θα ξεκινήσουμε σχεδιάζοντας της χωροθεσία μεμονωμένων διατάξεων Θα σχεδιάσουμε τα διάφορα επίπεδα της διάταξης (του τρανζίστορ). Τα ΟΚ κατασκευάζονται
10o ΕΡΓΑΣΤΗΡΙΟ Στοιχεία Χωροθεσίας (Layout) CMOS Εισαγωγή Θα ξεκινήσουμε σχεδιάζοντας της χωροθεσία μεμονωμένων διατάξεων Θα σχεδιάσουμε τα διάφορα επίπεδα της διάταξης (του τρανζίστορ). Τα ΟΚ κατασκευάζονται
Φυσική για Μηχανικούς
 Εικόνα: Επισκευή μιας πλακέτας κυκλωμάτων ενός υπολογιστή. Χρησιμοποιούμε καθημερινά αντικείμενα που περιέχουν ηλεκτρικά κυκλώματα, συμπεριλαμβανομένων και κάποιων με πολύ μικρότερες πλακέτες από την εικονιζόμενη.
Εικόνα: Επισκευή μιας πλακέτας κυκλωμάτων ενός υπολογιστή. Χρησιμοποιούμε καθημερινά αντικείμενα που περιέχουν ηλεκτρικά κυκλώματα, συμπεριλαμβανομένων και κάποιων με πολύ μικρότερες πλακέτες από την εικονιζόμενη.
ΘΕΜΑ 1 ο (3 μονάδες):
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΠΑΤΡΑΣ 9/0/00 ΘΕΜΑ ο ( μονάδες): Για τον ενισχυτή του παρακάτω σχήματος δίνονται: 0, 0.7, kω, 0 kω, Ε kω, L kω, β fe 00, e kω. (α) Να προσδιορίσετε τις τιμές των αντιστάσεων,
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΠΑΤΡΑΣ 9/0/00 ΘΕΜΑ ο ( μονάδες): Για τον ενισχυτή του παρακάτω σχήματος δίνονται: 0, 0.7, kω, 0 kω, Ε kω, L kω, β fe 00, e kω. (α) Να προσδιορίσετε τις τιμές των αντιστάσεων,
ΗΥ-121: Ηλεκτρονικά Κυκλώματα Γιώργος Δημητρακόπουλος. Βασικές Αρχές Ηλεκτρικών Κυκλωμάτων
 Πανεπιστήμιο Κρήτης Τμήμα Επιστήμης Υπολογιστών ΗΥ-121: Ηλεκτρονικά Κυκλώματα Γιώργος Δημητρακόπουλος Άνοιξη 2008 Βασικές Αρχές Ηλεκτρικών Κυκλωμάτων Ηλεκτρικό ρεύμα Το ρεύμα είναι αποτέλεσμα της κίνησης
Πανεπιστήμιο Κρήτης Τμήμα Επιστήμης Υπολογιστών ΗΥ-121: Ηλεκτρονικά Κυκλώματα Γιώργος Δημητρακόπουλος Άνοιξη 2008 Βασικές Αρχές Ηλεκτρικών Κυκλωμάτων Ηλεκτρικό ρεύμα Το ρεύμα είναι αποτέλεσμα της κίνησης
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Εργαστήριο Ηλεκτρονικής. Ψηφιακά Ηλεκτρονικά. Οικογένειες Ολοκληρωμένων Κυκλωμάτων Ψηφιακής Λογικής
 Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Οικογένειες Ολοκληρωμένων Κυκλωμάτων Ψηφιακής Λογικής Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Περιεχόμενα Βασικά ηλεκτρικά χαρακτηριστικά
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Οικογένειες Ολοκληρωμένων Κυκλωμάτων Ψηφιακής Λογικής Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Περιεχόμενα Βασικά ηλεκτρικά χαρακτηριστικά
ΗΜΥ-210: Λογικός Σχεδιασμός Εαρινό Εξάμηνο Κυκλώματα CMOS. Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 ΗΜΥ-210: Λογικός Σχεδιασμός Εαρινό Εξάμηνο 2005 Κυκλώματα CMOS Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Κυκλώματα CMOS Περίληψη Τρανζίστορ και μοντέλα διακόπτη ίκτυα CMOS
ΗΜΥ-210: Λογικός Σχεδιασμός Εαρινό Εξάμηνο 2005 Κυκλώματα CMOS Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Κυκλώματα CMOS Περίληψη Τρανζίστορ και μοντέλα διακόπτη ίκτυα CMOS
Εργαστηριακή άσκηση. Κανόνες σχεδίασης και κατασκευαστικές λεπτομέρειες στη σχεδίασης μασκών (layout) και προσομοίωσης κυκλώματος VLSI
 Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΠΑΤΡΑΣ 21/01/2011 ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΠΑΤΡΑΣ /0/0 ΘΕΜΑ ο (5 μονάδες) Για τον ενισχυτή του παρακάτω σχήματος δίνονται: 0 Ω, Ε kω, Β 00 kω, 4 kω, L kω, e 5 kω και 00 (α) Να προσδιορίσετε την ενίσχυση τάσης (A
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΠΑΤΡΑΣ /0/0 ΘΕΜΑ ο (5 μονάδες) Για τον ενισχυτή του παρακάτω σχήματος δίνονται: 0 Ω, Ε kω, Β 00 kω, 4 kω, L kω, e 5 kω και 00 (α) Να προσδιορίσετε την ενίσχυση τάσης (A
Ο πυκνωτής είναι μια διάταξη αποθήκευσης ηλεκτρικού φορτίου, επομένως και ηλεκτρικής ενέργειας.
 ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Ο πυκνωτής Ο πυκνωτής είναι μια διάταξη αποθήκευσης ηλεκτρικού φορτίου, επομένως και ηλεκτρικής ενέργειας. Η απλούστερη μορφή πυκνωτή είναι ο επίπεδος πυκνωτής, ο οποίος
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Ο πυκνωτής Ο πυκνωτής είναι μια διάταξη αποθήκευσης ηλεκτρικού φορτίου, επομένως και ηλεκτρικής ενέργειας. Η απλούστερη μορφή πυκνωτή είναι ο επίπεδος πυκνωτής, ο οποίος
Κεφάλαιο 11. Κυκλώματα Χρονισμού
 Κεφάλαιο 11. Κυκλώματα Χρονισμού Σύνοψη Στο κεφάλαιο αυτό αναλύεται η λειτουργία των κυκλωμάτων χρονισμού. Τα κυκλώματα αυτά παρουσιάζουν πολύ μεγάλο πρακτικό ενδιαφέρον και απαιτείται να λειτουργούν με
Κεφάλαιο 11. Κυκλώματα Χρονισμού Σύνοψη Στο κεφάλαιο αυτό αναλύεται η λειτουργία των κυκλωμάτων χρονισμού. Τα κυκλώματα αυτά παρουσιάζουν πολύ μεγάλο πρακτικό ενδιαφέρον και απαιτείται να λειτουργούν με
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α ΗΜΕΡΟΜΗΝΙΑ: ΑΡΧΩΝ ΜΑΡΚΟΣ-ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ-KΥΡΙΑΚΑΚΗΣ ΓΙΩΡΓΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α ΗΜΕΡΟΜΗΝΙΑ: 19-10-2014 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ-ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ-KΥΡΙΑΚΑΚΗΣ ΓΙΩΡΓΟΣ ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α ΗΜΕΡΟΜΗΝΙΑ: 19-10-2014 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ-ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ-KΥΡΙΑΚΑΚΗΣ ΓΙΩΡΓΟΣ ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4
Επιπλέον, για ευκολία στις πράξεις ορίζουμε τις παρακάτω μεταβλητές
 Αναστροφέας με φορτίο Enhancement OSFE Η απλούστερη υλοποίηση OSFE αναστροφέα με ενεργό φορτίο χρησιμοποιεί δύο N-OSFES. Στην ανάλυση που ακολουθεί θα διαπιστώσουμε ότι η χαρακτηριστική μεταφοράς απέχει
Αναστροφέας με φορτίο Enhancement OSFE Η απλούστερη υλοποίηση OSFE αναστροφέα με ενεργό φορτίο χρησιμοποιεί δύο N-OSFES. Στην ανάλυση που ακολουθεί θα διαπιστώσουμε ότι η χαρακτηριστική μεταφοράς απέχει
α) = β) Α 1 = γ) δ) Μονάδες 5
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: 19-10-2014 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ-ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ-ΚΥΡΙΑΚΑΚΗΣ ΓΙΩΡΓΟΣ ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4 να γράψετε
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: 19-10-2014 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ-ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ-ΚΥΡΙΑΚΑΚΗΣ ΓΙΩΡΓΟΣ ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4 να γράψετε
4.2 Αναπαράσταση δυαδικών τιμών στα ψηφιακά κυκλώματα
 ΚΕΦΑΛΑΙΟ 4 ΤΕΧΝΟΛΟΓΙΕΣ ΥΛΟΠΟΙΗΣΗΣ 4.1 Εισαγωγή Για την υλοποίηση των λογικών πυλών χρησιμοποιήθηκαν αρχικά ηλεκτρονικές λυχνίες κενού και στη συνέχεια κρυσταλλοδίοδοι και διπολικά τρανζίστορ. Τα ολοκληρωμένα
ΚΕΦΑΛΑΙΟ 4 ΤΕΧΝΟΛΟΓΙΕΣ ΥΛΟΠΟΙΗΣΗΣ 4.1 Εισαγωγή Για την υλοποίηση των λογικών πυλών χρησιμοποιήθηκαν αρχικά ηλεκτρονικές λυχνίες κενού και στη συνέχεια κρυσταλλοδίοδοι και διπολικά τρανζίστορ. Τα ολοκληρωμένα
Μικροηλεκτρονική - VLSI
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 5: Αντιστροφέας CMOS Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 5: Αντιστροφέας CMOS Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες Χρήσης
Ψηφιακά Ηλεκτρονικά. Μάθηµα 5ο.. Λιούπης
 Ψηφιακά Ηλεκτρονικά Μάθηµα 5ο. Λιούπης Τεχνολογία CMOS Υλοποιεί την πλειοψηφία των µοντέρνων ψηφιακών κυκλωµάτων λογικές πύλες µνήµες επεξεργαστές άλλα σύνθετα κυκλώµατα Συνδυάζει συµπληρωµατικά pmos και
Ψηφιακά Ηλεκτρονικά Μάθηµα 5ο. Λιούπης Τεχνολογία CMOS Υλοποιεί την πλειοψηφία των µοντέρνων ψηφιακών κυκλωµάτων λογικές πύλες µνήµες επεξεργαστές άλλα σύνθετα κυκλώµατα Συνδυάζει συµπληρωµατικά pmos και
ΛΥΣΕΙΣ ΕΞΕΤΑΣΗΣ ΣΤΟ ΜΑΘΗΜΑ «ΗΛΕΚΤΡΟΝΙΚΑ ΙΙ» ΗΜΕΡΟΜΗΝΙΑ: 23/06/2016 ΜΟΝΟ ΓΙΑ ΤΟΥΣ ΕΠΙ ΠΤΥΧΙΩ ΦΟΙΤΗΤΕΣ
 ΛΥΣΕΙΣ ΕΞΕΤΑΣΗΣ ΣΤΟ ΜΑΘΗΜΑ «ΗΛΕΚΤΡΟΝΙΚΑ ΙΙ» ΗΜΕΡΟΜΗΝΙΑ: /6/6 ΘΕΜΑ ο (5 μονάδες Για τον ενισχυτή του παρακάτω σχήματος δίνονται: =, = 6 kω, = kω και = = Ε = = kω, ενώ για το τρανζίστορ δίνονται: = 78, β
ΛΥΣΕΙΣ ΕΞΕΤΑΣΗΣ ΣΤΟ ΜΑΘΗΜΑ «ΗΛΕΚΤΡΟΝΙΚΑ ΙΙ» ΗΜΕΡΟΜΗΝΙΑ: /6/6 ΘΕΜΑ ο (5 μονάδες Για τον ενισχυτή του παρακάτω σχήματος δίνονται: =, = 6 kω, = kω και = = Ε = = kω, ενώ για το τρανζίστορ δίνονται: = 78, β
ΛΥΣΕΙΣ ΕΞΕΤΑΣΗΣ ΣΤΟ ΜΑΘΗΜΑ «ΗΛΕΚΤΡΟΝΙΚΑ ΙΙ» ΗΜΕΡΟΜΗΝΙΑ: 26/01/2017
 ΤΕΙ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΔΙΔΑΣΚΩΝ: Λ ΜΠΙΣΔΟΥΝΗΣ ΛΥΣΕΙΣ ΕΞΕΤΑΣΗΣ ΣΤΟ ΜΑΘΗΜΑ «ΗΛΕΚΤΡΟΝΙΚΑ ΙΙ» ΗΜΕΡΟΜΗΝΙΑ: 6/0/07 ΘΕΜΑ ο ( μονάδες) Για τον ενισχυτή του παρακάτω σχήματος δίνονται:
ΤΕΙ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΔΙΔΑΣΚΩΝ: Λ ΜΠΙΣΔΟΥΝΗΣ ΛΥΣΕΙΣ ΕΞΕΤΑΣΗΣ ΣΤΟ ΜΑΘΗΜΑ «ΗΛΕΚΤΡΟΝΙΚΑ ΙΙ» ΗΜΕΡΟΜΗΝΙΑ: 6/0/07 ΘΕΜΑ ο ( μονάδες) Για τον ενισχυτή του παρακάτω σχήματος δίνονται:
Εργαστήριο Εισαγωγής στη Σχεδίαση Συστημάτων VLSI
 Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
Ε.Μ.Π. - ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΜΙΚΡΟΫΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΧΕΔΙΑΣΗ ΣΥΣΤΗΜΑΤΩΝ VLSI
Λογικά Κυκλώματα CMOS. Διάλεξη 5
 Λογικά Κυκλώματα CMOS Διάλεξη 5 Δομή της διάλεξης Εισαγωγή Η τεχνολογία αντιστροφέων CMOS Λειτουργία του κυκλώματος Χαρακτηριστική μεταφοράς τάσης Περιθώρια θορύβου Κατανάλωση ισχύος Οι πύλες CMOS NOR
Λογικά Κυκλώματα CMOS Διάλεξη 5 Δομή της διάλεξης Εισαγωγή Η τεχνολογία αντιστροφέων CMOS Λειτουργία του κυκλώματος Χαρακτηριστική μεταφοράς τάσης Περιθώρια θορύβου Κατανάλωση ισχύος Οι πύλες CMOS NOR
Κυκλώματα αποθήκευσης με ρολόι
 Κυκλώματα αποθήκευσης με ρολόι Latches και Flip-Flops Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης 1 Γιατί χρειαζόμαστε τα ρολόγια Συνδιαστική λογική Η έξοδος εξαρτάται μόνο
Κυκλώματα αποθήκευσης με ρολόι Latches και Flip-Flops Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης 1 Γιατί χρειαζόμαστε τα ρολόγια Συνδιαστική λογική Η έξοδος εξαρτάται μόνο
ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ ΠΡΟΣΠΑΘΕΙΑ ΣΑΣ ΚΙ 2014
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
Κατανάλωση ισχύος ψηφιακών κυκλωμάτων
 Κατανάλωση ισχύος ψηφιακών κυκλωμάτων Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Γ. Δημητρακόπουλος ΗΥ422 1 Δυναμική κατανάλωση ισχύος Σε κάθε κύκλο μετακινούμε το διακόπτη
Κατανάλωση ισχύος ψηφιακών κυκλωμάτων Γιώργος Δημητρακόπουλος Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Γ. Δημητρακόπουλος ΗΥ422 1 Δυναμική κατανάλωση ισχύος Σε κάθε κύκλο μετακινούμε το διακόπτη
1. Ιδανικό κύκλωμα LC εκτελεί ηλεκτρικές ταλαντώσεις και η χρονική εξίσωση του φορτίου του πυκνωτή
 Εισαγωγικές ασκήσεις στις ηλεκτρικές ταλαντώσεις 1. Ιδανικό κύκλωμα L εκτελεί ηλεκτρικές ταλαντώσεις και η χρονική εξίσωση του φορτίου του πυκνωτή δίνεται από τη σχέση q = 10 6 συν(10 ) (S.I.). Ο συντελεστής
Εισαγωγικές ασκήσεις στις ηλεκτρικές ταλαντώσεις 1. Ιδανικό κύκλωμα L εκτελεί ηλεκτρικές ταλαντώσεις και η χρονική εξίσωση του φορτίου του πυκνωτή δίνεται από τη σχέση q = 10 6 συν(10 ) (S.I.). Ο συντελεστής
Σχεδίαση CMOS Ψηφιακών Ολοκληρωμένων Κυκλωμάτων
 Σχεδίαση CMOS Ψηφιακών Ολοκληρωμένων Κυκλωμάτων Ενότητα: Ασκήσεις Αγγελική Αραπογιάννη Τμήμα Πληροφορικής και Τηλεπικοινωνιών Σελίδα 2 1. Άσκηση 1... 5 2. Άσκηση 2... 5 3. Άσκηση 3... 7 4. Άσκηση 4...
Σχεδίαση CMOS Ψηφιακών Ολοκληρωμένων Κυκλωμάτων Ενότητα: Ασκήσεις Αγγελική Αραπογιάννη Τμήμα Πληροφορικής και Τηλεπικοινωνιών Σελίδα 2 1. Άσκηση 1... 5 2. Άσκηση 2... 5 3. Άσκηση 3... 7 4. Άσκηση 4...
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ. Δρ. Δ. Λαμπάκης (2 η σειρά διαφανειών)
 ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (2 η σειρά διαφανειών) Τα ψηφιακά ηλεκτρονικά κυκλώματα χωρίζονται σε κατηγορίες ( λογικές οικογένειες ) ανάλογα με την τεχνολογία κατασκευής
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (2 η σειρά διαφανειών) Τα ψηφιακά ηλεκτρονικά κυκλώματα χωρίζονται σε κατηγορίες ( λογικές οικογένειες ) ανάλογα με την τεχνολογία κατασκευής
V Vin $N PULSE 1.8V p 0.1p 1n 2n M M1 $N 0002 $N 0001 Vout $N 0002 MpTSMC180 + L=180n + W=720n + AD=0.324p + AS=0.
 Εργασία Μικροηλεκτρονικής 2013-2014 Θέμα: Σχεδίαση και Ανάλυση CMOS Αντιστροφέα και CMOS Λογικών Κυκλωμάτων στο SPICE Ονοματεπώνυμο: Αλέξανδρος Γεώργιος Μουντογιαννάκης Σχολή: Τμήμα Επιστήμης Υπολογιστών
Εργασία Μικροηλεκτρονικής 2013-2014 Θέμα: Σχεδίαση και Ανάλυση CMOS Αντιστροφέα και CMOS Λογικών Κυκλωμάτων στο SPICE Ονοματεπώνυμο: Αλέξανδρος Γεώργιος Μουντογιαννάκης Σχολή: Τμήμα Επιστήμης Υπολογιστών
Το χρονικό διάστημα μέσα σε μια περίοδο που η ενέργεια του μαγνητικού πεδίου αυξάνεται ισούται με:
 Κυκλώματα, Επαναληπτικό ΤΕΣΤ. ΘΕΜΑ Α. Στο κύκλωμα του σχήματος, ο πυκνωτής το χρονική στιγμή =0 που κλείνουμε το διακόπτη φέρει φορτίο q=q. Α. H ενέργεια του ηλεκτρικού πεδίου του πυκνωτή είναι ίσος με
Κυκλώματα, Επαναληπτικό ΤΕΣΤ. ΘΕΜΑ Α. Στο κύκλωμα του σχήματος, ο πυκνωτής το χρονική στιγμή =0 που κλείνουμε το διακόπτη φέρει φορτίο q=q. Α. H ενέργεια του ηλεκτρικού πεδίου του πυκνωτή είναι ίσος με
Κεφάλαιο Η6. Κυκλώματα συνεχούς ρεύματος
 Κεφάλαιο Η6 Κυκλώματα συνεχούς ρεύματος Ανάλυση κυκλωμάτων Τα απλά ηλεκτρικά κυκλώματα μπορεί να περιέχουν μπαταρίες, αντιστάτες, και πυκνωτές σε διάφορες συνδεσμολογίες. Κάποια κυκλώματα μπορούμε να τα
Κεφάλαιο Η6 Κυκλώματα συνεχούς ρεύματος Ανάλυση κυκλωμάτων Τα απλά ηλεκτρικά κυκλώματα μπορεί να περιέχουν μπαταρίες, αντιστάτες, και πυκνωτές σε διάφορες συνδεσμολογίες. Κάποια κυκλώματα μπορούμε να τα
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ. Δρ. Δ. Λαμπάκης (8 η σειρά διαφανειών)
 ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (8 η σειρά διαφανειών) Τα μοντέρνα ψηφιακά κυκλώματα (λογικές πύλες, μνήμες, επεξεργαστές και άλλα σύνθετα κυκλώματα) υλοποιούνται σήμερα
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (8 η σειρά διαφανειών) Τα μοντέρνα ψηφιακά κυκλώματα (λογικές πύλες, μνήμες, επεξεργαστές και άλλα σύνθετα κυκλώματα) υλοποιούνται σήμερα
Κεφάλαιο 4 o και 6 ο. Γ. Τσιατούχας. VLSI Systems and Computer Architecture Lab. Καθυστέρηση ιάδοσης Σήματος 2
 ΚΥΚΛΩΜΑΤΑ VSI Πανεπιστήμιο Ιωαννίνων Καθυστέρηση Διάδοσης Σήματος Κεφάλαιο 4 o και 6 ο Τμήμα Μηχανικών Η/Υ και Πληροφορικής Γ. Τσιατούχας ΚΥΚΛΩΜΑΤΑ VSI Διάρθρωση VSI Sysems ad omuer rchiecure ab. Παρασιτικές
ΚΥΚΛΩΜΑΤΑ VSI Πανεπιστήμιο Ιωαννίνων Καθυστέρηση Διάδοσης Σήματος Κεφάλαιο 4 o και 6 ο Τμήμα Μηχανικών Η/Υ και Πληροφορικής Γ. Τσιατούχας ΚΥΚΛΩΜΑΤΑ VSI Διάρθρωση VSI Sysems ad omuer rchiecure ab. Παρασιτικές
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I 3 η Εργαστηριακή Άσκηση
 Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I 3 η Εργαστηριακή Άσκηση Μελέτη της Κατανάλωσης Ενέργειας και Φυσικός Σχεδιασμός Πυλών CMOS Πολύπλοκης Λογικής Άδειες Χρήσης Το παρόν υλικό διατίθεται με τους
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I 3 η Εργαστηριακή Άσκηση Μελέτη της Κατανάλωσης Ενέργειας και Φυσικός Σχεδιασμός Πυλών CMOS Πολύπλοκης Λογικής Άδειες Χρήσης Το παρόν υλικό διατίθεται με τους
3.1 Η δίοδος στο κύκλωμα. Στατική και δυναμική χαρακτηριστική
 1 3. Κυκλώματα διόδων 3.1 Η δίοδος στο κύκλωμα. Στατική και δυναμική χαρακτηριστική Στην πράξη η δίοδος προσεγγίζεται με τμηματική γραμμικοποίηση, όπως στο σχήμα 3-1, όπου η δυναμική αντίσταση της διόδου
1 3. Κυκλώματα διόδων 3.1 Η δίοδος στο κύκλωμα. Στατική και δυναμική χαρακτηριστική Στην πράξη η δίοδος προσεγγίζεται με τμηματική γραμμικοποίηση, όπως στο σχήμα 3-1, όπου η δυναμική αντίσταση της διόδου
Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άδεια
 Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άδεια χρήσης άλλου τύπου, αυτή πρέπει να αναφέρεται ρητώς. 4.1
Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άδεια χρήσης άλλου τύπου, αυτή πρέπει να αναφέρεται ρητώς. 4.1
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Εργαστήριο Ηλεκτρονικής. Ψηφιακά Ηλεκτρονικά. Δίοδοι, BJT και MOSFET ως Διακόπτες 2
 Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Δίοδοι, BJT και MOSFET ως Διακόπτες Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Ιδανικός διακόπτης ΙΔΑΝΙΚΟΣ ΔΙΑΚΟΠΤΗΣ ΠΡΑΓΜΑΤΙΚΟΣ ΔΙΑΚΟΠΤΗΣ
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Δίοδοι, BJT και MOSFET ως Διακόπτες Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Ιδανικός διακόπτης ΙΔΑΝΙΚΟΣ ΔΙΑΚΟΠΤΗΣ ΠΡΑΓΜΑΤΙΚΟΣ ΔΙΑΚΟΠΤΗΣ
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ. Δρ. Δ. Λαμπάκης (11 η σειρά διαφανειών)
 ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (11 η σειρά διαφανειών) Μελέτη των Παρασιτικών Χωρητικοτήτων και της Καθυστέρησης στα Κυκλώματα CMOS Με βάση το εργαλείο σχεδιασμού Microwind
ΣΧΕΔΙΑΣΗ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΗΛΕΚΤΡΟΝΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ Δρ. Δ. Λαμπάκης (11 η σειρά διαφανειών) Μελέτη των Παρασιτικών Χωρητικοτήτων και της Καθυστέρησης στα Κυκλώματα CMOS Με βάση το εργαλείο σχεδιασμού Microwind
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΠΑΤΡΑΣ 06/02/2009 ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ
 ΘΕΜΑ ο (.5 μονάδες): Για τον ενισχυτή του παρακάτω σχήματος δίνονται: V 0V, V E 0.7 V, kω, 00 kω, kω, 0 kω, β h e 00, h e.5 kω. (α) Να προσδιορίσετε το σημείο λειτουργίας Q (I, V E ) του τρανζίστορ. (β)
ΘΕΜΑ ο (.5 μονάδες): Για τον ενισχυτή του παρακάτω σχήματος δίνονται: V 0V, V E 0.7 V, kω, 00 kω, kω, 0 kω, β h e 00, h e.5 kω. (α) Να προσδιορίσετε το σημείο λειτουργίας Q (I, V E ) του τρανζίστορ. (β)
Ενότητα 3 ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ
 Ενότητα 3 ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ Γενικές Γραμμές Οικογένειες Ψηφιακής Λογικής Τάση τροφοδοσίας Λογικά επίπεδα - Περιθώριo θορύβου Χρόνος μετάβασης Καθυστέρηση διάδοσης Κατανάλωση ισχύος Γινόμενο
Ενότητα 3 ΨΗΦΙΑΚΑ ΟΛΟΚΛΗΡΩΜΕΝΑ ΚΥΚΛΩΜΑΤΑ Γενικές Γραμμές Οικογένειες Ψηφιακής Λογικής Τάση τροφοδοσίας Λογικά επίπεδα - Περιθώριo θορύβου Χρόνος μετάβασης Καθυστέρηση διάδοσης Κατανάλωση ισχύος Γινόμενο
Πόλωση των Τρανζίστορ
 Πόλωση των Τρανζίστορ Πόλωση λέμε την κατάλληλη συνεχή τάση που πρέπει να εφαρμόσουμε στο κύκλωμα που περιλαμβάνει κάποιο ηλεκτρονικό στοιχείο (π.χ τρανζίστορ), έτσι ώστε να εξασφαλίσουμε την ομαλή λειτουργία
Πόλωση των Τρανζίστορ Πόλωση λέμε την κατάλληλη συνεχή τάση που πρέπει να εφαρμόσουμε στο κύκλωμα που περιλαμβάνει κάποιο ηλεκτρονικό στοιχείο (π.χ τρανζίστορ), έτσι ώστε να εξασφαλίσουμε την ομαλή λειτουργία
Φυσική για Μηχανικούς
 Εικόνα: Επισκευή μιας πλακέτας κυκλωμάτων ενός υπολογιστή. Χρησιμοποιούμε καθημερινά αντικείμενα που περιέχουν ηλεκτρικά κυκλώματα, συμπεριλαμβανομένων και κάποιων με πολύ μικρότερες πλακέτες από την εικονιζόμενη.
Εικόνα: Επισκευή μιας πλακέτας κυκλωμάτων ενός υπολογιστή. Χρησιμοποιούμε καθημερινά αντικείμενα που περιέχουν ηλεκτρικά κυκλώματα, συμπεριλαμβανομένων και κάποιων με πολύ μικρότερες πλακέτες από την εικονιζόμενη.
ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΙΚΩΝ ΜΕΤΡΗΣΕΩΝ Ι. Σημειώσεις Εργαστηριακών Ασκήσεων
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Τομέας Ηλεκτρικών Βιομηχανικών Διατάξεων και Συστημάτων Αποφάσεων ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΙΚΩΝ ΜΕΤΡΗΣΕΩΝ Ι Σημειώσεις Εργαστηριακών
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Τομέας Ηλεκτρικών Βιομηχανικών Διατάξεων και Συστημάτων Αποφάσεων ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΙΚΩΝ ΜΕΤΡΗΣΕΩΝ Ι Σημειώσεις Εργαστηριακών
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 6: Παθητικά στοιχεία αποθήκευσης ενέργειας Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 978-960-93-7110-0 κωδ.
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 6: Παθητικά στοιχεία αποθήκευσης ενέργειας Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 978-960-93-7110-0 κωδ.
Ψηφιακή Λογική και Σχεδίαση
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 26-7 Ψηφιακή Λογική και Σχεδίαση (σχεδίαση συνδυαστικών κυκλωμάτων) http://mixstef.github.io/courses/comparch/ Μ.Στεφανιδάκης Το τρανζίστορ
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 26-7 Ψηφιακή Λογική και Σχεδίαση (σχεδίαση συνδυαστικών κυκλωμάτων) http://mixstef.github.io/courses/comparch/ Μ.Στεφανιδάκης Το τρανζίστορ
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ. Το ιδανικό κύκλωμα LC του σχήματος εκτελεί αμείωτες ηλεκτρικές ταλαντώσεις, με περίοδο
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση 1. Ιδανικό κύκλωμα LC εκτελεί αμείωτες ηλεκτρικές ταλαντώσεις. Να αποδείξετε ότι η στιγμιαία τιμή i της έντασης του ρεύματος στο κύκλωμα δίνεται σε συνάρτηση με το στιγμιαίο
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση 1. Ιδανικό κύκλωμα LC εκτελεί αμείωτες ηλεκτρικές ταλαντώσεις. Να αποδείξετε ότι η στιγμιαία τιμή i της έντασης του ρεύματος στο κύκλωμα δίνεται σε συνάρτηση με το στιγμιαίο
Άσκηση 7 1. Άσκηση 7: Θεώρημα επαλληλίας
 Άσκηση 7 1 Άσκηση 7: Θεώρημα επαλληλίας α) Θεωρητικό μέρος Έχουμε ένα κύκλωμα με δύο διεγέρσεις, δύο πηγές τάσης (Σχήμα 1). Στο κύκλωμα αυτό αναπτύσσονται έξι αποκρίσεις, τρία ρεύματα και τρεις τάσεις,
Άσκηση 7 1 Άσκηση 7: Θεώρημα επαλληλίας α) Θεωρητικό μέρος Έχουμε ένα κύκλωμα με δύο διεγέρσεις, δύο πηγές τάσης (Σχήμα 1). Στο κύκλωμα αυτό αναπτύσσονται έξι αποκρίσεις, τρία ρεύματα και τρεις τάσεις,
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I
 Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I 1 η Εργαστηριακή Άσκηση Σχεδιασμός και Προσομοίωση Βασικών Κυκλωμάτων Τεχνολογίας CMOS Άδειες Χρήσης Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I 1 η Εργαστηριακή Άσκηση Σχεδιασμός και Προσομοίωση Βασικών Κυκλωμάτων Τεχνολογίας CMOS Άδειες Χρήσης Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης
ΠΑΡΑΔΕΙΓΜΑΤΑ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΜΕΤΑΓΩΓΗ ΚΥΚΛΩΜΑΤΩΝ
 ΜΕΤΑΓΩΓΗ ΑΠΟ ΤΟ ΕΝΑ ΚΥΚΛΩΜΑ LC ΣΤΟ ΑΛΛΟ. ΔΥΟ ΠΥΚΝΩΤΕΣ ΚΑΙ ΕΝΑ ΠΗΝΙΟ. Στο κύκλωμα του σχήματος το πηνίο έχει συντελεστή αυτεπαγωγής L = (A) (B) mh, ο πυκνωτής () έχει χωρητικότητα C = μf, ενώ ο πυκνωτής
ΜΕΤΑΓΩΓΗ ΑΠΟ ΤΟ ΕΝΑ ΚΥΚΛΩΜΑ LC ΣΤΟ ΑΛΛΟ. ΔΥΟ ΠΥΚΝΩΤΕΣ ΚΑΙ ΕΝΑ ΠΗΝΙΟ. Στο κύκλωμα του σχήματος το πηνίο έχει συντελεστή αυτεπαγωγής L = (A) (B) mh, ο πυκνωτής () έχει χωρητικότητα C = μf, ενώ ο πυκνωτής
(α) Σχ. 5/30 Σύμβολα πυκνωτή (α) με πολικότητα, (β) χωρίς πολικότητα
 5. ΗΛΕΚΤΡΟΝΙΚΑ ΕΞΑΡΤΗΜΑΤΑ Ι ( ΠΥΚΝΩΤΕΣ) Πυκνωτές O πυκνωτής είναι ένα ηλεκτρικό εξάρτημα το οποίο έχει την ιδιότητα να απορροφά και να αποθηκεύει ηλεκτρική ενέργεια και να την απελευθερώνει, σε προκαθορισμένο
5. ΗΛΕΚΤΡΟΝΙΚΑ ΕΞΑΡΤΗΜΑΤΑ Ι ( ΠΥΚΝΩΤΕΣ) Πυκνωτές O πυκνωτής είναι ένα ηλεκτρικό εξάρτημα το οποίο έχει την ιδιότητα να απορροφά και να αποθηκεύει ηλεκτρική ενέργεια και να την απελευθερώνει, σε προκαθορισμένο
«Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο
 ΤΕΙ Δυτικής Ελλάδας Τμήμα Μηχανικών Πληροφορικής ΤΕ Εργαστήριο Σχεδίασης Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων «Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο 2016-2017 Διάλεξη 5 η :
ΤΕΙ Δυτικής Ελλάδας Τμήμα Μηχανικών Πληροφορικής ΤΕ Εργαστήριο Σχεδίασης Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων «Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο 2016-2017 Διάλεξη 5 η :
ΘΕΜΑ 1 ο (3.5 μονάδες) V CC R C1 R C2. R s. v o v s R L. v i I 1 I 2 ΛΥΣΗ R 10 10
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΠΑΤΡΑΣ 0/0/0 ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΝ ΕΦΑΡΜΟΓΝ0/0/0 ΣΕΙΡΑ B: 6:00 8:0 (Λ ΕΣ ) ΘΕΜΑ ο (.5 μονάδες) Οι -παράμεροι των τρανζίστορ του ενισχυτή του παρακάτω σχήματος είναι: e 5 k,
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΠΑΤΡΑΣ 0/0/0 ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΝ ΕΦΑΡΜΟΓΝ0/0/0 ΣΕΙΡΑ B: 6:00 8:0 (Λ ΕΣ ) ΘΕΜΑ ο (.5 μονάδες) Οι -παράμεροι των τρανζίστορ του ενισχυτή του παρακάτω σχήματος είναι: e 5 k,
Σχεδίαση κυκλωμάτων ακολουθιακής λογικής
 Σχεδίαση κυκλωμάτων ακολουθιακής λογικής Βασικές αρχές Σχεδίαση Latches και flip-flops Γιώργος Δημητρακόπουλος Δημοκρίτειο Πανεπιστήμιο Θράκης Φθινόπωρο 2013 Ψηφιακά ολοκληρωμένα κυκλώματα 1 Ακολουθιακή
Σχεδίαση κυκλωμάτων ακολουθιακής λογικής Βασικές αρχές Σχεδίαση Latches και flip-flops Γιώργος Δημητρακόπουλος Δημοκρίτειο Πανεπιστήμιο Θράκης Φθινόπωρο 2013 Ψηφιακά ολοκληρωμένα κυκλώματα 1 Ακολουθιακή
Πανεπιστήµιο Αιγαίου Τµήµα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστηµάτων. 3η Άσκηση Logical Effort - Ένα ολοκληρωµένο παράδειγµα σχεδίασης
 Πανεπιστήµιο Αιγαίου Τµήµα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστηµάτων Εισαγωγή σε VLSI 3η Άσκηση Logical Effort - Ένα ολοκληρωµένο παράδειγµα σχεδίασης Μανόλης Καλλίγερος (kalliger@aegean.gr)
Πανεπιστήµιο Αιγαίου Τµήµα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστηµάτων Εισαγωγή σε VLSI 3η Άσκηση Logical Effort - Ένα ολοκληρωµένο παράδειγµα σχεδίασης Μανόλης Καλλίγερος (kalliger@aegean.gr)
Σε έναν επίπεδο πυκνωτή οι μεταλλικές πλάκες έχουν εμβαδό 0,2 m 2, και απέχουν απόσταση 8,85 mm ενώ μεταξύ των οπλισμών του μεσολαβεί αέρας.
 ΠΥΚΝΩΤΕΣ ΑΣΚΗΣΕΙΣ ΤΡΑΠΕΖΑΣ ΘΕΜΑ Δ Σε έναν επίπεδο πυκνωτή οι μεταλλικές πλάκες έχουν εμβαδό 0,2 m 2, και απέχουν απόσταση 8,85 mm ενώ μεταξύ των οπλισμών του μεσολαβεί αέρας Υπολογίστε τη χωρητικότητα
ΠΥΚΝΩΤΕΣ ΑΣΚΗΣΕΙΣ ΤΡΑΠΕΖΑΣ ΘΕΜΑ Δ Σε έναν επίπεδο πυκνωτή οι μεταλλικές πλάκες έχουν εμβαδό 0,2 m 2, και απέχουν απόσταση 8,85 mm ενώ μεταξύ των οπλισμών του μεσολαβεί αέρας Υπολογίστε τη χωρητικότητα
3 η διάλεξη Συσκευές στο Πυρήτιο
 3 η διάλεξη Συσκευές στο Πυρήτιο 1 2 3 4 5 6 7 8 9 Η δίοδος συναντάται ως δομή σε κάθε MOS τρανζίστορ. Αποτελείται από δυο ομοιογενείς περιοχές n και p πυριτίου, οι οποίες διαχωρίζονται από ένα χώρο μετάβασης
3 η διάλεξη Συσκευές στο Πυρήτιο 1 2 3 4 5 6 7 8 9 Η δίοδος συναντάται ως δομή σε κάθε MOS τρανζίστορ. Αποτελείται από δυο ομοιογενείς περιοχές n και p πυριτίου, οι οποίες διαχωρίζονται από ένα χώρο μετάβασης
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΠΑΤΡΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ 17/06/2011 ΣΕΙΡΑ Β: 16:00 18:30 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ
 ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ 7/0/0 ΣΕΙΡΑ Β: :00 8:0 ΘΕΜΑ ο (4 μονάδες) Ο ενισχυτής του διπλανού σχήματος περιλαμβάνει ένα τρανζίστορ τύπου npn (Q ) και ένα τρανζίστορ τύπου pnp (Q ), για τα οποία δίνονται:
ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ 7/0/0 ΣΕΙΡΑ Β: :00 8:0 ΘΕΜΑ ο (4 μονάδες) Ο ενισχυτής του διπλανού σχήματος περιλαμβάνει ένα τρανζίστορ τύπου npn (Q ) και ένα τρανζίστορ τύπου pnp (Q ), για τα οποία δίνονται:
HY330 Ψηφιακά Κυκλώματα - Εισαγωγή στα Συστήματα VLSI. Σταθερές Μνήμες Αρχιτεκτονικές Μνήμης RAM
 HY330 Ψηφιακά Κυκλώματα - Εισαγωγή στα Συστήματα VLSI Διδάσκων: Χ. Σωτηρίου, Βοηθοί: θα ανακοινωθούν http://inf-server.inf.uth.gr/courses/ce330 1 ΗΥ330 - Διάλεξη 12η - Κυκλώματα Μνήμης Περιεχόμενα Είδη
HY330 Ψηφιακά Κυκλώματα - Εισαγωγή στα Συστήματα VLSI Διδάσκων: Χ. Σωτηρίου, Βοηθοί: θα ανακοινωθούν http://inf-server.inf.uth.gr/courses/ce330 1 ΗΥ330 - Διάλεξη 12η - Κυκλώματα Μνήμης Περιεχόμενα Είδη
Λογικά Κυκλώματα NMOS. Διάλεξη 4
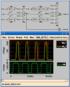 Λογικά Κυκλώματα NMOS Διάλεξη 4 Δομή της διάλεξης Η Σχεδίαση του Αντιστροφέα NMOS με Ωμικό Φόρτο Η Στατική Σχεδίαση του Αντιστροφέα NMOS με Κορεσμένο Φόρτο ΟΑντιστροφέαςΝMOS με Γραμμικό Φόρτο ΟΑντιστροφέαςΝMOS
Λογικά Κυκλώματα NMOS Διάλεξη 4 Δομή της διάλεξης Η Σχεδίαση του Αντιστροφέα NMOS με Ωμικό Φόρτο Η Στατική Σχεδίαση του Αντιστροφέα NMOS με Κορεσμένο Φόρτο ΟΑντιστροφέαςΝMOS με Γραμμικό Φόρτο ΟΑντιστροφέαςΝMOS
Ανάλυση Ηλεκτρικών Κυκλωμάτων
 Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 3: Συνδυασμός αντιστάσεων και πηγών Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ. ΕΥΔΟΞΟΣ:
Ανάλυση Ηλεκτρικών Κυκλωμάτων Κεφάλαιο 3: Συνδυασμός αντιστάσεων και πηγών Οι διαφάνειες ακολουθούν το βιβλίο του Κων/νου Παπαδόπουλου «Ανάλυση Ηλεκτρικών Κυκλωμάτων» ISBN: 9789609371100 κωδ. ΕΥΔΟΞΟΣ:
ΣΧΕ ΙΑΣΜΟΣ ΟΛΟΚΛΗΡΩΜΕΝΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΣΧΕ ΙΑΣΜΟΣ ΟΛΟΚΛΗΡΩΜΕΝΩΝ ΚΥΚΛΩΜΑΤΩΝ Ι ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ Λάµπρος Μπισδούνης Πάτρα 1996 ΠΕΡΙΕΧΟΜΕΝΑ 1. Σχεδιασµός και εξοµοίωση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΣΧΕ ΙΑΣΜΟΣ ΟΛΟΚΛΗΡΩΜΕΝΩΝ ΚΥΚΛΩΜΑΤΩΝ Ι ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ Λάµπρος Μπισδούνης Πάτρα 1996 ΠΕΡΙΕΧΟΜΕΝΑ 1. Σχεδιασµός και εξοµοίωση
i Το τρανζίστορ αυτό είναι τύπου NMOS. Υπάρχει και το συμπληρωματικό PMOS. ; Τι συμβαίνει στο τρανζίστορ PMOS; Το τρανζίστορ MOS(FET)
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 25-6 Το τρανζίστορ MOS(FET) πύλη (gate) Ψηφιακή και Σχεδίαση πηγή (source) καταβόθρα (drai) (σχεδίαση συνδυαστικών κυκλωμάτων) http://di.ioio.gr/~mistral/tp/comparch/
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Αρχιτεκτονική Υπολογιστών 25-6 Το τρανζίστορ MOS(FET) πύλη (gate) Ψηφιακή και Σχεδίαση πηγή (source) καταβόθρα (drai) (σχεδίαση συνδυαστικών κυκλωμάτων) http://di.ioio.gr/~mistral/tp/comparch/
ΛΥΣΕΙΣ ΕΞΕΤΑΣΗΣ ΣΤΟ ΜΑΘΗΜΑ «ΗΛΕΚΤΡΟΝΙΚΑ ΙΙ» ΗΜΕΡΟΜΗΝΙΑ: 05/02/2013
 ΘΕΜΑ ο (.5 μονάδες) Για τον ενισχυτή του παρακάτω σχήματος δίνονται: Β 90 kω, C kω, Ε E kω, kω, V CC V, V B 0.70 V και Ι Β 0 μα. Επίσης, για τα δύο τρανζίστορ του ενισχυτή δίνονται: β h e h e 00 και h
ΘΕΜΑ ο (.5 μονάδες) Για τον ενισχυτή του παρακάτω σχήματος δίνονται: Β 90 kω, C kω, Ε E kω, kω, V CC V, V B 0.70 V και Ι Β 0 μα. Επίσης, για τα δύο τρανζίστορ του ενισχυτή δίνονται: β h e h e 00 και h
Άσκηση 6 ΔΙΟΔΟΣ ZENER ΚΑΙ ΠΟΛΛΑΠΛΑΣΙΑΣΤΕΣ ΤΑΣΗΣ
 Άσκηση 6 ΔΙΟΔΟΣ ZENER ΚΑΙ ΠΟΛΛΑΠΛΑΣΙΑΣΤΕΣ ΤΑΣΗΣ Αυτό έργο χορηγείται με άδεια Creative Commons Attribution-NonCommercial-ShareAlike Greece 3.0. Ονοματεπώνυμο: Μητρόπουλος Σπύρος Α.Ε.Μ.: 3215 Εξάμηνο: Β'
Άσκηση 6 ΔΙΟΔΟΣ ZENER ΚΑΙ ΠΟΛΛΑΠΛΑΣΙΑΣΤΕΣ ΤΑΣΗΣ Αυτό έργο χορηγείται με άδεια Creative Commons Attribution-NonCommercial-ShareAlike Greece 3.0. Ονοματεπώνυμο: Μητρόπουλος Σπύρος Α.Ε.Μ.: 3215 Εξάμηνο: Β'
Ηλεκτρονική. Ενότητα 9: Τρανζίστορ Επίδρασης Πεδίου (FET) Αγγελική Αραπογιάννη Τμήμα Πληροφορικής και Τηλεπικοινωνιών
 Ηλεκτρονική Αγγελική Αραπογιάννη Τμήμα Πληροφορικής και Τηλεπικοινωνιών Περιεχόμενο ενότητας (1 από 2) Τύποι τρανζίστορ επίδρασης πεδίου (JFET, MOSFET, MESFET). Ομοιότητες και διαφορές των FET με τα διπολικά
Ηλεκτρονική Αγγελική Αραπογιάννη Τμήμα Πληροφορικής και Τηλεπικοινωνιών Περιεχόμενο ενότητας (1 από 2) Τύποι τρανζίστορ επίδρασης πεδίου (JFET, MOSFET, MESFET). Ομοιότητες και διαφορές των FET με τα διπολικά
ΤΟΠΟΛΟΓΙΕΣ ΣΥΣΤΟΙΧΙΑΣ ΔΙΑΛΕΞΗ 5
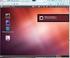 ΤΟΠΟΛΟΓΙΕΣ ΣΥΣΤΟΙΧΙΑΣ ΔΙΑΛΕΞΗ 5 Cascode Κυκλώματα (1/2) Χρησιμοποιούμε ένα κοινήςπύλης/βάσης τρανζίστορ για να: Βελτιώσουμε την αντίσταση εξόδου ενός άλλου τρανζίστορ. V drain Μειώσουμε το φαινόμενο Gate-to-
ΤΟΠΟΛΟΓΙΕΣ ΣΥΣΤΟΙΧΙΑΣ ΔΙΑΛΕΞΗ 5 Cascode Κυκλώματα (1/2) Χρησιμοποιούμε ένα κοινήςπύλης/βάσης τρανζίστορ για να: Βελτιώσουμε την αντίσταση εξόδου ενός άλλου τρανζίστορ. V drain Μειώσουμε το φαινόμενο Gate-to-
ΜΕΡΟΣ Α: Απαραίτητες γνώσεις
 ΜΕΡΟΣ Α: Απαραίτητες γνώσεις Φίλτρα RC Τα φίλτρα RC είναι από τις σπουδαίες εφαρμογές των πυκνωτών. Τα πιο απλά φίλτρα αποτελούνται από έναν πυκνωτή και μία αντίσταση σε σειρά. Με μια διαφορετική ματιά
ΜΕΡΟΣ Α: Απαραίτητες γνώσεις Φίλτρα RC Τα φίλτρα RC είναι από τις σπουδαίες εφαρμογές των πυκνωτών. Τα πιο απλά φίλτρα αποτελούνται από έναν πυκνωτή και μία αντίσταση σε σειρά. Με μια διαφορετική ματιά
Άσκηση 10 Στοιχεία ηλεκτρονικής τεχνολογίας
 Άσκηση 10 Στοιχεία ηλεκτρονικής τεχνολογίας ΔΙΟΔΟΣ Οι περισσότερες ηλεκτρονικές συσκευές όπως οι τηλεοράσεις, τα στερεοφωνικά συγκροτήματα και οι υπολογιστές χρειάζονται τάση dc για να λειτουργήσουν σωστά.
Άσκηση 10 Στοιχεία ηλεκτρονικής τεχνολογίας ΔΙΟΔΟΣ Οι περισσότερες ηλεκτρονικές συσκευές όπως οι τηλεοράσεις, τα στερεοφωνικά συγκροτήματα και οι υπολογιστές χρειάζονται τάση dc για να λειτουργήσουν σωστά.
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I
 Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI I Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα
