1. Σκοπός της άσκησης Στοιχεία θεωρίας Γεωμετρική οπτική Ο νόμος της ανάκλασης Ο νόμος της διάθλασης...
|
|
|
- Καλλιστράτης Παπαγεωργίου
- 9 χρόνια πριν
- Προβολές:
Transcript
1 1. Λεπτοί Φακοί Σελίδα 1. Σκοπός της άσκησης Στοιχεία θεωρίας Γεωμετρική οπτική Ο νόμος της ανάκλασης Ο νόμος της διάθλασης Είδωλα & παραξονική προσέγγιση Είδη φακών & τύπος κατασκευαστών των λεπτών φακών Θεμελιώδης εξίσωση φακών, μεγέθυνση & γραφικός προσδιορισμός ειδώλων Παραδείγματα Εστιακή απόσταση επιπεδόκοιλου φακού Είδωλα σφαιρικών κατόπτρων Συστήματα φακών Μεγεθυντής δέσμης. 3. Πειραματική διάταξη Πειραματική διαδικασία & ανάλυση μετρήσεων Προσδιορισμός εστιακής απόστασης συγκλίνοντος φακού & μεγέθους αντικειμένου Προσδιορισμός εστιακής απόστασης συγκλίνοντος φακού με τη μέθοδο Bessel Προσδιορισμός εστιακής απόστασης αποκλίνοντος φακού μέσω συστήματος φακών Προσδιορισμός εστιακής απόστασης αποκλίνοντος φακού με τη μέθοδο διαμέτρου φωτεινής δέσμης laser & μεγεθυντή δέσμης Βιβλιογραφία
2 Λεπτοί Φακοί 1. Σκοπός της άσκησης. Η άσκηση αυτή είναι αφιερωμένη στην εξοικείωση με τα βασικά στοιχεία της απεικονιστικής λειτουργίας των λεπτών φακών όπως αυτά προβλέπονται από τη Γεωμετρική Οπτική. Εφαρμόζονται τέσσερις μέθοδοι μέτρησης της εστιακής απόστασης λεπτών φακών τόσο συγκλινόντων όσο και αποκλινόντων. Ο προσδιορισμός των ζητούμενων μεγεθών και των σφαλμάτων τους γίνεται γραφικά, φέρνοντάς μας σε επαφή με μεθοδολογίες που θα χρησιμοποιηθούν κατ επανάληψη και στις υπόλοιπες ασκήσεις. 2. Στοιχεία θεωρίας. 2.1 Γεωμετρική οπτική. Στη Γεωμετρική Οπτική δεχόμαστε ότι το φως αποτελείται από ακτίνες που εκκινώντας από κάποια φωτεινή λ Σχήμα 1. πηγή διαδίδονται προς διάφορες κατευθύνσεις και κάμπτονται απότομα λόγω της διάθλασης ή ανάκλασής τους σε D διάφορα οπτικά στοιχεία. Θεωρούμε ότι σε ομογενή μέσα οι φωτεινές ακτίνες διαδίδονται ευθύγραμμα και αγνοούμε τον κυματικό χαρακτήρα του φωτός, εφαρμόζοντας τους νόμους της ανάκλασης και της διάθλασης χωρίς περιορισμούς. Σε L όλα τα οπτικά συστήματα, το φως διαδίδεται πάντα μέσα από κάποιο αριθμό οπών, διαφραγμάτων ή σχισμών από τις οποίες διέρχεται ένα μέρος του προσπίπτοντος κυματομετώπου. Η Γεωμετρική Οπτική μπορεί να θεωρηθεί ως το όριο της Κυματικής Οπτικής στο οποίο η περίθλαση στα στοιχεία αυτά είναι αμελητέα. Στο παράδειγμα του σχήματος 1, επίπεδο κύμα προσπίπτει σε οπή διαμέτρου D και διαδίδεται μέχρι την οθόνη που απέχει από αυτή απόσταση L. Εάν τα φαινόμενα περίθλασης είναι αμελητέα τότε το διερχόμενο κύμα θα συνεχίσει να είναι επίπεδο και οι διαστάσεις της διαδιδόμενης δέσμης θα είναι ίσες με αυτές της οπής. Διαφορετικά θα παρατηρήσουμε αποκλίσεις από την ευθύγραμμη διάδοση. Αποδεικνύεται ότι για να ισχύει η Γεωμετρική Οπτική πρέπει οι διαστάσεις του ανοίγματος να είναι πολύ μεγαλύτερες του μήκους κύματος λ της ακτινοβολίας. Ακριβέστερα, θα πρέπει να ικανοποιείται η σχέση, D Lλ. (1) Σε ότι ακολουθεί αποδεχόμαστε την ισχύ της (1). 2.2 Ο νόμος της ανάκλασης. Υποθέστε ότι φωτεινή ακτίνα (ή φωτεινή δέσμη) διαδίδεται σε κάποιο διαφανές μέσο (π.χ. αέρας) και προσπίπτει σε επίπεδη και λεία επιφάνεια. Η επιφάνεια αυτή μπορεί να είναι είτε αδιαφανής είτε απλώς η μεσεπιφάνεια μεταξύ δύο διαφανών υλικών. Κατά την ανάκλαση το φως αλλάζει διεύθυνση διάδοσης αλλά παραμένει εντός του ιδίου μέσου. Ο νόμος της ανάκλασης μπορεί να διατυπωθεί ως εξής: Κατά την ανάκλαση, (α) η προσπίπτουσα ακτίνα, η ανακλώμενη ακτίνα και η κάθετη στην ανακλαστική επιφάνεια στο σημείο πρόσπτωσης βρίσκονται επί του αυτού επιπέδου το οποίο ονομάζουμε επίπεδο πρόσπτωσης, και (β) η γωνία πρόσπτωσης θ π ισούται με τη γωνία ανάκλασης θ π, δηλαδή ισχύει: θ π =θ α. (2) Λεπτοί φακοί 1/12
3 Ανακλαστική Επιφάνεια Επίπεδο πρόσπτωσης Ανακλώμενη ακτίνα θ α θ π θ π θ α Κάθετη στην επιφάνεια στο σημείο πρόσπτωσης Προπίπτουσα ακτίνα Σχήμα 2. Ως γωνίες πρόσπτωσης και ανάκλασης ορίζουμε αυτές που σχηματίζονται από την κάθετη στην επιφάνεια και την προσπίπτουσα και ανακλώμενη ακτίνα αντίστοιχα. Η διάχυτη ανάκλαση (ή απλά διάχυση) του φωτός από τραχιές επιφάνειες εξηγείται μέσω της εφαρμογής του νόμου της ανάκλασης σε κάθε στοιχειώδη επιφάνεια που μπορεί να θεωρηθεί επίπεδη. 2.3 Ο νόμος της διάθλασης. Υποθέστε τώρα ότι φωτεινή ακτίνα προσπίπτει στην επίπεδη και λεία μεσεπιφάνεια μεταξύ δύο διαφανών υλικών. Στην περίπτωση αυτή, εκτός από ανάκλαση, παρατηρείται και διάθλαση δηλαδή αλλαγή τόσο της διεύθυνσης διάδοσης του φωτός όσο και του μέσου διάδοσης. Ο νόμος της διάθλασης μπορεί να διατυπωθεί ως εξής: Κατά τη διάθλαση, (α) η προσπίπτουσα ακτίνα, η διαθλώμενη ακτίνα και η κάθετη στη διαθλαστική επιφάνεια στο σημείο πρόσπτωσης βρίσκονται επί του αυτού επιπέδου (επίπεδο πρόσπτωσης) και (β) η γωνία πρόσπτωσης θ π συνδέεται με τη γωνία διάθλασης θ δ μέσω της σχέσης, n π sinθ π =n δ sinθ δ. (3) n π n δ Ανακλαστική/ ιαθλαστική Επιφάνεια Επίπεδο πρόσπτωσης ιαθλώμενη ακτίνα θ α θ δ θ π n π θ π θ α Κάθετη στην επιφάνεια στο σημείο πρόσπτωσης n π <n δ Προπίπτουσα ακτίνα n δ θ δ Σχήμα 3. Στη σχέση (3) (που είναι γνωστή ως νόμος του Snell) η γωνία διάθλασης ορίζεται ανάλογα με αυτές της πρόσπτωσης και ανάκλασης, δηλαδή είναι η γωνία μεταξύ της κάθετης στην επιφάνεια και Λεπτοί φακοί 2/12
4 της διαθλώμενης ακτίνας. Οι δείκτες διάθλασης n π και n δ χαρακτηρίζουν το κάθε διαφανές υλικό και ορίζονται από τη σχέση, c λ n ο (4) co λ όπου c o και λ ο η ταχύτητα και το μήκος κύματος του φωτός στο κενό και c και λ η ταχύτητα και το μήκος κύματός του στο διαφανές υλικό. Μεταξύ δύο υλικών, αυτό με το μεγαλύτερο δείκτη διάθλασης ονομάζεται οπτικά πυκνότερο. Ο δείκτης διάθλασης του κενού είναι προφανώς ίσος με 1. Ο δείκτης διάθλασης του αέρα είναι Όμως η ακρίβεια προσδιορισμού του δείκτη διάθλασης διαφανών υλικών μέσω των πειραμάτων των εργαστηρίων Κυμάνσεων & Οπτικής περιορίζεται συνήθως στα δύο δεκαδικά ψηφία και για το λόγο αυτό θεωρούμε από εδώ και στο εξής ότι n αέρα 1. Πρέπει επίσης να τονιστεί ότι, ακόμη και για το ίδιο διαφανές υλικό, ο δείκτης διάθλασης έχει έ- ντονη εξάρτηση από το μήκος κύματος του φωτός. Η εξάρτηση αυτή θα μελετηθεί διεξοδικά στην άσκηση του φασματοσκοπίου. Εάν n π <n δ, (πέρασμα από οπτικά αραιότερο σε οπτικά πυκνότερο μέσο) τότε θ π >θ δ και η διαθλώμενη ακτίνα πλησιάζει την κάθετη στη μεσεπιφάνεια. Αντίθετα, εάν n π >n δ, (πέρασμα από οπτικά πυκνότερο σε οπτικά αραιότερο μέσο) τότε θ π <θ δ και η διαθλώμενη ακτίνα απομακρύνεται από την κάθετη στη μεσεπιφάνεια. 2.4 Είδωλα & παραξονική προσέγγιση. Στο σχήμα 4 από το σημείο S εκπέμπεται Μάτι Παρατηρητή αποκλίνουσα δέσμη φωτεινών ακτίνων η οποία α- S νακλάται από την επιφάνεια του επίπεδου κατόπτρου σύμφωνα με το νόμο της ανάκλασης και εισέρχεται στο μάτι του παρατηρητή. Σε αυτόν δημιουργείται η εντύπωση ότι οι ακτίνες εκκινούν από το σημείο S το οποίο είναι το είδωλο του S. Το είδωλο αυτό είναι φανταστικό, αφού σχηματίζεται από τις προεκτάσεις ακτίνων και όχι από τις ίδιες τις ακτίνες. Παρ όλα αυτά, όπως γνωρίζουμε από θ π θ α την καθημερινή μας εμπειρία, τα φανταστικά είδωλα Σχήμα 4. μπορούμε να τα δούμε. Δεν μπορούν όμως να S' σχηματιστούν σε οθόνη. Αυτό μπορεί να συμβεί μόνο για τα πραγματικά είδωλα, δηλαδή αυτά που δημιουργούνται από τις ίδιες τις ακτίνες και όχι τις προεκτάσεις τους. Οι λείες επιφάνειες χωρίζονται σε δύο μεγάλες κατηγορίες, τις ασφαιρικές (ελλειπτικές, παραβολικές κλπ) και τις σφαιρικές. Τα ασφαιρικά στοιχεία εμφανίζουν καλύτερες ιδιότητες απεικόνισης αλλά παρουσιάζουν κατασκευαστικές δυσκολίες. Εδώ θα αναφερθούμε μόνο σε σφαιρικά κάτοπτρα και φακούς που παρουσιάζουν σειρά σφαλμάτων κατά την εστίαση/απεικόνιση. Τα σφάλματα αυτά ελαχιστοποιούνται εάν ισχύει η λεγόμενη παραξονική προσέγγιση ότι δηλαδή: Οι φωτεινές ακτίνες βρίσκονται κοντά στον άξονα του συστήματος και σχηματίζουν μικρές γωνίες με αυτόν. Στο σχήμα 5 παρατηρούμε ότι η εάν η φωτεινή δέσμη έχει μεγάλη εγκάρσια διάστάση, συγκρίσιμη με του σφαιρικού φακού, δεν ε- στιάζονται όλες οι φωτεινές ακτίνες στο ίδιο σημείο, όπως θα συνέβαινε εάν οι επιφάνειές του ήταν παραβολικές. Λόγω του ότι τα σφάλμα αυτό οφείλεται στο σφαιρικό σχήμα των δύο επιφανειών Σχήμα 5. Λεπτοί φακοί 3/12
5 του φακού ονομάζεται σφάλμα σφαιρικότητας ή σφαιρική εκτροπή. Όταν όμως οι διαστάσεις της δέσμης είναι μικρές όλες οι ακτίνες εστιάζονται με πολύ καλή προσέγγιση στο ίδιο σημείο. 2.5 Είδη φακών & τύπος κατασκευαστών των λεπτών φακών. Οι δύο μεγάλες κατηγορίες φακών είναι οι συγκλίνοντες (συγκεντρωτικοί) και οι αποκλίνοντες (αποκεντρωτικοί). Οι πρώτοι εστιάζουν προσπίπτουσα παράλληλη (α) Συγκεντρωτικός Εστιακή απόσταση, >0 (β) Αποκεντρωτικός φωτεινή δέσμη (σχήμα 6(α)) ενώ οι αποκλίνοντες την α- πεστιάζουν (σχήμα 6(β)). Η δράση Ο Εστία και των δύο είναι αποτέλεσμα <0 του νόμου της διάθλασης και της καμπυλότητας που παρουσιάζουν οι επιφάνειές τους. Ο υπολογισμός των χαρακτηριστικών τους απλοποιείται κατά πολύ εάν θεωρήσουμε ότι είναι λεπτοί, δηλαδή ότι το πάχος τους είναι πολύ μικρότερο της εστιακής τους απόστασης. Η τελευταία συμβολίζεται Εστιακό επίπεδο με και ορίζεται ως η από- σταση μεταξύ του φακού (ακριβέστερα του οπτικού του κέντρου Ο) και του σημείου - εστίας - ό- που συγκλίνουν όλες οι φωτεινές Οπτικός άξονας ακτίνες μιας παράλληλης φωτεινής δέσμης (ή οι προεκτάσεις Οπτικό κέντρο τους). Λόγω της αντίστροφης πορείας του φωτός κάθε φακός έχει δύο εστίες εκατέρωθεν αυτού. Σε Συμβολισμός Σχήμα 6. λεπτό φακό και οι δύο απέχουν ίση απόσταση από αυτόν, δηλαδή οι δεξιά και η αριστερή εστιακή απόσταση είναι ίσες. Συμβολίζοντας με n γ το δείκτη διάθλασης του γυαλιού από το οποίο είναι κατασκευασμένος και υποθέτοντας ότι περιβάλλεται εξ ολοκλήρου από διαφανές μέσο με δείκτη διάθλασης n περ, η εστιακή απόσταση λεπτού φακού δίνεται από τον λεγόμενο τύπο των κατασκευαστών των λεπτών φακών που γράφεται 1 n n R1 R 2 (5) Στην (5) R 1 και R 2 είναι οι ακτίνες καμπυλότητας των επιφανειών που συναντούν οι φωτεινές ακτίνες (πρώτη και δεύτερη αντίστοιχα). Τόσο αυτές όσο και η εστιακή απόσταση μπορούν να πάρουν θετικές ή αρνητικές τιμές. Οι συμβάσεις προσήμων φαίνονται στο σχήμα 7. Έτσι λοιπόν, εάν το κέντρο καμπυλότητας C μιας επιφάνειας βρίσκεται από τη μεριά πρόσπτωσης Κατεύθυνση πρόσπτωσης φωτεινών ακτίνων Σχήμα 7. C R<0 R Λεπτοί φακοί 4/12 R>0 C
6 των φωτεινών ακτίνων τότε η ακτίνα αυτή είναι αρνητική. Διαφορετικά είναι θετική. Εάν η επιφάνεια είναι επίπεδη η ακτίνα καμπυλότητάς της είναι άπειρη. Όσο για την εστιακή απόσταση όπως αυτή προκύπτει από την (5), εάν αυτή είναι θετική τότε μιλάμε για συγκλίνοντα ή θετικό φακό. Στην αντίθετη περίπτωση ο φακός είναι αποκλίνων ή αρνητικός. Προσέξτε ότι το πρόσημο της και η δράση του φακού δεν εξαρτώνται μόνον από τα πρόσημα των ακτίνων καμπυλότητας αλλά και από το σχετικό δείκτη διάθλασης n σχ =n γ /n περ. Στη συνηθέστερη περίπτωση όπου n σχ >1, οι συγκλίνοντες φακοί είναι λεπτότεροι στα άκρα και παχύτεροι στο κέντρο τους, ενώ οι αποκλίνοντες παχύτεροι στα άκρα και λεπτότεροι στο κέντρο. Σημειώστε ακόμη ότι, εφόσον ο δείκτης διάθλασης εξαρτάται από το μήκος κύματος, η εστιακή απόσταση είναι διαφορετική για κάθε χρώμα. Αυτό το σφάλμα των φακών ονομάζεται χρωματική εκτροπή. A>0 n σχ >1, >0 A>0 n σχ >1, <0 a>0 (I) O a>0 b<0 (I) B>0 b>0 (II) (III) (III) (II) (i) B<0 (ii) Σχήμα Θεμελιώδης εξίσωση φακών, μεγέθυνση & γραφικός προσδιορισμός ειδώλων. Θεωρούμε παρακάτω την περίπτωση n σχ >1. Στα παραδείγματα του σχήματος 8 αντικείμενο απέχει από το συγκλίνοντα φακό απόσταση a. Η απόσταση του ειδώλου, b, από αυτόν δίνεται από τη θεμελιώδη εξίσωση των λεπτών φακών (6) a b Εάν συμβολίσουμε το μέγεθος του αντικειμένου με Α και του ειδώλου με Β, η μεγέθυνση Μ δίνεται από τη σχέση, B b M. (7) A a Τα μεγέθη a, b, Β, Μ μπορούν να είναι είτε θετικά είτε αρνητικά (όπως και η ). Οι συμβάσεις προσήμων φαίνονται στο Πίνακα 1. Πίνακας 1. Συμβάσεις προσήμων για λεπτούς σφαιρικούς φακούς. Μέγεθος Πρόσημο + a Από τη μεριά πρόσπτωσης των ακτίνων (πραγματικό αντικείμενο) Μετά το φακό ως προς τη μεριά πρόσπτωσης των ακτίνων (φανταστικό αντικείμενο) b Μετά το φακό ως προς τη μεριά πρόσπτωσης των ακτίνων ( πραγματικό είδωλο) Από τη μεριά πρόσπτωσης των ακτίνων (φανταστικό είδωλο) B Ίδιας κατεύθυνσης με το Α Αντίθετης κατεύθυνσης σε σχέση με το Α Μ Μη-αντιστροφή ειδώλου ως προς αντικείμενο Αντιστροφή ειδώλου ως προς αντικείμενο Για το γραφικό προσδιορισμό του ειδώλου ενός σημείου του αντικειμένου αρκεί να βρούμε το σημείο τομής δύο φωτεινών ακτίνων (ή των προεκτάσεών τους) που εκκινούν από αυτό. Χρησιμοποιούμε συνήθως το πλέον απομεμακρυσμένο από τον οπτικό άξονα σημείο και τουλάχιστον δύο από τις τρεις κύριες ακτίνες (Ι), (ΙΙ) και (ΙΙΙ) του σχήματος 8. Σύμφωνα με αυτές: Λεπτοί φακοί 5/12
7 (Ι) Προσπίπτουσα φωτεινή ακτίνα παράλληλη στον οπτικό άξονα περνά, η ίδια ή η προέκτασή της, μετά το φακό από τη μία εστία του. (ΙΙ) Η διεύθυνση προσπίπτουσας φωτεινής ακτίνας που περνά από το οπτικό κέντρο λεπτού φακού δεν υφίσταται καμία μεταβολή. (ΙΙΙ) Προσπίπτουσα φωτεινή ακτίνα που διέρχεται, η ίδια (>0) ή η προέκτασή της (<0), από την άλλη εστία του φακού παραλληλίζεται μετά από αυτόν. 2.7 Παραδείγματα Εστιακή απόσταση επιπεδόκοιλου φακού. Η δράση ενός φακού προφανώς δεν αλλάζει εάν εναλλαγεί η σειρά με την οποία η φωτεινή δέσμη συναντά τις δύο επιφάνειές του (αν και τα σφάλματα εξαρτώνται από τη σειρά αυτή). Θεωρήστε το παράδειγμα του σχήματος 9 όπου σημειώνεται η κατεύθυνση της προσπίπτουσας δέσμης και Σχήμα 9. R 1 R 2 <0 R 1 >0 R 2 οι δύο τρόποι που μπορεί να τοποθετηθεί ο επιπεδόκοιλος φακός. Στην περίπτωση (α) το φως συναντά πρώτα την επίπεδη επιφάνεια στην οποία αντιστοιχούμε την ακτίνα R 1. Η δεύτερη επιφάνεια έχει αρνητική ακτίνα καμπυλότητας R 2 <0. Έστω ότι ο φακός περιβάλλεται από αέρα συνεπώς n περ =1 και n σχ =n γ >1. Θέτοντας R 2 = R και χρησιμοποιώντας την (5) η εστιακή απόσταση γράφεται, 1 1 R n (8) R n 1 Στην περίπτωση (β) από την άλλη μεριά η δέσμη προσπίπτει πρώτα στην καμπύλη επιφάνεια. Τώρα, είναι η ακτίνα αυτής της επιφάνειας που θα ονομάσουμε R 1 και μάλιστα είναι θετική R 1 = R >0. Η επίπεδη επιφάνεια είναι η δεύτερη που συναντά το φως συνεπώς R 2. Εύκολα επιβεβαιώνεται ότι εισάγοντας αυτές τις ακτίνες στη (5) καταλήγουμε ξανά στη σχέση (8) και η εστιακή απόσταση είναι πάλι θετική. (α) (β) Είδωλα σφαιρικών κατόπτρων. Οι σχέσεις (6) και (7) ισχύουν και για τα σφαιρικά κάτοπτρα είτε είναι κοίλα, όπως αυτό του σχήματος 10, είτε κυρτά. Στην παραξονική προσέγγιση η εστιακή απόσταση των κατόπτρων δίνεται από τη σχέση, R (9) 2 όπου R η ακτίνα καμπυλότητας του κατόπτρου. Οι συμβάσεις των προσήμων είναι ίδιες με αυτές των φακών εκτός από αυτές που αφορούν την απόσταση κέντρου κατόπτρου-ειδώλου, b, όπου αντιστρέφονται. Τα κάτοπτρα έχουν το πλεονέκτημα ότι δεν εμφανίζουν χρωματική εκτροπή όπως οι φακοί μια και κατά την ανάκλαση δεν Α (ΙΙ) Σχήμα 10. a (Ι) (ΙIΙ) C Β R<0 F b>0 >0 O Λεπτοί φακοί 6/12
8 υπάρχει εξάρτηση από το μήκος κύματος Συστήματα φακών. Πολλές φορές η χρήση ενός και μόνο φακού δεν αρκεί για να φέρει το επιθυμητό αποτέλεσμα. Γι αυτό και καταφεύγουμε σε συστήματα φακών. Εδώ θα περιοριστούμε στους δύο φακούς. Στο παράδειγμα του σχήματος 11 έχουμε επιλέξει να είναι και οι δύο συγκλίνοντες. Γενικά, για να βρούμε το τελικό είδωλο ενός αντικειμένου Α εργαζόμαστε ως εξής: Πρώτα βρίσκουμε το είδωλο Β 1 του αντικειμένου ως προς τον πρώτο φακό χωρίς την παρουσία του άλλου (σχήμα 11(α)). Θεωρούμε στη συνέχεια το είδωλο αυτό ως αντικείμενο για το δεύτερο φακό και βρίσκουμε το τελικό είδωλο Β 2 χρησιμοποιώντας ξανά τους τρεις κανόνες της παραγράφου 2.5. Στο σχήμα 11(β) η απόσταση d μεταξύ των φακών είναι μεγαλύτερη από την απόσταση πρώτου φακού-πρώτου ειδώλου b 1. Έτσι, η απόσταση πρώτου ειδώλου-δεύτερου φακού (για τον οποίο είναι το αντικείμενο) a 2 = d - b 1 > 0 και το ενδιάμεσο αντικείμενο (Β 1 ) είναι πραγματικό. Αντίθετα, στο σχήμα 11(γ) η απόσταση d έχει επιλεγεί έτσι ώστε a 2 = d - b 1 < 0 οπότε το ενδιάμεσο αντικείμενο είναι φανταστικό (δημιουργείται από προεκτάσεις ακτίνων). Παρακάτω θα χρησιμοποιήσουμε ένα σύστημα δύο φακών (ενός συγκλίνοντος και ενός α- ποκλίνοντος) για τη μέτρηση της εστιακής απόστασης του αποκλίνοντος φακού. Ο λόγος για τον οποίο καταφεύγουμε σε αυτή τη σχετικά περίπλοκη μέθοδο είναι ότι η μέτρηση της εστιακής απόστασης αποκλινόντων φακών δεν μπορεί να πραγματοποιηθεί άμεσα (διότι από μόνοι τους δεν δημιουργούν πραγματικά είδωλα) Μεγεθυντής δέσμης. Μία ενδιαφέρουσα περίπτωση συστήματος φακών είναι ο μεγεθυντής δέσμης που φαίνεται στο σχήμα 12. Αποτελείται από δύο συγκλίνοντες φακούς εστιακών αποστάσεων 1 και 2 > 1 τοποθετημένους σε απόσταση L= (10) Εάν παράλληλη δέσμη διαμέτρου d προσπέσει πρώτα στο φακό μικρότερης εστιακής απόστασης, στην έξοδο του συστήματος η δέσμη θα είναι πάλι παράλληλη αλλά με διαφορετική διάμετρο, έστω D. d 1 Σχήμα D Λεπτοί φακοί 7/12
9 Από ομοιότητα τριγώνων έχουμε D 2 (11) d 1 Συνεπώς η διάμετρος εξόδου είναι μεγεθυσμένη σε σχέση με τη διάμετρο εισόδου κατά το παράγοντα 2 / 1. Εάν το φως εισέλθει από την αντίθετη μεριά του συστήματος τότε θα έχουμε σμίκρυνση κατά τον παράγοντα 1 / 2, δηλαδή θα έχουμε ένα τηλεσκόπιο Keppler. 3. Πειραματική διάταξη. Στο σχήμα 13 φαίνονται τα όργανα και στοιχεία που θα χρησιμοποιήσετε στην άσκηση. Υπάρχουν δύο φωτεινές πηγές. Σε τρία πειράματα θα χρησιμοποιηθεί λάμπα πυρακτώσεως και στο τελευταίο laser He/Ne (λ=632.8 nm). Οι φακοί και η χιλιοστομετρική οθόνη τοποθετούνται σε κατάλληλες βάσεις (συνήθως μαγνητικής) στήριξης που μπορούν να μετακινηθούν κατά μήκος μιας Laser He/Ne Λάμπα πυρακτώσεως Σχήμα 13. Οπτική ράγα Συγκλίνοντες φακοί Οθόνη & είδωλο νήματος πυρακτώσεως Αποκλίνοντες φακοί σε βάση οπτικής τράπεζας (ράγας) στην οποία τοποθετούνται και οι φωτεινές πηγές. Φροντίζετε πάντα η όλη διάταξη (φωτεινή πηγή, φακοί και οθόνη) να είναι ευθυγραμμισμένα για την καλύτερη εκτέλεση των πειραμάτων. Οι αποστάσεις μετρώνται με μετροταινία ή απευθείας από την κλίμακα που είναι ενσωματωμένη στην οπτική ράγα. Σημειώστε τέλος ότι σε κάποιες ασκήσεις ως αντικείμενο προς απεικόνιση θα χρησιμοποιηθεί το νήμα πυρακτώσεως της λάμπας. Το νήμα βρίσκεται στο ε- σωτερικό της λάμπας και σε απόσταση 2.2 cm από την εμπρόσθια πλευρά της από όπου εξέρχεται το φως. Την απόσταση αυτή θα πρέπει να την συνυπολογίζετε στον υπολογισμό της απόστασης α- ντικειμένου-φακού. 4. Πειραματική διαδικασία & ανάλυση μετρήσεων. 4.1 Προσδιορισμός εστιακής απόστασης συγκλίνοντος φακού & μεγέθους αντικειμένου. Στο πείραμα αυτό ένας συγκλίνων φακός δημιουργεί σε οθόνη το πραγματικό είδωλο ενός αντικειμένου. Μεταβάλλοντας την απόσταση μεταξύ αντικειμένου και φακού, a, μεταβάλλεται προφανώς η απόσταση μεταξύ φακού και ειδώλου, b, αλλά και το μέγεθός του Β, συνεπώς και η μεγέθυνση Μ. Σκοπός μας είναι να προσδιορίσουμε τόσο την εστιακή απόσταση όσο και το μέγεθος του αντικειμένου Α. Για την πρώτη θα βασιστούμε στη σχέση (6) των λεπτών φακών η οποία μπορεί να γραφεί και ως a b = (a + b) (12) δηλαδή έχει μορφή ευθείας y=κ x με y= a b, x = a + b και κλίση κ =. Αντίστοιχα για το μέγεθος του αντικειμένου χρησιμοποιούμε τη σχέση (7) της μεγέθυνσης (κατ απόλυτη τιμή), την οποία γράφουμε ως Λεπτοί φακοί 8/12
10 Β = Α Μ (13) που είναι πάλι της μορφής y=κ x με y= Β, x= Μ = b/a και κλίση κ= Α. Ως αντικείμενο θα χρησιμοποιήσετε το ίδιο το νήμα πυρακτώσεως της φωτεινής πηγής. Ακολουθήστε τα εξής βήματα: 1. Επιλέξτε έναν από τους διαθέσιμους συγκλίνοντες φακούς και σημειώστε την ονομαστική τιμή της εστιακής του απόστασης. Επιλέξτε κατά προτίμηση φακό μεγάλης εστιακής απόστασης (π.χ 127 mm ή 252 mm). 2. Τοποθετήστε την βάση με την χιλιοστομετρική οθόνη απεικόνισης του ειδώλου σε κάποια απόσταση από την εμπρόσθια επιφάνεια της λάμπας πυρακτώσεως. Μετρείστε την απόσταση αυτή και προσθέστε τα 2.2 cm, δηλαδή την απόσταση μεταξύ εμπρόσθιας πλευράς της λάμπας και του νήματος πυρακτώσεως. Συμβολίζουμε τη συνολική αυτή απόσταση με. 3. Τοποθετήστε τη βάση με το συγκλίνοντα φακό μεταξύ της λάμπας και της οθόνης και μετακινήστε την έως ότου εμφανιστεί στην οθόνη το ευκρινές είδωλο του νήματος. Μετρείστε την απόσταση μεταξύ φακού και ειδώλου b και υπολογίστε την απόσταση a = b. 4. Μετρείστε στην οθόνη το μέγεθος του ειδώλου, έστω Β. 5. Επαναλάβατε τα βήματα 2 και 3 για ακόμη 6-9 διαφορετικές αποστάσεις i. Συγκεντρώστε τις μετρήσεις i, a i, b i και Β i σε πίνακα. 6. Κατά την ανάλυση των μετρήσεων στο σπίτι, αναπτύξτε τον πίνακα ώστε, εκτός από τις τιμές a i, b i και Β i να περιέχει και τις τιμές a i + b i, a i b i και Μ i = b i /a i. 7. Κατασκευάστε τις γραφικές παραστάσεις a i b i = F(a i + b i ) και Β i = F( Μ i ) (mm-χαρτί) που α- ναμένουμε να είναι ευθείες με σημείο οδηγό το (0,0) [δηλαδή πρέπει να περνούν - τόσο οι κύριες όσο και οι βοηθητικές - υποχρεωτικά από αυτό και πρέπει να συμπεριλαμβάνεται στο διάγραμμα]. Βρείτε τις κλίσεις κ= και κ= Α και τα σφάλματά τους από τα διαγράμματα. Ειδικά για της εστιακή απόσταση, βρείτε και την απόκλιση από την αναμενόμενη τιμή που σημειώσατε. Συζητείστε την απόκλιση αυτή σε σχέση με το σφάλμα που προέκυψε πειραματικά. 4.2 Προσδιορισμός εστιακής απόστασης συγκλίνοντος φακού με τη μέθοδο Bessel. Στόχος μας και εδώ είναι ο προσδιορισμός της εστιακής απόστασης συγκλίνοντος φακού αλλά αυτή τη φορά με τη μέθοδο Bessel. Η τελευταία βασίζεται στο γεγονός ότι, εάν ισχύει =a+b 4, υπάρχουν δύο θέσεις του φακού για τις οποίες δημιουργείται πραγματικό είδωλο. Χρησιμοποιώντας την (6), οι δύο αποστάσεις αντικειμένου-φακού για τις οποίες συμβαίνει αυτό ικανοποιούν την εξίσωση a 2 2 a + = 0. Ορίζοντας την απόσταση d μεταξύ των δύο θέσεων, έστω Ο 1 και Ο 2 (σχήμα 14) καταλήγουμε στη σχέση 2 2 d, 4 (14) 4 Η (14) μπορεί να γραφεί και στη μορφή 2 d 2 = (4 ) που παριστάνει ευθεία της μορφής y=κ x με y= 2 d 2, x=4 και κλίση κ=. Από την (14) προκύπτει ότι για =4 οι δύο θέσεις συμπίπτουν, ενώ για >4 βρίσκονται συμμετρικά ως προς τις σταθερές θέσεις του αντικειμένου Α και του ειδώλου Β. Συνεπώς ισχύει ότι a 1 = b 2, και a 2 = b 1 οπότε οι μεγεθύνσεις Μ 1 = b 1 /a 1 και Μ 2 = b 2 /a 2 για την πρώτη και δεύτερη θέση αντίστοιχα συνδέονται μέσω της σχέσης Μ 1 Μ 2 =1. Στη μία λοιπόν θέση το είδωλο είναι μεγαλύτερο του αντικειμένου και στην άλλη μικρότερο. Η μέθοδος παρουσιάζει το πλεονέκτημα ότι, εφόσον μετρώνται οι αποστάσεις και d μεταξύ αντικειμένου-ειδώλου και των δύο θέσεων Λεπτοί φακοί 9/12 (i) (ii) a 1 Σχήμα 14. O 1 a 2 d O 2 b 1 b 2
11 του φακού αντίστοιχα αλλά όχι οι αποστάσεις a και b απευθείας, μπορεί να εφαρμοστεί και στην περίπτωση μη-λεπτών φακών. Ως αντικείμενο θα χρησιμοποιήσετε πάλι το νήμα πυρακτώσεως της φωτεινής πηγής. Εργαστείτε κατά προτίμηση με τον ίδιο φακό του προηγουμένου πειράματος και φροντίστε ώστε για ό- λες τις μετρήσεις να ικανοποιείται η συνθήκη 4. Μην αμελήσετε επίσης να λάβετε υπ όψη την απόσταση των 2.2 cm μεταξύ της εμπρόσθιας πλευράς της λάμπας και του νήματος πυρακτώσεως στον υπολογισμό της απόστασης. Ακολουθήστε τα εξής βήματα: 1. Τοποθετήστε την βάση με την οθόνη απεικόνισης του ειδώλου σε απόσταση. 2. Τοποθετήστε τη βάση με το συγκλίνοντα φακό μεταξύ της λάμπας και της οθόνης και μετακινήστε την έως ότου εμφανιστεί στην οθόνη ευκρινές είδωλο του νήματος μεγαλύτερο του αντικειμένου. Σημειώστε τη θέση αυτή. 3. Χωρίς μεταβολή της μετακινήστε ξανά τη βάση με το φακό έως ότου εμφανιστεί στην οθόνη ευκρινές είδωλο του νήματος μικρότερο του αντικειμένου. Σημειώστε και αυτή τη θέση και βρείτε τη διαφορά d μεταξύ των δύο θέσεων. 4. Επαναλάβατε τα βήματα 2 και 3 για 6-9 φορές ακόμη. Συγκεντρώστε τις μετρήσεις i, και d i σε πίνακα. 5. Κατά την ανάλυση των μετρήσεων στο σπίτι, αναπτύξτε τον πίνακα ώστε, εκτός από τις τιμές i, και d i να περιέχει και τις τιμές 4 i και i 2 d i Κατασκευάστε τη γραφική παράσταση i 2 d i 2 = F(4 i ) (σημείο οδηγός το (0,0)) σε mm-χαρτί και βρείτε την κλίση κ= και το σφάλμα της. Βρείτε και την απόκλιση από την αναμενόμενη τιμή. Συζητείστε την απόκλιση αυτή σε σχέση με το σφάλμα που προέκυψε πειραματικά και συγκρίνετε το σφάλμα της μεθόδου Bessel με αυτό της προηγούμενης μεθόδου. 4.3 Προσδιορισμός εστιακής απόστασης αποκλίνοντος φακού μέσω συστήματος φακών. Όπως είπαμε και στην παράγραφο η μέτρηση της εστιακής απόστασης αποκλινόντων φακών δεν μπορεί να πραγματοποιηθεί άμεσα διότι από μόνοι τους δεν δημιουργούν πραγματικά είδωλα. Για το λόγο αυτό καταφεύγουμε εδώ σε σύστημα ενός συγκλίνοντος ( 1 >0) και ενός αποκλίνοντος ( 2 <0) φακού (με το φως να προσπίπτει πρώτα στον συγκλίνοντα). Ένα τέτοιο σύστημα μπορεί να παράγει πραγματικό τελικό είδωλο εάν ισχύουν οι δύο παρακάτω συνθήκες: (Ι) το ενδιάμεσο αντικείμενο είναι φανταστικό (συνεπώς a 2 = d - b 1 < 0) και (ΙΙ) 2 > a 2. Οι ορισμοί των αποστάσεων φαίνονται στα σχήματα 15(α,β). Ως αντικείμενο χρησιμοποιήστε πάλι το νήμα πυρακτώσεως. Εργαστείτε με συγκλίνοντα φακό σχετικά μεγάλης εστιακής α- πόστασης και τον αμφίκοιλο φακό Φ4 για τον οποίο η αναμενόμενη τιμή της εστιακής απόστασης είναι -167 mm. Ακολουθήστε τα εξής βήματα: Λεπτοί φακοί 10/12
12 1. Τοποθετήστε τη βάση με το συγκλίνοντα φακό σε σταθερή απόσταση a 1 από το νήμα. Η απόσταση αυτή δεν χρειάζεται να μετρηθεί αλλά πρέπει να είναι τέτοια ώστε η απόσταση b 1 (που πρέπει να μετρηθεί αλλά είναι σταθερή σε όλη της διάρκεια του πειράματος) να είναι αρκετά μεγάλη ώστε να έχετε μεγάλη περιοχή μετρήσεων. Βρείτε τη θέση του πρώτου ειδώλου και σημειώστε τη. 2. Τοποθετήστε τη βάση με τον αποκλίνοντα φακό σε θέση που βρίσκεται μεταξύ του συγκλίνοντα φακού και της θέσης που σημειώσατε στο βήμα 1. Μετρήστε την απόσταση d μεταξύ των δύο φακών και υπολογίστε το μέγεθος a 2 = d b 1 <0. Φροντίστε ώστε η απόσταση a 2 που προκύπτει να είναι (κατ απόλυτη τιμή) μικρότερη από την αναμενόμενη τιμή της εστιακής απόστασης του Φ4. 3. Βρείτε τη θέση του τελικού ειδώλου μετακινώντας τη βάση με την οθόνη και μετρήστε την απόστασή του, b 2, από τον αποκλίνοντα φακό. 4. Επαναλάβατε τα βήματα 2 και 3 για 6-9 φορές ακόμη για διάφορες τιμές d i προσέχοντας ώστε να ισχύουν πάντα οι συνθήκες (Ι) και (ΙΙ). Συγκεντρώστε τις μετρήσεις a 2i, και b 2i σε πίνακα. 5. Κατά την ανάλυση των μετρήσεων στο σπίτι, αναπτύξτε τον πίνακα ώστε, εκτός από τις τιμές a 2i, και b 2i, να περιέχει και τις τιμές a 2i + b 2i και a 2i b 2i <0. 6. Κατασκευάστε τη γραφική παράσταση a 2i b 2i = F(a 2i + b 2i ) (mm-χαρτί) που αναμένεται να είναι ευθεία με σημείο οδηγό το (0,0) και αρνητική κλίση ίση με 2. Βρείτε τη κλίση και το σφάλμα της. Βρείτε και την απόκλιση από την αναμενόμενη τιμή. Συζητείστε την απόκλιση αυτή σε σχέση με το σφάλμα που προέκυψε πειραματικά. 4.4 Προσδιορισμός εστιακής απόστασης αποκλίνοντος φακού με τη μέθοδο διαμέτρου φωτεινής δέσμης laser & μεγεθυντή δέσμης. Στο πείραμα αυτό θα προσδιορίσουμε την εστιακή απόσταση αποκλίνοντος φακού (του επιπεδόκοιλου Φ5) με διαφορετική μέθοδο. Έστω D ο η D o d διάμετρος παράλληλης δέσμης Laser He/Ne D που προσπίπτει στο φακό και D η διάμετρος της αποκλίνουσας 1 2 δέσμης μετά το φακό (τον οποίο θεωρούμε λεπτό). Μέσω του Σχήμα σχήματος 16 και ομοιότητας τριγώνων έχουμε, D D 1 1 (15) Do Do Η σχέση (15) στη δεύτερη μορφή της παριστάνει ευθεία y=κ x + c με y= D/D ο, x=,σταθερά c=1 και κλίση κ=1/. Συνεπώς έχει σημείο οδηγό το σημείο (0,1). Για τον προσδιορισμό της πρέπει να μετρήσουμε την αρχική διάμετρο της δέσμης D ο καθώς και τη διάμετρό της D μετά το φακό σε διάφορες αποστάσεις από αυτόν. Αντιμετωπίζουμε όμως το πρόβλημα ότι η δέσμη laser έχει πολύ μικρή διατομή d (της τάξης του 1 mm) και οι μετρήσεις των διαμέτρων είναι δύσκολες και ανακριβείς. Για το λόγο αυτό πριν προχωρήσουμε χρησιμοποιούμε ένα μεγεθυντή δέσμης του τύπου που αναπτύχθηκε στην παράγραφο 2.7.4, δηλαδή με δύο συγκλίνοντες φακούς εστιακών αποστάσεων 1 και 2 > 1 τοποθετημένους σε απόσταση L= Είναι η διάμετρος της εξερχόμενης από το μεγεθυντή δέσμης που θα προσπέσει στον επιπεδόκοιλο φακό. Η διάμετρος αυτή θα είναι ίση με D ο =d 2 / 1. Από τους διαθέσιμους φακούς χρησιμοποιήστε αυτούς που σας δίνουν τη μεγαλύτερη δυνατή μεγέθυνση. Στο σχήμα 16 φαίνεται σχηματικά η διάταξη στο σύνολό της. Ακολουθήστε τα παρακάτω βήματα: Λεπτοί φακοί 11/12
13 1. Αντικαταστήστε τη λάμπα πυρακτώσεως με το laser He/Ne στην οπτική ράγα και θέστε το σε λειτουργία. 2. Τοποθετήστε τη βάση με το συγκλίνοντα φακό μικρότερης εστιακής απόστασης 1 όσο κοντύτερα γίνεται στην έξοδο του laser. Κατόπιν τοποθετήστε την άλλη βάση με το συγκλίνοντα φακό μεγαλύτερης εστιακής απόστασης 2 σε απόσταση από το πρώτο ίση με το άθροισμα των αναγραφόμενων εστιακών τους αποστάσεων. Ελέγξτε με χιλιοστομετρική οθόνη ότι πράγματι η εξερχόμενη από το σύστημα δέσμη διατηρεί τη ίδια διάμετρο σε κοντινές, μέσες και μακρινές αποστάσεις. Εάν όχι μετακινείστε ελαφρά τη βάση του δεύτερο φακού έως ότου το επιτύχετε. Τότε μετρήστε αυτή τη διάμετρο D ο. 3. Τοποθετήστε τη βάση με τον επιπεδόκοιλο φακό Φ5 μετά τον φακό 2 και όσο κοντύτερα γίνεται. Τοποθετήστε τη βάση με τη χιλιοστομετρική οθόνη σε απόσταση από τον Φ5. Μετρήστε την απόσταση και τη διάμετρο της δέσμης D. 4. Κρατώντας της θέση του Φ5 σταθερή μετακινήστε την οθόνη σε διάφορες θέσεις i και μετρήστε τις διαμέτρους D i (6-9 φορές). Συγκεντρώστε τις μετρήσεις i και D i καθώς και την D ο σε πίνακα. 5. Κατά την ανάλυση των μετρήσεων στο σπίτι, αναπτύξτε τον πίνακα ώστε, εκτός από τις τιμές i και D i να περιέχει και τις τιμές D i /D ο. 6. Κατασκευάστε τη γραφική παράσταση D i /D ο = F( i ) (mm-χαρτί) με σημείο οδηγό το (0,1). Βρείτε την κλίση και το σφάλμα της και από αυτά την (κατ απόλυτη τιμή) εστιακή απόσταση του Φ5 και το σφάλμα της. Βρείτε και την απόκλιση από την αναμενόμενη τιμή η οποία είναι ίση με -360 mm. Συζητείστε την απόκλιση αυτή σε σχέση με το σφάλμα που προέκυψε πειραματικά. 5. Βιβλιογραφία. [1] D. Halliday& R. Resnick, Φυσική, Τόμος Β (1976). [2] Γ. Ασημέλλης, Μαθήματα Οπτικής, Σύγχρονη Γνώση (2008). [3] E. Hecht, Optics, Addison-Wesley, MA, Second Edition (1987). [4] Α. Χριστοδουλλίδης, Εργαστηριακά Πειράματα Φυσικής 3, Πανεπιστήμιο Ιωαννίνων (2005). (αντίτυπα υπάρχουν στο αναγνωστήριο). Λεπτοί φακοί 12/12
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0
 Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Σημειώσεις. Εργαστηρίου. Κυμάνσεων & Οπτικής
 Σημειώσεις Εργαστηρίου Κυμάνσεων & Οπτικής Ιωάννινα 01 Πανεπιστήμιο Ιωαννίνων Τμήμα Φυσικής Ασκήσεις 1. Λεπτοί Φακοί -3. Πόλωση του Φωτός Ι & ΙΙ 4. Ανάκλαση & Διάθλαση του Φωτός 5-6. Συμβολή & Περίθλαση
Σημειώσεις Εργαστηρίου Κυμάνσεων & Οπτικής Ιωάννινα 01 Πανεπιστήμιο Ιωαννίνων Τμήμα Φυσικής Ασκήσεις 1. Λεπτοί Φακοί -3. Πόλωση του Φωτός Ι & ΙΙ 4. Ανάκλαση & Διάθλαση του Φωτός 5-6. Συμβολή & Περίθλαση
Μελέτη συστήματος φακών με τη Μέθοδο του Newton
 Μελέτη συστήματος φακών με τη Μέθοδο του Newton.Σκοπός Σκοπός της άσκησης είναι η μελέτη της εστιακής απόστασης συστήματος φακών, η εύρεση της ισοδύναμης εστιακής απόστασης του συστήματος αυτού καθώς και
Μελέτη συστήματος φακών με τη Μέθοδο του Newton.Σκοπός Σκοπός της άσκησης είναι η μελέτη της εστιακής απόστασης συστήματος φακών, η εύρεση της ισοδύναμης εστιακής απόστασης του συστήματος αυτού καθώς και
Εφαρμοσμένη Οπτική. Γεωμετρική Οπτική
 Εφαρμοσμένη Οπτική Γεωμετρική Οπτική Κύρια σημεία του μαθήματος Η προσέγγιση της γεωμετρικής οπτικής Νόμοι της ανάκλασης και της διάθλασης Αρχή του Huygens Αρχή του Fermat Αρχή της αντιστρεψιμότητας (principle
Εφαρμοσμένη Οπτική Γεωμετρική Οπτική Κύρια σημεία του μαθήματος Η προσέγγιση της γεωμετρικής οπτικής Νόμοι της ανάκλασης και της διάθλασης Αρχή του Huygens Αρχή του Fermat Αρχή της αντιστρεψιμότητας (principle
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ. G. Mitsou
 ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ Διάθλαση σε σφαιρική επιφάνεια Φακοί Ορισμοί Λεπτοί φακοί Συγκλίνοντες φακοί Δημιουργία ειδώλων Αποκλίνοντες φακοί Γενικοί τύποι φακών Σύστημα λεπτών φακών σε επαφή Ασκήσεις Διάθλαση
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ Διάθλαση σε σφαιρική επιφάνεια Φακοί Ορισμοί Λεπτοί φακοί Συγκλίνοντες φακοί Δημιουργία ειδώλων Αποκλίνοντες φακοί Γενικοί τύποι φακών Σύστημα λεπτών φακών σε επαφή Ασκήσεις Διάθλαση
Σημειώσεις. Εργαστηρίου. Κυμάνσεων & Οπτικής
 Σημειώσεις Εργαστηρίου Κυμάνσεων & Οπτικής Ιωάννινα 013 Πανεπιστήμιο Ιωαννίνων Τμήμα Φυσικής Ασκήσεις 1. Ανάκλαση & Διάθλαση του Φωτός. Λεπτοί Φακοί 3-4. Συμβολή & Περίθλαση του Φωτός Ι & ΙΙ 5-6. Πόλωση
Σημειώσεις Εργαστηρίου Κυμάνσεων & Οπτικής Ιωάννινα 013 Πανεπιστήμιο Ιωαννίνων Τμήμα Φυσικής Ασκήσεις 1. Ανάκλαση & Διάθλαση του Φωτός. Λεπτοί Φακοί 3-4. Συμβολή & Περίθλαση του Φωτός Ι & ΙΙ 5-6. Πόλωση
Φύση του φωτός. Θεωρούμε ότι το φως έχει διττή φύση: διαταραχή που διαδίδεται στο χώρο. μήκος κύματος φωτός. συχνότητα φωτός
 Γεωμετρική Οπτική Φύση του φωτός Θεωρούμε ότι το φως έχει διττή φύση: ΚΥΜΑΤΙΚΗ Βασική ιδέα Το φως είναι μια Η/Μ διαταραχή που διαδίδεται στο χώρο Βασική Εξίσωση Φαινόμενα που εξηγεί καλύτερα (κύμα) μήκος
Γεωμετρική Οπτική Φύση του φωτός Θεωρούμε ότι το φως έχει διττή φύση: ΚΥΜΑΤΙΚΗ Βασική ιδέα Το φως είναι μια Η/Μ διαταραχή που διαδίδεται στο χώρο Βασική Εξίσωση Φαινόμενα που εξηγεί καλύτερα (κύμα) μήκος
Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα. Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ
 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ Πουλιάσης Αντώνης Φυσικός M.Sc. 2 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Γεωμετρική
Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ Πουλιάσης Αντώνης Φυσικός M.Sc. 2 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Γεωμετρική
ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ
 ΕΡΑΣΤΗΡΙ ΕΦΑΡΜΣΜΕΝΗΣ ΠΤΙΚΗΣ Άσκηση 1: Λεπτοί φακοί Εξεταζόμενες γνώσεις. Εξίσωση κατασκευαστών των φακών. Συστήματα φακών. Διαγράμματα κύριων ακτινών. Είδωλα και μεγέθυνση σε λεπτούς φακούς. Α. Λεπτοί
ΕΡΑΣΤΗΡΙ ΕΦΑΡΜΣΜΕΝΗΣ ΠΤΙΚΗΣ Άσκηση 1: Λεπτοί φακοί Εξεταζόμενες γνώσεις. Εξίσωση κατασκευαστών των φακών. Συστήματα φακών. Διαγράμματα κύριων ακτινών. Είδωλα και μεγέθυνση σε λεπτούς φακούς. Α. Λεπτοί
7.1 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ
 7.1 ΑΣΚΗΣΗ 7 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ ΘΕΩΡΙΑ Όταν φωτεινή παράλληλη δέσμη διαδιδόμενη από οπτικό μέσο α με δείκτη διάθλασης n 1 προσπίπτει σε άλλο οπτικό μέσο β με δείκτη διάθλασης n 2 και
7.1 ΑΣΚΗΣΗ 7 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ ΘΕΩΡΙΑ Όταν φωτεινή παράλληλη δέσμη διαδιδόμενη από οπτικό μέσο α με δείκτη διάθλασης n 1 προσπίπτει σε άλλο οπτικό μέσο β με δείκτη διάθλασης n 2 και
Ο15. Κοίλα κάτοπτρα. 2. Θεωρία. 2.1 Γεωμετρική Οπτική
 Ο15 Κοίλα κάτοπτρα 1. Σκοπός Σκοπός της άσκησης είναι η εύρεση της εστιακής απόστασης κοίλου κατόπτρου σχετικά μεγάλου ανοίγματος και την μέτρηση του σφάλματος της σφαιρικής εκτροπής... Θεωρία.1 Γεωμετρική
Ο15 Κοίλα κάτοπτρα 1. Σκοπός Σκοπός της άσκησης είναι η εύρεση της εστιακής απόστασης κοίλου κατόπτρου σχετικά μεγάλου ανοίγματος και την μέτρηση του σφάλματος της σφαιρικής εκτροπής... Θεωρία.1 Γεωμετρική
1. Ιδιότητες φακών. 1 Λεπτοί φακοί. 2 Απριλίου Βασικές έννοιες
 . Ιδιότητες φακών 2 Απριλίου 203 Λεπτοί φακοί. Βασικές έννοιες Φακός είναι ένα οπτικό σύστημα με δύο διαθλαστικές επιφάνειες. Ο απλούστερος φακός έχει δύο σφαιρικές επιφάνειες αρκετά κοντά η μία με την
. Ιδιότητες φακών 2 Απριλίου 203 Λεπτοί φακοί. Βασικές έννοιες Φακός είναι ένα οπτικό σύστημα με δύο διαθλαστικές επιφάνειες. Ο απλούστερος φακός έχει δύο σφαιρικές επιφάνειες αρκετά κοντά η μία με την
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 www.pmoira.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 www.pmoira.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
Generated by Foxit PDF Creator Foxit Software http://www.foxitsoftware.com For evaluation only. ΑΣΚΗΣΗ 10 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΟΥ
 ΑΣΚΗΣΗ 0 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΟΥ . Γεωμετρική οπτική ΜΕΡΟΣ ΠΡΩΤΟ ΒΑΣΙΚΕΣ ΘΕΩΡΗΤΙΚΕΣ ΓΝΩΣΕΙΣ Η Γεωμετρική οπτική είναι ένας τρόπος μελέτης των κυμάτων και χρησιμοποιείται για την εξέταση μερικών
ΑΣΚΗΣΗ 0 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΟΥ . Γεωμετρική οπτική ΜΕΡΟΣ ΠΡΩΤΟ ΒΑΣΙΚΕΣ ΘΕΩΡΗΤΙΚΕΣ ΓΝΩΣΕΙΣ Η Γεωμετρική οπτική είναι ένας τρόπος μελέτης των κυμάτων και χρησιμοποιείται για την εξέταση μερικών
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ
 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ Μάθημα προς τους ειδικευόμενους γιατρούς στην Οφθαλμολογία, Στο Κ.Οφ.Κ.Α. την 18/11/2003. Υπό: Δρος Κων. Ρούγγα, Οφθαλμιάτρου. 1. ΑΝΑΚΛΑΣΗ ΤΟΥ ΦΩΤΟΣ Όταν μια φωτεινή ακτίνα ή
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ Μάθημα προς τους ειδικευόμενους γιατρούς στην Οφθαλμολογία, Στο Κ.Οφ.Κ.Α. την 18/11/2003. Υπό: Δρος Κων. Ρούγγα, Οφθαλμιάτρου. 1. ΑΝΑΚΛΑΣΗ ΤΟΥ ΦΩΤΟΣ Όταν μια φωτεινή ακτίνα ή
ΟΠΤΙΚΑ ΣΤΟΙΧΕΙΑ : ΚΑΤΟΠΤΡΑ ΔΙΟΠΤΡΑ ΦΑΚΟΙ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΟΠΤΙΚΑ ΣΤΟΙΧΕΙΑ : ΚΑΤΟΠΤΡΑ ΔΙΟΠΤΡΑ ΦΑΚΟΙ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ.
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΟΠΤΙΚΑ ΣΤΟΙΧΕΙΑ : ΚΑΤΟΠΤΡΑ ΔΙΟΠΤΡΑ ΦΑΚΟΙ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ.
Γεωμετρική Οπτική ΚΕΦΑΛΑΙΟ 34
 Γεωμετρική Οπτική ΚΕΦΑΛΑΙΟ 34 Γεωμετρική Οπτική Γνωρίζουμε τα βασικά Δηλαδή, πως το φως διαδίδεται και αλληλεπιδρά με σώματα διαστάσεων πολύ μεγαλύτερων από το μήκος κύματος. Ανάκλαση: Προσπίπτουσα ακτίνα
Γεωμετρική Οπτική ΚΕΦΑΛΑΙΟ 34 Γεωμετρική Οπτική Γνωρίζουμε τα βασικά Δηλαδή, πως το φως διαδίδεται και αλληλεπιδρά με σώματα διαστάσεων πολύ μεγαλύτερων από το μήκος κύματος. Ανάκλαση: Προσπίπτουσα ακτίνα
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ. Ανάκλαση. Κάτοπτρα. Διάθλαση. Ολική ανάκλαση. Φαινόμενη ανύψωση αντικειμένου. Μετατόπιση ακτίνας. Πρίσματα
 ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ Ανάκλαση Κάτοπτρα Διάθλαση Ολική ανάκλαση Φαινόμενη ανύψωση αντικειμένου Μετατόπιση ακτίνας Πρίσματα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ - Ανάκλαση Επιστροφή σε «γεωμετρική οπτική» Ανάκλαση φωτός ονομάζεται
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ Ανάκλαση Κάτοπτρα Διάθλαση Ολική ανάκλαση Φαινόμενη ανύψωση αντικειμένου Μετατόπιση ακτίνας Πρίσματα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ - Ανάκλαση Επιστροφή σε «γεωμετρική οπτική» Ανάκλαση φωτός ονομάζεται
ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ
 ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ ΑΣΚΗΣΗ 3-2016 1 Σκοπός Σε αυτή την άσκηση ο φοιτητής χειρίζεται βασικά οπτικά όργανα όπως είναι οι λεπτοί φακοί. Στο πρώτο μέρος υπολογίζεται η εστιακή απόσταση
ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ ΑΣΚΗΣΗ 3-2016 1 Σκοπός Σε αυτή την άσκηση ο φοιτητής χειρίζεται βασικά οπτικά όργανα όπως είναι οι λεπτοί φακοί. Στο πρώτο μέρος υπολογίζεται η εστιακή απόσταση
ΑΣΚΗΣΗ 8 Μελέτη φακών
 Απαραίτητα όργανα και υλικά ΑΣΚΗΣΗ 8 Μελέτη φακών 8. Απαραίτητα όργανα και υλικά. Οπτική τράπεζα.. Πέτασμα. 3. Συγκεντρωτικός φακός. 4. Φωτεινή πηγή. 5. Διάφραγμα με δακτύλιο και οπή. 6. Φίλτρο κόκκινο
Απαραίτητα όργανα και υλικά ΑΣΚΗΣΗ 8 Μελέτη φακών 8. Απαραίτητα όργανα και υλικά. Οπτική τράπεζα.. Πέτασμα. 3. Συγκεντρωτικός φακός. 4. Φωτεινή πηγή. 5. Διάφραγμα με δακτύλιο και οπή. 6. Φίλτρο κόκκινο
ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ
 ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ ΑΣΚΗΣΗ 3-2017 1 Σκοπός Σε αυτή την άσκηση ο φοιτητής χειρίζεται βασικά οπτικά όργανα όπως είναι οι λεπτοί φακοί. Στο πρώτο μέρος υπολογίζεται η εστιακή απόσταση
ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ ΑΣΚΗΣΗ 3-2017 1 Σκοπός Σε αυτή την άσκηση ο φοιτητής χειρίζεται βασικά οπτικά όργανα όπως είναι οι λεπτοί φακοί. Στο πρώτο μέρος υπολογίζεται η εστιακή απόσταση
4. Ανάκλαση & Διάθλαση του Φωτός
 4. Ανάκλαση & Διάθλαση του Φωτός Σελίδα 1. Σκοπός της άσκησης... 1. Στοιχεία θεωρίας... 1.1 Ανάκλαση & διάθλαση του φωτός: κρίσιμη γωνία πρόσπτωσης... 1. Συντελεστές ανακλαστικότητας & διαπερατότητας φωτεινής
4. Ανάκλαση & Διάθλαση του Φωτός Σελίδα 1. Σκοπός της άσκησης... 1. Στοιχεία θεωρίας... 1.1 Ανάκλαση & διάθλαση του φωτός: κρίσιμη γωνία πρόσπτωσης... 1. Συντελεστές ανακλαστικότητας & διαπερατότητας φωτεινής
ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ. Διάθλαση μέσω πρίσματος - Φασματοσκοπικά χαρακτηριστικά πρίσματος.
 Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ. Διάθλαση μέσω πρίσματος - Φασματοσκοπικά χαρακτηριστικά πρίσματος. 1. Σκοπός Όταν δέσμη λευκού φωτός προσπέσει σε ένα πρίσμα τότε κάθε μήκος κύματος διαθλάται σύμφωνα με τον αντίστοιχο
Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ. Διάθλαση μέσω πρίσματος - Φασματοσκοπικά χαρακτηριστικά πρίσματος. 1. Σκοπός Όταν δέσμη λευκού φωτός προσπέσει σε ένα πρίσμα τότε κάθε μήκος κύματος διαθλάται σύμφωνα με τον αντίστοιχο
Μεγεθυντικός φακός. 1. Σκοπός. 2. Θεωρία. θ 1
 Μεγεθυντικός φακός 1. Σκοπός Οι μεγεθυντικοί φακοί ή απλά μικροσκόπια (magnifiers) χρησιμοποιούνται για την παρατήρηση μικροσκοπικών αντικειμένων ώστε να γίνουν καθαρά παρατηρήσιμες οι λεπτομέρειες τους.
Μεγεθυντικός φακός 1. Σκοπός Οι μεγεθυντικοί φακοί ή απλά μικροσκόπια (magnifiers) χρησιμοποιούνται για την παρατήρηση μικροσκοπικών αντικειμένων ώστε να γίνουν καθαρά παρατηρήσιμες οι λεπτομέρειες τους.
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ
 ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση =0.0 mm είναι τοποθετημένο σε απόσταση =1,0 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές φωτίζεται
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση =0.0 mm είναι τοποθετημένο σε απόσταση =1,0 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές φωτίζεται
ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ
 ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ Άσκηση 4: Σφάλματα φακών: Ι Σφαιρική εκτροπή Εξεταζόμενες γνώσεις: σφάλματα σφαιρικής εκτροπής. Α. Γενικά περί σφαλμάτων φακών Η βασική σχέση του Gauss 1/s +1/s = 1/f που
ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ Άσκηση 4: Σφάλματα φακών: Ι Σφαιρική εκτροπή Εξεταζόμενες γνώσεις: σφάλματα σφαιρικής εκτροπής. Α. Γενικά περί σφαλμάτων φακών Η βασική σχέση του Gauss 1/s +1/s = 1/f που
ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ ιάθλαση µέσω πρίσµατος Φασµατοσκοπικά χαρακτηριστικά πρίσµατος
 Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ ιάθλαση µέσω πρίσµατος Φασµατοσκοπικά χαρακτηριστικά πρίσµατος 1. Εισαγωγή Όταν δέσµη λευκού φωτός προσπέσει σε ένα πρίσµα τότε κάθε µήκος κύµατος διαθλάται σύµφωνα µε τον αντίστοιχο
Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ ιάθλαση µέσω πρίσµατος Φασµατοσκοπικά χαρακτηριστικά πρίσµατος 1. Εισαγωγή Όταν δέσµη λευκού φωτός προσπέσει σε ένα πρίσµα τότε κάθε µήκος κύµατος διαθλάται σύµφωνα µε τον αντίστοιχο
EΡΩΤΗΣΕΙΣ ΑΣΚΗΣΕΙΣ ΠΡΟΒΛΗΜΑΤΑ ΣΤΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΑΝΑΚΛΑΣΗ ΔΙΑΘΛΑΣΗ ΟΛΙΚΗ ΑΝΑΚΛΑΣΗ
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΠΟΥ ΔΙΑΔΙΔΕΤΑΙ ΤΟ ΦΩΣ
 1 ΦΩΣ Στο μικρόκοσμο θεωρούμε ότι το φως έχει δυο μορφές. Άλλοτε το αντιμετωπίζουμε με τη μορφή σωματιδίων που ονομάζουμε φωτόνια. Τα φωτόνια δεν έχουν μάζα αλλά μόνον ενέργεια. Άλλοτε πάλι αντιμετωπίζουμε
1 ΦΩΣ Στο μικρόκοσμο θεωρούμε ότι το φως έχει δυο μορφές. Άλλοτε το αντιμετωπίζουμε με τη μορφή σωματιδίων που ονομάζουμε φωτόνια. Τα φωτόνια δεν έχουν μάζα αλλά μόνον ενέργεια. Άλλοτε πάλι αντιμετωπίζουμε
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ
 ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση d=0.20 mm είναι τοποθετημένο σε απόσταση =1,20 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση d=0.20 mm είναι τοποθετημένο σε απόσταση =1,20 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές
Υπολογισμός της εστιακής απόστασης f λεπτού συμμετρικού συγκλίνοντος φακού απο τη γραμμική μεγέθυνση Μ
 ΟΜΑΔΑ ΟΝΟΜΑΤΕΠΩΝΥΜΑ ΜΑΘΗΤΩΝ 1)... 2)... 3)... ΗΜΕΡΟΜΗΝΙΑ : Υπολογισμός της εστιακής απόστασης f λεπτού συμμετρικού συγκλίνοντος φακού απο τη γραμμική μεγέθυνση Μ Με το πείραµα αυτό θα προσδιορίσουµε: Σκοπός
ΟΜΑΔΑ ΟΝΟΜΑΤΕΠΩΝΥΜΑ ΜΑΘΗΤΩΝ 1)... 2)... 3)... ΗΜΕΡΟΜΗΝΙΑ : Υπολογισμός της εστιακής απόστασης f λεπτού συμμετρικού συγκλίνοντος φακού απο τη γραμμική μεγέθυνση Μ Με το πείραµα αυτό θα προσδιορίσουµε: Σκοπός
ΚΕΦΑΛΑΙΟ 2ο: ΜΗΧΑΝΙΚΑ- ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ.
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
5 Δεκεμβρίου 2015 ΛΥΚΕΙΟ:... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: ΜΟΝΑΔΕΣ:
 ΤΟΠΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 2016 ΦΥΣΙΚΗ 5 Δεκεμβρίου 2015 ΛΥΚΕΙΟ:..... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1.. 2.. 3.. ΜΟΝΑΔΕΣ: Το πρόβλημα Μελέτη οπτικών ιδιοτήτων διαφανούς υλικού με τη βοήθεια πηγής φωτός laser Είστε στο δωμάτιό
ΤΟΠΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 2016 ΦΥΣΙΚΗ 5 Δεκεμβρίου 2015 ΛΥΚΕΙΟ:..... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1.. 2.. 3.. ΜΟΝΑΔΕΣ: Το πρόβλημα Μελέτη οπτικών ιδιοτήτων διαφανούς υλικού με τη βοήθεια πηγής φωτός laser Είστε στο δωμάτιό
25 Ιανουαρίου 2014 ΛΥΚΕΙΟ:... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: ΜΟΝΑΔΕΣ:
 ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗ 25 Ιανουαρίου 2014 ΛΥΚΕΙΟ:..... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1.. 2..... 3..... ΜΟΝΑΔΕΣ: Το πρόβλημα Ένας φίλος σας βρήκε ένα μικρό, πολύ όμορφο τεμάχιο διαφανούς στερεού και ζητά τη γνώμη
ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗ 25 Ιανουαρίου 2014 ΛΥΚΕΙΟ:..... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1.. 2..... 3..... ΜΟΝΑΔΕΣ: Το πρόβλημα Ένας φίλος σας βρήκε ένα μικρό, πολύ όμορφο τεμάχιο διαφανούς στερεού και ζητά τη γνώμη
Σφάλματα φακών (Σφαιρικό - Χρωματικό).
 O12 Σφάλματα φακών (Σφαιρικό - Χρωματικό). 1. Σκοπός Στην άσκηση αυτή υπολογίζονται πειραματικά δυο από τα πιο σημαντικά οπτικά σφάλματα (η αποκλίσεις) που παρουσιάζονται όταν φωτεινές ακτίνες διέλθουν
O12 Σφάλματα φακών (Σφαιρικό - Χρωματικό). 1. Σκοπός Στην άσκηση αυτή υπολογίζονται πειραματικά δυο από τα πιο σημαντικά οπτικά σφάλματα (η αποκλίσεις) που παρουσιάζονται όταν φωτεινές ακτίνες διέλθουν
ΕΚΦΕ ΕΥΒΟΙΑΣ. ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΓΙΑ ΤΗΝ ΕΠΙΛΟΓΗ ΟΜΑΔΑΣ ΜΑΘΗΤΩΝ ΓΙΑ ΤΗΝ 13 η ΕΥΡΩΠΑΪΚΗ ΟΛΥΜΠΙΑΔΑ ΕΠΙΣΤΗΜΩΝ EUSO 2015 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ
 ΕΚΦΕ ΕΥΒΟΙΑΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΓΙΑ ΤΗΝ ΕΠΙΛΟΓΗ ΟΜΑΔΑΣ ΜΑΘΗΤΩΝ ΓΙΑ ΤΗΝ 13 η ΕΥΡΩΠΑΪΚΗ ΟΛΥΜΠΙΑΔΑ ΕΠΙΣΤΗΜΩΝ EUSO 2015 Διάρκεια: 60 min ΣΑΒΒΑΤΟ 06/12/2014 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Μαθητές: Σχολική Μονάδα 1.
ΕΚΦΕ ΕΥΒΟΙΑΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΓΙΑ ΤΗΝ ΕΠΙΛΟΓΗ ΟΜΑΔΑΣ ΜΑΘΗΤΩΝ ΓΙΑ ΤΗΝ 13 η ΕΥΡΩΠΑΪΚΗ ΟΛΥΜΠΙΑΔΑ ΕΠΙΣΤΗΜΩΝ EUSO 2015 Διάρκεια: 60 min ΣΑΒΒΑΤΟ 06/12/2014 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Μαθητές: Σχολική Μονάδα 1.
Διάθλαση φωτός και ολική ανάκλαση: Εύρεση του δείκτη διάθλασης και της γωνίας ολικής ανάκλασης
 3 Διάθλαση φωτός και ολική ανάκλαση: Εύρεση του δείκτη διάθλασης και της γωνίας ολικής ανάκλασης Μέθοδος Σε σώμα διαφανές ημικυλινδρικού σχήματος είναι εύκολο να επιβεβαιωθεί ο νόμος του Sell και να εφαρμοστεί
3 Διάθλαση φωτός και ολική ανάκλαση: Εύρεση του δείκτη διάθλασης και της γωνίας ολικής ανάκλασης Μέθοδος Σε σώμα διαφανές ημικυλινδρικού σχήματος είναι εύκολο να επιβεβαιωθεί ο νόμος του Sell και να εφαρμοστεί
ΚΕΦΑΛΑΙΟ 11Α «Γεωμετρική οπτική - οπτικά όργανα» Εισαγωγή - Ανάκλαση
 ΚΕΦΑΛΑΙΟ Α «Γεωμετρική οπτική - οπτικά όργανα» Εισαγωγή - Ανάκλαση Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Ηφύσητουφωτός 643-77 Netwon Huygens 69-695 Το φως είναι δέσμη σωματιδίων Το φως
ΚΕΦΑΛΑΙΟ Α «Γεωμετρική οπτική - οπτικά όργανα» Εισαγωγή - Ανάκλαση Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Ηφύσητουφωτός 643-77 Netwon Huygens 69-695 Το φως είναι δέσμη σωματιδίων Το φως
Κεφάλαιο 32 Φως: Ανάκλασηκαι ιάθλαση. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 32 Φως: Ανάκλασηκαι ιάθλαση Γεωµετρική θεώρηση του Φωτός Ανάκλαση ηµιουργίαειδώλουαπόκάτοπτρα. είκτης ιάθλασης Νόµος του Snell Ορατό Φάσµα και ιασπορά Εσωτερική ανάκλαση Οπτικές ίνες ιάθλαση σε
Κεφάλαιο 32 Φως: Ανάκλασηκαι ιάθλαση Γεωµετρική θεώρηση του Φωτός Ανάκλαση ηµιουργίαειδώλουαπόκάτοπτρα. είκτης ιάθλασης Νόµος του Snell Ορατό Φάσµα και ιασπορά Εσωτερική ανάκλαση Οπτικές ίνες ιάθλαση σε
ΑΝΑΚΛΑΣΗ. β' νόμος της ανάκλασης: Η γωνία πρόσπτωσης και η γωνία ανάκλασης είναι ίσες.
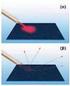 ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
Σχηματισμός ειδώλων. Εισαγωγή
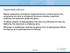 Σχηματισμός ειδώλων Είδωλα πραγματικών αντικειμένων σχηματίζονται όταν οι ακτίνες φωτός (που εκπέμπονται από αυτά τα αντικέιμενα) συναντούν επίπεδες ή καμπύλες επιφάνειες που βρίσκονται μεταξύ δύο μέσων.
Σχηματισμός ειδώλων Είδωλα πραγματικών αντικειμένων σχηματίζονται όταν οι ακτίνες φωτός (που εκπέμπονται από αυτά τα αντικέιμενα) συναντούν επίπεδες ή καμπύλες επιφάνειες που βρίσκονται μεταξύ δύο μέσων.
Κυματική οπτική. Συμβολή Περίθλαση Πόλωση
 Κυματική οπτική Η κυματική οπτική ασχολείται με τη μελέτη φαινομένων τα οποία δεν μπορούμε να εξηγήσουμε επαρκώς με τις αρχές της γεωμετρικής οπτικής. Στα φαινόμενα αυτά περιλαμβάνονται τα εξής: Συμβολή
Κυματική οπτική Η κυματική οπτική ασχολείται με τη μελέτη φαινομένων τα οποία δεν μπορούμε να εξηγήσουμε επαρκώς με τις αρχές της γεωμετρικής οπτικής. Στα φαινόμενα αυτά περιλαμβάνονται τα εξής: Συμβολή
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0
 Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Φυσική IΙ. Ενότητα 13: Γεωμετρική οπτική. Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών
 Φυσική IΙ Ενότητα 13: Γεωμετρική οπτική Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Η κυματική φύση του φωτός: διάθλαση, ανάκλαση, απορρόφηση Γωνίες πρόσπτωσης, ανάκλασης
Φυσική IΙ Ενότητα 13: Γεωμετρική οπτική Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Η κυματική φύση του φωτός: διάθλαση, ανάκλαση, απορρόφηση Γωνίες πρόσπτωσης, ανάκλασης
ΚΕΦΑΛΑΙΟ 1 - ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ
 ΚΕΦΑΛΑΙΟ 1 - ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ Σύμφωνα με την ηλεκτρομαγνητική θεωρία του Maxwell, το φως είναι εγκάρσιο ηλεκτρομαγνητικό κύμα. Η θεωρία αυτή α. δέχεται ότι κάθε φωτεινή πηγή εκπέμπει φωτόνια.
ΚΕΦΑΛΑΙΟ 1 - ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ Σύμφωνα με την ηλεκτρομαγνητική θεωρία του Maxwell, το φως είναι εγκάρσιο ηλεκτρομαγνητικό κύμα. Η θεωρία αυτή α. δέχεται ότι κάθε φωτεινή πηγή εκπέμπει φωτόνια.
1) Η εξάρτηση του δείκτη διάθλασης n από το μήκος κύματος για το κρύσταλλο του ιωδιούχου ρουβιδίου (RbI) παρουσιάζεται στο παρακάτω σχήμα.
 1) Η εξάρτηση του δείκτη διάθλασης n από το μήκος κύματος για το κρύσταλλο του ιωδιούχου ρουβιδίου (RbI) παρουσιάζεται στο παρακάτω σχήμα. Για τους δείκτες διάθλασης n 1 και n 2 ισχύει: n 2 = (11 / 10)
1) Η εξάρτηση του δείκτη διάθλασης n από το μήκος κύματος για το κρύσταλλο του ιωδιούχου ρουβιδίου (RbI) παρουσιάζεται στο παρακάτω σχήμα. Για τους δείκτες διάθλασης n 1 και n 2 ισχύει: n 2 = (11 / 10)
ιατµηµατικό µεταπτυχιακό πρόγραµµα «Οπτική και Όραση» Ασκήσεις Οπτική Ι ιδάσκων: ηµήτρης Παπάζογλου Email: dpapa@iesl.forth.gr
 ιατµηµατικό µεταπτυχιακό πρόγραµµα «Οπτική και Όραση» Ασκήσεις Οπτική Ι ιδάσκων: ηµήτρης Παπάζογλου Email: dpapa@iesl.forth.gr 1. Να σχεδιάσετε την διάδοση των ακτίνων στα παρακάτω οπτικά συστήµατα F F
ιατµηµατικό µεταπτυχιακό πρόγραµµα «Οπτική και Όραση» Ασκήσεις Οπτική Ι ιδάσκων: ηµήτρης Παπάζογλου Email: dpapa@iesl.forth.gr 1. Να σχεδιάσετε την διάδοση των ακτίνων στα παρακάτω οπτικά συστήµατα F F
ΑΝΑΚΛΑΣΗ. β' νόμος της ανάκλασης: Η γωνία πρόσπτωσης και η γωνία ανάκλασης είναι ίσες.
 ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
papost/
 Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
7α Γεωμετρική οπτική - οπτικά όργανα
 7α Γεωμετρική οπτική - οπτικά όργανα Εισαγωγή ορισμοί Φύση του φωτός Πηγές φωτός Δείκτης διάθλασης Ανάκλαση Δημιουργία ειδώλων από κάτοπτρα Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/katsiki Ηφύσητουφωτός
7α Γεωμετρική οπτική - οπτικά όργανα Εισαγωγή ορισμοί Φύση του φωτός Πηγές φωτός Δείκτης διάθλασης Ανάκλαση Δημιουργία ειδώλων από κάτοπτρα Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/katsiki Ηφύσητουφωτός
Q 40 th International Physics Olympiad, Merida, Mexico, July 2009
 ΠΕΙΡΑΜΑΤΙΚΟ ΠΡΟΒΛΗΜΑ No. 1 ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΟΥ ΜΗΚΟΥΣ ΚΥΜΑΤΟΣ ΦΩΤΟΣ ASER ΥΛΙΚΑ ΚΑΙ ΟΡΓΑΝΑ Επιπρόσθετα με τα υλικά 1), 2) και 3), αναμένεται να χρησιμοποιήσετε τα ακόλουθα: 4) Φακός ενσωματωμένος μέσα σε
ΠΕΙΡΑΜΑΤΙΚΟ ΠΡΟΒΛΗΜΑ No. 1 ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΟΥ ΜΗΚΟΥΣ ΚΥΜΑΤΟΣ ΦΩΤΟΣ ASER ΥΛΙΚΑ ΚΑΙ ΟΡΓΑΝΑ Επιπρόσθετα με τα υλικά 1), 2) και 3), αναμένεται να χρησιμοποιήσετε τα ακόλουθα: 4) Φακός ενσωματωμένος μέσα σε
γ) Να σχεδιάσετε τις γραφικές παραστάσεις απομάκρυνσης - χρόνου, για τα σημεία Α, Β και Γ, τα οποία απέχουν από το ελεύθερο άκρο αντίστοιχα,,
 1. Κατά μήκος μιας ελαστικής χορδής μεγάλου μήκους που το ένα άκρο της είναι ακλόνητα στερεωμένο, διαδίδονται δύο κύματα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι μετρημένα σε και
1. Κατά μήκος μιας ελαστικής χορδής μεγάλου μήκους που το ένα άκρο της είναι ακλόνητα στερεωμένο, διαδίδονται δύο κύματα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι μετρημένα σε και
Διάθλαση φωτεινής δέσμης σε διαφανές υλικό (Επιβεβαίωση, αξιοποίηση του νόμου Snell)
 Διάθλαση φωτεινής δέσμης σε διαφανές υλικό (Επιβεβαίωση, αξιοποίηση του νόμου Snell) 1. Σκοπός Αξιοποιώντας τις μετρήσεις των γωνιών πρόσπτωσης, διάθλασης α και δ αντίστοιχα μίας πολύ στενής φωτεινής δέσμης
Διάθλαση φωτεινής δέσμης σε διαφανές υλικό (Επιβεβαίωση, αξιοποίηση του νόμου Snell) 1. Σκοπός Αξιοποιώντας τις μετρήσεις των γωνιών πρόσπτωσης, διάθλασης α και δ αντίστοιχα μίας πολύ στενής φωτεινής δέσμης
Εστιομετρία φακών και κατόπτρων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ, ΑΣΤΡΟΝΟΜΙΑΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΑΣΤΡΟΝΟΜΙΑΣ ΚΑΙ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ Εστιομετρία
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ, ΑΣΤΡΟΝΟΜΙΑΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΑΣΤΡΟΝΟΜΙΑΣ ΚΑΙ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ Εστιομετρία
ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΟΛΟΓΙΑΣ ΟΠΤΙΚΩΝ ΟΡΓΑΝΩΝ
 ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΟΛΟΓΙΑΣ ΟΠΤΙΚΩΝ ΟΡΓΑΝΩΝ Άσκηση 4. Διαφράγματα. Θεωρία Στο σχεδιασμό οπτικών οργάνων πρέπει να λάβει κανείς υπόψη και άλλες παραμέτρους πέρα από το πού και πώς σχηματίζεται το είδωλο ενός
ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΟΛΟΓΙΑΣ ΟΠΤΙΚΩΝ ΟΡΓΑΝΩΝ Άσκηση 4. Διαφράγματα. Θεωρία Στο σχεδιασμό οπτικών οργάνων πρέπει να λάβει κανείς υπόψη και άλλες παραμέτρους πέρα από το πού και πώς σχηματίζεται το είδωλο ενός
Φυσικά Μεγέθη Μονάδες Μέτρησης
 ΓΝΩΣΤΙΚΟ ΑΝΤΙΚΕΙΜΕΝΟ: ΦΥΣΙΚΗ A ΛΥΚΕΙΟΥ ΚΟΙΝΟΥ ΚΟΡΜΟΥ ΤΑΞΗ: Α Λυκείου Προσανατολισμού 1,3,4. ΚΕΦΑΛΑΙΑ ΕΝΟΤΗΤΕΣ ΜΑΘΗΣΙΑΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ Οι μαθητές και οι μαθήτριες να είναι σε θέση να: ΑΝΤΙΣΤΟΙΧΑ
ΓΝΩΣΤΙΚΟ ΑΝΤΙΚΕΙΜΕΝΟ: ΦΥΣΙΚΗ A ΛΥΚΕΙΟΥ ΚΟΙΝΟΥ ΚΟΡΜΟΥ ΤΑΞΗ: Α Λυκείου Προσανατολισμού 1,3,4. ΚΕΦΑΛΑΙΑ ΕΝΟΤΗΤΕΣ ΜΑΘΗΣΙΑΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ Οι μαθητές και οι μαθήτριες να είναι σε θέση να: ΑΝΤΙΣΤΟΙΧΑ
Μέτρηση καμπυλότητας σφαιρικών και τοροειδών επιφανειών με οπτικές και μηχανικές μεθόδους
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ, ΑΣΤΡΟΝΟΜΙΑΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΑΣΤΡΟΝΟΜΙΑΣ ΚΑΙ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ Μέτρηση
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ, ΑΣΤΡΟΝΟΜΙΑΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΑΣΤΡΟΝΟΜΙΑΣ ΚΑΙ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ Μέτρηση
Προγραμματισμός Ύλης Έτους Τάξη Α Κοινός Κορμός
 Προγραμματισμός Ύλης Έτους Τάξη Α Κοινός Κορμός Μάθημα: Φυσική Τμήματα:,.. Τάξη: Α Ομάδα Προσανατολισμού 1,3,4 Καθηγητές: Περ. Εβδομ: 2 ΚΕΦΑΛΑΙΑ ΕΝΟΤΗΤΕΣ ΥΛΗ ΠΕΡΙΟΔΟΙ ΗΜΕΡΟΜΗΝΙΕΣ Φυσικά Μεγέθη Μονάδες
Προγραμματισμός Ύλης Έτους Τάξη Α Κοινός Κορμός Μάθημα: Φυσική Τμήματα:,.. Τάξη: Α Ομάδα Προσανατολισμού 1,3,4 Καθηγητές: Περ. Εβδομ: 2 ΚΕΦΑΛΑΙΑ ΕΝΟΤΗΤΕΣ ΥΛΗ ΠΕΡΙΟΔΟΙ ΗΜΕΡΟΜΗΝΙΕΣ Φυσικά Μεγέθη Μονάδες
OΠΤIKH. Επειδή είναι πάντα υ<c (
 OΠΤIKH Η ταχύτητα του φωτός δεν είναι πάντα ίδια αλλά αλλάζει όταν το φως από ένα μέσο περνά σε κάποιο άλλο. Αν c είναι η ταχύτητα του φωτός στο κενό και υ η ταχύτητά του σε ένα άλλο υλικό τότε, ορίζουμε
OΠΤIKH Η ταχύτητα του φωτός δεν είναι πάντα ίδια αλλά αλλάζει όταν το φως από ένα μέσο περνά σε κάποιο άλλο. Αν c είναι η ταχύτητα του φωτός στο κενό και υ η ταχύτητά του σε ένα άλλο υλικό τότε, ορίζουμε
Γεωμετρική Οπτική. Πρόκειται δηλαδή για μια ισοφασική επιφάνεια που ονομάζεται μέτωπο κύματος.
 Γεωμετρική Οπτική Στη Γεωμετρική Οπτική επεξεργαζόμαστε τα φαινόμενα ωσάν το φως να αποτελείται μόνο από σωματίδια, ώστε να εξασφαλίζεται την εύκολη ερμηνεία των φαινομένων της ευθύγραμμης διάδοσης του
Γεωμετρική Οπτική Στη Γεωμετρική Οπτική επεξεργαζόμαστε τα φαινόμενα ωσάν το φως να αποτελείται μόνο από σωματίδια, ώστε να εξασφαλίζεται την εύκολη ερμηνεία των φαινομένων της ευθύγραμμης διάδοσης του
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ
 ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ ΕΠΙΛΟΓΗ ΘΕΜΑΤΩΝ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ «Β ΘΕΜΑΤΑ ΦΩΣ» ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β ΛΥΚΕΙΟΥ Χ. Δ. ΦΑΝΙΔΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 04-05 ΠΟΡΕΙΑ ΑΚΤΙΝΑΣ. Β. Στο διπλανό
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ ΕΠΙΛΟΓΗ ΘΕΜΑΤΩΝ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ «Β ΘΕΜΑΤΑ ΦΩΣ» ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β ΛΥΚΕΙΟΥ Χ. Δ. ΦΑΝΙΔΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 04-05 ΠΟΡΕΙΑ ΑΚΤΙΝΑΣ. Β. Στο διπλανό
Περίθλαση από ακµή και από εµπόδιο.
 ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 63 6. Άσκηση 6 Περίθλαση από ακµή και από εµπόδιο. 6.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης αυτής, καθώς και των δύο εποµένων, είναι η γνωριµία των σπουδαστών
ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 63 6. Άσκηση 6 Περίθλαση από ακµή και από εµπόδιο. 6.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης αυτής, καθώς και των δύο εποµένων, είναι η γνωριµία των σπουδαστών
Πειραματικός υπολογισμός του μήκους κύματος μονοχρωματικής ακτινοβολίας
 Πειραματικός υπολογισμός του μήκους κύματος μονοχρωματικής ακτινοβολίας Τάξη : Γ Λυκείου Βασικές έννοιες και σχέσεις Μήκος κύματος - Μονοχρωματική ακτινοβολία - Συμβολή ηλεκτρομαγνητικών κυμάτων - Κροσσοί
Πειραματικός υπολογισμός του μήκους κύματος μονοχρωματικής ακτινοβολίας Τάξη : Γ Λυκείου Βασικές έννοιες και σχέσεις Μήκος κύματος - Μονοχρωματική ακτινοβολία - Συμβολή ηλεκτρομαγνητικών κυμάτων - Κροσσοί
Φυσική Εικόνας & Ήχου Ι (Ε)
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική Εικόνας & Ήχου Ι (Ε) Ενότητα 3: Γενικά περί φακών Αθανάσιος Αρααντινός Τμήμα Φωτογραφίας & Οπτικοακουστικών Τεχνών Το περιεχόμενο
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική Εικόνας & Ήχου Ι (Ε) Ενότητα 3: Γενικά περί φακών Αθανάσιος Αρααντινός Τμήμα Φωτογραφίας & Οπτικοακουστικών Τεχνών Το περιεχόμενο
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
Εισαγωγή Στοιχεία Θεωρίας
 Εισαγωγή Σκοπός της άσκησης αυτής είναι η εισαγωγή στην τεχνογνωσία των οπτικών ινών και η μελέτη τους κατά τη διάδοση μιας δέσμης laser. Συγκεκριμένα μελετάται η εξασθένιση που υφίσταται το σήμα στην
Εισαγωγή Σκοπός της άσκησης αυτής είναι η εισαγωγή στην τεχνογνωσία των οπτικών ινών και η μελέτη τους κατά τη διάδοση μιας δέσμης laser. Συγκεκριμένα μελετάται η εξασθένιση που υφίσταται το σήμα στην
Εισαγωγή στο φως. Εισαγωγή
 Εισαγωγή στο φως Το φως είναι απαραίτητο για όλες σχεδόν τις μορφές ζωής στη Γη. (Σήμερα γνωρίζουμε ότι) Το φως είναι μια μορφή ηλεκτρομαγνητικής ακτινοβολίας. Μέσω του φωτός μεταφέρεται ενέργεια από την
Εισαγωγή στο φως Το φως είναι απαραίτητο για όλες σχεδόν τις μορφές ζωής στη Γη. (Σήμερα γνωρίζουμε ότι) Το φως είναι μια μορφή ηλεκτρομαγνητικής ακτινοβολίας. Μέσω του φωτός μεταφέρεται ενέργεια από την
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
Q 40 th International Physics Olympiad, Merida, Mexico, July 2009
 ΠΕΙΡΑΜΑΤΙΚΟ ΠΡΟΒΛΗΜΑ No. 2 ΔΕΙΚΤΗΣ ΔΙΑΘΛΑΣΗΣ ΚΡΥΣΤΑΛΛΟΥ (MCA) Σκοπός αυτού του πειράματος είναι ο υπολογισμός του δείκτη διάθλασης ενός κρυσταλλικού υλικού (mica). ΟΡΓΑΝΑ ΚΑΙ ΥΛΙΚΑ Επιπρόσθετα από τα υλικά
ΠΕΙΡΑΜΑΤΙΚΟ ΠΡΟΒΛΗΜΑ No. 2 ΔΕΙΚΤΗΣ ΔΙΑΘΛΑΣΗΣ ΚΡΥΣΤΑΛΛΟΥ (MCA) Σκοπός αυτού του πειράματος είναι ο υπολογισμός του δείκτη διάθλασης ενός κρυσταλλικού υλικού (mica). ΟΡΓΑΝΑ ΚΑΙ ΥΛΙΚΑ Επιπρόσθετα από τα υλικά
ΕΥΘΥΓΡΑΜΜΗ ΔΙΑΔΟΣΗ ΤΟΥ ΦΩΤΟΣ
 ΕΥΘΥΓΡΑΜΜΗ ΔΙΑΔΟΣΗ ΤΟΥ ΦΩΤΟΣ Όταν προσπίπτει φως σε μια διεπιφάνεια που σχηματίζεται μεταξύ δύο οπτικά διαφορετικών μέσων, ένα μέρος του υφίσταται ανάκλαση ενώ το υπόλοιπο διέρχεται από το πρώτο στο δεύτερο
ΕΥΘΥΓΡΑΜΜΗ ΔΙΑΔΟΣΗ ΤΟΥ ΦΩΤΟΣ Όταν προσπίπτει φως σε μια διεπιφάνεια που σχηματίζεται μεταξύ δύο οπτικά διαφορετικών μέσων, ένα μέρος του υφίσταται ανάκλαση ενώ το υπόλοιπο διέρχεται από το πρώτο στο δεύτερο
ΑΝΑΚΛΑΣΗ ΕΠΙΠΕΔΟΙ ΚΑΘΡΕΦΤΕΣ ΕΙΔΩΛΟ
 1 ο ΕΚΦΕ (Ν. ΣΜΥΡΝΗΣ) Δ Δ/ΝΣΗΣ Δ. Ε. ΑΘΗΝΑΣ 1 ΑΝΑΚΛΑΣΗ ΕΠΙΠΕΔΟΙ ΚΑΘΡΕΦΤΕΣ ΕΙΔΩΛΟ Α. ΣΤΟΧΟΙ Η ικανότητα συναρμολόγησης μιας απλής πειραματικής διάταξης. Η ικανότητα χρήσης καθρέφτη και πηγής laser. Η κατανόηση
1 ο ΕΚΦΕ (Ν. ΣΜΥΡΝΗΣ) Δ Δ/ΝΣΗΣ Δ. Ε. ΑΘΗΝΑΣ 1 ΑΝΑΚΛΑΣΗ ΕΠΙΠΕΔΟΙ ΚΑΘΡΕΦΤΕΣ ΕΙΔΩΛΟ Α. ΣΤΟΧΟΙ Η ικανότητα συναρμολόγησης μιας απλής πειραματικής διάταξης. Η ικανότητα χρήσης καθρέφτη και πηγής laser. Η κατανόηση
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
Πειραματική μελέτη λεπτών σφαιρικών φακών
 Πειραματική μελέτη λεπτών σφαιρικών φακών Τάξη - Τµήµα: Ονόµατα µαθητών οµάδας: ) 2).. 3) 4) Πειραματική μελέτη λεπτών σφαιρικών φακών Στόχοι της εργαστηριακής άσκησης ) Μέτρηση των γεωµετρικών χαρακτηριστικών
Πειραματική μελέτη λεπτών σφαιρικών φακών Τάξη - Τµήµα: Ονόµατα µαθητών οµάδας: ) 2).. 3) 4) Πειραματική μελέτη λεπτών σφαιρικών φακών Στόχοι της εργαστηριακής άσκησης ) Μέτρηση των γεωµετρικών χαρακτηριστικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Εργαστήριο Φυσικής ΙΙΙ - Οπτική. Πέτρος Ρακιτζής. Τμήμα Φυσικής
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Εργαστήριο Φυσικής ΙΙΙ - Οπτική Πέτρος Ρακιτζής Φ-08: Εργαστήριο Φυσικής ΙΙΙ Οπτική. Σκοπός. ΜΕΛΕΤΗ ΛΕΠΤΩΝ ΦΑΚΩΝ Εξοικείωση με βασικές αρχές γεωμετρικής οπτικής
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Εργαστήριο Φυσικής ΙΙΙ - Οπτική Πέτρος Ρακιτζής Φ-08: Εργαστήριο Φυσικής ΙΙΙ Οπτική. Σκοπός. ΜΕΛΕΤΗ ΛΕΠΤΩΝ ΦΑΚΩΝ Εξοικείωση με βασικές αρχές γεωμετρικής οπτικής
7α Γεωµετρική οπτική - οπτικά όργανα
 7α Γεωµετρική οπτική - οπτικά όργανα Εισαγωγή ορισµοί Φύση του φωτός Πηγές φωτός είκτης διάθλασης Ανάκλαση ηµιουργία ειδώλων από κάτοπτρα Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Η φύση του
7α Γεωµετρική οπτική - οπτικά όργανα Εισαγωγή ορισµοί Φύση του φωτός Πηγές φωτός είκτης διάθλασης Ανάκλαση ηµιουργία ειδώλων από κάτοπτρα Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Η φύση του
Φωτογραφική μηχανή - Αρχή λειτουργίας.
 Ο25 Φωτογραφική μηχανή - Αρχή λειτουργίας. 1 Σκοπός Στην άσκηση αυτή γίνεται μία παρουσίαση των βασικών στοιχείων της φωτογραφικής μηχανής (φακός φωτοφράκτης - διάφραγμα αισθητήρας) καθώς και μία σύντομη
Ο25 Φωτογραφική μηχανή - Αρχή λειτουργίας. 1 Σκοπός Στην άσκηση αυτή γίνεται μία παρουσίαση των βασικών στοιχείων της φωτογραφικής μηχανής (φακός φωτοφράκτης - διάφραγμα αισθητήρας) καθώς και μία σύντομη
ΜΕΘΟΔΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ ΚΕΦΑΛΑΙΟΥ 3
 ΜΕΘΟΔΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ ΚΕΦΑΛΑΙΟΥ 3 Η ταχύτητα του φωτός στο κενό ή στον αέρα είναι σταθερή και ίση με c o =3.10 8 m/s Η ταχύτητα του φωτός οπουδήποτε αλλού είναι c και ισχύει πάντα ότι c
ΜΕΘΟΔΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ ΚΕΦΑΛΑΙΟΥ 3 Η ταχύτητα του φωτός στο κενό ή στον αέρα είναι σταθερή και ίση με c o =3.10 8 m/s Η ταχύτητα του φωτός οπουδήποτε αλλού είναι c και ισχύει πάντα ότι c
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ. Ερωτήσεις κλειστού τύπου. Ερωτήσεις ανοικτού τύπου
 ΟΠΤΙΚΗ Περιεχόμενα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ... 2 Ερωτήσεις κλειστού τύπου... 2 Ερωτήσεις ανοικτού τύπου... 2 Ασκήσεις... 3 ΚΥΜΑΤΙΚΗ ΟΠΤΙΚΗ... 4 Ερωτήσεις κλειστού τύπου... 4 Ερωτήσεις ανοικτού τύπου... 4 Ασκήσεις...
ΟΠΤΙΚΗ Περιεχόμενα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ... 2 Ερωτήσεις κλειστού τύπου... 2 Ερωτήσεις ανοικτού τύπου... 2 Ασκήσεις... 3 ΚΥΜΑΤΙΚΗ ΟΠΤΙΚΗ... 4 Ερωτήσεις κλειστού τύπου... 4 Ερωτήσεις ανοικτού τύπου... 4 Ασκήσεις...
MEΡΙΚΑ ΣΤΟΙΧΕΙΑ ΓΕΩΜΕΤΡΙΚΗΣ ΟΠΤΙΚΗΣ
 MEΡΙΚΑ ΣΤΟΙΧΕΙΑ ΓΕΩΜΕΤΡΙΚΗΣ ΟΠΤΙΚΗΣ Δ. Χατζηδημητρίου Βιβλιογραφία: Introduction to Optics, Pedrotti et al., 006, 3 rd edition, εκδ. Benjamin Cummings Optics and Photonics, An Introduction F. G. Smith
MEΡΙΚΑ ΣΤΟΙΧΕΙΑ ΓΕΩΜΕΤΡΙΚΗΣ ΟΠΤΙΚΗΣ Δ. Χατζηδημητρίου Βιβλιογραφία: Introduction to Optics, Pedrotti et al., 006, 3 rd edition, εκδ. Benjamin Cummings Optics and Photonics, An Introduction F. G. Smith
Ασκήσεις (Ηλεκτρισμός-Οπτική) Κ.-Α. Θ. Θωμά
 Ασκήσεις (Ηλεκτρισμός-Οπτική) Ηλεκτρισμός 6 η. Ηλεκτρόνια κινούμενα με ταχύτητα 0 m / sec εισέρχονται σε χώρο μαγνητικού πεδίου όπου διαγράφουν κυκλική τροχιά ακτίνας 0.0m. Να βρεθεί η ένταση του μαγνητικού
Ασκήσεις (Ηλεκτρισμός-Οπτική) Ηλεκτρισμός 6 η. Ηλεκτρόνια κινούμενα με ταχύτητα 0 m / sec εισέρχονται σε χώρο μαγνητικού πεδίου όπου διαγράφουν κυκλική τροχιά ακτίνας 0.0m. Να βρεθεί η ένταση του μαγνητικού
Όλα τα θέματα των εξετάσεων έως και το 2014 σε συμβολή, στάσιμα, ηλεκτρομαγνητικά κύματα, ανάκλαση - διάθλαση ΑΝΑΚΛΑΣΗ ΔΙΑΘΛΑΣΗ
 ΑΝΑΚΛΑΣΗ ΔΙΑΘΛΑΣΗ Ερωτήσεις Πολλαπλής επιλογής 1. To βάθος µιας πισίνας φαίνεται από παρατηρητή εκτός της πισίνας µικρότερο από το πραγµατικό, λόγω του φαινοµένου της: α. ανάκλασης β. διάθλασης γ. διάχυσης
ΑΝΑΚΛΑΣΗ ΔΙΑΘΛΑΣΗ Ερωτήσεις Πολλαπλής επιλογής 1. To βάθος µιας πισίνας φαίνεται από παρατηρητή εκτός της πισίνας µικρότερο από το πραγµατικό, λόγω του φαινοµένου της: α. ανάκλασης β. διάθλασης γ. διάχυσης
ΠΕΙΡΑΜΑΤΙΚΗ ΔΙΑΔΙΚΑΣΙΑ
 Εισαγωγή Σκοπός της εργαστηριακής άσκησης είναι η μελέτη του ηλεκτροοπτικού φαινομένου (φαινόμενο Pockels) σε θερμοκρασία περιβάλλοντος για κρύσταλλο KDP και ο προσδιορισμός της τάσης V λ/4. Στοιχεία Θεωρίας
Εισαγωγή Σκοπός της εργαστηριακής άσκησης είναι η μελέτη του ηλεκτροοπτικού φαινομένου (φαινόμενο Pockels) σε θερμοκρασία περιβάλλοντος για κρύσταλλο KDP και ο προσδιορισμός της τάσης V λ/4. Στοιχεία Θεωρίας
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΤΑΙΧΜΙΟ Επαναληπτικό στη Φυσική 1. Θέµα 1 ο
 ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΤΑΙΧΜΙΟ Επαναληπτικό στη Φυσική 1 Θέµα 1 ο 1. Το διάγραµµα του διπλανού σχήµατος παριστάνει τη χρονική µεταβολή της αποµάκρυνσης ενός σώµατος που εκτελεί απλή αρµονική ταλάντωση. Ποια από
ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΤΑΙΧΜΙΟ Επαναληπτικό στη Φυσική 1 Θέµα 1 ο 1. Το διάγραµµα του διπλανού σχήµατος παριστάνει τη χρονική µεταβολή της αποµάκρυνσης ενός σώµατος που εκτελεί απλή αρµονική ταλάντωση. Ποια από
[1] ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΤΑΞΗ : B ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΠΡΙΛΙΟΣ 2017
![[1] ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΤΑΞΗ : B ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΠΡΙΛΙΟΣ 2017 [1] ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΤΑΞΗ : B ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΠΡΙΛΙΟΣ 2017](/thumbs/65/53071279.jpg) [1] ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΤΑΞΗ : B ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΠΡΙΛΙΟΣ 2017 ΘΕΜΑ 1 Ο : Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και
[1] ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΤΑΞΗ : B ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΠΡΙΛΙΟΣ 2017 ΘΕΜΑ 1 Ο : Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και
ΑΣΚΗΣΗ 4 ΠΕΡΙΘΛΑΣΗ ΑΠΟ ΑΠΛΗ ΣΧΙΣΜΗ
 ΑΣΚΗΣΗ 4 ΠΕΡΙΘΛΑΣΗ ΑΠΟ ΑΠΛΗ ΣΧΙΣΜΗ 1 Σκοπός Στην άσκηση αυτή μελετάται η περίθλαση δέσμης φωτός ενός laser He-Ne από απλή σχισμή. Στο πρώτο μέρος της άσκησης προσδιορίζεται το πλάτος της σχισμής από την
ΑΣΚΗΣΗ 4 ΠΕΡΙΘΛΑΣΗ ΑΠΟ ΑΠΛΗ ΣΧΙΣΜΗ 1 Σκοπός Στην άσκηση αυτή μελετάται η περίθλαση δέσμης φωτός ενός laser He-Ne από απλή σχισμή. Στο πρώτο μέρος της άσκησης προσδιορίζεται το πλάτος της σχισμής από την
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 210-7722479 - e-mail:
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 210-7722479 - e-mail:
ΕΡΩΤΗΣΕΙΣ-ΑΣΚΗΣΕΙΣ ΣΤΗ ΦΥΣΗ ΦΩΤΟΣ
 ΕΡΩΤΗΣΕΙΣ-ΑΣΚΗΣΕΙΣ ΣΤΗ ΦΥΣΗ ΦΩΤΟΣ 1.. Ποιες από τις παρακάτω προτάσεις είναι σωστές (Σ) και ποιες λανθασμένες (Λ); α. Στη διάθλαση όταν το φως διέρχεται από ένα οπτικά πυκνότερο υλικό σε ένα οπτικά αραιότερο
ΕΡΩΤΗΣΕΙΣ-ΑΣΚΗΣΕΙΣ ΣΤΗ ΦΥΣΗ ΦΩΤΟΣ 1.. Ποιες από τις παρακάτω προτάσεις είναι σωστές (Σ) και ποιες λανθασμένες (Λ); α. Στη διάθλαση όταν το φως διέρχεται από ένα οπτικά πυκνότερο υλικό σε ένα οπτικά αραιότερο
Φύση και διάδοση φωτός
 Σημειώσεις Γενικής Φυσικής - ΒΕΤ Μ. Μπενής / 2016 Κυματική Φύση και διάδοση φωτός Ακτινικό μοντέλο διάδοσης. Στο κεφάλαιο των κυμάτων αναπαραστήσαμε τη διάδοση των κυμάτων με τα κυματομέτωπα. Μια απλούστευση
Σημειώσεις Γενικής Φυσικής - ΒΕΤ Μ. Μπενής / 2016 Κυματική Φύση και διάδοση φωτός Ακτινικό μοντέλο διάδοσης. Στο κεφάλαιο των κυμάτων αναπαραστήσαμε τη διάδοση των κυμάτων με τα κυματομέτωπα. Μια απλούστευση
Φυσική ΘΕΜΑ 1 ΘΕΜΑ 2 ΘΕΜΑ 3
 Φυσική ΘΕΜΑ 1 1) Υπάρχουν δύο διαφορετικά είδη φορτίου που ονομάστηκαν θετικό και αρνητικό ηλεκτρικό φορτίο αντίστοιχα. Τα σώματα που έχουν θετικό φορτίο λέμε ότι είναι θετικά φορτισμένα (π.χ. μια γυάλινη
Φυσική ΘΕΜΑ 1 1) Υπάρχουν δύο διαφορετικά είδη φορτίου που ονομάστηκαν θετικό και αρνητικό ηλεκτρικό φορτίο αντίστοιχα. Τα σώματα που έχουν θετικό φορτίο λέμε ότι είναι θετικά φορτισμένα (π.χ. μια γυάλινη
Φυσική Εικόνας & Ήχου ΙΙ (Ε)
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική Εικόνας & Ήχου ΙΙ (Ε) Ενότητα 3: Σφάλματα φακών (Σφαιρικό - Χρωματικό) Αθανάσιος Αραβαντινός Τμήμα Φωτογραφίας & Οπτικοακουστικών
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική Εικόνας & Ήχου ΙΙ (Ε) Ενότητα 3: Σφάλματα φακών (Σφαιρικό - Χρωματικό) Αθανάσιος Αραβαντινός Τμήμα Φωτογραφίας & Οπτικοακουστικών
Η συμβολή του φωτός και η μέτρηση του μήκους κύματος μονοχρωματικής ακτινοβολίας
 Η συμβολή του φωτός και η μέτρηση του μήκους κύματος μονοχρωματικής ακτινοβολίας Α. Στόχοι Οι μαθητές: Να παρατηρήσουν το φαινόμενο της συμβολής / περίθλασης Να αξιοποιήσουν το φαινόμενο της περίθλασης
Η συμβολή του φωτός και η μέτρηση του μήκους κύματος μονοχρωματικής ακτινοβολίας Α. Στόχοι Οι μαθητές: Να παρατηρήσουν το φαινόμενο της συμβολής / περίθλασης Να αξιοποιήσουν το φαινόμενο της περίθλασης
Μέτρηση μήκους κύματος μονοχρωματικής ακτινοβολίας
 Μέτρηση μήκους κύματος μονοχρωματικής ακτινοβολίας Όταν φωτεινή δέσμη φωτός συναντά στην πορεία του εμπόδια ή περνάει από λεπτές σχισμές υφίσταται περίθλαση, φτάνει δηλαδή σε σημεία που δεν προβλέπονται
Μέτρηση μήκους κύματος μονοχρωματικής ακτινοβολίας Όταν φωτεινή δέσμη φωτός συναντά στην πορεία του εμπόδια ή περνάει από λεπτές σχισμές υφίσταται περίθλαση, φτάνει δηλαδή σε σημεία που δεν προβλέπονται
δ) Αν ένα σηµείο του θετικού ηµιάξονα ταλαντώνεται µε πλάτος, να υπολογίσετε την απόσταση του σηµείου αυτού από τον πλησιέστερο δεσµό. ΑΣΚΗΣΗ 4 Μονοχρ
 ΑΣΚΗΣΗ 1 Κατά µήκος µιας ελαστικής χορδής µεγάλου µήκους που το ένα άκρο της είναι ακλόνητα στερεωµένο, διαδίδονται δύο κύµατα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι µετρηµένα σε
ΑΣΚΗΣΗ 1 Κατά µήκος µιας ελαστικής χορδής µεγάλου µήκους που το ένα άκρο της είναι ακλόνητα στερεωµένο, διαδίδονται δύο κύµατα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι µετρηµένα σε
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β και Γ ΛΥΚΕΙΟΥ.
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β και Γ ΛΥΚΕΙΟΥ. ΑΝΤΙΚΕΙΜΕΝΟ : ΤΟ ΦΩΣ,( ΚΕΦ. Γ ΛΥΚΕΙΟΥ και ΚΕΦ.3 Β ΛΥΚΕΙΟΥ) ΘΕΜΑ Α Να επιλέξετε την σωστή πρόταση χωρίς να δικαιολογήσετε την απάντηση σας.. Οι Huygens
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Β και Γ ΛΥΚΕΙΟΥ. ΑΝΤΙΚΕΙΜΕΝΟ : ΤΟ ΦΩΣ,( ΚΕΦ. Γ ΛΥΚΕΙΟΥ και ΚΕΦ.3 Β ΛΥΚΕΙΟΥ) ΘΕΜΑ Α Να επιλέξετε την σωστή πρόταση χωρίς να δικαιολογήσετε την απάντηση σας.. Οι Huygens
ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ
 ΦΥΣΙΚΗ Γ.Π. Γ Λυκείου / Το Φως 1. Η υπεριώδης ακτινοβολία : a) δεν προκαλεί αμαύρωση της φωτογραφικής πλάκας. b) είναι ορατή. c) χρησιμοποιείται για την αποστείρωση ιατρικών εργαλείων. d) έχει μήκος κύματος
ΦΥΣΙΚΗ Γ.Π. Γ Λυκείου / Το Φως 1. Η υπεριώδης ακτινοβολία : a) δεν προκαλεί αμαύρωση της φωτογραφικής πλάκας. b) είναι ορατή. c) χρησιμοποιείται για την αποστείρωση ιατρικών εργαλείων. d) έχει μήκος κύματος
Οπτική και κύματα Δημήτρης Παπάζογλου dpapa@materials.uoc.gr Τμήμα Επιστήμης και Τεχνολογίας Υλικών Πανεπιστήμιο Κρήτης Γεωμετρική Οπτική
 Οπτική και κύματα Δημήτρης Παπάζογλου dpapa@maerals.uoc.gr Τμήμα Επιστήμης και Τεχνολογίας Υλικών Πανεπιστήμιο Κρήτης Γεωμετρική Οπτική Η ιδέα την απεικόνισης Σημειακή πηγή Στιγματική απεικόνιση Η ανακατεύθυνση
Οπτική και κύματα Δημήτρης Παπάζογλου dpapa@maerals.uoc.gr Τμήμα Επιστήμης και Τεχνολογίας Υλικών Πανεπιστήμιο Κρήτης Γεωμετρική Οπτική Η ιδέα την απεικόνισης Σημειακή πηγή Στιγματική απεικόνιση Η ανακατεύθυνση
ΙΔΙΟΤΗΤΕΣ ΜΑΓΝΗΤΙΚΩΝ ΦΑΚΩΝ. Ηλεκτροστατικοί και Μαγνητικοί Φακοί Βασική Δομή Μαγνητικών Φακών Υστέρηση Λεπτοί Μαγνητικοί Φακοί Εκτροπές Φακών
 ΙΔΙΟΤΗΤΕΣ ΜΑΓΝΗΤΙΚΩΝ ΦΑΚΩΝ Βασική Δομή Μαγνητικών Φακών Υστέρηση Λεπτοί Μαγνητικοί Φακοί Εκτροπές Φακών ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ ΓΥΑΛΙΝΟΙ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΟΙ ΦΑΚΟΙ Οι φακοί χρησιμοποιούνται για να εκτρέψουν μία
ΙΔΙΟΤΗΤΕΣ ΜΑΓΝΗΤΙΚΩΝ ΦΑΚΩΝ Βασική Δομή Μαγνητικών Φακών Υστέρηση Λεπτοί Μαγνητικοί Φακοί Εκτροπές Φακών ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ ΓΥΑΛΙΝΟΙ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΟΙ ΦΑΚΟΙ Οι φακοί χρησιμοποιούνται για να εκτρέψουν μία
