9.2 Μελετώντας τρισδιάστατα γραφικά στο επίπεδο Oi sunartήseiv Contour Plot kai DensityPlot
|
|
|
- Ευφρανωρ Δουμπιώτης
- 6 χρόνια πριν
- Προβολές:
Transcript
1 trisdiastatastoepipedo_.nb 9. Μελετώντας τρισδιάστατα γραφικά στο επίπεδο 9.. Oi sunartήseiv Contour Plot kai DensityPlot Me thn ContourPlot[f[x,y], {x,xmin,xmax},{y,ymin,ymax}] scediάzoume thn f[x,y] pάnw sto epίpedo Oxy, dίnontav sto shmeίo (x,y) έna crώma (sunήqwv apόcrwsh tou gkrίzou) pou antistoiceί sthn timή f[x,y]. Ta shmeίa pou έcoun megalύterh timή f[x,y] eίnai pio jwteinά enώ autά pou έcoun mikrόterh eίnai pio skoteinά. P.c y^d, 8x,, 3<, 8y,, <D; Parathroύme apocrώseiv tou grί(to leukό den to metrάme, ousiastikά έcoume mazί me to leukό ). H na to poύme diajoretikά: To pedίo timώn(ston άxona Oz) έcei cwristeί se + ίsou mήkouv diastήmata έstw D,D,..,D. Kάqe diάsthma paίrnei έna crώma tou gkrί xekinώntav apo to maύro. Όsa shmeίa (x,y) tou epipέdou apeikonίzontai(mέsw thv f) mέsa sto ίdio diάsthma D i qa pάroun thn ίdia apόcrwsh! 'Etsi pάnw sto epίpedo Oxy emjanίzontai crwmatikέv lwrίdev,ta isouyή epίpeda, ta opoίa diacwrίzontai metaxύ touv apo kάpoiev kampύlev pou lέgontai isouyeίv(contours). Όla ta shmeίa miav isouyή kampύlhv paίrnoun thn ίdia akribώv timή me thn f! Fusikά epeidή upάrcoun άpeira shmeίa (x,y) mέsa sto orqogώnio scediasmoύ D={x,xmin,xmax}Χ{y,ymin,ymax}, to Mathematica qa dialέxei deigmatoleiptikά lίga shmeίa apo to D kai me bάsh tiv timέv touv qa scediάsei tiv isouyeίv kampύlev. Ta shmeίa autά lέgontai Plot- Points. Fusikά to apotέlesma pou paίrnoume έcei όpwv blέpoume pollέv atέleiev. Gia parάdeigma oi isouyeίv kampύlev den eίnai όso qa perimέname omalέv. EpίshV mporoύme na parathrήsoume όti h leukή lwrίda sta dexiά eίnai sto kάtw mέrov thv kommatiasmέnh! Autό wjeίletai kurίwv sto gegonόv όti h proepilegmέnh timή tou PlotPoints eίnai 5. Opόte apo to diάsthma D epilέgontai 5Χ5 to plήqov shmeίa pou den eίnai arketά an h f[x,y] έcei apόtomev "lakoύbev" kai "lojίskouv" sto D. Qa prospaqήsoume na antimetwpίsoume autέv tiv atέleiev. AV doύme όmwv prώta, poiέv eίnai oi epilogέv thv ContourPlot:
2 trisdiastatastoepipedo_.nb 8AspectRatio, Axes False, AxesLabel None, AxesOrigin Automatic, AxesStyle Automatic, Background Automatic, ColorFunction Automatic, ColorFunctionScaling True, ColorOutput Automatic, Compiled True, ContourLines True, Contours, ContourShading True, ContourSmoothing True, ContourStyle Automatic, DefaultColor Automatic, Epilog 8<, Frame True, FrameLabel None, FrameStyle Automatic, FrameTicks Automatic, ImageSize Automatic, PlotLabel None, PlotPoints 5, PlotRange Automatic, PlotRegion Automatic, Prolog 8<, RotateLabel True, Ticks Automatic, DefaultFont $DefaultFont, DisplayFunction $DisplayFunction, FormatType $FormatType, TextStyle $TextStyle< AllάzontaV kάpoia apo ta parapάnw carakthristikά mporoύme na έcoume έna kalό apotέlesma. P.c mporoύme na epitrέyoume sto Mathematica na kάnei kalύterh deigmatoleiyίa paίrnontav perissόtera shmeίa. WV apotέlesma qa έcoume pio akribeίv isouyeίv kampύlev. P.c gr = ContourPlot@Sin@x^ y^d, 8x,, 3<, 8y,, <, PlotPoints 3D; Mporoύme epίshv na zhtήsoume perissόterev isouyeίv(kai άra perissόterev apocrώseiv) megalώnontav thn proepilegmέnh timή tou Contours pou eίnai (ή akribέstera + όpwv proanajέrame). P.c
3 trisdiastatastoepipedo_.nb 3 gr = Show@gr, Contours D; Prosέxte όti auxάnontav to plήqov twn Contours cάnetai h akrίbeia sto scediasmό twn isouyώn!!! Άra qa prέpei na auxήsoume xanά ta PlotPoints gia na petύcoume thn akrίbeia ston scediasmό! An tώra qέloume mόno tiv diabaqmίseiv cwrίv tiv isouyeίv qa grάjame ContourLines->False p.c
4 trisdiastatastoepipedo_.nb 4 gr = Show@gr, ContourLines FalseD; Sίgoura polύ pio katanohtό apotέlesma! MerikέV jorέv den mav endiajέroun tόso oi apocrώseiv όso oi ίdiev oi isouyeίv! Parakάtw dίnoume έna tέtoio parάdeigma. Me ContourShading->False exajanίzoume tiv apocώseiv enώ me ContourStyle->({RGBColor[#,,]}&)/@Range[,.95,.5] dίnoume diajoretikέv apocrώseiv(όsa eίnai kai ta Contours) tou kόkkinou stiv antίstoicev isouyeίv kampύlev.
5 trisdiastatastoepipedo_.nb 5 gr3 = Show@gr, ContourShading > False, ContourStyle H8RGBColor@#,, D< &L ê@ Range@,.95,.5DD; Edώ me έntono kόkkino eίnai oi isouyeίv pou brίskontai pio yhlά apo tiv άllev. Qa mporoύsame tώra na emjanίsoume kai ta isouyή epίpeda me diabaqmίseiv tou kίtrinou-kόkkinou(me thn boήqeia thv Color- FunctionØ(RGBColor[,#,]&) ) kai tiv ContourLines kόkkinev kai diakekommέnev p.c
6 trisdiastatastoepipedo_.nb 6 gr4 = Show@gr, ContourShading True, ColorFunction HRGBColor@, #, D &L, ContourStyle H8RGBColor@#,, D, Dashing@8.5,.5<D< &Lê@ Range@,.95,.5DD; Den prέpei na xecάsoume na anajέroume thn Contours->{z,z,z3,...} me thn opoίa epilέgoume na mpoύn isouyeίv mόno stiv sugkekrimmέnev timέv tou z. P.c qa prospaqήsoume na diereunίsoume thn f kontά sto shmeίo (,) meletώntav mόno kάpoiev qetikέv isouyeίv me timέv kontά sto f[x,y]= p.c :ContoursØ84 9,9 7, 6 <Gia akrίbeia megalώnoume kai to plήqov twn deigmatoleiptikώn shmeίwn(plotpointsø4)
7 trisdiastatastoepipedo_.nb 7 gr5 = ContourPlot@Sin@x^ y^d, 8x,.,.<, 8y,.,.<, Contours 84 9,9 7, 6 <, PlotPoints 4, ContourStyle 88RGBColor@,, D<, 8RGBColor@,, D<, 8RGBColor@,, D<<D; Me maύro crώma eίnai όlev oi timέv thv sunάrthshv <4 9, me endiάmeso gkrί oi timέv metaxύ 4 9 και 9 7 k.o.k H DensityPlot den prospaqeί na scediάsei kάpoiev isouyeίv kampύlev όpwv h ContourPlot. AplώV parάgei έna plέgma(mesh)kai kάpoiev apocrώseiv mέsa se autό. H proepilegmέnev apocrώseiv eίnai tou gkrί. Skoteinά gkrί crhsimopoioύntai gia baqoulώmata thv f[x,y] dhl. gia mikrέv timέv kai anoikta gkrί gia megάlev timέv. P.c
8 trisdiastatastoepipedo_.nb 8 DensityPlot@Sin@x^ y^d, 8x,, 3<, 8y,, <D; ΌpwV blέpoume crhsimopoioύntai 5 PlotPoints se kάqe έna apo ta diastήmata twn x kai y antίstoica. Gia megalύterh akrίbeia sta crώmata mporoύme na bάloume megalύterh timή p.c PlotPoints->{5,5}
9 trisdiastatastoepipedo_.nb 9 gr = DensityPlot@Sin@x^ y^d, 8x,, 3<, 8y,, <, PlotPoints 85, 5<D; ΌpwV blέpoume den gίnetai kammίa prospάqeia na schmatistoύn kapoia isouyή epίpeda AplώV se kάqe deigmatolhptikό shmeίo apo ta 5 ä5 upologίzetai h antίstoich timή thv f kai sthn sunέceia autή metatrέpetai se mia apόcrwsh tou gkrί. Me Mesh->False mporoύme na exajanίsoume to plέgma kai na meίnei mόno h apόcrwsh:
10 trisdiastatastoepipedo_.nb gr = Show@gr, Mesh FalseD; Me thn ColorFunction mporoύme na allάxoume katά boύlhsh tiv apocrώseiv:
11 trisdiastatastoepipedo_.nb gr3 = Show@gr, ColorFunction HRGBColor@, #, D &LD; An qέloume na emjanίzontai oposdήpote kai to plέgma qa ήtan skόpimo na dialέgame me thn boήqeia thv MeshStyle έna diajoretikό crώma grammώn plέgmatov ή pio leptέv grammέv plέgmatov ή diakekommέnev ή kάpoia apo ta prohgoύmena:
12 trisdiastatastoepipedo_.nb gr4 = Show@gr, MeshStyle 8GrayLevel@.9D, Dashing@8.5,.5<D<, ColorFunction HRGBColor@, #, D &LD; Genikά h DensityPlot mav scediάzei mia epijάneia tou cώrou όpwv qa thn έblepe έnav parathrhtήv pou briskόtan akribώv apo pάnw thv! ΊswV qa anarwtiέste giatί na crhsimopoiήsoume thn DensityPlot ajoύ upάrcei h ContourPlot. H apάnthsh eίnai όti upάrcoun kakέv periptώseiv pou h ContourPlot sthn prospάqeia thv na zwgrajίsei ta isouyή epίpeda den bgάzei kάpoia kάpoio κατανοητό grάjhma dhl. mav epistrέjei anakribέv grάjhma. Genikά qa prέpei na eίmaste se qέsh na paίrnoume όlev tiv plhrojorίev pou mav creiάzontαι sthn melέth mav kάnontav katάllhlo sunduasmό όlwn twn dunatotήtwn p.c Askhsh: Na meletήsoume thn sumperijorά thv x^ + 3 y^ gia {x,-4,4} kai {y,-4,4}. Lύsh:Crhsimopoioύme thn Plot3D se sunduasmό me thn ContourPlot:
13 trisdiastatastoepipedo_.nb 3 Plot3D@ x^+ 3y^, 8x, 4, 4<, 8y, 4, 4<D; Blέpoume όti upάrcei έna baqoύlwma allά den xέroume pou akribώv. H ContourPlot qa bohqήsei ston entopismό tou: ContourPlot@ x^+ 3y^, 8x, 4, 4<, 8y, 4, 4<, ColorFunction HRGBColor@, #, D &L, Contours 3, PlotPoints 3D;
14 trisdiastatastoepipedo_.nb 4 Dhl. eίnai to shmeίo (,)! Qa mporoύsame na crhsimopoίhsoume kai thn ContourPlot se sunduasmό me thn DensityPlot wv exήv: Θέτουµε την DensityPlot κάτω απο την ContourPlot και στην πρώτη βάζουµε MeshØFalse ενώ στην δεύτερη ContourShadingØFalse(για να εµφανιστούν µόνο οι ισουψείς καµπύλες) cg = ContourPlot@ x^ + 3 y^, 8x, 4, 4<, 8y, 4, 4<, ContourShading False, DisplayFunction Identity, PlotPoints 3, Contours 3D; dg = DensityPlot@ x^+ 3y^, 8x, 4, 4<, 8y, 4, 4<, PlotPoints 3, Mesh False, DisplayFunction Identity, ColorFunction HGrayLevel@If@.5 + # >,,.5 + #DD &LD; Show@dg, cg, DisplayFunction $DisplayFunctionD; Me If[.5+#>,,.5+#] jwtίsame katά.5 perissόtero ta skoteinά merh tou DensityPlot gia na έcoume perissόterh jwteinόthta sta shmeίa gύrw apo to (,).
Χρησιµοποιούµε διαφορετικές εντολές ανάλογα µε τον τρόπο που περιγράφεται η επιφάνεια που µελετάµε. Έτσι έχουµε τις παρακάτω περιπτώσεις:
 trisdiastatesparastaseis.nb 9.3 Τρισδιάστατες Γραφικές Παραστάσεις Υπάρχει αρκετή οµοιότητα στις εντολές και στις επιλογές για την γραφική παράσταση επιφανειών και καµπυλών στο χώρο, µε τις αντίστοιχες
trisdiastatesparastaseis.nb 9.3 Τρισδιάστατες Γραφικές Παραστάσεις Υπάρχει αρκετή οµοιότητα στις εντολές και στις επιλογές για την γραφική παράσταση επιφανειών και καµπυλών στο χώρο, µε τις αντίστοιχες
Ενότητα 5: Γραφικές Παραστάσεις
 Συμβολικές Γλώσσες Προγραμματισμού Ενότητα 5: Γραφικές Παραστάσεις Νικόλαος Καραμπετάκης Τμήμα Μαθηματικών Άδειες Χρήσης è Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. è Για
Συμβολικές Γλώσσες Προγραμματισμού Ενότητα 5: Γραφικές Παραστάσεις Νικόλαος Καραμπετάκης Τμήμα Μαθηματικών Άδειες Χρήσης è Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. è Για
Συμβολικές Γλώσσες Προγραμματισμού. Ενότητα 2: Ξενάγηση στο Mathematica. Νικόλαος Καραμπετάκης Τμήμα Μαθηματικών
 Συμβολικές Γλώσσες Προγραμματισμού Ενότητα 2: Ξενάγηση στο Mathematica Νικόλαος Καραμπετάκης Τμήμα Μαθηματικών Άδειες Χρήσης è Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. è
Συμβολικές Γλώσσες Προγραμματισμού Ενότητα 2: Ξενάγηση στο Mathematica Νικόλαος Καραμπετάκης Τμήμα Μαθηματικών Άδειες Χρήσης è Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. è
Ομάδα Γ. Ο υπολογιστής ως επιστημονικό εργαλείο Εργασία η ιουργία γραφικών αραστάσεων ε την
 Ομάδα Γ. Ο υπολογιστής ως επιστημονικό εργαλείο Εργασία η ιουργία γραφικών αραστάσεων ε την 1 1 Λίστες Πίνακες Λίστες αντικειμένων Η λίστα στη Mathematica είναι ισοδύναμη με ένα μαθηματικό πίνακα. Για
Ομάδα Γ. Ο υπολογιστής ως επιστημονικό εργαλείο Εργασία η ιουργία γραφικών αραστάσεων ε την 1 1 Λίστες Πίνακες Λίστες αντικειμένων Η λίστα στη Mathematica είναι ισοδύναμη με ένα μαθηματικό πίνακα. Για
Εργαστήριο 4. Άóêçóç 1. Άóêçóç 2. Χημικοί. Plot Sec x, x, 2 π, 2π. p1 Plot Abs 1 Abs x, x, 3, 3. 1 In[3]:= f x_ : 2 π. p2 Plot f x, x, 3,
![Εργαστήριο 4. Άóêçóç 1. Άóêçóç 2. Χημικοί. Plot Sec x, x, 2 π, 2π. p1 Plot Abs 1 Abs x, x, 3, 3. 1 In[3]:= f x_ : 2 π. p2 Plot f x, x, 3, Εργαστήριο 4. Άóêçóç 1. Άóêçóç 2. Χημικοί. Plot Sec x, x, 2 π, 2π. p1 Plot Abs 1 Abs x, x, 3, 3. 1 In[3]:= f x_ : 2 π. p2 Plot f x, x, 3,](/thumbs/59/43970587.jpg) Εργαστήριο 4 Χημικοί Άóêçóç. In[]:= Plot Sec x, x, π, π 6 4 Out[]= -6-4 - 4 6 - -4-6 Άóêçóç. In[]:= p Plot Abs Abs x, x, 3, 3.0.5 Out[]= -3 - - 3 In[3]:= f x_ : π x p Plot f x, x, 3, 3 0.4 0.3 Out[4]=
Εργαστήριο 4 Χημικοί Άóêçóç. In[]:= Plot Sec x, x, π, π 6 4 Out[]= -6-4 - 4 6 - -4-6 Άóêçóç. In[]:= p Plot Abs Abs x, x, 3, 3.0.5 Out[]= -3 - - 3 In[3]:= f x_ : π x p Plot f x, x, 3, 3 0.4 0.3 Out[4]=
ΜΑΘΗΜΑ 2, Έλεγχος ροής προγράμματος ΒΑΣΙΚΗ ΣΥΝΤΑΞΗ:
 ΜΑΘΗΜΑ 2, 080312 Έλεγχος ροής προγράμματος Μπορούμε να χρησιμοποιήσουμε μια σειρά από λογικούς ελέγχους (συγκρίσεις) και με βάση το αποτέλεσμά τους γίνεται η λήψη αποφάσεων για τη συνέχεια του προγράμματος
ΜΑΘΗΜΑ 2, 080312 Έλεγχος ροής προγράμματος Μπορούμε να χρησιμοποιήσουμε μια σειρά από λογικούς ελέγχους (συγκρίσεις) και με βάση το αποτέλεσμά τους γίνεται η λήψη αποφάσεων για τη συνέχεια του προγράμματος
ΠΡΑΚΤΙΚΟΣ Ο ΗΓΟΣ ΓΙΑ ΤΗ MATHEMATICA
 ΓΕΩΡΓΙΟΣ ΘΕΟ ΩΡΟΥ Τµήµα Φυσικής Αριστοτέλειο Πανεπιστήµιο Θεσσαλονίκης ΧΡΙΣΤΙΝΑ ΘΕΟ ΩΡΟΥ Μαθηµατικός ΠΡΑΚΤΙΚΟΣ Ο ΗΓΟΣ ΓΙΑ ΤΗ MATHEMATICA ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Θεσσαλονίκη 004 Copyright
ΓΕΩΡΓΙΟΣ ΘΕΟ ΩΡΟΥ Τµήµα Φυσικής Αριστοτέλειο Πανεπιστήµιο Θεσσαλονίκης ΧΡΙΣΤΙΝΑ ΘΕΟ ΩΡΟΥ Μαθηµατικός ΠΡΑΚΤΙΚΟΣ Ο ΗΓΟΣ ΓΙΑ ΤΗ MATHEMATICA ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Θεσσαλονίκη 004 Copyright
10/2013. Mod: 02D-EK/BT. Production code: CTT920BE
 10/2013 Mod: 02D-EK/BT Production code: CTT920BE GR ΕΓΧΕΙΡΙ ΙΟ ΧΡΗΣΗΣ ΚΑΙ ΣΥΝΤΗΡΗΣΗΣ σελ. 1 ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ ΚΕΦ 1 ΕΙΣΑΓΩΓΗ... 3 ΚΕΦ 2 ΕΓΚΑΤΑΣΤΑΣΗ... 3 2.1 ΜΕΤΑΚΙΝΗΣΗ ΚΑΙ ΑΠΟΣΥΣΚΕΥΑΣΙΑ...3 2.2 ΗΛΕΚΤΡΙΚΗ
10/2013 Mod: 02D-EK/BT Production code: CTT920BE GR ΕΓΧΕΙΡΙ ΙΟ ΧΡΗΣΗΣ ΚΑΙ ΣΥΝΤΗΡΗΣΗΣ σελ. 1 ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ ΚΕΦ 1 ΕΙΣΑΓΩΓΗ... 3 ΚΕΦ 2 ΕΓΚΑΤΑΣΤΑΣΗ... 3 2.1 ΜΕΤΑΚΙΝΗΣΗ ΚΑΙ ΑΠΟΣΥΣΚΕΥΑΣΙΑ...3 2.2 ΗΛΕΚΤΡΙΚΗ
Σηµειώσεις για το πρόγραµµα Mathematica
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΝΑΥΠΗΓΩΝ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Σηµειώσεις για το πρόγραµµα Mathematica Νίκος Θεµελής Νοέµβριος 008 Σκοπός του φυλλαδίου είναι να παρέχει βασικές γνώσεις για την χρήση
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΝΑΥΠΗΓΩΝ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Σηµειώσεις για το πρόγραµµα Mathematica Νίκος Θεµελής Νοέµβριος 008 Σκοπός του φυλλαδίου είναι να παρέχει βασικές γνώσεις για την χρήση
ISTORIKH KATASKEUH PRAGMATIKWN ARIJMWN BIBLIOGRAFIA
 ΛΟΓΙΣΜΟΣ CALCULUS Διαφορικός Λογισμός, Απειροστικός Λογισμός 1670 1740 Ουράνια Μηχανική Isaac Newton 1648-1727 Gottfried Wilhelm Leibniz 1646-1716 απειροστάπολύ μικρά μεγέθη, άπειροπάρα πολύ μεγάλο, όριο
ΛΟΓΙΣΜΟΣ CALCULUS Διαφορικός Λογισμός, Απειροστικός Λογισμός 1670 1740 Ουράνια Μηχανική Isaac Newton 1648-1727 Gottfried Wilhelm Leibniz 1646-1716 απειροστάπολύ μικρά μεγέθη, άπειροπάρα πολύ μεγάλο, όριο
Ομάδα Γ. Ο υπολογιστής ως επιστημονικό εργαλείο
 Ομάδα Γ. Ο υπολογιστής ως επιστημονικό εργαλείο Λίστες - Πίνακες Η λίστα στη Mathematica είναι ισοδύναμη με ένα μαθηματικό πίνακα. Για να ορίσουμε τη λίστα χρησιμοποιούμε άγκιστρα {}, μέσα στα οποία βάζουμε
Ομάδα Γ. Ο υπολογιστής ως επιστημονικό εργαλείο Λίστες - Πίνακες Η λίστα στη Mathematica είναι ισοδύναμη με ένα μαθηματικό πίνακα. Για να ορίσουμε τη λίστα χρησιμοποιούμε άγκιστρα {}, μέσα στα οποία βάζουμε
Κεφάλαιο 1 Εισαγωγή σε Mathematica
 Σελίδα 1 από 37 Κεφάλαιο 1 Εισαγωγή σε Mathematica 1.1 Πότε δηµιουργήθηκε το Mathematica ; 2 1.2 Αριθµητικοί υπολογισµοί 2 1.2.1. Τελεστές 2 1.2.2 Εκφράσεις στo Mathematica 4 1.2.3 Ποιοι είναι οι τύποι
Σελίδα 1 από 37 Κεφάλαιο 1 Εισαγωγή σε Mathematica 1.1 Πότε δηµιουργήθηκε το Mathematica ; 2 1.2 Αριθµητικοί υπολογισµοί 2 1.2.1. Τελεστές 2 1.2.2 Εκφράσεις στo Mathematica 4 1.2.3 Ποιοι είναι οι τύποι
3. Τρισδιάστατα γραφικά
 3. Τρισδιάστατα γραφικά 3.1 Τρισδιάστατες γραφικές παραστάσεις συναρτήσεων δύο μεταβλητών. Μία συνάρτηση δύο μεταβλητών μπορεί να θεωρηθεί ως μία τρισδιάστατη επιφάνεια. Η βασική εντολή σχεδίασης, του
3. Τρισδιάστατα γραφικά 3.1 Τρισδιάστατες γραφικές παραστάσεις συναρτήσεων δύο μεταβλητών. Μία συνάρτηση δύο μεταβλητών μπορεί να θεωρηθεί ως μία τρισδιάστατη επιφάνεια. Η βασική εντολή σχεδίασης, του
Statistik gia QhmikoÔc MhqanikoÔc EKTIMHSH PARA
 Statistik gia QhmikoÔc MhqanikoÔc EKTIMHSH PARAMETRWN - 2 20 Maòou 200 t.m. X me mèsh tim µ t.m. X 2 me mèsh tim µ 2 Diaforˆ µ µ 2? [X kai X 2 anexˆrthtec] DeÐgma {x, x 2,..., x n } x DeÐgma {x 2, x 22,...,
Statistik gia QhmikoÔc MhqanikoÔc EKTIMHSH PARAMETRWN - 2 20 Maòou 200 t.m. X me mèsh tim µ t.m. X 2 me mèsh tim µ 2 Diaforˆ µ µ 2? [X kai X 2 anexˆrthtec] DeÐgma {x, x 2,..., x n } x DeÐgma {x 2, x 22,...,
Statistik gia PolitikoÔc MhqanikoÔc EKTIMHSH PAR
 Statistik gia PolitikoÔc MhqanikoÔc EKTIMHSH PARAMETRWN - 2 8 DekembrÐou 202 t.m. X me mèsh tim µ t.m. X 2 me mèsh tim µ 2 Diaforˆ µ µ 2? [X kai X 2 anexˆrthtec] DeÐgma {x, x 2,..., x n } x DeÐgma {x 2,
Statistik gia PolitikoÔc MhqanikoÔc EKTIMHSH PARAMETRWN - 2 8 DekembrÐou 202 t.m. X me mèsh tim µ t.m. X 2 me mèsh tim µ 2 Diaforˆ µ µ 2? [X kai X 2 anexˆrthtec] DeÐgma {x, x 2,..., x n } x DeÐgma {x 2,
Από την Άλγεβρα των Υπολογισµών στα Υπολογιστικά Συστήµατα Άλγεβρας.
 Από την Άλγεβρα των Υπολογισµών στα Υπολογιστικά Συστήµατα Άλγεβρας Επικ. Καθηγητής Νικόλαος Καραµπετάκης Τµήµα Μαθηµατικών Αριστοτέλειο Πανεπιστήµιο Θεσσαλονίκης Θεσσαλονίκη 54006 Email : karampet@math.auth.gr
Από την Άλγεβρα των Υπολογισµών στα Υπολογιστικά Συστήµατα Άλγεβρας Επικ. Καθηγητής Νικόλαος Καραµπετάκης Τµήµα Μαθηµατικών Αριστοτέλειο Πανεπιστήµιο Θεσσαλονίκης Θεσσαλονίκη 54006 Email : karampet@math.auth.gr
bab.la Φράσεις: Ταξίδι Τρώγοντας έξω ελληνικά-ελληνικά
 Τρώγοντας έξω : Στην είσοδο Θα ήθελα να κρατήσω ένα τραπέζι για _[αριθμός ατόμων]_ στις _[ώρα]_. (Tha íthela na kratíso éna trapézi ya _[arithmós atómon]_ στις _[óra]_.) Θα ήθελα να κρατήσω ένα τραπέζι
Τρώγοντας έξω : Στην είσοδο Θα ήθελα να κρατήσω ένα τραπέζι για _[αριθμός ατόμων]_ στις _[ώρα]_. (Tha íthela na kratíso éna trapézi ya _[arithmós atómon]_ στις _[óra]_.) Θα ήθελα να κρατήσω ένα τραπέζι
ΑΠΑΝΤΗΣΕΙΣ ΑΛΓΕΒΡΑΣ Α ΛΥΚΕΙΟΥ
 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΑΠΑΝΤΗΣΕΙΣ ΑΛΓΕΒΡΑΣ Α ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ ο : ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ. Σωστό. Σωστό. Σωστό 4. Λάθος 5. Σωστό 6. Λάθος 7. Σωστό 8. Λάθος 9. Σωστό 0. Λάθος. Λάθος a. Σωστό b. Λάθος c. Λάθος
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΑΠΑΝΤΗΣΕΙΣ ΑΛΓΕΒΡΑΣ Α ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ ο : ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ. Σωστό. Σωστό. Σωστό 4. Λάθος 5. Σωστό 6. Λάθος 7. Σωστό 8. Λάθος 9. Σωστό 0. Λάθος. Λάθος a. Σωστό b. Λάθος c. Λάθος
_Toc90831498 1. ΑΘΡΟΙΣΜΑΤΑ ΚΑΙ ΓΙΝΟΜΕΝΑ ΣΤΟ MATHEMATICA. 2 2. ΑΚΟΛΟΥΘΙΕΣ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ ΣΤΟ MATHEMATICA. 3
 _Toc9083498. ΑΘΡΟΙΣΜΑΤΑ ΚΑΙ ΓΙΝΟΜΕΝΑ ΣΤΟ MATHEMATICA.. ΑΚΟΛΟΥΘΙΕΣ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ ΣΤΟ MATHEMATICA. 3 3. ΣΕΙΡΕΣ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ ΣΤΟ MATHEMATICA. 8 4. ΣΥΝΑΡΤΗΣΕΙΣ ΣΤΟ MATHEMATICA. 5. ΌΡΙΑ ΠΡΑΓΜΑΤΙΚΩΝ
_Toc9083498. ΑΘΡΟΙΣΜΑΤΑ ΚΑΙ ΓΙΝΟΜΕΝΑ ΣΤΟ MATHEMATICA.. ΑΚΟΛΟΥΘΙΕΣ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ ΣΤΟ MATHEMATICA. 3 3. ΣΕΙΡΕΣ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ ΣΤΟ MATHEMATICA. 8 4. ΣΥΝΑΡΤΗΣΕΙΣ ΣΤΟ MATHEMATICA. 5. ΌΡΙΑ ΠΡΑΓΜΑΤΙΚΩΝ
Diakritˆ Majhmatikˆ I. Leutèrhc KuroÔshc (EÔh Papaðwˆnnou)
 Diakritˆ Majhmatikˆ I Leutèrhc KuroÔshc (EÔh Papaðwˆnnou) PlhroforÐec... Tetˆrth, 09.00-11.00, Paraskeu, 18.00-20.00 SÔggramma 1: Λ. Κυρούσης, Χ. Μπούρας, Π. Σπυράκης. Διακριτά Μαθηματικά: Τα Μαθηματικά
Diakritˆ Majhmatikˆ I Leutèrhc KuroÔshc (EÔh Papaðwˆnnou) PlhroforÐec... Tetˆrth, 09.00-11.00, Paraskeu, 18.00-20.00 SÔggramma 1: Λ. Κυρούσης, Χ. Μπούρας, Π. Σπυράκης. Διακριτά Μαθηματικά: Τα Μαθηματικά
11 OktwbrÐou 2012. S. Malefˆkh Genikì Tm ma Majhmatikˆ gia QhmikoÔc
 Mˆjhma 7 0 11 OktwbrÐou 2012 Orismìc sunart sewn mèsw orismènwn oloklhrwmˆtwn To orismèno olokl rwma prosfèrei ènan nèo trìpo orismoô sunˆrthshc afoô to orismèno olokl rwma mia suneqoôc sunˆrthshc f (t),
Mˆjhma 7 0 11 OktwbrÐou 2012 Orismìc sunart sewn mèsw orismènwn oloklhrwmˆtwn To orismèno olokl rwma prosfèrei ènan nèo trìpo orismoô sunˆrthshc afoô to orismèno olokl rwma mia suneqoôc sunˆrthshc f (t),
PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II DIAFORIKES EXISWSEIS DEUTERHS KAI ANWTERHS TAXHS
 PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II DIAFORIKES EXISWSEIS DEUTERHS KAI ANWTERHS TAXHS 1. Grammikèc diaforikèc exis seic deôterhc kai an terhc tˆxhc
PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II DIAFORIKES EXISWSEIS DEUTERHS KAI ANWTERHS TAXHS 1. Grammikèc diaforikèc exis seic deôterhc kai an terhc tˆxhc
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΤΩΝ ΥΛΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗ ΙΙ Εξετάσεις Ιουνίου 2002
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΤΩΝ ΥΛΙΚΩΝ Εξετάσεις Ιουνίου (α) Αναπτύξτε την µέθοδο του τραπεζίου για τον αριθµητικό υπολογισµό του ολοκληρώµατος: b I( f ) = f ( x) a όπου f (x) συνεχής και ολοκληρώσιµη
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΤΩΝ ΥΛΙΚΩΝ Εξετάσεις Ιουνίου (α) Αναπτύξτε την µέθοδο του τραπεζίου για τον αριθµητικό υπολογισµό του ολοκληρώµατος: b I( f ) = f ( x) a όπου f (x) συνεχής και ολοκληρώσιµη
ΑΤΣΑΛΑΚΗ ΞΑΝΘΟΥΛΑ ΕΡΓΑΣΤΗΡΙΟ 2
 EXERSICE 1 #include #define ROWS 20 #define COLUMNS 5 int better(int array[][columns],int rows); int main(void) int rows,grades[rows][columns],i,j,k=0,l=0; printf("\nhow many students are there
EXERSICE 1 #include #define ROWS 20 #define COLUMNS 5 int better(int array[][columns],int rows); int main(void) int rows,grades[rows][columns],i,j,k=0,l=0; printf("\nhow many students are there
SUNARTHSEIS POLLWN METABLHTWN. 5h Seirˆ Ask sewn. Allag metablht n sto diplì olokl rwma
 PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II SUNARTHSEIS POLLWN METABLHTWN 5h Seirˆ Ask sewn Allag metablht n sto diplì olokl rwma Jèma. Qrhsimopoi ntac
PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II SUNARTHSEIS POLLWN METABLHTWN 5h Seirˆ Ask sewn Allag metablht n sto diplì olokl rwma Jèma. Qrhsimopoi ntac
Σηµειώσεις για το πρόγραµµα Mathematica
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΝΑΥΠΗΓΩΝ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Σηµειώσεις για το πρόγραµµα Mathematica Νίκος Θεµελής Νοέµβριος 008 Σκοπός του φυλλαδίου είναι να παρέχει βασικές γνώσεις για την χρήση
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΝΑΥΠΗΓΩΝ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Σηµειώσεις για το πρόγραµµα Mathematica Νίκος Θεµελής Νοέµβριος 008 Σκοπός του φυλλαδίου είναι να παρέχει βασικές γνώσεις για την χρήση
PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II DIAFORIKES EXISWSEIS.
 PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II DIAFORIKES EXISWSEIS 6h Seirˆ Ask sewn OmogeneÐc grammikèc diaforikèc exis seic me stajeroôc suntelestèc Jèma
PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II DIAFORIKES EXISWSEIS 6h Seirˆ Ask sewn OmogeneÐc grammikèc diaforikèc exis seic me stajeroôc suntelestèc Jèma
KATASTATIKO 3. XRHSIMOPOIHSH TVN OIKONOMIKVN MESVN, KOINH VFELEIA
 1 of 5 20.10.2005 08:48 KATASTATIKO Tou Eurvpai_kouß Keßntrou Episthmonikhßw, Oikoumenikhßw kai Politistikhßw Sunergasißaw - Ellhnogermanikhß Prvtoboulißa Würzburg 1. ONOMASIA KAI EDRA TOU SULLOGOU (1)
1 of 5 20.10.2005 08:48 KATASTATIKO Tou Eurvpai_kouß Keßntrou Episthmonikhßw, Oikoumenikhßw kai Politistikhßw Sunergasißaw - Ellhnogermanikhß Prvtoboulißa Würzburg 1. ONOMASIA KAI EDRA TOU SULLOGOU (1)
Συλλογή απο σταθερές και εντολές του Mathematica (Κυρίως για την έκδοση 6)
 Συλλογή απο σταθερές και εντολές του Mathematica (Κυρίως για την έκδοση 6) Σταθερές Pi, E, I, Infinity. Το τελευταίο το γράφουµε \[Infinity]. Π.χ. Sum[1/n^2, {n, Infinity}]. Ακριβείς Αριθµητικές Ποσότητες
Συλλογή απο σταθερές και εντολές του Mathematica (Κυρίως για την έκδοση 6) Σταθερές Pi, E, I, Infinity. Το τελευταίο το γράφουµε \[Infinity]. Π.χ. Sum[1/n^2, {n, Infinity}]. Ακριβείς Αριθµητικές Ποσότητες
25 OktwbrÐou 2012 (5 h ebdomˆda) S. Malefˆkh Genikì Tm ma Majhmatikˆ gia QhmikoÔc
 Mˆjhma 9 0 25 OktwbrÐou 2012 (5 h ebdomˆda) Diaforikèc Exis seic TÔpoi Diaforik n exis sewn H pio apl diaforik exðswsh y = f (x) Diaforikèc Exis seic TÔpoi Diaforik n exis sewn H pio apl diaforik exðswsh
Mˆjhma 9 0 25 OktwbrÐou 2012 (5 h ebdomˆda) Diaforikèc Exis seic TÔpoi Diaforik n exis sewn H pio apl diaforik exðswsh y = f (x) Diaforikèc Exis seic TÔpoi Diaforik n exis sewn H pio apl diaforik exðswsh
PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II DIAFORIKES EXISWSEIS.
 PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II DIAFORIKES EXISWSEIS h Seirˆ Ask sewn Diaforikèc eis seic > diaforikèc
PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II DIAFORIKES EXISWSEIS h Seirˆ Ask sewn Diaforikèc eis seic > diaforikèc
Παρουσίαση του Mathematica
 Παρουσίαση του Mathematica Εργαστήριο Σκυλίτσης Θεοχάρης Καλαματιανός Ρωμανός Καπλάνης Αθανάσιος Ιόνιο Πανεπιστήμιο (www.ionio.gr)( Εισαγωγή Σύμβολα πράξεων ή συναρτήσεων: Πρόσθεση + Αφαίρεση - Πολλαπλασιασμός
Παρουσίαση του Mathematica Εργαστήριο Σκυλίτσης Θεοχάρης Καλαματιανός Ρωμανός Καπλάνης Αθανάσιος Ιόνιο Πανεπιστήμιο (www.ionio.gr)( Εισαγωγή Σύμβολα πράξεων ή συναρτήσεων: Πρόσθεση + Αφαίρεση - Πολλαπλασιασμός
Θέµα 1 (15%): (απαιτούµενος χρόνος < 15 λεπτά)
 Θέµα 1 (15%): (απαιτούµενος χρόνος < 15 λεπτά) Εκτελέστε µε το χέρι το παρακάτω πρόγραµµα και γράψτε όλες τις ενδιάµεσες τιµές και τις τιµές που τυπώνονται: int m,n; m=2; n=1; m=m+5; if (m>=9) m=m-8; n=n+7;
Θέµα 1 (15%): (απαιτούµενος χρόνος < 15 λεπτά) Εκτελέστε µε το χέρι το παρακάτω πρόγραµµα και γράψτε όλες τις ενδιάµεσες τιµές και τις τιµές που τυπώνονται: int m,n; m=2; n=1; m=m+5; if (m>=9) m=m-8; n=n+7;
Diˆsthma empistosônhc thc mèshc tim c µ. Statistik gia Hlektrolìgouc MhqanikoÔc EKTIMHSH EKTIMHSH PARAMETRWN - 2. Dhm trhc Kougioumtz c.
 Statistik gia Hlektrolìgouc MhqanikoÔc EKTIMHSH PARAMETRWN - 2 6 Maòou 2010 EktÐmhsh Diast matoc empistosônhc Melet same thn ektim tria ˆθ paramètrou θ: An gnwrðzoume thn katanom thc X kai eðnai F X (x;
Statistik gia Hlektrolìgouc MhqanikoÔc EKTIMHSH PARAMETRWN - 2 6 Maòou 2010 EktÐmhsh Diast matoc empistosônhc Melet same thn ektim tria ˆθ paramètrou θ: An gnwrðzoume thn katanom thc X kai eðnai F X (x;
Work12 REMARKS script file lab10 ask1-5 tabbing, ls2, urlparse, times, dates_correct
 Work12 REMARKS script le lab10 ask1-5 tabbing, ls2, urlparse, times, dates_correct #Username : imanousi #lename : tabbing.imanousi #To script eisagei ena tab sthn arxh kathe grammhs #tou arxeiou pou dinetai
Work12 REMARKS script le lab10 ask1-5 tabbing, ls2, urlparse, times, dates_correct #Username : imanousi #lename : tabbing.imanousi #To script eisagei ena tab sthn arxh kathe grammhs #tou arxeiou pou dinetai
ΟΜΟΣΠΟΝΔΙΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑΔΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2019 Β ΦΑΣΗ
 ΤΑΞΗ: 3 η ΤΑΞΗ ΕΠΑ.Λ. ΜΑΘΗΜΑ: ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΥΠΟΛΟΓΙΣΤΩΝ / ΕΙΔΙΚΟΤΗΤΑΣ Ημερομηνία: Σάββατο 20 Απριλίου 2019 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α Α1. 1. Λάθος 2. Λάθος 3. Σωστό 4. Λάθος 5. Σωστό Α2. print(x
ΤΑΞΗ: 3 η ΤΑΞΗ ΕΠΑ.Λ. ΜΑΘΗΜΑ: ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΥΠΟΛΟΓΙΣΤΩΝ / ΕΙΔΙΚΟΤΗΤΑΣ Ημερομηνία: Σάββατο 20 Απριλίου 2019 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α Α1. 1. Λάθος 2. Λάθος 3. Σωστό 4. Λάθος 5. Σωστό Α2. print(x
Να διορθωθούν τα εξής αρχεία scr2.chgeorg, scr2.gmotsias, scr2.ngrammen. cat scr2.*
 vassik@aetos:~/work/online$ cat scr2.* Τροποπoίηση/Συμπλήρωση του ask2 Δεχεται ονόματα αρχείων ως παραμέτρους Στο 1 ο αρχείο που δίνεται ως παράμετρος, γράφονται μέσα τα ονόματα και τα περιεχόμενα των
vassik@aetos:~/work/online$ cat scr2.* Τροποπoίηση/Συμπλήρωση του ask2 Δεχεται ονόματα αρχείων ως παραμέτρους Στο 1 ο αρχείο που δίνεται ως παράμετρος, γράφονται μέσα τα ονόματα και τα περιεχόμενα των
Ενότητα: «Επίλυση προβληµάτων στα Μαθηµατικά Mathematica Παραδείγµατα»
 Ενότητα: «Επίλυση προβληµάτων στα Μαθηµατικά Mathematica Παραδείγµατα» Οδηγός χρήσης του Mathematica. ιδακτικές εφαρµογές σε θέµατα Μαθηµατικών και Θετικών Επιστηµών ιδάσκων: Το Mathematica ως γνωστικό
Ενότητα: «Επίλυση προβληµάτων στα Μαθηµατικά Mathematica Παραδείγµατα» Οδηγός χρήσης του Mathematica. ιδακτικές εφαρµογές σε θέµατα Μαθηµατικών και Θετικών Επιστηµών ιδάσκων: Το Mathematica ως γνωστικό
Jerinì SqoleÐo Fusik c sthn EkpaÐdeush 28 IounÐou - 1 IoulÐou 2010 EstÐa Episthm n Pˆtrac
 Kbantik Perigraf tou Kìsmou mac KwnstantÐnoc Sfètsoc Kajhght c Fusik c Genikì Tm ma, Panepist mio Patr n Jerinì SqoleÐo Fusik c sthn EkpaÐdeush 28 IounÐou - 1 IoulÐou 2010 EstÐa Episthm n Pˆtrac Ti ennooôme
Kbantik Perigraf tou Kìsmou mac KwnstantÐnoc Sfètsoc Kajhght c Fusik c Genikì Tm ma, Panepist mio Patr n Jerinì SqoleÐo Fusik c sthn EkpaÐdeush 28 IounÐou - 1 IoulÐou 2010 EstÐa Episthm n Pˆtrac Ti ennooôme
Συστήματα Μικροϋπολογιστών
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ Η/Υ Συστήματα Μικροϋπολογιστών 3η Oμάδα Ασκήσεων Δημητρίου Ανδριάνα 03110684 Σκούρα Ελένη 03110721 1 η 4 η Άσκηση i) Στο πρόβλημα
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ Η/Υ Συστήματα Μικροϋπολογιστών 3η Oμάδα Ασκήσεων Δημητρίου Ανδριάνα 03110684 Σκούρα Ελένη 03110721 1 η 4 η Άσκηση i) Στο πρόβλημα
JEMATA EXETASEWN Pragmatik Anˆlush I
 JEMATA EXETASEWN Pragmatik Anˆlush I JEMA 1o. A)(M. 1.5) Na qarakthrðsete (me aitiolìghsh) tic protˆseic pou akoloujoôn me thn èndeixh Swstì Lˆjoc: (i) 'Estw x 0 tètoio ste x < ε, gia kˆje ε > 0. Tìte
JEMATA EXETASEWN Pragmatik Anˆlush I JEMA 1o. A)(M. 1.5) Na qarakthrðsete (me aitiolìghsh) tic protˆseic pou akoloujoôn me thn èndeixh Swstì Lˆjoc: (i) 'Estw x 0 tètoio ste x < ε, gia kˆje ε > 0. Tìte
ΕΥΣΤΑΘΕΙΑ ΙΑΤΟΙΧΙΣΜΟΥ ΠΛΟΙΟΥ ΚΑΙ ΥΠΟΒΑΘΡΟ ΚΑΝΟΝΙΣΜΩΝ. Σηµειώσεις για το πρόγραµµα Mathematica
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΝΑΥΠΗΓΩΝ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΥΣΤΑΘΕΙΑ ΙΑΤΟΙΧΙΣΜΟΥ ΠΛΟΙΟΥ ΚΑΙ ΥΠΟΒΑΘΡΟ ΚΑΝΟΝΙΣΜΩΝ Σηµειώσεις για το πρόγραµµα Mathematica ρ. Νίκος Θεµελής Νοέµβριος 009 Σκοπός των σηµειώσεων
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΝΑΥΠΗΓΩΝ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΥΣΤΑΘΕΙΑ ΙΑΤΟΙΧΙΣΜΟΥ ΠΛΟΙΟΥ ΚΑΙ ΥΠΟΒΑΘΡΟ ΚΑΝΟΝΙΣΜΩΝ Σηµειώσεις για το πρόγραµµα Mathematica ρ. Νίκος Θεµελής Νοέµβριος 009 Σκοπός των σηµειώσεων
aapostol.scr2, scr2.kdeligia
 vassik@aetos:~/work/online$ cat scr2.* Τροποπoίηση/Συμπλήρωση του ask2 Δέχεται ονόματα αρχείων ως παραμέτρους Στο 1 ο αρχείο που δίνεται ως παράμετρος, γράφονται μέσα τα ονόματα και τα περιεχόμενα των
vassik@aetos:~/work/online$ cat scr2.* Τροποπoίηση/Συμπλήρωση του ask2 Δέχεται ονόματα αρχείων ως παραμέτρους Στο 1 ο αρχείο που δίνεται ως παράμετρος, γράφονται μέσα τα ονόματα και τα περιεχόμενα των
Εφαρμοσμένα Μαθηματικά ΙΙ Πρόοδος Ι. Λυχναρόπουλος
 /4/05 Εφαρμοσμένα Μαθηματικά ΙΙ Πρόοδος Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) Αν z z 0 δείξτε ότι: z z ( z ) Παραγωγίζουμε την z z 0 ως προς θεωρώντας ότι η z είναι συνάρτηση των και : z z z z z z 0 () z
/4/05 Εφαρμοσμένα Μαθηματικά ΙΙ Πρόοδος Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) Αν z z 0 δείξτε ότι: z z ( z ) Παραγωγίζουμε την z z 0 ως προς θεωρώντας ότι η z είναι συνάρτηση των και : z z z z z z 0 () z
MÐa SÔntomh Eisagwgă stic SÔgqronec JewrÐec Isìthtac
 MÐa SÔntomh Eisagwgă stic SÔgqronec JewrÐec Isìthtac Nikìlac BroÔsalhc nicholas.vrousalis@lmh.ox.ac.uk 29 OktwbrÐou 2007 1 KĹpoiec basikèc diakrðseic 1.1 Ish Mèrimna Φέροµαι εξίσου στην Α και στον Β vs.
MÐa SÔntomh Eisagwgă stic SÔgqronec JewrÐec Isìthtac Nikìlac BroÔsalhc nicholas.vrousalis@lmh.ox.ac.uk 29 OktwbrÐou 2007 1 KĹpoiec basikèc diakrðseic 1.1 Ish Mèrimna Φέροµαι εξίσου στην Α και στον Β vs.
Εφαρμοσμένα Μαθηματικά για Μηχανικούς
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Εφαρμοσμένα Μαθηματικά για Μηχανικούς Σημειώσεις: Δειγματοληψία Γιώργος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών Kefˆlaio 5 DeigmatolhyÐa 'Estw èna sônolo periodikˆ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Εφαρμοσμένα Μαθηματικά για Μηχανικούς Σημειώσεις: Δειγματοληψία Γιώργος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών Kefˆlaio 5 DeigmatolhyÐa 'Estw èna sônolo periodikˆ
Στατιστική για Χημικούς Μηχανικούς
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Στατιστική για Χημικούς Μηχανικούς Ενότητα 3: Έλεγχος Υποθέσεων Κουγιουμτζής Δημήτρης Τμήμα Χημικών Μηχανικών Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Στατιστική για Χημικούς Μηχανικούς Ενότητα 3: Έλεγχος Υποθέσεων Κουγιουμτζής Δημήτρης Τμήμα Χημικών Μηχανικών Άδειες Χρήσης Το παρόν εκπαιδευτικό
Modern Greek Extension
 Centre Number 2015 HIGHER SCHOOL CERTIFICATE EXAMINATION Student Number Modern Greek Extension Written Examination Total marks 40 General Instructions Reading time 10 minutes Working time 1 hour and 50
Centre Number 2015 HIGHER SCHOOL CERTIFICATE EXAMINATION Student Number Modern Greek Extension Written Examination Total marks 40 General Instructions Reading time 10 minutes Working time 1 hour and 50
ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ, , 3 Ο ΕΞΑΜΗΝΟ ΑΠΑΝΤΗΣΕΙΣ ΕΡΓΑΣΙΑΣ #3: ΠΑΡΕΜΒΟΛΗ ΕΠΙΜΕΛΕΙΑ: Σ. Μισδανίτης
 ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ, 6-7, 3 Ο ΕΞΑΜΗΝΟ ΑΠΑΝΤΗΣΕΙΣ ΕΡΓΑΣΙΑΣ #3: ΠΑΡΕΜΒΟΛΗ ΕΠΙΜΕΛΕΙΑ: Σ. Μισδανίτης. Επιλέξτε αυθαίρετα µία συνάρτηση ( x και τέσσερα ζευγάρια σημείων ( x, ( x, έτσι ώστε τα σημεία x να μην
ΑΡΙΘΜΗΤΙΚΗ ΑΝΑΛΥΣΗ, 6-7, 3 Ο ΕΞΑΜΗΝΟ ΑΠΑΝΤΗΣΕΙΣ ΕΡΓΑΣΙΑΣ #3: ΠΑΡΕΜΒΟΛΗ ΕΠΙΜΕΛΕΙΑ: Σ. Μισδανίτης. Επιλέξτε αυθαίρετα µία συνάρτηση ( x και τέσσερα ζευγάρια σημείων ( x, ( x, έτσι ώστε τα σημεία x να μην
Statistik gia PolitikoÔc MhqanikoÔc ELEGQOS UPOJ
 Statistik gia PolitikoÔc MhqanikoÔc ELEGQOS UPOJESEWN 18 DekembrÐou 2012 'Elegqoc Upojèsewn 1 Statistik upìjesh 2 Statistik elègqou kai perioq apìrriyhc 3 Apìfash elègqou Statistik upìjesh mhdenik upìjesh
Statistik gia PolitikoÔc MhqanikoÔc ELEGQOS UPOJESEWN 18 DekembrÐou 2012 'Elegqoc Upojèsewn 1 Statistik upìjesh 2 Statistik elègqou kai perioq apìrriyhc 3 Apìfash elègqou Statistik upìjesh mhdenik upìjesh
Σύνοψη είτε τις ολοκληρωµένες απαντήσεις
 1 of 22 12/12/2012 11:18 µµ απαντήσεις Σύνοψη είτε τις ολοκληρωµένες απαντήσεις ΤΜΗΜΑ (επιλέξτε το τµήµα σας) 1 1% Β ΕΦΑΡΜΟΣΜΕΝΩΝ ΤΕΧΝΩΝ 15 13% Β ΗΛΕΚΤΡΟΛΟΓΩΝ 18 16% Β ΗΛΕΚΤΡΟΝΙΚΩΝ 21 18% Β ΜΗΧΑΝΟΛΟΓΩΝ
1 of 22 12/12/2012 11:18 µµ απαντήσεις Σύνοψη είτε τις ολοκληρωµένες απαντήσεις ΤΜΗΜΑ (επιλέξτε το τµήµα σας) 1 1% Β ΕΦΑΡΜΟΣΜΕΝΩΝ ΤΕΧΝΩΝ 15 13% Β ΗΛΕΚΤΡΟΛΟΓΩΝ 18 16% Β ΗΛΕΚΤΡΟΝΙΚΩΝ 21 18% Β ΜΗΧΑΝΟΛΟΓΩΝ
ΣΗΜΕΙΩΣΕΙΣ ΥΠΟΛΟΓΙΣΤΙΚΗΣ ΦΥΣΙΚΗΣ. Κων/νος Κόκκοτας Τμήμα Φυσικής, ΑΠΘ
 ΣΗΜΕΙΩΣΕΙΣ ΥΠΟΛΟΓΙΣΤΙΚΗΣ ΦΥΣΙΚΗΣ Κων/νος Κόκκοτας Τμήμα Φυσικής, ΑΠΘ 18 Μαρτίου 2011 ii Περιεχόμενα 0.1 ΔΙΑΦΟΡΙΚΕΣΕΞΙΣΩΣΕΙΣ & Mathematica... 1 0.1.1 ΑναλυτικήΕπίλυσηΔΕ... 1 0.1.2 ΑριθμητικήΕπίλυσηΔΕ...
ΣΗΜΕΙΩΣΕΙΣ ΥΠΟΛΟΓΙΣΤΙΚΗΣ ΦΥΣΙΚΗΣ Κων/νος Κόκκοτας Τμήμα Φυσικής, ΑΠΘ 18 Μαρτίου 2011 ii Περιεχόμενα 0.1 ΔΙΑΦΟΡΙΚΕΣΕΞΙΣΩΣΕΙΣ & Mathematica... 1 0.1.1 ΑναλυτικήΕπίλυσηΔΕ... 1 0.1.2 ΑριθμητικήΕπίλυσηΔΕ...
9. α 2 + β 2 ±2αβ. 10. α 2 ± αβ + β (1 + α) ν > 1+να, 1 <α 0, ν 2. log α. 14. log α x = ln x. 19. x 1 <x 2 ln x 1 < ln x 2
 UpenjumÐseic gia thn Jetik kai Teqnologik KateÔjunsh Kajhght c: N.S. Maurogi nnhc 1 Tautìthtec - Anisìthtec 1. (α ± ) = α ± α +. (α ± ) 3 = α 3 ± 3α +3α ± 3 3. α 3 ± 3 =(α ± ) ( α α + ) 4. (α + + γ) =
UpenjumÐseic gia thn Jetik kai Teqnologik KateÔjunsh Kajhght c: N.S. Maurogi nnhc 1 Tautìthtec - Anisìthtec 1. (α ± ) = α ± α +. (α ± ) 3 = α 3 ± 3α +3α ± 3 3. α 3 ± 3 =(α ± ) ( α α + ) 4. (α + + γ) =
thlèfwno: , H YHFIAKH TAXH A' GumnasÐou Miqˆlhc TzoÔmac Sq. Sumb. kl.
 A' GumnasÐou Sq. Sumb. kl. PE03 GiatÐ epibˆlletai h eisagwg thc sôgqronhc teqnologðac sthn ekpaðdeush. Η Πληροφοριοποίηση της κοινωνίας. Η αυξανόμενη πολυπλοκότητα του εκπαιδευτικού συστήματος. Η σημερινή
A' GumnasÐou Sq. Sumb. kl. PE03 GiatÐ epibˆlletai h eisagwg thc sôgqronhc teqnologðac sthn ekpaðdeush. Η Πληροφοριοποίηση της κοινωνίας. Η αυξανόμενη πολυπλοκότητα του εκπαιδευτικού συστήματος. Η σημερινή
Η-Υ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ. Εργαστήριο 8 Ασκήσεις Πινάκων Ταξινόμηση Αναζήτηση. Γιώργος Λαμπρινίδης
 Εργαστήριο 8 Ασκήσεις Πινάκων Ταξινόμηση Αναζήτηση Γιώργος Λαμπρινίδης amprinidis@pharm.uoa.gr Παραδείγματα στους πίνακες (1) Έστω ότι έχετε το εξής: int a[20]; for(i = 0; i < 20; i++) a[i] = i+1; Ποιες
Εργαστήριο 8 Ασκήσεις Πινάκων Ταξινόμηση Αναζήτηση Γιώργος Λαμπρινίδης amprinidis@pharm.uoa.gr Παραδείγματα στους πίνακες (1) Έστω ότι έχετε το εξής: int a[20]; for(i = 0; i < 20; i++) a[i] = i+1; Ποιες
2.3 Επιπλέον συναρτήσεις για δισδιάστατα γραφικά
 2.3 Επιπλέον συναρτήσεις για δισδιάστατα γραφικά 2.3.1 Γραφική παράσταση καμπύλης που ορίζεται με παραμετρικές εξισώσεις Μερικές φορές, οι καμπύλες ορίζονται παραμετρικά, για παράδειγμα μπορεί οι συντεταγμένες
2.3 Επιπλέον συναρτήσεις για δισδιάστατα γραφικά 2.3.1 Γραφική παράσταση καμπύλης που ορίζεται με παραμετρικές εξισώσεις Μερικές φορές, οι καμπύλες ορίζονται παραμετρικά, για παράδειγμα μπορεί οι συντεταγμένες
ΣΥΝΑΡΤΗΣΕΙΣ Παραδείγματα χρήσης συναρτήσεων
 ΣΥΝΑΡΤΗΣΕΙΣ Παραδείγματα χρήσης συναρτήσεων ΠΟΛΛΕΣ ΕΝΤΟΛΕΣ ΕΠΙΣΤΡΟΦΗΣ Να γραφτεί ένα πρόγραμμα που να διπλασιάζει ένα ποσό που του δίνει ο χρήστης μεταξύ 0 και 1000. Να ελέγχει εάν το ποσό που εισήχθη
ΣΥΝΑΡΤΗΣΕΙΣ Παραδείγματα χρήσης συναρτήσεων ΠΟΛΛΕΣ ΕΝΤΟΛΕΣ ΕΠΙΣΤΡΟΦΗΣ Να γραφτεί ένα πρόγραμμα που να διπλασιάζει ένα ποσό που του δίνει ο χρήστης μεταξύ 0 και 1000. Να ελέγχει εάν το ποσό που εισήχθη
Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ
 Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ Ενότητα: Ο δυϊκός χώρος Όνομα Καθηγητή: Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ Ενότητα: Ο δυϊκός χώρος Όνομα Καθηγητή: Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
2.2.7 Τίτλος στη γραφική παράσταση
 2.2.7 Τίτλος στη γραφική παράσταση Η επιλογή title τοποθετεί μία επικεφαλίδα (τίτλο) στη γραφική παράσταση. title = None (προεπιλογή) title = επικεφαλίδα δεν θέτει καμία επικεφαλίδα θέτει ως επικεφαλίδα
2.2.7 Τίτλος στη γραφική παράσταση Η επιλογή title τοποθετεί μία επικεφαλίδα (τίτλο) στη γραφική παράσταση. title = None (προεπιλογή) title = επικεφαλίδα δεν θέτει καμία επικεφαλίδα θέτει ως επικεφαλίδα
Κεφάλαιο Γραφικές απεικονίσεις. 4.1 Γραφικά στις δύο διαστάσεις Σχεδιάζοντας συμβολικές εκφράσεις και συναρτήσεις
 Κεφάλαιο 4 4. Γραφικές απεικονίσεις Η γραφική απεικόνιση ενός μαθηματικού αντικειμένου είναι ένα από τα ισχυρότερα εργαλεία ενός ΣΣΥ. Τα περισσότερα ΣΣΥ έχουν ένα δικό τους σύστημα γραφικών για να σχεδιάζουν
Κεφάλαιο 4 4. Γραφικές απεικονίσεις Η γραφική απεικόνιση ενός μαθηματικού αντικειμένου είναι ένα από τα ισχυρότερα εργαλεία ενός ΣΣΥ. Τα περισσότερα ΣΣΥ έχουν ένα δικό τους σύστημα γραφικών για να σχεδιάζουν
"ΓΛΩΣΣΑ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Η/Υ" (ΕΜ102), ΕΡΓΑΣΙΑ 1η
 "ΓΛΩΣΣΑ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Η/Υ" (ΕΜ102), ΕΡΓΑΣΙΑ 1η Σε αυτήν την εργασία καλείστε να κατασκευάσετε τον πηγαίο κώδικα γλώσσας C για το εκτελέσιµο αρχείο µε ό- νοµα ATM, που όταν εκτελείται σε κονσόλα προσοµοιώνει
"ΓΛΩΣΣΑ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Η/Υ" (ΕΜ102), ΕΡΓΑΣΙΑ 1η Σε αυτήν την εργασία καλείστε να κατασκευάσετε τον πηγαίο κώδικα γλώσσας C για το εκτελέσιµο αρχείο µε ό- νοµα ATM, που όταν εκτελείται σε κονσόλα προσοµοιώνει
242 -ΕισαγωγήστουςΗ/Υ
 1 242 -ΕισαγωγήστουςΗ/Υ ΤµήµαΜαθηµατικών, Πανεπιστήµιο Ιωαννίνων Άρτια Α.Μ. (0-2-4-6-8) Πίνακες σαν παράµετροι 2 Πίνακες σαν παράµετροι 3 Πίνακες σαν παράµετροι Περνάµε ένα πίνακα σαν παράµετρο σε µια
1 242 -ΕισαγωγήστουςΗ/Υ ΤµήµαΜαθηµατικών, Πανεπιστήµιο Ιωαννίνων Άρτια Α.Μ. (0-2-4-6-8) Πίνακες σαν παράµετροι 2 Πίνακες σαν παράµετροι 3 Πίνακες σαν παράµετροι Περνάµε ένα πίνακα σαν παράµετρο σε µια
Δομημένος Προγραμματισμός
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Δομημένος Προγραμματισμός Ενότητα: Συναρτήσεις - προγράμματα - Μέρος Α Δ. Ε. Μετάφας Τμ. Ηλεκτρονικών Μηχ. Τ.Ε. Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Δομημένος Προγραμματισμός Ενότητα: Συναρτήσεις - προγράμματα - Μέρος Α Δ. Ε. Μετάφας Τμ. Ηλεκτρονικών Μηχ. Τ.Ε. Άδειες Χρήσης
Τίτλος Μαθήματος: Γραμμική Άλγεβρα Ι
 Τίτλος Μαθήματος: Γραμμική Άλγεβρα Ι Ενότητα: Θέματα Εξετάσεων Όνομα Καθηγητή : Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Τίτλος Μαθήματος: Γραμμική Άλγεβρα Ι Ενότητα: Θέματα Εξετάσεων Όνομα Καθηγητή : Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
GLB0049 GLB0050 GLB0051
 GLB0049 GLB0050 GLB0051 ΕΓΧΕΙΡΙ ΙΟ ΧΡΗΣΗΣ ΠΛΗΝΡΥΡΙΩΝ Σελ. 321 PERIECOMENA KEF.1 ΠΡΟΛΟΓΟΣ... 323 KEF.2 ΜΕΤΑΚΙΝΗΣΗ ΚΑΙ ΜΕΤΑΦΟΡΑ ΤΗΣ ΣΥΣΚΕΥΗΣ... 323 2.1 METAFORA KAI SUSKEUASIA... 323 2.2 METAKINHSH... 324
GLB0049 GLB0050 GLB0051 ΕΓΧΕΙΡΙ ΙΟ ΧΡΗΣΗΣ ΠΛΗΝΡΥΡΙΩΝ Σελ. 321 PERIECOMENA KEF.1 ΠΡΟΛΟΓΟΣ... 323 KEF.2 ΜΕΤΑΚΙΝΗΣΗ ΚΑΙ ΜΕΤΑΦΟΡΑ ΤΗΣ ΣΥΣΚΕΥΗΣ... 323 2.1 METAFORA KAI SUSKEUASIA... 323 2.2 METAKINHSH... 324
Eisagwgă sto PICTEX: Mèroc prÿto
 EÖtupon TeÔqoc No. 1 Septèmbrioc 1998 9 Eisagwgă sto PICTEX: Mèroc prÿto Apìstoloc Surìpouloc 28ης Οκτωβρίου 366 67100Ξάνθη 1. Eisagwgă Το PICTEX είναι μια συλλογή από μακροεντολές του TEX με τις οποίες
EÖtupon TeÔqoc No. 1 Septèmbrioc 1998 9 Eisagwgă sto PICTEX: Mèroc prÿto Apìstoloc Surìpouloc 28ης Οκτωβρίου 366 67100Ξάνθη 1. Eisagwgă Το PICTEX είναι μια συλλογή από μακροεντολές του TEX με τις οποίες
2. Δισδιάστατα γραφικά
 2. Δισδιάστατα γραφικά 2.1 Δισδιάστατες γραφικές παραστάσεις συναρτήσεων μίας μεταβλητής. Η βασική εντολή σχεδίασης, του Sage, μιας γραφικής παράστασης μίας συνάρτησης μίας μεταβλητής είναι η συνάρτηση
2. Δισδιάστατα γραφικά 2.1 Δισδιάστατες γραφικές παραστάσεις συναρτήσεων μίας μεταβλητής. Η βασική εντολή σχεδίασης, του Sage, μιας γραφικής παράστασης μίας συνάρτησης μίας μεταβλητής είναι η συνάρτηση
Οι κανόνες που περιγράφουν τη ϕύση ϕαίνεται ότι είναι γραµµένοι µε µαθηµατικά. Richard Feynmann
 Στη Μαρία 2 Οι κανόνες που περιγράφουν τη ϕύση ϕαίνεται ότι είναι γραµµένοι µε µαθηµατικά. Richard Feynmann 2 Πρόλογος Μη χάνετε την πίστη σας. Τα µαθηµατικά µας είναι ένα ισχυρό ϕρούριο. Stan Ulam Στο
Στη Μαρία 2 Οι κανόνες που περιγράφουν τη ϕύση ϕαίνεται ότι είναι γραµµένοι µε µαθηµατικά. Richard Feynmann 2 Πρόλογος Μη χάνετε την πίστη σας. Τα µαθηµατικά µας είναι ένα ισχυρό ϕρούριο. Stan Ulam Στο
Ομάδα Γ. Ο υπολογιστής ως επιστημονικό εργαλείο
 Ομάδα Γ. Ο υπολογιστής ως επιστημονικό εργαλείο Πρόβλημα 10 a : Κλίση καμπύλης Πρόβλημα 10 b : Εμβαδόν καμπύλης Πρόβλημα 10 c : Βολές Πρόβλημα 10 d : Κινήσεις Πλανητών Πρόβλημα 10 e : Απλό μαθηματικό εκκρεμές
Ομάδα Γ. Ο υπολογιστής ως επιστημονικό εργαλείο Πρόβλημα 10 a : Κλίση καμπύλης Πρόβλημα 10 b : Εμβαδόν καμπύλης Πρόβλημα 10 c : Βολές Πρόβλημα 10 d : Κινήσεις Πλανητών Πρόβλημα 10 e : Απλό μαθηματικό εκκρεμές
D d2 c(x) dx 2. EI d4 v(x) dx 4. d 2 q(t) t + ω 2 p(t) m. +2ξω 0 d 4 X(x) dt 2. K d q(t) =p d (t) M d. + C d. (x) = p(x) a s e a s.
 v D d2 c(x) dx 2 d 2 u(t) dt 2 θ(x) =v (x) κ(x) =θ (x) M d d 2 q(t) dt 2 M(x) =EIκ (x) Q(x) = M (x) p(x) =Q (x) (x) = p(x) EI EI d4 v(x) dx 4 V dc(x) dx kc(x) =0 ΕΦΑΡΜΟΣΜΕΝΑ ΜΑΘΗΜΑΤΙΚΑ ΙΙ ΓΙΑ ΠΟΛΙΤΙΚΟΥΣ
v D d2 c(x) dx 2 d 2 u(t) dt 2 θ(x) =v (x) κ(x) =θ (x) M d d 2 q(t) dt 2 M(x) =EIκ (x) Q(x) = M (x) p(x) =Q (x) (x) = p(x) EI EI d4 v(x) dx 4 V dc(x) dx kc(x) =0 ΕΦΑΡΜΟΣΜΕΝΑ ΜΑΘΗΜΑΤΙΚΑ ΙΙ ΓΙΑ ΠΟΛΙΤΙΚΟΥΣ
Εισαγωγή στη Mathematica
 1 Εισαγωγή στη Mathematica Η Mathematica είναι ένα αλγεβρικό υπολογιστικό σύστηµα το οποίο εκτελεί αριθµητικούς, συµβολικούς και γραφικούς υπολογισµούς. Η ειδοποιός διαφορά της από τις κοινές γλώσσες προγραµµατισµού
1 Εισαγωγή στη Mathematica Η Mathematica είναι ένα αλγεβρικό υπολογιστικό σύστηµα το οποίο εκτελεί αριθµητικούς, συµβολικούς και γραφικούς υπολογισµούς. Η ειδοποιός διαφορά της από τις κοινές γλώσσες προγραµµατισµού
ΚΕΦ.3 ΣΥΣΤΑΣΕΙΣ ΑΣΦΑΛΕΙΑΣ...
 GLB0047 GR σελ. 221 ΠΙΝΑΚΑΣ ΚΕΦ.1 ΕΙΣΑΓΩΓΉ... 223 1.1 ΕΠΙΚΙΝ ΥΝΕΣ ΠΕΡΙΟΧΕΣ... 223 ΚΕΦ.2 ΕΓΚΑΤΆΣΤΑΣΗ... 224 2.1 ΜΕΤΑΚΙΝΗΣΗ ΚΑΙ ΑΠΟΣΥΣΚΕΥΑΣΙΑ... 224 2.2 ΗΛΕΚΤΡΙΚΗ ΣΥΝ ΕΣΜΟΛΟΓΙΑ ΓΙΑ ΣΥΣΚΕΥΕΣ ΧΩΡΙΣ ΚΑΛΩ ΙΟ...
GLB0047 GR σελ. 221 ΠΙΝΑΚΑΣ ΚΕΦ.1 ΕΙΣΑΓΩΓΉ... 223 1.1 ΕΠΙΚΙΝ ΥΝΕΣ ΠΕΡΙΟΧΕΣ... 223 ΚΕΦ.2 ΕΓΚΑΤΆΣΤΑΣΗ... 224 2.1 ΜΕΤΑΚΙΝΗΣΗ ΚΑΙ ΑΠΟΣΥΣΚΕΥΑΣΙΑ... 224 2.2 ΗΛΕΚΤΡΙΚΗ ΣΥΝ ΕΣΜΟΛΟΓΙΑ ΓΙΑ ΣΥΣΚΕΥΕΣ ΧΩΡΙΣ ΚΑΛΩ ΙΟ...
Eisagwg sthn KosmologÐa
 Eisagwg sthn KosmologÐa BasileÐou S. Gerogiˆnnh Kajhght Tm matoc Fusik c PanepisthmÐou Patr n Patra 2009 Kefˆlaio 1 Eisagwgikˆ 1.1 Gwniakì mègejoc, parsèk, ètoc fwtìc O parathrht c tou Sq matoc 1.1 parathreð
Eisagwg sthn KosmologÐa BasileÐou S. Gerogiˆnnh Kajhght Tm matoc Fusik c PanepisthmÐou Patr n Patra 2009 Kefˆlaio 1 Eisagwgikˆ 1.1 Gwniakì mègejoc, parsèk, ètoc fwtìc O parathrht c tou Sq matoc 1.1 parathreð
Παράγοντες που επηρεάζουν την οδική ασφάλεια των εργαζομένων δικυκλιστών
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Μηχανολόγων Μηχανικών Μονάδα Εργονομίας Παράγοντες που επηρεάζουν την οδική ασφάλεια των εργαζομένων δικυκλιστών Ναθαναήλ Δημήτρης, Επικ. Καθηγητής Το παρόν υλικό αποτελεί
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Μηχανολόγων Μηχανικών Μονάδα Εργονομίας Παράγοντες που επηρεάζουν την οδική ασφάλεια των εργαζομένων δικυκλιστών Ναθαναήλ Δημήτρης, Επικ. Καθηγητής Το παρόν υλικό αποτελεί
A[0] = 0; /* To μηδέν δεν έχει διαιρέτες */ for (i=1; i<n; i++) { S=0; for (d=1; d<=i; d++) if (i % d == 0) S += d; A[i] = S; }
![A[0] = 0; /* To μηδέν δεν έχει διαιρέτες */ for (i=1; i<n; i++) { S=0; for (d=1; d<=i; d++) if (i % d == 0) S += d; A[i] = S; } A[0] = 0; /* To μηδέν δεν έχει διαιρέτες */ for (i=1; i<n; i++) { S=0; for (d=1; d<=i; d++) if (i % d == 0) S += d; A[i] = S; }](/thumbs/102/153319538.jpg) TEI Λάρισας / ΣΤΕΦ Τμ. Τεχνολογίας Πληροφορικής & Τηλεπικοινωνιών B Εξεταστική Περίοδος, 19 Φεβρουαρίου 2009 ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ι Ηλίας. Κ. Σάββας Α 1) Να γράψετε ένα πρόγραμμα το οποίο να γεμίζει ένα ακέραιο
TEI Λάρισας / ΣΤΕΦ Τμ. Τεχνολογίας Πληροφορικής & Τηλεπικοινωνιών B Εξεταστική Περίοδος, 19 Φεβρουαρίου 2009 ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ι Ηλίας. Κ. Σάββας Α 1) Να γράψετε ένα πρόγραμμα το οποίο να γεμίζει ένα ακέραιο
2. ΕΝΤΟΛΕΣ ΕΛΕΓΧΟΥ (Α' μέρος: if)
 2. ΕΝΤΟΛΕΣ ΕΛΕΓΧΟΥ (Α' μέρος: if) 2.1. Τελεστές ΠΡΑΞΗ ΤΕΛΕΣΤΗΣ Ισότητα = = Μεγαλύτερο από > Μικρότερο από < Μεγαλύτερο ή ίσο από >= Μικρότερο ή ίσο από
2. ΕΝΤΟΛΕΣ ΕΛΕΓΧΟΥ (Α' μέρος: if) 2.1. Τελεστές ΠΡΑΞΗ ΤΕΛΕΣΤΗΣ Ισότητα = = Μεγαλύτερο από > Μικρότερο από < Μεγαλύτερο ή ίσο από >= Μικρότερο ή ίσο από
ΜΗΧΑΝΙΚΗ ΟΡΑΣΗ. 3η ΕΡΓΑΣΙΑ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΡΗΤΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΡΗΤΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΔΙΑΤΜΗΜΑΤΙΚΟ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΠΡΟΗΓΜΕΝΑ ΣΥΣΤΗΜΑΤΑ ΠΑΡΑΓΩΓΗΣ ΑΥΤΟΜΑΤΙΣΜΟΥ & ΡΟΜΠΟΤΙΚΗΣ 01 ΜΗΧΑΝΙΚΗ ΟΡΑΣΗ 3η ΕΡΓΑΣΙΑ ΣΠΟΥΔΑΣΤΕΣ:
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΡΗΤΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΔΙΑΤΜΗΜΑΤΙΚΟ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΠΡΟΗΓΜΕΝΑ ΣΥΣΤΗΜΑΤΑ ΠΑΡΑΓΩΓΗΣ ΑΥΤΟΜΑΤΙΣΜΟΥ & ΡΟΜΠΟΤΙΚΗΣ 01 ΜΗΧΑΝΙΚΗ ΟΡΑΣΗ 3η ΕΡΓΑΣΙΑ ΣΠΟΥΔΑΣΤΕΣ:
Διγραφία και Greeklish
 Εισαγωγή στην Κοινωνιογλωσσολογία Πανεπιστήμιο Αθηνών Τμήμα Επικοινωνίας και ΜΜΕ Σπύρος Α. Μοσχονάς Διγραφία και Greeklish 14/3/2012 1 Ορισμός» Greeklish είναι η παράσταση της ελληνικής γραφής με λατινικά
Εισαγωγή στην Κοινωνιογλωσσολογία Πανεπιστήμιο Αθηνών Τμήμα Επικοινωνίας και ΜΜΕ Σπύρος Α. Μοσχονάς Διγραφία και Greeklish 14/3/2012 1 Ορισμός» Greeklish είναι η παράσταση της ελληνικής γραφής με λατινικά
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Μηχανική Μάθηση. Ενότητα 10: Θεωρία Βελτιστοποίησης. Ιωάννης Τσαμαρδίνος Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Ενότητα 10: Θεωρία Βελτιστοποίησης Ιωάννης Τσαμαρδίνος Τμήμα Επιστήμης Υπολογιστών To genikì prìblhma, na broôme to mègisto elˆqisto miac sunˆrthshc
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Ενότητα 10: Θεωρία Βελτιστοποίησης Ιωάννης Τσαμαρδίνος Τμήμα Επιστήμης Υπολογιστών To genikì prìblhma, na broôme to mègisto elˆqisto miac sunˆrthshc
Αποτελέσματα. ΜΟΔΙΠ Πανεπιστημίου Κρήτης Ερωτηματολόγιο 533569 'Γλώσσα Προγραμματισμού ΙΙ' Ερωτηματολόγιο 533569
 Αποτελέσματα Ερωτηματολόγιο 533569 Σύνολο εγγραφών σε αυτό το ερώτημα: 9 Σύνολο εγγραφών στο ερωτηματολόγιο: 9 Ποσοστό συνόλου: 100.00% σελίδα 1 / 49 Ομάδα: Ερωτηματολόγιο Ερώτηση: S0. Θέλετε να συμπληρώσετε
Αποτελέσματα Ερωτηματολόγιο 533569 Σύνολο εγγραφών σε αυτό το ερώτημα: 9 Σύνολο εγγραφών στο ερωτηματολόγιο: 9 Ποσοστό συνόλου: 100.00% σελίδα 1 / 49 Ομάδα: Ερωτηματολόγιο Ερώτηση: S0. Θέλετε να συμπληρώσετε
ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ. (Σηµειώσεις) Γ. Βουγιατζής Λέκτορας του τµήµατος Φυσικής, Α.Π.Θ.
 ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ στο MATHEMATICA 4. (Σηµειώσεις).5.5 - - -.5 - -.5 Γ. Βουγιατζής Λέκτορας του τµήµατος Φυσικής, Α.Π.Θ. Με την Ενίσχυση του Προγράµµατος ΕΠΕΑΕΚ ΙΙ : «Εισαγωγή εξιοτήτων Πληροφορικής και
ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ στο MATHEMATICA 4. (Σηµειώσεις).5.5 - - -.5 - -.5 Γ. Βουγιατζής Λέκτορας του τµήµατος Φυσικής, Α.Π.Θ. Με την Ενίσχυση του Προγράµµατος ΕΠΕΑΕΚ ΙΙ : «Εισαγωγή εξιοτήτων Πληροφορικής και
Τεχνογλωσσία 8 Β' Εξάμηνο. Λογικός Προγραμματισμός Prolog. Άσκηση: Διορθωτής Εκφράσεων
 Τεχνογλωσσία 8 Β' Εξάμηνο Λογικός Προγραμματισμός Prolog Άσκηση: Διορθωτής Εκφράσεων Σκοπός της άσκησης είναι ο σχεδιασμός και η υλοποίηση συστήματος διορθωτή εκφράσεων βασισμένη στο φορμαλισμό της prolog
Τεχνογλωσσία 8 Β' Εξάμηνο Λογικός Προγραμματισμός Prolog Άσκηση: Διορθωτής Εκφράσεων Σκοπός της άσκησης είναι ο σχεδιασμός και η υλοποίηση συστήματος διορθωτή εκφράσεων βασισμένη στο φορμαλισμό της prolog
05/2012. Mod: D115-EK(230_3) Production code: GL80(230V/3)
 05/2012 Mod: D115-EK(230_3) Production code: GL80(230V/3) GR σελ. 1 ΠΙΝΑΚΑΣ ΚΕΦ.1 ΕΙΣΑΓΩΓΉ... 3 1.1 ΕΠΙΚΙΝ ΥΝΕΣ ΠΕΡΙΟΧΕΣ... 3 ΚΕΦ.2 ΕΓΚΑΤΆΣΤΑΣΗ... 4 2.1 ΜΕΤΑΚΙΝΗΣΗ ΚΑΙ ΑΠΟΣΥΣΚΕΥΑΣΙΑ... 4 2.2 ΗΛΕΚΤΡΙΚΗ
05/2012 Mod: D115-EK(230_3) Production code: GL80(230V/3) GR σελ. 1 ΠΙΝΑΚΑΣ ΚΕΦ.1 ΕΙΣΑΓΩΓΉ... 3 1.1 ΕΠΙΚΙΝ ΥΝΕΣ ΠΕΡΙΟΧΕΣ... 3 ΚΕΦ.2 ΕΓΚΑΤΆΣΤΑΣΗ... 4 2.1 ΜΕΤΑΚΙΝΗΣΗ ΚΑΙ ΑΠΟΣΥΣΚΕΥΑΣΙΑ... 4 2.2 ΗΛΕΚΤΡΙΚΗ
Η ΕΕΧ στα MME. Επιστολή προς τον Πρωθυπουργό για τη χρήση δακρυγόνων. 22 Ιανουαρίου Επιμέλεια: Δρ Σπύρος Κιτσινέλης Υπεύθυνος Επικοινωνίας ΕΕΧ
 Η ΕΕΧ στα MME Επιστολή προς τον Πρωθυπουργό για τη χρήση δακρυγόνων Επιμέλεια: Δρ Σπύρος Κιτσινέλης Υπεύθυνος Επικοινωνίας ΕΕΧ 22 Ιανουαρίου 2019 Επιστολή της Ένωσης Ελλήνων Χημικών προς τον Αλέξη Τσίπρα
Η ΕΕΧ στα MME Επιστολή προς τον Πρωθυπουργό για τη χρήση δακρυγόνων Επιμέλεια: Δρ Σπύρος Κιτσινέλης Υπεύθυνος Επικοινωνίας ΕΕΧ 22 Ιανουαρίου 2019 Επιστολή της Ένωσης Ελλήνων Χημικών προς τον Αλέξη Τσίπρα
ΜΕΛΕΤΗ Σ.Α.Ε. µε χρήση του CONTROL SYSTEM TOOLBOX του MATLAB
 Σ.Ν.. ΕΡΓΑΣΤΗΡΙΑ ΗΛΕΚΤΡΟΤΕΧΝΙΑΣ ο Έτος ΘΕΩΡΙΑ ΚΥΚΛΩΜΑΤΩΝ ΙΙ ΜΕΛΕΤΗ Σ.Α.Ε. µε χρήση του CONTROL SYSTEM TOOLBOX του MATLAB - Σύντοµη εισαγωγή στο Control System Toolbox - Παρουσίαση Εφαρµογών ( συνοδεύεται
Σ.Ν.. ΕΡΓΑΣΤΗΡΙΑ ΗΛΕΚΤΡΟΤΕΧΝΙΑΣ ο Έτος ΘΕΩΡΙΑ ΚΥΚΛΩΜΑΤΩΝ ΙΙ ΜΕΛΕΤΗ Σ.Α.Ε. µε χρήση του CONTROL SYSTEM TOOLBOX του MATLAB - Σύντοµη εισαγωγή στο Control System Toolbox - Παρουσίαση Εφαρµογών ( συνοδεύεται
Δομημένος Προγραμματισμός
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Δομημένος Προγραμματισμός Ενότητα: Συναρτήσεις - προγράμματα - Μέρος Β Δ. Ε. Μετάφας Τμ. Ηλεκτρονικών Μηχ. Τ.Ε. Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Δομημένος Προγραμματισμός Ενότητα: Συναρτήσεις - προγράμματα - Μέρος Β Δ. Ε. Μετάφας Τμ. Ηλεκτρονικών Μηχ. Τ.Ε. Άδειες Χρήσης
- 1 2π. - z2 2. ii = True
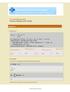 1η Γραπτή Εργασία Νικόλαος Μανάρας (Α.Μ. 52209) Άσκηση 1η ü Ερώτηµα (α) f@z_d:= 1 2π 1 2 z2 p =Table@8n, D@f@zD, 8z, n
1η Γραπτή Εργασία Νικόλαος Μανάρας (Α.Μ. 52209) Άσκηση 1η ü Ερώτηµα (α) f@z_d:= 1 2π 1 2 z2 p =Table@8n, D@f@zD, 8z, n
ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s
 P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t
P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t
88x Ø 0, y Ø 0<, 8x Ø 0, y Ø 32<, 8x Ø 12, y Ø 8<, 8x Ø 28, y Ø 0<<
 2η Γραπτή Εργασία Νικόλαος Μανάρας (Α.Μ. 52209). Άσκηση 7, σελ. 8 "Mathematica & Εφαρµογές" Στ. Τραχανά ü Ποιοτική µελέτη δυναµικού συστήµατος. Περίπτωση της "επικράτησης του ισχυρότερου". Να γίνει ποιοτική
2η Γραπτή Εργασία Νικόλαος Μανάρας (Α.Μ. 52209). Άσκηση 7, σελ. 8 "Mathematica & Εφαρµογές" Στ. Τραχανά ü Ποιοτική µελέτη δυναµικού συστήµατος. Περίπτωση της "επικράτησης του ισχυρότερου". Να γίνει ποιοτική
ΣΥΣΧΕΤΙΣΕΙΣ ΚΛΑΣΕΩΝ (Class relationships)
 ΣΥΣΧΕΤΙΣΕΙΣ ΚΛΑΣΕΩΝ (Class relationships) Σκοπός Σκοπός των συσχετίσεων είναι να αναπαριστούν την αλληλεπίδραση μεταξύ των κλάσεων και των αντικειμένων. Απεικονίζονται διαγραμματικά με μία γραμμή μεταξύ
ΣΥΣΧΕΤΙΣΕΙΣ ΚΛΑΣΕΩΝ (Class relationships) Σκοπός Σκοπός των συσχετίσεων είναι να αναπαριστούν την αλληλεπίδραση μεταξύ των κλάσεων και των αντικειμένων. Απεικονίζονται διαγραμματικά με μία γραμμή μεταξύ
22o YNE PIO I O O IA 22nd INTERNATIONAL CONFERENCE OF PHILOSOPHY
 IE NH ETAIPEIA E HNIKH I O O IA 5, 17456 - TEL: +30210 9956955, +30210 7277545, +30210 7277548 FAX: +30210 9923281, +30210 7248979 website: http://www.hri.org/iagp/, http://www.iagp.gr E-mail: kboud714@ppp.uoa.gr
IE NH ETAIPEIA E HNIKH I O O IA 5, 17456 - TEL: +30210 9956955, +30210 7277545, +30210 7277548 FAX: +30210 9923281, +30210 7248979 website: http://www.hri.org/iagp/, http://www.iagp.gr E-mail: kboud714@ppp.uoa.gr
Ergasthriak 'Askhsh 2
 Kefˆlaio 2 Ergasthriak 'Askhsh 2 Οπου θα δούμε πώς μπορούμε να ορίζουμε δικές μας διαδικασίες και θα παρουσιάσουμε τις primitive διαδικασίες χειρισμού λιστών, τις μεταβλητές και τα side effects. 2.1 P
Kefˆlaio 2 Ergasthriak 'Askhsh 2 Οπου θα δούμε πώς μπορούμε να ορίζουμε δικές μας διαδικασίες και θα παρουσιάσουμε τις primitive διαδικασίες χειρισμού λιστών, τις μεταβλητές και τα side effects. 2.1 P
Τα προγράμματα αυτά σήμερα είναι τα εξής:
 Η Επιτροπη Ευρωπαικών Προγραμμάτων του Πανεπιστημίου Νεάπολις (ΕΠΝ) αποτελείται από Ερευνητές, Συμβούλους, Νομικό Σύμβουλο, Ακαδημαϊκούς και Διοικητικούς, των οποίων ο κύριος στόχος είναι να εντοπίσουν,
Η Επιτροπη Ευρωπαικών Προγραμμάτων του Πανεπιστημίου Νεάπολις (ΕΠΝ) αποτελείται από Ερευνητές, Συμβούλους, Νομικό Σύμβουλο, Ακαδημαϊκούς και Διοικητικούς, των οποίων ο κύριος στόχος είναι να εντοπίσουν,
ΔΙΚΤΥΑ ΕΠΙΚΟΙΝΩΝΙΩΝ Εργαστηριακή Άσκηση 6 Δρομολόγηση Διανύσματος Αποστάσεων
 ΔΙΚΤΥΑ ΕΠΙΚΟΙΝΩΝΙΩΝ Εργαστηριακή Άσκηση 6 Δρομολόγηση Διανύσματος Αποστάσεων Σε αυτή την άσκηση θα μελετηθεί η επίδοση του πρωτοκόλλου δρομολόγησης διανύσματος αποστάσεων (distance vector, DV). Η λειτουργία
ΔΙΚΤΥΑ ΕΠΙΚΟΙΝΩΝΙΩΝ Εργαστηριακή Άσκηση 6 Δρομολόγηση Διανύσματος Αποστάσεων Σε αυτή την άσκηση θα μελετηθεί η επίδοση του πρωτοκόλλου δρομολόγησης διανύσματος αποστάσεων (distance vector, DV). Η λειτουργία
GENIKEUMENA OLOKLHRWMATA
 PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA I GENIKEUMENA OLOKLHRWMATA Anplhrwt c Kjhght c: Dr. Pppˆc G. Alèndroc GENIKEUMENA OLOKLHRWMATA H ènnoi tou orismènou
PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA I GENIKEUMENA OLOKLHRWMATA Anplhrwt c Kjhght c: Dr. Pppˆc G. Alèndroc GENIKEUMENA OLOKLHRWMATA H ènnoi tou orismènou
24o YNE PIO I O O IA 24th INTERNATIONAL CONFERENCE OF PHILOSOPHY
 IE NH ETAIPEIA E HNIKH I O O IA 5, 17456 - H H YMMETOXH N 1 (N μ 29/02/2012 ) (.,,,,.): KATOIKIA : TH E NO TH E NO KATOIKIA : KINHTO TH E NO: NA META X TO : μ YNE PO AKPOATH KAI YNE PO PO O OY YNO EYEI
IE NH ETAIPEIA E HNIKH I O O IA 5, 17456 - H H YMMETOXH N 1 (N μ 29/02/2012 ) (.,,,,.): KATOIKIA : TH E NO TH E NO KATOIKIA : KINHTO TH E NO: NA META X TO : μ YNE PO AKPOATH KAI YNE PO PO O OY YNO EYEI
Εισαγωγή στο Mathematica
 Εισαγωγή στο Mathematica Author: Michalis Xenos Revision. - Greece, 7// Τι είναι το MATHΕMAΤΙCA Το ΜΑΤΗΕΜATICA είναι ένα πακέτο συμβολικής άλγεβρας, δηλαδή ένα πρόγραμμα που μπορεί να κάνει αλγεβρικές
Εισαγωγή στο Mathematica Author: Michalis Xenos Revision. - Greece, 7// Τι είναι το MATHΕMAΤΙCA Το ΜΑΤΗΕΜATICA είναι ένα πακέτο συμβολικής άλγεβρας, δηλαδή ένα πρόγραμμα που μπορεί να κάνει αλγεβρικές
5 η ΕΝΟΤΗΤΑ Γραφήματα στο MATLAB
 ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΜΠ ΜΕΘΟΔΟΙ ΕΠΙΛΥΣΗΣ ΜΕ Η/Υ 5 η ΕΝΟΤΗΤΑ Γραφήματα στο MATLAB Ν.Δ. Λαγαρός Μ. Φραγκιαδάκης Α. Στάμος Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες Χρήσης Creative
ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΜΠ ΜΕΘΟΔΟΙ ΕΠΙΛΥΣΗΣ ΜΕ Η/Υ 5 η ΕΝΟΤΗΤΑ Γραφήματα στο MATLAB Ν.Δ. Λαγαρός Μ. Φραγκιαδάκης Α. Στάμος Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες Χρήσης Creative
Fortran και Αντικειµενοστραφής προγραµµατισµός.
 Fortran και Αντικειµενοστραφής προγραµµατισµός www.corelab.ntua.gr/courses/fortran_naval/naval δάσκοντες: ΆρηςΠαγουρτζής (pagour@cs.ntua.gr) (Επίκουρος Καθηγητής ΣΗΜΜΥ ) ώρασούλιου (dsouliou@mail.ntua.gr)
Fortran και Αντικειµενοστραφής προγραµµατισµός www.corelab.ntua.gr/courses/fortran_naval/naval δάσκοντες: ΆρηςΠαγουρτζής (pagour@cs.ntua.gr) (Επίκουρος Καθηγητής ΣΗΜΜΥ ) ώρασούλιου (dsouliou@mail.ntua.gr)
ΟΔΗΓΙΑ 92/50/ΕΟΚ ΤΟΥ ΣΥΜΒΟΥΛΙΟΥ της 18ης Ιουνίου 1992 για το συντονισμό των διαδικασιών σύναψης δημόσιων συμβάσεων υπηρεσιών
 ΟΔΗΓΙΑ 92/50/ΕΟΚ ΤΟΥ ΣΥΜΒΟΥΛΙΟΥ της 18ης Ιουνίου 1992 για το συντονισμό των διαδικασιών σύναψης δημόσιων συμβάσεων υπηρεσιών ΤΟ ΣΥΜΒΟΥΛΙΟ ΤΩΝ ΕΥΡΩΠΑΪΚΩΝ ΚΟΙΝΟΤΗΤΩΝ, Έχοντας υπόψη: τη συνθήκη για την ίδρυση
ΟΔΗΓΙΑ 92/50/ΕΟΚ ΤΟΥ ΣΥΜΒΟΥΛΙΟΥ της 18ης Ιουνίου 1992 για το συντονισμό των διαδικασιών σύναψης δημόσιων συμβάσεων υπηρεσιών ΤΟ ΣΥΜΒΟΥΛΙΟ ΤΩΝ ΕΥΡΩΠΑΪΚΩΝ ΚΟΙΝΟΤΗΤΩΝ, Έχοντας υπόψη: τη συνθήκη για την ίδρυση
