Statistik gia QhmikoÔc MhqanikoÔc EKTIMHSH PARA
|
|
|
- Βηθζαθά Κόρακας
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Statistik gia QhmikoÔc MhqanikoÔc EKTIMHSH PARAMETRWN Maòou 200
2 t.m. X me mèsh tim µ t.m. X 2 me mèsh tim µ 2 Diaforˆ µ µ 2? [X kai X 2 anexˆrthtec] DeÐgma {x, x 2,..., x n } x DeÐgma {x 2, x 22,..., x 2n2 } x 2 Ektim tria thc µ µ 2 : x x 2 Katanom thc x x 2? [όπως για x] Gnwstèc diasporèc σ 2 kai σ2 2 Upojètoume ( X N(µ, σ 2 ) X 2 N(µ 2, σ 2 2 )) ( >30 >30) ( x x 2 N µ µ 2, ) σ 2 An σ 2 = σ2 2 = σ2 (omoskedastikèc katanomèc) diasporˆ: σ 2 ( + )
3 D.e. thc µ µ 2, gnwstˆ σ 2 kai σ2 2 H diadikasða eðnai ìpwc gia d.e. thc µ: µ µ µ 2 ektim tria x x x 2 mèsh tim thc µ µ µ 2 σ diasporˆ thc n σ2 σ d.e. x ±z σ 2 α/2 n ( x x 2 ) ±z α/2 DiadikasÐa ektðmhshc d.e. thc µ µ 2 Epilog tou α, σ, σ 2 gnwstˆ, x x 2 apì to deðgma. 2 EÔresh krðsimhc tim c z α/2 apì ton pðnaka gia tupik kanonik katanom. 3 Antikatˆstash [ ston tôpo ] σ 2 x x 2 z α/2 σ 2, x x 2 + z α/2
4 Parˆdeigma: Por dec hlðou tou gaiˆnjraka tôpoc A tôpoc B A/A x i xi 2 x 2i x2i SÔnolo
5 Parˆdeigma (sunèqeia) DÐnetai ìti h diasporˆ eðnai koin kai gnwst σ 2 = 0.38 Zhtˆme d.e. gia µ µ 2 Katanom thc x x 2? kai eðnai mikrˆ 6 Iστoγραμμα πoρωδoυς ηλιoυ για κoιτασμα A 6 Iστoγραμμα pioρωδoυς ηλιoυ για κoιτασμα B 7 Θηκoγραμμα πoρωδoυς ηλιoυ για τα 2 κoιτασματα συχνoτητα 4 3 συχνoτητα ευρoς ευρoς A B X N(µ, 0.38) kai X 2 N(µ 2, 0.38)
6 Parˆdeigma (sunèqeia) x = 5.67, x 2 = 5.38 x x 2 = 0.29 DiadikasÐa ektðmhshc tou d.e. thc µ µ 2 α = 0.95, σ = 0.38, x x 2 = KrÐsimh tim : z = Φ (0.975) =.96. σ 2 3 ( x x 2 ) ± z α/ ± ( ) [ 0.073, 0.653] = Sumperˆsmata Se epðpedo empistosônhc 95% de mporoôme na poôme pwc to por dec hlðou diafèrei shmantikˆ stouc gaiˆnjrakec apì ta dôo koitˆsmata. To diˆsthma [ 0.073, 0.653] eðnai sqedìn jetikì allˆ de dðnei statistikˆ shmantik diaforˆ = aôxhsh twn,.
7 'Agnwstec diasporèc σ 2 kai σ2 2 PerÐptwsh : megˆla deðgmata (, > 30) s 2 σ 2 kai s 2 2 σ 2 2 : x x 2 z α/2 s 2 + s2 2, x x 2 + z α/2 s 2 + s2 2
8 'Agnwstec diasporèc σ 2 kai σ2 2 (sunèqeia) PerÐptwsh 2: mikrˆ deðgmata ( < 30) kai X N(µ, σ 2 ) X 2 N(µ 2, σ 2 ) kai omoskedastikèc katanomèc: σ 2 = σ2 2 = σ2 UpologÐzoume pr ta thn ektðmhsh thc koin c diasporˆc s 2 = ( )s 2 + ( )s s 2 eðnai amerìlhpth ektim tria thc koin c diasporˆc σ 2 Ektim tria diasporˆc thc µ µ 2 : s 2 ( + ) t ( x x 2 ) (µ µ 2 ) t n + 2 s + ( α)% d.e.: ( x x 2 ) ± t n + 2, α/2 s + n n2
9 'Agnwstec diasporèc σ 2 kai σ2 2 (sunèqeia) DiadikasÐa ektðmhshc d.e. thc µ µ 2 Epilog tou α, s kai x x 2 apì to deðgma. 2 EÔresh krðsimhc tim c t n + 2, α/2 apì ton pðnaka gia katanom student. 3 Antikatˆstash ston tôpo ( x x 2 ) ± t n + 2, α/2 s + n n2 PerÐptwsh 3: mikrˆ deðgmata ( < 30) kai σ 2 = σ2 2 = σ2 kai (X N(µ, σ 2 ) X 2 N(µ 2, σ 2 )) Mh-parametrik mèjodoc PerÐptwsh 4: mikrˆ deðgmata ( < 30) kai σ 2 σ2 2 Den upˆrqei gnwst mèjodoc ektðmhshc d.e. (qrhsimopoioôntai teqnikèc epanadeigmatolhyðac)
10 Parˆdeigma:por dec hlðou gaiˆnjraka, dôo koitˆsmata Oi diasporèc tou por dec hlðou stouc gaiˆnjrakec apì ta koitˆsmata A kai B eðnai ˆgnwstec Mikrˆ deðgmata ( = 25, = 20) kai katanomèc twn X, X 2 kanonikèc [ιστογράμματα, θηκογράμματα] x x 2 = 0.29 s 2 = s2 2 = s 2 s2 2 σ 2 = σ2 2 = σ2 s 2 = = s = DiadikasÐa ektðmhshc tou d.e. thc µ µ 2 α = 0.95, x x 2 = 0.29, s = KrÐsimh tim : t 43,0.975 = ( x x 2 ) ± t n + 2, α/2 s n + n = ± [ 0.07, 0.65] To mèso por dec hlðou gaianjrˆkwn de diafèrei shmantikˆ sta dôo koitˆsmata
11 EktÐmhsh diast matoc empistosônhc thc µ µ 2 diasporèc katanom, katanom thc x x 2 diˆsthma empistosônhc twn X,X 2 twn X,X 2 gnwstèc kanonik z ( x x 2 ) (µ µ 2 ) σ 2 gnwstèc mh kanonik megˆla z ( x x 2 ) (µ µ 2 ) σ 2 N(0, ) ( x x 2 ) ± z α/2 σ 2 N(0, ) ( x x 2 ) ± z α/2 σ 2 gnwstèc mh kanonik mikrˆ ˆgnwstec ˆnisec/Ðsec ˆgnwstec Ðsec ˆgnwstec Ðsec ˆgnwstec ˆnisec megˆla z ( x x 2 ) (µ µ 2 ) s 2 + s2 2 n2 kanonik mikrˆ t ( x x 2 ) (µ µ 2 ) N(0, ) ( x x 2 ) ± z α/2 s 2 + s2 2 n2 s n + t n + 2 ( x x 2 ) ± t n + 2, α/2 s mh kanonik mikrˆ mikrˆ n +
12 p : AnalogÐa stoiqeðwn me mia idiìthta ston èna plhjusmì p 2 : AnalogÐa stoiqeðwn me mia idiìthta ston ˆllo plhjusmì Diaforˆ p p 2? DeÐgma : mègejoc kai m epituqðec ˆp = m DeÐgma 2: mègejoc kai m 2 epituqðec ˆp 2 = m 2 Ektim tria thc p p 2 : ˆp ˆp 2 DÐnetai ìti gia megˆla kai ( p ( p ) ˆp ˆp 2 N p p 2, + p ) 2( p 2 ) z (ˆp ˆp 2 ) (p p 2 ) N(0, ) p ( p ) + p 2( p 2 ) kai antikajistoôme p ˆp p 2 ˆp 2
13 Diˆsthma empistosônhc thc p p 2 (sunèqeia) ( α)% d.e. thc p p 2 (ˆp ˆp 2 ) ± z α/2 ˆp ( ˆp ) + ˆp 2( ˆp 2 ). Enallaktikˆ me qr sh koin c analogðac ˆp = ˆp +ˆp 2 +n : 2 σ 2ˆp ˆp 2 = ˆp( ˆp)( + ( ) (ˆp ˆp 2 ) ± z n α/2 ˆp( ˆp) + ) 2 DiadikasÐa ektðmhshc d.e. thc p p 2 Epilog tou α, ˆp, ˆp 2 apì to deðgma. 2 EÔresh krðsimhc tim c z α/2 apì ton pðnaka gia tupik kanonik katanom. 3 Antikatˆstash ston tôpo (ˆp ˆp 2 ) ± z α/2 ˆp ( ˆp ) + ˆp 2( ˆp 2 )
14 Parˆdeigma EKTIMHSH PARAMETRWN - 2 Diaforˆ sto posostì skouriasmènwn rabd n qˆluba se dôo apoj kec? Apoj kh A: m = 2 stic = 00 eðnai skouriasmènec Apoj kh B: m 2 = 26 stic = 20 eðnai skouriasmènec ˆp = 2 00 = 0.2 ˆp 2 = = 0.27 DiadikasÐa ektðmhshc tou d.e. thc p p 2 α = 0.95, ˆp ˆp 2 = = KrÐsimh tim : z =.96 3 (ˆp ˆp 2 ) ± z ˆp ( ˆp ) α/2 + ˆp 2( ˆp 2 ) = ± [ 0.98, 0.004] An kai h diaforˆ tou posostoô skouriasmènwn rabd n sto ergostˆsio B eðnai katˆ perðpou 0% megalôterh, se epðpedo empistosônhc 95% den eðnai statistikˆ shmantik.
15 'Askhsh EKTIMHSH PARAMETRWN - 2 Εγιναν μετρήσεις της συγκέντρωσης διαλυμένου οξυγόνου (Δ.Ο.) σε δύο ποτάμια (σε mg/l) Βρείτε 95% διάστημα εμπιστοσύνης για τη διαφορά των μέσων συγκεντρώσεων Δ.Ο. στα δύο ποτάμια υποθέτοντας πρώτα ότι η διασπορά είναι γνωστή (0. (mg/l) 2 ) και ίδια για τα δύο δείγματα και μετά χρησιμοποιώντας τις εκτιμήσεις των διασπορών από τα δείγματα. Μπορούμε να πούμε πως η μέση συγκέντρωση Δ.Ο. είναι ίδια στα δύο ποτάμια (στην κάθε περίπτωση); 2 Για το ίδιο πρόβλημα, σε 200 μετρήσεις στο πρώτο ποτάμι βρέθηκαν 26 τιμές κάτω από την κρίσιμη τιμή.6 mg/l και σε 200 μετρήσεις στο δεύτερο ποτάμι βρέθηκαν 8 τιμές κάτω από την κρίσιμη τιμή. Μπορούμε να πούμε σε επίπεδο 95% ότι η συγκέντρωση Δ.Ο. βρίσκεται σε μη επιθυμητά επίπεδα πιό συχνά στο πρώτο ποτάμι από ότι στο δεύτερο;
Statistik gia PolitikoÔc MhqanikoÔc EKTIMHSH PAR
 Statistik gia PolitikoÔc MhqanikoÔc EKTIMHSH PARAMETRWN - 2 8 DekembrÐou 202 t.m. X me mèsh tim µ t.m. X 2 me mèsh tim µ 2 Diaforˆ µ µ 2? [X kai X 2 anexˆrthtec] DeÐgma {x, x 2,..., x n } x DeÐgma {x 2,
Statistik gia PolitikoÔc MhqanikoÔc EKTIMHSH PARAMETRWN - 2 8 DekembrÐou 202 t.m. X me mèsh tim µ t.m. X 2 me mèsh tim µ 2 Diaforˆ µ µ 2? [X kai X 2 anexˆrthtec] DeÐgma {x, x 2,..., x n } x DeÐgma {x 2,
Diˆsthma empistosônhc thc mèshc tim c µ. Statistik gia Hlektrolìgouc MhqanikoÔc EKTIMHSH EKTIMHSH PARAMETRWN - 2. Dhm trhc Kougioumtz c.
 Statistik gia Hlektrolìgouc MhqanikoÔc EKTIMHSH PARAMETRWN - 2 6 Maòou 2010 EktÐmhsh Diast matoc empistosônhc Melet same thn ektim tria ˆθ paramètrou θ: An gnwrðzoume thn katanom thc X kai eðnai F X (x;
Statistik gia Hlektrolìgouc MhqanikoÔc EKTIMHSH PARAMETRWN - 2 6 Maòou 2010 EktÐmhsh Diast matoc empistosônhc Melet same thn ektim tria ˆθ paramètrou θ: An gnwrðzoume thn katanom thc X kai eðnai F X (x;
Θεωρία Πιθανοτήτων και Στατιστική
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεωρία Πιθανοτήτων και Στατιστική Ενότητα 2: Εκτίμηση Παραμέτρων Κουγιουμτζής Δημήτρης Τμήμα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεωρία Πιθανοτήτων και Στατιστική Ενότητα 2: Εκτίμηση Παραμέτρων Κουγιουμτζής Δημήτρης Τμήμα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών
Statistik gia PolitikoÔc MhqanikoÔc ELEGQOS UPOJ
 Statistik gia PolitikoÔc MhqanikoÔc ELEGQOS UPOJESEWN 18 DekembrÐou 2012 'Elegqoc Upojèsewn 1 Statistik upìjesh 2 Statistik elègqou kai perioq apìrriyhc 3 Apìfash elègqou Statistik upìjesh mhdenik upìjesh
Statistik gia PolitikoÔc MhqanikoÔc ELEGQOS UPOJESEWN 18 DekembrÐou 2012 'Elegqoc Upojèsewn 1 Statistik upìjesh 2 Statistik elègqou kai perioq apìrriyhc 3 Apìfash elègqou Statistik upìjesh mhdenik upìjesh
Statistik gia QhmikoÔc MhqanikoÔc EKTIMHSH PARA
 Statistik gia QhmikoÔc MhqanikoÔc EKTIMHSH PARAMETRWN - 1 12 AprilÐou 2013 Eisagwgikˆ sthn ektðmhsh paramètrwn t.m. X me katanom F X (x; θ) Parˆmetroc θ: ˆgnwsth θ µ, σ 2, p DeÐgma {x 1,..., x n }: gnwstì
Statistik gia QhmikoÔc MhqanikoÔc EKTIMHSH PARAMETRWN - 1 12 AprilÐou 2013 Eisagwgikˆ sthn ektðmhsh paramètrwn t.m. X me katanom F X (x; θ) Parˆmetroc θ: ˆgnwsth θ µ, σ 2, p DeÐgma {x 1,..., x n }: gnwstì
Στατιστική για Χημικούς Μηχανικούς
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Στατιστική για Χημικούς Μηχανικούς Ενότητα 3: Έλεγχος Υποθέσεων Κουγιουμτζής Δημήτρης Τμήμα Χημικών Μηχανικών Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Στατιστική για Χημικούς Μηχανικούς Ενότητα 3: Έλεγχος Υποθέσεων Κουγιουμτζής Δημήτρης Τμήμα Χημικών Μηχανικών Άδειες Χρήσης Το παρόν εκπαιδευτικό
Θεωρία Πιθανοτήτων και Στατιστική
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεωρία Πιθανοτήτων και Στατιστική Ενότητα 3: Συσχέτιση & Γραμμική Παλινδρόμηση Κουγιουμτζής Δημήτρης Τμήμα Ηλεκτρολόγων Μηχανικών & Μηχανικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεωρία Πιθανοτήτων και Στατιστική Ενότητα 3: Συσχέτιση & Γραμμική Παλινδρόμηση Κουγιουμτζής Δημήτρης Τμήμα Ηλεκτρολόγων Μηχανικών & Μηχανικών
Στατιστική για Χημικούς Μηχανικούς
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Στατιστική για Χημικούς Μηχανικούς Ενότητα 4: Συσχέτιση & Γραμμική Παλινδρόμηση Κουγιουμτζής Δημήτρης Τμήμα Χημικών Μηχανικών Άδειες Χρήσης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Στατιστική για Χημικούς Μηχανικούς Ενότητα 4: Συσχέτιση & Γραμμική Παλινδρόμηση Κουγιουμτζής Δημήτρης Τμήμα Χημικών Μηχανικών Άδειες Χρήσης
Εφαρμοσμένα Μαθηματικά για Μηχανικούς
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Εφαρμοσμένα Μαθηματικά για Μηχανικούς Σημειώσεις: Δειγματοληψία Γιώργος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών Kefˆlaio 5 DeigmatolhyÐa 'Estw èna sônolo periodikˆ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Εφαρμοσμένα Μαθηματικά για Μηχανικούς Σημειώσεις: Δειγματοληψία Γιώργος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών Kefˆlaio 5 DeigmatolhyÐa 'Estw èna sônolo periodikˆ
Τίτλος Μαθήματος: Γραμμική Άλγεβρα Ι
 Τίτλος Μαθήματος: Γραμμική Άλγεβρα Ι Ενότητα: Θέματα Εξετάσεων Όνομα Καθηγητή : Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Τίτλος Μαθήματος: Γραμμική Άλγεβρα Ι Ενότητα: Θέματα Εξετάσεων Όνομα Καθηγητή : Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II DIAFORIKES EXISWSEIS DEUTERHS KAI ANWTERHS TAXHS
 PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II DIAFORIKES EXISWSEIS DEUTERHS KAI ANWTERHS TAXHS 1. Grammikèc diaforikèc exis seic deôterhc kai an terhc tˆxhc
PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II DIAFORIKES EXISWSEIS DEUTERHS KAI ANWTERHS TAXHS 1. Grammikèc diaforikèc exis seic deôterhc kai an terhc tˆxhc
11 OktwbrÐou 2012. S. Malefˆkh Genikì Tm ma Majhmatikˆ gia QhmikoÔc
 Mˆjhma 7 0 11 OktwbrÐou 2012 Orismìc sunart sewn mèsw orismènwn oloklhrwmˆtwn To orismèno olokl rwma prosfèrei ènan nèo trìpo orismoô sunˆrthshc afoô to orismèno olokl rwma mia suneqoôc sunˆrthshc f (t),
Mˆjhma 7 0 11 OktwbrÐou 2012 Orismìc sunart sewn mèsw orismènwn oloklhrwmˆtwn To orismèno olokl rwma prosfèrei ènan nèo trìpo orismoô sunˆrthshc afoô to orismèno olokl rwma mia suneqoôc sunˆrthshc f (t),
PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II DIAFORIKES EXISWSEIS.
 PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II DIAFORIKES EXISWSEIS 6h Seirˆ Ask sewn OmogeneÐc grammikèc diaforikèc exis seic me stajeroôc suntelestèc Jèma
PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II DIAFORIKES EXISWSEIS 6h Seirˆ Ask sewn OmogeneÐc grammikèc diaforikèc exis seic me stajeroôc suntelestèc Jèma
Στατιστική για Χημικούς Μηχανικούς
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Στατιστική για Χημικούς Μηχανικούς Ενότητα 1: Περιγραφική Στατιστική Κουγιουμτζής Δημήτρης Τμήμα Χημικών Μηχανικών Άδειες Χρήσης Το παρόν
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Στατιστική για Χημικούς Μηχανικούς Ενότητα 1: Περιγραφική Στατιστική Κουγιουμτζής Δημήτρης Τμήμα Χημικών Μηχανικών Άδειες Χρήσης Το παρόν
Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ
 Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ Ενότητα: Ο δυϊκός χώρος Όνομα Καθηγητή: Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ Ενότητα: Ο δυϊκός χώρος Όνομα Καθηγητή: Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
SUNARTHSEIS POLLWN METABLHTWN. 5h Seirˆ Ask sewn. Allag metablht n sto diplì olokl rwma
 PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II SUNARTHSEIS POLLWN METABLHTWN 5h Seirˆ Ask sewn Allag metablht n sto diplì olokl rwma Jèma. Qrhsimopoi ntac
PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II SUNARTHSEIS POLLWN METABLHTWN 5h Seirˆ Ask sewn Allag metablht n sto diplì olokl rwma Jèma. Qrhsimopoi ntac
ISTORIKH KATASKEUH PRAGMATIKWN ARIJMWN BIBLIOGRAFIA
 ΛΟΓΙΣΜΟΣ CALCULUS Διαφορικός Λογισμός, Απειροστικός Λογισμός 1670 1740 Ουράνια Μηχανική Isaac Newton 1648-1727 Gottfried Wilhelm Leibniz 1646-1716 απειροστάπολύ μικρά μεγέθη, άπειροπάρα πολύ μεγάλο, όριο
ΛΟΓΙΣΜΟΣ CALCULUS Διαφορικός Λογισμός, Απειροστικός Λογισμός 1670 1740 Ουράνια Μηχανική Isaac Newton 1648-1727 Gottfried Wilhelm Leibniz 1646-1716 απειροστάπολύ μικρά μεγέθη, άπειροπάρα πολύ μεγάλο, όριο
APEIROSTIKOS LOGISMOS I
 1 OktwbrÐou 2012 Kwdikìc Maj matoc: 101 (U) 'Etoc didaskalðac: 2012-2013, Qeimerinì Exˆmhno Hmèrec didaskalðac: Deut. - Tet. - Par., 11:00-13:00 Didˆskontec Tm ma 1 o (AM pou l gei se 0,1,2) Amf 21, BasÐleioc
1 OktwbrÐou 2012 Kwdikìc Maj matoc: 101 (U) 'Etoc didaskalðac: 2012-2013, Qeimerinì Exˆmhno Hmèrec didaskalðac: Deut. - Tet. - Par., 11:00-13:00 Didˆskontec Tm ma 1 o (AM pou l gei se 0,1,2) Amf 21, BasÐleioc
JEMATA EXETASEWN Pragmatik Anˆlush I
 JEMATA EXETASEWN Pragmatik Anˆlush I JEMA 1o. A)(M. 1.5) Na qarakthrðsete (me aitiolìghsh) tic protˆseic pou akoloujoôn me thn èndeixh Swstì Lˆjoc: (i) 'Estw x 0 tètoio ste x < ε, gia kˆje ε > 0. Tìte
JEMATA EXETASEWN Pragmatik Anˆlush I JEMA 1o. A)(M. 1.5) Na qarakthrðsete (me aitiolìghsh) tic protˆseic pou akoloujoôn me thn èndeixh Swstì Lˆjoc: (i) 'Estw x 0 tètoio ste x < ε, gia kˆje ε > 0. Tìte
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΤΩΝ ΥΛΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗ ΙΙ Εξετάσεις Ιουνίου 2002
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΤΩΝ ΥΛΙΚΩΝ Εξετάσεις Ιουνίου (α) Αναπτύξτε την µέθοδο του τραπεζίου για τον αριθµητικό υπολογισµό του ολοκληρώµατος: b I( f ) = f ( x) a όπου f (x) συνεχής και ολοκληρώσιµη
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΤΩΝ ΥΛΙΚΩΝ Εξετάσεις Ιουνίου (α) Αναπτύξτε την µέθοδο του τραπεζίου για τον αριθµητικό υπολογισµό του ολοκληρώµατος: b I( f ) = f ( x) a όπου f (x) συνεχής και ολοκληρώσιµη
Diakritˆ Majhmatikˆ I. Leutèrhc KuroÔshc (EÔh Papaðwˆnnou)
 Diakritˆ Majhmatikˆ I Leutèrhc KuroÔshc (EÔh Papaðwˆnnou) PlhroforÐec... Tetˆrth, 09.00-11.00, Paraskeu, 18.00-20.00 SÔggramma 1: Λ. Κυρούσης, Χ. Μπούρας, Π. Σπυράκης. Διακριτά Μαθηματικά: Τα Μαθηματικά
Diakritˆ Majhmatikˆ I Leutèrhc KuroÔshc (EÔh Papaðwˆnnou) PlhroforÐec... Tetˆrth, 09.00-11.00, Paraskeu, 18.00-20.00 SÔggramma 1: Λ. Κυρούσης, Χ. Μπούρας, Π. Σπυράκης. Διακριτά Μαθηματικά: Τα Μαθηματικά
Θεωρία Πιθανοτήτων και Στατιστική
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεωρία Πιθανοτήτων και Στατιστική Ενότητα 1: Περιγραφική Στατιστική Κουγιουμτζής Δημήτρης Τμήμα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεωρία Πιθανοτήτων και Στατιστική Ενότητα 1: Περιγραφική Στατιστική Κουγιουμτζής Δημήτρης Τμήμα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών
1 η Σειρά Ασκήσεων Θεόδωρος Αλεξόπουλος. Αναγνώριση Προτύπων και Νευρωνικά Δίκτυα
 Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μετσόβιο Πολυτεχνείο Αναγνώριση Προτύπων και Νευρωνικά Δίκτυα η Σειρά Ασκήσεων Θεόδωρος Αλεξόπουλος Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό
Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μετσόβιο Πολυτεχνείο Αναγνώριση Προτύπων και Νευρωνικά Δίκτυα η Σειρά Ασκήσεων Θεόδωρος Αλεξόπουλος Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό
Mègisth ro - elˆqisth tom
 15 DekembrÐou 2009 DÐnetai grˆfoc (N, A) me ìria ro c x ij [b ij, c ij ] gia kˆje akm (i, j) kai dôo epilegmènouc kìmbouc s kai t. Jèloume na upologðsoume th ro sto grˆfo, ste na megistopoieðtai h apìklish
15 DekembrÐou 2009 DÐnetai grˆfoc (N, A) me ìria ro c x ij [b ij, c ij ] gia kˆje akm (i, j) kai dôo epilegmènouc kìmbouc s kai t. Jèloume na upologðsoume th ro sto grˆfo, ste na megistopoieðtai h apìklish
PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II DIAFORIKES EXISWSEIS.
 PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II DIAFORIKES EXISWSEIS h Seirˆ Ask sewn Diaforikèc eis seic > diaforikèc
PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II DIAFORIKES EXISWSEIS h Seirˆ Ask sewn Diaforikèc eis seic > diaforikèc
Pragmatik Anˆlush ( ) TopologÐa metrik n q rwn Ask seic
 Pragmatik Anˆlush (2010 11) TopologÐa metrik n q rwn Ask seic Omˆda A' 1. 'Estw (X, ρ) metrikìc q roc kai F, G uposônola tou X. An to F eðnai kleistì kai to G eðnai anoiktì, deðxte ìti to F \ G eðnai kleistì
Pragmatik Anˆlush (2010 11) TopologÐa metrik n q rwn Ask seic Omˆda A' 1. 'Estw (X, ρ) metrikìc q roc kai F, G uposônola tou X. An to F eðnai kleistì kai to G eðnai anoiktì, deðxte ìti to F \ G eðnai kleistì
GENIKEUMENA OLOKLHRWMATA
 PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA I GENIKEUMENA OLOKLHRWMATA Anplhrwt c Kjhght c: Dr. Pppˆc G. Alèndroc GENIKEUMENA OLOKLHRWMATA H ènnoi tou orismènou
PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA I GENIKEUMENA OLOKLHRWMATA Anplhrwt c Kjhght c: Dr. Pppˆc G. Alèndroc GENIKEUMENA OLOKLHRWMATA H ènnoi tou orismènou
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Φωνής Άσκηση 2η Στυλιανού Ιωάννης Τμήμα Επιστήμης Υπολογιστών HU578: 2 η Seirˆ Ask sewn AporÐec: yannis@csd.uoc.gr 1. (aþ) Sac dðdetai o anadromikìc
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Φωνής Άσκηση 2η Στυλιανού Ιωάννης Τμήμα Επιστήμης Υπολογιστών HU578: 2 η Seirˆ Ask sewn AporÐec: yannis@csd.uoc.gr 1. (aþ) Sac dðdetai o anadromikìc
25 OktwbrÐou 2012 (5 h ebdomˆda) S. Malefˆkh Genikì Tm ma Majhmatikˆ gia QhmikoÔc
 Mˆjhma 9 0 25 OktwbrÐou 2012 (5 h ebdomˆda) Diaforikèc Exis seic TÔpoi Diaforik n exis sewn H pio apl diaforik exðswsh y = f (x) Diaforikèc Exis seic TÔpoi Diaforik n exis sewn H pio apl diaforik exðswsh
Mˆjhma 9 0 25 OktwbrÐou 2012 (5 h ebdomˆda) Diaforikèc Exis seic TÔpoi Diaforik n exis sewn H pio apl diaforik exðswsh y = f (x) Diaforikèc Exis seic TÔpoi Diaforik n exis sewn H pio apl diaforik exðswsh
Jerinì SqoleÐo Fusik c sthn EkpaÐdeush 28 IounÐou - 1 IoulÐou 2010 EstÐa Episthm n Pˆtrac
 Kbantik Perigraf tou Kìsmou mac KwnstantÐnoc Sfètsoc Kajhght c Fusik c Genikì Tm ma, Panepist mio Patr n Jerinì SqoleÐo Fusik c sthn EkpaÐdeush 28 IounÐou - 1 IoulÐou 2010 EstÐa Episthm n Pˆtrac Ti ennooôme
Kbantik Perigraf tou Kìsmou mac KwnstantÐnoc Sfètsoc Kajhght c Fusik c Genikì Tm ma, Panepist mio Patr n Jerinì SqoleÐo Fusik c sthn EkpaÐdeush 28 IounÐou - 1 IoulÐou 2010 EstÐa Episthm n Pˆtrac Ti ennooôme
L mma thc 'Antlhshc. A. K. Kapìrhc
 L mma thc 'Antlhshc A. K. Kapìrhc 12 MartÐou 2009 2 Perieqìmena 1 Το Λήμμα της Άντλησης για μη κανονικές γλώσσες 5 1.1 Μη κανονικές γλώσσες..................................... 5 1.2 Λήμμα άντλησης για
L mma thc 'Antlhshc A. K. Kapìrhc 12 MartÐou 2009 2 Perieqìmena 1 Το Λήμμα της Άντλησης για μη κανονικές γλώσσες 5 1.1 Μη κανονικές γλώσσες..................................... 5 1.2 Λήμμα άντλησης για
9.2 Μελετώντας τρισδιάστατα γραφικά στο επίπεδο Oi sunartήseiv Contour Plot kai DensityPlot
 trisdiastatastoepipedo_.nb 9. Μελετώντας τρισδιάστατα γραφικά στο επίπεδο 9.. Oi sunartήseiv Contour Plot kai DensityPlot Me thn ContourPlot[f[x,y], {x,xmin,xmax},{y,ymin,ymax}] scediάzoume thn f[x,y]
trisdiastatastoepipedo_.nb 9. Μελετώντας τρισδιάστατα γραφικά στο επίπεδο 9.. Oi sunartήseiv Contour Plot kai DensityPlot Me thn ContourPlot[f[x,y], {x,xmin,xmax},{y,ymin,ymax}] scediάzoume thn f[x,y]
Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ
 Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ Ενότητα: Διγραμμικές και Τετραγωνικές μορφές Όνομα Καθηγητή: Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ Ενότητα: Διγραμμικές και Τετραγωνικές μορφές Όνομα Καθηγητή: Ανδρέας Αρβανιτογεώργος Τμήμα: Μαθηματικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Anaplhrwt c Kajhght c : Dr. Pappˆc G. Alèxandroc PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA I
 PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA I. Aìristo Olokl rwma 2. Orismèno Olokl rwma 3. Diaforetik èkfrash tou aìristou oloklhr matoc H Sunˆrthsh F ()
PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA I. Aìristo Olokl rwma 2. Orismèno Olokl rwma 3. Diaforetik èkfrash tou aìristou oloklhr matoc H Sunˆrthsh F ()
Tm ma Fusik c Mˆjhma: Pijanìthtec -Sfˆlmata-Statistik PerÐodoc: Febrouˆrioc 2008
 Tm ma Fusik c Mˆjhma: Pijanìthtec -Sfˆlmata-Statistik PerÐodoc: Febrouˆrioc 2008 Jèma 1. a 'Enac upologist c dèqetai kajhmerinˆ e-mail. Apì prohgoômena dedomèna gnwrðzoume ìti ta 7/10 twn e-mailc pou stèlnontai
Tm ma Fusik c Mˆjhma: Pijanìthtec -Sfˆlmata-Statistik PerÐodoc: Febrouˆrioc 2008 Jèma 1. a 'Enac upologist c dèqetai kajhmerinˆ e-mail. Apì prohgoômena dedomèna gnwrðzoume ìti ta 7/10 twn e-mailc pou stèlnontai
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Μηχανική Μάθηση. Ενότητα 10: Θεωρία Βελτιστοποίησης. Ιωάννης Τσαμαρδίνος Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Ενότητα 10: Θεωρία Βελτιστοποίησης Ιωάννης Τσαμαρδίνος Τμήμα Επιστήμης Υπολογιστών To genikì prìblhma, na broôme to mègisto elˆqisto miac sunˆrthshc
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Ενότητα 10: Θεωρία Βελτιστοποίησης Ιωάννης Τσαμαρδίνος Τμήμα Επιστήμης Υπολογιστών To genikì prìblhma, na broôme to mègisto elˆqisto miac sunˆrthshc
10/2013. Mod: 02D-EK/BT. Production code: CTT920BE
 10/2013 Mod: 02D-EK/BT Production code: CTT920BE GR ΕΓΧΕΙΡΙ ΙΟ ΧΡΗΣΗΣ ΚΑΙ ΣΥΝΤΗΡΗΣΗΣ σελ. 1 ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ ΚΕΦ 1 ΕΙΣΑΓΩΓΗ... 3 ΚΕΦ 2 ΕΓΚΑΤΑΣΤΑΣΗ... 3 2.1 ΜΕΤΑΚΙΝΗΣΗ ΚΑΙ ΑΠΟΣΥΣΚΕΥΑΣΙΑ...3 2.2 ΗΛΕΚΤΡΙΚΗ
10/2013 Mod: 02D-EK/BT Production code: CTT920BE GR ΕΓΧΕΙΡΙ ΙΟ ΧΡΗΣΗΣ ΚΑΙ ΣΥΝΤΗΡΗΣΗΣ σελ. 1 ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ ΚΕΦ 1 ΕΙΣΑΓΩΓΗ... 3 ΚΕΦ 2 ΕΓΚΑΤΑΣΤΑΣΗ... 3 2.1 ΜΕΤΑΚΙΝΗΣΗ ΚΑΙ ΑΠΟΣΥΣΚΕΥΑΣΙΑ...3 2.2 ΗΛΕΚΤΡΙΚΗ
Εφαρμοσμένα Μαθηματικά για Μηχανικούς
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Εφαρμοσμένα Μαθηματικά για Μηχανικούς Σημειώσεις: Μετασχηματισμός Z Γιώργος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών Kefˆlaio 7 Metasqhmatismìc Z 7. Orismìc tou metasqhmatismoô
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Εφαρμοσμένα Μαθηματικά για Μηχανικούς Σημειώσεις: Μετασχηματισμός Z Γιώργος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών Kefˆlaio 7 Metasqhmatismìc Z 7. Orismìc tou metasqhmatismoô
Eisagwg sthn KosmologÐa
 Eisagwg sthn KosmologÐa BasileÐou S. Gerogiˆnnh Kajhght Tm matoc Fusik c PanepisthmÐou Patr n Patra 2009 Kefˆlaio 1 Eisagwgikˆ 1.1 Gwniakì mègejoc, parsèk, ètoc fwtìc O parathrht c tou Sq matoc 1.1 parathreð
Eisagwg sthn KosmologÐa BasileÐou S. Gerogiˆnnh Kajhght Tm matoc Fusik c PanepisthmÐou Patr n Patra 2009 Kefˆlaio 1 Eisagwgikˆ 1.1 Gwniakì mègejoc, parsèk, ètoc fwtìc O parathrht c tou Sq matoc 1.1 parathreð
Ergasthriak 'Askhsh 2
 Kefˆlaio 2 Ergasthriak 'Askhsh 2 Οπου θα δούμε πώς μπορούμε να ορίζουμε δικές μας διαδικασίες και θα παρουσιάσουμε τις primitive διαδικασίες χειρισμού λιστών, τις μεταβλητές και τα side effects. 2.1 P
Kefˆlaio 2 Ergasthriak 'Askhsh 2 Οπου θα δούμε πώς μπορούμε να ορίζουμε δικές μας διαδικασίες και θα παρουσιάσουμε τις primitive διαδικασίες χειρισμού λιστών, τις μεταβλητές και τα side effects. 2.1 P
PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II SUNARTHSEIS POLLWN METABLHTWN.
 PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II SUNARTHSEIS POLLWN METABLHTWN h Seirˆ Ask sewn Akrìtata pragmatik n sunart sewn 1. Na brejoôn ta topikˆ akrìtata
PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II SUNARTHSEIS POLLWN METABLHTWN h Seirˆ Ask sewn Akrìtata pragmatik n sunart sewn 1. Na brejoôn ta topikˆ akrìtata
PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II SUNARTHSEIS POLLWN METABLHTWN EPIKAMPULIA OLOKLHRWMATA
 PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II SUNARTHSEIS POLLWN METLHTWN EPIKAMPULIA OLOKLHRWMATA 1. EpikampÔlio Olokl rwma 1ou eðdouc Efarmogèc 2. Dianusmatikˆ
PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II SUNARTHSEIS POLLWN METLHTWN EPIKAMPULIA OLOKLHRWMATA 1. EpikampÔlio Olokl rwma 1ou eðdouc Efarmogèc 2. Dianusmatikˆ
ΜΑΘΗΜΑ 2, Έλεγχος ροής προγράμματος ΒΑΣΙΚΗ ΣΥΝΤΑΞΗ:
 ΜΑΘΗΜΑ 2, 080312 Έλεγχος ροής προγράμματος Μπορούμε να χρησιμοποιήσουμε μια σειρά από λογικούς ελέγχους (συγκρίσεις) και με βάση το αποτέλεσμά τους γίνεται η λήψη αποφάσεων για τη συνέχεια του προγράμματος
ΜΑΘΗΜΑ 2, 080312 Έλεγχος ροής προγράμματος Μπορούμε να χρησιμοποιήσουμε μια σειρά από λογικούς ελέγχους (συγκρίσεις) και με βάση το αποτέλεσμά τους γίνεται η λήψη αποφάσεων για τη συνέχεια του προγράμματος
Εφαρμοσμένα Μαθηματικά για Μηχανικούς
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Εφαρμοσμένα Μαθηματικά για Μηχανικούς Σημειώσεις: Μετασχηματισμός Laplace Γιώργος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών Kefˆlaio 8 Metasqhmatismìc Laplace 8. Orismìc
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Εφαρμοσμένα Μαθηματικά για Μηχανικούς Σημειώσεις: Μετασχηματισμός Laplace Γιώργος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών Kefˆlaio 8 Metasqhmatismìc Laplace 8. Orismìc
bab.la Φράσεις: Ταξίδι Τρώγοντας έξω ελληνικά-ελληνικά
 Τρώγοντας έξω : Στην είσοδο Θα ήθελα να κρατήσω ένα τραπέζι για _[αριθμός ατόμων]_ στις _[ώρα]_. (Tha íthela na kratíso éna trapézi ya _[arithmós atómon]_ στις _[óra]_.) Θα ήθελα να κρατήσω ένα τραπέζι
Τρώγοντας έξω : Στην είσοδο Θα ήθελα να κρατήσω ένα τραπέζι για _[αριθμός ατόμων]_ στις _[ώρα]_. (Tha íthela na kratíso éna trapézi ya _[arithmós atómon]_ στις _[óra]_.) Θα ήθελα να κρατήσω ένα τραπέζι
Anagn rish ProtÔpwn & Neurwnikˆ DÐktua Probl mata 2
 Jeìdwroc Alexìpouloc, Anaplhrwt c Kajhght c Theodoros Alexopoulos, Associate Professor EJNIKO METSOBIO POLUTEQNEIO NATIONAL TECHNICAL UNIVERSITY SQOLH EFARMOSMENWN MAJHMATIKWN KAI DEPARTMENT OF PHYSICS
Jeìdwroc Alexìpouloc, Anaplhrwt c Kajhght c Theodoros Alexopoulos, Associate Professor EJNIKO METSOBIO POLUTEQNEIO NATIONAL TECHNICAL UNIVERSITY SQOLH EFARMOSMENWN MAJHMATIKWN KAI DEPARTMENT OF PHYSICS
thlèfwno: , H YHFIAKH TAXH A' GumnasÐou Miqˆlhc TzoÔmac Sq. Sumb. kl.
 A' GumnasÐou Sq. Sumb. kl. PE03 GiatÐ epibˆlletai h eisagwg thc sôgqronhc teqnologðac sthn ekpaðdeush. Η Πληροφοριοποίηση της κοινωνίας. Η αυξανόμενη πολυπλοκότητα του εκπαιδευτικού συστήματος. Η σημερινή
A' GumnasÐou Sq. Sumb. kl. PE03 GiatÐ epibˆlletai h eisagwg thc sôgqronhc teqnologðac sthn ekpaðdeush. Η Πληροφοριοποίηση της κοινωνίας. Η αυξανόμενη πολυπλοκότητα του εκπαιδευτικού συστήματος. Η σημερινή
6h Seirˆ Ask sewn. EpikampÔlia oloklhr mata
 PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II SUNARTHSEIS POLLWN METLHTWN 6h Seirˆ Ask sewn EpikampÔlia oloklhr mata 1 Jèma 1. Na upologisjeð to epikampôlio
PANEPISTHMIO DUTIKHS ATTIKHS SQOLH MHQANIKWN TMHMA POLITIKWN MHQANIKWN ANWTERA MAJHMATIKA II SUNARTHSEIS POLLWN METLHTWN 6h Seirˆ Ask sewn EpikampÔlia oloklhr mata 1 Jèma 1. Na upologisjeð to epikampôlio
Ask seic me ton Metasqhmatismì Laplace
 Ask seic me ton Metasqhmatismì Laplace Epimèleia: Gi rgoc Kafentz c Upoy. Didˆktwr Tm m. H/U Panepist mio Kr thc 8 IounÐou 4. 'Estw to s ma { A, t T x(t), alloô () (aþ) Na upologðsete to metasq. Fourier
Ask seic me ton Metasqhmatismì Laplace Epimèleia: Gi rgoc Kafentz c Upoy. Didˆktwr Tm m. H/U Panepist mio Kr thc 8 IounÐou 4. 'Estw to s ma { A, t T x(t), alloô () (aþ) Na upologðsete to metasq. Fourier
Farkas. αx+(1 α)y C. λx+(1 λ)y i I A i. λ 1,...,λ m 0 me λ 1 + +λ m = m. i=1 λ i = 1. i=1 λ ia i A. j=1 λ ja j A. An µ := λ λ k = 0 a λ k
 Kefˆlaio 1 DiaqwrÐzon UperepÐpedo L mma Farkas 1.1 Kurtˆ SÔnola 'Ena uposônolo C tou R n onomˆzetai kurtì an, gia kˆje x,y C kai kˆje λ [0,1], αx+(1 α)y C. An a i, i = 1,2,...,m eðnai dianôsmata ston R
Kefˆlaio 1 DiaqwrÐzon UperepÐpedo L mma Farkas 1.1 Kurtˆ SÔnola 'Ena uposônolo C tou R n onomˆzetai kurtì an, gia kˆje x,y C kai kˆje λ [0,1], αx+(1 α)y C. An a i, i = 1,2,...,m eðnai dianôsmata ston R
9. α 2 + β 2 ±2αβ. 10. α 2 ± αβ + β (1 + α) ν > 1+να, 1 <α 0, ν 2. log α. 14. log α x = ln x. 19. x 1 <x 2 ln x 1 < ln x 2
 UpenjumÐseic gia thn Jetik kai Teqnologik KateÔjunsh Kajhght c: N.S. Maurogi nnhc 1 Tautìthtec - Anisìthtec 1. (α ± ) = α ± α +. (α ± ) 3 = α 3 ± 3α +3α ± 3 3. α 3 ± 3 =(α ± ) ( α α + ) 4. (α + + γ) =
UpenjumÐseic gia thn Jetik kai Teqnologik KateÔjunsh Kajhght c: N.S. Maurogi nnhc 1 Tautìthtec - Anisìthtec 1. (α ± ) = α ± α +. (α ± ) 3 = α 3 ± 3α +3α ± 3 3. α 3 ± 3 =(α ± ) ( α α + ) 4. (α + + γ) =
KATASTATIKO 3. XRHSIMOPOIHSH TVN OIKONOMIKVN MESVN, KOINH VFELEIA
 1 of 5 20.10.2005 08:48 KATASTATIKO Tou Eurvpai_kouß Keßntrou Episthmonikhßw, Oikoumenikhßw kai Politistikhßw Sunergasißaw - Ellhnogermanikhß Prvtoboulißa Würzburg 1. ONOMASIA KAI EDRA TOU SULLOGOU (1)
1 of 5 20.10.2005 08:48 KATASTATIKO Tou Eurvpai_kouß Keßntrou Episthmonikhßw, Oikoumenikhßw kai Politistikhßw Sunergasißaw - Ellhnogermanikhß Prvtoboulißa Würzburg 1. ONOMASIA KAI EDRA TOU SULLOGOU (1)
Eukleideiec Gewmetriec
 Eukleideiec Gewmetriec 1. Ta stoiqeða tou EukleÐdh To pio shmantikì biblðo sthn IstorÐa twn Majhmatik n allˆ kai èna apì ta pio shmantikˆ sthn IstorÐa tou anjr pinou politismoô eðnai ta StoiqeÐa tou EukleÐdh.
Eukleideiec Gewmetriec 1. Ta stoiqeða tou EukleÐdh To pio shmantikì biblðo sthn IstorÐa twn Majhmatik n allˆ kai èna apì ta pio shmantikˆ sthn IstorÐa tou anjr pinou politismoô eðnai ta StoiqeÐa tou EukleÐdh.
Κλασσική Ηλεκτροδυναμική II
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασσική Ηλεκτροδυναμική II Πεδία Σημειακών Φορτίων Διδάσκων : Καθ. Κ. Ταμβάκης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασσική Ηλεκτροδυναμική II Πεδία Σημειακών Φορτίων Διδάσκων : Καθ. Κ. Ταμβάκης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Στατιστική για Πολιτικούς Μηχανικούς
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Στατιστική για Πολιτικούς Μηχανικούς Ενότητα 3: Εκτίμηση παραμέτρων (μέρος 2 ο ) Κουγιουμτζής Δημήτριος Τμήμα Πολιτικών Μηχανικών Άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Στατιστική για Πολιτικούς Μηχανικούς Ενότητα 3: Εκτίμηση παραμέτρων (μέρος 2 ο ) Κουγιουμτζής Δημήτριος Τμήμα Πολιτικών Μηχανικών Άδειες
Å Ó Ó ÐÅÉÑÁÌÁÔÉÊÏ ËÕÊÅÉÏ. ÁóêÞóåéò. ôçò ÅÕÁÃÃÅËÉÊÇÓ Ó ÏËÇÓ ÓÌÕÑÍÇÓ Å ÅÔÏÓ É ÉÄÑÕÓÇÓ
 ÐÅÉÑÁÌÁÔÉÊÏ ËÕÊÅÉÏ ôçò ÅÕÁÃÃÅËÉÊÇÓ Ó ÏËÇÓ ÓÌÕÑÍÇÓ Å Ó Ó Å ÅÔÏÓ É ÉÄÑÕÓÇÓ 1733 ÔÁÎÇ Ã MáèçìáôéêÜ ÃåíéêÞò Ðáéäåßáò ÁóêÞóåéò EEEbbBBeee ÊáèçãçôÞò: Í.Ó. ÌáõñïãéÜííçò Ó ïëéêü ôïò 2008-2009 Πειραματικο Λυκειο
ÐÅÉÑÁÌÁÔÉÊÏ ËÕÊÅÉÏ ôçò ÅÕÁÃÃÅËÉÊÇÓ Ó ÏËÇÓ ÓÌÕÑÍÇÓ Å Ó Ó Å ÅÔÏÓ É ÉÄÑÕÓÇÓ 1733 ÔÁÎÇ Ã MáèçìáôéêÜ ÃåíéêÞò Ðáéäåßáò ÁóêÞóåéò EEEbbBBeee ÊáèçãçôÞò: Í.Ó. ÌáõñïãéÜííçò Ó ïëéêü ôïò 2008-2009 Πειραματικο Λυκειο
f(x) =x x 2 = x x 2 x =0 x(x 1) = 0,
 NÐkoc E. AggourÐdhc To Je rhma tou Sarkovskii Panepist mio Kr thc Tm ma Majhmatik n 2 Thn kritik epitrop apotèlesan oi Ajanasìpouloc KwnstantÐnoc Katsoprin khc Emmanou l Kwst khc Ge rgioc (epiblèpwn) touc
NÐkoc E. AggourÐdhc To Je rhma tou Sarkovskii Panepist mio Kr thc Tm ma Majhmatik n 2 Thn kritik epitrop apotèlesan oi Ajanasìpouloc KwnstantÐnoc Katsoprin khc Emmanou l Kwst khc Ge rgioc (epiblèpwn) touc
Hmiomˆdec telest n sônjeshc kai pðnakec Hausdorff se q rouc analutik n sunart sewn
 ARISTOTELEIO PANEPISTHMIO JESSALONIKHS SQOLH JETIKWN EPISTHMWN TMHMA MAJHMATIKWN TOMEAS MAJHMATIKHS ANALUSHS PETROS GALANOPOULOS Hmiomˆdec telest n sônjeshc kai pðnakec Hausdorff se q rouc analutik n sunart
ARISTOTELEIO PANEPISTHMIO JESSALONIKHS SQOLH JETIKWN EPISTHMWN TMHMA MAJHMATIKWN TOMEAS MAJHMATIKHS ANALUSHS PETROS GALANOPOULOS Hmiomˆdec telest n sônjeshc kai pðnakec Hausdorff se q rouc analutik n sunart
Ergasthriak 'Askhsh 3
 Kefˆlaio 3 Ergasthriak 'Askhsh 3 Οπου θα δούμε τις λογικές συναρτήσεις και θα εμβαθύνουμε λίγο περισσότερο στις λίστες και τις μεταβλητές. 3.1 Logikèc Sunart seic Οι λογικές συναρτήσεις (logical ή boolean
Kefˆlaio 3 Ergasthriak 'Askhsh 3 Οπου θα δούμε τις λογικές συναρτήσεις και θα εμβαθύνουμε λίγο περισσότερο στις λίστες και τις μεταβλητές. 3.1 Logikèc Sunart seic Οι λογικές συναρτήσεις (logical ή boolean
MÐa SÔntomh Eisagwgă stic SÔgqronec JewrÐec Isìthtac
 MÐa SÔntomh Eisagwgă stic SÔgqronec JewrÐec Isìthtac Nikìlac BroÔsalhc nicholas.vrousalis@lmh.ox.ac.uk 29 OktwbrÐou 2007 1 KĹpoiec basikèc diakrðseic 1.1 Ish Mèrimna Φέροµαι εξίσου στην Α και στον Β vs.
MÐa SÔntomh Eisagwgă stic SÔgqronec JewrÐec Isìthtac Nikìlac BroÔsalhc nicholas.vrousalis@lmh.ox.ac.uk 29 OktwbrÐou 2007 1 KĹpoiec basikèc diakrðseic 1.1 Ish Mèrimna Φέροµαι εξίσου στην Α και στον Β vs.
Κεϕάλαιο 2 ΕΚΤΙΜΗΣΗ ΠΑΡΑΜΕΤΡΩΝ. 2.1 Σηµειακή Εκτίµηση. {x 1,..., x n } της X από ένα δείγµα µεγέθους n. Τότε η σηµειακή εκτίµηση της θ δίνεται
 Κεϕάλαιο 2 ΕΚΤΙΜΗΣΗ ΠΑΡΑΜΕΤΡΩΝ Οι στατιστικές δείγµατος που υπολογίζονται από τα δεδοµένα που έχουν συλλεχθεί, όπως η δειγµατική µέση τιµή x και η δειγµατική διασπορά s 2, χρησιµοποιούνται για την εκτίµηση
Κεϕάλαιο 2 ΕΚΤΙΜΗΣΗ ΠΑΡΑΜΕΤΡΩΝ Οι στατιστικές δείγµατος που υπολογίζονται από τα δεδοµένα που έχουν συλλεχθεί, όπως η δειγµατική µέση τιµή x και η δειγµατική διασπορά s 2, χρησιµοποιούνται για την εκτίµηση
MELETH TWN RIZWN TWN ASSOCIATED ORJOGWNIWN
 IWANNH D. STAMPOLA MAJHMATIKOU MELETH TWN RIZWN TWN ASSOCIATED ORJOGWNIWN q-poluwnumwn DIDAKTORIKH DIATRIBH TMHMA MAJHMATIKWN SQOLH JETIKWN EPISTHMWN PANEPISTHMIO PATRWN PATRA 2004 Stouc goneðc mou kai
IWANNH D. STAMPOLA MAJHMATIKOU MELETH TWN RIZWN TWN ASSOCIATED ORJOGWNIWN q-poluwnumwn DIDAKTORIKH DIATRIBH TMHMA MAJHMATIKWN SQOLH JETIKWN EPISTHMWN PANEPISTHMIO PATRWN PATRA 2004 Stouc goneðc mou kai
AM = 1 ( ) AB + AΓ BΓ+ AE = AΔ+ BE. + γ =2 β + γ β + γ tìte α// β. OΓ+ OA + OB MA+ MB + M Γ+ MΔ =4 MO. OM =(1 λ) OA + λ OB
 Peiramatiko Lukeio Euaggelikhc Sqolhc Smurnhc Taxh B, Majhmatika Jetikhc kai Teqnologikhc Kateujunshc, Askhseic Kajhght c: Shmei seic gia sqolik qr sh. MporoÔn na anaparaqjoôn kai na dianemhjoôn eleôjera
Peiramatiko Lukeio Euaggelikhc Sqolhc Smurnhc Taxh B, Majhmatika Jetikhc kai Teqnologikhc Kateujunshc, Askhseic Kajhght c: Shmei seic gia sqolik qr sh. MporoÔn na anaparaqjoôn kai na dianemhjoôn eleôjera
G. A. Cohen ** stìqo thn kubernhtik nomojesða kai politik, den upˆrqei tðpota to qarakthristikì sth morf thc.)
 Εκεί που βρίσκεται η πράξη: Περί του πεδίου της διανεμητικής δικαιοσύνης G. A. Cohen ** Mετάφραση: Νικόλας Βρούσαλης Ι Σε αυτή την εργασία υπερασπίζομαι έναν ισχυρισμό που μπορεί να εκφραστεί με ένα οικείο
Εκεί που βρίσκεται η πράξη: Περί του πεδίου της διανεμητικής δικαιοσύνης G. A. Cohen ** Mετάφραση: Νικόλας Βρούσαλης Ι Σε αυτή την εργασία υπερασπίζομαι έναν ισχυρισμό που μπορεί να εκφραστεί με ένα οικείο
Εφαρμοσμένα Μαθηματικά για Μηχανικούς
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Εφαρμοσμένα Μαθηματικά για Μηχανικούς Σημειώσεις: Βασικές Έννοιες Σημάτων και Συστημάτων Γιώργος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών Kefˆlaio 2 Basikèc ènnoiec
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Εφαρμοσμένα Μαθηματικά για Μηχανικούς Σημειώσεις: Βασικές Έννοιες Σημάτων και Συστημάτων Γιώργος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών Kefˆlaio 2 Basikèc ènnoiec
JewrÐa UpologismoÔ. Grammatikèc QwrÐc Sumfrazìmena kai Autìmata StoÐbac
 M. G. Lagoudˆkhc Τμημα ΗΜΜΥ, Πολυτεχνειο Κρητης SelÐda 1 apì 33 JewrÐa UpologismoÔ Grammatikèc QwrÐc Sumfrazìmena kai Autìmata StoÐbac M. G. Lagoudˆkhc Τμημα ΗΜΜΥ, Πολυτεχνειο Κρητης SelÐda 2 apì 33 Epanˆlhyh
M. G. Lagoudˆkhc Τμημα ΗΜΜΥ, Πολυτεχνειο Κρητης SelÐda 1 apì 33 JewrÐa UpologismoÔ Grammatikèc QwrÐc Sumfrazìmena kai Autìmata StoÐbac M. G. Lagoudˆkhc Τμημα ΗΜΜΥ, Πολυτεχνειο Κρητης SelÐda 2 apì 33 Epanˆlhyh
Ανάλυση ις. συστήματα
 Σήματα Συστήματα Ανάλυση ourier για σήματα και συνεχούς χρόνου Λυμένες ασκήσει ις Κνσταντίνος Κοτρόπουλος Τμήμα Πληροφορικής συστήματα Θεσσαλονίκη, Ιούνιος 3 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Σήματα Συστήματα Ανάλυση ourier για σήματα και συνεχούς χρόνου Λυμένες ασκήσει ις Κνσταντίνος Κοτρόπουλος Τμήμα Πληροφορικής συστήματα Θεσσαλονίκη, Ιούνιος 3 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
5. (12 i)(3+4i) 6. (1 + i)(2+i) 7. (4 + 6i)(7 3i) 8. (1 i)(2 i)(3 i)
 Peiramatiko Lukeio Euaggelikhc Sqolhc Smurnhc Taxh G, Majhmatika Jetikhc kai Teqnologikhc Kateujunshc, Askhseic Kajhght c: Oi shmei seic autèc eðnai gia sqolik qr sh. MporoÔn na anaparaqjoôn kai na dianemhjoôn
Peiramatiko Lukeio Euaggelikhc Sqolhc Smurnhc Taxh G, Majhmatika Jetikhc kai Teqnologikhc Kateujunshc, Askhseic Kajhght c: Oi shmei seic autèc eðnai gia sqolik qr sh. MporoÔn na anaparaqjoôn kai na dianemhjoôn
Modern Greek Extension
 Centre Number 2015 HIGHER SCHOOL CERTIFICATE EXAMINATION Student Number Modern Greek Extension Written Examination Total marks 40 General Instructions Reading time 10 minutes Working time 1 hour and 50
Centre Number 2015 HIGHER SCHOOL CERTIFICATE EXAMINATION Student Number Modern Greek Extension Written Examination Total marks 40 General Instructions Reading time 10 minutes Working time 1 hour and 50
2+sin^2(x+2)+cos^2(x+2) Δ ν =[1 1 2 ν 1, ν ) ( ( π (x α) ημ β α π ) ) +1 + a 2
 Parathr seic sta Jèmata Jetik c kai Teqnologik c KateÔjunshc tou ètouc 7 Peiramatikì LÔkeio Euaggelik c Sqol c SmÔrnhc 1 IounÐou 7 PerÐlhyh Oi shmei seic autèc anafèrontai sta jèmata Majhmatik n Jetik
Parathr seic sta Jèmata Jetik c kai Teqnologik c KateÔjunshc tou ètouc 7 Peiramatikì LÔkeio Euaggelik c Sqol c SmÔrnhc 1 IounÐou 7 PerÐlhyh Oi shmei seic autèc anafèrontai sta jèmata Majhmatik n Jetik
ErgasÐa Statistik c. Mìsqoglou Stulianìc. 1 Πρόλογος 2
 ErgasÐa Statistik c Mìsqoglou Stulianìc stelios@moschoglou.com AEM: 6978 23 IounÐou 2009 Perieqìmena 1 Πρόλογος 2 2 Μελέτη Α 2 2.1 Πίνακας μέτρων κεντρικής τάσης και μεταβλητότητας........ 2 2.2 Θηκογράμματα.............................
ErgasÐa Statistik c Mìsqoglou Stulianìc stelios@moschoglou.com AEM: 6978 23 IounÐou 2009 Perieqìmena 1 Πρόλογος 2 2 Μελέτη Α 2 2.1 Πίνακας μέτρων κεντρικής τάσης και μεταβλητότητας........ 2 2.2 Θηκογράμματα.............................
2012-2013 ΘΡΗΣΚΕΥΤΙΚΑ ΛΥΚΕΙΟΥ
 ΘΡΗΣΚΕΥΤΙΚΑ ΛΥΚΕΙΟΥ A ΤΑΞΗ Σεπτέμβριος 2012 Γ ΤΑΞΗ 1. Γνωριμία Παρουσίαση ύλης Εισαγωγή στη Θεία Λειτουργία (σελ. 24-34) 2. Κληρικοί Ιερά άμφια Ιερά λειτουργικά σκεύη (σελ. 35 53) 3. Προετοιμασία για την
ΘΡΗΣΚΕΥΤΙΚΑ ΛΥΚΕΙΟΥ A ΤΑΞΗ Σεπτέμβριος 2012 Γ ΤΑΞΗ 1. Γνωριμία Παρουσίαση ύλης Εισαγωγή στη Θεία Λειτουργία (σελ. 24-34) 2. Κληρικοί Ιερά άμφια Ιερά λειτουργικά σκεύη (σελ. 35 53) 3. Προετοιμασία για την
Να διορθωθούν τα εξής αρχεία scr2.chgeorg, scr2.gmotsias, scr2.ngrammen. cat scr2.*
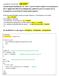 vassik@aetos:~/work/online$ cat scr2.* Τροποπoίηση/Συμπλήρωση του ask2 Δεχεται ονόματα αρχείων ως παραμέτρους Στο 1 ο αρχείο που δίνεται ως παράμετρος, γράφονται μέσα τα ονόματα και τα περιεχόμενα των
vassik@aetos:~/work/online$ cat scr2.* Τροποπoίηση/Συμπλήρωση του ask2 Δεχεται ονόματα αρχείων ως παραμέτρους Στο 1 ο αρχείο που δίνεται ως παράμετρος, γράφονται μέσα τα ονόματα και τα περιεχόμενα των
H mèjodoc Sturm. Mˆjhma AkoloujÐec Sturm
 Mˆjhma 2 H mèjodoc Sturm Το θεώρημα του Sturm μας δίνει έναν τρόπο καταμέτρησης των πραγματικών ριζών ενός πολυωνύμου σε δοσμένο διάστημα που τηρεί κάποιες συνθήκες. Εισάγουμε την έννοια της ακολουθίας
Mˆjhma 2 H mèjodoc Sturm Το θεώρημα του Sturm μας δίνει έναν τρόπο καταμέτρησης των πραγματικών ριζών ενός πολυωνύμου σε δοσμένο διάστημα που τηρεί κάποιες συνθήκες. Εισάγουμε την έννοια της ακολουθίας
Shmei seic sto mˆjhma Analutik GewmetrÐa
 Shmei seic sto mˆjhma Analutik GewmetrÐa Didˆskwn: Lˆppac D. Ejnikì Kapodistriakì Panepist mio Ajhn n B' MEROS 3 EPIFANEIES sto QWRO Epifˆneia gia thn perigraf thc qreiˆzontai dôo parˆmetroi mia eidik
Shmei seic sto mˆjhma Analutik GewmetrÐa Didˆskwn: Lˆppac D. Ejnikì Kapodistriakì Panepist mio Ajhn n B' MEROS 3 EPIFANEIES sto QWRO Epifˆneia gia thn perigraf thc qreiˆzontai dôo parˆmetroi mia eidik
Θέµα 1 (15%): (απαιτούµενος χρόνος < 15 λεπτά)
 Θέµα 1 (15%): (απαιτούµενος χρόνος < 15 λεπτά) Εκτελέστε µε το χέρι το παρακάτω πρόγραµµα και γράψτε όλες τις ενδιάµεσες τιµές και τις τιµές που τυπώνονται: int m,n; m=2; n=1; m=m+5; if (m>=9) m=m-8; n=n+7;
Θέµα 1 (15%): (απαιτούµενος χρόνος < 15 λεπτά) Εκτελέστε µε το χέρι το παρακάτω πρόγραµµα και γράψτε όλες τις ενδιάµεσες τιµές και τις τιµές που τυπώνονται: int m,n; m=2; n=1; m=m+5; if (m>=9) m=m-8; n=n+7;
BeltistopoÐhsh. Dr. Dhm trhc Swthrìpouloc. Tm ma Thlepikoinwniak Susthmˆtwn kai DiktÔwn. Tetˆrth, 7 OktwbrÐou 2009
 BeltistopoÐhsh Μάθημα 1ο Dr. Dhm trhc Swthrìpouloc Tm ma Thlepikoinwniak Susthmˆtwn kai DiktÔwn Tetˆrth, 7 OktwbrÐou 2009 Majhmatikìc Programmatismìc Μαθηματικός προγραμματισμός (Mathematical Programming):
BeltistopoÐhsh Μάθημα 1ο Dr. Dhm trhc Swthrìpouloc Tm ma Thlepikoinwniak Susthmˆtwn kai DiktÔwn Tetˆrth, 7 OktwbrÐou 2009 Majhmatikìc Programmatismìc Μαθηματικός προγραμματισμός (Mathematical Programming):
Anaz thsh eustaj n troqi n se triplˆ sust mata swmˆtwn
 Tmhma Fusikhc Aristoteleio Panepisthmio Jessalonikhc Ptuqiakh Ergasia Anaz thsh eustaj n troqi n se triplˆ sust mata swmˆtwn Ajanˆsioc MourtetzÐkoglou A.E.M.:13119 epiblèpwn kajhght c G. Bougiatz c 8 IoulÐou
Tmhma Fusikhc Aristoteleio Panepisthmio Jessalonikhc Ptuqiakh Ergasia Anaz thsh eustaj n troqi n se triplˆ sust mata swmˆtwn Ajanˆsioc MourtetzÐkoglou A.E.M.:13119 epiblèpwn kajhght c G. Bougiatz c 8 IoulÐou
Δομημένος Προγραμματισμός
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Δομημένος Προγραμματισμός Ενότητα: Συναρτήσεις - προγράμματα - Μέρος Α Δ. Ε. Μετάφας Τμ. Ηλεκτρονικών Μηχ. Τ.Ε. Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Δομημένος Προγραμματισμός Ενότητα: Συναρτήσεις - προγράμματα - Μέρος Α Δ. Ε. Μετάφας Τμ. Ηλεκτρονικών Μηχ. Τ.Ε. Άδειες Χρήσης
ibemo Kazakhstan Republic of Kazakhstan, West Kazakhstan Oblast, Aksai, Pramzone, BKKS office complex Phone: ; Fax:

στο Αριστοτέλειο υλικού.
 Σήματα Συστήματα Μετασχηματισμός Κωνσταντίνος Κοτρόπουλος Τμήμα Πληροφορικής Θεσσαλονίκη, Ιούνιος 203 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Σήματα Συστήματα Μετασχηματισμός Κωνσταντίνος Κοτρόπουλος Τμήμα Πληροφορικής Θεσσαλονίκη, Ιούνιος 203 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
HU215 - Frontist rio : Seirèc Fourier
 HU5 - Frontist rio : Seirèc Fourier Epimèleia: Gi rgoc P. Kafentz c Upoy. Didˆktwr Tm m. H/U Panepist mio Kr thc MartÐou 4. Na sqediˆsete to fˆsma plˆtouc kai to fˆsma fˆshc tou s matoc xt + cosπt sinπt
HU5 - Frontist rio : Seirèc Fourier Epimèleia: Gi rgoc P. Kafentz c Upoy. Didˆktwr Tm m. H/U Panepist mio Kr thc MartÐou 4. Na sqediˆsete to fˆsma plˆtouc kai to fˆsma fˆshc tou s matoc xt + cosπt sinπt
aapostol.scr2, scr2.kdeligia
 vassik@aetos:~/work/online$ cat scr2.* Τροποπoίηση/Συμπλήρωση του ask2 Δέχεται ονόματα αρχείων ως παραμέτρους Στο 1 ο αρχείο που δίνεται ως παράμετρος, γράφονται μέσα τα ονόματα και τα περιεχόμενα των
vassik@aetos:~/work/online$ cat scr2.* Τροποπoίηση/Συμπλήρωση του ask2 Δέχεται ονόματα αρχείων ως παραμέτρους Στο 1 ο αρχείο που δίνεται ως παράμετρος, γράφονται μέσα τα ονόματα και τα περιεχόμενα των
Συστήματα Μικροϋπολογιστών
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ Η/Υ Συστήματα Μικροϋπολογιστών 3η Oμάδα Ασκήσεων Δημητρίου Ανδριάνα 03110684 Σκούρα Ελένη 03110721 1 η 4 η Άσκηση i) Στο πρόβλημα
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ Η/Υ Συστήματα Μικροϋπολογιστών 3η Oμάδα Ασκήσεων Δημητρίου Ανδριάνα 03110684 Σκούρα Ελένη 03110721 1 η 4 η Άσκηση i) Στο πρόβλημα
Ta Jewr mata Alexander kai Markov thc JewrÐac Kìmbwn
 Ta Jewr mata Alexander kai Markov thc JewrÐac Kìmbwn Πατεράκης Αντώνης Αθήνα, Ιούλιος 2008 Eisagwgikèc 'Ennoiec Kìmboi Ενας κόμβος (knot) K είναι η εικόνα ενός ομοιομορφισμού h του κύκλου S 1 στο χώρο
Ta Jewr mata Alexander kai Markov thc JewrÐac Kìmbwn Πατεράκης Αντώνης Αθήνα, Ιούλιος 2008 Eisagwgikèc 'Ennoiec Kìmboi Ενας κόμβος (knot) K είναι η εικόνα ενός ομοιομορφισμού h του κύκλου S 1 στο χώρο
0 1/16 1/8 1/16 1/16 1 1/32 1/16 1/8 1/16 2 1/32 1/32 1/16 1/8 3 1/32 1/32 1/32 1/16
 ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΙΘΑΝΟΤΗΤΕΣ, ΚΑΘ: ΣΤΑΥΡΟΣ ΤΟΥΜΠΗΣ ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ, 7/6/ ΟΝΟΜΑ ΦΟΙΤΗΤΗ:.............................. OdhgÐe. Συμπληρώστε το όνομά σας άνω, και παραδώστε
ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΙΘΑΝΟΤΗΤΕΣ, ΚΑΘ: ΣΤΑΥΡΟΣ ΤΟΥΜΠΗΣ ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ, 7/6/ ΟΝΟΜΑ ΦΟΙΤΗΤΗ:.............................. OdhgÐe. Συμπληρώστε το όνομά σας άνω, και παραδώστε
Αποτελέσματα. ΜΟΔΙΠ Πανεπιστημίου Κρήτης Ερωτηματολόγιο 533569 'Γλώσσα Προγραμματισμού ΙΙ' Ερωτηματολόγιο 533569
 Αποτελέσματα Ερωτηματολόγιο 533569 Σύνολο εγγραφών σε αυτό το ερώτημα: 9 Σύνολο εγγραφών στο ερωτηματολόγιο: 9 Ποσοστό συνόλου: 100.00% σελίδα 1 / 49 Ομάδα: Ερωτηματολόγιο Ερώτηση: S0. Θέλετε να συμπληρώσετε
Αποτελέσματα Ερωτηματολόγιο 533569 Σύνολο εγγραφών σε αυτό το ερώτημα: 9 Σύνολο εγγραφών στο ερωτηματολόγιο: 9 Ποσοστό συνόλου: 100.00% σελίδα 1 / 49 Ομάδα: Ερωτηματολόγιο Ερώτηση: S0. Θέλετε να συμπληρώσετε
Σύνοψη είτε τις ολοκληρωµένες απαντήσεις
 1 of 22 12/12/2012 11:18 µµ απαντήσεις Σύνοψη είτε τις ολοκληρωµένες απαντήσεις ΤΜΗΜΑ (επιλέξτε το τµήµα σας) 1 1% Β ΕΦΑΡΜΟΣΜΕΝΩΝ ΤΕΧΝΩΝ 15 13% Β ΗΛΕΚΤΡΟΛΟΓΩΝ 18 16% Β ΗΛΕΚΤΡΟΝΙΚΩΝ 21 18% Β ΜΗΧΑΝΟΛΟΓΩΝ
1 of 22 12/12/2012 11:18 µµ απαντήσεις Σύνοψη είτε τις ολοκληρωµένες απαντήσεις ΤΜΗΜΑ (επιλέξτε το τµήµα σας) 1 1% Β ΕΦΑΡΜΟΣΜΕΝΩΝ ΤΕΧΝΩΝ 15 13% Β ΗΛΕΚΤΡΟΛΟΓΩΝ 18 16% Β ΗΛΕΚΤΡΟΝΙΚΩΝ 21 18% Β ΜΗΧΑΝΟΛΟΓΩΝ
Upologistikˆ Zht mata se Sumbibastikèc YhfoforÐec
 Panepisthmio Patrwn - Poluteqnikh Sqolh Tm ma Mhqanik n Hlektronik n Upologist n kai Plhroforik c Upologistikˆ Zht mata se Sumbibastikèc YhfoforÐec Dhmhtrioc Kalaðtzhc Diplwmatik ErgasÐa sto plaðsio tou
Panepisthmio Patrwn - Poluteqnikh Sqolh Tm ma Mhqanik n Hlektronik n Upologist n kai Plhroforik c Upologistikˆ Zht mata se Sumbibastikèc YhfoforÐec Dhmhtrioc Kalaðtzhc Diplwmatik ErgasÐa sto plaðsio tou
PERIEQŸOMENA I YHFIAKH THLEORASH 11 1 EISAGWGH STHN YHFIAKH THLEORASH Eisagwg Analogikì bðnteo
 PERIEQŸOMENA I YHFIAKH THLEORASH 11 1 EISAGWGH STHN YHFIAKH THLEORASH 13 1.1 Eisagwg......................... 13 1.2 Analogikì bðnteo..................... 14 1.2.1 Analogikì s ma bðnteo.............. 14
PERIEQŸOMENA I YHFIAKH THLEORASH 11 1 EISAGWGH STHN YHFIAKH THLEORASH 13 1.1 Eisagwg......................... 13 1.2 Analogikì bðnteo..................... 14 1.2.1 Analogikì s ma bðnteo.............. 14
AntistoÐqish Ontologi n
 AntistoÐqish Ontologi n BasÐlhc Sphliìpouloc 1,2 vspiliop@iit.demokritos.gr 1 Tm ma Mhqanik n Plhroforiak n kai Epikoinwniak n Susthmˆtwn, Ergast rio Teqnht c NohmosÔnhc, Panepist mio AigaÐou 2 InstitoÔto
AntistoÐqish Ontologi n BasÐlhc Sphliìpouloc 1,2 vspiliop@iit.demokritos.gr 1 Tm ma Mhqanik n Plhroforiak n kai Epikoinwniak n Susthmˆtwn, Ergast rio Teqnht c NohmosÔnhc, Panepist mio AigaÐou 2 InstitoÔto
"ΓΛΩΣΣΑ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Η/Υ" (ΕΜ102), ΕΡΓΑΣΙΑ 1η
 "ΓΛΩΣΣΑ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Η/Υ" (ΕΜ102), ΕΡΓΑΣΙΑ 1η Σε αυτήν την εργασία καλείστε να κατασκευάσετε τον πηγαίο κώδικα γλώσσας C για το εκτελέσιµο αρχείο µε ό- νοµα ATM, που όταν εκτελείται σε κονσόλα προσοµοιώνει
"ΓΛΩΣΣΑ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Η/Υ" (ΕΜ102), ΕΡΓΑΣΙΑ 1η Σε αυτήν την εργασία καλείστε να κατασκευάσετε τον πηγαίο κώδικα γλώσσας C για το εκτελέσιµο αρχείο µε ό- νοµα ATM, που όταν εκτελείται σε κονσόλα προσοµοιώνει
στο Αριστοτέλειο υλικού.
 Σήματα Συστήματα Μετασχηματισμός aplace Λυμένες ασκήσεις Κωνσταντίνος Κοτρόπουλος Τμήμα Πληροφορικής Θεσσαλονίκη, Ιούνιος 03 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Σήματα Συστήματα Μετασχηματισμός aplace Λυμένες ασκήσεις Κωνσταντίνος Κοτρόπουλος Τμήμα Πληροφορικής Θεσσαλονίκη, Ιούνιος 03 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Φυλλο 3, 9 Απριλιου Ροδόλφος Μπόρης
 FÔlla Majhmatik c PaideÐac Φυλλο 3, 9 Απριλιου 2010 StoiqeiojeteÐtai me to L A TEX 2ε Epimèleia: N.S. Maurogi nnhc, Dr Majhmatik n Peiramatikì LÔkeio Euaggelik c Sqol c SmÔrnhc mavrogiannis@gmail.com 1
FÔlla Majhmatik c PaideÐac Φυλλο 3, 9 Απριλιου 2010 StoiqeiojeteÐtai me to L A TEX 2ε Epimèleia: N.S. Maurogi nnhc, Dr Majhmatik n Peiramatikì LÔkeio Euaggelik c Sqol c SmÔrnhc mavrogiannis@gmail.com 1
Work12 REMARKS script file lab10 ask1-5 tabbing, ls2, urlparse, times, dates_correct
 Work12 REMARKS script le lab10 ask1-5 tabbing, ls2, urlparse, times, dates_correct #Username : imanousi #lename : tabbing.imanousi #To script eisagei ena tab sthn arxh kathe grammhs #tou arxeiou pou dinetai
Work12 REMARKS script le lab10 ask1-5 tabbing, ls2, urlparse, times, dates_correct #Username : imanousi #lename : tabbing.imanousi #To script eisagei ena tab sthn arxh kathe grammhs #tou arxeiou pou dinetai
Shmei seic Sunarthsiak c Anˆlushc
 Shmei seic Sunarthsiak c Anˆlushc Apìstoloc Giannìpouloc 1 Panepisthmio Krhthc Tmhma Majhmatikwn Anoixh 2003 1 Tm. Majhmatik n, Panep. Ajhn n 2 Perieqìmena 1 Μετρικοί χώροι 5 1.1 Ορισμός................................................
Shmei seic Sunarthsiak c Anˆlushc Apìstoloc Giannìpouloc 1 Panepisthmio Krhthc Tmhma Majhmatikwn Anoixh 2003 1 Tm. Majhmatik n, Panep. Ajhn n 2 Perieqìmena 1 Μετρικοί χώροι 5 1.1 Ορισμός................................................
Upologistik Fusik Exetastik PerÐodoc IanouarÐou 2013
 Upologistik Fusik Exetastik PerÐodoc IanouarÐou 03 Patra, 6 Ianouariou 03 Jèma A. Na exhg sete grafikˆ thn mèjodo thc diqotìmhshc. B. Na exhg sete grafikˆ thn mèjodo Runge Kutta. Jèma. DiatÔpwsh Oi migadikèc
Upologistik Fusik Exetastik PerÐodoc IanouarÐou 03 Patra, 6 Ianouariou 03 Jèma A. Na exhg sete grafikˆ thn mèjodo thc diqotìmhshc. B. Na exhg sete grafikˆ thn mèjodo Runge Kutta. Jèma. DiatÔpwsh Oi migadikèc
A[0] = 0; /* To μηδέν δεν έχει διαιρέτες */ for (i=1; i<n; i++) { S=0; for (d=1; d<=i; d++) if (i % d == 0) S += d; A[i] = S; }
![A[0] = 0; /* To μηδέν δεν έχει διαιρέτες */ for (i=1; i<n; i++) { S=0; for (d=1; d<=i; d++) if (i % d == 0) S += d; A[i] = S; } A[0] = 0; /* To μηδέν δεν έχει διαιρέτες */ for (i=1; i<n; i++) { S=0; for (d=1; d<=i; d++) if (i % d == 0) S += d; A[i] = S; }](/thumbs/102/153319538.jpg) TEI Λάρισας / ΣΤΕΦ Τμ. Τεχνολογίας Πληροφορικής & Τηλεπικοινωνιών B Εξεταστική Περίοδος, 19 Φεβρουαρίου 2009 ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ι Ηλίας. Κ. Σάββας Α 1) Να γράψετε ένα πρόγραμμα το οποίο να γεμίζει ένα ακέραιο
TEI Λάρισας / ΣΤΕΦ Τμ. Τεχνολογίας Πληροφορικής & Τηλεπικοινωνιών B Εξεταστική Περίοδος, 19 Φεβρουαρίου 2009 ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ι Ηλίας. Κ. Σάββας Α 1) Να γράψετε ένα πρόγραμμα το οποίο να γεμίζει ένα ακέραιο
Σύγχρονα ακολουθιακά κυκλώματα. URL:
 DeÔtero Ex mhno FoÐthshc Σύγχρονα ακολουθιακά κυκλώματα Ge rgioc. Alexandrìpouloc Lèktorac P.D. 47/8 e-mail: alexandg@uop.gr URL: http://users.iit.demokritos.gr/~alexandg Tm ma Epist mhc kai TeqnologÐac
DeÔtero Ex mhno FoÐthshc Σύγχρονα ακολουθιακά κυκλώματα Ge rgioc. Alexandrìpouloc Lèktorac P.D. 47/8 e-mail: alexandg@uop.gr URL: http://users.iit.demokritos.gr/~alexandg Tm ma Epist mhc kai TeqnologÐac
SofÐa ZafeirÐdou: GewmetrÐec
 Tm ma Majhmatik n Panepist mio Patr n Bohjhtikèc Shmei seic gia to mˆjhma GewmetrÐec SofÐa ZafeirÐdou Anaplhr tria Kajhg tria Pˆtra 2018 Oi shmei seic autèc grˆfthkan gia tic anˆgkec tou maj matoc GewmetrÐa.
Tm ma Majhmatik n Panepist mio Patr n Bohjhtikèc Shmei seic gia to mˆjhma GewmetrÐec SofÐa ZafeirÐdou Anaplhr tria Kajhg tria Pˆtra 2018 Oi shmei seic autèc grˆfthkan gia tic anˆgkec tou maj matoc GewmetrÐa.
