Θεωρία τησ Πληροφορίασ (Θ) ΔΙΔΑΚΩΝ: Δρ. Αναςτάςιοσ Πολίτησ
|
|
|
- Βασιλεύς Ζάχος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Θεωρία τησ Πληροφορίασ (Θ) Ενότητα 3: Κωδικοποίηςη Πηγήσ ΔΙΔΑΚΩΝ: Δρ. Αναςτάςιοσ Πολίτησ ΧΟΛΗ ΣΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΣΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗ ΣΕ
2 Άδειεσ Χρήςησ Σο παρόν εκπαιδευτικό υλικό υπόκειται ςε άδειεσ χρήςησ Creative Commons. Για εκπαιδευτικό υλικό, όπωσ εικόνεσ, που υπόκειται ςε άλλου τφπου άδειασ χρήςησ, η άδεια χρήςησ αναφζρεται ρητώσ. Θεωρία της Πληρουορίας - ΣΜΗΜΑ ΜHΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗ ΣΕ
3 Χρηματοδότηςη Σο παρόν εκπαιδευτικό υλικό ζχει αναπτυχθεί ςτα πλαίςια του εκπαιδευτικοφ ζργου του διδάςκοντα. Σο ζργο «Ανοικτά Ακαδημαϊκά Μαθήματα ςτο ΣΕΙ Κεντρικήσ Μακεδονίασ» ζχει χρηματοδοτήςει μόνο τη αναδιαμόρφωςη του εκπαιδευτικοφ υλικοφ. Σο ζργο υλοποιείται ςτο πλαίςιο του Επιχειρηςιακοφ Προγράμματοσ «Εκπαίδευςη και Δια Βίου Μάθηςη» και ςυγχρηματοδοτείται από την Ευρωπαϊκή Ζνωςη (Ευρωπαϊκό Κοινωνικό Σαμείο) και από εθνικοφσ πόρουσ. Θεωρία της Πληρουορίας- ΣΜΗΜΑ ΜHΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗ ΣΕ
4 Ενότητα 3 Κωδικοποίηση Πηγής ΔΙΔΑΚΩΝ: Δρ. Αναστάσιος Πολίτης Θεωρία της Πληρουορίας - ΣΜΗΜΑ ΜHΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗ ΣΕ
5 Κωδικοποίηση Πηγής Coder Decoder Μεταξύ πομπού και καναλιού παρεμβάλλεται ο κωδικοποιητής (coder). Έργο του: η αντικατάσταση των συμβόλων πληροφορίας της πηγής με εναλλακτικά σύμβολα ή λέξεις. 5
6 Κωδικοποίηση Πηγής Λόγοι για την κωδικοποίηση: Συμπίεση στόχος η μείωση του συνολικού μήκους του μηνύματος εξοικονόμηση χώρου αποθήκευσης. μείωση του χρόνου αποστολής. περιορίζει την απαιτούμενη χωρητικότητα διαύλου για την μεταφορά πληροφοριών. Ασφάλεια ο κωδικοποιητής αντιστοιχεί τα σύμβολα πηγής με σύνολο λέξεων που είναι γνωστά μόνο στον πομπό και δέκτη. αποφυγή υποκλοπής και κατανόησης. Ανίχνευση και διόρθωση σφαλμάτων αντικατάσταση συμβόλων πηγής με λέξεις μεγαλύτερου μεγέθους, που περιλαμβάνουν πληροφορίες για το αρχικό μήνυμα. εισαγωγή πλεονάζουσας πληροφορίας. αντίθετη αρχή λειτουργίας με την συμπίεση. Θα μας απασχολήσει η κωδικοποίηση με στόχο την συμπίεση! 6
7 Ορισμοί Ορισμός 1: Κωδικοποίηση είναι η αντικατάσταση συμβόλων ή ομάδων συμβόλων πληροφορίας με νέα εναλλακτικά σύμβολα ή ομάδες συμβόλων. Όρισμός 2: Κώδικας είναι ο αλγόριθμος με τον οποίο πραγματοποιείται η κωδικοποίηση, δηλαδή, η αντικατάσταση συμβόλων από νέα σύμβολα. Ορισμός 3: Τα νέα διακεκριμένα σύμβολα w 1, w 2,, w M που προκύπτουν κατά την κωδικοποίηση ονομάζονται κωδικά σύμβολα. Το πλήθος τους Μ μπορεί να είναι πεπερασμένο ή άπειρο. Ορισμός 4: Το σύνολο W={w 1, w 2,, w M } όλων των κωδικών συμβόλων λέγεται αλφάβητο κωδικοποίησης. Ορισμός 5: Ο κώδικας που έχει M κωδικά σύμβολα ονομάζεται M-αδικός κώδικας. 7
8 Κωδικοποίηση Morse Παραδείγματα Απεικόνιση γραμμάτων αλφαβήτου σε κωδικές λέξεις που σχηματίζονται από τελείες, παύλες και κενά διαστήματα. Κωδικά σύμβολα:. κενό Πλήθος κωδικών συμβόλων M=3 Αλφάβητο Κωδικοποίησης W={., -, κενό} Ο κώδικας Morse είναι ένας 3-αδικός κώδικας. 8
9 Παραδείγματα Κωδικοποίηση ASCII-7 (American Standard Code for Information Interchange) Κωδικά σύμβολα: 0 και 1 Πλήθος κωδικών συμβόλων M=2 Αλφάβητο Κωδικοποίησης W={0,1} Ο κώδικας ASCII-7 είναι ένας 2-αδικός κώδικας 9
10 Ταξινόμηση Κωδίκων Ταξινόμηση με κριτήριο τις απώλειες Κώδικες χωρίς απώλειες Η απεικόνιση της πηγής είναι ένα-προς-ένα (δηλαδή ένα σύμβολο αλφαβήτου πηγής αντιστοιχεί σε ένα σύμβολο αλφαβήτου κωδικοποίησης ή μια κωδική λέξη). Η αποκωδικοποίηση του κωδικού μηνύματος θα μας δώσει το αρχικό μήνυμα (καμία απώλεια). π.χ. Κώδικας Morse. Κώδικες με απώλειες Η απεικόνιση συμβόλων πηγής σε κωδικά σύμβολα είναι πολλά-σεένα. η αποκωδικοποίηση ενδέχεται να μας δώσει διαφορετικό μήνυμα από αυτό που μεταδόθηκε. π.χ. Κωδικοποίηση έγχρωμης εικόνας σε αντίστοιχη με διαβαθμίσεις του γκρί. Θα μας απασχολήσουν ΜΟΝΟ κώδικες χωρίς απώλειες. 10
11 Ταξινόμηση Κωδίκων Ταξινόμηση με κριτήριο το μήκος των κωδικών λέξεων Σταθερού μήκους το μήκος των κωδικών λέξεων είναι σταθερό για κάθε σύμβολο της πηγής Χ. π.χ. ASCII-7 (κάθε χαρακτήρας πηγής κωδικοποιείται με έναν συνδυασμό από 7 δυαδικών ψηφίων). Μεταβλητού μήκους χρησιμοποιούνται για την συμπίεση δεδομένων. Τα σύμβολα πηγής με μεγαλύτερη πιθανότητα εμφάνισης, κωδικοποιούνται με μικρότερου μήκους κωδικές λέξεις. π.χ. Κώδικας Morse το γράμμα Ε που είναι το πιο σύνηθες στην αγγλική αντιστοιχίζεται με μικρότερη κωδική λέξη από το γράμμα Q που είναι το πιο σπάνια εμφανιζόμενο. Δεν μας απασχολούν διαδικασίες ανίχνευσης και διόρθωσης σφαλμάτων Το κανάλι είναι «αθόρυβο» είναι το κανάλι που δέχεται ως είσοδο ένα σύνολο από «κωδικούς χαρακτήρες» και αναπαράγει στην έξοδο του τους χαρακτήρες αυτούς χωρίς πιθανότητα λάθους. (Βλ. Ιδανικός Δίαυλος) 11
12 Αθόρυβη (Noiseless )Κωδικοποίηση Στόχος είναι: η ελαχιστοποίηση του μέσου μήκους της κωδικής λέξης. Συνοπτικά, τα «συστατικά» του προβλήματος της «αθόρυβης κωδικοποίησης» είναι: Η πηγή εισόδου (Χ, P X ) στον ιδανικό δίαυλο με αλφάβητο πηγής Χ={x 1, x 2,, x N } και κατανομή πιθανοτήτων P X ={p 1, p 2,, p N }. Το αλφάβητο κωδικοποίησης W ={w 1, w 2,, w Μ }. Σε κάθε σύμβολο x i πρόκειται να ανατεθεί μία πεπερασμένη ακολουθία από κωδικά σύμβολα η οποία αποτελεί την κωδική λέξη. Π.χ. το σύμβολο x 1 μπορεί να αντιστοιχηθεί στην κωδική λέξη w 1 w 2 και το x 2 στην λέξη w 3 w 7 w 3 w 8. 12
13 Σχεδιαστικά Ζητήματα Κωδίκων Έστω ο παρακάτω δυαδικός κώδικας: x 1 10 x x 3 0 x 4 10 Ποιό είναι το πρόβλημα του κώδικα αυτού; Τα σύμβολα της πηγής x 1 και x 4 αντιστοιχίζονται στην ίδια κωδική λέξη. Ο δέκτης θα παρουσιάζει δυσκολία αποκωδικοποίησης της λέξης «10». Κατά τον σχεδιασμό θα πρέπει να αποφεύγονται τέτοιες αντιστοιχίσεις που οδηγούν σε «σύγχιση» τον δέκτη. Ορισμός: ένας κώδικας που αντιστοιχεί κάθε σύμβολο της πηγής σε διαφορετική κωδική λέξη, λέγεται ευκρινής. Εξασφαλίζουμε την παραπάνω σχεδιαστική απαίτηση αποφεύγοντας να αναθέσουμε την ίδια κωδική λέξη σε παραπάνω από ένα σύμβολα πηγής. 13
14 Σχεδιαστικά Ζητήματα Κωδίκων Έστω ο παρακάτω δυαδικός κώδικας: x 1 0 x x 3 01 x 4 10 Ποιό είναι το πρόβλημα του κώδικα αυτού; Στον δέκτη καταφθάνει η ακολουθία κωδικών συμβόλων «010». Ποιό σύμβολο ή ακολουθία συμβόλων θα προκύψει κατά την αποκωδικοποίηση; Απ.: x 2, x 1 x 4, x 3 x 1 Ο δέκτης δεν είναι σε θέση να αντιληφθεί με απόλυτη βεβαιότητα την αρχή και το τέλος μιας κωδικής λέξης. Είναι επιθυμητό να εξαλειφθούν καταστάσεις σύγχισης όπως η παραπάνω. Ορισμός: ένας κώδικας για τον οποίο κάθε κωδική λέξη αναγνωρίζεται με βεβαιότητα μέσα σε μία μακρά ακολουθία κωδικών συμβόλων λέγεται μονοσήματος. 14
15 Σχεδιαστικά Ζητήματα Κωδίκων Ένας τρόπος για την εξασφάλιση της μονοσημαντικότητας ενός κώδικα, είναι καμία κωδική λέξη να είναι πρόθεμα μιας άλλης. Η ιδιότητα αυτή λέγεται προθεματική ιδιότητα. Προσοχή! ένας κώδικας στον οποίο καμία κωδική λέξη δεν είναι πρόθεμα μιας άλλης, λέμε ότι έχει την προθεματική ιδιότητα. Ένας κώδικας για τον οποίο ισχύει η προθεματική ιδιότητα ονομάζεται στιγμιαία αποκωδικοποιήσιμος. (instantaneous) Πρακτικά, ένας στιγμιαία αποκωδικοποιήσιμος κώδικας επιτρέπει την αποκωδικοποίηση των κωδικών λέξεων που βρίσκονται σε μια ακολουθία χωρίς να χρειάζεται να εξεταστούν οι γειτονικές (στιγμιαία). x 1 x 2 x Λαμβανόμενη ακολουθία: Αποκωδικοποίηση: x 2 x 1 x 1 x 1 x 3 x 1 15
16 Σχεδιαστικά Ζητήματα Κωδίκων Κάθε στιγμιαία αποκωδικοποιήσιμος κώδικας είναι και μονοσήμαντος. Δεν ισχύει το αντίστροφο! Παράδειγμα x 1 1 x 2 x 3 x Δεν ισχύει η προθεματική ιδιότητα μη στιγμιαία αποκωδικοποιήσιμος, αλλά ο κώδικας είναι μονοσήμαντος! Κάθε μονοσήμαντος κώδικας είναι και ευκρινής. Δεν ισχύει το αντίστροφο! Παράδειγμα x 1 0 x 2 x 3 x Ο κώδικας είναι ευκρινής αλλά η ακολουθία 0110 οδηγεί είτε σε x 2 x 3 είτε σε x 1 x 4 x 1 Κάθε ευκρινής κώδικας σταθερού μήκους είναι και στιγμιαία αποκωδικοποιήσημος. 16
17 Γενικά ισχύει: Σχεδιαστικά Ζητήματα Κωδίκων Κ: όλοι οι κώδικες Ε: Ευκρινείς Μ: Μονοσήμαντοι Σ: Στιγμιαία Απαοκωδικοποιήσιμοι Περιπτώσεις: Ένας Σ κώδικας είναι αυτομάτως και Μ και Ε. Ένας Μ κώδικας είναι αυτομάτως και Ε αλλά μπορεί να μην είναι Σ. Ένας Ε κώδικας μπορεί να μην είναι Μ ή/και Σ. (Στην περίπτωση σταθερού μήκους είναι αυτομάτως και Σ και Μ) Ένας κώδικας που δεν είναι Σ μπορεί να είναι Μ. Ένας κώδικας που δεν είναι Μ μπορεί να είναι Ε. Ένας κώδικας που δέν είναι Ε δεν είναι Σ και Μ. 17
18 Εφαρμογές Εφαρμογή Ι: Να ταξινομηθούν οι παρακάτω κώδικες. Σύμβολο Κώδικας Α Κώδικας Β Κώδικας Γ Κώδικας Δ x x x x Ταξινόμιση Κώδικας Α Κώδικας Β Κώδικας Γ Κώδικας Δ Ευκρινής x Μονοσήμαντος x x Στιγμιαία αποκωδικοποιήσιμος x x x 18
19 Εφαρμογές Εφαρμογή ΙΙ: Να ταξινομηθούν οι παρακάτω κώδικες. Σύμβολο Κώδικας Α Κώδικας Β Κώδικας Γ Κώδικας Δ Κώδικας E x x x x Ταξινόμιση Κώδικας Α Κώδικας Β Κώδικας Γ Κώδικας Δ Κώδικας E ευκρινής Μονοσήμαντος X Στιγμιαία αποκωδικοποιήσιμος X X 19
20 Έλεγχος Μονοσημαντικότητας Ένας κώδικας που δεν είναι στιγμιαία αποκωδικοποιήσιμος μπορεί να είναι μονοσήμαντος. Είναι δυνατόν να ελέγξουμε πολύπλοκους κώδικες ως προς την μονοσημαντικότητα ακολουθώντας έναν έλεγχο που ονομάζεται Έλεγχος Sardinas-Patterson και παρουσιάζεται εδώ χωρίς απόδειξη. Η τεχνική βασίζεται στην διαδοχική κατασκευή συνόλων και έλεγχο των στοιχείων τους. Έστω ότι διαθέτουμε τον παρακάτω κώδικα: Κώδικας x 1 a Παρατηρούμε οτι ο κώδικας δεν είναι στιγμιαία αποκωδικοποιήσιμος: η κωδική λέξη (σύμβολο) «a» είναι πρόθεμα των «ad» και «abb». x 2 x 3 x 4 x 5 x 6 x 7 c ad abb bad deb bbcde 20
21 Έλεγχος Μονοσημαντικότητας Κατασκευάζουμε βήμα-βήμα μία ακολουθία από σύνολα S 0, S 1, S 2,, S n όπως παρακάτω: Το πρώτο σύνολο S 0 έχει ως στοιχεία τις αρχικές κωδικές λέξεις. Για την κατασκευή του S 1 συγκρίνουμε όλες τις κωδικές λέξεις μέσα στο S 0. Εάν μια κωδική λέξη είναι πρόθεμα μιας άλλης, τότε το επίθεμα (αυτό που απομένει δηλαδή) της τελευταίας εισάγεται ως στοιχείο στο S 1. Κώδικας Σύνολα x 1 x 2 x 3 x 4 x 5 x 6 x 7 a c ad abb bad deb bbcde S 0 S 1 a c ad abb bad deb bbcde d bb Κατόπιν εκτελούμε τον ακόλουθο έλεγχο: Υπάρχει κάποιο στοιχείο των δύο συνόλων που είναι ίδια; Ναι; Τότε ο κώδικας δεν είναι μονοσήμαντος. Όχι; Η διαδικασία συνεχίζεται όπως παρακάτω. 21
22 Έλεγχος Μονοσημαντικότητας Για τα υπόλοιπα σύνολα S n, n>1 συγκρίνουμε τα στοιχεία των S 0 και S n-1 και ψαχνουμε για κωδικές λέξεις του ενός συνόλου που είναι πρόθεμα του άλλου. Το επίθεμα τοποθετείται στο νέο σύνολο. Περιπτώσεις: Εάν δεν βρεθούν επιθέματα τότε το S n είναι το κενό σύνολο και η διαδικασία σταματά. Ο κώδικας είναι μονοσήμαντος. Εάν το προκύπτον σύνολο S n είναι ίσο με κάποιο από τα προηγούμενα σύνολα εκτός του S 0 η διαδικασία σταματά. Ο κώδικας είναι μονοσήμαντος. Εάν κάποιο από τα στοιχεία του S n είναι ίδιο με κάποιο από τα στοιχεία του S 0 η διαδικασία σταματά. Ο κώδικας δεν είναι μονοσήμαντος. Εάν δεν συμβεί τίποτε από τα παραπάνω η διαδικασία συνεχίζεται ομοίως. 22
23 Έλεγχος Μονοσημαντικότητας Κώδικας x 1 x 2 x 3 x 4 x 5 x 6 x 7 a c ad abb bad deb bbcde Σύνολα S 0 S 1 S 2 S 3 S 4 S 5 S 6 S 7 S 8 a d eb de b ad d eb {empty} c ad abb bad deb bbcde bb cde bcde Ο παραπάνω κώδικας δεν είναι στιγμιαία αποκωδικοποιήσιμος διότι ένα στοιχείο του S 5 είναι ίδιο με ένα στοιχείο του S 0 («ad»). 23
24 Εφαρμογές Εφαρμογή Ι: Να ελεγχθεί ως προς την μονοσημαντικότητα ο παρακάτω κώδικας: x x x 3 x 4 x 5 x 6 x 7 x Εφαρμογή ΙΙ: Να ελεγχθεί ως προς την μονοσημαντικότητα ο παρακάτω κώδικας: x1 S0 S1 S2 S3 S4 S5 S6 S7 S8 S9 S10 x 2 x 3 x 4 x 5 x 6 x 7 x 8 abc abcd e dba bace ceac ceab eabd Απ: S0 S1 S2 S3 S4 S5 S abc d ba ce ac c eac ac c eac ac abcd abd ab cd eab ab cd eab ab e dba bace ceac ceab eabd Απ: d ba ce d 24
25 Δενδροδιάγραμμα Απόφασης Ένας στιγμιαία αποκωδικοποιήσιμος κώδικας μπορεί να αναπαρασταθεί με ένα δενδροδιάγραμμα. Δενδροδιάγραμμα: γράφος με τα εξής στοιχεία: ρίζα κόμβους ή φύλλα ένας κόμβος λέγεται φύλο όταν αναπαριστά ένα σύμβολο πηγής. ακμές (κατευθυνόμενες). Παράδειγμα: 25
26 Δενδροδιάγραμμα Απόφασης Χαρακτηριστικά δενδροδιαγράμματος: επίπεδα όσα και το μήκος της μεγαλύτερης κωδικής λέξης (μη συμπεριλαμβανομένου του επιπέδου της ρίζας) λέγεται και ύψος του δένδρου φύλλα όσα και τα σύμβολα της πηγής (μπορεί και να μην είναι στο υψηλότερο επίπεδο) κατευθυνόμενες ακμές που εκκινούν από κάθε κόμβο το πολύ όσες και τα κωδικά σύμβολα Σύμβολα πηγής Επίπεδο 3 Επίπεδο 2 Ακμές = Μ Επίπεδο 1 Επίπεδο 0 26
27 Δενδροδιάγραμμα Απόφασης Το δενδροδιάγραμμα είναι σημαντικό εργαλείο για την γρήγορη αποκωδικοποίηση ενός κωδικού μηνύματος. Διαδικασία αποκωδικοποίησης ενός μηνύματος: 1. Ξεκινάμε από την ρίζα 2. Με την λήψη ενός κωδικού συμβόλου, μεταβαίνουμε στον κόμβο του αμέσως υψηλότερου επιπέδου μέσω της ακμής που αντιστοιχεί στο ληφθέν σύμβολο. 3. Επαναλαμβάνουμε το 2 ο βήμα μέχρι να φθάσουμε σε φύλλο και καταγράφουμε το σύμβολο της πηγής που αντιστοιχεί σε αυτό. 4. Μεταβαίνουμε στην ρίζα του δένδρου και επαναλαμβάνουμε την διαδικασία 27
28 Δενδροδιάγραμμα Απόφασης Παράδειγμα: λαμβάνουμε την ακολουθία « » Ακολουθία Συμβόλων Πηγής: ΒΔΓ 28
29 Εφαρμογές Εφαρμογή Ι: Έστω ο στιγμιαία αποκωδικοποιήσιμος κώδικας {010,101,111,001} που κωδικοποιεί μία πηγή με αλφάβητο {A,B,C,D}. Να φτιάξετε το δενδροδιάγραμμα. Να αποκωδικοποιηθεί το μήνυμα με τη χρήση του δενδροδιαγράμματος. Απ.: DADA Εφαρμογή ΙΙ: Έστω ο στιγμιαία αποκωδικοποιήσιμος κώδικας {a,c,d,bb,bad,eb,bcde} που κωδικοποιεί μία πηγή με αλφάβητο {x 1,x 2,x 3,x 4,x 5,x 6,x 7 }. Να φτιάξετε το δενδροδιάγραμμα. Να αποκωδικοποιηθεί το μήνυμα cbbbcdebaddad με τη χρήση του δενδροδιαγράμματος. Απ.: x 2 x 4 x 7 x 5 x 3 x 1 x 3 29
30 Οι Ταυτοανισότητες Kraft - McMillan Ταυτοανισότητα McMillan: Τα μήκη των κωδικών λέξεων l 1,l 2,,l N ενός μονοσήμαντου Μ-αδικού κώδικα θα πρέπει να ικανοποιούν την ταυτοανισότητα: N i1 M 1 Ταυτοανισότητα Kraft: Υπάρχει στιγμιαία αποκωδικοποιήσιμος Μ-αδικός κώδικας με μήκη κωδικών λέξεων l 1,l 2,,l N, αν και μόνο αν ισχύει η παρακάτω ταυτοανισότητα: N i1 M Και οι δύο ταυτοανισότητες αναφέρονται στην ύπαρξη ή όχι στιγμιαίου αποκωδικοποιήσιμου κώδικα (Kraft) ή μονοσήμαντου (McMillan) εφόσον γνωρίζουμε τα μήκη l i των κωδικών λέξεων: l i l i 1 30
31 Παραδείγματα Έστω ο στιγμιαία αποκωδικοποιήσιμος κώδικας: Κώδικας Μήκη A 0 1 B C D N i1 M l i Έστω ο μονοσήμαντος κώδικας: Κώδικας Μήκη A B C D N i1 M l i Έστω ο κώδικας: Κώδικας Μήκη A 0 1 B C D N i1 M l i
32 Οι Ταυτοανισότητες Kraft - McMillan Παρατηρήσεις: Οι ταυτοανισότητες Kraft-McMillan δεν λένε ότι: ένας συγκεκριμένος Μ-αδικός κώδικας με συγκεκριμένα μήκη κωδικών λέξεων είναι στιγμιαία αποκωδικοποιήσιμος ή μονοσήμαντος. Εάν ξέρουμε ότι ένας συγκεκριμένος Μ-αδικός κώδικας με δεδομένα μήκη κωδικών λέξεων είναι μονοσήμαντος τότε θα υπάρχει και στιγμιαία αποκωδικοποιήσιμος κώδικας με αυτά τα μήκη λέξεων. Ένας μονοσήμαντος κώδικας δεν παρουσιάζει ενδιαφέρον διότι θα υπάρχει στιγμιαία αποκωδικοποιήσιμος κώδικας με τα ίδια μήκη λέξεων που θα αποκωδικοποιείται με μεγαλύτερη ευκολία. 32
33 Οι Ταυτοανισότητες Kraft - McMillan Εάν η ταυτοανισότητα Kraft ισχύει ως ανισότητα τότε ο κώδικας έχει πλεόνασμα (redundancy) Πρακτικά μπορούμε να προσθέσουμε και νέα κωδική λέξη. N i1 M l i Εάν η ταυτοανισότητα Kraft ισχύει ως ισότητα τότε ο κώδικας θεωρείται ολόκληρος (complete) χωρίς πλεονασμό Πρακτικά δεν μπορούμε να προσθέσουμε και νέα κωδική λέξη. N i1 M l i 1 Ποιόν από τους δύο κώδικες θα επιλέγατε; Θα μπορούσατε να προτείνετε έναν καλύτερο; 33
34 Μέσο Μήκος Κώδικα Εάν θεωρήσουμε: Πηγή πληροφορίας με Αλφάβητο Χ={x 1,x 2,,x N } και Κατανομή P X ={p 1,p 2,,p N } M-αδικό Κώδικα με Αλφάβητο W={w 1,w 2,,w M } Ότι κάθε σύμβολο της πηγής x i αντιστοιχίζεται σε μία κωδική λέξη u i με μήκος l i Ορίζουμε Μέσο Μήκος Κώδικα: L N i1 p i l i Εκφράζει το μέσο αριθμό των κωδικών συμβόλων ανά σύμβολο πηγής. Παράδειγμα ASCII-7 μέσο μήκος: 7-bit δεν υπολογίζονται οι πιθανότητες εμφάνισης των συμβόλων πηγής σύμβολα με μικρή πιθανότητα εμφάνισης κωδικοποιούνται όπως και τα σύμβολα με μεγάλη πιθανότητα εμφάνισης Δεν είναι η βέλτιστη λύση στην «αθόρυβη κωδικοποίηση» 34
35 Βέλτιστος Κώδικας Είναι ο στιγμιαία αποκωδικοποιήσιμος κώδικας με το μικρότερο μέσο μήκος κώδικα: L * l 1, min l 2 { L} min Ο σχεδιασμός του βέλτιστου κώδικα απαιτεί τον προσδιορισμό των μηκών των κωδικών λέξεων που ελαχιστοποιούν το μέσο μήκος. { N,..., ln l1, l2,..., ln i1 p i l } Αποδεικνύεται ότι τα μήκη των κωδικών λέξεων του βέλτιστου στιγμιαία αποκωδικοποιήσιμου κώδικα είναι ίσα με: i l * i log ( p ) 1 M i i N Άρα, για δυαδικό κώδικα θα ισχύει: * L H ( X ) 35
36 Εφαρμογές Εφαρμογή Ι: Υπάρχει δυαδικός στιγμιαία αποκωδικοποιήσιμος κώδικας με κωδικές λέξεις μήκους {1,4,3,3,2,3}; Απ.: 19/16, όχι δεν υπάρχει. Εφαρμογή ΙΙ: Υπάρχει τριαδικός στιγμιαία αποκωδικοποιήσιμος κώδικας με κωδικές λέξεις μήκους {1,2,3,3,2,3}; Απ.: 18/27, υπάρχει. Εφαρμογή ΙΙΙ: Ποιοί από τους παρακάτω στιγμιαία αποκωδικοποιήσιμους κώδικες έχουν πλεονασμό και ποιοί όχι. I II III Απ.: Οι ΙΙ και ΙΙΙ έχουν. Ο Ι δεν έχει. Για τον ΙΙ: {010} Για τον ΙΙΙ: {0000} Αναφέρατε από μια κωδική λέξη που μπορούμε να προσθέσουμε στους κώδικες με πλεονασμό για να τους μετατρέψουμε σε ολόκληρους. 36
37 Εφαρμογές Εφαρμογή ΙV (Εξεταστική 2007): Παρακάτω δίνεται πίνακας με 4 κώδικες κωδικοποίησης τεσσάρων συμβόλων πηγής, καθώς και οι πιθανότητες εμφάνισης των συμβόλων. a) Να ταξινομηθούν οι κώδικες. b) Να υπολογιστεί το μέσο μήκος τους. c) Εάν έπρεπε να επιλέξουμε έναν από τους παρακάτω κώδικες ποιος θα ήταν ο βέλτιστος και γιατί? x i p i I II III IV A B C D
38 Ασκήσεις Επανάληψης Εφαρμογή Ι (Εξεταστική 2010): Δίνεται ο εξής κώδικας: Α:000, Β:001, Γ:01, Δ:10, Ε:11. Μπορούμε να προσθέσουμε ένα ακόμα σύμβολο Ζ (με την κατάλληλη κωδικοποίηση) έτσι ώστε ο νέος κώδικας που θα προκύψει να είναι στιγμιαία αποκωδικοποιήσιμος; Απ: Ναί Εφαρμογή ΙΙ (Εξεταστική 2009): α) Έστω ότι για έναν τριαδικό κώδικα γνωρίζουμε τα μήκη των κωδικών λέξεων που είναι τα εξής {1,2,3,1,2,3,1}. Ο κώδικας αυτός i) Είναι σίγουρα στιγμιαία αποκωδικοποιήσιμος ii) Σίγουρα δεν είναι στιγμιαία αποκωδικοποιήσιμος iii) Μπορεί ναι, μπορεί και όχι (πρέπει να γνωρίζουμε τις κωδικές λέξεις για να αποφανθούμε) β) Επιλύστε το παραπάνω ερώτημα για έναν κώδικα με τα εξής μήκη {1,2,3,3,2,3}. Εφαρμογή ΙΙΙ (Εξεταστική 2009): Έστω Μ-αδικός ευκρινής κώδικας σταθερού μήκους (k κωδικών λέξεων με μήκος l η κάθε μία) α) Τι πρέπει να προσέξουμε στην κατασκευή της νέας κωδικής λέξης έτσι ώστε ο νέος κώδικας να είναι στιγμιαία αποκωδικοποιήσιμος; β) Σε ποιά περίπτωση δεν μπορεί να κατασκευαστεί στιγμιαία αποκωδικοποιήσιμος κώδικας με τον παραπάνω τρόπο; Απ: α) το ii), β) το iii) 38
39 Ασκήσεις Επανάληψης Εφαρμογή ΙV (Εξεταστική 2009): Έστω ότι δίνεται ένας κώδικας ο οποίος είναι μονοσήμαντος αλλά όχι στιγμιαία αποκωδικοποιήσιμος. Μας ζητείται να μετατρέψουμε τον κώδικα αυτό σε στιγμιαία αποκωδικοποιήσιμο με την παρακάτω διαδικασία: Σε μερικές (ή όλες) τις κωδικές λέξεις αλλάζουμε τα σύμβολα τους (όσα επιθυμούμε και όπως εμείς επιθυμούμε) χωρίς όμως να προσθέσουμε ή να αφαιρέσουμε σύμβολο. (π.χ. Εάν είναι δυαδικός κώδικας κάποια μηδενκά μπορώ να τα κάνω άσσους και το αντίστροφο) Πότε μπορούμε με την παραπάνω διαδικασία να μετατρέψουμε έναν μονοσήμαντο αλλά μη στιγμιαία αποκωδικοποιήσιμο κώδικα σε στιγμιαία αποκωδικοποήσιμο: Ποτέ (κανένας μονοσήμαντος και μή στιγμιαία αποκωδικοποιήσιμος κώδικας δεν μπορεί να μετατραπεί σε στιγμιαία αποκωδικοποιήσιμο με την παραπάνω διαδικασία). Μερικές φορές (μπορεί να γίνει, αλλά για κάποιους μονοσήμαντους και μη στιγμαία αποκωδικοποιήσιμους κώδικες μόνο). Πάντα (μπορεί να γίνει για όλους τους μονοσήμαντους και μη στιγμιαία αποκωδικοποιήσιμους κώδικες). Απ: Πάντα 39
40 Σέλος Ενότητας Θεωρία της Πληρουορίας - ΣΜΗΜΑ ΜHΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗ ΣΕ
Κωδικοποίηση Πηγής. Δρ. Α. Πολίτης
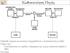 Κωδικοποίηση Πηγής Coder Decoder Μεταξύ πομπού και καναλιού παρεμβάλλεται ο κωδικοποιητής (coder). Έργο του: η αντικατάσταση των συμβόλων πληροφορίας της πηγής με εναλλακτικά σύμβολα ή λέξεις. Κωδικοποίηση
Κωδικοποίηση Πηγής Coder Decoder Μεταξύ πομπού και καναλιού παρεμβάλλεται ο κωδικοποιητής (coder). Έργο του: η αντικατάσταση των συμβόλων πληροφορίας της πηγής με εναλλακτικά σύμβολα ή λέξεις. Κωδικοποίηση
Κωδικοποίηση Πηγής. Η λειτουργία ενός συστήματος επικοινωνίας (γενικό διάγραμμα):
 Κωδικοποίηση Πηγής Η λειτουργία ενός συστήματος επικοινωνίας (γενικό διάγραμμα): Coder Decoder Μεταξύ πομπού-καναλιού παρεμβάλλεται ο κωδικοποιητής (coder). Έργο του: η αντικατάσταση των συμβόλων πληροφορίας
Κωδικοποίηση Πηγής Η λειτουργία ενός συστήματος επικοινωνίας (γενικό διάγραμμα): Coder Decoder Μεταξύ πομπού-καναλιού παρεμβάλλεται ο κωδικοποιητής (coder). Έργο του: η αντικατάσταση των συμβόλων πληροφορίας
Θεωρία τησ Πληροφορίασ (Θ) ΔΙΔΑΚΩΝ: Δρ. Αναςτάςιοσ Πολίτησ
 Θεωρία τησ Πληροφορίασ (Θ) Ενότητα 4: Συμπίεςη χωρίσ Απώλειεσ ΔΙΔΑΚΩΝ: Δρ. Αναςτάςιοσ Πολίτησ ΧΟΛΗ ΣΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΣΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗ ΣΕ Άδειεσ Χρήςησ Σο παρόν εκπαιδευτικό υλικό υπόκειται
Θεωρία τησ Πληροφορίασ (Θ) Ενότητα 4: Συμπίεςη χωρίσ Απώλειεσ ΔΙΔΑΚΩΝ: Δρ. Αναςτάςιοσ Πολίτησ ΧΟΛΗ ΣΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΣΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗ ΣΕ Άδειεσ Χρήςησ Σο παρόν εκπαιδευτικό υλικό υπόκειται
Συμπίεση χωρίς Απώλειες
 Συμπίεση χωρίς Απώλειες Στόχοι της συμπίεσης δεδομένων: Μείωση του απαιτούμενου χώρου αποθήκευσης των δεδομένων. Περιορισμός της απαιτούμενης χωρητικότητας διαύλου επικοινωνίας για την μετάδοση. μείωση
Συμπίεση χωρίς Απώλειες Στόχοι της συμπίεσης δεδομένων: Μείωση του απαιτούμενου χώρου αποθήκευσης των δεδομένων. Περιορισμός της απαιτούμενης χωρητικότητας διαύλου επικοινωνίας για την μετάδοση. μείωση
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ. Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Διακριτές Πηγές Πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Διακριτές Πηγές Πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
Δομές Δεδομένων και Αλγόριθμοι
 Δομές Δεδομένων και Αλγόριθμοι Χρήστος Γκόγκος ΤΕΙ Ηπείρου Χειμερινό Εξάμηνο 2014-2015 Παρουσίαση 20 Huffman codes 1 / 12 Κωδικοποίηση σταθερού μήκους Αν χρησιμοποιηθεί κωδικοποίηση σταθερού μήκους δηλαδή
Δομές Δεδομένων και Αλγόριθμοι Χρήστος Γκόγκος ΤΕΙ Ηπείρου Χειμερινό Εξάμηνο 2014-2015 Παρουσίαση 20 Huffman codes 1 / 12 Κωδικοποίηση σταθερού μήκους Αν χρησιμοποιηθεί κωδικοποίηση σταθερού μήκους δηλαδή
Εισαγωγή στην Πληροφορική & τον Προγραμματισμό
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στην Πληροφορική & τον Προγραμματισμό Ενότητα 3 η : Κωδικοποίηση & Παράσταση Δεδομένων Ι. Ψαρομήλιγκος Χ. Κυτάγιας Τμήμα
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στην Πληροφορική & τον Προγραμματισμό Ενότητα 3 η : Κωδικοποίηση & Παράσταση Δεδομένων Ι. Ψαρομήλιγκος Χ. Κυτάγιας Τμήμα
Πληροφορική. Ενότητα 4 η : Κωδικοποίηση & Παράσταση Δεδομένων. Ι. Ψαρομήλιγκος Τμήμα Λογιστικής & Χρηματοοικονομικής
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Πληροφορική Ενότητα 4 η : Κωδικοποίηση & Παράσταση Δεδομένων Ι. Ψαρομήλιγκος Τμήμα Λογιστικής & Χρηματοοικονομικής Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Πληροφορική Ενότητα 4 η : Κωδικοποίηση & Παράσταση Δεδομένων Ι. Ψαρομήλιγκος Τμήμα Λογιστικής & Χρηματοοικονομικής Άδειες Χρήσης
Θεωρία Πληροφορίας. Διάλεξη 4: Διακριτή πηγή πληροφορίας χωρίς μνήμη. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Θεωρία Πληροφορίας Διάλεξη 4: Διακριτή πηγή πληροφορίας χωρίς μνήμη Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Διακριτή πηγή πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
Θεωρία Πληροφορίας Διάλεξη 4: Διακριτή πηγή πληροφορίας χωρίς μνήμη Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Διακριτή πηγή πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 7β: Όρια Αλγόριθμων Ταξινόμησης Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commos.
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 7β: Όρια Αλγόριθμων Ταξινόμησης Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commos.
Εισαγωγή στους Ηλεκτρονικούς Υπολογιστές. 5 ο Μάθημα. Λεωνίδας Αλεξόπουλος Λέκτορας ΕΜΠ. url:
 στους Ηλεκτρονικούς Υπολογιστές 5 ο Μάθημα Λεωνίδας Αλεξόπουλος Λέκτορας ΕΜΠ email: leo@mail.ntua.gr url: http://users.ntua.gr/leo Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
στους Ηλεκτρονικούς Υπολογιστές 5 ο Μάθημα Λεωνίδας Αλεξόπουλος Λέκτορας ΕΜΠ email: leo@mail.ntua.gr url: http://users.ntua.gr/leo Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Εισαγωγή στην Επιστήμη των Υπολογιστών
 Εισαγωγή στην Επιστήμη των Υπολογιστών Ενότητα 2: Αποθήκευση Δεδομένων: Κώδικες, 1ΔΩ Τμήμα: Αγροτικής Οικονομίας & Ανάπτυξης Διδάσκων: Θεόδωρος Τσιλιγκιρίδης Μαθησιακοί Στόχοι Η Ενότητα 2 διαπραγματεύεται
Εισαγωγή στην Επιστήμη των Υπολογιστών Ενότητα 2: Αποθήκευση Δεδομένων: Κώδικες, 1ΔΩ Τμήμα: Αγροτικής Οικονομίας & Ανάπτυξης Διδάσκων: Θεόδωρος Τσιλιγκιρίδης Μαθησιακοί Στόχοι Η Ενότητα 2 διαπραγματεύεται
Λογική Δημήτρης Πλεξουσάκης Φροντιστήριο 6: Προτασιακός Λογισμός: Μέθοδος Επίλυσης Τμήμα Επιστήμης Υπολογιστών
 Λογική Δημήτρης Πλεξουσάκης Φροντιστήριο 6: Προτασιακός Λογισμός: Μέθοδος Επίλυσης Τμήμα Επιστήμης Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται στην άδεια χρήσης Creative Commons και
Λογική Δημήτρης Πλεξουσάκης Φροντιστήριο 6: Προτασιακός Λογισμός: Μέθοδος Επίλυσης Τμήμα Επιστήμης Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται στην άδεια χρήσης Creative Commons και
Τεχνολογία Πολυμέσων. Ενότητα # 7: Θεωρία πληροφορίας Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 7: Θεωρία πληροφορίας Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα.
Τεχνολογία Πολυμέσων Ενότητα # 7: Θεωρία πληροφορίας Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα.
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2014-2015 Ρυθμός κωδικοποίησης Ένας κώδικας που απαιτεί L bits για την κωδικοποίηση μίας συμβολοσειράς N συμβόλων που εκπέμπει μία πηγή έχει ρυθμό κωδικοποίησης (μέσο μήκος λέξης) L
Συμπίεση Δεδομένων 2014-2015 Ρυθμός κωδικοποίησης Ένας κώδικας που απαιτεί L bits για την κωδικοποίηση μίας συμβολοσειράς N συμβόλων που εκπέμπει μία πηγή έχει ρυθμό κωδικοποίησης (μέσο μήκος λέξης) L
Κεφάλαιο 2 Πληροφορία και εντροπία
 Κεφάλαιο 2 Πληροφορία και εντροπία Άσκηση. Έστω αλφάβητο Α={0,} και δύο πηγές p και q. Έστω οτι p(0)=-r, p()=r, q(0)=-s και q()=s. Να υπολογιστούν οι σχετικές εντροπίες Η(Α,p/q) και Η(Α,q/p). Να γίνει
Κεφάλαιο 2 Πληροφορία και εντροπία Άσκηση. Έστω αλφάβητο Α={0,} και δύο πηγές p και q. Έστω οτι p(0)=-r, p()=r, q(0)=-s και q()=s. Να υπολογιστούν οι σχετικές εντροπίες Η(Α,p/q) και Η(Α,q/p). Να γίνει
Θέματα Συστημάτων Πολυμέσων
 Θέματα Συστημάτων Πολυμέσων Ενότητα # 6: Στοιχεία Θεωρίας Πληροφορίας Διδάσκων: Γεώργιος K. Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Θέματα Συστημάτων Πολυμέσων Ενότητα # 6: Στοιχεία Θεωρίας Πληροφορίας Διδάσκων: Γεώργιος K. Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Τεχνολογία Πολυμέσων. Ενότητα # 9: Κωδικοποίηση εντροπίας Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 9: Κωδικοποίηση εντροπίας Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του
Τεχνολογία Πολυμέσων Ενότητα # 9: Κωδικοποίηση εντροπίας Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του
Υπολογιστικά & Διακριτά Μαθηματικά
 Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 3: Σύνολα Συνδυαστική Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 3: Σύνολα Συνδυαστική Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ
 ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ Ενότητα 10: Συνδυασμοί μηχανών Turing Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ Ενότητα 10: Συνδυασμοί μηχανών Turing Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Θεωρία Υπολογισμού Ενότητα 8: Πεπερασμένα Αυτόματα Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Θεωρία Υπολογισμού Ενότητα 8: Πεπερασμένα Αυτόματα Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος
 Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος Χιωτίδης Γεώργιος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος Χιωτίδης Γεώργιος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Πανεπιστήμιο Δυτικής Μακεδονίας. Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών. Ψηφιακή Σχεδίαση
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 9: Ελαχιστοποίηση και Κωδικοποίηση Καταστάσεων, Σχεδίαση με D flip-flop, Σχεδίαση με JK flip-flop, Σχεδίαση με T flip-flop Δρ. Μηνάς
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 9: Ελαχιστοποίηση και Κωδικοποίηση Καταστάσεων, Σχεδίαση με D flip-flop, Σχεδίαση με JK flip-flop, Σχεδίαση με T flip-flop Δρ. Μηνάς
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Θεωρία Υπολογισμού Ενότητα 14: Γραμματικές Χωρίς Συμφραζόμενα Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Θεωρία Υπολογισμού Ενότητα 14: Γραμματικές Χωρίς Συμφραζόμενα Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Εισαγωγή στους Ηλεκτρονικούς Υπολογιστές. 6 ο Μάθημα. Λεωνίδας Αλεξόπουλος Λέκτορας ΕΜΠ. url:
 στους Ηλεκτρονικούς Υπολογιστές 6 ο Μάθημα Λεωνίδας Αλεξόπουλος Λέκτορας ΕΜΠ email: leo@mail.ntua.gr url: http://users.ntua.gr/leo Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
στους Ηλεκτρονικούς Υπολογιστές 6 ο Μάθημα Λεωνίδας Αλεξόπουλος Λέκτορας ΕΜΠ email: leo@mail.ntua.gr url: http://users.ntua.gr/leo Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Θεωρία Υπολογισμού Ενότητα 7: Πεπερασμένη αναπαράσταση γλωσσών Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Θεωρία Υπολογισμού Ενότητα 7: Πεπερασμένη αναπαράσταση γλωσσών Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
ΠΛΗΡΟΦΟΡΙΚΗ Ι Ενότητα 8: Συστήματα αρίθμησης
 ΠΛΗΡΟΦΟΡΙΚΗ Ι Ενότητα 8: Συστήματα αρίθμησης Μιχάλης Δρακόπουλος Σχολή Θετικών επιστημών Τμήμα Μαθηματικών ΠΛΗΡΟΦΟΡΙΚΗ Ι (MATLAB) Ενότητα 8 Σημειώσεις βασισμένες στο βιβλίο Το MATLAB στην Υπολογιστική
ΠΛΗΡΟΦΟΡΙΚΗ Ι Ενότητα 8: Συστήματα αρίθμησης Μιχάλης Δρακόπουλος Σχολή Θετικών επιστημών Τμήμα Μαθηματικών ΠΛΗΡΟΦΟΡΙΚΗ Ι (MATLAB) Ενότητα 8 Σημειώσεις βασισμένες στο βιβλίο Το MATLAB στην Υπολογιστική
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Διακριτές Πηγές Πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 3 : Πηγές Πληροφορίας Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Διακριτές Πηγές Πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
Ψηφιακή Σχεδίαση. Ενότητα: ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ No:01. Δρ. Μηνάς Δασυγένης. Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών
 Ψηφιακή Σχεδίαση Ενότητα: ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ No:01 Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Εργαστήριο Ψηφιακών Συστημάτων και Αρχιτεκτονικής Υπολογιστών http:
Ψηφιακή Σχεδίαση Ενότητα: ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ No:01 Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Εργαστήριο Ψηφιακών Συστημάτων και Αρχιτεκτονικής Υπολογιστών http:
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 10 : Κωδικοποίηση καναλιού Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Απόσταση και βάρος Hamming Τεχνικές και κώδικες ανίχνευσης &
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 10 : Κωδικοποίηση καναλιού Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Απόσταση και βάρος Hamming Τεχνικές και κώδικες ανίχνευσης &
Υπολογιστικά & Διακριτά Μαθηματικά
 Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 8: Σχέσεις - Πράξεις Δομές Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 8: Σχέσεις - Πράξεις Δομές Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
Τηλεπικοινωνιακά Συστήματα ΙΙ
 Τηλεπικοινωνιακά Συστήματα ΙΙ Διάλεξη 11: Κωδικοποίηση Πηγής Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Αλγόριθμοι κωδικοποίησης πηγής Αλγόριθμος Fano Αλγόριθμος Shannon Αλγόριθμος Huffman
Τηλεπικοινωνιακά Συστήματα ΙΙ Διάλεξη 11: Κωδικοποίηση Πηγής Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Αλγόριθμοι κωδικοποίησης πηγής Αλγόριθμος Fano Αλγόριθμος Shannon Αλγόριθμος Huffman
Υπολογιστικά & Διακριτά Μαθηματικά
 Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 4: Διατάξεις Μεταθέσεις Συνδυασμοί Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 4: Διατάξεις Μεταθέσεις Συνδυασμοί Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Εισαγωγή στους Ηλεκτρονικούς Υπολογιστές. 4 ο Μάθημα. Λεωνίδας Αλεξόπουλος Λέκτορας ΕΜΠ. url:
 στους Ηλεκτρονικούς Υπολογιστές 4 ο Μάθημα Λεωνίδας λεξόπουλος Λέκτορας ΕΜΠ email: leo@mail.ntua.gr url: http://users.ntua.gr/leo Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
στους Ηλεκτρονικούς Υπολογιστές 4 ο Μάθημα Λεωνίδας λεξόπουλος Λέκτορας ΕΜΠ email: leo@mail.ntua.gr url: http://users.ntua.gr/leo Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
2 n N: 0, 1,..., n A n + 1 A
 Θεωρία Υπολογισμού Ενότητα 5: Τεχνικές απόδειξης & Κλειστότητα Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Θεωρία Υπολογισμού Ενότητα 5: Τεχνικές απόδειξης & Κλειστότητα Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα. Αρχιτεκτονική-Ι. Ενότητα 1: Εισαγωγή στην Αρχιτεκτονική -Ι
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Αρχιτεκτονική-Ι Ενότητα 1: Εισαγωγή στην Αρχιτεκτονική -Ι Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Αρχιτεκτονική-Ι Ενότητα 1: Εισαγωγή στην Αρχιτεκτονική -Ι Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Δίαυλος Πληροφορίας. Δρ. Α. Πολίτης
 Δίαυλος Πληροφορίας Η λειτουργία του διαύλου πληροφορίας περιγράφεται από: Τον πίνακα διαύλου μαθηματική περιγραφή. Το διάγραμμα διάυλου παραστατικός τρόπος περιγραφής. Πίνακας Διαύλου Κατασκευάζεται με
Δίαυλος Πληροφορίας Η λειτουργία του διαύλου πληροφορίας περιγράφεται από: Τον πίνακα διαύλου μαθηματική περιγραφή. Το διάγραμμα διάυλου παραστατικός τρόπος περιγραφής. Πίνακας Διαύλου Κατασκευάζεται με
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Θεωρία Υπολογισμού Ενότητα 26: Καθολική Μηχανή Turing Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που
Θεωρία Υπολογισμού Ενότητα 26: Καθολική Μηχανή Turing Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που
Κατηγορίες Συμπίεσης. Συμπίεση με απώλειες δεδομένων (lossy compression) π.χ. συμπίεση εικόνας και ήχου
 Συμπίεση Η συμπίεση δεδομένων ελαττώνει το μέγεθος ενός αρχείου : Εξοικονόμηση αποθηκευτικού χώρου Εξοικονόμηση χρόνου μετάδοσης Τα περισσότερα αρχεία έχουν πλεονασμό στα δεδομένα τους Είναι σημαντική
Συμπίεση Η συμπίεση δεδομένων ελαττώνει το μέγεθος ενός αρχείου : Εξοικονόμηση αποθηκευτικού χώρου Εξοικονόμηση χρόνου μετάδοσης Τα περισσότερα αρχεία έχουν πλεονασμό στα δεδομένα τους Είναι σημαντική
Ψηφιακή Επεξεργασία Εικόνας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 6 : Κωδικοποίηση & Συμπίεση εικόνας Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 6 : Κωδικοποίηση & Συμπίεση εικόνας Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό
7ο ΕΡΓΑΣΤΗΡΙΟ AAAABBBBAAAAABBBBBBCCCCCCCCCCCCCCBBABAAAABBBBBBCCCCD
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΛΑΜΙΑΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΣΧΕΔΙΑΣΜΟΣ ΚΑΙ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2010 11 Ιστοσελίδα μαθήματος: http://eclass.teilam.gr/di288 1 Συμπίεση
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΛΑΜΙΑΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΣΧΕΔΙΑΣΜΟΣ ΚΑΙ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2010 11 Ιστοσελίδα μαθήματος: http://eclass.teilam.gr/di288 1 Συμπίεση
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Θεωρία Υπολογισμού Ενότητα 2: Σύνολα και σχέσεις Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Θεωρία Υπολογισμού Ενότητα 2: Σύνολα και σχέσεις Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Τίτλος Μαθήματος: ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ
 Τίτλος Μαθήματος: ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 5: Ασκήσεις Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Τίτλος Μαθήματος: ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 5: Ασκήσεις Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Υπολογιστικά & Διακριτά Μαθηματικά
 Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 10: Αριθμητική υπολοίπων - Κυκλικές ομάδες: Διαιρετότητα - Ευκλείδειος αλγόριθμος - Κατάλοιπα Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 10: Αριθμητική υπολοίπων - Κυκλικές ομάδες: Διαιρετότητα - Ευκλείδειος αλγόριθμος - Κατάλοιπα Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΣΤΑΤΙΣΤΙΚΗ ΕΠΙΧΕΙΡΗΣΕΩΝ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΤΑΤΙΣΤΙΚΗ ΕΠΙΧΕΙΡΗΣΕΩΝ Ενότητα # 7: Θεωρία Πιθανοτήτων (Πείραμα Τύχης) Εβελίνα Κοσσιέρη Τμήμα Λογιστικής και Χρηματοοικονομικής
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΤΑΤΙΣΤΙΚΗ ΕΠΙΧΕΙΡΗΣΕΩΝ Ενότητα # 7: Θεωρία Πιθανοτήτων (Πείραμα Τύχης) Εβελίνα Κοσσιέρη Τμήμα Λογιστικής και Χρηματοοικονομικής
ΘΕΜΑ : ΣΥΣΤΗΜΑΤΑ ΑΡΙΘΜΗΣΗΣ. ΔΙΑΡΚΕΙΑ: 1 περιόδους. 22/1/ :11 Όνομα: Λεκάκης Κωνσταντίνος καθ. Τεχνολογίας
 ΘΕΜΑ : ΣΥΣΤΗΜΑΤΑ ΑΡΙΘΜΗΣΗΣ ΔΙΑΡΚΕΙΑ: 1 περιόδους 22/1/2010 10:11 καθ. Τεχνολογίας 22/1/2010 10:12 Παραδείγματα Τι ονομάζουμε αριθμητικό σύστημα? Το σύνολο από ψηφία (αριθμοί & χαρακτήρες). Που χρησιμεύουν
ΘΕΜΑ : ΣΥΣΤΗΜΑΤΑ ΑΡΙΘΜΗΣΗΣ ΔΙΑΡΚΕΙΑ: 1 περιόδους 22/1/2010 10:11 καθ. Τεχνολογίας 22/1/2010 10:12 Παραδείγματα Τι ονομάζουμε αριθμητικό σύστημα? Το σύνολο από ψηφία (αριθμοί & χαρακτήρες). Που χρησιμεύουν
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 014-015 Μοναδικά Αποκωδικοποιήσιμοι Κώδικες Δρ. Ν. Π. Σγούρος Έλεγος μοναδικής Αποκωδικοποίησης Γενικοί ορισμοί Έστω δύο κωδικές λέξεις α,β με μήκη,m και
Συμπίεση Δεδομένων 014-015 Μοναδικά Αποκωδικοποιήσιμοι Κώδικες Δρ. Ν. Π. Σγούρος Έλεγος μοναδικής Αποκωδικοποίησης Γενικοί ορισμοί Έστω δύο κωδικές λέξεις α,β με μήκη,m και
Εισαγωγή στους Ηλεκτρονικούς Υπολογιστές. 3 ο Μάθημα. Λεωνίδας Αλεξόπουλος Λέκτορας ΕΜΠ. url:
 Εισαγωγή στους Ηλεκτρονικούς Υπολογιστές 3 ο Μάθημα Λεωνίδας Αλεξόπουλος Λέκτορας ΕΜΠ email: leo@mail.ntua.gr url: http://users.ntua.gr/leo Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Εισαγωγή στους Ηλεκτρονικούς Υπολογιστές 3 ο Μάθημα Λεωνίδας Αλεξόπουλος Λέκτορας ΕΜΠ email: leo@mail.ntua.gr url: http://users.ntua.gr/leo Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Υπολογιστικά & Διακριτά Μαθηματικά
 Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 5: Αναδρομικές σχέσεις - Υπολογισμός Αθροισμάτων Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 5: Αναδρομικές σχέσεις - Υπολογισμός Αθροισμάτων Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Μελετάμε την περίπτωση όπου αποθηκεύουμε ένα (δυναμικό) σύνολο στοιχειών. Ένα στοιχείο γράφεται ως, όπου κάθε.
 Ψηφιακά Δένδρα Μελετάμε την περίπτωση όπου αποθηκεύουμε ένα (δυναμικό) σύνολο στοιχειών τα οποία είναι ακολουθίες συμβάλλων από ένα πεπερασμένο αλφάβητο Ένα στοιχείο γράφεται ως, όπου κάθε. Μπορούμε να
Ψηφιακά Δένδρα Μελετάμε την περίπτωση όπου αποθηκεύουμε ένα (δυναμικό) σύνολο στοιχειών τα οποία είναι ακολουθίες συμβάλλων από ένα πεπερασμένο αλφάβητο Ένα στοιχείο γράφεται ως, όπου κάθε. Μπορούμε να
Αρχιτεκτονική Υπολογιστών Ασκήσεις Εργαστηρίου
 Αρχιτεκτονική Υπολογιστών Ασκήσεις Εργαστηρίου Ενότητα: ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ Νο 03 Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Εργαστήριο Ψηφιακών Συστημάτων και
Αρχιτεκτονική Υπολογιστών Ασκήσεις Εργαστηρίου Ενότητα: ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ Νο 03 Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Εργαστήριο Ψηφιακών Συστημάτων και
Σχεδίαση με Ηλεκτρονικούς Υπολογιστές
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Σχεδίαση με Ηλεκτρονικούς Υπολογιστές Ενότητα # 2: Εργαστήριο 2 - Η διανυσματική μορφή (vector) Καθηγητής Ιωάννης Γ. Παρασχάκης Δρ. Μηχ.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Σχεδίαση με Ηλεκτρονικούς Υπολογιστές Ενότητα # 2: Εργαστήριο 2 - Η διανυσματική μορφή (vector) Καθηγητής Ιωάννης Γ. Παρασχάκης Δρ. Μηχ.
Δομές Δεδομένων. Ενότητα 13: B-Δέντρα/AVL-Δέντρα. Καθηγήτρια Μαρία Σατρατζέμη. Τμήμα Εφαρμοσμένης Πληροφορικής. Δομές Δεδομένων
 Ενότητα 13: B-Δέντρα/AVL-Δέντρα Καθηγήτρια Μαρία Σατρατζέμη Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε
Ενότητα 13: B-Δέντρα/AVL-Δέντρα Καθηγήτρια Μαρία Σατρατζέμη Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε
Κ15 Ψηφιακή Λογική Σχεδίαση 2: Δυαδικό Σύστημα / Αναπαραστάσεις
 Κ15 Ψηφιακή Λογική Σχεδίαση 2: Δυαδικό Σύστημα / Αναπαραστάσεις Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Δυαδικό Σύστημα Αρίθμησης Περιεχόμενα 1 Δυαδικό
Κ15 Ψηφιακή Λογική Σχεδίαση 2: Δυαδικό Σύστημα / Αναπαραστάσεις Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Δυαδικό Σύστημα Αρίθμησης Περιεχόμενα 1 Δυαδικό
Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών
 Δομημένος Προγραμματισμός Ενότητα 3(γ): Εργαστηριακή Άσκηση Αναπλ. Καθηγητής: Κωνσταντίνος Στεργίου Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Δομημένος Προγραμματισμός Ενότητα 3(γ): Εργαστηριακή Άσκηση Αναπλ. Καθηγητής: Κωνσταντίνος Στεργίου Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Στατιστική Επιχειρήσεων Ι
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Τεχνολογικό Εκπαιδευτικό Ίδρυμα Πειραιά Στατιστική Επιχειρήσεων Ι Ενότητα 2: Τυχαίες Μεταβλητές Μιλτιάδης Χαλικιάς, Επίκουρος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων Άδειες Χρήσης Το
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Τεχνολογικό Εκπαιδευτικό Ίδρυμα Πειραιά Στατιστική Επιχειρήσεων Ι Ενότητα 2: Τυχαίες Μεταβλητές Μιλτιάδης Χαλικιάς, Επίκουρος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων Άδειες Χρήσης Το
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Θεωρία Υπολογισμού Ενότητα 4: Ισοδυναμία, διάταξη, άπειρα σύνολα Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Θεωρία Υπολογισμού Ενότητα 4: Ισοδυναμία, διάταξη, άπειρα σύνολα Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Αναγνώριση Προτύπων Ι
 Αναγνώριση Προτύπων Ι Ενότητα 1: Μέθοδοι Αναγνώρισης Προτύπων Αν. Καθηγητής Δερματάς Ευάγγελος Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Αναγνώριση Προτύπων Ι Ενότητα 1: Μέθοδοι Αναγνώρισης Προτύπων Αν. Καθηγητής Δερματάς Ευάγγελος Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Ψηφιακή Μετάδοση Αναλογικών Σηµάτων
 Ψηφιακή Μετάδοση Αναλογικών Σηµάτων Τα σύγχρονα συστήµατα επικοινωνίας σε πολύ µεγάλο ποσοστό διαχειρίζονται σήµατα ψηφιακής µορφής, δηλαδή, σήµατα που δηµιουργούνται από ακολουθίες δυαδικών ψηφίων. Τα
Ψηφιακή Μετάδοση Αναλογικών Σηµάτων Τα σύγχρονα συστήµατα επικοινωνίας σε πολύ µεγάλο ποσοστό διαχειρίζονται σήµατα ψηφιακής µορφής, δηλαδή, σήµατα που δηµιουργούνται από ακολουθίες δυαδικών ψηφίων. Τα
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Θεωρία Υπολογισμού Ενότητα 24: Μη Ντεντερμινιστικές Μηχανές Turing Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
Θεωρία Υπολογισμού Ενότητα 24: Μη Ντεντερμινιστικές Μηχανές Turing Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ
 ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ Ενότητα 1: Εισαγωγή Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ Ενότητα 1: Εισαγωγή Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Μάθημα Εισαγωγή στις Τηλεπικοινωνίες Κωδικοποίηση πηγής- καναλιού Μάθημα 9o
 Μάθημα Εισαγωγή στις Τηλεπικοινωνίες Κωδικοποίηση πηγής- καναλιού Μάθημα 9o ΕΘΝΙΚΟ & ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τομέας Επικοινωνιών και Επεξεργασίας Σήματος Τμήμα Πληροφορικής & Τηλεπικοινωνιών
Μάθημα Εισαγωγή στις Τηλεπικοινωνίες Κωδικοποίηση πηγής- καναλιού Μάθημα 9o ΕΘΝΙΚΟ & ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τομέας Επικοινωνιών και Επεξεργασίας Σήματος Τμήμα Πληροφορικής & Τηλεπικοινωνιών
ΓΡΑΜΜΙΚΟΣ & ΔΙΚΤΥΑΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ
 ΓΡΑΜΜΙΚΟΣ & ΔΙΚΤΥΑΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ενότητα 21: Δυϊκή Θεωρία, Θεώρημα Συμπληρωματικής Χαλαρότητας και τρόποι χρήσης του Σαμαράς Νικόλαος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΓΡΑΜΜΙΚΟΣ & ΔΙΚΤΥΑΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ενότητα 21: Δυϊκή Θεωρία, Θεώρημα Συμπληρωματικής Χαλαρότητας και τρόποι χρήσης του Σαμαράς Νικόλαος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Αρχές Τηλεπικοινωνιών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Αρχές Τηλεπικοινωνιών Ενότητα #12: Δειγματοληψία, κβαντοποίηση και κωδικοποίηση Χ. ΚΑΡΑΪΣΚΟΣ Τμήμα Μηχανικών Αυτοματισμών Τ.Ε.
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Αρχές Τηλεπικοινωνιών Ενότητα #12: Δειγματοληψία, κβαντοποίηση και κωδικοποίηση Χ. ΚΑΡΑΪΣΚΟΣ Τμήμα Μηχανικών Αυτοματισμών Τ.Ε.
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Cretive Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύπ
 Θεωρία Υπολογισμού Ενότητα 11: Κλειστότητα, ΠΑ & καν. εκφράσεις Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Cretive Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Θεωρία Υπολογισμού Ενότητα 11: Κλειστότητα, ΠΑ & καν. εκφράσεις Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Cretive Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Στατιστική Επιχειρήσεων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Στατιστική Επιχειρήσεων Ενότητα # 2: Στατιστικοί Πίνακες Εβελίνα Κοσσιέρη Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Στατιστική Επιχειρήσεων Ενότητα # 2: Στατιστικοί Πίνακες Εβελίνα Κοσσιέρη Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης
Περιεχόμενα Ορισμός και λειτουργία των μηχανών Turing Θεωρία Υπολογισμού Ενότητα 20: Μηχανές Turing: Σύνθεση και Υπολογισμοί Επ. Καθ. Π. Κατσαρός Τμήμ
 Θεωρία Υπολογισμού Ενότητα 20: Μηχανές Turing: Σύνθεση και Υπολογισμοί Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
Θεωρία Υπολογισμού Ενότητα 20: Μηχανές Turing: Σύνθεση και Υπολογισμοί Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
Αρχιτεκτονική Υπολογιστών Ασκήσεις Εργαστηρίου
 Αρχιτεκτονική Υπολογιστών Ασκήσεις Εργαστηρίου Ενότητα: ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ Νο 01 Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Εργαστήριο Ψηφιακών Συστημάτων και
Αρχιτεκτονική Υπολογιστών Ασκήσεις Εργαστηρίου Ενότητα: ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ Νο 01 Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Εργαστήριο Ψηφιακών Συστημάτων και
d k 10 k + d k 1 10 k d d = k i=0 d i 10 i.
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ. ΕΝΟΤΗΤΑ: Διανύσματα στους Rn, Cn, διανύσματα στο χώρο (1) ΔΙΔΑΣΚΩΝ: Βλάμος Παναγιώτης ΙΟΝΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΝΟΤΗΤΑ: Διανύσματα στους, C, διανύσματα στο χώρο (1) ΙΟΝΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΔΙΔΑΣΚΩΝ: Βλάμος Παναγιώτης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΝΟΤΗΤΑ: Διανύσματα στους, C, διανύσματα στο χώρο (1) ΙΟΝΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΔΙΔΑΣΚΩΝ: Βλάμος Παναγιώτης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Ανάκτηση Πληροφορίας
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Ανάκτηση Πληροφορίας Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #08 Συµπίεση Κειµένων Φοίβος Μυλωνάς fmylonas@ionio.gr Ανάκτηση Πληροφορίας 1 Άδεια χρήσης
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Ανάκτηση Πληροφορίας Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #08 Συµπίεση Κειµένων Φοίβος Μυλωνάς fmylonas@ionio.gr Ανάκτηση Πληροφορίας 1 Άδεια χρήσης
Αρχιτεκτονική Υπολογιστών Ασκήσεις Εργαστηρίου
 Αρχιτεκτονική Υπολογιστών Ασκήσεις Εργαστηρίου Ενότητα: ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ No 05 Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Εργαστήριο Ψηφιακών Συστημάτων και
Αρχιτεκτονική Υπολογιστών Ασκήσεις Εργαστηρίου Ενότητα: ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ No 05 Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Εργαστήριο Ψηφιακών Συστημάτων και
Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών
 Δομημένος Προγραμματισμός Ενότητα 2(γ): Εργαστηριακή Άσκηση Αναπλ. Καθηγητής: Κωνσταντίνος Στεργίου Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Δομημένος Προγραμματισμός Ενότητα 2(γ): Εργαστηριακή Άσκηση Αναπλ. Καθηγητής: Κωνσταντίνος Στεργίου Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ
 ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ Ενότητα 8: Ιδιότητες Γραμματικών χωρίς Συμφραζόμενα Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ Ενότητα 8: Ιδιότητες Γραμματικών χωρίς Συμφραζόμενα Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Υπολογιστικά & Διακριτά Μαθηματικά
 Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 9: Εσωτερική πράξη και κλάσεις ισοδυναμίας - Δομές Ισομορφισμοί Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 9: Εσωτερική πράξη και κλάσεις ισοδυναμίας - Δομές Ισομορφισμοί Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Ψηφιακή Σχεδίαση. Ενότητα: ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ No:07. Δρ. Μηνάς Δασυγένης. Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών
 Ψηφιακή Σχεδίαση Ενότητα: ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ No:07 Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Εργαστήριο Ψηφιακών Συστημάτων και Αρχιτεκτονικής Υπολογιστών http:
Ψηφιακή Σχεδίαση Ενότητα: ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ No:07 Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Εργαστήριο Ψηφιακών Συστημάτων και Αρχιτεκτονικής Υπολογιστών http:
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Θεωρία Υπολογισμού Ενότητα 13: Ελαχιστοποίηση αυτομάτων Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που
Θεωρία Υπολογισμού Ενότητα 13: Ελαχιστοποίηση αυτομάτων Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα. Συστήματα Αυτομάτου Ελέγχου. Ενότητα Α: Γραμμικά Συστήματα
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Συστήματα Αυτομάτου Ελέγχου Ενότητα Α: Γραμμικά Συστήματα Όνομα Καθηγητή: Ραγκούση Μαρία Τμήμα: Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Συστήματα Αυτομάτου Ελέγχου Ενότητα Α: Γραμμικά Συστήματα Όνομα Καθηγητή: Ραγκούση Μαρία Τμήμα: Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες
Προγραμματισμός Ηλεκτρονικών Υπολογιστών 1
 Προγραμματισμός Ηλεκτρονικών Υπολογιστών 1 Ενότητα 3: Άλγεβρα Βοole και Λογικές Πράξεις Δρ. Φραγκούλης Γεώργιος Τμήμα Ηλεκτρολογίας Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Προγραμματισμός Ηλεκτρονικών Υπολογιστών 1 Ενότητα 3: Άλγεβρα Βοole και Λογικές Πράξεις Δρ. Φραγκούλης Γεώργιος Τμήμα Ηλεκτρολογίας Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Θεωρία Υπολογισμού Ενότητα 21: Υπολογισμοί ΜΤ - Αναδρομικές Γλώσσες Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
Θεωρία Υπολογισμού Ενότητα 21: Υπολογισμοί ΜΤ - Αναδρομικές Γλώσσες Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 6β: Ταξινόμηση με εισαγωγή και επιλογή Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creatve
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 6β: Ταξινόμηση με εισαγωγή και επιλογή Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creatve
Ψηφιακή Λογική Σχεδίαση
 Ψηφιακή Λογική Σχεδίαση Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα Αδειοδότησης Το παρόν
Ψηφιακή Λογική Σχεδίαση Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα Αδειοδότησης Το παρόν
Ασκήσεις Φροντιστηρίου «Υπολογιστική Νοημοσύνη Ι» 5 o Φροντιστήριο
 Πρόβλημα ο Ασκήσεις Φροντιστηρίου 5 o Φροντιστήριο Δίνεται το παρακάτω σύνολο εκπαίδευσης: # Είσοδος Κατηγορία 0 0 0 Α 2 0 0 Α 0 Β 4 0 0 Α 5 0 Β 6 0 0 Α 7 0 Β 8 Β α) Στον παρακάτω κύβο τοποθετείστε τα
Πρόβλημα ο Ασκήσεις Φροντιστηρίου 5 o Φροντιστήριο Δίνεται το παρακάτω σύνολο εκπαίδευσης: # Είσοδος Κατηγορία 0 0 0 Α 2 0 0 Α 0 Β 4 0 0 Α 5 0 Β 6 0 0 Α 7 0 Β 8 Β α) Στον παρακάτω κύβο τοποθετείστε τα
Θεωρία Υπολογισμού Αλφάβητα, Γλώσσες, Κανονικές Εκφράσεις
 1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Θεωρία Υπολογισμού Ενότητα 6 : Αλφάβητα, Γλώσσες, Κανονικές Εκφράσεις Αλέξανδρος Τζάλλας 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο Τμήμα Μηχανικών
1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Θεωρία Υπολογισμού Ενότητα 6 : Αλφάβητα, Γλώσσες, Κανονικές Εκφράσεις Αλέξανδρος Τζάλλας 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο Τμήμα Μηχανικών
Διαχείριση Χρόνου & Δίκτυα στη Διοίκηση Έργων. Κηρυττόπουλος Κωνσταντίνος Επ. Καθηγητής ΕΜΠ
 Διαχείριση Χρόνου & Δίκτυα στη Διοίκηση Έργων Κηρυττόπουλος Κωνσταντίνος Επ. Καθηγητής ΕΜΠ Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
Διαχείριση Χρόνου & Δίκτυα στη Διοίκηση Έργων Κηρυττόπουλος Κωνσταντίνος Επ. Καθηγητής ΕΜΠ Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
Εισαγωγή στην Επιστήμη των Υπολογιστών
 Εισαγωγή στην Επιστήμη των Υπολογιστών Ενότητα 2: Αποθήκευση Δεδομένων: Αριθμητική του Υπολογιστή, Αριθμητικά Συστήματα Μετατροπές, 2ΔΩ Τμήμα: Αγροτικής Οικονομίας & Ανάπτυξης Διδάσκων: Θεόδωρος Τσιλιγκιρίδης
Εισαγωγή στην Επιστήμη των Υπολογιστών Ενότητα 2: Αποθήκευση Δεδομένων: Αριθμητική του Υπολογιστή, Αριθμητικά Συστήματα Μετατροπές, 2ΔΩ Τμήμα: Αγροτικής Οικονομίας & Ανάπτυξης Διδάσκων: Θεόδωρος Τσιλιγκιρίδης
EE728 (22Α004) - Προχωρημένα Θέματα Θεωρίας Πληροφορίας 3η σειρά ασκήσεων Διακριτά και Συνεχή Κανάλια. Παράδοση: Έως 22/6/2015
 EE728 (22Α004) - Προχωρημένα Θέματα Θεωρίας Πληροφορίας Φυλλάδιο 13 Δ. Τουμπακάρης 30 Μαΐου 2015 EE728 (22Α004) - Προχωρημένα Θέματα Θεωρίας Πληροφορίας 3η σειρά ασκήσεων Διακριτά και Συνεχή Κανάλια Παράδοση:
EE728 (22Α004) - Προχωρημένα Θέματα Θεωρίας Πληροφορίας Φυλλάδιο 13 Δ. Τουμπακάρης 30 Μαΐου 2015 EE728 (22Α004) - Προχωρημένα Θέματα Θεωρίας Πληροφορίας 3η σειρά ασκήσεων Διακριτά και Συνεχή Κανάλια Παράδοση:
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία
 ΗΜΥ 100 Εισαγωγή στην Τεχνολογία Στέλιος Τιμοθέου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ ΜΑΣ ΣΗΜΕΡΑ Συστήματα αρίθμησης Δυαδικό αριθμητικό
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία Στέλιος Τιμοθέου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ ΜΑΣ ΣΗΜΕΡΑ Συστήματα αρίθμησης Δυαδικό αριθμητικό
Εισαγωγή στις Τηλεπικοινωνίες
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στις Τηλεπικοινωνίες Ενότητα 4: Κβάντιση και Κωδικοποίηση Σημάτων Όνομα Καθηγητή: Δρ. Ηρακλής Σίμος Τμήμα: Ηλεκτρονικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στις Τηλεπικοινωνίες Ενότητα 4: Κβάντιση και Κωδικοποίηση Σημάτων Όνομα Καθηγητή: Δρ. Ηρακλής Σίμος Τμήμα: Ηλεκτρονικών
ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ. Ενότητα 9: Απείρως επαναλαμβανόμενα παίγνια. Ρεφανίδης Ιωάννης Τμήμα Εφαρμοσμένης Πληροφορικής
 Ενότητα 9: Απείρως επαναλαμβανόμενα παίγνια Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Ενότητα 9: Απείρως επαναλαμβανόμενα παίγνια Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Θεωρία Υπολογισμού Ενότητα 10: Ισοδυναμία ντετερμινιστικών και μη ντετερμινιστικών αυτομάτων Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Θεωρία Υπολογισμού Ενότητα 10: Ισοδυναμία ντετερμινιστικών και μη ντετερμινιστικών αυτομάτων Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Οργάνωση Υπολογιστών
 Οργάνωση Υπολογιστών Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών 1 Άδειες Χρήσης Το παρόν υλικό
Οργάνωση Υπολογιστών Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών 1 Άδειες Χρήσης Το παρόν υλικό
ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ. Ενότητα 5: Παραδείγματα. Ρεφανίδης Ιωάννης Τμήμα Εφαρμοσμένης Πληροφορικής
 Ενότητα 5: Παραδείγματα Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύπου άδειας
Ενότητα 5: Παραδείγματα Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύπου άδειας
Αρχεία και Βάσεις Δεδομένων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αρχεία και Βάσεις Δεδομένων Διάλεξη 13η: Κλείσιμο Συνόλου Γνωρισμάτων - Ελάχιστη κάλυψη - Αποσύνθεση - Συναρτησιακές Εξαρτήσεις Δημήτρης Πλεξουσάκης Τμήμα Επιστήμης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αρχεία και Βάσεις Δεδομένων Διάλεξη 13η: Κλείσιμο Συνόλου Γνωρισμάτων - Ελάχιστη κάλυψη - Αποσύνθεση - Συναρτησιακές Εξαρτήσεις Δημήτρης Πλεξουσάκης Τμήμα Επιστήμης
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Θεωρία Υπολογισμού Ενότητα 18: Λήμμα Άντλησης για ΓΧΣ Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που
Θεωρία Υπολογισμού Ενότητα 18: Λήμμα Άντλησης για ΓΧΣ Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που
Ασκήσεις μελέτης της 4 ης διάλεξης. ), για οποιοδήποτε μονοπάτι n 1
 Οικονομικό Πανεπιστήμιο Αθηνών, Τμήμα Πληροφορικής Μάθημα: Τεχνητή Νοημοσύνη, 2016 17 Διδάσκων: Ι. Ανδρουτσόπουλος Ασκήσεις μελέτης της 4 ης διάλεξης 4.1. (α) Αποδείξτε ότι αν η h είναι συνεπής, τότε h(n
Οικονομικό Πανεπιστήμιο Αθηνών, Τμήμα Πληροφορικής Μάθημα: Τεχνητή Νοημοσύνη, 2016 17 Διδάσκων: Ι. Ανδρουτσόπουλος Ασκήσεις μελέτης της 4 ης διάλεξης 4.1. (α) Αποδείξτε ότι αν η h είναι συνεπής, τότε h(n
Υπολογιστές Ι. Άδειες Χρήσης. Εισαγωγή. Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης Υπολογιστές Ι Εισαγωγή Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης Υπολογιστές Ι Εισαγωγή Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Πανεπιστήμιο Δυτικής Μακεδονίας. Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών. Διακριτά Μαθηματικά. Ενότητα 4: Εισαγωγή / Σύνολα
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Διακριτά Μαθηματικά Ενότητα 4: Εισαγωγή / Σύνολα Αν. Καθηγητής Κ. Στεργίου e-mail: kstergiou@uowm.gr Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Άδειες
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Διακριτά Μαθηματικά Ενότητα 4: Εισαγωγή / Σύνολα Αν. Καθηγητής Κ. Στεργίου e-mail: kstergiou@uowm.gr Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Άδειες
