5 ο Εργαστήριο Δομές Επανάληψης (συνέχεια)
|
|
|
- Δείμος Βονόρτας
- 8 χρόνια πριν
- Προβολές:
Transcript
1 5 ο Εργαστήριο Δομές Επανάληψης (συνέχεια) Κύκλος 270 ο 3*(π/2) rad (3*HALF_PI) 180 ο π rad (PI) 0 ο 0 rad 360 ο 2π rad (TWO_PI) hyp x opp adj 90 ο π/2 rad (HALF_PI) sin(x) = opp / hyp cos(x) = adj/hyp Οι συντεταγμένες (Χ, Υ) κάθε σημείου στην περίμετρο ενός κύκλου υπολογίζονται με βάση τη γωνία x, το κέντρο του κύκλου (centerx, centery) και την ακτίνα του (radius) ως εξής: Χ = centerx + (radius * cos(x)); Y = centery + (radius * sin(x)); Σχεδιάζοντας έναν κύκλο με τριγωνομετρία Μέγεθος καμβά Ορισμός χρώματος φόντου Πάχος γραμμής Δήλωση μεταβλητής για ακτίνα κύκλου Μεταβλητές για δήλωση του κέντρου του κύκλου Ορισμός χρώματος γραμμής Ορισμός να μην έχουν χρώμα γεμίσματος τα σχήματα Σχεδίαση κύκλου Αλλαγή χρώματος γραμμής Επανάληψη από 0 έως 360 μοίρες με βήμα αύξησης 5 μοίρες Μετατροπή από μοίρες σε ακτίνια (radians) Υπολογισμός συντεταγμένων σημείου στη περίμετρο του κύκλου Σχεδίαση σημείου 1
2 Σχεδιάζοντας έναν κύκλο με τριγωνομετρία (animation) float radius = 100; int centx = 250; int centy = 150; float x, y; float lastx = -999; float lasty = -999; float ang = 0; void setup(){ size(500,300); framerate(10); background(255); strokeweight(5); smooth(); stroke(0, 30); nofill(); ellipse(centx,centy,radius*2,radius*2); stroke(20, 50, 70); void draw(){ if (ang <= 360 ) { float rad = radians(ang); x = centx + (radius * cos(rad)); y = centy + (radius * sin(rad)); point(x,y); ang += 5; Το ίδιο πρόγραμμα με το παραπάνω παράδειγμα αλλά τώρα βλέπουμε σε animation τη σχεδίαση κάθε σημείου πάνω στην περίμετρο του κύκλου. 2
3 Μετατρέποντας έναν κύκλο σε σπείρα Ορισμός αρχικής τιμής ακτίνας σε 10 Ορισμός αρχικής τιμής lastx, lasty σε Επανάληψη από 0 μοίρες έως 1440 μοίρες. Θα γίνουν 1440/360=4 πλήρης περιστροφές για τη σχεδίαση της σπείρας. Η ακτίνα του κύκλου αυξάνεται κατά 0.5 μοίρες σε κάθε επανάληψη Για να σχεδιαστεί η σπείρα σχεδιάζεται κάθε φορά μια γραμμή με αρχικό σημείο το x,y που υπολογίστηκε στη τρέχουσα επανάληψη και τελικό σημείο αυτό που υπολογίστηκε στην προηγούμενη επανάληψη και αποθηκεύτηκε στις μεταβλητές lastx, lasty. Ο έλεγχος με την if διασφαλίζει ότι στην πρώτη επανάληψη δεν θα σχεδιαστεί γραμμή αλλά μόνο από τη δεύτερη επανάληψη και μετά. Αυτό χρειάζεται γιατί για να σχεδιαστεί μια γραμμή πρέπει να έχουν υπολογιστεί συντεταγμένες δύο σημείων. Δοκιμάστε να αλλάξετε το βήμα αύξησης της ακτίνας του κύκλου, τον αριθμό πλήρων περιστροφών για να δείτε το αποτέλεσμα που προκύπτει. 3
4 random() Παράγει τυχαίους αριθμούς. Κάθε φορά που η random() καλείται, επιστρέφει μια τυχαία τιμή εντός του καθορισμένου εύρους. Εάν μόνο μία παράμετρος περνά στη συνάρτηση, θα επιστρέψει έναν float μεταξύ μηδέν και τη τιμή της παραμέτρου. Για παράδειγμα, η random(5) επιστρέφει τιμές μεταξύ 0 και 5 (ξεκινώντας από το μηδέν, και μέχρι, αλλά μη συμπεριλαμβανομένης της τιμής 5). Εάν έχουν καθοριστεί δύο παράμετροι, η συνάρτηση θα επιστρέψει έναν float με μια τιμή μεταξύ των δύο τιμών. Για παράδειγμα, η random(-5, 10.2) επιστρέφει τιμές που ξεκινούν από -5 έως (αλλά μη συμπεριλαμβανομένης) Παράδειγμα for (int i = 0; i < 100; i++) { float r = random(50); stroke(r*5); line(50, i, 50+r, i); noise() Επιστρέφει την τιμή του θορύβου Perlin σε συγκεκριμένες συντεταγμένες. O θόρυβος Perlin είναι μια τυχαία γεννήτρια ακολουθίας αριθμών, που παράγει όμως μια πιο φυσική, αρμονική διαδοχή των αριθμών από εκείνη της λειτουργίας βασικής συνάρτησης random(). Εφευρέθηκε από τον Ken Perlin στη δεκαετία του 1980 και έχει χρησιμοποιηθεί σε εφαρμογές γραφικών για να δημιουργήσει διαδικαστικές υφές, σχήματα, εδάφη, και άλλες φαινομενικά οργανικές μορφές. Σε αντίθεση με την random() λειτουργία, o θόρυβος Perlin ορίζεται σε ένα άπειρο χώρο n-διαστάσεων, όπου κάθε ζεύγος συντεταγμένων αντιστοιχεί σε μια σταθερή ημι-τυχαία τιμή (σταθερή μόνο για την διάρκεια ζωής του προγράμματος). Η προκύπτουσα τιμή θα είναι πάντα μεταξύ 0.0 και 1.0. Η Processing μπορεί να υπολογίσει 1Δ, 2Δ και 3Δ θόρυβο, ανάλογα με τον αριθμό των συντεταγμένων που δίνονται. Γενικά, όσο μικρότερη είναι η διαφορά μεταξύ των συντεταγμένων, τόσο ομαλότερη η προκύπτουσα ακολουθία θορύβου. Βήματα από έως 0.03 λειτουργούν καλύτερα για τις περισσότερες εφαρμογές, αλλά αυτό θα διαφέρει ανάλογα με τη χρήση. Παράδειγμα float xoff = 0.0; void draw() { background(204); xoff = xoff +.01; float n = noise(xoff) * width; line(n, 0, n, height); 4
5 Δημιουργία σπείρας με θόρυβο και τυχαίους αριθμούς 5
6 100 σπείρες με θόρυβο Ορισμός μικρού πάχους γραμμής Επανάληψη από 0 έως 100 για να σχεδιαστούν 100 σπείρες. Η random(10) θα παράγει έναν τυχαίο αριθμό από το 0 έως το 10. Αυτός ο τυχαίος αριθμός θα είναι ο θόρυβος που θα εφαρμοστεί στην ακτίνα των κύκλων. Το χρώμα της γραμμής ορίζεται με τυχαίο τρόπο. Η γωνία έναρξης ορίζεται με τυχαίο τρόπο. Η γωνία τερματισμού ορίζεται με τυχαίο τρόπο αλλά θα είναι μεγαλύτερη από Το βήμα αύξησης της γωνίας ορίζεται με τυχαίο τρόπο. Επανάληψή με βάση τις τυχαίες τιμές που παράχθηκαν. Σε κάθε επανάληψη ο θόρυβος αυξάνεται κατά 0.05 Υπολογισμός της ακτίνας με βάση τις τυχαίες τιμές και χρήση της noise(). 6
6 ο Εργαστήριο Σχεδιάζοντας σχήματα από σημεία κορυφών, Θόρυβος-Τυχαίοι Αριθμοί (συνέχεια)
 6 ο Εργαστήριο Σχεδιάζοντας σχήματα από σημεία κορυφών, Θόρυβος-Τυχαίοι Αριθμοί (συνέχεια) Σχεδιάζοντας σχήματα από σημεία κορυφών Με nofill() δηλώνουμε ότι το σχήμα δεν θα έχει γέμισμα με χρώμα Η beginshape()
6 ο Εργαστήριο Σχεδιάζοντας σχήματα από σημεία κορυφών, Θόρυβος-Τυχαίοι Αριθμοί (συνέχεια) Σχεδιάζοντας σχήματα από σημεία κορυφών Με nofill() δηλώνουμε ότι το σχήμα δεν θα έχει γέμισμα με χρώμα Η beginshape()
4 ο Εργαστήριο Τυχαίοι Αριθμοί, Μεταβλητές Συστήματος
 4 ο Εργαστήριο Τυχαίοι Αριθμοί, Μεταβλητές Συστήματος Μεταβλητές Συστήματος Η Processing χρησιμοποιεί κάποιες μεταβλητές συστήματος, όπως τις ονομάζουμε, για να μπορούμε να παίρνουμε πληροφορίες από το
4 ο Εργαστήριο Τυχαίοι Αριθμοί, Μεταβλητές Συστήματος Μεταβλητές Συστήματος Η Processing χρησιμοποιεί κάποιες μεταβλητές συστήματος, όπως τις ονομάζουμε, για να μπορούμε να παίρνουμε πληροφορίες από το
7 ο Εργαστήριο Θόρυβος 2Δ, Μετακίνηση, Περιστροφή
 7 ο Εργαστήριο Θόρυβος 2Δ, Μετακίνηση, Περιστροφή O θόρυβος 2Δ μας δίνει τη δυνατότητα να δημιουργίας υφής 2Δ. Στο παρακάτω παράδειγμα, γίνεται σχεδίαση γραμμών σε πλέγμα 300x300 με μεταβαλόμενη τιμή αδιαφάνειας
7 ο Εργαστήριο Θόρυβος 2Δ, Μετακίνηση, Περιστροφή O θόρυβος 2Δ μας δίνει τη δυνατότητα να δημιουργίας υφής 2Δ. Στο παρακάτω παράδειγμα, γίνεται σχεδίαση γραμμών σε πλέγμα 300x300 με μεταβαλόμενη τιμή αδιαφάνειας
1 ο Εργαστήριο Συντεταγμένες, Χρώματα, Σχήματα
 1 ο Εργαστήριο Συντεταγμένες, Χρώματα, Σχήματα 1. Σύστημα Συντεταγμένων Το σύστημα συντεταγμένων που έχουμε συνηθίσει από το σχολείο τοποθετούσε το σημείο (0,0) στο σημείο τομής των δυο αξόνων Χ και Υ.
1 ο Εργαστήριο Συντεταγμένες, Χρώματα, Σχήματα 1. Σύστημα Συντεταγμένων Το σύστημα συντεταγμένων που έχουμε συνηθίσει από το σχολείο τοποθετούσε το σημείο (0,0) στο σημείο τομής των δυο αξόνων Χ και Υ.
2 ο Εργαστήριο Αλληλεπίδραση και Animation
 2 ο Εργαστήριο Αλληλεπίδραση και Animation Τα προγράμματα που έχουμε δει μέχρι τώρα εκτελούν τον κώδικά τους μία φορά και το πρόγραμμα σταματάει. Ένα πρόγραμμα που δημιουργεί animation ή ανταποκρίνεται
2 ο Εργαστήριο Αλληλεπίδραση και Animation Τα προγράμματα που έχουμε δει μέχρι τώρα εκτελούν τον κώδικά τους μία φορά και το πρόγραμμα σταματάει. Ένα πρόγραμμα που δημιουργεί animation ή ανταποκρίνεται
> μεγαλύτερο <= μικρότερο ή ίσο < μικρότερο == ισότητα >= μεγαλύτερο ή ίσο!= διαφορετικό
 5 ο Εργαστήριο Λογικοί Τελεστές, Δομές Ελέγχου Λογικοί Τελεστές > μεγαλύτερο = μεγαλύτερο ή ίσο!= διαφορετικό Οι λογικοί τελεστές χρησιμοποιούνται για να ελέγξουμε
5 ο Εργαστήριο Λογικοί Τελεστές, Δομές Ελέγχου Λογικοί Τελεστές > μεγαλύτερο = μεγαλύτερο ή ίσο!= διαφορετικό Οι λογικοί τελεστές χρησιμοποιούνται για να ελέγξουμε
3 ο Εργαστήριο Μεταβλητές, Τελεστές
 3 ο Εργαστήριο Μεταβλητές, Τελεστές Μια μεταβλητή έχει ένα όνομα και ουσιαστικά είναι ένας δείκτης σε μια συγκεκριμένη θέση στη μνήμη του υπολογιστή. Στη θέση μνήμης στην οποία δείχνει μια μεταβλητή αποθηκεύονται
3 ο Εργαστήριο Μεταβλητές, Τελεστές Μια μεταβλητή έχει ένα όνομα και ουσιαστικά είναι ένας δείκτης σε μια συγκεκριμένη θέση στη μνήμη του υπολογιστή. Στη θέση μνήμης στην οποία δείχνει μια μεταβλητή αποθηκεύονται
Εργαστήριο 9 Συναρτήσεις στη PASCAL. Η έννοια του κατακερματισμού. Συναρτήσεις. Σκοπός
 Εργαστήριο 9 Συναρτήσεις στη PASCAL Η έννοια του κατακερματισμού. Συναρτήσεις. Σκοπός 7.1 ΕΠΙΔΙΩΞΗ ΤΗΣ ΕΡΓΑΣΙΑΣ Η έννοια της συνάρτησης ως υποπρογράμματος είναι τόσο βασική σε όλες τις γλώσσες προγραμματισμού,
Εργαστήριο 9 Συναρτήσεις στη PASCAL Η έννοια του κατακερματισμού. Συναρτήσεις. Σκοπός 7.1 ΕΠΙΔΙΩΞΗ ΤΗΣ ΕΡΓΑΣΙΑΣ Η έννοια της συνάρτησης ως υποπρογράμματος είναι τόσο βασική σε όλες τις γλώσσες προγραμματισμού,
8 ο Εργαστήριο Ευθυγράμμιση σε πλέγμα
 8 ο Εργαστήριο Ευθυγράμμιση σε πλέγμα Στο παρακάτω παράδειγμα το ο καμβάς χωρίζεται σε τετράγωνα. Σε κάθε τετράγωνο σχεδιάζεται μια διαγώνιος είτε από την πάνω-αριστερή στην κάτω-δεξιά γωνία είτε από την
8 ο Εργαστήριο Ευθυγράμμιση σε πλέγμα Στο παρακάτω παράδειγμα το ο καμβάς χωρίζεται σε τετράγωνα. Σε κάθε τετράγωνο σχεδιάζεται μια διαγώνιος είτε από την πάνω-αριστερή στην κάτω-δεξιά γωνία είτε από την
0 SOLID_LINE 1 DOTTED_LINE 2 CENTER_LINE 3 DASHED_LINE 4 USERBIT_LINE
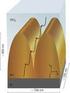 1. Η κωδικοποίηση των χρωµάτων για σύστηµα γραφικών µε 16 χρώµατα Κωδικός Χρώµα Χρώµατος 0 BLACK 1 BLUE 2 GREEN 3 CYAN 4 RED 5 MAGENTA 6 BROWN 7 LIGHTGRAY 8 DARKGRAY 9 LIGHTBLUE 10 LIGHTGREEN 11 LIGHTCYAN
1. Η κωδικοποίηση των χρωµάτων για σύστηµα γραφικών µε 16 χρώµατα Κωδικός Χρώµα Χρώµατος 0 BLACK 1 BLUE 2 GREEN 3 CYAN 4 RED 5 MAGENTA 6 BROWN 7 LIGHTGRAY 8 DARKGRAY 9 LIGHTBLUE 10 LIGHTGREEN 11 LIGHTCYAN
Θέματα Προγραμματισμού Η/Υ
 Πρόγραμμα Μεταπτυχιακών Σπουδών Πληροφορική και Υπολογιστική Βιοϊατρική Θέματα Προγραμματισμού Η/Υ Ενότητα 8: Θεματική Ενότητα: Συναρτήσεις ΘΕΜΑΤΑ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Η/Υ Θεματική Ενότητα 8 Συναρτήσεις Πληροφορική
Πρόγραμμα Μεταπτυχιακών Σπουδών Πληροφορική και Υπολογιστική Βιοϊατρική Θέματα Προγραμματισμού Η/Υ Ενότητα 8: Θεματική Ενότητα: Συναρτήσεις ΘΕΜΑΤΑ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Η/Υ Θεματική Ενότητα 8 Συναρτήσεις Πληροφορική
Κεφάλαιο 3 Βασική Σχεδίαση και Επεξεργασία
 Περιεχόμενα Πρόλογος... 7 Εισαγωγή... 9 Κεφάλαιο 1: Στοιχεία Λειτουργίας του Υπολογιστή και του προγράμματος AutoCAD... 11 Κεφάλαιο 2: Στοιχεία Λειτουργικού Συστήματος... 15 Κεφάλαιο 3: Βασική Σχεδίαση
Περιεχόμενα Πρόλογος... 7 Εισαγωγή... 9 Κεφάλαιο 1: Στοιχεία Λειτουργίας του Υπολογιστή και του προγράμματος AutoCAD... 11 Κεφάλαιο 2: Στοιχεία Λειτουργικού Συστήματος... 15 Κεφάλαιο 3: Βασική Σχεδίαση
Κεφάλαιο 1: Κινηματική των Ταλαντώσεων
 Κεφάλαιο : Κινηματική των Ταλαντώσεων Κεφάλαιο : Κινηματική των Ταλαντώσεων. Φαινομενολογικός ορισμός ταλαντώσεων Μεταβολές σε φυσικά φαινόμενα που χαρακτηρίζονται από μια κανονική επανάληψη κατά ορισμένα
Κεφάλαιο : Κινηματική των Ταλαντώσεων Κεφάλαιο : Κινηματική των Ταλαντώσεων. Φαινομενολογικός ορισμός ταλαντώσεων Μεταβολές σε φυσικά φαινόμενα που χαρακτηρίζονται από μια κανονική επανάληψη κατά ορισμένα
3.1 ΤΡΙΓΩΝΟΜΕΤΡΙΚΗ ΑΡΙΘΜΟΙ ΓΩΝΙΑΣ
 ΚΕΦΑΛΑΙΟ Ο : ΤΡΙΓΩΝΟΜΕΤΡΙΑ. ΤΡΙΓΩΝΟΜΕΤΡΙΚΗ ΑΡΙΘΜΟΙ ΓΩΝΙΑΣ ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ ΟΞΕΙΑΣ ΓΩΝΙΑΣ έ _ ά ί ί _ ά ί έ _ ά ί _ ά ί _ ά έ _ ά ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ ΤΥΧΑΙΑΣ ΓΩΝΙΑΣ y y y όπου η απόσταση του
ΚΕΦΑΛΑΙΟ Ο : ΤΡΙΓΩΝΟΜΕΤΡΙΑ. ΤΡΙΓΩΝΟΜΕΤΡΙΚΗ ΑΡΙΘΜΟΙ ΓΩΝΙΑΣ ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ ΟΞΕΙΑΣ ΓΩΝΙΑΣ έ _ ά ί ί _ ά ί έ _ ά ί _ ά ί _ ά έ _ ά ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ ΤΥΧΑΙΑΣ ΓΩΝΙΑΣ y y y όπου η απόσταση του
Προγραµµατιστικές Τεχνικές
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Αγρονόµων Τοπογράφων Μηχανικών Προγραµµατιστικές Τεχνικές Βασίλειος Βεσκούκης ρ. Ηλεκτρολόγος Μηχανικός & Μηχανικός Υπολογιστών ΕΜΠ v.vescoukis@cs.ntua.gr Ρωµύλος Κορακίτης
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Αγρονόµων Τοπογράφων Μηχανικών Προγραµµατιστικές Τεχνικές Βασίλειος Βεσκούκης ρ. Ηλεκτρολόγος Μηχανικός & Μηχανικός Υπολογιστών ΕΜΠ v.vescoukis@cs.ntua.gr Ρωµύλος Κορακίτης
Κεφάλαιο , 3.2: Συναρτήσεις II. (Διάλεξη 12)
 Κεφάλαιο 3.5-3.6, 3.2: Συναρτήσεις II (Διάλεξη 12) 12-1 Ανασκόπηση Δομής Προγράμματος με Συναρτήσεις 1 void PrintMessage (); Πρότυπο (Δήλωση) Συνάρτησης (Δηλώνουν τι επιπλέον συναρτήσεις θα χρησιμοποιήσουμε
Κεφάλαιο 3.5-3.6, 3.2: Συναρτήσεις II (Διάλεξη 12) 12-1 Ανασκόπηση Δομής Προγράμματος με Συναρτήσεις 1 void PrintMessage (); Πρότυπο (Δήλωση) Συνάρτησης (Δηλώνουν τι επιπλέον συναρτήσεις θα χρησιμοποιήσουμε
Κεφάλαιο 1: Κίνηση και γεωμετρικά σχήματα
 Ασκήσεις της Ενότητας 2 : Ζωγραφίζοντας με το ΒΥΟΒ -1- α. Η χρήση της πένας Κεφάλαιο 1: Κίνηση και γεωμετρικά σχήματα Υπάρχουν εντολές που μας επιτρέπουν να επιλέξουμε το χρώμα της πένας, καθώς και το
Ασκήσεις της Ενότητας 2 : Ζωγραφίζοντας με το ΒΥΟΒ -1- α. Η χρήση της πένας Κεφάλαιο 1: Κίνηση και γεωμετρικά σχήματα Υπάρχουν εντολές που μας επιτρέπουν να επιλέξουμε το χρώμα της πένας, καθώς και το
Γλώσσα Προγραμματισμού C
 Προγραμματισμός HY: Γλώσσα Προγραμματισμού C Δρ. Ηλίας Κ. Σάββας, Αναπληρωτής Καθηγητής, Τμήμα Μηχανικών Πληροφορικής Τ.Ε., T.E.I. Θεσσαλίας Email: savvas@teilar.gr URL: http://teilar.academia.edu/iliassavvas
Προγραμματισμός HY: Γλώσσα Προγραμματισμού C Δρ. Ηλίας Κ. Σάββας, Αναπληρωτής Καθηγητής, Τμήμα Μηχανικών Πληροφορικής Τ.Ε., T.E.I. Θεσσαλίας Email: savvas@teilar.gr URL: http://teilar.academia.edu/iliassavvas
Γραφικά υπολογιστών Εργαστήριο 10 Εισαγωγή στα Sprites
 Γραφικά υπολογιστών Εργαστήριο 10 Εισαγωγή στα Sprites Σκοπός της 10ης άσκησης είναι να μάθουμε να χρησιμοποιούμε sprites και να φτιάξουμε ένα παιχνίδι που χρησιμοποιεί συγκρούσεις. Θα δούμε επίσης μερικά
Γραφικά υπολογιστών Εργαστήριο 10 Εισαγωγή στα Sprites Σκοπός της 10ης άσκησης είναι να μάθουμε να χρησιμοποιούμε sprites και να φτιάξουμε ένα παιχνίδι που χρησιμοποιεί συγκρούσεις. Θα δούμε επίσης μερικά
Μηχανολογικό Σχέδιο. Εργαστηριακή Άσκηση 1 Σχέδιο 1 2. Σπύρος Ερμίδης. Σχολή Ναυπηγών Μηχανολόγων Μηχανικών Ε.Μ.Π
 Σχολή Ναυπηγών Μηχανολόγων Μηχανικών Ε.Μ.Π Μηχανολογικό Σχέδιο Εργαστηριακή Άσκηση 1 Σχέδιο 1 2 Σπύρος Ερμίδης Η παρουσίαση προετοιμάστηκε το ακ. έτος 2014 15 από τον Σερράο Απόστολο (nm11046@mail.ntua.gr)
Σχολή Ναυπηγών Μηχανολόγων Μηχανικών Ε.Μ.Π Μηχανολογικό Σχέδιο Εργαστηριακή Άσκηση 1 Σχέδιο 1 2 Σπύρος Ερμίδης Η παρουσίαση προετοιμάστηκε το ακ. έτος 2014 15 από τον Σερράο Απόστολο (nm11046@mail.ntua.gr)
21. ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 4 - ΔΗΜΙΟΥΡΓΩΝΤΑΣ ΜΕ ΤΟ BYOB BYOB. Αλγόριθμος Διαδικασία Παράμετροι
 21. ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 4 - ΔΗΜΙΟΥΡΓΩΝΤΑΣ ΜΕ ΤΟ BYOB BYOB Αλγόριθμος Διαδικασία Παράμετροι Τι είναι Αλγόριθμος; Οι οδηγίες που δίνουμε με λογική σειρά, ώστε να εκτελέσουμε μια διαδικασία ή να επιλύσουμε ένα
21. ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 4 - ΔΗΜΙΟΥΡΓΩΝΤΑΣ ΜΕ ΤΟ BYOB BYOB Αλγόριθμος Διαδικασία Παράμετροι Τι είναι Αλγόριθμος; Οι οδηγίες που δίνουμε με λογική σειρά, ώστε να εκτελέσουμε μια διαδικασία ή να επιλύσουμε ένα
Κεφάλαιο 3.5-3.6, 3.2: Συναρτήσεις II. ( ιάλεξη 12) ιδάσκων: ηµήτρης Ζεϊναλιπούρ
 Κεφάλαιο 3.5-3.6, 3.2: Συναρτήσεις II ( ιάλεξη 12) ιδάσκων: ηµήτρης Ζεϊναλιπούρ 12-1 Ανασκόπηση οµής Προγράµµατος µε Συναρτήσεις #include 1 void PrintMessage (); Πρότυπο ( ήλωση) Συνάρτησης (
Κεφάλαιο 3.5-3.6, 3.2: Συναρτήσεις II ( ιάλεξη 12) ιδάσκων: ηµήτρης Ζεϊναλιπούρ 12-1 Ανασκόπηση οµής Προγράµµατος µε Συναρτήσεις #include 1 void PrintMessage (); Πρότυπο ( ήλωση) Συνάρτησης (
Προγραμματισμός με Logo στο MicroWorlds Pro
 1 Προγραμματισμός με Logo στο MicroWorlds Pro Η Logo είναι μια γλώσσα προγραμματισμού ειδικά σχεδιασμένη για τους μαθητές. Το πιο βασικό ίσως εργαλείο της Logo είναι η χελώνα. Κάποιες βασικές εντολές της
1 Προγραμματισμός με Logo στο MicroWorlds Pro Η Logo είναι μια γλώσσα προγραμματισμού ειδικά σχεδιασμένη για τους μαθητές. Το πιο βασικό ίσως εργαλείο της Logo είναι η χελώνα. Κάποιες βασικές εντολές της
Create Sprite at Runtime
 Create Sprite at Runtime (with ActionScript 3.0) Free Flash Demos Tested on Adobe CS4 Το σενάριο: Να φτιάξεις ένα sprite (που στον «μουσαμά» του να υπάρχει μια ζωγραφιά, π.χ. ένα τετράγωνο). Αυτό να το
Create Sprite at Runtime (with ActionScript 3.0) Free Flash Demos Tested on Adobe CS4 Το σενάριο: Να φτιάξεις ένα sprite (που στον «μουσαμά» του να υπάρχει μια ζωγραφιά, π.χ. ένα τετράγωνο). Αυτό να το
ΕΡΓΑΣΤΗΡΙΟ ΠΟΛΥΜΕΣΩΝ ΚΑΙ ΓΡΑΦΙΚΩΝ
 ΕΡΓΑΣΤΗΡΙΟ ΠΟΛΥΜΕΣΩΝ ΚΑΙ ΓΡΑΦΙΚΩΝ Εισαγωγή /4 Το σχήμα και το μέγεθος των δισδιάστατων αντικειμένων περιγράφονται με τις καρτεσιανές συντεταγμένες x, y. Με εφαρμογή γεωμετρικών μετασχηματισμών στο μοντέλο
ΕΡΓΑΣΤΗΡΙΟ ΠΟΛΥΜΕΣΩΝ ΚΑΙ ΓΡΑΦΙΚΩΝ Εισαγωγή /4 Το σχήμα και το μέγεθος των δισδιάστατων αντικειμένων περιγράφονται με τις καρτεσιανές συντεταγμένες x, y. Με εφαρμογή γεωμετρικών μετασχηματισμών στο μοντέλο
Βασικές Εντολές MicroWorlds Pro.
 Βασικές Εντολές MicroWorlds Pro. 1. μπροστά (μπ) αριθμός Μετακινεί τη χελώνα προς τα εμπρός. π.χ. μπροστά 100 2. πίσω (πι) αριθμός Μετακινεί τη χελώνα προς τα πίσω. π.χ. πι 30 3. δεξιά (δε) αριθμός Στρέφει
Βασικές Εντολές MicroWorlds Pro. 1. μπροστά (μπ) αριθμός Μετακινεί τη χελώνα προς τα εμπρός. π.χ. μπροστά 100 2. πίσω (πι) αριθμός Μετακινεί τη χελώνα προς τα πίσω. π.χ. πι 30 3. δεξιά (δε) αριθμός Στρέφει
Μεθόδων Επίλυσης Προβλημάτων
 ΕΠΛ 032.3: 3: Προγραμματισμός Μεθόδων Επίλυσης Προβλημάτων Αχιλλέας Αχιλλέως, Τμήμα Πληροφορικής, Πανεπιστήμιο Κύπρου Email: achilleas@cs.ucy.ac.cy Κεφάλαιο 9 Συναρτήσεις Μέρος II Θέματα ιάλεξης Μη- ομημένος
ΕΠΛ 032.3: 3: Προγραμματισμός Μεθόδων Επίλυσης Προβλημάτων Αχιλλέας Αχιλλέως, Τμήμα Πληροφορικής, Πανεπιστήμιο Κύπρου Email: achilleas@cs.ucy.ac.cy Κεφάλαιο 9 Συναρτήσεις Μέρος II Θέματα ιάλεξης Μη- ομημένος
ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Η/Υ Ακαδημαϊκό έτος 2001-2002 ΤΕΤΡΑΔΙΟ ΕΡΓΑΣΤΗΡΙΟΥ #4
 ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Η/Υ Ακαδημαϊκό έτος 2001-2002 ΤΕΤΡΑΔΙΟ ΕΡΓΑΣΤΗΡΙΟΥ #4 «Προγραμματισμός Η/Υ» - Τετράδιο Εργαστηρίου #4 2 Γενικά Στο Τετράδιο #4 του Εργαστηρίου θα αναφερθούμε σε θέματα διαχείρισης πινάκων
ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Η/Υ Ακαδημαϊκό έτος 2001-2002 ΤΕΤΡΑΔΙΟ ΕΡΓΑΣΤΗΡΙΟΥ #4 «Προγραμματισμός Η/Υ» - Τετράδιο Εργαστηρίου #4 2 Γενικά Στο Τετράδιο #4 του Εργαστηρίου θα αναφερθούμε σε θέματα διαχείρισης πινάκων
ΜΕΘΟΔΟΛΟΓΙΑ ΣΤΗΝ ΟΜΑΛΗ ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ ΚΕΝΤΡΟΜΟΛΟΣ ΔΥΝΑΜΗ
 ΜΕΘΟΔΟΛΟΓΙΑ ΣΤΗΝ ΟΜΑΛΗ ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ ΚΕΝΤΡΟΜΟΛΟΣ ΔΥΝΑΜΗ 1.Οι περισσότερες ασκήσεις είναι απλή εφαρμογή των τύπων Συνήθως από ένα μέγεθος όπως η συχνότητα f ή η γωνιακή ταχύτητα ω μπορούμε να υπολογίσουμε
ΜΕΘΟΔΟΛΟΓΙΑ ΣΤΗΝ ΟΜΑΛΗ ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ ΚΕΝΤΡΟΜΟΛΟΣ ΔΥΝΑΜΗ 1.Οι περισσότερες ασκήσεις είναι απλή εφαρμογή των τύπων Συνήθως από ένα μέγεθος όπως η συχνότητα f ή η γωνιακή ταχύτητα ω μπορούμε να υπολογίσουμε
Άσκηση 1: Λύση: Για το άθροισμα ισχύει: κι επειδή οι μέσες τιμές των Χ και Υ είναι 0: Έτσι η διασπορά της Ζ=Χ+Υ είναι:
 Άσκηση 1: Δύο τυχαίες μεταβλητές Χ και Υ έχουν στατιστικές μέσες τιμές 0 και διασπορές 25 και 36 αντίστοιχα. Ο συντελεστής συσχέτισης των 2 τυχαίων μεταβλητών είναι 0.4. Να υπολογισθούν η διασπορά του
Άσκηση 1: Δύο τυχαίες μεταβλητές Χ και Υ έχουν στατιστικές μέσες τιμές 0 και διασπορές 25 και 36 αντίστοιχα. Ο συντελεστής συσχέτισης των 2 τυχαίων μεταβλητών είναι 0.4. Να υπολογισθούν η διασπορά του
4 3 Απόκρυψη /Εμφάνιση
 ΤΟ ΠΕΡΙΙΒΑΛΛΟΝ Ο ΟΠΤΙΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΙΣΜΟΥ TURTLEART 2 4 3 Απόκρυψη /Εμφάνιση πλακιδίων εντολών από την περιοχή «3» Σβήσιμο Γραφικών τοποθέτηση χελώνας στο κέντρο 1 5 1 2 3 Οι εντολές ομαδοποιημένες κατά
ΤΟ ΠΕΡΙΙΒΑΛΛΟΝ Ο ΟΠΤΙΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΙΣΜΟΥ TURTLEART 2 4 3 Απόκρυψη /Εμφάνιση πλακιδίων εντολών από την περιοχή «3» Σβήσιμο Γραφικών τοποθέτηση χελώνας στο κέντρο 1 5 1 2 3 Οι εντολές ομαδοποιημένες κατά
Γραμμικά Συστήματα. δεν είναι λύση του συστήματος. β) Ποιο από τα παραπάνω ζεύγη είναι λύση του συστήματος
 8808Δίνεται η εξίσωση x y 7 Γραμμικά Συστήματα α) Να επαληθεύσετε ότι το ζεύγος αριθμών x, y 4, είναι μια λύση της εξίσωσης β) Να αποδείξετε ότι το 4, 88Δίνεται η εξίσωση x y 8 δεν είναι λύση του συστήματος
8808Δίνεται η εξίσωση x y 7 Γραμμικά Συστήματα α) Να επαληθεύσετε ότι το ζεύγος αριθμών x, y 4, είναι μια λύση της εξίσωσης β) Να αποδείξετε ότι το 4, 88Δίνεται η εξίσωση x y 8 δεν είναι λύση του συστήματος
Γραμμικά Συστήματα Δίνεται η εξίσωση 4x y 11(1). α) Ποια από τα ζεύγη (2, 3),(0, 11), (1, 8) κα (7, 0) είναι λύση της εξίσωσης (1);
 8808Δίνεται η εξίσωση x y 7 Γραμμικά Συστήματα α) Να επαληθεύσετε ότι το ζεύγος αριθμών x, y, είναι μια λύση της εξίσωσης β) Να αποδείξετε ότι το, 88Δίνεται η εξίσωση x y 8 δεν είναι λύση του συστήματος
8808Δίνεται η εξίσωση x y 7 Γραμμικά Συστήματα α) Να επαληθεύσετε ότι το ζεύγος αριθμών x, y, είναι μια λύση της εξίσωσης β) Να αποδείξετε ότι το, 88Δίνεται η εξίσωση x y 8 δεν είναι λύση του συστήματος
ΑΣΚΗΣΕΙΣ ΣΤΗΝ LOGO ΓΙΑ ΤΗΝ Γ ΤΑΞΗ
 ΑΣΚΗΣΕΙΣ ΣΤΗΝ LOGO ΓΙΑ ΤΗΝ Γ ΤΑΞΗ ΑΣΚΗΣΕΙΣ 1. Γράψτε πρόγραμμα σχεδίασης ενός τετραγώνου πλευράς 100. 2. Γράψτε πρόγραμμα σχεδίασης ενός ισόπλευρου τριγώνου πλευράς 100. 3. Γράψτε πρόγραμμα σχεδίασης ενός
ΑΣΚΗΣΕΙΣ ΣΤΗΝ LOGO ΓΙΑ ΤΗΝ Γ ΤΑΞΗ ΑΣΚΗΣΕΙΣ 1. Γράψτε πρόγραμμα σχεδίασης ενός τετραγώνου πλευράς 100. 2. Γράψτε πρόγραμμα σχεδίασης ενός ισόπλευρου τριγώνου πλευράς 100. 3. Γράψτε πρόγραμμα σχεδίασης ενός
Τυχαιοκρατικοί Αλγόριθμοι
 Πιθανότητες και Αλγόριθμοι Ανάλυση μέσης περίπτωσης Μελέτα τη συμπεριφορά ενός αλγορίθμου σε μια «μέση» είσοδο (ως προς κάποια κατανομή) Τυχαιοκρατικός αλγόριθμος Λαμβάνει τυχαίες αποφάσεις καθώς επεξεργάζεται
Πιθανότητες και Αλγόριθμοι Ανάλυση μέσης περίπτωσης Μελέτα τη συμπεριφορά ενός αλγορίθμου σε μια «μέση» είσοδο (ως προς κάποια κατανομή) Τυχαιοκρατικός αλγόριθμος Λαμβάνει τυχαίες αποφάσεις καθώς επεξεργάζεται
Κεφάλαιο 6: Ζωγραφική
 Κεφάλαιο 6: Ζωγραφική... Σε αυτό το κεφάλαιο: 6.1 Ζωγραφική 6.2 Απλά ζωγράφισε 6.3 Χρώμα, σκιά και μέγεθος 6.4 Παράδειγμα... «Ζωγραφίζω πράγματα που σκέφτομαι, όχι πράγματα που βλέπω!» (Πικάσο) 6.1 Ζωγραφική
Κεφάλαιο 6: Ζωγραφική... Σε αυτό το κεφάλαιο: 6.1 Ζωγραφική 6.2 Απλά ζωγράφισε 6.3 Χρώμα, σκιά και μέγεθος 6.4 Παράδειγμα... «Ζωγραφίζω πράγματα που σκέφτομαι, όχι πράγματα που βλέπω!» (Πικάσο) 6.1 Ζωγραφική
ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ. Τι είναι ; Συναρτήσεις. Παράδειγμα #1. double convert ( double cm ) { double inch;
 ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ Τι είναι ; Συναρτήσεις Αυτόνομα τμήματα κώδικα (υποπρογράμματα) που πραγματοποιούν μια καθορισμένη εργασία. Χρήσιμες για περιπτώσεις που ο ίδιος υπολογισμός επαναλαμβάνεται πολλές φορές
ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ Τι είναι ; Συναρτήσεις Αυτόνομα τμήματα κώδικα (υποπρογράμματα) που πραγματοποιούν μια καθορισμένη εργασία. Χρήσιμες για περιπτώσεις που ο ίδιος υπολογισμός επαναλαμβάνεται πολλές φορές
Το μεσαίο πλήκτρο ενεργοποιεί τα Osnaps μόνο αν η μεταβλητή MBUTTONPAN έχει τιμή 1.
 ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΣΗΜΕΙΑ ΕΛΞΗΣ Ο μηχανισμός OBJECT SNAP ή OSNAP (έλξη σε αντικείμενα) μας επιτρέπει να προσδιορίζουμε, όποτε χρειάζεται, σημεία σε χαρακτηριστικές θέσεις πάνω σε αντικείμενα του σχεδίου μας,
ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΣΗΜΕΙΑ ΕΛΞΗΣ Ο μηχανισμός OBJECT SNAP ή OSNAP (έλξη σε αντικείμενα) μας επιτρέπει να προσδιορίζουμε, όποτε χρειάζεται, σημεία σε χαρακτηριστικές θέσεις πάνω σε αντικείμενα του σχεδίου μας,
Γενικός τρόπος σύνταξης: Όνομα_συνάρτησης(όρισμα1,όρισμα2,,όρισμαΝ) Η ονομασία τους είναι δεσμευμένη. Παραδείγματος χάριν: sin(x) cos(x) tan(x) exp(x)
 Εσωτερικές (built-in) συναρτήσεις του Matlab Γενικός τρόπος σύνταξης: Όνομα_συνάρτησης(όρισμα1,όρισμα2,,όρισμαΝ) Επιτελούν διάφορες προκαθορισμένες λειτουργίες Η ονομασία τους είναι δεσμευμένη Παραδείγματος
Εσωτερικές (built-in) συναρτήσεις του Matlab Γενικός τρόπος σύνταξης: Όνομα_συνάρτησης(όρισμα1,όρισμα2,,όρισμαΝ) Επιτελούν διάφορες προκαθορισμένες λειτουργίες Η ονομασία τους είναι δεσμευμένη Παραδείγματος
Ανάπτυξη και Σχεδίαση Λογισμικού
 Ανάπτυξη και Σχεδίαση Λογισμικού Η γλώσσα προγραμματισμού C Γεώργιος Δημητρίου Συναρτήσεις (Functions) Οι βασικές λειτουργικές ενότητες ενός προγράμματος C Καλούνται με ορίσματα που αντιστοιχούνται σε
Ανάπτυξη και Σχεδίαση Λογισμικού Η γλώσσα προγραμματισμού C Γεώργιος Δημητρίου Συναρτήσεις (Functions) Οι βασικές λειτουργικές ενότητες ενός προγράμματος C Καλούνται με ορίσματα που αντιστοιχούνται σε
Ο χώρος όπου βρίσκονται οι εντολές (πλακίδια) με τις οποίες δημιουργούμε τα προγράμματά μας
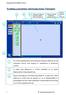 ΤΟ ΠΕΡΙΙΒΑΛΛΟΝ ΟΠΤΙΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΙΣΜΟΥ TURTLEART 2 4 3 Απόκρυψη /Εμφάνιση πλακιδίων εντολών από την περιοχή «3» Σβήσιμο Γραφικών τοποθέτηση χελώνας στο κέντρο Διακοπή εκτέλεσης του προγρ/τος 1 5 1 2
ΤΟ ΠΕΡΙΙΒΑΛΛΟΝ ΟΠΤΙΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΙΣΜΟΥ TURTLEART 2 4 3 Απόκρυψη /Εμφάνιση πλακιδίων εντολών από την περιοχή «3» Σβήσιμο Γραφικών τοποθέτηση χελώνας στο κέντρο Διακοπή εκτέλεσης του προγρ/τος 1 5 1 2
Γραφικά με υπολογιστές
 Γραφικά με Υπολογιστές Ενότητα # 3: Εισαγωγή Φοίβος Μυλωνάς Τμήμα Πληροφορικής Φοίβος Μυλωνάς Γραφικά με υπολογιστές 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Γραφικά με Υπολογιστές Ενότητα # 3: Εισαγωγή Φοίβος Μυλωνάς Τμήμα Πληροφορικής Φοίβος Μυλωνάς Γραφικά με υπολογιστές 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Οδηγίες για το Geogebra Μωυσιάδης Πολυχρόνης Δόρτσιος Κώστας
 Οδηγίες για το Geogebra Μωυσιάδης Πολυχρόνης Δόρτσιος Κώστας Η πρώτη οθόνη μετά την εκτέλεση του προγράμματος διαφέρει κάπως από τα προηγούμενα λογισμικά, αν και έχει αρκετά κοινά στοιχεία. Αποτελείται
Οδηγίες για το Geogebra Μωυσιάδης Πολυχρόνης Δόρτσιος Κώστας Η πρώτη οθόνη μετά την εκτέλεση του προγράμματος διαφέρει κάπως από τα προηγούμενα λογισμικά, αν και έχει αρκετά κοινά στοιχεία. Αποτελείται
Εργαστήριο #12. Βήμα 1 ο. Βήμα 2 ο. Βήμα 3 ο. Βήμα 4 ο.
 Εργαστήριο #12 Από τα προηγούμενα εργαστήρια: Το εργαστήριο αυτό είναι ανεξάρτητο από τα προηγούμενα επειδή όμως ασχολείται με τη γλώσσα JavaScript, βεβαιωθείτε ότι έχετε διαβάσει το εισαγωγικό Παράρτημα
Εργαστήριο #12 Από τα προηγούμενα εργαστήρια: Το εργαστήριο αυτό είναι ανεξάρτητο από τα προηγούμενα επειδή όμως ασχολείται με τη γλώσσα JavaScript, βεβαιωθείτε ότι έχετε διαβάσει το εισαγωγικό Παράρτημα
7.2.1 Εκτίμηση της Καμπύλης Παλινδρόμησης της Μεταβλητής Υ πάνω στην Μεταβλητή Χ
 7.2.1 Εκτίμηση της Καμπύλης Παλινδρόμησης της Μεταβλητής Υ πάνω στην Μεταβλητή Χ Για να προσδιορισθεί η καμπύλη παλινδρόμησης, η οποία αποτελείται από όλα τα ζεύγη σημείων τα οποία μπορούν προσδιορισθούν
7.2.1 Εκτίμηση της Καμπύλης Παλινδρόμησης της Μεταβλητής Υ πάνω στην Μεταβλητή Χ Για να προσδιορισθεί η καμπύλη παλινδρόμησης, η οποία αποτελείται από όλα τα ζεύγη σημείων τα οποία μπορούν προσδιορισθούν
Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε 3Δ. 3ο Μάθημα Αποκοπή. Γραφικα. Ευάγγελος Σπύρου
 Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε 3Δ Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε
Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε 3Δ Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε
ΣΕΤ ΑΣΚΗΣΕΩΝ 2. Προθεσμία: Τετάρτη 23/11/2016, 21:00
 ΣΕΤ ΑΣΚΗΣΕΩΝ 2 ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ I, ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2016-2017 Προθεσμία: Τετάρτη 23/11/2016, 21:00 Διαβάστε πριν ξεκινήσετε Διαβάστε την εκφώνηση προσεκτικά και σχεδιάστε το πρόγραμμά σας στο
ΣΕΤ ΑΣΚΗΣΕΩΝ 2 ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ I, ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2016-2017 Προθεσμία: Τετάρτη 23/11/2016, 21:00 Διαβάστε πριν ξεκινήσετε Διαβάστε την εκφώνηση προσεκτικά και σχεδιάστε το πρόγραμμά σας στο
ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ. ΘΕΜΑ 2ο
 ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΘΕΜΑ ο _6950 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να είναι αδύνατο. β) Να παραστήσετε γραφικά
ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΘΕΜΑ ο _6950 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να είναι αδύνατο. β) Να παραστήσετε γραφικά
ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ ΤΗΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
 ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ ΤΗΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΘΕΜΑ ο _6950 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του
ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ ΤΗΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΘΕΜΑ ο _6950 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ. Μια παράσταση που περιέχει πράξεις με μεταβλητές (γράμματα) και αριθμούς καλείται αλγεβρική, όπως για παράδειγμα η : 2x+3y-8
 ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
3) το παράθυρο Πίνακας τιμών όπου εμφανίζονται οι τιμές που παίρνουν οι παράμετροι
 Ο Δ Η Γ Ι Ε Σ Γ Ι Α Τ Ο M O D E L L U S 0.0 4. 0 5 Για να κατεβάσουμε το πρόγραμμα Επιλέγουμε Download στη διεύθυνση: http://modellus.co/index.php/en/download. Στη συνέχεια εκτελούμε το ModellusX_windows_0_4_05.exe
Ο Δ Η Γ Ι Ε Σ Γ Ι Α Τ Ο M O D E L L U S 0.0 4. 0 5 Για να κατεβάσουμε το πρόγραμμα Επιλέγουμε Download στη διεύθυνση: http://modellus.co/index.php/en/download. Στη συνέχεια εκτελούμε το ModellusX_windows_0_4_05.exe
Παιδαγωγικό σενάριο : Μελέτη της συνάρτησης y=αx
 Παιδαγωγικό σενάριο : Μελέτη της συνάρτησης y=αx Στόχος: Το παιδαγωγικό σενάριο αναφέρεται στη μελέτη της συνάρτησης y=αx και στη κατανόηση της κλίσης ευθείας. Λογισμικό: Για την εφαρμογή του σεναρίου
Παιδαγωγικό σενάριο : Μελέτη της συνάρτησης y=αx Στόχος: Το παιδαγωγικό σενάριο αναφέρεται στη μελέτη της συνάρτησης y=αx και στη κατανόηση της κλίσης ευθείας. Λογισμικό: Για την εφαρμογή του σεναρίου
5. Σε ορθογώνιο σύστημα αξόνων να σχεδιαστούν οι ευθείες που έχουν εξισώσεις τις: β. y = 4 δ. x = y
 . Δύο φίλοι, ο Μάρκος και ο Βασίλης, έχουν άθροισμα ηλικιών 7 χρόνια, και ο Μάρκος είναι μεγαλύτερος από το Βασίλη. Μπορείτε να υπολογίσετε την ηλικία του καθενός; Να δικαιολογήσετε την απάντησή σας. β.
. Δύο φίλοι, ο Μάρκος και ο Βασίλης, έχουν άθροισμα ηλικιών 7 χρόνια, και ο Μάρκος είναι μεγαλύτερος από το Βασίλη. Μπορείτε να υπολογίσετε την ηλικία του καθενός; Να δικαιολογήσετε την απάντησή σας. β.
Μορφοποίηση εικόνων. Εισαγωγή. Στόχος κεφαλαίου
 Περιεχόμενα Κεφάλαιο 1: Προετοιμασία παρουσίασης...1 Κεφάλαιο 2: Διαχείριση διαφανειών...18 Κεφάλαιο 3: Διαχείριση γραφικών...31 Κεφάλαιο 4: Επεξεργασία εικόνων με το Adobe Photoshop...56 Κεφάλαιο 5: Μορφοποίηση
Περιεχόμενα Κεφάλαιο 1: Προετοιμασία παρουσίασης...1 Κεφάλαιο 2: Διαχείριση διαφανειών...18 Κεφάλαιο 3: Διαχείριση γραφικών...31 Κεφάλαιο 4: Επεξεργασία εικόνων με το Adobe Photoshop...56 Κεφάλαιο 5: Μορφοποίηση
Graphics.h Διασύνδεση με τη Βιβλιοθήκη Γραφικών
 Graphics.h Διασύνδεση με τη Βιβλιοθήκη Γραφικών Βήμα 1 Θα πρέπει να κατεβάσετε τα παρακάτω αρχεία: A) graphics.h http://www.uniqueness-template.com/devcpp/graphics.h Αποθήκευση στο: C:\Dev-Cpp\include
Graphics.h Διασύνδεση με τη Βιβλιοθήκη Γραφικών Βήμα 1 Θα πρέπει να κατεβάσετε τα παρακάτω αρχεία: A) graphics.h http://www.uniqueness-template.com/devcpp/graphics.h Αποθήκευση στο: C:\Dev-Cpp\include
Μπορούμε να χρησιμοποιήσουμε τις παρακάτω μορφές συντεταγμένων με οποιοδήποτε συνδυασμό θέλουμε. Καρτεσιανές συντεταγμένες
 ΣΥΝΤΕΤΑΓΜΕΝΕΣ Όταν σχεδιάζουμε, πρέπει να προσδιορίζουμε σημεία πάνω σε ένα επίπεδο. Μπορούμε να εντοπίσουμε οποιοδήποτε σημείο στο χώρο, αν ορίσουμε πρώτα ένα απόλυτο, σταθερό σημείο και να μετρήσουμε
ΣΥΝΤΕΤΑΓΜΕΝΕΣ Όταν σχεδιάζουμε, πρέπει να προσδιορίζουμε σημεία πάνω σε ένα επίπεδο. Μπορούμε να εντοπίσουμε οποιοδήποτε σημείο στο χώρο, αν ορίσουμε πρώτα ένα απόλυτο, σταθερό σημείο και να μετρήσουμε
Κεφάλαιο 5. 5 Συστήματα συντεταγμένων
 Κεφάλαιο 5 5 Συστήματα συντεταγμένων Στις Γεωεπιστήμες η μορφή της γήινης επιφάνειας προσομοιώνεται από μια επιφάνεια, που ονομάζεται γεωειδές. Το γεωειδές είναι μια ισοδυναμική επιφάνεια του βαρυτικού
Κεφάλαιο 5 5 Συστήματα συντεταγμένων Στις Γεωεπιστήμες η μορφή της γήινης επιφάνειας προσομοιώνεται από μια επιφάνεια, που ονομάζεται γεωειδές. Το γεωειδές είναι μια ισοδυναμική επιφάνεια του βαρυτικού
Φύλλα εργασίας. MicroWorlds Pro. Πολυμεσικές Εφαρμογές με την χρήση της γλώσσας LOGO Στο Γυμνάσιο. Β. Χ. Χρυσοχοΐδης
 Φύλλα εργασίας MicroWorlds Pro Πολυμεσικές Εφαρμογές με την χρήση της γλώσσας LOGO Στο Γυμνάσιο Β. Χ. Χρυσοχοΐδης Πρόεδρος Συλλόγου Εκπαιδευτικών Πληροφορικής Φλώρινας 2 «Σχεδίαση και ανάπτυξη δραστηριοτήτων
Φύλλα εργασίας MicroWorlds Pro Πολυμεσικές Εφαρμογές με την χρήση της γλώσσας LOGO Στο Γυμνάσιο Β. Χ. Χρυσοχοΐδης Πρόεδρος Συλλόγου Εκπαιδευτικών Πληροφορικής Φλώρινας 2 «Σχεδίαση και ανάπτυξη δραστηριοτήτων
SVG Εργαστήριο 1. Εισαγωγή στα διανυσματικά γραφικά SVG
 SVG Εργαστήριο 1. Εισαγωγή στα διανυσματικά γραφικά SVG Χρήση SVG Τα SVG γραφικά, Scalable Vector Graphics, αναφέρονται σε διανυσματικά γραφικά που μένουν αναλοίωτα σε οποιαδήποτε αλλαγή των διαστάσεών
SVG Εργαστήριο 1. Εισαγωγή στα διανυσματικά γραφικά SVG Χρήση SVG Τα SVG γραφικά, Scalable Vector Graphics, αναφέρονται σε διανυσματικά γραφικά που μένουν αναλοίωτα σε οποιαδήποτε αλλαγή των διαστάσεών
ΥΠΟΛΟΓΙΣΤΕΣ ΙI. Άδειες Χρήσης. Τύποι δεδομένων, μεταβλητές, πράξεις. Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης ΥΠΟΛΟΓΙΣΤΕΣ ΙI Τύποι δεδομένων, μεταβλητές, πράξεις Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης Το παρόν εκπαιδευτικό
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης ΥΠΟΛΟΓΙΣΤΕΣ ΙI Τύποι δεδομένων, μεταβλητές, πράξεις Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης Το παρόν εκπαιδευτικό
Εισαγωγή στην πληροφορική
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Αγρονόμων Τοπογράφων Μηχανικών Εισαγωγή στην πληροφορική Βασίλειος Βεσκούκης Δρ. Ηλεκτρολόγος Μηχανικός & Μηχανικός Υπολογιστών ΕΜΠ v.vescoukis@cs.ntua.gr Η γλώσσα προγραμματισμού
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Αγρονόμων Τοπογράφων Μηχανικών Εισαγωγή στην πληροφορική Βασίλειος Βεσκούκης Δρ. Ηλεκτρολόγος Μηχανικός & Μηχανικός Υπολογιστών ΕΜΠ v.vescoukis@cs.ntua.gr Η γλώσσα προγραμματισμού
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Β ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ
 1 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Β ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ ΘΕΜΑ ο GI_V_ALG 16950 1.1 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να είναι αδύνατο. β)
1 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Β ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ ΘΕΜΑ ο GI_V_ALG 16950 1.1 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να είναι αδύνατο. β)
ΥΠΟΛΟΓΙΣΤΕΣ Ι. Τι χρειάζεται η εντολή DO ; ΕΠΑΝΑΛΗΨΕΙΣ ΕΝΤΟΛΗ DO. Όταν απαιτείται να εκτελεστεί πολλές φορές το ίδιο τμήμα ενός προγράμματος.
 ΥΠΟΛΟΓΙΣΤΕΣ Ι Τι χρειάζεται η εντολή DO ; ΕΠΑΝΑΛΗΨΕΙΣ ΕΝΤΟΛΗ DO Όταν απαιτείται να εκτελεστεί πολλές φορές το ίδιο τμήμα ενός προγράμματος. Τετριμμένο παράδειγμα: Κατασκευάστε πρόγραμμα που θα εμφανίζει
ΥΠΟΛΟΓΙΣΤΕΣ Ι Τι χρειάζεται η εντολή DO ; ΕΠΑΝΑΛΗΨΕΙΣ ΕΝΤΟΛΗ DO Όταν απαιτείται να εκτελεστεί πολλές φορές το ίδιο τμήμα ενός προγράμματος. Τετριμμένο παράδειγμα: Κατασκευάστε πρόγραμμα που θα εμφανίζει
Συλλογή & Επεξεργασία Δεδομένων Εργαστήριο 9 Ανάλυση Fourier: Από τη Θεωρία στην Πρακτική Εφαρμογή των Μαθηματικών
 Συλλογή & Επεξεργασία Δεδομένων Εργαστήριο 9 Ανάλυση Fourier: Από τη Θεωρία στην Πρακτική Εφαρμογή των Μαθηματικών Τύπων. Σύστημα Συλλογής & Επεξεργασίας Μετρήσεων Σκοπός Βασική δομή ενός προγράμματος
Συλλογή & Επεξεργασία Δεδομένων Εργαστήριο 9 Ανάλυση Fourier: Από τη Θεωρία στην Πρακτική Εφαρμογή των Μαθηματικών Τύπων. Σύστημα Συλλογής & Επεξεργασίας Μετρήσεων Σκοπός Βασική δομή ενός προγράμματος
ΥΠΟΛΟΓΙΣΤΕΣ ΙI. Άδειες Χρήσης. Συναρτήσεις I Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης ΥΠΟΛΟΓΙΣΤΕΣ ΙI Συναρτήσεις I Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Άδειες Χρήσης ΥΠΟΛΟΓΙΣΤΕΣ ΙI Συναρτήσεις I Διδάσκοντες: Αν. Καθ. Δ. Παπαγεωργίου, Αν. Καθ. Ε. Λοιδωρίκης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Δομημένος Προγραμματισμός. Τμήμα Επιχειρηματικού Σχεδιασμού και Πληροφοριακών Συστημάτων
 Δομημένος Προγραμματισμός Τμήμα Επιχειρηματικού Σχεδιασμού και Πληροφοριακών Συστημάτων www.bpis.teicrete.gr Τμήμα Επιχειρηματικού Σχεδιασμού και Πληροφοριακών Συστημάτων www.bpis.teicrete.gr 2 Παρατηρήσεις
Δομημένος Προγραμματισμός Τμήμα Επιχειρηματικού Σχεδιασμού και Πληροφοριακών Συστημάτων www.bpis.teicrete.gr Τμήμα Επιχειρηματικού Σχεδιασμού και Πληροφοριακών Συστημάτων www.bpis.teicrete.gr 2 Παρατηρήσεις
Πληροφορική ΙΙ Θεματική Ενότητα 8
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Πληροφορική ΙΙ Θεματική Ενότητα 8 Συναρτήσεις Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά Το έργο
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Πληροφορική ΙΙ Θεματική Ενότητα 8 Συναρτήσεις Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά Το έργο
ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ Ενότητα 3: ΣΥΝΕΛΙΞΗ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ Ενότητα 3: ΣΥΝΕΛΙΞΗ Aναστασία Βελώνη Τμήμα Η.Υ.Σ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ Ενότητα 3: ΣΥΝΕΛΙΞΗ Aναστασία Βελώνη Τμήμα Η.Υ.Σ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΜΑΘΗΜΑ: ΠΛΗΡΟΦΟΡΙΚΗ ΤΑΞΗ: Γ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΣΕ ΓΛΩΣΣΑ LOGO ΠΕΡΙΒΑΛΛΟΝ MICROWORLDS PRO
 ΜΑΘΗΜΑ: ΠΛΗΡΟΦΟΡΙΚΗ ΤΑΞΗ: Γ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΣΕ ΓΛΩΣΣΑ LOGO ΠΕΡΙΒΑΛΛΟΝ MICROWORLDS PRO 1. Δημιουργήστε τα παρακάτω σχήματα: Όλα τα σχήματα έχουν πλευρά 100, εκτός από το δωδεκάγωνο που έχει πλευρά 80. Τον
ΜΑΘΗΜΑ: ΠΛΗΡΟΦΟΡΙΚΗ ΤΑΞΗ: Γ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΣΕ ΓΛΩΣΣΑ LOGO ΠΕΡΙΒΑΛΛΟΝ MICROWORLDS PRO 1. Δημιουργήστε τα παρακάτω σχήματα: Όλα τα σχήματα έχουν πλευρά 100, εκτός από το δωδεκάγωνο που έχει πλευρά 80. Τον
Οδηγίες σχεδίασης στο περιβάλλον Blender
 Οδηγίες σχεδίασης στο περιβάλλον Blender Στον πραγματικό κόσμο, αντιλαμβανόμαστε τα αντικείμενα σε τρεις κατευθύνσεις ή διαστάσεις. Τυπικά λέμε ότι διαθέτουν ύψος, πλάτος και βάθος. Όταν θέλουμε να αναπαραστήσουμε
Οδηγίες σχεδίασης στο περιβάλλον Blender Στον πραγματικό κόσμο, αντιλαμβανόμαστε τα αντικείμενα σε τρεις κατευθύνσεις ή διαστάσεις. Τυπικά λέμε ότι διαθέτουν ύψος, πλάτος και βάθος. Όταν θέλουμε να αναπαραστήσουμε
ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ. Τύποι δεδομένων ΤΥΠΟΙ ΔΕΔΟΜΕΝΩΝ ΠΡΑΞΕΙΣ ΜΕΤΑΒΛΗΤΕΣ. Ακέραιοι αριθμοί (int) Πράξεις μεταξύ ακεραίων αριθμών
 ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ ΤΥΠΟΙ ΔΕΔΟΜΕΝΩΝ ΠΡΑΞΕΙΣ ΜΕΤΑΒΛΗΤΕΣ 1 Τύποι δεδομένων Η γλώσσα προγραμματισμού C++ υποστηρίζει τους παρακάτω τύπους δεδομένων: 1) Ακέραιοι αριθμοί (int). 2) Πραγματικοί αριθμοί διπλής ακρίβειας
ΥΠΟΛΟΓΙΣΤΕΣ ΙΙ ΤΥΠΟΙ ΔΕΔΟΜΕΝΩΝ ΠΡΑΞΕΙΣ ΜΕΤΑΒΛΗΤΕΣ 1 Τύποι δεδομένων Η γλώσσα προγραμματισμού C++ υποστηρίζει τους παρακάτω τύπους δεδομένων: 1) Ακέραιοι αριθμοί (int). 2) Πραγματικοί αριθμοί διπλής ακρίβειας
Εισαγωγή στην Αριθμητική Ανάλυση
 Εισαγωγή στην Αριθμητική Ανάλυση Εισαγωγή στη MATLAB ΔΙΔΑΣΚΩΝ: ΓΕΩΡΓΙΟΣ ΑΚΡΙΒΗΣ ΒΟΗΘΟΙ: ΔΗΜΗΤΡΙΑΔΗΣ ΣΩΚΡΑΤΗΣ, ΣΚΟΡΔΑ ΕΛΕΝΗ E-MAIL: SDIMITRIADIS@CS.UOI.GR, ESKORDA@CS.UOI.GR Τι είναι Matlab Είναι ένα περιβάλλον
Εισαγωγή στην Αριθμητική Ανάλυση Εισαγωγή στη MATLAB ΔΙΔΑΣΚΩΝ: ΓΕΩΡΓΙΟΣ ΑΚΡΙΒΗΣ ΒΟΗΘΟΙ: ΔΗΜΗΤΡΙΑΔΗΣ ΣΩΚΡΑΤΗΣ, ΣΚΟΡΔΑ ΕΛΕΝΗ E-MAIL: SDIMITRIADIS@CS.UOI.GR, ESKORDA@CS.UOI.GR Τι είναι Matlab Είναι ένα περιβάλλον
Γραφικά Υπολογιστών: Σχεδίαση γραμμών (Bresenham), Σχεδίασης Κύκλων, Γέμισμα Πολυγώνων
 1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Σχεδίαση γραμμών (Bresenham), Σχεδίασης Κύκλων, Γέμισμα Πολυγώνων Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιγραφή
1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Σχεδίαση γραμμών (Bresenham), Σχεδίασης Κύκλων, Γέμισμα Πολυγώνων Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιγραφή
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΗΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΗΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΘΕΜΑ ο _6950 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΗΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΘΕΜΑ ο _6950 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να
Ενσωματωμένα Συστήματα
 Ενσωματωμένα Συστήματα για εφαρμογές πραγματικού χρόνου Εφαρμογές με τον Arduino Ιωάννης Καλόμοιρος Αναπληρωτής Καθηγητής Τμήμα Μηχανικών Πληροφορικής Μάθημα 10 1 Συναρτήσεις αναλογικής εξόδου: PWM Το
Ενσωματωμένα Συστήματα για εφαρμογές πραγματικού χρόνου Εφαρμογές με τον Arduino Ιωάννης Καλόμοιρος Αναπληρωτής Καθηγητής Τμήμα Μηχανικών Πληροφορικής Μάθημα 10 1 Συναρτήσεις αναλογικής εξόδου: PWM Το
5ο Μάθημα Αλγόριθμοι Σχεδίασης Βασικών Σχημάτων
 5ο Μάθημα Αλγόριθμοι Σχεδίασης Βασικών Σχημάτων Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Ευθεία Κύκλος Έλλειψη Σύνοψη του σημερινού μαθήματος 1 Εισαγωγή 2 Ευθεία 3 Κύκλος
5ο Μάθημα Αλγόριθμοι Σχεδίασης Βασικών Σχημάτων Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Ευθεία Κύκλος Έλλειψη Σύνοψη του σημερινού μαθήματος 1 Εισαγωγή 2 Ευθεία 3 Κύκλος
δίου ορισμού, μέσου του τύπου εξαρτημένης μεταβλητής του πεδίου τιμών που λέγεται εικόνα της f για x α f α.
 3.1 Η έννοια της συνάρτησης Ορισμοί Συνάρτηση f από ένα συνόλου Α σε ένα σύνολο Β είναι μια αντιστοιχία των στοιχείων του Α στα στοιχεία του Β, κατά την οποία κάθε στοιχείο του Α αντιστοιχεί σε ένα μόνο
3.1 Η έννοια της συνάρτησης Ορισμοί Συνάρτηση f από ένα συνόλου Α σε ένα σύνολο Β είναι μια αντιστοιχία των στοιχείων του Α στα στοιχεία του Β, κατά την οποία κάθε στοιχείο του Α αντιστοιχεί σε ένα μόνο
MAΘΗΜΑΤΙΚΑ. κριτήρια αξιολόγησης B ΓΥΜΝΑΣΙΟΥ. Πέτρος Μάρκος
 B ΓΥΜΝΑΣΙΟΥ Πέτρος Μάρκος κριτήρια αξιολόγησης MAΘΗΜΑΤΙΚΑ Διαγωνίσματα σε κάθε μάθημα και επαναληπτικά σε κάθε κεφάλαιο Διαγωνίσματα σε όλη την ύλη για τις τελικές εξετάσεις Αναλυτικές απαντήσεις σε όλα
B ΓΥΜΝΑΣΙΟΥ Πέτρος Μάρκος κριτήρια αξιολόγησης MAΘΗΜΑΤΙΚΑ Διαγωνίσματα σε κάθε μάθημα και επαναληπτικά σε κάθε κεφάλαιο Διαγωνίσματα σε όλη την ύλη για τις τελικές εξετάσεις Αναλυτικές απαντήσεις σε όλα
Προγραμματιστικές Ασκήσεις, Φυλλάδιο 1
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΣΕ C Προγραμματιστικές Ασκήσεις, Φυλλάδιο Εκφώνηση: 9/3/0 Παράδοση: 5/4/0,.59 Άσκηση 0 η : Το πρόβλημα της βελόνας του Buffon Θέμα της εργασίας
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΣΕ C Προγραμματιστικές Ασκήσεις, Φυλλάδιο Εκφώνηση: 9/3/0 Παράδοση: 5/4/0,.59 Άσκηση 0 η : Το πρόβλημα της βελόνας του Buffon Θέμα της εργασίας
Τα στοιχεία του παιχνιδιού : Σκηνικό
 Περιγραφή των φύλλων δραστηριοτήτων διδασκαλίας γνωστικού αντικειμένου Φύλλο δραστηριοτήτων 1 Αναφέρεται στο στόχο σχεδίασης του παιχνιδιού. (Στόχος Α) Σκηνικό Τα στοιχεία του παιχνιδιού : (Ρακέτα) Χαρακτήρες
Περιγραφή των φύλλων δραστηριοτήτων διδασκαλίας γνωστικού αντικειμένου Φύλλο δραστηριοτήτων 1 Αναφέρεται στο στόχο σχεδίασης του παιχνιδιού. (Στόχος Α) Σκηνικό Τα στοιχεία του παιχνιδιού : (Ρακέτα) Χαρακτήρες
12. Συναρτήσεις (Μέρος ΙI)
 Προγραμματισμός Μεθόδων Επίλυσης Προβλημάτων 12. Συναρτήσεις (Μέρος ΙI) Ιωάννης Κατάκης Σήμερα o Συναρτήσεις χωρίς παραμέτρους o Συναρτήσεις με παραμέτρους Χωρίς επιστροφή τιμής Με επιστροφή τιμής o Εμβέλεια
Προγραμματισμός Μεθόδων Επίλυσης Προβλημάτων 12. Συναρτήσεις (Μέρος ΙI) Ιωάννης Κατάκης Σήμερα o Συναρτήσεις χωρίς παραμέτρους o Συναρτήσεις με παραμέτρους Χωρίς επιστροφή τιμής Με επιστροφή τιμής o Εμβέλεια
Απλή Δομή Επιλογής. Ο κώδικας. //με χρήση μεταβλητών. delay (3000);
 Απλή Δομή Επιλογής Να κατασκευάσετε το κύκλωμα το οποίο θα υλοποιεί τα φανάρια. Στη συνέχεια να αναπτύξετε τον κατάλληλο κώδικα ώστε όταν ανάβει το κόκκινο θα ανάβει και το άσπρο, όταν θα σβήνει το κόκκινο
Απλή Δομή Επιλογής Να κατασκευάσετε το κύκλωμα το οποίο θα υλοποιεί τα φανάρια. Στη συνέχεια να αναπτύξετε τον κατάλληλο κώδικα ώστε όταν ανάβει το κόκκινο θα ανάβει και το άσπρο, όταν θα σβήνει το κόκκινο
Προγραμματισμός Η/Υ (ΤΛ2007 )
 Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε.Ι. Κρήτης Προγραμματισμός Η/Υ (ΤΛ2007 ) Δρ. Μηχ. Νικόλαος Πετράκης (npet@chania.teicrete.gr) Ιστοσελίδα Μαθήματος: https://eclass.chania.teicrete.gr/ Εξάμηνο: Εαρινό 2014-15
Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε.Ι. Κρήτης Προγραμματισμός Η/Υ (ΤΛ2007 ) Δρ. Μηχ. Νικόλαος Πετράκης (npet@chania.teicrete.gr) Ιστοσελίδα Μαθήματος: https://eclass.chania.teicrete.gr/ Εξάμηνο: Εαρινό 2014-15
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Σχολή Οικονομίας Διοίκησης και Πληροφορικής Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Αρχές Τηλ/ων Συστημάτων Μπατιστάτος Μιχάλης Εργαστήριο 8 ο : Διαμόρφωση
Σχολή Οικονομίας Διοίκησης και Πληροφορικής Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Αρχές Τηλ/ων Συστημάτων Μπατιστάτος Μιχάλης Εργαστήριο 8 ο : Διαμόρφωση
Συναρτησιακός Προγραμματισμός 2008 Λύσεις στο Πρώτο Φύλλο Ασκήσεων
 Συναρτησιακός Προγραμματισμός 2008 Λύσεις στο Πρώτο Φύλλο Ασκήσεων 1. Χρησιμοποιείστε λ-εκφράσεις και τη συνάρτηση sumf στις Σημ.1, Ενότ.3.5, για να εκφράσετε το P 10 i=1p i j=1 (i + j)2, χωρίς να ορίσετε
Συναρτησιακός Προγραμματισμός 2008 Λύσεις στο Πρώτο Φύλλο Ασκήσεων 1. Χρησιμοποιείστε λ-εκφράσεις και τη συνάρτηση sumf στις Σημ.1, Ενότ.3.5, για να εκφράσετε το P 10 i=1p i j=1 (i + j)2, χωρίς να ορίσετε
Τράπεζα Θεμάτων Διαβαθμισμένης Δυσκολίας- Άλγεβρα Β ΓΕ.Λ.-Σχολικό έτος 2014-2015 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΔΙΑΒΑΘΜΙΣΜΕΝΗΣ ΔΥΣΚΟΛΙΑΣ. Σχολικό έτος: 2014-2015
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΔΙΑΒΑΘΜΙΣΜΕΝΗΣ ΔΥΣΚΟΛΙΑΣ Α Λ Γ Ε Β Ρ Α Β Λ Υ Κ Ε Ι Ο Υ Σχολικό έτος: 014-015 Τα θέματα εμπλουτίζονται με την δημοσιοποίηση και των νέων θεμάτων από το Ι.Ε.Π. Γ ε ν ι κ ή Ε π ι μ έ λ ε ι
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΔΙΑΒΑΘΜΙΣΜΕΝΗΣ ΔΥΣΚΟΛΙΑΣ Α Λ Γ Ε Β Ρ Α Β Λ Υ Κ Ε Ι Ο Υ Σχολικό έτος: 014-015 Τα θέματα εμπλουτίζονται με την δημοσιοποίηση και των νέων θεμάτων από το Ι.Ε.Π. Γ ε ν ι κ ή Ε π ι μ έ λ ε ι
Αριθμητική Επίλυση Συνήθων Διαφορίκών Εξισώσεων 3ο Εργαστήριο 27/03/2015 1
 Αριθμητική Επίλυση Συνήθων Διαφορίκών Εξισώσεων 3ο Εργαστήριο 7/3/5 Σκοπός αυτού του εργαστηρίου είναι να δούμε πως μπορούμε να επιλύσουμε συστήματα διαφορικών εξισώσεων, με την χρήση του Matlab. Συστήματα
Αριθμητική Επίλυση Συνήθων Διαφορίκών Εξισώσεων 3ο Εργαστήριο 7/3/5 Σκοπός αυτού του εργαστηρίου είναι να δούμε πως μπορούμε να επιλύσουμε συστήματα διαφορικών εξισώσεων, με την χρήση του Matlab. Συστήματα
Πληρουορική Γ Γσμμασίοσ
 Πληρουορική Γ Γσμμασίοσ Προγραμματισμός και Αλγόριθμοι Από το και τημ Χελώμα στημ Ευριπίδης Βραχνός http://evripides.mysch.gr/ 2014 2015 1 Προγραμματισμός Ζάννειο Πρότυπο Πειραματικό Γυμνάσιο Πειραιά Ενότητα:
Πληρουορική Γ Γσμμασίοσ Προγραμματισμός και Αλγόριθμοι Από το και τημ Χελώμα στημ Ευριπίδης Βραχνός http://evripides.mysch.gr/ 2014 2015 1 Προγραμματισμός Ζάννειο Πρότυπο Πειραματικό Γυμνάσιο Πειραιά Ενότητα:
ΘΕΜΑ 2 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να είναι αδύνατο.
 α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να είναι αδύνατο. (Μονάδες 10) β) Να παραστήσετε γραφικά στο επίπεδο τις δυο εξισώσεις
α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να είναι αδύνατο. (Μονάδες 10) β) Να παραστήσετε γραφικά στο επίπεδο τις δυο εξισώσεις
με παραμέτρους α, β, γ R α) Να επιλέξετε τιμές για τις παραμέτρους α, β, γ, ώστε το σύστημα αυτό να έχει μοναδική λύση το ζεύγος (1,-4).
 Δίνεται το σύστημα: x 2y= 9 ax+ βy= γ με παραμέτρους α, β, γ R α) Να επιλέξετε τιμές για τις παραμέτρους α, β, γ, ώστε το σύστημα αυτό να έχει μοναδική λύση το ζεύγος (1,-4). (Μονάδες 13) β) Να επιλέξετε
Δίνεται το σύστημα: x 2y= 9 ax+ βy= γ με παραμέτρους α, β, γ R α) Να επιλέξετε τιμές για τις παραμέτρους α, β, γ, ώστε το σύστημα αυτό να έχει μοναδική λύση το ζεύγος (1,-4). (Μονάδες 13) β) Να επιλέξετε
Επαναληπτικές Διαδικασίες
 Επαναληπτικές Διαδικασίες Οι επαναληπτικές δομές ( εντολές επανάληψης επαναληπτικά σχήματα ) χρησιμοποιούνται, όταν μια ομάδα εντολών πρέπει να εκτελείται αρκετές- πολλές φορές ανάλογα με την τιμή μιας
Επαναληπτικές Διαδικασίες Οι επαναληπτικές δομές ( εντολές επανάληψης επαναληπτικά σχήματα ) χρησιμοποιούνται, όταν μια ομάδα εντολών πρέπει να εκτελείται αρκετές- πολλές φορές ανάλογα με την τιμή μιας
Μηχανικό Στερεό. Μια εργασία για την Επανάληψη
 Μηχανικό Στερεό. Μια εργασία για την Επανάληψη Απλές προτάσεις Για τον έλεγχο της κατανόησης και εφαρμογής των εννοιών Δογραματζάκης Γιάννης 9/5/2013 Απλές προτάσεις για τον έλεγχο της κατανόησης και εφαρμογής
Μηχανικό Στερεό. Μια εργασία για την Επανάληψη Απλές προτάσεις Για τον έλεγχο της κατανόησης και εφαρμογής των εννοιών Δογραματζάκης Γιάννης 9/5/2013 Απλές προτάσεις για τον έλεγχο της κατανόησης και εφαρμογής
ΔΟΜΗΜΕΝΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ
 ΔΟΜΗΜΕΝΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Μάθημα 4ο Τμήμα Διοίκησης Επιχειρήσεων α εξάμηνο Β. Φερεντίνος Συναρτήσεις (functions) 56 Τεμαχισμός του προγράμματος σε μικρότερα κομμάτια που είναι πιο κατανοητά, πιο εύκολα
ΔΟΜΗΜΕΝΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Μάθημα 4ο Τμήμα Διοίκησης Επιχειρήσεων α εξάμηνο Β. Φερεντίνος Συναρτήσεις (functions) 56 Τεμαχισμός του προγράμματος σε μικρότερα κομμάτια που είναι πιο κατανοητά, πιο εύκολα
Φύλλο Εργασίας 3. Μια γρήγορη επανάληψη από τα προηγούμενα
 3 Φύλλο Εργασίας 3 Στο φύλλο εργασιών 3 θα ασχοληθούμε με τις λίστες μια δομή της γλώσσας python που έχει την δομή ενός πίνακα. Θα χρησιμοποιήσουμε τις βασικές εντολές από τις λίστες και θα κατασκευάσουμε
3 Φύλλο Εργασίας 3 Στο φύλλο εργασιών 3 θα ασχοληθούμε με τις λίστες μια δομή της γλώσσας python που έχει την δομή ενός πίνακα. Θα χρησιμοποιήσουμε τις βασικές εντολές από τις λίστες και θα κατασκευάσουμε
Μαθηματικός Ορισμός Διδιάστατου Χώρου (R 2 )
 Μαθηματικός Ορισμός Διδιάστατου Χώρου (R 2 ) Είναι ένα σύνολο σημείων με συντεταγμένες (x,y) Τα x και y έχουν τις εξής ιδιότητες: Το καθένα από αυτά διατρέχει το σύνολο των πραγματικών αριθμών Είναι ανεξάρτητα
Μαθηματικός Ορισμός Διδιάστατου Χώρου (R 2 ) Είναι ένα σύνολο σημείων με συντεταγμένες (x,y) Τα x και y έχουν τις εξής ιδιότητες: Το καθένα από αυτά διατρέχει το σύνολο των πραγματικών αριθμών Είναι ανεξάρτητα
Γ ΓΥΜΝΑΣΙΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΜΕ ΤΗ ΓΛΩΣΣΑ MicroWorlds Pro
 Για να μπορέσουμε να εισάγουμε δεδομένα από το πληκτρολόγιο αλλά και για να εξάγουμε εμφανίσουμε αποτελέσματα στην οθόνη του υπολογιστή χρησιμοποιούμε τις εντολές Εισόδου και Εξόδου αντίστοιχα. Σύνταξη
Για να μπορέσουμε να εισάγουμε δεδομένα από το πληκτρολόγιο αλλά και για να εξάγουμε εμφανίσουμε αποτελέσματα στην οθόνη του υπολογιστή χρησιμοποιούμε τις εντολές Εισόδου και Εξόδου αντίστοιχα. Σύνταξη
Κλήση Συναρτήσεων ΚΛΗΣΗ ΣΥΝΑΡΤΗΣΕΩΝ. Γεώργιος Παπαϊωάννου ( )
 ΚΛΗΣΗ ΣΥΝΑΡΤΗΣΕΩΝ Γεώργιος Παπαϊωάννου (2013-16) gepap@aueb.gr Περιγραφή: Μορφές μεταβίβασης ορισμάτων σε συναρτήσεις (και μεθόδους) και οι επιπτώσεις τους Επιστροφή τιμών από κλήση συναρτήσεων Υπερφόρτωση
ΚΛΗΣΗ ΣΥΝΑΡΤΗΣΕΩΝ Γεώργιος Παπαϊωάννου (2013-16) gepap@aueb.gr Περιγραφή: Μορφές μεταβίβασης ορισμάτων σε συναρτήσεις (και μεθόδους) και οι επιπτώσεις τους Επιστροφή τιμών από κλήση συναρτήσεων Υπερφόρτωση
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - 2 ο ΘΕΜΑ
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - ο ΘΕΜΑ ΚΕΦΑΛΑΙΟ 1 ο : ΣΥΣΤΗΜΑΤΑ 1. α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να είναι αδύνατο. β) Να παραστήσετε
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - ο ΘΕΜΑ ΚΕΦΑΛΑΙΟ 1 ο : ΣΥΣΤΗΜΑΤΑ 1. α) Να κατασκευάσετε ένα γραμμικό σύστημα δυο εξισώσεων με δυο αγνώστους με συντελεστές διάφορους του μηδενός, το οποίο να είναι αδύνατο. β) Να παραστήσετε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΑΝΑΠΤΥΞΗ ΚΑΙ ΣΧΕΔΙΑΣΗ ΛΟΓΙΣΜΙΚΟΥ Η γλώσσα προγραμματισμού C ΕΡΓΑΣΤΗΡΙΟ 3: Πίνακες, βρόχοι, συναρτήσεις 1 Ιουνίου 2017 Το σημερινό εργαστήριο
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΑΝΑΠΤΥΞΗ ΚΑΙ ΣΧΕΔΙΑΣΗ ΛΟΓΙΣΜΙΚΟΥ Η γλώσσα προγραμματισμού C ΕΡΓΑΣΤΗΡΙΟ 3: Πίνακες, βρόχοι, συναρτήσεις 1 Ιουνίου 2017 Το σημερινό εργαστήριο
FORTRAN & Αντικειμενοστραφής Προγραμματισμός ΣΝΜΜ 2017
 FORTRAN & Αντικειμενοστραφής Προγραμματισμός ΣΝΜΜ 2017 Μ4. Συναρτήσεις, Υπορουτίνες, Ενότητες - Ασκήσεις Γεώργιος Παπαλάμπρου Επικ. Καθηγητής ΕΜΠ Εργαστήριο Ναυτικής Μηχανολογίας george.papalambrou@lme.ntua.gr
FORTRAN & Αντικειμενοστραφής Προγραμματισμός ΣΝΜΜ 2017 Μ4. Συναρτήσεις, Υπορουτίνες, Ενότητες - Ασκήσεις Γεώργιος Παπαλάμπρου Επικ. Καθηγητής ΕΜΠ Εργαστήριο Ναυτικής Μηχανολογίας george.papalambrou@lme.ntua.gr
