Αρχές ροής υπογείων υδάτων
|
|
|
- ψυχή Δασκαλόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 ΚΕΦΑΛΑΙΟ 2 Αρχές ροής υπογείων υδάτων 2.1 Το εφαρμοσμένο πρόβλημα Το κίνητρο για να μελετήσουμε αρχές της υπόγειας ροής μάς το δίνουν μια σειρά ερωτημάτων που ανακύπτουν σε περιστατικά ρύπανσης των υπογείων υδάτων. Μερικά από τα πιο συνηθισμένα είναι τα εξής: Προς τα πού κινείται το υπόγειο νερό; πόσο γρήγορα κινείται; (Εδώ, έμμεσα ρωτάμε πόσο γρήγορα μπορεί το νερό να συμπαρασύρει ένα ρύπο.) Πόσον όγκο νερού μπορούμε να αντλήσουμε; (Αυτό το ερώτημα ενδιαφέρει γιατί ένα πιθανό μέτρο αποκατάστασης είναι και η άντληση από ρυπασμένους υδροφορείς, σε συνδυασμό με επεξεργασία του αντλούμενου νερού.) Πόση μάζα ρύπου μεταφέρει το υπόγειο νερό που κινείται ή που αντλούμε; Για να απαντήσουμε τις πιο πάνω ερωτήσεις ή για να καταλαβαίνουμε ποιοι παράγοντες επηρεάζουν τις απαντήσεις στα πιο πάνω ερωτήματα, πρέπει να μελετήσουμε το μηχανικό φαινόμενο της υπόγειας ροής. Η ροή υπογείων υδάτων (groundwater flow) αποτελεί αντικείμενο των ευρύτερων θεματικών ενοτήτων ρευστομηχανική (fluid mechanics) και ροή σε πορώδες μέσο (flow in porous media), από τις οποίες θα χρησιμοποιήσουμε λίγες θεμελιώδεις έννοιες. 2.2 Το μηχανικό φαινόμενο Για να αναλύσουμε το μηχανικό φαινόμενο της ροής των υπογείων υδάτων, χρειάζεται να ξέρουμε το αίτιο της κίνησής τους. Είναι σκόπιμο να αναζητήσουμε το μέγεθος εκείνο το οποίο αν γνωρίζαμε σε κάθε σημείο του πεδίου ροής θα ξέραμε πώς κινείται το νερό. Για την ανάλυση φυσικών φαινομένων ροής (μάζα ή όγκος ρευστού, μάζα ρύπου, θερμότητα, ηλεκτρισμός), συνήθως ορίζουμε μια κλίση δυναμικού, ορίζουμε δηλαδή ένα μέγεθος (δυναμικό) του οποίου η αλλαγή στο χώρο (κλίση) προκαλεί ροή της ποσότητας που μας ενδιαφέρει. Για τα προβλήματα ροής ρευστών, το μέγεθος του οποίου η αλλαγή προκαλεί ροή είναι η συνολική μηχανική ενέργεια ανά μονάδα μάζας ρευστού. Το δυναμικό ρευστού, Φ, για μοναδιαία μάζα (και σταθερή πυκνότητα) σε ένα σημείο του πεδίου ροής δίνεται ως (Freeze and Cherry, 1979): 2 v p p0 Φ = gz + + (2.1) 2 ρ όπου g είναι η επιτάχυνση της βαρύτητας, z είναι η απόσταση από κάποιο οριζόντιο επίπεδο αναφοράς, v είναι η ταχύτητα του ρευστού, p είναι η πίεση του ρευστού, p 0 είναι μια πίεση αναφοράς, συνήθως η ατμοσφαιρική, και ρ είναι η πυκνότητα του ρευστού. Λαμβάνοντας την ατμοσφαιρική πίεση αναφοράς p 0 = 0, και για προβλήματα ροής όπου οι ταχύτητες είναι μικρές, όπως συμβαίνει στα προβλήματα της υπόγειας ροής, ο όρος της κινητικής ενέργειας είναι αμελητέος, κι έτσι απλοποιείται η έκφραση για το δυναμικό: Σημειώσεις Μαθήματος Αποκατάσταση Ρυπασμένων Χώρων, Μαρίνα Πανταζίδου 2-1
2 pg Φ = gz + = gh γ (2.2) Στην εξίσωση (2.2) εισάγεται ένα καινούριο μέγεθος, το υδραυλικό φορτίο, h, που είναι το μέτρο της μηχανικής ενέργειας, ή, ισοδύναμα, το μέτρο δυναμικού. Η διαφορά του υδραυλικού φορτίου είναι το μέγεθος που μας επιτρέπει να αποφανθούμε αν το νερό κινείται ή όχι. Έτσι, αν εξετάζουμε δύο σημεία Α και Β, διακρίνουμε μεταξύ δύο περιπτώσεων: Δh ΑΒ = 0 το νερό δεν κινείται μεταξύ Α και Β Προσοχή όμως! Το δεδομένο Δh ΑΒ =0 δεν παρέχει επαρκή πληροφορία για να συμπεράνουμε ότι επικρατούν υδροστατικές συνθήκες, καθώς το νερό μπορεί να κινείται κάθετα στο διάστημα ΑΒ. Δh ΑΒ 0 (ύπαρξη υδραυλικής κλίσης) το νερό κινείται μεταξύ Α και Β Επίσης ξέρουμε και τη φορά της κίνησης, από το σημείο υψηλού δυναμικού στο σημείο χαμηλού δυναμικού, αφού στην κατεύθυνση της κίνησης του νερού χάνεται ενέργεια. Προσοχή όμως! δεν έχουμε επαρκή πληροφορία για να συμπεράνουμε ότι η διεύθυνση της κίνησης συμπίπτει με το διάστημα ΑΒ, απλά ξέρουμε ότι η ταχύτητα του υπόγειου νερού έχει μια συνιστώσα στη διεύθυνση που ορίζει το διάστημα ΑΒ. Για να έχουμε μια συνολική εικόνα για το πεδίο ροής, χρειαζόμαστε χάρτες με ισοδυναμικές καμπύλες. Ο λόγος που εισάγουμε ένα επί πλέον μέγεθος, δηλαδή το υδραυλικό φορτίο, είναι πρακτικός, επειδή έτσι γίνεται δυνατή η απαλοιφή της επιτάχυνσης της βαρύτητας από όλα τα μέλη της εξίσωσης (2.2) που δίνει: h = z + p/γ w (2.3) Η εξίσωση (2.3) μας επιτρέπει να υπολογίζουμε το υδραυλικό φορτίο h, σε κάθε σημείο του πεδίου ροής, ως το άθροισμα του υψομετρικού φορτίου, z, και του πιεζομετρικού φορτίου, p/γ w. Σημειώνεται ότι το υδραυλικό φορτίο έχει μονάδες μήκους [], όπως βέβαια και κάθε μέλος της εξίσωσης (2.3). Για κάθε σημείο του πεδίου ροής μπορούμε να υπολογίσουμε το υδραυλικό φορτίο αν γνωρίζουμε την πίεση, p, σε αυτό το σημείο και μετρώντας την απόστασή του, z, από το επίπεδο αναφοράς. Το υδραυλικό φορτίο είναι το μέγεθος που αναζητούσαμε, δηλαδή εκείνο που όταν το γνωρίζουμε σε κάθε σημείο του πεδίου ροής, ξέρουμε πώς κινείται το νερό. Έτσι η εξίσωση (2.3) είναι πολύ χρήσιμη, αφού μας επιτρέπει να υπολογίζουμε το μέγεθος-κλειδί για τα προβλήματα ροής στα σημεία που μας ενδιαφέρουν. Πρέπει να τονιστεί ότι τα παραπάνω περιγράφουν τη ροή ως αποτέλεσμα μεταβολών της μηχανικής ενέργειας του ρευστού. Υπάρχουν και άλλου είδους διαφορές ενέργειας (κλίσεις δυναμικού) που προκαλούν ροή των ρευστών, όπως διαφορές θερμοκρασίας, ηλεκτρικού δυναμικού και συγκεντρώσεων χημικών ουσιών. Σε αυτές τις περιπτώσεις έχουμε συζευγμένα φαινόμενα ροής (ωσμωτικά φαινόμενα) που δεν αποτελούν αντικείμενο αυτών των σημειώσεων και για τα οποία ο ενδιαφερόμενος αναγνώστης μπορεί να ανατρέξει στη βιβλιογραφία (itchell and Soga, 2005). Σημειώσεις Μαθήματος Αποκατάσταση Ρυπασμένων Χώρων, Μαρίνα Πανταζίδου 2-2
3 Παράδειγμα 2.1: δύο φρέατα που καταλήγουν από το ίδιο βάθος Στο Σχήμα 2.1 απεικονίζονται δύο φρέατα που καταλήγουν στο ίδιο βάθος, ενώ η στάθμη του νερού στο καθένα είναι διαφορετική. Ο σκοπός του απλού αυτού παραδείγματος είναι να βοηθήσει στην εξοικείωση με τα μεγέθη υδραυλικό, υψομετρικό και πιεζομετρικό φορτίο. 15m A 1 A1,A2 στάθμη νερού στα φρέατα B1 14m Από τον ορισμό του υδραυλικού φορτίου (2.3): h Α1 = z Α1 + p A1 /γ w = 15m+0 h Β1 = z Β1 + p Β1 /γ w = 14m+0 Σύμβαση-παραδοχή p A1 = p Β1 = ατμοσφαιρική =0 A 2 3m B2 h A1 = h A2 (γιατί;) h A2 = z Α2 + p A2 /γ w p A2 /γ w =15m-3m=12m αυθαίρετο επίπεδο αναφοράς Σχήμα 2.1: Μετρήσεις στάθμης υπογείων υδάτων σε δύο φρέατα Α και Β. Το συμπέρασμα στο οποίο μπορούμε να καταλήξουμε με τις πληροφορίες του Σχήματος 2.1 είναι ότι υπάρχει οριζόντια συνιστώσα της ροής με φορά από το φρέαρ Α (h A2 = 15m) προς το φρέαρ Β (h B2 = 14m). Το Σχήμα 2.1 θα μπορούσε να απεικονίζει ισοδύναμα δύο πιεζόμετρα στα οποία μετράμε το ύψος της στήλης του νερού (πχ το μήκος A1,A2 ), το οποίο μας δίνει το πιεζομετρικό ύψος του νερού στο σημείο όπου εγκαταστήσαμε το πιεζόμετρο (δηλαδή στο Α 2 ). Όπως προαναφέρθηκε, για να έχουμε μια συνολική εικόνα για το πεδίο ροής, χρειαζόμαστε χάρτες με ισοδυναμικές καμπύλες, τους οποίους μπορούμε να κατασκευάσουμε αν έχουμε εγκαταστήσει αρκετά φρέατα παρατήρησης και μετρήσει τη στάθμη του νερού στο καθένα. Στο εφαρμοσμένο όμως πρόβλημα, δεν μας ενδιαφέρει μόνο προς τα πού κινείται το νερό, αλλά και το πόσο γρήγορα κινείται. Την απάντηση μας δίνει ο νόμος του Darcy, όπως θα δούμε στην επόμενη ενότητα. Σημειώσεις Μαθήματος Αποκατάσταση Ρυπασμένων Χώρων, Μαρίνα Πανταζίδου 2-3
4 2.3 Ταχύτητα υπόγειας ροής ο νόμος του Darcy Στα μέσα του 19 ου αιώνα, o Darcy προσδιόρισε μια εμπειρική σχέση που συνδέει την ταχύτητα του νερού στο έδαφος με τα χαρακτηριστικά της ροής, με τη βοήθεια πειραμάτων ροής σε εδαφικές στήλες. Στη συνέχεια θα περιγράψουμε αυτή τη σχέση με τη βοήθεια του Σχήματος 2.2 1, αφού ορίσουμε πρώτα κάποια βασικά μεγέθη. Δh 1,2 p 2 /γ w p 1 /γ w 2 h 2 h 1 z 2 επίπεδο αναφοράς 1 z 1 διατομή επιφάνειας Α Σχήμα 2.2: Σκαρίφημα πειραματικής διάταξης ροής διαμέσου εδαφικής στήλης: το εδαφικό δείγμα συγκρατείται με πλέγματα στα σημεία 1 και 2. (Ποια είναι η κατεύθυνση της κίνησης του νερού; Από το σημείο 2 στο σημείο 1 ή από το 1 στο 2; Γιατί;) Η παροχή, Q [μονάδες: όγκος/χρόνος, 3 /T], είναι ο όγκος νερού που διέρχεται από μια διατομή στη μονάδα του χρόνου. Η μέση ταχύτητα ροής, v [/T], είναι ο λόγος της παροχής προς την επιφάνεια της διατομής, Α (επισήμανση: η επιφάνεια Α είναι κάθετη στη διεύθυνση ροής). Αναφορικά με το Σχήμα 2.2, έχοντας μετρήσει την παροχή, βρίσκουμε τη μέση ταχύτητα ως: v = Q /A (2.4) Ο Darcy βρήκε πειραματικά ότι η ταχύτητα είναι ανάλογη της υδραυλικής κλίσης, i: v i = Δh 1,2 / (2.5) (δηλαδή της κλίσης του υδραυλικού φορτίου), η οποία ορίζεται ως η διαφορά υδραυλικού φορτίου μεταξύ δύο σημείων, Δh 1,2, δια το μήκος ροής μεταξύ των δύο 1 Στο Σχήμα 2.2 σημειώνονται, για εξάσκηση, τα μεγέθη υδραυλικό φορτίο, πιεζομετρικό φορτίο και υψομετρικό φορτίο για τα σημεία 1 και 2. Για τον υπολογισμό της ταχύτητας ροής επαρκεί η γνώση της διαφοράς υδραυλικού φορτίου μεταξύ των σημείων 1 και 2. Σημειώσεις Μαθήματος Αποκατάσταση Ρυπασμένων Χώρων, Μαρίνα Πανταζίδου 2-4
5 αυτών σημείων,. (Προσοχή! Το μήκος ροής, όχι την απόσταση των δύο σημείων! Στο απλό μονοδιάστατο παράδειγμα ροής του Σχήματος 2.2, το μήκος ροής συμπίπτει με την απόσταση.) Την αναλογική σχέση που βρήκε ο Darcy μπορούμε να την εκφράσουμε ως ισότητα, εισάγοντας το μέγεθος της υδραυλικής αγωγιμότητας, k, που περιγράφει την ευκολία κίνησης του νερού διαμέσου των εδαφικών πόρων: v 1,2 = k i 1,2 (2.6) Στη γενική περίπτωση όπου δεν γνωρίζουμε την φορά της κίνησης του νερού, η (2.6) γράφεται με αρνητικό πρόσημο, που δηλώνει ότι η κίνηση του νερού γίνεται στην κατεύθυνση που μειώνεται το υδραυλικό φορτίο: v 1 2 = -k (h 2 -h 1 )/ (2.7) Για την επίλυση πρακτικών προβλημάτων, από αυτήν την ενότητα συγκρατούμε για την παροχή και τη μέση ταχύτητα τις σχέσεις: Q = k i A (2.8) και v = k i (2.9) Υδραυλική αγωγιμότητα Η υδραυλική αγωγιμότητα εκφράζει συνδυασμένα τις ιδιότητες του πορώδους μέσου και του ρευστού, δηλ. του εδάφους και του νερού στα προβλήματα υπόγειας ροής. Η συμβολή του μέσου και του ρευστού μπορεί να διαχωριστεί με την πιο κάτω έκφραση για την υδραυλική αγωγιμότητα: k = K ρ g / μ (2.10) όπου K είναι η απόλυτη περατότητα, που είναι ιδιότητα του εδάφους, ενώ ρ και μ είναι η πυκνότητα και το ιξώδες του ρευστού, αντίστοιχα. Η υδραυλική αγωγιμότητα των φυσικών εδαφών παρουσιάζει πολύ μεγάλη διακύμανση: 10 έως 12 τάξεις μεγέθους από τα χαλίκια έως την άργιλο. Ξαναγυρνώντας στην εξίσωση (2.9), αξίζει να τονίσουμε ότι η ταχύτητα της κίνησης του υπόγειου νερού εξαρτάται και από την υδραυλική αγωγιμότητα, δηλαδή το είδος του εδάφους, αλλά και από την υδραυλική κλίση, δηλαδή τα χαρακτηριστικά του πεδίου ροής. Για συνθήκες φυσικής ροής (πχ όχι για συνθήκες άντλησης), οι ackay et al. (1985) δίνουν ένα αναμενόμενο εύρος ταχυτήτων 1 έως 1000 μέτρα το χρόνο για περατά στρώματα (άμμους και χαλίκια), ενώ εκτιμούν ως πιο συνήθη μια διακύμανση μεταξύ 10 και 100 μέτρων το χρόνο Τι αγνοεί πότε ισχύει ο νόμος του Darcy O νόμος του Darcy, ή, ισοδύναμα, η εξίσωση (2.9), στην ουσία αγνοεί το πορώδες μέσο, θεωρώντας ροή διαμέσου της συνολικής επιφάνειας της διατομής. Αγνοεί δηλαδή την ύπαρξη των εδαφικών κόκκων, που καταλαμβάνουν ένα ποσοστό της διατομής το οποίο δεν είναι διαθέσιμο για ροή. Γι αυτόν το λόγο, όταν αναφερόμαστε στην ταχύτητα που δίνει η εξίσωση (2.9), την προσδιορίζουμε ως ταχύτητα Darcy ή φαινόμενη ταχύτητα. Εύκολα μπορούμε να πειστούμε ότι αυτή δεν είναι η πραγματική ταχύτητα του υπόγειου νερού, αφού η παροχή δεν διαιρείται με την επιφάνεια της πραγματικής διατομής που αντιστοιχεί στη ροή (δηλ. την επιφάνεια που αντιστοιχεί στους εδαφικούς πόρους) αλλά με την επιφάνεια της Σημειώσεις Μαθήματος Αποκατάσταση Ρυπασμένων Χώρων, Μαρίνα Πανταζίδου 2-5
6 συνολικής διατομής. Θέλοντας να πλησιάσουμε πιο κοντά στην πραγματικότητα, ορίζουμε τη μέση γραμμική ταχύτητα, v, ως το λόγο της παροχής προς την επιφάνεια των πόρων, A v : v Q Q v = = = (2.11) A A n n V όπου n είναι το πορώδες του εδαφικού υλικού, το οποίο εκφράζει το λόγο του όγκου των εδαφικών πόρων προς το συνολικό όγκο εδαφικού δείγματος (V v /V). Σημειώνεται ότι η αντικατάσταση της επιφάνειας των πόρων σε μια διατομή, A v, με το γινόμενο A n προϋποθέτει ότι ο λόγος της επιφάνειας των πόρων προς τη συνολική επιφάνεια εκφράζεται, για κάθε διατομή, από το πορώδες. Η μέση γραμμική ταχύτητα, v, μας είναι χρήσιμη γιατί περιγράφει την κίνηση του νερού διαμέσου της επιφάνειας που είναι διαθέσιμη για ροή. Γι αυτό, αν υποθέσουμε ότι εμφανίζεται στο ανάντη άκρο της εδαφικής στήλης του Σχήματος 2.2 (δηλαδή στο σημείο 1) ένας ρύπος και θέλουμε να υπολογίσουμε σε πόσο χρόνο θα εμφανιστεί το κατάντη άκρο (σημείο 2), μπορούμε να υπολογίσουμε το χρόνο άφιξης, Τ, του ρύπου με τη σχέση: T = (2.12) v Η σχέση (2.12) θα δώσει μια ικανοποιητική απάντηση στο ερώτημά μας, με την προϋπόθεση ότι ο ρύπος θα κινηθεί κυρίως λόγω της κίνησης του υπόγειου νερού, μια προσέγγιση που, όπως θα δούμε στο Κεφάλαιο 4, είναι ικανοποιητική για συγκεκριμένες συνθήκες. Στο ίδιο αυτό κεφάλαιο, θα συναντήσουμε ξανά τη μέση γραμμική ταχύτητα, v, και θα της αποδώσουμε έναν συνώνυμο όρο που περιγράφει με ακρίβεια τη συμβολή της στην εξάπλωση των ρύπων στο υπόγειο νερό. Επί πλέον, ο νόμος του Darcy ισχύει για στρωτή ροή, προϋπόθεση η οποία ικανοποιείται για τιμές του αδιάστατου αριθμού Reynolds, R=ρvd/μ, που δεν ξεπερνούν ένα εύρος τιμών 1 έως 10 (σημειώνεται ότι ο αριθμός Reynolds ορίζεται για σωλήνα διαμέτρου d), περιορισμός που ικανοποιείται στις περισσότερες περιπτώσεις φυσικής ροής σε εδάφη. Τέλος, όπως προαναφέρθηκε, ο νόμος του Darcy περιγράφει πλήρως τη ροή όταν δεν υπάρχει θερμική, χημική ή ηλεκτρική κλίση δυναμικού. 2.4 Εξισώσεις ροής Η προηγούμενη ενότητα παρουσίασε ένα νόμο που μπορεί να βοηθήσει στην επίλυση απλών μονοδιάστατων προβλημάτων ροής σε κορεσμένο έδαφος, για συνθήκες μόνιμης ροής, δηλαδή όταν δεν υπάρχουν μεταβολές στο χρόνο (η ταχύτητα σε κάθε σημείο παραμένει σταθερή). Για πιο πολύπλοκα προβλήματα, χρειάζεται να επιλυθούν οι διαφορικές εξισώσεις ροής οι οποίες προκύπτουν με βάση την αρχή της διατήρησης της μάζας του νερού, και οι οποίες διαφοροποιούνται για ροή σε κορεσμένο ή ακόρεστο έδαφος. Επί πλέον, σε περιπτώσεις ταυτόχρονης ροής ρευστών, η αρχή της διατήρησης της μάζας εφαρμόζεται για κάθε ρευστό ξεχωριστά και με αυτόν τον τρόπο προκύπτουν οι συζευγμένες διαφορικές εξισώσεις πολυφασικής ροής. Οι εξισώσεις αυτές δεν αποτελούν αντικείμενο αυτών των σημειώσεων και ο ενδιαφερόμενος αναγνώστης παραπέμπεται στη βιβλιογραφία (Dullien, 1992). Εδώ θα αναφερθεί απλώς η σχέση της πολυφασικής ροής με τα Σημειώσεις Μαθήματος Αποκατάσταση Ρυπασμένων Χώρων, Μαρίνα Πανταζίδου 2-6
7 προβλήματα ρύπανσης του υπεδάφους σε περιπτώσεις διαρροής ρύπων που δεν αναμειγνύονται με το νερό. Τέτοιοι ρύποι είναι τα πετρελαιοειδή ή οι οργανικοί διαλύτες, στους οποίους αναφερόμαστε με τον όρο μη υδατική φάση και με τους οποίους θα ασχοληθούμε στο Κεφάλαιο 3. (Δεν βλάπτει όμως να τονιστεί από τώρα ότι, ενώ οι δύο φάσεις δεν αναμειγνύονται, η μη υδατική φάση πάντα διαλύεται σε κάποιο βαθμό στο νερό, βλέπε Ενότητα 3.4.) Έτσι, σε κάποια περιστατικά ρυπασμένων χώρων, ενδιαφέρει η διφασική (νερό-μη υδατική φάση) ή τριφασική ροή (αέρας-νερό-μη υδατική φάση). 2.5 Προβλήματα Παράδειγμα 2.2: ροή σε ανομοιογενές έδαφος Για το πεδίο ροής που εικονίζεται στο Σχήμα 2.3, ζητείται να υπολογιστεί η παροχή (για επιφάνεια, κάθετη στην οριζόντια διεύθυνση ροής, ίση με 1 m 2 ) όταν η υδραυλική αγωγιμότητα είναι 8640 m/ημ και 432 m/ημ για τα στρώματα 1 και 2, αντίστοιχα. Επίσης, ζητείται να υπολογιστεί το υδραυλικό φορτίο στα σημεία Η και Μ. Οι επιφάνειες ΑΒ και ΓΔ είναι αδιαπέρατες (συνοριακή συνθήκη: γνωστή, σταθερή παροχή, Q = 0), ενώ οι επιφάνειες ΑΓ και ΒΔ είναι ισοδυναμικές επιφάνειες (συνοριακή συνθήκη: γνωστό όπως δίνεται στο Σχήμα 2.3 σταθερό υδραυλικό φορτίο). A h=5m Η Μ B h=1m Γ Δ x=0 x =1 x =1.5 x=2.5m Σχήμα 2.3: Ανομοιογενές εδαφικό στρώμα και συνοριακές συνθήκες πεδίου ροής. Η ανομοιογένεια του εδάφους δεν επιτρέπει να χρησιμοποιήσουμε απ ευθείας τις εξισώσεις της Ενότητας 2.3 για όλο το πεδίο ροής, αλλά μπορούμε να τις χρησιμοποιήσουμε για κάθε στρώμα ξεχωριστά. Ξεκινάμε παρατηρώντας ότι η συνολική πτώση υδραυλικού φορτίου μεταξύ των επιφανειών ΑΓ και ΒΔ, ή ισοδύναμα μεταξύ των σημείων Α και Β αφού στο πρόβλημά μας οι κατακόρυφες επιφάνειες είναι και ισοδυναμικές γραμμές, ισούται με το άθροισμα της πτώσης υδραυλικού φορτίου σε κάθε ένα στρώμα (παρατήρηση που δεν θα χρησιμοποιηθεί για την απάντηση των ερωτημάτων της άσκησης): Δh A + Δh Μ + Δh ΜΒ = h A h Β = 4m Παρατηρούμε επίσης ότι, λόγω συνέχειας, από κάθε στρώμα περνάει η ίδια παροχή, Q: Q = Q A = Q Μ = Q ΜΒ Στη συνέχεια, γράφουμε την έκφραση που δίνει την παροχή για κάθε στρώμα ξεχωριστά: Σημειώσεις Μαθήματος Αποκατάσταση Ρυπασμένων Χώρων, Μαρίνα Πανταζίδου 2-7
8 Q A ha h = k 1 A k1 0.5m k2 1m h h Q = k 2 h h k = k A = Q ( h h ) = h h 10 ( 5m h ) = h h 50m + h = 11h (1) 1 2 A A = Q 0.5m 1m B h h = k 2 h h = k 1 A A ( h h ) h h = 10h 10m = h = 11h 10m (2) B B B Επιλύοντας το σύστημα των εξισώσεων (1) και (2), βρίσκουμε h Μ = 1.33m και h Η = 4.67m. Σημειώνεται ότι η μεγαλύτερη πτώση υδραυλικού φορτίου (δηλαδή η μεγαλύτερη απώλεια ενέργειας) λαμβάνει χώρα στο στρώμα χαμηλότερης υδραυλικής αγωγιμότητας. Οι συνοριακές συνθήκες σε αυτό το πρόβλημα αναγκάζουν το νερό να περάσει με την ίδια ταχύτητα (αφού η παροχή πρέπει να μείνει σταθερή και η διατομή είναι σταθερή) από όλα τα στρώματα, με αποτέλεσμα να παρατηρείται η μεγάλη απώλεια ενέργειας στο χαμηλότερης περατότητας στρώμα. Αντίθετα, σε ένα πιο ρεαλιστικά ανομοιογενές, διδιάστατο ή τριδιάστατο πρόβλημα, το νερό θα κινηθεί κυρίως διαμέσου των πιο περατών στρώσεων, αποφεύγοντας τις λιγότερο περατές στρώσεις. Για τη συνολική παροχή, αρκεί να υπολογίσουμε την παροχή σε ένα στρώμα: ha h 5m 4.67m 2 3 QA = k 1 A = 8640m / ημ 1m Q = 2880m /ημ 1m A Παράδειγμα 2.3: ροή σε πεδίο με περατό διάφραγμα Το Σχήμα 2.4 απεικονίζει τις γραμμές ίσου υδραυλικού φορτίου (υπό κλίμακα η μονάδα μέτρησης και για το μήκος και για το υδραυλικό φορτίο είναι το μέτρο) σε εδαφικό σχηματισμό με υδραυλική αγωγιμότητα k = 10-5 cm/s = 8.64x10-3 m/ημ και τη θέση ενός περατού διαφράγματος-αντιδραστήρα πάχους 0.5 m με υδραυλική αγωγιμότητα k = 10-3 cm/s = m/ημ. Ως υλικό πλήρωσης του περατού διαφράγματος έχει επιλεγεί ένα μίγμα από ρινίσματα σιδήρου και άμμο, για να επιτευχθεί η μείωση της συγκέντρωσης τριχλωροαιθυλενίου που έχει ανιχνευτεί στην περιοχή. Ζητείται να υπολογιστεί ο χρόνος που θα παραμείνει το τριχλωροαιθυλένιο μέσα στο διάφραγμα. περατό διάφραγμα Σχήμα 2.4: Ισοδυναμικές καμπύλες όπως προκύπτουν από την εγκατάσταση περατού διαφράγματος σε ομοιογενές έδαφος. Προσοχή! - μόνο το μήκος του διαφράγματος δίνεται σωστά από την κλίμακα (σε m), το πάχος του όχι. Σημειώσεις Μαθήματος Αποκατάσταση Ρυπασμένων Χώρων, Μαρίνα Πανταζίδου 2-8
9 Για να βρούμε την υδραυλική κλίση στο περατό διάφραγμα θα μπορούσαμε να ακολουθήσουμε δύο προσεγγίσεις που σχολιάζονται στη συνέχεια με τη βοήθεια του Σχήματος 2.5, που δίνει ένα σκαρίφημα των ισοδυναμικών καμπυλών που περιβάλλουν το περατό διάφραγμα. περατό διάφραγμα Σχήμα 2.5: Σημεία στα οποία ενδιαφέρει η τιμή του υδραυλικού φορτίου. Προσέγγιση Ι Υποθέτουμε ότι η υδραυλική κλίση στην περιοχή του διαφράγματος (δηλ. μεταξύ Η και Μ) είναι ίδια με τη μέση κλίση μεταξύ των δύο ισοδυναμικών γραμμών (δηλ. μεταξύ Α και Β). Μπορούμε να στηρίξουμε αυτήν την προσέγγιση αν μπορούμε να επιχειρηματολογήσουμε ότι είτε (α) δίνει αποτελέσματα ικανοποιητικής ακρίβειας ή (β) αν τα αποτελέσματα δεν είναι μεν ακριβή, αλλά η απάντηση είναι υπέρ της ασφάλειας. Προσέγγιση ΙΙ Θεωρούμε τη ροή στην περιοχή του περατού διαφράγματος λίγο-πολύ ως μονοδιάστατη, κάτι που μπορεί να υποστηριχτεί από τις χονδρικώς παράλληλες ισοδυναμικές γραμμές στην περιοχή του διαφράγματος. Σε αυτήν την περίπτωση, θα λύσουμε ένα πρόβλημα με τρία στρώματα με διαφορετική υδραυλική αγωγιμότητα (ΑΗ, ΗΜ, ΜΒ). Με γνωστές τις υδραυλικές αγωγιμότητες και το υδραυλικό φορτίο στα Α και Β, θα βρούμε το υδραυλικό φορτίο στα σημεία Η και Μ, όπως ακριβώς στο Παράδειγμα 2.2. Για λόγους εξάσκησης, αλλά κυρίως σύγκρισης, θα επιχειρήσουμε και τις δύο προσεγγίσεις. Προσέγγιση Ι Στην περιοχή του διαφράγματος, οι ισοδυναμικές γραμμές απέχουν (χρησιμοποιούμε την κλίμακα στο Σχήμα 2.4) 16.7m. Η υδραυλική κλίση στην περιοχή του διαφράγματος δίνεται από τη διαφορά υδραυλικού φορτίου μεταξύ δύο ισοδυναμικών γραμμών δια το μήκος ροής (που ισούται με την απόσταση) μεταξύ των ισοδυναμικών γραμμών: i = Δh A, B A, B 0.1m = 16.7m = Θα βρούμε το χρόνο παραμονής του ρύπου μέσα στο διάφραγμα, δηλαδή το χρόνο άφιξης του ρύπου στην κατάντη επιφάνεια του διαφράγματος, υπολογίζοντας τη μέση γραμμική ταχύτητα του νερού μέσα στο διάφραγμα. Ξεκινάμε υπολογίζοντας την ταχύτητα Darcy (φαινόμενη ταχύτητα): m m v = kδιαϕρ i = = ημ ημ Υποθέτοντας για το πορώδες του διαφράγματος μια τιμή ίση με n=0.4, βρίσκουμε τη μέση γραμμική ταχύτητα: v m v = = n ημ Σημειώσεις Μαθήματος Αποκατάσταση Ρυπασμένων Χώρων, Μαρίνα Πανταζίδου 2-9
10 και στη συνέχεια το χρόνο παραμονής του τριχλωροαιθυλενίου στο διάφραγμα: T = διαϕρ v = 0.5m = 38ημ 0.013m ημ Προσέγγιση ΙΙ Ακολουθώντας τα βήματα του Παραδείγματος 2.2, υπολογίζουμε το υδραυλικό φορτίο στα σημεία Η και Μ, κι έτσι βρίσκουμε h Μ = m και h Η = m. Για αυτές τις τιμές, η υδραυλική κλίση μεταξύ των σημείων Η και Μ είναι , εκατό φορές μικρότερη σε σχέση με την προσέγγιση Ι, και άρα ο χρόνος παραμονής στο διάφραγμα θα είναι εκατό φορές μεγαλύτερος, ξεπερνάει δηλαδή τη μια δεκαετία (3800 μέρες). Με άλλα λόγια, η προσέγγιση Ι δεν είναι ακριβής, αλλά είναι υπέρ της ασφαλείας. Βέβαια σε μια πραγματική εφαρμογή, θα καταλήγαμε στο συμπέρασμα ότι επειδή δεν αναμένεται να χρειάζονται τόσο μεγάλοι χρόνοι παραμονής, δεν χρειάζεται να κατασκευαστεί ένα συνεχές διάφραγμα. Για το συγκεριμένο πρόβλημα, προτείνεται ένα διάφραγμα με εναλλασσόμενα αδιαπέρατα και περατά τμήματα (funnel and gate), έτσι ώστε το νερό να περνάει με μεγαλύτερη ταχύτητα μέσα από τα περατά τμήματα. Το προτέρημα αυτού του εναλλακτικού σχεδιασμού είναι ότι εξοικονομείται υλικό πλήρωσης του περατού διαφράγματος. 2.6 Κύρια σημεία του κεφαλαίου Για την ενότητα της ροής υπογείων υδάτων, είναι σημαντική η εξοικείωση με την έννοια του υδραυλικού φορτίου, που είναι το μέγεθος-κλειδί για την κατανόηση και επίλυση των προβλημάτων ροής. Το υδραυλικό φορτίο είναι το μέτρο της μηχανικής ενέργειας του ρευστού. Στα προβλήματα υπόγειας ροής υπολογίζουμε δυο συνεισφορές στη συνολική μηχανική ενέργειας του ρευστού: την ενέργεια λόγω θέσης του ρευστού στο βαρυτικό πεδίο και την ενέργεια λόγω πίεσης. Αγνοούμε δηλαδή τη συμβολή της κινητικής ενέργειας επειδή οι ταχύτητες είναι μικρές. Όσον αφορά το εφαρμοσμένο αντικείμενο της ροής υπογείων υδάτων, σε αυτό το κεφάλαιο είδαμε τις σχέσεις που μας επιτρέπουν να υπολογίζουμε, για απλά μονοδιάστατα προβλήματα, τα βασικά μεγέθη που ενδιαφέρουν σε περιστατικά ρύπανσης, δηλαδή την παροχή και την ταχύτητα. Ειδικά για την ταχύτητα, είναι πολύ σημαντική η διάκριση μεταξύ της φαινόμενης ταχύτητας, που αναφέρεται σε ολόκληρη τη διατομή, και της μέσης γραμμικής ταχύτητας, που αναφέρεται στη διατομή που αντιστοιχεί τους εδαφικούς πόρους και γι αυτό μπορεί να προσεγγίσει καλύτερα την κίνηση ενός ρύπου εξ αιτίας της κίνησης του υπόγειου νερού. Η σχέση μεταξύ κίνησης ρύπου και κίνησης υπόγειου νερού αντιμετωπίζεται συστηματικά στο Κεφάλαιο Βιβλιογραφικές αναφορές Freeze, R.A. and J.A. Cherry (1979). Groundwater, Prentice all. ackay, D.., P.V. Roberts and J.A. Cherry (1985). Transport of organic contaminants in groundwater, Environmental Science and Technology, 19:5: Βιβλιογραφία Dullien, F.A.. (1992). Porous media: fluid transport and pore structure, 2 nd edition, Academic Press. itchell, J.K. and K. Soga (2005). Fundamentals of soil behavior, 3 rd edition, Wiley. Σημειώσεις Μαθήματος Αποκατάσταση Ρυπασμένων Χώρων, Μαρίνα Πανταζίδου 2-10
Περιβαλλοντική Γεωτεχνική Θεματική Ενότητα 4 Υπόγεια Ροή
 Περιβαλλοντική Γεωτεχνική Θεματική Ενότητα 4 Υπόγεια Ροή Λυμένες ασκήσεις Χρόνος παραμονής ρύπου σε περατό διάφραγμα Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Σχολή Πολιτικών Μηχανικών Άδειες Χρήσης Το
Περιβαλλοντική Γεωτεχνική Θεματική Ενότητα 4 Υπόγεια Ροή Λυμένες ασκήσεις Χρόνος παραμονής ρύπου σε περατό διάφραγμα Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Σχολή Πολιτικών Μηχανικών Άδειες Χρήσης Το
Περιβαλλοντική Γεωτεχνική Θεματική Ενότητα 4 Υπόγεια Ροή
 Περιβαλλοντική Γεωτεχνική Θεματική Ενότητα 4 Υπόγεια Ροή Λυμένες ασκήσεις Πρόβλημα ροής σε ανομοιογενές έδαφος Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Σχολή Πολιτικών Μηχανικών Άδειες Χρήσης Το παρόν
Περιβαλλοντική Γεωτεχνική Θεματική Ενότητα 4 Υπόγεια Ροή Λυμένες ασκήσεις Πρόβλημα ροής σε ανομοιογενές έδαφος Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Σχολή Πολιτικών Μηχανικών Άδειες Χρήσης Το παρόν
Υπόγεια ροή. Παρουσίαση 2 από 4: Νόμος Darcy
 Υπόγεια ροή Παρουσίαση 2 από 4: Νόμος Darcy 1 Κύρια ερωτήματα ροής & νόμος Darcy Πόσον όγκο νερού μπορούμε να αντλήσουμε; Σχετικά μεγέθη: ταχύτητα, παροχή σε απλά μονοδιάστατα προβλήματα, τα βρίσκουμε
Υπόγεια ροή Παρουσίαση 2 από 4: Νόμος Darcy 1 Κύρια ερωτήματα ροής & νόμος Darcy Πόσον όγκο νερού μπορούμε να αντλήσουμε; Σχετικά μεγέθη: ταχύτητα, παροχή σε απλά μονοδιάστατα προβλήματα, τα βρίσκουμε
Υπόγεια ροή. Παρουσίαση 1 από 4: Κατεύθυνση κίνησης υπόγειου νερού. Περιεχόμενα
 Υπόγεια ροή Παρουσίαση 1 από 4: Κατεύθυνση κίνησης υπόγειου νερού Περιεχόμενα 1) Εισαγωγή (κίνητρο μελέτης υπόγειας ροής) 2) Αναζήτηση απάντησης στην ερώτηση «προς τα πού κινείται το υπόγειο νερό» 1 Βασικό
Υπόγεια ροή Παρουσίαση 1 από 4: Κατεύθυνση κίνησης υπόγειου νερού Περιεχόμενα 1) Εισαγωγή (κίνητρο μελέτης υπόγειας ροής) 2) Αναζήτηση απάντησης στην ερώτηση «προς τα πού κινείται το υπόγειο νερό» 1 Βασικό
ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ
 ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Θεματική Ενότητα 4 Υπόγεια ροή Νόμος Darcy Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Θεματική Ενότητα 4 Υπόγεια ροή Νόμος Darcy Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ
 ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Θεματική Ενότητα 4 Υπόγεια ροή Κατεύθυνση κίνησης υπόγειου νερού Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Θεματική Ενότητα 4 Υπόγεια ροή Κατεύθυνση κίνησης υπόγειου νερού Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Υπόγεια ροή. Εξισώσεις (μονοφασικής) ροής Εξισώσεις πολυφασικής ροής
 Υπόγεια ροή Εξισώσεις (μονοφασικής) ροής Εξισώσεις πολυφασικής ροής Ποια προβλήματα λύνονται με ποια εργαλεία; Μονοδιάστατα προβλήματα (ή μονοδιάστατη απλοποίηση -D πεδίων ροής), σταθερή υδραυλική κλίση
Υπόγεια ροή Εξισώσεις (μονοφασικής) ροής Εξισώσεις πολυφασικής ροής Ποια προβλήματα λύνονται με ποια εργαλεία; Μονοδιάστατα προβλήματα (ή μονοδιάστατη απλοποίηση -D πεδίων ροής), σταθερή υδραυλική κλίση
Υπόγεια ροή. Παρουσίαση 3 από 4: Ταχύτητα κίνησης υπόγειου νερού & ρύπου. (Tαχύτητα μεταγωγής)
 Υπόγεια ροή Παρουσίαση 3 από : Ταχύτητα κίνησης υπόγειου νερού & ρύπου (Tαχύτητα μεταγωγής) Απλό μοντέλο εδαφικής στήλης: συμπαγής κύλινδρος επιφάνειας Α με πολλά κυλινδρικά ανοίγματα R=0.5cm R=1cm =100cm
Υπόγεια ροή Παρουσίαση 3 από : Ταχύτητα κίνησης υπόγειου νερού & ρύπου (Tαχύτητα μεταγωγής) Απλό μοντέλο εδαφικής στήλης: συμπαγής κύλινδρος επιφάνειας Α με πολλά κυλινδρικά ανοίγματα R=0.5cm R=1cm =100cm
ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ
 ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Θεματική Ενότητα Υπόγεια ροή Ταχύτητα κίνησης υπόγειου νερού και ρύπου Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Θεματική Ενότητα Υπόγεια ροή Ταχύτητα κίνησης υπόγειου νερού και ρύπου Άδειες Χρήσης Το παρόν εκπαιδευτικό
Mεταφορά διαλυμένου ρύπου σε κορεσμένο έδαφος: Μαθηματική περιγραφή
 Mεταφορά διαλυμένου ρύπου σε κορεσμένο έδαφος: Μαθηματική περιγραφή Βασικό ερώτημα: Πού θα πάει ο ρύπος; Παρουσίαση από 4 Μεταφορά λόγω μεταγωγής+διάχυσης+διασποράς Ροή μάζας λόγω μεταγωγής Ροή μάζας ρύπου
Mεταφορά διαλυμένου ρύπου σε κορεσμένο έδαφος: Μαθηματική περιγραφή Βασικό ερώτημα: Πού θα πάει ο ρύπος; Παρουσίαση από 4 Μεταφορά λόγω μεταγωγής+διάχυσης+διασποράς Ροή μάζας λόγω μεταγωγής Ροή μάζας ρύπου
Mεταφορά διαλυμένου ρύπου σε κορεσμένο έδαφος: Μαθηματική περιγραφή
 Mεταφορά διαλυμένου ρύπου σε κορεσμένο έδαφος: Μαθηματική περιγραφή Βασικό ερώτημα: Πού θα πάει ο ρύπος; Παρουσίαση 3 από 4 Tρία λυμένα παραδείγματα & μαθησιακοί στόχοι (έως τώρα) Τρία ερωτήματα μεταφοράς
Mεταφορά διαλυμένου ρύπου σε κορεσμένο έδαφος: Μαθηματική περιγραφή Βασικό ερώτημα: Πού θα πάει ο ρύπος; Παρουσίαση 3 από 4 Tρία λυμένα παραδείγματα & μαθησιακοί στόχοι (έως τώρα) Τρία ερωτήματα μεταφοράς
ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ
 ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Θεματική Ενότητα 4 Υπόγεια ροή Εξισώσεις ροής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Θεματική Ενότητα 4 Υπόγεια ροή Εξισώσεις ροής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
. Υπολογίστε το συντελεστή διαπερατότητας κατά Darcy, την ταχύτητα ροής και την ταχύτητα διηθήσεως.
 Μάθημα: Εδαφομηχανική Ι, 7 ο εξάμηνο. Διδάσκων: Ιωάννης Ορέστης Σ. Γεωργόπουλος, Επιστημονικός Συνεργάτης Τμήματος Πολιτικών Έργων Υποδομής, Δρ Πολιτικός Μηχανικός Ε.Μ.Π. Θεματική περιοχή: Υδατική ροή
Μάθημα: Εδαφομηχανική Ι, 7 ο εξάμηνο. Διδάσκων: Ιωάννης Ορέστης Σ. Γεωργόπουλος, Επιστημονικός Συνεργάτης Τμήματος Πολιτικών Έργων Υποδομής, Δρ Πολιτικός Μηχανικός Ε.Μ.Π. Θεματική περιοχή: Υδατική ροή
Τρία ερωτήματα μεταφοράς. Που πρέπει να γίνουν «άσκηση», και να λυθεί η άσκηση για να απαντηθεί το ερώτημα...
 Τρία ερωτήματα μεταφοράς Που πρέπει να γίνουν «άσκηση», και να λυθεί η άσκηση για να απαντηθεί το ερώτημα... Ερώτημα Άσκηση Lundell-Sällfors and Sällfors (2000) Τι μπορώ να «πετάξω»; Πού πρέπει να εστιάσω;
Τρία ερωτήματα μεταφοράς Που πρέπει να γίνουν «άσκηση», και να λυθεί η άσκηση για να απαντηθεί το ερώτημα... Ερώτημα Άσκηση Lundell-Sällfors and Sällfors (2000) Τι μπορώ να «πετάξω»; Πού πρέπει να εστιάσω;
ΑΠΟΚΑΤΑΣΤΑΣΗ ΡΥΠΑΣΜΕΝΩΝ ΧΩΡΩΝ ΣΧΟΛΙΑ ΓΙΑ ΤΕΧΝΟΛΟΓΙΕΣ ΓΙΑ ΤΙΣ ΟΠΟΙΕΣ ΔΙΝΟΝΤΑΙ ΑΡΙΘΜΗΤΙΚΑ ΠΑΡΑΔΕΙΓΜΑΤΑ
 ΑΠΟΚΑΤΑΣΤΑΣΗ ΡΥΠΑΣΜΕΝΩΝ ΧΩΡΩΝ ΣΧΟΛΙΑ ΓΙΑ ΤΕΧΝΟΛΟΓΙΕΣ ΓΙΑ ΤΙΣ ΟΠΟΙΕΣ ΔΙΝΟΝΤΑΙ ΑΡΙΘΜΗΤΙΚΑ ΠΑΡΑΔΕΙΓΜΑΤΑ Σχόλια για 1. άντληση με επεξεργασία - Δοκιμασμένη τεχνολογία - Κατ αρχήν κατάλληλη για κάθε είδος ρύπου
ΑΠΟΚΑΤΑΣΤΑΣΗ ΡΥΠΑΣΜΕΝΩΝ ΧΩΡΩΝ ΣΧΟΛΙΑ ΓΙΑ ΤΕΧΝΟΛΟΓΙΕΣ ΓΙΑ ΤΙΣ ΟΠΟΙΕΣ ΔΙΝΟΝΤΑΙ ΑΡΙΘΜΗΤΙΚΑ ΠΑΡΑΔΕΙΓΜΑΤΑ Σχόλια για 1. άντληση με επεξεργασία - Δοκιμασμένη τεχνολογία - Κατ αρχήν κατάλληλη για κάθε είδος ρύπου
ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ
 ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Θεματική Ενότητα 7 Μεταφορά ρύπων στο υπόγειο νερό Μεταφορά λόγω μεταγωγής και υδροδυναμικής διασποράς Άδειες
ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Θεματική Ενότητα 7 Μεταφορά ρύπων στο υπόγειο νερό Μεταφορά λόγω μεταγωγής και υδροδυναμικής διασποράς Άδειες
Το πρόβλημα. 15m. ταμιευτήρας. κανάλι
 Το πρόβλημα Μετά από ατύχημα, ρύπος (τριχλωροαιθένιο διαλυμένο στο νερό) διαρρέει στον ταμιευτήρα στο πιο κάτω σχήμα. Υπάρχει ανησυχία για το πόσο γρήγορα θα επηρεαστεί κανάλι στα κατάντη αν δεν ληφθούν
Το πρόβλημα Μετά από ατύχημα, ρύπος (τριχλωροαιθένιο διαλυμένο στο νερό) διαρρέει στον ταμιευτήρα στο πιο κάτω σχήμα. Υπάρχει ανησυχία για το πόσο γρήγορα θα επηρεαστεί κανάλι στα κατάντη αν δεν ληφθούν
Περιβαλλοντική Γεωτεχνική Θεματική Ενότητα 7 Μεταφορά ρύπων στο υπόγειο νερό
 Περιβαλλοντική Γεωτεχνική Θεματική Ενότητα 7 Μεταφορά ρύπων στο υπόγειο νερό Λυμένες ασκήσεις Πότε θα φτάσει η ρύπανση στο κανάλι; Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Σχολή Πολιτικών Μηχανικών Άδειες
Περιβαλλοντική Γεωτεχνική Θεματική Ενότητα 7 Μεταφορά ρύπων στο υπόγειο νερό Λυμένες ασκήσεις Πότε θα φτάσει η ρύπανση στο κανάλι; Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Σχολή Πολιτικών Μηχανικών Άδειες
ΕΠΙΔΡΑΣΗ ΤΗΣ ΡΟΗΣ ΝΕΡΟΥ ΣΕ ΕΦΑΡΜΟΓΕΣ ΤΗΣ ΕΔΑΦΟΜΗΧΑΝΙΚΗΣ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΜΕΤΑΛΛΕΙΩΝ ΜΕΤΑΛΛΟΥΡΓΩΝ ΤΟΜΕΑΣ ΓΕΩΛΟΓΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΗΡΩΩΝ ΠΟΛΥΤΕΧΝΕΙΟΥ 9 15780 ΖΩΓΡΑΦΟΥ ΑΘΗΝΑ ΕΔΑΦΟΜΗΧΑΝΙΚΗ & ΣΤΟΙΧΕΙΑ ΘΕΜΕΛΙΩΣΕΩΝ Διδάσκων: Κωνσταντίνος Λουπασάκης,
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΜΕΤΑΛΛΕΙΩΝ ΜΕΤΑΛΛΟΥΡΓΩΝ ΤΟΜΕΑΣ ΓΕΩΛΟΓΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΗΡΩΩΝ ΠΟΛΥΤΕΧΝΕΙΟΥ 9 15780 ΖΩΓΡΑΦΟΥ ΑΘΗΝΑ ΕΔΑΦΟΜΗΧΑΝΙΚΗ & ΣΤΟΙΧΕΙΑ ΘΕΜΕΛΙΩΣΕΩΝ Διδάσκων: Κωνσταντίνος Λουπασάκης,
Εργαστήριο Μηχανικής Ρευστών. Εργασία 1 η : Πτώση πίεσης σε αγωγό κυκλικής διατομής
 Εργαστήριο Μηχανικής Ρευστών Εργασία 1 η : Πτώση πίεσης σε αγωγό κυκλικής διατομής Ονοματεπώνυμο:Κυρκιμτζής Γιώργος Σ.Τ.Ε.Φ. Οχημάτων - Εξάμηνο Γ Ημερομηνία εκτέλεσης Πειράματος : 12/4/2000 Ημερομηνία
Εργαστήριο Μηχανικής Ρευστών Εργασία 1 η : Πτώση πίεσης σε αγωγό κυκλικής διατομής Ονοματεπώνυμο:Κυρκιμτζής Γιώργος Σ.Τ.Ε.Φ. Οχημάτων - Εξάμηνο Γ Ημερομηνία εκτέλεσης Πειράματος : 12/4/2000 Ημερομηνία
Υπόγεια Υδραυλική. 1 η Εργαστηριακή Άσκηση Εφαρμογή Νόμου Darcy
 Υπόγεια Υδραυλική 1 η Εργαστηριακή Άσκηση Εφαρμογή Νόμου Darcy Τα υπόγεια υδατικά συστήματα Τα υπόγεια υδατικά συστήματα είναι συγκεντρώσεις υπόγειου νερού, που εμφανίζουν τα χαρακτηριστικά της υπόγειας
Υπόγεια Υδραυλική 1 η Εργαστηριακή Άσκηση Εφαρμογή Νόμου Darcy Τα υπόγεια υδατικά συστήματα Τα υπόγεια υδατικά συστήματα είναι συγκεντρώσεις υπόγειου νερού, που εμφανίζουν τα χαρακτηριστικά της υπόγειας
ΕΔΑΦΟΜΗΧΑΝΙΚΗ & ΣΤΟΙΧΕΙΑ ΘΕΜΕΛΙΩΣΕΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΜΕΤΑΛΛΕΙΩΝ ΜΕΤΑΛΛΟΥΡΓΩΝ ΤΟΜΕΑΣ ΓΕΩΛΟΓΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΗΡΩΩΝ ΠΟΛΥΤΕΧΝΕΙΟΥ 9 15780 ΖΩΓΡΑΦΟΥ ΑΘΗΝΑ ΕΔΑΦΟΜΗΧΑΝΙΚΗ & ΣΤΟΙΧΕΙΑ ΘΕΜΕΛΙΩΣΕΩΝ Διδάσκοντες: Βασίλειος Παπαδόπουλος,
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΜΕΤΑΛΛΕΙΩΝ ΜΕΤΑΛΛΟΥΡΓΩΝ ΤΟΜΕΑΣ ΓΕΩΛΟΓΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΗΡΩΩΝ ΠΟΛΥΤΕΧΝΕΙΟΥ 9 15780 ΖΩΓΡΑΦΟΥ ΑΘΗΝΑ ΕΔΑΦΟΜΗΧΑΝΙΚΗ & ΣΤΟΙΧΕΙΑ ΘΕΜΕΛΙΩΣΕΩΝ Διδάσκοντες: Βασίλειος Παπαδόπουλος,
Moντελοποίηση Ανοιχτά Ασκήσεις ερωτήματα προς επίλυση 1
 Moντελοποίηση Ανοιχτά ερωτήματα Ασκήσεις προς επίλυση 1 Ερώτημα Άσκηση Lundell-Sällfors and Sällfors (2000) Τι μπορώ να «πετάξω»; Πού πρέπει να εστιάσω; 2 Μοντελοποίηση: βασικά συστατικά Στοιχεία κατάστρωσης
Moντελοποίηση Ανοιχτά ερωτήματα Ασκήσεις προς επίλυση 1 Ερώτημα Άσκηση Lundell-Sällfors and Sällfors (2000) Τι μπορώ να «πετάξω»; Πού πρέπει να εστιάσω; 2 Μοντελοποίηση: βασικά συστατικά Στοιχεία κατάστρωσης
ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ
 ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Θεματική Ενότητα 5 Μοντελοποίηση Προβλήματα μεταγωγής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Θεματική Ενότητα 5 Μοντελοποίηση Προβλήματα μεταγωγής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Περατότητα και Διήθηση διαμέσου των εδαφών
 Περατότητα και Διήθηση διαμέσου των εδαφών Costas Sachpazis, (M.Sc., Ph.D.) Διάρκεια = 17 λεπτά 1 Τι είναι Περατότητα των εδαφών? Ένα μέτρο για το πόσο εύκολα ένα ρευστό (π.χ., νερό) μπορεί να περάσει
Περατότητα και Διήθηση διαμέσου των εδαφών Costas Sachpazis, (M.Sc., Ph.D.) Διάρκεια = 17 λεπτά 1 Τι είναι Περατότητα των εδαφών? Ένα μέτρο για το πόσο εύκολα ένα ρευστό (π.χ., νερό) μπορεί να περάσει
Παραδείγματα μεταφοράς για εφαρμογές αποκατάστασης & σχόλια. Άντληση και επεξεργασία, φυσική εξασθένηση, διάλυση κηλίδας NAPL, περατά διαφράγματα
 Παραδείγματα μεταφοράς για εφαρμογές αποκατάστασης & σχόλια Άντληση και επεξεργασία, φυσική εξασθένηση, διάλυση κηλίδας NAPL, περατά διαφράγματα Σχόλια για άντληση με επεξεργασία Δοκιμασμένη τεχνολογία
Παραδείγματα μεταφοράς για εφαρμογές αποκατάστασης & σχόλια Άντληση και επεξεργασία, φυσική εξασθένηση, διάλυση κηλίδας NAPL, περατά διαφράγματα Σχόλια για άντληση με επεξεργασία Δοκιμασμένη τεχνολογία
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Σελίδα 1 από 6
 ΘΕΜΑ Α Στις παρακάτω ερωτήσεις να επιλέξετε τη σωστή απάντηση 1) Το δοχείο του σχήματος 1 είναι γεμάτο με υγρό και κλείνεται με έμβολο Ε στο οποίο ασκείται δύναμη F. Όλα τα μανόμετρα 1,, 3, 4 δείχνουν
ΘΕΜΑ Α Στις παρακάτω ερωτήσεις να επιλέξετε τη σωστή απάντηση 1) Το δοχείο του σχήματος 1 είναι γεμάτο με υγρό και κλείνεται με έμβολο Ε στο οποίο ασκείται δύναμη F. Όλα τα μανόμετρα 1,, 3, 4 δείχνουν
Απώλειες φορτίου Συντελεστής τριβής Ο αριθμός Reynolds Το διάγραμμα Moody Εφαρμογές
 Απώλειες φορτίου Συντελεστής τριβής Ο αριθμός Reynolds Το διάγραμμα Moody Εφαρμογές Στο σχήμα έχουμε ροή σε ένα ιδεατό ρευστό. Οι σωλήνες πάνω στον αγωγό (μανομετρικοί σωλήνες) μετρούν μόνο το ύψος πίεσης
Απώλειες φορτίου Συντελεστής τριβής Ο αριθμός Reynolds Το διάγραμμα Moody Εφαρμογές Στο σχήμα έχουμε ροή σε ένα ιδεατό ρευστό. Οι σωλήνες πάνω στον αγωγό (μανομετρικοί σωλήνες) μετρούν μόνο το ύψος πίεσης
ΥΔΡΑΥΛΙΚΕΣ ΑΠΩΛΕΙΕΣ ΚΑΤΑ ΤΗΝ ΡΟΗ ΝΕΡΟΥ ΣΕ ΚΛΕΙΣΤΟ ΑΓΩΓΟ
 Α.Ε.Ι. ΠΕΙΡΑΙΑ Τ.Τ. ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΡΕΥΣΤΩΝ 8 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΥΔΡΑΥΛΙΚΕΣ ΑΠΩΛΕΙΕΣ ΚΑΤΑ ΤΗΝ ΡΟΗ ΝΕΡΟΥ ΣΕ ΚΛΕΙΣΤΟ ΑΓΩΓΟ Σκοπός του πειράματος είναι να μελετηθεί
Α.Ε.Ι. ΠΕΙΡΑΙΑ Τ.Τ. ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΡΕΥΣΤΩΝ 8 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΥΔΡΑΥΛΙΚΕΣ ΑΠΩΛΕΙΕΣ ΚΑΤΑ ΤΗΝ ΡΟΗ ΝΕΡΟΥ ΣΕ ΚΛΕΙΣΤΟ ΑΓΩΓΟ Σκοπός του πειράματος είναι να μελετηθεί
ΚΙΝΗΣΗ ΤΟΥ Ε ΑΦΙΚΟΥ ΝΕΡΟΥ
 ΚΙΝΗΣΗ ΤΟΥ Ε ΑΦΙΚΟΥ ΝΕΡΟΥ Το εδαφικό νερό υπό την επίδραση διαφόρων δυνάµεων βρίσκεται σε συνεχή κίνηση και µπορεί να κινηθεί προς διάφορες κατευθύνσεις. Οι δυνάµεις οφείλονται στη βαρύτητα, Στην πίεση
ΚΙΝΗΣΗ ΤΟΥ Ε ΑΦΙΚΟΥ ΝΕΡΟΥ Το εδαφικό νερό υπό την επίδραση διαφόρων δυνάµεων βρίσκεται σε συνεχή κίνηση και µπορεί να κινηθεί προς διάφορες κατευθύνσεις. Οι δυνάµεις οφείλονται στη βαρύτητα, Στην πίεση
Υπόγεια Υδραυλική και Υδρολογία
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: ΝΟΜΟΣ ΤΟΥ DARCY Καθηγητής Κωνσταντίνος Λ. Κατσιφαράκης Αναπληρωτής Καθηγητής Νικόλαος Θεοδοσίου ΑΠΘ Άδειες Χρήσης Το παρόν
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: ΝΟΜΟΣ ΤΟΥ DARCY Καθηγητής Κωνσταντίνος Λ. Κατσιφαράκης Αναπληρωτής Καθηγητής Νικόλαος Θεοδοσίου ΑΠΘ Άδειες Χρήσης Το παρόν
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ. Ρευστά. Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός. https://physicscourses.wordpress.com
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ Ρευστά Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός https://physicscourses.wordpress.com Βασικές έννοιες Πρώτη φορά συναντήσαμε τη φυσική των ρευστών στη Β Γυμνασίου. Εκεί
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ Ρευστά Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός https://physicscourses.wordpress.com Βασικές έννοιες Πρώτη φορά συναντήσαμε τη φυσική των ρευστών στη Β Γυμνασίου. Εκεί
2g z z f k k z z f k k z z V D 2g 2g 2g D 2g f L ka D
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΟΜΕΑΣ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ & ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΜΑΘΗΜΑ: ΥΔΡΑΥΛΙΚΗ ΚΑΙ ΥΔΡΑΥΛΙΚΑ ΕΡΓΑ ΕΞΕΤΑΣΗ ΠΡΟΟΔΟΥ ΝΟΕΜΒΡΙΟΥ 017 Άσκηση 1 1. Οι δεξαμενές Α και Β, του Σχήματος 1, συνδέονται με σωλήνα
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΟΜΕΑΣ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ & ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΜΑΘΗΜΑ: ΥΔΡΑΥΛΙΚΗ ΚΑΙ ΥΔΡΑΥΛΙΚΑ ΕΡΓΑ ΕΞΕΤΑΣΗ ΠΡΟΟΔΟΥ ΝΟΕΜΒΡΙΟΥ 017 Άσκηση 1 1. Οι δεξαμενές Α και Β, του Σχήματος 1, συνδέονται με σωλήνα
ΚΟΡΕΣΜΕΝΟ ΕΔΑΦΟΣ ΜΕΤΑΦΟΡΑ ΡΥΠΟΥ ΛΟΓΩ ΜΕΤΑΓΩΓΗΣ. Σχόλιο: ίδια έκφραση για ροή ρευστού σε αγωγό ή πορώδες μέσο V V
 ΚΟΡΕΣΜΕΝΟ ΕΔΑΦΟΣ ΜΕΤΑΦΟΡΑ ΡΥΠΟΥ ΛΟΓΩ ΜΕΤΑΓΩΓΗΣ Ροή μάζας ρύπου = Μάζα / (χρόνος επιφάνεια) = (όγκος συγκέντρωση) / (χρόνος επιφάνεια) = (παροχή συγκέντρωση) / (επιφάνεια) Για μονοδιάστατη ροή, η φαινόμενη
ΚΟΡΕΣΜΕΝΟ ΕΔΑΦΟΣ ΜΕΤΑΦΟΡΑ ΡΥΠΟΥ ΛΟΓΩ ΜΕΤΑΓΩΓΗΣ Ροή μάζας ρύπου = Μάζα / (χρόνος επιφάνεια) = (όγκος συγκέντρωση) / (χρόνος επιφάνεια) = (παροχή συγκέντρωση) / (επιφάνεια) Για μονοδιάστατη ροή, η φαινόμενη
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΥΔΡΟΛΟΓΙΑ 6. ΥΔΡΟΛΟΓΙΑ ΥΠΟΓΕΙΩΝ ΝΕΡΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΥΔΡΟΛΟΓΙΑ 6. ΥΔΡΟΛΟΓΙΑ ΥΠΟΓΕΙΩΝ ΝΕΡΩΝ 6.1 ΓΕΝΙΚΑ Το νερό που υπάρχει στη φύση και χρησιμοποιείται από τον άνθρωπο: - Επιφανειακό: Το νερό των
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΥΔΡΟΛΟΓΙΑ 6. ΥΔΡΟΛΟΓΙΑ ΥΠΟΓΕΙΩΝ ΝΕΡΩΝ 6.1 ΓΕΝΙΚΑ Το νερό που υπάρχει στη φύση και χρησιμοποιείται από τον άνθρωπο: - Επιφανειακό: Το νερό των
Περιβαλλοντική Γεωτεχνική Άσκηση από διαγώνισμα
 Περιβαλλοντική Γεωτεχνική Άσκηση από διαγώνισμα 007-008 Στο πιο κάτω σχήμα φαίνεται η διερευνητική γεώτρηση Α η οποία διανοίχθηκε από λάθος, όπως αποδείχθηκε εκ των υστέρων, διαμέσου της κορεσμένης ζώνης
Περιβαλλοντική Γεωτεχνική Άσκηση από διαγώνισμα 007-008 Στο πιο κάτω σχήμα φαίνεται η διερευνητική γεώτρηση Α η οποία διανοίχθηκε από λάθος, όπως αποδείχθηκε εκ των υστέρων, διαμέσου της κορεσμένης ζώνης
Υποστηρικτικό υλικό για την εργασία «Πειραματική διάταξη για τη μελέτη της ροής ρευστού σε σωλήνα» του Σπύρου Χόρτη.
 Υποστηρικτικό υλικό για την εργασία «Πειραματική διάταξη για τη μελέτη της ροής ρευστού σε σωλήνα» του Σπύρου Χόρτη. Η εργασία δημοσιεύτηκε στο 9ο τεύχος του περιοδικού Φυσικές Επιστήμες στην Εκπαίδευση,
Υποστηρικτικό υλικό για την εργασία «Πειραματική διάταξη για τη μελέτη της ροής ρευστού σε σωλήνα» του Σπύρου Χόρτη. Η εργασία δημοσιεύτηκε στο 9ο τεύχος του περιοδικού Φυσικές Επιστήμες στην Εκπαίδευση,
Σχέσεις εδάφους νερού Σχέσεις μάζας όγκου των συστατικών του εδάφους Εδαφική ή υγρασία, τρόποι έκφρασης
 Γεωργική Υδραυλική Αρδεύσεις Σ. Αλεξανδρής Περιγραφή Μαθήματος Σχέσεις εδάφους νερού Σχέσεις μάζας όγκου των συστατικών του εδάφους Εδαφική ή υγρασία, τρόποι έκφρασης Χαρακτηριστική Χ ή καμπύλη υγρασίας
Γεωργική Υδραυλική Αρδεύσεις Σ. Αλεξανδρής Περιγραφή Μαθήματος Σχέσεις εδάφους νερού Σχέσεις μάζας όγκου των συστατικών του εδάφους Εδαφική ή υγρασία, τρόποι έκφρασης Χαρακτηριστική Χ ή καμπύλη υγρασίας
ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ
 ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Θεματική Ενότητα 3 Μηχανισμοί Εξάπλωσης της Ρύπανσης Εξέλιξη διαρροής στο υπέδαφος Άδειες Χρήσης Το παρόν
ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Θεματική Ενότητα 3 Μηχανισμοί Εξάπλωσης της Ρύπανσης Εξέλιξη διαρροής στο υπέδαφος Άδειες Χρήσης Το παρόν
Περιβαλλοντική Γεωτεχνική Θεματική Ενότητα 7 Μεταφορά ρύπων στο υπόγειο νερό
 Περιβαλλοντική Γεωτεχνική Θεματική Ενότητα 7 Μεταφορά ρύπων στο υπόγειο νερό Εξισώσεις και λύσεις για τη μεταφορά ρύπων Α Μέρος Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Σχολή Πολιτικών Μηχανικών Άδειες
Περιβαλλοντική Γεωτεχνική Θεματική Ενότητα 7 Μεταφορά ρύπων στο υπόγειο νερό Εξισώσεις και λύσεις για τη μεταφορά ρύπων Α Μέρος Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Σχολή Πολιτικών Μηχανικών Άδειες
ΘΕΜΑ 1: ίδεται η περιγραφή µίας κίνησης ενός µονοδιάστατου Συνεχούς κατά Lagrange
 ΜΗΧΑΝΙΚΗ ΤΟΥ ΣΥΝΕΧΟΥΣ ΜΕΣΟΥ Σχολή Πολιτικών Μηχανικών, Εξ. ιδ. 04 Καθηγητής Ι. Βαρδουλάκης, Σ.Ε.Μ.Φ.Ε. 8:30 π.µ., Πέµπτη 8 Ιουλίου 004 ΘΕΜΑ : ίδεται η περιγραφή µίας κίνησης ενός µονοδιάστατου Συνεχούς
ΜΗΧΑΝΙΚΗ ΤΟΥ ΣΥΝΕΧΟΥΣ ΜΕΣΟΥ Σχολή Πολιτικών Μηχανικών, Εξ. ιδ. 04 Καθηγητής Ι. Βαρδουλάκης, Σ.Ε.Μ.Φ.Ε. 8:30 π.µ., Πέµπτη 8 Ιουλίου 004 ΘΕΜΑ : ίδεται η περιγραφή µίας κίνησης ενός µονοδιάστατου Συνεχούς
A3. Το δοχείο του σχήματος 1 είναι γεμάτο με υγρό και κλείνεται με έμβολο Ε στο οποίο ασκείται δύναμη F.
 ΘΕΜΑ Α ΘΕΜΑΤΑ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ-ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ- ΚΕΦΑΛΑΙΟ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ' ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 23 ΜΑΪΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ
ΘΕΜΑ Α ΘΕΜΑΤΑ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ-ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ- ΚΕΦΑΛΑΙΟ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ' ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 23 ΜΑΪΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ
Πρόβλεψη εξέλιξης ρύπανσης. Βασικά ερωτήματα: Πού θα πάει ο ρύπος; Πώς θα συμπεριφερθεί; Τι θα απογίνει;
 Πρόβλεψη εξέλιξης ρύπανσης Βασικά ερωτήματα: Πού θα πάει ο ρύπος; Πώς θα συμπεριφερθεί; Τι θα απογίνει; Τι θα απογίνει ο ρύπος; Μηχανισμοί που εμπλέκονται στην εξάπλωση των ρύπων στο έδαφος και στο υπόγειο
Πρόβλεψη εξέλιξης ρύπανσης Βασικά ερωτήματα: Πού θα πάει ο ρύπος; Πώς θα συμπεριφερθεί; Τι θα απογίνει; Τι θα απογίνει ο ρύπος; Μηχανισμοί που εμπλέκονται στην εξάπλωση των ρύπων στο έδαφος και στο υπόγειο
Περιστατικό ρύπανσης και αποκατάστασης υπεδάφους: Αεροδρόμιο Ναυτικής Βάσης στην Καλιφόρνια. (Moffett Field)
 Περιστατικό ρύπανσης και αποκατάστασης υπεδάφους: Αεροδρόμιο Ναυτικής Βάσης στην Καλιφόρνια (Moffett Field) San Francisco San Francisco Bay Moffett Field 2 3 Κατοικίες Kαθαρές Βιομηχανίες ΝΑΣΑ Κόλπος του
Περιστατικό ρύπανσης και αποκατάστασης υπεδάφους: Αεροδρόμιο Ναυτικής Βάσης στην Καλιφόρνια (Moffett Field) San Francisco San Francisco Bay Moffett Field 2 3 Κατοικίες Kαθαρές Βιομηχανίες ΝΑΣΑ Κόλπος του
Διαγώνισμα Φυσικής Γ Λυκείου 5/3/2017
 Διαγώνισμα Φυσικής Γ Λυκείου 5/3/2017 ΦΡΟΝΤΙΣΤΗΡΙΟ ΕΠΙΛΟΓΗ Θέμα Α 1) Το δοχείο του σχήματος 1 είναι γεμάτο με υγρό και κλείνεται με έμβολο Ε στο οποίο ασκείται δύναμη F. Όλα τα μανόμετρα 1,2,3,4 δείχνουν
Διαγώνισμα Φυσικής Γ Λυκείου 5/3/2017 ΦΡΟΝΤΙΣΤΗΡΙΟ ΕΠΙΛΟΓΗ Θέμα Α 1) Το δοχείο του σχήματος 1 είναι γεμάτο με υγρό και κλείνεται με έμβολο Ε στο οποίο ασκείται δύναμη F. Όλα τα μανόμετρα 1,2,3,4 δείχνουν
ΑΓΩΓΟΣ VENTURI. Σχήμα 1. Διάταξη πειραματικής συσκευής σωλήνα Venturi.
 Α.Ε.Ι. ΠΕΙΡΑΙΑ Τ.Τ. ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΡΕΥΣΤΩΝ 7 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΑΓΩΓΟΣ VENTURI ΣΚΟΠΟΣ ΤΗΣ ΑΣΚΗΣΗΣ Σκοπός της άσκησης είναι η κατανόηση της χρήσης της συσκευής
Α.Ε.Ι. ΠΕΙΡΑΙΑ Τ.Τ. ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΡΕΥΣΤΩΝ 7 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΑΓΩΓΟΣ VENTURI ΣΚΟΠΟΣ ΤΗΣ ΑΣΚΗΣΗΣ Σκοπός της άσκησης είναι η κατανόηση της χρήσης της συσκευής
Περιβαλλοντική Γεωτεχνική. Θεματική Ενότητα 7 Μεταφορά ρύπων στο υπόγειο νερό
 Περιβαλλοντική Γεωτεχνική Θεματική Ενότητα 7 Μεταφορά ρύπων στο υπόγειο νερό Λυμένες ασκήσεις Πότε θα επηρεαστεί η γεώτρηση από τη ρύπανση στα ανάντη; Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Σχολή Πολιτικών
Περιβαλλοντική Γεωτεχνική Θεματική Ενότητα 7 Μεταφορά ρύπων στο υπόγειο νερό Λυμένες ασκήσεις Πότε θα επηρεαστεί η γεώτρηση από τη ρύπανση στα ανάντη; Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Σχολή Πολιτικών
ΑΓΩΓΟΣ VENTURI. Σχήμα 1. Διάταξη πειραματικής συσκευής σωλήνα Venturi.
 Α.Ε.Ι. ΠΕΙΡΑΙΑ Τ.Τ. ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΡΕΥΣΤΩΝ 7 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΑΓΩΓΟΣ VENTURI ΣΚΟΠΟΣ ΤΗΣ ΑΣΚΗΣΗΣ Σκοπός της άσκησης είναι η κατανόηση της χρήσης της συσκευής
Α.Ε.Ι. ΠΕΙΡΑΙΑ Τ.Τ. ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΡΕΥΣΤΩΝ 7 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΑΓΩΓΟΣ VENTURI ΣΚΟΠΟΣ ΤΗΣ ΑΣΚΗΣΗΣ Σκοπός της άσκησης είναι η κατανόηση της χρήσης της συσκευής
Διαγώνισμα Φυσικής Γ Λυκείου ~~ Ρευστά ~~
 Διαγώνισμα Φυσικής Γ Λυκείου ~~ Ρευστά ~~ Διάρκεια: 3 ώρες Θέμα Α 1) Το δοχείο του σχήματος 1 είναι γεμάτο με υγρό και κλείνεται με έμβολο Ε στο οποίο ασκείται δύναμη F. Όλα τα μανόμετρα 1,2,3,4 δείχνουν
Διαγώνισμα Φυσικής Γ Λυκείου ~~ Ρευστά ~~ Διάρκεια: 3 ώρες Θέμα Α 1) Το δοχείο του σχήματος 1 είναι γεμάτο με υγρό και κλείνεται με έμβολο Ε στο οποίο ασκείται δύναμη F. Όλα τα μανόμετρα 1,2,3,4 δείχνουν
Κινηματική ρευστών. Ροή ρευστού = η κίνηση του ρευστού, μέσα στο περιβάλλον του
 301 Κινηματική ρευστών Ροή ρευστού = η κίνηση του ρευστού, μέσα στο περιβάλλον του Είδη ροής α) Σταθερή ή μόνιμη = όταν σε κάθε σημείο του χώρου οι συνθήκες ροής, ταχύτητα, θερμοκρασία, πίεση και πυκνότητα,
301 Κινηματική ρευστών Ροή ρευστού = η κίνηση του ρευστού, μέσα στο περιβάλλον του Είδη ροής α) Σταθερή ή μόνιμη = όταν σε κάθε σημείο του χώρου οι συνθήκες ροής, ταχύτητα, θερμοκρασία, πίεση και πυκνότητα,
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 4 ο ΔΙΑΓΩΝΙΣΜΑ ΡΕΥΣΤΑ - ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 4 ο ΔΙΑΓΩΝΙΣΜΑ ΡΕΥΣΤΑ - ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
Ορμή και Δυνάμεις. Θεώρημα Ώθησης Ορμής
 501 Ορμή και Δυνάμεις Θεώρημα Ώθησης Ορμής «Η μεταβολή της ορμής ενός σώματος είναι ίση με την ώθηση της δύναμης που ασκήθηκε στο σώμα» = ή Το θεώρημα αυτό εφαρμόζεται διανυσματικά. 502 Θεώρημα Ώθησης
501 Ορμή και Δυνάμεις Θεώρημα Ώθησης Ορμής «Η μεταβολή της ορμής ενός σώματος είναι ίση με την ώθηση της δύναμης που ασκήθηκε στο σώμα» = ή Το θεώρημα αυτό εφαρμόζεται διανυσματικά. 502 Θεώρημα Ώθησης
ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ
 ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Θεματική Ενότητα 6 Αλληλεπίδραση ρύπων με το έδαφος Εισαγωγή Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Θεματική Ενότητα 6 Αλληλεπίδραση ρύπων με το έδαφος Εισαγωγή Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ
 ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Θεματική Ενότητα 7 Μεταφορά ρύπων στο υπόγειο νερό Σχόλια για λυμένα προβλήματα Μαθησιακοί στόχοι Άδειες Χρήσης
ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Θεματική Ενότητα 7 Μεταφορά ρύπων στο υπόγειο νερό Σχόλια για λυμένα προβλήματα Μαθησιακοί στόχοι Άδειες Χρήσης
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΑΝΤΛΗΤΙΚΩΝ ΕΓΚΑΤΑΣΤΑΣΕΩΝ
 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΑΝΤΛΗΤΙΚΩΝ ΕΓΚΑΤΑΣΤΑΣΕΩΝ Εισαγωγικά Στην περίπτωση που επιθυμείται να διακινηθεί υγρό από μία στάθμη σε μία υψηλότερη στάθμη, απαιτείται η χρήση αντλίας/ αντλιών. Γενικώς, ονομάζεται δεξαμενή
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΑΝΤΛΗΤΙΚΩΝ ΕΓΚΑΤΑΣΤΑΣΕΩΝ Εισαγωγικά Στην περίπτωση που επιθυμείται να διακινηθεί υγρό από μία στάθμη σε μία υψηλότερη στάθμη, απαιτείται η χρήση αντλίας/ αντλιών. Γενικώς, ονομάζεται δεξαμενή
ΥΔΡΑΥΛΙΚΗ ΑΝΟΙΚΤΩΝ ΑΓΩΓΩΝ
 Τμήμα Δασολογίας & Διαχείρισης Περιβάλλοντος & Φυσικών Πόρων Εργαστήριο Διευθέτησης Ορεινών Υδάτων και Διαχείρισης Κινδύνου Προπτυχιακό Πρόγραμμα Σπουδών ΥΔΡΑΥΛΙΚΗ ΑΝΟΙΚΤΩΝ ΑΓΩΓΩΝ Κεφάλαιο 2 ο : Είδη ροής
Τμήμα Δασολογίας & Διαχείρισης Περιβάλλοντος & Φυσικών Πόρων Εργαστήριο Διευθέτησης Ορεινών Υδάτων και Διαχείρισης Κινδύνου Προπτυχιακό Πρόγραμμα Σπουδών ΥΔΡΑΥΛΙΚΗ ΑΝΟΙΚΤΩΝ ΑΓΩΓΩΝ Κεφάλαιο 2 ο : Είδη ροής
Υπολογισμός Διαπερατότητας Εδαφών
 ΠΑΡΟΥΣΙΑΣΗ ΤΗΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΔΟΚΙΜΗΣ: Υπολογισμός Διαπερατότητας Εδαφών Επιστημονικός Συνεργάτης: Δρ. Αλέξανδρος Βαλσαμής, Πολιτικός Μηχανικός Εργαστηριακός Υπεύθυνος: Παναγιώτης Καλαντζάκης, Καθηγητής
ΠΑΡΟΥΣΙΑΣΗ ΤΗΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΔΟΚΙΜΗΣ: Υπολογισμός Διαπερατότητας Εδαφών Επιστημονικός Συνεργάτης: Δρ. Αλέξανδρος Βαλσαμής, Πολιτικός Μηχανικός Εργαστηριακός Υπεύθυνος: Παναγιώτης Καλαντζάκης, Καθηγητής
Αλληλεπίδραση ρύπων εδάφους
 Αλληλεπίδραση ρύπων εδάφους Παρουσίαση 1 από 4 Περιεχόμενα 1) Kίνητρο μελέτης αλληλεπίδρασης 2) Έννοιες και όροι 3) Προαπαιτούμενα από φυσικοχημεία & εδαφομηχανική Πώς κατανέμεται ο ρύπος στις εδαφικές
Αλληλεπίδραση ρύπων εδάφους Παρουσίαση 1 από 4 Περιεχόμενα 1) Kίνητρο μελέτης αλληλεπίδρασης 2) Έννοιες και όροι 3) Προαπαιτούμενα από φυσικοχημεία & εδαφομηχανική Πώς κατανέμεται ο ρύπος στις εδαφικές
Εργαστήριο Μηχανικής Ρευστών. Εργασία 2 η Κατανομή πίεσης σε συγκλίνοντα αποκλίνοντα αγωγό.
 Εργαστήριο Μηχανικής Ρευστών Εργασία 2 η Κατανομή πίεσης σε συγκλίνοντα αποκλίνοντα αγωγό. Κυρκιμτζής Γιώργος Σ.Τ.Ε.Φ. Οχημάτων - Εξάμηνο Γ Ημ/νία παράδοσης Εργασίας: Τετάρτη 24 Μαΐου 2 1 Θεωρητική Εισαγωγή:
Εργαστήριο Μηχανικής Ρευστών Εργασία 2 η Κατανομή πίεσης σε συγκλίνοντα αποκλίνοντα αγωγό. Κυρκιμτζής Γιώργος Σ.Τ.Ε.Φ. Οχημάτων - Εξάμηνο Γ Ημ/νία παράδοσης Εργασίας: Τετάρτη 24 Μαΐου 2 1 Θεωρητική Εισαγωγή:
Περιβαλλοντική Γεωτεχνική Θεματική Ενότητα 7 Μεταφορά ρύπων στο υπόγειο νερό
 Περιβαλλοντική Γεωτεχνική Θεματική Ενότητα 7 Μεταφορά ρύπων στο υπόγειο νερό Εξισώσεις και λύσεις για τη μεταφορά ρύπων Β Μέρος Μ. Πανταζίδου Αναπληρώτρια Καθηγήτρια ΕΜΠ Σχολή Πολιτικών Μηχανικών Άδειες
Περιβαλλοντική Γεωτεχνική Θεματική Ενότητα 7 Μεταφορά ρύπων στο υπόγειο νερό Εξισώσεις και λύσεις για τη μεταφορά ρύπων Β Μέρος Μ. Πανταζίδου Αναπληρώτρια Καθηγήτρια ΕΜΠ Σχολή Πολιτικών Μηχανικών Άδειες
ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ 7-9
 ΤΕΙ ΙΟΝΙΩΝ ΝΗΣΩΝ Τμήμα Τεχνολόγων Περιβάλλοντος Κατεύθυνση Τεχνολογιών Φυσικού Περιβάλλοντος ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ 7-9 Μετρήσεις ταχύτητας ροής αέρα με τη βοήθεια σωλήνα Prandtl και απεικόνιση του πεδίου
ΤΕΙ ΙΟΝΙΩΝ ΝΗΣΩΝ Τμήμα Τεχνολόγων Περιβάλλοντος Κατεύθυνση Τεχνολογιών Φυσικού Περιβάλλοντος ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ 7-9 Μετρήσεις ταχύτητας ροής αέρα με τη βοήθεια σωλήνα Prandtl και απεικόνιση του πεδίου
Λαμβάνονται υπόψη οι απώλειες. διατομή και θεώρηση
 Δρ Μ.Σπηλιώτη λώ Λαμβάνονται υπόψη οι απώλειες ενέργειας Eνιαία ταχύτητα σε όλη τη διατομή και θεώρηση συντελεστή διόρθωσης κινητικής ενέργειας Αρχικά σε όγκο ελέγχου Σε διακλαδιζόμενους αγωγούς δεν συμπίπτουν
Δρ Μ.Σπηλιώτη λώ Λαμβάνονται υπόψη οι απώλειες ενέργειας Eνιαία ταχύτητα σε όλη τη διατομή και θεώρηση συντελεστή διόρθωσης κινητικής ενέργειας Αρχικά σε όγκο ελέγχου Σε διακλαδιζόμενους αγωγούς δεν συμπίπτουν
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 4 o ΔΙΑΓΩΝΙΣΜΑ ΜΑΡΤΙΟΣ 2019: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 4 ο ΔΙΑΓΩΝΙΣΜΑ ΡΕΥΣΤΑ - ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ A Α1α. (β) Α1β. (β) Αα. (γ) Αβ. (α) Αα. (γ) Αβ. (δ) Α4α. (α) Α4β. (γ) Α5. α. Σ β. Λ γ. Λ δ. Σ ΘΕΜΑ Β Β1.
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 4 ο ΔΙΑΓΩΝΙΣΜΑ ΡΕΥΣΤΑ - ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ A Α1α. (β) Α1β. (β) Αα. (γ) Αβ. (α) Αα. (γ) Αβ. (δ) Α4α. (α) Α4β. (γ) Α5. α. Σ β. Λ γ. Λ δ. Σ ΘΕΜΑ Β Β1.
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 η & 2 η : ΟΡΙΑΚΟ ΣΤΡΩΜΑ
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 η & 2 η : ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 η & 2 η : ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού
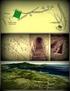
(1) ταχύτητα, v δεδομένη την πιο πάνω κατανομή θερμοκρασίας; 6. Γιατί είναι σωστή η προσέγγιση του ερωτήματος [2]; Ποια είναι η
![(1) ταχύτητα, v δεδομένη την πιο πάνω κατανομή θερμοκρασίας; 6. Γιατί είναι σωστή η προσέγγιση του ερωτήματος [2]; Ποια είναι η (1) ταχύτητα, v δεδομένη την πιο πάνω κατανομή θερμοκρασίας; 6. Γιατί είναι σωστή η προσέγγιση του ερωτήματος [2]; Ποια είναι η](/thumbs/62/47887680.jpg) ΜΕΤΑΦΟΡΑ ΘΕΡΜΟΤΗΤΑΣ Σειρά Ασκήσεων σε Συναγωγή Θερμότητας Οι λύσεις θα παρουσιαστούν στις παραδόσεις του μαθήματος μετά την επόμενη εβδομάδα. Για να σας φανούν χρήσιμες στην κατανόηση της ύλης του μαθήματος,
ΜΕΤΑΦΟΡΑ ΘΕΡΜΟΤΗΤΑΣ Σειρά Ασκήσεων σε Συναγωγή Θερμότητας Οι λύσεις θα παρουσιαστούν στις παραδόσεις του μαθήματος μετά την επόμενη εβδομάδα. Για να σας φανούν χρήσιμες στην κατανόηση της ύλης του μαθήματος,
h 1 M 1 h 2 M 2 P = h (2) 10m = 1at = 1kg/cm 2 = 10t/m 2
 ΕΡΓΑΣΤΗΡΙΟ 4 Ο Ενότητα: Βασικές υδραυλικές έννοιες Πίεση απώλειες πιέσεως Ι. Υδροστατική πίεση Η υδροστατική πίεση, είναι η πίεση που ασκεί το νερό, σε κατάσταση ηρεμίας, στα τοιχώματα του δοχείου που
ΕΡΓΑΣΤΗΡΙΟ 4 Ο Ενότητα: Βασικές υδραυλικές έννοιες Πίεση απώλειες πιέσεως Ι. Υδροστατική πίεση Η υδροστατική πίεση, είναι η πίεση που ασκεί το νερό, σε κατάσταση ηρεμίας, στα τοιχώματα του δοχείου που
Ανάθεση εργασίας για το εργαστηριακό μέρος του μαθήματος «Μηχανική των Ρευστών»
 Ανάθεση εργασίας για το εργαστηριακό μέρος του μαθήματος «Μηχανική των Ρευστών» : Στρωτή και τυρβώδης ροή σε λείο σωλήνα Συντάκτες: Α. Φιλιός, Κ. Μουστρής, Κ.-Σ. Νίκας 1 Αντικείμενο της εργαστηριακής άσκησης
Ανάθεση εργασίας για το εργαστηριακό μέρος του μαθήματος «Μηχανική των Ρευστών» : Στρωτή και τυρβώδης ροή σε λείο σωλήνα Συντάκτες: Α. Φιλιός, Κ. Μουστρής, Κ.-Σ. Νίκας 1 Αντικείμενο της εργαστηριακής άσκησης
Ονοματεπώνυμο: Μάθημα: Ύλη: Επιμέλεια διαγωνίσματος: Αξιολόγηση: Φυσική Προσανατολισμού Ρευστά Ιωάννης Κουσανάκης
 Ονοματεπώνυμο: Μάθημα: Ύλη: Επιμέλεια διαγωνίσματος: Αξιολόγηση: Φυσική Προσανατολισμού Ρευστά Ιωάννης Κουσανάκης ΘΕΜΑ Α Α1. Το ανοιχτό κυλινδρικό δοχείο του σχήματος βρίσκεται εντός πεδίο βαρύτητας με
Ονοματεπώνυμο: Μάθημα: Ύλη: Επιμέλεια διαγωνίσματος: Αξιολόγηση: Φυσική Προσανατολισμού Ρευστά Ιωάννης Κουσανάκης ΘΕΜΑ Α Α1. Το ανοιχτό κυλινδρικό δοχείο του σχήματος βρίσκεται εντός πεδίο βαρύτητας με
Ειδική Ενθαλπία, Ειδική Θερµότητα και Ειδικός Όγκος Υγρού Αέρα
 θερµοκρασία που αντιπροσωπεύει την θερµοκρασία υγρού βολβού. Το ποσοστό κορεσµού υπολογίζεται από την καµπύλη του σταθερού ποσοστού κορεσµού που διέρχεται από το συγκεκριµένο σηµείο. Η απόλυτη υγρασία
θερµοκρασία που αντιπροσωπεύει την θερµοκρασία υγρού βολβού. Το ποσοστό κορεσµού υπολογίζεται από την καµπύλη του σταθερού ποσοστού κορεσµού που διέρχεται από το συγκεκριµένο σηµείο. Η απόλυτη υγρασία
Προστασία Υδροφόρων Οριζόντων Τρωτότητα. Άσκηση 1
 Προστασία Υδροφόρων Οριζόντων Τρωτότητα Άσκηση 1 Σε μια περιοχή αναπτύσσεται υδροφόρος ορίζοντας, του οποίου η πιεζομετρία παρουσιάζεται στο χάρτη. Στην ίδια περιοχή υπάρχει γεώτρηση ύδρευσης για παρακείμενο
Προστασία Υδροφόρων Οριζόντων Τρωτότητα Άσκηση 1 Σε μια περιοχή αναπτύσσεται υδροφόρος ορίζοντας, του οποίου η πιεζομετρία παρουσιάζεται στο χάρτη. Στην ίδια περιοχή υπάρχει γεώτρηση ύδρευσης για παρακείμενο
ΜΗΧΑΝΙΚΗ ΡΕΥΣΤΩΝ. Πτώση πίεσης σε αγωγό σταθερής διατομής 2η εργαστηριακή άσκηση. Βλιώρα Ευαγγελία
 ΜΗΧΑΝΙΚΗ ΡΕΥΣΤΩΝ Πτώση πίεσης σε αγωγό σταθερής διατομής 2η εργαστηριακή άσκηση Βλιώρα Ευαγγελία ΘΕΣΣΑΛΟΝΙΚΗ 2014 Σκοπός της εργαστηριακής άσκησης Σκοπός της εργαστηριακής άσκησης είναι ο υπολογισμός της
ΜΗΧΑΝΙΚΗ ΡΕΥΣΤΩΝ Πτώση πίεσης σε αγωγό σταθερής διατομής 2η εργαστηριακή άσκηση Βλιώρα Ευαγγελία ΘΕΣΣΑΛΟΝΙΚΗ 2014 Σκοπός της εργαστηριακής άσκησης Σκοπός της εργαστηριακής άσκησης είναι ο υπολογισμός της
Το μισό του μήκους του σωλήνα, αρκετά μεγάλη απώλεια ύψους.
 Πρόβλημα Λάδι πυκνότητας 900 kg / και κινηματικού ιξώδους 0.000 / s ρέει διαμέσου ενός κεκλιμένου σωλήνα στην κατεύθυνση αυξανομένου υψομέτρου, όπως φαίνεται στο παρακάτω Σχήμα. Η πίεση και το υψόμετρο
Πρόβλημα Λάδι πυκνότητας 900 kg / και κινηματικού ιξώδους 0.000 / s ρέει διαμέσου ενός κεκλιμένου σωλήνα στην κατεύθυνση αυξανομένου υψομέτρου, όπως φαίνεται στο παρακάτω Σχήμα. Η πίεση και το υψόμετρο
Η αστοχία στα εδαφικά υλικά Νόμος Τριβής Coulomb
 Η αστοχία στα εδαφικά υλικά Νόμος Τριβής Coulomb Ν u Τ 81 Η αστοχία στα εδαφικά υλικά Νόμος Τριβής Coulomb 82 Η αστοχία στα εδαφικά υλικά Νόμος Τριβής Coulomb 83 Η αστοχία στα εδαφικά υλικά Νόμος Τριβής
Η αστοχία στα εδαφικά υλικά Νόμος Τριβής Coulomb Ν u Τ 81 Η αστοχία στα εδαφικά υλικά Νόμος Τριβής Coulomb 82 Η αστοχία στα εδαφικά υλικά Νόμος Τριβής Coulomb 83 Η αστοχία στα εδαφικά υλικά Νόμος Τριβής
Να υπολογίσετε τη μάζα 50 L βενζίνης. Δίνεται η σχετική πυκνότητά της, ως προς το νερό ρ σχ = 0,745.
 1 Παράδειγμα 101 Να υπολογίσετε τη μάζα 10 m 3 πετρελαίου, στους : α) 20 ο C και β) 40 ο C. Δίνονται η πυκνότητά του στους 20 ο C ρ 20 = 845 kg/m 3 και ο συντελεστής κυβικής διαστολής του β = 9 * 10-4
1 Παράδειγμα 101 Να υπολογίσετε τη μάζα 10 m 3 πετρελαίου, στους : α) 20 ο C και β) 40 ο C. Δίνονται η πυκνότητά του στους 20 ο C ρ 20 = 845 kg/m 3 και ο συντελεστής κυβικής διαστολής του β = 9 * 10-4
website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Νευτώνια και μη Νευτώνια ρευστά Μαάιτα Τζαμάλ-Οδυσσέας 15 Απριλίου 2019 1 Καταστατικές εξισώσεις Νευτώνιου ρευστού Νευτώνια ή Νευτωνικά
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Νευτώνια και μη Νευτώνια ρευστά Μαάιτα Τζαμάλ-Οδυσσέας 15 Απριλίου 2019 1 Καταστατικές εξισώσεις Νευτώνιου ρευστού Νευτώνια ή Νευτωνικά
Ηλεκτρομαγνητισμός. Ηλεκτρικό δυναμικό. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Ηλεκτρικό δυναμικό Νίκος Ν. Αρπατζάνης Ηλεκτρικό δυναμικό Θα συνδέσουμε τον ηλεκτρομαγνητισμό με την ενέργεια. Χρησιμοποιώντας την αρχή διατήρησης της ενέργειας μπορούμε να λύνουμε διάφορα
Ηλεκτρομαγνητισμός Ηλεκτρικό δυναμικό Νίκος Ν. Αρπατζάνης Ηλεκτρικό δυναμικό Θα συνδέσουμε τον ηλεκτρομαγνητισμό με την ενέργεια. Χρησιμοποιώντας την αρχή διατήρησης της ενέργειας μπορούμε να λύνουμε διάφορα
Εθνικό Μετσόβιο Πολυτεχνείο - Σχολή Πολιτικών Μηχανικών Περιβαλλοντική Γεωτεχνική - 2 η σειρά ασκήσεων - 25 Οκτωβρίου, 2018
 Καλόν είναι μαζί με τις απαντήσεις να παραδίνετε και την εκφώνηση. Είναι απαραίτητο όταν χρειάζεται να σημειώσετε/μετρήσετε κάτι πάνω στο σχήμα. Υπενθύμιση: οι απαντήσεις σας να είναι σε συρραμμένα φύλλα,
Καλόν είναι μαζί με τις απαντήσεις να παραδίνετε και την εκφώνηση. Είναι απαραίτητο όταν χρειάζεται να σημειώσετε/μετρήσετε κάτι πάνω στο σχήμα. Υπενθύμιση: οι απαντήσεις σας να είναι σε συρραμμένα φύλλα,
Τα τρία βασικά προβλήματα της Υδραυλικής
 Τα τρία βασικά προβλήματα της Υδραυλικής Α βασικό πρόβλημα,, παροχή γνωστή απλός υπολογισμός απωλειών όχι δοκιμές (1): L1 = 300, d1 = 0.6 m, (): L = 300, d = 0.4 m Q = 0.5m 3 /s, H=?, k=0.6 mm Διατήρηση
Τα τρία βασικά προβλήματα της Υδραυλικής Α βασικό πρόβλημα,, παροχή γνωστή απλός υπολογισμός απωλειών όχι δοκιμές (1): L1 = 300, d1 = 0.6 m, (): L = 300, d = 0.4 m Q = 0.5m 3 /s, H=?, k=0.6 mm Διατήρηση
ΙΔΙΟΤΗΤΕΣ ΤΟΥ ΕΔΑΦΟΥΣ
 ΙΔΙΟΤΗΤΕΣ ΤΟΥ ΕΔΑΦΟΥΣ Το αντικείμενο της εδαφομηχανικής είναι η μελέτη των εδαφών, με στόχο την κατανόηση και πρόβλεψη της συμπεριφοράς του εδάφους για μία ποικιλία σκοπών: συμπεριλαμβανομένων των θεμελίων
ΙΔΙΟΤΗΤΕΣ ΤΟΥ ΕΔΑΦΟΥΣ Το αντικείμενο της εδαφομηχανικής είναι η μελέτη των εδαφών, με στόχο την κατανόηση και πρόβλεψη της συμπεριφοράς του εδάφους για μία ποικιλία σκοπών: συμπεριλαμβανομένων των θεμελίων
1 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΕΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ
 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΕΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού Οριακού
η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΕΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού Οριακού
ΔΥΝΑΜΙΚΗ ΘΑΛΑΣΣΙΩΝ ΚΑΤΑΣΚΕΥΩΝ
 ΔΥΝΑΜΙΚΗ ΘΑΛΑΣΣΙΩΝ ΚΑΤΑΣΚΕΥΩΝ ΤΑΛΑΝΤΩΣΕΙΣ ΚΥΛΙΝΔΡΙΚΗΣ ΚΑΤΑΣΚΕΥΗΣ ΛΟΓΩ ΔΙΝΩΝ Γ. Σ. ΤΡΙΑΝΤΑΦYΛΛΟΥ ΚΑΘΗΓΗΤΗΣ ΕΜΠ Διατύπωση των εξισώσεων Θεωρούμε κύλινδρο διαμέτρου D, μήκους l, και μάζας m. Ο κύλινδρος συγκρατειται
ΔΥΝΑΜΙΚΗ ΘΑΛΑΣΣΙΩΝ ΚΑΤΑΣΚΕΥΩΝ ΤΑΛΑΝΤΩΣΕΙΣ ΚΥΛΙΝΔΡΙΚΗΣ ΚΑΤΑΣΚΕΥΗΣ ΛΟΓΩ ΔΙΝΩΝ Γ. Σ. ΤΡΙΑΝΤΑΦYΛΛΟΥ ΚΑΘΗΓΗΤΗΣ ΕΜΠ Διατύπωση των εξισώσεων Θεωρούμε κύλινδρο διαμέτρου D, μήκους l, και μάζας m. Ο κύλινδρος συγκρατειται
Γραμμή ενέργειας σε ένα αγωγό (χωρίς αντλία)
 Γραμμή ενέργειας σε ένα αγωγό (χωρίς αντλία) Γραμμή ενεργείας: ο γεωμετρικός τόπος του ύψος θέσης, του ύψους πίεσης και του ύψους κινητικής ενέργειας Πάντοτε πτωτική από τη διατήρηση της ενέργειας Δεν
Γραμμή ενέργειας σε ένα αγωγό (χωρίς αντλία) Γραμμή ενεργείας: ο γεωμετρικός τόπος του ύψος θέσης, του ύψους πίεσης και του ύψους κινητικής ενέργειας Πάντοτε πτωτική από τη διατήρηση της ενέργειας Δεν
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΔΙΑΤΜΗΜΑΤΟ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΣΧΕΔΙΑΣΜΟΣ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΥΠΟΓΕΙΩΝ ΕΡΓΩΝ»
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΔΙΑΤΜΗΜΑΤΟ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΣΧΕΔΙΑΣΜΟΣ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΥΠΟΓΕΙΩΝ ΕΡΓΩΝ» ΜΑΘΗΜΑ: ΗΛΕΚΤΡΟΜΗΧΑΝΟΛΟΓΙΚΕΣ ΕΓΚΑΤΑΣΤΑΣΕΙΣ ΔΙΔΑΣΚΩΝ: Επικ. Καθ. Δ. ΜΑΘΙΟΥΛΑΚΗΣ ΘΕΜΑΤΑ ΤΕΤΡΑΜΗΝΟΥ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΔΙΑΤΜΗΜΑΤΟ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΣΧΕΔΙΑΣΜΟΣ ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΥΠΟΓΕΙΩΝ ΕΡΓΩΝ» ΜΑΘΗΜΑ: ΗΛΕΚΤΡΟΜΗΧΑΝΟΛΟΓΙΚΕΣ ΕΓΚΑΤΑΣΤΑΣΕΙΣ ΔΙΔΑΣΚΩΝ: Επικ. Καθ. Δ. ΜΑΘΙΟΥΛΑΚΗΣ ΘΕΜΑΤΑ ΤΕΤΡΑΜΗΝΟΥ
Περιβαλλοντική Γεωτεχνική Θεματική Ενότητα 8 Τεχνολογίες αποκατάστασης υπεδάφους
 Περιβαλλοντική Γεωτεχνική Θεματική Ενότητα 8 Τεχνολογίες αποκατάστασης υπεδάφους Λυμένες ασκήσεις Απαιτούμενος χρόνος και όγκος άντλησης Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Σχολή Πολιτικών Μηχανικών
Περιβαλλοντική Γεωτεχνική Θεματική Ενότητα 8 Τεχνολογίες αποκατάστασης υπεδάφους Λυμένες ασκήσεις Απαιτούμενος χρόνος και όγκος άντλησης Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Σχολή Πολιτικών Μηχανικών
ΛΥΜΕΝΕΣ ΕΦΑΡΜΟΓΕΣ ΣΤΟ 2 ο ΚΕΦΑΛΑΙΟ
 ΛΥΜΕΝΕΣ ΕΦΑΡΜΟΓΕΣ ΣΤΟ 2 ο ΚΕΦΑΛΑΙΟ 1. Έστω συνάρτηση ζήτησης με τύπο Q = 200 4P. Να βρείτε: α) Την ελαστικότητα ως προς την τιμή όταν η τιμή αυξάνεται από 10 σε 12. 1ος τρόπος Αν P 0 10 τότε Q 0 200 410
ΛΥΜΕΝΕΣ ΕΦΑΡΜΟΓΕΣ ΣΤΟ 2 ο ΚΕΦΑΛΑΙΟ 1. Έστω συνάρτηση ζήτησης με τύπο Q = 200 4P. Να βρείτε: α) Την ελαστικότητα ως προς την τιμή όταν η τιμή αυξάνεται από 10 σε 12. 1ος τρόπος Αν P 0 10 τότε Q 0 200 410
Όλα τα θέματα είναι ισοδύναμα από άποψη βαθμού. Σύνολο: 10.5 (προβλήματα: 4x2.5=10, κρίση επίτευξης στόχων βλέπε πιο κάτω: 0.5)
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ - ΤΟΜΕΑΣ ΓΕΩΤΕΧΝΙΚΗΣ ΔΙΑΓΩΝΙΣΜΑ ΣΤΟ ΜΑΘΗΜΑ: ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ (9 ο Εξ. ΠΜ) Ακαδ. έτος: 2014-15 16 Φεβρουαρίου 2015 Διάρκεια: 2.5 h Όνομα: Οδηγίες/επεξηγήσεις/συμβουλές
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ - ΤΟΜΕΑΣ ΓΕΩΤΕΧΝΙΚΗΣ ΔΙΑΓΩΝΙΣΜΑ ΣΤΟ ΜΑΘΗΜΑ: ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ (9 ο Εξ. ΠΜ) Ακαδ. έτος: 2014-15 16 Φεβρουαρίου 2015 Διάρκεια: 2.5 h Όνομα: Οδηγίες/επεξηγήσεις/συμβουλές
ΚΕΦΑΛΑΙΟ 3 Ο ΡΕΥΣΤΑ ΣΕ ΚΙΝΗΣΗ
 166 Α. ΕΡΩΤΗΣΕΙΣ ΑΝΟΙΚΤΟΥ ΤΥΠΟΥ: ΚΕΦΑΛΑΙΟ 3 Ο ΡΕΥΣΤΑ ΣΕ ΚΙΝΗΣΗ 1. Να αναφέρεται παραδείγματα φαινομένων που μπορούν να ερμηνευτούν με την μελέτη των ρευστών σε ισορροπία. 2. Ποια σώματα ονομάζονται ρευστά;
166 Α. ΕΡΩΤΗΣΕΙΣ ΑΝΟΙΚΤΟΥ ΤΥΠΟΥ: ΚΕΦΑΛΑΙΟ 3 Ο ΡΕΥΣΤΑ ΣΕ ΚΙΝΗΣΗ 1. Να αναφέρεται παραδείγματα φαινομένων που μπορούν να ερμηνευτούν με την μελέτη των ρευστών σε ισορροπία. 2. Ποια σώματα ονομάζονται ρευστά;
Υπολογισμός συνάρτησης μεταφοράς σε Υδραυλικά συστήματα. Αντίσταση ροής υγρού. Μανομετρικό Υψος h. Υψος h2. Ροή q
 Υπολογισμός συνάρτησης μεταφοράς σε Υδραυλικά συστήματα. Αντίσταση ροής υγρού Υψος h Μανομετρικό Υψος h Υψος h Σχήμα.4 Ροή q Ας υποθέσουμε ότι έχουμε δύο δεξαμενές που επικοινωνούν με ένα σωλήνα όπως ακριβώς
Υπολογισμός συνάρτησης μεταφοράς σε Υδραυλικά συστήματα. Αντίσταση ροής υγρού Υψος h Μανομετρικό Υψος h Υψος h Σχήμα.4 Ροή q Ας υποθέσουμε ότι έχουμε δύο δεξαμενές που επικοινωνούν με ένα σωλήνα όπως ακριβώς
Στο διπλανό σχήμα το έμβολο έχει βάρος Β, διατομή Α και ισορροπεί. Η δύναμη που ασκείται από το υγρό στο έμβολο είναι
 Ερωτήσεις θεωρίας - Θέμα Β Εκφώνηση 1η Στο διπλανό σχήμα το έμβολο έχει βάρος Β, διατομή Α και ισορροπεί. Η δύναμη που ασκείται από το υγρό στο έμβολο είναι α) β) γ) Λύση Εκφώνηση 2η Στο διπλανό υδραυλικό
Ερωτήσεις θεωρίας - Θέμα Β Εκφώνηση 1η Στο διπλανό σχήμα το έμβολο έχει βάρος Β, διατομή Α και ισορροπεί. Η δύναμη που ασκείται από το υγρό στο έμβολο είναι α) β) γ) Λύση Εκφώνηση 2η Στο διπλανό υδραυλικό
ΡΕΥΣΤΑ. Φυσική Θετικού Προσανατολισμου Γ' Λυκείου
 ΡΕΥΣΤΑ ΕΙΣΑΓΩΓΗ Ρευστά Με τον όρο ρευστά εννοούμε τα ΥΓΡΑ και τα ΑΕΡΙΑ τα οποία, αντίθετα από τα στερεά, δεν έχουν καθορισμένο όγκο ούτε σχήμα. Τα υγρά είναι ασυμπίεστα και τα αέρια συμπιεστά. Τα υγρά
ΡΕΥΣΤΑ ΕΙΣΑΓΩΓΗ Ρευστά Με τον όρο ρευστά εννοούμε τα ΥΓΡΑ και τα ΑΕΡΙΑ τα οποία, αντίθετα από τα στερεά, δεν έχουν καθορισμένο όγκο ούτε σχήμα. Τα υγρά είναι ασυμπίεστα και τα αέρια συμπιεστά. Τα υγρά
2 Μετάδοση θερμότητας με εξαναγκασμένη μεταφορά
 2 Μετάδοση θερμότητας με εξαναγκασμένη μεταφορά 2.1 Εισαγωγή Η θερμοκρασιακή διαφορά μεταξύ δυο σημείων μέσα σ' ένα σύστημα προκαλεί τη ροή θερμότητας και, όταν στο σύστημα αυτό περιλαμβάνεται ένα ή περισσότερα
2 Μετάδοση θερμότητας με εξαναγκασμένη μεταφορά 2.1 Εισαγωγή Η θερμοκρασιακή διαφορά μεταξύ δυο σημείων μέσα σ' ένα σύστημα προκαλεί τη ροή θερμότητας και, όταν στο σύστημα αυτό περιλαμβάνεται ένα ή περισσότερα
Χαμηλής περατότητας διαφράγματα (περιορισμός εξάπλωσης ρύπων): Σχόλια
 Χαμηλής περατότητας διαφράγματα (περιορισμός εξάπλωσης ρύπων): Σχόλια Μεγάλη εμπειρία εφαρμογής σε χώρους υγειονομικής ταφής απορριμμάτων (ΧΥΤΑ) ο όγκος του διαφεύγοντος στραγγίσματος και η επιβράδυνση
Χαμηλής περατότητας διαφράγματα (περιορισμός εξάπλωσης ρύπων): Σχόλια Μεγάλη εμπειρία εφαρμογής σε χώρους υγειονομικής ταφής απορριμμάτων (ΧΥΤΑ) ο όγκος του διαφεύγοντος στραγγίσματος και η επιβράδυνση
ΟΡΙΑΚΟ ΣΤΡΩΜΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΘΕΩΡΗΤΙΚΗ ΑΝΑΛΥΣΗ. Σημειώσεις. Επιμέλεια: Άγγελος Θ. Παπαϊωάννου, Ομοτ. Καθηγητής ΕΜΠ
 ΟΡΙΑΚΟ ΣΤΡΩΜΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΘΕΩΡΗΤΙΚΗ ΑΝΑΛΥΣΗ Σημειώσεις Επιμέλεια: Άγγελος Θ. Παπαϊωάννου, Ομοτ. Καθηγητής ΕΜΠ Αθήνα, Απρίλιος 13 1. Η Έννοια του Οριακού Στρώματος Το οριακό στρώμα επινοήθηκε για
ΟΡΙΑΚΟ ΣΤΡΩΜΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΘΕΩΡΗΤΙΚΗ ΑΝΑΛΥΣΗ Σημειώσεις Επιμέλεια: Άγγελος Θ. Παπαϊωάννου, Ομοτ. Καθηγητής ΕΜΠ Αθήνα, Απρίλιος 13 1. Η Έννοια του Οριακού Στρώματος Το οριακό στρώμα επινοήθηκε για
Αρχές μεταφοράς ρύπων
 ΚΕΦΑΛΑΙΟ 4 Αρχές μεταφοράς ρύπων 4.1 Διεργασίες μεταφοράς ρύπων Η γενικότερη έννοια της μεταφοράς περιλαμβάνει κάθε διεργασία που συντελεί στη μετακίνηση μάζας ή ενέργειας. Στα προβλήματα ρύπανσης του
ΚΕΦΑΛΑΙΟ 4 Αρχές μεταφοράς ρύπων 4.1 Διεργασίες μεταφοράς ρύπων Η γενικότερη έννοια της μεταφοράς περιλαμβάνει κάθε διεργασία που συντελεί στη μετακίνηση μάζας ή ενέργειας. Στα προβλήματα ρύπανσης του
ΦΥΣΙΚΗ -ΚΛΙΜΑΤΙΚΗ ΑΛΛΑΓΗ ΚΑΙ ΓΕΩΡΓΙΑ
 Γιάννης Λ. Τσιρογιάννης Γεωργικός Μηχανικός M.Sc., PhD Επίκουρος Καθηγητής ΤΕΙ Ηπείρου Τμ. Τεχνολόγων Γεωπόνων Κατ. Ανθοκομίας Αρχιτεκτονικής Τοπίου ΦΥΣΙΚΗ -ΚΛΙΜΑΤΙΚΗ ΑΛΛΑΓΗ ΚΑΙ ΓΕΩΡΓΙΑ Υδραυλική Έκδοση
Γιάννης Λ. Τσιρογιάννης Γεωργικός Μηχανικός M.Sc., PhD Επίκουρος Καθηγητής ΤΕΙ Ηπείρου Τμ. Τεχνολόγων Γεωπόνων Κατ. Ανθοκομίας Αρχιτεκτονικής Τοπίου ΦΥΣΙΚΗ -ΚΛΙΜΑΤΙΚΗ ΑΛΛΑΓΗ ΚΑΙ ΓΕΩΡΓΙΑ Υδραυλική Έκδοση
8 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ
 8.1 8 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΩΣΤΙΚΟ ΕΔΡΑΝΟ ΟΛΙΣΘΗΣΗΣ 8.1. Εισαγωγή Το απλό επίπεδο ωστικό έδρανο ολίσθησης (Σχήμα 8.1) είναι ίσως η απλούστερη περίπτωση εφαρμογής της εξίσωσης Reynolds που περιγράφει τη
8.1 8 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΩΣΤΙΚΟ ΕΔΡΑΝΟ ΟΛΙΣΘΗΣΗΣ 8.1. Εισαγωγή Το απλό επίπεδο ωστικό έδρανο ολίσθησης (Σχήμα 8.1) είναι ίσως η απλούστερη περίπτωση εφαρμογής της εξίσωσης Reynolds που περιγράφει τη
Α.Σ.ΠΑΙ.Τ.Ε. / ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΦΕΒΡΟΥΑΡΙΟΥ 2014 ΜΑΘΗΜΑ ΦΥΣΙΚΗ Ι Μαρούσι Καθηγητής Σιδερής Ε.
 Α.Σ.ΠΑΙ.Τ.Ε. / ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΦΕΒΡΟΥΑΡΙΟΥ 2014 Μαρούσι 04-02-2014 Καθηγητής Σιδερής Ε. ΘΕΜΑ 1 ο (βαθμοί 4) (α) Θέλετε να κρεμάσετε μια ατσάλινη δοκό που έχει
Α.Σ.ΠΑΙ.Τ.Ε. / ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΦΕΒΡΟΥΑΡΙΟΥ 2014 Μαρούσι 04-02-2014 Καθηγητής Σιδερής Ε. ΘΕΜΑ 1 ο (βαθμοί 4) (α) Θέλετε να κρεμάσετε μια ατσάλινη δοκό που έχει
Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου. Στραγγίσεις (Θεωρία) Ενότητα 9 : Η ασταθής στράγγιση των εδαφών Ι Δρ.
 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Στραγγίσεις (Θεωρία) Ενότητα 9 : Η ασταθής στράγγιση των εδαφών Ι Δρ Μενέλαος Θεοχάρης 61 Γενικά Η ροή του υπόγειου νερού ονομάζεται ασταθής,
Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Στραγγίσεις (Θεωρία) Ενότητα 9 : Η ασταθής στράγγιση των εδαφών Ι Δρ Μενέλαος Θεοχάρης 61 Γενικά Η ροή του υπόγειου νερού ονομάζεται ασταθής,
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΜΗΧΑΝΙΚΗ ΡΕΥΣΤΩΝ
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΜΗΧΑΝΙΚΗ ΡΕΥΣΤΩΝ Στις παρακάτω ερωτήσεις Α-Α4 να σημειώσετε την σωστή απάντηση Α. Νερό διαρρέει έναν κυλινδρικό σωλήνα, ο οποίος στενεύει σε κάποιο σημείο του χωρίς να διακλαδίζεται. Ποια
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΜΗΧΑΝΙΚΗ ΡΕΥΣΤΩΝ Στις παρακάτω ερωτήσεις Α-Α4 να σημειώσετε την σωστή απάντηση Α. Νερό διαρρέει έναν κυλινδρικό σωλήνα, ο οποίος στενεύει σε κάποιο σημείο του χωρίς να διακλαδίζεται. Ποια
Γραμμή ενέργειας σε ένα αγωγό (χωρίς αντλία)
 Γραμμή ενέργειας σε ένα αγωγό (χωρίς αντλία) Γραμμή ενεργείας: ο γεωμετρικός τόπος του ύψος θέσης, του ύψους πίεσης και του ύψους κινητικής ενέργειας Πάντοτε πτωτική από τη διατήρηση της ενέργειας Δεν
Γραμμή ενέργειας σε ένα αγωγό (χωρίς αντλία) Γραμμή ενεργείας: ο γεωμετρικός τόπος του ύψος θέσης, του ύψους πίεσης και του ύψους κινητικής ενέργειας Πάντοτε πτωτική από τη διατήρηση της ενέργειας Δεν
