ΦΥΣΙΚΗ. Ενότητα 8: Ηλεκτρική Δυναμική Ενέργεια-Θεώρημα Έργου- Ενέργειας-Ηλεκτρικό Δυναμικό-Ισοδυναμικές Επιφάνειες
|
|
|
- Λητώ Γερμανός
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗ Ενότητα 8: Ηλεκτρική Δυναμική Ενέργεια-Θεώρημα Έργου- Ενέργειας-Ηλεκτρικό Δυναμικό-Ισοδυναμικές Επιφάνειες Τσόκας Γρηγόρης Καθηγητής Εφαρμοσμένης Γεωφυσικής, Τομέας Γεωφυσικής Παπαζάχος Κωνσταντίνος Καθηγητής Γεωφυσικής, Τομέας Γεωφυσικής
2 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Cetive Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύπου άδειας χρήσης, η άδεια χρήσης αναφέρεται ρητώς.
3 Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το έργο «Ανοικτά Ακαδημαϊκά Μαθήματα στο» έχει χρηματοδοτήσει μόνο την αναδιαμόρφωση του εκπαιδευτικού υλικού. Το έργο υλοποιείται στο πλαίσιο του Επιχειρησιακού Προγράμματος «Εκπαίδευση και Δια Βίου Μάθηση» και συγχρηματοδοτείται από την Ευρωπαϊκή Ένωση (Ευρωπαϊκό Κοινωνικό Ταμείο) και από εθνικούς πόρους. 3
4 Ενημέρωση Η διδασκαλία του μαθήματος, πολλά από τα σχήματα και όλες οι ασκήσεις προέρχονται από το βιβλίο: «Πανεπιστημιακή» του Hugh Young των Εκδόσεων Παπαζήση, οι οποίες μας επέτρεψαν τη χρήση των σχετικών σχημάτων και ασκήσεων. 4
5 ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ- Έστω δύναμη που ενεργεί πάνω σε σωμάτιο που κινείται από το σημείο στο σημείο, τότε η δύναμη παράγει έργο το οποίο είναι W F d l Fcos dl Όπου dl είναι το στοιχείο μήκους της τροχιάς και φ είναι η γωνία μεταξύ F και dl σε κάθε σημείο. Εάν το πεδίο δυνάμεων είναι διατηρητικό τότε το έργο μπορεί να δοθεί ως συνάρτηση μιας δυναμικής ενέργειας.
6 ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ- Ας υποθέσουμε το σωματίδιο μας που μεταφέρεται από τη θέση στη θέση με αντίστοιχη δυναμική ενέργεια και, τότε το έργο που παράγεται από τη δύναμη είναι W Επομένως το έργο μπορεί να είναι θετικό ή αρνητικό ανάλογα με το πιο σημείο έχει μεγαλύτερη δυναμική ενέργεια. ΜΗΧΑΝΙΚΟ ΑΝΑΛΟΓΟ Όταν αφήσουμε μια μπάλα να πέσει ελεύθερα μέσα στο γήινο πεδίο βαρύτητας αυτή θα κινηθεί από σημείο με μεγαλύτερη δυναμική ενέργεια σε σημείο με χαμηλότερη, τότε Η ΔΥΝΑΜΗ ΠΑΡΑΓΕΙ ΘΕΤΙΚΟ ΕΡΓΟ. Όταν όμως πετάμε τη μπάλα προς τα πάνω τότε Η ΒΑΡΥΤΙΚΗ ΔΥΝΑΜΗ ΠΑΡΑΓΕΙ ΑΡΝΗΤΙΚΟ ΕΡΓΟ.
7 ΘΕΩΡΗΜΑ ΕΡΓΟΥ- ΕΝΕΡΓΕΙΑΣ- Η μεταβολή της κινητικής ενέργειας (K -K )είναι ίση με το συνολικό έργο που παράγεται στο σωμάτιο Επομένως το συνολικό έργο είναι K -K = - Απ όπου K + =K + ΔΗΛΑΔΗ Η ΣΥΝΟΛΙΚΗ ΕΝΕΡΓΕΙΑ ΠΑΡΑΜΕΝΕΙ ΑΝΑΛΟΙΩΤΗ ΑΛΛΑ ΟΙ ΣΥΝΙΣΤΩΣΕΣ ΤΗΣ ΜΠΟΡΕΙ ΝΑ ΜΕΤΑΒΑΛΛΟΝΤΑΙ ΕΤΣΙ ΩΣΤΕ ΤΟ ΑΘΡΟΙΣΜΑ ΤΟΥΣ ΝΑ ΕΙΝΑΙ ΣΤΑΘΕΡΟ.
8 ΘΕΩΡΗΜΑ ΕΡΓΟΥ- ΕΝΕΡΓΕΙΑΣ- Ηλεκτροστατική περίπτωση ομογενούς πεδίου Ας υποθέσουμε ένα δοκιμαστικό φορτίο που κινείται από το σημείο στο σημείο του σχήματος. Το πεδίο εξασκεί μια σταθερή δύναμη μέτρου F= E, η οποία διευθύνεται προς τα κάτω. Παράγεται έργο από το πεδίο (ή τη δύναμη), το οποίο είναι W Fd Ed
9 ΘΕΩΡΗΜΑ ΕΡΓΟΥ- ΕΝΕΡΓΕΙΑΣ-3 Η συνιστώσα κατά τον y της δύναμης είναι Fy=- E ενώ δεν υπάρχουν συνιστώσες κατά x και z. Το έργο είναι ανεξάρτητο από τη διαδρομή. Η δυναμική ενέργεια του ηλεκτρικού πεδίου είναι = Ey ακριβώς όπως η δυναμική ενέργεια για τη δύναμη βαρύτητας F y =-mg είναι =mgy Όταν το δοκιμαστικό μας φορτίο κινείται από το στο, το πεδίο παράγει έργο πάνω στο φορτίο, το οποίο είναι W Ey Ey E ( y y )
10 ΘΕΩΡΗΜΑ ΕΡΓΟΥ- ΕΝΕΡΓΕΙΑΣ-4 ΘΕΤΙΚΟ ΦΟΡΤΙΟ W E ( y y ) Όταν το y είναι μεγαλύτερο του y τότε το δοκιμαστικό ας φορτίο κινείται στην ίδια κατεύθυνση με αυτή του πεδίου και το έργο είναι θετικό. Όταν όμως y <y τότε το πεδίο παράγει αρνητικό έργο.
11 ΘΕΩΡΗΜΑ ΕΡΓΟΥ- ΕΝΕΡΓΕΙΑΣ-5 y y ) Ey ( ) Ey ( y E - y ) E ( ) y y ) E ( ( ) Ey ( ) Ey ( W ΑΡΝΗΤΙΚΟ ΦΟΡΤΙΟ Όταν το δοκιμαστικό μας φορτίο είναι αρνητικό τότε η δυναμική ενέργεια αυξάνει όταν το σωμάτιο κινείται προς τη φορά του πεδίου και το έργο που παράγει το πεδίο είναι αρνητικό ΔΗΛΑΔΗ ΠΑΜΕ ΑΝΤΙΘΕΤΑ ΜΕ ΤΗ «ΘΕΛΗΣΗ» ΤΟΥ ΠΕΔΙΟΥ, ΠΡΕΠΕΙ ΝΑ ΚΑΤΑΒΑΛΟΥΜΕ ΕΜΕΙΣ ΕΡΓΟ ΓΙΑ ΝΑ ΓΙΝΕΙ ΑΥΤΟ ΚΑΙ ΟΧΙ ΤΟ ΠΕΔΙΟ.
12 ΘΕΩΡΗΜΑ ΕΡΓΟΥ- ΕΝΕΡΓΕΙΑΣ-6 Η δυναμική ενέργεια ελαττώνεται όταν το φορτίο κινείται αντίθετα με το πεδίο. ΤΩΡΑ ΟΜΩΣ ΤΟ ΠΕΔΙΟ ΤΟ ΤΡΑΒΑΕΙ ΤΟ ΦΟΡΤΙΟ άρα αυτό καταβάλει έργο. Το σωματίδιο υπακούει στο πεδίο. Το έργο που παράγει το πεδίο στο σωματίδιο είναι θετικό. ( ) Ey ( ) Ey W ( ) Ey ( ) Ey ( ) E ( y y ) ( ) E ( y ) E y
13 ΘΕΩΡΗΜΑ ΕΡΓΟΥ- ΕΝΕΡΓΕΙΑΣ-7 ΕΡΓΟ ΠΟΥ ΠΑΡΑΓΕΤΑΙ ΟΤΑΝ ΔΟΚΙΜΑΣΤΙΚΟ ΦΟΡΤΙΟ ΚΙΝΕΙΤΑΙ ΜΕΣΑ ΣΤΟ ΠΕΔΙΟ ΠΟΥ ΔΗΜΙΟΥΡΓΕΙ ΣΤΑΤΙΚΟ ΜΕΜΟΝΩΜΕΝΟ ΣΗΜΕΙΑΚΟ ΦΟΡΤΙΟ ΠΡΩΤΑ ΘΑ ΔΟΥΜΕ ΤΙ ΓΙΝΕΤΑΙ ΓΙΑ ΑΚΤΙΝΙΚΗ ΚΙΝΗΣΗ Νόμος του Coulom F 4 W F d 4 d 4 ( )
14 ΘΕΩΡΗΜΑ ΕΡΓΟΥ- ΕΝΕΡΓΕΙΑΣ-8 ΟΜΩΣ ΤΟ ΕΡΓΟ ΠΑΡΑΜΕΝΕΙ ΤΟ ΙΔΙΟ ΓΙΑ ΟΛΕΣ ΤΙΣ ΔΥΝΑΤΕΣ ΤΡΟΧΙΕΣ; Αν δούμε μια πιο γενική μετατόπιση από το στο, τα οποία τώρα δεν είναι πάνω στην ίδια ακτινική διεύθυνση. Η δύναμη αναλύεται σε δύο συνιστώσες, μία κάθετη στην τροχιά και μία εφαπτόμενη. Από αυτές μόνο η εφαπτομενική συνιστώσα παράγει έργο εφόσον μπορεί να μεταβάλει το μέτρο της ταχύτητας ενώ η κάθετη μεταβάλει μόνο τη διεύθυνση της ταχύτητας.
15 ΘΕΩΡΗΜΑ ΕΡΓΟΥ- ΕΝΕΡΓΕΙΑΣ-9 Τα παραπάνω εκφράζονται μαθηματικά με τη θεώρηση του έργου ως εσωτερικό γινόμενου της δύναμης επί την μετατόπιση (Δηλαδή με το γινόμενο της προβολής της δύναμης στη μετατόπιση ΕΠΙ τη μετατόπιση). W F dl Fcos dl Fd Το έργο που παράγεται για κάθε μικρή μετατόπιση dl εξαρτάται μόνο από τη μεταβολή της ακτινικής απόστασης των δύο φορτίων d
16 ΘΕΩΡΗΜΑ ΕΡΓΟΥ- ΕΝΕΡΓΕΙΑΣ- Αφού το έργο εξαρτάται μόνο από τη μεταβολή της ακτινικής απόστασης μεταξύ αρχικής και τελικής θέσης, τότε ισχύει η εξίσωση που βρήκαμε για κίνηση κατά τη διεύθυνση κάποιας ακτίνας. W = 4πε
17 ΘΕΩΡΗΜΑ ΕΡΓΟΥ- ΕΝΕΡΓΕΙΑΣ- ΓΙΑ ΝΑ ΕΙΝΑΙ ΣΥΝΕΠΕΙΣ ΜΕΤΑΞΥ ΤΟΥΣ ΟΙ ΕΞΙΣΩΣΕΙΣ ΠΡΕΠΕΙ Η ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ ΝΑ ΕΙΝΑΙ 4 Δηλαδή : W F d 4 d 4 ( )
18 ΘΕΩΡΗΜΑ ΕΡΓΟΥ- ΕΝΕΡΓΕΙΑΣ- Η δυναμική ενέργεια ορίζεται πάντα ως προς ένα σημείο αναφοράς, δηλαδή ένα σημείο το οποίο =. Στην τελευταία εξίσωση έχουμε = όταν Άρα η παριστά το έργο που προσφέρεται από το πεδίο του φορτίου στο φορτίο για να μεταφερθεί αυτό από μια συγκεκριμένη θέση στο άπειρο. Εάν τα και έχουν ίδιο πρόσημο τότε η αλληλεπίδραση είναι απωστική και το έργο για να πάει το στο άπειρο είναι θετικό και από τον ορισμό ΘΕΤΙΚΗ ΕΙΝΑΙ ΚΑΙ Η ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ ΣΕ ΚΑΘΕ ΠΕΠΕΡΑΣΜΕΝΗ ΑΠΟΣΤΑΣΗ. W F d 4 d 4 ( ), W 4
19 ΘΕΩΡΗΜΑ ΕΡΓΟΥ- ΕΝΕΡΓΕΙΑΣ-3 Εάν τα και έχουν αντίθετο πρόσημο τότε το έργο για να πάει το στο άπειρο είναι αρνητικό και από τον ορισμό ΑΡΝΗΤΙΚΗ ΕΙΝΑΙ ΚΑΙ Η ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ. W F d 4 (- ) d 4 ( ), W ΜΕ ΑΛΛΑ ΛΟΓΙΑ: ΕΜΕΙΣ ΠΡΕΠΕΙ ΝΑ ΕΦΑΡΜΟΣΟΥΜΕ ΕΞΩΤΕΡΙΚΗ ΔΥΝΑΜΗ ΓΙΑ ΝΑ ΑΠΟΚΟΛΛΗΣΟΥΜΕ ΤΟ ΕΝΑ ΦΟΡΤΙΟ ΑΠΟ ΤΗΝ ΕΛΞΗ ΤΟΥ ΑΛΛΟΥ ΚΑΙ ΝΑ ΤΟ ΠΑΜΕ ΣΤΟ ΑΠΕΙΡΟ.
20 ΘΕΩΡΗΜΑ ΕΡΓΟΥ- ΕΝΕΡΓΕΙΑΣ-4 ΓΕΝΙΚΕΥΣΗ Έστω ότι το πεδίο μας Ε δημιουργείται από πολλά σημειακά φορτία,, 3, τα οποία βρίσκονται σε αποστάσεις,, 3,.. από το δοκιμαστικό φορτίο ΔΗΛΑΔΗ το Ε είναι το άθροισμα των πεδίων των επιμέρους φορτίων Το έργο που παράγεται στο για κάποια μετατόπισή του είναι το άθροισμα των έργων που παράγουν τα επιμέρους πεδία Ε,Ε, Ε 3...
21 ΘΕΩΡΗΜΑ ΕΡΓΟΥ- ΕΝΕΡΓΕΙΑΣ-5 ΕΠΟΜΕΝΩΣ ΚΑΙ Η ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ ΣΕ ΣΗΜΕΙΟ ΤΟΥ ΧΩΡΟΥ ΤΟΥ ΠΕΔΙΟΥ ΤΗΣ ΟΜΑΔΑΣ ΤΩΝ ΦΟΡΤΙΩΝ ΕΙΝΑΙ: ΤΟ ΑΘΡΟΙΣΜΑ ΤΩΝ ΕΠΙΜΕΡΟΥΣ ΔΥΝΑΜΙΚΩΝ ΕΝΕΡΓΕΙΩΝ 4 π 3 4 π 3 i i i ΔΗΛΑΔΗ Η ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ ΕΞΑΡΤΑΤΑΙ ΑΠΟ ΤΙΣ ΑΠΟΣΤΑΣΕΙΣ ΤΩΝ ΕΠΙΜΕΡΟΥΣ ΦΟΡΤΙΩΝ ΤΗΣ ΣΥΛΛΟΓΗΣ ΑΠΟ ΤΟ ΣΗΜΕΙΟ α
22 ΘΕΩΡΗΜΑ ΕΡΓΟΥ- ΕΝΕΡΓΕΙΑΣ-6 ΤΟ ΤΕΛΕΥΤΑΙΟ ΑΠΟΤΕΛΕΣΜΑ ΕΙΝΑΙ ΠΟΛΥ ΣΗΜΑΝΤΙΚΟ ΓΙΑΤΙ ΜΠΟΡΟΥΜΕ ΝΑ ΘΕΩΡΗΣΟΥΜΕ ΟΠΟΙΑΔΗΠΟΤΕ ΚΑΤΑΝΟΜΗ ΦΟΡΤΙΩΝ ΩΣ ΣΥΛΛΟΓΗ ΣΗΜΕΙΑΚΩΝ ΦΟΡΤΙΩΝ. Π.Χ. ΜΠΟΡΟΥΜΕ ΝΑ ΘΕΩΡΗΣΟΥΜΕ ΤΟ ΣΥΝΟΛΙΚΟ ΦΟΡΤΙΟ ΣΦΑΙΡΑΣ ΩΣ ΑΘΡΟΙΣΜΑ ΣΗΜΕΙΑΚΩΝ ΦΟΡΤΙΩΝ ΚΑΤΑΝΕΜΗΜΕΝΩΝ ΣΤΗΝ ΕΠΙΦΑΝΕΙΑ ΤΗΣ.
23 ΘΕΩΡΗΜΑ ΕΡΓΟΥ- ΕΝΕΡΓΕΙΑΣ-7 ΕΩΣ ΤΩΡΑ ΘΕΩΡΗΣΑΜΕ ΤΟ ΠΕΔΙΟ Ε ΣΥΛΛΟΓΗΣ ΦΟΡΤΙΩΝ ΚΑΙ ΤΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ ΠΟΥ ΣΥΝΔΕΕΤΑΙ ΜΕ ΤΑ ΦΟΡΤΙΑ ΑΥΤΑ ΚΑΘ ΕΑΥΤΑ Ας θεωρήσουμε τα φορτία,, 3 σε άπειρη απόσταση μεταξύ τους και ότι στη συνέχεια αυτά πλησιάζουν σε αποστάσεις ij το ένα από το άλλο. ΤΟΤΕ ΤΟ ΣΥΣΤΗΜΑ ΑΠΟΚΤΑ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ 4 π i ij Μετράμε κάθε ζεύγος μια μόνο φορά i j
24 ΕΠΑΝΑΛΗΨΗ Όταν συμπιέζουμε το ελατήριο δαπανούμε έργο (εμείς το βάζουμε εξωτερικά αρνητικό έργο). Αυτό αποθηκεύεται ως δυναμική ενέργεια. Αν αφήσουμε το ελατήριο ελεύθερο, τότε θα εκτελεστεί έργο (θετικό) γιατί από θέση υψηλής δυναμικής ενέργειας θα μεταπέσει σε θέση χαμηλής. Το ίδιο συμβαίνει όταν ωθούμε το θετικό δοκιμαστικό φορτίο προς μια θετικά φορτισμένη σφαίρα.
25 ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ- W W i i i π 4 π Είναι η δυναμική ενέργεια που συνδέεται με δοκιμαστικό φορτίο δια του φορτίου. ΑΝΑΦΕΡΕΤΑΙ ΣΕ ΚΑΠΟΙΟ ΣΗΜΕΙΟ ΤΟΥ ΠΕΔΙΟΥ ΥΠΕΝΘΥΜΙΖΕΤΑΙ: Ένταση πεδίου είναι η δύναμη ανά μονάδα φορτίου ΣΥΛΛΟΓΗ ΦΟΡΤΙΩΝ ΕΡΓΟ ΑΝΑ ΜΟΝΑΔΑ ΦΟΡΤΙΟΥ ΕΙΝΑΙ ΔΙΑΦΟΡΑ ΔΥΝΑΜΙΚΟΥ
26 ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ- Όταν έχουμε συνεχή κατανομή φορτίων κατά μήκος γραμμής ή καθ έκταση ή μέσα σε ορισμένο όγκο ΤΟΤΕ: d 4 π Όπου είναι απόσταση του στοιχείου φορτίου από το σημείο στο οποίο θα υπολογίσουμε το δυναμικό. Το ολοκλήρωμα αναφέρεται στο χώρο που καταλαμβάνει η κατανομή. ΜΟΝΑΔΕΣ : Ενέργεια ανά φορτίο J/C= (olt) Alessndo olt (745-87) Τα βολτόμετρα μπορούν σήμερα να μετρήσουν έως -. Τα συνηθισμένα μπορούν έως -6 =μ
27 ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ-3 ΑΝ θέλουμε να δουλέψουμε με την ένταση του πεδίου και όχι με τα δυναμικά, μπορούμε να καταλήξουμε σε σχέση που συνδέει το δυναμικό με αυτή W F d l E d l W E d l W W E d l E d l ΑΛΛΟΙΩΣ: Για να μεταφέρουμε το φορτίο από το στο χρειαζόμαστε μια εξωτερική δύναμη ανά μονάδα φορτίου -Ε. Το έργο που παράγεται από αυτή την εξωτερική δύναμη είναι η διαφορά δυναμικού E d l
28 ΠΑΡΑΔΕΙΓΜΑ 4- Ένα πρωτόνιο (φορτίο,6 x -9 C) κινείται μέσα σε γραμμικό επιταχυντή από το σημείο στο σημείο πάνω σε ευθεία γραμμή, διανύοντας απόσταση d=,5 m. Το ηλεκτρικό πεδίο είναι ομογενές κατά μήκος αυτής της γραμμής με κατεύθυνση από το στο και έχει ένταση μέτρου Ε=,5 x 7 N/C. Να βρεθούν: α) η δύναμη στο πρωτόνιο β) το έργο που παράγει το πεδίο για αυτή τη μετακίνηση γ) η διαφορά δυναμικού - + E
29 ΠΑΡΑΔΕΙΓΜΑ 4- α) η δύναμη στο πρωτόνιο F= E=(,6 x -9 )(,5 x 7 ) C x N/C=,4 x - N β) Έργο που παράγει το πεδίο για τη μετακίνηση από το στο W=Fd=(,4 x - )(,5) N x m=, x - J γ) Διαφορά δυναμικού - - =W/=(, x - )/(,6 x -9 ) J/C = 7,5 x 6
30 ΠΑΡΑΔΕΙΓΜΑ 4-3/ Ένα ηλεκτρικό δίπολο αποτελείται από δύο σημειακά φορτία + nc και - nc, σε απόσταση cm μεταξύ τους. Να υπολογιστούν τα δυναμικά στα σημεία,, και c του σχήματος.
31 i i i π 4 π 4 π Στο σημείο α C Nm 9,4,6 ) / (9, 4 π ΠΑΡΑΔΕΙΓΜΑ 4-3/
32 ΠΑΡΑΔΕΙΓΜΑ 4-3/3 4 π Στο σημείο (9, Nm / C ) 93,4,4 4 π Στο σημείο c (9, Nm / C ),3,3
33 ΠΑΡΑΔΕΙΓΜΑ 4-4/ Φέρουμε φορτίο +4 nc στα σημεία,, και c του σχήματος. Να υπολογιστούν οι δυναμικές ενέργειες που συνδέονται με το φορτίο. ( 4 9 )( 9 )C J C 3,6 6 J ( 4 9 )(93 )C J C 7,7 6 J +4 nc +4 nc
34 ΠΑΡΑΔΕΙΓΜΑ 4-4/ c c Αν μεταφέρουμε το φορτίο κατά μήκος της μεσοκαθέτου δεν παράγεται έργο γιατί παντού πάνω η δυναμική ενέργεια είναι Αν από σημείο της μεσοκαθέτου μεταφέρουμε το φορτίο στο άπειρο, όποια διαδρομή και αν ακολουθήσουμε, το έργο είναι γιατί η αρχική και η τελική τιμή δυναμικού και δυναμικής ενέργειας είναι ΠΡΟΣΟΧΗ ΟΛΕΣ ΟΙ ΤΙΜΕΣ ΑΝΑΦΕΡΟΝΤΑΙ ΣΕ ΣΤΑΘΜΗ ΣΤΟ ΑΠΕΙΡΟ +4 nc
35 ΠΑΡΑΔΕΙΓΜΑ 4-5/ Ένα σωμάτιο μάζας m=5 g και φορτίου = nc ξεκινά από την ηρεμία στο σημείο α και κινείται κατά μήκος της ευθείας που ενώνει τα δύο σταθερά φορτία. Ποιά είναι η ταχύτητά του όταν φτάσει στο σημείο.
36 m K K K m ) ( υ K m ΠΑΡΑΔΕΙΓΜΑ 4-5/ Αρχή διατήρησης της ενέργειας
37 7 ) 35 ( m C C Nm m C C Nm m ) ( υ s m 4,6 kg C 5 ) 7 )( ( υ 3 9 ΠΑΡΑΔΕΙΓΜΑ 4-5/3
38 ΠΑΡΑΔΕΙΓΜΑ 4-6/ Έστω στερεά αγώγιμη σφαίρα με φορτίο. Να υπολογιστεί το δυναμικό σε κάθε σημείο μέσα και έξω από τη σφαίρα. Σε άλλο παράδειγμα χρησιμοποιήσαμε το νόμο του Guss για να δείξουμε ότι ΕΞΩΤΕΡΙΚΑ το πεδίο είναι το ίδιο με αυτό ενός σημειακού φορτίου στο κέντρο της σφαίρας. ΕΣΩΤΕΡΙΚΑ της σφαίρας το πεδίο είναι παντού μηδέν ΘΕΩΡΟΥΜΕ = ΟΤΑΝ ΑΠΕΙΡΟ
39 ΠΑΡΑΔΕΙΓΜΑ 4-6/ ΤΟΤΕ για σημείο εκτός της σφαίρας και σε απόσταση από αυτή, η σφαίρα θα «φαίνεται» σαν σημειακό φορτίο ΣΤΗΝ ΕΠΙΦΑΝΕΙΑ ΤΗΣ ΣΦΑΙΡΑΣ 4 π R ΕΣΩΤΕΡΙΚΑ της σφαίρας το πεδίο είναι παντού μηδέν. Επομένως δεν παράγεται έργο κατά τη μετακίνηση δοκιμαστικού φορτίου μεταξύ δύο οποιονδήποτε σημείων στην περιοχή αυτή. ΤΟ ΔΥΝΑΜΙΚΟ ΕΙΝΑΙ ΙΔΙΟ ΓΙΑ ΟΠΟΙΑΔΗΠΟΤΕ ΣΗΜΕΙΟ ΜΕΣΑ ΣΤΗ ΣΦΑΙΡΑ ΚΑΙ ΙΣΟ ΜΕ ΑΥΤΟ ΣΤΗΝ ΕΠΙΦΑΝΕΙΑ ΤΗΣ ΣΦΑΙΡΑΣ ΤΟ ΠΕΔΙΟ ΣΤΗΝ ΕΠΙΦΑΝΕΙΑ ΘΑ ΕΧΕΙ ΜΕΤΡΟ E 4 π R 4 π
40 ΠΑΡΑΔΕΙΓΜΑ 4-6/3
41 ΠΡΑΚΤΙΚΗ ΕΦΑΡΜΟΓΗ- ΤΟ ΜΕΓΙΣΤΟ ΔΥΝΑΜΙΚΟ ΣΤΟ ΟΠΟΙΟ ΜΠΟΡΕΙ ΝΑ ΤΕΘΕΙ ΑΓΩΓΟΣ ΣΤΟΝ ΑΕΡΑ ΤΑ ΜΟΡΙΑ ΤΟΥ ΑΕΡΑ ΙΟΝΙΖΟΝΤΑΙ ΓΙΑ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ 3 x 6 N/C. Δηλαδή σε τέτοιο πεδίο ο αέρας καθίσταται αγώγιμος. Από το προηγούμενο παράδειγμα έχουμε ότι το δυναμικό στην επιφάνεια της σφαίρας είναι =ER εφόσον E 4 π R 4 π R R R Δηλαδή το μέγιστο δυναμικό σχετίζεται με το μέγιστο πεδίο (αυτό που θα προκαλέσει ιονισμό) με τη σχέση m =E m R
42 ΠΡΑΚΤΙΚΗ ΕΦΑΡΜΟΓΗ- ΓΙΑ ΣΦΑΙΡΑ ΑΚΤΙΝΑΣ cm m =( - )(3 x 6 ) [mn/c]=3 Δηλαδή κανένας τρόπος δεν υπάρχει να υψώσουμε το δυναμικό της σφαίρας ακτίνας cm πέραν της τιμής των 3. ΑΝ ΞΕΠΕΡΑΣΟΥΜΕ ΤΗΝ ΤΙΜΕ ΑΥΤΗ Ο ΑΕΡΑΣ ΠΟΥ ΠΕΡΙΒΑΛΕΙ ΤΗ ΣΦΑΙΡΑ ΙΟΝΙΖΕΤΑΙ (ΓΙΝΕΤΑΙ ΑΓΩΓΙΜΟΣ) ΚΑΙ ΤΟ ΦΟΡΤΙΟ ΘΑ ΔΙΑΦΥΓΕΙ ΜΕΣΩ ΤΟΥ ΑΕΡΑ (ΑΣΤΡΑΠΗ). Αυτός είναι και ο λόγος που στις μηχανές υψηλής τάσης χρησιμοποιούνται ως πόλοι σφαίρες σχετικά μεγάλων ακτινών. Π.χ. Οι γεννήτριες n de Gf. AN KANOYME THN AKTINA 3 m ΤΟΤΕ m =9 M
43 ΠΡΑΚΤΙΚΗ ΕΦΑΡΜΟΓΗ-3
44 ΠΡΑΚΤΙΚΗ ΕΦΑΡΜΟΓΗ-4 Η σχέση m =E m R Μας λέει ότι το μέγιστο δυναμικό εξαρτάται από την ακτίνα, επομένως αν η ακτίνα είναι πολύ μικρή, τότε και το μέγιστο δυναμικό είναι μικρό. Δηλαδή κοντά σε αντικείμενα με οξείες απολήξεις αν αυτά φορτιστούν παράγονται σπινθήρες. Το ρεύμα που δημιουργείται και η ακτινοβολία λέγεται κορόνα. Γι αυτό οι κεραίες έχουν συνήθως μπαλάκι στην άκρη ή κάτι που να μεγαλώνει τον όγκο.
45 ΠΑΡΑΔΕΙΓΜΑ 4-7/ Έστω φορτισμένες παράλληλες πλάκες όπως στο σχήμα. Να υπολογιστεί το δυναμικό σε κάθε σημείο μεταξύ των πλακών. x Θέτουμε το σημείο των αξόνων στην κάτω πλάκα. Τότε η δυναμική ενέργεια για δοκιμαστικό φορτίο σε απόσταση y από την κάτω πλάκα είναι = Ey
46 ΠΑΡΑΔΕΙΓΜΑ 4-7/ = Ey / =Ey= y x Θεωρούμε = και επομένως και = στο σημείο y= δηλαδή στην κάτω πλάκα. y =Ey Αλλά και αν επιλέγαμε μια διαφορετική του μηδενός τιμή στην κάτω πλάκα τότε πάλι θα είχαμε y - =Ey. Το δυναμικό ελαττώνεται γραμμικά καθώς κινούμαστε από την πάνω πλάκα προς τη κάτω (γιατί μειώνεται το y) και εκεί παίρνει την τιμή.
47 ΠΑΡΑΔΕΙΓΜΑ 4-7/3 y - =Ey. Στο σημείο : y=d και y = α - =Ed και E=( α - )/d= /d ΠΡΟΣΟΧΗ ΑΥΤΟ ΙΣΧΥΕΙ ΜΟΝΟ ΓΙΑ ΕΠΙΠΕΔΗ ΓΕΩΜΕΤΡΙΑ ΚΑΙ ΟΧΙ ΓΙΑ ΟΜΟΚΕΝΤΡΕΣ ΣΦΑΙΡΕΣ ΚΑΙ ΟΜΟΚΕΝΤΡΟΥΣ ΚΥΛΙΝΔΡΟΥΣ ΜΟΝΑΔΑ ΠΕΔΙΟΥ /m= N/C x Σε παραδείγματα που αναλύσαμε στα προηγούμενα μαθήματα είχαμε βρει ότι το πεδίο μεταξύ των πλακών είναι Ε=σ/ε. Η σχέση που έχουμε τώρα δίνει το πεδίο ως συνάρτηση του δυναμικού και είναι πολύ πιο εύχρηστη στην πράξη γιατί το δυναμικό μετριέται με ένα βολτόμετρο ενώ δεν υπάρχουν όργανα που να μετρούν την επιφανειακή πυκνότητα φορτίου.
48 ΠΑΡΑΔΕΙΓΜΑ 4-8/ Να βρεθεί το δυναμικό σε απόσταση από πολύ μακριά γραμμική κατανομή φορτίου και σε ίδια απόσταση από μεγάλου μήκους φορτισμένο κύλινδρο. Φορτίο ανά μονάδα μήκους = λ
49 ΠΑΡΑΔΕΙΓΜΑ 4-8/ ΑΠΟ ΠΡΟΗΓΟΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΧΟΥΜΕ ΒΡΕΙ E 4 π Το δυναμικό μεταξύ δύο σημείων σε ακτινικές αποστάσεις από την κατανομή είναι d E dl ΔΕΝ ΜΠΟΡΟΥΜΕ ΝΑ ΘΕΩΡΗΣΟΥΜΕ ΟΤΙ = ΟΤΑΝ ΑΠΕΙΡΟ ΓΙΑΤΙ ΤΟΤΕ ln E ln
50 ΠΑΡΑΔΕΙΓΜΑ 4-8/3 ΔΗΛΑΔΗ ΑΝ ΤΟ ΔΥΝΑΜΙΚΟ ΕΙΝΑΙ ΜΗΔΕΝ ΣΤΟ ΑΠΕΙΡΟ ΤΟΤΕ ΑΥΤΌ ΕΙΝΑΙ ΑΠΕΙΡΟ ΣΕ ΚΑΘΕ ΠΕΠΕΡΑΣΜΕΝΗ ΑΠΟΣΤΑΣΗ ΕΠΟΜΕΝΩΣ ΟΡΙΖΟΥΜΕ ΤΟ ΔΥΝΑΜΙΚΟ ΝΑ ΕΙΝΑΙ ΜΗΔΕΝ ΣΕ ΜΙΑ ΑΥΘΑΙΡΕΤΗ ΑΠΟΣΤΑΣΗ = ln Η παραπάνω εξίσωση δίνει το δυναμικό στο πεδίο μιας ευθύγραμμης κατανομής φορτίων ΕΠΙΠΛΕΟΝ ΜΑΣ ΔΙΝΕΙ ΤΟ ΔΥΝΑΜΙΚΟ ΓΙΑ ΤΟ ΠΕΔΙΟ ΚΥΛΙΝΔΡΟΥ ΕΞΩ ΟΜΩΣ ΑΠΟ ΤΟΝ ΚΥΛΙΝΔΡΟ ΔΗΛΑΔΗ ΟΤΑΝ R<
51 ΠΑΡΑΔΕΙΓΜΑ 4-8/4 ΑΝ ΓΙΑ ΤΟΝ ΚΥΛΙΝΔΡΟ ΔΙΑΛΕΞΟΥΜΕ R= ΔΗΛΑΔΗ ΟΡΙΖΟΥΜΕ ΤΟ ΔΥΝΑΜΙΚΟ ΝΑ ΕΙΝΑΙ ΜΗΔΕΝ ΠΑΝΩ ΣΤΗΝ ΕΠΙΦΑΝΕΙΑ ΤΟΥ ΚΥΛΙΝΔΡΟΥ, ΤΟΤΕ ΕΧΟΥΜΕ: ln R
52 ΠΑΡΑΔΕΙΓΜΑ 4-9/ Να βρεθεί το δυναμικό σε σημείο Ρ του άξονα ομοιόμορφα φορτισμένου δακτυλίου με φορτίο Q σε απόσταση x από το κέντρο του.
53 ΠΑΡΑΔΕΙΓΜΑ 4-9/ Όλο το φορτίο είναι σε απόσταση : x 4 x Q Σε μεγάλη απόσταση 4 ΔΗΛΑΔΗ ΕΧΟΥΜΕ ΠΑΛΙ ΤΟ ΣΥΜΠΕΡΑΣΜΑ ΠΟΥ ΕΞΗΓΑΜΕ ΟΤΑΝ ΕΞΕΤΑΖΑΜΕ ΤΟ ΠΕΔΙΟ ΤΟΥ ΦΟΡΤΙΣΜΕΝΟΥ ΔΑΚΤΥΛΙΟΥ Ο ΔΑΚΤΥΛΙΟΣ ΑΠΟ ΜΑΚΡΥΑ ΦΑΙΝΕΤΑΙ ΣΑΝ ΣΗΜΕΙΑΚΟ ΦΟΡΤΙΟ Q x
54 ΠΑΡΑΔΕΙΓΜΑ 4-/ Να βρεθεί το δυναμικό σε σημείο Ρ της μεσοκαθέτου λεπτής ράβδου μήκους α, ομοιόμορφα φορτισμένης με συνολικό φορτίο Q. d 4 x dq y Όμως dq Q dy d 4 Q x dy y
55 ΠΑΡΑΔΕΙΓΜΑ 4-/ ( x ) Q x dy y Q ln x x Όταν το x είναι πολύ μεγάλο το τείνει στο ΓΕΝΙΚΑ ΣΤΑ ΠΡΟΗΓΟΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ ΦΑΙΝΕΤΑΙ ΟΤΙ ΟΙ ΥΠΟΛΟΓΙΣΜΟΙ ΤΩΝ ΔΥΝΑΜΙΚΩΝ ΕΙΝΑΙ ΑΠΛΟΥΣΤΕΡΑ ΠΡΟΒΛΗΜΑΤΑ ΑΠΟ ΟΤΙ ΟΙ ΥΠΟΛΟΓΙΣΜΟΙ ΤΩΝ ΠΕΔΙΩΝ. ΑΥΤΟ ΟΦΕΙΛΕΤΑΙ ΣΤΟ ΟΤΙ ΤΟ ΔΥΝΑΜΙΚΟ ΕΙΝΑΙ ΒΑΘΜΩΤΗ ΠΟΣΟΤΗΤΑ.
56 ΙΣΟΔΥΝΑΜΙΚΕΣ ΕΠΙΦΑΝΕΙΕΣ- Κάθε επιφάνεια, στη οποία το δυναμικό έχει την ίδια τιμή σε όλα τα σημεία της λέγεται ισοδυναμική. ΕΧΟΥΜΕ ΔΗΛΑΔΗ ΕΠΟΠΤΙΚΗ ΕΙΚΟΝΑ ΤΟΥ ΠΕΔΙΟΥ ΟΠΩΣ ΜΕ ΤΙΣ ΓΡΑΜΜΕΣ ΠΕΔΙΟΥ (ΔΥΝΑΜΙΚΕΣ ΓΡΑΜΜΕΣ). Αν έχουμε ένα δοκιμαστικό φορτίο που κινείται πάνω σε ισοδυναμική επιφάνεια τότε το πεδίο Ε δεν παράγει έργο γιατί η δυναμική ενέργεια είναι παντού ίδια. ΕΠΟΜΕΝΩΣ το πεδίο Ε δεν έχει συνιστώσα εφαπτόμενη προς την ισοδυναμική επιφάνεια γιατί τέτοια συνιστώσα θα παρήγαγε έργο κατά την κίνηση του φορτίου πάνω στην επιφάνεια. ΟΙ ΔΥΝΑΜΙΚΕΣ ΓΡΑΜΜΕΣ ΚΑΙ ΟΙ ΙΣΟΔΥΝΑΜΙΚΕΣ ΕΠΙΦΑΝΕΙΕΣ ΕΙΝΑΙ ΠΑΝΤΑ ΚΑΘΕΤΕΣ ΜΕΤΑΞΥ ΤΟΥΣ.
57 ΙΣΟΔΥΝΑΜΙΚΕΣ ΕΠΙΦΑΝΕΙΕΣ- ΤΟ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΜΟΛΙΣ ΕΞΩ ΑΠΟ ΤΟΝ ΑΓΩΓΟ ΠΡΕΠΕΙ ΝΑ ΕΙΝΑΙ ΚΑΘΕΤΟ ΣΤΗΝ ΕΠΙΦΑΝΕΙΑ ΤΟΥ ΑΓΩΓΟΥ ΑΠΟΔΕΙΞΗ : Θεωρούμε παραλληλόγραμμο βρόχο μερικώς μέσα και μερικώς έξω από τον αγωγό και δοκιμαστικό φορτίο που τον διατρέχει. Επειδή το πεδίο είναι διατηρητικό, το έργο που θα παράγει πάνω στο δοκιμαστικό φορτίο για αυτή την κλειστή διαδρομή θα πρέπει να είναι μηδέν.
58 ΙΣΟΔΥΝΑΜΙΚΕΣ ΕΠΙΦΑΝΕΙΕΣ-3 Έχουμε όμως ότι Ε= παντού μέσα στον αγωγό. ΟΜΩΣ ΕΦΟΣΟΝ ΣΥΜΒΑΙΝΕΙ ΑΥΤΟ ΤΟΤΕ ΚΑΙ Η ΣΥΝΙΣΤΩΣΑ ΤΟΥ Ε Η ΕΦΑΠΤΟΜΕΝΗ ΑΜΕΣΩΣ ΕΞΩ ΑΠΟ ΤΟΝ ΑΓΩΓΟ ΠΡΕΠΕΙ ΝΑ ΕΙΝΑΙ. ΑΝ ΔΕΝ ΗΤΑΝ ΕΤΣΙ ΤΟΤΕ ΤΟ ΕΡΓΟ ΓΙΑ ΚΛΕΙΣΤΗ ΔΙΑΔΡΟΜΗ (ΔΗΛΑΔΗ ΓΙΑ ΤΗΝ ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΗ ΤΡΟΧΙΑ ΤΟΥ ΔΟΚΙΜΑΣΤΙΚΟΥ ΦΟΡΤΙΟΥ) ΜΕΡΙΚΩΣ ΜΕΣΑ ΚΑΙ ΜΕΡΙΚΩΣ ΕΞΩ ΑΠΟ ΤΟ ΑΓΩΓΟ ΔΕΝ ΘΑ ΗΤΑΝ.
59 ΙΣΟΔΥΝΑΜΙΚΕΣ ΕΠΙΦΑΝΕΙΕΣ-4 Χ Χ Αυτό είναι Αδύνατο γιατί έρχεται σε αντίθεση με τη διατηρητική φύση του ηλεκτρικού πεδίου. ΕΠΟΜΕΝΩΣ ΥΠΑΡΧΕΙ ΜΟΝΟ ΚΑΘΕΤΗ ΣΥΝΙΣΤΩΣΑ ΣΤΗΝ ΕΠΙΦΑΝΕΙΑ ΤΟΥ ΑΓΩΓΟΥ. ΜΕ ΑΛΛΑ ΛΟΓΙΑ ΚΑΘΕ ΑΓΩΓΙΜΗ ΕΠΙΦΑΝΕΙΑ ΕΙΝΑΙ ΜΙΑ ΙΣΟΔΥΝΑΜΙΚΗ ΕΠΙΦΑΝΕΙΑ. ΟΤΑΝ ΕΧΟΥΜΕ ΑΓΩΓΙΜΕΣ ΕΠΙΦΑΝΕΙΕΣ ΟΙ ΓΡΑΜΜΕΣ ΤΟΥ ΠΕΔΙΟΥ ΣΤΑΜΑΤΟΥΝ ΕΚΕΙ.
60 ΙΣΟΔΥΝΑΜΙΚΕΣ ΕΠΙΦΑΝΕΙΕΣ-5
61 ΙΣΟΔΥΝΑΜΙΚΕΣ ΕΠΙΦΑΝΕΙΕΣ-6 ΕΔΩ ΒΛΕΠΟΥΜΕ ΤΙΣ ΙΣΟΔΥΝΑΜΙΚΕΣ ΓΡΑΜΜΕΣ ΠΑNΩ ΣΤΗΝ ΕΠΙΦΑΝΕΙΑ ΤΗΣ ΓΗΣ. Η ΕΥΡΕΣΗ ΚΑΙ Η ΧΑΡΤΟΓΡΑΦΗΣΗ ΤΟΥΣ ΑΠΟΤΕΛΕΙ ΜΙΑ ΑΠΟ ΤΙΣ ΜΕΘΟΔΟΥΣ ΜΕΛΕΤΗΣ TΗΣ ΔΟΜΗΣ ΤΟΥ ΕΣΩΤΕΡΙΚΟΥ ΤΗΣ ΓΗΣ. ΜΕ ΑΛΛΑ ΛΟΓΙΑ ΜΙΑ ΜΕΘΟΔΟ ΤΗΣ ΕΦΑΡΜΟΣΜΕΝΗΣ ΓΕΩΦΥΣΙΚΗΣ
62 ΙΣΟΔΥΝΑΜΙΚΕΣ ΕΠΙΦΑΝΕΙΕΣ-7 ΓΙΑ ΗΛΕΚΤΡΟΣΤΑΤΙΚΕΣ ΣΥΝΘΗΚΕΣ, όταν ένας αγωγός περιέχει μια κοιλότητα, η οποία δεν περιέχει φορτίο, τότε δεν μπορεί να υπάρξει φορτίο οπουδήποτε πάνω στην επιφάνεια μιας κοιλότητας. Η επιφάνεια της κοιλότητας, ας την πούμε Α, είναι ισοδυναμική επιφάνεια γιατί είναι επιφάνεια αγωγού. Υποθέτουμε επίσης ότι το σημείο Ρ της κοιλότητας έχει διαφορετικό δυναμικό και έστω Β η ισοδυναμική επιφάνεια στην οποία ανήκει το Ρ. Θεωρούμε τώρα μια γκαουσιανή επιφάνεια μεταξύ των δύο ισοδυναμικών.
63 ΙΣΟΔΥΝΑΜΙΚΕΣ ΕΠΙΦΑΝΕΙΕΣ-8 ΤΟ ΠΕΔΙΟ ΠΡΕΠΕΙ ΝΑ ΚΑΤΕΥΘΥΝΕΤΑΙ ΑΠΟ ΣΤΗ ΜΙΑ ΙΣΟΔΥΝΑΜΙΚΗ ΕΠΙΦΑΝΕΙΑ ΠΡΟΣ ΤΗΝ ΑΛΛΗ ΜΕ ΦΟΡΑ ΠΟΥ ΕΞΑΡΤΑΤΑΙ ΑΠΟ ΤΟ ΠΟΙΑ ΕΧΕΙ ΜΕΓΑΛΥΤΕΡΗ ΤΙΜΗ ΡΟΗ ΜΕΣΑ ΑΠΟ ΤΗ ΓΚΑΟΥΣΙΑΝΗ ΑΤΟΠΟ ΓΙΑΤΙ ΔΕΝ ΠΕΡΙΕΧΕΤΑΙ ΦΟΡΤΙΟ ΜΕΣΑ ΣΤΗ ΓΚΑΟΥΣΙΑΝΗ ΤΟ ΔΥΝΑΜΙΚΟ ΜΕΣΑ ΣΤΗΝ ΚΟΙΛΟΤΗΤΑ ΕΙΝΑΙ ΠΑΝΤΟΥ ΙΔΙΟ ΚΑΙ ΜΑΛΙΣΤΑ ΙΣΟ ΜΕ ΑΥΤΟ ΣΤΗΝ ΕΠΙΦΑΝΕΙΑ ΤΗΣ ΚΟΙΛΟΤΗΤΑΣ
64 ΙΣΟΔΥΝΑΜΙΚΕΣ ΕΠΙΦΑΝΕΙΕΣ-9 ΤΟ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΚΑΙ ΤΟ ΔΥΝΑΜΙΚΟ ΣΥΝΔΕΟΝΤΑΙ ΜΕΤΑΞΥ ΤΟΥΣ Όμως, - είναι το δυναμικό του ως προς το. Δηλαδή η μεταβολή του δυναμικού όταν ένα φορτίο κινείται από το στο E d l d E d l d Αν Ε είναι η συνιστώσα του πεδίου η παράλληλη προς τη στοιχειώδη μετατόπιση dl d E dl
65 ΙΣΟΔΥΝΑΜΙΚΕΣ ΕΠΙΦΑΝΕΙΕΣ- d E E d dl dl Δηλαδή το πεδίο κατά τη διεύθυνση dl είναι ο ρυθμός μεταβολής του δυναμικού στην ίδια διεύθυνση Σε καρτεσιανό σύστημα συντεταγμένων θα έχουμε E x x, E y y, E z z Και έτσι E ( x i y j z k ) ΧΡΗΣΙΜΟΠΟΙΩΝΤΑΣ ΤΗ ΓΕΝΙΚΕΥΜΕΝΗ ΠΑΡΑΓΩΓΟ (ΒΑΘΜΙΔΑ) ΔΗΛΑΔΗ ΤΟΝ ΤΕΛΕΣΤΗ ΑΝΑΔΕΛΤΑ, ΕΧΟΥΜΕ E
66 ΙΣΟΔΥΝΑΜΙΚΕΣ ΕΠΙΦΑΝΕΙΕΣ- Όλα τα σημεία μιας ισοϋψούς του τοπογραφικού χάρτη είναι στο ίδιο βαρυτικό δυναμικό (σε πρώτη προσέγγιση) γιατί απέχουν το ίδιο από το κέντρο της Γης. Μπορούμε να παραλληλίσουμε τις ισοϋψείς με τις ισοδυναμικές γραμμές στο ηλεκτρικό πεδίο. Το νερό κυλά λόγω βαρύτητας επίσης σε χαμηλότερα σημεία και η ροή του είναι κάθετη στις γραμμές του τοπογραφικού χάρτη, έτσι προσομοιώνουμε τις υδάτινες γραμμές ροής με τις γραμμές του ηλεκτρικού πεδίου (δυναμικές γραμμές). Οι επιφάνειες των λιμνών έχουν το ίδιο υψομέτρο παντού. Ακριβώς όπως οι επιφάνειες των αγωγών ευρίσκονται στο ίδιο δυναμικό.
67 ΙΣΟΔΥΝΑΜΙΚΕΣ ΕΠΙΦΑΝΕΙΕΣ- Το ηλεκτρικό πεδίο είναι η «κλίση» του δυναμικού σε κάθε σημείο και βρίσκεται ακριβώς όπως η τοπογραφική κλίση E Εν προκειμένω E x x Όπου Δx είναι η απόσταση μεταξύ δύο ισοδυναμικών Οι γραμμές του πεδίου κατευθύνονται πάντα προς την «κατηφόρα» δηλαδή από σημείο υψηλότερου δυναμικού προς σημείο με χαμηλότερο.
68 ΠΑΡΑΔΕΙΓΜΑΤΑ- ΠΕΔΙΟ ΣΗΜΕΙΑΚΟΥ ΦΟΡΤΙΟΥ 4 π E x E 4 π z 4 π ΠΕΔΙΟ ΕΞΩΤΕΡΙΚΑ ΦΟΡΤΙΣΜΕΝΟΥ ΚΥΛΙΝΔΡΟΥ R ln (ln R ln ) E Εφόσον θεωρήσαμε ως δυναμικό αναφορά (=), το δυναμικό στην επιφάνεια του κυλίνδρου z ln ln
69 ΠΑΡΑΔΕΙΓΜΑΤΑ- Όταν ένα σωμάτιο κινείται μέσα σε ηλεκτρικό πεδίο από μια θέση με δυναμικό σε μια άλλη με δυναμικό τότε η δυναμική του ενέργεια μεταβάλλεται κατά Δ ( ) Αν το φορτίο είναι ίσο με το φορτίου ηλεκτρονίου (δηλαδή ίσο με το κβάντο φορτίου=,6 Χ -9 C) και η διαφορά δυναμικού ίση με Δ=(,6 Χ -9 C)()=,6 Χ -9 J Η ΠΟΣΟΤΗΤΑ ΑΥΤΗ ΟΡΙΖΕΤΑΙ ΩΣ ΗΛΕΚΤΡΟΝΙΟΒΟΛΤ (e) e=,6 Χ -9 J
70 ΑΣΚΗΣΗ 4- Σημειακό φορτίο Q=+8 μc τοποθετείται με σταθερή πρόσδεση στην αρχή των αξόνων. Ένα δεύτερο σημειακό φορτίο =-.5 μc με μάζα 3 X -4 kg τοποθετείται στον άξονα των σε απόσταση,8 m από την αρχή. Α) Ποιά είναι η ηλεκτρική δυναμική ενέργεια του ζεύγους των φορτίων;(να θεωρηθεί ότι η δυναμική ενέργεια είναι όταν τα φορτία είναι σε άπειρη απόσταση.) Β) Το δεύτερο φορτίο ελευθερώνεται σε ηρεμία. Ποια θα είναι η ταχύτητά του σε απόσταση, m από την αρχή των αξόνων. B A Β Α
71 ΑΣΚΗΣΗ 4-7 Σε πόση απόσταση από σημειακό φορτίο =6 X - C έχουμε δυναμικό: α) β) 4
72 ΑΣΚΗΣΗ 4-7 Ένας απλός τύπος λυχνίας κενού (δίοδος) αποτελείται από δύο ηλεκτρόδια σε κάψουλα υψηλού κενού. Ένα ηλεκτρόδιο, η κάθοδος, διατηρείται σε υψηλή θερμοκρασία και έτσι εκπέμπει ηλεκτρόνια από την επιφάνειά της. Το άλλο ηλεκτρόδιο, η άνοδος βρίσκεται σε υψηλότερο δυναμικό. Υποθέτουμε ότι η κάθοδος είναι κυλινδρική με ακτίνα.5 cm και η άνοδος είναι επίσης κύλινδρος, ομοαξονικός της καθόδου, με ακτίνα.45 cm. Το δυναμικό της ανόδου είναι κατά 36 υψηλότερο της καθόδου. Ένα ηλεκτρόνιο αφήνει την κάθοδο από την κατάσταση της ηρεμίας και βομβαρδίζει την άνοδο. Με πόση ταχύτητα προσκρούει στην άνοδο;.5 cm.45 cm
73 ΣΥΝΟΨΗ- Σε ηλεκτροστατικές συνθήκες το έργο που παράγεται από το πεδίο πάνω σε σωματίδιο που κινείται μέσα σε αυτό μπορεί να παρασταθεί από συνάρτηση δυναμικής ενέργειας. W 4 π 3 4 π 3 i i i Το δυναμικό είναι η δυναμική ενέργεια ανά μονάδα φορτίου.
74 ΣΥΝΟΨΗ- Η διαφορά δυναμικού μεταξύ δύο σημείων είναι επίσης το γραμμικό ολοκλήρωμα του πεδίου Ισοδυναμική επιφάνεια είναι η επιφάνεια πάνω στην οποία το δυναμικό έχει παντού την ίδια τιμή Οι ισοδυναμικές επιφάνειες και οι γραμμές πεδίου (ή δυναμικές γραμμές) είναι κάθετες μεταξύ τους. Το πεδίο μπορεί να εκφραστεί σε N/C αλλά μας είναι πολύ πιο χρήσιμη η μονάδα /m. E d l
75 ΣΥΝΟΨΗ-3 Το πεδίο είναι η δυναμικού. κλίση (γενικευμένη παράγωγος) του E Το ηλεκτρονιοβόλτ είναι η ενέργεια που χρειάζεται ένα σωματίδιο για να διασχίσει διαφορά δυναμικού ίση με.
76 Σημείωμα Αναφοράς Copyight, Παπαζάχος Κωνσταντίνος. Τσόκας Γρηγόριος. «. Ηλεκτρική Δυναμική Ενέργεια- Θεώρημα Έργου-Ενέργειας-Ηλεκτρικό Δυναμικό-Ισοδυναμικές Επιφάνειες». Έκδοση:.. Θεσσαλονίκη 4. Διαθέσιμο από τη δικτυακή διεύθυνση:
77 Σημείωμα Αδειοδότησης Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης Cetive Commons Αναφορά - Παρόμοια Διανομή [] ή μεταγενέστερη, Διεθνής Έκδοση. Εξαιρούνται τα αυτοτελή έργα τρίτων π.χ. φωτογραφίες, διαγράμματα κ.λ.π., τα οποία εμπεριέχονται σε αυτό και τα οποία αναφέρονται μαζί με τους όρους χρήσης τους στο «Σημείωμα Χρήσης Έργων Τρίτων». Ο δικαιούχος μπορεί να παρέχει στον αδειοδόχο ξεχωριστή άδεια να χρησιμοποιεί το έργο για εμπορική χρήση, εφόσον αυτό του ζητηθεί. []
78 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Τέλος Ενότητας Επεξεργασία: Βεντούζη Χρυσάνθη Θεσσαλονίκη, Χειμερινό Εξάμηνο 3-4
79 Διατήρηση Σημειωμάτων Οποιαδήποτε αναπαραγωγή ή διασκευή του υλικού θα πρέπει να συμπεριλαμβάνει: το Σημείωμα Αναφοράς το Σημείωμα Αδειοδότησης τη δήλωση Διατήρησης Σημειωμάτων το Σημείωμα Χρήσης Έργων Τρίτων (εφόσον υπάρχει) μαζί με τους συνοδευόμενους υπερσυνδέσμους.
Ενημέρωση. Η διδασκαλία του μαθήματος, όλες οι ασκήσεις προέρχονται από το βιβλίο: «Πανεπιστημιακή
 Ενημέρωση Η διδασκαλία του μαθήματος, πολλά από τα σχήματα και όλες οι ασκήσεις προέρχονται από το βιβλίο: «Πανεπιστημιακή Φυσική» του Hugh Young των Εκδόσεων Παπαζήση, οι οποίες μας επέτρεψαν τη χρήση
Ενημέρωση Η διδασκαλία του μαθήματος, πολλά από τα σχήματα και όλες οι ασκήσεις προέρχονται από το βιβλίο: «Πανεπιστημιακή Φυσική» του Hugh Young των Εκδόσεων Παπαζήση, οι οποίες μας επέτρεψαν τη χρήση
Ορίζοντας την δυναμική ενέργεια σαν: Για μετακίνηση του φορτίου ανάμεσα στις πλάκες: Ηλεκτρικό Δυναμικό 1
 Ηλεκτρική Δυναμική Ενέργεια Ένα ζεύγος παράλληλων φορτισμένων μεταλλικών πλακών παράγει ομογενές ηλεκτρικό πεδίο Ε. Το έργο που παράγεται πάνω σε θετικό δοκιμαστικό φορτίο είναι: W W Fl q y q l q y Ορίζοντας
Ηλεκτρική Δυναμική Ενέργεια Ένα ζεύγος παράλληλων φορτισμένων μεταλλικών πλακών παράγει ομογενές ηλεκτρικό πεδίο Ε. Το έργο που παράγεται πάνω σε θετικό δοκιμαστικό φορτίο είναι: W W Fl q y q l q y Ορίζοντας
ΦΥΣΙΚΗ. Ενότητα 3: Οι νόμοι του Νεύτωνα
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗ Ενότητα 3: Οι νόμοι του Νεύτωνα Παπαζάχος Κωνσταντίνος Καθηγητής Γεωφυσικής, Τομέας Γεωφυσικής Τσόκας Γρηγόρης Καθηγητής Εφαρμοσμένης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗ Ενότητα 3: Οι νόμοι του Νεύτωνα Παπαζάχος Κωνσταντίνος Καθηγητής Γεωφυσικής, Τομέας Γεωφυσικής Τσόκας Γρηγόρης Καθηγητής Εφαρμοσμένης
ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ
 ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν μια
ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν μια
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν
ΦΥΣΙΚΗ. Ενότητα 2: Ταχύτητα - Επιτάχυνση
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗ Ενότητα 2: Ταχύτητα - Επιτάχυνση Παπαζάχος Κωνσταντίνος Καθηγητής Γεωφυσικής, Τομέας Γεωφυσικής Τσόκας Γρηγόρης Καθηγητής Εφαρμοσμένης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗ Ενότητα 2: Ταχύτητα - Επιτάχυνση Παπαζάχος Κωνσταντίνος Καθηγητής Γεωφυσικής, Τομέας Γεωφυσικής Τσόκας Γρηγόρης Καθηγητής Εφαρμοσμένης
ΘΕΩΡΙΑ ΜΗΧΑΝΙΚΩΝ ΤΑΛΑΝΤΩΣΕΩΝ ΚΑΙ ΕΛΑΣΤΙΚΑ ΚΥΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΘΕΩΡΙΑ ΜΗΧΑΝΙΚΩΝ ΤΑΛΑΝΤΩΣΕΩΝ ΚΑΙ ΕΛΑΣΤΙΚΑ ΚΥΜΑΤΑ Ενότητα 1: Στοιχεία Διανυσματικού Λογισμού Σκορδύλης Εμμανουήλ Καθηγητής Σεισμολογίας,
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΘΕΩΡΙΑ ΜΗΧΑΝΙΚΩΝ ΤΑΛΑΝΤΩΣΕΩΝ ΚΑΙ ΕΛΑΣΤΙΚΑ ΚΥΜΑΤΑ Ενότητα 1: Στοιχεία Διανυσματικού Λογισμού Σκορδύλης Εμμανουήλ Καθηγητής Σεισμολογίας,
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
ΦΥΣΙΚΗ. Ενότητα 1: Εισαγωγή στη Φυσική-Ακρίβεια & Σημαντικά Ψηφία- Βαθμωτά Μεγέθη-Διανυσματικά Μεγέθη
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗ Ενότητα 1: Εισαγωγή στη -Ακρίβεια & Σημαντικά Ψηφία- Βαθμωτά Μεγέθη-Διανυσματικά Μεγέθη Παπαζάχος Κωνσταντίνος Καθηγητής Γεωφυσικής,
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗ Ενότητα 1: Εισαγωγή στη -Ακρίβεια & Σημαντικά Ψηφία- Βαθμωτά Μεγέθη-Διανυσματικά Μεγέθη Παπαζάχος Κωνσταντίνος Καθηγητής Γεωφυσικής,
ΦΥΣΙΚΗ. Ενότητα 4: Κινητική ενέργεια-έργο-ισχύς- Δυναμική ενέργεια
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗ Ενότητα 4: Κινητική ενέργεια-έργο-ισχύς- Δυναμική ενέργεια Παπαζάχος Κωνσταντίνος Καθηγητής Γεωφυσικής, Τομέας Γεωφυσικής Τσόκας
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗ Ενότητα 4: Κινητική ενέργεια-έργο-ισχύς- Δυναμική ενέργεια Παπαζάχος Κωνσταντίνος Καθηγητής Γεωφυσικής, Τομέας Γεωφυσικής Τσόκας
ΦΥΣΙΚΗ ΙΙΙ. Ενότητα: Ηλεκτροστατική ΜΑΪΝΤΑΣ ΞΑΝΘΟΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ
 ΦΥΣΙΚΗ ΙΙΙ Ενότητα: Ηλεκτροστατική ΜΑΪΝΤΑΣ ΞΑΝΘΟΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ Σελίδα 2 ΑΣΚΗΣΕΙΣ... 4 Σελίδα 3 ΑΣΚΗΣΕΙΣ Ηλεκτροστατική 1. Στις κορυφές κανονικού n-πλεύρου τοποθετούνται ίδια φορτία q. Να δειχθεί ότι η
ΦΥΣΙΚΗ ΙΙΙ Ενότητα: Ηλεκτροστατική ΜΑΪΝΤΑΣ ΞΑΝΘΟΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ Σελίδα 2 ΑΣΚΗΣΕΙΣ... 4 Σελίδα 3 ΑΣΚΗΣΕΙΣ Ηλεκτροστατική 1. Στις κορυφές κανονικού n-πλεύρου τοποθετούνται ίδια φορτία q. Να δειχθεί ότι η
Γενική Φυσική. Ενότητα 5: Έργο, ενέργεια. Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Μαθηματικών
 Γενική Φυσική Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Μαθηματικών Έργο - Ενέργεια Βασική έννοια. Μηχανική, Ηλεκτρομαγνητική, Χημική, Θερμική, Πυρηνική, κ.α. Δυνατότητα μετατροπής της μίας μορφής
Γενική Φυσική Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Μαθηματικών Έργο - Ενέργεια Βασική έννοια. Μηχανική, Ηλεκτρομαγνητική, Χημική, Θερμική, Πυρηνική, κ.α. Δυνατότητα μετατροπής της μίας μορφής
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ. Γενικά Μαθηματικά Ι. Ενότητα 6: Ακρότατα Συνάρτησης. Λουκάς Βλάχος Τμήμα Φυσικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Ακρότατα Συνάρτησης Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Ακρότατα Συνάρτησης Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού. Ιωάννης Γκιάλας 14 Μαρτίου 2014
 Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού Ιωάννης Γκιάλας 14 Μαρτίου 2014 Έργο ηλεκτροστατικής δύναμης W F Δl W N i i1 F Δl i Η μετατόπιση Δl περιγράφεται από ένα διάνυσμα που
Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού Ιωάννης Γκιάλας 14 Μαρτίου 2014 Έργο ηλεκτροστατικής δύναμης W F Δl W N i i1 F Δl i Η μετατόπιση Δl περιγράφεται από ένα διάνυσμα που
Λογισμός 3. Ενότητα 19: Θεώρημα Πεπλεγμένων (γενική μορφή) Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 19: Θεώρημα Πεπλεγμένων (γενική μορφή) Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 19: Θεώρημα Πεπλεγμένων (γενική μορφή) Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 13 Ηλεκτρικό (Βαθμωτό) δυναμικό ΦΥΣ102 1 Διαφορά δυναμικού Η Ηλεκτροστατική Δύναμη
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 13 Ηλεκτρικό (Βαθμωτό) δυναμικό ΦΥΣ102 1 Διαφορά δυναμικού Η Ηλεκτροστατική Δύναμη
Γενικά Μαθηματικά Ι. Ενότητα 1: Συναρτήσεις και Γραφικές Παραστάσεις. Λουκάς Βλάχος Τμήμα Φυσικής ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1: Συναρτήσεις και Γραφικές Παραστάσεις Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1: Συναρτήσεις και Γραφικές Παραστάσεις Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Κλασική Hλεκτροδυναμική
 Κλασική Hλεκτροδυναμική Ενότητα 1: Εισαγωγή Ανδρέας Τερζής Σχολή Θετικών επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι μια σύντομη επανάληψη στις βασικές έννοιες της ηλεκτροστατικής.
Κλασική Hλεκτροδυναμική Ενότητα 1: Εισαγωγή Ανδρέας Τερζής Σχολή Θετικών επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι μια σύντομη επανάληψη στις βασικές έννοιες της ηλεκτροστατικής.
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα αυτής της
Φυσική για Μηχανικούς Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα αυτής της
Γενική Φυσική Ενότητα: Δυναμική Άκαμπτου Σώματος
 Γενική Φυσική Ενότητα: Δυναμική Άκαμπτου Σώματος Όνομα Καθηγητή: Γεώργιος Βούλγαρης Τμήμα: Μαθηματικό Σελίδα 2 1. Ερωτήσεις Δυναμικής Άκαμπτου Σώματος... 4 1.1 Ερώτηση 1... 4 1.2 Ερώτηση 2... 4 1.3 Ερώτηση
Γενική Φυσική Ενότητα: Δυναμική Άκαμπτου Σώματος Όνομα Καθηγητή: Γεώργιος Βούλγαρης Τμήμα: Μαθηματικό Σελίδα 2 1. Ερωτήσεις Δυναμικής Άκαμπτου Σώματος... 4 1.1 Ερώτηση 1... 4 1.2 Ερώτηση 2... 4 1.3 Ερώτηση
Γενικά Μαθηματικά Ι. Ενότητα 9: Κίνηση Σε Πολικές Συντεταγμένες. Λουκάς Βλάχος Τμήμα Φυσικής ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 9: Κίνηση Σε Πολικές Συντεταγμένες Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Ceative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 9: Κίνηση Σε Πολικές Συντεταγμένες Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Ceative
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΤΕΧΝΙΚΕΣ ΥΠΟΛΟΓΙΣΜΟΥ ΗΛΕΚΤΡΙΚΟΥ ΔΥΝΑΜΙΚΟΥ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΤΕΧΝΙΚΕΣ ΥΠΟΛΟΓΙΣΜΟΥ ΗΛΕΚΤΡΙΚΟΥ ΔΥΝΑΜΙΚΟΥ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Υπόγεια Υδραυλική και Υδρολογία
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 8: Συστήματα πηγαδιών Μέθοδος εικόνων Καθηγητής Κωνσταντίνος Λ. Κατσιφαράκης Αναπληρωτής Καθηγητής Νικόλαος Θεοδοσίου ΑΠΘ Άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 8: Συστήματα πηγαδιών Μέθοδος εικόνων Καθηγητής Κωνσταντίνος Λ. Κατσιφαράκης Αναπληρωτής Καθηγητής Νικόλαος Θεοδοσίου ΑΠΘ Άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΑΝΟΙΚΤΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΚΑΔΗΜΑΪΚΑ ΘΕΣΣΑΛΟΝΙΚΗΣ ΜΑΘΗΜΑΤΑ Γενικά Μαθηματικά Ι Ενότητα 11 : Ακολουθίες και Σειρές Λουκάς Βλάχος Τμήμα Φυσικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα : Ακολουθίες και Σειρές Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Ceative Commos. Για
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα : Ακολουθίες και Σειρές Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Ceative Commos. Για
ΦΥΣΙΚΗ. Ενότητα 9: Πυκνωτές-Ενέργεια Πυκνωτή-Διηλεκτρικά
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗ Ενότητα 9: Πυκνωτές-Ενέργεια Πυκνωτή-Διηλεκτρικά Τσόκας Γρηγόρης Καθηγητής Εφαρμοσμένης Γεωφυσικής, Τομέας Γεωφυσικής Παπαζάχος
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗ Ενότητα 9: Πυκνωτές-Ενέργεια Πυκνωτή-Διηλεκτρικά Τσόκας Γρηγόρης Καθηγητής Εφαρμοσμένης Γεωφυσικής, Τομέας Γεωφυσικής Παπαζάχος
Ηλεκτρομαγνητισμός. Ηλεκτρικό δυναμικό. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Ηλεκτρικό δυναμικό Νίκος Ν. Αρπατζάνης Ηλεκτρικό δυναμικό Θα συνδέσουμε τον ηλεκτρομαγνητισμό με την ενέργεια. Χρησιμοποιώντας την αρχή διατήρησης της ενέργειας μπορούμε να λύνουμε διάφορα
Ηλεκτρομαγνητισμός Ηλεκτρικό δυναμικό Νίκος Ν. Αρπατζάνης Ηλεκτρικό δυναμικό Θα συνδέσουμε τον ηλεκτρομαγνητισμό με την ενέργεια. Χρησιμοποιώντας την αρχή διατήρησης της ενέργειας μπορούμε να λύνουμε διάφορα
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Γενικά Μαθηματικά Ι. Ενότητα 8: Εφαρμογές Σειρών Taylor. Λουκάς Βλάχος Τμήμα Φυσικής ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 8: Εφαρμογές Σειρών Tylor Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Cretive Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 8: Εφαρμογές Σειρών Tylor Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Cretive Commons.
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ. Ενότητα 2: Ο νόμος του Gauss. Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε.
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ενότητα 2: Ο νόμος του Gauss Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ενότητα 2: Ο νόμος του Gauss Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Λογισμός 4 Ενότητα 13
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 3: Το επικαμπύλιο ολοκλήρωμα. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 3: Το επικαμπύλιο ολοκλήρωμα. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Λογισμός 3. Ενότητα 18: Θεώρημα Πεπλεγμένων (Ειδική περίπτωση) Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 18: Θεώρημα Πεπλεγμένων (Ειδική περίπτωση) Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑ ΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 18: Θεώρημα Πεπλεγμένων (Ειδική περίπτωση) Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Γενικά Μαθηματικά Ι. Ενότητα 12: Κριτήρια Σύγκλισης Σειρών. Λουκάς Βλάχος Τμήμα Φυσικής ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Κριτήρια Σύγκλισης Σειρών Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Κριτήρια Σύγκλισης Σειρών Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΦΥΣΙΚΗ. Ενότητα 7: ΠΕΡΙΣΤΡΟΦΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΓΥΡΩ ΑΠΟ ΣΤΑΘΕΡΟ ΑΞΟΝΑ. Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε.
 ΦΥΣΙΚΗ Ενότητα 7: ΠΕΡΙΣΤΡΟΦΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΓΥΡΩ ΑΠΟ ΣΤΑΘΕΡΟ ΑΞΟΝΑ Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΦΥΣΙΚΗ Ενότητα 7: ΠΕΡΙΣΤΡΟΦΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΓΥΡΩ ΑΠΟ ΣΤΑΘΕΡΟ ΑΞΟΝΑ Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Εφαρμοσμένη Βελτιστοποίηση
 Εφαρμοσμένη Βελτιστοποίηση Ενότητα 2: Συναρτήσεις Χώροι - Μεταβλητές Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα Αδειοδότησης Το
Εφαρμοσμένη Βελτιστοποίηση Ενότητα 2: Συναρτήσεις Χώροι - Μεταβλητές Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα Αδειοδότησης Το
ΦΥΣΙΚΗ. Ενότητα 2: ΔΙΑΝΥΣΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ. Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε.
 ΦΥΣΙΚΗ Ενότητα 2: ΔΙΑΝΥΣΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΦΥΣΙΚΗ Ενότητα 2: ΔΙΑΝΥΣΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Γενικά Μαθηματικά Ι. Ενότητα 15: Ολοκληρώματα Με Ρητές Και Τριγωνομετρικές Συναρτήσεις Λουκάς Βλάχος Τμήμα Φυσικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Ολοκληρώματα Με Ρητές Και Τριγωνομετρικές Συναρτήσεις Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Ολοκληρώματα Με Ρητές Και Τριγωνομετρικές Συναρτήσεις Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Γενικά Μαθηματικά Ι. Ενότητα 5: Παράγωγος Πεπλεγμένης Συνάρτησης, Κατασκευή Διαφορικής Εξίσωσης. Λουκάς Βλάχος Τμήμα Φυσικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Παράγωγος Πεπλεγμένης Συνάρτησης, Κατασκευή Διαφορικής Εξίσωσης Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Παράγωγος Πεπλεγμένης Συνάρτησης, Κατασκευή Διαφορικής Εξίσωσης Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Λογισμός 4 Ενότητα 19
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 19: Το Θεώρημα του Gauss. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 19: Το Θεώρημα του Gauss. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Γενικά Μαθηματικά Ι. Ενότητα 7: Σειρές Taylor, Maclaurin. Λουκάς Βλάχος Τμήμα Φυσικής ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 7: Σειρές Taylor, Maclaurin Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 7: Σειρές Taylor, Maclaurin Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ Γ.Ο.Ι. ΧΩΡΟΥΣ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ Γ.Ο.Ι. ΧΩΡΟΥΣ
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Γενική Φυσική Ενότητα: Ταλαντώσεις
 Γενική Φυσική Ενότητα: Ταλαντώσεις Όνομα Καθηγητή: Γεώργιος Βούλγαρης Τμήμα: Μαθηματικό Σελίδα 2 1. Ερωτήσεις Ταλαντώσεων... 4 1.1 Ερώτηση 1... 4 2. Ασκήσεις Ταλαντώσεων... 4 2.1 Άσκηση 1... 4 2.2 Άσκηση
Γενική Φυσική Ενότητα: Ταλαντώσεις Όνομα Καθηγητή: Γεώργιος Βούλγαρης Τμήμα: Μαθηματικό Σελίδα 2 1. Ερωτήσεις Ταλαντώσεων... 4 1.1 Ερώτηση 1... 4 2. Ασκήσεις Ταλαντώσεων... 4 2.1 Άσκηση 1... 4 2.2 Άσκηση
Ηλεκτρομαγνητισμός. Ηλεκτρικό πεδίο νόμος Gauss. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Νόμος Gauss Ο νόµος του Gauss εκφράζει τη σχέση μεταξύ της συνολικής ηλεκτρικής ροής που διέρχεται από μια κλειστή επιφάνεια και του φορτίου
Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Νόμος Gauss Ο νόµος του Gauss εκφράζει τη σχέση μεταξύ της συνολικής ηλεκτρικής ροής που διέρχεται από μια κλειστή επιφάνεια και του φορτίου
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Ηλεκτρομαγνητισμός
 Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Ηλεκτρομαγνητισμός Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών 7/15/2014 Ο νόμος του Gauss Νόμος Gauss Ο νόμος
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Ηλεκτρομαγνητισμός Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών 7/15/2014 Ο νόμος του Gauss Νόμος Gauss Ο νόμος
Ηλεκτρικό φορτίο Ηλεκτρικό Πεδίο
 Ηλεκτρικό Φορτίο Ν.Coulomb Όπου χρειάζεται στις παρακάτω ασκήσεις θεωρείστε δεδομένες τις τιμές των μεγεθών: k ηλ = 9.10 9 Nm 2 /C 2, e = 1,6.10-19 C, m e = 9,1.10-31 kg, m p = 1,7.10-27 kg, g = 10 m/s
Ηλεκτρικό Φορτίο Ν.Coulomb Όπου χρειάζεται στις παρακάτω ασκήσεις θεωρείστε δεδομένες τις τιμές των μεγεθών: k ηλ = 9.10 9 Nm 2 /C 2, e = 1,6.10-19 C, m e = 9,1.10-31 kg, m p = 1,7.10-27 kg, g = 10 m/s
ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ
 2η ΕΒΔΟΜΑΔΑ 1. Ηλεκτρική δυναμική ενέργεια (electric potentil energy) 2. Ηλεκτρικό δυναμικό (electric potentil) 3. Διαφορά δυναμικού (potentil difference) 4. Σχέση ηλεκτρικού δυναμικού με το ηλεκτρικό
2η ΕΒΔΟΜΑΔΑ 1. Ηλεκτρική δυναμική ενέργεια (electric potentil energy) 2. Ηλεκτρικό δυναμικό (electric potentil) 3. Διαφορά δυναμικού (potentil difference) 4. Σχέση ηλεκτρικού δυναμικού με το ηλεκτρικό
ΗΛΕΚΤΡΙΚΟ ΥΝΑΜΙΚΟ (ΚΕΦΑΛΑΙΟ 23)
 ΗΛΕΚΤΡΙΚΟ ΥΝΑΜΙΚΟ (ΚΕΦΑΛΑΙΟ 23) Υπενθύμιση/Εισαγωγή: Λέμε ότι ένα πεδίο δυνάμεων είναι συντηρητικό (ή διατηρητικό) όταν το έργο που παράγεται από το πεδίο δυνάμεων κατά τη μετατόπιση ενός σώματος από μία
ΗΛΕΚΤΡΙΚΟ ΥΝΑΜΙΚΟ (ΚΕΦΑΛΑΙΟ 23) Υπενθύμιση/Εισαγωγή: Λέμε ότι ένα πεδίο δυνάμεων είναι συντηρητικό (ή διατηρητικό) όταν το έργο που παράγεται από το πεδίο δυνάμεων κατά τη μετατόπιση ενός σώματος από μία
Ηλεκτρική δυναμική ενέργεια
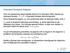 Ηλεκτρική δυναμική ενέργεια Όταν ένα δοκιμαστικό φορτίο βρεθεί μέσα σε ένα ηλεκτρικό πεδίο, δέχεται μια ηλεκτρική δύναμη: F e =q o E. Η ηλεκτρική δύναμη είναι συντηρητική. Έστω δοκιμαστικό φορτίο, q 0,
Ηλεκτρική δυναμική ενέργεια Όταν ένα δοκιμαστικό φορτίο βρεθεί μέσα σε ένα ηλεκτρικό πεδίο, δέχεται μια ηλεκτρική δύναμη: F e =q o E. Η ηλεκτρική δύναμη είναι συντηρητική. Έστω δοκιμαστικό φορτίο, q 0,
Φυσική ΙΙΙ. Ενότητα 4: Ηλεκτρικά Κυκλώματα. Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής
 Φυσική ΙΙΙ Ενότητα 4: Ηλεκτρικά Κυκλώματα Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Ηλεκτρεγερτική δύναμη. emf Ιστορική ονομασία που δόθηκε από τον Faraday. (Η αιτία που τείνει να δημιουργήσει
Φυσική ΙΙΙ Ενότητα 4: Ηλεκτρικά Κυκλώματα Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Ηλεκτρεγερτική δύναμη. emf Ιστορική ονομασία που δόθηκε από τον Faraday. (Η αιτία που τείνει να δημιουργήσει
1.Η δύναμη μεταξύ δύο φορτίων έχει μέτρο 120 N. Αν η απόσταση των φορτίων διπλασιαστεί, το μέτρο της δύναμης θα γίνει:
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΩΝ ΕΠΙΛΟΓΩΝ Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο 1.Η δύναμη μεταξύ δύο φορτίων έχει μέτρο 10 N. Αν η απόσταση των φορτίων διπλασιαστεί, το μέτρο της δύναμης θα γίνει: (α)
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΩΝ ΕΠΙΛΟΓΩΝ Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο 1.Η δύναμη μεταξύ δύο φορτίων έχει μέτρο 10 N. Αν η απόσταση των φορτίων διπλασιαστεί, το μέτρο της δύναμης θα γίνει: (α)
Φυσική ΙΙΙ. Ενότητα 4: Ηλεκτρικά Κυκλώματα. Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής
 Φυσική ΙΙΙ Ενότητα 4: Ηλεκτρικά Κυκλώματα Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Ασκήσεις ΦΙΙΙ Ηλεκτρικά Κυκλώματα Γ. Βούλγαρης 2 Ασκήσεις κατανομές φορτίου 1) Ένα γραμμικό φορτίο με
Φυσική ΙΙΙ Ενότητα 4: Ηλεκτρικά Κυκλώματα Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Ασκήσεις ΦΙΙΙ Ηλεκτρικά Κυκλώματα Γ. Βούλγαρης 2 Ασκήσεις κατανομές φορτίου 1) Ένα γραμμικό φορτίο με
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΑ ΠΕΔΙΑ ΣΤΗΝ ΥΛΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΑ ΠΕΔΙΑ ΣΤΗΝ ΥΛΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
ΦΥΣΙΚΗ. Ενότητα 8: ΠΕΡΙΣΤΡΟΦΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΓΥΡΩ ΑΠΟ ΣΤΑΘΕΡΟ ΑΞΟΝΑ. Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε.
 ΦΥΣΙΚΗ Ενότητα 8: ΠΕΡΙΣΤΡΟΦΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΓΥΡΩ ΑΠΟ ΣΤΑΘΕΡΟ ΑΞΟΝΑ Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΦΥΣΙΚΗ Ενότητα 8: ΠΕΡΙΣΤΡΟΦΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΓΥΡΩ ΑΠΟ ΣΤΑΘΕΡΟ ΑΞΟΝΑ Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Γενική Φυσική Ενότητα: Εισαγωγή στην Ειδική Θεωρία της Σχετικότητας
 Γενική Φυσική Ενότητα: Εισαγωγή στην Ειδική Θεωρία της Σχετικότητας Όνομα Καθηγητή: Γεώργιος Βούλγαρης Τμήμα: Μαθηματικό Σελίδα 2 1. Ασκήσεις στην Εισαγωγή στην Ειδική Θεωρία της Σχετικότητας... 4 1.1
Γενική Φυσική Ενότητα: Εισαγωγή στην Ειδική Θεωρία της Σχετικότητας Όνομα Καθηγητή: Γεώργιος Βούλγαρης Τμήμα: Μαθηματικό Σελίδα 2 1. Ασκήσεις στην Εισαγωγή στην Ειδική Θεωρία της Σχετικότητας... 4 1.1
ΦΥΣΙΚΗ ΙΙΙ. Ενότητα: Μαγνητοστατική ΜΑΪΝΤΑΣ ΞΑΝΘΟΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ
 ΦΥΣΙΚΗ ΙΙΙ Ενότητα: Μαγνητοστατική ΜΑΪΝΤΑΣ ΞΑΝΘΟΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ Σελίδα 2 ΑΣΚΗΣΕΙΣ... 4 Σελίδα 3 ΑΣΚΗΣΕΙΣ Μαγνητοστατική. Σωματίδιο μάζας m φορτίου Q βρίσκεται αρχικά ακίνητο μέσα σε ομογενές μαγνητικό
ΦΥΣΙΚΗ ΙΙΙ Ενότητα: Μαγνητοστατική ΜΑΪΝΤΑΣ ΞΑΝΘΟΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ Σελίδα 2 ΑΣΚΗΣΕΙΣ... 4 Σελίδα 3 ΑΣΚΗΣΕΙΣ Μαγνητοστατική. Σωματίδιο μάζας m φορτίου Q βρίσκεται αρχικά ακίνητο μέσα σε ομογενές μαγνητικό
Φυσική IΙ. Ενότητα 3: Ο Νόμος του Gauss. Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών
 Φυσική IΙ Ενότητα 3: Ο Νόμος του Gauss Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Ορισμός και ερμηνεία των δυναμικών γραμμών Παραδείγματα δυναμικών γραμμών σημειακού φορτίου,
Φυσική IΙ Ενότητα 3: Ο Νόμος του Gauss Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Ορισμός και ερμηνεία των δυναμικών γραμμών Παραδείγματα δυναμικών γραμμών σημειακού φορτίου,
Εκμετάλλευση και Προστασία των Υπόγειων Υδατικών Πόρων
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εκμετάλλευση και Προστασία των Υπόγειων Υδατικών Πόρων Ενότητα 10: Οριοθέτηση ζωνών προστασίας γεωτρήσεων Μέθοδος ιχνηλάτισης σωματιδίων
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εκμετάλλευση και Προστασία των Υπόγειων Υδατικών Πόρων Ενότητα 10: Οριοθέτηση ζωνών προστασίας γεωτρήσεων Μέθοδος ιχνηλάτισης σωματιδίων
Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Γ. Ολοκληρωτικός Λογισμός
 Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Γ. Ολοκληρωτικός Λογισμός Κεφάλαιο Γ.08.4: Υπολογισμός Όγκων Όνομα Καθηγητή: Γεώργιος Ν. Μπροδήμας Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Τίτλος Μαθήματος: Μαθηματική Ανάλυση Ενότητα Γ. Ολοκληρωτικός Λογισμός Κεφάλαιο Γ.08.4: Υπολογισμός Όγκων Όνομα Καθηγητή: Γεώργιος Ν. Μπροδήμας Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Φυσική ΙΙΙ. Ενότητα 3: Επαγωγή. Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής
 Φυσική ΙΙΙ Ενότητα 3: Επαγωγή Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Χρονικά μεταβαλλόμενο πεδίο. Κυκλικό πηνίο με 100 σπείρες και αντίσταση =5 Ω, τοποθετείται γύρω από σωληνοειδές όπως
Φυσική ΙΙΙ Ενότητα 3: Επαγωγή Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Χρονικά μεταβαλλόμενο πεδίο. Κυκλικό πηνίο με 100 σπείρες και αντίσταση =5 Ω, τοποθετείται γύρω από σωληνοειδές όπως
Ασκήσεις 2 ου Κεφαλαίου, Νόμος του Gauss
 Ασκήσεις 2 ου Κεφαλαίου, Νόμος του Guss 22.36.Μία αγώγιμη σφαίρα με φορτίο q έχει ακτίνα α. Η σφαίρα βρίσκεται στο εσωτερικό μίας κοίλης ομόκεντρης αγώγιμης σφαίρας με εσωτερική ακτίνα και εξωτερική ακτίνα.
Ασκήσεις 2 ου Κεφαλαίου, Νόμος του Guss 22.36.Μία αγώγιμη σφαίρα με φορτίο q έχει ακτίνα α. Η σφαίρα βρίσκεται στο εσωτερικό μίας κοίλης ομόκεντρης αγώγιμης σφαίρας με εσωτερική ακτίνα και εξωτερική ακτίνα.
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 11 Εισαγωγή στην Ηλεκτροδυναμική Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο ΦΥΣ102 1 Στατικός
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 11 Εισαγωγή στην Ηλεκτροδυναμική Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο ΦΥΣ102 1 Στατικός
Εκκλησιαστικό Δίκαιο. Ενότητα 10η: Ιερά Σύνοδος της Ιεραρχίας και Διαρκής Ιερά Σύνοδος Κυριάκος Κυριαζόπουλος Τμήμα Νομικής Α.Π.Θ.
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 10η: Ιερά Σύνοδος της Ιεραρχίας και Διαρκής Ιερά Σύνοδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 10η: Ιερά Σύνοδος της Ιεραρχίας και Διαρκής Ιερά Σύνοδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙIΙ ΜΕΤΑΒΑΤΙΚΑ ΦΑΙΝΟΜΕΝΑ ΣΤΑ ΣΗΕ Λαμπρίδης Δημήτρης Κατσανού Βάνα Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Γενικά Μαθηματικά Ι. Ενότητα 19: Υπολογισμός Εμβαδού και Όγκου Από Περιστροφή (2 ο Μέρος) Λουκάς Βλάχος Τμήμα Φυσικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 19: Υπολογισμός Εμβαδού και Όγκου Από Περιστροφή ( ο Μέρος) Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 19: Υπολογισμός Εμβαδού και Όγκου Από Περιστροφή ( ο Μέρος) Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙΙ Μάθημα ασκήσεων 2: Ηλεκτρικά χαρακτηριστικά γραμμών μεταφοράς Λαμπρίδης Δημήτρης Ανδρέου Γεώργιος Δούκας
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙΙ Μάθημα ασκήσεων 2: Ηλεκτρικά χαρακτηριστικά γραμμών μεταφοράς Λαμπρίδης Δημήτρης Ανδρέου Γεώργιος Δούκας
Κεφάλαιο 23 Ηλεκτρικό Δυναµικό. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 23 Ηλεκτρικό Δυναµικό Διαφορά Δυναµικού-Δυναµική Ενέργεια Σχέση Ηλεκτρικού Πεδίου και Ηλεκτρικού Δυναµικού Ηλεκτρικό Δυναµικό Σηµειακών Φορτίων Δυναµικό Κατανοµής Φορτίων Ισοδυναµικές Επιφάνειες
Κεφάλαιο 23 Ηλεκτρικό Δυναµικό Διαφορά Δυναµικού-Δυναµική Ενέργεια Σχέση Ηλεκτρικού Πεδίου και Ηλεκτρικού Δυναµικού Ηλεκτρικό Δυναµικό Σηµειακών Φορτίων Δυναµικό Κατανοµής Φορτίων Ισοδυναµικές Επιφάνειες
1. Ηλεκτρικό Φορτίο. Ηλεκτρικό Φορτίο και Πεδίο 1
 . Ηλεκτρικό Φορτίο Το ηλεκτρικό φορτίο είναι ένα από τα βασικά χαρακτηριστικά των σωματιδίων από τα οποία οικοδομείται η ύλη. Υπάρχουν δύο είδη φορτίου (θετικό αρνητικό). Κατά την φόρτιση το φορτίο δεν
. Ηλεκτρικό Φορτίο Το ηλεκτρικό φορτίο είναι ένα από τα βασικά χαρακτηριστικά των σωματιδίων από τα οποία οικοδομείται η ύλη. Υπάρχουν δύο είδη φορτίου (θετικό αρνητικό). Κατά την φόρτιση το φορτίο δεν
ΗΛΕΚΤΡΟΝΙΚΗ IΙ Ενότητα 6
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΗΛΕΚΤΡΟΝΙΚΗ IΙ Ενότητα 6: Ανάδραση Χατζόπουλος Αλκιβιάδης Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχ. Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΗΛΕΚΤΡΟΝΙΚΗ IΙ Ενότητα 6: Ανάδραση Χατζόπουλος Αλκιβιάδης Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχ. Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό
Δυναμική και Έλεγχος E-L Ηλεκτρομηχανικών Συστημάτων
 Δυναμική και Έλεγχος E-L Ηλεκτρομηχανικών Συστημάτων Ενότητα : Περιγραφή Δυναμικών Συστημάτων Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών
Δυναμική και Έλεγχος E-L Ηλεκτρομηχανικών Συστημάτων Ενότητα : Περιγραφή Δυναμικών Συστημάτων Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Γενικά Μαθηματικά Ι. Ενότητα 2: Τριγωνομετρικές, Εκθετικές και Σύνθετες Συναρτήσεις. Λουκάς Βλάχος Τμήμα Φυσικής ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Τριγωνομετρικές, Εκθετικές και Σύνθετες Συναρτήσεις Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Τριγωνομετρικές, Εκθετικές και Σύνθετες Συναρτήσεις Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Φυσική ΙΙΙ. Ενότητα 4: Ηλεκτρικά Κυκλώματα. Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής
 Φυσική ΙΙΙ Ενότητα 4: Ηλεκτρικά Κυκλώματα Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Ασκήσεις ΦΙΙΙ Γ. Βούλγαρης 2 Ταχύτητα ολίσθησης σε σύρμα από χαλκό. Διάμετρος δ=1,6 mm Ρεύμα 10 Α Πυκνότητα
Φυσική ΙΙΙ Ενότητα 4: Ηλεκτρικά Κυκλώματα Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Ασκήσεις ΦΙΙΙ Γ. Βούλγαρης 2 Ταχύτητα ολίσθησης σε σύρμα από χαλκό. Διάμετρος δ=1,6 mm Ρεύμα 10 Α Πυκνότητα
Ατομικά Δίκτυα Αρδεύσεων
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2 : Διήθηση-Εξίσωση Kostiakov Ευαγγελίδης Χρήστος Τμήμα Αγρονόμων & Τοπογράφων Μηχανικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2 : Διήθηση-Εξίσωση Kostiakov Ευαγγελίδης Χρήστος Τμήμα Αγρονόμων & Τοπογράφων Μηχανικών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Λογισμός 4 Ενότητα 17
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 17: Το επί-επιφάνειο ολοκλήρωμα διανυσματικών πεδίων. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 17: Το επί-επιφάνειο ολοκλήρωμα διανυσματικών πεδίων. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Υπόγεια Υδραυλική και Υδρολογία
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 4: Αναλυτική επίλυση του μαθηματικού ομοιώματος: Σύμμορφη Απεικόνιση Καθηγητής Κωνσταντίνος Λ. Κατσιφαράκης Αναπληρωτής Καθηγητής
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 4: Αναλυτική επίλυση του μαθηματικού ομοιώματος: Σύμμορφη Απεικόνιση Καθηγητής Κωνσταντίνος Λ. Κατσιφαράκης Αναπληρωτής Καθηγητής
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β Τάξης ΓΕΛ 4 ο ΓΕΛ ΚΟΖΑΝΗΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΣΤΕΦΑΝΟΥ Μ. ΦΥΣΙΚΟΣ
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β Τάξης ΓΕΛ 4 ο ΓΕΛ ΚΟΖΑΝΗΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΣΤΕΦΑΝΟΥ Μ. ΦΥΣΙΚΟΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ - ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ Δυναμική ενέργεια δυο φορτίων Δυναμική ενέργεια τριών ή περισσοτέρων
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β Τάξης ΓΕΛ 4 ο ΓΕΛ ΚΟΖΑΝΗΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΣΤΕΦΑΝΟΥ Μ. ΦΥΣΙΚΟΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ - ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ Δυναμική ενέργεια δυο φορτίων Δυναμική ενέργεια τριών ή περισσοτέρων
Hλεκτρικό. Πεδίο. Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ
 Hλεκτρικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SRWAY, Physics fo scientists nd enginees YOUNG H.D., Univesity
Hλεκτρικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SRWAY, Physics fo scientists nd enginees YOUNG H.D., Univesity
Ιστορία της μετάφρασης
 ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Μεταφραστές και πρωτότυπα. Ελένη Κασάπη ΤΜΗΜΑ ΑΓΓΛΙΚΗΣ ΓΛΩΣΣΑΣ ΚΑΙ ΦΙΛΟΛΟΓΙΑΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Μεταφραστές και πρωτότυπα. Ελένη Κασάπη ΤΜΗΜΑ ΑΓΓΛΙΚΗΣ ΓΛΩΣΣΑΣ ΚΑΙ ΦΙΛΟΛΟΓΙΑΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ. Λογισμός 4. Ενότητα 6: Εφαρμογές του Fubini. Μιχ. Γ. Μαριάς Τμήμα Μαθηματικών
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Εφαρμογές του Fubini. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Εφαρμογές του Fubini. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Φυσική (Ε) Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 2: Θεωρία ταλαντώσεων (Συνοπτική περιγραφή) Αικατερίνη Σκουρολιάκου. Τμήμα Ενεργειακής Τεχνολογίας
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική (Ε) Ενότητα 2: Θεωρία ταλαντώσεων (Συνοπτική περιγραφή) Αικατερίνη Σκουρολιάκου Τμήμα Ενεργειακής Τεχνολογίας Το περιεχόμενο του
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική (Ε) Ενότητα 2: Θεωρία ταλαντώσεων (Συνοπτική περιγραφή) Αικατερίνη Σκουρολιάκου Τμήμα Ενεργειακής Τεχνολογίας Το περιεχόμενο του
Δυναμική και Έλεγχος E-L Ηλεκτρομηχανικών Συστημάτων
 Δυναμική και Έλεγχος E-L Ηλεκτρομηχανικών Συστημάτων Ενότητα 5: Παραδείγματα Περιγραφής Δυναμικών Συστημάτων III Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας
Δυναμική και Έλεγχος E-L Ηλεκτρομηχανικών Συστημάτων Ενότητα 5: Παραδείγματα Περιγραφής Δυναμικών Συστημάτων III Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας
ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23
 ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23 Ροή (γενικά): Ηλεκτρική Ροή Η ποσότητα ενός μεγέθους που διέρχεται από μία επιφάνεια. Ε Ε dα dα θ Ε Ε θ Ηλεκτρική ροή dφ Ε μέσω στοιχειώδους επιφάνειας da (αφού da στοιχειώδης
ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23 Ροή (γενικά): Ηλεκτρική Ροή Η ποσότητα ενός μεγέθους που διέρχεται από μία επιφάνεια. Ε Ε dα dα θ Ε Ε θ Ηλεκτρική ροή dφ Ε μέσω στοιχειώδους επιφάνειας da (αφού da στοιχειώδης
Γενικά Μαθηματικά Ι. Ενότητα 14: Ολοκλήρωση Κατά Παράγοντες, Ολοκλήρωση Ρητών Συναρτήσεων Λουκάς Βλάχος Τμήμα Φυσικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1: Ολοκλήρωση Κατά Παράγοντες, Ολοκλήρωση Ρητών Συναρτήσεων Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 1: Ολοκλήρωση Κατά Παράγοντες, Ολοκλήρωση Ρητών Συναρτήσεων Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Προστασία Σ.Η.Ε. Ενότητα 3: Ηλεκτρονόμοι απόστασης. Νικόλαος Βοβός Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών
 Προστασία Σ.Η.Ε Ενότητα 3: Ηλεκτρονόμοι απόστασης Νικόλαος Βοβός Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών 1 Σημείωμα Αδειοδότησης Το παρόν υλικό διατίθεται με τους όρους
Προστασία Σ.Η.Ε Ενότητα 3: Ηλεκτρονόμοι απόστασης Νικόλαος Βοβός Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών 1 Σημείωμα Αδειοδότησης Το παρόν υλικό διατίθεται με τους όρους
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
ΔΙΑΓΩΝΙΣΜΑ ΣΤO HΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΚΑΙ ΣΤΟΥΣ ΠΥΚΝΩΤΕΣ Επώνυμο: Όνομα: Τμήμα: Αγρίνιο
 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ B ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤO HΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΚΑΙ ΣΤΟΥΣ ΠΥΚΝΩΤΕΣ Επώνυμο: Όνομα: Τμήμα: Αγρίνιο 30-03-014 ΘΕΜΑ 1 ο Α) Να επιλέξετε τη σωστή απάντηση σε καθεμία από τις επόμενες προτάσεις
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ B ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤO HΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΚΑΙ ΣΤΟΥΣ ΠΥΚΝΩΤΕΣ Επώνυμο: Όνομα: Τμήμα: Αγρίνιο 30-03-014 ΘΕΜΑ 1 ο Α) Να επιλέξετε τη σωστή απάντηση σε καθεμία από τις επόμενες προτάσεις
Μαθηματικά Και Στατιστική Στη Βιολογία
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μαθηματικά Και Στατιστική Στη Βιολογία Ενότητα 8 : Μιγαδικοί Αριθμοί & Ακολουθίες Αριθμών Στέφανος Σγαρδέλης Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μαθηματικά Και Στατιστική Στη Βιολογία Ενότητα 8 : Μιγαδικοί Αριθμοί & Ακολουθίες Αριθμών Στέφανος Σγαρδέλης Άδειες Χρήσης Το παρόν εκπαιδευτικό
Γενικά Μαθηματικά Ι. Ενότητα 17: Αριθμητική Ολοκλήρωση, Υπολογισμός Μήκους Καμπύλης Λουκάς Βλάχος Τμήμα Φυσικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 7: Αριθμητική Ολοκλήρωση, Υπολογισμός Μήκους Καμπύλης Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 7: Αριθμητική Ολοκλήρωση, Υπολογισμός Μήκους Καμπύλης Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Κλασική Ηλεκτροδυναμική
 Κλασική Ηλεκτροδυναμική Ενότητα 17: Μαγνητοστατική σε υλικά Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να ολοκληρώσει τα στοιχεία θεωρίας που αφορούν
Κλασική Ηλεκτροδυναμική Ενότητα 17: Μαγνητοστατική σε υλικά Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να ολοκληρώσει τα στοιχεία θεωρίας που αφορούν
