«Εκτίμηση αγοραίων αξιών ακινήτων με τη χρήση μοντέλου πολλαπλής γραμμικής παλινδρόμησης, εφαρμογή στην πόλη της Θεσσαλονίκης και της Βαρκελώνης»
|
|
|
- Ἡρακλείδης Λούλης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ - ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΑΓΡΟΝΟΜΩΝ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΤΕΧΝΙΚΕΣ ΚΑΙ ΜΕΘΟΔΟΙ ΣΤΗΝ ΑΝΑΛΥΣΗ, ΣΧΕΔΙΑΣΗ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗ ΤΟΥ ΧΩΡΟΥ» ΚΑΤΕΥΘΥΝΣΗ «ΚΤΗΜΑΤΟΛΟΓΙΟ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗ ΧΩΡΙΚΩΝ ΔΕΔΟΜΕΝΩΝ» Μεταπτυχιακή διατριβή «Εκτίμηση αγοραίων αξιών ακινήτων με τη χρήση μοντέλου πολλαπλής γραμμικής παλινδρόμησης, εφαρμογή στην πόλη της Θεσσαλονίκης και της Βαρκελώνης» ΕΥΡΩΠΗ Β. ΑΝΑΣΤΑΣΙΑΔΟΥ Διπλ. Αγρονόμος τοπογράφος μηχανικός Α.Π.Θ. Υπεύθυνος Διατριβής: Αρβανίτης Απόστολος, Καθηγητής Α.Π.Θ. Εξεταστική επιτροπή Αρβανίτης Α. Καθηγητής Λαφαζάνη Π. Αναπλ. Καθηγήτρια Παπαδοπούλου Μ. Αναπλ. Καθηγήτρια Θεσσαλονίκη, Μάρτιος 2013
2 ΕΥΧΑΡΙΣΤΙΕΣ Η παρούσα μεταπτυχιακή διατριβή με τίτλο «Εκτίμηση αγοραίων αξιών ακινήτων με τη χρήση μοντέλου πολλαπλής γραμμικής παλινδρόμησης, εφαρμογή στην πόλη της Θεσσαλονίκης και της Βαρκελώνης» εκπονήθηκε στα πλαίσια του προγράμματος μεταπτυχιακών σπουδών με τίτλο «Κτηματολόγιο και Διαχείριση Χωρικών Δεδομένων» της κατεύθυνσης «Τεχνικές μέθοδοι στη Ανάλυση, Σχεδίαση & Διαχείριση του Χώρου» του Τμήματος Αγρονόμων Τοπογράφων Μηχανικών του Αριστοτελείου Πανεπιστημίου Θεσσαλονίκης. Με το πέρας της μεταπτυχιακής διπλωματικής εργασίας θα ήθελα να ευχαριστήσω θερμά τον Καθηγητή Αρβανίτη Απόστολο αρχικά για την εμπιστοσύνη που μου έδειξε με την ανάθεση της μεταπτυχιακής εργασίας, αλλά κυρίως για την πολύτιμη καθοδήγηση, επιμονή και υποστήριξη του, η οποία ήταν καθοριστικής σημασίας για την έκβαση της μεταπτυχιακής διατριβής. Επίσης, θα ήθελα να ευχαριστήσω εγκάρδια την Επίκουρο Καθηγήτρια Λαφαζάνη Περιστέρα, η οποία έδειξε εξαιρετικό διδακτικό ενδιαφέρον κατά τη διάρκεια της συνεργασίας μας και αφιέρωσε πολύτιμο χρόνο για τη δική μου καθοδήγηση στο δύσκολο αντικείμενο της στατιστικής ανάλυσης, με τις επιστημονικές συμβουλές και γνώσεις της. Τέλος, δε θα ήθελα να παραλείψω να ευχαριστήσω τη Γεωργοπούλου Ελισάβετ για την πολύτιμη συμβολή της και τον Διδάκτορα Μισιρλόγλου Συμεών, Διπλωματούχο Αγρονόμο Τοπογράφο Μηχανικό για την άριστη συνεργασία, το ενδιαφέρον του και τις συμβουλές του στη διάρκεια της εργασίας μέχρι και την τελική της παράδοση. Κλείνοντας το παρόν σημείωμα, αισθάνομαι την ανάγκη να ευχαριστήσω την οικογένεια μου και όλους τους δικούς μου ανθρώπους που με τη στήριξη και την υπομονή τους με βοήθησαν για την υλοποίηση ενός ακόμη στόχου στην ακαδημαϊκή μου πορεία. Θεσσαλονίκη, Μάρτιος 2013 Αναστασιάδου Ευρώπη
3 ΠΕΡΙΛΗΨΗ Η εκτίμηση της αξίας κατοικιών αποτελεί μία καθημερινή διαδικασία σε πολλούς τομείς μίας κοινωνίας. Πραγματοποιούνται εκτιμήσεις αξιών για αγοραπωλησίες, για λήψεις δανείων, για επενδυτικές κινήσεις ή ακόμη για φορολογικούς σκοπούς προς όφελος του κράτους. Στην παρούσα εργασία γίνεται προσπάθεια αυτοματοποίησης και ελέγχου της εκτίμησης αγοραίων αξιών ακινήτων μέσω γραμμικού μοντέλου εκτίμησης, με τη βοήθεια της στατιστικής και των βασικών αρχών εκτίμησης ακινήτων. Ο κύριος στόχος της παρούσας μεταπτυχιακής διατριβής διακρίνεται σε δύο βασικά σκέλη. Αρχικά, επιδιώκεται με τη βοήθεια ενός στατιστικού δείγματος η αναζήτηση των μεταβλητών που ερμηνεύουν τον τρόπο με τον οποίο διαμορφώνεται η αγοραία αξία των ακινήτων, ενώ δεύτερο στόχο αποτελεί η διερεύνηση των διαφοροποιήσεων που υφίστανται οι μεταβλητές ως προς τον αριθμό και το είδος τους ανάλογα με την περιοχή μελέτης. Μέσω των διαφοροποιήσεων που αναμένεται να υπάρχουν, διαφαίνεται η επίδραση του χώρου και της γεωγραφικής θέσης στα βάρη των μεταβλητών που διαμορφώνουν τις αγοραίες αξίες των ακινήτων, καθώς πρόκειται για ένα γεωγραφικό και οικονομικό φαινόμενο. Η εφαρμογή πραγματοποιείται σε δύο περιοχές της Θεσσαλονίκης (κέντρο και Εύοσμος)και σε τρεις περιοχές της Βαρκελώνης (Eixample, Sant Marti και Badalona). Η επιλογή των πέντε περιοχών μελέτης δεν γίνεται τυχαία, καθώς η κάθε μία από τις παραπάνω έχει χαρακτηριστικά που τη διαφοροποιούν από τις υπόλοιπες περιοχές σε κοινωνικό, οικονομικό, πληθυσμιακό και ιστορικό επίπεδο και τις καθιστούν άξιες μελέτης. Πηγή δεδομένων για την έρευνα αποτελεί η συγκέντρωση πέντε στατιστικών δειγμάτων μέσω του διαδικτύου. Ως μεταβλητές θεωρούνται οι αγοραίες αξίες των προς μελέτη οριζόντιων ιδιοκτησιών και οι τιμές που αντιστοιχίζονται στα βασικά χαρακτηριστικά τους γνωρίσματα όπως εμβαδόν, παλαιότητα, όροφος, γωνιακή θέση, ύπαρξη ανελκυστήρα, θέση στάθμευσης, είδος θέρμανσης, αριθμός δωματίων, αριθμός μπάνιων και βαθμός συντήρησης τους. Για το σχηματισμό των μοντέλων εκτίμησης αγοραίων αξιών αξιοποιείται σε πρώτο στάδιο η μέθοδος της πολλαπλής γραμμικής παλινδρόμησης με τη βοήθεια του στατιστικού εργαλείου SPSS 18. Για τον έλεγχο αξιοπιστίας των μοντέλων πραγματοποιούνται έλεγχοι επτά παραδοχών των γραμμικών μοντέλων ενώ ταυτόχρονα αξιοποιούνται μέθοδοι εκτίμησης της προβλεπτικής τους ικανότητας. Τελικό προϊόν της διαδικασίας είναι η δημιουργία πέντε γραμμικών εξισώσεων παλινδρόμησης που βοηθούν τον υπολογισμό των εκτιμώμενων αξιών ακινήτων. Σε δεύτερο στάδιο πραγματοποιείται ο σχηματισμός του ίδιου μοντέλου με τη βοήθεια της πολλαπλής γραμμικής παλινδρόμησης σε περιβάλλον ArcGIS10, με την ταυτόχρονη χαρτογράφηση των ακινήτων του δείγματος για τις δύο περιοχές μελέτης της Θεσσαλονίκης. Τα συμπεράσματα που προκύπτουν στο τέλος της εργασίας επικεντρώνονται στη μαθηματική και φυσική ερμηνεία των μοντέλων, στη σύγκριση των μεταβλητών που διαμορφώνουν τις τελικές αξίες ακινήτων στο εσωτερικό κάθε πόλης ξεχωριστά και στη i
4 συνέχεια σε επίπεδο κτηματαγοράς των δύο πόλεων. Τέλος, αξιολογούνται τα πλεονεκτήματα και μειονεκτήματα της δημιουργίας γραμμικών μοντέλων στο SPSS και σε περιβάλλον ArcGIS. Από τις πέντε τελικές εξισώσεις πολλαπλής παλινδρόμησης προκύπτει ότι η μοντελοποίηση αγοραίων αξιών ακινήτων είναι μία ιδιαίτερα ευαίσθητη διαδικασία, καθώς τα μεγέθη είναι συνεχώς μεταβαλλόμενα, ωστόσο με μία σταθερά ενημερωμένη βάση δεδομένων σε τοπικό επίπεδο μπορεί να δώσει ορθά και αξιόπιστα αποτελέσματα για κάθε χρήση ιδιωτική ή κρατική. Λέξεις κλειδιά: αγοραία αξία ακινήτου, πολλαπλή γραμμική παλινδρόμηση, στατιστική ανάλυση, Γεωγραφικά συστήματα Πληροφοριών ii
5 ARISTOTLE UNIVERSITY OF THESSALONIKI School of Rural & Surveying Engineering (RSE) Postgraduate Studies Cadastre and Spatial Analysis E. Anastasiadou Thessaloniki, March 2013 Estimation of Property Market Value with the Use of a Multiple Linear Regression Model: A Case Study of Thessaloniki and Barcelona ABSTRACT Estimating the value of property is a daily task in multiple areas within any given society. Estimations of this sort are conducted for real estate transactions, loans, and investments, as well as for determining property tax rates, etc. The present study proposes a method of automatizing and validating the estimation of the market values of properties with the use of a linear model of estimation, aided by statistics, and with the application of elementary principles of estimating property value. The main focus of the present M.Sc. thesis is twofold: first, using a statistical sample of properties, to determine the variables that explain the ways in which the market value of property is estimated; and second, to study the differentiations that these variables present in terms of their quantity and type, depending on a given geographical area under study. Analysis of expected differentiations of this sort shows that geographical location clearly affects the weight of variables that determine the market values of properties, as the nature of these variables is evidently geographical and economic. The proposed model has been applied to two areas in the Thessaloniki region (central Thessaloniki and Evosmos) and three areas in the Barcelona region (Eixample, Sant Marti and Badalona). None of the areas was randomly selected; the selection was made based on distinctive social, financial, historical, and population features which differentiate these five areas from others, thus exhibiting interesting research potentials. The data used in the research were acquired from five online statistical samples. The model considers as variables the market values of the horizontal properties under study, as well as their prices based on their features such as surface area, year of construction, floor, corner position, elevator, parking spot, type of heating, number of rooms, number of bathrooms, and level of maintenance. The formulation of the five models for estimating market values, one for each area, consists of two stages. The first stage is to utilize the multiple linear regression method, with the help of the SPSS 18 statistical software. In order to verify the validity of the models, tests of the seven assumptions of linear models are carried out, while at the same time methods for assessing their prediction ability are utilized. The product resulting from this procedure is the formulation of five linear regression equations, which assist in calculating the estimated market values of properties. The second stage involves the formulation of the same model with the help of multiple linear regression in ArcGIS 10 iii
6 environment, while at the same time the sample properties reflecting the two studied areas of Thessaloniki were mapped. The conclusions drawn at the end of the study focus on analyzing the models on mathematical and geographical terms; the variables are compared based on the way they form the final market values of properties within each specific city separately, as well as on the level of the real estate markets of both cities comparatively. Finally, the conclusions evaluate the advantages and disadvantages of creating linear models in SPSS and in ArcGIS environment. From the resulting five multiple regression equations it is concluded that the modelization of property market values is a particularly delicate procedure, as the parameters affecting property value constantly change; still, with the use of a database regularly updated on a local level, the modelization can indeed provide correct and reliable results that be applied to all uses in both the private and public sectors. Keywords: property market value; multiple linear regression; statistical analysis; Geographical Information Systems (GIS) iv
7 ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ ΠΕΡΙΛΗΨΗ... i ABSTRACT... iii ΕΙΣΑΓΩΓΗ ο ΚΕΦΑΛΑΙΟ ΤΟ ΑΣΤΙΚΟ ΑΚΙΝΗΤΟ ΩΣ ΑΝΤΙΚΕΙΜΕΝΟ ΜΕΛΕΤΗΣ 1.1 Μονάδα αναφοράς Αγοραία αξία ακινήτου Παράγοντες που επηρεάζουν την αξία ενός αστικού ακινήτου Γενικοί παράγοντες επίδρασης Ειδικοί παράγοντες επίδρασης Εφαρμογή ο ΚΕΦΑΛΑΙΟ ΠΕΡΙΟΧΕΣ ΜΕΛΕΤΗΣ 2.1 Περιοχές μελέτης στην πόλη της Θεσσαλονίκης Πρώτη περιοχή μελέτης Κέντρο Θεσσαλονίκης Δεύτερη περιοχή μελέτης Δημοτική Ενότητα Ευόσμου Περιοχές μελέτης στην πόλη της Βαρκελώνης Τρίτη περιοχή μελέτης Eixample Βαρκελώνης Τέταρτη περιοχή μελέτης Sant Marti Βαρκελώνης Τέταρτη περιοχή μελέτης Badalona Βαρκελώνης ο ΚΕΦΑΛΑΙΟ ΣΤΑΤΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ ΤΟΥ ΠΡΟΒΛΗΜΑΤΟΣ 3.1 Θεωρητικό υπόβαθρο Εφαρμογή Επιλογή στατιστικής μεθόδου Σχηματισμός του δείγματος Μέγεθος δείγματος Διαδικασία δειγματοληψίας Κατηγοριοποίηση και ποσοτικοποίηση των ανεξάρτητων μεταβλητών Μεθοδολογικό πλαίσιο Συμπεράσματα... 45
8 4 ο ΚΕΦΑΛΑΙΟ ΔΗΜΙΟΥΡΓΙΑ ΜΑΘΗΜΑΤΙΚΟΥ ΜΟΝΤΕΛΟΥ ΜΕΣΩ ΠΟΛΛΑΠΛΗΣ ΓΡΑΜΜΙΚΗΣ ΠΑΛΙΝΔΡΟΜΗΣΗΣ ΜΕ ΣΚΟΠΟ ΤΟΝ ΑΥΤΟΜΑΤΟΠΟΙΗΜΕΝΟ ΥΠΟΛΟΓΙΣΜΟ ΤΗΣ ΑΓΟΡΑΙΑΣ ΑΞΙΑΣ ΔΙΑΜΕΡΙΣΜΑΤΩΝ ΕΦΑΡΜΟΓΗ ΣΤΗΝ ΠΟΛΗ ΤΗΣ ΘΕΣΣΑΛΟΝΙΚΗΣ 4.1 Περιβάλλον εργασίας για τη στατιστική εφαρμογή - SPSS Εφαρμογή πολλαπλής γραμμικής παλινδρόμησης για ένα τμήμα του κέντρου της Θεσσαλονίκης (Πρώτο μοντέλο) Δημιουργία παλινδρομικού μοντέλου σε περιβάλλον spss Έλεγχος ικανοποίησης προϋποθέσεων αρχικού μοντέλου πολλαπλής γραμμικής παλινδρόμησης Σημαντικότητα ανεξάρτητων μεταβλητών Ανεξαρτησία οντοτήτων Πολυσυγγραμικότητα ή Συγγραμικότητα Κανονικότητα Ισότητα διακυμάνσεων/ομοσκεδαστικότητα Γραμμικότητα Ακραίες οντότητες και οντότητες επίδρασης Χρήση δεικτών για τον εντοπισμό των ακραίων οντοτήτων Χρήση δεικτών για τον εντοπισμό των οντοτήτων επίδρασης Χρήση γραφημάτων για τον εντοπισμό οντοτήτων επίδρασης Χρήση κατανομών για τον εντοπισμό οντοτήτων επίδρασης Έλεγχος προβλεπτικής ικανότητας του αρχικού μοντέλου Μέθοδος των διαστημάτων πρόβλεψης Μέθοδος του διαχωρισμού των δεδομένων (Data Splitting) Μέθοδος εύρεσης του βέλτιστου αριθμού σημαντικών μεταβλητών Διαδοχικές προσεγγίσεις για σχηματισμό τελικού μοντέλου Έλεγχος ικανοποίησης προϋποθέσεων τελικού μοντέλου πολλαπλής γραμμικής παλινδρόμησης Σημαντικότητα ανεξάρτητων μεταβλητών Ανεξαρτησία οντοτήτων Πολυσυγγραμικότητα ή Συγγραμικότητα Κανονικότητα Ισότητα διακυμάνσεων/ομοσκεδαστικότητα Γραμμικότητα
9 Ακραίες οντότητες και οντότητες επίδρασης Έλεγχος προβλεπτικής ικανότητας του τελικού μοντέλου Μέθοδος των διαστημάτων πρόβλεψης Μέθοδος του διαχωρισμού των δεδομένων (Data Splitting) Μέθοδος εύρεσης του βέλτιστου αριθμού σημαντικών μεταβλητών Ερμηνεία μοντέλου για την περιοχή του κέντρου Εφαρμογή πολλαπλής γραμμικής παλινδρόμησης για τη Δημοτική Ενότητα Ευόσμου (Δεύτερο μοντέλο) Διερεύνηση γραμμικής σχέσης μεταξύ της εξαρτημένης μεταβλητής Υ και των ανεξάρτητων Χ i Γραφήματα συσχέτισης των Χi με την Υ Συντελεστές μερικής συσχέτισης Εφαρμογή πολλαπλής γραμμικής παλινδρόμησης και δημιουργία τελικού μοντέλου Έλεγχος ικανοποίησης παραδοχών του γραμμικού μοντέλου Σημαντικότητα ανεξάρτητων μεταβλητών Ανεξαρτησία οντοτήτων Πολυσυγγραμικότητα ή συγγραμικότητα Κανονικότητα Ισότητα διακυμάνσεων ή ομοσκεδαστικότητα Γραμμικότητα Ακραίες οντότητες και οντότητες επίδρασης Έλεγχος προβλεπτικής ικανότητας του μοντέλου Μέθοδος των διαστημάτων πρόβλεψης Μέθοδος του διαχωρισμού των δεδομένων (Data Splitting) Μέθοδος εύρεσης του βέλτιστου αριθμού σημαντικών μεταβλητών Ερμηνεία μοντέλου για την περιοχή του Ευόσμου Συμπεράσματα ο ΚΕΦΑΛΑΙΟ ΔΗΜΙΟΥΡΓΙΑ ΜΑΘΗΜΑΤΙΚΟΥ ΜΟΝΤΕΛΟΥ ΜΕΣΩ ΤΗΣ ΠΟΛΛΑΠΛΗΣ ΓΡΑΜΜΙΚΗΣ ΠΑΛΙΝΔΡΟΜΗΣΗΣ ΜΕ ΣΚΟΠΟ ΤΟΝ ΑΥΤΟΜΑΤΟΠΟΙΗΜΕΝΟ ΥΠΟΛΟΓΙΣΜΟ ΤΗΣ ΑΓΟΡΑΙΑΣ ΑΞΙΑΣ ΤΩΝ ΔΙΑΜΕΡΙΣΜΑΤΩΝ ΕΦΑΡΜΟΓΗ ΣΤΗΝ ΠΟΛΗ ΤΗΣ ΒΑΡΚΕΛΩΝΗΣ 5.1 Εφαρμογή πολλαπλής γραμμικής παλινδρόμησης για την περιοχή Eixample (Τρίτο μοντέλο)
10 5.1.1 Διερεύνηση γραμμικής σχέσης μεταξύ της εξαρτημένης μεταβλητής Υ και των ανεξάρτητων Χ i Γραφήματα συσχέτισης των Χ i με την Υ Συντελεστές μερικής συσχέτισης Εφαρμογή της πολλαπλής γραμμικής παλινδρόμησης και δημιουργία τελικού μοντέλου Έλεγχος ικανοποίησης παραδοχών του γραμμικού μοντέλου Σημαντικότητα ανεξάρτητων μεταβλητών Ανεξαρτησία οντοτήτων Πολυσυγγραμικότητα ή συγγραμικότητα Κανονικότητα Ισότητα διακυμάνσεων ή ομοσκεδαστικότητα Γραμμικότητα Ακραίες οντότητες και οντότητες επίδρασης Έλεγχος προβλεπτικής ικανότητας του μοντέλου Μέθοδος των διαστημάτων πρόβλεψης Μέθοδος του διαχωρισμού των δεδομένων (Data Splitting) Μέθοδος εύρεσης του βέλτιστου αριθμού σημαντικών μεταβλητών Ερμηνεία μοντέλου για την περιοχή Eixample Εφαρμογή πολλαπλής γραμμικής παλινδρόμησης για την περιοχή Sant Marti (Τέταρτο μοντέλο) Διερεύνηση γραμμικής σχέσης μεταξύ της εξαρτημένης μεταβλητής Υ και των ανεξάρτητων Χ i Γραφήματα συσχέτισης των Χ i με την Υ Συντελεστές μερικής συσχέτισης Εφαρμογή της πολλαπλής γραμμικής παλινδρόμησης και δημιουργία τελικού μοντέλου Έλεγχος ικανοποίησης παραδοχών του γραμμικού μοντέλου Σημαντικότητα ανεξάρτητων μεταβλητών Ανεξαρτησία οντοτήτων Πολυσυγγραμικότητα ή συγγραμικότητα Κανονικότητα Ισότητα διακυμάνσεων ή ομοσκεδαστικότητα Γραμμικότητα Ακραίες οντότητες και οντότητες επίδρασης
11 5.2.4 Έλεγχος προβλεπτικής ικανότητας του μοντέλου Μέθοδος των διαστημάτων πρόβλεψης Μέθοδος του διαχωρισμού των δεδομένων (Data Splitting) Μέθοδος εύρεσης του βέλτιστου αριθμού σημαντικών μεταβλητών Ερμηνεία μοντέλου για την περιοχή Sant Marti Εφαρμογή πολλαπλής γραμμικής παλινδρόμησης για την περιοχή Badalona (Πέμπτο μοντέλο) Διερεύνηση γραμμικής σχέσης μεταξύ της εξαρτημένης μεταβλητής Υ και των ανεξάρτητων Χ i Γραφήματα συσχέτισης των Χ i με την Υ Συντελεστές μερικής συσχέτισης Εφαρμογή της πολλαπλής γραμμικής παλινδρόμησης και δημιουργία τελικού μοντέλου Έλεγχος ικανοποίησης παραδοχών του γραμμικού μοντέλου Σημαντικότητα ανεξάρτητων μεταβλητών Ανεξαρτησία οντοτήτων Πολυσυγγραμικότητα ή συγγραμικότητα Κανονικότητα Ισότητα διακυμάνσεων ή ομοσκεδαστικότητα Γραμμικότητα Ακραίες οντότητες και οντότητες επίδρασης Έλεγχος προβλεπτικής ικανότητας του μοντέλου Μέθοδος των διαστημάτων πρόβλεψης Μέθοδος του διαχωρισμού των δεδομένων (Data Splitting) Μέθοδος εύρεσης του βέλτιστου αριθμού σημαντικών μεταβλητών Ερμηνεία μοντέλου για την περιοχή Badalona Συμπεράσματα ο ΚΕΦΑΛΑΙΟ ΤΑ ΓΕΩΓΡΑΦΙΚΑ ΣΥΣΤΗΜΑΤΑ ΠΛΗΡΟΦΟΡΙΩΝ ΚΑΙ Η ΜΕΘΟΔΟΣ ΤΗΣ ΠΟΛΛΑΠΛΗΣ ΓΡΑΜΜΙΚΗΣ ΠΑΛΙΝΔΡΟΜΗΣΗΣ 6.1 Εισαγωγή δεδομένων στο Γεωγραφικό Σύστημα Πληροφοριών Δημιουργία χωρικής βάσης δεδομένων Εφαρμογή της πολλαπλής γραμμικής παλινδρόμησης στην περιοχή του κέντρου της Θεσσαλονίκης Διαδικασία πολλαπλής γραμμικής παλινδρόμησης
12 6.2.2 Παρουσίαση και ερμηνεία των αποτελεσμάτων Δημιουργία νέου επιπέδου της OLS διαδικασίας Γενική επίδοση του μοντέλου Σχολιασμός των συντελεστών πολλαπλής παλινδρόμησης Έλεγχος στατιστικής σημαντικότητας των ανεξάρτητων μεταβλητών Έλεγχος συγγραμμικότητας/πολυσυγγραμμικότητας Έλεγχος κανονικότητας των υπολοίπων Έλεγχος ανεξαρτησίας των υπολοίπων Εφαρμογή της πολλαπλής γραμμικής παλινδρόμησης στην περιοχή του Ευόσμου Θεσσαλονίκης Συμπεράσματα ο ΚΕΦΑΛΑΙΟ ΣΥΜΠΕΡΑΣΜΑΤΑ & ΠΡΟΤΑΣΕΙΣ 7.1 Συμπεράσματα Προτάσεις ΒΙΒΛΙΟΓΡΑΦΙΚΕΣ ΠΑΡΑΠΟΜΠΕΣ
13 ΕΙΣΑΓΩΓΗ Στην παρούσα εισαγωγή πραγματοποιείται μία συνοπτική παρουσίαση του περιεχομένου όλων των κεφαλαίων που έπονται, ώστε με αυτόν τον τρόπο να γίνει κατανοητή προς των αναγνώστη η δομή της εργασίας και ο τρόπος που διαρθρώνονται τα επιμέρους κεφάλαια. Πιο συγκεκριμένα, στο πρώτο κεφάλαιο γίνεται αναφορά στη σημασία μελέτης της κατοικίας και ειδικότερα στον ελλαδικό χώρο, ενώ επισημαίνεται η χωρική μονάδα αναφοράς της παρούσας εφαρμογής. Επίσης, γίνεται η εισαγωγή στην έννοια της αγοραίας αξίας, όπου στόχο αποτελεί η προσέγγιση της και αναλύονται με λεπτομέρεια οι παράγοντες που διαμορφώνουν τις αγοραίες αξίες διαμερισμάτων σε αστικό περιβάλλον. Στο δεύτερο κεφάλαιο, πραγματοποιείται η περιγραφή των λόγων για τους οποίους επιλέγεται ως δεύτερη ευρωπαϊκή πόλη η Βαρκελώνη και αναλύονται οι ομοιότητες και οι διαφορές της αγοράς ακινήτων σε σχέση με τη Θεσσαλονίκη. Στη συνέχεια, για κάθε μία από τις πέντε περιοχές μελέτης δίνονται χάρτες για τον ορισμό της θέσης τους και στοιχεία που αναφέρονται στα πληθυσμιακά τους χαρακτηριστικά και στον τρόπο διαμόρφωσης του αστικού ιστού τους. Το τρίτο κεφάλαιο περιέχει τα στάδια της μεθοδολογίας όλης της εφαρμογής, με αναφορές στον προσδιορισμό των μεταβλητών, στο σχηματισμό του δείγματος, την ποσοτικοποίηση και κατηγοριοποίηση των μεταβλητών και στην επιλογή της μεθόδου στατιστικής ανάλυσης για τις πέντε περιοχές μελέτης. Όλες οι επιλογές δικαιολογούνται και στηρίζονται στη μελέτη του αντίστοιχου θεωρητικού υποβάθρου. Στο τέταρτο και πέμπτο κεφάλαιο της εργασίας πραγματοποιείται η εκτέλεση της πολλαπλής γραμμικής παλινδρόμησης σε περιβάλλον εργασίας SPSS 18 για την περιοχή της Θεσσαλονίκης και της Βαρκελώνης αντίστοιχα. Περιγράφονται αναλυτικά όλα τα βήματα της διαδικασίας και οι έλεγχοι υποθέσεων που απαιτούνται για την αξιολόγηση των μοντέλων. Στο τέλος κάθε κεφαλαίου πραγματοποιούνται συγκρίσεις και διατυπώνονται συμπεράσματα για την ποιότητα του κάθε μοντέλου. Το έκτο κεφάλαιο αναφέρεται στα Γεωγραφικά Συστήματα Πληροφοριών και στην αντίστοιχη εφαρμογή πολλαπλής γραμμικής παλινδρόμησης σε περιβάλλον ArcMap 10. Η εφαρμογή στο συγκεκριμένο λογισμικό πραγματοποιείται μόνο για της περιοχές της Θεσσαλονίκης διότι προσφέρεται το ανάλογο χαρτογραφικό υπόβαθρο. Τέλος, στο έβδομο κεφάλαιο γίνεται η μία συλλογική αξιολόγηση και αποτίμηση του εγχειρήματος με αναλυτική έκθεση των συμπερασμάτων και των προτάσεων για μελλοντική προσπάθεια και συνέχιση στο συγκεκριμένο επιστημονικό πεδίο. 1
14 ΚΕΦΑΛΑΙΟ 1 Ο ΤΟ ΑΣΤΙΚΟ ΑΚΙΝΗΤΟ ΩΣ ΑΝΤΙΚΕΙΜΕΝΟ ΜΕΛΕΤΗΣ Η εκτίμηση της αξίας των ακινήτων πραγματοποιείται καθημερινά για μία πολύ μεγάλη ποικιλία περιπτώσεων, όπως ζητήματα τραπεζών (λήψη δανείων, υποθήκες κ.λπ.), αγοραπωλησίες, λογιστικές καταστάσεις, φορολογία ακίνητης περιουσίας, απαλλοτριώσεις, δουλείες, διανομές, κληρονομικά, εταιρίες επενδύσεων κ.α. Είναι σαφές ότι πρόκειται για ένα επίκαιρο ζήτημα με πολλά περιθώρια μελέτης, το οποίο απασχολεί πολλούς κλάδους της επιστήμης. Αποτελεί κοινό τόπο πως κάθε ιδιοκτησία είναι μοναδική. Ωστόσο η ανάγκη διενέργειας πολλών εκτιμήσεων καθημερινά για την ικανοποίηση των παραπάνω σκοπών οδηγεί στην ανάγκη εφαρμογής της σύγχρονης τεχνολογίας προκειμένου να γίνει μια μορφή αυτοματοποίησης της διαδικασίας με στόχο τον καλύτερο έλεγχο των αποτελεσμάτων. Πιο συγκεκριμένα, ένα μαθηματικό μοντέλο εκτίμησης αξιών επιτυγχάνει την προσέγγιση της προβλεπόμενης αξίας του ακινήτου και ταυτόχρονα θέτει τα ανώτερα και κατώτερα όρια μέσα στα οποία θα πρέπει να βρίσκεται η αγοραία αξία του. Μία διαδικασία αυτοματοποιημένης εκτίμησης αγοραίων αξιών υποβάλλεται σε συγκεκριμένους χρονικούς και χωρικούς περιορισμούς, διότι αποτελεί ένα δυναμικό γεωγραφικό και οικονομικό φαινόμενο. Οι χρονικοί περιορισμοί οφείλονται στα δεδομένα της κτηματαγοράς που μεταβάλλονται δυναμικά ανάλογα με τις κοινωνικοοικονομικές εξελίξεις σε τοπικό ή διεθνές επίπεδο, ενώ οι χωρικοί περιορισμοί αφορούν την άμεση σύνδεση της αξίας ενός ακινήτου με τη γεωγραφική του θέση. Η ανάγκη περαιτέρω μελέτης της εκτίμησης των ακινήτων με μία σταθερή και αυτοματοποιημένη διαδικασία πηγάζει ταυτόχρονα και από έναν ακόμη βασικό παράγοντα. Η απόκτηση κυριότητας σε ακίνητα αποτελεί μία ιδιαίτερη αγορά με πολύ 2
15 Κ ε φ ά λ α ι ο 1 ο σημαντική επίδραση στις μακροοικονομικές εξελίξεις και τη χρηματοοικονομική σταθερότητα. Χαρακτηριστικό είναι το παράδειγμα της Ελλάδας, της οποίας τα νοικοκυριά παραδοσιακά για χρόνια τοποθετούν τις αποταμιεύσεις τους στα ακίνητα. Πιο συγκεκριμένα, σύμφωνα με στοιχεία της Τράπεζας της Ελλάδος που αναφέρονται στο έτος 2008 οι επενδύσεις στην αγορά κατοικίας αποτελούσαν το ¼ περίπου του συνόλου των επενδύσεων, ενώ το ποσοστό πλούτου των Ελλήνων που έχει τοποθετηθεί στα ακίνητα είναι 80 90% σε σχέση με τη συνολική τους περιουσία. Παρόμοια, εκτιμήσεις της Eurobank EFG Research, στο 4 ο τρίμηνο του 2008 έδειξαν ότι το 81,8% των περιουσιακών στοιχείων των νοικοκυριών είναι ακίνητα, το 17% είναι καταθέσεις και μόνο το 1,2% είναι μετοχές. Συνεπώς, η συστηματική παρακολούθηση και ανάλυση των εξελίξεων και των προοπτικών της αγοράς αυτής έχει επομένως πολύ μεγάλη σημασία για την πληρέστερη αξιολόγηση των μακροοικονομικών συνθηκών και προοπτικών της οικονομίας. Έπειτα από την παραπάνω εισαγωγή που αφορά στην ανάγκη εκτίμησης των αγοραίων αξιών με τη βοήθεια μαθηματικού μοντέλου εκτίμησης, το πρώτο κεφάλαιο εστιάζεται στη χωρική μονάδα αναφοράς που αξιοποιείται στην παρούσα εφαρμογή με την ταυτόχρονη επεξήγηση των βασικών συνιστωσών που οδηγούν στην επιλογή της, ενώ στη συνέχεια, προσδιορίζεται με ακρίβεια ο ορισμός της αξίας που επιτυγχάνεται να προσεγγιστεί (αγοραία αξία των ακινήτων) και οι κύριοι παράγοντες που τη διαμορφώνουν. 1.1 ΜΟΝΑΔΑ ΑΝΑΦΟΡΑΣ Ο όρος «εκτίμηση της αξίας ακινήτων» είναι πολύ γενικός και δε δίνει σαφή απάντηση για τη μονάδα αναφοράς που εξετάζεται. Για την έννοια του ακινήτου δίνονται περισσότεροι από ένας ορισμοί ανάλογα με τη νομική ή οικονομική σκοπιά από την οποία εξετάζεται. Σύμφωνα με τον Αστικό Κώδικα (Αρθ. 948 Α.Κ.) «ακίνητα πράγματα είναι το έδαφος και τα συστατικά αυτού μέρη», ενώ σύμφωνα με το Ζεντέλη, 2001 «με την έννοια ακίνητο ορίζεται το ιδεατό ή πραγματικό τμήμα του χώρου, που τεκμηριώνει αυτοτελές ή εξ αδιαιρέτου ιδιοκτησιακό δικαίωμα. Έτσι το ακίνητο είναι ένα περιουσιακό στοιχείο, που απεικονίζει το συμβατικό δικαίωμα της ιδιοκτησίας». Από οικονομική άποψη το ακίνητο είναι αυτό που περιλαμβάνει όλους τους συντελεστές παραγωγής, δηλαδή με άλλα λόγια είναι ίσο με το έδαφος, την εργασία, το κεφάλαιο και την επιχειρηματικότητα. Η έννοια του ακινήτου ταξινομείται σε επιμέρους κατηγορίες ανάλογα με τη χρήση του. Οι κατηγορίες των ακινήτων σύμφωνα με τα τεχνικά στοιχεία της Εμπορικής Τράπεζας είναι: 1. κατοικίες 2. εμπορικά ακίνητα 1 3. ξενοδοχεία 4. αποθήκες και οικόπεδα ή αγροτεμάχια που προορίζονται για ανάπτυξη αποθηκευτικών χώρων 1 Ως εμπορικά ακίνητα θεωρούνται τα γραφεία, καταστήματα, εμπορικά κέντρα ή τα οικόπεδα/αγροτεμάχια που προορίζονται για εμπορική ανάπτυξη και χωρίζονται σε αυτά με υψηλή ή μικρή εμπορευσιμότητα και σε εκείνα με μη ενεργή αγορά ακινήτων Μεταπτυχιακή διατριβή 3
16 Α σ τ ι κ ό α κ ί ν η τ ο 5. βιομηχανικές, αγροτικές, κτηνοτροφικές εγκαταστάσεις και οικόπεδα ή αγροτεμάχια που προορίζονται για βιομηχανική ανάπτυξη. Η παρούσα εφαρμογή περιορίζεται αποκλειστικά στη μελέτη ακινήτων με χρήση την κατοικία. Ο βασικότερος λόγος, για τον οποίο επιλέγεται η κατοικία ως αντικείμενο μελέτης είναι το παράδειγμα της Ελλάδας κατά το οποίο παρουσιάζεται ένα πολύ μεγάλο ποσοστό ιδιοκατοίκησης της τάξης του 80,1%, ενώ παρόμοια ποσοστά συναντώνται επίσης στις χώρες της Ανατολικής και Νότιας Ευρώπης. Η κατοικία καλύπτει σε πολύ μεγάλο βαθμό την ανάγκη στέγασης αλλά ταυτόχρονα θεωρείται ως μία ασφαλής επένδυση για πολλές οικογένειες και νοικοκυριά. Πολλούς συνεπώς αφορά η πορεία των τιμών της κτηματαγοράς και αποτελεί ένα ιδιαίτερα σημαντικό ζήτημα σε κάθε κοινωνία, όχι μόνο εντός των ορίων της Ελλάδας, αλλά και εκτός. (Σαμπανιώτης, 2012) (Αρβανιτίδης κα., 2008) Οι κατοικίες στο χώρο διακρίνονται σε δύο κύριες κατηγορίες. Στις κατοικίες σε αστικό περιβάλλον και σε αγροτικό περιβάλλον αντίστοιχα. Η βασική διαφοροποίηση των δύο χώρων συνδέεται άμεσα με την πυκνότητα του πληθυσμού και της απασχόλησης. Η παρούσα εφαρμογή εστιάζεται στις κατοικίες εντός του αστικού ιστού. Οι έντονοι μετασχηματισμοί στις οικονομικές, κοινωνικές δομές, οι διαρθρωτικές αλλαγές στην απασχόληση με τη μείωση του πρωτογενούς τομέα και η ανατίμηση της αστικής γης, οδήγησαν έντονο ρυθμό αστικοποίησης, με άμεση συνέπεια την έντονη ανοικοδόμηση και τον πολλαπλασιασμό των κατοικιών. (Ζεντέλης, 2001) Η μελέτη του αστικού χώρου έχει ιδιαίτερο ενδιαφέρον καθώς σύμφωνα με την Ανανιάδου, 1997 πρόκειται για ένα χώρο πολύ δυναμικό, με τον άνθρωπο δράστη και επηρεαζόμενο, όχι θεατή, παράγοντα δημιουργίας κοινωνικά και ατομικά. Η διαμόρφωση αξιών ακινήτων σε αστικό περιβάλλον διαφοροποιείται ανάλογα με τη συνοικία, τη γειτονιά ή ακόμη και με το δρόμο στον οποίο τα ακίνητα έχουν πρόσοψη. Συνεπώς, έχει μεγάλο ενδιαφέρον η δημιουργία μοντέλων εκτίμησης αξιών ακινήτων σε ένα τόσο ποικιλόμορφο περιβάλλον όπως ο αστικός χώρος. Επίσης, μία πόλη προσφέρει μεγάλο πλήθος δεδομένων για επεξεργασία, προσφέροντας με αυτόν τον τρόπο πολλές ερευνητικές δυνατότητες. Η τελευταία υποδιαίρεση αφορά στις οριζόντιες, κάθετες ιδιοκτησίες και τα οικόπεδα που προορίζονται για οικιστική ανάπτυξη. Αντικείμενο μελέτης αποτελούν στην προκειμένη περίπτωση, οι οριζόντιες ιδιοκτησίες, στις οποίες υπάρχει αποκλειστική κυριότητα σε όροφο ή διαμέρισμα μιας οικοδομής και αντίστοιχα συγκυριότητα στα κοινόχρηστα μέρη της οικοδομής. (Αρβανίτης, 2000) Η ομοιομορφία που παρουσιάζουν οι οριζόντιες ιδιοκτησίες ως προς τα χαρακτηριστικά που διαμορφώνουν την αξία τους, τις καθιστούν το καταλληλότερο αντικείμενο μελέτης. Συνεπώς, μονάδα αναφοράς αποτελούν αποκλειστικά οι οριζόντιες ιδιοκτησίες σε αστικό περιβάλλον. 1.2 ΑΓΟΡΑΙΑ ΑΞΙΑ ΑΚΙΝΗΤΟΥ Στον ελλαδικό χώρο η εκτίμηση της αξίας ενός ακινήτου πραγματοποιείται με διαφορετική μεθοδολογία ανάλογα το σκοπό που εξυπηρετεί. Η αξία ενός ακινήτου μπορεί να προκύψει βάσει του «συστήματος αντικειμενικού προσδιορισμού» - φορολογητέα αξία, 4
17 Κ ε φ ά λ α ι ο 1 ο ή από εκτιμήσεις της Εφορίας για την φορολογικούς σκοπούς, του Σώματος Ορκωτών Εκτιμητών (ΣΟΕ) για αγοραπωλησίες, επενδύσεις, χορήγηση δανείων, της Κτηματικής Εταιρείας του Δημοσίου (ΚΕΔ) για απαλλοτριώσεις κ.α. με αποτέλεσμα να προκύπτουν διαφορετικές τιμές για το ίδιο ακίνητο προκαλώντας συχνά αντιθέσεις. Δημιουργείται συνεπώς η ανάγκη συστηματικού προσδιορισμού της αξίας με βάση έναν αντικειμενικό και αντιπροσωπευτικό τρόπο, ο οποίος ταυτόχρονα να προσφέρει κοινωνική δικαιοσύνη όσον αφορά τη φορολόγηση. (Ζεντέλης, 2001) Από την ύπαρξη πολλών ειδών αξιών, όπως η αγοραία αξία, η αξία υπάρχουσας χρήσης, η εύλογη αξία, η πραγματική/τρέχουσα αξία κλπ. η αξία που αποτελεί στόχο κάθε εκτιμητή είναι η αγοραία αξία των ακινήτων και επιδιώκεται να προσεγγιστεί μέσω αυτοματοποιημένης διαδικασίας στην παρούσα μεταπτυχιακή διατριβή. Παρακάτω, παρατίθενται ορισμένοι βασικοί ορισμοί της αγοραίας αξίας των ακινήτων, σύμφωνα με το Ελληνικό Ινστιτούτο Εκτιμητικής (ΕΛ.Ι.Ε.), ώστε να είναι ξεκάθαρη στο εξής η έννοια της. Ο ορισμός που δίνεται από το Ευρωπαϊκό Συμβούλιο είναι: «Ως Αγοραία Αξία θα νοείται η τιμή στην οποία η γη και τα κτίρια θα μπορούσαν να πωληθούν στο πλαίσιο μίας ιδιωτικής σύμβασης μεταξύ ενός πρόθυμου πωλητή και ενός αγοραστή που κινείται εντός των πλαισίων της αγοράς κατά την ημερομηνία της εκτίμησης, με βάση την υπόθεση ότι το ακίνητο εκτίθεται δημόσια στην αγορά, ότι οι συνθήκες στην αγορά επιτρέπουν την τακτική πώληση και ότι μία κανονική περίοδος, λαμβάνοντας υπόψη τη φύση και μορφή του ακινήτου, είναι διαθέσιμη για τη διαπραγμάτευση της πώλησης». (ΕΛ.Ι.Ε., 2007) Ο εγκεκριμένος ορισμός IVSC/TEGoVA καλούμενος ως ο Ορισμός είναι: «Η Αγοραία Αξία είναι το εκτιμώμενο ποσό για το οποίο μία ιδιοκτησία θα μπορούσε να ανταλλαχθεί κατά την ημερομηνία της εκτίμησης μεταξύ ενός πρόθυμου αγοραστή και ενός πρόθυμου πωλητή σε μία συναλλαγή εντός των πλαισίων της αγοράς μετά από κατάλληλη προώθηση όπου τα συμβαλλόμενα μέρη έχουν το καθένα ενεργήσει με επίγνωση, σωφροσύνη και χωρίς εξαναγκασμό». (ΕΛ.Ι.Ε., 2007) 1.3 ΠΑΡΑΓΟΝΤΕΣ ΠΟΥ ΕΠΗΡΕΑΖΟΥΝ ΤΗΝ ΑΞΙΑ ΕΝΟΣ ΑΣΤΙΚΟΥ ΑΚΙΝΗΤΟΥ Οι παράγοντες που επιδρούν στην αξία ενός ακινήτου είναι πάρα πολλοί και σχετίζονται όχι μόνο με τα ιδιαίτερα χαρακτηριστικά της κάθε ιδιοκτησίας ως οντότητα, αλλά ταυτόχρονα συνδέονται με παράγοντες που αφορούν την τοπική κτηματαγορά στο σύνολο της. Η συμβολή του κάθε παράγοντα στη διαμόρφωση της αξίας είναι άγνωστη, διότι είναι μεγάλος ο αριθμός τους και ταυτόχρονα δε συμπεριφέρονται με τον ίδιο τρόπο στο χρόνο και στο χώρο. Για την προσπάθεια προσέγγισης της αγοραίας αξίας ακινήτων μέσα από την κατασκευή ενός μαθηματικού μοντέλου, απαραίτητη προϋπόθεση είναι η μελέτη όλων των παραγόντων που επιδρούν στις αξίες σε ένα θεωρητικό αρχικά επίπεδο ώστε στη συνέχεια να γίνει προσπάθεια συμμετοχής τους στην εφαρμογή. Στη συνέχεια λοιπόν αναφέρεται ένα πλήθος παραγόντων, αφού αρχικά ταξινομηθούν σε γενικούς και ειδικούς. Μεταπτυχιακή διατριβή 5
18 Α σ τ ι κ ό α κ ί ν η τ ο Γενικοί παράγοντες επίδρασης Ο πρώτος και κύριος παράγοντας που επιδρά στη διαμόρφωση αξιών ακινήτων είναι η θέση. Με τον όρο θέση εννοούνται τα γενικότερα χαρακτηριστικά γνωρίσματα της εκάστοτε περιοχής, είτε αυτά είναι ιστορικά, είτε πολεοδομικά, είτε γεωμορφολογικά και περιβαλλοντικά. Για την εκτίμηση αγοραίων αξιών που βρίσκονται σε αστικό περιβάλλον λαμβάνονται υπόψη και υπολογίζονται σημαντικά οι παρακάτω παράγοντες. Κοινωνικοοικονομικό επίπεδο Το κοινωνικοοικονομικό επίπεδο κάθε περιοχής συνδέεται άμεσα με την ιστορική διαμόρφωση του αστικού χώρου και την πληθυσμιακή κατανομή κατά περιόδους (π.χ. εγκατάσταση μεταναστών). Οι κοινωνικές δομές της κάθε περιοχής και η κοινωνική διαστρωμάτωση και σύνθεση του πληθυσμού κατά ηλικία, φύλλο και οικογενειακή κατάσταση έχει μία έμμεση επίδραση στις αγοραίες αξίες. Επίσης, σημαντική επίδραση διαδραματίζει το βιοτικό επίπεδο του μέσου ατόμου της περιοχής (εισόδημα). (Πλουμιστού, 2010) Πολεοδομική οργάνωση Ο πολεοδομικός σχεδιασμός μίας συνοικίας του αστικού ιστού καθορίζει τους κοινόχρηστους χώρους και τους χώρους πρασίνου που διαθέτει, τη διαρρύθμιση και τα πλάτη των δρόμων και των πεζοδρομίων, την ύπαρξη προκηπίων, τις χρήσεις, την εμπορικότητα, το μέγεθος και το σχήμα των οικοδομικών τετραγώνων, το μέγιστο επιτρεπόμενο ύψος των κτισμάτων κ.ο.κ. Συνεπώς, η πολεοδομική οργάνωση κάθε περιοχής διαμορφώνει μία γενικότερη εικόνα που επιδρά σημαντικά στην τιμή εκκίνησης μίας οριζόντιας ιδιοκτησίας. Οικιστική πυκνότητα Η οικιστική πυκνότητα κάθε περιοχής συνδέεται έμμεσα με τη διαμόρφωση της αξίας μιας οριζόντιας ιδιοκτησίας, καθώς υψηλές πυκνότητες οδηγούν πιθανά σε χαμηλότερη ποιότητα αστικού περιβάλλοντος και σε έντονη συμφόρηση. Από την άλλη μεριά, αυξημένος πληθυσμός συνεπάγεται αύξηση των υπηρεσιών και εξυπηρετήσεων μίας περιοχής που πάντα έχει θετική επίδραση στις αξίες των ακινήτων. Η οικιστική πυκνότητα κάθε περιοχής είναι αρκετά σημαντικός παράγοντας, γι αυτό πολλά στατιστικά δείγματα συλλέγοντα για την παραγωγή δεικτών όπως δείκτης πυκνοκατοίκησης (άτομα ανά δωμάτιο κατοικίας) ή το εμβαδόν διαμερίσματος ανά άτομο. (Καρανικόλας, 2010) Δίκτυα μεταφορών Στα πλαίσια μιας πόλης, οι αποστάσεις που μπορεί να χρειάζεται να διανύει κανείς για να προσέλθει στο χώρο εργασίας ή σε χώρους ψυχαγωγίας είναι ανάλογες με το μέγεθος της πόλης. Συνεπώς, η μετακίνηση με τη βοήθεια των συστημάτων μεταφοράς αποκτά ιδιαίτερη σημασία και βαρύτητα. Όσο μεγαλύτερη είναι η προσπελασιμότητα και η προσβασιμότητα σε μία περιοχή με τη χρήση της δημόσιας συγκοινωνίας, τόσο μεγαλύτερη αξία αποκτά η κάθε ιδιοκτησία. Επίσης, αναλόγως με το μέγεθος της πόλης και τις ανάγκες 6
19 Κ ε φ ά λ α ι ο 1 ο της, τα μέσα μαζικής μεταφοράς μπορεί να είναι υπέργεια δίκτυα (λεωφορεία, τραμ) ή και υπόγεια (μετρό), με άμεση συνέπεια στην ταχύτητα μετακίνησης προς τα σημεία εξυπηρέτησης και στο κόστος. Συντελεστής εμπορικότητας Βασικός παράγοντας για τη διαμόρφωση αξιών είναι η απόσταση από κεντρικά σημεία όπου συγκεντρώνονται οι υπηρεσίες και η εξυπηρέτηση των πολιτών. Όσο υψηλότερος είναι ο συντελεστής εμπορικότητας, τόσο αυξάνεται η αξία των διαμερισμάτων, ως προς αυτό το χαρακτηριστικό. Γενικά, αυξάνεται η αξία μίας ιδιοκτησίας όσο πιο κοντά βρίσκεται σε σχέση με σημεία ενδιαφέροντος, όπως σχολεία, νοσοκομεία, φαρμακεία, ΚΕΠ, κλπ. Περιβαλλοντική επιβάρυνση Η ποιότητα ζωής είναι ένα χαρακτηριστικό που ο καθένας θέλει να του προσφέρει ο χώρος κατοικίας του. Η περιβαλλοντική συνείδηση λοιπόν διαδραματίζει σημαντικό ρόλο στη διαμόρφωση των αξιών ακινήτων. Αρχικά, η περιβαλλοντική επιβάρυνση μίας περιοχής μπορεί να πηγάζει από το έντονο κυκλοφοριακό πρόβλημα. Μεγάλα επίπεδα ατμοσφαιρικής ρύπανσης είναι η πρώτη συνέπεια ενός τέτοιου φαινομένου. Σύμφωνα με τον Καρανικόλα, 2010 η επίδραση των ατμοσφαιρικών ρύπων στις αγοραίες αξίες των ακινήτων είναι μεγάλη και μελλοντικά πρόκειται να διευρυνθεί, καθώς οι πολίτες ευαισθητοποιούνται όλο και περισσότερο για τη διεκδίκηση καθαρότερου περιβάλλοντος. Είναι ένας πολύ σημαντικός παράγοντας επίδρασης, καθώς οι αέριοι ρύποι αποτελούν ένα έντονο πρόβλημα των σύγχρονων μεγαλουπόλεων. Συνέπεια του κυκλοφοριακού προβλήματος σε μία κεντρική οδό είναι επίσης τα μεγάλα επίπεδα ηχορύπανσης. Ωστόσο, σύμφωνα με τον Αραβαντινό, 2007 τα μεγάλα επίπεδα θορύβου οφείλονται γενικά στις μεταφορές και όχι μόνο στο οδικό δίκτυο. Επισημαίνει ότι περίπου 170εκ. άτομα από τον πληθυσμό της Ευρωπαϊκής Ένωσης εκτίθεται σε επίπεδα θορύβου που προκαλούν σοβαρή ενόχληση. Από τα παραπάνω άτομα το 88% υφίσταται θόρυβο από την οδική κυκλοφορία, το 8% από τις σιδηροδρομικές μεταφορές και το υπόλοιπο 4% από τις αεροπορικές. Η ηχορύπανση συνεπώς επιδρά σημαντικά στις αξίες των ακινήτων, καθώς παρατηρούνται χαρακτηριστικά παραδείγματα, όπου κατρακυλούν οι αξίες σε νεόδμητες οικοδομές που εμφανίζουν έντονα το φαινόμενο της ηχορύπανσης (π.χ. κατοικίες επί της περιφερειακής οδού της Θεσσαλονίκης). Τέλος, μεγάλη περιβαλλοντική επιβάρυνση υφίσταται συνοικίες ή προάστια που είναι τοποθετημένα κοντά σε βιομηχανικές περιοχές (έντονη ατμοσφαιρική ρύπανση) ή κοντά σε δίκτυα υψηλής τάσης ρεύματος (φόβος για πρόκληση ασθενειών), με αποτέλεσμα να υπάρχει επίσης πτώση στην τιμή εκκίνησης των κατοικιών που βρίσκονται στις συγκεκριμένες περιοχές. Αστικό πράσινο Το αστικό πράσινο, σε όλες τις μορφές του παρέχει πολλά θετικά οφέλη στην ποιότητα ζωής κάθε κοινωνίας. Σύμφωνα με τον Καρανικόλα, 2010 τα σπίτια που βρίσκονται κοντά σε περιοχές πρασίνου, προτιμώνται από τα υπόλοιπα που δεν έχουν αυτό το Μεταπτυχιακή διατριβή 7
20 Α σ τ ι κ ό α κ ί ν η τ ο χαρακτηριστικό, με μία τάση για αύξηση της τιμής, η οποία κινείται στο 7% περίπου. Σπίτια κοντά σε δημόσια πάρκα ή σε ανοιχτούς ελεύθερους χώρους προσελκύουν περισσότερους υποψήφιους αγοραστές, οι οποίοι είναι διατεθειμένοι να πληρώσουν περισσότερο για το συγκεκριμένο χαρακτηριστικό Ειδικοί παράγοντες επίδρασης Οι παραπάνω ανθρωπογεωγραφικοί παράγοντες λαμβάνονται υπόψη σε κάθε εκτίμηση μιας ιδιοκτησίας. Είναι χαρακτηριστικά της γενικότερης περιοχής και διαμορφώνουν ουσιαστικά μία τιμή εκκίνησης χαμηλή ή υψηλή ανάλογα με την περιοχή μελέτης. Οι παράγοντες που αναλύονται παρακάτω αναφέρονται στα ιδιαίτερα χαρακτηριστικά της κάθε οριζόντιας ιδιοκτησίας που την καθιστούν μοναδική και διαφοροποιούν την αξίας της σε σύγκριση με όλες τις υπόλοιπες ιδιοκτησίες της ίδιας περιοχής μελέτης. Πρωταρχικό ρόλο στη διαμόρφωση της αγοραίας αξίας μιας ιδιοκτησίας έχει το μέγεθος της. Η σχέση μεταξύ αξίας και εμβαδού δεν είναι όμως ανάλογη. Σύμφωνα με τη βιβλιογραφία το μέγεθος είναι μία ιδιαίτερη παράμετρος επίδρασης, καθώς τα μικρότερα από το σύνηθες μέγεθος ακίνητα λαμβάνουν ένα θετικό συντελεστή και αυξάνουν την τιμή τους ανά τετραγωνικό μέτρο, ενώ στην περίπτωση των μεγαλύτερων ακινήτων ο συντελεστής μεγέθους είναι αρνητικός και μπορεί να έχει ιδιαίτερα υψηλό βάρος επί της τελικής διαμόρφωσης της τιμής. (Καρανικόλας, 2010) Ορισμένες ακόμη ειδικές παράμετροι που επιδρούν στη διαμόρφωση της αξίας είναι η παλαιότητα του κτίσματος στο οποίο ανήκει η οριζόντια ιδιοκτησία και ο όροφος της. Η παλαιότητα έχοντας μία αρνητική συσχέτιση με την αξία, ενώ ο όροφος έχοντας μία θετική επίδραση. Άμεση συνέπεια του ορόφου ενός διαμερίσματος σε συνδυασμό με τη θέση του σε ένα κτίσμα (πρόσοψη σε οδό ή στον ακάλυπτο χώρο της οικοδομής) είναι επίσης η θέα του. Τα διαμερίσματα που βρίσκονται στους υψηλότερους ορόφους και έχουν πρόσοψη σε κύρια οδό είναι πιθανότερο να έχουν καλύτερη θέα από τα ακριβώς ίδια διαμερίσματα χαμηλότερων ορόφων και άρα μεγαλύτερη αξία. Επίσης, δύο διαμερίσματα που βρίσκονται στον ίδιο όροφο, αλλά το ένα από τα δύο είναι σε γωνιακή θέση έχουν διαφορετική αξία. Βασικός παράγοντας στη διαμόρφωση της αξίας είναι επίσης η ποιότητα κατασκευής της οικοδομής, η οποία τις περισσότερες φορές συνδέεται με την παλαιότητα της οικοδομής. Η ποιότητα του κτίσματος δεν αφορά μόνο την κατηγοριοποίηση τους βάσει της πολυτέλειας στην κατασκευή, αλλά κυρίως βάσει της στατικής επάρκειας τους και της αντισεισμικής μελέτης. Αντίστοιχα, σε επίπεδο διαμερίσματος σημαντική επίδραση έχει η κατάσταση του ακινήτου, δηλαδή ο βαθμός συντήρησης του στις περιπτώσεις των παλιών οικοδομών και η ποιότητα των βασικών του στοιχείων όσον αφορά τις νεόδμητες. Πιο συγκεκριμένα, η ποιότητα των κουφωμάτων, η ύπαρξη πόρτας ασφαλείας, οι υδραυλικές και ηλεκτρολογικές εγκαταστάσεις, το υλικό δαπέδου κλπ. Η γενικότερη κατάσταση του ακινήτου κρίνεται επίσης από την ενεργειακή απόδοση του. Το είδος θέρμανσης που διαθέτει (ατομική ή κεντρική θέρμανση, πετρέλαιο, φυσικό αέριο, ή ηλεκτρικά σώματα, 8
21 Κ ε φ ά λ α ι ο 1 ο τζάκι, κλιματισμός) και ο προσανατολισμός του είναι μόνο μερικά από τα στοιχεία που διαμορφώνουν την ενέργεια που απόδοση. Ένα από τα κυριότερα σύγχρονα προβλήματα του αστικού χώρου είναι η έλλειψη θέσεων στάθμευσης. Το μέγεθος του προβλήματος οδηγεί σε αύξηση των αγοραίων αξιών κατοικιών, όταν στην περιοχή ή στη γειτονιά που ανήκουν είναι εύκολη η αναζήτηση θέσεων στάθμευσης. Ακόμη περισσότερο πριμοδοτούνται όπως είναι φυσικό τα ακίνητα που διαθέτουν ιδιωτική θέση στάθμευσης. Τέλος, διαμερίσματα προς πώληση τα οποία έχουν αυθαιρεσίες βάσει του γενικού πολεοδομικού κανονισμού αποφεύγονται με άμεση επίδραση στη διαμόρφωση της αγοραίας αξίας τους Εφαρμογή Λαμβάνοντας υπόψη τους παραπάνω παράγοντες προκύπτει το συμπέρασμα ότι η εκτίμηση της αξίας ενός ακινήτου είναι ιδιαίτερα πολύπλοκη και η μοντελοποίηση της ακόμη δυσκολότερη. Σύμφωνα με τον Scarrett, 1991 καμία ιδιοκτησία δε μπορεί να είναι πανομοιότυπη με κάποια άλλη, ακόμη και εάν κατασκευαστικά είναι ίδιες, διότι καταλαμβάνουν ξεχωριστή θέση στο χώρο. Μπορεί για παράδειγμα να διαφέρει η πρόσοψη τους, η πλευρά του δρόμου στην οποία βρίσκονται, ο βαθμός συντήρησης τους κλπ. Όπως χαρακτηριστικά αναφέρει, σε πολλές περιπτώσεις πολύ μικρές διαφορές, οι οποίες δεν είναι πάντα εύκολα αναγνωρίσιμες, μπορεί να έχουν πολύ μεγάλη επίδραση στη διαμόρφωση της αξίας δύο ιδιοκτησιών. Η μοναδικότητα της κάθε ιδιοκτησίας αποτελεί τροχοπέδη στην ακριβή εκτίμηση της αξίας μέσω ενός μαθηματικού μοντέλου και ο μόνος τρόπος για να ξεπεραστεί είναι με τη βοήθεια παραδοχών, ώστε να γίνει μίας μορφής γενίκευση στην εκτίμηση. Η βασική παραδοχή που πραγματοποιείται αφορά τον παράγοντα γεωγραφική θέση. Συνεπώς, επιλέγονται περιοχές μελέτης, οι οποίες όσο είναι εφικτό διατηρούν «σταθερούς» τους γενικούς παράγοντες που διαμορφώνουν την αξία και διαφοροποιούνται μόνο ως προς τους ειδικούς. Συνεπώς, στόχος είναι ο σχηματισμός μοντέλων τα οποία να εμπεριέχουν την επίδραση της γεωγραφικής τους θέσης με έμμεσο τρόπο αποτυπωμένη στο μαθηματικό μοντέλο και την επίδραση των υπόλοιπων παραγόντων (εμβαδόν, παλαιότητα, όροφος κλπ.) με άμεσο τρόπο ως ξεχωριστές μεταβλητές. Πρόκειται για τη βασική αρχή στην οποία στηρίζεται όλη η μεθοδολογία που περιγράφεται στη συνέχεια. Επίσης, στην παρούσα εφαρμογή λαμβάνονται υπόψη μόνο εκείνοι οι παράγοντες που είναι διαθέσιμοι ως πρωτογενής πληροφορία, διότι πολύ δύσκολα μία βάση δεδομένων εμπεριέχει συγκεντρωμένα όλα τα στοιχεία που περιγράφονται αναλυτικά παραπάνω. Μεταπτυχιακή διατριβή 9
22 ΚΕΦΑΛΑΙΟ 2 Ο ΠΕΡΙΟΧΕΣ ΜΕΛΕΤΗΣ Η κύρια περιοχή μελέτης στην οποία αποφασίζεται να εκτελεστεί η εφαρμογή είναι η πόλη της Θεσσαλονίκης. Εν συνεχεία, η ανάγκη διεύρυνσης της έρευνας πέρα από τα σύνορα μίας πόλης για την εξαγωγή πληρέστερων συμπερασμάτων οδηγεί στην αναζήτηση μίας δεύτερης ευρωπαϊκής πόλης, η οποία να παρουσιάζει ορισμένα κοινά στοιχεία, όσο αυτό είναι δυνατό, όσον αφορά τα γεωμορφολογικά της στοιχεία, τη γενικότερη μορφή του αστικού δικτύου και τη διαμόρφωση του αστικού της χώρου στο πέρασμα των χρόνων. Ταυτόχρονα θα πρέπει να δημιουργεί ενδιαφέρον η σημερινή κατάσταση διαμόρφωσης των αγοραίων αξιών της. Η καταλληλότερη ευρωπαϊκή πόλη που πληροί σε μεγαλύτερο βαθμό τα παραπάνω κριτήρια είναι η Βαρκελώνη της Ισπανίας. Μεσογειακές πόλεις - λιμάνια και οι δύο, παραθαλάσσιες με παρόμοιο κλίμα, οι οποίες είναι πληθυσμιακά οι δεύτερες μεγαλύτερες πόλεις στη χώρα τους. Η Θεσσαλονίκη και η Βαρκελώνη συγκαταλέγονται στις πόλεις ύστερης εκβιομηχάνισης, όπου η συγκρότηση και μεγέθυνση τους συνδέεται με την ανάπτυξη της βιομηχανίας. Ωστόσο η διαμόρφωση της σημερινής τους κατάστασης συνδέεται κυρίως με τις ιστορικές συγκυρίες και τα παρεπόμενα τους (έλευση προσφύγων, μετακίνηση πληθυσμών κλπ) οι οποίες αποδίδονται κυρίως στην αναπαραγωγή κυρίαρχων κοινωνικών και οικονομικών δομών στο εσωτερικό των χωρών. (Μαλούτας, 2002) Οι δύο πόλεις διαφέρουν σαφώς ως προς την κλίμακα τους και τις διαρθρωτικές αλλαγές που έλαβαν χώρα κάτω από ένα οργανωμένο πλάνο αστικής μεγέθυνσης. Επίσης, μεταμορφώνονται στην πάροδο του χρόνου με διαφορετικούς ρυθμούς ανάπλασης, με αποτέλεσμα η κάθε μία να διαθέτει σήμερα τα δικά της χαρακτηριστικά και ιδιαιτερότητες όσον αφορά την κατοικία, την αρχιτεκτονική και εν τέλει τη διαμόρφωση των αξιών των ακινήτων τους. 10
23 Κ ε φ ά λ α ι ο 2 ο Τα μοντέλα εκτίμησης αξιών δεν μπορούν να πραγματοποιηθούν σε εκτάσεις ανάλογες μίας πόλης όπως η Θεσσαλονίκη ή ακόμη περισσότερο η Βαρκελώνη, εξαιτίας της τεράστιας ανομοιογένειας που υπάρχει στις αξίες των κατοικιών από συνοικία σε συνοικία, ακόμη και από γειτονιά σε γειτονιά. Στην παρούσα εφαρμογή η έρευνα βασίζεται στα δεδομένα πέντε διαφορετικών περιοχών μελέτης. Πιο συγκεκριμένα, οι δύο πρώτες περιοχές μελέτης ανήκουν στην πόλη της Θεσσαλονίκης και οι τρεις επόμενες στην πόλη της Βαρκελώνης. Στο κεφάλαιο γίνεται μία προσπάθεια να περιγραφούν με τη βοήθεια χαρτών τα χωρικά όρια των περιοχών μελέτης και με τη βοήθεια επίσημων στατιστικών δεδομένων και ιστορικών στοιχείων να περιγραφούν τα υπόλοιπα χαρακτηριστικά γνωρίσματα τους που τις καθιστούν κατάλληλες για έρευνα. Η ιστορία των περιοχών μελέτης δεν αποτελεί θέμα της διατριβής, παρόλα αυτά η μελέτη σε πολύ μικρό βαθμό της πορείας διαμόρφωσης του αστικού τους χώρου κάνει περισσότερο κατανοητή την επιλογή των περιοχών, την ύπαρξη και το βαθμό των αντιθέσεων τους, αλλά και το ζητούμενο που είναι η διαμόρφωση των αξιών των οριζόντιων ιδιοκτησιών τους. 2.1 ΠΕΡΙΟΧΕΣ ΜΕΛΕΤΗΣ ΣΤΗΝ ΠΟΛΗ ΤΗΣ ΘΕΣΣΑΛΟΝΙΚΗΣ Η Θεσσαλονίκη βρίσκεται στο νοτιοανατολικό άκρο της Ευρώπης και αποτελεί μία πόλη πολυκύμαντη με μεγάλο ενδιαφέρον ιστορικό, πολιτισμικό και οικονομικό. Η ιστορία της πόλης αποδεικνύει ότι η Θεσσαλονίκη είναι μία πόλη εξαιρετικά παλιά αλλά ταυτόχρονα εντυπωσιακά νέα με συνεχή αστική ζωή για περισσότερους από 23 αιώνες. Η ζωντάνια της είναι χαρακτηριστική, ενώ στη σύγχρονη εποχή η Θεσσαλονίκη είναι μια μεγαλούπολη που αποτελεί το διοικητικό και οικονομικό κέντρο της βόρειας Ελλάδας και είναι μία από τις σπουδαιότερες πόλεις της βαλκανικής χερσονήσου. Το πολεοδομικό συγκρότημα της Θεσσαλονίκης αποτελείται από έξι Δήμους και έχει πληθυσμό κατοίκους σύμφωνα με την τελευταία απογραφή του Η Θεσσαλονίκη του σήμερα αποτελείται κατά το πέρασμα στον 21 ο αιώνα από μια πολυκεντρική δομή, με την ταυτόχρονη όμως ισχυρή παρουσία του κέντρου που παραμένει ζωντανό και συγκεντρώνει μία πληθώρα χρήσεων κατοικίας, εμπορίου, εργασίας και ψυχαγωγίας. Στην ανατολική Θεσσαλονίκη κατά μήκος των μεγάλων αρτηριών εισόδου στην πόλη εγκαθίστανται μεγάλα εμπορικά κέντρα, κινηματογράφοι, περιοχές αναψυχής, νυχτερινά κέντρα και πολυτελή ξενοδοχεία, ενώ αντίστοιχα στη δυτική είσοδο της πόλης εγκαθίστανται κτιριακά συγκροτήματα για τα ΚΤΕΛ, τα ΚΤΕΟ, τα ΤΕΙ αλλά και ξενοδοχεία και νέα συγκροτήματα πολυκατοικιών. Τέλος, στο κέντρο αλλά και συνολικά σε όλες τις συνοικίες της πολυπολιτισμικής Θεσσαλονίκης σήμερα τοποθετούνται πολλά σημεία ενδιαφέροντος πολιτιστικού ενδιαφέροντος αλλά και αναψυχής, όπως το πολιτιστικό συγκρότημα της Μονής Λαζαριστών (Σταυρούπολη), Θέατρο Γης (Δήμος Θεσσαλονίκης), ΧΑΝΘ, θέατρα, αποθήκες στο λιμάνι, Αρχαιολογικό μουσείο, μουσείο Βυζαντινού πολιτισμού κλπ. (Καυκαλάς κ.α., 2008) 2 Μεταπτυχιακή διατριβή 11
24 Π ε ρ ι ο χ έ ς μ ε λ έ τ η ς Εικόνα 2.1: Η πόλη της Θεσσαλονίκης με τα διοικητικά όρια της (Πηγή: geodata.gov.gr) Η πρώτη περιοχή μελέτης που επιλέγεται από το πολεοδομικό συγκρότημα της πόλης αναφέρεται σε ένα μικρό σύνολο οικοδομικών τετραγώνων στο κέντρο της πόλης, που ανήκει στο Δήμο Θεσσαλονίκης συνολικής έκτασης 0,8km 2, ενώ η δεύτερη περιοχή μελέτης αναφέρεται στη Δημοτική ενότητα Ευόσμου στη δυτική Θεσσαλονίκη, συνολικής έκτασης περίπου 9km 2. Τα όρια της κάθε περιοχής, οι ιδιαιτερότητες τους και οι λόγοι για τους οποίους επιλέγονται περιγράφονται στα υποκεφάλαια που ακολουθούν Πρώτη περιοχή μελέτης - Κέντρο Θεσσαλονίκης Το κέντρο της Θεσσαλονίκης χαρακτηρίζεται από μεγάλη ανομοιογένεια 3, όσον αφορά τα δημογραφικά οικονομικοκοινωνικά χαρακτηριστικά και τις αξίες των ακινήτων κατά προέκταση. Συνεπώς, στόχο για την πρώτη περιοχή μελέτης (1 η εφαρμογή) αποτελεί η αναζήτηση μόνο ενός τμήματος του κέντρου της Θεσσαλονίκης που να παρουσιάζει όσο το δυνατό μεγαλύτερη ομοιογένεια στα χαρακτηριστικά των διαμερισμάτων της. Για παράδειγμα, αποφεύγεται να επιλεγεί περιοχή του κέντρου της Θεσσαλονίκης όπου βρίσκονται οδοί με έντονη εμπορικότητα 4, καθώς τα ακίνητα που έχουν πρόσοψη σε αυτές εμφανίζουν εξάρσεις ως προς τις αξίες τους. Η περιοχή μελέτης που επιλέγεται με βάσει τα παραπάνω κριτήρια ανήκει στην πρώτη δημοτική κοινότητα του Δήμου Θεσσαλονίκης και τοποθετείται μεταξύ μίας ζώνης από την οδό Καραολή και Δημητρίου των Κυπρίων μέχρι την οδό Εθνικής Αμύνης, και εκτείνεται μεταξύ της Εγνατίας και της Αγ. Δημητρίου. (Εικόνα 2.2). 3 Χαρακτηριστικό είναι το παράδειγμα της παλαιάς παραλίας, στην οποία οι τιμές κυμαίνονται μεταξύ και /τμ, στην περιοχή Διοικητήριο μεταξύ 800και /τμ, στην πλατεία Αριστοτέλους με /τμ κ.ο.κ. (Στοιχεία στο πλαίσιο ημερίδας του Ελληνικού Ινστιτιούτου Εκτιμητικής) 4 Αγ. Σοφίας, Τσιμισκή, Μητροπόλεως, Λεωφόρος Νίκης, Π. Πατρών γερμανού κλπ. 12
25 Κ ε φ ά λ α ι ο 2 ο Εικόνα2.2: Πρώτη περιοχή μελέτης στο κέντρο της πόλης (πορτοκαλί επιφάνεια) και σύγκριση της έκτασης της με τη συνολική έκταση του Δήμου Θεσσαλονίκης. Πηγή: δορυφορική απεικόνιση από Google earth Το πρώτο χαρακτηριστικό της επιλεγείσας περιοχής είναι η εμφάνιση αυξημένης χρήσης κατοικιών και όχι γραφείων και εμπορικών χώρων σε σύγκριση με το υπόλοιπο κέντρο της πόλης. Επίσης, η περιοχή επάνω από την Εγνατία θεωρείται περισσότερο υποβαθμισμένη και οι τιμές των κατοικιών βρίσκονται σε χαμηλότερα επίπεδα, συγκριτικά με το υπόλοιπο κέντρο. Ωστόσο πρόκειται για ένα θετικό χαρακτηριστικό, διότι συνεπάγεται πιο ομαλοποιημένη διαμόρφωση των αξιών. Επίσης, σύμφωνα με τις διατυπώσεις μεσιτικών γραφείων η περιοχή παρουσιάζει μία ανθεκτικότητα όσον αφορά τις αγοροπωλησίες που λαμβάνουν χώρα και προσελκύει το ενδιαφέρον ενός σημαντικού μέρους της πόλης είτε για ιδιοκατοίκηση είτε για επένδυση. Παρόλα αυτά, ο κύριος λόγος για τον οποίο είναι ενδιαφέρουσα η αναζήτηση της διαμόρφωσης των αξιών στη συγκεκριμένη περιοχή είναι το ενδιαφέρον που παρουσιάζει όσον αφορά την προσέλκυση μεγάλου πλήθους φοιτητών κάθε χρόνο και η μεγάλη πληθυσμιακή πυκνότητα που είναι αξιοσημείωτη σε σχέση με τα διεθνώς αποδεκτά όρια για τη βιωσιμότητα στις πόλεις. Σύμφωνα με ειδικούς της αγοράς ακινήτων 5, οι τιμές στα ενοίκια στις πλέον πυκνοκατοικημένες περιοχές Εγνατία, Αγίου Δημητρίου Κασσάνδρου ξεκινούν από 100 και φθάνουν τα 450 στα ανακαινισμένα διαμερίσματα. Επισημαίνουν επίσης ότι η περιοχή εμφανίζει ενδιαφέρον για τον φοιτητικό κόσμο, ο οποίος την προτιμά λόγω της γειτνίασης της με το χώρο των πανεπιστημίων, προκαλώντας έτσι κάποια κίνηση στην κατά τα άλλα λιμνάζουσα κτηματαγορά της Θεσσαλονίκης. 5. Αστέριος Παπαγεωργίου κτηματομεσίτης ( ton_sti_thessaloniki) Μεταπτυχιακή διατριβή 13
26 Περιοχές μελέτης Στην πρώτη περιοχή μελέτης, αναμένονται στην πλειοψηφία τους πολυώροφες οικοδομές μεγάλων ηλικιών, χωρίς θέσεις στάθμευσης, με μικρούς εξώστες, ρετιρέ στους τελευταίους ορόφους και έλλειψη ανελκυστήρα σε πολλές από αυτές. Διαμερίσματα σε πολύ κακή κατάσταση, αλλά και διαμερίσματα ανακαινισμένα με θέα και κοντά στα πανεπιστήμια. Επίσης, στη συγκεκριμένη ζώνη δεν αναμένονται μεγάλες εξάρσεις σε τιμές, καθώς γεωγραφικά ανήκουν όλα τα διαμερίσματα, λίγο ή πολύ στην ίδια κατηγορία Δεύτερη περιοχή μελέτης Δημοτική ενότητα Ευόσμου Ο Δήμος Κορδελιού - Ευόσμου τοποθετείται στη βορειοδυτική πλευρά του πολεοδομικού συγκροτήματος της Θεσσαλονίκης και προήλθε από τη συνένωση των πρώην Δήμων Ελευθέριου Κορδελιού και Ευόσμου. Καταλαμβάνει συνολική έκταση 14 km2 περίπου και αποτελεί αντιπροσωπευτικό δείγμα των δυτικών συνοικιών της πόλης. Στην περιοχή του Δήμου Κορδελιού - Ευόσμου βρίσκεται η δυτική είσοδος της πόλης και περικλείεται από πολύ κεντρικές οδούς όπως η Μοναστηρίου, η εσωτερική περιφερειακή και η Εγνατία Οδός. Ο Δήμος Κορδελιού - Ευόσμου χαρακτηρίζεται από μία σειρά ιδιαίτερων γνωρισμάτων, άλλων θετικών και άλλων αρνητικών με αποτέλεσμα να καθίσταται όλη η περιοχή άξια για περαιτέρω μελέτη σε διάφορους τομείς κοινωνικού, εκπαιδευτικού και οικονομικού ενδιαφέροντος. Εικόνα2.3: Απεικόνιση Δημοτική ενότητας Ευόσμου (κίτρινο χρώμα) σε σύγκριση με τη συνολική έκταση του Δήμου Κορδελιού - Ευόσμου (κόκκινο περίγραμμα). Πηγή: δορυφορική απεικόνιση από Google earth 14
27 Κ ε φ ά λ α ι ο 2 ο Όπως αναφέρεται στα κριτήρια επιλογής της πρώτης περιοχής μελέτης, έτσι και από το Δήμο Κορδελιού Ευόσμου επιλέγεται ένα τμήμα του ως περιοχή μελέτης για περισσότερη ομοιομορφία στο εσωτερικό της. Τη συγκεκριμένη περιοχή αποτελούν τα σύνορα της Δημοτικής Ενότητας Ευόσμου (Εικόνα 2.3), καθώς η Δ.Ε. Ελευθέριου Κορδελιού τοποθετείται δυτικότερα και είναι περισσότερο υποβαθμισμένη περιοχή, ως προς τις αξίες πώλησης ανά τετραγωνικό μέτρο των κατοικιών. Ένα από τα βασικότερα θετικά γνωρίσματα της περιοχής του Ευόσμου είναι η προσέλκυση τα τελευταία χρόνια πολλών νέων ζευγαριών και οικογενειών που αναζητούν μία οικονομική πρώτη κατοικία. Η τεράστια ανοικοδόμηση και η ραγδαία οικιστική ανάπτυξη της περιοχής, αλλά ταυτόχρονα οι σαφώς χαμηλότερες τιμές ανά τετραγωνικό μέτρο που επικράτησαν σε σύγκριση με τα διαμερίσματα του κέντρου ή ακόμη περισσότερο της ανατολικής Θεσσαλονίκης, οδήγησαν τα νέα ζευγάρια να προτιμήσουν νεοδόμητες οικοδομές με ιδιωτικές θέσεις στάθμευσης και μεγάλους χώρους στη δυτική Θεσσαλονίκη. Ο χαμηλός δείκτης πληθυσμιακής γήρανσης άλλωστε οδηγεί μία περιοχή στη διαρκή εξέλιξη και στη δημιουργία ενός σύγχρονου και λειτουργικού κέντρου με ποικίλες δραστηριότητες σε όλους τους τομείς μίας κοινωνίας. Τα βασικότερα προβλήματα του Δήμου πηγάζουν από τη θέση την οποία βρίσκεται, όσον αφορά τη ρύπανση από τη βιομηχανική περιοχή και όλα τα μειονεκτήματα της αστικής δυτικής Θεσσαλονίκης, όπως διαμορφώθηκαν κυρίως από τη μετανάστευση και την αυθαίρετη δόμηση. Κτίσματα άναρχα τοποθετημένα, πολλά εκ των οποίων σε πολλά σημεία του Δήμου δεν έχουν ακόμη αντικατασταθεί με νέες οικοδομές. Επιπλέον, την τελευταία εικοσαετία, οι χαμηλές τιμές αγοράς των ακινήτων προσέλκυσαν οικογένειες ομογενών από την πρώην ΕΣΣΔ και οικονομικούς μετανάστες. Τα παραπάνω κριτήρια κρίθηκε ότι ικανοποιεί ο πρώην Δήμος Ευόσμου για μία ποικιλία παραγόντων. Από έρευνα στο διαδίκτυο που θα αποτελέσει την πηγή των δεδομένων παρουσιάζει μεγαλύτερο μέγεθος ακινήτων προς πώληση, άρα ευκολία συγκέντρωσης μεγαλύτερου δείγματος. Ταυτόχρονα, είναι μία περιοχή που εμφανίζει μία πολύ μεγάλη ανοικοδόμηση τα τελευταία χρόνια, άρα θα υπάρχουν στο δείγμα πολλές νεοδόμητες οικοδομές, που δεν χαρακτηρίζονται πολυτελείς κατοικίες αλλά είναι σπίτια σε πολύ καλή κατάσταση με θέση στάθμευσης και καινούριες τεχνολογίες σε κουφώματα κλπ. Παρόλα αυτά η βασικότερη αιτία επιλογής σχετίζεται με τα δεδομένα που προκύπτουν από τα στοιχεία της Ελληνικής Στατιστικής Αρχής 6 (ΕΛ.ΣΤΑΤ.). Σύμφωνα με την επίσημη απογραφή πληθυσμού του 2011, ο πρώην Δήμος Ευόσμου και νυν Δημοτική Ενότητα Ευόσμου είναι τρίτη σε πληθυσμό, ακολουθώντας το Δήμο Θεσσαλονίκης και Καλαμαριάς με μία αύξηση όμως της τάξης του 32% περίπου σε σχέση με την αντίστοιχη απογραφή του Οι πρώτοι έξι δήμοι σε πληθυσμό της Περιφερειακής Ενότητας Θεσσαλονίκης και οι αλλαγές που έλαβαν χώρα αποτυπώνονται στον παρακάτω πίνακα. 6 National Statistical Service of Greece Μεταπτυχιακή διατριβή 15
28 Π ε ρ ι ο χ έ ς μ ε λ έ τ η ς Πίνακας 2.1 : Δεδομένα της ΕΛ.ΣΤΑΤ. για τους πρώτους έξι πολυπληθέστερους δήμους της Θεσσαλονίκης ΑΥΞΗΣΗ/ ΜΕΙΩΣΗ % 1 Δ. ΘΕΣΣΑΛΟΝΙΚΗΣ 284,898 Δ. ΘΕΣΣΑΛΟΝΙΚΗΣ 260,08-8,7% 2 Δ. ΚΑΛΑΜΑΡΙΑΣ 55,04 Δ. ΚΑΛΑΜΑΡΙΑΣ 58,651 6,2% 3 Δ. ΕΥΟΣΜΟΥ 30,289 Δ.Ε. ΕΥΟΣΜΟΥ 44,375 31,7% 4 Δ. ΣΥΚΕΩΝ 30,257 Δ.Ε. ΣΥΚΕΩΝ 30,014-0,8% 5 Δ. ΑΠΕΛΟΚΗΠΩΝ 28,285 Δ.Ε. ΑΜΠΕΛΟΚΗΠΩΝ 27,356-3,3% 6 Δ. ΝΕΑΠΟΛΕΩΣ 26,534 Δ.Ε. ΝΕΑΠΟΛΕΩΣ 25,732-3% *Δ. : ΔΗΜΟΣ, Δ.Ε.: ΔΗΜΟΤΙΚΗ ΕΝΟΤΗΤΑ Παρατηρείται ότι είναι η πολυπληθέστερη περιοχή όλης της Δυτικής Θεσσαλονίκης και ότι εμφανίζει τόσο μεγάλη αύξηση πληθυσμού μέσα στην τελευταία δεκαετία, όταν οι υπόλοιπες πέντε πέραν της Καλαμαριάς εμφανίζουν μείωση. Σύμφωνα με τα παραπάνω στοιχεία, θα έχει ενδιαφέρον η δεύτερη περιοχή μελέτης που θα αναζητηθούν οι παράγοντες που επηρεάζουν την αγοραία αξία των ακινήτων να είναι η περιοχή του Ευόσμου. 2.2 ΠΕΡΙΟΧΕΣ ΜΕΛΕΤΗΣ ΣΤΗΝ ΠΟΛΗ ΤΗΣ ΒΑΡΚΕΛΩΝΗΣ Η Βαρκελώνη τοποθετείται στο νοτιοδυτικό τμήμα της Ευρώπης και αποτελεί πρωτεύουσα της αυτόνομης κοινότητας της Καταλονίας. Είναι η δεύτερη μεγαλύτερη πόλη της Ισπανίας σε πληθυσμό και έκταση, μετά τη Μαδρίτη. Ο συνολικός πληθυσμός της είναι περίπου κάτοικοι στο Δήμο της Βαρκελώνης και περίπου λαμβάνοντας υπόψη όλη τη μητροπολιτική περιοχή. Την πόλη χαρακτηρίζει η τέχνη, η αρχιτεκτονική και ο δυναμισμός. Μία πόλη με έντονο τουρισμό, η οποία αποτελεί ένα χαρακτηριστικό παράδειγμα αστικού σχεδιασμού, καθώς αναμορφώνεται τις τελευταίες δεκαετίες στη λογική μίας συμπαγούς πόλης. Σύμφωνα με τον Rowe, 2006 η Βαρκελώνη είναι μία από τις πιο ενεργές πόλεις του κόσμου την τελευταία εικοσιπενταετία όσον αφορά τον αστικό σχεδιασμό. Από τα πρώτα μικρά οικοδομικά τετράγωνα του 1980 στις σημερινές μεγάλης κλίμακας κατασκευές, οι οποίες συναντούν τις προκλήσεις της παγκόσμιας οικονομίας. Η ανάπτυξη της Βαρκελώνης αντανακλά έναν ταχέως αναπτυσσόμενο κόσμο, γεμάτο αλλαγές. Παρόλα αυτά πέρα από τη βιτρίνα των αλλαγών, νόημα έχουν οι ουσιαστικές αλλαγές που έχουν γίνει στη Βαρκελώνη και την έχουν μεταμορφώσει. Το 1992 φιλοξενεί τους ολυμπιακούς αγώνες που αποτέλεσαν αφορμή για την υλοποίηση ενός μαζικού προγράμματος αναγέννησης της πόλης. Οδοποιία, συγκοινωνιακές μελέτες, κατασκευή βιβλιοθηκών, αναδιαμόρφωση υποβαθμισμένων περιοχών, επέκταση του μετρό είναι μόνο μερικά από τα προγράμματα αστικής αναμόρφωσης που έλαβαν χώρα. Το 10% της πόλης αποτελεί χώρους πρασίνου, ενώ αναρίθμητες είναι οι πλατείες και οι πεζόδρομοι. Από τις τρεις περιοχές μελέτης της Βαρκελώνης, οι δύο πρώτες (Eixample και Sant Marti) ανήκουν στο Δήμο Βαρκελώνης, ενώ η τρίτη (Badalona) αποτελεί προάστιο της 16
29 Κεφάλαιο 2ο πόλης, όπως φαίνεται από την παρακάτω εικόνα. Τα ιδιαίτερα χαρακτηριστικά της κάθε μίας και ο λόγος για τον οποίο επιλέγονται σε σύγκριση με άλλες περιοχές αναλύονται παρακάτω. Εικόνα2.4: Απεικόνιση των 10 συνοικιών του μητροπολιτικού Δήμου της Βαρκελώνης (Πηγή: ) Τρίτη περιοχή μελέτης Eixample Βαρκελώνης To Eixample, το οποίο στα Καταλανικά σημαίνει «επέκταση», χτίστηκε κατά τη διάρκεια του 19ου αιώνα στην πρώτη μεγάλη επέκταση της Βαρκελώνης πέρα από τα τείχη της πόλης. Αποτελεί το επακόλουθο της βιομηχανικής ανάπτυξης και της δημογραφικής έκρηξης της εποχής, ενώ η κατασκευή του συνέπεσε με την έκρηξη του τοπικού πλούτου στην περιοχή. Σαν αποτέλεσμα, η περιοχή Eixample φιλοξενεί μερικά από τα πολυτελέστερα κτίρια και έχει μερικές από τις καλύτερες κατοικίες της Βαρκελώνης, καθώς οι πλούσιες τοπικές οικογένειες της εποχής, θέλοντας να επιδείξουν την κοινωνική τάξη και τον πλούτο τους, ανέθεσαν την κατασκευή μεγαλειωδών κτιρίων σε αρχιτέκτονες του μοντερνισμού, διασημότερος από τους οποίους είναι ο Gaudi. Σήμερα η περιοχή τοποθετείται κεντρικά, καθώς περικλείεται μεταξύ της Παλαιάς πόλης (Ciutat Vella) και των περιοχών Sants, Les Corts, Gracia, Sant Marti, Horta Guinardo Μεταπτυχιακή διατριβή 17
30 Περιοχές μελέτης και Sant Gervasi, ενώ διοικητικά χωρίζεται σε πέντε επιμέρους «γειτονιές», κάθε μία από τις οποίες έχει μερικά στοιχεία του την κάνουν μοναδική. Εικόνα2.5: Απεικόνιση περιοχής Eixample. Πηγή: δορυφορική απεικόνιση από Google earth Ο συνολικός πληθυσμός της περιοχής σύμφωνα με την απογραφή του 2009 ήταν κάτοικοι (η μεγαλύτερη σε πληθυσμό περιοχή) σε έκταση 7,50 km2, άρα πρόκειται για μία πυκνοδομημένη περιοχή της Βαρκελώνης. Επίσης, είναι μία όμορφη και καλαίσθητη περιοχή, η οποία κατά τη διάρκεια της ημέρας είναι γεμάτη με έντονη δραστηριότητα σε γραφεία, καταστήματα, πολυτελείς μπουτίκ, εστιατόρια και γκαλερί. Είναι ασφαλής με μεγάλη προσφορά ακινήτων πολύ καλής ποιότητας κυρίως στο ανατολικό Eixample που είναι μία από τις πιο ιδιαίτερες κατοικήσιμες περιοχές της πόλης. Το βράδυ ένας μεγάλος αριθμός μπαρ και εστιατορίων κυριαρχεί κυρίως στο δυτικό Eixample. Τα σπίτια είναι αρκετά παλιά, αλλά ταυτόχρονα καλά διατηρημένα. Η γειτονιά Fort Pius τον τελευταίο καιρό ξεχωρίζει για τον αυξημένο αριθμό ασιατών, κυρίως Κινέζων, με συνέπεια την απότομη ανάπτυξη της κινέζικης αγοράς με τον ταυτόχρονο πολλαπλασιασμό των καταστημάτων. Γενικά η περιοχή χαρακτηρίζεται από ευκατάστατες γειτονιές, αλλά ταυτόχρονα φιλοξενεί πλέον μεγάλο ποσοστό κατοίκων που είναι μετανάστες και άρα χαμηλότερων εισοδημάτων. Το ιδιαίτερο γνώρισμα της περιοχής είναι η μορφή των οικοδομικών τετραγώνων με τις χαρακτηριστικές αποτμήσεις στις γωνίες, σχηματίζοντας οκτάγωνα (Εικόνα 2.6), καθώς και οι ευθείς και μακρύς δρόμοι με τις μεγάλες λεωφόρους. Χάρη στις πρωτοποριακές ιδέες Καταλανών αρχιτεκτόνων η περιοχή και γενικότερα η πόλη έχει ένα πλήρως ιπποδάμειο ρυμοτομικό σύστημα. Τα οικοδομικά τετράγωνα είναι πολύ μεγάλα, με μεγάλους ελεύθερους χώρους στο κέντρο και χωρίζονται με δρόμους τουλάχιστον τριών 18
31 Κεφάλαιο 2ο λωρίδων και φαρδιά πεζοδρόμια7. Τα παραπάνω χαρακτηριστικά προσφέρουν διαμερίσματα με θέα, περισσότερες θέσεις στάθμευσης και δρόμους που αναπνέουν. Σε κάθε διασταύρωση οι δρόμοι φαίνονται μεγαλύτεροι, υπάρχει καλύτερη ορατότητα και καλύτερη κυκλοφορία του αέρα σε μία μεγάλη πόλη που το έχει ανάγκη. Οι ιδιαιτερότητες της περιοχής όπως τα οικοδομικά της τετράγωνα επηρεάζουν σαφώς και τις αξίες των ακινήτων που βρίσκονται εκεί σε υψηλότερα επίπεδα. Η μεγάλη επιφάνεια της περιοχής Eixample περιλαμβάνει μια εντυπωσιακή λίστα από κύρια αξιοθέατα με κυριότερη τη Sagrada Familia του Γκαουντί, ίσως το πιο εντυπωσιακό αρχιτεκτονικό στοιχείο της Βαρκελώνης, με αποτέλεσμα να δομείται μία υπέροχη περιοχή που φιλοξενεί μερικά από τα καλύτερα διαμερίσματα της πόλης. Εικόνα 2.6 : Αεροφωτογραφία Βαρκελώνης που απεικονίζει τη χαρακτηριστική ρυμοτομία της Το μεγάλο σε έκταση εύρος της περιοχής, τα μοντέρνα κτίρια, η ξεχωριστή ρυμοτομία, η έντονη δραστηριότητα κατά τη διάρκεια της ημέρας και της νύχτας, οι διαφορετικές κοινωνικές τάξεις που αλληλεπιδρούν και οι υψηλές αξίες που συναντώνται δημιουργούν μεγάλο ενδιαφέρον για την αγορά ακινήτων της περιοχής και για την εύρεση των πραγματικών παραγόντων που διαμορφώνουν τις τελικές αξίες πώλησης των διαμερισμάτων Τέταρτη περιοχή μελέτης - Sant Marti Βαρκελώνης To Sant Marti είναι μία από τις δέκα συνοικίες του Δήμου Βαρκελώνης και τοποθετείται στο ανατολικό τμήμα του Δήμου. Πρόκειται για μία παραθαλάσσια συνοικία, η οποία από ξηράς συνορεύει βόρεια με το Sant Andreu και το Horta Guinardo, δυτικά με το Eixampleκαι το Ciutat Vella και ανατολικά με το St Adria de Besos. Από το 1714 ήταν ένα αυτόνομο χωριό, το οποίο το 1897 ξεκίνησε να αποτελεί κομμάτι της Βαρκελώνης. Σήμερα η συνοικία Sant Marti χωρίζεται σε δέκα επιμέρους γειτονιές και σύμφωνα με την 7 Μεταπτυχιακή διατριβή 19
32 Περιοχές μελέτης απογραφή του 2005 ο πληθυσμός της είναι κάτοικοι. Αποτελεί τη δεύτερη μεγαλύτερη συνοικία της Βαρκελώνης μετά το Eixample, όπου σε συνδυασμό με το μέγεθος της την καθιστά την έκτη μεγαλύτερη σε πληθυσμιακή πυκνότητα. Εικόνα 2.7: Απεικόνιση περιοχής Sant Marti. Πηγή: δορυφορική απεικόνιση από Google earth Το χαρακτηριστικό γνώρισμα της περιοχής που τη διαφοροποιεί από όλες τις υπόλοιπες είναι η ανάδειξη της ως μίας από τις βιομηχανικές ζώνες της Βαρκελώνης με πολυάριθμα εργοστάσια και αποθήκες. Ο χαρακτηρισμός της ως βιομηχανικό κέντρο της Βαρκελώνης, στις αρχές του 20ου αιώνα βασιζόταν στη συγκέντρωση των περισσότερων εργοστασίων όλης της Καταλονίας. Όπως είναι αναμενόμενο οι πρώτοι κάτοικοι της περιοχής ανήκουν στην εργατική τάξη της πόλης (Καταλανοί) ή σε μετανάστες από όλη της Ισπανία. Όπως αναφέρεται και παραπάνω, σταθμό στην εξέλιξη της περιοχής αποτέλεσαν οι Ολυμπιακοί αγώνες του 1992 γιατί έδωσαν μεγάλα κίνητρα για αλλαγές. Η συνοικία Sant Marti κυριολεκτικά μεταμορφώθηκε. Πολλά από τα παλιά εργοστάσια επανασχεδιάστηκαν ή αντικαταστάθηκαν με νέες μοντέρνες κατοικήσιμες περιοχές όπως το Diagonal Mar, εμπορικά κέντρα, πάρκα, νέοι χώροι εργασίας και πανεπιστήμια. Ένα νέο σχέδιο με όνομα δίνει χώρο σε νέες εταιρίες και πολλές καινούριες θέσεις εργασίας στο σημερινό Sant Marti. Επικρατεί το πνεύμα της καινοτομίας, μοντέρνες οικοδομές κτίζονται, νέες εγκαταστάσεις και ζώνες πρασίνου, ενώ οι αλλαγές αποτελούν καθημερινό φαινόμενο. Η ρυμοτομία του Sant Marti βασίζεται στο μοντέλο που υπάρχει στο Eixample αν και το πλήθος των ακινήτων είναι πολύ διαφορετικό. Η ισχυρή αίσθηση της κοινότητας που επικρατούσε και συνεχίζει να επικρατεί, το βιομηχανικό παρελθόν της, οι τεράστιες εξελίξεις που έλαβαν χώρα, τα σχέδια για περαιτέρω ανάπτυξη της περιοχής, η παραθαλάσσια αίγλη της, η έντονη εμπορικότητα και η πολύ μικρή απόσταση της από το κέντρο της πόλης την καθιστά μία ιδιαίτερη περιοχή για την πόλη της Βαρκελώνης και άξια μελέτης. Τα παραπάνω χαρακτηριστικά της δεν υπάρχει 20
33 Κ ε φ ά λ α ι ο 2 ο αμφιβολία ότι έχουν θετική επίδραση στην αγορά ακινήτων του Sant Μarti, η οποία επιδιώκεται να ερευνηθεί μέσω στατιστικού μοντέλου στα επόμενα κεφάλαια Πέμπτη περιοχή μελέτης Badalona Βαρκελώνης Η Badalona αποτελεί προάστιο της Βαρκελώνης, το οποίο τοποθετείται μόνο 10km μακριά από την πόλη στο βορειοανατολικό τμήμα της. Αποτελεί μία αστική περιοχή (2010) κατοίκων και είναι ο τρίτος πιο πυκνοδομημένος δήμος της Καταλονίας μετά τη Βαρκελώνη και το L Hospitalet de Llobreget. Σήμερα χωρίζεται σε εννέα επιμέρους γειτονιές. Είναι μία από τις παλαιότερες πόλεις της περιοχής με πλούσια καλλιτεχνική και ιστορική κληρονομιά. Η περιοχή είναι τουριστική και φιλοξενεί αρκετά ξενοδοχεία καθώς η σύνδεση της με το κέντρο της Βαρκελώνης πραγματοποιείται με όλα τα δυνατά μέσα μαζικής μεταφοράς, μετρό, προαστιακό, λεωφορείο και τραμ. Εικόνα 2.8: Απεικόνιση της περιοχής Badalona. Πηγή: Η Badalona ήταν μία από τις πιο σημαντικές κωμοπόλεις κατά τη διάρκεια ανάπτυξης της βιομηχανίας στην Ισπανία από το 19 ο αιώνα και έπειτα. Η δύναμη της πηγάζει από την αλιεία, την κατασκευή μάλλινων και βαμβακερών αγαθών, γυαλιού και διαφόρων ποτών και προϊόντων όπως η ζάχαρη. Την περιοχή κατοικούν άνθρωποι της μεσαίας ή εργατικής τάξης, αν και οι αξίες των διαμερισμάτων είναι πολύ υψηλότερες από αντίστοιχες περιοχές στην πόλη της Θεσσαλονίκης. Τα χαρακτηριστικά που τη διαφοροποιούν σε σύγκριση με τις υπόλοιπες περιοχές και την κάνουν ενδιαφέρουσα ως προς τη μελέτη του τρόπου διαμόρφωσης των αξιών της είναι ποικίλα. Αρχικά, αποτελεί μία αυτόνομη περιοχή που η δομή της στο εσωτερικό αντιπροσωπεύει μία μικρή πόλη, παρόλο που απέχει πολύ μικρή απόσταση από την έντονη Μεταπτυχιακή διατριβή 21
34 Π ε ρ ι ο χ έ ς μ ε λ έ τ η ς ζωή και δραστηριότητα της Βαρκελώνης. Το κέντρο της, το λιμάνι, οι παραθαλάσσιες κατοικίες και το βιομηχανικό παρελθόν, της δίνουν χαρακτηριστικά που την καθιστούν σίγουρα ενδιαφέρουσα. Η κατοικία στη Badalona έχει επίσης τη μορφή των οριζόντιων ιδιοκτησιών που τοποθετούνται σε πολυώροφες οικοδομές και άρα δίνεται η δυνατότητα να συγκεντρωθεί ένα αξιόλογο μέγεθος στατιστικού δείγματος. Τέλος, σε μία περιοχή αυτής της κατηγορίας είναι περισσότερες οι πιθανότητες η διαμόρφωση των αξιών ακινήτων να είναι ομαλοποιημένη, χωρίς ιδιαίτερες εξάρσεις, γεγονός που μόνο θετική επίδραση μπορεί να έχει στη μοντελοποίηση της εκτίμησης αγοραίων αξιών στην περιοχή. 22
35 ΚΕΦΑΛΑΙΟ 3 Ο ΣΤΑΤΙΣΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ ΤΟΥ ΠΡΟΒΛΗΜΑΤΟΣ Κάθε είδους στατιστική μελέτη απαιτεί μια ιδιαίτερα χρονοβόρα και αναπόφευκτη προεργασία. Έπειτα από τον προσδιορισμό του προβλήματος και την ανάλυση όλων των δεδομένων, τα βασικά βήματα αυτής της προεργασίας είναι η επιλογή της κατάλληλης στατιστικής μεθοδολογίας, ο προσδιορισμός των μεταβλητών, η κατηγοριοποίηση και ποσοτικοποίηση τους και τέλος ο σχηματισμός του δείγματος. Κάθε ένα από τα παραπάνω βήματα πρέπει να επεξηγείται ώστε να είναι δικαιολογημένη κάθε επιλογή του ερευνητή, καθώς αντικατοπτρίζει την πρόθεση που έχει για τη στατιστική ανάλυση και τα αποτελέσματα που αποζητά. Μία καλή προεργασία οδηγεί σε λιγότερα προβλήματα όταν ξεκινήσει η επεξεργασία του δείγματος και εξοικονομεί χρόνο και ενέργεια για κάθε ερευνητή. Στο πρώτο μέρος του κεφαλαίου που ακολουθεί αναλύεται το θεωρητικό υπόβαθρο στο οποίο στηρίζεται ο βασικός κορμός της προετοιμασίας των δεδομένων, ενώ στο δεύτερο μέρος περιγράφεται η μεθοδολογία, οι περιορισμοί και οι παραδοχές που λαμβάνουν χώρα στην παρούσα εφαρμογή. 3.1 ΘΕΩΡΗΤΙΚΟ ΥΠΟΒΑΘΡΟ Προϋπόθεση για την υλοποίηση μίας στατιστικής μελέτης αποτελεί η διερεύνηση του προβλήματος σε βάθος, σε συνδυασμό με την ταυτόχρονη μελέτη μεγάλου όγκου σχετικής βιβλιογραφίας, έτσι ώστε να γίνει αντιληπτή η βασική μεθοδολογία που θα δώσει τα ζητούμενα αποτελέσματα. Πιο συγκεκριμένα, για την επιλογή της κατάλληλης μεθόδου γίνεται αρχικά μία διερεύνηση της σχέσης μεταξύ των μεταβλητών και στη συνέχεια επιλέγεται μία ή και περισσότερες στατιστικές μεθοδολογίες που υπάρχουν στη διεθνή βιβλιογραφία. Παρόλο που η ύπαρξη παραδειγμάτων για κάθε στατιστική μεθοδολογία διευκολύνει τον ερευνητή να κατανοήσει εάν το εκάστοτε μοντέλο είναι επαρκές για το 23
36 Κ ε φ ά λ α ι ο 3 ο δικό του στατιστικό πρόβλημα, θα πρέπει να λαμβάνεται υπόψη ότι αναλόγως με το είδος και το πλήθος των μεταβλητών, αλλά και με τις ιδιαιτερότητες της κάθε περίπτωσης, τα δεδομένα προσαρμόζονται διαφορετικά στο στατιστικό μοντέλο. Η συγκεκριμένη διαπίστωση οδηγεί στο συμπέρασμα ότι εάν υπάρχουν περισσότερα από ένα μοντέλα που θεωρητικά δίνουν λύση στο πρόβλημα, τότε για την επίλυση του μπορούν να εφαρμοστούν όλα και να επιλεγεί εν τέλει εκείνο ή εκείνα με την καλύτερη προσαρμογή των δεδομένων. Σε κάθε περίπτωση γίνονται παραδοχές και υπάρχουν περιορισμοί που πρέπει να ληφθούν υπόψη, καθώς κάθε πραγματικό θα πρέπει να αποδοθεί κατά το δυνατό καλύτερα, από ένα μοντέλο, δηλ. από μία θεωρητική μαθηματική κατασκευή. Το στάδιο που έπεται της επιλογής μεθόδου στατιστικής ανάλυσης είναι η αναζήτηση και ο σχηματισμός του δείγματος. Στις περιπτώσεις, όπου μελετώνται ορισμένα χαρακτηριστικά του γεωγραφικού χώρου πρέπει κάθε φορά να γίνεται ξεκάθαρη η δυναμική του φαινομένου. Ένα γεωγραφικό φαινόμενο χαρακτηρίζεται από το χρόνο κατά τον οποίο συμβαίνει, τα κοινωνικά, οικονομικά και πολιτικά χαρακτηριστικά τα οποία επιδρούν στο φαινόμενο με οποιονδήποτε τρόπο εκείνη την περίοδο και φυσικά τη χωρική μονάδα αναφοράς, όπου γίνεται η αναζήτηση των δεδομένων για το σχηματισμό του δείγματος. Η λεπτομερής μελέτη του χώρου και των ποσοτικών ή ποιοτικών χαρακτηριστικών που περιγράφουν το φαινόμενο στη συγκεκριμένη περιοχή μελέτης οδηγεί στη συλλογή των στοιχείων εκείνων που καθρεφτίζουν την ουσία του γεωγραφικού φαινομένου που μελετάται σε όλες τις πτυχές του και αποτελεί την πρώτη και ιδιαίτερα δύσκολη διαδικασία που πρέπει να πραγματοποιηθεί. Είναι γεγονός ότι για να μελετηθεί με τον πλέον ασφαλή τρόπο ένα φαινόμενο μέσω της στατιστικής ανάλυσης, θα πρέπει να εισαχθεί στο μοντέλο κάθε άτομο ή κάθε αντικείμενο του γεωγραφικού χώρου, δηλαδή να συμμετέχει στη μελέτη όλος ο πληθυσμός 8. Παρόλα αυτά είναι πρακτικά δύσκολη η συλλογή των δεδομένων που αναφέρονται στον πληθυσμό για λόγους κόστους, ταχύτητας, αδυναμίας ύπαρξης δεδομένων, ακόμη και για έλλειψη αναγκαιότητας στην ύπαρξη απόλυτης ακρίβειας. Η δυσκολία μπορεί να προσπεραστεί μέσω της χρησιμοποίησης μόνο ενός τμήματος του πληθυσμού επιλεγόμενου τυχαία, του δείγματος. (Ψωινός, 1999) Σύμφωνα με τον Πραμαγγιούλη, 2008 «Δειγματοληπτική έρευνα είναι η στατιστική έρευνα χαρακτηριστικών ενός πεπερασμένου πληθυσμού η οποία βασίζεται σε πληροφορίες που συλλέγονται από μέρος (δείγμα) αυτού του πληθυσμού». Σύμφωνα με Λαφαζάνη, 2010 θα πρέπει να πληρούνται δύο βασικές προϋποθέσεις προκειμένου να γίνει ορθός σχηματισμός του δείγματος: Πρώτον, θα πρέπει για κάθε εφαρμογή το μέγεθος n του δείγματος να είναι «μεγάλο», έτσι ώστε από τη μία μεριά να προσεγγίζονται πιο αντιπροσωπευτικά αποτελέσματα και από την άλλη μεριά να υπάρχει το περιθώριο να γίνονται στατιστικές δοκιμασίες για την έκβαση καλύτερου αποτελέσματος. Με άλλα λόγια «το περιθώριο σφάλματος είναι συνάρτηση του μεγέθους του δείγματος», άρα μικρό δείγμα σημαίνει μεγαλύτερη αβεβαιότητα για το αποτέλεσμα. 8 «Ως πληθυσμός ορίζεται το σύνολο ατόμων ή αντικειμένων με ένα ή περισσότερα κοινά χαρακτηριστικά». (Λαφαζάνη, 2003) Μεταπτυχιακή διατριβή 24
37 Σ τ α τ ι σ τ ι κ ή π ρ ο σ έ γ γ ι σ η Δεύτερον, θα πρέπει το δείγμα να είναι σίγουρα αντιπροσωπευτικό του πληθυσμού, δηλαδή τα άτομα του δείγματος να συλλέγονται με ένα αμερόληπτο τυχαίο τρόπο, ώστε όλα τα άτομα του πληθυσμού να έχουν τις ίδιες ακριβώς πιθανότητες να επιλεγούν, από τη μία, και από την άλλη να αποδίδονται κατά το δυνατό οι διαφοροποιήσεις του πληθυσμού. Σύμφωνα με το Δημητριάδη, 2002 «Ο χρυσός κανόνας για τη σωστή επιλογή του μεγέθους του δείγματος πρέπει να είναι ο εξής: Το μέγεθος του δείγματος πρέπει να είναι τόσο, ώστε να συνδυάζεται η μέγιστη δυνατή αξιοπιστία των αποτελεσμάτων με τη μέγιστη δυνατή οικονομία σε χρόνο και χρήμα.» Το κατάλληλο μέγεθος του δείγματος μπορεί να βρεθεί με τη βοήθεια περισσότερο χονδροειδών υπολογισμών, οι οποίοι συνδέονται με τον αριθμό των μεταβλητών που χρησιμοποιούνται και την ακρίβεια που απαιτείται στα εξαγόμενα αποτελέσματα. Πιο συγκεκριμένα, σύμφωνα με Δημητριάδης, 2010 στην περίπτωση πολλαπλής γραμμικής παλινδρόμησης ως ελάχιστα αποδεκτό όριο μπορούν να θεωρηθούν οι πέντε (5) οντότητες για κάθε μία ανεξάρτητη μεταβλητή που συμμετέχει στο μοντέλο, ενώ ως επιθυμητό όριο μπορούν να θεωρηθούν οι 15 οντότητες για κάθε μία ανεξάρτητη μεταβλητή. Η τεχνική λήψης ενός δείγματος μπορεί να διαφέρει ανάλογα με τον πληθυσμό και στηρίζεται σε επιστημονικά κριτήρια για τη συγκρότηση του. Οι τεχνικές δειγματοληψίας κατηγοριοποιούνται στις ακόλουθες. (Δαφέρμος, 2005) 1. Απλή τυχαία δειγματοληψία 2. Συστηματική δειγματοληψία 3. Δειγματοληψία κατά στρώματα 4. Δειγματοληψία κατά ομάδες 5. Δειγματοληψία κατά στάδια Παρόλα αυτά η μελέτη των δεδομένων δεν αφορά μόνο τον εντοπισμό τους αλλά παράλληλα την οργάνωση, κατηγοριοποίηση και ταξινόμηση τους, ώστε να μελετηθούν σε τέτοιο βαθμό που να συμμετέχουν με τον καλύτερο δυνατό τρόπο στη στατιστική ανάλυση με στόχο να δώσουν αξιόπιστα αποτελέσματα και λύση στο κάθε ερώτημα του μελετητή. Πολλές είναι οι κατηγορίες που μπορεί να ανήκει το κάθε δεδομένο όπως πρωτογενή δευτερογενή, πρωτοβάθμια δευτεροβάθμια, ποιοτικά ή ποσοτικά, σταθερές ή μεταβλητές. (Λαφαζάνη, 2010) Η συγκεκριμένη διαδικασία ονομάζεται κατηγοριοποίηση και ποσοτικοποίηση των μεταβλητών που περιγράφουν το γεωγραφικό φαινόμενο και είναι το τελευταίο, απαραίτητο βήμα πριν την έναρξη της στατιστικής ανάλυσης. Σύμφωνα με όλα τα παραπάνω σχόλια σχετικά με την προεργασία μιας στατιστικής ανάλυσης παρατίθεται το παρακάτω σχεδιάγραμμα που παρουσιάζει διαγραμματικά τα βασικά στάδια που απαιτούνται. 25
38 Κ ε φ ά λ α ι ο 3 ο 1. Κατανόηση του προς εξέταση φαινομένου 2. Προσδιορισμός μεταβλητών 3. Μελέτη σχετικής βιβλιογραφίας 4. Επιλογή στατιστικής μεθόδου ανάλυσης 5. Σχηματισμός δείγματος με τη βοήθεια περιορισμών και κριτηρίων 6. Κατηγοριοποίηση και ποσοτικοποίηση μεταβλητών 7. Στατιστική ανάλυση Διάγραμμα 3.1: Διαγραμματική απεικόνιση της στατιστικής προεργασίας 3.2 ΕΦΑΡΜΟΓΗ Τα παραπάνω επτά στάδια για τη στατιστική προσέγγιση ενός προβλήματος αναλύονται λεπτομερώς παρακάτω για το γεωγραφικό φαινόμενο που μας ενδιαφέρει και αφορά την προεκτίμηση αγοραίων αξιών ακινήτων. Τα βήματα που προαναφέρονται μαζί με τα ιδιαίτερα χαρακτηριστικά της στατιστικής μεθόδου που επιλέγεται και τους περιορισμούς και προϋποθέσεις της εφαρμογής αποτελούν το βασικό μεθοδολογικό κορμό της εργασίας, στον οποίο στηρίζεται η παρούσα εφαρμογή Επιλογή στατιστικής μεθόδου Το φαινόμενο που εξετάζεται στα πλαίσια της παρούσας μεταπτυχιακής διατριβής χαρακτηρίζεται πολυκριτηριακό και απαιτεί τη χρήση ενός μαθηματικού μοντέλου που να μπορεί να λάβει υπόψη του ένα σύνολο πολλών διαφορετικών μεταβλητών και να διερευνά τις σχέσεις μεταξύ τους. Πιο συγκεκριμένα, το ζητούμενο είναι η πρόβλεψη της αγοραίας αξίας των οριζόντιων ιδιοκτησιών με βάση τις τιμές ενός συνόλου μεταβλητών από τις οποίες εξαρτάται η αγοραία αξία. Σύμφωνα με τις τεχνικές πολυμεταβλητής ανάλυσης πρόκειται για την πρόβλεψη της συμπεριφοράς μιας μεταβλητής (εξαρτημένη), όταν είναι γνωστή η συμπεριφορά (δηλ. οι τιμές) ενός συνόλου άλλων μεταβλητών (ανεξάρτητων). Μεταπτυχιακή διατριβή 26
39 Σ τ α τ ι σ τ ι κ ή π ρ ο σ έ γ γ ι σ η Ένας από τους τρόπους αντιμετώπισης τέτοιων προβλημάτων είναι η τεχνική της πολλαπλής γραμμικής παλινδρόμησης, και αυτή επιλέγεται. Σύμφωνα με Λαφαζάνη, 2008 στα προβλήματα πολλαπλής παλινδρόμησης υπάρχει πάντοτε μία σαφής διάκριση μεταξύ των ανεξάρτητων και της εξαρτημένης μεταβλητής. Οι τιμές που παίρνουν οι ανεξάρτητες τυχαίες μεταβλητές μπορούν να καθοριστούν με ακρίβεια από τον ερευνητή, ενώ η εξαρτημένη που είναι και αυτή μία τυχαία μεταβλητή, μπορεί να πάρει για κάθε «ελεγχόμενη» τιμή της ανεξάρτητης μεταβλητής μία οποιαδήποτε τιμή μεταξύ ορισμένων «λογικών» ορίων. Η γενική εξίσωση ενός πολλαπλού γραμμικού παλινδρομικού μοντέλου είναι της μορφής:,όπου b 0 είναι ο σταθερός όρος, b 1,, b κ οι μερικοί συντελεστές πολλαπλής παλινδρόμησης (partial regression coefficients), χ 1, χ 2,, χ κ οι κ ανεξάρτητες μεταβλητές (predictor variables) και e το σφάλμα του παλινδρομικού μοντέλου. Στην παρούσα εφαρμογή η αντίστοιχη εξίσωση γραμμικής παλινδρόμησης είναι της μορφής: Αγοραία αξία ακινήτων = σταθερός όρος + b1 * (Εμβαδόν) b2 * (Παλαιότητα) + b3 * (Όροφος)+ + bκ * (Θέση στάθμευσης) Για την εφαρμογή της πολλαπλής γραμμικής παλινδρόμησης, όπως φαίνεται και από την παραπάνω εξίσωση, γίνεται αρχικά η υπόθεση ότι η σχέση που συνδέει την αγοραία αξία των ακινήτων με τις μεταβλητές από τις οποίες αυτή εξαρτάται είναι γραμμική. Η θεώρηση της σύνδεσης με γραμμικό τρόπο αποτελεί την πρώτη παραδοχή που γίνεται στο μοντέλο. Στη διεθνή βιβλιογραφία συναντάται η χρήση της γραμμικής πολλαπλής παλινδρόμησης σε ποικιλία φαινομένων που αφορούν πρόβλεψη αξίας γης, τιμής κόστους κατασκευής κλπ. Μολοταύτα μέσω της διαδικασίας εκτέλεσης της παλινδρόμησης θα φανεί ξεκάθαρα στην πορεία εάν υφίσταται η αρχική υπόθεση για ύπαρξη γραμμικότητας και για το ποιες από τις μεταβλητές που λαμβάνουν μέρος στο μοντέλο επιδρούν θετικά ή αρνητικά στη διαμόρφωση της αγοραίας αξίας. Αποτελεί κοινό τόπο ότι ένας από τους παράγοντες που επηρεάζει σημαντικά την αξία των ακινήτων είναι η θέση τους. Παρόλα αυτά όταν ένας εκτιμητής ακινήτων επιθυμεί να υπολογίσει την αγοραία αξία ενός διαμερίσματος αστικού περιβάλλοντος μία από τις μεθόδους που μπορεί να εφαρμόσει είναι κατά κύριο λόγο η συγκριτική μέθοδος εκτίμησης, κάνοντας ταυτόχρονα την παραδοχή για ύπαρξη χωρικής ομοιομορφίας στα δεδομένα που συλλέγει. Η εφαρμογή της μεθόδου σύμφωνα με το Ζεντέλη, 2001 βασίζεται στη γνώση αντίστοιχων αξιών άλλων παρεμφερών ή κατά το δυνατόν παρόμοιων ακινήτων. Η συλλογή ενός ικανού αριθμού πρόσφατων αγοραπωλησιών αφορά ακίνητα που βρίσκονται στην ίδια περιοχή ή στον ίδιο δρόμο έτσι ώστε να θεωρείται ότι η επίδραση της θέσης είναι όμοια για όλα τα ακίνητα. Με παρόμοια λογική επιλέγεται να εφαρμοστεί το μοντέλο της παλινδρόμησης στις πέντε περιοχές μελέτης και με το παραπάνω κριτήριο επιλέγονται και τα πέντε δείγματα. Για τη δυνατότητα εκτέλεσης της μεθόδου γίνεται 27
40 Κ ε φ ά λ α ι ο 3 ο συνεπώς η παραδοχή ότι οι περιοχές μελέτης χαρακτηρίζονται στο εσωτερικό τους από χωρική ομοιομορφία. Στόχος είναι μέσω της εφαρμογής πολλαπλής γραμμικής παλινδρόμησης να εντοπιστούν ποιες είναι οι μεταβλητές που επηρεάζουν εν τέλει την αγοραία αξία των οριζόντιων ιδιοκτησιών και εν συνεχεία να φανεί εάν αυτές οι μεταβλητές είναι όμοιες ή διαφορετικές για κάθε περιοχή μελέτης. Η πολλαπλή γραμμική παλινδρόμηση επιλέγεται έναντι άλλων μεθόδων στατιστικής ανάλυσης, όπως για παράδειγμα της μη γραμμικής πολλαπλής παλινδρόμησης εξαιτίας του γεγονότος ότι πρόκειται για μία εξαιρετικά διαδεδομένη, σίγουρα πιο προσιτή μέθοδο, η οποία πλεονεκτεί στο γεγονός ότι είναι ελεγχόμενη και μπορεί με τη βοήθεια παραδοχών που πρέπει να ικανοποιούνται να οδηγήσει σε στατιστικά ορθά αποτελέσματα και σε ένα μοντέλο που θα συνοδεύεται από αξιοπιστία και σταθερότητα. Πρόκειται λοιπόν για ένα πολύ σημαντικό στατιστικό εργαλείο, το οποίο αφήνει το περιθώριο αποφάσεων στον ερευνητή, έχει δοκιμαστεί σε παρόμοιες εφαρμογές και μπορεί κανείς να το εμπιστευτεί Σχηματισμός του δείγματος Στην παρούσα εφαρμογή τον πληθυσμό μεγέθους Ν αποτελεί το σύνολο των οριζόντιων ιδιοκτησιών που βρίσκονται στις αντίστοιχες περιοχές μελέτης, όπως αυτές ορίζονται στο κεφάλαιο 2 και είναι προς πώληση τη συγκεκριμένη χρονική περίοδο της έρευνας. Όπως γίνεται αντιληπτό, η συγκέντρωση όλων αυτών των στοιχείων μπορεί να χαρακτηριστεί αδύνατη, καθώς δεν υπάρχει κάποιος αρμόδιος φορέας που να διαθέτει τη ζητούμενη πληροφορία συγκεντρωτικά. Στόχος είναι να σχηματιστεί το κατάλληλο στατιστικό δείγμα, ώστε να πληροί τις προϋποθέσεις μεγέθους που έχουν τεθεί και να δώσει ισάξια λύση στα ερωτήματα που καλείται να απαντήσει η παρούσα μεταπτυχιακή διατριβή. Ο σχηματισμός του δείγματος είναι μία ιδιαίτερα σοβαρή διαδικασία καθώς η έκβαση ενός αξιόπιστου αποτελέσματος και ο σχηματισμός ενός ισχυρού μαθηματικού μοντέλου εξαρτάται άμεσα από αυτό. Για τη συγκέντρωση του δείγματος και στις πέντε περιοχές αξιοποιείται η δειγματοληψία κατά στρώματα (ή στρωματοποιημένη δειγματοληψία). Πρόκειται για διαδικασία κατά την οποία πραγματοποιείται διαίρεση του πληθυσμού σε μη επικαλυπτόμενα στρώματα και επιλέγεται ένα απλό τυχαίο δείγμα από κάθε στρώμα. (Ψωινός, 2001). Η συγκεκριμένη διαδικασία δειγματοληψίας εφαρμόζεται στην παρούσα μελέτη, καθώς οι διαφορετικές περιοχές της πόλης της Θεσσαλονίκης και της Βαρκελώνης αντιστοιχούν στα διαφορετικά στρώματα, τα οποία στο εσωτερικό τους είναι ομοιογενή (όσο πιο πολύ γίνεται), ενώ μεταξύ τους είναι διαφορετικά (όσο πιο πολύ γίνεται). Η διαίρεση και κατηγοριοποίηση των περιοχών περιγράφεται αναλυτικά στο δεύτερο κεφάλαιο, ενώ παρακάτω φαίνεται σχηματικά 9 η λογική της στρωματοποιημένης δειγματοληψίας, στις δύο περιοχές μελέτης της Θεσσαλονίκης και στη μία από τις τρεις περιοχές της Βαρκελώνης, αντιπροσωπευτικά. 9 Οι τρεις εικόνες αποτελούν απλό σκαρίφημα επεξήγησης με τη βοήθεια πολυγώνων και όχι χάρτη των περιοχών Μεταπτυχιακή διατριβή 28
41 Σ τ α τ ι σ τ ι κ ή π ρ ο σ έ γ γ ι σ η Εικόνα 3.1: Σκαρίφημα επεξήγησης μεθοδολογίας δειγματοληψίας για την πρώτη περιοχή μελέτης Εικόνα 3.2: Σκαρίφημα επεξήγησης μεθοδολογίας δειγματοληψίας για τη δεύτερη περιοχή μελέτης Εάν θεωρηθεί ότι στην εικόνα 3.1 απεικονίζεται όλος ο δήμος Θεσσαλονίκης, η πρώτη διαίρεση σε στρώματα που πραγματοποιείται (με τα γράμματα Α, Β) είναι η 29
42 Κ ε φ ά λ α ι ο 3 ο διοικητική διαίρεση, σύμφωνα με την οποία διαχωρίζεται ο Δήμος σε δύο δημοτικές ενότητες. Εν συνεχεία, η δημοτική ενότητα της Θεσσαλονίκης (Α) διαιρείται σε επιπλέον στρώματα, τα οποία αντιστοιχίζονται στις πέντε βασικές δημοτικές κοινότητες (Α1, Α2, Α3, Α4, Α5), όπως ορίζονται από το πρόγραμμα «Καλλικράτης». Παρόλα αυτά στο στρώμα Α1 που είναι το κέντρο της πόλης υπάρχουν διαφοροποιήσεις και έντονη ποικιλομορφία σε όλα τα επίπεδα, άρα μεγάλη διακύμανση στις αξίες των ακινήτων που τοποθετούνται στο συγκεκριμένο στρώμα. Για αυτό το λόγο πραγματοποιείται επιπλέον στρωματοποίηση (Α11, Α12, Α13, Α14), ώστε να υπάρχει όσο γίνεται περισσότερη ομοιομορφία στο εσωτερικό του κάθε στρώματος. Στη συνέχεια, η περιοχή A12 διαιρείται σε περαιτέρω στρώματα, καθώς στο εσωτερικό της υπάρχουν διαμερίσματα με πρόσοψη σε κεντρικούς δρόμους, σε στενά δρομάκια του κέντρου, σε πλατείες κλπ. Για το σχηματισμό του δείγματος συλλέγονται διαμερίσματα από κάθε επιμέρους υποπεριοχή, προκειμένου να είναι αντιπροσωπευτικό το δείγμα της πρώτης περιοχής μελέτης. Η εικόνα 3.2 θεωρείται ότι απεικονίζει όλο το Δήμο Ελευθέριου Κορδελιού στο δυτικό τμήμα της πόλης. Ο πρώτος διαχωρισμός που δημιουργεί τα πρώτα στρώματα στηρίζεται στη διοικητική διαίρεση στις δύο δημοτικές ενότητες του δήμου, Δημοτική ενότητα Ελευθερίου Κορδελιού και Δημοτική ενότητα Ευόσμου (Α, Β). Στην περίπτωση της δημοτικής ενότητας του Ευόσμου πραγματοποιούνται επιπλέον διαιρέσεις, οι οποίες διαμορφώνονται βάσει των γενικών χαρακτηριστικών και αντικειμενικών αξιών στην περιοχή και δημιουργείται ένα ακόμη επίπεδο στρωματοποίησης (Β1, Β2, Β3, Β4). Για να προσεγγίζεται καλύτερα ο πληθυσμός από το δείγμα, συλλέγονται διαμερίσματα από κάθε κατηγορία Β1, Β2 κλπ και εν συνεχεία ενώνονται για να αποτελέσουν το αντιπροσωπευτικό δείγμα της δεύτερης περιοχής μελέτης. Με τη ίδια ακριβώς λογική δημιουργούνται τα επίπεδα στρωματοποίησης για τις τρεις περιοχές μελέτης της Βαρκελώνης. Χαρακτηριστικό είναι το παράδειγμα της κεντρικής περιοχής Eixample που αποτελεί την τρίτη περιοχή μελέτης της εφαρμογής (Σκαρίφημα 3.3). Η πρώτη διαίρεση σε στρώματα (γράμματα Α, Β κλπ) αποτελεί τη διοικητική διαίρεση που διαφοροποιεί τους αντίστοιχους «Δήμους» για τα δεδομένα της Ελλάδας. Στη συνέχεια ο Δήμος Βαρκελώνης χωρίζεται σε περιοχές (Α1, Α2, Α3.. Α10), οι οποίες διαφέρουν γεωγραφικά σε μεγάλο βαθμό, διότι είναι ανομοιογενείς όσον αφορά τη θέση, το εισόδημα των κατοίκων, την κοινωνική τους θέση και τα χαρακτηριστικά των κατοικιών. Συγκεκριμένα, το στρώμα Α5 αποτελεί την περιοχή Eixample η οποία διαιρείται σε περισσότερα στρώματα (υποπεριοχές). Απλό τυχαίο δείγμα συλλέγεται από τα έξι στρώματα Α51, Α52, Α53, Α54, Α55 και Α56 ώστε με την ένωση τους να αποτελέσουν το αντιπροσωπευτικό δείγμα της τρίτης περιοχής μελέτης. Μεταπτυχιακή διατριβή 30
43 Σ τ α τ ι σ τ ι κ ή π ρ ο σ έ γ γ ι σ η Εικόνα 3.3: Σκαρίφημα επεξήγησης μεθοδολογίας δειγματοληψίας για την Τρίτη περιοχή μελέτης Μέγεθος δείγματος Για τον έλεγχο του μεγέθους του δείγματος συμμετέχουν στο μοντέλο για την τελική διαμόρφωση της αγοραίας αξίας των ακινήτων. Όπως έχει αναφερθεί παραπάνω ως ελάχιστα αποδεκτό όριο θεωρούνται οι οντότητες για κάθε ανεξάρτητη μεταβλητή. Στην παρούσα εφαρμογή, όπως αναφέρεται αναλυτικά παρακάτω, ο αριθμός των μεταβλητών που θεωρείται ότι επηρεάζει τη διαμόρφωση της αγοραίας αξίας των διαμερισμάτων για την πόλη της Θεσσαλονίκης, με βάση την πηγή συλλογής των δεδομένων είναι συνολικά οκτώ (8), ενώ για την πόλη της Βαρκελώνης είναι συνολικά εννέα (9). Σύμφωνα με όρια που τίθενται στην ενότητα 3.1, για την περίπτωση της Θεσσαλονίκης ισχύει: Μέγεθος δείγματος n 5*8 που πρέπει να υπάρχει τουλάχιστον είναι 40. Μέγεθος δείγματος n 15*8 που θεωρείται ιδιαίτερα ικανοποιητικό είναι 120. Λαμβάνοντας υπόψη τα παραπάνω αλλά και με εμπόδιο τη μεγάλη δυσκολία εντοπισμού ακινήτων με χωρική αναφορά στις δύο περιοχές της Θεσσαλονίκης, το μέγεθος του δείγματος που συλλέγεται είναι 60 οντότητες ανά περιοχή μελέτης. Το μέγεθος του δείγματος θεωρείται ικανοποιητικό εφόσον βρίσκεται πάνω από το κατώτατο όριο ανοχής αλλά και εξαιτίας των δυσκολιών που παρατηρούνται, της απόρριψης εγγραφών για όσο το δυνατό καλύτερη αξιοπιστία του δείγματος και των δυνατοτήτων της παρούσας έρευνας. Ικανοποιητικό μπορεί επίσης να θεωρηθεί, διότι σύμφωνα με τη βιβλιογραφία (π.χ. 31
44 Κ ε φ ά λ α ι ο 3 ο Δαφέρμος, 2005) μεγάλα στατιστικά δείγματα θεωρούνται εκείνα που ξεπερνούν τις 30 οντότητες. Για την περίπτωση της Βαρκελώνης ισχύει αντίστοιχα: Μέγεθος δείγματος n 5*9 που πρέπει να υπάρχει τουλάχιστον είναι 45. Μέγεθος δείγματος n 15*9 που θεωρείται ιδιαίτερα ικανοποιητικό είναι 135. Τα μεγέθη των δειγμάτων που συλλέγονται είναι διαφορετικά για κάθε μία περιοχή της πόλης της Βαρκελώνης. Πιο συγκεκριμένα, για την περιοχή Eixample συλλέγονται 75 οριζόντιες ιδιοκτησίες, για την περιοχή Sant Marti συλλέγονται 60 και για την περιοχή Badalona συλλέγονται 80. Ο κύριος λόγος για τον οποίο συλλέγονται στις δύο από τις τρεις περιοχές μεγαλύτερα δείγματα οφείλεται κατά κύριο λόγο στο γεγονός ότι είναι διαθέσιμες περισσότερες εγγραφές. Συνεπώς, για τους ίδιους λόγους που αναφέρονται παραπάνω και βάσει της θεωρίας τα δείγματα των τριών τελευταίων περιοχών θεωρούνται ικανοποιητικά και ικανά να δημιουργήσουν μοντέλα προεκτίμησης των αγοραίων αξιών. Φυσικά, η τελευταία διαπίστωση θα πρέπει να επαληθευτεί μέσω της στατιστικής ανάλυσης που ακολουθεί Διαδικασία δειγματοληψίας Κρίνεται αδύνατο από την αρχή της μελέτης ενός φαινομένου να είναι ξεκάθαρες όλες οι πτυχές του. Αυτές ανακαλύπτονται σταδιακά κατά τη διαδικασία συλλογής των δεδομένων και της επεξεργασίας τους μέσω της στατιστικής ανάλυσης. Η διαδικασία συλλογής του δείγματος αποτελεί την πρώτη φάση προβληματισμού καθώς κάνουν την εμφάνιση τους εμπόδια και σημεία που πρέπει να οριοθετηθούν μέσω της λήψης αποφάσεων. Παρακάτω αναφέρονται όλα τα σημεία προβληματισμού και διατυπώνονται οι περιορισμοί και οι αποφάσεις της κεντρικής μεθοδολογίας της εφαρμογής. Πρωταρχικό ζήτημα προς διερεύνηση είναι η πηγή συλλογής των δεδομένων. Από την ελληνική βιβλιογραφία γνωρίζουμε ότι ένας εκτιμητής μπορεί να συλλέξει δεδομένα από εργολάβους, μηχανικούς, εκτιμητές, μεσίτες, έντυπες και ηλεκτρονικές αγγελίες, κατά τόπους εφορίες κλπ. Καμία από τις παραπάνω πηγές δεν αποτελεί οργανωμένη βάση δεδομένων σε επίπεδο είτε τοπικό, είτε εθνικό. Συνεπώς, η απουσία οργανωμένης τράπεζας πληροφοριών από οποιονδήποτε ιδιωτικό ή δημόσιο φορέα οδηγεί σε μία μόνο επιλογή που είναι το διαδίκτυο. Σήμερα, η οργάνωση των ιστοσελίδων που περιέχουν αγγελίες εμπλουτίζεται ιδιαίτερα με τη χρήση ακριβούς γεωγραφικής θέσης, φωτογραφικού υλικού και μεγάλου πλήθους αγγελιών που εισάγονται από ιδιώτες και κυρίως από μεγάλα μεσιτικά γραφεία σε όλη την πόλη. Η εύρεση κάθε είδους πληροφορίας μέσω του διαδικτύου αποτελεί το μέλλον, συνεπώς μία σύγχρονη έρευνα δε μπορεί να μη συγχρονίζεται με αυτό. Ταυτόχρονα, θέλοντας κανείς να αντιμετωπίσει την εφαρμογή με μία πιο σφαιρική σκοπιά που να δίνει τη δυνατότητα για δημιουργία παρόμοιων εφαρμογών πέρα από τα σύνορα της Θεσσαλονίκης, αλλά και της Ελλάδας κατ επέκταση θα κατέληγε και πάλι στην επιλογή των αγγελιών μέσω διαδικτύου. Πρόκειται για ένα προσιτό προς όλους τρόπο συλλογής δεδομένων, που σίγουρα ξεπερνά τα σύνορα και δίνει Μεταπτυχιακή διατριβή 32
45 Σ τ α τ ι σ τ ι κ ή π ρ ο σ έ γ γ ι σ η τη δυνατότητα στον εκάστοτε ερευνητή να διευρύνει τις ερευνητικές του ανησυχίες σε ευρύτερο πεδίο, καθώς με αυτόν τον τρόπο πετυχαίνει ομοιομορφία στις ανεξάρτητες μεταβλητές που συλλέγει και μπορεί να συγκρίνει τη μέθοδο σε πολύ διαφορετικές γεωγραφικά περιοχές. Πέρα από τα θετικά γνωρίσματα της συλλογής δεδομένων από το διαδίκτυο, σε μία τέτοια προσπάθεια ελλοχεύουν ταυτόχρονα κίνδυνοι, οι οποίοι πρέπει να εντοπιστούν και να αποφευχθούν μέσω περιορισμών κατά τη συλλογή του δείγματος. Σε κάθε περίπτωση, η συλλογή κάθε μιας οριζόντιας ιδιοκτησίας θα πρέπει να συνοδεύεται από κριτική σκέψη, ώστε να αποφευχθούν σε πρώτη φάση τα σκόπιμα ή όχι χονδροειδή λάθη, με την παρουσία παράλογων τιμών στις μεταβλητές σε σχέση με το υπόλοιπο δείγμα, αναντιστοιχίας εικόνας με περιγραφική πληροφορία κλπ. Στις περιπτώσεις που εντοπίζονται τέτοιου είδους λάθη διαγράφονται απευθείας και αποφεύγεται η συμμετοχή τους στη στατιστική ανάλυση. Προσπερνώντας τα χονδροειδή λάθη που μπορεί να υπάρχουν στο δείγμα πρέπει να ληφθεί υπόψη και μία άλλη κατηγορία σφαλμάτων. Ένα βασικό γνώρισμα της λήψης του δείγματος είναι η ύπαρξη λαθών που οφείλονται στον τρόπο μέτρησης της κάθε μεταβλητής, ο οποίος είναι πολύ πιθανό να είναι υποκειμενικός. Σε αυτή την περίπτωση ο αριθμός των παραπάνω περιπτώσεων είναι άγνωστος και ο εντοπισμός τους είναι αδύνατος με αποτέλεσμα να γίνεται η βασική παραδοχή ότι τα σφάλματα είναι τυχαία και όχι συστηματικά, ενώ για να ισχύει η παραπάνω πρόταση ισχύουν οι παρακάτω προϋποθέσεις : 1. Τα στατιστικά μεγέθη των τιμών που προκύπτουν κατά τη μέτρηση είναι ίσα με τα στατιστικά μεγέθη των πραγματικών τιμών και 2. Οι μετρήσεις είναι μεταξύ τους ανεξάρτητες, δηλαδή δεν επηρεάζεται η τιμή της μίας μέτρησης από τις άλλες (Λαφαζάνη, 2010) Πολύ βασικό κομμάτι της διαδικασίας λήψης του δείγματος αποτελεί επίσης η ακριβής χωρική τοποθέτηση όλων των διαμερισμάτων. Πρόκειται για εφαρμογή με γεωγραφικό χαρακτήρα, συνεπώς η απόδοση της θέσης του δείγματος και η οπτικοποίηση του οδηγεί σε μία ολοκληρωμένη μελέτη και κάνει σαφή τα χωρικά της όρια. Πρακτικά στην πόλη της Θεσσαλονίκης όπου είναι διαθέσιμο χωρικό υπόβαθρο 10 (shapefiles), απορρίπτονται οι αγγελίες οι οποίες δεν περιέχουν χωρική αναφορά, διότι στα πλαίσια της εφαρμογής στη συνέχεια γίνεται μία προσπάθεια εφαρμογής της μεθόδου σε περιβάλλον Γεωγραφικών Συστημάτων Πληροφοριών, το οποίο επιβάλλει την ύπαρξη θέσης του δείγματος. Επίσης, δε μπορεί να αποκλειστεί μελλοντικά η δυνατότητα επέκτασης της εφαρμογής με την πιθανή χρήση αποστάσεων και γεωγραφικών δεδομένων που να προστεθούν στην ήδη υπάρχουσα μελέτη. Τέλος, ως ένα βαθμό η ηλεκτρονική αγγελία που είναι πλήρης (δηλ. περιλαμβάνει και τη χωρική αναφορά στο χάρτη της πόλης) δείχνει μία 10 Η χωρική αναφορά των διαμερισμάτων στην παρούσα έρευνα παραμένει δυστυχώς πλεονέκτημα μόνο της Θεσσαλονίκης, διότι η απουσία χωρικού υποβάθρου για την πόλη της Βαρκελώνης αποτέλεσε τροχοπέδη. 33
46 Κ ε φ ά λ α ι ο 3 ο συνέπεια και σοβαρότητα του ιδιοκτήτη που την ανέβασε, άρα θεωρητικά κρίνεται περισσότερο αξιόπιστη. Επίσης, στα πλαίσια της παρούσας εφαρμογής κρίνεται απαραίτητη η συλλογή μόνο των αγγελιών όπου περιέχουν φωτογραφικό υλικό του διαμερίσματος. Ο βασικός λόγος είναι ότι μέσω των φωτογραφιών διαφαίνεται η γενική κατάσταση του ακινήτου (ποιότητα δαπέδων, ανακαινισμένο μπάνιο κλπ.) και άρα δίνεται η δυνατότητα για την εισαγωγή άλλης μίας μεταβλητής, η οποία αναφέρεται στην κατάσταση του ακινήτου και στο βαθμό συντήρησης του. Για την ορθή επιλογή δείγματος, ένας παράγοντας που πρέπει επίσης να εξεταστεί διεξοδικά σχετικά με την πηγή των δεδομένων είναι η ιστοσελίδα ή οι ιστοσελίδες από τις οποίες θα αντληθεί η πληροφορία και σε τι υπερέχουν αυτές από άλλες, οι οποίες εν τέλει δεν επιλέγονται. Βασικό κριτήριο στην παρούσα εργασία για την τελική επιλογή υπήρξε το πόσο διαδεδομένος είναι ο ιστότοπος, το πλήθος αγγελιών που προσφέρει, η οργανωμένη και αναλυτική παρουσίαση των ακινήτων του και τέλος η ύπαρξη ή όχι χρέωσης του ιδιώτη ή επαγγελματία που ενδιαφέρεται να πωλήσει ένα ακίνητο. Για τους παραπάνω λόγους ο ιστότοπος που τελικά επιλέγεται για τη Θεσσαλονίκη είναι ο spitogatos.gr διότι διαθέτει μία ιδιαίτερα μεγάλη βάση δεδομένων με εκατοντάδες χιλιάδες αγγελίες για όλη την Ελλάδα, φωτογραφικό υλικό και ελκύει εξαιτίας των πολλών μηνιαίων επισκεπτών, της οργάνωσης του και των υπηρεσιών και δυνατοτήτων που προσφέρει ένα πολύ μεγάλο αριθμό από επαγγελματίες μεσίτες, μεγάλα κτηματομεσιτικά γραφεία, αλλά και ιδιώτες. Επίσης, για κάθε αγγελία υπάρχει αυτόματη λήξη της έπειτα από ένα διάστημα από την ημερομηνία καταχώρησης και είναι στην ευχέρεια του ιδιώτη ή μεσίτη εάν θα την ανανεώσει, γεγονός που επιβεβαιώνει το πόσο ενημερωμένα είναι τα δεδομένα των αγγελιών και επιβεβαιώνεται η σοβαρότητα που απαιτείται από τους ενδιαφερόμενους. Επίσης, με την επιλογή του spitogatos.gr ικανοποιείται ο στόχος που τίθεται παραπάνω για δυνατότητα εφαρμογής της μελέτης από κάθε μελετητή που βρίσκεται εκτός συνόρων, διότι οι αγγελίες του spitogatos.gr αυτόματα προβάλλονται στην ιστοσελίδα που αποτελεί την αγγλική εκδοχή του. Ταυτόχρονα, για την ύπαρξη ομοιομορφίας των δεδομένων που συλλέγονται, η οποία είναι απαραίτητη για τη μετέπειτα επεξεργασία τους, γίνεται μία προσπάθεια να μην επιλεγούν άλλοι ιστότοποι ως πηγές πληροφοριών, εκτός από την περίπτωση του Δήμου Ευόσμου, όπου εξαιτίας μη συγκέντρωσης του επιθυμητού αριθμού δείγματος (λόγω μικρότερης προσφοράς αξιόπιστων και με φωτογραφικό υλικό αγγελιών στη συγκεκριμένη περιοχή) ένας μικρός αριθμός αγγελιών αντλούνται από άλλο ιστότοπο 11. Αντίστοιχα για τη Βαρκελώνη αξιοποιείται η ιστοσελίδα fotocasa.com, η οποία συγκεντρώνει ένα πάρα πολύ μεγάλο πλήθος ακινήτων, τα περισσότερα εκ των οποίων διαθέτουν πλούσιο και αντιπροσωπευτικό φωτογραφικό υλικό, χωρική τοποθέτηση, πλήθος πληροφοριών για τα διαμερίσματα και χάρτες, οι οποίοι διευκολύνουν πάρα πολύ την ορθή συλλογή των δεδομένων. Η ιστοσελίδα παρόλο που παρέχει τις πληροφορίες στην ισπανική γλώσσα προτιμήθηκε έναντι των αντίστοιχων αγγλικών ιστότοπων εξαιτίας της καλύτερης οργάνωσης της, αλλά κυρίως εξαιτίας του μεγάλου πλήθους δεδομένων της Μεταπτυχιακή διατριβή 34
47 Σ τ α τ ι σ τ ι κ ή π ρ ο σ έ γ γ ι σ η Ένα επιπλέον στοιχείο που πρέπει να διευκρινιστεί αφορά την εξαρτημένη μεταβλητή, η οποία όπως παρέχεται από τις ηλεκτρονικές αγγελίες ισοδυναμεί με τη ζητούμενη τιμή πώλησης των διαμερισμάτων του δείγματος. Είναι αναμενόμενο να υπάρχει μία διαφορά μεταξύ της αγοραίας αξίας του ακινήτου και της τιμής που δίνεται στο διαδίκτυο, σε μερικά ακίνητα μεγαλύτερη, σε άλλα μικρότερη και σε άλλα μηδενική. Σύμφωνα με ειδικούς της αγοράς ακινήτων 12 της Θεσσαλονίκης, η τελική τιμή πώλησης, όπως αυτή έχει διαμορφωθεί σήμερα με τις υπάρχουσες συνθήκες στην κτηματαγορά, διαφέρει σημαντικά από την αρχικά ζητούμενη. Η διαφορά συνήθως κυμαίνεται σε μείωση από 10 έως 20% και εξαρτάται συνήθως από τον τρόπο εξόφλησης του ποσού και από τη μειωμένη ζήτηση. Ακραίες διαφορές εντοπίζονται και στις ενοικιάσεις επαγγελματικών χώρων, των οποίων οι τιμές μπορεί να μειωθούν και κατά 50%. Στα πλαίσια της εργασίας κρίνεται αδύνατη η γνώση της ακριβούς τιμής αγοραπωλησίας του κάθε ακινήτου, οπότε προτιμάται να μη γίνει η οποιαδήποτε αυθαίρετη αλλαγή των αρχικών τιμών και ορίζεται ως παραδοχή ότι οι ζητούμενες τιμές πώλησης είναι και οι αγοραίες αξίες των ακινήτων. Σύμφωνα με τις παραπάνω παραγράφους, στα πλαίσια της παρούσας έρευνας, η συλλογή των δεδομένων αποτελεί σίγουρα σημείο προβληματισμού, καθώς θα πρέπει να συνδυάζονται απαραίτητα πρώτον η συλλογή ενός μεγάλου αριθμού δεδομένων, το οποίο να είναι ενημερωμένο για να αντικατοπτριστεί όσο είναι εφικτό η σημερινή κατάσταση στην αγορά ακινήτων, δεύτερον να γίνεται η χωρική τοποθέτηση των διαμερισμάτων και τρίτον να υπάρχει φωτογραφικό υλικό. Εξαιτίας των παραπάνω περιορισμών που τίθενται και επιλογής της Βαρκελώνης ως επιπλέον πόλη έρευνας δικαιολογείται για ακόμη μία φορά η συλλογή των δεδομένων από το διαδίκτυο. Παρόλα αυτά, ακόμη και εάν η μελέτη περιοριζόταν αυστηρά στα σύνορα της Θεσσαλονίκης, οι αγγελίες από τον έντυπο τύπο δε θα ήταν επαρκείς διότι δε συνοδεύονται από φωτογραφικό υλικό και δεν γίνεται απόλυτη γεωγραφική αναφορά. Επίσης, η συλλογή του δείγματος από επιτόπια έρευνα, δηλαδή λήψη συνεντεύξεων σε μεσίτες ή μέσω ερωτηματολογίων (συνήθης τρόπος συλλογής δείγματος από ένα πληθυσμό στις στατιστικές μελέτες), δε θα ήταν εφικτή διότι οι μεν μεσίτες τις περισσότερες φορές δεν είναι εύκολα συνεργάσιμοι λόγω καχυποψίας και κυρίως όταν έχει να κάνει με μεγάλο αριθμό πληροφορίας, ενώ τα ερωτηματολόγια δεν θα μπορούσαν να έχουν πρακτική εφαρμογή στην παρούσα μελέτη. Αξιόπιστα δεδομένα κατέχουν όλες οι τράπεζες μέσω των εκτιμήσεων και επανεκτιμήσεων που πραγματοποιούνται για τη λήψη δανείων, τα οποία όμως δεν είναι πρωτογενή και όχι διαθέσιμα. Τέλος, στον ελλαδικό χώρο δεν υπάρχει αρμόδιος δημόσιος φορέας που να διαθέτει μία βάση δεδομένων με το σύνολο των αγοραπωλησιών που πραγματοποιούνται, ώστε να μπορούσαν να αξιοποιηθούν για παρόμοια εφαρμογή Κατηγοριοποίηση και ποσοτικοποίηση των ανεξάρτητων μεταβλητών Στην παρούσα εργασία, έχει γίνει κατανοητό από προηγούμενα κεφάλαια ότι η μονάδα αναζήτησης δεδομένων είναι το διαμέρισμα και ζητείται να προσδιοριστούν τα διαστήματα πρόβλεψης της αγοραίας αξίας ακινήτων μέσω μίας σειράς μεταβλητών. Η 12 Συνέντευξη του Χ. Μπακιρτζόγλου, Αγρονόμου Τοπογράφου Μηχανικού και Εκτιμητή Ακινήτων. 35
48 Κ ε φ ά λ α ι ο 3 ο διαδικασία συλλογής των δεδομένων και η επεξεργασία τους πραγματοποιείται σε πέντε ξεχωριστά σύνολα δεδομένων τα οποία ως μονάδα έχουν το διαμέρισμα αλλά πρόκειται για διακριτά σύνολα. Παρόλο που η κάθε περιοχή έχει τα δικά της χαρακτηριστικά γνωρίσματα και ιδιαιτερότητες όσον αφορά τη θέση τους και τα πολεοδομικά τους χαρακτηριστικά, οι ιδιοκτησίες έχουν την ίδια ακριβώς λογική. Πρόκειται για περιοχές με πολυώροφες οικοδομές, οι οποίες εμπεριέχουν ένα μεγάλο αριθμό οριζόντιων ιδιοκτησιών η κάθε μία και η τιμή τους εξαρτάται από τους ίδιου παράγοντες. Παρόλα αυτά εξετάζοντας τα δεδομένα που παρέχονται από τους δύο ιστότοπους προκύπτει το συμπέρασμα ότι η υπάρχει μία σχετική ομοιομορφία στα δεδομένα τους. Με άλλα λόγια οι περισσότερες μεταβλητές είναι κοινές και για τις δύο πόλεις, ενώ υπάρχουν και κάποιες μεταβλητές οι οποίες βρίσκονται μόνο στη μία ή μόνο στην άλλη πόλη. Για αυτό το λόγο επιλέγεται να δημιουργηθούν δύο διαφορετικά μοντέλα μεταβλητών, ένα για κάθε πόλη, προκειμένου να είναι αντιπροσωπευτικά και να εξεταστεί η κάθε πόλη μεμονωμένα ανάλογα με τις ιδιαιτερότητες της, όσον αφορά την αγορά ακινήτων. Συνεπώς, η επιλογή των τελικών ανεξάρτητων μεταβλητών θα είναι μίας μορφής για τα δύο σύνολα της Θεσσαλονίκης και μίας άλλης μορφής για τα τρία σύνολα της Βαρκελώνης. Η σύγκριση των στατιστικών αποτελεσμάτων που θα προκύψουν από το μαθηματικό μοντέλο θα αποτελεί ταυτόχρονα ένα ιδιαίτερα ενδιαφέρον αντικείμενο σχολιασμού αφού από τη μία μεριά θα φανούν με άμεσο τρόπο οι ομοιότητες και διαφορές της αγοράς ακινήτων στις δύο ευρωπαϊκές πόλεις και από την άλλη μεριά θα εντοπιστούν οι ομοιότητες και διαφορές μεταξύ των περιοχών μελέτης της κάθε πόλης ξεχωριστά. Επίσης, πρέπει να γίνει σαφές από την αρχή του κεφαλαίου ότι η επιλογή των μεταβλητών στηρίζεται στην σκοπιά με την οποία προσεγγίζεται το θέμα θεωρητικά. Η ανάλυση που θα ακολουθήσει και η μαθηματική προσέγγιση του προβλήματος θα δείξουν στην πραγματικότητα, ποιες από τις μεταβλητές επηρεάζουν την αγοραία αξία των διαμερισμάτων των δειγμάτων και ποιες είναι ικανές να δημιουργήσουν ένα όσο το δυνατό πιο ισχυρό μοντέλο για την μετέπειτα πρόβλεψη αξιών ακινήτων. Ο αριθμός των ανεξάρτητων μεταβλητών που θα συμμετέχουν στην παρούσα μελέτη είναι συνολικά οκτώ για την Θεσσαλονίκη και εννέα για τη Βαρκελώνη. Οι μεταβλητές συγκεντρώνονται έπειτα από τη μελέτη της βιβλιογραφίας και από τα δεδομένα που είναι διαθέσιμα στις ιστοσελίδες των ηλεκτρονικών αγγελιών. Πρόκειται για τις ανεξάρτητες μεταβλητές, δηλαδή τις μεταβλητές εκείνες που θεωρούμε ότι επιδρούν στην εξαρτημένη μεταβλητή (αγοραία αξία ακινήτων) και αποτελούν την αιτία που επηρεάζουν τη συμπεριφορά της (Λαφαζάνη,2010). Οι προαναφερθείσες μεταβλητές φαίνονται στους πίνακες 3.1 και 3.2. Μεταπτυχιακή διατριβή 36
49 Σ τ α τ ι σ τ ι κ ή π ρ ο σ έ γ γ ι σ η Πίνακας 3.1: Ανεξάρτητες μεταβλητές των οποίων η επίδραση στην αγοραία αξία των ακινήτων εξετάζεται για την πόλη της Θεσσαλονίκης Σύνολο ανεξάρτητων μεταβλητών 1 Εμβαδόν 2 Παλαιότητα 3 Όροφος 4 Θέση Διαμερίσματος/Γωνιακό ή όχι 5 Ύπαρξη ή απουσία ανελκυστήρα 6 Είδος Θέρμανσης 7 Κατάσταση ακινήτου 8 Ύπαρξη ή όχι θέσης στάθμευσης Πίνακας 3.2: Ανεξάρτητες μεταβλητές των οποίων η επίδραση στην αγοραία αξία των ακινήτων εξετάζεται για την πόλη της Βαρκελώνης Σύνολο ανεξάρτητων μεταβλητών 1 Εμβαδόν 2 Παλαιότητα 3 Όροφος 4 Ύπαρξη ή απουσία ανελκυστήρα 5 Είδος Θέρμανσης 6 Κατάσταση ακινήτου 7 Ύπαρξη ή όχι θέσης στάθμευσης 8 Αριθμός Δωματίων 9 Αριθμός Μπάνιων Όπως είναι ορατό από τους παραπάνω πίνακες, οι μεταβλητές που διαφέρουν μεταξύ των δύο πόλεων είναι οι ακόλουθες: 1. Θέση διαμερίσματος/γωνιακό ή όχι: Πρόκειται για ένα παράγοντα επίδρασης της αξίας ενός ακινήτου, ο οποίος επισημαίνεται πάντα στα χαρακτηριστικά των διαμερισμάτων της Θεσσαλονίκης και καθόλου στην πόλη της Βαρκελώνης. Πρόκειται για μία μεταβλητή που κρίνοντας από την αναφορά της στον ισπανικό ιστότοπο δεν διαδραματίζει τόσο σημαντικό ρόλο στη διαμόρφωση αξιών των διαμερισμάτων, όσο στην πόλη της Θεσσαλονίκης. 2. Αριθμός Δωματίων: Πρόκειται για ένα παράγοντα διαμόρφωσης της αξίας, ο οποίος υπάρχει ως πληροφορία και στις δύο πόλεις, με τη διαφορά ότι οι τιμές που δέχεται στην περιοχή της Βαρκελώνης παρουσιάζουν ποικιλομορφία και άρα φαίνεται να επιδρούν σημαντικά στη διαμόρφωση της αξίας των ακινήτων. Στις δύο περιοχές μελέτης της Θεσσαλονίκης τα διαμερίσματα διαθέτουν στη μεγαλύτερη 37
50 Κ ε φ ά λ α ι ο 3 ο πλειοψηφία τους δύο δωμάτια, σε αντίθεση με τα διαμερίσματα της Βαρκελώνης που έχουν μεγαλύτερα εμβαδά και διαφορετική διάταξη. 3. Αριθμός Μπάνιων: Όμοια για το συγκεκριμένο χαρακτηριστικό των διαμερισμάτων της Βαρκελώνης παρατηρούνται τιμές από ένα έως και τρία μπάνια με τιμές οι οποίες μοιράζονται σχεδόν ισόποσα στο μέγεθος των δειγμάτων. Αντίθετα, το τμήμα του κέντρου που επιλέγεται για το Δήμο Θεσσαλονίκης και ο πρώην Δήμος Ευόσμου έχουν στη μεγάλη πλειοψηφία τους μόνο ένα μπάνιο. Συνεπώς, πρόκειται για μία μεταβλητή που φαίνεται να επιδρά στη διαμόρφωση των αξιών μόνο της μία πόλης. Παρακάτω δίνονται τα γενικότερα χαρακτηριστικά της εξαρτημένης και των ανεξάρτητων μεταβλητών και περιγράφονται οι ποσοτικοποιήσεις που πραγματοποιούνται στην παρούσα εφαρμογή. Αγοραία αξία: Πρόκειται για μία συνεχή ποσοτική μεταβλητή, η οποία μετριέται σε χιλιάδες ευρώ, δηλαδή αναφέρεται στο συνολικό ποσό πώλησης και όχι στην τιμή ανά τμ. Εμβαδόν: Πρόκειται για μία συνεχή ποσοτική μεταβλητή, η οποία ως μονάδα μέτρησης έχει τα τετραγωνικά μέτρα (τμ). Στη συγκεκριμένη μεταβλητή, δίνεται κάθε φορά η τιμή που εμφανίζεται στην αντίστοιχη ιστοσελίδα, χωρίς δυστυχώς να γίνεται σαφές στην πηγή δεδομένων εάν αναφέρεται στο καθαρό ή μεικτό εμβαδόν του διαμερίσματος. Παλαιότητα: Είναι επίσης μία συνεχής ποσοτική μεταβλητή, διότι αφορά το χρόνο με μονάδα μέτρησης τα έτη που πέρασαν από τη χρονιά που αποπερατώθηκε η κατασκευή της οικοδομής. Το διαδίκτυο ως τιμή παλαιότητας δίνει πάντοτε τη χρονιά ανέγερσης της οικοδομής, δεδομένο όμως που επεξεργάζεται στη συνέχεια για να δοθεί ως τιμή μεταβλητής ο αριθμός των ετών. Όπως γίνεται κατανοητό και θα φανεί παρακάτω από τις εξισώσεις που προκύπτουν, πρόκειται για μία μεταβλητή που συσχετίζεται αρνητικά με την εξαρτημένη μεταβλητή του μοντέλου, διότι όσο αυξάνεται η τιμή της παλαιότητας, τόσο μειώνεται και η αγοραία αξία του διαμερίσματος. Όροφος: Η μεταβλητή που αναφέρεται στον όροφο είναι μία ποιοτική μεταβλητή, η οποία παραμένει στατιστικά επεξεργάσιμη έπειτα από την ποσοτικοποίηση της βάσει συγκεκριμένων κριτηρίων. Πιο συγκεκριμένα, τα διαμερίσματα που βρίσκονται στο ισόγειο ή στον ημιώροφο οικοδομής παίρνουν την τιμή ένα (1), ο πρώτος όροφος παίρνει την τιμή δύο (2), ο δεύτερος όροφος την τιμή τρία (3) κ.ο.κ. Τέλος, τα διαμερίσματα που αποτελούν εσοχές οικοδομής (ρετιρέ) δέχονται δύο επιπλέον μονάδες σε σχέση με τον όροφο που ήδη τοποθετούνται, διότι πρόκειται για διαμερίσματα που έχουν στη γενική περίπτωση καλύτερη θέα, μεγάλο μπαλκόνι σε σχέση με όλα τα άλλα διαμερίσματα της οικοδομής και κατά συνέπεια η αξία τους ανά τετραγωνικό μέτρο είναι μεγαλύτερη. Η ιδιαιτερότητα των ρετιρέ εντοπίζεται μόνο στην Θεσσαλονίκη και όχι στη Βαρκελώνη (τουλάχιστον όσον αφορά το δείγμα που συλλέχθηκε). Μεταπτυχιακή διατριβή 38
51 Σ τ α τ ι σ τ ι κ ή π ρ ο σ έ γ γ ι σ η Ανελκυστήρας: Πρόκειται για μία δίτιμη ονομαστική μεταβλητή, η οποία παίρνει ως τιμές, την ύπαρξη ανελκυστήρα στην οικοδομή και τη μη ύπαρξη. Για να μπορέσει να συμμετέχει σε στατιστική ανάλυση μία τέτοιου είδους μεταβλητή θα πρέπει να γίνει η ποσοτικοποίηση της με τρόπο ώστε να αντιστοιχίζεται ένας αριθμός σε κάθε μία από τις δύο περιπτώσεις, οι μεταβλητές αυτής της κατηγορίας χαρακτηρίζονται ως ψευδομεταβλητές (dummy variables). Οι τιμές που δίνονται είναι αντίστοιχα 0 και 1 (0 για τη μη ύπαρξη ανελκυστήρα και 1 για την ύπαρξη ανελκυστήρα). Πρόκειται για μία μεταβλητή της οποίας η επίδραση αναμένεται να είναι μεγαλύτερη στα κέντρα των δύο πόλεων, καθώς λόγω παλαιότητας των οικοδομών (μη σύγχρονες οικοδομές άρα περισσότερες πιθανότητες για απουσία ανελκυστήρα) η διασπορά των τιμών που δέχεται η μεταβλητή πιθανολογείται να είναι σημαντική. Θέση Διαμερίσματος/Γωνιακό ή όχι: Όμοια με την παραπάνω μεταβλητή, η θέση του διαμερίσματος είναι μία δίτιμη ονομαστική μεταβλητή, η οποία ως πληροφορία δίνει τη θέση του διαμερίσματος σε σχέση με την οικοδομή για τα κτίρια φυσικά που είναι τοποθετημένα στη γωνία των οικοδομικών τετραγώνων στα οποία ανήκουν. Όπως η θέση ενός οικοπέδου στο οικοδομικό τετράγωνο (δηλαδή εάν είναι γωνιακό, μεσαίο, τυφλό κλπ) είναι σημαντική, με όμοιο τρόπο η θέση ενός διαμερίσματος στην οικοδομή είναι εξίσου σημαντική για τη διαμόρφωση της αξίας του και κατά συνέπεια και της τιμής πώλησης του. Το διαμέρισμα που έχει πρόσωπο σε οδό έχει σαφέστατα μεγαλύτερη αξία σε σχέση με ένα διαμέρισμα ίδιων τετραγωνικών μέτρων, του ίδιου ορόφου που βλέπει στον ακάλυπτο χώρο 13. Με όμοιο τρόπο τα διαμερίσματα που έχουν πρόσωπο σε δύο οδούς είναι μεγαλύτερης αξίας σε σχέση με αυτά που δεν είναι γωνιακά. Κατά τη συγκριτική μέθοδο εκτίμησης των διαμερισμάτων λαμβάνεται πάντοτε υπόψη το συγκεκριμένο χαρακτηριστικό, συνεπώς κρίνεται σημαντική η συμμετοχή της συγκεκριμένης μεταβλητής στο μοντέλο της Θεσσαλονίκης και άρα άξια μελέτης η επίδραση που μπορεί να έχει στη διαμόρφωση των αγοραίων αξιών των ακινήτων. Θέρμανση: Η μεταβλητή που αφορά το είδος θέρμανσης του κάθε διαμερίσματος είναι μία ποιοτική μεταβλητή που παίρνει παραπάνω από δύο διακριτές τιμές και μετριέται σε τακτική κλίμακα. Τα διαμερίσματα αρχικά ιεραρχούνται ως προς το είδος θέρμανσης που διαθέτουν και στη συνέχεια πραγματοποιείται η ποσοτικοποίηση τους. Για να γίνει αυτού του είδους η ποσοτικοποίηση μελετούνται τα δύο δείγματα της Θεσσαλονίκης, έπειτα τα τρία δείγματα της Βαρκελώνης και κρίνεται η σχετική κατάταξη που θα πραγματοποιηθεί. Για την πόλη της Θεσσαλονίκης η μεταβλητή θέρμανση διακρίνεται στις κατηγορίες «Καθόλου θέρμανση», «Κεντρική θέρμανση», «Αυτόνομη θέρμανση» και τέλος «Αυτόνομη θέρμανση με ταυτόχρονη παρουσία τζακιού». Οι τέσσερις ψευδομεταβλητές που δημιουργούνται αντιστοιχίζονται για τις δύο περιοχές μελέτης της Θεσσαλονίκης στις τιμές 0, 1, 2, 3 αντίστοιχα. Όσον αφορά την πόλη της Βαρκελώνης, η μεταβλητή «θέρμανση» διακρίνεται στα κατηγορίες «Καθόλου θέρμανση», «Κλιματισμός», «Θέρμανση» (πετρέλαιο ή φυσικό 13 Η μόνη πληροφορία που αφορά τη θέση της οριζόντιας ιδιοκτησίας στην οικοδομή είναι η μεταβλητή «γωνιακό διαμέρισμα ή όχι». Για παράδειγμα, δεν υπήρξε εφικτή η συλλογή δεδομένων για το εάν ένα διαμέρισμα «βλέπει στην κεντρική οδό ή στον ακάλυπτο χώρο της οικοδομής. 39
52 Κ ε φ ά λ α ι ο 3 ο αέριο)και «Θέρμανση και κλιματισμός» με αύξουσα σειρά από τη δυσμενέστερη προς την ευμενέστερη περίπτωση. Οι συγκεκριμένες κατηγορίες διαμορφώνονται σύμφωνα με την παρεχόμενη πληροφορία από τον ιστότοπο που αναφέρεται στα διαμερίσματα της Βαρκελώνης. Οι αντίστοιχες τέσσερις ψευδομεταβλητές που δημιουργούνται αντιστοιχίζονται για τις τρεις περιοχές μελέτης της Βαρκελώνης στις τιμές 0, 1, 2, 3 αντίστοιχα. Συμπερασματικά τα διαμερίσματα διαχωρίζονται ως προς τη μεταβλητή «θέρμανση» σε διαφορετικές μεταξύ τους κατηγορίες ανάλογα με την περιοχή μελέτης. Επιβεβαιώνεται για ακόμη μία φορά το γεγονός ότι τα ιδιαίτερα χαρακτηριστικά γνωρίσματα της κάθε περιοχής οδηγούν σε διαφορετικές τιμές των μεταβλητών. Κατάσταση Ακινήτου: Η μεταβλητή «κατάσταση ακινήτου» επιλέγεται να χρησιμοποιηθεί διότι κρίνεται ιδιαιτέρως σημαντική η επίδραση της στη διαμόρφωση της αγοραίας αξίας των ακινήτων. Όπως είναι γνωστό για να γίνει εκτίμηση ενός ακινήτου είναι απαραίτητη η επίσκεψη στο ακίνητο με σκοπό την καταγραφή της υπάρχουσας κατάστασης, του βαθμού συντήρησης του διαμερίσματος και γενικότερα την «αίσθηση» που αυτό αφήνει στον εκτιμητή. Στην παρούσα έρευνα μία τέτοια διαδικασία δεν ήταν εφικτό να πραγματοποιηθεί. Παρόλα αυτά έγινε πολύ σύντομα αντιληπτό ότι κυρίως στην περιοχή του κέντρου της Θεσσαλονίκης και της Βαρκελώνης υπήρχε ανεξάρτητα από την παλαιότητα του ακινήτου μεγάλη ποικιλομορφία και διαφορετικός βαθμός συντήρησης των διαμερισμάτων. Όπως είναι λογικό δυο γειτονικά διαμερίσματα στην ίδια οικοδομή έχουν μεγάλη διαφορά στην αξία τους ανά τμ, όταν το ένα από τα δύο έχει καινούρια κουφώματα, πόρτα ασφαλείας, ανακαινισμένα δάπεδα, μπάνιο, συντήρηση υδραυλικών και ηλεκτρικών εγκαταστάσεων κλπ., ενώ το άλλο είναι ακριβώς όπως ήταν πριν σαράντα ή πενήντα χρόνια (για οικοδομές μεγάλης ηλικίας). Μπορεί με άλλα λόγια να έχει λιγότερη βαρύτητα στη διαμόρφωση της αγοραίας αξίας ενός διαμερίσματος η παλαιότητα της οικοδομής, όταν ο αγοραστής επιλέγει ένα πλήρως ανακαινισμένο διαμέρισμα στο κέντρο της πόλης, με όλα τα θετικά όπου αυτό συνεπάγεται κυρίως για ειδικές κατηγορίες ατόμων όπως οι φοιτητές. Κρίνεται απαραίτητη λοιπόν η συμμετοχή της παραπάνω μεταβλητής ενώ οι τιμές που επιλέγεται να παίρνει περιγράφονται αναλυτικά παρακάτω. Αρχικά, πρόκειται για μία πολυμερή ποιοτική μεταβλητή που παίρνει παραπάνω από δύο διακριτές τιμές, η ποσοτικοποίηση των οποίων πραγματοποιείται με υποκειμενικά κριτήρια. Οι κατηγορίες όπου διακρίνεται η κατάσταση του ακινήτου είναι «κακή κατάσταση», «μέτρια κατάσταση», «καλή κατάσταση» και «πολύ καλή κατάσταση». Το κριτήριο για τον παραπάνω διαχωρισμό είναι η εικόνα που παρουσιάζει το ακίνητο στο φωτογραφικό υλικό 14 που υπάρχει στην ηλεκτρονική αγγελία του και τα σημεία που οδηγούν στην τελική απόφαση είναι η γενική εντύπωση που αφήνει το ακίνητο, η ύπαρξη ή όχι καινούριων κουφωμάτων, εσωτερικών πορτών, πόρτας ασφαλείας, δαπέδων (όπου αυτό κρίνεται απαραίτητο), η ποιότητα της κουζίνας και του μπάνιου και τέλος η εικόνα που ο ιδιοκτήτης επιλέγει να προβάλλει για το ακίνητο του. Ένα πλήρως ανακαινισμένο διαμέρισμα άμεσα κατατάσσεται στην κατηγορία «πολύ καλή κατάσταση», ένα παλαιό και 14 Για τον παραπάνω λόγο δεν συμμετείχε στο μοντέλο κανένα ακίνητο, το οποίο δεν είχε επισυναπτόμενες φωτογραφίες του εσωτερικού του χώρου Μεταπτυχιακή διατριβή 40
53 Σ τ α τ ι σ τ ι κ ή π ρ ο σ έ γ γ ι σ η σε πολύ κακή κατάσταση συντήρησης κατατάσσεται στην κατηγορία «σε κακή κατάσταση», ενώ για την επιλογή σε μέτρια ή καλή κατάσταση γίνεται επιλογή βάσει του βαθμού ικανοποίησης των παραπάνω κριτηρίων. Για την ποσοτικοποίηση της μεταβλητής δημιουργούνται ισάριθμες με το πλήθος των κατηγοριών της ονομαστικής μεταβλητής ψευδομεταβλητές με την ακόλουθη αντιστοίχιση τιμών : Κακή κατάσταση Τιμή 1 Μέτρια κατάσταση Τιμή 2 Καλή κατάσταση Τιμή 3 Πολύ καλή κατάσταση Τιμή 4 Σημαντικό είναι να σημειωθεί ότι για τον έλεγχο της ποσοτικοποίησης που πραγματοποιείται έγιναν ορισμένες απαραίτητες δοκιμές ώστε να προκύψει η επικρατέστερη βάσει της επίδρασης στο μοντέλο και να ακολουθήσει στη συνέχεια η ίδια λογική και στα πέντε μοντέλα της εφαρμογής. Στάθμευση: Πρόκειται για μία κοινή για τις πέντε περιοχές μελέτης μεταβλητή, η οποία ανήκει στην κατηγορία των δίτιμων ποιοτικών μεταβλητών και χρίζει ποσοτικοποίησης. Η τιμή των ψευδομεταβλητών, όπως αναφέρθηκε και παραπάνω είναι 0 και 1 για την περίπτωση μη ύπαρξης και ύπαρξης στάθμευσης αντίστοιχα. Η μεταβλητή της στάθμευσης κρίνεται απαραίτητο να ενταχθεί στο σχηματισμό του μοντέλου, καθώς στην πόλη της Θεσσαλονίκης και της Βαρκελώνης, όπως και σε πολλές άλλες μεγάλες πόλεις, η στάθμευση των οχημάτων αποτελεί ένα ουσιαστικό πρόβλημα. Είναι εύλογο συνεπώς, ο εκάστοτε αγοραστής να επιδιώκει να βρει κατοικία με δική της θέσης στάθμευσης και φυσικά να αποζημιώνει το συγκεκριμένο προνόμιο. Από τη μελέτη των δύο δειγμάτων παρατηρείται ότι το 87% των διαμερισμάτων στην περιοχή του Ευόσμου έχουν θέση στάθμευσης, το 3% μόνο των διαμερισμάτων στην περιοχή του κέντρου της Θεσσαλονίκης, το 9% στην περιοχή Eixample το 7% στην περιοχή Sant Marti και το 29% στην Badalona. Αριθμός Δωματίων: Η μεταβλητή που αναφέρεται στον αριθμό των δωματίων είναι μία συνεχής ποσοτική μεταβλητή, η οποία χρησιμοποιείται μόνο στις τρεις περιοχές μελέτης της Βαρκελώνης και δέχεται ως τιμές τους ακέραιους αριθμούς που αναφέρονται στα αριθμό των δωματίων του κάθε διαμερίσματος (υπνοδωμάτια, αποθήκες κλπ). Αριθμός Μπάνιων: Όμοια, η μεταβλητή που αναφέρεται στον αριθμό των μπάνιων είναι μία συνεχής ποσοτική μεταβλητή, η οποία χρησιμοποιείται μόνο στις τρεις περιοχές μελέτης της Βαρκελώνης και λαμβάνει τιμές, όπως αυτές δίνονται από τον αντίστοιχο ιστότοπο
54 Κ ε φ ά λ α ι ο 3 ο Σύμφωνα με αντίστοιχη μεθοδολογία που εφαρμόζεται στην περιοχή των Μεσογείων Αττικής, λαμβάνονται επιπλέον ανεξάρτητες μεταβλητές, όπως θέα της ιδιοκτησίας, τζάκι, σοφίτα, πισίνα και εάν είναι ή όχι διαμπερές. (Παπαευθυμίου κα., 2010) Στη στατιστική ανάλυση που ακολουθεί δεν εισάγονται μεταβλητές, όπως το τζάκι (0,1), η σοφίτα (0,1)και η πισίνα(0,1), διότι πρώτον δεν υφίστανται τα συγκεκριμένα χαρακτηριστικά στις επιλεγείσες περιοχές μελέτης και δεύτερον διότι οι παραπάνω πληροφορίες δεν είναι διαθέσιμες από τον ιστότοπο που αποτελεί την πηγή των δεδομένων. Όπως γίνεται αντιληπτό, η κάθε εφαρμογή που αφορά εκτιμήσεις ακινήτων είναι μοναδική και εξαρτάται από τα ιδιαίτερα χαρακτηριστικά της κάθε περιοχής και από την πηγή των απαραίτητων πληροφοριών. Συγκεντρωτικά, οι μεταβλητές που συμμετέχουν στο μοντέλο και για τις δύο πόλεις μαζί με τις ποσοτικοποιήσεις τους παρουσιάζονται στους ακόλουθους πίνακες: Πίνακας3.3: Μεταβλητές που συμμετέχουν στο μοντέλο για την πόλη της Θεσσαλονίκης Μεταβλητές Περιγραφή Τιμές 1. Μεταβλητή [Χ1] Εμβαδόν ακινήτου Τετραγωνικά μέτρα 2. Μεταβλητή [Χ2] Παλαιότητα Έτος ανέγερσης 3. Μεταβλητή [Χ3] Όροφος Αριθμός ορόφου 4. Μεταβλητή [Χ4] Γωνιακό διαμέρισμα Υφίσταται = 1 Δεν υφίσταται = 0 5. Μεταβλητή [Χ5] Ανελκυστήρας Υφίσταται = 1 Δεν υφίσταται = 0 6. Μεταβλητή [Χ6] Είδος θέρμανσης Καθόλου θέρμανση = 0 Κεντρική θέρμανση = 1 Αυτόνομη θέρμανση = 2 Αυτόνομη θέρμανση με τζάκι = 3 7. Μεταβλητή [Χ7] Κατάσταση ακινήτου Κακή κατάσταση = 1 Μέτρια κατάσταση = 2 Καλή κατάσταση = 3 Πολύ καλή κατάσταση = 4 8. Μεταβλητή [Χ8] Θέση στάθμευσης Υφίσταται = 1 Δεν υφίσταται = 0 Μεταπτυχιακή διατριβή 42
55 Σ τ α τ ι σ τ ι κ ή π ρ ο σ έ γ γ ι σ η Πίνακας3.4: Μεταβλητές που συμμετέχουν στο μοντέλο για την πόλη της Βαρκελώνης Μεταβλητές Περιγραφή Τιμές 1. Μεταβλητή [AREA] Εμβαδόν ακινήτου Τετραγωνικά μέτρα 2. Μεταβλητή [AGE] Παλαιότητα Έτος ανέγερσης 3. Μεταβλητή [FLOOR] Όροφος Αριθμός ορόφου 4. Μεταβλητή [ELEV] Ανελκυστήρας Υφίσταται = 1 Δεν υφίσταται = 0 5. Μεταβλητή [HEATING] Είδος θέρμανσης Καθόλου θέρμανση = 0 Κλιματισμός = 1 Θέρμανση = 2 Θέρμανση και Κλιματισμός = 3 6. Μεταβλητή [QUALITY] Κατάσταση ακινήτου Κακή κατάσταση = 1 Μέτρια κατάσταση = 2 Καλή κατάσταση = 3 Πολύ καλή κατάσταση = 4 7. Μεταβλητή [PARKING] Θέση στάθμευσης Υφίσταται = 1 Δεν υφίσταται = 0 8. Μεταβλητή [ROOM] Αριθμός Δωματίων Αριθμός Δωματίων 9. Μεταβλητή [BATH] Αριθμός Μπάνιων Αριθμός Μπάνιων Μεθοδολογικό πλαίσιο Περιεκτικά η κύρια μεθοδολογία της παρούσας εφαρμογής βασίζεται στην παρακάτω συλλογιστική πορεία που αποτυπώνεται με διαγραμματικό τρόπο. Η μεθοδολογία χωρίζεται σε τρία βασικά σκέλη. Πρώτο μέρος της διαδικασίας αποτελεί η προεργασία της στατιστικής μελέτης. Προσδιορισμός μεταβλητών, συλλογή δείγματος, εύρεση κατάλληλης μεθόδου ανάλυσης, επιλογή στατιστικού λογισμικού και επεξεργασία των δεδομένων του δείγματος ώστε να είναι έτοιμα για επεξεργασία. Δεύτερο σκέλος αποτελεί η διαδικασία που μεσολαβεί από την πρώτη προσέγγιση του μοντέλου, με την εκτέλεση της πολλαπλής γραμμικής παλινδρόμησης, μέχρι την επιλογή του τελικού που να πληρεί όλες οι παραδοχές του γραμμικού μοντέλου. Πιο αναλυτικά, οι έλεγχοι που πρέπει να γίνουν αφορούν τη σημαντικότητα των ανεξάρτητων μεταβλητών, την ανεξαρτησία των οντοτήτων, τον έλεγχο πολυσυγγραμικότητας, κανονικότητας, σταθερότητας των διακυμάνσεων, τον έλεγχο γραμμικότητας, τον εντοπισμό των ακραίων οντοτήτων ή οντοτήτων επίδρασης και τέλος τον έλεγχο της προβλεπτικής δύναμης του μοντέλου. Τέλος, το τρίτο στάδιο της εφαρμογής αποτελεί η χωρική απεικόνιση του δείγματος και η εφαρμογή της μεθόδου σε περιβάλλον Γεωγραφικών Συστημάτων Πληροφοριών Η διαδικασία περιγράφεται αναλυτικά στο έκτο κεφάλαιο της διατριβής. 43
56 Κ ε φ ά λ α ι ο 3 ο ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΠΡΟΒΛΗΜΑΤΟΣ Μελέτη Θεωριών περί Εκτιμήσεως ακινήτων Έρευνα κατάλληλης πηγής δεδομένων για το δείγμα ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΜΕΤΑΒΛΗΤΩΝ ΚΑΙ ΣΥΛΛΟΓΗ ΔΕΙΓΜΑΤΟΣ Μελέτη Θεωριών περί στατιστικ ής ανάλυση ς ΕΥΡΕΣΗ ΚΑΤΑΛΛΗΛΗΣ ΜΕΘΟΔΟΥ ΑΝΑΛΥΣΗΣ Απαιτείται πολυμεταβλητή ανάλυση ΕΦΑΡΜΟΓΗ ΠΟΛΛΑΠΛΗΣ ΓΡΑΜΜΙΚΗΣ ΠΑΛΙΝΔΡΟΜΗΣΗΣ ΥΠΟΨΗΦΙΟ ΤΕΛΙΚΟ ΜΟΝΤΕΛΟ Δημιουργία κατάλληλης Βάσης Δεδομένων Διαδοχικές προσεγγίσεις και επαναπροσδιορισμος των μεταβλητών ΠΡΩΤΗ ΠΡΟΣΕΓΓΙΣΗ ΕΛΕΓΧΟΙ ΑΚΡΑΙΩΝ ΤΙΜΩΝ 1. ΣΗΜΑΝΤΙΚΟΤΗΤΑ ΑΝΕΞΑΡΤΗΤΩΝ ΜΕΤΑΒΛΗΤΩΝ 2. ΑΝΕΞΑΡΤΗΣΙΑ ΟΝΤΟΤΗΤΩΝ 3. ΠΟΛΥΣΥΓΓΡΑΜΙΚΟΤΗΤΑ / ΣΥΓΓΡΑΜΙΚΟΤΗΤΑ 4. ΚΑΝΟΝΙΚΟΤΗΤΑ 5. ΣΤΑΘΕΡΟΤΗΤΑ ΔΙΑΚΥΜΑΝΣΕΩΝ 6. ΓΡΑΜΜΙΚΟΤΗΤΑ 7. ΑΚΡΑΙΕΣ ΟΝΤΟΤΗΤΕΣ ΚΑΙ ΟΝΤΟΤΗΤΕΣ ΕΠΙΔΡΑΣΗΣ ΕΛΕΓΧΟΙ ΠΡΟΒΛΕΠΤΙΚΗΣ ΙΚΑΝΟΤΗΤΑΣ ΤΕΛΙΚΟ ΜΟΝΤΕΛΟ ΕΡΜΗΝΕΙΑ ΑΠΟΤΕΛΕΣΜΑΤΩΝ ΧΩΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ / OLS ArcGIS Μεταπτυχιακή διατριβή 44
57 Σ τ α τ ι σ τ ι κ ή π ρ ο σ έ γ γ ι σ η 3.3 ΣΥΜΠΕΡΑΣΜΑΤΑ Η εύρεση της αγοραστικής αξίας ενός ακινήτου με αντικειμενικά κριτήρια είναι από μόνη της μία πολύπλοκη και λεπτομερής διαδικασία που για να προσεγγιστεί με τον καλύτερο δυνατό τρόπο πρέπει να καλύπτονται πολλές προϋποθέσεις. Είναι απαραίτητη η συλλογή ενός μεγάλου αριθμού πληροφοριών σχετικά με τα γενικά και ειδικά χαρακτηριστικά του ακινήτου, είναι απαραίτητη η αυτοψία και η μελέτη της κτηματαγοράς. Συνεπώς, η εύρεση της κατάλληλης μεθοδολογίας που θα οδηγήσει σε μία πολύ καλή προεκτίμηση της αξίας είναι ομοίως πολύ πολύπλοκη. Από τη μελέτη της σχετικής βιβλιογραφίας περί εκτιμήσεων ακινήτων και της μεθοδολογίας ανάλυσης των δεδομένων θεωρείται ότι έγινε μία ιδιαίτερα ικανοποιητική προσπάθεια επιλογής ενός σημαντικού αριθμού κατάλληλων μεταβλητών (λαμβάνοντας υπόψη την έλλειψη τέτοιου είδους πληροφοριών στον ελλαδικό χώρο) αλλά και κατάλληλης στατιστικής μεθόδου για την προσέγγιση του επιθυμητού αποτελέσματος. Ένα μειονέκτημα της προσπάθειας είναι αδιαμφισβήτητα το μέγεθος του δείγματος. Κατά τη διάρκεια λήψης του, εμφανίζεται μία σειρά παραγόντων που αποτελούν τροχοπέδη στην εύρεση μεγαλύτερου αριθμού ακινήτων. Αρχικά, πρόβλημα αποτελεί το μέγεθος των περιοχών μελέτης, διότι βάσει μεθοδολογίας οφείλει να είναι όσο το δυνατό μικρότερο για την ύπαρξη σχετικής χωρικής ομοιομορφίας και για την ύπαρξη κοινών γενικών χαρακτηριστικών. Περιορισμός στην έκταση των περιοχών, συνεπάγεται μείωση των προς πώληση διαμερισμάτων στη συγκεκριμένη περιοχή, άρα μικρότερο δείγμα. Εμπόδιο παράλληλα αποτελούν οι βασικές παραδοχές που τίθενται βάσει μεθοδολογίας. Η πληρότητα των παραγόντων που αναφέρονται παραπάνω, δηλαδή πληρότητα στις τιμές των μεταβλητών, απόδοση θέσης και ύπαρξη φωτογραφικού υλικού, μειώνουν τον αριθμό του δείγματος, αλλά βοηθούν στο σχηματισμό ενός δείγματος πιο αξιόπιστου και ικανού να δώσει απαντήσεις στα ερωτήματα. 45
58 ΚΕΦΑΛΑΙΟ 4 Ο ΔΗΜΙΟΥΡΓΙΑ ΜΑΘΗΜΑΤΙΚΟΥ ΜΟΝΤΕΛΟΥ ΜΕΣΩ ΤΗΣ ΠΟΛΛΑΠΛΗΣ ΓΡΑΜΜΙΚΗΣ ΠΑΛΙΝΔΡΟΜΗΣΗΣ ΜΕ ΣΚΟΠΟ ΤΟΝ ΑΥΤΟΜΑΤΟΠΟΙΗΜΕΝΟ ΥΠΟΛΟΓΙΣΜΟ ΤΗΣ ΑΓΟΡΑΙΑΣ ΑΞΙΑΣ ΤΩΝ ΔΙΑΜΕΡΙΣΜΑΤΩΝ ΕΦΑΡΜΟΓΗ ΣΤΗΝ ΠΟΛΗ ΤΗΣ ΘΕΣΣΑΛΟΝΚΗΣ Η στατιστική ανάλυση δεδομένων υλοποιείται με τη βοήθεια των στατιστικών μεθόδων και με τη χρήση των κατάλληλων λογισμικών. Ωστόσο, στην πράξη δεν καθοδηγείται από αυτά, αλλά δημιουργείται και ελέγχεται με ενεργητικό τρόπο από τον εκάστοτε ερευνητή. Ποιος είναι ο αντικειμενικός στόχος; Ποια είναι τα δεδομένα που πρέπει να συλλεχθούν βάσει αυτού; Σε ποια ερωτήματα δίνουν απάντηση αυτά τα δεδομένα; Ο ερευνητής κατά τη διάρκεια της ανάλυσης έρχεται αντιμέτωπος με μία σειρά αποφάσεων που πρέπει να λάβει. Οι περισσότερες από τις οποίες πρέπει να δικαιολογούνται και να αναλύονται προσεκτικά. Ωστόσο, άλλες αποφάσεις επιλέγονται αυθαίρετα, καθώς δεν υπάρχει μόνο μία σωστή οδός, αλλά αντίθετα ένα πλήθος εξίσου αποδεκτών εναλλακτικών λύσεων. (Howitt & Cramer, 2006) Στο κεφάλαιο που ακολουθεί γίνεται μία προσπάθεια παρουσίασης όλης της διαδικασίας εκτέλεσης μίας πολλαπλής γραμμικής παλινδρόμησης σε περιβάλλον SPSS και παρουσιάζονται όλες οι παραδοχές, προϋποθέσεις και βήματα που απαιτούνται ώστε να επιλεγούν έπειτα από προσεγγίσεις οι τελικές εξισώσεις των δύο μοντέλων και η ερμηνεία τους. Λαμβάνονται επίσης αποφάσεις κατά τη διάρκεια της στατιστικής ανάλυσης, οι οποίες στηρίζονται σε βασικές αρχές της στατιστικής, αλλά και σε δοκιμές που λαμβάνουν χώρα ώστε να ακολουθείται κάθε φορά η βέλτιστη οδός. Από την ερμηνεία του μοντέλου στόχος είναι, με τη βοήθεια ενός πλήθους γραφημάτων, πινάκων και δεικτών να γίνει 46
59 Κ ε φ ά λ α ι ο 4 ο κατανοητή η επίδραση της κάθε μεταβλητής στην διαμόρφωση της αγοραίας αξίας των ακινήτων. 4.1 ΠΕΡΙΒΑΛΛΟΝ ΕΡΓΑΣΙΑΣ ΓΙΑ ΤΗ ΣΤΑΤΙΣΤΙΚΗ ΕΦΑΡΜΟΓΗ SPSS Η στατιστική χρησιμοποιείται σήμερα ολοένα και περισσότερο σε όλες τις επιστήμες κοινωνικού, οικονομικού, γεωγραφικού κλπ ενδιαφέροντος με αποτέλεσμα να γίνεται επιτακτική η ανάγκη βελτίωσης των λογισμικών που την υποστηρίζουν. Τα συγκεκριμένα λογισμικά έχουν τη δυνατότητα εισαγωγής, επεξεργασίας, ανάλυσης και παρουσίασης των αποτελεσμάτων σύντομα, με ποικίλους τρόπους όπως γραφήματα και πίνακες και σε ένα φιλικό προς το χρήστη περιβάλλον εργασίας. Παράλληλα, το επιπλέον χαρακτηριστικό το οποίο σίγουρα προσφέρουν πέραν της ταχύτητας είναι ο μεγάλος όγκος δεδομένων που μπορούν πλέον να επεξεργαστούν και η ευκολία της επεξεργασίας τους. Υπάρχει μία ποικιλία λογισμικών πακέτων στατιστικής όπως το SPSS, E-views, Minitab Assistat, Ezanova, Knme, Microsiris, Winidams εκ των οποίων τα πέντε τελευταία αποτελούν και «ελεύθερα» στατιστικά πακέτα - free software (Χατζηπέτρου, 2008). Για την παρούσα εφαρμογή επιλέγεται να χρησιμοποιηθεί το SPSS 18.0, καθώς είναι ίσως το πιο διαδεδομένο στατιστικό πρόγραμμα ανάλυσης δεδομένων. Παράλληλα, βασικό κριτήριο για την επιλογή του αποτέλεσε η πλατιά βιβλιογραφία που το συνοδεύει καθώς πρόκειται για ένα εξαιρετικά διαδεδομένο στατιστικό εργαλείο αλλά και η άποψη που εκφράζεται στη διεθνή βιβλιογραφία, ότι αποτελεί ένα κορυφαίο πακέτο ανάλυσης, το οποίο καλύπτει ένα πολύ μεγάλο εύρος στατιστικών τεχνικών, από τις πιο απλές μέχρι τις πιο σημαντικές και προχωρημένες. Τέλος, η ταχύτητα και η ευχρηστία του δίνουν τη δυνατότητα σε όλους τους χρήστες να εξερευνήσουν τις εναλλακτικές λύσεις που έχουν. (Howitt & Cramer, 2006) Για την ορθή χρήση του SPSS ακολουθούνται τέσσερα βασικά βήματα, τα οποία καθιστούν ολοκληρωμένη τη διαδικασία μελέτης ενός στατιστικού φαινομένου. Σε πρώτο στάδιο πραγματοποιείται η εισαγωγή του αρχείου δεδομένων στο SPSS. Το SPSS μπορεί να διαβάζει μία μεγάλη ποικιλία αρχείων που προέρχονται από διάφορους τύπους λογισμικού: αρχεία λογιστικών φύλλων, αρχεία βάσεων δεδομένων, αρχεία κειμένου, αρχεία του ίδιου του SPSS, που έχουν παραχθεί σε άλλα λειτουργικά συστήματα, καθώς και αρχεία άλλων στατιστικών πακέτων. Σε δεύτερο στάδιο γίνεται ο μετασχηματισμός των δεδομένων, όπου αυτό είναι απαραίτητο. Δηλαδή, διορθώσεις όπως επανακωδικοποίηση μεταβλητών, παραγωγή νέων, ένωση με άλλα αρχεία κλπ. Τρίτο στάδιο αποτελεί η ανάλυση των δεδομένων μέσω της επιλογής και εκτέλεσης στατιστικών διαδικασιών και της παραγωγής διαγραμμάτων υψηλής ευκρίνειας. Τελευταίο στάδιο αποτελεί η διαχείριση των παραγόμενων αποτελεσμάτων και η ερμηνεία τους, ώστε να κριθεί αποδεκτό ή όχι το μοντέλο που παράχθηκε. (Γναρδέλλης, 2006) 4.2 ΕΦΑΡΜΟΓΗ ΠΟΛΛΑΠΛΗΣ ΓΡΑΜΜΙΚΗΣ ΠΑΛΙΝΔΡΟΜΗΣΗΣ ΓΙΑ ΕΝΑ ΤΜΗΜΑ ΤΟΥ ΚΕΝΤΡΟΥ ΤΗΣ ΘΕΣΣΑΛΟΝΙΚΗΣ (ΠΡΩΤΟ ΜΟΝΤΕΛΟ) Αρχικά, πριν την έναρξη επεξεργασίας των δεδομένων μία πρώτη προσέγγιση στο περιεχόμενο του δείγματος επιτυγχάνεται εξετάζοντας τις τιμές του. Ορισμένα γενικά συμπεράσματα σχετικά με τα ιδιαίτερα χαρακτηριστικά της περιοχής είναι αρχικά ο μέσος όρος της ζητούμενης τιμής πώλησης από τους ιδιοκτήτες ανά τμ είναι /τμ., τιμή η Μεταπτυχιακή διατριβή 47
60 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ οποία χαρακτηρίζεται γενικά χαμηλή και δείχνει από τη μία μεριά την υποβάθμιση της συγκεκριμένης περιοχής του κέντρου που βρίσκεται επάνω από την οδό Εγνατία και την επίπτωση της οικονομικής κρίσης στο χώρο της αγοράς ακινήτων. Στο στατιστικό δείγμα του κέντρου παρατηρείται επίσης ότι συμπεριλαμβάνονται ακίνητα νεοδόμητα, κτίρια παλιά, πολύ παλιά και διατηρητέα. Ένα από τα βασικότερα χαρακτηριστικά του κέντρου άλλωστε είναι η έλλειψη ομοιομορφίας, η οποία είναι εμφανής από την ποικιλία που εμφανίζεται σε ουσιαστικά χαρακτηριστικά, όπως είναι η ύπαρξη ασανσέρ, το είδος θέρμανσης, ο βαθμός συντήρησης του διαμερίσματος κλπ. Επίσης, παρουσία νεοδόμητων οικοδομών στο δείγμα δίνει ενδιαφέρον για τα τελικά αποτελέσματα που θα προκύψουν. Για την έναρξη της επεξεργασίας η διαδικασία που προηγείται όλων είναι η δημιουργία ενός αρχείου.xls του οποίου η δομή είναι κατάλληλη για τη μετέπειτα επεξεργασία στο SPSS. Τοποθετούνται όλα τα δεδομένα του δείγματος που συλλέχθηκε με τις ποσοτικοποιημένες τους τιμές σε δέκα συνολικά στήλες του λογιστικού φύλλου, εκ των οποίων η πρώτη περιέχει μία αύξουσα αρίθμηση των διαμερισμάτων του δείγματος, η δεύτερη περιέχει τις αγοραίες αξίες των ακινήτων (εξαρτημένη μεταβλητή) και οι υπόλοιπες οκτώ περιέχουν τις ανεξάρτητες μεταβλητές που περιγράφονται αναλυτικά στο προηγούμενο κεφάλαιο. Οι γραμμές του λογιστικού φύλλου είναι συνολικά 61, καθώς στην πρώτη γραμμή βρίσκονται οι ετικέτες των μεταβλητών (ΑΑ, Υ, Χ1,Χ2,..Χ8) και ακολουθούν οι 60 οντότητες του δείγματος Δημιουργία παλινδρομικού μοντέλου σε περιβάλλον spss Στο παρόν υποκεφάλαιο περιγράφεται η διαδικασία εφαρμογής πολλαπλής παλινδρόμησης σε μορφή διαδοχικών βημάτων, σε περιβάλλον SPSS, ώστε να προκύψουν οι πίνακες και τα γραφήματα εκείνα που με τη μελέτη τους και την αξιολόγηση τους θα οδηγήσουν στο τελικό μοντέλο πολλαπλής παλινδρόμησης. ΒΗΜΑ 1 ο : Εισαγωγή δεδομένων στο περιβάλλον εργασίας Η εισαγωγή στο περιβάλλον του SPSS, γίνεται όταν ανοίξει το λογισμικό PASW Statistics 18. Εμφανίζεται αυτόματα το παράθυρο Data Editor (επεξεργασία δεδομένων του SPSS), δηλαδή μορφολογικά ένα λογιστικό φύλλο στο οποίο θα γίνει στη συνέχεια η καταχώριση των δεδομένων. Από το πλαίσιο διαλόγου Open File επιλέγεται ο τύπος αρχείου.xls και με την επιλογή του αρχείου εμφανίζονται όλα τα δεδομένα τοποθετημένα σε γραμμές και στήλες. (Εικόνα 4.1) Οι οριζόντιες γραμμές αποτελούν τις περιπτώσεις (cases) ή αλλιώς οντότητες και οι κατακόρυφες στήλες αποτελούν τις μεταβλητές (Variables), διότι για κάθε στήλη ενός αρχείου του Excel δημιουργείται μία μεταβλητή του αρχείου του SPSS. Όπως είναι ορατό από την εικόνα 4.1. η πρώτη στήλη των δεδομένων (AA)αποτελεί μία αύξουσα αρίθμηση των οντοτήτων. Υπάρχει η δυνατότητα μέσω της δεύτερης καρτέλας με όνομα Variable View (καρτέλα με βάση την ορολογία των λογιστικών φύλλων) να οριστούν οι ιδιότητες των μεταβλητών. Πιο συγκεκριμένα μπορούν να δοθούν στοιχεία, όπως το όνομα (Variable Names), ο τύπος της μεταβλητής (Variable Types αριθμός, αλφαριθμητικό, ημερομηνία κλπ), το πλάτος των στοιχείων που θα καταχωρούνται για κάθε μεταβλητή (Column Width), ο αριθμός των δεκαδικών ψηφίων, η ετικέτα της (value labels), η στοίχιση της (alignment), 48
61 Κ ε φ ά λ α ι ο 4 ο το επίπεδο μέτρησης μιας μεταβλητής 17 (Measurement level Διατεταγμένες, ονομαστικές μεταβλητές και μεταβλητές κλίμακας) κ.α. Εξαιτίας της εισαγωγής των δεδομένων μέσω ενός αρχείου Excel και όχι χειρονακτικά, τα στοιχεία της συγκεκριμένης καρτέλας είναι ήδη συμπληρωμένα βάσει της μορφής που είχαν στο λογιστικό φύλλο. Εικόνα 4.1: Καταχώρηση της βάσης δεδομένων σε περιβάλλον SPSS ΒΗΜΑ 2 ο : Δημιουργία γραφημάτων συσχέτισης της εξαρτημένης μεταβλητής Υ με τις ανεξάρτητες Χ i Πριν τη διαδικασία εκτέλεσης της πολλαπλής γραμμικής παλινδρόμησης και τη μελέτη των αποτελεσμάτων (report) που θα προκύψουν κρίνεται σημαντικό σε πρώτη φάση να οπτικοποιηθεί μέσω διαγράμματος η ύπαρξη ή όχι γραμμικής σχέσης μεταξύ της εξαρτημένης και των ανεξάρτητων μεταβλητών. Δίνεται η δυνατότητα με άλλα λόγια μέσω ενός διαγράμματος που παρέχει το λογισμικό να δοθεί μία πρώτη ουσιαστική εικόνα για τη σύνδεση που υπάρχει. Η ανάλυση συσχέτισης προηγείται της ανάλυσης παλινδρόμησης, διότι με βάσει το διάγραμμα επιλέγονται οι μεταβλητές εκείνες που θα λάβουν εν τέλει μέρος στη διαδικασία και απορρίπτονται εκείνες που δείχνουν μη γραμμική σχέση με την αξία των διαμερισμάτων. Τα γραφήματα συσχέτισης παράλληλα δείχνουν την ένταση και την κατεύθυνση της σχέσης. Το διάγραμμα που παρουσιάζεται παρακάτω δεν ερμηνεύεται αυθαίρετα αλλά βάσει ορισμένων κανόνων οι οποίοι αναλύονται στη συνέχεια. Το κατάλληλο διάγραμμα που θα δείξει γραφικά την ύπαρξη της σχέσης μεταξύ των μεταβλητών ανήκει στην κατηγορία των διαγραμμάτων διασποράς ή σκέδασης (scatterplots). Τα διαγράμματα διασποράς χρησιμοποιούνται για το διαγραμματικό προσδιορισμό της σχέσης που υπάρχει μεταξύ δύο ποσοτικών μεταβλητών οι οποίες αναφέρονται στο ίδιο σύνολο παρατηρήσεων. (Γναρδέλλης, 2006) Η διαδικασία εμφάνισης του σε περιβάλλον SPSS 18.0 περιγράφεται αναλυτικά παρακάτω. 17 Τα πραγματικά επίπεδα μέτρησης των μεταβλητών είναι είτε μεταβλητές κλίμακας, είτε διατεταγμένες μεταβλητές. Παρόλα αυτά επιλέγεται για όλες τις τιμές να αναγνωρίζονται ως μεταβλητές κλίμακας (Scale), διότι είναι η γενική κατηγορία και αντιστοιχεί σε ποσοτικά μεγέθη. Μεταπτυχιακή διατριβή 49
62 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Αρχικά εισάγονται όλα τα δεδομένα του δείγματος σε ένα νέο αρχείο *.sav (Βλ. ΒΗΜΑ 1 ο ) και από το Μενού του Data Editor επιλέγεται Graphs Legacy Dialogs Scatter/Dot Matrix (Εικόνα 4.2) Εικόνα4.2 : Διαδικασία εμφάνισης του διαγράμματος διασποράς Scatter/Dot για τον έλεγχο της σχέσης των μεταβλητών, σε περιβάλλον SPSS 18.0 Στο παράθυρο διαλόγου που εμφανίζεται γίνεται εισαγωγή όλων των μεταβλητών του μοντέλου στο δεξί υποπλαίσιο διαλόγου και με την επιλογή ΟΚ εμφανίζεται η εικόνα των διαγραμμάτων διασποράς (Διάγραμμα 4.1). Είναι εφικτό να κατασκευαστούν ξεχωριστά τα επτά γραφήματα που δείχνουν τη σχέση της κάθε ανεξάρτητης μεταβλητής με την εξαρτημένη, η εντολή matrix όμως οδηγεί στην παρακάτω εικόνα που απεικονίζει σε ένα μόνο γράφημα τις σχέσεις μεταξύ των μεταβλητών. 50
63 Κ ε φ ά λ α ι ο 4 ο Διάγραμμα 4.1: Γράφημα Matrix Scatter Plot για δείγμα 60 ακινήτων και για τις οκτώ ανεξάρτητες μεταβλητές Γραμμική είναι μία συσχέτιση, όπως φαίνεται στις παρακάτω απεικονίσεις όταν τα σημεία όλων των παρατηρήσεων συγκεντρώνονται γύρω από μία ευθεία και αντίστοιχα μη γραμμική όταν τα σημεία τείνουν να συγκεντρώνονται γύρω από μία καμπύλη. Ο βαθμός της συσχέτισης, δηλαδή το πόσο ισχυρή ή όχι είναι η γραμμική συσχέτιση συνδέεται κάθε φορά με το εάν είναι έντονα συγκεντρωμένα τα σημεία γύρω από την ευθεία γραμμή ή εάν είναι περισσότερο διασκορπισμένα. Τέλος, στην περίπτωση που όλα τα σημεία βρίσκονται πάνω στην ευθεία η συσχέτιση ονομάζεται πλήρης. (Ζήμερας, 2003) Εικόνα4.3: Χαρακτηριστικά παραδείγματα συσχέτισης μεταξύ μιας εξαρτημένης και μίας ανεξάρτητης μεταβλητής (Πηγή εικόνων: Ζήμερος, 2003) Χαρακτηριστικά είναι τα παραδείγματα της παραπάνω εικόνας, στα οποία ξεκινώντας την περιγραφή από αριστερά προς τα δεξιά, αρχικά απεικονίζεται μία αρνητική γραμμική συσχέτιση, στη συνέχεια μία θετική γραμμική συσχέτιση, ύπαρξη καμίας συσχέτισης και τέλος μια μη γραμμική συσχέτιση. Σύμφωνα με τα παραπάνω παραδείγματα και τα γραφήματα διασποράς της εικόνας 4.1, είναι ορατό ότι η εξαρτημένη μεταβλητή που αντιστοιχεί στην αγοραία αξία των ακινήτων δείχνει να μην έχει καμία γραμμική σχέση με τις ανεξάρτητες μεταβλητές Χ4 και Χ6, οι οποίες αντιστοιχούν στις μεταβλητές «Γωνιακό διαμέρισμα» και «Είδος θέρμανσης», αντίστοιχα. Με βάση τα παραπάνω δεδομένα το μοντέλο της πολλαπλής γραμμικής παλινδρόμησης θα τρέξει με τις υπόλοιπες έξι μεταβλητές, ενώ οι Χ4 και Χ6 δεν υπάρχει λόγος να συμπεριληφθούν στη διαδικασία. Η επίδραση των έξι κύριων μεταβλητών μένει να διερευνηθεί μέσω της ανάλυσης που ακολουθεί, διότι η τελική επιλογή του μοντέλου εξαρτάται από μία μεγάλη ποικιλία παραγόντων. ΒΗΜΑ 3 ο : Εύρεση μερικής συσχέτισης της κάθε ανεξάρτητης μεταβλητής Χi με την εξαρτημένη Y Ο έλεγχος που προηγείται με το διάγραμμα σκέδασης είναι ουσιαστικός γιατί αποτελεί το πρώτο βασικό μεθοδολογικό βήμα. Πέραν όμως της οπτικοποιημένης «χονδροειδούς» εικόνας που παρέχει το διάγραμμα υπάρχει ένας ακόμη έλεγχος αυστηρότερος και ακριβέστερος. Μέσω του Μενού Analyze Correlate Partial ανοίγει ένα νέο παράθυρο στο οποίο εισάγεται κάθε φορά η εξαρτημένη μεταβλητή με μία από τις ανεξάρτητες και υπολογίζεται η «καθαρή» συσχέτιση της κάθε μίας με την εξαρτημένη. Συνολικά προκύπτουν οκτώ πίνακες της παρακάτω μορφής με το ποσοστό που ερμηνεύει η κάθε μεταβλητή στο μοντέλο. Μεταπτυχιακή διατριβή 51
64 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Σύμφωνα με τον πίνακα 4.1 το εμβαδόν των διαμερισμάτων στην περιοχή του κέντρου της Θεσσαλονίκης ερμηνεύει το 79% της αξίας του διαμερίσματος. Με άλλα λόγια συμμετέχει στην διαμόρφωση της τιμής κατά 79%. Η σχέση είναι ιδιαίτερα μεγάλη και γίνεται σαφές ότι είναι το εμβαδόν θα συμμετέχει στο παλινδρομικό μοντέλο που πρόκειται να σχηματιστεί. Πίνακας 4.1 : Ποσοστό μερικής συσχέτισης της αγοραίας αξίας και του εμβαδού στην περιοχή του κέντρου της Θεσσαλονίκης Correlations Control Variables Y X1 X2 & X3 & X4 & X5 & X6 & X7 & Χ8 Y Correlation 1,000,790 Significance (2-tailed).,000 df 0 52 X1 Correlation,790 1,000 Significance (2-tailed),000. df 52 0 Με όμοια διαδικασία προκύπτουν οι αντίστοιχες μερικές συσχετίσεις και των υπόλοιπων ανεξάρτητων μεταβλητών με την εξαρτημένη και είναι ορατές στον παρακάτω πίνακα. Πίνακας 4.2 : Μερικές συσχετίσεις μεταξύ των μεταβλητών στην περιοχή του κέντρου Μεταβλητές Συσχέτιση Επίπεδο στατιστικής σημαντικότητας Χ1 Y 0,790 0,000 Χ2 Y -0,493 0,000 Χ3 Y 0,052 0,727 Χ4 Y 0,123 0,412 Χ5 Y 0,186 0,210 Χ6 Y 0,083 0,579 Χ7- Y 0,399 0,006 Χ8 - Y 0,208 0,161 Αποδεικνύεται με έναν ακόμη πιο ακριβή τρόπο ότι οι μεταβλητές Χ4, Χ5 και Χ6 δεν έχουν καμία γραμμική σχέση με την εξαρτημένη μεταβλητή και άρα δεν υπάρχει κανένας λόγος να συμμετέχουν στη διαδικασία εκτέλεσης της πολλαπλής παλινδρόμησης. 52
65 Κ ε φ ά λ α ι ο 4 ο ΒΗΜΑ 4 ο : Διαδικασία εκτέλεσης της πολλαπλής γραμμικής παλινδρόμησης Από το Μενού Analyze επιλέγεται Regression Linear και εμφανίζεται το παράθυρο Linear Regression όπως φαίνεται στην παρακάτω εικόνα. Επιλέγεται αρχικά η εξαρτημένη μεταβλητή, η οποία μεταφέρεται στην περιοχή Dependent και το σύνολο των ανεξάρτητων μεταβλητών στην περιοχή Independent(s). Εικόνα 4.4: Επιλογή εξαρτημένης μεταβλητής, ανεξάρτητων μεταβλητών και μεθόδου εκτέλεσης της πολλαπλής γραμμικής παλινδρόμησης Στο πεδίο Method πρέπει να επιλεγεί η διαδικασία με την οποία θα εφαρμοστεί η πολλαπλή γραμμική παλινδρόμηση. Η επιλογή της μεθόδου είναι ιδιαίτερα σημαντική σε αυτό το βήμα, διότι θα καθοριστεί στην ουσία η μορφή της εξίσωσης του μοντέλου. Οι μέθοδοι που μπορεί να εφαρμόσει το SPSS είναι η μέθοδος Enter, Remove, Forward, Backward και Stepwise. Στην προκειμένη περίπτωση επιλέγεται η μέθοδος Stepwise για τους λόγους που περιγράφονται στην ακόλουθη παράγραφο. Σύμφωνα με τον Αγγελίδη, 2009 με τη μέθοδο Enter ο χρήστης εισάγει μόνος τις μεταβλητές που επιθυμεί, με την εντολή Forward το SPSS επιλέγει τις μεταβλητές που θα συμμετέχουν στο μοντέλο με κριτήριο επιλογής τα αντίστοιχα b να είναι στατιστικά σημαντικά τουλάχιστον στο επίπεδο του 20% (p. Value 0.2), ξεκινώντας από αυτή που έχει το μικρότερο p. Value και με την εντολή Backward με ακριβώς αντίστροφο τρόπο αρχικά εισάγονται όλες οι μεταβλητές στο μοντέλο και αφαιρούνται διαδοχικά με κριτήριο η τιμή p. value να είναι > 0.2 ξεκινώντας από αυτήν που έχει τη μεγαλύτερη τιμή. Τέλος, η μέθοδος Stepwise (μέθοδος που επιλέγεται στη συγκεκριμένη περίπτωση) είναι η πιο αξιόπιστη από τις παραπάνω διότι αποτελεί μία μέθοδο βέλτιστης επιλογής των μεταβλητών σύμφωνα με τον Γναρδέλλη, Η επιλογή των μεταβλητών γίνεται κατά βήματα και κάθε νέο βήμα θεωρείται ως μοντέλο. Πιο συγκεκριμένα, σε κάθε βήμα της Μεταπτυχιακή διατριβή 53
66 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ διαδικασίας αξιολογούνται οι μεταβλητές που βρίσκονται ήδη στην εξίσωση, σύμφωνα με τα κριτήρια επιλογής για απαλοιφή. Εάν τα p-value είναι μικρότερα από 0,05, δηλαδή το 5% επίπεδο σημαντικότητας, τότε οι μεταβλητές θεωρούνται στατιστικά σημαντικές. Στην αντίθετη περίπτωση που η τιμή p-value είναι μεγαλύτερη από 0,05 τότε οι μεταβλητές κρίνονται ακατάλληλες. Η διαδικασία ελέγχου της τιμής p-value πραγματοποιείται μέχρι να μην είναι κατάλληλη για προσθήκη ή απαλοιφή καμία από τις μεταβλητές του σετ των μεταβλητών (Πραμαγγιούλης, 2008) και (Dennis, 2006). Η μέθοδος της διαδοχικής επιλογής συνήθως χρησιμοποιείται όταν το μοντέλο είναι πειραματικό και δεν είναι γνωστή η συνεισφορά της κάθε μεταβλητής στην ερμηνεία του. (Δημητριάδης, 2010) ΒΗΜΑ 5 ο : Δημιουργία περιγραφικών στατιστικών μέτρων της διαδικασίας Linear Regression Από το παράθυρο διαλόγου Statistics (Εικ. 4.5) επιλέγονται όλα τα στοιχεία που είναι επιθυμητό να εμφανίζονται έπειτα από τις διαδοχικές προσεγγίσεις που θα πραγματοποιηθούν στη συνέχεια για το σχηματισμό του τελικού μοντέλου, ώστε να αποτελέσουν κύρια πηγή αξιολόγησης των αποτελεσμάτων. Εικόνα 4.5: Πλαίσιο διαλόγου Linear regression: Statistics Από την παραπάνω εικόνα, η επιλογή των Estimates δίνει τον πίνακα συντελεστών δηλαδή το σταθερό όρο, τους μερικούς συντελεστές παλινδρόμησης, τις τιμές του t test, και το επίπεδο σημαντικότητας του αντίστοιχου μερικού συντελεστή παλινδρόμησης (Sig.) βάσει του οποίου γίνεται η επιλογή ή αντίστοιχα η απόρριψη της μηδενικής υπόθεσης που σχετίζεται με τους συντελεστές. Η επιλογή Confidence intervals δίνει τα κατώτερα και ανώτερα άκρα του διαστήματος εμπιστοσύνης των συντελεστών που έχουν υπολογιστεί, η επιλογή Model Fit δίνει δύο βασικούς πίνακες εκ των οποίων ο πρώτος Model Summary, περιλαμβάνει το συντελεστή πολλαπλής συσχέτισης (R), το δείκτη προσδιορισμού (R Square), το διορθωμένο δείκτη προσδιορισμού (Adjusted R Square) και το τυπικό σφάλμα της εκτίμησης, ενώ ο δεύτερος ANOVA περιλαμβάνει το άθροισμα τετραγώνων της 54
67 Κ ε φ ά λ α ι ο 4 ο παλινδρόμησης και των σφαλμάτων, το συνολικό άθροισμα τετραγώνων, τους βαθμούς ελευθερίας, το μέσο των προηγούμενων αθροισμάτων, την τιμή του F κριτηρίου και το Sig.(στάθμη στατιστικής σημαντικότητας). Στη συνέχεια, η επιλογή Part and partial correlations δίνει τους τμηματικούς και μερικούς συντελεστές συσχέτισης, η επιλογή descriptives εμφανίζει δύο πίνακες, εκ των οποίων ο ένας Descriptive Statistics παρέχει τη μέση τιμή και την τυπική απόκλιση όλων των μεταβλητών, ενώ ο δεύτερος πίνακας Correlation δίνει τους συντελεστές συσχέτισης μεταξύ όλων των μεταβλητών, καθώς επίσης και τις στάθμες στατιστικής σημαντικότητας για όλους τους συντελεστές συσχέτισης που υπολογίστηκαν. Η επιλογή Collinearity diagnostics προσθέτει δύο βασικές τιμές, τον παράγοντα ανοχής Tolerance και τον παράγοντα πληθωριστικής διακύμανσης VIF, οι οποίοι όπως θα φανεί και σε παρακάτω υποκεφάλαιο αποτελούν κριτήριο για την ύπαρξη συγγραμμικότητας ή πολυσυγγραμμικότητας. Τελευταίες είναι δύο επιλογές, αρχικά ο δείκτης Durbin Watson, ο οποίος προστίθεται στον πίνακα Model Summary και αποτελεί δείκτη ελέγχου της ύπαρξης ανεξαρτησίας των οντοτήτων και τέλος η επιλογή Casewise diagnostics Outliers Outside τιμή 2 όπου αναφέρεται στις οντότητες που έχουν υπόλοιπο ± 2 και θα οδηγήσει σε μετέπειτα έλεγχο για το πόσο ικανοποιητικό είναι το μοντέλο (πιθανόν και μία πιο ελαστική επιλογή όπως η τιμή ± 3 να ήταν ικανοποιητική, εξαιτίας της ύπαρξης πραγματικών δεδομένων). (Αγγελίδης, 2009) ΒΗΜΑ 6 ο : Διαγράμματα που παράγονται κατά τη διαδικασία Linear Regression Σύμφωνα με τον Γναρδέλλη, 2006 η διαδικασία ανάλυσης παλινδρόμησης δίνει τη δυνατότητα παραγωγής διαγραμμάτων, κυρίως για τον έλεγχο της εγκυρότητας του υποδείγματος. Από το παράθυρο διαλόγου Plots (Εικ. 4.6) αρχικά επιλέγεται να εμφανιστούν όλα τα διαγράμματα μερικής συσχέτισης και το ιστόγραμμα των κανονικοποιημένων υπολοίπων (z-τιμές), αφού θεωρούμε ότι ακολουθούν την κανονική κατανομή. Επίσης, ορίζεται η δημιουργία ενός διαγράμματος όπου στον Υ άξονα έχει τα τυποποιημένα κατά Student διαγραμμένα υπόλοιπα (SDRESID)και στον Χ άξονα τις τυποποιημένες εκτιμώμενες τιμές (ZPRED)και ένα ακόμη διάγραμμα, στο οποίο στον άξονα Y έχει τις τυποποιημένες εκτιμώμενες τιμές και στον άξονα Χ την εξαρτημένη μεταβλητή του υποδείγματος (DEPENDNT). (Εικόνα 4.7) Μεταπτυχιακή διατριβή 55
68 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Εικόνα 4.6: Πλαίσιο διαλόγου Linear Regression: Plot. Δημιουργία πρώτου διαγράμματος διασποράς Εικόνα 4.7: Πλαίσιο διαλόγου Linear Regression: Plot. Δημιουργία δεύτερου διαγράμματος διασποράς ΒΗΜΑ 7 ο : Αποθήκευση νέων μεταβλητών που παράγονται από τη διαδικασία Linear Regression Από το παράθυρο διαλόγου Save (Εικ. 4.8) τσεκάρονται όλες οι επιλογές που δίνονται στο πλαίσιο διαλόγου, ώστε να αποθηκευτούν νέες μεταβλητές και διαγνωστικά στατιστικά μέτρα τα οποία παράγονται έπειτα από την εκτέλεση της πολλαπλής γραμμικής παλινδρόμησης. Οι νέες μεταβλητές αφορούν τις εκτιμώμενες τιμές, τα υπόλοιπα της παλινδρόμησης, καθώς και ορισμένες αποστάσεις και στατιστικά μέτρα που χρησιμοποιούνται για τον εντοπισμό «ασυνήθιστων» παρατηρήσεων με ισχυρή επίδραση στη διαμόρφωση του υποδείγματος. Η πρώτη κατηγορία επιλογών με τον τίτλο Predicted Values οδηγεί στην αποθήκευση των εκτιμώμενων τιμών (Unstandardized), των τυποποιημένων εκφράσεων των εκτιμώμενων τιμών (Standardized), των προσαρμοσμένων τιμών των εκτιμήσεων (Adjusted) και των τυπικών σφαλμάτων των εκτιμώμενων τιμών (S.E. of mean predictions). Η κατηγορία με τον τίτλο Distances οδηγεί στον υπολογισμό συγκεκριμένων στατιστικών μέτρων. Αρχικά, η απόσταση Mahalahobis αποτελεί μέτρο της απόκλισης των Χ i τιμών μιας οντότητας από τις αντίστοιχες μέσες τιμές των ανεξάρτητων μεταβλητών. Η επιλογή Cook s αποτελεί μέτρο της διαφοροποίησης των υπολοίπων όταν μία από τις οντότητες της ανάλυσης αποκλειστεί από τον υπολογισμό των συντελεστών της 56
69 Κ ε φ ά λ α ι ο 4 ο παλινδρόμησης. Τέλος, η επιλογή Leverage values αποτελεί μέτρο της επίδρασης μιας οντότητας στην προσαρμογή του υποδείγματος. Η επιλογή των Prediction Intervals αναφέρεται στα διαστήματα εμπιστοσύνης (ανώτατο και κατώτερο όριο) των εκτιμούμενων τιμών που αντιστοιχούν είτε όταν πρόκειται για τις μέσες τιμές υποπληθυσμών της Υ στις διάφορες τιμές των ανεξάρτητων μεταβλητών, είτε όταν πρόκειται για τις ατομικές τιμές της Υ (Mean και Individual αντίστοιχα)για τις ίδιες τιμές των ανεξάρτητων μεταβλητών. Στο πεδίο Confidence Interval ορίζεται το ακριβές διάστημα εμπιστοσύνης 95% για τις δύο προηγούμενες εκδοχές των εκτιμούμενων τιμών. Η κατηγορία των υπολοίπων (residuals) αναφέρεται στις τιμές των υπολοίπων δηλαδή στις διαφορές των εκτιμώμενων τιμών από τις παρατηρούμενες (Unstandardized)και στις τιμές των υπολοίπων έπειτα από το μετασχηματισμό τους. Πιο συγκεκριμένα, τα τυποποιημένα υπόλοιπα (Standardized residuals) είναι τα υπόλοιπα διαιρούμενα με την τυπική τους απόκλιση. Τα τυποποιημένα κατά Student υπόλοιπα (Studentized residuals) αναφέρονται στις τιμές των υπολοίπων που διαιρούνται με μία εκτίμηση της τυπικής τους απόκλισης η οποία μεταβάλλεται από οντότητα σε οντότητα ανάλογα με την απόσταση κάθε οντότητας από τις μέσες τιμές των ανεξάρτητων μεταβλητών. Τα διαγραμμένα υπόλοιπα (Deleted residuals) είναι το υπόλοιπο για κάθε οντότητα όταν αυτή δε συμμετέχει στον υπολογισμό των συντελεστών της παλινδρόμησης. Tα τυποποιημένα κατά Student διαγραμμένα υπόλοιπα είναι τα κατά student υπόλοιπα, όταν όμως η οντότητα δεν περιλαμβάνεται στους υπολογισμούς. Η τελευταία κατηγορία Influence Statistics αναφέρεται στις μεταβολές που προκύπτουν στους συντελεστές της παλινδρόμησης και στις εκτιμώμενες από το υπόδειγμα τιμές όταν μία οντότητα απομακρυνθεί από την ανάλυση. Ως BfBeta(s) ορίζονται οι διαφορές στους συντελεστές παλινδρόμησης όταν μία παρατήρηση απομακρυνθεί από την ανάλυση, ενώ οι αντίστοιχες τυποποιημένες τιμές (Standardized BfBeta) αναφέρονται στις τυποποιημένες διαφορές στους συντελεστές παλινδρόμησης. Ως DfFit ορίζεται η διαφορά στην εκτιμώμενη τιμή μιας οντότητας όταν αυτή απομακρυνθεί από την ανάλυση και αντίστοιχα η τυποποιημένη διαφορά υπολογίζεται μέσω της επιλογής του Standardized DfFit. Η τελευταία δυνατότητα που προσφέρεται (Covariance ratio) υπολογίζει το λόγο της ορίζουσας του πίνακα των συνδιακυμάνσεων όταν μία συγκεκριμένη οντότητα δε συμπεριλαμβάνεται στην ανάλυση προς την ορίζουσα του πίνακα των συνδιακυμάνσεων με όλες τις οντότητες να συμμετέχουν στην ανάλυση. (Γναρδέλλης, 2006) Μεταπτυχιακή διατριβή 57
70 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Εικόνα 4.8: Πλαίσιο διαλόγου Linear Regression: Save ΒΗΜΑ 8 ο : Επιλογές της διαδικασίας Linear Regression Στο παράθυρο διαλόγου Options (Εικ. 4.9) ορίζονται ουσιαστικά τα κριτήρια εισόδου εξόδου των μεταβλητών στο μοντέλο. Στην προκειμένη περίπτωση η μεταβλητή συμμετέχει στο μοντέλο αν το επίπεδο σημαντικότητας (significance level) για κάθε F τιμή είναι μικρότερο από την τιμή που δίνεται στο παράθυρο Entry (0.05). Αντίθετα αφαιρείται αν το επίπεδο σημαντικότητας για κάθε F τιμή είναι μεγαλύτερο από την τιμή που δίνεται στο παράθυρο Removal (0.10) 18. Είναι δηλαδή η ανοχή που δίνεται στη μέθοδο διαδοχικής επιλογής (stepwise) για την επιλογή των μεταβλητών, όπως αναφέρθηκε παραπάνω. 18 Οι τιμές που ορίζουν τα κριτήρια εισόδου και εξόδου των μεταβλητών στο μοντέλο και επιλέχθηκαν παραπάνω είναι οι προεπιλεγμένες τιμές του προγράμματος για την εφαρμογή της πολλαπλή γραμμικής παλινδρόμησης 58
71 Κ ε φ ά λ α ι ο 4 ο Εικόνα 4.9: Πλαίσιο διαλόγου Linear Regression: Options Η επιλογή της ένδειξης Include constant in equation γίνεται για να εμφανιστεί ο σταθερός όρος του μοντέλου στην εξίσωση παλινδρόμησης και η επιλογή της ένδειξης Exclude cases listwise γίνεται με σκοπό την συμμετοχή μόνο των οντοτήτων που έχουν έγκυρες τιμές για όλες τις μεταβλητές στην ανάλυση. (Δημητριάδης, 2010) ΒΗΜΑ 9 ο : Εμφάνιση αποτελεσμάτων σε περιβάλλον εργασίας Viewer Με την ολοκλήρωση των επιλογών που έγιναν στο πλαίσιο διαλόγου Linear Regression τα αποτελέσματα της διαδικασίας με τη μέθοδο Stepwise εμφανίζονται στο παράθυρο του Viewer. Το συγκεκριμένο περιβάλλον εργασίας δίνει τη δυνατότητα διαχείρισης και επεξεργασίας των αποτελεσμάτων για τη λήψη αποφάσεων και εξαγωγή τους σε διάφορες μορφές αρχείων. Η εξίσωση παλινδρόμησης που αποτελεί μία πρώτη προσέγγιση του προβλήματος είναι η ακόλουθη: Υ = , ,846 Χ ,365 Χ7-920,315 Χ2 δηλ., Αγοραία αξία = , ,846 * (Εμβαδόν) ,365 * (Κατάσταση ακινήτου) - 920,315 * (Παλαιότητα),με συντελεστή προσδιορισμού R 2 = 0,72. Μεταπτυχιακή διατριβή 59
72 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Έλεγχος ικανοποίησης προϋποθέσεων αρχικού μοντέλου πολλαπλής γραμμικής παλινδρόμησης Βασικός στόχος από την αρχή της συγκεκριμένης προσπάθειας είναι η δημιουργία μίας αξιόπιστης παλινδρομικής εξίσωσης που να ικανοποιεί τη δυνατότητα πρόβλεψης αγοραίων αξιών ακινήτων στις αντίστοιχες περιοχές μελέτης. Ο έλεγχος της αξιοπιστίας και του επιτυχούς σχηματισμού του μοντέλου ελέγχεται με μία σειρά διαδικασιών μέσω του SPSS που καθρεφτίζουν όλο το θεωρητικό υπόβαθρο που συνοδεύει τα μοντέλα πολλαπλής γραμμικής παλινδρόμησης. Η σειρά ελέγχων που ακολουθούν εκτελούνται στο αρχικό μοντέλο για να ελεγχθεί η αξιοπιστία του και η δύναμη της προβλεπτικής του ικανότητας Σημαντικότητα ανεξάρτητων μεταβλητών Ένα ουσιαστικό ερώτημα προς απάντηση είναι η ύπαρξη ή όχι στατιστικής σημαντικότητας των ανεξάρτητων μεταβλητών του μοντέλου. Σύμφωνα με τον Μισιρλόγλου, 2011 η λεγόμενη «σημαντικότητα των μεταβλητών» αναφέρεται στις μεταβλητές εκείνες που είναι ικανές να βοηθήσουν στην προβλεπτική ικανότητα του μοντέλου και μέσα από το λογισμικό του spss δίνεται με τη βοήθεια του ελέγχου γραφημάτων μερικής παλινδρόμησης (Partial Plots) και μέσω των τιμών t. Παρακάτω αναλύονται και οι δύο τρόποι ελέγχου. Γραφήματα Μερικής Παλινδρόμησης (Partial Residual Plots) Τιμές t Διαγράμματα μερικής συσχέτισης Τα διαγράμματα μερικής συσχέτισης απεικονίζουν την πραγματική, «καθαρή» σχέση μεταξύ της εξαρτημένης και κάθε μίας από τις ανεξάρτητες μεταβλητές που λαμβάνουν μέρος στο σχηματισμό του μοντέλου, απαλλαγμένες όμως από οποιαδήποτε επίδραση σε σχέση με τις άλλες ανεξάρτητες μεταβλητές. Τα διαγράμματα μερικής συσχέτισης δείχνουν ξεκάθαρα την ύπαρξη γραμμικότητας μεταξύ εξαρτημένης και ανεξάρτητων. Πρακτικά σημαίνει ότι υπολογίζονται τα υπόλοιπα της παλινδρόμησης μεταξύ της μεταβλητής Y και των άλλων ανεξάρτητων μεταβλητών, στη συνέχεια υπολογίζονται τα υπόλοιπα της παλινδρόμησης μεταξύ της Xi και των άλλων ανεξάρτητων μεταβλητών και τέλος κατασκευάζεται το διάγραμμα διασποράς μεταξύ των δύο μεταβλητών των υπολοίπων. (Λαφαζάνη, 2003 & Γναρδέλλης, 2006) 60
73 Κ ε φ ά λ α ι ο 4 ο Τα παρακάτω διαγράμματα αποτελούν το σύνολο των διαγραμμάτων μερικής συσχέτισης της εξαρτημένης μεταβλητής Y με όλες τις ανεξάρτητες μεταβλητές του μοντέλου. Στην ουσία, τα διαγράμματα παρέχουν μια διαγραμματική απεικόνιση της μερικής συσχέτισης κάθε ανεξάρτητης μεταβλητής με την εξαρτημένη. Οι μεταβλητές τις οποίες κράτησε εν τέλει το λογισμικό είναι τρεις από τις οκτώ. Με τα παρακάτω διαγράμματα βεβαιώνεται οπτικά η σημαντικότητα των ανεξάρτητων μεταβλητών και η ύπαρξη ή όχι γραμμικότητας. Διάγραμμα 1 Διάγραμμα 2 Διάγραμμα 3 Διάγραμμα 4 Μεταπτυχιακή διατριβή 61
74 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα 5 Διάγραμμα 6 Διάγραμμα 7 Διάγραμμα 8 Διάγραμμα 4.2: Διαγράμματα μερικής παλινδρόμησης ως προς όλες τις ανεξάρτητες μεταβλητές Xi για την περιοχή του κέντρου της Θεσσαλονίκης - Διάγραμμα 1: Απεικονίζει τη σχέση που υπάρχει μεταξύ της αγοραίας αξίας των ακινήτων και του εμβαδού των διαμερισμάτων, η οποία είναι γραμμική. Παρατηρούνται δύο οντότητες (31 και 34) που βρίσκονται εκτός της ζώνης σταθερού πλάτους και άρα είναι πιθανές ακραίες οντότητες. 62
75 Κ ε φ ά λ α ι ο 4 ο - Διάγραμμα 2: Απεικονίζει τη σχέση που υπάρχει μεταξύ της αγοραίας αξίας των ακινήτων και της παλαιότητας των διαμερισμάτων, η οποία είναι γραμμική. Όμοια, επισημαίνονται οι δύο οντότητες 31 και 34, ως πιθανές ακραίες οντότητες. - Διάγραμμα 3: Απεικονίζει τη σχέση που υπάρχει μεταξύ της αγοραίας αξίας των ακινήτων και του ορόφου των διαμερισμάτων, η οποία δεν είναι γραμμική - Διάγραμμα 4: Απεικονίζει τη σχέση που υπάρχει μεταξύ της αγοραίας αξίας των ακινήτων της θέσης στην οικοδομή του κάθε διαμερίσματος (γωνιακό/όχι), η οποία δεν είναι γραμμική - Διάγραμμα 5: Απεικονίζει τη σχέση που υπάρχει μεταξύ της αγοραίας αξίας των ακινήτων και της ύπαρξης ή όχι ανελκυστήρα, η οποία δεν είναι γραμμική - Διάγραμμα 6: Απεικονίζει τη σχέση που υπάρχει μεταξύ της αγοραίας αξίας των ακινήτων και του είδους θέρμανσης των διαμερισμάτων, η οποία δεν είναι γραμμική - Διάγραμμα 7: Απεικονίζει τη σχέση που υπάρχει μεταξύ της αγοραίας αξίας των ακινήτων και του βαθμού συντήρησης τους, η οποία είναι γραμμική. Όμοια, με το διάγραμμα 1 και 2, επισημαίνονται οι δύο οντότητες 31 και 34, ως πιθανές ακραίες οντότητες. - Διάγραμμα 8: Απεικονίζει τη σχέση που υπάρχει μεταξύ της αγοραίας αξίας των ακινήτων και της ιδιωτικής θέσης στάθμευσης, η οποία δεν είναι γραμμική Η διαγραμματική απεικόνιση των μερικών συσχετίσεων μόνο των τριών μεταβλητών είναι αρκετή στο συγκεκριμένο στάδιο, διότι μόνο αυτές ενδιαφέρουν για την αξιολόγηση του μοντέλου. Παρ όλα αυτά παρατίθενται όλες για να τονιστούν για ακόμη μία φορά οι διαφορές που υπάρχουν όσον αφορά την επίδραση των μεταβλητών. Τιμές t Οι τιμές t εξάγονται έπειτα από την εκτέλεση της γραμμικής πολλαπλής παλινδρόμησης και είναι ορατές στον πίνακα των συντελεστών παλινδρόμησης (Coefficients), ο οποίος σύμφωνα με τον Πραμαγγιούλη, 2008 είναι ο πίνακας εκτίμησης των παραμέτρων του μοντέλου αλλά και ελέγχου στατιστικής σημαντικότητας καθεμίας μεταβλητής. Όπως φαίνεται και από τον παρακάτω πίνακα κάθε γραμμή του αναφέρεται στους συντελεστές κάθε μίας από τις ανεξάρτητες μεταβλητές που συσχετίζονται με την εξαρτημένη μεταβλητή και επιδρούν στη διαμόρφωση της τιμής της με διαφορετική βαρύτητα η κάθε μία από αυτές. Μεταπτυχιακή διατριβή 63
76 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Πίνακας4.3: Πίνακας Coefficients που περιλαμβάνει τις τιμές μεταβλητών t των ανεξάρτητων Coefficients a Model Unstandardized Standardized 95,0% Confidence Collinearity Coefficients Coefficients Interval for B Correlations Statistics Lower Upper Zero- B Std. Error Beta t Sig. Bound Bound order Partial Part Tolerance VIF 3 (Constant) , ,749 -,575, , ,746 X1 1595, ,167,722 9,902, , ,702,716,798,700,938 1,066 X , ,896,284 3,570, , ,001,292,431,252,786 1,271 X2-920, ,517 -,257-3,235, , ,359 -,469 -,397 -,789 1,268,229 Η πέμπτη στήλη του πίνακα (t) οδηγεί στον έλεγχο της στατιστικής σημαντικότητας των συντελεστών με τη χρήση των t-tests που ελέγχουν εάν κάθε συντελεστής διαφέρει από την τιμή 0. Έτσι Μηδενική υπόθεση Ηο : Οι μερικοί συντελεστές παλινδρόμησης είναι μηδέν έναντι της εναλλακτικής υπόθεσης Η1: Τουλάχιστον ένας συντελεστής παλινδρόμησης διαφέρει από το μηδέν. Οι τιμές Sig. του πίνακα (παρατηρούμενο επίπεδο σημαντικότητας) που αντιστοιχούν στο στατιστικό έλεγχο για τη στατιστική σημαντικότητα ή όχι των ανεξάρτητων μεταβλητών είναι <0,05 με αποτέλεσμα να απορρίπτεται η μηδενική υπόθεση, οπότε και οι τρεις μεταβλητές είναι στατιστικά σημαντικές και κατάλληλες για το μοντέλο. Σύμφωνα με τον Δαφέρμο, 2005 η σημαντικότητα μιας ανεξάρτητης μεταβλητής είναι μεγάλη όταν οι τιμές του t είναι > Ι±2Ι και όσο πιο μεγάλη είναι η τιμή από το δύο τόσο πιο σημαντική είναι. Από τον παραπάνω πίνακα προκύπτει ότι και οι τρεις μεταβλητές είναι στατιστικά σημαντικές με την Χ1 (εμβαδόν διαμερίσματος) να συμβάλλει σημαντικότερα στην ερμηνεία της εξαρτημένης μεταβλητής, τη μεταβλητή Χ7 (κατάσταση ακινήτου) να ακολουθεί και τέλος τη Χ2 (παλαιότητα οικοδομής) Ανεξαρτησία οντοτήτων Ο όρος ανεξαρτησία των οντοτήτων σημαίνει ότι η συμμετοχή στο δείγμα μίας οντότητας δε θα πρέπει να επηρεάζει καθόλου τη συμμετοχή μιας άλλης οντότητας. Σύμφωνα με τον Γναρδέλλη, 2006 η πρώτη προϋπόθεση της ανεξαρτησίας των παρατηρήσεων διασφαλίζεται κατά το σχεδιασμό, ο οποίος αποτελεί την πρώτη φάση μιας μελέτης. Θεωρείται δεδομένο ότι κατά τη συλλογή ενός δείγματος οι οντότητες δεν έχουν προκύψει από επαναλαμβανόμενες μετρήσεις της ίδιας μεταβλητής. Σύμφωνα με τη βιβλιογραφία ο έλεγχος της παραδοχής της ανεξαρτησίας ελέγχεται με δύο τρόπους. Αρχικά, με τη βοήθεια του δείκτη Durbin Watson και στη συνέχεια με το 64
77 dimension0 Κ ε φ ά λ α ι ο 4 ο γράφημα σκέδασης (scatterplot) των τυποποιημένων κατά student υπολοίπων με τη σειρά καταγραφής των οντοτήτων. Δείκτης Durbin Watson Ο δείκτης Durbin Watson εμφανίζεται στα αποτελέσματα της ανάλυσης στον πίνακα Model Summary (Πίνακας 4.4) όπως φαίνεται παρακάτω. Με τη βοήθεια του δείκτη ελέγχεται εάν τα τυποποιημένα υπόλοιπα είναι ανεξάρτητα μεταξύ τους, δηλαδή ελέγχεται η ανεξαρτησία των αντίστοιχων οντοτήτων. Η θεωρία αναφέρει ότι ο έλεγχος των αυτοσυσχετίσεων (δηλαδή έλεγχος της ανεξαρτησίας των υπολοίπων) με τη χρήση του δείκτη γίνεται με τη βοήθεια συγκεκριμένων ορίων που κρίνουν το αποτέλεσμα. Πιο συγκεκριμένα, οι τιμές του δείκτη Durbin Watson κυμαίνονται μεταξύ 0 και 4 (0<D<4). Όταν οι τιμές του δείκτη βρίσκονται μεταξύ του 0 και του 2 δείχνουν θετική αυτοσυσχέτιση και όσο τείνουν στο 0 χαρακτηρίζονται από έντονη θετική συσχέτιση. Αντίστοιχα, όταν οι τιμές του δείκτη βρίσκονται μεταξύ 2 και 4 δείχνουν αρνητική αυτοσυσχέτιση και όσο τείνουν στο πάνω όριο χαρακτηρίζονται από έντονη αρνητική συσχέτιση. Παρόλα αυτά ζητούμενη σε κάθε μελέτη είναι η ανεξαρτησία των οντοτήτων, η οποία εξασφαλίζεται όταν η τιμή του δείκτη βρίσκεται μεταξύ 1.5 και 2.5. Πίνακας4.4: Δείκτης Durbin Watson στον πίνακα Model Summary Model Summary d Model Change Statistics Adjusted Std. Error R R R of the Square F Sig. F Durbin- R Square Square Estimate Change Change df1 df2 Change Watson 1,716 a,512, ,023,512 60, ,000 2,817 b,668, ,911,156 26, ,000 3,849 c,720, ,523,052 10, ,002 2,224 a. Predictors: (Constant), X1 b. Predictors: (Constant), X1, X2 c. Predictors: (Constant), X1, X2, X7 d. Dependent Variable: Y Η τιμή του δείκτη Durbin Watson όπως φαίνεται από τον παραπάνω πίνακα είναι 2,224, βρίσκεται κοντά στο πάνω όριο που τίθεται από την θεωρία (1,5<2,224<2,5) και προδίδει ανεξαρτησία των οντοτήτων. Μεταπτυχιακή διατριβή 65
78 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα Σκέδασης : Studentized Residuals vs Sequence Πρόκειται για ένα διάγραμμα σκέδασης, το οποίο στόχο έχει την ανίχνευση της παραδοχής της ανεξαρτησίας μέσω της παρακάτω λογικής. Θεωρούμε μία νοητή γραμμή στο σημείο μηδέν, που χωρίζει τα θετικά τυποποιημένα υπόλοιπα από τα αρνητικά. Τα σημεία θα πρέπει να είναι τοποθετημένα τυχαία πάνω και κάτω από τη γραμμή και ταυτόχρονα να μη σχηματίζουν συσσωρεύσεις και πρότυπα. Με άλλα λόγια δε θα πρέπει η τιμή των υπολοίπων να εξαρτάται από τη σειρά με την οποία καταχωρήθηκαν μία προς μία οι οντότητες. (Δαφέρμος, 2005) Ο σχηματισμός του διαγράμματος γίνεται μέσω του βήματος Graphs Legacy Dialogs Scatter/Dot Simple Scatter Y: Studentized Residual, X: A/A (Εικόνα 4.10) Εικόνα 4.10: Δημιουργία διαγράμματος σκέδασης (Studentized Residuals vs Sequence) Το διάγραμμα σκέδασης που προκύπτει αποτυπώνεται παρακάτω (Διάγραμμα 4.3), και παράλληλα γίνεται επεξεργασία του ώστε να φανεί η τυχαία κατανομή γύρω από τη γραμμή 0. 66
79 Κ ε φ ά λ α ι ο 4 ο Διάγραμμα 4.3: Διάγραμμα σκέδασης (Studentized Residuals vs Sequence) Το διάγραμμα 4.3 παρουσιάζει τα επιθυμητά αποτελέσματα, διότι πρόκειται για μία τυχαία κατανομή των υπολοίπων, η οποία τοποθετείται με ομοιόμορφο τρόπο επάνω και κάτω από τη γραμμή του μηδέν και ταυτόχρονα βρίσκεται εντός μίας ζώνης σταθερού πλάτους (μεταξύ του ±2). Παρατηρείται ότι οι οντότητες 31 και 34 βρίσκονται εκτός της ζώνης σταθερού πλάτους ±2 και άρα είναι πιθανή η απομάκρυνση τους ως πιθανές ακραίες οντότητες σε επόμενο βήμα της εφαρμογής. Παρόλα αυτά, σύμφωνα με το δείκτη Durbin Watson και με το γράφημα σκέδασης των τυποποιημένων υπολοίπων κατά student με τη σειρά καταχώρησης των οντοτήτων (Α/Α) γίνεται σαφές ότι το αρχικό μοντέλο πρόβλεψης των αγοραίων αξιών ακινήτων για την περιοχή του κέντρου της Θεσσαλονίκης πληροί το έλεγχο της ανεξαρτησίας των οντοτήτων Πολυσυγγραμικότητα ή Συγγραμικότητα Πρόβλημα πολυσυγγραμικότητας ή συγγραμικότητας (multicollinearity or collinearity & Singularity) υπάρχει σε εκείνες τις περιπτώσεις όπου κάποιες από τις ανεξάρτητες μεταβλητές X i είναι γραμμικά εξαρτημένες μεταξύ τους, με αποτέλεσμα να δημιουργείται πρόβλημα στα αποτελέσματα που προκύπτουν από την εκτέλεση της πολλαπλής γραμμικής παλινδρόμησης. Σύμφωνα με Λαφαζάνη, 2011 το πρόβλημα πολυσυγγραμικότητας οδηγεί σε αύξηση των τυπικών σφαλμάτων των συντελεστών παλινδρόμησης με αποτέλεσμα οι συντελεστές αυτοί να μη θεωρούνται αξιόπιστοι για το μοντέλο. Μία σειρά από δείκτες και συντελεστές που αναλύονται παρακάτω βοηθούν στον έλεγχο ύπαρξης ή όχι πολυσυγγραμικότητας και εντοπίζουν την ανεξάρτητη μεταβλητή που συσχετίζεται με άλλη ή άλλες ή τις ομάδες ισχυρά συσχετισμένων μεταβλητών. Μεταπτυχιακή διατριβή 67
80 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Σύμφωνα με τον Μούτσικα, 2004 ένας απλός τρόπος αντιμετώπισης της πολυσυγγραμικότητας είναι η αφαίρεση ορισμένων ανεξάρτητων μεταβλητών, με την ταυτόχρονη όμως μείωση της πληροφορίας. Πιο συγκεκριμένα, στο μοντέλο θα πρέπει να κρατηθεί μόνο μία από τις ανεξάρτητες μεταβλητές όπου συσχετίζονται γραμμικά. Επισημαίνει επίσης ότι επειδή δεν είναι πάντα μία εύκολη διαδικασία, υπάρχουν και εναλλακτικές μέθοδοι (πχ. Principal components regression). Στην περίπτωση όπου οι παρακάτω συντελεστές και δείκτες δείξουν πρόβλημα πολυσυγγραμικότητας, τότε θα πρέπει να γίνει αφαίρεση της αντίστοιχης ανεξάρτητης μεταβλητής. Παράγοντας ανοχής (Tolerance factor) & Παράγοντας πληθωριστικής διακύμανασης (Variance inflation factor) Το SPSS υπολογίζει τον παράγοντα ανοχής και πληθωριστικής διακύμανσης μέσα από τον πίνακα των συντελεστών παλινδρόμησης (Coefficients), όπως φαίνεται παρακάτω (Πίνακας 4.5). Όταν η τιμή του παράγοντα ανοχής είναι μικρότερη από μία κρίσιμη τιμή, τότε η αντίστοιχη μεταβλητή X i απορρίπτεται από το μοντέλο πολλαπλής παλινδρόμησης, διότι είναι γραμμικός συνδυασμός των άλλων ανεξάρτητων μεταβλητών. Γενικά, οι τιμές του δείκτη tolerance βρίσκονται στο διάστημα [0,1]. Οριακή τιμή για τον έλεγχο αποτελεί το 0,5. Τιμές μεγαλύτερες από 0,5 είναι ικανοποιητικές για την παραδοχή της πολυσυγγραμικότητας, ενώ τιμές μικρότερες του 0,5 φανερώνουν ότι η μεταβλητή αποτελεί γραμμικό συνδυασμό των υπόλοιπων ανεξάρτητων μεταβλητών. Επίσης, η τιμή (1 tolerance)% μίας μεταβλητής είναι το ποσοστό της μεταβλητότητας της μεταβλητής, το οποίο μπορούν να εξηγήσουν οι υπόλοιπες ανεξάρτητες μεταβλητές του μοντέλου. (Αγγελίδης, 2009) Στην προκειμένη περίπτωση, οι τιμές του παράγοντα ανοχής για τις τρεις ανεξάρτητες μεταβλητές Εμβαδόν, Βαθμός συντήρησης ακινήτου και Παλαιότητα είναι αντίστοιχα 0.938, 0.786, 0.789, συνεπώς δεν υπάρχει πρόβλημα πολυσυγγραμικότητας σύμφωνα με τον πρώτο έλεγχο. Αντίστοιχα, η τιμή του παράγοντα πληθωριστικής διακύμανσης μεγαλώνει όταν ο παράγοντας T i μικραίνει. Σύμφωνα με την ηλεκτρονική βοήθεια του SPSS, τιμή μεγαλύτερη του 2, δείχνει ένα δείκτη που θεωρείται συνήθως προβληματικός. Σύμφωνα με τον Αγγελίδη, 2009 οριακή τιμή για τον δείκτη VIF είναι το 5, ενώ πιο ελαστική ανοχή θα μπορούσε να είναι και η τιμή 10. Σύμφωνα με τον πίνακα 4.5, οι αντίστοιχες τιμές VIF 1, VIF 7, VIF 2 είναι 1.066, 1.271, Παρατηρείται ότι όλες είναι εντός του ορίου που αναφέρει η θεωρία, άρα και ο έλεγχος του δεύτερου δείκτη δεν παρουσιάζει πρόβλημα συγγραμικότητας μεταξύ των ανεξάρτητων μεταβλητών. 68
81 n1 Κ ε φ ά λ α ι ο 4 ο Πίνακας4.5: Πίνακας Coefficients, όπου δίνονται οι δείκτες για τον έλεγχο συγγραμικότητας Tolerance & VIF Coefficients a Model Unstandardized Standardized 95,0% Confidence Collinearity Coefficients Coefficients Interval for B Correlations Statistics Lower Upper Zero- B Std. Error Beta t Sig. Bound Bound order Partial Part Tolerance VIF 3 (Constant) , ,749 -,575, , ,746 X1 1595, ,167,722 9,902, , ,702,716,798,700,938 1,066 X , ,896,284 3,570, , ,001,292,431,252,786 1,271 X2-920, ,517 -,257-3,235, , ,359 -,469 -,397 -,789 1,268,229 Έλεγχος ιδιοτιμών (Eigenvalues) & Δεσμευμένοι δείκτες (Condition indexes) Στον πίνακα Collinearity Diagnostics όπως φαίνεται παρακάτω δύο στήλες (Eigenvalue και condition index ) αποτελούν επίσης μέτρα για τη διάγνωση συγγραμικότητας. Όσον αφορά το δείκτη των ιδιοτιμών (Eigenvalues) τιμές οι οποίες βρίσκονται πολύ κοντά στο 0 φανερώνουν γραμμική συσχέτιση των ανεξάρτητων μεταβλητών. Όπως παρατηρείται από τον πίνακα 4.6 οι τιμές του δείκτη για κάθε μία ανεξάρτητη μεταβλητή δεν είναι πάρα πολύ κοντά στην τιμή του μηδέν και άρα δεν εμφανίζεται πρόβλημα πολυσυγγραμμικότητας σύμφωνα με τις τιμές Eigenvalues. Όσον αφορά τους δεσμευμένους δείκτες, τιμές μεγαλύτερες του 15 παρουσιάζουν ένα πιθανό πρόβλημα, ενώ εάν ξεπεράσουν την τιμή 30, τότε υπάρχει σίγουρα μεγάλο πρόβλημα συγγραμικότητας. (Αγγελίδης, 2009) Όμοια από τα στοιχεία του πίνακα διαπιστώνεται ότι οι τιμές των δεσμευμένων δεικτών δεν ξεπερνούν την τιμή 15 και άρα δεν εμφανίζουν κάποια ένδειξη ύπαρξης πολυσυγγραμμικότητας. Πίνακας4.6: Πίνακας Collinearity diagnostics, όπου δίνονται οι δείκτες για τον έλεγχο συγγραμικότητας Eigenvalue και Condition Index Collinearity Diagnostics a Model Dimension Condition Variance Proportions Eigenvalue Index (Constant) X1 X7 X ,640 1,000,00,01,01,01 2,219 4,076,00,01,43,13 3,122 5,458,00,56,05,23 4,019 13,773 1,00,42,50,63 Μεταπτυχιακή διατριβή 69
82 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Κανονικότητα Σύμφωνα με τον Σιάρδο, 2000 η κανονικότητα δεν θα πρέπει να αποκλείεται όταν η κατανομή των υπολοίπων δεν εμφανίζεται απόλυτα κανονική. Επισημαίνει, επίσης ότι η ανεπιτυχής προσαρμογή του υποδείγματος της παλινδρόμησης, η μεταβλητότητα στη διακύμανση, ο μικρός αριθμός των διαθέσιμων υπολοίπων κ.α. δε βοηθούν στην ακριβή διαπίστωση της κανονικότητας. Για αυτό το λόγο για την ικανοποίηση του ελέγχου της κανονικότητας σε ένα παλινδρομικό μοντέλο προτείνει την χρησιμοποίηση περισσότερων τρόπων. Ταυτόχρονα, σύμφωνα με το Δαφέρμο, 2005 για τους τρόπους ελέγχου της κανονικότητας θα πρέπει αρχικά να ληφθεί υπόψη το μέγεθος του δείγματος. Στις περιπτώσεις εκείνες που το δείγμα είναι μικρότερο από 30 παρατηρήσεις, χρησιμοποιούνται τα συνήθη residuals ή τα standardized residuals. Αντίθετα, όταν το δείγμα είναι μεγάλο, δηλαδή μεγαλύτερο από 30 παρατηρήσεις για την παραδοχή της κανονικότητας αξιοποιούνται τα studentized residuals. Το χαρακτηριστικό τους είναι ότι στα μεγάλα δείγματα τα studentized residuals ακολουθούν την κανονική κατανομή και συνεπώς πρέπει να ελεγχθεί εάν αυτό συμβαίνει στην προκειμένη περίπτωση. Ωστόσο, είναι σαφές ότι εάν ληφθούν υπόψη τα Studentized Deleted Residuals η παραδοχή της κανονικότητας ελέγχεται με ακόμη πιο ακριβή τρόπο. Για τον έλεγχο αρχικά αξιοποιείται το ιστόγραμμα των Studentized Deleted Residuals που έχει ήδη παραχθεί μέσω της διαδικασίας Analyze Regression Linear. Επίσης, μέσω της εντολής Analyze Descriptive Statistics Explore και των επιλογών που φαίνονται αναλυτικά στην εικόνα 4.11 παράγονται για τον έλεγχο της κανονικότητας τέσσερα ακόμη διαγράμματα και ένας πίνακας. Συγκεντρωτικά, οι τρόποι ελέγχου είναι οι ακόλουθοι: 1) Φυλλογράφημα των υπολοίπων (Εντολή Explore) 2) Test of normality : Kolmogorv Smirnov, Lillefors, Shapiro Wilk (Εντολή Explore) 3) Normal Q-Q Plot of Studentized deleted residuals (Εντολή Explore) 4) Detrended normal Q-Q Plot Studentized Deleted residuals (Εντολή Explore) 5) Histogram Studentized Deleted Residuals (Εντολή Explore) 6) Histogram standardized residuals (Εκτέλεση πολλαπλής γραμμικής παλινδρόμησης) 7) Normal P-P Plot of regression standardized residuals (Εκτέλεση πολλαπλής γραμμικής παλινδρόμησης) 8) Θηκόγραμμα των υπολοίπων (Boxplot of Residuals) (Εντολή Explore) 70
83 Κ ε φ ά λ α ι ο 4 ο Εικόνα4.11: Βήματα εκτέλεσης της διαδικασίας Explore Φυλλογράφημα των υπολοίπων [Stem And- Leaf- Plot of residuals Studentized deleted residuals] Το φυλλογράφημα των υπολοίπων, όπως φαίνεται και από την παρακάτω εικόνα έχει τη μορφή του ιστογράμματος στραμμένου 90 ο με τη φορά των δεικτών του ρολογιού. Τα δεδομένα ταξινομούνται, δίνοντας αρχικά προτεραιότητα στην τιμή του ακέραιου μέρους τους και μετά στην τιμή του δεκαδικού, σε οριζόντιες σειρές. Επίσης οι τιμές χωρίζονται σε δύο τμήματα, τον κορμό (stem) και το φύλλο (leaf). Μεταπτυχιακή διατριβή 71
84 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Το φυλλογράφημα παρέχει πληροφορίες που αφορούν τον προσδιορισμό του εύρους των τιμών μιας κατανομής, τον εντοπισμό του διαστήματος που παρατηρείται η μεγαλύτερη συγκέντρωση τιμών, την παρουσία ή όχι ασυμμετρίας στη μορφή της κατανομής και μία πρώτη προσέγγιση στην ύπαρξη ή όχι ακραίων τιμών. (Μισιρλόγλου, 2011) Studentized Deleted Residual Stem-and-Leaf Plot Frequency Stem & Leaf 4, , , , , , , , , Stem width: 1,00000 Each leaf: 1 case(s) Διάγραμμα 4.4: Φυλλογράφημα των υπολοίπων για την περιοχή του κέντρου της Θεσσαλονίκης (αρχικό δείγμα 60 οντοτήτων) Σύμφωνα με το φυλλογράφημα που παράγεται, μέσω της εντολής Explore, για την περιοχή του κέντρου δεν επισημαίνονται ακραίες τιμές και όλα τα Studentized Deleted Residuals ακολουθούν την κανονική κατανομή, όπως φαίνεται από την γνωστή καμπανοειδή μορφή που σχηματίζεται, στραμμένη όμως κατά 90 ο. Test of normality : Kolmogorv Smirnov, Lillefors, Shapiro Wilk Από τον παρακάτω πίνακα το στατιστικό κριτήριο Shapiro Wilk επιλέγεται να εφαρμοστεί στα μικρά δείγματα, ενώ το Kolmogorov Smirnov στα μεγάλα δείγματα (μεγαλύτερα των 30 οντοτήτων). Πίνακας4.7: Πίνακας Tests of Normality Kolmogorv Smirnov, Lillefors, Shapiro Wilk Tests of Normality Kolmogorov-Smirnov a Shapiro-Wilk Statistic df Sig. Statistic df Sig. Studentized Deleted Residual,067 60,200 *,978 60,345 72
85 Κ ε φ ά λ α ι ο 4 ο Ο έλεγχος της υπόθεσης της κανονικότητας των υπολοίπων γίνεται με τη χρήση του ελέγχου Kolmogorov Smirnov: Μηδενική Υπόθεση Ho: Τα υπόλοιπα κατανέμονται κανονικά και Εναλλακτική Υπόθεση H1: Τα υπόλοιπα δεν κατανέμονται κανονικά. Το τεστ για την κανονικότητα των Kolmogorov Smirnov και των Shapiro Wilk δίνει επίπεδο στατιστικής σημαντικότητας (Sig.) 20% και 34,5% αντίστοιχα, δηλαδή μεγαλύτερο του 5%. Συνεπώς, δεν μπορεί να απορριφθεί η υπόθεση ότι τα Studentized Deleted Residuals ακολουθούν την κανονική κατανομή. Normal Q-Q Plot of Studentized deleted Residuals Ο συγκεκριμένος τρόπος ελέγχου γίνεται μέσω της σύγκρισης της παρατηρούμενης αθροιστικής κατανομής των υπολοίπων προς την προσδοκώμενη αθροιστική κατανομή τους, παρατηρώντας τον τρόπο διασποράς τους ως προς την ευθεία γραμμή της κανονικής θεωρητικής κατανομής. (Σιάρδος, 2000) Διάγραμμα 4.5: Διάγραμμα κανονικότητας Normal Q-Q Plot of Studentized deleted Residuals για τον έλεγχο της κανονικότητας των υπολοίπων Μεταπτυχιακή διατριβή 73
86 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Από το παραπάνω γράφημα παρατηρείται ότι υπάρχουν διαφοροποιήσεις στα σημεία του διαγράμματος σε σχέση με τη γραμμή που ορίζει την πλήρη κανονικότητα, οι οποίες όμως δεν απορρίπτουν την περίπτωση της κανονικής κατανομής. Detrended normal Q-Q Plot Studentized Deleted residuals Το διάγραμμα «Detrended normal Q-Q Plot Studentized Deleted residual» (Διάγραμμα 4.6) απεικονίζει στον άξονα Χ τις παρατηρούμενες τιμές των Studentized Deleted Residuals, στον άξονα Υ τα ποσοστιαία σημεία μίας τυπικής κανονικής κατανομής και παρουσιάζει την απόκλιση των υπολοίπων από την κανονική κατανομή. Στο παρακάτω διάγραμμα εμφανίζεται μία τάση συγκέντρωσης των σημείων, η οποία οδηγεί στο συμπέρασμα ότι πιθανόν να πρέπει να απομακρυνθούν ορισμένα σημεία για τη βελτίωση της κανονικότητας στο μοντέλο. Διάγραμμα 4.6: Διάγραμμα Detrended normal Q-Q Plot Studentized Deleted residuals για τον έλεγχο της κανονικότητας των υπολοίπων Histogram Studentized Deleted Residuals Στο παρακάτω ιστόγραμμα (Διάγραμμα 4.7), το οποίο παράγεται μέσω της διαδικασίας Explore, εμφανίζεται μία μορφή κανονικότητας με ορισμένες εξαιρέσεις εκτροπών. Επίσης, στο διάγραμμα φαίνεται ότι υπάρχουν τιμές των υπολοίπων που ξεπερνούν την τιμή 2, γεγονός που συνεπάγεται την ανάγκη βελτιστοποίησης του μοντέλου. 74
87 Κ ε φ ά λ α ι ο 4 ο Διάγραμμα 4.7: Ιστόγραμμα των Studentized Deleted Residuals για τον έλεγχο της κανονικότητας των υπολοίπων Histogram Standardized Residuals Διάγραμμα 4.8: Ιστόγραμμα των Standartized Residuals για τον έλεγχο της κανονικότητας των υπολοίπων Μεταπτυχιακή διατριβή 75
88 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Υπάρχουν διάφορες γραφικές μέθοδοι για τον έλεγχο της κανονικότητας, εκ των οποίων το ιστόγραμμα συχνοτήτων του παραπάνω διαγράμματος (Διάγραμμα 4.8) χρησιμοποιείται πάρα πολύ συχνά στη συνήθη στατιστική ανάλυση. Πρόκειται για διάγραμμα που δημιουργήθηκε από την κύρια διαδικασία εκτέλεσης της γραμμικής παλινδρόμηση και όπως φαίνεται και από αυτό το διάγραμμα υπάρχουν ακραίες οντότητες που επιδρούν στην κανονικότητα του μοντέλου. Διάγραμμα Normal P-P Plot of regression standardized residuals Το παρακάτω γράφημα αναμενόμενης παρατηρούμενης αθροιστικής συχνότητας, δείχνει ότι η πλειοψηφία των παρατηρήσεων συγκεντρώνονται γύρω από την ευθεία γραμμή, με ελάχιστες αποκλίσεις που δεν επηρεάζουν όμως σημαντικά την κανονικότητα. Διάγραμμα 4.9: Διάγραμμα Normal P-P Plot of regression standardized residuals για τον έλεγχο της κανονικότητας των υπολοίπων Θηκόγραμμα των υπολοίπων (Boxplot of Residuals) Το θηκόγραμμα είναι ένας χαρακτηριστικός τύπος γραφήματος, ο οποίος βοηθά στην αναγνώριση των ακραίων τιμών του δείγματος 19 και στον προσδιορισμό με άμεσο τρόπο της θέσης των δεδομένων ως προς τη διάμεσο. Στο θηκόγραμμα στο σημείο που βρίσκεται 19 Ακραίες ή ασυνήθιστες λέγονται οι τιμές που είναι είτε πολύ μεγαλύτερες είτε πολύ μικρότερες από τον κύριο όγκο των δεδομένων. 76
89 Κ ε φ ά λ α ι ο 4 ο η διάμεσος υπάρχει μία οριζόντια γραμμή (Βλ. Διάγραμμα 4.10), η οποία βοηθά στον προσδιορισμό της ασυμμετρίας της κατανομής στο δείγμα. Διάγραμμα 4.10: Θηκόγραμμα για τον εντοπισμό των ακραίων τιμών του δείγματος μέσω της διαδικασίας Explore Στην προκειμένη περίπτωση, η διάμεσος του θηκογράμματος που αναφέρεται στο παλινδρομικό μοντέλο του κέντρου βρίσκεται στο κέντρο του ορθογωνίου, αλλά παρατηρείται ότι η μέγιστη τιμή της παρατήρησης των Studentized Deleted Residuals βρίσκεται μεταξύ των τιμών 2 και 3. Συνεπώς, είναι πιθανό να υπάρχουν οντότητες που εάν αγνοηθούν από το μοντέλο, μπορούν να βελτιώσουν την κανονικότητα του μοντέλου Ισότητα διακυμάνσεων/ομοσκεδαστικότητα Ο έλεγχος της ομοσκεδαστικότητας πραγματοποιείται για να ελεγχθεί η σχέση ανάμεσα στα υπόλοιπα και στις προβλεπόμενες από το μοντέλο τιμές. Η ανυπαρξία σχέσης ονομάζεται ομοσκεδαστικότητα και φανερώνει μία σταθερότητα στη διασπορά. (Δαφέρμος, 2005). Ο έλεγχος πραγματοποιείται μέσω της ερμηνείας των ακόλουθων διαγραμμάτων: Studentized Deleted Residuals vs Standardized Predicted Values Studentized Residuals vs Standardized Predicted Values Standardized Predicted Values vs Dependent Variable Στα δύο πρώτα διαγράμματα ο ομοσκεδαστικότητα ικανοποιείται όταν οι κουκκίδες των σημείων είναι τυχαία κατανεμημένες στο διάγραμμα. Αντίθετα, πρόβλημα ετεροσκεδασικότητας, δηλαδή ύπαρξη σχέσης μεταξύ των υπολοίπων (residuals) και των Μεταπτυχιακή διατριβή 77
90 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ προβλεπόμενων από το μοντέλο τιμών (predicted values), υφίσταται όταν εμφανίζονται πρότυπα και τάσεις στα δύο πρώτα διαγράμματα. Τα δύο πρώτα διαγράμματα ταιριάζουν πολύ διότι, το πρώτο (Διάγραμμα 4.11) που κατασκευάστηκε κατά τη διαδικασία εκτέλεσης της πολλαπλής γραμμικής παλινδρόμησης έχει στον Υ άξονα τα διαγραμμένα κατά student υπόλοιπα και στον Χ άξονα τις τυποποιημένες εκτιμώμενες/προβλεπόμενες τιμές του δείγματος των 60 τιμών, ενώ από την άλλη μεριά το δεύτερο διάγραμμα (Διάγραμμα 4.12) στον άξονα Y έχει τα κατά Student υπόλοιπα και στον άξονα Χ, τις τυποποιημένες προβλεπόμενες τιμές του δείγματος. Διάγραμμα 4.11: Διάγραμμα σκέδασης των Studentized Deleted Residuals με τα Standardized Predicted Values Το διάγραμμα 4.11 δείχνει τα σημεία τοποθετημένα μέσα σε μία σταθερή ζώνη γύρω από το 0 με εύρος από το -2 έως το 2. Παρατηρείται ότι οι οντότητες με Α/Α 31 και 34 ξεφεύγουν από τα όρια που έχουν τεθεί στο διάγραμμα και παρατηρείται μία μικρή τάση συγκέντρωσης των σημείων. Συνεπώς, παρόλο που οριακά ισχύει η ισότητα των διακυμάνσεων, υποδεικνύονται οντότητες που με την πιθανή απομάκρυνση τους να υπάρξει βελτίωση του διαγράμματος. Η ίδια λογική ακριβώς ισχύει και στο παρακάτω διάγραμμα, το οποίο όπως παρατηρείται δίνει τις ίδιες πληροφορίες. 78
91 Κ ε φ ά λ α ι ο 4 ο Διάγραμμα 4.12: Διάγραμμα σκέδασης των Studentized Residuals με τα Standardized Predicted Values Το τρίτο διάγραμμα απεικονίζει τη διασπορά των εκτιμώμενων τιμών έναντι των παρατηρούμενων. Πιο συγκεκριμένα, στον άξονα Υ βρίσκονται οι τυποποιημένες προβλεπόμενες τιμές, ενώ στον άξονα Χ οι παρατηρούμενες. Η ευθεία στο κέντρο αντιπροσωπεύει την ευθεία των ελαχίστων τετραγώνων και τα σημεία συσσωρεύονται με ομοιόμορφο τρόπο γύρω από αυτήν μέσα σε μία ζώνη σταθερού πλάτους. Στο διάγραμμα παρατηρούνται δύο οντότητες, οι οποίες οριακά είναι εκτός του εύρους (οντότητες 31 και 38). Μεταπτυχιακή διατριβή 79
92 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα 4.13: Διάγραμμα σκέδασης των τυποποιημένων προβλεπόμενων τιμών έναντι των παρατηρούμενων Εν κατακλείδι σύμφωνα με τα διαγράμματα 4.11, 4.12 και 4.13 ικανοποιείται η απαίτηση της ομοσκεδαστικότητας Γραμμικότητα Η ύπαρξη γραμμικής σχέσης μεταξύ των μεταβλητών Υ με τις Χ i είναι ίσως η πρώτη βασική υπόθεση που γίνεται για το μοντέλο πολλαπλής παλινδρόμησης. Ο έλεγχος της συγκεκριμένης παραδοχής πραγματοποιείται με τη βοήθεια τεσσάρων κατηγοριών διαγραμμάτων. Η οπτική ερμηνεία και αξιολόγηση τους δίνουν απαντήσεις για την ύπαρξη γραμμικότητας ή όχι. Τα διαγράμματα που αξιοποιούνται είναι τα ακόλουθα: 1) Διαγράμματα σκέδασης της εξαρτημένης μεταβλητής με κάθε ανεξάρτητη. Πρόκειται για το διάγραμμα 4.1, το οποίο παρουσιάστηκε σαν πρωταρχικό βήμα πριν αναλυθούν τα αποτελέσματα της εκτέλεσης της παλινδρόμησης, διότι δίνει μία πρώτη εικόνα της σχέσης μεταξύ εξαρτημένης και κάθε ανεξάρτητης μεταβλητής. Σύμφωνα με το διάγραμμα Matrix, υπάρχει γραμμικότητα μεταξύ της εξαρτημένης μεταβλητής Υ και των ανεξάρτητων μεταβλητών Χ1 (Εμβαδόν), Χ2 (Παλαιότητα) και Χ7 (Κατάσταση ακινήτου). 2) Διάγραμμα σκέδασης των διαγραμμένων κατά student υπολοίπων με τις τυποποιημένες προβλεπόμενες τιμές (Studentized deleted residuals vs standardized predicted values), το οποίο είναι το διάγραμμα 4.11 που χρησιμοποιείται για τον έλεγχο της ισότητας/σταθερότητας των διακυμάνσεων. Το διάγραμμα παρουσιάζει γραμμικότητα, αλλά υποδεικνύει ότι υπάρχουν πιθανοί τρόποι βελτίωσης, αφαιρώντας τα κατάλληλα σημεία. 3) Διαγράμματα μερικής παλινδρόμησης/ συσχέτισης (Partial Regression Plots) τα οποία αξιοποιήθηκαν για τον έλεγχο σημαντικότητας των ανεξάρτητων μεταβλητών Χi (Βλ Διαγράμματα με αριθμούς 1,2,7 στο διάγραμμα 4.2). Βασικό χαρακτηριστικό των διαγραμμάτων μερικής συσχέτισης είναι ότι αποτελούν ίσως τον πιο αξιόπιστο έλεγχο της γραμμικότητας, όσο και της καλής προσαρμογής του υποδείγματος της παλινδρόμησης (Σιάρδος, 2000) 4) Διάγραμμα σκέδασης των κατά student υπολοίπων με τις τυποποιημένες προβλεπόμενες τιμές (Studentized residual vs standardized predicted values),το οποίο είναι το διάγραμμα 4.12 που χρησιμοποιείται για τον έλεγχο της ισότητας/σταθερότητας των διακυμάνσεων Σύμφωνα με όλα τα παραπάνω διαγράμματα που έχουν μελετηθεί σε προηγούμενα στάδια, ισχύει η ύπαρξη γραμμικότητας μεταξύ της αγοραίας αξίας των ακινήτων με το εμβαδό, την παλαιότητα και την κατάσταση του ακινήτου (π.χ. Partial Plots), με την ταυτόχρονη όμως υπόδειξη οντοτήτων που είναι πιθανή η απομάκρυνση τους για τη βελτιστοποίηση του μοντέλου. 80
93 Κ ε φ ά λ α ι ο 4 ο Ακραίες οντότητες και οντότητες επίδρασης Στο σύνολο ενός δείγματος πολλές είναι οι φορές ύπαρξης παρατηρήσεων με διαφορετική συμπεριφορά σε σχέση με όλες τις υπόλοιπες. Οι λόγοι μπορεί να είναι ακόμη και τυχαίο λάθος κατά τη συλλογή του δείγματος ή κατά τη διάρκεια επεξεργασίας του από το μελετητή. Οποιαδήποτε και αν είναι η αιτία που τις καθιστά αποκομμένες, θα πρέπει να γίνει έλεγχος τους είτε με τη βοήθεια δεικτών, κατανομών ή διαγραμμάτων ώστε να κριθεί εάν πρέπει να απομακρυνθούν ή όχι από το δείγμα. Αυτού του είδους οι παρατηρήσεις διακρίνονται σε δύο βασικές κατηγορίες. Η πρώτη κατηγορία περιλαμβάνει τις ακραίες τιμές που έχουν πολύ μικρή επίδραση στα αποτελέσματα της ανάλυσης και ονομάζονται ακραίες οντότητες (outliers). Η δεύτερη κατηγορία περιλαμβάνει τις παρατηρήσεις που φτάνουν στο σημείο να επηρεάσουν ριζικά την ανάλυση παλινδρόμησης και κατ επέκταση τους συντελεστές παλινδρόμησης 20 και ονομάζονται οντότητες επίδρασης (influential points). Όπως γίνεται σαφές για το σχηματισμό ενός γραμμικού μοντέλου πολλαπλής παλινδρόμησης θα πρέπει να απομακρυνθεί κάθε είδους παρατήρηση που επηρεάζει αισθητά το αποτέλεσμα και για αυτό οι έλεγχοι που ακολουθούν είναι ιδιαίτερα σημαντικοί. Σύμφωνα με το Δαφέρμο, 2005 ο έλεγχος ύπαρξης των outliers γίνεται με τη βοήθεια της απόστασης Mahalanobis (Mahalanobis distance D i 2 ) και του Levarage h i (centered leverage). Επίσης τρία γραφήματα βοηθούν στον εντοπισμό τους και είναι τα διαγράμματα σκέδασης 1) Cook s distance με Centered Leverage Values 2) Standardized DFFITS με την αύξουσα σειρά των παρατηρήσεων A/A και 3) Standardized DFBETA X i με A/A. Ο έλεγχος των influential points γίνεται με τη βοήθεια της απόστασης Cook (Cook s Distance : CD i ), του μέτρου DFFITS (Standardized DFFITS), του μέτρου DFBetas (Standardized DFBetas), της κατανομής t (Διαδικασία BONFERRONI), της κατανομής F και με τη βοήθεια των ίδιων ειδικών γραφημάτων που αναφέρθηκαν παραπάνω για τον έλεγχο των outliers, δηλ. 1) Cook s distance με Centered Leverage Values 2) Standardized DFFITS με την αύξουσα σειρά των παρατηρήσεων A/A και 3) Standardized DFBETA X i με A/A. Όλοι οι παραπάνω έλεγχοι πραγματοποιούνται αναλυτικά στα υποκεφάλαια που ακολουθούν Χρήση δεικτών για τον εντοπισμό των ακραίων οντοτήτων (outliers) Οι οντότητες του δείγματος που αποτελούν ακραίες οντότητες έχουν άμεση επίδραση στην κλίση της ευθείας παλινδρόμησης και όχι στους συντελεστές παλινδρόμησης (Δαφέρμος, 2005). Η εύρεση τους δε σημαίνει άμεση απομάκρυνση του σημείου, αλλά περαιτέρω διερεύνηση για την πιθανότητα να αποτελεί οντότητα επίδρασης. Οι δύο δείκτες που ελέγχονται είναι η απόσταση Mahalanobis και η τιμή Leverage. 20 «είναι μία παρατήρηση η οποία όταν απαλειφθεί από την ανάλυση, προκαλεί μία ουσιαστική αλλαγή σε τουλάχιστον έναν από τους συντελεστές μερικής παλινδρόμησης.» Δαφέρμος, 2005 Μεταπτυχιακή διατριβή 81
94 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Απόσταση Mahalanobis 2 Το βασικό χαρακτηριστικό της απόστασης Mahalanobis D i είναι ότι ο υπολογισμός της στηρίζεται αποκλειστικά στις τιμές των ανεξάρτητων μεταβλητών και όχι της εξαρτημένης. Κατά τη διαδικασία εκτέλεσης της πολλαπλής γραμμικής παλινδρόμησης, όπως φαίνεται από την εικόνα 4.8, επιλέγεται να υπολογιστούν αυτόματα όλες οι αποστάσεις, δείκτες και μέτρα που αξιοποιούνται στον έλεγχο των ακραίων τιμών, οι τιμές των οποίων εισάγονται σε νέες στήλες στο παράθυρο του Data Editor. Σε αυτές τις τιμές που υπολογίζονται αυτόματα είναι το μέτρο Mahalanobis που εκφράζει της απόσταση κάθε οντότητας από το κέντρο βάρους όλων των άλλων οντοτήτων. Μεγάλη τιμή της απόστασης συνεπάγεται πιθανότητα ύπαρξης ακραίας οντότητας. Παρόλα αυτά δεν πραγματοποιείται ο συγκεκριμένος έλεγχος, διότι σύμφωνα με την ίδια πηγή (Δαφέρμος, 2005) στην τιμή Leverage δίνεται μεγαλύτερη βαρύτητα και ο έλεγχος της καλύπτει και τον έλεγχο της απόστασης Mahalanobis. Centered Leverage Στην περίπτωση του SPSS, σύμφωνα με τον Δαφέρμο, 2005 σημασία έχει ο υπολογισμός του κεντραρισμένου Leverage, η τιμή του οποίου δίνεται από τη σχέση Centered Leverage = h i - = - όπου h i η τιμή Leverage, n ο αριθμός του δείγματος και D i 2 η απόσταση Mahalanobis. Σύμφωνα με τη διεθνή βιβλιογραφία επισημαίνονται τα εξής κριτήρια ελέγχου για την τιμή Leverage: 1) Δεν θα πρέπει να ξεπερνά την τιμή, όπου p είναι ο αριθμός των συντελεστών παλινδρόμησης μαζί με το σταθερό όρο και n το μέγεθος του δείγματος. 2) Θα πρέπει οι τιμές Levarage να βρίσκονται στο διάστημα (0, ), δηλαδή στο (0, 0,98) 3) Τιμές μικρότερες του 0,2 δεν θεωρούνται ακραίες τιμές για τις προβλεπόμενες τιμές 4) Τιμές μεγαλύτερες του 0,2 και μικρότερες του 0,5 χαρακτηρίζονται επικίνδυνες και πρέπει να εξετάζονται εκτενέστερα για την πιθανή απομάκρυνση τους 5) Τιμές μεγαλύτερες από την τιμή 0,5 πρέπει να αποφεύγονται Σύμφωνα με το τρίτο κριτήριο οι τιμές δε θα πρέπει να ξεπερνούν την τιμή 0,2. Από τον έλεγχο όλων των οντοτήτων της στήλης LEV στην επιφάνεια του Data Εditor, καμία οντότητα δεν ξεπερνά την τιμή 0,2. Συνεπώς, σύμφωνα με τον πρώτο έλεγχο εύρεσης ακραίων οντοτήτων, δεν υπάρχει καμία οντότητα που να θεωρείται αποκομμένη σε σχέση με τις υπόλοιπες οντότητες του δείγματος. 82
95 Κ ε φ ά λ α ι ο 4 ο Χρήση δεικτών για τον εντοπισμό των οντοτήτων επίδρασης Αποστάσεις Cook CD i Πρόκειται για μέτρο, το οποίο υπολογίζει για κάθε οντότητα τις αλλαγές που συμβαίνουν στις εκτιμήσεις των παλινδρομικών συντελεστών όταν η συγκεκριμένη απαλειφθεί από το παλινδρομικό μοντέλο. Ως ανοχή για τον έλεγχο θεωρείται η μονάδα, καθώς αποστάσεις CDi > 1 σηματοδοτούν ύπαρξη οντότητας επίδρασης. (Δαφέρμος, 2005) Σύμφωνα με τα δεδομένα που προκύπτουν από την εκτέλεση πολλαπλής παλινδρόμησης όλες οι τιμές Cook είναι μικρότερες της μονάδας και άρα δεν υποδεικνύονται οντότητες επίδρασης. Μέτρα DfFits Πρόκειται για μέτρο, το οποίο εκφράζει την επίδραση της κάθε οντότητας στις εκτιμήσεις των παλινδρομικών συντελεστών και ο υπολογισμός του δίνεται από την παρακάτω σχέση. DfFits i = *SDR με hi τιμή Leverage και SDR τα κατά Student διαγραμμένα υπόλοιπα. Σύμφωνα με Δαφέρμο, 2005 στα μεγάλα δείγματα (n>30) κριτήριο για την εύρεση των οντοτήτων επίδρασης είναι η σύγκριση των Standardized DfFits με την τιμή 2* = 0,52, ενώ για τα μικρά δείγματα (n 30) η οριακή τιμή είναι η μονάδα. Πιο συγκεκριμένα, όταν τα Standardized > 2*, τότε θεωρείται ότι η περίπτωση i αποτελεί οντότητα επίδρασης. Με βάση τα στοιχεία του Data Editor και τη στήλη SDF παρατηρείται ότι οι οντότητες 12, 29, 31, 38, 39 και 44 έχουν Standardized DfFits κατά απόλυτη τιμή μεγαλύτερα του 0,52. Οι τιμές αντίστοιχα είναι SDF 12 = 0,86 και SDF 29 = 0,58, SDF 31 = 0,58 SDF 38 = 0,74, SDF 39 = 0,61 και SDF 44 = 0,81. Μέτρα DfBetas Πρόκειται για το μέτρο που εκφράζει την επίδραση της κάθε οντότητας στην εκτίμηση του κάθε παλινδρομικού συντελεστή ξεχωριστά. Για τον υπολογισμό αυτής της επίδρασης πραγματοποιούνται δύο παλινδρομικές αναλύσεις, εκ των οποίων η πρώτη συμπεριλαμβάνει την i οντότητα, ενώ η δεύτερη όχι. Ο υπολογισμός της διαφοράς των δύο τιμών οδηγεί σε τρεις τιμές DfBetas (συνολικά στο μοντέλο συμμετέχουν τρεις ανεξάρτητες μεταβλητές) για κάθε οντότητα του μοντέλου. (Δαφέρμος, 2005) Για τον έλεγχο αξιοποιούνται οι απόλυτες τιμές των τυποποιημένων DfBetas (Standardized DfBetas), οι οποίες συγκρίνονται με μία ποσότητα οριακή για την ύπαρξη οντοτήτων επίδρασης. Πιο συγκεκριμένα, ο Δαφέρμος, 2005 αναφέρει ότι για μεγάλα δείγματα (n>30) απόλυτες τιμές standardized DfBetas μεγαλύτερες από την ποσότητα θεωρούνται οντότητες επίδρασης. Μεταπτυχιακή διατριβή 83
96 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ > = 0,258 Συγκρίνοντας τις τιμές που υπολογίζονται αυτοματοποιημένα από το SPSS με την οριακή τιμή 0,258 εμφανίζονται τα ακόλουθα αποτελέσματα: 1) Οι οντότητες 5, 12, 29, 30, 36, 38, και 44 με αντίστοιχες τιμές των Standardized DfBetas SDB1 5 = 0,27, SDB1 12 = 0,81, SDB1 29 = 0,47, SDB1 30 = 0,29, SDB1 36 = 0,29, SDB1 38 = 0,51 και SDB1 44 = 0,34 ξεπερνούν την οριακή τιμή που τέθηκε και άρα είναι υποψήφιες οντότητες επίδρασης. 2) Οι οντότητες 1, 7, 19, 39, 44, 45, και 47 με αντίστοιχες τιμές των Standardized DfBetas SDB2 1 = 0,32, SDB2 7 = 0,30, SDB2 19 = 0,28, SDB2 39 = 0,48, SDB2 44 = 0,53, SDB2 45 = 0,41 και SDB2 47 = 0,38 όμοια ξεπερνούν την οριακή τιμή και πιθανόν να πρέπει να απομακρυνθούν από το μοντέλο, διότι επιδρούν στο συντελεστή της παλαιότητας στην εξίσωση του παλινδρομικού μοντέλου. 3) Οι οντότητες 12, 19, 31, 34, 38 και 50 με αντίστοιχες τιμές των Standardized DfBetas SDB7 12 = 0,29, SDB7 19 = 0,36, SDB7 31 = 0,40, SDB7 34 = 0,39, SDB7 38 = 0,31 και SDB7 50 = 0,31 ξεπερνούν την οριακή τιμή που τέθηκε και άρα είναι υποψήφιες οντότητες επίδρασης Χρήση γραφημάτων για τον εντοπισμό οντοτήτων επίδρασης Η διαγραμματική απεικόνιση πάντοτε δίνει μία πιο ξεκάθαρη διάσταση των μεγεθών που πρόκειται να συγκριθούν. Τα παρακάτω τρία διαγράμματα σκέδασης βοηθούν στην οπτικοποίηση των ακραίων οντοτήτων και υποψήφιων οντοτήτων επίδρασης. Διάγραμμα σκέδασης των αποστάσεων Cook με κεντραρισμένες τιμές Leverage Στο διάγραμμα σκέδασης 4.14 τοποθετείται κάθε σημείο βάσει της τιμής Leverage και Cook, ώστε με βάσει τις οριακές τιμές ανοχής να φανούν οι ακραίες οντότητες και οντότητες επίδρασης. Σε ένα διάγραμμα Cook vs Leverage είναι πιθανό να φανούν τα εξής αποτελέσματα: - Κάθε οντότητα να έχει απόσταση Cook μικρότερη της μονάδας και τιμή Centered Leverage μικρότερη του 0,2. Σε αυτή την περίπτωση δεν ασκείται επίδραση από καμία παρατήρηση που να χαρακτηρίζεται στατιστικώς σημαντική. - Στη δεύτερη κατηγορία ανήκει η περίπτωση ύπαρξης μίας ή περισσότερων παρατηρήσεων με τιμή Leverage που περνά την τιμή 0,2 και δεν ξεπερνά την τιμή 0,5 όσον αφορά τον Χ άξονα. Σε αυτήν την περίπτωση οι παρατηρήσεις που ξεφεύγουν από το όριο επηρεάζουν την κλίση της ευθείας παλινδρόμησης και όχι το ίδιο το μοντέλο. (Δαφέρμος, 2005) Μένει να αξιολογηθεί εάν η συγκεκριμένη επίδραση κρίνεται από τον ερευνητή ως στατιστικά σημαντική ή όχι. 84
97 Κ ε φ ά λ α ι ο 4 ο - Πιθανή είναι επίσης η εμφάνιση οντοτήτων με τιμές Cook ιδιαίτερα μεγάλες και πιθανόν μεγαλύτερες της μονάδας ενώ η κάθε τιμή που αντιστοιχεί στην Centered Leverage να είναι εντός των επιτρεπόμενων ορίων. Πρόκειται για μία δυσχερέστερη περίπτωση σε σχέση με τις προηγούμενες κατά την οποία δεν υπάρχει επίδραση στην γραμμή παλινδρόμησης, αλλά υπάρχει σημαντική επίδραση στους συντελεστές γραμμικής παλινδρόμησης, άρα στο ίδιο το μοντέλο. Μία τέτοια παρατήρηση αποτελεί οντότητα επίδρασης και εξετάζεται σοβαρά η άμεση απομάκρυνση της. - Η τέταρτη και τελευταία περίπτωση αναφέρεται στο ενδεχόμενο μία τιμή να έχει ιδιαίτερα μεγάλες και τις δύο τιμές, με αποτέλεσμα να είναι υποψήφια οντότητα επίδρασης που επιβάλλεται η απομάκρυνση της από το μοντέλο. Διάγραμμα 4.14: Διάγραμμα σκέδασης των αποστάσεων Cook με τις Centered leverage τιμές Στο διάγραμμα 4.14 καμία παρατήρηση του μοντέλου δεν ξεπερνά τις οριακές τιμές 1 και 0,2, άρα δεν ασκείται από καμία οντότητα ουσιαστική επίδραση στην κλίση της εξίσωσης παλινδρόμησης, αλλά ούτε στο παλινδρομικό μοντέλο. Μεταπτυχιακή διατριβή 85
98 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα σκέδασης των τυποποιημένων DfFits με την ακολουθία των παρατηρήσεων Α/Α Πρόκειται για διάγραμμα διαφορετικού τύπου (Sequence Chart), το οποίο δείχνει τον τρόπο που εξελίσσεται ο δείκτης Standardized DfFits σύμφωνα με τη σειρά καταχώρησης των παρατηρήσεων. Η κατασκευή του γραφήματος γίνεται μέσω του βήματος Analyze Forecasting Sequence Charts. Στη θέση των μεταβλητών (Variables) εισάγεται η τιμή Standardized DfFits, ενώ στον άξονα των Χ τοποθετείται η αύξουσα σειρά εισαγωγής των οντοτήτων στο δείγμα, όπως φαίνεται στην εικόνα Εικόνα 4.12: Διαδικασία δημιουργίας διαγράμματος σειράς (Sequence) Το αποτέλεσμα της διαδικασίας απεικονίζεται στο διάγραμμα Με κόκκινη γραμμή στο σημείο μηδέν τοποθετείται η αρχή μέτρησης των τιμών, ενώ οι υποψήφιες οντότητες επίδρασης είναι εκείνες που ξεπερνούν την κρίσιμη τιμή 0,52 (Βλ ). Παρατηρούνται πλέον διαγραμματικά οι έξι συνολικά οντότητες (με ΑΑ 12, 29, 31, 38, 39 και 44) που βρίσκονται εκτός της ζώνης που τέθηκε. Οι οντότητες 29, 31 και 38 ξεπερνούν ελάχιστα την τιμή 0,52, ενώ οι οντότητες 12, 39 και 44 φαίνεται να απέχουν αισθητά από το σύνολο των υπόλοιπων οντοτήτων. Όπως φαίνεται υποδεικνύονται αρκετές οντότητες, οι οποίες πιθανόν με την απομάκρυνση τους να οδηγήσουν στη βελτίωση του μοντέλου ως προς την αξιοπιστίας τους την αντιπροσωπευτικότητα του και την δύναμη της προβλεπτικής του ικανότητας. 86
99 Κ ε φ ά λ α ι ο 4 ο Διάγραμμα 4.15: Διάγραμμα Sequence των DfFits με την αύξουσα σειρά του δείγματος Διάγραμμα σκέδασης των τυποποιημένων DfBetas με την ακολουθία των παρατηρήσεων Α/Α Πρόκειται για ένα αντίστοιχο διάγραμμα με αυτό των Standardized DfFit έναντι της σειράς καταχώρησης των περιπτώσεων, με τη διαφορά ότι στον άξονα των Y γίνεται εισαγωγή περισσότερων από μίας μεταβλητών, οι οποίες απεικονίζονται με διαφορετικό χρωματισμό. Δημιουργείται ένα Sequence διάγραμμα (Analyze Forecasting Sequence Charts) με μεταβλητές στον άξονα Υ τις Standardized DfBetas και για τους τρεις συντελεστές του παλινδρομικού μοντέλου (δηλ. DFBeta1, DfBeta2 και DFBeta7), όταν στον Χ άξονα τοποθετείται η σειρά καταχώρησης των παρατηρήσεων Α/Α (Διάγραμμα 4.16). Η ανοχή που δίνεται για τα μεγάλα δείγματα είναι ίση με 0,258 (Βλ ) και οι οντότητες που ξεπερνούν το όριο απεικονίζονται στο παρακάτω διάγραμμα. Με πορτοκαλί γραμμή ορίζεται το πάνω και κάτω όριο έτσι ώστε να είναι ευκολότερα ορατές οι αποκλίσεις των οντοτήτων και τα μεγέθη των αποκλίσεων αυτών. Όπως παρατηρείται μεγαλύτερη επίδραση στον συντελεστή του εμβαδού παρουσιάζει η οντότητα 12 και 38, ενώ έπονται οι 44, 29, 30, 36 και 5 κατά φθίνουσα σειρά επίδρασης. Όσον αφορά τη μεταβλητή Χ2 (Παλαιότητα) μεγαλύτερη επίδραση δείχνει να έχει η οντότητα 44 και έπονται οι 39, 45, 47, 1, 7 και 19. Τέλος, όσον αφορά την μεταβλητή κατάσταση ακινήτου μεγαλύτερη επίδραση εμφανίζει η οντότητα 31 και έπονται οι 34, 19, 38, 50, και 12. Μεταπτυχιακή διατριβή 87
100 Σχηματισμός μοντέλου Διάγραμμα 4.16: Διάγραμμα Sequence των DfBetas με την αύξουσα σειρά του δείγματος Χρήση κατανομών για τον εντοπισμό οντοτήτων επίδρασης t κατανομή H t κατανομή μπορεί να βοηθήσει μέσω της διαδικασίας Bonferroni στον εντοπισμό των οντοτήτων επίδρασης με τη χρήση των Studentized Deleted Residuals που έχουν ήδη υπολογιστεί και βρίσκονται στα δεδομένα του Data Editor. Με τη βοήθεια της κατανομής t αλλά και F που ακολουθεί θα ληφθεί η τελική απόφαση για το εάν οι υποψήφιες οντότητες επίδρασης θα πρέπει να αφαιρεθούν από το μοντέλο ή όχι. Όπου ti ορίζεται η τιμή των Studentized Deleted Residuals, τα οποία ακολουθούν την κανονική κατανομή με βαθμούς ελευθερίας n-p-1 = =55. Πρώτο βήμα αποτελεί ο εντοπισμός της οντότητας με το μεγαλύτερο Studentized Deleted Residual (max SDR)ώστε να συγκριθεί με την κρίσιμη τιμή που ορίζει η διαδικασία Bonferroni και είναι ίση με t κρίσιμη = t(1 - ; n-p-1) t (0,99958 ; 55) = 2,669 βάσει των στατιστικών πινάκων της t κατανομής με α το επίπεδο στατιστικής σημαντικότητας (α= 0,05), n το μέγεθος του δείγματος και p τον αριθμό των συντελεστών παλινδρόμησης μαζί με το σταθερό όρο. 88
101 Κ ε φ ά λ α ι ο 4 ο Από τα δεδομένα του Data Editor προκύπτει ότι η οντότητα με τη μεγαλύτερη τιμή Studentized Deleted Residual κατά απόλυτη τιμή είναι η = = 2,25285, άρα ισχύει η μηδενική υπόθεση Η ο : Το Studentized Deleted Residual με τη μεγαλύτερη απόλυτη τιμή είναι μία οντότητα επίδρασης και με εναλλακτική υπόθεση Η 1 : Studentized Deleted Residual με τη μεγαλύτερη απόλυτη τιμή οντότητα επίδρασης =2,25285 ΔΕΝ =2,25285 είναι Επειδή όμως = 2,25285 <2,669 ισχύει η μηδενική υπόθεση Η ο και η οντότητα 34 δεν αποτελεί οντότητα επίδρασης. F κατανομή Η F κατανομή μπορεί με τη βοήθεια των τιμών Cook να εντοπίσει την ύπαρξη ή όχι οντοτήτων επίδρασης στο μοντέλο που σχηματίζεται, διότι θεωρείται ότι οι τιμές Cook ακολουθούν την κατανομή F(1-a;p;n-p). Με την ίδια λογική που περιγράφηκε παραπάνω αρχικά επιλέγεται από τα δεδομένα που υπολογίστηκαν κατά την εκτέλεση της πολλαπλής γραμμικής παλινδρόμησης, η τιμή Cook που είναι η μεγαλύτερη σε μέγεθος σε σύγκρισή με όλες τις υπόλοιπες. Η μέγιστη τιμή Cook (max CDi)στη συνέχεια συγκρίνεται με την κρίσιμη τιμή F(1-a; p; n-p) = F(0,95; 4; 56) και ανάλογα με το εκατοστημόριο το οποίο βρίσκεται φαίνεται ο βαθμός επίδρασης της στο μοντέλο. Εάν το εκατοστημόριο στο οποίο ανήκει είναι μικρότερο του 20%, τότε δεν ασκείται σημαντική επίδραση στο μοντέλο. Εάν βρίσκεται πολύ κοντά ή ξεπερνά το 50%, τότε η παρατήρηση αποτελεί οντότητα επίδρασης και εξετάζεται η αφαίρεση της από το μοντέλο. Η μέγιστη απόσταση Cook ανήκει στην οντότητα 12 και είναι ίση με CD 12 = 0, Από τους στατιστικούς πίνακες της F κατανομής παρατηρείται ότι η τιμή βρίσκεται στο 25,5% εκατοστημόριο της συγκεκριμένης κατανομής, δηλαδή δεν πλησιάζει σε καμία περίπτωση το 50% και άρα η οντότητα δε μπορεί να χαρακτηριστεί οντότητα επίδρασης. Σύμφωνα με τους δύο ελέγχους κρίνεται ότι καμία από τις υποψήφιες οντότητες επίδρασης στο αρχικό δείγμα των 60 οντοτήτων δε χρειάζεται να απομακρυνθεί από το μοντέλο Έλεγχος προβλεπτικής ικανότητας του αρχικού μοντέλου Έπειτα από την ολοκλήρωση της στατιστικής ανάλυσης ακολουθεί ο έλεγχος της προβλεπτικής δύναμης του μοντέλου. Για τον έλεγχο της προβλεπτικής ικανότητας αξιοποιούνται τρεις μέθοδοι. Η μέθοδος των διαστημάτων πρόβλεψης, η μέθοδος του διαχωρισμού των δεδομένων και τέλος η μέθοδος εύρεσης του βέλτιστου αριθμού των σημαντικών μεταβλητών. Μεταπτυχιακή διατριβή 89
102 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Μέθοδος των διαστημάτων πρόβλεψης Για την πραγματοποίηση του ελέγχου θα πρέπει αρχικά να συλλεχθούν ορισμένα νέα διαμερίσματα με όμοιο ακριβώς τρόπο με αυτόν που συλλέχθηκε το δείγμα. Απαραίτητη προϋπόθεση είναι ότι οι νέες οντότητες θα πρέπει να ανήκουν αυστηρά στον ίδιο πληθυσμό από τον οποίο προέρχεται το αρχικό δείγμα. Οι 60 εγγραφές του αρχικού μοντέλου μαζί με τις πέντε νέες εγγραφές εισάγονται στο περιβάλλον του Data Editor και στη συνέχεια εκτελείται η πολλαπλή γραμμική παλινδρόμησης (Analyze Regression Linear) επιλέγοντας όμως μόνο τις πρώτες 60 εγγραφές. Τα αποτελέσματα της παλινδρόμησης που προκύπτουν δεν αφορούν μόνο τις 60 οντότητες, αλλά και τις 65. Ο έλεγχος πραγματοποιείται συγκρίνοντας τις παρατηρούμενες τιμές Υ των πέντε νέων οντοτήτων με το διάστημα πρόβλεψης που ορίζεται στο SPSS από τις τιμές (LICI, UICI). Όταν βρίσκονται εντός του διαστήματος πρόβλεψης, τότε το δείγμα θεωρείται ότι ανταποκρίνεται στην πραγματικότητα. Σύμφωνα με τα αποτελέσματα όλες οι νέες οντότητες περνούν τον έλεγχο της πρόβλεψης, διότι οι αγοραίες αξίες που είναι γνωστές τιμές βρίσκονται εντός των διαστημάτων πρόβλεψης. Συνεπώς, το αρχικό δείγμα των 60 οντοτήτων ανταποκρίνεται στην πραγματικότητα < < < < < < < < Παρόλα αυτά, τα παραπάνω στοιχεία δείχνουν ένα αρκετά μεγάλο εύρος στο διάστημα πρόβλεψης ( ) σχετικά με τις αξίες των ακινήτων, γεγονός που σημαίνει ότι το μοντέλο δεν έχει ισχυρή προβλεπτική ικανότητα και άρα απαιτείται η βελτιστοποίηση του Μέθοδος του διαχωρισμού των δεδομένων (Data Splitting) Πρόκειται για ακόμη μία σημαντική διαδικασία ελέγχου της προβλεπτικής ικανότητας του μοντέλου η οποία εκτελείται σε δύο στάδια. Σε πρώτη φάση επιλέγεται με τυχαία σειρά το 70% περίπου των οντοτήτων και εκτελείται μόνο με αυτές η διαδικασία της πολλαπλής γραμμικής παλινδρόμησης. Στη συνέχεια επιλέγεται το υπόλοιπο 30% των οντοτήτων και με τη χρήση της εξίσωσης που προκύπτει από το πρώτο βήμα υπολογίζεται μία νέα στήλη προβλεπόμενων τιμών. Εάν η σύγκριση της με τις παρατηρούμενες τιμές 90
103 Κ ε φ ά λ α ι ο 4 ο είναι ικανοποιητική και άρα υπάρχει ισχυρή συσχέτιση, τότε το μοντέλο είναι αξιόπιστο και θεωρείται ότι έχει υψηλή προβλεπτική ικανότητα. Η διαδικασία εκτέλεσης των δύο βημάτων είναι η ακόλουθη: 1 ο ΒΗΜΑ: Στο αρχείο *.sav τοποθετούνται μόνο οι τέσσερις μεταβλητές (Υ, Χ1, Χ2, Χ7) και εκτελείται η διαδικασία Μενού Data Select Cases Random Sample Approximately 70% of all cases. Ο αριθμός των οντοτήτων που επιλέγεται τυχαία από το δείγμα είναι 47/60. Η διαδικασία για την επιλογή μόνο ορισμένων οντοτήτων (70%) πραγματοποιείται μέσω μίας νέας στήλης, η οποία έχει το όνομα filter_$ και παίρνει την τιμή 1 για τις οντότητες που είναι ενεργές και την τιμή 0 για εκείνες που είναι ανενεργές. Στη συνέχεια εκτελείται η διαδικασία της πολλαπλής παλινδρόμησης με τα γνωστά βήματα (Βλ )και εξάγεται μία νέα, διαφορετική εξίσωση παλινδρόμησης. Υ = , ,255 Χ ,058 Χ7-739,826 Χ2 με R = 0,870, R 2 = 0,758, R 2 adj = 0,741, Δείκτη Durbin Watson = 1,934, τιμές VIF μικρότερες του 2 και τιμές t μεγαλύτερες του. Πρόκειται δηλαδή για ένα καλό και αξιόπιστο μοντέλο. Τέλος, ο έλεγχος της ανεξαρτησίας των οντοτήτων με τη βοήθεια του διαγράμματος Studentized Residual vs AA (Sequence) επιβεβαιώνει ότι πρόκειται για ένα μοντέλο που πληροί όλες τις βασικές παραδοχές μιας γραμμικής παλινδρόμησης (Διάγραμμα 4.17). Μεταπτυχιακή διατριβή 91
104 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα 4.17: Διάγραμμα σκέδασης των Studentized Residual vs AA (Sequence) για τις 47 μόνο οντότητες του δείγματος 2 ο ΒΗΜΑ: Για την επιλογή των υπόλοιπων οντοτήτων, οι οποίες στο προηγούμενο βήμα ήταν ανενεργές (13/60) και την ταυτόχρονη απενεργοποίηση του 70% ακολουθείται η παρακάτω διαδικασία. Από το Μενού Data Select Cases If Condition is satisfied filter_$ = 0. Με την επιλογή των 13 οντοτήτων και την εντολή Compute Variables εισάγεται στο πεδίο target Variable η τιμή PRED και στο πεδίο Numeric Expression η εξίσωση παλινδρόμησης που παράγεται κατά το πρώτο βήμα (Εικόνα4.13). Παρατηρείται ότι προστέθηκε μία επιπλέον στήλη στον Data Editor με τον τίτλο PRED για όλο το δείγμα των 60 οντοτήτων. Εικόνα 4.13: Διαδικασία υπολογισμού των 60 προβλεπόμενων τιμών με βάση την παλινδρομική εξίσωση των 47 οντοτήτων Στη συνέχεια, μέσω της εντολής Μενού Analyze Correlation Bivariate εισάγονται οι προβλεπόμενες τιμές που υπολογίστηκαν (PRED)με τις παρατηρούμενες (Y)για να φανεί άμεσα ο βαθμός συσχέτισης τους (Εικόνα 4.14). 92
105 Κ ε φ ά λ α ι ο 4 ο Εικόνα 4.14: Εντολή Analyze, Correlation, Bivariate για τον υπολογισμό της συσχέτισης μεταξύ PRED και Υ Η τιμή του Pearson Correlation είναι ίση με 0,363 και άρα εμφανίζεται μία πολύ αδύναμη προβλεπτική δύναμη στο μοντέλο. Η συσχέτιση μεταξύ της προβλεπόμενης και παρατηρούμενης τιμής είναι μικρότερη από 50% και φανερώνει την ανάγκη πραγματοποίησης διαδικασιών βελτιστοποίησης του μοντέλου προκειμένου να δίνει αποτελέσματα που να ανταποκρίνονται στην πραγματικότητα. Διάγραμμα 4.18: Διάγραμμα Bivariate συσχέτισης μεταξύ των προβλεπόμενων και παρατηρούμενων τιμών Μεταπτυχιακή διατριβή 93
106 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Για την επιβεβαίωση της αξιολόγησης κατασκευάζεται και το διάγραμμα σκέδασης μεταξύ των PRED και Υ, ώστε να οπτικοποιηθεί το αποτέλεσμα (Διάγραμμα 4.18). Όπως είναι ξεκάθαρο δεν εμφανίζεται καμία συσχέτιση μεταξύ των προβλεπόμενων και παρατηρούμενων τιμών Μέθοδος εύρεσης του βέλτιστου αριθμού σημαντικών μεταβλητών Υπάρχει συγκεκριμένη διαδικασία στο SPSS σύμφωνα με την οποία ελέγχεται εάν οι μεταβλητές που επιλέγονται ως στατιστικώς σημαντικές κατά την εκτέλεση της γραμμικής πολλαπλής παλινδρόμησης (π.χ. στην περίπτωση της πρώτης περιοχής μελέτης οι μεταβλητές Y, X1, X7 και X2) επαρκούν ή είναι περισσότερες ή λιγότερες σε αριθμό από αυτές που πραγματικά ερμηνεύουν το φαινόμενο. Η διαδικασία που αναλύεται παρακάτω γίνεται μέσω διαδικασίας σύνταξης εντολής (File New Syntax) και με τη χρήση του κριτηρίου Mallow s Prediction Criterion. Πρόκειται για κριτήριο το οποίο ελέγχει το βέλτιστο αριθμό των παραμέτρων σε ένα μοντέλο παλινδρόμησης, διότι όπως είναι λογικό πρέπει να αποφεύγονται τα μοντέλα που έχουν υπερβολικά μεγάλο ή μικρό αριθμό παραμέτρων. Ο μόνος τρόπος εμφάνισης του συγκεκριμένου κριτηρίου, σύμφωνα με την ηλεκτρονική βοήθεια υποστήριξης της IBM, γίνεται μέσα από το πλαίσιο εντολών του SPSS (Syntax Window) και όχι από τη γνωστή διαδικασία μέσω του παραθύρου διαλόγου Linear Regresssion. Οι εντολές (Syntax) που εκτελούνται κατά τη διαδικασία της παλινδρόμησης (Analyze Regression Linear Method Stepwise OK) είναι οι ακόλουθες: REGRESSION /MISSING LISTWISE /STATISTICS COEFF OUTS R ANOVA /CRITERIA = PIN (.05) POUT (.10) /NOORIGIN /DEPENDENT Y /METHOD = STEPWISE. Σύμφωνα με την ηλεκτρονική βοήθεια υποστήριξης της IBM 21 προσθέτοντας SELECTION στην υποεντολή (subcommand) /STATISTICS εμφανίζονται στον πίνακα Model Summary τα κριτήρια Mallow's CP, Akaike Information Criterion (AIC), το Amemiya Prediction Criterion, και το Schwartz Bayesian Criterion. Συνεπώς πληκτρολογούνται οι παρακάτω εντολές και στη συνέχεια με το εικονίδιο Selection «τρέχει» η διαδικασία. REGRESSION VARIABLES = Y X1 X2 X7 /MISSING LISTWISE /STATISTICS COEFF OUTS R ANOVA SELECTION /CRITERIA = PIN (.05) POUT (.10) /NOORIGIN /DEPENDENT Y /METHOD = STEPWISE
107 Κ ε φ ά λ α ι ο 4 ο Μπορεί να πραγματοποιηθεί αποθήκευση του κώδικα, ώστε να μπορεί να χρησιμοποιηθεί σε άλλη παρόμοια εφαρμογή με την κατάληξη *.sps. Από τον πίνακα 4.8 και από την τιμή τέσσερα (4) που εμφανίζεται στην τελευταία γραμμή της στήλης Mallow s Prediction Criteria είναι ξεκάθαρο ότι ο βέλτιστος αριθμός μεταβλητών που υποδεικνύει το κριτήριο είναι τέσσερις. Συνεπώς, ο τρίτος έλεγχος της διαδικασίας ελέγχου της προβλεπτικής ικανότητας, παρουσιάζει ένα μοντέλο με ικανοποιητική προβλεπτική ικανότητα. Πίνακας4.8: Πίνακας Model Summary που περιλαμβάνει το κριτήριο πρόβλεψης Mallow Model Summary Model Selection Criteria Std. Error Akaike Amemiya Mallows' Schwarz R Adjusted of the Information Prediction Prediction Bayesian R Square R Square Estimate Criterion Criterion Criterion Criterion 1,716 a,512, , ,895,522 41, ,083 2,817 b,668, , ,746,367 12, ,029 3,849 c,720, , ,468,319 4, , Διαδοχικές προσεγγίσεις για σχηματισμό τελικού μοντέλου Εκτελώντας διαδοχικά όλους τους ελέγχους που απαιτούνται για την επικύρωση του μοντέλου πολλαπλής γραμμικής παλινδρόμησης προκύπτει το συμπέρασμα ότι το αρχικό μοντέλο εκτίμησης αξιών στην πρώτη περιοχή μελέτης είναι ιδιαίτερα ικανοποιητικό. Ισχύει η παραδοχή της σημαντικότητας των ανεξάρτητων μεταβλητών, η ανεξαρτησία των οντοτήτων, η ισότητα των διακυμάνσεων, η κανονικότητα των υπολοίπων, η γραμμικότητα ενώ ταυτόχρονα δεν υπάρχει καμία ένδειξη πολυσυγγραμικότητας στο μοντέλο. Επίσης, ο συντελεστής προσδιορισμού R 2 είναι αρκετά υψηλός και φανερώνει ότι μόνο το 28 % της «αρχικής» πληροφορίας που αναφέρεται στην εξαρτημένη μεταβλητή Υ οφείλεται σε άλλους παράγοντες διαφορετικούς των μεταβλητών Χ1, Χ7 και Χ2. Παρόλα αυτά, προβλήματα συναντώνται στην προβλεπτική δύναμη του μοντέλου, καθώς και στο γεγονός ότι εμφανίζονται οντότητες σε όλα τα διαγράμματα σκέδασης που ξεπερνούν τα επιτρεπόμενα όρια που τίθενται. Γι αυτό το λόγο στη συνέχεια επιχειρείται η αφαίρεση των οντοτήτων από το μοντέλο που θεωρούνται απομακρυσμένες σε σύγκριση με το σύνολο των υπόλοιπων οντοτήτων. Ωστόσο, η διαδοχική τους απομάκρυνση δεν είναι δεδομένο ότι φέρνει θετικά αποτελέσματα στο μοντέλο. Ένδειξη βελτίωσης του μοντέλου αποτελεί ο συντελεστής προσδιορισμού R 2, ο οποίος όταν αυξάνεται, ενώ οι οντότητες του δείγματος μειώνονται δείχνει ότι η λήψη της συγκεκριμένης απόφασης είναι ορθή. Ταυτόχρονα, σημαντικό κριτήριο αποτελούν οι δείκτες και τα διαγράμματα που Μεταπτυχιακή διατριβή 95
108 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ περιγράφονται παραπάνω, καθώς θα πρέπει να ικανοποιούν κάθε φορά τις αντίστοιχες παραδοχές. Πρόκειται για μία χρονοβόρα και ιδιαίτερα πολύπλοκη διαδικασία, η οποία σύμφωνα με το Δαφέρμο, 2005 πρέπει κάθε ερευνητής να είναι πολύ προσεκτικός κατά τη διαγραφή η τροποποίηση των ακραίων οντοτήτων (outliers), διότι συμπεριφέρονται συχνά όπως η Λερναία Ύδρα. Με άλλα λόγια, μπορεί να αφαιρεθούν οντότητες που να οδηγούν αρχικά σε βελτίωση του μοντέλου βάσει των κριτηρίων που αναφέρονται παραπάνω αλλά να δημιουργούν διαρκώς νέες ακραίες οντότητες, οι οποίες με την απομάκρυνση τους εν συνεχεία να μην οδηγούν στα επιθυμητά προσδοκώμενα αποτελέσματα. Γι αυτό το λόγο για την εύρεση του τελικού βέλτιστου μοντέλου ακολουθούνται ποικίλα σενάρια απομάκρυνσης ακραίων οντοτήτων και επιλέγεται στο τέλος αυτό που θεωρείται καλύτερο σε σχέση με τα υπόλοιπα. Συνολικά στο μοντέλο εκτελούνται επτά διαδοχικές παλινδρομικές αναλύσεις και σχηματίζονται επτά νέες παλινδρομικές εξισώσεις με την αφαίρεση των ακόλουθων οντοτήτων. Παλινδρ. Ανάλυση Οντότητα R R 2 1η (Ν = 60) - 0,849 0,720 2 η 31 0,862 0,744 3η 37 0,871 0,759 4η 33 0,884 0,781 5η 30 0,895 0,802 6η 36 0,900 0,811 7η (Ν = 54) 48 0,906 0,821 Σύμφωνα με τα στοιχεία του πίνακα, το υποψήφιο τελικό μοντέλο αποτελείται από 54 οντότητες με συντελεστή προσδιορισμού R 2 = 0,821, σαφώς μεγαλύτερο από το συντελεστή της πρώτης προσέγγισης του μοντέλου (0,720). Η τελική μορφή της εξίσωσης παλινδρόμησης είναι η ακόλουθη: Υ = , ,748 Χ1 1153,296 Χ ,720 Χ7 με συντελεστή προσδιορισμού R 2 = 0,821. Ακολουθεί ο έλεγχος όλων των παραδοχών που τίθενται βάσει μεθοδολογίας για το μοντέλο των 54 οντοτήτων, έτσι ώστε να φανεί εάν αποτελεί το τελικό μοντέλο εκτίμησης αγοραίων αξιών στην πρώτη περιοχή μελέτης. 96
109 Κ ε φ ά λ α ι ο 4 ο Έλεγχος ικανοποίησης προϋποθέσεων τελικού μοντέλου πολλαπλής γραμμικής παλινδρόμησης Στα ακόλουθα υποκεφάλαια πραγματοποιούνται οι ίδιοι έλεγχοι στο μοντέλο των 54 οντοτήτων και ταυτόχρονα σχολιάζονται οι αλλαγές και οι βελτιώσεις, όπου αυτές υπάρχουν, σε σύγκριση με τα δεδομένα που παρήχθησαν κατά την πρώτη παλινδρομική ανάλυση. Η ικανοποίηση όλων των ελέγχων οδηγεί σε ένα αξιόπιστο και με ισχυρή προβλεπτική ικανότητα παλινδρομικό μοντέλο Σημαντικότητα ανεξάρτητων μεταβλητών Η στατιστική σημαντικότητα των ανεξάρτητων μεταβλητών στο γραμμικό μοντέλο παλινδρόμησης αποδεικνύεται μέσω δύο διαφορετικών μεθόδων. Ο πρώτος στηρίζεται στην οπτική ερμηνεία των διαγραμμάτων μερικής παλινδρόμησης (Partial Plots) και ο δεύτερος στις t τιμές του πίνακα των συντελεστών (Coefficients). Τα διαγράμματα και ο πίνακας των συντελεστών αποτελούν προϊόντα της κύριας εκτέλεσης πολλαπλής γραμμικής παλινδρόμησης, όπως περιγράφεται στην ενότητα Διαγράμματα μερικής συσχέτισης Τα διαγράμματα μερικής συσχέτισης 4.19, 4.20 και 4.21 φανερώνουν ξεκάθαρες γραμμικές συσχετίσεις της αγοραίας αξίας των ακινήτων με το εμβαδόν (Χ1), την παλαιότητα (Χ2) και την κατάσταση του ακινήτου (Χ7). Ο βαθμός στατιστικής σημαντικότητα της κάθε μεταβλητής διαφαίνεται μέσω του εύρους ζώνης που περιλαμβάνει το 95% των παρατηρήσεων. Το εμβαδόν (Χ1) αποτελεί τη πιο σημαντική μεταβλητή του μοντέλου, με την παλαιότητα (Χ2) να ακολουθεί και τέλος την κατάσταση του ακινήτου (Χ7) με μία μικρότερη συμβολή. Μεταπτυχιακή διατριβή 97
110 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα 4.19: Διάγραμμα μερικής παλινδρόμησης μεταξύ της αξίας και του εμβαδού Διάγραμμα 4.20: Διάγραμμα μερικής παλινδρόμησης μεταξύ της αξίας και της παλαιότητας Διάγραμμα 4.21: Διάγραμμα μερικής παλινδρόμησης μεταξύ της αξίας και της κατάστασης του ακινήτου 98
111 Κεφάλαιο 4ο Το γενικό συμπέρασμα που προκύπτει είναι ότι ο πρώτος έλεγχος του μοντέλου που αφορά τη στατιστική σημαντικότητα των ανεξάρτητων μεταβλητών ικανοποιείται. Συγκρίνοντας τα τρία διαγράμματα με τα αντίστοιχα του αρχικού μοντέλου, παρατηρείται αρχικά πως καμία οντότητα δεν βρίσκεται εκτός των ζωνών που περιέχουν το 95% των παρατηρήσεων. Παράλληλα, είναι ξεκάθαρο ότι έχουν αυξηθεί οι συσχετίσεις μεταξύ των τριών ανεξάρτητων μεταβλητών με την εξαρτημένη, σε σύγκριση με την πρώτη προσέγγιση, και άρα το μοντέλο των 54 οντοτήτων είναι βελτιωμένο ως προς το συγκεκριμένο χαρακτηριστικό. Τιμές t Η αξιολόγηση των t τιμών του παρακάτω πίνακα οδηγεί σε σαφή συμπεράσματα όσον αφορά τη στατιστική σημαντικότητα των ανεξάρτητων μεταβλητών. Πιο συγκεκριμένα, συγκρίνοντας τις απόλυτες τιμές των t τιμών που δίνονται πραγματοποιείται μία κατάταξη ως προς το βαθμό στατιστικής σημαντικότητας της κάθε μεταβλητής. Οριακή τιμή για τη στατιστική σημαντικότητα είναι η τιμή. Τιμές μικρότερες του χαρακτηρίζονται στατιστικά μη σημαντικές και απορρίπτονται από το μοντέλο. Πίνακας 4.9: Πίνακας Coefficients που περιλαμβάνει τις τιμές t των ανεξάρτητων μεταβλητών Coefficients Model Standardize Unstandardized d 95,0% Confidence Coefficients Coefficients Interval for B B 3 a Std. Error Constant , ,079 X1 1888, ,261 X2-1153,296 X7 8184,720 Beta t Sig. Collinearity Correlations Lower Upper Zero- Bound Bound order Partial Statistics Part Tolerance VIF -,539, , ,294,779 12,914, , ,522,794,877,772,983 1, ,552 -,326-4,835, , ,151 -,468 -,564 -,289,784 1, ,914,177 2,633, , ,158,280,349,157,787 1,271 Όπως παρατηρείται από τα στοιχεία του πίνακα 4.9 μεγαλύτερη τιμή t παρουσιάζει η μεταβλητή Χ1 (Εμβαδόν), ακολουθεί η μεταβλητή Χ2 (Παλαιότητα) και έπεται η μεταβλητή Χ7 (Κατάσταση ακινήτου), η οποία βρίσκεται εντός επιτρεπόμενων ορίων, αλλά παρουσιάζει αρκετά μικρότερη στατιστική σημαντικότητα. Συγκρίνοντας τις τιμές t του τελικού μοντέλου με το αρχικό παρατηρείται ότι σαφώς αυξάνεται ο βαθμός στατιστικής σημαντικότητας των τριών ανεξάρτητων μεταβλητών, καθώς πρόκειται για καλύτερο μοντέλο. Μεταπτυχιακή διατριβή 99
112 Σχηματισμός μοντέλου Σύμφωνα με τα αποτελέσματα και των δύο μεθόδων ελέγχου, ισχύει η πρώτη παραδοχή του μοντέλου με ιδιαίτερα ικανοποιητικό τρόπο, λαμβάνοντας υπόψη ότι τα δεδομένα προέρχονται από την πραγματική αγορά ακινήτων της Θεσσαλονίκης Ανεξαρτησία οντοτήτων Η παραδοχή της ανεξαρτησίας συνεπάγεται το σχηματισμό ενός μοντέλου στο οποίο η συμμετοχή μίας οντότητας, δεν επηρεάζει τη συμμετοχή μία άλλης οντότητας του δείγματος. Η ύπαρξη ανεξαρτησίας των υπολοίπων, ουσιαστικά σημαίνει απουσία αυτοσυσχέτισης στο μοντέλο και ελέγχεται με δύο διαφορετικούς τρόπους σε περιβάλλον SPSS. Ο πρώτος αναφέρεται στο στατιστικό δείκτη Durbin Watson και ο δεύτερος στο διάγραμμα διασποράς των Studentized Residuals με τη σειρά καταχώρησης των δεδομένων (Α/Α). Δείκτης Durbin Watson Η τιμή του στατιστικού δείκτη Durbin Watson υποδεικνύει ύπαρξη ανεξαρτησίας των οντοτήτων όταν είναι μεγαλύτερη από 1,5 και μικρότερη από 2,5. Στην προκειμένη περίπτωση σύμφωνα με τα στοιχεία του πίνακα 4.10 η τιμή του δείκτη είναι 1,978, συνεπώς ικανοποιείται η συνθήκη της ανεξαρτησίας στο μοντέλο των 54 οντοτήτων. Πίνακας 4.10: Δείκτης Durbin Watson στον πίνακα Model Summary d Model Summary Model Change Statistics R Adjusted Std. Error R R R of the Square F Square Square Estimate Change Change df1 df2 Sig. F Durbin- Change Watson,794 a,631, ,590,631 88, ,000 2,892 b,797, ,484,165 41, ,000 3,906 c,821, ,915,025 6, , ,978 Διάγραμμα Σκέδασης : Studentized Residuals vs Sequence Το διάγραμμα σκέδασης της εικόνας 4.22 παρουσιάζει μία ομοιόμορφη κατανομή, χωρίς την παρουσία προτύπων. Όλες οι τιμές των Studentized Residuals βρίσκονται εντός του εύρους (το αρχικό μοντέλο περιείχε οντότητες που ήταν εκτός της σταθερής ζώνης ) και η τιμή τους δε συνδέεται με τη σειρά με την οποία εισήχθησαν στο δείγμα. Συνεπώς, το παρακάτω διάγραμμα των Studentized Residuals έναντι της σειράς καταχώρησης των δεδομένων φανερώνει την ανεξαρτησία των οντοτήτων, όπως ακριβώς συνέβη με τον στατιστικό δείκτη Durbin Watson. 100
113 Κ ε φ ά λ α ι ο 4 ο Διάγραμμα 4.22: Διάγραμμα σκέδασης (Studentized Residuals vs Sequence) Πολυσυγγραμικότητα ή Συγγραμικότητα Το πρόβλημα πολυσυγγραμικότητας αναφέρεται στην περίπτωση όπου οι ανεξάρτητες μεταβλητές συνδέονται μεταξύ τους με γραμμικό τρόπο. Η συσχέτιση των ανεξάρτητων μεταβλητών επιβεβαιώνεται ή απορρίπτεται με τη βοήθεια τεσσάρων στατιστικών δεικτών, του παράγοντα ανοχής (Tolerance Factor), του παράγοντα πληθωριστικής διακύμανσης (Variance Inflation Factor), των ιδιοτιμών (Eigenvalues) και των δεσμευμένων δεικτών (Condition Indexes). Παράγοντας ανοχής (Tolerance factor) & Παράγοντας πληθωριστικής διακύμανασης (Variance inflation factor) Σύμφωνα με τα στοιχεία του πίνακα 4.11 η τιμή του παράγοντα ανοχής (Tolerance) για τη μεταβλητή Χ1 (Εμβαδόν) είναι ίση με 0,983, για τη μεταβλητή Χ2 (Παλαιότητα) είναι ίση με 0,784 και για τη μεταβλητή Χ7 (Κατάσταση ακινήτου) είναι ίση με 0,787. Όταν οι τιμές του δείκτη είναι μεγαλύτερες από την τιμή 0,5 έως και τη μονάδα, τότε δεν υπάρχει πρόβλημα πολυσυγγραμικότητας μεταξύ των ανεξάρτητων μεταβλητών. Στην προκειμένη περίπτωση όλες οι τιμές είναι κοντά στη μονάδα, άρα ικανοποιείται ο έλεγχος, βάσει του πρώτου δείκτη. Ο παράγοντας πληθωριστικής διακύμανσης VIF θα πρέπει να είναι μεγαλύτερος του δύο για να μην υπάρχει πρόβλημα πολυσυγγραμικότητας. Σύμφωνα με τα στοιχεία του πίνακα, όλες οι τιμές είναι περίπου ίσες με τη μονάδα (1,018, 1,275 και 1,271) και άρα ικανοποιείται ο έλεγχος βάσει του δεύτερου ελέγχου. Μεταπτυχιακή διατριβή 101
114 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Πίνακας 4.11: Πίνακας Coefficients, όπου δίνονται οι δείκτες για τον έλεγχο συγγραμικότητας Tolerance & VIF Coefficients a Model Unstandardized Standardized 95,0% Confidence Collinearity Coefficients Coefficients Interval for B Correlations Statistics Lower Upper Zero- B Std. Error Beta t Sig. Bound Bound order Partial Part Tolerance VIF 3 Constant , ,079 -,539, , ,294 X1 1888, ,261,779 12,914, , ,522,794,877,772,983 1,018 X2-1153, ,552 -,326-4,835, , ,151 -,468 -,564 -,289,784 1,275 X7 8184, ,914,177 2,633, , ,158,280,349,157,787 1,271 Έλεγχος ιδιοτιμών (Eigenvalues) & Δεσμευμένοι δείκτες (Condition indexes) Όταν οι τιμές Eigenvalues είναι πολύ κοντά στη μηδενική τιμή, τότε υπάρχει πρόβλημα πολυσυγγραμικότητας. Σύμφωνα με τα στοιχεία του πίνακα 4.12 μόνο η τιμή 0,21 προσεγγίζει το μηδέν, παρόλα αυτά η συγκεκριμένη προσέγγιση δε θεωρείται στατιστικά σημαντική, ώστε να δημιουργεί πρόβλημα πολυσυγγραμικότητας. Αντίστοιχα, όσον αφορά τους δεσμευμένους δείκτες, δε θα πρέπει να ξεπερνούν την τιμή 15. Σύμφωνα με τα παρακάτω στοιχεία, όλες οι τιμές είναι μικρότερες του 15 (μέγιστη τιμή 13,267) και άρα ικανοποιείται η παραδοχή βάσει και του τέταρτου ελέγχου. Πίνακας 4.12: Πίνακας Collinearity diagnostics, όπου δίνονται οι δείκτες για τον έλεγχο συγγραμικότητας Eigenvalue και Condition Index Collinearity Diagnostics a Model Dimension Condition Variance Proportions Eigenvalue Index (Constant) X1 X2 X ,647 1,000,00,01,01,01 2,226 4,018,00,01,15,41 3,106 5,868,00,64,23,10 4,021 13,267 1,00,35,62,47 102
115 Κ ε φ ά λ α ι ο 4 ο Κανονικότητα Για τον έλεγχο της κανονικότητας των υπολοίπων αξιοποιούνται τα Studentized Deleted Residuals μέσω της διαδικασίας Explore (Analyze Descriptive Statistics Explore), διότι ακολουθούν την κανονική κατανομή. Παρακάτω αναλύονται οι οκτώ διαφορετικοί τρόποι ελέγχου της κανονικότητα των υπολοίπων του τελικού μοντέλου για την πρώτη περιοχή μελέτης, στην πόλη της Θεσσαλονίκης. Φυλλογράφημα των υπολοίπων [Stem And- Leaf- Plot of residuals Studentized deleted residuals] Το παρακάτω φυλλογράφημα των υπολοίπων δεν εμφανίζει καμία ακραία οντότητα και ταυτόχρονα έχει τη γνωστή καμπανοειδή μορφή της κανονικής κατανομής, στραμμένης κατά 90 ο. Συνεπώς, ο πρώτος τρόπος ελέγχου που είναι το φυλλογράφημα των υπολοίπων, παρουσιάζει μία κανονική κατανομή. Studentized Deleted Residual Stem-and-Leaf Plot Frequency Stem & Leaf 2, , , , , , , , Stem width: 1,00000 Each leaf: 1 case(s) Διάγραμμα 4.23: Φυλλογράφημα των υπολοίπων για την περιοχή του κέντρου Test of normality : Kolmogorv Smirnov, Lillefors, Shapiro Wilk Ο δεύτερος τρόπος ελέγχου αναφέρεται στο στατιστικό κριτήριο Kolmogorov Smirnov και στο Shapiro Wilk. Για τα δείγματα που χαρακτηρίζονται μεγάλα (n>30) αρκεί η ικανοποίηση μόνο του πρώτου κριτηρίου. Ο έλεγχος της υπόθεσης της κανονικότητας των υπολοίπων γίνεται με τη χρήση του ελέγχου Kolmogorov Smirnov: Μηδενική Υπόθεση Ho: Τα υπόλοιπα κατανέμονται κανονικά και Εναλλακτική Υπόθεση H1: Τα υπόλοιπα δεν κατανέμονται κανονικά. Μεταπτυχιακή διατριβή 103
116 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Το τεστ για την κανονικότητα των Kolmogorov Smirnov δίνει επίπεδο στατιστικής σημαντικότητας (Sig.) 20%, δηλαδή μεγαλύτερο του 5% και άρα δε μπορεί να απορριφθεί η υπόθεση ότι τα Studentized Deleted Residuals ακολουθούν την κανονική κατανομή. Πίνακας4.13: Πίνακας Tests of Normality Kolmogorv Smirnov, Lillefors, Shapiro Wilk Tests of Normality Kolmogorov-Smirnov a Shapiro-Wilk Statistic df Sig. Statistic df Sig. Studentized Deleted Residual,067 54,200 *,978 54,424 Normal Q-Q Plot of Studentized deleted Residuals Στο παρακάτω διάγραμμα (Διάγραμμα 4.24) η γραμμή αντιπροσωπεύει τη θεωρητική κανονική κατανομή και άρα εξετάζεται η διασπορά των σημείων σε σχέση με την ευθεία γραμμή. Στο παρακάτω διάγραμμα παρατηρούνται μερικές διαφοροποιήσεις στα σημεία σε σχέση με τη γραμμή που ορίζει την πλήρη κανονικότητα, οι οποίες όμως βρίσκονται εντός των επιτρεπόμενων ορίων και άρα δεν απορρίπτουν την κανονικότητα των Studentized Deleted Residuals. Διάγραμμα 4.24: Διάγραμμα κανονικότητας Normal Q-Q Plot των Studentized Deleted Residuals για τον έλεγχο της κανονικότητας των υπολοίπων 104
117 Κ ε φ ά λ α ι ο 4 ο Detrended normal Q-Q Plot Studentized Deleted residuals Το παρακάτω διάγραμμα απεικονίζει στον άξονα Χ τις παρατηρούμενες τιμές των Studentized Deleted Residuals, ενώ στον άξονα των Υ τα ποσοστιαία σημεία μιας τυπικής κανονικής κατανομής. Όλα τα σημεία του διαγράμματος κατανέμονται τυχαία πάνω και κάτω από τη γραμμή που βρίσκεται στην τιμή μηδέν με μία αμελητέα συσσώρευση σημείων στο κέντρο του διαγράμματος. Η πιο απομακρυσμένη τιμή βρίσκεται στο 0,4, συνεπώς σύμφωνα με το διάγραμμα δεν υπάρχουν ακραίες οντότητες και ικανοποιείται η παραδοχή της κανονικότητας των υπολοίπων. Διάγραμμα 4.25: Διάγραμμα Detrended normal Q-Q Plot Studentized Deleted Residuals για τον έλεγχο της κανονικότητας των υπολοίπων Histogram Studentized Deleted Residuals Στο παρακάτω ιστόγραμμα συχνοτήτων (Διάγραμμα 4.26) με τα Studentized Deleted Residuals φαίνεται ότι προσεγγίζεται η κανονική κατανομή των υπολοίπων. Ορισμένες εκτροπές που εμφανίζονται σε σχέση με τη θεωρητική καμπύλη δεν εμποδίζουν την ικανοποίηση της παραδοχής της κανονικότητας στο τελικό μοντέλο της πρώτης περιοχής μελέτης. Μεταπτυχιακή διατριβή 105
118 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα 4.26: Ιστόγραμμα των Studentized Deleted Residuals για τον έλεγχο της κανονικότητας των υπολοίπων Histogram Standardized Residuals Διάγραμμα 4.27: Ιστόγραμμα των Standardized Residuals για τον έλεγχο της κανονικότητας των υπολοίπων 106
119 Κ ε φ ά λ α ι ο 4 ο Το παραπάνω ιστόγραμμα συχνοτήτων δημιουργείται μέσω της κύριας διαδικασίας εκτέλεσης της πολλαπλής γραμμικής παλινδρόμησης και όχι μέσω της διαδικασίας Explore. To ιστόγραμμα εμφανίζει όμοια με το διάγραμμα 4.26 ορισμένες εκτροπές από τη θεωρητική καμπύλη της κανονικής κατανομής, οι οποίες όμως δε επηρεάζουν την παραδοχή της κανονικότητας. Διάγραμμα Normal P-P Plot of regression standardized residuals Το διάγραμμα που ακολουθεί παράγεται μέσω της βασικής διαδικασίας εκτέλεσης της πολλαπλής γραμμικής παλινδρόμησης και εμφανίζει σημεία που βρίσκονται πάνω ή σε πολύ μικρή απόσταση από την ευθεία γραμμή που αντιπροσωπεύει την πλήρη κανονικότητα. Οι παρατηρούμενες αποκλίσεις από την ευθεία γραμμή δεν επηρεάζουν σημαντικά την κανονικότητα. Συνεπώς, το πέμπτο γράφημα ικανοποιεί την υπόθεση της κανονικότητας. Διάγραμμα 4.28: Διάγραμμα Normal P-P Plot of regression Standardized Residuals για τον έλεγχο της κανονικότητας των υπολοίπων Θηκόγραμμα των υπολοίπων (Boxplot of Residuals) Αρχικά στο παρακάτω θηκόγραμμα δεν εντοπίζεται καμία ακραία οντότητα. Επίσης η διάμεσος βρίσκεται στο μέσο του ορθογωνίου παραλληλογράμμου με αποτέλεσμα να περιγράφει μία συμμετρική κατανομή των υπολοίπων που είναι στοιχείο κανονικότητας. Μεταπτυχιακή διατριβή 107
120 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα 4.29: Θηκόγραμμα για τον εντοπισμό των ακραίων οντοτήτων του δείγματος μέσω της διαδικασίας Explore Ισότητα διακυμάνσεων ή ομοσκεδαστικότητα Ο πέμπτος έλεγχος αναφέρεται στην ύπαρξη ισότητας των διακυμάνσεων και πραγματοποιείται με τη βοήθεια των ακόλουθων τριών διαγραμμάτων σκέδασης: Studentized Deleted Residuals vs Standardized Predicted Values Studentized Residuals vs Standardized Predicted Values Standardized Predicted Values vs Dependent Variable 108
121 Κ ε φ ά λ α ι ο 4 ο Διάγραμμα 4.30: Διάγραμμα σκέδασης των Studentized Deleted Residuals με τα Standardized Predicted Values (αριστερά) και διάγραμμα σκέδασης των Studentized Residuals με τα Standardized Predicted Values (δεξιά) Τα δύο πρώτα διαγράμματα διασποράς παρουσιάζουν μία τυχαία κατανομή των σημείων με ομοιόμορφο τρόπο, πάνω και κάτω από τη νοητή γραμμή που διέρχεται από το μηδέν. Το βασικό χαρακτηριστικό των διαγραμμάτων που τα διαφοροποιεί από τα αντίστοιχα διαγράμματα του αρχικού μοντέλου είναι το γεγονός ότι όλα τα σημεία βρίσκονται εντός του σταθερού εύρους. Συμπεραίνεται ότι από το αρχικό δείγμα αφαιρέθηκαν οι κατάλληλες οντότητες, έτσι ώστε να βελτιωθεί η αξιοπιστία του μοντέλου. Τα δύο πρώτα διαγράμματα επιβεβαιώνουν την ύπαρξη ισότητας των διακυμάνσεων, αλλά ταυτόχρονα επιβεβαιώνουν την ικανοποίηση της γραμμικότητας του μοντέλου (Βλ ). Το τρίτο διάγραμμα (Διάγραμμα 4.31) απεικονίζει τη διασπορά των παρατηρούμενων (Υ) και τυποποιημένων εκτιμώμενων τιμών (Standardized Predicted Value). Η ευθεία γραμμή που τοποθετείται στο κέντρο του διαγράμματος αντιπροσωπεύει την ευθεία των ελαχίστων τετραγώνων, ενώ η ζώνη που δημιουργείται γύρω από την ευθεία γραμμή αντιπροσωπεύει το 95% των παρατηρήσεων. Από το γεγονός ότι όλα τα σημεία είναι τοποθετημένα με τυχαίο τρόπο μέσα στο συγκεκριμένο εύρος ζώνης συμπεραίνεται ότι ικανοποιείται επιτυχώς και βάσει του τρίτου διαγράμματος η ισότητα των διακυμάνσεων. Διάγραμμα 4.31: Διάγραμμα σκέδασης των τυποποιημένων προβλεπόμενων τιμών έναντι των παρατηρούμενων Μεταπτυχιακή διατριβή 109
122 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Γραμμικότητα Η επιβεβαίωση της γραμμικής σύνδεσης των τριών ανεξάρτητων μεταβλητών (Χ1, Χ2 και Χ7)με την εξαρτημένη μεταβλητή Υ είναι ένας ιδιαίτερα σημαντικός έλεγχος. Η ικανοποίηση του στηρίζεται στην αξιολόγηση και οπτική ερμηνεία διαφορετικών μεταξύ τους διαγραμμάτων σκέδασης, τα οποία θα πρέπει να συνηγορούν στο σύνολο τους την ύπαρξη γραμμικότητα στο μοντέλο των 54 οντοτήτων. Η πρώτη κατηγορία διαγραμμάτων είναι τα διαγράμματα σκέδασης μεταξύ της εξαρτημένης και των ανεξάρτητων μεταβλητών Χi. Το διάγραμμα Matrix Scatter Plot 4.1 απεικονίζει αυτή την κατηγορία διαγραμμάτων, αλλά για το αρχικό δείγμα των 60 οντοτήτων. Προβλέπεται τα αντίστοιχα διαγράμματα του τελικού μοντέλου των 54 οντοτήτων να ικανοποιούν εξίσου ή και σε περισσότερο βαθμό τη συνθήκη της γραμμικότητας. Σύμφωνα με το διάγραμμα που ακολουθεί και ανταποκρίνεται στο τελικό μοντέλο παρατηρείται ότι όλα τα τετραγωνίδια παρουσιάζουν μία πολύ ικανοποιητική γραμμική συσχέτιση μεταξύ της κάθε μίας ανεξάρτητης μεταβλητής με την εξαρτημένη Υ. Η ισχυρότερη συσχέτιση είναι προφανές ότι εμφανίζεται στην περίπτωση του εμβαδού (Χ1) με την αγοραία αξία, έπεται η συσχέτιση της παλαιότητας (Χ2) με την Υ και ακολουθεί ασθενέστερη η συσχέτιση της κατάστασης του ακινήτου (Χ7) με την Υ. Είναι σαφές, ότι η πρώτη κατηγορία διαγραμμάτων επιβεβαιώνει την ύπαρξη γραμμικότητας στο τελικό μοντέλο των 54 οντοτήτων. Διάγραμμα 4.32: Διάγραμμα σκέδασης των ανεξάρτητων μεταβλητών (Χ1, Χ2 και Χ7) με τις τιμές της εξαρτημένης μεταβλητής Υ για το δείγμα των 54 οντοτήτων 110
123 Κ ε φ ά λ α ι ο 4 ο Δεύτερη βασική κατηγορία διαγραμμάτων ελέγχου της γραμμικότητας αποτελούν τα διαγράμματα μερικής συσχέτισης, τα οποία όπως φαίνεται από την ενότητα επιβεβαιώνουν την ύπαρξη γραμμικής σχέσης μεταξύ της εξαρτημένης και των ανεξάρτητων μεταβλητών. Το τρίτο διάγραμμα ελέγχου αποτελεί το διάγραμμα σκέδασης των Studentized Deleted Residuals με τα Standardized Predicted Values, ενώ το τέταρτο και τελευταίο διάγραμμα αποτελεί το παρόμοιο του διάγραμμα σκέδασης μεταξύ των Studentized Residuals και των Standardized Predicted Values. Η οπτική ερμηνεία και των δύο πραγματοποιείται στο υποκεφάλαιο αποδεικνύοντας ότι ικανοποιείται η παραδοχή της γραμμικότητας. Έπειτα από την ολοκλήρωση του ελέγχου της γραμμικότητας έπεται μόνο ένας βασικός έλεγχος του μοντέλου, ο οποίος αναφέρεται στην ύπαρξη ακραίων οντοτήτων ή οντοτήτων επίδρασης Ακραίες οντότητες και οντότητες επίδρασης Όπως αναφέρεται αναλυτικά και στο αρχικό μοντέλο της πρώτης περιοχής μελέτης για τον εντοπισμό των ακραίων οντοτήτων αξιοποιείται η απόσταση Mahalanobis (Mahalanobis Distance Di 2 ) και η τιμή Centered Leverage. Αντίστοιχα για τον εντοπισμό των οντοτήτων επίδρασης αξιοποιούνται οι αποστάσεις Cook (Cook s Distance: CD i ), το μέτρο DFFITS (Standardized DFFITS) και το μέτρο DFBetas (Standardized DFBetas). Για την οπτικοποίηση τους αξιοποιούνται τα διαγράμματα Cook s distance με Centered Leverage Values, Standardized DFFITS με την αύξουσα σειρά των παρατηρήσεων A/A και Standardized DFBETA X i με A/A. Τέλος, η απομάκρυνση των υποψήφιων οντοτήτων που προκύπτουν από τους προηγούμενους ελέγχους επιλέγεται με τη βοήθεια της κατανομής t (Διαδικασία BONFERRONI) και της κατανομής F. Centered Leverage Για την εύρεση των ακραίων οντοτήτων με τη βοήθεια του δείκτη Centered Leverage αξιοποιούνται οι τιμές που παράγονται από το SPSS κατά την κύρια διαδικασία εκτέλεσης της πολλαπλής γραμμικής παλινδρόμησης και είναι τοποθετημένες στη στήλη LEV_1 του Data Editor. Οριακή τιμή του δείκτη αποτελεί το 0,2, όπου τιμές που την ξεπερνούν υποδεικνύουν οντότητες που πιθανόν είναι ακραίες και άρα διερευνάται εκτενέστερα η πιθανή απομάκρυνση τους από το μοντέλο. Από τον έλεγχο όλων των τιμών της στήλης LEV στην επιφάνεια του Data Εditor, καμία δεν ξεπερνά την οριακή τιμή του δείκτη, συνεπώς καμία οντότητα του τελικού μοντέλου δεν είναι ακραία οντότητα. Με τον έλεγχο του δείκτη Centered Leverage, ικανοποιείται ταυτόχρονα και ο δείκτης Mahalanobis. Μεταπτυχιακή διατριβή 111
124 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Αποστάσεις Cook CD i Η αντίστοιχη κρίσιμη τιμή του δείκτη Cook είναι η μονάδα. Μόνο τιμές που είναι μεγαλύτερες της μονάδας υποδεικνύουν την ύπαρξη οντοτήτων επίδρασης. Σύμφωνα με τα δεδομένα που προκύπτουν από την εκτέλεση πολλαπλής παλινδρόμησης όλες οι τιμές Cook είναι μικρότερες της μονάδας και συνεπώς δεν υποδεικνύεται καμία οντότητα επίδρασης. Μέτρα DfFits Για τον εντοπισμό των οντοτήτων επίδρασης υπολογίζεται η Standardized DfFits κρίσιμη βάσει του ακόλουθου τύπου: DfFits i = 2* = 0,54 Με βάση τα στοιχεία του Data Editor και τη στήλη SDF παρατηρείται ότι οι οντότητες 12, 29, 38 και 44 έχουν Standardized DfFits κατά απόλυτη τιμή μεγαλύτερα του 0,54. Οι τιμές αντίστοιχα είναι SDF 12 = 0,86 και SDF 29 = 0,57, SDF 38 = 0,60 και SDF 44 = 0,81. Οι παρατηρήσεις 29 και 38 έχουν τιμή μέτρου DfFit πάρα πολύ κοντά στην οριακή τιμή και άρα η επίδραση τους δε θεωρείται στατιστικώς σημαντική. Οι τιμές των 38 και 44 είναι μεγαλύτερες, χωρίς όμως να ξεπερνούν την τιμή 1. Η τελική απόφαση θα κριθεί από τους ελέγχους που ακολουθούν και κυρίως από την ανίχνευση τιμών επίδρασης μέσω της κατανομής t και F. Μέτρα DfBetas Για τον έλεγχο αξιοποιούνται οι απόλυτες τιμές των Standardized DfBetas, οι οποίες συγκρίνονται με μία κρίσιμη τιμή για την ύπαρξη οντοτήτων επίδρασης. Η κρίσιμη τιμή για τις περιπτώσεις των μεγάλων δειγμάτων (n>30) δίνεται από την ακόλουθη σχέση: > = 0,272 Αναλυτικά για τον έλεγχο που αφορά τη μεταβλητή X1 λαμβάνεται υπόψη η στήλη SDB1_1 του Data Editor, η οποία επισημαίνει τις οντότητες με Α/Α 12 (0,813), 29 (0,471) και 39 (0,341) ως υποψήφιες οντότητες επίδρασης. Για τον έλεγχο που αφορά τη μεταβλητή X2 λαμβάνεται υπόψη η στήλη με τίτλο SDB2_1 του Data Editor, η οποία επισημαίνει τις οντότητες 1 (0,325), 7 (0,304), 34 (0,483), 39 (0,528), 40 (0,406) και 42 (0,385) ως υποψήφιες οντότητες επίδρασης. Τέλος, για τον έλεγχο που αφορά τη μεταβλητή Χ7 αξιοποιείται η στήλη με τίτλο SDB7_1 του Data Editor, η οποία με τη σειρά της επισημαίνει τις οντότητες 12 (0,293), 19 (0,357) και 44 (0,309) ως υποψήφιες οντότητες επίδρασης. Καμία από τις παραπάνω οντότητες δεν απομακρύνεται εάν αρχικά δεν ολοκληρωθούν οι έλεγχοι των κατανομών t και F, οι οποίοι οδηγούν στην τελική απόφαση για την διαγραφή οντοτήτων. 112
125 Κ ε φ ά λ α ι ο 4 ο Όπως παρατηρείται από τους παραπάνω ελέγχους, ο αριθμός των υποψήφιων οντοτήτων επίδρασης σε σύγκριση με το αρχικό μοντέλο έχει μειωθεί σημαντικά. Διάγραμμα σκέδασης των αποστάσεων Cook με κεντραρισμένες τιμές Leverage Από το διάγραμμα που απεικονίζει τις αποστάσεις Cook με τις Centered Leverage τιμές διαφαίνεται ότι όλες οι τιμές των οντοτήτων είναι τοποθετημένες εντός των επιτρεπόμενων ορίων (κόκκινες γραμμές) και άρα δεν υποδεικνύεται καμία οντότητα που να επηρεάζει σημαντικά την κλίση της ευθείας παλινδρόμησης ή τους συντελεστές της παλινδρομικής εξίσωσης. Διάγραμμα 4.33: Διάγραμμα σκέδασης των αποστάσεων Cook με τις Centered Leverage τιμές Διάγραμμα σκέδασης των τυποποιημένων DfFits με την ακολουθία των παρατηρήσεων Α/Α Όμοια στο παρακάτω διάγραμμα σκέδασης των τυποποιημένων DfFits με την σειρά εισαγωγής των οντοτήτων, οπτικοποιούνται οι αποκλίσεις από την οριακή τιμή 0,54 και διαφαίνεται γραμμικά το μέγεθος κάθε απόκλισης. Παρατηρείται ότι οι οντότητες 12, 29, 38, 44 και 47 ξεπερνούν το όριο που έχει τεθεί με μεγαλύτερη την απόκλιση της οντότητας 12. Για την καλύτερη κατανόηση της απόκλισης τοποθετούνται οι δύο πορτοκαλί οριζόντιες γραμμές, οι οποίες αντιπροσωπεύουν τα θεωρητικά όρια που έχουν τεθεί για την ύπαρξη οντοτήτων επίδρασης βάσει του δείκτη DfFits. Μεταπτυχιακή διατριβή 113
126 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα 4.34: Διάγραμμα Sequence των Standardized DfFits με την αύξουσα σειρά του δείγματος Διάγραμμα σκέδασης των τυποποιημένων DfBetas με την ακολουθία των παρατηρήσεων Α/Α Διάγραμμα 4.35: Διάγραμμα Sequence των Standardized DfBeta με την αύξουσα σειρά του δείγματος 114
127 Κ ε φ ά λ α ι ο 4 ο Όμοια στην περίπτωση του διαγράμματος απεικόνισης των τιμών DfBetas, οπτικοποιείται ο βαθμός απόκλισης των υποψήφιων οντοτήτων επίδρασης, οι οποίοι έχουν ήδη επισημανθεί. Πιο συγκεκριμένα, οι τιμές που αποκλίνουν περισσότερο από όλες τις υπόλοιπες είναι οι 12 ως προς τη μεταβλητή Χ1,οι 39, 44 και 47 ως προς την Χ2 ενώ καμία τους δεν ξεπερνά την τιμή της μονάδας. Συνεπώς, είναι σαφές ότι υπάρχει επίδραση η οποία πιθανόν να μην χαρακτηρίζεται στατιστικά σημαντική για ένα μοντέλο που έχει περάσει όλους τους ελέγχους γραμμικότητας, πολυσυγγραμμικότητας, κανονικότητας κλπ. Παρόλα αυτά με τους ελέγχους των κατανομών που ακολουθούν θα φανεί εάν είναι οι παραπάνω οντότητες επίδρασης ή όχι. t κατανομή Τα Studentized Deleted Residuals μέσω της διαδικασίας Bonferroni και της t κατανομής μπορούν να βοηθήσουν στον εντοπισμό των οντοτήτων επίδρασης. Όπου t i ορίζεται η τιμή των Studentized Deleted Residuals, τα οποία ακολουθούν την κανονική κατανομή με βαθμούς ελευθερίας: β.ε. = n-p-1 = =49 Η κρίσιμη τιμή που ορίζει η διαδικασία Bonferroni και είναι ίση με: t κρίσιμη = t(1 - ; n-p-1) t (0, ; 49) = 3, με α το επίπεδο στατιστικής σημαντικότητας (α= 0,05), n το μέγεθος του δείγματος (n =54) και p τον αριθμό των συντελεστών παλινδρόμησης μαζί με το σταθερό όρο (p = 4). Επόμενο βήμα αποτελεί ο εντοπισμός της οντότητας με το μεγαλύτερο Studentized Deleted Residual (max SDR)ώστε να συγκριθεί με την οριακή τιμή που προέκυψε παραπάνω. Από τα δεδομένα του Data Editor προκύπτει ότι η οντότητα με τη μεγαλύτερη απόλυτη τιμή Studentized Deleted Residual κατά απόλυτη τιμή είναι η = = 1,7989. Ορίζεται η μηδενική υπόθεση Ηο: Το Studentized Deleted Residual με τη μεγαλύτερη απόλυτη τιμή είναι μία οντότητα επίδρασης, με εναλλακτική υπόθεση = 1,7989 ΔΕΝ Η1: Studentized Deleted Residual με τη μεγαλύτερη απόλυτη τιμή = 1,7989 είναι οντότητα επίδρασης Επειδή όμως = 1,7989 <3,2656 ισχύει η μηδενική υπόθεση Ηο και η οντότητα 50 δεν αποτελεί οντότητα επίδρασης. 22 Η τελική τιμή προκύπτει μέσω των στατιστικών πινάκων Μεταπτυχιακή διατριβή 115
128 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ F κατανομή Οι τιμές Cook θεωρείται ότι ακολουθούν την κατανομή F(1-a;p;n-p), συνεπώς με τη βοήθεια της κατανομής μπορούν να εντοπιστούν οι οντότητες επίδρασης εάν και εφόσον υπάρχουν. Με την ίδια λογική που περιγράφεται παραπάνω υπολογίζεται αρχικά η κρίσιμη τιμή F και στη συνέχεια συγκρίνεται με την τιμή Cook που είναι η μεγαλύτερη σε μέγεθος συγκριτικά με όλες τις υπόλοιπες. F κρίσιμη =F(1-a; p; n-p) = F(0,95; 4; 50) = 2,57 Η μέγιστη απόσταση Cook ανήκει στην οντότητα 37 και είναι ίση με CD 37 = 0, Από τους στατιστικούς πίνακες της F κατανομής παρατηρείται ότι η τιμή βρίσκεται στο 25,70% εκατοστημόριο της συγκεκριμένης κατανομής, δηλαδή δεν πλησιάζει σε καμία περίπτωση το 50% και άρα η οντότητα δε μπορεί να χαρακτηριστεί οντότητα επίδρασης. Σύμφωνα με τους δύο ελέγχους καμία από τις υποψήφιες οντότητες επίδρασης των προηγούμενων ελέγχων δε χρειάζεται να απομακρυνθεί από το μοντέλο και άρα αυτή είναι η τελική μορφή του με συνολικά 54 οντότητες Έλεγχος προβλεπτικής ικανότητας του τελικού μοντέλου Το μοντέλο των 54 οντοτήτων είναι αξιόπιστο, καθώς ικανοποιεί τους επτά διαδοχικούς ελέγχους που το αξιολογούν βάσει μεθοδολογίας. Παράλληλα, το μοντέλο των 54 οντοτήτων είναι καλύτερο από το αρχικό μοντέλο ως προς όλες τις παραδοχές που έχουν τεθεί. Παρόλα αυτά για την τελική επικύρωση του απαιτούνται οι τρεις έλεγχοι που ακολουθούν και υπολογίζουν την προβλεπτική του δύναμη Μέθοδος των διαστημάτων πρόβλεψης Οι οντότητες που αξιοποιούνται για τον αντίστοιχο έλεγχο του αρχικού μοντέλου, χρησιμοποιούνται και στην συγκεκριμένη περίπτωση. Ουσιαστικά ελέγχεται εάν οι παρατηρούμενες τιμές των τεσσάρων νέων οντοτήτων βρίσκονται εντός των διαστημάτων πρόβλεψης που προκύπτουν με την εκτέλεση πολλαπλής γραμμικής παλινδρόμησης για τις 54 οντότητες του δείγματος. Σύμφωνα με τα αποτελέσματα που φαίνονται παρακάτω όλες οι αξίες βρίσκονται εντός του διαστήματος πρόβλεψης και άρα το μοντέλο θεωρείται ότι έχει ικανοποιητική προβλεπτική ικανότητα < < < < < < < <
129 Κεφάλαιο 4ο Το εύρος του διαστήματος πρόβλεψης είναι μικρότερο από το αντίστοιχο του αρχικού μοντέλου, αλλά παραμένει μεγάλο σε μέγεθος εάν λάβει κανείς υπόψη, ότι οι αξίες των ακινήτων στην περιοχή μελέτης δεν είναι υψηλές Μέθοδος του διαχωρισμού των δεδομένων (Data Splitting) Για την εφαρμογή της μεθόδου Data Splitting, όπως αναφέρεται και στην ενότητα , η διαδικασία χωρίζεται σε δύο κύρια στάδια, τα οποία περιγράφονται αναλυτικά παρακάτω: 1ο ΒΗΜΑ Επιλέγεται από το δείγμα των 54 οντοτήτων το 70% περίπου των περιπτώσεων με τυχαία σειρά επιλογής. Το SPSS κατά την εκτέλεση της διαδικασίας επιλέγει συνολικά 42/54 οντότητες. Με το νέο δείγμα διαμερισμάτων εκτελείται η διαδικασία της πολλαπλής γραμμικής παλινδρόμησης και προκύπτει η παρακάτω εξίσωση: Υ = , ,344 Χ1 1053,732 Χ ,084 Χ7 με R = 0,923, R2 = 0,853, Radj2 = 0,841, Δείκτη Durbin Watson = 1,715, τιμές VIF μικρότερες του 2 και τιμές t μεγαλύτερες του. Πρόκειται δηλαδή για ένα καλό και αξιόπιστο μοντέλο. Όσον αφορά τον έλεγχο ανεξαρτησίας των οντοτήτων, ο διάγραμμα Studentized Residuals με τη σειρά καταχώρησης των οντοτήτων επιβεβαιώνει ότι πρόκειται για ένα μοντέλο που πληροί όλες τις βασικές παραδοχές μιας γραμμικής παλινδρόμησης. (Διάγραμμα 4.36). Μεταπτυχιακή διατριβή 117
130 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα 4.36: Διάγραμμα σκέδασης των Studentized Residual vs AA (Sequence) για τις 42 μόνο οντότητες του δείγματος 2 ο ΒΗΜΑ Στη συνέχεια της διαδικασίας με τη χρήση των υπόλοιπων 12 οντοτήτων και με την αξιοποίηση της εξίσωσης παλινδρόμησης που προκύπτει από το πρώτο βήμα εκτελείται η εντολή Compute Variables. Δημιουργείται μία νέα στήλη PRED για το σύνολο των 54 οντοτήτων και στη συνέχεια μέσω του βήματος Analyze Correlation Bivariate υπολογίζεται η συσχέτιση Pearson μεταξύ της στήλης PRED και των παρατηρούμενων τιμών Υ. Η συσχέτιση που εμφανίζουν είναι ίση με 0,65, σαφώς βελτιωμένη σε σύγκριση με την αντίστοιχη τιμή του αρχικού μοντέλου, η οποία ήταν ίση με 0,363. Όμοια, πολύ μεγαλύτερη συσχέτιση διακρίνεται στο παρακάτω διάγραμμα σε σχέση με το διάγραμμα PRED με τις παρατηρούμενες τιμές Υ του αρχικού μοντέλου (Διάγραμμα 4.18). Διάγραμμα 4.37: Διάγραμμα Bivariate συσχέτισης μεταξύ των προβλεπόμενων και παρατηρούμενων τιμών Γενικά, η δεύτερη μέθοδος ελέγχου της προβλεπτικής δύναμης του μοντέλου παρουσιάζει ένα μοντέλο με ασθενή προβλεπτική ικανότητα, η οποία διαφαίνεται και από το αρκετά μεγάλο εύρος των διαστημάτων πρόβλεψης σε σύγκριση με τις αξίες των ακινήτων της περιοχής. 118
131 n0 Κ ε φ ά λ α ι ο 4 ο Μέθοδος εύρεσης του αριθμού των σημαντικών μεταβλητών Με τη βοήθεια του κριτηρίου Mallow s ελέγχεται εάν οι μεταβλητές οι οποίες επιλέγονται από τον αλγόριθμο ως στατιστικά σημαντικές είναι ο βέλτιστος αριθμός μεταβλητών για το συγκεκριμένο μοντέλο. Μέσω της διαδικασίας που περιγράφεται αναλυτικά στην ενότητα παράγεται ο παρακάτω πίνακας (Πίνακας 4.14) Πίνακας 4.14: Πίνακας Model Summary που περιλαμβάνει το κριτήριο πρόβλεψης Mallow Model Summary Model Selection Criteria Std. Error Akaike Amemiya Mallows' Schwarz R Adjusted of the Information Prediction Prediction Bayesian R Square R Square Estimate Criterion Criterion Criterion Criterion 1,794 a,631, , ,457,397 53, ,435 2,892 b,797, , ,343,227 8, ,310 3,906 c,821, , ,333,207 4, ,289 Στην προκειμένη περίπτωση η τρίτη γραμμή της στήλης Mallow s Prediction Criterion δίνει τον αριθμό τέσσερα, όσες δηλαδή είναι οι ανεξάρτητες μεταβλητές μαζί με την εξαρτημένη. Συνεπώς, όλοι οι έλεγχοι συνηγορούν σε ένα αξιόπιστο και με ισχυρή προβλεπτική ικανότητα μοντέλο Ερμηνεία μοντέλου για την περιοχή του κέντρου Το χαρακτηριστικό γνώρισμα ενός γραμμικού μοντέλου είναι ότι υπόκειται σε περιορισμούς - κριτήρια που οφείλουν να ικανοποιούνται ώστε να θεωρείται αξιόπιστο και να έχει νόημα ο σχηματισμός του. Σε πρώτη φάση έγινε εκτέλεση της πολλαπλής γραμμικής παλινδρόμησης με όλο το δείγμα, συνολικού μεγέθους 60 παρατηρήσεων, ώστε από τη λεπτομερή μελέτη των αποτελεσμάτων που προέκυψαν να βρεθούν τρόποι βελτίωσης του. Έπειτα από έξι προσπάθειες (εναπομείναν δείγμα 54 παρατηρήσεων) βρέθηκε το μοντέλο που ικανοποιεί όλα τα κριτήρια που θέτει η πολλαπλή γραμμική παλινδρόμηση και άρα χαρακτηρίζεται ως το τελικό αποδεκτό δείγμα για την πρώτη περιοχή μελέτης που είναι ένα τμήμα του κέντρου της Θεσσαλονίκης. Η τελική εξίσωση παλινδρόμησης είναι η ακόλουθη: Υ = , ,748 Χ1 1153,296 Χ ,720 Χ7 δηλαδή, Αγοραία Αξία ακινήτων = , ,748 * (Εμβαδόν) 1153,296 * (Παλαιότητα) ,720 * (Κατάσταση Ακινήτου) με συντελεστή προσδιορισμού R 2 = 0,821. Μεταπτυχιακή διατριβή 119
132 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Πρόκειται για μία μαθηματική σχέση που απαιτήθηκε σημαντική προσπάθεια για το σχηματισμό της, η οποία όμως αποκτά ουσιαστική σημασία μόνο όταν ερμηνεύεται. Η εξίσωση δείχνει ότι σύμφωνα με το δείγμα που μελετήθηκε, τρεις είναι πρακτικά οι μεταβλητές που συμβάλλουν στη διαμόρφωση της αγοραίας αξίας των ακινήτων σε ένα τμήμα του ιστορικού κέντρου της Θεσσαλονίκης (πρώτη περιοχή μελέτης), το εμβαδόν (Χ1), η παλαιότητα (Χ2) και η κατάσταση του ακινήτου (Χ7). Παρατηρείται ότι οι δύο εκ των τριών συντελεστών με τους οποίους πολλαπλασιάζονται οι μεταβλητές έχουν θετικά πρόσημα και η μία έχει αρνητικό. Τα πρόσημα έχουν ιδιαίτερη σημασία διότι δείχνουν την αρνητική ή θετική επίδραση που έχουν οι μεταβλητές στην διαμόρφωση της εξαρτημένης μεταβλητής. Πιο συγκεκριμένα, το εμβαδόν και η κατάσταση του ακινήτου ασκούν θετική επίδραση στην εξαρτημένη μεταβλητή, διότι όσο αυξάνεται η τιμή τους, τόσο περισσότερο αυξάνεται η τιμή της αγοραίας αξίας, ενώ η παλαιότητα ασκεί αρνητική επίδραση, διότι όσο αυξάνεται η τιμή της, τόσο μειώνεται η τιμή πώλησης του ακινήτου. Ποιος όμως είναι ο βαθμός επίδρασης της κάθε μεταβλητής ξεχωριστά; Σε αυτό το ερώτημα δε μπορεί να απαντήσει το κατά απόλυτη τιμή μέγεθος των συντελεστών που πολλαπλασιάζονται με τις μεταβλητές. Αυτό που στην πραγματικότητα δείχνουν οι συντελεστές είναι πόσες μονάδες αυξάνεται η εξαρτημένη μεταβλητή του μοντέλου (αγοραία αξία ακινήτων), με την αύξηση μίας μονάδας της κάθε ανεξάρτητης μεταβλητής, όταν όλες οι υπόλοιπες μένουν σταθερές. Ο συντελεστής πολλαπλής συσχέτισης R δείχνει τη συσχέτιση ανάμεσα στις παρατηρούμενες και στις προβλεπόμενες τιμές της εξαρτημένης μεταβλητής (Λαφαζάνη, 2003). Στην προκειμένη περίπτωση, σύμφωνα με τον πίνακα 4.2, η τιμή του είναι ίση με R=0,906 και δείχνει μία πολύ έντονη σχέση μεταξύ της αγοραίας αξίας των ακινήτων και των τριών ανεξάρτητων μεταβλητών. Η δε τιμή του συντελεστή προσδιορισμού είναι ίση με R 2 =0,821 και με τη σειρά της δείχνει μία πάρα πολύ καλή προσαρμογή του μοντέλου στα δεδομένα. Ο συντελεστής προσδιορισμού ουσιαστικά εκφράζει το ποσοστό της συνολικής διακύμανσης της εξαρτημένης μεταβλητής Υ που ερμηνεύεται από τις τρεις ανεξάρτητες μεταβλητές. Για παράδειγμα, η τιμή R 2 =0,821 σημαίνει ότι το 82,1% της συνολικής διακύμανσης της αγοραίας αξίας των ακινήτων οφείλεται στις πληροφορίες που περιλαμβάνουν οι τρεις ανεξάρτητες μεταβλητές (εμβαδόν, παλαιότητα και κατάσταση ακινήτου), η κάθε μία ξεχωριστά και όλες μαζί. Μία πιο λεπτομερής ανάλυση της συμβολής της κάθε μίας ανεξάρτητης μεταβλητής στη διασπορά της εξαρτημένης μεταβλητής γίνεται με τη βοήθεια των στοιχείων του πίνακα 4.2 που παρουσιάζει τους αντίστοιχους συντελεστές προσδιορισμού κατά τη διαδικασία εκτέλεσης της βηματικής (stepwise) διαδικασίας. Σύμφωνα με τα δεδομένα του πίνακα η μεταβλητή που καταχωρείται πρώτη και συμβάλει περισσότερο (σε σύγκριση με τις υπόλοιπες τρεις μεταβλητές) στη διαμόρφωση της εξαρτημένης μεταβλητής είναι το εμβαδόν με ποσοστό 63,1%. Ακολουθεί η παλαιότητα, η οποία είναι υπεύθυνη για το 16,6% της διακύμανσης της εξαρτημένης μεταβλητής. Τρίτη σε σειρά είναι η μεταβλητή που αφορά το βαθμό συντήρησης του ακινήτου με ποσοστό συνεισφοράς 2,4%. Αθροίζοντας όλα τα ποσοστά υπολογίζεται το συνολικό ποσοστό της διασποράς που πιστώνεται στην εξαρτημένη μεταβλητή από το σύνολο των τριών ανεξάρτητων μεταβλητών. 120
133 Κ ε φ ά λ α ι ο 4 ο Η τιμή του συντελεστή προσδιορισμού R 2 αναφέρεται στο δείγμα των 54 παρατηρήσεων. Θέλοντας κανείς να εκτιμήσει την προβλεπτική δύναμη του παλινδρομικού μοντέλου στο πληθυσμό θα πρέπει να προσεγγίσει έναν άλλο συντελεστή που ονομάζεται προσαρμοσμένος συντελεστής προσδιορισμού (Adjusted R 2 ) και ελέγχει την προσαρμογή του μοντέλου σε ένα διαφορετικό δείγμα που προέρχεται φυσικά από τον ίδιο ακριβώς πληθυσμό ή την προσαρμογή του μοντέλου στον πληθυσμό. Η τιμή του προσαρμοσμένου συντελεστή προσδιορισμού σύμφωνα με τον πίνακα 4.2 είναι μικρότερη από τον συντελεστή προσδιορισμού R 2, αλλά παραμένει ιδιαίτερα υψηλή. Συγκεκριμένα, ο προσαρμοσμένος συντελεστής προσδιορισμού είναι Adjusted R 2 = 0,811, άρα το 81,1% της συνολικής διακύμανσης της αγοραίας αξίας οφείλεται στις τρεις μεταβλητές για τον πληθυσμό της περιοχής του κέντρου. Συνεπώς, το μοντέλο με κριτήριο το δείκτη Adjusted R 2 έχει ιδιαίτερα υψηλή προβλεπτική δύναμη. Για την εύρεση των μεταβλητών από τις οποίες εξαρτάται η αγοραία αξία των ακινήτων συλλέχθηκαν από το διαδίκτυο οκτώ συνολικά μεταβλητές. Η τελική μορφή του μοντέλου απέδειξε ότι στο συγκεκριμένο δείγμα μόνο τρεις από τις οκτώ θεωρούνται στατιστικά σημαντικές, μέσω της βηματικής διαδικασίας. Ο αριθμός των μεταβλητών που τελικά συμμετέχουν στην εξίσωση παλινδρόμησης είναι ικανοποιητικός, διότι μπορεί να είναι μικρότερος από τις αρχικές, αλλά οι τρεις επιλεγμένες έχουν ουσιαστική συμβολή στο μοντέλο και έχουν σημαντική «ατομική» αξία. Σύμφωνα με τον Myer (1990), τα βέλτιστα παλινδρομικά μοντέλα είναι εκείνα που έχουν το μικρότερο, κατά το δυνατόν, αριθμό ανεξάρτητων μεταβλητών άλλα από τα οποία δεν απουσιάζουν σημαντικές ανεξάρτητες μεταβλητές με σημαντική ατομική συμβολή στο μοντέλο. Συνεπώς, η συμμετοχή περισσότερων ανεξάρτητων μεταβλητών που να έχουν ασήμαντη επίδραση στο μοντέλο, είναι λάθος και μπορεί να δημιουργήσει μεγαλύτερα προβλήματα όσον αφορά την προβλεπτική ικανότητα του μοντέλου. Πέραν της μαθηματικής προσέγγισης στο θέμα σημαντική είναι και η καθαρά γεωγραφική ερμηνεία ή αλλιώς η φυσική ερμηνεία του αποτελέσματος, όταν όλες οι μεταβλητές παίρνουν την τιμή μηδέν. Μία πιθανή πρόβλεψη για την τιμή που έχει η αγοραία αξία των ακινήτων όταν όλες οι μεταβλητές μηδενίζονται θα ήταν να είναι ίση με το μηδέν ή με μία θετική τιμή που να εκφράζει την τιμή έναρξης κάθε περιοχής η οποία στη συνέχεια προσαρμόζεται με τις υπόλοιπες τιμές. Στην πράξη όταν όλες οι ανεξάρτητες μεταβλητές μηδενίζονται εμφανίζεται η εξαρτημένη μεταβλητή να είναι ίση με αρνητικό αριθμό. Με μία πρώτη προσέγγιση θα μπορούσε κανείς να συμπεράνει ότι δεν έχει κάποια φυσική σημασία ή υπόσταση εφόσον δε μπορεί να ληφθεί υπόψη ως τιμή εκκίνησης της αγοραίας αξίας. Παρόλα αυτά υφίσταται φυσική ερμηνεία του σταθερού όρου, διότι ο σταθερός όρος εκφράζει την «υπερτιμημένη λογική» ή υπεραξία της γεωγραφικής περιοχής. Προφανώς, η υπεραξία αυτή αποδίδεται από τις τιμές των ανεξάρτητων μεταβλητών που ερμηνεύουν το γεωγραφικό φαινόμενο. Επομένως: Θετικός σταθερός όρος μεταβλητών = «λογική υπεραξία» = «λογικές» τιμές των ανεξάρτητων Μεταπτυχιακή διατριβή 121
134 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Αρνητικός σταθερός όρος = «υπερτιμημένη υπεραξία» = «μη λογικές τιμές» των ανεξάρτητων μεταβλητών Τέλος, δεν πρέπει να παραληφθεί να αναφερθεί στα συμπεράσματα της πρώτης στατιστικής ανάλυσης, ότι η συμμετοχή πραγματικών δεδομένων του χώρου, δεν μπορεί σε καμία περίπτωση να οδηγεί σε ιδανικά νούμερα και αποτελέσματα. Η πληροφορία που εμπεριέχει το δείγμα είναι ιδιαίτερα πολύπλοκη και αυτός είναι και ο λόγος όπου η ανάλυση που πραγματοποιήθηκε κρίνεται ικανοποιητική και επαρκεί για την δυνατότητα προβλέψεων εντός των ορίων του συγκεκριμένου πληθυσμού. 122
135 Κ ε φ ά λ α ι ο 4 ο 4.3 ΕΦΑΡΜΟΓΗ ΠΟΛΛΑΠΛΗΣ ΓΡΑΜΜΙΚΗΣ ΠΑΛΙΝΔΡΟΜΗΣΗΣ ΓΙΑ ΤΗ ΔΗΜΟΤΙΚΗ ΕΝΟΤΗΤΑ ΕΥΟΣΜΟΥ (ΔΕΥΤΕΡΟ ΜΟΝΤΕΛΟ) Μία πρώτη επαφή με τη νέα περιοχή μελέτης πραγματοποιείται μέσω της εξέτασης του δείγματος και των γενικών χαρακτηριστικών που εντοπίζονται. Σύμφωνα με τις 60 οντότητες που συλλέχθηκαν από τον πληθυσμό που αποτελεί όλος ο πρώην Δήμος Ευόσμου παρατηρούνται διαμερίσματα κατά κύριο λόγο νεόδμητα, καθώς ο μέσος όρος ηλικίας τους είναι τα οκτώμισι (8,5) έτη. Σαν επακόλουθο της ηλικίας τους είναι φυσικά η γενική καλή κατάσταση τους(τα περισσότερα ανήκουν στην κατηγορία της καλής ή πολύ καλής κατάστασης), η ύπαρξη ανελκυστήρα στο 95% των διαμερισμάτων, η ύπαρξη θέσης στάθμευσης στο 87% των διαμερισμάτων και η ύπαρξη αυτόνομης θέρμανσης στα περισσότερα από αυτά. Με άλλα λόγια μπορεί να πει κανείς ότι είναι μία περιοχή που εμφανίζει μία ομοιομορφία στα χαρακτηριστικά των διαμερισμάτων της όπως και στη διακύμανση των ζητούμενων τιμών πώλησης τους. Η μικρότερη τιμή πώλησης που εντοπίζεται είναι στα 700 /τμ και η καλύτερη κατοικία δεν ξεπερνά τα 1800 /τμ. γι αυτό ο μέσος όρος όλου του δείγματος κυμαίνεται 1100 /τμ. Η ανάλυση του δείγματος και ο τρόπος διαμόρφωσης των τιμών αποδεικνύει ότι από τη μία μεριά πρόκειται για μία περιοχή η οποία γνώρισε τεράστια ανοικοδόμηση τα τελευταία χρόνια, η οποία όμως κινείται σε χαμηλές τιμές λόγω θέσης στο πολεοδομικό συγκρότημα της Θεσσαλονίκης (δυτικά προάστια) και φυσικά λόγω των αλλαγών που έφερε η οικονομική κρίση στη χώρα. Παρακάτω πραγματοποιούνται οι ίδιες διαδικασίες στατιστικής ανάλυσης όπως περιγράφηκαν στο υποκεφάλαιο 4.2 με τη διαφορά ότι πλέον η ανάλυση εστιάζεται συνοπτικότερα στα κύρια βήματα της μεθοδολογίας, στους ελέγχους όλων των παραδοχών, στον έλεγχο της προβλεπτικής δύναμης του μοντέλου και τέλος στην ερμηνεία του μοντέλου για την δεύτερη σε σειρά περιοχή μελέτης Διερεύνηση γραμμικής σχέσης μεταξύ της εξαρτημένης μεταβλητής Υ και των ανεξάρτητων Χi Η πρώτη διερεύνηση που είναι πρωταρχικής σημασίας να γίνει πριν την ανάλυση παλινδρόμησης είναι η εύρεση της σχέσης που συνδέει την εξαρτημένη με τις ανεξάρτητες μεταβλητές. Μία μεταβλητή για να ληφθεί υπόψη στη διαδικασία παλινδρόμησης θα πρέπει να εμφανίζει θετική ή αρνητική γραμμική σχέση με την εξαρτημένη. Για τον έλεγχο αξιοποιούνται τα διαγράμματα σκέδασης της κάθε ανεξάρτητης μεταβλητής με την εξαρτημένη και οι συντελεστές μερικής συσχέτισης Γραφήματα συσχέτισης των Χi με την Υ Σύμφωνα με το διάγραμμα 4.38 εμφανίζεται αρχικά μία ξεκάθαρη γραμμική συσχέτιση μεταξύ της αξίας των ακινήτων (Υ) και του εμβαδού του διαμερίσματος (Χ1), ενώ ασθενέστερη γραμμική συσχέτιση διαφαίνεται μεταξύ της αξίας (Υ), της παλαιότητας (Χ2) και των ορόφων (Χ3) των διαμερισμάτων. Μεταπτυχιακή διατριβή 123
136 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Οι δίτιμες μεταβλητές, οι οποίες περιγράφουν εάν το διαμέρισμα είναι γωνιακό, έχει ανελκυστήρα ή θέση στάθμευσης (Χ4, Χ5 και Χ8) δείχνουν ότι δεν έχουν καμία γραμμική σχέση με την εξαρτημένη μεταβλητή, οπότε συνεχίζει να διερευνάται εάν θα συμμετέχουν στην εκτέλεση της παλινδρόμησης. Παρατηρώντας τις τιμές που παίρνουν οι δίτιμες μεταβλητές (δεν κατανέμονται με ποσοστό περίπου 50 και 50% αλλά συγκεντρώνονται στη μία εκ των δύο περιπτώσεων) μπορεί κανείς να καταλήξει στο ίδιο συμπέρασμα. Τέλος, οι μεταβλητές Χ6 και Χ7 δεν είναι ξεκάθαρο ένα συνδέονται γραμμικά ή όχι, οπότε προτιμάται η συμμετοχή τους στο μοντέλο για να φανεί ποια είναι η πραγματική τους σχέση με την εξαρτημένη μεταβλητή και εάν είναι στατιστικά σημαντικές ή όχι. Διάγραμμα 4.38: Γράφημα Matrix Scatter Plot για δείγμα 60 ακινήτων στην περιοχή μελέτης του πρώην Δήμου Ευόσμου Συντελεστές μερικής συσχέτισης Η χρήση των συντελεστών μερικής συσχέτισης, ο υπολογισμός των οποίων περιγράφηκε στο υποκεφάλαιο οδηγεί σε σαφέστερα συμπεράσματα σχετικά με την ύπαρξη συσχέτισης και με το βαθμό της. Από τον πίνακα 4.15 που ακολουθεί είναι ορατή μία έντονα θετική συσχέτιση μεταξύ της αξίας και του εμβαδού, μία αρνητική γραμμική συσχέτιση μεταξύ της αξίας και της παλαιότητας, καμία συσχέτιση μεταξύ της Υ και των Χ5, Χ6, Χ8, ενώ ασθενέστερη είναι η συσχέτιση μεταξύ της Y και των Χ3, Χ4 και Χ7. 124
137 Κ ε φ ά λ α ι ο 4 ο Πίνακας4.15: Πίνακας με τις μερικές συσχετίσεις της εξαρτημένης μεταβλητής με κάθε μία ανεξάρτητη στο δείγμα των 60 οντοτήτων Μεταβλητές Συσχέτιση Επίπεδο στατιστικής σημαντικότητας Χ1 - Y 0,811 0,000 Χ2 - Y -0,170 0,223 Χ3 - Y 0,241 0,082 Χ4 - Y 0,124 0,378 Χ5 - Y 0,024 0,866 Χ6 - Y 0,035 0,803 Χ7 - Y 0,163 0,244 Χ8 - Y 0,074 0,599 Εν κατακλείδι, δείγματα γραμμικότητας, φαίνονται στις μεταβλητές Χ1, Χ2, Χ3, Χ4, Χ6 και Χ7, ενώ οι μεταβλητές Χ5 και Χ8 δεν εμφανίζουν καμία γραμμική σχέση. Συνεπώς, στην εκτέλεση πολλαπλής γραμμικής παλινδρόμησης για τη δεύτερη περιοχή μελέτης συμμετέχουν μόνο οι Χ1, Χ2, Χ3, Χ4, Χ6 και Χ7 ανεξάρτητες μεταβλητές. Ο πίνακας των συσχετίσεων και τα διαγράμματα σκέδασης με την αφαίρεση των ακραίων οντοτήτων από το δείγμα, επαναπροσδιορίζονται και βελτιώνονται κάθε φορά. Παρακάτω θα παρατεθούν οι αντίστοιχες τιμές του τελικού μοντέλου ώστε να γίνουν εμφανείς οι διαφορές τους Εφαρμογή πολλαπλής γραμμικής παλινδρόμησης και δημιουργία τελικού μοντέλου Στόχος είναι να εκτελεστεί η διαδικασία της παλινδρόμησης για τις 60 οντότητες με τη βηματική μέθοδο (stepwise) ώστε με τη χρήση των κατάλληλων γραφημάτων να εντοπιστούν οι οντότητες εκείνες που επιδρούν στους συντελεστές της εξίσωσης και να αφαιρεθούν σταδιακά. Με την ολοκλήρωση των επιλογών που γίνονται στο πλαίσιο διαλόγου Linear Regression δημιουργείται η πρώτη εξίσωση πολλαπλής παλινδρόμησης που αποτελεί μία πρώτη προσέγγιση του προβλήματος: Υ = , ,754 Χ1-1156,521 Χ ,594 Χ3 δηλαδή, Αγοραία αξία = , ,754* (Εμβαδόν) -1156,521* (Παλαιότητα) ,594* (Όροφος) με R 2 = 0,743 Η εξίσωση οδηγεί στο συμπέρασμα ότι στην περιοχή του Ευόσμου οι μεταβλητές που επηρεάζουν την αξία των διαμερισμάτων είναι το εμβαδόν, η παλαιότητα και ο αριθμός των ορόφων. Πρόκειται για μία καλή πρώτη προσέγγιση, η οποία χαρακτηρίζεται Μεταπτυχιακή διατριβή 125
138 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ από υψηλό συντελεστή προσδιορισμού, συνεπώς το μοντέλο προσαρμόζεται ικανοποιητικά στα δεδομένα του δείγματος. Το διάγραμμα σκέδασης που ακολουθεί απεικονίζει το βαθμό τυχαιότητας του δείγματος και όπως φαίνεται από το εύρος ζώνης που έχει καθοριστεί ±2 επισημαίνει τις οντότητες που υπερβαίνουν τη ζώνη ανοχής. Διάγραμμα 4.39: Διάγραμμα σκέδασης των Studentized Deleted Residuals με τα Standardized Predicted Values Όλες οι οντότητες που ξεπερνούν τα όρια είναι υποψήφιες για απομάκρυνση από το μοντέλο. Παρόλα αυτά η διαδικασία γίνεται σταδιακά με αφαίρεση αρχικά της οντότητας 28, διότι είναι η πιο απομακρυσμένη σε σχέση με τις υπόλοιπες. Στην τελική απόφαση οδηγούν ταυτόχρονα τα διαγράμματα μερικής συσχέτισης καθώς και το διάγραμμα σκέδασης των αποστάσεων Cook με τις Centered Leverage τιμές. Οι οντότητες που αφαιρούνται για τη βελτιστοποίηση του μοντέλου σε ξεχωριστά βήματα είναι συνολικά 12, όπως φαίνεται στον ακόλουθο πίνακα. Παλινδρ. Ανάλυση Οντότητα R R 2 1η (Ν = 60) - 0,862 0,743 2η 45 0,878 0,771 3η 28 0,882 0,778 4η 17 0,859 0,738 5η 23 0,868 0,753 6η 39 0,890 0,
139 Κ ε φ ά λ α ι ο 4 ο 7η 51 0,897 0,804 8η 39, 3 0,908 0,825 9η 42, 2 0,916 0,840 10η 5 0,924 0,855 11η 1 0,942 0,887 Κάθε μία απομάκρυνση από τις παραπάνω οντότητες οδηγεί σε σαφώς καλύτερο μοντέλο έως ότου καμία παρατήρηση να μην ξεφεύγει από τα όρια ανοχών που έχουν τεθεί. Η τελική μορφή εξίσωσης παλινδρόμησης που αντιπροσωπεύει τις 48 οντότητες από τις 60 είναι η ακόλουθη: Υ = , ,631 Χ1-586,040 Χ ,792 Χ ,754 Χ ,241 Χ6 δηλαδή, Αγοραία αξία = = , ,631 * (Εμβαδόν) - 586,040 * (Παλαιότητα) ,792 * (Όροφος) ,754* (Κατάσταση Ακινήτου) ,241* (Είδος Θέρμανσης) με R 2 = 0,887 Είναι σαφές ότι η αφαίρεση των ακραίων οντοτήτων είχε θετικά αποτελέσματα στο μοντέλο, διότι βελτιώθηκε πάρα πολύ η τιμή του συντελεστή προσδιορισμού και ταυτόχρονα αυξήθηκε ο αριθμός των μεταβλητών που θεωρούνται στατιστικά σημαντικές. Παρατηρείται ότι από τις πέντε μεταβλητές που θεωρήθηκε ότι συνδέονται γραμμικά με την αξία των ακινήτων μόνο η μεταβλητή Χ4 δεν θεωρήθηκε από τον αλγόριθμο στατιστικά σημαντική, ενώ οι υπόλοιπες πέντε (Χ1, Χ2, Χ3, Χ6, Χ7) επιδρούν στη διαμόρφωση της αξίας των ακινήτων. Οι αναθεωρημένοι συντελεστές μερικής συσχέτισης (Πίνακας 4.16) δείχνουν ότι κάθε ανεξάρτητη μεταβλητή συσχετίζεται εντονότερα με την εξαρτημένη έπειτα από την αφαίρεση των 12 οντοτήτων. Πίνακας4.16: Σύγκριση μερικών συσχετίσεων μεταξύ του πρώτου μοντέλου των 60 οντοτήτων και του τελικού μοντέλου των 48 οντοτήτων Μεταβλητές Πρώτη προσέγγιση Τελική Προσέγγιση Χ1 0,811 0,926 Χ2-0,170-0,259 Χ3 0,241 0,313 Χ6 0,035 0,337 Χ7 0,163 0,416 Μεταπτυχιακή διατριβή 127
140 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Παρακάτω τεκμηριώνεται με τους απαραίτητους ελέγχους η αξιοπιστία του προτεινόμενου μοντέλου Έλεγχος ικανοποίησης παραδοχών του γραμμικού μοντέλου Το μοντέλο των 48 οντοτήτων αξιολογείται βάσει επτά διαδοχικών ελέγχων, βάσει μεθοδολογίας, ώστε να αποδειχθεί η αξιοπιστία του και ο βαθμός προβλεπτικής του ικανότητας Σημαντικότητα ανεξάρτητων μεταβλητών Ο έλεγχος της στατιστικής σημαντικότητας των ανεξάρτητων μεταβλητών, δηλαδή η «καθαρή» αξία και συμβολή της κάθε μεταβλητής στο μοντέλο, είναι πρωταρχικής σημασίας. Ο έλεγχος γίνεται μέσω γραφημάτων με τη βοήθεια των διαγραμμάτων μερικής συσχέτισης και στη συνέχεια με την ανάγνωση των t τιμών που βρίσκονται στον πίνακα Coefficients του.spv αρχείου. Διαγράμματα μερικής συσχέτισης Τα διαγράμματα μερικής συσχέτισης δείχνουν ξεκάθαρα την πραγματική σχέση μεταξύ της εξαρτημένης και κάθε μίας από τις ανεξάρτητες μεταβλητές. Η συγκέντρωση και η πυκνότητα που είναι κατανεμημένες οι οντότητες φανερώνει ταυτόχρονα την ένταση της σχέσης και με αυτόν τον τρόπο είναι ορατός ο βαθμός επίδρασης της κάθε μεταβλητής. Παρατηρείται ότι στα παρακάτω διαγράμματα όλες οι οντότητες είναι εντός της ζώνης που ορίζεται από το SPSS στο 95%, γεγονός που οφείλεται στην απομάκρυνση των ακραίων οντοτήτων κατά τη διαδικασία βελτιστοποίησης του μοντέλου. 128
141 Κ ε φ ά λ α ι ο 4 ο Διάγραμμα 4.40: Διάγραμμα μερικής παλινδρόμησης μεταξύ της αξίας και του εμβαδού Διάγραμμα 4.41: Διάγραμμα μερικής παλινδρόμησης μεταξύ της αξίας και της παλαιότητας Διάγραμμα 4.42: Διάγραμμα μερικής παλινδρόμησης μεταξύ της αξίας και του ορόφου Μεταπτυχιακή διατριβή 129
142 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα 4.43: Διάγραμμα μερικής παλινδρόμησης μεταξύ της αξίας και της κατάστασης του ακινήτου Διάγραμμα 4.44: Διάγραμμα μερικής παλινδρόμησης μεταξύ της αξίας και του είδους θέρμανσης 130
143 Κ ε φ ά λ α ι ο 4 ο Σύμφωνα με τα διαγράμματα η πιο ισχυρή σύνδεση εντοπίζεται όπως είναι λογικό μεταξύ της αξίας των ακινήτων και του εμβαδού τους. Ασθενέστερη είναι η σχέση μεταξύ της αξίας και των υπόλοιπων τεσσάρων μεταβλητών, ενώ η λιγότερο ισχυρή σύνδεση υπάρχει με το είδος θέρμανσης των ακινήτων. Παρόλο που δεν είναι ιδιαίτερα σημαντική η συνεισφορά της Χ6 μεταβλητής στο μοντέλο, οι αλγόριθμοι του στατιστικού λογισμικού SPSS την κρίνουν στατιστικά σημαντική και ταυτόχρονα στο διάγραμμα 4.44 διακρίνεται γραμμικότητα. Συνεπώς σύμφωνα με τα πέντε διαγράμματα μερικής παλινδρόμησης όλες οι μεταβλητές είναι στατιστικά σημαντικές. t τιμές Η σημαντικότητα των ανεξάρτητων μεταβλητών συνδέεται ταυτόχρονα με την προβλέπουσα ή ερμηνευτική δύναμη που έχει η κάθε μεταβλητή στο μοντέλο. Σύμφωνα με τον πίνακα 4.17 οι τιμές t που αντιστοιχούν στις μεταβλητές Χ1, Χ3, Χ4, Χ6 και Χ7 έχουν τιμές μεγαλύτερες του Ι±2Ι και τα επίπεδα στατιστικής σημαντικότητας είναι μικρότερα του 0,05 με αποτέλεσμα οι τέσσερις μεταβλητές να θεωρούνται στατιστικά σημαντικές. Η μεταβλητή Χ2 παρουσιάζει τιμή t κατά απόλυτη τιμή ίση με 1,910 και επίπεδο στατιστικής σημαντικότητας 0,063. Το γεγονός ότι η απόκλιση από την οριακή τιμή (Ι±2Ι) είναι πολύ μικρή οδηγεί στο συμπέρασμα ότι δεν υπάρχει στο μοντέλο πρόβλημα στατιστικής σημαντικότητας των ανεξάρτητων μεταβλητών. Πίνακας4.17: Πίνακας Coefficients που περιλαμβάνει τις τιμές t των ανεξάρτητων μεταβλητών Coefficients a Model Unstandardized Standardized 95,0% Confidence Collinearity Coefficients Coefficients Interval for B Correlations Statistics Lower Upper Zero- B Std. Error Beta t Sig. Bound Bound order Partial Part Tolerance VIF 5 (Constant) , ,379-4,113, , ,571 X1 1277,631 79,684,913 16,034, , ,438,868,927,832,832 1,203 X2-586, ,882 -,147-1,910, ,352 33,272,007 -,283 -,453 2,206,099 X3 1788, ,368,117 2,167, , ,451,321,317,112,918 1,089 Χ7 5901, ,841,163 2,393, , ,021,141,346,124,578 1,729 X6 7479, ,987,127 2,175, , ,379,275,318,113,789 1,267 Μεταπτυχιακή διατριβή 131
144 dimension0 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Συμπερασματικά, δεν εμφανίζεται να υπάρχει πρόβλημα στατιστικής σημαντικότητας των ανεξάρτητων μεταβλητών του μοντέλου Ανεξαρτησία οντοτήτων Ο έλεγχος ανεξαρτησίας των παρατηρήσεων εξασφαλίζεται με δύο τρόπους. Ο πρώτος είναι μέσω του στατιστικού δείκτη Durbin Watson, ο οποίος πρέπει να κυμαίνεται μεταξύ των τιμών 1,5 και 2,5. Ο δεύτερος έλεγχος είναι οπτικός και γίνεται με τη βοήθεια του διαγράμματος σκέδασης των κατά Student υπολοίπων με την σειρά εισαγωγής τους στο μοντέλο. Δείκτης Durbin Watson Σύμφωνα με τον πίνακα Model summary (Πίνακας 4.18) η τιμή του στατιστικού δείκτη είναι ίση με 2,213 <2,5. Συνεπώς, στην περίπτωση του Ευόσμου οι οντότητες του δείγματος είναι ασυσχέτιστες μεταξύ τους. Πίνακας4.18: Πίνακας Model Summary, ο οποίο περιέχει την τιμή του στατιστικού δείκτη Durbin Watson Model Summary Model Change Statistics Adjusted Std. Error R R R of the Square F Sig. F Durbin- R Square Square Estimate Change Change df1 df2 Change Watson 1,868 a,754, ,525, , ,000 2,917 b,840, ,556,086 24, ,000 3,928 c,862, ,160,022 7, ,011 4,935 d,874, ,714,012 4, ,048 5,942 e,887, ,764,013 4, ,035 2,213 Διάγραμμα σκέδασης Studentized residuals vs Sequence Το διάγραμμα σκέδασης της παρακάτω μορφής δείχνει εάν η τιμή των υπολοίπων επηρεάζεται ή όχι από την σειρά με την οποία καταχωρήθηκαν οι οντότητες στο δείγμα. 132
145 Κ ε φ ά λ α ι ο 4 ο Στο διάγραμμα 4.45 φαίνεται μία τυχαία κατανομή των οντοτήτων πάνω και κάτω από τη νοητή γραμμή που διέρχεται από το μηδέν, χωρίς το σχηματισμό συσσωρεύσεων και προτύπων που να υποδηλώνουν πρόβλημα ανεξαρτησίας των παρατηρήσεων. Οι παρατηρήσεις είναι τοποθετημένες με ομοιόμορφο τρόπο και βρίσκονται εντός μιας ζώνης σταθερού πλάτους (μεταξύ του ±2). Διάγραμμα 4.45: Διάγραμμα σκέδασης των Studentized Residuals με τα A/A για τον Εύοσμο Θεσσαλονίκης Συμπερασματικά, σύμφωνα και με τους δύο τρόπους ελέγχου γίνεται ξεκάθαρο ότι το τελικό μοντέλο πρόβλεψης των αγοραίων αξιών ακινήτων για την περιοχή του Ευόσμου της Θεσσαλονίκης δεν εμφανίζει κανένα πρόβλημα μη ανεξαρτησίας των παρατηρήσεων Πολυσυγγραμικότητα ή Συγγραμικότητα Η γραμμική εξάρτηση μίας ανεξάρτητης μεταβλητής ή περισσότερων με μία άλλη ανεξάρτητη μεταβλητή αποτελεί ένα πρόβλημα πολυσυγγραμικότητας. Ο βαθμός εξάρτησης φυσικά διαφέρει ανάλογα με το φαινόμενο που εξετάζεται και για αυτό το λόγο υπάρχουν συγκεκριμένα μέτρα και στατιστικοί δείκτες για τον υπολογισμό του. Παρακάτω αναλύονται τέσσερις στατιστικοί δείκτες εκ των οποίων οι δύο πρώτοι (παράγοντας ανοχής και παράγοντας πληθωριστικής διακύμανσης) εντοπίζονται στον πίνακα Coefficients, ενώ οι δύο επόμενοι (έλεγχος ιδιοτιμών και δεσμευμένοι δείκτες) εντοπίζονται στον πίνακα Collinearity diagnostics του στατιστικού πακέτου SPSS. Μεταπτυχιακή διατριβή 133
146 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Παράγοντας ανοχής (Tolerance factor) & Παράγοντας πληθωριστικής διακύμανασης (Variance inflation factor) Σύμφωνα με τον πίνακα 4.19 η τιμή του παράγοντα ανοχής (Tolerance factor) για τη μεταβλητή Εμβαδό (Χ1) είναι ίση με 0,832, για τη μεταβλητή Παλαιότητα (Χ2) 0,453, για τη μεταβλητή Όροφος (Χ3) 0,918, για τη μεταβλητή Κατάσταση ακινήτου (Χ7) 0,578 και τέλος για τη μεταβλητή Είδος Θέρμανσης (Χ6) είναι ίση με 0,789. Όταν οι τιμές του παράγοντα είναι κοντά στο μηδέν, τότε είναι έντονο το φαινόμενο πολυσυγγραμμικότητας. Αντίθετα τιμές μεγαλύτερες του 0,5 και μέχρι τη μονάδα αποδεικνύουν ότι η ανεξάρτητη μεταβλητή δεν παρουσιάζει κανένα πρόβλημα πολυσυγγραμμικότητας. Στην προκειμένη περίπτωση όλες οι τιμές είναι μεγαλύτερες από την οριακή τιμή 0,5, πέραν της Χ2, η οποία όμως είναι οριακά μικρότερη και θεωρείται ότι στατιστικώς δεν παραβιάζει την παραδοχή της πολυσυγγραμμικότητας. Επίσης, σύμφωνα με τη Norusis, 2000 πρόβλημα μπορεί να υπάρχει στην περίπτωση όπου η ανοχή είναι μικρότερη ή ίση με 0,10. Συνεπώς, σύμφωνα με τον πρώτο έλεγχο δεν εμφανίζεται κανένα πρόβλημα πολυσυγγραμμικότητας στο μοντέλο. Πίνακας4.19: Πίνακας Coefficients ο οποίος περιλαμβάνει τις τιμές VIF και Tolerance Coefficients a Model Unstandardized Standardized 95,0% Confidence Collinearity Coefficients Coefficients Interval for B Correlations Statistics Lower Upper Zero- B Std. Error Beta t Sig. Bound Bound order Partial Part Tolerance VIF 5 (Constant) , ,379-4,113, , ,571 X1 1277,631 79,684,913 16,034, , ,438,868,927,832,832 1,203 X2-586, ,882 -,147-1,910, ,352 33,272,007 -,283 -,099,453 2,206 X3 1788, ,368,117 2,167, , ,451,321,317,112,918 1,089 Χ7 5901, ,841,163 2,393, , ,021,141,346,124,578 1,729 X6 7479, ,987,127 2,175, , ,379,275,318,113,789 1,267 Όσον αφορά το δεύτερο έλεγχο με τη βοήθεια του παράγοντα πληθωριστικής διακύμανσης VIF, όπως φαίνεται από τις τιμές του παραπάνω πίνακα οι τέσσερις στις πέντε είναι μικρότερες της τιμής 2 που αποτελεί την αυστηρότερη ανοχή σύμφωνα με τη βιβλιογραφία. Όσον αφορά την τιμή της μεταβλητής Χ2, η οποία είναι ίση με 2,206 δεν θεωρείται προβληματική, διότι όπως αναφέρθηκε και στο υποκεφάλαιο ορισμένες θεωρίες σχετικά με το δείκτη VIF ορίζουν ως κρίσιμη τιμή την τιμή του 5 και άλλες την τιμή 10. Συνεπώς, εφόσον οι δείκτες VIF όλων των μεταβλητών είναι εντός των επιτρεπόμενων ορίων δεν παρατηρείται κανένα πρόβλημα συγγραμμικότητας μεταξύ τους. 134
147 Κ ε φ ά λ α ι ο 4 ο Έλεγχος ιδιοτιμών (Eigenvalues) & Δεσμευμένοι δείκτες (Condition indexes) Οι τιμές του δείκτη Eigenvalue (Πίνακας 4.20) παρουσιάζουν πιθανό πρόβλημα διασυσχέτισης όσο πιο κοντά στην τιμή του μηδέν βρίσκονται. Σε αντίθεση με το δείκτη Tolerance, ο οποίος υποδεικνύει ως πιθανόν προβληματική τη μεταβλητή Χ2, ο δείκτης Eigenvalue φανερώνει τη μεταβλητή Χ6. Η μεταβλητή του Είδους θέρμανσης έχει μία τιμή που βρίσκεται πιο κοντά στο μηδέν, σε σύγκριση με τις υπόλοιπες άρα μπορεί να θεωρηθεί πιθανή για απομάκρυνση. Η απόφαση θα παρθεί αφού ολοκληρωθούν όλοι οι έλεγχοι. Πίνακας4.20: Πίνακας Colllinearity Diagnostics που περιλαμβάνει τις τιμές Eigenvalue και Condition Index Collinearity Diagnostics a Model Dimension Eigenvalue Condition Index Variance Proportions (Constant) X1 X2 X3 Χ7 X ,369 1,000,00,00,00,01,00,00 2,410 3,619,00,00,37,01,00,00 3,147 6,051,00,01,00,97,01,01 4,035 12,395,01,64,14,01,21,05 5,033 12,705,00,33,05,00,08,64 6,007 28,032,98,02,43,01,70,29 Οι τιμές των δεσμευμένων δεικτών για να μην υπάρχει καμία ένδειξη πολυσυγγραμμικότητας πρέπει να είναι μικρότερες της τιμής 15. Στην περίπτωση που είναι μεταξύ των τιμών 15 και 30, τότε είναι πιθανό να υπάρχει πρόβλημα πολυσυγγραμμικότητας, ενώ εάν υπερβούν την τιμή 30 τότε η ανεξάρτητη μεταβλητή πρέπει να αφαιρεθεί από το μοντέλο, διότι αποτελεί γραμμικό συνδυασμό των άλλων ανεξάρτητων μεταβλητών. Στην προκειμένη περίπτωση, παρουσιάζεται πιθανότητα να έχει πρόβλημα η μεταβλητή Χ6, η οποία έχει τιμή δεσμευμένου δείκτη κοντά στο πάνω όριο της ανοχής. Παρόλα αυτά επειδή τα δεδομένα του δείγματος αποτελούν ρεαλιστικά δεδομένα της αγοράς ακινήτων της Θεσσαλονίκης η απομάκρυνση της μεταβλητής Χ6 από το μοντέλο θα επιβαλλόταν μόνο εάν ο δεσμευμένος δείκτης (Condition index)ξεπερνούσε την τιμή 30. Λαμβάνοντας υπόψη όλους τους δείκτες, οι μεταβλητές που έχουν ενδείξεις για ύπαρξη συγγραμμικότητας είναι κυρίως η Χ6 και πολύ λιγότερο η Χ2. Παρόλα αυτά οι αποκλίσεις δεν μαρτυρούν σοβαρό πρόβλημα συγγραμμικότητας, συνεπώς δεν υποδεικνύεται η αφαίρεση καμίας ανεξάρτητης μεταβλητής. Μεταπτυχιακή διατριβή 135
148 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Κανονικότητα Είναι πρωταρχικής σημασίας η ικανοποίηση της κανονικότητας σε κάθε στατιστική διαδικασία, καθώς αποτελεί μία από τις πιο σημαντικές συνθήκες. Η κανονικότητα όπως αναφέρθηκε και στο υποκεφάλαιο ελέγχεται με πολλούς διαφορετικούς τρόπους. Μερικοί από αυτούς είναι περισσότερο χονδρικοί όπως το φυλλογράφημα των υπολοίπων, ενώ άλλοι είναι περισσότερο ακριβής. Σημαντικό είναι να ικανοποιούνται όλοι οι έλεγχοι ένας προς ένας. Για τα μεγάλα δείγματα (μεγαλύτερα των 30 οντοτήτων) για την παραδοχή της κανονικότητας αξιοποιούνται τα Studentized Deleted Residuals, διότι ακολουθούν την κανονική κατανομή. Παρακάτω περιγράφονται αναλυτικά οι οκτώ διαφορετικοί έλεγχοι και τα αποτελέσματα που προκύπτουν για το τελικό παλινδρομικό μοντέλο. Φυλλογράφημα των υπολοίπων [Stem And- Leaf- Plot of residuals Studentized deleted residuals] Σύμφωνα με το φυλλογράφημα που παράχθηκε από τη διαδικασία Explore για την περιοχή του Ευόσμου (Διάγραμμα 4.46) δεν επισημαίνονται ακραίες τιμές. Επίσης, παρατηρείται από τη γνωστή καμπανοειδή μορφή που σχηματίζεται, στραμμένη κατά 90 ο, ότι τα Studentized Deleted Residuals ακολουθούν την κανονική κατανομή. Studentized Deleted Residual Stem-and-Leaf Plot Frequency Stem & Leaf 2, , , , , , , , Stem width: 1,00000 Each leaf: 1 case(s) Διάγραμμα 4.46: Φυλλογράφημα των υπολοίπων για την περιοχή του Ευόσμου Συνεπώς ο πρώτος έλεγχος ικανοποιεί την παραδοχή της κανονικότητας για το σύνολο των 48 οντοτήτων της περιοχής του Ευόσμου. 136
149 Κ ε φ ά λ α ι ο 4 ο Test of normality : Kolmogorv Smirnov, Lillefors, Shapiro Wilk Εξαιτίας του μεγάλου δείγματος για τον έλεγχο της κανονικότητας αξιοποιείται το στατιστικό κριτήριο των Kolmogorov Smirnov και όχι των Shapiro Wilk (Πίνακας 4.21). Ο έλεγχος της υπόθεσης της κανονικότητας των υπολοίπων σύμφωνα με το στατιστικό κριτήριο Kolmogorov Smirnov: Μηδενική Υπόθεση Ho: Τα υπόλοιπα κατανέμονται κανονικά και Εναλλακτική Υπόθεση H1: Τα υπόλοιπα δεν κατανέμονται κανονικά. Το τεστ για την κανονικότητα των Kolmogorov Smirnov δίνει επίπεδο στατιστικής σημαντικότητας (Sig.) 20%, δηλαδή μεγαλύτερο του 5%. Συνεπώς, δεν μπορεί να απορριφθεί η υπόθεση ότι τα Studentized Deleted Residuals ακολουθούν την κανονική κατανομή. Πίνακας4.21: Πίνακας Tests of Normality Kolmogorv Smirnov, Lillefors, Shapiro Wilk Tests of Normality Kolmogorov-Smirnov a Shapiro-Wilk Statistic df Sig. Statistic df Sig. Studentized Deleted Residual,105 48,200 *,967 48,191 a. Lilliefors Significance Correction *. This is a lower bound of the true significance. Normal Q-Q Plot of Studentized deleted Residuals Το διάγραμμα 4.47 που παράγεται μέσω της διαδικασίας Explore (Analyze Descriptive Statistics Explore) απεικονίζει στον άξονα Χ τις παρατηρούμενες τιμές των Studentized Deleted Residuals, ενώ στον άξονα Υ τις αναμενόμενες τιμές τους. Κύριος στόχος δεν είναι η εμφάνιση ιδανικής περίπτωσης κανονικής κατανομής (σε κανένα φαινόμενο οικονομικού κοινωνικού ενδιαφέροντος δε μπορεί να εμφανιστεί με απόλυτο τρόπο)αλλά η όσο το δυνατό προσέγγιση της. Στο γράφημα παρατηρείται ότι τα σημεία τείνουν στη γραμμή που ορίζει την πλήρη κανονικότητα (διχοτόμος) με πολύ μικρές αποκλίσεις. Άμεσο συμπέρασμα είναι ότι το διάγραμμα μεταξύ των παρατηρούμενων και προσδοκώμενων τιμών των υπολοίπων αναφέρεται σε μία κανονική κατανομή. Μεταπτυχιακή διατριβή 137
150 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα 4.47: Διάγραμμα κανονικότητας Normal Q-Q Plot of Studentized deleted Residuals για τον έλεγχο της κανονικότητας των υπολοίπων Detrended normal Q-Q Plot Studentized Deleted residuals Το διάγραμμα 4.48 απεικονίζει στον άξονα Χ τις παρατηρούμενες τιμές των Studentized Deleted Residuals, ενώ στον άξονα Υ τα ποσοστιαία σημεία μίας τυπικής κανονικής κατανομής που αποτελούν τυποποιημένες μονάδες. Η ανάγνωση του διαγράμματος μπορεί να οδηγήσει σε ιδιαίτερα ακριβή συμπεράσματα σχετικά με την κανονικότητα των υπολοίπων, διότι πρόκειται για ένα ιδιαίτερα σημαντικό διάγραμμα της διαδικασίας Explore. Παρουσιάζονται στο διάγραμμα 4.48 κουκκίδες τυχαία κατανεμημένες πάνω και κάτω από την οριζόντια γραμμή που διέρχεται από την τιμή μηδέν, σε ένα σταθερό εύρος πλάτους περίπου. Επίσης, είναι φανερό ότι δεν παρατηρείται κανενός είδους συσσώρευση σημείων που να προκαλεί τη δημιουργία προτύπων. Τα λεγόμενα «τσαμπιά» (εμφάνιση μεγάλης πυκνότητας σε σημεία) αντιπροσωπεύουν μαθηματικές συναρτήσεις διαφορετικής μορφής που δείχνουν ύπαρξη προβλήματος κανονικότητας. Συνεπώς, στην προκειμένη περίπτωση ικανοποιείται η παραδοχή της κανονικότητας, χωρίς καμία ένδειξη πιθανού προβλήματος. 138
151 Κ ε φ ά λ α ι ο 4 ο Διάγραμμα 4.48: Διάγραμμα Detrended Νormal Q-Q Plot Studentized Deleted Ρesiduals για τον έλεγχο της κανονικότητας των υπολοίπων Histogram Studentized Deleted Residuals Μεταπτυχιακή διατριβή 139
152 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα 4.49: Ιστόγραμμα των Studentized Deleted Residuals για τον έλεγχο της κανονικότητας των υπολοίπων Στο παραπάνω ιστόγραμμα (Διάγραμμα 4.49), το οποίο παράχθηκε μέσω της διαδικασίας Explore, γίνεται σαφές ότι προσεγγίζεται ικανοποιητικά η κανονική κατανομή και πέραν ορισμένων εκτροπών από την καμπύλη, παρουσιάζεται κανονικότητα. Histogram Standardized Residuals Πρόκειται για ιστόγραμμα συχνοτήτων που δημιουργείτε από την κύρια διαδικασία εκτέλεσης της γραμμικής παλινδρόμηση και όπως φαίνεται από την καμπύλη κανονικής κατανομής που προσαρμόζεται στο ιστόγραμμα η κανονικότητα προσεγγίζεται ικανοποιητικά. Διάγραμμα 4.50: Ιστόγραμμα των Standardized Residuals για τον έλεγχο της κανονικότητας των υπολοίπων Διάγραμμα Normal P-P Plot of regression standardized residuals Το παρακάτω γράφημα αναμενόμενης παρατηρούμενης αθροιστικής πιθανότητας, δείχνει ότι η πλειοψηφία των παρατηρήσεων προσεγγίζει, με μικρές αποκλίσεις, ικανοποιητικά την ευθεία γραμμή και άρα το διάγραμμα φανερώνει ύπαρξη κανονικότητας. 140
153 Κ ε φ ά λ α ι ο 4 ο Διάγραμμα 4.51: Διάγραμμα Normal P-P Plot of regression Standardized Residuals για τον έλεγχο της κανονικότητας των υπολοίπων Θηκόγραμμα των υπολοίπων (Boxplot of Residuals) Είναι ορατό από το διάγραμμα 4.52 ότι η διάμεσος του θηκογράμματος που αναφέρεται στο παλινδρομικό μοντέλο βρίσκεται στο κέντρο του ορθογωνίου, άρα πρόκειται για μία συμμετρική κατανομή. Επίσης, καμία απομονωμένη ή ακραία τιμή δεν παρατηρείται στο θηκόγραμμα. Μεταπτυχιακή διατριβή 141
154 Σχηματισμός μοντέλου Διάγραμμα 4.52: Θηκόγραμμα για τον εντοπισμό των ακραίων τιμών του δείγματος μέσω της διαδικασίας Explore Σύμφωνα με όλους τους τρόπους ελέγχου που προηγήθηκαν, δεν παρατηρείται καμία πιθανή ένδειξη μη κανονικότητας των υπολοίπων και άρα το δεύτερο σε σειρά μοντέλο που αναφέρεται στην περιοχή του Ευόσμου Θεσσαλονίκης θεωρείται ότι ικανοποιεί επαρκώς την παραδοχή της κανονικότητας Ισότητα διακυμάνσεων ή ομοσκεδαστικότητα Η ικανοποίηση της παραδοχής της ομοσκεδαστικότητας πραγματοποιείται με τη βοήθεια των ακόλουθων τριών διαγραμμάτων σκέδασης: Studentized Deleted Residuals vs Standardized Predicted Values Studentized Residuals vs Standardized Predicted Values Standardized Predicted Values vs Dependent Variable Τα δύο πρώτα διαγράμματα είναι της ίδιας μορφής και η απεικόνιση τους δίνει παρόμοια αποτελέσματα. Όπως φαίνεται παρακάτω, τα δύο διαγράμματα φανερώνουν μία τυχαία κατανομή και όχι κάποιας μορφής συσσώρευση ή πρότυπο. Επίσης, θετικό στοιχείο για την ικανοποίηση της παραδοχής είναι το μικρό εύρος ζώνης ( ) που είναι τοποθετημένες οι τιμές. Τα παρακάτω γραφήματα καλύπτουν ικανοποιητικά την παραδοχή ομοσκεδαστικότητας αλλά ταυτόχρονα και της γραμμικότητας του μοντέλου. της 142
155 Κ ε φ ά λ α ι ο 4 ο Διάγραμμα 4.53: Διάγραμμα σκέδασης των Studentized Deleted Residuals με τα Standardized Predicted Values (αριστερά) και διάγραμμα σκέδασης των Studentized Residuals με τα Standardized Predicted Values (δεξιά) Το διάγραμμα διασποράς των εκτιμώμενων και παρατηρούμενων τιμών (Διάγραμμα 4.54) παρουσιάζει τα υπόλοιπα κατανεμημένα κανονικά και με σταθερή διακύμανση. Όλα τα σημεία κατανέμονται με ομοιόμορφο τρόπο πάνω και κάτω από την ευθεία των ελαχίστων τετραγώνων σε μία ζώνη σταθερού πλάτους και συνεπώς ικανοποιείται επιτυχώς η παραδοχή της ισότητας των διασπορών. Διάγραμμα 4.54: Διάγραμμα σκέδασης των Standardized Predicted Values με τις τιμές της εξαρτημένης μεταβλητής Υ Εφόσον η διασπορά των υπολοίπων στα διαγράμματα 4.53 και 4.54, σύμφωνα με την οπτική τους ερμηνεία, είναι τυχαία και ομοιόμορφη ικανοποιείται η απαίτηση της ομοσκεδαστικότητας Γραμμικότητα Ο έλεγχος της γραμμικότητας πραγματοποιείται στην παρούσα διατριβή με οπτική ερμηνεία τεσσάρων διαφορετικών διαγραμμάτων σκέδασης. Διαγράμματα σκέδασης ανεξάρτητων μεταβλητών με την εξαρτημένη Studentized Deleted Residuals με Standardized Predicted Values Studentized Residuals με Standardized Predicted Values Partial Plots Μεταπτυχιακή διατριβή 143
156 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ H πρώτη κατηγορία διαγραμμάτων αποτελεί βασικό κριτήριο για την επιλογή των ανεξάρτητων μεταβλητών που συμμετέχουν στο μοντέλο. Ένας έλεγχος αυτής της κατηγορίας είναι το διάγραμμα 4.38 του υποκεφαλαίου για δείγμα 60 οντοτήτων. Το αντίστοιχο διάγραμμα Matrix για το δείγμα των 48 οντοτήτων και για τις τελικές πέντε μεταβλητές είναι το ακόλουθο. Διάγραμμα 4.55: Διάγραμμα σκέδασης των ανεξάρτητων μεταβλητών με τις τιμές της εξαρτημένης μεταβλητής Υ για Σύμφωνα με το διάγραμμα 4.55 παρατηρείται η πιο χονδρική σύνδεση των μεταβλητών Χ1, Χ2, Χ3, Χ6 και Χ7 με την Υ. έντονη γραμμικότητα παρουσιάζει η Χ1 με την Υ, λιγότερο ισχυρή γραμμική σχέση παρουσιάζει η Χ2 και Χ3 με την Υ και τέλος ασθενέστερη αλλά υπαρκτή είναι η σχέση μεταξύ των Χ6 και Χ7 με την Υ. Οι μεταβλητές Χ6 και Χ7 παίρνουν τιμές μόνο μεταξύ τεσσάρων κατηγοριών (πχ. 0, 1, 2, 3, 4) με αποτέλεσμα να μην είναι τόσο εύκολα ορατή η γραμμική σχέση, όπως συμβαίνει στην περίπτωση του εμβαδού, όπου η διασπορά των τιμών είναι μεγάλη. Συνεπώς, το τελικό διάγραμμα Μatrix των 48 οντοτήτων παρουσιάζει γραμμικότητα. Το δεύτερο και τρίτο σε σειρά διάγραμμα ελέγχου της γραμμικότητας έχει ήδη εξεταστεί μέσω της παραδοχής της ομοσκεδασιμότητας στο υποκεφάλαιο Σύμφωνα με τα δύο διαγράμματα της εικόνας 4.53 είναι ορατή η ικανοποίηση της γραμμικότητας του μοντέλου. 144
157 Κ ε φ ά λ α ι ο 4 ο Τέλος, η τρίτη κατηγορία διαγραμμάτων είναι τα διαγράμματα μερικής παλινδρόμησης (Partial Plots) τα οποία εξετάστηκαν λεπτομερώς στο υποκεφάλαιο (παραδοχή σημαντικότητας ανεξάρτητων μεταβλητών). Σύμφωνα με τα διαγράμματα 4.40, 4.41, 4.42, 4.43 και 4.44 όλες οι μεταβλητές έχουν γραμμική σχέση με την εξαρτημένη. Συμπερασματικά, ισχύει η ύπαρξη γραμμικότητας μεταξύ της αγοραίας αξίας των ακινήτων με το εμβαδό, την παλαιότητα, τον όροφο, την κατάσταση του ακινήτου και το είδος θέρμανσης Ακραίες οντότητες και οντότητες επίδρασης Οι έλεγχοι που ακολουθούν για τον εντοπισμό και την απομάκρυνση των οντοτήτων επίδρασης είναι ιδιαίτερα σημαντικοί. Με τη βοήθεια δεικτών, γραφημάτων και κατανομών διερευνάται η ύπαρξη οντοτήτων που επιδρούν ριζικά στην ανάλυση παλινδρόμησης και στους συντελεστές της. Σε πρώτο στάδιο ελέγχεται η ύπαρξη ακραίων τιμών (Outliers) και ακολουθεί η αναζήτηση εάν κάποια ή κάποιες από αυτές τις τιμές είναι πιθανή οντότητα επίδρασης (influential point). Εάν είναι, τότε ο τελικός έλεγχος για την απομάκρυνση της γίνεται με τη βοήθεια της t και F κατανομής. Ο έλεγχος ύπαρξης των outliers γίνεται με τη βοήθεια της απόστασης Mahalanobis (Mahalanobis distance D i 2 ) και του Levarage h i (centered leverage). Ο έλεγχος των influential points γίνεται με τη βοήθεια της απόστασης Cook (Cook s Distance : CD i ), του μέτρου DFFITS (Standardized DFFITS), του μέτρου DFBetas (Standardized DFBetas), των γραφημάτων, Cook s distance με Centered Leverage Values, Standardized DFFITS με την αύξουσα σειρά των παρατηρήσεων A/A και Standardized DFBETA X i με A/A. Η απομάκρυνση των υποψήφιων οντοτήτων επίδρασης ελέγχεται με τη βοήθεια της κατανομής t (Διαδικασία BONFERRONI) και της κατανομής F. Centered Leverage Αρχικά, ελέγχονται οι τιμές του δείκτη Centered Leverage μέσω της στήλης LEV_1 και της κρίσιμης τιμής 0,20. Από τον έλεγχο όλων των οντοτήτων με την τιμή 0,20προκύπτει ότι οι οντότητες 4(0,35)και 17 (0,39) υπερβαίνουν το όριο και θεωρούνται υποψήφιες ακραίες οντότητες. Σύμφωνα με τη διεθνή βιβλιογραφία τιμές μεγαλύτερες του 0,2 και μικρότερες του 0,5 χαρακτηρίζονται επικίνδυνες και πρέπει να εξετάζονται εκτενέστερα για πιθανή τους απομάκρυνση. Συνεπώς παρακάτω εξετάζεται εάν οι οντότητες 4 και 17 αποτελούν οντότητες επίδρασης. Αποστάσεις Cook CD i Πρόκειται για το πρώτο μέτρο εντοπισμού των οντοτήτων επίδρασης, το οποίο υπολογίζει για κάθε οντότητα τις αλλαγές που συμβαίνουν στις εκτιμήσεις των παλινδρομικών συντελεστών όταν η συγκεκριμένη απαλειφθεί από το παλινδρομικό Μεταπτυχιακή διατριβή 145
158 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ μοντέλο. Κρίσιμη τιμή για τις αποστάσεις Cook θεωρείται η μονάδα, συνεπώς οι τιμές της στήλης COO_1 για όλες τις οντότητες θα πρέπει να συγκριθούν με τη μονάδα. Σύμφωνα με τα δεδομένα που προκύπτουν από την εκτέλεση πολλαπλής παλινδρόμησης όλες οι τιμές Cook είναι πολύ μικρότερες της μονάδας και συνεπώς καμία από τις δύο ακραίες τιμές δεν αποτελεί οντότητα επίδρασης. Μέτρα DfFits Το μέτρο DfFits εκφράζει την επίδραση της κάθε περίπτωσης (case) στις εκτιμήσεις των παλινδρομικών συντελεστών και αποτελεί άλλη μία μέθοδο εντοπισμού των πιθανών οντοτήτων επίδρασης. Για τον έλεγχο λαμβάνεται υπόψη η στήλη SDF_1 του Data Editor, η οποία αναφέρεται στα Standardized DfFits και συγκρίνεται με την κρίσιμη τιμή για τα μεγάλα δείγματα 23 (n>30)η οποία είναι η ακόλουθη: Standardized DfFits κρίσιμη = 2* = 0,71 Έπειτα από τη μελέτη των απόλυτων τιμών των Standardized DfFits όλων των οντοτήτων, καμία από τις οντότητες δεν ξεπερνά την οριακή τιμή και άρα δεν υπάρχει καμία ένδειξη ύπαρξης οντοτήτων επίδρασης. Μέτρα DfBetas Τα μέτρα DfBetas εκφράζουν την επίδραση των περιπτώσεων (cases) στην εκτίμηση του κάθε παλινδρομικού συντελεστή ξεχωριστά. Για τον έλεγχο αξιοποιούνται οι απόλυτες τιμές των Standardized DfBetas και στη συνέχεια συγκρίνονται με μία κρίσιμη τιμή για την ύπαρξη οντοτήτων επίδρασης. Η κρίσιμη τιμή για τις περιπτώσεις των μεγάλων δειγμάτων (n>30) δίνεται από την ακόλουθη σχέση: Standardized DfBetas κρίσιμη = = 0,29 Συγκεκριμένα, για τη μεταβλητή Χ1 ελέγχεται η στήλη με τίτλο SDB1_1 του Data Editor, για τη μεταβλητή Χ2 η στήλη SDB2_1 κοκ. Σύμφωνα με τα δεδομένα που προκύπτουν από την παλινδρομική ανάλυση των 48 οντοτήτων, τα Standardized DfBetas(Χ1) υποδεικνύουν ως υποψήφιες οντότητες επίδρασης εκείνες με Α/Α 14 και 60, τα Standardized DfBetas(Χ2) υποδεικνύουν την οντότητα 56, τα Standardized DfBetas(Χ3) τις οντότητες 21, 40 και 60, τα Standardized DfBetas(Χ6) τις 40 και 49 και τέλος τα Standardized DfBetas(Χ7) υποδεικνύουν τις οντότητες 8 και 60. Από τις οντότητες που αναφέρθηκαν παραπάνω, μόνο η οντότητα με Α/Α 8 αποτελεί ταυτοχρόνως ακραία τιμή βάσει των αντίστοιχων δεικτών. Οι υπόλοιπες οντότητες 14, 21, 40, 49 και60 πιθανόν να επιδρούν σημαντικά στη διαμόρφωση των συντελεστών και άρα σε όλο το μοντέλο. Παρόλα αυτά καμία από τις παραπάνω οντότητες δεν απομακρύνεται εάν αρχικά δεν ολοκληρωθούν όλες οι μέθοδοι εντοπισμού των οντοτήτων επίδρασης του μοντέλου. 23 Αντίστοιχα για τα μικρά δείγματα (n<30) η οριακή τιμή είναι ίση με τη μονάδα 146
159 Κ ε φ ά λ α ι ο 4 ο Διάγραμμα σκέδασης των αποστάσεων Cook με κεντραρισμένες τιμές Leverage Οι παραπάνω δείκτες και μέτρα γίνονται πολύ πιο κατανοητά μέσω της σχετικής θέσης που έχουν κάθε φορά οι οντότητες σε διαγράμματα. Παρακάτω ακολουθεί η σχεδίαση τριών διαφορετικών διαγραμμάτων για να ξεχωρίσουν οπτικά οι ακραίες τιμές και οι οντότητες επίδρασης. Το πρώτο διάγραμμα παρουσιάζει στον άξονα Χ τις τιμές Centered Leverage και τον άξονα Y τις αντίστοιχες τιμές Cook. Διάγραμμα 4.56: Διάγραμμα σκέδασης των αποστάσεων Cook με τις Centered Leverage τιμές Στο διάγραμμα 4.56 καμία παρατήρηση του μοντέλου δεν ξεπερνά την οριακή τιμή 1 για την απόσταση Cook, ενώ οι οντότητες 4 και 17, όπως επισημαίνονται στο διάγραμμα, βρίσκονται μεταξύ των τιμών 0,20 και 0,5. Η απομάκρυνση τους πρόκειται να ελεγχθεί μέσω των κατανομών t και F. Διάγραμμα σκέδασης των τυποποιημένων DfFits με την ακολουθία των παρατηρήσεων Το παρακάτω Sequence διάγραμμα απεικονίζει στον άξονα Υ τις τιμές Standardized DfFits, ενώ στον άξονα των Χ την αύξουσα σειρά εισαγωγής των οντοτήτων στο δείγμα. Για την ανάγνωση του διαγράμματος φέρουμε μία νοητή γραμμή στο μηδέν και στη συνέχεια παρατηρούμε τις εξάρσεις που υπάρχουν προχωρώντας από την πρώτη ως την τελευταία οντότητα. Μεταπτυχιακή διατριβή 147
160 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα 4.57: Διάγραμμα Sequence των Standardized DfFits με την αύξουσα σειρά του δείγματος Παραπάνω αναφέρθηκε ότι οριακή κρίσιμη τιμή για τα Standardized DfFits είναι η τιμή 0,71. Όπως φαίνεται και από το διάγραμμα καμία οντότητα δεν παρουσιάζει τιμή μεγαλύτερη του 0,71. Συνεπώς, δεν υπάρχει καμία ένδειξη για οντότητες επίδρασης βάσει του συγκεκριμένου κριτηρίου. Διάγραμμα σκέδασης των τυποποιημένων DfBetas με την ακολουθία των παρατηρήσεων Στο Sequence διάγραμμα (Διάγραμμα 4.58) ο άξονας Y απεικονίζει τα Standardized Dfbetas και ο άξονας Χ τη σειρά καταχώρησης των παρατηρήσεων. Για κάθε συντελεστή του παλινδρομικού μοντέλου (στη συγκεκριμένη περίπτωση πέντε συντελεστές) δημιουργείται ένα ξεχωριστό διάγραμμα και αποδίδεται με διαφορετικό χρωματισμό. Η ανοχή που έχει υπολογιστεί είναι ίση με 0,29 και υποψήφιες οντότητες επίδρασης είναι εκείνες που ξεπερνούν τη συγκεκριμένη τιμή. Σύμφωνα με το διάγραμμα 4.42 οι τιμές που αποκλίνουν περισσότερο από όλες τις υπόλοιπες είναι οι 14 και 60 ως προς τη μεταβλητή Χ1, η 56 ως προς τη μεταβλητή Χ2, οι 21, 40, 60 ως προς τη μεταβλητή Χ3, οι 40 και 49 ως προς τη Χ6 και οι 8 και 60 ως προς τη Χ7. Οι μεγαλύτερες σε μέγεθος αποκλίσεις παρατηρούνται στη μεταβλητή Χ6 και ακολουθεί η μεταβλητή Χ3. Είναι σαφές ότι υπάρχει επίδραση η οποία για να αποφασιστεί εάν είναι στατιστικώς σημαντική ή όχι θα πρέπει να ολοκληρωθούν οι έλεγχοι με τη βοήθεια των κατανομών που ακολουθούν. 148
161 Κεφάλαιο 4ο Διάγραμμα 4.58: Διάγραμμα Sequence των Standardized DfBeta με την αύξουσα σειρά του δείγματος t κατανομή Τα Studentized Deleted Residuals μέσω της διαδικασίας Bonferroni και της t κατανομής μπορούν να βοηθήσουν στον εντοπισμό των οντοτήτων επίδρασης. Όπου ti ορίζεται η τιμή των Studentized Deleted Residuals, τα οποία ακολουθούν την κανονική κατανομή με βαθμούς ελευθερίας: β.ε. = n-p-1 = =41 Η κρίσιμη τιμή που ορίζει η διαδικασία Bonferroni και είναι ίση με: t κρίσιμη = t(1 - ; n-p-1) t (0, ; 41) = 3,29824 με α το επίπεδο στατιστικής σημαντικότητας (α= 0,05), n το μέγεθος του δείγματος (n =48) και p τον αριθμό των συντελεστών παλινδρόμησης μαζί με το σταθερό όρο (p = 6). 24 Η τελική τιμή προκύπτει μέσω των στατιστικών πινάκων Μεταπτυχιακή διατριβή 149
162 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Επόμενο βήμα αποτελεί ο εντοπισμός της οντότητας με το μεγαλύτερο Studentized Deleted Residual (max SDR)ώστε να συγκριθεί με την οριακή τιμή που προέκυψε παραπάνω. Από τα δεδομένα του Data Editor προκύπτει ότι η οντότητα με τη μεγαλύτερη απόλυτη τιμή Studentized Deleted Residual κατά απόλυτη τιμή είναι η = = 1,9349. Ορίζεται η μηδενική υπόθεση Ηο: Το Studentized Deleted Residual με τη μεγαλύτερη απόλυτη τιμή είναι μία οντότητα επίδρασης, με εναλλακτική υπόθεση =1,9349 ΔΕΝ Η1: Studentized Deleted Residual με τη μεγαλύτερη απόλυτη τιμή =1,9349 είναι οντότητα επίδρασης Επειδή όμως = 1,9349 <3,298 ισχύει η μηδενική υπόθεση Ηο και η οντότητα 20 δεν αποτελεί οντότητα επίδρασης. F κατανομή Οι τιμές Cook θεωρείται ότι ακολουθούν την κατανομή F(1-a;p;n-p), συνεπώς με τη βοήθεια της κατανομής μπορούν να εντοπιστούν οι οντότητες επίδρασης εάν και εφόσον υπάρχουν. Με την ίδια λογική που περιγράφηκε παραπάνω υπολογίζεται αρχικά η κρίσιμη τιμή F και στη συνέχεια συγκρίνεται με την τιμή Cook που είναι η μεγαλύτερη σε μέγεθος σε σύγκρισή με όλες τις υπόλοιπες. F κρίσιμη =F(1-a; p; n-p) = F(0,95; 6; 42) = 2,3375 Η μέγιστη απόσταση Cook ανήκει στην οντότητα 40 και είναι ίση με CD 40 = 0,0653. Από τους στατιστικούς πίνακες της F κατανομής παρατηρείται ότι η τιμή βρίσκεται στο 23,37% εκατοστημόριο της συγκεκριμένης κατανομής, δηλαδή δεν πλησιάζει σε καμία περίπτωση το 50% και άρα η οντότητα δε μπορεί να χαρακτηριστεί οντότητα επίδρασης. Σύμφωνα με τους δύο ελέγχους κρίνεται ότι καμία από τις υποψήφιες οντότητες επίδρασης των προηγούμενων ελέγχων δε χρειάζεται να απομακρυνθεί από το μοντέλο και άρα αυτή είναι η τελική μορφή του με συνολικά 48 οντότητες Έλεγχος προβλεπτικής ικανότητας του μοντέλου Σύμφωνα με τις παραπάνω διαδικασίες σχηματίστηκε ένα γραμμικό μοντέλο πολλών μεταβλητών, το οποίο πληροί όλους τους περιορισμούς των μοντέλων της κατηγορίας του και κρίνεται ιδιαίτερα ικανοποιητικό. Οι δύο πρώτοι έλεγχοι που ακολουθούν πραγματοποιούνται για να φανεί η δύναμη πρόβλεψης του συγκεκριμένου μοντέλου και ο τρίτος για να επιβεβαιωθεί εάν το μοντέλο έχει πλεονάζουσα ή ελλιπή πληροφορία σχετικά με τις μεταβλητές που διαμορφώνουν την αγοραία αξία. 150
163 Κ ε φ ά λ α ι ο 4 ο Μέθοδος των διαστημάτων πρόβλεψης Η μέθοδος των διαστημάτων πρόβλεψης πραγματοποιείται με τη βοήθεια νέων οντοτήτων που συλλέγονται από τον ίδιο ακριβώς πληθυσμό από τον οποίο προήλθε το δείγμα. Μέσω διαδικασίας που περιγράφηκε στο υποκεφάλαιο συγκρίνονται οι τιμές Υ των νέων εγγραφών με το διάστημα πρόβλεψης που δίνεται από το SPSS (LICI, UICI). Εάν η γνωστή, ζητούμενη τιμή πώλησης βρίσκεται εντός του διαστήματος πρόβλεψης, τότε το δείγμα θεωρείται ότι ανταποκρίνεται στην πραγματικότητα. Πιο συγκεκριμένα, συλλέγονται για τον έλεγχο τέσσερα νέα διαμερίσματα και μαζί με τις 48 οντότητες του δείγματος εκτελείται η διαδικασία. Τα αποτελέσματα είναι τα ακόλουθα: < < < < < < < < Παρατηρείται ότι όλες οι αξίες βρίσκονται εντός του διαστήματος πρόβλεψης και άρα το μοντέλο θεωρείται ικανοποιητικό και ικανό να αξιοποιηθεί για να δώσει τιμές σε διαμερίσματα με άγνωστη αγοραία αξία. Παράλληλα, το μικρό εύρος του διαστήματος εμπιστοσύνης αποδεικνύει ότι το μοντέλο είναι ιδιαιτέρως καλό και η περιοχή εμφανίζει ομοιογένεια στον τρόπο που διαμορφώνονται οι αξίες των ακινήτων της Μέθοδος του διαχωρισμού των δεδομένων (Data Splitting) Η διαδικασία εκτελείται σε δύο στάδια, όπως περιγράφεται στο κεφάλαιο , με στόχο μέσω του διαχωρισμού των 48 οντοτήτων σε δύο μέρη, στο τέλος να υπάρχει ισχυρή συσχέτιση. 1 ο ΒΗΜΑ: Επιλέγεται από το δείγμα των 48 οντοτήτων το 70% περίπου των παρατηρήσεων με τυχαία σειρά επιλογής. Το SPSS κατά την εκτέλεση της διαδικασίας επιλέγει συνολικά 33 οντότητες. Με το νέο δείγμα διαμερισμάτων εκτελείται η διαδικασία της πολλαπλής γραμμικής παλινδρόμησης και προκύπτει η παρακάτω εξίσωση παλινδρόμησης: Υ = , ,720 Χ1 677,690 Χ ,182 Χ ,698 Χ6 Μεταπτυχιακή διατριβή 151
164 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ με R = 0,948, R 2 = 0,899, R adj 2 = 0,885 και δείκτη Durbin Watson = 2,023. Επίσης όλες οι υπόλοιπες τιμές των δεικτών είναι εντός επιτρεπόμενων ορίων και κινούνται στα ίδια πλαίσια στα οποία βρίσκεται το μοντέλο των 48 οντοτήτων. Συνεπώς, πρόκειται για ένα καλό και αξιόπιστο μοντέλο. Όσον αφορά τον έλεγχο ανεξαρτησίας των οντοτήτων, το διάγραμμα Studentized Residual vs AA (Sequence) επιβεβαιώνει ότι πρόκειται για ένα μοντέλο που πληρεί όλες τις βασικές παραδοχές μιας γραμμικής παλινδρόμησης (Διάγραμμα 4.59). Διάγραμμα 4.59: Διάγραμμα σκέδασης των Studentized Residual vs AA (Sequence) για τις 33 μόνο οντότητες του δείγματος 2 ο ΒΗΜΑ: Στη συνέχεια της διαδικασίας επιλέγονται οι υπόλοιπες 15 οντότητες και με τη χρήση της εξίσωσης παλινδρόμησης που προκύπτει από το πρώτο βήμα εκτελείται η εντολή Compute Variables. Δημιουργείται μία νέα στήλη PRED για το σύνολο των 48 οντοτήτων και όχι μόνο για τις 15. Η συσχέτιση μεταξύ της παρατηρούμενης και της προβλεπόμενης τιμής PRED είναι ίση με 0,916, συνεπώς η προβλεπτική ικανότητα του μοντέλου των 48 οντοτήτων είναι πολύ ικανοποιητική. Για την επιβεβαίωση της αξιολόγησης κατασκευάζεται και το διάγραμμα σκέδασης μεταξύ των PRED και Υ, ώστε να οπτικοποιηθεί το αποτέλεσμα (Διάγραμμα 4. 60). 152
165 Κ ε φ ά λ α ι ο 4 ο Διάγραμμα 4.60: Διάγραμμα Bivariate συσχέτισης μεταξύ των προβλεπόμενων και παρατηρούμενων τιμών Είναι εμφανής ο ισχυρός βαθμός συσχέτισης των δύο τιμών και άρα η δύναμη πρόβλεψης του μοντέλου Μέθοδος εύρεσης του βέλτιστου αριθμού σημαντικών μεταβλητών Με τη βοήθεια του κριτηρίου Mallow s ελέγχεται εάν οι μεταβλητές οι οποίες επιλέγονται από τον αλγόριθμο ως στατιστικά σημαντικές είναι επαρκείς για να ερμηνεύσουν το φαινόμενο ή εάν είναι περισσότερες ή λιγότερες. Μέσω της διαδικασίας που περιγράφεται αναλυτικά στο υποκεφάλαιο παράγεται ο παρακάτω πίνακας (Πίνακας 4.22). Η διαδικασία ορίζει ότι ο αριθμός των μεταβλητών, ο οποίος ερμηνεύει ικανοποιητικά την αγοραία αξία των ακινήτων είναι έξι (6). Στην προκειμένη περίπτωση ταυτίζεται με τον αριθμό των μεταβλητών που επιλέχθηκαν και δομούν την τελική μορφή της εξίσωσης παλινδρόμησης, συνεπώς όλοι οι έλεγχοι συνηγορούν στο σχηματισμό ενός αξιόπιστου και με ικανοποιητική προβλεπτική ικανότητα μοντέλου. Μεταπτυχιακή διατριβή 153
166 dimension0 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Πίνακας4.22: Πίνακας Model Summary που περιλαμβάνει το κριτήριο πρόβλεψης Mallow Model Summary Model Selection Criteria Std. Error Akaike Amemiya Mallows' Schwarz R Adjusted of the Information Prediction Prediction Bayesian R Square R Square Estimate Criterion Criterion Criterion Criterion 1,868 a,754, , ,599,268 47, ,342 2,917 b,840, , ,903,181 17, ,516 3,928 c,862, , ,800,163 11, ,285 4,935 d,874, , ,399,155 8, ,755 5,942 e,887, , ,274,145 6, , Ερμηνεία μοντέλου για την περιοχή του Ευόσμου Το μοντέλο της δεύτερης περιοχής μελέτης σχηματίζεται ολοκληρωτικά έπειτα από την αφαίρεση 12 οντοτήτων και την απομάκρυνση τριών μεταβλητών. Αποδεικνύεται η αρχική υπόθεση ότι η αγοραία αξία των ακινήτων συνδέεται γραμμικά με μία σειρά μεταβλητών, άλλοι από τους οποίους έχουν σχέση με το κτίριο στο οποίο ανήκει η οριζόντια ιδιοκτησία και άλλοι με τα ιδιαίτερα χαρακτηριστικά του διαμερίσματος. Το βασικό χαρακτηριστικό γνώρισμα της συγκεκριμένης περιοχής είναι η ομοιομορφία που παρατηρείται στα γενικά χαρακτηριστικά των διαμερισμάτων και κατά συνέπεια στον τρόπο διαμόρφωσης των αξιών τους. Η ομοιομορφία συνδέεται ταυτόχρονα με τη γεωγραφική θέση τους, διότι κάθε διαμέρισμα δεν υπερέχει ουσιαστικά σε σύγκριση με τα υπόλοιπα. Κανένα δε διαθέτει μία ιδιαίτερα προνομιακή θέση, ώστε να δημιουργούνται εξάρσεις και ανομοιογένειες. Συμπέρασμα το οποίο προκύπτει από το δεύτερο μοντέλο είναι ότι όσο η θέση διατηρείται «σταθερά», τόσο τα υπόλοιπα χαρακτηριστικά του διαμερίσματος επιδρούν στη διαμόρφωση της αξίας του και άρα αποτυπώνονται στην εξίσωση παλινδρόμησης. Επίσης η λογική της προσέγγισης του μοντέλου με τη διαδοχική αφαίρεση οντοτήτων επίδρασης είναι ουσιαστικής σημασίας, διότι όπως αποδεικνύεται από τη στατιστική ανάλυση, οι 60 οντότητες υποδείκνυαν τρεις μεταβλητές να συνδέονται γραμμικά, ενώ στο τέλος με την αφαίρεση των δώδεκα οντοτήτων διατηρήθηκαν πέντε. Συνεπώς, η στατιστική ανάλυση είναι μία ιδιαίτερα ευαίσθητη διαδικασία, η οποία καθοδηγούμενη με το βέλτιστο τρόπο (πάντα όμως με βάσει του περιορισμούς που τίθενται από τη θεωρία) μπορεί να προσεγγίσει την πραγματικότητα. Επιπρόσθετα, όλοι οι έλεγχοι που γίνονται στο υποψήφιο τελικό μοντέλο, βάσει μεθοδολογίας, οδηγούν στην ικανοποίηση των παραδοχών. Στην προκειμένη περίπτωση όλες οι συνθήκες ικανοποιούνται άψογα, πέραν της σημαντικότητας της μεταβλητής Χ2, η οποία βρισκόταν στο όριο (βάσει θεωρίας) και της συγγραμμικότητας της Χ6, η οποία ήταν εντός ορίων αλλά αρκετά κοντά στην ανοχή. Οι δύο αυτές περιπτώσεις δε δημιουργούν 154
167 Κ ε φ ά λ α ι ο 4 ο κανένα απολύτως πρόβλημα για δύο λόγους. Ο πρώτος είναι το γεγονός ότι οι τιμές που αναφέρονται βρίσκονται πολύ κοντά στο όριο και δεν απέχουν πολύ περισσότερο, ώστε να θεωρηθεί στατιστικά απαράδεκτο και ο δεύτερος είναι το γεγονός ότι η μελέτη βασίζεται σε πραγματικά δεδομένα, τα οποία συλλέγονται διαδικτυακά και άρα κανείς δε μπορεί να περιμένει το «τέλειο» μοντέλο, διότι δεν μπορεί να υπάρξει. Η ίδια ακριβώς επιτυχία υπάρχει και στην περίπτωση διερεύνησης της προβλεπτικής δύναμης του μοντέλου, καθώς και οι τρεις τρόποι οδηγούν στο ίδιο συμπέρασμα, δηλαδή στο σχηματισμό ενός μοντέλου με σημαντική προβλεπτική ικανότητα. Το σχόλιο που μπορεί να γίνει για το μοντέλο του Ευόσμου είναι ότι στη μέθοδο των διαστημάτων πρόβλεψης του υποκεφαλαίου , το διάστημα μέσα στο οποίο πρέπει να βρίσκονται οι γνωστές αγοραίες αξίες είναι ιδιαίτερα μικρό της τάξης των Το εύρος των είναι πιθανότερο να οφείλεται στην ομοιογένεια που αναφέρθηκε παραπάνω και προφανώς είναι χαρακτηριστική στη συγκεκριμένη περιοχή μελέτης. Η τελική μορφή της παλινδρομικής εξίσωσης είναι η ακόλουθη: Υ = , ,631 Χ1-586,040 Χ ,792 Χ ,754 Χ ,241 Χ6 δηλαδή, Αγοραία Αξία ακινήτων = , ,631 * (Εμβαδόν) - 586,040 * (Παλαιότητα) ,792* (Όροφος) ,754* (Κατάσταση ακινήτων) ,241* (Είδος Θέρμανσης) με R 2 = 0,887. Λαμβάνοντας υπόψη το συντελεστή προσδιορισμού R 2, παρατηρείται μία πολύ καλή προσαρμογή του μοντέλου στα δεδομένα και άρα ένα μεγάλο τμήμα της αξίας ερμηνεύεται από τις πέντε μεταβλητές (Χ1, Χ2, Χ3, Χ7 και Χ6). Η ίδια διαπίστωση γίνεται και για τον προσαρμοσμένο συντελεστή προσδιορισμού (Adjusted R 2 ), ο οποίος σύμφωνα με τον πίνακα 4.12 είναι ίσος με 0,873. Το ποσοστό 87,3 % αντιπροσωπεύει τη συνολική διακύμανση της αγοραίας αξίας που οφείλεται στις πέντε μεταβλητές της εξίσωσης για κάθε άλλο δείγμα του πληθυσμού του Ευόσμου και επιβεβαιώνει την ισχυρή προβλεπτική δύναμη του μοντέλου. Εστιάζοντας στις ανεξάρτητες μεταβλητές ο πίνακας 4.12 εμπεριέχει τους συντελεστές προσδιορισμού R 2 κάθε μοντέλου κατά την εκτέλεση της βηματικής διαδικασίας (stepwise) δείχνοντας τη συμβολή της κάθε μίας στη διαμόρφωση των αξιών. Πιο συγκεκριμένα, η μεταβλητή που συμβάλει περισσότερο στη διαμόρφωση της αγοραίας αξίας είναι το εμβαδόν με ποσοστό 75,4%. Ακολουθεί η παλαιότητα, η οποία είναι υπεύθυνη για το 8,6% της διακύμανσης της εξαρτημένης μεταβλητής, ο όροφος με ποσοστό συνεισφοράς 2,2%, η κατάσταση του ακινήτου με ποσοστό 1,2% και τέλος το είδος θέρμανσης με ποσοστό συνεισφοράς 1,3%. Τέλος, όσον αφορά το σταθερό όρο της παλινδρομικής εξίσωσης διαδραματίζει τον ίδιο ρόλο με την περιοχή του κέντρου της Θεσσαλονίκης, δηλαδή το ρόλο της εξισορρόπησης των τιμών που διαμορφώνονται από τις μεταβλητές πολλαπλασιασμένες με το συντελεστή τους. Το πρόσημο του είναι αρνητικό και η τιμή του ίση με 55602,763. Μεταπτυχιακή διατριβή 155
168 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Συνεπώς, η αγοραία αξία ενός διαμερίσματος κάθε φορά για την περιοχή του Ευόσμου είναι περίπου κατά μικρότερη από αυτήν που διαμορφώνεται από τις ανεξάρτητες μεταβλητές του μοντέλου πολλαπλασιασμένες με τους συντελεστές τους. 4.4 ΣΥΜΠΕΡΑΣΜΑΤΑ Από την ολοκληρωμένη πλέον μελέτη των δύο περιοχών της Θεσσαλονίκης μπορούν να προκύψουν ποικίλα συμπεράσματα σχετικά με τη στατιστική ανάλυση τους και τις τελικές εξισώσεις παλινδρόμησης, επισημαίνοντας ταυτόχρονα τις ομοιότητες και τις διαφορές των δύο μοντέλων. Η ιδιαιτερότητα του κέντρου της Θεσσαλονίκης, με τις παλιές κατοικίες, την έλλειψη θέσεων στάθμευσης και τα πολλές φορές μέτρια σε βαθμό συντήρησης διαμερίσματα αντικατοπτρίζεται στην τελική εξίσωση παλινδρόμησης. Υπάρχει μία σαφώς μεγάλη γραμμική σχέση μεταξύ της αξίας και του εμβαδού των διαμερισμάτων, ακολουθεί μία εξίσου σημαντική επίδραση της ηλικίας των οικοδομών στη διαμόρφωση της ζητούμενης τιμής πώλησης, η οποία φυσικά συνοδεύεται από έναν τρίτο παράγοντα επίδρασης που είναι ο βαθμός συντήρησης και ποιότητας του εσωτερικού χώρου του διαμερίσματος. Όπως φαίνεται για τα διαμερίσματα του κέντρου, βάσει του συγκεκριμένου δείγματος, δεν λαμβάνεται ισχυρά υπόψη ο όροφος της οικοδομής, το είδος θέρμανσης, η θέση στάθμευσης, η ύπαρξη ανελκυστήρα και τέλος εάν είναι γωνιακό ή όχι. Όσον αφορά την ύπαρξη ανελκυστήρα, το 90% των διαμερισμάτων του κέντρου αυτής της περιοχής διαθέτουν ανελκυστήρα, συνεπώς η συνολική διασπορά των τιμών της αγοραίας αξίας είναι λογικό να μην επηρεάζεται από τη συγκεκριμένη μεταβλητή. Όμοια διαπίστωση γίνεται για τη μεταβλητή που αφορά τη θέση στάθμευσης (3% των διαμερισμάτων κατέχουν ιδιωτική θέση στάθμευσης), και εάν το διαμέρισμά είναι γωνιακό ή όχι (5% του δείγματος είναι γωνιακά). Οι δύο μεταβλητές που απομένουν είναι ο όροφος της οικοδομής και το είδος θέρμανσης που ενώ είναι γνωστό ότι η επίδραση τους είναι σημαντική στη διαμόρφωση της αξίας μίας οριζόντιας ιδιοκτησίας, στη συγκεκριμένη μελέτη δεν κρίνονται στατιστικά σημαντικές και δεν συσχετίζονται γραμμικά με την εξαρτημένη μεταβλητή Υ. Επίσης, η μεγάλη ανομοιογένεια στα πολεοδομικά χαρακτηριστικά του κέντρου με τους πολύ κεντρικούς δρόμους από τη μία μεριά, τα πολύ στενά δρομάκια από την άλλη ή την έλλειψη προκηπίων οδηγεί εκ νέου στο συμπέρασμα ότι είναι υπαρκτή μία τοπική ανομοιογένεια που βασίζεται στη θέση και η οποία εμποδίζει τον ομαλό σχηματισμό ενός γραμμικού μοντέλου που να επικεντρώνεται σε όλο το φάσμα των παραγόντων που έχουν να κάνουν με την ποιότητα του διαμερίσματος ως ξέχωρη οντότητα. Μία διαφορετική εικόνα παρουσιάζεται στο μοντέλο του Ευόσμου, καθώς η πιο ομαλοποιημένη κατάσταση όσον αφορά την επίδραση της θέσης, οδηγεί σε ένα μοντέλο με συνολικά πέντε ανεξάρτητες μεταβλητές. Οι αξίες των διαμερισμάτων στον Εύοσμο, όπως φαίνεται από το μοντέλο, εξαρτώνται με γραμμικό τρόπο από το εμβαδόν τους, την παλαιότητα τους, τον όροφο στον οποίο ανήκουν, το είδος θέρμανσης που διαθέτουν και τέλος τη γενικότερη κατάσταση του ακινήτου. Οι μεταβλητές που αποκλείονται από το μοντέλο είναι αρχικά η γωνιακή θέση του διαμερίσματος (33% γωνιακά διαμερίσματα) και η ύπαρξη θέσης στάθμευσης (87% διαθέτουν θέση στάθμευσης), καθώς τα ποσοστά 156
169 Κ ε φ ά λ α ι ο 4 ο εμφάνισης των παραπάνω χαρακτηριστικών στις δίτιμες μεταβλητές δεν είναι ικανά να επιδράσουν στη διαμόρφωση της διακύμανσης της αγοραίας αξίας των ακινήτων. Συμπεραίνεται ότι τα τελευταία χρόνια η πολύ γρήγορη ανοικοδόμηση της περιοχής του Ευόσμου με ένα μέσο όρο ηλικίας των οικοδομών τα 9 έτη, οδηγεί σε πολλές ομοιότητες όσον αφορά τα πολεοδομικά χαρακτηριστικά της και τις ποιότητες κατασκευής των οικοδομών με αποτέλεσμα να διαφαίνεται καθαρότερα η συμβολή των ιδιαίτερων χαρακτηριστικών των διαμερισμάτων (εμβαδόν, παλαιότητα, όροφος, θέρμανση κλπ) στη διαμόρφωση των αξιών τους. Τα δύο μοντέλα σαν γενικό συμπέρασμα χαρακτηρίζονται καλά, παρόλα αυτά ο βαθμός ικανοποίησης των υποθέσεων της κύριας μεθοδολογίας διαφέρει από μοντέλο σε μοντέλο. Χαρακτηριστική είναι η υπόθεση που αφορά τη γραμμικότητα και τη σημαντικότητα των ανεξάρτητων μεταβλητών. Οι μεταβλητές του κέντρου είναι μεν λιγότερες σε αριθμό, συνδέονται όμως ισχυρότερα με τη μεταβλητή Υ, σε σχέση με την περιοχή του Ευόσμου. Τα διαγράμματα μερικής συσχέτισης και οι αντίστοιχοι συντελεστές αντικατοπτρίζουν τη συγκεκριμένη διαπίστωση. Από την άλλη μεριά στην περιοχή του κέντρου ο συντελεστή προσδιορισμού είναι κατά 7% περίπου μικρότερος από τον αντίστοιχο του κέντρου, γεγονός που σημαίνει ότι στην περίπτωση του Ευόσμου ένα μικρότερο ποσοστό της συνολικής διακύμανσης της αγοραίας αξίας οφείλεται σε άλλους παράγοντες πέραν από αυτούς που παρουσιάζονται στην εξίσωση παλινδρόμησης, άρα το μοντέλο του Ευόσμου πλησιάζει περισσότερο την πραγματικότητα. Αυτό το γεγονός αντικατοπτρίζεται ταυτόχρονα μέσω του πολύ μικρού εύρους του διαστήματος πρόβλεψης και του αποτελέσματος που προκύπτει από τη μέθοδο διαχωρισμού των δεδομένων, τα οποία φανερώνουν ότι το μοντέλο του Ευόσμου έχει μεγαλύτερη δυνατότητα πρόβλεψης αγοραίων αξιών σε σύγκριση με το μοντέλο του κέντρου της Θεσσαλονίκης. Μεταπτυχιακή διατριβή 157
170 ΚΕΦΑΛΑΙΟ 5 Ο ΔΗΜΙΟΥΡΓΙΑ ΜΑΘΗΜΑΤΙΚΟΥ ΜΟΝΤΕΛΟΥ ΜΕΣΩ ΤΗΣ ΠΟΛΛΑΠΛΗΣ ΓΡΑΜΜΙΚΗΣ ΠΑΛΙΝΔΡΟΜΗΣΗΣ ΜΕ ΣΚΟΠΟ ΤΟΝ ΑΥΤΟΜΑΤΟΠΟΙΗΜΕΝΟ ΥΠΟΛΟΓΙΣΜΟ ΤΗΣ ΑΓΟΡΑΙΑΣ ΑΞΙΑΣ ΤΩΝ ΔΙΑΜΕΡΙΣΜΑΤΩΝ ΕΦΑΡΜΟΓΗ ΣΤΗΝ ΠΟΛΗ ΤΗΣ ΒΑΡΚΕΛΩΝΗΣ Η διαδικασία εκτέλεσης της πολλαπλής γραμμικής παλινδρόμησης πραγματοποιείται για τρεις νέες περιοχές στην πόλη της Βαρκελώνης. Σχηματίζονται συνολικά τρία νέα μοντέλα που αναφέρονται στον τρόπο που διαμορφώνονται οι αξίες των διαμερισμάτων στην κάθε μία περιοχή ξεχωριστά. Τα βήματα που ακολουθούνται είναι όμοια με εκείνα που εκτελούνται στην πόλη της Θεσσαλονίκης ακολουθώντας την ίδια κύρια μεθοδολογία, ενώ τα συμπεράσματα που προκύπτουν στο τέλος του κεφαλαίου δίνουν μία ξεκάθαρη εικόνα σχετικά με τη σχέση που συνδέει τη θέση των διαμερισμάτων σε μία πόλη με τις μεταβλητές που έχουν μεγαλύτερη βαρύτητα στη διαμόρφωση των αξιών. 5.1 ΕΦΑΡΜΟΓΗ ΠΟΛΛΑΠΛΗΣ ΓΡΑΜΜΙΚΗΣ ΠΑΛΙΝΔΡΟΜΗΣΗΣ ΓΙΑ ΤΗΝ ΠΕΡΙΟΧΗ EIXAMPLE (ΤΡΙΤΟ ΜΟΝΤΕΛΟ) Το τρίτο μοντέλο αναφέρεται σε μία ιδιαίτερα χαρακτηριστική περιοχή του κέντρου της Βαρκελώνης. Το πλούσιο φωτογραφικό υλικό των διαμερισμάτων μέσω της αναζήτησης τους διαδικτυακά οδηγεί στο συμπέρασμα ότι τα κτίρια της συγκεκριμένης περιοχής είναι ιδιαίτερα κομψά, παραδοσιακά και πολλά από αυτά χαρακτηρίζονται πολυτελή. Πρόκειται για μία εμπορική περιοχή με πολλά κτίρια τουριστικού ενδιαφέροντος και επαγγελματικούς χώρους της υψηλής κοινωνικής τάξης. Παρόλη τη μεγάλη παλαιότητα των κατοικιών (μέσος όρος ηλικίας των διαμερισμάτων του δείγματος είναι τα 49 έτη) τα χαρακτηριστικά που 158
171 Κ ε φ ά λ α ι ο 5 ο προαναφέρθηκαν διαμορφώνουν την υψηλή αξία τους. Συγκεκριμένα, ο μέσος όρος αξίας πώλησης ανά τετραγωνικό μέτρο είναι περίπου 3.500,00 με μέγιστη τιμή τα ,00 /τμ και ελάχιστη τα 1000,00 /τμ. Τα μεγέθη αυτά αντικατοπτρίζουν μία μεγάλη ανομοιογένεια στο δείγμα, η οποία όμως είναι χαρακτηριστική για το ιστορικό κέντρο πόλεων όπως της Θεσσαλονίκης και της Βαρκελώνης. Στο τρίτο μοντέλο που αναφέρεται στην περιοχή Eixample εφαρμόζεται μία διαφοροποίηση σε σύγκριση με τις υπόλοιπες περιοχές. Πιο συγκεκριμένα, κρίνεται απαραίτητη η διαφορετική ποσοτικοποίηση της μεταβλητής «Κατάσταση ακινήτου» έτσι ώστε να εξομαλυνθεί η ιδιότητα ορισμένων διαμερισμάτων που είτε λόγω θέσης (υπέροχη θέα, θέα σε ιστορικό τουριστικό κτίσμα κλπ) είτε λόγω υπερπολυτελούς κατάστασης και ποιότητας έχουν εξαιρετικά μεγάλη αξία ανά τμ. Γι αυτό το σκοπό τα διαμερίσματα με τα παραπάνω χαρακτηριστικά αντί για την τιμή τέσσερα (4) δέχονται την τιμή πέντε (5). Η αλλαγή προέκυψε έπειτα από δοκιμές και προσπάθειες έτσι ώστε η μεθοδολογία και οι ποσοτικοποιήσεις που προηγούνται της εκτέλεσης να προσαρμοστούν στις τόσο διαφορετικές ανάγκες της περιοχής Eixample και φυσικά να οδηγήσουν σε ένα μοντέλο που να ανταποκρίνεται στην πραγματικότητα Διερεύνηση γραμμικής σχέσης μεταξύ της εξαρτημένης μεταβλητής Υ και των ανεξάρτητων Χ i Το δείγμα της πρώτης περιοχής μελέτης από την πόλη της Βαρκελώνης αποτελείται από 75 περιπτώσεις, στις οποίες αναφέρονται εννέα συνολικά μεταβλητές. Το αρχικό βήμα της διαδικασίας περιλαμβάνει την εισαγωγή των δεδομένων στο στατιστικό πακέτο SPSS και την αναζήτηση της σχέσης που συνδέει την εξαρτημένη μεταβλητή με τις ανεξάρτητες. Η διερεύνηση πραγματοποιείται με τη βοήθεια των διαγραμμάτων διασποράς της εξαρτημένης με όλες τις ανεξάρτητες μεταβλητές και με τη βοήθεια των συντελεστών μερικής συσχέτισης. Η ανάγνωση των διαγραμμάτων και η εκτίμηση της συσχέτισης στηρίζεται σε ορισμένα βασικά κριτήρια, αλλά δίνεται πάντα ένα μεγαλύτερο περιθώριο για πιθανή μεταβολή των σχέσεων εξαιτίας της απομάκρυνσης των ακραίων παρατηρήσεων Γραφήματα συσχέτισης των Χ i με την Υ Σύμφωνα με το διάγραμμα 5.1 η εντονότερη γραμμική συσχέτιση εντοπίζεται μεταξύ της εξαρτημένης μεταβλητής Υ και του εμβαδού (AREA). Ακολουθούν οι μεταβλητές AGE, FLOOR, HEATING, QUALITY, ROOMS και BATH. Αντίθετα, γραμμικότητα δεν παρουσιάζεται μεταξύ της Υ και των ELEV και PARKING. Οι σχέσεις που παρουσιάζονται μέσω του διαγράμματος φαίνεται ότι σε καμία περίπτωση δεν είναι ιδιαίτερα ισχυρές, παρόλα αυτά δε μπορεί να απορριφθεί καμία μεταβλητή πέραν των δύο που αναφέρθηκαν. Συνεπώς, με κριτήριο τα διαγράμματα σκέδασης στο μοντέλο συμμετέχουν οι επτά από τις εννέα μεταβλητές. Σε κάθε ένα τετραγωνίδιο της πρώτης σειράς παρατηρείται μία οντότητα (πάνω δεξιά) η οποία ξεχωρίζει σε σχέση με όλες τις υπόλοιπες. Η πιθανή απομάκρυνση της στη συνέχεια της διαδικασίας είναι πιθανό να αλλάξει την κατάσταση που παρατηρείται στα διαγράμματα και να ανατραπεί η πρώτη εικόνα των συσχετίσεων. Άλλωστε είναι ίσως και Μεταπτυχιακή διατριβή 159
172 Σχηματισμός μοντέλου αναμενόμενο να υπάρξουν αλλαγές σε ένα δείγμα με τόσο μεγάλη ανομοιογένεια στα διαμερίσματα του. Διάγραμμα 5.1: Γράφημα Matrix Scatter Plot για δείγμα 75 ακινήτων και για τις εννέα ανεξάρτητες μεταβλητές Συντελεστές μερικής συσχέτισης Η σχέση της κάθε μεταβλητής με την εξαρτημένη απαλλαγμένη όμως από τη σχέση που τη συνδέει με τις υπόλοιπες μεταβλητές φαίνεται στον παρακάτω πίνακα μέσω των συντελεστών μερικής συσχέτισης. Γενικά παρατηρούνται συσχετίσεις πολύ μικρού βαθμού, με μικρότερη τη σχέση που συνδέει την αξία με τη θέρμανση των διαμερισμάτων. Η συσχέτιση της τάξης του 2,6 % με επίπεδο στατιστικής σημαντικότητας α = 0,833 αποδεικνύει ότι η θέρμανση έχει ελάχιστη επίδραση στην τελική διαμόρφωση των αξιών και δεν χαρακτηρίζεται στατιστικώς σημαντική μεταβλητή. Είναι αναμενόμενο ότι για να μπορέσει να αποτελέσει μοντέλο πρόβλεψης αξιών η περιοχή του κέντρου της Βαρκελώνης (Eixample), απαιτείται πιθανόν η απομάκρυνση ακραίων οντοτήτων, έτσι ώστε να αυξηθεί ο βαθμός συσχέτισης των μεταβλητών με την εξαρτημένη μεταβλητή. 160
173 Κ ε φ ά λ α ι ο 5 ο Πίνακας 5.1: Πίνακας με τις μερικές συσχετίσεις της εξαρτημένης μεταβλητής με κάθε μία ανεξάρτητη στο δείγμα των 75 οντοτήτων Μεταβλητές Συσχέτιση Επίπεδα στατιστικής σημαντικότητας AREA -Y 0,527 0,000 AGE - Y -0,115 0,355 FLOOR - Y 0,229 0,063 ELEV - Y 0,147 0,234 HEATING - Y 0,026 0,833 QUALITY - Y 0,296 0,015 PARKING - Y 0,115 0,356 ROOMS - Y 0,139 0,263 BATH - Y 0,194 0,116 Τα διαγράμματα συσχέτισης όπως αναφέρεται και παραπάνω υποδεικνύουν την απομάκρυνση του ασανσέρ (ELEV) και της θέσης στάθμευσης (PARKING), ενώ ο πίνακας των μερικών συσχετίσεων, ο οποίος είναι πιο αυστηρός, υποδεικνύει την απομάκρυνση της θέρμανσης (HEATING). Συνεπώς, σύμφωνα με το πρώτο βήμα διερεύνησης της γραμμικότητας προκύπτει το συμπέρασμα ότι στο μοντέλο υπάρχει λόγος να συμμετέχουν έξι από τις εννέα μεταβλητές,του εμβαδού(area), της ηλικίας (AGE), του ορόφου (FLOOR), της κατάστασης του ακινήτου (QUALITY), του αριθμού των δωματίων (ROOMS)και των μπάνιων (BATH) Εφαρμογή της πολλαπλής γραμμικής παλινδρόμησης και δημιουργία τελικού μοντέλου Με τις έξι πλέον μεταβλητές, το δείγμα των 75 οντοτήτων και τη βηματική μέθοδο (Stepwise Method) εκτελείται η γραμμική πολλαπλή παλινδρόμηση μέσω του Μενού Analyze Regression Linear. Τα αποτελέσματα της πρώτης εκτέλεσης αποτελούν τη βάση για τη λήψη αποφάσεων σχετικά με τη βελτιστοποίηση του μοντέλου μέχρι ένα κατ εκτίμηση βέλτιστο μοντέλο. Η πρώτη εξίσωση παλινδρόμησης είναι η ακόλουθη: με R 2 = 0,603 Υ = , ,885 AREA ,846 QUALITY ,972 FLOOR Η εξίσωση οδηγεί στο συμπέρασμα ότι οι τιμές των διαμερισμάτων της περιοχής Eixample εξαρτώνται σε ένα ποσοστό 60% από το εμβαδόν τους, το βαθμό συντήρησης τους και από τον όροφο που βρίσκονται. Ο μη υψηλός συντελεστής προσδιορισμού φανερώσει μία όχι καλή προσαρμογή των δεδομένων του δείγματος και αφήνει αρκετά περιθώρια βελτίωσης για το μοντέλο. Μία πάρα πολύ καλή εικόνα της ποιότητας του μπορεί να φανεί από τα δύο διαγράμματα που ακολουθούν και φανερώνουν ύπαρξη ακραίων οντοτήτων. Μεταπτυχιακή διατριβή 161
174 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα 5.2: (Αριστερά) Διάγραμμα σκέδασης των Studentized Deleted Residual με τα Standardized Predicted Values. (Δεξιά) Ιστόγραμμα συχνοτήτων των τυποποιημένων υπολοίπων Από το πρώτο διάγραμμα αριστερά φαίνεται ότι όλα τα σημεία κατανέμονται εντός μίας σταθερής ζώνης γύρω από το μηδέν (±2), εκτός από την οντότητα 10, η οποία απέχει κατά πολύ από τα όρια ανοχής. Παράλληλα, ύπαρξη ακραίων οντοτήτων φανερώνει και το δεύτερο διάγραμμα κανονικής κατανομής των υπολοίπων. Συνεπώς, η πρώτη οντότητα που απομακρύνεται για τη δημιουργία ενός πιο αξιόπιστου μοντέλου είναι η οντότητα με Α/Α 10. Με όμοιο τρόπο λαμβάνουν χώρα διαδοχικές αφαιρέσεις οντοτήτων με στόχο τη βελτίωση προσαρμογής των δεδομένων του δείγματος, και την ικανοποίηση όλων των παραδοχών του γραμμικού μοντέλου. Οι διαδοχικές παλινδρομήσεις που εκτελούνται αποτυπώνονται στον ακόλουθο πίνακα: Παλινδρ. Ανάλυση Οντότητα R R 2 1η (Ν = 75) - 0,777 0,603 2η 10 0,866 0,750 3η 59 0,886 0,785 4η 46 0,895 0,802 5η 26 0,906 0,821 6η 51, 13 0,912 0,831 7η 24 0,921 0,849 8η 14 0,930 0,865 9η 22 0,932 0,868 10η 43 0,930 0,865 11η 5 0,933 0,870 12η (Ν = 63) 74 0,936 0,
175 Κ ε φ ά λ α ι ο 5 ο Παρατηρείται ότι η διαδοχική αφαίρεση οντοτήτων οδηγεί σε αύξηση του συντελεστή προσδιορισμού R 2. Συνεπώς, θεωρείται ικανοποιητική η διαδικασία βελτιστοποίησης του μοντέλου. Έπειτα από την απομάκρυνση των οντοτήτων η τελική μορφή της παλινδρομικής εξίσωσης είναι: Υ = , ,834 AREA ,950 QUALITY ,568 BATH με R 2 = 0,876 Το νέο δείγμα των 63 οντοτήτων έχει μία σαφώς καλύτερη προσαρμογή των δεδομένων του δείγματος, εφόσον ο συντελεστής προσδιορισμού έχει αυξηθεί σημαντικά και παρουσιάζει ως στατιστικά σημαντικές άλλες μεταβλητές από εκείνες που το αρχικό μοντέλο παρουσίασε. Οι μεταβλητές που φαίνεται ότι συνδέονται γραμμικά με την αγοραία αξία των ακινήτων βάσει της παλινδρομικής εξίσωσης είναι το εμβαδόν, η κατάσταση του ακινήτου και τέλος ο αριθμός των μπάνιων. Σημαντικό είναι να αναφερθεί ότι έπειτα από την αφαίρεση της πρώτης οντότητας με Α/Α 10 μέχρι και την αφαίρεση του δωδέκατου σημείου, οι μεταβλητές που θεωρούνται από το δείγμα ως στατιστικώς σημαντικές είναι οι τρεις που τελικά συγκροτούν την παλινδρομική εξίσωση. Το συγκεκριμένο γεγονός μπορεί να συμπεράνει κανείς ότι δίνει την αίσθηση μίας σταθερότητας και άρα ενός πιθανώς αξιόπιστου μοντέλου παλινδρόμησης. Η αποδεδειγμένη όμως αξιοπιστία του μοντέλου φαίνεται από τον έλεγχο των παραδοχών που έχουν ήδη αναλυθεί και των ελέγχων προβλεπτικής δύναμης του μοντέλου, οι οποίοι περιγράφονται στα επόμενα κεφάλαια αναλυτικά Έλεγχος ικανοποίησης παραδοχών του γραμμικού μοντέλου Με τη βοήθεια διαγραμμάτων και πινάκων ακολουθούν επτά έλεγχοι, οι οποίοι αναφέρονται στις βασικές παραδοχές που πρέπει να ισχύουν στις περιπτώσεις των γραμμικών μοντέλων. Για τη διατήρηση του μοντέλου που αποτελεί έπειτα από διαδικασίες τη βέλτιστη λύση θα πρέπει να ικανοποιούνται όλες οι παραδοχές και μάλιστα όσο είναι εφικτό όχι με οριακό τρόπο Σημαντικότητα ανεξάρτητων μεταβλητών Ο πρώτος έλεγχος αφορά τη σημαντικότητα των ανεξάρτητων μεταβλητών και υλοποιείται με δύο διαφορετικούς τρόπους. Μέσω των διαγραμμάτων μερικής συσχέτισης και μέσω των t τιμών από τον πίνακα των συντελεστών (Coefficient Table). Μεταπτυχιακή διατριβή 163
176 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διαγράμματα μερικής συσχέτισης Τα τρία διαγράμματα μερικής παλινδρόμησης που ακολουθούν φανερώνουν τη γραμμική σχέση των ανεξάρτητων μεταβλητών (AREA, QUALITY, BATH) με την εξαρτημένη Υ, απαλλαγμένη όμως από τις μεταξύ τους συσχετίσεις. Παράλληλα, όσο πιο ισχυρά γραμμική είναι η σχέση, τόσο πιο σημαντική είναι η ανεξάρτητη μεταβλητή για το μοντέλο. Τα διαγράμματα 5.3, 5.4, 5.5 δείχνουν ισχυρές, ξεκάθαρες γραμμικές σχέσεις με εντονότερη τη συσχέτιση μεταξύ της αγοραίας αξίας των ακινήτων με το εμβαδόν τους. Λιγότερο έντονη αλλά εξίσου ισχυρή είναι η σχέση με την κατάσταση του ακινήτου και στη συνέχεια με τον αριθμό των μπάνιων. Το εύρος ζώνης, μέσα στο οποίο είναι τοποθετημένες οι κουκίδες, ορίζεται στο 95% από το λογισμικό και τοποθετείται για να είναι περισσότερο ορατές και ξεκάθαρες οι οντότητες που ξεφεύγουν. Όπως φαίνεται από τα διαγράμματα καμία τιμή δεν βρίσκεται εκτός της ζώνης, ενώ οι πιο απομακρυσμένες είναι οριακά εντός της. Σύμφωνα με τον πρώτο τρόπο ελέγχου οι τρείς ανεξάρτητες μεταβλητές χαρακτηρίζονται στατιστικά σημαντικές. Διάγραμμα 5.3: Διάγραμμα μερικής παλινδρόμησης μεταξύ της αξίας και του εμβαδού 164
177 Κ ε φ ά λ α ι ο 5 ο Διάγραμμα 5.4: Διάγραμμα μερικής παλινδρόμησης μεταξύ της αξίας και της κατάστασης του ακινήτου Διάγραμμα 5.5: Διάγραμμα μερικής παλινδρόμησης μεταξύ της αξίας και του αριθμού των μπάνιων Μεταπτυχιακή διατριβή 165
178 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ t τιμές Ο δεύτερος τρόπος ελέγχου γίνεται με τη βοήθεια των τιμών t του παρακάτω πίνακα. Όσο μεγαλύτερη είναι η τιμή των t τιμών από το ±2, τόσο μεγαλύτερη είναι η σημαντικότητα της συγκεκριμένης μεταβλητής. Πίνακας 5.2: Πίνακας Coefficients που περιλαμβάνει τις τιμές t των ανεξάρτητων μεταβλητών Coefficients a Model Unstandardized Standardized 95,0% Confidence Interval Collinearity Coefficients Coefficients for B Correlations Statistics Upper Zero- Part B Std. Error Beta t Sig. Lower Bound Bound order ial Part Tolerance VIF 3 (Constant) , ,391-4,985, , ,523 AREA 2469, ,826,586 9,966, , ,733,861,792,457,607 1,646 QUALITY 26702, ,551,298 5,865, , ,583,627,607,269,816 1,225 BATH 49806, ,066,261 4,568, , ,552,706,511,209,644 1,552 Στην προκειμένη περίπτωση οι μεταβλητές AREA, QUALITY και BATH αντιστοιχίζονται στις τιμές 9,97, 5,87 και 4,57 αντίστοιχα, οι οποίες είναι αρκετά μεγαλύτερες της οριακή τιμής και άρα όλες χαρακτηρίζονται στατιστικά σημαντικές. Ο βαθμός σημαντικότητας τους για το μοντέλο μεγαλώνει όσο μεγαλύτερες είναι οι τιμές, άρα η σημαντικότητα τους είναι φθίνουσα από την πρώτη (AREA) προς την τελευταία (ΒΑΤΗ). Συμπερασματικά, η παραδοχή της σημαντικότητας των ανεξάρτητων μεταβλητών ικανοποιείται σε πολύ καλό επίπεδο Ανεξαρτησία οντοτήτων Η ανεξαρτησία των οντοτήτων εξασφαλίζεται με δύο τρόπους στην παρούσα εφαρμογή. Ο πρώτος αφορά το δείκτη Durbin Watson και ο δεύτερος αφορά την οπτική ερμηνεία του διαγράμματος σκέδασης των Studentized Residuals με τη σειρά εισαγωγής των δεδομένων στο μοντέλο Α/Α. Με την ικανοποίηση μόνο και των δύο μπορεί να γίνει δεκτή η παραδοχή της ανεξαρτησίας. Δείκτης Durbin Watson Η θεωρία αναφέρει ότι ο δείκτης Durbin Watson οφείλει να κυμαίνεται μεταξύ των τιμών 1,5 και 2,5 ώστε να θεωρούνται οι οντότητες που συμμετέχουν στο μοντέλο στατιστικά ανεξάρτητες. Σύμφωνα με τα στοιχεία του πίνακα ο δείκτης λαμβάνει την τιμή 2,382, η οποία είναι μικρότερη της τιμής 2,5 και άρα υπάρχει σαφής ανεξαρτησία των οντοτήτων. 166
179 Κεφάλαιο 5ο Πίνακας 5.3: Πίνακας Model Summary, ο οποίος περιέχει την τιμή του στατιστικού δείκτη Durbin Watson d Model Summary Model Change Statistics R Std. Error R R R of the Square F Square Square Estimate Change Change df1 df2 Sig. F Durbin- Change Watson 1,861 a 2,912 b,832, ,814,091 32, ,000 c,876, ,252,044 20, ,000 3 Adjusted,936,742, ,220, , ,000 2,382 Διάγραμμα σκέδασης Studentized residuals vs Sequence Στο διάγραμμα 5.6 δε διαφαίνεται κανένα πρότυπο ή συσσώρευση. Αντίθετα οι τιμές των Studentized Residuals είναι τυχαία κατανεμημένες με ομοιόμορφο τρόπο εντός μιας ζώνης με συγκεκριμένο πλάτος. Παρατηρούνται δύο μόνο οντότητες να βρίσκονται εκτός των τιμών ± 2, οι οποίες όμως ανήκουν στο 5% των παρατηρήσεων που επιτρέπεται να βρίσκονται εκτός της ζώνης (5% *63 και άρα δεν υπάρχει καμία πιθανή ένδειξη συσχέτισης των παρατηρήσεων. Διάγραμμα 5.6: Διάγραμμα σκέδασης των Studentized Residuals με τα A/A για την περιοχή Eixample της Βαρκελώνης Μεταπτυχιακή διατριβή 167
180 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Κρίνοντας από τους δύο ελέγχους οι οντότητες θεωρούνται ασυσχέτιστες και ικανοποιείται με επιτυχία η παραδοχή της ανεξαρτησίας Πολυσυγγραμικότητα ή Συγγραμικότητα Πρόβλημα πολυσυγγραμμικότητας εμφανίζεται σε ένα γραμμικό μοντέλο, όταν οι ανεξάρτητες μεταβλητές είναι γραμμικά εξαρτημένες μεταξύ τους. Η ύπαρξη πολυσυγγραμμικότητας οδηγεί σε πρόβλημα αξιοπιστίας των συντελεστών της γραμμικής εξίσωσης, συνεπώς όπως γίνεται κατανοητό είναι ένας ιδιαίτερα σημαντικός έλεγχος. Για την παραδοχή της απουσίας πολυσυγγραμικότητας αξιοποιούνται τέσσερις διαφορετικοί στατιστικοί δείκτες. Ο παράγοντας ανοχής, πληθωριστικής διακύμανσης, οι ιδιοτιμές και οι δεσμευμένοι δείκτες. Παράγοντας ανοχής (Tolerance factor) & Παράγοντας πληθωριστικής διακύμανασης (Variance inflation factor) Ο πρώτος στατιστικός δείκτης ονομάζεται Tolerance Factor και όταν οι τιμές του κυμαίνονται μεταξύ του 0,5 και της μονάδας, δεν υπάρχει κανένα πρόβλημα πολυσυγγραμικότητας στο μοντέλο. Η τιμή του δείκτη Tolerance για την μεταβλητή AREA είναι ίση με 0,607, για τη μεταβλητή QUALITY 0,816 και για τη μεταβλητή BATH είναι ίση με 0,644. Όπως προκύπτει από τη σύγκριση των τιμών με τις ανοχές του δείκτη, καμία μεταβλητή δεν αποτελεί γραμμικό συνδυασμό άλλων ανεξάρτητων μεταβλητών. Πίνακας 5.4: Πίνακας Coefficients ο οποίος περιλαμβάνει τις τιμές VIF και Tolerance Coefficients a Model Unstandardized Standardized 95,0% Confidence Interval Collinearity Coefficients Coefficients for B Correlations Statistics Upper Zero- Part B Std. Error Beta t Sig. Lower Bound Bound order ial Part Tolerance VIF 3 (Constant) , ,391-4,985, , ,523 AREA 2469, ,826,586 9,966, , ,733,861,792,457,607 1,646 QUALITY 26702, ,551,298 5,865, , ,583,627,607,269,816 1,225 BATH 49806, ,066,261 4,568, , ,552,706,511,209,644 1,552 Ο δεύτερος στατιστικός δείκτης ονομάζεται παράγοντας πληθωριστικής διακύμανσης (VIF) και δεν φανερώνει πρόβλημα πολυσυγγραμικότητας όταν οι τιμές που δέχεται είναι μικρότερες της οριακής τιμής δύο. Στην προκειμένη περίπτωση η τιμή του 168
181 Κ ε φ ά λ α ι ο 5 ο δείκτη VIF για την μεταβλητή AREA είναι ίση με 1,646, για τη μεταβλητή QUALITY 1,225 και για τη μεταβλητή BATH είναι ίση με 1,552. Συνεπώς και ο δεύτερος στατιστικός δείκτης ελέγχου δεν παρουσιάζει πρόβλημα πολυσυγγραμικότητας. Έλεγχος ιδιοτιμών (Eigenvalues) & Δεσμευμένοι δείκτες (Condition indexes) Ο δείκτης Eigenvalue φανερώνει πρόβλημα διασυσχέτισης όταν οι τιμές του βρίσκονται πολύ κοντά στην τιμή μηδέν. Από την άλλη μεριά, οι δεσμευμένοι δείκτες (Condition indexes) εμφανίζουν πιθανό πρόβλημα όταν οι τιμές τους ξεπερνούν την τιμή δεκαπέντε. Σύμφωνα με τον Πίνακα 5.5 και οι δύο δείκτες βρίσκονται εντός των ορίων ανοχής. Πιο συγκεκριμένα, οι τιμές του δείκτη Eigenvalue δεν προσεγγίζουν την τιμή μηδέν, ενώ η μέγιστη τιμή δεσμευμένου δείκτη είναι ίση με 10,542, δηλαδή μικρότερη της οριακής τιμής 15. Συνεπώς, τέσσερις διαφορετικοί στατιστικοί δείκτες καταλήγουν σε ένα κοινό συμπέρασμα, ότι δηλαδή δεν υφίσταται κανένα πρόβλημα πολυσυγγραμικότητας. Πίνακας 5.5: Πίνακας Colllinearity Diagnostics που περιλαμβάνει τις τιμές Eigenvalue και Condition Index Collinearity Diagnostics a Model Dimension Variance Proportions Eigenvalue Condition Index (Constant) AREA QUALITY BATH 3 1 3,793 1,000,00,00,01,01 2,107 5,965,03,02,94,14 3,066 7,572,56,01,04,58 4,034 10,542,41,97,02, Κανονικότητα Η παραδοχή της κανονικότητας των υπολοίπων είναι ένας πολύ σημαντικός έλεγχος, ο οποίος για την εξακρίβωση του απαιτεί οκτώ διαφορετικούς τρόπους εξέτασης. Η κατασκευή των πέντε από τα επτά διαγράμματα και του ενός πίνακα πραγματοποιείται μέσω της διαδικασίας Explore του στατιστικού εργαλείου SPSS, τα δύο διαγράμματα που υπολείπονται παράγονται από την αρχή, διότι είναι προϊόντα της παλινδρομικής ανάλυσης. Μεταπτυχιακή διατριβή 169
182 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Φυλλογράφημα των υπολοίπων [Stem And- Leaf- Plot of residuals Studentized deleted residuals] Σύμφωνα με το φυλλογράφημα που φαίνεται παρακάτω (Διάγραμμα 5.7) ισχύει η παραδοχή της κανονικότητας, διότι δεν παρατηρούνται ακραίες τιμές και ταυτόχρονα σχηματίζεται η γνωστή καμπανοειδής μορφή της κανονικής κατανομής, στραμμένη κατά 90 ο. Studentized Deleted Residual Stem-and-Leaf Plot Frequency Stem & Leaf 2, , , , , , Stem width: 1,00000 Each leaf: 1 case(s) Διάγραμμα 5.7: Φυλλογράφημα των υπολοίπων για την περιοχή Eixample της Βαρκελώνης Test of normality : Kolmogorv Smirnov, Lillefors, Shapiro Wilk Από τα δύο στατιστικά κριτήρια του πίνακα 5.6 αξιοποιείται το κριτήριο Kolmogorov Smirnov διότι το δείγμα των 63 οντοτήτων χαρακτηρίζεται μεγάλο (n>30). Ο έλεγχος της υπόθεσης της κανονικότητας των υπολοίπων σύμφωνα με το στατιστικό κριτήριο Kolmogorov Smirnov: Μηδενική Υπόθεση Ho: Τα υπόλοιπα κατανέμονται κανονικά και Εναλλακτική Υπόθεση H1: Τα υπόλοιπα δεν κατανέμονται κανονικά. Το τεστ για την κανονικότητα των Kolmogorov Smirnov δίνει επίπεδο στατιστικής σημαντικότητας (Sig.) 20%, δηλαδή μεγαλύτερο του 5%. Συνεπώς, δεν μπορεί να απορριφθεί η υπόθεση ότι τα Studentized Deleted Residuals ακολουθούν την κανονική κατανομή. Πίνακας 5.6: Πίνακας Tests of Normality Kolmogorv Smirnov, Lillefors, Shapiro Wilk Tests of Normality Kolmogorov-Smirnov a Shapiro-Wilk Statistic df Sig. Statistic df Sig. Studentized Deleted Residual,050 63,200 *,991 63,
183 Κ ε φ ά λ α ι ο 5 ο Normal Q-Q Plot of Studentized deleted Residuals Διάγραμμα 5.8: Διάγραμμα κανονικότητας Normal Q-Q Plot of Studentized deleted Residuals για τον έλεγχο της κανονικότητας των υπολοίπων Στο παραπάνω διάγραμμα η γραμμή που αποτελεί και τη διχοτόμο των αξόνων ορίζει την πλήρη κανονικότητα. Όσο μεγαλύτερη είναι η προσέγγιση της συγκεκριμένης γραμμής σημαίνει ότι τα Studentized Residuals ακολουθούν την κανονική κατανομή. Στην προκειμένη περίπτωση σχεδόν όλες οι κουκίδες είναι τοποθετημένες πάνω στη γραμμή της κανονικής κατανομής. Συνεπώς, δεν υπάρχει καμία αμφιβολία ότι το μοντέλο των 63 οντοτήτων της περιοχής Eixample της Βαρκελώνης ακολουθεί την κανονική κατανομή. Detrended normal Q-Q Plot Studentized Deleted residuals Το διάγραμμα 5.9 παρουσιάζει όλα τα σημεία κατανεμημένα τυχαία πάνω και κάτω από τη γραμμή του μηδέν. Δεν υπάρχουν συσσωρεύσεις, πρότυπα και όλα τα σημεία βρίσκονται εντός μίας μικρής απόστασης από τη μηδενική τιμή (μέγιστη απόσταση στον άξονα Υ η τιμή 0,2). Συνεπώς, σύμφωνα με το διάγραμμα 5.9 ικανοποιείται η παραδοχή της κανονικότητας. Μεταπτυχιακή διατριβή 171
184 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα 5.9: Διάγραμμα Detrended Νormal Q-Q Plot Studentized Deleted Ρesiduals για τον έλεγχο της κανονικότητας των υπολοίπων Histogram Studentized Deleted Residuals Στο παρακάτω ιστόγραμμα των συχνοτήτων με τα Studentized Deleted Residuals είναι σαφές ότι ακολουθείται η κανονική κατανομή των υπολοίπων και άρα ικανοποιείται η παραδοχή της κανονικότητας. 172
185 Κ ε φ ά λ α ι ο 5 ο Διάγραμμα 5.10: Ιστόγραμμα των Studentized Deleted Residuals για τον έλεγχο της κανονικότητας των υπολοίπων Histogram Standardized Residuals Διάγραμμα 5.11: Ιστόγραμμα των Standardized Residuals για τον έλεγχο της κανονικότητας των υπολοίπων Το παραπάνω ιστόγραμμα (Διάγραμμα 5.11)κατασκευάζεται κατά τη διαδικασία εκτέλεσης της πολλαπλής γραμμικής παλινδρόμησης και όπως φαίνεται από την καμπύλη της κανονικής κατανομής η κανονικότητα είναι ξεκάθαρη και προσεγγίζεται σε πάρα πολύ μεγάλο βαθμό. Διάγραμμα Normal P-P Plot of regression standardized residuals Το παρακάτω γράφημα αναμενόμενης παρατηρούμενης αθροιστικής πιθανότητας παράγεται κατά τη διαδικασία εκτέλεσης της πολλαπλής γραμμικής παλινδρόμησης και παρουσιάζει όλα τα σημεία των οντοτήτων, με ελάχιστες αποκλίσεις, να βρίσκονται επάνω στην ευθεία γραμμή. Το άμεσο συμπέρασμα είναι ότι η παραδοχή της κανονικότητας ικανοποιείται σε μεγάλο βαθμό. Μεταπτυχιακή διατριβή 173
186 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα 5.12: Διάγραμμα Normal P-P Plot of regression Standardized Residuals για τον έλεγχο της κανονικότητας των υπολοίπων Θηκόγραμμα των υπολοίπων (Boxplot of Residuals) Στο τελευταίο διάγραμμα το οποίο ονομάζεται θηκόγραμμα των υπολοίπων δεν εντοπίζεται καμία ακραία τιμή. Η διάμεσος του θηκογράμματος που αναφέρεται στο παλινδρομικό μοντέλο βρίσκεται στο κέντρο του ορθογωνίου, άρα πρόκειται για μία συμμετρική κατανομή που αποτελεί στοιχείο κανονικότητας. 174
187 Κ ε φ ά λ α ι ο 5 ο Διάγραμμα 5.13: Θηκόγραμμα για τον εντοπισμό των ακραίων τιμών του δείγματος μέσω της διαδικασίας Explore Εν κατακλείδι, όλοι οι έλεγχοι που προηγούνται φανερώνουν ότι τα υπόλοιπα ακολουθούν την κανονική κατανομή και άρα ικανοποιείται επιτυχώς η παραδοχή της κανονικότητας στο τρίτο σε σειρά μοντέλο της παρούσας διατριβής Ισότητα διακυμάνσεων ή ομοσκεδαστικότητα Η ύπαρξη ομοσκεδασιμότητας ελέγχεται μέσω οπτικής ερμηνείας με τη βοήθεια τριών διαγραμμάτων. Τα δύο πρώτα είναι της ίδια κατηγορίας διαγράμματα διασποράς, όπου στο ένα εμφανίζεται η σχέση μεταξύ των Studentized Deleted Residuals με τις τυποποιημένες προβλεπόμενες τιμές, ενώ στο δεύτερο η σχέση μεταξύ των Studentized Residuals με τις τυποποιημένες προβλεπόμενες τιμές. Ένδειξη ετεροσκεδασιμότητας αποτελεί η εμφάνιση προτύπων και τάσεων στο διάγραμμα διασποράς. Το τρίτο διάγραμμα ελέγχου απεικονίζει τη διασπορά των τυποποιημένων εκτιμώμενων τιμών έναντι των παρατηρούμενων και η παραδοχή ικανοποιείται όταν τα σημεία συγκεντρώνονται με ομοιόμορφο τρόπο πάνω και κάτω από την ευθεία των ελαχίστων τετραγώνων. Η διασπορά των 63 κουκίδων στα διαγράμματα 5.14 είναι ξεκάθαρο ότι είναι τυχαία, διότι τα σημεία δεν παρουσιάζουν κανενός είδους συσσώρευση και τάση. Επίσης, είναι σχεδόν όλα τοποθετημένα εντός μίας ζώνης που σχηματίζεται με εύρος ± 2 πάνω και κάτω από το μηδέν. Συνεπώς, δεν υφίσταται κανένα πρόβλημα ομοσκεδασιμότητας. Διάγραμμα 5.14: Διάγραμμα σκέδασης των Studentized Deleted Residuals με τα Standardized Predicted Values (αριστερά) και διάγραμμα σκέδασης των Studentized Residuals με τα Standardized Predicted Values (δεξιά) Μεταπτυχιακή διατριβή 175
188 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα 5.15: Διάγραμμα σκέδασης των Standardized Predicted Values με τις τιμές της εξαρτημένης μεταβλητής Υ Το τρίτο διάγραμμα (Διάγραμμα 5.15) ανταποκρίνεται εξίσου ικανοποιητικά στην παραδοχή της ομοσκεδασιμότητας, εφόσον όλα τα σημεία είναι με ομοιόμορφο τρόπο κατανεμημένα κατά μήκος της ευθείας των ελαχίστων τετραγώνων και σε πολύ μικρή απόσταση από αυτήν, χωρίς αποκλίσεις Γραμμικότητα Η ύπαρξη γραμμικότητας σε ένα μοντέλο πολλαπλής γραμμικής παλινδρόμησης είναι απαραίτητη προϋπόθεση και γι αυτό ο έλεγχος της δεν ικανοποιείται μόνο με ένα τρόπο, αλλά με τέσσερις διαφορετικούς. Ύπαρξη ή όχι γραμμικότητας μεταξύ της εξαρτημένης και των ανεξάρτητων μεταβλητών φανερώνουν τα διαγράμματα σκέδασης τους. Ακολουθεί το διάγραμμα Matrix Scatter Plot το οποίο απεικονίζει όλα τα διαγράμματα διασποράς της εξαρτημένης με τις ανεξάρτητες μεταβλητές στο τελικό δείγμα των 63 οντοτήτων. Σύμφωνα με το διάγραμμα οι σχέσεις παρουσιάζουν γραμμικότητα και άρα ο πρώτος τρόπος ελέγχου συνηγορεί στην ικανοποίηση της παραδοχής της γραμμικότητας. 176
189 Κ ε φ ά λ α ι ο 5 ο Διάγραμμα 5.16: Διάγραμμα σκέδασης των ανεξάρτητων μεταβλητών με τις τιμές της εξαρτημένης μεταβλητής Υ για δείγμα 63 οντοτήτων Ο δεύτερος τρόπος ελέγχου πραγματοποιείται με τη βοήθεια των διαγραμμάτων μερικής συσχέτισης, τα οποία έχουν ήδη αναλυθεί στο υποκεφάλαιο , διότι καθρεφτίζουν ταυτόχρονα το βαθμό σημαντικότητας των ανεξάρτητων μεταβλητών. Σύμφωνα λοιπόν με τα διαγράμματα 5.3, 5.4 και 5.5 ισχύει η γραμμικότητα στο μοντέλο των τριών μεταβλητών. Τέλος, ο τρίτος και τέταρτος τρόπος ελέγχου πραγματοποιείται με τη βοήθεια των διαγραμμάτων 5.14 (αριστερό και δεξί διάγραμμα), τα οποία όπως αναφέρεται στο υποκεφάλαιο ικανοποιούν τις προϋποθέσεις που πρέπει να ικανοποιούν και άρα δεν παρουσιάζουν κανένα πιθανό πρόβλημα στη γραμμικότητα του μοντέλου. Συνεπώς, όλα τα παραπάνω διαγράμματα συνηγορούν στο συμπέρασμα ότι υπάρχει γραμμικότητα μεταξύ της αγοραίας αξίας των ακινήτων και του εμβαδού, της κατάστασης των διαμερισμάτων και του αριθμού των μπάνιων τους Ακραίες οντότητες και οντότητες επίδρασης Μέχρι αυτό το σημείο οι έξι έλεγχοι που προηγούνται παρουσιάζουν ένα αξιόπιστο μοντέλο, το οποίο καλύπτει όλες της προϋποθέσεις που τίθενται βάσει μεθοδολογίας. Ο τελευταίος έλεγχος γίνεται με στόχο να επιβεβαιωθεί ότι καμία ακραία τιμή δεν επιδρά στην κλίση της εξίσωσης παλινδρόμησης και καμία οντότητα επίδρασης δεν μεταβάλλει Μεταπτυχιακή διατριβή 177
190 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ ριζικά τους συντελεστές παλινδρόμησης. Πρόκειται δηλαδή για ένα σημαντικό έλεγχο, καθώς από το αποτέλεσμα του κρίνεται εάν το τελικό μοντέλο των 63 περιπτώσεων θα πρέπει να μεταβληθεί με την αφαίρεση επιπλέον οντοτήτων ή όχι. Οι έλεγχοι χωρίζονται σε τρία βασικά μέρη. Το πρώτο αφορά τον εντοπισμό των ακραίων τιμών (Outliers) με τη βοήθεια της απόστασης Mahalanobis (Mahalanobis distance D 2 i ) και της τιμής Levarage h i (centered leverage). Η δεύτερη φάση εστιάζει στην εύρεση των οντοτήτων που αποτελούν πιθανές οντότητες επίδρασης (influential points) με τη βοήθεια της απόστασης Cook (Cook s Distance : CD i ), του μέτρου DFFITS (Standardized DFFITS) και του μέτρου DFBetas (Standardized DFBetas), ενώ ολοκληρώνεται το στάδιο με την οπτικοποίηση τους με τη βοήθεια των διαγραμμάτων Cook s distance με Centered Leverage Values, Standardized DFFITS με την αύξουσα σειρά των οντοτήτων A/A και Standardized DFBETA X i με A/A. Τρίτο και τελευταίο στάδιο αποτελεί η τελική απόφαση σχετικά με την απομάκρυνση ή όχι των πιθανών οντοτήτων επίδρασης και των ακραίων τιμών που έχουν ήδη εντοπιστεί με τη βοήθεια των κατανομών t και F. Centered Leverage Αρχικά, ελέγχονται οι τιμές του δείκτη Centered Leverage μέσω της στήλης LEV_1 και της κρίσιμης τιμής που είναι ίση με 0,2. Από τον έλεγχο όλων των οντοτήτων προκύπτει ότι καμία τιμή δεν ξεπερνά την κρίσιμη τιμή 0,2 και άρα καμία οντότητα στο δείγμα των 63 οντοτήτων δε χαρακτηρίζεται ακραία. Με τον έλεγχο του δείκτη Centered Leverage, ικανοποιείται ταυτόχρονα και ο έλεγχος του δείκτη Mahalanobis. Αποστάσεις Cook CD i Πρόκειται για το πρώτο μέτρο εντοπισμού των οντοτήτων επίδρασης, το οποίο υπολογίζει για κάθε οντότητα τις αλλαγές που συμβαίνουν στις εκτιμήσεις των παλινδρομικών συντελεστών όταν η συγκεκριμένη απαλειφθεί από το παλινδρομικό μοντέλο. Κρίσιμη τιμή για τις αποστάσεις Cook θεωρείται η μονάδα, συνεπώς οι τιμές της στήλης COO_1 για όλες τις οντότητες θα πρέπει να συγκριθούν με τη μονάδα. Σύμφωνα με τα δεδομένα που προκύπτουν από την εκτέλεση πολλαπλής παλινδρόμησης όλες οι τιμές Cook είναι πολύ μικρότερες της μονάδας και συνεπώς καμία οντότητα δεν αποτελεί οντότητα επίδρασης. Μέτρα DfFits Το μέτρο DfFits εκφράζει την επίδραση της κάθε οντότητας στις εκτιμήσεις των παλινδρομικών συντελεστών και αποτελεί άλλη μία μέθοδο εντοπισμού των πιθανών οντοτήτων επίδρασης. Στην πράξη χρησιμοποιούνται οι τιμές των Standardized DfFits, οι οποίες εκφράζονται στο περιβάλλον εργασίας του Data Editor με το όνομα SDF_1. Η αντίστοιχη κρίσιμη τιμή για τα μεγάλα δείγματα είναι η ακόλουθη: 178
191 Κ ε φ ά λ α ι ο 5 ο Standardized DfFits κρίσιμη = 2* = 0,50 Η σύγκριση των Standardized DfFits όλων των οντοτήτων με την οριακή τιμή υποδεικνύει ως πιθανές οντότητες επίδρασης την 11 (0,96), την 17 (0,59) και την 71 (0,59). Η τελική απόφαση για την απομάκρυνση τους λαμβάνεται έπειτα από τους ελέγχους της t και F κατανομής. Μέτρα DfBetas Αντίστοιχα, τα μέτρα DfBetas εκφράζουν την επίδραση των οντοτήτων στην εκτίμηση του κάθε παλινδρομικού συντελεστή ξεχωριστά. Η κρίσιμη τιμή για τις περιπτώσεις των μεγάλων δειγμάτων υπολογίζεται βάσει της ακόλουθης σχέσης: Standardized DfBetas κρίσιμη = = 0,25 ενώ για τον έλεγχο αξιοποιούνται οι απόλυτες τιμές των Standardized DfBetas των τριών μεταβλητών. Αναλυτικά, για τη μεταβλητή AREA ελέγχεται η στήλη με τίτλο SDB1_1 του Data Editor, για τη μεταβλητή QUALITY η στήλη SDB6_1 και για τη μεταβλητή BATH η στήλη SDB8_1. Σύμφωνα με τη σύγκριση των τιμών του δείγματος με την οριακή τιμή (0,25), τα Standardized DfBetas(AREA) υποδεικνύουν ως υποψήφιες οντότητες επίδρασης εκείνες με Α/Α 11(0,65), 61(0,46) και 68 (0,26), τα Standardized DfBetas(QUALITY) υποδεικνύουν την οντότητα 7(0,34), την 11 (0,73), την 17 (0,51), την 57 (0,35) και την 60 (0,27) και τέλος τα Standardized DfBetas(BATH) υποδεικνύουν τις οντότητες 7 ( 0,29), 38 (0,34), 61 (0,32) και 71 (0,38). Συνοψίζοντας τα παραπάνω στοιχεία προκύπτει ότι η πιθανή ακραία οντότητα 61 (Mahalanobis Method) συναντάται και ως πιθανή οντότητα επίδρασης βάσει των SDfBetas(AREA) και SDfBetas(BATH). Επίσης, ως πιθανές οντότητες επίδρασης σύμφωνα με τα SDfFits και SDfBetas χαρακτηρίζονται συγκεντρωτικά οι 7, 11, 17, 38, 57, 60, 61, 68, 71. Οι αποκλίσεις από τις κρίσιμες τιμές διαφέρουν όπως είναι λογικό από ελάχιστες έως μεγαλύτερες, οπότε είναι πιθανό να χρειαστεί η απομάκρυνση μόνο μερικών από τις προαναφερθείσες οντότητες ή και καμία. Διάγραμμα σκέδασης των αποστάσεων Cook με κεντραρισμένες τιμές Leverage Το διάγραμμα Cook έναντι των Centered Leverage οπτικοποιεί τα μεγέθη που έχουν ήδη αναλυθεί στις προηγούμενες ενότητες. Η ταυτόχρονη απόδοση των δύο μεγεθών οδηγεί σε άμεσα συμπεράσματα σχετικά με το ποιες οντότητες επηρεάζουν τους συντελεστές της παλινδρόμησης και ποιες την κλίση της ευθείας. Από το διάγραμμα 5.17, όλες οι οντότητες είναι εντός των ανοχών που επισημαίνονται με κόκκινη γραμμή. Συνεπώς δεν παρατηρείται καμία ακραία τιμή ή οντότητα επίδρασης. Μεταπτυχιακή διατριβή 179
192 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα 5.17: Διάγραμμα σκέδασης των αποστάσεων Cook με τις Centered Leverage τιμές Διάγραμμα σκέδασης των τυποποιημένων DfFits με την ακολουθία των παρατηρήσεων 180
193 Κ ε φ ά λ α ι ο 5 ο Διάγραμμα 5.18: Διάγραμμα Sequence των Standardized DfFits με την αύξουσα σειρά του δείγματος Όμοια με το παραπάνω διάγραμμα των Standardized DfFits οπτικοποιούνται οι τιμές που ξεπερνούν την οριακή τιμή 0,50 (όπως υπολογίζεται στην αντίστοιχη ενότητα), διότι εμφανίζονται με τη μορφή των εξάρσεων. Τη μεγαλύτερη απόκλιση από το μηδέν φαίνεται να έχει η οντότητα 11, ενώ οι οντότητες 17 και 71 οριακά ξεπερνούν την οριακή τιμή. Συμπεραίνεται, ότι σύμφωνα με τις τιμές των Standardized DfFits η πιο πιθανή οντότητα επίδρασης είναι η οντότητα με Α/Α 11. Διάγραμμα σκέδασης των τυποποιημένων DfBetas με την ακολουθία των παρατηρήσεων Οι οντότητες που εμφανίζουν εξάρσεις στο Διάγραμμα 5.19 είναι διαφορετικές για κάθε μία μεταβλητή. Οι πιο έντονες εξάρσεις συνδέονται με το συντελεστή του εμβαδού (μπλε γραμμή) και με το συντελεστή της κατάστασης του ακινήτου (πράσινη γραμμή). Οι πιθανές οντότητες επίδρασης και οι απόλυτες τιμές των αποστάσεων τους από την τιμή μηδέν έχουν ήδη αναφερθεί, διότι εντοπίστηκαν μία προς μία σε προηγούμενη ενότητα. Διάγραμμα 5.19: Διάγραμμα Sequence των Standardized DfBeta με την αύξουσα σειρά του δείγματος Μεταπτυχιακή διατριβή 181
194 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Πιο συγκεκριμένα, οι δύο κίτρινες οριζόντιες γραμμές ορίζουν την οριακή τιμή και με αυτόν τον τρόπο είναι ορατό ότι οι οντότητες 11, 61 και 68 είναι πιθανό να επιδρούν στο συντελεστή του εμβαδού (με μεγαλύτερη απόκλιση της οντότητας 11), οι οντότητες 7, 11, 17, 57 και 60 είναι πιθανό να επιδρούν στο συντελεστή της κατάστασης του ακινήτου (με μεγαλύτερη απόκλιση της οντότητας 11) και οι οντότητες 7, 38, 61 και 71 (με πολύ μικρές αποκλίσεις από την οριακή τιμή). Παρόλα αυτά λαμβάνοντας υπόψη ότι για μικρά δείγματα (n <30) η οριακή τιμή ισούται με τη μονάδα, είναι πολύ πιθανό οι εξάρσεις που αποτυπώνονται παραπάνω να μην έχουν ουσιαστική επίδραση στους συντελεστές του παλινδρομικού μοντέλου. Οι κατανομές που ακολουθούν δίνουν την οριστική απάντηση σχετικά με την απομάκρυνση ή όχι οντοτήτων από το μοντέλο. t κατανομή Τα Studentized Deleted Residuals μέσω της διαδικασίας Bonferroni και της t κατανομής μπορούν να βοηθήσουν στον εντοπισμό των οντοτήτων επίδρασης. Όπου t i ορίζεται η τιμή των Studentized Deleted Residuals, τα οποία ακολουθούν την κανονική κατανομή με βαθμούς ελευθερίας: β.ε. = n-p-1 = =58 Η κρίσιμη τιμή που ορίζει η διαδικασία Bonferroni και είναι ίση με: t κρίσιμη = t(1 - ; n-p-1) t (0, ; 58) = 3, με α το επίπεδο στατιστικής σημαντικότητας (α= 0,05), n το μέγεθος του δείγματος (n =58) και p τον αριθμό των συντελεστών παλινδρόμησης μαζί με το σταθερό όρο (p = 4). Επόμενο βήμα αποτελεί ο εντοπισμός της οντότητας με το μεγαλύτερο Studentized Deleted Residual (max SDR)ώστε να συγκριθεί με την οριακή τιμή που προέκυψε παραπάνω. Από τα δεδομένα του Data Editor προκύπτει ότι η οντότητα με τη μεγαλύτερη τιμή Studentized Deleted Residual κατά απόλυτη τιμή είναι η = = 2, Ορίζεται η μηδενική υπόθεση Ηο: Το Studentized Deleted Residual με τη μεγαλύτερη απόλυτη τιμή είναι μία οντότητα επίδρασης, με εναλλακτική υπόθεση =2,28874 ΔΕΝ Η1: Studentized Deleted Residual με τη μεγαλύτερη απόλυτη τιμή =2,28874 είναι οντότητα επίδρασης Επειδή όμως = 2,28874 <3,2378ισχύει η μηδενική υπόθεση Ηο και η οντότητα 11 δεν αποτελεί οντότητα επίδρασης. 25 Η τελική τιμή προκύπτει μέσω των στατιστικών πινάκων 182
195 Κ ε φ ά λ α ι ο 5 ο F κατανομή Οι τιμές Cook θεωρείται ότι ακολουθούν την κατανομή F(1-a;p;n-p), συνεπώς με τη βοήθεια της κατανομής μπορούν να εντοπιστούν οι οντότητες επίδρασης εάν και εφόσον υπάρχουν. Με την ίδια λογική που περιγράφηκε παραπάνω υπολογίζεται αρχικά η κρίσιμη τιμή F και στη συνέχεια συγκρίνεται με την τιμή Cook που είναι η μεγαλύτερη σε μέγεθος σε σύγκρισή με όλες τις υπόλοιπες. F κρίσιμη =F(1-a; p; n-p) = F(0,95; 4; 59) = 2,534 Η μέγιστη απόσταση Cook ανήκει στην οντότητα 11 και είναι ίση με CD 11 = 0, Από τους στατιστικούς πίνακες της F κατανομής παρατηρείται ότι η τιμή βρίσκεται στο 25.34% εκατοστημόριο της συγκεκριμένης κατανομής, δηλαδή δεν πλησιάζει σε καμία περίπτωση το 50% και άρα η οντότητα δε μπορεί να χαρακτηριστεί οντότητα επίδρασης. Σύμφωνα με τους δύο ελέγχους κρίνεται ότι καμία από τις υποψήφιες οντότητες επίδρασης των προηγούμενων ελέγχων δε χρειάζεται να απομακρυνθεί από το μοντέλο και άρα αυτή είναι η τελική μορφή του με συνολικά 63 οντότητες Έλεγχος προβλεπτικής ικανότητας του μοντέλου Οι τρεις έλεγχοι που ακολουθούν αποδεικνύουν την προβλεπτική δύναμη του μοντέλου και το καθιστούν κατάλληλο για πρόβλεψη αγοραίων αξιών νέων διαμερισμάτων προς πώληση. Οι έλεγχοι στηρίζονται στις ακόλουθες μεθόδους: Μέθοδος των διαστημάτων πρόβλεψης Μέθοδος του διαχωρισμού των δεδομένων (Data Splitting) Μέθοδος εύρεσης του αριθμού των σημαντικών μεταβλητών Μέθοδος των διαστημάτων πρόβλεψης Για τη μέθοδο των διαστημάτων πρόβλεψης συλλέγονται από τον ίδιο πληθυσμό τέσσερα νέα διαμερίσματα, τα οποία προστίθενται στο υπάρχον δείγμα των 63 οντοτήτων. Στη συνέχεια, εκτελείται η διαδικασία της πολλαπλής παλινδρόμησης επιλέγοντας μόνο τις 63 οντότητες του αρχικού δείγματος. Τα αποτελέσματα της εκτέλεσης αφορούν τις 67 οντότητες και παρέχουν τις στήλες LICI_1 και UICI_1 με τα πάνω και κάτω όρια των διαστημάτων εμπιστοσύνης. Τα αποτελέσματα είναι τα ακόλουθα: < < < < < < < < Μεταπτυχιακή διατριβή 183
196 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Παρατηρείται ότι όλες οι αξίες βρίσκονται εντός του διαστήματος πρόβλεψης και άρα το μοντέλο θεωρείται ικανοποιητικό και ικανό να αξιοποιηθεί για να δώσει τιμές σε διαμερίσματα με άγνωστη αγοραία αξία. Το εύρος των διαστημάτων εμπιστοσύνης είναι σχετικά μεγάλο αλλά και ανάλογο των αξιών ακινήτων της περιοχής. Πιθανή αιτία του εύρους του, όπως αναφέρεται και στην περίπτωση του κέντρου της Θεσσαλονίκης είναι η ανομοιογένεια που παρουσιάζεται σε ανάλογες περιοχές Μέθοδος του διαχωρισμού των δεδομένων (Data Splitting) Η διαδικασία εκτελείται σε δύο κύρια βήματα από τα οποία το πρώτο αναφέρεται σε ένα μόνο τυχαίο αριθμό του δείγματος ενώ το δεύτερο στο υπόλοιπο. Μέσω του βαθμού συσχέτισης του πρώτου μέρους με το δεύτερο επιτυγχάνεται η εύρεση της προβλεπτικής δύναμης του μοντέλου. 1 ο ΒΗΜΑ: Επιλέγεται από το δείγμα των 63 οντοτήτων το 70% περίπου των παρατηρήσεων με τυχαία σειρά επιλογής. Το SPSS κατά την εκτέλεση της διαδικασίας επιλέγει συνολικά 50 οντότητες. Με το νέο δείγμα διαμερισμάτων εκτελείται η διαδικασία της πολλαπλής γραμμικής παλινδρόμησης και προκύπτει η παρακάτω εξίσωση παλινδρόμησης: Υ = , ,590 Χ ,076 Χ ,538 Χ9 με R = 0,936, R 2 = 0,877, R 2 adj = 0,869 και δείκτη Durbin Watson = 2,246 τιμές VIF μικρότερες του 2 και τιμές t μεγαλύτερες του. Ταυτόχρονα, όλες οι υπόλοιπες τιμές των δεικτών είναι εντός επιτρεπόμενων ορίων και κινούνται στα ίδια πλαίσια στα οποία βρίσκεται το μοντέλο των 63 οντοτήτων. Συνεπώς, πρόκειται για ένα μοντέλο 50 οντοτήτων, το οποίο χαρακτηρίζεται αξιόπιστο. Όσον αφορά τον έλεγχο ανεξαρτησίας των οντοτήτων, το διάγραμμα Studentized Residual vs AA (Sequence) παρουσιάζει μία τυχαία κατανομή των κουκκίδων, χωρίς την εμφάνιση προτύπων. Συνεπώς και γραφικά το μοντέλο θεωρείται καλό και πληρεί όλες τις κύριες προδιαγραφές που απαιτούνται στα μοντέλο γραμμικής παλινδρόμησης. 184
197 Κ ε φ ά λ α ι ο 5 ο Διάγραμμα 5.20: Διάγραμμα σκέδασης των Studentized Residual vs AA (Sequence) για τις 50 μόνο οντότητες του δείγματος 2 ο ΒΗΜΑ: Στη συνέχεια επιλέγονται οι υπόλοιπες 13 οντότητες μέσω της διαδικασίας που περιγράφεται στο κεφάλαιο και με τη χρήση της εξίσωσης παλινδρόμησης που προκύπτει από το πρώτο βήμα εκτελείται η εντολή Compute Variables. Δημιουργείται μία νέα στήλη προβλεπόμενων τιμών PRED για το σύνολο των 63 οντοτήτων και όχι μόνο για τις 13. Η συσχέτιση που προκύπτει μεταξύ της παρατηρούμενης και της προβλεπόμενης τιμής PRED (Analyze Correlation Bivariate ) είναι ίση με 0,927. Πρόκειται για ένα πολύ υψηλό βαθμό συσχέτισης και άρα η προβλεπτική ικανότητα του μοντέλου των 63 οντοτήτων είναι ιδιαίτερα ικανοποιητική. Για την επιβεβαίωση της αξιολόγησης κατασκευάζεται και το διάγραμμα σκέδασης μεταξύ των PRED και Υ, ώστε να οπτικοποιηθεί το αποτέλεσμα. Στο παρακάτω διάγραμμα (Διάγραμμα 5.21) είναι ορατή η μεγάλη συσχέτιση μεταξύ των προβλεπόμενων τιμών που παράγονται μέσω της μεθόδου του διαχωρισμού και των παρατηρούμενων τιμών και ως επακόλουθο η δύναμη πρόβλεψης του μοντέλου. Μεταπτυχιακή διατριβή 185
198 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα 5.21: Διάγραμμα Bivariate συσχέτισης μεταξύ των προβλεπόμενων και παρατηρούμενων τιμών Μέθοδος εύρεσης του βέλτιστου αριθμού σημαντικών μεταβλητών Με τη βοήθεια του κριτηρίου Mallow s ελέγχεται εάν οι μεταβλητές οι οποίες επιλέγονται από τον αλγόριθμο ως στατιστικά σημαντικές είναι επαρκείς για να ερμηνεύσουν το φαινόμενο ή όχι. Το αποτέλεσμα φαίνεται από την τιμή που δίνεται στο Mallows Prediction Criterion στο τελευταίο μοντέλο της βηματικής διαδικασίας. Πίνακας 5.7: Πίνακας Model Summary που περιλαμβάνει το κριτήριο πρόβλεψης Mallow Model Summary Model Selection Criteria Std. Error Akaike Amemiya Mallows' Schwarz R Adjusted of the Information Prediction Prediction Bayesian R Square R Square Estimate Criterion Criterion Criterion Criterion 1,861 a,742, , ,728,275 63, ,015 2,912 b,832, , ,572,185 22, ,001 3,936 c,876, , ,493,141 4, ,
199 Κ ε φ ά λ α ι ο 5 ο Στην προκειμένη περίπτωση η τρίτη γραμμή της στήλης Mallows Prediction Criterion δίνει τον αριθμό τέσσερα, όσες δηλαδή είναι συνολικά οι ανεξάρτητες μεταβλητές μαζί με την εξαρτημένη. Συνεπώς, όλοι οι έλεγχοι οδηγούν στο συμπέρασμα ότι το μοντέλο που σχηματίζεται είναι αξιόπιστο και με ισχυρή προβλεπτική δύναμη Ερμηνεία μοντέλου για την περιοχή Eixample Το τρίτο μοντέλο πολλαπλής γραμμικής παλινδρόμησης αναφέρεται σε μία ιδιαίτερα ανομοιογενή και πολύπλοκη περιοχή του κέντρου της Βαρκελώνης, την περιοχή Eixample. Πρόκειται για κατοικίες που χτίστηκαν περίπου στα μέσα του περασμένου αιώνα (δηλαδή ιδιαίτερα παλαιές κατοικίες), αλλά τοποθετούνται σε μία περιοχή που μπορεί να χαρακτηριστεί κυρίως εμπορική και τουριστική. Συνεπώς είναι πρακτικά ιδιαίτερα δύσκολη η μοντελοποίηση της όσον αφορά τις αξίες των ακινήτων, διότι η θέση επιδρά σημαντικά. Παρόλα αυτά κατά την εκτέλεση της διαδικασίας ένα δείγμα 75 διαμερισμάτων δημιουργεί μέσω της μεθοδολογίας της παρούσας εργασίας ένα μοντέλο το οποίο ικανοποιεί σε πάρα πολύ μεγάλο βαθμό όλα τα κριτήρια που επιτάσσει η διεθνής και εγχώρια βιβλιογραφία σχετικά με τα γραμμικά μοντέλα πολλών μεταβλητών. Ξεκινώντας με 75 οντότητες και έπειτα από την αφαίρεση 12 συνολικά ακραίων οντοτήτων σχηματίζεται η παλινδρομική εξίσωση της παρακάτω μορφής: με R 2 = 0,876 Υ = , ,834 AREA ,950 QUALITY ,568 BATH Η εξίσωση παρουσιάζει την εξάρτηση της αγοραίας αξίας των ακινήτων από τρεις μεταβλητές, το εμβαδόν, την ποιότητα του διαμερίσματος και των αριθμό των μπάνιων που διαθέτει. Ποιοι όμως μπορεί να είναι οι λόγοι για τους οποίους, οι υπόλοιπες μεταβλητές δε φαίνεται να επιδρούν στη διαμόρφωση της αξίας; Δε θεωρούνται στατιστικώς σημαντικές η παλαιότητα, ο αριθμός των ορόφων, η ύπαρξη ανελκυστήρα, το είδος θέρμανσης, η θέση στάθμευσης και τέλος ο αριθμός των δωματίων. Από τις προαναφερθείσες μεταβλητές μπορεί να γίνει σαφώς κατανοητή η μη συμμετοχή της ύπαρξης ανελκυστήρα, διότι περίπου ένα 90% από το δείγμα διαθέτει ανελκυστήρα, καθώς και η ύπαρξη θέσης στάθμευσης, διότι περίπου μόνο ένα 8% διαθέτει. Η μεταβλητή παλαιότητα, όπως φαίνεται από το σχηματισμό του μοντέλου δεν διαδραματίζει ιδιαίτερα σημαντικό ρόλο, διότι ο μέσος όρος των ηλικιών του δείγματος είναι περίπου τα 49 έτη, συνεπώς όλα τα ακίνητα θεωρούνται παλαιά και μικρές μεταβολές στην ηλικία τους δεν επηρεάζουν σε πολύ μεγάλο βαθμό την αξία τους. Η ίδια λογική ισχύει και για την περίπτωση του είδους θέρμανσης, διότι στην περίπτωση της Βαρκελώνης η βάση δεδομένων αναφέρεται στην ύπαρξη θέρμανσης και όχι στο είδος της (αυτόνομη, κεντρική κλπ.). Με άλλα λόγια δεν πριμοδοτείται η αυτόνομη θέρμανση, η θέρμανση με φυσικό αέριο ή πιθανόν η ύπαρξη τζακιού. Παρατηρείται ένα 65% των διαμερισμάτων να έχει θέρμανση, ενώ το 35% είτε δεν έχει θέρμανση είτε έχει μόνο κλιματισμό. Επίσης, θα πρέπει κανείς να λάβει υπόψη του ότι τα διαμερίσματα της περιοχής Eixample έχουν δυσανάλογες αγοραίες αξίες σε σχέση με τα βασικά χαρακτηριστικά τους. Τα διαμερίσματα πωλούνται ακριβότερα σε σύγκριση με άλλα παρόμοια άλλης περιοχής Μεταπτυχιακή διατριβή 187
200 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ κυρίως λόγω πολύ καλής θέσης, θέας κοκ. Τέλος, όσον αφορά τον όροφο του διαμερίσματος, παρατηρείται ότι αποτελεί μία στατιστικώς σημαντική μεταβλητή κατά την πρώτη προσέγγιση του μοντέλου, άρα υπάρχει ένας εμφανής βαθμός συσχέτισης ο οποίος εν τέλει δεν επαρκεί για να συμπεριληφθεί η μεταβλητή στο μοντέλο των 63 οντοτήτων. Όσον αφορά τις μεταβλητές που επηρεάζουν την αγοραία αξία των ακινήτων στην περιοχή Eixample της Βαρκελώνης τίθεται το ερώτημα του ποιος είναι ο βαθμός επίδρασης και συσχέτισης τους με την εξαρτημένη μεταβλητή. Σύμφωνα με το συντελεστή προσδιορισμού R 2 = 0.876, το 87,6% της συνολικής διακύμανσης της αγοραίας αξίας των ακινήτων οφείλεται στις πληροφορίες που περιλαμβάνουν οι τρεις ανεξάρτητες μεταβλητές. Πιο συγκεκριμένα, με βάσει τα στοιχεία του πίνακα 5.3 και τη βηματική διαδικασία (Stepwise), η μεταβλητή που συμβάλει περισσότερο στη διαμόρφωση της εξαρτημένης μεταβλητής είναι το εμβαδόν με ποσοστό 74,2%. Στη συνέχεια, ακολουθεί η κατάσταση του ακινήτου, η οποία είναι υπεύθυνη για το 8,4% της διακύμανσης της εξαρτημένης μεταβλητής και τέλος ο αριθμός των μπάνιων των διαμερισμάτων με ποσοστό συνεισφοράς 5%. Το άθροισμα όλων των παραπάνω ποσοστών είναι ίσο με το συνολικό ποσοστό διασποράς της εξαρτημένης μεταβλητής από την επίδραση των τριών ανεξάρτητων μεταβλητών. Ο συντελεστής προσδιορισμού R 2, όπως διαπιστώνεται παραπάνω, είναι ιδιαίτερα μεγάλος και παρουσιάζει μία πολύ καλή προσαρμογή του μοντέλου στα δεδομένα. Ωστόσο, η τιμή του αναφέρεται αποκλειστικά στο δείγμα των 63 οντοτήτων. Στην περίπτωση του προσαρμοσμένου συντελεστή προσδιορισμού Adjusted R 2 το μέγεθος προσαρμογής των του μοντέλου στα δεδομένα αναφέρεται σε οποιοδήποτε δείγμα προέρχεται από τον πληθυσμό ή ακόμη και σε ολόκληρο τον πληθυσμό του μοντέλου. Η τιμή του Adjusted R 2 σύμφωνα με τον πίνακα 5.3 είναι ίση με 0,870, άρα το 87% της συνολικής διακύμανσης της αγοραίας αξίας οφείλεται στις τρεις μεταβλητές για τον πληθυσμό της περιοχής Eixample της Βαρκελώνης. Το ποσοστό θεωρείται ιδιαίτερα υψηλό και φανερώνει ικανοποιητική προβλεπτική δύναμη στο μοντέλο. 188
201 Κ ε φ ά λ α ι ο 5 ο 5.2 ΕΦΑΡΜΟΓΗ ΠΟΛΛΑΠΛΗΣ ΓΡΑΜΜΙΚΗΣ ΠΑΛΙΝΔΡΟΜΗΣΗΣ ΓΙΑ ΤΗΝ ΠΕΡΙΟΧΗ SANT MARTI (ΤΕΤΑΡΤΟ ΜΟΝΤΕΛΟ) Το τέταρτο μοντέλο αφορά την περιοχή Sant Marti της Βαρκελώνης, η οποία βρίσκεται στο βορειοανατολικό τμήμα της παλιάς πόλης. Όπως έχει ήδη επισημανθεί η περιοχή χαρακτηρίζεται γενικά από πολυώροφες οικοδομές που κατοικούνται κυρίως από οικογένειες της μεσαίας τάξης. Συνεπώς αναμένονται όχι ιδιαίτερα υψηλές αγοραίες αξίες, για τα δεδομένα της Βαρκελώνης, και σίγουρα όχι πολυτελείς κατοικίες. Η πρώτη σάρωση των δεδομένων του δείγματος μπορεί πολύ εύκολα να δώσει απαντήσεις σχετικά με τα γενικά χαρακτηριστικά των κατοικιών. Πρόκειται όντως για πολυώροφες οικοδομές οι οποίες στην μεγάλη πλειοψηφία τους χρονολογούνται στη δεκαετία του 70 και πωλούνται κατά μέσο όρο στα 1900 με 2000 /τμ. Το 98% των οικοδομών του δείγματος διαθέτει ανελκυστήρα, ενώ μόνο ένα 7% διαθέτει ιδιόκτητη θέση στάθμευσης. Βασικό χαρακτηριστικό των κατοικιών είναι ότι ένα πολύ μεγάλο ποσοστό δεν διαθέτει θέρμανση ( ), το 14% θερμαίνεται με τη χρήση κλιματιστικού και το υπόλοιπο 45% περίπου θερμαίνεται με κανονικές εγκαταστάσεις πομπών, ή και επιπλέον με τη χρήση κλιματιστικού. Τέλος, αξιολογώντας με τη βοήθεια φωτογραφικού υλικού τα διαμερίσματα του δείγματος η γενική ποιότητα τους κυμαίνεται μεταξύ μέτριας και καλής. Στη συνέχεια του κεφαλαίου ακολουθούν όλα τα βήματα της στατιστικής ανάλυσης των δεδομένων, οι έλεγχοι των παραδοχών του γραμμικού μοντέλου και τα συμπεράσματα που προκύπτουν για την τέταρτη περιοχή μελέτης Διερεύνηση γραμμικής σχέσης μεταξύ της εξαρτημένης μεταβλητής Υ και των ανεξάρτητων Χi Η αναζήτηση του τρόπου σύνδεσης της εξαρτημένης μεταβλητής με τις ανεξάρτητες είναι μία πρώτη εικόνα των αποτελεσμάτων που θα προκύψουν αργότερα και προκύπτει με τη βοήθεια των γραφημάτων διασποράς των Xi με την Υ και με τους συντελεστές μερικής συσχέτισης. Τα γραφήματα και τα ποσοστά της μερικής συσχέτισης φανερώνουν τις θετικές ή αρνητικές συσχετίσεις, καθώς και το βαθμό τους. Δεν θα πρέπει να παρακάμπτεται το γεγονός ότι τα αποτελέσματα που προκύπτουν αναφέρονται στο δείγμα των 60 οντοτήτων και είναι λοιπόν πολύ πιθανό να δεδομένα να αλλάξουν σημαντικά έπειτα από την αφαίρεση ακραίων οντοτήτων Γραφήματα συσχέτισης των Χ i με την Υ Η απόδοση όλων των διαγραμμάτων συσχέτισης σε ένα μόνο διάγραμμα (Matrix) δίνει τη δυνατότητα εκτίμησης όλων των συσχετίσεων μεμονωμένα, αλλά προσφέρει και μία άμεση σύγκριση της επίδρασης των εννέα ανεξάρτητων μεταβλητών ταυτόχρονα. Το διάγραμμα 5.22 αποτυπώνει στην πρώτη σειρά γραφημάτων διασποράς τη σύνδεση της εξαρτημένης μεταβλητής Y που αντιστοιχίζεται στην αγοραία αξία των ακινήτων με τις εννέα ανεξάρτητες μεταβλητές διαδοχικά. Σαφής γραμμική σχέση παρατηρείται στην περίπτωση του εμβαδού (AREA) και της παλαιότητας (AGE). Ακολουθούν, σύμφωνα με το διάγραμμα ο αριθμός των ορόφων (FLOOR), η θέρμανση (HEATING), η κατάσταση του ακινήτου (QUALITY) και ο αριθμός των δωματίων (ROOM). Αντιθέτως, καμία γραμμική Μεταπτυχιακή διατριβή 189
202 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ σχέση δε διαφαίνεται στην ύπαρξη ανελκυστήρα (ELEV), θέσης στάθμευσης (PARKING)και στον αριθμό των μπάνιων (BATH). Τα διαγράμματα διασποράς που αποτελούν το πρώτο κριτήριο επιλογής των μεταβλητών που θα συμμετέχουν στην εκτέλεση της στατιστικής ανάλυσης υποδεικνύει τις μεταβλητές, Εμβαδόν, Παλαιότητα, Όροφος, Θέρμανση, Κατάσταση ακινήτου και Αριθμός δωματίων, δηλαδή έξι από τις εννέα μεταβλητές. Διάγραμμα 5.22: Γράφημα Matrix Scatter Plot για δείγμα 60 ακινήτων και για τις εννέα ανεξάρτητες μεταβλητές Συντελεστές μερικής συσχέτισης Πιθανότερο σενάριο είναι το κριτήριο των συντελεστών μερικής συσχέτισης να υποδείξει λιγότερες μεταβλητές ως γραμμικά συνδεδεμένες με την αγοραία αξία των ακινήτων, καθώς πρόκειται για αυστηρότερο και ακριβέστερο έλεγχο (βασίζεται σε ποσοτικό μέγεθος και όχι σε οπτική ερμηνεία). Τα παρακάτω αποτελέσματα της διαδικασίας (Analyze, Correlate, Partial) φανερώνουν τους «καθαρούς» βαθμούς συσχέτισης της εξαρτημένης μεταβλητής με τις ανεξάρτητες μεταβλητές. Σύμφωνα με τον πίνακα, οι μεταβλητές εμβαδόν, παλαιότητα και 190
203 Κ ε φ ά λ α ι ο 5 ο είδος θέρμανσης παρουσιάζουν σημαντικό βαθμό συσχέτισης με την εξαρτημένη μεταβλητή, συγκρινόμενες με όλες τις υπόλοιπες. Ακολουθούν ο αριθμός των δωματίων, πολύ λιγότερο η θέση στάθμευσης, η κατάσταση του ακινήτου και ο αριθμός του ορόφου, ενώ καμία συσχέτιση δεν εμφανίζει η ύπαρξη ανελκυστήρα και ο αριθμός μπάνιων της κατοικίας. Πίνακας 5.8: Μερικές συσχετίσεις μεταξύ των μεταβλητών στην περιοχή Sant Marti της Βαρκελώνης που αναφέρεται στο δείγμα των 60 οντοτήτων Μεταβλητές Συσχέτιση Επίπεδο στατιστικής σημαντικότητας AREA 0,468 0,000 AGE -0,493 0,000 FLOOR 0,142 0,316 ELEV 0,025 0,861 HEATING 0,529 0,000 QUALITY 0,163 0,247 PARKING 0,200 0,156 ROOMS 0,360 0,009 BATH 0,001 0,997 Λαμβάνοντας υπόψη μόνο τα δεδομένα του πίνακα οι μεταβλητές που εμφανίζουν γραμμική σχέση με την αγοραία αξία και άρα πρέπει να συμμετέχουν στη διαδικασία του SPSS είναι οι AREA, AGE, HEATING και ROOMS. Παρόλα αυτά, υπολογίζοντας ταυτόχρονα τα αποτελέσματα από το πρώτο κριτήριο, εν τέλει επιλέγονται οι μεταβλητές AREA, AGE, FLOOR, HEATING, QUALITY, PARKING και ROOMS (επτά από τις εννέα), έτσι ώστε να μην υπάρχει περίπτωση αμφισβήτησης των επιλογών και το ίδιο το SPSS μέσω των αλγορίθμων του να επιβεβαιώσει ή να διαψεύσει τη αρχική επιλογή των τεσσάρων μεταβλητών. Με αυτόν τον τρόπο επιτυγχάνεται και ένας τρόπος ελέγχου του βαθμού σημαντικότητας των συσχετίσεων που παρουσιάζονται στον πίνακα Εφαρμογή της πολλαπλής γραμμικής παλινδρόμησης και δημιουργία τελικού μοντέλου Η πρώτη προσέγγιση της εξίσωσης παλινδρόμησης πραγματοποιείται με τη βηματική (stepwise)διαδικασία μέσω του βήματος (Analyze Regression Linear) για το σύνολο των 60 περιπτώσεων. Τα αποτελέσματα είναι τα ακόλουθα: Υ = 44607, ,448 AREA 1404,751 AGE ,772 HEATING ,382 ROOM με R 2 = 0,705 Μεταπτυχιακή διατριβή 191
204 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Η εξίσωση επιβεβαιώνει απόλυτα τη διαπίστωση που γίνεται στο υποκεφάλαιο σχετικά με τους συντελεστές μερικής συσχέτισης. Οι ανεξάρτητες μεταβλητές με τα τέσσερα μεγαλύτερα ποσοστά συσχέτισης εμφανίζονται στο μοντέλο των 60 οντοτήτων. Μεγαλύτερη συνεισφορά φαίνεται να έχει το εμβαδόν των ακινήτων και ακολουθούν η παλαιότητα, το είδος θέρμανσης και ο αριθμός των δωματίων. Επίσης, κρίνοντας από το συντελεστή προσδιορισμού του οποίου η τιμή είναι ιδιαίτερα μεγάλη για πρώτη προσέγγιση, συμπεραίνεται ότι είναι ικανοποιητικός και ο βαθμός προσαρμογής του μοντέλου στα δεδομένα. Παρόλα αυτά επιβάλλονται προσπάθειες για τη βελτίωση του, λαμβάνοντας υπόψη και τα παρακάτω δύο διαγράμματα. Διάγραμμα 5.23: (Αριστερά) Διάγραμμα σκέδασης των Studentized Deleted Residual με τα Standardized Predicted Values. (Δεξιά) Ιστόγραμμα συχνοτήτων των τυποποιημένων υπολοίπων Το διάγραμμα σκέδασης (αριστερά) και το ιστόγραμμα συχνοτήτων (δεξιά) υποδεικνύουν οντότητες οι οποίες είναι εκτός των ανοχών που τίθενται. Ως επακόλουθο, πραγματοποιούνται διαδοχικές προσεγγίσεις της τελικής παλινδρομικής εξίσωσης μέσω της αφαίρεσης των ακραίων οντοτήτων. Πιο συγκεκριμένα, η αφαίρεση ξεκινά από την οντότητα με Α/Α 55, η οποία ξεχωρίζει στο διάγραμμα 5.23 (αριστερά) και ακολουθούν οι 5, 51, 44, 60 και 42. Τα κριτήρια αφαίρεσης βασίζονται στην οπτική ερμηνεία του διαγράμματος σκέδασης των Studentized Deleted Residuals με τα τυποποιημένα προβλεπόμενα υπόλοιπα και με την ερμηνεία των διαγραμμάτων μερικής συσχέτισης. Τα αποτελέσματα της διαδοχικής αφαίρεσης οντοτήτων φαίνεται στον ακόλουθο πίνακα: 192
205 Κ ε φ ά λ α ι ο 5 ο Παλινδρ. Ανάλυση Ακραία οντότητα R R 2 1η (Ν = 60) - 0,839 0,705 2η -55 0,855 0,732 3η -5 0,862 0,742 4η -51 0,896 0,803 5η -44 0,910 0,828 6η -60 0,925 0,855 7η (Ν = 54) -42 0,926 0,857 Παρατηρείται ότι όσο αφαιρούνται οντότητες, τόσο αυξάνεται η τιμή του συντελεστή προσδιορισμού R 2. Συνεπώς, η αφαίρεση οντοτήτων έχει θετική συμβολή στην αξιοπιστία του μοντέλου. Το τελικό μοντέλο με αριθμό δείγματος 54 οντοτήτων δείχνει να μην απαιτεί την αφαίρεση άλλων σημείων και παρουσιάζει ικανοποιητικές τιμές δεικτών. Η εξίσωση παλινδρόμησης του υποψήφιου τελικού μοντέλου είναι η ακόλουθη: Υ = 55351, ,445 AGE +1778,897 AREA ,012 HEATING με R 2 = 0,857 Το νέο μοντέλο διαθέτει ένα σαφώς καλύτερο συντελεστή προσδιορισμού, ο οποίος πληροφορεί ότι το 85,7 % της συνολικής διακύμανσης της αγοραίας αξίας οφείλεται στις τρεις ανεξάρτητες μεταβλητές. Παράλληλα, παρατηρείται ότι με την αφαίρεση έξι σημείων αλλάζει ο αριθμός των μεταβλητών που θεωρούνται στατιστικώς σημαντικές. Η μείωση των μεταβλητών δεν έχει αρνητική επίδραση στο μοντέλο, διότι αποδεικνύεται ότι οι τρεις από τις τέσσερις μόνο ανεξάρτητες μεταβλητές έχουν ουσιαστική συμβολή στο μοντέλο και έχουν «ατομική» αξία. Τέλος, αναζητώντας εκ νέου τους συντελεστές μερικής συσχέτισης (Πίνακας 5.9) του δείγματος των 54 οντοτήτων διαφαίνεται μία εντονότερη συσχέτιση σε σύγκριση με το πρώτο μοντέλο των 60 οντοτήτων. Συμπεραίνεται λοιπόν ότι η τελική παλινδρομική εξίσωση περιγράφει ένα σαφώς πιο αξιόπιστο μοντέλο. Πίνακας 5.9: Σύγκριση μερικών συσχετίσεων μεταξύ του πρώτου μοντέλου των 60 οντοτήτων και του τελικού μοντέλου των 54 οντοτήτων Μεταβλητές Πρώτη προσέγγιση Τελική προσέγγιση AREA 0,468 0,665 AGE -0,493 0,608 HEATING 0,529 0,547 Μεταπτυχιακή διατριβή 193
206 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Ακολουθούν οι επτά συνολικά έλεγχοι που αφορούν την ποιότητα του μοντέλου και οι τρεις επιπλέον για την επιβεβαίωση της προβλεπτικής του ικανότητας Έλεγχος ικανοποίησης παραδοχών του γραμμικού μοντέλου Με την ίδια διαδικασία που περιγράφεται αναλυτικά σε προηγούμενα κεφάλαια ελέγχονται όλα τα γραφήματα και οι δείκτες που παράγονται από την ανάλυση παλινδρόμησης. Παράλληλα δημιουργούνται επιπλέον στατιστικοί δείκτες και διαγράμματα, μέσω διαφορετικών διαδικασιών, όπως για παράδειγμα η εντολή Explore για την παραδοχή της κανονικότητας Σημαντικότητα ανεξάρτητων μεταβλητών Η στατιστική σημαντικότητα των ανεξάρτητων μεταβλητών διαφαίνεται μέσω δύο κύριων τρόπων. Ο πρώτος είναι τα διαγράμματα μερικής παλινδρόμησης, όπου μέσω της ανάγνωσης τους ερμηνεύουν το βαθμό στατιστικής σημαντικότητας, ενώ ο δεύτερος είναι οι t τιμές του πίνακα των συντελεστών (Coefficiets), οι απόλυτες τιμές των οποίων συγκρίνονται με μία κρίσιμη τιμή. Διαγράμματα μερικής συσχέτισης Τα διαγράμματα μερικής συσχέτισης 5.24, 5.25, 5.26 φανερώνουν ξεκάθαρες γραμμικές συσχετίσεις της αγοραίας αξίας των ακινήτων με το εμβαδόν, την παλαιότητα και το είδος θέρμανσης. Το εύρος της ζώνης μέσα στο οποίο βρίσκεται το 95% των παρατηρήσεων είναι περίπου όμοιο στην περίπτωση του Εμβαδού και της Παλαιότητας, ενώ μεγαλώνει στην περίπτωση του Είδους θέρμανσης. Η συγκεκριμένη παρατήρηση καθορίζει και το βαθμό στατιστικής σημαντικότητας των ανεξάρτητων μεταβλητών. Συνεπώς, στην περιοχή Sant Marti της Βαρκελώνης, το Εμβαδόν των διαμερισμάτων και η Παλαιότητα τους είναι εξίσου σημαντικές στη διαμόρφωση της τελικής τους αξίας. Οι δύο οντότητες που σε κάθε διάγραμμα βρίσκονται εκτός της ζώνης του 95% των παρατηρήσεων ανήκουν στο επιτρεπόμενο 5% και άρα δεν απαιτείται η αφαίρεση τους από το μοντέλο. Τα διαγράμματα συνεπώς παρουσιάζουν τρεις μεταβλητές με ιδιαίτερα ικανοποιητική στατιστική σημαντικότητα, οι οποίες επιδρούν ουσιαστικά στη αγοραία αξία των ακινήτων και παρουσιάζουν ένα επαρκές μοντέλο. Ταυτόχρονα, φανερώνουν την ύπαρξη γραμμικότητας, η οποία αποτελεί προϋπόθεση για την μετέπειτα αξιολόγηση του μοντέλου. 194
207 Κ ε φ ά λ α ι ο 5 ο Διάγραμμα 5.24: Διάγραμμα μερικής παλινδρόμησης μεταξύ της αξίας και του εμβαδού Διάγραμμα 5.25: Διάγραμμα μερικής παλινδρόμησης μεταξύ της αξίας και της παλαιότητας Μεταπτυχιακή διατριβή 195
208 Σχηματισμός μοντέλου Διάγραμμα 5.26: Διάγραμμα μερικής παλινδρόμησης μεταξύ της αξίας και του είδους θέρμανσης t τιμές Οι απόλυτες τιμές των t δεδομένων του παρακάτω πίνακα καθορίζουν εάν μία μεταβλητή είναι στατιστικώς σημαντική, αλλά καθορίζουν ταυτόχρονα την κατάταξη των μεταβλητών με κριτήριο το βαθμό σημαντικότητας τους. Τοποθετώντας τις μεταβλητές κατά αύξουσα τιμή των t θα είναι πρώτη η παλαιότητα με t = , το εμβαδόν με t =9.965 και τέλος το είδος θέρμανσης με t = Όλες οι τιμές είναι ιδιαίτερα κοντά, χωρίς κάποια να ξεχωρίζει και μάλιστα είναι αρκετά μεγαλύτερες της οριακής τιμής tοριακή= (τιμές μεγαλύτερες του θεωρούνται στατιστικά σημαντικές). Συνεπώς, στατιστικώς σημαντικότερη είναι η παλαιότητα (AGE), ακολουθεί το εμβαδόν (AREA) και στη συνέχεια το είδος θέρμανσης (HEATING). Κρίνοντας από τα αποτελέσματα και των δύο μεθόδων ελέγχου, οι τρεις ανεξάρτητες μεταβλητές του μοντέλου είναι στατιστικά σημαντικές με ιδιαίτερα ικανοποιητικό τρόπο για δεδομένα που προέρχονται από την πραγματική αγορά ακινήτων της Βαρκελώνης. 196
209 dimension0 Κ ε φ ά λ α ι ο 5 ο Πίνακας 5.10: Πίνακας Coefficients που περιλαμβάνει τις τιμές t των ανεξάρτητων μεταβλητών Coefficients a Model Unstandardized Standardized 95,0% Confidence Collinearity Coefficients Coefficients Interval for B Correlations Statistics Lower Upper Zero- B Std. Error Beta t Sig. Bound Bound order Partial Part Tolerance VIF 3 (Constant) 55351, ,828 3,814, , ,944 AGE -1592, ,591 -,554-10,105, , ,913 -,601 -,819 -,541,954 1,049 AREA 1778, ,520,539 9,965, , ,464,554,816,534,979 1,022 HEATING 14071, ,542,395 7,159, , ,918,569,711,383,943 1, Ανεξαρτησία οντοτήτων Η παραδοχή της ανεξαρτησίας των οντοτήτων είναι ιδιαίτερα σημαντική, διότι αποκλείει την περίπτωση η συμμετοχή μίας οντότητας να επηρεάζει τη συμμετοχή μίας άλλης οντότητας του δείγματος, γεγονός το οποίο εκφράζεται από την ανεξαρτησία των υπολοίπων. Για την ικανοποίηση της παραδοχής αξιοποιείται ο δείκτης Durbin Watson και το διάγραμμα διασποράς των Studentized Residuals με τη σειρά καταχώρησης των δεδομένων (Α/Α). Δείκτης Durbin Watson Η τιμή του στατιστικού δείκτη Durbin Watson όταν βρίσκεται μεταξύ των τιμών 1,5 και 2,5 υποδεικνύει ότι υπάρχει ανεξαρτησία μεταξύ των οντοτήτων. Στην προκειμένη περίπτωση η τιμή του στατιστικού δείκτη είναι ίση με 1,869, συνεπώς ικανοποιείται η συνθήκη της ανεξαρτησίας για το μοντέλο των 54 οντοτήτων. Πίνακας 5.11: Δείκτης Durbin Watson στον πίνακα Model Summary Model Summary d Model Change Statistics Adjusted Std. Error R R R of the Square F Sig. F Durbin- R Square Square Estimate Change Change df1 df2 Change Watson 1,601 a,361, ,058,361 29, ,000 2,842 b,710, ,365,348 61, ,000 3,926 c,857, ,326,147 51, ,000 1,869 Μεταπτυχιακή διατριβή 197
210 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα σκέδασης Studentized residuals vs Sequence Διάγραμμα 5.27: Διάγραμμα σκέδασης (Studentized Residuals vs Sequence) Το διάγραμμα 5.27 παρουσιάζει μια ομοιόμορφη κατανομή, χωρίς την παρουσία συσσωρεύσεων και προτύπων. Όλες οι τιμές των Studentized Residuals βρίσκονται εντός του εύρους ± 2 (πάνω και κάτω από την τιμή 0) και η τιμή τους δεν εξαρτάται από τη σειρά με την οποία καταχωρήθηκαν στο δείγμα. Συνεπώς, το διάγραμμα των Studentized Residuals έναντι της τάξης καταχώρησης των δεδομένων φανερώνει την ανεξαρτησία των οντοτήτων, όπως έγινε και με την περίπτωση του στατιστικού δείκτη Durbin Watson Πολυσυγγραμικότητα ή Συγγραμικότητα Στο παρόν υποκεφάλαιο ελέγχεται η ύπαρξη συσχέτισης μεταξύ των ανεξάρτητων μεταβλητών. Η ύπαρξη πολυσυγγραμικότητας οδηγεί σε αύξηση των τυπικών σφαλμάτων των συντελεστών παλινδρόμησης και άρα είναι ένα ιδιαίτερα σημαντικό πρόβλημα για την αξιοπιστία του μοντέλου. Ο έλεγχος πραγματοποιείται με τη βοήθεια τεσσάρων στατιστικών δεικτών, του παράγοντα ανοχής (Tolerance factor) του παράγοντα πληθωριστικής διακύμανσης (Variance Inflation Factor), των ιδιοτιμών (Eigenvalues) και των δεσμευμένων δεικτών (Condition Indexes). Παράγοντας ανοχής (Tolerance factor) & Παράγοντας πληθωριστικής διακύμανασης (Variance Inflation Factor) Σύμφωνα με τον πίνακα 5.12 η τιμή του παράγοντα ανοχής (Tolerance factor) για τη μεταβλητή AGE είναι ίση με 0,954, για τη μεταβλητή AREA 0,979 και για τη μεταβλητή 198
211 Κ ε φ ά λ α ι ο 5 ο HEATING 0,943. Όταν οι τιμές του παράγοντα Tolerance είναι κοντά στο μηδέν, τότε είναι έντονο το φαινόμενο πολυσυγγραμμικότητας. Αντίθετα τιμές μεγαλύτερες του 0,5 και μέχρι τη μονάδα αποδεικνύουν ότι η ανεξάρτητη μεταβλητή δεν παρουσιάζει κανένα πρόβλημα πολυσυγγραμμικότητας. Στην προκειμένη περίπτωση η τιμές είναι κοντά στη μονάδα, άρα ισχύει η παραδοχή της έλλειψης πολυσυγγραμικότητας. Πίνακας 5.12: Πίνακας Coefficients ο οποίος περιλαμβάνει τις τιμές VIF και Tolerance Coefficients a Model Unstandardized Standardized 95,0% Confidence Collinearity Coefficients Coefficients Interval for B Correlations Statistics Lower Upper Zero- B Std. Error Beta t Sig. Bound Bound order Partial Part Tolerance VIF 3 (Constant) 55351, ,828 3,814, , ,944 AGE -1592, ,591 -,554-10,105, , ,913 -,601 -,819 -,541,954 1,049 AREA 1778, ,520,539 9,965, , ,464,554,816,534,979 1,022 HEATING 14071, ,542,395 7,159, , ,918,569,711,383,943 1,060 Ο παράγοντας πληθωριστικής διακύμανσης VIF φανερώνει αντίστοιχα πρόβλημα πολυσυγγραμικότητας, όταν οι τιμές του είναι μεγαλύτερες της τιμής δύο. Σύμφωνα με τα στοιχεία του πίνακα 5.12 οι τιμές VIF των τριών ανεξάρτητων μεταβλητών είναι όλες κοντά στη μονάδα. Συνεπώς και ο δεύτερος στατιστικός δείκτης δεν παρουσιάζει κανένα πρόβλημα πολυσυγγραμικότητας. Έλεγχος ιδιοτιμών (Eigenvalues) & Δεσμευμένοι δείκτες (Condition indexes) Οι τιμές Eigenvalues αποτελούν ένδειξη πιθανού προβλήματος, όταν βρίσκονται πάρα πολύ κοντά στην τιμή μηδέν. Στην προκειμένη περίπτωση μόνο η μεταβλητή HEATING έχει τιμή που προσεγγίζει το μηδέν, παρόλα αυτά η συγκεκριμένη προσέγγιση δε θεωρείται στατιστικά σημαντική για να δημιουργεί πρόβλημα πολυσυγγραμικότητας. Αντίστοιχα οι δεσμευμένοι δείκτες όταν είναι μικρότεροι από την τιμή 15 δεν εμφανίζουν κανένα πρόβλημα πολυσυγγραμικότητας των ανεξάρτητων μεταβλητών, ενώ όταν η τιμή τους είναι μεταξύ 15 και 30 υπάρχει πιθανότητα η συγκεκριμένη μεταβλητή να αποτελεί πρόβλημα για το μοντέλο. Για τιμές μεγαλύτερες από 30 θα πρέπει να ελέγχεται η πιθανή απομάκρυνση της εκάστοτε μεταβλητής. Σύμφωνα με τον πίνακα 5.13, οι τιμές του δείκτη για τις μεταβλητές AGE και AREA είναι πολύ μικρότερες από την οριακή τιμή, ενώ η μεταβλητή HEATING την ξεπερνά για πολύ λίγο. Συνεπώς, ο τέταρτος στατιστικός δείκτης, όπως και όλοι οι προηγούμενοι, δεν φανερώνουν πρόβλημα συσχέτισης των ανεξάρτητων μεταβλητών και άρα ικανοποιείται και η τρίτη παραδοχή του μοντέλου. Μεταπτυχιακή διατριβή 199
212 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Πίνακας5.13: Πίνακας Colllinearity Diagnostics που περιλαμβάνει τις τιμές Eigenvalue και Condition Index Collinearity Diagnostics a Model Dimension Condition Variance Proportions Eigenvalue Index (Constant) AGE AREA HEATING 3 1 3,430 1,000,00,01,00,03 2,461 2,728,00,05,00,80 3,095 6,019,04,91,07,17 4,015 15,358,95,03,93, Κανονικότητα Ο έλεγχος κανονικότητας των υπολοίπων αποτελεί την τέταρτη προϋπόθεση που οφείλει να ικανοποιείται για το σχηματισμό ενός αξιόπιστου γραμμικού μοντέλου. Για την παραδοχή της κανονικότητας αξιοποιούνται τα Studentized Deleted Residuals μέσω της διαδικασίας Explore (Analyze Descriptive Statistics Explore), τα οποία ακολουθούν την κανονική κατανομή. Ακολουθούν οκτώ διαφορετικοί τρόποι επιβεβαίωσης της ύπαρξης κανονικότητας, οι περισσότεροι από τους οποίους είναι διαγραμματικοί και ένας αφορά έλεγχο στατιστικού κριτηρίου. Φυλλογράφημα των υπολοίπων [Stem And- Leaf- Plot of residuals Studentized deleted residuals] Το φυλλογράφημα των υπολοίπων που απεικονίζεται παρακάτω δεν εμφανίζει καμία ακραία οντότητα και παρουσιάζει τη γνωστή καμπανοειδή μορφή της κανονικής κατανομής, στραμμένη κατά 90 ο. Η ύπαρξη συμμετρίας στη μορφή της κατανομής οδηγεί στο συμπέρασμα ότι το φυλλογράφημα μαρτυρά της ύπαρξη κανονικότητας. Studentized Deleted Residual Stem-and-Leaf Plot Frequency Stem & Leaf 1, , , , , , , , , Stem width: 1,00000 Each leaf: 1 case(s) 200
213 Κ ε φ ά λ α ι ο 5 ο Διάγραμμα 5.28: Φυλλογράφημα των υπολοίπων για την περιοχή Sant Marti της Βαρκελώνης Test of normality : Kolmogorv Smirnov, Lillefors, Shapiro Wilk Ο δεύτερος έλεγχος αναφέρεται στο στατιστικό κριτήριο Kolmogorov Smirnov και στο Shapiro Wilk. Για δείγματα που χαρακτηρίζονται μεγάλα (n>30) αρκεί η αξιοποίηση μόνο του πρώτου. Συνεπώς, ο έλεγχος της υπόθεσης της κανονικότητας των υπολοίπων γίνεται με τη χρήση του ελέγχου Kolmogorov Smirnov με: Μηδενική Υπόθεση Ho: Τα υπόλοιπα κατανέμονται κανονικά και Εναλλακτική Υπόθεση H1: Τα υπόλοιπα δεν κατανέμονται κανονικά. Σύμφωνα με τον πίνακα 5.14, το τεστ για την κανονικότητα των Kolmogorov Smirnov δίνει επίπεδο στατιστικής σημαντικότητας (Sig.) 20%, δηλαδή μεγαλύτερο του 5%. Συνεπώς, δεν μπορεί να απορριφθεί η υπόθεση ότι τα Studentized Deleted Residuals ακολουθούν την κανονική κατανομή. Πίνακας 5.14: Πίνακας Tests of Normality Kolmogorv Smirnov, Lillefors, Shapiro Wilk Tests of Normality Kolmogorov-Smirnov a Shapiro-Wilk Statistic df Sig. Statistic df Sig. Studentized Deleted Residual,068 54,200 *,991 54,960 a. Lilliefors Significance Correction *. This is a lower bound of the true significance. Normal Q-Q Plot of Studentized deleted Residuals Η γραμμή του διαγράμματος 5.29 αντιπροσωπεύει την θεωρητική κανονική κατανομή. Συνεπώς γα τον έλεγχο της κανονικότητας θα πρέπει να εξεταστεί η διασπορά των σημείων σε σχέση με την ευθεία γραμμή. Από το παρακάτω γράφημα παρατηρείται ότι υπάρχουν μερικές διαφοροποιήσεις στα σημεία του διαγράμματος σε σχέση με τη γραμμή που ορίζει την πλήρη κανονικότητα, οι οποίες όμως δεν απορρίπτουν την περίπτωση της κανονικής κατανομής. Μεταπτυχιακή διατριβή 201
214 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα 5.29: Διάγραμμα κανονικότητας Normal Q-Q Plot of Studentized Deleted Residuals για τον έλεγχο της κανονικότητας των υπολοίπων Detrended normal Q-Q Plot Studentized Deleted residuals 202
215 Κ ε φ ά λ α ι ο 5 ο Διάγραμμα 5.30: Διάγραμμα Detrended Νormal Q-Q Plot Studentized Deleted Ρesiduals για τον έλεγχο της κανονικότητας των υπολοίπων Το διάγραμμα Detrended normal Q-Q Plot Studentized Deleted Residual (Διάγραμμα 5.30) απεικονίζει στον άξονα Χ τις παρατηρούμενες τιμές των Studentized Deleted Residuals, ενώ στον άξονα Υ τα ποσοστιαία σημεία μίας τυπικής κανονικής κατανομής. Όλα τα σημεία κατανέμονται τυχαία πάνω και κάτω από το μηδέν, χωρίς την εμφάνιση προτύπων. Επίσης, η πιο απομακρυσμένη τιμή βρίσκεται στο 0,4, συνεπώς σύμφωνα με το διάγραμμα δεν υπάρχουν ακραίες οντότητες και ικανοποιείται η παραδοχή της κανονικότητας των υπολοίπων. Histogram Studentized Deleted Residuals Στο παρακάτω ιστόγραμμα (Διάγραμμα 5.31) των συχνοτήτων με τα Studentized Deleted Residuals, είναι ξεκάθαρο ότι προσεγγίζεται η κανονική κατανομή των υπολοίπων και πέραν ορισμένων εκτροπών από τη θεωρητική καμπύλη, ικανοποιείται η παραδοχή της κανονικότητας. Διάγραμμα 5.31: Ιστόγραμμα των Studentized Deleted Residuals για τον έλεγχο της κανονικότητας των υπολοίπων Μεταπτυχιακή διατριβή 203
216 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Histogram Standardized Residuals Διάγραμμα 5.32: Ιστόγραμμα των Standardized Residuals για τον έλεγχο της κανονικότητας των υπολοίπων Το παραπάνω ιστόγραμμα συχνοτήτων δημιουργείτε από την κύρια διαδικασία εκτέλεσης της γραμμικής παλινδρόμησης και χρησιμοποιείται ιδιαίτερα πολύ στη συνήθη στατιστική ανάλυση. Η καμπύλη κανονικής κατανομής που προσαρμόζεται στο ιστόγραμμα φανερώνει την ικανοποίηση της παραδοχής της κανονικότητας. Διάγραμμα Normal P-P Plot of regression standardized residuals Το Normal P-P Plot Standardized Residual είναι ένα διάγραμμα αναμενόμενης παρατηρούμενης αθροιστικής πιθανότητας, το οποίο παράγεται μέσω της βασικής διαδικασίας εκτέλεσης της παλινδρόμησης. Παρατηρείται ότι η πλειοψηφία των παρατηρήσεων συγκεντρώνονται γύρω από την ευθεία γραμμή, με αποκλίσεις που δεν επηρεάζουν όμως σημαντικά την κανονικότητα. Συνεπώς, το έκτο στη σειρά γράφημα παρουσιάζει υπόλοιπα τα οποία ακολουθούν την κανονική κατανομή. 204
217 Κ ε φ ά λ α ι ο 5 ο Διάγραμμα 5.33: Διάγραμμα Normal P-P Plot of regression Standardized Residuals για τον έλεγχο της κανονικότητας των υπολοίπων Θηκόγραμμα των υπολοίπων (Boxplot of Residuals) Διάγραμμα 5.34: Θηκόγραμμα για τον εντοπισμό των ακραίων τιμών του δείγματος μέσω της διαδικασίας Explore Μεταπτυχιακή διατριβή 205
218 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Όπως φαίνεται από το παρακάτω θηκόγραμμα (Διάγραμμα 5.34) η διάμεσος του τοποθετείται στο μέσο του ορθογωνίου παραλληλογράμμου με αποτέλεσμα να περιγράφει μία συμμετρική κανονική κατανομή. Επίσης, δεν εμφανίζεται καμία ακραία τιμή άνω και κάτω από το ορθογώνιο, γεγονός που είναι ιδιαίτερα σημαντικό, διότι σε επόμενο βήμα ακολουθεί ο έλεγχος των ακραίων τιμών και οντοτήτων επίδρασης. Το γενικό συμπέρασμα που προκύπτει από τους οκτώ ελέγχους που προηγούνται είναι ότι στο τέταρτο μοντέλο που αναφέρεται στην περιοχή Sant Marti της βαρκελώνης, ικανοποιείται η παραδοχή κανονικότητας των υπολοίπων επιτυχημένα Ισότητα διακυμάνσεων ή ομοσκεδαστικότητα Η ικανοποίηση της παραδοχής της ομοσκεδασιμότητας πραγματοποιείται με τη βοήθεια των ακόλουθων τριών διαγραμμάτων σκέδασης: Studentized Deleted Residuals vs Standardized Predicted Values (Διάγραμμα 5.35 αριστερά) Studentized Residuals vs Standardized Predicted Values (Διάγραμμα 5.35 δεξιά) Standardized Predicted Values vs Dependent Variable (Διάγραμμα 5.36) Αρχικά, τα δύο διαγράμματα διασποράς παρουσιάζουν μία τυχαία κατανομή των κουκκίδων τους, με ομοιόμορφο τρόπο, πάνω και κάτω από τη νοητή γραμμή στο σημείο μηδέν. Παράλληλα το σύνολο των 54 σημείων βρίσκεται εντός της ζώνης εύρους ±2, πέραν δύο κουκκίδων οι οποίες όμως είναι μέσα στο διάστημα ±3, όπου βρίσκεται το 99,73% των παρατηρήσεων. Συνεπώς δεν υπάρχει καμία ένδειξη προβλήματος, αντίθετα αποδεικνύεται η ύπαρξη ομοσκεδασιμότητας στο μοντέλο των 54 οντοτήτων. Διάγραμμα 5.35: Διάγραμμα σκέδασης των Studentized Deleted Residuals με τα Standardized Predicted Values (αριστερά) και διάγραμμα σκέδασης των Studentized Residuals με τα Standardized Predicted Values (δεξιά) 206
219 Κ ε φ ά λ α ι ο 5 ο Το τρίτο διάγραμμα απεικονίζει τη διασπορά των παρατηρούμενων (Υ) και τυποποιημένων εκτιμώμενων τιμών (Standardized Predicted Value). Η γραμμή στο κέντρο του διαγράμματος αντιπροσωπεύει την ευθεία των ελαχίστων τετραγώνων και η ζώνη που δημιουργείται γύρω από την ευθεία αντιπροσωπεύει το 95% των παρατηρήσεων. Κρίνοντας από το γεγονός ότι όλα τα σημεία συγκεντρώνονται με ομοιόμορφο τρόπο γύρω από την ευθεία των ελαχίστων τετραγώνων και τοποθετούνται εντός ζώνης, προκύπτει το συμπέρασμα ότι ικανοποιείται επιτυχώς η απαίτηση της ομοσκεδασιμότητας. Τα δύο πρώτα διαγράμματα (Διάγραμμα 5.35) με τον τρόπο με τον οποίο διαμορφώνονται δηλώνουν ταυτόχρονα ότι οι τρεις ανεξάρτητες μεταβλητές του μοντέλου των 54 οντοτήτων συσχετίζονται γραμμικά και άρα ικανοποιούν τη συνθήκη της γραμμικότητας, που αποτελεί επίσης μία πολύ σημαντική προϋπόθεση του μοντέλου (Βλ ). Διάγραμμα 5.36: Διάγραμμα σκέδασης των Standardized Predicted Values με τις τιμές της εξαρτημένης μεταβλητής Υ Μεταπτυχιακή διατριβή 207
220 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Γραμμικότητα Η υπόθεση που γίνεται στο πρώτο στάδιο της εργασίας, πάνω στην οποία στηρίζεται όλη η μεθοδολογία, είναι η ύπαρξη γραμμικής σχέσης μεταξύ της εξαρτημένης και των ανεξάρτητων μεταβλητών. Η επιβεβαίωση της γραμμικότητας πραγματοποιείται με τη βοήθεια τεσσάρων διαφορετικών κατηγοριών διαγραμμάτων διασποράς, τα περισσότερα εκ των οποίων έχουν ήδη ερμηνευτεί σε προηγούμενα στάδια ελέγχου των μοντέλων. Ο πρώτος τρόπος ελέγχου πραγματοποιείται με τη βοήθεια των διαγραμμάτων σκέδασης μεταξύ της εξαρτημένης και των ανεξάρτητων μεταβλητών Xi. Στο υποκεφάλαιο το γράφημα Matrix Scatter Plot αναφέρεται στο αρχικό δείγμα των 60 οντοτήτων και για τις εννέα μεταβλητές. Το ακόλουθο αντίστοιχο διάγραμμα αναφέρεται στο τελικό μοντέλο των 54 οντοτήτων, για τις τρεις μόνο ανεξάρτητες μεταβλητές. Οι συσχετίσεις που απεικονίζονται σε κάθε τετραγωνίδιο αφορούν τη συσχέτιση που υφίσταται μεταξύ της κάθε ανεξάρτητης μεταβλητής με την εξαρτημένη αλλά ταυτόχρονα και με όλες τις άλλες ανεξάρτητες μεταβλητές. Το διάγραμμα αποκαλύπτει την ύπαρξη γραμμικότητας, η οποία είναι φυσικά ισχυρότερη στην περίπτωση του εμβαδού και της ηλικίας. Διάγραμμα 5.37: Διάγραμμα σκέδασης των ανεξάρτητων μεταβλητών (AREA, AGE, HEATING)με τις τιμές της εξαρτημένης μεταβλητής Υ για το δείγμα των 54 οντοτήτων Το δεύτερο διάγραμμα ελέγχου αποτελεί το διάγραμμα σκέδασης των Studentized Deleted Residuals με τα Standartized Predicted Values, ενώ το τρίτο αποτελεί το παρόμοιο του διάγραμμα σκέδασης μεταξύ των Studenized Residuals και των Standartized Predicted 208
221 Κ ε φ ά λ α ι ο 5 ο Values. Η οπτική ερμηνεία των δύο έχει προηγηθεί στο προηγούμενο κεφάλαιο ( ), αποδεικνύοντας ότι ισχύει η παραδοχή της γραμμικότητας. Τελευταία βασική κατηγορία ελέγχου της γραμμικότητας αποτελούν τα διαγράμματα μερικής συσχέτισης, τα οποία όπως φαίνεται από το υποκεφάλαιο φανερώνου εύκολα τη γραμμικότητα του μοντέλου. Έπειτα από την επιβεβαίωση της γραμμικότητας από το σύνολο των διαγραμμάτων που προαναφέρονται, απομένει μόνο ένας έλεγχος (έλεγχος ύπαρξης ακραίων οντοτήτων) για την οριστική αποδοχή του τέταρτου μοντέλου ως αξιόπιστο Ακραίες οντότητες και οντότητες επίδρασης Ο εντοπισμός των οντοτήτων που απέχουν από το σύνολο των υπόλοιπων περιπτώσεων με αποτέλεσμα να επιδρούν είτε στην κλίση της ευθείας παλινδρόμησης, είτε στους συντελεστές των μεταβλητών είναι η ακόλουθη διαδικασία. Όπως αναφέρεται και στα προηγούμενα μοντέλα για τον εντοπισμό των ακραίων οντοτήτων (outliers) αξιοποιείται η απόσταση Mahalanobis (Mahalanobis distance Di2) και η τιμή Centered Leverage. Για τον εντοπισμό των οντοτήτων επίδρασης (influential points)αξιοποιούνται αντίστοιχα οι αποστάσεις Cook (Cook s Distance : CD i ), το μέτρο DFFITS (Standardized DFFITS) και το μέτρο DFBetas (Standardized DFBetas). Για την οπτικοποίηση των ακραίων οντοτήτων αξιοποιούνται τα διαγράμματα Cook s distance με Centered Leverage Values, Standardized DFFITS με την αύξουσα σειρά των παρατηρήσεων A/A και Standardized DFBETA X i με A/A. Τέλος, η απομάκρυνση των υποψήφιων οντοτήτων που προκύπτουν από τους προηγούμενους ελέγχους ελέγχεται με τη βοήθεια της κατανομής t (Διαδικασία BONFERRONI) και της κατανομής F. Σε όλους τους παρακάτω ελέγχους υπολογίζεται αρχικά η κρίσιμη τιμή των δεικτών, βάσει μεθοδολογίας (κριτήριο αποτελεί το μέγεθος του δείγματος και ο αριθμός των μεταβλητών) και στη συνέχεια συγκρίνεται με τις αντίστοιχες τιμές του δείκτη σε κάθε οντότητα. Centered Leverage Οι τιμές του δείκτη Centered Leverage ελέγχονται με κριτήριο την τιμή 0,2, η οποία αποτελεί οριακή τιμή. Σύμφωνα με Δαφέρμο, 2005 όταν οι τιμές του δείκτη Centered Leverage είναι μικρότερες από 0,2, τότε δεν υπάρχει ένδειξη ακραίας οντότητας. Από τον έλεγχο όλων των τιμών Centered Leverage στη στήλη LEV_1, καμία οντότητα δεν ξεπερνά την κρίσιμη τιμή, άρα δεν υπάρχει καμία ένδειξη ύπαρξης ακραίας οντότητας 26. Με τον έλεγχο του δείκτη Centered Leverage, ικανοποιείται ταυτόχρονα και ο δείκτης Mahalanobis. 26 Στο διάγραμμα Cook με Centered Leverage οπτικοποιείται το γεγονός ότι όλες οι τιμές είναι μικρότερες του 0,2 Μεταπτυχιακή διατριβή 209
222 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Αποστάσεις Cook CD i Η αντίστοιχη κρίσιμη τιμή στην περίπτωση των αποστάσεων Cook είναι η μονάδα, ενώ η στήλη που περιέχει τις τιμές Cook του δείγματος για κάθε οντότητα είναι η COO_1. Σύμφωνα με τα δεδομένα που προκύπτουν από την εκτέλεση πολλαπλής παλινδρόμησης όλες οι τιμές Cook είναι πολύ μικρότερες της μονάδας και συνεπώς καμία οντότητα δε χαρακτηρίζεται οντότητα επίδρασης. Μέτρα DfFits Για τον εντοπισμό των οντοτήτων επίδρασης υπολογίζεται η Standardized DfFits κρίσιμη βάσει του ακόλουθου τύπου: Standardized DfFits κρίσιμη = 2* = 0,54 Για τον έλεγχο λαμβάνεται υπόψη η στήλη SDF_1 του Data Editor, η οποία φανερώνει ότι οι οντότητες με Α/Α 36 (0,86) και 54 (0,75) ξεπερνούν την οριακή τιμή. Όπως παρατηρείται οι τιμές δεν απέχουν σημαντικά από την τιμή 0,54, οπότε είναι πολύ πιθανό να μην αποτελούν οι οντότητες 36 και 54 πρόβλημα για την αξιοπιστία του μοντέλου. Παρόλα αυτά θεωρούνται υποψήφιες οντότητες επίδρασης και η αξιολόγηση με την ολοκλήρωση όλων των ελέγχων θα δείξει αν απομακρύνονται ή όχι. Μέτρα DfBetas Για τον έλεγχο αξιοποιούνται οι απόλυτες τιμές των Standardized DfBetas και στη συνέχεια συγκρίνονται με την κρίσιμη τιμή για την ύπαρξη οντοτήτων επίδρασης. Η κρίσιμη τιμή για τις περιπτώσεις των μεγάλων δειγμάτων (n>30) δίνεται από την ακόλουθη σχέση: Standardized DfBetas κρίσιμη = = 0,27 Αναλυτικά, για τον έλεγχο που αφορά τη μεταβλητή AREA λαμβάνεται υπόψη η στήλη με τίτλο SDB1_1 του Data Editor, η οποία επισημαίνει τις οντότητες με Α/Α 8 (0,35), 16 (0,32) και 36 (0,59) ως υποψήφιες οντότητες επίδρασης. Για τον έλεγχο που αφορά τη μεταβλητή AGE λαμβάνεται υπόψη η στήλη με τίτλο SDB2_1 του Data Editor, η οποία επισημαίνει ως υποψήφιες οντότητες επίδρασης τις 36 (0,54) και 54 (0,58). Τέλος, για τον έλεγχο που αφορά τη μεταβλητή HEATING αξιοποιείται η στήλη με τίτλο SDB5_1 του Data Editor, η οποία με τη σειρά της επισημαίνει τις οντότητες 21 (0,45) και 54 (0,43) ως υποψήφιες οντότητες επίδρασης. Από το σύνολο των οντοτήτων που επισημαίνονται παραπάνω, μόνο οι οντότητες με Α/Α 36 και 54 έχουν τις μεγαλύτερες αποκλίσεις και ταυτόχρονα εντοπίζονται σε περισσότερους από έναν δείκτες (DFits, DfBetas (1), DfBetas(2) και DfBetas (5)). Παρόλα αυτά καμία από τις παραπάνω οντότητες δεν απομακρύνεται εάν αρχικά δεν ολοκληρωθούν όλες οι μέθοδοι εντοπισμού των οντοτήτων επίδρασης του μοντέλου. 210
223 Κ ε φ ά λ α ι ο 5 ο Διάγραμμα σκέδασης των αποστάσεων Cook με κεντραρισμένες τιμές Leverage Οι έλεγχοι που πραγματοποιούνται παραπάνω με τη βοήθεια των Cook αποστάσεων, των τιμών Centered Leverage, των DfFits και των DfBetas, μπορούν να οπτικοποιηθούν στα αντίστοιχα διαγράμματα προκειμένου να γίνουν ευκολότερα κατανοητές οι αποκλίσεις και ο βαθμός τους σε σύγκριση με το σύνολο των υπόλοιπων οντοτήτων. Διάγραμμα 5.38: Διάγραμμα σκέδασης των αποστάσεων Cook με τις Centered Leverage τιμές Σύμφωνα με το διάγραμμα 5.38, που απεικονίζει τις αποστάσεις Cook με τις Centered Leverage τιμές οπτικοποιείται το γεγονός ότι όλες οι τιμές των οντοτήτων είναι τοποθετημένες εντός των επιτρεπόμενων ορίων και άρα δεν υποδεικνύεται καμία οντότητα που να επηρεάζει σημαντικά την κλίση της ευθείας παλινδρόμησης ή τους συντελεστές της παλινδρομικής εξίσωσης. Διάγραμμα σκέδασης των τυποποιημένων DfFits με την ακολουθία των παρατηρήσεων Όμοια στο παρακάτω διάγραμμα σκέδασης των τυποποιημένων DfFits με την ακολουθία των παρατηρήσεων, οπτικοποιούνται οι δύο οντότητες που εντοπίζονται βάσει του αριθμητικού ελέγχου παραπάνω. Οι οντότητες 36 και 54 ξεπερνούν την οριακή τιμή και ξεχωρίζουν αισθητά σε σχέση με τις υπόλοιπες 52 περιπτώσεις. Μεταπτυχιακή διατριβή 211
224 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα 5.39: Διάγραμμα Sequence των Standardized DfFits με την αύξουσα σειρά του δείγματος Για την καλύτερη κατανόηση της απόκλισης από τις οριακές τιμές ±0,544, τοποθετούνται οι δύο κίτρινες οριζόντιες γραμμές, οι οποίες θέτουν τα θεωρητικά όρια για την ύπαρξη οντοτήτων επίδρασης. Σημαντική επισήμανση είναι βέβαια ότι ακόμη και οι ακραίες οντότητες (36 & 54) δεν ξεπερνούν την μονάδα, η οποία τίθεται ως όριο στα μικρά δείγματα και άρα είναι πολύ πιθανό να μην απαιτηθεί η απομάκρυνση τους. Διάγραμμα σκέδασης των τυποποιημένων DfBetas με την ακολουθία των παρατηρήσεων Όμοια στην περίπτωση του διαγράμματος απεικόνισης των τιμών DfBetas, οπτικοποιείται ο βαθμός απόκλισης των υποψήφιων οντοτήτων επίδρασης, οι οποίοι έχουν ήδη επισημανθεί. Οι οντότητες ταξινομημένες κατά βαθμό απόκλισης τους από την οριακή τιμή είναι οι 16 (Μπλε γραμμή), 8 (Μπλε γραμμή), 54 (Καφέ γραμμή), 21 (καφέ γραμμή), 36 (Πράσινη γραμμή), 54 (Πράσιμη γραμμή) και 36 (Μπλε γραμμή). 212
225 Κεφάλαιο 5ο Διάγραμμα 5.40: Διάγραμμα Sequence των Standardized DfBeta με την αύξουσα σειρά του δείγματος Στους ελέγχους των δύο κατανομών που ακολουθούν στηρίζεται η απομάκρυνση ή όχι των παραπάνω υποψήφιων οντοτήτων επίδρασης. t κατανομή Τα Studentized Deleted Residuals μέσω της διαδικασίας Bonferroni και της t κατανομής μπορούν να βοηθήσουν στον εντοπισμό των οντοτήτων επίδρασης. Όπου ti ορίζεται η τιμή των Studentized Deleted Residuals, τα οποία ακολουθούν την κανονική κατανομή με βαθμούς ελευθερίας: β.ε. = n-p-1 = =49 Η κρίσιμη τιμή που ορίζει η διαδικασία Bonferroni και είναι ίση με: t κρίσιμη = t(1 - ; n-p-1) t (0, ; 49) = 3, με α το επίπεδο στατιστικής σημαντικότητας (α= 0,05), n το μέγεθος του δείγματος (n =54) και p τον αριθμό των συντελεστών παλινδρόμησης μαζί με το σταθερό όρο (p = 4). Επόμενο βήμα αποτελεί ο εντοπισμός της οντότητας με το μεγαλύτερο Studentized Deleted Residual (max SDR)ώστε να συγκριθεί με την οριακή τιμή που προέκυψε παραπάνω. 27 Η τελική τιμή προκύπτει μέσω των στατιστικών πινάκων Μεταπτυχιακή διατριβή 213
226 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Από τα δεδομένα του Data Editor προκύπτει ότι η οντότητα με τη μεγαλύτερη απόλυτη τιμή Studentized Deleted Residual κατά απόλυτη τιμή είναι η = = 2,5064. Ορίζεται η μηδενική υπόθεση Ηο: Το Studentized Deleted Residual με τη μεγαλύτερη απόλυτη τιμή είναι μία οντότητα επίδρασης, με εναλλακτική υπόθεση =2,5064 ΔΕΝ Η1: Studentized Deleted Residual με τη μεγαλύτερη απόλυτη τιμή = 2,5064 είναι οντότητα επίδρασης Επειδή όμως = 2,5064 <3,2656 ισχύει η μηδενική υπόθεση Ηο και η οντότητα 56 δεν αποτελεί οντότητα επίδρασης. F κατανομή Οι τιμές Cook θεωρείται ότι ακολουθούν την κατανομή F(1-a;p;n-p), συνεπώς με τη βοήθεια της κατανομής μπορούν να εντοπιστούν οι οντότητες επίδρασης εάν και εφόσον υπάρχουν. Με την ίδια λογική που περιγράφεται παραπάνω υπολογίζεται αρχικά η κρίσιμη τιμή F και στη συνέχεια συγκρίνεται με την τιμή Cook που είναι η μεγαλύτερη σε μέγεθος συγκριτικά με όλες τις υπόλοιπες. F κρίσιμη =F(1-a; p; n-p) = F(0,95; 4; 50) = 2,57 Η μέγιστη απόσταση Cook ανήκει στην οντότητα 36 και είναι ίση με CD 36 = 0,1776. Από τους στατιστικούς πίνακες της F κατανομής παρατηρείται ότι η τιμή βρίσκεται στο 25,70% εκατοστημόριο της συγκεκριμένης κατανομής, δηλαδή δεν πλησιάζει σε καμία περίπτωση το 50% και άρα η οντότητα δε μπορεί να χαρακτηριστεί οντότητα επίδρασης. Από τις δύο μέγιστες τιμές των Studentized Deleted Residual και Cook που εντοπίζονται γίνεται σαφές ότι οι οντότητες 36 και 54 ξεχωρίζουν σε σχέση με τις υπόλοιπες σε κάθε έλεγχο που επιχειρείται να πραγματοποιηθεί. Παρόλα αυτά σύμφωνα με τους δύο ελέγχους καμία από τις υποψήφιες οντότητες επίδρασης των προηγούμενων ελέγχων δε χρειάζεται να απομακρυνθεί από το μοντέλο και άρα αυτή είναι η τελική μορφή του με συνολικά 54 οντότητες Έλεγχος προβλεπτικής ικανότητας του μοντέλου Το μοντέλο των 54 οντοτήτων είναι αξιόπιστο, καθώς ικανοποιεί τους επτά διαδοχικούς ελέγχους της μεθοδολογίας και δεν παρουσιάζει δείγματα μη καλής προβλεπτικής δύναμης. Παρόλα αυτά για την επιβεβαίωση της προβλεπτικής του ικανότητας πραγματοποιούνται οι έλεγχοι που ακολουθούν Μέθοδος των διαστημάτων πρόβλεψης Για τον έλεγχο των διαστημάτων πρόβλεψης συλλέγονται τέσσερις νέες οντότητες, οι οποίες προέρχονται από τον ίδιο πληθυσμό από τον οποίο συλλέγεται το δείγμα. Στη συνέχεια οι νέες περιπτώσεις προστίθεται στο δείγμα των 54 οντοτήτων στο περιβάλλον εργασίας του SPSS. Εκτελείται η πολλαπλή γραμμική παλινδρόμηση μόνο για τις 54 πρώτες οντότητες και στη συνέχεια πραγματοποιείται η σύγκριση των γνωστών αγοραίων αξιών 214
227 Κ ε φ ά λ α ι ο 5 ο ακινήτων των τεσσάρων νέων οντοτήτων με το διάστημα πρόβλεψης (LICI, UICI) που προκύπτει από τη διαδικασία. Τα αποτελέσματα είναι τα ακόλουθα: < < < < < < < < Παρατηρείται ότι όλες οι αξίες βρίσκονται εντός του διαστήματος πρόβλεψης και άρα το μοντέλο θεωρείται πως έχει ικανοποιητική προβλεπτική δύναμη. Παράλληλα, το εύρος των διαστημάτων εμπιστοσύνης κατά μέσο όρο (περίπου ) αποδεικνύει ότι το μοντέλο είναι ιδιαιτέρως καλό και η περιοχή εμφανίζει σίγουρα μικρότερη ανομοιογένεια στον τρόπο που διαμορφώνονται οι αξίες των ακινήτων της, σε σύγκριση με την περιοχή Eixample της Βαρκελώνης Μέθοδος του διαχωρισμού των δεδομένων (Data Splitting) Στη συγκεκριμένη μέθοδο ελέγχου της προβλεπτικής δύναμης του μοντέλου, το δείγμα των 54 οντοτήτων χωρίζεται σε δύο τυχαία τμήματα. Με το πρώτο τμήμα του δείγματος εκτελείται η διαδικασία της πολλαπλής γραμμικής παλινδρόμησης με σκοπό να ελεγχθεί η ποιότητα του μοντέλου. Η εξίσωση παλινδρόμησης που δημιουργείται από το πρώτο στάδιο αξιοποιείται στο δεύτερο δίνοντας νέες τιμές εκτίμησης για όλες τις οντότητες. Εάν οι νέες προβλεπόμενες τιμές συσχετίζονται ισχυρά με τις παρατηρούμενες, τότε το μοντέλο χαρακτηρίζεται από ισχυρή προβλεπτική ικανότητα. 1 ο ΒΗΜΑ Επιλέγεται από το δείγμα των 54 οντοτήτων το 70% περίπου των παρατηρήσεων με τυχαία σειρά επιλογής. Το SPSS κατά την εκτέλεση της διαδικασίας επιλέγει συνολικά 42 οντότητες. Με το νέο δείγμα διαμερισμάτων εκτελείται η διαδικασία της πολλαπλής γραμμικής παλινδρόμησης και προκύπτει η παρακάτω εξίσωση παλινδρόμησης: Υ = 60228, ,136 AREA 1545,496 AGE ,768 HEATING Μεταπτυχιακή διατριβή 215
228 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ με R = 0,921, R 2 = 0,848, R 2 adj = 0,836 και δείκτη Durbin Watson = 1,912, τιμές VIF μικρότερες του 2 και τιμές t μεγαλύτερες του. Ταυτόχρονα, όλες οι υπόλοιπες τιμές των δεικτών είναι εντός επιτρεπόμενων ορίων. Συνεπώς, πρόκειται για ένα καλό και αξιόπιστο μοντέλο. Όσον αφορά τον έλεγχο ανεξαρτησίας των οντοτήτων, το διάγραμμα Studentized Residual vs AA (Sequence) επιβεβαιώνει ότι πρόκειται για ένα μοντέλο που πληρεί όλες τις βασικές παραδοχές μιας γραμμικής παλινδρόμησης (Διάγραμμα 4.43). Διάγραμμα 5.41: Διάγραμμα σκέδασης των Studentized Residual vs AA (Sequence) για τις 42 μόνο οντότητες του δείγματος ( ) 2 ο ΒΗΜΑ Στη συνέχεια της διαδικασίας με τη χρήση των υπόλοιπων 12 οντοτήτων και με τη χρήση της εξίσωσης παλινδρόμησης που προκύπτει από το πρώτο βήμα εκτελείται η εντολή Compute Variables. Δημιουργείται μία νέα στήλη PRED για το σύνολο των 54 οντοτήτων και στη συνέχεια μέσω του βήματος Analyze Correlation Bivariate υπολογίζεται η συσχέτιση Pearson μεταξύ της νέας στήλης PRED και των παρατηρούμενων τιμών Υ. Η συσχέτιση τους είναι ίση με 0,933, συνεπώς η προβλεπτική ικανότητα του μοντέλου των 54 οντοτήτων είναι πολύ ικανοποιητική. Για την επιβεβαίωση της αξιολόγησης κατασκευάζεται και το διάγραμμα σκέδασης μεταξύ των PRED και Υ, ώστε να οπτικοποιηθεί το αποτέλεσμα (Διάγραμμα 5.42). 216
229 Κ ε φ ά λ α ι ο 5 ο Διάγραμμα 5.42 : Διάγραμμα Bivariate συσχέτισης μεταξύ των προβλεπόμενων και παρατηρούμενων τιμών Είναι εμφανής ο ισχυρός βαθμός συσχέτισης των δύο τιμών και άρα η δύναμη πρόβλεψης του μοντέλου Μέθοδος εύρεσης του βέλτιστου αριθμού σημαντικών μεταβλητών Με τη βοήθεια του κριτηρίου Mallow s ελέγχεται εάν οι μεταβλητές οι οποίες επιλέγονται από τον αλγόριθμο ως στατιστικά σημαντικές είναι επαρκείς για να ερμηνεύσουν το φαινόμενο ή εάν είναι περισσότερες ή λιγότερες. Μέσω της διαδικασίας που περιγράφεται αναλυτικά στο υποκεφάλαιο παράγεται ο παρακάτω πίνακας (Πίνακας 5.15). Η διαδικασία ορίζει ότι ο αριθμός των μεταβλητών, ο οποίος ερμηνεύει ικανοποιητικά την αγοραία αξία των ακινήτων είναι τέσσερις (4). Στην προκειμένη περίπτωση ταυτίζεται με τον αριθμό των μεταβλητών που δομούν την τελική μορφή της εξίσωσης παλινδρόμησης, συνεπώς όλοι οι έλεγχοι συνηγορούν στο σχηματισμό ενός αξιόπιστου και με ικανοποιητική προβλεπτική ικανότητα μοντέλου. Μεταπτυχιακή διατριβή 217
230 dimension0 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Πίνακας 5.15: Πίνακας Model Summary που περιλαμβάνει το κριτήριο πρόβλεψης Mallow Model Summary Model Selection Criteria Std. Error Akaike Amemiya Mallows' Schwarz R Adjusted of the Information Prediction Prediction Bayesian R Square R Square Estimate Criterion Criterion Criterion Criterion 1,601 a,361, , ,895, , ,873 2,842 b,710, , ,328,324 53, ,295 3,926 c,857, , ,228,166 4, , Ερμηνεία μοντέλου για την περιοχή Sant Marti Το τέταρτο μοντέλο εκτίμησης ακινήτων αναφέρεται σε δείγμα 54 οντοτήτων έπειτα από την αφαίρεση έξι οντοτήτων για τη βελτιστοποίηση του. Ο αριθμός των μεταβλητών που σύμφωνα με τη στατιστική ανάλυση επιδρά στη διαμόρφωση των αξιών της τοπικής κτηματαγοράς είναι το εμβαδόν, η παλαιότητα και τέλος το είδος θέρμανσης που χρησιμοποιείται. Είναι σαφές ότι δεν απουσιάζει η συμβολή των υπόλοιπων παραγόντων στη διαμόρφωση της τιμής. Ωστόσο, η συνεισφορά τους σύμφωνα με το δείγμα των 60 οντοτήτων δεν είναι στατιστικά σημαντική ώστε να εισαχθούν στην παλινδρομική εξίσωση. Στόχος της στατιστικής ανάλυσης πάντα είναι η δημιουργία ενός αξιόπιστου μοντέλου, το οποίο να ανταποκρίνεται στην πραγματικότητα και να παρουσιάζει όσο γίνεται μεγαλύτερη προβλεπτική ικανότητα. Η αφαίρεση των έξι οντοτήτων, οδηγεί σε σαφώς καλύτερα γραφήματα, τιμές των στατιστικών δεικτών και γενικότερα σε ένα καλύτερο μοντέλο σε σύγκριση με την πρώτη προσέγγιση, παρόλο που ο αρχικός αριθμός των ανεξάρτητων μεταβλητών ήταν τέσσερις (AREA, AGE, HEATING, ROOM)και έγιναν στη συνέχεια τρεις (AREA, AGE, HEATING). Το βασικό χαρακτηριστικό του τέταρτου μοντέλου είναι ότι η πραγματοποίηση όλων των παραδοχών γίνεται σε πολύ ικανοποιητικό βαθμό. Κανένας από τους επτά κύριους ελέγχους της μεθοδολογίας δεν αφήνει περιθώρια αμφισβήτησης, καθώς όλοι οι στατιστικοί δείκτες απέχουν αρκετά από τις οριακές τιμές και τα διαγράμματα περιγράφουν ξεκάθαρη γραμμικότητα, κανονικότητα κλπ. Η ίδια εικόνα παρατηρείται και στο δεύτερο τμήμα, το οποίο αναφέρεται στις μεθόδου ελέγχους της προβλεπτικής του δύναμης. Συνεπώς, πρόκειται για ένα καλό μοντέλο, του οποίου η τελική εξίσωση παλινδρόμησης είναι η ακόλουθη: με R 2 = 0,857. Υ = 55351, ,445 AGE +1778,897 AREA ,012 HEATING 218
231 Κ ε φ ά λ α ι ο 5 ο Κρίνοντας από το συντελεστή προσδιορισμού R 2 υπάρχει μία πολύ καλή προσαρμογή του μοντέλου στα δεδομένα και άρα ένα μεγάλο τμήμα της αξίας ερμηνεύεται από τις τρεις μεταβλητές του μοντέλου (AREA, AGE, HEATING). Πιο συγκεκριμένα, το 85,7% της συνολικής διακύμανσης της αγοραίας αξίας των ακινήτων οφείλεται στα πληροφορίες που περιλαμβάνουν οι τρεις μεταβλητές. Όμοια, όσον αφορά τον προσαρμοσμένο συντελεστή προσδιορισμού (Adjusted R 2 ), το 84,8% αντιπροσωπεύει τη συνολική διακύμανση της αγοραίας αξίας που οφείλεται στις παραπάνω μεταβλητές για κάθε άλλο δείγμα του ίδιου πληθυσμού της περιοχής μελέτης Sant Marti, γεγονός που ταυτόχρονα φανερώνει την υψηλή προβλεπτική ικανότητα του μοντέλου. Ο πίνακας 5.11 παρουσιάζει ταυτόχρονα τη συμβολή της κάθε μίας ανεξάρτητης μεταβλητής στη διαμόρφωση των αξιών μέσω των συντελεστών προσδιορισμού R 2 κάθε μοντέλου κατά την εκτέλεση της βηματικής διαδικασίας (stepwise). Αναλυτικά, η μεταβλητή που συμβάλει περισσότερο στη διαμόρφωση της αγοραίας αξίας είναι η παλαιότητα με ποσοστό 36,1%. Ακολουθεί το εμβαδόν, το οποίο είναι υπεύθυνο για το 34,9% της διακύμανσης της εξαρτημένης μεταβλητής και τέλος το είδος θέρμανσης με ποσοστό συνεισφοράς 14,7%. Παρατηρείται ένας πολύ μεγάλος βαθμός επίδρασης της παλαιότητας, ο οποίος είναι περίπου ισόποσος με την επίδραση του εμβαδού στη διαμόρφωση της αξίας. Σημαντική είναι επίσης και η επίδραση του είδους θέρμανσης διότι οι κατοικίες της περιοχής Sant Marti, όπως φαίνεται από το δείγμα, υστερούν στην ποιότητα της θέρμανσης που παρέχουν και άρα πριμοδοτείται η ικανοποίηση του συγκεκριμένου χαρακτηριστικού. Το τελευταίο προς σχολιασμό χαρακτηριστικό που αφορά την εξίσωση πολλαπλής παλινδρόμησης είναι ο ρόλος του σταθερού της όρου. Ο σταθερός όρος έχει το ρόλο της εξισορρόπησης της αξίας μέσω της μαθηματικής εξίσωσης. Στην προκειμένη περίπτωση η τιμή του σταθερού όρου είναι θετική και ίση με 55351,061. Η βασική μαθηματική ερμηνεία είναι ότι η τιμή κάθε διαμερίσματος στην περιοχή Sant Marti της Βαρκελώνης είναι περίπου κατά μεγαλύτερη από αυτήν που διαμορφώνεται από τις ανεξάρτητες μεταβλητές του μοντέλου πολλαπλασιασμένες με τους συντελεστές τους. Ο σταθερός θετικός όρος εκφράζει την ύπαρξη λογικών τιμών των ανεξάρτητων μεταβλητών που προδίδουν την απουσία υπεραξίας. Μεταπτυχιακή διατριβή 219
232 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ 5.3 ΕΦΑΡΜΟΓΗ ΠΟΛΛΑΠΛΗΣ ΓΡΑΜΜΙΚΗΣ ΠΑΛΙΝΔΡΟΜΗΣΗΣ ΓΙΑ ΤΗΝ ΠΕΡΙΟΧΗ BADALONA (ΠΕΜΠΤΟ ΜΟΝΤΕΛΟ) Η περιοχή Badalona της Βαρκελώνης αποτελεί προάστιο της πόλης, το οποίο όμως δε φιλοξενεί τα υψηλά στρώματα αλλά ένα μεγάλο αριθμό της μεσαίας τάξης. Πρόκειται για μια περιοχή, η οποία δεν ανήκει στον Μητροπολιτικό Δήμο της Βαρκελώνης, ενώ τα γενικά χαρακτηριστικά της αντιστοιχούν περισσότερο στον Εύοσμο της Θεσσαλονίκης (αν φυσικά μπορεί να υπάρξει σύγκριση, καθώς τα μεγέθη και η κλίμακα τους είναι διαφορετικά). Σύμφωνα με το δείγμα των 80 διαμερισμάτων, η ηλικία των πολυκατοικιών της περιοχής είναι κατά μέσο όρο εικοσαετίας, γεγονός που σημαίνει ότι η επέκταση της περιοχής πραγματοποιείται περίπου τη δεκαετία του 90. Κάθε διαμέρισμα διαθέτει κατά μέσο όρο τρία δωμάτια και η γενικότερη κατάσταση των διαμερισμάτων χαρακτηρίζεται καλή. Το 69% μόνο διαθέτει ανελκυστήρα, ενώ ένα 30% περίπου διαθέτει θέση στάθμευσης. Οι περισσότερες οριζόντιες ιδιοκτησίες διαθέτουν θέρμανση (το είδος της οποίας δεν προσδιορίζεται) και ο μέσος όρος της αξίας τους είναι ανά τετραγωνικό μέτρο περίπου 2300 /τμ. Τα παραπάνω χαρακτηριστικά έχουν ιδιαίτερο ενδιαφέρον, διότι οι τιμές κάθε μεταβλητής μοιράζονται. Για παράδειγμα, δεν εμφανίζονται ποσοστά 90% και άνω στις περιπτώσεις των δίτιμων μεταβλητών (Βλ. δεύτερο μοντέλο)και άρα έχει ιδιαίτερο ενδιαφέρον η τελική διαμόρφωση της εξίσωσης παλινδρόμησης. Παρακάτω αναλύονται όλα τα στάδια της μεθοδολογίας για τη διαμόρφωση ενός αξιόπιστου μοντέλου πρόβλεψης των αγοραίων αξιών ακινήτων στην περιοχή Badalona της Βαρκελώνης Διερεύνηση γραμμικής σχέσης μεταξύ της εξαρτημένης μεταβλητής Υ και των ανεξάρτητων Χ i Πρώτο βήμα αποτελεί η εύρεση της σχέσης (γραμμικής ή όχι) μεταξύ της εξαρτημένης μεταβλητής Υ και των εννέα ανεξάρτητων μεταβλητών Χi. Αρχικά, η οπτική ερμηνεία των διαγραμμάτων διασποράς της μεταβλητής Υ με κάθε ανεξάρτητη βοηθά στον εντοπισμό ενός αριθμού μεταβλητών, οι οποίες δείχνουν να έχουν γραμμική εξάρτηση. Στη συνέχεια, η ερμηνεία της μερική συσχέτισης της κάθε μεταβλητής με την Υ, δίνει ένα νέο αριθμό μεταβλητών. Η ένωση των δύο, οδηγεί τελικά στον αριθμό των μεταβλητών που υπάρχει στατιστικός λόγος να συμμετέχουν στη διαδικασία παλινδρόμησης Γραφήματα συσχέτισης των Χ i με την Υ Από το γράφημα Matrix Scatter Plot της παρακάτω εικόνας διαφαίνεται ότι η αξία των διαμερισμάτων συνδέεται γραμμικά με τις μεταβλητές AREA, AGE, FLOOR,HEATING, QUALITY και ROOM. Λιγότερο ισχυρή φαίνεται να είναι η συσχέτιση της με τις δίτιμες μεταβλητές ELEV και PARKING, σχέση η οποία όμως δεν αποκλείεται καθώς και στις δύο περιπτώσεις η διασπορά των τιμών είναι περίπου 70% με 30%. Όσον αφορά τη μεταβλητή BATH, στην περιοχή της Badalona λαμβάνει μόνο τις τιμές 1 (60/80) και 2 (40/80), με μία διασπορά όμως που θα μπορούσε να την χαρακτηρίσει στατιστικώς σημαντική για το μοντέλο. 220
233 Κεφάλαιο 5ο Διάγραμμα 5.43: Γράφημα Matrix Scatter Plot για δείγμα 80 ακινήτων στην περιοχή Badalona της Βαρκελώνης Συνεπώς, η ερμηνεία του διαγράμματος οδηγεί στο συμπέρασμα ότι όλες οι μεταβλητές εμφανίζουν γραμμικότητα με την αξία των διαμερισμάτων (άλλες μεγαλύτερη και άλλες μικρότερη) και δεν θα ήταν φρόνιμο να μη συμμετέχει κάποια από τις παραπάνω στην εκτέλεση της γραμμικής παλινδρόμησης Συντελεστές μερικής συσχέτισης Η πρώτη εικόνα που παρουσιάζεται από τους συντελεστές μερικής συσχέτισης του παρακάτω πίνακα, είναι ότι παρουσιάζουν ιδιαίτερα χαλαρές γραμμικές συνδέσεις. Η μέγιστη τιμή «καθαρής» σχέσης παρουσιάζεται μεταξύ της Υ και των μεταβλητών QUALITY και BATH, γεγονός περίεργο εάν λάβει κανείς υπόψη του ότι έπονται σε βαθμό συσχέτισης μεταβλητές όπως το εμβαδόν των διαμερισμάτων, η θέρμανση και ο όροφος τους. Παρόλα αυτά παρατηρώντας τις τιμές των συντελεστών συσχέτισης σχετικά και όχι απόλυτα, θα πρέπει να ληφθούν όλες υπόψη στη διαδικασία εκτέλεσης της πολλαπλής γραμμικής παλινδρόμησης, πέραν της μεταβλητής AGE και PARKING, οι οποίες δεν παρουσιάζουν σχεδόν καμία γραμμική σύνδεση. Για την τελική απόφαση λαμβάνονται υπόψη ταυτόχρονα τα διαγράμματα σκέδασης (Διάγραμμα 5.43), τα οποία δεν αποκλείουν καμία μεταβλητή από το μοντέλο. Συνεπώς στην περιοχή Badalona της Βαρκελώνης όλες οι μεταβλητές θεωρείται ότι Μεταπτυχιακή διατριβή 221
234 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ μπορούν με τις κατάλληλες προσεγγίσεις να συμμετέχουν στην τελική εξίσωση παλινδρόμησης του πέμπτου μοντέλου της παρούσας διατριβής. Πίνακας 5.16: Πίνακας με τις μερικές συσχετίσεις της εξαρτημένης μεταβλητής με κάθε μία ανεξάρτητη στο δείγμα των 80 οντοτήτων Μεταβλητές Συσχέτιση Επίπεδο στατιστικής σημαντικότητας AREA 0,268 0,023 AGE -0,090 0,453 FLOOR 0,163 0,172 ELEV 0,265 0,025 HEATING 0,282 0,017 QUALITY 0,422 0,000 PARKING 0,032 0,792 ROOMS 0,282 0,016 BATH 0,443 0, Εφαρμογή της πολλαπλής γραμμικής παλινδρόμησης και δημιουργία τελικού μοντέλου Εκτελείται η διαδικασία πολλαπλής γραμμικής παλινδρόμησης με τη βοήθεια του στατιστικού εργαλείου SPSS και με τη χρήση της βηματικής μεθόδου (stepwise). Το δείγμα αριθμεί συνολικά 80 οντότητες και συμμετέχουν εννέα συνολικά ανεξάρτητες μεταβλητές. Έπειτα από την ολοκλήρωση των επιλογών που πραγματοποιούνται στο πλαίσιο διαλόγου Linear Regression παράγεται η ακόλουθη πρώτη προσέγγιση της εξίσωσης πολλαπλής παλινδρόμησης. Υ = , ,829 AREA ,057 QUALITY ,625 BATH ,707 ELEV ,616 HEATING ,216 ROOM με R 2 = 0,814 Η πρώτη προσέγγιση της εξίσωσης παλινδρόμησης είναι ιδιαίτερα ικανοποιητική, διότι παρατηρείται ότι συνολικά έξι από τις εννέα μεταβλητές συσχετίζονται γραμμικά με την αξία των διαμερισμάτων. Πιο συγκεκριμένα, οι μεταβλητές AREA, QUALITY, BATH, ELEV, HEATING και ROOM χαρακτηρίζονται στατιστικά σημαντικές βάσει των περιορισμών που θέτει το SPSS και με βάση τη βηματική διαδικασία. Αντίθετα, όπως ορίζεται από την 222
235 Κ ε φ ά λ α ι ο 5 ο παλινδρομική εξίσωση, οι μεταβλητές AGE, FLOOR και PARKING, δε συμμετέχουν σημαντικά στη διαμόρφωση της αξίας των διαμερισμάτων. Ταυτόχρονα, κρίνοντας από τη τιμή του συντελεστή προσδιορισμού R 2 = 0,814 το μοντέλο προσαρμόζεται πάρα πολύ καλά στα δεδομένα του δείγματος και ένα μεγάλο ποσοστό της συνολικής διακύμανσης της εξαρτημένης μεταβλητής Υ εκφράζεται από τις έξι ανεξάρτητες μεταβλητές. Αναζητώντας ακραίες οντότητες μέσω του διαγράμματος σκέδασης των Studentized Deleted Residuals με τις τυποποιημένες προβλεπόμενες τιμές των υπολοίπων (Διάγραμμα 5.44) διαφαίνεται ότι μόνο δύο από τις ογδόντα τιμές (2,5%) ξεπερνούν ελάχιστα την τιμή ±2. Συνεπώς, δεν θεωρείται θεωρητικά απαραίτητη η απομάκρυνση καμίας οντότητας από το μοντέλο. Διάγραμμα 5.44: Διάγραμμα σκέδασης των Studentized Deleted Residuals με τα Standardized Predicted Values Ταυτόχρονα, ρίχνοντας μία ματιά σε όλες τους δείκτες και διαγράμματα, δεν διαφαίνεται κάποια ιδιαίτερη έξαρση ή απόκλιση από τα όρια ανοχής που τίθενται βάσει μεθοδολογίας. Συνεπώς, η πρώτη προσέγγιση του μοντέλου με τις 80 οντότητες αποτελεί ταυτόχρονα και την υποψήφια τελική προσέγγιση, εάν φυσικά κριθούν ικανοποιητικοί όλοι οι έλεγχοι που ακολουθούν στα επόμενα κεφάλαια. Μεταπτυχιακή διατριβή 223
236 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Έλεγχος ικανοποίησης παραδοχών του γραμμικού μοντέλου Στα υποκεφάλαια που ακολουθούν ελέγχεται η ικανοποίηση των βασικών κριτηρίων ενός γραμμικού μοντέλου. Εάν το αποτέλεσμα είναι θετικό, τότε το μοντέλο κρίνεται ικανοποιητικό, ενώ εάν κάποιος από τους ελέγχους έχει αρνητικό αποτέλεσμα, τότε είτε διαγράφεται κάποια μεταβλητή, είτε αφαιρούνται οντότητες που επιδρούν αρνητικά στο σχηματισμό ενός αξιόπιστου μοντέλου Σημαντικότητα ανεξάρτητων μεταβλητών Ο έλεγχος στατιστικής σημαντικότητας των ανεξάρτητων μεταβλητών συνδέεται με το βαθμό συμβολής της κάθε μεταβλητής στο μοντέλο και ελέγχεται με τη βοήθεια των διαγραμμάτων μερικής συσχέτισης και των τιμών t του πίνακα Coefficients (Πίνακας 5.17) του αρχείου *.spv. Διαγράμματα μερικής συσχέτισης Τα διαγράμματα μερικής συσχέτισης που ακολουθούν (5.45, 5.46, 5.47, 5.48, 5.49 και 5.50)αποκαλύπτουν την ύπαρξη γραμμικότητας μεταξύ της εξαρτημένης μεταβλητής Υ και των έξι ανεξάρτητων μεταβλητών και ταυτόχρονα μαρτυρούν την επάρκεια του παλινδρομικού μοντέλου. Γίνεται κατανοητό ότι τα σημεία κατά μεγάλη προσέγγιση έχουν γραμμική πορεία και επιβεβαιώνεται η ύπαρξη σημαντικότητας των ανεξάρτητων μεταβλητών, ο βαθμός της οποίας όμως διαφέρει από μεταβλητή σε μεταβλητή. Διάγραμμα 5.45: Διάγραμμα μερικής παλινδρόμησης μεταξύ της αξίας και του εμβαδού 224
237 Κ ε φ ά λ α ι ο 5 ο Διάγραμμα 5.46: Διάγραμμα μερικής παλινδρόμησης μεταξύ της αξίας και της κατάστασης του ακινήτου Διάγραμμα 5.47: Διάγραμμα μερικής παλινδρόμησης μεταξύ της αξίας και του αριθμού των μπάνιων Μεταπτυχιακή διατριβή 225
238 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα 5.48: Διάγραμμα μερικής παλινδρόμησης μεταξύ της αξίας και της ύπαρξης ανελκυστήρα Διάγραμμα 5.49: Διάγραμμα μερικής παλινδρόμησης μεταξύ της αξίας και του είδους θέρμανσης 226
239 Κ ε φ ά λ α ι ο 5 ο Διάγραμμα 5.50: Διάγραμμα μερικής παλινδρόμησης μεταξύ της αξίας και του αριθμού των δωματίων Από την αξιολόγηση των συντελεστών μερικής συσχέτισης του πίνακα 5.16 γίνεται σαφές ότι υφίσταται γραμμική σχέση, η οποία όμως δεν είναι τόσο ισχυρή. Η ισχυρότερη σχέση σε σύγκριση με τις υπόλοιπες εμφανίζεται μεταξύ της Υ και των μεταβλητών QUALITY και BATH, η οποία φαίνεται και από τις τιμές R 2 Linear = και R 2 Linear =0.232 (R = 0,47 και R= 0,48) αντίστοιχα. Επίσης, το γεγονός ότι σχεδόν όλες οι τιμές βρίσκονται εντός του εύρους της ζώνης που περιλαμβάνει το 95% των παρατηρήσεων (μόνο μία ή δύο σε σύνολο 80 κουκκίδων ξεφεύγουν ελάχιστα) είναι θετικό σημάδι σχετικά με τις ακραίες οντότητες, ενώ ταυτόχρονα παραπέμπουν σε ύπαρξη ομοιομορφίας στο μοντέλο. Η ερμηνεία των παραπάνω διαγραμμάτων δεν μπορεί να απορρίψει σε καμία περίπτωση την παραδοχή της σημαντικότητας των ανεξάρτητων μεταβλητών, διότι παρόλο που οι σχέσεις είναι λιγότερο ισχυρές από τα προηγούμενα μοντέλα που έχουν μελετηθεί, ισχύουν όλες οι προϋποθέσεις για την ικανοποίηση της συνθήκης. t τιμές Η στατιστική σημαντικότητα των ανεξάρτητων μεταβλητών είναι τόσο μεγάλη, όσο μεγαλύτερες είναι οι τιμές t του πίνακα Coefficient από την οριακή τιμή ±2. Τοποθετώντας όλες τις μεταβλητές κατά αύξουσα σειρά βάσει της τιμής t διαφαίνεται ο βαθμός σημαντικότητας της κάθε μίας. Πιο συγκεκριμένα, η μεταβλητή με τη μικρότερη τιμή είναι η AREA και ακολουθούν οι μεταβλητές ROOM, ELEV, HEATING, QUALITY και BATH (Πίνακας 5.17). Μεταπτυχιακή διατριβή 227
240 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Πίνακας 5.17: Πίνακας Coefficients που περιλαμβάνει τις τιμές t των ανεξάρτητων μεταβλητών Coefficients a Model Unstandardized Standardized 95,0% Confidence Collinearity Coefficients Coefficients Interval for B Correlations Statistics Lower Upper Zero- B Std. Error Beta t Sig. Bound Bound order Partial Part Tolerance VIF 6 (Constant) ,216 -, ,129 4, , ,231 AREA 537, ,308,200 2,043,045 13, ,600,756,233,103,267 3,752 QUALITY 22528, ,863,283 4,595, , ,450,577,474,232,672 1,489 BATH 52057, ,617,337 4,696, , ,235,747,482,237,495 2,019 ELEV 20987, ,339,129 2,343, , ,665,456,264,118,838 1,193 HEATING 10606, ,804,177 2,805, , ,740,446,312,142,641 1,559 ROOM 17074, ,422,195 2,311, , ,326,560,261,117,360 2,775 Παράλληλα, παρατηρώντας τις τιμές Sig. του πίνακα (παρατηρούμενο επίπεδο σημαντικότητας) που αντιστοιχούν στο στατιστικό έλεγχο για τη στατιστική σημαντικότητα είναι όλες μικρότερες του 0,05 με αποτέλεσμα οι έξι ανεξάρτητες μεταβλητές να θεωρούνται στατιστικά σημαντικές Ανεξαρτησία οντοτήτων Η επόμενη υπόθεση που πρέπει να ικανοποιείται είναι η ύπαρξη ανεξαρτησίας των οντοτήτων, σύμφωνα με την οποία η ύπαρξη μίας οντότητας στο δείγμα δε θα πρέπει να επηρεάζει τη συμμετοχή μίας άλλης. Ο έλεγχος ανεξαρτησίας των παρατηρήσεων σε περιβάλλον SPSS εξασφαλίζεται με δύο τρόπους. Ο πρώτος είναι μέσω του στατιστικού δείκτη Durbin Watson, ο οποίος πρέπει να κυμαίνεται μεταξύ των τιμών 1,5 και 2,5, ενώ ο δεύτερος έλεγχος είναι οπτικός και γίνεται με τη βοήθεια του διαγράμματος σκέδασης των κατά Student υπολοίπων με την σειρά εισαγωγής τους στο μοντέλο. Δείκτης Durbin Watson Σύμφωνα με τα στοιχεία του πίνακα Model Summary ο στατιστικός δείκτης Durbin Watson του τελευταίου μοντέλου μέσω της βηματικής διαδικασίας έχει τιμή 1,70. Το μέγεθος του δείκτη βρίσκεται κοντά στο κάτω όριο, αλλά δεν παύει να είναι μεταξύ των δύο οριακών τιμών 1,5 και 2,5. Συνεπώς, οι οντότητες στο δείγμα των 80 παρατηρήσεων στην περιοχή Badalona της Βαρκελώνης είναι ασυσχέτιστες μεταξύ τους, βάσει του πρώτου εκ των δύο ελέγχων. 228
241 ion0 Κ ε φ ά λ α ι ο 5 ο Πίνακας 5.18: Πίνακας Model Summary, ο οποίος περιέχει την τιμή του στατιστικού δείκτη Durbin Watson Model Summary g Model Change Statistics R R Adjusted Std. Error of Square F Sig. F Durbin- R Square R Square the Estimate Change Change df1 df2 Change Watson 1,756 a,571, ,212, , ,000 2,832 b,692, ,114,121 30, ,000 3,878 c,771, ,473,079 26, ,000 4,888 d,788, ,566,017 5, ,018 5,894 e,800, ,593,012 4, ,039 6,902 f,814, ,590,014 5, ,024 1,700 Διάγραμμα σκέδασης Studentized residuals vs Sequence Διάγραμμα 5.51: Διάγραμμα σκέδασης των Studentized Residuals με τη συνέχεια των οντοτήτων A/A για την περιοχή Badalona της Βαρκελώνης Μεταπτυχιακή διατριβή 229
242 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Στο διάγραμμα 5.51 αποτυπώνεται ξεκάθαρα η ανεξαρτησία των οντοτήτων στο πέμπτο μοντέλο πολλαπλής παλινδρόμησης. Είναι εμφανής η τυχαία κατανομή των υπολοίπων, τα οποία είναι τοποθετημένα μεταξύ της ζώνης σταθερού πλάτους ±2. Επίσης, όλα τα σημεία τοποθετούνται με ομοιόμορφο τρόπο πάνω και κάτω από την τιμή του μηδέν, ενώ δεν εμφανίζονται συσσωρεύσεις και τάσεις. Σύμφωνα με το δείκτη Durbin Watson και με το γράφημα σκέδασης των τυποποιημένων κατά student υπολοίπων, με τη σειρά των παρατηρήσεων (Α/Α) γίνεται σαφές ότι το τελικό μοντέλο πρόβλεψης των αγοραίων αξιών ακινήτων πληροί τον έλεγχο της ανεξαρτησίας των οντοτήτων Πολυσυγγραμικότητα ή Συγγραμικότητα Η σύνδεση των ανεξάρτητων μεταβλητών μεταξύ τους με γραμμικό τρόπο αποτελεί ένα πρόβλημα πολυσυγγραμικότητας. Η υπόθεση της μη ύπαρξης πολυσυγγραμικότητας στο μοντέλο εντοπίζεται με τη βοήθεια τεσσάρων στατιστικών δεικτών. Οι δύο πρώτοι βρίσκονται στον πίνακα Coefficients και είναι ο παράγοντας ανοχής Tolerance και ο παράγοντας πληθωριστικής διακύμανσης VIF, ενώ οι δύο τελευταίοι βρίσκονται στον πίνακα Collinearity Diagnostics και είναι ο δείκτης Eigenvalue και ο δεσμευμένος δείκτης (Condition Index). Παράγοντας ανοχής (Tolerance factor) & Παράγοντας πληθωριστικής διακύμανασης (Variance inflation factor) Όταν οι τιμές του παράγοντα Tolerance είναι κοντά στο μηδέν, τότε το φαινόμενο πολυσυγγραμμικότητας είναι έντονο και πιθανόν θα πρέπει να ελεγχθεί η απομάκρυνση της αντίστοιχης ανεξάρτητης μεταβλητής. Αντίθετα τιμές μεγαλύτερες του 0,5 και μέχρι τη μονάδα αποδεικνύουν ότι η ανεξάρτητη μεταβλητή δεν παρουσιάζει κανένα πρόβλημα πολυσυγγραμμικότητας. Σύμφωνα με τα στοιχεία του πίνακα 5.19 η τιμή του δείκτη για τη μεταβλητή AREA είναι ίση με 0,267, για τη μεταβλητή QUALITY 0,672, για τη μεταβλητή BATH 0,495, για τη μεταβλητή ELEV 0,838, για τη μεταβλητή HEATING 0,641, και τέλος για τη μεταβλητή ROOM 0,360. Παρατηρείται ότι οι τρεις από τις έξι τιμές βρίσκονται ανάμεσα στην τιμή 0,5 και στη μονάδα, ενώ οι υπόλοιπες τρεις δεν πλησιάζουν την τιμή μηδέν. Συνεπώς, ο πρώτος δείκτης ελέγχου δεν παρουσιάζει κανένα πρόβλημα πολυσυγγραμικότητας των μεταβλητών. Τα όρια ανοχής για το στατιστικό δείκτη VIF ποικίλουν ανάλογα με την προς μελέτη βιβλιογραφική αναφορά. Οι τιμές που συναντώνται κατά φθίνουσα σειρά είναι 10, 7,5 (ηλεκτρονική βοήθεια του ArcGIS), 5 (Αγγελίδης, 2009) και 2 (ηλεκτρονική βοήθεια του SPSS). Οι τιμές του στατιστικού δείκτη σύμφωνα με τα στοιχεία του πίνακα 5.19 κυμαίνονται από 3,75 στη μεταβλητή AREA, 2,77 στη μεταβλητή ROOM, 2,019 στη μεταβλητή BATH και σε τιμές μικρότερες του δύο σε όλες τις υπόλοιπες μεταβλητές. Παρατηρείται ότι οι όλες οι τιμές είναι ιδιαίτερα χαμηλές σε σχέση με τα όρια ανοχής, 230
243 Κ ε φ ά λ α ι ο 5 ο συνεπώς σύμφωνα με το δείκτη VIF δεν παρουσιάζεται πρόβλημα συγγραμικότητας μεταξύ των ανεξάρτητων μεταβλητών. Πίνακας 5.19: Πίνακας Coefficients ο οποίος περιλαμβάνει τις τιμές VIF και Tolerance Coefficients a Model Unstandardized Standardized 95,0% Confidence Collinearity Coefficients Coefficients Interval for B Correlations Statistics Lower Upper Zero- B Std. Error Beta t Sig. Bound Bound order Partial Part Tolerance VIF 6 (Constant) ,216 -, ,129 4, , ,231 AREA 537, ,308,200 2,043,045 13, ,600,756,233,103,267 3,752 QUALITY 22528, ,863,283 4,595, , ,450,577,474,232,672 1,489 BATH 52057, ,617,337 4,696, , ,235,747,482,237,495 2,019 ELEV 20987, ,339,129 2,343, , ,665,456,264,118,838 1,193 HEATING 10606, ,804,177 2,805, , ,740,446,312,142,641 1,559 ROOM 17074, ,422,195 2,311, , ,326,560,261,117,360 2,775 Έλεγχος ιδιοτιμών (Eigenvalues) & Δεσμευμένοι δείκτες (Condition indexes) Ο δείκτης ιδιοτιμών (Eigenvalues) υπονοεί πρόβλημα πολυσυγγραμκότητας, όταν οι τιμές του βρίσκονται πολύ κοντά στην τιμή μηδέν. Στην προκειμένη περίπτωση, όλες οι τιμές θεωρείται ότι δεν προσεγγίζουν σε μεγάλο βαθμό το μηδέν, συνεπώς δεν υπάρχει πρόβλημα συσχέτισης μεταξύ των ανεξάρτητων μεταβλητών. Πίνακας 5.20: Πίνακας Colllinearity Diagnostics που περιλαμβάνει τις τιμές Eigenvalue και Condition Index Collinearity Diagnostics a Model Dimension Condition Variance Proportions Eigenvalue Index (Constant) AREA QUALITY BATH ELEV HEATING ROOM 6 1 6,342 1,000,00,00,00,00,01,00,00 2,277 4,785,00,00,01,00,33,37,00 3,216 5,420,01,01,00,01,63,18,01 4,074 9,232,13,05,22,19,03,11,00 5,042 12,244,04,02,33,48,01,25,14 6,035 13,393,39,18,34,25,00,03,01 7,013 21,852,43,74,09,07,00,06,83 Μεταπτυχιακή διατριβή 231
244 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Στην περίπτωση των δεσμευμένων δεικτών, τιμές μεγαλύτερες του 15 παρουσιάζουν ένα πιθανό πρόβλημα, ενώ εάν ξεπεράσουν την τιμή 30, τότε υπάρχει σίγουρα μεγάλο πρόβλημα συγγραμικότητας. Σύμφωνα με τα στοιχεία του πίνακα η τιμή 21,85 ξεπερνά την τιμή ανοχής 15 αλλά προσεγγίζει περισσότερο το κάτω όριο (15)σε σχέση με το ανώτερο όριο (30). Λαμβάνοντας ταυτόχρονα υπόψη τους τρεις προηγούμενους ελέγχους, οι οποίοι παρουσιάζουν ένα μοντέλο που δεν έχει πρόβλημα συσχέτισης των μεταβλητών του, θεωρείται ότι η τιμή 21 δεν είναι τόσο υψηλή, ώστε να υποδεικνύει πρόβλημα πολυσυγγραμικότητας Κανονικότητα Η υπόθεση της κανονικότητας στο γραμμικό μοντέλο ικανοποιείται με τη βοήθεια οκτώ διαδοχικών ελέγχων, οι επτά από τους οποίους είναι διαγραμματικοί. Για την παραδοχή της κανονικότητας αξιοποιούνται τα Studentized Deleted Residuals, μέσω της διαδικασίας Explore και τα τυποποιημένα υπόλοιπα (Standardized Residuals) μέσω της κύριας διαδικασίας εκτέλεσης της πολλαπλής γραμμικής παλινδρόμησης. Φυλλογράφημα των υπολοίπων [Stem And- Leaf- Plot of residuals Studentized deleted residuals] Studentized Deleted Residual Stem-and-Leaf Plot Frequency Stem & Leaf 2, , , , , , Stem width: 1,00000 Each leaf: 1 case(s) Διάγραμμα 5.52: Φυλλογράφημα των υπολοίπων για την περιοχή του Ευόσμου Ο πρώτος έλεγχος αφορά το φυλλογράφημα των υπολοίπων που παράγεται μέσω της διαδικασίας Explore. Σύμφωνα με το παραπάνω διάγραμμα δεν επισημαίνεται καμία ακραία οντότητα, ενώ παράλληλα παρατηρείται ο σχηματισμός της γνωστής καμπανοειδούς μορφής στραμμένης κατά 90 ο. Συνεπώς, ο πρώτος έλεγχος ικανοποιεί την υπόθεση της κανονικότητας για το σύνολο των 80 οντοτήτων. 232
245 Κ ε φ ά λ α ι ο 5 ο Test of normality : Kolmogorv Smirnov, Lillefors, Shapiro Wilk Το μεγάλο δείγμα του πέμπτου μοντέλου (n>30) απαιτεί για τον έλεγχο της κανονικότητας τη χρήση του στατιστικού κριτηρίου των Kolmogorov Smirnov. Για τον έλεγχο της υπόθεσης της κανονικότητας των υπολοίπων σύμφωνα με το στατιστικό κριτήριο Kolmogorov Smirnov ισχύει η: Μηδενική Υπόθεση Ho: Τα υπόλοιπα κατανέμονται κανονικά και Εναλλακτική Υπόθεση H1: Τα υπόλοιπα δεν κατανέμονται κανονικά. Το τεστ για την κανονικότητα των Kolmogorov Smirnov δίνει επίπεδο στατιστικής σημαντικότητας (Sig.) 20% (Πίνακας 5.21), δηλαδή μεγαλύτερο του 5%. Συνεπώς, δεν μπορεί να απορριφθεί η υπόθεση ότι τα Studentized Deleted Residuals ακολουθούν την κανονική κατανομή. Πίνακας 5.21: Πίνακας Tests of Normality Kolmogorv Smirnov, Lillefors, Shapiro Wilk Tests of Normality Kolmogorov-Smirnov a Shapiro-Wilk Statistic df Sig. Statistic df Sig. Studentized Deleted Residual,064 80,200 *,986 80,529 a. Lilliefors Significance Correction *. This is a lower bound of the true significance. Normal Q-Q Plot of Studentized deleted Residuals Το διάγραμμα Normal Q-Q παράγεται μέσω της διαδικασίας Explore, με τη χρήση των Studentized Deleted Residuals, όπως αναφέρεται παραπάνω. Απεικονίζει τις παρατηρούμενες τιμές στον άξονα Χ έναντι των εκτιμώμενων τιμών τους. Η γραμμή του διαγράμματος 5.53 ορίζει την τέλεια κανονική κατανομή, συνεπώς η ποιότητα της κανονικότητας του μοντέλου εξαρτάται από τον τρόπο που κατανέμονται τα σημεία σε σχέση με την γραμμή της κανονικότητας. Στην προκειμένη περίπτωση όλα τα σημεία στο κέντρο της γραμμής βρίσκονται τοποθετημένα πάνω στη γραμμή, ενώ στις άκρες της τείνουν πάνω σε αυτή με πολύ μικρές αποκλίσεις. Το συμπέρασμα που μπορεί να προκύψει από την παρακάτω απεικόνιση των παρατηρούμενων έναντι των προσδοκώμενων τιμών είναι ότι ικανοποιείται η υπόθεση της κανονικότητας των υπολοίπων. Μεταπτυχιακή διατριβή 233
246 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα 5.53: Διάγραμμα κανονικότητας Normal Q-Q Plot of Studentized deleted Residuals για τον έλεγχο της κανονικότητας των υπολοίπων Detrended normal Q-Q Plot Studentized Deleted residuals 234
247 Κ ε φ ά λ α ι ο 5 ο Διάγραμμα 5.54: Διάγραμμα Detrended Νormal Q-Q Plot Studentized Deleted Ρesiduals για τον έλεγχο της κανονικότητας των υπολοίπων Το διάγραμμα 5.54 απεικονίζει στον άξονα Χ τις παρατηρούμενες τιμές των Studentized Deleted Residuals, ενώ στον άξονα Υ τα ποσοστιαία σημεία μίας τυπικής κανονικής κατανομής που αποτελούν τυποποιημένες μονάδες και παράγεται μέσω της διαδικασίας Explore. Τα σημεία στο διάγραμμα παρατηρείται ότι είναι τυχαία κατανεμημένα πάνω και κάτω από την οριζόντια γραμμή που διέρχεται από την τιμή μηδέν, σε ένα σταθερό εύρος πλάτους περίπου. Επίσης, δεν παρατηρείται κανενός είδους συσσώρευση σημείων που να προκαλεί τη δημιουργία προτύπων. Συνεπώς, σύμφωνα με το τρίτο διάγραμμα ελέγχου ικανοποιείται η παραδοχή της κανονικότητας, χωρίς κάποια ένδειξη πιθανού προβλήματος. Histogram Studentized Deleted Residuals Διάγραμμα 5.55: Ιστόγραμμα των Studentized Deleted Residuals για τον έλεγχο της κανονικότητας των υπολοίπων Στο παραπάνω ιστόγραμμα (Διάγραμμα 5.55), το οποίο παράγεται μέσω της διαδικασίας Explore, γίνεται σαφές ότι προσεγγίζεται σε πολύ μεγάλο βαθμό η κανονική κατανομή και άρα υπάρχει κανονικότητα των υπολοίπων. Histogram Standardized Residuals Πρόκειται για το αντίστοιχο ιστόγραμμα συχνοτήτων των τυποποιημένων υπολοίπων που δημιουργείτε από την κύρια διαδικασία εκτέλεσης της γραμμικής παλινδρόμηση. Σύμφωνα με το ιστόγραμμα (Διάγραμμα 5.56) και την καμπύλη Μεταπτυχιακή διατριβή 235
248 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ κανονικής κατανομής που προσαρμόζεται σε αυτό διακρίνεται η κανονικότητα του μοντέλου. Διάγραμμα 5.56: Ιστόγραμμα των Standardized Residuals για τον έλεγχο της κανονικότητας των υπολοίπων Διάγραμμα Normal P-P Plot of regression standardized residuals 236
249 Κ ε φ ά λ α ι ο 5 ο Διάγραμμα 5.57: Διάγραμμα Normal P-P Plot of regression Standardized Residuals για τον έλεγχο της κανονικότητας των υπολοίπων Το παραπάνω γράφημα αναμενόμενης παρατηρούμενης αθροιστικής πιθανότητας, παρουσιάζει μία πάρα πολύ καλή προσαρμογή των παρατηρήσεων πάνω στην ευθεία γραμμή, με μικρές αποκλίσεις από αυτήν. Συνεπώς και το διάγραμμα Normal P-P Plot φανερώνει την ύπαρξη κανονικότητας του μοντέλου. Θηκόγραμμα των υπολοίπων (Boxplot of Residuals) Ο πρώτος ρόλος του θηκογράμματος που αφορά την υπόδειξη ακραίων ή απομονωμένων οντοτήτων, όπως φαίνεται από το διάγραμμα, δεν εμφανίζει κανένα πρόβλημα στο δείγμα των 80 παρατηρήσεων. Επίσης, το διάγραμμα παρουσιάζει τη διάμεσο του θηκογράμματος που αναφέρεται στο παλινδρομικό μοντέλο να μη βρίσκεται στο κέντρο του ορθογωνίου. Η συγκεκριμένη διαπίστωση συνεπάγεται μία κατανομή, η οποία δεν είναι απόλυτα συμμετρική. Παρόλα αυτά η υπόθεση της κανονικότητας ικανοποιείται και με το τελευταίο διάγραμμα ελέγχου. Διάγραμμα 5.58: Θηκόγραμμα για τον εντοπισμό των ακραίων τιμών του δείγματος μέσω της διαδικασίας Explore Μεταπτυχιακή διατριβή 237
250 Σχηματισμός μοντέλου Ισότητα διακυμάνσεων ή ομοσκεδαστικότητα Η ικανοποίηση της παραδοχής της ομοσκεδασιμότητας πραγματοποιείται με τη βοήθεια των ακόλουθων τριών διαγραμμάτων σκέδασης: Studentized Deleted Residuals vs Standardized Predicted Values Studentized Residuals vs Standardized Predicted Values Standardized Predicted Values vs Dependent Variable Τα δύο πρώτα διαγράμματα είναι της ίδιας μορφής και η απεικόνιση τους δίνει παρόμοια αποτελέσματα. Όπως φαίνεται παρακάτω, τα δύο διαγράμματα φανερώνουν μία τυχαία κατανομή και όχι κάποιας μορφής συσσώρευση ή πρότυπο. Επίσης, θετικό στοιχείο για την ικανοποίηση της παραδοχής είναι το μικρό εύρος ζώνης ( ) που είναι τοποθετημένες οι τιμές, με εξαίρεση δύο παρατηρήσεις από τις 80 (2,5%) που βρίσκονται οριακά έξω από το συγκεκριμένο εύρος. Συνεπώς, τα παρακάτω γραφήματα καλύπτουν ικανοποιητικά την παραδοχή της ομοσκεδασιμότητας αλλά ταυτόχρονα και της γραμμικότητας του μοντέλου (όπως αναφέρεται και παρακάτω Βλ ). Διάγραμμα 5.59: Διάγραμμα σκέδασης των Studentized Deleted Residuals με τα Standardized Predicted Values (αριστερά) και διάγραμμα σκέδασης των Studentized Residuals με τα Standardized Predicted Values (δεξιά) 238
251 Κ ε φ ά λ α ι ο 5 ο Το διάγραμμα διασποράς των τυποποιημένων εκτιμώμενων τιμών έναντι των παρατηρούμενων τιμών της εξαρτημένης μεταβλητής Υ(Διάγραμμα 5.59) παρουσιάζει τα σημεία κατανεμημένα κανονικά και με σταθερή διακύμανση. Όλα τα σημεία κατανέμονται με ομοιόμορφο τρόπο πάνω και κάτω από την ευθεία των ελαχίστων τετραγώνων σε μία ζώνη σταθερού πλάτους, με μικρές αποκλίσεις. Συνεπώς ικανοποιείται επιτυχώς η παραδοχή της ισότητας των διασπορών. Διάγραμμα 5.59: Διάγραμμα σκέδασης των Standardized Predicted Values με τις τιμές της εξαρτημένης μεταβλητής Υ Λαμβάνοντας υπόψη την οπτική ερμηνεία των τριών παραπάνω διαγραμμάτων, η υπόθεση ύπαρξης ομοσκεδασιμότητας στο γραμμικό μοντέλο ικανοποιείται Γραμμικότητα Η ύπαρξη γραμμικότητας σε ένα μοντέλο πολλαπλής γραμμικής παλινδρόμησης αποτελεί την πρώτη υπόθεση που οφείλει να ικανοποιείται και ελέγχεται με την ερμηνεία των κατάλληλων κατηγοριών διαγραμμάτων. Η πρώτη κατηγορία αναφέρεται στα διαγράμματα σκέδασης μεταξύ της εξαρτημένης και όλων των ανεξάρτητων μεταβλητών. Το διάγραμμα Matrix Scatter Plot της εικόνας 5.43 αναφέρεται στο τελικό δείγμα των 80 οντοτήτων και όπως έχει ήδη επισημανθεί εμφανίζει γραμμικότητα μεταξύ της Υ και των έξι ανεξάρτητων μεταβλητών AREA, QUALITY, HEATING, ELEV, BATH και ROOM. Μεταπτυχιακή διατριβή 239
252 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Η δεύτερη κατηγορία αναφέρεται στα διαγράμματα μερικής παλινδρόμησης, τα οποία έχουν ήδη παραχθεί στο κεφάλαιο , διότι ταυτόχρονα αντικατοπτρίζουν τη σημαντικότητα της κάθε μεταβλητής στη διαμόρφωση της αγοραίας αξίας των ακινήτων. Τα διαγράμματα 5.45, 5.46, 5.47, 5.48, 5.49 και 5.50 παρουσιάζουν μία όχι ιδιαίτερα ισχυρή γραμμική σύνδεση της Υ με τις ανεξάρτητες μεταβλητές, σε καμία περίπτωση όμως δεν απορρίπτεται η ύπαρξη γραμμικότητας στο μοντέλο των έξι μεταβλητών. Τέλος, τα δύο τελευταία διαγράμματα ελέγχου της γραμμικότητας του μοντέλου είναι τα γραφήματα της εικόνας 5.59 (αριστερό και δεξί διάγραμμα) τα οποία όπως αναφέρεται στο αντίστοιχο κεφάλαιο ελέγχου της ομοσκεδασιμότητας του μοντέλου, παρουσιάζουν την ύπαρξη γραμμικότητας. Συνεπώς, όλα τα παραπάνω διαγράμματα συνηγορούν στο συμπέρασμα ότι υπάρχει γραμμικότητα μεταξύ της αγοραίας αξίας των ακινήτων και του εμβαδού, της κατάστασης των διαμερισμάτων, του είδους θέρμανσης, της ύπαρξης ανελκυστήρα, του αριθμού των δωματίων και τέλος του αριθμού των μπάνιων τους Ακραίες οντότητες και οντότητες επίδρασης Το γεγονός ότι στην περιοχή της Badalona Βαρκελώνης δεν απαιτήθηκε αρχικά να αφαιρεθεί καμία οντότητα για το σχηματισμό της τελικής παλινδρομικής εξίσωσης σημαίνει ότι στον παρόν έλεγχο αυξάνονται οι πιθανότητες να υπάρχουν αρκετές υποψήφιες ακραίες οντότητες. Τα διαδοχικά βήματα εντοπισμού των ακραίων οντοτήτων που ακολουθούν πρόκειται να αποκαλύψουν εάν ισχύει η αρχική υπόθεση για μεγαλύτερο πλήθος υποψήφιων ακραίων οντοτήτων, σε σχέση με τα προηγούμενα μοντέλα, λόγω της ιδιαιτερότητας του παρόντος. Συνοπτικά αναφέρεται ότι για τον εντοπισμό των ακραίων οντοτήτων (outliers) αξιοποιείται η απόσταση Mahalanobis (Mahalanobis distance Di2) και η τιμή Centered Leverage, ενώ για τον εντοπισμό των οντοτήτων επίδρασης (influential points)αξιοποιούνται αντίστοιχα οι αποστάσεις Cook (Cook s Distance : CD i ), το μέτρο DFFITS (Standardized DFFITS) και το μέτρο DFBetas (Standardized DFBetas). Οι δύο τελευταίοι έλεγχοι γίνονται με τη βοήθεια της t και F κατανομής. Centered Leverage Η κρίσιμη τιμή του δείκτη Centered Leverage είναι ίση με την τιμή 0,2, καθώς σύμφωνα με τη βιβλιογραφία τιμές μικρότερες του 0,2 δεν φανερώνουν την ύπαρξη ακραίων οντοτήτων. Όταν οι τιμές είναι μεγαλύτερες του 0,2 και μικρότερες του 0,5 τότε υπάρχουν ενδείξεις ότι μπορεί η οντότητα να είναι ακραία και θα πρέπει να εξεταστεί εκτενέστερα για την πιθανή απομάκρυνση της. Από τον έλεγχο όλων των τιμών Centered Leverage στη στήλη LEV_1, διαπιστώνεται ότι οι οντότητες με A/A 21 (0,26) και 62 (0,27) ξεπερνούν την οριακή τιμή 0,2. Παρόλα αυτά 240
253 Κ ε φ ά λ α ι ο 5 ο επειδή οι τιμές Centered Leverage είναι πολύ κοντά στην οριακή τιμή πιθανότερο είναι να μη δημιουργούν ουσιαστικά προβλήματα στο μοντέλο και να μην είναι απαραίτητη η απομάκρυνση τους. Με την μη εύρεση ακραίων οντοτήτων μέσω του δείκτη Centered Leverage, ικανοποιείται ταυτόχρονα και ο έλεγχος του δείκτη Mahalanobis. Αποστάσεις Cook CD i Η αντίστοιχη κρίσιμη τιμή στην περίπτωση των αποστάσεων Cook είναι η μονάδα, ενώ η στήλη που περιέχει τις τιμές Cook του δείγματος για κάθε οντότητα είναι η COO_1. Συγκρίνοντας τις 80 τιμές Cook του δείγματος προκύπτει ότι καμία οντότητα δεν ξεπερνά την οριακή τιμή και συνεπώς σύμφωνα με τον δείκτη Cook καμία οντότητα δεν αποτελεί οντότητα επίδρασης. Παρακάτω ακολουθεί και η διαγραμματική απεικόνιση των τιμών Cook, όπου οπτικοποιείται η παραπάνω διαπίστωση. Μέτρα DfFits Για τον εντοπισμό των οντοτήτων επίδρασης αρχικά υπολογίζεται η Standardized DfFits κρίσιμη βάσει του ακόλουθου τύπου: Standardized DfFits κρίσιμη = 2* = 0, 59 Στη συνέχεια, η τιμή 0,59 συγκρινόμενη με τις τιμές της στήλης SDF_1 του Data Editor παρουσιάζει τις οντότητες με Α/Α 13 (0,65), 21 (1,25), 29 (0,62), 42 (0,77), 45 (0,62), 62 (1,15) και 70 (0,69) να την ξεπερνούν. Όπως παρατηρείται οι οντότητες 13, 29, 42, 45 και 70 ξεπερνούν για πολύ λίγο της οριακή τιμή, σε αντίθεση με τις οντότητες 21 και 62, οι οποίες έχουν περίπου διπλάσια τιμή της οριακής. Επίσης, διαπιστώνεται ότι οι οντότητες 21 και 62 που έχουν αναφερθεί νωρίτερα στην περίπτωση του δείκτη Centered Leverage είναι εκείνες που είναι πολύ πιθανό να επιδρούν στην ανάλυση παλινδρόμησης και κατ επέκταση στους συντελεστές παλινδρόμησης. Μέτρα DfBetas Για τον έλεγχο των μέτρων DfBetas αξιοποιούνται οι τιμές των Standardized DfBetas και στη συνέχεια συγκρίνονται με την κρίσιμη τιμή για την ύπαρξη οντοτήτων επίδρασης. Η κρίσιμη τιμή για τις περιπτώσεις των μεγάλων δειγμάτων (n>30) δίνεται από την ακόλουθη σχέση: Standardized DfBetas κρίσιμη = = 0, 22 Μεταπτυχιακή διατριβή 241
254 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Αναλυτικά, για τον έλεγχο που αφορά τη μεταβλητή AREA λαμβάνεται υπόψη η στήλη με τίτλο SDB1_1 του Data Editor, η οποία επισημαίνει τις οντότητες με Α/Α 21(0,64), 42 (0,57), 62 (0,68), και 75 (0,44) ως υποψήφιες οντότητες επίδρασης. Για τον έλεγχο που αφορά τη μεταβλητή ELEV λαμβάνεται υπόψη η στήλη με τίτλο SDB4_1 του Data Editor, η οποία επισημαίνει ως υποψήφιες οντότητες επίδρασης τις 51 (0,40), 62 (0,45) και 70 (0,44). Εν συνεχεία, για τον έλεγχο που αφορά τη μεταβλητή HEATING αξιοποιείται η στήλη με τίτλο SDB5_1 του Data Editor, η οποία με τη σειρά της επισημαίνει τις οντότητες 2 (0,29), 45 (0,26), 73 (0,26) και 77 (0,26) ως υποψήφιες οντότητες επίδρασης. Για τη μεταβλητή QUALITY αξιοποιείται η στήλη SDB6_1, η οποία υποδεικνύει τις οντότητες 2 (0,30), 21 (0,36), 29 (0,40) και 62 (0,70). Για τον έλεγχο που αφορά τη μεταβλητή ROOM λαμβάνεται υπόψη η στήλη με τίτλο SDB8_1 του Data Editor, η οποία επισημαίνει ως υποψήφιες οντότητες επίδρασης τις 42 (0,30), 62 (0,62) και 64 (0,34). Τέλος, όσον αφορά τη μεταβλητή BATH λαμβάνεται υπόψη η στήλη με τίτλο SDB9_1, η οποία επισημαίνει τις οντότητες με Α/Α 3 (0,31), 13 (0,34), 21 (0,48), 70 (0,48), 75 (0,46) και 77 (0,44). Από τον μεγάλο αριθμό των οντοτήτων που ξεπερνούν την τιμή 0,22 επιβεβαιώνεται ότι στο συγκεκριμένο μοντέλο είναι πιθανό να απαιτηθεί στο τέλος η απομάκρυνση ορισμένων οντοτήτων για την βελτιστοποίηση του μοντέλου, επιβεβαιώνοντας ταυτόχρονα και την αρχική υπόθεση. Οι οντότητες που εμφανίζονται στα περισσότερα μέτρα είναι οι 21, 62, 64 και 75, συνεπώς είναι οι παρατηρήσεις, των οποίων η απομάκρυνση από το μοντέλο είναι πιθανότερη. Από τους ελέγχους των κατανομών t και F που ακολουθούν πρόκειται να διαπιστωθεί εάν η επίδραση τους είναι στατιστικά σημαντική, ώστε να πρέπει να αφαιρεθούν. Διάγραμμα σκέδασης των αποστάσεων Cook με κεντραρισμένες τιμές Leverage 242
255 Κ ε φ ά λ α ι ο 5 ο Διάγραμμα 5.60: Διάγραμμα σκέδασης των αποστάσεων Cook με τις Centered leverage τιμές Όπως αναφέρεται παραπάνω δύο από τις 80 οντότητες έχουν τιμή Centered Leverage που ξεπερνά την τιμή 0,2, ενώ καμία οντότητα δεν ξεφεύγει από την οριακή τιμή των αποστάσεων Cook. Το διάγραμμα 5.60 που ακολουθεί οπτικοποιεί τα συγκεκριμένα στοιχεία για να φανεί ταυτόχρονα η διασπορά όλων των περιπτώσεων και τα μεγέθη των αποκλίσεων. Ο αριθμός των σημείων που ξεπερνούν την κρίσιμη τιμή είναι αρκετά μικρός εάν λάβει κανείς υπόψη ότι αποτελεί μόνο το 2,5% του συνόλου. Διάγραμμα σκέδασης των τυποποιημένων DfFits με την ακολουθία των παρατηρήσεων Όμοια στο παρακάτω διάγραμμα σκέδασης των τυποποιημένων DfFits με την ακολουθία των παρατηρήσεων, οπτικοποιούνται οι επτά οντότητες που ξεπερνούν την τιμή 0,59 (13, 21, 29, 42, 45, 62 και 70). Παρατηρώντας το διάγραμμα 5.61 εντοπίζονται δύο μεγάλες εξάρσεις, οι οποίες ξεπερνούν την μονάδα και υποδεικνύουν τις οντότητες 21 και 62. Πέραν των συγκεκριμένων δύο περιπτώσεων, όλα τα υπόλοιπα σημεία φαίνεται οπτικά να μην παρουσιάζουν ιδιαίτερες αποκλίσεις. Διάγραμμα 5.61: Διάγραμμα Sequence των DfFits με την αύξουσα σειρά του δείγματος Μεταπτυχιακή διατριβή 243
256 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Διάγραμμα σκέδασης των τυποποιημένων DfBetas με την ακολουθία των παρατηρήσεων Διάγραμμα 5.62: Διάγραμμα Sequence των DfBetas με την αύξουσα σειρά του δείγματος Όμοια στην περίπτωση του διαγράμματος απεικόνισης των τιμών DfBetas, οπτικοποιείται ο βαθμός απόκλισης των υποψήφιων οντοτήτων επίδρασης. Οι μεγαλύτερες εξάρσεις παρατηρούνται στην οντότητα 62 (AREA, QUALITY, ROOM), καθώς και στην 21 (AREA), ενώ όλες οι υπόλοιπες βρίσκονται μεταξύ των τιμών ± 0,50. Στους ελέγχους των δύο κατανομών που ακολουθούν στηρίζεται η απομάκρυνση ή όχι των παραπάνω υποψήφιων οντοτήτων επίδρασης. t κατανομή Τα Studentized Deleted Residuals μέσω της διαδικασίας Bonferroni και της t κατανομής μπορούν να βοηθήσουν στον εντοπισμό των οντοτήτων επίδρασης. Όπου t i ορίζεται η τιμή των Studentized Deleted Residuals, τα οποία ακολουθούν την κανονική κατανομή με βαθμούς ελευθερίας: β.ε. = n-p-1 = = 72 Η κρίσιμη τιμή που ορίζει η διαδικασία Bonferroni και είναι ίση με: 244
257 Κ ε φ ά λ α ι ο 5 ο t κρίσιμη = t(1 - ; n-p-1) t (0, ; 72) = 3,22 με α το επίπεδο στατιστικής σημαντικότητας (α= 0,05), n το μέγεθος του δείγματος (n =80) και p τον αριθμό των συντελεστών παλινδρόμησης μαζί με το σταθερό όρο (p = 7). Επόμενο βήμα αποτελεί ο εντοπισμός της οντότητας με το μεγαλύτερο Studentized Deleted Residual (max SDR)ώστε να συγκριθεί με την οριακή τιμή που προέκυψε παραπάνω. Από τα δεδομένα του Data Editor προκύπτει ότι η οντότητα με τη μεγαλύτερη απόλυτη τιμή Studentized Deleted Residual κατά απόλυτη τιμή είναι η = = 2,34. Ορίζεται η μηδενική υπόθεση Ηο: Το Studentized Deleted Residual με τη μεγαλύτερη απόλυτη τιμή μία οντότητα επίδρασης, με εναλλακτική υπόθεση =2,34 ΔΕΝ είναι Η1: Studentized Deleted Residual με τη μεγαλύτερη απόλυτη τιμή = 2,34 είναι οντότητα επίδρασης Επειδή όμως = 2,34 <3,22 ισχύει η μηδενική υπόθεση Ηο και η οντότητα 45 δεν αποτελεί οντότητα επίδρασης. Το γεγονός ότι η οντότητα με την πιο μεγάλη τιμή Studentized Deleted Residual δεν αποτελεί οντότητα επίδρασης, αποκλείει την πιθανότητα οι υποψήφιες οντότητες επίδρασης των προηγούμενων βημάτων να επηρεάζουν την ανάλυση παλινδρόμησης και κατ επέκταση τους συντελεστές της παλινδρομικής εξίσωσης. F κατανομή Οι τιμές Cook θεωρείται ότι ακολουθούν την κατανομή F(1-a;p;n-p), συνεπώς με τη βοήθεια της κατανομής μπορούν να εντοπιστούν οι οντότητες επίδρασης εάν και εφόσον υπάρχουν. Με την ίδια λογική που περιγράφηκε παραπάνω υπολογίζεται αρχικά η κρίσιμη τιμή F και στη συνέχεια συγκρίνεται με την τιμή Cook που είναι η μεγαλύτερη σε μέγεθος σε σύγκρισή με όλες τις υπόλοιπες. F κρίσιμη =F(1-a; p; n-p) = F(0,95; 7; 73) = 2,15 Η μέγιστη απόσταση Cook ανήκει στην οντότητα 21 και είναι ίση με CD 21 = 0,21. Από τους στατιστικούς πίνακες της F κατανομής παρατηρείται ότι η τιμή βρίσκεται στο 21,50% εκατοστημόριο της συγκεκριμένης κατανομής, δηλαδή δεν πλησιάζει σε καμία περίπτωση το 50% και άρα η οντότητα δε μπορεί να χαρακτηριστεί οντότητα επίδρασης. Σύμφωνα με τους δύο ελέγχους καμία από τις υποψήφιες οντότητες επίδρασης των προηγούμενων ελέγχων δε δημιουργεί ουσιαστικό πρόβλημα στους συντελεστές παλινδρόμησης και άρα δε χρειάζεται να απομακρυνθεί από το μοντέλο. Οι επτά διαδοχικοί έλεγχοι οδηγούν στο συμπέρασμα ότι το τελικό μοντέλο εκτίμησης αξιών για την περιοχή Badalona της Βαρκελώνης στηρίζεται σε δείγμα 80 παρατηρήσεων και συμπεριλαμβάνει έξι ανεξάρτητες οντότητες. Μεταπτυχιακή διατριβή 245
258 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ Έλεγχος προβλεπτικής ικανότητας του μοντέλου Η ικανοποίηση των βασικών υποθέσεων του παλινδρομικού μοντέλου αποτελεί ένα πρώτο βήμα της διαδικασίας, το οποίο ακολουθείται από μερικές διαδικασίες που εστιάζουν αποκλειστικά στον έλεγχο της προβλεπτικής δύναμης του μοντέλου. Εάν οι παρακάτω μέθοδοι που ακολουθούν «μετρήσουν» μεγάλη προβλεπτική ικανότητα, τότε το μοντέλο της Badalona με τις 80 οντότητες και τις έξι ανεξάρτητες μεταβλητές είναι το τελικό μοντέλο εκτίμησης της αξίας των ακινήτων στην πέμπτη περιοχή μελέτης Μέθοδος των διαστημάτων πρόβλεψης Για τη χρήση της μεθόδου που αναφέρεται στα διαστήματα πρόβλεψης συλλέγονται πέντε επιπλέον οριζόντιες ιδιοκτησίες από τον ίδιο πληθυσμό που ανήκει το δείγμα των 80 οντοτήτων. Εκτελείται η διαδικασία πολλαπλής παλινδρόμησης μόνο για τις 80 πρώτες οντότητες του δείγματος και στη συνέχεια συγκρίνονται οι γνωστές αξίες των πέντε νέων οντοτήτων με τα διαστήματα πρόβλεψης που προκύπτουν από τη στατιστικά ανάλυση(lici, UICI). Τα αποτελέσματα που είναι ορατά παρακάτω, αποδεικνύουν ότι το πέμπτο μοντέλο ανταποκρίνεται στην πραγματικότητα, καθώς όλες οι παρατηρούμενες αγοραίες αξίες βρίσκονται εντός των διαστημάτων πρόβλεψης. Το εύρος των διαστημάτων πρόβλεψης θεωρείται σχετικά μεγάλο, διότι είναι της τάξης των , γεγονός που δε μπορεί να δικαιολογηθεί απόλυτα εξαιτίας των ιδιαίτερα ικανοποιητικών ελέγχων που έχουν προηγηθεί και της ύπαρξης ομοιογένειας στο μοντέλο. Μία πιθανή αιτία μπορεί να είναι ο μεγάλος αριθμός ανεξάρτητων μεταβλητών που επιδρούν στο μοντέλο και προφανώς δημιουργούν μικρότερη σταθερότητα όσον αφορά την πρόβλεψη αξιών νέων ακινήτων < < < < < < < < < < Μέθοδος του διαχωρισμού των δεδομένων (Data Splitting) Η μέθοδος Data Splitting έχει στόχο μέσω του διαχωρισμού των δεδομένων σε δύο τμήματα, να δημιουργήσει ένα μοντέλο με το πρώτο μέρος του δείγματος και να εντοπίσει τη συσχέτιση του με το δεύτερο μέρος του δείγματος. Εάν η συσχέτιση Pearson είναι ισχυρή σημαίνει ότι υφίσταται ισχυρή προβλεπτική ικανότητα στο μοντέλο. 246
259 Κ ε φ ά λ α ι ο 5 ο 1 ο ΒΗΜΑ: Επιλέγεται από το δείγμα των 80 οντοτήτων το 70% περίπου των παρατηρήσεων με τυχαία σειρά επιλογής. Το SPSS κατά την εκτέλεση της διαδικασίας επιλέγει συνολικά 62 οντότητες. Με το νέο δείγμα διαμερισμάτων εκτελείται η διαδικασία της πολλαπλής γραμμικής παλινδρόμησης και προκύπτει η παρακάτω εξίσωση παλινδρόμησης: Υ = , ,869 BATH ,860 QUALITY ,280 ELEV ,784 HEATING ,686 ROOM με R = 0,897, R 2 = 0,805, Radj 2 = 0,787 και δείκτη Durbin Watson = Επίσης όλες οι υπόλοιπες τιμές των δεικτών είναι εντός επιτρεπόμενων ορίων και κινούνται στα ίδια πλαίσια στα οποία βρίσκεται το μοντέλο των 80 οντοτήτων. Συνεπώς, πρόκειται για ένα καλό και αξιόπιστο μοντέλο. Όσον αφορά τον έλεγχο ανεξαρτησίας των οντοτήτων, το διάγραμμα Studentized Residual vs AA (Sequence) επιβεβαιώνει ότι πρόκειται για ένα μοντέλο που πληροί όλες τις βασικές παραδοχές μιας γραμμικής παλινδρόμησης (Διάγραμμα 5.63). Διάγραμμα 5.63: Διάγραμμα σκέδασης των Studentized Residual vs AA (Sequence) για τις 62 μόνο οντότητες του δείγματος Μεταπτυχιακή διατριβή 247
260 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ 2 ο ΒΗΜΑ: Στη συνέχεια της διαδικασίας επιλέγονται οι υπόλοιπες 18 οντότητες και με τη χρήση της εξίσωσης παλινδρόμησης που προκύπτει από το πρώτο βήμα εκτελείται η εντολή Compute Variables. Δημιουργείται μία νέα στήλη PRED για το σύνολο των 80 οντοτήτων. Η συσχέτιση μεταξύ της παρατηρούμενης και της προβλεπόμενης τιμής PRED είναι ίση με 0,896, συνεπώς η προβλεπτική ικανότητα του μοντέλου των 80 οντοτήτων είναι ιδιαίτερα ικανοποιητική. Για την επιβεβαίωση της αξιολόγησης κατασκευάζεται και το διάγραμμα σκέδασης μεταξύ των PRED και Υ, ώστε να οπτικοποιηθεί το αποτέλεσμα (Διάγραμμα 5.64). Διάγραμμα 5.64: Διάγραμμα Bivariate συσχέτισης μεταξύ των προβλεπόμενων και παρατηρούμενων τιμών Είναι εμφανής ο ισχυρός βαθμός συσχέτισης των δύο τιμών και άρα η δύναμη πρόβλεψης του μοντέλου Μέθοδος εύρεσης του βέλτιστου αριθμού σημαντικών μεταβλητών Με τη βοήθεια του κριτηρίου Mallow s ελέγχεται εάν οι μεταβλητές οι οποίες επιλέγονται από τον αλγόριθμο ως στατιστικά σημαντικές είναι επαρκείς για να ερμηνεύσουν το φαινόμενο ή εάν είναι περισσότερες ή λιγότερες. 248
261 n0 Κ ε φ ά λ α ι ο 5 ο Μέσω της διαδικασίας που περιγράφεται αναλυτικά στο υποκεφάλαιο παράγεται ο παρακάτω πίνακας (Πίνακας 5.22). Σύμφωνα με τα στοιχεία του κριτηρίου πρόβλεψης Mallow ο αριθμός των μεταβλητών, ο οποίο ερμηνεύει ικανοποιητικά την αγοραία αξία των ακινήτων στην περιοχή Badalona είναι επτά (7). Το αποτέλεσμα ταυτίζεται με τον αριθμό των μεταβλητών του μοντέλου (Υ, AREA, QUALITY, ELEV, HEATING, ROOM, BATH) και άρα η τρίτη μέθοδος ελέγχου συνηγορεί σε ένα αξιόπιστο μοντέλο πρόβλεψης. Πίνακας 5.22: Πίνακας Model Summary που περιλαμβάνει το κριτήριο πρόβλεψης Mallow Model Summary Model Selection Criteria Std. Error Akaike Amemiya Mallows' Schwarz R Adjusted of the Information Prediction Prediction Bayesian R Square R Square Estimate Criterion Criterion Criterion Criterion 1,756 a,571, , ,714,451 91, ,478 2,832 b,692, , ,259,332 46, ,405 3,878 c,771, , ,393,253 17, ,921 4,888 d,788, , ,387,240 13, ,297 5,894 e,800, , ,743,233 10, ,036 6,902 f,814, , ,094,222 7, ,768 Όλα τα βήματα ελέγχου του μοντέλου ικανοποιούν τις παραδοχές και τις απαιτήσεις που έχουν τεθεί με αποτέλεσμα να ολοκληρώνεται με επιτυχία και το τελευταίο μοντέλο εκτίμησης αγοραίων αξιών της παρούσας εφαρμογής Ερμηνεία μοντέλου για την περιοχή Badalona Η συνολική επισκόπηση του τελευταίου μοντέλου αποκτά ιδιαίτερο ενδιαφέρον, λαμβάνοντας υπόψη ότι για το σχηματισμό της τελικής εξίσωσης παλινδρόμησης δεν απαιτείται η προσέγγιση διαδοχικών μοντέλων μέσω της αφαίρεσης ακραίων οντοτήτων. Η πρώτη εκτέλεση της πολλαπλής γραμμικής παλινδρόμησης με δείγμα 80 οντοτήτων οδηγεί σε ένα μοντέλο εκτίμησης αξιών το οποίο χαρακτηρίζεται από έναν ιδιαίτερα υψηλό συντελεστή προσδιορισμού R 2 και από έξι ανεξάρτητες μεταβλητές που επιδρούν σε διαφορετικό βαθμό στη διαμόρφωση των αξιών της περιοχής μελέτης. Ταυτόχρονα, το γεγονός ότι ικανοποιούνται όλες οι υποθέσεις που πρέπει να ισχύουν κατά το σχηματισμό ενός γραμμικού μοντέλου με πολλές μεταβλητές, οδηγούν στο συμπέρασμα ότι η απομάκρυνση περιπτώσεων δεν αποτελεί αυτοσκοπό σε μία στατιστική ανάλυση. Είναι πολλές φορές ο δρόμος για τη βελτιστοποίηση του μοντέλου, αλλά δεν είναι πάντα Μεταπτυχιακή διατριβή 249
262 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ απαραίτητη. Κάθε μοντέλο, όσα κοινά χαρακτηριστικά φαίνεται να έχει με άλλα, είναι μοναδικό και απαιτείται κριτική ικανότητα και γνώση της βασικής μεθοδολογίας ώστε εάν χρειαστεί να δοθεί μία λύση, η οποία να διαφέρει από άλλα παρόμοια μοντέλα. Στην περίπτωση της περιοχής Badalona ικανοποιούνται όλες οι παραδοχές που τίθενται βάσει μεθοδολογίας. Ο έλεγχος της ανεξαρτησίας, της πολυσυγγραμικότητας, της κανονικότητας και ομοσκεδασιμότητας δίνουν άψογα αποτελέσματα. Ο έλεγχος της σημαντικότητας των μεταβλητών και της γραμμικότητας, οι οποίοι στηρίζονται σε μεγάλο βαθμό από την ερμηνεία των διαγραμμάτων μερικής συσχέτισης, ικανοποιούνται αλλά παρουσιάζουν ασθενέστερες σχέσεις από ότι θα ήταν επιθυμητό για το μοντέλο. Παρόλα αυτά δεν αποκλείεται η σημαντικότητα των μεταβλητών και η γραμμικότητα του μοντέλου, η οποία είναι ξεκάθαρη. Η προβλεπτική ικανότητα του μοντέλου, η οποία διερευνάται μέσω των τριών μεθόδων παρουσιάζουν ένα μοντέλο με σημαντική προβλεπτική ικανότητα. Η περιοχή Badalona θεωρείται ότι εμφανίζει ομαλότητα ως προς τον τρόπο με τον οποίο διαμορφώνονται οι αξίες των ακινήτων της, κρίνοντας από το γεγονός ότι έξι διαφορετικές μεταβλητές συσχετίζονται γραμμικά με την αγοραία αξία. Παράλληλα, ο σχηματισμός μοντέλου που περιλαμβάνει έξι ανεξάρτητες μεταβλητές μαρτυρά ότι η περιοχή μελέτης χαρακτηρίζεται από ομοιομορφία ως προς της γεωγραφική θέση, δηλαδή κανένα διαμέρισμα δε διαθέτει μία ιδιαίτερα προνομιακή θέση σε σύγκριση με τα υπόλοιπα του δείγματος των 80 οντοτήτων, ώστε να δημιουργούνται εξάρσεις και ανομοιογένειες. Συνεπώς, αυξάνεται σημαντικά ο ρόλος και η επίδραση των ιδιαίτερων χαρακτηριστικών της κάθε οριζόντιας ιδιοκτησίας. Σύμφωνα με την ακόλουθη εξίσωση παλινδρόμησης, η αγοραία αξία των διαμερισμάτων εξαρτάται από το εμβαδόν τους, τον βαθμό συντήρησης τους, το είδος θέρμανσης που διαθέτουν, την ύπαρξη ασανσέρ και τέλος τον αριθμό των δωματίων και των μπάνιων τους. Υ = , ,829 AREA ,057 QUALITY ,625 BATH ,707 ELEV ,616 HEATING ,216 ROOM με R 2 = 0,814 Λαμβάνοντας υπόψη το συντελεστή προσδιορισμού R 2, παρατηρείται μία ικανοποιητική προσαρμογή του μοντέλου στα δεδομένα και άρα ένα αρκετά μεγάλο τμήμα της αξίας ερμηνεύεται από τις έξι μεταβλητές. Πιο συγκεκριμένα, το 81,4% της συνολικής διακύμανσης της αγοραίας αξίας των ακινήτων οφείλεται στις πληροφορίες που περιλαμβάνουν οι έξι ανεξάρτητες μεταβλητές (AREA, QUALITY, BATH, ELEV, HEATING, ROOM), η κάθε μία ξεχωριστά και όλες μαζί. Η ίδια διαπίστωση γίνεται και για τον προσαρμοσμένο συντελεστή προσδιορισμού (Adjusted R 2 ), ο οποίος σύμφωνα με τα στοιχεία του πίνακα 5.18 είναι ίσος με 0,798. Το ποσοστό 79,8 % αντιπροσωπεύει τη συνολική διακύμανση της αγοραίας αξίας που οφείλεται στις παραπάνω μεταβλητές για 250
263 Κ ε φ ά λ α ι ο 5 ο κάθε άλλο δείγμα του ίδιου πληθυσμού της περιοχής Badalona, γεγονός που ταυτόχρονα επιβεβαιώνει την ικανοποιητική προβλεπτική δύναμη του πέμπτου μοντέλου. Εστιάζοντας στις ανεξάρτητες μεταβλητές ο πίνακας 5.18 εμπεριέχει τους συντελεστές προσδιορισμού R 2 κάθε μοντέλου κατά την εκτέλεση της βηματικής διαδικασίας (stepwise) δείχνοντας τη συμβολή της κάθε μίας στη διαμόρφωση των αξιών. Πιο συγκεκριμένα, η μεταβλητή που συμβάλει περισσότερο στη διαμόρφωση της αγοραίας αξίας είναι το εμβαδόν με ποσοστό 57%. Ακολουθεί η κατάσταση του ακινήτου, η οποία είναι υπεύθυνη για το 12,1% της διακύμανσης της εξαρτημένης μεταβλητής, ο αριθμός των μπάνιων με ποσοστό συνεισφοράς 7,9%, ο ανελκυστήρας με ποσοστό 1,7%, το είδος θέρμανσης με ποσοστό 1,2% και τέλος ο αριθμός των δωματίων με ποσοστό συνεισφοράς 1,4%. 5.4 ΣΥΜΠΕΡΑΣΜΑΤΑ Έπειτα από τη μελέτη όλων των αποτελεσμάτων προκύπτει το γενικό συμπέρασμα ότι κάθε περιοχή ή γειτονιά της Βαρκελώνης ανάλογα με τα ιδιαίτερα χαρακτηριστικά της γνωρίσματα (πληθυσμιακά, ιστορικά, κατασκευαστικά κλπ) διαμορφώνει διαφορετικά μοντέλα εκτίμησης αξιών ακινήτων. Οι τρεις εξισώσεις παλινδρόμησης των περιοχών Eixample, Sant Marti και Badalona ποικίλουν αρχικά ως προς τον αριθμό και το είδος των ανεξάρτητων μεταβλητών που συνδέονται γραμμικά και δεύτερον ποικίλουν ως προς τα βάρη των κοινών τους μεταβλητών. Στην προκειμένη περίπτωση διαμορφώνονται τρία πολύ διαφορετικά μεταξύ τους μοντέλα τα οποία αντικατοπτρίζουν τις διαφορές των περιοχών μελέτης της Βαρκελώνης. Η βασική ιδιαιτερότητα της περιοχής Eixample είναι η πολύ μεγάλη ανομοιογένεια στα διαμερίσματα της. Από τη μία μεριά ισόγεια διαμερίσματα σε κακή κατάσταση και από την άλλη μεριά πολυτελείς κατοικίες με υπέροχη θέα και τιμές πώλησης που ξεπερνούν κατά πολύ το μέσο όρο των υπόλοιπων διαμερισμάτων. Πολύ μεγάλες αξίες, οι οποίες δε συνδέονται τόσο με τα χαρακτηριστικά γνωρίσματα των κατοικιών, αλλά με τη γεωγραφική θέση τους μέσα στο πολεοδομικό συγκρότημα της πόλης. Σύμφωνα με το τελικό μοντέλο δείγματος 63 οντοτήτων οι αξίες των διαμερισμάτων της περιοχής Eixample εξαρτώνται στο μεγαλύτερο ποσοστό από το εμβαδόν τους, ακολουθεί η κατάσταση των ακινήτων και έπεται με μικρότερο ποσοστό συμβολής ο αριθμός των μπάνιων που διαθέτουν. Από το μοντέλο αποκλείονται εξίσου σημαντικές μεταβλητές, όπως η παλαιότητα, ο όροφος, ο αριθμός δωματίων, η ύπαρξη ανελκυστήρα, θέσης στάθμευσης και το είδος θέρμανσης. Από τις προαναφερθείσες οι μεταβλητές ELEV (περίπου το 90% των διαμερισμάτων διαθέτουν ανελκυστήρα) και PARKING (περίπου το 9% διαθέτουν θέση στάθμευσης) δεν επιδρούν στη συνολική διακύμανση της αγοραίας αξίας εξαιτίας της συγκέντρωσης μεγάλων ποσοστών σε μία από τις δύο δυνατές τιμές, ενώ οι μεταβλητές AGE, FLOOR, και HEATING φανερώνουν ύπαρξη συσχέτισης, η οποία όμως δεν είναι τόσο ισχυρή ώστε να συμμετέχουν στο μοντέλο. Παρόλο που το μοντέλο θεωρεί μόνο τρεις από τις εννέα μεταβλητές στατιστικά σημαντικές, είναι πάρα πολύ ικανοποιητικό από τη σκοπιά της στατιστικής, λαμβάνοντας υπόψη την ύπαρξη ανομοιογένειας. Οι έλεγχοι όλων των Μεταπτυχιακή διατριβή 251
264 Σ χ η μ α τ ι σ μ ό ς μ ο ν τ έ λ ο υ υποθέσεων είναι ιδιαίτερα ικανοποιητικοί με πιο εντυπωσιακά τα γραφήματα που αντιστοιχούν στον έλεγχο της παραδοχής της κανονικότητας, διότι προσεγγίζεται περισσότερο από κάθε άλλο μοντέλο η πλήρης κανονικότητα. Η δεύτερη περιοχή μελέτης χαρακτηρίζεται από μεγαλύτερη ομοιογένεια και περιλαμβάνει κατοικίες χωρίς ιδιαίτερες εξάρσεις στις τιμές τους. Το ιδιαίτερο χαρακτηριστικό της είναι η συμβολή της παλαιότητας στη διαμόρφωση των αξιών, η οποία έχει την ίδια περίπου βαρύτητα με τη μεταβλητή «Εμβαδόν διαμερίσματος», ενώ σε κάθε άλλο μοντέλο η συμβολή της παλαιότητας κινείται σε αρκετά μικρότερα ποσοστά. Αναλυτικότερα, η εξίσωση παλινδρόμησης φανερώνει μία γραμμική σύνδεση της αγοραίας αξίας των ακινήτων με το εμβαδόν, την παλαιότητα και τέλος το είδος θέρμανσης των διαμερισμάτων, ενώ αποκλείονται από το μοντέλο μεταβλητές όπως ο αριθμός των ορόφων, η ύπαρξη ανελκυστήρα, θέσης στάθμευσης, ο αριθμός των δωματίων, των μπάνιων και η κατάσταση του ακινήτου. Όμοια με άλλα μοντέλα οι μεταβλητές ELEV (98% διαθέτουν ανελκυστήρα)και PARKING (7% διαθέτουν θέση στάθμευσης) έχουν συγκεντρωτικό χαρακτήρα και δεν είναι εφικτό να διαμορφώνουν τη διασπορά των αξιών. Η μεταβλητή ROOM παρουσιάζει ικανοποιητικό βαθμό συσχέτισης με τη μεταβλητή Υ, κρίνοντας από τους μερικούς συντελεστές που υπολογίζονται παραπάνω και από την πρώτη προσέγγιση του μοντέλου, κατά την οποία θεωρείται στατιστικά σημαντική. Παρόλα αυτά με την αφαίρεση ακραίων οντοτήτων η σχέση εξασθενεί και η μεταβλητή δεν συμμετέχει τελικά στο μοντέλο. Τέλος, οι υπόλοιπες μεταβλητές FLOOR, QUALITY, BATH, δε δείχνουν καμία γραμμική σχέση από την πρώτη προσέγγιση. Η ποιότητα του μοντέλου είναι εξίσου ικανοποιητική, καθώς υφίσταται σημαντικότητα των μεταβλητών, ύπαρξη ανεξαρτησίας, βέβαιη απουσία πολυσυγγραμικότητας, σταθερότητα της διακύμανσης και ύπαρξη κανονικότητας. Ο βαθμός προβλεπτικής ικανότητας του μοντέλου είναι ισχυρότερος σε σύγκριση με τις υπόλοιπες περιοχές μελέτης της Βαρκελώνης, ενώ το εύρος του διαστήματος πρόβλεψης είναι αντίστοιχα το μικρότερο σε σχέση με τα υπόλοιπα δύο. Το ιδιαίτερο χαρακτηριστικό γνώρισμα του τέταρτου μοντέλου που αντιστοιχεί στην περιοχή Sant Mart είναι η ύπαρξη θετικού σταθερού όρου, καθώς όπως φαίνεται εξομαλύνεται με αυτόν τον τρόπο η σημαντική αρνητική επίδραση της παλαιότητας στο μοντέλο. Η τρίτη περιοχή της Βαρκελώνης αποτελεί ένα προάστιο της πόλης, με το δικό του κέντρο και τα δικά του χαρακτηριστικά γνωρίσματα. Είναι το μόνο μοντέλο της Βαρκελώνης, το οποίο φανερώνει γραμμική σχέση μεταξύ της εξαρτημένης μεταβλητής Υ και έξι ανεξάρτητων μεταβλητών. Πιο συγκεκριμένα, η αξία των ακινήτων της περιοχής, βάσει της παλινδρομικής εξίσωσης εξαρτάται από τον εμβαδόν, την κατάσταση του ακινήτου, την ύπαρξη ανελκυστήρα, το είδος θέρμανσης, των αριθμό των δωματίων και τον αριθμό των μπάνιων. Αποκλείονται από το μοντέλο μεταβλητές όπως η παλαιότητα, ο αριθμός του ορόφου και η ύπαρξη θέσης στάθμευσης. Κρίνοντας από τους συντελεστές μερικής συσχέτισης, οι μεταβλητές AGE και PARKING έχουν μικρότερη από 10% «καθαρή» γραμμική σχέση με την Υ, ενώ η μεταβλητή FLOOR περίπου 16%. Η δεύτερη επίσης βασική ιδιαιτερότητα του μοντέλου είναι ότι προσαρμόζεται πάρα πολύ ικανοποιητικά στα δεδομένα από την πρώτη προσέγγιση, αφήνοντας το περιθώριο να πραγματοποιηθούν οι έλεγχοι όλων των υποθέσεων χωρίς την αφαίρεση καμίας ακραίας οντότητας. Οι έλεγχοι ικανοποιούνται και σχηματίζεται ένα μοντέλο με δείγμα 80 οντοτήτων, το οποίο έχει 252
265 Κ ε φ ά λ α ι ο 5 ο ικανοποιητική προβλεπτική δύναμη βάσει των μεθόδων που αξιοποιούνται. Οι συνδέσεις παρόλα αυτά είναι ασθενέστερες σε σύγκριση με τις άλλες δύο περιοχές και παρουσιάζεται μεγαλύτερη αστάθεια στους απαραίτητους ελέγχους του μοντέλου. Παρόλα αυτά το μοντέλο από καθαρά στατιστική σκοπιά είναι αποδεκτό, ενώ ταυτόχρονα ικανοποιεί σε μεγάλο βαθμό την αρχική υπόθεση που αναφέρεται στο γεγονός ότι οι συγκεκριμένες μεταβλητές επιδρούν, άλλες περισσότερο και άλλες λιγότερο, στη διαμόρφωση των αγοραίων αξιών. Μεταπτυχιακή διατριβή 253
266 ΚΕΦΑΛΑΙΟ 6 Ο ΤΑ ΓΕΩΓΡΑΦΙΚΑ ΣΥΣΤΗΜΑΤΑ ΠΛΗΡΟΦΟΡΙΩΝ ΚΑΙ Η ΜΕΘΟΔΟΣ ΤΗΣ ΠΟΛΛΑΠΛΗΣ ΓΡΑΜΜΙΚΗΣ ΠΑΛΙΝΔΡΟΜΗΣΗΣ Λαμβάνοντας κανείς υπόψη ότι το φαινόμενο που εξετάζεται εντάσσεται σε μία γεωγραφική περιοχή, είναι επιθυμητό στο παρόν κεφάλαιο να εξεταστεί η εφαρμογή της πολλαπλής γραμμικής παλινδρόμησης σε ένα περιβάλλον Γεωγραφικών Συστημάτων Πληροφοριών (Γ.Σ.Π.). Με αυτόν τον τρόπο γίνεται προσδιορισμός των θέσεων όλων των οντοτήτων διαμερισμάτων ενώ τα αποτελέσματα που προκύπτουν από την ανάλυση θα μπορούν να φαίνονται αποτυπωμένα στο χώρο. Σύμφωνα με το Μάλλιο, 2009 το βασικό πλεονέκτημα της χρήσης Γ.Σ.Π. στη στατιστική ανάλυση δεδομένων είναι η συνδυασμένη χρήση των πληροφοριών των χαρακτηριστικών ενός στοιχείου με την ταυτόχρονη πληροφορία της θέσης του. Από τη μία μεριά τα πακέτα λογισμικού επικεντρώνονται στην απεικόνιση στοιχείων και στη χωρική τους ανάλυση, αλλά έχουν περιορισμένες δυνατότητες σε θέματα οικονομετρικής ανάλυσης, ενώ από την άλλη μεριά τα εξειδικευμένα πακέτα στατιστικής μελέτης δεν παρέχουν τις δυνατότητες ενός GIS. Στόχο λοιπόν αποτελεί η εύρεση του κατάλληλου λογισμικού Γ.Σ.Π. και σε πρώτο στάδιο η δημιουργία του χωρικού υποβάθρου για τη μετέπειτα ανάλυση. Το λογισμικό που επιλέγεται ως το καταλληλότερο για την οπτικοποίηση του δείγματος είναι το ArcGIS 10 για ποικίλους λόγους. Αρχικά, πρόκειται για ένα πακέτο Γεωγραφικού Συστήματος Πληροφοριών (Geographical Information System) που είναι ιδιαίτερα διαδεδομένο, με ευρύ πεδίο χρήσης και ιδιαίτερα αξιόπιστο σε μικρές αλλά και σε μεγάλες εφαρμογές. Το περιβάλλον του είναι φιλικό προς το χρήστη και προσφέρει μία πλούσια εργαλειοθήκη που δίνει πολλές δυνατότητες προς αξιοποίηση. Το περιβάλλον εργασίας του ArcMap 10 είναι το πλέον κατάλληλο, διότι δίνει τη δυνατότητα εφαρμογής 254
267 Κ ε φ ά λ α ι ο 6 ο της πολλαπλής γραμμικής παλινδρόμησης προκειμένου να φανεί εάν και κατά πόσο συμπίπτουν οι αναλύσεις που προκύπτουν και από τα δύο πακέτα. Στο πρώτο μέρος του κεφαλαίου αναλύεται η διαδικασία δημιουργίας του χωρικού υποβάθρου, μέσω της κατασκευής μίας γεωβάσης που θα εμπεριέχει τα σχηματικά αρχεία shapefile όλων των κτιρίων του δείγματος και για τις δύο περιοχές μελέτης. Στη συνέχεια, στο δεύτερο μέρος δίνονται τα βήματα εφαρμογής μιας πολλαπλής γραμμικής παλινδρόμησης, η ερμηνεία των αποτελεσμάτων που εξάγονται και η σύγκριση τους με τα αποτελέσματα που προκύπτουν από το SPSS ΕΙΣΑΓΩΓΗ ΔΕΔΟΜΕΝΩΝ ΣΤΟ ΓΕΩΓΡΑΦΙΚΟ ΣΥΣΤΗΜΑ ΠΛΗΡΟΦΟΡΙΩΝ Η διαδικασία εισαγωγής των δεδομένων σε ένα Σύστημα Γεωγραφικών Πληροφοριών, δεν είναι μία ιδιαίτερα απλή διαδικασία, διότι είναι συνήθως χρονοβόρα (εξαρτάται βέβαια από τον όγκο των δεδομένων) και απαιτεί σωστή οργάνωση της δομής με την οποία θα εισαχθούν οι χωρικές και περιγραφικές πληροφορίες ώστε να αποφευχθούν προβλήματα στο μέλλον. Σε πρώτο στάδιο είναι βασικό να ξεκαθαριστεί ποιο είναι το χαρτογραφικό υπόβαθρο πάνω στο οποίο θα απεικονιστεί η χωρική πληροφορία του δείγματος και στη συνέχεια ποια είναι η χωρική μονάδα ψηφιοποίησης του δείγματος. Για τις ανάγκες της παρούσας εργασίας το σύνολο των χωρικών δεδομένων που είναι διαθέσιμα στην περιοχή του κέντρου της Θεσσαλονίκης είναι τα ΟΤ της περιοχής μελέτης και όλα τα κτίρια που βρίσκονται σε κάθε ΟΤ, ενώ στην περιοχή του Ευόσμου είναι διαθέσιμα μόνο τα ΟΤ της περιοχής μελέτης. Η μορφή των παραπάνω δεδομένων είναι διανυσματική (vector αρχεία) και όχι ψηφιδωτή με αποτέλεσμα να είναι άμεσα επεξεργάσιμα από το ArcGIS 10, το οποίο αναγνωρίζει τα σχηματικά αρχεία (shapefiles) και τα εμφανίζει άμεσα στο περιβάλλον του. Η γεωμετρία και των δύο κατηγοριών (ΟΤ, κτίσματα) είναι η μορφή των πολυγώνων (polygons). Η τοποθέτηση των διαμερισμάτων του δείγματος με τη συνοδεία, όλων των περιγραφικών χαρακτηριστικών τους πραγματοποιείται στη συνέχεια μέσω της διαδικασίας ψηφιοποίησης τους βάσει των παραπάνω χαρτογραφικών επιπέδων. Παρόλα αυτά η ψηφιοποίηση διαμερισμάτων είναι ανέφικτη, διότι τα δεδομένα που είναι διαθέσιμα δεν αναφέρονται στις τρεις διαστάσεις, ώστε να είναι για παράδειγμα δυνατή η αποτύπωση ενός διαμερίσματος του τρίτου ορόφου της οικοδομής, αλλά στις δύο. Συνεπώς, ως μονάδα ψηφιοποίησης του δείγματος πλέον θεωρείται το κτίριο στο οποίο βρίσκεται η κάθε οριζόντια ιδιοκτησία και όχι το ίδιο το διαμέρισμα. Σαν πρώτο βήμα της διαδικασίας για την οπτικοποίηση των πληροφοριών της διατριβής δομείται μία προσωπική γεωβάση, η οποία είναι συγκεκριμένη μορφή αποθήκευσης χωρικών δεδομένων σχεδιασμένη από το ArcGIS και αποτελείται από ένα σύνολο ομάδων οντοτήτων. Τα χωρικά και περιγραφικά δεδομένα αποθηκεύονται σε πίνακες της Microsoft Access και με αυτόν τον τρόπο γίνεται η διαχείριση και επεξεργασία τους, χωρίς τη συμμετοχή άλλου λογισμικού. (Ανδρουλακάκης κα., 2003) Μεταπτυχιακή διατριβή 255
268 Γ. Σ. Π. Συγκεντρωτικά, για τις ανάγκες της παρούσας εργασίας το σύνολο των χωρικών δεδομένων που συμμετέχουν είναι για την περιοχή του κέντρου τα Οικοδομικά Τετράγωνα (ΟΤ) όλης της περιοχής μελέτης, το σύνολο των κτίριων που βρίσκονται εντός τους και τα κτίρια που αντιστοιχούν στα διαμερίσματα του δείγματος, δηλαδή συνολικά τρεις ομάδες οντοτήτων (feature classes), ενώ για την περιοχή του Ευόσμου τα ΟΤ όλης της περιοχής μελέτης και τα κτίρια του δείγματος. Τα επιφανειακά γεωγραφικά χαρακτηριστικά μαζί με τις ιδιότητες τους φαίνονται στους πίνακες που ακολουθούν: Πίνακας 6.1.: Ιδιότητες του χαρτογραφικού επιπέδου των κτιρίων για την περιοχή του κέντρου ΚΤΙΡΙΑ δείγματος (κέντρο) Ιδιότητα 1 kt_id Κωδικός κτιρίων Ιδιότητα 2 Y Αγοραία αξία ακινήτων Ιδιότητα 3 X1 Εμβαδόν Ιδιότητα 4 X2 Παλαιότητα Ιδιότητα 5 X3 Όροφος Ιδιότητα 6 X4 Θέση Διαμερίσματος (Γωνιακό/όχι) Ιδιότητα 7 X5 Ανελκυστήρας Ιδιότητα 8 X6 Είδος Θέρμανσης Ιδιότητα 9 X7 Κατάσταση Ακινήτου Ιδιότητα 10 X8 Ύπαρξη ή όχι θέσης στάθμευσης Ιδιότητα 13 ADDRESS Διεύθυνση Πίνακας 6.2.: Ιδιότητες του χαρτογραφικού επιπέδου των κτιρίων για την περιοχή του Ευόσμου ΚΤΙΡΙΑ δείγματος (πρώην Δήμος Ευόσμου) Ιδιότητα 1 ktiria_id Κωδικός Κτιρίων Ιδιότητα 2 Y Αγοραία αξία ακινήτων Ιδιότητα 3 X1 Εμβαδόν Ιδιότητα 4 X2 Παλαιότητα Ιδιότητα 5 X3 Όροφος Ιδιότητα 6 X4 Θέση διαμερίσματος (Γωνιακό/όχι) Ιδιότητα 7 X5 Ανελκυστήρας Ιδιότητα 8 X6 Είδος Θέρμανσης Ιδιότητα 9 X7 Κατάσταση ακινήτου Ιδιότητα 10 X8 Θέση στάθμευσης Ιδιότητα 13 ADDRESS Διεύθυνση 256
269 Κ ε φ ά λ α ι ο 6 ο Δημιουργία Χωρικής Βάσης Δεδομένων 28 Το σχήμα της γεωβάσης δημιουργείται μέσα σε περιβάλλον ArcCatalog 10 με τον ακόλουθο τρόπο : 1) Με δεξί κλικ μέσα στο φάκελο εργασίας επιλέγεται New Personal Geodatabase και δίνεται το όνομα thesis_ken. 2) Ακολουθεί η δημιουργία ενός set χωρικών δεδομένων (Feature Dataset), μέσω του οποίου ορίζονται όλες οι κοινές ιδιότητες των ομάδων οντοτήτων που θα δημιουργηθούν στη συνέχεια, όπως για παράδειγμα το προβολικό σύστημα στο οποίο ανήκουν (Εικόνα 6.1). Στο αριστερό παράθυρο της εικόνας φαίνεται η επιλογή του προβολικού συστήματος, Greek Grid ΕΓΣΑ 87, ενώ στη δεύτερη εικόνα απεικονίζονται τα χαρακτηριστικά του προβολικού συστήματος μέσω των ιδιοτήτων του σετ δεδομένων που δημιουργείται. Εικόνα 6.1: Επιλογή προβολικού συστήματος 28 Η διαδικασία που περιγράφεται στο παρόν υποκεφάλαιο πραγματοποιείται με όμοιο τρόπο και για τις δύο περιοχές μελέτης. Μεταπτυχιακή διατριβή 257
270 Γ. Σ. Π. 3) Στη συνέχεια, με δεξί κλικ δημιουργείται όμοια το χαρτογραφικό επίπεδο των κτιρίων (New Feature Class)και ορίζονται μέσα από τα αναρτημένα παράθυρα οι ιδιότητες που αναφέρονται παραπάνω (Βλ. Πίνακα 6.1 & 6.2), η γεωμετρία τους (σημείο, γραμμή ή επιφάνεια)και ο τύπος τους (ακέραιος αριθμός, διπλής ακρίβειας, κείμενο κλπ) (Εικόνα 6.2). Στη συγκεκριμένη περίπτωση, ως γεωμετρία ορίζεται η επιφάνεια (polygon feature) και ως τύπος των δεδομένων 29 εισαγωγής ορίζεται για τον μοναδικό κωδικό αριθμό κάθε κτιρίου (kt_id) ένας ακέραιος αριθμός, για όλες τις μεταβλητές (Χ1 Χ10) ένας αριθμός διπλής ακρίβειας και για τη διεύθυνση (ADDRESS) ένα κείμενο. Εικόνα 6.2: Διαδικασία δημιουργίας του επιπέδου των κτιρίων μέσα από το περιβάλλον του Arc Catalog 29 Η επιλογή του τύπου τους είναι ιδιαίτερα σημαντική, διότι στη συνέχεια θα εκτελεστεί με τη χρήση των συγκεκριμένων τιμών γραμμική πολλαπλή παλινδρόμηση. Η επιλογή text τύπος δεν είναι επιθυμητή, διότι δε θα μπορούν να εκτελεστούν μαθηματικές πράξεις. 258
271 Κ ε φ ά λ α ι ο 6 ο 4) Στο Feature Dataset που δημιουργείται με το όνομα kentro πρέπει να εισαχθεί το ήδη υπάρχον σχηματικό αρχείο των ΟΤ και το σχηματικό αρχείο του συνόλου των κτιρίων μέσα σε αυτά,ώστε και αυτά να ανήκουν από την αρχή της εργασίας μέσα στην ίδια γεωβάση. Με δεξί κλικ επιλέγεται η εντολή Import Feature Class (Single) 30 και από το παράθυρο που εμφανίζεται επιλέγεται αρχικά το χαρακτηριστικό που θέλουμε να μετατρέψουμε από shapefile σε οντότητα της γεωβάσης, στη συνέχεια ορίζεται η θέση μέσα στη γεωβάση που θα τοποθετηθεί και τέλος το όνομα του χαρτογραφικού επιπέδου έπειτα από τη μετατροπή (Εικόνα 6.3). Εικόνα 6.3: Διαδικασία μετατροπής των δοθέντων σχηματικών αρχείων σε χαρτογραφικά επίπεδα της γεωβάσης 5) Σε περιβάλλον Arc Map εισάγονται και τα τρία χαρτογραφικά επίπεδα(file Add data). Τα επίπεδα των ΟΤ και όλων των κτιρίων είναι πλήρη έχοντας σε αντιστοιχία τη χωρική με την περιγραφική πληροφορία μέσω του πίνακα των περιγραφικών χαρακτηριστικών (Attribute Table). Με τη βοήθεια της Εργαλειοθήκης Editor του ArcMap 10 και των διευθύνσεων των διαμερισμάτων τοποθετούνται ένα προς ένα τα κτίρια εκείνα που έπειτα από τις διαδοχικές επιλύσεις σε περιβάλλον SPSS 18 διατηρήθηκαν και συγκρότησαν το 30 Σημ: Σε περιβάλλον ArcMap η διαδικασία υλοποιείται με τα βήματα: Arc Toolbox Conversion Tools to Geodatabase Feature Class to Feature Class Μεταπτυχιακή διατριβή 259
272 Γ.Σ.Π. τελικό μοντέλο (στην περιοχή του Ευόσμου συνολικά 48/60 και στην περιοχή του κέντρου 54/60) Με το πέρας της διαδικασίας και την ταυτόχρονη εισαγωγή των περιγραφικών δεδομένων, η θέση των διαμερισμάτων που μελετούνται φαίνεται στις παρακάτω εικόνες (Εικόνα 6.4 & 6.5), ενώ τα περιγραφικά δεδομένα της περιοχής του κέντρου παρουσιάζονται στην εικόνα 6.6 Εικόνα 6.4: Απεικόνιση των 54/60 κτιρίων του δείγματος για την περιοχή του κέντρου Εικόνα 6.5: Τα ΟΤ που ανήκουν στον πρώην Δήμο Ευόσμου, καθώς και τα 48 κτίρια που τοποθετήθηκαν πάνω στο χάρτη 260
273 Κ ε φ ά λ α ι ο 6 ο Ο πίνακας των περιγραφικών χαρακτηριστικών των κτιρίων του δείγματος περιλαμβάνει αρχικά όλες τις ιδιότητες που αναφέρονται στην ενότητα 6.1 αλλά ταυτόχρονα και επιπλέον στήλες που εισάγονται αυτόματα μέσω του ArcGIS κατά τη δημιουργία των πολυγώνων, όπως το μήκος του περιγράμματος τους, το εμβαδόν τους και ένας κωδικός ObjectId. Εικόνα 6.6: Ο πίνακας των περιγραφικών χαρακτηριστικών 6.2 ΕΦΑΡΜΟΓΗ ΤΗΣ ΠΟΛΛΑΠΛΗΣ ΓΡΑΜΜΙΚΗΣ ΠΑΛΙΝΔΡΟΜΗΣΗΣ ΣΤΗΝ ΠΕΡΙΟΧΗ ΤΟΥ ΚΕΝΤΡΟΥ ΤΗΣ ΘΕΣΣΑΛΟΝΙΚΗΣ Τα λογισμικά που υποστηρίζουν Γ.Σ.Π., όπως το ArcGIS, πέρα από τη χωρική ανάλυση (spatial analysis) επεκτείνουν τις δυνατότητες τους με τις πιο πρόσφατες εκδόσεις τους και σε ευρύτερα πεδία. Η αντίστοιχη διαδικασία εφαρμογής μιας γραμμικής πολλαπλής παλινδρόμησης (Analyze Linear Regression) σε περιβάλλον SPSS 18 αντιστοιχίζεται στο ArcGIS από την εφαρμογή OLS (Ordinary Least Squares) η οποία και αναπτύχθηκε στις επόμενες εκδόσεις του ArcGIS 9.3. Η δυνατότητα υλοποίησης της εφαρμογής που περιγράφεται παραπάνω βρίσκεται μέσα στις κύριες εντολές της εργαλειοθήκης του ArcGIS 10 και συγκεκριμένα στο ArcToolbox Spatial Statistics Tools Modeling Spatial Relationships Ordinary Least Squares. H OLS μέθοδος χαρακτηρίζεται εφαρμογή πολλαπλής γραμμικής παλινδρόμησης, αλλά σε ένα επίπεδο «υπερτοπικό» (global ordinary least square linear regression 31 ), 31 Μεταπτυχιακή διατριβή 261
274 Γ. Σ. Π. σύμφωνα με το οποίο θεωρείται ότι υπάρχει στην εκάστοτε περιοχή μελέτης χωρική ομοιομορφία Διαδικασία πολλαπλής γραμμικής παλινδρόμησης Τα βασικά βήματα της διαδικασίας δεν διαφέρουν ουσιαστικά από αυτά που πραγματοποιούνται στο στατιστικό πακέτο SPSS 18, καθώς η λογική είναι ακριβώς η ίδια 33 : ΒΗΜΑ 1 ο : Επιλογή της εξαρτημένης μεταβλητής Υ ΒΗΜΑ 2 ο : Επιλογή των ανεξάρτητων μεταβλητών Χi ΒΗΜΑ 3 ο : Διερεύνηση των ανεξάρτητων μεταβλητών ΒΗΜΑ 4 ο : Εφαρμόζεται η διαδικασία της γραμμικής παλινδρόμησης που παρέχει το ArcGIS 10 με διαφορετικούς συνδυασμούς ανεξάρτητων μεταβλητών μέχρι την επιλογή του καταλληλότερου μοντέλου πολλαπλής παλινδρόμησης για τις ανάγκες της εφαρμογής. Ο σχηματισμός του μοντέλου μέσω του SPSS 18 δίνει τη δυνατότητα στην παρούσα φάση επεξεργασίας να αποφευχθεί η αναλυτική διαδικασία εφαρμογής πολλαπλής γραμμικής παλινδρόμησης μέσω του ArcGIS, δηλαδή τη δημιουργία του μοντέλου εκ νέου με τις διαδοχικές προσεγγίσεις που απαιτούνται στο ενδιάμεσο. Σε αντικατάσταση, εισάγονται στο μοντέλο μόνο εκείνες οι εγγραφές που θεωρούνται σημαντικές στο σχηματισμό του μοντέλου και επιλέγονται μόνο οι στατιστικά σημαντικές μεταβλητές που βοηθούν στην ερμηνεία της εξαρτημένης μεταβλητής στο προηγούμενο κεφάλαιο (Κεφάλαιο 4 ο ). Με τον παραπάνω τρόπο επιτυγχάνεται και η σύγκριση των αποτελεσμάτων ώστε να φανούν οι ομοιότητες ή οι διαφορές στις μαθηματικές εξισώσεις των δύο λογισμικών πακέτων. Σε περιβάλλον ArcMap 10 με το εργαλείο εισαγωγής δεδομένων Add Data εισάγονται τα τρία επίπεδα της γεωβάσης της περιοχής του κέντρου (επίπεδα των ΟΤ, των οικοδομών και των κτιρίων του δείγματος). Στη συνέχεια, μέσω του ArcToobox ανοίγει το παράθυρο εφαρμογής της γραμμικής παλινδρόμησης Ordinary Least Squares, όπως φαίνεται στην παρακάτω εικόνα. 32 Βλέπε Κεφάλαιο
275 Κ ε φ ά λ α ι ο 6 ο Εικόνα 6.7: Παράθυρο εφαρμογής της γραμμικής παλινδρόμησης OLS Στο πεδίο Input Feature Class εισάγεται το χαρτογραφικό επίπεδο που περιέχει την απαιτούμενη πληροφορία, δηλαδή το σύνολο της εξαρτημένης και των ανεξάρτητων μεταβλητών, το οποίο είναι τα «κτίρια». Στο πεδίο Unique ID Field εισάγεται η ιδιότητα του πίνακα των κτιρίων που η τιμή της είναι μοναδική για κάθε εγγραφή του πίνακα(θα πρέπει υποχρεωτικά να είναι ακέραιος αριθμός). Ιδιότητα επιλογής kt_id. Στη συνέχεια, ζητείται το όνομα και η θέση του νέου χαρτογραφικού επιπέδου που θα δημιουργηθεί έπειτα από την εφαρμογή της γραμμικής πολλαπλής παλινδρόμησης (Output Feature Class) και τέλος, στα δύο επόμενα πεδία ζητείται από τη μία μεριά η ιδιότητα του πίνακα των κτιρίων που αποτελεί την εξαρτημένη μεταβλητή και από την άλλη το σύνολο των ανεξάρτητων μεταβλητών που συμμετέχουν στο μοντέλο. Επίσης, υπάρχει η δυνατότητα επιλογής της παραγωγής ή όχι δύο ακόμη πινάκων Coefficient Output Table και Diagnostic Output Table. Με την επιλογή OK εφαρμόζεται η διαδικασία της πολλαπλής παλινδρόμησης και εμφανίζονται στο κύριο περιβάλλον εργασίας του ArcMap 10 τα παρακάτω αποτελέσματα Παρουσίαση και ερμηνεία των αποτελεσμάτων Τα εξαγόμενα δεδομένα της εφαρμογής, τα οποία περιγράφονται και αναλύονται παρακάτω δίνουν τη δυνατότητα στον κάθε χρήστη που δεν έχει χρησιμοποιήσει κάποιο ισχυρό στατιστικό λογισμικό νωρίτερα να αξιολογήσει σε ένα πολύ ικανοποιητικό επίπεδο Μεταπτυχιακή διατριβή 263
276 Γ. Σ. Π. το μοντέλο που σχημάτισε και να προεκτείνει την ανάλυση του ώστε να έχει με διαδοχικές προσεγγίσεις το βέλτιστο δυνατό μοντέλο. Συνοπτικά, τα αποτελέσματα της διαδικασίας είναι τα ακόλουθα : 1) Ένα νέο επίπεδο (shapefile) που περιέχει μία προτεινόμενη διάταξη των τυποποιημένων υπολοίπων της διαδικασίας (Βλ ) 2) Η αναφορά των αποτελεσμάτων (Message) με όλη τη στατιστική και διαγνωστική πληροφορία (Βλ έως ) 3) Δημιουργία Πίνακα (Coefficient Output Table) που περιέχει ουσιαστικά ένα τμήμα του παραθύρου της αναφοράς (Summary of OLS results) είναι προαιρετικό. 4) Δημιουργία Πίνακα (Diagnostic Output Table) που περιέχει όλες τις τιμές και τους διαγνωστικούς δείκτες που ταυτόχρονα υπάρχουν και στο παράθυρο της αναφοράς είναι προαιρετικό. 5) Δυνατότητα χειροκίνητου σχηματισμού γραφημάτων για την οπτικοποίηση των παραδοχών που πρέπει να καλύπτονται μέσα από τις βασικές εντολές που διαθέτει το ArcGIS Δημιουργία νέου επιπέδου της OLS διαδικασίας Ένα από τα εξαγόμενα αποτελέσματα είναι η δημιουργία ενός νέου χαρτογραφικού επιπέδου, το οποίο αποτελεί θεματικό χάρτη των υπολοίπων της OLS διαδικασίας και ο πίνακας περιγραφικών χαρακτηριστικών που αντιστοιχεί σε αυτό (Εικόνα 6.8 & 6.9). Εικόνα 6.8: Νέος χάρτης των OLS υπολοίπων με το υπόμνημα του 264
277 Κ ε φ ά λ α ι ο 6 ο Εικόνα 6.9: Πίνακας περιγραφικών χαρακτηριστικών του νέου χαρτογραφικού επιπέδου που προέκυψε από την OLS διαδικασία Με την εκτέλεση της διαδικασίας, η πρώτη εικόνα που εμφανίζεται είναι ο χάρτης της περιοχής μελέτης με μία ταξινόμηση να έχει πραγματοποιηθεί στα κτίρια που αντιστοιχούν στα διαμερίσματα του δείγματος. Ο παραπάνω χάρτης συνοδεύεται από τον πίνακα περιγραφικών δεδομένων, ο οποίος περιέχει μεταξύ άλλων τις προβλεπόμενες/εκτιμούμενες τιμές (estimated values), τις τιμές των υπολοίπων (διαφορά προβλεπόμενης από την παρατηρούμενη τιμή) (residuals) και τις τιμές των τυποποιημένων υπολοίπων (Std residuals), οι οποίες υπολογίζονται εάν διαιρεθεί η τιμή του υπολοίπου με την εκτιμούμενη τυπική απόκλιση των υπολοίπων. Με βάση την τιμή των τυποποιημένων υπολοίπων (Std Residuals) γίνεται η ταξινόμηση των κτιρίων σε επτά διαφορετικές κλάσεις, οι οποίες με αυτόν τον τρόπο αποτελούν ένδειξη για το ποια είναι η κατανομή των υπολοίπων (residuals) και εάν το μοντέλο ταιριάζει λίγο ή πολύ στα δεδομένα. Σύμφωνα με το Δαφέρμο, 2005 όταν η κατανομή των υπολοίπων είναι περίπου κανονική, τότε το 95% των τυποποιημένων υπολοίπων θα βρίσκονται μέσα στο διάστημα -2 έως +2, όταν η κατανομή είναι κανονική τότε το 99% των τυποποιημένων υπολοίπων βρίσκεται στο διάστημα από -2,58 έως +2,58. Από την παραπάνω ταξινόμηση προκύπτει ότι όλες οι τιμές των τυποποιημένων υπολοίπων είναι μικρότερες από δύο και άρα το μοντέλο ταιριάζει ικανοποιητικά στα δεδομένα (Max 1,58 Min -1,75). Μεταπτυχιακή διατριβή 265
278 Γ.Σ.Π. Εικόνα 6.10: Απεικόνιση μέσω της επιλογής Statistics της μέγιστης και ελάχιστης τιμής των Std Residuals Γενική επίδοση του μοντέλου Οι έλεγχοι που πραγματοποιούνται στη συνέχεια αναφέρονται όλοι στα στοιχεία της παρακάτω εικόνας που εμφανίζει το βασικό εξαγόμενο αποτέλεσμα, τον πίνακα αναφοράς των στατιστικών αποτελεσμάτων της εφαρμογής (Message window report of statistical results). Παράλληλα, για τους δείκτες και τα στοιχεία που είναι κοινά και στις δύο εφαρμογές πολλαπλής γραμμικής παλινδρόμησης (SPSS και ArcGIS)γίνεται ιδιαίτερη αναφορά. Εικόνα 6.11: Αναφορά των στατιστικών αποτελεσμάτων της OLS μεθόδου 266
279 Κ ε φ ά λ α ι ο 6 ο Η πρώτη είδους αξιολόγηση αναφέρεται στη γενική επίδοση του μοντέλου, δηλαδή στην τιμή του συντελεστή προσδιορισμού (R 2 )και στον προσαρμοσμένο συντελεστή προσδιορισμού (Adjusted R 2 ). Οι τιμές που προκύπτουν και φαίνονται στην παραπάνω εικόνα είναι R 2 = Adjusted R 2 = Οι δύο τιμές είναι όμοιες με τις αντίστοιχες που υπολογίστηκαν στο SPSS 18 στο προηγούμενο κεφάλαιο και παρουσιάζουν μία σαφέστατα καλή προσαρμογή στα δεδομένα και έντονη προβλεπτική δύναμη. Σύμφωνα με τις τιμές, το 81% της διακύμανσης της εξαρτημένης μεταβλητής ερμηνεύεται από την εξίσωση πολλαπλής παλινδρόμησης που προέκυψε Σχολιασμός των συντελεστών πολλαπλής παλινδρόμησης Επόμενο βήμα αξιολόγησης του μοντέλου αποτελεί η πρώτη στήλη του πίνακα, στην οποία αποδίδονται οι μερικοί συντελεστές πολλαπλής συσχέτισης που αντικατοπτρίζουν τη σχέση της κάθε μίας ανεξάρτητης μεταβλητής με την εξαρτημένη. Όπως φαίνεται και παραπάνω, η μία μεταβλητή (Χ2 - παλαιότητα) έχει μία αρνητική σχέση με την εξαρτημένη μεταβλητή, ενώ οι μεταβλητές Χ1 (εμβαδόν) και Χ7 (βαθμός συντήρησης ακινήτου) έχουν θετική συσχέτιση με την αγοραία αξία των ακινήτων. Οι συντελεστές που φαίνονται στο παραπάνω απόσπασμα είναι όμοιοι με αυτούς που προέκυψαν μέσω της εφαρμογής του SPSS, όπως και όλα τα υπόλοιπα στοιχεία του πίνακα με τη διαφορά ότι η αναφορά των Μεταπτυχιακή διατριβή 267
280 Γ. Σ. Π. αποτελεσμάτων σε ArcGIS 10 δίνει μεγαλύτερη ακρίβεια με την εμφάνιση περισσότερων δεκαδικών ψηφίων σε κάθε τιμή Έλεγχος στατιστικής σημαντικότητας των ανεξάρτητων μεταβλητών Ένδειξη της καλής μοντελοποίησης της εφαρμογής αποτελούν τα δεδομένα της τέταρτης στήλης p-values 34, όπου ενημερώνουν σχετικά με την ύπαρξη στατιστικής σημαντικότητας των ανεξάρτητων μεταβλητών. Ο έλεγχος t- test χρησιμοποιείται για να αξιολογήσει τη στατιστική σημαντικότητα των ανεξάρτητων μεταβλητών με τη μηδενική υπόθεση ότι ο συντελεστής της κάθε ανεξάρτητης μεταβλητής να είναι μηδέν. Όταν οι τιμές που δίνονται στη στήλη probability είναι πολύ μικρές(<0.05), τότε η πιθανότητα οι συντελεστές να είναι μηδέν είναι επίσης πολύ μικρή. Οι τιμές που παρατηρούμε στη συγκεκριμένη στήλη είναι όλες πολύ κοντά στο μηδέν με αποτέλεσμα να θεωρούνται όλες οι μεταβλητές στατιστικά σημαντικές. Τέλος, οι οδηγίες του ArcGIS 10 ενημερώνουν ότι κριτήριο για κάποιον να αξιολογήσει τις τιμές Probability με άμεσο τρόπο είναι η ύπαρξη ή όχι αστερίσκου (*) δίπλα από αυτές που σημαίνει ότι είναι στατιστικά σημαντικές ή όχι αντίστοιχα. Σύμφωνα με τα αποτελέσματα της αναφοράς δίπλα από τις τιμές probability και στις τρεις ανεξάρτητες μεταβλητής εμφανίζεται το σύμβολο (*), άρα επιβεβαιώνεται η ύπαρξη στατιστικής σημαντικότητας Έλεγχος συγγραμμικότητας/πολυσυγγραμμικότητας Όπως αναφέρεται αναλυτικά και στο τέταρτο κεφάλαιο, ένας από τους απαραίτητους ελέγχους που πραγματοποιούνται είναι της ύπαρξης του φαινομένου συγγραμμικότητας ή πολυσυγγραμμικότητας. Ο έλεγχος της ύπαρξης δηλαδή κάποιας γραμμικής σχέσης μεταξύ των ανεξάρτητων μεταβλητών μπορεί να γίνει με μία σειρά συγκεκριμένων δεικτών, από τους οποίους μόνο ο δείκτης της πληθωριστικής διασποράς (VIF)παρέχεται στα εξαγόμενα αποτελέσματα της OLS διαδικασίας. Για το δείκτη VIF υπάρχουν κανόνες ανοχής από διάφορους επιστήμονες που ασχολούνται με τη στατιστική, οι οποίοι πολλές φορές ορίζουν ιδιαίτερα υψηλά όρια. Για παράδειγμα, μία συνήθης τιμή ανοχής VIF είναι η τιμή δέκα, η οποία θεωρείται ότι δείχνει πρόβλημα συγγραμμικότητας της i μεταβλητής (O Brien, 2007). Σύμφωνα με την διαδικτυακή βοήθεια του ArcGIS 10, αλλά σύμφωνα και με το μήνυμα αναφοράς που φαίνεται στην εικόνα 6.11 ορίζεται η οριακή τιμή 7,5. Όπως φαίνεται από την τελευταία στήλη του πίνακα οι τιμές VIF κυμαίνονται μεταξύ των 1, και 1,274840, οι οποίες είναι πολύ μικρότερες από την τιμή 7,5, άρα δεν υπάρχει ένδειξη ύπαρξης πολυσυγγραμμικότητας. Η αντίστοιχη τιμή ανοχής του δείκτη VIF που λήφθηκε υπόψη στην εφαρμογή στο SPSS είναι η τιμή 2, σύμφωνα με την οποία και πάλι ικανοποιείται ο έλεγχος πολυσυγγραμμικότητας. 34 Πρόκειται για την πιθανότητα που ελέγχει τη μηδενική υπόθεση: ο συντελεστής προσδιορισμού του μοντέλου να είναι ίσος με μηδέν (Λαμπρόπουλος κα. 2007) 268
281 Κ ε φ ά λ α ι ο 6 ο Έλεγχος κανονικότητας των υπολοίπων Επόμενη σημαντική αξιολόγηση του μοντέλου είναι ο έλεγχος της κανονικότητας των υπολοίπων που επιτυγχάνεται στο ArcMap 10 μέσω της στατιστικής των Jarque και Bera (JB - statistic). Η στατιστική Jarque και Bera ακολουθεί την κανονική κατανομή X 2, με δύο βαθμούς ελευθερίας και μηδενική υπόθεση ότι η μεταβλητή ακολουθεί την κανονική κατανομή (Τσαρδούνης, 2006). Πιο συγκεκριμένα, ο έλεγχος υπολογίζει την ασυμμετρία και την κύρτωση και στη συνέχεια συγκρίνει τα δεδομένα αυτά με τις θεωρητικές τιμές που ισχύουν στην κανονική κατανομή, δηλαδή με την τιμή μηδέν, εφόσον στην κανονική κατανομή δεν υπάρχει ασυμμετρία (Τσιώνας, 2009). Πιο συγκεκριμένα, σύμφωνα με τον οδηγό του ArcGIS κριτήριο αποτελεί η τιμή της πιθανότητας (p-value), η οποία όταν είναι μικρότερη από 0,05 για επίπεδο εμπιστοσύνης 95% είναι δείκτης μη κανονικής κατανομής των υπολοίπων. Σύμφωνα με την παραπάνω αναφορά η τιμή είναι ίση με 0, >0,05 άρα τα υπόλοιπα ακολουθούν την κανονική κατανομή. Επίσης, ένα άμεσο κριτήριο αξιολόγησης είναι η ύπαρξη ενός αστερίσκου στην εγγραφή της Jarque και Bera στατιστικής, όπου δηλώνει τη μη ύπαρξη κανονικής κατανομής, ενώ η απουσία αστερίσκου το αντίθετο. Για την οπτικοποίηση του αποτελέσματος, παρακάτω κατασκευάστηκε το ιστόγραμμα των τυποποιημένων υπολοίπων σε περιβάλλον ArcGIS 10 (Μενού View Graphs Create Histogram) και ταυτόχρονα παρατίθεται το ίδιο διάγραμμα, όπως προκύπτει από το στατιστικό πακέτο SPSS, στο οποίο είναι προσαρμοσμένη και η καμπύλη της κανονικής κατανομής. Εικόνα 6.12: Απεικόνιση της κατανομής των υπολοίπων, όπως σχηματίστηκε από τη δημιουργία γραφημάτων του ArcGIS Μεταπτυχιακή διατριβή 269
282 Γ. Σ. Π. Εικόνα 6.13: Απεικόνιση της κατανομής των υπολοίπων με την ταυτόχρονη εμφάνιση της κανονικής κατανομής μέσω του SPSS 18 Από τα παραπάνω ιστογράμματα μπορεί να οδηγηθεί κανείς στο συμπέρασμα ότι προσεγγίζεται ικανοποιητικά η κανονική κατανομή, εάν λάβει κανείς υπόψη του ότι τα δεδομένα είναι ρεαλιστικά από την κτηματαγορά της Θεσσαλονίκης Έλεγχος ανεξαρτησίας των υπολοίπων Ο έλεγχος της ανεξαρτησίας των υπολοίπων σχετίζεται άμεσα με τη χωρική αυτοσυσχέτιση, καθώς ανεξαρτησία των υπολοίπων πρακτικά σημαίνει ότι η σειρά με την οποία εισάγονται στο μοντέλο τα δεδομένα του δείγματος δεν θα πρέπει να επηρεάζει την τιμή των υπολοίπων (Δαφέρμος, 2005). Σύμφωνα με Goodchild, 1986 με τη γενική έννοια του όρου, η χωρική αυτοσυσχέτιση ασχολείται με το βαθμό με τον οποίο τα αντικείμενα ή οι δραστηριότητες σε κάποια θέση είναι παρόμοια με άλλα αντικείμενα ή δραστηριότητες που βρίσκονται κοντά σε αυτό. Επίσης, προτείνει μία σειρά από δείκτες και άλλα κριτήρια που οδηγούν στην αξιολόγηση της σχέσης που περιγράφεται παραπάνω, όπως δείκτης Geary, δείκτης Moran, ονομαστικά χαρακτηριστικά κλπ. Ο Anselin, 1995 αναφέρει χαρακτηριστικά ότι, θετική τιμή του δείκτη Moran σημαίνει συγκέντρωση χωρικά παρόμοιων τιμών, ενώ μία αρνητική τιμή στο δείκτη Moran σημαίνει συγκέντρωση χωρικά διαφορετικών τιμών. Από την άλλη μεριά, η Πλεξίδα, 2010 αναφέρει ότι τιμή του δείκτη Moran κοντά στο 0 σημαίνει έλλειψη χωρικής εξάρτησης μεταξύ των παρατηρήσεων που γειτνιάζουν. 270
283 Κ ε φ ά λ α ι ο 6 ο Σε περιβάλλον ArcGIS 10 το εργαλείο που χρησιμοποιείται για να καλύψει το συγκεκριμένο έλεγχο είναι ο υπερτοπικός δείκτης Moran s I 36 μέσω της διαδικασίας που παρουσιάζεται παρακάτω. ΒΗΜΑ 1 ο : Μέσω της εργαλειοθήκης του ArcGIS 10, ArcToolBox Spatial Statistic Tools Analyzing Patterns Spatial autocorrelation (Morans I) ΒΗΜΑ 2 Ο : Στο παράθυρο διαλόγου που εμφανίζεται στην οθόνη (Εικόνα 6.14) επιλέγεται το επίπεδο της OLS διαδικασίας ως επίπεδο εισαγωγής με βασική ιδιότητα το μοναδικό αριθμό των κτιρίων, και με εξαγόμενα αποτελέσματα τα προεπιλεγμένα του ArcGIS 10. Εικόνα 6.14: Διαδικασία υπολογισμού του δείκτη Morans ΒΗΜΑ 3 Ο : Ερμηνεία των αποτελεσμάτων Σε αυτό το στάδιο γίνεται αξιολόγηση της τιμής του δείκτη Morans με τη συνδρομή και ορισμένων άλλων τιμών που υπολογίζονται, όπως η τιμή p-value και z-score. Σύμφωνα με τις παρακάτω εικόνες η τιμή Moran s I είναι θετική (0,604676), το οποίο σημαίνει ότι σύμφωνα με το λογισμικό του ArcGIS 10 ότι υπάρχει θετική χωρική αυτοσυσχέτιση και εξαιτίας της τιμής που είναι πολύ κοντά στη μονάδα διαπιστώνεται ότι υπάρχει ισχυρή σχέση. Γενικά, μπορεί κανείς να συμπεράνει ότι για τις τιμές των δεικτών Moran s όπου είναι κοντά στην τιμή +1, η θέση που εξετάζεται έχει πολύ κοντινές τιμές με τις γειτονικές της, ενώ στην περίπτωση που η τιμή προσεγγίζει το -1, τότε η συγκεκριμένη θέση παρουσιάζει τιμή ακραία σε σχέση με τις γειτονικές της. (Γκριτζάπη, 2011) 36 Τα κριτήρια που πρέπει να ικανοποιούνται για τον έλεγχο της ανεξαρτησίας των υπολοίπων σε περιβάλλον SPSS αναλύονται στο τέταρτο κεφάλαιο Μεταπτυχιακή διατριβή 271
284 Γ. Σ. Π. Εικόνα 6.15: Αποτελέσματα ελέγχου ανεξαρτησίας των υπολοίπων Πρόβλημα δημιουργεί και η τιμή z-score, για την οποία σύμφωνα με την ηλεκτρονική βοήθεια του λογισμικoύ ArcGIS 10 υπάρχουν τα όρια -1,96 και +1,96, όπου τιμές χαμηλότερες από την κατώτερη τιμή σημαίνουν ότι το σημείο θεωρείται ότι έχει ακραία τιμή και τιμές μεγαλύτερες της θετικής τιμής σημαίνουν ότι το εξεταζόμενο σημείο δε διαφέρει σημαντικά από τα γειτονικά του. Η τιμή που δίνεται παραπάνω είναι ίση με 6, που πρακτικά οδηγεί στο συμπέρασμα ότι υπάρχει πρόβλημα στην ανεξαρτησία των υπολοίπων. Παρόλα αυτά, δε μπορεί να μη γίνει ταυτόχρονα σύγκριση με τα αποτελέσματα που προέκυψαν μέσω του στατιστικού προγράμματος SPSS, διότι ο συγκεκριμένος έλεγχος δίνει δύο τελείως διαφορετικά αποτελέσματα, ενώ αναφέρονται ακριβώς στα ίδια δεδομένα του δείγματος. Ο κύριος δείκτης που ελέγχει την παραδοχή της ανεξαρτησίας στο SPSS είναι ο δείκτης Durbin Watson, ο οποίος πρέπει να βρίσκεται μεταξύ των τιμών 1,5 και 2,5 όπως αναλυτικά αναφέρεται και στο κεφάλαιο 4. Στην περιοχή του κέντρου η τιμή του δείκτη είναι ίση με 1,978 που δείχνει ότι δεν υπάρχει κανένα πρόβλημα αυτοσυσχέτισης των υπολοίπων. 272
285 Κ ε φ ά λ α ι ο 6 ο 6.3 ΕΦΑΡΜΟΓΗ ΤΗΣ ΠΟΛΛΑΠΛΗΣ ΓΡΑΜΜΙΚΗΣ ΠΑΛΙΝΔΡΟΜΗΣΗΣ ΣΤΗ ΠΕΡΙΟΧΗ ΤΟΥ ΕΥΟΣΜΟΥ ΘΕΣΣΑΛΟΝΙΚΗΣ Στη δεύτερη περιοχή μελέτης, η εκτέλεση της διαδικασίας για την εφαρμογή της πολλαπλής γραμμικής παλινδρόμησης σε περιβάλλον εργασίας ArcGIS 10 και οι έλεγχοι που πραγματοποιούνται για την αξιολόγηση της εξίσωσης παλινδρόμησης είναι όμοιες με τα βήματα που ακολουθούνται παραπάνω. Γι αυτό το λόγο θα παρουσιαστούν συνοπτικά μόνο τα αποτελέσματα της εκτέλεσης της γραμμικής παλινδρόμησης και θα αξιολογηθούν. Δημιουργία νέου επιπέδου της OLS διαδικασίας Παρακάτω παρουσιάζεται ο χάρτης της OLS διαδικασίας με τα υπόλοιπα της διαδικασίας ταξινομημένα βάσει της τιμής των τυποποιημένων υπολοίπων και ο πίνακας περιγραφικών χαρακτηριστικών του νέου χαρτογραφικού επιπέδου που περιλαμβάνει τις υπολογισμένες τιμές των υπολοίπων και των τυποποιημένων υπολοίπων, έπειτα από την εκτέλεση της διαδικασίας. (Εικόνα 6.16 & 6.17) Εικόνα 6.16: Νέος χάρτης των OLS υπολοίπων που αναφέρεται στην περιοχή του πρώην Δήμου Ευόσμου Μεταπτυχιακή διατριβή 273
286 Γ. Σ. Π. Εικόνα 6.17: Πίνακας περιγραφικών χαρακτηριστικών του νέου χαρτογραφικού επιπέδου που προέκυψε από την OLS διαδικασία Η ταξινόμηση που επιλέγεται να γίνει αυτοματοποιημένα από το πρόγραμμα, οδηγεί σε επτά διαφορετικές κλάσεις, οι οποίες αντικατοπτρίζουν στην ουσία την κατανομή των υπολοίπων. Από την παραπάνω ταξινόμηση παρατηρείται ότι όλες οι τιμές βρίσκονται μέσα στο διάστημα 1.68 και που σημαίνει, όπως αναφέρεται και στο , ότι η κατανομή είναι κανονική και το μοντέλο ταιριάζει ικανοποιητικά στα δεδομένα. Γενική επίδοση του μοντέλου Σύμφωνα με τα στοιχεία που προκύπτουν από το μήνυμα της αναφοράς της OLS διαδικασίας (Εικόνα 6.18) προκύπτει η τιμή του συντελεστή προσδιορισμού R 2 ίση με 0, και η τιμή προσαρμοσμένου συντελεστή προσδιορισμού (Adjusted R 2 ) ίση με 0,
287 Κ ε φ ά λ α ι ο 6 ο Εικόνα 6.18: Αναφορά των στατιστικών αποτελεσμάτων της OLS μεθόδου Η πρώτη παρατήρηση είναι ότι και οι δύο τιμές είναι όμοιες με τις αντίστοιχες που υπολογίζονται στο SPSS 18 του προηγούμενου κεφαλαίου, γεγονός που σημαίνει ότι και στην περιοχή του Ευόσμου υπάρχει ταύτιση των αποτελεσμάτων. Η διαπίστωση βάσει των τιμών είναι ότι παρουσιάζεται μία καλή προσαρμογή στα δεδομένα και ότι είναι εμφανής μία έντονη προβλεπτική δύναμη. Σύμφωνα με τις τιμές, το 87% της διακύμανσης της εξαρτημένης μεταβλητής ερμηνεύεται από την εξίσωση πολλαπλής παλινδρόμησης που προέκυψε. Σχολιασμός των συντελεστών πολλαπλής παλινδρόμησης Σημαντική είναι η απόδοση των συντελεστών πολλαπλής παλινδρόμησης, διότι αποτελούν τα βασικά στοιχεία της εξίσωσης του μοντέλου. Όπως ακριβώς και από το SPSS η τιμή του συντελεστή που αναφέρεται στο εμβαδόν (Χ1)είναι 1277, και παρουσιάζει μία θετική συσχέτιση καθώς όσο ανεβαίνει η τιμή των τμ, τόσο αυξάνεται η αξία του διαμερίσματος, ακολουθεί η τιμή του συντελεστή που αναφέρεται στην παλαιότητα (Χ2) είναι ίση με -586, και παρουσιάζει μία αρνητική γραμμική συσχέτιση, διότι όσο αυξάνεται η παλαιότητα, τόσο μειώνεται η αγοραία αξία του ακινήτου, η τιμή του συντελεστή που αναφέρεται στον όροφο (Χ3) του διαμερίσματος η οποία είναι 1788, και έχει θετική συσχέτιση με την εξαρτημένη μεταβλητή, η τιμή του συντελεστή που αναφέρεται στο είδος θέρμανσης (Χ6) του διαμερίσματος η οποία είναι ίση με 7479, και όμοια έχει θετική συσχέτιση με την εξαρτημένη μεταβλητή και τέλος η τιμή του συντελεστή που αναφέρεται στην κατάσταση του ακινήτου, η οποία είναι 5901, και συσχετίζεται θετικά με την εξαρτημένη μεταβλητή. Μεταπτυχιακή διατριβή 275
288 Γ. Σ. Π. Έλεγχος στατιστικής σημαντικότητας των ανεξάρτητων μεταβλητών Όμοια με την περιοχή του κέντρου η σημαντικότητα των ανεξάρτητων μεταβλητών κρίνεται βάσει των τιμών της στήλης p-values, οι οποίες θα πρέπει να βρίσκονται πολύ κοντά στο μηδέν. Σύμφωνα με τα αποτελέσματα Χ0 : 0, Χ1: 0, Χ2: 0, Χ3: 0, Χ6: 0, Χ7: 0, οι μεταβλητές Χ1, Χ3, Χ6 και Χ7 θεωρούνται στατιστικά σημαντικές και η διαπίστωση επιβεβαιώνεται από τα όρια που θέτει το ArcGIS, καθώς έχει τοποθετήσει (*) δίπλα από κάθε τιμή. Η μεταβλητή Χ2 παρατηρείται ότι ξεπερνά για λίγο την τιμή 0,05. Γνωρίζοντας από τη θεωρία των εκτιμήσεων ακινήτων ότι η παλαιότητα επιδρά στη διαμόρφωση των αξιών, η παραπάνω παρατήρηση (0,063) λαμβάνεται υπόψη αλλά δεν εμποδίζει τη θεώρηση της Χ2 ως στατιστικά σημαντικής για το μοντέλο. Έλεγχος συγγραμμικότητας/πολυσυγγραμμικότητας Ο έλεγχος της ύπαρξης γραμμικής σχέσης μεταξύ των ανεξάρτητων μεταβλητών, δηλαδή ο έλεγχος ύπαρξης πολυσυγγραμμικότητας, όπως αναφέρεται και παραπάνω, εξαρτάται από την τιμή του δείκτη VIF. Σύμφωνα με τα αποτελέσματα της OLS διαδικασίας, οι τιμές VIF για τις μεταβλητές είναι ίσες με VIF (X1) = VIF (X2) = VIF (X3) = VIF (X6) = VIF (X7) = Η τιμή που θεωρείται οριακή σύμφωνα με το ArcGIS είναι 7,5. Όπως παρατηρούμε από τις παραπάνω τιμές είναι όλες πολύ μικρότερες από την οριακή τιμή, άρα στο μοντέλο της περιοχής του Ευόσμου δεν υπάρχει κανένα πρόβλημα πολυσυγγραμμικότητας. Έλεγχος κανονικότητας των υπολοίπων Ο επόμενος βασικός έλεγχος αφορά την κανονικότητα των υπολοίπων και ικανοποιείται με τη στατιστική των Jarque και Bera. 276
289 Κ ε φ ά λ α ι ο 6 ο Σύμφωνα με τον διαδικτυακό οδηγό του ArcGIS την απάντηση δίνει η τιμή p-value, η οποία δεν πρέπει να είναι μικρότερη από 0,05 για επίπεδο εμπιστοσύνης 95%. Η τιμή που δίνεται είναι ίση με 0, > 0,05, άρα τα υπόλοιπα ακολουθούν την κανονική κατανομή. Ταυτόχρονα, στο μήνυμα της αναφοράς δεν υπάρχει (*) δίπλα από την εγγραφή της Jarque και Bera στατιστικής, άρα και το λογισμικό δεν εντοπίζει πρόβλημα κανονικότητας. Όμοια με την περιοχή του κέντρου, παρακάτω δίνεται το ιστόγραμμα των τυποποιημένων υπολοίπων(standardized residuals) 38, ώστε να είναι και οπτικά εμφανής η ύπαρξη κανονικότητας. Εικόνα 6.19: Απεικόνιση της κατανομής των υπολοίπων, όπως σχηματίστηκε από τη δημιουργία γραφημάτων του ArcGIS 10 Από το παραπάνω ιστόγραμμα, είναι ορατό ότι η κατανομή των υπολοίπων προσεγγίζει ικανοποιητικά την κανονική κατανομή και στην δεύτερη περιοχή μελέτης, τον πρώην Δήμο Ευόσμου. Για λόγους άμεσης σύγκρισης με το αντίστοιχο διάγραμμα που προκύπτει από το SPSS 18, παρατίθεται το ιστόγραμμα παρακάτω με ταυτόχρονη όμως προσαρμογή της καμπύλης της κανονικής κατανομής Μενού View Graphs Create Histogram Μεταπτυχιακή διατριβή 277
290 Γ. Σ. Π. Εικόνα 6.20: Απεικόνιση της κατανομής των υπολοίπων με την ταυτόχρονη εμφάνιση της κανονικής κατανομής μέσω του SPSS 18 Έλεγχος της ανεξαρτησίας των υπολοίπων Όπως στην περιοχή του κέντρου για τον έλεγχο της ανεξαρτησίας των υπολοίπων θα πρέπει να χρησιμοποιηθεί η διαδικασία υπολογισμού του δείκτη Moran s. Μέσω της διαδικασίας ArcToolBox Spatial Statistic Tools Analyzing Patterns Spatial autocorrelation (Morans I) παράγονται τα αποτελέσματα που φαίνονται στην παρακάτω εικόνα. Εικόνα 6.21: Μήνυμα αναφοράς από τον έλεγχο ανεξαρτησίας των υπολοίπων 278
291 Κ ε φ ά λ α ι ο 6 ο Εικόνα 6.22: Αποτέλεσμα ελέγχου χωρικής αυτοσυσχέτισης σε μορφή html αρχείου αναφοράς Σύμφωνα με τις παραπάνω εικόνες η τιμή Moran s I είναι αρνητική (- 0,032427), το οποίο σημαίνει ότι, σύμφωνα με το λογισμικό του ArcGIS 10, υπάρχει έλλειψη χωρικής εξάρτισης μεταξύ των παρατηρήσεων που γειτνιάζουν. Παράλληλα, ικανοποιητική κρίνεται η τιμή z-score, η οποία είναι ίση με -0,162099, διότι βρίσκεται εντός των επιτρεπτών ορίων που είναι Min -1,96 και Max 1,96. Τέλος, η ύπαρξη ανεξαρτησίας μεταξύ των υπολοίπων είναι ορατή από το παραπάνω διάγραμμα που απεικονίζει την κατηγορία που ανήκει το δείγμα και φανερώνει την έλλειψη χωρικής αυτοσυσχέτισης. 6.4 ΣΥΜΠΕΡΑΣΜΑΤΑ Το βασικό συμπέρασμα που εξάγεται από την παραπάνω ανάλυση είναι ότι ικανοποιείται ο βασικός στόχος της εφαρμογής πολλαπλής γραμμικής παλινδρόμησης σε περιβάλλον Γ.Σ.Π., ο οποίος είναι να ελεγχθεί η παραγωγή ακριβών και σωστών αποτελεσμάτων, όμοιων με τα αποτελέσματα που προκύπτουν από το εξειδικευμένο πακέτο στατιστικής ανάλυσης SPSS. Πράγματι, βάσει των αποτελεσμάτων της ανάλυσης, το ArcGIS 10 αντιμετωπίζει το πρόβλημα με τη χρήση των ελαχίστων τετραγώνων και δίνει όμοια αποτελέσματα με τη διαδικασίας μέσω του SPSS. Ταυτόχρονα παράγεται ικανός όγκος πληροφορίας, ώστε να ελέγχεται ταυτόχρονα και η αξιοπιστία του αποτελέσματος, Μεταπτυχιακή διατριβή 279
Μοντέλο πρόβλεψης αγοραίων αξιών ακινήτων βάσει των μεθόδων OLS και GWR με χρήση GIS Η περίπτωση του Δήμου Θεσσαλονίκης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΣΤΗ ΔΙΟΙΚΗΣΗ ΕΠΙΧΕΙΡΗΣΕΩΝ ΓΙΑ ΣΤΕΛΕΧΗ (EMBA) Διατριβή μεταπτυχιακού Μοντέλο πρόβλεψης αγοραίων αξιών ακινήτων
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΣΤΗ ΔΙΟΙΚΗΣΗ ΕΠΙΧΕΙΡΗΣΕΩΝ ΓΙΑ ΣΤΕΛΕΧΗ (EMBA) Διατριβή μεταπτυχιακού Μοντέλο πρόβλεψης αγοραίων αξιών ακινήτων
Περιεχόμενα. 1: Ιστορική προσέγγιση της οικονομικής θεωρίας και της έννοιας της προσόδου. Το υπόβαθρο των εκτιμήσεων στο σκηνικό του χθες
 Περιεχόμενα Εισαγωγή.................................................................. xiii 1: Ιστορική προσέγγιση της οικονομικής θεωρίας και της έννοιας της προσόδου. Το υπόβαθρο των εκτιμήσεων στο σκηνικό
Περιεχόμενα Εισαγωγή.................................................................. xiii 1: Ιστορική προσέγγιση της οικονομικής θεωρίας και της έννοιας της προσόδου. Το υπόβαθρο των εκτιμήσεων στο σκηνικό
5 ο Πανελλήνιο Συνέδριο Αγρονόμων και Τοπογράφων Μηχανικών
 5 ο Πανελλήνιο Συνέδριο Αγρονόμων και Τοπογράφων Μηχανικών ΑΝΑΠΤΥΞΗ ΣΥΣΤΗΜΑΤΟΣ ΜΑΖΙΚΩΝ ΕΚΤΙΜΗΣΕΩΝ ΑΞΙΩΝ ΟΙΚΙΣΤΙΚΩΝ ΑΚΙΝΗΤΩΝ ΜΕ ΧΡΗΣΗ ΤΕΧΝΟΛΟΓΙΩΝ GIS ΕΦΑΡΜΟΓΗ ΣΤΟ ΔΗΜΟ ΧΑΛΑΝΔΡΙΟΥ ΑΤΤΙΚΗΣ Ελευθερία Ανδρέου,
5 ο Πανελλήνιο Συνέδριο Αγρονόμων και Τοπογράφων Μηχανικών ΑΝΑΠΤΥΞΗ ΣΥΣΤΗΜΑΤΟΣ ΜΑΖΙΚΩΝ ΕΚΤΙΜΗΣΕΩΝ ΑΞΙΩΝ ΟΙΚΙΣΤΙΚΩΝ ΑΚΙΝΗΤΩΝ ΜΕ ΧΡΗΣΗ ΤΕΧΝΟΛΟΓΙΩΝ GIS ΕΦΑΡΜΟΓΗ ΣΤΟ ΔΗΜΟ ΧΑΛΑΝΔΡΙΟΥ ΑΤΤΙΚΗΣ Ελευθερία Ανδρέου,
1ο ΣΤΑΔΙΟ ΓΕΝΕΣΗ ΜΕΤΑΚΙΝΗΣΕΩΝ
 ΠΡΟΒΛΗΜΑ 1ο ΣΤΑΔΙΟ ΓΕΝΕΣΗ ΜΕΤΑΚΙΝΗΣΕΩΝ πόσες μετακινήσεις δημιουργούνται σε και για κάθε κυκλοφοριακή ζώνη; ΟΡΙΣΜΟΙ μετακίνηση μετακίνηση με βάση την κατοικία μετακίνηση με βάση άλλη πέρα της κατοικίας
ΠΡΟΒΛΗΜΑ 1ο ΣΤΑΔΙΟ ΓΕΝΕΣΗ ΜΕΤΑΚΙΝΗΣΕΩΝ πόσες μετακινήσεις δημιουργούνται σε και για κάθε κυκλοφοριακή ζώνη; ΟΡΙΣΜΟΙ μετακίνηση μετακίνηση με βάση την κατοικία μετακίνηση με βάση άλλη πέρα της κατοικίας
1η Ελληνο - Γαλλική & Διεθνής Συνάντηση, SD-MED:
 Ε ΘΝΙΚΟ Μ ΕΤΣΟΒΙΟ Π ΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ & ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΓΡΑΦΙΑΣ & ΠΕΡΙΦΕΡΕΙΑΚΟΥ ΣΧΕΔΙΑΣΜΟΥ 1η Ελληνο - Γαλλική & Διεθνής Συνάντηση, SD-MED: «Πολιτικές χωρικού σχεδιασμού και διευθέτησης
Ε ΘΝΙΚΟ Μ ΕΤΣΟΒΙΟ Π ΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ & ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΓΡΑΦΙΑΣ & ΠΕΡΙΦΕΡΕΙΑΚΟΥ ΣΧΕΔΙΑΣΜΟΥ 1η Ελληνο - Γαλλική & Διεθνής Συνάντηση, SD-MED: «Πολιτικές χωρικού σχεδιασμού και διευθέτησης
ΕΚΤΙΜΗΣΗ ΕΜΠΟΡΙΚΗΣ ΑΞΙΑΣ ΔΙΑΜΕΡΙΣΜΑΤΟΣ Α ΟΡΟΦΟΥ, ΣΤΗΝ ΟΔΟ ΛΑΜΠΡΟΥ ΠΟΡΦΥΡΑ 3 & ΚΑΛΥΜΝΟΥ, ΣΤΗ ΣΥΝΟΙΚΙΑ ΧΑΤΖΗΚΥΡΙΑΚΕΙΟ ΤΟΥ ΔΗΜΟΥ ΠΕΙΡΑΙΑ
 ΕΚΤΙΜΗΣΗ ΕΜΠΟΡΙΚΗΣ ΑΞΙΑΣ ΔΙΑΜΕΡΙΣΜΑΤΟΣ Α ΟΡΟΦΟΥ, ΣΤΗΝ ΟΔΟ ΛΑΜΠΡΟΥ ΠΟΡΦΥΡΑ 3 & ΚΑΛΥΜΝΟΥ, ΣΤΗ ΣΥΝΟΙΚΙΑ ΧΑΤΖΗΚΥΡΙΑΚΕΙΟ ΤΟΥ ΔΗΜΟΥ ΠΕΙΡΑΙΑ ΥΠΕΥΘΥΝΟΣ ΜΗΧΑΝΙΚΟΣ: ΑΘΑΝΑΣΙΟΣ Θ. ΑΡΙΔΑΣ ΔΙΠΛΩΜΑΤΟΥΧΟΣ ΠΟΛΙΤΙΚΟΣ ΜΗΧΑΝΙΚΟΣ
ΕΚΤΙΜΗΣΗ ΕΜΠΟΡΙΚΗΣ ΑΞΙΑΣ ΔΙΑΜΕΡΙΣΜΑΤΟΣ Α ΟΡΟΦΟΥ, ΣΤΗΝ ΟΔΟ ΛΑΜΠΡΟΥ ΠΟΡΦΥΡΑ 3 & ΚΑΛΥΜΝΟΥ, ΣΤΗ ΣΥΝΟΙΚΙΑ ΧΑΤΖΗΚΥΡΙΑΚΕΙΟ ΤΟΥ ΔΗΜΟΥ ΠΕΙΡΑΙΑ ΥΠΕΥΘΥΝΟΣ ΜΗΧΑΝΙΚΟΣ: ΑΘΑΝΑΣΙΟΣ Θ. ΑΡΙΔΑΣ ΔΙΠΛΩΜΑΤΟΥΧΟΣ ΠΟΛΙΤΙΚΟΣ ΜΗΧΑΝΙΚΟΣ
ΜΕΘΟΔΟΣ ΣΥΓΚΡΙΤΙΚΩΝ ΣΤΟΙΧΕΙΩΝ
 ΜΕΘΟΔΟΣ ΣΥΓΚΡΙΤΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Θ Ε Ω Ρ Ι Α Κ Α Ι Α Σ Κ Η Σ Ε Ι Σ Σεμινάριο Εκτιμήσεων Ακίνητης Περιουσίας, ΣΠΜΕ, 2018 Συγκριτική Μέθοδος (Comparative method) H Συγκριτική Μέθοδος είναι ίσως η πιο σημαντική
ΜΕΘΟΔΟΣ ΣΥΓΚΡΙΤΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Θ Ε Ω Ρ Ι Α Κ Α Ι Α Σ Κ Η Σ Ε Ι Σ Σεμινάριο Εκτιμήσεων Ακίνητης Περιουσίας, ΣΠΜΕ, 2018 Συγκριτική Μέθοδος (Comparative method) H Συγκριτική Μέθοδος είναι ίσως η πιο σημαντική
ΝΑΥΤΙΛΙΑΚΟΙ ΚΥΚΛΟΙ ΚΑΙ ΧΡΗΜΑΤΟΔΟΤΗΣΗ ΝΑΥΤΙΛΙΑΚΩΝ ΕΠΕΝΔΥΣΕΩΝ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ Σχολή Διοίκησης και Οικονομίας Μεταπτυχιακή διατριβή ΝΑΥΤΙΛΙΑΚΟΙ ΚΥΚΛΟΙ ΚΑΙ ΧΡΗΜΑΤΟΔΟΤΗΣΗ ΝΑΥΤΙΛΙΑΚΩΝ ΕΠΕΝΔΥΣΕΩΝ ΔΗΜΗΤΡΗΣ ΤΡΥΦΩΝΟΣ Λεμεσός, Μάιος 2017 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ Σχολή Διοίκησης και Οικονομίας Μεταπτυχιακή διατριβή ΝΑΥΤΙΛΙΑΚΟΙ ΚΥΚΛΟΙ ΚΑΙ ΧΡΗΜΑΤΟΔΟΤΗΣΗ ΝΑΥΤΙΛΙΑΚΩΝ ΕΠΕΝΔΥΣΕΩΝ ΔΗΜΗΤΡΗΣ ΤΡΥΦΩΝΟΣ Λεμεσός, Μάιος 2017 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
ΑΡΧΙΤΕΚΤΟΝΙΚΟΙ ΚΑΙ ΠΟΛΕΟΔΟΜΙΚΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΣΤΗ ΘΕΣΣΑΛΟΝΙΚΗ ΛΟΓΩ ΤΟΥ ΦΑΙΝΟΜΕΝΟΥ ΤΗΣ ΜΕΤΑΝΑΣΤΕΥΣΗΣ Μέρος Α
 ΤΕΧΝΙΚΟ ΕΠΙΜΕΛΗΤΗΡΙΟ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΜΟΝΙΜΗ ΕΠΙΤΡΟΠΗ ΑΡΧΙΤΕΚΤΟΝΙΚΩΝ ΘΕΜΑΤΩΝ ΟΜΑΔΑ ΕΡΓΑΣΙΑΣ ΜΕ ΑΝΤΙΚΕΙΜΕΝΟ: ΑΡΧΙΤΕΚΤΟΝΙΚΟΙ ΚΑΙ ΠΟΛΕΟΔΟΜΙΚΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΣΤΗ ΘΕΣΣΑΛΟΝΙΚΗ ΛΟΓΩ ΤΟΥ ΦΑΙΝΟΜΕΝΟΥ
ΤΕΧΝΙΚΟ ΕΠΙΜΕΛΗΤΗΡΙΟ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΜΟΝΙΜΗ ΕΠΙΤΡΟΠΗ ΑΡΧΙΤΕΚΤΟΝΙΚΩΝ ΘΕΜΑΤΩΝ ΟΜΑΔΑ ΕΡΓΑΣΙΑΣ ΜΕ ΑΝΤΙΚΕΙΜΕΝΟ: ΑΡΧΙΤΕΚΤΟΝΙΚΟΙ ΚΑΙ ΠΟΛΕΟΔΟΜΙΚΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΣΤΗ ΘΕΣΣΑΛΟΝΙΚΗ ΛΟΓΩ ΤΟΥ ΦΑΙΝΟΜΕΝΟΥ
REPORT 2017-Q3 ΠΑΡΑΤΗΡΗΤΗΡΙΟ ΑΞΙΩΝ ΔΙΑΜΕΡΙΣΜΑΤΑ
 REPORT 2017-Q3 ΠΑΡΑΤΗΡΗΤΗΡΙΟ ΑΞΙΩΝ ΔΙΑΜΕΡΙΣΜΑΤΑ ΕΊΔΟΣ ΑΚΙΝΉΤΩΝ: Διαμερίσματα στην Αττική (5 περιοχές) ΠΑΡΑΤΉΡΗΣΗ: Ζητούμενες τιμές πώλησης (Market Values) ΧΡΌΝΟΣ ΜΕΛΈΤΗΣ: 3ο τρίμηνο 2017 ΠΕΡΊΟΔΟΣ ΣΎΓΚΡΙΣΗΣ:
REPORT 2017-Q3 ΠΑΡΑΤΗΡΗΤΗΡΙΟ ΑΞΙΩΝ ΔΙΑΜΕΡΙΣΜΑΤΑ ΕΊΔΟΣ ΑΚΙΝΉΤΩΝ: Διαμερίσματα στην Αττική (5 περιοχές) ΠΑΡΑΤΉΡΗΣΗ: Ζητούμενες τιμές πώλησης (Market Values) ΧΡΌΝΟΣ ΜΕΛΈΤΗΣ: 3ο τρίμηνο 2017 ΠΕΡΊΟΔΟΣ ΣΎΓΚΡΙΣΗΣ:
ΕΚΤΙΜΗΣΗ ΕΜΠΟΡΙΚΗΣ ΑΞΙΑΣ ΑΝΟΙΚΤΗΣ ΘΕΣΕΩΣ ΣΤΑΘΜΕΥΣΗΣ ΣΤΗΝ ΟΔΟ ΟΝΕΙΡΩΝ 5, ΣΤΑ ΠΕΥΚΑ ΔΗΜΟΥ ΝΕΑΠΟΛΗΣ ΣΥΚΕΩΝ ΘΕΣΣΑΛΟΝΙΚΗΣ
 ΕΚΤΙΜΗΣΗ ΕΜΠΟΡΙΚΗΣ ΑΞΙΑΣ ΑΝΟΙΚΤΗΣ ΘΕΣΕΩΣ ΣΤΑΘΜΕΥΣΗΣ ΣΤΗΝ ΟΔΟ ΟΝΕΙΡΩΝ 5, ΣΤΑ ΠΕΥΚΑ ΔΗΜΟΥ ΝΕΑΠΟΛΗΣ ΣΥΚΕΩΝ ΘΕΣΣΑΛΟΝΙΚΗΣ ΥΠΕΥΘΥΝΟΣ ΜΗΧΑΝΙΚΟΣ: ΑΘΑΝΑΣΙΟΣ Θ. ΑΡΙΔΑΣ ΔΙΠΛΩΜΑΤΟΥΧΟΣ ΠΟΛΙΤΙΚΟΣ ΜΗΧΑΝΙΚΟΣ MSc East
ΕΚΤΙΜΗΣΗ ΕΜΠΟΡΙΚΗΣ ΑΞΙΑΣ ΑΝΟΙΚΤΗΣ ΘΕΣΕΩΣ ΣΤΑΘΜΕΥΣΗΣ ΣΤΗΝ ΟΔΟ ΟΝΕΙΡΩΝ 5, ΣΤΑ ΠΕΥΚΑ ΔΗΜΟΥ ΝΕΑΠΟΛΗΣ ΣΥΚΕΩΝ ΘΕΣΣΑΛΟΝΙΚΗΣ ΥΠΕΥΘΥΝΟΣ ΜΗΧΑΝΙΚΟΣ: ΑΘΑΝΑΣΙΟΣ Θ. ΑΡΙΔΑΣ ΔΙΠΛΩΜΑΤΟΥΧΟΣ ΠΟΛΙΤΙΚΟΣ ΜΗΧΑΝΙΚΟΣ MSc East
ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ. «Η πολεοδομική εξέλιξη της Χαλκίδας» Ευσταθοπούλου Αγγελική (ΑΜ) Παπαβασιλείου Βασιλική (ΑΜ) Επίβλεψη Τσουκάτου Στέλλα
 ΑΝΩΤΑΤΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΔΟΜΙΚΩΝ ΕΡΓΩΝ ΑΡΧΙΤΕΚΤΟΝΙΚΟΣ ΤΟΜΕΑΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ «Η πολεοδομική εξέλιξη της Χαλκίδας» Ευσταθοπούλου Αγγελική
ΑΝΩΤΑΤΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΔΟΜΙΚΩΝ ΕΡΓΩΝ ΑΡΧΙΤΕΚΤΟΝΙΚΟΣ ΤΟΜΕΑΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ «Η πολεοδομική εξέλιξη της Χαλκίδας» Ευσταθοπούλου Αγγελική
ΠΙΛΟΤΙΚΗ ΕΦΑΡΜΟΓΗ ΑΥΤΟΝΟΜΩΝ ΣΥΣΤΗΜΑΤΩΝ ΠΛΟΗΓΗΣΗΣ ΓΙΑ ΤΗΝ ΠΑΡΑΓΩΓΗ ΥΨΗΛΗΣ ΑΝΑΛΥΣΗΣ ΟΡΘΟΦΩΤΟΓΡΑΦΙΩΝ ΓΕΩΡΓΙΚΩΝ ΕΚΤΑΣΕΩΝ
 Σχολή Μηχανικής & Τεχνολογίας Τμήμα Πολιτικών & Μηχανικών Γεωπληροφορικής Μεταπτυχιακή διατριβή ΠΙΛΟΤΙΚΗ ΕΦΑΡΜΟΓΗ ΑΥΤΟΝΟΜΩΝ ΣΥΣΤΗΜΑΤΩΝ ΠΛΟΗΓΗΣΗΣ ΓΙΑ ΤΗΝ ΠΑΡΑΓΩΓΗ ΥΨΗΛΗΣ ΑΝΑΛΥΣΗΣ ΟΡΘΟΦΩΤΟΓΡΑΦΙΩΝ ΓΕΩΡΓΙΚΩΝ
Σχολή Μηχανικής & Τεχνολογίας Τμήμα Πολιτικών & Μηχανικών Γεωπληροφορικής Μεταπτυχιακή διατριβή ΠΙΛΟΤΙΚΗ ΕΦΑΡΜΟΓΗ ΑΥΤΟΝΟΜΩΝ ΣΥΣΤΗΜΑΤΩΝ ΠΛΟΗΓΗΣΗΣ ΓΙΑ ΤΗΝ ΠΑΡΑΓΩΓΗ ΥΨΗΛΗΣ ΑΝΑΛΥΣΗΣ ΟΡΘΟΦΩΤΟΓΡΑΦΙΩΝ ΓΕΩΡΓΙΚΩΝ
Περιεχόμενα. Πρόλογος... 15
 Περιεχόμενα Πρόλογος... 15 Κεφάλαιο 1 ΘΕΩΡΗΤΙΚΑ ΚΑΙ ΦΙΛΟΣΟΦΙΚΑ ΟΝΤΟΛΟΓΙΚΑ ΚΑΙ ΕΠΙΣΤΗΜΟΛΟΓΙΚΑ ΖΗΤΗΜΑΤΑ ΤΗΣ ΜΕΘΟΔΟΛΟΓΙΑΣ ΕΡΕΥΝΑΣ ΤΟΥ ΠΡΑΓΜΑΤΙΚΟΥ ΚΟΣΜΟΥ... 17 Το θεμελιώδες πρόβλημα των κοινωνικών επιστημών...
Περιεχόμενα Πρόλογος... 15 Κεφάλαιο 1 ΘΕΩΡΗΤΙΚΑ ΚΑΙ ΦΙΛΟΣΟΦΙΚΑ ΟΝΤΟΛΟΓΙΚΑ ΚΑΙ ΕΠΙΣΤΗΜΟΛΟΓΙΚΑ ΖΗΤΗΜΑΤΑ ΤΗΣ ΜΕΘΟΔΟΛΟΓΙΑΣ ΕΡΕΥΝΑΣ ΤΟΥ ΠΡΑΓΜΑΤΙΚΟΥ ΚΟΣΜΟΥ... 17 Το θεμελιώδες πρόβλημα των κοινωνικών επιστημών...
Εκτίμηση και διαχείριση Εμπορικών Κέντρων με χρήση Γεωγραφικών Συστημάτων Πληροφοριών. Θεσσαλονίκης
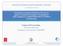 ΔΙΑΧΕΙΡΙΣΗ ΚΑΙ ΑΞΙΟΠΟΙΗΣΗ ΑΚΙΝΗΤΩΝ, ΕΠΕΝΔΥΣΕΙΣ - ΠΡΟΟΠΤΙΚΕΣ 11-12 Μαΐου 2009, Θεσσαλονίκη Εκτίμηση και διαχείριση Εμπορικών Κέντρων με χρήση Γεωγραφικών Συστημάτων Πληροφοριών (GIS), εφαρμογή στο MEDITERRANEAN
ΔΙΑΧΕΙΡΙΣΗ ΚΑΙ ΑΞΙΟΠΟΙΗΣΗ ΑΚΙΝΗΤΩΝ, ΕΠΕΝΔΥΣΕΙΣ - ΠΡΟΟΠΤΙΚΕΣ 11-12 Μαΐου 2009, Θεσσαλονίκη Εκτίμηση και διαχείριση Εμπορικών Κέντρων με χρήση Γεωγραφικών Συστημάτων Πληροφοριών (GIS), εφαρμογή στο MEDITERRANEAN
ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ- ΤΜΗΜΑ ΑΡΧΙΤΕΚΤΟΝΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΠΟΛΕΟΔΟΜΙΚΟΥ ΚΑΙ ΧΩΡΟΤΑΞΙΚΟΥ ΣΧΕΔΙΑΣΜΟΥ
 ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ- ΤΜΗΜΑ ΑΡΧΙΤΕΚΤΟΝΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΠΟΛΕΟΔΟΜΙΚΟΥ ΚΑΙ ΧΩΡΟΤΑΞΙΚΟΥ ΣΧΕΔΙΑΣΜΟΥ ΕΞΑΜΗΝΟ 5 ο Ακαδημαϊκό έτος 2016-2017 ΥΠΟΧΡΕΩΤΙΚΟ ΜΑΘΗΜΑ : ΠΟΛΕΟΔΟΜΙΑ Ι ΕΙΣΑΓΩΓΗ
ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ- ΤΜΗΜΑ ΑΡΧΙΤΕΚΤΟΝΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΠΟΛΕΟΔΟΜΙΚΟΥ ΚΑΙ ΧΩΡΟΤΑΞΙΚΟΥ ΣΧΕΔΙΑΣΜΟΥ ΕΞΑΜΗΝΟ 5 ο Ακαδημαϊκό έτος 2016-2017 ΥΠΟΧΡΕΩΤΙΚΟ ΜΑΘΗΜΑ : ΠΟΛΕΟΔΟΜΙΑ Ι ΕΙΣΑΓΩΓΗ
ΘΕΜΑ ΕΞΑΜΗΝΟΥ «Το φαινόμενο της αστικοποίησης στο Δήμο Ζωγράφου»
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΡΧΙΤΕΚΤΟΝΩΝ ΜΗΧΑΝΙΚΩΝ Δ.Π.Μ.Σ. «ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΣΧΕΔΙΑΣΜΟΣ ΤΟΥ ΧΩΡΟΥ» ΚΑΤΕΥΘΥΝΣΗ: «ΠΟΛΕΟΔΟΜΙΑ-ΧΩΡΟΤΑΞΙΑ» ΜΑΘΗΜΑ: «ΓΕΩΓΡΑΦΙΚΕΣ ΔΥΝΑΜΙΚΕΣ ΚΑΙ ΣΥΓΧΡΟΝΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΤΟΥ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΡΧΙΤΕΚΤΟΝΩΝ ΜΗΧΑΝΙΚΩΝ Δ.Π.Μ.Σ. «ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΣΧΕΔΙΑΣΜΟΣ ΤΟΥ ΧΩΡΟΥ» ΚΑΤΕΥΘΥΝΣΗ: «ΠΟΛΕΟΔΟΜΙΑ-ΧΩΡΟΤΑΞΙΑ» ΜΑΘΗΜΑ: «ΓΕΩΓΡΑΦΙΚΕΣ ΔΥΝΑΜΙΚΕΣ ΚΑΙ ΣΥΓΧΡΟΝΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΤΟΥ
ΒΕΛΤΙΩΣΗ ΔΙΕΡΓΑΣΙΩΝ ΕΡΓΑΣΤΗΡΙΟΥ ΕΛΕΓΧΟΥ ΠΟΙΟΤΗΤΑΣ ΚΑΙ ΕΦΑΡΜΟΓΗ ΕΡΓΑΛΕΙΩΝ ΔΙΑΣΦΑΛΙΣΗΣ ΠΟΙΟΤΗΤΑΣ ΣΕ ΜΕΤΑΛΛΟΒΙΟΜΗΧΑΝΙΑ
 Σχολή Mηχανικής και Τεχνολογίας Πτυχιακή εργασία ΒΕΛΤΙΩΣΗ ΔΙΕΡΓΑΣΙΩΝ ΕΡΓΑΣΤΗΡΙΟΥ ΕΛΕΓΧΟΥ ΠΟΙΟΤΗΤΑΣ ΚΑΙ ΕΦΑΡΜΟΓΗ ΕΡΓΑΛΕΙΩΝ ΔΙΑΣΦΑΛΙΣΗΣ ΠΟΙΟΤΗΤΑΣ ΣΕ ΜΕΤΑΛΛΟΒΙΟΜΗΧΑΝΙΑ Στέλιος Καράσαββας Λεμεσός, Μάιος 2017
Σχολή Mηχανικής και Τεχνολογίας Πτυχιακή εργασία ΒΕΛΤΙΩΣΗ ΔΙΕΡΓΑΣΙΩΝ ΕΡΓΑΣΤΗΡΙΟΥ ΕΛΕΓΧΟΥ ΠΟΙΟΤΗΤΑΣ ΚΑΙ ΕΦΑΡΜΟΓΗ ΕΡΓΑΛΕΙΩΝ ΔΙΑΣΦΑΛΙΣΗΣ ΠΟΙΟΤΗΤΑΣ ΣΕ ΜΕΤΑΛΛΟΒΙΟΜΗΧΑΝΙΑ Στέλιος Καράσαββας Λεμεσός, Μάιος 2017
ΕΕΟ 11. Η χρήση στατιστικών εργαλείων στην εκτιμητική
 ΕΕΟ 11 Η χρήση στατιστικών εργαλείων στην εκτιμητική 1. Εισαγωγή 2. Προϋποθέσεις χρήσης των Αυτοματοποιημένων Εκτιμητικών Μοντέλων (ΑΕΜ) 3. Περιορισμοί στη χρήση των ΑΕΜ εφόσον έχουν πληρωθεί οι προϋποθέσεις
ΕΕΟ 11 Η χρήση στατιστικών εργαλείων στην εκτιμητική 1. Εισαγωγή 2. Προϋποθέσεις χρήσης των Αυτοματοποιημένων Εκτιμητικών Μοντέλων (ΑΕΜ) 3. Περιορισμοί στη χρήση των ΑΕΜ εφόσον έχουν πληρωθεί οι προϋποθέσεις
ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΑΚΙΝΗΤΩΝ
 ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΑΚΙΝΗΤΩΝ Ακίνητο κατά το άρθρο 948 Α.Κ. είναι το έδαφος και τα συστατικά του μέρη. Κινητό είναι ότι δεν είναι ακίνητο. Ως έδαφος νοείται ορισμένο τμήμα της επιφάνειας της γης που πληρεί
ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΑΚΙΝΗΤΩΝ Ακίνητο κατά το άρθρο 948 Α.Κ. είναι το έδαφος και τα συστατικά του μέρη. Κινητό είναι ότι δεν είναι ακίνητο. Ως έδαφος νοείται ορισμένο τμήμα της επιφάνειας της γης που πληρεί
ΑΡΧΙΤΕΚΤΟΝΙΚΟΙ ΚΑΙ ΠΟΛΕΟΔΟΜΙΚΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΣΤΗ ΘΕΣΣΑΛΟΝΙΚΗ ΛΟΓΩ ΤΟΥ ΦΑΙΝΟΜΕΝΟΥ ΤΗΣ ΜΕΤΑΝΑΣΤΕΥΣΗΣ
 Νέες Πολιτείες ΙΙΙ : Λαχανόκηποι Μενεμένης Στα ενδιάμεσα όρια της πόλης Στην περιοχή Λαχανόκηποι, που ανήκει στα διοικητικά όρια του Δήμου Μενεμένης, εντοπίστηκε ένας τρίτος, εντελώς νέος για τα δεδομένα
Νέες Πολιτείες ΙΙΙ : Λαχανόκηποι Μενεμένης Στα ενδιάμεσα όρια της πόλης Στην περιοχή Λαχανόκηποι, που ανήκει στα διοικητικά όρια του Δήμου Μενεμένης, εντοπίστηκε ένας τρίτος, εντελώς νέος για τα δεδομένα
ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΘΕΩΡΙΑ ΚΑΙ ΕΦΑΡΜΟΓΗ ΤΟΥ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΣΤΗ ΛΗΨΗ ΑΠΟΦΑΣΕΩΝ (1)
 ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΘΕΩΡΙΑ ΚΑΙ ΕΦΑΡΜΟΓΗ ΤΟΥ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΣΤΗ ΛΗΨΗ ΑΠΟΦΑΣΕΩΝ (1) 1 Προέλευση και ιστορία της Επιχειρησιακής Έρευνας Αλλαγές στις επιχειρήσεις Τέλος του 19ου αιώνα: βιομηχανική
ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΘΕΩΡΙΑ ΚΑΙ ΕΦΑΡΜΟΓΗ ΤΟΥ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΣΤΗ ΛΗΨΗ ΑΠΟΦΑΣΕΩΝ (1) 1 Προέλευση και ιστορία της Επιχειρησιακής Έρευνας Αλλαγές στις επιχειρήσεις Τέλος του 19ου αιώνα: βιομηχανική
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ. Πτυχιακή διατριβή
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πτυχιακή διατριβή Η ΣΥΓΚΕΝΤΡΩΣΗ ΤΩΝ ΒΑΡΕΩΝ ΜΕΤΑΛΛΩΝ ΣΤΟ ΕΔΑΦΟΣ ΚΑΙ ΜΕΘΟΔΟΙ ΠΡΟΣΔΙΟΡΙΣΜΟΥ ΤΟΥΣ Μιχαήλ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πτυχιακή διατριβή Η ΣΥΓΚΕΝΤΡΩΣΗ ΤΩΝ ΒΑΡΕΩΝ ΜΕΤΑΛΛΩΝ ΣΤΟ ΕΔΑΦΟΣ ΚΑΙ ΜΕΘΟΔΟΙ ΠΡΟΣΔΙΟΡΙΣΜΟΥ ΤΟΥΣ Μιχαήλ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΧΩΡΟΤΑΞΙΑΣ, ΠΟΛΕΟΔΟΜΙΑΣ ΚΑΙ ΠΕΡΙΦΕΡΕΙΑΚΗΣ ΑΝΑΠΤΥΞΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΧΩΡΟΤΑΞΙΑΣ, ΠΟΛΕΟΔΟΜΙΑΣ ΚΑΙ ΠΕΡΙΦΕΡΕΙΑΚΗΣ ΑΝΑΠΤΥΞΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΕΠΕΝΔΥΣΕΙΣ ΚΑΙ ΠΕΡΙΦΕΡΕΙΑΚΗ ΑΝΑΠΤΥΞΗ» ΠΕΡΙΓΡΑΦΕΣ ΜΑΘΗΜΑΤΩΝ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΧΩΡΟΤΑΞΙΑΣ, ΠΟΛΕΟΔΟΜΙΑΣ ΚΑΙ ΠΕΡΙΦΕΡΕΙΑΚΗΣ ΑΝΑΠΤΥΞΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΕΠΕΝΔΥΣΕΙΣ ΚΑΙ ΠΕΡΙΦΕΡΕΙΑΚΗ ΑΝΑΠΤΥΞΗ» ΠΕΡΙΓΡΑΦΕΣ ΜΑΘΗΜΑΤΩΝ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ
Ανάλυση και Σχεδιασμός Μεταφορών Ι Γένεση Μετακινήσεων
 Γένεση Μετακινήσεων Παναγιώτης Παπαντωνίου Δρ. Πολιτικός Μηχανικός, Συγκοινωνιολόγος ppapant@upatras.gr Πάτρα, 2017 Εισαγωγή Αθροιστικά μοντέλα (Aggregate models) Ανάλυση κατά ζώνη πόσες μετακινήσεις ξεκινούν
Γένεση Μετακινήσεων Παναγιώτης Παπαντωνίου Δρ. Πολιτικός Μηχανικός, Συγκοινωνιολόγος ppapant@upatras.gr Πάτρα, 2017 Εισαγωγή Αθροιστικά μοντέλα (Aggregate models) Ανάλυση κατά ζώνη πόσες μετακινήσεις ξεκινούν
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ Επιβλέπων Καθηγητής: Δρ. Νίκος Μίτλεττον Η ΣΧΕΣΗ ΤΟΥ ΜΗΤΡΙΚΟΥ ΘΗΛΑΣΜΟΥ ΜΕ ΤΗΝ ΕΜΦΑΝΙΣΗ ΣΑΚΧΑΡΩΔΗ ΔΙΑΒΗΤΗ ΤΥΠΟΥ 2 ΣΤΗΝ ΠΑΙΔΙΚΗ ΗΛΙΚΙΑ Ονοματεπώνυμο: Ιωσηφίνα
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ Επιβλέπων Καθηγητής: Δρ. Νίκος Μίτλεττον Η ΣΧΕΣΗ ΤΟΥ ΜΗΤΡΙΚΟΥ ΘΗΛΑΣΜΟΥ ΜΕ ΤΗΝ ΕΜΦΑΝΙΣΗ ΣΑΚΧΑΡΩΔΗ ΔΙΑΒΗΤΗ ΤΥΠΟΥ 2 ΣΤΗΝ ΠΑΙΔΙΚΗ ΗΛΙΚΙΑ Ονοματεπώνυμο: Ιωσηφίνα
ΜΕΡΟΣ ΙII ΝΙΚΟΣ ΧΡΙΣΤΟ ΟΥΛΑΚΗΣ ΦΟΡΟΛΟΓΙΑ ΠΕΡΙΟΥΣΙΑΣ
 ΦΟΡΟΛΟΓΙΚΕΣ ΠΟΛΙΤΙΚΕΣ ΜΕΡΟΣ ΙII ΝΙΚΟΣ ΧΡΙΣΤΟ ΟΥΛΑΚΗΣ ΦΟΡΟΛΟΓΙΑ ΠΕΡΙΟΥΣΙΑΣ ΙΑΛΕΞΗ #8 ΑΚΑ. ΕΤΟΣ 2016-17 ιακρίνουμε δύο κατηγορίες: (α) τους φόρους κατοχής περιουσίας έχουν ως βάση την αξία, τον όγκο ή άλλο
ΦΟΡΟΛΟΓΙΚΕΣ ΠΟΛΙΤΙΚΕΣ ΜΕΡΟΣ ΙII ΝΙΚΟΣ ΧΡΙΣΤΟ ΟΥΛΑΚΗΣ ΦΟΡΟΛΟΓΙΑ ΠΕΡΙΟΥΣΙΑΣ ΙΑΛΕΞΗ #8 ΑΚΑ. ΕΤΟΣ 2016-17 ιακρίνουμε δύο κατηγορίες: (α) τους φόρους κατοχής περιουσίας έχουν ως βάση την αξία, τον όγκο ή άλλο
Σχολή Διοίκησης και Οικονομίας. Μεταπτυχιακή διατριβή
 Σχολή Διοίκησης και Οικονομίας Μεταπτυχιακή διατριβή Samsung και Apple: Αναλύοντας τη χρηματοοικονομική πληροφόρηση των ηγετών της τεχνολογίας και η επίδραση των εξωτερικών και ενδοεπιχειρησιακών παραγόντων
Σχολή Διοίκησης και Οικονομίας Μεταπτυχιακή διατριβή Samsung και Apple: Αναλύοντας τη χρηματοοικονομική πληροφόρηση των ηγετών της τεχνολογίας και η επίδραση των εξωτερικών και ενδοεπιχειρησιακών παραγόντων
ο εκτοπισμός της κατοικίας από το Γκαζοχώρι
 Δ.Π.Μ.Σ. ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΣΧΕΔΙΑΣΜΟΣ ΧΩΡΟΥ ΚΑΤΕΥΘΥΝΣΗ Β : ΠΟΛΕΟΔΟΜΙΑ και ΧΩΡΟΤΑΞΙΑ ΓΕΩΓΡΑΦΙΚΕΣ ΔΥΝΑΜΙΚΕΣ και ΣΥΓΧΡΟΝΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΤΟΥ ΕΛΛΗΝΙΚΟΥ ΧΩΡΟΥ ο εκτοπισμός της κατοικίας από το Γκαζοχώρι φοιτήτρια:
Δ.Π.Μ.Σ. ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΣΧΕΔΙΑΣΜΟΣ ΧΩΡΟΥ ΚΑΤΕΥΘΥΝΣΗ Β : ΠΟΛΕΟΔΟΜΙΑ και ΧΩΡΟΤΑΞΙΑ ΓΕΩΓΡΑΦΙΚΕΣ ΔΥΝΑΜΙΚΕΣ και ΣΥΓΧΡΟΝΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΤΟΥ ΕΛΛΗΝΙΚΟΥ ΧΩΡΟΥ ο εκτοπισμός της κατοικίας από το Γκαζοχώρι φοιτήτρια:
Εντολή: αγορά ακινήτου στο (τοποθεσία)
 Εντολή: αγορά ακινήτου στο (τοποθεσία) Σύνοψη Αναφορικά με την υπόθεση που μας ανατέθηκε από τον εντολέα μας (όνομα) του (όνομα πατρός) και της (όνομα μητρός) σχετικά με την αγορά ακινήτου στην θέση (τοποθεσία)
Εντολή: αγορά ακινήτου στο (τοποθεσία) Σύνοψη Αναφορικά με την υπόθεση που μας ανατέθηκε από τον εντολέα μας (όνομα) του (όνομα πατρός) και της (όνομα μητρός) σχετικά με την αγορά ακινήτου στην θέση (τοποθεσία)
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΗΣ ΕΠΙΣΤΗΜΗΣ ΑΜΕΣΕΣ ΞΕΝΕΣ ΕΠΕΝΔΥΣΕΙΣ ΣΕ ΕΥΡΩΠΑΙΚΕΣ ΧΩΡΕΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΗΣ ΕΠΙΣΤΗΜΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΣΤΗΝ ΟΙΚΟΝΟΜΙΚΗ ΚΑΙ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΣΤΡΑΤΗΓΙΚΗ ΑΜΕΣΕΣ ΞΕΝΕΣ ΕΠΕΝΔΥΣΕΙΣ ΣΕ ΕΥΡΩΠΑΙΚΕΣ ΧΩΡΕΣ Αθανάσιος Νταραβάνογλου Διπλωματική
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΗΣ ΕΠΙΣΤΗΜΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΣΤΗΝ ΟΙΚΟΝΟΜΙΚΗ ΚΑΙ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΣΤΡΑΤΗΓΙΚΗ ΑΜΕΣΕΣ ΞΕΝΕΣ ΕΠΕΝΔΥΣΕΙΣ ΣΕ ΕΥΡΩΠΑΙΚΕΣ ΧΩΡΕΣ Αθανάσιος Νταραβάνογλου Διπλωματική
ΠΑΡΑΡΤΗΜΑ ΠΑΡΟΥΣΙΑΣΗ ΜΕΘΟΔΩΝ ΑΠΟΤΙΜΗΣΗΣ ΑΚΙΝΗΤΩΝ
 ΠΑΡΑΡΤΗΜΑ ΠΑΡΟΥΣΙΑΣΗ ΜΕΘΟΔΩΝ ΑΠΟΤΙΜΗΣΗΣ ΑΚΙΝΗΤΩΝ Η επιλογή της κατάλληλης εκτιμητικής μεθόδου ακινήτων αποτελεί μία «λεπτή» διαδικασία που εξαρτάται κυρίως από τη φύση και τις προοπτικές του κάθε ακινήτου.
ΠΑΡΑΡΤΗΜΑ ΠΑΡΟΥΣΙΑΣΗ ΜΕΘΟΔΩΝ ΑΠΟΤΙΜΗΣΗΣ ΑΚΙΝΗΤΩΝ Η επιλογή της κατάλληλης εκτιμητικής μεθόδου ακινήτων αποτελεί μία «λεπτή» διαδικασία που εξαρτάται κυρίως από τη φύση και τις προοπτικές του κάθε ακινήτου.
Ο ΤΟΠΟΣ ΕΓΚΑΤΑΣΤΑΣΗΣ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ
 Ο ΤΟΠΟΣ ΕΓΚΑΤΑΣΤΑΣΗΣ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ Οι κλασικές προσεγγίσεις αντιμετωπίζουν τη διαδικασία της επιλογής του τόπου εγκατάστασης των επιχειρήσεων ως αποτέλεσμα επίδρασης ορισμένων μεμονωμένων παραγόντων,
Ο ΤΟΠΟΣ ΕΓΚΑΤΑΣΤΑΣΗΣ ΤΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ Οι κλασικές προσεγγίσεις αντιμετωπίζουν τη διαδικασία της επιλογής του τόπου εγκατάστασης των επιχειρήσεων ως αποτέλεσμα επίδρασης ορισμένων μεμονωμένων παραγόντων,
ΔΙΕΥΘΥΝΣΗ ΤΕΧΝΙΚΩΝ ΥΠΗΡΕΣΙΩΝ A.Π. / ΔΤΥ ΠΡΟΣ : Πρόεδρο ΔΣ
 1 ΠΡΟΣ : Πρόεδρο ΔΣ ΘΕΜΑ : ΣΧΕΤ : Πολεοδομική μελέτη περιοχής Bοσπόρου Γνωμοδότηση ΣΧΟΠ (πράξη 222 /συνεδρία 19 η / 01. 06. 99) Α. Ο Δήμος προσπαθώντας να αντιμετωπίσει τα έντονα προβλήματα των αντικρουόμενων
1 ΠΡΟΣ : Πρόεδρο ΔΣ ΘΕΜΑ : ΣΧΕΤ : Πολεοδομική μελέτη περιοχής Bοσπόρου Γνωμοδότηση ΣΧΟΠ (πράξη 222 /συνεδρία 19 η / 01. 06. 99) Α. Ο Δήμος προσπαθώντας να αντιμετωπίσει τα έντονα προβλήματα των αντικρουόμενων
ΓΕΩΠΟΝΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙO ΑΘΗΝΩΝ ΤΜΗΜΑ ΑΞΙΟΠΟΙΗΣΗΣ ΦΥΣΙΚΩΝ ΠΟΡΩΝ & ΓΕΩΡΓΙΚΗΣ ΜΗΧΑΝΙΚΗΣ
 ΓΕΩΠΟΝΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙO ΑΘΗΝΩΝ ΤΜΗΜΑ ΑΞΙΟΠΟΙΗΣΗΣ ΦΥΣΙΚΩΝ ΠΟΡΩΝ & ΓΕΩΡΓΙΚΗΣ ΜΗΧΑΝΙΚΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΕΦΑΡΜΟΓΕΣ ΤΗΣ ΓΕΩΠΛΗΡΟΦΟΡΙΚΗΣ ΣΤΟΥΣ ΦΥΣΙΚΟΥΣ ΠΟΡΟΥΣ» «Χωρικά μοντέλα πρόβλεψης αναβλάστησης
ΓΕΩΠΟΝΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙO ΑΘΗΝΩΝ ΤΜΗΜΑ ΑΞΙΟΠΟΙΗΣΗΣ ΦΥΣΙΚΩΝ ΠΟΡΩΝ & ΓΕΩΡΓΙΚΗΣ ΜΗΧΑΝΙΚΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΕΦΑΡΜΟΓΕΣ ΤΗΣ ΓΕΩΠΛΗΡΟΦΟΡΙΚΗΣ ΣΤΟΥΣ ΦΥΣΙΚΟΥΣ ΠΟΡΟΥΣ» «Χωρικά μοντέλα πρόβλεψης αναβλάστησης
ΕΡΓΑΣΤΗΡΙΟ ΧΩΡΟΤΑΞΙΚΟΥ ΣΧΕΔΙΑΣΜΟΥ Μάθημα 2Σ6 01. ΔΙΔΑΣΚΟΝΤΕΣ: Ελένη ΑΝΔΡΙΚΟΠΟΥΛΟΥ, Γρηγόρης ΚΑΥΚΑΛΑΣ Χ Ε Ι Μ Ε Ρ Ι Ν Ο Ε Ξ Α Μ Η Ν Ο
 ΕΡΓΑΣΤΗΡΙΟ ΧΩΡΟΤΑΞΙΚΟΥ ΣΧΕΔΙΑΣΜΟΥ Μάθημα 2Σ6 01 ΔΙΔΑΣΚΟΝΤΕΣ: Ελένη ΑΝΔΡΙΚΟΠΟΥΛΟΥ, Γρηγόρης ΚΑΥΚΑΛΑΣ Χ Ε Ι Μ Ε Ρ Ι Ν Ο Ε Ξ Α Μ Η Ν Ο 2 0 1 3-2014 1 Α. ΟΙΚΙΣΤΙΚΗ ΑΝΑΠΤΥΞΗ ΚΑΙ ΚΑΤΟΙΚΙΑ Δίκτυο οικισμών και
ΕΡΓΑΣΤΗΡΙΟ ΧΩΡΟΤΑΞΙΚΟΥ ΣΧΕΔΙΑΣΜΟΥ Μάθημα 2Σ6 01 ΔΙΔΑΣΚΟΝΤΕΣ: Ελένη ΑΝΔΡΙΚΟΠΟΥΛΟΥ, Γρηγόρης ΚΑΥΚΑΛΑΣ Χ Ε Ι Μ Ε Ρ Ι Ν Ο Ε Ξ Α Μ Η Ν Ο 2 0 1 3-2014 1 Α. ΟΙΚΙΣΤΙΚΗ ΑΝΑΠΤΥΞΗ ΚΑΙ ΚΑΤΟΙΚΙΑ Δίκτυο οικισμών και
Πρόλογος... xv. Κεφάλαιο 1. Εισαγωγικές Έννοιες... 1
 Πρόλογος... xv Κεφάλαιο 1. Εισαγωγικές Έννοιες... 1 1.1.Ιστορική Αναδρομή... 1 1.2.Βασικές Έννοιες... 5 1.3.Πλαίσιο ειγματοληψίας (Sampling Frame)... 9 1.4.Κατηγορίες Ιατρικών Μελετών.... 11 1.4.1.Πειραµατικές
Πρόλογος... xv Κεφάλαιο 1. Εισαγωγικές Έννοιες... 1 1.1.Ιστορική Αναδρομή... 1 1.2.Βασικές Έννοιες... 5 1.3.Πλαίσιο ειγματοληψίας (Sampling Frame)... 9 1.4.Κατηγορίες Ιατρικών Μελετών.... 11 1.4.1.Πειραµατικές
ΣΗΜΕΡΑ ΠΕΔΙΟ ΔΡΑΣΗΣ & ΠΡΟΒΛΗΜΑΤΑ
 ΕΚΤΙΜΗΣΕΙΣ ΑΚΙΝΗΤΩΝ ΣΤΗΝ ΕΛΛΑΔΑ ΣΗΜΕΡΑ ΠΕΔΙΟ ΔΡΑΣΗΣ & ΠΡΟΒΛΗΜΑΤΑ Μαριάνα Γκόγκου Αρχιτέκτονας μηχανικός Α.Π.Θ. Εκτιμητής μέλος ΕΛ.Ι.Ε. ΑΝΤΙΚΕΙΜΕΝΟ ΤΗΣ ΕΚΤΙΜΗΣΗΣ Αντικείμενο της εκτίμησης αποτελεί το περιουσιακό
ΕΚΤΙΜΗΣΕΙΣ ΑΚΙΝΗΤΩΝ ΣΤΗΝ ΕΛΛΑΔΑ ΣΗΜΕΡΑ ΠΕΔΙΟ ΔΡΑΣΗΣ & ΠΡΟΒΛΗΜΑΤΑ Μαριάνα Γκόγκου Αρχιτέκτονας μηχανικός Α.Π.Θ. Εκτιμητής μέλος ΕΛ.Ι.Ε. ΑΝΤΙΚΕΙΜΕΝΟ ΤΗΣ ΕΚΤΙΜΗΣΗΣ Αντικείμενο της εκτίμησης αποτελεί το περιουσιακό
Γεωγραφικά Πληροφοριακά Συστήµατα (Geographical Information Systems GIS)
 Γεωγραφικά Πληροφοριακά Συστήµατα (Geographical Information Systems GIS) ρ. ΧΑΛΚΙΑΣ ΧΡΙΣΤΟΣ xalkias@hua.gr Χ. Χαλκιάς - Εισαγωγή στα GIS 1 Ορισµοί ΓΠΣ Ένα γεωγραφικό πληροφοριακό σύστηµα Geographic Information
Γεωγραφικά Πληροφοριακά Συστήµατα (Geographical Information Systems GIS) ρ. ΧΑΛΚΙΑΣ ΧΡΙΣΤΟΣ xalkias@hua.gr Χ. Χαλκιάς - Εισαγωγή στα GIS 1 Ορισµοί ΓΠΣ Ένα γεωγραφικό πληροφοριακό σύστηµα Geographic Information
ΠΕΡΙΟΧΗ ΜΕΛΕΤΗΣ: ΟΙΚΟΣΜΟΣ ΕΡΓΑΤΙΚΩΝ ΚΑΤΟΙΚΙΩΝ «ΠΥΛΗΣ ΑΞΙΟΥ»
 Ομάδα Εργασίας: Κόντου Χριστίνα, Λαζαρίδης Χριστόφορος, Μπουλταδάκη Άννα, Πάσχου Μαρία, Παυλίδου Ιωάννα, Τσιολάκη Φανή ΠΕΡΙΟΧΗ ΜΕΛΕΤΗΣ: ΟΙΚΟΣΜΟΣ ΕΡΓΑΤΙΚΩΝ ΚΑΤΟΙΚΙΩΝ «ΠΥΛΗΣ ΑΞΙΟΥ» Η περιοχή μελέτης ανήκει
Ομάδα Εργασίας: Κόντου Χριστίνα, Λαζαρίδης Χριστόφορος, Μπουλταδάκη Άννα, Πάσχου Μαρία, Παυλίδου Ιωάννα, Τσιολάκη Φανή ΠΕΡΙΟΧΗ ΜΕΛΕΤΗΣ: ΟΙΚΟΣΜΟΣ ΕΡΓΑΤΙΚΩΝ ΚΑΤΟΙΚΙΩΝ «ΠΥΛΗΣ ΑΞΙΟΥ» Η περιοχή μελέτης ανήκει
Μεταπτυχιακή διατριβή. Ανδρέας Παπαευσταθίου
 Σχολή Γεωτεχνικών Επιστημών και Διαχείρισης Περιβάλλοντος Μεταπτυχιακή διατριβή Κτίρια σχεδόν μηδενικής ενεργειακής κατανάλωσης :Αξιολόγηση συστημάτων θέρμανσης -ψύξης και ΑΠΕ σε οικιστικά κτίρια στην
Σχολή Γεωτεχνικών Επιστημών και Διαχείρισης Περιβάλλοντος Μεταπτυχιακή διατριβή Κτίρια σχεδόν μηδενικής ενεργειακής κατανάλωσης :Αξιολόγηση συστημάτων θέρμανσης -ψύξης και ΑΠΕ σε οικιστικά κτίρια στην
επιπτώσεις της : συντάχθηκε πριν τους νόµους 3843/10 & 4014/11)
 εκτίµηση & πολεοδοµικόςέλεγχος ήαλλιώς η ΠΟΛΕΟ ΟΜΙΚΗ ΠΑΡΑΜΕΤΡΟΣ καιοι επιπτώσεις της στην ΠΩΛΗΣΗ ΤΩΝ ΑΚΙΝΗΤΩΝ (ΠΡΟΣΟΧΗ : συντάχθηκε πριν τους νόµους 3843/10 & 4014/11) ΠΑΠΩΤΗΣ ΑΡΗΣ Αγρ. Τοπογράφος µηχανικός
εκτίµηση & πολεοδοµικόςέλεγχος ήαλλιώς η ΠΟΛΕΟ ΟΜΙΚΗ ΠΑΡΑΜΕΤΡΟΣ καιοι επιπτώσεις της στην ΠΩΛΗΣΗ ΤΩΝ ΑΚΙΝΗΤΩΝ (ΠΡΟΣΟΧΗ : συντάχθηκε πριν τους νόµους 3843/10 & 4014/11) ΠΑΠΩΤΗΣ ΑΡΗΣ Αγρ. Τοπογράφος µηχανικός
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ. Πτυχιακή εργασία ΕΤΟΙΜΑΣΙΑ ΔΕΛΤΙΟΥ ΠΟΣΟΤΗΤΩΝ ΜΕ ΤΗ ΧΡΗΣΗ ΛΟΓΙΣΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ Πτυχιακή εργασία ΕΤΟΙΜΑΣΙΑ ΔΕΛΤΙΟΥ ΠΟΣΟΤΗΤΩΝ ΜΕ ΤΗ ΧΡΗΣΗ ΛΟΓΙΣΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ Χρύσω Κωνσταντίνου Λεμεσός 2016 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ Πτυχιακή εργασία ΕΤΟΙΜΑΣΙΑ ΔΕΛΤΙΟΥ ΠΟΣΟΤΗΤΩΝ ΜΕ ΤΗ ΧΡΗΣΗ ΛΟΓΙΣΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ Χρύσω Κωνσταντίνου Λεμεσός 2016 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
ΝΑΥΠΛΙΟ Η ΤΑΥΤΟΤΗΤΑ ΤΗΣ ΠΟΛΗΣ ΠΟΛΕΟΔΟΜΙΚΟΣ ΣΧΕΔΙΑΣΜΟΣ ΜΕΛΕΤΕΣ ΚΑΙ ΕΡΓΑ ΑΝΑΠΛΑΣΗΣ ΗΠΑΛΙΑΠΟΛΗ ΒΥΖΑΝΤΙΟ ΚΑΙ ΠΡΟΝΟΙΑ
 ΝΑΥΠΛΙΟ Η ΤΑΥΤΟΤΗΤΑ ΤΗΣ ΠΟΛΗΣ ΠΟΛΕΟΔΟΜΙΚΟΣ ΣΧΕΔΙΑΣΜΟΣ ΜΕΛΕΤΕΣ ΚΑΙ ΕΡΓΑ ΑΝΑΠΛΑΣΗΣ ΗΠΑΛΙΑΠΟΛΗ ΒΥΖΑΝΤΙΟ ΚΑΙ ΠΡΟΝΟΙΑ 1 Η ΝΕΩΤΕΡΗ ΕΠΕΚΤΑΣΗ ΤΗΣ ΠΟΛΗΣ 2 Τα εργαλεία ανάγνωσης της ταυτότητας της πόλης. Τα εργαλεία
ΝΑΥΠΛΙΟ Η ΤΑΥΤΟΤΗΤΑ ΤΗΣ ΠΟΛΗΣ ΠΟΛΕΟΔΟΜΙΚΟΣ ΣΧΕΔΙΑΣΜΟΣ ΜΕΛΕΤΕΣ ΚΑΙ ΕΡΓΑ ΑΝΑΠΛΑΣΗΣ ΗΠΑΛΙΑΠΟΛΗ ΒΥΖΑΝΤΙΟ ΚΑΙ ΠΡΟΝΟΙΑ 1 Η ΝΕΩΤΕΡΗ ΕΠΕΚΤΑΣΗ ΤΗΣ ΠΟΛΗΣ 2 Τα εργαλεία ανάγνωσης της ταυτότητας της πόλης. Τα εργαλεία
ΔΕΛΤΙΟ ΑΠΟΤΕΛΕΣΜΑΤΩΝ ΔΕΙΚΤΗ SET18: ΜΕΤΑΒΟΛΗ ΑΞΙΑΣ ΓΗΣ ΚΑΙ ΠΑΡΟΔΙΩΝ ΟΙΚΟΠΕΔΩΝ
 ΔΕΛΤΙΟ ΑΠΟΤΕΛΕΣΜΑΤΩΝ ΔΕΙΚΤΗ ΟΡΙΣΜΟΣ ΣΚΟΠΙΜΟΤΗΤΑ Ο δείκτης εκτιμά την μεταβολή των αξιών γης στην άμεση ζώνη επιρροής του άξονα και σε επιλεγμένα σημεία. Ως έτος βάσης για την εκτίμηση των μεταβολών αξιών
ΔΕΛΤΙΟ ΑΠΟΤΕΛΕΣΜΑΤΩΝ ΔΕΙΚΤΗ ΟΡΙΣΜΟΣ ΣΚΟΠΙΜΟΤΗΤΑ Ο δείκτης εκτιμά την μεταβολή των αξιών γης στην άμεση ζώνη επιρροής του άξονα και σε επιλεγμένα σημεία. Ως έτος βάσης για την εκτίμηση των μεταβολών αξιών
ΓΕΝΙΚΕΣ ΑΡΧΕΣ ΓΙΑ ΕΚΤΙΜΗΣΕΙΣ - ΓΝΩΜΑΤΕΥΣΕΙΣ - ΚΑΤΑΝΟΜΗ ΤΗΣ ΥΛΗΣ
 ΓΕΝΙΚΕΣ ΑΡΧΕΣ ΓΙΑ ΕΚΤΙΜΗΣΕΙΣ - ΓΝΩΜΑΤΕΥΣΕΙΣ - ΚΑΤΑΝΟΜΗ ΤΗΣ ΥΛΗΣ ΟΙ κυριότερες από τις αιτίες για τις οποίες πραγματοποιούνται οι εκτιμήσεις η οι γνωματεύσεις από έναν κατάλληλο εκτιμητικό φορέα η έναν
ΓΕΝΙΚΕΣ ΑΡΧΕΣ ΓΙΑ ΕΚΤΙΜΗΣΕΙΣ - ΓΝΩΜΑΤΕΥΣΕΙΣ - ΚΑΤΑΝΟΜΗ ΤΗΣ ΥΛΗΣ ΟΙ κυριότερες από τις αιτίες για τις οποίες πραγματοποιούνται οι εκτιμήσεις η οι γνωματεύσεις από έναν κατάλληλο εκτιμητικό φορέα η έναν
ΕΚΤΙΜΗΣΕΙΣ ΑΚΙΝΗΤΩΝ ΣΤΗΝ ΕΛΛΑΔΑ ΣΗΜΕΡΑ ΠΕΔΙΟ ΔΡΑΣΗΣ & ΠΡΟΒΛΗΜΑΤΑ. Μαριάνα Γκόγκου Αρχιτέκτονας μηχανικός Α.Π.Θ. REV
 ΕΚΤΙΜΗΣΕΙΣ ΑΚΙΝΗΤΩΝ ΣΤΗΝ ΕΛΛΑΔΑ ΣΗΜΕΡΑ ΠΕΔΙΟ ΔΡΑΣΗΣ & ΠΡΟΒΛΗΜΑΤΑ Μαριάνα Γκόγκου Αρχιτέκτονας μηχανικός Α.Π.Θ. REV Εκτιμητής μέλος ΕΛ.Ι.Ε. - Σ.ΕΚ.Ε. Μ.Π.Ε. Υπ. Οικονομικών ΑΝΤΙΚΕΙΜΕΝΟ ΤΗΣ ΕΚΤΙΜΗΣΗΣ Αντικείμενο
ΕΚΤΙΜΗΣΕΙΣ ΑΚΙΝΗΤΩΝ ΣΤΗΝ ΕΛΛΑΔΑ ΣΗΜΕΡΑ ΠΕΔΙΟ ΔΡΑΣΗΣ & ΠΡΟΒΛΗΜΑΤΑ Μαριάνα Γκόγκου Αρχιτέκτονας μηχανικός Α.Π.Θ. REV Εκτιμητής μέλος ΕΛ.Ι.Ε. - Σ.ΕΚ.Ε. Μ.Π.Ε. Υπ. Οικονομικών ΑΝΤΙΚΕΙΜΕΝΟ ΤΗΣ ΕΚΤΙΜΗΣΗΣ Αντικείμενο
ΤΟ ΜΟΝΤΕΛΟ Οι Υποθέσεις Η Απλή Περίπτωση για λi = μi 25 = Η Γενική Περίπτωση για λi μi..35
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΤΟΜΕΑΣ ΣΤΑΤΙΣΤΙΚΗΣ ΚΑΙ ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΑΝΑΛΥΣΗ ΤΩΝ ΣΥΣΧΕΤΙΣΕΩΝ ΧΡΕΟΚΟΠΙΑΣ ΚΑΙ ΤΩΝ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΤΟΜΕΑΣ ΣΤΑΤΙΣΤΙΚΗΣ ΚΑΙ ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΑΝΑΛΥΣΗ ΤΩΝ ΣΥΣΧΕΤΙΣΕΩΝ ΧΡΕΟΚΟΠΙΑΣ ΚΑΙ ΤΩΝ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πτυχιακή Διατριβή Η ΣΥΝΕΙΣΦΟΡΑ ΤΟΥ CΗ 4 ΣΤΟ ΦΑΙΝΟΜΕΝΟ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πτυχιακή Διατριβή Η ΣΥΝΕΙΣΦΟΡΑ ΤΟΥ CΗ 4 ΣΤΟ ΦΑΙΝΟΜΕΝΟ
Ανάλυση και Σχεδιασμός Μεταφορών Ι Δειγματοληψία - Μέθοδοι συλλογής στοιχείων
 Δειγματοληψία - Μέθοδοι συλλογής στοιχείων Παναγιώτης Παπαντωνίου Δρ. Πολιτικός Μηχανικός, Συγκοινωνιολόγος ppapant@upatras.gr Πάτρα, 2017 Στόχοι Βασικές έννοιες στατιστικής Μέθοδοι συλλογής στοιχείων
Δειγματοληψία - Μέθοδοι συλλογής στοιχείων Παναγιώτης Παπαντωνίου Δρ. Πολιτικός Μηχανικός, Συγκοινωνιολόγος ppapant@upatras.gr Πάτρα, 2017 Στόχοι Βασικές έννοιες στατιστικής Μέθοδοι συλλογής στοιχείων
Εργαστήριο Χωροταξικού Σχεδιασμού. 6 η Διάλεξη Β. Διάγνωση της υπάρχουσας κατάστασης Οικιστική ανάπτυξη και Κατοικία Εισήγηση: Ελένη Ανδρικοπούλου
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Διδακτική ομάδα: Ελένη Ανδρικοπούλου, Γρηγόρης Καυκαλάς 6 η Διάλεξη Β. Διάγνωση της υπάρχουσας κατάστασης Οικιστική ανάπτυξη και Κατοικία
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Διδακτική ομάδα: Ελένη Ανδρικοπούλου, Γρηγόρης Καυκαλάς 6 η Διάλεξη Β. Διάγνωση της υπάρχουσας κατάστασης Οικιστική ανάπτυξη και Κατοικία
ΕΤΑΙΡΙΚΗ ΚΟΙΝΩΝΙΚΗ ΕΥΘΥΝΗ ΣΤΗΝ ΝΑΥΤΙΛΙΑΚΗ ΒΙΟΜΗΧΑΜΙΑ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ Μεταπτυχιακή διατριβή ΕΤΑΙΡΙΚΗ ΚΟΙΝΩΝΙΚΗ ΕΥΘΥΝΗ ΣΤΗΝ ΝΑΥΤΙΛΙΑΚΗ ΒΙΟΜΗΧΑΜΙΑ Ανδρούλα Γιαπάνη Λεμεσός, Φεβρουάριος 2018 0 i ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ Μεταπτυχιακή διατριβή ΕΤΑΙΡΙΚΗ ΚΟΙΝΩΝΙΚΗ ΕΥΘΥΝΗ ΣΤΗΝ ΝΑΥΤΙΛΙΑΚΗ ΒΙΟΜΗΧΑΜΙΑ Ανδρούλα Γιαπάνη Λεμεσός, Φεβρουάριος 2018 0 i ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
Εισόδημα Κατανάλωση 1500 500 1600 600 1300 450 1100 400 600 250 700 275 900 300 800 352 850 400 1100 500
 Εισόδημα Κατανάλωση 1500 500 1600 600 1300 450 1100 400 600 250 700 275 900 300 800 352 850 400 1100 500 Πληθυσμός Δείγμα Δείγμα Δείγμα Ο ρόλος της Οικονομετρίας Οικονομική Θεωρία Διατύπωση της
Εισόδημα Κατανάλωση 1500 500 1600 600 1300 450 1100 400 600 250 700 275 900 300 800 352 850 400 1100 500 Πληθυσμός Δείγμα Δείγμα Δείγμα Ο ρόλος της Οικονομετρίας Οικονομική Θεωρία Διατύπωση της
Ο ΔΗΜΟΣ ΝΟΤΙΑΣ ΚΥΝΟΥΡΙΑΣ ΣΤΟ ΔΡΟΜΟ ΓΙΑ ΤΟ ΔΗΜΟ ΤΟΥ ΜΕΛΛΟΝΤΟΣ
 ΣΥΝΕΔΡΙΟ ΟΛΟΚΛΗΡΩΜΕΝΗΣ ΤΟΠΙΚΗΣ ΑΝΑΠΤΥΞΗΣ Ο ΔΗΜΟΣ ΝΟΤΙΑΣ ΚΥΝΟΥΡΙΑΣ ΣΤΟ ΔΡΟΜΟ ΓΙΑ ΤΟ ΔΗΜΟ ΤΟΥ ΜΕΛΛΟΝΤΟΣ ΕΛΕΝΗ ΜΑΙΣΤΡΟΥ 1 Η ΠΡΟΣΤΑΣΙΑ ΚΑΙ ΑΝΑΔΕΙΞΗ ΤΗΣ ΠΟΛΙΤΙΣΤΙΚΗΣ ΚΛΗΡΟΝΟΜΙΑΣ ΩΣ ΕΡΓΑΛΕΙΟ ΒΙΩΣΙΜΗΣ ΑΝΑΠΤΥΞΗΣ
ΣΥΝΕΔΡΙΟ ΟΛΟΚΛΗΡΩΜΕΝΗΣ ΤΟΠΙΚΗΣ ΑΝΑΠΤΥΞΗΣ Ο ΔΗΜΟΣ ΝΟΤΙΑΣ ΚΥΝΟΥΡΙΑΣ ΣΤΟ ΔΡΟΜΟ ΓΙΑ ΤΟ ΔΗΜΟ ΤΟΥ ΜΕΛΛΟΝΤΟΣ ΕΛΕΝΗ ΜΑΙΣΤΡΟΥ 1 Η ΠΡΟΣΤΑΣΙΑ ΚΑΙ ΑΝΑΔΕΙΞΗ ΤΗΣ ΠΟΛΙΤΙΣΤΙΚΗΣ ΚΛΗΡΟΝΟΜΙΑΣ ΩΣ ΕΡΓΑΛΕΙΟ ΒΙΩΣΙΜΗΣ ΑΝΑΠΤΥΞΗΣ
Αδραμυττίου 45, Νέα Σμύρνη Αττική, 11145
 Αδραμυττίου 45, Αττική, 11145 Αγοραία Αξία Πώλησης 196,000 Εύρος εκτιμώμενης αξίας από 176,000 έως 215,000 Μέθοδος Εκτίμησης: Ο υπολογισμός της εμπορικής αξίας του ακινήτου έχει γίνει με τη συγκριτική
Αδραμυττίου 45, Αττική, 11145 Αγοραία Αξία Πώλησης 196,000 Εύρος εκτιμώμενης αξίας από 176,000 έως 215,000 Μέθοδος Εκτίμησης: Ο υπολογισμός της εμπορικής αξίας του ακινήτου έχει γίνει με τη συγκριτική
ΔΕΛΤΙΟ ΑΠΟΤΕΛΕΣΜΑΤΩΝ ΔΕΙΚΤΗ SET18: ΜΕΤΑΒΟΛΗ ΑΞΙΑΣ ΓΗΣ ΚΑΙ ΠΑΡΟΔΙΩΝ ΟΙΚΟΠΕΔΩΝ
 ΔΕΛΤΙΟ ΑΠΟΤΕΛΕΣΜΑΤΩΝ ΔΕΙΚΤΗ ΟΡΙΣΜΟΣ ΣΚΟΠΙΜΟΤΗΤΑ Ο δείκτης εκτιμά την μεταβολή των αξιών γης στην άμεση ζώνη επιρροής του άξονα και σε επιλεγμένα σημεία. Ως έτος βάσης για την εκτίμηση των μεταβολών αξιών
ΔΕΛΤΙΟ ΑΠΟΤΕΛΕΣΜΑΤΩΝ ΔΕΙΚΤΗ ΟΡΙΣΜΟΣ ΣΚΟΠΙΜΟΤΗΤΑ Ο δείκτης εκτιμά την μεταβολή των αξιών γης στην άμεση ζώνη επιρροής του άξονα και σε επιλεγμένα σημεία. Ως έτος βάσης για την εκτίμηση των μεταβολών αξιών
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ Μ.Ν. Ντυκέν, Πανεπιστήμιο Θεσσαλίας Τ.Μ.Χ.Π.Π.Α. Ε. Αναστασίου, Πανεπιστήμιο Θεσσαλίας Τ.Μ.Χ.Π.Π.Α. ΔΙΑΛΕΞΗ 07 & ΔΙΑΛΕΞΗ 08 ΣΗΜΠΕΡΑΣΜΑΤΙΚΗ ΣΤΑΤΙΣΤΙΚΗ Βόλος, 016-017 ΕΙΣΑΓΩΓΗ ΣΤΗΝ
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ Μ.Ν. Ντυκέν, Πανεπιστήμιο Θεσσαλίας Τ.Μ.Χ.Π.Π.Α. Ε. Αναστασίου, Πανεπιστήμιο Θεσσαλίας Τ.Μ.Χ.Π.Π.Α. ΔΙΑΛΕΞΗ 07 & ΔΙΑΛΕΞΗ 08 ΣΗΜΠΕΡΑΣΜΑΤΙΚΗ ΣΤΑΤΙΣΤΙΚΗ Βόλος, 016-017 ΕΙΣΑΓΩΓΗ ΣΤΗΝ
ΠΛΗΘΥΣΜΙΑΚΟΣ ΘΕΜΑΤΙΚΟΣ ΑΤΛΑΝΤΑΣ ΤΗ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΜΕ ΒΑΣΗ ΤΟ ΝΕΟ ΣΧ ΔΙΟΙΚΗΤΙΚΗΣ ΔΙΑΙΡΕΣΗΣ ΚΑΛΛΙΚΡΑΤΗΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΕΡΡΩΝ ΤΜΗΜΑ ΓΕΩΠΛΗΡΟΦΟΡΙΚΗΣ & ΤΟΠΟΓΡΑΦΙΑΣ Υπεύθυνη Δήλωση Η παρακάτω υπογράφουσα δηλώνω ότι είμαι συγγραφέα τη παρούσα πτυχιακή εργασία. Κάθε τη, είναι πλήρω αναγνωρισμένη
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΕΡΡΩΝ ΤΜΗΜΑ ΓΕΩΠΛΗΡΟΦΟΡΙΚΗΣ & ΤΟΠΟΓΡΑΦΙΑΣ Υπεύθυνη Δήλωση Η παρακάτω υπογράφουσα δηλώνω ότι είμαι συγγραφέα τη παρούσα πτυχιακή εργασία. Κάθε τη, είναι πλήρω αναγνωρισμένη
Πτυχιακή διατριβή. Η επίδραση της τασιενεργής ουσίας Ακεταλδεΰδης στη δημιουργία πυρήνων συμπύκνωσης νεφών (CCN) στην ατμόσφαιρα
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πτυχιακή διατριβή Η επίδραση της τασιενεργής ουσίας Ακεταλδεΰδης στη δημιουργία πυρήνων συμπύκνωσης νεφών (CCN)
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πτυχιακή διατριβή Η επίδραση της τασιενεργής ουσίας Ακεταλδεΰδης στη δημιουργία πυρήνων συμπύκνωσης νεφών (CCN)
ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ ΠΡΩΤΟ
 ΠΕΡΙΕΧΟΜΕΝΑ Εισαγωγή 1. Γενικά... 25 2. Έννοια και Είδη Μεταβλητών... 26 3. Κλίμακες Μέτρησης Μεταβλητών... 29 3.1 Ονομαστική κλίμακα... 30 3.2. Τακτική κλίμακα... 31 3.3 Κλίμακα ισοδιαστημάτων... 34 3.4
ΠΕΡΙΕΧΟΜΕΝΑ Εισαγωγή 1. Γενικά... 25 2. Έννοια και Είδη Μεταβλητών... 26 3. Κλίμακες Μέτρησης Μεταβλητών... 29 3.1 Ονομαστική κλίμακα... 30 3.2. Τακτική κλίμακα... 31 3.3 Κλίμακα ισοδιαστημάτων... 34 3.4
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ. Πτυχιακή εργασία ΑΓΧΟΣ ΚΑΙ ΚΑΤΑΘΛΙΨΗ ΣΕ ΓΥΝΑΙΚΕΣ ΜΕ ΚΑΡΚΙΝΟΥ ΤΟΥ ΜΑΣΤΟΥ ΜΕΤΑ ΑΠΟ ΜΑΣΤΕΚΤΟΜΗ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ Πτυχιακή εργασία ΑΓΧΟΣ ΚΑΙ ΚΑΤΑΘΛΙΨΗ ΣΕ ΓΥΝΑΙΚΕΣ ΜΕ ΚΑΡΚΙΝΟΥ ΤΟΥ ΜΑΣΤΟΥ ΜΕΤΑ ΑΠΟ ΜΑΣΤΕΚΤΟΜΗ ΧΡΥΣΟΒΑΛΑΝΤΗΣ ΒΑΣΙΛΕΙΟΥ ΛΕΜΕΣΟΣ 2014 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ Πτυχιακή εργασία ΑΓΧΟΣ ΚΑΙ ΚΑΤΑΘΛΙΨΗ ΣΕ ΓΥΝΑΙΚΕΣ ΜΕ ΚΑΡΚΙΝΟΥ ΤΟΥ ΜΑΣΤΟΥ ΜΕΤΑ ΑΠΟ ΜΑΣΤΕΚΤΟΜΗ ΧΡΥΣΟΒΑΛΑΝΤΗΣ ΒΑΣΙΛΕΙΟΥ ΛΕΜΕΣΟΣ 2014 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
Παρατηρητήριο ΤΟΜΕΑΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΚΑΙ ΠΑΡΑΚΟΛΟΥΘΗΣΗΣ ΕΡΓΩΝ & ΧΡΗΜΑΤΟΔΟΤΗΣΕΩΝ ΕΓΝΑΤΙΑ ΟΔΟΣ Α.Ε ΕΝΗΜΕΡΩΤΙΚΟ ΔΕΛΤΙΟ
 Παρατηρητήριο ΤΟΜΕΑΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΚΑΙ ΠΑΡΑΚΟΛΟΥΘΗΣΗΣ ΕΡΓΩΝ & ΧΡΗΜΑΤΟΔΟΤΗΣΕΩΝ ΕΓΝΑΤΙΑ ΟΔΟΣ Α.Ε ΕΝΗΜΕΡΩΤΙΚΟ ΔΕΛΤΙΟ ΠΙΛΟΤΙΚΗ ΜΕΛΕΤΗ ΜΕΤΑΒΟΛΩΝ ΧΡΗΣΕΩΝ ΚΑΙ ΑΞΙΩΝ ΓΗΣ ΣΕ ΕΠΙΛΕΓΜΕΝΕΣ ΑΣΤΙΚΕΣ ΠΕΡΙΟΧΕΣ ΤΗΣ ΑΜΕΣΗΣ
Παρατηρητήριο ΤΟΜΕΑΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΚΑΙ ΠΑΡΑΚΟΛΟΥΘΗΣΗΣ ΕΡΓΩΝ & ΧΡΗΜΑΤΟΔΟΤΗΣΕΩΝ ΕΓΝΑΤΙΑ ΟΔΟΣ Α.Ε ΕΝΗΜΕΡΩΤΙΚΟ ΔΕΛΤΙΟ ΠΙΛΟΤΙΚΗ ΜΕΛΕΤΗ ΜΕΤΑΒΟΛΩΝ ΧΡΗΣΕΩΝ ΚΑΙ ΑΞΙΩΝ ΓΗΣ ΣΕ ΕΠΙΛΕΓΜΕΝΕΣ ΑΣΤΙΚΕΣ ΠΕΡΙΟΧΕΣ ΤΗΣ ΑΜΕΣΗΣ
þÿ P u b l i c M a n a g e m e n t ÃÄ ½ ¼ÌÃ
 Neapolis University HEPHAESTUS Repository School of Economic Sciences and Business http://hephaestus.nup.ac.cy Master Degree Thesis 2017 þÿ ±À Ç Ä Â µæ±á¼ ³ Â Ä þÿ P u b l i c M a n a g e m e n t ÃÄ ½
Neapolis University HEPHAESTUS Repository School of Economic Sciences and Business http://hephaestus.nup.ac.cy Master Degree Thesis 2017 þÿ ±À Ç Ä Â µæ±á¼ ³ Â Ä þÿ P u b l i c M a n a g e m e n t ÃÄ ½
Γεώργιος ΚΑΡΙΩΤΗΣ, Ελευθέριος ΠΑΝΑΓΙΩΤΟΠΟΥΛΟΣ. Νικόλαος ΔΕΜΙΡΤΖΗΟΓΛΟΥ, Δήμητρα ΤΟΠΑΛΙΔΟΥ. Αγρονόμοι Τοπογράφοι Μηχανικοί Καθηγητές Εφαρμογών
 Αυτοματοποίηση και Τοπική Αυτοδιοίκηση. Η Χωρική πληροφορία και το διοικητικό πλαίσιο, Σχεδιασμός και Ανάπτυξη, μια νέα διδακτική ενότητα. Μελέτη περίπτωσης: Σχεδιασμός λαϊκής αγοράς. Γεώργιος ΚΑΡΙΩΤΗΣ,
Αυτοματοποίηση και Τοπική Αυτοδιοίκηση. Η Χωρική πληροφορία και το διοικητικό πλαίσιο, Σχεδιασμός και Ανάπτυξη, μια νέα διδακτική ενότητα. Μελέτη περίπτωσης: Σχεδιασμός λαϊκής αγοράς. Γεώργιος ΚΑΡΙΩΤΗΣ,
ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 7. ΚΕΦΑΛΑΙΟ 1: Εισαγωγικές Έννοιες 13
 ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 7 ΚΕΦΑΛΑΙΟ 1: Εισαγωγικές Έννοιες 13 1.1. Εισαγωγή 13 1.2. Μοντέλο ή Υπόδειγμα 13 1.3. Η Ανάλυση Παλινδρόμησης 16 1.4. Το γραμμικό μοντέλο Παλινδρόμησης 17 1.5. Πρακτική χρησιμότητα
ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 7 ΚΕΦΑΛΑΙΟ 1: Εισαγωγικές Έννοιες 13 1.1. Εισαγωγή 13 1.2. Μοντέλο ή Υπόδειγμα 13 1.3. Η Ανάλυση Παλινδρόμησης 16 1.4. Το γραμμικό μοντέλο Παλινδρόμησης 17 1.5. Πρακτική χρησιμότητα
ΜΗΤΡΙΚΟΣ ΘΗΛΑΣΜΟΣ ΚΑΙ ΓΝΩΣΤΙΚΗ ΑΝΑΠΤΥΞΗ ΜΕΧΡΙ ΚΑΙ 10 ΧΡΟΝΩΝ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ ΜΗΤΡΙΚΟΣ ΘΗΛΑΣΜΟΣ ΚΑΙ ΓΝΩΣΤΙΚΗ ΑΝΑΠΤΥΞΗ ΜΕΧΡΙ ΚΑΙ 10 ΧΡΟΝΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ Ονοματεπώνυμο Κεντούλλα Πέτρου Αριθμός Φοιτητικής Ταυτότητας 2008761539 Κύπρος
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΝΟΣΗΛΕΥΤΙΚΗΣ ΜΗΤΡΙΚΟΣ ΘΗΛΑΣΜΟΣ ΚΑΙ ΓΝΩΣΤΙΚΗ ΑΝΑΠΤΥΞΗ ΜΕΧΡΙ ΚΑΙ 10 ΧΡΟΝΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ Ονοματεπώνυμο Κεντούλλα Πέτρου Αριθμός Φοιτητικής Ταυτότητας 2008761539 Κύπρος
ΓΕΩΓΡΑΦΙΚΑ ΣΥΣΤΗΜΑΤΑ ΠΛΗΡΟΦΟΡΙΩΝ ΚΑΙ ΧΑΡΤΟΓΡΑΦΗΣΗ ΦΥΣΙΚΩΝ ΠΟΡΩΝ
 ΓΕΩΓΡΑΦΙΚΑ ΣΥΣΤΗΜΑΤΑ ΠΛΗΡΟΦΟΡΙΩΝ ΚΑΙ ΧΑΡΤΟΓΡΑΦΗΣΗ ΦΥΣΙΚΩΝ ΠΟΡΩΝ ΓΕΩΓΡΑΦΙΚΑ ΣΥΣΤΗΜΑΤΑ ΠΛΗΡΟΦΟΡΙΩΝ Τα Γεωγραφικά Συστήματα Πληροφοριών (G.I.S.), επιτυγχάνουν με τη βοήθεια υπολογιστών την ανάπτυξη και τον
ΓΕΩΓΡΑΦΙΚΑ ΣΥΣΤΗΜΑΤΑ ΠΛΗΡΟΦΟΡΙΩΝ ΚΑΙ ΧΑΡΤΟΓΡΑΦΗΣΗ ΦΥΣΙΚΩΝ ΠΟΡΩΝ ΓΕΩΓΡΑΦΙΚΑ ΣΥΣΤΗΜΑΤΑ ΠΛΗΡΟΦΟΡΙΩΝ Τα Γεωγραφικά Συστήματα Πληροφοριών (G.I.S.), επιτυγχάνουν με τη βοήθεια υπολογιστών την ανάπτυξη και τον
ΖΩΝΟΠΟΙΗΣΗ ΤΗΣ ΚΑΤΟΛΙΣΘΗΤΙΚΗΣ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑΣ ΣΤΟ ΟΡΟΣ ΠΗΛΙΟ ΜΕ ΤΗ ΣΥΜΒΟΛΗ ΔΕΔΟΜΕΝΩΝ ΣΥΜΒΟΛΟΜΕΤΡΙΑΣ ΜΟΝΙΜΩΝ ΣΚΕΔΑΣΤΩΝ
 EΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΕΙΟ Τμήμα Μηχανικών Μεταλλείων-Μεταλλουργών ΖΩΝΟΠΟΙΗΣΗ ΤΗΣ ΚΑΤΟΛΙΣΘΗΤΙΚΗΣ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑΣ ΜΕ ΤΗ ΣΥΜΒΟΛΗ ΔΕΔΟΜΕΝΩΝ ΣΥΜΒΟΛΟΜΕΤΡΙΑΣ ΜΟΝΙΜΩΝ ΣΚΕΔΑΣΤΩΝ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Κιτσάκη Μαρίνα
EΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΕΙΟ Τμήμα Μηχανικών Μεταλλείων-Μεταλλουργών ΖΩΝΟΠΟΙΗΣΗ ΤΗΣ ΚΑΤΟΛΙΣΘΗΤΙΚΗΣ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑΣ ΜΕ ΤΗ ΣΥΜΒΟΛΗ ΔΕΔΟΜΕΝΩΝ ΣΥΜΒΟΛΟΜΕΤΡΙΑΣ ΜΟΝΙΜΩΝ ΣΚΕΔΑΣΤΩΝ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Κιτσάκη Μαρίνα
Η Επίδραση των Events στην Απόδοση των Μετοχών
 Χρηματοοικονομικά και Διοίκηση Μεταπτυχιακή διατριβή Η Επίδραση των Events στην Απόδοση των Μετοχών Άντρεα Φωτίου Λεμεσός, Μάιος 2018 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΔΙΟΙΚΗΣΗΣ
Χρηματοοικονομικά και Διοίκηση Μεταπτυχιακή διατριβή Η Επίδραση των Events στην Απόδοση των Μετοχών Άντρεα Φωτίου Λεμεσός, Μάιος 2018 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΔΙΟΙΚΗΣΗΣ
ΓΕΩΓΡΑΦΙΚΕΣ ΔΥΝΑΜΙΚΕΣ ΚΑΙ ΣΥΓΧΡΟΝΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΤΟΥ ΕΛΛΗΝΙΚΟΥ ΧΩΡΟΥ
 ΕΜΠ ΣΧΟΛΗ ΑΡΧΙΤΕΚΤΟΝΩΝ ΜΗΧΑΝΙΚΩΝ Πρόγραμμα Διατμηματικών Μεταπτυχιακών Σπουδών Εξειδίκευσης ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΣΧΕΔΙΑΣΜΟΣ ΤΟΥ ΧΩΡΟΥ ΓΕΩΓΡΑΦΙΚΕΣ ΔΥΝΑΜΙΚΕΣ ΚΑΙ ΣΥΓΧΡΟΝΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΤΟΥ ΕΛΛΗΝΙΚΟΥ ΧΩΡΟΥ Σοφία
ΕΜΠ ΣΧΟΛΗ ΑΡΧΙΤΕΚΤΟΝΩΝ ΜΗΧΑΝΙΚΩΝ Πρόγραμμα Διατμηματικών Μεταπτυχιακών Σπουδών Εξειδίκευσης ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΣΧΕΔΙΑΣΜΟΣ ΤΟΥ ΧΩΡΟΥ ΓΕΩΓΡΑΦΙΚΕΣ ΔΥΝΑΜΙΚΕΣ ΚΑΙ ΣΥΓΧΡΟΝΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΤΟΥ ΕΛΛΗΝΙΚΟΥ ΧΩΡΟΥ Σοφία
ΑΣΤΙΚΕΣ ΑΝΑΠΛΑΣΕΙΣ ΚΑΙ ΠΡΑΣΙΝΟΣ ΣΧΕΔΙΑΣΜΟΣ
 ΠΡΟΓΡΑΜΜΑ ΔΙΑ ΒΙΟΥ ΜΑΘΗΣΗΣ: ΑΣΤΙΚΕΣ ΑΝΑΠΛΑΣΕΙΣ ΚΑΙ ΠΡΑΣΙΝΟΣ ΣΧΕΔΙΑΣΜΟΣ ΠΡΑΣΙΝΟΣ ΣΧΕΔΙΑΣΜΟΣ ΚΑΙ ΑΝΑΣΧΕΔΙΑΣΜΟΣ ΑΣΤΙΚΩΝ ΠΕΡΙΟΧΩΝ ΜΑΘΗΜΑ VI: ΠΟΛΗ ΕΝΕΡΓΕΙΑ ΑΠΟΡΡΙΜΑΤΑ ΔΙΔ. Β. ΤΡΟΒΑ αν. καθ. Τμ. Αρχιτεκτόνων,
ΠΡΟΓΡΑΜΜΑ ΔΙΑ ΒΙΟΥ ΜΑΘΗΣΗΣ: ΑΣΤΙΚΕΣ ΑΝΑΠΛΑΣΕΙΣ ΚΑΙ ΠΡΑΣΙΝΟΣ ΣΧΕΔΙΑΣΜΟΣ ΠΡΑΣΙΝΟΣ ΣΧΕΔΙΑΣΜΟΣ ΚΑΙ ΑΝΑΣΧΕΔΙΑΣΜΟΣ ΑΣΤΙΚΩΝ ΠΕΡΙΟΧΩΝ ΜΑΘΗΜΑ VI: ΠΟΛΗ ΕΝΕΡΓΕΙΑ ΑΠΟΡΡΙΜΑΤΑ ΔΙΔ. Β. ΤΡΟΒΑ αν. καθ. Τμ. Αρχιτεκτόνων,
Χωρική Ανάλυση Συμπεριφοράς Ασφάλειας Οδηγών με Δεδομένα από Έξυπνα Κινητά Τηλέφωνα
 Χωρική Ανάλυση Συμπεριφοράς Ασφάλειας Οδηγών με Δεδομένα από Έξυπνα Κινητά Τηλέφωνα Ηλίας Αλέξανδρος Παρμακσίζογλου Επιβλέπων: Γιώργος Γιαννής, Καθηγητής ΕΜΠ Αθήνα, Μάρτιος 2018 Εθνικό Μετσόβιο Πολυτεχνείο
Χωρική Ανάλυση Συμπεριφοράς Ασφάλειας Οδηγών με Δεδομένα από Έξυπνα Κινητά Τηλέφωνα Ηλίας Αλέξανδρος Παρμακσίζογλου Επιβλέπων: Γιώργος Γιαννής, Καθηγητής ΕΜΠ Αθήνα, Μάρτιος 2018 Εθνικό Μετσόβιο Πολυτεχνείο
SOURCE DF SUM OF SQUARES MEAN SQUARE F VALUE PR F MODEL (a) 2.882 E04 (e) (g) (h) ERROR (b) (d) (f) TOTAL (c) 4.063 E04 R SQUARE (i) PARAMETER
 ΑΣΚΗΣΕΙΣ. Θεωρήστε το παράδειγμα που αναφέρεται στη συσχέτιση του βαθμού ικανοποίησης των εργαζομένων σε ένα εργαστήριο σε σχέση με τις οκτώ μεταβλητές που ορίστηκαν εκεί. (Χ =ηλικία, Χ =φύλο, Χ =εβδομαδιαίος
ΑΣΚΗΣΕΙΣ. Θεωρήστε το παράδειγμα που αναφέρεται στη συσχέτιση του βαθμού ικανοποίησης των εργαζομένων σε ένα εργαστήριο σε σχέση με τις οκτώ μεταβλητές που ορίστηκαν εκεί. (Χ =ηλικία, Χ =φύλο, Χ =εβδομαδιαίος
ΜΕΘΟΔΟΣ (RESIDUAL METHOD)
 Σεμινάριο Εκτιμήσεων Ακίνητης Περιουσίας, ΣΠΜΕ, 2018 ΥΠΟΛΕΙΜΜΑΤΙΚΗ ΜΕΘΟΔΟΣ (RESIDUAL METHOD) Θ Ε Ω Ρ Ι Α Κ Α Ι Α Σ Κ Η Σ Ε Ι Σ Υπολειμματική μέθοδος Η υπολειμματική μέθοδος βασίζεται στη βέλτιστη αξιοποίηση
Σεμινάριο Εκτιμήσεων Ακίνητης Περιουσίας, ΣΠΜΕ, 2018 ΥΠΟΛΕΙΜΜΑΤΙΚΗ ΜΕΘΟΔΟΣ (RESIDUAL METHOD) Θ Ε Ω Ρ Ι Α Κ Α Ι Α Σ Κ Η Σ Ε Ι Σ Υπολειμματική μέθοδος Η υπολειμματική μέθοδος βασίζεται στη βέλτιστη αξιοποίηση
Τ.Ε.Ι. ΑΝΑΤΟΛΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΚΑΙ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ
 Τ.Ε.Ι. ΑΝΑΤΟΛΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΚΑΙ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΕΙΣΗΓΗΤΗΣ: Δρ. Ιωάννης Σ. Τουρτούρας Μηχανικός Παραγωγής & Διοίκησης Δ.Π.Θ. Χρηματοδότηση Το παρόν εκπαιδευτικό
Τ.Ε.Ι. ΑΝΑΤΟΛΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΚΑΙ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΕΙΣΗΓΗΤΗΣ: Δρ. Ιωάννης Σ. Τουρτούρας Μηχανικός Παραγωγής & Διοίκησης Δ.Π.Θ. Χρηματοδότηση Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΕΚΤΙΜΗΤΙΚΗΣ
 ΕΛΛΗΝΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΕΚΤΙΜΗΤΙΚΗΣ 2000 2017 Διημερίδα: «Ο ΑΤΜ στην Εκτίμηση, Αξιοποίηση και Διαχείριση της Ακίνητης Περιουσίας» ΠΑΝΕΛΛΗΝΙΟΣ ΣΥΛΛΟΓΟΣ ΔΙΠΛΩΜΑΤΟΥΧΩΝ ΑΓΡΟΝΟΜΩΝ & ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ 23 & 24
ΕΛΛΗΝΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΕΚΤΙΜΗΤΙΚΗΣ 2000 2017 Διημερίδα: «Ο ΑΤΜ στην Εκτίμηση, Αξιοποίηση και Διαχείριση της Ακίνητης Περιουσίας» ΠΑΝΕΛΛΗΝΙΟΣ ΣΥΛΛΟΓΟΣ ΔΙΠΛΩΜΑΤΟΥΧΩΝ ΑΓΡΟΝΟΜΩΝ & ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ 23 & 24
ΠΡΟΤΑΣΗ ΑΝΑΠΤΥΞΗΣ OIKOΔΟΜΙΚΟΥ ΤΕΤΡΑΓΩΝΟΥ ΣΤΗΝ ΚΑΛΑΜΑΤΑ ΟΔΟΣ ΛΑΚΩΝΙΚΗΣ & ΒΑΣ. ΓΕΩΡΓΙΟΥ
 ΠΡΟΤΑΣΗ ΑΝΑΠΤΥΞΗΣ OIKOΔΟΜΙΚΟΥ ΤΕΤΡΑΓΩΝΟΥ ΣΤΗΝ ΚΑΛΑΜΑΤΑ ΟΔΟΣ ΛΑΚΩΝΙΚΗΣ & ΒΑΣ. ΓΕΩΡΓΙΟΥ ΜΕ ΛΙΓΑ ΛΟΓΙΑ Η επιχειρηματική δραστηριότητα των εταιρειών συμφερόντων Π.ΤΣΙΓΑΡΙΔΗ ξεκίνησε το 1975 με αιχμή τον κατασκευαστικό
ΠΡΟΤΑΣΗ ΑΝΑΠΤΥΞΗΣ OIKOΔΟΜΙΚΟΥ ΤΕΤΡΑΓΩΝΟΥ ΣΤΗΝ ΚΑΛΑΜΑΤΑ ΟΔΟΣ ΛΑΚΩΝΙΚΗΣ & ΒΑΣ. ΓΕΩΡΓΙΟΥ ΜΕ ΛΙΓΑ ΛΟΓΙΑ Η επιχειρηματική δραστηριότητα των εταιρειών συμφερόντων Π.ΤΣΙΓΑΡΙΔΗ ξεκίνησε το 1975 με αιχμή τον κατασκευαστικό
Η πόλη και οι λειτουργίες της.
 Η πόλη και οι λειτουργίες της. Η έννοια του οικισµού. Τον αστικό χώρο χαρακτηρίζουν τα εξής δύο κύρια στοιχεία: 1. Το «κέλυφος», το οποίο αποτελείται από οικοδομικούς όγκους και τεχνικό εξοπλισμό συσσωρευμένους
Η πόλη και οι λειτουργίες της. Η έννοια του οικισµού. Τον αστικό χώρο χαρακτηρίζουν τα εξής δύο κύρια στοιχεία: 1. Το «κέλυφος», το οποίο αποτελείται από οικοδομικούς όγκους και τεχνικό εξοπλισμό συσσωρευμένους
Η εκπόνηση της εργασίας θα γίνει σε ομάδες των 2-3 ατόμων
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΣΥΣΤΗΜΑΤΑ ΓΕΩΓΡΑΦΙΚΩΝ ΠΛΗΡΟΦΟΡΙΩΝ (εαρινό εξάμηνο 2009-2010) ΔΙΔΑΣΚΟΝΤΕΣ: Γιάννης Θεοδωρίδης Νίκος Πελέκης ΥΠΕΥΘΥΝΟΣ ΕΡΓΑΣΤΗΡΙΩΝ: Δρ. Ηλίας Φρέντζος Η εκπόνηση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΣΥΣΤΗΜΑΤΑ ΓΕΩΓΡΑΦΙΚΩΝ ΠΛΗΡΟΦΟΡΙΩΝ (εαρινό εξάμηνο 2009-2010) ΔΙΔΑΣΚΟΝΤΕΣ: Γιάννης Θεοδωρίδης Νίκος Πελέκης ΥΠΕΥΘΥΝΟΣ ΕΡΓΑΣΤΗΡΙΩΝ: Δρ. Ηλίας Φρέντζος Η εκπόνηση
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ. Πτυχιακή εργασία ΟΛΙΣΘΗΡΟΤΗΤΑ ΚΑΙ ΜΑΚΡΟΥΦΗ ΤΩΝ ΟΔΟΔΤΡΩΜΑΤΩΝ ΚΥΚΛΟΦΟΡΙΑΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ Πτυχιακή εργασία ΟΛΙΣΘΗΡΟΤΗΤΑ ΚΑΙ ΜΑΚΡΟΥΦΗ ΤΩΝ ΟΔΟΔΤΡΩΜΑΤΩΝ ΚΥΚΛΟΦΟΡΙΑΣ Χριστοδούλου Αντρέας Λεμεσός 2014 2 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ Πτυχιακή εργασία ΟΛΙΣΘΗΡΟΤΗΤΑ ΚΑΙ ΜΑΚΡΟΥΦΗ ΤΩΝ ΟΔΟΔΤΡΩΜΑΤΩΝ ΚΥΚΛΟΦΟΡΙΑΣ Χριστοδούλου Αντρέας Λεμεσός 2014 2 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Δυτικής Μακεδονίας Western Macedonia University of Applied Sciences Κοίλα Κοζάνης Kozani GR 50100
 Ποσοτικές Μέθοδοι Τεχνολογικό Εκπαιδευτικό Ίδρυμα Δυτικής Μακεδονίας Western Macedonia University of Applied Sciences Κοίλα Κοζάνης 50100 Kozani GR 50100 Απλή Παλινδρόμηση Η διερεύνηση του τρόπου συμπεριφοράς
Ποσοτικές Μέθοδοι Τεχνολογικό Εκπαιδευτικό Ίδρυμα Δυτικής Μακεδονίας Western Macedonia University of Applied Sciences Κοίλα Κοζάνης 50100 Kozani GR 50100 Απλή Παλινδρόμηση Η διερεύνηση του τρόπου συμπεριφοράς
þÿ ½ ÁÉÀ ºµ½ÄÁ¹º ÀÁ à ³³¹Ã Ä þÿ Á³±½Éù±º  ±»»±³  ¼ ÃÉ þÿà» Á Æ Á¹±º Í ÃÅÃÄ ¼±Ä Â.
 Neapolis University HEPHAESTUS Repository School of Economic Sciences and Business http://hephaestus.nup.ac.cy Master Degree Thesis 2016-02 þÿ ½ ÁÉÀ ºµ½ÄÁ¹º ÀÁ à ³³¹Ã Ä þÿ Á³±½Éù±º  ±»»±³  ¼ ÃÉ þÿà»
Neapolis University HEPHAESTUS Repository School of Economic Sciences and Business http://hephaestus.nup.ac.cy Master Degree Thesis 2016-02 þÿ ½ ÁÉÀ ºµ½ÄÁ¹º ÀÁ à ³³¹Ã Ä þÿ Á³±½Éù±º  ±»»±³  ¼ ÃÉ þÿà»
Άρθρο 32: Προσδιορισμός αξίας ακινήτων φυσικών προσώπων
 Άρθρο 32: Προσδιορισμός αξίας ακινήτων φυσικών προσώπων 1. Ως φορολογητέα αξία των ακινήτων ή των εμπράγματων σε αυτά δικαιωμάτων των φυσικών προσώπων ορίζεται το γινόμενο που προκύπτει από τις τιμές εκκίνησης
Άρθρο 32: Προσδιορισμός αξίας ακινήτων φυσικών προσώπων 1. Ως φορολογητέα αξία των ακινήτων ή των εμπράγματων σε αυτά δικαιωμάτων των φυσικών προσώπων ορίζεται το γινόμενο που προκύπτει από τις τιμές εκκίνησης
Συνολικός Χάρτης Πόλης
 Στα πλαίσια εφαρµογής της οδηγίας 2002/49/ΕΚ, για την αντιµετώπιση των σοβαρών περιβαλλοντικών προβληµάτων που αντιµετωπίζουν οι πόλεις, εξαιτίας του οδικού Θορύβου, µε σοβαρές επιπτώσεις στην ανθρώπινη
Στα πλαίσια εφαρµογής της οδηγίας 2002/49/ΕΚ, για την αντιµετώπιση των σοβαρών περιβαλλοντικών προβληµάτων που αντιµετωπίζουν οι πόλεις, εξαιτίας του οδικού Θορύβου, µε σοβαρές επιπτώσεις στην ανθρώπινη
Οι συγκοινωνιακές προκλήσεις της Αστικής Σήραγγας Ηλιούπολης
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών Τομέας Μεταφορών και Συγκοινωνιακής Υποδομής Οι συγκοινωνιακές προκλήσεις της Αστικής Σήραγγας Ηλιούπολης Γ. Γιαννής, Καθηγητής ΕΜΠ Π. Παπαντωνίου,
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών Τομέας Μεταφορών και Συγκοινωνιακής Υποδομής Οι συγκοινωνιακές προκλήσεις της Αστικής Σήραγγας Ηλιούπολης Γ. Γιαννής, Καθηγητής ΕΜΠ Π. Παπαντωνίου,
ΔΕΙΓΜΑ ΠΡΙΝ ΤΙΣ ΔΙΟΡΘΩΣΕΙΣ
 Εισαγωγή Μέρος Πρώτο: Αστικά και Περιφερειακά Οικονομικά Υποδείγματα και Μέθοδοι ΚΕΦΑΛΑΙΟ 1 Χωροθέτηση δραστηριοτήτων: η χωροθέτηση της επιχείρησης στη θεωρία 1. 1 Εισαγωγή 1.2 Κλασικά και νεοκλασικά υποδείγματα
Εισαγωγή Μέρος Πρώτο: Αστικά και Περιφερειακά Οικονομικά Υποδείγματα και Μέθοδοι ΚΕΦΑΛΑΙΟ 1 Χωροθέτηση δραστηριοτήτων: η χωροθέτηση της επιχείρησης στη θεωρία 1. 1 Εισαγωγή 1.2 Κλασικά και νεοκλασικά υποδείγματα
iii ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος
 iii ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος xi 1 Αντικείμενα των Πιθανοτήτων και της Στατιστικής 1 1.1 Πιθανοτικά Πρότυπα και Αντικείμενο των Πιθανοτήτων, 1 1.2 Αντικείμενο της Στατιστικής, 3 1.3 Ο Ρόλος των Πιθανοτήτων
iii ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος xi 1 Αντικείμενα των Πιθανοτήτων και της Στατιστικής 1 1.1 Πιθανοτικά Πρότυπα και Αντικείμενο των Πιθανοτήτων, 1 1.2 Αντικείμενο της Στατιστικής, 3 1.3 Ο Ρόλος των Πιθανοτήτων
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ. Πτυχιακή εργασία EDQNM ΙΣΟΤΡΟΠΙΚΗΣ ΤΥΡΒΗΣ. Μιχάλης Πιερής
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ Πτυχιακή εργασία EDQNM ΙΣΟΤΡΟΠΙΚΗΣ ΤΥΡΒΗΣ Μιχάλης Πιερής Λεμεσός 2016 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΤΜΗΜΑ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ Πτυχιακή εργασία EDQNM ΙΣΟΤΡΟΠΙΚΗΣ ΤΥΡΒΗΣ Μιχάλης Πιερής Λεμεσός 2016 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΤΜΗΜΑ
ισόγειο βρίσκεται άλλοτε σε άμεση επαφή με το υπόγειο και άλλοτε το χρησιμοποιεί σαν βοηθητικό χώρο εξωτερικά προσπελάσιμο από το κεντρικό
 τεχνική έκθεση Η μορφή, ο τόπος, το ρέμα ο οικισμός, το κέντρο του. Ο άλλοτε τυπικός αγροτικός οικισμός γραμμικός με μικρή πλατεία στο μέσο του μήκους του, έπειτα οι μεταγενέστερες επεκτάσεις (σύγχρονες
τεχνική έκθεση Η μορφή, ο τόπος, το ρέμα ο οικισμός, το κέντρο του. Ο άλλοτε τυπικός αγροτικός οικισμός γραμμικός με μικρή πλατεία στο μέσο του μήκους του, έπειτα οι μεταγενέστερες επεκτάσεις (σύγχρονες
ΤΕΙ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ Μεταπτυχιακό Τμήμα Τραπεζικής & Χρηματοοικονομικής
 ΤΕΙ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ Μεταπτυχιακό Τμήμα Τραπεζικής & Χρηματοοικονομικής Πολλαπλό Γραμμικό Υπόδειγμα Παλινδρόμησης Τα υποδείγματα του απλού γραμμικού υποδείγματος της παλινδρόμησης (simple linear regression
ΤΕΙ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ Μεταπτυχιακό Τμήμα Τραπεζικής & Χρηματοοικονομικής Πολλαπλό Γραμμικό Υπόδειγμα Παλινδρόμησης Τα υποδείγματα του απλού γραμμικού υποδείγματος της παλινδρόμησης (simple linear regression
Συγκριτική μέθοδος. 5.1. Γενικά
 5 Συγκριτική μέθοδος 5.1. Γενικά Η συγκριτική μέθοδος εκτίμησης ακινήτων είναι η πιο βασική μέθοδος εκτίμησης της αξίας των ακινήτων. Θεωρείται η μητέρα όλων των μεθόδων εκτίμησης και συνηθίζεται να εφαρμόζεται
5 Συγκριτική μέθοδος 5.1. Γενικά Η συγκριτική μέθοδος εκτίμησης ακινήτων είναι η πιο βασική μέθοδος εκτίμησης της αξίας των ακινήτων. Θεωρείται η μητέρα όλων των μεθόδων εκτίμησης και συνηθίζεται να εφαρμόζεται
A. Georgiou*, D. Skarlatos. Civil Engineering & Geomatics Dept., Cyprus University of Technology,
 Ανάπτυξη μεθοδολογικού εργαλείου με τη χρήση ΓΣΠ για την εύρεση κατάλληλων περιοχών για την χωροθέτηση φωτοβολταϊκού πάρκου: Η περίπτωση της Επαρχίας Λεμεσού στη Κύπρο A. Georgiou*, D. Skarlatos Civil
Ανάπτυξη μεθοδολογικού εργαλείου με τη χρήση ΓΣΠ για την εύρεση κατάλληλων περιοχών για την χωροθέτηση φωτοβολταϊκού πάρκου: Η περίπτωση της Επαρχίας Λεμεσού στη Κύπρο A. Georgiou*, D. Skarlatos Civil
ΣΧΕΔΙΑΣΜΟΣ ΕΠΙΓΕΙΟΥ ΣΥΣΤΗΜΑΤΟΣ ΑΛΥΣΟΚΙΝΗΣΗΣ ΓΙΑ ΜΕΤΑΦΟΡΑ ΤΡΟΛΕΪ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ Πτυχιακή εργασία ΣΧΕΔΙΑΣΜΟΣ ΕΠΙΓΕΙΟΥ ΣΥΣΤΗΜΑΤΟΣ ΑΛΥΣΟΚΙΝΗΣΗΣ ΓΙΑ ΜΕΤΑΦΟΡΑ ΤΡΟΛΕΪ Μάριος Σταυρίδης Λεμεσός, Ιούνιος 2017 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ Πτυχιακή εργασία ΣΧΕΔΙΑΣΜΟΣ ΕΠΙΓΕΙΟΥ ΣΥΣΤΗΜΑΤΟΣ ΑΛΥΣΟΚΙΝΗΣΗΣ ΓΙΑ ΜΕΤΑΦΟΡΑ ΤΡΟΛΕΪ Μάριος Σταυρίδης Λεμεσός, Ιούνιος 2017 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
Περίληψη Διδακτορικής Διατριβής ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΤΜΗΜΑ ΠΕΡΙΒΑΛΛΟΝΤΟΣ. Πανεπιστήμιο Αιγαίου. Τμήμα Περιβάλλοντος. Ευστράτιος Γιαννούλης
 Μοντελοποίηση και βελτιστοποίηση του ενεργειακού συστήματος με την χρήση κατανεμημένης παραγωγής και ανανεώσιμων πηγών ενέργειας. H τεχνολογική διάσταση Περίληψη Διδακτορικής Διατριβής ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ
Μοντελοποίηση και βελτιστοποίηση του ενεργειακού συστήματος με την χρήση κατανεμημένης παραγωγής και ανανεώσιμων πηγών ενέργειας. H τεχνολογική διάσταση Περίληψη Διδακτορικής Διατριβής ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ. Πτυχιακή εργασία ΔΙΕΡΕΥΝΗΣΗ ΤΟΥ ΚΛΙΜΑΤΟΣ ΑΣΦΑΛΕΙΑΣ ΤΩΝ ΑΣΘΕΝΩΝ ΣΤΟ ΝΟΣΟΚΟΜΕΙΟ
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ Πτυχιακή εργασία ΔΙΕΡΕΥΝΗΣΗ ΤΟΥ ΚΛΙΜΑΤΟΣ ΑΣΦΑΛΕΙΑΣ ΤΩΝ ΑΣΘΕΝΩΝ ΣΤΟ ΝΟΣΟΚΟΜΕΙΟ ΑΝΔΡΕΑΣ ΛΕΩΝΙΔΟΥ Λεμεσός, 2012 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΥΓΕΙΑΣ Πτυχιακή εργασία ΔΙΕΡΕΥΝΗΣΗ ΤΟΥ ΚΛΙΜΑΤΟΣ ΑΣΦΑΛΕΙΑΣ ΤΩΝ ΑΣΘΕΝΩΝ ΣΤΟ ΝΟΣΟΚΟΜΕΙΟ ΑΝΔΡΕΑΣ ΛΕΩΝΙΔΟΥ Λεμεσός, 2012 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ. Πτυχιακή εργασία
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πτυχιακή εργασία ΑΝΑΛΥΣΗ ΚΟΣΤΟΥΣ-ΟΦΕΛΟΥΣ ΓΙΑ ΤΗ ΔΙΕΙΣΔΥΣΗ ΤΩΝ ΑΝΑΝΕΩΣΙΜΩΝ ΠΗΓΩΝ ΕΝΕΡΓΕΙΑΣ ΣΤΗΝ ΚΥΠΡΟ ΜΕΧΡΙ ΤΟ 2030
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πτυχιακή εργασία ΑΝΑΛΥΣΗ ΚΟΣΤΟΥΣ-ΟΦΕΛΟΥΣ ΓΙΑ ΤΗ ΔΙΕΙΣΔΥΣΗ ΤΩΝ ΑΝΑΝΕΩΣΙΜΩΝ ΠΗΓΩΝ ΕΝΕΡΓΕΙΑΣ ΣΤΗΝ ΚΥΠΡΟ ΜΕΧΡΙ ΤΟ 2030
Οικονομετρία Ι. Ενότητα 6: Πολλαπλό Γραμμικό Υπόδειγμα Παλινδρόμησης. Δρ. Χαϊδώ Δριτσάκη Τμήμα Λογιστικής & Χρηματοοικονομικής
 Οικονομετρία Ι Ενότητα 6: Πολλαπλό Γραμμικό Υπόδειγμα Παλινδρόμησης Δρ. Χαϊδώ Δριτσάκη Τμήμα Λογιστικής & Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Οικονομετρία Ι Ενότητα 6: Πολλαπλό Γραμμικό Υπόδειγμα Παλινδρόμησης Δρ. Χαϊδώ Δριτσάκη Τμήμα Λογιστικής & Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Περιεχόμενα. Αστικά και περιφερειακά οικονομικά υποδείγματα και μέθοδοι... 37
 Περιεχόμενα Εισαγωγικό σημείωμα του επιμελητή, Δημήτρης Σκούρας....................... 23 Εισαγωγή................................................................................ 25 Η λογική και η οργάνωση
Περιεχόμενα Εισαγωγικό σημείωμα του επιμελητή, Δημήτρης Σκούρας....................... 23 Εισαγωγή................................................................................ 25 Η λογική και η οργάνωση
Μεθοδολογία των Επιστημών του Ανθρώπου: Στατιστική
 Μεθοδολογία των Επιστημών του Ανθρώπου: Στατιστική Ενότητα 2: Βασίλης Γιαλαμάς Σχολή Επιστημών της Αγωγής Τμήμα Εκπαίδευσης και Αγωγής στην Προσχολική Ηλικία Περιεχόμενα ενότητας Παρουσιάζονται οι βασικές
Μεθοδολογία των Επιστημών του Ανθρώπου: Στατιστική Ενότητα 2: Βασίλης Γιαλαμάς Σχολή Επιστημών της Αγωγής Τμήμα Εκπαίδευσης και Αγωγής στην Προσχολική Ηλικία Περιεχόμενα ενότητας Παρουσιάζονται οι βασικές
Μεταπτυχιακή διατριβή
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Μεταπτυχιακή διατριβή «100% Α.Π.Ε.» : ΤΕΧΝΙΚΕΣ ΚΑΙ ΟΙΚΟΝΟΜΙΚΕΣ ΠΡΟΚΛΗΣΕΙΣ ΓΙΑ ΤΗΝ ΠΛΗΡΗ ΥΠΟΚΑΤΑΣΤΑΣΗ ΤΩΝ ΣΥΜΒΑΤΙΚΩΝ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Μεταπτυχιακή διατριβή «100% Α.Π.Ε.» : ΤΕΧΝΙΚΕΣ ΚΑΙ ΟΙΚΟΝΟΜΙΚΕΣ ΠΡΟΚΛΗΣΕΙΣ ΓΙΑ ΤΗΝ ΠΛΗΡΗ ΥΠΟΚΑΤΑΣΤΑΣΗ ΤΩΝ ΣΥΜΒΑΤΙΚΩΝ
