Σπειρώματα. Περιεχόμενα. Είδη σύνδεσης. Τύποι σύνδεσης. 1. Μόνιμες συνδέσεις. 2. Λυόμενες συνδέσεις. Εισαγωγή. Σπειρώματα - ονοματολογία

Transcript

1 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ναυπηγών Μηχανολόγων Μηχανικών Περιεχόμενα Εισαγωγή Σπειρώματα Κοχλίες Σχεδίαση και διαστασιολόγηση σπειρωμάτων Κοχλίες Τύποι σύνδεσης 1. Μόνιμες συνδέσεις Συγκόλληση Κόλληση Γυρωτικός ήλος (περτσίνι) Είδη σύνδεσης 2. Λυόμενες συνδέσεις 2.1 Κοχλίες - περαστοί - σε τυφλή οπή - φυτευτοί 2.2 Σύνδεσμοι χωρίς σπείρωμα - σφήνες σφήνα - πείροι

2 Εφαρμογές σπειρωμάτων 1. Σπειρώματα σύνδεσης. Εφαρμογές σπειρωμάτων 1. Σπειρώματα σύνδεσης. 2. Σπειρώματα κίνησης. Στοιχείο A Στοιχείο B Στοιχείο Γ Σπειρώματα Εξωτερικό σπείρωμα Εσωτερικό σπείρωμα Σπείρωμα το οποίο δημιουργείται στο εξωτερικού ενός κυλινδρικού σώματος. Σπείρωμα το οποίο δημιουργείται στο εσωτερικό μιας κυλινδρικής οπής. Το σπείρωμα παράγεται αν μια ευθεία με γωνία κλίσης α περιτυλιχθεί γύρω από έναν κύλινδρο. y/x=tan a = P / 2 π r όπου P είναι η αξονική μετάθεση ενός σημείου κατά μία πλήρη περιστροφή πάνω στην ελικοειδή γραμμή, η οποία ονομάζεται βήμα του σπειρώματος.

3 Δεξιόστροφο Σπείρωμα το οποίο συσφίγγει όταν σπείρωμα περιστρέφεται δεξιόστροφα. Αρσερόσροφο Αριστερόστροφο Σπείρωμα το οποίο συσφίγγει σπείρωμα όταν στρέφεται αριστερόστροφα. Κορυφή Πυρήνας Γωνία κορυφής Τα σημεία πάνω στον εξωτερικό κύλινδρο του σπειρώματος. Τα σημεία πάνω στον εσωτερικό κύλινδρο του σπειρώματος. Η γωνία που δημιουργείται από δύο διαδοχικές κορυφές. Στη μηχανολογία χρησιμοποιούμε συνήθως δεξιόστροφα σπειρώματα. Γωνία κορυφής Αν κάποιο σπείρωμα είναι αριστερόστροφο τότε πρέπει να αναγράφεται κατάλληλη ένδειξη με τοπική σημείωση κατά τη διαστασιολόγησή του Πυρήνας Κορυφή Πυρήνας Κορυφή Εξωτερική Η μέγιστη διάμετρος ενός εξωτερικού ή διάμετρος εσωτερικού σπειρώματος. Εσωτερική διάμετρος ή διάμετρος πυρήνα Η ελάχιστη διάμετρος ενός εξωτερικού ή εσωτερικού σπειρώματος. Απόσταση κορυφών Βήμα Η απόσταση μεταξύ δύο διαδοχικών κορυφών του σπειρώματος. Η απόσταση κατά την οποία θα προχωρήσει ο κοχλίας αν περιστραφεί κατά 360 ο (μία πλήρη στροφή). Για σπειρώματα με μία αρχή, ίση με την απόσταση κορυφών. Εσω ωτ. διάμ. Εξωτ τ. διαμ. Εσωτ τ. διαμ. Εξωτ τ. διαμ. Απόσταση κορυφών Απόσταση κορυφών

4 Σπειρώματα Παράγον Σχήμα Σπειρώματα Το προφίλ του σπειρώματος. Στους κοχλίες κίνησης πολλές φορές χρησιμοποιούμε σπειρώματα με δύο ή περισσότερες αρχές, δηλαδή δύο ή περισσότερες ελικοειδής γραμμές παράλληλες μεταξύ τους. Σε μια πλήρη περιστροφή έχουμε πολλαπλάσια προχώρηση (διαδρομή) σε σχέση με το κοχλία μίας αρχής. Το παράγον σχήμα μπορεί να είναι τρίγωνο, τετράγωνο, τραπέζιο, ανισοσκελές τραπέζιο, ημικύκλιο. Οδηγούμαστε σε διαφορετικού είδους σπειρώματα. Παράγον Σχήμα Μετρικό τριγωνικό Παράγον Σχήμα Whitworth τριγωνικό Κατατομή ισόπλευρου τριγώνου ργ με γωνία 60 ο 60 ο Κατατομή τριγώνου με γωνία κορυφών 55 ο 55 ο Ονομαστική διάμετρος σε mm Ονομαστική διάμετρος σε ίντσες

5 Παράγον Σχήμα Μετρικό Τραπεζοειδές Κατατομή τραπεζίου με γωνία των μη παράλληλων πλευρών 30 ο Ονομαστική διάμετρος σε mm Παράγον Σχήμα Μετρικό Πριονωτό Κατατομή ανισοσκελούς τραπεζίου με γωνίες 33 ο και 3 ο Απεικόνιση σπειρωμάτων Μετρικό και Whitworth τριγωνικό: Σπειρώματα σύνδεσης Ορθογωνικά, Τραπεζοειδή, Πριονωτά, Στρογγυλά: Σπειρώματα κίνησης Ευρεία τυποποίηση σπειρωμάτων. Γιατί? 1. Κανονική σχεδίαση 2. Σχηματική σχεδίαση 3. Απλοποιημένη σχεδίαση

6 Μετρικό Σπείρωμα - Κανονική σχεδίαση Κανονική σχεδίαση Χρήση κεκλιμένων γραμμών για την απεικόνιση των σημείων που βρίσκονται στις κορυφές και στον πυρήνα. Κορυφές και πυρήνας ενώνονται με έντονα V. Τυποποίηση η σπειρωμάτων.. Ανώφελη η κανονική σχεδίασή τους. Τελείωμα (ξεθύμασμα) σπειρώματος Βήμα 60 o Σχηματική σχεδίαση Χρησιμοποιούμε εναλλασσόμενες πλήρεις και ημιτελείς γραμμές για την απεικόνιση των κορυφών και του πυρήνα του σπειρώματος. Απλοποιημένη η σχεδίαση Χρησιμοποιούμε παχειά συνεχή γραμμή για την απεικόνιση των κορυφών και λεπτή συνεχή γραμμή για την απεικόνιση του πυρήνα του σπειρώματος. Τελείωμα (ξεθύμασμα) σπειρώματος Βήμα Πυρήνας (παχειά γραμμή) Κορυφές (λεπτή γραμμή) Πυρήνας Κορυφή

7 Απλοποιημένη η σχεδίαση Τυποποιημένα σπειρώματα Χρησιμοποιούμε παχειά συνεχή γραμμή για την απεικόνιση των κορυφών και λεπτή συνεχή γραμμή για την απεικόνιση του πυρήνα του σπειρώματος. Προσοχή, οι γραμμές διαγράμμισης φτάνουν μέχρι την εσωτερική διάμετρο του σπειρώματος! Τομή Συνεργασία εσωτερικού και εξωτερικού σπειρώματος είναι δυνατή μόνο αν και τα δύο σπειρώματα έχουν ίση ονομαστική διάμετρο και βήμα. Πιν. Α-11-8 Βιβλίο, Σελ. 100 ISO (μετρικό) σπείρωμα Μετρικό λεπτό σπείρωμα Ονομαστική Εξωτερική Βήμα Εσωτερική διάμετρος διάμετρος διάμετρος M Κανονικό βήμα 1.25 mm M mm Πλεονεκτήματα: - Μικρότερη ρη δύναμη κοχλίωσης - Μεγαλύτερη ασφάλεια σε αποκοχλίωση Μειονεκτήματα: - Μεγαλύτερος χρόνος κοχλίωσης - Κίνδυνος παραμόρφωσης και καταστροφής του σπειρώματος

8 Βήματα σχεδιασμού εξωτερικού σπειρώματος Βήματα σχεδιασμού κοχλιοτομημένης οπής Σχεδιασμός λοξότμησης 45 ο Σχεδιασμός τελειώματος σε 30 o με τον οριζόντιο άξονα Σχεδιασμός κύκλου που παριστά την εξωτερική διάμετρο. 1. Διαμπερής κοχλιοτομημένη οπή Τομή Σχεδιασμός κύκλου που παριστά την εξωτερική διάμετρο. Πυρήνας Εξ. διάμετρος ς. Εσ. διάμετρος άμετρος Εξ. δι ιάμετρος Εσ. δι Κορυφή Σχεδιασμός τόξου κύκλου που παριστά την εσωτερική διάμετρο. Οι γραμμές διαγράμμισης φτάνουν ως την γραμμή κορυφών. Σχεδιασμός τόξου κύκλου που παριστά την εσωτερική διάμετρο. Βήματα σχεδιασμού κοχλιοτομημένης οπής Βήματα σχεδιασμού κοχλιοτομημένης οπής 2. Τυφλή κοχλιοτομημένη οπή Σχεδιασμός τόξου κύκλου που παριστά την εξωτερική διάμετρο. 2. Τυφλή κοχλιοτομημένη οπή Εξ. δι άμετρος Εσ. διά άμετρος Βάθος σπειρώματος Βάθος οπής Σχεδιασμός κύκλου που παριστά την εσωτερική διάμετρο. Τομή

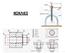
9 Διαστασιολόγηση Διαστασιολόγηση Κοχλιοτομημένη οπή Χρήση τοπικής σημείωσης για τον ορισμό του είδους σπειρώματος, της ονομαστικής διάστασης και του βήματος (για λεπτά σπειρώματα) Χρήση τυπικής μεθόδου για τον ορισμό του μήκους σπειρώματος. M10 Κανονικό σπείρωμα M Λεπτό σπείρωμα Χρήση τοπικής σημείωσης για τον ορισμό: 1. Είδους σπειρώματος 2. Ονομαστικής διάστασης 3. Βήματος (λεπτό σπείρωμα) M10 Προσοχή, η απόσταση του πέρατος κοχλιοτόμησης από το πέρας της οπής ορίζεται από τους κανονισμούς! l Χρήση τυπικής μεθόδου για τον ορισμό: 1. Βάθους οπής 2. Βάθους σπειρώματος Μέτρηση σπειρωμάτων Κοχλίας: Ονοματολογία Κοχλίας είναι ένας κύλινδρος με σπείρωμα και κεφαλή. Κοχλίας με εξαγωνική κεφαλή και περικόχλιο Ύψος κεφαλής Μήκος κορμού Άνοιγμα κλειδιού

10 Κοχλίας: Ονοματολογία Κοχλίας: Τυποποιημένο τεμάχιο Περαστός Σε τυφλή οπή κορμού Εξαγωνικός κοχλίας με μετρικό σπείρωμα Πιν. Α-12-8, Σελ. 125 Κοχλίας : Σχεδιασμός Περικόχλιο : Σχεδιασμός Σχεδιασμός κεφαλής Σχεδιασμός κορμού Σχεδιασμός πλάγιας όψης Οι διαστάσεις του περικοχλίου δίδονται στους πίνακες του βιβλίου r=e/4, e, η διαγώνιος του εξαγώνου r=3/4 e K Μήκος κορμού S Ύψος κεφαλής Άνοιγμα κλειδιού Οι διακεκομμένες γραμμές που απεικονίζουν το εσωτερικό σπείρωμα παραλείπονται για σπείρωμα παραλείπονται για λόγους σαφήνειας.

11 Κοχλίας : Εφαρμογή - Διαστασιολόγηση Μ10 x 40, DIN 601 Φυτευτός κοχλίας : Ονοματολογία Φυτευτός κοχλίας (μπουζόνι) είναι ένας κοχλίας χωρίς κεφαλή με σπείρωμα και στα δύο άκρα.. Σε κατασκευαστικά σχέδια και σχέδια συναρμολόγησης προστίθεται και η απαιτούμενη ροπή σύσφιγξης. Σχεδιαστική απεικόνιση Μήκος Φυτευτός κοχλίας : Τυποποίηση Φυτευτός κοχλίας : Βήματα σχεδιασμού Λοξότμηση Τελείωμα Λοξότμηση 45 ο σπειρώματος (30 ο ) 45 ο Εξ. Διάμ. Εσ. Διάμ. Μήκος φυτευτού κοχλία

12 Φυτευτός κοχλίας : Εφαρμογή Είδη κοχλίων - Διαστάσεις 1. Άνοιγμα οπής. 2. Κοχλιοτόμηση. 3. Κοχλίωση μπουζονιού. 4. Τοποθέτηση του τεμαχίου προς συναρμολόγηση. 5. Τοποθέτηση ροδέλας και κοχλίωση του περικοχλίου.. Οι κοχλίες δεν σχεδιάζονται σε τομή. Κεφαλωτοί κοχλίες : Ονοματολογία Εξαγωνικοί Με κωνική, ημιστρόγγυλη, κυλινδρική κεφαλή με εγκοπή Κοίλης κυλινδρικής κεφαλής (allen) Κοινές ροδέλλες Παράκυκλοι (Ροδέλλες) Ροδέλλες ασφαλείας