Τίτλος Μαθήματος: Γενική Φυσική (Ηλεκτρομαγνητισμός) Διδάσκων: Επίκουρος Καθηγητής Δημήτριος Βλάχος
|
|
|
- Περσεφόνη Γαλάνη
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Τίτλος Μαθήματος: Γενική Φυσική (Ηλεκτρομαγνητισμός) Ενότητα: ΧΩΡΗΤΙΚΟΤΗΤΑ ΚΑΙ ΔΙΗΛΕΚΤΡΙΚΑ Διδάσκων: Επίκουρος Καθηγητής Δημήτριος Βλάχος Τμήμα: Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής
2 1 ΚΕΦΑΛΑΙΟ 5 ΧΩΡΗΤΙΚΟΤΗΤΑ ΚΑΙ ΔΙΗΛΕΚΤΡΙΚΑ 5.1 Εισαγωγικά Στο εδάφιο 1.3 μιλήσαμε για τις κατηγορίες των υλικών βάση της ικανότητάς τους να επιτρέπουν στο εσωτερικό τους την διέλευση ηλεκτρικών φορτίων. Ονομάσαμε μονωτές τα υλικά τα οποία δεν επιτρέπουν την διέλευση φορτίου, και αγωγούς αυτά που την επιτρέπουν. Όταν ένας μονωτής τοποθετηθεί ανάμεσα από δυο αγωγούς, τα υλικά απαρτίζουν ένα σύστημα που ονομάζεται πυκνωτής. Το μονωτικό υλικό το οποίο υπάρχει μεταξύ των αγωγών ονομάζεται διηλεκτρικό. Εάν οι δυο αγωγοί είναι φορτισμένοι με αντίθετα φορτία Q και Q, μια διαφορά δυναμικού αναπτύσσεται μεταξύ των δυο αγωγών του πυκνωτή, η οποία είναι ανάλογη προς την απόλυτη τιμή του φορτίου Q. H χωρητικότητα ενός πυκνωτή, είναι η ικανότητα αποθήκευσης ηλεκτρικού φορτίου στους αγωγούς του και ορίζεται με το πηλίκο της απόλυτης τιμής του φορτίου Q ως προς την διαφορά δυναμικού μεταξύ των δύο αγωγών. Q (5.1) Οι μονάδες χωρητικότητας στο IS είναι το Faad (F), όπου 1F=1/. Tο 1 F είναι πολύ μεγάλη χωρητικότητα και γι αυτό οι συνήθεις μονάδες χωρητικότητας των πυκνωτών είναι το μf=10 6 F, το nf=10 9 F και το pf=10 1 F. Οι αγωγοί του πυκνωτή ονομάζονται και οπλισμοί, ενώ η διαφορά δυναμικού ονομάζεται τάση του πυκνωτή. Οι πυκνωτές χρησιμοποιούνται στα ηλεκτρικά κυκλώματα για αποθήκευση ηλεκτρικού φορτίου και επομένως ηλεκτρικής δυναμικής ενέργειας. Στην πραγματικότητα η διαφορά δυναμικού ορίζεται ως Δ= a, όμως προς χάριν απλότητας, στη συνέχεια θα αναφέρεται ως.
3 5. Επίπεδος πυκνωτής Υπάρχουν διάφοροι τύποι πυκνωτών. Ο πιο κοινός πυκνωτής είναι ο επίπεδος πυκνωτής που φαίνεται στο σχ. 5.1 και αποτελείται από δυο παράλληλες αγώγιμες πλάκες ίσου εμβαδού Α οι οποίες απέχουν απόσταση d και είναι φορτισμένες με αντίθετα φορτία Q και Q. Η τιμή του ηλεκτρικού πεδίου Ε μέσα στον πυκνωτή ορίζεται ως Q E (5.) όπου σ είναι η επιφανειακή πυκνότητα φορτίου στους οπλισμούς και ε η διηλεκτρική σταθερά του κενού. (Η σχέση αυτή λαμβάνεται από τον νόμο του Gauss. Βλέπε κεφ. 13). Οι δυναμικές γραμμές του πεδίου Ε του πυκνωτή είναι παράλληλες μεταξύ τους και το πεδίο δίνεται ως d E (5.3) d όπου d/d η μεταβολή του δυναμικού κατά μήκος των δυναμικών γραμμών. Για να υπολογίσουμε την διαφορά δυναμικού μεταξύ των οπλισμών του πυκνωτή ολοκληρώνουμε την εξ. 5.3 και παίρνουμε Ed E (5.4) T αρνητικό πρόσημο δηλώνει ότι η διαφορά δυναμικού κατά μήκος των δυναμικών γραμμών είναι αρνητική, διότι καθώς απομακρυνόμαστε από τον θετικά φορτισμένο οπλισμό και πλησιάζουμε τον αρνητικά φορτισμένο οπλισμό, το δυναμικό ελαττώνεται. Τελικά η απόλυτη τιμή της διαφοράς δυναμικού στα άκρα του πυκνωτή ή αλλιώς η τάση του πυκνωτή ορίζεται ως 5. Q E (5.5) Q Q E Σχήμα 5.1 Επίπεδος πυκνωτής με φορτίο Q ομοιόμορφα κατανεμημένο στους οπλισμούς του, οι οποίοι απέχουν απόσταση. Από την εξ.15.1 του ορισμού της χωρητικότητας και την εξ. 5.5 καταλήγουμε στην (5.6)
4 3 η οποία μας δίνει την χωρητικότητα του επίπεδου πυκνωτή συναρτήσει της διηλεκτρικής σταθεράς του κενού, του εμβαδού και της απόστασης των οπλισμών. Γενικά η χωρητικότητα ενός πυκνωτή εξαρτάται από την γεωμετρία των οπλισμών και το διηλεκτρικό υλικό που βρίσκεται ανάμεσά τους. Άλλα συνήθη είδη πυκνωτών είναι ο κυλινδρικός και ο σφαιρικός πυκνωτής. Παράδειγμα 5.1 Επίπεδος πυκνωτής Σε έναν τύπο πληκτρολογίου υπολογιστή, το κάθε πλήκτρο συνδέεται με ένα μικρό μεταλλικό πλακίδιο που παίζει το ρόλο του ενός οπλισμού επίπεδου πυκνωτή αέρος. Αν πιεστεί το πλήκτρο, η απόσταση των οπλισμών μειώνεται και η χωρητικότητα του πυκνωτή αυξάνεται. Κατάλληλο ηλεκτρικό κύκλωμα ανιχνεύει τη μεταβολή της χωρητικότητας και έτσι γίνεται αντιληπτό ότι το πλήκτρο πατήθηκε. Έστω η επιφάνεια του κάθε πλακιδίου είναι 50mm και η απόσταση μεταξύ των πλακιδίων είναι 0.600mm πριν πατηθεί το πλήκτρο. Αν η ελάχιστη χωρητικότητα που ανιχνεύεται από το κύκλωμα είναι 0.50pF, πόσο πρέπει να μετακινηθεί το πλακίδιο για να ανιχνεύσει το κύκλωμα ότι το πλήκτρο πατήθηκε; Λύση Η χωρητικότητα του πλήκτρου με τα δυο πλακίδια είναι Q (1) και το φορτίο σε κάθε πλακίδιο είναι Q () όπου σ η επιφανειακή πυκνότητα φορτίου. Επίσης επειδή ο πυκνωτής είναι επίπεδος ισχύει E (3) και E. (4) ο Η εξ. 1 λόγω των,3 και 4 γίνεται (4) Κατά το πάτημα του πλήκτρου τα Α και ε ο δεν αλλάζουν. Μειώνεται όμως η απόσταση και επομένως αυξάνεται η χωρητικότητα κατά Δ=0.50pF. Εάν η μεταβολή της απόστασης είναι Δ, τότε ισχύει
5 4 (5) Από την εξ. 4 μπορούμε να υπολογίσουμε την, δηλαδή την χωρητικότητα όταν το πλήκτρο δεν είναι πατημένο. Έτσι /Nm 5010 m m F Η αρχική χωρητικότητα είναι 0.740pF και η απόσταση των οπλισμών είναι =0.600mm. Από την εξ. 5 έχουμε για την μεταβολή της απόστασης Δ όταν το πλήκτρο πατιέται προκαλείται μεταβολή στην χωρητικότητα Δ=0.50pF και μπορούμε να γράψουμε F Επομένως όταν πατήσουμε το πλήκτρο και μετακινηθεί προς τα κάτω κατά 0.153mm το /Nm 5010 m m m κύκλωμα ανιχνεύει το πάτημα του πλήκτρου και στην οθόνη του υπολογιστή αναγράφεται ένα γράμμα, ή εκτελείται οποιαδήποτε άλλη λειτουργία. Παράδειγμα 5. Σφαιρικός πυκνωτής Σφαιρικός πυκνωτής αποτελείται από σφαιρικό αγωγό ακτίνας a που περιβάλλεται από σφαιρικό αγώγιμο κέλυφος ακτίνας με τον ενδιάμεσο χώρο να είναι κενός, όπως φαίνεται στο σχ. 5.. Χρησιμοποιώντας τον νόμο του Gauss να υπολογιστεί η Q Σχήμα 5. Σφαιρικός πυκνωτής με φορτίο Q και ακτίνες οπλισμών a και αντίστοιχα (παράδειγμα 5.). a Ε χωρητικότητα του πυκνωτή αν το φορτίο του εσωτερικού σφαιρικού οπλισμού είναι Q. Λύση Εφαρμόζοντας τον νόμο του Gauss για κλειστή σφαιρική επιφάνεια με ακτίνα που περικλείει το φορτίο Q του εσωτερικού οπλισμού έχουμε Q Q Q E. ds EdS E ds E4 E Q 1 Q 4 Η διαφορά δυναμικού μεταξύ των οπλισμών α και είναι Q
6 5 1 Q Q 1 Q 1 Q Q 1 1 a Ed d d ( ) ( ) a a a a a Q Q ( ) ( ) a a a a 4 a 4 a a Η διαφορά δυναμικού = a, είναι θετική διότι a >. Επομένως η χωρητικότητα του σφαιρικού πυκνωτή είναι Παράδειγμα 5.3 Κυλινδρικός πυκνωτής Κυλινδρικός πυκνωτής αποτελείται από δυο ομοαξονικούς κυλινδρικούς αγωγούς ακτίνων a και αντίστοιχα με τον ενδιάμεσο χώρο να είναι κενός. Ο πυκνωτής έχει μήκος και είναι ομοιόμορφα φορτισμένος με πυκνότητα φορτίου λ ανά μονάδα μήκους στον εσωτερικό κύλινδρο και λ στον εξωτερικό όπως φαίνεται στο σχ Υπολογίστε την χωρητικότητα αν οι κυλινδρικοί οπλισμοί έχουν μήκος. Λύση Η χωρητικότητα του πυκνωτή ορίζεται ως Q (1) Το φορτίο στους οπλισμούς του πυκνωτή δίνεται από την σχέση Q () Η διαφορά δυναμικού μεταξύ των οπλισμών α και είναι Ed (3) a a Σχήμα 5.3 Κυλινδρικός πυκνωτής με φορτίο λ ανά μονάδα μήκους και ακτίνες οπλισμών a και αντίστοιχα (παράδειγμα 5.3). λ a Ε λ
7 6 Για να υπολογίσουμε το λοιπόν θα πρέπει να ξέρουμε πως μεταβάλλεται το Ε στο χώρο μεταξύ των οπλισμών του πυκνωτή. Χρησιμοποιώντας το νόμο του Gauss για μια κυλινδρική επιφάνεια ακτίνας που περιβάλει τον οπλισμό α με πυκνότητα φορτίου λ όπως φαίνεται στο σχ. 5.3, έχουμε Q 1 E.dS EdS E ds E E (4) Πρέπει να σημειώσουμε ότι στον πιο πάνω υπολογισμό της ηλεκτρικής ροής μέσα από την κυλινδρική επιφάνεια Gauss δεν συνεισφέρουν οι βάσεις της κυλινδρικής επιφάνειας γιατί το διάνυσμα Ε δεν τις διαπερνά μιας και δεν είναι φορτισμένες. Έτσι ροή υπάρχει μόνο διαμέσου της παράπλευρης επιφάνειας. Αντικαθιστώντας την εξ. 4 στην εξ. 3 παίρνουμε (5) a a a a 1 d d n n Η διαφορά δυναμικού είναι αρνητική γιατί από το θετικό δυναμικό του οπλισμού α καταλήγουμε στο αρνητικό δυναμικό του οπλισμού. Οι εξ., 5 στην εξ. 1 δίνουν a n n a n a n 5.3 Συνδεσμολογία πυκνωτών Όταν σ ένα ηλεκτρικό κύκλωμα, δηλαδή σε μια κλειστή αγώγιμη διαδρομή, (θα αναφερθούμε λεπτομερώς στα ηλεκτρικά κυκλώματα σε επόμενο κεφάλαιο), υπάρχουν δύο πυκνωτές, η συνδεσμολογία μεταξύ τους μπορεί να γίνει είτε παράλληλα ο ένας προς τον άλλο a Q 1 Q 1 Q Q Q Q 1 _ Σχήμα 5.4 Σχεδιάγραμμα σύνδεσης δυο πυκνωτών σε α) παράλληλη σύνδεση και β) σύνδεση εν σειρά. είτε σε σειρά. Ο πυκνωτής στα ηλεκτρικά κυκλώματα συμβολίζεται με δυο κάθετες (α) 1 _ Q 1 Q (β)
8 7 παράλληλες γραμμές. Στο σχήμα 5.4 φαίνονται σχηματικά οι δυο διαφορετικοί τρόποι σύνδεσης. Για την παράλληλη συνδεσμολογία του κυκλώματος στο σχ.5.4α η ολική χωρητικότητα ολ είναι όπου ολ Qολ (5.7) Qολ Q1 Q (5.8) Η εξ.5.8 στην 5.7 δίνει Q1 Q Q1 Q ολ ολ 1 (5.9α) Δηλαδή η συνολική χωρητικότητα δυο πυκνωτών παράλληλα συνδεδεμένων είναι το άθροισμα των επιμέρους χωρητικοτήτων. Γενικότερα για Ν πυκνωτές ισχύει ολ 1... N (5.9β) Για συνδεσμολογία σε σειρά όπως φαίνεται στο κύκλωμα του σχ. 5.4β οι επιμέρους τάσεις στα άκρα των πυκνωτών είναι 1 και όπου 1 (5.10) Τα φορτία που αναπτύσσονται επαγωγικά στους οπλισμούς των πυκνωτών που είναι συνδεμένοι θα πρέπει να είναι ίσα και αντίθετα Q και Q. Έτσι λοιπόν η εξ μπορεί να γραφτεί Q Q (5.11) 1 Όμως για την ολική χωρητικότητα ισχύει ολ Q 5.10 Q ολ Q Q Q 1 ολ 1 Γενικά για Ν πυκνωτές συνδεδεμένους σε σειρά ισχύει (5.1β) ολ 1 N (5.1α) Αξίζει να τονίσουμε ότι παράλληλα συνδεδεμένοι πυκνωτές έχουν πάντα την ίδια διαφορά δυναμικού στα άκρα τους, ενώ πυκνωτές συνδεδεμένοι σε σειρά έχουν πάντα ίδιο φορτίο στους οπλισμούς τους.
9 8 Παράδειγμα 5.4 Σύνδεση πυκνωτών Θεωρείστε ότι έχουμε τον συνδυασμό των πυκνωτών που δείχνει το σχ α) Ποια είναι η ισοδύναμη χωρητικότητα μεταξύ των σημείων α και, αν 1 =5μF, =3μF, 3 =0μF και 4 =5μF; β) Προσδιορίστε το φορτίο κάθε πυκνωτή, αν a =4.8. Λύση ως α) Η συνολική χωρητικότητα δίνεται ολ 1 34 (1) επειδή οι πυκνωτές 1, και 34 είναι παράλληλοι συνδεδεμένοι μεταξύ τους. Η χωρητικότητα 34 είναι η συνολική χωρητικότητα των πυκνωτών 3 και 4 οι οποίοι είναι συνδεδεμένοι σε σειρά. Έτσι ισχύει () Η εξ. στην 1 δίνει 3 4 5μF 5μF ολ 1 5μF 3μF 8μF 4μF ολ 1μF 0μF 5μF 3 4 β) Το φορτίο του πυκνωτή 1 είναι Q 5μF 4.8 Q 4μ 1 1 a 1 Ομοίως το φορτίο του πυκνωτή είναι Q 3μF 4.8 Q 14.4μ a Οι πυκνωτές 3 και 4 οι οποίοι είναι συνδεδεμένοι εν σειρά έχουν το ίδιο φορτίο στους οπλισμούς τους, άρα Q3 Q4 34 a 4μF μ a Σχήμα 5.5 Σύνδεση πυκνωτών (παράδειγμα 5.4)
10 9 Παράδειγμα 5.5 Να βρεθεί η συνολική χωρητικότητα του κυκλώματος των πυκνωτών. Αν η διαφορά δυναμικού μεταξύ των σημείων Α και Β είναι 100, ποια είναι η διαφορά δυναμικού μεταξύ των σημείων Α και D; Δίνονται 1 =4.0μF, =1.0μF, 3 =3.0μF και 4 =1.0μF. Λύση Βλέποντας το σχ. 5.6 παρατηρούμε ότι ο πυκνωτής 1 και η συνολική χωρητικότητα 34 των πυκνωτών 1, και 3 είναι παράλληλα συνδεδεμένα μεταξύ τους. Άρα ισχύει ολ 1 34 (1) Για την 34 χωρητικότητα ισχύει ( ) ( 3 4 4) 3 4 Η εξ. στην 1 δίνει ( ) ( ) ( ) (4μF16μF) (1μF 4μF) 16μF ολ 1 11μF 16μF ολ μF Για την διαφορά δυναμικού B ισχύει B D DB (3) Το φορτίο Q 1 στον πυκνωτή 1 είναι Q (4) 1 1 B Το φορτίο Q στον πυκνωτή είναι το ίδιο με αυτό της συνολικής χωρητικότητας 34 γιατί είναι συνδεμένοι σε σειρά. Έτσι ισχύει Q και (5) D B 1 () D 3 4 Σχήμα 5.6 Σύνδεση πυκνωτών (παράδειγμα 5.5)
11 10 Q (6) 34 DB Οι εξισώσεις 5 και 6 δίνουν 3 D D 34 DB D ( 3 4)( B D ) B D 3 4 ( 1) D B D D B D 3μF 1μF 4μF D 5 1μF 3μF 1μF 16μF 5.4 Ενέργεια του πυκνωτή Ο ρόλος των πυκνωτών στα ηλεκτρικά κυκλώματα είναι να αποθηκεύουν ηλεκτρική ενέργεια την οποία μπορούν ανά πάσα στιγμή να την παρέχουν σαν ωφέλιμο έργο. Ας υποθέσουμε ότι κατά την διάρκεια φόρτισης ενός πυκνωτή χωρητικότητας, το φορτίο στους οπλισμούς του είναι q ενώ η τάση του είναι όπως φαίνεται στο σχ Το έργο που απαιτείται για την μεταφορά ενός στοιχειώδους θετικού φορτίου dq από τον οπλισμό φορτίου q στον οπλισμό q (ο οποίος έχει υψηλότερο δυναμικό) είναι (5.4) dw df dq. E dw dq (5.13) Όμως το φορτίο στα άκρα του πυκνωτή είναι q την δεδομένη στιγμή της φόρτισης και άρα ισχύει =q/, και επομένως η εξ γίνεται q dw dq (5.14) q F dq q E Σχήμα 5.7 Φόρτιση επίπεδου πυκνωτή με μετακίνηση φορτίου dq από τον αρνητικό οπλισμό στον θετικό όταν στα άκρα του πυκνωτή υπάρχει φορτίο q και τάση.
12 11 Αν το μέγιστο φορτίο που μπορεί να δεχθεί ο πυκνωτής είναι Q, το συνολικό έργο που θα πρέπει να δαπανηθεί από την πηγή ηλεκτρικής ενέργειας του κυκλώματος για την πλήρη φόρτιση του πυκνωτή είναι 0 0 Q Q 1 W q dq q W Q (5.15) Το έργο της εξ αποθηκεύεται ως ηλεκτροστατική ενέργεια στους οπλισμούς του πυκνωτή η οποία μπορεί να αποβεί χρήσιμη κατά την εκφόρτισή του. Από την εξ. 5.1 και βάση της εξ η ηλεκτροστατική ενέργεια U του πυκνωτή είναι U 1 1 Q (5.16) Μία άλλη έκφραση για την ηλεκτρική ενέργεια του πυκνωτή προκύπτει από την εξ λόγω των εξισώσεων 5.4 και 6. Έτσι μπορούμε να γράψουμε 1 1 (5.17) ο U E U οe όπου περιγράφουμε την ενέργεια του πυκνωτή συναρτήσει του ηλεκτρικού πεδίου Ε μεταξύ των οπλισμών του. Παράδειγμα 5.6 Υποθέστε ότι ένας πυκνωτής έχει χωρητικότητα και η μέγιστη τάση που μπορούμε να εφαρμόσουμε μεταξύ των οπλισμών του χωρίς να καταστραφεί ο πυκνωτής, είναι. Συγκρίνετε τη μέγιστη ενέργεια που μπορεί να αποθηκευτεί σε μια σύνδεση εν σειρά δυο τέτοιων πυκνωτών με την μέγιστη ενέργεια που μπορεί να αποθηκευτεί σε μια παράλληλη σύνδεση αυτών των πυκνωτών. Λύση Η μέγιστη ενέργεια ενός πυκνωτή δίνεται από την εξίσωση U max 1 max (1) όπου max είναι η μέγιστη διαφορά δυναμικού που μπορεί να εφαρμοστεί στα άκρα του πυκνωτή. Όταν οι δυο πυκνωτές είναι συνδεδεμένοι σε σειρά, έχουν συνολική χωρητικότητα
13 1 ολ 1 ολ 1 () Η μέγιστη διαφορά δυναμικού στον κάθε πυκνωτή είναι, και αφού είναι συνδεδεμένοι σε σειρά η συνολική διαφορά δυναμικού θα είναι το άθροισμα των επιμέρους δυναμικών, άρα ολ 1 ολ (3) Η εξ. 1 βάση των και 3 δίνει U ( σειρα) ( ) U ( ) max 1 max σειρα (4) Όταν οι δυο πυκνωτές είναι συνδεδεμένοι παράλληλα, έχουν συνολική χωρητικότητα ολ 1 ολ (5) Στην παράλληλη σύνδεση η διαφορά δυναμικού στα άκρα των πυκνωτών είναι κοινή ίση με. Άρα για την μέγιστη ενέργεια του συστήματος των δυο πυκνωτών η εξ. 1 δίνει U ( παραλληλα) U ( ) max 1 max παραλληλα (6) Από τις εξισώσεις 4 και 6 συμπεραίνουμε ότι η μέγιστη ενέργεια του συστήματος των δυο πυκνωτών είναι ίδια ανεξάρτητα εάν αυτοί είναι συνδεδεμένοι σε σειρά ή παράλληλα. 5.5 Διηλεκτρικά Όπως αναφέραμε πιο πάνω το υλικό που υπάρχει μεταξύ των οπλισμών ενός πυκνωτή ονομάζεται διηλεκτρικό και η ύπαρξή του εκεί σκοπεύει στην μόνωση των δυο οπλισμών. Έτσι είναι δυνατόν να συγκρατούνται τα ετερώνυμα φορτία στους οπλισμούς του πυκνωτή και επομένως να δημιουργείται ηλεκτρικό πεδίο στο χώρο του διηλεκτρικού, καθιστώντας τον πυκνωτή μια διάταξη αποθήκευσης ηλεκτρικής ενέργειας. Ο χώρος μεταξύ των οπλισμών του πυκνωτή έχει μια συγκεκριμένη διηλεκτρική σταθερά ε που είναι διαφορετική από αυτή του κενού ε ο, και εξαρτάται από το διηλεκτρικό δηλαδή το μονωτικό υλικό. Μάλιστα η σχέση που συνδέει τα ε και ε ο είναι ο (5.18) ο Η σταθερά κ ονομάζεται σχετική διηλεκτρική σταθερά γιατί συγκρίνει την διηλεκτρική σταθερά του υλικού με αυτήν του κενού (πολλές φορές το κ ονομάζεται απλώς διηλεκτρική
14 13 σταθερά). Ας δούμε ποιες αλλαγές επιφέρει το διηλεκτρικό υλικό σε έναν επίπεδο πυκνωτή. Η χωρητικότητα του επίπεδου πυκνωτή δίνεται από την εξ Εάν αντί για κενό τοποθετήσουμε ένα μονωτικό υλικό μεταξύ των οπλισμών με διηλεκτρική σταθερά ε θα έχουμε μια νέα χωρητικότητα 5.18 (5.19) Το κενό που είναι και αυτό στην ουσία ένα διηλεκτρικό έχει κ=1. Ο αέρας επίσης είναι διηλεκτρικό με κ~1. Άλλα μονωτικά υλικά έχουν τιμές του κ>1. Το χαρτί για παράδειγμα έχει 3.7, το νερό 80, ενώ το τιτανιούχο βάριο 100! Στον πίνακα 5.1 φαίνονται οι τιμές της σχετικής διηλεκτρικής διαφόρων μονωτικών υλικών. Από τα παραπάνω και την εξ καταλαβαίνουμε ότι το διηλεκτρικό υλικό μπορεί να αυξήσει την χωρητικότητα ενός πυκνωτή πολλές φορές. Αυτή η ιδιότητά του διηλεκτρικού έχει σαν συνέπεια την αύξηση Πίνακας 5.1 Προσεγγιστικές τιμές της σχετικής διηλεκτρικής διαφόρων υλικών Υλικό κ Υλικό κ Κενό 1 (ακριβώς) Γυαλί 510 Αέρας (ξηρός) Πορσελάνη 6 Τεφλόν.1 Σιλικόνη 1 Πολυεθυλένιο.5 Γερμάνιο 16 Μαρμαρυγία (Μίκα) 36 Γλυκερίνη 4.5 Πλεξιγκλάς 3.4 Νερό 80 Χαρτί 3.7 Τιτανιούχο στρόντιο 310 Βακελίτης 4.9 Τιτανιούχο βάριο 100 του φορτίου στους οπλισμούς και επομένως της ενέργειας του πυκνωτή (βλέπε εξ. 5.15). Επίσης το διηλεκτρικό είναι απαραίτητο στοιχείο σε έναν πυκνωτή, διότι όπως προαναφέραμε, μονώνει τον έναν οπλισμό από τον άλλο και επιτρέπει να υπάρχει διαφορά δυναμικού (τάση) στα άκρα του πυκνωτή. Έτσι ο πυκνωτής λειτουργεί ως πηγή ηλεκτρικής ενέργειας, χρήσιμη σε ηλεκτρικά κυκλώματα όπως θα δούμε πιο κάτω. Η τάση στα άκρα ενός πυκνωτή δεν μπορεί να αυξάνεται απεριόριστα, διότι οι μονωτικές ιδιότητες ενός διηλεκτρικού έχουν κάποιο όριο. Εάν η διαφορά δυναμικού γίνει υπερβολικά μεγάλη, τότε και το ηλεκτρικό πεδίο στο διηλεκτρικό μεγαλώνει, με αποτέλεσμα τα φορτία από τον
15 14 θετικό οπλισμό του πυκνωτή να κινηθούν προς τον αρνητικό οπλισμό και αντίστροφα διαμέσου του διηλεκτρικού. Τότε γίνονται εκκενώσεις και το διηλεκτρικό καταρρέει, οι μονωτικές του ιδιότητες χάνονται ανεπιστρεπτί οπότε γίνεται διηλεκτρική κατάρρευση και τελικά ο πυκνωτής καταστρέφεται. Γι αυτό τον λόγο ο κατασκευαστής κάθε πυκνωτή αναφέρει την μέγιστη τάση λειτουργίας του, ώστε να μην πολώνεται ποτέ ο πυκνωτής με μεγαλύτερη τάση και καταστρέφεται. Ας δούμε όμως πιο αναλυτικά τι συμβαίνει όταν ένα διηλεκτρικό τοποθετείται ανάμεσα στους οπλισμούς ενός επίπεδου πυκνωτή. Αρχικά ας θεωρήσουμε κενό χώρο ανάμεσα στους οπλισμούς όπως φαίνεται στο σχ. 5.8α. Λόγω του ηλεκτρικού πεδίου Ε ο του υλικό του διηλεκτρικού ως μονωτής πολώνεται με αποτέλεσμα να δημιουργούνται ηλεκτρικά δίπολα προσανατολισμένα ως προς το Ε ο (βλέπε φόρτιση μονωτή, κεφ. 1, σχ. 1.5). Τα δίπολα αυτά δημιουργούν ένα νέο ηλεκτρικό πεδίο Ε στο χώρο του διηλεκτρικού που είναι αντίθετης φοράς αυτής του Ε ο όπως φαίνεται με τα διακεκομμένα βέλη στο σχ. 5.8β. Η γενεσιουργός αιτία του πεδίου Ε είναι στην ουσία τα επαγωγικά φορτία q που αναπτύσσονται στις περιοχές γειτνίασης του διηλεκτρικού με του οπλισμούς του πυκνωτή. Έτσι τελικά το συνολικό ηλεκτρικό πεδίο που δημιουργείται στον πυκνωτή όταν επέρχεται ηλεκτροστατική ισορροπία είναι E = E E (5.0) Εφόσον το διηλεκτρικό ελαττώνει το πεδίο θα ελαττώνει και την τάση στα άκρα του πυκνωτή διότι από την εξ. 5.4 παίρνουμε E ( E E) E E (5.1) όπου η αρχική τάση στα άκρα του πυκνωτή χωρίς το διηλεκτρικό (με κενό ανάμεσα
16 15 Σχήμα 5.8 (α) Επίπεδος πυκνωτής με φορτίο Q, χωρητικότητα και διηλεκτρικό το κενό. (β) Διηλεκτρικό τοποθετείται μεταξύ των οπλισμών μεταβάλλοντας την χωρητικότητα σε και μειώνοντας την τάση στα άκρα σε. (γ) Στην ηλεκτροστατική ισορροπία το ηλεκτρικό πεδίο Ε είναι μικρότερο του αρχικού Ε ο πριν την παρένθεση του διηλεκτρικού. στους οπλισμούς) και η τάση λόγω της πόλωσης του διηλεκτρικού. Επειδή ελαττώνεται η τάση σε αλλά το φορτίο Q στους οπλισμούς δεν αλλάζει, το διηλεκτρικό μεγαλώνει την χωρητικότητα του πυκνωτή διότι Q μιας και >. Q Q E = q q (5.) Το συμπέρασμα αυτό το εξάγαμε ήδη από την εξ Έτσι λοιπόν η διηλεκτρική σταθερά ε αυξάνει την χωρητικότητα μειώνοντας ταυτόχρονα την τάση του πυκνωτή. Με αυτόν τον τρόπο μπορούμε να φορτίσουμε και να αποθηκεύσουμε περισσότερο φορτίο στους οπλισμούς, αυξάνοντας την τάση μέχρι τα επιτρεπτά όρια του κατασκευαστή. E Q Q E = q q E = E E Q Q (a) (β) (γ) Παράδειγμα 5.7 Ένας επίπεδος πυκνωτής με αέρα έχει χωρητικότητα 1.3pF. Η απόσταση των πλακών διπλασιάζεται και ανάμεσά τους τοποθετείται κερί. Η νέα χωρητικότητα είναι.57pf. Εάν η σχετική διηλεκτρική σταθερά του αέρα είναι κ α =1, βρείτε την σχετική διηλεκτρική σταθερά του κεριού. Λύση
17 16 Η χωρητικότητα του επίπεδου πυκνωτή με μονωτικό υλικό τον αέρα, δίνεται από την σχέση α α (1) όπου ε α η διηλεκτρική σταθερά του αέρα, Α το εμβαδόν των πλακών του πυκνωτή και η απόσταση των πλακών. Αυξάνοντας την απόσταση των πλακών σε και τοποθετώντας κερί ανάμεσα από τις πλάκες, η νέα χωρητικότητα είναι () κ κ όπου ε κ η διηλεκτρική σταθερά του κεριού. Διαιρώντας κατά μέλη τις εξισώσεις 1 και παίρνουμε (3) κ κ κ κ κ κ α α α α α α Η εξ. 3 συνδέει την διηλεκτρική σταθερά του κεριού με αυτήν του αέρα. Επειδή ζητάμε την σχετική διηλεκτρική σταθερά του κεριού, εάν διαιρέσουμε την εξ. 3 με την διηλεκτρική σταθερά του κενού ε ο παίρνουμε.57f κ α κ α κ κ ο ο 1.3 F Επειδή το κερί έχει μεγαλύτερη σχετική διηλεκτρική σταθερά από τον αέρα γι αυτό τον λόγο αυξάνει την χωρητικότητα του πυκνωτή. Παράδειγμα 5.8 Επίπεδος πυκνωτής με μονωτικό υλικό τον αέρα (κ1) είναι φορτισμένος με ηλεκτρικό φορτίο Q. Στα άκρα του πυκνωτή συνδέεται βολτόμετρο που δείχνει τάση =45. Ξαφνικά εισάγεται διηλεκτρικό μεταξύ των πλακών του πυκνωτή και η ένδειξη του βολτομέτρου αλλάζει σε α) Ποια είναι η σχετική διηλεκτρική σταθερά του διηλεκτρικού; β) Ποια θα είναι η ένδειξη του βολτομέτρου εάν το διηλεκτρικό συρθεί προς τα έξω, ώστε να γεμίζει μόνο το ένα τρίτο του χώρου μεταξύ των πλακών; Λύση Η χωρητικότητα του επίπεδου πυκνωτή δίνεται από την εξ. 5.4 ως
18 17 α α (1) όπου α είναι η χωρητικότητα του πυκνωτή έχοντας ως διηλεκτρικό τον αέρα, ε α η διηλεκτρική σταθερά του αέρα, Α το εμβαδόν του κάθε οπλισμού και η απόσταση μεταξύ των οπλισμών. Όταν εισάγεται στον πυκνωτή το νέο διηλεκτρικό με διηλεκτρική σταθερά ε ισχύει δ δ () Το ηλεκτρικό φορτίο του πυκνωτή δεν αλλάζει με την τοποθέτηση του νέου διηλεκτρικού και έτσι ισχύει Q αα δ δ (3) όπου δ είναι η διαφορά δυναμικού στα άκρα του πυκνωτή μετά την εισαγωγή του διηλεκτρικού. Από την εξ. 3 παίρνουμε (4) () α α α δ α δ α δ α δ δ δ Η σχετική διηλεκτρική σταθερά του διηλεκτρικού ορίζεται ως δ (5) α Η εξ. 5 λόγω της ε δίνει δ δ β) Εάν το διηλεκτρικό τοποθετηθεί σε μια νέα θέση ώστε τα δύο τρίτα του πυκνωτή να έχουν ως διηλεκτρικό τον αέρα, ενώ το υπόλοιπο ένα τρίτο του πυκνωτή να έχει διηλεκτρικό το υλικό με κ=3.91, στην ουσία έχουμε μια διάταξη που όπως φαίνεται στο σχ. Q Α/3 (a) ε α ε δ Q (β) α δ Σχήμα 5.9 α)επίπεδος πυκνωτής με διηλεκτρικό και β) ισοδυναμία πυκνωτών με παράλληλη σύνδεση και διαφορετικά διηλεκτρικά (παράδειγμα 5.8)
19 18 5.9α. Αυτή η χωρητικότητα ισοδυναμεί με την παράλληλη σύνδεση δύο πυκνωτών με διηλεκτρικά σταθεράς ε α και ε δ αντίστοιχα όπως δείχνει το σχ. 5.9β. από δυο πυκνωτές σε. Η συνολική χωρητικότητα είναι τελικά (1) / 3 / 3 α δ α δ α δ ( ) ( α δ) (6) Όμως η εξ. 5 στην 6 δίνει (1) α ( α α) α( ) ( ) (7) Επειδή ισχύει α Q / α, τελικά παίρνουμε από την εξ. 7 Q ( ) (8) 3 α Εάν η τάση του πυκνωτή με τα δυο διαφορετικά διηλεκτρικά (σχ. 5.8α) είναι τότε ισχύει Q (9) Διαιρώντας κατά μέλη τις εξισώσεις 8 και 9 έχουμε α 1 ( ).8 α ΠΡΟΒΛΗΜΑΤΑ ΚΕΦΑΛΑΙΟΥ 5 1. Επίπεδος πυκνωτής. Επίπεδος πυκνωτής αέρος έχει χωρητικότητα 500pF και φορτίο μέτρου 0.00μ στον κάθε οπλισμό του. Οι οπλισμοί (πλάκες) βρίσκονται σε απόσταση 0.400mm μεταξύ τους. α) Πόση είναι η διαφορά δυναμικού μεταξύ των οπλισμών; β) Πόση είναι η επιφάνεια κάθε οπλισμού; γ) Πόσο είναι το μέτρο του ηλεκτρικού πεδίου μεταξύ των πλακών; δ) Πόση είναι η επιφανειακή πυκνότητα φορτίου στον κάθε οπλισμό; Απάντηση: α) 400, β) 0.06m, γ) /m και δ) /m.
20 19. Ηλεκτρικό πεδίο επίπεδου πυκνωτή. Επίπεδος πυκνωτής με φορτίο Q ομοιόμορφα κατανεμημένο στους οπλισμούς του εμβαδού Α, οι οποίοι απέχουν απόσταση, δημιουργούν ομοιογενές ηλεκτρικό πεδίο Ε όπως φαίνεται στο σχήμα. Χρησιμοποιώντας τον νόμο του Gauss αποδείξτε τη σχέση E. (Θεωρείστε κλειστή Q Q E κυβική επιφάνεια να περιβάλλει μέρος του ενός οπλισμού, όπως φαίνεται στο σχήμα, και ότι το φορτίο κατανέμεται εξίσου και στις δυο πλευρές του κάθε οπλισμού). 3. Σύνδεση πυκνωτών. Τρεις επίπεδοι πυκνωτές είναι συνδεδεμένοι παράλληλα. Το εμβαδόν κάθε πλάκας είναι Α και η απόσταση μεταξύ τους είναι d. α) Πόση πρέπει να είναι η απόσταση μεταξύ των πλακών ενός μόνο πυκνωτή εμβαδού Α, ώστε η χωρητικότητά του να είναι ίδια με εκείνη του παράλληλου συνδυασμού; β) Πόση πρέπει να είναι η απόσταση, εάν οι τρεις πυκνωτές είναι συνδεδεμένοι στη σειρά; Απάντηση: α) d/3 και β) 3d. a 4. Σύνδεση πυκνωτών Στο κύκλωμα του σχήματος, 1 =.00μF, =4.00μF και 3 =9.00μF. Η εφαρμοσμένη διαφορά δυναμικού a =48. Υπολογίστε α) το φορτίο του καθενός πυκνωτή, β) την διαφορά δυναμικού μεταξύ των πλακών κάθε πυκνωτή. Απάντηση: α) Q 1 =57.6μ, Q =115.μ, Q 3 =17.8μ, β) 1 = =8.8, 3 = Κύκλωμα πυκνωτών. Οι πυκνωτές του σχήματος 1 =3.00μF, =6.00μF, 3 =6.00μF και 4 =3.00μF συνδέονται όπως στο διάγραμμα με 1 d τον διακόπτη S ανοικτό. Η εφαρμοσμένη διαφορά δυναμικού είναι a =400. α) Πόση είναι η a 3 S 4 διαφορά δυναμικού cd ; β) Πόση είναι η διαφορά c
21 0 δυναμικού στα άκρα του καθενός πυκνωτή αφού κλείσει ο διακόπτης S; Απάντηση: α) 134 και β) Όλες ίσες με Διηλεκτρικό σε επίπεδο πυκνωτή. Δυο παράλληλες πλάκες εμβαδού 110cm φορτίζονται με το ίδιο φορτίο 890n αλλά με αντίθετο πρόσημο. Το ηλεκτρικό πεδίο μέσα στο διηλεκτρικό, το οποίο γεμίζει το χώρο ανάμεσα στις πλάκες είναι 1.4Μ/m. Υπολογίστε την σχετική διηλεκτρική σταθερά του υλικού κ. Απάντηση: 6.5.
22 Ανοικτά Ακαδημαϊκά Μαθήματα Πανεπιστήμιο Ιωαννίνων Τέλος Ενότητας
23 Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το έργο «Ανοικτά Ακαδημαϊκά Μαθήματα στο Πανεπιστήμιο Ιωαννίνων» έχει χρηματοδοτήσει μόνο τη αναδιαμόρφωση του εκπαιδευτικού υλικού. Το έργο υλοποιείται στο πλαίσιο του Επιχειρησιακού Προγράμματος «Εκπαίδευση και Δια Βίου Μάθηση» και συγχρηματοδοτείται από την Ευρωπαϊκή Ένωση (Ευρωπαϊκό Κοινωνικό Ταμείο) και από εθνικούς πόρους. Σημειώματα Σημείωμα Αναφοράς pyight Πανεπιστήμιο Ιωαννίνων, Διδάσκων: Επίκουρος Καθηγητής Δημήτριος Βλάχος. «Γενική Φυσική (Ηλεκτρομαγνητισμός). ΧΩΡΗΤΙΚΟΤΗΤΑ ΚΑΙ ΔΙΗΛΕΚΤΡΙΚΑ». Έκδοση: 1.0. Ιωάννινα 014. Διαθέσιμο από τη δικτυακή διεύθυνση: Σημείωμα Αδειοδότησης Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης eative mmns Αναφορά Δημιουργού Παρόμοια Διανομή, Διεθνής Έκδοση 4.0 [1] ή μεταγενέστερη. [1]
ΧΩΡΗΤΙΚΟΤΗΤΑ και ΔΙΗΛΕΚΤΡΙΚΑ (ΚΕΦ 24)
 ΧΩΡΗΤΙΚΟΤΗΤΑ και ΔΙΗΛΕΚΤΡΙΚΑ (ΚΕΦ 24) ΧΩΡΗΤΙΚΟΤΗΤΑ Ένας πυκνωτής έχει ως σκοπό να αποθηκεύει ηλεκτρική ενέργεια που μπορεί να ελευθερώνεται με ελεγχόμενο τρόπο σε βραχύ χρονικό διάστημα. Ένας πυκνωτής
ΧΩΡΗΤΙΚΟΤΗΤΑ και ΔΙΗΛΕΚΤΡΙΚΑ (ΚΕΦ 24) ΧΩΡΗΤΙΚΟΤΗΤΑ Ένας πυκνωτής έχει ως σκοπό να αποθηκεύει ηλεκτρική ενέργεια που μπορεί να ελευθερώνεται με ελεγχόμενο τρόπο σε βραχύ χρονικό διάστημα. Ένας πυκνωτής
ΧΩΡΗΤΙΚΟΤΗΤΑ και ΔΙΗΛΕΚΤΡΙΚΑ
 ΧΩΡΗΤΙΚΟΤΗΤΑ και ΔΙΗΛΕΚΤΡΙΚΑ ΧΩΡΗΤΙΚΟΤΗΤΑ Ένας πυκνωτής έχει ως σκοπό να αποθηκεύει ηλεκτρική ενέργεια που μπορεί να ελευθερώνεται με ελεγχόμενο τρόπο σε βραχύ χρονικό διάστημα. Αποτελείται από 2 χωρικά
ΧΩΡΗΤΙΚΟΤΗΤΑ και ΔΙΗΛΕΚΤΡΙΚΑ ΧΩΡΗΤΙΚΟΤΗΤΑ Ένας πυκνωτής έχει ως σκοπό να αποθηκεύει ηλεκτρική ενέργεια που μπορεί να ελευθερώνεται με ελεγχόμενο τρόπο σε βραχύ χρονικό διάστημα. Αποτελείται από 2 χωρικά
Πυκνωτές και διηλεκτρικά. Ιωάννης Γκιάλας 21 Μαρτίου 2014
 Πυκνωτές και διηλεκτρικά Ιωάννης Γκιάλας 1 Μαρτίου 014 Μεταλλικά σώματα (τυχαίου σχήματος) που συνδέονται με τους πόλους μίας μπαταρίας Φορτίο πυκνωτή = φορτίο ενός οπλισμού Δυναμικό πυκνωτή η διαφορά
Πυκνωτές και διηλεκτρικά Ιωάννης Γκιάλας 1 Μαρτίου 014 Μεταλλικά σώματα (τυχαίου σχήματος) που συνδέονται με τους πόλους μίας μπαταρίας Φορτίο πυκνωτή = φορτίο ενός οπλισμού Δυναμικό πυκνωτή η διαφορά
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΑ ΠΕΔΙΑ ΣΤΗΝ ΥΛΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΑ ΠΕΔΙΑ ΣΤΗΝ ΥΛΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
4η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1. Ασκήσεις 4 ου Κεφαλαίου
 4η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ Ασκήσεις 4 ου Κεφαλαίου. Ένας επίπεδος πυκνωτής αποτελείται από δύο παράλληλους οπλισμούς, οι οποίοι απέχουν μεταξύ τους.8 mm και έχουν εμβαδόν 7.6 cm
4η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ Ασκήσεις 4 ου Κεφαλαίου. Ένας επίπεδος πυκνωτής αποτελείται από δύο παράλληλους οπλισμούς, οι οποίοι απέχουν μεταξύ τους.8 mm και έχουν εμβαδόν 7.6 cm
Κεφάλαιο 24 Χωρητικότητα, Διηλεκτρικά, Αποθήκευση Ηλεκτρικής Ενέργειας. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 24 Χωρητικότητα, Διηλεκτρικά, Αποθήκευση Ηλεκτρικής Ενέργειας Περιεχόμενα 24 Πυκνωτές Προσδιορισμός Χωρητικότητας Πυκνωτή Παράλληλη και σε σειρά σύνδεση πυκνωτών Αποθήκευση Ηλεκτρικής Ενέργειας
Κεφάλαιο 24 Χωρητικότητα, Διηλεκτρικά, Αποθήκευση Ηλεκτρικής Ενέργειας Περιεχόμενα 24 Πυκνωτές Προσδιορισμός Χωρητικότητας Πυκνωτή Παράλληλη και σε σειρά σύνδεση πυκνωτών Αποθήκευση Ηλεκτρικής Ενέργειας
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα. ΔΙΑΛΕΞΗ 14 Πυκνωτές Διηλεκτρικά
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 14 Πυκνωτές Διηλεκτρικά ΦΥΣ102 1 Πυκνωτές Ένας πυκνωτής αποτελείται από δύο αγωγούς
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 14 Πυκνωτές Διηλεκτρικά ΦΥΣ102 1 Πυκνωτές Ένας πυκνωτής αποτελείται από δύο αγωγούς
(α) 1. (β) Το σύστημα βρίσκεται υπό διαφορά δυναμικού 12 V: U ολ = 1 2 C ολ(δv) 2 = J.
 4 η Ομάδα Ασκήσεων Δύο πυκνωτές C=5 μf και C=40 μf συνδέονται παράλληλα στους ακροδέκτες πηγών τάσης VS=50 V και VS=75 V αντίστοιχα και φορτίζονται Στην συνέχεια αποσυνδέονται και συνδέονται μεταξύ τους,
4 η Ομάδα Ασκήσεων Δύο πυκνωτές C=5 μf και C=40 μf συνδέονται παράλληλα στους ακροδέκτες πηγών τάσης VS=50 V και VS=75 V αντίστοιχα και φορτίζονται Στην συνέχεια αποσυνδέονται και συνδέονται μεταξύ τους,
ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΧΩΡΗΤΙΚΟΤΗΤΑ ΚΑΙ ΔΙΗΛΕΚΤΡΙΚΑ
 ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΧΩΡΗΤΙΚΟΤΗΤΑ ΚΑΙ ΔΙΗΛΕΚΤΡΙΚΑ 1 1. ΧΩΡΗΤΙΚΟΤΗΤΑ ΚΑΙ ΠΥΚΝΩΤΕΣ Ένας πυκνωτής είναι μια διάταξη που αποθηκεύει ηλεκτρικό φορτίο. Οι πυκνωτές μπορεί να διαφέρουν σε σχήμα και μέγεθος αλλά
ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΧΩΡΗΤΙΚΟΤΗΤΑ ΚΑΙ ΔΙΗΛΕΚΤΡΙΚΑ 1 1. ΧΩΡΗΤΙΚΟΤΗΤΑ ΚΑΙ ΠΥΚΝΩΤΕΣ Ένας πυκνωτής είναι μια διάταξη που αποθηκεύει ηλεκτρικό φορτίο. Οι πυκνωτές μπορεί να διαφέρουν σε σχήμα και μέγεθος αλλά
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Χωρητικότητα Εικόνα: Όλες οι παραπάνω συσκευές είναι πυκνωτές, οι οποίοι αποθηκεύουν ηλεκτρικό φορτίο και ενέργεια. Ο πυκνωτής είναι ένα είδος κυκλώματος που μπορούμε να συνδυάσουμε
Φυσική για Μηχανικούς Χωρητικότητα Εικόνα: Όλες οι παραπάνω συσκευές είναι πυκνωτές, οι οποίοι αποθηκεύουν ηλεκτρικό φορτίο και ενέργεια. Ο πυκνωτής είναι ένα είδος κυκλώματος που μπορούμε να συνδυάσουμε
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Ασκήσεις 2 ου Κεφαλαίου, Νόμος του Gauss
 Ασκήσεις 2 ου Κεφαλαίου, Νόμος του Guss 22.36.Μία αγώγιμη σφαίρα με φορτίο q έχει ακτίνα α. Η σφαίρα βρίσκεται στο εσωτερικό μίας κοίλης ομόκεντρης αγώγιμης σφαίρας με εσωτερική ακτίνα και εξωτερική ακτίνα.
Ασκήσεις 2 ου Κεφαλαίου, Νόμος του Guss 22.36.Μία αγώγιμη σφαίρα με φορτίο q έχει ακτίνα α. Η σφαίρα βρίσκεται στο εσωτερικό μίας κοίλης ομόκεντρης αγώγιμης σφαίρας με εσωτερική ακτίνα και εξωτερική ακτίνα.
Κεφάλαιο Η4. Χωρητικότητα και διηλεκτρικά
 Κεφάλαιο Η4 Χωρητικότητα και διηλεκτρικά Κυκλώματα και στοιχεία κυκλωμάτων Τα ηλεκτρικά κυκλώματα αποτελούν τη βάση για το μεγαλύτερο μέρος των συσκευών που χρησιμοποιούνται στην κοινωνία μας. Τα ηλεκτρικά
Κεφάλαιο Η4 Χωρητικότητα και διηλεκτρικά Κυκλώματα και στοιχεία κυκλωμάτων Τα ηλεκτρικά κυκλώματα αποτελούν τη βάση για το μεγαλύτερο μέρος των συσκευών που χρησιμοποιούνται στην κοινωνία μας. Τα ηλεκτρικά
Φυσική ΙΙΙ. Ενότητα 4: Ηλεκτρικά Κυκλώματα. Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής
 Φυσική ΙΙΙ Ενότητα 4: Ηλεκτρικά Κυκλώματα Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Ασκήσεις ΦΙΙΙ Ηλεκτρικά Κυκλώματα Γ. Βούλγαρης 2 Ασκήσεις κατανομές φορτίου 1) Ένα γραμμικό φορτίο με
Φυσική ΙΙΙ Ενότητα 4: Ηλεκτρικά Κυκλώματα Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Ασκήσεις ΦΙΙΙ Ηλεκτρικά Κυκλώματα Γ. Βούλγαρης 2 Ασκήσεις κατανομές φορτίου 1) Ένα γραμμικό φορτίο με
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΤΕΧΝΙΚΕΣ ΥΠΟΛΟΓΙΣΜΟΥ ΗΛΕΚΤΡΙΚΟΥ ΔΥΝΑΜΙΚΟΥ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΤΕΧΝΙΚΕΣ ΥΠΟΛΟΓΙΣΜΟΥ ΗΛΕΚΤΡΙΚΟΥ ΔΥΝΑΜΙΚΟΥ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ
 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
Ηλεκτρομαγνητισμός. Ηλεκτρικό πεδίο νόμος Gauss. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Νόμος Gauss Ο νόµος του Gauss εκφράζει τη σχέση μεταξύ της συνολικής ηλεκτρικής ροής που διέρχεται από μια κλειστή επιφάνεια και του φορτίου
Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Νόμος Gauss Ο νόµος του Gauss εκφράζει τη σχέση μεταξύ της συνολικής ηλεκτρικής ροής που διέρχεται από μια κλειστή επιφάνεια και του φορτίου
Ο πυκνωτής είναι μια διάταξη αποθήκευσης ηλεκτρικού φορτίου, επομένως και ηλεκτρικής ενέργειας.
 ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Ο πυκνωτής Ο πυκνωτής είναι μια διάταξη αποθήκευσης ηλεκτρικού φορτίου, επομένως και ηλεκτρικής ενέργειας. Η απλούστερη μορφή πυκνωτή είναι ο επίπεδος πυκνωτής, ο οποίος
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Ο πυκνωτής Ο πυκνωτής είναι μια διάταξη αποθήκευσης ηλεκτρικού φορτίου, επομένως και ηλεκτρικής ενέργειας. Η απλούστερη μορφή πυκνωτή είναι ο επίπεδος πυκνωτής, ο οποίος
Εφαρμογές Νόμος Gauss, Ηλεκτρικά πεδία. Ιωάννης Γκιάλας 7 Μαρτίου 2014
 Εφαρμογές Νόμος Gauss, Ηλεκτρικά πεδία Ιωάννης Γκιάλας 7 Μαρτίου 14 Άσκηση: Ηλεκτρικό πεδίο διακριτών φορτίων Δύο ίσα θετικά φορτία q βρίσκονται σε απόσταση α μεταξύ τους. Να βρεθεί η ακτίνα του κύκλου,
Εφαρμογές Νόμος Gauss, Ηλεκτρικά πεδία Ιωάννης Γκιάλας 7 Μαρτίου 14 Άσκηση: Ηλεκτρικό πεδίο διακριτών φορτίων Δύο ίσα θετικά φορτία q βρίσκονται σε απόσταση α μεταξύ τους. Να βρεθεί η ακτίνα του κύκλου,
ΠΥΚΝΩΤΕΣ. Ένα τέτοιο σύστημα ονομάζεται πυκνωτής και οι δύο αγωγοί οπλισμοί του πυκνωτή
 Δύο κομμάτια μέταλλο (αγωγοί) πολύ κοντά μεταξύ τους αλλά δεν ακουμπούν. Χωρίζονται από αέρα ή αλλο μονωτικό. Φορτίο +Q υπάρχει στον ένα αγωγό και Q στον άλλο οπότε το σύστημα ως σύνολο είναι ουδέτερο.
Δύο κομμάτια μέταλλο (αγωγοί) πολύ κοντά μεταξύ τους αλλά δεν ακουμπούν. Χωρίζονται από αέρα ή αλλο μονωτικό. Φορτίο +Q υπάρχει στον ένα αγωγό και Q στον άλλο οπότε το σύστημα ως σύνολο είναι ουδέτερο.
Δυνάμεις μεταξύ ηλεκτρικών φορτίων
 Φυσική ενικής Παιδείας Β Λυκείου Δυνάμεις μεταξύ εκτρικών φορτίων- 3. Δυνάμεις μεταξύ εκτρικών φορτίων Φυσική ενικής Παιδείας Β Λυκείου Δυνάμεις μεταξύ εκτρικών φορτίων-. Νόμος του Coulomb Ανάμεσα σε δύο
Φυσική ενικής Παιδείας Β Λυκείου Δυνάμεις μεταξύ εκτρικών φορτίων- 3. Δυνάμεις μεταξύ εκτρικών φορτίων Φυσική ενικής Παιδείας Β Λυκείου Δυνάμεις μεταξύ εκτρικών φορτίων-. Νόμος του Coulomb Ανάμεσα σε δύο
Πυκνότητα φορτίου. dq dv. Μικρή Περιοχή. φορτίου. Χωρική ρ Q V. Επιφανειακή σ. dq da Γραµµική λ Q A. σ = dq dl. Q l. Γ.
 Πυκνότητα φορτίου Πυκνότητα φορτίου Οµοιόµορφη Μικρή Περιοχή Χωρική ρ Q V ρ= dq dv Επιφανειακή σ Q A σ = dq da Γραµµική λ Q l λ= dq dl Γ. Βούλγαρης 1 Παράσταση της έντασης Ηλεκτρικού Πεδίου. Η Εφαπτόµενη
Πυκνότητα φορτίου Πυκνότητα φορτίου Οµοιόµορφη Μικρή Περιοχή Χωρική ρ Q V ρ= dq dv Επιφανειακή σ Q A σ = dq da Γραµµική λ Q l λ= dq dl Γ. Βούλγαρης 1 Παράσταση της έντασης Ηλεκτρικού Πεδίου. Η Εφαπτόµενη
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ ΤΕΛΕΙΟΥΣ ΑΓΩΓΟΥΣ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ ΤΕΛΕΙΟΥΣ ΑΓΩΓΟΥΣ
ΘΕΜΑΤΑ ΠΑΛΑΙΟΤΕΡΩΝ ΕΞΕΤΑΣΕΩΝ
 ΘΕΜΑΤΑ ΠΑΛΑΙΟΤΕΡΩΝ ΕΞΕΤΑΣΕΩΝ Όπως θα παρατηρήσετε, τα θέματα αφορούν σε θεωρία που έχει διδαχθεί στις παραδόσεις και σε ασκήσεις που είτε προέρχονται από τα λυμένα παραδείγματα του βιβλίου, είτε έχουν
ΘΕΜΑΤΑ ΠΑΛΑΙΟΤΕΡΩΝ ΕΞΕΤΑΣΕΩΝ Όπως θα παρατηρήσετε, τα θέματα αφορούν σε θεωρία που έχει διδαχθεί στις παραδόσεις και σε ασκήσεις που είτε προέρχονται από τα λυμένα παραδείγματα του βιβλίου, είτε έχουν
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS 1 1. ΗΛΕΚΤΡΙΚΗ ΡΟΗ O νόμος του Gauss και o νόμος του Coulomb είναι δύο εναλλακτικές διατυπώσεις της ίδιας βασικής σχέσης μεταξύ μιας κατανομής φορτίου και του
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS 1 1. ΗΛΕΚΤΡΙΚΗ ΡΟΗ O νόμος του Gauss και o νόμος του Coulomb είναι δύο εναλλακτικές διατυπώσεις της ίδιας βασικής σχέσης μεταξύ μιας κατανομής φορτίου και του
E = E 0 + E = E 0 P ϵ 0. = 1 + χ r. = Q E 0 l
 Πυκνωτής με διηλεκτρικό Πυκνωτής με ορθογώνιους οπλισμούς εμβαδού A και απόσταση μεταξύ των οπλισμών l έχει ϕορτίο Q. Η επιϕανειακή πυκνότητα ϕορτίου σε κάθε οπλισμό θα είνα σ = ±Q/A. Το ηλεκτρικό πεδίο
Πυκνωτής με διηλεκτρικό Πυκνωτής με ορθογώνιους οπλισμούς εμβαδού A και απόσταση μεταξύ των οπλισμών l έχει ϕορτίο Q. Η επιϕανειακή πυκνότητα ϕορτίου σε κάθε οπλισμό θα είνα σ = ±Q/A. Το ηλεκτρικό πεδίο
Κεφάλαιο Η2. Ο νόµος του Gauss
 Κεφάλαιο Η2 Ο νόµος του Gauss Ο νόµος του Gauss Ο νόµος του Gauss µπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού του ηλεκτρικού πεδίου. Ο νόµος του Gauss βασίζεται στο γεγονός ότι η ηλεκτρική
Κεφάλαιο Η2 Ο νόµος του Gauss Ο νόµος του Gauss Ο νόµος του Gauss µπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού του ηλεκτρικού πεδίου. Ο νόµος του Gauss βασίζεται στο γεγονός ότι η ηλεκτρική
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
ΔΥΝΑΜΙΚΟ ΔΙΑΦΟΡΑ ΔΥΝΑΜΙΚΟΥ
 ΔΥΝΑΜΙΚΟ ΔΙΑΦΟΡΑ ΔΥΝΑΜΙΚΟΥ Υποθέστε ότι έχουμε μερικά ακίνητα φορτισμένα σώματα (σχ.). Τα σώματα αυτά δημιουργούν γύρω τους ηλεκτρικό πεδίο. Αν σε κάποιο σημείο Α του ηλεκτρικού πεδίου τοποθετήσουμε ένα
ΔΥΝΑΜΙΚΟ ΔΙΑΦΟΡΑ ΔΥΝΑΜΙΚΟΥ Υποθέστε ότι έχουμε μερικά ακίνητα φορτισμένα σώματα (σχ.). Τα σώματα αυτά δημιουργούν γύρω τους ηλεκτρικό πεδίο. Αν σε κάποιο σημείο Α του ηλεκτρικού πεδίου τοποθετήσουμε ένα
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ, Αγωγοί Διηλεκτρικά. Ν. Τράκας, Ι. Ράπτης Ζωγράφου 27.3.
 ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) 8-9 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Αγωγοί Διηλεκτρικά Ν. Τράκας Ι. Ράπτης Ζωγράφου 7.3.9 Να επιστραφούν λυμένες μέχρι.4.9 οι ασκήσεις 3 4 5 [ΠΡΟΣΟΧΗ: Οι λύσεις
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) 8-9 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Αγωγοί Διηλεκτρικά Ν. Τράκας Ι. Ράπτης Ζωγράφου 7.3.9 Να επιστραφούν λυμένες μέχρι.4.9 οι ασκήσεις 3 4 5 [ΠΡΟΣΟΧΗ: Οι λύσεις
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Ηλεκτρομαγνητισμός
 Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Ηλεκτρομαγνητισμός Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών 7/15/2014 Κυκλώματα και στοιχεία κυκλωμάτων Χωρητικότητα
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Ηλεκτρομαγνητισμός Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών 7/15/2014 Κυκλώματα και στοιχεία κυκλωμάτων Χωρητικότητα
Κεφάλαιο 24 Χωρητικότητα, Διηλεκτρικά, Dielectrics, Αποθήκευση Ηλεκτρικής Ενέργειας. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 24 Χωρητικότητα, Διηλεκτρικά, Dielectrics, Αποθήκευση Ηλεκτρικής Ενέργειας Περιεχόµενα 24 Πυκνωτές Προσδιορισµός Χωρητικότητας Πυκνωτή Παράλληλη και σε σειρά σύνδεση πυκνωτών Αποθήκευση Ηλεκτρικής
Κεφάλαιο 24 Χωρητικότητα, Διηλεκτρικά, Dielectrics, Αποθήκευση Ηλεκτρικής Ενέργειας Περιεχόµενα 24 Πυκνωτές Προσδιορισµός Χωρητικότητας Πυκνωτή Παράλληλη και σε σειρά σύνδεση πυκνωτών Αποθήκευση Ηλεκτρικής
Από τι αποτελείται ένας πυκνωτής
 Πυκνωτές Οι πυκνωτές είναι διατάξεις οι οποίες αποθηκεύουν ηλεκτρικό φορτίο. Xρησιµοποιούνται ως «αποθήκες ενέργειας» που µπορούν να φορτίζονται µε αργό ρυθµό και µετά να εκφορτίζονται ακαριαία, παρέχοντας
Πυκνωτές Οι πυκνωτές είναι διατάξεις οι οποίες αποθηκεύουν ηλεκτρικό φορτίο. Xρησιµοποιούνται ως «αποθήκες ενέργειας» που µπορούν να φορτίζονται µε αργό ρυθµό και µετά να εκφορτίζονται ακαριαία, παρέχοντας
1)Σε ένα πυκνωτή, η σχέση μεταξύ φορτίου Q και τάσης V μεταξύ των οπλισμών του, απεικονίζεται στο διάγραμμα.
 1)Σε ένα πυκνωτή, η σχέση μεταξύ φορτίου Q και τάσης V μεταξύ των οπλισμών του, απεικονίζεται στο διάγραμμα. Να επιλέξετε τη σωστή απάντηση. Η χωρητικότητα του πυκνωτή είναι: α. 5 F, β. 1 / 5 μf, γ. 5
1)Σε ένα πυκνωτή, η σχέση μεταξύ φορτίου Q και τάσης V μεταξύ των οπλισμών του, απεικονίζεται στο διάγραμμα. Να επιλέξετε τη σωστή απάντηση. Η χωρητικότητα του πυκνωτή είναι: α. 5 F, β. 1 / 5 μf, γ. 5
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Ενημέρωση. Η διδασκαλία του μαθήματος, όλες οι ασκήσεις προέρχονται από το βιβλίο: «Πανεπιστημιακή
 Ενημέρωση Η διδασκαλία του μαθήματος, πολλά από τα σχήματα και όλες οι ασκήσεις προέρχονται από το βιβλίο: «Πανεπιστημιακή Φυσική» του Hugh Young των Εκδόσεων Παπαζήση, οι οποίες μας επέτρεψαν τη χρήση
Ενημέρωση Η διδασκαλία του μαθήματος, πολλά από τα σχήματα και όλες οι ασκήσεις προέρχονται από το βιβλίο: «Πανεπιστημιακή Φυσική» του Hugh Young των Εκδόσεων Παπαζήση, οι οποίες μας επέτρεψαν τη χρήση
ΦΥΣΙΚΗ ΙΙΙ. Ενότητα: Ηλεκτροστατική ΜΑΪΝΤΑΣ ΞΑΝΘΟΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ
 ΦΥΣΙΚΗ ΙΙΙ Ενότητα: Ηλεκτροστατική ΜΑΪΝΤΑΣ ΞΑΝΘΟΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ Σελίδα 2 ΑΣΚΗΣΕΙΣ... 4 Σελίδα 3 ΑΣΚΗΣΕΙΣ Ηλεκτροστατική 1. Στις κορυφές κανονικού n-πλεύρου τοποθετούνται ίδια φορτία q. Να δειχθεί ότι η
ΦΥΣΙΚΗ ΙΙΙ Ενότητα: Ηλεκτροστατική ΜΑΪΝΤΑΣ ΞΑΝΘΟΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ Σελίδα 2 ΑΣΚΗΣΕΙΣ... 4 Σελίδα 3 ΑΣΚΗΣΕΙΣ Ηλεκτροστατική 1. Στις κορυφές κανονικού n-πλεύρου τοποθετούνται ίδια φορτία q. Να δειχθεί ότι η
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Χωρητικότητα Εικόνα: Όλες οι παραπάνω συσκευές είναι πυκνωτές, οι οποίοι αποθηκεύουν ηλεκτρικό φορτίο και ενέργεια. Ο πυκνωτής είναι ένα είδος κυκλώματος που μπορούμε να συνδυάσουμε
Φυσική για Μηχανικούς Χωρητικότητα Εικόνα: Όλες οι παραπάνω συσκευές είναι πυκνωτές, οι οποίοι αποθηκεύουν ηλεκτρικό φορτίο και ενέργεια. Ο πυκνωτής είναι ένα είδος κυκλώματος που μπορούμε να συνδυάσουμε
Σε έναν επίπεδο πυκνωτή οι μεταλλικές πλάκες έχουν εμβαδό 0,2 m 2, και απέχουν απόσταση 8,85 mm ενώ μεταξύ των οπλισμών του μεσολαβεί αέρας.
 ΠΥΚΝΩΤΕΣ ΑΣΚΗΣΕΙΣ ΤΡΑΠΕΖΑΣ ΘΕΜΑ Δ Σε έναν επίπεδο πυκνωτή οι μεταλλικές πλάκες έχουν εμβαδό 0,2 m 2, και απέχουν απόσταση 8,85 mm ενώ μεταξύ των οπλισμών του μεσολαβεί αέρας Υπολογίστε τη χωρητικότητα
ΠΥΚΝΩΤΕΣ ΑΣΚΗΣΕΙΣ ΤΡΑΠΕΖΑΣ ΘΕΜΑ Δ Σε έναν επίπεδο πυκνωτή οι μεταλλικές πλάκες έχουν εμβαδό 0,2 m 2, και απέχουν απόσταση 8,85 mm ενώ μεταξύ των οπλισμών του μεσολαβεί αέρας Υπολογίστε τη χωρητικότητα
Φυσική IΙ. Ενότητα 6: Πυκνωτές. Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών
 Φυσική IΙ Ενότητα 6: Πυκνωτές Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Ορισμός χωρητικότητας πυκνωτή Ανάλυση γεωμετρίας και χαρακτηριστικών μεγεθών επίπεδου πυκνωτή
Φυσική IΙ Ενότητα 6: Πυκνωτές Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Ορισμός χωρητικότητας πυκνωτή Ανάλυση γεωμετρίας και χαρακτηριστικών μεγεθών επίπεδου πυκνωτή
ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙΙ Μάθημα ασκήσεων 8: Καλώδια Λαμπρίδης Δημήτρης Ανδρέου Γεώργιος Δούκας Δημήτριος Τμήμα Ηλεκτρολόγων Μηχανικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙΙ Μάθημα ασκήσεων 8: Καλώδια Λαμπρίδης Δημήτρης Ανδρέου Γεώργιος Δούκας Δημήτριος Τμήμα Ηλεκτρολόγων Μηχανικών
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Ηλεκτρομαγνητισμός
 Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Ηλεκτρομαγνητισμός Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών 7/15/2014 Ο νόμος του Gauss Νόμος Gauss Ο νόμος
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Ηλεκτρομαγνητισμός Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών 7/15/2014 Ο νόμος του Gauss Νόμος Gauss Ο νόμος
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ. Ενότητα 4: Χωρητικότητα και διηλεκτρικά. Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε.
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ενότητα 4: Χωρητικότητα και διηλεκτρικά Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ενότητα 4: Χωρητικότητα και διηλεκτρικά Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού. Ιωάννης Γκιάλας 14 Μαρτίου 2014
 Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού Ιωάννης Γκιάλας 14 Μαρτίου 2014 Έργο ηλεκτροστατικής δύναμης W F Δl W N i i1 F Δl i Η μετατόπιση Δl περιγράφεται από ένα διάνυσμα που
Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού Ιωάννης Γκιάλας 14 Μαρτίου 2014 Έργο ηλεκτροστατικής δύναμης W F Δl W N i i1 F Δl i Η μετατόπιση Δl περιγράφεται από ένα διάνυσμα που
4η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1. Ασκήσεις 4 ου Κεφαλαίου
 4η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ Ασκήσεις 4 ου Κεφαλαίου. (α) Βρείτε την ισοδύναμη χωρητικότητα μεταξύ των άκρων α και β της συνδεσμολογίας του σχήματος. Θεωρήστε ότι = 5 μ, = μ, και =
4η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ Ασκήσεις 4 ου Κεφαλαίου. (α) Βρείτε την ισοδύναμη χωρητικότητα μεταξύ των άκρων α και β της συνδεσμολογίας του σχήματος. Θεωρήστε ότι = 5 μ, = μ, και =
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ. Ενότητα 2: Ο νόμος του Gauss. Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε.
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ενότητα 2: Ο νόμος του Gauss Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ενότητα 2: Ο νόμος του Gauss Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Ηλεκτρισμός & Μαγνητισμός
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρισμός & Μαγνητισμός Το ρεύμα μετατώπισης Διδάσκων : Επίκ. Καθ. Ν. Νικολής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης reative
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρισμός & Μαγνητισμός Το ρεύμα μετατώπισης Διδάσκων : Επίκ. Καθ. Ν. Νικολής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης reative
Ηλεκτρικό φορτίο Ηλεκτρικό Πεδίο
 Ηλεκτρικό Φορτίο Ν.Coulomb Όπου χρειάζεται στις παρακάτω ασκήσεις θεωρείστε δεδομένες τις τιμές των μεγεθών: k ηλ = 9.10 9 Nm 2 /C 2, e = 1,6.10-19 C, m e = 9,1.10-31 kg, m p = 1,7.10-27 kg, g = 10 m/s
Ηλεκτρικό Φορτίο Ν.Coulomb Όπου χρειάζεται στις παρακάτω ασκήσεις θεωρείστε δεδομένες τις τιμές των μεγεθών: k ηλ = 9.10 9 Nm 2 /C 2, e = 1,6.10-19 C, m e = 9,1.10-31 kg, m p = 1,7.10-27 kg, g = 10 m/s
Α) Η επιφάνεια Gauss έχει ακτίνα r μεγαλύτερη ή ίση της ακτίνας του κελύφους, r α.
 1. Ένα σφαιρικό κέλυφος που θεωρούμε ότι έχει αμελητέο πάχος έχει ακτίνα α και φέρει φορτίο Q, ομοιόμορφα κατανεμημένο στην επιφάνειά του. Βρείτε την ένταση του ηλεκτρικού πεδίου στο εξωτερικό και στο
1. Ένα σφαιρικό κέλυφος που θεωρούμε ότι έχει αμελητέο πάχος έχει ακτίνα α και φέρει φορτίο Q, ομοιόμορφα κατανεμημένο στην επιφάνειά του. Βρείτε την ένταση του ηλεκτρικού πεδίου στο εξωτερικό και στο
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ. Ν. Τράκας, Ι. Ράπτης 2/4/2018
 ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) 7-8 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Ν. Τράκας Ι. Ράπτης /4/8 Παράδοση των 3 4 5 μέχρι /4/8 [Σε χειρόγραφη μορφή στο μάθημα ή σε μορφή ενιαίου αρχείου PDF στις
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) 7-8 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Ν. Τράκας Ι. Ράπτης /4/8 Παράδοση των 3 4 5 μέχρι /4/8 [Σε χειρόγραφη μορφή στο μάθημα ή σε μορφή ενιαίου αρχείου PDF στις
ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23
 ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23 Ροή (γενικά): Ηλεκτρική Ροή Η ποσότητα ενός μεγέθους που διέρχεται από μία επιφάνεια. Ε Ε dα dα θ Ε Ε θ Ηλεκτρική ροή dφ Ε μέσω στοιχειώδους επιφάνειας da (αφού da στοιχειώδης
ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23 Ροή (γενικά): Ηλεκτρική Ροή Η ποσότητα ενός μεγέθους που διέρχεται από μία επιφάνεια. Ε Ε dα dα θ Ε Ε θ Ηλεκτρική ροή dφ Ε μέσω στοιχειώδους επιφάνειας da (αφού da στοιχειώδης
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 11 Εισαγωγή στην Ηλεκτροδυναμική Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο ΦΥΣ102 1 Στατικός
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 11 Εισαγωγή στην Ηλεκτροδυναμική Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο ΦΥΣ102 1 Στατικός
ΦΥΣΙΚΗ ΓΙΑ ΜΗΧΑΝΙΚΟΥΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΗΛΕΚΤΡΙΣΜΟΣ ΜΑΓΝΗΤΙΣΜΟΣ
 ΦΥΣΙΚΗ ΓΙΑ ΜΗΧΑΝΙΚΟΥΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΗΛΕΚΤΡΙΣΜΟΣ ΜΑΓΝΗΤΙΣΜΟΣ Μοντέλο ατόμου m p m n =1,7x10-27 Kg m e =9,1x10-31 Kg Πυρήνας: πρωτόνια (p + ) και νετρόνια (n) Γύρω από τον πυρήνα νέφος ηλεκτρονίων (e -
ΦΥΣΙΚΗ ΓΙΑ ΜΗΧΑΝΙΚΟΥΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΗΛΕΚΤΡΙΣΜΟΣ ΜΑΓΝΗΤΙΣΜΟΣ Μοντέλο ατόμου m p m n =1,7x10-27 Kg m e =9,1x10-31 Kg Πυρήνας: πρωτόνια (p + ) και νετρόνια (n) Γύρω από τον πυρήνα νέφος ηλεκτρονίων (e -
ΔΙΑΛΕΞΗ 2 Νόμος Gauss, κίνηση σε ηλεκτρικό πεδίο. Ι. Γκιάλας Χίος, 28 Φεβρουαρίου 2014
 ΔΙΑΛΕΞΗ 2 Νόμος Gauss, κίνηση σε ηλεκτρικό πεδίο Ι. Γκιάλας Χίος, 28 Φεβρουαρίου 214 Ασκηση συνολικό φορτίο λεκτρικό φορτίο Q είναι κατανεμημένο σε σφαιρικό όγκο ακτίνας R με πυκνότητα ορτίου ανάλογη του
ΔΙΑΛΕΞΗ 2 Νόμος Gauss, κίνηση σε ηλεκτρικό πεδίο Ι. Γκιάλας Χίος, 28 Φεβρουαρίου 214 Ασκηση συνολικό φορτίο λεκτρικό φορτίο Q είναι κατανεμημένο σε σφαιρικό όγκο ακτίνας R με πυκνότητα ορτίου ανάλογη του
Ανάστροφη πόλωση της επαφής p n
 Ανάστροφη πόλωση της επαφής p n Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo Επαφή p n Ανάστροφη πόλωση Πολώνουμε
Ανάστροφη πόλωση της επαφής p n Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo Επαφή p n Ανάστροφη πόλωση Πολώνουμε
Φυσική IΙ. Ενότητα 3: Ο Νόμος του Gauss. Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών
 Φυσική IΙ Ενότητα 3: Ο Νόμος του Gauss Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Ορισμός και ερμηνεία των δυναμικών γραμμών Παραδείγματα δυναμικών γραμμών σημειακού φορτίου,
Φυσική IΙ Ενότητα 3: Ο Νόμος του Gauss Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Ορισμός και ερμηνεία των δυναμικών γραμμών Παραδείγματα δυναμικών γραμμών σημειακού φορτίου,
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
(α) Σχ. 5/30 Σύμβολα πυκνωτή (α) με πολικότητα, (β) χωρίς πολικότητα
 5. ΗΛΕΚΤΡΟΝΙΚΑ ΕΞΑΡΤΗΜΑΤΑ Ι ( ΠΥΚΝΩΤΕΣ) Πυκνωτές O πυκνωτής είναι ένα ηλεκτρικό εξάρτημα το οποίο έχει την ιδιότητα να απορροφά και να αποθηκεύει ηλεκτρική ενέργεια και να την απελευθερώνει, σε προκαθορισμένο
5. ΗΛΕΚΤΡΟΝΙΚΑ ΕΞΑΡΤΗΜΑΤΑ Ι ( ΠΥΚΝΩΤΕΣ) Πυκνωτές O πυκνωτής είναι ένα ηλεκτρικό εξάρτημα το οποίο έχει την ιδιότητα να απορροφά και να αποθηκεύει ηλεκτρική ενέργεια και να την απελευθερώνει, σε προκαθορισμένο
Ανάστροφη πόλωση της επαφής p n
 Ανάστροφη πόλωση της επαφής p n Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo Επαφή p n Ανάστροφη πόλωση Πολώνουμε
Ανάστροφη πόλωση της επαφής p n Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo Επαφή p n Ανάστροφη πόλωση Πολώνουμε
ΑΡΧΙΚΗ ΚΑΤΑΣΤΑΣΗ 1 ΠΥΚΝΩΤΗ :
 ΤΕΙ ΧΑΛΚΙΔΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΙΚΩΝ ΜΕΤΡΗΣΕΩΝ Α/Α ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ : ΑΣΚΗΣΗ 5 η Τίτλος Άσκησης : ΜΕΤΡΗΣΗ ΧΩΡΗΤΙΚΟΤΗΤΑΣ ΜΕ ΑΜΕΣΕΣ ΚΑΙ ΕΜΜΕΣΕΣ ΜΕΘΟΔΟΥΣ Θεωρητική Ανάλυση Πυκνωτής
ΤΕΙ ΧΑΛΚΙΔΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΗΛΕΚΤΡΙΚΩΝ ΜΕΤΡΗΣΕΩΝ Α/Α ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ : ΑΣΚΗΣΗ 5 η Τίτλος Άσκησης : ΜΕΤΡΗΣΗ ΧΩΡΗΤΙΚΟΤΗΤΑΣ ΜΕ ΑΜΕΣΕΣ ΚΑΙ ΕΜΜΕΣΕΣ ΜΕΘΟΔΟΥΣ Θεωρητική Ανάλυση Πυκνωτής
Κεφάλαιο 22 Νόµος του Gauss. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 22 Νόµος του Gauss Περιεχόµενα Κεφαλαίου 22 Ηλεκτρική Ροή Ο Νόµος του Gauss Εφαρµογές του Νόµου του Gauss Πειραµατικές επιβεβαιώσεις για τους Νόµους των Gauss και Coulomb 22-1 Ηλεκτρική Ροή Ηλεκτρική
Κεφάλαιο 22 Νόµος του Gauss Περιεχόµενα Κεφαλαίου 22 Ηλεκτρική Ροή Ο Νόµος του Gauss Εφαρµογές του Νόµου του Gauss Πειραµατικές επιβεβαιώσεις για τους Νόµους των Gauss και Coulomb 22-1 Ηλεκτρική Ροή Ηλεκτρική
2. Δυναμικό και χωρητικότητα αγωγού.
 . Δυναμικό και χωρητικότητα αγωγού. Σε όλα τα σηµεία ενός αγωγού, σε ηλεκτροστατική ισορροπία, το δυναµικό είναι σταθερό. Για παράδειγµα, στην φορτισµένη σφαίρα του διπλανού σχήµατος τα σηµεία Α και Β
. Δυναμικό και χωρητικότητα αγωγού. Σε όλα τα σηµεία ενός αγωγού, σε ηλεκτροστατική ισορροπία, το δυναµικό είναι σταθερό. Για παράδειγµα, στην φορτισµένη σφαίρα του διπλανού σχήµατος τα σηµεία Α και Β
( ) Στοιχεία που αποθηκεύουν ενέργεια Ψ = N Φ. διαφορικές εξισώσεις. Πηνίο. μαγνητικό πεδίο. του πηνίου (κάθε. ένα πηνίο Ν σπειρών:
 Στοιχεία που αποθηκεύουν ενέργεια Λέγονται επίσης και δυναμικά στοιχεία Οι v- χαρακτηριστικές τους δεν είναι αλγεβρικές, αλλά ολοκληρο- διαφορικές εξισώσεις. Πηνίο: Ουσιαστικά πρόκειται για έναν περιεστραμμένο
Στοιχεία που αποθηκεύουν ενέργεια Λέγονται επίσης και δυναμικά στοιχεία Οι v- χαρακτηριστικές τους δεν είναι αλγεβρικές, αλλά ολοκληρο- διαφορικές εξισώσεις. Πηνίο: Ουσιαστικά πρόκειται για έναν περιεστραμμένο
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Κλασική Hλεκτροδυναμική
 Κλασική Hλεκτροδυναμική Ενότητα 1: Εισαγωγή Ανδρέας Τερζής Σχολή Θετικών επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι μια σύντομη επανάληψη στις βασικές έννοιες της ηλεκτροστατικής.
Κλασική Hλεκτροδυναμική Ενότητα 1: Εισαγωγή Ανδρέας Τερζής Σχολή Θετικών επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι μια σύντομη επανάληψη στις βασικές έννοιες της ηλεκτροστατικής.
στη θέση 1. Κάποια χρονική στιγμή μεταφέρουμε το διακόπτη από τη θέση 1 στη
 ΠΥΚΝΩΤΗΣ ΣΥΝΔΕΔΕΜΕΝΟΣ ΠΑΡΑΛΛΗΛΑ ΜΕ ΠΗΓΗ. Στο διπλανό κύκλωμα η πηγή έχει ΗΕΔ = V και ο διακόπτης είναι αρχικά στη θέση. Κάποια χρονική στιγμή μεταφέρουμε το διακόπτη από τη θέση στη θέση και αρχίζουν οι
ΠΥΚΝΩΤΗΣ ΣΥΝΔΕΔΕΜΕΝΟΣ ΠΑΡΑΛΛΗΛΑ ΜΕ ΠΗΓΗ. Στο διπλανό κύκλωμα η πηγή έχει ΗΕΔ = V και ο διακόπτης είναι αρχικά στη θέση. Κάποια χρονική στιγμή μεταφέρουμε το διακόπτη από τη θέση στη θέση και αρχίζουν οι
1. Ιδανικό κύκλωμα LC εκτελεί ηλεκτρικές ταλαντώσεις και η χρονική εξίσωση του φορτίου του πυκνωτή
 Εισαγωγικές ασκήσεις στις ηλεκτρικές ταλαντώσεις 1. Ιδανικό κύκλωμα L εκτελεί ηλεκτρικές ταλαντώσεις και η χρονική εξίσωση του φορτίου του πυκνωτή δίνεται από τη σχέση q = 10 6 συν(10 ) (S.I.). Ο συντελεστής
Εισαγωγικές ασκήσεις στις ηλεκτρικές ταλαντώσεις 1. Ιδανικό κύκλωμα L εκτελεί ηλεκτρικές ταλαντώσεις και η χρονική εξίσωση του φορτίου του πυκνωτή δίνεται από τη σχέση q = 10 6 συν(10 ) (S.I.). Ο συντελεστής
Ηλεκτρική δυναμική ενέργεια
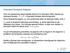 Ηλεκτρική δυναμική ενέργεια Όταν ένα δοκιμαστικό φορτίο βρεθεί μέσα σε ένα ηλεκτρικό πεδίο, δέχεται μια ηλεκτρική δύναμη: F e =q o E. Η ηλεκτρική δύναμη είναι συντηρητική. Έστω δοκιμαστικό φορτίο, q 0,
Ηλεκτρική δυναμική ενέργεια Όταν ένα δοκιμαστικό φορτίο βρεθεί μέσα σε ένα ηλεκτρικό πεδίο, δέχεται μια ηλεκτρική δύναμη: F e =q o E. Η ηλεκτρική δύναμη είναι συντηρητική. Έστω δοκιμαστικό φορτίο, q 0,
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 2002
 ΘΕΜΑ 1ο ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Η αντίσταση ενός µεταλλικού
ΘΕΜΑ 1ο ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Η αντίσταση ενός µεταλλικού
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Πρόβλημα 4.9.
 Πρόβλημα 4.9. Να βρεθεί το δυναμικό V() παντού στο χώρο ενός θετικά φορτισμένου φύλλου απείρων διαστάσεων με επιφανειακή πυκνότητα φορτίου σ. Πάρτε τον άξονα κάθετα στο φύλλο και θεωρήστε ότι το φύλλο
Πρόβλημα 4.9. Να βρεθεί το δυναμικό V() παντού στο χώρο ενός θετικά φορτισμένου φύλλου απείρων διαστάσεων με επιφανειακή πυκνότητα φορτίου σ. Πάρτε τον άξονα κάθετα στο φύλλο και θεωρήστε ότι το φύλλο
ΔΙΑΓΩΝΙΣΜΑ ΣΤO HΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΚΑΙ ΣΤΟΥΣ ΠΥΚΝΩΤΕΣ Επώνυμο: Όνομα: Τμήμα: Αγρίνιο
 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ B ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤO HΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΚΑΙ ΣΤΟΥΣ ΠΥΚΝΩΤΕΣ Επώνυμο: Όνομα: Τμήμα: Αγρίνιο 30-03-014 ΘΕΜΑ 1 ο Α) Να επιλέξετε τη σωστή απάντηση σε καθεμία από τις επόμενες προτάσεις
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ B ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤO HΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΚΑΙ ΣΤΟΥΣ ΠΥΚΝΩΤΕΣ Επώνυμο: Όνομα: Τμήμα: Αγρίνιο 30-03-014 ΘΕΜΑ 1 ο Α) Να επιλέξετε τη σωστή απάντηση σε καθεμία από τις επόμενες προτάσεις
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 2002
 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Η αντίσταση
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Η αντίσταση
ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 3 ΙΟΥΝΙΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΘΕΜΑ 1ο ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 3 ΙΟΥΝΙΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και
ΘΕΜΑ 1ο ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 3 ΙΟΥΝΙΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και
ΦΥΕ14 - ΕΡΓΑΣΙΑ 6 Προθεσμία αποστολής: 4/7/2006
 ΦΥΕ14 - ΕΡΓΑΣΙΑ 6 Προθεσμία αποστολής: 4/7/2006 Άσκηση 1 Δύο σφαίρες με ίσες μάζες m είναι δεμένες με νήματα μήκους l από το ίδιο σημείο της οροφής Σ. Αν η κάθε σφαίρα φέρει φορτίο q να βρεθεί η γωνία
ΦΥΕ14 - ΕΡΓΑΣΙΑ 6 Προθεσμία αποστολής: 4/7/2006 Άσκηση 1 Δύο σφαίρες με ίσες μάζες m είναι δεμένες με νήματα μήκους l από το ίδιο σημείο της οροφής Σ. Αν η κάθε σφαίρα φέρει φορτίο q να βρεθεί η γωνία
ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙΙ Μάθημα ασκήσεων 2: Ηλεκτρικά χαρακτηριστικά γραμμών μεταφοράς Λαμπρίδης Δημήτρης Ανδρέου Γεώργιος Δούκας
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΣΥΣΤΗΜΑΤΑ ΗΛΕΚΤΡΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΙΙ Μάθημα ασκήσεων 2: Ηλεκτρικά χαρακτηριστικά γραμμών μεταφοράς Λαμπρίδης Δημήτρης Ανδρέου Γεώργιος Δούκας
ΣΗΜΕΙΩΣΕΙΣ ΦΥΣΙΚΗΣ Γ ΓΥΜΝΑΣΙΟΥ
 ΣΗΜΕΙΩΣΕΙΣ ΦΥΣΙΚΗΣ Γ ΓΥΜΝΑΣΙΟΥ Κεφάλαιο 2 - Ηλεκτρικό Ρεύμα Επιμέλεια: Αγκανάκης Παναγιώτης, Φυσικός https://physicscourses.wordpress.com/ Με ποιες θεμελιώδεις έννοιες συνδέεται το ηλεκτρικό ρεύμα; Το
ΣΗΜΕΙΩΣΕΙΣ ΦΥΣΙΚΗΣ Γ ΓΥΜΝΑΣΙΟΥ Κεφάλαιο 2 - Ηλεκτρικό Ρεύμα Επιμέλεια: Αγκανάκης Παναγιώτης, Φυσικός https://physicscourses.wordpress.com/ Με ποιες θεμελιώδεις έννοιες συνδέεται το ηλεκτρικό ρεύμα; Το
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Στοιχεία Ηλεκτρικών Κυκλωμάτων
 Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Στοιχεία Ηλεκτρικών Κυκλωμάτων Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Νόμος Faraday Η μεταβαλλόμενη μαγνητική
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Στοιχεία Ηλεκτρικών Κυκλωμάτων Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Νόμος Faraday Η μεταβαλλόμενη μαγνητική
Φυσική ΙΙΙ. Ενότητα 4: Ηλεκτρικά Κυκλώματα. Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής
 Φυσική ΙΙΙ Ενότητα 4: Ηλεκτρικά Κυκλώματα Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Ασκήσεις ΦΙΙΙ Γ. Βούλγαρης 2 Ταχύτητα ολίσθησης σε σύρμα από χαλκό. Διάμετρος δ=1,6 mm Ρεύμα 10 Α Πυκνότητα
Φυσική ΙΙΙ Ενότητα 4: Ηλεκτρικά Κυκλώματα Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Ασκήσεις ΦΙΙΙ Γ. Βούλγαρης 2 Ταχύτητα ολίσθησης σε σύρμα από χαλκό. Διάμετρος δ=1,6 mm Ρεύμα 10 Α Πυκνότητα
ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 23 ΜΑΪΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6)
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΘΕΜΑ 1ο ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 23 ΜΑΪΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΘΕΜΑ 1ο ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 23 ΜΑΪΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας
ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 23 ΜΑΪΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ : ΦΥΣΙΚΗ
 ΘΕΜΑ 1ο ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 23 ΜΑΪΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ : ΦΥΣΙΚΗ Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα
ΘΕΜΑ 1ο ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 23 ΜΑΪΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ : ΦΥΣΙΚΗ Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα
Ηλεκτροτεχνία Ηλ. Μηχανές & Εγκαταστάσεις πλοίου (Θ)
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας Ηλεκτροτεχνία Ηλ. Μηχανές & Εγκαταστάσεις πλοίου (Θ) Ενότητα 3: Τα στοιχεία του Πυκνωτή και του Πηνίου Δ.Ν. Παγώνης Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Αθήνας Ηλεκτροτεχνία Ηλ. Μηχανές & Εγκαταστάσεις πλοίου (Θ) Ενότητα 3: Τα στοιχεία του Πυκνωτή και του Πηνίου Δ.Ν. Παγώνης Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ. Το ιδανικό κύκλωμα LC του σχήματος εκτελεί αμείωτες ηλεκτρικές ταλαντώσεις, με περίοδο
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση 1. Ιδανικό κύκλωμα LC εκτελεί αμείωτες ηλεκτρικές ταλαντώσεις. Να αποδείξετε ότι η στιγμιαία τιμή i της έντασης του ρεύματος στο κύκλωμα δίνεται σε συνάρτηση με το στιγμιαίο
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση 1. Ιδανικό κύκλωμα LC εκτελεί αμείωτες ηλεκτρικές ταλαντώσεις. Να αποδείξετε ότι η στιγμιαία τιμή i της έντασης του ρεύματος στο κύκλωμα δίνεται σε συνάρτηση με το στιγμιαίο
Φ Υ Σ Ι Κ Η Τ Α Ξ Η Σ Β 1 ο υ Κ Υ Κ Λ Ο Υ
 Φ Υ Σ Ι Κ Η Τ Α Ξ Η Σ Β 1 ο υ Κ Υ Κ Λ Ο Υ Ε π ι σ η μ ά ν σ ε ι ς Η Λ Ε Κ Τ Ρ Ι Σ Μ Ο Σ a. Σ τ α τ ι κ ό ς Η λ ε κ τ ρ ι σ µ ό ς Ερ.1 Τι είναι το ηλεκτρικό φορτίο; Απ.1 Κανείς δεν γνωρίζει τι είναι το
Φ Υ Σ Ι Κ Η Τ Α Ξ Η Σ Β 1 ο υ Κ Υ Κ Λ Ο Υ Ε π ι σ η μ ά ν σ ε ι ς Η Λ Ε Κ Τ Ρ Ι Σ Μ Ο Σ a. Σ τ α τ ι κ ό ς Η λ ε κ τ ρ ι σ µ ό ς Ερ.1 Τι είναι το ηλεκτρικό φορτίο; Απ.1 Κανείς δεν γνωρίζει τι είναι το
2π 10 4 s,,,q=10 6 συν10 4 t,,,i= 10 2 ημ 10 4 t,,,i=± A,,, s,,,
 1. Ο πυκνωτής του σχήματος έχει χωρητικότητα C=5μF και φορτίο Q=1μC, ενώ το πηνίο έχει συντελεστή αυτεπαγωγής L=2 mh. Τη χρονική στιγμή t=0 κλείνουμε το διακόπτη και το κύκλωμα εκτελεί ηλεκτρική ταλάντωση.
1. Ο πυκνωτής του σχήματος έχει χωρητικότητα C=5μF και φορτίο Q=1μC, ενώ το πηνίο έχει συντελεστή αυτεπαγωγής L=2 mh. Τη χρονική στιγμή t=0 κλείνουμε το διακόπτη και το κύκλωμα εκτελεί ηλεκτρική ταλάντωση.
ΦΥΣΙΚΗ. Ενότητα 9: Πυκνωτές-Ενέργεια Πυκνωτή-Διηλεκτρικά
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗ Ενότητα 9: Πυκνωτές-Ενέργεια Πυκνωτή-Διηλεκτρικά Τσόκας Γρηγόρης Καθηγητής Εφαρμοσμένης Γεωφυσικής, Τομέας Γεωφυσικής Παπαζάχος
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗ Ενότητα 9: Πυκνωτές-Ενέργεια Πυκνωτή-Διηλεκτρικά Τσόκας Γρηγόρης Καθηγητής Εφαρμοσμένης Γεωφυσικής, Τομέας Γεωφυσικής Παπαζάχος
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα αυτής της
Φυσική για Μηχανικούς Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα αυτής της
Ορίζοντας την δυναμική ενέργεια σαν: Για μετακίνηση του φορτίου ανάμεσα στις πλάκες: Ηλεκτρικό Δυναμικό 1
 Ηλεκτρική Δυναμική Ενέργεια Ένα ζεύγος παράλληλων φορτισμένων μεταλλικών πλακών παράγει ομογενές ηλεκτρικό πεδίο Ε. Το έργο που παράγεται πάνω σε θετικό δοκιμαστικό φορτίο είναι: W W Fl q y q l q y Ορίζοντας
Ηλεκτρική Δυναμική Ενέργεια Ένα ζεύγος παράλληλων φορτισμένων μεταλλικών πλακών παράγει ομογενές ηλεκτρικό πεδίο Ε. Το έργο που παράγεται πάνω σε θετικό δοκιμαστικό φορτίο είναι: W W Fl q y q l q y Ορίζοντας
Κλασική Ηλεκτροδυναμική
 Κλασική Ηλεκτροδυναμική Ενότητα 14: Ολοκλήρωση πολυπολικής ανάπτυξης και διηλεκτρικά Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να ολοκληρώσει την πολυπολική
Κλασική Ηλεκτροδυναμική Ενότητα 14: Ολοκλήρωση πολυπολικής ανάπτυξης και διηλεκτρικά Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να ολοκληρώσει την πολυπολική
ΦΥΣΙΚΗ Β ΤΑΞΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 2003 ΕΚΦΩΝΗΣΕΙΣ
 ΦΥΣΙΚΗ Β ΤΑΞΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 003 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1 - και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Η χαρακτηριστική
ΦΥΣΙΚΗ Β ΤΑΞΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 003 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1 - και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Η χαρακτηριστική
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Β ΤΑΞΗ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΘΕΜΑ 1ο ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 3 ΜΑΪΟΥ 00 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΘΕΜΑ 1ο ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 3 ΜΑΪΟΥ 00 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον
1ο Επαναληπτικό Διαγώνισμα Φυσικής Γενικής Παιδείας Β τάξης Λυκείου.
 ο Επαναληπτικό Διαγώνισμα Φυσικής Γενικής Παιδείας Β τάξης Λυκείου Θέμα Α: (Για τις ερωτήσεις Α έως και Α να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ο Επαναληπτικό Διαγώνισμα Φυσικής Γενικής Παιδείας Β τάξης Λυκείου Θέμα Α: (Για τις ερωτήσεις Α έως και Α να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη σωστή
Hλεκτρικό. Πεδίο. Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ
 Hλεκτρικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SRWAY, Physics fo scientists nd enginees YOUNG H.D., Univesity
Hλεκτρικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SRWAY, Physics fo scientists nd enginees YOUNG H.D., Univesity
Δυνάμεις μεταξύ ηλεκτρικών φορτίων ΘΕΜΑ Δ
 Δυνάμεις μεταξύ ηλεκτρικών φορτίων ΘΕΜΑ Δ 4_15580 Δύο σημειακά ηλεκτρικά φορτία Q 1 = μc και Q = 8 μc, συγκρατούνται ακλόνητα πάνω σε οριζόντιο μονωτικό δάπεδο, στα σημεία Α και Β αντίστοιχα, σε απόσταση
Δυνάμεις μεταξύ ηλεκτρικών φορτίων ΘΕΜΑ Δ 4_15580 Δύο σημειακά ηλεκτρικά φορτία Q 1 = μc και Q = 8 μc, συγκρατούνται ακλόνητα πάνω σε οριζόντιο μονωτικό δάπεδο, στα σημεία Α και Β αντίστοιχα, σε απόσταση
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ
 ΘΕΜΑ 1ο ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Η αντίσταση ενός µεταλλικού αγωγού που
ΘΕΜΑ 1ο ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Η αντίσταση ενός µεταλλικού αγωγού που
ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ
 ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ Νόμος του Coulomb Έστω δύο ακίνητα σημειακά φορτία, τα οποία βρίσκονται σε απόσταση μεταξύ τους. Τα φορτία αυτά αλληλεπιδρούν μέσω δύναμης F, της οποίας
ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ Νόμος του Coulomb Έστω δύο ακίνητα σημειακά φορτία, τα οποία βρίσκονται σε απόσταση μεταξύ τους. Τα φορτία αυτά αλληλεπιδρούν μέσω δύναμης F, της οποίας
