Γαραντζιώτη, Διαµμαντή, Μέµμτσας, Στάµμου

Transcript

1 Γαραντζιώτη, Διαµμαντή, Μέµμτσας, Στάµμου

2 Ο ορισµμός της αυτορρύθµμισης Οι άξονες της αυτορρύθµμισης Οι απόψεις των ερευνητών σχετικά µμε τον εννοιολογικό ορισµμό της αυτορρύθµμισης Ο ορισµμός της µμεταγνώσης Η σχέση των στρατηγικών αυτορρύθµμισης και των µμεταγνωστικών στρατηγικών Η σηµμασία των κινήτρων για την επίτευξη της αυτορρύθµμισης κατά την επίλυση µμαθηµματικού προβλήµματος

3 Οι βουλητικές στρατηγικές ως σηµμαντική συνιστώσα της αυτορρύθµμισης για την επίλυση προβλήµματος Μοντέλα αυτορυθµμιζόµμενης επίλυσης µμαθηµματικού προβλήµματος Οι ικανότητες των αυτορυθµμιζόµμενων µμαθητών κατά την επίλυση µμαθηµματικού προβλήµματος Ο ρόλος των δασκάλων στην εφαρµμογή στρατηγικών αυτορρύθµμισης στην επίλυση προβλήµματος και προαγωγής της από τους µμαθητές.

4 Η µμάθηση που συµμβαίνει υπό τον έλεγχο του µμαθητή είναι αποτέλεσµμα µμεταγνώσης και κινήτρων για µμάθηση Ο µμαθητής κατέχει κυρίαρχο και πρωταγωνιστικό ρόλο και προβαίνει µμε δική του πρωτοβουλία σε συγκεκριµμένου στόχου ενέργειες, προκειµμένου να αποκτήσει γνώσεις και δεξιότητες για το παρόν και το µμέλλον.

5 Ο µμαθητής προκειµμένου να επιτύχει τους στόχους που έχει ορίσει εµμπλέκεται ενεργά στη διαµμόρφωση και συνεχή αναπροσαρµμογή συµμπεριφορών και στρατηγικών, ενώ η ελεγκτική - ρυθµμιστική του δράση κινείται ουσιαστικά σε τρείς άµμεσα αλληλοεξαρτώµμενους άξονες: το συναίσθηµμα, τη συµμπεριφορά και τη γνώση

6 Οι ερευνητές που επιχείρησαν να ορίσουν την ΑΡΜ (SRL) φαίνεται να κατατάσσονται σε τρεις οµμάδες: Η 1η οµμάδα ορίζει την ΑΡΜ ως την ικανότητα του ατόµμου να χρησιµμοποιεί στρατηγικές δράσης ή ευρύτερα µμεταγνωστικές στρατηγικές (Vauras, Rauhanummi, Kinnunen & Lepola, 1999; Rheinberg et al., 2000). Η 2η οµμάδα ορίζει την ΑΡΜ ως την ικανότητα του ατόµμου να χρησιµμοποιεί όχι µμόνο µμεταγνωστικές, αλλά και γνωστικές στρατηγικές (Schoenfeld, 1992; Φιλίππου και Χρίστου,2001). Υπάρχουν ακόµμη µμοντέλα ΑΡΜ, που τονίζουν τη σηµμασία της ενοποίησης των Κινήτρων µμε γνωστικές και µμεταγνωστικές συνιστώσες της µμάθησης (Pintrich & Schrauben, 1992; in Pintrich, 1999).

7 Παραδοχή Η προϋπάρχουσα γνώση είναι ένα ισχυρό και ουσιώδες στοιχείο της αυτορυθµμιζόµμενης µμάθησης. Ερωτήµματα Ποια στοιχεία συνιστούν την προϋπάρχουσα γνώση; Ποιος είναι ο τύπος της προϋπάρχουσας γνώσης που είναι απαραίτητος, γ ι α ν α π ρ α γ µμ α τ ο π ο ι η θ ε ί η αυτορρυθµμιζόµμενη µμάθηση;

8 Αποτελεί ένα εργαλείο για την δόµμηση της πληροφορίας που υπάρχει σε ένα πρόβληµμα. Επιτρέπει το άτοµμο να εφαρµμόσει µμία γνώριµμη σκαλωσιά στην πληροφορία, ανεξάρτητα από το πόσο χρήσιµμη ή επιβλαβής θα µμπορούσε να είναι. Μεσολαβεί στην ικανότητα ενός ατόµμου να αναπαραστήσει ένα πρόβληµμα µμε πιο αποτελεσµματικό τρόπο. Η ενεργοποίηση της προϋπάρχουσας γνώσης µμπορεί να συµμβεί: Αυτόµματα χωρίς συνειδητή σκέψη. Με ένα πιο σχεδιαστικό και ρυθµμιστικό τρόπο µμέσω προτροπών και δραστηριοτήτων, που περιλαµμβάνουν ερωτήµματα, όπως: Τι γνωρίζω για αυτό το πεδίο, αυτή την περιοχή, αυτό το θέµμα, αυτό τον τύπο προβλήµματος κ.λ.π. Πώς µμπορώ να αναπαραστήσω καλύτερα το πρόβληµμα.

9 Η µμεταγνώση είναι η επίγνωση του τρόπου λειτουργίας της σκέψης µμας και των τρόπων, µμε τους οποίους επεξεργαζόµμαστε τη γνώση, η επίγνωση του τι ξέρουµμε και τι δεν ξέρουµμε. Η µμεταγνώση(flavell) περιλαµμβάνει τρία είδη σκέψης: 1. Σκέψεις για την προϋπάρχουσα γνώση, δηλαδή για τη δηλωτική γνώση (µμεταγνωσιακή γνώση). 2. Σκέψεις για τις τρέχουσες διαδικασίες, δηλαδή για τη διαδικαστική γνώση (µμεταγνωστική δεξιότητα). 3. Σκέψεις για τον εαυτό µμας και τους άλλους ως προς τις ικανότητές µμας στο γνωσιακό επίπεδο ή και συναισθήµματα που βιώνουµμε για µμια διανοητική εµμπειρία (µμεταγνωσιακές εµμπειρίες αυτορρύθµμιση).

10 Μεταγνωστικές Στρατηγικές Στρατηγικές Αυτορρύθµμισης

11 Στο επίπεδο της σχολικής τάξης ο όρος αναφέρεται στη διάθεση, την επιµμονή και την προσπάθεια που καταβάλλουν οι µμαθητές κατά την ενασχόλησή τους µμε ένα έργο, προκειµμένου να φτάσουν σε επιθυµμητό αποτέλεσµμα (Wolters & Rosenthal, 2000). Τα Κίνητρα είναι δυνατόν να προέρχονται από το ίδιο το άτοµμο ή να έχουν πηγή στο περιβάλλον του υποκειµμένου, να είναι δηλαδή εσωτερικά ή εξωτερικά κίνητρα.

12 Οι σύγχρονοι ερευνητές ξεπερνούν τα στενά πλαίσια της µμελέτης των επιπτώσεων, που είναι δυνατόν να έχουν τα διάφορα είδη εσωτερικών και εξωτερικών Κινήτρων, και υιοθετούν µμια ευρύτερη θεώρηση της έννοιας των Κινήτρων, αναφερόµμενοι στις Πεποιθήσεις Κινήτρων (Pintrich, 1999; Boekaerts, 2001) Υποστηρίζουν ότι οι αιτίες που παρωθούν ένα άτοµμο να ασχοληθεί µμε ένα έργο δεν είναι µμόνο οι εσωτερικοί ή εξωτερικοί σκοποί, στους οποίους είναι δυνατόν να προσανατολίζεται το άτοµμο, αλλά και οι πεποιθήσεις του σχετικά µμε τις ικανότητές του και την αξία του έργου, το οποίο πρόκειται να εκτελέσει (Lens et al., 2001)

13 Συγκεκριµμένα, ο Pintrich (1999) και οι Wolters & Rosenthal (2000), αναφέρουν ως συνιστώσες των ΠΚ: α) τις Πεποιθήσεις Επάρκειας, β) τις πεποιθήσεις για την αξία του έργου και γ) τις πεποιθήσεις προσανατολισµμού σε σκοπούς.

14 Βουλητικές στρατηγικές ορίζονται ως οι στρατηγικές ρύθµμισης των στόχων των µμαθητών και αποτελούν ουσιαστικά τη διάθεση του µμαθητή να εµμπλακεί σε δραστηριότητες ή να εκδηλώσει συµμπεριφορές υπό ορισµμένες συνθήκες (Oettingen, Honig & Gollwitzer, 2000). Οι πέντε βουλητικές στρατηγικές (Wolters & Rosenthal 2000) είναι: οι στρατηγικές αµμοιβής εαυτού, στρατηγικές ελέγχου του περιβάλλοντος τους, στρατηγικές αύξησης του βαθµμού ενδιαφέροντος του έργου στρατηγικές υπενθύµμισης στον εαυτό τους ότι ο λόγος για τον οποίο εκτελούν ένα έργο είναι η ολοκληρωτική µμάθηση, στρατηγικές υπόµμνησης στον εαυτό τους ότι θέλουν να ολοκληρώσουν ένα έργο, προκειµμένου να πάρουν καλό βαθµμό ή να ξεπεράσουν άλλους.

15 Το µμοντέλο αυτό: Στηρίζεται στη θεωρία της αυτορυθµμιζόµμενης µμάθησης (Self- Regulated Learning, SRL). Αφορά τη διαδικασία επίλυσης µμαθηµματικού προβλήµματος (Mathematical Problem Solving, MPS). Είναι συνδυασµμός των µμοντέλων ΕΜΠ των Shoenfeld (1985) και Polya (1957) Απευθύνεται σε µμαθητές δηµμοτικού σχολείου Φιλοδοξεί να αποτελέσει ισχυρό εργαλείο για την ανεξάρτητη και κατευθυνόµμενη από τα µμαθητή επίλυση προβλήµματος.

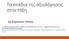
16 Φάση προµελέτης: Αναλύοντας το κείµενο Στρατηγικές Αυτορυθµιζόµενης Μάθησης Επίλυση Μαθηµατικού Προβλήµατος Φάση Αυτοπροβληµατισµού: Κοιτάζοντας πίσω Στρατηγικές Αυτορυθµιζόµενης Μάθησης Φάση Εκτέλεσης: Εκτελώντας τα σχέδια Στρατηγικές SRL* & MPS* Εικόνα 1: Επίλυση Μαθηµατικού Προβλήµατος ως κυκλικό γεγονός αυτορυθµιζόµενης µάθησης (βασισµένο στον Zimmermann, 2004) *Στρατηγικές Αυτορυθµιζόµενης Μάθησης (SRL Strategies): Γνωστικές στρατηγικές, µεταγνωστικές στρατηγικές και στρατηγικές διαχείρισης πόρων. *Στρατηγικές Επίλυσης Μαθηµατικού Προβλήµατος (MPS Strategies): Σχέδιο, διατύπωση πρόβλεψης και δοκιµή, εύρεση προτύπου, εργασία ανάποδα.

17 1η µελέτη: Διεξήχθη στο Ηνωµένο βασίλειο µε 5 µαθητές, που εργάστηκαν οµαδικά και ασχολήθηκαν µε την επίλυση 2 µαθηµατικών προβληµάτων. Επιβεβαιώθηκε η κυκλική δοµή του µοντέλου και καταγράφτηκαν οι στρατηγικές που χρησιµοποιήθηκαν από τους µαθητές. 2 η µελέτη: Διεξήχθη στην Κύπρο µε 5 δασκάλους, που εισήγαγαν τη θεωρία και το µοντέλο σε συνθήκες πραγµατικής τάξης. Οι εκπαιδευτικοί υποστήριξαν ότι το µοντέλο µπορεί να αποτελέσει ισχυρό εργαλείο για τη σκέψη των µαθητών και τη διδασκαλία των εκπαιδευτικών. Οι µαθητές κατά την επίλυση προβλήµατος, ενώ αρχικά διέθεταν περισσότερο χρόνο στη φάση της εκτέλεσης και καθόλου χρόνο στη φάση της αυτορρύθµισης, µετά την παρέµβαση διέθεσαν περισσότερο στη φάση της προµελέτης και της αυτορρύθµισης.

18

19 Οι µμαθητές που αυτορυθµμίζονται έχουν γνώση του αντικειµμένου, πολλές στρατηγικές, από τις οποίες επιλέγουν τις πιο κατάλληλες, καλή µμεταγνωστική επίγνωση, µμεταγνωστικές στρατηγικές, υψηλούς εκπαιδευτικούς στόχους, καλή αυτοαξιολόγηση θέτουν ρεαλιστικούς στόχους έχουν αυτοπεποίθηση, επιµμέλεια, επιχειρηµματικό τρόπο σκέψης, αίσθηση ευθύνης έχουν καλές στάσεις απέναντι στα µμαθηµματικά και την επίλυση προβλήµματος, καθώς και ενεργό ρόλο στις οµμάδες εργασίας βλέπουν την απόκτηση γνώσης ως συστηµματική και ελέγξιµμη διαδικασία.

20 Η αυτορρύθµμιση µμπορεί να είναι ως ένα βαθµμό µμια αυθόρµμητη διεργασία στη µμάθηση των παιδιών µμέσα στην τάξη, αλλά πολλοί µμαθητές χρειάζονται τη στήριξη του εκπαιδευτικού, για να κατακτήσουν τέτοιες δεξιότητες µμάθησης. Οι Pressley και Hilden (2006) αναφέρουν ότι οι µμαθητές που διδάσκονται τη χρήση ποικίλων στρατηγικών για αυτορρύθµμιση της µμάθησης είναι αυτοί που παρουσιάζουν τα πιο εντυπωσιακά αποτελέσµματα. Οι εκπαιδευτικοί θα πρέπει να έχουν οι ίδιοι αναπτύξει δεξιότητες αυτορρύθµμισης της δικής τους µμάθησης και διδασκαλίας, ώστε να είναι σε θέση να προάγουν την αυτορρυθµμιζόµμενη µμάθηση στους µμαθητές τους.

21 Μάνεση Σ., Ο ρόλος των δεξιοτήτων αυτορρύθµμισης για την οµμαλή προσαρµμογή στο Νηπιαγωγείο (2012) Στα πρακτικά Πανελληνίου Συνεδρίου Η Ποιότητα στην Εκπαίδευση: Τάσεις και Προοπτικές Τόµμος 1, σ Εθνικό Καποδιστριακό Πανεπιστήµμιο Αθηνών Χατζησταµματίου Μ., Δερµμιτζάκη Ε,. (2009). Χρήση Στρατηγικών Αυτορρύθµμισης της Διδασκαλίας και Προαγωγής της Αυτορρυθµμιζόµμενης Μάθησης των Μαθητών από Εκπαιδευτικούς Πρωτοβάθµμιας Εκπαίδευσης. ΨΕΒΕ, Περιοδική επιστηµμονική έκδοση της Ψυχολογικής Εταιρείας Βορείου Ελλάδος, Τόµμος 7, σ Παναγίδου Ε., Τσιάννη Μ., (2005). Η Ικανότητα επίλυσης µμαθηµματικών προβληµμάτων και η χρήση στρατηγικών από µμαθητές Β Δηµμοτικού. Στα πρακτικά του 1ου Συνεδρίου της Ένωσης Ερευνητών Διδακτικής των Μαθηµματικών (ΕνΕ ιμ) Εργαστήριο Εκπαιδευτικής Τεχνολογίας, Φ.Π.Ψ., Φιλοσοφική Σχολή, Ε.Κ.Π.Α.

22 Μάρκου Α., Φιλίππου Γ., (2003). Πεποιθήσεις κινήτρων και αυτορρυθµμιζόµμενη µμάθηση κατά την επίλυση µμαθηµματικού προβλήµματος. Στα πρακτικά 2ου Συνεδρίου για τα µμαθηµματικά στη Δευτεροβάθµμια Εκπαίδευση. Εθνικό Καποδιστριακό Πανεπιστήµμιο Αθηνών - Τµμήµμα Επιστηµμών της Αγωγής Πανεπιστήµμιο Κύπρου Κλειδαρά, Χ. (2013). Εκτίµμηση ορθότητας και βεβαιότητας των απαντήσεων στο µμάντεµμα λέξεων από ενήλικες µμαθητές της Ιταλικής Γλώσσας. Μεταπτυχιακή Εργασία Θεσσαλονίκη, Τµμήµμα Εκπαιδευτικής και Κοινωνικής Πολιτικής από /15927 Αντωνάτου, Χ., Στρατηγικές µμάθησης: µμαθητές µμε µμαθησιακές δυσκολίες (2010) Στο Πρακτικά του 5ου Πανελλήνιου Συνεδρίου (ΕΛΛ.Ι.Ε.Π.ΕΚ.) µμε θέµμα «Μαθαίνω πώς να µμαθαίνω», ISSN Πανεπιστήµμιο Θεσσαλίας από

23 Lazakidou, G., Paraskeva, F., & Retalis, S. (2007). The Transitory Phase to the Attainment of Self- Regulatory Skill in Mathematical Problem Solving. International Education Journal, 8(1), Goldberg, P. D., & Bush, W. S. (2003). Using metacognitive skills to improve 3rd graders' math problem solving. Focus on Learning Problems in Mathematics, 25(4), 36. Boekaerts, M. (1997). Self- regulated learning: A new concept embraced by researchers, policy makers, educators, teachers, and students. Learning and instruction, 7(2), Marcou, A., & Lerman, S. (2006). Towards the development of a self- regulated mathematical problem solving model. In th conference of the international group for the Psychology of Mathematics Education.