Λύση α) Αν θεωρήσουµε ότι δεν περνάµε το παραπάνω κείµενο από stoplist και stemming, το ανεστραµµένο ευρετήριο θα έχει ως εξής:
|
|
|
- Ὕδρα Γκόφας
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών HY463 - Συστήµατα Ανάκτησης Πληροφοριών Εαρινό Εξάµηνο 3 η Σειρά Ασκήσεων Ανάθεση: 1 Απριλίου Παράδοση: 14 Απριλίου Άσκηση 1 (3 βαθµοί) (Ενότητα: Ευρετηρίαση Κειµένου) Θεωρείστε ένα έγγραφο το οποίο περιέχει τα εξής λόγια του Βενιαµίν Φραγκλίνου: «Όποιος θυσιάζει την ελευθερία για την ασφάλεια δεν αξίζει ούτε την ελευθερία ούτε την ασφάλεια.» (α) Φτιάξτε το ανεστραµµένο ευρετήριο αυτού του εγγράφου. (β) Φτιάξτε το δένδρο καταλήξεων του εγγράφου θεωρώντας ως σηµεία ευρετηρίου (index points) τις αρχές των λέξεων (µπορείτε να δώσετε κατευθείαν το PATRICIA tree). (γ) Σχολιάστε το µέγεθος των (α) και (β) ως προς το µέγεθος του εγγράφου. Λύση α) Αν θεωρήσουµε ότι δεν περνάµε το παραπάνω κείµενο από stoplist και stemming, το ανεστραµµένο ευρετήριο θα έχει ως εξής: Ανεστραµµένο ευρετήριο : ασφάλεια : 39, 87 αξίζει : 52 για : 31 δεν : 48 ελευθερία : 21, 68 θυσιάζει : 8 όποιος : 1 ούτε : 59, 78 την : 17, 35, 64, 83 <> σ 9 β). 2 ξ α δ γ ε γ ο ο τ 10 5 θ 8 ε α γ 15 ε ο 13 <> α
2 Ασφαλώς θα µπορούσαµε να περάσουµε το κείµενο από stoplist, οπότε θα αγνοούσαµε λέξεις όπως το «για», «δεν», «την». γ) Το µέγεθος του ανεστραµµένου ευρετηρίου είναι µικρότερο από το µέγεθος του κανονικού αρχείου για ένα σχετικά µεγάλο κείµενο. Ο λόγος είναι ότι τα strings που επαναλαµβάνονται, αντί να καταλαµβάνουν χώρο όσο είναι το µέγεθος του string επί τον αριθµό των επαναλήψεων, καταλαµβάνουν τόσο χώρο όσο το µέγεθος του string συν τον αριθµό των επαναλήψεων επί το µέγεθος ενός ακέραιου αριθµού. Το δικό µας κείµενο όµως είναι σχετικά µικρό και επειδή δεν έχουµε βγάλει και τα stopwords, τα οποία είναι σχετικά µικρά (3 µε 4 χαρακτήρες και θα µας βόλευε να τα κρατάµε σαν strings) ουσιαστικά από άποψη χώρου το ανεστραµµένο ευρετήριο είναι λίγο χειρότερο από το κανονικό text. Έτσι ενώ το κείµενο είναι 95 χαρακτήρες και αρά θα χρειαστούµε 95 bytes, για το ανεστραµµένο ευρετήριο χρειαζόµαστε 106 bytes. Όσον αφορά το Patricia tree, είναι καταδικασµένο να καταλαµβάνει πολύ περισσότερο χώρο από το χώρο που θα καταλάµβανε το αρχείο. Ο λόγος είναι ότι για κάθε κόµβο χρειάζεται να καταλαµβάνουµε 4 bytes για να αποθηκεύουµε ένα ακέραιο, και για κάθε ακµή χρειαζόµαστε 5 bytes, αφού ουσιαστικά χρειάζεται να κρατάµε ένα δείκτη και ένα χαρακτήρα. Μετρώντας για το συγκεκριµένο κείµενο βρίσκουµε ότι χρειαζόµαστε 213 bytes. Αν το κείµενο µας ήταν ακόµα πιο µεγάλο η κατάσταση θα χειροτέρευε ακόµα περισσότερο µιας και θα έπρεπε για κάθε νέο πρόθεµα που θα εισάγαµε να δεσµεύσουµε 18 bytes επιπλέον (δύο ακµές, ένα επιπλέον occurrence και ένα node). Άσκηση 2 (5 βαθµοί) (Ενότητα: Ευρετηρίαση Κειµένου) Θέλετε να σχεδιάσετε ένα ΣΑΠ που να βασίζεται στο διανυσµατικό µοντέλο για µια συλλογή κειµένων συνολικού µεγέθους στο δίσκο 1 Gigabyte. Έστω ότι το µέσο µέγεθος των λέξεων που εµφανίζονται στα κείµενα είναι 10 χαραχτήρες και ότι το πλήθος των διαφορετικών λέξεων της συλλογής είναι (α) Ποιο το αναµενόµενο (µέγιστο) µέγεθος του ανεστραµµένου ευρετηρίου για τη συλλογή αυτή; (β) Ποιο το αναµενόµενο (µέγιστο) µέγεθος του ανεστραµµένου ευρετηρίου αν χρησιµοποιήσετε block addressing µε µέγεθος block ίσο µε 200 λέξεις; Τι ποσοστό µείωσης έχουµε, σε σχέση µε το (α); (γ) Αν έπρεπε το ευρετήριο να καταλαµβάνει το πολύ 1 MB (π.χ. για να χωράει στην κύρια µνήµη ενός κινητού τηλεφώνου) πως θα σχεδιάζατε το ανεστραµµένο ευρετήριο; (δ) Αν έπρεπε να καταλαµβάνει το πολύ 100 Κ τι θα κάνατε; (ε) Αν έπρεπε να καταλαµβάνει το πολύ 10 Κ τι θα κάνατε; (στ) Αν έπρεπε να υποστηρίξετε και phrase queries (µέγιστου µήκους 4 διαδοχικών λέξεων) και είχατε στη διάθεση σας µόνο 1 Μbyte µνήµης και επιλέγατε αντί για ανεστραµµένο ευρετήριο να είχατε αρχείο υπογραφών πως θα το σχεδιάζατε; Λύση Κατ αρχήν θεωρούµε, είτε ότι στη γλώσσα µας δεν µας ενδιαφέρουν τα stopwords, είτε ότι ήδη στην συλλογή του 1Gbyte που έχουµε ήδη αφαιρέσει τα stopwords (αν τα είχαµε στη συλλογή µας το 10byte/λέξη θα φαινόταν λίγο υπερβολικό). Ακόµα θα κάνουµε τις εξής θεωρήσεις : Σαν οccurencies στους κόµβους των inverted lists θα κρατάµε σε ποιο document βρίσκεται ο όρος, σε ποιες θέσεις µέσα στο κέιµενο εµφανίζεται και το tf-idf βάρος του όρου στο έγγραφο. Έτσι στην παρακάτω ανάλυση µας θεωρούµε ότι η συλλογή µας καθώς και το vocabulary αποτελούνται από µηstopword λέξεις που γίνονται όλες indexing. Η συλλογή µας αποτελείται από 1 GByte = bytes και µε µέσο όρο 10bytes/λέξη η συλλογή µας περιέχει λέξεις (δεν θεωρούµε κενά
3 µεταξύ λέξεων, αν θέλαµε να πάρουµε υπ όψιν κενά η ανάλυση θα ήταν παρόµοια αφού µετά από κάθε λέξη θα παίρναµε υπ όψιν µας ένα κενό). Γνωρίζουµε ότι η συλλογή µας περιέχει διαφορετικές λέξεις και συνεπώς κάθε λέξη εµφανίζεται κατά µέσο όρο / = φορές. Τέλος δεν αγνοούµε το µέγεθος των pointers (θα µπορούσαµε να λάβουµε υπ όψιν 4Bytes επιβάρυνση για κάθε pointer µε συνακόλουθες µικρές αλλαγές στα νούµερα παρακάτω). α) Για το vocabulary του ευρετηρίου θέλουµε να αποθηκεύσουµε τις διαφορετικές λέξεις των 10byte και άρα θέλουµε χώρο bytes = 100 KB. Αν για κάθε vocabulary entry κρατήσουµε και 4 bytes για το document frequency, το vocabulary θα καταλαµβάνει µόνο του χώρο 140Κ. Για κάθε µια entry από τις θα αποθηκεύσουµε τόσα occurencies σε όλα τα κείµενα όσες φορές εµφανίζεται η λέξη και ήδη αναφέραµε ότι κάθε λέξη εµφανίζεται κατά µέσο όρο φορές και άρα θέλει integers για να αποθηκευτούν όλα τα occurencies µιας λέξης. Συνεπώς για ένα entry του vocabulary θέλουµε * 4 bytes = bytes = 40 KB. Αυτό µόνο για τις θέσεις των εµφανίσεων της ίδιας λέξης. Εκτός από αυτό πρέπει να αποθηκεύσουµε το σε ποια έγγραφα υπάρχουν αυτές οι εµφανίσεις καθώς και το tf-idf βάρος της (εµφάνισης της) λέξης στο κείµενο. Επειδή ψάχνουµε το µέγιστο µέγεθος ευρετηρίου που µπορεί να έχουµε θα κάνουµε την χειρότερη από άποψη χώρου υπόθεση, ότι κάθε εµφάνιση µιας λέξης βρίσκεται σε διαφορετικό κείµενο και άρα θέλουµε (για κάθε λέξη) integers για να κρατάµε τα id του κειµένων που αυτή εµφανίζεται και άλλους integers για τα tf-idf βάρη. Συνεπώς για ένα entry του vocabulary θέλουµε (µιλάµε πάντα κατά µέσο όρο) 40Κ για τις θέσεις των εµφανίσεων στα κείµενα, 40Κ για τα id των documents και άλλα 40Κ για τα βάρη. Σύνολο 120Κ για κάθε µια από τις entries του vocabulary. Συνεπώς για όλες τις inverted lists θέλουµε χώρο 120K * = bytes = 1,2 G. Εν κατακλείδι για το ανεστραµένο αρχείο θέλουµε 1,2G + 140Κ = 1200,14 Μbytes. β) To να χρησιµοποιήσουµε block addressing µε µέγεθος block = 200 λέξεις * 10 byte/λέξη = 2000 bytes δεν έχει σαν αποτέλεσµα καµία βελτίωση στο µέγεθος του ευρετηρίου σε σχέση µε το ερώτηµα (α). Αυτό συµβαίνει διότι µε µέγεθος block 2000 bytes, η 1G συλλογή µας χωρίζεται σε blocks (περίπου), τα οποία είναι πάρα πολλά σε σχέση µε το πλήθος των διαφορετικών λέξεων της συλλογής µας. Με την υπόθεση ότι οι εµφανίσεις µιας λέξης κατανέµονται οµοιόµορφα µέσα στο κείµενο, µια λέξη εµφανίζεται κάθε άλλες άρα µια λέξη εµφανίζεται κάθε / 200 = 50blocks. Κατά συνέπεια τo πλήθος των occurencies κάθε λέξης θα παραµείνει το ίδιο αφού ναι µεν πλέον ένας integer occurence θα δηλώνει θέση µπλόκ και όχι θέση στο κείµενο αλλά επειδή µε µεγάλη πιθανότητα οι εµφανίσεις της ίδιας λέξης θα είναι σε διαφορετικά µπλοκ το πλήθος των µπλοκς που θα εµφανίζεται µια λέξη θα είναι και θέλουµε τόσο χώρο όσο και στο (α). Κάνουµε πάλι την χείριστη υπόθεση ότι κάθε µπλοκ (και συνεπώς κάθε εµφάνιση λέξης) είναι σε διαφορετικό κείµενο, και άρα πάλι θέλουµε 3 ακέραιους (αριθµό µπλοκ, id εγγράφου, tf-idf βάρος) ανά κόµβο λίστας, έχοντας κόµβους για κάθε µια από τις λέξεις. Συνεπώς και πάλι για το ανεστραµµένο αρχείο θέλουµε 1200,14 Μbytes. γ) Σε αυτό το ερώτηµα θα χωρίσουµε τη συλλογή των εγγράφων µας σε µεγάλα µπλοκς, ώστε να χωρούν πολλές εµφανίσεις της ίδιας λέξης σε ένα block, και για κάθε λέξη στο ευρετήριο θα κρατούµε µόνο ακεραίους που θα είναι τα µπλοκ που βρέθηκε η λέξη. Το vocabulary του ευρετηρίου από µόνο του (και χωρίς document frequency πληροφορία) καταλαµβάνει 100Κ και άρα έχουµε ακόµα 900Κ στην διάθεσή µας. Αυτά τα 900Κ θα κατανεµηθούν σε εγγραφές (µια για κάθε λέξη) και έτσι κάθε inverted list θα έχει περίπου 90 bytes (µέσο όρο) χώρο για πληροφορίες σχετικές µε την λέξη. Σε αυτά τα
4 90 bytes πρέπει να περιγραφούν και οι (κατά µέσο όρο) εµφανίσεις της λέξης. Αν θεωρήσουµε, όπως παραπάνω, ότι για κάθε µπλοκ θα κρατούµε 4 bytes, τότε θέλουµε 22,5 µπλοκς (90=22,5*4) που θα έχουν τις εµφανίσεις της λέξης. Άρα σε ένα µπλοκ θέλουµε να εµφανίζεται η λέξη / 22,5 = 444,44 φορές κατά µέσο όρο.όπως αναφέραµε και στο ερώτηµα (β) η ιδια λέξη εµφανίζεται κάθε άλλες λέξεις και άρα για να περιέχει ένα µπλοκ 444,44 φορές την ίδια λέξη πρέπει να περιέχει συνολικά * 444,44 λέξεις = λέξεις. Η κάθε λέξη είναι 10 bytes και άρα ένα µπλοκ πρέπει να έχει µέγεθος bytes = 44,44 Mbyte. Συνεπώς µε µπλοκ των 44,44 Mbyte, το ευρετήριο (κρατώντας πληροφορία µόνο 4 byte/block) έχει µέγεθος 90 bytes (ανά εγγραφή) * διαφορετικές εγγραφές + 100Κ (το vocabulary) = 1Μbyte. Αν θέλαµε να κρατάµε πιο πολύ πληροφορία ανά µπλοκ, π.χ ένα ακόµη byte (έστω έναν pointer σε µια άλλη δοµή στο δίσκο η οποία θα κρατά βάρη ή/και άλλη πληροφορία), τότε για παράδειγµα θα έπρεπε να έχουµε τα µισά µπλοκ σε πλήθος (αφού θα κρατούσαµε την διπλάσια πληροφορία) και συνεπώς διπλάσιο µέγεθος µπλοκ. δ) Το να καταλαµβάνει το ευρετηρίο 100Κ σηµαίνει ότι το vocabulary ίσα που χωράει στη µνήµη αφού αυτό από µόνο του είναι 100Κ. εν έχουµε πολλές επιλογές παρά να κρατάµε στη µνήµη pointers για θέσεις στο δίσκο όπου βρίσκεται η υπόλοιπη πληροφορία του ευρετηρίου. Όµως το vocabulary καταλαµβάνει και τα 100Κ και δεν αφήνει χώρο για τίποτα άλλο. Μπορούµε να εφαρµόσουµε stemming στο vocabulary ώστε το µέγεθος της µέσης λέξης να µετατραπεί από 10 σε 6 bytes. Έτσι θα περισσεύουν 4 bytes ανά λέξη που θα µπορούσε να µπει ο pointer και πάλι να έχουµε 100K χώρο. Ακόµα και εάν έχει εφαρµοστεί stemming ήδη, το µεγεθος της µέσης λέξης (10 bytes) µας αφήνει περιθώρια να την κόψουµε και να εφαρµόσουµε την ιδέα µας. Έχουµε βέβαια το πρόβληµα ότι για µια λέξη που έχει κοινό πρόθεµα µε κάποια του vocabulary µας πρέπει να φτάσουµε ώς το δίσκο για να καταλάβουµε ότι αποτύχαµε. ε) Όλες οι ιδέες που παρουσιάζονται (blocks,stemming και η παρούσα ιδέα) µπορούν βέβαια να εφαρµοστούν µόνες τους ή συνδυασµένες σε όλα τα ερωτήµατα. Αυτό που µπορούµε να κάνουµε όταν έχουµε τόσο µικρή µνήµη όσο 10Κ είναι να «σπάσουµε» το ευρετήριο του προηγούµενου ερωτήµατος σε δέκα κοµµάτια και να έχουµε 1 κοµµάτι κάθε φορά στη µνήµη. Αν δεν περιέχει τη λέξη που ψάχνουµε πάµε στο δίσκο και φορτώνουµε ένα άλλο κοµµάτι. Η παραπάνω διαδικασία είναι πάρα πολύ αργή και µια βελτιστοποίηση είναι να χωρέσουµε κάποιες από τις λέξεις (π.χ. 900) αλφαβητικά επιλέγοντάς τες όσο περισσότερο οµοιόµορφα µπορούµε από όλο το σύνολο του vocabulary. Ανάµεσα σε λέξεις (π.χ κάθε 10 λέξεις) θα κρατούµε έναν pointer σε ένα τµήµα του vocabulary που είναι 10Κ και αλφαβητικά ανάµεσα στην λέξη πριν από τον pointer και στην επόµενη. Το παρακάτω σχήµα δείχνει τι εννοώ. αστο -----> λαλα.... κλασµα ωµεγα
5 Αν ψάχνουµε µια λέξη λεξικογραφικά ανάµεσα σε «αστο» και «λαλα» ακολουθούµε τον pointer και φορτώνουµε εκείνο το κοµµάτι του vocabulary που βρίσκεται λεξικογραφικά ανάµεσα σε «αστο» και «λαλα» και περιέχει ίσως την λέξη που θέλουµε. Αν χρειάζεται µπορούµε να προσθέσουµε και άλλα επίπεδα indexing (δηλαδή αυτό το τµήµα που θα φορτώσουµε να έχει και αυτό pointers σε λεξικογραφικά εµπεριέχοντα τµήµατα). Όπως και να έχει το τελευταίο επίπεδο indexing του vocabulary πρεπει να περιέχει pointers στον δίσκο για περαιτέρω πληροφορία (pointers π.χ. σε inverted lists). στ) Το µέγεθος του αρχείου υπογραφών είναι τα bit masks των µπλοκ συν ένας pointer για κάθε µπλοκ. Για να µην έχουµε conflicted hashes δυο block σε ίδιο bit mask, θα χρησιµοποιήσουµε Β = log(10.000)=10, όπου Β το πλήθος των bits ανά mask. Για κάθε µπλοκ θα αποθηκέυουµε λοιπόν 10 bits = 1,25 bytes (κατά µέσο όρο) + 4bytes o pointer στο block της µάσκας. Σε αυτό το σηµείο µπορούµε να θεωρήσουµε είτε ότι θα δώσουµε εν τέλει 1byte = 8 bit ανά mask, µε αναµενόµενη τετραπλασίαση των false drops (αφού 8 bits µπορουν να κωδικοποιήσουν έως 2 8 = 256 masks = ¼ των διαφορετικών λέξεων), είτε ότι η αρχιτεκτονική της µηχανής µας, µας επιτρέπει να γράφουµε σειριακά bits µέσα σε ένα byte και οπότε µπορεί να υπάρξει ένα byte, στο οποίο µερικά bit ανήκουν σε ένα mask ενώ τα υπόλοιπα σε άλλο. Εµείς (λόγω και του περιορισµού χώρου) θα επιλέξουµε να δώσουµε 1 byte ανα mask. Συνεπώς στο αρχείο υπογραφών για κάθε µπλοκ κειµένου µας χρειαζόµαστε 1+4 = 5 bytes. Το 1 ΜΒ = bytes της µνήµης, µας αφήνει περιθώριο να έχουµε συνολικά blocks. Άρα χωρίζουµε το 1G τις συλλογής µας σε blocks των bytes (= 5KB). Άρα κάθε µπλοκ θα έχει β = 500 λέξεις (αφού η λέξη είναι 10 bytes). Κλείνοντας παρατηρούµε πως µπορούµε να εφαρµόσουµε και overlapping µεταξύ των blocks σε πλήθος λέξεων εξαρτώµενο από το proximity των proximity queries ή το µέσο µέγεθος των phrase queries. Άσκηση 3 (2 βαθµοί) To Google θέλει να υποστηρίξει εξατοµικευµένη διαβάθµιση των ιστοσελίδων στους χρήστες του. Κάθε χρήστης να µπορεί να ορίζει ένα ή περισσότερα προφίλ. Κάθε προφίλ (ενός χρήστη) θα έχει ένα όνοµα (π.χ. ψυχαγωγία, my Master, MyMusic, computer science, κλπ) το οποίο ο χρήστης θα δίδει αρχικά. Η διαδικασία της αναζήτησης θα τροποποιηθεί ως εξής: ίπλα στο πλαίσιο διατύπωσης επερωτήσεων του Google, θα υπάρχει ένα µενού το οποίο θα εµφανίζει όλα τα ονόµατα προφίλ που έχει δηλώσει ο χρήστης καθώς και την προεπιλεγµένη επιλογή «ΧωρίςΠροφίλ». Η αναζήτηση µε επιλογή «ΧωρίςΠροφίλ» θα διενεργείται όπως γίνεται σήµερα. Αν ο χρήστης έχει επιλέξει ένα προφίλ, τότε δίπλα σε κάθε στοιχείο της απάντησης (σύνδεσµο προς ιστοσελίδα) της κάθε απάντησης θα εµφανίζονται δυο κοµβία: ένα good και ένα bad. Ανάλογα µε το περιεχόµενο της κάθε σελίδα και τις προτιµήσεις του χρήστη (και για το συγκεκριµένο προφίλ), ο χρήστης θα µπορεί να πατήσει το good ή το bad για όποιες σελίδες το επιθυµεί. Βάσει αυτής της ανατροφοδότησης το Google πρέπει να παρέχει εξατοµικευµένη διαβάθµιση σελίδων.. (α) Πως θα αξιοποιούσατε τα good και bad εισόδους του χρήστη ώστε να υποστηρίξετε εξατοµικευµένη ανάκτηση; Μπορείτε να περιγράψετε παραπάνω από ένα τρόπους. (β) Για κάθε προφίλ ενός χρήστη τι θα αποθηκεύατε; Λάβετε υπόψη ότι εκατοµµύρια χρήστες χρησιµοποιούν το Google καθώς και το γεγονός ότι το Google ευρετηριάζει περίπου 9 δις σελίδες. (γ) Ποιο θα ήταν το µεγαλύτερο τεχνικό πρόβληµα για την υποστήριξη αυτής της λειτουργικότητας; Αν προτείνατε παραπάνω από µια µέθοδο απαντήστε αυτό το ερώτηµα για κάθε µία µέθοδο και αναφέρετε τη µέθοδο που θα επιλέγατε (και δικαιολογείστε).
6 Λύση Ακολουθούν 2 λύσεις που µπορούν να θεωρηθούν σαν συµπληρωµατικές η µία ως προς την άλλη (χωρίς να σηµαίνει πως δεν υπάρχουν κι άλλες λύσεις). 1 η Λύση: α) Θα µπορούσαµε για να αξιοποιήσουµε την good/bad πληροφορία ως εξής: Για ένα προφίλ όπου ο χρήστης έχει δώσει προτιµήσεις θα µπορούσαµε να τροποποιούµε το ranking των απαντήσεων που δίνουµε λαµβάνοντας υπ όψιν τις προηγούµενες απαντήσεις του χρήστη στο προφίλ αυτό. Σε µια απόλυτη περίπτωση θα µπορούσαµε να εµφανίζουµε πρωτα τα good αποτελέσµατα στον χρήστη (ταξινοµηµένα ως προς το µεταξύ τους ranking), έπειτα τα ουδέτερα αποτελέσµατα (αυτά που δεν απάντησε ούτε good είτε bad) και αυτά ταξινοµηµένα ως προς το µεταξύ τους ranking και στο τέλος τα bad αποτελέσµατα (αν και αυτά µπορούµε και να τα παραλείψουµε). Αυτή η προσέγγιση όµως υστερεί από την άποψη ότι δεν εκµεταλλευόµαστε την επανεπιλογή ενός εγγράφου σαν good (αυτό θα σήµαινε ότι του χρήστη του αρέσει πολύ) και επίσης όταν στο ίδιο προφίλ για διαφορετικά queries ο χρήστης έχει δώσει το ίδιο έγγραφο σαν good και bad η παραπάνω προσέγγιση θα το κατατάξει σύµφωνα µε την τελευταία αξιολόγηση του χρήστη (αφού π.χ. για ένα έγγραφο η παραπάνω προσέγγιση θα διατηρεί 2 λίστες µε good και bad έγγραφα και θα προσθέτει/αφαιρεί από αυτές καθώς και θα µετακινεί έγγραφα από την µια λίστα στην άλλη). Μια αλλη προσέγγιση θα ήταν τα good και bad να είχαν µια έννοια ψήφων. Το good θα ήταν θετική ψήφος για ένα έγγραφο (+1) ενώ το bad αρνητική (-1 και όταν ένα έγγραφο εχει <0 σύνολο ψήφων (ή π.χ. <-5) να µην εµφανίζεται καθόλου). Έτσι τώρα για κάθε προφίλ υπάρχει µια λίστα µε έγγραφα κατεταγµένα ως προς σύνολο ψήφων και θα εµφανίζονται πρώτα τα έγγραφα που θα έχουν το ίδιο σύνολο ψήφων (κατεταγµένα ως προς το ranking του ΣΑΠ) πριν εµφανιστούν έγγραφα µε µικρότερο σύνολο ψήφων κ.ο.κ. Μια βελτιστοποίηση της πιο πάνω ιδέας θα ήταν να προσπαθήσουµε να ευνοήσουµε documents τα οποία µοιάζουν (π.χ. όσον αφορά στο cossim µέτρο) µε τα good διανύσµατά µας άρα κατά την διαδικασία της απάντησης παρουσιάζουµε στον χρήστη τα έγγραφα µε το υψηλότερο σύνολο ψήφων και αυτά (που µας επέστρεψε το ΣΑΠ και) που µοιάζουν πολύ µε κάποιο έγγραφο από αυτά της υψηλής προτίµησης (τα παρουσιάζουµε όλα µαζί ταξινοµηµένα ως προς το ranking του ΣΑΠ). Έπειτα «κατεβαίνουµε» επίπεδο ψήφων και παρουσιάζουµε (κατεταγµένα ως προς το ranking) αυτά που εχουν αµέσως λιγότερους ψήφους και αυτά που µας επέστρεψε το ΣΑΠ και «µοιάζουν» µε τα πρώτα κ.οκ. Εναλλακτικά µια προσέγγιση που θα απορρίψω στο ερώτηµα (γ) έχει να κάνει µε το να διατηρούµε και πληροφορία όπως το σε ποιο query έδωσε το feedback ο χρήστης.έτσι διατηρώντας για κάθε διαφορετικό query διαφορετική λίστα µε good και bad έγγραφα και όταν ο χρήστης έκανε ένα query που µοιάζει µε ένα(ή περισσότερα) query για τα οποία έχουµε good και bad έγγραφα του επιστρέφουµε τα έγγραφα που ξέρουµε ότι είναι good (και έγγραφα που µοιάζουν µε αυτά) και όχι αυτά που είναι bad (ή έγγραφα που µοιάζουν µε αυτά). (Ακόµα µια προσέγγιση που είναι ουτοπική φαίνεται στο ερώτηµα (β)). β) Σύµφωνα µε την πιο πάνω προσέγγιση των ψήφων για κάθε προφίλ χρήστη θα αποθηκεύαµε µια λίστα µε τα id s των εγγράφων για τα οποία έχει δώσει feedback ο χρήστης και έναν αριθµό που δηλώνει τις «ψήφους» κάθε εγγράφου. (Σε ένα κόσµο όπου το αποθηκευτικό κόστός θα ήταν αµελητέο θα µπορούσαµε να διατηρούµε και πληροφορία όπως το σε ποιο query έδωσε το feedback ο χρήστης ή ακόµα και να έχουµε διαφορετικές συλλογές διανυσµάτων εγγράφων για κάθε προφίλ µε τα βάρη των διανυσµάτων των εγγράφων κάθε
7 συλλογής να έχουν γίνει train από το feedback του χρήστη ώστε να εµφανίζονται ψηλά τα έγγραφα που θέλουµε στο συγκεκριµένο προφίλ) γ) Το κυριότερο πρόβληµα είναι το πρόβληµα χώρου (για κάθε προφίλ κάθε χρήστη µια λίστα µε όλα τα id s των εγγράφων για τα οποία ο χρήστης έχει δώσει απάντηση). Επίσης υπάρχει και ένα επιπλέον υπολογιστικό κόστος στην αποτίµηση των επερωτήσεων (για να τροποποιηθούν τα αποτελέσµατα σύµφωνα µε τις λίστες όπως περιγράψαµε παραπάνω). Θα επέλεγα τον τρόπο που περιέγραψα πιο πάνω (µε µια λίστα µε Document_id s ψήφους ανά προφίλ) γιατί φαίνεται ο πιο εφικτός σε σχέση µε το να είχαµε διαφορετικές συλλογές διανυσµάτων εγγράφων για κάθε προφίλ, καθενός χρήστη το οποίο θα πολλαπλασίαζε τα 9 δις διανύσµατα σελίδων που έχει το Google σήµερα * κάθε προφίλ * κάθε χρήστη. Το να κρατάµε πληροφορία όπως το σε ποιο query έδωσε το feedback ο χρήστης είναι επίσης πάρα πολύ σπάταλο αφού θέλει µια λίστα για κάθε query (!), που γίνεται σε κάθε προφίλ από κάθε χρήστη. 2 η Λύση: α) Κάθε φορά που ο χρήστης εκτελεί µια επερώτηση, τα έγγραφα που επιστρέφονται εξετάζονται από το χρήστη και κρίνονται από αυτόν ως good ή bad. Οι λέξεις εξάγονται αυτόµατα από τα έγγραφα που αξιολογήθηκαν και χρησιµοποιούνται για να τροποποιήσουν την αρχική επερώτηση. Η επαναδιατύπωση των επερωτήσεων µπορεί να γίνει µε πολλούς τρόπους. Μπορεί να προστεθούν ή να αφαιρεθούν όροι στην επερώτηση ή ρυθµιστούν τα βάρη των όρων του διανύσµατος επερώτησης, ώστε τα βάρη των συναφών όρων να σταθµιστούν υψηλότερα. Σε συστήµατα που χρησιµοποιείται το διανυσµατικό µοντέλο για την αναπαράσταση των εγγράφων και των επερωτήσεων, η όλη διαδικασία της ανάδρασης συνάφειας µπορεί να θεωρηθεί ως µια προσπάθεια να µετακινήσουµε το διάνυσµα επερώτησης πλησιέστερα στα διανύσµατα που αναπαριστάνουν τα αξιολογηµένα ως συναφή έγγραφα. Πολλοί αλγόριθµοι έχουν χρησιµοποιηθεί για να κάνουν αυτήν την τροποποίηση, µε την αρχική ιδέα να έχει δοθεί από το Roccio. H τροποποιηµένη επερώτηση επαναδιατυπώνεται στην µηχανή αναζήτησης και ένα νέο σύνολο από έγγραφα επιστρέφεται και η διαδικασία προχωράει. Η όλη αυτή διαδικασία θα γίνει εξατοµικευµένη ανάκτηση εάν αυτή η κρίση σχετικά µε τη συνάφεια των εγγράφων αντιγραφεί σε ένα προφίλ χρήστη και χρησιµοποιηθούν στις επόµενες αναζητήσεις για να βελτιωθεί η ανάκτηση εγγράφων και οι διαβαθµίσεις των αποτελεσµάτων αναζήτησης. Η αξιολόγηση των µη-συναφών σελίδων µπορεί να χρησιµοποιηθεί ως φιλτράρισµα, ώστε η µηχανή αναζήτησης να µην τις επιστρέφει στα αποτελέσµατα των επερωτήσεων του αντίστοιχου προφίλ. β) Το σύστηµα πρέπει να ρυθµίζει την επερώτηση που δόθηκε από τον χρήστη σύµφωνα µε το αντίστοιχο προφίλ χρήστη. Ο κλασικός τρόπος είναι ανάλογα µε το προφίλ που έχει επιλέξει ο χρήστης (το έχει δηµιουργήσει ο ίδιος) να αποθηκευτεί και το αντίστοιχο διάνυσµα που αντανακλά τις κρίσεις του χρήστη στα επιστρεφόµενα έγγραφα. Έτσι κάθε φορά που είναι να εκτελεστεί µία επερώτηση, θα διάνυσµα της τελικής επερώτησης θα είναι της µορφής q = q * (1+p), όπου q το αρχικό διάνυσµα της επερώτησης και p το διάνυσµα του συγκεκριµένου προφίλ. Αυτό το διάνυσµα θα περιέχει τις υψηλότερες τιµές βάρους για τους όρους εκείνους που κρίθηκαν συναφή µε τη διαδικασία που περιγράψαµε προηγουµένως. Επίσης µπορούµε να χρησιµοποιήσουµε το προφίλ όχι ως µέθοδος επαναδιατύπωσης της επερώτησης αλλά για να προσδιορίσουµε καλύτερα την αναζήτηση. ηλαδή µέσα από τους όρους που έχουν υψηλότερο βάρος στο διάνυσµα του προφίλ, η µηχανή αναζήτησης θα αντιστοιχεί την επερώτηση εισόδου σε ένα σύνολο από ενδιαφέρουσες κατηγορίες, βασισµένες στο προφίλ χρήστη, και περιορίζει την περιοχή αναζήτησης σε αυτές τις κατηγορίες.
8 γ) Το µεγαλύτερο πρόβληµα για την υποστήριξη αυτής της λειτουργικότητας είναι η δυσκολία απόκτησης ανάδρασης συνάφειας µε σαφή τρόπο από τους χρήστες σε εξατοµικευµένες διαδικτυακές µηχανές αναζήτησης, λόγο του τεράστιου µεγέθους του ιστού, ο οποίος αποτελείται από δισεκατοµµύρια έγγραφα. Είναι ιδιαίτερα χρονοβόρο και σχεδόν αδύνατο να συλλεχθούν κρίσεις συνάφειας από τον κάθε χρήστη, για κάθε σελίδα που επιστρέφεται ως αποτέλεσµα µίας επερώτησης. Οι χρήστες γενικά απεχθάνονται να έχουν να ξοδέψουν χρόνο και προσπάθεια υποβάλλοντας δεδοµένα σε οποιοδήποτε σύστηµα, ιδιαίτερα αν τα πλεονεκτήµατα δεν είναι αµέσως εµφανή. Επίσης οι χρήστες αποφεύγουν να δώσουν προσωπικές πληροφορίες στους ανώνυµους servers για λόγους απορρήτου και ασφάλειας. Τέλος ένα ακόµα πρόβληµα βρίσκεται στην διατήρηση της αποδοτικότητας. Υπάρχει χρονική πολυπλοκότητα όσο µεγαλώνει το µέγεθος των προφίλ των χρηστών (π.χ αυξανόµενος αριθµός λέξεων, ενδιαφέρων κατηγοριών και περιοχών).
Φροντιστήριο 4. Άσκηση 1. Λύση. Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών HY463 - Συστήµατα Ανάκτησης Πληροφοριών Εαρινό Εξάµηνο
 Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών HY463 - Συστήµατα Ανάκτησης Πληροφοριών 2007-2008 Εαρινό Εξάµηνο Άσκηση 1 Φροντιστήριο 4 Θεωρείστε ένα έγγραφο με περιεχόμενο «αυτό είναι ένα κείμενο και
Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών HY463 - Συστήµατα Ανάκτησης Πληροφοριών 2007-2008 Εαρινό Εξάµηνο Άσκηση 1 Φροντιστήριο 4 Θεωρείστε ένα έγγραφο με περιεχόμενο «αυτό είναι ένα κείμενο και
Παλαιότερες ασκήσεις
 Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών HY6 - Συστήµατα Ανάκτησης Πληροφοριών Παλαιότερες ασκήσεις η Σειρά Ασκήσεων (Αξιολόγηση της Αποτελεσµατικότητας της Ανάκτησης) Άσκηση ( η σειρά ασκήσεων
Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών HY6 - Συστήµατα Ανάκτησης Πληροφοριών Παλαιότερες ασκήσεις η Σειρά Ασκήσεων (Αξιολόγηση της Αποτελεσµατικότητας της Ανάκτησης) Άσκηση ( η σειρά ασκήσεων
Λύσεις 1 ης Σειράς Ασκήσεων (Αξιολόγηση της Αποτελεσµατικότητας της Ανάκτησης)
 Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών ΗΥ-6 Συστήµατα Ανάκτησης Πληροφοριών 7-8 Εαρινό Εξάµηνο Άσκηση Λύσεις ης Σειράς Ασκήσεων (Αξιολόγηση της Αποτελεσµατικότητας της Ανάκτησης) Θεωρείστε µια
Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών ΗΥ-6 Συστήµατα Ανάκτησης Πληροφοριών 7-8 Εαρινό Εξάµηνο Άσκηση Λύσεις ης Σειράς Ασκήσεων (Αξιολόγηση της Αποτελεσµατικότητας της Ανάκτησης) Θεωρείστε µια
Λύση (από: Τσιαλιαμάνης Αναγνωστόπουλος Πέτρος) (α) Το trie του λεξιλογίου είναι
 Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών HY463 - Συστήματα Ανάκτησης Πληροφοριών 2006-2007 Εαρινό Εξάμηνο 3 η Σειρά ασκήσεων (Ευρετηρίαση, Αναζήτηση σε Κείμενα και Άλλα Θέματα) (βαθμοί 12: όποιος
Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών HY463 - Συστήματα Ανάκτησης Πληροφοριών 2006-2007 Εαρινό Εξάμηνο 3 η Σειρά ασκήσεων (Ευρετηρίαση, Αναζήτηση σε Κείμενα και Άλλα Θέματα) (βαθμοί 12: όποιος
Οργάνωση αρχείων: πως είναι τοποθετηµένες οι εγγραφές ενός αρχείου όταν αποθηκεύονται στο δίσκο
 Κατακερµατισµός 1 Οργάνωση Αρχείων (σύνοψη) Οργάνωση αρχείων: πως είναι τοποθετηµένες οι εγγραφές ενός αρχείου όταν αποθηκεύονται στο δίσκο 1. Αρχεία Σωρού 2. Ταξινοµηµένα Αρχεία Φυσική διάταξη των εγγραφών
Κατακερµατισµός 1 Οργάνωση Αρχείων (σύνοψη) Οργάνωση αρχείων: πως είναι τοποθετηµένες οι εγγραφές ενός αρχείου όταν αποθηκεύονται στο δίσκο 1. Αρχεία Σωρού 2. Ταξινοµηµένα Αρχεία Φυσική διάταξη των εγγραφών
Η ακρίβεια ορίζεται σαν το πηλίκο των ευρεθέντων συναφών εγγράφων προς τα ευρεθέντα έγγραφα. Άρα για τα τρία συστήµατα έχουµε τις εξής τιµές:
 Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών HY463 - Συστήµατα Ανάκτησης Πληροφοριών 2005-2006 Εαρινό Εξάµηνο 1 η Σειρά Ασκήσεων (Αξιολόγηση Αποτελεσµατικότητας Ανάκτησης) Άσκηση 1 (4 βαθµοί) Θεωρείστε
Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών HY463 - Συστήµατα Ανάκτησης Πληροφοριών 2005-2006 Εαρινό Εξάµηνο 1 η Σειρά Ασκήσεων (Αξιολόγηση Αποτελεσµατικότητας Ανάκτησης) Άσκηση 1 (4 βαθµοί) Θεωρείστε
Posting File. D i. tf key1 [position1 position2 ] D j tf key2... D l.. tf keyl
![Posting File. D i. tf key1 [position1 position2 ] D j tf key2... D l.. tf keyl Posting File. D i. tf key1 [position1 position2 ] D j tf key2... D l.. tf keyl](/thumbs/26/8690994.jpg) ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΗΥ463 Συστήµατα Ανάκτησης Πληροφοριών Εργασία: Ανεστραµµένο Ευρετήριο Εισαγωγή Σκοπός της εργασίας είναι η δηµιουργία ενός ανεστραµµένου ευρετηρίου για τη µηχανή αναζήτησης Μίτος, το
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΗΥ463 Συστήµατα Ανάκτησης Πληροφοριών Εργασία: Ανεστραµµένο Ευρετήριο Εισαγωγή Σκοπός της εργασίας είναι η δηµιουργία ενός ανεστραµµένου ευρετηρίου για τη µηχανή αναζήτησης Μίτος, το
Εισαγωγή στην Πληροφορική. Α σ κ ή σ ε ι ς σ τ η ν ι α χ ε ί ρ ι σ η Μ ν ή µ η ς. Αντώνης Σταµατάκης
 Εισαγωγή στην Πληροφορική Α σ κ ή σ ε ι ς σ τ η ν ι α χ ε ί ρ ι σ η Μ ν ή µ η ς Αντώνης Σταµατάκης Μονάδες µέτρησης µνήµης Η βασική µονάδα µέτρησης της µνήµης στα υπολογιστικά συστήµατα είναι το µπάιτ
Εισαγωγή στην Πληροφορική Α σ κ ή σ ε ι ς σ τ η ν ι α χ ε ί ρ ι σ η Μ ν ή µ η ς Αντώνης Σταµατάκης Μονάδες µέτρησης µνήµης Η βασική µονάδα µέτρησης της µνήµης στα υπολογιστικά συστήµατα είναι το µπάιτ
Τεχνικές ταξινόµησης αποτελεσµάτων µηχανών αναζήτησης µε βάση την ιστορία του χρήστη
 Τεχνικές ταξινόµησης αποτελεσµάτων µηχανών αναζήτησης µε βάση την ιστορία του χρήστη Όνοµα: Νικολαΐδης Αντώνιος Επιβλέπων: Τ. Σελλής Περίληψη ιπλωµατικής Εργασίας Συνεπιβλέποντες: Θ. αλαµάγκας, Γ. Γιαννόπουλος
Τεχνικές ταξινόµησης αποτελεσµάτων µηχανών αναζήτησης µε βάση την ιστορία του χρήστη Όνοµα: Νικολαΐδης Αντώνιος Επιβλέπων: Τ. Σελλής Περίληψη ιπλωµατικής Εργασίας Συνεπιβλέποντες: Θ. αλαµάγκας, Γ. Γιαννόπουλος
Ανάκτηση Πληροφορίας
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Ανάκτηση Πληροφορίας Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #11 Suffix Arrays Φοίβος Μυλωνάς fmylonas@ionio.gr Ανάκτηση Πληροφορίας 1 Άδεια χρήσης Το παρόν
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Ανάκτηση Πληροφορίας Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #11 Suffix Arrays Φοίβος Μυλωνάς fmylonas@ionio.gr Ανάκτηση Πληροφορίας 1 Άδεια χρήσης Το παρόν
Φροντιστήριο 5. Το πρώτο πράγµα λοιπόν που πρέπει να κάνουµε είναι να βρούµε τις πιθανότητες εµφάνισης των συµβόλων. Έτσι έχουµε:
 Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών HY463 - Συστήµατα Ανάκτησης Πληροφοριών 2006-2007 Εαρινό Εξάµηνο Φροντιστήριο 5 Άσκηση 1 Θεωρείστε το αλφάβητο {α,β,γ,δ,ε} και την εξής φράση: «α α β γ
Πανεπιστήµιο Κρήτης, Τµήµα Επιστήµης Υπολογιστών HY463 - Συστήµατα Ανάκτησης Πληροφοριών 2006-2007 Εαρινό Εξάµηνο Φροντιστήριο 5 Άσκηση 1 Θεωρείστε το αλφάβητο {α,β,γ,δ,ε} και την εξής φράση: «α α β γ
Αριθµητική Ανάλυση 1 εκεµβρίου / 43
 Αριθµητική Ανάλυση 1 εκεµβρίου 2014 Αριθµητική Ανάλυση 1 εκεµβρίου 2014 1 / 43 Κεφ.5. Αριθµητικός Υπολογισµός Ιδιοτιµών και Ιδιοδιανυσµάτων ίνεται ένας πίνακας A C n n και Ϲητούνται να προσδιορισθούν οι
Αριθµητική Ανάλυση 1 εκεµβρίου 2014 Αριθµητική Ανάλυση 1 εκεµβρίου 2014 1 / 43 Κεφ.5. Αριθµητικός Υπολογισµός Ιδιοτιµών και Ιδιοδιανυσµάτων ίνεται ένας πίνακας A C n n και Ϲητούνται να προσδιορισθούν οι
Λύσεις Παλιών Θεµάτων. Συστήµατα Παράλληλης Επεξεργασίας, 9ο εξάµηνο Υπεύθ. Καθ. Νεκτάριος Κοζύρης
 Λύσεις Παλιών Θεµάτων Συστήµατα Παράλληλης Επεξεργασίας, 9ο εξάµηνο Υπεύθ. Καθ. Νεκτάριος Κοζύρης Θέµα Φεβρουάριος 2003 1) Έστω ένας υπερκύβος n-διαστάσεων. i. Να βρεθεί ο αριθµός των διαφορετικών τρόπων
Λύσεις Παλιών Θεµάτων Συστήµατα Παράλληλης Επεξεργασίας, 9ο εξάµηνο Υπεύθ. Καθ. Νεκτάριος Κοζύρης Θέµα Φεβρουάριος 2003 1) Έστω ένας υπερκύβος n-διαστάσεων. i. Να βρεθεί ο αριθµός των διαφορετικών τρόπων
Συστήματα Ανάκτησης Πληροφοριών ΗΥ-463
 ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ COMPUTER SCIENCE DEPARTMENT UNIVERSITY OF CRETE Συστήματα Ανάκτησης Πληροφοριών ΗΥ-463 4 η Σειρά Ασκήσεων Ψαράκη Μαρία-Γεωργία ΜΕΤ 556 psaraki@csd.uoc.gr Εαρινό Εξάμηνο 2008-2009
ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ COMPUTER SCIENCE DEPARTMENT UNIVERSITY OF CRETE Συστήματα Ανάκτησης Πληροφοριών ΗΥ-463 4 η Σειρά Ασκήσεων Ψαράκη Μαρία-Γεωργία ΜΕΤ 556 psaraki@csd.uoc.gr Εαρινό Εξάμηνο 2008-2009
Ανάκτηση Πληροφορίας
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Ανάκτηση Πληροφορίας Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #10 εικτοδότηση και Αναζήτηση Φοίβος Μυλωνάς fmylonas@ionio.gr Ανάκτηση Πληροφορίας 1 Άδεια
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Ανάκτηση Πληροφορίας Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #10 εικτοδότηση και Αναζήτηση Φοίβος Μυλωνάς fmylonas@ionio.gr Ανάκτηση Πληροφορίας 1 Άδεια
Επεξεργασία Ερωτήσεων
 Εισαγωγή στην Επεξεργασία Ερωτήσεων 1 Εισαγωγή ΣΔΒΔ Σύνολο από προγράµµατα για τη διαχείριση της ΒΔ Αρχεία ευρετηρίου Κατάλογος ΒΑΣΗ ΔΕΔΟΜΕΝΩΝ Αρχεία δεδοµένων συστήµατος Σύστηµα Βάσεων Δεδοµένων (ΣΒΔ)
Εισαγωγή στην Επεξεργασία Ερωτήσεων 1 Εισαγωγή ΣΔΒΔ Σύνολο από προγράµµατα για τη διαχείριση της ΒΔ Αρχεία ευρετηρίου Κατάλογος ΒΑΣΗ ΔΕΔΟΜΕΝΩΝ Αρχεία δεδοµένων συστήµατος Σύστηµα Βάσεων Δεδοµένων (ΣΒΔ)
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΛΥΣΗ ΣΤΗΝ ΕΥΤΕΡΗ ΑΣΚΗΣΗ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΛΥΣΗ ΣΤΗΝ ΕΥΤΕΡΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑ ΒΑΣΕΙΣ Ε ΟΜΕΝΩΝ ΑΚΑ. ΕΤΟΣ 2012-13 Ι ΑΣΚΟΝΤΕΣ Ιωάννης Βασιλείου Καθηγητής, Τοµέας Τεχνολογίας
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΛΥΣΗ ΣΤΗΝ ΕΥΤΕΡΗ ΑΣΚΗΣΗ ΜΑΘΗΜΑ ΒΑΣΕΙΣ Ε ΟΜΕΝΩΝ ΑΚΑ. ΕΤΟΣ 2012-13 Ι ΑΣΚΟΝΤΕΣ Ιωάννης Βασιλείου Καθηγητής, Τοµέας Τεχνολογίας
Ασκήσεις Φροντιστηρίου «Υπολογιστική Νοηµοσύνη Ι» 7ο Φροντιστήριο 15/1/2008
 Ασκήσεις Φροντιστηρίου «Υπολογιστική Νοηµοσύνη Ι» 7ο Φροντιστήριο 5//008 Πρόβληµα ο Στα παρακάτω ερωτήµατα επισηµαίνουµε ότι perceptron είναι ένας νευρώνας και υποθέτουµε, όπου χρειάζεται, τη χρήση δικτύων
Ασκήσεις Φροντιστηρίου «Υπολογιστική Νοηµοσύνη Ι» 7ο Φροντιστήριο 5//008 Πρόβληµα ο Στα παρακάτω ερωτήµατα επισηµαίνουµε ότι perceptron είναι ένας νευρώνας και υποθέτουµε, όπου χρειάζεται, τη χρήση δικτύων
Ο ΑΤΔ Λεξικό. Σύνολο στοιχείων με βασικές πράξεις: Δημιουργία Εισαγωγή Διαγραφή Μέλος. Υλοποιήσεις
 Ο ΑΤΔ Λεξικό Σύνολο στοιχείων με βασικές πράξεις: Δημιουργία Εισαγωγή Διαγραφή Μέλος Υλοποιήσεις Πίνακας με στοιχεία bit (0 ή 1) (bit vector) Λίστα ακολουθιακή (πίνακας) ή συνδεδεμένη Είναι γνωστό το μέγιστο
Ο ΑΤΔ Λεξικό Σύνολο στοιχείων με βασικές πράξεις: Δημιουργία Εισαγωγή Διαγραφή Μέλος Υλοποιήσεις Πίνακας με στοιχεία bit (0 ή 1) (bit vector) Λίστα ακολουθιακή (πίνακας) ή συνδεδεμένη Είναι γνωστό το μέγιστο
Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών HY463 - Συστήματα Ανάκτησης Πληροφοριών Εαρινό Εξάμηνο. Φροντιστήριο 3.
 Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών HY6 - Συστήματα Ανάκτησης Πληροφοριών 007 008 Εαρινό Εξάμηνο Φροντιστήριο Retrieval Models Άσκηση Θεωρείστε μια συλλογή κειμένων που περιέχει τα ακόλουθα
Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών HY6 - Συστήματα Ανάκτησης Πληροφοριών 007 008 Εαρινό Εξάμηνο Φροντιστήριο Retrieval Models Άσκηση Θεωρείστε μια συλλογή κειμένων που περιέχει τα ακόλουθα
ζωγραφίζοντας µε τον υπολογιστή
 ζωγραφίζοντας µε τον υπολογιστή Μια από τις εργασίες που µπορούµε να κάνουµε µε τον υπολογιστή είναι και η ζωγραφική. Για να γίνει όµως αυτό πρέπει ο υπολογιστής να είναι εφοδιασµένος µε το κατάλληλο πρόγραµµα.
ζωγραφίζοντας µε τον υπολογιστή Μια από τις εργασίες που µπορούµε να κάνουµε µε τον υπολογιστή είναι και η ζωγραφική. Για να γίνει όµως αυτό πρέπει ο υπολογιστής να είναι εφοδιασµένος µε το κατάλληλο πρόγραµµα.
Περίληψη ιπλωµατικής Εργασίας
 Περίληψη ιπλωµατικής Εργασίας Θέµα: Εναλλακτικές Τεχνικές Εντοπισµού Θέσης Όνοµα: Κατερίνα Σπόντου Επιβλέπων: Ιωάννης Βασιλείου Συν-επιβλέπων: Σπύρος Αθανασίου 1. Αντικείµενο της διπλωµατικής Ο εντοπισµός
Περίληψη ιπλωµατικής Εργασίας Θέµα: Εναλλακτικές Τεχνικές Εντοπισµού Θέσης Όνοµα: Κατερίνα Σπόντου Επιβλέπων: Ιωάννης Βασιλείου Συν-επιβλέπων: Σπύρος Αθανασίου 1. Αντικείµενο της διπλωµατικής Ο εντοπισµός
Σηµειώσεις στις σειρές
 . ΟΡΙΣΜΟΙ - ΓΕΝΙΚΕΣ ΕΝΝΟΙΕΣ Σηµειώσεις στις σειρές Στην Ενότητα αυτή παρουσιάζουµε τις βασικές-απαραίτητες έννοιες για την µελέτη των σειρών πραγµατικών αριθµών και των εφαρµογών τους. Έτσι, δίνονται συστηµατικά
. ΟΡΙΣΜΟΙ - ΓΕΝΙΚΕΣ ΕΝΝΟΙΕΣ Σηµειώσεις στις σειρές Στην Ενότητα αυτή παρουσιάζουµε τις βασικές-απαραίτητες έννοιες για την µελέτη των σειρών πραγµατικών αριθµών και των εφαρµογών τους. Έτσι, δίνονται συστηµατικά
ΔΟΜΗΜΕΝΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Κεφάλαιο 8 : H γλώσσα προγραµµατισµού Pascal 1 ο Μέρος σηµειώσεων (Ενότητες 8.1 & 8.2 σχολικού βιβλίου)
 ΔΟΜΗΜΕΝΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Κεφάλαιο 8 : H γλώσσα προγραµµατισµού Pascal 1 ο Μέρος σηµειώσεων (Ενότητες 8.1 & 8.2 σχολικού βιβλίου) 1. Εισαγωγή Χαρακτηριστικά της γλώσσας Τύποι δεδοµένων Γλώσσα προγραµµατισµού
ΔΟΜΗΜΕΝΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Κεφάλαιο 8 : H γλώσσα προγραµµατισµού Pascal 1 ο Μέρος σηµειώσεων (Ενότητες 8.1 & 8.2 σχολικού βιβλίου) 1. Εισαγωγή Χαρακτηριστικά της γλώσσας Τύποι δεδοµένων Γλώσσα προγραµµατισµού
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ. ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ, 5 ο εξάµηνο
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ και ΥΠΟΛΟΓΙΣΤΩΝ ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ, 5 ο εξάµηνο ΦΕΒΡΟΥΑΡΙΟΣ 2006 ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ και ΥΠΟΛΟΓΙΣΤΩΝ ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ, 5 ο εξάµηνο ΦΕΒΡΟΥΑΡΙΟΣ 2006 ΘΕΜΑΤΑ ΚΑΙ ΛΥΣΕΙΣ
Τα δεδοµένα συνήθως αποθηκεύονται σε αρχεία στο δίσκο Για να επεξεργαστούµε τα δεδοµένα θα πρέπει αυτά να βρίσκονται στη
 Ευρετήρια 1 Αρχεία Τα δεδοµένα συνήθως αποθηκεύονται σε αρχεία στο δίσκο Για να επεξεργαστούµε τα δεδοµένα θα πρέπει αυτά να βρίσκονται στη µνήµη. Η µεταφορά δεδοµένων από το δίσκο στη µνήµη και από τη
Ευρετήρια 1 Αρχεία Τα δεδοµένα συνήθως αποθηκεύονται σε αρχεία στο δίσκο Για να επεξεργαστούµε τα δεδοµένα θα πρέπει αυτά να βρίσκονται στη µνήµη. Η µεταφορά δεδοµένων από το δίσκο στη µνήµη και από τη
Προτεινόμενες Λύσεις 1 ης Σειράς Ασκήσεων (Αξιολόγηση της Αποτελεσματικότητας της Ανάκτησης & Μοντέλα Ανάκτησης)
 Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών ΗΥ463 Συστήματα Ανάκτησης Πληροφοριών 28-29 Εαρινό Εξάμηνο Προτεινόμενες Λύσεις 1 ης Σειράς Ασκήσεων (Αξιολόγηση της Αποτελεσματικότητας της Ανάκτησης &
Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών ΗΥ463 Συστήματα Ανάκτησης Πληροφοριών 28-29 Εαρινό Εξάμηνο Προτεινόμενες Λύσεις 1 ης Σειράς Ασκήσεων (Αξιολόγηση της Αποτελεσματικότητας της Ανάκτησης &
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ Τ Μ Η Μ Α Π Λ Η Ρ Ο Φ Ο Ρ Ι Κ Η Σ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ Τ Μ Η Μ Α Π Λ Η Ρ Ο Φ Ο Ρ Ι Κ Η Σ ΕΠΛ 035 - ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΑΛΓΟΡΙΘΜΟΙ ΓΙΑ ΗΛΕΚΤΡΟΛΟΓΟΥΣ ΜΗΧΑΝΙΚΟΥΣ ΚΑΙ ΜΗΧΑΝΙΚΟΥΣ ΥΠΟΛΟΓΙΣΤΩΝ Ακαδηµαϊκό έτος 2017-2018 Υπεύθυνος εργαστηρίου: Γεώργιος
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ Τ Μ Η Μ Α Π Λ Η Ρ Ο Φ Ο Ρ Ι Κ Η Σ ΕΠΛ 035 - ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΑΛΓΟΡΙΘΜΟΙ ΓΙΑ ΗΛΕΚΤΡΟΛΟΓΟΥΣ ΜΗΧΑΝΙΚΟΥΣ ΚΑΙ ΜΗΧΑΝΙΚΟΥΣ ΥΠΟΛΟΓΙΣΤΩΝ Ακαδηµαϊκό έτος 2017-2018 Υπεύθυνος εργαστηρίου: Γεώργιος
Επαναληπτικές δοµές. µτ α.τ. Όχι. ! απαγορεύεται µέσα σε µία ΓΙΑ να µεταβάλλουµε τον µετρητή! διότι δεν θα ξέρουµε µετά πόσες επαναλήψεις θα γίνουν
 Επαναληπτικές δοµές Η λογική των επαναληπτικών διαδικασιών εφαρµόζεται όπου µία ακολουθία εντολών εφαρµόζεται σε ένα σύνολο περιπτώσεων που έχουν κάτι κοινό. Όταν ψάχνουµε θέση για να παρκάρουµε κοντά
Επαναληπτικές δοµές Η λογική των επαναληπτικών διαδικασιών εφαρµόζεται όπου µία ακολουθία εντολών εφαρµόζεται σε ένα σύνολο περιπτώσεων που έχουν κάτι κοινό. Όταν ψάχνουµε θέση για να παρκάρουµε κοντά
2η Οµάδα Ασκήσεων. 250 km db/km. 45 km 0.22 db/km 1:2. T 75 km 0.22 db/km 1:2. 75 km db/km. 1:2 225 km 0.22 db/km
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΙΚΤΥΑ ΟΠΤΙΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Καθηγητής Συβρίδης η Οµάδα Ασκήσεων Άσκηση 1η Στη ζεύξη που φαίνεται
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΙΚΤΥΑ ΟΠΤΙΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Καθηγητής Συβρίδης η Οµάδα Ασκήσεων Άσκηση 1η Στη ζεύξη που φαίνεται
Σχήµα 3.1: Εισαγωγή shift register σε βρόγχο for-loop.
 Η δοµή «Shift register» 1. Η δοµή «Shift register» εισάγεται στο βρόγχο for-loop αλλά και σε άλλους βρόγχους που θα δούµε στη συνέχεια, όπως ο βρόγχος «While loop». Ο τρόπος εισαγωγής και λειτουργίας της
Η δοµή «Shift register» 1. Η δοµή «Shift register» εισάγεται στο βρόγχο for-loop αλλά και σε άλλους βρόγχους που θα δούµε στη συνέχεια, όπως ο βρόγχος «While loop». Ο τρόπος εισαγωγής και λειτουργίας της
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Θεµατική Ενότητα ΠΛΗ 21: Ψηφιακά Συστήµατα Ακαδηµαϊκό Έτος 2009 2010 Γραπτή Εργασία #3 Παράδοση: 28 Μαρτίου 2010 Άσκηση 1 (15 µονάδες) Ένας επεξεργαστής υποστηρίζει τόσο
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Θεµατική Ενότητα ΠΛΗ 21: Ψηφιακά Συστήµατα Ακαδηµαϊκό Έτος 2009 2010 Γραπτή Εργασία #3 Παράδοση: 28 Μαρτίου 2010 Άσκηση 1 (15 µονάδες) Ένας επεξεργαστής υποστηρίζει τόσο
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ Τεχνικές κατασκευής δένδρων επιθεµάτων πολύ µεγάλου µεγέθους και χρήσης
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ Τεχνικές κατασκευής δένδρων επιθεµάτων πολύ µεγάλου µεγέθους και χρήσης
Αλγόριθµοι δροµολόγησης µε µέσα µαζικής µεταφοράς στο µεταφορικό δίκτυο των Αθηνών
 1 Αλγόριθµοι δροµολόγησης µε µέσα µαζικής µεταφοράς στο µεταφορικό δίκτυο των Αθηνών ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ της Κωτσογιάννη Μαριάννας Περίληψη 1. Αντικείµενο- Σκοπός Αντικείµενο της διπλωµατικής αυτής εργασίας
1 Αλγόριθµοι δροµολόγησης µε µέσα µαζικής µεταφοράς στο µεταφορικό δίκτυο των Αθηνών ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ της Κωτσογιάννη Μαριάννας Περίληψη 1. Αντικείµενο- Σκοπός Αντικείµενο της διπλωµατικής αυτής εργασίας
πίνακας σελίδων Bit Παρουσίας Αριθμός Πλαισίου
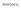 Ασκήσεις Ένα υπολογιστικό σύστημα που χρησιμοποιεί σελιδοποίηση διαθέτει λογικό χώρο διευθύνσεων 12 bit και υποστηρίζεται από 2 πλαίσια φυσικής μνήμης. Την παρούσα στιγμή ο πίνακας σελίδων είναι ο εξής:
Ασκήσεις Ένα υπολογιστικό σύστημα που χρησιμοποιεί σελιδοποίηση διαθέτει λογικό χώρο διευθύνσεων 12 bit και υποστηρίζεται από 2 πλαίσια φυσικής μνήμης. Την παρούσα στιγμή ο πίνακας σελίδων είναι ο εξής:
3 Αναδροµή και Επαγωγή
 3 Αναδροµή και Επαγωγή Η ιδέα της µαθηµατικής επαγωγής µπορεί να επεκταθεί και σε άλλες δοµές εκτός από το σύνολο των ϕυσικών N. Η ορθότητα της µαθηµατικής επαγωγής ϐασίζεται όπως ϑα δούµε λίγο αργότερα
3 Αναδροµή και Επαγωγή Η ιδέα της µαθηµατικής επαγωγής µπορεί να επεκταθεί και σε άλλες δοµές εκτός από το σύνολο των ϕυσικών N. Η ορθότητα της µαθηµατικής επαγωγής ϐασίζεται όπως ϑα δούµε λίγο αργότερα
1. Financial New Times Year MAXk {FREQij} D D D D
 Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών HY46 - Συστήματα Ανάκτησης Πληροφοριών 2004-2005 Εαρινό Εξάμηνο 2 η Σειρά ασκήσεων (Μοντέλα Ανάκτησης Πληροφοριών και Ευρετήρια) Ανάθεση: 6 Μαρτίου Παράδοση:
Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών HY46 - Συστήματα Ανάκτησης Πληροφοριών 2004-2005 Εαρινό Εξάμηνο 2 η Σειρά ασκήσεων (Μοντέλα Ανάκτησης Πληροφοριών και Ευρετήρια) Ανάθεση: 6 Μαρτίου Παράδοση:
ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ. Δοµές Δεδοµένων
 ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ AM: Δοµές Δεδοµένων Πτυχιακή Εξεταστική Ιούλιος 2014 Διδάσκων : Ευάγγελος Μαρκάκης 09.07.2014 ΥΠΟΓΡΑΦΗ ΕΠΟΠΤΗ: Διάρκεια εξέτασης : 2 ώρες
ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ AM: Δοµές Δεδοµένων Πτυχιακή Εξεταστική Ιούλιος 2014 Διδάσκων : Ευάγγελος Μαρκάκης 09.07.2014 ΥΠΟΓΡΑΦΗ ΕΠΟΠΤΗ: Διάρκεια εξέτασης : 2 ώρες
Τα δεδομένα (περιεχόμενο) μιας βάσης δεδομένων αποθηκεύεται στο δίσκο
 Κατακερματισμός 1 Αποθήκευση εδομένων (σύνοψη) Τα δεδομένα (περιεχόμενο) μιας βάσης δεδομένων αποθηκεύεται στο δίσκο Παραδοσιακά, μία σχέση (πίνακας/στιγμιότυπο) αποθηκεύεται σε ένα αρχείο Αρχείο δεδομένων
Κατακερματισμός 1 Αποθήκευση εδομένων (σύνοψη) Τα δεδομένα (περιεχόμενο) μιας βάσης δεδομένων αποθηκεύεται στο δίσκο Παραδοσιακά, μία σχέση (πίνακας/στιγμιότυπο) αποθηκεύεται σε ένα αρχείο Αρχείο δεδομένων
Ενότητα 2: Η κρυφή µνήµη και η λειτουργία της
 Ενότητα 2: Η κρυφή µνήµη και η λειτουργία της Στην ενότητα αυτή θα αναφερθούµε εκτενέστερα στη λειτουργία και την οργάνωση της κρυφής µνήµης. Θα προσδιορίσουµε τις βασικές λειτουργίες που σχετίζονται µε
Ενότητα 2: Η κρυφή µνήµη και η λειτουργία της Στην ενότητα αυτή θα αναφερθούµε εκτενέστερα στη λειτουργία και την οργάνωση της κρυφής µνήµης. Θα προσδιορίσουµε τις βασικές λειτουργίες που σχετίζονται µε
µπιτ Λύση: Κάθε οµάδα των τεσσάρων µπιτ µεταφράζεται σε ένα δεκαεξαδικό ψηφίο 1100 C 1110 E Άρα το δεκαεξαδικό ισοδύναµο είναι CE2
 ! Βρείτε το δεκαεξαδικό ισοδύναµο του σχήµατος µπιτ 110011100010 Λύση: Κάθε οµάδα των τεσσάρων µπιτ µεταφράζεται σε ένα δεκαεξαδικό ψηφίο 1100 C 1110 E 0010 2 Άρα το δεκαεξαδικό ισοδύναµο είναι CE2 2 !
! Βρείτε το δεκαεξαδικό ισοδύναµο του σχήµατος µπιτ 110011100010 Λύση: Κάθε οµάδα των τεσσάρων µπιτ µεταφράζεται σε ένα δεκαεξαδικό ψηφίο 1100 C 1110 E 0010 2 Άρα το δεκαεξαδικό ισοδύναµο είναι CE2 2 !
Άρα, Τ ser = (A 0 +B 0 +B 0 +A 0 ) επίπεδο 0 + (A 1 +B 1 +A 1 ) επίπεδο 1 + +(B 5 ) επίπεδο 5 = 25[χρονικές µονάδες]
![Άρα, Τ ser = (A 0 +B 0 +B 0 +A 0 ) επίπεδο 0 + (A 1 +B 1 +A 1 ) επίπεδο 1 + +(B 5 ) επίπεδο 5 = 25[χρονικές µονάδες] Άρα, Τ ser = (A 0 +B 0 +B 0 +A 0 ) επίπεδο 0 + (A 1 +B 1 +A 1 ) επίπεδο 1 + +(B 5 ) επίπεδο 5 = 25[χρονικές µονάδες]](/thumbs/27/10818274.jpg) Α. Στο παρακάτω διάγραµµα εµφανίζεται η εκτέλεση ενός παράλληλου αλγόριθµου που λύνει το ίδιο πρόβληµα µε έναν ακολουθιακό αλγόριθµο χωρίς πλεονασµό. Τα Α i και B i αντιστοιχούν σε ακολουθιακά υποέργα
Α. Στο παρακάτω διάγραµµα εµφανίζεται η εκτέλεση ενός παράλληλου αλγόριθµου που λύνει το ίδιο πρόβληµα µε έναν ακολουθιακό αλγόριθµο χωρίς πλεονασµό. Τα Α i και B i αντιστοιχούν σε ακολουθιακά υποέργα
ΠΛΗΡΟΦΟΡΙΑΚΑ & ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΑ ΣΥΣΤΗΜΑΤΑ
 Οικονοµικό Πανεπιστήµιο Αθηνών Τµήµα ιοικητικής Επιστήµης & Τεχνολογίας ΠΛΗΡΟΦΟΡΙΑΚΑ & ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΑ ΣΥΣΤΗΜΑΤΑ Κεφάλαιο 2 Αριθµητικά Συστήµατα και Αριθµητική Υπολογιστών Γιώργος Γιαγλής Περίληψη Κεφαλαίου
Οικονοµικό Πανεπιστήµιο Αθηνών Τµήµα ιοικητικής Επιστήµης & Τεχνολογίας ΠΛΗΡΟΦΟΡΙΑΚΑ & ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΑ ΣΥΣΤΗΜΑΤΑ Κεφάλαιο 2 Αριθµητικά Συστήµατα και Αριθµητική Υπολογιστών Γιώργος Γιαγλής Περίληψη Κεφαλαίου
Στην ενότητα αυτή θα µελετηθούν τα εξής επιµέρους θέµατα:
 Τεχνικές Κατακερµατισµού Στην ενότητα αυτή θα µελετηθούν τα εξής επιµέρους θέµατα: Τεχνικές Κατακερµατισµού ιαχείριση Συγκρούσεων µε Αλυσίδωση ιαχείριση Συγκρούσεων µε Ανοικτή ιεύθυνση ιπλός Κατακερµατισµός,
Τεχνικές Κατακερµατισµού Στην ενότητα αυτή θα µελετηθούν τα εξής επιµέρους θέµατα: Τεχνικές Κατακερµατισµού ιαχείριση Συγκρούσεων µε Αλυσίδωση ιαχείριση Συγκρούσεων µε Ανοικτή ιεύθυνση ιπλός Κατακερµατισµός,
Κατακερματισμός. 4/3/2009 Μ.Χατζόπουλος 1
 Κατακερματισμός 4/3/2009 Μ.Χατζόπουλος 1 H ιδέα που βρίσκεται πίσω από την τεχνική του κατακερματισμού είναι να δίνεται μια συνάρτησης h, που λέγεται συνάρτηση κατακερματισμού ή παραγωγής τυχαίων τιμών
Κατακερματισμός 4/3/2009 Μ.Χατζόπουλος 1 H ιδέα που βρίσκεται πίσω από την τεχνική του κατακερματισμού είναι να δίνεται μια συνάρτησης h, που λέγεται συνάρτηση κατακερματισμού ή παραγωγής τυχαίων τιμών
Κεφ.11: Ευρετήρια και Κατακερματισμός
 Κεφ.11: Ευρετήρια και Κατακερματισμός Database System Concepts, 6 th Ed. See www.db-book.com for conditions on re-use Κεφ. 11: Ευρετήρια-Βασική θεωρία Μηχανισμοί ευρετηρίου χρησιμοποιούνται για την επιτάχυνση
Κεφ.11: Ευρετήρια και Κατακερματισμός Database System Concepts, 6 th Ed. See www.db-book.com for conditions on re-use Κεφ. 11: Ευρετήρια-Βασική θεωρία Μηχανισμοί ευρετηρίου χρησιμοποιούνται για την επιτάχυνση
Σχήµα 2.1: Εισαγωγή array στο Front Panel.
 Arrays (Πίνακες) 1. Στο LAbVIEW η εισαγωγή πινάκων γίνεται µε τα arrays. Για να εισάγουµε ένα array στο Front Panel κάνουµε δεξί κλικ σε αυτό και επιλέγουµε την εντολή «Array» από το µενού «Array, Matrix
Arrays (Πίνακες) 1. Στο LAbVIEW η εισαγωγή πινάκων γίνεται µε τα arrays. Για να εισάγουµε ένα array στο Front Panel κάνουµε δεξί κλικ σε αυτό και επιλέγουµε την εντολή «Array» από το µενού «Array, Matrix
Linear Hashing. Linear vs other Hashing
 Linear Hashing Τµήµα Πληροφορικής & Τηλ/νών, ΕΚΠΑ Υλοποίηση Συστηµάτων Βάσεων εδοµένων http://www.di.uoa.gr/~k18 Linear vs other Hashing Σεαντίθεσηµετοστατικόκατακερµατισµό, τα buckets αυξάνονται καθώς
Linear Hashing Τµήµα Πληροφορικής & Τηλ/νών, ΕΚΠΑ Υλοποίηση Συστηµάτων Βάσεων εδοµένων http://www.di.uoa.gr/~k18 Linear vs other Hashing Σεαντίθεσηµετοστατικόκατακερµατισµό, τα buckets αυξάνονται καθώς
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών. HY-217: Πιθανότητες - Χειµερινό Εξάµηνο 2012 ιδάσκων : Π. Τσακαλίδης. Λύσεις Τρίτης Σειράς Ασκήσεων
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-1: Πιθανότητες - Χειµερινό Εξάµηνο 01 ιδάσκων : Π Τσακαλίδης Λύσεις Τρίτης Σειράς Ασκήσεων Ηµεροµηνία Ανάθεσης : /10/01 Ηµεροµηνία Παράδοσης : /11/01
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-1: Πιθανότητες - Χειµερινό Εξάµηνο 01 ιδάσκων : Π Τσακαλίδης Λύσεις Τρίτης Σειράς Ασκήσεων Ηµεροµηνία Ανάθεσης : /10/01 Ηµεροµηνία Παράδοσης : /11/01
 ΑΣΚΗΣΗ 5 η Η σειριακή επικοινωνία ΙΙ 1.1 ΣΚΟΠΟΣ Σκοπός της άσκησης αυτής είναι η κατανόηση σε βάθος των λειτουργιών που παρέχονται από το περιβάλλον LabView για τον χειρισµό της σειριακής επικοινωνίας
ΑΣΚΗΣΗ 5 η Η σειριακή επικοινωνία ΙΙ 1.1 ΣΚΟΠΟΣ Σκοπός της άσκησης αυτής είναι η κατανόηση σε βάθος των λειτουργιών που παρέχονται από το περιβάλλον LabView για τον χειρισµό της σειριακής επικοινωνίας
Δοµές Δεδοµένων. 18η Διάλεξη Ισορροπηµένα δέντρα. Ε. Μαρκάκης
 Δοµές Δεδοµένων 18η Διάλεξη Ισορροπηµένα δέντρα Ε. Μαρκάκης Περίληψη Επανάληψη των Τυχαιοποιηµένων ΔΔΑ, Στρεβλών ΔΔΑ, Δέντρων 2-3-4 Δέντρα κόκκινου-µαύρου Λίστες Παράλειψης Χαρακτηριστικά επιδόσεων - συµπεράσµατα
Δοµές Δεδοµένων 18η Διάλεξη Ισορροπηµένα δέντρα Ε. Μαρκάκης Περίληψη Επανάληψη των Τυχαιοποιηµένων ΔΔΑ, Στρεβλών ΔΔΑ, Δέντρων 2-3-4 Δέντρα κόκκινου-µαύρου Λίστες Παράλειψης Χαρακτηριστικά επιδόσεων - συµπεράσµατα
ΜΥΕ003: Ανάκτηση Πληροφορίας. Διδάσκουσα: Ευαγγελία Πιτουρά Κεφάλαιο 5: Στατιστικά Συλλογής. Συμπίεση.
 ΜΥΕ003: Ανάκτηση Πληροφορίας Διδάσκουσα: Ευαγγελία Πιτουρά Κεφάλαιο 5: Στατιστικά Συλλογής. Συμπίεση. 1 Κεφ. 4-5 Τι θα δούμε σήμερα Κατασκευή ευρετηρίου Στατιστικά για τη συλλογή Συμπίεση 2 ΣΤΑΤΙΣΤΙΚΑ
ΜΥΕ003: Ανάκτηση Πληροφορίας Διδάσκουσα: Ευαγγελία Πιτουρά Κεφάλαιο 5: Στατιστικά Συλλογής. Συμπίεση. 1 Κεφ. 4-5 Τι θα δούμε σήμερα Κατασκευή ευρετηρίου Στατιστικά για τη συλλογή Συμπίεση 2 ΣΤΑΤΙΣΤΙΚΑ
Ν. Μ. Μισυρλής. Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών. Καθηγητής: Ν. Μ. Μισυρλής 29 Μαΐου / 18
 Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής 29 Μαΐου 2017 1 / 18 Βέλτιστα (στατικά) δυαδικά δένδρα αναζήτησης Παράδειγµα: Σχεδιασµός προγράµµατος
Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής 29 Μαΐου 2017 1 / 18 Βέλτιστα (στατικά) δυαδικά δένδρα αναζήτησης Παράδειγµα: Σχεδιασµός προγράµµατος
Δυναμικά Πολυεπίπεδα Ευρετήρια (Β-δένδρα) Μ.Χατζόπουλος 1
 Δυναμικά Πολυεπίπεδα Ευρετήρια (Β-δένδρα) Μ.Χατζόπουλος 1 Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ.Χατζόπουλος 2 Δένδρο αναζήτησης είναι ένας ειδικός τύπος δένδρου που χρησιμοποιείται για να καθοδηγήσει την αναζήτηση μιας
Δυναμικά Πολυεπίπεδα Ευρετήρια (Β-δένδρα) Μ.Χατζόπουλος 1 Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ.Χατζόπουλος 2 Δένδρο αναζήτησης είναι ένας ειδικός τύπος δένδρου που χρησιμοποιείται για να καθοδηγήσει την αναζήτηση μιας
Εργαστήριο ΨΗΦΙΑΚΗ ΛΟΓΙΚΗ. Εισαγωγή
 Εισαγωγή Εργαστήριο ΨΗΦΙΑΚΗ ΛΟΓΙΚΗ Ξεκινάµε την εργαστηριακή µελέτη της Ψηφιακής Λογικής των Η/Υ εξετάζοντας αρχικά τη µορφή των δεδοµένων που αποθηκεύουν και επεξεργάζονται οι υπολογιστές και προχωρώντας
Εισαγωγή Εργαστήριο ΨΗΦΙΑΚΗ ΛΟΓΙΚΗ Ξεκινάµε την εργαστηριακή µελέτη της Ψηφιακής Λογικής των Η/Υ εξετάζοντας αρχικά τη µορφή των δεδοµένων που αποθηκεύουν και επεξεργάζονται οι υπολογιστές και προχωρώντας
ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ. Εξωτερική Αναζήτηση και Β-δέντρα Κεφάλαιο 16. Ε. Μαρκάκης Επίκουρος Καθηγητής
 ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ Εξωτερική Αναζήτηση και Β-δέντρα Κεφάλαιο 16 Ε. Μαρκάκης Επίκουρος Καθηγητής Περίληψη Ακολουθιακή πρόσβαση Β-δέντρα Υλοποίηση πίνακα συµβόλων µε Β-δέντρα Αναζήτηση Εισαγωγή Δοµές Δεδοµένων
ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ Εξωτερική Αναζήτηση και Β-δέντρα Κεφάλαιο 16 Ε. Μαρκάκης Επίκουρος Καθηγητής Περίληψη Ακολουθιακή πρόσβαση Β-δέντρα Υλοποίηση πίνακα συµβόλων µε Β-δέντρα Αναζήτηση Εισαγωγή Δοµές Δεδοµένων
ΑΝΑΖΗΤΗΣΗ ΣΕ ΗΛΕΚΤΡΟΝΙΚΕΣ ΒΙΒΛΙΟΘΗΚΕΣ
 ΑΝΑΖΗΤΗΣΗ ΣΕ ΗΛΕΚΤΡΟΝΙΚΕΣ ΒΙΒΛΙΟΘΗΚΕΣ Μία από τις πιο σηµαντικές υπηρεσίες που προσφέρει το διαδίκτυο στην επιστηµονική κοινότητα είναι η αποµακρυσµένη πρόσβαση των χρηστών σε ηλεκτρονικές βιβλιοθήκες
ΑΝΑΖΗΤΗΣΗ ΣΕ ΗΛΕΚΤΡΟΝΙΚΕΣ ΒΙΒΛΙΟΘΗΚΕΣ Μία από τις πιο σηµαντικές υπηρεσίες που προσφέρει το διαδίκτυο στην επιστηµονική κοινότητα είναι η αποµακρυσµένη πρόσβαση των χρηστών σε ηλεκτρονικές βιβλιοθήκες
Εργασία Μαθήματος Αξία: 40% του τελικού σας βαθμού Ανάθεση: Παράδοση:
 Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών ΗΥ463 Συστήματα Ανάκτησης Πληροφοριών 2009-2010 Φθινοπωρινό Εξάμηνο Εργασία Μαθήματος Αξία: 40% του τελικού σας βαθμού Ανάθεση: Παράδοση: Σκοπός αυτής της
Πανεπιστήμιο Κρήτης, Τμήμα Επιστήμης Υπολογιστών ΗΥ463 Συστήματα Ανάκτησης Πληροφοριών 2009-2010 Φθινοπωρινό Εξάμηνο Εργασία Μαθήματος Αξία: 40% του τελικού σας βαθμού Ανάθεση: Παράδοση: Σκοπός αυτής της
ΒΑΣΕΙΣ Ε ΟΜΕΝΩΝ. Επίπεδα Αφαίρεσης Σ Β. Αποθήκευση Εγγραφών - Ευρετήρια. ρ. Βαγγελιώ Καβακλή ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ, Επίπεδο Όψεων.
 ΒΑΣΕΙΣ Ε ΟΜΕΝΩΝ Χειµερινό Εξάµηνο 2002 Αποθήκευση Εγγραφών - Ευρετήρια ρ Βαγγελιώ Καβακλή ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ, ΤΜΗΜΑ ΠΟΛΙΤΙΣΜΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΑΣ Επίπεδα Αφαίρεσης Σ Β Επίπεδο Όψεων Όψη Όψη
ΒΑΣΕΙΣ Ε ΟΜΕΝΩΝ Χειµερινό Εξάµηνο 2002 Αποθήκευση Εγγραφών - Ευρετήρια ρ Βαγγελιώ Καβακλή ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ, ΤΜΗΜΑ ΠΟΛΙΤΙΣΜΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΑΣ Επίπεδα Αφαίρεσης Σ Β Επίπεδο Όψεων Όψη Όψη
Δυναμικός Κατακερματισμός. Βάσεις Δεδομένων Ευαγγελία Πιτουρά 1
 Δυναμικός Κατακερματισμός Βάσεις Δεδομένων 2018-2019 1 Κατακερματισμός Πρόβλημα στατικού κατακερματισμού: Έστω Μ κάδους και r εγγραφές ανά κάδο - το πολύ Μ * r εγγραφές (αλλιώς μεγάλες αλυσίδες υπερχείλισης)
Δυναμικός Κατακερματισμός Βάσεις Δεδομένων 2018-2019 1 Κατακερματισμός Πρόβλημα στατικού κατακερματισμού: Έστω Μ κάδους και r εγγραφές ανά κάδο - το πολύ Μ * r εγγραφές (αλλιώς μεγάλες αλυσίδες υπερχείλισης)
ΘΕΜΑ 2. (2,5 µονάδες) Θεωρήστε τρεις κρυφές µνήµες των 512 πλαισίων µε 8 λέξεις ανά πλαίσιο και οργανώσεις αντίστοιχα:
 ΑΡΧΙΤΕΤΟΝΙΗ ΥΠΟΛΟΓΙΣΤΩΝ 2 Σεπτεµβρίου 2006 ΘΕΜΑ 1. (2 µονάδες) Θεωρούµε δύο υπολογιστές Υ1 και Υ2 που έχουν υλοποιηθεί µε τους επεξεργαστές Ε 1 και Ε 2 αντίστοιχα που έχουν την ίδια αρχιτεκτονική σε επίπεδο
ΑΡΧΙΤΕΤΟΝΙΗ ΥΠΟΛΟΓΙΣΤΩΝ 2 Σεπτεµβρίου 2006 ΘΕΜΑ 1. (2 µονάδες) Θεωρούµε δύο υπολογιστές Υ1 και Υ2 που έχουν υλοποιηθεί µε τους επεξεργαστές Ε 1 και Ε 2 αντίστοιχα που έχουν την ίδια αρχιτεκτονική σε επίπεδο
Λύση: Λύση: Λύση: Λύση:
 1. Ένας δίαυλος έχει ρυθµό δεδοµένων 4 kbps και καθυστέρηση διάδοσης 20 msec. Για ποια περιοχή µηκών των πλαισίων µπορεί η µέθοδος παύσης και αναµονής να έχει απόδοση τουλάχιστον 50%; Η απόδοση θα είναι
1. Ένας δίαυλος έχει ρυθµό δεδοµένων 4 kbps και καθυστέρηση διάδοσης 20 msec. Για ποια περιοχή µηκών των πλαισίων µπορεί η µέθοδος παύσης και αναµονής να έχει απόδοση τουλάχιστον 50%; Η απόδοση θα είναι
Κεφάλαιο 14. Δομές Ευρετηρίων για Αρχεία. Copyright 2007 Ramez Elmasri and Shamkant B. Navathe Ελληνική Έκδοση,
 Δίαβλος, Επιμέλεια Μ.Χατζόπουλος Διαφάνεια 14-1 Κεφάλαιο 14 Δομές Ευρετηρίων για Αρχεία Copyright 2007 Ramez Elmasri and Shamkant B. Navathe Ελληνική Έκδοση, Διαβλος, Επιμέλεια Μ.Χατζόπουλος 1 Θα μιλήσουμε
Δίαβλος, Επιμέλεια Μ.Χατζόπουλος Διαφάνεια 14-1 Κεφάλαιο 14 Δομές Ευρετηρίων για Αρχεία Copyright 2007 Ramez Elmasri and Shamkant B. Navathe Ελληνική Έκδοση, Διαβλος, Επιμέλεια Μ.Χατζόπουλος 1 Θα μιλήσουμε
Σύνοψη Προηγούµενου. Γλώσσες χωρίς Συµφραζόµενα (2) Ισοδυναµία CFG και PDA. Σε αυτό το µάθηµα. Αυτόµατα Στοίβας Pushdown Automata
 Σύνοψη Προηγούµενου Γλώσσες χωρίς Συµφραζόµενα (2) Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Αυτόµατα Στοίβας Pushdown utomata Ισοδυναµία µε τις Γλώσσες χωρίς Συµφραζόµενα:
Σύνοψη Προηγούµενου Γλώσσες χωρίς Συµφραζόµενα (2) Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Αυτόµατα Στοίβας Pushdown utomata Ισοδυναµία µε τις Γλώσσες χωρίς Συµφραζόµενα:
ΛΥΣΕΙΣ 2 ης ΣΕΙΡΑΣ ΑΣΚΗΣΕΩΝ
 ΛΥΣΕΙΣ 2 ης ΣΕΙΡΑΣ ΑΣΚΗΣΕΩΝ Άσκηση 1 Θεωρείστε μια συλλογή κειμένων που περιέχει τα ακόλουθα 5 έγγραφα: Έγγραφο 1: «Computer Games» Έγγραφο 2: «Computer Games Computer Games» Έγγραφο 3: «Games Theory and
ΛΥΣΕΙΣ 2 ης ΣΕΙΡΑΣ ΑΣΚΗΣΕΩΝ Άσκηση 1 Θεωρείστε μια συλλογή κειμένων που περιέχει τα ακόλουθα 5 έγγραφα: Έγγραφο 1: «Computer Games» Έγγραφο 2: «Computer Games Computer Games» Έγγραφο 3: «Games Theory and
Σύνθετη Άσκηση για Απώλειες και ιασπορά
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΟΠΤΙΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ ΚΑΙ ΟΠΤΙΚΑ ΙΚΤΥΑ Καθηγητής. Συβρίδης Σύνθετη Άσκηση για Απώλειες και ιασπορά
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΟΠΤΙΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ ΚΑΙ ΟΠΤΙΚΑ ΙΚΤΥΑ Καθηγητής. Συβρίδης Σύνθετη Άσκηση για Απώλειες και ιασπορά
Εισαγωγή στην Επεξεργασία Ερωτήσεων. Βάσεις Δεδομένων Ευαγγελία Πιτουρά 1
 Εισαγωγή στην Επεξεργασία Ερωτήσεων 1 Επεξεργασία Ερωτήσεων Θα δούμε την «πορεία» μιας SQL ερώτησης (πως εκτελείται) Ερώτηση SQL Ερώτηση ΣΒΔ Αποτέλεσμα 2 Βήματα Επεξεργασίας Τα βασικά βήματα στην επεξεργασία
Εισαγωγή στην Επεξεργασία Ερωτήσεων 1 Επεξεργασία Ερωτήσεων Θα δούμε την «πορεία» μιας SQL ερώτησης (πως εκτελείται) Ερώτηση SQL Ερώτηση ΣΒΔ Αποτέλεσμα 2 Βήματα Επεξεργασίας Τα βασικά βήματα στην επεξεργασία
Κεφάλαιο 14. οµές Ευρετηρίων για Αρχεία. ιαφάνεια 14-1
 ιαφάνεια 14-1 Κεφάλαιο 14 οµές Ευρετηρίων για Αρχεία Copyright 2007 Ramez Elmasri and Shamkant B. NavatheΕλληνικήΈκδοση, ιαβλος, Επιµέλεια Μ.Χατζόπουλος 1 Θα µιλήσουµε για Τύποι Ταξινοµηµένων Ευρετηρίων
ιαφάνεια 14-1 Κεφάλαιο 14 οµές Ευρετηρίων για Αρχεία Copyright 2007 Ramez Elmasri and Shamkant B. NavatheΕλληνικήΈκδοση, ιαβλος, Επιµέλεια Μ.Χατζόπουλος 1 Θα µιλήσουµε για Τύποι Ταξινοµηµένων Ευρετηρίων
3.1 εκαδικό και υαδικό
 Εισαγωγή στην επιστήµη των υπολογιστών Υπολογιστές και εδοµένα Κεφάλαιο 3ο Αναπαράσταση Αριθµών 1 3.1 εκαδικό και υαδικό εκαδικό σύστηµα 2 1 εκαδικό και υαδικό υαδικό Σύστηµα 3 3.2 Μετατροπή Για τη µετατροπή
Εισαγωγή στην επιστήµη των υπολογιστών Υπολογιστές και εδοµένα Κεφάλαιο 3ο Αναπαράσταση Αριθµών 1 3.1 εκαδικό και υαδικό εκαδικό σύστηµα 2 1 εκαδικό και υαδικό υαδικό Σύστηµα 3 3.2 Μετατροπή Για τη µετατροπή
Αλγόριθµοι για την παραγοντοποίηση ακεραίων αριθµών
 Αλγόριθµοι για την παραγοντοποίηση ακεραίων αριθµών Αλέξανδρος Γ. Συγκελάκης 3 Απριλίου 2006 Μέθοδος Συνεχών Κλασµάτων. Θεωρητικό Υπόβαθρο Συνεχών Κλασµάτων Περίληψη Στο κοµµάτι αυτό ϑα περιγράψουµε µία
Αλγόριθµοι για την παραγοντοποίηση ακεραίων αριθµών Αλέξανδρος Γ. Συγκελάκης 3 Απριλίου 2006 Μέθοδος Συνεχών Κλασµάτων. Θεωρητικό Υπόβαθρο Συνεχών Κλασµάτων Περίληψη Στο κοµµάτι αυτό ϑα περιγράψουµε µία
HY118- ιακριτά Μαθηµατικά
 HY118- ιακριτά Μαθηµατικά Τρίτη, 19/04/2016 Το υλικό των Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr 1 Συνδυαστική 2 Πείραµα Πείραµα: Οποιαδήποτε διαδικασία που µπορεί να οδηγήσει σε ένα αριθµό παρατηρήσιµων
HY118- ιακριτά Μαθηµατικά Τρίτη, 19/04/2016 Το υλικό των Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr 1 Συνδυαστική 2 Πείραµα Πείραµα: Οποιαδήποτε διαδικασία που µπορεί να οδηγήσει σε ένα αριθµό παρατηρήσιµων
ΕΝΟΤΗΤΑ 6 ΛΙΣΤΕΣ ΠΑΡΑΛΕΙΨΗΣ (SKIP LISTS)
 ΕΝΟΤΗΤΑ 6 ΛΙΣΤΕΣ ΠΑΡΑΛΕΙΨΗΣ (SKIP LISTS) Ταχεία Αναζήτηση Σε πίνακα: δυαδική αναζήτηση (binary search) σε ταξινοµηµένο πίνακα O(log n) Σε δένδρο: αναζήτηση σε ισοζυγισµένο δένδρο O(log n) Σε λίστα: Μπορούµε
ΕΝΟΤΗΤΑ 6 ΛΙΣΤΕΣ ΠΑΡΑΛΕΙΨΗΣ (SKIP LISTS) Ταχεία Αναζήτηση Σε πίνακα: δυαδική αναζήτηση (binary search) σε ταξινοµηµένο πίνακα O(log n) Σε δένδρο: αναζήτηση σε ισοζυγισµένο δένδρο O(log n) Σε λίστα: Μπορούµε
Κεφάλαιο 5ο: Εντολές Επανάληψης
 Χρήστος Τσαγγάρης ΕΕ ΙΠ Τµήµατος Μαθηµατικών, Πανεπιστηµίου Αιγαίου Κεφάλαιο 5ο: Εντολές Επανάληψης Η διαδικασία της επανάληψης είναι ιδιαίτερη συχνή, αφού πλήθος προβληµάτων µπορούν να επιλυθούν µε κατάλληλες
Χρήστος Τσαγγάρης ΕΕ ΙΠ Τµήµατος Μαθηµατικών, Πανεπιστηµίου Αιγαίου Κεφάλαιο 5ο: Εντολές Επανάληψης Η διαδικασία της επανάληψης είναι ιδιαίτερη συχνή, αφού πλήθος προβληµάτων µπορούν να επιλυθούν µε κατάλληλες
Αριθµητική Γραµµική ΑλγεβραΚεφάλαιο 4. Αριθµητικός Υπολογισµός Ιδιοτιµών 2 Απριλίου και2015 Ιδιοδιανυσµάτων 1 / 50
 Αριθµητική Γραµµική Αλγεβρα Κεφάλαιο 4. Αριθµητικός Υπολογισµός Ιδιοτιµών και Ιδιοδιανυσµάτων ΕΚΠΑ 2 Απριλίου 205 Αριθµητική Γραµµική ΑλγεβραΚεφάλαιο 4. Αριθµητικός Υπολογισµός Ιδιοτιµών 2 Απριλίου και205
Αριθµητική Γραµµική Αλγεβρα Κεφάλαιο 4. Αριθµητικός Υπολογισµός Ιδιοτιµών και Ιδιοδιανυσµάτων ΕΚΠΑ 2 Απριλίου 205 Αριθµητική Γραµµική ΑλγεβραΚεφάλαιο 4. Αριθµητικός Υπολογισµός Ιδιοτιµών 2 Απριλίου και205
ΠΑΡΑΡΤΗΜΑ: QUIZ ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ
 ΠΑΡΑΡΤΗΜΑ: QUIZ ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ (Οι ερωτήσεις µε κίτρινη υπογράµµιση είναι εκτός ύλης για φέτος) ΕΙΣΑΓΩΓΗ Q1. Οι Πρωταρχικοί τύποι (primitive types) στη Java 1. Είναι όλοι οι ακέραιοι και όλοι οι πραγµατικοί
ΠΑΡΑΡΤΗΜΑ: QUIZ ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ (Οι ερωτήσεις µε κίτρινη υπογράµµιση είναι εκτός ύλης για φέτος) ΕΙΣΑΓΩΓΗ Q1. Οι Πρωταρχικοί τύποι (primitive types) στη Java 1. Είναι όλοι οι ακέραιοι και όλοι οι πραγµατικοί
Πανεπιστήµιο Θεσσαλίας
 Πανεπιστήµιο Θεσσαλίας Τµήµα Πληροφορικής Ενότητα 8η: Συσκευές Ε/Ε - Αρτηρίες Άσκηση 1: Υπολογίστε το µέσο χρόνο ανάγνωσης ενός τµήµατος των 512 bytes σε µια µονάδα σκληρού δίσκου µε ταχύτητα περιστροφής
Πανεπιστήµιο Θεσσαλίας Τµήµα Πληροφορικής Ενότητα 8η: Συσκευές Ε/Ε - Αρτηρίες Άσκηση 1: Υπολογίστε το µέσο χρόνο ανάγνωσης ενός τµήµατος των 512 bytes σε µια µονάδα σκληρού δίσκου µε ταχύτητα περιστροφής
Εισαγωγή στην. Εισαγωγή Σ Β. Αρχεία ευρετηρίου Κατάλογος. συστήματος. Αρχεία δεδομένων
 Εισαγωγή στην Επεξεργασία Ερωτήσεων 1 Εισαγωγή Σ Β Σύνολο από προγράμματα για τη διαχείριση της Β Αρχεία ευρετηρίου Κατάλογος ΒΑΣΗ Ε ΟΜΕΝΩΝ Αρχεία δεδομένων συστήματος Σύστημα Βάσεων εδομένων (ΣΒ ) 2 :
Εισαγωγή στην Επεξεργασία Ερωτήσεων 1 Εισαγωγή Σ Β Σύνολο από προγράμματα για τη διαχείριση της Β Αρχεία ευρετηρίου Κατάλογος ΒΑΣΗ Ε ΟΜΕΝΩΝ Αρχεία δεδομένων συστήματος Σύστημα Βάσεων εδομένων (ΣΒ ) 2 :
Εισαγωγή στον Προγραµµατισµό. Ανάλυση (ή Επιστηµονικοί8 Υπολογισµοί)
 Εισαγωγή στον Προγραµµατισµό Αριθµητική Ανάλυση (ή Επιστηµονικοί Υπολογισµοί) ιδάσκοντες: Καθηγητής Ν. Μισυρλής, Επίκ. Καθηγητής Φ.Τζαφέρης ΕΚΠΑ 8 εκεµβρίου 2014 Ανάλυση (ή Επιστηµονικοί8 Υπολογισµοί)
Εισαγωγή στον Προγραµµατισµό Αριθµητική Ανάλυση (ή Επιστηµονικοί Υπολογισµοί) ιδάσκοντες: Καθηγητής Ν. Μισυρλής, Επίκ. Καθηγητής Φ.Τζαφέρης ΕΚΠΑ 8 εκεµβρίου 2014 Ανάλυση (ή Επιστηµονικοί8 Υπολογισµοί)
Ανάκληση Πληποφοπίαρ. Information Retrieval. Διδάζκων Δημήηριος Καηζαρός
 Ανάκληση Πληποφοπίαρ Information Retrieval Διδάζκων Δημήηριος Καηζαρός Διάλεξη 4η: 04/03/2017 1 Phrase queries 2 Ερωτήματα φράσεως Έστω ότι επιθυμούμε ν απαντήσουμε ερωτήματα της μορφής stanford university
Ανάκληση Πληποφοπίαρ Information Retrieval Διδάζκων Δημήηριος Καηζαρός Διάλεξη 4η: 04/03/2017 1 Phrase queries 2 Ερωτήματα φράσεως Έστω ότι επιθυμούμε ν απαντήσουμε ερωτήματα της μορφής stanford university
Το εσωτερικό ενός Σ Β
 Επεξεργασία Ερωτήσεων 1 Εισαγωγή ΜΕΡΟΣ 1 Γενική Εικόνα του Μαθήµατος Μοντελοποίηση (Μοντέλο Ο/Σ, Σχεσιακό, Λογικός Σχεδιασµός) Προγραµµατισµός (Σχεσιακή Άλγεβρα, SQL) ηµιουργία/κατασκευή Εισαγωγή εδοµένων
Επεξεργασία Ερωτήσεων 1 Εισαγωγή ΜΕΡΟΣ 1 Γενική Εικόνα του Μαθήµατος Μοντελοποίηση (Μοντέλο Ο/Σ, Σχεσιακό, Λογικός Σχεδιασµός) Προγραµµατισµός (Σχεσιακή Άλγεβρα, SQL) ηµιουργία/κατασκευή Εισαγωγή εδοµένων
ΑΣΚΗΣΕΙΣ ΘΕΩΡΙΑΣ. ΘΕΜΑ 1 Δίνεται το παρακάτω τμήμα δηλώσεων ενός προγράμματος σε «ΓΛΩΣΣΑ»: ΜΕΤΑΒΛΗΤΕΣ ΠΡΑΓΜΑΤΙΚΕΣ: Π[10] ΛΟΓΙΚΕΣ: ΒΡΕΘΗΚΕ ΑΚΕΡΑΙΕΣ: i
![ΑΣΚΗΣΕΙΣ ΘΕΩΡΙΑΣ. ΘΕΜΑ 1 Δίνεται το παρακάτω τμήμα δηλώσεων ενός προγράμματος σε «ΓΛΩΣΣΑ»: ΜΕΤΑΒΛΗΤΕΣ ΠΡΑΓΜΑΤΙΚΕΣ: Π[10] ΛΟΓΙΚΕΣ: ΒΡΕΘΗΚΕ ΑΚΕΡΑΙΕΣ: i ΑΣΚΗΣΕΙΣ ΘΕΩΡΙΑΣ. ΘΕΜΑ 1 Δίνεται το παρακάτω τμήμα δηλώσεων ενός προγράμματος σε «ΓΛΩΣΣΑ»: ΜΕΤΑΒΛΗΤΕΣ ΠΡΑΓΜΑΤΙΚΕΣ: Π[10] ΛΟΓΙΚΕΣ: ΒΡΕΘΗΚΕ ΑΚΕΡΑΙΕΣ: i](/thumbs/95/123398278.jpg) ΑΣΚΗΣΕΙΣ ΘΕΩΡΙΑΣ ΘΕΜΑ 1 Δίνεται το παρακάτω τμήμα δηλώσεων ενός προγράμματος σε «ΓΛΩΣΣΑ»: ΜΕΤΑΒΛΗΤΕΣ ΠΡΑΓΜΑΤΙΚΕΣ: Π[10] ΛΟΓΙΚΕΣ: ΒΡΕΘΗΚΕ ΑΚΕΡΑΙΕΣ: i Να μετατρέψετε τις ενέργειες που δίνονται παρακάτω σε
ΑΣΚΗΣΕΙΣ ΘΕΩΡΙΑΣ ΘΕΜΑ 1 Δίνεται το παρακάτω τμήμα δηλώσεων ενός προγράμματος σε «ΓΛΩΣΣΑ»: ΜΕΤΑΒΛΗΤΕΣ ΠΡΑΓΜΑΤΙΚΕΣ: Π[10] ΛΟΓΙΚΕΣ: ΒΡΕΘΗΚΕ ΑΚΕΡΑΙΕΣ: i Να μετατρέψετε τις ενέργειες που δίνονται παρακάτω σε
/ / 38
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-37: Εφαρµοσµένες Στοχαστικές ιαδικασίες - Εαρινό Εξάµηνο 205-6 ιδάσκων : Π. Τσακαλίδης Φροντιστήριο 0 Επιµέλεια : Σοφία Σαββάκη Ασκηση. Ο Κώστας πηγαίνει
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-37: Εφαρµοσµένες Στοχαστικές ιαδικασίες - Εαρινό Εξάµηνο 205-6 ιδάσκων : Π. Τσακαλίδης Φροντιστήριο 0 Επιµέλεια : Σοφία Σαββάκη Ασκηση. Ο Κώστας πηγαίνει
Κώδικας σχεδίασης Λογισµικής ιαγραµµατικής Οντολογίας
 Κώδικας σχεδίασης Λογισµικής ιαγραµµατικής Οντολογίας Αρχιµήδης ΙΙΙ Υποέργο 18 2013 Ενα µάγµα µπορεί να εξελιχθεί κάτω από την επίδραση τριών ειδών επιρροών. Την εξέλιξη αυτή συµβολίζουµε µε ένα απλό τόξο
Κώδικας σχεδίασης Λογισµικής ιαγραµµατικής Οντολογίας Αρχιµήδης ΙΙΙ Υποέργο 18 2013 Ενα µάγµα µπορεί να εξελιχθεί κάτω από την επίδραση τριών ειδών επιρροών. Την εξέλιξη αυτή συµβολίζουµε µε ένα απλό τόξο
ΛΕΙΤΟΥΡΓΙΚΑ ΣΥΣΤΗΜΑΤΑ ΙΙ - UNIX. Συστήματα Αρχείων. Διδάσκoντες: Καθ. Κ. Λαμπρινουδάκης Δρ. Α. Γαλάνη
 ΛΕΙΤΟΥΡΓΙΚΑ ΣΥΣΤΗΜΑΤΑ ΙΙ - UNIX Μάθημα: Λειτουργικά Συστήματα Συστήματα Αρχείων Διδάσκoντες: Καθ. Κ. Λαμπρινουδάκης (clam@unipi.gr) Δρ. Α. Γαλάνη (agalani@unipi.gr) Λειτουργικά Συστήματα 1 Αρχεία με Χαρτογράφηση
ΛΕΙΤΟΥΡΓΙΚΑ ΣΥΣΤΗΜΑΤΑ ΙΙ - UNIX Μάθημα: Λειτουργικά Συστήματα Συστήματα Αρχείων Διδάσκoντες: Καθ. Κ. Λαμπρινουδάκης (clam@unipi.gr) Δρ. Α. Γαλάνη (agalani@unipi.gr) Λειτουργικά Συστήματα 1 Αρχεία με Χαρτογράφηση
8.1 Θεωρητική εισαγωγή
 ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 8 ΣΤΟΙΧΕΙΑ ΜΝΗΜΗΣ ΚΑΤΑΧΩΡΗΤΕΣ Σκοπός: Η µελέτη της λειτουργίας των καταχωρητών. Θα υλοποιηθεί ένας απλός στατικός καταχωρητής 4-bit µε Flip-Flop τύπου D και θα µελετηθεί
ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 8 ΣΤΟΙΧΕΙΑ ΜΝΗΜΗΣ ΚΑΤΑΧΩΡΗΤΕΣ Σκοπός: Η µελέτη της λειτουργίας των καταχωρητών. Θα υλοποιηθεί ένας απλός στατικός καταχωρητής 4-bit µε Flip-Flop τύπου D και θα µελετηθεί
(1) 98! 25! = 4 100! 23! = 4
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-217: Πιθανότητες - Χειµερινό Εξάµηνο 2015 ιδάσκων : Π. Τσακαλίδης Φροντιστήριο 5 Συνδυαστική Ανάλυση ΙΙ και Εισαγωγή στις ιακριτές Τυχαίες Μεταβλητές
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-217: Πιθανότητες - Χειµερινό Εξάµηνο 2015 ιδάσκων : Π. Τσακαλίδης Φροντιστήριο 5 Συνδυαστική Ανάλυση ΙΙ και Εισαγωγή στις ιακριτές Τυχαίες Μεταβλητές
Ορια Συναρτησεων - Ορισµοι
 Ορια Συναρτησεων - Ορισµοι Λυγάτσικας Ζήνων Βαρβάκειο Ενιαίο Πειραµατικό Λύκειο 3 Σεπτεµβρίου 205 Εισαγωγή Στην παράγραφο αυτή ϑα δούµε πως προκύπτει η ιδέα του ορίου στην προσπά- ϑεια να ορίσουµε την
Ορια Συναρτησεων - Ορισµοι Λυγάτσικας Ζήνων Βαρβάκειο Ενιαίο Πειραµατικό Λύκειο 3 Σεπτεµβρίου 205 Εισαγωγή Στην παράγραφο αυτή ϑα δούµε πως προκύπτει η ιδέα του ορίου στην προσπά- ϑεια να ορίσουµε την
Σχήµα 6.1: Εισαγωγή της εντολής Read From Spreadsheet File στο Block Diagram.
 Εισαγωγή αρχείων δεδοµένων 1. Η εισαγωγή αρχείων δεδοµένων στο LaVIEW γίνεται στο Block Diagram µε την εντολή Read From Spreadsheet File. 2. Εισάγουµε την εντολή Read From Spreadsheet File στο Block Diagram
Εισαγωγή αρχείων δεδοµένων 1. Η εισαγωγή αρχείων δεδοµένων στο LaVIEW γίνεται στο Block Diagram µε την εντολή Read From Spreadsheet File. 2. Εισάγουµε την εντολή Read From Spreadsheet File στο Block Diagram
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών. ΗΥ-217: Πιθανότητες-Χειµερινό Εξάµηνο ιδάσκων : Π. Τσακαλίδης
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-27: Πιθανότητες-Χειµερινό Εξάµηνο 205- ιδάσκων : Π. Τσακαλίδης Λύσεις Τέταρτης Σειράς Ασκήσεων Ασκηση. (αʹ) Σύµφωνα µε το αξίωµα της κανονικοποίησης,
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-27: Πιθανότητες-Χειµερινό Εξάµηνο 205- ιδάσκων : Π. Τσακαλίδης Λύσεις Τέταρτης Σειράς Ασκήσεων Ασκηση. (αʹ) Σύµφωνα µε το αξίωµα της κανονικοποίησης,
Πρόβληµα 2 (15 µονάδες)
 ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΚΡΥΠΤΟΓΡΑΦΙΑ ΚΑΙ ΕΦΑΡΜΟΓΕΣ, 2013-2014 ΔΙΔΑΣΚΩΝ: Ε. Μαρκάκης Πρόβληµα 1 (5 µονάδες) 2 η Σειρά Ασκήσεων Προθεσµία Παράδοσης: 19/1/2014 Υπολογίστε
ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΚΡΥΠΤΟΓΡΑΦΙΑ ΚΑΙ ΕΦΑΡΜΟΓΕΣ, 2013-2014 ΔΙΔΑΣΚΩΝ: Ε. Μαρκάκης Πρόβληµα 1 (5 µονάδες) 2 η Σειρά Ασκήσεων Προθεσµία Παράδοσης: 19/1/2014 Υπολογίστε
Data Focus Business Solutions σελ. 1/10
 Data Focus Business Solutions σελ. 1/10 1. ΕΓΚΑΤΑΣΤΑΣΗ ΕΦΑΡΜΟΓΗΣ Data Focus Κάθε εφαρµογή της Data Focus, δεδοµένου του ότι είναι πλήρως ανεπτυγµένη σε παραθυρικό περιβάλλον, συνοδεύεται από ένα CD εγκατάστασης.
Data Focus Business Solutions σελ. 1/10 1. ΕΓΚΑΤΑΣΤΑΣΗ ΕΦΑΡΜΟΓΗΣ Data Focus Κάθε εφαρµογή της Data Focus, δεδοµένου του ότι είναι πλήρως ανεπτυγµένη σε παραθυρικό περιβάλλον, συνοδεύεται από ένα CD εγκατάστασης.
ΗΥ460 Συστήµατα Διαχείρισης Βάσεων Δεδοµένων Χειµερινό Εξάµηνο 2016 Διδάσκοντες: Βασίλης Χριστοφίδης
 ΗΥ460 Συστήµατα Διαχείρισης Βάσεων Δεδοµένων Χειµερινό Εξάµηνο 2016 Διδάσκοντες: Βασίλης Χριστοφίδης 2 η Σειρά Ασκήσεων Ηµεροµηνία Παράδοσης: 14/11/2016 Άσκηση 1 (10 µονάδες) Εξωτερική Ταξινόµηση Θεωρείστε
ΗΥ460 Συστήµατα Διαχείρισης Βάσεων Δεδοµένων Χειµερινό Εξάµηνο 2016 Διδάσκοντες: Βασίλης Χριστοφίδης 2 η Σειρά Ασκήσεων Ηµεροµηνία Παράδοσης: 14/11/2016 Άσκηση 1 (10 µονάδες) Εξωτερική Ταξινόµηση Θεωρείστε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών. HY-217: Πιθανότητες - Χειµερινό Εξάµηνο 2015 ιδάσκων : Π. Τσακαλίδης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-: Πιθανότητες - Χειµερινό Εξάµηνο 0 ιδάσκων : Π. Τσακαλίδης Φροντιστήριο - Συνδυαστική Ανάλυση Επιµέλεια : Σοφία Σαββάκη Θεωρία. Η ϐασική αρχή της απαρίθµησης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-: Πιθανότητες - Χειµερινό Εξάµηνο 0 ιδάσκων : Π. Τσακαλίδης Φροντιστήριο - Συνδυαστική Ανάλυση Επιµέλεια : Σοφία Σαββάκη Θεωρία. Η ϐασική αρχή της απαρίθµησης
HY118- ιακριτά Μαθηµατικά. Μαθηµατική επαγωγή. 11 Επαγωγή
 Επαγωγή HY8- ιακριτά Μαθηµατικά Τρίτη, /03/06 Μαθηµατική Επαγωγή Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University
Επαγωγή HY8- ιακριτά Μαθηµατικά Τρίτη, /03/06 Μαθηµατική Επαγωγή Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University
5.1 Θεωρητική εισαγωγή
 ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 5 ΚΩ ΙΚΟΠΟΙΗΣΗ BCD Σκοπός: Η κατανόηση της µετατροπής ενός τύπου δυαδικής πληροφορίας σε άλλον (κωδικοποίηση/αποκωδικοποίηση) µε τη µελέτη της κωδικοποίησης BCD
ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ - ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 5 ΚΩ ΙΚΟΠΟΙΗΣΗ BCD Σκοπός: Η κατανόηση της µετατροπής ενός τύπου δυαδικής πληροφορίας σε άλλον (κωδικοποίηση/αποκωδικοποίηση) µε τη µελέτη της κωδικοποίησης BCD
lab9grades Άσκηση 1 - Σωστοί τύποι (παραµέτρων και επιστρεφόµενης τιµής) της series_cosh.
 ΑΕΜ ΒΑΘΜΟΣ ΣΧΟΛΙΑ - Μέτρια σχόλια. 00497 PASS - Σωστοί τύποι (παραµέτρων και επιστρεφόµενης τιµής) της factorial. - Σωστοί τύποι (παραµέτρων και επιστρεφόµενης τιµής) της series_cosh. - Καλά ονόµατα µεταβλητών
ΑΕΜ ΒΑΘΜΟΣ ΣΧΟΛΙΑ - Μέτρια σχόλια. 00497 PASS - Σωστοί τύποι (παραµέτρων και επιστρεφόµενης τιµής) της factorial. - Σωστοί τύποι (παραµέτρων και επιστρεφόµενης τιµής) της series_cosh. - Καλά ονόµατα µεταβλητών
Επίλυση προβληµάτων. Περιγραφή προβληµάτων Αλγόριθµοι αναζήτησης Αλγόριθµοι τυφλής αναζήτησης Αλγόριθµοι ευρετικής αναζήτησης
 Επίλυση προβληµάτων Περιγραφή προβληµάτων Αλγόριθµοι αναζήτησης Αλγόριθµοι τυφλής αναζήτησης Αλγόριθµοι ευρετικής αναζήτησης! Παιχνίδια δύο αντιπάλων Προβλήµατα ικανοποίησης περιορισµών Γενικά " Ντετερµινιστικά
Επίλυση προβληµάτων Περιγραφή προβληµάτων Αλγόριθµοι αναζήτησης Αλγόριθµοι τυφλής αναζήτησης Αλγόριθµοι ευρετικής αναζήτησης! Παιχνίδια δύο αντιπάλων Προβλήµατα ικανοποίησης περιορισµών Γενικά " Ντετερµινιστικά
Αναγνώριση υποθεµάτων αρχείων Αντιγραφή κειµένου Αντιγραφη εικόνων Αντιγραφή video
 Σύντοµες οδηγίες Αναγνώριση υποθεµάτων αρχείων Αντιγραφή κειµένου Αντιγραφη εικόνων Αντιγραφή video 2 ο Ε.Κ.Φ.Ε. Ηρακλείου Κρήτης Περιεχόµενα Πλήκτρα που θα χρησιµοποιήσουµε...3 Αναγνώριση υποθεµάτων αρχείων...4
Σύντοµες οδηγίες Αναγνώριση υποθεµάτων αρχείων Αντιγραφή κειµένου Αντιγραφη εικόνων Αντιγραφή video 2 ο Ε.Κ.Φ.Ε. Ηρακλείου Κρήτης Περιεχόµενα Πλήκτρα που θα χρησιµοποιήσουµε...3 Αναγνώριση υποθεµάτων αρχείων...4
ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ. Πίνακες Συµβόλων Κεφάλαιο 12 ( ) Ε. Μαρκάκης Επίκουρος Καθηγητής
 ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ Πίνακες Συµβόλων Κεφάλαιο 12 (12.1-12.4) Ε. Μαρκάκης Επίκουρος Καθηγητής Περίληψη Πίνακες συµβόλων Διεπαφή πίνακα συµβόλων Αναζήτηση µε αριθµοδείκτη Ακολουθιακή αναζήτηση Δυαδική αναζήτηση
ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ Πίνακες Συµβόλων Κεφάλαιο 12 (12.1-12.4) Ε. Μαρκάκης Επίκουρος Καθηγητής Περίληψη Πίνακες συµβόλων Διεπαφή πίνακα συµβόλων Αναζήτηση µε αριθµοδείκτη Ακολουθιακή αναζήτηση Δυαδική αναζήτηση
Copyright 2007 Ramez Elmasri and Shamkant B. Navathe, Ελληνική Έκδοση, Δίαβλος, Επιμέλεια Μ.Χατζόπουλος Διαφάνεια 14-1
 Δίαβλος, Επιμέλεια Μ.Χατζόπουλος Διαφάνεια 14-1 Κεφάλαιο 14 Δομές Ευρετηρίων για Αρχεία Copyright 2007 Ramez Elmasri and Shamkant B. Navathe Ελληνική Έκδοση, Διαβλος, Επιμέλεια Μ.Χατζόπουλος Θα μιλήσουμε
Δίαβλος, Επιμέλεια Μ.Χατζόπουλος Διαφάνεια 14-1 Κεφάλαιο 14 Δομές Ευρετηρίων για Αρχεία Copyright 2007 Ramez Elmasri and Shamkant B. Navathe Ελληνική Έκδοση, Διαβλος, Επιμέλεια Μ.Χατζόπουλος Θα μιλήσουμε
