ΜΕΛΕΤΗ ΕΛΑΤΗΡΙΩΝ. Α. Μελέτη του νόμου του Hooke
|
|
|
- Ίσις Αποστόλου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Σκοπός της άσκησης Σε αυτή την άσκηση θα μελετήσουμε την συμπεριφορά ελατηρίων. Θα μελετηθεί ο νόμος του Hooke και θα χρησιμοποιηθεί αυτός ώστε να προσδιοριστεί η σταθερά του ελατηρίου. Η σταθερά του ελατηρίου θα προσδιοριστεί και από την περίοδο της ταλάντωσης σώματος κρεμασμένου στο άκρο του ελατηρίου. Επιπλέον, θα μελετηθεί η συνδεσμολογία ελατηρίων. Α. Μελέτη του νόμου του Hooke Στοιχεία από την θεωρία Όταν σε ένα υλικό εφαρμοστεί συμπίεση ή εφελκυσμός μπορεί να προκληθούν μεταβολές της απόστασης μεταξύ των μορίων σε σχέση με τις αποστάσεις ισορροπίας. Μικρές μεταβολές της απόστασης μεταξύ των μορίων γύρω από την θέση ισορροπίας έχουν σαν αποτέλεσμα την αύξηση της δυναμικής ενέργειας των μορίων. Η δύναμη που ασκείται στο κάθε μόριο έχει την μορφή: F = K l (1) όπου Κ είναι μία σταθερά αναλογίας. H σχέση (1) αποτελεί ορισμό της απλής αρμονικής ταλάντωσης και ορίστηκε σε μικροσκοπική κλίμακα αφού το l αφορά διαφορά αποστάσεων ανάμεσα στα μόρια. Όμως η σχέση αυτή ισχύει 1
2 και μακροσκοπικά οπότε το l αθροιστικά μετράει την μεταβολή της διάστασης του υλικού. Η σχέση (1) αποτελεί τον νόμο του Hooke: οι παραμορφώσεις των υλικών είναι ανάλογες με το αίτιο το οποίο τις προκαλεί. Ο νόμος του Hooke πριν από την θεωρητική του επαλήθευση έχει αποδειχθεί πειραματικά. Ο νόμος του Hooke ισχύει για μεταβολές μέχρι μιας ορισμένης τιμής που ονομάζεται όριο ελαστικότητας. Πέραν της τιμής αυτής έχουμε πλαστικές ή μόνιμες παραμορφώσεις, οι οποίες δεν περιγράφονται από την σχέση (1). Για ελατήριο, το Κ ονομάζεται κατευθύνουσα δύναμη ή σκληρότητα ή σταθερά του ελατηρίου. Θεωρητική βάση του πειράματος Ένα ελατήριο είναι τοποθετημένο κατακόρυφα και στο κάτω άκρο του προστίθενται βάρη: B = mg (2) Για κάθε βάρος μετράμε την παραμόρφωση (επιμήκυνση) του ελατηρίου, L : L= L L O (3) όπου L O και L είναι το μήκος του ελατηρίου πριν κρεμάσουμε το βάρος και αφού κρεμάσουμε το βάρος αντίστοιχα. 2
3 Αφού η σχέση (1) είναι γραμμική, η συνάρτηση B=f(ΔL) θα είναι μια ευθεία γραμμή της οποίας η κλίση θα είναι η σταθερά του ελατηρίου.! Προσοχή: Σε όλα τα πειραματικά στάδια θα πρέπει να επιλέγονται προσεκτικά τα βάρη που θα κρεμαστούν στο κάθε ελατήριο ώστε να μην καταστρέψουν το ελατήριο. Το ελατήριο δεν θα πρέπει να επιμηκυνθεί περισσότερο από δύο φορές το φυσικό του μήκος ώστε να μην παραμορφωθεί ανελαστικά. Όταν ένα ελατήριο επιμηκύνεται χωρίς να ξεπερνιέται το ελαστικό όριο του φυσικού του μήκους L o, η επιμήκυνση ΔL είναι ανάλογη του βάρους-φορτίου mg. Η σταθερά αναλογίας Κ στην εξίσωση: mg = K L (4) είναι η σταθερά του ελατηρίου. Η σταθερά Κ μπορεί να μετρηθεί λοιπόν με μέτρηση της επιμήκυνσης του ελατηρίου όταν κρεμιέται μάζα m σε αυτό. 3
4 Εκτέλεση του πειράματος 1. Επιλέξτε προσεκτικά τις μάζες που θα κρεμάσετε στο ελατήριο. 2. Συνδέστε την κρεμάστρα μαζών στην βάση του δείκτη και τοποθετήστε την πρώτη μάζα. Καταγράψτε την επιμήκυνση και το βάρος της μάζας που κρεμάσατε. Μην ξεχάσετε να συμπεριλάβετε την μάζας της κρεμάστρας. 3. Προσθέστε 4 ακόμα μάζες και κάθε φορά καταγράψτε την επιμήκυνση και το βάρος της μάζας που κρέμεται από το ελατήριο. α/α m (kg) B (N) L (m) ΔL=L-L O (m) Φτιάξτε το διάγραμμα Δύναμη-Επιμήκυνση, B=f(ΔL). 5. Προσδιορίστε την εξίσωση της ευθείας με την μέθοδο των ελαχίστων τετραγώνων. Σιγουρευτείτε ότι χρησιμοποιήσατε κατάλληλες μεταβλητές, αριθμούς και μονάδες. 4
5 6. Η κλίση της ευθείας Δύναμη-Επιμήκυνση ισούται με την σταθερά του ελατηρίου. Η τεταγμένη επί την αρχή εκφράζει την δύναμη που είναι απαραίτητη για να αρχίσει να επιμηκύνεται το ελατήριο και ονομάζεται αρχική τάση. Καταχωρήστε τα αποτελέσματά σας: Σταθερά του ελατηρίου = Αρχική τάση = 5
6 Β. Μελέτη συμπεριφοράς ελατηρίων Θεωρητική βάση του πειράματος Το ελατήριο είναι τοποθετημένο κατακόρυφα και στο κάτω άκρο του προστίθενται βάρη Β. Αφήνουμε το ελατήριο να πάρει την νέα θέση ισορροπίας του. Μετά εκτρέπουμε ελαφρά το κάτω άκρο του ελατηρίου (προς τα κάτω) και το αφήνουμε ελεύθερο. Αφού οι σχέση (1) περιγράφει μιαν αρμονική ταλάντωση, η κίνηση που θα εκτελέσει το κάτω άκρο του ελατηρίου θα είναι επίσης μια αρμονική ταλάντωση. Αποδεικνύεται, ότι η περίοδος της αρμονικής αυτής ταλάντωσης, όταν το ελατήριο είναι αβαρές, δίνεται από την σχέση: T m = 2π (5) K Από την σχέση αυτή μπορούμε να βρούμε το Κ μετρώντας την περίοδο ταλάντωσης Τ. Τα ελατήρια όμως δεν είναι αβαρή. Έχουν κάποια μάζα κατανεμημένη γραμμικά σε όλο το μήκος του ελατηρίου. Η μάζα αυτή δεν λαμβάνεται υπόψη όταν κάνουμε υπολογισμούς με την σχέση (5) και φυσικά η σταθερά Κ του ελατηρίου που υπολογίζεται από την σχέση αυτή θα έχει κάποιο σφάλμα. Θα μπορούσε κάποιος να προτείνει να προσθέσουμε την μάζα του ελατηρίου, Μ, στην σχέση (5), έτσι ώστε η σχέση να διορθωθεί και να γίνει: T m+ M = 2π. K Όμως αυτό είναι λάθος! Η σχέση (5) αναφέρεται σε αβαρές ελατήριο και μάζα στο κάτω άκρο του ελατηρίου. Η μάζα όμως Μ είναι κατανεμημένη σε όλο το μήκος του ελατηρίου και όχι μόνο στο κάτω άκρο του. Είναι δυνατόν να 6
7 αποδειχθεί θεωρητικά ότι μόνο το 1/3 της μάζας του ελατηρίου συνεισφέρει στην ταλάντωση. Έτσι η σχέση (5) πρέπει να γραφεί με την μορφή: T m+ M/3 = 2π. (6) K Εκτέλεση του πειράματος Μελέτη ενός ελατηρίου 1. Κρεμάστε το ελατήριο από το οριζόντιο στήριγμα και μετρήστε την απόσταση από την βάση του ελατηρίου στην επιφάνεια του εργαστηριακού πάγκου. Καταγράψτε αυτή την τιμή H ο =. 2. Κρεμάστε τώρα στο ελεύθερο άκρο του ελατηρίου βάρος 0.3 kp και επαναλάβετε την διαδικασία του βήματος 1. H 1 =. 3. Βρείτε την επιμήκυνση του ελατηρίου αφαιρώντας τις παραπάνω δύο μετρήσεις ΔL = H ο - H 1 =. 4. Υπολογίστε την σταθερά του ελατηρίου. K =. 5. Στη συνέχεια θα προσδιορίσουμε την σταθερά του ελατηρίου με μια άλλη μέθοδο: 7
8 Με το ελατήριο φορτισμένο με βάρος 150 p εκτρέψτε ελαφρά το ελατήριο από την θέση ισορροπίας και μετρήστε τον χρόνο 10 πλήρων αιωρήσεων (10 Τ ). Βρείτε την περίοδο Τ. T =. 6. Από την σχέση (5) βρείτε την σταθερά του ελατηρίου K. K =. 7. Συγκρίνετε τις δύο τιμές. Ποια τιμή του K νομίζετε ότι είναι πιο σωστή; Εξηγήστε γιατί. 8. Ζυγίστε το ελατήριο και βρείτε την μάζα του Μ. 9. Χρησιμοποιώντας την σχέση (6) και την περίοδο της ταλάντωσης που μετρήθηκε, βρείτε ξανά την σταθερά Κ του ελατηρίου. K =. 10. Συγκρίνετε την με την τιμή που βρήκατε στην εργασία 5. Προσεγγίζουν οι δύο τιμές; Συνδεσμολογία ελατηρίων 1. Επιλέξτε ένα ελατήριο, A, από αυτά που διαθέτετε. Κρεμάστε μία μάζα στο ελεύθερο άκρο του και προσδιορίστε την σταθερά του: 8
9 K A =. 2. Προσδιορίστε το μέσο του ελατηρίου και κρεμάστε από εκεί την μάζα. Προσδιορίστε την σταθερά του ελατηρίου με το μισό μήκος: K A/2 =. Τι συμπεραίνετε; Πως θα μπορούσατε να επιβεβαιώσετε το συμπέρασμα σας; 3. Επιλέξτε ένα άλλο ελατήριο, B, και προσδιορίστε την σταθερά του. K B =. 4. Κρεμάστε στη συνέχεια το πρώτο ελατήριο, A, στην οριζόντια βάση και στο ελεύθερο άκρο του κρεμάστε το δεύτερο ελατήριο, B. Κρεμάστε μία μάζα στο ελεύθερο άκρο του δεύτερου ελατηρίου και προσδιορίστε την σταθερά του συστήματος των δύο ελατηρίων. K AB =. Τι συμπεραίνετε για την σταθερά του συστήματος των ελατηρίων που έχουν συνδεθεί σε σειρά; 5. Μπορείτε να επαναλάβετε αντίστοιχη διαδικασία για να βρείτε την σταθερά συστήματος ελατηρίων που έχουν συνδεθεί παράλληλα; K AB =. 9
Άσκηση 5 Υπολογισμός της σταθεράς ελατηρίου
 Άσκηση 5 Υπολογισμός της σταθεράς ελατηρίου Σύνοψη Σκοπός της συγκεκριμένης άσκησης είναι ο υπολογισμός της σταθεράς ενός ελατηρίου. Αυτό θα γίνει με δύο τρόπους: από την κλίση της (πειραματικής) ευθείας
Άσκηση 5 Υπολογισμός της σταθεράς ελατηρίου Σύνοψη Σκοπός της συγκεκριμένης άσκησης είναι ο υπολογισμός της σταθεράς ενός ελατηρίου. Αυτό θα γίνει με δύο τρόπους: από την κλίση της (πειραματικής) ευθείας
ΤΟΠΙΚΟΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO Ε.Κ.Φ.Ε. Νέας Σμύρνης
 ΤΟΠΙΚΟΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 14-15 Ε.Κ.Φ.Ε. Νέας Σμύρνης Εξέταση στη Φυσική ΛΥΚΕΙΟ: Τριμελής ομάδα μαθητών: 1.. 3. Αναπληρωματικός: Θέματα: Ηλ. Μαυροματίδης Β Σειρά Θεμάτων (Φυσική) Μέτρηση της
ΤΟΠΙΚΟΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 14-15 Ε.Κ.Φ.Ε. Νέας Σμύρνης Εξέταση στη Φυσική ΛΥΚΕΙΟ: Τριμελής ομάδα μαθητών: 1.. 3. Αναπληρωματικός: Θέματα: Ηλ. Μαυροματίδης Β Σειρά Θεμάτων (Φυσική) Μέτρηση της
Ο ΝΟΜΟΣ ΤΟΥ HOOKE ΣΤΟΧΟΙ
 Ο ΝΟΜΟΣ ΤΟΥ HOOKE ΣΤΟΧΟΙ Να αποδείξεις πειραματικά ότι η επιμήκυνση ενός ελατηρίου είναι ανάλογη της δύναμης που την προκαλεί. Να υπολογίσεις την σταθερά k (σκληρότητα) του ελατηρίου. Να γίνει κατανοητή
Ο ΝΟΜΟΣ ΤΟΥ HOOKE ΣΤΟΧΟΙ Να αποδείξεις πειραματικά ότι η επιμήκυνση ενός ελατηρίου είναι ανάλογη της δύναμης που την προκαλεί. Να υπολογίσεις την σταθερά k (σκληρότητα) του ελατηρίου. Να γίνει κατανοητή
Προσδιορισμός της σταθεράς ενός ελατηρίου.
 Μ3 Προσδιορισμός της σταθεράς ενός ελατηρίου. 1 Σκοπός Στην άσκηση αυτή θα προσδιοριστεί η σταθερά ενός ελατηρίου χρησιμοποιώντας στην ακολουθούμενη διαδικασία τον νόμο του Hooke και τη σχέση της περιόδου
Μ3 Προσδιορισμός της σταθεράς ενός ελατηρίου. 1 Σκοπός Στην άσκηση αυτή θα προσδιοριστεί η σταθερά ενός ελατηρίου χρησιμοποιώντας στην ακολουθούμενη διαδικασία τον νόμο του Hooke και τη σχέση της περιόδου
ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ. A. Στάσιμα κύματα σε χορδές
 Σκοπός της άσκησης Σε αυτή την άσκηση θα μελετήσουμε τα στάσιμα κύματα σε χορδές και σωλήνες. A. Στάσιμα κύματα σε χορδές Εισαγωγή Μία γεννήτρια ημιτονοειδούς σήματος διεγείρει έναν δονητή ο οποίος δημιουργεί
Σκοπός της άσκησης Σε αυτή την άσκηση θα μελετήσουμε τα στάσιμα κύματα σε χορδές και σωλήνες. A. Στάσιμα κύματα σε χορδές Εισαγωγή Μία γεννήτρια ημιτονοειδούς σήματος διεγείρει έναν δονητή ο οποίος δημιουργεί
Εκφώνηση 1. α). β). γ). Επιλέξτε τη σωστή πρόταση και αιτιολογείστε.
 Εκφώνηση 1 Στο σχήμα το σώμα μάζας ισορροπεί χαμηλότερα κατά h από τη θέση φυσικού μήκους του ελατηρίου. Από τη θέση φυσικού μήκους του ελατηρίου αφήνουμε σώμα ίσης μάζας ( ) να κάνει ελεύθερη πτώση στην
Εκφώνηση 1 Στο σχήμα το σώμα μάζας ισορροπεί χαμηλότερα κατά h από τη θέση φυσικού μήκους του ελατηρίου. Από τη θέση φυσικού μήκους του ελατηρίου αφήνουμε σώμα ίσης μάζας ( ) να κάνει ελεύθερη πτώση στην
6 Δεκεμβρίου 2014 ΛΥΚΕΙΟ:... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: ΜΟΝΑΔΕΣ:
 ΤΟΠΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 2015 ΦΥΣΙΚΗ 6 Δεκεμβρίου 2014 ΛΥΚΕΙΟ:.... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1.. 2.. 3.. ΜΟΝΑΔΕΣ: Το πρόβλημα Φτιάξτε ένα ρολόι με ένα σύστημα ελατηρίου-βαριδίου που ταλαντώνεται ελεύθερα Τα όργανα
ΤΟΠΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ EUSO 2015 ΦΥΣΙΚΗ 6 Δεκεμβρίου 2014 ΛΥΚΕΙΟ:.... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1.. 2.. 3.. ΜΟΝΑΔΕΣ: Το πρόβλημα Φτιάξτε ένα ρολόι με ένα σύστημα ελατηρίου-βαριδίου που ταλαντώνεται ελεύθερα Τα όργανα
Φυσική (Ε) Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 4: Προσδιορισμός της σταθεράς ενός ελατηρίου. Αικατερίνη Σκουρολιάκου. Τμήμα Ενεργειακής Τεχνολογίας
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική (Ε) Ενότητα 4: Προσδιορισμός της σταθεράς ενός ελατηρίου Αικατερίνη Σκουρολιάκου Τμήμα Ενεργειακής Τεχνολογίας Το περιεχόμενο του
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική (Ε) Ενότητα 4: Προσδιορισμός της σταθεράς ενός ελατηρίου Αικατερίνη Σκουρολιάκου Τμήμα Ενεργειακής Τεχνολογίας Το περιεχόμενο του
Υπολογισμός της σταθεράς του ελατηρίου
 Άσκηση 5 Υπολογισμός της σταθεράς του ελατηρίου Σκοπός: Ο υπολογισμός της σταθεράς ενός ελατηρίου. Αυτό θα γίνει με δύο τρόπους: 1. Από την κλίση μιας πειραματικής καμπύλης 2. Από τον τύπο της περιόδου
Άσκηση 5 Υπολογισμός της σταθεράς του ελατηρίου Σκοπός: Ο υπολογισμός της σταθεράς ενός ελατηρίου. Αυτό θα γίνει με δύο τρόπους: 1. Από την κλίση μιας πειραματικής καμπύλης 2. Από τον τύπο της περιόδου
ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ ΜΕ ΤΗ ΧΡΗΣΗ ΤΟΥ MULTILOG
 1 ο ΕΚΦΕ (Ν. ΣΜΥΡΝΗΣ) Δ Δ/ΝΣΗΣ Δ. Ε. ΑΘΗΝΑΣ 1 Α. ΣΤΟΧΟΙ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ ΜΕ ΤΗ ΧΡΗΣΗ ΤΟΥ MULTILOG Η πραγματοποίηση αρμονικής ταλάντωσης μικρού πλάτους με τη χρήση μάζας δεμένης σε ελατήριο. Η εφαρμογή
1 ο ΕΚΦΕ (Ν. ΣΜΥΡΝΗΣ) Δ Δ/ΝΣΗΣ Δ. Ε. ΑΘΗΝΑΣ 1 Α. ΣΤΟΧΟΙ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ ΜΕ ΤΗ ΧΡΗΣΗ ΤΟΥ MULTILOG Η πραγματοποίηση αρμονικής ταλάντωσης μικρού πλάτους με τη χρήση μάζας δεμένης σε ελατήριο. Η εφαρμογή
European Union Science Olympiad EUSO 2014 ΤΟΠΙΚΟΣ ΜΑΘΗΤΙΚΟΣ ΙΑΓΩΝΙΣΜΟΣ ΠΕΙΡΑΜΑΤΙΚΗ ΟΚΙΜΑΣΙΑ ΣΤΗ ΦΥΣΙΚΗ. Σάββατο 7 ΕΚΕΜΒΡΙΟΥ 2013 ΕΚΦΕ ΑΧΑΪΑΣ (ΑΙΓΙΟΥ)
 12 η ΕΥΡΩΠΑΪΚΗ ΟΛΥΜΠΙΑ Α ΕΠΙΣΤΗΜΩΝ EUSO 2014 ΤΟΠΙΚΟΣ ΜΑΘΗΤΙΚΟΣ ΙΑΓΩΝΙΣΜΟΣ ΠΕΙΡΑΜΑΤΙΚΗ ΟΚΙΜΑΣΙΑ ΣΤΗ ΦΥΣΙΚΗ Σάββατο 7 ΕΚΕΜΒΡΙΟΥ 2013 ΕΚΦΕ ΑΧΑΪΑΣ (ΑΙΓΙΟΥ) ( ιάρκεια εξέτασης 60 min) Μαθητές: Σχολική Μονάδα
12 η ΕΥΡΩΠΑΪΚΗ ΟΛΥΜΠΙΑ Α ΕΠΙΣΤΗΜΩΝ EUSO 2014 ΤΟΠΙΚΟΣ ΜΑΘΗΤΙΚΟΣ ΙΑΓΩΝΙΣΜΟΣ ΠΕΙΡΑΜΑΤΙΚΗ ΟΚΙΜΑΣΙΑ ΣΤΗ ΦΥΣΙΚΗ Σάββατο 7 ΕΚΕΜΒΡΙΟΥ 2013 ΕΚΦΕ ΑΧΑΪΑΣ (ΑΙΓΙΟΥ) ( ιάρκεια εξέτασης 60 min) Μαθητές: Σχολική Μονάδα
α. β. γ. δ. Μονάδες 5 α. β. γ. δ. Μονάδες 5 α. ελαστική β. ανελαστική γ. πλαστική δ. έκκεντρη
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 27/09/2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 27/09/2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
Θέματα Παγκύπριων Εξετάσεων
 Θέματα Παγκύπριων Εξετάσεων 2009 2014 Σελίδα 1 από 24 Ταλαντώσεις 1. Το σύστημα ελατήριο-σώμα εκτελεί απλή αρμονική ταλάντωση μεταξύ των σημείων Α και Β. (α) Ο χρόνος που χρειάζεται το σώμα για να κινηθεί
Θέματα Παγκύπριων Εξετάσεων 2009 2014 Σελίδα 1 από 24 Ταλαντώσεις 1. Το σύστημα ελατήριο-σώμα εκτελεί απλή αρμονική ταλάντωση μεταξύ των σημείων Α και Β. (α) Ο χρόνος που χρειάζεται το σώμα για να κινηθεί
Θέμα: Πειραματική Μελέτη του απλού εκκρεμούς ΟΝΟΜΑ ΟΜΑΔΑΣ: ΜΕΛΗ ΟΜΑΔΑΣ: Ε.Κ.Φ.Ε Κέρκυρας -1-
 Θέμα: Πειραματική Μελέτη του απλού εκκρεμούς ΟΝΟΜΑ ΟΜΑΔΑΣ: ΜΕΛΗ ΟΜΑΔΑΣ: 1) 2) 3) 4) Ε.Κ.Φ.Ε Κέρκυρας -1- ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: ΤΟ ΑΠΛΟ ΕΚΚΡΕΜΕΣ Α. Θεωρητική εισαγωγή Το απλό εκκρεμές είναι μια διάταξη που
Θέμα: Πειραματική Μελέτη του απλού εκκρεμούς ΟΝΟΜΑ ΟΜΑΔΑΣ: ΜΕΛΗ ΟΜΑΔΑΣ: 1) 2) 3) 4) Ε.Κ.Φ.Ε Κέρκυρας -1- ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: ΤΟ ΑΠΛΟ ΕΚΚΡΕΜΕΣ Α. Θεωρητική εισαγωγή Το απλό εκκρεμές είναι μια διάταξη που
γ. Πόση επιτάχυνση θα έχει το σώμα τη στιγμή που έχει απομάκρυνση 0,3 m;
 ΘΕΜΑ Γ 1. Ένα σώμα εκτελεί αρμονική ταλάντωση με εξίσωση 0,6 ημ 8 S.I.. α. Να βρείτε την περίοδο και τον αριθμό των ταλαντώσεων που εκτελεί το σώμα σε ένα λεπτό της ώρας. β. Να γράψετε τις εξισώσεις της
ΘΕΜΑ Γ 1. Ένα σώμα εκτελεί αρμονική ταλάντωση με εξίσωση 0,6 ημ 8 S.I.. α. Να βρείτε την περίοδο και τον αριθμό των ταλαντώσεων που εκτελεί το σώμα σε ένα λεπτό της ώρας. β. Να γράψετε τις εξισώσεις της
4. Σώμα Σ 1 μάζας m 1 =1kg ισορροπεί πάνω σε λείο κεκλιμένο επίπεδο που σχηματίζει με τον ορίζοντα γωνία φ=30 ο. Το σώμα Σ 1 είναι δεμένο στην άκρη
 1. Δίσκος μάζας Μ=1 Kg είναι στερεωμένος στο πάνω άκρο κατακόρυφου ελατηρίου, σταθεράς k=200 N/m. Το άλλο άκρο του ελατηρίου είναι στερεωμένο σε οριζόντιο δάπεδο. Πάνω στο δίσκο κάθεται ένα πουλί με μάζα
1. Δίσκος μάζας Μ=1 Kg είναι στερεωμένος στο πάνω άκρο κατακόρυφου ελατηρίου, σταθεράς k=200 N/m. Το άλλο άκρο του ελατηρίου είναι στερεωμένο σε οριζόντιο δάπεδο. Πάνω στο δίσκο κάθεται ένα πουλί με μάζα
Υπολογισμός της σταθεράς ελατηρίου
 Εργαστηριακή Άσκηση 6 Υπολογισμός της σταθεράς ελατηρίου Βαρσάμης Χρήστος Στόχος: Υπολογισμός της σταθεράς ελατηρίου, k. Πειραματική διάταξη: Κατακόρυφο ελατήριο, σειρά πλακιδίων μάζας m. Μέθοδος: α) Εφαρμογή
Εργαστηριακή Άσκηση 6 Υπολογισμός της σταθεράς ελατηρίου Βαρσάμης Χρήστος Στόχος: Υπολογισμός της σταθεράς ελατηρίου, k. Πειραματική διάταξη: Κατακόρυφο ελατήριο, σειρά πλακιδίων μάζας m. Μέθοδος: α) Εφαρμογή
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΕΛΑΤΗΡΙΟ-ΚΡΟΥΣΗ. Σε όσες ασκήσεις απαιτείται δίνεται επιτάχυνση βαρύτητας g=10 m/s 2.
 ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΕΛΑΤΗΡΙΟ-ΚΡΟΥΣΗ Σε όσες ασκήσεις απαιτείται δίνεται επιτάχυνση βαρύτητας g=10 m/s 2. ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Η δύναμη επαναφοράς που ασκείται σε ένα σώμα μάζας m που εκτελεί απλή αρμονική
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΕΛΑΤΗΡΙΟ-ΚΡΟΥΣΗ Σε όσες ασκήσεις απαιτείται δίνεται επιτάχυνση βαρύτητας g=10 m/s 2. ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Η δύναμη επαναφοράς που ασκείται σε ένα σώμα μάζας m που εκτελεί απλή αρμονική
Ένωση Ελλήνων Φυσικών ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗΣ 2011 Πανεπιστήμιο Αθηνών Εργαστήριο Φυσικών Επιστημών, Τεχνολογίας, Περιβάλλοντος.
 Θεωρητικό Μέρος Θέμα 1 ο A Λυκείου 1 Μαρτίου 011 Στις ερωτήσεις A, B, και Γ, μια μόνο απάντηση είναι σωστή. Γράψτε στο τετράδιό σας το κεφαλαίο γράμμα της ερώτησης και το μικρό γράμμα της σωστής απάντησης.
Θεωρητικό Μέρος Θέμα 1 ο A Λυκείου 1 Μαρτίου 011 Στις ερωτήσεις A, B, και Γ, μια μόνο απάντηση είναι σωστή. Γράψτε στο τετράδιό σας το κεφαλαίο γράμμα της ερώτησης και το μικρό γράμμα της σωστής απάντησης.
Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
Φυσική κατεύθυνσης Γ Λυκείου. MultiLog Pro
 Φυσική κατεύθυνσης Γ Λυκείου Πειραµατική µελέτη της απλής αρµονικής ταλάντωσης µε το: MultiLog Pro Ε.Κ.Φ.Ε ΛΕΣΒΟΥ Σχολικό έτος 2009-2010 Ε.Κ.Φ.Ε ΛΕΣΒΟΥ Σελίδα 2 / 12 ver. 1.0 Όργανα υο µάζες των 500 g
Φυσική κατεύθυνσης Γ Λυκείου Πειραµατική µελέτη της απλής αρµονικής ταλάντωσης µε το: MultiLog Pro Ε.Κ.Φ.Ε ΛΕΣΒΟΥ Σχολικό έτος 2009-2010 Ε.Κ.Φ.Ε ΛΕΣΒΟΥ Σελίδα 2 / 12 ver. 1.0 Όργανα υο µάζες των 500 g
Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς
 Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς 1. Δύο σώματα ίδιας μάζας εκτελούν Α.Α.Τ. Στο διάγραμμα του σχήματος παριστάνεται η συνισταμένη δύναμη που ασκείται σε κάθε σώμα σε συνάρτηση
Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς 1. Δύο σώματα ίδιας μάζας εκτελούν Α.Α.Τ. Στο διάγραμμα του σχήματος παριστάνεται η συνισταμένη δύναμη που ασκείται σε κάθε σώμα σε συνάρτηση
Όταν το ελατήριο έχει μάζα
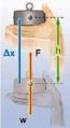 Όταν το ελατήριο έχει μάζα Εισαγωγή Αφορμή για την παρούσα ανάρτηση ήταν η θέση που διατύπωσε ο Γιάννης ο Κυριακόπουλος όσον αφορά στην συχνότητα ταλάντωσης ενός σώματος, το οποίο είναι δεμένο σε ελατήριο
Όταν το ελατήριο έχει μάζα Εισαγωγή Αφορμή για την παρούσα ανάρτηση ήταν η θέση που διατύπωσε ο Γιάννης ο Κυριακόπουλος όσον αφορά στην συχνότητα ταλάντωσης ενός σώματος, το οποίο είναι δεμένο σε ελατήριο
Νόµος Hooke. Α Τρόπος. Πειραµατική διαδικασία :
 Νόµος Hooke Γνωστικοί στόχοι : 1) Να αντιληφθούν οι µαθητές την αναλογική σχέση της επιµήκυνσης και της δύναµης στις ελαστικές παραµορφώσεις. 2) Να κατασκευάσουν τη γραφική παράσταση της δύναµης συναρτήσει
Νόµος Hooke Γνωστικοί στόχοι : 1) Να αντιληφθούν οι µαθητές την αναλογική σχέση της επιµήκυνσης και της δύναµης στις ελαστικές παραµορφώσεις. 2) Να κατασκευάσουν τη γραφική παράσταση της δύναµης συναρτήσει
Μελέτη της ευθύγραμμης ομαλά μεταβαλλόμενης κίνησης σώματος με χρήση συστήματος φωτοπύλης-χρονομέτρου. Περιγραφή - Θεωρητικές προβλέψεις - Σχεδιασμός
 Εργαστήριο Φυσικής Λυκείου Επιμέλεια: Κ. Παπαμιχάλης Μελέτη της ευθύγραμμης ομαλά μεταβαλλόμενης κίνησης σώματος με χρήση συστήματος φωτοπύλης-χρονομέτρου Περιγραφή - Θεωρητικές προβλέψεις - Σχεδιασμός
Εργαστήριο Φυσικής Λυκείου Επιμέλεια: Κ. Παπαμιχάλης Μελέτη της ευθύγραμμης ομαλά μεταβαλλόμενης κίνησης σώματος με χρήση συστήματος φωτοπύλης-χρονομέτρου Περιγραφή - Θεωρητικές προβλέψεις - Σχεδιασμός
ΘΕΜΑ Α A1. Στις ερωτήσεις 1 9 να επιλέξετε το γράμμα που αντιστοιχεί στη σωστή απάντηση, χωρίς να αιτιολογήσετε την επιλογή σας.
 ΜΑΘΗΜΑ / Προσανατολισμός / ΤΑΞΗ ΑΡΙΘΜΟΣ ΦΥΛΛΟΥ ΕΡΓΑΣΙΑΣ: ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ : ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ: ΦΥΣΙΚΗ/ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ / Γ ΛΥΚΕΙΟΥ 1 Ο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ( ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ) ΘΕΜΑ Α A1. Στις ερωτήσεις
ΜΑΘΗΜΑ / Προσανατολισμός / ΤΑΞΗ ΑΡΙΘΜΟΣ ΦΥΛΛΟΥ ΕΡΓΑΣΙΑΣ: ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ : ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ: ΦΥΣΙΚΗ/ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ / Γ ΛΥΚΕΙΟΥ 1 Ο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ( ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ) ΘΕΜΑ Α A1. Στις ερωτήσεις
Φύλλο Εργασίας 3 Μετρήσεις μάζας Τα διαγράμματα
 Φύλλο Εργασίας 3 Μετρήσεις μάζας Τα διαγράμματα α. Παρατηρώ, Πληροφορούμαι, Ενδιαφέρομαι Τι πρέπει να κάνουμε για να μετρήσουμε οποιοδήποτε μέγεθος; Πρέπει να ορίσουμε: 1. Μια ομοειδή ποσότητα ως μονάδα
Φύλλο Εργασίας 3 Μετρήσεις μάζας Τα διαγράμματα α. Παρατηρώ, Πληροφορούμαι, Ενδιαφέρομαι Τι πρέπει να κάνουμε για να μετρήσουμε οποιοδήποτε μέγεθος; Πρέπει να ορίσουμε: 1. Μια ομοειδή ποσότητα ως μονάδα
ΜΕΤΡΗΣΗ ΕΜΒΑΔΟΥ. Σχεδιασμός - Περιγραφή
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 ΜΕΤΡΗΣΗ ΕΜΒΑΔΟΥ Πώς θα μετρήσουμε την επιφάνεια ενός θρανίου, ενός φύλλου, ή του πουκάμισου που φοράμε; Την έννοια της «επιφάνειας» τη συναντάμε στα αντικείμενα της καθημερινότητάς
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 ΜΕΤΡΗΣΗ ΕΜΒΑΔΟΥ Πώς θα μετρήσουμε την επιφάνεια ενός θρανίου, ενός φύλλου, ή του πουκάμισου που φοράμε; Την έννοια της «επιφάνειας» τη συναντάμε στα αντικείμενα της καθημερινότητάς
Ένωση Ελλήνων Φυσικών ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗΣ 2011 Πανεπιστήμιο Αθηνών Εργαστήριο Φυσικών Επιστημών, Τεχνολογίας, Περιβάλλοντος.
 Θεωρητικό Μέρος Θέμα 1 ο A Λυκείου 1 Μαρτίου 011 Στις ερωτήσεις A, B, Γ, και Δ μια μόνο απάντηση είναι σωστή. Γράψτε στο τετράδιό σας το κεφαλαίο γράμμα της ερώτησης και το μικρό γράμμα της σωστής απάντησης.
Θεωρητικό Μέρος Θέμα 1 ο A Λυκείου 1 Μαρτίου 011 Στις ερωτήσεις A, B, Γ, και Δ μια μόνο απάντηση είναι σωστή. Γράψτε στο τετράδιό σας το κεφαλαίο γράμμα της ερώτησης και το μικρό γράμμα της σωστής απάντησης.
Διαγώνισμα στη Φυσική Θετικού Προσανατολισμού στα κεφάλαια Ταλαντώσεις-κρούσεις κύματα και Doppler. Κυριακή
 Θέμα ο. Διαγώνισμα στη Φυσική Θετικού Προσανατολισμού στα κεφάλαια Ταλαντώσεις-κρούσεις κύματα και Doppler. Κυριακή 4--06 Στα θέματα Α, Α, Α3,Α4 επιλέξτε το γράμμα που απαντά στην ερώτηση και γράψτε το
Θέμα ο. Διαγώνισμα στη Φυσική Θετικού Προσανατολισμού στα κεφάλαια Ταλαντώσεις-κρούσεις κύματα και Doppler. Κυριακή 4--06 Στα θέματα Α, Α, Α3,Α4 επιλέξτε το γράμμα που απαντά στην ερώτηση και γράψτε το
Κεφάλαιο 10: Νόμος του Hooke-Αρμονική ταλάντωση σπειρoειδούς ελατηρίου
 Κεφάλαιο 1: Νόμος του Hooke-Αρμονική ταλάντωση σπειρoειδούς ελατηρίου Σύνοψη Πειραματική επαλήθευση του νόμου του Hooke, προσδιορισμός της σταθερής k του ελατηρίου μέσω μέτρησης της περιόδου αρμονικών
Κεφάλαιο 1: Νόμος του Hooke-Αρμονική ταλάντωση σπειρoειδούς ελατηρίου Σύνοψη Πειραματική επαλήθευση του νόμου του Hooke, προσδιορισμός της σταθερής k του ελατηρίου μέσω μέτρησης της περιόδου αρμονικών
ΤΑΛΑΝΤΩΣΕΙΣ (23 ΠΕΡΙΟΔΟΙ)
 α (cm/s ) ΚΕΦΑΛΑΙΟ 3 Κατηγορία Α ΤΑΛΑΝΤΩΣΕΙΣ (3 ΠΕΡΙΟΔΟΙ) 1. Να προσδιορίσετε ποια από τα πιο κάτω φυσικά μεγέθη μπορεί να έχουν την ίδια κατεύθυνση για ένα απλό αρμονικό ταλαντωτή: α. θέση και ταχύτητα,
α (cm/s ) ΚΕΦΑΛΑΙΟ 3 Κατηγορία Α ΤΑΛΑΝΤΩΣΕΙΣ (3 ΠΕΡΙΟΔΟΙ) 1. Να προσδιορίσετε ποια από τα πιο κάτω φυσικά μεγέθη μπορεί να έχουν την ίδια κατεύθυνση για ένα απλό αρμονικό ταλαντωτή: α. θέση και ταχύτητα,
Θέμα 1 ο (Μονάδες 25)
 ΙΙΑΑΓΓΩΝΝΙΙΣΣΜΑΑ ΦΦΥΥΣΣΙΙΚΚΗΗΣΣ ΚΚΑΑΤΤΕΕΥΥΘΘΥΥΝΝΣΣΗΗΣΣ ΑΑΠΟΟΦΦΟΟΙΙΤΤΩΝΝ 0055 -- -- 00 Θέμα ο. Ένα σημειακό αντικείμενο που εκτελεί ΑΑΤ μεταβαίνει από τη θέση ισορροπίας του σε ακραία θέση σε χρόνο s. Η
ΙΙΑΑΓΓΩΝΝΙΙΣΣΜΑΑ ΦΦΥΥΣΣΙΙΚΚΗΗΣΣ ΚΚΑΑΤΤΕΕΥΥΘΘΥΥΝΝΣΣΗΗΣΣ ΑΑΠΟΟΦΦΟΟΙΙΤΤΩΝΝ 0055 -- -- 00 Θέμα ο. Ένα σημειακό αντικείμενο που εκτελεί ΑΑΤ μεταβαίνει από τη θέση ισορροπίας του σε ακραία θέση σε χρόνο s. Η
Μεταξύ της τάσης και της ελαστικής παραμόρφωσης ενός σώματος υπάρχει μια απλή σχέση, ο νόμος του Hooke:
 Άσκηση Μ Σπειροειδές ελατήριο Νόμος του Hooe και εξίσωση δυνάμεων Μεταξύ της τάσης και της ελαστικής παραμόρφωσης ενός σώματος υπάρχει μια απλή σχέση, ο νόμος του Hooe: Οι ελαστικές τάσεις και οι παραμορφώσεις
Άσκηση Μ Σπειροειδές ελατήριο Νόμος του Hooe και εξίσωση δυνάμεων Μεταξύ της τάσης και της ελαστικής παραμόρφωσης ενός σώματος υπάρχει μια απλή σχέση, ο νόμος του Hooe: Οι ελαστικές τάσεις και οι παραμορφώσεις
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Στ.
 1.1. Μηχανικές Ταλαντώσεις. Ομάδα Στ. 101) Δυο σώματα αφήνονται να κινηθούν. Δυο σώματα Σ 1 και Σ 2, ίδιας μάζας m=2kg, συγκρατιόνται σε λείο κεκλιμένο επίπεδο απέχοντας κατά D=1,5m από την κορυφή του
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Στ. 101) Δυο σώματα αφήνονται να κινηθούν. Δυο σώματα Σ 1 και Σ 2, ίδιας μάζας m=2kg, συγκρατιόνται σε λείο κεκλιμένο επίπεδο απέχοντας κατά D=1,5m από την κορυφή του
7. Αντιστοιχίστε τα διανύσματα των δυνάμεων με τις τιμές τους:
 1. Σημειώστε με Σ τη σωστή και με Λ τη λάθος πρόταση: a. Η δύναμη προκαλεί μεταβολή στη θερμοκρασία των σωμάτων. b. Η παραμόρφωση είναι αποτέλεσμα της επίδρασης της δύναμης. c. Για να σταματήσει ένα σώμα
1. Σημειώστε με Σ τη σωστή και με Λ τη λάθος πρόταση: a. Η δύναμη προκαλεί μεταβολή στη θερμοκρασία των σωμάτων. b. Η παραμόρφωση είναι αποτέλεσμα της επίδρασης της δύναμης. c. Για να σταματήσει ένα σώμα
Δύναμη - Παραμόρφωση
 Δύναμη - Παραμόρφωση Τάση (σ): περιγράφει το αίτιο τη δύναμη που ασκείται σε όρους δύναμης προς επιφάνεια. Παραμόρφωση: περιγράφει το αποτέλεσμα Για μικρές τάσεις και παραμορφώσεις η σχέση τάσης παραμόρφωσης
Δύναμη - Παραμόρφωση Τάση (σ): περιγράφει το αίτιο τη δύναμη που ασκείται σε όρους δύναμης προς επιφάνεια. Παραμόρφωση: περιγράφει το αποτέλεσμα Για μικρές τάσεις και παραμορφώσεις η σχέση τάσης παραμόρφωσης
ΤΟΠΙΚΟΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΕΥΡΩΠΑΪΚΗΣ ΟΛΥΜΠΙΑΔΑΣ ΕΠΙΣΤΗΜΩΝ - EUSO 2017
 1ο και 2ο ΕΚΦΕ Ηρακλείου ΤΟΠΙΚΟΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΕΥΡΩΠΑΪΚΗΣ ΟΛΥΜΠΙΑΔΑΣ ΕΠΙΣΤΗΜΩΝ - EUSO 2017 Σάββατο 3 Δεκεμβρίου 2016 Διαγωνισμός στη Φυσική (Διάρκεια 1 ώρα) ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΩΝ 1)... 2)...
1ο και 2ο ΕΚΦΕ Ηρακλείου ΤΟΠΙΚΟΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΕΥΡΩΠΑΪΚΗΣ ΟΛΥΜΠΙΑΔΑΣ ΕΠΙΣΤΗΜΩΝ - EUSO 2017 Σάββατο 3 Δεκεμβρίου 2016 Διαγωνισμός στη Φυσική (Διάρκεια 1 ώρα) ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΩΝ 1)... 2)...
ΑΠΛΟ ΑΡΜΟΝΙΚΟ ΣΑΛΑΝΣΩΣΗ - ΤΣΗΜΑ ΕΛΑΣΗΡΙΟΤ ΩΜΑΣΟ
 ΑΠΛΟ ΑΡΜΟΝΙΚΟ ΣΑΛΑΝΣΩΣΗ - ΤΣΗΜΑ ΕΛΑΣΗΡΙΟΤ ΩΜΑΣΟ α) Ένα σώμα που μπορεί να εκτελεί απλή αρμονική ταλάντωση ονομάζεται απλός αρμονικός ταλαντωτής. Το σύστημα ελατήριο-μάζα είναι απλός αρμονικός ταλαντωτής,
ΑΠΛΟ ΑΡΜΟΝΙΚΟ ΣΑΛΑΝΣΩΣΗ - ΤΣΗΜΑ ΕΛΑΣΗΡΙΟΤ ΩΜΑΣΟ α) Ένα σώμα που μπορεί να εκτελεί απλή αρμονική ταλάντωση ονομάζεται απλός αρμονικός ταλαντωτής. Το σύστημα ελατήριο-μάζα είναι απλός αρμονικός ταλαντωτής,
Όλα τα θέματα των πανελληνίων στις μηχανικές ταλαντώσεις έως και το 2014 ΣΑΛΑΝΣΩΕΙ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΣΑΛΑΝΣΩΗ ΒΑΙΚΕ ΕΝΝΟΙΕ. Ερωτήσεις Πολλαπλής Επιλογής
 έως και το 04 ΣΑΛΑΝΣΩΕΙ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΣΑΛΑΝΣΩΗ ΒΑΙΚΕ ΕΝΝΟΙΕ Ερωτήσεις Πολλαπλής Επιλογής. Να μεταφέρετε στο τετράδιό σας τον παρακάτω πίνακα που αναφέρεται στην απλή αρμονική ταλάντωση και να συμπληρώσετε
έως και το 04 ΣΑΛΑΝΣΩΕΙ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΣΑΛΑΝΣΩΗ ΒΑΙΚΕ ΕΝΝΟΙΕ Ερωτήσεις Πολλαπλής Επιλογής. Να μεταφέρετε στο τετράδιό σας τον παρακάτω πίνακα που αναφέρεται στην απλή αρμονική ταλάντωση και να συμπληρώσετε
5. Δείξτε με λεκτικούς ισχυρισμούς ότι ο χρόνος κίνησης από τη θέση x = + A στην θέση
 Στα μεγέθη και στις περιγραφές των κινήσεων που ακολουθούν δεν γίνεται λεπτομερής ορισμός. Θεωρούνται καλώς ορισμένα (για τους σχετικούς φυσικά). Γενικά οι περιγραφές είναι σχετικά «χαλαρές» και επί της
Στα μεγέθη και στις περιγραφές των κινήσεων που ακολουθούν δεν γίνεται λεπτομερής ορισμός. Θεωρούνται καλώς ορισμένα (για τους σχετικούς φυσικά). Γενικά οι περιγραφές είναι σχετικά «χαλαρές» και επί της
ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΚΑΙ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΜΕ ΑΙΤΙΟΛΟΓΗΣΗ ΜΕΡΟΣ 2. έχει το φυσικό του μήκος και η πάνω άκρη του είναι δεμένη σε σταθερό σημείο.
 ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΚΑΙ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΜΕ ΑΙΤΙΟΛΟΓΗΣΗ ΜΕΡΟΣ. Ένα ιδανικό ελατήριο σταθεράς = 00 N/ που έχει τον άξονα του κατακόρυφο έχει το φυσικό του μήκος και η πάνω άκρη του είναι δεμένη σε
ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΚΑΙ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΜΕ ΑΙΤΙΟΛΟΓΗΣΗ ΜΕΡΟΣ. Ένα ιδανικό ελατήριο σταθεράς = 00 N/ που έχει τον άξονα του κατακόρυφο έχει το φυσικό του μήκος και η πάνω άκρη του είναι δεμένη σε
Ταλαντώσεις. =+ και έχει θετική ταχύτητα. Να γραφεί η εξίσωση κίνησης του.
 Ταλαντώσεις Άσκηση 1 η Ένα σώμα εκτελεί απλή αρμονική ταλάντωση και την χρονική στιγμή t=0s βρίσκεται στην θέση =+ και έχει θετική ταχύτητα. Να γραφεί η εξίσωση κίνησης του. Για t=0s, =+, υ>0 =+ 2 = =
Ταλαντώσεις Άσκηση 1 η Ένα σώμα εκτελεί απλή αρμονική ταλάντωση και την χρονική στιγμή t=0s βρίσκεται στην θέση =+ και έχει θετική ταχύτητα. Να γραφεί η εξίσωση κίνησης του. Για t=0s, =+, υ>0 =+ 2 = =
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ
 4 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 7 Ιανουαρίου, 00 Ώρα: 0.00.00 Οδηγίες: ) Το δοκίμιο αποτελείται από έξι (6) σελίδες και πέντε (5) θέματα. ) Να απαντήσετε τα ερωτήματα όλων
4 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 7 Ιανουαρίου, 00 Ώρα: 0.00.00 Οδηγίες: ) Το δοκίμιο αποτελείται από έξι (6) σελίδες και πέντε (5) θέματα. ) Να απαντήσετε τα ερωτήματα όλων
Απλή αρμονική ταλάντωση με χρήση Multilog
 1 Εργαστηριακή Διδασκαλία των Φυσικών εργασιών στα Γενικά Λύκεια Περίοδος 2006 2007 Φυσική Κατεύθυνσης Γ Λυκείου Ενδεικτική προσέγγιση της εργαστηριακή δραστηριότητας : Απλή αρμονική ταλάντωση με χρήση
1 Εργαστηριακή Διδασκαλία των Φυσικών εργασιών στα Γενικά Λύκεια Περίοδος 2006 2007 Φυσική Κατεύθυνσης Γ Λυκείου Ενδεικτική προσέγγιση της εργαστηριακή δραστηριότητας : Απλή αρμονική ταλάντωση με χρήση
Φροντιστήρια Εν-τάξη Σελίδα 1 από 6
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 11/09/2016 ΘΕΜΑ Α Να γράψετε στο τετραδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Ένα
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 11/09/2016 ΘΕΜΑ Α Να γράψετε στο τετραδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Ένα
Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΣΕ ΣΥΝΘΕΤΗ ΚΙΝΗΣΗ ΣΥΣΤΗΜΑΤΟΣ ΔΥΟ ΣΩΜΑΤΩΝ (ΤΑΛΑΝΤΩΣΗ + ΟΜΑΛΑ ΜΕΤΑΒΑΛΛΟΜΕΝΗ ΚΙΝΗΣΗ) Όνομα:...
 A A N A B P Y T A 9 5 0 Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΣΕ ΣΥΝΘΕΤΗ ΚΙΝΗΣΗ ΣΥΣΤΗΜΑΤΟΣ ΔΥΟ ΣΩΜΑΤΩΝ (ΤΑΛΑΝΤΩΣΗ + ΟΜΑΛΑ ΜΕΤΑΒΑΛΛΟΜΕΝΗ ΚΙΝΗΣΗ) Όνομα: Μέρος ο Στο διπλανό σχήμα βλέπετε ένα σύστημα
A A N A B P Y T A 9 5 0 Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΣΕ ΣΥΝΘΕΤΗ ΚΙΝΗΣΗ ΣΥΣΤΗΜΑΤΟΣ ΔΥΟ ΣΩΜΑΤΩΝ (ΤΑΛΑΝΤΩΣΗ + ΟΜΑΛΑ ΜΕΤΑΒΑΛΛΟΜΕΝΗ ΚΙΝΗΣΗ) Όνομα: Μέρος ο Στο διπλανό σχήμα βλέπετε ένα σύστημα
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Ε.
 1.1. Μηχανικές. Ομάδα Ε. 1.1.81. Δυο ΑΑΤ και μία Ταλάντωση. Ένα σώμα μάζας 1kg ηρεμεί σε λείο κεκλιμένο επίπεδο κλίσεως θ=30, δεμένο στο άκρο ελατηρίου σταθεράς k 1 =40Ν/m, ενώ εφάπτεται στο ε- λεύθερο
1.1. Μηχανικές. Ομάδα Ε. 1.1.81. Δυο ΑΑΤ και μία Ταλάντωση. Ένα σώμα μάζας 1kg ηρεμεί σε λείο κεκλιμένο επίπεδο κλίσεως θ=30, δεμένο στο άκρο ελατηρίου σταθεράς k 1 =40Ν/m, ενώ εφάπτεται στο ε- λεύθερο
Α. Για ποιο από τα δυο σώματα καταναλώσαμε περισσότερη ενέργεια;
 1. Στην κάτω άκρη ενός ιδανικού ελατήριου είναι δεμένο ένα σώμα που έχει μάζα m 1 = m και ισορροπεί. Στην κάτω άκρη ενός άλλου ομοίου ελατήριου είναι δεμένο ένα άλλο σώμα που έχει μάζα m 2 = 4m και ισορροπεί.
1. Στην κάτω άκρη ενός ιδανικού ελατήριου είναι δεμένο ένα σώμα που έχει μάζα m 1 = m και ισορροπεί. Στην κάτω άκρη ενός άλλου ομοίου ελατήριου είναι δεμένο ένα άλλο σώμα που έχει μάζα m 2 = 4m και ισορροπεί.
1 η ΑΣΚΗΣΗ Γ ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΗ
 1 η ΑΣΚΗΣΗ Γ ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΗ Αβαρές και μη εκτατό νήμα είναι δεμένο στο ένα άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 100 N/m, το άλλο άκρο του οποίου είναι στερεωμένο στο έδαφος. Το ελεύθερο άκρο
1 η ΑΣΚΗΣΗ Γ ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΗ Αβαρές και μη εκτατό νήμα είναι δεμένο στο ένα άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 100 N/m, το άλλο άκρο του οποίου είναι στερεωμένο στο έδαφος. Το ελεύθερο άκρο
4. Το βάρος ενός αντικειμένου είναι 98Ν. Πόση είναι η μάζα του; a. 9,8kg b. 46kg c. 10kg d. 1kg
 1. Στη θέση Α είναι ένα ελατήριο με κρεμασμένο στην άκρη του ένα σώμα. Στη θέση Β είναι το ίδιο ελατήριο με το ίδιο σώμα στην άκρη. Τι μπορεί να συμβαίνει ώστε η επιμήκυνση στη θέση Α να μην είναι ίδια
1. Στη θέση Α είναι ένα ελατήριο με κρεμασμένο στην άκρη του ένα σώμα. Στη θέση Β είναι το ίδιο ελατήριο με το ίδιο σώμα στην άκρη. Τι μπορεί να συμβαίνει ώστε η επιμήκυνση στη θέση Α να μην είναι ίδια
Τοπικός Διαγωνισμός EUSO2019 Πειραματική δοκιμασία Φυσικής
 ΕΚΦΕ Νέας Ιωνίας ΕΚΦΕ Χαλανδρίου Τοπικός Διαγωνισμός EUSO2019 Πειραματική δοκιμασία Φυσικής Ένα «ακατάλληλο» δυναμόμετρο! 8 Δεκεμβρίου 2018 ΣΧΟΛΙΚΗ ΜΟΝΑΔΑ: ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1) 2). 3).. Τα δυναμόμετρα Το
ΕΚΦΕ Νέας Ιωνίας ΕΚΦΕ Χαλανδρίου Τοπικός Διαγωνισμός EUSO2019 Πειραματική δοκιμασία Φυσικής Ένα «ακατάλληλο» δυναμόμετρο! 8 Δεκεμβρίου 2018 ΣΧΟΛΙΚΗ ΜΟΝΑΔΑ: ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1) 2). 3).. Τα δυναμόμετρα Το
ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ
 ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ 1. Κατακόρυφο ελατήριο σταθεράς k=1000 N /m έχει το κάτω άκρο του στερεωμένο σε ακίνητο σημείο. Στο πάνω άκρο του ελατηρίου έχει προσδεθεί σώμα Σ 1 μάζας m 1 =8 kg, ενώ ένα δεύτερο
ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ 1. Κατακόρυφο ελατήριο σταθεράς k=1000 N /m έχει το κάτω άκρο του στερεωμένο σε ακίνητο σημείο. Στο πάνω άκρο του ελατηρίου έχει προσδεθεί σώμα Σ 1 μάζας m 1 =8 kg, ενώ ένα δεύτερο
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ
 28 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 15 Δεκεμβρίου, 2013 Ώρα: 10:00-13:00 Οδηγίες: 1) Το δοκίμιο αποτελείται από πέντε (5) σελίδες και πέντε (5) θέματα. 2) Να απαντήσετε σε
28 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 15 Δεκεμβρίου, 2013 Ώρα: 10:00-13:00 Οδηγίες: 1) Το δοκίμιο αποτελείται από πέντε (5) σελίδες και πέντε (5) θέματα. 2) Να απαντήσετε σε
1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI).
 1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI). Να βρείτε: α. το πλάτος της απομάκρυνσης, της ταχύτητας και της επιτάχυνσης. β.
1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI). Να βρείτε: α. το πλάτος της απομάκρυνσης, της ταχύτητας και της επιτάχυνσης. β.
Το παρακάτω διάγραμμα παριστάνει την απομάκρυνση y ενός σημείου Μ (x Μ =1,2 m) του μέσου σε συνάρτηση με το χρόνο.
 ΟΔΗΓΙΕΣ: 1. Η επεξεργασία των θεμάτων θα γίνει γραπτώς σε χαρτί Α4 ή σε τετράδιο που θα σας δοθεί (το οποίο θα παραδώσετε στο τέλος της εξέτασης). Εκεί θα σχεδιάσετε και όσα γραφήματα ζητούνται στο Θεωρητικό
ΟΔΗΓΙΕΣ: 1. Η επεξεργασία των θεμάτων θα γίνει γραπτώς σε χαρτί Α4 ή σε τετράδιο που θα σας δοθεί (το οποίο θα παραδώσετε στο τέλος της εξέτασης). Εκεί θα σχεδιάσετε και όσα γραφήματα ζητούνται στο Θεωρητικό
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ(ΘΕΡΙΝΑ)
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ(ΘΕΡΙΝΑ) 5/01/2019 ΟΙΚΟΝΟΜΟΥ ΓΙΩΡΓΟΣ ΚΑΡΑΒΟΚΥΡΟΣ ΧΡΗΣΤΟΣ- ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ(ΘΕΡΙΝΑ) 5/01/2019 ΟΙΚΟΝΟΜΟΥ ΓΙΩΡΓΟΣ ΚΑΡΑΒΟΚΥΡΟΣ ΧΡΗΣΤΟΣ- ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
Προκριµατικός διαγωνισµός για την 11 th EUSO 2013 στην Φυσική ΑΙΓΑΛΕΩ. Ονοµατεπώνυµα. Σχολείο: Ηµεροµηνία: Σάββατο 8/12/2012.
 Ε.Κ.Φ.Ε. ΑΙΓΑΛΕΩ Προκριµατικός διαγωνισµός για την 11 th EUSO 2013 στην Φυσική Ονοµατεπώνυµα µελών οµάδας 1) 2) 3) ιάρκεια: 45 λεπτά Σχολείο: Ηµεροµηνία: Σάββατο 8/12/2012 Ο νόµος του Hooke Θεωρητικές
Ε.Κ.Φ.Ε. ΑΙΓΑΛΕΩ Προκριµατικός διαγωνισµός για την 11 th EUSO 2013 στην Φυσική Ονοµατεπώνυµα µελών οµάδας 1) 2) 3) ιάρκεια: 45 λεπτά Σχολείο: Ηµεροµηνία: Σάββατο 8/12/2012 Ο νόµος του Hooke Θεωρητικές
ΛΥΣΕΙΣ ΕΞΕΤΑΣΗΣ ΣΤΟ ΜΑΘΗΜΑ «ΤΕΧΝΟΛΟΓΙΑ ΜΕΤΡΗΣΕΩΝ» ΗΜΕΡΟΜΗΝΙΑ: 28/01/2013
 ΛΥΣΕΙΣ ΕΞΕΤΑΣΗΣ ΣΤΟ ΜΑΘΗΜΑ «ΤΕΧΝΟΛΟΓΙΑ ΜΕΤΡΗΣΕΩΝ» ΗΜΕΡΟΜΗΝΙΑ: 8/0/0 ΘΕΜΑ ο ( μονάδες) H διάταξη του παρακάτω σχήματος χρησιμοποιείται για τη μέτρηση της θερμοκρασίας σε ηλεκτρικό φούρνο και περιλαμβάνει
ΛΥΣΕΙΣ ΕΞΕΤΑΣΗΣ ΣΤΟ ΜΑΘΗΜΑ «ΤΕΧΝΟΛΟΓΙΑ ΜΕΤΡΗΣΕΩΝ» ΗΜΕΡΟΜΗΝΙΑ: 8/0/0 ΘΕΜΑ ο ( μονάδες) H διάταξη του παρακάτω σχήματος χρησιμοποιείται για τη μέτρηση της θερμοκρασίας σε ηλεκτρικό φούρνο και περιλαμβάνει
ΕΡΓΑΣΤΗΡΙΑΚΟ ΚΕΝΤΡΟ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΣΕΡΡΩΝ ΤΟΠΙΚΟΣ ΜΑΘΗΤΙΚΟΣ ΙΑΓΩΝΙΣΜΟΣ ΠΕΙΡΑΜΑΤΩΝ ΦΥΣΙΚΗΣ. ΣΧΟΛΕΙΟ:. Μαθητές/τριες που συµµετέχουν:
 14 η Ευρωπαϊκή Ολυµπιάδα Επιστηµών EUSO 2016 ΤΟΠΙΚΟΣ ΜΑΘΗΤΙΚΟΣ ΙΑΓΩΝΙΣΜΟΣ ΠΕΙΡΑΜΑΤΩΝ ΦΥΣΙΚΗΣ ΣΧΟΛΕΙΟ:. Μαθητές/τριες που συµµετέχουν: (1) (2) (3) Σέρρες 05/12/2015 Σύνολο µορίων:..... ΜΕΤΡΗΣΗ ΤΗΣ ΣΤΑΘΕΡΑΣ
14 η Ευρωπαϊκή Ολυµπιάδα Επιστηµών EUSO 2016 ΤΟΠΙΚΟΣ ΜΑΘΗΤΙΚΟΣ ΙΑΓΩΝΙΣΜΟΣ ΠΕΙΡΑΜΑΤΩΝ ΦΥΣΙΚΗΣ ΣΧΟΛΕΙΟ:. Μαθητές/τριες που συµµετέχουν: (1) (2) (3) Σέρρες 05/12/2015 Σύνολο µορίων:..... ΜΕΤΡΗΣΗ ΤΗΣ ΣΤΑΘΕΡΑΣ
Ποιο είναι το πλάτος της ταλάντωσης ;
 Ποιο είναι το πλάτος της ταλάντωσης ; 1. Ένα σώμα είναι δεμένο στο δεξιό άκρο οριζόντιου ιδανικού ελατηρίου και στο αριστερό άκρο οριζόντιου νήματος και ηρεμεί σε ισορροπία όπως δείχνει το σχήμα. Το ελατήριο
Ποιο είναι το πλάτος της ταλάντωσης ; 1. Ένα σώμα είναι δεμένο στο δεξιό άκρο οριζόντιου ιδανικού ελατηρίου και στο αριστερό άκρο οριζόντιου νήματος και ηρεμεί σε ισορροπία όπως δείχνει το σχήμα. Το ελατήριο
ΕΝΕΡΓΕΙΑ ΚΑΙ ΤΑΛΑΝΤΩΣΗ
 ΕΝΕΡΓΕΙΑ ΚΑΙ ΤΑΛΑΝΤΩΣΗ 1. Ελατήριο σταθεράς K τοποθετείται κατακόρυφα με το πάνω άκρο του στερεωμένο σε ακλόνητο σημείο. Ένα σώμα μάζας M=1 kg δένεται στο κάτω άκρο του ελατηρίου και η επιμήκυνση που προκαλεί
ΕΝΕΡΓΕΙΑ ΚΑΙ ΤΑΛΑΝΤΩΣΗ 1. Ελατήριο σταθεράς K τοποθετείται κατακόρυφα με το πάνω άκρο του στερεωμένο σε ακλόνητο σημείο. Ένα σώμα μάζας M=1 kg δένεται στο κάτω άκρο του ελατηρίου και η επιμήκυνση που προκαλεί
1. Σημειώστε με Σ και Λ για σωστή ή λάθος πρόταση: a. Μηχανική ενέργεια είναι η ενέργεια που έχουν οι μηχανές. b. Η μηχανική ενέργεια μπορεί να είναι
 1. Σημειώστε με Σ και Λ για σωστή ή λάθος πρόταση: a. Μηχανική ενέργεια είναι η ενέργεια που έχουν οι μηχανές. b. Η μηχανική ενέργεια μπορεί να είναι μόνο κινητική ή μόνο δυναμική. c. Η διαφορά κινητικής
1. Σημειώστε με Σ και Λ για σωστή ή λάθος πρόταση: a. Μηχανική ενέργεια είναι η ενέργεια που έχουν οι μηχανές. b. Η μηχανική ενέργεια μπορεί να είναι μόνο κινητική ή μόνο δυναμική. c. Η διαφορά κινητικής
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2007 ΓΙΑ ΤΑ ΑΝΩΤΕΡΑ ΚΑΙ ΑΝΩΤΑΤΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΙΔΡΥΜΑΤΑ Μάθημα: ΦΥΣΙΚΗ Ηµεροµηνία και
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2007 ΓΙΑ ΤΑ ΑΝΩΤΕΡΑ ΚΑΙ ΑΝΩΤΑΤΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΙΔΡΥΜΑΤΑ Μάθημα: ΦΥΣΙΚΗ Ηµεροµηνία και
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ.
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Ε.
 .. Μηχανικές. Ομάδα Ε...8. Δυο ΑΑΤ και μία Ταλάντωση. Ένα σώμα μάζας kg ηρεμεί σε λείο κεκλιμένο επίπεδο κλίσεως θ=30, δεμένο στο άκρο ελατηρίου σταθεράς k =40Ν/m, ενώ εφάπτεται στο ε- λεύθερο άκρο ενός
.. Μηχανικές. Ομάδα Ε...8. Δυο ΑΑΤ και μία Ταλάντωση. Ένα σώμα μάζας kg ηρεμεί σε λείο κεκλιμένο επίπεδο κλίσεως θ=30, δεμένο στο άκρο ελατηρίου σταθεράς k =40Ν/m, ενώ εφάπτεται στο ε- λεύθερο άκρο ενός
Επαναληπτικό Διαγώνισμα Φυσικής Προσανατολισμού Γ Λυκείου ~~ Διάρκεια: 3 ώρες ~~
 Επαναληπτικό Διαγώνισμα Φυσικής Προσανατολισμού Γ Λυκείου ~~ Διάρκεια: 3 ώρες ~~ Θέμα Α 1. Σε χορδή έχει δημιουργηθεί στάσιμο κύμα. Δύο σημεία Α και Β που δεν είναι δεσμοί απέχουν μεταξύ τους απόσταση
Επαναληπτικό Διαγώνισμα Φυσικής Προσανατολισμού Γ Λυκείου ~~ Διάρκεια: 3 ώρες ~~ Θέμα Α 1. Σε χορδή έχει δημιουργηθεί στάσιμο κύμα. Δύο σημεία Α και Β που δεν είναι δεσμοί απέχουν μεταξύ τους απόσταση
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ
 ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 27 η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 16 Δεκεμβρίου, 2012 Απενεργοποιήστε τα κινητά σας τηλέφωνα!!! Παρακαλώ διαβάστε πρώτα τα πιο κάτω, πριν απαντήσετε
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 27 η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 16 Δεκεμβρίου, 2012 Απενεργοποιήστε τα κινητά σας τηλέφωνα!!! Παρακαλώ διαβάστε πρώτα τα πιο κάτω, πριν απαντήσετε
Εργαστηριακή Άσκηση 4 Προσδιορισμός του μέτρου στρέψης υλικού με τη μέθοδο του στροφικού εκκρεμούς.
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Όνομα : Κάραλης Νικόλας Α/Μ: 09104042 Εργαστηριακή Άσκηση 4 Προσδιορισμός του μέτρου στρέψης υλικού με τη μέθοδο του στροφικού
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Όνομα : Κάραλης Νικόλας Α/Μ: 09104042 Εργαστηριακή Άσκηση 4 Προσδιορισμός του μέτρου στρέψης υλικού με τη μέθοδο του στροφικού
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΣΕΠΤΕΜΒΡΙΟΣ 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΣΕΠΤΕΜΒΡΙΟΣ 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 ΘΕΜΑ 1 Ο : Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΣΕΠΤΕΜΒΡΙΟΣ 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 ΘΕΜΑ 1 Ο : Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας
2 ο Διαγώνισμα Γ Λυκείου
 ο Διαγώνισμα Γ Λυκείου 03-09-08 Διάρκεια Εξέτασης 3 ώρες Ονοματεπώνυμο. Αξιολόγηση : Θέμα Α Στις ερωτήσεις Α ως και Α4 επιλέξτε την σωστή απάντηση: Α. Όταν ένα κινούμενο σώμα συγκρουστεί κεντρικά και ελαστικά
ο Διαγώνισμα Γ Λυκείου 03-09-08 Διάρκεια Εξέτασης 3 ώρες Ονοματεπώνυμο. Αξιολόγηση : Θέμα Α Στις ερωτήσεις Α ως και Α4 επιλέξτε την σωστή απάντηση: Α. Όταν ένα κινούμενο σώμα συγκρουστεί κεντρικά και ελαστικά
Υπολογισμός της σταθεράς του ελατηρίου
 ΑΣΚΗΣΗ 5 Υπολογισμός της σταθεράς του ελατηρίου Σκοπός είναι ο υπολογισμός της σταθεράς k ενός ελατηρίου. Θα γίνει με δύο τρόπους: Από το νόμο του Hooke F = k x, βρίσκοντας την κλίση μιας πειραματικής
ΑΣΚΗΣΗ 5 Υπολογισμός της σταθεράς του ελατηρίου Σκοπός είναι ο υπολογισμός της σταθεράς k ενός ελατηρίου. Θα γίνει με δύο τρόπους: Από το νόμο του Hooke F = k x, βρίσκοντας την κλίση μιας πειραματικής
Κρούσεις. Ομάδα Δ. Κρούσεις Μια κρούση και οι τριβές Κρούση σφαίρας με άλλη ακίνητη.
 . Ομάδα Δ. 4.1.41. Μια κρούση και οι τριβές. Σε οριζόντιο επίπεδο ηρεμούν δυο σώματα Α και Β με μάζες m=1kg και Μ=3kg αντίστοιχα, τα οποία απέχουν απόσταση d=4,75m. Το Β είναι δεμένο στο άκρο ιδανικού
. Ομάδα Δ. 4.1.41. Μια κρούση και οι τριβές. Σε οριζόντιο επίπεδο ηρεμούν δυο σώματα Α και Β με μάζες m=1kg και Μ=3kg αντίστοιχα, τα οποία απέχουν απόσταση d=4,75m. Το Β είναι δεμένο στο άκρο ιδανικού
ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ ΠΡΟΣΠΑΘΕΙΑ ΣΑΣ ΚΙ 2014
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Αντικείμενο: Ταλαντώσεις Χρόνος Εξέτασης: 3 ώρες Θέμα 1ο Στις παρακάτω ερωτήσεις 1-5 να γράψετε τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Αντικείμενο: Ταλαντώσεις Χρόνος Εξέτασης: 3 ώρες Θέμα 1ο Στις παρακάτω ερωτήσεις 1-5 να γράψετε τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
Ημερομηνία: Παρασκευή 27 Οκτωβρίου 2017 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΑΠΟ /0/07 ΕΩΣ //07 η ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Παρασκευή 7 Οκτωβρίου 07 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις
ΑΠΟ /0/07 ΕΩΣ //07 η ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Παρασκευή 7 Οκτωβρίου 07 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24 Εκφώνηση άσκησης 6. Ένα σώμα, μάζας m, εκτελεί απλή αρμονική ταλάντωση έχοντας ολική ενέργεια Ε. Χωρίς να αλλάξουμε τα φυσικά χαρακτηριστικά του συστήματος, προσφέρουμε στο σώμα
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24 Εκφώνηση άσκησης 6. Ένα σώμα, μάζας m, εκτελεί απλή αρμονική ταλάντωση έχοντας ολική ενέργεια Ε. Χωρίς να αλλάξουμε τα φυσικά χαρακτηριστικά του συστήματος, προσφέρουμε στο σώμα
Γραπτές προαγωγικές εξετάσεις, περιόδου Μαΐου-Ιουνίου στη ΦΥΣΙΚΗ
 Γραπτές προαγωγικές εξετάσεις, περιόδου Μαΐου-Ιουνίου στη ΦΥΣΙΚΗ ΘΕΜΑ 1 ο Ποιες λέξεις συμπληρώνουν σωστά τις παρακάτω προτάσεις: Α. Όταν ένα σώμα ασκεί δύναμη σ ένα άλλο σώμα (δράση), τότε και το δεύτερο
Γραπτές προαγωγικές εξετάσεις, περιόδου Μαΐου-Ιουνίου στη ΦΥΣΙΚΗ ΘΕΜΑ 1 ο Ποιες λέξεις συμπληρώνουν σωστά τις παρακάτω προτάσεις: Α. Όταν ένα σώμα ασκεί δύναμη σ ένα άλλο σώμα (δράση), τότε και το δεύτερο
1. Ένα σώμα A μάζας, κινούμενο με ταχύτητα πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική κατεύθυνση του άξονα x Ox, συγκρούεται με ακίνητο σώμα Β.
 ΚΡΟΥΣΕΙΣ ΕΠΑΝΑΛΗΨΗ 1. Ένα σώμα A μάζας, κινούμενο με ταχύτητα πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική κατεύθυνση του άξονα x Ox, συγκρούεται με ακίνητο σώμα Β. Α) Αν η κρούση είναι μετωπική και ελαστική
ΚΡΟΥΣΕΙΣ ΕΠΑΝΑΛΗΨΗ 1. Ένα σώμα A μάζας, κινούμενο με ταχύτητα πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική κατεύθυνση του άξονα x Ox, συγκρούεται με ακίνητο σώμα Β. Α) Αν η κρούση είναι μετωπική και ελαστική
Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 Μάθημα/Τάξη: ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Κεφάλαιο: ΤΑΛΑΝΤΩΣΕΙΣ - ΚΡΟΥΣΕΙΣ Ονοματεπώνυμο Μαθητή: Ημερομηνία: Επιδιωκόμενος Στόχος: 70/100 Θέμα A Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης
Μάθημα/Τάξη: ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Κεφάλαιο: ΤΑΛΑΝΤΩΣΕΙΣ - ΚΡΟΥΣΕΙΣ Ονοματεπώνυμο Μαθητή: Ημερομηνία: Επιδιωκόμενος Στόχος: 70/100 Θέμα A Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης
Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις
 Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις ~ Διάρκεια: 3 ώρες ~ Θέμα Α Α1. Η ορμή συστήματος δύο σωμάτων που συγκρούονται διατηρείται: α. Μόνο στην πλάγια κρούση. β. Μόνο στην έκκεντρη
Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις ~ Διάρκεια: 3 ώρες ~ Θέμα Α Α1. Η ορμή συστήματος δύο σωμάτων που συγκρούονται διατηρείται: α. Μόνο στην πλάγια κρούση. β. Μόνο στην έκκεντρη
ΚΕΦΑΛΑΙΟ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ
 55 ΚΕΦΑΛΑΙΟ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ Α. ΠΡΟΣΘΕΣΗ ΔΥΝΑΜΕΩΝ ΝΟΜΟΣ ΤΟΥ HOOKE 1. Να σχεδιάσετε δύο αντίρροπες δυνάμεις F 1=5N και F 2=15N με κλίμακα 1cm/2,5N και να βρείτε την συνισταμένη τους. (Απ.: 10
55 ΚΕΦΑΛΑΙΟ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ Α. ΠΡΟΣΘΕΣΗ ΔΥΝΑΜΕΩΝ ΝΟΜΟΣ ΤΟΥ HOOKE 1. Να σχεδιάσετε δύο αντίρροπες δυνάμεις F 1=5N και F 2=15N με κλίμακα 1cm/2,5N και να βρείτε την συνισταμένη τους. (Απ.: 10
ΕΡΓΑΣΙΑ ΣΤΟ ΠΡΩΤΟ ΚΕΦΑΛΑΙΟ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ.
 ΕΡΓΑΣΙΑ ΣΤΟ ΠΡΩΤΟ ΚΕΦΑΛΑΙΟ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ. ΕΡΩΤΗΣΗ 1 Στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 400 N/m είναι κρεμασμένο σώμα μάζας m = 1 kg. Το σύστημα ελατήριο-σώμα εξαναγκάζεται
ΕΡΓΑΣΙΑ ΣΤΟ ΠΡΩΤΟ ΚΕΦΑΛΑΙΟ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ. ΕΡΩΤΗΣΗ 1 Στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 400 N/m είναι κρεμασμένο σώμα μάζας m = 1 kg. Το σύστημα ελατήριο-σώμα εξαναγκάζεται
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 24/09/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 017-018 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΟΠ / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 4/09/017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 017-018 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΟΠ / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 4/09/017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
ΑΣΚΗΣΗ 1: ΜΕΤΡΗΣΕΙΣ ΚΑΙ ΥΠΟΛΟΓΙΣΜΟΙ ΒΑΣΙΚΩΝ ΜΕΓΕΘΩΝ ΤΗΣ ΜΗΧΑΝΙΚΗΣ
 ΑΣΚΗΣΗ 1: ΜΕΤΡΗΣΕΙΣ ΚΑΙ ΥΠΟΛΟΓΙΣΜΟΙ ΒΑΣΙΚΩΝ ΜΕΓΕΘΩΝ ΤΗΣ ΜΗΧΑΝΙΚΗΣ (A) ΜΕΤΡΗΣΗ ΠΥΚΝΟΤΗΤΑΣ ΣΤΕΡΕΟΥ (B) ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΗΣ ΕΠΙΤΑΧΥΝΣΗΣ ΤΗΣ ΒΑΡΥΤΗΤΑΣ (Γ) ΜΕΤΡΗΣΗ ΜΕΓΕΘΩΝ ΣΕ ΠΕΡΙΣΤΡΟΦΗ 1 Σκοπός Στην άσκηση αυτή
ΑΣΚΗΣΗ 1: ΜΕΤΡΗΣΕΙΣ ΚΑΙ ΥΠΟΛΟΓΙΣΜΟΙ ΒΑΣΙΚΩΝ ΜΕΓΕΘΩΝ ΤΗΣ ΜΗΧΑΝΙΚΗΣ (A) ΜΕΤΡΗΣΗ ΠΥΚΝΟΤΗΤΑΣ ΣΤΕΡΕΟΥ (B) ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΗΣ ΕΠΙΤΑΧΥΝΣΗΣ ΤΗΣ ΒΑΡΥΤΗΤΑΣ (Γ) ΜΕΤΡΗΣΗ ΜΕΓΕΘΩΝ ΣΕ ΠΕΡΙΣΤΡΟΦΗ 1 Σκοπός Στην άσκηση αυτή
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΥΓΟΥΣΤΟΥ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 5
 ΑΡΧΗ ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Ο : ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΥΓΟΥΣΤΟΥ 08 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 5 Στις παρακάτω ερωτήσεις έως 4 να γράψετε στο τετράδιό σας τον
ΑΡΧΗ ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Ο : ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΥΓΟΥΣΤΟΥ 08 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 5 Στις παρακάτω ερωτήσεις έως 4 να γράψετε στο τετράδιό σας τον
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2011
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2011 Μάθημα: ΦΥΣΙΚΗ 4ωρο Τ.Σ. Ημερομηνία και ώρα εξέτασης: Πέμπτη, 2 Ιουνίου 2011 07:30
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2011 Μάθημα: ΦΥΣΙΚΗ 4ωρο Τ.Σ. Ημερομηνία και ώρα εξέτασης: Πέμπτη, 2 Ιουνίου 2011 07:30
ΚΕΦΑΛΑΙΟ 1ο: ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ.
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ. β) Πόσο είναι το μέτρο της δύναμης που δέχεται η ράβδος από την άρθρωση
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση 1. (Ισορροπία στερεού σώματος) Ομογενής ράβδος ΑΒ μήκους L=4m και βάρους w=100n ισορροπεί οριζόντια στηριζόμενη σε κατακόρυφο τοίχο με άρθρωση και στο σημείο της Λ σε υποστήριγμα
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Άσκηση 1. (Ισορροπία στερεού σώματος) Ομογενής ράβδος ΑΒ μήκους L=4m και βάρους w=100n ισορροπεί οριζόντια στηριζόμενη σε κατακόρυφο τοίχο με άρθρωση και στο σημείο της Λ σε υποστήριγμα
ΜΕΛΕΤΗ ΤΗΣ ΚΙΝΗΣΗΣ ΡΑΒΔΟΥ ΓΥΡΩ ΑΠΟ ΣΤΑΘΕΡΟ ΑΞΟΝΑ ΜΕΤΡΗΣΗ ΤΗΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΤΗΣ ΡΑΒΔΟΥ
 ΜΕΛΕΤΗ ΤΗΣ ΚΙΝΗΣΗΣ ΡΑΒΔΟΥ ΓΥΡΩ ΑΠΟ ΣΤΑΘΕΡΟ ΑΞΟΝΑ ΜΕΤΡΗΣΗ ΤΗΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΤΗΣ ΡΑΒΔΟΥ Συνοπτική περιγραφή Μελετάμε την κίνηση μιας ράβδου που μπορεί να περιστρέφεται γύρω από σταθερό οριζόντιο άξονα,
ΜΕΛΕΤΗ ΤΗΣ ΚΙΝΗΣΗΣ ΡΑΒΔΟΥ ΓΥΡΩ ΑΠΟ ΣΤΑΘΕΡΟ ΑΞΟΝΑ ΜΕΤΡΗΣΗ ΤΗΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΤΗΣ ΡΑΒΔΟΥ Συνοπτική περιγραφή Μελετάμε την κίνηση μιας ράβδου που μπορεί να περιστρέφεται γύρω από σταθερό οριζόντιο άξονα,
ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ στις αμείωτες μηχανικές ΤΑΛΑΝΤΩΣΕΙΣ- ΚΡΟΥΣΕΙΣ (1) ΟΝΟΜΑΤΕΠΩΝΥΜΟ
 ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ στις αμείωτες μηχανικές ΤΑΛΑΝΤΩΣΕΙΣ- ΚΡΟΥΣΕΙΣ (1) ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΘΕΜΑ Α Α1.Ένα σώμα μάζας m είναι δεμένο και ισορροπεί στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k 1 του
ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ στις αμείωτες μηχανικές ΤΑΛΑΝΤΩΣΕΙΣ- ΚΡΟΥΣΕΙΣ (1) ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΘΕΜΑ Α Α1.Ένα σώμα μάζας m είναι δεμένο και ισορροπεί στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k 1 του
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) 23 ΜΑΪOY 2016 ΕΚΦΩΝΗΣΕΙΣ
 ΘΕΜΑ Α ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) 3 ΜΑΪOY 016 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και, δίπλα, το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει
ΘΕΜΑ Α ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) 3 ΜΑΪOY 016 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και, δίπλα, το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει
Μεταβολές της Δυναμικής Ενέργειας στην κατακόρυφη κίνηση σώματος εξαρτημένου από ελατήριο. Με τη βοήθεια λογισμικού LoggerProGR
 Μεταβολές της Δυναμικής Ενέργειας στην κατακόρυφη κίνηση σώματος εξαρτημένου από ελατήριο. Με τη βοήθεια λογισμικού LoggerProGR τόχοι Οι μαθητές να υπολογίζουν το έργο δύναμης που το μέτρο της δεν μένει
Μεταβολές της Δυναμικής Ενέργειας στην κατακόρυφη κίνηση σώματος εξαρτημένου από ελατήριο. Με τη βοήθεια λογισμικού LoggerProGR τόχοι Οι μαθητές να υπολογίζουν το έργο δύναμης που το μέτρο της δεν μένει
Σάββατο 12 Νοεμβρίου Απλή Αρμονική Ταλάντωση - Κρούσεις. Σύνολο Σελίδων: Επτά (7) - Διάρκεια Εξέτασης: 3 ώρες. Θέμα Α.
 Γ Τάξης Γενικού Λυκείου Σάββατο 1 Νοεμβρίου 016 Απλή Αρμονική Ταλάντωση - Κρούσεις Σύνολο Σελίδων: Επτά (7) - Διάρκεια Εξέτασης: 3 ώρες Ονοματεπώνυμο: Θέμα Α. Στις ημιτελείς προτάσεις Α.1 Α.4 να γράψετε
Γ Τάξης Γενικού Λυκείου Σάββατο 1 Νοεμβρίου 016 Απλή Αρμονική Ταλάντωση - Κρούσεις Σύνολο Σελίδων: Επτά (7) - Διάρκεια Εξέτασης: 3 ώρες Ονοματεπώνυμο: Θέμα Α. Στις ημιτελείς προτάσεις Α.1 Α.4 να γράψετε
Ένωση Ελλήνων Φυσικών ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗΣ 2011 Πανεπιστήμιο Αθηνών Εργαστήριο Φυσικών Επιστημών, Τεχνολογίας, Περιβάλλοντος.
 Θεωρητικό Μέρος A Λυκείου 1 Μαρτίου 011 Θέμα 1 ο Στις ερωτήσεις A, B, και Γ, μια μόνο απάντηση είναι σωστή. Γράψτε στο τετράδιό σας το κεφαλαίο γράμμα της ερώτησης και το μικρό γράμμα της σωστής απάντησης.
Θεωρητικό Μέρος A Λυκείου 1 Μαρτίου 011 Θέμα 1 ο Στις ερωτήσεις A, B, και Γ, μια μόνο απάντηση είναι σωστή. Γράψτε στο τετράδιό σας το κεφαλαίο γράμμα της ερώτησης και το μικρό γράμμα της σωστής απάντησης.
1. Ένα σώμα μάζας είναι στερεωμένο στην άκρη οριζοντίου ιδανικού ελατηρίου, του οποίου το άλλο άκρο είναι ακλόνητα στερεωμένο.
 1. Ένα σώμα μάζας είναι στερεωμένο στην άκρη οριζοντίου ιδανικού ελατηρίου σταθεράς, του οποίου το άλλο άκρο είναι ακλόνητα στερεωμένο. Το σώμα εκτελεί απλή αρμονική ταλάντωση, κατά τη διεύθυνση του άξονα
1. Ένα σώμα μάζας είναι στερεωμένο στην άκρη οριζοντίου ιδανικού ελατηρίου σταθεράς, του οποίου το άλλο άκρο είναι ακλόνητα στερεωμένο. Το σώμα εκτελεί απλή αρμονική ταλάντωση, κατά τη διεύθυνση του άξονα
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 19 Ταλαντώσεις Απλή αρμονική κίνηση ΦΥΣ102 1 Ταλαντώσεις Ελατηρίου Όταν ένα αντικείμενο
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 19 Ταλαντώσεις Απλή αρμονική κίνηση ΦΥΣ102 1 Ταλαντώσεις Ελατηρίου Όταν ένα αντικείμενο
ΕΚΦΕ Τρικάλων. Πειραματική Δοκιμασία στη Φυσική. Τοπικός Μαθητικός Διαγωνισμός. Τρίκαλα, Σάββατο, 8 Δεκεμβρίου 2012
 1 Τοπικός Μαθητικός Διαγωνισμός 11η Ευρωπαϊκή Ολυμπιάδα Επιστημών EUSO 2013 11Η ΕΥΡΩΠΑΪΚΗ ΟΛΥΜΠΙΑΔΑ ΕΠΙΣΤΗΜΩΝ EUSO 2013 ΕΚΦΕ Τρικάλων Πειραματική Δοκιμασία στη Φυσική Τοπικός Μαθητικός Διαγωνισμός Τρίκαλα,
1 Τοπικός Μαθητικός Διαγωνισμός 11η Ευρωπαϊκή Ολυμπιάδα Επιστημών EUSO 2013 11Η ΕΥΡΩΠΑΪΚΗ ΟΛΥΜΠΙΑΔΑ ΕΠΙΣΤΗΜΩΝ EUSO 2013 ΕΚΦΕ Τρικάλων Πειραματική Δοκιμασία στη Φυσική Τοπικός Μαθητικός Διαγωνισμός Τρίκαλα,
