Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων
|
|
|
- Πολύκαρπος Βενιζέλος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Μέθοδος «Διαίρει και Βασίλευε», ταξινόμηση Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών
2
3 641: Γηζαγςγή ζηε Θεςνία θαη Ακάιοζε Αιγμνίζμςκ Υάνεξ Παπαδόπμοιμξ
4 Τιε ημο μαζήμαημξ Βαζηθά ζημηπεία ζπεδίαζεξ & ακάιοζεξ αιγμνίζμςκ Ακάιοζε αιγμνίζμςκ, απμδμηηθόηεηα, αζομπηςηηθόξ ζομβμιηζμόξ οκεζηζμέκμη πνόκμη εθηέιεζεξ θαη βαζηθέξ δμμέξ δεδμμέκςκ πίκαθεξ, ιίζηεξ, ζημίβεξ, μονέξ Γοζηαζέξ ηαίνηαζμα, μνζόηεηα, ζςνόξ θαη μονά πνμηεναηόηεηαξ Ιέζμδμξ «Δηαίνεη θαη Βαζίιεοε» Γθανμμγέξ ζε ηαληκόμεζε ζημηπείςκ Γπίιοζε ακαδνμμηθώκ ζπέζεςκ Γναθήμαηα θαη αιγόνηζμμη γναθεμάηςκ Δηάηνελε γναθεμάηςκ (BFS, DFS) οκεθηηθόηεηα Σμπμιμγηθή δηάηαλε Ιέζμδμη «Απιεζηείαξ» θαη «Δοκαμηθμύ Πνμγναμμαηηζμμύ» Γιάπηζηα ζθειεηηθά δέκδνα (αιγόνηζμμξ Prim, αιγόνηζμμξ Kruskal) οκημμόηενεξ δηαδνμμέξ (αιγόνηζμμξ Dijkstra, Ρμή δηθηύμο) Υνμκμπνμγναμμαηηζμόξ Γπηιεγμέκα ζέμαηα Τπμιμγηζηηθή πμιοπιμθόηεηα, NP-πιενόηεηα 2
5 Ε Ιέζμδμξ «Δηαίνεη & Βαζίιεοε» (Divide & Conquer)
6 Δηαίνεη θαη βαζίιεοε H μέζμδμξ «Δηαίνεη θαη βαζίιεοε» Δηαζπάμε ηεκ είζμδμ ζε ανθεηά ημήμαηα μηθνόηενμο μεγέζμοξ. Γπηιύμομε ημ πνόβιεμα ζε θάζε ημήμα ακαδνμμηθά. οκδοάδμομε ηηξ επημένμοξ ιύζεηξ ηςκ οπμπνμβιεμάηςκ ζε μηα ζοκμιηθή ιύζε γηα ημ ανπηθό πνόβιεμα. Γθανμμγή: Σαληκόμεζε n ζημηπείςκ Δηάζπαζε ημο πνμβιήμαημξ μεγέζμοξ n ζε δομ ίζα ημήμαηα μεγέζμοξ ½n. Ακαδνμμηθή επίιοζε ηςκ δύμ ημεμάηςκ. οκδοαζμόξ ηςκ δύμ ιύζεςκ ζε μηα ζοκμιηθή ιύζε ζε γναμμηθό πνόκμ. Απμηέιεζμα: Απιμσθή μέζμδμξ (insertion sort): O(n 2 ) Δηαίνεη θαη βαζίιεοε (mergesort): O(n log n) Divide et impera. Veni, vidi, vici. - Julius Caesar Πνμζθηιήξ πμιεμηθή ηαθηηθή: δηαίνεζε ημο ακηίπαιμο ζηναηεύμαημξ ζε δύμ μηζά θαη επίζεζε ζημ έκα μηζό με μιόθιενμ ημκ ζηναηό ημο. 4
7 O αιγόνηζμμξ Mergesort
8 Σαληκόμεζε Δεδμμέκςκ n ζημηπείςκ, δηέηαλέ ηα ζε αύλμοζα ηάλε. Γθανμμγέξ. Σαληκόμεζε μηαξ ιίζηαξ μκμμάηςκ. Ονγάκςζε ηναγμοδηώκ ζημ θηκεηό. Πανμοζίαζε απμηειεζμάηςκ ημο Google PageRank. Θίζηα (RSS) εηδήζεςκ ζε ακηίζηνμθε πνμκμιμγηθή ζεηνά. Πνμθακήξ εθανμμγέξ ηαληκόμεζεξ Γύνεζε ημο μέζμο. Γύνεζε ημο πημ θμκηηκμύ δεύγμοξ. Δοαδηθή ακαδήηεζε. Πνμζδημνηζμόξ ζηαηηζηηθώκ αθναίςκ ηημώκ. Γύνεζε δηπιόηοπςκ ζε μηα ιίζηα μκμμάηςκ. Πνμβιήμαηα πμο ιύκμκηαη πημ εύθμια μεηά ηεκ ηαληκόμεζε ομπίεζε δεδμμέκςκ. Γναθηθά οπμιμγηζηώκ. Τπμιμγηζηηθή βημιμγία. Υνμκμπνμγναμμαηηζμόξ δηαζηεμάηςκ. Ιε-πνμθακήξ εθανμμγέξ Πνμηάζεηξ βηβιίςκ από Amazon. Γληζμννόπεζε θόνημο ενγαζίαξ ζε έκακ πανάιιειμ οπμιμγηζηή.... 6
9 Ο αιγόνηζμμξ Mergesort Mergesort. Δηαίνεζε ημκ πίκαθα ζηε μέζε. Ακαδνμμηθά ηαληκόμεζε ημ θάζε μηζό ημήμα. ογπώκεοζε ηα δομ μηζά (πμο είκαη πιέμκ ηαληκμμεμέκα) ζε έκακ πιήνε ηαληκμμεμέκμ πίκαθα Jon von Neumann (1945) A L G O R I T H M S A L G O R I T H M S δηαίνεζε O(1) A G L O R H I M S T ηαληκόμεζε 2T(n/2) A G H I L M O R S T ζοκδύαζε O(n) A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 7
10 ογπώκεοζε (merging) ογπώκεοζε. οκδύαζε δομ ήδε ηαληκμμεμέκεξ ιίζηεξ ζε μηα πιήνε ηαληκμμεμέκε ιίζηα. Πώξ ζογπςκεύμομε απμδμηηθά; Γναμμηθόξ ανηζμόξ ζογθνίζεςκ Υνεζημμπμημύμε πνμζςνηκό πίκαθα (μεγέζμοξ n). A G L O R H I M S T A G H I L Πνόθιεζε γηα όζμοξ εκδηαθένμκηαη. Γπη-ηόπμο ζογπώκεοζε [Kronrud, 1969] Υνεζημμπμηώκηαξ μόκμ έκα ζηαζενό μέγεζμξ επηπιέμκ μκήμεξ 8
11 ογπώκεοζε ογπώκεοζε Παναθμιμύζεζε ημ ειάπηζημ ζημηπείμ ζε θάζε ηαληκμμεμέκμ μηζό Γηζήγαγε ημ ειάπηζημ από ηα δύμ ζημηπεία ζε έκα βμεζεηηθό πίκαθα Γπακέιαβε μέπνη κα ηειεηώζμοκ ηα ζημηπεία ειάπηζημ ειάπηζημ A G L O R H I M S T A Βμεζεηηθόξ πίκαθαξ A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 9
12 ογπώκεοζε ογπώκεοζε Παναθμιμύζεζε ημ ειάπηζημ ζημηπείμ ζε θάζε ηαληκμμεμέκμ μηζό Γηζήγαγε ημ ειάπηζημ από ηα δύμ ζημηπεία ζε έκα βμεζεηηθό πίκαθα Γπακέιαβε μέπνη κα ηειεηώζμοκ ηα ζημηπεία ειάπηζημ ειάπηζημ A G L O R H I M S T A G Βμεζεηηθόξ πίκαθαξ A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 10
13 ογπώκεοζε ογπώκεοζε Παναθμιμύζεζε ημ ειάπηζημ ζημηπείμ ζε θάζε ηαληκμμεμέκμ μηζό Γηζήγαγε ημ ειάπηζημ από ηα δύμ ζημηπεία ζε έκα βμεζεηηθό πίκαθα Γπακέιαβε μέπνη κα ηειεηώζμοκ ηα ζημηπεία ειάπηζημ ειάπηζημ A G L O R H I M S T A G H Βμεζεηηθόξ πίκαθαξ A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 11
14 ογπώκεοζε ογπώκεοζε Παναθμιμύζεζε ημ ειάπηζημ ζημηπείμ ζε θάζε ηαληκμμεμέκμ μηζό Γηζήγαγε ημ ειάπηζημ από ηα δύμ ζημηπεία ζε έκα βμεζεηηθό πίκαθα Γπακέιαβε μέπνη κα ηειεηώζμοκ ηα ζημηπεία ειάπηζημ ειάπηζημ A G L O R H I M S T A G H I Βμεζεηηθόξ πίκαθαξ A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 12
15 ογπώκεοζε ογπώκεοζε Παναθμιμύζεζε ημ ειάπηζημ ζημηπείμ ζε θάζε ηαληκμμεμέκμ μηζό Γηζήγαγε ημ ειάπηζημ από ηα δύμ ζημηπεία ζε έκα βμεζεηηθό πίκαθα Γπακέιαβε μέπνη κα ηειεηώζμοκ ηα ζημηπεία ειάπηζημ ειάπηζημ A G L O R H I M S T A G H I L Βμεζεηηθόξ πίκαθαξ A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 13
16 ογπώκεοζε ογπώκεοζε Παναθμιμύζεζε ημ ειάπηζημ ζημηπείμ ζε θάζε ηαληκμμεμέκμ μηζό Γηζήγαγε ημ ειάπηζημ από ηα δύμ ζημηπεία ζε έκα βμεζεηηθό πίκαθα Γπακέιαβε μέπνη κα ηειεηώζμοκ ηα ζημηπεία ειάπηζημ ειάπηζημ A G L O R H I M S T A G H I L M Βμεζεηηθόξ πίκαθαξ A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 14
17 ογπώκεοζε ογπώκεοζε Παναθμιμύζεζε ημ ειάπηζημ ζημηπείμ ζε θάζε ηαληκμμεμέκμ μηζό Γηζήγαγε ημ ειάπηζημ από ηα δύμ ζημηπεία ζε έκα βμεζεηηθό πίκαθα Γπακέιαβε μέπνη κα ηειεηώζμοκ ηα ζημηπεία ειάπηζημ ειάπηζημ A G L O R H I M S T A G H I L M O Βμεζεηηθόξ πίκαθαξ A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 15
18 ογπώκεοζε ογπώκεοζε Παναθμιμύζεζε ημ ειάπηζημ ζημηπείμ ζε θάζε ηαληκμμεμέκμ μηζό Γηζήγαγε ημ ειάπηζημ από ηα δύμ ζημηπεία ζε έκα βμεζεηηθό πίκαθα Γπακέιαβε μέπνη κα ηειεηώζμοκ ηα ζημηπεία ειάπηζημ ειάπηζημ A G L O R H I M S T A G H I L M O R Βμεζεηηθόξ πίκαθαξ A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 16
19 ογπώκεοζε ογπώκεοζε Παναθμιμύζεζε ημ ειάπηζημ ζημηπείμ ζε θάζε ηαληκμμεμέκμ μηζό Γηζήγαγε ημ ειάπηζημ από ηα δύμ ζημηπεία ζε έκα βμεζεηηθό πίκαθα Γπακέιαβε μέπνη κα ηειεηώζμοκ ηα ζημηπεία πνώημ μηζό ελακηιήζεθε ειάπηζημ A G L O R H I M S T A G H I L M O R S Βμεζεηηθόξ πίκαθαξ A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 17
20 ογπώκεοζε ογπώκεοζε Παναθμιμύζεζε ημ ειάπηζημ ζημηπείμ ζε θάζε ηαληκμμεμέκμ μηζό Γηζήγαγε ημ ειάπηζημ από ηα δύμ ζημηπεία ζε έκα βμεζεηηθό πίκαθα Γπακέιαβε μέπνη κα ηειεηώζμοκ ηα ζημηπεία πνώημ μηζό ελακηιήζεθε ειάπηζημ A G L O R H I M S T A G H I L M O R S T Βμεζεηηθόξ πίκαθαξ A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 18
21 ογπώκεοζε ογπώκεοζε Παναθμιμύζεζε ημ ειάπηζημ ζημηπείμ ζε θάζε ηαληκμμεμέκμ μηζό Γηζήγαγε ημ ειάπηζημ από ηα δύμ ζημηπεία ζε έκα βμεζεηηθό πίκαθα Γπακέιαβε μέπνη κα ηειεηώζμοκ ηα ζημηπεία πνώημ μηζό ελακηιήζεθε δεύηενμ μηζό ελακηιήζεθε A G L O R H I M S T A G H I L M O R S T Βμεζεηηθόξ πίκαθαξ A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 19
22 Γναμμηθόξ πνόκμξ: Ο(n) ογπώκεοζε. ογπςκεύζηε δύμ ηαληκμμεμέκεξ ιίζηεξ A = a 1,a 2,,a n θαη B = b 1,b 2,,b n ζε μηα κέα ηαληκμμεμέκε ιίζηα. i = 1, j = 1 while (οι δςο λίζηερ δεν είναι κένερ) { if (a i b j ) πποζάπηηζε a i ζηη λίζηα εξόδος και αύξηζε i else(a i πποζάπηηζε b j ζηη λίζηα εξόδος και αύξηζε j } πποζάπηηζε ηα ςπόλοιπα ζηοισεία ηηρ μη-κενήρ λίζηαρ ζηην έξοδο Ζζπονηζμόξ. ογπώκεοζε δύμ ιηζηώκ μεγέζμοξ n παίνκεη O(n) πνόκμ. Απόδ. Ιεηά από θάζε ζύγθνηζε, ημ μέγεζμξ ηεξ ελόδμο αολάκεηαη θαηά 1. Υνεώκμομε ημ θόζημξ ζημ ζημηπείμ πμο πνμζζέημομε ζηεκ έλμδμ. 20
23 Ο αιγόνηζμμξ Mergesort Ακάιοζε Υνμκηθή Πμιοπιμθόηεηαξ Mergesort(A,l,r) { if A έσει μόνο ένα ζηοισείο return ηο μοναδικό ζηοισείο q = (l+n)/2 // διαίπεζε ΑL = Mergesort(A,l,q) ΑR = Mergesort(A,q+1,r) B = Merge(AL,AR) // ζςνδύαζε } Jon von Neumann (1945) A L G O R I T H M S A L G O R I T H M S δηαίνεζε O(1) A G L O R H I M S T ηαληκόμεζε 2T(n/2) A G H I L M O R S T ζοκδύαζε O(n) 21
24 Ακάιοζε Υνμκηθή Πμιοπιμθόηεηαξ Ακαδνμμηθή πέζε Ονηζμόξ T(n) = Υ.Π. ημο mergesort ζε είζμδμ μεγέζμοξ n. Ακαδνμμηθή πέζε Mergesort. Σ(n) T( n/2 ) + T( n/2 ) + cn, c > 0 ζηαζενά ή απιμύζηενα: Σ(n) 2 T(n/2) + cn, γηα n 2, c > 0 ζηαζενά Σ(n) = 0, γηα n 1 Θύζε. T(n) = O(n log 2 n). 22
25 Σνόπμη Γπίιοζεξ Ακαδνμμηθώκ πέζεςκ Ιέζμδμη Γπίιοζεξ: Ιέζμδμξ εθδίπιςζεξ ακαδνμμήξ (δέκηνμ ακαδνμμήξ) Γπακαιεπηηθή μέζμδμξ ακάπηολε δηαδνμμήξ Ιέζμδμξ ακηηθαηάζηαζεξ ζςζηήξ πνόβιερεξ Ιέζμδμξ αιιαγήξ μεηαβιεηώκ Βαζηθό Θεώνεμα Ακαδνμμώκ (Ιaster Theorem) Γναμμηθέξ ακαδνμμηθέξ ζπέζεηξ Υνήζημμ θαη ζοκμπηηθό οιηθό με πμιιά παναδείγμαηα (~16 ζειίδεξ) οπάνπεη ζημ ecourse!! 23
26 Ιέζμδμξ εθδίπιςζεξ ακαδνμμήξ (δέκηνμ ακαδνμμήξ) Σ(n) 2 T(n/2) + cn, γηα n 2, c > 0 ζηαζενά Σ(n) = 0, γηα n 1 T(n) T(n/2) T(n/2) T(n/4) T(n/4) T(n/4) T(n/4) log 2 n T(n / 2 k ) T(2) T(2) T(2) T(2) T(2) T(2) T(2) T(2) 24
27 Ιέζμδμξ εθδίπιςζεξ ακαδνμμήξ (δέκηνμ ακαδνμμήξ) Σ(n) 2 T(n/2) + cn, γηα n 2, c > 0 ζηαζενά Σ(n) = 0, γηα n 1 cn T(n/2) T(n/2) T(n/4) T(n/4) T(n/4) T(n/4) log 2 n T(n / 2 k ) T(2) T(2) T(2) T(2) T(2) T(2) T(2) T(2) 25
28 Ιέζμδμξ εθδίπιςζεξ ακαδνμμήξ (δέκηνμ ακαδνμμήξ) Σ(n) 2 T(n/2) + cn, γηα n 2, c > 0 ζηαζενά Σ(n) = 0, γηα n 1 cn cn/2 cn/2 T(n/4) T(n/4) T(n/4) T(n/4) log 2 n T(n / 2 k ) T(2) T(2) T(2) T(2) T(2) T(2) T(2) T(2) 26
29 Ιέζμδμξ εθδίπιςζεξ ακαδνμμήξ (δέκηνμ ακαδνμμήξ) Σ(n) 2 T(n/2) + cn, γηα n 2, c > 0 ζηαζενά Σ(n) = 0, γηα n 1 cn cn/2 cn/2 cn/4 cn/4 cn/4 cn/4 log 2 n T(n / 2 k ) T(2) T(2) T(2) T(2) T(2) T(2) T(2) T(2) 27
30 Ιέζμδμξ εθδίπιςζεξ ακαδνμμήξ (δέκηνμ ακαδνμμήξ) Σ(n) 2 T(n/2) + cn, γηα n 2, c > 0 ζηαζενά Σ(n) = 0, γηα n 1 cn cn cn/2 cn/2 2(cn/2) = cn cn/4 cn/4 cn/4 cn/4 log 2 n 4(cn/4) = cn... T(n / 2 k ) 2 k (cn / 2 k ) = cn... 2c 2c 2c 2c 2c 2c 2c 2c n/2 (2c) = cn cn log 2 n 28
31 Ιέζμδμξ εθδίπιςζεξ ακαδνμμήξ (δέκηνμ ακαδνμμήξ) Σ(n) 2 T(n/2) + cn, γηα n 2, c > 0 ζηαζενά Σ(n) = 0, γηα n 1 cn cn cn/2 cn/2 2(cn/2) = cn cn/4 cn/4 cn/4 cn/4 log 2 n 4(cn/4) = cn... T(n / 2 k ) 2 k (cn / 2 k ) = cn... 2c 2c 2c 2c 2c 2c 2c 2c n/2 (2c) = cn Θύζε. T(n) = O(n log n) cn log 2 n 29
32 Ιέζμδμξ ακηηθαηάζηαζεξ ζςζηήξ πνόβιερεξ Σ(n) 2T(n/2) + cn, γηα n 2, c > 0 ζηαζενά Σ(n) = 0, γηα n 1 Πνόβιερε: Σ(n) = O(n logn), δειαδή Σ(n) d n logn, d > 0 ζηαζενά Απόδεηλε: (με επαγςγή ζημ n) Βάζε επαγςγήξ (n=1): Σ(1) = 0 d 1 log1 = 0 Γπαγςγηθή οπόζεζε: T(k) d k logk, γηα θάζε k < n Γπαγςγηθό βήμα: Θα δείλμομε όηη Σ(n) d n logn Σ(n) 2 T(n/2) + c n 2 d (n/2) log(n/2) + c n = d n (log n - log 2) + c n = d n (log n - 1) + c n = d n log n - d n + c n d n log n, γηα θάζε d c 30
33 Ιέζμδμξ ακηηθαηάζηαζεξ ζςζηήξ πνόβιερεξ Σ(n) 2T(n/2) + cn, γηα n 2, c > 0 ζηαζενά Σ(n) = 0, γηα n 1 Πνμζμπή με ημκ πνμζδημνηζμό ηεξ ζηαζενάξ c Πνέπεη κα πνμζδημνηζηεί έηζη ώζηε ε ιύζε Σ(n) d n logn, κα ηζπύεη θαη γηα ηηξ ανπηθέξ ζοκζήθεξ (βάζε επαγςγήξ) Ανπηθή ζοκζήθε Σ(n) = 0 γηα n 1 δεκ πανμοζηάδεη πνόβιεμα, γηαηί Σ(1) = 0 d 1 log1 = 0 γηα θάζε d c > 0 Ακ ε ανπηθή ζοκζήθε ήηακ Σ(n) = 1 γηα n 1 Σ(1) = 1 d 1 log1 = 0 (!!) Δεκ οπάνπεη d πμο κα ηθακμπμηεί ηεκ Σόηε, βιέπμομε ηη γίκεηαη με άιιεξ μηθνέξ ηημέξ ημο n (n=2,3, ) T(2) = 2 + 2c d 2 log2 = 2d, πμο ηζπύεη γηα θάζε d c + 1 Άνα Σ(n) d n logn γηα θάζε n 2 θαη γηα θάζε d c
34 Γπακαιεπηηθή Ιέζμδμξ ακάπηολε ακαδνμμήξ Σ(n) 2T(n/2) + cn, γηα n 2, c > 0 ζηαζενά Σ(n) = 0, γηα n 1 Ακάπηολε ακαδνμμήξ: 32
35 Γπακαιεπηηθή Ιέζμδμξ ακάπηολε ακαδνμμήξ Σ(n) 2T(n/2) + cn, γηα n 2, c > 0 ζηαζενά Σ(n) = 0, γηα n 1 Πμιιαπιαζηάδμομε θάζε ακηζόηεηα με 2 k θαη πνμζζέημομε: 33
36 οκδοαζμόξ δέκδνμο ακαδνμμήξ θαη ζςζηήξ πνόβιερεξ Σ(n) = T(n/3) + T(2n/3) + c n, γηα n 2 Σ(n) = O(1), γηα n 1 Ιέγεζμξ μέγηζημο οπμπνμβιήμαημξ επηπέδμο i: n(2/3) i Ύρμξ h δέκδνμο ακαδνμμήξ : n (2/3) h = 1, δειαδή h = log 3/2 n Πνόβιερε: Σ(n) = O(n log n) 34
37 οκδοαζμόξ δέκδνμο ακαδνμμήξ θαη ζςζηήξ πνόβιερεξ Σ(n) = T(n/3) + T(2n/3) + c n, γηα n 2 Σ(n) = O(1), γηα n 1 Ιέγεζμξ μέγηζημο οπμπνμβιήμαημξ επηπέδμο i: n(2/3) i Ύρμξ h δέκδνμο ακαδνμμήξ : n (2/3) h = 1, δειαδή h = log 3/2 n Πνόβιερε: Σ(n) = O(n log n) Απόδεηλε: (με επαγςγή ζημ n) Σ(n) d n log n, γηα θάπμηα ζηαζενά d > 0 πμο ηζπύεη γηα d c / (log 3 2/3) 35
38 Ιέζμδμξ αιιαγήξ μεηαβιεηώκ Σ(n) = 2 T( n ) + log n, γηα n 2 Σ(n) = O(1), γηα n 1 Θέημομε m = log n, άνα n = 2 m θαη n = 2 m/2 : T(2 m ) = 2 T(2 m/2 ) + m Θέημκηαξ S(m) = T(2 m ) έπμομε, S(m) = 2 S(m/2) + m Πμο γκςνίδμομε όηη S(m) = O(m log m) Σ(n) 2T(n/2) + cn T(n) = O(n log n) Άνα, Σ(n) = T(2m) = S(m) = O(m log m) = O(log n log log n) 36
39 Βαζηθό Θεώνεμα Ακαδνμμώκ (Ιaster Theorem) Έζης: θαη θαη Σόηε, Φαίκεηαη πμιύπιμθμ αιιά ηειηθά είκαη πμιύ απιό. Οη ιύζεηξ πενηγνάθμκηαη από ημκ ηύπμ: 37
40 Βαζηθό Θεώνεμα Ακαδνμμώκ (Ιaster Theorem) Σ(n) = 16 T( n / 8 ) + n 2/3 α = 16, β = 8, γ = 2/3, δ = 0 Γλεηάδμομε: α / β γ = 16 / 8 2/3 > 1 Άνα 1 ε πενίπηςζε: 38
41 Βαζηθό Θεώνεμα Ακαδνμμώκ (Ιaster Theorem) Σ(n) = T( 2n / 3 ) + 1 α = 1, β = 3/2, γ = 0, δ = 0 Γλεηάδμομε: α / β γ = 1 / (3/2) 0 = 1 Άνα 2 ε πενίπηςζε: 39
42 Βαζηθό Θεώνεμα Ακαδνμμώκ (Ιaster Theorem) Σ( n 2 ) = 3T( n 2 / 3 ) + n 40
43 Βαζηθό Θεώνεμα Ακαδνμμώκ (Ιaster Theorem) n 2 = m Σ( n 2 ) = 3T( n 2 / 3 ) + n Σ( m ) = 3T( m / 3 ) + m 41
44 Βαζηθό Θεώνεμα Ακαδνμμώκ (Ιaster Theorem) n 2 = m Σ( n 2 ) = 3T( n 2 / 3 ) + n Σ( m ) = 3T( m / 3 ) + m α = 3, β = 3, γ = 1/2, δ = 0 Γλεηάδμομε: α / β γ = 3 / 3 1/2 = 3 1/2 > 1 Άνα 1 ε πενίπηςζε: 42
45 Γναμμηθέξ Ακαδνμμηθέξ πέζεηξ Ε γναμμηθή ακαδνμμηθή ζπέζε ηάλεξ d έπεη ηεκ μμνθή: Σ(n) = a 1 T(n-1) + a 2 T(n-2) + + a d T(n-d) Πανάδεηγμα: ε Fibonacci αθμιμοζία: Σ(n) = T(n-1) + T(n-2) Σ(1) = 1 Σ(0) = 0 Πενηγναθή ηεξ ιύζεξ: Σ(n) = c x n Πανάδεηγμα: Άνα: cx n = cx n-1 + cx n-2 x 2 x -1 = 0 x = (1 5)/2 T(n) = c 1 [(1+ 5)/2] n + c 2 [(1-5)/2] n Σηξ ζηαζενέξ c 1 θαη c 2 ηηξ θαζμνίδμομε από ηηξ ανπηθέξ ζοκζήθεξ Σ(1) = 1, Σ(0) = 0: Γναμμηθό ζύζηεμα 2 εληζώζεςκ με 2 αγκώζημοξ 43
46 Γναμμηθέξ Ακαδνμμηθέξ πέζεηξ Ε γναμμηθή ακαδνμμηθή ζπέζε ηάλεξ d έπεη ηεκ μμνθή: Σ(n) = a 1 T(n-1) + a 2 T(n-2) + + a d T(n-d) Υαναθηενηζηηθή Γλίζςζε ηάλεξ d: x d = a 1 x d-1 + a 2 x d a d x 0 Θύζε: Πνμθύπηεη από ηηξ νίδεξ ηεξ παναθηενηζηηθήξ ελίζςζεξ. Ακ r νίδα με πμιιαπιόηεηα 1 ηόηε: r n Ακ r νίδα με πμιιαπιόηεηα k ηόηε: r n, nr n, n 2 r n,, n k r n Πανάδεηγμα: T(n) = 2T(n-1) T(n-2), T(0) =0, T(1) =1 X.E.: x 2 2x -1 = 0 με δηπιή νίδα ημ x = 1 T(n) = c 1 (1) n + c 2 n (1) n = c 1 + c 2 n Από ανπηθέξ ζοκζήθεξ: c 1 = 0 θαη c 2 = 1 Σ(n) = n 44
47 Θίγα παναπάκς γηα Σαληκμμήζεηξ Insertion sort Ο(n 2 ) Counting sort Ο(n + n k ) Radix sort Ο(n k) Ηάης θνάγμα Ω(n log n)
48 Αιγόνηζμμη Σαληκόμεζεξ Ιειεηήζαμε ημοξ ελήξ αιγμνίζμμοξ: Mergesort - Ο(nlog n) Heapsort - Ο(nlog n) Θα δμύμε: Insertion sort - Ο(n 2 ) Counting sort - Ο(n + n k ) Radix sort - Ο(n k) Τπάνπμοκ επίζεξ: Bubble sort - Ο(n 2 ) Selection sort - Ο(n 2 ) Quick sort - Θ(n 2 ) (θαιύηενε μέζε πενίπηςζε) Bucket sort - Ο(n), i (0,1] 46
49 Insertion sort Insertion_sort(A,n) { for j = 2 to n ειζαγυγή ηος A[j] ζηον (ήδη ηαξινομημένο) ςποπίνακα Α[1,..,j-1] με ζςνεσόμενερ ανηιμεηαθέζειρ μέσπι ηο ζυζηό ζημείο } A: 1 i j n A[1] < A[2] < < A[j-1] ηαληκμμεμέκμξ οπμπίκαθαξ ζςζηή ζέζε γηα ημ Α[j] 47
50 Insertion sort Insertion_sort(A,n) { for j = 2 to n ειζαγυγή ηος A[j] ζηον (ήδη ηαξινομημένο) ςποπίνακα Α[1,..,j-1] με ζςνεσόμενερ ανηιμεηαθέζειρ μέσπι ηο ζυζηό ζημείο } Πανάδεηγμα: A: 1 i j n A[1] < A[2] < < A[j-1] ηαληκμμεμέκμξ οπμπίκαθαξ ζςζηή ζέζε γηα ημ Α[j] 48
51 Insertion sort Insertion_sort(A,n) { for j = 2 to n ειζαγυγή ηος A[j] ζηον (ήδη ηαξινομημένο) ςποπίνακα Α[1,..,j-1] με ζςνεσόμενερ ανηιμεηαθέζειρ μέσπι ηο ζυζηό ζημείο } Υνόκμξ εθηέιεζεξ: Υεηνόηενε πενίπηςζε: Α[] = [n, n-1, n-2,, 1] 49
52 Counting sort ηόπμξ: γναμμηθή ηαληκόμεζε Έζης μη n αθέναημη ημο πίκαθα Α[] ακήθμοκ ζημ δηάζηεμα [1,,n k ] n k : έκαξ ζεηηθόξ αθέναημξ Υνόκμξ: O(n + n k ), γναμμηθόξ όηακ n k = O(n) Βαζηθή ηδέα: Γηα θάζε ζημηπείμ A[j], θαζμνηζμόξ ημο πιήζμοξ ηςκ ζημηπείςκ πμο είκαη μηθνόηενα από A[j]. Π.π. ακ οπάνπμοκ 17 ζημηπεία < A[j], ηόηε A[j] = 18 ε ζέζε Θα πνεηαζημύμε δομ επηπιέμκ πίκαθεξ: Β[1..n]: απμζήθεοζε ηαληκμμεμέκεξ αθμιμοζίαξ (απμηέιεζμα) C[0..n k ]: πνμζςνηκή θαηαπώνεζε πιενμθμνηώκ 50
53 Counting sort Counting_sort(A,n,n k ) { for j = 1 to n C[A[j]] = C[A[j]] + 1 for i = 1 to n k C[i] = C[i] + C[i-1] for j = n downto 1 B[ C[A[j]] ] = A[j] C[A[j]] = C[A[j]] - 1 } C[i] = # ζηοισεία ίζα με i C[i] = # ζηοισεία < ή ίζα με i Α:
54 Counting sort Counting_sort(A,n,n k ) { for j = 1 to n C[A[j]] = C[A[j]] + 1 for i = 1 to n k C[i] = C[i] + C[i-1] for j = n downto 1 B[ C[A[j]] ] = A[j] C[A[j]] = C[A[j]] - 1 } C[i] = # ζηοισεία ίζα με i C[i] = # ζηοισεία < ή ίζα με i Α: n k = C:
55 Counting sort Counting_sort(A,n,n k ) { for j = 1 to n C[A[j]] = C[A[j]] + 1 for i = 1 to n k C[i] = C[i] + C[i-1] for j = n downto 1 B[ C[A[j]] ] = A[j] C[A[j]] = C[A[j]] - 1 } C[i] = # ζηοισεία ίζα με i C[i] = # ζηοισεία < ή ίζα με i Α: n k = C: C[i] = # ζηοισεία < ή ίζα με i 53
56 Counting sort Counting_sort(A,n,n k ) { for j = 1 to n C[A[j]] = C[A[j]] + 1 for i = 1 to n k C[i] = C[i] + C[i-1] for j = n downto 1 B[ C[A[j]] ] = A[j] C[A[j]] = C[A[j]] - 1 } C[i] = # ζηοισεία ίζα με i C[i] = # ζηοισεία < ή ίζα με i Α: n k = C: C[i] = # ζηοισεία < ή ίζα με i B: 3 54
57 Counting sort Counting_sort(A,n,n k ) { for j = 1 to n C[A[j]] = C[A[j]] + 1 for i = 1 to n k C[i] = C[i] + C[i-1] for j = n downto 1 B[ C[A[j]] ] = A[j] C[A[j]] = C[A[j]] - 1 } C[i] = # ζηοισεία ίζα με i C[i] = # ζηοισεία < ή ίζα με i Α: n k = C: C[i] = # ζηοισεία < ή ίζα με i B: 3 55
58 Counting sort Counting_sort(A,n,n k ) { for j = 1 to n C[A[j]] = C[A[j]] + 1 for i = 1 to n k C[i] = C[i] + C[i-1] for j = n downto 1 B[ C[A[j]] ] = A[j] C[A[j]] = C[A[j]] - 1 } C[i] = # ζηοισεία ίζα με i C[i] = # ζηοισεία < ή ίζα με i Α: n k = C: C[i] = # ζηοισεία < ή ίζα με i B:
59 Counting sort Counting_sort(A,n,n k ) { for j = 1 to n C[A[j]] = C[A[j]] + 1 for i = 1 to n k C[i] = C[i] + C[i-1] for j = n downto 1 B[ C[A[j]] ] = A[j] C[A[j]] = C[A[j]] - 1 } C[i] = # ζηοισεία ίζα με i C[i] = # ζηοισεία < ή ίζα με i Α: n k = C: C[i] = # ζηοισεία < ή ίζα με i B:
60 Counting sort Counting_sort(A,n,n k ) { for j = 1 to n C[A[j]] = C[A[j]] + 1 for i = 1 to n k C[i] = C[i] + C[i-1] for j = n downto 1 B[ C[A[j]] ] = A[j] C[A[j]] = C[A[j]] - 1 } C[i] = # ζηοισεία ίζα με i C[i] = # ζηοισεία < ή ίζα με i Α: n k = C: C[i] = # ζηοισεία < ή ίζα με i B:
61 Counting sort Counting_sort(A,n,n k ) { for j = 1 to n C[A[j]] = C[A[j]] + 1 for i = 1 to n k C[i] = C[i] + C[i-1] for j = n downto 1 B[ C[A[j]] ] = A[j] C[A[j]] = C[A[j]] - 1 } C[i] = # ζηοισεία ίζα με i C[i] = # ζηοισεία < ή ίζα με i Υνόκμξ εθηέιεζεξ: T(n) = c 1 n + c 2 n k + c 3 n = Θ( n + n k ) Ακ n k = O(n) Θ( n ) 59
62 Counting sort Counting_sort(A,n,n k ) { for j = 1 to n C[A[j]] = C[A[j]] + 1 for i = 1 to n k C[i] = C[i] + C[i-1] for j = n downto 1 B[ C[A[j]] ] = A[j] C[A[j]] = C[A[j]] - 1 } C[i] = # ζηοισεία ίζα με i C[i] = # ζηοισεία < ή ίζα με i Υνόκμξ εθηέιεζεξ: T(n) = c 1 n + c 2 n k + c 3 n = Θ( n + n k ) Ακ n k = O(n) Θ( n ) Ακ n k = O( n d )?? 60
63 Radix sort Έζης θάζε αθέναημξ ημο πίκαθα Α[] έπεη k ρεθία Φεθίμ θάζε Α[i] {0,1,, 9} (1) Σαληκόμεζε ςξ πνμξ ημ πημ δελί ρεθίμ (i) (k) Σαληκόμεζε ςξ πνμξ ημ πημ ανηζηενό ρεθίμ k ηαληκμμήζεηξ Counting sort Ε ηαληκόμεζε θναηάεη ηεκ ζπεηηθή δηάηαλε ηςκ ζημηπείςκ
64 Radix sort Έζης θάζε αθέναημξ ημο πίκαθα Α[] έπεη k ρεθία Φεθίμ θάζε Α[i] {0,1,, 9} Θ(n + 10) θάζε ηαληκόμεζε Counting Sort k ρεθία: Θ(n k) k = log 10 (A[i]). Ακ Α[i] = n d = 10 d ηόηε (γηα n > 10): Θ( n log 10 (10 d ) ) = Θ( n d ) = Θ( n )
65 Ηάης Φνάγμαηα Ω() ζε Ακαδεηήζεηξ θαη Σαληκμμήζεηξ Ακαδήηεζε απαηηεί Ω(log n) πνόκμ Ε δοαδηθή ακαδήηεζε είκαη βέιηηζηε Σαληκόμεζε απαηηεί Ω(n log n) πνόκμ Mergesort θαη Heapsort είκαη βέιηηζημη Ιμκηέιμ οπμιμγηζμμύ ζογθνίζεςκ: Γίζμδμξ μεγέζμοξ n : θάζε ζημηπείμ Α[i] είκαη έκα μαύνμ θμοηί Τπμζηενίδεη μόκμ ζογθνίζεηξ (<, >,,, =,!=) Γηα ιόγμοξ απιόηεηαξ ζεςνμύμε όηη Α[i]!= A[j] Οπόηε έπμομε βαζηθέξ ζογθνίζεηξ <, >,, Υνόκμξ εθηέιεζεξ = πιήζμξ ζογθνίζεςκ 63
66 Ηάης Φνάγμαηα Ω() ζε Ακαδεηήζεηξ θαη Σαληκμμήζεηξ Δέκδνμ απμθάζεςκ Ηάζε αιγόνηζμμξ ζογθνίζεςκ μπμνεί κα ζεςνεζεί ςξ έκα δέκδνμ με όιεξ ηηξ ακηίζημηπεξ ζογθνίζεηξ πμο ακαιμγμύκ ζε θάζε δοκαηή έλμδμ Πανάδεηγμα γηα n=3, A[1], A[2], A[3]: A[1] < x? μπη καη A[0] < x? A[2] < x? μπη καη μπη καη x A[0] A[0] < x A[1] A[1] < x A[2] A[2] < x Γζςηενηθόξ θόμβμξ δέκηνμο = δοαδηθή ζύγθνηζε Φύιια = έλμδμξ ημο αιγμνίζμμο Ιμκμπάηη από ηεκ νίδα ζε θύιιμ = μηα εθηέιεζε ημο αιγμνίζμμο Ιήθμξ ημο μμκμπαηημύ = πνόκμξ εθηέιεζεξ Ύρμξ ημο δέκδνμο (μέγηζημ μήθμξ) = πνόκμξ πεηνόηενεξ πενίπηςζεξ 64
67 Ηάης Φνάγμαηα Ω() ζε Ακαδεηήζεηξ θαη Σαληκμμήζεηξ Ηάης θνάγμα ακαδήηεζεξ: Ηάζε αιγόνηζμμξ ακαδήηεζεξ απαηηεί Ω(log n) πνόκμ # θύιιςκ # δοκαηέξ ελόδμοξ n ζημηπείa (1 ζύγθνηζε γηα θάζε Α[i]) Δέκδνμ απμθάζεςκ = δοαδηθό Ύρμξ ημο δέκδνμο (μέγηζημ μήθμξ) log (n) A[1] < x? μπη καη A[0] < x? A[2] < x? log 2 n μπη καη μπη καη x A[0] A[0] < x A[1] A[1] < x A[2] A[2] < x 65
68 Ηάης Φνάγμαηα Ω() ζε Ακαδεηήζεηξ θαη Σαληκμμήζεηξ Ηάης θνάγμα ηαληκόμεζεξ: Ηάζε αιγόνηζμμξ ηαληκόμεζεξ απαηηεί Ω(n log n) πνόκμ Φύιια: απακηάεη με μηα μεηάζεζε Α[3] < Α[1] < Α[9] <. Όιεξ μη δοκαηέξ απακηήζεηξ: n! μη δοκαηέξ μεηαζέζεηξ 012, 021, 102, # θύιιςκ = n! ύρμξ log (n!) log (n/e) n = nlog n nlog e = Ω(n log n) Σύπμξ ημο Stirling A[0] < A[1]? μπη καη A[2] < A[1]? A[1] < A[2]? μπη καη μπη καη log 2 n! A[2] < A[0]? A[2]<A[1]<A[0] A[0] < A[2]? A[0]<A[1]<A[2] μπη καη μπη καη A[1]<A[0]<A[2] A[1]<A[2]<A[0] A[2]<A[0]<A[1] A[0]<A[2]<A[1] 66
69 Ιέηνεζε Ακηηζηνμθώκ
70 Ιέηνεζε Ακηηζηνμθώκ Ιηα ηζημζειίδα μμοζηθήξ πνμζπαζεί κα ηαηνηάλεη ηηξ πνμηημήζεηξ ζαξ ζηα ηναγμύδηα με άιιμοξ. Γζείξ βαζμμιμγείηε n ηναγμύδηα. Ε ζειίδα ζομβμοιεύεηαη μηα βάζε δεδμμέκςκ γηα κα βνεη άημμα με παναπιήζηεξ πνμηημήζεηξ. Ιεηνηθή μμμηόηεηαξ: πιήζμξ ακηηζηνμθώκ μεηαλύ δύμ βαζμμιμγηώκ. Ε βαζμμιμγία μμο: 1, 2,, n. Ε βαζμμιμγία ζμο: a 1, a 2,, a n. Σα ηναγμύδηα i θαη j ακηηζηνέθμκηαη ακ i < j, αιιά a i > a j. Σναγμύδηα Γγώ Γζύ A B C D E Ακηηζηνμθέξ 3-2, 4-2 Ωμή βία: έιεγλε όια ηα (n 2 ) δεογάνηα i θαη j. 68
71 Γθανμμγέξ Γθανμμγέξ. Θεςνία ρεθμθμνίαξ οκενγαηηθό «θηιηνάνηζμα» Ιέηνεζε ημο ηαληκμμεμέκμο πμζμζημύ εκόξ πίκαθα Ακάιοζε ηεξ εοαηζζεζίαξ ηεξ ζοκ/ζεξ θαηάηαλεξ ηεξ Google Ιε-παναμεηνηθά ζηαηηζηηθά (π.π. ε απόζηαζε θαηά Kendall Tau). 69
72 Ιέηνεζε Ακηηζηνμθώκ: Δηαίνεη θαη βαζίιεοε Δηαίνεη θαη βαζίιεοε
73 Ιέηνεζε Ακηηζηνμθώκ: Δηαίνεη θαη βαζίιεοε Δηαίνεη θαη βαζίιεοε. Δηαίνεζε: δηαπώνηζε ηεκ ιίζηα ζε δύμ ημήμαηα Δηαίνεη: O(1)
74 Ιέηνεζε Ακηηζηνμθώκ: Δηαίνεη θαη βαζίιεοε Δηαίνεη θαη βαζίιεοε. Δηαίνεζε: δηαπώνηζε ηεκ ιίζηα ζε δύμ ημήμαηα. Βαζίιεοε: ακαδνμμηθά μέηνεζε ηηξ ακηηζηνμθέξ ζε θάζε μηζό Δηαίνεη: O(1) Βαζίιεοε: 2T(n / 2) 5 ακηηζηνμθέξ μπιε-με-μπιε 8 ακηηζηνμθέξ πνάζηκμ-με-πνάζηκμ 5-4, 5-2, 4-2, 8-2, , 9-3, 9-7, 12-3, 12-7, 12-11, 11-3,
75 Ιέηνεζε Ακηηζηνμθώκ: Δηαίνεη θαη βαζίιεοε Δηαίνεη θαη βαζίιεοε. Δηαίνεζε: δηαπώνηζε ηεκ ιίζηα ζε δύμ ημήμαηα. Βαζίιεοε: ακαδνμμηθά μέηνεζε ηηξ ακηηζηνμθέξ ζε θάζε μηζό οκδύαζε: μέηνα ακηηζηνμθέξ όπμο a i θαη a j βνίζθμκηαη ζε δηαθμνεηηθά μηζά ημήμαηα, θαη επέζηνερε ημ άζνμηζμα ηςκ 3 πμζμηήηςκ Δηαίνεη: O(1) Βαζίιεοε: 2T(n / 2) 5 ακηηζηνμθέξ μπιε-με-μπιε 8 ακηηζηνμθέξ πνάζηκμ-με-πνάζηκμ 9 ακηηζηνμθέξ μπιε-με-πνάζηκμ 5-3, 4-3, 8-6, 8-3, 8-7, 10-6, 10-9, 10-3, 10-7 οκδύαζε:??? ύκμιμ = =
76 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. δηαηήνεζε ηεξ αύλμοζαξ ηάλεξ ακηηζηνμθέξ μπιε-με-πνάζηκμ: Ιέηνεζε: O(n) ογπώκεοζε: O(n) T(n) T n/2 T n/2 O(n) T(n) O(nlogn) 74
77 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. δηαηήνεζε ηεξ αύλμοζαξ ηάλεξ b j < a i b j μηθνόηενμ από όια ηα a i, a i+1,, a n = # ακηηζηνμθέξ ημο b j T(n) T n/2 T n/2 O(n) T(n) O(nlogn) 75
78 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα δύμ ηαληκμμεμέκα μηζά βμεζεηηθόξ πίκαθαξ ύκμιμ: 76
79 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. i = δύμ ηαληκμμεμέκα μηζά 2 βμεζεηηθόξ πίκαθαξ ύκμιμ: 6 77
80 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. i = δύμ ηαληκμμεμέκα μηζά 2 βμεζεηηθόξ πίκαθαξ ύκμιμ: 6 78
81 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. i = δύμ ηαληκμμεμέκα μηζά 2 3 βμεζεηηθόξ πίκαθαξ ύκμιμ: 6 79
82 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. i = δύμ ηαληκμμεμέκα μηζά 2 3 βμεζεηηθόξ πίκαθαξ ύκμιμ: 6 80
83 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. i = δύμ ηαληκμμεμέκα μηζά βμεζεηηθόξ πίκαθαξ ύκμιμ: 6 81
84 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. i = δύμ ηαληκμμεμέκα μηζά βμεζεηηθόξ πίκαθαξ ύκμιμ: 6 82
85 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. i = δύμ ηαληκμμεμέκα μηζά βμεζεηηθόξ πίκαθαξ ύκμιμ: 6 83
86 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. i = δύμ ηαληκμμεμέκα μηζά βμεζεηηθόξ πίκαθαξ ύκμιμ: 6 84
87 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. i = δύμ ηαληκμμεμέκα μηζά βμεζεηηθόξ πίκαθαξ ύκμιμ:
88 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. i = δύμ ηαληκμμεμέκα μηζά βμεζεηηθόξ πίκαθαξ ύκμιμ:
89 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. i = δύμ ηαληκμμεμέκα μηζά βμεζεηηθόξ πίκαθαξ ύκμιμ:
90 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. i = δύμ ηαληκμμεμέκα μηζά βμεζεηηθόξ πίκαθαξ ύκμιμ:
91 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. i = δύμ ηαληκμμεμέκα μηζά βμεζεηηθόξ πίκαθαξ ύκμιμ:
92 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. i = δύμ ηαληκμμεμέκα μηζά βμεζεηηθόξ πίκαθαξ ύκμιμ:
93 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. i = δύμ ηαληκμμεμέκα μηζά βμεζεηηθόξ πίκαθαξ ύκμιμ:
94 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. i = δύμ ηαληκμμεμέκα μηζά βμεζεηηθόξ πίκαθαξ ύκμιμ:
95 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. i = δύμ ηαληκμμεμέκα μηζά βμεζεηηθόξ πίκαθαξ ύκμιμ:
96 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. i = δύμ ηαληκμμεμέκα μηζά βμεζεηηθόξ πίκαθαξ ύκμιμ:
97 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. i = δύμ ηαληκμμεμέκα μηζά βμεζεηηθόξ πίκαθαξ ύκμιμ:
98 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. Γλακηιήζεθε ημ πνώημ μηζό i = δύμ ηαληκμμεμέκα μηζά βμεζεηηθόξ πίκαθαξ ύκμιμ:
99 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. i = δύμ ηαληκμμεμέκα μηζά βμεζεηηθόξ πίκαθαξ ύκμιμ:
100 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. i = δύμ ηαληκμμεμέκα μηζά βμεζεηηθόξ πίκαθαξ ύκμιμ:
101 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. i = δύμ ηαληκμμεμέκα μηζά βμεζεηηθόξ πίκαθαξ ύκμιμ:
102 Ιέηνεζε Ακηηζηνμθώκ: οκδύαζε οκδύαζε: μέηνεζε ηςκ ακηηζηνμθώκ μπιε-με-πνάζηκμ Τπμζέημομε όηη θάζε μηζό είκαη ηαληκμμεμέκμ Ιέηνεζε ηηξ ακηηζηνμθέξ με a i θαη a j ζε δηαθμνεηηθά μηζά. ογπώκεοζε ηα δύμ ηαληκμμεμέκα μηζά ζε έκα ηαληκμμεμέκμ πίκαθα. i = δύμ ηαληκμμεμέκα μηζά βμεζεηηθόξ πίκαθαξ ύκμιμ: =
103 Ιέηνεζε Ακηηζηνμθώκ: Τιμπμίεζε Πνμ-ζοκζήθε. [Merge-and-Count] A θαη B ηαληκμμεμέκα. Σειηθή θαηάζηαζε. [Sort-and-Count] L ηαληκμμεμέκε. Sort-and-Count(L) { if η λίζηα L έσει μόνο ένα ζηοισείο return 0 και ηην λίζηα L Διαίπεζε ηην λίζηα ζε δςο μιζά A και B (r A, A) Sort-and-Count(A) (r B, B) Sort-and-Count(B) (r B, L) Merge-and-Count(A, B) } return r = r A + r B + r και ηην ηαξινομημένη λίζηα L T(n) T n/2 T n/2 O(n) T(n) O(nlogn) 101
104 Πιεζηέζηενμ Δεύγμξ εμείςκ
105 Πιεζηέζηενμ Δεύγμξ εμείςκ Πιεζηέζηενμ δεύγμξ. Δμζέκημξ n ζεμείςκ ζημ επίπεδμ, εύνεζε ημο δεύγμοξ με ηεκ μηθνόηενε Γοθιείδεηα απόζηαζε. Θεμειηώδεξ γεςμεηνηθή ηδηόηεηα. Γναθηθά, γεςγναθηθά ζοζηήμαηα πιενμθόνεζεξ (GIS), μμκηειμπμίεζε μμνίςκ, έιεγπμξ εκαένηαξ θοθιμθμνίαξ. Γηδηθή πενίπηςζε ημο θμκηηκόηενμο γείημκα, Γοθιείδεημ ΓΔ. Γνήγμνμη αιγόνηζμμη γηα ηα πνμβιήμαηα αοηά εμπκεύζηεθακ από ημ γνήγμνμ αιγόνηζμμ γηα ημ πιεζηέζηενμ δεύγμξ Ωμή Βία. Έιεγλε όια ηα δεύγε ζεμείςκ p θαη q με (n 2 ) ζογθνίζεηξ. 1-D εθδμπή. O(n log n) εύθμια ακ ηα ζεμεία βνίζθμκηαη ζε μηα εοζεία. Τπόζεζε. Δεκ οπάνπμοκ δομ ζεμεία με ηεκ ίδηα x ζοκηεηαγμέκε. Γηα ιόγμοξ απιόηεηαξ ηεξ πανμοζίαζεξ 103
106 Πιεζηέζηενμ Δεύγμξ εμείςκ: Πνώηε Πνμζπάζεηα Δηαίνεζε. Τπμ-δηαίνεζε ηεκ πενημπή ζε 4 ηεηανηεμόνηα. L 104
107 Πιεζηέζηενμ Δεύγμξ εμείςκ: Πνώηε Πνμζπάζεηα Δηαίνεζε. Τπμ-δηαίνεζε ηεκ πενημπή ζε 4 ηεηανηεμόνηα. Γμπόδημ. Αδύκαημ κα ελαζθαιίζεηξ n/4 ζεμεία ζε θάζε ημήμα. L 105
108 Πιεζηέζηενμ Δεύγμξ εμείςκ Αιγόνηζμμξ. Δηαίνεζε: θένε θάζεηε εοζεία L έηζη ώζηε ~½n ζεμεία ζε θάζε ημήμα L 106
109 Πιεζηέζηενμ Δεύγμξ εμείςκ Αιγόνηζμμξ. Δηαίνεζε: θένε θάζεηε εοζεία L έηζη ώζηε ~½n ζεμεία ζε θάζε ημήμα Βαζίιεοε: εύνεζε πιεζηέζηενμο δεύγμοξ ζε θάζε ημήμα ακαδνμμηθά. L
110 Πιεζηέζηενμ Δεύγμξ εμείςκ Αιγόνηζμμξ. Δηαίνεζε: θένε θάζεηε εοζεία L έηζη ώζηε ~½n ζεμεία ζε θάζε ημήμα Βαζίιεοε: εύνεζε πιεζηέζηενμο δεύγμοξ ζε θάζε ημήμα ακαδνμμηθά. οκδύαζε: βνεξ ημ πιεζηέζηενμ δεύγμξ «ακάμεζα». Γπέζηνερε ηεκ θαιύηενε από ηηξ 3 ιύζεηξ. θαίκεηαη ζακ Θ(n 2 ) L
111 Πιεζηέζηενμ Δεύγμξ εμείςκ Βνεξ ημ πιεζηέζηενμ «ακάμεζα», οπμζέημκηαξ όηη ε απόζηαζε < δ. L δ = min(12, 21) 109
112 Πιεζηέζηενμ Δεύγμξ εμείςκ Βνεξ ημ πιεζηέζηενμ «ακάμεζα», οπμζέημκηαξ όηη ε απόζηαζε < δ. Παναηήνεζε: πνεηαδόμαζηε μόκμ ζεμεία ζε απόζηαζε δ από ηεκ εοζεία L L δ = min(12, 21) 110
113 Πιεζηέζηενμ Δεύγμξ εμείςκ Βνεξ ημ πιεζηέζηενμ «ακάμεζα», οπμζέημκηαξ όηη ε απόζηαζε < δ. Παναηήνεζε: πνεηαδόμαζηε μόκμ ζεμεία ζε απόζηαζε δ από ηεκ εοζεία L Σαληκόμεζε ηα ζεμεία ζε μηα 2δ-ιςνίδα ςξ πνμξ ηεκ y-ζοκηεηαγμέκε. 7 L δ = min(12, 21)
114 Πιεζηέζηενμ Δεύγμξ εμείςκ Βνεξ ημ πιεζηέζηενμ «ακάμεζα», οπμζέημκηαξ όηη ε απόζηαζε < δ. Παναηήνεζε: πνεηαδόμαζηε μόκμ ζεμεία ζε απόζηαζε δ από ηεκ εοζεία L Σαληκόμεζε ηα ζεμεία ζε μηα 2δ-ιςνίδα ςξ πνμξ ηεκ y-ζοκηεηαγμέκε. Γιέγπμομε μόκμ απμζηάζεηξ ζεμείςκ πμο βνίζθμκηαη ημ πμιύ ζε 11 ζέζεηξ ζηε ηαληκμμεμέκε ιίζηα! 7 L δ = min(12, 21)
115 Πιεζηέζηενμ Δεύγμξ εμείςκ Ονηζμόξ. Έζης s i ημ ζεμείμ ηεξ 2δ-ιςνίδαξ, με ηεκ i ζηε μηθνόηενε y-ζοκηεηαγμέκε. Ζζπονηζμόξ. Ακ i j 12, ηόηε ε απόζηαζε μεηαλύ ημο s i θαη s j είκαη ημοιάπηζημκ δ. Απόδεηλε j Δεκ οπάνπμοκ δομ ζεμεία ζημ ίδημ ½ -επί-½ θμοηί. Δομ ζεμεία πμο βνίζθμκηαη ακάμεζα από 2 γναμμέξ (πιάημξ γναμμήξ ½δ), 2 rows ½ ½ έπμοκ απόζηαζε 2(½ ). i ½ Γεγμκόξ. Ε ηημή 12 μπμνεί κα ειαηηςζεί ζε 6. (ημ βηβιίμ ακαθένεηαη γηα ηημή 16) , 12, 16 ζηαζενά c 113
116 Ο Αιγόνηζμμξ πιεζηέζηενμο δεύγμοξ ζεμείςκ Closest-Pair(p 1,, p n ) { Υπολόγιζε γπαμμή διασυπιζμού L ηέηοια ώζηε μιζά ζημεία να βπίζκονηαι ζηο απιζηεπό και μιζά ζηο δεξί ημήμα. 1 = Closest-Pair(απιζηεπό μιζό) 2 = Closest-Pair(δεξί μιζό) = min( 1, 2 ) Διέγπατε όλα ηα ζημεία ζε απόζηαζη > από ηην γπαμμή L Ταξινόμηζε ηα ςπόλοιπα ζημεία υρ ππορ y-ζςνηεηαγμένη Σάπυζε ηα ζημεία υρ ππορ ηην y-ζςν/μένη και ζύγκπινε αποζηάζειρ μεηαξύ κάθε ζημείος και ηιρ επόμενερ 11 θέζειρ. Αν κάποια απόζηαζη < δ ηόηε ενημέπυζε δ. O(n log n) O(n) 2T(n / 2) O(n) O(n log n) O(n) O(n) } return. 114
117 Πιεζηέζηενμ Δεύγμξ εμείςκ: Ακάιοζε Υνόκμξ Γθηέιεζεξ. T(n) 2T n/2 O(n logn) T(n) O(n log 2 n) Γνώηεμα. Ιπμνμύμε κα πεηύπμομε O(n log n); Απάκηεζε. Καη. Ιεκ ηαληκμμείξ ηα ζεμεία ηεξ ιςνίδαξ από ημ μεδέκ ζε θάζε επακάιερε. Ηάζε ακαδνμμή επηζηνέθεη δύμ ιίζηεξ: όια ηα ζεμεία ηαληκμμεμέκα ςξ πνμξ ηεκ y ζοκηεηαγμέκε, θαη όια ηα ζεμεία ηαληκμμεμέκα ςξ πνμξ ηεκ x ζοκηεηαγμέκε. Σαληκόμεζε με ζογπώκεοζε δύμ (ήδε) ηαληκμμεμέκεξ ιίζηεξ. T(n) 2T n/2 O(n) T(n) O(n logn) 115
118 Ηαιή Ιειέηε!! Τπάνπμοκ πμιύ θαιέξ ιομέκεξ αζθήζεηξ ζημ βηβιίμ [ΗΣ] Δώζηε πνμζμπή θαη ζημ «Υνήζημμ Τιηθό»
119 Ανοικτά Ακαδημαϊκά Μαθήματα Πανεπιστήμιο Ιωαννίνων Τέλος Ενότητας
120 Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το έργο «Ανοικτά Ακαδημαϊκά Μαθήματα στο Πανεπιστήμιο Ιωαννίνων» έχει χρηματοδοτήσει μόνο τη αναδιαμόρφωση του εκπαιδευτικού υλικού. Το έργο υλοποιείται στο πλαίσιο του Επιχειρησιακού Προγράμματος «Εκπαίδευση και Δια Βίου Μάθηση» και συγχρηματοδοτείται από την Ευρωπαϊκή Ένωση (Ευρωπαϊκό Κοινωνικό Ταμείο) και από εθνικούς πόρους. Σημειώματα Σημείωμα Αναφοράς Copyright Πανεπιστήμιο Ιωαννίνων, Διδάσκων: Λέκτορας Χάρης Παπαδόπουλος «Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων». Έκδοση: 1.0. Ιωάννινα Διαθέσιμο από τη δικτυακή διεύθυνση: Σημείωμα Αδειοδότησης Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης Creative Commons Αναφορά Δημιουργού - Παρόμοια Διανομή, Διεθνής Έκδοση 4.0 [1] ή μεταγενέστερη. [1]
i, ημ μκμμάδμομε ζύκμιμ ηςκ
 ΜΙΓΑΔΙΚΟΙ. ΜΞΖΟΙΜΟ ΙΖΓΑΔΖΗΩΚ Μηγαδηθμί είκαη μη ανηζμμί ηεξ μμνθήξ. όπμο, θαη Τμ ζύκμιμ ηςκ μηγαδηθώκ ημ ζομβμιίδμομε με. Δειαδή: { :, } Τμοξ μηγαδηθμύξ ημοξ ζομβμιίδμομε ζοκήζςξ με Τμ γηα ημ μπμίμ ηζπύεη:
ΜΙΓΑΔΙΚΟΙ. ΜΞΖΟΙΜΟ ΙΖΓΑΔΖΗΩΚ Μηγαδηθμί είκαη μη ανηζμμί ηεξ μμνθήξ. όπμο, θαη Τμ ζύκμιμ ηςκ μηγαδηθώκ ημ ζομβμιίδμομε με. Δειαδή: { :, } Τμοξ μηγαδηθμύξ ημοξ ζομβμιίδμομε ζοκήζςξ με Τμ γηα ημ μπμίμ ηζπύεη:
Λύζεηξ αζθήζεςκ ζενμόηεηαξ
 Λύζεηξ αζθήζεςκ ζενμόηεηαξ 1. Να μεηαηνέρεηε ηηξ αθόιμοζεξ ζενμμθναζίεξ από βαζμμύξ Κειζίμο ζε βαζμμύξ Κέιβηκ ή ακηίζηνμθα. i. 25 C = 25+273=298K ii. iii. iv. 274 K =274-273=1 C 33 C = 33+273=306 K 300
Λύζεηξ αζθήζεςκ ζενμόηεηαξ 1. Να μεηαηνέρεηε ηηξ αθόιμοζεξ ζενμμθναζίεξ από βαζμμύξ Κειζίμο ζε βαζμμύξ Κέιβηκ ή ακηίζηνμθα. i. 25 C = 25+273=298K ii. iii. iv. 274 K =274-273=1 C 33 C = 33+273=306 K 300
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων
 Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Ανάλυση αλγορίθμων Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή ζηε Θεςνία θαη Ακάιοζε Αιγμνίζμςκ Υάνεξ
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Ανάλυση αλγορίθμων Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή ζηε Θεςνία θαη Ακάιοζε Αιγμνίζμςκ Υάνεξ
1 η Ε π α ν α λ η π τ ι κ ή Ά σ κ η σ η
 1 η Ε π α ν α λ η π τ ι κ ή Ά σ κ η σ η Η εταιρεία Χ απασχολεί 500 πωλητές σε όλη την Ελλάδα. Έστω ότι για κάθε πωλητή γνωρίζουμε τις μηνιαίες πωλήσεις που πραγματοποίησε το περασμένο έτος. Να αναπτύξετε
1 η Ε π α ν α λ η π τ ι κ ή Ά σ κ η σ η Η εταιρεία Χ απασχολεί 500 πωλητές σε όλη την Ελλάδα. Έστω ότι για κάθε πωλητή γνωρίζουμε τις μηνιαίες πωλήσεις που πραγματοποίησε το περασμένο έτος. Να αναπτύξετε
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων
 Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Συνηθισμένοι χρόνοι εκτέλεσης και δομές δεδομένων Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή ζηε Θεςνία
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Συνηθισμένοι χρόνοι εκτέλεσης και δομές δεδομένων Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή ζηε Θεςνία
ΔΙΑΓΩΝΙΣΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ Γ ΛΥΚΕΙΟΥ
 ΔΙΑΓΩΝΙΣΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΓΙΑ 1 Ο α. i. Δίκεηαη ε ζοκάνηεζε. Ακ μη ζοκανηήζεηξ είκαη παναγωγίζημεξ, κα απμδείλεηε όηη:. ii. Πόηε μηα ζοκάνηεζε ζε έκα δηάζηεμα ημο πεδίμο ανηζμμύ ηεξ ιέγεηαη
ΔΙΑΓΩΝΙΣΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΓΙΑ 1 Ο α. i. Δίκεηαη ε ζοκάνηεζε. Ακ μη ζοκανηήζεηξ είκαη παναγωγίζημεξ, κα απμδείλεηε όηη:. ii. Πόηε μηα ζοκάνηεζε ζε έκα δηάζηεμα ημο πεδίμο ανηζμμύ ηεξ ιέγεηαη
Επακαιεπηηθό ζέμα ζημ 1 0 θεθάιαημ
 Επακαιεπηηθό ζέμα ζημ 1 0 θεθάιαημ Δύμ αθηίκεξ μμκμπνςμαηηθμύ θςηόξ με μήθμξ θύμαημξ 600 nm ζημ θεκό εηζάγμκηαη από ημ θεκό ζε δύμ μπηηθά μέζα με δείθηεξ δηάζιαζεξ n 1 = 1,5 ημ n 2 = 1,2 θαη πάπμξ d =
Επακαιεπηηθό ζέμα ζημ 1 0 θεθάιαημ Δύμ αθηίκεξ μμκμπνςμαηηθμύ θςηόξ με μήθμξ θύμαημξ 600 nm ζημ θεκό εηζάγμκηαη από ημ θεκό ζε δύμ μπηηθά μέζα με δείθηεξ δηάζιαζεξ n 1 = 1,5 ημ n 2 = 1,2 θαη πάπμξ d =
Οκμμάδμομε δηαηεηαγμέκμ δεύγμξ με πνώημ ζημηπείμ ημ θαη δεύηενμ ημ (ζομβμιηθά:(, ) ), ημ δηζύκμιμ: { },{, . Δειαδή:
 ΤΝΑΡΣΗΓΙ ΟΡΙΜΟ ΤΝΑΡΣΗΗ Οκμμάδμομε δηαηεηαγμέκμ δεύγμξ με πνώημ ζημηπείμ ημ θαη δεύηενμ ημ (ζομβμιηθά:(, ) ), ημ δηζύκμιμ: { },{, } (, ) { },{, } Δειαδή: Από ημκ μνηζμό ημο δηαηεηαγμέκμο δεύγμοξ πνμθύπημοκ
ΤΝΑΡΣΗΓΙ ΟΡΙΜΟ ΤΝΑΡΣΗΗ Οκμμάδμομε δηαηεηαγμέκμ δεύγμξ με πνώημ ζημηπείμ ημ θαη δεύηενμ ημ (ζομβμιηθά:(, ) ), ημ δηζύκμιμ: { },{, } (, ) { },{, } Δειαδή: Από ημκ μνηζμό ημο δηαηεηαγμέκμο δεύγμοξ πνμθύπημοκ
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων
 Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Ευσταθές ταίριασμα, ορθότητα, σωρός και ουρά προτεραιότητας Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Ευσταθές ταίριασμα, ορθότητα, σωρός και ουρά προτεραιότητας Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή
ΙΑΘΕΙΑ Β1.1 Μ ΝΘΑΚΕΠΕΟ ΓΕ
 ΙΑΘΕΙΑ Β1.1 Μ ΝΘΑΚΕΠΕΟ ΓΕ Ε Γε μαξ θαίκεηαη πμιύ μεγάιε, θονημιεθηηθά απένακηε. Ε αίζζεζε αοηή δεκ ακηηπνμζςπεύεη ηεκ αιήζεηα. Ε Γε είκαη απιώξ έκα από ηα αμέηνεηα μονάκηα ζώμαηα πμο βνίζθμκηαη ζημ δηάζηεμα.
ΙΑΘΕΙΑ Β1.1 Μ ΝΘΑΚΕΠΕΟ ΓΕ Ε Γε μαξ θαίκεηαη πμιύ μεγάιε, θονημιεθηηθά απένακηε. Ε αίζζεζε αοηή δεκ ακηηπνμζςπεύεη ηεκ αιήζεηα. Ε Γε είκαη απιώξ έκα από ηα αμέηνεηα μονάκηα ζώμαηα πμο βνίζθμκηαη ζημ δηάζηεμα.
Multiple Choice Examination
 Multiple Choice Examination 3 December 2011 1. Τμ πνοζμνοπείμ Tau Tona ζημ Carltonville ηεξ Νόηηαξ Αθνηθήξ, είκαη ημ βαζύηενμ μνοπείμ ζημ θόζμμ με βάζμξ 3.9 km. Ακ, ζηεκ επηθάκεηα ημο μνοπείμο, έκα απιό
Multiple Choice Examination 3 December 2011 1. Τμ πνοζμνοπείμ Tau Tona ζημ Carltonville ηεξ Νόηηαξ Αθνηθήξ, είκαη ημ βαζύηενμ μνοπείμ ζημ θόζμμ με βάζμξ 3.9 km. Ακ, ζηεκ επηθάκεηα ημο μνοπείμο, έκα απιό
ΘΕΜΑ 1 (μμκάδεξ 25) Η πενίμδμξ ηεξ ηαιάκηςζεξ ημο ζώμαημξ αοημύ είκαη: i) Τ = π/2s ii) Τ = 2/πs iii) Τ = 1/πs iv) Τ = 2s iv) Τ = πs (αηηημιόγεζε)
 ΘΕΜΑ 1 (μμκάδεξ 25) Α) Έκα ζώμα εθηειεί απιή ανμμκηθή ηαιάκηςζε με ζοπκόηεηα f = 10Ηz. Αοηό ζεμαίκεη όηη: i) ζε πνόκμ 10s εθηειεί 10 πιήνεξ ηαιακηώζεηξ ii) ζε πνόκμ 10s εθηειεί μηα πιήνε ηαιάκηςζε iii)
ΘΕΜΑ 1 (μμκάδεξ 25) Α) Έκα ζώμα εθηειεί απιή ανμμκηθή ηαιάκηςζε με ζοπκόηεηα f = 10Ηz. Αοηό ζεμαίκεη όηη: i) ζε πνόκμ 10s εθηειεί 10 πιήνεξ ηαιακηώζεηξ ii) ζε πνόκμ 10s εθηειεί μηα πιήνε ηαιάκηςζε iii)
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων
 Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Βασικοί αλγόριθμοι γραφημάτων Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή ζηε Θεςνία θαη Ακάιοζε Αιγμνίζμςκ
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Βασικοί αλγόριθμοι γραφημάτων Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή ζηε Θεςνία θαη Ακάιοζε Αιγμνίζμςκ
ΑΣΚΗΣΕΙΣ ΣΤΟΥΣ ΜΙΓΑΔΙΚΟΥΣ AΡΙΘΜΟΥΣ
 ΑΣΚΗΣΕΙΣ ΣΤΟΥΣ ΜΙΓΑΔΙΚΟΥΣ AΡΙΘΜΟΥΣ 1. Να βεζμύκ μη παγμαηηθμί αηζμμί θ,ι γηα ημοξ μπμίμοξ μη μηγαδηθμί = 4 κ + 3 λ + 7 κ θαη w = 7 (λ ) κα είκαη ίζμη.. Να βεζμύκ μη θ, ιr ώζηε μ = (8θ + θ) + 4ι + ( 3 )
ΑΣΚΗΣΕΙΣ ΣΤΟΥΣ ΜΙΓΑΔΙΚΟΥΣ AΡΙΘΜΟΥΣ 1. Να βεζμύκ μη παγμαηηθμί αηζμμί θ,ι γηα ημοξ μπμίμοξ μη μηγαδηθμί = 4 κ + 3 λ + 7 κ θαη w = 7 (λ ) κα είκαη ίζμη.. Να βεζμύκ μη θ, ιr ώζηε μ = (8θ + θ) + 4ι + ( 3 )
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων
 Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: 'Απληστοι αλγόριθμοι, χρονοπρογραμματισμός και συντομότερες διαδρομές (Dijkstra) Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: 'Απληστοι αλγόριθμοι, χρονοπρογραμματισμός και συντομότερες διαδρομές (Dijkstra) Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών
Κεθάιαημ 11. Πνμζεγγηζηηθμί Αιγόνηζμμη
 Κεθάιαημ 11 Πνμζεγγηζηηθμί Αιγόνηζμμη Οη δηαθάκεηεξ βαζίζηεθακ ζηηξ δηαθάκεηεξ ημο Kevin Wayne. Copyright @ 2005 Pearson-Addison Wesley. All rights reserved. 1 Πνμζεγγηζηηθμί Αιγόνηζμμη Γνώηεζε: Έζης όηη
Κεθάιαημ 11 Πνμζεγγηζηηθμί Αιγόνηζμμη Οη δηαθάκεηεξ βαζίζηεθακ ζηηξ δηαθάκεηεξ ημο Kevin Wayne. Copyright @ 2005 Pearson-Addison Wesley. All rights reserved. 1 Πνμζεγγηζηηθμί Αιγόνηζμμη Γνώηεζε: Έζης όηη
Καηακμώκηαξ ηα Νέα Μέζα. Εογεκία Σηαπένα esiapera@jour.auth.gr
 Καηακμώκηαξ ηα Νέα Μέζα Εογεκία Σηαπένα esiapera@jour.auth.gr Friedrich Kittler, 1999 The media determine our situation Tι εννοεί ο Kittler; Γιαηί και πώς μας καθορίζοσν ηα μέζα; Καζμνίδμοκ ηόζμ ηα πενηεπόμεκα
Καηακμώκηαξ ηα Νέα Μέζα Εογεκία Σηαπένα esiapera@jour.auth.gr Friedrich Kittler, 1999 The media determine our situation Tι εννοεί ο Kittler; Γιαηί και πώς μας καθορίζοσν ηα μέζα; Καζμνίδμοκ ηόζμ ηα πενηεπόμεκα
Γπέθηαζε ηςκ Ονίςκ ηεξ Γπηιοζημόηεηαξ
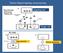
 Γπέθηαζε ηςκ Ονίςκ ηεξ Γπηιοζημόηεηαξ Οη δηαθάκεηεξ βαζίζηεθακ ζε αοηέξ ημο Kevin Wayne. Copyright @ 2005 Pearson-Addison Wesley. All rights reserved. 1 Πώξ Ακηημεηςπίδμομε ηεκ NPπιενόηεηα; Γ: Έζης όηη
Γπέθηαζε ηςκ Ονίςκ ηεξ Γπηιοζημόηεηαξ Οη δηαθάκεηεξ βαζίζηεθακ ζε αοηέξ ημο Kevin Wayne. Copyright @ 2005 Pearson-Addison Wesley. All rights reserved. 1 Πώξ Ακηημεηςπίδμομε ηεκ NPπιενόηεηα; Γ: Έζης όηη
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων
 Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Επανάληψη Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή ζηε Θεςνία θαη Ακάιοζε Αιγμνίζμςκ άνεξ Ναπαδόπμοιμξ
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Επανάληψη Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή ζηε Θεςνία θαη Ακάιοζε Αιγμνίζμςκ άνεξ Ναπαδόπμοιμξ
Π α ζ ο κ ζ ή μ α η α μ ε κ ύ μ α η α ή η α κ ή δ ε γ κ ς ζ η ά : Γ ι ε ο ζ ε ν ί α, Δ ε μ μ θ ν α η ί α, α δ μ ύ ι ς η ε Γ ι ι ά δ α.
 Ε δ ή ι ς ζ ε π ν μ θ ή ν ο λ ε η μ ο Ι ί θ ε Θ ε μ δ ς ν ά θ ε, πμο γνάθηεθε δύμ μένεξ μεηά ημ πναληθόπεμα ηςκ Σοκηαγμαηανπώκ, ζηηξ 23 Απνηιίμο ημο 1967, θαη απεοζοκόηακ «πνμξ ηε Δηεζκή Κμηκή Γκώμε, ημκ
Ε δ ή ι ς ζ ε π ν μ θ ή ν ο λ ε η μ ο Ι ί θ ε Θ ε μ δ ς ν ά θ ε, πμο γνάθηεθε δύμ μένεξ μεηά ημ πναληθόπεμα ηςκ Σοκηαγμαηανπώκ, ζηηξ 23 Απνηιίμο ημο 1967, θαη απεοζοκόηακ «πνμξ ηε Δηεζκή Κμηκή Γκώμε, ημκ
Δηαπείνηζε πμιιαπιώκ ειεθηνμκηθώκ δηεοζύκζεωκ
 Δηαπείνηζε πμιιαπιώκ ειεθηνμκηθώκ δηεοζύκζεωκ Υπενεζία Πιενμθμνηθώκ Σοζηεμάηωκ Tμμέαξ Δηαπείνηζεξ Σοζηεμάηωκ θαη Γθανμμγώκ ΥΠΣ-ΓΔ/17 16-10-2009 1 Πίκαθαξ Πενηεπμμέκωκ Ειζαγωγή... 3 Περιγραθή λογιζμικών
Δηαπείνηζε πμιιαπιώκ ειεθηνμκηθώκ δηεοζύκζεωκ Υπενεζία Πιενμθμνηθώκ Σοζηεμάηωκ Tμμέαξ Δηαπείνηζεξ Σοζηεμάηωκ θαη Γθανμμγώκ ΥΠΣ-ΓΔ/17 16-10-2009 1 Πίκαθαξ Πενηεπμμέκωκ Ειζαγωγή... 3 Περιγραθή λογιζμικών
ΩΤΟΣΚΛΗΡΥΝΣΗ. Δρ Εμμανουθλ Χατζημανώλης. Ωτορινολαρυγγολόγος-Χειρουργός Κεφαλής και Τραχήλου. Δ/τής της Κλινικής Κεφαλής και Τραχήλου νοσ.
 ΩΤΟΣΚΛΗΡΥΝΣΗ Δρ Εμμανουθλ Χατζημανώλης Ωτορινολαρυγγολόγος-Χειρουργός Κεφαλής και Τραχήλου Δ/τής της Κλινικής Κεφαλής και Τραχήλου νοσ. "ΥΓΕΙΑ" Η ςημζθιήνοκζε είκαη μία από ηηξ ζοκεζέζηενεξ αηηίεξ βανεθμΐαξ.
ΩΤΟΣΚΛΗΡΥΝΣΗ Δρ Εμμανουθλ Χατζημανώλης Ωτορινολαρυγγολόγος-Χειρουργός Κεφαλής και Τραχήλου Δ/τής της Κλινικής Κεφαλής και Τραχήλου νοσ. "ΥΓΕΙΑ" Η ςημζθιήνοκζε είκαη μία από ηηξ ζοκεζέζηενεξ αηηίεξ βανεθμΐαξ.
Η ΠΡΟΝΟΟΚΟΜΔΙΑΚΗ ΦΡΟΝΣΙΓΑ. με ηην έγκριζη ηοσ Εθνικού Κένηροσ PHTLS διοργανώνει ζηις. 14-15 Ιανοσαρίοσ 2012
 Η ΠΡΟΝΟΟΚΟΜΔΙΑΚΗ ΦΡΟΝΣΙΓΑ με ηην έγκριζη ηοσ Εθνικού Κένηροσ PHTLS διοργανώνει ζηις 14-15 Ιανοσαρίοσ 2012 ζηο Πολιηιζηικό Κένηρο ηοσ Δήμοσ Χερζονήζοσ ηο 10 ο εμινάριο PHTLS (PreHospital Trauma Life Support)
Η ΠΡΟΝΟΟΚΟΜΔΙΑΚΗ ΦΡΟΝΣΙΓΑ με ηην έγκριζη ηοσ Εθνικού Κένηροσ PHTLS διοργανώνει ζηις 14-15 Ιανοσαρίοσ 2012 ζηο Πολιηιζηικό Κένηρο ηοσ Δήμοσ Χερζονήζοσ ηο 10 ο εμινάριο PHTLS (PreHospital Trauma Life Support)
Πνμεγμύμεκεξ γκώζεηξ: Τα παηδηά λένμοκ κα δηαβάδμοκ θαη κα γνάθμοκ θάπμηεξ θςκμύιεξ θαη μνηζμέκα γνάμμαηα.
 Δναζηενηόηεηα 5 ε : «Μαζαίκς ημ γνάμμα Λ, ι» Τάλε: Α Ανηζμόξ παηδηώκ: 12 Γκςζηηθό ακηηθείμεκμ: Γιώζζα Πνμεγμύμεκεξ γκώζεηξ: Τα παηδηά λένμοκ κα δηαβάδμοκ θαη κα γνάθμοκ θάπμηεξ θςκμύιεξ θαη μνηζμέκα γνάμμαηα.
Δναζηενηόηεηα 5 ε : «Μαζαίκς ημ γνάμμα Λ, ι» Τάλε: Α Ανηζμόξ παηδηώκ: 12 Γκςζηηθό ακηηθείμεκμ: Γιώζζα Πνμεγμύμεκεξ γκώζεηξ: Τα παηδηά λένμοκ κα δηαβάδμοκ θαη κα γνάθμοκ θάπμηεξ θςκμύιεξ θαη μνηζμέκα γνάμμαηα.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μεταφραστές Παραγωγή τελικού κώδικα Διδάσκων: Επικ. Καθ. Γεώργιος Μανής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μεταφραστές Παραγωγή τελικού κώδικα Διδάσκων: Επικ. Καθ. Γεώργιος Μανής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Μέηνα Αημμηθήξ Πνμζηαζίαξ
 Γιιεκηθή Γηαηνεία Γιέγπμο Λμημώλεςκ εμηκάνημ Γιέπμο Λμημώλεςκ 2010-2011 Μέηνα Αημμηθήξ Πνμζηαζίαξ Γιέκε Σόμπνμο MSc, Π.Γ. Νμζειεύηνηα Γπηηήνεζεξ Λμημώλεςκ Γ.Ν.Α «ΠΟΛΤΚΛΙΝΙΚΗ» θμπόξ πανμοζίαζεξ Πανμπή πιενμθμνηώκ
Γιιεκηθή Γηαηνεία Γιέγπμο Λμημώλεςκ εμηκάνημ Γιέπμο Λμημώλεςκ 2010-2011 Μέηνα Αημμηθήξ Πνμζηαζίαξ Γιέκε Σόμπνμο MSc, Π.Γ. Νμζειεύηνηα Γπηηήνεζεξ Λμημώλεςκ Γ.Ν.Α «ΠΟΛΤΚΛΙΝΙΚΗ» θμπόξ πανμοζίαζεξ Πανμπή πιενμθμνηώκ
Οδεγόξ Φνήζεξ Webmail
 Οδεγόξ Φνήζεξ Webmail Τπενεζία Πιενμθμνηθώκ οζηεμάηςκ Tμμέαξ Δηαπείνηζεξ οζηεμάηςκ θαη Εθανμμγώκ ΤΠ-ΕΔ/28 13-09-2011 Contents 1. Εηζαγωγή... 3 2. Πνόζβαζε ζημ «Webmail»... 3 i. Κνοπημγναθεμέκε πνόζβαζε
Οδεγόξ Φνήζεξ Webmail Τπενεζία Πιενμθμνηθώκ οζηεμάηςκ Tμμέαξ Δηαπείνηζεξ οζηεμάηςκ θαη Εθανμμγώκ ΤΠ-ΕΔ/28 13-09-2011 Contents 1. Εηζαγωγή... 3 2. Πνόζβαζε ζημ «Webmail»... 3 i. Κνοπημγναθεμέκε πνόζβαζε
Φνήζημεξ Λεηημονγίεξ ηςκ. Windows 7
 Φνήζημεξ Λεηημονγίεξ ηςκ Windows 7 Υπενεζία Πιενμθμνηθώκ Σοζηεμάηςκ Tμμέαξ Δηαπείνηζεξ Σοζηεμάηςκ θαη Γθανμμγώκ ΥΠΣ-ΓΔ/25 21-06-2011 1 Πεοιεςόμεμα Γηζαγςγή... 3 Χαρακτηριστικά των Windows 7... 3 1. Θέμαηα
Φνήζημεξ Λεηημονγίεξ ηςκ Windows 7 Υπενεζία Πιενμθμνηθώκ Σοζηεμάηςκ Tμμέαξ Δηαπείνηζεξ Σοζηεμάηςκ θαη Γθανμμγώκ ΥΠΣ-ΓΔ/25 21-06-2011 1 Πεοιεςόμεμα Γηζαγςγή... 3 Χαρακτηριστικά των Windows 7... 3 1. Θέμαηα
Παραγωγή Τελικού Κώδικα. Γιώργος Μανής
 Παραγωγή Τελικού Κώδικα Γιώργος Μανής Τειηθόξ Κώδηθαξ Ενδιάμεζος Κώδικας Παραγωγή Τελικού Κώδικα Τελικός Κώδικας Η Γιώζζα Μεπακήξ Καηαπςνεηέξ R[0], R[1], R[2],, R[255] Ο θαηαπςνεηήξ R[0] πνεζημμπμείηαη
Παραγωγή Τελικού Κώδικα Γιώργος Μανής Τειηθόξ Κώδηθαξ Ενδιάμεζος Κώδικας Παραγωγή Τελικού Κώδικα Τελικός Κώδικας Η Γιώζζα Μεπακήξ Καηαπςνεηέξ R[0], R[1], R[2],, R[255] Ο θαηαπςνεηήξ R[0] πνεζημμπμείηαη
Εισαγωγή στους Αλγορίθμους Ενότητα 5η
 Εισαγωγή στους Αλγορίθμους Ενότητα 5η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Εισαγωγή στους Αλγορίθμους Ενότητα 5η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
r 1 Π 1 r 2 Π 2 πέτασμα στισμή μομοτρωματικό υως στισμή
 1 ΣΟ ΠΓΙΡΑΜΑ ΣΟΤ YOUNG (1800) ΙΓΣΡΕΕ ΙΕΗΟΤ ΗΤΙΑΣΟ ΙΟΚΟΥΡΩΙΑΣΖΗΕ ΑΗΣΖΚΟΒΟΘΖΑ. Γεκηθά μηα ζοζθεοή πμο ζπεμαηίδεη θνμζζμύξ ζομβμιήξ μκμμάδεηαη ζομβμιόμεηνμ. Ε ανπή ιεηημονγίαξ εκόξ ζομβμιόμεηνμο δηαηνέζεςξ
1 ΣΟ ΠΓΙΡΑΜΑ ΣΟΤ YOUNG (1800) ΙΓΣΡΕΕ ΙΕΗΟΤ ΗΤΙΑΣΟ ΙΟΚΟΥΡΩΙΑΣΖΗΕ ΑΗΣΖΚΟΒΟΘΖΑ. Γεκηθά μηα ζοζθεοή πμο ζπεμαηίδεη θνμζζμύξ ζομβμιήξ μκμμάδεηαη ζομβμιόμεηνμ. Ε ανπή ιεηημονγίαξ εκόξ ζομβμιόμεηνμο δηαηνέζεςξ
Κεθάλαιο 3 Κρσπηογραθία δημόζιοσ κλειδιού και πιζηοποίηζη ασθεμηικόηηηας μημσμάηφμ
 Κεθάλαιο 3 Κρσπηογραθία δημόζιοσ κλειδιού και πιζηοποίηζη ασθεμηικόηηηας μημσμάηφμ Giannis F. Marias 1 Περίληυη Πνμζεγγίζεηξ ςξ πνμξ ηεκ πηζημπμίεζε μεκομάηςκ Σοκανηήζεηξ αζθαιμύξ θαηαθενμαηηζμμύ θαη HMAC
Κεθάλαιο 3 Κρσπηογραθία δημόζιοσ κλειδιού και πιζηοποίηζη ασθεμηικόηηηας μημσμάηφμ Giannis F. Marias 1 Περίληυη Πνμζεγγίζεηξ ςξ πνμξ ηεκ πηζημπμίεζε μεκομάηςκ Σοκανηήζεηξ αζθαιμύξ θαηαθενμαηηζμμύ θαη HMAC
Πνμθόπημξ Mαγηάηεξ, 11-8-2013
 Πακεπηζηήμημ Αζεκώκ, Τμήμα Φανμαθεοηηθήξ ΝΓΓ ΠΡΟΟΠΣΙΚΓ ΑΞΙΟΠΟΙΗΗ ΣΟΤ ΓΛΑΙΟΛΑΔΟΤ ΜΓ ΒΑΗ ΣΑ ΤΓΓΙΟΠΡΟΣΑΣΓΤΣΙΚΑ ΣΟΤ ΥΑΡΑΚΣΗΡΙΣΙΚΑ. TA ΑΠΟΣΓΛΓΜΑΣΑ ΣΗ ΜΓΛΓΣΗ ΘΑΟΤ-ΚΑΒΑΛΑ Πνμθόπημξ Mαγηάηεξ, 11-8-2013 Φανμαθμγκςζία
Πακεπηζηήμημ Αζεκώκ, Τμήμα Φανμαθεοηηθήξ ΝΓΓ ΠΡΟΟΠΣΙΚΓ ΑΞΙΟΠΟΙΗΗ ΣΟΤ ΓΛΑΙΟΛΑΔΟΤ ΜΓ ΒΑΗ ΣΑ ΤΓΓΙΟΠΡΟΣΑΣΓΤΣΙΚΑ ΣΟΤ ΥΑΡΑΚΣΗΡΙΣΙΚΑ. TA ΑΠΟΣΓΛΓΜΑΣΑ ΣΗ ΜΓΛΓΣΗ ΘΑΟΤ-ΚΑΒΑΛΑ Πνμθόπημξ Mαγηάηεξ, 11-8-2013 Φανμαθμγκςζία
1. Camtasia. 2. Audacity. 3. Movie Maker
 1. Camtasia 2. Audacity 3. Movie Maker Από ημ Γεςθεκηνηθό ζημ Ηιημθεκηνηθό Σύζηεμα Από ημ Γεςθεκηνηθό ζημ Ηιημθεκηνηθό Σύζηεμα Πενηπόμεκα: Γεςθεκηνηθό Σύζηεμα Ηιημθεκηνηθό Σύζηεμα Σύγθνηζε Τη γκςνίδμομε
1. Camtasia 2. Audacity 3. Movie Maker Από ημ Γεςθεκηνηθό ζημ Ηιημθεκηνηθό Σύζηεμα Από ημ Γεςθεκηνηθό ζημ Ηιημθεκηνηθό Σύζηεμα Πενηπόμεκα: Γεςθεκηνηθό Σύζηεμα Ηιημθεκηνηθό Σύζηεμα Σύγθνηζε Τη γκςνίδμομε
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων
 Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Ελάχιστα σκελετικά δένδρα (αλγόριθμοι Prim και Kruskal), κωδικοποίηση Huffman Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Ελάχιστα σκελετικά δένδρα (αλγόριθμοι Prim και Kruskal), κωδικοποίηση Huffman Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών
Θμγμηεπκία γηα Παηδηά Ζ
 Θμγμηεπκία γηα Παηδηά Ζ Γκόηεηα 2: Παναμύζη Δεμήηνεξ Πμιίηεξ πμιή Ακζνςπηζηηθώκ θαη Ημηκςκηθώκ Γπηζηεμώκ Σ.Γ.Γ.Α.Π.Ε. 1 θμπμί εκόηεηαξ Ηαηακόεζε ηςκ βαζηθώκ εηδώκ ηςκ Θασθώκ Αθεγήζεςκ-Δηάθνηζε/Αλημπμίεζε
Θμγμηεπκία γηα Παηδηά Ζ Γκόηεηα 2: Παναμύζη Δεμήηνεξ Πμιίηεξ πμιή Ακζνςπηζηηθώκ θαη Ημηκςκηθώκ Γπηζηεμώκ Σ.Γ.Γ.Α.Π.Ε. 1 θμπμί εκόηεηαξ Ηαηακόεζε ηςκ βαζηθώκ εηδώκ ηςκ Θασθώκ Αθεγήζεςκ-Δηάθνηζε/Αλημπμίεζε
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων. Ενότητα: Βασικά στοιχεία σχεδίασης & ανάλυσης αλγορίθμων
 Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Βασικά στοιχεία σχεδίασης & ανάλυσης αλγορίθμων Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή ζηε Θεςνία
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Βασικά στοιχεία σχεδίασης & ανάλυσης αλγορίθμων Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή ζηε Θεςνία
Αλάιπζε Αιγνξίζκωλ. Κεθ. 13: Τπραίνη Αιγόξηζκνη
 Μενηθέξ δηαθάκεηεξ βαζίδμκηαη ζε δηαθάκεηεξ ημο Kevin Wayne. Copyright @ 2005 Pearson-Addison Wesley. All rights reserved. Αλάιπζε Αιγνξίζκωλ Κεθ. 13: Τπραίνη Αιγόξηζκνη 1 Σοπαίμη Αιγόνηζμμη Έκαξ ησταίος
Μενηθέξ δηαθάκεηεξ βαζίδμκηαη ζε δηαθάκεηεξ ημο Kevin Wayne. Copyright @ 2005 Pearson-Addison Wesley. All rights reserved. Αλάιπζε Αιγνξίζκωλ Κεθ. 13: Τπραίνη Αιγόξηζκνη 1 Σοπαίμη Αιγόνηζμμη Έκαξ ησταίος
641: πεδίαζε θαη Ακάιοζε Αιγμνίζμςκ. Υάνεξ Παπαδόπμοιμξ
 641: πεδίαζε θαη Ακάιοζε Αιγμνίζμςκ Υάνεξ Παπαδόπμοιμξ Δηαδηθαζηηθά Μαζήμαημξ Δηδαζθαιία: Πέμπηε 11:00-14:00 Γπηπιέμκ: Ονηζμέκεξ Πέμπηεξ/Παναζθεοέξ 16:00-19:00 Ακαπιενώζεηξ μαζεμάηςκ / ομπιενςμαηηθέξ αζθήζεηξ
641: πεδίαζε θαη Ακάιοζε Αιγμνίζμςκ Υάνεξ Παπαδόπμοιμξ Δηαδηθαζηηθά Μαζήμαημξ Δηδαζθαιία: Πέμπηε 11:00-14:00 Γπηπιέμκ: Ονηζμέκεξ Πέμπηεξ/Παναζθεοέξ 16:00-19:00 Ακαπιενώζεηξ μαζεμάηςκ / ομπιενςμαηηθέξ αζθήζεηξ
Μελέηη Ηλεκηοικήπ Εγκαηάζηαζηπ. Δκπαιδεςηήρ: αββίδεο Μηράιεο. Σερληθή ρνιή Απγόξνπ. Μάθημα: Σερλνινγία Ηιεθηξηθώλ Εγθαηαζηάζεσλ
 Μελέηη Ηλεκηοικήπ Εγκαηάζηαζηπ Δκπαιδεςηήρ: Σερληθή ρνιή Απγόξνπ Μάθημα: Σερλνινγία Ηιεθηξηθώλ Εγθαηαζηάζεσλ Εμδεικηική βιβλιξγοαθία 1. Τεσνολογία Ηλεκηπικών Δγκαηαζηάζευν - Μεπορ Α, ΥΑΠ, ΓΜΤΔΔ 1988 2.
Μελέηη Ηλεκηοικήπ Εγκαηάζηαζηπ Δκπαιδεςηήρ: Σερληθή ρνιή Απγόξνπ Μάθημα: Σερλνινγία Ηιεθηξηθώλ Εγθαηαζηάζεσλ Εμδεικηική βιβλιξγοαθία 1. Τεσνολογία Ηλεκηπικών Δγκαηαζηάζευν - Μεπορ Α, ΥΑΠ, ΓΜΤΔΔ 1988 2.
Κα ακαγκςνίζμομε ημ ηηηάκημ ένγμ (όιςκ) ηςκ ενγαδμμέκςκ ζημ CERN. Να απμθηήζμομε βηςμαηηθέξ γκώζεηξ γηα πενίπιμθεξ έκκμηεξ ηςκ Φοζηθώκ Γπηζηεμώκ.
 Ζηαιία Γιβεηία Μη ζηόπμη μαξ Να πνμβιεμαηηζημύμε γηα ηεκ απανπή ημο ζύμπακημξ. Κα ακαγκςνίζμομε ημ ηηηάκημ ένγμ (όιςκ) ηςκ ενγαδμμέκςκ ζημ CERN. Να απμθηήζμομε βηςμαηηθέξ γκώζεηξ γηα πενίπιμθεξ έκκμηεξ
Ζηαιία Γιβεηία Μη ζηόπμη μαξ Να πνμβιεμαηηζημύμε γηα ηεκ απανπή ημο ζύμπακημξ. Κα ακαγκςνίζμομε ημ ηηηάκημ ένγμ (όιςκ) ηςκ ενγαδμμέκςκ ζημ CERN. Να απμθηήζμομε βηςμαηηθέξ γκώζεηξ γηα πενίπιμθεξ έκκμηεξ
ΕΞΟΡΤΞΗ & ΚΑΣΑΚΕΤΕ ΣΗΝ ΕΤΡΩΠΗ ΜΑΘΗΜΑ 43
 ΕΞΟΡΤΞΗ & ΚΑΣΑΚΕΤΕ ΣΗΝ ΕΤΡΩΠΗ ΜΑΘΗΜΑ 43 Κα ακαθένεηε 5 εονςπασθέξ πώνεξ θαη κα βνείηε ημ είδμξ ημο μνοθημύ ημοξ πιμύημο. Πμημη πανάγμκηεξ επηηνέπμοκ ηεκ θαηαζθεοή μεγάιςκ ηεπκηθώκ ένγςκ; Ε ελόνολε (ελαγςγή
ΕΞΟΡΤΞΗ & ΚΑΣΑΚΕΤΕ ΣΗΝ ΕΤΡΩΠΗ ΜΑΘΗΜΑ 43 Κα ακαθένεηε 5 εονςπασθέξ πώνεξ θαη κα βνείηε ημ είδμξ ημο μνοθημύ ημοξ πιμύημο. Πμημη πανάγμκηεξ επηηνέπμοκ ηεκ θαηαζθεοή μεγάιςκ ηεπκηθώκ ένγςκ; Ε ελόνολε (ελαγςγή
Άπιεζημη αιγόνηζμμη. Μάνζα Σηδένε
 Άπιεζημη αιγόνηζμμη Μάνζα Σηδένε Πξνηεηλόκελε βηβιηνγξαθία: S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani «Αιγόξηζκνη» Κιεηδάξηζκνο 2009 Κεθάιαην 5. http://www.cs.berkeley.edu/~vazirani/algorithms/chap5.pdf
Άπιεζημη αιγόνηζμμη Μάνζα Σηδένε Πξνηεηλόκελε βηβιηνγξαθία: S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani «Αιγόξηζκνη» Κιεηδάξηζκνο 2009 Κεθάιαην 5. http://www.cs.berkeley.edu/~vazirani/algorithms/chap5.pdf
Μυοπάθεια και τατίνες
 Μυοπάθεια και τατίνες ΧΡΗΣΟ Ν. ΠΑΝΑΓΟΤΛΗ ΔΙΕΤΘΤΝΣΗ ΚΑΡΔΙΟΛΟΓΟ ΚΑΡΔΙΟΛΟΓΙΚΗ ΚΛΙΝΙΚΗ ΙΑΣΡΕΙΟ ΤΠΕΡΣΑΗ ΚΑΙ ΛΙΠΙΔΙΩΝ ΓΕΝΙΚΟ ΝΟΟΚΟΜΕΙΟ ΑΘΗΝΩΝ Γ. ΓΕΝΝΗΜΑΣΑ ηαηίκεξ Μεηώκμοκ ηεκ LDLπμι. 30-55%, ηα Σνηγι. 10-30%
Μυοπάθεια και τατίνες ΧΡΗΣΟ Ν. ΠΑΝΑΓΟΤΛΗ ΔΙΕΤΘΤΝΣΗ ΚΑΡΔΙΟΛΟΓΟ ΚΑΡΔΙΟΛΟΓΙΚΗ ΚΛΙΝΙΚΗ ΙΑΣΡΕΙΟ ΤΠΕΡΣΑΗ ΚΑΙ ΛΙΠΙΔΙΩΝ ΓΕΝΙΚΟ ΝΟΟΚΟΜΕΙΟ ΑΘΗΝΩΝ Γ. ΓΕΝΝΗΜΑΣΑ ηαηίκεξ Μεηώκμοκ ηεκ LDLπμι. 30-55%, ηα Σνηγι. 10-30%
Μμκηειμπμίεζε θαη Aκάιοζε Βημσαηνηθώκ θαη Φοζηθώκ Σοζηεμάηςκ
 Μμκηειμπμίεζε θαη Aκάιοζε Βημσαηνηθώκ θαη Φοζηθώκ Σοζηεμάηςκ Γκδμπακεπηζηεμηαθό Δίθηομ Πακεπηζηεμίμο Παηνώκ Γπηζηεμμκηθόξ Υπεύζοκμξ:Τάζμξ Μπμύκηεξ Τμήμα Μαζεμαηηθώκ MATHEMATICS DEPARTMENT Laboratory of
Μμκηειμπμίεζε θαη Aκάιοζε Βημσαηνηθώκ θαη Φοζηθώκ Σοζηεμάηςκ Γκδμπακεπηζηεμηαθό Δίθηομ Πακεπηζηεμίμο Παηνώκ Γπηζηεμμκηθόξ Υπεύζοκμξ:Τάζμξ Μπμύκηεξ Τμήμα Μαζεμαηηθώκ MATHEMATICS DEPARTMENT Laboratory of
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων
 Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Επιλεγμένα θέματα: Υπολογιστική πολυπλοκότητα και ΝΡ-πληρότητα Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Επιλεγμένα θέματα: Υπολογιστική πολυπλοκότητα και ΝΡ-πληρότητα Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή
ΜΑΘΕΜΑ Β2.1 Ε ΤΝΘΓΕ ΣΕ ΑΣΜΟΦΑΖΡΑ, Ε ΑΣΜΟΦΑΖΡΑ, ΟΖ ΑΝΓΜΟΖ.
 ΜΑΘΕΜΑ Β2.1 Ε ΤΝΘΓΕ ΣΕ ΑΣΜΟΦΑΖΡΑ, Ε ΑΣΜΟΦΑΖΡΑ, ΟΖ ΑΝΓΜΟΖ. Αημόζθαιοα: έκαξ ΑΓΡΖΟ ςθεακόξ, μ μπμίμξ γίκεηαη όιμ θαη πημ ΑΡΑΖΟ θαζώξ ακεβαίκμομε Σμ 90% Σεξ μάδαξ ηεξ αημόζθαηναξ είκαη ζογθεκηνςμέκμ ζηα πνώηα
ΜΑΘΕΜΑ Β2.1 Ε ΤΝΘΓΕ ΣΕ ΑΣΜΟΦΑΖΡΑ, Ε ΑΣΜΟΦΑΖΡΑ, ΟΖ ΑΝΓΜΟΖ. Αημόζθαιοα: έκαξ ΑΓΡΖΟ ςθεακόξ, μ μπμίμξ γίκεηαη όιμ θαη πημ ΑΡΑΖΟ θαζώξ ακεβαίκμομε Σμ 90% Σεξ μάδαξ ηεξ αημόζθαηναξ είκαη ζογθεκηνςμέκμ ζηα πνώηα
Μικροβιολογία & Υγιεινή Τροφίμων
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μικροβιολογία & Υγιεινή Τροφίμων Μικροοργανισμοί που ελέγχονται ανά είδος τροφίμου Διδάσκοντες: Καθ. Χρυσάνθη Παπαδοπούλου, Λέκτορας Ηρακλής Σακκάς Άδειες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μικροβιολογία & Υγιεινή Τροφίμων Μικροοργανισμοί που ελέγχονται ανά είδος τροφίμου Διδάσκοντες: Καθ. Χρυσάνθη Παπαδοπούλου, Λέκτορας Ηρακλής Σακκάς Άδειες
ΙΑΘΕΙΑ Α1.3 Ε ΥΡΕΕ ΣΩΚ ΥΑΡΣΩΚ ΣΕΚ ΗΑΘΕΙΓΡΖΚΕ ΔΩΕ. Ελένη Παλούμπα, Χημικός, Πειραματικό Γσμνάσιο Σπάρτης
 ΙΑΘΕΙΑ Α1.3 Ε ΥΡΕΕ ΣΩΚ ΥΑΡΣΩΚ ΣΕΚ ΗΑΘΕΙΓΡΖΚΕ ΔΩΕ ΣΖ ΠΑΡΟΤΖΑΔΓΖ Ο ΥΑΡΣΕ; Ε ΓΡΩΣΕΕ ΑΤΣΕ ΙΑ ΟΔΕΓΓΖ ΣΟΚ ΣΙΣΛΟ. Ο ΣΖΣΘΟ ΔΖΚΓΖ ΠΘΕΡΟΦΟΡΖΓ ΓΖΑ ΣΟ ΠΕΡΙΕΧΟΜΕΝΟ ΣΟΤ ΥΑΡΣΕ. ΥΑΡΣΗ ΓΙΑ ΣΗ ΜΟΡΦΟΛΟΓΙΑ ΣΟΤ ΔΓΑΦΟΤ ΥΑΡΣΗ
ΙΑΘΕΙΑ Α1.3 Ε ΥΡΕΕ ΣΩΚ ΥΑΡΣΩΚ ΣΕΚ ΗΑΘΕΙΓΡΖΚΕ ΔΩΕ ΣΖ ΠΑΡΟΤΖΑΔΓΖ Ο ΥΑΡΣΕ; Ε ΓΡΩΣΕΕ ΑΤΣΕ ΙΑ ΟΔΕΓΓΖ ΣΟΚ ΣΙΣΛΟ. Ο ΣΖΣΘΟ ΔΖΚΓΖ ΠΘΕΡΟΦΟΡΖΓ ΓΖΑ ΣΟ ΠΕΡΙΕΧΟΜΕΝΟ ΣΟΤ ΥΑΡΣΕ. ΥΑΡΣΗ ΓΙΑ ΣΗ ΜΟΡΦΟΛΟΓΙΑ ΣΟΤ ΔΓΑΦΟΤ ΥΑΡΣΗ
Τπμιμγηζμόξ ηεξ ηαπύηεηαξ ηεξ πεμηθήξ ακηίδναζεξ ημο Mg με HCl
 ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ 2 Τπμιμγηζμόξ ηεξ ηαπύηεηαξ ηεξ πεμηθήξ ακηίδναζεξ ημο Mg με HCl (με ηε βμήζεηα ημο θαηαγναθέα loggerpro) θμπόξ Η δεμημονγία ηεξ θαμπύιεξ μεηαβμιήξ ηεξ ζογθέκηνςζεξ εκόξ πνμσόκημξ, ζηεκ
ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ 2 Τπμιμγηζμόξ ηεξ ηαπύηεηαξ ηεξ πεμηθήξ ακηίδναζεξ ημο Mg με HCl (με ηε βμήζεηα ημο θαηαγναθέα loggerpro) θμπόξ Η δεμημονγία ηεξ θαμπύιεξ μεηαβμιήξ ηεξ ζογθέκηνςζεξ εκόξ πνμσόκημξ, ζηεκ
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων
 Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Μέθοδος "δυναμικού προγραμματισμού": Ροή δικτύου, χρονοπρογραμματισμός και σακίδια Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Μέθοδος "δυναμικού προγραμματισμού": Ροή δικτύου, χρονοπρογραμματισμός και σακίδια Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών
ΕΙΗΓΗΗ: Σα Πληροθοριακά σζηήμαηα ηων Νοζοκομείων ζηην Ελλάδα ηης κρίζης: Ο ρόλος ηοσ cloud computing & ηοσ Εζωηερικού Ελέγτοσ
 3ο Πανελλήνιο σνέδριο Διατείριζης Κρίζεων ζηον Σομέα Yγείας ΟΡΓΑΝΩΗ: Ελληνική Εηαιρεία Διατείριζης Κρίζεων ζηον Σομέα Τγείας, 13 15/11/2015, Ξενοδοτείο Divani Caravel, Αθήνα. Προθορική Ανακοίνωζη Νο. 33
3ο Πανελλήνιο σνέδριο Διατείριζης Κρίζεων ζηον Σομέα Yγείας ΟΡΓΑΝΩΗ: Ελληνική Εηαιρεία Διατείριζης Κρίζεων ζηον Σομέα Τγείας, 13 15/11/2015, Ξενοδοτείο Divani Caravel, Αθήνα. Προθορική Ανακοίνωζη Νο. 33
Δηάιελε 6: Δηαπείνηζε Μκήμεξ & Δοκαμηθέξ Δμμέξ Δεδμμέκςκ
 Δηάιελε 6: Δηαπείνηζε Μκήμεξ & Δοκαμηθέξ Δμμέξ Δεδμμέκςκ Σηεκ εκόηεηα αοηή ζα μειεηεζμύκ ηα ελήξ επημένμοξ ζέμαηα: Δοκαμηθέξ Δμμέξ Δεδμμέκςκ Γεκηθά Δοκαμηθή Δέζμεοζε/Απμδέζμεοζε Μκήμεξ Δμμή ηύπμο structure
Δηάιελε 6: Δηαπείνηζε Μκήμεξ & Δοκαμηθέξ Δμμέξ Δεδμμέκςκ Σηεκ εκόηεηα αοηή ζα μειεηεζμύκ ηα ελήξ επημένμοξ ζέμαηα: Δοκαμηθέξ Δμμέξ Δεδμμέκςκ Γεκηθά Δοκαμηθή Δέζμεοζε/Απμδέζμεοζε Μκήμεξ Δμμή ηύπμο structure
Tνόπμη δηαθοηηανηθήξ επηθμηκςκίαξ
 Tνόπμη δηαθοηηανηθήξ επηθμηκςκίαξ Από απόζηαζε: -Γκδμθνηκήξ -Παναθνηκήξ Signaling cell Target cell Με επαθή Gap junction Notch signaling εμαημδόηεζε μέζς θακαιηώκ ηόκηςκ: Κακάιηα ηόκηςκ ςξ δηαθόπηεξ Πένα
Tνόπμη δηαθοηηανηθήξ επηθμηκςκίαξ Από απόζηαζε: -Γκδμθνηκήξ -Παναθνηκήξ Signaling cell Target cell Με επαθή Gap junction Notch signaling εμαημδόηεζε μέζς θακαιηώκ ηόκηςκ: Κακάιηα ηόκηςκ ςξ δηαθόπηεξ Πένα
Γηζαγωγή ζηεκ Πιεζοζμηαθή Οηθμιμγία. Α. Φακηηκμύ
 Γηζαγωγή ζηεκ Πιεζοζμηαθή Οηθμιμγία Α. Φακηηκμύ http://www.aua.gr/fantinou/ Πιεζοζμόξ- πενημπή ύκμιμ αηόμωκ ημο ηδίμο είδμοξ πμο δμοκ ζε μία πενημπή (μέγεζμξ πιεζοζμμύ) Ονημζέηεζε μηαξ πενημπήξ δύζθμιε
Γηζαγωγή ζηεκ Πιεζοζμηαθή Οηθμιμγία Α. Φακηηκμύ http://www.aua.gr/fantinou/ Πιεζοζμόξ- πενημπή ύκμιμ αηόμωκ ημο ηδίμο είδμοξ πμο δμοκ ζε μία πενημπή (μέγεζμξ πιεζοζμμύ) Ονημζέηεζε μηαξ πενημπήξ δύζθμιε
Κοσμάς Λιάμος Γενικός Ιατρός Επιμελητής Β Περιυερειακό Ιατρείο Βελβεντού Κέντρο Τγείας ερβίων
 «Ο νυιμξ ημο γηαηνμφ πνςημβάζμηαξ θνμκηίδαξ ογείαξ ζηεκ πνυιερε θαη πνχημε δηάγκςζε ημο θανθίκμο ημο πκεφμμκα» Κοσμάς Λιάμος Γενικός Ιατρός Επιμελητής Β Περιυερειακό Ιατρείο Βελβεντού Κέντρο Τγείας ερβίων
«Ο νυιμξ ημο γηαηνμφ πνςημβάζμηαξ θνμκηίδαξ ογείαξ ζηεκ πνυιερε θαη πνχημε δηάγκςζε ημο θανθίκμο ημο πκεφμμκα» Κοσμάς Λιάμος Γενικός Ιατρός Επιμελητής Β Περιυερειακό Ιατρείο Βελβεντού Κέντρο Τγείας ερβίων
Κοιμό Γεωγραφικό Υπόβαθρο για το WISE
 Κοιμό Γεωγραφικό Υπόβαθρο για το WISE Νονιήξ Γ. Γεςζεζία ΓΝΓ Ημοθμοβίκμξ Α. Γζκηθό Ιεηζόβημ Νμιοηεπκείμ Οαιαπώνεξ Ι. Γεςζεζία ΓΝΓ Πη είκαη ημ θμηκό γεςγναθηθό οπόβαζνμ γηα ημ WISE Απμηειείηαη από : A.
Κοιμό Γεωγραφικό Υπόβαθρο για το WISE Νονιήξ Γ. Γεςζεζία ΓΝΓ Ημοθμοβίκμξ Α. Γζκηθό Ιεηζόβημ Νμιοηεπκείμ Οαιαπώνεξ Ι. Γεςζεζία ΓΝΓ Πη είκαη ημ θμηκό γεςγναθηθό οπόβαζνμ γηα ημ WISE Απμηειείηαη από : A.
Εισαγωγή στους Αλγορίθμους
 Εισαγωγή στους Αλγορίθμους Ενότητα 5η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Η Μέθοδος «Διαίρει & Βασίλευε» Η Μέθοδος
Εισαγωγή στους Αλγορίθμους Ενότητα 5η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Η Μέθοδος «Διαίρει & Βασίλευε» Η Μέθοδος
H ΑΞΙΑ ΣΗ ΓΛΙΑ ΚΑΙ ΣΟΤ ΓΛΑΙΟΛΑΔΟΤ ΜΤΘΟΙ & ΠΡΑΓΜΑΣΙΚΟΣΗΣΑ. << Γιηά & Λάδη >>
 H ΑΞΙΑ ΣΗ ΓΛΙΑ ΚΑΙ ΣΟΤ ΓΛΑΙΟΛΑΔΟΤ ΜΤΘΟΙ & ΠΡΑΓΜΑΣΙΚΟΣΗΣΑ > ΜΟΛΑΟΙ 9 Οθηςβνίμο 2011 Καηεγμνίεξ θνηηενίςκ πνμζηαζίαξ, αλημιόγεζεξ θαη επηιμγήξ, Έληνα Πανζέκμο Γιαημιάδμο Κνηηήνηα πμηόηεηαξ
H ΑΞΙΑ ΣΗ ΓΛΙΑ ΚΑΙ ΣΟΤ ΓΛΑΙΟΛΑΔΟΤ ΜΤΘΟΙ & ΠΡΑΓΜΑΣΙΚΟΣΗΣΑ > ΜΟΛΑΟΙ 9 Οθηςβνίμο 2011 Καηεγμνίεξ θνηηενίςκ πνμζηαζίαξ, αλημιόγεζεξ θαη επηιμγήξ, Έληνα Πανζέκμο Γιαημιάδμο Κνηηήνηα πμηόηεηαξ
ΑΓΠΠ 2o Γπαμαληπηικό Διαγώμιζμα
 ΑΓΠΠ 2o Γπαμαληπηικό Διαγώμιζμα Οκμμαηεπχκομμ: ΘΓΜΑ 1 A. Κα γνάρεηε ημοξ θακυκεξ πμο πνέπεη κα αθμιμοζμφκηαη ζηε πνήζε ηςκ εμθςιεομέκςκ βνυπςκ. Β1. Na γίκεη μ πμιιαπιαζηαζμυξ 15 * 45 αιά Ρχζηθα Β2. Nα
ΑΓΠΠ 2o Γπαμαληπηικό Διαγώμιζμα Οκμμαηεπχκομμ: ΘΓΜΑ 1 A. Κα γνάρεηε ημοξ θακυκεξ πμο πνέπεη κα αθμιμοζμφκηαη ζηε πνήζε ηςκ εμθςιεομέκςκ βνυπςκ. Β1. Na γίκεη μ πμιιαπιαζηαζμυξ 15 * 45 αιά Ρχζηθα Β2. Nα
ΓΗΔΕΘΩΟΓΖΟ ΠΕΟ ΝΑΖΔΑΓΩΓΖΗΕΟ ΟΜΘΕΟ, ΑΝΘ. Αθαδεμασθό έημξ: 2008-2009. (πνμκμιμγηθή ζεηνά)
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΣΙΑ ΠΑΙΔΑΓΩΓΙΚΗ ΣΧΟΛΗ ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ Δήμηηοα Κξγκίδξρ, Κξζμηηόοιζζα Τηλ.: 2310 99 1290, Fax: 2310 99 5061 e-mail: info@educ.auth.gr Κτίριο: Πύργος (3 ος όροφος) Θεσσαλονίκη,
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΣΙΑ ΠΑΙΔΑΓΩΓΙΚΗ ΣΧΟΛΗ ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ Δήμηηοα Κξγκίδξρ, Κξζμηηόοιζζα Τηλ.: 2310 99 1290, Fax: 2310 99 5061 e-mail: info@educ.auth.gr Κτίριο: Πύργος (3 ος όροφος) Θεσσαλονίκη,
HY-335 : Δίθηοα Υπμιμγηζηώκ
 W N net works R E O T HY-335 : Δίθηοα Υπμιμγηζηώκ K Επίπεδο Δικηύου Αλγόριθμοι Δρομολόγηζη Scalability issues Multiple domains Ιανία Παπαδμπμύιε Τμήμα Γπηζηήμεξ Υπμιμγηζηώκ Πακεπηζηήμημ Ηνήηεξ Φεημενηκό
W N net works R E O T HY-335 : Δίθηοα Υπμιμγηζηώκ K Επίπεδο Δικηύου Αλγόριθμοι Δρομολόγηζη Scalability issues Multiple domains Ιανία Παπαδμπμύιε Τμήμα Γπηζηήμεξ Υπμιμγηζηώκ Πακεπηζηήμημ Ηνήηεξ Φεημενηκό
ΓΤΡΩΠΗ. 5 ή 6 ΕΙΓΞΓΟ ΑΓΞΜΝΜΞΖΗΕ ΓΗΔΞΜΙΕ ΖΠΑΘΖΗΜ ΝΑΚΜΞΑΙΑ ΒΓΚΓΠΖΑ-ΦΘΩΞΓΚΠΖΑ-ΟΖΓΚΑ-ΞΩΙΕ ΑΚΑΩΞΕΟΓΖΟ : 5ΕΙΓΞΓΟ : ΗΑΘΓ ΠΞΖΠΕ 6ΕΙΓΞΓΟ : KAΘΓ ΠΞΖΠΕ
 ΓΤΡΩΠΗ 5 ή 6 ΕΙΓΞΓΟ ΑΓΞΜΝΜΞΖΗΕ ΓΗΔΞΜΙΕ ΖΠΑΘΖΗΜ ΝΑΚΜΞΑΙΑ ΒΓΚΓΠΖΑ-ΦΘΩΞΓΚΠΖΑ-ΟΖΓΚΑ-ΞΩΙΕ ΑΚΑΩΞΕΟΓΖΟ : 5ΕΙΓΞΓΟ : ΗΑΘΓ ΠΞΖΠΕ 6ΕΙΓΞΓΟ : KAΘΓ ΠΞΖΠΕ Ννόγναμμα 1 ε ΙΓΞΑ: ΑΘΕΚΑ ΙΖΘΑΚΜ ή ΙΝΜΘΜΚΖΑ ή ΒΓΚΓΠΖΑ Νηήζε γηα
ΓΤΡΩΠΗ 5 ή 6 ΕΙΓΞΓΟ ΑΓΞΜΝΜΞΖΗΕ ΓΗΔΞΜΙΕ ΖΠΑΘΖΗΜ ΝΑΚΜΞΑΙΑ ΒΓΚΓΠΖΑ-ΦΘΩΞΓΚΠΖΑ-ΟΖΓΚΑ-ΞΩΙΕ ΑΚΑΩΞΕΟΓΖΟ : 5ΕΙΓΞΓΟ : ΗΑΘΓ ΠΞΖΠΕ 6ΕΙΓΞΓΟ : KAΘΓ ΠΞΖΠΕ Ννόγναμμα 1 ε ΙΓΞΑ: ΑΘΕΚΑ ΙΖΘΑΚΜ ή ΙΝΜΘΜΚΖΑ ή ΒΓΚΓΠΖΑ Νηήζε γηα
Αμαμεώζιμες πηγές εμέργειας
 Αμαμεώζιμες πηγές εμέργειας Τι είμαι η αμαμεώζιμη εμέργεια; Η ακακεώζημε εκένγεηα πνμένπεηαη από θοζηθέξ πεγέξ θαη ακαπιενώκεηαη θοζηθά. Ακακεώζημεξ πεγέξ εκένγεηαξ ζεςνμύκηαη ημ θςξ ημο ήιημο, μη άκεμμη
Αμαμεώζιμες πηγές εμέργειας Τι είμαι η αμαμεώζιμη εμέργεια; Η ακακεώζημε εκένγεηα πνμένπεηαη από θοζηθέξ πεγέξ θαη ακαπιενώκεηαη θοζηθά. Ακακεώζημεξ πεγέξ εκένγεηαξ ζεςνμύκηαη ημ θςξ ημο ήιημο, μη άκεμμη
Τίτλος Μαθήματος: Θεωρία Πολυπλοκότητας. Ενότητα: H κλάση ΝΡ. Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος. Τμήμα: Μαθηματικών
 Τίτλος Μαθήματος: Θεωρία Πολυπλοκότητας Ενότητα: H κλάση ΝΡ Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών Θεςνία Νμιοπιμθόηεηαξ άνεξ Ναπαδόπμοιμξ Αιγμνηζμηθέξ Πεπκηθέξ θαη Γμπόδηα Αιγμνηζμηθέξ
Τίτλος Μαθήματος: Θεωρία Πολυπλοκότητας Ενότητα: H κλάση ΝΡ Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών Θεςνία Νμιοπιμθόηεηαξ άνεξ Ναπαδόπμοιμξ Αιγμνηζμηθέξ Πεπκηθέξ θαη Γμπόδηα Αιγμνηζμηθέξ
Τβοιδικό Ιζξδύμαμξ Μξμηέλξ transistor BJT & εκηζποηέξ. Ειεθηνμκηθή Γ Σάλε /Β ελάμεκμ Γπίθ. Ηαζεγήηνηα Γ. Ηαναγηάκκε
 Τβοιδικό Ιζξδύμαμξ Μξμηέλξ tansst BJT & εκηζποηέξ Ειεθηνμκηθή Γ Σάλε /Β ελάμεκμ Γπίθ. Ηαζεγήηνηα Γ. Ηαναγηάκκε Ιζξδύμαμα Κρκλώμαηα? Πίνακας σύνθετων αντιστάσεων z z z z y y y y Πίνακας σύνθετων Γύθμιμξ
Τβοιδικό Ιζξδύμαμξ Μξμηέλξ tansst BJT & εκηζποηέξ Ειεθηνμκηθή Γ Σάλε /Β ελάμεκμ Γπίθ. Ηαζεγήηνηα Γ. Ηαναγηάκκε Ιζξδύμαμα Κρκλώμαηα? Πίνακας σύνθετων αντιστάσεων z z z z y y y y Πίνακας σύνθετων Γύθμιμξ
Κεφάλαιο 4. Διαίρει και Βασίλευε (Divide and Conquer) Παύλος Εφραιμίδης V1.1,
 Κεφάλαιο 4 Διαίρει και Βασίλευε (Divide and Conquer) Παύλος Εφραιμίδης V1.1, 2015-01-19 Χρησιμοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne. 1 Διαίρει και Βασίλευε (Divide-and-Conquer) Διαίρει-και-βασίλευε
Κεφάλαιο 4 Διαίρει και Βασίλευε (Divide and Conquer) Παύλος Εφραιμίδης V1.1, 2015-01-19 Χρησιμοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne. 1 Διαίρει και Βασίλευε (Divide-and-Conquer) Διαίρει-και-βασίλευε
Κεφάλαιο 4. Διαίρει και Βασίλευε (Divide and Conquer) Χρησιµοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne.
 Κεφάλαιο 4 Διαίρει και Βασίλευε (Divide and Conquer) Χρησιµοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne. 1 Διαίρει και Βασίλευε (Divide-and-Conquer) Διαίρει-και-βασίλευε (γενικά) Χωρίζουµε
Κεφάλαιο 4 Διαίρει και Βασίλευε (Divide and Conquer) Χρησιµοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne. 1 Διαίρει και Βασίλευε (Divide-and-Conquer) Διαίρει-και-βασίλευε (γενικά) Χωρίζουµε
Σωλήμες Ηλεκηρικώμ Εγκαηαζηάζεωμ. Εκπαιδεσηής: Σαββίδης Μιτάλης. Τετνική Στολή Ασγόροσ. Μάθημα: Τετνολογία Ηλεκηρικών Εγκαηαζηάζεων
 Σωλήμες Ηλεκηρικώμ Εγκαηαζηάζεωμ Εκπαιδεσηής: Σαββίδης Μιτάλης Τετνική Στολή Ασγόροσ Μάθημα: Τετνολογία Ηλεκηρικών Εγκαηαζηάζεων Εμδεικηική βιβλιογραθία 1. Τετνολογία Ηλεκηρικών Εγκαηαζηάζεων - Μερος Α,
Σωλήμες Ηλεκηρικώμ Εγκαηαζηάζεωμ Εκπαιδεσηής: Σαββίδης Μιτάλης Τετνική Στολή Ασγόροσ Μάθημα: Τετνολογία Ηλεκηρικών Εγκαηαζηάζεων Εμδεικηική βιβλιογραθία 1. Τετνολογία Ηλεκηρικών Εγκαηαζηάζεων - Μερος Α,
H XHMEIA EINAI ΙΑΓΖΗΕ
 H XHMEIA EINAI ΙΑΓΖΗΕ Ναροσσίαση Νειραμάτων από τοσς μαθητές τοσ τμήματος Α1 τοσ ΘΡΗΓΖΜΡ ΒΑΙΜΡ Νείραμα 1 ο ΜΙΖΘΖΑ ΙΓ ΕΘΖΜ (He) Μανία Καιιηβνεηάθε Γθπκέμκηαξ ήιημ, επεηδή έπεη μηθνόηενμ μμνηαθό βάνμξ από
H XHMEIA EINAI ΙΑΓΖΗΕ Ναροσσίαση Νειραμάτων από τοσς μαθητές τοσ τμήματος Α1 τοσ ΘΡΗΓΖΜΡ ΒΑΙΜΡ Νείραμα 1 ο ΜΙΖΘΖΑ ΙΓ ΕΘΖΜ (He) Μανία Καιιηβνεηάθε Γθπκέμκηαξ ήιημ, επεηδή έπεη μηθνόηενμ μμνηαθό βάνμξ από
HY-335 : Δίθηοα Υπμιμγηζηώκ
 W N net works R E O T HY-335 : Δίθηοα Υπμιμγηζηώκ Δπίπεδο Γικηύος K Δνμμμιμγεηέξ, addressing, layers, εκζοιάθςζε Μανία Παπαδμπμύιε Τμήμα Γπηζηήμεξ Υπμιμγηζηώκ Πακεπηζηήμημ Κνήηεξ Φεημενηκό ελάμεκμ 2011-2012
W N net works R E O T HY-335 : Δίθηοα Υπμιμγηζηώκ Δπίπεδο Γικηύος K Δνμμμιμγεηέξ, addressing, layers, εκζοιάθςζε Μανία Παπαδμπμύιε Τμήμα Γπηζηήμεξ Υπμιμγηζηώκ Πακεπηζηήμημ Κνήηεξ Φεημενηκό ελάμεκμ 2011-2012
ΜΑΘΗΜΑ Β 5.1 ΟΡΓΑΝΙΜΩΝ Η ΓΓΩΓΡΑΦΙΚΗ ΚΑΣΑΝΟΜΗ ΣΩΝ. Ελέμη Γ. Παλούμπα, Χημικός, Πειραματικό Γυμμάσιο Σπάρτης
 ΜΑΘΗΜΑ Β 5.1 Η ΓΓΩΓΡΑΦΙΚΗ ΚΑΣΑΝΟΜΗ ΣΩΝ Ελέμη Γ. Παλούμπα, Χημικός, Πειραματικό Γυμμάσιο Σπάρτης ΟΡΓΑΝΙΜΩΝ Βηόζθαηνα: ημ ελςηενηθό πενίβιεμα ημο πιακήηε. Πενηιαμβάκεη ημκ αένα, ημ έδαθμξ,ηo μηθμιμγηθό ζύζηεμα
ΜΑΘΗΜΑ Β 5.1 Η ΓΓΩΓΡΑΦΙΚΗ ΚΑΣΑΝΟΜΗ ΣΩΝ Ελέμη Γ. Παλούμπα, Χημικός, Πειραματικό Γυμμάσιο Σπάρτης ΟΡΓΑΝΙΜΩΝ Βηόζθαηνα: ημ ελςηενηθό πενίβιεμα ημο πιακήηε. Πενηιαμβάκεη ημκ αένα, ημ έδαθμξ,ηo μηθμιμγηθό ζύζηεμα
ΜΤΟΚΑΡΔΙΟΠΑΘΕΙΕ MΤΟΚΑΡΔΙΣΙΔΑ ΜΕΛΕΣΗ ΜΕ ΓΑΔΟΛΙΝΙΟ
 ΜΤΟΚΑΡΔΙΟΠΑΘΕΙΕ MΤΟΚΑΡΔΙΣΙΔΑ ΜΕΛΕΣΗ ΜΕ ΓΑΔΟΛΙΝΙΟ ΙΑΞΖΑ Β. ΗΑΘΑΚΠΔΕ ΗΑΞΔΖΜΘΜΓΜΟ ΖΑΟΩ GENERAL ΜΤΟΚΑΡΔΙΟΠΑΘΕΙΕ - ΣΑΞΙΝΟΜΗΗ Κμζήμαηα ημο μομθανδίμο άγκςζηεξ (πνςημπαζείξ) ή γκςζηήξ (δεοηενμπαζείξ ή εηδηθέξ)
ΜΤΟΚΑΡΔΙΟΠΑΘΕΙΕ MΤΟΚΑΡΔΙΣΙΔΑ ΜΕΛΕΣΗ ΜΕ ΓΑΔΟΛΙΝΙΟ ΙΑΞΖΑ Β. ΗΑΘΑΚΠΔΕ ΗΑΞΔΖΜΘΜΓΜΟ ΖΑΟΩ GENERAL ΜΤΟΚΑΡΔΙΟΠΑΘΕΙΕ - ΣΑΞΙΝΟΜΗΗ Κμζήμαηα ημο μομθανδίμο άγκςζηεξ (πνςημπαζείξ) ή γκςζηήξ (δεοηενμπαζείξ ή εηδηθέξ)
Ψηφιακός Τόπος Εργασίας Γνγμδόηεξ Πνμζςπηθή Σειίδα Γνγαδόμεκμξ Πνμζςπηθή Σειίδα Μηνύματα Θέση Εργασίας Λαγωνικό Βιογραυικό
 www.intrajobs.gr Ψηφιακός Τόπος Εργασίας Γνγαδόμεκμξ Πνμζςπηθή Σειίδα Μηνύματα Γνγμδόηεξ Πνμζςπηθή Σειίδα Βιογραυικό Λαγωνικό Θέση Εργασίας αγμνά Data Base Βιογραυικών Θέσεων Εργασίας αγμνά HR SERVICES
www.intrajobs.gr Ψηφιακός Τόπος Εργασίας Γνγαδόμεκμξ Πνμζςπηθή Σειίδα Μηνύματα Γνγμδόηεξ Πνμζςπηθή Σειίδα Βιογραυικό Λαγωνικό Θέση Εργασίας αγμνά Data Base Βιογραυικών Θέσεων Εργασίας αγμνά HR SERVICES
GANODERMA LUCIDUM «μακηηάνη ηςκ ζεώκ» Τμ θαζμιηθό θάνμαθμ ηεξ θύζεξ
 GANODERMA LUCIDUM «μακηηάνη ηςκ ζεώκ» Τμ θαζμιηθό θάνμαθμ ηεξ θύζεξ Ο «βαζιλιάπ» ηωμ βξηάμωμ Τμ Γακόδενμα (ιαμπενό δένμα) είκαη εδώδημμ μακηηάνη γκςζηό εδώ θαη πηιηάδεξ πνόκηα ζηεκ Ηίκα, ηεκ Ζαπςκία θαη
GANODERMA LUCIDUM «μακηηάνη ηςκ ζεώκ» Τμ θαζμιηθό θάνμαθμ ηεξ θύζεξ Ο «βαζιλιάπ» ηωμ βξηάμωμ Τμ Γακόδενμα (ιαμπενό δένμα) είκαη εδώδημμ μακηηάνη γκςζηό εδώ θαη πηιηάδεξ πνόκηα ζηεκ Ηίκα, ηεκ Ζαπςκία θαη
ΓΑΣΡΟΟΙΟΦΑΓΙΚΗ ΠΑΛΙΝΔΡΟΜΗΗ ΚΑΙ ΑΝΑΠΝΓΤΣΙΚΟ ΤΣΗΜΑ. Δν. Δεμήηνεξ Καπεηάκμξ Γπημειεηήξ A Γαζηνεκηενμιμγηθή Κιηκηθή Γ.Ν. «Γεώνγημξ Παπακηθμιάμο»
 ΓΑΣΡΟΟΙΟΦΑΓΙΚΗ ΠΑΛΙΝΔΡΟΜΗΗ ΚΑΙ ΑΝΑΠΝΓΤΣΙΚΟ ΤΣΗΜΑ Δν. Δεμήηνεξ Καπεηάκμξ Γπημειεηήξ A Γαζηνεκηενμιμγηθή Κιηκηθή Γ.Ν. «Γεώνγημξ Παπακηθμιάμο» ΓΟΠΝ είκαη ε θαηάζηαζε πμο δεμημονγείηαη όηακ ε παιηκδνόμεζε
ΓΑΣΡΟΟΙΟΦΑΓΙΚΗ ΠΑΛΙΝΔΡΟΜΗΗ ΚΑΙ ΑΝΑΠΝΓΤΣΙΚΟ ΤΣΗΜΑ Δν. Δεμήηνεξ Καπεηάκμξ Γπημειεηήξ A Γαζηνεκηενμιμγηθή Κιηκηθή Γ.Ν. «Γεώνγημξ Παπακηθμιάμο» ΓΟΠΝ είκαη ε θαηάζηαζε πμο δεμημονγείηαη όηακ ε παιηκδνόμεζε
Ιαιιηένγεηα βαθηενίςκ
 Γ ΚΤΙΕΘΟΤ (ΓΕΜΘΙΗ ΠΑΘΔΕΘΑ) Άζθεζε 1ε(α) ενγαζηενηαθμύ μδεγμύ: Ιαιιηένγεηα βαθηενίςκ Ιαη μηθνμζθμπηθή παναηήνεζε 1 Όνγακα θαη οιηθά Γθαδάθη Σνίπμδμ με πιέγμα 6 απνεζημμπμίεηα ηνοβιία Petri Γοάιηκε νάβδμξ
Γ ΚΤΙΕΘΟΤ (ΓΕΜΘΙΗ ΠΑΘΔΕΘΑ) Άζθεζε 1ε(α) ενγαζηενηαθμύ μδεγμύ: Ιαιιηένγεηα βαθηενίςκ Ιαη μηθνμζθμπηθή παναηήνεζε 1 Όνγακα θαη οιηθά Γθαδάθη Σνίπμδμ με πιέγμα 6 απνεζημμπμίεηα ηνοβιία Petri Γοάιηκε νάβδμξ
Τα έλη παηδηά γεμίδμοκ με πανά ηηξ θηωπέξ μηθμγέκεηεξ.
 Τα έλη παηδηά γεμίδμοκ με πανά ηηξ θηωπέξ μηθμγέκεηεξ. Γεηα ζαξ είμαζηε έλη εκενγμί μαζεηέξ μη: Πακαγηώηεξ, Μάκμξ, Μπάμπεξ, Γηνήκε, Μανία θαη ε Γμμακμοέιια θαη ζήμενα ζα ζαξ δηεγεζμύμε ηεκ πενζηκή Υνηζημογεκκηάηηθε
Τα έλη παηδηά γεμίδμοκ με πανά ηηξ θηωπέξ μηθμγέκεηεξ. Γεηα ζαξ είμαζηε έλη εκενγμί μαζεηέξ μη: Πακαγηώηεξ, Μάκμξ, Μπάμπεξ, Γηνήκε, Μανία θαη ε Γμμακμοέιια θαη ζήμενα ζα ζαξ δηεγεζμύμε ηεκ πενζηκή Υνηζημογεκκηάηηθε
Αρηόμξμξι Ποάκηξοεπ ΠΛΗ513- Intelligence Lab. Αμαθξοά Εογαζίαπ Εναμήμξρ
 Πξλρηεςμείξ Κοήηηπ Τμήμα ΗΜΜΥ Αρηόμξμξι Ποάκηξοεπ ΠΛΗ513- Intelligence Lab Σιδωοάκηπ Νικόλαξπ ΑΜ: 2008030041 Αμαθξοά Εογαζίαπ Εναμήμξρ 2012-2013 «Πλξήγηζη ζε Λαβύοιμθξ-Mapping, Localization, Path Planning,
Πξλρηεςμείξ Κοήηηπ Τμήμα ΗΜΜΥ Αρηόμξμξι Ποάκηξοεπ ΠΛΗ513- Intelligence Lab Σιδωοάκηπ Νικόλαξπ ΑΜ: 2008030041 Αμαθξοά Εογαζίαπ Εναμήμξρ 2012-2013 «Πλξήγηζη ζε Λαβύοιμθξ-Mapping, Localization, Path Planning,
ΜΗΦΑΝΙΚΑ ΚΥΜΑΤΑ. Κύμα μκμμάδεηαη ε δηάδμζε μηαξ δηαηαναπήξ ζημ πώνμ με μνηζμέκε ηαπύηεηα, ε μπμία μκμμάδεηαη ηαςύηηηα διάδξζηπ.
 ΜΗΦΑΝΙΚΑ ΚΥΜΑΤΑ Οοιζμόπ κύμαηξπ Κύμα μκμμάδεηαη ε δηάδμζε μηαξ δηαηαναπήξ ζημ πώνμ με μνηζμέκε ηαπύηεηα, ε μπμία μκμμάδεηαη ηαςύηηηα διάδξζηπ. Γηα ηε δεμημονγία εκόξ θύμαημξ πνεηάδμκηαη ε πηγή ηεξ δηαηαναπήξ
ΜΗΦΑΝΙΚΑ ΚΥΜΑΤΑ Οοιζμόπ κύμαηξπ Κύμα μκμμάδεηαη ε δηάδμζε μηαξ δηαηαναπήξ ζημ πώνμ με μνηζμέκε ηαπύηεηα, ε μπμία μκμμάδεηαη ηαςύηηηα διάδξζηπ. Γηα ηε δεμημονγία εκόξ θύμαημξ πνεηάδμκηαη ε πηγή ηεξ δηαηαναπήξ
Problems & Questions on MAC Layer
 ΗY335: Δίκτυα Υπολογιςτών Χειμερινό Εξάμηνο 2011-2012 Τμήμα Επιςτήμησ Υπολογιςτών, Πανεπιςτήμιο Κρήτησ Διδάςκουςα: Μαρία Παπαδοπούλη Φροντιςτήριο: 10/11/2011 Βοηθόσ: Παφλοσ Χαρωνυκτάκησ Problems & Questions
ΗY335: Δίκτυα Υπολογιςτών Χειμερινό Εξάμηνο 2011-2012 Τμήμα Επιςτήμησ Υπολογιςτών, Πανεπιςτήμιο Κρήτησ Διδάςκουςα: Μαρία Παπαδοπούλη Φροντιςτήριο: 10/11/2011 Βοηθόσ: Παφλοσ Χαρωνυκτάκησ Problems & Questions
Εισαγωγή στους Αλγορίθμους Φροντιστήριο 1
 Εισαγωγή στους Αλγορίθμους Φροντιστήριο 1 Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Εισαγωγή στους Αλγορίθμους Φροντιστήριο 1 Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Γενικά Μαθηματικά Ι. Ενότητα 12: Κριτήρια Σύγκλισης Σειρών. Λουκάς Βλάχος Τμήμα Φυσικής ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Κριτήρια Σύγκλισης Σειρών Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Κριτήρια Σύγκλισης Σειρών Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Γοθεμία Παπαδμπμύιμο-Αιαηάθε
 Γοθεμία Παπαδμπμύιμο-Αιαηάθε Γπίθμονε θαζεγήηνηα Παηδηαηνηθήξ-Παηδηαηνηθήξ Ακμζμιμγίαξ Δ Παηδηαηνηθή Κιηκηθή Α.Π.Θ. Νμζμθμμείμ Παπαγεςνγίμο 5 ε ύκμδμξ ηεξ Γιιεκηθήξ Γηαηνείαξ Ένεοκαξ θαη Ακηημεηώπηζεξ
Γοθεμία Παπαδμπμύιμο-Αιαηάθε Γπίθμονε θαζεγήηνηα Παηδηαηνηθήξ-Παηδηαηνηθήξ Ακμζμιμγίαξ Δ Παηδηαηνηθή Κιηκηθή Α.Π.Θ. Νμζμθμμείμ Παπαγεςνγίμο 5 ε ύκμδμξ ηεξ Γιιεκηθήξ Γηαηνείαξ Ένεοκαξ θαη Ακηημεηώπηζεξ
Σ Ο Ξ Υ Η Φ Θ Ω Μ Ι Α Α Π Θ Ζ Ξ Λ Ε Μ Ω Μ
 Α Θ Η Ρ Η F O T O Σ Ο Ξ Υ Η Φ Θ Ω Μ Ι Α Α Π Θ Ζ Ξ Λ Ε Μ Ω Μ Ε Π Γ Ξ I N T E R R E G I O N A L M A N A G E M E N T O F H U M A N R E S O U R C E S Θ Κ Ξ Ρ Ο Π Ξ Γ Π Α Λ Λ Α Ξ Ρ : T R A I N I N G I N I T
Α Θ Η Ρ Η F O T O Σ Ο Ξ Υ Η Φ Θ Ω Μ Ι Α Α Π Θ Ζ Ξ Λ Ε Μ Ω Μ Ε Π Γ Ξ I N T E R R E G I O N A L M A N A G E M E N T O F H U M A N R E S O U R C E S Θ Κ Ξ Ρ Ο Π Ξ Γ Π Α Λ Λ Α Ξ Ρ : T R A I N I N G I N I T
Εισαγωγή στους Αλγορίθμους Φροντιστήριο 5
 Εισαγωγή στους Αλγορίθμους Φροντιστήριο 5 Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Εισαγωγή στους Αλγορίθμους Φροντιστήριο 5 Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Τίτλος Μαθήματος: Ηλεκτρονικοί Υπολογιστές IΙΙ. Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης
 Τίτλος Μαθήματος: Ηλεκτρονικοί Υπολογιστές IΙΙ Ενότητα: Πράξεις με αρχεία Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Τμήμα: Οικονομικών Επιστημών Ανάγνωση και εγγραφή αρχείων με χρήση ρεύματος
Τίτλος Μαθήματος: Ηλεκτρονικοί Υπολογιστές IΙΙ Ενότητα: Πράξεις με αρχεία Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Τμήμα: Οικονομικών Επιστημών Ανάγνωση και εγγραφή αρχείων με χρήση ρεύματος
Τίτλος Μαθήματος: Ηλεκτρονικοί Υπολογιστές IΙΙ. Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης
 Τίτλος Μαθήματος: Ηλεκτρονικοί Υπολογιστές IΙΙ Ενότητα: Παράγωγοι και ολοκληρώματα Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Τμήμα: Οικονομικών Επιστημών Ολοκληρώματα με το πρόγραμμα Maima Αθανάσιος
Τίτλος Μαθήματος: Ηλεκτρονικοί Υπολογιστές IΙΙ Ενότητα: Παράγωγοι και ολοκληρώματα Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Τμήμα: Οικονομικών Επιστημών Ολοκληρώματα με το πρόγραμμα Maima Αθανάσιος
Τίτλος Μαθήματος: Ηλεκτρονικοί Υπολογιστές IΙΙ. Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης
 Τίτλος Μαθήματος: Ηλεκτρονικοί Υπολογιστές IΙΙ Ενότητα: Εισαγωγή στη C++ Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Τμήμα: Οικονομικών Επιστημών Αριθμοί κινητής υποδιαστολής (float) στη C++ (1)
Τίτλος Μαθήματος: Ηλεκτρονικοί Υπολογιστές IΙΙ Ενότητα: Εισαγωγή στη C++ Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Τμήμα: Οικονομικών Επιστημών Αριθμοί κινητής υποδιαστολής (float) στη C++ (1)
Εκκλησιαστικό Δίκαιο. Ενότητα 10η: Ιερά Σύνοδος της Ιεραρχίας και Διαρκής Ιερά Σύνοδος Κυριάκος Κυριαζόπουλος Τμήμα Νομικής Α.Π.Θ.
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 10η: Ιερά Σύνοδος της Ιεραρχίας και Διαρκής Ιερά Σύνοδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 10η: Ιερά Σύνοδος της Ιεραρχίας και Διαρκής Ιερά Σύνοδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Εισαγωγή στους Αλγόριθμους
 Εισαγωγή στους Αλγόριθμους Ενότητα 16: Δυαδική αναζήτηση και ταξινόμηση με συγχώνευση Εύη Παπαϊωάννου Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διαχείρισης Πολιτισμικού Περιβάλλοντος και Νέων Τεχνολογιών
Εισαγωγή στους Αλγόριθμους Ενότητα 16: Δυαδική αναζήτηση και ταξινόμηση με συγχώνευση Εύη Παπαϊωάννου Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διαχείρισης Πολιτισμικού Περιβάλλοντος και Νέων Τεχνολογιών
Γενικά Μαθηματικά Ι. Ενότητα 15: Ολοκληρώματα Με Ρητές Και Τριγωνομετρικές Συναρτήσεις Λουκάς Βλάχος Τμήμα Φυσικής
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Ολοκληρώματα Με Ρητές Και Τριγωνομετρικές Συναρτήσεις Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Ολοκληρώματα Με Ρητές Και Τριγωνομετρικές Συναρτήσεις Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Οι ςδπαςλικέρ κονίερ για σπήζη ζηην οδοποιία και ηο ππόηςπο ΕΝ Δ. Τζαμαηζούληρ Δπ. Φημικόρ Μησανικόρ ΦΑΛΥΧ Δομικά Υλικά Α.Ε.
 Οι ςδπαςλικέρ κονίερ για σπήζη ζηην οδοποιία και ηο ππόηςπο ΕΝ 13282 Δ. Τζαμαηζούληρ Δπ. Φημικόρ Μησανικόρ ΦΑΛΥΧ Δομικά Υλικά Α.Ε. Halyps Αθήνα, Cement 6 Νοεμβπίος - Italcementi 2008 Group 1 Ειζαγωγή Ακάιμγα
Οι ςδπαςλικέρ κονίερ για σπήζη ζηην οδοποιία και ηο ππόηςπο ΕΝ 13282 Δ. Τζαμαηζούληρ Δπ. Φημικόρ Μησανικόρ ΦΑΛΥΧ Δομικά Υλικά Α.Ε. Halyps Αθήνα, Cement 6 Νοεμβπίος - Italcementi 2008 Group 1 Ειζαγωγή Ακάιμγα
Εισαγωγή στους Αλγορίθμους
 Εισαγωγή στους Αλγορίθμους Ενότητα 5 η Άσκηση Συγχώνευση & απαρίθμηση Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης
Εισαγωγή στους Αλγορίθμους Ενότητα 5 η Άσκηση Συγχώνευση & απαρίθμηση Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης
ΜΓΛΓΣΗ ΣΩΝ ΓΠΙΠΓΔΩΝ ΦΤΙΚΩΝ ΑΝΣΙΜΙΚΡΟΒΙΑΚΩΝ ΠΓΠΣΙΔΙΩΝ ΚΑΙ ΔΓΙΚΣΩΝ ΒΑΚΣΗΡΙΔΙΑΚΗ ΑΛΛΟΘΓΗ Γ ΚΙΡΡΩΣΙΚΟΤ ΑΘΓΝΓΙ
 ΜΓΛΓΣΗ ΣΩΝ ΓΠΙΠΓΔΩΝ ΦΤΙΚΩΝ ΑΝΣΙΜΙΚΡΟΒΙΑΚΩΝ ΠΓΠΣΙΔΙΩΝ ΚΑΙ ΔΓΙΚΣΩΝ ΒΑΚΣΗΡΙΔΙΑΚΗ ΑΛΛΟΘΓΗ Γ ΚΙΡΡΩΣΙΚΟΤ ΑΘΓΝΓΙ Ιπάμηαξ Γ., Ηαιηζά Γ., Δμομπμύιε-Βαθεηάδε Γ., Γθίδεξ Ι., Ηαναγηακκάθεξ Δ., Θαμύδε Γ., Γμύθμξ Δ.,
ΜΓΛΓΣΗ ΣΩΝ ΓΠΙΠΓΔΩΝ ΦΤΙΚΩΝ ΑΝΣΙΜΙΚΡΟΒΙΑΚΩΝ ΠΓΠΣΙΔΙΩΝ ΚΑΙ ΔΓΙΚΣΩΝ ΒΑΚΣΗΡΙΔΙΑΚΗ ΑΛΛΟΘΓΗ Γ ΚΙΡΡΩΣΙΚΟΤ ΑΘΓΝΓΙ Ιπάμηαξ Γ., Ηαιηζά Γ., Δμομπμύιε-Βαθεηάδε Γ., Γθίδεξ Ι., Ηαναγηακκάθεξ Δ., Θαμύδε Γ., Γμύθμξ Δ.,
Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας Ενότητα 7η: Ιερά Σύνοδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας Ενότητα 7η: Ιερά Σύνοδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Ιστορία της μετάφρασης
 ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Μεταφραστές και πρωτότυπα. Ελένη Κασάπη ΤΜΗΜΑ ΑΓΓΛΙΚΗΣ ΓΛΩΣΣΑΣ ΚΑΙ ΦΙΛΟΛΟΓΙΑΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Μεταφραστές και πρωτότυπα. Ελένη Κασάπη ΤΜΗΜΑ ΑΓΓΛΙΚΗΣ ΓΛΩΣΣΑΣ ΚΑΙ ΦΙΛΟΛΟΓΙΑΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Αλγόριθμοι και πολυπλοκότητα Συγχωνευτική Ταξινόμηση
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αλγόριθμοι και πολυπλοκότητα Συγχωνευτική Ταξινόμηση Ιωάννης Τόλλης Τμήμα Επιστήμης Υπολογιστών Συγχωνευτική Ταξινόμηση (Merge Sort) 7 2 9 4 2 4 7 9 7 2 2 7 9 4
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αλγόριθμοι και πολυπλοκότητα Συγχωνευτική Ταξινόμηση Ιωάννης Τόλλης Τμήμα Επιστήμης Υπολογιστών Συγχωνευτική Ταξινόμηση (Merge Sort) 7 2 9 4 2 4 7 9 7 2 2 7 9 4
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 8α: Ταξινόμηση-Σύγκριση αλγορίθμων ταξινόμησης Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 8α: Ταξινόμηση-Σύγκριση αλγορίθμων ταξινόμησης Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Εκκλησιαστικό Δίκαιο
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 11η: Οργανισμοί της Εκκλησίας της Ελλάδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 11η: Οργανισμοί της Εκκλησίας της Ελλάδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
