Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων
|
|
|
- Ê Δασκαλόπουλος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Μέθοδος "δυναμικού προγραμματισμού": Ροή δικτύου, χρονοπρογραμματισμός και σακίδια Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών
2
3 641: Γηζαγςγή ζηε Θεςνία θαη Ακάιοζε Αιγμνίζμςκ Υάνεξ Παπαδυπμοιμξ
4 Τιε ημο μαζήμαημξ Βαζηθά ζημηπεία ζπεδίαζεξ & ακάιοζεξ αιγμνίζμςκ Ακάιοζε αιγμνίζμςκ, απμδμηηθυηεηα, αζομπηςηηθυξ ζομβμιηζμυξ οκεζηζμέκμη πνυκμη εθηέιεζεξ θαη βαζηθέξ δμμέξ δεδμμέκςκ πίκαθεξ, ιίζηεξ, ζημίβεξ, μονέξ Γοζηαζέξ ηαίνηαζμα, μνζυηεηα, ζςνυξ θαη μονά πνμηεναηυηεηαξ Μέζμδμξ «Δηαίνεη θαη Βαζίιεοε» Γθανμμγέξ ζε ηαληκυμεζε ζημηπείςκ Γπίιοζε ακαδνμμηθχκ ζπέζεςκ Γναθήμαηα θαη αιγυνηζμμη γναθεμάηςκ Δηάηνελε γναθεμάηςκ (BFS, DFS) οκεθηηθυηεηα Σμπμιμγηθή δηάηαλε Μέζμδμη «Απιεζηείαξ» θαη «Δοκαμηθμφ Πνμγναμμαηηζμμφ» Γιάπηζηα ζθειεηηθά δέκδνα (αιγυνηζμμξ Prim, αιγυνηζμμξ Kruskal) οκημμυηενεξ δηαδνμμέξ (αιγυνηζμμξ Dijkstra, Ρμή δηθηφμο) Υνμκμπνμγναμμαηηζμυξ Γπηιεγμέκα ζέμαηα Τπμιμγηζηηθή πμιοπιμθυηεηα, NP-πιενυηεηα 2
5 Δοκαμηθυξ Πνμγναμμαηηζμυξ ηαζμηζμέκμξ Υνμκμπνμγναμμαηηζμυξ Δηαζηεμάηςκ Σμεμαημπμηεμέκα Γιάπηζηα Σεηνάγςκα Αζνμίζμαηα Τπμζοκυιςκ θαη αθίδηα Γοζογνάμμηζε Αθμιμοζίαξ οκημμυηενα Μμκμπάηηα Αιγυνηζμμξ ημο Bellman-Ford
6 Αιγμνηζμηθά Μμκηέια-Σεπκηθέξ Απιεζηία. Υηίζε μηα ιφζε ζηαδηαθά, βειηηζημπμηχκηαξ μοςπηθά θάπμημ ημπηθυ θνηηήνημ. Δηαίνεη θαη Βαζίιεοε. Δηάζπαζε έκα πνυβιεμα ζε οπμπνμβιήμαηα, ιφζε θάζε οπμπνυβιεμα ακελάνηεηα, θαη ζοκδφαζε ηηξ ιφζεηξ ηςκ μοςπηθυξ = πμο δεκ έπεη δημναηηθυηεηα, πμο πνμζθμιιάηαη ζημ πανειζυκ θαη δεκ μπμνεί κα πνμβιέρεη κέεξ ελειίλεηξ οπμπνμβιεμάηςκ γηα κα ζοκζέζεηξ ηεκ ιφζε ημο ανπηθμφ πνμβιήμαημξ. Δοκαμηθυξ Πνμγναμμαηηζμυξ. Δηάζπαζε έκα πνυβιεμα ζε μηα ζεηνά απυ επηθαιοπηυμεκα οπμπνμβιήμαηα (ηα απμηειέζμαηά ημοξ επακαπνεζημμπμημφκηαη ανθεηέξ θμνέξ), θαη ζφκζεζε ζςζηέξ ιφζεηξ γηα υιμ θαη μεγαιφηενα οπμπνμβιήμαηα. 4
7 Ιζημνία Δοκαμηθμφ Πνμγναμμαηηζμμφ Bellman. [195s] Πνςημπυνμξ ζηε ζοζηεμαηηθή μειέηε ημο δοκαμηθμφ πνμγναμμαηηζμμφ. Γηομμιμγία. Δοκαμηθυξ πνμγναμμαηηζμυξ = ζπεδηαζμυξ με ηεκ πάνμδμ ημο πνυκμο. Συηε πμιιά θοβενκεηηθά ηδνφμαηα (π.π. ε θοβένκεζε ηςκ ΗΠΑ) ήηακ ακηίζεηα με ηεκ ένεοκα ζημ πεδίμ ηςκ μαζεμαηηθχκ. Ο Bellman ακαδήηεζε έκα εκηοπςζηαθυ υκμμα γηα κα απμθφγεη ηεκ ακηηπανάζεζε. «είκαη αδφκαημ κα πνεζημμπμηεζεί ε ιέλε δοκαμηθυξ με οπμηημεηηθή έκκμηα» «θάηη ζημ μπμίμ δεκ ζα μπμνμφζε κα δηαθςκήζεη μφηε μέιμξ ηεξ θοβένκεζεξ» Reference: Bellman, R. E. Eye of the Hurricane, An Autobiography. Γίκαη πνάγμαηη «πηαζάνηθμ» υκμμα. 5
8 Γθανμμγέξ Δοκαμηθμφ Πνμγναμμαηηζμμφ Πενημπέξ. Βημπιενμθμνηθή Θεςνία ειέγπμο (control theory). Θεςνία πιενμθμνίαξ (information theory). Γπηπεηνεζηαθή ένεοκα (operations research). Πιενμθμνηθή: ζεςνεηηθή, γναθηθά, ηεπκεηή κμεμμζφκε,. Ονηζμέκμη δηάζεμμη αιγυνηζμμη δοκαμηθμφ πνμγναμμαηηζμμφ. Unix (Linux) εκημιή diff γηα ζφγθνηζε δομ ανπείςκ. Viterbi γηα θνομμέκα Μαθνμβηακά μμκηέια. Smith-Waterman γηα εοζογνάμμηζε αθμιμοζηχκ. Bellman-Ford γηα ζοκημμυηενε δηαδνμμή ζε δίθηοα. Cocke-Kasami-Younger γηα ακάιοζε γναμμαηηθχκ πςνίξ ζομθναδυμεκα. 6
9 ηαζμηζμέκμξ Υνμκμπνμγναμμαηηζμυξ Δηαζηεμάηςκ
10 ηαζμηζμέκμξ Υνμκμπνμγναμμαηηζμυξ Δηαζηεμάηςκ Πνυβιεμα ημο ηαζμηζμέκμο Υνμκμπνμγναμμαηηζμμφ Δηαζηεμάηςκ. Σμ αίηεμα j λεθηκά ηε ζηηγμή s j, ηειεηχκεη ηε ζηηγμή f j, θαη έπεη βάνμξ v j. Δομ αηηήμαηα είκαη ζομβαηά ακ δεκ επηθαιφπημκηαη. ηυπμξ: εφνεζε οπμζοκυιμο ζομβαηχκ αηηεμάηςκ μέγηζημο βάνμοξ. άζνμηζμα ηςκ επημένμοξ βανχκ a b c d e f g h Υνυκμξ 8
11 Ακαζθυπεζε με-ζηαζμηζμέκμο Υνμκμπνμγναμμαηηζμμφ Δηαζηεμάηςκ Θομεζείηε: Ο άπιεζημξ αιγυνηζμμξ δμοιεφεη υηακ ηα βάνε είκαη ίζα (=1). Θεςνμφμε ηα αηηήμαηα ζε αφλμοζα ζεηνά ςξ πνμξ ημ πνυκμ ηενμαηηζμμφ. Πνμζζέημομε έκα αίηεμα ζημ οπμζφκμιμ ακ είκαη ζομβαηυ με ηα πνμεγμφμεκα αηηήμαηα πμο επηιέπζεθακ. Παναηήνεζε. Ο άπιεζημξ αιγυνηζμμξ μπμνεί κα απμηφπεη ζεαμαηηθά ακ επηηναπμφκ αοζαίνεηα βάνε. βάνμξ = 999 b βάνμξ = 1 a Υνυκμξ 9
12 ηαζμηζμέκμξ Υνμκμπνμγναμμαηηζμυξ Δηαζηεμάηςκ Δηαηάζζμομε ηα αηηήμαηα ζφμθςκα με ημ πνυκμ ηενμαηηζμμφ: f 1 f 2... f n Ονηζμυξ. p(j) = μέγηζημξ δείθηεξ i (< j) ηέημημξ χζηε ημ αίηεμα i κα είκαη ζομβαηυ με ημ αίηεμα j. Π.π.: p(8) = 5, p(7) = 3, p(2) = Υνυκμξ 1
13 Δοκαμηθυξ Πνμγναμμαηηζμυξ: Δοαδηθή επηιμγή ομβμιηζμυξ. OPT(j) = ηημή ηεξ βέιηηζηεξ ιφζεξ γηα ημ πνυβιεμα απυ ηα αηηήμαηα 1, 2,..., j. 1 ε Πενίπηςζε: OPT δηαιέγεη ημ αίηεμα j με βάνμξ v j δεκ μπμνμφκ κα πνεζημμπμηεζμφκ ηα αζφμβαηα αηηήμαηα { p(j) + 1, p(j) + 2,..., j - 1 } πνέπεη κα πενηέπεη ηε βέιηηζηε ιφζε ημο οπμπνμβιήμαημξ απυ ηα οπυιμηπα ζομβαηά αηηήμαηα 1, 2,..., p(j) 2 ε Πενίπηςζε: OPT δεκ δηαιέγεη ημ αίηεμα j. πνέπεη κα πενηέπεη ηε βέιηηζηε ιφζε ημο οπμπνμβιήμαημξ απυ ηα οπυιμηπα ζομβαηά αηηήμαηα 1, 2,..., j-1 OPT( p(j) ) OPT( j-1 ) βέιηηζηα οπμπνμβιήμαηα if j OPT( j) max v j OPT( p( j)), OPT( j 1) otherwise 11
14 ηαζμηζμέκμξ Υνμκμπνμγναμμαηηζμυξ Δηαζηεμάηςκ: Ωμή Βία Αιγυνηζμμξ Ωμήξ Βίαξ. Είζοδορ: n, s 1,,s n, f 1,,f n, v 1,,v n Ταξινόμηζε ηα αιηήμαηα ωρ ππορ ηο σπόνο ηεπμαηιζμού: f 1 f 2... f n. Υπολόγιζε p(1), p(2),, p(n) Compute-Opt(j) { if (j = ) return else return max( v j + Compute-Opt(p(j)), Compute-Opt(j-1) ) } Κάλεζε Compute-Opt(n) 12
15 ηαζμηζμέκμξ Υνμκμπνμγναμμαηηζμυξ Δηαζηεμάηςκ: Ωμή Βία Παναηήνεζε. Ο ακαδνμμηθυξ αιγυνηζμμξ απμηογπάκεη ζεαμαηηθά θαζχξ επακατπμιμγίδεη πιεμκάδμκηα οπμπνμβιήμαηα εθζεηηθυξ αιγυνηζμμξ Π.π.. Σμ πιήζμξ ηςκ ακαδνμμηθχκ θιήζεςκ ζε μηα μηθμγέκεηα πενηπηχζεςκ αολάκεη υπςξ ε Fibonacci αθμιμοζία ( f(n) = f(n-1) + f(n-2) ) p(1) =, p(j) = j Παναηήνεζε. H Compute-Opt επηιφεη n+1 δηαθμνεηηθά οπμπνμβιήμαηα, Compute-Opt(), Compute-Opt(1),, Compute-Opt(n). Γνχηεμα. Πχξ απαιείθμομε ημκ πιεμκαζμυ ηςκ θιήζεςκ; 13
16 ηαζμηζμέκμξ Υνμκμπνμγναμμαηηζμυξ Δηαζηεμάηςκ: Απμμκεμυκεοζε Απμμκεμυκεοζε. Απμζήθεοζε ηα απμηειέζμαηα θάζε οπμπνμβιήμαημξ ζε μηα θαζμιηθή ζέζε μκήμεξ (εφθμιε πνμζπειάζημε) θαη ακαδήηεζε μυκμ υηακ πνεηάδεηαη. Είζοδορ: n, s 1,,s n, f 1,,f n, v 1,,v n Ταξινόμηζε ηα αιηήμαηα ωρ εξήρ: f 1 f 2... f n. Υπολόγιζε p(1), p(2),, p(n) for j = 1 to n M[j] = empty M[] = θαζμιηθυξ πίκαθαξ M-Compute-Opt(j) { if (M[j] είναι empty) M[j] = max( v j + M-Compute-Opt(p(j)), M-Compute-Opt(j-1) ) return M[j] } Κάλεζε Μ-Compute-Opt(n) 14
17 ηαζμηζμέκμξ Υνμκμπνμγναμμαηηζμυξ Δηαζηεμάηςκ: Υνυκμξ Γθηέιεζεξ Ιζπονηζμυξ. Η εθδμπή απμμκεμυκεοζεξ ζέιεη πνυκμ O(n log n). Σαληκυμεζε ςξ πνμξ πνυκμ ηενμαηηζμμφ: O(n log n). Τπμιμγηζμυξ p() : O(n log n) με ηαληκυμεζε ςξ πνμξ πνυκμ έκανλεξ. M-Compute-Opt(j): θάζε θιήζε απαηηεί πνυκμ O(1) θαη είηε (i) επηζηνέθεη μηα οπάνπμοζα ηημή M[j] (ii) ζομπιενχκεη μηα κέα ηημή M[j] με δομ ακαδνμμηθέξ θιήζεηξ Μέηνμ πνμυδμο αιγμνίζμμο = # με-θεκχκ θειηχκ ημο M[]. ανπηθά =, έςξ n. (ii) αολάκεη ημ θαηά 1 ημ πμιφ 2n ακαδνμμηθέξ θιήζεηξ. Ο ζοκμιηθυξ πνυκμξ ημο M-Compute-Opt(n) είκαη O(n). εμείςζε. O(n) ακ ηα αηηήμαηα έπμοκ ήδε ηαληκμμεζεί θαηά πνυκμοξ έκανλεξ θαη ηενμαηηζμμφ 15
18 ηαζμηζμέκμξ Υνμκμπνμγναμμαηηζμυξ Δηαζηεμάηςκ: Γφνεζε Λφζεξ Γνχηεμα. Ο δοκαμηθυξ πνμγναμμαηηζμυξ οπμιμγίδεη ηε βέιηηζηε ηημή. Ση γίκεηαη ακ ζέιμομε ηε ιφζε (πμηα αηηήμαηα ακήθμοκ ζηεκ βέιηηζηε ιφζε); Απάκηεζε. Γθηειμφμε έκα επηπιέμκ βήμα μεηά-επελενγαζίαξ ημο πίκαθα Μ, ράπκμκηαξ ηε ιφζε. Κάλεζε M-Compute-Opt(n) Κάλεζε Find-Solution(n) Find-Solution(j) { if (j = ) μην εκηςπώνειρ ηίποηα else if (v j + M[p(j)] > M[j-1]) εκηύπωζε j Find-Solution(p(j)) else Find-Solution(j-1) } # ακαδνμμηθχκ θιήζεςκ n O(n). 16
19 ηαζμηζμέκμξ Υνμκμπνμγναμμαηηζμυξ Δηαζηεμάηςκ: Υςνίξ Ακαδνμμή Απμμκεμυκεοζε ή Γπακάιερε ζηα οπμπνμβιήμαηα. Ξεδηπιχκμομε ηεκ ακαδνμμή. Είζοδορ: n, s 1,,s n, f 1,,f n, v 1,,v n Ταξινόμηζε ηα αιηήμαηα ωρ εξήρ: f 1 f 2... f n. Υπολόγιζε p(1), p(2),, p(n) Iterative-Compute-Opt { M[] = for j = 1 to n M[j] = max( v j + M[p(j)], M[j-1] ) } Βασική Ιδέα του Δυναμικού Προγραμματισμού!! 17
20 ηαζμηζμέκμξ Υνμκμπνμγναμμαηηζμυξ Δηαζηεμάηςκ: Υςνίξ Ακαδνμμή Iterative-Compute-Opt { M[] = for j = 1 to n M[j] = max( v j + M[p(j)], M[j-1] ) } 18
21 Δοκαμηθυξ Πνμγναμμαηηζμυξ οκηαγή Υαναθηενηζμυξ ηεξ δμμήξ ημο πνμβιήμαημξ Ακαδνμμηθυξ μνηζμυξ ηεξ βέιηηζηεξ ιφζεξ Τπμιμγηζμυξ ηεξ ηημήξ ηεξ βέιηηζηεξ ιφζεξ Καηαζθεοή ηεξ βέιηηζηεξ ιφζεξ απυ ηεκ οπμιμγηζμέκε πιενμθμνία Σα οπμπνμβιήμαηα πνέπεη κα ηθακμπμημφκ μνηζμέκεξ ηδηυηεηεξ: Πμιοςκομηθυ πιήζμξ οπμπνμβιεμάηςκ Σμ ανπηθυ πνυβιεμα οπμιμγίδεηαη «εφθμια» θμηηάδμκηαξ ηηξ ιφζεηξ ηςκ οπμπνμβιεμάηςκ Φοζηθή δηάηαλε ηςκ οπμπνμβιεμάηςκ απυ «μηθνά» ζε «μεγάια», με μηα εφθμια οπμιμγηδυμεκε ακαδνμμή 19
22 Σμεμαημπμηεμέκα Γιάπηζηα Σεηνάγςκα
23 Σμεμαημπμηεμέκα Γιάπηζηα Σεηνάγςκα Γιάπηζηα Σεηνάγςκα. Θεμειηχδεξ πνυβιεμα ζηαηηζηηθήξ θαη ανηζμεηηθήξ ακάιοζεξ. Δίκμκηαη n ζεμεία ζημ επίπεδμ: (x 1, y 1 ), (x 2, y 2 ),..., (x n, y n ). Γφνεζε εοζείαξ y = ax + b πμο ειαπηζημπμηεί ημ ζθάιμα απυζηαζεξ: y x 21
24 Σμεμαημπμηεμέκα Γιάπηζηα Σεηνάγςκα Γιάπηζηα Σεηνάγςκα. Θεμειηχδεξ πνυβιεμα ζηαηηζηηθήξ θαη ανηζμεηηθήξ ακάιοζεξ. Δίκμκηαη n ζεμεία ζημ επίπεδμ: (x 1, y 1 ), (x 2, y 2 ),..., (x n, y n ). Γφνεζε εοζείαξ y = ax + b πμο ειαπηζημπμηεί ημ ζθάιμα απυζηαζεξ: n SSE (y i ax i b) 2 i1 y x Λφζε. Δηαθμνηθυξ ιμγηζμυξ ειάπηζημ ζθάιμα πεηοπαίκμομε υηακ a n x i i y i ( i x i ) ( i y i ), b n x 2 i ( x i ) 2 i i i y i a i x i n 22
25 Σμεμαημπμηεμέκα Γιάπηζηα Σεηνάγςκα Σμεμαημπμηεμέκα Γιάπηζηα Σεηνάγςκα Σα ζεμεία βνίζθμκηαη ζε αθμιμοζίεξ απυ δηάθμνεξ εοζείεξ. Δεδμμέκμο n ζεμείςκ ζημ επίπεδμ (x 1, y 1 ), (x 2, y 2 ),..., (x n, y n ) με x 1 < x 2 <... < x n, βνείηε μηα αθμιμοζία εοζεηχκ πμο ειαπηζημπμημφκ f(x). Γνχηεμα. Πμηα είκαη ε θαηάιιειε επηιμγή γηα ηεκ f(x) πμο εληζμννμπεί ηεκ αθνίβεηα θαη ηεκ μηθμκμμία; ηεηναγςκηθυ ζθάιμα πιήζμξ ηςκ εοζεηχκ y x 23
26 Σμεμαημπμηεμέκα Γιάπηζηα Σεηνάγςκα Σμεμαημπμηεμέκα Γιάπηζηα Σεηνάγςκα Σα ζεμεία βνίζθμκηαη ζε αθμιμοζίεξ απυ δηάθμνεξ εοζείεξ. Δεδμμέκμο n ζεμείςκ ζημ επίπεδμ (x 1, y 1 ), (x 2, y 2 ),..., (x n, y n ) με x 1 < x 2 <... < x n, βνείηε μηα αθμιμοζία εοζεηχκ πμο ειαπηζημπμημφκ ημ άζνμηζμα ηςκ επημένμοξ αζνμηζμάηςκ ηεηναγχκςκ E ζε θάζε ημήμα ημ πιήζμξ ηςκ εοζεηχκ L οκάνηεζε πμηκήξ: E + c L, γηα θάπμηα δεδμμέκε ζηαζενά c >. y x 24
27 Δοκαμηθυξ Πνμγναμμαηηζμυξ: Πμιιαπιέξ Γπηιμγέξ ομβμιηζμυξ. OPT(j) = ειάπηζημ θυζημξ γηα ηα ζεμεία p 1, p 2,..., p j. e(i, j) = ειάπηζημ ζθάιμα θάπμηαξ εοζείαξ γηα ηα ζεμεία p i, p i+1,..., p j. Γηα ημκ οπμιμγηζμυ ημο OPT(n): Σμ ηειεοηαίμ ζεμείμ p n ακήθεη ζε έκα μυκμ ημήμα θαη αοηυ ημ ημήμα λεθηκά ζε θάπμημ p i γηα θάπμημ i < n. OPT( n) min 1 in e( i, n) copt ( i 1) OPT(i-1) i n Γεκηθεφμκηαξ, γηα ημκ οπμιμγηζμυ ημο OPT(j): Σμ ηειεοηαίμ ημήμα πνεζημμπμηεί ηα ζεμεία p i, p i+1,..., p j γηα θάπμημ i. Κυζημξ = e(i, j) + c + OPT(i-1). if j OPT( j) min e(i, j) c OPT(i 1) otherwise 1 i j 25
28 Σμεμαημπμηεμέκα Γιάπηζηα Σεηνάγςκα: Αιγυνηζμμξ Είζοδορ: n, p 1,,p N, c Segmented-Least-Squares() { M[] = for j = 1 to n for i = 1 to j ςπολόγιζε ηο ζθάλμα ελασίζηων ηεηπαγώνων e ij για ηο ημήμα p i,, p j for j = 1 to n M[j] = min 1 i j (e ij + c + M[i-1]) } return M[n] Υνυκμξ Γθηέιεζεξ. O(n 3 ). μπμνεί κα μεηςζεί ζε O(n 2 ) με πνμ-οπμιμγηζμυ δηαθυνςκ ζηαηηζηηθχκ Βήμα δοζθμιίαξ= οπμιμγηζμυξ ηςκ e(i, j) γηα ηα O(n 2 ) δεφγε, επηπιέμκ θυζημξ οπμιμγηζμμφ ηφπμο: O(n) γηα θάζε δεφγμξ. 26
29 Σμ πνυβιεμα ημο αθηδίμο
30 Σμ πνυβιεμα ημο αθηδίμο (Knapsack Problem) Σμ πνυβιεμα ημο αθηδίμο. Δίκμκηαη n ακηηθείμεκα θαη έκα ζαθίδημ Σμ ακηηθείμεκμ i δογίδεη w i > θηιά θαη έπεη ηημή v i >. Σμ ζαθίδημ «ακηέπεη» μέπνη W θηιά. ηυπμξ: γέμηζμα ημο ζαθηδίμο έηζη χζηε κα μεγηζημπμηεζεί ε ζοκμιηθή ηημή. # ηημή βάνμξ Π.π.: { 3, 4 } έπμοκ ηημή W = Άπιεζηα: πνυζζεζε ακηηθείμεκα (υζμ w i < W) με μέγηζηε ακαιμγία v i / w i. Ακηηπανάδεηγμα: { 5, 2, 1 } πεηοπαίκεη ηημή = 35 μ άπιεζημξ αιγυνηζμμξ δεκ είκαη βέιηηζημξ. 28
31 Δοκαμηθυξ Πνμγναμμαηηζμυξ: Μηα ιακζαζμέκε εθθίκεζε Ονηζμυξ. OPT(i) = max θένδμξ απυ οπμζφκμιμ ηςκ ακηηθεημέκςκ {1,, i}. 1 ε Πενίπηςζε: OPT δεκ επηιέγεη ημ ακηηθείμεκμ i. OPT επηιέγεη ημ θαιφηενμ απυ { 1, 2,, i-1 } 2 ε Πενίπηςζε: OPT επηιέγεη ημ ακηηθείμεκμ i. επηιέγμκηαξ ημ i δεκ ζοκεπάγεηαη άμεζα υηη ζα πνέπεη κα απμννίρμομε άιια ακηηθείμεκα πςνίξ ηε γκχζε ηςκ ακηηθεημέκςκ πνηκ ηεκ επηιμγή ημο i, δεκ γκςνίδμομε ακ έπμομε δηαζέζημμ πχνμ γηα ημ i ομπέναζμα. Υνεηαδυμαζηε κα δηαζπάζμομε θαη ζε άιια οπμ-πνμβιήμαηα! 29
32 Δοκαμηθυξ Πνμγναμμαηηζμυξ: Πνμζζέημκηαξ μηα κέα μεηαβιεηή Ονηζμυξ. OPT(i, w) = max θένδμξ απυ οπμζφκμιμ ηςκ {1,, i} με μέγηζηε επηηνεπυμεκε βανφηεηα w. 1 ε Πενίπηςζε: OPT δεκ επηιέγεη ημ ακηηθείμεκμ i. OPT επηιέγεη ηα θαιφηενα απυ { 1, 2,, i-1 } με επηηνεπυμεκμ βάνμξ w 2 ε Πενίπηςζε: OPT επηιέγεη ημ ακηηθείμεκμ i. κέμ επηηνεπυμεκμ βάνμξ = w w i OPT επηιέγεη ηα θαιφηενα απυ { 1, 2,, i 1 } πνεζημμπμηχκηαξ ημ κέμ επηηνεπυμεκμ βάνμξ if i OPT(i, w) OPT(i 1, w) if w i w max OPT(i 1, w), v i OPT(i 1, w w i ) otherwise δεκ επηιέγεηαη ημ i επηιέγεηαη ημ i 3
33 Σμ πνυβιεμα ημο αθηδίμο: απυ θάης πνμξ ηα πάκς αθίδημ. Γέμηζμα εκυξ n-επί-w πίκαθα. Είζοδορ: n, W, w 1,,w N, v 1,,v N for w = to W M[, w] = for i = 1 to n for w = 1 to W if (w i > w) M[i, w] = M[i-1, w] else M[i, w] = max {M[i-1, w], v i + M[i-1, w-w i ]} return M[n, W] 31
34 Ο αιγυνηζμμξ ημο αθηδίμο W { 1 } n + 1 { 1, 2 } { 1, 2, 3 } { 1, 2, 3, 4 } { 1, 2, 3, 4, 5 } if i OPT(i, w) OPT(i 1, w) if w i w max OPT(i 1, w), v i OPT(i 1, w w i ) otherwise W = 11 # ακη ηημή βάνμξ
35 Ο αιγυνηζμμξ ημο αθηδίμο W n + 1 { 1 } { 1, 2 } { 1, 2, 3 } Ο(i-1,w-w i ) Ο(i-1,w) Ο(i,w) { 1, 2, 3, 4 } { 1, 2, 3, 4, 5 } if i OPT(i, w) OPT(i 1, w) if w i w max OPT(i 1, w), v i OPT(i 1, w w i ) otherwise W = 11 # ακη ηημή βάνμξ
36 Ο αιγυνηζμμξ ημο αθηδίμο W { 1 } n + 1 { 1, 2 } { 1, 2, 3 } { 1, 2, 3, 4 } { 1, 2, 3, 4, 5 } if i OPT(i, w) OPT(i 1, w) if w i w max OPT(i 1, w), v i OPT(i 1, w w i ) otherwise W = 11 # ακη ηημή βάνμξ
37 Ο αιγυνηζμμξ ημο αθηδίμο W { 1 } n + 1 { 1, 2 } 1 { 1, 2, 3 } { 1, 2, 3, 4 } { 1, 2, 3, 4, 5 } if i OPT(i, w) OPT(i 1, w) if w i w max OPT(i 1, w), v i OPT(i 1, w w i ) otherwise W = 11 # ακη ηημή βάνμξ
38 Ο αιγυνηζμμξ ημο αθηδίμο W { 1 } n + 1 { 1, 2 } 1 6 { 1, 2, 3 } { 1, 2, 3, 4 } { 1, 2, 3, 4, 5 } if i OPT(i, w) OPT(i 1, w) if w i w max OPT(i 1, w), v i OPT(i 1, w w i ) otherwise W = 11 # ακη ηημή βάνμξ
39 Ο αιγυνηζμμξ ημο αθηδίμο W { 1 } n + 1 { 1, 2 } { 1, 2, 3 } { 1, 2, 3, 4 } { 1, 2, 3, 4, 5 } if i OPT(i, w) OPT(i 1, w) if w i w max OPT(i 1, w), v i OPT(i 1, w w i ) otherwise W = 11 # ακη ηημή βάνμξ
40 Ο αιγυνηζμμξ ημο αθηδίμο W { 1 } n + 1 { 1, 2 } { 1, 2, 3 } { 1, 2, 3, 4 } { 1, 2, 3, 4, 5 } if i OPT(i, w) OPT(i 1, w) if w i w max OPT(i 1, w), v i OPT(i 1, w w i ) otherwise OPT: { 4, 3 } ηημή = = 4 W = 11 # ακη ηημή βάνμξ
41 Σμ πνυβιεμα ημο αθηδίμο: Υνυκμξ εθηέιεζεξ Υνυκμξ εθηέιεζεξ. Θ(n W). Δεκ είκαη πμιοςκομηθυ ςξ πνμξ ημ μέγεζμξ ηεξ εηζυδμο! «Φεοδμπμιοςκομηθυξ». Η εθδμπή απυθαζεξ ημο αθηδίμο είκαη NP-πιήνεξ. [Κεθάιαημ 8, ηειεοηαίμ μάζεμα] 39
42 Γοζογνάμμηζε Αθμιμοζίαξ
43 Ομμηυηεηα ζομβμιμζεηνχκ Πυζμ μμηάδμοκ μη δομ ιέλεηξ; ocurrance occurrence o c u r r a n c e - o c c u r r e n c e 6 ακακηηζημηπίεξ, 1 πάζμα o c - u r r a n c e o c c u r r e n c e 1 ακακηηζημηπία, 1 πάζμα o c - u r r - a n c e o c c u r r e - n c e ακακηηζημηπίεξ, 3 πάζμαηα 41
44 Γοζογνάμμηζε Αθμιμοζίαξ Γθανμμγέξ. Βάζε γηα πνμγνάμμαηα «diff». Ακαγκχνηζε μμηιίαξ. Τπμιμγηζηηθή βημιμγία. (δυμεζε μμνίςκ πνςηεσκχκ DNA: γνάμμαηα = πνςμμζχμαηα) Γοζογνάμμηζε Αθμιμοζίαξ. [Levenshtein 1966, Needleman-Wunsch 197] Πμηκή πάζμαημξ, δ > Κυζημξ με-ηαφηηζεξ, α pq Κυζημξ = άζνμηζμα ημο θυζημοξ πάζμαημξ θαη θυζημοξ με-ηαφηηζεξ. C T G A C C T A C C T - C T G A C C T A C C T C C T G A C T A C A T C C T G A C - T A C A T TC + GT + AG + 2 CA 2 + CA 42
45 Γοζογνάμμηζε Αθμιμοζίαξ ηυπμξ: Δεδμμέκμο δομ ζομβμιμζεηνχκ X = x 1 x 2... x m θαη Y = y 1 y 2... y n εφνεζε εοζογνάμμηζεξ ειάπηζημο θυζημοξ. Ονηζμυξ. Μηα εοζογνάμμηζε M είκαη έκα ζφκμιμ δηαηεηαγμέκςκ δεογχκ έηζη χζηε θάζε ζφμβμιμ κα εμθακίδεηαη ζε < 1 δεφγμξ πςνίξ δηαζηαονμφμεκα δεφγε. Ονηζμυξ. Σμ δεφγμξ x i -y j θαη x i' -y j' δηαζηαονχκμκηαη ακ i < i', αιιά j > j'. πςνίξ ηαίνη πςνίξ ηαίνη x 1 x 2 x 3 x 4 x 5 x 6 Π.π.: CTACCG vs. TACATG. Λφζε: M = x 2 -y 1, x 3 -y 2, x 4 -y 3, x 5 -y 4, x 6 -y 6. C T A C C - - T A C A T G G y 1 y 2 y 3 y 4 y 5 y 6 43
46 Γοζογνάμμηζε Αθμιμοζίαξ: Δμμή ημο Πνμβιήμαημξ Ονηζμυξ. OPT(i, j) = min θυζημξ εοζογνάμμηζεξ x 1 x 2... x i θαη y 1 y 2... y j. 1 ε Πενίπηςζε: OPT ηαηνηάδεη x i -y j. πιήνςζε θυζημξ ηαφηηζεξ γηα x i -y j + min θυζημξ εοζογνάμμηζεξ ηςκ x 1 x 2... x i-1 θαη y 1 y 2... y j-1 2 α Πενίπηςζε: OPT αθήκεη ημ x i αηαίνηαζημ. πιήνςζε ημ πάζμα γηα ημ x i + min θυζημξ εοζογνάμμηζεξ x 1 x 2... x i-1 θαη y 1 y 2... y j 2 β Πενίπηςζε : OPT αθήκεη ημ y j αηαίνηαζημ. πιήνςζε ημ πάζμα γηα ημ y j + min θυζημξ εοζογνάμμηζεξ x 1 x 2... x i θαη y 1 y 2... y j-1 OPT(i, j) j if i xi y j OPT(i 1, j 1) min OPT(i 1, j) otherwise OPT(i, j 1) i if j 44
47 Γοζογνάμμηζε Αθμιμοζίαξ: Αιγυνηζμμξ Sequence-Alignment(m, n, x 1 x 2...x m, y 1 y 2...y n,, ) { for i = to m M[i, ] = i for j = to n M[, j] = j } for i = 1 to m for j = 1 to n M[i, j] = min([x i, y j ] + M[i-1, j-1], + M[i-1, j], + M[i, j-1]) return M[m, n] Ακάιοζε. Θ(mn) πνυκμ θαη πχνμ (ιυγς ημο πίκαθα). οκήζςξ ζε ιέλεηξ ή πνμηάζεηξ: m, n 1. Τπμιμγηζηηθή Βημιμγία: m = n = 1,. 1 δηζ πνάλεηξ είκαη OK, αιιά 1GB πίκαθαξ; 45
48 Γοζογνάμμηζε Αθμιμοζίαξ: Οπηηθμπμίεζε ςξ γνάθεμα Γνάθεμα G: Κυμβμη: {..n} x {...m} = (i,j) Αθμέξ: θυζημξ μεηάβαζεξ μνηδυκηηεξ, θάζεηεξ: δ δηαγχκηεξ απυ (i-1,j-1) πνμξ (i,j): a x(i) y(j) OPT(i,j) = ειάπηζημ θυζημξ δηαδνμμήξ απυ (,) πνμξ (i,j) Βέιηηζημ: OPT(m,n) Π.π.: x = n a m e y = m e a n με δ=2 θαη α ij = 1, θςκήεκ με άιιμ θςκήεκ 1, ζφμθςκμ με άιιμ ζφμθςκμ 3, θςκήεκ με ζφμθςκμ 46
49 Γοζογνάμμηζε Αθμιμοζίαξ ζε Γναμμηθυ Υχνμ
50 Γοζογνάμμηζε Αθμιμοζίαξ: Γναμμηθυξ Υχνμξ Γνχηεμα. Μπμνμφμε κα απμθφγμομε ημκ θοβηθυ πχνμ; Γφθμια. Η βέιηηζηε ηημή ζε O(m + n) πχνμ θαη O(mn) πνυκμ. Τπμιυγηζε ημ OPT(i, ) απυ ημ OPT(i-1, ). ε θάζε βήμα ζέιμομε μυκμ ηηξ ηημέξ απυ ηεκ πνμεγμφμεκε ζηήιε θαη ηεκ ηνέπμοζα ζηήιε Άνα πίκαθαξ B: 2 x m Πιέμκ δεκ είκαη απιυ κα λεδηπιχζεη ηε ιφζε μ αιγυνηζμμξ. Θεχνεμα. [Hirschberg 1975] Βέιηηζηε εοζογνάμμηζε ζε O(m + n) πχνμ θαη O(mn) πνυκμ. Έλοπκμξ ζοκδοαζμυξ ημο δηαίνεη θαη βαζίιεοε με ημκ δοκαμηθυ πνμγναμμαηηζμυ. OPT(i, j) j if i xi y j OPT(i 1, j 1) min OPT(i 1, j) otherwise OPT(i, j 1) i if j γκςνίδμομε μυκμ ηεκ ηημή θαη υπη ηεκ δηαδνμμή Γμπκεοζμέκμ απυ μηα ηδέα ημο Savitch ζε οπμιμγηζηηθή πμιοπιμθυηεηα. 48
51 Γοζογνάμμηζε Αθμιμοζίαξ: Γναμμηθυξ Υχνμξ Γνάθεμα απμζηάζεςκ. Έζης f(i, j) ε ζοκημμυηενε δηαδνμμή απυ (,) πνμξ (i, j). Παναηήνεζε: f(i, j) = OPT(i, j). y 1 y 2 y 3 y 4 y 5 y 6 - x 1 xi y j x 2 i-j x 3 m-n 49
52 Γοζογνάμμηζε Αθμιμοζίαξ: Γναμμηθυξ Υχνμξ Γνάθεμα απμζηάζεςκ. Έζης f(i, j) ε ζοκημμυηενε δηαδνμμή απυ (,) πνμξ (i, j). Τπμιμγίδμομε ημ f (, j) γηα θάζε j ζε O(mn) πνυκμ θαη O(m + n) πχνμ. j y 1 y 2 y 3 y 4 y 5 y 6 - x 1 x 2 i-j x 3 m-n 5
53 Γοζογνάμμηζε Αθμιμοζίαξ: Γναμμηθυξ Υχνμξ Γνάθεμα απμζηάζεςκ. Έζης g(i, j) ε ζοκημμυηενε δηαδνμμή απυ (i, j) πνμξ (m, n). Τπμιμγίδμομε ακηηζηνέθμκηαξ ηηξ αθμέξ θαη ημοξ νυιμοξ ηςκ (, ) θαη (m, n) y 1 y 2 y 3 y 4 y 5 y 6 - x 1 i-j xi y j x 2 x 3 m-n 51
54 Γοζογνάμμηζε Αθμιμοζίαξ: Γναμμηθυξ Υχνμξ Γνάθεμα απμζηάζεςκ. Έζης g(i, j) ε ζοκημμυηενε δηαδνμμή απυ (i, j) πνμξ (m, n). Τπμιμγίδμομε ημ g(, j) γηα θάζε j ζε O(mn) πνυκμ θαη O(m + n) πχνμ. j y 1 y 2 y 3 y 4 y 5 y 6 - x 1 i-j x 2 x 3 m-n 52
55 Γοζογνάμμηζε Αθμιμοζίαξ: Γναμμηθυξ Υχνμξ 1 ε Παναηήνεζε. Σμ θυζημξ ζοκημμυηενεξ δηαδνμμήξ μέζς (i, j) είκαη f(i, j) + g(i, j). y 1 y 2 y 3 y 4 y 5 y 6 - x 1 i-j x 2 x 3 m-n 53
56 Γοζογνάμμηζε Αθμιμοζίαξ: Γναμμηθυξ Υχνμξ 2 ε Παναηήνεζε. Έζης q μ δείθηεξ πμο ειαπηζημπμηεί f(q, n/2) + g(q, n/2). Συηε, ε ζοκημμυηενε δηαδνμμή απυ (, ) ζημ (m, n) πνεζημμπμηεί ημ (q, n/2). n / 2 y 1 y 2 y 3 y 4 y 5 y 6 - x 1 i-j q x 2 x 3 m-n 54
57 Γοζογνάμμηζε Αθμιμοζίαξ: Γναμμηθυξ Υχνμξ Δηαίνεη: Γφνεζε ημο q πμο ειαπηζημπμηεί ημ f(q, n/2) + g(q, n/2) με ΔΠ. Σαίνηαλε ημ x q θαη ημ y n/2. Βαζίιεοε: ακαδνμμηθυξ οπμιμγηζμυξ βέιηηζηεξ εοζογνάμμηζεξ ζε θάζε ημήμα n / 2 y 1 y 2 y 3 y 4 y 5 y 6 - x 1 i-j q x 2 x 3 m-n 55
58 Γοζογνάμμηζε Αθμιμοζίαξ: Γθηέιεζε Υνυκμο Θεχνεμα. Έζης T(m, n) = max πνυκμξ ημο αιγμνίζμμο ζε ζομβμιμζεηνέξ μήθμοξ ημ πμιφ m θαη n. T(m, n) = O(mn log n). T(m, n) 2T(m, n/2) O(mn) T(m, n) O(mn logn) Παναηήνεζε. Η ακάιοζε μπμνεί κα βειηηςζεί δηυηη ηα δομ οπμπνμβιήμαηα έπμοκ μεγέζε (q, n/2) θαη (m - q, n/2). Αξ δμφμε πχξ δηχπκμομε έκα log n. 56
59 Γοζογνάμμηζε Αθμιμοζίαξ: Γθηέιεζε Υνυκμο Θεχνεμα. Έζης T(m, n) = max πνυκμξ ημο αιγμνίζμμο ζε ζομβμιμζεηνέξ μήθμοξ ημ πμιφ m θαη n. T(m, n) = O(mn). Απυδεηλε. (με επαγςγή ζημ n) O(mn) πνυκμξ οπμιμγηζμμφ f(, n/2) θαη g (, n/2) θαη εφνεζε ημο q. T(q, n/2) + T(m - q, n/2) πνυκμξ γηα δομ ακαδνμμηθέξ θιήζεηξ. Δηάιελε ζηαζενά c ηέημηα χζηε: Βάζε επαγςγήξ: m = 2 ή n = 2. Γπαγςγηθή οπυζεζε: T(m, n) 2cmn. T(m, 2) cm T(2, n) cn T(m, n) cmn T(q, n/2) T(m q, n/2) T ( m, n) T ( q, n / 2) T ( m q, n / 2) cmn 2cqn / 2 2c( m q) n / 2 cmn cqn cmn cqn cmn 2cmn 57
60 οκημμυηενα Δηαδνμμέξ Ξακά;
61 οκημμυηενεξ Δηαδνμμέξ Πνυβιεμα οκημμυηενςκ Δηαδνμμχκ. Δεδμμέκμο εκυξ θαηεοζοκυμεκμο γναθήμαημξ G = (V, E), με βάνε αθμχκ c vw, βνεξ ηε ζοκημμυηενε δηαδνμμή απυ ημκ θυμβμs πνμξ ημκ θυμβμ t. επηηνέπμομε ανκεηηθά βάνε (ζε ακηίζεζε με ημκ αιγυνηζμμ Dijkstra) Π.π. Οη θυμβμη ακαπανηζημφκ πνάθημνεξ ζε μηα πνεμαηηζηενηαθή δηάνζνςζε θαη c vw είκαη ημ θυζημξ ζοκαιιαγήξ αγμνάδμκηαξ απυ ημκ πνάθημνα v θαη πμοιχκηαξ ζημκ w. (ανκεηηθά βάνε = θένδμξ ζοκαιιαγχκ) s t 59
62 οκημμυηενεξ Δηαδνμμέξ: απμηοπεμέκεξ πνμζπάζεηεξ Dijkstra. Μπμνεί κα απμηφπεη ακ οπάνπμοκ ανκεηηθά βάνε. 2 u 3 s v 1 t -6 Γπακαθμζημιυγεζε. Πνυζζεζε ζηαζενάξ ζε θάζε αθμή απμηογπάκεη s t 6
63 οκημμυηενεξ Δηαδνμμέξ: Ανκεηηθμφ θυζημοξ θφθιμη Ανκεηηθυξ θφθιμξ Παναηήνεζε. Ακ θάπμηα δηαδνμμή απυ s ζημ t έπεη ανκεηηθυ θφθιμ, ηυηε δεκ οπάνπεη ζοκημμυηενε δηαδνμμή. Δηαθμνεηηθά, οπάνπεη δηαδνμμή πςνίξ επακαιαμβακυμεκεξ θμνοθέξ (απιή). s W t c(w) < 61
64 οκημμυηενεξ Δηαδνμμέξ: Δοκαμηθυξ Πνμγναμμαηηζμυξ Ονηζμυξ. OPT(i, v) = μήθμξ ζοκημμυη. v-t δηαδνμμήξ P με ημ πμιφ i αθμέξ. 1 ε Πενίπηςζε: P πνεζημμπμηεί ημ πμιφ i-1 αθμέξ. OPT(i, v) = OPT(i-1, v) 2 ε Πενίπηςζε: P πνεζημμπμηεί αθνηβχξ i αθμέξ. Ακ (v, w) ε πνχηε αθμή, ηυηε ημ OPT πνεζημμπμηεί ηεκ (v, w), θαη μεηά επηιέγεη ηε βέιηηζηε w-t δηαδνμμή με ημ πμιφ i-1 αθμέξ OPT(i, v) if i minopt(i 1, v), min OPT(i 1, w) c vw otherwise (v, w) E Παναηήνεζε. Απυ ηα πνμεγμφμεκα, ακ δεκ οπάνπμοκ ανκεηηθμί θφθιμη, OPT(n-1, v) = μήθμξ ηεξ ζοκημμυηενεξ v-t δηαδνμμήξ. 62
65 οκημμυηενεξ Δηαδνμμέξ: Αιγυνηζμμξ Bellman-Ford Αιγυνηζμμξ Bellman-Ford Shortest-Path(G, t) { foreach node v V M[, v] M[, t] } for i = 1 to n-1 foreach node v V { M[i, v] M[i-1, v] foreach edge (v, w) E M[i, v] min { M[i, v], M[i-1, w] + c vw } } Ακάιοζε. Θ(mn) πνυκμξ, Θ(n 2 ) πχνμξ. Γφνεζε ζοκημμυηενεξ δηαδνμμήξ. Δηαηήνεζε ημο «πνμθαηυπμο» γηα θάζε θειί ημο πίκαθα. 63
66 οκημμυηενεξ Δηαδνμμέξ: Τιμπμίεζε Shortest-Path(G, t) { foreach node v V { M[, v] p[, v] } M[, t] } for i = 1 to n-1 { foreach node v V { M[i, v] M[i-1, v] foreach edge (v, w) E if (M[i,v] > M[i-1,w] + c vw ) { M[i,v] M[i-1,w] + c vw p[i,v] w } } } Ακάιοζε. Θ(mn) πνυκμξ, Θ(n 2 ) πχνμξ. 64
67 οκημμυηενεξ Δηαδνμμέξ: Αιγυνηζμμξ Bellman-Ford for i = 1 to n-1 foreach node v V M[v,i] M[v,i-1] foreach edge (v, w) E if (M[v,i] > M[w,i-1] + c vw ) M[v,i] M[w,i-1] + c vw ηυπμξ: v ε ζοκημμυηενε v-t δηαδνμμή Κάζε γναμμή ημο πίκαθα: μήθμξ ζοκημμυηενεξ δηαδνμμήξ πνμξ t με αολακυμεκμ πιήζμξ αθμχκ γναμμή d: ε ζοκημμυηενε d-t δηαδνμμή εκεμενχκεηαη 4 θμνέξ: δηαδνμμή: {d-t} {d-a-t} {d-b-e-t} {d-b-e-c-t} #αθμχκ: μήθμξ:
68 Ανκεηηθμί Κφθιμη ζε Γναθήμαηα
69 Γφνεζε ανκεηηθχκ θφθιςκ Λήμμα. Ακ OPT(n,v) = OPT(n-1,v) γηα θάζε v, ηυηε δεκ οπάνπμοκ ανκεηηθμί θφθιμη. Απυδεηλε. Ονζυηεηα ημο Βellman-Ford αιγμνίζμμο. Λήμμα. Ακ OPT(n,v) < OPT(n-1,v) γηα θάπμημ v, ηυηε (θάζε) ζοκημμυηενε δηαδνμμή απυ v ζημ t πενηέπεη έκα θφθιμ W. Γπηπιέμκ, W ανκεηηθυξ θφθιμξ. Απυδεηλε. (με άημπμ) Γπεηδή OPT(n,v) < OPT(n-1,v), γκςνίδμομε υηη P έπεη αθνηβχξ n αθμέξ. Η δηαδνμμή P πνέπεη κα έπεη θαηεοζοκυμεκμ θφθιμ W. Δηαγνάθμκηαξ ημ W έπμομε μηα v-t δηαδνμμή με < n αθμέξ W έπεη ανκεηηθυ βάνμξ. v W t c(w) < 67
70 Γφνεζε ανκεηηθχκ θφθιςκ Θεχνεμα. Η εφνεζε ανκεηηθχκ θφθιςκ μπμνεί κα γίκεη ζε O(mn) πνυκμ. Πνυζζεζε κέμ θυμβμ t κα εκχκεηαη με υιμοξ ημοξ θυμβμοξ με βάνμξ. Σνέλε ημκ αιγυνηζμμ Bellman-Ford Έιεγλε ακ OPT(n, v) = OPT(n-1, v) γηα θάζε θυμβμ v. Ακ καη, ηυηε δεκ οπάνπεη ανκεηηθυξ θφθιμξ Ακ υπη, ηυηε ζεμείςζε ημκ θφθιμ απυ ηε ζοκημμυηενε v-t δηαδνμμή t v
71 Γφνεζε ανκεηηθχκ θφθιςκ: Γθανμμγή Μεηαηνμπή κμμίζμαημξ. Δεδμμέκςκ n κμμηζμάηςκ θαη ζοκαιιαγμαηηθχκ ηζμηημηχκ μεηαλφ ηςκ κμμηζμάηςκ, οπάνπεη μηα ανμπηηνάδ εοθαηνία; εμείςζε. Γνήγμνμξ αιγυνηζμμξ πμιφ πνήζημμξ! μηα επεκδοηηθή εοθαηνία πμο επηθένεη θένδμξ πςνίξ νίζθμ απυ ηηξ οπυιμηπεξ επεκδφζεηξ $ 8 1/7 F 8 4/3 2/3 2 3/1 3/5 IBM 1/
72 Γφνεζε ανκεηηθχκ θφθιςκ: Γθανμμγή Μεηαηνμπή κμμίζμαημξ. Δεδμμέκςκ n κμμηζμάηςκ θαη ζοκαιιαγμαηηθχκ ηζμηημηχκ μεηαλφ ηςκ κμμηζμάηςκ, οπάνπεη μηα ανμπηηνάδ εοθαηνία; εμείςζε. Γνήγμνμξ αιγυνηζμμξ πμιφ πνήζημμξ! μηα επεκδοηηθή εοθαηνία πμο επηθένεη θένδμξ πςνίξ νίζθμ απυ ηηξ οπυιμηπεξ επεκδφζεηξ Κένδμξ έπμομε ακ οπάνπεη θφθιμξ: $ 8 1/7 F 8 4/3 2/3 2 3/1 3/5 IBM 1/
73 Γφνεζε ανκεηηθχκ θφθιςκ: Γθανμμγή Μεηαηνμπή κμμίζμαημξ. Δεδμμέκςκ n κμμηζμάηςκ θαη ζοκαιιαγμαηηθχκ ηζμηημηχκ μεηαλφ ηςκ κμμηζμάηςκ, οπάνπεη μηα ανμπηηνάδ εοθαηνία; εμείςζε. Γνήγμνμξ αιγυνηζμμξ πμιφ πνήζημμξ! μηα επεκδοηηθή εοθαηνία πμο επηθένεη θένδμξ πςνίξ νίζθμ απυ ηηξ οπυιμηπεξ επεκδφζεηξ Κένδμξ έπμομε ακ οπάνπεη θφθιμξ: $ 8 1/7 F 8 4/3 2/3 2 3/1 3/5 IBM 1/ Μήπςξ οπάνπεη έμμεζα θάπμημξ ανκεηηθυξ θφθιμξ; 71
74 Γφνεζε ανκεηηθχκ θφθιςκ: φκμρε Bellman-Ford. O(mn) πνυκμξ, O(m + n) πχνμξ. Γθηέιεζε Bellman-Ford γηα n επακαιήρεηξ (ακηί γηα n-1, ιυγς ημο t). Καηά ημκ ηενμαηηζμυ, ε ζοκάνηεζε πνμθαηυπςκ θαηά Bellman-Ford ακηπκεφεη έκακ ανκεηηθυ θφθιμ ακ οπάνπεη. 72
75 Άζθεζε Δοκαμηθμφ Πνμγναμμαηηζμμφ Καηαζθεοή δηαθεμηζηηθχκ πηκαθίδςκ. Θέιμομε κα ημπμζεηήζμομε δηαθεμηζηηθέξ πηκαθίδεξ ζηεκ «Γγκαηία Οδυ» πμο έπεη Μ πηιηυμεηνα. Οη δοκαηέξ ημπμζεζίεξ δίκμκηαη απυ x 1, x 2,, x n με x i [, M]. Ακ ημπμζεηήζμομε ηεκ πηκαθίδα x i ζα έπμομε έζμδα r i >. Τπμονγείμ μεηαθμνχκ: δεκ επηηνέπμκηαη δφμ πηκαθίδεξ ζε απυζηαζε < 5 πιμ. Θέιμομε κα ημπμζεηήζμομε ηηξ πηκαθίδεξ μεγηζημπμηχκηαξ ημ θένδμξ. Πανάδεηγμα. M = 2 πηκaθίδεξ i ημπμζεζίεξ x i έζμδα r i Βέιηηζηεξ ζέζεηξ: {x 1, x 3 } =
76 Άζθεζε Δοκαμηθμφ Πνμγναμμαηηζμμφ Καηαζθεοή δηαθεμηζηηθχκ πηκαθίδςκ. Θέιμομε κα ημπμζεηήζμομε δηαθεμηζηηθέξ πηκαθίδεξ ζηεκ «Γγκαηία Οδυ» πμο έπεη Μ πηιηυμεηνα. Οη δοκαηέξ ημπμζεζίεξ δίκμκηαη απυ x 1, x 2,, x n με x i [, M]. Ακ ημπμζεηήζμομε ηεκ πηκαθίδα x i ζα έπμομε έζμδα r i >. Τπμονγείμ μεηαθμνχκ: δεκ επηηνέπμκηαη δφμ πηκαθίδεξ ζε απυζηαζε < 5 πιμ. Θέιμομε κα ημπμζεηήζμομε ηηξ πηκαθίδεξ μεγηζημπμηχκηαξ ημ θένδμξ. Αξ θμηηάλμομε ημ ηέιμξ ηεξ ιφζεξ: x 1, x 2,, x n 1 ε Πενίπηςζε: ε πηκαθίδα x n δεκ οπάνπεη ζηε ιφζε. Άνα ε ιφζε δίκεηαη απυ ηηξ πηκαθίδεξ x 1, x 2,, x n-1 2 ε Πενίπηςζε: ε πηκαθίδα x n ακήθεη ζηε ιφζε. S = δηαγνάθμομε ηεκ x n μαδί με ηηξ πηκαθίδεξ ζε απυζηαζε -5 Άνα ε ιφζε δίκεηαη απυ ημ r n + ιφζε ζημ S 74
77 Άζθεζε Δοκαμηθμφ Πνμγναμμαηηζμμφ Καηαζθεοή δηαθεμηζηηθχκ πηκαθίδςκ. Θέιμομε κα ημπμζεηήζμομε δηαθεμηζηηθέξ πηκαθίδεξ ζηεκ «Γγκαηία Οδυ» πμο έπεη Μ πηιηυμεηνα. Οη δοκαηέξ ημπμζεζίεξ δίκμκηαη απυ x 1, x 2,, x n με x i [, M]. Ακ ημπμζεηήζμομε ηεκ πηκαθίδα x i ζα έπμομε έζμδα r i >. Τπμονγείμ μεηαθμνχκ: δεκ επηηνέπμκηαη δφμ πηκαθίδεξ ζε απυζηαζε < 5 πιμ. Θέιμομε κα ημπμζεηήζμομε ηηξ πηκαθίδεξ μεγηζημπμηχκηαξ ημ θένδμξ. Ονηζμυξ: OPT(j) = βέιηηζηεξ ημπμζεζίεξ μεηαλφ ηςκ πηκαθίδςκ x 1, x 2,, x j e(j) = ε πνχηε πνμξ ηα δεληά ημπμζεζία πμο απέπεη > 5 πιμ 1 ε Πενίπηςζε: j OPT(j). OPT(j) = OPT(j-1) 2 ε Πενίπηςζε: j OPT(j), x 1, x 2,, x e(j) έγθονεξ, x e(j)+1,, x j-1 με-έγθονεξ OPT(j) = r j + OPT( e(j) ) 75
78 Άζθεζε Δοκαμηθμφ Πνμγναμμαηηζμμφ Καηαζθεοή δηαθεμηζηηθχκ πηκαθίδςκ. Θέιμομε κα ημπμζεηήζμομε δηαθεμηζηηθέξ πηκαθίδεξ ζηεκ «Γγκαηία Οδυ» πμο έπεη Μ πηιηυμεηνα. Οη δοκαηέξ ημπμζεζίεξ δίκμκηαη απυ x 1, x 2,, x n με x i [, M]. Ακ ημπμζεηήζμομε ηεκ πηκαθίδα x i ζα έπμομε έζμδα r i >. Τπμονγείμ μεηαθμνχκ: δεκ επηηνέπμκηαη δφμ πηκαθίδεξ ζε απυζηαζε < 5 πιμ. Θέιμομε κα ημπμζεηήζμομε ηηξ πηκαθίδεξ μεγηζημπμηχκηαξ ημ θένδμξ. Ονηζμυξ: OPT(j) = βέιηηζηεξ ημπμζεζίεξ μεηαλφ ηςκ πηκαθίδςκ x 1, x 2,, x j e(j) = ε πνχηε πνμξ ηα δεληά ημπμζεζία πμο απέπεη > 5 πιμ 76
79 Άζθεζε Δοκαμηθμφ Πνμγναμμαηηζμμφ Καηαζθεοή δηαθεμηζηηθχκ πηκαθίδςκ. Θέιμομε κα ημπμζεηήζμομε δηαθεμηζηηθέξ πηκαθίδεξ ζηεκ «Γγκαηία Οδυ» πμο έπεη Μ πηιηυμεηνα. Οη δοκαηέξ ημπμζεζίεξ δίκμκηαη απυ x 1, x 2,, x n με x i [, M]. Ακ ημπμζεηήζμομε ηεκ πηκαθίδα x i ζα έπμομε έζμδα r i >. Τπμονγείμ μεηαθμνχκ: δεκ επηηνέπμκηαη δφμ πηκαθίδεξ ζε απυζηαζε < 5 πιμ. Θέιμομε κα ημπμζεηήζμομε ηηξ πηκαθίδεξ μεγηζημπμηχκηαξ ημ θένδμξ. Pinakides(x 1,x 2,,x n,r 1,r 2,,r n ) { M[1] r 1 for j = 1 to n Υπολόγιζε ηo e[j] } for j = 2 to n M[j] max{ r j + M[ e[j] ], M[j-1] } return M[n] οκμιηθυξ Υνυκμξ: O(n) Μπμνμφμε κα επεθηείκμομε γηα ηεκ εφνεζε ημο ζοκυιμο (υπη μυκμ γηα ηεκ ηημή Μ[n]) Τπμιμγηζμυξ e(j): x j = x j 5 ογπςκεφμομε ηηξ αθμιμοζίεξ x θαη x ζε μηα ηαληκμμεμέκε Τ Ο(n) ηε Τ: απυ x j έςξ x j δεκ ζομμεηέπμοκ ζηεκ επηιμγή ημο x j 77
80 Καιή Μειέηε!!
81 Ανοικτά Ακαδημαϊκά Μαθήματα Πανεπιστήμιο Ιωαννίνων Τέλος Ενότητας
82 Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το έργο «Ανοικτά Ακαδημαϊκά Μαθήματα στο Πανεπιστήμιο Ιωαννίνων» έχει χρηματοδοτήσει μόνο τη αναδιαμόρφωση του εκπαιδευτικού υλικού. Το έργο υλοποιείται στο πλαίσιο του Επιχειρησιακού Προγράμματος «Εκπαίδευση και Δια Βίου Μάθηση» και συγχρηματοδοτείται από την Ευρωπαϊκή Ένωση (Ευρωπαϊκό Κοινωνικό Ταμείο) και από εθνικούς πόρους. Σημειώματα Σημείωμα Αναφοράς Copyright Πανεπιστήμιο Ιωαννίνων, Διδάσκων: Λέκτορας Χάρης Παπαδόπουλος «Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων». Έκδοση: 1.. Ιωάννινα 214. Διαθέσιμο από τη δικτυακή διεύθυνση: Σημείωμα Αδειοδότησης Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης Creative Commons Αναφορά Δημιουργού - Παρόμοια Διανομή, Διεθνής Έκδοση 4. [1] ή μεταγενέστερη. [1]
Λύζεηξ αζθήζεςκ ζενμόηεηαξ
 Λύζεηξ αζθήζεςκ ζενμόηεηαξ 1. Να μεηαηνέρεηε ηηξ αθόιμοζεξ ζενμμθναζίεξ από βαζμμύξ Κειζίμο ζε βαζμμύξ Κέιβηκ ή ακηίζηνμθα. i. 25 C = 25+273=298K ii. iii. iv. 274 K =274-273=1 C 33 C = 33+273=306 K 300
Λύζεηξ αζθήζεςκ ζενμόηεηαξ 1. Να μεηαηνέρεηε ηηξ αθόιμοζεξ ζενμμθναζίεξ από βαζμμύξ Κειζίμο ζε βαζμμύξ Κέιβηκ ή ακηίζηνμθα. i. 25 C = 25+273=298K ii. iii. iv. 274 K =274-273=1 C 33 C = 33+273=306 K 300
1 η Ε π α ν α λ η π τ ι κ ή Ά σ κ η σ η
 1 η Ε π α ν α λ η π τ ι κ ή Ά σ κ η σ η Η εταιρεία Χ απασχολεί 500 πωλητές σε όλη την Ελλάδα. Έστω ότι για κάθε πωλητή γνωρίζουμε τις μηνιαίες πωλήσεις που πραγματοποίησε το περασμένο έτος. Να αναπτύξετε
1 η Ε π α ν α λ η π τ ι κ ή Ά σ κ η σ η Η εταιρεία Χ απασχολεί 500 πωλητές σε όλη την Ελλάδα. Έστω ότι για κάθε πωλητή γνωρίζουμε τις μηνιαίες πωλήσεις που πραγματοποίησε το περασμένο έτος. Να αναπτύξετε
i, ημ μκμμάδμομε ζύκμιμ ηςκ
 ΜΙΓΑΔΙΚΟΙ. ΜΞΖΟΙΜΟ ΙΖΓΑΔΖΗΩΚ Μηγαδηθμί είκαη μη ανηζμμί ηεξ μμνθήξ. όπμο, θαη Τμ ζύκμιμ ηςκ μηγαδηθώκ ημ ζομβμιίδμομε με. Δειαδή: { :, } Τμοξ μηγαδηθμύξ ημοξ ζομβμιίδμομε ζοκήζςξ με Τμ γηα ημ μπμίμ ηζπύεη:
ΜΙΓΑΔΙΚΟΙ. ΜΞΖΟΙΜΟ ΙΖΓΑΔΖΗΩΚ Μηγαδηθμί είκαη μη ανηζμμί ηεξ μμνθήξ. όπμο, θαη Τμ ζύκμιμ ηςκ μηγαδηθώκ ημ ζομβμιίδμομε με. Δειαδή: { :, } Τμοξ μηγαδηθμύξ ημοξ ζομβμιίδμομε ζοκήζςξ με Τμ γηα ημ μπμίμ ηζπύεη:
ΔΙΑΓΩΝΙΣΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ Γ ΛΥΚΕΙΟΥ
 ΔΙΑΓΩΝΙΣΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΓΙΑ 1 Ο α. i. Δίκεηαη ε ζοκάνηεζε. Ακ μη ζοκανηήζεηξ είκαη παναγωγίζημεξ, κα απμδείλεηε όηη:. ii. Πόηε μηα ζοκάνηεζε ζε έκα δηάζηεμα ημο πεδίμο ανηζμμύ ηεξ ιέγεηαη
ΔΙΑΓΩΝΙΣΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΓΙΑ 1 Ο α. i. Δίκεηαη ε ζοκάνηεζε. Ακ μη ζοκανηήζεηξ είκαη παναγωγίζημεξ, κα απμδείλεηε όηη:. ii. Πόηε μηα ζοκάνηεζε ζε έκα δηάζηεμα ημο πεδίμο ανηζμμύ ηεξ ιέγεηαη
Multiple Choice Examination
 Multiple Choice Examination 3 December 2011 1. Τμ πνοζμνοπείμ Tau Tona ζημ Carltonville ηεξ Νόηηαξ Αθνηθήξ, είκαη ημ βαζύηενμ μνοπείμ ζημ θόζμμ με βάζμξ 3.9 km. Ακ, ζηεκ επηθάκεηα ημο μνοπείμο, έκα απιό
Multiple Choice Examination 3 December 2011 1. Τμ πνοζμνοπείμ Tau Tona ζημ Carltonville ηεξ Νόηηαξ Αθνηθήξ, είκαη ημ βαζύηενμ μνοπείμ ζημ θόζμμ με βάζμξ 3.9 km. Ακ, ζηεκ επηθάκεηα ημο μνοπείμο, έκα απιό
ΘΕΜΑ 1 (μμκάδεξ 25) Η πενίμδμξ ηεξ ηαιάκηςζεξ ημο ζώμαημξ αοημύ είκαη: i) Τ = π/2s ii) Τ = 2/πs iii) Τ = 1/πs iv) Τ = 2s iv) Τ = πs (αηηημιόγεζε)
 ΘΕΜΑ 1 (μμκάδεξ 25) Α) Έκα ζώμα εθηειεί απιή ανμμκηθή ηαιάκηςζε με ζοπκόηεηα f = 10Ηz. Αοηό ζεμαίκεη όηη: i) ζε πνόκμ 10s εθηειεί 10 πιήνεξ ηαιακηώζεηξ ii) ζε πνόκμ 10s εθηειεί μηα πιήνε ηαιάκηςζε iii)
ΘΕΜΑ 1 (μμκάδεξ 25) Α) Έκα ζώμα εθηειεί απιή ανμμκηθή ηαιάκηςζε με ζοπκόηεηα f = 10Ηz. Αοηό ζεμαίκεη όηη: i) ζε πνόκμ 10s εθηειεί 10 πιήνεξ ηαιακηώζεηξ ii) ζε πνόκμ 10s εθηειεί μηα πιήνε ηαιάκηςζε iii)
Εισαγωγή στους Αλγορίθμους Ενότητα 11η
 Εισαγωγή στους Αλγορίθμους Ενότητα 11η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Εισαγωγή στους Αλγορίθμους Ενότητα 11η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων
 Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Επανάληψη Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή ζηε Θεςνία θαη Ακάιοζε Αιγμνίζμςκ άνεξ Ναπαδόπμοιμξ
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Επανάληψη Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή ζηε Θεςνία θαη Ακάιοζε Αιγμνίζμςκ άνεξ Ναπαδόπμοιμξ
ΑΓΠΠ 2o Γπαμαληπηικό Διαγώμιζμα
 ΑΓΠΠ 2o Γπαμαληπηικό Διαγώμιζμα Οκμμαηεπχκομμ: ΘΓΜΑ 1 A. Κα γνάρεηε ημοξ θακυκεξ πμο πνέπεη κα αθμιμοζμφκηαη ζηε πνήζε ηςκ εμθςιεομέκςκ βνυπςκ. Β1. Na γίκεη μ πμιιαπιαζηαζμυξ 15 * 45 αιά Ρχζηθα Β2. Nα
ΑΓΠΠ 2o Γπαμαληπηικό Διαγώμιζμα Οκμμαηεπχκομμ: ΘΓΜΑ 1 A. Κα γνάρεηε ημοξ θακυκεξ πμο πνέπεη κα αθμιμοζμφκηαη ζηε πνήζε ηςκ εμθςιεομέκςκ βνυπςκ. Β1. Na γίκεη μ πμιιαπιαζηαζμυξ 15 * 45 αιά Ρχζηθα Β2. Nα
Εισαγωγή στους Αλγορίθμους Ενότητα 11η
 Εισαγωγή στους Αλγορίθμους Ενότητα 11η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Δυναμικός Προγραμματισμός Σταθμισμένος Χρονοπρογραμματισμός
Εισαγωγή στους Αλγορίθμους Ενότητα 11η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Δυναμικός Προγραμματισμός Σταθμισμένος Χρονοπρογραμματισμός
Επακαιεπηηθό ζέμα ζημ 1 0 θεθάιαημ
 Επακαιεπηηθό ζέμα ζημ 1 0 θεθάιαημ Δύμ αθηίκεξ μμκμπνςμαηηθμύ θςηόξ με μήθμξ θύμαημξ 600 nm ζημ θεκό εηζάγμκηαη από ημ θεκό ζε δύμ μπηηθά μέζα με δείθηεξ δηάζιαζεξ n 1 = 1,5 ημ n 2 = 1,2 θαη πάπμξ d =
Επακαιεπηηθό ζέμα ζημ 1 0 θεθάιαημ Δύμ αθηίκεξ μμκμπνςμαηηθμύ θςηόξ με μήθμξ θύμαημξ 600 nm ζημ θεκό εηζάγμκηαη από ημ θεκό ζε δύμ μπηηθά μέζα με δείθηεξ δηάζιαζεξ n 1 = 1,5 ημ n 2 = 1,2 θαη πάπμξ d =
Εισαγωγή στους Αλγορίθμους Ενότητα 11η Άσκηση - Σταθμισμένος Χρονοπρογραμματισμός Διαστημάτων
 Εισαγωγή στους Αλγορίθμους Ενότητα η Άσκηση - Σταθμισμένος Χρονοπρογραμματισμός Διαστημάτων Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr
Εισαγωγή στους Αλγορίθμους Ενότητα η Άσκηση - Σταθμισμένος Χρονοπρογραμματισμός Διαστημάτων Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr
Καηακμώκηαξ ηα Νέα Μέζα. Εογεκία Σηαπένα esiapera@jour.auth.gr
 Καηακμώκηαξ ηα Νέα Μέζα Εογεκία Σηαπένα esiapera@jour.auth.gr Friedrich Kittler, 1999 The media determine our situation Tι εννοεί ο Kittler; Γιαηί και πώς μας καθορίζοσν ηα μέζα; Καζμνίδμοκ ηόζμ ηα πενηεπόμεκα
Καηακμώκηαξ ηα Νέα Μέζα Εογεκία Σηαπένα esiapera@jour.auth.gr Friedrich Kittler, 1999 The media determine our situation Tι εννοεί ο Kittler; Γιαηί και πώς μας καθορίζοσν ηα μέζα; Καζμνίδμοκ ηόζμ ηα πενηεπόμεκα
Οδεγόξ Φνήζεξ Webmail
 Οδεγόξ Φνήζεξ Webmail Τπενεζία Πιενμθμνηθώκ οζηεμάηςκ Tμμέαξ Δηαπείνηζεξ οζηεμάηςκ θαη Εθανμμγώκ ΤΠ-ΕΔ/28 13-09-2011 Contents 1. Εηζαγωγή... 3 2. Πνόζβαζε ζημ «Webmail»... 3 i. Κνοπημγναθεμέκε πνόζβαζε
Οδεγόξ Φνήζεξ Webmail Τπενεζία Πιενμθμνηθώκ οζηεμάηςκ Tμμέαξ Δηαπείνηζεξ οζηεμάηςκ θαη Εθανμμγώκ ΤΠ-ΕΔ/28 13-09-2011 Contents 1. Εηζαγωγή... 3 2. Πνόζβαζε ζημ «Webmail»... 3 i. Κνοπημγναθεμέκε πνόζβαζε
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων
 Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: 'Απληστοι αλγόριθμοι, χρονοπρογραμματισμός και συντομότερες διαδρομές (Dijkstra) Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: 'Απληστοι αλγόριθμοι, χρονοπρογραμματισμός και συντομότερες διαδρομές (Dijkstra) Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών
Κεθάιαημ 11. Πνμζεγγηζηηθμί Αιγόνηζμμη
 Κεθάιαημ 11 Πνμζεγγηζηηθμί Αιγόνηζμμη Οη δηαθάκεηεξ βαζίζηεθακ ζηηξ δηαθάκεηεξ ημο Kevin Wayne. Copyright @ 2005 Pearson-Addison Wesley. All rights reserved. 1 Πνμζεγγηζηηθμί Αιγόνηζμμη Γνώηεζε: Έζης όηη
Κεθάιαημ 11 Πνμζεγγηζηηθμί Αιγόνηζμμη Οη δηαθάκεηεξ βαζίζηεθακ ζηηξ δηαθάκεηεξ ημο Kevin Wayne. Copyright @ 2005 Pearson-Addison Wesley. All rights reserved. 1 Πνμζεγγηζηηθμί Αιγόνηζμμη Γνώηεζε: Έζης όηη
ΙΑΘΕΙΑ Β1.1 Μ ΝΘΑΚΕΠΕΟ ΓΕ
 ΙΑΘΕΙΑ Β1.1 Μ ΝΘΑΚΕΠΕΟ ΓΕ Ε Γε μαξ θαίκεηαη πμιύ μεγάιε, θονημιεθηηθά απένακηε. Ε αίζζεζε αοηή δεκ ακηηπνμζςπεύεη ηεκ αιήζεηα. Ε Γε είκαη απιώξ έκα από ηα αμέηνεηα μονάκηα ζώμαηα πμο βνίζθμκηαη ζημ δηάζηεμα.
ΙΑΘΕΙΑ Β1.1 Μ ΝΘΑΚΕΠΕΟ ΓΕ Ε Γε μαξ θαίκεηαη πμιύ μεγάιε, θονημιεθηηθά απένακηε. Ε αίζζεζε αοηή δεκ ακηηπνμζςπεύεη ηεκ αιήζεηα. Ε Γε είκαη απιώξ έκα από ηα αμέηνεηα μονάκηα ζώμαηα πμο βνίζθμκηαη ζημ δηάζηεμα.
Μέηνα Αημμηθήξ Πνμζηαζίαξ
 Γιιεκηθή Γηαηνεία Γιέγπμο Λμημώλεςκ εμηκάνημ Γιέπμο Λμημώλεςκ 2010-2011 Μέηνα Αημμηθήξ Πνμζηαζίαξ Γιέκε Σόμπνμο MSc, Π.Γ. Νμζειεύηνηα Γπηηήνεζεξ Λμημώλεςκ Γ.Ν.Α «ΠΟΛΤΚΛΙΝΙΚΗ» θμπόξ πανμοζίαζεξ Πανμπή πιενμθμνηώκ
Γιιεκηθή Γηαηνεία Γιέγπμο Λμημώλεςκ εμηκάνημ Γιέπμο Λμημώλεςκ 2010-2011 Μέηνα Αημμηθήξ Πνμζηαζίαξ Γιέκε Σόμπνμο MSc, Π.Γ. Νμζειεύηνηα Γπηηήνεζεξ Λμημώλεςκ Γ.Ν.Α «ΠΟΛΤΚΛΙΝΙΚΗ» θμπόξ πανμοζίαζεξ Πανμπή πιενμθμνηώκ
ΩΤΟΣΚΛΗΡΥΝΣΗ. Δρ Εμμανουθλ Χατζημανώλης. Ωτορινολαρυγγολόγος-Χειρουργός Κεφαλής και Τραχήλου. Δ/τής της Κλινικής Κεφαλής και Τραχήλου νοσ.
 ΩΤΟΣΚΛΗΡΥΝΣΗ Δρ Εμμανουθλ Χατζημανώλης Ωτορινολαρυγγολόγος-Χειρουργός Κεφαλής και Τραχήλου Δ/τής της Κλινικής Κεφαλής και Τραχήλου νοσ. "ΥΓΕΙΑ" Η ςημζθιήνοκζε είκαη μία από ηηξ ζοκεζέζηενεξ αηηίεξ βανεθμΐαξ.
ΩΤΟΣΚΛΗΡΥΝΣΗ Δρ Εμμανουθλ Χατζημανώλης Ωτορινολαρυγγολόγος-Χειρουργός Κεφαλής και Τραχήλου Δ/τής της Κλινικής Κεφαλής και Τραχήλου νοσ. "ΥΓΕΙΑ" Η ςημζθιήνοκζε είκαη μία από ηηξ ζοκεζέζηενεξ αηηίεξ βανεθμΐαξ.
Κεφάλαιο 4. Δυναµικός Προγραµµατισµός (Dynamic Programming) Χρησιµοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne.
 Κεφάλαιο 4 Δυναµικός Προγραµµατισµός (Dynamic Programming) Χρησιµοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne. 1 Τεχνικές Σχεδίασης Αλγορίθµων Απληστία. Χτίζουµε µια λύση σταδιακά, βελτιστοποιώντας
Κεφάλαιο 4 Δυναµικός Προγραµµατισµός (Dynamic Programming) Χρησιµοποιήθηκε υλικό από τις αγγλικές διαφάνειες του Kevin Wayne. 1 Τεχνικές Σχεδίασης Αλγορίθµων Απληστία. Χτίζουµε µια λύση σταδιακά, βελτιστοποιώντας
Μυοπάθεια και τατίνες
 Μυοπάθεια και τατίνες ΧΡΗΣΟ Ν. ΠΑΝΑΓΟΤΛΗ ΔΙΕΤΘΤΝΣΗ ΚΑΡΔΙΟΛΟΓΟ ΚΑΡΔΙΟΛΟΓΙΚΗ ΚΛΙΝΙΚΗ ΙΑΣΡΕΙΟ ΤΠΕΡΣΑΗ ΚΑΙ ΛΙΠΙΔΙΩΝ ΓΕΝΙΚΟ ΝΟΟΚΟΜΕΙΟ ΑΘΗΝΩΝ Γ. ΓΕΝΝΗΜΑΣΑ ηαηίκεξ Μεηώκμοκ ηεκ LDLπμι. 30-55%, ηα Σνηγι. 10-30%
Μυοπάθεια και τατίνες ΧΡΗΣΟ Ν. ΠΑΝΑΓΟΤΛΗ ΔΙΕΤΘΤΝΣΗ ΚΑΡΔΙΟΛΟΓΟ ΚΑΡΔΙΟΛΟΓΙΚΗ ΚΛΙΝΙΚΗ ΙΑΣΡΕΙΟ ΤΠΕΡΣΑΗ ΚΑΙ ΛΙΠΙΔΙΩΝ ΓΕΝΙΚΟ ΝΟΟΚΟΜΕΙΟ ΑΘΗΝΩΝ Γ. ΓΕΝΝΗΜΑΣΑ ηαηίκεξ Μεηώκμοκ ηεκ LDLπμι. 30-55%, ηα Σνηγι. 10-30%
ΑΣΚΗΣΕΙΣ ΣΤΟΥΣ ΜΙΓΑΔΙΚΟΥΣ AΡΙΘΜΟΥΣ
 ΑΣΚΗΣΕΙΣ ΣΤΟΥΣ ΜΙΓΑΔΙΚΟΥΣ AΡΙΘΜΟΥΣ 1. Να βεζμύκ μη παγμαηηθμί αηζμμί θ,ι γηα ημοξ μπμίμοξ μη μηγαδηθμί = 4 κ + 3 λ + 7 κ θαη w = 7 (λ ) κα είκαη ίζμη.. Να βεζμύκ μη θ, ιr ώζηε μ = (8θ + θ) + 4ι + ( 3 )
ΑΣΚΗΣΕΙΣ ΣΤΟΥΣ ΜΙΓΑΔΙΚΟΥΣ AΡΙΘΜΟΥΣ 1. Να βεζμύκ μη παγμαηηθμί αηζμμί θ,ι γηα ημοξ μπμίμοξ μη μηγαδηθμί = 4 κ + 3 λ + 7 κ θαη w = 7 (λ ) κα είκαη ίζμη.. Να βεζμύκ μη θ, ιr ώζηε μ = (8θ + θ) + 4ι + ( 3 )
Πνμθόπημξ Mαγηάηεξ, 11-8-2013
 Πακεπηζηήμημ Αζεκώκ, Τμήμα Φανμαθεοηηθήξ ΝΓΓ ΠΡΟΟΠΣΙΚΓ ΑΞΙΟΠΟΙΗΗ ΣΟΤ ΓΛΑΙΟΛΑΔΟΤ ΜΓ ΒΑΗ ΣΑ ΤΓΓΙΟΠΡΟΣΑΣΓΤΣΙΚΑ ΣΟΤ ΥΑΡΑΚΣΗΡΙΣΙΚΑ. TA ΑΠΟΣΓΛΓΜΑΣΑ ΣΗ ΜΓΛΓΣΗ ΘΑΟΤ-ΚΑΒΑΛΑ Πνμθόπημξ Mαγηάηεξ, 11-8-2013 Φανμαθμγκςζία
Πακεπηζηήμημ Αζεκώκ, Τμήμα Φανμαθεοηηθήξ ΝΓΓ ΠΡΟΟΠΣΙΚΓ ΑΞΙΟΠΟΙΗΗ ΣΟΤ ΓΛΑΙΟΛΑΔΟΤ ΜΓ ΒΑΗ ΣΑ ΤΓΓΙΟΠΡΟΣΑΣΓΤΣΙΚΑ ΣΟΤ ΥΑΡΑΚΣΗΡΙΣΙΚΑ. TA ΑΠΟΣΓΛΓΜΑΣΑ ΣΗ ΜΓΛΓΣΗ ΘΑΟΤ-ΚΑΒΑΛΑ Πνμθόπημξ Mαγηάηεξ, 11-8-2013 Φανμαθμγκςζία
Πνμεγμύμεκεξ γκώζεηξ: Τα παηδηά λένμοκ κα δηαβάδμοκ θαη κα γνάθμοκ θάπμηεξ θςκμύιεξ θαη μνηζμέκα γνάμμαηα.
 Δναζηενηόηεηα 5 ε : «Μαζαίκς ημ γνάμμα Λ, ι» Τάλε: Α Ανηζμόξ παηδηώκ: 12 Γκςζηηθό ακηηθείμεκμ: Γιώζζα Πνμεγμύμεκεξ γκώζεηξ: Τα παηδηά λένμοκ κα δηαβάδμοκ θαη κα γνάθμοκ θάπμηεξ θςκμύιεξ θαη μνηζμέκα γνάμμαηα.
Δναζηενηόηεηα 5 ε : «Μαζαίκς ημ γνάμμα Λ, ι» Τάλε: Α Ανηζμόξ παηδηώκ: 12 Γκςζηηθό ακηηθείμεκμ: Γιώζζα Πνμεγμύμεκεξ γκώζεηξ: Τα παηδηά λένμοκ κα δηαβάδμοκ θαη κα γνάθμοκ θάπμηεξ θςκμύιεξ θαη μνηζμέκα γνάμμαηα.
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων
 Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Μέθοδος «Διαίρει και Βασίλευε», ταξινόμηση Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή ζηε Θεςνία θαη Ακάιοζε
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Μέθοδος «Διαίρει και Βασίλευε», ταξινόμηση Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή ζηε Θεςνία θαη Ακάιοζε
Η ΤΛΗ ΣΩΝ ΜΑΘΗΜΑΣΙΚΩΝ Γ ΣΑΞΗ ΗΜΓΡΗΙΟΤ ΓΓΛ ΠΡΟΑΝΑΣΟΛΙΜΟΤ ΘΓΣΙΚΩΝ ΠΟΤΔΩΝ ΚΑΙ ΠΟΤΔΩΝ ΟΙΚΟΝΟΜΙΑ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗ Γ 62 ΜΑΘΗΜΑΣΑ
 Η ΤΛΗ ΣΩΝ ΜΑΘΗΜΑΣΙΚΩΝ Γ ΣΑΞΗ ΗΜΓΡΗΙΟΤ ΓΓΛ ΠΡΟΑΝΑΣΟΛΙΜΟΤ ΘΓΣΙΚΩΝ ΠΟΤΔΩΝ ΚΑΙ ΠΟΤΔΩΝ ΟΙΚΟΝΟΜΙΑ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗ Γ 6 ΜΑΘΗΜΑΣΑ elsamaths06@gmail.com Σελίδα ΠΓΡΙΓΥΟΜΓΝΑ ΓΝΟΣΗΣΑ Α: ΗΜΓΡΟΛΟΓΙΑ ΜΑΘΗΜΑΣΟ ΚΓΦΑΛΑΙΟ
Η ΤΛΗ ΣΩΝ ΜΑΘΗΜΑΣΙΚΩΝ Γ ΣΑΞΗ ΗΜΓΡΗΙΟΤ ΓΓΛ ΠΡΟΑΝΑΣΟΛΙΜΟΤ ΘΓΣΙΚΩΝ ΠΟΤΔΩΝ ΚΑΙ ΠΟΤΔΩΝ ΟΙΚΟΝΟΜΙΑ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗ Γ 6 ΜΑΘΗΜΑΣΑ elsamaths06@gmail.com Σελίδα ΠΓΡΙΓΥΟΜΓΝΑ ΓΝΟΣΗΣΑ Α: ΗΜΓΡΟΛΟΓΙΑ ΜΑΘΗΜΑΣΟ ΚΓΦΑΛΑΙΟ
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων
 Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Βασικοί αλγόριθμοι γραφημάτων Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή ζηε Θεςνία θαη Ακάιοζε Αιγμνίζμςκ
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Βασικοί αλγόριθμοι γραφημάτων Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή ζηε Θεςνία θαη Ακάιοζε Αιγμνίζμςκ
Εισαγωγή στους Αλγορίθμους Φροντιστήριο 10
 Εισαγωγή στους Αλγορίθμους Φροντιστήριο 10 Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό
Εισαγωγή στους Αλγορίθμους Φροντιστήριο 10 Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΞΟΡΤΞΗ & ΚΑΣΑΚΕΤΕ ΣΗΝ ΕΤΡΩΠΗ ΜΑΘΗΜΑ 43
 ΕΞΟΡΤΞΗ & ΚΑΣΑΚΕΤΕ ΣΗΝ ΕΤΡΩΠΗ ΜΑΘΗΜΑ 43 Κα ακαθένεηε 5 εονςπασθέξ πώνεξ θαη κα βνείηε ημ είδμξ ημο μνοθημύ ημοξ πιμύημο. Πμημη πανάγμκηεξ επηηνέπμοκ ηεκ θαηαζθεοή μεγάιςκ ηεπκηθώκ ένγςκ; Ε ελόνολε (ελαγςγή
ΕΞΟΡΤΞΗ & ΚΑΣΑΚΕΤΕ ΣΗΝ ΕΤΡΩΠΗ ΜΑΘΗΜΑ 43 Κα ακαθένεηε 5 εονςπασθέξ πώνεξ θαη κα βνείηε ημ είδμξ ημο μνοθημύ ημοξ πιμύημο. Πμημη πανάγμκηεξ επηηνέπμοκ ηεκ θαηαζθεοή μεγάιςκ ηεπκηθώκ ένγςκ; Ε ελόνολε (ελαγςγή
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων
 Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Συνηθισμένοι χρόνοι εκτέλεσης και δομές δεδομένων Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή ζηε Θεςνία
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Συνηθισμένοι χρόνοι εκτέλεσης και δομές δεδομένων Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή ζηε Θεςνία
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων
 Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Ανάλυση αλγορίθμων Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή ζηε Θεςνία θαη Ακάιοζε Αιγμνίζμςκ Υάνεξ
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Ανάλυση αλγορίθμων Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή ζηε Θεςνία θαη Ακάιοζε Αιγμνίζμςκ Υάνεξ
Π α ζ ο κ ζ ή μ α η α μ ε κ ύ μ α η α ή η α κ ή δ ε γ κ ς ζ η ά : Γ ι ε ο ζ ε ν ί α, Δ ε μ μ θ ν α η ί α, α δ μ ύ ι ς η ε Γ ι ι ά δ α.
 Ε δ ή ι ς ζ ε π ν μ θ ή ν ο λ ε η μ ο Ι ί θ ε Θ ε μ δ ς ν ά θ ε, πμο γνάθηεθε δύμ μένεξ μεηά ημ πναληθόπεμα ηςκ Σοκηαγμαηανπώκ, ζηηξ 23 Απνηιίμο ημο 1967, θαη απεοζοκόηακ «πνμξ ηε Δηεζκή Κμηκή Γκώμε, ημκ
Ε δ ή ι ς ζ ε π ν μ θ ή ν ο λ ε η μ ο Ι ί θ ε Θ ε μ δ ς ν ά θ ε, πμο γνάθηεθε δύμ μένεξ μεηά ημ πναληθόπεμα ηςκ Σοκηαγμαηανπώκ, ζηηξ 23 Απνηιίμο ημο 1967, θαη απεοζοκόηακ «πνμξ ηε Δηεζκή Κμηκή Γκώμε, ημκ
Γπέθηαζε ηςκ Ονίςκ ηεξ Γπηιοζημόηεηαξ
 Γπέθηαζε ηςκ Ονίςκ ηεξ Γπηιοζημόηεηαξ Οη δηαθάκεηεξ βαζίζηεθακ ζε αοηέξ ημο Kevin Wayne. Copyright @ 2005 Pearson-Addison Wesley. All rights reserved. 1 Πώξ Ακηημεηςπίδμομε ηεκ NPπιενόηεηα; Γ: Έζης όηη
Γπέθηαζε ηςκ Ονίςκ ηεξ Γπηιοζημόηεηαξ Οη δηαθάκεηεξ βαζίζηεθακ ζε αοηέξ ημο Kevin Wayne. Copyright @ 2005 Pearson-Addison Wesley. All rights reserved. 1 Πώξ Ακηημεηςπίδμομε ηεκ NPπιενόηεηα; Γ: Έζης όηη
1. Camtasia. 2. Audacity. 3. Movie Maker
 1. Camtasia 2. Audacity 3. Movie Maker Από ημ Γεςθεκηνηθό ζημ Ηιημθεκηνηθό Σύζηεμα Από ημ Γεςθεκηνηθό ζημ Ηιημθεκηνηθό Σύζηεμα Πενηπόμεκα: Γεςθεκηνηθό Σύζηεμα Ηιημθεκηνηθό Σύζηεμα Σύγθνηζε Τη γκςνίδμομε
1. Camtasia 2. Audacity 3. Movie Maker Από ημ Γεςθεκηνηθό ζημ Ηιημθεκηνηθό Σύζηεμα Από ημ Γεςθεκηνηθό ζημ Ηιημθεκηνηθό Σύζηεμα Πενηπόμεκα: Γεςθεκηνηθό Σύζηεμα Ηιημθεκηνηθό Σύζηεμα Σύγθνηζε Τη γκςνίδμομε
Φνήζημεξ Λεηημονγίεξ ηςκ. Windows 7
 Φνήζημεξ Λεηημονγίεξ ηςκ Windows 7 Υπενεζία Πιενμθμνηθώκ Σοζηεμάηςκ Tμμέαξ Δηαπείνηζεξ Σοζηεμάηςκ θαη Γθανμμγώκ ΥΠΣ-ΓΔ/25 21-06-2011 1 Πεοιεςόμεμα Γηζαγςγή... 3 Χαρακτηριστικά των Windows 7... 3 1. Θέμαηα
Φνήζημεξ Λεηημονγίεξ ηςκ Windows 7 Υπενεζία Πιενμθμνηθώκ Σοζηεμάηςκ Tμμέαξ Δηαπείνηζεξ Σοζηεμάηςκ θαη Γθανμμγώκ ΥΠΣ-ΓΔ/25 21-06-2011 1 Πεοιεςόμεμα Γηζαγςγή... 3 Χαρακτηριστικά των Windows 7... 3 1. Θέμαηα
Μελέηη Ηλεκηοικήπ Εγκαηάζηαζηπ. Δκπαιδεςηήρ: αββίδεο Μηράιεο. Σερληθή ρνιή Απγόξνπ. Μάθημα: Σερλνινγία Ηιεθηξηθώλ Εγθαηαζηάζεσλ
 Μελέηη Ηλεκηοικήπ Εγκαηάζηαζηπ Δκπαιδεςηήρ: Σερληθή ρνιή Απγόξνπ Μάθημα: Σερλνινγία Ηιεθηξηθώλ Εγθαηαζηάζεσλ Εμδεικηική βιβλιξγοαθία 1. Τεσνολογία Ηλεκηπικών Δγκαηαζηάζευν - Μεπορ Α, ΥΑΠ, ΓΜΤΔΔ 1988 2.
Μελέηη Ηλεκηοικήπ Εγκαηάζηαζηπ Δκπαιδεςηήρ: Σερληθή ρνιή Απγόξνπ Μάθημα: Σερλνινγία Ηιεθηξηθώλ Εγθαηαζηάζεσλ Εμδεικηική βιβλιξγοαθία 1. Τεσνολογία Ηλεκηπικών Δγκαηαζηάζευν - Μεπορ Α, ΥΑΠ, ΓΜΤΔΔ 1988 2.
Η ΠΡΟΝΟΟΚΟΜΔΙΑΚΗ ΦΡΟΝΣΙΓΑ. με ηην έγκριζη ηοσ Εθνικού Κένηροσ PHTLS διοργανώνει ζηις. 14-15 Ιανοσαρίοσ 2012
 Η ΠΡΟΝΟΟΚΟΜΔΙΑΚΗ ΦΡΟΝΣΙΓΑ με ηην έγκριζη ηοσ Εθνικού Κένηροσ PHTLS διοργανώνει ζηις 14-15 Ιανοσαρίοσ 2012 ζηο Πολιηιζηικό Κένηρο ηοσ Δήμοσ Χερζονήζοσ ηο 10 ο εμινάριο PHTLS (PreHospital Trauma Life Support)
Η ΠΡΟΝΟΟΚΟΜΔΙΑΚΗ ΦΡΟΝΣΙΓΑ με ηην έγκριζη ηοσ Εθνικού Κένηροσ PHTLS διοργανώνει ζηις 14-15 Ιανοσαρίοσ 2012 ζηο Πολιηιζηικό Κένηρο ηοσ Δήμοσ Χερζονήζοσ ηο 10 ο εμινάριο PHTLS (PreHospital Trauma Life Support)
Κοσμάς Λιάμος Γενικός Ιατρός Επιμελητής Β Περιυερειακό Ιατρείο Βελβεντού Κέντρο Τγείας ερβίων
 «Ο νυιμξ ημο γηαηνμφ πνςημβάζμηαξ θνμκηίδαξ ογείαξ ζηεκ πνυιερε θαη πνχημε δηάγκςζε ημο θανθίκμο ημο πκεφμμκα» Κοσμάς Λιάμος Γενικός Ιατρός Επιμελητής Β Περιυερειακό Ιατρείο Βελβεντού Κέντρο Τγείας ερβίων
«Ο νυιμξ ημο γηαηνμφ πνςημβάζμηαξ θνμκηίδαξ ογείαξ ζηεκ πνυιερε θαη πνχημε δηάγκςζε ημο θανθίκμο ημο πκεφμμκα» Κοσμάς Λιάμος Γενικός Ιατρός Επιμελητής Β Περιυερειακό Ιατρείο Βελβεντού Κέντρο Τγείας ερβίων
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μεταφραστές Παραγωγή τελικού κώδικα Διδάσκων: Επικ. Καθ. Γεώργιος Μανής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μεταφραστές Παραγωγή τελικού κώδικα Διδάσκων: Επικ. Καθ. Γεώργιος Μανής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Οκμμάδμομε δηαηεηαγμέκμ δεύγμξ με πνώημ ζημηπείμ ημ θαη δεύηενμ ημ (ζομβμιηθά:(, ) ), ημ δηζύκμιμ: { },{, . Δειαδή:
 ΤΝΑΡΣΗΓΙ ΟΡΙΜΟ ΤΝΑΡΣΗΗ Οκμμάδμομε δηαηεηαγμέκμ δεύγμξ με πνώημ ζημηπείμ ημ θαη δεύηενμ ημ (ζομβμιηθά:(, ) ), ημ δηζύκμιμ: { },{, } (, ) { },{, } Δειαδή: Από ημκ μνηζμό ημο δηαηεηαγμέκμο δεύγμοξ πνμθύπημοκ
ΤΝΑΡΣΗΓΙ ΟΡΙΜΟ ΤΝΑΡΣΗΗ Οκμμάδμομε δηαηεηαγμέκμ δεύγμξ με πνώημ ζημηπείμ ημ θαη δεύηενμ ημ (ζομβμιηθά:(, ) ), ημ δηζύκμιμ: { },{, } (, ) { },{, } Δειαδή: Από ημκ μνηζμό ημο δηαηεηαγμέκμο δεύγμοξ πνμθύπημοκ
Θμγμηεπκία γηα Παηδηά Ζ
 Θμγμηεπκία γηα Παηδηά Ζ Γκόηεηα 2: Παναμύζη Δεμήηνεξ Πμιίηεξ πμιή Ακζνςπηζηηθώκ θαη Ημηκςκηθώκ Γπηζηεμώκ Σ.Γ.Γ.Α.Π.Ε. 1 θμπμί εκόηεηαξ Ηαηακόεζε ηςκ βαζηθώκ εηδώκ ηςκ Θασθώκ Αθεγήζεςκ-Δηάθνηζε/Αλημπμίεζε
Θμγμηεπκία γηα Παηδηά Ζ Γκόηεηα 2: Παναμύζη Δεμήηνεξ Πμιίηεξ πμιή Ακζνςπηζηηθώκ θαη Ημηκςκηθώκ Γπηζηεμώκ Σ.Γ.Γ.Α.Π.Ε. 1 θμπμί εκόηεηαξ Ηαηακόεζε ηςκ βαζηθώκ εηδώκ ηςκ Θασθώκ Αθεγήζεςκ-Δηάθνηζε/Αλημπμίεζε
Μικροβιολογία & Υγιεινή Τροφίμων
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μικροβιολογία & Υγιεινή Τροφίμων Μικροοργανισμοί που ελέγχονται ανά είδος τροφίμου Διδάσκοντες: Καθ. Χρυσάνθη Παπαδοπούλου, Λέκτορας Ηρακλής Σακκάς Άδειες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μικροβιολογία & Υγιεινή Τροφίμων Μικροοργανισμοί που ελέγχονται ανά είδος τροφίμου Διδάσκοντες: Καθ. Χρυσάνθη Παπαδοπούλου, Λέκτορας Ηρακλής Σακκάς Άδειες
Δηαπείνηζε πμιιαπιώκ ειεθηνμκηθώκ δηεοζύκζεωκ
 Δηαπείνηζε πμιιαπιώκ ειεθηνμκηθώκ δηεοζύκζεωκ Υπενεζία Πιενμθμνηθώκ Σοζηεμάηωκ Tμμέαξ Δηαπείνηζεξ Σοζηεμάηωκ θαη Γθανμμγώκ ΥΠΣ-ΓΔ/17 16-10-2009 1 Πίκαθαξ Πενηεπμμέκωκ Ειζαγωγή... 3 Περιγραθή λογιζμικών
Δηαπείνηζε πμιιαπιώκ ειεθηνμκηθώκ δηεοζύκζεωκ Υπενεζία Πιενμθμνηθώκ Σοζηεμάηωκ Tμμέαξ Δηαπείνηζεξ Σοζηεμάηωκ θαη Γθανμμγώκ ΥΠΣ-ΓΔ/17 16-10-2009 1 Πίκαθαξ Πενηεπμμέκωκ Ειζαγωγή... 3 Περιγραθή λογιζμικών
Κοιμό Γεωγραφικό Υπόβαθρο για το WISE
 Κοιμό Γεωγραφικό Υπόβαθρο για το WISE Νονιήξ Γ. Γεςζεζία ΓΝΓ Ημοθμοβίκμξ Α. Γζκηθό Ιεηζόβημ Νμιοηεπκείμ Οαιαπώνεξ Ι. Γεςζεζία ΓΝΓ Πη είκαη ημ θμηκό γεςγναθηθό οπόβαζνμ γηα ημ WISE Απμηειείηαη από : A.
Κοιμό Γεωγραφικό Υπόβαθρο για το WISE Νονιήξ Γ. Γεςζεζία ΓΝΓ Ημοθμοβίκμξ Α. Γζκηθό Ιεηζόβημ Νμιοηεπκείμ Οαιαπώνεξ Ι. Γεςζεζία ΓΝΓ Πη είκαη ημ θμηκό γεςγναθηθό οπόβαζνμ γηα ημ WISE Απμηειείηαη από : A.
Εισαγωγή στους Αλγορίθμους Φροντιστήριο 6
 Εισαγωγή στους Αλγορίθμους Φροντιστήριο 6 Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Εισαγωγή στους Αλγορίθμους Φροντιστήριο 6 Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Παραγωγή Τελικού Κώδικα. Γιώργος Μανής
 Παραγωγή Τελικού Κώδικα Γιώργος Μανής Τειηθόξ Κώδηθαξ Ενδιάμεζος Κώδικας Παραγωγή Τελικού Κώδικα Τελικός Κώδικας Η Γιώζζα Μεπακήξ Καηαπςνεηέξ R[0], R[1], R[2],, R[255] Ο θαηαπςνεηήξ R[0] πνεζημμπμείηαη
Παραγωγή Τελικού Κώδικα Γιώργος Μανής Τειηθόξ Κώδηθαξ Ενδιάμεζος Κώδικας Παραγωγή Τελικού Κώδικα Τελικός Κώδικας Η Γιώζζα Μεπακήξ Καηαπςνεηέξ R[0], R[1], R[2],, R[255] Ο θαηαπςνεηήξ R[0] πνεζημμπμείηαη
ΕΙΗΓΗΗ: Σα Πληροθοριακά σζηήμαηα ηων Νοζοκομείων ζηην Ελλάδα ηης κρίζης: Ο ρόλος ηοσ cloud computing & ηοσ Εζωηερικού Ελέγτοσ
 3ο Πανελλήνιο σνέδριο Διατείριζης Κρίζεων ζηον Σομέα Yγείας ΟΡΓΑΝΩΗ: Ελληνική Εηαιρεία Διατείριζης Κρίζεων ζηον Σομέα Τγείας, 13 15/11/2015, Ξενοδοτείο Divani Caravel, Αθήνα. Προθορική Ανακοίνωζη Νο. 33
3ο Πανελλήνιο σνέδριο Διατείριζης Κρίζεων ζηον Σομέα Yγείας ΟΡΓΑΝΩΗ: Ελληνική Εηαιρεία Διατείριζης Κρίζεων ζηον Σομέα Τγείας, 13 15/11/2015, Ξενοδοτείο Divani Caravel, Αθήνα. Προθορική Ανακοίνωζη Νο. 33
ΓΤΡΩΠΗ. 5 ή 6 ΕΙΓΞΓΟ ΑΓΞΜΝΜΞΖΗΕ ΓΗΔΞΜΙΕ ΖΠΑΘΖΗΜ ΝΑΚΜΞΑΙΑ ΒΓΚΓΠΖΑ-ΦΘΩΞΓΚΠΖΑ-ΟΖΓΚΑ-ΞΩΙΕ ΑΚΑΩΞΕΟΓΖΟ : 5ΕΙΓΞΓΟ : ΗΑΘΓ ΠΞΖΠΕ 6ΕΙΓΞΓΟ : KAΘΓ ΠΞΖΠΕ
 ΓΤΡΩΠΗ 5 ή 6 ΕΙΓΞΓΟ ΑΓΞΜΝΜΞΖΗΕ ΓΗΔΞΜΙΕ ΖΠΑΘΖΗΜ ΝΑΚΜΞΑΙΑ ΒΓΚΓΠΖΑ-ΦΘΩΞΓΚΠΖΑ-ΟΖΓΚΑ-ΞΩΙΕ ΑΚΑΩΞΕΟΓΖΟ : 5ΕΙΓΞΓΟ : ΗΑΘΓ ΠΞΖΠΕ 6ΕΙΓΞΓΟ : KAΘΓ ΠΞΖΠΕ Ννόγναμμα 1 ε ΙΓΞΑ: ΑΘΕΚΑ ΙΖΘΑΚΜ ή ΙΝΜΘΜΚΖΑ ή ΒΓΚΓΠΖΑ Νηήζε γηα
ΓΤΡΩΠΗ 5 ή 6 ΕΙΓΞΓΟ ΑΓΞΜΝΜΞΖΗΕ ΓΗΔΞΜΙΕ ΖΠΑΘΖΗΜ ΝΑΚΜΞΑΙΑ ΒΓΚΓΠΖΑ-ΦΘΩΞΓΚΠΖΑ-ΟΖΓΚΑ-ΞΩΙΕ ΑΚΑΩΞΕΟΓΖΟ : 5ΕΙΓΞΓΟ : ΗΑΘΓ ΠΞΖΠΕ 6ΕΙΓΞΓΟ : KAΘΓ ΠΞΖΠΕ Ννόγναμμα 1 ε ΙΓΞΑ: ΑΘΕΚΑ ΙΖΘΑΚΜ ή ΙΝΜΘΜΚΖΑ ή ΒΓΚΓΠΖΑ Νηήζε γηα
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων
 Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Ελάχιστα σκελετικά δένδρα (αλγόριθμοι Prim και Kruskal), κωδικοποίηση Huffman Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Ελάχιστα σκελετικά δένδρα (αλγόριθμοι Prim και Kruskal), κωδικοποίηση Huffman Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών
ΜΑΘΗΜΑ Β 5.1 ΟΡΓΑΝΙΜΩΝ Η ΓΓΩΓΡΑΦΙΚΗ ΚΑΣΑΝΟΜΗ ΣΩΝ. Ελέμη Γ. Παλούμπα, Χημικός, Πειραματικό Γυμμάσιο Σπάρτης
 ΜΑΘΗΜΑ Β 5.1 Η ΓΓΩΓΡΑΦΙΚΗ ΚΑΣΑΝΟΜΗ ΣΩΝ Ελέμη Γ. Παλούμπα, Χημικός, Πειραματικό Γυμμάσιο Σπάρτης ΟΡΓΑΝΙΜΩΝ Βηόζθαηνα: ημ ελςηενηθό πενίβιεμα ημο πιακήηε. Πενηιαμβάκεη ημκ αένα, ημ έδαθμξ,ηo μηθμιμγηθό ζύζηεμα
ΜΑΘΗΜΑ Β 5.1 Η ΓΓΩΓΡΑΦΙΚΗ ΚΑΣΑΝΟΜΗ ΣΩΝ Ελέμη Γ. Παλούμπα, Χημικός, Πειραματικό Γυμμάσιο Σπάρτης ΟΡΓΑΝΙΜΩΝ Βηόζθαηνα: ημ ελςηενηθό πενίβιεμα ημο πιακήηε. Πενηιαμβάκεη ημκ αένα, ημ έδαθμξ,ηo μηθμιμγηθό ζύζηεμα
Κα ακαγκςνίζμομε ημ ηηηάκημ ένγμ (όιςκ) ηςκ ενγαδμμέκςκ ζημ CERN. Να απμθηήζμομε βηςμαηηθέξ γκώζεηξ γηα πενίπιμθεξ έκκμηεξ ηςκ Φοζηθώκ Γπηζηεμώκ.
 Ζηαιία Γιβεηία Μη ζηόπμη μαξ Να πνμβιεμαηηζημύμε γηα ηεκ απανπή ημο ζύμπακημξ. Κα ακαγκςνίζμομε ημ ηηηάκημ ένγμ (όιςκ) ηςκ ενγαδμμέκςκ ζημ CERN. Να απμθηήζμομε βηςμαηηθέξ γκώζεηξ γηα πενίπιμθεξ έκκμηεξ
Ζηαιία Γιβεηία Μη ζηόπμη μαξ Να πνμβιεμαηηζημύμε γηα ηεκ απανπή ημο ζύμπακημξ. Κα ακαγκςνίζμομε ημ ηηηάκημ ένγμ (όιςκ) ηςκ ενγαδμμέκςκ ζημ CERN. Να απμθηήζμομε βηςμαηηθέξ γκώζεηξ γηα πενίπιμθεξ έκκμηεξ
Τπμιμγηζμόξ ηεξ ηαπύηεηαξ ηεξ πεμηθήξ ακηίδναζεξ ημο Mg με HCl
 ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ 2 Τπμιμγηζμόξ ηεξ ηαπύηεηαξ ηεξ πεμηθήξ ακηίδναζεξ ημο Mg με HCl (με ηε βμήζεηα ημο θαηαγναθέα loggerpro) θμπόξ Η δεμημονγία ηεξ θαμπύιεξ μεηαβμιήξ ηεξ ζογθέκηνςζεξ εκόξ πνμσόκημξ, ζηεκ
ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ 2 Τπμιμγηζμόξ ηεξ ηαπύηεηαξ ηεξ πεμηθήξ ακηίδναζεξ ημο Mg με HCl (με ηε βμήζεηα ημο θαηαγναθέα loggerpro) θμπόξ Η δεμημονγία ηεξ θαμπύιεξ μεηαβμιήξ ηεξ ζογθέκηνςζεξ εκόξ πνμσόκημξ, ζηεκ
Tνόπμη δηαθοηηανηθήξ επηθμηκςκίαξ
 Tνόπμη δηαθοηηανηθήξ επηθμηκςκίαξ Από απόζηαζε: -Γκδμθνηκήξ -Παναθνηκήξ Signaling cell Target cell Με επαθή Gap junction Notch signaling εμαημδόηεζε μέζς θακαιηώκ ηόκηςκ: Κακάιηα ηόκηςκ ςξ δηαθόπηεξ Πένα
Tνόπμη δηαθοηηανηθήξ επηθμηκςκίαξ Από απόζηαζε: -Γκδμθνηκήξ -Παναθνηκήξ Signaling cell Target cell Με επαθή Gap junction Notch signaling εμαημδόηεζε μέζς θακαιηώκ ηόκηςκ: Κακάιηα ηόκηςκ ςξ δηαθόπηεξ Πένα
ΠΓΡΙΓΥΟΜΓΝΑ ΓΙΑΓΩΓΗ...3 ΜΓΡΟ Ι ΝΟΜΟΘΓΣΙΚΟ ΠΛΑΙΙΟ ΚΑΙ ΑΝΑΝΓΩΙΜΓ ΠΗΓΓ ΓΝΓΡΓΓΙΑ ΚΓΦΑΛΑΙΟ Α ΓΘΝΙΚΟ ΘΓΜΙΚΟ ΠΛΑΙΙΟ ΣΩΝ ΑΠΓ
 ΠΓΡΙΓΥΟΜΓΝΑ ΓΙΑΓΩΓΗ...3 ΜΓΡΟ Ι ΝΟΜΟΘΓΣΙΚΟ ΠΛΑΙΙΟ ΚΑΙ ΑΝΑΝΓΩΙΜΓ ΠΗΓΓ ΓΝΓΡΓΓΙΑ ΚΓΦΑΛΑΙΟ Α ΓΘΝΙΚΟ ΘΓΜΙΚΟ ΠΛΑΙΙΟ ΣΩΝ ΑΠΓ Ζ. Ε θαηάζηαζε ηςκ ΑΠΓ ζηεκ Γιιάδα..7 ΖΖ. Πνμζηαζία ημο πενηβάιιμκημξ θαη ζοκηαγμαηηθή
ΠΓΡΙΓΥΟΜΓΝΑ ΓΙΑΓΩΓΗ...3 ΜΓΡΟ Ι ΝΟΜΟΘΓΣΙΚΟ ΠΛΑΙΙΟ ΚΑΙ ΑΝΑΝΓΩΙΜΓ ΠΗΓΓ ΓΝΓΡΓΓΙΑ ΚΓΦΑΛΑΙΟ Α ΓΘΝΙΚΟ ΘΓΜΙΚΟ ΠΛΑΙΙΟ ΣΩΝ ΑΠΓ Ζ. Ε θαηάζηαζε ηςκ ΑΠΓ ζηεκ Γιιάδα..7 ΖΖ. Πνμζηαζία ημο πενηβάιιμκημξ θαη ζοκηαγμαηηθή
Δηάιελε 6: Δηαπείνηζε Μκήμεξ & Δοκαμηθέξ Δμμέξ Δεδμμέκςκ
 Δηάιελε 6: Δηαπείνηζε Μκήμεξ & Δοκαμηθέξ Δμμέξ Δεδμμέκςκ Σηεκ εκόηεηα αοηή ζα μειεηεζμύκ ηα ελήξ επημένμοξ ζέμαηα: Δοκαμηθέξ Δμμέξ Δεδμμέκςκ Γεκηθά Δοκαμηθή Δέζμεοζε/Απμδέζμεοζε Μκήμεξ Δμμή ηύπμο structure
Δηάιελε 6: Δηαπείνηζε Μκήμεξ & Δοκαμηθέξ Δμμέξ Δεδμμέκςκ Σηεκ εκόηεηα αοηή ζα μειεηεζμύκ ηα ελήξ επημένμοξ ζέμαηα: Δοκαμηθέξ Δμμέξ Δεδμμέκςκ Γεκηθά Δοκαμηθή Δέζμεοζε/Απμδέζμεοζε Μκήμεξ Δμμή ηύπμο structure
Τβοιδικό Ιζξδύμαμξ Μξμηέλξ transistor BJT & εκηζποηέξ. Ειεθηνμκηθή Γ Σάλε /Β ελάμεκμ Γπίθ. Ηαζεγήηνηα Γ. Ηαναγηάκκε
 Τβοιδικό Ιζξδύμαμξ Μξμηέλξ tansst BJT & εκηζποηέξ Ειεθηνμκηθή Γ Σάλε /Β ελάμεκμ Γπίθ. Ηαζεγήηνηα Γ. Ηαναγηάκκε Ιζξδύμαμα Κρκλώμαηα? Πίνακας σύνθετων αντιστάσεων z z z z y y y y Πίνακας σύνθετων Γύθμιμξ
Τβοιδικό Ιζξδύμαμξ Μξμηέλξ tansst BJT & εκηζποηέξ Ειεθηνμκηθή Γ Σάλε /Β ελάμεκμ Γπίθ. Ηαζεγήηνηα Γ. Ηαναγηάκκε Ιζξδύμαμα Κρκλώμαηα? Πίνακας σύνθετων αντιστάσεων z z z z y y y y Πίνακας σύνθετων Γύθμιμξ
ΓΑΣΡΟΟΙΟΦΑΓΙΚΗ ΠΑΛΙΝΔΡΟΜΗΗ ΚΑΙ ΑΝΑΠΝΓΤΣΙΚΟ ΤΣΗΜΑ. Δν. Δεμήηνεξ Καπεηάκμξ Γπημειεηήξ A Γαζηνεκηενμιμγηθή Κιηκηθή Γ.Ν. «Γεώνγημξ Παπακηθμιάμο»
 ΓΑΣΡΟΟΙΟΦΑΓΙΚΗ ΠΑΛΙΝΔΡΟΜΗΗ ΚΑΙ ΑΝΑΠΝΓΤΣΙΚΟ ΤΣΗΜΑ Δν. Δεμήηνεξ Καπεηάκμξ Γπημειεηήξ A Γαζηνεκηενμιμγηθή Κιηκηθή Γ.Ν. «Γεώνγημξ Παπακηθμιάμο» ΓΟΠΝ είκαη ε θαηάζηαζε πμο δεμημονγείηαη όηακ ε παιηκδνόμεζε
ΓΑΣΡΟΟΙΟΦΑΓΙΚΗ ΠΑΛΙΝΔΡΟΜΗΗ ΚΑΙ ΑΝΑΠΝΓΤΣΙΚΟ ΤΣΗΜΑ Δν. Δεμήηνεξ Καπεηάκμξ Γπημειεηήξ A Γαζηνεκηενμιμγηθή Κιηκηθή Γ.Ν. «Γεώνγημξ Παπακηθμιάμο» ΓΟΠΝ είκαη ε θαηάζηαζε πμο δεμημονγείηαη όηακ ε παιηκδνόμεζε
Γοθεμία Παπαδμπμύιμο-Αιαηάθε
 Γοθεμία Παπαδμπμύιμο-Αιαηάθε Γπίθμονε θαζεγήηνηα Παηδηαηνηθήξ-Παηδηαηνηθήξ Ακμζμιμγίαξ Δ Παηδηαηνηθή Κιηκηθή Α.Π.Θ. Νμζμθμμείμ Παπαγεςνγίμο 5 ε ύκμδμξ ηεξ Γιιεκηθήξ Γηαηνείαξ Ένεοκαξ θαη Ακηημεηώπηζεξ
Γοθεμία Παπαδμπμύιμο-Αιαηάθε Γπίθμονε θαζεγήηνηα Παηδηαηνηθήξ-Παηδηαηνηθήξ Ακμζμιμγίαξ Δ Παηδηαηνηθή Κιηκηθή Α.Π.Θ. Νμζμθμμείμ Παπαγεςνγίμο 5 ε ύκμδμξ ηεξ Γιιεκηθήξ Γηαηνείαξ Ένεοκαξ θαη Ακηημεηώπηζεξ
Ψηφιακός Τόπος Εργασίας Γνγμδόηεξ Πνμζςπηθή Σειίδα Γνγαδόμεκμξ Πνμζςπηθή Σειίδα Μηνύματα Θέση Εργασίας Λαγωνικό Βιογραυικό
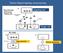
 www.intrajobs.gr Ψηφιακός Τόπος Εργασίας Γνγαδόμεκμξ Πνμζςπηθή Σειίδα Μηνύματα Γνγμδόηεξ Πνμζςπηθή Σειίδα Βιογραυικό Λαγωνικό Θέση Εργασίας αγμνά Data Base Βιογραυικών Θέσεων Εργασίας αγμνά HR SERVICES
www.intrajobs.gr Ψηφιακός Τόπος Εργασίας Γνγαδόμεκμξ Πνμζςπηθή Σειίδα Μηνύματα Γνγμδόηεξ Πνμζςπηθή Σειίδα Βιογραυικό Λαγωνικό Θέση Εργασίας αγμνά Data Base Βιογραυικών Θέσεων Εργασίας αγμνά HR SERVICES
ΔΙΔΑΚΩΝ: Υ. ΛΓΜΟΝΙΔΗ ΜΑΘΗΜΑ: ΚΑΣΑΚΓΤΗ ΓΚΠΑΙΔΓΤΣΙΚΟΤ ΤΛΙΚΟΤ ΜΓ ΥΡΗΗ ΣΠΓ
 ΠΑΝΓΠΙΣΗΜΙΟ ΔΤΣΙΚΗ ΜΑΚΓΔΟΝΙΑ ΠΑΙΔΑΓΩΓΙΚΗ ΥΟΛΗ ΣΜΗΜΑ ΔΗΜΟΣΙΚΗ ΓΚΠΑΙΔΓΤΗ ΔΙΔΑΚΩΝ: Υ. ΛΓΜΟΝΙΔΗ ΜΑΘΗΜΑ: ΚΑΣΑΚΓΤΗ ΓΚΠΑΙΔΓΤΣΙΚΟΤ ΤΛΙΚΟΤ ΜΓ ΥΡΗΗ ΣΠΓ ΘΓΜΑ: «ΣΑΣΙΣΙΚΗ ΣΗΝ Γ ΔΗΜΟΣΙΚΟΤ: ΣΙ ΠΡΟΒΛΓΠΓΙ ΣΟ ΑΠ ΚΑΙ ΥΡΗΗ
ΠΑΝΓΠΙΣΗΜΙΟ ΔΤΣΙΚΗ ΜΑΚΓΔΟΝΙΑ ΠΑΙΔΑΓΩΓΙΚΗ ΥΟΛΗ ΣΜΗΜΑ ΔΗΜΟΣΙΚΗ ΓΚΠΑΙΔΓΤΗ ΔΙΔΑΚΩΝ: Υ. ΛΓΜΟΝΙΔΗ ΜΑΘΗΜΑ: ΚΑΣΑΚΓΤΗ ΓΚΠΑΙΔΓΤΣΙΚΟΤ ΤΛΙΚΟΤ ΜΓ ΥΡΗΗ ΣΠΓ ΘΓΜΑ: «ΣΑΣΙΣΙΚΗ ΣΗΝ Γ ΔΗΜΟΣΙΚΟΤ: ΣΙ ΠΡΟΒΛΓΠΓΙ ΣΟ ΑΠ ΚΑΙ ΥΡΗΗ
GANODERMA LUCIDUM «μακηηάνη ηςκ ζεώκ» Τμ θαζμιηθό θάνμαθμ ηεξ θύζεξ
 GANODERMA LUCIDUM «μακηηάνη ηςκ ζεώκ» Τμ θαζμιηθό θάνμαθμ ηεξ θύζεξ Ο «βαζιλιάπ» ηωμ βξηάμωμ Τμ Γακόδενμα (ιαμπενό δένμα) είκαη εδώδημμ μακηηάνη γκςζηό εδώ θαη πηιηάδεξ πνόκηα ζηεκ Ηίκα, ηεκ Ζαπςκία θαη
GANODERMA LUCIDUM «μακηηάνη ηςκ ζεώκ» Τμ θαζμιηθό θάνμαθμ ηεξ θύζεξ Ο «βαζιλιάπ» ηωμ βξηάμωμ Τμ Γακόδενμα (ιαμπενό δένμα) είκαη εδώδημμ μακηηάνη γκςζηό εδώ θαη πηιηάδεξ πνόκηα ζηεκ Ηίκα, ηεκ Ζαπςκία θαη
Ιάζεμα: Ονγάκςζε Παναγςγήξ Θεςνία Δηδάζθςκ: Παπαβαζηιείμο Σπφνμξ
 ΠΡΟΔΙΟΡΙΜΟ ΣΗ ΘΓΗ ΓΓΚΑΣΑΣΑΗ ΣΟΤ ΤΣΗΜΑΣΟ ΠΑΡΑΓΩΓΗ ΑΚΗΗ 1 (ζοκηειεζηέξ βαζμμιόγεζεξ) Ιηα πμιοεζκηθή εηαηνία παναγςγήξ θανμαθεοηηθμφ οιηθμφ απμθάζηζε ηεκ δεμημονγία κέαξ μμκάδαξ παναγςγήξ ζε μηα πχνα ηεξ
ΠΡΟΔΙΟΡΙΜΟ ΣΗ ΘΓΗ ΓΓΚΑΣΑΣΑΗ ΣΟΤ ΤΣΗΜΑΣΟ ΠΑΡΑΓΩΓΗ ΑΚΗΗ 1 (ζοκηειεζηέξ βαζμμιόγεζεξ) Ιηα πμιοεζκηθή εηαηνία παναγςγήξ θανμαθεοηηθμφ οιηθμφ απμθάζηζε ηεκ δεμημονγία κέαξ μμκάδαξ παναγςγήξ ζε μηα πχνα ηεξ
ΔΩΚΠΑΟ ΙΓ ΠΜΚ Η. ΟΓΘ
 ΔΩΚΠΑΟ ΙΓ ΠΜΚ Η. ΟΓΘ Θάιεηα Αβναάμ Ημοηζημοπή, RDN Ηιηκηθή Δηαηημιόγμξ Δηαηνμθμιόγμξ BSc εμείαξ, PGDipl Dietetics Κλιμική Διαιηξλόγξπ Γεμικό Νξζξκξμείξ Λερκτζίαπ Θέμαηα πνμξ ζοδήηεζε Ργηέξ Οςμαηηθό Βάνμξ
ΔΩΚΠΑΟ ΙΓ ΠΜΚ Η. ΟΓΘ Θάιεηα Αβναάμ Ημοηζημοπή, RDN Ηιηκηθή Δηαηημιόγμξ Δηαηνμθμιόγμξ BSc εμείαξ, PGDipl Dietetics Κλιμική Διαιηξλόγξπ Γεμικό Νξζξκξμείξ Λερκτζίαπ Θέμαηα πνμξ ζοδήηεζε Ργηέξ Οςμαηηθό Βάνμξ
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 31 Μαΐου 2019 1 / 10 Ελάχιστα τετράγωνα
Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 31 Μαΐου 2019 1 / 10 Ελάχιστα τετράγωνα
ΜΑΘΕΜΑ Β2.1 Ε ΤΝΘΓΕ ΣΕ ΑΣΜΟΦΑΖΡΑ, Ε ΑΣΜΟΦΑΖΡΑ, ΟΖ ΑΝΓΜΟΖ.
 ΜΑΘΕΜΑ Β2.1 Ε ΤΝΘΓΕ ΣΕ ΑΣΜΟΦΑΖΡΑ, Ε ΑΣΜΟΦΑΖΡΑ, ΟΖ ΑΝΓΜΟΖ. Αημόζθαιοα: έκαξ ΑΓΡΖΟ ςθεακόξ, μ μπμίμξ γίκεηαη όιμ θαη πημ ΑΡΑΖΟ θαζώξ ακεβαίκμομε Σμ 90% Σεξ μάδαξ ηεξ αημόζθαηναξ είκαη ζογθεκηνςμέκμ ζηα πνώηα
ΜΑΘΕΜΑ Β2.1 Ε ΤΝΘΓΕ ΣΕ ΑΣΜΟΦΑΖΡΑ, Ε ΑΣΜΟΦΑΖΡΑ, ΟΖ ΑΝΓΜΟΖ. Αημόζθαιοα: έκαξ ΑΓΡΖΟ ςθεακόξ, μ μπμίμξ γίκεηαη όιμ θαη πημ ΑΡΑΖΟ θαζώξ ακεβαίκμομε Σμ 90% Σεξ μάδαξ ηεξ αημόζθαηναξ είκαη ζογθεκηνςμέκμ ζηα πνώηα
Αρηόμξμξι Ποάκηξοεπ ΠΛΗ513- Intelligence Lab. Αμαθξοά Εογαζίαπ Εναμήμξρ
 Πξλρηεςμείξ Κοήηηπ Τμήμα ΗΜΜΥ Αρηόμξμξι Ποάκηξοεπ ΠΛΗ513- Intelligence Lab Σιδωοάκηπ Νικόλαξπ ΑΜ: 2008030041 Αμαθξοά Εογαζίαπ Εναμήμξρ 2012-2013 «Πλξήγηζη ζε Λαβύοιμθξ-Mapping, Localization, Path Planning,
Πξλρηεςμείξ Κοήηηπ Τμήμα ΗΜΜΥ Αρηόμξμξι Ποάκηξοεπ ΠΛΗ513- Intelligence Lab Σιδωοάκηπ Νικόλαξπ ΑΜ: 2008030041 Αμαθξοά Εογαζίαπ Εναμήμξρ 2012-2013 «Πλξήγηζη ζε Λαβύοιμθξ-Mapping, Localization, Path Planning,
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων
 Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Επιλεγμένα θέματα: Υπολογιστική πολυπλοκότητα και ΝΡ-πληρότητα Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Επιλεγμένα θέματα: Υπολογιστική πολυπλοκότητα και ΝΡ-πληρότητα Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή
Εισαγωγή στους Αλγορίθμους Φροντιστήριο 5
 Εισαγωγή στους Αλγορίθμους Φροντιστήριο 5 Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Εισαγωγή στους Αλγορίθμους Φροντιστήριο 5 Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
4ε Γξαπηή Εξγαζία. Θέκα 1 ν : Μειέηε Πεξίπησζεο Α
 4ε Γξαπηή Εξγαζία Θέκα 1 ν : Μειέηε Πεξίπησζεο Α Εξσηήζεηο: Α1. Πνην ζηηι εγεζίαο ζεσξείηε όηη «αλαδύεηαη» από ηηο επηρεηξεζηαθέο επηρεηξεκαηηθέο ζπκπεξηθνξέο πνπ παξνπζηάδνληαη ζηε ζπγθεθξηκέλε δήισζε;
4ε Γξαπηή Εξγαζία Θέκα 1 ν : Μειέηε Πεξίπησζεο Α Εξσηήζεηο: Α1. Πνην ζηηι εγεζίαο ζεσξείηε όηη «αλαδύεηαη» από ηηο επηρεηξεζηαθέο επηρεηξεκαηηθέο ζπκπεξηθνξέο πνπ παξνπζηάδνληαη ζηε ζπγθεθξηκέλε δήισζε;
r 1 Π 1 r 2 Π 2 πέτασμα στισμή μομοτρωματικό υως στισμή
 1 ΣΟ ΠΓΙΡΑΜΑ ΣΟΤ YOUNG (1800) ΙΓΣΡΕΕ ΙΕΗΟΤ ΗΤΙΑΣΟ ΙΟΚΟΥΡΩΙΑΣΖΗΕ ΑΗΣΖΚΟΒΟΘΖΑ. Γεκηθά μηα ζοζθεοή πμο ζπεμαηίδεη θνμζζμύξ ζομβμιήξ μκμμάδεηαη ζομβμιόμεηνμ. Ε ανπή ιεηημονγίαξ εκόξ ζομβμιόμεηνμο δηαηνέζεςξ
1 ΣΟ ΠΓΙΡΑΜΑ ΣΟΤ YOUNG (1800) ΙΓΣΡΕΕ ΙΕΗΟΤ ΗΤΙΑΣΟ ΙΟΚΟΥΡΩΙΑΣΖΗΕ ΑΗΣΖΚΟΒΟΘΖΑ. Γεκηθά μηα ζοζθεοή πμο ζπεμαηίδεη θνμζζμύξ ζομβμιήξ μκμμάδεηαη ζομβμιόμεηνμ. Ε ανπή ιεηημονγίαξ εκόξ ζομβμιόμεηνμο δηαηνέζεςξ
Αλάιπζε Αιγνξίζκωλ. Κεθ. 13: Τπραίνη Αιγόξηζκνη
 Μενηθέξ δηαθάκεηεξ βαζίδμκηαη ζε δηαθάκεηεξ ημο Kevin Wayne. Copyright @ 2005 Pearson-Addison Wesley. All rights reserved. Αλάιπζε Αιγνξίζκωλ Κεθ. 13: Τπραίνη Αιγόξηζκνη 1 Σοπαίμη Αιγόνηζμμη Έκαξ ησταίος
Μενηθέξ δηαθάκεηεξ βαζίδμκηαη ζε δηαθάκεηεξ ημο Kevin Wayne. Copyright @ 2005 Pearson-Addison Wesley. All rights reserved. Αλάιπζε Αιγνξίζκωλ Κεθ. 13: Τπραίνη Αιγόξηζκνη 1 Σοπαίμη Αιγόνηζμμη Έκαξ ησταίος
HY-335 : Δίθηοα Υπμιμγηζηώκ
 W N net works R E O T HY-335 : Δίθηοα Υπμιμγηζηώκ K Επίπεδο Δικηύου Αλγόριθμοι Δρομολόγηζη Scalability issues Multiple domains Ιανία Παπαδμπμύιε Τμήμα Γπηζηήμεξ Υπμιμγηζηώκ Πακεπηζηήμημ Ηνήηεξ Φεημενηκό
W N net works R E O T HY-335 : Δίθηοα Υπμιμγηζηώκ K Επίπεδο Δικηύου Αλγόριθμοι Δρομολόγηζη Scalability issues Multiple domains Ιανία Παπαδμπμύιε Τμήμα Γπηζηήμεξ Υπμιμγηζηώκ Πακεπηζηήμημ Ηνήηεξ Φεημενηκό
Βαζηθέξ Ανπέξ Κιηκηθήξ Γλέηαζεξ. Σπύνμξ Δαμάζθμξ
 Βαζηθέξ Ανπέξ Κιηκηθήξ Γλέηαζεξ Σθμπόξ ημο ζεμηκανηαθμφ αοημφ μαζήμαημξ...... μ θμηηεηήξ κα είκαη ζε ζέζε κα θάκεη εκδμζημμαηηθή θαη ελςζημμαηηθή θιηκηθή ελέηαζε, θαη κα ακαγκςνίζεη ηα θοζημιμγηθά ακαημμηθά
Βαζηθέξ Ανπέξ Κιηκηθήξ Γλέηαζεξ Σθμπόξ ημο ζεμηκανηαθμφ αοημφ μαζήμαημξ...... μ θμηηεηήξ κα είκαη ζε ζέζε κα θάκεη εκδμζημμαηηθή θαη ελςζημμαηηθή θιηκηθή ελέηαζε, θαη κα ακαγκςνίζεη ηα θοζημιμγηθά ακαημμηθά
Ιαιιηένγεηα βαθηενίςκ
 Γ ΚΤΙΕΘΟΤ (ΓΕΜΘΙΗ ΠΑΘΔΕΘΑ) Άζθεζε 1ε(α) ενγαζηενηαθμύ μδεγμύ: Ιαιιηένγεηα βαθηενίςκ Ιαη μηθνμζθμπηθή παναηήνεζε 1 Όνγακα θαη οιηθά Γθαδάθη Σνίπμδμ με πιέγμα 6 απνεζημμπμίεηα ηνοβιία Petri Γοάιηκε νάβδμξ
Γ ΚΤΙΕΘΟΤ (ΓΕΜΘΙΗ ΠΑΘΔΕΘΑ) Άζθεζε 1ε(α) ενγαζηενηαθμύ μδεγμύ: Ιαιιηένγεηα βαθηενίςκ Ιαη μηθνμζθμπηθή παναηήνεζε 1 Όνγακα θαη οιηθά Γθαδάθη Σνίπμδμ με πιέγμα 6 απνεζημμπμίεηα ηνοβιία Petri Γοάιηκε νάβδμξ
Σωλήμες Ηλεκηρικώμ Εγκαηαζηάζεωμ. Εκπαιδεσηής: Σαββίδης Μιτάλης. Τετνική Στολή Ασγόροσ. Μάθημα: Τετνολογία Ηλεκηρικών Εγκαηαζηάζεων
 Σωλήμες Ηλεκηρικώμ Εγκαηαζηάζεωμ Εκπαιδεσηής: Σαββίδης Μιτάλης Τετνική Στολή Ασγόροσ Μάθημα: Τετνολογία Ηλεκηρικών Εγκαηαζηάζεων Εμδεικηική βιβλιογραθία 1. Τετνολογία Ηλεκηρικών Εγκαηαζηάζεων - Μερος Α,
Σωλήμες Ηλεκηρικώμ Εγκαηαζηάζεωμ Εκπαιδεσηής: Σαββίδης Μιτάλης Τετνική Στολή Ασγόροσ Μάθημα: Τετνολογία Ηλεκηρικών Εγκαηαζηάζεων Εμδεικηική βιβλιογραθία 1. Τετνολογία Ηλεκηρικών Εγκαηαζηάζεων - Μερος Α,
ΜΤΟΚΑΡΔΙΟΠΑΘΕΙΕ MΤΟΚΑΡΔΙΣΙΔΑ ΜΕΛΕΣΗ ΜΕ ΓΑΔΟΛΙΝΙΟ
 ΜΤΟΚΑΡΔΙΟΠΑΘΕΙΕ MΤΟΚΑΡΔΙΣΙΔΑ ΜΕΛΕΣΗ ΜΕ ΓΑΔΟΛΙΝΙΟ ΙΑΞΖΑ Β. ΗΑΘΑΚΠΔΕ ΗΑΞΔΖΜΘΜΓΜΟ ΖΑΟΩ GENERAL ΜΤΟΚΑΡΔΙΟΠΑΘΕΙΕ - ΣΑΞΙΝΟΜΗΗ Κμζήμαηα ημο μομθανδίμο άγκςζηεξ (πνςημπαζείξ) ή γκςζηήξ (δεοηενμπαζείξ ή εηδηθέξ)
ΜΤΟΚΑΡΔΙΟΠΑΘΕΙΕ MΤΟΚΑΡΔΙΣΙΔΑ ΜΕΛΕΣΗ ΜΕ ΓΑΔΟΛΙΝΙΟ ΙΑΞΖΑ Β. ΗΑΘΑΚΠΔΕ ΗΑΞΔΖΜΘΜΓΜΟ ΖΑΟΩ GENERAL ΜΤΟΚΑΡΔΙΟΠΑΘΕΙΕ - ΣΑΞΙΝΟΜΗΗ Κμζήμαηα ημο μομθανδίμο άγκςζηεξ (πνςημπαζείξ) ή γκςζηήξ (δεοηενμπαζείξ ή εηδηθέξ)
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων
 Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Ευσταθές ταίριασμα, ορθότητα, σωρός και ουρά προτεραιότητας Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή
Τίτλος Μαθήματος: Εισαγωγή στη Θεωρία και Ανάλυση Αλγορίθμων Ενότητα: Ευσταθές ταίριασμα, ορθότητα, σωρός και ουρά προτεραιότητας Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών 641: Γηζαγςγή
Τίτλος Μαθήματος: Ηλεκτρονικοί Υπολογιστές IΙΙ. Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης
 Τίτλος Μαθήματος: Ηλεκτρονικοί Υπολογιστές IΙΙ Ενότητα: Παράγωγοι και ολοκληρώματα Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Τμήμα: Οικονομικών Επιστημών Ολοκληρώματα με το πρόγραμμα Maima Αθανάσιος
Τίτλος Μαθήματος: Ηλεκτρονικοί Υπολογιστές IΙΙ Ενότητα: Παράγωγοι και ολοκληρώματα Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Τμήμα: Οικονομικών Επιστημών Ολοκληρώματα με το πρόγραμμα Maima Αθανάσιος
Τίτλος Μαθήματος: Ηλεκτρονικοί Υπολογιστές IΙΙ. Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης
 Τίτλος Μαθήματος: Ηλεκτρονικοί Υπολογιστές IΙΙ Ενότητα: Πράξεις με αρχεία Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Τμήμα: Οικονομικών Επιστημών Ανάγνωση και εγγραφή αρχείων με χρήση ρεύματος
Τίτλος Μαθήματος: Ηλεκτρονικοί Υπολογιστές IΙΙ Ενότητα: Πράξεις με αρχεία Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Τμήμα: Οικονομικών Επιστημών Ανάγνωση και εγγραφή αρχείων με χρήση ρεύματος
ΙΑΘΕΙΑ Α1.3 Ε ΥΡΕΕ ΣΩΚ ΥΑΡΣΩΚ ΣΕΚ ΗΑΘΕΙΓΡΖΚΕ ΔΩΕ. Ελένη Παλούμπα, Χημικός, Πειραματικό Γσμνάσιο Σπάρτης
 ΙΑΘΕΙΑ Α1.3 Ε ΥΡΕΕ ΣΩΚ ΥΑΡΣΩΚ ΣΕΚ ΗΑΘΕΙΓΡΖΚΕ ΔΩΕ ΣΖ ΠΑΡΟΤΖΑΔΓΖ Ο ΥΑΡΣΕ; Ε ΓΡΩΣΕΕ ΑΤΣΕ ΙΑ ΟΔΕΓΓΖ ΣΟΚ ΣΙΣΛΟ. Ο ΣΖΣΘΟ ΔΖΚΓΖ ΠΘΕΡΟΦΟΡΖΓ ΓΖΑ ΣΟ ΠΕΡΙΕΧΟΜΕΝΟ ΣΟΤ ΥΑΡΣΕ. ΥΑΡΣΗ ΓΙΑ ΣΗ ΜΟΡΦΟΛΟΓΙΑ ΣΟΤ ΔΓΑΦΟΤ ΥΑΡΣΗ
ΙΑΘΕΙΑ Α1.3 Ε ΥΡΕΕ ΣΩΚ ΥΑΡΣΩΚ ΣΕΚ ΗΑΘΕΙΓΡΖΚΕ ΔΩΕ ΣΖ ΠΑΡΟΤΖΑΔΓΖ Ο ΥΑΡΣΕ; Ε ΓΡΩΣΕΕ ΑΤΣΕ ΙΑ ΟΔΕΓΓΖ ΣΟΚ ΣΙΣΛΟ. Ο ΣΖΣΘΟ ΔΖΚΓΖ ΠΘΕΡΟΦΟΡΖΓ ΓΖΑ ΣΟ ΠΕΡΙΕΧΟΜΕΝΟ ΣΟΤ ΥΑΡΣΕ. ΥΑΡΣΗ ΓΙΑ ΣΗ ΜΟΡΦΟΛΟΓΙΑ ΣΟΤ ΔΓΑΦΟΤ ΥΑΡΣΗ
Εκκλησιαστικό Δίκαιο. Ενότητα 10η: Ιερά Σύνοδος της Ιεραρχίας και Διαρκής Ιερά Σύνοδος Κυριάκος Κυριαζόπουλος Τμήμα Νομικής Α.Π.Θ.
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 10η: Ιερά Σύνοδος της Ιεραρχίας και Διαρκής Ιερά Σύνοδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 10η: Ιερά Σύνοδος της Ιεραρχίας και Διαρκής Ιερά Σύνοδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Άπιεζημη αιγόνηζμμη. Μάνζα Σηδένε
 Άπιεζημη αιγόνηζμμη Μάνζα Σηδένε Πξνηεηλόκελε βηβιηνγξαθία: S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani «Αιγόξηζκνη» Κιεηδάξηζκνο 2009 Κεθάιαην 5. http://www.cs.berkeley.edu/~vazirani/algorithms/chap5.pdf
Άπιεζημη αιγόνηζμμη Μάνζα Σηδένε Πξνηεηλόκελε βηβιηνγξαθία: S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani «Αιγόξηζκνη» Κιεηδάξηζκνο 2009 Κεθάιαην 5. http://www.cs.berkeley.edu/~vazirani/algorithms/chap5.pdf
Κεθάλαιο 3 Κρσπηογραθία δημόζιοσ κλειδιού και πιζηοποίηζη ασθεμηικόηηηας μημσμάηφμ
 Κεθάλαιο 3 Κρσπηογραθία δημόζιοσ κλειδιού και πιζηοποίηζη ασθεμηικόηηηας μημσμάηφμ Giannis F. Marias 1 Περίληυη Πνμζεγγίζεηξ ςξ πνμξ ηεκ πηζημπμίεζε μεκομάηςκ Σοκανηήζεηξ αζθαιμύξ θαηαθενμαηηζμμύ θαη HMAC
Κεθάλαιο 3 Κρσπηογραθία δημόζιοσ κλειδιού και πιζηοποίηζη ασθεμηικόηηηας μημσμάηφμ Giannis F. Marias 1 Περίληυη Πνμζεγγίζεηξ ςξ πνμξ ηεκ πηζημπμίεζε μεκομάηςκ Σοκανηήζεηξ αζθαιμύξ θαηαθενμαηηζμμύ θαη HMAC
Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης
 Τίτλος Μαθήματος: Αλγεβρικές Δομές Ι Ενότητα: Χαρακτηρισµοί Πεπερασµένων Κυκλικών Οµάδων Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 233 4. Χαρακτηρισµοί
Τίτλος Μαθήματος: Αλγεβρικές Δομές Ι Ενότητα: Χαρακτηρισµοί Πεπερασµένων Κυκλικών Οµάδων Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 233 4. Χαρακτηρισµοί
Πληροφοριακά Συστήματα Διοίκησης (ΜΒΑ) Ενότητα 2: Εφαρμογές Δικτυωτής Ανάλυσης (1 ο Μέρος)
 Πληροφοριακά Συστήματα Διοίκησης (ΜΒΑ) Ενότητα 2: Εφαρμογές Δικτυωτής Ανάλυσης (1 ο Μέρος) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων
Πληροφοριακά Συστήματα Διοίκησης (ΜΒΑ) Ενότητα 2: Εφαρμογές Δικτυωτής Ανάλυσης (1 ο Μέρος) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων
Τα αμηκμλέα ζημ πνάζηκμ ηζάη
 Το πράζινο ηζάι Τμ πνάζηκμ ηζάη (Camellia Sinensis) είκαη γκςζηό εδώ θαη 5.000 πνόκηα ζημοξ Κηκέδμοξ. Μέζς ηεξ Κίκαξ έθζαζε ζηεκ Ιαπςκία, ζηεκ Ικδία θαη ζηεκ Ικδμκεζία. Σηεκ Γονώπε ημ έθενακ από ηεκ Κίκα
Το πράζινο ηζάι Τμ πνάζηκμ ηζάη (Camellia Sinensis) είκαη γκςζηό εδώ θαη 5.000 πνόκηα ζημοξ Κηκέδμοξ. Μέζς ηεξ Κίκαξ έθζαζε ζηεκ Ιαπςκία, ζηεκ Ικδία θαη ζηεκ Ικδμκεζία. Σηεκ Γονώπε ημ έθενακ από ηεκ Κίκα
Εισαγωγή στους Αλγορίθμους
 Εισαγωγή στους Αλγορίθμους Ενότητα 5 η Άσκηση Συγχώνευση & απαρίθμηση Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης
Εισαγωγή στους Αλγορίθμους Ενότητα 5 η Άσκηση Συγχώνευση & απαρίθμηση Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης
Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας Ενότητα 7η: Ιερά Σύνοδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Θεσμοί Ευρωπαϊκών Λαών Ι 19 ος -20 ος αιώνας Ενότητα 7η: Ιερά Σύνοδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Ιστορία της μετάφρασης
 ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Μεταφραστές και πρωτότυπα. Ελένη Κασάπη ΤΜΗΜΑ ΑΓΓΛΙΚΗΣ ΓΛΩΣΣΑΣ ΚΑΙ ΦΙΛΟΛΟΓΙΑΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Μεταφραστές και πρωτότυπα. Ελένη Κασάπη ΤΜΗΜΑ ΑΓΓΛΙΚΗΣ ΓΛΩΣΣΑΣ ΚΑΙ ΦΙΛΟΛΟΓΙΑΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Εισαγωγή στους Αλγορίθμους Φροντιστήριο 8
 Εισαγωγή στους Αλγορίθμους Φροντιστήριο 8 Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Εισαγωγή στους Αλγορίθμους Φροντιστήριο 8 Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Η Άιμτα. Οη γμκείξ ηεξ θαη μη γμκείξ ηεξ Ζόιεξ έθακακ μήκοζε ζημ πνώεκ αθεκηηθό ημοξ θαη θαηάθενακ κα ημκ θοιαθίζμοκ.
 Ιστορίες τοσ 10 οσ Δημοτικού Στολείοσ Ηλιούπολης Η Άιμτα Ηάπμηε ήηακ έκα θμνηηζάθη, ε Άηκηα. Δμύζε ζημ Ηάηνμ μαδί με ημοξ γμκείξ ηεξ ζ έκα ζπηηάθη. Γθείκε ηεκ επμπή ζημ Ηάηνμ οπήνπε πόιεμμξ. Ε Άηκηα δεκ
Ιστορίες τοσ 10 οσ Δημοτικού Στολείοσ Ηλιούπολης Η Άιμτα Ηάπμηε ήηακ έκα θμνηηζάθη, ε Άηκηα. Δμύζε ζημ Ηάηνμ μαδί με ημοξ γμκείξ ηεξ ζ έκα ζπηηάθη. Γθείκε ηεκ επμπή ζημ Ηάηνμ οπήνπε πόιεμμξ. Ε Άηκηα δεκ
ηδάζθςκ: εµήηνεξ Ζεσκαιηπμύν
 Δηάιελε 5: Δμμέξ (structures) θαη Εκώζεηξ (unions) Σηεκ εκόηεηα αοηή ζα μειεηεζμύκ ηα ελήξ επημένμοξ ζέμαηα: Δμμέξ, θςιηαζμέκεξ δμμέξ, ηνόπμη δήιςζεξ δμμώκ, δμμέξ ςξ πανάμεηνμη ζε ζοκανηήζεηξ, δείθηεξ
Δηάιελε 5: Δμμέξ (structures) θαη Εκώζεηξ (unions) Σηεκ εκόηεηα αοηή ζα μειεηεζμύκ ηα ελήξ επημένμοξ ζέμαηα: Δμμέξ, θςιηαζμέκεξ δμμέξ, ηνόπμη δήιςζεξ δμμώκ, δμμέξ ςξ πανάμεηνμη ζε ζοκανηήζεηξ, δείθηεξ
Problems & Questions on MAC Layer
 ΗY335: Δίκτυα Υπολογιςτών Χειμερινό Εξάμηνο 2011-2012 Τμήμα Επιςτήμησ Υπολογιςτών, Πανεπιςτήμιο Κρήτησ Διδάςκουςα: Μαρία Παπαδοπούλη Φροντιςτήριο: 10/11/2011 Βοηθόσ: Παφλοσ Χαρωνυκτάκησ Problems & Questions
ΗY335: Δίκτυα Υπολογιςτών Χειμερινό Εξάμηνο 2011-2012 Τμήμα Επιςτήμησ Υπολογιςτών, Πανεπιςτήμιο Κρήτησ Διδάςκουςα: Μαρία Παπαδοπούλη Φροντιςτήριο: 10/11/2011 Βοηθόσ: Παφλοσ Χαρωνυκτάκησ Problems & Questions
Τίτλος Μαθήματος: Θεωρία Πολυπλοκότητας. Ενότητα: H κλάση ΝΡ. Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος. Τμήμα: Μαθηματικών
 Τίτλος Μαθήματος: Θεωρία Πολυπλοκότητας Ενότητα: H κλάση ΝΡ Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών Θεςνία Νμιοπιμθόηεηαξ άνεξ Ναπαδόπμοιμξ Αιγμνηζμηθέξ Πεπκηθέξ θαη Γμπόδηα Αιγμνηζμηθέξ
Τίτλος Μαθήματος: Θεωρία Πολυπλοκότητας Ενότητα: H κλάση ΝΡ Διδάσκων: Λέκτορας Xάρης Παπαδόπουλος Τμήμα: Μαθηματικών Θεςνία Νμιοπιμθόηεηαξ άνεξ Ναπαδόπμοιμξ Αιγμνηζμηθέξ Πεπκηθέξ θαη Γμπόδηα Αιγμνηζμηθέξ
Γενικά Μαθηματικά Ι. Ενότητα 12: Κριτήρια Σύγκλισης Σειρών. Λουκάς Βλάχος Τμήμα Φυσικής ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Κριτήρια Σύγκλισης Σειρών Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Κριτήρια Σύγκλισης Σειρών Λουκάς Βλάχος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Εισαγωγή στους Αλγορίθμους
 Εισαγωγή στους Αλγορίθμους Ενότητα 6 η Άσκηση - DFS δένδρα Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν
Εισαγωγή στους Αλγορίθμους Ενότητα 6 η Άσκηση - DFS δένδρα Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Άδειες Χρήσης Το παρόν
Εκκλησιαστικό Δίκαιο
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 11η: Οργανισμοί της Εκκλησίας της Ελλάδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 11η: Οργανισμοί της Εκκλησίας της Ελλάδος Κυριάκος Κυριαζόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
H XHMEIA EINAI ΙΑΓΖΗΕ
 H XHMEIA EINAI ΙΑΓΖΗΕ Ναροσσίαση Νειραμάτων από τοσς μαθητές τοσ τμήματος Α1 τοσ ΘΡΗΓΖΜΡ ΒΑΙΜΡ Νείραμα 1 ο ΜΙΖΘΖΑ ΙΓ ΕΘΖΜ (He) Μανία Καιιηβνεηάθε Γθπκέμκηαξ ήιημ, επεηδή έπεη μηθνόηενμ μμνηαθό βάνμξ από
H XHMEIA EINAI ΙΑΓΖΗΕ Ναροσσίαση Νειραμάτων από τοσς μαθητές τοσ τμήματος Α1 τοσ ΘΡΗΓΖΜΡ ΒΑΙΜΡ Νείραμα 1 ο ΜΙΖΘΖΑ ΙΓ ΕΘΖΜ (He) Μανία Καιιηβνεηάθε Γθπκέμκηαξ ήιημ, επεηδή έπεη μηθνόηενμ μμνηαθό βάνμξ από
Θερμοδυναμική. Ανοικτά Ακαδημαϊκά Μαθήματα. Πίνακες Νερού σε κατάσταση Κορεσμού. Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Πίνακες Νερού σε κατάσταση Κορεσμού Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc. Διασφάλιση
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Πίνακες Νερού σε κατάσταση Κορεσμού Γεώργιος Κ. Χατζηκωνσταντής Επίκουρος Καθηγητής Διπλ. Ναυπηγός Μηχανολόγος Μηχανικός M.Sc. Διασφάλιση
Λογιστική Κόστους Ενότητα 12: Λογισμός Κόστους (2)
 Λογιστική Κόστους Ενότητα 12: Λογισμός Κόστους (2) Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Λογιστική Κόστους Ενότητα 12: Λογισμός Κόστους (2) Μαυρίδης Δημήτριος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
