Ανάπτυξη Συστήµατος Σχεδιασµού Ενεργειών µε την Γλώσσα JAVA
|
|
|
- Ἥβη Ζωγράφου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ - ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ Ανάπτυξη Συστήµατος Σχεδιασµού Ενεργειών µε την Γλώσσα JAVA ιπλωµατική Εργασία του Dimitar Sht. Shterionov (ΑΕΜ: 1171) Επιβλέπων Καθηγητής: ηµήτριος Βράκας ΘΕΣΣΑΛΟΝΙΚΗ ΙΟΥΛΙΟΣ 2008
2
3 Πρόλογος Με τις τεχνικές της Τεχνητής Νοηµοσύνης (ΤΝ) µπορούν να δοθούν λύσεις σε πολλά προβλήµατα που υπάρχουν στις µέρες µας, όπως η αυτόµατη καθοδήγηση πρακτόρων (robots, softbots), εύρεση βέλτιστου µονοπατιού, σχεδιασµός ενεργειών κ.α. Ο σχεδιασµός ενεργειών συνίσταται στην ανάλυση ενός προβλήµατος και στην δηµιουργία ενός πλάνου η εκτέλεση του οποίου επιλύει το συγκεκριµένο πρόβληµα. Ο προσδιορισµός ενός προβλήµατος και το πεδίο στο οποίο αυτό υπάρχει πρέπει να γίνει µε τυποποιηµένο τρόπο, παρέχοντας έτσι γενικότητα από άποψη χρήσης διαφορετικών συστηµάτων επίλυσης και ανάγνωσης από διαφορετικούς χρήστες. Αυτό πετυχαίνεται µε την χρήση της γλώσσας PDDL (McDermott 1998). Ο σκοπός αυτής της εργασίας είναι η κατασκευή ενός συστήµατος σχεδιασµού ενεργειών γραµµένο στην γλώσσα JAVA. Η γλώσσα αυτή, επιτρέπει τα συστήµατα που γράφονται σε αυτήν να εκτελούνται σε διάφορες υπολογιστικές αρχιτεκτονικές ανεξάρτητα από το λειτουργικό σύστηµα. Έτσι το σύστηµα σχεδιασµού ενεργειών θα µπορεί να λειτουργήσει σε όλους τους είδους υπολογιστικών συστηµάτων. Η πτυχιακή εργασία εκπονήθηκε στο Εργαστήριο Γλωσσών Προγραµµατισµού και Τεχνολογίας Λογισµικού, του Αριστοτέλειου Πανεπιστήµιου Θεσσαλονίκης, και η υλοποίησή του πραγµατοποιήθηκε σε συνεργασία µε την οµάδα Λογικού Προγραµµατισµού και Ευφυών Συστηµάτων (LPIS). Για την εκπόνηση αυτής της εργασίας συνέβαλλαν πολλοί άνθρωποι τους οποίους θα ήθελα να ευχαριστήσω. Πρώτα θα ήθελα να ευχαριστήσω τον κύριο ηµήτριο Βράκας, Λέκτορα του τµήµατος Πληροφορικής του ΑΠΘ για την ανάθεση της εργασίας, τις συµβουλές, τις καθοδηγήσεις και τις δυνατότητες που µου προσέφερε. Επίσης, θα ήθελα να ευχαριστήσω τον κ. Ιωάννη Βλαχάβα, διευθυντή του εργαστηρίου, για την παροχή του απαραίτητου εργαστηριακού εξοπλισµού καθώς και για τη δηµιουργία ευχάριστου και δηµιουργικού κλίµατος εργασίας µέσα στο εργαστήριο. Θα ήθελα να ευχαριστήσω πάρα πολύ αυτούς που είναι µακριά και όµως βρίσκουν τρόπους να µε υποστηρίζουν και να µε βοηθούν την οικογένειά µου, και την δεσποινίδα Τσβέτα Τσόγκοβα για τους ελέγχους που έκανε και την δύναµη που µου δίνει. ηµήταρ Στ. Στεριόνοβ
4
5 Περιεχόµενα 1 ΕΙΣΑΓΩΓΗ ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕ ΙΑΣΜΟ ΕΝΕΡΓΕΙΩΝ ΣΧΕ ΙΟ ΚΑΙ ΣΧΕ ΙΑΣΜΟΣ ΓΛΩΣΣΕΣ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΣΧΕ ΙΑΣΜΟΥ ΕΝΕΡΓΕΙΩΝ ΤΟ ΜΟΝΤΕΛΟ STRIPS Η ΓΛΩΣΣΑ PDDL ΣΥΣΤΗΜΑΤΑ ΣΧΕ ΙΑΣΜΟΥ ΕΝΕΡΓΕΙΩΝ Η ΓΛΩΣΣΑ JAVA ΙΣΤΟΡΙΚΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ Η ανεξαρτησία από την πλατφόρµα γραφής και εκτέλεσης του πηγαίου κώδικα ιαχείριση Μνήµης ΤΟ ΣΥΝΤΑΚΤΙΚΟ ΤΗΣ JAVA APPLETS ΚΑΙ SERVLETS Applets Servlets ΤΑ ΓΡΑΦΙΚΑ ΤΗΣ JAVA Η ΟΜΗ ARRAYLIST Η ΑΡΧΙΤΕΚΤΟΝΙΚΗ TWOX ΤΟ ΓΡΑΦΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΣΥΝΤΑΚΤΙΚΗ ΑΝΑΛΥΗ ΤΩΝ ΑΡΧΕΙΩΝ PDDL Ο ΣΧΕ ΙΑΣΤΗΣ ΕΝΕΡΓΕΙΩΝ ΥΛΟΠΟΙΗΣΗ ΤΟΥ ΣΥΣΤΗΜΑΤΟΣ ΣΧΕ ΙΑΣΜΟΥ ΕΝΕΡΓΕΙΩΝ Η ΥΛΟΠΟΙΗΣΗ ΤΟΥ PARSER
6 6.2 ΟΙ ΑΛΓΟΡΙΘΜΟΙ ΑΝΑΖΗΤΗΣΗΣ Υλοποίηση του αλγορίθµου αναζήτησης πρώτα σε βάθος Υλοποίηση του αλγορίθµου αναζήτησης πρώτα σε πλάτος Υλοποίηση του αλγορίθµου επαναληπτικής εµβάθυνσης Υλοποίηση του αλγορίθµου Identidem Υλοποίηση του αλγορίθµου FF Η λύση του προβλήµατος ΥΛΟΠΟΙΗΣΗ ΤΗΣ ΙΑΣΥΝ ΕΣΗΣ ΜΕ ΤΟΝ ΧΡΗΣΤΗ ΕΠΙΛΟΓΟΣ ΣΥΜΠΕΡΑΣΜΑΤΑ ΜΕΛΛΟΝΤΙΚΗ ΕΡΓΑΣΙΑ ΕΠΙΛΟΓΟΣ ΒΙΒΛΙΟΓΡΑΦΙΑ...89 ΠΑΡΑΡΤΗΜΑ Α Ο ΚΩ ΙΚΑΣ ΤΟΥ ΣΥΣΤΗΜΑΤΟΣ
7 1 Εισαγωγή Η περίπλοκες διαδικασίες που υπάρχουν στο σηµερινό κόσµο χρειάζονται περίπλοκους τρόπους εκτέλεσης. Υπάρχουν διάφορα συστήµατα και τεχνικές οι οποίες συµβάλλουν στην επίτευξη γρήγορης και αποδοτικής επίλυσης διάφορων προβληµάτων. Η Τεχνητή Νοηµοσύνη (ΤΝ) είναι µία περιοχή της επιστήµης της Πληροφορικής η οποία ασχολείται µε την προσοµοίωση της ανθρώπινης νοηµοσύνης µέσω υπολογιστικών µοντέλων. Το επίπεδο εξέλιξης στο οποίο έχει φθάσει η ΤΝ προσφέρει ένα πλήθος τεχνικών οι οποίες απαλλάσσουν τις ανθρώπινες δυνάµεις από δύσκολες, χρονοβόρες και επικίνδυνες δουλειές και αναλαµβάνουν τις ευθύνες για τις επιτεύξεις διάφορων στόχων. Κάποια από τα προβλήµατα µε τα οποία ασχολείται η ΤΝ είναι: Η αναπαράσταση γνώσης Σχεδιασµός και χρονοπρογραµµατισµός Μάθηση Επεξεργασία φυσικής γλώσσας, Μετακίνηση και έλεγχος κινήσεων, κ.α. Στο παρόν σύγγραµµα αναλύεται η ανάπτυξη ενός συστήµατος σχεδιασµού ενεργειών µε την γλώσσα JAVA το οποίο επεξεργάζεται εντολές της γλώσσας PDDL και κατασκευάζει πλάνα ενεργειών για την επίτευξη προκαθορισµένων στόχων. Το σύστη- µα αυτό θα πρέπει να είναι σε θέση να κατανοεί τις εντολές PDDL και να τα µετατρέπει σε κατάλληλη µορφή για επόµενη επεξεργασία, να κατασκευάζει σωστά ένα πλάνο ε- νεργειών και να το παρουσιάζει στον χρήστη του µε κατανοητό για αυτόν τρόπο. Η περιγραφή της εργασίας δοµείται ως εξής: 1. Πρώτο κεφάλαιο Εισαγωγή (είναι το παρόν κεφάλαιο) 2. εύτερο κεφάλαιο Εισαγωγή στον σχεδιασµό ενεργειών Αναλύεται το θεωρητικό υπόβαθρο του σχεδιασµού ενεργειών, περιγράφονται τις έννοιες των όρων «πλάνο», «ενέργεια», «κατάσταση». ίνεται στη συνέχεια µία σύντοµη παρουσίαση διάφορων συστηµάτων σχεδιασµού ενεργειών και πα
8 ρουσιάζεται συνοπτικά η γλώσσα PDDL συγκρίνοντάς την µε το µοντέλο STRIPS. 3. Τρίτο κεφάλαιο Συστήµατα σχεδιασµού ενεργειών Παρουσιάζεται το θεωρητικό µοντέλο ενός συστήµατος σχεδιασµού µε την γλώσσα PDDL. Στη συνέχεια αναλυτικά παρουσιάζονται πέντε αλγορίθµους αναζήτησης οι οποίοι χρησιµοποιούνται στο σύστηµα που κατασκευάστηκε. Αυτοί είναι οι τρεις τυφλοί αλγόριθµοι DFS, BFS και Iterative Deepening (ID), και δύο ευρετικοί (heuristic) αλγόριθµοι Identidem και FF Search. 4. Τέταρτο κεφάλαιο Η Γλώσσα JAVA Παρουσιάζεται η γλώσσα µε την οποία έχει προγραµµατιστεί το σύστηµα. ίνονται γενικά ιστορικά στοιχεία της γλώσσας, τα χαρακτηριστικά της, η συντακτική. Ακόµα παρουσιάζονται κλάσεις και δοµές της γλώσσας οι οποίες έχουν ά- µεση σχέση µε την υλοποίηση του συστήµατος σχεδιασµού ενεργειών η φόρ- µα (JForm) και η δοµή του ArrayList δυναµικός πίνακας. 5. Πέµπτο κεφάλαιο Η λύση του θέµατος της εργασίας Πως αντιµετωπίσθηκε το τεθειµένο θέµα, και ποια είναι η λύση σε αυτό. Περιγράφονται τα γενικότερα χαρακτηριστικά του συστήµατος, και τα τµήµατά του, η αρχιτεκτονική του και πως πρέπει να λειτουργεί αυτό σαν ενιαίο σύστηµα αλλά έτσι και κάθε τµήµα του ξεχωριστά. 6. Έκτο κεφάλαιο Η υλοποίηση του συστήµατος σχεδιασµού ενεργειών Πως υλοποιήθηκε το σύστηµα, θέµα αυτής της διπλωµατικής εργασίας. Πως λειτουργεί και ποια τµήµατα κώδικα είναι υπεύθυνα για τις ξεχωριστές του λειτουργίες. Πως σχετίζονται οι κλάσεις του και πως ο χρήστης αλληλεπιδρά µε αυτό. Παριστάνονται επεξιγηµένα τµήµατα κώδικα προς τον αναγνώστη για την καλύτερη κατανόηση του τρόπου υλοποίησης του συστήµατος οπως και εικόνες που εποπτικά παρουσιάζουν κάποιες λειτουργίες του συστήµατος. 7. Έβδοµο κεφάλαιο Συµπεράσµατα.- Επίλογος ο οποίος περιλαµβάνει συµπεράσµατα για την εργασία, προβλήµατα τα οποία υπήρξαν κατά την υλοποίηση, δυνατές µελλοντικές µελέτες και επεκτάσεις πάνω σε αυτό το σύστηµα. 8. Παράρτηµα Α Τµήµατα κώδικα που δείχνουν τον τρόπο υλοποίησης του συστήµατος - 4 -
9 2 Εισαγωγή στο σχεδιασµό ενεργειών 2.1 Σχέδιο και σχεδιασµός Σχέδιο (Plan) είναι µία λίστα από βήµατα, τα οποία αν εκτελεστούν µε την κατάλληλη σειρά παράγεται ένα επιθυµητό αποτέλεσµα. Το αποτέλεσµα, το οποίο προσπαθούµε να πετύχουµε, καλείται στόχος (goal), τα βήµατα που εκτελούνται ενέργειες και ο προσδιορισµός της κατάλληλης σειράς (ακολουθίας) εκτέλεσης των βηµάτων σχεδιασµός. Τα προβλήµατα σχεδιασµού ενεργειών είναι αυτά των οποίων είναι γνωστή η τελική κατάσταση, και για να επιλυθούν πρέπει να βρεθεί η σωστή ακολουθία ενεργειών (το πλάνο/σχέδιο the plan). Σχεδιασµός και σχέδια χρειάζονται σε κάθε το- µέα της ζωής µας και στην καθηµερινότητά µας (πχ. προγραµµατισµός διακοπών, ε- κτέλεση µιας συνταγής φαγητού, κ.ά.), και σε κάθε εκτέλεση ενός υπολογιστικού προγράµµατος (πχ. οι αλγόριθµοι). Το σχέδιο, όπως αναφέρθηκε παραπάνω, είναι µία ακολουθία βηµάτων τα οποία οδηγούν στην ολοκλήρωση κάποιου στόχου. Για παράδειγµα σε ένα εργοστάσιο παραγωγής αυτοκινήτων υπάρχει µια σειρά από γεγονότα και κανόνες τα οποία πρέπει να εκτελεστούν και να τηρούνται προκειµένου να κατασκευαστεί ένα αυτοκίνητο: πρώτα πρέπει να υπάρχει το σκίτσο, στο οποίο να αναφέρονται οι διαστάσεις του αυτοκίνητου. Στη συνέχεια πρέπει να αποφασιστούν και να παραγγελθούν τα απαραίτητα υλικά. Ό- ταν όλα τα υλικά και εξαρτήµατα είναι διαθέσιµα ξεκινάει η δηµιουργία κάθε κοµµατιού του αυτοκινήτου µηχανή, σκελετός αυτοκινήτου, συσπανσιόν κ.ά. Στη συνέχεια αυτά τα κοµµάτια συναρµολογούνται ακλουθώντας απαραίτητα µία ορισµένη σειρά (π.χ. πρώτα τα αµορτισέρ µετά οι ρόδες). Όταν όλες οι απαιτήσεις που έχουµε θέσει στην αρχή πληρούνται τότε έχουµε πετύχει τον τελικό µας στόχο. Άλλο παράδειγµα είναι ο αλγόριθµος και η εκτέλεσή του : begin - 5 -
10 int x, y, z; readln(x); readln(y); z:=x+y; write( The result of x+y is: ); writeln(z); end Πρώτα δηλώνονται οι µεταβλητές, µετά διαβάζονται, εκτελείται η πράξη και στη συνέχεια τυπώνεται το αποτέλεσµα, το οποίο είναι και ο στόχος µας. Και στα δύο παραπάνω παραδείγµατα φαίνεται πώς υπάρχουν κάποιες συνθήκες οι οποίες πρέπει να τηρούνται έτσι ώστε να µπορεί να συνεχιστεί η ορθή εκτέλεση του πλάνου (πριν διαβαστούν οι µεταβλητές, αυτές πρέπει να δηλωθούν, πριν ξεκινήσει η συναρµολόγηση του αυτοκινήτου τα απαραίτητα κοµµάτια πρέπει να είναι διαθέσιµα). Οι συνθήκες/προϋποθέσεις (preconditions), και οι ενέργειες (actions) είναι τα δοµικά στοιχεία ενός πλάνου. Συνθήκες/προϋποθέσεις σε κάθε βήµα του σχεδίου πρέπει να αληθεύουν κάποια γεγονότα για να είναι δυνατόν να εκτελεστεί το επόµενο βήµα του σχεδίου. Αυτά τα δεδοµένα (συνθήκες/ προϋποθέσεις) είναι ένα ενδιάµεσο αποτέλεσµα, το οποίο παράγεται µετά από κάθε ενέργεια και χρειάζεται για την εκτέλεση της επόµενης. Με αυτή την λογική µπορεί να υποτεθεί ότι ο τελικός στόχος αναλύεται σε υπο-στόχους. Ενέργεια είναι η µετάβαση από ένα στάδιο σε άλλο. Η ενέργεια (action) παίρνει ως είσοδο ένα σύνολο από προϋποθέσεις και παράγει κάποιο άλλο σύνολο δεδοµένων ή γεγονότων το οποίο στο επόµενο βήµα εκτέλεσης του πλάνου χρειάζεται ως είσοδο ή (στο τελευταίο βήµα εκτέλεσης) είναι το επιθυµητό στόχο (the goal). Τα πλάνα εκτελούντα από µια οντότητα η οποία ονοµάζεται µε το γενικό όνοµα «πράκτορας» ( agent ). Οι πράκτορες µπορεί να είναι είτε βιολογικοί (π.χ. άνθρωπος), είτε υπολογιστικές µονάδες (computer units) λογισµικοί, ροµποτικοί. Ο πράκτορας, εκτελώντας το πλάνο δρα σε έναν κόσµο υποσύνολο του πραγµατικού. Ο κόσµος αυτός καλείται κόσµος προβλήµατος (problem world). Περιέχει όλες τις απαραίτητες ο
11 ντότητες (αντικείµενα, γεγονότα), οι οποίες χρειάζονται για την επίλυση του προβλήµατος και πάνω σε αυτόν εκτελούνται οι ενέργειες. Το πρόβληµα που πρόκειται να επιλυθεί περιλαµβάνει δύο (τουλάχιστον) καταστάσεις του κόσµου αρχική και τελική. Η αρχική κατάσταση (initial state) είναι η κατάσταση του κόσµου προτού ξεκινήσει η ε- κτέλεση του πλάνου, και η τελική κατάσταση (Goal/Final state), η οποία εκτός από µοναδική µπορεί να είναι και ένα σύνολο καταστάσεων, είναι αυτή στην οποία βρίσκεται ο κόσµος όταν το πρόβληµα έχει επιλυθεί. Άρα ένα πλάνο είναι το λογικό µονοπάτι το οποίο οδηγεί από την αρχική κατάσταση του κόσµου στην τελική του κατάσταση, εκτελώντας ενδιάµεσα διάφορες ενέργειες οι οποίες τον αλλάζουν. Σε κάθε βήµα του πλάνου πρέπει να διευκρινίζεται πώς οι ενέργειες παραµορφώνουν τον κόσµο του προβλή- µατος. Εικόνα 2.1. Η αντίληψη του πράκτορα, η σχεδίαση του πλάνου και η εφαρµογή των ε- νεργειών του πάνω στον κόσµο Ο κόσµος του προβλήµατος µπορεί να είναι στατικός ή δυναµικός. Στατικός κόσµος είναι αυτός, στον οποίον δεν δρουν εξωτερικά παράγοντα τα οποία να αλλάζουν την - 7 -
12 κατάστασή του κατά την πορεία εκτέλεσης του πλάνου. Αλλαγή της κατάστασης γίνεται µόνο από τον πράκτορα. Σε έναν δυναµικό κόσµο η ενδιάµεση κατάστασή του αλλάζεται και από άλλα παράγοντα. Μια άλλη διάκριση για τον κόσµο µπορεί να γίνει µε βάση την πιθανότητα επιτυχίας των ενεργειών του πράκτορα. Αν πάντα είναι γνωστό το τελικό αποτέλεσµα κάθε ενέργειας τότε ο κόσµος καλείται προκαθορισµένος/ντετερµινιστικός (deterministic). Αν όµως µετά από κάθε ενέργεια υπάρχει περίπτωση τα αποτελέσµατα να διαφέρουν, και σε κάθε δυνατό αποτέλεσµα να αντιστοιχεί κάποια πιθανότητα, τότε ο κόσµος ονο- µάζεται µη-προκαθορισµένος/µη-ντετερµινιστικός (non deterministic) ή στοχαστικός (stochastic). Για παράδειγµα ο πραγµατικός κόσµος είναι µη-ντετερµινιστικός και δυναµικός, ενώ αν θέσουµε ένα ροµπότ σε κλειστό χώρο όπου υπάρχουν κάποια κιβώτια, και ο πράκτορας (το ροµπότ) πρέπει να µετακινεί τα κιβώτια αυτά, τα οποία δεν µειώνονται ούτε αυξάνονται µε την πάροδο του χρόνου τότε αυτός ο κόσµος είναι στατικός και προκαθορισµένος. Έστω x είναι µια κατάσταση του κόσµου, η οποία ανήκει στο σύνολο όλων των δυνατών καταστάσεων Χ. Είναι πολύ σηµαντικό το Χ να είναι πεπερασµένο και να περιέχει µόνο πληροφορίες για το κόσµο οι οποίες είναι χρήσιµες για την επίλυση του προβλήµατος. Για παράδειγµα αν θέσουµε ένα ροµποτάκι να κινείται στην Γαλλία, ας πού- µε από το Παρίσι µέχρι το Λιον, δεν πρέπει να περιλαµβάνονται πληροφορίες για το αν στην Κίνα πουλιέται κάποια µάρκα λάµπες. Από την άλλη πλευρά η περιγραφή του κόσµου του προβλήµατος πρέπει να είναι αρκετά εφοδιασµένη µε πληροφορίες έτσι ώστε να είναι δυνατή η σωστή επίλυση του προβλήµατος. Αν συµπεριλαµβάνονται άσχετες πληροφορίες µπορεί εύκολα να µετατραπεί ένα πρόβληµα από τέτοιο που µπορεί εύκολα να επιλυθεί από κάποιους αλγορίθµους σε τέτοιο που είναι αδύνατον να λυθεί. Αν u είναι ενέργεια, τότε: x =f(x,u) (1) όπου x είναι η καινούργια κατάσταση, x είναι η παλιά και f µια συνάρτηση µετάβασης. Όπως είναι δυνατόν για µία κατάσταση του κόσµου να υπάρχουν πολλές ενέργειες, έτσι είναι δυνατόν για µία ενέργεια να υπάρχουν πολλές καταστάσεις. Συνεπάγεται ότι αν U είναι το σύνολο των ενεργειών τότε: - 8 -
13 (2) όπου U(x) είναι οι δυνατές ενέργειες για την συγκεκριµένη κατάσταση x. Με τον παραπάνω συλλογισµό µπορεί να παρασταθεί ο τελικός στόχος ενός προβλήµατος σχεδιασµού ως X G X. Ένα πρόβληµα σχεδιασµού αναπαριστάται από µια τριάδα <I, Χ, G>, όπου Ι είναι η αρχική κατάσταση του κόσµου η οποία περιγράφει πλήρως τα αντικείµενα, απαραίτητα για την εκτέλεση του πλάνου. Χ είναι το σύνολο όλων των δυνατών ενεργειών που είναι δυνατόν να εκτελέσει ο πράκτορας πάνω στον κόσµο στο οποίον δρα. Κάθε x (ενέργεια) πρέπει να περιέχει πλήρη περιγραφή των προϋποθέσεων, και µία λίστα γεγονότων τα οποία θα επιφέρουν στον κόσµο. G είναι ο στόχος. Αυτός µπορεί να είναι µία λίστα από γεγονότα και αντικείµενα τα οποία να είναι παρόντα στην (τελική) κατάσταση του κόσµου. Με αυτό τον τρόπο µία τελική κατάσταση µπορεί να είναι µοναδική (µία µόνο κατάσταση του κόσµου) αλλά µπορεί να υπάρχουν και πολλές καταστάσεις οι οποίες να θεωρούνται τελικές. Π.χ. στο µπιλιάρδο δεν έχει σηµασία σε ποίο pocket µπαίνουν οι µπάλες πολλές δυνατές τελικές καταστάσεις. Αν όµως έχουµε 6 µπάλες αριθµηµένες από 1 έως 6 και το κάθε pocket έχει αριθµό 1, 2... ή 6 και πρέπει κάθε µπάλα να µπει στο αντίστοιχό της pocket µία µόνο τελική κατάσταση. Η λύση του προβλήµατος µπορεί να θεωρηθεί ως µία δυάδα <X G, C>, όπου: X G είναι µία διάταξη ενεργειών x i. Ο αριθµός των ενεργειών στην λίστα X G καλείται µήκος του πλάνου. Το C είναι ένα σύνολο από περιορισµούς το οποίο δηλώνει κάποια σειρά διάταξης µεταξύ των ενεργειών π.χ. x 4 εκτελείται µετά από x 3 και πριν από x 9, η µπάλα 3 µπαίνει στο pocket 3 πριν η µπάλα 4 να µπει στο pocket 4 κ.ο.κ. Έτσι ένα πλάνο µπορεί να είναι γραµµικό (linear plan) όταν µε βάση το C οι ενέργειες στην λύση ακολουθούν µια αυστηρή διάταξη ή να είναι - 9 -
14 παράλληλο (parallel plan) όταν µπορεί µία ενέργεια να εκτελεστεί πριν, µετά ή παράλληλα µε µία άλλη χωρίς αυτό να επηρεάσει το τελικό αποτέλεσµα. Στην απλούστερη µορφή του πλάνου η κατάσταση του κόσµου είναι σε κάθε περίπτωση σαφώς καθορισµένη ως µία ακολουθία από την αρχική κατάσταση και τις µεταβολές του κόσµου µε βάση των επιτρεπόµενων ενεργειών. Αυτός ο κόσµος είναι προκαθορισµένος. Με την υπόθεση ενός τέτοιου κόσµου είναι εύκολα να λυθούν πολλά απλά προβλήµατα, όµως µε την µοντελοποίηση ενός σύνθετου κόσµου ο οποίος να πλησιάζει την πραγµατικότητα η επίλυση ενός προβλήµατος σχεδιασµού γίνεται δυσκολότερη. Οι πράκτορες πρέπει να παίρνουν υπ όψη τους γεγονότα και δεδοµένα τα οποία δεν υπήρξαν στην αρχική κατάσταση και δεν εξαρτώνται από τις ενέργειες που εκτελούν, και τις πιθανότητες να διαφέρουν τα αποτελέσµατα µιας ενέργειας µετά από κάθε της εκτέλεση αν και δεν έχει αλλάξει ο κόσµος του προβλήµατος. Η µη ντετερµινιστικότητα του κόσµου προέρχεται µε βάση δύο παραγόντων: Πρώτα, κάθε κατορθωτό µοντέλο του κόσµου µπορεί να είναι ελλιπές και µε αυτόν τον τρόπο γεγονότα τα οποία πραγµατικά είναι προκαθορισµένα µπορεί να θεωρηθούν µη-προκαθορισµένα. Π.χ. δεν ξέρουµε πότε κάποιος θα µας πάρει τηλέφωνο ή θα έρθει στο σπίτι µας και αυτά τα γεγονότα µπορεί να θεωρηθούν ως µη-ντετερµινιστικά Αν όµως κωδικοποιήσουµε στο µοντέλο του κόσµο και το γεγονός ότι κάθε πρωΐ στις 9:00 έρχεται ο διανοµέας εφηµερίδων και κάθε δύο µέρες ο µπαµπάς παίρνει τηλέφωνο, τότε ο κόσµος είναι ντετερµινιστικός. εύτερον, πολλές ενέργειες από την φύση τους είναι µη ντετερµινιστικές το ρίξι- µο δύο ζαριών και η άθροιση των ενδείξεών τους έχει 11 πιθανές λύσεις. Το να πετάξεις ένα σκουπίδι από πολύ µακριά στοχεύοντας έναν κάδο απορριµµάτων δεν είναι σίγουρο ότι πάντα θα πετύχει. Είναι σηµαντικό να σηµειωθεί ότι αν και µπορεί να έχουµε ένα προκαθορισµένο κόσµο το να µη ξέρουµε την αιτία των γεγονότων µπορεί να µας προκαλέσει να θεωρήσουµε αυτά τα γεγονότα µη ντετερµινιστικά. [3] Τα περισσότερα προβλήµατα τα οποία παράγονται από και πρέπει να εφαρµοστούν σε έναν µη προκαθορισµένο και δυναµικό κόσµο είναι πολύ σύνθετα και δύσκολα να λυθεί. Για τον λόγο αυτό θα επικεντρωθούµε στην µελέτη των τρόπων επίλυσης ντετερµινιστικών προβληµάτων σχεδιασµού. Με την αύξηση των απαιτήσεων των ανθρώπων τα προβλήµατα αυτά, αν και από την φύση τους ντετερµινιστικά, γίνονται δύσκολα για επίλυση από τους ίδιους τους ανθρώπους και για αυτό έχουν φτιαχτεί διάφορα υπο
15 λογιστικά συστήµατα και γλώσσες σχεδιασµού ενεργειών τα οποία µειώνουν το κόστος και τον χρόνο σχεδιασµού. 2.2 Γλώσσες και συστήµατα σχεδιασµού ενεργειών Τα συστήµατα σχεδιασµού ενεργειών έχουν ως σκοπό την παραγωγή ενός πλάνου, µε την χρήση διάφορων αλγορίθµων πάνω σε ένα πεδίο στο οποίο ορίζεται το πρόβλη- µα και δρα ο πράκτορας. Τα συστήµατα αυτά κατηγοριοποιούνται µε βάση τα χαρακτηριστικά τους σε 11 κατηγορίες 1) Planners based on Binary Decision Diagrams (BDDs) Συστήµατα σχεδιασµού βασιζόµενα σε ιαγράµµατα υαδικής Απόφασης. Τα διαγράµµατα αυτά είναι µία δοµή δεδοµένων η οποία παριστάνει εκφράσεις ή συναρτήσεις δυαδικής λογικής (Boolean expressions/functions). Μια Boolean συνάρτηση µπορεί να παρασταθεί ως ένας κατευθυνόµενος, άκυκλος γράφος µε ρίζα, ο οποίος συνίσταται από αποφάσεις σε κάθε κόµβο και δύο τερµατικούς κόµβους οι οποίοι ονοµάζονται 0-terminal και 1-terminal. Τα συστή- µατα αυτά βασίζονται στην απόφαση η οποία παίρνεται µε βάση την δυαδική λογική σε κάθε κόµβο των BDDs. Εικόνα 2. ιάγραµµα υαδικής Απόφασης
16 2) Graph-based Planners Σχεδιαστές βασιζόµενοι σε γράφους. Αυτοί η σχεδιαστές βασίζονται στους αλγορίθµους γράφων. Όταν δηλωθεί ένα πρόβληµα οι σχεδιαστές αυτού του τύπου σχεδιάζουν και σχολιάζουν µία συµπαγή δο- µή η οποία ονοµάζεται γράφο σχεδίου (Planning Graph). Το τελικό πλάνο µπορεί να θεωρηθεί ως µία «ροή» τιµών αλήθειας µέσω του γράφου. Οι γράφοι σχεδίου έχουν την ιδιότητα να µεταδίδουν τις χρήσιµες πληροφορίες για την αναζήτηση µε βάση τους περιορισµούς (constraining) κατά την κατασκευή του γράφου. Στη συνέχεια οι σχεδιαστές βασιζόµενοι στους γράφους εξετάζουν αυτές τις πληροφορίες για την επιτυχή αναζήτηση της λύσης του προβλήµατος. 3) Heuristic Search Planners Σχεδιαστές ευρετικής αναζήτησης Αναζητούν την επόµενη κατάσταση του κόσµου µε την χρήση ευρετικών µηχανισµών οι οποίοι µπορούν να εξαχθούν απευθείας από την κωδικοποίηση του προβλή- µατος και των κανονικών αλγορίθµων αναζήτησης. Η επιτυχία τους εξαρτάται από διάφορους παράγοντες όπως η επιλογή του ευρετικού µηχανισµού, του αλγορίθµου αναζήτησης και της κατεύθυνσης αναζήτησης. 4) Integrated Planners & Schedulers Ολοκληρωµένοι σχεδιαστές και προγραµµατιστές 5) Interactive Planners Αλληλεπιδραστικοί σχεδιαστές παρέχουν την δυνατότητα ο χρήστης να εισάγει διάφορα δεδοµένα κατά την εκτέλεση του σχεδιασµού. 6) Knowledge-based & HTN (hierarchical transition network) Planners Σχεδιαστές βασιζόµενοι σε γνώσεις και δίκτυα ιεραρχικής µετάβασης για να βρουν την λύση του προβλήµατος σχεδιασµού αυτοί οι σχεδιαστές χρησιµοποιούν οτιδήποτε γνώσεις υπάρχουν για το πεδίο εφαρµογής (domain). Αυτά τα συστήµατα µπορούν να χειριστούν µεγάλα µοντέλα πεδίων (domain models) και χαρακτηρίζονται από τους πολλαπλούς τύπους γνώσεων. Αυτές οι γνώσεις µπορεί να περιλαµβάνουν δοµές στόχου και προβλήµατος, διάφορους τύπους περιορισµών, τεχνικές ελέγχου αναζήτησης και σε περίπτωση ασυνεπών ή ελλείπων γνώσεων να τους αποκτούν από τους χρήστες. Οι HTN planners σχεδιάζουν ένα αφηρηµένο δίκτυο το οποίο παριστάνει το πρόβληµα το οποίο πρόκειται να λυθεί. Στη συνέχεια επεκτείνουν το δίκτυο µε ιεραρχικό τρόπο αυξάνοντας τις λεπτοµέρειες και µειώνοντας την αφαίρεση (abstraction) έως ότου αυτό να περιέχει εκτελέσιµες ενέργειες. Με αυ
17 τόν τον τρόπο µειώνεται αποτελεσµατικά ο χώρος αναζήτησης και δίνεται δυνατότητα στον χρήστη να ελέγχει τον τύπο των αποτελεσµάτων. 7) Multi-agent Planners Πολιπρακτορικοί σχεδιαστές Το σχέδιο παράγεται µε την συνεργασία µεταξύ πολλαπλών πρακτόρων. 8) Planning as Satisfiability (SAT) Ο σχεδιασµός σαν ικανοποίηση. 9) Temporal Planners Χρονικοί Σχεδιαστές Οι σχεδιαστές αυτοί χρησιµοποιούνται για πεδία όπου απαιτείται ιδιαίτερη αντίληψη χρόνου, όταν υπάρχει ανάγκη να χειριστούν ενέργειες διαφορετικών διαρκειών οι οποίες µπορεί να επικαλύπτονται. 10) Planners handling Uncertainty Σχεδιαστές που διαχειρίζουν την αβεβαιότητα Αυτοί οι σχεδιαστές διαθέτουν την ικανότητα να χειριστούν κόσµους µε αβεβαιότητα και µη πλήρους κόσµους. Και στις δύο περιπτώσεις ο κόσµος µπορεί να είναι δυναµικός. 11) Case Based Planners Σχεδιαστές βασιζόµενοι σε Περιπτώσεις σε αυτή την περίπτωση χρησιµοποιούνται πλάνα που έχουν κατασκευαστεί προηγουµένως για να δηµιουργηθεί το καινούριο σχέδιο. Τα παλιά πλάνα έχουν καταχωρηθεί στη µνήµη µε την µορφή περιπτώσεων και ξαναχρησιµοποιούνται στην επίλυση παροµοίων µελλοντικών προβληµάτων. Χαρακτηρίζονται από την σηµαντική µείωση του χρόνου επίλυσης. [4] Παρακάτω δίνονται δύο πίνακες που περιέχουν γλώσσες και συστήµατα σχεδιασµού ενεργειών. Πίνακας 1. ιάφορα συστήµατα, τα οποία έχουν προσπαθήσει να ενσωµατώσουν σχεδιαστικές τεχνικές και να τις εφαρµόσουν στους αντίστοιχους τοµείς. [2] STRIPS (Fikes & Nilsson 1971) HACKER (Sussman 1973) Simple Robot Control Simple Program Generation NOAH (Sacerdoti 1977) Mechanical Engineers Apprentice Supervision NONLIN (Tate 1977) NASL (McDermott 1978) OPM (Hayes-Roth & Hayes-Roth 1979) ISIS-II (Fox et. al. 1981) Electricity Turbine Overhaul Electronic Circuit Design Journey Planning Job shop Scheduling (Turbine Production)
18 MOLGEN (Stefik 1981a) SIPE (Wilkins 1983) NONLIN+ (Tate & Whiter 1984) DEVISER (Vere 1983) FORBIN (Miller et. al. 1985) Experiment Planning in Molecular Genetics Aircraft Carrier Mission Planning Naval Logistics Voyager Spacecraft Mission Sequencing Factory Control Πίνακας 2. Πρόσφατα συστήµατα σχεδιασµού (planners). [4] 1 BLACKBOX (by Henry Kautz, the University of Washington) BDDPlan (by Hans-Peter Stört) CAPLAN (University of Kaiserslautern, Germany) DISCOPLAN (by Alfonso Gerevini, and Lenhart K. Schubert) LISA (by Alfonso Gerevini and Ivan Serina) O-Plan (by Austin Tate) PARIS (by Ralph Bergmann) PDDL/PDDL 2.1 created by the AIPS-98 Planning Committee, headed by Drew McDermott SAPA (by Rao Kambhampati's Yochan research group at Arizona State University) Graph-based and SAT planner planning by means of BDDs (Binary Decision Diagrams Case based planner a collection of techniques for inferring state constraints (or invariants) and operator-parameter domains A Library of Scheduling Algorithms Knowledge based planner Case based planner an action-centered language, inspired by the STRIPS formulations of planning problems a domain-independent heuristic forward chaining planner 1 Σ.Σ. Στο πίνακα 2 αναφέρεται ένα μικρό μέρος τών συστημάτων και γλωσσών σχεδιασμού. Για πλήρη αναφορά δείτε την
19 2.3 Το µοντέλο STRIPS. Η περιγραφή τόσο των καταστάσεων όσο και των ενεργειών καθορίζει αποφασιστικά τα είδη των προβληµάτων σχεδιασµού που µπορεί να περιγραφούν και φυσικά τις δυνατότητες που πρέπει να έχουν τα αντίστοιχα συστήµατα σχεδιασµού που θα τα επιλύσουν. Θα µπορούσε να χρησιµοποιηθεί η προτασιακή λογική για την περιγραφή ε- νεργειών αλλά αυτή δεν µπορεί να εκφράσει γενικότητα, λόγω έλλειψης µεταβλητών. Για να περιγραφεί η γενικότητα χρειάζεται κατηγορηµατική λογική πρώτης τάξης η ο- ποία όµως δεν µπορεί να περιγράψει ενέργειες µε µη αιτιοκρατικά (µη ντετερµινιστικά) αποτελέσµατα. Π.χ. το ρίξιµο των ζαριών του προηγούµενου παραδείγµατος. Όπως δείχνουν και οι παραπάνω πίνακες υπάρχει ένα µεγάλο φάσµα γλωσσών και συστηµάτων σχεδιασµού, κάθε ένα από τα οποία προσφέρει δυνατότητες επίλυσης διάφορων κατηγορηµάτων προβληµάτων. Ένα από τα δηµοφιλέστατα µοντέλα περιγραφής προβληµάτων σχεδιασµού είναι το µοντέλο STRIPS (Stanford Research Institute Planning System), το οποίο χρησιµοποιήθηκε από τον σχεδιαστή STRIPS που καθοδηγούσε το ροµπότ SHAKEY. Αυτό το µοντέλο χαρακτηρίζεται από απλότητα και φυσικότητα, έχει στοιχεία προτασιακής λογικής και είναι κατάλληλο για επίλυση προβληµάτων χωρίς αβεβαιότητα. Επιπλέον έχει αποδειχθεί ότι προβλήµατα κατηγορηµατικής λογικής µε πεπερασµένο και σταθερό α- ριθµό αντικειµένων µπορούν ισοδύναµα να αναπαρασταθούν στο µοντέλο αυτό. Στην αρχική του µορφή δεν υποστήριζε την αναπαράσταση χρονικών και άλλων περιορισµών, ωστόσο στη συνέχεια εµφανίστηκαν πολυάριθµες επεκτάσεις του µε πιο πλούσιες εκφραστικές δυνατότητες, όπως η γλώσσα PDDL. Στο µοντέλο STRIPS ο κόσµος παριστάνεται από ένα σύνολο καλά ορισµένων τύπων (well formed formulas wffs) της κατηγορηµατικής λογικής πρώτης τάξεως. Τα βασικά στοιχεία από τα οποία δηµιουργείται η λύση του προβλήµατος είναι οι τελεστές (operators). Για παράδειγµα, για ένα ροµπότ κάθε τελεστής αντιστοιχεί σε µία ρουτίνα ενεργειών (action routine), η ακολούθηση της οποίας αναγκάζει το ροµπότ να δρα στον κόσµο. Π.χ. µπορεί να υπάρχει µία ρουτίνα η οποία να αναγκάζει το ροµπότ να περνάει από µια πόρτα, άλλη να σπρώχνει κουτιά, κ.ά
20 Κάποια παλαιότερα συστήµατα 2 βασιζότανε αποκλειστικά στις τυπικές µεθόδους απόδειξης θεωρηµάτων για την αναζήτηση της κατάλληλης ακολουθίας τελεστών. Αυτά όµως δεν µπορούσαν να λύνουν µη τετριµµένα προβλήµατα. Το µοντέλο STRIPS όµως διαχωρίζει τις διαδικασίες απόδειξης θεωρηµάτων και τις διαδικασίες αναζήτησης σε µοντέλα καταστάσεων του κόσµου και µε αυτόν τον τρόπο ξεπερνά αυτά τα προβλήµατα. Αυτός ο διαχωρισµός επιτρέπει την εφαρµογή διάφορων στρατηγικών για τις δύο αυτές δραστηριότητες µε αποτέλεσµα η βελτιστοποίηση της ολόκληρης απόδοσης του συστήµατος. a) Οι µέθοδοι απόδειξης θεωρηµάτων χρησιµοποιούνται µόνο για την επαλήθευση αν κάποιος τελεστής είναι εφαρµόσιµος στην κατάσταση του κόσµου και αν έχουµε πετύχει τους στόχους. b) Για την αναζήτηση στον κόσµο, το STRIPS χρησιµοποιεί means-end στρατηγικές αναλύσεις όµοιες µε αυτές του GPS (General Problem Solver) Ο συνδυασµός των means-end στρατηγικών ανάλυσης και των τυπικών µεθόδων απόδειξης θεωρηµάτων προσθέτει την δυνατότητα εφαρµογής του µοντέλου αυτού πάνω σε πιο σύνθετους και γενικούς κόσµους και προσφέρει πιο δυνατές ευριστικές µηχανικές από αυτές των προγραµµάτων απόδειξης θεωρηµάτων. Το πρόβληµα σχεδιασµού για το STRIPS ορίζεται από την αρχική κατάσταση του κόσµου, το σύνολο υπαρχόντων τελεστών και την επιρροή τους στην κατάσταση του κόσµου, και την τελική κατάσταση (goal state). Όπως αναφέρθηκε παραπάνω το STRIPS απεικονίζει το µοντέλο του κόσµου µε ένα σύνολο από καλά ορισµένους τύπους (well formed formulas - wffs). Π.χ. για να περιγραφεί ο κόσµος στον οποίον υπάρχει ένα ροµπότ στο σηµείο α και υπάρχουν κιβώτια Β και Γ τα οποία βρίσκονται στα σηµεία β και γ µπορεί να χρησιµοποιηθούν τα εξής wffs: AT_Robot(α) AT(B, β) AT(Γ, γ). 2 Βλ. Green, C. Application of theorem proving to problem solving. Proc. Int'l. Joint Conf. Artificial Intelligence, Washington, D.C. (May 1969)
21 Μπορεί να συµπεριληφθεί και το wffs για να δηλωθεί τον κανόνα ότι ένα αντικείµενο το οποίο βρίσκεται σε ένα σηµείο δεν βρίσκεται ταυτόχρονα σε άλλο. Με την χρήση wffs κατηγορηµατικής λογικής πρώτης τάξεως µπορεί να περιγραφούν αρκετά ικανοποιητικά µοντέλα του κόσµου και τα ήδη υπάρχοντα προγράµµατα απόδειξης θεωρηµάτων µπορεί να χρησιµοποιηθούν για απαντήσεις σχετικές µε τα µοντέλα αυτά. Η τελική κατάσταση (ο στόχος) µπορεί να περιγραφεί µε την χρήση τέτοιων τύπων. Π.χ. «Τα κιβώτια Β και Γ να βρίσκονται στο σηµείο α και το κιβώτιο Β να είναι πάνω από το Γ» µπορεί να δηλωθεί ως εξής: (AT(B, α) ^ AT(Γ, α))^over(b, Γ). Ένα πρόβληµα έχει λυθεί όταν παραχθεί κατάσταση του µοντέλου του κόσµου η οποία να ικανοποιεί το wff του στόχου. Η στρατηγική αναζήτησης Σε ένα πολύ απλό σύστηµα επίλυσης προβληµάτων µπορεί αρχικά όλοι οι δυνατοί τελεστές να εφαρµοστούν στην αρχική κατάσταση του κόσµου έτσι ώστε να παραχθούν όλες οι δυνατές επόµενες καταστάσεις. Στη συνέχεια να εφαρµόζονται όλοι οι δυνατοί τελεστές στην καινούρια κατάσταση (όπως σε ένα αλγόριθµο Breath-first) µέχρι να παραχθεί µία κατάσταση όπου ο wff του στόχου αποδεικνύεται σαν θεώρηµα (αληθεύει). Όµως σε πολύπλοκους κόσµους ο αριθµός των τελεστών µπορεί να είναι πολύ µεγάλος, ένα τέτοιο σύστηµα µπορεί να δηµιουργήσει ανεπιθύµητα µεγάλο δέντρο καταστάσεων του κόσµου και το σύστηµα να καταστεί µη πρακτικό. Αντίθετα το STRIPS υιοθετεί από το GPS την στρατηγική για εξαγωγή «διαφορών» µεταξύ της τρέχουσας και της τελικής κατάστασης του κόσµου, και την εύρεση τελεστών οι οποίοι να µειώσουν αυτή την διαφορά. Αν υποθέσουµε ότι το Χ 0 είναι η αρχική κατάσταση του κόσµου το µοντέλο STRIPS αρχίζει µε την υποβολή του µηχανισµού απόδειξης θεωρηµάτων εξετάζοντας αν η κατάσταση του στόχου G 0 προέρχεται απευθείας από την Χ 0. Σε αυτήν την περίπτωση η αρχική κατάσταση είναι και η λύση του προβλήµατος. Αν σε κάποιο σηµείο
22 όµως αποτύχει ο µηχανισµός απόδειξης θεωρηµάτων θεωρείται ότι η µέχρι στιγµής α- πόδειξη, η οποία είναι µη πλήρης, είναι η διαφορά µεταξύ της Χ 0 και G 0. Στη συνέχεια αναζητούνται τελεστές οι οποίοι µειώνουν αυτή την διαφορά, δηλαδή θα επιτρέψουν τον µηχανισµό να συνεχίσει την απόδειξη. Ας θεωρηθεί το τετριµµένο απλό παράδειγµα στο οποίο ο στόχος είναι ένα ροµπότ να πάει στο σηµείο β. Το wffs του στόχου είναι ΑΤ_Robot(β), και η µόνη περίπτωση στην οποία η απόδειξη δεν θα αποτύχει είναι όταν το ροµπότ βρίσκεται ήδη στο σηµείο β. Αν το ροµπότ δεν είναι στο σηµείο β τότε ο τελεστής goto(m, n) είναι κατάλληλος για να µειώσει την διαφορά, επιτρέποντας η απόδειξη να συνεχιστεί, και έτσι µπορεί να ταυτιστεί µε τον goto(m, β). H τεχνική η οποία χρησιµοποιεί το µοντέλο STRIPS είναι η εξής: a) Αν δεν βρεθεί απόδειξη, το STRIPS χρησιµοποιεί την µη πλήρης απόδειξη ως διαφορά και θέτει (υπό) υπό- στόχους µε βάση τις προϋποθέσεις τους. b) Αν το STRIPS βρεθεί στιγµιότυπο του G το οποίο παράγεται κατευθείαν από (ή είναι µέρος του) X 0, τότε ο τελεστής χρησιµοποιείται για να µετατραπεί το Χ 0 σε Χ 1. Στο παραπάνω παράδειγµα το στιγµιότυπο G ήταν εκείνο µε βάση του οποίου να αληθεύει το ΑΤ_Robot(m). Παρακάτω ακολουθεί ένα παράδειγµα διατυπωµένο µε το µοντέλο STRIPS. Το πρόβληµα συµπεριλαµβάνει φόρτωση και εκφόρτωση φορτίων σε και από αεροπλάνα και η µεταφορά τους από ένα αεροδρόµιο σε ένα άλλο Το πρόβληµα αυτό µπορεί να δηλωθεί µε την χρήση τριών ενεργειών «Φόρτωση», «Εκφόρτωση», «Μεταφορά» ( Load, Unload, Fly ): Είναι δυνατές 3 ενέργειες: Φόρτωση, Εκφόρτωση, Μεταφορά Μεταβλητές: a: Αεροδρόµιο, c: Φορτίο (Cargo), p: Αεροπλάνο (Plane), from (από): start, to (µέχρι): destination δυνατές αντικαταστάσεις a, from, to: JFK John F. Kennedy Airport New York SFO San Francisco International Airport c: C1, C2 p: P1, P2-18 -
23 Action (Load (c, p, a), PRECOND: At (c, a) At (p, a) Cargo (c) Plane (p) airport (a) EFFECT: At (c, a) In (c, p)) Action (Unload (c, p, a), PRECOND: In (c, p) At (p, a) Cargo (c) Plane (p) Airport (a) EFFECT: At (c, a) In (c, p)) Action (Fly (p, from, to), PRECOND: At (p, from) Plane (p) Airport (from) Airport (to) EFFECT: At (p, from) At (p, to)) Initial State: Init (At (C1, SFO) At (C2, JFK) At (P1, SFO) At (P2, JFK) Cargo (C1) Cargo (C2) Plane (P1) Plane (P2) Airport (JFK) Airport (SFO)) Goal State: Goal (At (C1, JFK) At (C2, SFO)) Init (At (C1, SFO) At (C2, JFK) At (P1, SFO) At (P2, JFK) Cargo (C1) Cargo (C2) Plane (P1) Plane (P2) Airport (JFK) Airport (SFO)) - First Action: Load (C1, P1, SFO) Action (Load (C1, P1, SFO), PRECOND: At (C1, SFO) At (P1, SFO) Cargo (C1) Plane (P1) airport (SFO) EFFECT: At (C1, SFO) In (C1, P1)) S1 (In (C1, P1) At (C2, JFK) At (P1, SFO) At (P2, JFK) Cargo (C1) Cargo (C2) Plane (P1) Plane (P2) Airport (JFK) Airport (SFO)) - Second Action: Fly (P1, SFO, JFK) Action (Fly (P1, SFO, JFK), PRECOND: At (P1, SFO) Plane (P1) Airport (SFO) Airport (JFK) EFFECT: At (P1, SFO) At (P1, JFK)) S2 (In (C1, P1) At (C2, JFK) At (P1, JFK) At (P2, JFK) Cargo (C1) Cargo (C2) Plane (P1) Plane (P2) Airport (JFK) Airport (SFO)) - Third Action: Load (C2,P2,JFK) Action (Load (C2, P2, JFK), PRECOND: At (C2, JFK) At (P2, JFK) Cargo (C2) Plane (P2) airport (JFK) EFFECT: At (C2, JFK) In (C2, P2)) S3 (In (C1, P1) In (C2, P2) At (P1, JFK) At (P2, JFK) Cargo (C1) Cargo (C2) Plane (P1) Plane (P2) Airport (JFK) Airport (SFO))
24 - Fourth Action: Fly (P2, JFK, SFO) Action (Fly (P2, JFK, SFO), PRECOND: At (P2, JFK) Plane (P2) Airport (JFK) Airport (SFO) EFFECT: At (P2, JFK) At (P2, SFO)) S4 (In (C1, P1) In (C2, P2) At (P1, JFK) At (P2, SFO) Cargo (C1) Cargo (C2) Plane (P1) Plane (P2) Airport (JFK) Airport (SFO)) - Fifth Action: Unload (C1, P1, JFK) Action (Unload (C1, P1, JFK), PRECOND: In (C1, P1) At (P1, JFK) Cargo (C1) Plane (P1) Airport (JFK) EFFECT: At (C1, JFK) In (C1, P1)) S5 (At (C1, JFK) In (C2, P2) At (P1, JFK) At (P2, SFO) Cargo (C1) Cargo (C2) Plane (P1) Plane (P2) Airport (JFK) Airport (SFO)) - Sixth Action: Unload (C2, P2, SFO) Action (Unload (C2, P2, SFO), PRECOND: In (C2, P2) At (P2, SFO) Cargo (C2) Plane (P2) Airport (SFO) EFFECT: At (C2, SFO) In (C2, P2)) S6 (At (C1, JFK) At (C2, SFO) At (P1, JFK) At (P2, SFO) Cargo (C1) Cargo (C2) Plane (P1) Plane (P2) Airport (JFK) Airport (SFO)) Goal (At (C1, JFK) At (C2, SFO)) Μία κατάσταση s ικανοποιεί τον στόχο αν περιλαµβάνει όλα τα στοιχεία του (και περισσότερα). Στην περίπτωση αυτήν η S6 ικανοποιεί τον στόχο (goal) [10]. Στη συνέχεια η µελέτη θα επικεντρωθεί στην γλώσσα PDDL. 2.4 Η γλώσσα PDDL Το µοντέλο STRIPS περιγράφει ικανοποιητικά τα προβλήµατα σχεδιασµού. Ένας άλλος τρόπος περιγραφής των προβληµάτων σχεδιασµού είναι η χρήση της γλώσσας PDDL (the Planning Domain Definition Language 3 ) η οποία δηµιουργήθηκε από AIPS- 98 Competition Committee για δύο γενικούς σκοπούς: 3 Σ.σ. Η σηνδομογραφία PDDL σηναντάται σε κάποιες αναφορές και ως Planning Domain Description Language
25 I. Για να επιτρέπει στους συµµετέχοντες να ορίζουν πεδία (domains) και προβλή- µατα σχεδιασµού σε µία κοινή γλώσσα. II. Να βοηθήσει στην ανάπτυξη ενός συνόλου προβληµάτων σ αυτήν την κοινή γλώσσα για να µπορούν να τεστάρουν τους διάφορους σχεδιαστές (planners). Η PDDL παρέχει ένα ευρύ φάσµα συντακτικών χαρακτηριστικών, αλλά οι περισσότεροι σχεδιαστές δεν µπορούν να τους χρησιµοποιούν. Αυτοί χρησιµοποιούν ένα υποσύνολο αυτών των χαρακτηριστικών και αυτό δηλώνεται στον ορισµό του πεδίου προβλήµατος. Στη σχεδίαση µε την γλώσσα PDDL υπάρχουν πέντε βασικά συστατικά: Είναι τα αντικείµενα (objects), τα κατηγορήµατα (predicates), η αρχική κατάσταση (initial state), η περιγραφή του κόσµου στην τελική κατάσταση (goal specification) και οι ενέργειες/τελεστές (actions/operators). 1. Αντικείµενα είναι όλα που υπάρχουν στον κόσµο του προβλήµατος. Σε σχέση µε τον πραγµατικό κόσµο είναι όλα αυτά που µας ενδιαφέρουν και έχουν κάποια επιρροή στην διατύπωση και στην επίλυση του προβλήµατός µας. 2. Κατηγορήµατα ή σχέσεις (predicates/relations) είναι οι ιδιότητες των αντικειµένων τα οποία µας ενδιαφέρουν (είναι χρήσιµα για το πρόβληµα). Αυτά µπορεί να είναι είτε αληθές είτε ψευδές. 3. Αρχική λέγεται η κατάσταση του κόσµου προβλήµατος στην οποία διατυπώνεται το πρόβληµα και από την οποία αρχίζει η επίλυσή του. 4. Η τελική κατάσταση µπορεί να διαφέρει από πρόβληµα σε πρόβληµα (αν και να αναφέρονται στον ίδιο πεδίο προβλήµατος µε ίδιες αρχικές καταστάσεις). Συνεπώς ο στόχος είναι µία περιγραφή µιας κατάστασης του κόσµου, συνήθως µη πλήρης. 5. Οι ενέργειες/τελεστές είναι τα γεγονότα τα οποία αλλάζουν τον κόσµο. Στην γραφή ενός προγράµµατος µε την γλώσσα PDDL τα συστατικά αυτά διαιρούνται σε δύο µέρη (δύο αρχεία) το αρχείο του πεδίου και το αρχείο του στιγµιότυπου του προβλήµατος domain file και problem file. Στο πρώτο αρχείο δηλώνονται οι κλάσεις των αντικειµένων, τα κατηγορήµατα/οι σχέσεις µεταξύ τους και οι επιτρεπόµενες ενέργειες περιγράφεται ο κόσµος. Στο δεύτερο αρχείο δηλώνονται τα αντικείµενα, η αρχική κατάσταση και η τελική κατάσταση
26 domain file (define (domain <όνοµα>) <κώδικας για τα κατηγορήµατα> <κώδικας για πρώτη ενέργεια>... <κώδικας για τελευταία ενέργεια> ) <όνοµα> - ένα αλφαριθµητικό που εκφράζει το όνοµα του πεδίου <κώδικας...> - PDDL κώδικας problem file (define (problem <όνοµα προβλήµατος>) (:domain <όνοµα πεδίου>) <κώδικας για τα αντικείµενα> <κώδικάς για την αρχική κατάσταση> <κώδικα για τελική κατάσταση> ) <όνοµα προβλήµατος/πεδίου> - ένα αλφαριθµητικό που εκφράζει το όνοµα του προβλήµατος/πεδίου <κώδικας...> - PDDL κώδικας Π.χ. Το πρόβληµα των πύργων του Hanoi: Όλοι οι δίσκοι από τον ένα πύργο πρέπει να περάσουν σε ένα άλλο µε την χρήση του ενδιάµεσου, και µόνο µετακινώντας έναν δίσκο την φορά. Υπάρχει ο περιορισµός ότι ένας δίσκος µπορεί να βρίσκεται πάνω µόνο σε µεγαλύτερο. Αρχική κατάσταση: Εικόνα 3 α. Οι πύργοι του Hanoi αρχική κατάσταση
27 Τελική κατάσταση (Goal state): Εικόνα 3 β. Οι πύργοι του Hanoi τελική κατάσταση. Domain: (define (domain hanoi) (:requirements :strips) (:predicates (clear?x) (on?x?y) (smaller?x?y)) (:action move :parameters (?disc?from?to) :precondition (and (smaller?to?disc) (on?disc?from) (clear?disc) (clear?to)) :effect (and (clear?from) (on?disc?to) (not (on?disc?from)) (not (clear?to))) )) Problem: (define (problem TEST) (:domain TEST-strips) (:objects object1 object2 object3 object4 object5) (:init
28 ) (object object1) (object object2) (object object3) (object object4) (object object5) (clear object2) (clear object3) (clear object5) (on object5 object4) (on object4 object1) (smaller object5 object4) (smaller object4 object1) (smaller object4 object2) (smaller object4 object3) (smaller object5 object1) (smaller object5 object2) (smaller object5 object3) ) (:goal (and (on object4 object2) (on object5 object4)) ) Τα κατηγορήµατα (predicates) δείχνουν κάποια ιδιότητα των αντικειµένων ή κάποια σχέση µεταξύ των κλάσεων και, όπως αναφέρθηκε προηγουµένως, δηλώνονται στο αρχείο πεδίου προβλήµατος (problem.pddl). Είναι δηλώσεις της µορφής: <όνοµα κατηγορήµατος>?κ1?κ2...?κ3, όπου το <όνοµα κατηγορήµατος> δηλώνει το τι σχέση υπάρχει µεταξύ των κλάσεων ή το τι ιδιότητα έχουν. Μετά το όνοµα είναι η αντίστοιχες κλάσεις. Το σύµβολο «?» δηλώνει ότι το επόµενο είναι µια µεταβλητή αντικείµενο της κλάσης. Στο παραπάνω παράδειγµα η δήλωση του predicate «smaller?x?y» υποθέτει ότι τα x και y είναι αντι
29 κείµενα κάποιων κλάσεων µεταξύ των οποίων ισχύει ότι το πρώτο είναι µικρότερο του δεύτερου. Με την λέξη «action» δηλώνεται µία ενέργεια η οποία αποτελείται από τέσσερα πεδία το όνοµά της, οι παράµετροι, η λίστα προϋποθέσεων και η λίστα των αποτελεσµάτων. Το όνοµα δηλώνεται µετά την λέξη κλειδί «action» και είναι ένα αλφαριθµητικό. Οι παράµετροι σχετίζονται µε τις κλάσεις αντικειµένων οι οποίες συµµετέχουν στην ενέργεια. Π.χ. η ενέργεια move (µετακίνησε) του παραπάνω παραδείγµατος έχει τρείς παραµέτρους -?disc υποδηλώνει την ύπαρξη ενός δίσκου ο οποίος πρόκειται να µετακινηθεί.?from δηλώνει την υποχρέωση µίας αρχικής θέσης του δίσκου από την ο- ποία θα µετακινηθεί και?to είναι ο προορισµός του δίσκου. Η λίστα των προϋποθέσεων ορίζει τις κατάλληλες για την εφαρµογή της ενέργειας, καταστάσεις του κόσµου. Ακόµα γίνεται η σύνδεση µεταξύ κλάσεων και παραµέτρων. Π.χ.... (on?disc?from) (clear?disc)... υποθέτει ότι στην τρέχουσα κατάσταση (γενικά στην κατάσταση στην οποία µπορεί να εφαρµοστεί η ενέργεια αυτή) υπάρχει ένα (τουλάχιστον) αντικείµενο της κλάσης disc, και αυτό βρίσκεται στην θέση η οποία δηλώνεται ως αρχική (?from), και ο δίσκος αυτός είναι άδειος από πάνω. Αν στην κατάσταση του κόσµου δεν υπάρχουν αυτές οι προϋποθέσεις τότε η ενέργεια αυτή δεν µπορεί να εκτελεστεί. Το αποτέλεσµα από την εκτέλεση της ενέργειας είναι µια καινούρια κατάσταση του κόσµου. Το πώς µετατρέπεται ο κόσµος µετά την εκτέλεση της ενέργειας δηλώνεται στην λίστα αποτελεσµάτων (effect list). Τα αποτελέσµατα µπορεί να είναι προσθέσεις ή αφαιρέσεις αντικειµένων από την αρχική (για την ενέργεια αυτή) κατάσταση. Π.χ....(on?disc?to) (not (on?disc?from))... δηλώνει ότι µετά την εκτέλεση ο δίσκος θα βρίσκεται στην θέση προορισµού και δεν θα βρίσκεται στην αρχική θέση. Η άρνηση δείχνεται µε την ειδική λέξη «not». Η διατύπωση του προβλήµατος συνίσταται στην περιγραφή ενός στιγµιότυπου του κόσµου µέσου του αρχείου προβλήµατος. Στο αρχείο αυτό περιγράφεται ο στόχος µε την διατύπωση γεγονότων τα οποία πρέπει να ισχύουν στο τέλος. Ο σχεδιαστής πρέπει µε την χρήση των ενεργειών οι οποίες έχουν δηλωθεί στο αρχείο του πεδίου προβλήµατος να βρει µια λογική ακολουθία από την αρχική κατάσταση στην κατάσταση η οποία περιγράφεται στο αρχείο του προβλήµατος. Κάθε πρόβληµα έχει ένα όνοµα µε το οποίο χαρακτηρίζεται και ένα πεδίο στο οποίο αντιστοιχεί το δεδοµένο πρόβληµα σε κάποιο υπάρχοντα πεδίο (domain). Στη συνέχεια
30 δηλώνεται για κάθε αντικείµενο το αντίστοιχό του όνοµα. Μετά είναι οι περιγραφές της αρχικής και της τελικής κατάστασης. Η περιγραφή της αρχικής κατάστασης πρέπει να είναι ένα πλήρες στιγµιότυπο του κόσµου, το οποίο περιγράφει ισχύοντα γεγονότα. Π.χ. (object object1) δηλώνει την ύπαρξη του αντικείµενο object1, (on object5 object4) δείχνει ότι την στιγµή αυτήν το αντικείµενο object5 βρίσκεται πάνω στο αντικείµενο object4, (smaller object4 object1) ορίζει ποιό από τα αντικείµενα είναι µεγαλύτερο, κ.τ.λ. Όπως φαίνεται υπάρχουν δύο τύποι γεγονότων τα οποία ισχύουν στην αρχική κατάσταση είναι τα στατικά και τα δυναµικά. Τα στατικά είναι αυτά τα οποία δεν αλλάζουν κατά την επίλυση του προβλή- µατος (object object1), (object object2), (smaller object4 object1). Τα δυναµικά όµως κατά την πορεία της εύρεσης του πλάνου αλλάζουν (on object5 object4), το οποίο κάποια στιγµή µπορεί να γίνει (on object4 object5) ή να µην ισχύει καθόλου, ή και πάλι να γίνει (on object5 object4). Το τελευταίο βήµα στην περιγραφή του προβλήµατος είναι η διατύπωση του στόχου. Αυτή γίνεται όπως στη περιγραφή της αρχικής κατάστασης µε τον ορισµό γεγονότων τα οποία πρέπει να ισχύουν ή/και γεγονότων τα οποία να µην ισχύουν στη τελική κατάσταση του κόσµου. Αυτή η περιγραφή δεν ορίζει µια πλήρης κατάσταση του κόσµου, αλλά µία υποκατάσταση. Η αρχική και η τελική καταστάσεις ορίζονται µετά τις λέξεις κλειδιά «init» και «goal». Παρακάτω ακολουθεί το παράδειγµα που αναφέρθηκε στο τµήµα (του κεφαλαίου αυτού) για το µοντέλο STRIPS φόρτωση και εκφόρτωση φορτίων σε και από αεροπλάνα και η µεταφορά τους από ένα αεροδρόµιο σε ένα άλλο. (define (domain air-cargo) (:requirements :typing :adl) (:types cargo plane airport) (:predicates (at?t - (either cargo plane)?a - airport) (in?c - cargo?p - plane)) (:action load :parameters (?c - cargo?p - plane?a - airport)
31 :precondition (and (at?c?a) (at?p?a)) :effect (and (not (at?c?a)) (in?c?p))) (:action unload :parameters (?c -cargo?p - plane?a - airport) :precondition (and (in?c?p) (at?p?a)) :effect (and (at?c?a) (not (in?c?p)))) ) (:action fly :parameters (?p - plane?a1?a2 - airport) :precondition (and (at?p?a1) (not (=?a1?a2))) :effect (and (not (at?p?a1)) (at?p?a2))) (define (problem sfo-jfk) (:domain air-cargo) (:objects c1 c2 - cargo sfo jfk - airport p1 p2 - plane) (:init (at c1 sfo) (at p1 sfo) (at c2 jfk) (at p2 jfk) ) (:goal (and (at c1 jfk) (at c2 sfo)))
32 - 28 -
33 3 Συστήµατα Σχεδιασµού Ε- νεργειών Στην καθηµερινότητά του ο άνθρωπος είναι αναγκασµένος να εκτελεί διάφορες διαδικασίες για να πετύχει συγκεκριµένους στόχος. Για την επιτυχή εκτέλεσή τους απαιτείται ο προσδιορισµός µιας ακολουθίας βηµάτων η σχεδίαση ενός πλάνου. Το πλάνο συνίσταται από διακεκριµένες ενέργειες, οι οποίες όταν εκτελούνται (ακολουθούνται) µετατρέπουν την τρέχουσα κατάσταση του κόσµου, έτσι ώστε ο στόχος (οι στόχοι) να «πλησιάζεται». Υπάρχουν απλές διαδικασίες οι οποίες δεν χρειάζονται αναλυτικό σχεδιασµό, όµως στην γρήγορα εξελίξιµη ζωή µας υπάρχουν στόχοι για την επίτευξη των οποίων ο σχεδιασµός ενός πλάνου µπορεί να ξεπεράσει τα όρια των ανθρώπινων δυνατοτήτων. Για το λόγο αυτό έχουν δηµιουργηθεί διάφορα συστήµατα και γλώσσες σχεδιασµού, έτσι ώστε να µην υπάρχουν εµπόδια στην δηµιουργία οτιδήποτε πλάνου. Άλλα αίτια σχετίζονται µε τους τοµείς της ροµποτικής (π.χ. προσδιορισµός της επόµενης κίνησης ενός ροµπότ), της οικονοµίας (π.χ. βελτιστοποίηση σχεδιασµός χρησιµοποιείται από εταιρίες οι οποίες χρειάζονται την πιο οικονοµική λύση, ή την πιο γρήγορη λύση), κ.α. Ενδεικτικό είναι το µοντέλο STRIPS (1971, Fikes and Nilson), το οποίο χρησιµοποιήθηκε στο SHAKEY το πρώτο ροµπότ, και προσδιορίζει την επόµενη κίνησή του µε βάση µια αρχική κατάσταση του κόσµου, µια τελική ο στόχος, και ένα σύνολο επιτρεπτών ενεργειών. Κάθε ενέργεια είναι µία τριάδα <Π, Λδ, Λπ> Π είναι το σύνολο των προϋποθέσεων οι οποίες πρέπει να ισχύουν στην κατάσταση πάνω στην οποία ε- φαρµόζεται η ενέργεια, Λδ είναι η λίστα διαιρέσεων περιέχει τα γεγονότα τα οποία θα αφαιρεθούν από την κατάσταση, και Λπ είναι η λίστα προσθηκών η οποία περιέχει τα γεγονότα που πρόκειται να προστεθούν στην τρέχουσα κατάσταση. Με την αφαίρεση υπαρχόντων και την προσθήκη καινούριων γεγονότων παράγεται η καινούρια κατάσταση. Η ιδέα αυτή επεκτείνεται στην συνέχεια, και βασίζοντας σε αυτήν έχει δηµιουργηθεί ένα πλήθος γλωσσών και εργαλείων. Μία από αυτές είναι η γλώσσα PDDL Planning Domain Definition Language (1998), είναι η γλώσσα, η οποία χρησιµοποιήθηκε
34 για την προδιαγραφή προβληµάτων (problem specification) στον διαγωνισµό AIPS-98. Υποστηρίζει τα ακόλουθα χαρακτηριστικά: Βασικές ενέργειες τύπου STRIPS Αποτελέσµατα υπό συνθήκη Γενική ποσοτικοποίηση δυναµικών κόσµων Αξιώµατα στο domain, πάνω σε θεωρήµατα Προδιαγραφή ασφαλών περιορισµών Προδιαγραφή ιεραρχικών ενεργειών, οι οποίες συνίστανται από υπό-ενέργειες και υπό-στόχους ιαχείριση πολλαπλών προβληµάτων σε πολλαπλά domains Η γλώσσα PDDL έχει ως στόχο να εκφράσει την φυσική δοµή ενός domain τις συνιστώσες του, τα κατηγορήµατά του, τις δυνατές ενέργειες, την µορφή των σύνθετων ενεργειών, και οι επιδράσεις των ενεργειών αυτών. Η PDDL χρησιµοποιεί δύο αρχεία του domain και του problem. Σε αυτό του domain περιγράφεται ο κόσµος πάνω στον οποίον δηλώνεται το πρόβληµα και οι επιτρεπτές ενέργειες, στο problem δηλώνονται στιγµιότυπα του κόσµου, τα οποία αντιστοιχούν σε µία αρχική κατάσταση και σε µία ή περισσότερες επιθυµητές τελικές καταστάσεις στόχου. Πίνακας 3.1: Παράδειγµα αρχείων pddl σχετικά µε πρόβληµα µετακίνησης µλοκ. (define (domain BLOCKS) (:requirements :strips) (:predicates (on?x?y) (ontable?x) (clear?x) (handempty) (holding?x) ) domain.pddl problem.pddl (define (problem BLOCKS-5-1) (:domain BLOCKS) (:objects A B C ) (:INIT (CLEAR B) (CLEAR A) (CLEAR C) (ONTABLE A) (ONTABLE B) (ONTABLE C)) (:goal (AND (ON B A) (ON C B) (ONTABLE A))) ) (:action move :parameters (?x?y?z) :precondition (and (clear?x) (clear?z) (on?x?y)) :effect (and (not (on?x?y)) (not (clear?z)) (on?x?z) (clear?y)))
35 (:action move_to_table :parameters (?x?y) :precondition (and (clear?x) (on?x?y)) :effect (and (not (on?x?y)) (ontable?x) (clear?y))) ) (:action move_from_table :parameters (?x?z) :precondition (and (clear?x) (clear?z) (ontable?x)) :effect (and (not (ontable?x)) (not (clear?z)) (on?x?z))) α) β) Εικόνα 3.1: Αρχική κατάσταση α) και κατάσταση του κόσµου η οποία παριστάνει τον στόχο β) του παραπάνω παραδείγµατος Η PDDL, όµως, είναι µόνο µία γλώσσα περιγραφής, η οποία επιτρέπει την δήλωση κάποιου προβλήµατος και ενός κόσµου πάνω στον οποίο υφίσταται το πρόβληµα. Από την άλλη, διάφορα συστήµατα έχουν φτιαχτεί για να επιτραπούν την διαχείριση και την αξιοποίησή της. Με βάση των αποτελεσµάτων από το parsing των δύο αρχείων pddl, τα συστήµατα αυτά (τα planners) ορίζουν τον χώρο αναζήτησης (ΧΑ). Σε αυτόν εφαρµόζουν έναν αλγόριθµο ο οποίος αναζητά ένα συγκεκριµένο σηµείο, το οποίο θεωρείται ως στόχο, και σε κατάλληλη µορφή παράγουν την ακολουθία ενεργειών. Τα planners διαφέρουν µεταξύ τους βασικά στο πώς ορίζουν τον χώρο αναζήτησης. Κάποιοι πλάνερς θεωρούν τα σηµεία στον χώρο αναζήτησης καταστάσεις του κόσµου του προβλή- µατος, οι οποίες χωρίζονται σε χρονικά διαστήµατα. Όταν σε µία κατάσταση εφαρµο
36 στεί ένας τελεστής η τρέχουσα κατάσταση αλλάζεται και η αναζήτηση συνεχίζεται στο επόµενο στάδιο από το καινούριο σηµείο του ΧΑ. Η λύση µπορεί να οριστεί ως η ακολουθία τελεστών, η οποία µπορεί να εφαρµοστεί στον ΧΑ ξεκινώντας από το αρχικό σηµείο και οδηγεί ή «µετακινεί» σε ένα (ή ένα σύνολο) σηµείο(ων) το οποίο ικανοποιεί την αρχική απαίτηση (the goal). Άλλο είδος συστηµάτων σχεδιασµού ορίζουν στους χώρους αναζήτησής τους ση- µεία τα οποία αντιστοιχούν σε µη πλήρως επεξεργασµένα πλάνα. Ένα σηµείο του ΧΑ µετατρέπεται σε άλλο εφαρµόζοντας τους κατάλληλους τελεστές και επεκτείνοντας το µερικώς αναπτυγµένο πλάνο. Σε αυτή την περίπτωση ο σκοπός του συστήµατος είναι η εύρεση µιας ακολουθίας µετασχηµατισµών από ένα αρχικό πλάνο µέχρι ένα πλήρες και λεπτοµερές πλάνο το οποίο ικανοποιεί τον στόχο. Ένα πλάνο θεωρείται πλήρες όταν έχει δηµιουργηθεί µια ακολουθία από πρωταρχικές ενέργειες, η εκτέλεση των οποίων οδηγεί σε κατάσταση µε όλους τους στόχους. [2] Ο σχεδιασµός ενεργειών στην ουσία καταλήγει σε πρόβληµα αναζήτησης στον ΧΑ, όπου εκτελείται κατάλληλος αλγόριθµος αναζήτησης ο οποίος ευρίσκει τις επόµενες καταστάσεις. Σε πολλά προβλήµατα η επέκταση του χώρου αναζήτησης έχει µέγεθος επίπονο για τις ικανότητες ενός υπολογιστικού συστήµατος (ή τουλάχιστον ξεπερνάει τα λογικά όρια). Παραδείγµατα είναι το σκάκι, τα προβλήµατα µετακίνησης µπλοκ: - στο σκάκι στην αρχή είναι δυνατές 10 κινήσεις (10 διαφορετικές καταστάσεις). Όταν ο πρώτος παίκτης επιλέξει την κίνησή του ο αντίπαλός του µπορεί και αυτός να επιλέξει µία από 10 κινήσεις συνολικά 10*10 = 100 καταστάσεις στην πρώτη κίνηση. Σε επόµενες κινήσεις οι δυνατές καταστάσεις µπορεί να φτάσουν µέχρι τα 256 = 16*16. Αν θεωρήσουµε ότι ο µέσος όρος των δυνατών καταστάσεων ανά στάδιο είναι 100 και η µνήµη η οποία χρειάζεται για την αποθήκευση µιας κατάστασης είναι 1 ΚΒ, η RAM ενός κανονικού σηµερινού υπολογιστή θα εξαντλούνταν µε την αποθήκευση των καταστάσεων µέχρι το τέταρτο γύρο. Αυτό το παράδειγµα δείχνει πως δεν υπάρχει δυνατότητα ο χώρος αναζήτησης να δηµιουργείται ολόκληρος και η αναζήτηση να πραγµατοποιείται πάνω σε αυτόν. Οπότε ακολουθείται άλλη συλλογιστική στην εύρεση λύσης ενός προβλήµατος σχεδιασµού από την αρχική κατάσταση (ή κάποια ενδιάµεση, η οποία στη συγκεκριµένη χρονική στιγµή θεωρείται αρχική) επιλέγεται η επόµενη η οποία θεωρείται καταλληλότερη από το σύνολο όλων των δυνατών καταστάσεων οι οποίες µπορεί να προκύψουν από την τρέχουσα. Αυτή η διαδικασία επαναλαµβάνεται µέχρι να βρεθεί µια η οποία περιέχει
37 σαν υποσύνολό της τα γεγονότα των στόχων. Με αυτόν τον τρόπο στην µνήµη διατηρείται µόνο το µέρος του ΧΑ, το οποίο χρειάζεται την δεδοµένη στιγµή. Η παρουσίαση των διαδικαστικών δικτύων στο σύστηµα Noah αλλάζει το πρόβλη- µα αναζήτησης. Σε αυτό το είδος συστηµάτων ο χώρος αναζήτησης δεν αποτελείται από ένα σύνολο καταστάσεων του κόσµου αλλά από µερικώς υλοποιηµένα πλάνα. Για κάθε µη-πρωτόγονη ενέργεια στο συγκεκριµένο δίκτυο το σύστηµα µπορεί να εφαρµόσει κάποια µέθοδο για να µετατρέπει την σύνθετη ενέργεια σε σύνολο άλλων πιο απλών ενεργειών ή/και πρωτόγονων γεγονότων.[2] Για την εύρεση της λύσης στον χώρο αναζήτησης εφαρµόζεται ένας αλγόριθµος αναζήτησης ο οποίος προσδιορίζει την ακολουθία επόµενων καταστάσεων. Οι αλγόριθµοι αυτοί διαφέρουν µεταξύ τους µε τον τρόπο προσδιορισµού της επόµενης κατάστασης και µπορούν να καταταχθούν σε δύο βασικές οµάδες: Ι. Αλγόριθµοι τυφλής αναζήτησης, ΙΙ. Ευριστικοί (heuristic) αλγόριθµοι αναζήτησης. Αυτοί της πρώτης οµάδας είναι απλοί αλλά εφαρµόσιµοι µόνο σε µικρά προβλήµατα. Όπως λέει και το όνοµά τους η αναζήτηση την οποία εκτελούν γίνεται «στα τυφλά» - χωρίς να αξιολογούν τις καταστάσεις. Αρχίζει από την αρχική κατάσταση και εφαρ- µόζοντας όλες τις δυνατές ενέργειες επιλέγει µια από τις παραγµένες καταστάσεις και την θέτει ως τρέχουσα. Αυτή η διαδικασία επαναλαµβάνεται µέχρι να βρεθεί µια κατάσταση η οποία ικανοποιεί τους στόχους, και είναι η βάση των αλγορίθµων τυφλής αναζήτησης. Τα συστήµατα σχεδιασµού τα οποία χρησιµοποιούν τέτοιους αλγορίθµους βασίζουν την εύρεση λύσης στη οπισθοδρόµηση (backtracking) όταν ο αλγόριθµος δεν µπορεί να προχωρήσει επιστρέφει σε προηγούµενο σηµείο και επαναλαµβάνει την αναζήτηση επιλέγοντας άλλη ενέργεια (και άρα άλλη κατάσταση). ύο είναι οι βασικοί αλγόριθµοι αυτής της κατηγορίας Α) ο αλγόριθµος αναζήτησης πρώτα σε βάθος (DFS Depth First Search) και Β) ο αλγόριθµος αναζήτησης πρώτα σε πλάτος (BFS Breadth First Search) Και οι δύο αλγόριθµοι αναζητούν την επόµενη κατάσταση από το πλήθος όλων των δυνατών καταστάσεων χωρίς να «νοιάζονται» για το αν αυτή πλησιάζει στην επίτευξη των στόχων ή όχι. Κάθε κατάσταση την οποία εξετάζουν καταγράφεται σε µια λίστα το κλειστό σύνολο (Closed set) και οι δυνατές καταστάσεις καταγράφονται στο µέτωπο αναζήτησης (Frontier set). Η διαφορά τους συνίσταται στο πότε επιλέγεται µία συγκεκριµένη κατάσταση. Στον DFS η επόµενη κατάσταση είναι πάντα αυτή η οποία παράγεται από την πρώτη δυνατή ενέργεια. Με αυτόν τον τρόπο ο αλγόριθµος εξετάζει πά
38 ντα τις καινούριες καταστάσεις προχωρεί στο βάθος. Οπισθοδρόµηση εκτελείται όταν στην τρέχουσα κατάσταση δεν µπορεί να εφαρµοστεί καµία ενέργεια χωρίς να επιστραφεί σε κατάσταση η οποία έχει εξεταστεί προηγουµένως. Σε αυτήν την περίπτωση ο αλγόριθµος επιλέγει την πρώτη κατάσταση από το κλειστό σύνολο και εφαρµόζει την αναζήτηση. Ολόκληρη η διαδικασία αυτή επαναλαµβάνεται µέχρι να βρεθεί κατάσταση η οποία ικανοποιεί τους στόχους. Το πλεονέκτηµά του είναι ότι αν υπάρχει ικανοποιητική (για τους στόχους) κατάσταση η οποία παράγεται, εφαρµόζοντας µια σειρά από ενέργειες οι οποίες είναι από τις πρώτες που µπορούν να εφαρµοστούν στην γονική κατάσταση (δεν χρειάζεται οπισθοδρόµηση) αυτός ο αλγόριθµος θα την βρει πολύ γρήγορα. Από την άλλη πλευρά όµως δεν βρίσκει την καλύτερη λύση. Στην ουσία αυτά τα χαρακτηριστικά του ανταλλάσσονται στον BFS ο οποίος επιλέγει για επόµενη κατάσταση αυτή την οποία δεν έχει εξετάσει. Ελέγχει όλες τις καταστάσεις οι οποίες έχουν παραχθεί από την προηγούµενη και αν δεν βρεθεί καµία που να ικανοποιεί τους στόχους περνάει στο επόµενο στάδιο, όπου για κάθε κατάσταση γονέα βρίσκονται οι δυνατές καταστάσεις παιδιών. Όταν εφαρµοστεί µια ενέργεια η παραγό- µενη κατάσταση καταγράφεται στο τέλος του µετώπου αναζήτησης σε αντίθεση µε τον DFS. Πλεονέκτηµα αυτού του αλγορίθµου είναι ότι πάντα βρίσκει την βέλτιστη λύση, όµως είναι αργός σε περίπτωση όταν η τελική κατάσταση δεν βρίσκεται κοντά στην αρχική ή το πλήθος των καταστάσεων παιδιά είναι πολύ µεγάλο. Πίνακας 3.2: Οι χώροι αναζήτησης και οι καταστάσεις οι οποίες έχουν εξετασθεί σε ένα θεωρητικό πρόβληµα, µε βάση τους αλγορίθµους DFS και BFS. DFS BFS Α) Τελική κατάσταση η Β2 Β) Τελική κατάσταση η C1-34 -
39 Tο παραπάνω παράδειγµα (το οποίο φαίνεται στον πίνακα 3.2) δείχνει δύο περιπτώσεις ενός προβλήµατος: περίπτωση Α µε τελική κατάσταση Β2 και περίπτωση Β µε τελική κατάσταση C1. Στην Α) ο αλγόριθµος DFS εξετάζει 5 καταστάσεις και η έκτη είναι η τελική, και ο BFS εξετάζει µόνο 2 καταστάσεις και στο τρίτο βήµα φθάνει στην Β2. Στην περίπτωση Β) ο DFS εξετάζει µόνο 2 καταστάσεις και η τελική είναι η τρίτη, και ο BFS εξετάζει τέσσερεις και η πέµπτη είναι η τελική. Αν χρησιµοποιούνταν ο DFS για την αναζήτηση πλάνου στο παραπάνω domain και υπήρχαν δύο τελικές καταστάσεις Β2 και C1, ο αλγόριθµος θα εύρισκε πρώτα την C1 η οποία είναι χειρότερη λύση σε σύγκριση µε την Β2, υπό την υπόθεση ότι µια λύση είναι καλύτερη όταν ο α- ριθµός των ενεργειών του πλάνου είναι µικρότερος, κάτι το οποίο δεν είναι πάντα σωστό να θεωρείται. Όπως φαίνεται και οι δύο αυτοί αλγόριθµοι εξετάζουν όλες τις δυνατές καταστάσεις µέχρι να βρουν αυτήν η οποία ικανοποιεί τους στόχους. Γεγονός το οποίο καθιστά αυτούς τους αλγορίθµους µη εφαρµόσιµους σε µεγάλα προβλήµατα προβλήµατα µε µεγάλους χώρους αναζήτησης. Για να είναι δυνατόν να λύνονται οτιδήποτε µεγέθους προβλήµατα χρειάζονται αλγόριθµοι οι οποίοι να βρίσκουν από την αρχή µια σωστή κατεύθυνση η οποία γρήγορα και χωρίς περιττές αναζητήσεις να οδηγεί στην τελική κατάσταση. Αυτοί είναι οι ευριστικοί αλγόριθµοι (heuristic algorithms) και για µεγάλα προβλήµατα έχουν πολύ καλύτερες αποδόσεις σε σύγκριση µε τους τυφλούς. Η βασική ιδέα στην οποία στηρίζονται είναι η αξιολόγηση των υποψήφιων καταστάσεων και η επιλογή της «καλύτερης». Η εκτίµηση δίνεται ως αποτέλεσµα µιας συνάρτησης ευριστική συνάρτηση (heuristic function), η οποία υπολογίζει την «απόσταση» από τις υ- ποψήφιες καταστάσεις µέχρι µια υποθετική τελική κατάσταση 4. Ο όρος «απόσταση» µπορεί να έχει διάφορες έννοιες: σε προβλήµατα λαβυρίνθων η απόσταση µπορεί να θεωρηθεί ως πραγµατικά η ευκλείδεια απόσταση µεταξύ της τρέχουσας θέσης και της εξόδου (βλ. εικόνα 3.2), σε άλλα προβλήµατα ο όρος έχει αφηρηµένη έννοια. 4 Σ.σ. - Αυτή η υποθετική τελική κατάσταση είναι μία κατάσταση η οποία έχει μόνο τους στόχους. Το σύνολο των γεγονότων της πρέπει να είναι υποσύνολο αυτού της πραγματικής τελικής κατάστασης
40 Υποψήφιες καταστάσεις Ενδείξεις για τον αριθµό των θέσεων µέχρι την έξοδο. Εικόνα 3.2: Λαβύρινθος µε δύο υποψήφιες θέσεις και η απόσταση τους µέχρι την έξοδο. Στην παραπάνω εικόνα φαίνεται ένας λαβύρινθος µε δύο υποψήφιες θέσεις για να προχωρήσει το ανθρωπάκι. Η ευκλείδεια απόστασή τους είναι: για την θέση µε τον κύκλο µε την πλήρη γραµµή και για την θέση µε τον κύκλο µε την διακεκοµµένη γραµµή. Ο πιο απλός αλγόριθµος ευριστικής αναζήτησης είναι ο Αλγόριθµος Αναρρίχησης Λόφων (Hill Climbing Algorithm), ο οποίος προσπαθεί να ελαχιστοποιήσει (ή µεγιστοποιήσει) την ευριστική συνάρτηση f(x). Από το πλήθος των δυνατών καταστάσεων, οι οποίες µπορεί να παραχθούν από την τρέχουσα, ο αναφερόµενος αλγόριθµος επιλέγει αυτήν µε την µικρότερη (ή την µεγαλύτερη) τιµή της ευριστικής της συνάρτησης, µε τάση πάντα προς την καλύτερη επιλογή. Αρχίζει από µια τυχαία επιλεγµένη κατάσταση (στις περισσότερες περιπτώσεις αυτή είναι η αρχική), και προσπαθώντας να την βελτιστοποιήσει έχοντας υπ όψην τους στόχους επιλέγει την επόµενη ενέργεια. Σε ένα ση- µείο όµως υπάρχει περίπτωση να µην βρίσκει κατάσταση µε καλύτερη εκτίµηση, και τότε ο αλγόριθµος τερµατίζεται 5. Αυτό το σηµείο καλείται τοπικό ελάχιστο (ή µέγιστο) και ο αλγόριθµος δεν είναι ικανός να το ξεπεράσει (τουλάχιστον όχι σε αυτή του τη µορφή, βλ. Εικόνα 3.3). Έχουν δηµιουργηθεί διάφορες παραλλαγές του αλγορίθµου αναρρίχησης λόφων οι οποίες ξεπερνούν το πρόβληµα του τοπικού ελαχίστου, έχουν αποδειχτεί επιτυχές και εφαρµόζονται στα συστήµατα σχεδιασµού, λύνοντας ογκώδη προβλήµατα σε πολύ καλούς χρόνους. 5 Σε κάποιες υλοποιήσεις του Hill Climbing σε αυτήν την περίπτωση ο αλγόριθμος αποτυγχάνει χωρίς να αναφέρει καμία λύση, σε άλλες όμως το σημείο αυτό μπορεί να θεωρηθεί σαν μια μερική (όχι βέλτιστη) λύση και να αναφερθεί ως αποτέλεσμα
41 Κατευθήνσεις (µη διακεκοµµένη γραµµή) του Hill Climbing, διακεκοµµένη προς την πραγµατική λύση - αρχική κατάσταση - τελική κατάσταση του Hill Climbing (τοπικό ελάχιστο) - πραγµατική τελική κατάσταση Εικόνα 3.3: Ο αλγόριθµος Hill Climbing πέφτει σε τοπικό ελάχιστο ξεκινόντας από την αρχική (µπλε σηµείο) κατάσταση, και δεν µπορεί να φθάσει στην πραγµατική λύση. Το αντικείµενο της τρέχουσας έρευνας είναι ένα σύστηµα σχεδιασµού ενεργειών, υλοποιηµένο σε JAVA, το οποίο συνδυάζει την γλώσσα PDDL Problem Domain Definition Language µε ένα πλήθος αλγορίθµων αναζήτησης. Προσφέρει στον χρήστη ένα γραφικό περιβάλλον παραθύρων µέσα του οποίου η διαχείριση των αρχείων και η παρακολούθηση της εκτέλεσης γίνεται µε βολικό τρόπο. Υποθετικά µπορεί να διαιρεθεί σε τρία µέρη το parser, το γραφικό περιβάλλον και οι αλγόριθµοι αναζήτησης. Η είσοδος στο σύστηµα συνίσταται από δύο αρχεία.pddl του πεδίου ορισµού (το domain.pddl) και του συγκεκριµένου προβλήµατος (το problem.pddl). Αυτά τα αρχεία επεξεργάζονται από το πάρσερ, ο οποίος τα διαβάζει και παράγει ενδιάµεσα αποτελέσµατα απαραίτητα στους αλγορίθµους για να προσδιοριστεί η ακολουθία ενεργειών το πλάνο. Τα παραγόµενα από το parser δεδοµένα είναι ένα σύνολο γεγονότων στο οποίο κάθε γεγονός εκπροσωπείται από ένα µοναδικό κωδικό, ένα σύνολο ενεργειών, όπου οι ενέργειες είναι τύπου STRING της µορφής <Π, Λδ, Λπ>, κάθε λίστα περιέχει τους κωδικούς των απαραίτητων γεγονότων, επιπρόσθετα περιέχεται και το όνοµα της ενέργειας. µία αρχική και µία τελική κατάσταση τα γεγονότα των οποίων ξανά εµφανίζονται µε τους κωδικούς τους. Στο πρόβληµα µπορεί να περιέχεται ένα σύνολο στόχων διάφορα γεγονότα συνδεδεµένα µεταξύ τους µε λογικούς τελεστές (AND, OR, NOT), αυτή η πληροφορία επεξεργάζεται από το πάρσερ ο οποίος στην συνέχεια παράγει µία ενιαία κατάσταση στόχων. Αφού το parser έχει δηµιουργήσει σε κατάλληλη µορφή την αρχική και την τελική καταστάσεις, και τα απαραίτητα γεγονότα και ενέργειες, το σύστηµα είναι σε θέση να µεταφέρει την επεξεργασία στο επόµενό του µέρος των αλγορίθµων αναζήτησης. Το παρών σύστηµα περιλαµβάνει αλγορίθµους και από την οµάδα των τυφλών και των ευριστικών. Το πλήθος αλγορίθµων προσφέρει τη δυνατότητα εκτέλεσης του ιδίου
42 προβλήµατος µε διάφορους τρόπους για να µπορεί ο χρήστης να την παρακολουθεί και να εξάγει συµπεράσµατα ό,τι αφορά στην ταχύτητα, την αξιοπιστία, την ικανότητα εύρεσης βέλτιστης λύσης κ.α. Στους αλγορίθµους περιλαµβάνονται τρεις τυφλούς και δύο ευρεστικούς. Οι τυφλοί είναι ο DFS, o BFS, o Iterative Deepening, και οι ευριστικοί είναι ο FF και ο Identidem. Για τους DFS και BFS έγινε λόγο ανωτέρως και δεν θα εξεταστούν στην συνέχεια. Ο Iterative Deepening είναι ένας συνδυασµός µεταξύ του DFS και του BFS, ο οποίος είναι στην ουσία ο DFS µε περιορισµό στο βάθος αριθµός καταστάσεων τις οποίες µπορεί να εξετάσει χωρίς να κάνει οπισθοδρόµηση. Ο DFS εξετάζει τους κόµβους (τις καταστάσεις) ένα προς ένα επιλέγοντας ως επόµενο τον κόµβο ο οποίος είναι στο επό- µενο επίπεδο, όταν φτάσει στο προκαθορισµένο οριακό βάθος η αναζήτηση συνεχίζεται στους κόµβους αδερφών. Με την τεχνική της οπισθοδρόµησης εξετάζονται όλοι οι κόµβοι σε βάθος µικρότερο από ή ίσο µε το οριακό. Αν σε έναν κύκλο δεν βρεθεί κατάσταση η οποία να ικανοποιεί τους στόχους ο αλγόριθµος αρχίζει από την αρχική κατάσταση αυξάνοντας το όριο βάθους κατά µία παράµετρος α. Ο αλγόριθµος αυτός παίρνει ως είσοδοι δύο παραµέτρους την α και την β. Η α είναι ένας πραγµατικός α- ριθµός ο οποίος προστίθεται στο συνολικό (τρέχον) όριο βάθους σε περίπτωση που δεν έχει βρεθεί µέχρι στιγµής λύση. Η β είναι ο αριθµός του αρχικού ορίου βάθους. Στο πρώτο κύκλο εκτέλεσης το όριο βάθους ισούται µε την β, στο δεύτερο µε την β+α, στο τρίτο µε την β+α+α, κ.ο.κ. Τα πλεονεκτήµατα αυτού του αλγορίθµου σχετίζονται µε την γρήγορη εύρεση λύσης αλλά µόνο αν αυτή υπάρχει στα επίπεδα κοντά στην αρχική κατάσταση. Από την άλλη πλευρά όµως αν η λύση βρίσκεται πολύ «βαθιά» η απόδοσή του µπορεί να καταλήξει και χειρότερη από τον DFS, λόγου του ότι οι ίδιες καταστάσεις εξετάζονται αρκετές φορές. Η ολική του απόδοση εξαρτάται από τους παραµέτρους εισόδου β και α. Οι δύο ευριστικοί αλγόριθµοι οι οποίοι περιλαµβάνονται στο συγκεκριµένο σύστη- µα σχεδιασµού ενεργειών είναι ο FF και ο Identidem. Ο πρώτος είναι ο αλγόριθµος του συστήµατος FF ο οποίος ξαναγράφτηκε για τις ανάγκες του παρόντος συστήµατος [12]. Είναι στην ουσία ο Αλγόριθµος Ενισχυµένης Αναρρίχησης Λόφων (Enforced Hill Climbing Algorithm). Ο Enforced Hill Climbing Algorithm είναι µία επέκταση του α- πλού αλγορίθµου Αναρρίχησης Λόφων, και ξεπερνάει το πρόβληµα του τοπικού ελαχίστου (ή µεγίστου). Όταν φθάσει σε τέτοιο σηµείο εφαρµόζεται ο BFS µέχρι να βρεθεί καλύτερη κατάσταση
43 - µία κατάσταση (1 αρχική κατάσταση, 2 τοπικό ελάχιστο, 3 κατάσταση την οποία εξετάζει ο BFS αλλά δεν έχει καλύτερη εκτίµηση, 4 κατάσταση µε καλύτερη εκτίµηση (σε σχέση µε την 2), 5 τελική κατάσταση). Εικόνα 5: Ο αλγόριθµος Enforced Hill Climbing. Στο τµήµα από την κατάσταση 1 (αρχική) µέχρι την κατάσταση 2 (τοπικό ακρότατο) εφαρµόζεται ο Hill Climbing. Όταν δεν µπορεί να βρεθεί καλύτερη κατάσταση εφαρµόζεται ο BFS στο τµήµα 2-4, η κατάσταση 3 εξετάζεται αλλά δεν έχει καλύτερη αποτίµηση και ο BFS συνεχίζει µέχρι την κατάσταση 4, από την οποία ξανά αρχίζει ο Hill Climbing. Η αξιολόγηση των καταστάσεων γίνεται µε βάση την ευριστική συνάρτηση (the heuristic function), η οποία αναθέτει έναν ακέραιο αριθµό σε κάθε µία. Η συνάρτηση αυτή υπολογίζει την απόσταση από την υποψήφια µέχρι την τελική κατάσταση. Ο υπολογισµός αυτός δεν είναι ακριβής (είναι πολύ δύσκολο να γίνει) άλλα προσεγγιστικός και γίνεται λύνοντας ένα «χαλαρό» πρόβληµα (relaxed problem), το οποίο στη συνέχεια οδηγεί στην κατασκευή ενός «χαλαρού» πλάνου (relaxed plan). Για να µπορεί να παραχθεί ένα τέτοιο πλάνο εφαρµόζοντας τις δυνατές ενέργειες αγνοώντας τις αρνητικές τους επιδράσεις η λίστα διαιρέσεων. Μία «χαλαρή» ενέργεια µπορεί να παρασταθεί από την τριάδα <Π, Λπ, Ø> - Π η λίστα προϋποθέσεων, Λπ η λίστα προσθηκών και στην θέση της λίστας διαιρέσεων είναι το κενό σύνολο. Η κατασκευή του χαλαρού πλάνου ακολουθεί τα επόµενα τρία βήµατα: Α) Ξεκίνησε από την αρχική κατάσταση Β) Επανέλαβε το: εφάρµοσε κάθε δυνατή χαλαρή ενέργεια στην κατάσταση αυτή και κατέγραψε το αποτέλεσµα στο επόµενο επίπεδο (layer). Γ) Αν έχεις φθάσει σε επίπεδο από όπου δεν µπορείς να εφαρµόσεις άλλη ενέργεια και δεν έχεις βρει κατάσταση η οποία να ικανοποιεί τους στόχους τότε το πρόβληµα δεν έχει λύση. Όταν το πλάνο είναι έτοιµο µετρούνται οι ενέργειες οι οποίες έχουν εφαρµοστεί στην δεδοµένη (υποψήφια) ενέργεια, ο αριθµός των οποίων είναι και η τιµή την οποία επιστρέφει η ευριστική συνάρτηση του FF. Αυτή η τιµή είναι µία προσέγγιση του πόσο απέχει η δεδοµένη κατάσταση από την τελική και χρησιµοποιείται για την σύγκριση µεταξύ δύο υποψήφιων καταστάσεων [13]
44 Η ίδια ευριστική συνάρτηση χρησιµοποιείται και στον επόµενο αλγόριθµο Identidem A New Local-Search Algorithm for Forward-Chainging Planning [14]. Αυτός χρησιµοποιεί την ευριστική συνάρτηση και αξιολογεί κάθε υποψήφια κατάσταση, αλλά δεν επιλέγει πάντα αυτή µε την καλύτερη τιµή η οποία απέχει λιγότερο από τους στόχους, αλλά µία από όλες τις δυνατές µε την µέθοδο της ρουλέτας. Από µία κατάσταση προσδιορίζεται µια γειτονιά καταστάσεων από την οποία επιλέγεται η επόµενη. Σε κάθε µία από αυτές ανατίθεται µία τιµή W i το µέγεθος τµήµατος της ρουλέτας το οποίο καταλαµβάνει, η οποία παράγεται από τον τύπο W i =, µε i να είναι ο δείκτης κατάσταση από την γειτονιά, και β το heuristic-bias. Από την γειτονία των δυνατών καταστάσεων αυτή µε την καλύτερη τιµή στην ευριστική συνάρτηση καταλαµβάνει µεγαλύτερο τµήµα της ρουλέτας, η επόµενη κατάσταση µικρότερο, κ.ο.κ. Η επόµενη κατάσταση επιλέγεται τυχαία από την ρουλέτα µε πιθανότητα η οποία προσδιορίζεται από τον τύπο:, όπου i = 1, 2, n, και n είναι το µέγεθος της γειτονιάς. Όταν επιλέγεται η επόµενη κατάσταση, µε πιθανότητα P i, δεν δίνεται σηµασία στην τιµή της (από την ευριστική συνάρτηση). Γεγονός το οποίο σε κάποιο βαθµό ξεπερνάει το πρόβληµα των τοπικών ακρότατων, αν και ακόµα υπάρχει η δυνατότητα ο αλγόριθ- µος να φθάσει σε σηµείο πέρα από το οποίο δεν µπορεί να προχωρήσει αδιέξοδο (dead-end). Σε τέτοια περίπτωση ο αλγόριθµος επανεκκινείται (restarts) και η πιθανότητα να ακολουθηθεί ακριβός η ίδια διαδροµή είναι πολύ µικρή διαδικασία, η οποία επαναλαµβάνεται µέχρι να βρεθεί λύση. Ο αλγόριθµος συνίσταται σε δύο τµήµατα: το τµήµα των επανεκκινήσεων και το τµήµα της επιλογής νέας κατάστασης. Το πρώτο τµήµα φαίνεται το παρακάτω πίνακα: Πίνακας 3.2. Το τµήµα του αλγορίθµου Identidem, υπεύθυνο για τις επανεκκινήσεις. In: (IntitialState, GoalState, Actions) Out: ένα πλάνο που είναι λύση του προβλήµατος. 1. State S = IitialState; 2. while (S δεν ικανοποιεί την GoalState) 3. S = Algorithm3(S); 4. if (Algorithm3 επιτυχής) then 5. S=S ; 6. else 7. S=I; 8. end 9. end while; return το πλάνο µέχρι την S
45 Το δεύτερο τµήµα είναι ο Algorithm3(), ο οποίος παίρνει έξι παραµέτρους µία κατάσταση (S) από την οποία ψάχνει καλύτερη, αριθµό επαναλήψεων (iterations), αριθµό δοκιµών (probes_at_depth) ανά δοκιµή, ένα όριο βάθους (depth_bound), αριθµό αποτυχηµένων προσπαθειών (failcount) και µέγιστο αριθµό αποτυχηµένων προσπαθειών (failbound), παράγει µία αυστιρά καλύτερη κατάσταση. Η έννοια των δοκιµών σχετίζεται µε το πόσες φορές θα προσπαθήσει ο αλγόριθµος να βρει καλύτερη κατάσταση, η µεταβλητή του ορίου βάθους (depth) δείχνει µέχρι τι βάθος να αναζητείται καλύτερη κατάσταση. Σε κάθε ανεπιτυχής επανάληψη (όταν δεν βρίσκεται καλύτερη κατάσταση) αυξάνεται ο µετρητής αποτυχηµένων προσπαθειών (failcount) και αν αυτός φτάσει στο όριο (failbound) ο Algorithm3 επιστρέφει αποτυχία. Πρέπει να δοθεί ιδιαίτερη προσοχή στις δύο έννοιες της επανεκκίνησης και της ε- πανάληψης. Οι επαναλήψεις έχουν ένα συγκεκριµένο αριθµό, ο οποίος µπορεί να περιορισθεί ιδιαίτερα είτε από το failbound, είτε από το depth, είτε από τον αριθµό των δοκιµών (probes). Όταν το τµήµα επιλογής επόµενης κατάστασης (Algorithm3) αποτύχει, τότε εκτελείται µία επανεκκίνηση σειρά µε αριθµό 7 στον πίνακα 3.2. Στον Πίνακα 3.3 φαίνεται ο τρόπος υλοποίησης του Algorithm3 στο σύστηµα. Πίνακας 3.3. Ο Algorithm3 το τµήµα του αλγορίθµου Identidem, υπέυθηνο για την εύρεση καινούργιας κατάστασης µε αυστηρώς καλύτερη ευριστική τιµή. In: S1, iterations, failcount, failbound, depth_bound, probes_at_depth Out: newstate κατάσταση µε αυστηρώς καλύτερη ευριστική τιµή 1. depth_bound = initial_depth_bound; 2. State tempstate, newstate; 3. for i = 0 to iterations do 4. for probes = 0 to probes_at_depth do 5. newstate = S1; 6. for depth = 0 to depth_bound do 7. tempstate = getneighbour(1.5, newstate) 6 ; 8. newstate = tempstate; 9. if heuristic(newstate)< heuristic(s1) then return newstate; 10. end for; 11. failcount++; 12. if (failcount = failbound) then return S1 7 ; 13. end for; 14. depth_bound += depth_bound; 15. end for; 16. return S1; 6 Σ.σ. - Η συνάρτηση getneighbour(β, S) βρίσκει γείτονα της τρέχουσας κατάστασης με βάση αυτήν και την παράμετρο β the heuristic bias
46 Το τρίτο µέρος του συστήµατος το οποίο παρουσιάζεται στο παρόν έγγραφο είναι το γραφικό του περιβάλλον. Συνίσταται από ένα κεντρικό παράθυρο µέσω του οποίου γίνεται η εισαγωγή των αρχείων pddl και η επιλογή διάφορων ρυθµίσεων, και δύο βοηθητικά στο ένα εκτυπώνονται τα αποτελέσµατα σε µορφή βολική προς τον χρήστη, και το δεύτερο περιέχει στατιστικά δεδοµένα και προδιαγραφές σε ότι αφορά στην µεταγλώττιση των δύο αρχείων εισόδου. Για λόγους ευελιξίας υπάρχει µενού µε ξεχωριστό τµήµα µε οδηγίες για την χρήση του συστήµατος. Το σύστηµα σχεδιασµού ενεργειών είναι σε θέσει να λύνει διάφορα από άποψη ό- γκου (το χώρου αναζήτησης) και πολυπλοκότητας προβλήµατα και επιπρόσθετα µπορεί να δώσει την επιλογή διαφορετικών λύσεων ικανοποιώντας διαφορετικές απαιτήσεις. Είναι εφαρµόσιµο σε πολλούς τοµείς της οικονοµικής, της πληροφορικής κ.α. 7 Σ.σ. - Όταν επιστρέφεται ίδια κατάσταση με αυτήν που έχει δοθεί στην είσοδο σημαίνει αποτυχία δεν μπορεί να βρεί καλύτερη κατάσταση
47 4 Η Γλώσσα JAVA. Η γλώσσα JAVA είναι µία από τις αποδοτικότερες γλώσσες προγραµµατισµού της εποχής µας. Οι λόγοι είναι διαφορετικοί και σχετίζονται µε: a. την µεταφερσιµότητα b. την αντικειµενοστρέφεια c. το εύκολο interface/διασύνδεση µε τον προγραµµατιστή d. τα κοινά στοιχεία µε την γλώσσα C/C++, γνωστή από παλαιά. e. είναι δωρεάν λογισµικό 4.1 Ιστορικά Η JAVA είναι µία γλώσσα προγραµµατισµού, η οποία εκδόθηκε από την εταιρία SUN Microsystems το Η συντακτική της προέρχεται από τις γλώσσες C και C++, και έχει απλότερο µοντέλο αντικειµένων. Τα προγράµµατα της JAVA µεταφράζονται σε µία ενδιάµεση µορφή (bytecode) η οποία είναι εκτελέσιµη από κάθε εικονική µηχανή JAVA (JVM JAVA Virtual Machine). Η JAVA είχε σχεδιαστεί από τον James Gosling τον Ιούνιο 1991 µε σκοπό να χρησιµοποιηθεί σε ένα από τα set-top box 8 projects του. Η αρχική ονοµασία ήταν Oak βαλανιδιά, αλλά στη συνέχεια το όνοµα άλλαξε σε JAVA, το οποίο επιλέχθηκε από µία λίστα αυθαίρετων λέξεων. Οι στόχοι του Gosling ήταν να δηµιουργήσει µία εικονική µηχανή και µία γλώσσα η οποία να λειτουργεί πάνω σε αυτήν και να µοιάζει µε την C και C++. Αυτή η αρχική έκδοση (η οποία από την SUN Microsystems βγήκε το 1995) ήταν η JAVA 1.0. Στη συνέχεια άρχιζαν να βγαίνουν διάφορες εκδώσεις οι οποίες προοριζότανε προς διάφορες πλατφόρµες και χρήστες. π.χ. J2ME έκδοση για κινητά τηλέφωνα, J2SΕ είναι η τυποποιηµένη (standard) έκδωση. 8 Σ.σ. - Set-top box είναι μία συσκευή, η οποία συνδέει μία τηλεόραση και μία εξωτερική πηγή μετατρέποντας το σήμα σε πληροφορία η οποία στη συνέχεια εκτυπώνεται στην οθόνη
48 Οι κύριοι στόχοι της είναι οι εξής: 1. Να χρησιµοποιεί αντικειµενοστραφής µεθοδολογία 2. Να επιτρέπει το ίδιο πρόγραµµα να εκτελείται σε διαφορετικά λειτουργικά συστήµατα. 3. Να διαθέτει ενσωµατωµένη (built-in) υποστήριξη για χρήση υπολογιστικών δικτύων. 4. Να µπορεί ασφαλώς να εκτελεί προγράµµατα, ο πηγαίος κώδικας των οποίων βρίσκεται σε αποµακρυσµένων υπολογιστών. 5. Να παρέχει ευκολία στην χρήση κάτι το οποίο πετυχαίνεται συµπεριλαµβάνοντας τα πλεονεκτήµατα άλλων αντικειµενοστραφών γλωσσών προγραµµατισµού. Η JAVA είναι ένα δωρεάν λογισµικό, κάτι το οποίο επιτρέπει τους χρήστες του να µην συµµορφώνονται µε οικονοµικές σχέσεις και περιορισµούς χρόνου (trial verstions) και δυνατοτήτων(demo verstions) στην χρήση της γλώσσας. Στις 13 Νοεµβρίου 2006 η SUN εκδόθηκε την JAVA ως δωρεάν λογισµικό υπό τους όρους χρήσης του GNU General Public License (GPL) 9, και κατά το Μάιο 2007 η εταιρία τελείωσε µε την διαδικασία γραφής του πυρήνα της JAVA σε ανοιχτό κώδικα (εκτός από ένα µικρό κοµµάτι, στο οποίο δεν έχει δικαιώµατα η SUN Microsystems). 4.2 Χαρακτηριστικά Η ανεξαρτησία από την πλατφόρµα γραφής και εκτέλεσης του πηγαίου κώδικα. Η JAVA είναι πολύ ισχυρή γλώσσα προγραµµατισµού επιτρέποντας την σχεδόν πλήρης διαχείριση των υπολογιστικών συστηµάτων. Ο κυριότερος λόγος είναι η ανεξαρτησία από την πλατφόρµα (platform independency) στην οποία γράφεται και εκτελείται ένα πρόγραµµα. Η ανεξαρτησία πλατφόρµας, σε γενικές γραµµές, σηµαίνει ότι προγράµµατα γραµµένα σε JAVA εκτελούνται µε παρόµοιο τρόπο σε κάθε υποστηριζόµενο υπολογιστικό σύστηµα (λογισµικό και υλικό). Ένα πρόγραµµα γράφεται σε ότι πλατφόρµα επιθυµεί ο χρήστης, µεταγλωττίζεται µία φορά και στη συνέχεια µπορεί να 9 Σ.σ - Η GNU General Public License είναι μία ευρέως διαδεδομένη άδεια για την χρήση λογισμικού ανοιχτού κώδικα, γραμμένη αρχικά από τον Richard Stallman
49 εκτελεστεί σε άλλο σύστηµα, είτε Windows, είτε Linux, είτε κινητό τηλέφωνο αρκεί αυτό να διαθέτει την απαραίτητη JAVA εικονική µηχανή JVM. Για την επίτευξη της ανεξαρτησίας εφαρµόζεται µία τεχνική η οποία µεταγλωττίζει το πηγαίο κώδικα µόνο µέχρι ένα σηµείο µετατρέποντάς το σε µία ενδιάµεση µορφή απλοποιηµένων ειδικών εντολών για την JAVA πλατφόρµα JAVA bytecode. Αυτός ο κώδικας στη συνέχεια διαβάζεται και εκτελείται από την JAVA εικονική µηχανή (JVM), η οποία είναι ένα πρόγραµµα, γραµµένο ειδικά για το συγκεκριµένο υπολογιστικό σύστηµα και µεταφράζει τα bytecode σε γλώσσα µηχανής υποστηριζόµενη από αυτό το υπολογιστικό σύστηµα. Υπάρχουν κάποιες εκδώσεις JVMs οι οποίες επιτρέπουν την µεταγλώττιση είτε πριν, είτε κατά την εκτέλεση του προγράµµατος, γεγονός ο οποίος αυξάνει την ταχύτητα εκτέλεσης ενός προγράµµατος. Στην αρχική έκδοση χρησιµοποιήθηκε µία διερµηνευτική εικονική µηχανή (interpreted virtual machine) η οποία είχε χαµηλή απόδοση (από άποψη χρόνου εκτέλεσης) σε σχέση µε προγράµµατα γραµµένα σε άλλες γλώσσες. Τώρα πια η ταχύτητα είναι πολύ υψηλότερη και ξεπερνάει αυτή άλλων γλωσσών προγραµµατισµού. ύο τεχνικές οι οποίες χρησιµοποιούνται για την επίτευξη υψηλότερων ταχυτήτων είναι η just-in-time compilation και η dynamic recompilation (δυναµική ξαναµεταγλώττηση). Στην πρώτη περίπτωση ο κώδικας µεταγλωττίζεται την ώρα της εκτέλεσης του προγράµµατος. Προσφέρει µεγαλύτερη ταχύτητα, αλλά προκαλεί overhead στην µεταγλώττιση. Κατά την δυναµική ξαναµεταγλώττηση η JVM αναλύει την συµπεριφορά του εκτελούµενου προγράµµατος και επιλέγει κρίσιµα σηµεία κώδικα για ξαναµεταγλώττηση ή για βελτιστοποίηση. Επιλεκτικά βελτιστοποιεί τέτοια κοµµάτια κώδικα τα οποία σπαταλάνε πολύ χρόνο, όπως για παράδειγµα εσωτερικούς βρόχους. Μια άλλη τεχνική η οποία χρησιµοποιεί αντίθετη λογική από τις παραπάνω είναι η στατική µεταγλώττιση (Static Compilation) η οποία µπορεί να παρακάµψει το στάδιο παραγωγής bytecode και κατευθείαν να παράγει κώδικα µηχανής του συγκεκριµένου υπολογιστικού συστήµατος. Με αυτήν την τεχνική πετυχαίνονται υψηλές ταχύτητες, αλλά χάνεται εντελώς η ανεξαρτησία πλατφόρµας
50 4.2.2 ιαχείριση Μνήµης Ένα από τα χαρακτηριστικά της γλώσσας JAVA είναι η αυτοµατική διαχείριση µνήµης. Σε κάποιες γλώσσες, όπως η C++, ο χρήστης (ο προγραµµατιστής) δεσµεύει ή αποδεσµεύει µνήµη για κάθε ένα αντικείµενο που δηµιουργεί. Μνήµη δεσµεύεται κάθε φορά που δηµιουργείται ένα αντικείµενο π.χ. Car opel = new Car();. Όµως για την α- ποδέσµευση της χρησιµοποιούµενης µνήµης υπεύθυνος είναι ο προγραµµατιστής ο ο- ποίος πρέπει να διαγράψει το αντίστοιχο αντικείµενο. Σε περίπτωση που αυτός ξεχάσει να το διαγράψει µπορεί να προκύψει «διαρροή µνήµης» - ανικανότητα δέσµευσης άλλης µνήµης, λόγου µην ύπαρξης. Αυτό συµβαίνει όταν δεν διαγράφονται αντικείµενα και η µνήµη δεν απελευθερώνεται. Άλλο φαινόµενο προκύπτει όταν ο προγραµµατιστής προσπαθεί να αποδεσµεύσει περιοχή της µνήµης που είναι ήδη ελεύθερη. Το αποτέλεσµα από αυτό το φαινόµενο είναι απροσδιόριστο και το πρόγραµµα µπορεί να γίνει ασταθές και να καταρρεύσει. Η JAVA διαθέτει ένα ειδικό µέρος το οποίο λέγεται garbage collector. Αυτό είναι υπεύθυνο για την διαχείριση της µνήµης η οποία δεσµεύεται από αχρησιµοποίητα αντικείµενα («σκουπίδια» - garbage ), και αποφεύγει σε ένα βαθµό περιπτώσεις όπως αυτές που αναφέρθηκαν παραπάνω. Για την δέσµευση της µνήµης είναι υπεύθυνος ο προγραµµατιστής κατά την δηµιουργία του αντικειµένου, αλλά η διαχείριση του κύκλου ζωής ενός αντικειµένου είναι ευθύνη της JAVA. Ένα πρόγραµµα ή ένα αντικείµενο α- ναφέρονται σε άλλο αντικείµενο µέσω της διεύθυνσής του στο σωρό µνήµης αντικειµένων. Όταν όµως δεν υπάρχει αναφορά σε αντικείµενο που υπάρχει στο σωρό, τότε το garbage collector είναι σε θέση να απελευθερώσει την αντίστοιχη περιοχή µνήµης. Λόγο λάθους του προγραµµατιστή πάλι µπορεί να συµβεί «διαρροή µνήµης», αν στο πρόγραµµα υπάρχει αναφορά σε αντικείµενο το οποίο δεν χρησιµοποιείται καθόλου πια. Επειδή το garbage collector είναι ενσωµατωµένο στη JAVA και είναι αόρατο για τον προγραµµατιστή αυτός δεν µπορεί να ελέγχει πότε και ποια αντικείµενα διαγράφονται. Κάτι το οποίο σε διάφορες περιπτώσεις µπορεί να φανεί χρήσιµο και σε άλλες όχι, µπορεί ακόµα και να θεωρηθεί µειονέκτηµα για την υλοποίηση κάποιου προγράµ- µατος. Η JAVA δεν υποστηρίζει δείκτες (pointers) όπως η C++, επειδή µπορεί ένας δείκτης να αναφέρεται σε περιοχή µνήµης η οποία να έχει ήδη απελευθερωθεί από το garbage collector και να υπάρχει άλλο αντικείµενο που να αντιστοιχεί στον δείκτη αυτόν. Από την άλλη, επειδή ένας προγραµµατιστής µπορεί να αναφερθεί σε µία απαγο
51 ρευµένη περιοχή µνήµης, αν η JAVA επέτρεπε την χρήση δεικτών δεν θα µπορούσε να εγγυάται την πλήρης ασφάλεια. 4.3 Το συντακτικό της JAVA Το συντακτικό της JAVA προέρχεται κυρίως από την C++, µε την διαφορά ότι η C++ συνδυάζει συντακτικό δοµηµένου, γενικού και αντικειµενοστραφούς προγραµµατισµού ενώ η JAVA έχει χτιστεί απόλυτα ως µία αντικειµενοστραφής γλώσσα. Το αποτέλεσµα αυτής της δοµής είναι το κάθε τι της JAVA να είναι ένα αντικείµενο και κάθε κώδικας εµπεριέχεται σε µία κλάση. Εξαίρεση αποτλεούν οι τύποι δεδοµένων integer (int), double, float, boolean αν και υπάρχουν κλάσεις που διαχειρίζουν πράξεις συγκεκριµένων τύπων η κλάση Integer, η κλάση String κ.α. Στο σχήµα 4.1. φαίνεται ένα παράδειγµα κώδικα µιας κλάσης της γλώσσας JAVA. // Hello.java public class Hello public static void main(string[] args) System.out.println("Hello, world!"); Σχήµα 4.1. Mία κλάση της γλώσσας JAVA η οποία εκτυπώνει ένα µήνυµα Η εκτέλεση ενός τέτοιου προγράµµατος (όσο και απλό να είναι) περιλαµβάνει την δηµιουργία ενός αρχείου κλάσης µε όνοµα class_name.java (όπου το class_name δηλώνει το όνοµα της κλάσης) το οποίο στη συνέχεια µεταγλωττίζεται σε bytecode και παράγεται ένα αρχείο class_name.class. Αυτό είναι και το κοµµάτι το οποίο εκτελείται στη συνέχεια. Έχοντας υπόψη το πρόγραµµα του σχήµατος 4.1. φαίνεται ότι κάθε εκτελέσιµη εντολή βρίσκεται µέσα στην κλάση, κάθε αρχείο κλάσης έχει την ίδια ονοµασία µε την ίδια την κλάση class_name = hallo, ο µεταγλωττιστής δηµιουργεί για κάθε κλάση ένα αρχείο µε το ίδιο όνοµα και το τελικό.class,
52 η λέξη κλειδί public δηλώνει ότι αυτή η µέθοδος µπορεί να καλείται και από εξωτερικές δοµές κλάσεις και µεθόδους, η λέξη static δηλώνει µία στατική µέθοδο η λέξη void υποδηλώνει µία µέθοδος η οποία δεν επιστρέφει τιµή, το όνοµα µεθόδου main δεν είναι µία λέξη κλειδί και σε κάποια περιβάλλοντα JAVA applets και Enterprise Java Beans δεν είναι απαραίτητη για να εκτελεστεί το πρόγραµµα Η κύρια µέθοδος (main() ) παίρνει ως είσοδο µία σειρά αντικειµένων της κλάσης String() 10. Προκαθορισµένα, το όνοµα του πίνακα εισόδου στην main() είναι arg, άλλα δεν απαγορεύεται η είσοδος πίνακα µε άλλο όνοµα. Μετά την έκδοση 5 της γλώσσας επιτρέπεται και η είσοδος συµβολοσειρά µε µη προκαθορισµένο αριθµό ορισµάτων, προσφέροντας δυναµικότητα στην είσοδο της main().σε πολλές περιπτώσεις η είσοδος αυτών των ορισµάτων γίνεται από την γραµµή εντολών (Command line). Όταν εκκινεί ένα πρόγραµµα η µηχανή του µεταγλωττιστή βρίσκει την main() µέθοδο και αρχίζει την εκτέλεση του προγράµµατος από αυτό το σηµείο. Σε αυτόνοµα (Stand-alone) προγράµ- µατα η κύρια µέθοδος πρέπει να προκαθοριστεί εξ αρχήν από τον προγραµµατιστή. Η εκτύπωση ενός µηνύµατος γίνεται µε την χρήση της System.out. println («µήνυ- µα»); όπου η out είναι µία στατική µέθοδος της κλάσης System. (Για την σύντοµη γραφή της εντολής System.out.println(); µπορεί να πληκτρολογείται η εντολή «sout» και στην συνέχεια να πατηθεί το space). Υπάρχει µία λέξη κλειδί η οποία αντιστοιχεί στην #include της C++. Είναι η import και επιτρέπει την εισαγωγή στο τρέχον πρόγραµµα διάφορων βιβλιοθηκών π.χ. import java.util.*; 10 Σ.σ. - Αν και σε κάποιες γλώσσες, όπως για παράδειγμα η Pascal, ένα αλφαριθμητικό παριστάνεται με έναν τύπο δεδομένων, η JAVA διαθέτει μία κλάση η String, η οποία παρέχει τις λειτουργίες απαραίτητες για την επεξεργασία αλφαριθμητικών
53 4.4 Applets και Servlets Applets Τα Applets είναι αυτόνοµα (µε την έννοια ότι δεν τρέχουν µαζί µε ένα σύνολο άλλων κλάσεων JAVA, αλλά µπορούν να εκτελούνται ξεχωριστά) προγράµµατα τα οποία ενσωµατώνονται σε άλλες εφαρµογές κυρίως web σελίδες. Η γραφή ενός τέτοιου προγράµµατος διαφέρει από την µορφή του σχήµατος 4.1. Τα προγράµµατα αυτού του είδους επεκτείνουν (extend) την αφηρηµένη κλάση Applet. Ένα σύντοµο παράδειγµα δείχνεται στο σχήµα 4.2, όπου φαίνεται ένα απλέτ το οποίο τυπώνει το µήνυµα «Hello, world!». // Hello.java import java.applet.applet; import java.awt.graphics; public class Hello extends Applet public void paint(graphics gc) gc.drawstring("hello, world!", 65, 95); Σχήµα 4.2. JAVA Applet το οποίο τυπώνει ένα µήνυµα. Η κλάση Hello επεκτείνει την κλάση Applet η οποία έχει ενσωµατωθεί στο πρόγραµµα µε την χρήση της εντολής import java.applet.applet;. Με αυτόν τον τρόπο δηλώνεται ότι ο µεταγλωττιστής πρέπει να συµπεριληφθεί την κλάση Applet και κατά την µεταγλώττιση να πραγµατοποιηθεί µία αναφορά προς αυτήν σαν να έχει γραφεί κατευθείαν στον πηγαίο κώδικα. Η κλάση Applet είναι ένα µέρος του AWT Abstract Window Toolkit µία σειρά εργαλείων η οποία προσφέρει στο Applet να εµφανίζει γραφική διασύνδεση χρηστών (GUI Graphical User Interface) και να αλληλεπιδρά µε αυτούς π.χ. µπορεί να εµφανίζει εκτός από αναγνωστικά µηνύµατα και εικόνες, µπορεί να παίρνει είσοδο από τον χρήστη. Για να εκτυπωθεί το επιθυµητό µήνυµα δεν χρησιµοποιείται πια η εντολή System.out.println(«µήνυµα 2»); αλλά η gc.drawstring( Hello, world!, 65, 95);. Η gc είναι ένα αντικείµενο της κλάσης Graphics η οποία ενσωµατώνεται στην αρχή του προ
54 γράµµατος µε την χρήση της import. Αυτή η κλάση παρακάµπτει (overrides) την µέθοδο paint(graphics) η οποία προέρχεται από την υπερκλάση για να επιτραπεί η εµφάνιση του επιθυµητού Applet. Αυτή η µέθοδος παίρνει σαν είσοδο ένα αντικείµενο της κλάσης Graphics το περιεχόµενο του οποίου στη συνέχεια εκτυπώνεται στο Applet. Στην περίπτωση του σχήµατος 4.2. η paint() εκτυπώνει την γραφική η οποία συνίσταται από µία συµβολοσειρά Hello, world!, οι δύο αριθµητικές ενδείξεις αφορούν στην θέση στην οθόνη όπου πρέπει να εκτυπωθεί (σε pixels) σε αυτό το παράδειγµα η αρχή του µηνύµατος θα εκτυπωθεί στο σηµείο 65x95 µετρώντας από την πάνω αριστερά γωνία. Στο σχήµα 4.3. δείχνεται µία σελίδα HTML η οποία τυπώνει το µήνυµα Hello world µε την χρήση Applets. Η δήλωση Applet συνίσταται στην εισαγωγή µιας ετικέτας - <applet code> </applet>, όπου δηλώνεται ποια είναι η πηγαία κλάση και οι διαστάσεις του παραθύρου όπου πρέπει να εµφανιστεί το Applet. <!-- Hello.html --> <html> <head> <title>hello World Applet</title> </head> <body> <applet code="hello" width="200" height="200"> </applet> </body> </html> Σχήµα 4.3. Ο κώδικας HTML στον οποίο ενσωµατώνεται το Applet του σχήµατος 4.2. Η ετικέτα του Applet έχει τρία πεδία του code όπου δηλώνεται η κλάση και που ακριβώς βρίσκεται αυτή, του width και του height, τα οποία ορίζουν την θέση της κλάσης µέσα στην ιστοσελίδα Servlets Σε γενικές γραµµές ένα Servlet µπορεί να θεωρηθεί ένα Applet το οποίο εκτελείται στην µεριά του server. Η τεχνολογία των Servlets επιτρέπει την επέκταση της λειτουργικότητας ενός Web server και της πρόσβασης σε υπάρχοντα επιχειρησιακά συστήµατα. Τα Servlets είναι JAVA προγράµµατα τα οποία σε ερώτηµα από τον χρήστη δηµιουργούν µία απόκριση η λειτουργία της οποίας βρίσκεται στο server. Στο σχήµα
55 φαίνεται µία κλάση Servlet η οποία εκτελεί την ίδια διεργασία όπως τα προηγούµενα παραδείγµατα. // Hello.java import java.io.*; import javax.servlet.*; public class Hello extends GenericServlet public void service(servletrequest request, ServletResponse response) throws ServletException, IOException response.setcontenttype("text/html"); final PrintWriter pw = response.getwriter(); pw.println("hello, world!"); pw.close(); Σχήµα 4.4. ένα Java applet. 4.5 Τα γραφικά της JAVA Οι δυνατότητες της JAVA είναι τεράστιες και δεν είναι δυνατόν να συµπεριφερθούν όλες σε µερικές σελίδες. Ένα µέρος το οποίο σχετίζεται στενά µε το πρόγραµµα το οποίο παρουσιάζεται στο παρών σύγγραµµα και γι αυτό πρέπει να τονιστεί είναι η βιβλιοθήκη Swing. Αυτή διαθέτει µεθόδους για δηµιουργία και διαχείριση γραφικών διασυνδέσεων χρηστών (GUI). Η Swing δηµιουργήθηκε το 1997 και προσφέρει ένα σύνολο πιο εξελιγµένων συστατικών από αυτά που υπήρχαν στο AWT (Abstract Window Toolkit) π.χ. JLabel αντί για το Label, JTextBox αντί για το TextBox. Η βιβλιοθήκη αυτή διαθέτει διαφορετικές εµφανίσεις παραθύρων σε σχέση µε την πλατφόρµα στην οποία εκτελείται, ταυτόχρονα υποστηρίζει όµως και την εµφάνιση κατά έναν προκαθορισµένο τρόπο ανεξάρτητο από την πλατφόρµα. Με την χρήση της βιβλιοθήκης Swing µπορούν να παράγονται παράθυρα τα συστατικά των οποίων µεταβάλλονται χωρίς ναι χρειάζεται ουσιαστική αλλαγή στον πηγαίο κώδικα του προγράµµατος, υποστηρίζει «pluggable look and feel» που είναι µία τεχνική η οποία επιτρέπει τις αλλαγές της γραφικής διασύνδεσης µε τον χρήστη (GUI) να γίνουν κατά τον χρόνο εκτέλεσης (run time). Ως βιβλιοθήκη της JAVA η Swing είναι ανεξάρτητη από την πλατφόρµα στην ο- ποία εκτελείται. Τα χαρακτηριστικά της δίνονται παρακάτω: Ανεξαρτησία από πλατφόρµες
56 Επεκτασιµότητα επιτρέπει την παράκαµψη (overriding) ή/και την επέκταση υπαρχόντων κλάσεών της. Συστατικο - στραφής (Component Oriented) και όχι αντικειµενοστραφής µε βασική µονάδα το συστατικό. Ένα συστατικό (component) είναι ένα αντικείµενο µε ορισµένο/γνωστό χαρακτηριστικό πρότυπο συµπεριφοράς π.χ. JButton ένα κουµπί το οποίο διαθέτει δύο βασικές καταστάσεις οι οποίες µπορεί να αντιστοιχιστούν µε ON και OFF (πατηµένο και µη πατηµένο). Προσαρµογή για κάθε συστατικό µπορούν να αλλάζονται διάφορα χαρακτηριστικά του για να επιτευχθούν τις ανάγκες του προγραµµατιστή π.χ. το µέγεθός του, η τοποθεσία του, το πάχος του πλαισίου, κ.α. Ρύθµισης επιτρέπεται χρήστες να προσφέρουν τις δικές τους αλλαγές χωρίς αυτό να επηρεάζει τον κώδικα του προγράµµατος. Μη χρήση της γραφικής διασύνδεσης µε τον χρήστη του λειτουργικού συστήµατος στο οποίο εκτελείται το πρόγραµµα. Η Swing «ζωγραφίζει» µε την χρήση της JA- VA 2D API τα αντίστοιχα συστατικά και όχι µε την χρήση των εργαλείων για την γραφική παράσταση διασύνδεσης του τοπικού µηχανήµατος. public class Swing_example extends javax.swing.jframe private int count = 0; /** Creates new form Swing_example */ public Swing_example() initcomponents(); private void initcomponents() jbutton1 = new javax.swing.jbutton(); jlabel1 = new javax.swing.jlabel(); setdefaultcloseoperation(javax.swing.windowconstants.exit_on_close); jbutton1.settext("jbutton1"); jbutton1.addactionlistener(new java.awt.event.actionlistener() public void actionperformed(java.awt.event.actionevent evt) jbutton1actionperformed(evt); ); jlabel1.settext(" ");
57 // </editor-fold> private void jbutton1actionperformed(java.awt.event.actionevent evt) // TODO add your handling code here: jbutton1.settext("press me please!"); jlabel1.settext("press " + (2 - count) + " more times to exit!"); if (count >= 2) System.exit(0); count++; /** args the command line arguments */ public static void main(string args[]) java.awt.eventqueue.invokelater(new Runnable() public void run() new Swing_example().setVisible(true); ); // Variables declaration - do not modify private javax.swing.jbutton jbutton1; private javax.swing.jlabel jlabel1; // End of variables declaration Σχ. 4.5.α. Ο κώδικας ενός παραθύρου Σχήµα 4.5.β το αποτέλεσµα της εκτέλεσης του κώδικα του σχήµατος 4.5.α
58 Στην οπτική σχεδίαση η βιβλιοθήκη Swing στηρίζεται στην σχεσιακή διάταξη των συστατικών, κάτι το οποίο σηµαίνει ότι η θέση και το µέγεθος κάθε συστατικού προσδιορίζεται σε σχέση µε το προηγούµενό του. Αυτό είναι σε αντίκρουση µε την απόλυτη διάταξη όπου η θέση και το µέγεθος παριστάνονται από τις πραγµατικές τους τιµές. Αυτός ο τρόπος διάταξης είναι παρόµοιος µε την διάταξη η οποία χρησιµοποιείται από τους φυλλοµετριτές (browsers) για την έκθεση του περιεχοµένου µιας HTML σελίδα. Στο σχήµα 4.5.α. παρατίθεται ένα κοµµάτι κώδικα το οποίο δηµιουργεί ένα παράθυρο µε ένα κουµπί και µία ετικέτα (JButton και JLabel). Όταν το κουµπί πατιέται το κείµενο της ετικέτας αλλάζει και µετά από δύο πατήµατα το πρόγραµµα τερµατίζεται (δυναµική αλλαγή των συστατικών). 4.6 Η δοµή ArrayList Στην βιβλιοθήκη java.util υπάρχει η κλάση ArrayList. Αυτή η κλάση παριστάνει µία δοµή δεδοµένων η οποία συνδυάζει τα πλεονεκτήµατα του πίνακα (array) και της συνδεδεµένης λίστας (list). Το βασικό του χαρακτηριστικό είναι η µεγάλου βαθµού δυνα- µικότητα ένα αντικείµενο της κλάσης ArrayList µπορεί να περιέχει έναν µη προκαθορισµένο αριθµό στοιχείων. Τα στοιχεία αυτά µπορεί να είναι µεταβλητές οτιδήποτε τύπου, ή αντικείµενα άλλων ή ίδιας κλάσεων. Όταν αρχικοποιείται ένα αντικείµενο της κλάσης αυτής δεν δηλώνεται προκαθορισµένο µέγεθος, αλλά αυτό προσδιορίζεται αυτόµατα στην συνέχεια. Η µέθοδος Array- List.size() επιστρέφει τον αριθµό αντικειµένων που περιέχονται. Η απόδοση της ArrayList συγκρίνοντάς την µε αυτή της συνδεδεµένης λίστας και του απλού πίνακα (array) φαίνεται στον πίνακα 4.1. Συνδεδεµένη Array (πίνακας) ArrayList (δυνα- Λίστα µικός πίνακας εικτοδότηση (Indexing) Θ(n) Θ(1) Θ(1) Πρόσθεση/ ιαγραφή στο τέλος Θ(1) N/A δεν υποστηρίζεται Θ(1) Πρόσθεση/ ιαγραφή στη µέση Θ(1) N/A δεν υποστηρίζεται Θ(n) Χαµένος χώρος (µέση τιµή) Θ(n) 0 Θ(n) Πίνακας 4.1. Απόδοση της ArrayList (δυναµικός πίνακας)
59 Για το συγκεκριµένο πρόγραµµα όπου τα αποτελέσµατα είναι διαφορετικών τύπων (κλάσεων) και απροσδιόριστου από την αρχή πλήθους η χρήση αυτής της δοµής επιτρέπει την πλήρης αποθήκευση και διαχείρισή τους. [15]
60 - 56 -
61 5 Η αρχιτεκτονική TWOX Το σύστηµα το οποίο παρουσιάζεται σε αυτό το σύγγραµµα είναι ένα σύστηµα σχεδιασµού ενεργειών (Action Planning System). Είναι ένα πλήρως αντικειµενοστραφής πρόγραµµα γραµµένο στην γλώσσα JAVA και συνίσταται από συνολικά 32 κλάσεις οι οποίες µπορούν να καταταχθούν σε τρείς γενικές οµάδες (επίπεδα): Ι. Το γραφικό περιβάλλον ΙΙ. Το parser ΙΙΙ. Ο σχεδιαστής ενεργειών Τα τρία επίπεδα αλληλεπιδρούν µεταξύ τους µε τον τρόπο που φαίνεται στο Εικόνα 5.1. Εικόνα 5.1. Σχέσεις µεταξύ των τριών επιπέδων του συστήµατος Τα δεδοµένα εισόδου διαχειρίζονται από ένα κεντρικό παράθυρο (µέρους του επιπέδου γραφικού περιβάλλοντος) και αποστέλλονται προς το parser ο οποίος διαβάζει και µετατρέπει τις εισόδους σε κατάλληλη για επεξεργασία µορφή. Η είσοδος στο σύστηµα συνίσταται κυρίως από δύο αρχεία κειµένου που περιέχουν εντολές PDDL τις οποίες αναγνωρίζει ο parser και τις µετατρέπει σε ένα σύνολο γεγονότων και ένα σύνο
62 λο ενεργειών. Στο επόµενο στάδιο ο σχεδιαστής ενεργειών εφαρµόζει το επιλεγέν αλγόριθµο αναζήτησης πάνω στα δεδοµένα που προέρχονται από το parser και βρίσκει την λύση του προβλήµατος. Η λύση αυτή είναι µία ακολουθία ενεργειών η οποία ικανοποιεί τις προδιαγραφές που δόθηκαν στην αρχή µέσω των δύο αρχείων εισόδου. 5.1 Το γραφικό περιβάλλον Το γραφικό περιβάλλον συνίσταται από πέντε παράθυρα µέσω των οποίων ο χρήστης µπορεί να εισάγει δεδοµένα στο σύστηµα και να παίρνει ενδιάµεσα και τελικά α- ποτελέσµατα. Είναι το κεντρικό παράθυρο, το παράθυρο στατιστικών/ενδιάµεσων πληροφοριών, το παράθυρο αποτελεσµάτων, το παράθυρο βοήθειας και το παράθυρο ρυθ- µίσεων. Στο παράθυρο βοήθειας (Help window) αναφέρονται πληροφορίες για να βοηθηθεί ο χρήστης στην διαχείριση του συστήµατος. Το κεντρικό παράθυρο δεν είναι περίπλοκο και οι διάφορες λειτουργικότητες είναι προσβάσηµες είτε από τα κουµπιά στην επιφάνειά του είτε από το µενού που διατίθεται. Προσφέροντας στον χρήστη µία καθαρή, από την µία πλευρά, και όµως ισχυρή από την άλλη διασύνδεση, αυτός µπορεί εύκολα να ελέγχει την λειτουργία του συστήµατος σχεδιασµού ενεργειών και να κατανοήσει τα αποτελέσµατα που του δίνονται. Η εύκολη κατανόηση των αποτελεσµάτων είναι ιδιαίτερα σηµαντική όταν επιλύονται µεγάλα σε όγκο και δύσκολα προβλήµατα. Εκτός από την λύση (σύνολο γεγονότων, διατεταγµένα σε σειρά από το πρώτο που πρέπει να εκτελεστεί προς το τελευταίο) το σύστηµα εκτυπώνει πληροφορίες που σχετίζονται µε την ενδιάµεση επεξεργασία των δεδοµένων και δεδοµένα δευτερεύουσας ση- µασίας, όπως όνοµα του πεδίου προβλήµατος (domain name), επιτρεπτές ενέργειες, στόχος κ.α.. Η λύση µπορεί να δοθεί στον χρήστη υπό δύο µορφές ως σειρά ενεργειών ή ως σειρά καταστάσεων του κόσµου προβλήµατος µία διάταξη η οποία δείχνει τις αλλαγές οι οποίες υποστεί ο κόσµος του προβλήµατος µετά από την εκτέλεση κάθε ενέργειας. Έτσι ο χρήστης έχει διαφορετικές απόψεις για την λύση. Στην εικόνα 5.1. φαίνεται ότι το επίπεδο αυτό αλληλεπιδρά µε τα υπόλοιπα δύο ε- λέγχοντας κάθε ένα από αυτά, άλλα δεν προσφέρει άµεση σύνδεση µεταξύ τους
63 5.2 Συντακτική Ανάλυη των αρχείων PDDL Ο συντακτικός αναλυτής (parser) είναι µια µηχανή η οποία εκτελεί την διαδικασία ανάλυσης µιας σειράς από λεκτικών µονάδων (tokens) µε σκοπό να προσδιορίσει µια γραµµατική δοµή µε βάση ένα σύνολο γραµµατικών κανόνων. Η µηχανή αυτή µετατρέπει το κείµενο που έχει διαβάσει σε µία µορφή (συνήθως ένα συντακτικό δένδρο) η οποία µπορεί να επεξεργαστεί σε επόµενα στάδια λειτουργίας του συστήµατος και ταυτόχρονα εκτελεί έλεγχο συντακτικής ορθότητας. Για την δηµιουργία των λεκτικών µονάδων («φράσεων» tokens) κάποια parser χρησιµοποιούν έναν λεκτικό αναλυτή (lexical analyzer) ο οποίος διαβάζει το κείµενο χαρακτήρα επί χαρακτήρα και αναγνωρίζουν τις δυνατές φράσεις. Σε όλα τα στάδια γίνεται αναφορά σε έναν πίνακα ο οποίος λέγεται πίνακας συµβόλων. [16][17] Στην εικόνα 5.2. φαίνονται τα στάδια ενός parser. Εικόνα 5.2. Τα στάδια ενός parser
64 Στο σύστηµα σχεδιασµού ενεργειών το οποίο παρουσιάζεται σε αυτό το σύγγραµµα τo parser εκτελεί την ανάγνωση και την επεξεργασία των δεδοµένων εισόδου διαβάζει τα δύο αρχεία και παράγει ένα σύνολο κατηγορηµάτων (predicates list), ένα σύνολο ενεργειών (action list) και δύο καταστάσεις του κόσµου την αρχική και την τελική. Η κάθε µία κατάσταση είναι ένα σύνολο ισχυόντων γεγονότων. Στο συγκεκριµένο σύστη- µα το τελικό αποτέλεσµα του parser είναι αυτή η συλλογή από γεγονότα, καταστάσεις και κατηγορήµατα η οποία περνάει ως είσοδο στο επόµενο στάδιο επεξεργασίας η εφαρµογή του αλγορίθµου αναζήτησης και η εύρεση τελικής λύσης. 5.3 Ο σχεδιαστής ενεργειών Μετά την µεταγλώττιση των δύο αρχείων εισόδου τα αποτελέσµατα περνιούνται σαν είσοδο στο τρίτο µέρος του συστήµατος όπου εκτελούνται µεθόδους για την εύρεση τελικής λύσης. Συγκεκριµένα εκτελείται ένα από τους πέντε αλγορίθµους αναζήτησης (τρεις τυφλούς και δύο ευρετικούς heuristic) σε έναν γράφο καταστάσεων. Ο αλγόριθµος και οι αντίστοιχες ρυθµίσεις επιλέγονται από το κεντρικό παράθυρο. Κάθε ένας από τους αλγορίθµους επιλέγει την επόµενη ενέργεια από το σύνολο των δυνατών ενεργειών. Στην ιδανική περίπτωση αν εφαρµοστεί η ενέργεια που επιλέχθηκε θα παραχθεί µία καινούρια κατάσταση η οποία θα απέχει όσο το δυνατόν λιγότερο από την κατάσταση στόχου. Η διαδικασία παραγωγής της καινούριας κατάστασης συνίσταται από τα εξής βήµατα: 1. Εύρεση της λίστας των ενεργειών που µπορούν να εφαρµοστούν στην τρέχουσα κατάσταση µία κατάσταση είναι ένα σύνολο ισχυόντων γεγονότων, µία ενέργεια µπορεί να θεωρηθεί ως ένα αντικείµενο το οποίο περιέχει τρία σύνολα γεγονότων η λίστα προϋποθέσεων, η λίστα προσθηκών και η λίστα διαγραφών. Η πρώτη δείχνει ποια γεγονότα πρέπει να ισχύουν για να µπορεί να εφαρµοστεί η ενέργεια και η δεύτερη και η τρίτη πως θα αλλάξει η τρέχουσα κατάσταση (δηλαδή πια αντικείµενα θα προστεθούν και ποια θα διαγραφούν). 2. Επιλογή µία από τις ενέργειες οι τυφλοί αλγόριθµοι έχουν έναν προκαθορισµένο τρόπο επιλογής της επόµενης ενέργειας ο οποίος δεν βασίζεται στην αξιολόγηση της υποψήφιας κατάστασης, αλλά στην εξαντλητική αναζήτηση κατάστασης µέχρι να βρεθεί µία λύση που να ικανοποιεί τους στόχους. Από την άλλη οι ευρετικοί αλγόριθµοι αξιολογούν κάθε υποψήφια κατάσταση και επιλέγουν
65 την ενέργεια που οδηγεί στην καλύτερη κατάσταση αυτή η οποία βρίσκεται πιο κοντά στην τελική λύση. 3. Εφαρµογή της ενέργειας και καταγραφή της στην τελική λίστα ενεργειών κάθε ενέργεια που εφαρµόζεται αλλάζει την κατάσταση του κόσµου µειώνοντας την απόσταση από την τελική κατάσταση (αυτή που θα ικανοποιεί τους στόχους). Όταν φθάσει στην τελική κατάσταση το σύστηµα πρέπει να προσφέρει στον χρήστη έναν πλάνο µε την ακολουθία των ενεργειών που πρέπει να εφαρ- µοστούν για να πετύχουν οι στόχοι. Όταν µία ενέργεια επιλεγεί για εκτέλεση από τον αντίστοιχο αλγόριθµο αυτή καταγράφεται σε µία λίστα. Η λίστα αυτή τελικά προσφέρεται σαν τελική λύση στον χρήστη. Το σύστηµα σχεδιασµού ε- νεργειών που αναλύεται σε αυτό το σύγγραµµα καταγράφει όχι µόνο τις ενέργειες, αλλά και τις καταστάσεις µέσω των οποίων πρέπει να περάσει ο κόσµος µέχρι αυτή που ικανοποιεί τους στόχους. Το σύστηµα αυτό προσφέρει την εφαρµογή των διαφορετικών αλγορίθµων πάνω σε ένα πρόβληµα έτσι ώστε να µπορεί ο χρήστης να κάνει σύγκριση των αποτελεσµάτων και των αποδόσεών τους. Ο συνδυασµός των λειτουργιών αυτών των µερών παράγει ένα σύστηµα σχεδιασµού ενεργειών γρήγορο, κατανοητό και εύκολο στην χρήση, γραµµένο σε γλώσσα η οποία προσφέρει την εκτέλεσή του σε οτιδήποτε λειτουργικό σύστηµα και οτιδήποτε αρχιτεκτονική
66 - 62 -
67 6 Υλοποίηση του Συστήµατος Σχεδιασµού Ενεργειών Μετά την ανάθεση του προβλήµατος δηµιουργία ενός συστήµατος σχεδιασµού ενεργειών µε την γλώσσα JAVA, υπήρξαν τρία βασικά θέµατα υλοποίησης πώς θα κατασκευαστεί το µέρος το οποίο θα διαβάζει και θα µετατρέπει την είσοδο (PDDL κώδικα) σε µορφή κατάλληλη για επόµενη επεξεργασία; ποια θα είναι ακριβώς η «επό- µενη επεξεργασία» των ήδη διαµορφωµένων δεδοµένων εισόδου και πώς θα γραφεί ως κώδικα; και µε τι τρόπο ο χρήστης θα αλληλεπιδρά µε το σύστηµα. Η απαντήσεις αυτών των ερωτηµάτων είναι συνδεδεµένες και εξαρτώνται η µία από την άλλη. 6.1 Η υλοποίηση του parser Για την λύση του πρώτου θέµατος έπρεπε να βρεθεί ένα PDDL parser ο οποίος να µπορεί να ξεχωρίζει λεκτικές µονάδες µε βάση της γραµµατικής της γλώσσας PDDL και να ανιχνεύει πιθανά συντακτικά λάθη. Το parser στη συνέχεια θα έπρεπε να παράγει τις λίστες κατηγορηµάτων και ενεργειών και τις καταστάσεις του κόσµου βασικά στοιχεία ενός σχεδιαστή ενεργειών. Στην υλοποίηση του παρόντος συστήµατος χρησιµοποιήθηκε ένα έτοιµο parser γραµµένο στην JAVA το οποίο µετατράπηκε κατάλληλα για να µπορεί να απαντάει στις απαιτήσεις του συστήµατος. Το parser αυτό έχει γραφθεί από τον Rakesh Garwal και µπορεί να βρεθεί στην ιστοσελίδα: Στο πίνακα 6.1. δίνεται ένα κοµµάτι κώδικα στο οποίο φαίνονται η διαφορές µεταξύ του αρχικού και του αλλαγµένου parser. Στην πρωτότυπη του µορφή το πώς θα αντιδράσει το parser εξαρτάται από την είσοδο του χρήστη ο κώδικας PDDL µπορεί να εισαχθεί από την κανονική είσοδο του συστήµατος (System.in) ως ακολουθία εντολών PDDL, ή να γίνει εισαγωγή των µονοπατιών δύο αρχείων κειµένου, τα οποία να περιέχουν τον κώδικα PDDL. Στην πρώτη περίπτωση χρησιµοποιείται η κονσόλα (console) και οι συµβολοσειρές εντολών περνιούνται σαν ορίσµατα στη κύρια µέθοδο main() /βλ
68 γραµµές 4, 10, 15, 28, 58 της στήλης Α., σχήµα 6.1./. Στο αλλαγµένο parser η είσοδος προέρχεται από την απευθείας επιλογή δύο αρχείων. Με αυτόν των τρόπο µειώνεται η δυνατότητα να συµβεί λάθος στην εισαγωγή, αν και πάλι υπάρχει έλεγχος ύπαρξης των αρχείων. Και στις δύο περιπτώσεις καλούνται οι µέθοδοι parse_domain_pddl(); και parse_problem_pddl(my_domain); /βλ. γραµµές 32 και 58 της Β. και 43 και 69 της στήλης Α./. Η µέθοδος parse_domain_pddl(); δεν απαιτεί δεδοµένα εισόδου, εκτελείται µε βάση µόνο το αρχείο του πεδίου ορισµού (το domain file) και παράγει ένα καινούριο αντικείµενο της κλάσης Domain. Στην περίπτωση της µεθόδου parse_problem_pddl(my_domain); η µεταβλητή my_domain είναι το αντικείµενο της κλάσης η οποία παριστάνει το πεδίου ορισµού, και το πρόβληµα µεταγλωττίζεται µε βάση τους κανόνες που ορίζει το domain. Πίνακας 6.1. Το parser σε πρωτότυπη µορφή και µε τις αλλαγές που χρειάστηκαν για να µπορεί να χρησιµοποιηθεί στο σύστηµα Α. Αρχική έκδοση του parser Β. Η κλάση Parse η οποία εκτελεί το parsing µε τις αλλαγές public class PDDL3Parser implements PDDL3ParserConstants public static void main(string args[]) PDDL3Parser parser = new PDDL3Parser(System.in); java.io.fileinputstream pddl_file; if( args.length == 0 ) System.out.println("PDDL2.1 Parser Version1.0:" + "Reading from standard input!!"); else if (args.length > 2 ) System.out.println("PDDL2.1 Parser Version1.0"); System.out.println("Usage: java PDDL3Parser domain.pddl [problem.pddl]"); return; else /*** Parse the Domain specification file ****/ try public class Parse 11 PDDL3Parser parser; public Parse() parser = new PDDL3Parser(System.in); public void Parse2(String domain_file, String problem_file) java.io.fileinputstream pddl_file; /*** Parse the Domain specification file ****/ try pddl_file = new java.io.fileinputstream(domain_file); parser.reinit(pddl_file); catch(java.io.filenotfoundexception e) System.out.println("File not found!!!"); return; 11 Οι τρεις τελείες δείχνουν ότι ο κώδικας δεν είναι πλήρες. Για τον πλήρη κώδικα αναφερθείτε στο CD στο τέλος του συγγράμματος
69 pddl_file = new java.io.fileinputstream(args[0]); parser.reinit(pddl_file); catch(java.io.filenotfoundexception e) System.out.println("File not found!!!"); return; /* * Try to parse the input file */ try my_domain = parser.parse_domain_pddl(); System.out.println("Parsed Succesfully!!"); catch( ParseException e) System.out.println("Exception!!!"); e.printstacktrace(); /**** Parse the problem file ****/ if( args.length == 2 ) try pddl_file = new java.io.fileinputstream(args[1]); parser.reinit(pddl_file); catch(java.io.filenotfoundexception e) System.out.println("File not found!!!"); return; try my_problem = parser.parse_problem_pddl(my_domain); System.out.println("Parsed Succesfully!!"); catch( ParseException e) System.out.println("Exception!!!"); e.printstacktrace(); /* * Try to parse the input file */ try my_domain = parser.parse_domain_pddl(); System.out.println("Parsed Succesfully"); catch( ParseException e) System.out.println("Exception!!! ); e.printstacktrace(); /**** Parse the problem file ****/ try pddl_file = new java.io.fileinputstream(problem_file); parser.reinit(pddl_file); catch(java.io.filenotfoundexception e) System.out.println("File not found!!!"); return; try my_problem = parser.parse_problem_pddl(my_domain); System.out.println("Parsed Succesfully!!"); catch( ParseException e) System.out.println("Exception!!!"); e.printstacktrace(); Στο πρώτο στάδιο το parser διαβάζει τις εισόδους και αναγνωρίζει λεξικές µονάδες µε βάση τη γραµµατική. Στη συνέχεια από αυτές τις λεξικές µονάδες παράγονται «φράσεις» και δεσµευµένες λέξεις. Σε επόµενο βήµα εκτελείται η διαδικασία της «γείωσης»
70 (grounding) κατά την οποία κάθε µεταβλητή παίρνει µία δυνατή τιµή της. Για παράδειγµα αν στο domain υπάρχει ο κανόνας move_from_to(x, y) όπου x και y είναι διαφορετικές µεταβλητές τύπου cube, και αν στο αρχείο προβλήµατος έχουν δηλωθεί τα αντικείµενα cubea και cubeb του τύπου cube, τότε θα παραχθούν δύο «γειωµένες» ενέργειες: move_from_to(cubea, cubeb) και move_from_to(cubeb, cubea). Όταν µεταγλωττιστούν τα αρχεία επιτυχώς παράγονται τέσσερα αποτελέσµατα: η αρχική κατάσταση (initial state), η κατάσταση στόχου (goal state), η λίστα µε τα κατηγορήµατα (predicate list) και η λίστα ενεργειών (action list). Το κάθε κατηγόρηµα είναι ένα αντικείµενο της κλάσης Predicate και µετά την «γείωση» για κάθε ένα κατηγόρηµα δηµιουργείται και ένα ή περισσότερα αντικείµενα της κλάσης GPredicate (Grounded Predicate). Στις ενέργειες και στις καταστάσεις ένα κατηγόρηµα υπάρχει µε το ID του ένας µοναδιαίος ακέραιος αριθµός. Όταν εκτελούνται πράξεις πάνω στα σύνολα ενεργειών ή καταστάσεων η αναφορά σε ένα κατηγόρηµα συνίσταται στην διατύπωση του ειδικού αριθµού του, και όµως όταν πρέπει να εκτυπωθεί κάποιο αποτέλεσµα (είτε ενδιάµεσο είτε τελικό) το οποίο να είναι κατανοητό στον τελικό χρήστη, για κάθε ID πού υπάρχει εκτυπώνεται το αντίστοιχο όνοµα κατηγορήµατος. Ένα παράδειγµα φαίνεται στο σχήµα
71 Σχήµα 6.1. Η λίστα των κατηγορηµάτων και η αρχική και η τελική καταστάσεις µαζί µε τις σχέσεις τους µε αυτήν. Στο σχήµα 6.1. φαίνεται µία λίστα η οποία περιέχει όλα τα δυνατά κατηγορήµατα ενός προβλήµατος (συγκεκριµένα είναι ένα πρόβληµα µεταφοράς κύβων) µαζί µε την τελική και την αρχική καταστάσεις. Παριστάνεται πως σε κάθε κατάσταση τα κατηγορήµατα υπάρχουν µε τους ειδικούς τους αριθµούς οι οποίοι αντιστοιχούνται στην λίστα κατηγορηµάτων. Στις λίστες προσθηκών, διαγραφών και προϋποθέσεων των ενεργειών τα κατηγορήµατα υπάρχουν υπό την ίδια µορφή. Συνοψίζοντας, η λειτουργία του parser είναι να διαβάζει τα αρχεία κειµένου που δίνονται σαν είσοδο, να διαχωρίζει φράσεις, δεσµευµένες λέξεις, µεταβλητές, ονόµατα κατηγορηµάτων και ενεργειών ανιχνεύοντας µία µία λεξικές µονάδες, να «γειώνει» τις µεταβλητές, και να κάνει ανίχνευση λαθών. Στο τέλος να παράγει την λίστα των δυνατών ενεργειών, την λίστα των δυνατών κατηγορηµάτων, την αρχική και την τελική καταστάσεις
72 6.2 Οι αλγόριθµοι αναζήτησης Όταν το parser ολοκληρώσει µε επιτυχία την επεξεργασία των αρχείων κώδικα PDDL τα δεδοµένα που παράγονται πρέπει να υποστούν άλλη επεξεργασία για να παραχθεί η λύση του προβλήµατος σχεδιασµού η ακολουθία ενεργειών η εφαρµογή των οποίων θα ικανοποιήσει τους στόχους. Η κλάση η οποία είναι υπεύθυνη για την αποστολή των δύο αρχείων εισόδου προς το parser, και την προώθηση των αποτελεσµάτων από το parser στο τµήµα των αλγορίθµων αναζήτησης είναι η Planner.java η οποία διαθέτει τις µεθόδους ParsIt() και BuildIt(). Η πρώτη καλεί το parser και φαίνεται στο σχήµα 6.2. public boolean ParseIt(String df, String pf) parsing.parse2(df, pf); 3. initial = parsing.getinitialstate(); 4. goal = parsing.getgoalstate(); 5. predicates = parsing.getpredicates(); 6. actions = parsing.getactions(); 7. return parsing.parsedsuccessfully(); 8. Σχήµα 6.2. Ο κώδικας της µεθόδου ParseIt(String df, String pf) υπεύθυνη για την µεταγλώττιση των αρχείων εισόδου df και pf Η γραµµή 2 καλεί την µέθοδο εκτέλεσης του parser (η Parse2() ) και οι υπόλοιπες παίρνουν τα αποτελέσµατα. Στην γραµµή 7 καλείται µία µέθοδος η οποία επιστρέφει την τιµή «αλήθεια» αν κατά την µεταγλώττιση δεν προέκυψε κάποιο λάθος και «ψευδές» στην αντίθετη περίπτωση. Η δεύτερη βασική µέθοδος της κλάσης Planner.java είναι η BuildIt() και παρουσιάζεται στο σχήµα 6.3. Στις εντολές των γραµµών 3 έως 9 δηµιουργείται και αρχικοποιείται το αντικείµενο plan της κλάσης BuildPlan(), η οποία περιέχει τους αλγορίθµους αναζήτησης. Η εντολή της γραµµής 10 καλή το plan να εκτελέσει τον επιλεγέν αλγόριθµο πάνω στα υπάρχοντα δεδοµένα. Κατά την εκτέλεσή του η µεταβλητή result (βλ. γραµµή 11) παίρνει µία τιµή «αληθές» ή «ψευδές» η οποία δηλώνει αν το πλάνο έχει δηµιουργηθεί επιτυχώς ή έχει αποτύχει. Με την εντολή της 11.d. δηµιουργείται το παράθυρο το οποίο εµφανίζει την λύση στον χρήστη µέσω ενός παραθύρου. Στις γραµµές 1, 2 δηµιουργείται µία µεταβλητή µετρητής του χρόνου η οποία (βλ. γραµµές 11.c, 11.d) βρίσκει το χρόνο που
73 χρειάστηκε για να ολοκληρωθεί η διαδικασία εύρεσης λύσης και στην συνέχεια εµφανίζεται στο παράθυρο έτσι ώστε ο χρήστης να µπορεί να συγκρίνει την απόδοση των διαφορετικών αλγορίθµων που δρουν στο ίδιο πεδίο ορισµού και στο ίδιο πρόβληµα. public boolean BuildIt(int Al) 1. long ElapsedTime; 2. ElapsedTime = System.nanoTime(); //Start Time; 3. BuildPlan plan = new BuildPlan(); 4. plan.setactionlist(actions); 5. plan.setpredicatelist(predicates); 6. plan.setinitialstate(initial); 7. plan.setgoalstate(goal); 8. plan.buildrelaxplan(); 9. plan.setparameters(parida, paridb, partime); 10. plan.getstatesequence(al); 11. if (plan.result) a. States = plan.getstatesequence1(); b. Actions = plan.getactionsequence(); c. ElapsedTime = System.nanoTime()-ElapsedTime; d. Solution = new SolutionWindow(Actions, States, ElapsedTime); return plan.buildsuccessfully(); 14. Σχήµα 6.3. Ο κώδικας της µεθόδου BuildIt(Al) υπεύθυνη για την κατασκευή του πλάνου. Η µεταβλητή Al δείχνει ποιος αλγόριθµος επέλεξε ο χρήστης. Η µεταβλητή Al παίρνει ακέραιες τιµές στο διάστηµα [0, 4] οι οποίες αντιστοιχούν στους πέντε αλγορίθµους 0 Depth First Search (DFS), 1 Bread First Search (BFS), 2 Iterative Deepening (ID), 3 Identidem και 4 FFSearch. Οι πρώτοι τρεις αλγόριθ- µοι είναι τυφλής αναζήτησης, ενώ οι άλλες δύο είναι ευρετικοί (heuristic) Υλοποίηση του αλγορίθµου αναζήτησης πρώτα σε βάθος Στο σχήµα 6.4. παρουσιάζονται ο ψευδοκώδικας και η µέθοδος που υλοποιεί τον αλγόριθµο αναζήτησης πρώτα σε βάθος (DFS) Πρώτα χρειάζεται να σηµειωθεί ότι σε αντίθεση µε το πρωταρχικό αλγόριθµο (όπως δηλώνεται στο σχήµα 6.4.α) ) στην υλοποίησή του έχει προστεθεί ένας περιορισµός χρόνου, έτσι ώστε, σε περίπτωση που ο αλγόριθµος παγιδευτεί σε τοπικό ακρότατο και
74 του χρειάζεται απαγορευτικό χρόνο για να βρει την λύση, η εκτέλεσή του σταµατάει επιστρέφοντας αποτυχία. Ο περιορισµός αυτός δηλώνεται από τον χρήστη, άλλα προεπιλεγµένα είναι 0 το οποίο αντιστοιχεί σε άπειρο χρόνο δηλαδή δεν υπάρχει καθόλου περιορισµός. 1. Βάλε την αρχική κατάσταση στο µέτωπο της αναζήτησης 2. Αν το µέτωπο της αναζήτησης είναι κενό τότε σταµάτησε (κριτήριο τερµατισµού 1) 3. Βγάλε την πρώτη κατάσταση από το µέτωπο της αναζήτησης 4. Αν είναι η κατάσταση µέλος του κλειστού συνόλου πήγαινε στο Αν η κατάσταση ικανοποιεί τους στόχους (είναι δηλαδή τελική) ανέφερε την λύση (κριτήριο τερµατισµού 2) 6. Εφάρµοσε τους τελεστές µετάβασης για να βρεις τις καταστάσεις-παιδιά 7. Βάλε τις καταστάσεις-παιδιά στην αρχή του µετώπου αναζήτησης 8. Βάλε την κατάσταση γονέα στο κλειστό σύνολο 9. Πήγαινε στο 2. α) ο ψευδοκώδικας του αλγορίθµου DFS public boolean dfs(state init, State fin, int time) long inittime, currtime; 3. inittime = 4. System.nanoTime()/ ; ArrayList Closed = new ArrayList(); 7. ArrayList Frontier=new ArrayList(); 8. Frontier.add((State) init); 9. State Current = new State(); 10. ArrayList ChildrenStates; 11. Current.addState(((State) Frontier.get(0)).this_state); 12. Current.addPrevStateSet(((State) Frontier.get(0)).previousSt); 13. while ((!Current.HasSubset(fin)) && (!Frontier.isEmpty())) Frontier.remove(0); 16. if (ArrayContains(Closed, Current)==(-1)) 17. a. ChildrenStates = new ArrayList(); b. ChildrenStates = Expand(Current); c. int i; d. for (i=childrenstates.size()-1; i>=0; i--) Frontier.add(0, ((State) ChildrenStates.get(i))); e. Closed.add((State)Current);
75 if (Frontier.isEmpty()) return false; 20. Current = new State(); 21. Current.addState(((State) Frontier.get(0)).this_state); 22. Current.addPrevStateSet(((State) Frontier.get(0)).previousSt); 23. if (time!=0) a. if ((((currtime=system.nanotime()) - inittime)/ ) >= time) b. c. System.out.println("Time Limit Exceeded!"); d. return false; e if (!Closed.isEmpty()) Closed.add((State) Current); 28. StateSequence = Current.getPrevStateSet(); 29. return true; return false; 32. β) η µέθοδος η οποία υλοποιεί τον αλγόριθµο DFS Σχήµα 6.4. Ο αλγόριθµος DFS α) ο ψευδοκώδικας του αλγορίθµου [8] και β) η υλοποίησή του. Τα υπόλοιπα αντιστοιχούν στις προδιαγραφές του ψευδοκώδικα. Αρχικά /βλ. γραµ- µές 6 και 7 του σχ. 6.4.β)/ δηµιουργούνται τα δύο σύνολα του µετώπου και το κλειστό (Frontier και Closed) στα οποία θα αποθηκεύονται οι καταστάσεις αντικείµενα της κλάσης State. Η πρώτη τρέχουσα κατάσταση τίθεται στην αρχική /βλ. γραµµές 9 έως 12/ από την οποία στην συνέχεια παράγονται οι καταστάσεις-παιδιά. Η παραγωγή των καταστάσεων-παιδιά υλοποιείται εφαρµόζοντας στην τρέχουσα κατάσταση όλες οι δυνατές ενέργειες και από τις καταστάσεις οι οποίες δηµιουργούνται παιδιά θεωρούνται αυτές που δεν έχουν ήδη καταγραφή στο κλειστό σύνολο, δηλαδή δεν βρίσκονται σε υψηλότερο επίπεδο από την τρέχουσα. Η διαδικασία αυτή καλείται επέκταση (expand) της τρέχουσας κατάστασης και υλοποιείται από την οµώνυµη µέθοδο /βλ. γραµµή 17.b)/. Ο αλγόριθµος τερµατίζεται σε δύο περιπτώσεις όταν δεν υπάρχει άλλη κατάσταση από την οποία να συνεχίσει η αναζήτηση (το σύνολο Frontier είναι άδειο) ή όταν µία λύση έχει βρεθεί όπως φαίνεται και από το σχήµα 6.4.α) σειρά 2 και σειρά 5. Στην
76 υλοποίηση αυτοί οι έλεγχοι εκτελούνται την ίδια στιγµή οπότε αν δεν υπάρχει άλλη κατάσταση στο µέτωπο αναζήτησης ή έχει βρεθεί λύση ο βρόχος για την εύρεση των καταστάσεων-παιδιά τερµατίζεται και αναφέρεται το αποτέλεσµα του αλγορίθµου true, αν έχει βρεθεί λύση του προβλήµατος και false αν το µέτωπο αναζήτηση είναι άδειο και η τρέχουσα κατάσταση δεν ικανοποιεί τους στόχους. Πρέπει να δοθεί ιδιαίτερη σηµασία στην γραµµή 17.d) του σχήµατος 6.4.β), αυτή είναι η ουσία, η οποία χαρακτηρίζει τον αλγόριθµο ως αλγόριθµος αναζήτησης πρώτα σε βάθος. for (i=childrenstates.size()-1; i>=0; i--) Frontier.add(0, ((State) ChildrenStates.get(i))); - κάθε κατάσταση παιδί που έχει παραχθεί από την τρέχουσα εισάγεται στην αρχή του µετώπου αναζήτησης. Με αυτόν τον τρόπο όταν σε επόµενη επανάληψη αναζητηθεί καινούρια κατάσταση αυτή θα είναι η πρώτη η οποία βρίσκεται στο αµέσως χαµηλότερο επίπεδο. /βλ. πίνακα 3.2/, µέχρι να εξαντληθούν όλες οι καταστάσεις του χαµηλότερου επιπέδου χωρίς να βρεθεί καµία που να ικανοποιεί τους στόχος οπότε ο αλγόριθµος κάνει οπισθοδρόµηση (backtracking) και παίρνει την πρώτη που δεν έχει εξεταστεί στο αµέσως παραπάνω επίπεδο από την οποία επαναλαµβάνεται όλη η διαδικασία. Η οπισθοδρόµηση στην ουσία συνίσταται από κάποια ιδιαίτερη διαδικασία, απλά επιλέγεται η επόµενη κατάσταση στο µέτωπο αναζήτησης η οποία απλά βρίσκεται σε υψηλότερο επίπεδο (σε περίπτωση που όλες που βρίσκονται σε χαµηλότερο επίπεδο έχουν εξεταστεί) Υλοποίηση του αλγορίθµου αναζήτησης πρώτα σε πλάτος Επόµενος είναι ο αλγόριθµος αναζήτησης πρώτα σε πλάτος (BFS), ο οποίος µοιάζει µε τον DFS, ό,τι αφορά στην υλοποίηση, µε την µόνη διαφορά στον τρόπο εισαγωγής των καταστάσεων-παιδιά στο µέτωπο αναζήτησης. Η παρακάτω γραµµή κώδικα δείχνει την διαδικασία αυτή: for (i=0; i<childrenstates.size(); i++) Frontier.add((State) ChildrenStates.get(i)); - στην περίπτωση του BFS οι καταστάσεις-παιδιά δεν µπαίνουν στην αρχή άλλα στο τέλος του µετώπου αναζήτησης, άρα επειδή η επόµενη κατάσταση που επιλέγεται είναι η πρώτη στο µέτωπο αυτή είναι η αµέσως γειτονική της τρέχουσας (αν έχουν αποµείνει τέτοιες), και µόνο όταν εξεταστούν όλες οι γειτονικές καταστάσεις του ιδίου επιπέδου τότε ο αλγόριθµος ελέγχει τις καταστάσεις του παρακάτω επιπέδου /βλ. πίνακα 3.2./
77 Τα υπόλοιπα σηµεία µεταξύ των δύο αλγορίθµων (DFS και BFS) είναι όµοια, για αυτό τον λόγο δεν θα αναφερθεί ο κώδικας του BFS Υλοποίηση του αλγορίθµου επαναληπτικής εµβάθυνσης Ο αλγόριθµος επαναληπτικής εµβάθυνσης (Iterative Deepening ID) εκτελεί τον DFS µε περιορισµένο βάθος το οποίο στην ουσία είναι ένας συνδυασµός µεταξύ του DFS και του BFS. Στο σχήµα 6.5. παρουσιάζονται ο ψευδοκώδικας και ο κώδικας (η µέθοδος id_search() ) αυτού του αλγορίθµου. 1. Όρισε το αρχικό βάθος αναζήτησης (ίσο µε 1) 2. Εφάρµοσε τον αλγόριθµο dfs µε περιορισµένο βάθος 3. Αν βρέθηκε η λύση σταµάτησε (κριτήριο τερµατισµού 1) 4. Αύξησε το βάθος κατά ποσότητα a 5. Πήγαινε στο 2. public boolean id_search(state init, State fin, int a, int b) //a - initial depth //b - increasing quntity int depth = a; while (!bounded_dfs (init, fin, depth)) depth+=b; return true; α) ο ψεύδοκωδικας του αλγορίθµου επαναληπτικής εµβάθυνσης β) η υλοποίηση του αλγορίθµου επαναληπτικής εµβάθυνσης Σχήµα 6.5. Ο αλγόριθµος Iterative Deepening (ID). Εκτός από την αρχική και την τελική κατάσταση παίρνει σαν ορίσµατα δύο παραµέτρους που σχετίζονται µε το βάθος η a και η b Ο αλγόριθµος αυτός είναι πολύ εύκολος για υλοποίηση επειδή χρησιµοποιεί το DFS. Στο σύστηµα που παρουσιάζεται σε αυτό το σύγγραµµα όµως δεν χρησιµοποιείται ο DFS κατευθείαν, αλλά µία παραλλαγή του η οποία παρέχει την δυνατότητα περιορισµού του βάθους. Ο περιορισµός αυτός πετυχαίνεται µε την επόµενη γραµµή κώδικα: if (Current.getPrevStateSet().size()<depth) - όπου η µεταβλητή depth δηλώνει το επιτρεπτό βάθος. Με αυτή την εντολή ελέγχεται αν η τρέχουσα κατάσταση έχει λιγότερους προγόνους από ό,τι ορίζει η depth αν ναι τότε επιτρέπεται η επέκταση της τρέχουσας κατάστασης και η εισαγωγή των καταστά
78 σεων-παιδιά στο µέτωπο αναζήτησης, αν όχι τότε δεν εκτελείται η επέκταση και δεν εισάγονται καταστάσεις οι οποίες βρίσκονται σε χαµηλότερο (βαθύτερο) επίπεδο. Η απόδοση του αλγορίθµου αυτού βασίζεται εντελώς στις τιµές των παραµέτρων a και b. Αν επιλεγεί ένα µικρό αρχικό βάθος (παράµετρος a) το οποίο δεν αυξάνεται πολύ γρήγορα (παράµετρος b) µπορεί να εκτελεστούν πάρα πολλές επαναλήψεις ξοδεύοντας πολύ χρόνο και χώρο οι ίδιες καταστάσεις θα εξετάζονται πάρα πολλές φορές. Αν όµως δοθούν τιµές για τους a και b πολύ µεγάλες τότε µια πιθανή λύσει η οποία όµως βρίσκεται σε υψηλότερο επίπεδο αλλά έξω από το µονοπάτι που εξετάζεται δεν θα µπορεί να ανιχνευθεί, χάνοντας έτσι και πολύ χρόνο και µία καλύτερη λύση Υλοποίηση του αλγορίθµου Identidem Η λειτουργία του αλγορίθµου αυτού περιγράφεται αναλυτικά στο κεφάλαιο 3, εδώ θα δοθεί σηµασία στον τρόπο υλοποίησής του. Αυτός ο αλγόριθµος υλοποιήθηκε µέσω µιας κύριας µεθόδου η οποία παριστάνει το εξωτερικό βρόχο του αλγορίθµου και µιας άλλης µεθόδου, υπεύθυνη για την επιλογή της επόµενης κατάστασης. Στην Εικόνα 6.1. δείχνεται πως αλληλεπιδρούν οι δύο αυτές µεθόδους µαζί µε τις δευτερεύουσες µεθόδους τους. Εικόνα 6.1. Οι µέθοδοι µέσω τις οποίες υλοποιείται ο αλγόριθµος Identidem a. Η µέθοδος getnumberofneighbours απλά επιστρέφει τον αριθµό των γειτόνων της τρέχουσας κατάστασης b. Η µέθοδος heuristic επιστρέφει µία τιµή, η οποία δείχνει πόσο απέχει η κατάσταση από µία υποθετική τελική κατάσταση. Θα αναλυθεί στη συνέχεια ως βασικό τµήµα του αλγορίθµου FFSearch
79 c. Η µέθοδος getneighbour() επιστρέφει µία κατάσταση του κόσµου η οποία είναι γειτονική της τρέχουσας. Αυτή επιλέγεται µε την µέθοδο της ρουλέτας (Roulette Rule) από το πλήθος όλων των δυνατών καταστάσεων οι οποίες µπορεί να παραχθούν από την τρέχουσα. Για κάθε δυνατή κατάσταση δίνεται ένας αριθµός ο οποίος δείχνει πόσο καλύτερη είναι αυτή σε σχέση µε τις υπόλοιπες. Το σχήµα 6.6. δείχνει τον κώδικα για την επίτευξη της ανάθεσης τιµής σε κάθε υποψήφια κατάσταση: for (int j =0; j<neighbourcandidates.size(); j++) Hi = Gspot.heuristic((State) NeighbourCandidates.get(j)); Wi = java.lang.math.pow((1.0/((double) Hi)), beta); NeighbourHeuristics.add(Hi); NHeuristicWs.add(Wi); Σχήµα 6.6. Ο βρόχος ο οποίος αναθέτει τιµή σε κάθε υποψήφια κατάσταση στη µέθοδο getneighbour() για κάθε υποψήφια κατάσταση η οποία περιέχεται στον πίνακα NeigbourCandidates υπολογίζεται ένα βάρος (Wi) χρησιµοποιώντας την βιβλιοθήκη Math της JAVA και την µέθοδο pow() η οποία υπολογίζει την τιµή (1 / την ευριστική τιµή της υποψήφιας κατάστασης) στη δύναµη της παραµέτρου β (beta). Επειδή η ευρετική συνάρτηση επιστρέφει την απόσταση της υποψήφιας κατάσταση µέχρι µία υποθετική τελική κατάσταση όσο πιο µικρή είναι αυτή τόσο καλύτερα, επο- µένως όσο µικρότερη είναι η τιµή Hi τόσο µεγαλύτερη είναι η Wi (το βάρος της κατάστασης). Τα βάρη και η τιµές Hi για κάθε υποψήφια κατάσταση καταχωρούνται στους πίνακες NHeuristicWs και NeighbourHeuristics. Στη συνέχεια δηµιουργείται ένας άλλος πίνακας τα στοιχεία του οποίου είναι οι υποψήφιες καταστάσεις και ο αριθµός των φορών που υπάρχει κάθε µία από αυτές στον πίνακα είναι ανάλογος προς το βάρος της. Για παράδειγµα αν οι καταστάσεις S1, S3 και S7 είναι υποψήφιες µε αντίστοιχα βάρη 0.5, 0.2 και 0.4 τότε ο πίνακας της ρουλέτας (Roulette) θα είναι όπως φαίνεται στην εικόνα 6.2.α)
80 α) S1 S3 S7 β) Εικόνα 6.2. Η ρουλέτα για τις υποψήφιες καταστάσεις S1, S3, S7. Στο τµήµα α) φαίνεται ο πίνακας όπως υλοποιείται στο πρόγραµµα µε πέντε θέσεις για την S1, µε δύο θέσεις για την S3, και για S7 τέσσερεις θέσεις. Στο τµήµα β) φαίνεται οπτικά η ρουλέτα. Για την επιστροφή µιας από τις γειτονικές καταστάσεις, επιλέγεται µία από την ρουλέτα µε βάση δύο παραµέτρων bet και initial_bet. Η µεταβλητή initial_bet δηλώνει την αρχική θέση του δείκτη (της ρουλέτας) και η bet πόσες θέσεις να µετακινηθεί αυτός. Επιλέγεται η κατάσταση στην οποία δείχνει ο δείκτης µετά το άθροισµα της bet µε την initial_bet. Στο σχήµα 6.7. φαίνεται η υλοποίηση της παραπάνω διαδικασίας 1. bet = generator.nextint(theroulette.size()); 2. initial_bet = generator.nextint(theroulette.size()); 3. if ((bet + initial_bet) >=theroulette.size()) 4. return ((State) NeighbourCandidates.get((Integer) theroulette.get(bet))); 5. return ((State) NeighbourCandidates.get((Integer) theroulette.get((bet+initial_bet)))); Σχήµα 6.7. Η επιλογή της κατάστασης που θα επιστραφεί. Με τις εντολές της γραµµής 1 και της γραµµής 2 δηµιουργούνται δύο αυθαίρετοι αριθµοί από 0 έως το µέγεθος της ρουλέτας. Αν το άθροισµά τους είναι µε
81 γαλύτερο του µέγεθος της ρουλέτας (γραµµή 3) τότε επιστρέφεται η κατάσταση της θέσης bet, αν όµως δεν αληθεύει ο παραπάνω έλεγχος τότε επιστρέφεται η κατάσταση στην θέση initial_bet+bet. d. Η µέθοδος Algorithm3 αρχικά προσπαθεί να βρει µία κατάσταση, έστω temp- State, η οποία να είναι γειτονική της τρέχουσας (επιστρέφεται από την µέθοδο getneighbour() ) και να µην έχει ελεγχθεί µέχρι τώρα. Οι προσπάθειές του περιορίζονται από τον αριθµό τον γειτόνων της. Αυτό πετυχαίνεται µε τον κώδικα του σχήµατος int NumberofNeighbours = getnumberofneighbours(newstate); 2. int NoNs = 0; 3. do NoNs++; 6. tempstate = new State(); 7. tempstate = this.getneighbour(1.5, newstate); while ((ArrayContains(Closed, tempstate) == 1) && (NoNs<NumberofNeighbours)); Σχήµα 6.8. Αναζήτηση γειτονικής κατάστασης η οποία να µη έχει εξεταστεί προηγουµένως Στη συνέχεια εξετάζεται αν αυτή η κατάσταση tempstate έχει καλύτερη ευριστική τιµή από την κατάσταση εισόδου, έστω S1, αν ναι τότε αυτή επιστρέφεται. Σε αντίθετη περίπτωση αυτή η διαδικασία εύρεσης καλύτερης κατάστασης συνεχίζεται µέχρι ένα προκαθορισµένο βάθος εκτελώντας έναν αριθµό δοκιµών σε κάθε επίπεδο. Αν και µέχρι το χαµηλότερο επιτρεπτό επίπεδο (περιορίζεται από την µεταβλητή depth, βλ. σχήµα 6.9) δεν βρεθεί καλύτερη κατάσταση σε σχέση µε την S1 τότε ο αλγόριθµος ξεκινάει πάλι ψάχνοντας γειτονική κατάσταση της S1. Πρέπει να σηµειωθεί ότι: 1. η κατάσταση S1 είναι διαφορετική από αυτήν η ο- ποία επιλέγεται ως τρέχουσα µετά από την εκτέλεση του κώδικα του σχήµατος 6.8. και 2. όταν ο αλγόριθµος ξεκινάει πάλι ψάχνοντας για γειτονική της S1 είναι σχεδόν βέβαιο ότι θα επιλεγεί άλλη γειτονική κατάσταση λόγο των δύο αυθαίρετων τιµών bet και initial_bet της µεθόδου getneighbour()
82 Οι τρεις βρόχους του αλγορίθµου Algorithm3() φαίνονται στο σχήµα 6.9 γραµµές 1, 3 και for (int i = 0; i<iterations; i++) for (int probes = 0; probes<probes_at_depth; probes++) Closed = new ArrayList(); 7. for (int depth = 0; depth<depth_bound; depth++) /*κώδικας του σχήµατος 5.9.*/ 10. if (ArrayContains(Closed, tempstate)==(-1)) newstate = new State(); 13. newstate.addstate(tempstate.this_state); 14. newstate.addprevstateset(tempstate.previousst); 15. if (Gspot.heuristic(newState)<Gspot.heuristic(S1)) 16. return newstate; 17. Closed.add((State) newstate); if (NoNs>=NumberofNeighbours) depth=depth_bound; failcount++; 22. if (failcount == failbound) return S1; depth_bound += depth_bound; return S1; Σχήµα 6.9. Ο αλγόριθµος Algorithm3(). Σε περίπτωση που ο αλγόριθµος αποτύχει περισσότερες φορές από ένα προκαθορισµένο όριο τότε τερµατίζεται µε αποτυχία επιστρέφοντας την κατάσταση από την οποία έχει ξεκινήσει /βλ. γραµµές 21 και 22/ e. Η τελευταία µέθοδος του αλγορίθµου Identidem είναι ο κύριος βρόχους. Αυτός παίρνει κάθε καινούρια κατάσταση και την θέτει ως είσοδο στην µέθοδο Algorithm3() για να µπορεί από αυτή στην συνέχεια να παραχθεί η επόµενη. Στο τέλος αυτής της µεθόδου επιστρέφεται η τελική λύση του προβλήµατος σχεδιασµού: StateSequence = Current.getPrevStateSet();
83 6.2.5 Υλοποίηση του αλγορίθµου FF Ο FF είναι ένας εύκολος ευρετικός αλγόριθµος ο οποίος υλοποιείται µε τρεις βασικές µεθόδους η κύρια µέθοδος FFSearch (State init, State fin), η ευριστική συνάρτηση µέθοδος της κλάσης Graphplan.java, και η FF_bfs(Current, fin, Hi) η οποία είναι εναλλακτική µέθοδος εύρεσης επόµενης κατάστασης σε περίπτωση που ο αλγόριθµος έχει παγιδευτεί σε τοπικό ακρότατο (δεν υπάρχει γειτονική κατάσταση µε καλύτερη ευρετική τιµή). Στο σχήµα δείχνεται ο βρόχος του αλγορίθµου, όπου αναζητείται από το σύνολο των καταστάσεων-παιδιά της τρέχουσας, µία κατάσταση µε καλύτερη ευρετική τιµή από την τρέχουσα. 1. int Hi = Integer.MAX_VALUE; 2. Candidates = Expand(Current); 3. for (int i = 0; i<candidates.size(); i++) if (this.arraycontains(closed, ((State) Candidates.get(i)))==(-1)) HiTemp = Gspot.heuristic((State) Candidates.get(i)); 8. if (HiTemp <= Hi) 9. //Finds the state with the best heuristic value from the candidates that may //occure from the current state 10. Temp = new State(); 11. Hi = HiTemp; 12. Temp.addState(((State) Candidates.get(i)).this_state); 13. Temp.addPrevStateSet(((State) Candidates.get(i)).previousSt); Σχήµα Βρόχος εύρεσης καλύτερης κατάστασης του αλγορίθµου FF Search Όταν βρεθεί καλύτερη κατάσταση η αναζήτηση συνεχίζεται από αυτήν µέχρι να βρεθεί κατάσταση η οποία να ικανοποιεί τους στόχους. Όµως µπορεί ο αλγόριθµος να «πέσει» σε τοπικό ελάχιστο δηλαδή να καταγραφεί µία κατάσταση η οποία να µην έχει παιδιά µε καλύτερη τιµή. Σε αυτήν την περίπτωση εκτελείται ο αλγόριθµος αναζήτηση πρώτα σε πλάτος µέχρι να βρεθεί κατάσταση µε καλύτερη ευρετική τιµή από το τοπικό ελάχιστο στο οποίο είχε παγιδευτεί ο FF Search. Αυτή η διαδικασία παριστάνεται από τον κώδικα του σχήµατος
84 1. else//in case of local minimum we do bfs 2. //until a state with better heuristic is found 3. Closed.add((State) Current); 4. Temp= new State(); 5. Temp = FF_bfs(Current, fin, Hi); 6. if (!Current.compare(Temp)) Current = new State(); 9. Current.addState(Temp.this_state); 10. Current.addPrevStateSet(Temp.previousSt); 11. Hi = Gspot.heuristic(Current); else return false; 14. Σχήµα Εκτέλεση του αλγορίθµου BFS σε περίπτωση που δεν µπορεί να βρεθεί κατάσταση µε καλύτερη ευρετική τιµή Η τιµή η οποία δηλώνει πόσο καλή είναι µία κατάσταση επιστρέφεται από την µέθοδο heuristic της κλάσης Graphplan.java. Σε αυτή η κλάση δηµιουργείται ένα «χαλαρό» (relaxed) πλάνο το οποίο χρησιµοποιείται για τον προσδιορισµό της απόστασης µεταξύ τρέχουσας και «χαλαρής» τελικής κατάστασης. Η κατασκευή ενός «χαλαρού» πλάνου συνίσταται στη εφαρµογή των δυνατών ε- νεργειών σε µία κατάσταση χωρίς να αφαιρούν από αυτήν τα γεγονότα που διαθέτονται στις λίστες διαγραφής τους. Η διαδικασία αυτή εκτελείται από την µέθοδο που φαίνεται στο σχήµα public State executerelax (State CurrentState, ArrayList gprecondlist) State newstate = new State(); 4. newstate.addstate(currentstate.this_state); 5. if (newstate.chkexistlist(this.precondlist)) 6. newstate.addnewpreds(this.addeffectlist); 7. return newstate; 8. Σχήµα Η µέθοδος executerelax της κλάσης GActoin.java η οποία εφαρµόζει µία ενέργεια στην τρέχουσα κατάσταση χωρίς να αφαιρεί όµως από αυτήν κανένα γεγονός
85 Η ευρετική τιµή η οποία επιστρέφεται είναι ο αριθµός των ενεργειών οι οποίες έ- χουν εφαρµοσθεί µέχρι να έχει παραχθεί κατάσταση η οποία να ικανοποιεί τους στόχους Η λύση του προβλήµατος Ποια όµως είναι η λύση του προβλήµατος και πώς αυτή επιστρέφεται για ανάγνωση από τον χρήστη; Σε όποιον και αλγόριθµο όταν δηµιουργούνται οι καταστάσεις-παιδιά η κάθε από αυτές διατηρεί µία λίστα από ακολουθούµενες καταστάσεις µε την αρχική (initial state) να βρίσκεται στην αρχή της. Κάθε µία από αυτές είναι κατάσταση γονέα της επόµενης και παιδί της προηγούµενης, αυτές οι σχέσεις φαίνονται στην εικόνα 6.3. Εικόνα 6.3. Σύνολο ακολουθούµενων καταστάσεων µαζί µε τις σχέσεις µεταξύ τους. Η Si είναι η αρχική (initial) και είναι η τελική Sf (final) κατάσταση Κάθε µία κατάσταση διατηρεί µία τέτοια ακολουθία, π.χ. η κατάσταση S3 έχει την λίστα Si, S1, S2, και η κατάσταση S4 Si, S1, S2, S3, έτσι η τελική κατάσταση είναι «ενηµερωµένη» για τα στάδια από τα οποία περνάει ο κόσµος του προβλήµατος µέχρι να φθάσει σε αυτήν. Αλλά ο στόχος ενός συστήµατος σχεδιασµού ενεργειών είναι η εύρεση µιας ακολουθίας από ενέργειες και όχι από καταστάσεις. Όµως αν υπάρχει η ακολουθία των καταστάσεων µπορεί κατευθείαν να βρεθεί η ακολουθία των ενεργειών οπότε οι δύο αυτές λίστες µπορεί να θεωρηθούν ισοδύναµες. Η αντιστοιχία «Κατάσταση Ενέργεια Επόµενη Κατάσταση» υλοποιείται µέσω της κλάσης State_Action_State.java η οποία διατηρεί αυτή τη σχέση και είναι σε θέση αν δοθούν δύο καταστάσεις να επιστρέψει την ενέργεια η οποία αλλάζει την πρώτη στην δεύτερη
86 6.3 Υλοποίηση της διασύνδεσης µε τον χρήστη. Η διασύνδεση µε τον χρήστη συνίσταται από ένα σύνολο παραθύρων, κλάσεις.java οι οποίες εκτείνουν (extends) την javax.swing.jframe κληρονοµούν τις ιδιότητες και τις µεθόδους της κλάσης JFrame, και τα οποία αλληλεπιδρούν µεταξύ τους. Υπάρχει ένα κεντρικό παράθυρο από το οποίο γίνεται ο έλεγχος ολόκληρου του συστήµατος εισαγωγή αρχείων PDDL, επιλογή αλγόριθµου, επιλογή ρυθµίσεων, προβολή των αποτελεσµάτων και πρόσθετων πληροφοριών. Κάθε λειτουργία του συστήµατος βρίσκεται υλοποιηµένη στο πεδίο ActionPerformed ενός κουµπιού και παίρνει εισόδους από τα υπόλοιπα στοιχεία του παραθύρου - jtextfiled, jcombobox, jlabel, jmenubar, jslider, jfilechooser, κ.α. Στην εικόνα 6.4. φαίνεται το κεντρικό παράθυρο. Τα δύο αρχεία κειµένου που περιέχουν εντολές PDDL εισάγονται µε την χρήση ε- νός επιλογέα αρχείων (jfilechooser) και τα µονοπάτια τους καταγράφονται στις δύο text field /βλ. σηµεία 7 και 8 της εικόνας 6.4/. Στη συνέχεια όταν πατηθεί το κουµπί «GO» /σηµείο 4 της εικόνας 6.4./ εκτελείται η µεταγλώττιση και αν ήταν επιτυχής ακολουθείται η δηµιουργία του πλάνου µε βάση του αλγορίθµου που επιλέχθηκε από την λίστα αλγορίθµων /σηµείο 3 της εικόνας 6.4./. Τα περιεχόµενα των δύο αρχείων εµφανίζονται στα text area /σηµεία 5 και 6 της εικόνας 6.4./ όπου ο χρήστης µπορεί να ελέγχει το περιεχόµενό τους και να κάνει αλλαγές. Σε περίπτωση όµως που ο χρήστης αλλάξει το περιεχόµενο των δύο αρχείων πρέπει αυτά να αποθηκευθούν και µετά να ξαναεισαχθούν στο σύστηµα µε την χρήση των σηµείων 1 και 2 που φαίνονται στην εικόνα Αλλιώς το σύστηµα δεν θα λάβει υπόψη τις αλλαγές
87 Εικόνα 6.4. Το κεντρικό παράθυρο του συστήµατος σχεδιασµού ενεργειών. Το κουµπί «GO» εκτελεί τις εντολές του σχήµατος Η εντολή της γραµµής 1. εκτελεί το parsing και της γραµµής 7 την εύρεση της λύσης (του πλάνου). 1. if (PDDL_planner.ParseIt(jTextField1.getText(), jtextfield2.gettext())) 2. //Checks if the parsing has been successfull 3. this.jlabel3.setvisible(true); 4. jbutton4.setenabled(true); 5. SolveSubMnu.setEnabled(true); 6. PDDL_planner.setBuildParameters(theOptions.ID_a, theoptions.id_b, theoptions.db_time); 7. if (PDDL_planner.BuildIt(jComboBox1.getSelectedIndex()) /*0-DFS, 1-BFS, 2-ID, 3-Identidem, 4-FF Search*/) 8. //Checks if the building of the plan is successfull 9. this.jlabel2.setvisible(true); 10. jbutton5.setenabled(true); 11. thesolution = PDDL_planner.theAnswer(); Σχήµα Ο κώδικας του κουµπιού «GO»
88 Αν όλη η διαδικασία έχει περάσει επιτυχώς εµφανίζεται ένα κουµπί «Solution», το πάτηµα του οποίου εµφανίζει το παράθυρο λύσης. Αυτό φαίνεται στην εικόνα 6.5. Εικόνα 6.5. Το παράθυρο προβολής της λύσης Η λύση δίνεται σε ένα πεδίο κειµένου (jtextarea) /βλ. σηµείο 1 της εικόνας 6.5/ και µπορεί να εµφανίζεται είτε σαν λίστα ενεργειών είτε σαν λίστα καταστάσεων του κόσµου. Αυτή η αλλαγή γίνεται µέσω του κουµπιού του σηµείου 3 στην εικόνα 6.5. Ένα µέτρο της απόδοσης του συστήµατος είναι ο χρόνος εύρεσης του πλάνου αυτός φαίνεται σε µία ετικέτα σηµείο 2 της εικόνας 6.5. Με την υλοποίηση µίας κατανοητής διασύνδεσης µε τον χρήστη το σύστηµα καθίσταται εύκολο στην χρήση και προσθέτοντας τις δυνατότητες που περιέχει διάφοροι αλγόριθµοι, ρυθµίσεις αυτό το σύστηµα σχεδιασµού ενεργειών γίνεται ένα ισχυρό εργαλείο επίλυσης προβληµάτων σχεδιασµού
Περιγραφή Προβλημάτων
 Τεχνητή Νοημοσύνη 02 Περιγραφή Προβλημάτων Φώτης Κόκκορας Τμ.Τεχν/γίας Πληροφορικής & Τηλ/νιών - ΤΕΙ Λάρισας Παραδείγματα Προβλημάτων κύβοι (blocks) Τρεις κύβοι βρίσκονται σε τυχαία διάταξη πάνω στο τραπέζι
Τεχνητή Νοημοσύνη 02 Περιγραφή Προβλημάτων Φώτης Κόκκορας Τμ.Τεχν/γίας Πληροφορικής & Τηλ/νιών - ΤΕΙ Λάρισας Παραδείγματα Προβλημάτων κύβοι (blocks) Τρεις κύβοι βρίσκονται σε τυχαία διάταξη πάνω στο τραπέζι
Πληροφορική 2. Τεχνητή νοημοσύνη
 Πληροφορική 2 Τεχνητή νοημοσύνη 1 2 Τι είναι τεχνητή νοημοσύνη; Τεχνητή νοημοσύνη (AI=Artificial Intelligence) είναι η μελέτη προγραμματισμένων συστημάτων τα οποία μπορούν να προσομοιώνουν μέχρι κάποιο
Πληροφορική 2 Τεχνητή νοημοσύνη 1 2 Τι είναι τεχνητή νοημοσύνη; Τεχνητή νοημοσύνη (AI=Artificial Intelligence) είναι η μελέτη προγραμματισμένων συστημάτων τα οποία μπορούν να προσομοιώνουν μέχρι κάποιο
Τεχνητή Νοημοσύνη. 2η διάλεξη (2015-16) Ίων Ανδρουτσόπουλος. http://www.aueb.gr/users/ion/
 Τεχνητή Νοημοσύνη 2η διάλεξη (2015-16) Ίων Ανδρουτσόπουλος http://www.aueb.gr/users/ion/ 1 Οι διαφάνειες αυτής της διάλεξης βασίζονται στα βιβλία: Τεχνητή Νοημοσύνη των Βλαχάβα κ.ά., 3η έκδοση, Β. Γκιούρδας
Τεχνητή Νοημοσύνη 2η διάλεξη (2015-16) Ίων Ανδρουτσόπουλος http://www.aueb.gr/users/ion/ 1 Οι διαφάνειες αυτής της διάλεξης βασίζονται στα βιβλία: Τεχνητή Νοημοσύνη των Βλαχάβα κ.ά., 3η έκδοση, Β. Γκιούρδας
Επίλυση προβληµάτων. Αλγόριθµοι Αναζήτησης
 Επίλυση προβληµάτων! Περιγραφή προβληµάτων Αλγόριθµοι αναζήτησης Αλγόριθµοι τυφλής αναζήτησης Αλγόριθµοι ευρετικής αναζήτησης Παιχνίδια δύο αντιπάλων Προβλήµατα ικανοποίησης περιορισµών Γενικά " Τεχνητή
Επίλυση προβληµάτων! Περιγραφή προβληµάτων Αλγόριθµοι αναζήτησης Αλγόριθµοι τυφλής αναζήτησης Αλγόριθµοι ευρετικής αναζήτησης Παιχνίδια δύο αντιπάλων Προβλήµατα ικανοποίησης περιορισµών Γενικά " Τεχνητή
Κεφάλαιο 7 : Είδη, Τεχνικές, και Περιβάλλοντα Προγραµµατισµού
 ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΥΠΟΛΟΓΙΣΤΩΝ Κεφάλαιο 7 : Είδη, Τεχνικές, και Περιβάλλοντα Προγραµµατισµού ( Απαντήσεις & Λύσεις Βιβλίου) 1. Σκοποί κεφαλαίου Κύκλος ανάπτυξης προγράµµατος Κατηγορίες γλωσσών προγραµµατισµού
ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΥΠΟΛΟΓΙΣΤΩΝ Κεφάλαιο 7 : Είδη, Τεχνικές, και Περιβάλλοντα Προγραµµατισµού ( Απαντήσεις & Λύσεις Βιβλίου) 1. Σκοποί κεφαλαίου Κύκλος ανάπτυξης προγράµµατος Κατηγορίες γλωσσών προγραµµατισµού
Α. Ερωτήσεις Ανάπτυξης
 οµηµένος Προγραµµατισµός-Κεφάλαιο 7 Σελίδα 1 α ό 10 ΕΝΟΤΗΤΑ ΙΙΙ (ΠΡΟΓΡΑΜΜΑΤΑ) ΚΕΦΑΛΑΙΟ 7: Είδη, Τεχνικές και Περιβάλλοντα Προγραµµατισµού Α. Ερωτήσεις Ανάπτυξης 1. Τι ονοµάζουµε γλώσσα προγραµµατισµού;
οµηµένος Προγραµµατισµός-Κεφάλαιο 7 Σελίδα 1 α ό 10 ΕΝΟΤΗΤΑ ΙΙΙ (ΠΡΟΓΡΑΜΜΑΤΑ) ΚΕΦΑΛΑΙΟ 7: Είδη, Τεχνικές και Περιβάλλοντα Προγραµµατισµού Α. Ερωτήσεις Ανάπτυξης 1. Τι ονοµάζουµε γλώσσα προγραµµατισµού;
Τεχνικές σχεδίασης προγραμμάτων, Προγραμματιστικά Περιβάλλοντα
 Τεχνικές σχεδίασης προγραμμάτων, Προγραμματιστικά Περιβάλλοντα Ενότητες βιβλίου: 6.4, 6.7 Ώρες διδασκαλίας: 1 Τεχνικές σχεδίασης προγραμμάτων Στο βιβλίο γίνεται αναφορά σε μία τεχνική για την ανάπτυξη
Τεχνικές σχεδίασης προγραμμάτων, Προγραμματιστικά Περιβάλλοντα Ενότητες βιβλίου: 6.4, 6.7 Ώρες διδασκαλίας: 1 Τεχνικές σχεδίασης προγραμμάτων Στο βιβλίο γίνεται αναφορά σε μία τεχνική για την ανάπτυξη
Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή
 Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή raniah@hua.gr 1 Περιγραφή Προβλημάτων Διαισθητικά, σε ένα πρόβλημα υπάρχει μια δεδομένη κατάσταση
Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή raniah@hua.gr 1 Περιγραφή Προβλημάτων Διαισθητικά, σε ένα πρόβλημα υπάρχει μια δεδομένη κατάσταση
Κεφάλαιο 10 ο Υποπρογράµµατα
 Κεφάλαιο 10 ο Υποπρογράµµατα Ανάπτυξη Εφαρµογών σε Προγραµµατιστικό Περιβάλλον Η αντιµετώπιση των σύνθετων προβληµάτων και η ανάπτυξη των αντίστοιχων προγραµµάτων µπορεί να γίνει µε την ιεραρχική σχεδίαση,
Κεφάλαιο 10 ο Υποπρογράµµατα Ανάπτυξη Εφαρµογών σε Προγραµµατιστικό Περιβάλλον Η αντιµετώπιση των σύνθετων προβληµάτων και η ανάπτυξη των αντίστοιχων προγραµµάτων µπορεί να γίνει µε την ιεραρχική σχεδίαση,
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ
 ΘΕΜΑ 1 ο (2.5 µονάδες) ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ Τελικές εξετάσεις 25 Ιουνίου 2003 ιάρκεια: 2 ώρες α) Σε ποια περίπτωση
ΘΕΜΑ 1 ο (2.5 µονάδες) ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ Τελικές εξετάσεις 25 Ιουνίου 2003 ιάρκεια: 2 ώρες α) Σε ποια περίπτωση
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 15 Ιουνίου 2009 1 / 26 Εισαγωγή Η ϑεωρία
Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 15 Ιουνίου 2009 1 / 26 Εισαγωγή Η ϑεωρία
ΥΣ02 Τεχνητή Νοημοσύνη Χειμερινό Εξάμηνο
 ΥΣ02 Τεχνητή Νοημοσύνη Χειμερινό Εξάμηνο 2010-2011 Πρώτη Σειρά Ασκήσεων (20% του συνολικού βαθμού στο μάθημα, Άριστα = 390 μονάδες) Ημερομηνία Ανακοίνωσης: 6/10/2010 Ημερομηνία Παράδοσης: 15/11/2010 σύμφωνα
ΥΣ02 Τεχνητή Νοημοσύνη Χειμερινό Εξάμηνο 2010-2011 Πρώτη Σειρά Ασκήσεων (20% του συνολικού βαθμού στο μάθημα, Άριστα = 390 μονάδες) Ημερομηνία Ανακοίνωσης: 6/10/2010 Ημερομηνία Παράδοσης: 15/11/2010 σύμφωνα
ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΜΑΘΗΜΑ 2 ΑΝΑΠΑΡΑΣΤΑΣΗ - ΤΕΧΝΙΚΕΣ ΤΝ (1)
 ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΜΑΘΗΜΑ 2 ΑΝΑΠΑΡΑΣΤΑΣΗ - ΤΕΧΝΙΚΕΣ ΤΝ (1) 2. ΑΝΑΠΑΡΑΣΤΑΣΗ ΠΡΟΒΛΗΜΑΤΟΣ H υλοποίηση ενός προβλήµατος σε σύστηµα Η/Υ που επιδεικνύει ΤΝ 1 απαιτεί: Την κατάλληλη περιγραφή του προβλήµατος
ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ ΜΑΘΗΜΑ 2 ΑΝΑΠΑΡΑΣΤΑΣΗ - ΤΕΧΝΙΚΕΣ ΤΝ (1) 2. ΑΝΑΠΑΡΑΣΤΑΣΗ ΠΡΟΒΛΗΜΑΤΟΣ H υλοποίηση ενός προβλήµατος σε σύστηµα Η/Υ που επιδεικνύει ΤΝ 1 απαιτεί: Την κατάλληλη περιγραφή του προβλήµατος
Κεφ. 2 Θέματα Θεωρητικής Επιστήμης Υπολογιστών. Κοντογιάννης Βασίλειος ΠΕ19
 Κεφ. 2 Θέματα Θεωρητικής Επιστήμης Υπολογιστών Κεφ. 2 Θεωρητική Επιστήμη Υπολογιστών 2.3.1.1 Έννοια προγράμματος Τι είναι πρόγραμμα και τι προγραμματισμός; Πρόγραμμα είναι το σύνολο εντολών που χρειάζεται
Κεφ. 2 Θέματα Θεωρητικής Επιστήμης Υπολογιστών Κεφ. 2 Θεωρητική Επιστήμη Υπολογιστών 2.3.1.1 Έννοια προγράμματος Τι είναι πρόγραμμα και τι προγραμματισμός; Πρόγραμμα είναι το σύνολο εντολών που χρειάζεται
FORTRAN και Αντικειμενοστραφής Προγραμματισμός
 FORTRAN και Αντικειμενοστραφής Προγραμματισμός Παραδόσεις Μαθήματος 2016 Δρ Γ Παπαλάμπρου Επίκουρος Καθηγητής ΕΜΠ georgepapalambrou@lmentuagr Εργαστήριο Ναυτικής Μηχανολογίας (Κτίριο Λ) Σχολή Ναυπηγών
FORTRAN και Αντικειμενοστραφής Προγραμματισμός Παραδόσεις Μαθήματος 2016 Δρ Γ Παπαλάμπρου Επίκουρος Καθηγητής ΕΜΠ georgepapalambrou@lmentuagr Εργαστήριο Ναυτικής Μηχανολογίας (Κτίριο Λ) Σχολή Ναυπηγών
ιδάσκων: ηµήτρης Ζεϊναλιπούρ
 Κεφάλαιο 1.3-1.4: Εισαγωγή Στον Προγραµµατισµό ( ιάλεξη 2) ιδάσκων: ηµήτρης Ζεϊναλιπούρ Περιεχόµενα Εισαγωγικές Έννοιες - Ορισµοί Ο κύκλος ανάπτυξης προγράµµατος Παραδείγµατα Πότε χρησιµοποιούµε υπολογιστή?
Κεφάλαιο 1.3-1.4: Εισαγωγή Στον Προγραµµατισµό ( ιάλεξη 2) ιδάσκων: ηµήτρης Ζεϊναλιπούρ Περιεχόµενα Εισαγωγικές Έννοιες - Ορισµοί Ο κύκλος ανάπτυξης προγράµµατος Παραδείγµατα Πότε χρησιµοποιούµε υπολογιστή?
Γλώσσες υψηλού επιπέδου Περιέχουν περισσότερες εντολές για την εκτέλεση πολύπλοκων εργασιών Τα προγράµµατα µεταφράζονται σε γλώσσα µηχανής είτε από το
 Σηµαντικά σηµεία κεφαλαίου Τα τρία στάδια επίλυσης ενός προβλήµατος: Ακριβής προσδιορισµό του προβλήµατος Ανάπτυξη του αντίστοιχου αλγορίθµου. ιατύπωση του αλγορίθµου σε κατανοητή µορφή από τον υπολογιστή.
Σηµαντικά σηµεία κεφαλαίου Τα τρία στάδια επίλυσης ενός προβλήµατος: Ακριβής προσδιορισµό του προβλήµατος Ανάπτυξη του αντίστοιχου αλγορίθµου. ιατύπωση του αλγορίθµου σε κατανοητή µορφή από τον υπολογιστή.
ΑΕΠΠ Ερωτήσεις θεωρίας
 ΑΕΠΠ Ερωτήσεις θεωρίας Κεφάλαιο 1 1. Τα δεδομένα μπορούν να παρέχουν πληροφορίες όταν υποβάλλονται σε 2. Το πρόβλημα μεγιστοποίησης των κερδών μιας επιχείρησης είναι πρόβλημα 3. Για την επίλυση ενός προβλήματος
ΑΕΠΠ Ερωτήσεις θεωρίας Κεφάλαιο 1 1. Τα δεδομένα μπορούν να παρέχουν πληροφορίες όταν υποβάλλονται σε 2. Το πρόβλημα μεγιστοποίησης των κερδών μιας επιχείρησης είναι πρόβλημα 3. Για την επίλυση ενός προβλήματος
Σου προτείνω να τυπώσεις τις επόμενες τέσσερις σελίδες σε ένα φύλο διπλής όψης και να τις έχεις μαζί σου για εύκολη αναφορά.
 AeppAcademy.com facebook.com/aeppacademy Γεια. Σου προτείνω να τυπώσεις τις επόμενες τέσσερις σελίδες σε ένα φύλο διπλής όψης και να τις έχεις μαζί σου για εύκολη αναφορά. Καλή Ανάγνωση & Καλή Επιτυχία
AeppAcademy.com facebook.com/aeppacademy Γεια. Σου προτείνω να τυπώσεις τις επόμενες τέσσερις σελίδες σε ένα φύλο διπλής όψης και να τις έχεις μαζί σου για εύκολη αναφορά. Καλή Ανάγνωση & Καλή Επιτυχία
ΚΕΦΑΛΑΙΟ 8 Η ΓΛΩΣΣΑ PASCAL
 8.1. Εισαγωγή ΚΕΦΑΛΑΙΟ 8 Η ΓΛΩΣΣΑ PACAL Πως προέκυψε η γλώσσα προγραμματισμού Pascal και ποια είναι τα γενικά της χαρακτηριστικά; Σχεδιάστηκε από τον Ελβετό επιστήμονα της Πληροφορικής Nicklaus Wirth to
8.1. Εισαγωγή ΚΕΦΑΛΑΙΟ 8 Η ΓΛΩΣΣΑ PACAL Πως προέκυψε η γλώσσα προγραμματισμού Pascal και ποια είναι τα γενικά της χαρακτηριστικά; Σχεδιάστηκε από τον Ελβετό επιστήμονα της Πληροφορικής Nicklaus Wirth to
ΜΑΘΗΜΑ: Εισαγωγή στις Αρχές της Επιστήμης των Η/Υ. 1 η ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ
 ΜΑΘΗΜΑ: Εισαγωγή στις Αρχές της Επιστήμης των Η/Υ 1 η ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Στόχος Θεματικής Ενότητας Οι μαθητές να περιγράφουν τους βασικούς τομείς της Επιστήμης των Υπολογιστών και να μπορούν
ΜΑΘΗΜΑ: Εισαγωγή στις Αρχές της Επιστήμης των Η/Υ 1 η ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Στόχος Θεματικής Ενότητας Οι μαθητές να περιγράφουν τους βασικούς τομείς της Επιστήμης των Υπολογιστών και να μπορούν
Η-Υ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ. Εργαστήριο 1 Εισαγωγή στη C. Σοφία Μπαλτζή s.mpaltzi@di.uoa.gr
 Η-Υ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Εργαστήριο 1 Εισαγωγή στη C Σοφία Μπαλτζή s.mpaltzi@di.uoa.gr Διαδικαστικά Ιστοσελίδα μαθήματος: http://eclass.uoa.gr/courses/f30/ Υποχρεωτική παρακολούθηση: Παρασκευή 14:00 16:00 στην
Η-Υ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Εργαστήριο 1 Εισαγωγή στη C Σοφία Μπαλτζή s.mpaltzi@di.uoa.gr Διαδικαστικά Ιστοσελίδα μαθήματος: http://eclass.uoa.gr/courses/f30/ Υποχρεωτική παρακολούθηση: Παρασκευή 14:00 16:00 στην
Περιεχόµενα. Ανασκόπηση - Ορισµοί. Ο κύκλος ανάπτυξης προγράµµατος. Γλώσσες Προγραµµατισµού Ασκήσεις
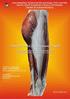 Προγραµµατισµός Η/Υ Ανασκόπηση - Ορισµοί Περιεχόµενα Ο κύκλος ανάπτυξης προγράµµατος Περιγραφή προβλήµατος Ανάλυση προβλήµατος Λογικό ιάγραµµα Ψευδοκώδικας Κωδικοποίηση Συντήρηση Γλώσσες Προγραµµατισµού
Προγραµµατισµός Η/Υ Ανασκόπηση - Ορισµοί Περιεχόµενα Ο κύκλος ανάπτυξης προγράµµατος Περιγραφή προβλήµατος Ανάλυση προβλήµατος Λογικό ιάγραµµα Ψευδοκώδικας Κωδικοποίηση Συντήρηση Γλώσσες Προγραµµατισµού
Μέθοδοι Σχεδίασης κίνησης
 Μέθοδοι Σχεδίασης κίνησης Τασούδης Σταύρος Ο προγραμματισμός τροχιάς(trajectory planning) είναι η κίνηση από το σημείο Α προς το σημείο Β αποφεύγοντας τις συγκρούσεις με την πάροδο του χρόνου. Αυτό μπορεί
Μέθοδοι Σχεδίασης κίνησης Τασούδης Σταύρος Ο προγραμματισμός τροχιάς(trajectory planning) είναι η κίνηση από το σημείο Α προς το σημείο Β αποφεύγοντας τις συγκρούσεις με την πάροδο του χρόνου. Αυτό μπορεί
Επιµέλεια Θοδωρής Πιερράτος
 Εισαγωγή στον προγραµµατισµό Η έννοια του προγράµµατος Ο προγραµµατισµός ασχολείται µε τη δηµιουργία του προγράµµατος, δηλαδή του συνόλου εντολών που πρέπει να δοθούν στον υπολογιστή ώστε να υλοποιηθεί
Εισαγωγή στον προγραµµατισµό Η έννοια του προγράµµατος Ο προγραµµατισµός ασχολείται µε τη δηµιουργία του προγράµµατος, δηλαδή του συνόλου εντολών που πρέπει να δοθούν στον υπολογιστή ώστε να υλοποιηθεί
Δομές Δεδομένων & Αλγόριθμοι
 Θέματα Απόδοσης Αλγορίθμων 1 Η Ανάγκη για Δομές Δεδομένων Οι δομές δεδομένων οργανώνουν τα δεδομένα πιο αποδοτικά προγράμματα Πιο ισχυροί υπολογιστές πιο σύνθετες εφαρμογές Οι πιο σύνθετες εφαρμογές απαιτούν
Θέματα Απόδοσης Αλγορίθμων 1 Η Ανάγκη για Δομές Δεδομένων Οι δομές δεδομένων οργανώνουν τα δεδομένα πιο αποδοτικά προγράμματα Πιο ισχυροί υπολογιστές πιο σύνθετες εφαρμογές Οι πιο σύνθετες εφαρμογές απαιτούν
Προβλήματα, αλγόριθμοι, ψευδοκώδικας
 Προβλήματα, αλγόριθμοι, ψευδοκώδικας October 11, 2011 Στο μάθημα Αλγοριθμική και Δομές Δεδομένων θα ασχοληθούμε με ένα μέρος της διαδικασίας επίλυσης υπολογιστικών προβλημάτων. Συγκεκριμένα θα δούμε τι
Προβλήματα, αλγόριθμοι, ψευδοκώδικας October 11, 2011 Στο μάθημα Αλγοριθμική και Δομές Δεδομένων θα ασχοληθούμε με ένα μέρος της διαδικασίας επίλυσης υπολογιστικών προβλημάτων. Συγκεκριμένα θα δούμε τι
Σχεδιασµός βασισµένος σε συνιστώσες
 Σχεδιασµός βασισµένος σε συνιστώσες 1 Ενδεικτικά περιεχόµενα του κεφαλαίου Ποια είναι τα "άτοµα", από τα οποία κατασκευάζονται οι υπηρεσίες; Πώς οργανώνουµε τις συνιστώσες σε ένα αρµονικό σύνολο; Τι είναι
Σχεδιασµός βασισµένος σε συνιστώσες 1 Ενδεικτικά περιεχόµενα του κεφαλαίου Ποια είναι τα "άτοµα", από τα οποία κατασκευάζονται οι υπηρεσίες; Πώς οργανώνουµε τις συνιστώσες σε ένα αρµονικό σύνολο; Τι είναι
Δομημένος Προγραμματισμός
 Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Δομημένος Προγραμματισμός Ενότητα 1: Εισαγωγή Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά Το έργο
Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ιονίων Νήσων Δομημένος Προγραμματισμός Ενότητα 1: Εισαγωγή Το περιεχόμενο του μαθήματος διατίθεται με άδεια Creative Commons εκτός και αν αναφέρεται διαφορετικά Το έργο
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΜΑΡΙΑ Σ. ΖΙΩΓΑ ΚΑΘΗΓΗΤΡΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟ
 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΙΜΕΛΕΙΑ: ΜΑΡΙΑ Σ. ΖΙΩΓΑ ΚΑΘΗΓΗΤΡΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ 6 ΟΥ ΚΕΦΑΛΑΙΟΥ ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟ 6.1 Τι ονοµάζουµε πρόγραµµα υπολογιστή; Ένα πρόγραµµα
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΙΜΕΛΕΙΑ: ΜΑΡΙΑ Σ. ΖΙΩΓΑ ΚΑΘΗΓΗΤΡΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ 6 ΟΥ ΚΕΦΑΛΑΙΟΥ ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟ 6.1 Τι ονοµάζουµε πρόγραµµα υπολογιστή; Ένα πρόγραµµα
Επίλυση προβλημάτων με αναζήτηση
 Επίλυση προβλημάτων με αναζήτηση Περιεχόμενα Μέθοδοι (πράκτορες) επίλυσης προβλημάτων Προβλήματα και Λύσεις Προβλήματα παιχνίδια Προβλήματα του πραγματικού κόσμου Αναζήτηση λύσεων Δέντρο αναζήτησης Στρατηγικές
Επίλυση προβλημάτων με αναζήτηση Περιεχόμενα Μέθοδοι (πράκτορες) επίλυσης προβλημάτων Προβλήματα και Λύσεις Προβλήματα παιχνίδια Προβλήματα του πραγματικού κόσμου Αναζήτηση λύσεων Δέντρο αναζήτησης Στρατηγικές
Ε Ι Α Γ Ω Γ Η Σ Ο Ν Π Ρ Ο Γ Ρ Α Μ Μ Α Σ Ι Μ Ο Κ Ε Υ Α Λ Α Ι Ο 6. Σο πρόγραμμα γράφεται σε κάποια γλώσσα προγραμματισμού.
 Κεφάλαιο 6 6.1 Η έννοια του προγράμματος Η επίλυση ενός προβλήματος με τον υπολογιστή περιλαμβάνει τρία σημαντικά στάδια : Σον ακριβή προσδιορισμό του προβλήματος Σην ανάπτυξη του αντίστοιχου αλγορίθμου
Κεφάλαιο 6 6.1 Η έννοια του προγράμματος Η επίλυση ενός προβλήματος με τον υπολογιστή περιλαμβάνει τρία σημαντικά στάδια : Σον ακριβή προσδιορισμό του προβλήματος Σην ανάπτυξη του αντίστοιχου αλγορίθμου
Εξελιγµένες Τεχνικές Σχεδιασµού
 Κεφάλαιο 16 Εξελιγµένες Τεχνικές Σχεδιασµού Τεχνητή Νοηµοσύνη - Β' Έκδοση Ι. Βλαχάβας, Π. Κεφαλάς, Ν. Βασιλειάδης, Φ. Κόκκορας, Η. Σακελλαρίου Σχεδιασµός Βασισµένος σε Γράφους Γράφος σχεδιασµού (1/2) Ο
Κεφάλαιο 16 Εξελιγµένες Τεχνικές Σχεδιασµού Τεχνητή Νοηµοσύνη - Β' Έκδοση Ι. Βλαχάβας, Π. Κεφαλάς, Ν. Βασιλειάδης, Φ. Κόκκορας, Η. Σακελλαρίου Σχεδιασµός Βασισµένος σε Γράφους Γράφος σχεδιασµού (1/2) Ο
ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ. Δοµές Δεδοµένων
 ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ AM: Δοµές Δεδοµένων Πτυχιακή Εξεταστική Ιούλιος 2014 Διδάσκων : Ευάγγελος Μαρκάκης 09.07.2014 ΥΠΟΓΡΑΦΗ ΕΠΟΠΤΗ: Διάρκεια εξέτασης : 2 ώρες
ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ AM: Δοµές Δεδοµένων Πτυχιακή Εξεταστική Ιούλιος 2014 Διδάσκων : Ευάγγελος Μαρκάκης 09.07.2014 ΥΠΟΓΡΑΦΗ ΕΠΟΠΤΗ: Διάρκεια εξέτασης : 2 ώρες
ΙΚΑΝΟΠΟΙΗΣΗ ΠΕΡΙΟΡΙΣΜΩΝ
 ΙΚΑΝΟΠΟΙΗΣΗ ΠΕΡΙΟΡΙΣΜΩΝ (ΜΕ ΒΑΣΗ ΤΟ ΚΕΦ. 6 ΤΟΥ ΒΙΒΛΙΟΥ «ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ» ΤΩΝ ΒΛΑΧΑΒΑ, ΚΕΦΑΛΑ, ΒΑΣΙΛΕΙΑ Η, ΚΟΚΚΟΡΑ & ΣΑΚΕΛΛΑΡΙΟΥ) Ι. ΧΑΤΖΗΛΥΓΕΡΟΥ ΗΣ ΠΡΟΒΛΗΜΑΤΑ ΙΚΑΝΟΠΟΙΗΣΗΣ ΠΕΡΙΟΡΙΣΜΩΝ Είναι γνωστές µερικές
ΙΚΑΝΟΠΟΙΗΣΗ ΠΕΡΙΟΡΙΣΜΩΝ (ΜΕ ΒΑΣΗ ΤΟ ΚΕΦ. 6 ΤΟΥ ΒΙΒΛΙΟΥ «ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ» ΤΩΝ ΒΛΑΧΑΒΑ, ΚΕΦΑΛΑ, ΒΑΣΙΛΕΙΑ Η, ΚΟΚΚΟΡΑ & ΣΑΚΕΛΛΑΡΙΟΥ) Ι. ΧΑΤΖΗΛΥΓΕΡΟΥ ΗΣ ΠΡΟΒΛΗΜΑΤΑ ΙΚΑΝΟΠΟΙΗΣΗΣ ΠΕΡΙΟΡΙΣΜΩΝ Είναι γνωστές µερικές
Επίλυση Προβλημάτων 1
 Επίλυση Προβλημάτων 1 Επίλυση Προβλημάτων Περιγραφή Προβλημάτων Αλγόριθμοι αναζήτησης Αλγόριθμοι τυφλής αναζήτησης Αναζήτηση πρώτα σε βάθος Αναζήτηση πρώτα σε πλάτος (ΒFS) Αλγόριθμοι ευρετικής αναζήτησης
Επίλυση Προβλημάτων 1 Επίλυση Προβλημάτων Περιγραφή Προβλημάτων Αλγόριθμοι αναζήτησης Αλγόριθμοι τυφλής αναζήτησης Αναζήτηση πρώτα σε βάθος Αναζήτηση πρώτα σε πλάτος (ΒFS) Αλγόριθμοι ευρετικής αναζήτησης
Κεφάλαιο 6. Ικανοποίηση Περιορισµών. Τεχνητή Νοηµοσύνη - Β' Έκδοση. Ι. Βλαχάβας, Π. Κεφαλάς, Ν. Βασιλειάδης, Φ. Κόκκορας, Η.
 Κεφάλαιο 6 Ικανοποίηση Περιορισµών Τεχνητή Νοηµοσύνη - Β' Έκδοση Ι. Βλαχάβας, Π. Κεφαλάς, Ν. Βασιλειάδης, Φ. Κόκκορας, Η. Σακελλαρίου Ικανοποίηση Περιορισµών Ένα πρόβληµα ικανοποίησης περιορισµών (constraint
Κεφάλαιο 6 Ικανοποίηση Περιορισµών Τεχνητή Νοηµοσύνη - Β' Έκδοση Ι. Βλαχάβας, Π. Κεφαλάς, Ν. Βασιλειάδης, Φ. Κόκκορας, Η. Σακελλαρίου Ικανοποίηση Περιορισµών Ένα πρόβληµα ικανοποίησης περιορισµών (constraint
ΠΛΗ 405 Τεχνητή Νοηµοσύνη
 ΠΛΗ 405 Τεχνητή Νοηµοσύνη Σχεδιασµός και ράση στον Πραγµατικό Κόσµο Τµήµα Ηλεκτρονικών Μηχανικών και Μηχανικών Υ ολογιστών Πολυτεχνείο Κρήτης Ε ανάληψη Γραφήµατα σχεδιασµού δοµή δεδοµένων για κατασκευή
ΠΛΗ 405 Τεχνητή Νοηµοσύνη Σχεδιασµός και ράση στον Πραγµατικό Κόσµο Τµήµα Ηλεκτρονικών Μηχανικών και Μηχανικών Υ ολογιστών Πολυτεχνείο Κρήτης Ε ανάληψη Γραφήµατα σχεδιασµού δοµή δεδοµένων για κατασκευή
ΚΕΦΑΛΑΙΟ 7 ΕΙ Η, ΤΕΧΝΙΚΕΣ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΑ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ
 ΚΕΦΑΛΑΙΟ 7 ΕΙ Η, ΤΕΧΝΙΚΕΣ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΑ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ 7.1. Ανάπτυξη Προγράµµατος Τι είναι το Πρόγραµµα; Το Πρόγραµµα: Είναι ένα σύνολο εντολών για την εκτέλεση ορισµένων λειτουργιών από τον υπολογιστή.
ΚΕΦΑΛΑΙΟ 7 ΕΙ Η, ΤΕΧΝΙΚΕΣ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΑ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ 7.1. Ανάπτυξη Προγράµµατος Τι είναι το Πρόγραµµα; Το Πρόγραµµα: Είναι ένα σύνολο εντολών για την εκτέλεση ορισµένων λειτουργιών από τον υπολογιστή.
ΚΕΦΑΛΑΙΟ 18. 18 Μηχανική Μάθηση
 ΚΕΦΑΛΑΙΟ 18 18 Μηχανική Μάθηση Ένα φυσικό ή τεχνητό σύστηµα επεξεργασίας πληροφορίας συµπεριλαµβανοµένων εκείνων µε δυνατότητες αντίληψης, µάθησης, συλλογισµού, λήψης απόφασης, επικοινωνίας και δράσης
ΚΕΦΑΛΑΙΟ 18 18 Μηχανική Μάθηση Ένα φυσικό ή τεχνητό σύστηµα επεξεργασίας πληροφορίας συµπεριλαµβανοµένων εκείνων µε δυνατότητες αντίληψης, µάθησης, συλλογισµού, λήψης απόφασης, επικοινωνίας και δράσης
<<ΔΗΜΗΤΡΗΣ ΜΑΝΩΛΗΣ ΦΥΣΙΚΟΣ ΜCs>> 1
 ΚΕΦΑΛΑΙΟ 7 ο ΠΡΟΓΡΑΜΜΑ : Το πρόγραμμα αποτελείται από μια σειρά οδηγιών, που ονομάζονται εντολές, για την εκτέλεση τέτοιου είδους πράξεων, καθώς επίσης και από ένα σύνολο πρόσθετων οδηγιών ελέγχου, που
ΚΕΦΑΛΑΙΟ 7 ο ΠΡΟΓΡΑΜΜΑ : Το πρόγραμμα αποτελείται από μια σειρά οδηγιών, που ονομάζονται εντολές, για την εκτέλεση τέτοιου είδους πράξεων, καθώς επίσης και από ένα σύνολο πρόσθετων οδηγιών ελέγχου, που
Ασκήσεις μελέτης της 4 ης διάλεξης. ), για οποιοδήποτε μονοπάτι n 1
 Οικονομικό Πανεπιστήμιο Αθηνών, Τμήμα Πληροφορικής Μάθημα: Τεχνητή Νοημοσύνη, 2016 17 Διδάσκων: Ι. Ανδρουτσόπουλος Ασκήσεις μελέτης της 4 ης διάλεξης 4.1. (α) Αποδείξτε ότι αν η h είναι συνεπής, τότε h(n
Οικονομικό Πανεπιστήμιο Αθηνών, Τμήμα Πληροφορικής Μάθημα: Τεχνητή Νοημοσύνη, 2016 17 Διδάσκων: Ι. Ανδρουτσόπουλος Ασκήσεις μελέτης της 4 ης διάλεξης 4.1. (α) Αποδείξτε ότι αν η h είναι συνεπής, τότε h(n
Ερωτήσεις πολλαπλής επιλογής - Κεφάλαιο 2. Α1. Ο αλγόριθμος είναι απαραίτητος μόνο για την επίλυση προβλημάτων πληροφορικής
 Ερωτήσεις πολλαπλής επιλογής - Κεφάλαιο 2 Α1. Ο αλγόριθμος είναι απαραίτητος μόνο για την επίλυση προβλημάτων πληροφορικής Α2. Ο αλγόριθμος αποτελείται από ένα πεπερασμένο σύνολο εντολών Α3. Ο αλγόριθμος
Ερωτήσεις πολλαπλής επιλογής - Κεφάλαιο 2 Α1. Ο αλγόριθμος είναι απαραίτητος μόνο για την επίλυση προβλημάτων πληροφορικής Α2. Ο αλγόριθμος αποτελείται από ένα πεπερασμένο σύνολο εντολών Α3. Ο αλγόριθμος
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ Ανάπτυξη μιας προσαρμοστικής πολιτικής αντικατάστασης αρχείων, με χρήση
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ Ανάπτυξη μιας προσαρμοστικής πολιτικής αντικατάστασης αρχείων, με χρήση
Κεφάλαιο 6 ο Εισαγωγή στον Προγραμματισμό 1
 Κεφάλαιο 6 ο Εισαγωγή στον Προγραμματισμό 1 Ποιες γλώσσες αναφέρονται ως φυσικές και ποιες ως τεχνητές; Ως φυσικές γλώσσες αναφέρονται εκείνες οι οποίες χρησιμοποιούνται για την επικοινωνία μεταξύ ανθρώπων,
Κεφάλαιο 6 ο Εισαγωγή στον Προγραμματισμό 1 Ποιες γλώσσες αναφέρονται ως φυσικές και ποιες ως τεχνητές; Ως φυσικές γλώσσες αναφέρονται εκείνες οι οποίες χρησιμοποιούνται για την επικοινωνία μεταξύ ανθρώπων,
ΠΛΗ 405 Τεχνητή Νοηµοσύνη 2006. Ε ανάληψη. δοµή δεδοµένων για κατασκευή ευρετικών συναρτήσεων Ο αλγόριθµος GraphPlan
 ΠΛΗ 405 Τεχνητή Νοηµοσύνη Σχεδιασµός και ράση στον Πραγµατικό Κόσµο Τµήµα Ηλεκτρονικών Μηχανικών και Μηχανικών Υ ολογιστών Πολυτεχνείο Κρήτης Ε ανάληψη Γραφήµατα σχεδιασµού δοµή δεδοµένων για κατασκευή
ΠΛΗ 405 Τεχνητή Νοηµοσύνη Σχεδιασµός και ράση στον Πραγµατικό Κόσµο Τµήµα Ηλεκτρονικών Μηχανικών και Μηχανικών Υ ολογιστών Πολυτεχνείο Κρήτης Ε ανάληψη Γραφήµατα σχεδιασµού δοµή δεδοµένων για κατασκευή
Θεωρητικές Ασκήσεις. ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ. 1 ο Μέρος
 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ. 1 ο Μέρος Θέμα 1 Δίνονται τα παρακάτω τμήματα αλγορίθμου Α. βαλίτσα Αληθής εισιτήριο Αληθής ταξίδι βαλίτσα και εισιτήριο Τι τιμή θα έχει η λογική μεταβλητή
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ. 1 ο Μέρος Θέμα 1 Δίνονται τα παρακάτω τμήματα αλγορίθμου Α. βαλίτσα Αληθής εισιτήριο Αληθής ταξίδι βαλίτσα και εισιτήριο Τι τιμή θα έχει η λογική μεταβλητή
Ασκήσεις μελέτης της 8 ης διάλεξης
 Οικονομικό Πανεπιστήμιο Αθηνών, Τμήμα Πληροφορικής Μάθημα: Τεχνητή Νοημοσύνη, 2017 18 Διδάσκων: Ι. Ανδρουτσόπουλος Ασκήσεις μελέτης της 8 ης διάλεξης 8.1. (i) Έστω ότι α και β είναι δύο τύποι της προτασιακής
Οικονομικό Πανεπιστήμιο Αθηνών, Τμήμα Πληροφορικής Μάθημα: Τεχνητή Νοημοσύνη, 2017 18 Διδάσκων: Ι. Ανδρουτσόπουλος Ασκήσεις μελέτης της 8 ης διάλεξης 8.1. (i) Έστω ότι α και β είναι δύο τύποι της προτασιακής
Επίλυση προβληµάτων. Περιγραφή προβληµάτων Αλγόριθµοι αναζήτησης Αλγόριθµοι τυφλής αναζήτησης Αλγόριθµοι ευρετικής αναζήτησης
 Επίλυση προβληµάτων Περιγραφή προβληµάτων Αλγόριθµοι αναζήτησης Αλγόριθµοι τυφλής αναζήτησης Αλγόριθµοι ευρετικής αναζήτησης! Παιχνίδια δύο αντιπάλων Προβλήµατα ικανοποίησης περιορισµών Γενικά " Ντετερµινιστικά
Επίλυση προβληµάτων Περιγραφή προβληµάτων Αλγόριθµοι αναζήτησης Αλγόριθµοι τυφλής αναζήτησης Αλγόριθµοι ευρετικής αναζήτησης! Παιχνίδια δύο αντιπάλων Προβλήµατα ικανοποίησης περιορισµών Γενικά " Ντετερµινιστικά
Αλγόριθμοι και Δομές Δεδομένων (Ι) (εισαγωγικές έννοιες)
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 2015-16 Αλγόριθμοι και Δομές Δεδομένων (Ι) (εισαγωγικές έννοιες) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Τι είναι
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 2015-16 Αλγόριθμοι και Δομές Δεδομένων (Ι) (εισαγωγικές έννοιες) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Τι είναι
ΠΑΙΓΝΙΑ Παιχνίδια Γενική Θεώρηση μεγιστοποιήσει την πιθανότητά
 ΠΑΙΓΝΙΑ Παιχνίδια Γενική Θεώρηση: Έστω ότι έχουμε τους παίκτες Χ και Υ. Ο κάθε παίκτης, σε κάθε κίνηση που κάνει, προσπαθεί να μεγιστοποιήσει την πιθανότητά του να κερδίσει. Ο Χ σε κάθε κίνηση που κάνει
ΠΑΙΓΝΙΑ Παιχνίδια Γενική Θεώρηση: Έστω ότι έχουμε τους παίκτες Χ και Υ. Ο κάθε παίκτης, σε κάθε κίνηση που κάνει, προσπαθεί να μεγιστοποιήσει την πιθανότητά του να κερδίσει. Ο Χ σε κάθε κίνηση που κάνει
Ανάλυση Απαιτήσεων Απαιτήσεις Λογισµικού
 ΧΑΡΟΚΟΠΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΜΑΤΙΚΗΣ Ανάλυση Απαιτήσεων Απαιτήσεις Λογισµικού Μάρα Νικολαϊδου Δραστηριότητες Διαδικασιών Παραγωγής Λογισµικού Καθορισµός απαιτήσεων και εξαγωγή προδιαγραφών
ΧΑΡΟΚΟΠΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΜΑΤΙΚΗΣ Ανάλυση Απαιτήσεων Απαιτήσεις Λογισµικού Μάρα Νικολαϊδου Δραστηριότητες Διαδικασιών Παραγωγής Λογισµικού Καθορισµός απαιτήσεων και εξαγωγή προδιαγραφών
ΚΕΦΑΛΑΙΟ 7 ο. Έτσι ο προγραµµατισµός µε τη ΓΛΩΣΣΑ εστιάζεται στην ανάπτυξη του αλγορίθµου και τη µετατροπή του σε σωστό πρόγραµµα.
 ΚΕΦΑΛΑΙΟ 7 ο 1. Επιλογή της κατάλληλης γλώσσας προγραµµατισµού Εκατοντάδες γλώσσες προγραµµατισµού χρησιµοποιούνται όπως αναφέρθηκε σήµερα για την επίλυση των προβληµάτων µε τον υπολογιστή, τη δηµιουργία
ΚΕΦΑΛΑΙΟ 7 ο 1. Επιλογή της κατάλληλης γλώσσας προγραµµατισµού Εκατοντάδες γλώσσες προγραµµατισµού χρησιµοποιούνται όπως αναφέρθηκε σήµερα για την επίλυση των προβληµάτων µε τον υπολογιστή, τη δηµιουργία
Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή
 Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή raniah@hua.gr 1 Αναζήτηση Δοθέντος ενός προβλήματος με περιγραφή είτε στον χώρο καταστάσεων
Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή raniah@hua.gr 1 Αναζήτηση Δοθέντος ενός προβλήματος με περιγραφή είτε στον χώρο καταστάσεων
Σύνθεση διαδικτυακών υπηρεσιών με χρήση τεχνικών σχεδιασμού ενεργειών
 Σύνθεση διαδικτυακών υπηρεσιών με χρήση τεχνικών σχεδιασμού ενεργειών Ουρανία Χατζή raniah@hua.gr Χαροκόπειο Πανεπιστήμιο 29 Νοεμβρίου 2007 Outline Web Service Overview Standards & Model Syntactic vs Semantic
Σύνθεση διαδικτυακών υπηρεσιών με χρήση τεχνικών σχεδιασμού ενεργειών Ουρανία Χατζή raniah@hua.gr Χαροκόπειο Πανεπιστήμιο 29 Νοεμβρίου 2007 Outline Web Service Overview Standards & Model Syntactic vs Semantic
Ορισµοί κεφαλαίου. Σηµαντικά σηµεία κεφαλαίου
 Ορισµοί κεφαλαίου Αλγόριθµος είναι µια πεπερασµένη σειρά ενεργειών, αυστηρά καθορισµένων και εκτελέσιµων σε πεπερασµένο χρόνο, που στοχεύουν στην επίλυση ενός προβλήµατος. Σηµαντικά σηµεία κεφαλαίου Κριτήρια
Ορισµοί κεφαλαίου Αλγόριθµος είναι µια πεπερασµένη σειρά ενεργειών, αυστηρά καθορισµένων και εκτελέσιµων σε πεπερασµένο χρόνο, που στοχεύουν στην επίλυση ενός προβλήµατος. Σηµαντικά σηµεία κεφαλαίου Κριτήρια
Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή
 Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή raniah@hua.gr 1 Ικανοποίηση Περιορισμών Κατηγορία προβλημάτων στα οποία είναι γνωστές μερικές
Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή raniah@hua.gr 1 Ικανοποίηση Περιορισμών Κατηγορία προβλημάτων στα οποία είναι γνωστές μερικές
3 Αλληλεπίδραση Αντικειμένων
 Αφαίρεση και Αρθρωσιμότητα 3 Αλληλεπίδραση Αντικειμένων Πώς συνεργάζονται τα αντικείμενα που δημιουργούμε Αφαίρεση (abstraction) είναι η δυνατότητα να αγνοούμε τις λεπτομέρειες και να εστιάζουμε την προσοχή
Αφαίρεση και Αρθρωσιμότητα 3 Αλληλεπίδραση Αντικειμένων Πώς συνεργάζονται τα αντικείμενα που δημιουργούμε Αφαίρεση (abstraction) είναι η δυνατότητα να αγνοούμε τις λεπτομέρειες και να εστιάζουμε την προσοχή
Μαλούτα Θεανώ Σελίδα 1
 ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΑΡΧΕΣ ΤΗΣ ΕΠΙΣΤΗΜΗΣ ΤΩΝ ΥΠΟΛΟΓΙΣΤΩΝ Α. ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΦΥΛΛΑΔΙΟ 6 ο ( Ενότητες 2.3 ) 1.Τι είναι πρόγραμμα; 2. Ποια είναι τα πλεονεκτήματα των γλωσσών υψηλού επιπέδου σε σχέση με τις γλώσσες
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΑΡΧΕΣ ΤΗΣ ΕΠΙΣΤΗΜΗΣ ΤΩΝ ΥΠΟΛΟΓΙΣΤΩΝ Α. ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΦΥΛΛΑΔΙΟ 6 ο ( Ενότητες 2.3 ) 1.Τι είναι πρόγραμμα; 2. Ποια είναι τα πλεονεκτήματα των γλωσσών υψηλού επιπέδου σε σχέση με τις γλώσσες
ΕΙΔΗ,ΤΕΧΝΙΚΕΣ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΑ ΠΡΟΓΡΑΜΜΑΤΙ- ΣΜΟΥ
 Κεφάλαιο 7 ΕΙΔΗ,ΤΕΧΝΙΚΕΣ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΑ ΠΡΟΓΡΑΜΜΑΤΙ- ΣΜΟΥ Ερωτήσεις 1. Να αναφέρετε διαφορές μεταξύ γλωσσών μηχανής και γλωσσών χαμηλού επιπέδου. Οι γλώσσες μηχανής κωδικοποιούν τις εντολές τους με ομάδες
Κεφάλαιο 7 ΕΙΔΗ,ΤΕΧΝΙΚΕΣ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΑ ΠΡΟΓΡΑΜΜΑΤΙ- ΣΜΟΥ Ερωτήσεις 1. Να αναφέρετε διαφορές μεταξύ γλωσσών μηχανής και γλωσσών χαμηλού επιπέδου. Οι γλώσσες μηχανής κωδικοποιούν τις εντολές τους με ομάδες
Μάριος Αγγελίδης Ενότητες βιβλίου: 2.1, 2.3, 6.1 (εκτός ύλης αλλά χρειάζεται για την συνέχεια) Ώρες διδασκαλίας: 1
 Ενότητα 1 Ενότητες βιβλίου: 2.1, 2.3, 6.1 (εκτός ύλης αλλά χρειάζεται για την συνέχεια) Ώρες διδασκαλίας: 1 Τι είναι αλγόριθμος Σύμφωνα με το σχολικό βιβλίο: Ορισμός: Μια πεπερασμένη σειρά ενεργειών, αυστηρά
Ενότητα 1 Ενότητες βιβλίου: 2.1, 2.3, 6.1 (εκτός ύλης αλλά χρειάζεται για την συνέχεια) Ώρες διδασκαλίας: 1 Τι είναι αλγόριθμος Σύμφωνα με το σχολικό βιβλίο: Ορισμός: Μια πεπερασμένη σειρά ενεργειών, αυστηρά
2 ΟΥ και 7 ΟΥ ΚΕΦΑΛΑΙΟΥ
 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΙΜΕΛΕΙΑ: ΜΑΡΙΑ Σ. ΖΙΩΓΑ ΚΑΘΗΓΗΤΡΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ 2 ΟΥ και 7 ΟΥ ΚΕΦΑΛΑΙΟΥ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΑΛΓΟΡΙΘΜΩΝ και ΔΟΜΗ ΑΚΟΛΟΥΘΙΑΣ 2.1 Να δοθεί ο ορισμός
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΙΜΕΛΕΙΑ: ΜΑΡΙΑ Σ. ΖΙΩΓΑ ΚΑΘΗΓΗΤΡΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ 2 ΟΥ και 7 ΟΥ ΚΕΦΑΛΑΙΟΥ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΑΛΓΟΡΙΘΜΩΝ και ΔΟΜΗ ΑΚΟΛΟΥΘΙΑΣ 2.1 Να δοθεί ο ορισμός
Ε ανάληψη. Ορισµοί της Τεχνητής Νοηµοσύνης (ΤΝ) Καταβολές. Ιστορική αναδροµή. Πράκτορες. Περιβάλλοντα. κριτήρια νοηµοσύνης
 ΠΛΗ 405 Τεχνητή Νοηµοσύνη Αναζήτηση Search Τµήµα Ηλεκτρονικών Μηχανικών και Μηχανικών Υ ολογιστών Πολυτεχνείο Κρήτης Ε ανάληψη Ορισµοί της Τεχνητής Νοηµοσύνης (ΤΝ) κριτήρια νοηµοσύνης Καταβολές συνεισφορά
ΠΛΗ 405 Τεχνητή Νοηµοσύνη Αναζήτηση Search Τµήµα Ηλεκτρονικών Μηχανικών και Μηχανικών Υ ολογιστών Πολυτεχνείο Κρήτης Ε ανάληψη Ορισµοί της Τεχνητής Νοηµοσύνης (ΤΝ) κριτήρια νοηµοσύνης Καταβολές συνεισφορά
Υπολογιστικό Πρόβληµα
 Υπολογιστικό Πρόβληµα Μετασχηµατισµός δεδοµένων εισόδου σε δεδοµένα εξόδου. Δοµή δεδοµένων εισόδου (έγκυρο στιγµιότυπο). Δοµή και ιδιότητες δεδοµένων εξόδου (απάντηση ή λύση). Τυπικά: διµελής σχέση στις
Υπολογιστικό Πρόβληµα Μετασχηµατισµός δεδοµένων εισόδου σε δεδοµένα εξόδου. Δοµή δεδοµένων εισόδου (έγκυρο στιγµιότυπο). Δοµή και ιδιότητες δεδοµένων εξόδου (απάντηση ή λύση). Τυπικά: διµελής σχέση στις
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ Τ Μ Η Μ Α Π Λ Η Ρ Ο Φ Ο Ρ Ι Κ Η Σ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ Τ Μ Η Μ Α Π Λ Η Ρ Ο Φ Ο Ρ Ι Κ Η Σ ΕΠΛ 035 - ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΑΛΓΟΡΙΘΜΟΙ ΓΙΑ ΗΛΕΚΤΡΟΛΟΓΟΥΣ ΜΗΧΑΝΙΚΟΥΣ ΚΑΙ ΜΗΧΑΝΙΚΟΥΣ ΥΠΟΛΟΓΙΣΤΩΝ Ακαδηµαϊκό έτος 2017-2018 Υπεύθυνος εργαστηρίου: Γεώργιος
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ Τ Μ Η Μ Α Π Λ Η Ρ Ο Φ Ο Ρ Ι Κ Η Σ ΕΠΛ 035 - ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΑΛΓΟΡΙΘΜΟΙ ΓΙΑ ΗΛΕΚΤΡΟΛΟΓΟΥΣ ΜΗΧΑΝΙΚΟΥΣ ΚΑΙ ΜΗΧΑΝΙΚΟΥΣ ΥΠΟΛΟΓΙΣΤΩΝ Ακαδηµαϊκό έτος 2017-2018 Υπεύθυνος εργαστηρίου: Γεώργιος
Σχεδιασµός. Planning. Το πρόβληµα τουσχεδιασµού
 Σχεδιασµός Planning Το πρόβληµα τουσχεδιασµού Κλασσικός σχεδιασµός: Πλήρως παρατηρήσιµα, αιτιοκρατικά, πεπερασµένα, στατικά και διακριτά περιβάλλοντα. Ευρετική συνάρτηση Αποσυνθέσιµα προβλήµατα Σχεδόν
Σχεδιασµός Planning Το πρόβληµα τουσχεδιασµού Κλασσικός σχεδιασµός: Πλήρως παρατηρήσιµα, αιτιοκρατικά, πεπερασµένα, στατικά και διακριτά περιβάλλοντα. Ευρετική συνάρτηση Αποσυνθέσιµα προβλήµατα Σχεδόν
ΠΑΝΕΠΙΣΤΗΜΙΟ AΙΓΑIΟΥ & ΑΕΙ ΠΕΙΡΑΙΑ Τ.Τ. Τμήματα Ναυτιλίας και Επιχειρηματικών Υπηρεσιών & Μηχ. Αυτοματισμού ΤΕ. Εισαγωγή στη Python
 ΠΑΝΕΠΙΣΤΗΜΙΟ AΙΓΑIΟΥ & ΑΕΙ ΠΕΙΡΑΙΑ Τ.Τ. Τμήματα Ναυτιλίας και Επιχειρηματικών Υπηρεσιών & Μηχ. Αυτοματισμού ΤΕ ΠΛΗΡΟΦΟΡΙΚΗ ΤΕΧΝΟΛΟΓΙΑ ΚΑΙ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Η/Υ Εισαγωγή στη Python Νικόλαος Ζ. Ζάχαρης Αναπληρωτής
ΠΑΝΕΠΙΣΤΗΜΙΟ AΙΓΑIΟΥ & ΑΕΙ ΠΕΙΡΑΙΑ Τ.Τ. Τμήματα Ναυτιλίας και Επιχειρηματικών Υπηρεσιών & Μηχ. Αυτοματισμού ΤΕ ΠΛΗΡΟΦΟΡΙΚΗ ΤΕΧΝΟΛΟΓΙΑ ΚΑΙ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Η/Υ Εισαγωγή στη Python Νικόλαος Ζ. Ζάχαρης Αναπληρωτής
Σύνοψη Θεωρίας ΟΡΙΣΜΟΣ ΚΑΙ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΑΛΓΟΡΙΘΜΩΝ
 1 ο ΓΥΜΝΑΣΙΟ ΘΕΡΜΗΣ Τάξη: Γ Μάθημα: Πληροφορική Εξεταστέα ύλη: Παρ11.1 & 11.2 Σύνοψη Θεωρίας ΟΡΙΣΜΟΣ ΚΑΙ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΑΛΓΟΡΙΘΜΩΝ Αλγόριθμος είναι μια πεπερασμένη σειρά ενεργειών που περιγράφει τη διαδικασία
1 ο ΓΥΜΝΑΣΙΟ ΘΕΡΜΗΣ Τάξη: Γ Μάθημα: Πληροφορική Εξεταστέα ύλη: Παρ11.1 & 11.2 Σύνοψη Θεωρίας ΟΡΙΣΜΟΣ ΚΑΙ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΑΛΓΟΡΙΘΜΩΝ Αλγόριθμος είναι μια πεπερασμένη σειρά ενεργειών που περιγράφει τη διαδικασία
Μηχανική Μάθηση Μερωνυµιών για Αναγνώριση Γεγονότων
 Μηχανική Μάθηση Μερωνυµιών για Αναγνώριση Γεγονότων Αναστάσιος Σκαρλατίδης 1,2 anskarl@iit.demokritos.gr επιβλέπων: Καθ. Βούρος Γ. 1 1 Τµήµα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστηµάτων Πανεπιστήµιο
Μηχανική Μάθηση Μερωνυµιών για Αναγνώριση Γεγονότων Αναστάσιος Σκαρλατίδης 1,2 anskarl@iit.demokritos.gr επιβλέπων: Καθ. Βούρος Γ. 1 1 Τµήµα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστηµάτων Πανεπιστήµιο
ΚΕΦΑΛΑΙΟ 2ο ΠΡΟΣΟΜΟΙΩΣΗ ΔΙΑΚΡΙΤΩΝ ΓΕΓΟΝΟΤΩΝ
 ΚΕΦΑΛΑΙΟ 2ο ΠΡΟΣΟΜΟΙΩΣΗ ΔΙΑΚΡΙΤΩΝ ΓΕΓΟΝΟΤΩΝ 2.1 Εισαγωγή Η μέθοδος που θα χρησιμοποιηθεί για να προσομοιωθεί ένα σύστημα έχει άμεση σχέση με το μοντέλο που δημιουργήθηκε για το σύστημα. Αυτό ισχύει και
ΚΕΦΑΛΑΙΟ 2ο ΠΡΟΣΟΜΟΙΩΣΗ ΔΙΑΚΡΙΤΩΝ ΓΕΓΟΝΟΤΩΝ 2.1 Εισαγωγή Η μέθοδος που θα χρησιμοποιηθεί για να προσομοιωθεί ένα σύστημα έχει άμεση σχέση με το μοντέλο που δημιουργήθηκε για το σύστημα. Αυτό ισχύει και
Τι είναι αλγόριθμος; Υποπρογράμματα (υποαλγόριθμοι) Βασικές αλγοριθμικές δομές
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 2015-16 Αλγόριθμοι και Δομές Δεδομένων (Ι) (εισαγωγικές έννοιες) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Τι είναι
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 2015-16 Αλγόριθμοι και Δομές Δεδομένων (Ι) (εισαγωγικές έννοιες) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Τι είναι
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Λογική. Δημήτρης Πλεξουσάκης
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Λογική Δημήτρης Πλεξουσάκης 2ο μέρος σημειώσεων: Συστήματα Αποδείξεων για τον ΠΛ, Μορφολογική Παραγωγή, Κατασκευή Μοντέλων Τμήμα Επιστήμης Υπολογιστών Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Λογική Δημήτρης Πλεξουσάκης 2ο μέρος σημειώσεων: Συστήματα Αποδείξεων για τον ΠΛ, Μορφολογική Παραγωγή, Κατασκευή Μοντέλων Τμήμα Επιστήμης Υπολογιστών Άδειες Χρήσης
Κεφ. 1: Εισαγωγή στην έννοια του Αλγορίθμου και στον Προγραμματισμό. Η έννοια του προβλήματος
 Η έννοια του προβλήματος 1. Αναφέρετε μερικά από τα προβλήματα που συναντάτε στην καθημερινότητά σας. Απλά προβλήματα Ποιο δρόμο θα ακολουθήσω για να πάω στο σχολείο; Πως θα οργανώσω μια εκδρομή; Πως θα
Η έννοια του προβλήματος 1. Αναφέρετε μερικά από τα προβλήματα που συναντάτε στην καθημερινότητά σας. Απλά προβλήματα Ποιο δρόμο θα ακολουθήσω για να πάω στο σχολείο; Πως θα οργανώσω μια εκδρομή; Πως θα
Προγραμματισμός Η/Υ. Προτεινόμενα θέματα εξετάσεων Εργαστήριο. Μέρος 1 ό. ΤΕΙ Λάρισας- Σχολή Τεχνολογικών Εφαρμογών Τμήμα Πολιτικών Έργων Υποδομής
 Προγραμματισμός Η/Υ Προτεινόμενα θέματα εξετάσεων Εργαστήριο Μέρος 1 ό ΤΕΙ Λάρισας- Σχολή Τεχνολογικών Εφαρμογών Τμήμα Πολιτικών Έργων Υποδομής Ιανουάριος 2011 Καλογιάννης Γρηγόριος Επιστημονικός/ Εργαστηριακός
Προγραμματισμός Η/Υ Προτεινόμενα θέματα εξετάσεων Εργαστήριο Μέρος 1 ό ΤΕΙ Λάρισας- Σχολή Τεχνολογικών Εφαρμογών Τμήμα Πολιτικών Έργων Υποδομής Ιανουάριος 2011 Καλογιάννης Γρηγόριος Επιστημονικός/ Εργαστηριακός
Ενότητα 13. Εισαγωγή στην Πληροφορική. Κεφάλαιο 13Α. Αρχεία. Χειµερινό Εξάµηνο ρ. Παναγιώτης Χατζηδούκας (Π..407/80) προγραµµατισµός
 Ενότητα 13 Εισαγωγή στην Πληροφορική Χειµερινό Εξάµηνο 2006-07 Προγραµµατισµός Κεφάλαιο 13Α: ηµιουργία Προγραµµάτων Υπολογιστή Κεφάλαιο 13Β: Γλώσσες Προγραµµατισµού και η ιαδικασία Προγραµµατισµού ρ. Παναγιώτης
Ενότητα 13 Εισαγωγή στην Πληροφορική Χειµερινό Εξάµηνο 2006-07 Προγραµµατισµός Κεφάλαιο 13Α: ηµιουργία Προγραµµάτων Υπολογιστή Κεφάλαιο 13Β: Γλώσσες Προγραµµατισµού και η ιαδικασία Προγραµµατισµού ρ. Παναγιώτης
Επεξεργασία Ερωτήσεων
 Εισαγωγή στην Επεξεργασία Ερωτήσεων 1 Εισαγωγή ΣΔΒΔ Σύνολο από προγράµµατα για τη διαχείριση της ΒΔ Αρχεία ευρετηρίου Κατάλογος ΒΑΣΗ ΔΕΔΟΜΕΝΩΝ Αρχεία δεδοµένων συστήµατος Σύστηµα Βάσεων Δεδοµένων (ΣΒΔ)
Εισαγωγή στην Επεξεργασία Ερωτήσεων 1 Εισαγωγή ΣΔΒΔ Σύνολο από προγράµµατα για τη διαχείριση της ΒΔ Αρχεία ευρετηρίου Κατάλογος ΒΑΣΗ ΔΕΔΟΜΕΝΩΝ Αρχεία δεδοµένων συστήµατος Σύστηµα Βάσεων Δεδοµένων (ΣΒΔ)
Δομές Δεδομένων. Ενότητα 1 - Εισαγωγή. Χρήστος Γκουμόπουλος. Πανεπιστήμιο Αιγαίου Τμήμα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστημάτων
 Δομές Δεδομένων Ενότητα 1 - Εισαγωγή Χρήστος Γκουμόπουλος Πανεπιστήμιο Αιγαίου Τμήμα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστημάτων Αντικείμενο μαθήματος Δομές Δεδομένων (ΔΔ): Στην επιστήμη υπολογιστών
Δομές Δεδομένων Ενότητα 1 - Εισαγωγή Χρήστος Γκουμόπουλος Πανεπιστήμιο Αιγαίου Τμήμα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστημάτων Αντικείμενο μαθήματος Δομές Δεδομένων (ΔΔ): Στην επιστήμη υπολογιστών
Επίλυση Προβλημάτων 1
 Επίλυση Προβλημάτων 1 Επίλυση Προβλημάτων Περιγραφή Προβλημάτων Αλγόριθμοι αναζήτησης Αλγόριθμοι τυφλής αναζήτησης Αναζήτηση πρώτα σε βάθος Αναζήτηση πρώτα σε πλάτος (ΒFS) Αλγόριθμοι ευρετικής αναζήτησης
Επίλυση Προβλημάτων 1 Επίλυση Προβλημάτων Περιγραφή Προβλημάτων Αλγόριθμοι αναζήτησης Αλγόριθμοι τυφλής αναζήτησης Αναζήτηση πρώτα σε βάθος Αναζήτηση πρώτα σε πλάτος (ΒFS) Αλγόριθμοι ευρετικής αναζήτησης
Διαδικασίες παραγωγής λογισμικού. Βασικές αρχές Τεχνολογίας Λογισμικού, 8η αγγ. έκδοση
 Διαδικασίες παραγωγής λογισμικού Περιεχόμενα Παρουσίαση μοντέλων διεργασίας ανάπτυξης λογισμικού Περιγραφή τριών γενικών μοντέλων διεργασίας ανάπτυξης λογισμικού Γενική περιγραφή των διαδικασιών που περιλαμβάνονται
Διαδικασίες παραγωγής λογισμικού Περιεχόμενα Παρουσίαση μοντέλων διεργασίας ανάπτυξης λογισμικού Περιγραφή τριών γενικών μοντέλων διεργασίας ανάπτυξης λογισμικού Γενική περιγραφή των διαδικασιών που περιλαμβάνονται
ΚΕΦΑΛΑΙΟ 5. Κύκλος Ζωής Εφαρμογών ΕΝΟΤΗΤΑ 2. Εφαρμογές Πληροφορικής. Διδακτικές ενότητες 5.1 Πρόβλημα και υπολογιστής 5.2 Ανάπτυξη εφαρμογών
 44 Διδακτικές ενότητες 5.1 Πρόβλημα και υπολογιστής 5.2 Ανάπτυξη εφαρμογών Διδακτικοί στόχοι Σκοπός του κεφαλαίου είναι οι μαθητές να κατανοήσουν τα βήματα που ακολουθούνται κατά την ανάπτυξη μιας εφαρμογής.
44 Διδακτικές ενότητες 5.1 Πρόβλημα και υπολογιστής 5.2 Ανάπτυξη εφαρμογών Διδακτικοί στόχοι Σκοπός του κεφαλαίου είναι οι μαθητές να κατανοήσουν τα βήματα που ακολουθούνται κατά την ανάπτυξη μιας εφαρμογής.
Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος
 Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος Χιωτίδης Γεώργιος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος Χιωτίδης Γεώργιος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Μοντέλα. χαρακτηριστικά χωρίς να συνοδεύεται από λεπτοµέρειες.
 Γλώσσες Περιγραφής Μοντέλα Ένα µοντέλο ενός κυκλώµατος είναι µία αναπαράσταση που παρουσιάζει χαρακτηριστικά χωρίς να συνοδεύεται από λεπτοµέρειες. Τα τυπικά µοντέλα έχουν καλά ορισµένη σύνταξη. Τα αυτόµατα
Γλώσσες Περιγραφής Μοντέλα Ένα µοντέλο ενός κυκλώµατος είναι µία αναπαράσταση που παρουσιάζει χαρακτηριστικά χωρίς να συνοδεύεται από λεπτοµέρειες. Τα τυπικά µοντέλα έχουν καλά ορισµένη σύνταξη. Τα αυτόµατα
Ψευδοκώδικας. November 7, 2011
 Ψευδοκώδικας November 7, 2011 Οι γλώσσες τύπου ψευδοκώδικα είναι ένας τρόπος περιγραφής αλγορίθμων. Δεν υπάρχει κανένας τυπικός ορισμός της έννοιας του ψευδοκώδικα όμως είναι κοινός τόπος ότι οποιαδήποτε
Ψευδοκώδικας November 7, 2011 Οι γλώσσες τύπου ψευδοκώδικα είναι ένας τρόπος περιγραφής αλγορίθμων. Δεν υπάρχει κανένας τυπικός ορισμός της έννοιας του ψευδοκώδικα όμως είναι κοινός τόπος ότι οποιαδήποτε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ
 ΘΕΜΑ 1 ο (2.5 µονάδες) ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ Τελικές εξετάσεις 17 Φεβρουαρίου 2004 ιάρκεια: 2 ώρες (15:00-17:00)
ΘΕΜΑ 1 ο (2.5 µονάδες) ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ Τελικές εξετάσεις 17 Φεβρουαρίου 2004 ιάρκεια: 2 ώρες (15:00-17:00)
ΠΑΡΑΡΤΗΜΑ: QUIZ ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ
 ΠΑΡΑΡΤΗΜΑ: QUIZ ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ (Οι ερωτήσεις µε κίτρινη υπογράµµιση είναι εκτός ύλης για φέτος) ΕΙΣΑΓΩΓΗ Q1. Οι Πρωταρχικοί τύποι (primitive types) στη Java 1. Είναι όλοι οι ακέραιοι και όλοι οι πραγµατικοί
ΠΑΡΑΡΤΗΜΑ: QUIZ ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ (Οι ερωτήσεις µε κίτρινη υπογράµµιση είναι εκτός ύλης για φέτος) ΕΙΣΑΓΩΓΗ Q1. Οι Πρωταρχικοί τύποι (primitive types) στη Java 1. Είναι όλοι οι ακέραιοι και όλοι οι πραγµατικοί
Κεφάλαιο 2.3: Προγραμματισμός. Επιστήμη ΗΥ Κεφ. 2.3 Καραμαούνας Πολύκαρπος
 Κεφάλαιο 2.3: Προγραμματισμός 1 2.3.1 Αναφορά σε γλώσσες προγραμματισμού και «Προγραμματιστικά Υποδείγματα» 2.3.1.1 Πρόγραμμα και Γλώσσες Προγραμματισμού Πρόγραμμα: σύνολο εντολών που χρειάζεται να δοθούν
Κεφάλαιο 2.3: Προγραμματισμός 1 2.3.1 Αναφορά σε γλώσσες προγραμματισμού και «Προγραμματιστικά Υποδείγματα» 2.3.1.1 Πρόγραμμα και Γλώσσες Προγραμματισμού Πρόγραμμα: σύνολο εντολών που χρειάζεται να δοθούν
ΚΕΦΑΛΑΙΟ 6 ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟ. Η επίλυση ενός προβλήματος με τον υπολογιστή περιλαμβάνει τρία εξίσου σημαντικά στάδια.
 ΚΕΦΑΛΑΙΟ 6 ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟ Η επίλυση ενός προβλήματος με τον υπολογιστή περιλαμβάνει τρία εξίσου σημαντικά στάδια. Τον ακριβή προσδιορισμό του προβλήματος. Την ανάπτυξη του αντίστοιχου αλγορίθμου.
ΚΕΦΑΛΑΙΟ 6 ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟ Η επίλυση ενός προβλήματος με τον υπολογιστή περιλαμβάνει τρία εξίσου σημαντικά στάδια. Τον ακριβή προσδιορισμό του προβλήματος. Την ανάπτυξη του αντίστοιχου αλγορίθμου.
Κεφάλαιο 5: Εισαγωγή στην Προσομοίωση
 Κεφάλαιο 5: Εισαγωγή στην Προσομοίωση Τεχνικές Εκτίμησης Υπολογιστικών Συστημάτων Γιάννης Γαροφαλάκης Αν. Καθηγητής Προσομοίωση Τεχνικές χρήσης υπολογιστών για τη «μίμηση» των λειτουργιών διαφόρων ειδών
Κεφάλαιο 5: Εισαγωγή στην Προσομοίωση Τεχνικές Εκτίμησης Υπολογιστικών Συστημάτων Γιάννης Γαροφαλάκης Αν. Καθηγητής Προσομοίωση Τεχνικές χρήσης υπολογιστών για τη «μίμηση» των λειτουργιών διαφόρων ειδών
for for for for( . */
 Εισαγωγή Στον Προγραµµατισµό «C» Βρόχοι Επανάληψης Πανεπιστήµιο Πελοποννήσου Τµήµα Πληροφορικής & Τηλεπικοινωνιών Νικόλαος Δ. Τσελίκας Νικόλαος Προγραµµατισµός Δ. Τσελίκας Ι Ο βρόχος for Η εντολή for χρησιµοποιείται
Εισαγωγή Στον Προγραµµατισµό «C» Βρόχοι Επανάληψης Πανεπιστήµιο Πελοποννήσου Τµήµα Πληροφορικής & Τηλεπικοινωνιών Νικόλαος Δ. Τσελίκας Νικόλαος Προγραµµατισµός Δ. Τσελίκας Ι Ο βρόχος for Η εντολή for χρησιµοποιείται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΙΑΤΜΗΜΑΤΙΚΟ ΠΜΣ «ΜΑΘΗΜΑΤΙΚΑ ΤΩΝ ΥΠΟΛΟΓΙΣΤΩΝ & ΤΩΝ ΑΠΟΦΑΣΕΩΝ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ 2006-2007 2η Σειρά Ασκήσεων ΑΠΑΝΤΗΣΕΙΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΙΑΤΜΗΜΑΤΙΚΟ ΠΜΣ «ΜΑΘΗΜΑΤΙΚΑ ΤΩΝ ΥΠΟΛΟΓΙΣΤΩΝ & ΤΩΝ ΑΠΟΦΑΣΕΩΝ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ 2006-2007 2η Σειρά Ασκήσεων ΑΠΑΝΤΗΣΕΙΣ 1. ίνεται το γνωστό πρόβληµα των δύο δοχείων: «Υπάρχουν δύο δοχεία
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΙΑΤΜΗΜΑΤΙΚΟ ΠΜΣ «ΜΑΘΗΜΑΤΙΚΑ ΤΩΝ ΥΠΟΛΟΓΙΣΤΩΝ & ΤΩΝ ΑΠΟΦΑΣΕΩΝ ΤΕΧΝΗΤΗ ΝΟΗΜΟΣΥΝΗ 2006-2007 2η Σειρά Ασκήσεων ΑΠΑΝΤΗΣΕΙΣ 1. ίνεται το γνωστό πρόβληµα των δύο δοχείων: «Υπάρχουν δύο δοχεία
ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΥΠΟΛΟΓΙΣΤΩΝ
 Εισαγωγή ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΥΠΟΛΟΓΙΣΤΩΝ Όπως για όλες τις επιστήμες, έτσι και για την επιστήμη της Πληροφορικής, ο τελικός στόχος της είναι η επίλυση προβλημάτων. Λύνονται όμως όλα τα προβλήματα;
Εισαγωγή ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΥΠΟΛΟΓΙΣΤΩΝ Όπως για όλες τις επιστήμες, έτσι και για την επιστήμη της Πληροφορικής, ο τελικός στόχος της είναι η επίλυση προβλημάτων. Λύνονται όμως όλα τα προβλήματα;
ΚΕΦΑΛΑΙΟ 10 ΥΠΟΠΡΟΓΡΑΜΜΑΤΑ
 ΚΕΦΑΛΑΙΟ 10 Όπως είδαμε και σε προηγούμενο κεφάλαιο μια από τις βασικότερες τεχνικές στον Δομημένο Προγραμματισμό είναι ο Τμηματικός Προγραμματισμός. Τμηματικός προγραμματισμός ονομάζεται η τεχνική σχεδίασης
ΚΕΦΑΛΑΙΟ 10 Όπως είδαμε και σε προηγούμενο κεφάλαιο μια από τις βασικότερες τεχνικές στον Δομημένο Προγραμματισμό είναι ο Τμηματικός Προγραμματισμός. Τμηματικός προγραμματισμός ονομάζεται η τεχνική σχεδίασης
Περιεχόµενα. Πληροφοριακά Συστήµατα: Κατηγορίες και Κύκλος Ζωής. Π.Σ. ιαχείρισης Πράξεων. Π.Σ. ιοίκησης. Κατηγορίες Π.Σ. Ο κύκλος ζωής Π.Σ.
 Πληροφοριακά Συστήµατα: Κατηγορίες και Κύκλος Ζωής Περιεχόµενα Κατηγορίες Π.Σ. ιαχείρισης Πράξεων ιοίκησης Υποστήριξης Αποφάσεων Έµπειρα Συστήµατα Ατόµων και Οµάδων Ο κύκλος ζωής Π.Σ. Ορισµός Φάσεις Χρήστες
Πληροφοριακά Συστήµατα: Κατηγορίες και Κύκλος Ζωής Περιεχόµενα Κατηγορίες Π.Σ. ιαχείρισης Πράξεων ιοίκησης Υποστήριξης Αποφάσεων Έµπειρα Συστήµατα Ατόµων και Οµάδων Ο κύκλος ζωής Π.Σ. Ορισµός Φάσεις Χρήστες
Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου. Πληροφορική II. Ενότητα 9 : Τεχνητή νοημοσύνη. Δρ. Γκόγκος Χρήστος
 1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Πληροφορική II Ενότητα 9 : Τεχνητή νοημοσύνη Δρ. Γκόγκος Χρήστος 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου Τμήμα Χρηματοοικονομικής & Ελεγκτικής
1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Πληροφορική II Ενότητα 9 : Τεχνητή νοημοσύνη Δρ. Γκόγκος Χρήστος 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου Τμήμα Χρηματοοικονομικής & Ελεγκτικής
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ
 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΙΜΕΛΕΙΑ: ΜΑΡΙΑ Σ. ΖΙΩΓΑ ΚΑΘΗΓΗΤΡΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ 10 ΟΥ ΚΕΦΑΛΑΙΟΥ ΥΠΟΠΡΟΓΡΑΜΜΑΤΑ 1. Πως ορίζεται ο τμηματικός προγραμματισμός; Τμηματικός προγραμματισμός
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΙΜΕΛΕΙΑ: ΜΑΡΙΑ Σ. ΖΙΩΓΑ ΚΑΘΗΓΗΤΡΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ 10 ΟΥ ΚΕΦΑΛΑΙΟΥ ΥΠΟΠΡΟΓΡΑΜΜΑΤΑ 1. Πως ορίζεται ο τμηματικός προγραμματισμός; Τμηματικός προγραμματισμός
Θεωρία Υπολογισμού και Πολυπλοκότητα Κανονικές Γλώσσες (1)
 Θεωρία Υπολογισμού και Πολυπλοκότητα Κανονικές Γλώσσες () Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Πεπερασμένα Αυτόματα (Κεφάλαιο., Sipser) Ορισμός πεπερασμένων αυτομάτων και ορισμός του
Θεωρία Υπολογισμού και Πολυπλοκότητα Κανονικές Γλώσσες () Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Πεπερασμένα Αυτόματα (Κεφάλαιο., Sipser) Ορισμός πεπερασμένων αυτομάτων και ορισμός του
Οργάνωση αρχείων: πως είναι τοποθετηµένες οι εγγραφές ενός αρχείου όταν αποθηκεύονται στο δίσκο
 Κατακερµατισµός 1 Οργάνωση Αρχείων (σύνοψη) Οργάνωση αρχείων: πως είναι τοποθετηµένες οι εγγραφές ενός αρχείου όταν αποθηκεύονται στο δίσκο 1. Αρχεία Σωρού 2. Ταξινοµηµένα Αρχεία Φυσική διάταξη των εγγραφών
Κατακερµατισµός 1 Οργάνωση Αρχείων (σύνοψη) Οργάνωση αρχείων: πως είναι τοποθετηµένες οι εγγραφές ενός αρχείου όταν αποθηκεύονται στο δίσκο 1. Αρχεία Σωρού 2. Ταξινοµηµένα Αρχεία Φυσική διάταξη των εγγραφών
Chapter 6. Problem Solving and Algorithm Design. Στόχοι Ενότητας. Επίλυση προβληµάτων. Εισαγωγή. Nell Dale John Lewis
 Στόχοι Ενότητας Chapter 6 Problem Solving and Algorithm Design Nell Dale John Lewis Αναγνώριση αν ένα πρόβληµα µπορεί να επιλυθεί µε τη χρήση υπολογιστή Περιγραφή της διαδικασίας επίλυσης προβληµάτων και
Στόχοι Ενότητας Chapter 6 Problem Solving and Algorithm Design Nell Dale John Lewis Αναγνώριση αν ένα πρόβληµα µπορεί να επιλυθεί µε τη χρήση υπολογιστή Περιγραφή της διαδικασίας επίλυσης προβληµάτων και
Επιλέξτε Σωστό ή Λάθος για καθένα από τα παρακάτω:
 Επιλέξτε Σωστό ή Λάθος για καθένα από τα παρακάτω: 1ο ΓΕΛ Καστοριάς Βασικές Έννοιες Αλγορίθμων Δομή Ακολουθίας (κεφ. 2 και 7 σχολικού βιβλίου) 1. Οι μεταβλητές αντιστοιχίζονται από τον μεταγλωττιστή κάθε
Επιλέξτε Σωστό ή Λάθος για καθένα από τα παρακάτω: 1ο ΓΕΛ Καστοριάς Βασικές Έννοιες Αλγορίθμων Δομή Ακολουθίας (κεφ. 2 και 7 σχολικού βιβλίου) 1. Οι μεταβλητές αντιστοιχίζονται από τον μεταγλωττιστή κάθε
3.1 Αριθμητικοί και Λογικοί Τελεστές, Μετατροπές Τύπου (Casting)
 Εργαστήριο 3: 3.1 Αριθμητικοί και Λογικοί Τελεστές, Μετατροπές Τύπου (Casting) Η C++, όπως όλες οι γλώσσες προγραμματισμού, χρησιμοποιεί τελεστές για να εκτελέσει τις αριθμητικές και λογικές λειτουργίες.
Εργαστήριο 3: 3.1 Αριθμητικοί και Λογικοί Τελεστές, Μετατροπές Τύπου (Casting) Η C++, όπως όλες οι γλώσσες προγραμματισμού, χρησιμοποιεί τελεστές για να εκτελέσει τις αριθμητικές και λογικές λειτουργίες.
