[1] Εύρεση διαµορφωµερών ελάχιστης ενέργειας µε χρήση του

HTML
DOWNLOAD

Μέγεθος: px

Εμφάνιση ξεκινά από τη σελίδα:

Download "[1] Εύρεση διαµορφωµερών ελάχιστης ενέργειας µε χρήση του"

Βεελζεβούλ Θεοτόκης
8 χρόνια πριν
Προβολές:

1 1 [1] Εύρεση διαµορφωµερών ελάχιστης ενέργειας µε χρήση του προγράµµατος Spartan 04 v (Wavefunction, Inc., (Ι) Κτίσατε (built 3D) την Αποµορφίνη µε την πρωτονιωµένη της µορφή και µε διαµόρφωση του δεσµού C-Ν + (δηλαδή, µεθινίου-αζώτου) α] ως αξονικού στο χώρο (axial, συντοµογραφία a) & β]ως ισηµερινού στο χώρο (equatorial, συντοµογραφία e) Ελαχιστοποιήστε ενεργειακά τη δοµή των δύο διαµορφωµερών (αξονικού και ισηµερινού) µε χρήση µοριακής µηχανικής (molecular mechanic s MMFF) {ελαχιστοποιεί τη συνολική τάση του µορίου, δηλαδή βελτιστοποιεί τη διάταξη των ατόµων του µορίου στο χώρο} και αποθηκεύσατε (save=>ogdoo2017) τα µόρια ως αρχείο Apoamm (για την περίπτωση του αξονικού διαµορφωµερούς) και ως αρχείο Apoemm (για την περίπτωση του ισηµερινού διαµορφωµερούς). (ΙΙ) Επαναλάβατε διαδοχικά την ίδια διαδικασία για τις ενώσεις µε κωδικούς Der1, Der2 και Der3. Αποθηκεύσατε (save=>ogdoo2017) τα µόρια ως αρχεία Der1amm, Der2amm, Der3amm (για τις περιπτώσεις των αξονικών διαµορφωµερών) και ως αρχεία Der1emm, Der2emm, Der3emm (για τις περιπτώσεις των ισηµερινών διαµορφωµερών). (ΙΙΙ) Ανοίξατε (open) διαδοχικά όλα τα αρχεία που έχετε φτιάξει και αποθηκεύσατέ τα µε καινούργια ονοµασία (save as=>ogdoo2017) ως αρχεία Apoaam1, Der1aam1, Der2aam1, Der3aam1 (για τις περιπτώσεις των αξονικών διαµορφωµερών) και ως αρχεία Apoeam1, Der1eam1, Der2eam1, Der3eam1 (για τις περιπτώσεις των ισηµερινών διαµορφωµερών). Ελαχιστοποιήστε ενεργειακά τις δοµές των δύο αυτών σειρών διαµορφωµερών (αξονικών και ισηµερινών) µε χρήση της ηµιεµπειρικής κβαντοµηχανικής µεθόδου ΑΜ1 (semiempirical quantum mechanic s Austin Model 1) {ελαχιστοποιεί τη συνολική ενέργεια του µορίου µε βελτιστοποίηση των µηκών των δεσµών καθώς και των τιµών των γωνιών και των δίεδρων γωνιών}.

2 2 Παρατήρηση: Η παραπάνω µεθοδολογία µοριακής προσοµοίωσης δυο σταδίων (molecular mechanics=>semiempirical quantum mechanics) για την εύρεση διαµορφωµερών ελάχιστης ενέργειας, ξεκινά από αριθµό (2-6) διαφορετικών/τυχαίων αρχικών διαµορφώσεων των υπό µελέτη ενώσεων. Κατ αυτόν τον τρόπο, µειώνεται ο κίνδυνος εγκλωβισµού σε ένα τοπικό ελάχιστο και οδηγούµαστε σε διαµορφώσεις της ένωσης που παρουσιάζουν απόκλιση ενέργειας το πολύ 10% από την ενέργεια του διαµορφωµερούς µε απόλυτα ελάχιστη ενέργεια (global energy minimum). Αυτό απεικονίζεται στο ακόλουθο σχήµα: Επισηµαίνεται ότι η εύρεση διαµορφωµερών ελάχιστης ενέργειας µε συστηµατική ανάλυση του διαµορφωσιακού χώρου είναι, πολλές φορές, χρονοβόρος αφού απαιτείτε ελαχιστοποίηση ενέργειας για κάθε ένα από τα πιθανά αρχικά διαµορφωµερή της υπό µελέτη ένωσης. Ο αριθµός των πιθανών αρχικών διαµορφωµερών αυξάνει εκθετικά µε τον αριθµό των περιστρεφόµενων (όχι τελικών) δεσµών του µορίου και µε τα βήµατα στρέψης των οριζόµενων από αυτούς δίεδρων γωνιών. Για παράδειγµα, στο µόριο της ένωσης Der3 µε 7 περιστρεφόµενους δεσµούς, αν ακολουθηθεί βήµα στρέψης 30 ο (δηλαδή, 360/30=12 βήµατα συνολικά) προκύπτουν 12 7 (περίπου 36 εκατοµµύρια) αρχικά διαµορφωµερή προς ενεργειακή ελαχιστοποίηση. Έτσι, συνήθως στην πράξη ακολουθείται τυχαία αναζήτηση (προσοµοίωση Monte Carlo), µια µορφή της οποίας χρησιµοποιήθηκε στην παρούσα άσκηση µοριακής προσοµοίωσης.

3 3 [2] Υπολογισµός λιποφιλίας µε χρήση του προγράµµατος MedChem Designer v (Simulations Plus, Inc., Σχεδιάσατε (draw 2D) τις ενώσεις Apo, Der1, Der2 και Der3 στη µη πρωτονιωµένη µορφή τους και καταγράψατε τις τιµές λογαρίθµου συντελεστή µερισµού [S+logP] καθώς και λογαρίθµου συντελεστή κατανοµής [S+logD 7.4 (default p=7.4)]. (σηµείωση: η πρωτονίωση καθώς και η διαµόρφωση δεν επηρεάζουν τα αποτελέσµατα των υπολογισµών).

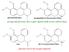
4 4 ΟΜΕΣ ΕΝΩΣΕΩΝ Apomorphine (Apo) N Apo in its protonated form + N [strong and eficacious DA receptor agonist (both in vitro and in-vivo)] Der1 N Der1 in its protonated form + N [ inactive in-vivo DA receptor agonist] Der2 N Der2 in its protonated form + N [active in-vivo DA receptor agonist] N Der3 in its protonated form + N Der3 [most active in-vivo DA receptor agonist]

5 5 [3] Συλλογή δεδοµένων Καταγράψατε τα αποτελέσµατα (output) των ενεργειών των αξονικών και των ισηµερινών διαµορφώσεων των ενώσεων από τους υπολογισµούς AM1. Καταγράψατε τις αποστάσεις των ατόµων σε αυτά τα διαµορφωµερή σύµφωνα µε το παρακάτω σχήµα: m- center Apo N+ m- m- center center N+ N+ Der1 Der2 m- center N+ Der3

6 Εργαστηριακή Εργασία Καταγράψατε στο τετράδιό σας όλα τα στοιχεία που συλλέξατε για τις ενώσεις Apo, Der1, Der2, Der3 και αναλύσατε/εξηγήσατε πιθανούς λόγους της παρατηρούµενης διαφοράς στην

6 6 Εργαστηριακή Εργασία Καταγράψατε στο τετράδιό σας όλα τα στοιχεία που συλλέξατε για τις ενώσεις Apo, Der1, Der2, Der3 και αναλύσατε/εξηγήσατε πιθανούς λόγους της παρατηρούµενης διαφοράς στην in-vivo εκδήλωση της ντοπαµινεργικής αγωνιστικής δράσης. Χρησιµοποιήσατε και το παρακάτω διάγραµµα κατανοµής κατά Boltzmann που είναι σε συνάρτηση µε τη διαφορά ενέργειας δυο διαµορφωµερών µιας ένωσης. F2/F1 = e (E1-E2)/RT (E1>E2)

7 7 Συνολική Καταγραφή Αποτελεσµάτων Apo S+logP= S+logD 7,4 = Conformer Conformation s Energy Distances (N-m & N-Center) Der1 S+logP= S+logD 7,4 = Conformer Conformation s Energy Distances (N-m & N-Center)

8 Der2 S+logP= S+logD 7,4 = 8 Conformer Conformation s Energy Distances (N-m & N-Center) Der3 S+logP= S+logD 7,4 = Conformer Conformation s Energy Distances (N-m & N-Center)

Σχετικά έγγραφα

[1] Εύρεση διαμορφωμερών ελάχιστης ενέργειας με χρήση του προγράμματος

1 [1] Εύρεση διαμορφωμερών ελάχιστης ενέργειας με χρήση του προγράμματος Spartan 08 v. 1.2.0 (Wavefunction, Inc., http://www.wavefun.com) (Ι) Κτίσατε (built 3D) την απομορφίνη (apo) και τα παράγωγά της