Σχεδιασμός και υλοποίηση μεθόδων. Intra πρόβλεψης για το Η.264
|
|
|
- Ευαδνη Καλύβας
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Σχεδιασμός και υλοποίηση μεθόδων Intra πρόβλεψης για το Η.264 Διπλωυατική εργασία: Πανεπιστήμιο Θεσσαλίας Τμήμα Μηχανικών Η/Υ, Τηλ & Δικτύων Οκτώβριος, 2007
2 Πανεπιστήμιο Θεσσαλίας ΒΙΒΛΙΟΘΗΚΗ & ΚΕΝΤΡΟ ΠΛΗΡΟΦΟΡΗΣΗΣ Ειδική Συλλογή «Γκρίζα Βιβλιογραφία» Αριθ. Εισ.: 5987/1 Ημερ. Εισ.: Δωρεά: Συγγραφέα Ταξιθετικός Κωδικός: ΠΤ - ΜΗΥΤΔ 2007 ΣΜΑ
3 Αρχικά, θα ήθελα να ευχαριστήσω τον καθηγητή του τμήματος Μηχανικών Η/Υ Τηλεπικοινωνιών και Δικτύων και βασικό επιβλέποντα της πτυχιακής αυτής εργασίας κ.γεώργιο Σταμούλη που μου έδωσε την ευκαιρία να πραγματοποιήσω αυτή την μελέτη. Η υποστήριξή του συντέλεοε στην έγκαιρη και έγκυρη ολοκλήρωση αυτής της μελέτης. Επιπρόσθετα, θα ήθελα να ευχαριστήσω την διδακτορική φοιτήτρια του τμήματος Κοζύρη Μαρία για τις εύστοχες υποδείξεις της σε θεωρητικά ζητήματα και για την καθοδήγηση της κατά τη διάρκεια της διπλωματικής εργασίας. Ακόμη Θα ήθελα να ευχαριστήσω το διδακτορικό φοιτητή του τμήματος Δαδαλιάρη Αντώνιο για την ανεκτίμητη βοήθεια του στην εκμάθηση χρήσιμων εργαλείων που συντέλεσαν στην εκπόνηση της διπλωματικής εργασίας και για τις παρατηρήσεις του σε ζητήματα υλοποίησης. Θα ήθελα να ευχαριστήσω επίσης όλους τους μεταπτυχιακούς και διδακτορικούς φοιτητές του γραφείου Ε5, φίλους και γνωστούς για την βοήθεια που μου παρείχαν όλο αυτό το διάστημα. Τέλος, ένα πολύ μεγάλο ευχαριστώ στην οικογένεια μου που με στήριξε με όλους τους δυνατούς τρόπους αυτά τα πέντε χρόνια στο Πανεπιστήμιο Θεσσαλίας, στο τμήμα Μηχανικών Η/Υ, Τηλεπικοινωνιών & Δικτύων ως προπτυχιακό φοιτητή.
4 1.Τι είναι το Η Πώς ένας κωδικοποιητής -αποκωδικοποιητής Η.264 λειτουργεί 2.1 Διαδικασία Κωόικοποιητή Πρόβλεψη Μετατροπή και κβαντοποίηοη Κωδικοποίηση bitstream 2.2 Διαδικασία Αποκωδικοποιητή Αποκωδικοποίηση bitstream Κλιμάκωση και αντίστροφη μετατροπή Αναδημιουργία 1. Δομή Η Profiles 1.2 Μορφή βίντεο 1.3 Μορφή κωδικοποιημένων δεδομένων 1.4 Φέτες (Slices) I καρέ (intra frames) Ρ καρέ (Predicted frames) Β καρέ (Bi- directional frames) SP & SI καρέ (SP και SI frames) 2. Η διαδικασία Κωδικοποίησης-Αποκωδικοποίησης 2.1 Διαδικασία κωδικοποίησης 2.2 Κωδικοποιητής Κωδικοποιητής (κατεύθυνση κωδικοποίησης) Κωδικοποιητής (κατεύθυνση αναδημιουργίας) 2.3 Αποκιοδικοποιητής 3. Το Η.264 στην πράξη 3.1 Απόδοση 3.2 Εφαρμογές 3.3 Κοινά στοιχεία με άλλα πρότυπα
5 1. Πρόβλεψη των intra macroblocks 2. 1 ρόποι πρόβλεψης 4X4 μπλοκ φωτεινότητας 2.1 Κάθετη Πρόβλεψη μπλοκ φωτεινότητας 4X4 (Vertical ) 2.2 Οριζόντια Πρόβλεψη μπλοκ φωτεινότητας 4X4 (Horizontal ) 2.3 Πρόβλεψη Μέσου όρου μπλοκ φωτεινότητας 4X4 (DC ) 2.4 Διαγώνια Κάτω αριστερά Πρόβλεψη μπλοκ φωτεινότητας 4X4 (Diagonal Down -Left ) 2.5 Διαγώνια Κάτω δεξιά Πρόβλεψη μπλοκ φωτεινότητας 4X4 (Diagonal Down- Right ) 2.6 Κάθετη δεξιά Πρόβλεψη μπλοκ φωτεινότητας 4X4 (Vertical Right ) 2.7 Οριζόντια Κάτω Πρόβλεψη μπλοκ φωτεινότητας 4X4 (Horizontal-Down ) 2.8 Κάθετη Αριστερά Πρόβλεψη μπλοκ φωτεινότητας 4X4 (Vertical-Left) 2.9 Πάνω οριζόντια Πρόβλεψη μπλοκ φωτεινότητας 4X4 (Horizontal- Up) 2.10 Χαρακτηριστικό παράδειγμα 3. Τρόποι πρόβλεψης 16X16 μπλοκ φωτεινότητας 3.1 Κάθετη Πρόβλεψη μπλοκ φωτεινότητας 16X16 (Vertical ) 3.2 Οριζόντια Πρόβλεψη μπλοκ φωτεινότητας 16X16 (Horizontal) 3.3 Πρόβλεψη μέσου όρου μπλοκ φωτεινότητας 16X16 (DC ) 3.4 Plane Πρόβλεψη μπλοκ φωτεινότητας 16X16 (Plane ) 3.5 Χαρακτηριστικό παράδειγμα 4. Intra prediction 4X4 vs. Intra Prediction 16X16 5.Τρόποι πρόβλεψης 8X8 μπλοκ χρώματος 6. Επιλογή κατάλληλου τρόπου 1. Εισαγωγή 2. Σχεδίαση τρόπων πρόβλεψης 4X4 μπλοκ φωτεινότητας 2.1 Μαθηματική αναπαράσταση τρόπων πρόβλεψης 4X4 μπλοκ φωτεινότητας σύμφωνα με το πρότυπο Η.264 και Τροποποίηση Κάθετη Πρόβλεψη μπλοκ φωτεινότητας 4X4 (Vertical ) Οριζόντια Πρόβλεψη μπλοκ φωτεινότητας 4X4 (Horizontal ) Πρόβλεψη Μέσου όρου μπλοκ φωτεινότητας 4X4 (DC)
6 2.1.4 Διαγώνια Κάτω αριστερά Πρόβλεψη μπλοκ φωτεινότητας 4X4 (Diagonal Down -Left) Διαγώνια Κάτω δεξιά Πρόβλεψη μπλοκ φωτεινόχητας 4X4 (Diagonal Down- Right) Κάθετη δεξιά Πρόβλεψη μπλοκ φωτεινότητας 4X4 (Vertical-Right) Οριζόντια Κάτω Πρόβλεψη μπλοκ φωτεινότητας 4X4 (Horizontal-Down ) Κάθετη Αριστερά Πρόβλεψη μπλοκ φωτεινότητας 4X4 (Vertical-Left) Πάνω οριζόντια Πρόβλεψη μπλοκ φωτεινότητας 4X4 3. Σχεδίαση τρόπων πρόβλεψης 16X16 μπλοκ φωτεινότητας 3.1 Μαθηματική αναπαράσταση τρόπων πρόβλεψης 16X16 μπλοκ φωτεινότητας σύμφωνα με το πρότυπο Η.264 και τροποποίηση Κάθετη Πρόβλεψη μπλοκ φωτεινότητας 16X Οριζόντια Πρόβλεψη μπλοκ φωτεινότητας 16X Πρόβλεψη μέσου όρου μπλοκ φωτεινότητας 16X Plane Πρόβλεψη μπλοκ φωτεινότητας 16X16 1. Εισαγωγή 2. Υλοποίηση μεθόδων πρόβλεψης για τα μπλοκ φωτεινότητας 4X4 3. Υλοποίηση μεθόδων πρόβλεψης για τα μπλοκ φωτεινότητας 16X16 1. Εισαγωγή 2. Design compiler 3. Πειραματικές μετρήσεις και αποτελέσματα
7
8 Η εργασία αυτή είναι αφιερωμένη στην οικογένεια μου.
9 i. Τι είναι το Η.264 To h.264 είναι ένα βιομηχανικό πρότυπο (standard) για την συμπίεση βίντεο, δηλαδή την διαδικασία κατά την οποία μετατρέπεται ψηφιακό βίντεο σε μια άλλη μορφή η οποία καταλαμβάνει λιγότερη χωρητικότητα όταν αποθηκεύεται ή μεταδίδεται. Η συμπίεση βίντεο (video coding) είναι μια απαραίτητη τεχνολογία για εφαρμογές όπως ψηφιακή τηλεόραση % DVD-video : mobile TV : video conferencing : internet video streaming To νέο αυτό πρότυπο έχει τίτλο Advanced Video Coding (AVC) και εκδίδεται από την International standard bodies ITU-T (International Telecommunication Union) και ISO/IEC (International Organization for standardization /International Electron technical Commission). Ορίζει μια σύνταξη για κωδικοποίηση βίντεο και μια μέθοδο για αποκωδικοποίηση αυτής της σύνταξης για να παράγει μια ακολουθία βίντεο που θα μπορεί να προβληθεί. Το πρότυπο αυτό δεν προσδιορίζει επακριβώς πώς να κωδικοποιείται (συμπιέζεται) βίντεο -αυτό αφήνεται στο κατασκευαστή του κωδικοποιητή βίντεο -αλλά στην πράξη τα βήματα που λαμβάνουν χώρα στον κωδικοποιητή είναι τα αντίθετα από αυτά συμβαίνουν κατά την διαδικασία αποκωδικοποίησης. Ένας κωδικοποιητής αναλαμβάνει να μετατρέψει βίντεο σε μια συμπιεσμένη μορφή και ένας αποκωδικοποίησής μετατρέπει συμπιεσμένο βίντεο πίσω στη μη συμπιεσμένη μορφή. Το σχήμα απεικονίζει την διαδικασία κωδικοποίησης και αποκωδικοποίησης.
10 To H.264/AVC πρώτα δημοσιεύτηκε το Χτίστηκε πάνω σε παλαιότερα πρότυπα όπως το MPEG-2 και MPEG-4 και προσφέρει την δυνατότητα για καλύτερη απόδοση συμπίεσης και μεγαλύτερη ευελιξία στην μεταφορά, στη συμπίεση και στην αποθήκευση βίντεο. VIDEO ENCODER > 7 VIDEO DECODER Scope of EC2!6*1/AVC standard 2. Πώς ένας κωδικοποιητής-αποκωδικοποιητής Η.264 λειτουργεί; Ένας κωδικοποιητής βίντεο Η.264 πραγματοποιεί τις διαδικασίες πρόβλεψης, μετατροπής και κωδικοποίησης (,-,/ για να παραγάγει ένα συμπιεσμένο Η.264 bitstream. Ένας αποκωδικοποιητής βίντεο Η.264 πραγματοποιεί τις συμπληρωματικές διαδικασίες της αποκωδικοποίησης, της αντίστροφης μετατροπής και της αναδημιουργίας για να παράγει μια αποκωδικοποιημένη ακολουθία βίντεο.
11 Ο κωδικοποιητής διαμερίζει ένα καρέ βίντεο στις μονάδες ενός macroblock 16x16 δειγμάτων. Διαμορφώνει μια πρόβλεψη του macroblock αυτού βαοιομένη οε στοιχεία που έχουν κωδικοποιηθεί προηγουμένως, είτε από το τρέχον καρέ (intra prediction) είτε από άλλα καρέ που έχουν ήδη κωδικοποιηθεί και μεταδοθεί (inter prediction). Ο κωδικοποιητής αφαιρεί την πρόβλεψη από το τρέχον μπλοκ (μπλοκ 16X16 ή 4X4) για να διαμορφώσει το μπλοκ υπολοίπων (residual block). Οι μέθοδοι πρόβλεψης που υποστηρίζονται από το Η.264 είναι πιο εύκαμπτες από εκείνες στα προηγούμενα πρότυπα, επιτρέποντας περισσότερο ακριβείς προβλέψεις και ως εκ τούτου αποδοτικότερη συμπίεση βίντεο. Η πρόβλεψη χρησιμοποιεί 16x16 και 4x4 μεγέθη μπλοκ για να προβλέψει το macroblock από γειτονικά δείγματα που έχουν κωδικοποιηθεί προηγουμένως μέσα στο ίδιο καρέ (οχ ή μα 0.?). Η πρόβλεψη χρησιμοποιεί μια σειρά μεγεθών μπλοκ (από 16x16 έως 4x4) για να προβλέψει τα δείγματα στο τρέχον καρέ από παρόμοιες περιοχές προηγουμένων κωδικοποιημένων καρέ (σχήμα 0.3). \5rονιοιιsIy codeci pixels ο 11 r t1 d i c t Tn O <U cil Current block (_ 1 (> X 1 (; > Ο Γ 1 X O J
12 Ένα μπλοκ με τα υπολειπόμενα δείγματα (residual block) μετασχηματίζεται χρησιμοποιώντας 4x4 ή 8x8 integer transform, μια προσεγγιστική μορφή του διακριτού μετασχηματισμού συνημίτονου (DCT). Η μετατροπή παράγει ένα σύνολο συντελεστών, κάθε ένας από τους οποίους είναι μια βεβαρημένη τιμή για κάθε σταθμισμένο σχέδιο βάσης. Όταν συνδυάζονται, τα σταθμισμένα σχέδια βάσης αναδημιουργούν το μπλοκ με τα υπολειπόμενα δείγματα. Το - επιδεικνύει πώς ο αντίστροφος DCT δημιουργεί έναν μπλοκ εικόνας με τη στάθμιση κάθε σχεδίου βάσης σύμφωνα με μια τιμή ενός συντελεστή και το συνδυασμό των βεβαρημένων σχεδίων βάσης. Το αποτέλεσμα της μετατροπής ενός μπλοκ με μετασχηματισμένους συντελεστές, κβαντοποιείται, δηλαδή κάθε συντελεστής διαιρείται με μια ακέραια τιμή. Η κβαντοποίηση μειώνει την ακρίβεια των συντελεστών μετατροπής σύμφωνα με μια παράμετρο κβαντοποίησης (QP). Τυπικά το αποτέλεσμα είναι ένα μπλοκ στο οποίο οι περισσότεροι ή όλοι οι συντελεστές είναι μηδέν, με μερικούς συντελεστές μη μηδενικούς. Ρύθμιση του QP σε μεγάλη τιμή σημαίνει ότι οι περισσότεροι συντελεστές παίρνουν τιμή μηδέν με συνέπεια την υψηλή συμπίεση εις βάρος της φτωχής αποκωδικοποιημένης ποιότητας εικόνας. Θέτοντας QP σε μια χαμηλή τιμή σημαίνει ότι περισσότεροι διαφορετικοί από το μηδέν συντελεστές παραμένουν μετά τον
13 κβαντισμό με συνέπεια την καλύτερη αποκωδικοποιημένη ποιότητα εικόνας αλλά τη χαμηλότερη συμπίεση. I ϋ I Μ Μ Μ * «" ι m m mm Η διαδικασία κωδικοποίησης βίντεο παράγει διάφορες τιμές που πρέπει να κωδικοποιηθούν για να διαμορφώσουν το συμπιεσμένο bitstream. Αυτές οι τιμές περιλαμβάνουν : κβαντοποιημένους συντελεστές μετατροπής : πληροφορίες για να επιτρέψει στον αποκωδικοποιητή να αναδημιουργήσει την πρόβλεψη πληροφορίες για τη δομή των συμπιεσμένων στοιχείων και τα Εργαλεία συμπίεσης που χρησιμοποιούνται κατά τη διάρκεια της κωδικοποίησης πληροφορίες για την πλήρη ακολουθία βίντεο.
14 Αυτές οι τιμές και οι παράμετροι (στοιχεία σύνταξης) μετατρέπονται σε δυαδικούς κώδικες χρησιμοποιώντας κωδικοποίηση μεταβλητού μήκους (CAVLC) ή/και αριθμητική κωδικοποίηση (CABAC). Κάθε μια από αυτές τις μεθόδους κωδικοποίησης παράγουν μια αποδοτική, συμπαγή δυαδική αναπαράσταση της πληροφορίας. Η κωδικοποιημένη ακολουθία μπορεί έπειτα να αποθηκευτεί ή/και να μεταδοθεί. Ένας αποκωδικοποιητής βίντεο λαμβάνει το συμπιεσμένο Η.264 bitstream, αποκωδικοποιεί κάθε ένα από τα συντακτικά στοιχεία και εξάγει τις πληροφορίες που περιγράφονται παραπάνω (κβαντοποιημένοι συντελεστές, πληροφορίες πρόβλεψης, κλπ). Αυτές οι πληροφορίες χρησιμοποιούνται έπειτα για να αντιστρέφουν τη διαδικασία κωδικοποίησης και αναδημιουργούν μια ακολουθία τηλεοπτικών εικόνων. Οι κβαντοποιημένοι συντελεστές κλιμακώνονται ξανά. Κάθε συντελεστής πολλαπλασιάζεται με μια ακέραια τιμή για να αποκαταστήσει την αρχική κλιμάκωση του. Μια αντίστροφη μετατροπή συνδυάζει τα τυποποιημένα σχέδια βάσης, που σταθμίζονται από τους επανακλιμακούμενους συντελεστές, για να αναδημιουργήσουν κάθε επιμέρους μπλοκ από τα υπολειπόμενα στοιχεία (residual block). Αυτά τα μπλοκ συνδυάζονται μαζί για να διαμορφώσουν το residual macroblock. Για κάθε μπλοκ, ο αποκωδικοποιητής διαμορφώνει μια ίδια πρόβλεψη με αυτή που δημιουργείται από τον κωδικοποιητή. Ο αποκωδικοποιητής προσθέτει την πρόβλεψη mro αποκωδικοποιημένο μπλοκ υπολοίπων (residual block) για να αναδημιουργήσει τελικά ένα αποκωδικοποιημένο macroblock που μπορεί έπειτα να επιδειχθεί ως τμήμα ενός τηλεοπτικού πλαισίου.
15 1. Δομή Η.264 Το Η.264 καθορίζει ένα σύνολο τριών Profiles όπου κάθε ένα από αυτά υποστηρίζει ένα ιδιαίτερο σύνολο λειτουργιών κωδικοποίησης και διευκρινίζει τι απαιτείται από έναν κωδικοποιητή ή έναν αποκωδικοιιοιητή που πειθαρχεί στο συγκεκριμένο profile. 1.1). To Baseline Profile υποστηρίζει infra, inter πρόβλεψη (χρησιμοποιώντας τις Ι-φέτες και τις Ρ-φέτες) και κωδικοποίηση εντροπίας με τους προσαρμοστικούς κώδικες μεταβλητού-μήκους για ένα καρέ (CAVLC). Οι πιθανές εψαρμογές του συγκεκριμένου profile περιλαμβάνουν τη βιντεοτηλεφωνία, συνεδρίαση μέσω video και ασύρματες επικοινωνίες To Main Profile περιλαμβάνει την υποστήριξη για interlaced βίντεο, για inter κωδικοποίηση χρησιμοποιώντας τις Β-φέτες, για inter κωδικοποίηση χρησιμοποιώντας τη σταθμισμένη πρόβλεψη και κωδικοποίηση εντροπίας που χρησιμοποιεί την αριθμητική κωδικοποίηση βασισμένη σε καρέ (CABAC). Οι πιθανές εφαρμογές του συγκεκριμένου profile περιλαμβάνουν τηλεοπτική ραδιοφωνική αναμετάδοση και τηλεοπτική αποθήκευση. To Extended Profile δεν υποστηρίζει το πεπλεγμένο βίντεο ή CABAC αλλά προσθέτει τρόπους για να επιτρέψει την αποδοτική εναλλαγή μεταξύ κωδικοποιημένων bitstream (SP και SI-φέτες) και τη βελτιωμένη ανθεκτικότητα λάθους. To Extended Profile μπορεί να είναι ιδιαίτερα χρήσιμο για εφαρμογές μέσων ροής. Εντούτοις, κάθε σχεδιάγραμμα έχει την ικανοποιητική ευελιξία να υποστηρίξει ένα ευρύ φάσμα εφαρμογών.
16 [ <,η I- I iif> til To H.264 υποστηρίζει την κωδικοποίηση και την αποκωδικοποίηση για 4:2:0 interlaced βίντεο και την προεπιλεγμένη μορφή δειγματοληψίας για 4:2:0 προοδευτικά καρέ. Με το προεπιλεγμένο σχήμα δειγματοληψίας, τα δείγματα χρώματος (Cb και Cr) ευθυγραμμίζονται οριζόντια με κάθε δεύτερο δείγμα φωτεινότητας και τοποθετούνται κάθετα μεταξύ δύο δειγμάτων φωτεινότητας. Ένα πεπλεγμένο καρέ αποτελείται από δύο τομείς που χωρίζεται εγκαίρως.
17 Το Η.264 κάνει μια διάκριση μεταξύ ενός στρώματος τηλεοπτικής κωδικοποίησης (VCL) και ενός στρώματος αφαίρεσης δικτύου (NAL). Η έξοδος της διαδικασίας κωδικοποίησης είναι δεδομένα VCL (μια ακολουθία από bits τα οποία αναπαριστούν τα κωδικοποιημένα δεδομένα βίντεο) τα οποία χαρτογραφούνται στις μονάδες NAL πριν από τη μετάδοση ή την αποθήκευση. Ένα καρέ βίντεο κωδικοποιείται σαν μια ή περισσότερες φέτες η καθεμία εκ των οποίων αποτελείται από ένα ή περισσότερα macroblock. Υπάρχει το ενδεχόμενο να υπάρχει ένα macroblock ανά καρέ ή ακόμη και μία φέτα ανά καρέ. Ο αριθμός των macroblocks ανά φέτα μπορεί να μην είναι συνεχόμενος μέσα σε ένα καρέ ; Υπάρχουν 5 διαφορετικές φέτες και κατ' επέκταση καρέ. : Αυτόνομα κωδικοποιημένα καρέ(κωδικοποιημένα ως εικόνες) : ; κυρ : Κωδικοποιημένα με βάση προβλεπτική κωδικοποίηση από άλλα Ρ ή I καρέ Παρεμβαλλόμενα (Interpolation) frames ανάμεσα σε Ρ και I frames
18 τα καρέ SP και SI επιτρέπουν την αποδοτική μετατροπή μεταξύ ίων τηλεοπτικών ρευμάτων και της αποδοτικής τυχαίας προσπέλασης για τους τηλεοπτικούς αποκωδικοιιοιητές. Το είδος αυτό των καρέ κάνει χρήση του intra frame-coding. Τα καρέ τύπου I είναι τα μόνα που είναι κωδικοποιημένα σεο σύνολό τους και η αποκωδικοποίηση μπορεί να γίνει χωρίς αναφορά σε κάποιο άλλο. Αποτελούν σημεία αναφοράς κατά την τυχαία προσπέλαση ενός σήματος. Επειδή η παρουσία τους είναι απαραίτητη σα σημείο χρονικής αναφοράς και για να αποφευχθεί η διάδοση των σφαλμάτων που δημιουργούν τα Ρ καρέ επιβάλλεται να μεταδίδονται ανά τακτά χρονικά καρέ. Έτσι υπάρχει ένα I καρέ τουλάχιστον κάθε 15 καρέ (δηλαδή δύο φόρες το δευτερόλεπτο αν η συχνότητα είναι 30 Ηζ). Η διαδικασία της κωδικοποίησης ενός I καρέ βασίζεται στη λογική του προτύπου JPEG. Η εικόνα χωρίζεται σε macroblocks και για κάθε μπλοκ ξεχωριστά εφαρμόζεται DCT, Κβαντοποίηση, Zig-Zag Scanning, Run-Length Encoding και Huffman Encoding. Τα καρέ τύπου Ρ είναι βασισμένα σε ένα προηγούμενο I ή Ρ καρέ. Με τη βοήθεια του motion compensation προβλέπουν τη νέα θέση όποιων macroblocks έχουν απλά μετακινηθεί και κωδικοποιούν τον αριθμό του macroblock, ένα διάνυσμα κίνησης και τη διαφορά (σφάλμα πρόβλεψης). Με τη σειρά τους μπορούν να αποτελόσουν και αυτά σημείο αναφοράς για επόμενα καρέ και αυτός είναι και ο λόγος που συμβάλλουν στην εισαγωγή και διάδοση σφαλμάτων, αφού η διαδικασία της πρόβλεψης κίνησης δεν μπορεί να είναι 100% ακριβής. Δεν έχουν το μέγεθος των I καρέ γιατί δεν έχουν περιγράφει με την ίδια ακρίβεια, δηλαδή παρουσιάζουν μεγαλύτερο ποσοστό συμπίεσης. Η διαδικασία λοιπόν της κωδικοποίησης τους περιλαμβάνει:
19 : σύγκριση macroblocks του τρέχοντος καρέ με αυτά του προηγουμένου και εύρεση της βέλτιστης ομοιότητας (motion estimation) : δημιουργία διανύσματος κίνησης, και υπολογισμός των διαφορών πρόβλεψης (motion compensation) : μετασχηματισμός DCT των διαφορών σε κάθε μπλοκ του νέου macroblock, κβαντοποίηση : Run-Length-Encoding και το αποτέλεσμα κωδικοποιείται με κωδικοποίηση Huffman, όπως και οτα I καρέ Τα καρέ τύπου Β είναι καρέ που δημιουργούνται λαμβάνοντας το μέσο όρο σε επίπεδο macroblock ενός προηγούμενου και ενός επόμενου καρέ 1 και Ρ (ένα από το κάθε είδος). Δε συντελούν τόσο πολύ στη διάδοση των σφαλμάτων γιατί δεν χρησιμοποιούνται ως σημεία αναφοράς και επιπλέον μειώνουν σημαντικά το σφάλμα παίρνοντας το μέσο όρο από δύο καρέ. Μπορούμε να πούμε ότι ο 'κύκλος της ζωής' τους περιορίζεται μόνο σε αυτά και δεν επεκτείνεται με το να κληροδοτούν πληροφορίες σε άλλα καρέ, κάτι που πολλές φορές σε συνδυασμό και με την υπολογιστική πολυπλοκότητα που απαιτούν για την κωδικοποίηση και αποκωδικοποίηση τα κάνει μη επιθυμητά από τους κατασκευαστές. Η διαδικασία της κωδικοποίησης περιλαμβάνει συνδυασμό των αντίστοιχων macroblocks που παρουσιάζουν μικρές διαφορές με τα αντίστοιχα των καρέ αναφοράς (προηγούμενο και επόμενο) δηλαδή αφαίρεση του μέσου όρου των άλλων δύο από το τρέχον καρέ, συνδυασμό των διανυσμάτων κίνησης των καρέ αναφοράς (που συνδυάζονται όπως και τα αντίστοιχα macroblocks, δηλαδή λαμβάνεται ο μέοος όρος τους) και στη συνέχεια την ίδια διαδικασία με τα I και Ρ καρέ για την κωδικοποίηση του macroblock που προκύπτει. Οι φέτες SP και φέτες SI μπορούν να χρησιμοποιηθούν για την ανθεκτικότητα λάθους, για τη μετατροπή μεταξύ των διαφορετικών streams και για γρήγορη προώθηση. Οι φέτες SP χρησιμοποιούνται για να
20 κωδικοποιήσουν την ίδια φέτα χρησιμοποιώντας δύο διαφορετικά καρέ αναφοράς. Οι δύο φέτες SP αποκωδικοποιούνται ακριβώς στα ίδια στοιχεία. Μια φέτα SI κωδικοποιείται έτσι ώστε να αποκωδικοποιήσει ακριβώς τα ίδια στοιχεία με μια αντίστοιχη φέτα SP. 2. Η διαδικασία Κωδικοποίησης -Αποκωδικοποίησης Ένα καρέ διαιρείται σε macroblocks (16x16 δειγμάτων). Τα macroblocks ομαδοποιούνται σε φέτες. Κάθε φέτα κωδικοποιείται είτε ως φέτα I, Ρ είτε Β (Υπάρχουν επίσης τύποι αποκαλούμενοι SI και SP). Σε μια φέτα I, όλα τα block κωδικοποιούνται ως block I. Σε μια φέτα Ρ, τα block κωδικοποιούνται ως block I ή Ρ. Σε μια φέτα Β, τα block κωδικοποιούνται ως block I, Ρ ή Β. Ο κωδικοποιητής περιλαμβάνει δύο κατευθύνσεις ροής πληροφοριών, μια αριστερά προς τα δεξιά (κωδικοποίηση) και μια δεξιά προς τα αριστερά (αναδημιουργία). Η κατεύθυνση ροής πληροφοριών στον αποκωδικοποιητή παρουσιάζεται από δεξιά στα αριστερά για να απεικονίσει τις ομοιότητες μεταξύ του κωδικοποιητή και του αποκωδικοποιητή. Πριν εξεταστεί λεπτομερώς το Η.264, θα περιγράφουμε τα κύρια βήματα στην κωδικοποίηση και την αποκωδικοποίηση ενός καρέ βίντεο. Η ακόλουθη περιγραφή απλοποιείται προκειμένου να παρασχεθεί μια επισκόπηση των διαδικασιών κωδικοποίησης και αποκωδικοποίησης. Ένα καρέ ή ένας τομέας εισαγωγής F υποβάλλεται σε επεξεργασία στις μονάδες ενός macroblock. Κάθε macroblock κωδικοποιείται με intra ή inter πρόβλεψη, και για κάθε μπλοκ στο macroblock, μια πρόβλεψη PRED (Ρ μέσα στο.. >') διαμορφώνεται βασισμένη στα αναδημιουργημένα δείγματα εικόνων. Στην intra πρόβλεψη, η PRED διαμορφώνεται από τα δείγματα στην τρέχουσα φέτα που έχουν κωδικοποιηθεί προηγουμένως, έχουν
21 αποκωδικοποιηθεϊ και έχουν αναδημιουργηθεί (uf'n στο οχήμα 1.3, σημειώστε ότι τα μη φιλτραρισμένα δείγματα χρησιμοποιούνται για να διαμορφώσουν PRED). Στην inter πρόβλεψη, η PRED διαμορφώνεται από την motion-compensated πρόβλεψη από μια ή δύο εικόνες αναφοράς που επιλέγονται από το σύνολο εικόνων αναφοράς. Στις εικόνες, η εικόνα αναφοράς παρουσιάζεται ως προηγούμενη κωδικοποιημένη εικόνα F'n_i αλλά η αναφορά πρόβλεψης για κάθε macroblock (στην inter πρόβλεψη) μπορεί να επιλεχτεί από μια επιλογή των προηγούμενων ή μελλοντικών εικόνων που έχουν κωόικοποιηθεΐ ήδη, αναδημιουργηθεί και φιλτραριστεί. FI πρόβλεψη PRED αφαιρείται από τον τρέχον μπλοκ για να παραχθεί το μπλοκ υπολειπομένων (residual block) D που μετασχηματίζεται και κβαντοποιείται για να δώσει X, ένα σύνολο κβαντοποιημένων συντελεστών μετατροπής οι οποίοι έχουν αναδιαταχτεί και κωδικοποιηθεί. Οι κωδικοποιημένοι συντελεστές μέσω της εντροπίας, μαζί με την πληροφορία που απαιτείται για να αποκωδικοποιηθεϊ κάθε μπλοκ μέσα στο macroblock διαμορφώνουν το συμπιεσμένο bitstream το οποίο εισάγεται σε ένα στρώμα αφαίρεσης δικτύων (NAL) για μετάδοση ή αποθήκευση. ι,
22 Ο κωδικοποιητής αναδημιουργεί κάθε μπλοκ για να παρέχει μια αναφορά για τις περαιτέρω προβλέψεις. Οι συντελεστές X κλιμακώνονται (Q ') και μετασχηματίζονται αντίστροφα (Τ1) για να παράγουν ένα υπολειπόμενο μπλοκ D'. διαφοράς. Το μπλοκ πρόβλεψης PRED προστίθεται στο D' για να δημιουργηθεί ένα αναδημιουργημένο μπλοκ uf'n (μια αποκωδικοποιημένη έκδοση του αρχικού μπλοκ, το υ δείχνει ότι δεν είναι φιλτραρισμένο). Ένα φίλτρο εφαρμόζεται για να μειώσει τα αποτελέσματα της διαμόρφωσης του μπλοκ και η αναδημιουργημένη εικόνα αναφοράς δημιουργείται από μια σειρά μπλοκ F'n. Ο αποκωδικοποιητής λαμβάνει ένα συμπιεσμένο bitstream από το NAL και αποκωδικοποιεί τα δεδομένα μέσω εντροπίας για να παραγάγει ένα σύνολο κβαντοποιημένων συντελεστών X. Αυτοί κλιμακώνονται και μετασχηματίζονται αντίστροφα για να δώσουν D'n (ίδιο με το D'n που παρουσιάζεται στον κωδικοποιητή). Χρησιμοποιώντας τις πληροφορίες κεφαλίδας που αποκωδικοποιούνται από το bitstream, ο αποκωδικοποιητής δημιουργεί ένα μπλοκ πρόβλεψης PRED, ίδιο με τον αρχικό PRED που διαμορφώνεται στον κωδικοποιητή. Το τελευταίο προστίθεται στο D',, για να παράγει uf'n που φιλτράρονται για να δημιουργήσουν κάθε αποκωόικοποιημένο μπλοκ F',.
23 Ίσως το μεγαλύτερο πλεονέκτημα του Η.264 σε σχέση τα προηγούμενα πρότυπα είναι η απόδοση στην συμπίεση. Έναντι των προτύπων όπως Mpeg- 2 και Mpeg-4, το Η.264 μπορεί να επιτύχει: : Καλύτερη ποιότητα εικόνας στο ίδιο συμπιεσμένο bitrate : Ένα χαμηλότερο συμπιεσμένο bitrate για την ίδια ποιότητα εικόνας. Παραδείγματος χάριν, ένα single-layer DVD μπορεί να αποθηκεύσει μια ταινία μήκους περίπου 2 ωρών σε MPEG- 2 μορφή. Χρησιμοποιώντας το Η.264, πρέπει να είναι δυνατό να αποθηκευτούν 4 ώρες ή περισσότερες της ταινίας σε ίδιο δίσκο (δηλ. χαμηλότερο bitrate). Εναλλακτικά, η μορφή συμπίεσης Η.264 μπορεί να μεταδώσει καλύτερη ποιότητα στο ίδιο bitrate έναντι Mpeg-2 και Mpeg-4 οπτικά p τ. Η βελτιωμένη απόδοση συμπίεσης Η.264 έρχεται στην τιμή μεγαλύτερου υπολογιστικού κόστος. Το Η.264 είναι περιπλοκότερο από τις προηγούμενες μεθόδους συμπίεσης και αυτό σημαίνει ότι μπορεί να πάρει σημαντικά περισσότερη ισχύς επεξεργασίας να συμπιέσει και αποσυμπιέσει το βίντεο Η.264.
24 Παρόλο τη βελτιωμένη απόδοση συμπίεσής του, το Η.264 προσφέρει μεγαλύτερη ευελιξία στις επιλογές συμπίεσης και της υποστήριξης μετάδοσης. Ένας κωδικοποιητής Η.264 μπορεί να επιλέξει από μια ευρεία ποικιλία εργαλείων συμπίεσης, καθιστώντας τον κατάλληλο για εφαρμογές από γο χαμηλός-ποσοστό δυαδικών ψηφίων και τη χαμηλή καθυστέρηση κινητής μετάδοσης. Τα πρότυπα παρέχουν ενσωματωμένη υποστήριξη για μετάδοση ή αποθήκευση, συμπεριλαμβανομένης μιας πακετοποιημένης συμπιεσμένης μορφής και των χαρακτηριστικών γνωρισμάτων που βοηθούν για να ελαχιστοποιηθεί η επίδραση των λαθών μετάδοσης. To H.264/AVC υιοθετείται για μια αυξανόμενη σειρά εφαρμογών, που περιλαμβάνουν: : Υψηλός καθορισμός DVD's (σχήματα hd-dvd και blu-ακτίνων) : Υψηλή τηλεοπτική αναμετάδοση καθορισμού στην Ευρώπη : Τα προϊόντα Apple : Τηλεοπτικές εφαρμογές του ΝΑΤΟ και των ΗΠΑ DoD : Κινητή τηλεοπτική αναμετάδοση : Βίντεο Διαδικτύου Ι Συνεδρίαση μέσω βίντεο
25 To h.264 έχει κοινά σημεία με άλλα πρότυπα. Αυτά είναι :* 16χ 16 macroblocks > Συμβατική 4:2:0 δειγματοληψία χρώματος και σύνδεση των στοιχείων φωτεινότητας και χρώματος : Μετατόπιση κίνησης μπλοκ ( block motion displacement ) : Διανύσματα κίνησης πέρα από τα όρια εικόνων ν Μεταβλητή κίνηση μεγέθους μπλοκ ν Μετατροπές μπλοκ : Κλιμακωτή κβαντοποίηοη : I, Ρ και Β τύποι εικόνας
26 1. Πρόβλεψη των intra macroblocks Όπως έχουμε ήδη δει, ένα καρέ εικόνας αρχικά χωρίζεται σε macroblocks ;. )μα. k00e macroblock αποτελείται από μικρότερα δομικά στοιχεία, τα οποία έχουμε ονομάσει μπλοκ.... Ένα μπλοκ στην ουσία είναι ένας δυσδιάστατος πίνακας και κάθε στοιχείο του είναι ένα pixel (σχήμα. Η τιμή κάθε pixel προκύπτει με την εφαρμογή των μεθόδων πρόβλεψης ενός macroblock. Υπάρχουν δυο μέθοδοι πρόβλεψης, η και η. Στην πρώτη, οι τιμές των pixels προκύπτουν από τιμές των pixels γειτονικών μπλοκ που βρίσκονται όμως στο ίδιο καρέ ενώ στη δεύτερη προκύπτουν από τιμές των pixels μπλοκ που βρίσκονται σε διαφορετικά καρέ αλλά στην ίδια θέση με το τρέχον. Για παράδειγμα, αν το τρέχον μπλοκ σε ένα καρέ είναι το μπλοκ που βρίσκεται πάνω και αριστερά, οι τιμές των pixels του τρέχοντος μπλοκ θα προκύψουν από μπλοκ μου βρίσκονται στην ίδια θέση με το τρέχον σε διαφορετικά καρέ.
27 Β Λ C Πιο συγκεκριμένα στην intra πρόβλεψη, οι τιμές των pixels ανήκουν σε γειτονικά μπλοκ τα οποία έχουν κωδικοποιηθεί προηγουμένως και ξαναδημιουργηθεί αλλά δεν είναι φιλτραρισμένα (υχήμα 2.3). Αυτό το μπλοκ πρόβλεψης Ρ αφαιρείται από το τρέχον μπλοκ πριν από την κωδικοποίηση. Για τα δείγματα φωτεινότητας (luma), το Ρ μπορεί να διαμορφωθεί για κάθε 4x4 μπλοκ ή για ένα 16x16 macroblock. Υπάρχουν συνολικά : 9 προαιρετικοί τρόποι πρόβλεψης για κάθε 4x4 luma μπλοκ ; υχήμα > 4 προαιρετικοί τρόποι για έναν luma 16x16 μπλοκ : και ένας τρόπος που εφαρμόζεται πάντα σε κάθε 4x4 μπλοκ χρώματος.
28 Μέθοδοι πρόβλεψης 4X4 luma μπλοκ. Mode 0 Mode 1 Mode 2 Mode 3 Mode 4 Mode 5 Mode 6 Mode 7 Mode 8 Vertical Horizontal DC (πάντα πραγματοποιείται Diagonal down -left Diagonal down -right Vertical right Horizontal-down Vertical left Horizontal-up Μέθοδοι πρόβλεψης 16X16 luma μπλοκ. Mode 0 Mode 1 Mode 2 Mode 3 Vertical Horizontal DC Plane
29 I 2. Τρόποι πρόβλεψης 4X4 μπλοκ ψωτεινότητας Το ' παρουσιάζει ένα luma macroblock και ένα 4x4 luma μπλοκ που πρέπει να προβλεφθεί. Τα δείγματα επάνω και αριστερά έχουν κωδικοποιηθεί προηγουμένως και αναδημιουργηθεί και είναι επομένως διαθέσιμα στον κωδικοποιητή και τον αποκωδικοποιητή για να διαμορφώσει μια αναφορά πρόβλεψης. Το μπλοκ πρόβλεψης Ρ υπολογίζεται σύμφωνα με τα δείγματα Α έως Μ στο., ως εξής. Η DC πρόβλεψη (τρόπος 0) τροποποιείται ανάλογα με το ποια δείγματα είναι διαθέσιμα. Οι άλλοι τρόποι (1-8) μπορούν μόνο χρησιμοποιηθούν μόνο εάν όλα τα απαραίτητα δείγματα πρόβλεψης είναι διαθέσιμα. Ο κωδικοποιητής μπορεί να επιλέξει τον τρόπο πρόβλεψης για κάθε μπλοκ που ελαχιστοποιεί το υπόλοιπο μεταξύ του Ρ και του μπλοκ που κωδικοποιείται.
30 Μ A B c D E F G H 1 α b d 1 J e r g [Ί κ j k 1 L rn n o P
31 Τα δείγματα A,B,C,D που βρίσκονται στο πάνω μέρος του πίνακα προεκτείνονται κάθετα Τα δείγματα I,J,Κ,L που βρίσκονται αριστερά του πίνακα προεκτείνονται οριζόντια
32 Όλα τα δείγματα στο μπλοκ προβλέπονται από το μέσο όρο των δειγμάτων A,B,C,D και I,J,K,L,χ.;χημυ. Τα δείγματα παρεμβάλλονται σε μια γωνία 45 μεταξύ του κάτω δεξιά δείγματος και άνω αριστερά
33 Τα δείγματα παρεκτείνονται σε μια γωνία 45 κάτω και προς τα αριστερά 4 ~ι τ - r - F - j χ\ \ V \ \ \ V V \ χ X X * \Χ\\ λ. 4 A X Παρέκταση διαγωνίως περίπου αριστερά και κάθετα (πλάτος/ύψος = 1/2)..
34 Παρέκταση διαγωνίως περίπου 26.6 οριζόντια και κάτω (πλάτος/ύψος = 1/2) Προέκταση (ή παρεμβολή) διαγωνίως περίπου δεξιά της κατακορύφου
35 Παρεμβολή διαγωνίως περίπου 26.6 επάνω και οριζόντια J : Ι:Ί El"1 _,.W,.Ψ - Οι εννέα τρόποι πρόβλεψης υπολογίζονται για την εικόνα του υχήμαιος 2.16 και τα μπλοκ πρόβλεψης Ρ που προκύπτουν από κάθε τρόπο απεικονίζονται στην εικόνα του χπ; 2..Το ποσό των απόλυτων σφαλμάτων (SAE) για κάθε μία πρόβλεψη δείχνει το μέγεθος του λάθους πρόβλεψης. Σε αυτή την περίπτωση, το καλύτερο ταίριασμα στο τρέχων καρέ δίνεται από τον τρόπο 8 (horizontal -up ) επειδή αυτός ο τρόπος δίνει το μικρότερο το SAE. Μια οπτική σύγκριση δείχνει ότι το μπλοκ Ρ εμφανίζεται αρκετά παρόμοιο με τα αρχικό 4x4 μπλοκ.
36 (!viri;3li. SAE=eIS ih :riz:*ntall 8AE idc;. $AE=v)7 3 iolv: -:oan. lrft'. $ E=223 - ldi.il.; c: /. ' -ight;. SAE= *[22 c iven'il-nyt), $AE=KE ί ihorizoira dvan. SAE-209 SAE=:E7 8 ;-cfizcn:a. p;. $AE=333
37 3. Τρόποι πρόβλεψης 16X16 μπλοκ φωτεινότητας Σαν εναλλακτική λύση των τρόπων για τα 4X4 μπλοκ φωτεινότητας που περιγράφονται ανωτέρω, ένα ολόκληρο μπλοκ φωτεινότητας 16x16 μπορεί να προβλεφθεί με μια εκτέλεση. Τέσσερις τρόποι είναι διαθέσιμοι σε αυτή την περίπτωση : Τρόπος 0 (κατακόρυφος) : Τρόπος 1 (οριζόντιος) : Τρόπος 2 (συνεχές ρεύμα): μέσος όρος ανώτερων και αριστερών δειγμάτων : Τρόπος 4 (επίπεδο): μια γραμμική λειτουργία εγκαθίσταται στα ανώτερα και αριστερά δείγματα. Τα δείγματα Η που βρίσκονται στο πάνω μέρος του πίνακα προεκτείνονται κάθετα J - ti...! Η Μ
38 Τα δείγματα V που βρίσκονται αριστερά του πίνακα προεκτείνονται οριζόντια I ιΐίοΐίευι :.ι ι Όλα τα δείγματα στο μπλοκ προβλέπονται από το μέσο όρο των δειγμάτων Η και V 2 '.DCι Η fv'eant'h+v}
39 Μια γραμμική επίπεδη συνάρτηση εγκαθίσταται στα ανώτερα και αριστερά δείγματα X και V. :? ψίοιτ-ί Το παρουσιάζει ένα μπλοκ φωτεινότητας μετά προηγουμένως κωδικοποιημένα δείγματα πάνω και αριστερά. Τα αποτελέσματα της πρόβλεψης δείχνουν ότι η καλύτερη αντιστοιχία δίνεται από τον τρόπο 3.
40 .. ί I or:o ίμ. ί -E = l ; : ;.! &. -E : 4
41 4. Intra prediction ίχ ί vs. Intra Prediction 16X16 Η πρόβλεψη για μπλοκ μεγέθους 4X4 είναι περισσότερη κατάλληλη για περιοχές που έχουν αρκετές λεπτομέρειες. Επίσης παρέχει περισσότερες επιλογές κατά τη διαδικασία πρόβλεψης ενός μπλοκ. Από τη άλλη η πρόβλεψη για μπλοκ μεγέθους 16X16 είναι κατάλληλη για περισσότερο ομαλές περιοχές. Η δουλεία του κωδικοποιητή είναι να συγκρίνει τα αποτελέσματα των διάφορων τρόπων και να επιλέξει την καλύτερη. Αυτό επιφέρει αρκετό κόστος. 5. Τρόποι πρόβλεψης 8X8 μπλοκ χρώματος Κάθε 8x8 τμήμα χρώματος ενός μπλοκ (macroblock) προβλέπεται από τα δείγματα χρώματος επάνω και αριστερά που έχουν κωδικοποιηθεί προηγουμένως και έχει αναδημιουργηθεί. Οι 4 τρόποι πρόβλεψης είναι παρόμοιοι με τους τρόπους πρόβλεψης μπλοκ φωτεινότητας 16x16 που περιγράφονται στην παράγραφο 3 εκτός από το ότι η διάταξη των αριθμών τρόπου είναι διαφορετική. Δηλαδή : Συνεχές ρεύμα (τρόπος 0), : οριζόντιος (τρόπος 1) : κατακόρυφος (τρόπος 2) ν Επίπεδη εφαρμογή συνάρτησης (τρόπος 3). Ο ίδιος τρόπος πρόβλεψης εφαρμόζεται πάντα και στους δύο μπλοκ χρώματος.
42 t>. tniaoy ί j κ ο γ α Λ λ r ι Λ ΰ ι του Η επιλογή κάθε τρόπου πρόβλεψης για κάθε 4x4 μπλοκ πρέπει να επιοημανθεί orov αποκωδικοποιητή και αυτό θα μπορούσε ενδεχομένως να απαιτεί έναν μεγάλο αριθμό από bits. Εντούτοις, οι τρόποι που τα γειτονικά 4x4 μπλοκ έχουν προβλεφθεί είναι ιδιαίτερα συσχετισμένοι. Παραδείγματος χάριν, ας θεωρήσουμε ότι τα μπλοκ Α,Β και Ε είναι το αριστερό μπλοκ, το πάνω μπλοκ και το τρέχον αντίστοιχα.. Εάν το Α και το Β προβλέφθηκαν χρησιμοποιώντας τον τρόπο 2, είναι πιθανό ότι ο καλύτερος τρόπος για το μπλοκ Ε (τρέχων μπλοκ) είναι επίσης ο τρόπος 2. Για κάθε τρέχοντα μπλοκ Ε, ο κωδικοποιητής και ο αποκωδικοποιητής υπολογίζουν την πιο πιθανή κατάσταση (most probable mode), δηλαδή την ελάχιστη από τις κατασγάσεις πρόβλεψης του Α και του Β. Εάν κάποιο από το Α ή το Β δεν είναι διαθέσιμα (είτε γιατί δεν είναι κωδικοποιημένα με κάποιον τρόπο πρόβλεψης μπλοκ φωτεινότητας είτε γιατί δεν είναι στην τρέχουσα φέτα )τότε η πμή της μεταβλητής most probable mode τίθεται 2 (συνεχές ρεύμα πρόβλεψη). Ο κωδικοποιητής στέλνει μια σημαία για κάθε 4x4 καρέ, την prev intra4x4 pred mode. Εάν η σημαία είναι «1», η περισσότερο πιθανή κατάσταση πρόβλεψης χρησιμοποιείται. Εάν η σημαία είναι «0», μια άλλη παράμετρος η rem intra4x4 pred mode στέλνεται για να δείξει αλλαγή του τρόπου. Εάν η rem intra4x4 pred mode είναι μικρότερη από την τρέχουσα περισσότερο πιθανή κατάσταση πρόβλεψης, τότε ο τρόπος πρόβλεψης τίθεται στο rem intra4x4 pred mode διαφορετικό ο τρόπος πρόβλεψης τίθεται rem intra4x4 pred mode+1.
43 Τέλος, όσον αφορά τα γειτονικά δείγματα, στις παρακάτω εικόνες (σχήμα απεικονίζονται δυο περιπτώσεις στις οποίες φαίνεται ποια δείγματα από τα γειτονικά μπλοκ χρησιμοποιούνται. Με κόκκινο χρώμα απεικονίζονται τα διαθέσιμα δείγματα. A OQ C D
44 1. Εισαγωγή Μέχρι τώρα έχουμε αναλύσει τα χαρακτηριστικά του προτύπου Η.264 όπως επίσης και τις βασικές αρχές λειτουργίας του. Ιδιαίτερη έμφαση έχει δοθεί στην διαδικασία πρόβλεψης intra και συγκεκριμένα στους εννέα διαφορετικούς τρόπους πρόβλεψης για τα μπλοκ φωτεινότητας μεγέθους 4X4. Δηλαδή Mode Ο Mode 1 Mode 2 Mode 3 Mode 4 Mode 5 Mode 6 Mode 7 Mode 8 Vertical Horizontal DC Diagonal down -left Diagonal down -right Vertical right Horizontal-down Vertical left Horizontal-up Επίσης αναφέραμε και τους 4 τρόπους πρόβλεψης για τα μπλοκ φωτεινότητας μεγέθους 16X16. Δηλαδή
45 Mode 0 Mode 1 M O C j 2 Μ o d a 3 Vertical Horizontal DC Plane Στην συνέχεια αυτού rou κεφαλαίου θα αναλύσουμε πως αυτοί οι τρόποι - συναρτήσεις περιγράφονται σε μαθηματική μορφή και θα εντρυφήσουμε σε θέματα υλοποίησης. 2. Σχεδίαση τρόπων πρόβλεψης 4X4 μπλοκ φωτεινότητας. Όπως έχουμε αναφέρει και σε προηγούμενο κεφάλαιο, κατά την διαδικασία της intra πρόβλεψης για ένα macroblock ενός καρέ βίντεο, πριν την κωδικοποίηση, υπολογίζονται και οι εννέα τρόποι πρόβλεψης ενός μπλοκ και στην συνέχεια επιλέγεται ο καλύτερος τρόπος από τους εννέα. Ως καλύτερος τρόπος χαρακτηρίζεται αυτός που έχει τον μικρότερο ποσό απόλυτων σφαλμάτων. Έπειτα το μπλοκ πρόβλεψης που προκύπτει αφαιρείται από το τρέχον μπλοκ και σχηματίζεται το μπλοκ υπολοίπων (residual block) το οποίο και κωδικοποιείται. Για να είναι εφικτή μια μέθοδος πρόβλεψης, πρέπει ορισμένα ή και όλα τα δείγματα από τα γειτονικά μπλοκ που βρίσκονται πέριξ του τρέχοντος μπλοκ να είναι διαθέσιμα. Το ποια δείγματα πρέπει να είναι διαθέσιμα εξαρτάται από την συνάρτηση - τρόπο πρόβλεψης. Για παράδειγμα, ο κάθετος τρόπος πρόβλεψης ενός μπλοκ 4X4 (vertical) απαιτεί να είναι διαθέσιμα τα δείγματα που βρίσκονται άνω του τρέχοντος μπλοκ. Σύμφωνα με το πρότυπο Η.264, τα 13 γειτονικά δείγματα τα οποία είναι ήδη κατασκευασμένα πριν τη διαδικασία του deblocking filter τοποθετούνται σε ένα πίνακα ρ[χ, y ] με
46 : χ = -1, y = (δείγματα M, I,J,K,I -σε πορτοκαλί φόντο) χ = 0..7, y = -1 (δείγματα Α,Β,ύήϋ,Ε,Ρ,Ο,Η -σε κόκκινο φόντο ) 1 η 1? ΐ! Γ, ή / Μ A Β ο D ε f '[h 1.1 κ L.1 1 ΓΓΙ 1;. ί 1 Γι α k h 1 i1 Δηλαδή το δείγμα Μ βρίσκεται στη θέση ρ[-1,-1], το δείγμα Α στη θέση ρ[0,- 1] και το δείγμα I βρίσκεται στη θέση ρ[-1,0]. Τα αποτελέσματα από την εφαρμογή κάθε τρόπου πρόβλεψης θα αποθηκεύονται κάθε φορά σε έναν δυσδιάστατο πίνακα pred4x4 [ χ, y ], με χ, y = Σε υια νλώοσα πεοιγραφήε υλικού όπωε είναι n VHDL,ένα κύκλωμα που θα πραγματοποιούσε ολόκληρη την διαδικασία την πρόβλεψης θα ήταν το κύκλωμα το οποίο θα δέχονταν ως είσοδο > ένα διάνυσμα με τα ήδη κατασκευασμένα δείγματα των γειτονικών μπλοκ του τρέχοντος πλαισίου *: ένα διάνυσμα ίδιου μεγέθους με το διάνυσμα των δειγμάτων το οποίο θα υποδηλώνει ποια δείγματα είναι διαθέσιμα και θα παράγει ως έξοδο ν τα εννέα διαφορετικά μπλοκ από τους εννέα διαφορετικούς τρόπους πρόβλεψης ν ένα διάνυσμα μεγέθους εννέα θέσεων το οποίο θα υποδηλώνει ποια συνάρτηση -- τρόπος έχει υλοποιηθεί
47 To block diagram του κυκλώματος που περιγράψαμε ποιο πάνω είναι το ακόλουθο Όσον αφορά τους τύπους και τα περιεχόμενα των διανυσμάτων εισόδου και εξόδου πρέπει να αναφέρουμε τα εξής στοιχεία: 1 1. το διάνυσμα Vector_with samples περιέχει τα δείγματα των γειτονικών μπλοκ του τρέχοντος πλαισίου. Τα δείγματα είναι τύπου byte.
48 2. το διάνυσμα Available_samples_vector έχει το ίδιο μέγεθος με το διάνυσμα Vector with samples. Σε κάθε του θέση μπορεί να πάρει είτε Ί' είτε Ό'. Το Ί' στην θέση j του πίνακα δείχνει ότι το δείγμα j είναι διαθέσιμο ενώ το Ό' στη ίδια θέση δείχνει ότι το δείγμα δεν είναι διαθέσιμο. Για παράδειγμα αν το Available_samplcs vector[2] = 'Γ, αυτό σημαίνει ότι το 3 δείγμα είναι διαθέσιμο για πρόβλεψη. 3. Τα διανύσματα Pred block X με Χ = 0,...8 είναι ένας δυσδιάστατος πίνακας μεγέθους 4X4. Κάθε θέση του συγκεκριμένου πίνακα θα περιέχει την τιμή του συγκεκριμένου δείγματος. Τα δείγματα είναι τύπου byte. 4. Το διάνυσμα Done vector έχει μέγεθος 9 -όσοι δηλαδή και οι τρόποι πρόβλεψης ενός 4X4 μπλοκ φωτεινότητας. Σε κάθε του θέση μπορεί να πάρει είτε Ί' είτε Ό'. Το Ί' στην θέση j του πίνακα υποδηλώνει ότι ο τρόπος πρόβλεψης με κωδικό αριθμό j έχει υλοποιηθεί ενώ το Ό' ότι δεν έχει υλοποιηθεί. Για παράδειγμα εάν το Done Vector[2] = 'l'( αυτό σημαίνει ότι η DC συνάρτηση έχει υλοποιηθεί.
49 Έστω ότι τα δείγματα των γειτονικών μπλοκ του τρέχοντος μπλοκ είναι τα ακόλουθα που φαίνονται στο παρακάτω σχήμα - με ετικέτες A,B,C,D,E,F,G,H,I,J/K,L,M. Τα δείγματα αυτά Οα τοποθετηθούν στο διάνυσμα Vector with samples με την εξής σειρά : 1 Μ A Β C D 1 a t.l d J f a h Κ j k 1 L m II o i-j M A B C D E F G H M I J K L Δηλαδή,στην θέση [0] του πίνακα βρίσκεται το δείγμα Μ,στην θέση 1 το δείγμα Α. Παρατηρούμε ότι το δείγμα Μ βρίσκεται σε 2 θέσεις του πίνακα. Αυτό γίνεται για ευκολία στην υλοποίηση. Για λόγους ευκολίας το διάνυσμα Vectorwithsamples θα το συμβολίζουμε s στην συνέχεια.
50 Τα δείγματα A,B,C,D που βρίσκονται στο πάνω μέρος του πίνακα προεκτείνονται κάθετα. Για να υλοποιηθεί αυτός ο τρόπος πρέπει αυτά τα δείγματα να είναι διαθέσιμα (τα δείγματα σε κίτρινο φόντο). Η μαθηματική αναπαράσταση της παραπάνω συνάρτησης σύμφωνα με το πρότυπο είναι: pred4x4, χ, y] = ρ χ, -11, με χ, y = Για τις ανάγκες της υλοποίησης η συνάρτηση μετατρέπεται σε: Pred block 0 χ, y ] = s (I) με χ, y =0.3 & 1=1..4
51 Τα δείγματα I,J,Κ,L που βρίσκονται αριστερά του πίνακα προεκτείνονται οριζόντια. Για να υλοποιηθεί αυτός ο τρόπος πρέπει αυτά τα δείγματα να είναι διαθέσιμα (τα δείγματα σε κίτρινο φόντο). Η μαθηματική αναπαράσταση της παραπάνω συνάρτησης σύμφωνα με το πρότυπο είναι: pred4x4, (χ, y = ρ -1, y, με χ, y = Για τις ανάγκες της υλοποίησης η συνάρτηση μετατρέπεται σε : Prod block 1 χ, y s (J) με x, y =0..3 8< J -11, 12, 13, 14
52 Όλα τα δείγματα στο μπλοκ ηροβλέπονται από το μέσο όρο των δειγμάτων A,B,C,D και I,J,K,L Για να υλοποιηθεί αυτός ο τρόπος πρέπει αυτά τα δείγματα να είναι διαθέσιμα (τα δείγματα σε κίτρινο φόντο). Αυτός ο τρόπος πρόβλεψης πραγματοποιείται πάντα. Είναι ο μοναδικός που μπορεί να το πετύχει αυτό. Ο τρόπος αυτός έχει τέσσερις υποπεριπτώσεις. Η μαθηματική αναπαράσταση της παραπάνω συνάρτησης σύμφωνα με το πρότυπο είναι: prcd4x4, χ, y ] = ( ρ 0, -1 + p 1, -1 ] + p 2, -1 + p 3, -1 ] + p -1,0] i p -1, 1 ] + p[ -1,2 ] + p -1,3 ] f 4 ) > > 3 με x, y = Εάν είναι διαθέσιμα μόνο τα δείγματα που βρίσκονται αριστερά τότε η μαθηματική αναπαράσταση της συνάρτησης είναι : prcd4x4,[ χ, y = ( ρ 1,0) t ρ -1, 1 ] t ρ -1,2 ] i p -1,3 ] i?)>> 2 με x, y
53 Εάν είναι διαθέσιμα μόνο τα δείγματα που βρίσκονται πάνω τότε η μαθηματική αναπαράσταση νης συνάρτησης είναι : pred4x4, χ, y = ( ρ 0, I ] ι ρ( 1,1 + ρ[ 2, -1 ] I ρ 3,1 ) (2 )>> 2 μι; χ, y = Εάν ένα είτε κανένα από τα δείγματα που βρίσκονται πάνω και αριστερά δεν είναι διαθέσιμα, τότε η μαθηματική αναπαράσταση της συνάρτησης είναι η ακόλουθη : pred4x4i χ, y 128 με χ, y = 0...3
54 Για τις ανάγκες της υλοποίησης η συνάρτηση μετατρέπεται σε Prod block 2 χ, y - ( >, s (I) l s (!) M) >> 3 με x, y =-0.3 & 1=1,2,3,4 & J= 11, 12, 13, 14 Prcd block 2[ x,y = (>_, s (J) + 2 ) >> 2 με x, y d 3 & J = ll, 12, 13, 14 Prcd block 2 x,y ] = ( Σ, s (I) +2 ) >>2 με x, y & 1=1,2,3,4 Prcd block 2[x,y =128 με x, y 0..3
55 Τα δείγματα παρεμβάλλονται σε μια γωνία 45 μεταξύ του κάτω δεξιά δείγματος και άνω αριστερά. Για να υλοποιηθεί αυτός ο τρόπος πρέπει τα δείγματα A,B,C,D & E,F,G,H να είναι διαθέσιμα (τα δείγματα σε κίτρινο φόντο). Η μαθηματική αναπαράσταση της παραπάνω συνάρτησης σύμφωνα με το πρότυπο είναι: pred4x4, χ, y - ( ρ 6, 1 τ 3 * ρ 7, ) >> 2 prcd4x4,[ χ, y -( ρ χ -t- y, -1 ] + 2 * ρ[ χ + y + 1, -1 ] T ρ χ + y τ 2, -1 t 2)>> 2 με x, y 0...3
56 Για τις ανάγκες της υλοποίησης η συνάρτηση μετατρέπεται σε: Pred block 3 x,y = (s(7) ι 3 * s (8) ι 2 )>>2 Prcri block 3 x,yp(s(x-tytl) t 2 s (x t y t 2) l s (x f y-l 3) l 2)> >2 με x, y = 0...3
57 Τα δείγματα προεκτείνονται σε μια γωνία 45 κάτω και προς τα αριστερά. Για να υλοποιηθεί αυτός ο τρόπος πρέπει τα δείγματα A,B,C,D & I,J,k,L & Μ να είναι διαθέσιμα (τα δείγματα σε κίτρινο φόντο). i >;: ί γ :1c Λ" ί:γ : μ^ι= ι=.=: -ι ί \ \\ \ \ V \ 1 \\\\ \ \ \ \ \ \ «\\ \\ \ 4 K \ Η μαθηματική αναπαράσταση της παραπάνω συνάρτησης σύμφωνα με το πρότυπο είναι: prcd4x4( x, y = (ρ χ y - 2, -1 f 2 * p x - y - 1, -11 f p x - y, ) >> 2 pred4x4i x, y - ( p -1, y x?! f 2 * p 1, y - x 1 p -1, y - x f 2 ) >> 2 prcd4x4i x, y ] - ( p 0, -1 ] T 2 * p -1, -T ] + p -1, 0 ] + 2 ) >> 2 pr. x, y 0...3
58 Για τις ανάγκες της υλοποίησης η συνάρτηση μετατρέπεται με αντικατάσταση σε: για ιις θέσεις (1,0),(2,1 ),(3,2) Prod block 4 x,y ] = ( s (0) -l 2* s (1) + s (2) +2 )>>2 για ιις ϋέοεις (2,0),(3,1) Prod block 4 x,y = (s(l) + 2*s(2) t s (3) T2)>>2 >- 5 C Prod block 4 x,y = ( s (2) + 2 s (3) f s (4) t 2 )>>2 για τις Οέαεις (0,1),(1,2),(2,3) Prod block 4 x,y] = ( s (9) f 2* s (10) + s (11) +2 )>>2 για ιις ϋέοεις (0,2),(1,3) Prod block 4 x,y = ( s (10) l 2* s (1 1) 1 s (12) T2 )>>2 για τη Οέοη (0,3) Prod block 4 x,y = (s(ll) τ 2* s (12) τ s(13)+2)>>2 για τις θέσεις (0,0),(1,1),(2,2),(3,3) Prod block 4[x,y = (s(l) t 2* s (0) + s (10) +2 )>>2 με x, y 0...3
59 Προέκταση διαγωνίως περίπου 26.6 αριστερά και κάθετα (πλάτος/ύψος 1/2). Για να υλοποιηθεί αυτός ο τρόπος πρέπει τα δείγματα A,B,C,D & I,J,k,L & Μ να είναι διαθέσιμα (τα δείγματα σε κίτρινο φόντο). Η μαθηματική αναπαράσταση της παραπάνω συνάρτησης σύμφωνα με το πρότυπο είναι: ΈαΓω η μεταβλητή zvr = (2 * χ) -y pred^l χί, χ, y =(p x-(y >> 1 ) 1, -1 + ρ[ χ - ( y >> 1 ), -1 ] + 1 ) >> 1 precmx-lil x,y I == ( p x - ( y >> 1 ) - 2, * p x (y>> 1 ) - 1, -1 ] + p x - (y >> 1), ) >> 2 prcddxdil x, y = ( p[ -1, 0 ( 2 * p -1,-1 ] f p[ 0, ) >> 2 pred4xd, x, y - ( p -1, y - 1 ] t 2 * p -!, y 2 l p 1, y - 3 ] * 2 ) >> 2 με x, y
60 Στους παραιιάνω τύπους παρατηρούμε ότι το y υπόκειται οε δεξιά ολίσθηση ενός ψηφίου. Εάν δώσουμε τιμές στις μεταβλητές x,y =0...3 τότε Στην περίπτωση όπου το zvr ισούται με 0,2,4,6 παρατηρούμε ότι θα επηρεάζονται οι θέσεις πίνακα που φαίνονται στον παραπάνω πίνακα. Σε αυτές τις περιπτώσεις το y ισούται με 0 ή 2. Εάν κάνουμε δεξιά ολίσθηση στο 0 παίρνουμε ξανά 0. Εάν κάνουμε στο 2, παίρνουμε 1. Στην περίπτωση όπου το zvr ισούται με 1,3,5 παρατηρούμε ότι θα επηρεάζονται οι θέσεις πίνακα που φαίνονται στον παραπάνω πίνακα. Σε αυτές τις περιπτώσεις το y ισούται με 1 ή 3. Εάν κάνουμε δεξιά ολίσθηση στο 1 παίρνουμε ξανά 0. Εάν κάνουμε στο 3, παίρνουμε 1. Συνεπώς οι τύποι του προτύπου απλοποιούνται ως εξής :
61 'ΙΙοιω η μεταβλητή zvr (2 * χ) y prcd4x4, χ, y 1 ( ρ χ 1, 1 t p x, ) >> 1 prcd4x4, x, y ] ( p x 2, 1 i p χ 1, 1 f 1 ) >> 1 prcd4x4, [ x, y I ( p x 2, * p x - 1, -1 f p[ x, - l + 2)>>2 prcd4x4, x, y ; ( p x - 3, -1-4? * p x - 2, -1 I + p x-1, ) >> 2 prcd4x4, x, y = ( p -1, * p -1, -1 I t p Ο, ) >> 2 prcd4x4, x, y ] - ( p 1, y 1 t 2 * p -1, y p -1, y - 3 t 2 ) >> 2 με x, y = 0...3
62 Για τις ανάγκες της υλοποίησης η συνάρτηση μετατρέπεται με αντικατάσταση σε Τοιω η μεταβλητή /VR (2 χ) y για πς θέσεις (Ο,Ο),(1,2) Prcd block 5[x,y = ( s (0) + s (1) +1 )>>1 για τις θέσεις (1,0),(2,2) Prcd block 5 x,y -( s (1) + s (2) + 1 )>>1 για τις θέσεις (2,0),(3,2) Prcd block 5[x,y] = ( s (?) + s (3) 11 )>>1 για τις θέσεις (3,0) Prod block 5 x,y] ( s s(3) + s (4) +1 )>>1 για ιις θέσεις (1,1),(2,3) Prcd block 5 x,y -( s (0) f 2* s (1) i s (2) + 2 )>>2 για τις θέσεις (2,1),(3,3) Prcd block 5 x,y = ( s (1) + 2* s (?) + s (3) + 2 )>>2 για τις θέσεις (3,1) Prcd block 5 x,y -( s (2) i 2* s (3) r s (4) + 2 )>>2 για τις θέσεις (0,1),(1,3) Prcd block 5 x,y = ( s (10) + 2* s (9) f s (l) + 2 )>>2 για τις θέσεις (0,2) Prcd block 5 x,yl = ( s (11) + 2* s (10) r s (9)+2 )>>2 για τις θέσεις (0,3) Prcd block 5 x,y) = ( s (12) + 2* s (11) τ s (10) + 2 )>>2 με x, y 0...3
63 Προέκταση διαγωνίως περίπου 26.6 οριζόντια και κάτω (πλάτος/ύψος = 1/2) ; Για να υλοποιηθεί αυτός ο τρόπος πρέπει τα δείγματα A,B,C,D & I,J,k,L & Μ να είναι διαθέσιμα (τα διαθέσιμα δείγματα σε κίτρινο φόντο). Η μαθηματική αναπαράσταση της παραπάνω συνάρτησης σύμφωνα με το πρότυπο είναι: Έοτω η μεταβλητή zlld = (2 * y) χ prcd4x4, χ, y I - ( p -1, y ( x >> 1 ) 1 ] t p[ 1, y - ( x >> 1 ) τ 1 ) >> 1 prcd4x4,[ x, y ] - ( p -1, y ( χ >> 1 ) - 2 t 2 * p -1, y ( χ >> 1 ) 1 J τ p [-1, y - (x >> i)] + 2) >> 2 prcd4x4 [ x, y - ( p[ -1, 0 T 2 * p -1, -1 + p 0, -1 ] t 2 ) >> 2 prcd4x4; x, y ( p x - 1, 1 ] τ 2 * p x 2,-1 t p[ x 3, -1 ] + 2 ) >> 2 με x, y = 0...3
64 Στους παραπάνω τύπους παρατηρούμε ότι το χ υπόκειται σε δεξιά ολίσθηση ενός ψηφίου. Εάν δώσουμε τιμές στις μεταβλητές x,y =0..,3 τότε Στην περίπτωση όπου το zhd ισούται με 0,2,4,6 παρατηρούμε ότι θα επηρεάζονται οι θέσεις πίνακα που φαίνονται στον παραπάνω πίνακα. Σε αυτές τις περιπτώσεις το χ ισούται με 0 ή 2. Εάν κάνουμε δεξιά ολίσθηση στο 0 παίρνουμε ξανά 0. Εάν κάνουμε στο 2, παίρνουμε 1. Στην περίπτωση όπου το zηd ισούται με 1,3,5 παρατηρούμε ότι θα επηρεάζονται οι θέσεις πίνακα που φαίνονται στον παραπάνω πίνακα. Σε αυτές τις περιπτώσεις το χ ισούται με 1 ή 3. Εάν κάνουμε δεξιά ολίσθηση στο 1 παίρνουμε ξανά 0. Εάν κάνουμε στο 3, παίρνουμε 1. Συνεπώς οι τύποι του προτύπου απλοποιούνται ως εξής :
65 Ί οιω η μειαβληιή /HD (2 * y) -χ prcd4x4, χ, y = ( ρ -1, y - 1 t p -1, y 4 1 ) > > 1 pred4x4, x, y ( p 1, y 2 \ t p 1, y 1 t 1 ) >> 1 prcd4x4,[ x, y ] ~: ( p -1, y? I + 2 * p. -1, y - 1 ] + p[ 1, y] f 2 ) >> 2 prcd4x4, x, y ] - ( p 1, y * p[ -1, y p -1, y-1] + 2 ) > > 2 prcd4x4, x, y = ( p -l, 0 f 2 * p -1, 1 + p[ 0, ) >> 2 prcd4x4, x, y I - ( p -1, y 1 4? * p -1, y - 2 t p -1, y - 3 ] + 2 ) >> 2 με x, y = 0...3
66 Για τις ανάγκες της υλοποίησης η συνάρτηση μετατρέπεται με αντικατάσταση σε Τοιω η μειαβληιή /111) = (2 y) -χ για τις θέσεις (0,0),(2,1) Prcd block 6 x,y -'( s(9) τ s(10) -ι 1 )>>1 για τις θέσεις (0,1),(2,2) Prcd block 6 x,y ( s (10) + s (11) +1 )>>1 για ιις θέσεις (0,2),(2,3) Prcd block 6 χ,y) ( S (11) Τ s (123) +1 )>>1 για ιις θέσεις (0,3) Prcd block 6[x,y) ( s (12) t s (13) +1 )>> 1 για τις θέσεις (1,1),(3,2) Prcd block 6[x,y 1 = ( s (9) + 2* s (10) t s (11) + 2 )>>2 για ιις θέσεις (1,2),(3,3) Prcd block 6[x,y -( s (10) t 2* s (11) + s (12) + 2 )>>2 για τις θέσεις (1,3) Prcd block 6(x,y = ( s (11) + 2* s (12) + s (13) + 2 )>>2 για τις θέσεις (1,0),(3,1) Prcd block 6 x,y] = ( s (10) + 2* s (11) + s (1) + 2 )>>2 για ιις Οέαεις (2,0) Prcd block 61 χ, y ] = ( s (2) + 2* s (1) + s (0) + 2 )>>2 για τις θέσεις (3,0) Prcd block 6 x,y - ( s (3) + 2* s (2) + s (1 )-t 2 )> >2 με x, y = 0...3
67 Προέκταση (ή παρεμβολή) διαγωνίως περίπου 26.6 δεξιά της κατακόρυφου. Για να υλοποιηθεί αυτός ο τρόπος πρέπει τα δείγματα A,B,C,D & E,F,G,H να είναι διαθέσιμα (τα διαθέσιμα δείγματα σε κίτρινο φόντο). Η μάθημάιική αναπαράσιαση της παραπάνω συνάρτησης σύμφωνα με το πρότυπο είναι: prcdtx^i x,y = (ρ[ χ f ( y >> 1 ),-1 ) + ρ[ x + (y>> 1 ) + 1,1 ] + 1)>>1 prcd4x4, x, y I = ( p x + ( y >> 1 ), -1 T 2 * p x I ( y >> 1 ) + 1, i p x + (y >> 1) + 2, \ +?)>>? με x, y = Στους παραπάνω τύπους παρατηρούμε ότι ίο y υπόκειται σε δεξιά ολίσθηση ενός ψηφίου.
68 Εάν δώσουμε τιμές στις μεταβλητές x,y =0.3 τότε Στην περίπτωση όπου το y ιοούται με 0,2 παρατηρούμε ότι θα επηρεάζονται οι θέσεις πίνακα που (ραίνονται στον παραπάνω πίνακα. Σε αυτές τις περιπτώσεις το y ισούται με 0 ή 2. Εάν κάνουμε δεξιά ολίσθηση στο 0 παίρνουμε ξανά 0. Εάν κάνουμε στο 2, παίρνουμε 1. Στην περίπτωση όπου το y ισούται με 1,3 παρατηρούμε ότι θα επηρεάζονται οι θέσεις πίνακα που φαίνονται στον παραπάνω πίνακα. Σε αυτές τις περιπτώσεις το y ισούιαι με 1 ή 3. Εάν κάνουμε δεξιά ολίσθηση στο 1 παίρνουμε ξανά 0. Εάν κάνουμε στο 3, παίρνουμε 1. Συνεπώς οι τύποι του προτύπου απλοποιούνται ως εξής : prcd4x4( χ, y = ( ρ χ, -1 I * ρ χ ι 1,-1 * 1) >>1 pred4x4,1 x, y - ( ρ[ χ+ 1, -1 ] + ρ[ χ + 2, -1 ] + 1) > > 1 prcd4x4, χ, y - ( ρ χ, 1 J + 2 * ρ[ χ + 1, -1 ] + ρ[ χ + 2, 1 ] + 2 ) >> 2 prcd4x4,[ x, y = ( ρ x+1, -1 ) + 2 * ρ χ + 2, -1 ] + ρ[ χ + 3, ) >> 2 με χ, y = 0...3
69 Για τις ανάγκες της υλοποίησης η συνάρτηση μετατρέπεται με αντικατάσταση σε για ιις θέσεις (0,0) Prod block 7 x,y = ( s (1) i s (2) 1 )»1 για τις θέσεις (1,0),(0,2) Prod block 7 x,y 1 -( S (2) s(3) i 1 )»1 για τις θέσεις (2,0),(1,2) Prod block 7 x,y]= ( s (3) i s (4) l 1 )»1 για ιις θέσεις (3,0),(2,2) Prod block 7[x,y ( s (4) t s (5) ll )> > 1 για τις θέσεις (3,2) Prod block 7[x,y = ( s (5) + s (6) ll )»1 γιο τις θέσεις (0,1) Prod block 7[x,y =( s (i) + 2*s(2) l s (3) + 2 )>>2 για τις θέσεις (1,1),(0,3) Prod block 7(x,y] ( s (2) + 2* s (3) + s (4) + 2 )> >2 για τις θέσεις (1,3),(2,1) Prod block 7[x,y1= ( s (3) τ 2* s (4) t s (5)+2 )>>2 για τις θέσεις (3,1),(2,3) Prod block 71x,y] ( s (4) i 7* s (b) i s (6)1-2 )>>2 για ιις θέσεις (3,3) Prod block 7 x,y = ( s (5) + 2* s (6) f s (7)+2 )>>2
70 Παρεμβολή διαγωνίως περίπου 26.6 επάνω και οριζόντια.. :. ). Για να υλοποιηθεί αυτός ο τρόπος πρέπει αυτά τα δείγματα να είναι διαθέσιμα (τα διαθέσιμα δείγματα σε κίτρινο φόντο). Η μαθηματική αναπαράσταση της παραπάνω συνάρτησης σύμφωνα με το πρότυπο είναι: Έστω η μεταβλητή zllu χ + 2 * y. pred4x4 x, y I = ( ρ -1, y Η ( x >> 1 ) + p -1, y + ( x >> 1 ) ) >> 1 prcd4x4, x, y ( p -1, y i ( x >> I ) τ 2 * p 1, y ι ( x >> 1 ) τ 1 i p[ -1, y f ( χ >> 1 ) t 2 2)>>? prcddxd, x, y = ( p -1,2 t 3 * p 1,3] 1 2 ) >> 2 pred4x4, x, y Pi -1, 3 I
71 Στους παραπάνω τύπους παρατηρούμε ότι το χ υπόκειται σε δεξιά ολίσθηση ενός ψηφίου. Εάν δώσουμε τιμές στις μεταβλητές x,y =0...3 τότε Στην περίπτωση όπου το zhu ισούται με 0,2,4 παρατηρούμε ότι θα επηρεάζονται οι θέσεις πίνακα που φαίνονται στον παραπάνω πίνακα. Σε αυτές τις περιπτώσεις το χ ισούται με 0 ή 2. Εάν κάνουμε δεξιά ολίσθηση στο 0 παίρνουμε ξανά 0. Εάν κάνουμε στο 2, παίρνουμε 1. Στην περίπτωση όπου το zhd ισούται με 1,3 παρατηρούμε ότι θα επηρεάζονται οι θέσεις πίνακα που φαίνονται στον παραπάνω πίνακα. Σε αυτές τις περιπτώσεις το χ ισούται με 1 ή 3. Εάν κάνουμε δεξιά ολίσθηση στο 1 παίρνουμε ξανά 0. Εάν κάνουμε στο 3, παίρνουμε 1. Συνεπώς οι τύποι του προτύπου απλοποιούνται ως εξής:
72 Ί:οιω η μεταβλτή /IIU - χ 4 2 r y. prcd4x4, χ, γ > > Λ Λ precmχί, χ, y - ( ρ 1, y ι 1 ( ρ 1, y ( 2 t 1 ) >> 1 prc;d4x4, χ, y ] ( μ 1, y 1 t- 2 * p[ -1, y t l +p[-l,yt2 + 2)>>? prcd4x4, 1 x, y! - ( p 1, y t 11 i 2 * p -1, y + 2 t p 1, y 4 3] t 2)>>2 prcd4x4 x, y - ( p -1, * p -1, ) > > 2 prcd4x4,[ x, y Pi -1, 3 1
73 Για πς ανάγκες της υλοποίησης η συνάρτηση μετατρέπεται με αντικατάσταση οε Τοιω η μεταβλητή 7I1U - (2 * y) χ για ιις Οέοεις (0,0) Prcd block 8[x,y ( s (10) 1 S (11) 11 )> > 1 για τις θέσεις (0,1),(2,0) Prcd block CO > X -( s (11) + s (12) H )> > 1 για τις Οέοεις (0,2),(2,1) Prcd block 8[x,y -=( s(12) t s (13) 1-1 )>>1 για ιic, Οέοεις (1,0) Pred block Β x,y 1 ( s (10) + 2* s (11) τ s (12)+2 )>>2 για τις Οέοεις (1,1 ),(3,0) Prcd block 81x,y] ( s (1 1) + 2» s (12) + s (13) + 2 )>>2 για τις Οέοεις (1,2),(3,1) Prcd block 8 x,y] = ( s (12) 3* s (13) t- 2 )>>2 για τις θέσεις (0,3), (1,3), (2,2), (2,3), (3,2), (3,3) Prcd block 8(x,y = s (13)
74 . Σχεδίαση ί jύγηι;ν ημύβλεψί'ΐς 16X16 μπλοκ ψωτεινότητας. Η διαδικασία κωδικοποίησης και αποκωδικοποίησης που ακολουθείται για τα μπλοκ ψωτεινότητας 16X16 είναι ίδια με αυτή των μπλοκ 4X4. Σύμφωνα με το ηρότυπο_ Η.264, τα 33 γειτονικά δείγματα τα οποία είναι ήδη κατασκευασμένα πριν τη διαδικασία του deblocking filter τοποθετούνται σε ένα πίνακα ρ[χ, y ] με : χ = -1, y = ν χ = , y = -1 Σε υια γλώσσα περιγραφής υλικού όπως είναι n VHDL. ένα κύκλωμα που θα πραγματοποιούσε ολόκληρη την διαδικασία την πρόβλεψης θα ήταν κύκλωμα το οποίο θα δέχονταν ως είσοδο : ένα διάνυσμα με τα ήδη κατασκευασμένα δείγματα των γειτονικών μπλοκ του τρέχοντος πλαισίου ν ένα διάνυσμα ίδιου μεγέθους με το διάνυομα των δειγμάτων το οποίο θα υποδηλώνει ποια δείγματα είναι διαθέσιμα και θα παράγει ως έξοδο ν τα τέσσερα διαψορετικά μπλοκ από τους τέσσερις διαφορετικούς τρόπους πρόβλεψης ένα διάνυσμα μεγέθους τεσσάρων θέσεων το οποίο θα υποδηλώνει ποια συνάρτηση - τρόπος έχει υλοποιηθεί To block diagram rou κυκλώματος που περιγράψαμε ποιο πάνω είναι το ακόλουθο:
75 Όσον αφορά ιούς τύπους και τα περιεχόμενα των διανυσμάτων εισόδου και εξόδου πρέπει να αναφέρουμε τα εξής στοιχεία: 1. το διάνυσμα Vcctor_withsamples περιέχει τα δείγματα των γειτονικών μπλοκ του τρέχοντος πλαισίου. Τα δείγματα είναι τύπου byte. 2. το διάνυσμα Available samples vector έχει το ίδιο μέγεθος με το διάνυσμα Vector with samples. Σε κάθε του θέση μπορεί να πάρει είτε Ί' είτε Ό'. Το Ί' στην θέση j του πίνακα δείχνει ότι το δείγμα j είναι διαθέσιμο ενώ το Ό' στη ίδια θέση δείχνει ότι το δείγμα δεν είναι διαθέσιμο. Για παράδειγμα αν το Available_samples vcctor[2] = Ί', αυτό σημαίνει ότι το 3 δείγμα είναι διαθέσιμο για πρόβλεψη. 3. Τα διανύσματα Predblock X με Χ = είναι ένας δυσδιάστατος πίνακας μεγέθους 16X16. Κάθε θέση του συγκεκριμένου πίνακα θα περιέχει την τιμή ίου συγκεκριμένου δείγματος. Τα δείγματα είναι τύπου byte. 4. Το διάνυσμα Done vector έχει μέγεθος 4 -όσοι δηλαδή και οι τρόποι πρόβλεψης ενός 16X16 μπλοκ φωτεινότητας. Σε κάθε του θέση μπορεί να πάρει είτε Ί' είτε Ό'. Το Ί' στην θέση j του πίνακα υποδηλώνει ότι ο τρόπος πρόβλεψης με κωδικό αριθμό j έχει
76 υλοποιηθεί ενώ το Ό' ότι δεν έχει υλοποιηθεί. Για παράδειγμα εάν το Done Vector[2] = 'r, αυτό σημαίνει ότι η DC συνάρτηση έχει υλοποιηθεί. Έστω Η και V τα δείγματα που βρίσκονται πάνω και αριστερά αντίστοιχα από το τρέχον μπλοκ 16X16. Στο διάνυσμα Vector with samples θα τοποθετηθεί στο στη θέση 1 το δείγμα pf-ι,-ι], στις θέσεις 1 έως 16 τα δείγματα Η, στη θέση 17 το δείγμα pf-ι,-ι] για λόγους ευκολίας στην υλοποίηση και στις θέσεις 18 έως 33 τα δείγματα V. Για λόγους ευκολίας το διάνυσμα Vectorwith samples θα το συμβολίζουμε s στην συνέχεια
77 Τα δείγματα Η που βρίσκονται στο πάνω μέρος του πίνακα προεκτείνονται κάθετα. Για να υλοποιηθεί αυτός ο τρόπος πρέπει τα δείγματα να είναι διαθέσιμα (τα δείγματα σε κίτρινο φόντο ). ι.,. ιιο-τ ZZ H 1 ' M ' < H μαθηματική αναπαράσταση της παραπάνω συνάρτησης σύμφωνα με το πρότυπο είναι: I rcd 16Χ 16, χ, y ρ χ, 1), με χ, y Για τις ανάγκες της υλοποίησης η συνάρτηση μετατρέπεται σε : Prod block 0 [χ, y s (I) με χ, y &
78 Τα δείγματα V που βρίοκονται αριστερά του πίνακα προεκτείνονται οριζόντια Για να υλοποιηθεί αυτός ο τρόπος πρέπει τα δείγματα να είναι διαθέσιμα (τα δείγματα σε κίτρινο φόντο ). I ιιίγι ι i ι Η μαθηματική αναπαράσταση της παραπάνω συνάρτησης σύμφωνα με το πρότυπο είναι: Prod 16Χ 16ι χ, y = ρ - 1, y j, με χ, y = Για τις ανάγκες της υλοποίησης η συνάρτηση μεταιρέπεται σε Prcd block 1 χ, y) = s (J),με x, y = & J= 18.33
79 Όλα τα δείγματα στο μπλοκ προβλέπονται από το μέσο όρο των δειγμάτων Η και V.Για να υλοποιηθεί αυτός ο τρόπος πρέπει αυτά τα δείγματα να είναι διαθέσιμα (τα διαθέσιμα δείγματα σε κίτρινο φόντο). 2.DC fv'*an H+V; Αυτός ο τρόπος πρόβλεψης πραγματοποιείται πάντα. Είναι ο μοναδικός που μπορεί να το πετύχει αυτό. Ο τρόπος αυτός έχει τέσσερις υποπεριπτώσεις. Η μαθηματική αναπαράσταση της παραπάνω συνάρτησης σύμφωνα με το πρότυπο είναι: Prcd 16Χ16, χ, y 1 - (Σ* ρ χ', 11 ι Σν ρ -1, y' + 16)>>5 με χ, y & χ', y' Εάν είναι διαθέσιμα μόνο τα δείγματα που βρίσκονται αριστερά τότε η μαθηματική αναπαράσταση της συνάρτησης είναι : Prcd 16X16ι χ, y - (Σν ρ -1, y' *Η)>>Ί με χ, y Li & y' 0 ί :>
80 Εάν είναι διαθέσιμα μόνο τα δείγματα που βρίσκονται πάνω τότε η μαθηματική αναπαράσταση της συνάρτησης είναι : Prod 16Χ16, χ, y (>> ρ [χ', 1 + 8)>>4 με χ, y & χ -0 lb (β) Εάν ένα είτε κανένα από τα δείγματα που βρίσκονται πάνω και αριστερά δεν είναι διαθέσιμα, τότε η μαθηματική αναπαράσταση της συνάρτησης είναι η ακόλουθη : Prcd 16X16, χ, y 1?8 με χ, y
81 Για τις ανάγκες της υλοποίησης η συνάρτηση μετατρέπεται σε: Prod block 3 x,y ( s (I) i >, s (J) l 16 ) >> 5 pr x, y & I I 16 & J 1/ 33 Prod block Γ> x,y (>., s (J) + 8 ) >> 4 pc x, y / 33 Prod block 2 x,y ( X, s (I) 4 ) >> 4 pc x, y 0 IS & 1116 Prod block?[x,y -l?8 pc x, y 0. IS
82 Επίπεδη γραμμική συνάρτηση (σχήμα 3.18). Για να υλοποιηθεί αυτός ο τρόπος πρέπει όλα τα δείγματα να είναι διαθέσιμα (τα δείγματα σε κίτρινο φόντο). : ;Ι.ιγτι Η μαθηματική αναπαράσταση της παραπάνω συνάρτησης σύμφωνα με το πρότυπο είναι: PrcdlGX 16, χ, y = Clip 1 ((a tb * (x-/) + c * (y /) I 16)»5) Clip 1 (x) Clip3 (0, x) X, /<x c;iip3(x, y, /) y, z>y /, αλλιώς a 16 '(P I, 151 τ P 116,11) b- (5*IIP37)>>6 c (5*V i 3?)>>6 II > > (x' i I) * (p 8 i x', 1 p [ 6 x', 1 ) V >, (y'+l) * (P 1-1, 81 y'i p r 1, 6 y' ) με x, y ώ x', y'-o.../
83 Για τις ανάγκες της υλοποίησης η συνάρτηση μετατρέπεται σε Prod block 3 x,y ClipX((a Tb * (x 7) t c * (y 7) t 16)>>!>) Clip 1 (x) Clip3(0,255,x) 0, εάν χ<0 Clip3(x) <T 233, εάν χ>233 X, αλλιώς a- 10 *(s(33)+s( 16) b- (5*H t 32)> >6 c (5*Vt 32)> >6 II- (>, (x't 1) *( s(9 l x') s(7 x')) V- (>:y (y'+l) * (s(26+y')-s(2d-y')) με x, y x', y' 0. /
84 ΙΟΙ Στο προηγούμενο κεφάλαιο, περιγράψαμε την μαθηματική αναπαράσταση των συναρτήσεων - τρόπων πρόβλεψης για τα μπλοκ φωτεινότητας μεγέθους 4X4 και 16X16 δειγμάτων. Πιο συγκεκριμένα αναφέραμε την μαθηματική αναπαράσταση των συναρτήσεων σύμφωνα με το πρότυπο Η.264. Στη συνέχεια επισημάναμε πως οι συναρτήσεις μετατρέπονται για τις ανάγκες τις υλοποίησης. 2. Υλοποίηση μεθόδων πρόβλεψης για τα μπλοκ φωτεινότητας 4X4 Εάν μελετήσουμε καλύτερα τις τροποποιημένες μαθηματικές αναπαραστάσεις των συναρτήσεων - τρόπων πρόβλεψης, θα παρατηρήσουμε ότι πολλές εκφράσεις οι οποίες αναθέτουν τιμή στα στοιχεία ενός μπλοκ εκτός από εκείνες για την dc πρόβλεψη είναι κοινές σε περισσότερους του ενός τρόπων πρόβλεψης. Οι διαφορετικές εκφράσεις είναι οι ακόλουθες. 1. (s(0) +s( 1) +1) >> 1 2. (s( 1) + s(2) + 1) >>1
85 3. (s(2) +s(3)+ 1) >> 1 4. (s(3) + s(4) + l) >>1 5. (s(4) + s( 5) + 1) >>1 6. (s(5) + s( 6) + 1) >>1 7. (s(7) +3 * s(8) + 2)>>2 8. (s( 12) +3 * s( 13) +2)>>2 9. (s(0) + 2* s( 1)+ s(2) + 2)>>2 10.(s( 1) + 2* s(2)+ s(3) + 2)>>2
86 ll.(s(2) + 2* s(3)+ s(4) + 2)>>2 12.(s(3) + 2* s(4)+ s(5) + 2)>>2 13.(s(4) + 2* s(5)+ s(6) + 2)>>2 14.(s(5) + 2* s(6)+ s(7) + 2)>>2 15.(s(6) + 2* s(7)+ s(8) + 2)>>2 16.(s(9) + 2* s(10)+ s(ll) + 2)>>2 17.(s( 10) + 2+ s( 11) + s(12) + 2)>>2 18.(s( 11) + 2* s(12)+ s(13) + 2)>>2
87 19.(s( 1) + 2* s(0)+ s(10) + 2)>>2 20.(s( 10) + 2* s(9)+ s(l) + 2)>>2 21.(s( 11) + 2* s( 10) + s(9) + 2)>>2 22.(s( 12) + 2* s( 11) + s(10) + 2)>>2 23.(s( 10) + 2* s(ll)+ s(l) + 2)>>2 24.(s(2) + 2* s(l)+ s(0) + 2)>>2 25.(s(3) + 2* s(2) + s( 1 ) + 2)>>2 26.(s(9) + s(10)+1)>>1
88 27.(s( 10) + s(11) + 1)>>1 28.(si 1) + s(12) + 1)>>1 29. (s( 12) +s( 13) +1)>>1 Τα στοιχεία του διανύοματος s() αναπαριστούν τις τιμές των γειτονικών δειγμάτων. Το πεδίο τιμών των δειγμάτων είναι από οτο δεκαδικό σύστημα. Επομένως στο δυαδικό σύστημα οι τιμές των δειγμάτων θα αποτελούνται από 8 bits (2b -255 διαφορετικοί συνδυασμοί). Από τα 29 παραπάνω αθροίσματα παρατηρούμε ότι υπάρχουν 3 διαφορετικά είδη αθροιορά των ' ( s(i) + s( j) + 1)»1 ^ (s( i) + 2 * s(j) + s( k ) +2 )>>2 - (s(i) + 3 *s(j ) +2 )>>2 Παρατηρήσεις: Για τις παραπάνω προσθέσεις Οα χρησιμοποιηθούν σαν δομικά στοιχεία αθροιστές 8,9,10 και 11 bits. Ο λόγος για τον οποίο χρησιμοποιούνται αθροιστές 9,10,11 bits ενώ τα δείγματα είναι 8 bits είναι για να μην χάνονται τα κρατούμενα (cout) και παραποιείται το αποτέλεσμα. Ο τελεστής & ενώνει το cout με το sum κάθε αθροιστή. Για παράδειγμα εάν cout='l' και sum-=' ' θα
89 δημιουργηθεί το 9bit σήμα cout & sum =' ' το οποίο θα αποτελέσει είσοδο σε έναν 9bit αθροιστή. Σαν δομικό στοιχείο των παραπάνω αθροιστών χρησιμοποιείται ο παρακάτω αθροιστής 1 bit ο οποίος απεικονίζεται στο U1 lit:1 που: U4 U6 U3 -MIL,,U ' ΙΊ ^ U5 Ο τελεστής >> συμβολίζει δεξιά ολίσθηση τόσο ψηφία όσα και ο αριθμός που ακολουθεί τον τελεστή. Για παράδειγμα, >>2 στο. 10 θα τον μετατρέψει σε 00 Η πράξη k* s(i) μπορεί να υλοποιηθεί ως εξής : 1. Εάν το k = 2J, j = 1... τότε η παραπάνω πράξη μπορεί να υπολογιστεί με αριστερή ολίσθηση j ψηφίων. Για παράδειγμα, 2 * s( 1), με s( 1) = 0 θα μετατραπεί σε Αλλιώς με πολλαπλασιασμό χρησιμοποιώντας σαν δομικό μπλοκ ένα πολλαπλασιαστή 8 bits είτε με διαδοχικές προσθέσεις χρησιμοποιώντας αθροιστές. Για παράδειγμα η
90 πράξη 3 * s(i) 0α γίνει είτε πολλαπλασιάζοντας το s(i) με το 3 είτε προσθέτοντας το s(i) 3 φορές. Τα κυκλώματα που πραγματοποιούν τις παραπάνω προσθέσεις είναι τα ακόλουθα: I I ια την dc πρόβλεψη όταν όλα τα δείγματα είναι διαθέσιμα
91 * Για την dc πρόβλεψη όταν είναι διαθέσιμα τα πάνω ή αριστερά δείγματα : Για το άθροισμα ( s(i) + s( j) + 1)>>1
92 I ια το άθροισμα (s(i) 4 2 * s(j) 4 s( k ) 4-2 )>>2 ^ Για το άθροισμα (s(i) 4-3 * s(j) 4-2 )>>2
93 3. Υλοποίηση ρ ε 0 ό ό co ν! ι ρ ό (3 λ ε ψ rj ς γιο το ρ π Λ ο κ φωτεινό π] ι ας! 6Χ 16 Για την υλοποίηοη των μεθόδων πρόβλεψης για τα μπλοκ 16X16, η φιλοοοφία της υλοποίηοης της dc συνάριησης είναι ίδια με αυτή για μπλοκ 4X4 με 32 δείγματα αυτή τη φορά. Όσον αφορά την plane συνάρτηση, η υλοποίησή της απαιτεί αθροιστές και πολλαπλασιαστές. Αρχικά θα πρέπει να υπολογιστούν τα αθροίσματα Η και V. Ο Υπολογισμός τους απαιτεί αφαιρέσεις μεταξύ των δειγμάτων, πολλαπλασιασμό του κάθε αποτελέσματος της αφαίρεσης και τέλος πρόσθεση όλων αυτών των αποτελεσμάτων. Έπειτα υπολογίζουμε τις μεταβλητές a, b, c. Εφόσον έχουμε υπολογίσει όλα ra προηγούμενα, δημιουργούμε ένα component το οποίο πραγματοποιεί τις προσθέσεις των τεσσάρων εισόδων, και στη συνέχεια αναθέτει orov πίνακα πρόβλεψης την κάθε τιμή.
94 i (jo γ ω γ Για τις ανάγκες της υλοποίησης της διπλωματικής εργασίας, χρησιμοποιήθηκαν εργαλεία της Synopsys τα οποία συντέλεσαν στην πραγματοποίηση πειραματικών μετρήσεων και στην εξαγωγή αποτελεσμάτων. Ένα από αυτά τα εργαλεία είναι ο Design compiler (DeCo). γ Design comριισιο Design Compiler (DC) είναι το λογισμικό που καλείται από το σύνολο των προγραμμάτων που προσφέρονται για την σύνθεση ψηφιακών κυκλωμάτων. Ο DC βελτιστοποιεί τις σχεδιάσεις με απώτερο στόχο την παροχή μικρότερων και γρηγορότερων αναπαραστάσεων μιας λογικής συνάριησης. Περιέχει υποεργαλεία τα οποία συνθέτουν τις HDL σχεδιάσεις σε τεχνολογικά εξαρτημένες σχεδιάσεις σε επίπεδο πυλών. Υποστηρίζει την δυνατότητα βελτιστοποίησης σχεδιάσεων είτε σε ιεραρχική είτε σε flat μορφή και μπορεί να συνθέσει τόσο ακολουθιακά όσο και συνδυαστικά κυκλώματα βελτιώνοντας την ταχύτητα απόκρισής τους, τον χώρο που καταλαμβάνουν και την ισχύ που καταναλώνουν. Στο. της επόμενης σελίδας παρουσιάζεται ο τρόπος με τον οποίο ο DC συμβάλλει στην συνολική ροή σχεδίασης :
95 :!'.illl H» 1 1 j l.'.ii.m *t"i Στο σημείο αυιό Οα δώσουμε και τον ιιρώτο «επίσημο» ορισμό της σύνθεσης ενός ψηφιακού κυκλώματος : «Σύνθεση ονομάζεται η διαδικασία κατά την οποία μετατρέπουμε μια σχεδίαση, η οποία μας δίνεται σε HDL κώδικα, σε ένα βέλτιστο nctlist σε επίπεδο πυλών το οποίο προσδιορίζεται πλήρως από μια τεχνολογική βιβλιοθήκη» Τα βήματα που ακολουθούμε κατά την διαδικασία της σύνθεσης ενός κυκλώματος, σε άμεση αντιστοιχία με το παραπάνω σχήμα, είναι τα εξής : 1) Δεχόμαστε ως είσοδο, αρχεία τα οποία περιγράφουν το κύκλωμά μας σε επίπεδο καταχωρητών (RTL - Register Transfer Level), δηλαδή αρχεία σε κάποια γλώσσα περιγραφής υλικού (HDL) όπως η Verilog και η VHDL.
96 2) Κατά την σύνθεση ο Design Compiler μεταφράζει την HDL περιγραφή σε συνθετικά στοιχεία της DesignWare βιβλιοθήκης, όπως είναι για παράδειγμα οι αθροιοτές και τα γενικά Boolean συνθετικά στοιχεία (τα οποία στο εξής θα αναφέρονται ως generic Boolean components ή πιο απλά GTECH components). Τα GTECH components δεν έχουν πληροφορίες όσον αφορά τον χρονισμό και την δυνατότητα οδήγησης και δεν προσδιορίζονται - αντιστοιχούν σε κάποια τεχνολογική βιβλιοθήκη. Ο DC χρησιμοποιεί τεχνολογικές (technology), συνθετικές (synthetic) και συμβολικές (symbolic) βιβλιοθήκες από το σημείο αυτό και μετέπειτα για την υλοποίηση της σύνθεσης και την παρουσίαση του αποτελέσματος ως γραφική αναπαράσταση. 3) Αφού γίνει η μετάφραση - μετατροπή του HDL κώδικα σε επίπεδο πυλών, ο DC βελτιστοποιεί την σχεδίαση και αντιστοιχίζει τα στοιχεία που την αποτελούν σε ένα συνδυασμό αποτελούμενο από συγκεκριμένα κελιά βιβλιοθηκών, βασιζόμενος στις επιλογές του χρήστη και τους περιορισμούς που αυτός έχει δώσει. Οι περιορισμοί αποτελούν στην ουσία τις σχεδιαστικές απαιτήσεις του χρήστη για τους στόχους που θέλει να πετύχει με βάση την απόδοση της σχεδίασης, δηλαδή αναφέρονται κατά κύριο λόγο στους χωρικούς και χρονικούς περιορισμούς υπό τους οποίους καλείται να επιτελεστεί η σύνθεση. Λ) Αφού ολοκληρωθεί η φάση αυτή, ακολουθώντας την ροή σχεδίασης που παρουσιάστηκε στο παραπάνω σχήμα, ελέγχουμε το αποτέλεσμα της σύνθεσης για να δούμε αν πληρεί τις απαιτήσεις που θέσαμε στην προηγούμενη φάση έτσι ώστε στην περίπτωση που παρουσιαστεί οποιοδήποτε πρόβλημα να το επιλύσουμε σε όσο το δυνατό πιο πρώιμο στάδιο του κύκλου σχεδίασης.
97 5) Μετά το πέρας του παραπάνω σταδίου, το κύκλωμά μας, όπως έχει πλέον διαμορφωθεί, είναι έτοιμο για την προσαγωγή του στα place & route εργαλεία ίου πακέτου που παρέχει η Synopsys, τα οποία σε γενικές γραμμές είναι αρμόδια για την τοποθέτηση και την διασύνδεση των επιμέρους κελιών στην σχεδίαση. Ο σχεδιαστής στο σημείο αυτό, έχει την δυνατότητα να επισημειώσει επιπρόσθετα στοιχεία, όπως οι καθυστερήσεις που παρουσιάζονται στις εσωτερικές διασυνδέσεις (interconnection delays) και να βάλει τον Design Compiler να επανασυνθέσει την σχεδίαση προκειμένου η ανάλυση χρονισμού να είναι πιο ακριβής. Ο Design Compiler διαβάζει και παράγει αρχεία που προσδιορίζουν σχεδιάσεις σε πολλαπλές μορφές που αποτελούν standards στην ηλεκτρονική σχεδίαση ψηφιακών κυκλωμάτων, συμπεριλαμβανομένων των αρχείων της Synopsys.db και eqn. Επιπρόσθετα ο DC προσφέρει άμεση σύνδεση με άλλα EDA (Electronic Design Automation) εργαλεία. Αυτό μας δίνει την δυνατότητα να μεταφέρουμε με ευκολία από εργαλείο σε εργαλείο τους περιορισμούς και τα αποτελέσματα που έχουμε ανακτήσει μέχρι την προκειμένη στιγμή. Στην συνέχεια θα αναφερθούμε, πιο αναλυτικά, στα εργαλεία που χρησιμοποιήθηκαν για την σύνθεση των κυκλωμάτων της παρούσας εργασίας (Design Vision) και τις βιβλιοθήκες που παρέχει η Synopsys και συνεπικουρούν στην επιτυχημένη σύνθεση ψηφιακών κυκλωμάτων. To Design Vision είναι μια γραφική διεπαφή (graphical user interface - GUI) για το περιβάλλον σύνθεσης της Synopsys και ένα εργαλείο το οποίο μπορεί να χρησιμοποιηθεί για την ανάλυση της σχεδίασής μας και την «αντιστοίχησή» της στην GTECH τεχνολογική βιβλιοθήκη σε επίπεδο πυλών. Το γραφικό περιβάλλον του Design Vision περιέχει μενού επιλογών τα οποία μας δίνουν την δυνατότητα να εκτελέσουμε το μεγαλύτερο ποσοστό των
98 εντολών που μπορούν να εκτελεστούν μέσα από το dc shell. Με άλλα λόγια το εργαλείο αυτό αποτελεί μια μετεξέλιξη του Design Analyzer το οποίο είναι μια ακόμη γραφική διεπαφή που προσφέρεται για την επικοινωνία με τον πυρήνα των εργαλείων της Synopsys. Στο σημείο αυτό πρέπει να αναφέρουμε πως όλες οι δυνατότητες του DC μπορούν να χρησιμοποιηθούν μέσα από την κονσόλα που μας προσφέρει το design vision, και αυτό συμβαίνει διότι τόσο ιο Design Vision όσο και ο Design Compiler χρησιμοποιούν την ίδια «μηχανή» ανάλυσης στατικού χρονισμού. Η μεθοδολογία που ακολουθείται είναι όμοια με αυτήν που περιγράψαμε παραπάνω, λόγω του γεγονότος πως το καλούν περιβάλλον είναι αυτό του Design Compiler. Η μεθοδολογία αυτή μπορεί να περιγράφει από το ακόλουθο σχήμα :
99 $ ο ο <ο cz 00 CO CO O >. GO Design Rule Constraints I Design Optimization Constraints Θα παρουσιάσουμε βήμα βήμα την πορεία που ακολουθείται βαοιζόμενη στο παρακάτω script που αποτελεί μια γενικευμένη εκδοχή αυτών που χρησιμοποιήθηκαν :
100 sol link library {/home/adadalia/umc013/umcel3h210t3 tc 120V 25C.db} set symbol library {/home/adadalia/umco 1 3/umce 1 3h21013 tc 120V 25C.sdb} set target library {/home/adadalia/umco 1 3/umce 13h21013 tc 120V 25C.db} analyze -format vhdl {/home/adadalia/vasilis/add/lypes.vhd} analyze -format vhdl {/home/adadalia/vasilis/add/and gate.vhd} analyze -format vhdl {/home/adadalia/vasllls/add/or gate.vhd) analyze -format vhdl {/home/adadalia/vasills/add/xor gate.vhd) analyze -format vhdl {/home/adadalia/vasills/add/adderl,vhd) analyze -format vhdl {/home/adadalia/vasllls/add/adder8.vhd} analyze -format vhdl {/home/adadalia/vasilis/add/adder9.vhd) analyze -format vhdl {/home/adadalia/vasius/add/adderlo.vhd) analyze -format vhdl {/home/adadalia/vasills/add/adderl 1.vhd) analyze -format vhdl {/home/adadalia/vasills/add/intra4x4.vhd} elaborate inlra circuit -library WORK current design intra circuit uniquify set flatten true -design intra^ circuit -effort high -minimize single output -phase true set max delay 1.0 [all outputs] set max transition 0.1 [all inputs] compile -map effort high -ungroup all -exact map report timing -path full -delay max -nworst 1 -max paths 1 -significant digits 3 - sort by group >> //home/adadalia/vasllis/add/time03.txt report area -nosplit >> /home/adadalia/vasills/add/areal.txt report cell -physical >> /home/adadalia/vasills/add/cell 1.txt Οι εντολές, με την σειρά που αναγράφονται, αποτελούν ένα τυπικό παράδειγμα ενός script το οποίο οδηγεί το Design Vision στην σύνθεση ενός ψηφιακού κυκλώματος και την αποθήκευση της νέας σχεδίασης στο δίσκο. Οι «εντολές» "link library" και "target library" προσδιορίζουν την θέση όπου βρίσκονται οι τεχνολογικές βιβλιοθήκες που προσδιορίζουν τα κελιά και άλλες πληροφορίες ανάλογα με τον «παροχέα» της τεχνολογίας, όπως τα ονόματα των κελιών τους σχεδιαστικούς κανόνες και τις συνθήκες λειτουργίας. Η
101 παράμετρος "symbol library" καθορίζει τα ούμβολα που είναι διαθέσιμα για την δημιουργία των κατάλληλων schematics. Για να ξεκινήσουμε να δουλεύουμε πάνω στην σχεδίαση, πρέπει αρχικά να διαβάσουμε ιην σχεδίασή μας από τον δίσκο στην ενεργή μνήμη του εργαλείου. Από το σημείο αυτό και έπειτα θα πραγματοποιηθούν όλες οι αλλαγές πριν η σχεδίασή μας αποθηκευτεί και πάλι στον δίσκο. Υπάρχουν δυο δυνατές επιλογές στην περίπτωση που θέλουμε να διαβάσουμε μια σχεδίαση : Analyze & Elaborate : Χρησιμοποιούμε αυτές τις εντολές για να διαβάσουμε HDL σχεδιάσεις και να τις μετατρέψουμε σε αρχεία βάσης δεδομένων στο format της Synopsys (.db). ^ Read : Η εντολή αυτή χρησιμοποιείται όταν θέλουμε να διαβάσουμε σχεδιάσεις που είναι ήδη σε.db μορφή. Η εντολή "analyze" εξετάζει το HDL αρχείο προκειμένου να δει εάν βρίσκεται σε σωστή συντακτική λογική και αν είναι δυνατό να υποστεί σύνθεση. Επιπρόσθετα μεταφράζει τα αρχεία μας σε ένα ενδιάμεσο format και τοποθετεί το αρχείο αυτό στον φάκελο που έχουμε προσδιορίσει ως φάκελο εργασίας (working directory). Η εντολή "elaborate" εξετάζει το «ενδιάμεσο» αρχείο και στην συνέχεια δημιουργεί την σχεδίαση σε μορφή.db αρχείου. Κατά την διάρκεια αυτής της διαδικασίας το πρόγραμμα καθορίζει ποια από τα «στοιχεία» της σχεδίασης πρέπει να αντικατασταθούν από συνθετικά «στοιχεία» της βιβλιοθήκης που έχουμε επιλέξει. Η εντολή "read" αποτελεί ένα συνδυασμό των παραπάνω εντολών, δεν πραγματοποιεί, όμως όοους ελέγχους πραγματοποιούν οι προκείμενες εντολές. Ακολούθως καλούμαστε να καθορίσουμε το περιβάλλον της σχεδίασης και τους περιορισμούς/παραμέτρους της σχεδίασης. Ο DC απαιτεί την
102 μοντελοποίηση ιου σχεδιασπκού περιβάλλοντος του κυκλώματος ώστε να προχωρήσει η διαδικασία της σύνθεσης. Με το μοντέλο αυτό καθορίζουμε τις εξωτερικές συνθήκες λειτουργίας (manufacturing process, temperature, voltage), loads, drives, fanouts, και wire load models. Ο καθορισμός όλων αυιών των παραμέτρων επηρεάζει άμεσα την σύνθεση του κυκλώματος και τα αποτελέσματα των βελτιστοποιήσεων που εφαρμόζει ο DC. Τέλος, με χρήση της εντολής "report" και μιας σειράς παράμερων λαμβάνουμε πληροφορίες για την σχεδίαση, τα κελιά, τον χώρο που καταλαμβάνει το κύκλωμα αλλά και το μέγιστο μονοπάτι που υπάρχει στο κύκλωμα (critical path). Ο υπολογισμός του critical path είναι επιθυμητός διότι είθισται ως εμπειρικός κανόνας να τοποθετείται ως περίοδος στα testbenches των κυκλωμάτων η ποσότητα critical path + 10%critical path. 3. Πειραματικές μετρήσεις και αποτελέσματα Για to κύκλωμα που υλοποιεί τις μεθόδους πρόβλεψης για μτιλοκ 4X4: Max delay it of cells Total cell area Data arrival time Max frequency ns 780 MHz ns 764 MHz ns 770 MHz ns 780 MHz ns 762 MHz ns 775 MHz
103 [1] 12] [3] [4] [5] ' [6] [7] vl [8 [9 I 10] HI] [12] /! V l pin lie Π'1Q ( : I'M it ill.it'll pi if [13] /Wfir ipapers/h32 3/Ejnercj11iciH26 l.pof [14] /\V'lit'?![ >:[- /H W3/H204 o,-:pl ηηϋ,ρι]! [15] : i/ ΓΐίΐριΊΊΐ:'/[i:>iriO../Sei u mi i 2.00 'J \nin
104 [16] 117] [18] [19] [20] Ι( [21] )4 - [22] / \
Τεχνολογία Πολυμέσων. Ενότητα # 14: Κωδικοποίηση βίντεο: Η.264 Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 14: Κωδικοποίηση βίντεο: Η.264 Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου
Τεχνολογία Πολυμέσων Ενότητα # 14: Κωδικοποίηση βίντεο: Η.264 Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου
ΤΕΙ ΚΡΗΤΗΣ ΤΜ. ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡ/ΚΗΣ & ΠΟΛΥΜΕΣΩΝ ΔΙΔΑΣΚΩΝ: Δρ. Γ. ΓΑΡΔΙΚΗΣ. Κωδικοποίηση εικόνας
 ΤΕΙ ΚΡΗΤΗΣ ΤΜ. ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡ/ΚΗΣ & ΠΟΛΥΜΕΣΩΝ ΔΙΔΑΣΚΩΝ: Δρ. Γ. ΓΑΡΔΙΚΗΣ 2 Κωδικοποίηση εικόνας Ακολουθία από ψηφιοποιημένα καρέ (frames) που έχουν συλληφθεί σε συγκεκριμένο ρυθμό frame rate (π.χ. 10fps,
ΤΕΙ ΚΡΗΤΗΣ ΤΜ. ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡ/ΚΗΣ & ΠΟΛΥΜΕΣΩΝ ΔΙΔΑΣΚΩΝ: Δρ. Γ. ΓΑΡΔΙΚΗΣ 2 Κωδικοποίηση εικόνας Ακολουθία από ψηφιοποιημένα καρέ (frames) που έχουν συλληφθεί σε συγκεκριμένο ρυθμό frame rate (π.χ. 10fps,
ΕΙΔΗ ΠΛΑΙΣΙΩΝ Ενδο-πλαισιακή κωδικοποίηση (Intra- frame Coding): Δια-πλαισιακή κωδικοποίηση (Inter-frame Coding):
 ΕΙΔΗ ΠΛΑΙΣΙΩΝ Ενδο-πλαισιακή κωδικοποίηση (Intraframe Coding): κάθε εικόνα αντιμετωπίζεται και κωδικοποιείται ανεξάρτητα από τις υπόλοιπες (όπως στο JPEG) Δια-πλαισιακή κωδικοποίηση (Inter-frame Coding):
ΕΙΔΗ ΠΛΑΙΣΙΩΝ Ενδο-πλαισιακή κωδικοποίηση (Intraframe Coding): κάθε εικόνα αντιμετωπίζεται και κωδικοποιείται ανεξάρτητα από τις υπόλοιπες (όπως στο JPEG) Δια-πλαισιακή κωδικοποίηση (Inter-frame Coding):
Τεράστιες ανάγκες σε αποθηκευτικό χώρο
 ΣΥΜΠΙΕΣΗ Τεράστιες ανάγκες σε αποθηκευτικό χώρο Παράδειγμα: CD-ROM έχει χωρητικότητα 650MB, χωρά 75 λεπτά ασυμπίεστου στερεοφωνικού ήχου, αλλά 30 sec ασυμπίεστου βίντεο. Μαγνητικοί δίσκοι χωρητικότητας
ΣΥΜΠΙΕΣΗ Τεράστιες ανάγκες σε αποθηκευτικό χώρο Παράδειγμα: CD-ROM έχει χωρητικότητα 650MB, χωρά 75 λεπτά ασυμπίεστου στερεοφωνικού ήχου, αλλά 30 sec ασυμπίεστου βίντεο. Μαγνητικοί δίσκοι χωρητικότητας
Αρχές κωδικοποίησης. Τεχνολογία Πολυμέσων και Πολυμεσικές Επικοινωνίες 08-1
 Αρχές κωδικοποίησης Απαιτήσεις κωδικοποίησης Είδη κωδικοποίησης Κωδικοποίηση εντροπίας Διαφορική κωδικοποίηση Κωδικοποίηση μετασχηματισμών Στρωματοποιημένη κωδικοποίηση Κβαντοποίηση διανυσμάτων Τεχνολογία
Αρχές κωδικοποίησης Απαιτήσεις κωδικοποίησης Είδη κωδικοποίησης Κωδικοποίηση εντροπίας Διαφορική κωδικοποίηση Κωδικοποίηση μετασχηματισμών Στρωματοποιημένη κωδικοποίηση Κβαντοποίηση διανυσμάτων Τεχνολογία
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ,
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 004 005, Χειµερινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ Η εξέταση αποτελείται από δύο µέρη. Το πρώτο περιλαµβάνει
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 004 005, Χειµερινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ Η εξέταση αποτελείται από δύο µέρη. Το πρώτο περιλαµβάνει
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2013-2014 JPEG 2000 Δρ. Ν. Π. Σγούρος 2 JPEG 2000 Βασικά χαρακτηριστικά Επιτρέπει συμπίεση σε εξαιρετικά χαμηλούς ρυθμούς όπου η συμπίεση με το JPEG εισάγει μεγάλες παραμορφώσεις Ενσωμάτωση
Συμπίεση Δεδομένων 2013-2014 JPEG 2000 Δρ. Ν. Π. Σγούρος 2 JPEG 2000 Βασικά χαρακτηριστικά Επιτρέπει συμπίεση σε εξαιρετικά χαμηλούς ρυθμούς όπου η συμπίεση με το JPEG εισάγει μεγάλες παραμορφώσεις Ενσωμάτωση
Τεχνολογία Πολυμέσων. Ενότητα # 8: Αρχές κωδικοποίησης Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 8: Αρχές κωδικοποίησης Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του
Τεχνολογία Πολυμέσων Ενότητα # 8: Αρχές κωδικοποίησης Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του
Συστήματα Πολυμέσων. Ενότητα 15: Συμπίεση Ψηφιακού Βίντεο. Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Συστήματα Πολυμέσων Ενότητα 15: Συμπίεση Ψηφιακού Βίντεο Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Συστήματα Πολυμέσων Ενότητα 15: Συμπίεση Ψηφιακού Βίντεο Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
Group (JPEG) το 1992.
 Μέθοδοι Συμπίεσης Εικόνας Πρωτόκολλο JPEG Συμπίεση Εικόνας: Μείωση αποθηκευτικού χώρου Ευκολία στη μεταφορά αρχείων Δημιουργήθηκε από την ομάδα Joint Photographic Experts Group (JPEG) το 1992. Ονομάστηκε
Μέθοδοι Συμπίεσης Εικόνας Πρωτόκολλο JPEG Συμπίεση Εικόνας: Μείωση αποθηκευτικού χώρου Ευκολία στη μεταφορά αρχείων Δημιουργήθηκε από την ομάδα Joint Photographic Experts Group (JPEG) το 1992. Ονομάστηκε
Δ11 Δ12. Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2013-2014 Κωδικοποιητές εικονοροής (Video) Δρ. Ν. Π. Σγούρος 2 Κωδικοποιητές Εικονοροών ITU-T VCEG H.261 (1990) ISO/IEC MPEG H.263 (1995/9 6) MPEG-2 (H.262) (1994/9 5) H.263+ (1997/98)
Συμπίεση Δεδομένων 2013-2014 Κωδικοποιητές εικονοροής (Video) Δρ. Ν. Π. Σγούρος 2 Κωδικοποιητές Εικονοροών ITU-T VCEG H.261 (1990) ISO/IEC MPEG H.263 (1995/9 6) MPEG-2 (H.262) (1994/9 5) H.263+ (1997/98)
Συµπίεση Εικόνας: Το πρότυπο JPEG
 ΒΕΣ : Συµπίεση και Μετάδοση Πολυµέσων ΒΕΣ Συµπίεση και Μετάδοση Πολυµέσων Συµπίεση Εικόνας: Το πρότυπο JPEG ΒΕΣ : Συµπίεση και Μετάδοση Πολυµέσων Εισαγωγή Σχεδιάστηκε από την οµάδα Joint Photographic Experts
ΒΕΣ : Συµπίεση και Μετάδοση Πολυµέσων ΒΕΣ Συµπίεση και Μετάδοση Πολυµέσων Συµπίεση Εικόνας: Το πρότυπο JPEG ΒΕΣ : Συµπίεση και Μετάδοση Πολυµέσων Εισαγωγή Σχεδιάστηκε από την οµάδα Joint Photographic Experts
ΒΕΣ 04: Συµπίεση και Μετάδοση Πολυµέσων. Περιεχόµενα. Βιβλιογραφία. Συµπίεση εικόνων: Το πρότυπο JPEG. Εισαγωγή. Ευθύς µετασχηµατισµός DCT
 ΒΕΣ : Συµπίεση και Μετάδοση Πολυµέσων Συµπίεση εικόνων: Το πρότυπο JPEG Περιεχόµενα Εισαγωγή Ο µετασχηµατισµός DCT Το πρότυπο JPEG Προετοιµασία εικόνας / µπλοκ Ευθύς µετασχηµατισµός DCT Κβαντισµός Κωδικοποίηση
ΒΕΣ : Συµπίεση και Μετάδοση Πολυµέσων Συµπίεση εικόνων: Το πρότυπο JPEG Περιεχόµενα Εισαγωγή Ο µετασχηµατισµός DCT Το πρότυπο JPEG Προετοιµασία εικόνας / µπλοκ Ευθύς µετασχηµατισµός DCT Κβαντισµός Κωδικοποίηση
Περιεχόµενα. ΕΠΛ 422: Συστήµατα Πολυµέσων. Βιβλιογραφία. Εισαγωγή. Συµπίεση εικόνων: Το πρότυπο JPEG. Εισαγωγή. Ευθύς µετασχηµατισµός DCT
 Περιεχόµενα ΕΠΛ : Συστήµατα Πολυµέσων Συµπίεση εικόνων: Το πρότυπο JPEG Εισαγωγή Ο µετασχηµατισµός DCT Το πρότυπο JPEG Προετοιµασία εικόνας / µπλοκ Ευθύς µετασχηµατισµός DCT Κβαντισµός Κωδικοποίηση ηµιουργία
Περιεχόµενα ΕΠΛ : Συστήµατα Πολυµέσων Συµπίεση εικόνων: Το πρότυπο JPEG Εισαγωγή Ο µετασχηµατισµός DCT Το πρότυπο JPEG Προετοιµασία εικόνας / µπλοκ Ευθύς µετασχηµατισµός DCT Κβαντισµός Κωδικοποίηση ηµιουργία
MPEG-4 : Διαδραστικές εφαρμογές πολυμέσων
 MPEG-4 : Διαδραστικές εφαρμογές πολυμέσων Συμπίεση οπτικοακουστικών δεδομένων για το Διαδίκτυο Οπτικοί δίσκοι Ψηφιακή τηλεόραση (επίγεια, δορυφορική) Συμβατότητα με MPEG-1 και MPEG-2 Συνθετική σκηνή Εισαγωγή
MPEG-4 : Διαδραστικές εφαρμογές πολυμέσων Συμπίεση οπτικοακουστικών δεδομένων για το Διαδίκτυο Οπτικοί δίσκοι Ψηφιακή τηλεόραση (επίγεια, δορυφορική) Συμβατότητα με MPEG-1 και MPEG-2 Συνθετική σκηνή Εισαγωγή
Κωδικοποίηση βίντεο (MPEG)
 (MEG) Εισαγωγή στο MEG-1 Κωδικοποίηση βίντεο οµή βίντεο Κωδικοποίηση ήχου Ροή δεδοµένων Τεχνολογία Πολυµέσων 11-1 Εισαγωγή στο MEG-1 MEG (Motion ictures Experts Group) ίντεο και ήχος υψηλής ποιότητας ιανοµή
(MEG) Εισαγωγή στο MEG-1 Κωδικοποίηση βίντεο οµή βίντεο Κωδικοποίηση ήχου Ροή δεδοµένων Τεχνολογία Πολυµέσων 11-1 Εισαγωγή στο MEG-1 MEG (Motion ictures Experts Group) ίντεο και ήχος υψηλής ποιότητας ιανοµή
ITU-T : H.261 (1990), H.262 (1996), H.263 (1995) MPEG-1, MPEG-2, MPEG-4. Αποθήκευση, Μετάδοση, Επικοινωνίες, ίκτυα
 Συµπίεση/κωδικοποίηση βίντεο ITU-T : H.261 (1990), H.262 (1996), H.263 (1995) Συνδιάσκεψη : ISDN, ATM, LANs, Internet, PSTN MPEG-1, MPEG-2, MPEG-4 Αποθήκευση, Μετάδοση, Επικοινωνίες, ίκτυα 1 H.261 : εισαγωγή
Συµπίεση/κωδικοποίηση βίντεο ITU-T : H.261 (1990), H.262 (1996), H.263 (1995) Συνδιάσκεψη : ISDN, ATM, LANs, Internet, PSTN MPEG-1, MPEG-2, MPEG-4 Αποθήκευση, Μετάδοση, Επικοινωνίες, ίκτυα 1 H.261 : εισαγωγή
Τεχνολογία Πολυμέσων. Ενότητα # 11: Κωδικοποίηση εικόνων: JPEG Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 11: Κωδικοποίηση εικόνων: JPEG Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου
Τεχνολογία Πολυμέσων Ενότητα # 11: Κωδικοποίηση εικόνων: JPEG Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου
Ραδιοτηλεοπτικά Συστήματα Ενότητα 4: Ψηφιοποίηση και συμπίεση σημάτων εικόνας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ραδιοτηλεοπτικά Συστήματα Ενότητα 4: Ψηφιοποίηση και συμπίεση σημάτων εικόνας Δρ. Νικόλαος- Αλέξανδρος Τάτλας Τμήμα Ηλεκτρονικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ραδιοτηλεοπτικά Συστήματα Ενότητα 4: Ψηφιοποίηση και συμπίεση σημάτων εικόνας Δρ. Νικόλαος- Αλέξανδρος Τάτλας Τμήμα Ηλεκτρονικών
Ψηφιακή Επεξεργασία Εικόνας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 9 : Κωδικοποίηση βίντεο Πρότυπο συμπίεσης MPEG Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 9 : Κωδικοποίηση βίντεο Πρότυπο συμπίεσης MPEG Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το
Τεχνολογία Πολυμέσων. Ενότητα # 12: Κωδικοποίηση βίντεο: H.26x Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
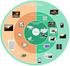 Τεχνολογία Πολυμέσων Ενότητα # 12: Κωδικοποίηση βίντεο: H.26x Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου
Τεχνολογία Πολυμέσων Ενότητα # 12: Κωδικοποίηση βίντεο: H.26x Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου
Κωδικοποίηση βίντεο (H.261 / DVI)
 Κωδικοποίηση βίντεο (H.261 / DVI) Αρχές κωδικοποίησης βίντεο Εισαγωγή στο H.261 Κωδικοποίηση βίντεο Ροή δεδοµένων Εισαγωγή στο DVI Κωδικοποίηση ήχου και εικόνων Κωδικοποίηση βίντεο Ροή δεδοµένων Τεχνολογία
Κωδικοποίηση βίντεο (H.261 / DVI) Αρχές κωδικοποίησης βίντεο Εισαγωγή στο H.261 Κωδικοποίηση βίντεο Ροή δεδοµένων Εισαγωγή στο DVI Κωδικοποίηση ήχου και εικόνων Κωδικοποίηση βίντεο Ροή δεδοµένων Τεχνολογία
χωρίςναδηµιουργείταιαίσθησηαπώλειαςτηςποιότηταςτηςανακατασκευασµένηςεικόνας.
 Το πρότυπο JPEG για κωδικοποίησηση εικόνας Το JPEG, που υιοθετήθηκε από την Joint Photographic Experts Group, είναι ένα πρότυπο που χρησιµοποιείταιευρέωςγιατησυµπίεσηακίνητωνεικόνων, µε µέσο λόγο συµπίεσης
Το πρότυπο JPEG για κωδικοποίησηση εικόνας Το JPEG, που υιοθετήθηκε από την Joint Photographic Experts Group, είναι ένα πρότυπο που χρησιµοποιείταιευρέωςγιατησυµπίεσηακίνητωνεικόνων, µε µέσο λόγο συµπίεσης
Πολυμέσα. Συμπίεση δεδομένων Κωδικοποίηση MPEG. Δρ. Γεώργιος Π. Παυλίδης ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ
 Πολυμέσα Συμπίεση δεδομένων Κωδικοποίηση MPEG Δρ. Γεώργιος Π. Παυλίδης Συμπίεση Δεδομένων Περιεχόμενα Γνωστοίαλγόριθμοισυμπίεσης MPEG Χρησιμοποίηση Εφαρμογές Εκμάθηση Σχεδίαση Διασύνδεση χρήστη Υπηρεσίες
Πολυμέσα Συμπίεση δεδομένων Κωδικοποίηση MPEG Δρ. Γεώργιος Π. Παυλίδης Συμπίεση Δεδομένων Περιεχόμενα Γνωστοίαλγόριθμοισυμπίεσης MPEG Χρησιμοποίηση Εφαρμογές Εκμάθηση Σχεδίαση Διασύνδεση χρήστη Υπηρεσίες
Ψηφιακή Επεξεργασία Εικόνας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 6 : Κωδικοποίηση & Συμπίεση εικόνας Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 6 : Κωδικοποίηση & Συμπίεση εικόνας Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό
Συστήµατα και Αλγόριθµοι Πολυµέσων
 Συστήµατα και Αλγόριθµοι Πολυµέσων Ιωάννης Χαρ. Κατσαβουνίδης Οµιλία #5: Αρχές Επεξεργασίας Σηµάτων Πολυµέσων 7 Νοεµβρίου 2005 Επανάληψη Θεωρία Πληροφορίας Εντροπία: H ( P) i= 0 Κωδικοποίηση Huffman 3
Συστήµατα και Αλγόριθµοι Πολυµέσων Ιωάννης Χαρ. Κατσαβουνίδης Οµιλία #5: Αρχές Επεξεργασίας Σηµάτων Πολυµέσων 7 Νοεµβρίου 2005 Επανάληψη Θεωρία Πληροφορίας Εντροπία: H ( P) i= 0 Κωδικοποίηση Huffman 3
Συµπίεση Ψηφιακών Εικόνων: Συµπίεση µε Απώλειες. Πρότυπα Συµπίεσης Εικόνων
 ΤΨΣ 5: Ψηφιακή Επεξεργασία Εικόνας ΤΨΣ 5 Ψηφιακή Επεξεργασία Εικόνας Συµπίεση Ψηφιακών Εικόνων: Συµπίεση µε απώλειες Πρότυπα Συµπίεσης Εικόνων Τµήµα ιδακτικής της Τεχνολογίας και Ψηφιακών Συστηµάτων Πανεπιστήµιο
ΤΨΣ 5: Ψηφιακή Επεξεργασία Εικόνας ΤΨΣ 5 Ψηφιακή Επεξεργασία Εικόνας Συµπίεση Ψηφιακών Εικόνων: Συµπίεση µε απώλειες Πρότυπα Συµπίεσης Εικόνων Τµήµα ιδακτικής της Τεχνολογίας και Ψηφιακών Συστηµάτων Πανεπιστήµιο
MPEG-4: Βασικά Χαρακτηριστικά
 MPEG-4 MPEG-4: Βασικά Χαρακτηριστικά Σχεδιάστηκε ώστε να καλύπτει ευρύ φάσμα ρυθμών, από 5 kbps εώς 10 Mbps Εκτός από τη συμπίεση δίνει έμφαση και στην αλληλεπίδραση με το χρήστη Χρησιμοποιεί αντικείμενα
MPEG-4 MPEG-4: Βασικά Χαρακτηριστικά Σχεδιάστηκε ώστε να καλύπτει ευρύ φάσμα ρυθμών, από 5 kbps εώς 10 Mbps Εκτός από τη συμπίεση δίνει έμφαση και στην αλληλεπίδραση με το χρήστη Χρησιμοποιεί αντικείμενα
MPEG-4: Διαδραστικές εφαρμογές πολυμέσων
 MPEG-4: Διαδραστικές εφαρμογές πολυμέσων Γιώργος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών http://www.csd.uoc.gr/~tziritas Άνοιξη 2016 1 Εισαγωγή Δημοσίευση 1998 (Intern. Telecom. Union) Επικοινωνίες με πολυμέσα,
MPEG-4: Διαδραστικές εφαρμογές πολυμέσων Γιώργος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών http://www.csd.uoc.gr/~tziritas Άνοιξη 2016 1 Εισαγωγή Δημοσίευση 1998 (Intern. Telecom. Union) Επικοινωνίες με πολυμέσα,
Αρχές κωδικοποίησης. Τεχνολογία Πολυµέσων 08-1
 Αρχές κωδικοποίησης Απαιτήσεις κωδικοποίησης Είδη κωδικοποίησης Βασικές τεχνικές κωδικοποίησης Κωδικοποίηση Huffman Κωδικοποίηση µετασχηµατισµών Κβαντοποίηση διανυσµάτων ιαφορική κωδικοποίηση Τεχνολογία
Αρχές κωδικοποίησης Απαιτήσεις κωδικοποίησης Είδη κωδικοποίησης Βασικές τεχνικές κωδικοποίησης Κωδικοποίηση Huffman Κωδικοποίηση µετασχηµατισµών Κβαντοποίηση διανυσµάτων ιαφορική κωδικοποίηση Τεχνολογία
Συµπίεση Δεδοµένων: Συµπίεση Ψηφιακού Βίντεο
 Συµπίεση Δεδοµένων: Συµπίεση Ψηφιακού Βίντεο Αλέξανδρος Ελευθεριάδης Αναπ. Καθηγητής & Marie Curie Chair Τµήµα Πληροφορικής και Τηλεπικοινωνιών Εθνικό και Καποδιστριακό Πανεπιστήµιο Αθηνών eleft@di.uoa.gr,
Συµπίεση Δεδοµένων: Συµπίεση Ψηφιακού Βίντεο Αλέξανδρος Ελευθεριάδης Αναπ. Καθηγητής & Marie Curie Chair Τµήµα Πληροφορικής και Τηλεπικοινωνιών Εθνικό και Καποδιστριακό Πανεπιστήµιο Αθηνών eleft@di.uoa.gr,
Δ10. Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 203-204 Κωδικοποίηση εικονοροής (Video) Δρ. Ν. Π. Σγούρος 2 Ανάλυση Οθονών Δρ. Ν. Π. Σγούρος 3 Πρωτόκολλα μετάδοσης εικονοροών Πρωτόκολλο Ρυθμός (Hz) Φίλμ 23.976 ATSC 24 PAL,DVB-SD,DVB-HD
Συμπίεση Δεδομένων 203-204 Κωδικοποίηση εικονοροής (Video) Δρ. Ν. Π. Σγούρος 2 Ανάλυση Οθονών Δρ. Ν. Π. Σγούρος 3 Πρωτόκολλα μετάδοσης εικονοροών Πρωτόκολλο Ρυθμός (Hz) Φίλμ 23.976 ATSC 24 PAL,DVB-SD,DVB-HD
Συστήματα Πολυμέσων. Ενότητα 7: Συμπίεση Εικόνας κατά JPEG. Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
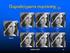 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 7: Συμπίεση Εικόνας κατά JPEG Θρασύβουλος Γ. Τσιάτσος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 7: Συμπίεση Εικόνας κατά JPEG Θρασύβουλος Γ. Τσιάτσος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Η ανάγκη για συμπίεση
 Πρότυπα συμπίεσης Η ανάγκη για συμπίεση High-Definition Television (HDTV) 1920x1080 30 frames per second (full motion) 8 bits για κάθε κανάλι χρώματος 1.5 Gb/sec! Κάθε κανάλι 6 MHz Max data rate: 19.2
Πρότυπα συμπίεσης Η ανάγκη για συμπίεση High-Definition Television (HDTV) 1920x1080 30 frames per second (full motion) 8 bits για κάθε κανάλι χρώματος 1.5 Gb/sec! Κάθε κανάλι 6 MHz Max data rate: 19.2
Μάθημα 7 ο. Συμπίεση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ 1
 Μάθημα 7 ο Συμπίεση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ 1 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας πληροφορίας Ανάγκες που καλύπτονται Εξοικονόμηση μνήμης Ελάττωση χρόνου και εύρους
Μάθημα 7 ο Συμπίεση Εικόνας ΤΜΗΥΠ / ΕΕΣΤ 1 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας πληροφορίας Ανάγκες που καλύπτονται Εξοικονόμηση μνήμης Ελάττωση χρόνου και εύρους
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 004 005, Χειµερινό Εξάµηνο Θεωρητικές Ασκήσεις (# 3): 1. Ο διακριτός µετασχηµατισµός συνηµίτονου (Discrete Cosine Transform)
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 4: ΣΥΣΤΗΜΑΤΑ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 004 005, Χειµερινό Εξάµηνο Θεωρητικές Ασκήσεις (# 3): 1. Ο διακριτός µετασχηµατισµός συνηµίτονου (Discrete Cosine Transform)
Κωδικοποίηση εικόνων κατά JPEG
 Κωδικοποίηση εικόνων κατά JPEG Εισαγωγή Προετοιµασία της εικόνας ρυθµός Ακολουθιακός απωλεστικός ρυθµός Εκτεταµένος απωλεστικός ρυθµός Μη απωλεστικός ρυθµός Ιεραρχικός ρυθµός Τεχνολογία Πολυµέσων 09-1
Κωδικοποίηση εικόνων κατά JPEG Εισαγωγή Προετοιµασία της εικόνας ρυθµός Ακολουθιακός απωλεστικός ρυθµός Εκτεταµένος απωλεστικός ρυθµός Μη απωλεστικός ρυθµός Ιεραρχικός ρυθµός Τεχνολογία Πολυµέσων 09-1
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία
 ΗΜΥ 100 Εισαγωγή στην Τεχνολογία Δρ. Στέλιος Τιμοθέου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ ΜΑΣ ΣΗΜΕΡΑ Αναλογικά και ψηφιακά συστήματα Μετατροπή
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία Δρ. Στέλιος Τιμοθέου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ ΜΑΣ ΣΗΜΕΡΑ Αναλογικά και ψηφιακά συστήματα Μετατροπή
3. ΤΕΧΝΙΚΕΣ ΣΥΜΠΙΕΣΗΣ ΠΟΛΥΜΕΣΩΝ
 3. ΤΕΧΝΙΚΕΣ ΣΥΜΠΙΕΣΗΣ ΠΟΛΥΜΕΣΩΝ ΑΝΑΓΚΗ ΣΥΜΠΙΕΣΗΣ ΔΕΔΟΜΕΝΩΝ Local Multimedia Π.χ. Μία ταινία 90 min απαιτεί 120 GB, και τα σημερινά μέσα αποθήκευσης < 25 GB. Άρα σήμερα είναι αδύνατη η αποθήκευση και η
3. ΤΕΧΝΙΚΕΣ ΣΥΜΠΙΕΣΗΣ ΠΟΛΥΜΕΣΩΝ ΑΝΑΓΚΗ ΣΥΜΠΙΕΣΗΣ ΔΕΔΟΜΕΝΩΝ Local Multimedia Π.χ. Μία ταινία 90 min απαιτεί 120 GB, και τα σημερινά μέσα αποθήκευσης < 25 GB. Άρα σήμερα είναι αδύνατη η αποθήκευση και η
Αναλογικά & Ψηφιακά Κυκλώματα ιαφάνειες Μαθήματος ρ. Μηχ. Μαραβελάκης Εμ.
 Αναλογικά & Ψηφιακά Κυκλώματα ιαφάνειες Μαθήματος ρ. Μηχ. Μαραβελάκης Εμ. 1 Εισαγωγή Αναλογικό σήμα (analog signal): συνεχής συνάρτηση στην οποία η ανεξάρτητη μεταβλητή και η εξαρτημένη μεταβλητή (π.χ.
Αναλογικά & Ψηφιακά Κυκλώματα ιαφάνειες Μαθήματος ρ. Μηχ. Μαραβελάκης Εμ. 1 Εισαγωγή Αναλογικό σήμα (analog signal): συνεχής συνάρτηση στην οποία η ανεξάρτητη μεταβλητή και η εξαρτημένη μεταβλητή (π.χ.
Τμήμα Λογιστικής. Εισαγωγή στους Ηλεκτρονικούς Υπολογιστές. Μαθήματα 6 και 7 Αναπαράσταση της Πληροφορίας στον Υπολογιστή. 1 Στέργιος Παλαμάς
 ΤΕΙ Ηπείρου Παράρτημα Πρέβεζας Τμήμα Λογιστικής Εισαγωγή στους Ηλεκτρονικούς Υπολογιστές Μαθήματα 6 και 7 Αναπαράσταση της Πληροφορίας στον Υπολογιστή 1 1. Αριθμοί: Το Δυαδικό Σύστημα Οι ηλεκτρονικοί υπολογιστές
ΤΕΙ Ηπείρου Παράρτημα Πρέβεζας Τμήμα Λογιστικής Εισαγωγή στους Ηλεκτρονικούς Υπολογιστές Μαθήματα 6 και 7 Αναπαράσταση της Πληροφορίας στον Υπολογιστή 1 1. Αριθμοί: Το Δυαδικό Σύστημα Οι ηλεκτρονικοί υπολογιστές
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 6 η : Συμπίεση Εικόνας. Καθ. Κωνσταντίνος Μπερμπερίδης Πολυτεχνική Σχολή Μηχανικών Η/Υ & Πληροφορικής
 Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 6 η : Συμπίεση Εικόνας Καθ. Κωνσταντίνος Μπερμπερίδης Πολυτεχνική Σχολή Μηχανικών Η/Υ & Πληροφορικής Σκοποί ενότητας Εισαγωγή στη συμπίεση εικόνας Μη απωλεστικες
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 6 η : Συμπίεση Εικόνας Καθ. Κωνσταντίνος Μπερμπερίδης Πολυτεχνική Σχολή Μηχανικών Η/Υ & Πληροφορικής Σκοποί ενότητας Εισαγωγή στη συμπίεση εικόνας Μη απωλεστικες
Συμπίεση Πολυμεσικών Δεδομένων
 Συμπίεση Πολυμεσικών Δεδομένων Εισαγωγή στο πρόβλημα και επιλεγμένες εφαρμογές Παράδειγμα 2: Συμπίεση Εικόνας ΔΠΜΣ ΜΥΑ, Ιούνιος 2011 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας
Συμπίεση Πολυμεσικών Δεδομένων Εισαγωγή στο πρόβλημα και επιλεγμένες εφαρμογές Παράδειγμα 2: Συμπίεση Εικόνας ΔΠΜΣ ΜΥΑ, Ιούνιος 2011 Εισαγωγή (1) Οι τεχνικές συμπίεσης βασίζονται στην απόρριψη της πλεονάζουσας
Περιεχόµενα. ΕΠΛ 422: Συστήµατα Πολυµέσων. Συµπίεση Βίντεο. Βιβλιογραφία. Αρχές συµπίεσης βίντεο
 Περιεχόµενα ΕΠΛ 422: Συστήµατα Πολυµέσων Συµπίεση Βίντεο Αρχές Συµπίεσης Τύποι πλαισίων Εκτίµηση και αντιστάθµιση κίνησης Θέµατα υλοποίησης Η261 Η263 MEG MEG-1 MEG-2 MEG-4 Βιβλιογραφία Καγιάφας [2000]:
Περιεχόµενα ΕΠΛ 422: Συστήµατα Πολυµέσων Συµπίεση Βίντεο Αρχές Συµπίεσης Τύποι πλαισίων Εκτίµηση και αντιστάθµιση κίνησης Θέµατα υλοποίησης Η261 Η263 MEG MEG-1 MEG-2 MEG-4 Βιβλιογραφία Καγιάφας [2000]:
Κεφάλαιο 3 Συμπίεση Βίντεο
 Κεφάλαιο 3 Συμπίεση Βίντεο Σύνοψη Στο κεφάλαιο αυτό εξετάζουμε τους βασικούς τρόπους με τους οποίους το πρότυπο MPEG (και συγκεκριμένα το MPEG-2) προβλέπει τη συμπίεση του σήματος βίντεο. Η ανάγκη για
Κεφάλαιο 3 Συμπίεση Βίντεο Σύνοψη Στο κεφάλαιο αυτό εξετάζουμε τους βασικούς τρόπους με τους οποίους το πρότυπο MPEG (και συγκεκριμένα το MPEG-2) προβλέπει τη συμπίεση του σήματος βίντεο. Η ανάγκη για
Ακαδηµαϊκό Έτος , Χειµερινό Εξάµηνο ιδάσκων Καθ.: Νίκος Τσαπατσούλης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ, ΤΜΗΜΑ Ι ΑΚΤΙΚΗΣ ΤΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΤΨΣ 50: ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ Ακαδηµαϊκό Έτος 005 006, Χειµερινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ Η εξέταση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ, ΤΜΗΜΑ Ι ΑΚΤΙΚΗΣ ΤΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΤΨΣ 50: ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ Ακαδηµαϊκό Έτος 005 006, Χειµερινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ Η εξέταση
Πληροφορική Ι. Μάθημα 9 ο Συμπίεση δεδομένων. Τμήμα Χρηματοοικονομικής & Ελεγκτικής ΤΕΙ Ηπείρου Παράρτημα Πρέβεζας. Δρ.
 Οι διαφάνειες έχουν βασιστεί στο βιβλίο «Εισαγωγή στην επιστήμη των υπολογιστών» του B. Forouzanκαι Firoyz Mosharraf(2 η έκδοση-2010) Εκδόσεις Κλειδάριθμος Τμήμα Χρηματοοικονομικής & Ελεγκτικής ΤΕΙ Ηπείρου
Οι διαφάνειες έχουν βασιστεί στο βιβλίο «Εισαγωγή στην επιστήμη των υπολογιστών» του B. Forouzanκαι Firoyz Mosharraf(2 η έκδοση-2010) Εκδόσεις Κλειδάριθμος Τμήμα Χρηματοοικονομικής & Ελεγκτικής ΤΕΙ Ηπείρου
Γιώργος Τζιρίτας Τµήµα Επιστήµης Υπολογιστών http://www.csd.uoc.gr/~tziritas
 Συµπίεση/κωδικοποίηση βίντεο Γιώργος Τζιρίτας Τµήµα Επιστήµης Υπολογιστών http://www.csd.uoc.gr/~tziritas Άνοιξη 2009 1 Εφαρµογή Απαίτηση Παρα- µόρφωση Μετάδοση Πρότυπο ικτυακό βίντεο 1,5 Mbps Υψηλή Internet
Συµπίεση/κωδικοποίηση βίντεο Γιώργος Τζιρίτας Τµήµα Επιστήµης Υπολογιστών http://www.csd.uoc.gr/~tziritas Άνοιξη 2009 1 Εφαρµογή Απαίτηση Παρα- µόρφωση Μετάδοση Πρότυπο ικτυακό βίντεο 1,5 Mbps Υψηλή Internet
Εισαγωγή στην επιστήμη των υπολογιστών
 Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 3ο Αναπαράσταση Αριθμών www.di.uoa.gr/~organosi 1 Δεκαδικό και Δυαδικό Δεκαδικό σύστημα 2 3 Δεκαδικό και Δυαδικό Δυαδικό Σύστημα
Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 3ο Αναπαράσταση Αριθμών www.di.uoa.gr/~organosi 1 Δεκαδικό και Δυαδικό Δεκαδικό σύστημα 2 3 Δεκαδικό και Δυαδικό Δυαδικό Σύστημα
Συστήματα Πολυμέσων. Ενότητα 3: Εισαγωγικά θέματα Συμπίεσης. Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
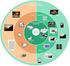 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 3: Εισαγωγικά θέματα Συμπίεσης Θρασύβουλος Γ. Τσιάτσος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 3: Εισαγωγικά θέματα Συμπίεσης Θρασύβουλος Γ. Τσιάτσος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Συμπίεση Βίντεο: Αρχές και Πρότυπα Συμπίεσης
 ΒΕΣ 04 Συμπίεση και Μετάδοση Πολυμέσων Συμπίεση Βίντεο: Αρχές και Πρότυπα Συμπίεσης Εισαγωγή Στη συμπίεση video αναζητείται μία χρυσή τομή (sweet spot) ανάμεσα στην ποιότητα και το εύρος ζώνης (bandwidth)
ΒΕΣ 04 Συμπίεση και Μετάδοση Πολυμέσων Συμπίεση Βίντεο: Αρχές και Πρότυπα Συμπίεσης Εισαγωγή Στη συμπίεση video αναζητείται μία χρυσή τομή (sweet spot) ανάμεσα στην ποιότητα και το εύρος ζώνης (bandwidth)
Συστήµατα και Αλγόριθµοι Πολυµέσων
 Συστήµατα και Αλγόριθµοι Πολυµέσων Ιωάννης Χαρ. Κατσαβουνίδης Οµιλία #12: Αρχιτεκτονική Texas Instruments OMAP (διπλού πυρήνα ARM + DSP) και Intel XScale 29 Νοεµβρίου 2005 Επανάληψη ιεθνές στάνταρ H.264/MPEG4-10/AVC
Συστήµατα και Αλγόριθµοι Πολυµέσων Ιωάννης Χαρ. Κατσαβουνίδης Οµιλία #12: Αρχιτεκτονική Texas Instruments OMAP (διπλού πυρήνα ARM + DSP) και Intel XScale 29 Νοεµβρίου 2005 Επανάληψη ιεθνές στάνταρ H.264/MPEG4-10/AVC
Θέματα Συστημάτων Πολυμέσων. Ενότητα # 8: MPEG Διδάσκων: Γεώργιος Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών
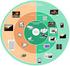 Θέματα Συστημάτων Πολυμέσων Ενότητα # 8: MPEG Διδάσκων: Γεώργιος Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Θέματα Συστημάτων Πολυμέσων Ενότητα # 8: MPEG Διδάσκων: Γεώργιος Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΑΝΑΠΤΥΞΗ ΚΑΙ ΣΧΕΔΙΑΣΗ ΛΟΓΙΣΜΙΚΟΥ Η γλώσσα προγραμματισμού C ΕΡΓΑΣΤΗΡΙΟ 3: Πίνακες, βρόχοι, συναρτήσεις 1 Ιουνίου 2017 Το σημερινό εργαστήριο
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΑΝΑΠΤΥΞΗ ΚΑΙ ΣΧΕΔΙΑΣΗ ΛΟΓΙΣΜΙΚΟΥ Η γλώσσα προγραμματισμού C ΕΡΓΑΣΤΗΡΙΟ 3: Πίνακες, βρόχοι, συναρτήσεις 1 Ιουνίου 2017 Το σημερινό εργαστήριο
Συστήµατα και Αλγόριθµοι Πολυµέσων
 Συστήµατα και Αλγόριθµοι Πολυµέσων Ιωάννης Χαρ. Κατσαβουνίδης Οµιλία #3: Αρχές Επεξεργασίας Σηµάτων Πολυµέσων 10 Οκτωβρίου 005 Επανάλειψη (1) ειγµατοληψία επανα-δειγµατοληψία Τεχνικές φίλτρων (συνέλειξη)
Συστήµατα και Αλγόριθµοι Πολυµέσων Ιωάννης Χαρ. Κατσαβουνίδης Οµιλία #3: Αρχές Επεξεργασίας Σηµάτων Πολυµέσων 10 Οκτωβρίου 005 Επανάλειψη (1) ειγµατοληψία επανα-δειγµατοληψία Τεχνικές φίλτρων (συνέλειξη)
Πολυμέσα. Συμπίεση δεδομένων Κωδικοποίηση JPEG. Δρ. Γεώργιος Π. Παυλίδης ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ
 Πολυμέσα Συμπίεση δεδομένων Δρ. Γεώργιος Π. Παυλίδης Συμπίεση Δεδομένων Περιεχόμενα Γνωστοίαλγόριθμοισυμπίεσης JPEG, Οικογένεια H.26x, H.32x Χρησιμοποίηση Εφαρμογές Εκμάθηση Σχεδίαση Διασύνδεση χρήστη
Πολυμέσα Συμπίεση δεδομένων Δρ. Γεώργιος Π. Παυλίδης Συμπίεση Δεδομένων Περιεχόμενα Γνωστοίαλγόριθμοισυμπίεσης JPEG, Οικογένεια H.26x, H.32x Χρησιμοποίηση Εφαρμογές Εκμάθηση Σχεδίαση Διασύνδεση χρήστη
Συστήματα Πολυμέσων. Ενότητα 2: Εισαγωγικά θέματα Ψηφιοποίησης. Θρασύβουλος Γ. Τσιάτσος Τμήμα Πληροφορικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Εισαγωγικά θέματα Ψηφιοποίησης Θρασύβουλος Γ. Τσιάτσος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 2: Εισαγωγικά θέματα Ψηφιοποίησης Θρασύβουλος Γ. Τσιάτσος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Εισαγωγή στην επιστήμη των υπολογιστών. Υπολογιστές και Δεδομένα Κεφάλαιο 2ο Αναπαράσταση Δεδομένων
 Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 2ο Αναπαράσταση Δεδομένων 1 2.1 Τύποι Δεδομένων Τα δεδομένα σήμερα συναντώνται σε διάφορες μορφές, στις οποίες περιλαμβάνονται αριθμοί,
Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 2ο Αναπαράσταση Δεδομένων 1 2.1 Τύποι Δεδομένων Τα δεδομένα σήμερα συναντώνται σε διάφορες μορφές, στις οποίες περιλαμβάνονται αριθμοί,
Αρχές Τηλεπικοινωνιών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Αρχές Τηλεπικοινωνιών Ενότητα #12: Δειγματοληψία, κβαντοποίηση και κωδικοποίηση Χ. ΚΑΡΑΪΣΚΟΣ Τμήμα Μηχανικών Αυτοματισμών Τ.Ε.
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Αρχές Τηλεπικοινωνιών Ενότητα #12: Δειγματοληψία, κβαντοποίηση και κωδικοποίηση Χ. ΚΑΡΑΪΣΚΟΣ Τμήμα Μηχανικών Αυτοματισμών Τ.Ε.
DIP_06 Συμπίεση εικόνας - JPEG. ΤΕΙ Κρήτης
 DIP_06 Συμπίεση εικόνας - JPEG ΤΕΙ Κρήτης Συμπίεση εικόνας Το μέγεθος μιας εικόνας είναι πολύ μεγάλο π.χ. Εικόνα μεγέθους Α4 δημιουργημένη από ένα σαρωτή με 300 pixels ανά ίντσα και με χρήση του RGB μοντέλου
DIP_06 Συμπίεση εικόνας - JPEG ΤΕΙ Κρήτης Συμπίεση εικόνας Το μέγεθος μιας εικόνας είναι πολύ μεγάλο π.χ. Εικόνα μεγέθους Α4 δημιουργημένη από ένα σαρωτή με 300 pixels ανά ίντσα και με χρήση του RGB μοντέλου
Τμήμα Μηχανικών Η/Υ και Πληροφορικής
 Τμήμα Μηχανικών Η/Υ και Πληροφορικής Εργαστήριο Επεξεργασίας Σημάτων και Τηλεπικοινωνιών Ασύρματες και Κινητές Επικοινωνίες Κωδικοποίηση καναλιού Τι θα δούμε στο μάθημα Σύντομη εισαγωγή Γραμμικοί κώδικες
Τμήμα Μηχανικών Η/Υ και Πληροφορικής Εργαστήριο Επεξεργασίας Σημάτων και Τηλεπικοινωνιών Ασύρματες και Κινητές Επικοινωνίες Κωδικοποίηση καναλιού Τι θα δούμε στο μάθημα Σύντομη εισαγωγή Γραμμικοί κώδικες
Ασκήσεις Φροντιστηρίου «Υπολογιστική Νοημοσύνη Ι» 5 o Φροντιστήριο
 Πρόβλημα ο Ασκήσεις Φροντιστηρίου 5 o Φροντιστήριο Δίνεται το παρακάτω σύνολο εκπαίδευσης: # Είσοδος Κατηγορία 0 0 0 Α 2 0 0 Α 0 Β 4 0 0 Α 5 0 Β 6 0 0 Α 7 0 Β 8 Β α) Στον παρακάτω κύβο τοποθετείστε τα
Πρόβλημα ο Ασκήσεις Φροντιστηρίου 5 o Φροντιστήριο Δίνεται το παρακάτω σύνολο εκπαίδευσης: # Είσοδος Κατηγορία 0 0 0 Α 2 0 0 Α 0 Β 4 0 0 Α 5 0 Β 6 0 0 Α 7 0 Β 8 Β α) Στον παρακάτω κύβο τοποθετείστε τα
Κεφάλαιο 2. Συστήματα Αρίθμησης και Αναπαράσταση Πληροφορίας. Περιεχόμενα. 2.1 Αριθμητικά Συστήματα. Εισαγωγή
 Κεφάλαιο. Συστήματα Αρίθμησης και Αναπαράσταση Πληροφορίας Περιεχόμενα. Αριθμητικά συστήματα. Μετατροπή αριθμών από ένα σύστημα σε άλλο.3 Πράξεις στο δυαδικό σύστημα.4 Πράξεις στο δεκαεξαδικό σύστημα.5
Κεφάλαιο. Συστήματα Αρίθμησης και Αναπαράσταση Πληροφορίας Περιεχόμενα. Αριθμητικά συστήματα. Μετατροπή αριθμών από ένα σύστημα σε άλλο.3 Πράξεις στο δυαδικό σύστημα.4 Πράξεις στο δεκαεξαδικό σύστημα.5
ΤΕΙ ΚΡΗΤΗΣ ΤΜ. ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡ/ΚΗΣ & ΠΟΛΥΜΕΣΩΝ ΔΙΔΑΣΚΩΝ: Δρ. Γ. ΓΑΡΔΙΚΗΣ. Εισαγωγή
 ΤΕΙ ΚΡΗΤΗΣ ΤΜ. ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡ/ΚΗΣ & ΠΟΛΥΜΕΣΩΝ ΔΙΔΑΣΚΩΝ: Δρ. Γ. ΓΑΡΔΙΚΗΣ 1 Εισαγωγή Το μάθημα «Αρχές Ψηφιακής Τηλεόρασης» εξετάζει τις τεχνολογίες και τους μηχανισμούς που παρεμβάλλονται για να διανεμηθεί
ΤΕΙ ΚΡΗΤΗΣ ΤΜ. ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡ/ΚΗΣ & ΠΟΛΥΜΕΣΩΝ ΔΙΔΑΣΚΩΝ: Δρ. Γ. ΓΑΡΔΙΚΗΣ 1 Εισαγωγή Το μάθημα «Αρχές Ψηφιακής Τηλεόρασης» εξετάζει τις τεχνολογίες και τους μηχανισμούς που παρεμβάλλονται για να διανεμηθεί
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 3 ο : Πολυπλεξία με διαίρεση
Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 3 ο : Πολυπλεξία με διαίρεση
ΠΛΗ21 Κεφάλαιο 1. ΠΛΗ21 Ψηφιακά Συστήματα: Τόμος Α Κεφάλαιο: 1 Εισαγωγή
 Ψηφιακά Συστήματα: Τόμος Α Κεφάλαιο: 1 Εισαγωγή Στόχοι του κεφαλαίου είναι να γνωρίσουμε: Τι είναι τα Αναλογικά κ τι τα Ψηφιακά Μεγέθη Τι είναι Σήμα, Αναλογικό Σήμα, Ψηφιακό Σήμα Τι είναι Δυαδικό Σήμα
Ψηφιακά Συστήματα: Τόμος Α Κεφάλαιο: 1 Εισαγωγή Στόχοι του κεφαλαίου είναι να γνωρίσουμε: Τι είναι τα Αναλογικά κ τι τα Ψηφιακά Μεγέθη Τι είναι Σήμα, Αναλογικό Σήμα, Ψηφιακό Σήμα Τι είναι Δυαδικό Σήμα
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ. Εργαστήριο 8 ο. Αποδιαμόρφωση PAM-PPM με προσαρμοσμένα φίλτρα
 Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Εργαστήριο 8 ο Αποδιαμόρφωση PAM-PPM με προσαρμοσμένα φίλτρα Βασική Θεωρία Σε ένα σύστημα μετάδοσης
Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Εργαστήριο 8 ο Αποδιαμόρφωση PAM-PPM με προσαρμοσμένα φίλτρα Βασική Θεωρία Σε ένα σύστημα μετάδοσης
Η κωδικοποίηση των συντελεστών DC
 Η κωδικοποίηση των συντελεστών DC Γιακάθευποπίνακαηδιαφορά, d,του DC συντελεστήτουαπότοσυντελεστή DC τουπροηγούµενουυποπίνακαοδηγούνταιστονκωδικοποιητήεντροπίας (variable length coding VLC). Στονκωδικοποιητήηδιαφοράκατατάσσεταιανάλογαµετοµέγεθόςτηςστοακόλουθοπίνακα,
Η κωδικοποίηση των συντελεστών DC Γιακάθευποπίνακαηδιαφορά, d,του DC συντελεστήτουαπότοσυντελεστή DC τουπροηγούµενουυποπίνακαοδηγούνταιστονκωδικοποιητήεντροπίας (variable length coding VLC). Στονκωδικοποιητήηδιαφοράκατατάσσεταιανάλογαµετοµέγεθόςτηςστοακόλουθοπίνακα,
Επεξεργασία Πολυµέσων. Δρ. Μαρία Κοζύρη Π.Μ.Σ. «Εφαρµοσµένη Πληροφορική» Τµήµα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Πανεπιστήµιο Θεσσαλίας
 Π.Μ.Σ. «Εφαρµοσµένη Πληροφορική» Τµήµα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Πανεπιστήµιο Θεσσαλίας Ενότητα 4: Συµπίεση Εικόνας 2 Συµπίεση Εικόνας Μείωση Πλεονασµού: Το σήµα εικόνας παρουσιάζει
Π.Μ.Σ. «Εφαρµοσµένη Πληροφορική» Τµήµα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Πανεπιστήµιο Θεσσαλίας Ενότητα 4: Συµπίεση Εικόνας 2 Συµπίεση Εικόνας Μείωση Πλεονασµού: Το σήµα εικόνας παρουσιάζει
Ασκήσεις Επεξεργασίας Εικόνας
 Ασκήσεις Επεξεργασίας Εικόνας. Εύρεση στοιχείων μιας περιοχής με ιδιότητα συγκεκριμένης γειτονιάς Άσκηση. Έστω δύο υποσύνολα πίνακα εικόνας S και S2 η οποία φαίνεται στο σχήμα παρακάτω. Για σύνολο τιμών
Ασκήσεις Επεξεργασίας Εικόνας. Εύρεση στοιχείων μιας περιοχής με ιδιότητα συγκεκριμένης γειτονιάς Άσκηση. Έστω δύο υποσύνολα πίνακα εικόνας S και S2 η οποία φαίνεται στο σχήμα παρακάτω. Για σύνολο τιμών
ΕΣΔ 200: ΔΗΜΙΟΥΡΓΙΑ ΠΕΡΙΕΧΟΜΕΝΟΥ ΙΙ. Ακαδημαϊκό Έτος 2011 2012, Χειμερινό Εξάμηνο Διδάσκων Καθ.: Νίκος Τσαπατσούλης
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΕΠΙΚΟΙΝΩΝΙΑΣ & ΣΠΟΥΔΩΝ ΔΙΑΔΙΚΤΥΟΥ ΕΣΔ 200: ΔΗΜΙΟΥΡΓΙΑ ΠΕΡΙΕΧΟΜΕΝΟΥ ΙΙ Ακαδημαϊκό Έτος 2011 2012, Χειμερινό Εξάμηνο Διδάσκων Καθ.: Νίκος Τσαπατσούλης ΕΡΩΤΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ, ΤΜΗΜΑ ΕΠΙΚΟΙΝΩΝΙΑΣ & ΣΠΟΥΔΩΝ ΔΙΑΔΙΚΤΥΟΥ ΕΣΔ 200: ΔΗΜΙΟΥΡΓΙΑ ΠΕΡΙΕΧΟΜΕΝΟΥ ΙΙ Ακαδημαϊκό Έτος 2011 2012, Χειμερινό Εξάμηνο Διδάσκων Καθ.: Νίκος Τσαπατσούλης ΕΡΩΤΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ
Τεχνολογία Πολυμέσων. Ενότητα # 10: Κωδικοποίηση ήχου Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 10: Κωδικοποίηση ήχου Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα.
Τεχνολογία Πολυμέσων Ενότητα # 10: Κωδικοποίηση ήχου Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα.
Θέματα Συστημάτων Πολυμέσων
 Θέματα Συστημάτων Πολυμέσων Ενότητα # 6: Στοιχεία Θεωρίας Πληροφορίας Διδάσκων: Γεώργιος K. Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Θέματα Συστημάτων Πολυμέσων Ενότητα # 6: Στοιχεία Θεωρίας Πληροφορίας Διδάσκων: Γεώργιος K. Πολύζος Τμήμα: Μεταπτυχιακό Πρόγραμμα Σπουδών Επιστήμη των Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Περιεχόµενα. ΕΠΛ 422: Συστήµατα Πολυµέσων. Γιατί Συµπίεση; Βιβλιογραφία
 Περιεχόµενα ΕΠΛ 422: Συστήµατα Πολυµέσων Συµπίεση εδοµένων: Εισαγωγή, Κατηγορίες Τεχνικών Συµπίεσης Βιβλιογραφία Γιατί Συµπίεση εδοµένων; Μερικά παραδείγµατα Ορισµός Συµπίεσης Συµπίεση και Πολυµεσικές
Περιεχόµενα ΕΠΛ 422: Συστήµατα Πολυµέσων Συµπίεση εδοµένων: Εισαγωγή, Κατηγορίες Τεχνικών Συµπίεσης Βιβλιογραφία Γιατί Συµπίεση εδοµένων; Μερικά παραδείγµατα Ορισµός Συµπίεσης Συµπίεση και Πολυµεσικές
Συστήματα Επικοινωνιών ΙI
 + Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Παλμοκωδική διαμόρφωση (PCM) I + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/ + Περιεχόμενα
+ Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Παλμοκωδική διαμόρφωση (PCM) I + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/ + Περιεχόμενα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΒΕΣ 04: ΣΥΜΠΙΕΣΗ ΚΑΙ ΜΕΤΑ ΟΣΗ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 2007 2008, Χειµερινό Εξάµηνο 6 Νοεµβρίου 2007 Φροντιστηριακή Άσκηση 2: (I) Εντροπία,
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΒΕΣ 04: ΣΥΜΠΙΕΣΗ ΚΑΙ ΜΕΤΑ ΟΣΗ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 2007 2008, Χειµερινό Εξάµηνο 6 Νοεµβρίου 2007 Φροντιστηριακή Άσκηση 2: (I) Εντροπία,
Ανάλυση Διατάξεων Εκπομπής σε Συστήματα Ψηφιακής Τηλεόρασης Υψηλής Ευκρίνειας
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΑΥΤΟΜΑΤΙΣΜΟΥ Ανάλυση Διατάξεων Εκπομπής σε Συστήματα Ψηφιακής Τηλεόρασης Υψηλής Ευκρίνειας Φλώρος Άγγελος ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΑΥΤΟΜΑΤΙΣΜΟΥ Ανάλυση Διατάξεων Εκπομπής σε Συστήματα Ψηφιακής Τηλεόρασης Υψηλής Ευκρίνειας Φλώρος Άγγελος ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ
Analog vs Digital. Δούρβας Ιωάννης ΙΩΑΝΝΗΣ ΔΟΥΡΒΑΣ
 Analog vs Digital Δούρβας Ιωάννης Ηλεκτρονικός Υπολογιστής ψηφιακή μηχανή Ο υπολογιστής αποτελείται από ένα σύνολο (εκατομμύρια) ηλεκτρικά κυκλώματα. Για τα ηλεκτρικά κυκλώματα υπάρχουν μόνο 2 καταστάσεις.
Analog vs Digital Δούρβας Ιωάννης Ηλεκτρονικός Υπολογιστής ψηφιακή μηχανή Ο υπολογιστής αποτελείται από ένα σύνολο (εκατομμύρια) ηλεκτρικά κυκλώματα. Για τα ηλεκτρικά κυκλώματα υπάρχουν μόνο 2 καταστάσεις.
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 4 ΠΑΛΜΟΚΩΔΙΚΗ ΔΙΑΜΟΡΦΩΣΗ - PCM (ΜΕΡΟΣ Α)
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 4 ΠΑΛΜΟΚΩΔΙΚΗ ΔΙΑΜΟΡΦΩΣΗ - PCM (ΜΕΡΟΣ Α) 3.1. ΣΚΟΠΟΣ ΑΣΚΗΣΗΣ Σκοπός της εργαστηριακής αυτής άσκησης είναι η μελέτη της παλμοκωδικής διαμόρφωσης που χρησιμοποιείται στα σύγχρονα τηλεπικοινωνιακά
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 4 ΠΑΛΜΟΚΩΔΙΚΗ ΔΙΑΜΟΡΦΩΣΗ - PCM (ΜΕΡΟΣ Α) 3.1. ΣΚΟΠΟΣ ΑΣΚΗΣΗΣ Σκοπός της εργαστηριακής αυτής άσκησης είναι η μελέτη της παλμοκωδικής διαμόρφωσης που χρησιμοποιείται στα σύγχρονα τηλεπικοινωνιακά
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ. Ενότητα 9: Πρότυπο Συμπίεσης Βίντεο MPEG
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ Ενότητα 9: Πρότυπο Συμπίεσης Βίντεο MPEG Ιωάννης Έλληνας Τμήμα Υπολογιστικών Συστημάτων Άδειες Χρήσης Το παρόν
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ Ενότητα 9: Πρότυπο Συμπίεσης Βίντεο MPEG Ιωάννης Έλληνας Τμήμα Υπολογιστικών Συστημάτων Άδειες Χρήσης Το παρόν
Κωδικοποίηση ήχου. Σύστημα ακοής MP3 / MP4 Κωδικοποίηση φωνής
 Κωδικοποίηση ήχου Σύστημα ακοής MP3 / MP4 Κωδικοποίηση φωνής T. Painter and A. Spanias, Perceptual Coding of Digital Audio, Proceedings of the IEEE, pp. 451-513, April 2000. P. Noll, MPEG digital audio
Κωδικοποίηση ήχου Σύστημα ακοής MP3 / MP4 Κωδικοποίηση φωνής T. Painter and A. Spanias, Perceptual Coding of Digital Audio, Proceedings of the IEEE, pp. 451-513, April 2000. P. Noll, MPEG digital audio
Μετάδοση Πολυμεσικών Υπηρεσιών Ψηφιακή Τηλεόραση
 Χειμερινό Εξάμηνο 2013-2014 Μετάδοση Πολυμεσικών Υπηρεσιών Ψηφιακή Τηλεόραση 5 η Παρουσίαση : Ψηφιακή Επεξεργασία Εικόνας Διδάσκων: Γιάννης Ντόκας Σύνθεση Χρωμάτων Αφαιρετική Παραγωγή Χρώματος Χρωματικά
Χειμερινό Εξάμηνο 2013-2014 Μετάδοση Πολυμεσικών Υπηρεσιών Ψηφιακή Τηλεόραση 5 η Παρουσίαση : Ψηφιακή Επεξεργασία Εικόνας Διδάσκων: Γιάννης Ντόκας Σύνθεση Χρωμάτων Αφαιρετική Παραγωγή Χρώματος Χρωματικά
Σύστημα Πλεονάσματος. Αναπαράσταση Πραγματικών Αριθμών. Αριθμητικές Πράξεις σε Αριθμούς Κινητής Υποδιαστολής
 Σύστημα Πλεονάσματος Αναπαράσταση Πραγματικών Αριθμών Αριθμητικές Πράξεις σε Αριθμούς Κινητής Υποδιαστολής Σύστημα Πλεονάσματος (Excess System) - 1 Είναι μια άλλη μια μορφή αναπαράστασης για αποθήκευση
Σύστημα Πλεονάσματος Αναπαράσταση Πραγματικών Αριθμών Αριθμητικές Πράξεις σε Αριθμούς Κινητής Υποδιαστολής Σύστημα Πλεονάσματος (Excess System) - 1 Είναι μια άλλη μια μορφή αναπαράστασης για αποθήκευση
Μετάδοση Πολυμεσικών Υπηρεσιών Ψηφιακή Τηλεόραση
 Χειμερινό Εξάμηνο 2013-2014 Μετάδοση Πολυμεσικών Υπηρεσιών Ψηφιακή Τηλεόραση 3 η Παρουσίαση : Συμπίεση Διδάσκων: Γιάννης Ντόκας Εισαγωγή 2 Συμπίεση πληροφορίας πολυμέσων 3 Γιατί χρειάζεται συμπίεση? 4
Χειμερινό Εξάμηνο 2013-2014 Μετάδοση Πολυμεσικών Υπηρεσιών Ψηφιακή Τηλεόραση 3 η Παρουσίαση : Συμπίεση Διδάσκων: Γιάννης Ντόκας Εισαγωγή 2 Συμπίεση πληροφορίας πολυμέσων 3 Γιατί χρειάζεται συμπίεση? 4
Πολυμέσα πάνω από κινητά δίκτυα
 Πολυμέσα πάνω από κινητά δίκτυα Γιώργος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών http://www.csd.uoc.gr/~tziritas Άνοιξη 2016 1 Πολυμέσα σε ασύρματα δίκτυα Οι πολυμεσικές επικοινωνίες μέσω φορητών συσκευών
Πολυμέσα πάνω από κινητά δίκτυα Γιώργος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών http://www.csd.uoc.gr/~tziritas Άνοιξη 2016 1 Πολυμέσα σε ασύρματα δίκτυα Οι πολυμεσικές επικοινωνίες μέσω φορητών συσκευών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ. Ενότητα 6: Κωδικοποίηση & Συμπίεση Εικόνας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ Ενότητα 6: Κωδικοποίηση & Συμπίεση Εικόνας Ιωάννης Έλληνας Τμήμα Υπολογιστικών Συστημάτων Άδειες Χρήσης Το
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ Ενότητα 6: Κωδικοποίηση & Συμπίεση Εικόνας Ιωάννης Έλληνας Τμήμα Υπολογιστικών Συστημάτων Άδειες Χρήσης Το
Κωδικοποίηση βίντεο (MPEG)
 Κωδικοποίηση βίντεο (MPEG) Εισαγωγή στο MPEG-2 Κωδικοποίηση βίντεο Κωδικοποίηση ήχου Ροή δεδοµένων Εισαγωγή στο MPEG-4 οµή σκηνών Κωδικοποίηση ήχου και βίντεο Τεχνολογία Πολυµέσων 11-1 Εισαγωγή στο MPEG-2
Κωδικοποίηση βίντεο (MPEG) Εισαγωγή στο MPEG-2 Κωδικοποίηση βίντεο Κωδικοποίηση ήχου Ροή δεδοµένων Εισαγωγή στο MPEG-4 οµή σκηνών Κωδικοποίηση ήχου και βίντεο Τεχνολογία Πολυµέσων 11-1 Εισαγωγή στο MPEG-2
Ιατρική Πληροφορική. Δρ. Π. ΑΣΒΕΣΤΑΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΒΙΟΪΑΤΡΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ Τ.Ε.
 Ιατρική Πληροφορική Δρ. Π. ΑΣΒΕΣΤΑΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΒΙΟΪΑΤΡΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ Τ.Ε. Οι διάφορες τεχνικές απεικόνισης (imaging modalities) της ανθρώπινης ανατομίας περιγράφονται κατά DICOM ως συντομογραφία
Ιατρική Πληροφορική Δρ. Π. ΑΣΒΕΣΤΑΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΒΙΟΪΑΤΡΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ Τ.Ε. Οι διάφορες τεχνικές απεικόνισης (imaging modalities) της ανθρώπινης ανατομίας περιγράφονται κατά DICOM ως συντομογραφία
Μάθημα Εισαγωγή στις Τηλεπικοινωνίες Κωδικοποίηση πηγής- καναλιού Μάθημα 9o
 Μάθημα Εισαγωγή στις Τηλεπικοινωνίες Κωδικοποίηση πηγής- καναλιού Μάθημα 9o ΕΘΝΙΚΟ & ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τομέας Επικοινωνιών και Επεξεργασίας Σήματος Τμήμα Πληροφορικής & Τηλεπικοινωνιών
Μάθημα Εισαγωγή στις Τηλεπικοινωνίες Κωδικοποίηση πηγής- καναλιού Μάθημα 9o ΕΘΝΙΚΟ & ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τομέας Επικοινωνιών και Επεξεργασίας Σήματος Τμήμα Πληροφορικής & Τηλεπικοινωνιών
Μοντέλο Επικοινωνίας Δεδομένων. Επικοινωνίες Δεδομένων Μάθημα 6 ο
 Μοντέλο Επικοινωνίας Δεδομένων Επικοινωνίες Δεδομένων Μάθημα 6 ο Εισαγωγή Με τη βοήθεια επικοινωνιακού σήματος, κάθε μορφή πληροφορίας (κείμενο, μορφή, εικόνα) είναι δυνατόν να μεταδοθεί σε απόσταση. Ανάλογα
Μοντέλο Επικοινωνίας Δεδομένων Επικοινωνίες Δεδομένων Μάθημα 6 ο Εισαγωγή Με τη βοήθεια επικοινωνιακού σήματος, κάθε μορφή πληροφορίας (κείμενο, μορφή, εικόνα) είναι δυνατόν να μεταδοθεί σε απόσταση. Ανάλογα
2 Η ΠΡΟΟΔΟΣ. Ενδεικτικές λύσεις κάποιων προβλημάτων. Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση
 2 Η ΠΡΟΟΔΟΣ Ενδεικτικές λύσεις κάποιων προβλημάτων Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση Ένας τροχός εκκινεί από την ηρεμία και επιταχύνει με γωνιακή ταχύτητα που δίνεται από την,
2 Η ΠΡΟΟΔΟΣ Ενδεικτικές λύσεις κάποιων προβλημάτων Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση Ένας τροχός εκκινεί από την ηρεμία και επιταχύνει με γωνιακή ταχύτητα που δίνεται από την,
Τεχνολογία Πολυμέσων. Ενότητα # 13: Κωδικοποίηση βίντεο: MPEG Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 13: Κωδικοποίηση βίντεο: MPEG Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου
Τεχνολογία Πολυμέσων Ενότητα # 13: Κωδικοποίηση βίντεο: MPEG Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου
E[ (x- ) ]= trace[(x-x)(x- ) ]
![E[ (x- ) ]= trace[(x-x)(x- ) ] E[ (x- ) ]= trace[(x-x)(x- ) ]](/thumbs/55/36021260.jpg) 1 ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Σε αυτό το μέρος της πτυχιακής θα ασχοληθούμε λεπτομερώς με το φίλτρο kalman και θα δούμε μια καινούρια έκδοση του φίλτρου πάνω στην εφαρμογή της γραμμικής εκτίμησης διακριτού
1 ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Σε αυτό το μέρος της πτυχιακής θα ασχοληθούμε λεπτομερώς με το φίλτρο kalman και θα δούμε μια καινούρια έκδοση του φίλτρου πάνω στην εφαρμογή της γραμμικής εκτίμησης διακριτού
Ένα αναλογικό σήμα περιέχει άπειρες πιθανές τιμές. Για παράδειγμα ένας απλός ήχος αν τον βλέπαμε σε ένα παλμογράφο θα έμοιαζε με το παρακάτω:
 Σημειώσεις Δικτύων Αναλογικά και ψηφιακά σήματα Ένα αναλογικό σήμα περιέχει άπειρες πιθανές τιμές. Για παράδειγμα ένας απλός ήχος αν τον βλέπαμε σε ένα παλμογράφο θα έμοιαζε με το παρακάτω: Χαρακτηριστικά
Σημειώσεις Δικτύων Αναλογικά και ψηφιακά σήματα Ένα αναλογικό σήμα περιέχει άπειρες πιθανές τιμές. Για παράδειγμα ένας απλός ήχος αν τον βλέπαμε σε ένα παλμογράφο θα έμοιαζε με το παρακάτω: Χαρακτηριστικά
Κωδικοποίηση και αποκωδικοποίηση µε χρήση του H.264/MPEG-4 για βίντεο µε µία ή περισσότερες λήψεις
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Κωδικοποίηση και αποκωδικοποίηση µε χρήση του H.264/MPEG-4 για βίντεο µε µία
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Κωδικοποίηση και αποκωδικοποίηση µε χρήση του H.264/MPEG-4 για βίντεο µε µία
Συµπίεση Δεδοµένων: Συµπίεση Ψηφιακού Βίντεο
 Συµπίεση Δεδοµένων: Συµπίεση Ψηφιακού Βίντεο Αλέξανδρος Ελευθεριάδης Αναπ. Καθηγητής & Marie Curie Chair Τµήµα Πληροφορικής και Τηλεπικοινωνιών Εθνικό και Καποδιστριακό Πανεπιστήµιο Αθηνών eleft@di.uoa.gr,
Συµπίεση Δεδοµένων: Συµπίεση Ψηφιακού Βίντεο Αλέξανδρος Ελευθεριάδης Αναπ. Καθηγητής & Marie Curie Chair Τµήµα Πληροφορικής και Τηλεπικοινωνιών Εθνικό και Καποδιστριακό Πανεπιστήµιο Αθηνών eleft@di.uoa.gr,
Εισαγωγή στην επιστήμη των υπολογιστών. Υπολογιστές και Δεδομένα Κεφάλαιο 2ο Αναπαράσταση Δεδομένων
 Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 2ο Αναπαράσταση Δεδομένων 1 Εισαγωγή Ο Υπολογιστής είναι μια μηχανή επεξεργασίας δεδομένων Πριν ασχοληθούμε με την επεξεργασία τους
Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 2ο Αναπαράσταση Δεδομένων 1 Εισαγωγή Ο Υπολογιστής είναι μια μηχανή επεξεργασίας δεδομένων Πριν ασχοληθούμε με την επεξεργασία τους
Προγραμματισμός Υπολογιστών
 Προγραμματισμός Υπολογιστών Αναπαράσταση Πληροφορίας Κ. Βασιλάκης, ΣΤΕΦ, ΤΕΙ Κρήτης Δεδομένα και πληροφορία Δεδομένα είναι ένα σύνολο διακριτών στοιχείων σχετικά με ένα συμβάν ή μια διαδικασία χωρίς κάποια
Προγραμματισμός Υπολογιστών Αναπαράσταση Πληροφορίας Κ. Βασιλάκης, ΣΤΕΦ, ΤΕΙ Κρήτης Δεδομένα και πληροφορία Δεδομένα είναι ένα σύνολο διακριτών στοιχείων σχετικά με ένα συμβάν ή μια διαδικασία χωρίς κάποια
Συστήματα Επικοινωνιών ΙI
 + Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Διαφορική Παλμοκωδική Διαμόρφωση + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/ +
+ Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI Διαφορική Παλμοκωδική Διαμόρφωση + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/ +
Σύστημα Πλεονάσματος και Αναπαράσταση Αριθμών Κινητής Υποδιαστολής
 Σύστημα Πλεονάσματος και Αναπαράσταση Αριθμών Κινητής Υποδιαστολής Σύστημα Πλεονάσματος (Excess System) - 1 Είναι μια άλλη μια μορφή αναπαράστασης για αποθήκευση θετικών και αρνητικών ακεραίων σε έναν
Σύστημα Πλεονάσματος και Αναπαράσταση Αριθμών Κινητής Υποδιαστολής Σύστημα Πλεονάσματος (Excess System) - 1 Είναι μια άλλη μια μορφή αναπαράστασης για αποθήκευση θετικών και αρνητικών ακεραίων σε έναν
