The Early Universe Big Bang Cosmology: Einstein Universe Friedmann-Lemaître Universe Einstein-deSitter Universe

CHAPTER (2) Electric Charges, Electric Charge Densities and Electric Field Intensity

CHAPTE () Electric Chrges, Electric Chrge Densities nd Electric Field Intensity Chrge Configurtion ) Point Chrge: The concept of the point chrge is used when the dimensions of n electric chrge distriution

wave energy Superposition of linear plane progressive waves Marine Hydrodynamics Lecture Oblique Plane Waves:

3.0 Marine Hydrodynamics, Fall 004 Lecture 0 Copyriht c 004 MIT - Department of Ocean Enineerin, All rihts reserved. 3.0 - Marine Hydrodynamics Lecture 0 Free-surface waves: wave enery linear superposition,

Exercises 10. Find a fundamental matrix of the given system of equations. Also find the fundamental matrix Φ(t) satisfying Φ(0) = I. 1.

Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given

Matrices and Determinants

Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z

D-Wave D-Wave Systems Inc.

D-Wave D-Wave sems Inc. Anaol Yu. mirnov D-Wave sems Inc. Vancouver Briish Columbia HE QUANUM COMPUING COMPANY M Decoherence and Noise Conrol in rongl Driven uperconducing Quanum Bis Collaboraion: M. Grajcar

6.4 Superposition of Linear Plane Progressive Waves

.0 - Marine Hydrodynamics, Spring 005 Lecture.0 - Marine Hydrodynamics Lecture 6.4 Superposition of Linear Plane Progressive Waves. Oblique Plane Waves z v k k k z v k = ( k, k z ) θ (Looking up the y-ais

Cosmological Space-Times

Cosmological Space-Times Lecture notes compiled by Geoff Bicknell based primarily on: Sean Carroll: An Introduction to General Relativity plus additional material 1 Metric of special relativity ds 2 =

4.4 Superposition of Linear Plane Progressive Waves

.0 Marine Hydrodynamics, Fall 08 Lecture 6 Copyright c 08 MIT - Department of Mechanical Engineering, All rights reserved..0 - Marine Hydrodynamics Lecture 6 4.4 Superposition of Linear Plane Progressive

Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit

Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal

BandPass (4A) Young Won Lim 1/11/14

BandPass (4A) Copyright (c) 22 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2 or any later version

Homework 8 Model Solution Section

MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx

General 2 2 PT -Symmetric Matrices and Jordan Blocks 1

General 2 2 PT -Symmetric Matrices and Jordan Blocks 1 Qing-hai Wang National University of Singapore Quantum Physics with Non-Hermitian Operators Max-Planck-Institut für Physik komplexer Systeme Dresden,

Practice Exam 2. Conceptual Questions. 1. State a Basic identity and then verify it. (a) Identity: Solution: One identity is csc(θ) = 1

Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the

16. 17. r t te 2t i t 1. 18 19 Find the derivative of the vector function. 19. r t e t cos t i e t sin t j ln t k. 31 33 Evaluate the integral.

SECTION.7 VECTOR FUNCTIONS AND SPACE CURVES.7 VECTOR FUNCTIONS AND SPACE CURVES A Click here for answers. S Click here for soluions. Copyrigh Cengage Learning. All righs reserved.. Find he domain of he

Appendix. The solution begins with Eq. (2.15) from the text, which we repeat here for 1, (A.1)

Aenix Aenix A: The equaion o he sock rice. The soluion egins wih Eq..5 rom he ex, which we reea here or convenience as Eq.A.: [ [ E E X, A. c α where X u ε, α γ, an c α y AR. Take execaions o Eq. A. as

Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013

Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering

Fourier Transform. Fourier Transform

ECE 307 Z. Aliyziioglu Eleril & Compuer Engineering Dep. Cl Poly Pomon The Fourier rnsform (FT is he exension of he Fourier series o nonperiodi signls. The Fourier rnsform of signl exis if sisfies he following

Potential Dividers. 46 minutes. 46 marks. Page 1 of 11

Potential Dividers 46 minutes 46 marks Page 1 of 11 Q1. In the circuit shown in the figure below, the battery, of negligible internal resistance, has an emf of 30 V. The pd across the lamp is 6.0 V and

Space-Time Symmetries

Chapter Space-Time Symmetries In classical fiel theory any continuous symmetry of the action generates a conserve current by Noether's proceure. If the Lagrangian is not invariant but only shifts by a

Every set of first-order formulas is equivalent to an independent set

Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent

1 2 3 4 5 6 7 8 9 10 2 12,999,976 km 9,136,765 km 1,276,765 km 499,892 km 245,066 km 112,907 km 36,765 km 24,159 km 7899 km 2408 km 76 km 12 14 16 3 6 11 1 12 7 1 2 5 4 3 9 10 8 18 20 21 22 23 24 25 26

2 3 4 5 6 7 8 9 10 12,999,976 km 9,136,765 km 1,276,765 km 499,892 km 245,066 km 112,907 km 36,765 km 24,159 km 7899 km 2408 km 76 km 12 14 16 9 10 1 8 12 7 3 1 6 2 5 4 3 11 18 20 21 22 23 24 26 28 30

Congruence Classes of Invertible Matrices of Order 3 over F 2

International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and

( ) ( t) ( 0) ( ) dw w. = = β. Then the solution of (1.1) is easily found to. wt = t+ t. We generalize this to the following nonlinear differential

Periodic oluion of van der Pol differenial equaion. by A. Arimoo Deparmen of Mahemaic Muahi Iniue of Technology Tokyo Japan in Seminar a Kiami Iniue of Technology January 8 9. Inroducion Le u conider a

PRODUCT FICHE. A Supplier name Morris MKV 64325

PRODUCT FICHE The information in the product data sheet is given in accordance with the Commission delegated Regulation (EU) No 65/2014 supplementing Directive of the European Parliament and of the Council

Tutorial problem set 6,

GENERAL RELATIVITY Tutorial problem set 6, 01.11.2013. SOLUTIONS PROBLEM 1 Killing vectors. a Show that the commutator of two Killing vectors is a Killing vector. Show that a linear combination with constant

ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Οικονομία. Διάλεξη 10η: Basics of Game Theory part 2 Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών

ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 0η: Basics of Game Theory part 2 Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Best Response Curves Used to solve for equilibria in games

Reminders: linear functions

Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U

Geodesic Equations for the Wormhole Metric

Geodesic Equations for the Wormhole Metric Dr R Herman Physics & Physical Oceanography, UNCW February 14, 2018 The Wormhole Metric Morris and Thorne wormhole metric: [M S Morris, K S Thorne, Wormholes

Anti-aliasing Prefilter (6B) Young Won Lim 6/8/12

ni-aliasing Prefiler (6B) Copyrigh (c) Young W. Lim. Permission is graned o copy, disribue and/or modify his documen under he erms of he GNU Free Documenaion License, Version. or any laer version published

ibemo Kazakhstan Republic of Kazakhstan, West Kazakhstan Oblast, Aksai, Pramzone, BKKS office complex Phone: ; Fax:

Laplace s Equation in Spherical Polar Coördinates

Laplace s Equation in Spheical Pola Coödinates C. W. David Dated: Januay 3, 001 We stat with the pimitive definitions I. x = sin θ cos φ y = sin θ sin φ z = cos θ thei inveses = x y z θ = cos 1 z = z cos1

Review Exercises for Chapter 7

8 Chapter 7 Integration Techniques, L Hôpital s Rule, and Improper Integrals 8. For n, I d b For n >, I n n u n, du n n d, dv (a) d b 6 b 6 (b) (c) n d 5 d b n n b n n n d, v d 6 5 5 6 d 5 5 b d 6. b 6

Calculus and Differential Equations page 1 of 17 CALCULUS and DIFFERENTIAL EQUATIONS

alculus and Diffrnial Equaions pag of 7 ALULUS and DIFFERENTIAL EQUATIONS Th following 55 qusions concrn calculus and diffrnial quaions. In his vrsion of h am, h firs choic is always h corrc on. In h acual

the total number of electrons passing through the lamp.

1. A 12 V 36 W lamp is lit to normal brightness using a 12 V car battery of negligible internal resistance. The lamp is switched on for one hour (3600 s). For the time of 1 hour, calculate (i) the energy

Example Sheet 3 Solutions

Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note

Strain gauge and rosettes

Strain gauge and rosettes Introduction A strain gauge is a device which is used to measure strain (deformation) on an object subjected to forces. Strain can be measured using various types of devices classified

Για να μιλήσουμε για περισσότερα από ένα πρόσωπα, ζώα ή πράγματα, συνήθως προσθέτουμε το s στο τέλος μίας λέξης. four sisters

Lesson 1 Two dogs nd one ll! 1 Red. Plurls Γι ν μιλήσουμε γι περισσότερ πό έν πρόσωπ, ζώ ή πράγμτ, συνήθως προσθέτουμε το s στο τέλος μίς λέξης. four sisters one sister two insects one insect Circle. 1

Hartree-Fock Theory. Solving electronic structure problem on computers

Hartree-Foc Theory Solving electronic structure problem on computers Hartree product of non-interacting electrons mean field molecular orbitals expectations values one and two electron operators Pauli

derivation of the Laplacian from rectangular to spherical coordinates

derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used

Lanczos and biorthogonalization methods for eigenvalues and eigenvectors of matrices

Lanzos and iorthogonalization methods for eigenvalues and eigenvetors of matries rolem formulation Many prolems are redued to solving the following system: x x where is an unknown numer А a matrix n n

Mean bond enthalpy Standard enthalpy of formation Bond N H N N N N H O O O

Q1. (a) Explain the meaning of the terms mean bond enthalpy and standard enthalpy of formation. Mean bond enthalpy... Standard enthalpy of formation... (5) (b) Some mean bond enthalpies are given below.

D Alembert s Solution to the Wave Equation

D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique

Μονοβάθμια Συστήματα: Εξίσωση Κίνησης, Διατύπωση του Προβλήματος και Μέθοδοι Επίλυσης. Απόστολος Σ. Παπαγεωργίου

Μονοβάθμια Συστήματα: Εξίσωση Κίνησης, Διατύπωση του Προβλήματος και Μέθοδοι Επίλυσης VISCOUSLY DAMPED 1-DOF SYSTEM Μονοβάθμια Συστήματα με Ιξώδη Απόσβεση Equation of Motion (Εξίσωση Κίνησης): Complete

Written Examination. Antennas and Propagation (AA ) April 26, 2017.

Written Examination Antennas and Propagation (AA. 6-7) April 6, 7. Problem ( points) Let us consider a wire antenna as in Fig. characterized by a z-oriented linear filamentary current I(z) = I cos(kz)ẑ

Parametrized Surfaces

Parametrized Surfaces Recall from our unit on vector-valued functions at the beginning of the semester that an R 3 -valued function c(t) in one parameter is a mapping of the form c : I R 3 where I is some

ECE Spring Prof. David R. Jackson ECE Dept. Notes 2

ECE 634 Spring 6 Prof. David R. Jackson ECE Dept. Notes Fields in a Source-Free Region Example: Radiation from an aperture y PEC E t x Aperture Assume the following choice of vector potentials: A F = =

1. Consider the three dimensional space with the line element. Determine the surface area of the sphere that corresponds to r = R.

Physics 43: Relativity Homework Assignment 4 Due 26 March 27 1. Consider the three dimensional space with the line element 2 = 1 1 r/r dr2 + r 2 (dθ 2 + sin 2 θ dφ 2 ) Determine the surface area of the

(1) Describe the process by which mercury atoms become excited in a fluorescent tube (3)

Q1. (a) A fluorescent tube is filled with mercury vapour at low pressure. In order to emit electromagnetic radiation the mercury atoms must first be excited. (i) What is meant by an excited atom? (1) (ii)

If ABC is any oblique triangle with sides a, b, and c, the following equations are valid. 2bc. (a) a 2 b 2 c 2 2bc cos A or cos A b2 c 2 a 2.

etion 6. Lw of osines 59 etion 6. Lw of osines If is ny oblique tringle with sides, b, nd, the following equtions re vlid. () b b os or os b b (b) b os or os b () b b os or os b b You should be ble to

Το άτομο του Υδρογόνου

Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες

ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007

Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο

HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:

HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying

.. ntsets ofa.. d ffeom.. orp ism.. na s.. m ooth.. man iod period I n open square. n t s e t s ofa \quad d ffeom \quad orp ism \quad na s \quad m o

G G - - -- - W - - - R S - q k RS ˆ W q q k M G W R S L [ RS - q k M S 4 R q k S [ RS [ M L ˆ L [M O S 4] L ˆ ˆ L ˆ [ M ˆ S 4 ] ˆ - O - ˆ q k ˆ RS q k q k M - j [ RS ] [ M - j - L ˆ ˆ ˆ O ˆ [ RS ] [ M

Math221: HW# 1 solutions

Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin

DiracDelta. Notations. Primary definition. Specific values. General characteristics. Traditional name. Traditional notation

DiracDelta Notations Traditional name Dirac delta function Traditional notation x Mathematica StandardForm notation DiracDeltax Primary definition 4.03.02.000.0 x Π lim ε ; x ε0 x 2 2 ε Specific values

Stresses in a Plane. Mohr s Circle. Cross Section thru Body. MET 210W Mohr s Circle 1. Some parts experience normal stresses in

ME 10W E. Evans Stresses in a Plane Some parts eperience normal stresses in two directions. hese tpes of problems are called Plane Stress or Biaial Stress Cross Section thru Bod z angent and normal to

The Euler Equations! λ 1. λ 2. λ 3. ρ ρu. E = e + u 2 /2. E + p ρ. = de /dt. = dh / dt; h = h( T ); c p. / c v. ; γ = c p. p = ( γ 1)ρe. c v.

hp://www.nd.ed/~gryggva/cfd-corse/ The Eler Eqaions The Eler Eqaions The Eler eqaions for D flow: + + p = x E E + p where Define E = e + / H = h + /; h = e + p/ Gréar Tryggvason Spring 3 Ideal Gas: p =

Areas and Lengths in Polar Coordinates

Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the

THE PUBLISHING HOUSE PROCEEDINGS OF THE ROMANIAN ACADEMY, Series A, OF THE ROMANIAN ACADEMY Volume 15, Number 2/2014, pp

THE PUBLISHING HOUSE PROCEEDINGS OF THE ROMANIAN ACADEMY, Series A, OF THE ROMANIAN ACADEMY Volume 5, Number /0, pp. 07 DOUBLY STOCHASTIC MODELS WITH ASYMMETRIC GARCH ERRORS Muhmmd SHERAZ Uniersiy o Buchres,

L F'(-c, 0) F(c, 0) M' D' x + d = 0 x - d = 0

Hperol Reference: Advnced Level Pure Mheics S.L. Green (4 h Ediion) Chper VII p.9 - p.0 Edied Mr. Frncis Hung Ls upded: Deceer 7, 0 M D N' N P(, ) L F'(-c, 0) F(c, 0) A'(-,0) B' B A(,0) L' M' D' + d 0

Differential equations

Differential equations Differential equations: An equation inoling one dependent ariable and its deriaties w. r. t one or more independent ariables is called a differential equation. Order of differential

( ) ( ) ( ) Fourier series. ; m is an integer. r(t) is periodic (T>0), r(t+t) = r(t), t Fundamental period T 0 = smallest T. Fundamental frequency ω

Fourier series e jm when m d when m ; m is an ineger. jm jm jm jm e d e e e jm jm jm jm r( is periodi (>, r(+ r(, Fundamenal period smalles Fundamenal frequeny r ( + r ( is periodi hen M M e j M, e j,

Second Order Partial Differential Equations

Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y

( )( ) La Salle College Form Six Mock Examination 2013 Mathematics Compulsory Part Paper 2 Solution

L Slle ollege Form Si Mock Emintion 0 Mthemtics ompulsor Prt Pper Solution 6 D 6 D 6 6 D D 7 D 7 7 7 8 8 8 8 D 9 9 D 9 D 9 D 5 0 5 0 5 0 5 0 D 5. = + + = + = = = + = =. D The selling price = $ ( 5 + 00)

Note: Please use the actual date you accessed this material in your citation.

MIT OpenCourseWare http://ocw.mit.edu 6.03/ESD.03J Electromagnetics and Applications, Fall 005 Please use the following citation format: Markus Zahn, 6.03/ESD.03J Electromagnetics and Applications, Fall

S :Silicon Sealed blank:no Silicon Seal 2.54/0.100" 5.05/0.199" Code 3.2/0.126" 5.7/0.224" 3.2/0.126" 7.4/0.291"

Specifications Acceptable Plug: φ2~φ0.30/0.021"~0.011" Dielectric Strength: AC700Vrms 1min Insulation Resistance: 1000MΩ Contact Resistance: 15mΩmax Current Rating: 1.0 A Operating Temp.: -55 ~+150 (In

6. MAXIMUM LIKELIHOOD ESTIMATION

6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ

ω = radians per sec, t = 3 sec

Secion. Linear and Angular Speed 7. From exercise, =. A= r A = ( 00 ) (. ) = 7,00 in 7. Since 7 is in quadran IV, he reference 7 8 7 angle is = =. In quadran IV, he cosine is posiive. Thus, 7 cos = cos

ΚΕΦΑΛΑΙΟ 1 Ο 1.1. ΕΛΑΣΤΙΚΟ ΣΤΕΡΕΟ

ΚΕΦΑΛΑΙΟ Ο.. ΕΛΑΣΤΙΚΟ ΣΤΕΡΕΟ Ο Robert Hooke έγρψε το 678, "he power of any spring is in the same proportion with the tension thereof". Αυτή η δήλωση είνι η βάση του πρώτου ρεολογικού νόµου γι ιδνικά ελστικά

ˆ ˆ Œ Ÿ Š Œ ƒˆ Šˆ ˆ Ÿ ˆ ˆ Š ˆˆ ƒ ˆ ˆˆ

Ó³ Ÿ. 2015.. 12, º 2(193).. 281Ä298 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ. ˆŸ ˆ ˆ Œ Ÿ Š Œ ƒˆ Šˆ ˆ Ÿ ˆ ˆ Š ˆˆ ƒ ˆ ˆˆ.. Ê 1 Œμ ±μ ± μ Ê É Ò Ê É É ³. Œ.. μ³μ μ μ, Œμ ± Í Œ Ì ²ÖÉ É ±μ É μ É Í ( ƒ) μ μ²ö É μ μ ÉÓ É ²Ó- ÊÕ ² ±Í

Š Š Œ Š Œ ƒˆ. Œ. ϵ,.. ÊÏ,.. µ ±Ê

ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2003.. 34.. 7 Š 524.8+[530.12:531.51] Š Š Œ Š Œ ƒˆ. Œ. ϵ,.. ÊÏ,.. µ ±Ê Ñ Ò É ÉÊÉ Ö ÒÌ ² µ, Ê ˆ 138 Š Šˆ Š Š ˆ ˆ Š Œ ƒˆˆ 140 Š Œ ƒˆÿ œ 141 Š Ÿ Š Œ ƒˆÿ 143 ˆ Ÿ Š Œ ƒˆÿ ˆ Œ 144 ˆŸ Ä ˆ Œ

CE 530 Molecular Simulation

C 53 olecular Siulation Lecture Histogra Reweighting ethods David. Kofke Departent of Cheical ngineering SUNY uffalo kofke@eng.buffalo.edu Histogra Reweighting ethod to cobine results taken at different

CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS

CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =

On the Einstein-Euler Equations

On the Einstein-Euler Equations Tetu Makino (Yamaguchi U, Japan) November 10, 2015 / Int l Workshop on the Multi-Phase Flow at Waseda U 1 1 Introduction. Einstein-Euler equations: (A. Einstein, Nov. 25,

The Simply Typed Lambda Calculus

Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and

Rektangulär fläns, Rectangular fin

Rekangulär fläns, Recangular fin. Z d f d αc d λ ( f ) (3 3) m αc λ α Z λz α λ Randvillkor, Boundary condiions: : d : λ ( f ) d unn och lång fläns, long and hin fin d d f Rekangulär fläns, recangular fin

5.4 The Poisson Distribution.

The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable

Chapter 6: Systems of Linear Differential. be continuous functions on the interval

Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations

Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in

Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that

3 Frequency Domain Representation of Continuous Signals and Systems

3 Frequency Domain Represenaion of Coninuous Signals and Sysems 3. Fourier Series Represenaion of Periodic Signals............. 2 3.. Exponenial Fourier Series.................... 2 3..2 Discree Fourier

( ) ρ ρ + + = + d dt. ME 309 Formula Sheet. dp g dz = ρ. = f +ΣΚ and HS. +α + z = +α + z. δ =δ = δ =θ= τ =ρ =ρ. Page 1 of 7. Basic Equations.

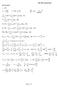Basic Eqaions ME 9 Fomla Shee R µ F F A A ηv V el η η A Vssem ( ) V el A F F V A ( ) S B XYZ XYZ el g F F a V V A S B / XYZ el M M A V ( ) S B el ( ) Q W ev e A hee V e g ino on el V consan (o invisci

(b) flat (continuous) fins on an array of tubes

(a) Individually finned ues () fla (coninuous) fins on an array of ues Eample Fins Fins on Segosaurus 3 Rekangulär fläns, Recangular fin. Z d f 4 Rekangulär fläns, Recangular fin. Z d f d αc d λ ( f )

Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------

Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin

Introduction: Big-Bang Cosmology

Introduction: Big-Bng Cosology Bsic Assuptions Principle of Reltivity: The lws of nture re the se everywhere nd t ll ties The Cosologicl principle: The universe is hoogeneous nd isotropic Spce tie is siply

Section 8.3 Trigonometric Equations

99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.

Assalamu `alaikum wr. wb.

LUMP SUM Assalamu `alaikum wr. wb. LUMP SUM Wassalamu alaikum wr. wb. Assalamu `alaikum wr. wb. LUMP SUM Wassalamu alaikum wr. wb. LUMP SUM Lump sum lump sum lump sum. lump sum fixed price lump sum lump

Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1

Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test

Approximation of distance between locations on earth given by latitude and longitude

Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth

Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3

Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all

ΠΕΡΙΕΧΟΜΕΝΑ ΓΕΝΙΚΗ ΘΕΩΡΙΑ ΣΧΕΤΙΚΟΤΗΤΑΣ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΣΤΟ ΚΕΝΟ ΠΑΡΑΓΩΓΗ ΒΑΡΥΤΙΚΩΝ ΚΥΜΑΤΩΝ ΑΠΟ ΠΗΓΕΣ ΑΝΙΧΝΕΥΣΗ ΒΑΡΥΤΙΚΩΝ ΚΥΜΑΤΩΝ

ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΤΖΩΡΤΖΗΣ ΔΗΜΗΤΡΗΣ Επιβλέπων καθηγητής:αναγνωστοπουλοσ Κ. ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ-ΣΕΜΦΕ 26 Σεπτεμβρίου 2016 ΠΕΡΙΕΧΟΜΕΝΑ ΓΕΝΙΚΗ ΘΕΩΡΙΑ ΣΧΕΤΙΚΟΤΗΤΑΣ ΒΑΡΥΤΙΚΑ ΚΥΜΑΤΑ ΣΤΟ ΚΕΝΟ ΠΑΡΑΓΩΓΗ ΒΑΡΥΤΙΚΩΝ

www.hepo.gr Αγαπητοί συνεργάτες,

/ΝΣΗ ΑΝΑΠΤΥΞΗΣ ΕΡΓΑΣΙΩΝ Αρµόδια: Ε. Παναγιωταροπούλου Τηλ.: 210 9982342 Fax : 210 9982402 e-mail: panagiotaropoulou@hepo.gr Url: ΚΥΠΡΟΣ - ΛΕΥΚΩΣΙΑ (13-15/12/2009) Αγαπητοί συνεργάτες, Εκατοντάδες ελληνικές

Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1

Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a

Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.

Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action

Chapter 6: Systems of Linear Differential. be continuous functions on the interval

Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations

Dark matter from Dark Energy-Baryonic Matter Couplings

Dark matter from Dark Energy-Baryonic Matter Coulings Alejandro Avilés 1,2 1 Instituto de Ciencias Nucleares, UNAM, México 2 Instituto Nacional de Investigaciones Nucleares (ININ) México January 10, 2010

Η αλληλεπίδραση ανάμεσα στην καθημερινή γλώσσα και την επιστημονική ορολογία: παράδειγμα από το πεδίο της Κοσμολογίας

Η αλληλεπίδραση ανάμεσα στην καθημερινή γλώσσα και την επιστημονική ορολογία: παράδειγμα από το πεδίο της Κοσμολογίας ΠΕΡΙΛΗΨΗ Αριστείδης Κοσιονίδης Η κατανόηση των εννοιών ενός επιστημονικού πεδίου απαιτεί

Lecture 12 Modulation and Sampling

EE 2 spring 2-22 Handou #25 Lecure 2 Modulaion and Sampling The Fourier ransform of he produc of wo signals Modulaion of a signal wih a sinusoid Sampling wih an impulse rain The sampling heorem 2 Convoluion

ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 6/5/2006

Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή

MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3)

1. MATH43 String Theory Solutions 4 x = 0 τ = fs). 1) = = f s) ) x = x [f s)] + f s) 3) equation of motion is x = 0 if an only if f s) = 0 i.e. fs) = As + B with A, B constants. i.e. allowe reparametrisations