( k) ( ) = ( ) ( ) ( ) ( ) A Ω P( B) P A B P A P B תכונות: A ו- B ב"ת, אזי: A, B ב "ת. בינומי: (ההסתברות לk הצלחות מתוך n ניסויים) n.
|
|
|
- Πολωνα Βιτάλη
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Ω קבוצת התוצאות האפשריות של הניסוי A קבוצת התוצאות המבוקשות של הניסוי A A מספר האיברים של P( A A Ω מבוא להסתברות ח' 434 ( P A B הסתברות מותנית: P( A B P( B > ( P A B P A B P A B P( B PB נוסחאת ההסתברות השלמה: PA PAB PB אם: B Ω B P( אזי: ( PB ( > PB ( Bj נוסחת בייס: P( B A P( A P( A B אם ( PB> PA אזי : P( B ובניסוח נוסף: P( B A P( A Ω A אזי: אם : A P( P( B Aj P( Aj j PA ( > P( B PA ( A ( P( A P A B P A P B P A B P( > + > P( > > B P( אזי : מאורעות בלתי תלויים: A ו- B ב"ת זה בזה אם: הערה: אם בנוסף C AB C A ו- B ב"ת אזי: A B ב "ת C C A B משתנה מקרה בדיד מודל ניסויי ברנולי עם פרמטר P בינומי: (ההסתברות ל הצלחות מתוך ניסויים מספר ההצלחות K P מספר הניסויים p q 3 B p גיאומטרי: (ההסתברות ל ניסויים עד להצלחה הראשונה PY ( p q Y Geom p j חוסר הזיכרון של הפילוג הגיאומטרי : עמוד מתוך
2 מבוא להסתברות ח' 434 N( P a< < b φ( b φ( a φ( φ( z N ( μ P e Pos פואסון : λ λ ( λ! קירוב פואסוני: כאשר גדול וp קטן (כאשר >p > אזי : B( p Pos ( λ p b משתנה מקרי רציף הוא משתנה מקרי רציף בהחלט אם קיימת ( ( הנקראת פונ' צפיפות. P a< < b a כך ש <. P < < Ω. פונק' צפיפות נקבעת ביחידות עד כדי מספר סופי או ניתן להימנות של נקודות.. 3 P( > t+ s > t P( > s פונקציית צפיפות למשתנה מקרי אחיד a< < b ( b a else פונקציית צפיפות למשתנה מקרי מעריכי/אקספוננציאלי λ λe > ( < ep λ חוסר הזיכרון של הצפיפות המעריכית : פונקציית צפיפות נורמלית כללית/גאוסית נוסחת התיקון: כללי: a b b a P( a z b P μ μ μ φ( μ < < < < φ( פונקציית צפיפות גאמה פונקציית צפיפות של סכום אקספוננציאלים r r λ λ e עבור r מתקבלת צפיפות > ( ( r! אקספוננציאלית רגילה. else Gamma r ( λ ( μ e ( π ( μ עמוד מתוך
3 מ" פונקציית התפלגות lm F. מבוא להסתברות ח' 434 P( < < lm F (. (ערך הפונקציה הוא הגבול מימין ( F פונקצייה לא יורדת (.3 F רציפה מימין (.4.5 (. 6 F פונק' רציפה אם מ"מ רציף (בהחלט אזי ( ' בנק F בערך הקפיצה P F lm F ( y c F ( F y משפט: רציף אזי: F' ( בכל בו ( גזירה. ( מ F ניסוח נוסף : u u F ( משפט: יהיה מ"מ פונק' התפלגות שלו. ( β α (נסמן α סכום הקפיצות α קיים קבוע F וקיימת פונק' התפלגות רציפה קיימת פונק' התפלגות בדידה c F ( αf ( + βf ( כך ש : y h אזי : משפט: יהי מ "מ בעל צפיפות ( ( h פונ' מונוטונית ממש וגזירה(בקטע נגדיר ( תהי ( ' Y ( y ( h ( y ( h ( y משפט: יהי מ "מ בעל צפיפות ( ( בתומך של יש מספר סופי של מקורות y גזירה כזו שלכל ' h ( אזי :... פונק תהי ' ( ( y y h y h Y תוחלת עבור מ"מ בדיד E P ( עבור מ "מ בינומי: E p E עבור מ"מ גיאומטרי: p עבור מ"מ פואסוני: E λ עמוד 3 מתוך
4 מבוא להסתברות ח' 434 ( ± q p p + q q λ! e λ ( q נוסחאת הבינום : ' תוחלת עבור מ"מ רציף * E בתנאי שהאינטגרל מוגדר היטב (יכול לקבל את הערך a ( b a עבור מ"מ אחיד: E (אמצע הקטע E עבור מ"מ אקספוננציאלי: λ עבור מ "מ גאוסי: E μ למה: אם צפיפות ( ( סימטרית סביב מספר כלומר a ( a+ ( E ( ( c β ( אם התוחלת קיימת אזי: a ( F( E F( + ( F ( F תוחלת עבור מ"מ מעורב F αf + F ( c E αey + βez אזי: Y F אם מ"מ מעורב כאשר EY h EY קיימת אזי: Z F Y h אם ( ( ( p תוחלת של פונקצייה של מ"מ מ "מ בעל צפיפות EY h m o m (!! eve N משפט : עבור מקרה בדיד : m m ( מומנטים E( תכונות יסודיות של תוחלת E( + a E + a E( c ce + + E g h Eg Eh עמוד 4 מתוך
5 מבוא להסתברות ח' 434 שונות Var E E m ( m שונות של מ"מ בדידים: λ λ Var pos ( Var pq B p q Var Geom( p p שונות של מ"מ רציפים: ( b a [ ] Var U a b Var ep( λ λ Var N μ תכונות של השונות Var : מ"מ מנוון אמ"מ cost Var ( + a Var ( Var ( c c Var (. s s Ee c c פונקציה יוצרת מומנטים אם מ"מעבור s נגדיר. s מוגדרת לכל ( s s יכולה להיות סופית או אינסופית. I { s ( s נסמן: {>. ( I לכל I קטע רציף הכולל את. s s e אם ל- יש צפיפות ( ( אזי: (התמרת לפלס של הצפיפות. Δ פעמים ברציפות ב- E משפט (נגזרות של פונקציה יוצרת מומנטים: ננחי ש I מכיל קטע פתוח סביב s וש- s ( גזירה ( ( m אזי קיים המומנט מסדר של ו- m! אזי : c ( s cs ( s אם ניתן לכתוב את כטור : δ δ < s < עמוד 5 מתוך
6 מבוא להסתברות ח' 434. Eh( ( ϕ ( פונקציה אופיינית t t מ"מ אזי: ( t Ee e ( t אם תכונות : ϕ ( t ( t ϕ ( מוגדר וסופי לכל ϕ ( ( ( ϕ m ( μ > a P ϕ קיימת אזי: בהנחה ש משפט: אי-שיוויון צ'בישב יהי מ"מ בעל תוחלת μ וסטיית תקן : P( μ > b b ניסוח נוסף כאשר : b a a משפט: אי-שיוויון ינסן יהי מ"מ ו- ( h פונק' קמורה בהנחה שהתוחלות קיימות וסופיות : E h.. תוספת:אם קיים קטע I כך ש- I P ו- h( קמורה בקטע עדיין מתקיים המשפט. ווקטור אקראי פונקציית ההסתברות של ו"א בדיד... ( נתונה ע"י: P... P... כלומר לחיתוך של פונקציות ההסתברויות הבדידות.... P P Y בדיד בדיד Y בדיד ( P P y P P... Y... y... אם הערה:מפונקציית ההסתברות המשותפת ניתן לחשב את פונקציות ההסתברות השוליות אך לא ניתן ע"י פונקציות ההסתברות השוליות (אפילו לא ע"י כולן לחשב את המשותפת. ( נקראת פונקציית הצפיפות המשותפת של... ווקטור אקראי רציף... (... בעלת (... (( P A... (... נקבעת ביחידות עד כדי קבוצות של שנפחן במימד הוא עמוד 6 מתוך
7 מבוא להסתברות ח' 434 ל - יש צפיפות : יש צפיפות משותפת הצפיפות האחידה ב- : D D A c צפיפות שולית: אם ל... ( עבור צפיפות אחידה- אם D תחום ב- בעל נפח (... D else VOL A P ( A ( D פונקציית התפלגות של ווקטור אקראי F... P Y Y ( ( y ( Y ( y lm F or ( lm F y P F y ( ( lm F y P Y y F ( ( ( + ( F b F b c F a b F a c Y y a b F u... u u... u Y Y... ( y F... F y y ווקטור אקראי בלתי תלוי F... (... (... F F F במקרה הרציף :... ב"ת אמ"מ ( במקרה הבדיד:... ב"ת אמ"מ P (... P... עבור ווקטור אחיד- הרכיבים לא יהיו ב"ת אם תחום האחידות לא יהיה מלבן (מקביל לצירים. קונבולוציה הגדרה: נתונות שתי פונקציות אינטגרביליות הפעולה: U V U V נקראת הקונבולוציה של U * V U+ V U u V u u U * V V * U Gamma ( r + s λ Gamma ( r λ * Gamma ( s λ PU חיוביים רק ב- שלם אזי : ( PV ( P + P ( P ( עבור מקרה בדיד: UV בדידים וב"ת U V U V עמוד 7 מתוך
8 י" מבוא להסתברות ח' 434 A Pos ( λ * Pos ( λ Pos ( λ+λ B ( p * B( m p B( + m p תוחלת של פונקצייה של ווקטור אקראי ( ו"א בעלת צפיפ h( Y אזי : ות יהי... ו-... ( ( (... E + Y E + EY EY... h ( E( Y אם ו- Y לא מתואמים אזי: E EY טרנספורמציה של ווקטור אקראי (... יהי ו"א בעלת צפיפות... y... ו-( y ( ( ( ( uv J uv S uv UV S Y S (... ( נתונה ע... (... (... (... הטרנספורמציה ההפוכה y y y y J y y S y y Y Y S ( Y ( עבור UV : U U ( Y ( U V ( Y JS U V J U V ( UV Y Y V V U V Y ({ < } P( A P A F A P < A Y ( y YA התפלגות מותנית מאורע עבור בדיד: > A P מ"מ אזי: ({ } P( A P Y y A P y A P y Y A ( y ( Y A F A A A A הגדרה : A E A A אם ו"א בעל צפיפות משותפת אזי: ( y Y ( Y EY ( y ובהתאם : yy ( Y C C נוסחאת התוחלת השלמה: ( ( + ( ( ( E E A P A E A P A Y Y y y Y ( y נוסחאת הצפיפות השלמה : ( y y y Y Y Y ( משפט: עמוד 8 מתוך
9 מבוא להסתברות ח' 434 E ( E( Y משפט ההחלקה: E קווריאנס Y cov ( Y E ( μ( Y μy הגדרה : בהנחה כי : < EY E < cov ( var ( cov Y E Y EEY אם Y בלתי מתואמים : cov Y E Y EEY + Y + Y cov ( + Y cov ( Y + cov ( Y cov ( a Y a cov ( Y cov ( Y cov ( Y cov ( + CY cov ( Y var ( + Y var + vary + cov ( Y ( Y cov Y Y Y משפט: לכל Y cov ( Y cov ( cov ( Y צורה נוספת : (Y ( corr Y קורלציה Y cov ( Y ρ Y הגדרה: Y Y > > : cov מוגדרת רק אם בנוסף להנחה של ρ Y Y ρ Y ρ Y ρy ρ ay sg a ρ Y ρ + C Y ρ Y עמוד 9 מתוך
10 צפיפות גאוסית רב-מימדית הגדרה : ו"א ( נקרא גאוסי סימטרי אם קיימת מטריצה סימטרית A... מבוא להסתברות ח' 434 A a : j j j C e. A כך ש: הרכיבים ב "ת A אלכסונית. לא כל A יכולה לשמש לתבנית ריבועית. (... ( הגדרה:מטריצה A מוגדרת חיובית אם והשיוויון מתקיים רק עבור ( צפיפות C e A מוגדרת חיובית. A טענה: מטריצה A מוגדרת חיובית אמ"מ כל הערכים העצמיים של < A מטריצה A מוגדרת חיובית אמ "מ כל המינוריים הראשיים של < A N אם ( ווקטור גאוסי אזי:... מ"מ גאוסי ( ווקטור גאוסי סימטרי אזי : גם יהיה ווקטור גאוסי סימטרי. לא סינגולרית et... ווקטור גאוסי סימטרי Y מטריצה ( y y C et e Y אם (... (... y A Y ווקטור גאוסי סימטרי: ( cost אזי: מסקנה:לכל מטריצה מוגדרת חיובית A יש מטריצה B מוגדרת חיובית כך שA B B A A Y A A ווקטור גאוסי סימסטרי עם ( ( N N( A A A A I ווקטור גאוסי עם מטריצה Y A A N ( j j ( עבור מטריצת קווריאנס ווקטור אקראי נגדיר את המטריצה מ"מ גאוסי Y Z YZ Y YY YZ עבור 3 : Z ZY ZZ מטריצה סימטרית. באלכסון מופיעות השונויות. עמוד מתוך
11 עבור (צירוף לינארי של הרכיבים: מסקנה: מטריצת הקווריאנס מוגדרת אי שלילית. E כתיבה אחרת של מטריצת הקווריאנס: נהפוך כל חלק לחוד מבוא להסתברות ח' 434 ( j Z j j j j j Z a a var Z cov Z Z cov a a aa j cov j aa a a Y אזי: ו- m m m m j j E ( E( E אם ל- יש מטריצת קווריאנס ווקטור גאוסי (לא בהכרח סימטרי ce ( μ A( μ A E μ אבל לא בהכרח להיפך. Y הערה כללית: אם Y ( ב"ת Y ( בלתי מתואמים כלומר שלבי פתרון:. זיהוי A :לדוגמא עבור : ( a E + b y EY + c E y EY a c ( a + b y + c y+... Y ce A Y ce c b ו μ ע"י מציאת נקודות קריטיות של הפונק' (בעצם מספיק של ה. ep b a b c a : c a bc Σ כללי להפיכת מטריצה:. זיהוי : A הפיכת מטריצה טרנספורמציה: a b לדוגמא: U a + by V c + Y c a b a c UV מתקבלת ע"י: ומטריצת הקווריאנס של Y c b UV עמוד מתוך
12 חזאי כללי Y ווקטור גאוסי מבוא להסתברות ח' 434 ( ( ( g כך שלכל h מתקיים: E( Y g( אם Y בלתי תלויים cost a a המינימום יושג עבור (Y E E Y g E Y h Yˆ L ( μ + μy Y μ ES E EY חזאי לינארי אופטימלי החזאי הלינארי האפוטימלי של Y באמצעות נתון ע"י: Yˆ μy L Y ρ Y ( μ כתיבה אחרת: עבור ווקטור גאוסי החזאי האופטימלי הוא הלינארי. סדרת משתנים מקריים בלתי תלויים מפולגים זהה- נסמן באופן כללי: E μ var ES S נגדיר: Y S S var S var var vary var var S μ S lm P μ > δ : δ > חוק המספרים הגדולים תהי ( סדרה של משתנים מקריים S בהסתברות כלומר μ אזי לכל S ; E μ;var ( משפט הגבול המרכזי ( סדרה של מ" יהי מ בלתי תלויים מפולגים זהה. S ( N μ נניח א. כלומר פונקציית ההתפלגות האופייניות של בהתפלגות. שואפות לזו של N S S μ S N μ ( μ כללי: N ( ב. מ "מ בעל תוחלת μ ושונות ויש סיבה להתייחס אליו כסכום של מספר גדול של משמעות : אם (. N μ אזי: עמוד מתוך
{ } { } { A חוקי דה-מורגן: הגדרה הסתברות מותנית P P P. נוסחת בייס ) :(Bayes P P נוסחת ההסתברות הכוללת:
 A A A = = A = = = = { A B} P{ A B} P P{ B} P { } { } { A P A B = P B A } P{ B} P P P B=Ω { A} = { A B} { B} = = 434 מבוא להסתברות ח', דפי נוסחאות, עמוד מתוך 6 חוקי דה-מורגן: הגדרה הסתברות מותנית נוסחת
A A A = = A = = = = { A B} P{ A B} P P{ B} P { } { } { A P A B = P B A } P{ B} P P P B=Ω { A} = { A B} { B} = = 434 מבוא להסתברות ח', דפי נוסחאות, עמוד מתוך 6 חוקי דה-מורגן: הגדרה הסתברות מותנית נוסחת
I. גבולות. x 0. מתקיים L < ε. lim אם ורק אם. ( x) = 1. lim = 1. lim. x x ( ) הפונקציה נגזרות Δ 0. x Δx
 דפי נוסחאות I גבולות נאמר כי כך שלכל δ קיים > ε לכל > lim ( ) L המקיים ( ) מתקיים L < ε הגדרת הגבול : < < δ lim ( ) lim ורק ( ) משפט הכריך (סנדוויץ') : תהיינה ( ( ( )g ( )h פונקציות המוגדרות בסביבה נקובה
דפי נוסחאות I גבולות נאמר כי כך שלכל δ קיים > ε לכל > lim ( ) L המקיים ( ) מתקיים L < ε הגדרת הגבול : < < δ lim ( ) lim ורק ( ) משפט הכריך (סנדוויץ') : תהיינה ( ( ( )g ( )h פונקציות המוגדרות בסביבה נקובה
רשימת משפטים והגדרות
 רשימת משפטים והגדרות חשבון אינפיניטיסימאלי ב' מרצה : למברג דן 1 פונקציה קדומה ואינטגרל לא מסויים הגדרה 1.1. (פונקציה קדומה) יהי f :,] [b R פונקציה. פונקציה F נקראת פונקציה קדומה של f אם.[, b] גזירה ב F
רשימת משפטים והגדרות חשבון אינפיניטיסימאלי ב' מרצה : למברג דן 1 פונקציה קדומה ואינטגרל לא מסויים הגדרה 1.1. (פונקציה קדומה) יהי f :,] [b R פונקציה. פונקציה F נקראת פונקציה קדומה של f אם.[, b] גזירה ב F
תורת ההסתברות 1 יובל קפלן סיכום הרצאות פרופ יורי קיפר בקורס "תורת ההסתברות 1" (80420) באוניברסיטה העברית,
 תורת ההסתברות יובל קפלן סיכום הרצאות פרופ יורי קיפר בקורס "תורת ההסתברות " (80420) באוניברסיטה העברית, 8 2007. תוכן מחברת זו הוקלד ונערך על-ידי יובל קפלן. אין המרצה אחראי לכל טעות שנפלה בו. סודר באמצעות
תורת ההסתברות יובל קפלן סיכום הרצאות פרופ יורי קיפר בקורס "תורת ההסתברות " (80420) באוניברסיטה העברית, 8 2007. תוכן מחברת זו הוקלד ונערך על-ידי יובל קפלן. אין המרצה אחראי לכל טעות שנפלה בו. סודר באמצעות
חורף תש''ע פתרון בחינה סופית מועד א'
 מד''ח 4 - חורף תש''ע פתרון בחינה סופית מועד א' ( u) u u u < < שאלה : נתונה המד''ח הבאה: א) ב) ג) לכל אחד מן התנאים המצורפים בדקו האם קיים פתרון יחיד אינסוף פתרונות או אף פתרון אם קיים פתרון אחד או יותר
מד''ח 4 - חורף תש''ע פתרון בחינה סופית מועד א' ( u) u u u < < שאלה : נתונה המד''ח הבאה: א) ב) ג) לכל אחד מן התנאים המצורפים בדקו האם קיים פתרון יחיד אינסוף פתרונות או אף פתרון אם קיים פתרון אחד או יותר
פתרון תרגיל 5 מבוא ללוגיקה ותורת הקבוצות, סתיו תשע"ד
 פתרון תרגיל 5 מבוא ללוגיקה ותורת הקבוצות, סתיו תשע"ד 1. לכל אחת מן הפונקציות הבאות, קבעו אם היא חח"ע ואם היא על (הקבוצה המתאימה) (א) 3} {1, 2, 3} {1, 2, : f כאשר 1 } 1, 3, 3, 3, { 2, = f לא חח"ע: לדוגמה
פתרון תרגיל 5 מבוא ללוגיקה ותורת הקבוצות, סתיו תשע"ד 1. לכל אחת מן הפונקציות הבאות, קבעו אם היא חח"ע ואם היא על (הקבוצה המתאימה) (א) 3} {1, 2, 3} {1, 2, : f כאשר 1 } 1, 3, 3, 3, { 2, = f לא חח"ע: לדוגמה
הרצאה. α α פלוני, וכדומה. הזוויות α ל- β שווה ל-
 מ'' ל'' Deprmen of Applied Mhemics Holon Acdemic Insiue of Technology PROBABILITY AND STATISTICS Eugene Knzieper All righs reserved 4/5 חומר לימוד בקורס "הסתברות וסטטיסטיקה" מאת יוג'ין קנציפר כל הזכויות
מ'' ל'' Deprmen of Applied Mhemics Holon Acdemic Insiue of Technology PROBABILITY AND STATISTICS Eugene Knzieper All righs reserved 4/5 חומר לימוד בקורס "הסתברות וסטטיסטיקה" מאת יוג'ין קנציפר כל הזכויות
1 תוחלת מותנה. c ארזים 3 במאי G מדיד לפי Y.1 E (X1 A ) = E (Y 1 A )
 הסתברות למתמטיקאים c ארזים 3 במאי 2017 1 תוחלת מותנה הגדרה 1.1 לכל משתנה מקרי X אינטגרבילית ותת סיגמא אלגברה G F קיים משתנה מקרי G) Y := E (X המקיים: E (X1 A ) = E (Y 1 A ).G מדיד לפי Y.1.E Y
הסתברות למתמטיקאים c ארזים 3 במאי 2017 1 תוחלת מותנה הגדרה 1.1 לכל משתנה מקרי X אינטגרבילית ותת סיגמא אלגברה G F קיים משתנה מקרי G) Y := E (X המקיים: E (X1 A ) = E (Y 1 A ).G מדיד לפי Y.1.E Y
( )( ) ( ) f : B C היא פונקציה חח"ע ועל מכיוון שהיא מוגדרת ע"י. מכיוון ש f היא פונקציהאז )) 2 ( ( = ) ( ( )) היא פונקציה חח"ע אז ועל פי הגדרת
 הרצאה 7 יהיו :, : C פונקציות, אז : C חח"ע ו חח"ע,אז א אם על ו על,אז ב אם ( על פי הגדרת ההרכבה )( x ) = ( )( x x, כךש ) x א יהיו = ( x ) x חח"ע נקבל ש מכיוון ש חח"ע נקבל ש מכיוון ש ( b) = c כך ש b ( ) (
הרצאה 7 יהיו :, : C פונקציות, אז : C חח"ע ו חח"ע,אז א אם על ו על,אז ב אם ( על פי הגדרת ההרכבה )( x ) = ( )( x x, כךש ) x א יהיו = ( x ) x חח"ע נקבל ש מכיוון ש חח"ע נקבל ש מכיוון ש ( b) = c כך ש b ( ) (
שדות תזכורת: פולינום ממעלה 2 או 3 מעל שדה הוא פריק אם ורק אם יש לו שורש בשדה. שקיימים 5 מספרים שלמים שונים , ראשוני. שעבורם
 תזכורת: פולינום ממעלה או מעל שדה הוא פריק אם ורק אם יש לו שורש בשדה p f ( m i ) = p m1 m5 תרגיל: נתון עבור x] f ( x) Z[ ראשוני שקיימים 5 מספרים שלמים שונים שעבורם p x f ( x ) f ( ) = נניח בשלילה ש הוא
תזכורת: פולינום ממעלה או מעל שדה הוא פריק אם ורק אם יש לו שורש בשדה p f ( m i ) = p m1 m5 תרגיל: נתון עבור x] f ( x) Z[ ראשוני שקיימים 5 מספרים שלמים שונים שעבורם p x f ( x ) f ( ) = נניח בשלילה ש הוא
תרגיל 13 משפטי רול ולגראנז הערות
 Mthemtics, Summer 20 / Exercise 3 Notes תרגיל 3 משפטי רול ולגראנז הערות. האם קיים פתרון למשוואה + x e x = בקרן )?(0, (רמז: ביחרו x,f (x) = e x הניחו שיש פתרון בקרן, השתמשו במשפט רול והגיעו לסתירה!) פתרון
Mthemtics, Summer 20 / Exercise 3 Notes תרגיל 3 משפטי רול ולגראנז הערות. האם קיים פתרון למשוואה + x e x = בקרן )?(0, (רמז: ביחרו x,f (x) = e x הניחו שיש פתרון בקרן, השתמשו במשפט רול והגיעו לסתירה!) פתרון
פתרון תרגיל מרחבים וקטורים. x = s t ולכן. ur uur נסמן, ur uur לכן U הוא. ur uur. ur uur
 פתרון תרגיל --- 5 מרחבים וקטורים דוגמאות למרחבים וקטורים שונים מושגים בסיסיים: תת מרחב צירוף לינארי x+ y+ z = : R ) בכל סעיף בדקו האם הוא תת מרחב של א } = z = {( x y z) R x+ y+ הוא אוסף הפתרונות של המערכת
פתרון תרגיל --- 5 מרחבים וקטורים דוגמאות למרחבים וקטורים שונים מושגים בסיסיים: תת מרחב צירוף לינארי x+ y+ z = : R ) בכל סעיף בדקו האם הוא תת מרחב של א } = z = {( x y z) R x+ y+ הוא אוסף הפתרונות של המערכת
{ } { } = { } ( ) { } { } { } ( v) { } { ( ) } כללי הגדרות: σ σ. ( x) ( y) E X Y ; 1. X = signal ; N = noise. ax, a X } } ( )
 For more please vs www.so.o ( כל המשפטים הנ"ל נכונים גם עבור וקטורים בעלי יותר מ- איברים. ( אם ו- בת"ס אז: F / ( / y F( ; / ( / y ( ρ ( η( E ; ρ :Covarace - Cov η Cov( כללי הגדרות: מטריצה מוגדרת חיובית
For more please vs www.so.o ( כל המשפטים הנ"ל נכונים גם עבור וקטורים בעלי יותר מ- איברים. ( אם ו- בת"ס אז: F / ( / y F( ; / ( / y ( ρ ( η( E ; ρ :Covarace - Cov η Cov( כללי הגדרות: מטריצה מוגדרת חיובית
חדוו"א 2 סיכום טענות ומשפטים
 חדוו"א 2 סיכום טענות ומשפטים 3 ביוני 2 n S(f, T ) := (t k+ t k ) inf k= סכום דרבו תחתון מוגדר על ידי [t k,t k+ ] f אינטגרל רימן חלוקות של קטע חלוקה של קטע [,] הינה אוסף סדור סופי של נקודות מהצורה: טענה.2
חדוו"א 2 סיכום טענות ומשפטים 3 ביוני 2 n S(f, T ) := (t k+ t k ) inf k= סכום דרבו תחתון מוגדר על ידי [t k,t k+ ] f אינטגרל רימן חלוקות של קטע חלוקה של קטע [,] הינה אוסף סדור סופי של נקודות מהצורה: טענה.2
תורת ההסתברות (1) 80420
 תורת ההסתברות (1) 80420 איתי שפירא 4 באוקטובר 2017 מתוך הרצאות מהאונברסיטה העברית 2017. i.j.shapira@gmail.com תוכן עניינים 0 מבוא והשלמות 6 0.1 נושאים מתורת הקבוצות.......................... 6 0.2 נושאים
תורת ההסתברות (1) 80420 איתי שפירא 4 באוקטובר 2017 מתוך הרצאות מהאונברסיטה העברית 2017. i.j.shapira@gmail.com תוכן עניינים 0 מבוא והשלמות 6 0.1 נושאים מתורת הקבוצות.......................... 6 0.2 נושאים
לדוגמה: במפורט: x C. ,a,7 ו- 13. כלומר בקיצור
 הרצאה מס' 1. תורת הקבוצות. מושגי יסוד בתורת הקבוצות.. 1.1 הקבוצה ואיברי הקבוצות. המושג קבוצה הוא מושג בסיסי במתמטיקה. אין מושגים בסיסים יותר, אשר באמצעותם הגדרתו מתאפשרת. הניסיון והאינטואיציה עוזרים להבין
הרצאה מס' 1. תורת הקבוצות. מושגי יסוד בתורת הקבוצות.. 1.1 הקבוצה ואיברי הקבוצות. המושג קבוצה הוא מושג בסיסי במתמטיקה. אין מושגים בסיסים יותר, אשר באמצעותם הגדרתו מתאפשרת. הניסיון והאינטואיציה עוזרים להבין
3-9 - a < x < a, a < x < a
 1 עמוד 59, שאלהמס', 4 סעיףג' תיקוני הקלדה שאלון 806 צריך להיות : ג. מצאאתמקומושלאיברבסדרהזו, שקטןב- 5 מסכוםכלהאיבריםשלפניו. עמוד 147, שאלהמס' 45 ישלמחוקאתהשאלה (מופיעהפעמיים) עמוד 184, שאלהמס', 9 סעיףב',תשובה.
1 עמוד 59, שאלהמס', 4 סעיףג' תיקוני הקלדה שאלון 806 צריך להיות : ג. מצאאתמקומושלאיברבסדרהזו, שקטןב- 5 מסכוםכלהאיבריםשלפניו. עמוד 147, שאלהמס' 45 ישלמחוקאתהשאלה (מופיעהפעמיים) עמוד 184, שאלהמס', 9 סעיףב',תשובה.
גבול ורציפות של פונקציה סקלרית שאלות נוספות
 08 005 שאלה גבול ורציפות של פונקציה סקלרית שאלות נוספות f ( ) f ( ) g( ) f ( ) ו- lim f ( ) ו- ( ) (00) lim ( ) (00) f ( בסביבת הנקודה (00) ) נתון: מצאו ) lim g( ( ) (00) ננסה להיעזר בכלל הסנדביץ לשם כך
08 005 שאלה גבול ורציפות של פונקציה סקלרית שאלות נוספות f ( ) f ( ) g( ) f ( ) ו- lim f ( ) ו- ( ) (00) lim ( ) (00) f ( בסביבת הנקודה (00) ) נתון: מצאו ) lim g( ( ) (00) ננסה להיעזר בכלל הסנדביץ לשם כך
אותות אקראיים סיכום הקורס עדכון אחרון: 12/10/2009
 www.hapeek.co.il אותות אקראיים 44 סיכום הקורס עדכון אחרון: //9 תוכן עניינים תוכן עניינים... חזרה על הסתברות...3 משתנים אקראיים... 4 וקטור אקראי... 6 וקטור אקראי גאוסי...7 משתנים אקראיים ווקטורים אקראיים...
www.hapeek.co.il אותות אקראיים 44 סיכום הקורס עדכון אחרון: //9 תוכן עניינים תוכן עניינים... חזרה על הסתברות...3 משתנים אקראיים... 4 וקטור אקראי... 6 וקטור אקראי גאוסי...7 משתנים אקראיים ווקטורים אקראיים...
פתרון תרגיל 8. מרחבים וקטורים פרישה, תלות \ אי-תלות לינארית, בסיס ומימד ... ( ) ( ) ( ) = L. uuruuruur. { v,v,v ( ) ( ) ( ) ( )
 פתרון תרגיל 8. מרחבים וקטורים פרישה, תלות \ אי-תלות לינארית, בסיס ומימד a d U c M ( יהי b (R) a b e ל (R M ( (אין צורך להוכיח). מצאו קבוצה פורשת ל. U בדקו ש - U מהווה תת מרחב ש a d U M (R) Sp,,, c a e
פתרון תרגיל 8. מרחבים וקטורים פרישה, תלות \ אי-תלות לינארית, בסיס ומימד a d U c M ( יהי b (R) a b e ל (R M ( (אין צורך להוכיח). מצאו קבוצה פורשת ל. U בדקו ש - U מהווה תת מרחב ש a d U M (R) Sp,,, c a e
צעד ראשון להצטיינות מבוא: קבוצות מיוחדות של מספרים ממשיים
 מבוא: קבוצות מיוחדות של מספרים ממשיים קבוצות של מספרים ממשיים צעד ראשון להצטיינות קבוצה היא אוסף של עצמים הנקראים האיברים של הקבוצה אנו נתמקד בקבוצות של מספרים ממשיים בדרך כלל מסמנים את הקבוצה באות גדולה
מבוא: קבוצות מיוחדות של מספרים ממשיים קבוצות של מספרים ממשיים צעד ראשון להצטיינות קבוצה היא אוסף של עצמים הנקראים האיברים של הקבוצה אנו נתמקד בקבוצות של מספרים ממשיים בדרך כלל מסמנים את הקבוצה באות גדולה
סרוקל רזע תרבוח 1 ילמיסיטיפניא ןובשח
 חוברת עזר לקורס חשבון אינפיטיסימלי 495 יולי 4 חוברת עזר לקורס חשבון אינפיטיסימלי 495 עמוד חוברת עזר לקורס חשבון אינפיטיסימלי 495 יולי 4 תוכן העניינים נושא עמוד נושא כללי 3 רציפות זהויות טריגונומטריות 4
חוברת עזר לקורס חשבון אינפיטיסימלי 495 יולי 4 חוברת עזר לקורס חשבון אינפיטיסימלי 495 עמוד חוברת עזר לקורס חשבון אינפיטיסימלי 495 יולי 4 תוכן העניינים נושא עמוד נושא כללי 3 רציפות זהויות טריגונומטריות 4
הרצאה 5 הגדרה D5.1 בין 1 N . כלומר, t N
 ROBABILITY A STATISTIS הסתברות וסטטיסטיקה יוג'ין מאת קנציפר ugee Kazieer All rights reserved 005/06 כל הזכויות שמורות 005/06 הרצאה 5 התפלגויות בדידות מיוחדות התפלגות אחידה ניסוי והתפלגות ברנולי התפלגות
ROBABILITY A STATISTIS הסתברות וסטטיסטיקה יוג'ין מאת קנציפר ugee Kazieer All rights reserved 005/06 כל הזכויות שמורות 005/06 הרצאה 5 התפלגויות בדידות מיוחדות התפלגות אחידה ניסוי והתפלגות ברנולי התפלגות
x a x n D f (iii) x n a ,Cauchy
 גבולות ורציפות גבול של פונקציה בנקודה הגדרה: קבוצה אשר מכילה קטע פתוח שמכיל את a תקרא סביבה של a. קבוצה אשר מכילה קטע פתוח שמכיל את a אך לא מכילה את a עצמו תקרא סביבה מנוקבת של a. יהו a R ו f פונקציה מוגדרת
גבולות ורציפות גבול של פונקציה בנקודה הגדרה: קבוצה אשר מכילה קטע פתוח שמכיל את a תקרא סביבה של a. קבוצה אשר מכילה קטע פתוח שמכיל את a אך לא מכילה את a עצמו תקרא סביבה מנוקבת של a. יהו a R ו f פונקציה מוגדרת
הסתברות לתלמידי מדעי-המחשב
 הסתברות לתלמידי מדעי-המחשב סיכום קורס מפי ד"ר לובה ספיר סמסטר א', תשע"ה אוניברסיטת בן-גוריון בנגב מס' קורס --93 סוכם ע"י: אסף של וש מקרא צבעים: כחול הגדרות ומונחים שמופיעים לראשונה; אדום משפט, למה, טענה;
הסתברות לתלמידי מדעי-המחשב סיכום קורס מפי ד"ר לובה ספיר סמסטר א', תשע"ה אוניברסיטת בן-גוריון בנגב מס' קורס --93 סוכם ע"י: אסף של וש מקרא צבעים: כחול הגדרות ומונחים שמופיעים לראשונה; אדום משפט, למה, טענה;
לוגיקה ותורת הקבוצות מבחן סופי אביב תשע"ב (2012) דפי עזר
 לוגיקה ותורת הקבוצות מבחן סופי אביב תשע"ב (2012) דפי עזר תורת הקבוצות: סימונים.N + = N \ {0} קבוצת המספרים הטבעיים; N Z קבוצת המספרים השלמים. Q קבוצת המספרים הרציונליים. R קבוצת המספרים הממשיים. הרכבת
לוגיקה ותורת הקבוצות מבחן סופי אביב תשע"ב (2012) דפי עזר תורת הקבוצות: סימונים.N + = N \ {0} קבוצת המספרים הטבעיים; N Z קבוצת המספרים השלמים. Q קבוצת המספרים הרציונליים. R קבוצת המספרים הממשיים. הרכבת
סיכום בנושא של דיפרנציאביליות ונגזרות כיווניות
 סיכום בנושא של דיפרנציאביליות ונגזרות כיווניות 25 בדצמבר 2016 תזכורת: תהי ) n f ( 1, 2,..., פונקציה המוגדרת בסביבה של f. 0 גזירה חלקית לפי משתנה ) ( = 0, אם קיים הגבול : 1 0, 2 0,..., בנקודה n 0 i f(,..,n,).lim
סיכום בנושא של דיפרנציאביליות ונגזרות כיווניות 25 בדצמבר 2016 תזכורת: תהי ) n f ( 1, 2,..., פונקציה המוגדרת בסביבה של f. 0 גזירה חלקית לפי משתנה ) ( = 0, אם קיים הגבול : 1 0, 2 0,..., בנקודה n 0 i f(,..,n,).lim
מתכנס בהחלט אם n n=1 a. k=m. k=m a k n n שקטן מאפסילון. אם קח, ניקח את ה- N שאנחנו. sin 2n מתכנס משום ש- n=1 n. ( 1) n 1
 1 טורים כלליים 1. 1 התכנסות בהחלט מתכנס. מתכנס בהחלט אם n a הגדרה.1 אומרים שהטור a n משפט 1. טור מתכנס בהחלט הוא מתכנס. הוכחה. נוכיח עם קריטריון קושי. יהי אפסילון גדול מ- 0, אז אנחנו יודעים ש- n N n>m>n
1 טורים כלליים 1. 1 התכנסות בהחלט מתכנס. מתכנס בהחלט אם n a הגדרה.1 אומרים שהטור a n משפט 1. טור מתכנס בהחלט הוא מתכנס. הוכחה. נוכיח עם קריטריון קושי. יהי אפסילון גדול מ- 0, אז אנחנו יודעים ש- n N n>m>n
יסודות לוגיקה ותורת הקבוצות למערכות מידע (סמסטר ב 2012)
 יסודות לוגיקה ותורת הקבוצות למערכות מידע (סמסטר ב 2012) דף פתרונות 6 נושא: תחשיב הפסוקים: הפונקציה,val גרירה לוגית, שקילות לוגית 1. כיתבו טבלאות אמת לפסוקים הבאים: (ג) r)).((p q) r) ((p r) (q p q r (p
יסודות לוגיקה ותורת הקבוצות למערכות מידע (סמסטר ב 2012) דף פתרונות 6 נושא: תחשיב הפסוקים: הפונקציה,val גרירה לוגית, שקילות לוגית 1. כיתבו טבלאות אמת לפסוקים הבאים: (ג) r)).((p q) r) ((p r) (q p q r (p
The No Arbitrage Theorem for Factor Models ג'רמי שיף - המחלקה למתמטיקה, אוניברסיטת בר-אילן
 .. The No Arbitrage Theorem for Factor Models ג'רמי שיף - המחלקה למתמטיקה, אוניברסיטת בר-אילן 03.01.16 . Factor Models.i = 1,..., n,r i נכסים, תשואות (משתנים מקריים) n.e[f j ] נניח = 0.j = 1,..., d,f j
.. The No Arbitrage Theorem for Factor Models ג'רמי שיף - המחלקה למתמטיקה, אוניברסיטת בר-אילן 03.01.16 . Factor Models.i = 1,..., n,r i נכסים, תשואות (משתנים מקריים) n.e[f j ] נניח = 0.j = 1,..., d,f j
תרגול 1 חזרה טורי פורייה והתמרות אינטגרליות חורף תשע"ב זהויות טריגונומטריות
 תרגול חזרה זהויות טריגונומטריות si π α) si α π α) α si π π ), Z si α π α) t α cot π α) t α si α cot α α α si α si α + α siα ± β) si α β ± α si β α ± β) α β si α si β si α si α α α α si α si α α α + α si
תרגול חזרה זהויות טריגונומטריות si π α) si α π α) α si π π ), Z si α π α) t α cot π α) t α si α cot α α α si α si α + α siα ± β) si α β ± α si β α ± β) α β si α si β si α si α α α α si α si α α α + α si
אינפי - 1 תרגול בינואר 2012
 אינפי - תרגול 4 3 בינואר 0 רציפות במידה שווה הגדרה. נאמר שפונקציה f : D R היא רציפה במידה שווה אם לכל > 0 ε קיים. f(x) f(y) < ε אז x y < δ אם,x, y D כך שלכל δ > 0 נביט במקרה בו D הוא קטע (חסום או לא חסום,
אינפי - תרגול 4 3 בינואר 0 רציפות במידה שווה הגדרה. נאמר שפונקציה f : D R היא רציפה במידה שווה אם לכל > 0 ε קיים. f(x) f(y) < ε אז x y < δ אם,x, y D כך שלכל δ > 0 נביט במקרה בו D הוא קטע (חסום או לא חסום,
אלגברה לינארית 2 משפטים וטענות
 אלגברה לינארית 2 משפטים וטענות סוכם ע"פ הרצאות פרופ' מ.קריבלביץ' 1.2 אידאלים של פולינומים הגדרה 1.13 יהי F שדה. קבוצת פולינומים [x] I F נקראת אידיאל ב [ x ] F אם מתקיים:.0 I.1.2 לכל f 1, f 2 I מתקיים.f
אלגברה לינארית 2 משפטים וטענות סוכם ע"פ הרצאות פרופ' מ.קריבלביץ' 1.2 אידאלים של פולינומים הגדרה 1.13 יהי F שדה. קבוצת פולינומים [x] I F נקראת אידיאל ב [ x ] F אם מתקיים:.0 I.1.2 לכל f 1, f 2 I מתקיים.f
אלגברה לינארית מטריצות מטריצות הפיכות
 מטריצות + [( αij+ β ij ] m λ [ λα ij ] m λ [ αijλ ] m + + ( + +C + ( + C i C m q m q ( + C C + C C( + C + C λ( ( λ λ( ( λ (C (C ( ( λ ( + + ( λi ( ( ( k k i חיבור מכפלה בסקלר מכפלה בסקלר קומוטטיב אסוציאטיב
מטריצות + [( αij+ β ij ] m λ [ λα ij ] m λ [ αijλ ] m + + ( + +C + ( + C i C m q m q ( + C C + C C( + C + C λ( ( λ λ( ( λ (C (C ( ( λ ( + + ( λi ( ( ( k k i חיבור מכפלה בסקלר מכפלה בסקלר קומוטטיב אסוציאטיב
לוגיקה ותורת הקבוצות פתרון תרגיל בית 4 אביב תשע"ו (2016)
 לוגיקה ותורת הקבוצות פתרון תרגיל בית 4 אביב תשע"ו (2016)............................................................................................................. חלק ראשון: שאלות שאינן להגשה 1. עבור
לוגיקה ותורת הקבוצות פתרון תרגיל בית 4 אביב תשע"ו (2016)............................................................................................................. חלק ראשון: שאלות שאינן להגשה 1. עבור
c ארזים 26 בינואר משפט ברנסייד פתירה. Cl (z) = G / Cent (z) = q b r 2 הצגות ממשיות V = V 0 R C אזי מקבלים הצגה מרוכבת G GL R (V 0 ) GL C (V )
 הצגות של חבורות סופיות c ארזים 6 בינואר 017 1 משפט ברנסייד משפט 1.1 ברנסייד) יהיו p, q ראשוניים. תהי G חבורה מסדר.a, b 0,p a q b אזי G פתירה. הוכחה: באינדוקציה על G. אפשר להניח כי > 1 G. נבחר תת חבורה
הצגות של חבורות סופיות c ארזים 6 בינואר 017 1 משפט ברנסייד משפט 1.1 ברנסייד) יהיו p, q ראשוניים. תהי G חבורה מסדר.a, b 0,p a q b אזי G פתירה. הוכחה: באינדוקציה על G. אפשר להניח כי > 1 G. נבחר תת חבורה
Logic and Set Theory for Comp. Sci.
 234293 - Logic and Set Theory for Comp. Sci. Spring 2008 Moed A Final [partial] solution Slava Koyfman, 2009. 1 שאלה 1 לא נכון. דוגמא נגדית מפורשת: יהיו } 2,(p 1 p 2 ) (p 2 p 1 ).Σ 2 = {p 2 p 1 },Σ 1 =
234293 - Logic and Set Theory for Comp. Sci. Spring 2008 Moed A Final [partial] solution Slava Koyfman, 2009. 1 שאלה 1 לא נכון. דוגמא נגדית מפורשת: יהיו } 2,(p 1 p 2 ) (p 2 p 1 ).Σ 2 = {p 2 p 1 },Σ 1 =
רשימת משפטים וטענות נכתב על ידי יהונתן רגב רשימת משפטים וטענות
 λ = 0 A. F n n ערך עצמי של A אם ורק אם A לא הפיכה..det(λ I ערך עצמי של λ F.A F n n n A) = 0 אם ורק אם: A v וקטור עצמי של Tהמתאים יהי T: V V אופרטור לינארי. אם λ F ערך עצמי של,T לערך העצמי λ, אזי λ הוא
λ = 0 A. F n n ערך עצמי של A אם ורק אם A לא הפיכה..det(λ I ערך עצמי של λ F.A F n n n A) = 0 אם ורק אם: A v וקטור עצמי של Tהמתאים יהי T: V V אופרטור לינארי. אם λ F ערך עצמי של,T לערך העצמי λ, אזי λ הוא
אותות אקראיים ורעש
 הפקולטה להנדסה אוניברסיטת תל אביב אותות אקראיים ורעש 052.3632 ע"פ סיכום הרצאות מסמסטר א' שנת תשס"ח מרצים: ד"ר אורי ארז פרופ' רם זמיר רישום: יגאל רג'ואן מהדורה.3 עריכה אחרונה 27.0.20 2 תוכן עניינים מבוא...5
הפקולטה להנדסה אוניברסיטת תל אביב אותות אקראיים ורעש 052.3632 ע"פ סיכום הרצאות מסמסטר א' שנת תשס"ח מרצים: ד"ר אורי ארז פרופ' רם זמיר רישום: יגאל רג'ואן מהדורה.3 עריכה אחרונה 27.0.20 2 תוכן עניינים מבוא...5
דף פתרונות 7 נושא: תחשיב הפסוקים: צורה דיסיונקטיבית נורמלית, מערכת קשרים שלמה, עקביות
 יסודות לוגיקה ותורת הקבוצות למערכות מידע (סמסטר ב 2012) דף פתרונות 7 נושא: תחשיב הפסוקים: צורה דיסיונקטיבית נורמלית, מערכת קשרים שלמה, עקביות 1. מצאו צורה דיסיונקטיבית נורמלית קנונית לפסוקים הבאים: (ג)
יסודות לוגיקה ותורת הקבוצות למערכות מידע (סמסטר ב 2012) דף פתרונות 7 נושא: תחשיב הפסוקים: צורה דיסיונקטיבית נורמלית, מערכת קשרים שלמה, עקביות 1. מצאו צורה דיסיונקטיבית נורמלית קנונית לפסוקים הבאים: (ג)
ל הזכויות שמורות לדפנה וסטרייך
 מרובע שכל זוג צלעות נגדיות בו שוות זו לזו נקרא h באיור שלעיל, הצלעות ו- הן צלעות נגדיות ומתקיים, וכן הצלעות ו- הן צלעות נגדיות ומתקיים. תכונות ה כל שתי זוויות נגדיות שוות זו לזו. 1. כל שתי צלעות נגדיות
מרובע שכל זוג צלעות נגדיות בו שוות זו לזו נקרא h באיור שלעיל, הצלעות ו- הן צלעות נגדיות ומתקיים, וכן הצלעות ו- הן צלעות נגדיות ומתקיים. תכונות ה כל שתי זוויות נגדיות שוות זו לזו. 1. כל שתי צלעות נגדיות
לוגיקה ותורת הקבוצות מבחן סופי אביב תשע"ד (2014) דפי עזר
 לוגיקה ותורת הקבוצות מבחן סופי אביב תשע"ד (2014) דפי עזר תורת הקבוצות: סימונים.N + = N \ {0} קבוצת המספרים הטבעיים; N Z קבוצת המספרים השלמים. Q קבוצת המספרים הרציונליים. R קבוצת המספרים הממשיים. הרכבת
לוגיקה ותורת הקבוצות מבחן סופי אביב תשע"ד (2014) דפי עזר תורת הקבוצות: סימונים.N + = N \ {0} קבוצת המספרים הטבעיים; N Z קבוצת המספרים השלמים. Q קבוצת המספרים הרציונליים. R קבוצת המספרים הממשיים. הרכבת
סיכום אינפי 2 19 ביוני 2010 מרצה: צביק איתמר, בעזרת סיכומים משיעוריו של נועם ברגר מתרגלים: ינאי ג', איב גודין
 סיכום אינפי 2 9 ביוני 200 מרצה: צביק איתמר, בעזרת סיכומים משיעוריו של נועם ברגר מתרגלים: ינאי ג', איב גודין אין המרצה או המתרגלים קשורים לסיכום זה בשום דרך. סוכם ע"י נגה רוטמן בשעות לא הגיוניות בעליל,
סיכום אינפי 2 9 ביוני 200 מרצה: צביק איתמר, בעזרת סיכומים משיעוריו של נועם ברגר מתרגלים: ינאי ג', איב גודין אין המרצה או המתרגלים קשורים לסיכום זה בשום דרך. סוכם ע"י נגה רוטמן בשעות לא הגיוניות בעליל,
תרגול מס' 6 פתרון מערכת משוואות ליניארית
 אנליזה נומרית 0211 סתיו - תרגול מס' 6 פתרון מערכת משוואות ליניארית נרצה לפתור את מערכת המשוואות יהי פתרון מקורב של נגדיר את השארית: ואת השגיאה: שאלה 1: נתונה מערכת המשוואות הבאה: הערך את השגיאה היחסית
אנליזה נומרית 0211 סתיו - תרגול מס' 6 פתרון מערכת משוואות ליניארית נרצה לפתור את מערכת המשוואות יהי פתרון מקורב של נגדיר את השארית: ואת השגיאה: שאלה 1: נתונה מערכת המשוואות הבאה: הערך את השגיאה היחסית
לוגיקה ותורת הקבוצות פתרון תרגיל בית 8 חורף תשע"ו ( ) ... חלק ראשון: שאלות שאינן להגשה נפריד למקרים:
 לוגיקה ותורת הקבוצות פתרון תרגיל בית 8 חורף תשע"ו ( 2016 2015 )............................................................................................................. חלק ראשון: שאלות שאינן להגשה.1
לוגיקה ותורת הקבוצות פתרון תרגיל בית 8 חורף תשע"ו ( 2016 2015 )............................................................................................................. חלק ראשון: שאלות שאינן להגשה.1
שאלה 1 V AB פתרון AB 30 R3 20 R
 תרגילים בתורת החשמל כתה יג שאלה א. חשב את המתח AB לפי משפט מילמן. חשב את הזרם בכל נגד לפי המתח שקיבלת בסעיף א. A 60 0 8 0 0.A B 8 60 0 0. AB 5. v 60 AB 0 0 ( 5.) 0.55A 60 א. פתרון 0 AB 0 ( 5.) 0 0.776A
תרגילים בתורת החשמל כתה יג שאלה א. חשב את המתח AB לפי משפט מילמן. חשב את הזרם בכל נגד לפי המתח שקיבלת בסעיף א. A 60 0 8 0 0.A B 8 60 0 0. AB 5. v 60 AB 0 0 ( 5.) 0.55A 60 א. פתרון 0 AB 0 ( 5.) 0 0.776A
c ארזים 15 במרץ 2017
 הסתברות למתמטיקאים c ארזים 15 במרץ 2017 הקורס הוא המשך של מבוא להסתברות שם דיברנו על מרחבים לכל היותר בני מניה. למשל, סדרת הטלות מטבע בלתי תלויות היא דבר שאי אפשר לממש במרחב בן מניה נסמן את התוצאה של ההטלה
הסתברות למתמטיקאים c ארזים 15 במרץ 2017 הקורס הוא המשך של מבוא להסתברות שם דיברנו על מרחבים לכל היותר בני מניה. למשל, סדרת הטלות מטבע בלתי תלויות היא דבר שאי אפשר לממש במרחב בן מניה נסמן את התוצאה של ההטלה
תורת המספרים 1 פירוק לגורמים ראשוניים סיכום הגדרות טענות ומשפטים אביב הגדרות 1.2 טענות
 תורת המספרים סיכום הגדרות טענות ומשפטים אביב 017 1 פירוק לגורמים ראשוניים 1.1 הגדרות חוג A C נקראת חוג אם: היא מכילה את 0 ואת 1 סגורה תחת חיבור, חיסור, וכפל הפיך A חוג. a A נקרא הפיך אם 0,a.a 1 A קבוצת
תורת המספרים סיכום הגדרות טענות ומשפטים אביב 017 1 פירוק לגורמים ראשוניים 1.1 הגדרות חוג A C נקראת חוג אם: היא מכילה את 0 ואת 1 סגורה תחת חיבור, חיסור, וכפל הפיך A חוג. a A נקרא הפיך אם 0,a.a 1 A קבוצת
אלגברה לינארית 1. המערכת הלא הומוגנית גם כן. יתרה מזאת כל פתרון של (A b) הוא מהצורה c + v כאשר v פתרון כלשהו של המערכת ההומוגנית
 אלגברה לינארית 1 Uטענה U: אם c פתרון של המערכת (A b) ו v פתרון של המערכת (0 A) אזי c + v פתרון של המערכת הלא הומוגנית גם כן. יתרה מזאת כל פתרון של (A b) הוא מהצורה c + v כאשר v פתרון כלשהו של המערכת ההומוגנית
אלגברה לינארית 1 Uטענה U: אם c פתרון של המערכת (A b) ו v פתרון של המערכת (0 A) אזי c + v פתרון של המערכת הלא הומוגנית גם כן. יתרה מזאת כל פתרון של (A b) הוא מהצורה c + v כאשר v פתרון כלשהו של המערכת ההומוגנית
תורת ההסתברות 2: (או הסתברות ותהליכים סטוכסטים)
 תורת ההסתברות : או הסתברות ותהליכים סטוכסטים סוכם על ידי תום חן tomhen@gmail.com בדצמבר 04 שימו לב יתכנו שגיאות בטקסט עידכונים יתבצעו במהלך הסמסטר נא לדווח שגיאות ל gidi.amir@gmail.com או לחלופין שלשמור
תורת ההסתברות : או הסתברות ותהליכים סטוכסטים סוכם על ידי תום חן tomhen@gmail.com בדצמבר 04 שימו לב יתכנו שגיאות בטקסט עידכונים יתבצעו במהלך הסמסטר נא לדווח שגיאות ל gidi.amir@gmail.com או לחלופין שלשמור
גירסה liran Home Page:
 גירסה 1.00 26.10.03 סיכום באלגברה א מסמך זה הורד מהאתר.hp://uderwar.liveds.co.il אין להפיץ מסמך זה במדיה כלשהי, ללא אישור מפורש מאת המחבר. מחבר המסמך איננו אחראי לכל נזק, ישיר או עקיף, שיגרם עקב השימוש
גירסה 1.00 26.10.03 סיכום באלגברה א מסמך זה הורד מהאתר.hp://uderwar.liveds.co.il אין להפיץ מסמך זה במדיה כלשהי, ללא אישור מפורש מאת המחבר. מחבר המסמך איננו אחראי לכל נזק, ישיר או עקיף, שיגרם עקב השימוש
חשבון אינפיניטסמלי מתקדם 1 סיכומי הרצאות
 חשבון אינפיניטסמלי מתקדם 1 סיכומי הרצאות 13 בינואר 211 מרצה: אילון לינדנשטראוס מתרגל: רון רוזנטל סוכם ע י: אור שריר פניות לתיקונים והערות: tnidtnid@gmail.com אתר הסיכומים שלי: http://bit.ly/huji_notes
חשבון אינפיניטסמלי מתקדם 1 סיכומי הרצאות 13 בינואר 211 מרצה: אילון לינדנשטראוס מתרגל: רון רוזנטל סוכם ע י: אור שריר פניות לתיקונים והערות: tnidtnid@gmail.com אתר הסיכומים שלי: http://bit.ly/huji_notes
חישוביות הרצאה 4 לא! זיהוי שפות ע''י מכונות טיורינג הוכחה: הגדרת! : f r
 ל' ' פונקציות פרימיטיביות רקורסיביות חישוביות הרצאה 4 האם כל פונקציה מלאה היא פרימיטיבית רקורסיבית? לא נראה שתי הוכחות: פונקציות רקורסיביות (המשך) זיהוי שפות ע''י מכונות טיורינג הוכחה קיומית: קיימות פונקציות
ל' ' פונקציות פרימיטיביות רקורסיביות חישוביות הרצאה 4 האם כל פונקציה מלאה היא פרימיטיבית רקורסיבית? לא נראה שתי הוכחות: פונקציות רקורסיביות (המשך) זיהוי שפות ע''י מכונות טיורינג הוכחה קיומית: קיימות פונקציות
מתמטיקה בדידה תרגול מס' 5
 מתמטיקה בדידה תרגול מס' 5 נושאי התרגול: פונקציות 1 פונקציות הגדרה 1.1 פונקציה f מ A (התחום) ל B (הטווח) היא קבוצה חלקית של A B המקיימת שלכל a A קיים b B יחיד כך ש. a, b f a A.f (a) = ιb B. a, b f או, בסימון
מתמטיקה בדידה תרגול מס' 5 נושאי התרגול: פונקציות 1 פונקציות הגדרה 1.1 פונקציה f מ A (התחום) ל B (הטווח) היא קבוצה חלקית של A B המקיימת שלכל a A קיים b B יחיד כך ש. a, b f a A.f (a) = ιb B. a, b f או, בסימון
תרגיל 7 פונקציות טריגונומטריות הערות
 תרגיל 7 פונקציות טריגונומטריות הערות. פתרו את המשוואות הבאות. לא מספיק למצוא פתרון אחד יש למצוא את כולם! sin ( π (א) = x sin (ב) = x cos (ג) = x tan (ד) = x) (ה) = tan x (ו) = 0 x sin (x) + sin (ז) 3 =
תרגיל 7 פונקציות טריגונומטריות הערות. פתרו את המשוואות הבאות. לא מספיק למצוא פתרון אחד יש למצוא את כולם! sin ( π (א) = x sin (ב) = x cos (ג) = x tan (ד) = x) (ה) = tan x (ו) = 0 x sin (x) + sin (ז) 3 =
תורת הקבוצות יובל קפלן סיכום הרצאות פרופ ארז לפיד בקורס "תורת הקבוצות" (80200) באוניברסיטה העברית,
 תורת הקבוצות יובל קפלן סיכום הרצאות פרופ ארז לפיד בקורס "תורת הקבוצות" (80200) באוניברסיטה העברית, 7 2006. תוכן מחברת זו הוקלד ונערך על-ידי יובל קפלן. אין המרצה אחראי לכל טעות שנפלה בו. סודר באמצעות L
תורת הקבוצות יובל קפלן סיכום הרצאות פרופ ארז לפיד בקורס "תורת הקבוצות" (80200) באוניברסיטה העברית, 7 2006. תוכן מחברת זו הוקלד ונערך על-ידי יובל קפלן. אין המרצה אחראי לכל טעות שנפלה בו. סודר באמצעות L
gcd 24,15 = 3 3 =
 מחלק משותף מקסימאלי משפט אם gcd a, b = g Z אז קיימים x, y שלמים כך ש.g = xa + yb במלים אחרות, אם ה כך ש.gcd a, b = xa + yb gcd,a b של שני משתנים הוא מספר שלם, אז קיימים שני מקדמים שלמים כאלה gcd 4,15 =
מחלק משותף מקסימאלי משפט אם gcd a, b = g Z אז קיימים x, y שלמים כך ש.g = xa + yb במלים אחרות, אם ה כך ש.gcd a, b = xa + yb gcd,a b של שני משתנים הוא מספר שלם, אז קיימים שני מקדמים שלמים כאלה gcd 4,15 =
חשבון אינפיניטסימלי 1
 חשבון אינפיניטסימלי 1 יובל קפלן סיכום הרצאות פרופ צליל סלע בקורס "חשבון אינפיניטסימלי 1" (80131) באוניברסיטה העברית, 7 2006. תוכן מחברת זו הוקלד ונערך על-ידי יובל קפלן. אין המרצה אחראי לכל טעות שנפלה בו.
חשבון אינפיניטסימלי 1 יובל קפלן סיכום הרצאות פרופ צליל סלע בקורס "חשבון אינפיניטסימלי 1" (80131) באוניברסיטה העברית, 7 2006. תוכן מחברת זו הוקלד ונערך על-ידי יובל קפלן. אין המרצה אחראי לכל טעות שנפלה בו.
בית הספר הגבוה לטכנולוגיה ירושלים אותות ומערכות הרצאות #2-3 ההערות מבוססות על אתר הקורס הפתוח של MIT 1
 בית הספר הגבוה לטכנולוגיה ירושלים אותות ומערכות הרצאות #2-3 ההערות מבוססות על אתר הקורס הפתוח של MIT 1 סקירת המצגת אותות ומערכות בזמן בדיד )DT( פונקצית מדרגה ופונקצית "הלם" )דגימה( a. ייצוג אותות בדידים
בית הספר הגבוה לטכנולוגיה ירושלים אותות ומערכות הרצאות #2-3 ההערות מבוססות על אתר הקורס הפתוח של MIT 1 סקירת המצגת אותות ומערכות בזמן בדיד )DT( פונקצית מדרגה ופונקצית "הלם" )דגימה( a. ייצוג אותות בדידים
{ : Halts on every input}
 אוטומטים - תרגול 13: רדוקציות, משפט רייס וחזרה למבחן E תכונה תכונה הינה אוסף השפות מעל.(property המקיימות תנאים מסוימים (תכונה במובן של Σ תכונה לא טריביאלית: תכונה היא תכונה לא טריוויאלית אם היא מקיימת:.
אוטומטים - תרגול 13: רדוקציות, משפט רייס וחזרה למבחן E תכונה תכונה הינה אוסף השפות מעל.(property המקיימות תנאים מסוימים (תכונה במובן של Σ תכונה לא טריביאלית: תכונה היא תכונה לא טריוויאלית אם היא מקיימת:.
תשובות מלאות לבחינת הבגרות במתמטיקה מועד ג' תשע"ד, מיום 0/8/0610 שאלונים: 315, מוצע על ידי בית הספר לבגרות ולפסיכומטרי של אבירם פלדמן
 תשובות מלאות לבחינת הבגרות במתמטיקה מועד ג' תשע"ד, מיום 0/8/0610 שאלונים: 315, 635865 מוצע על ידי בית הספר לבגרות ולפסיכומטרי של אבירם פלדמן שאלה מספר 1 נתון: 1. סדרה חשבונית שיש בה n איברים...2 3. האיבר
תשובות מלאות לבחינת הבגרות במתמטיקה מועד ג' תשע"ד, מיום 0/8/0610 שאלונים: 315, 635865 מוצע על ידי בית הספר לבגרות ולפסיכומטרי של אבירם פלדמן שאלה מספר 1 נתון: 1. סדרה חשבונית שיש בה n איברים...2 3. האיבר
פולינומים אורתוגונליים
 פולינומים אורתוגונליים מרצה: פרופ' זינובי גרינשפון סיכום: אלון צ'רני הקורס ניתן בסמסטר אביב 03, בר אילן פולינומים אורתוגונאליים תוכן עניינים תאריך 3.3.3 הרצאה מרחב מכפלה פנימית (הגדרה, תכונות, דוגמאות)
פולינומים אורתוגונליים מרצה: פרופ' זינובי גרינשפון סיכום: אלון צ'רני הקורס ניתן בסמסטר אביב 03, בר אילן פולינומים אורתוגונאליים תוכן עניינים תאריך 3.3.3 הרצאה מרחב מכפלה פנימית (הגדרה, תכונות, דוגמאות)
אלגברה לינארית 1 יובל קפלן
 אלגברה לינארית 1 יובל קפלן מחברת סיכום הרצאות ד"ר אלי בגנו בקורס "אלגברה לינארית 1" (80134) באוניברסיטה העברית, 7 2006 תוכן מחברת זו הוקלד ונערך על-ידי יובל קפלן אין המרצה אחראי לכל טעות שנפלה בו סודר
אלגברה לינארית 1 יובל קפלן מחברת סיכום הרצאות ד"ר אלי בגנו בקורס "אלגברה לינארית 1" (80134) באוניברסיטה העברית, 7 2006 תוכן מחברת זו הוקלד ונערך על-ידי יובל קפלן אין המרצה אחראי לכל טעות שנפלה בו סודר
טענה חשובה : העתקה לינארית הינה חד חד ערכית האפס ב- הוא הוקטור היחיד שמועתק לוקטור אפס של. נקבל מחד חד הערכיות כי בהכרח.
 1 תשע'א תירגול 8 אלגברה לינארית 1 טענה חשובה : העתקה לינארית הינה חד חד ערכית האפס ב- הוא הוקטור היחיד שמועתק לוקטור אפס של וקטור אם הוכחה: חד חד ערכית ויהי כך ש מכיוון שגם נקבל מחד חד הערכיות כי בהכרח
1 תשע'א תירגול 8 אלגברה לינארית 1 טענה חשובה : העתקה לינארית הינה חד חד ערכית האפס ב- הוא הוקטור היחיד שמועתק לוקטור אפס של וקטור אם הוכחה: חד חד ערכית ויהי כך ש מכיוון שגם נקבל מחד חד הערכיות כי בהכרח
(Derivative) של פונקציה
 נגזרת Drivtiv של פונקציה t הנגזרת היא המושג החשוב בקורס, ולה חשיבות מעשית רבה היא מכמתת את קצב השינוי של תופעה כלשהי פיסיקלית, כלכלית, וויזואלית דוגמאות: מהירות של עצם היא קצב השינוי במקומו, ולכן המהירות
נגזרת Drivtiv של פונקציה t הנגזרת היא המושג החשוב בקורס, ולה חשיבות מעשית רבה היא מכמתת את קצב השינוי של תופעה כלשהי פיסיקלית, כלכלית, וויזואלית דוגמאות: מהירות של עצם היא קצב השינוי במקומו, ולכן המהירות
סיכום- בעיות מינימוםמקסימום - שאלון 806
 סיכום- בעיות מינימוםמקסימום - שאלון 806 בבעיותמינימום מקסימוםישלחפשאתנקודותהמינימוםהמוחלטוהמקסימוםהמוחלט. בשאלות מינימוםמקסימוםחובהלהראותבעזרתטבלה אובעזרתנגזרתשנייהשאכן מדובר עלמינימוםאומקסימום. לצורךקיצורהתהליך,
סיכום- בעיות מינימוםמקסימום - שאלון 806 בבעיותמינימום מקסימוםישלחפשאתנקודותהמינימוםהמוחלטוהמקסימוםהמוחלט. בשאלות מינימוםמקסימוםחובהלהראותבעזרתטבלה אובעזרתנגזרתשנייהשאכן מדובר עלמינימוםאומקסימום. לצורךקיצורהתהליך,
הגדרה 0.1 טיעון הוא תקף אם בכל פעם שההנחות נכונות גם המסקנה נכונה.
 1 לוגיקה סיכום הגדרות משפטים ודברים חשובים אחרים תודה רבה לניצן פומרנץ על הסיכום הכולל של החומר הקדמה הגדרה 0.1 טיעון הוא תקף אם בכל פעם שההנחות נכונות גם המסקנה נכונה. הערה 0.2 נשים לב שלכל שפה יש רובד
1 לוגיקה סיכום הגדרות משפטים ודברים חשובים אחרים תודה רבה לניצן פומרנץ על הסיכום הכולל של החומר הקדמה הגדרה 0.1 טיעון הוא תקף אם בכל פעם שההנחות נכונות גם המסקנה נכונה. הערה 0.2 נשים לב שלכל שפה יש רובד
חשבון אינפיניטסמלי 2 סיכומי הרצאות
 חשבון אינפיניטסמלי סיכומי הרצאות 9 ביולי מרצה: פרופ מתניה בן ארצי מתרגל: מני אקא mennyk@mth.huji.c.il סוכם ע י: אור שריר פניות לתיקונים והערות: tnidtnid@gmil.com הערה לקראת המבחנים כרגע חסרים מספר דברים
חשבון אינפיניטסמלי סיכומי הרצאות 9 ביולי מרצה: פרופ מתניה בן ארצי מתרגל: מני אקא mennyk@mth.huji.c.il סוכם ע י: אור שריר פניות לתיקונים והערות: tnidtnid@gmil.com הערה לקראת המבחנים כרגע חסרים מספר דברים
חשבון אינפיניטסימלי 1 סיכום הרצאות באוניברסיטה חיפה, חוג לסטטיסטיקה.
 חשבון אינפיניטסימלי 1 סיכום הרצאות באוניברסיטה חיפה, חוג לסטטיסטיקה. מרצה: למברג דן תוכן העניינים 3 מספרים ממשיים 1 3.................................. סימונים 1. 1 3..................................
חשבון אינפיניטסימלי 1 סיכום הרצאות באוניברסיטה חיפה, חוג לסטטיסטיקה. מרצה: למברג דן תוכן העניינים 3 מספרים ממשיים 1 3.................................. סימונים 1. 1 3..................................
פונקציות מרוכבות בדצמבר 2012
 פונקציות מרוכבות 80519 אור דגמי, or@digmi.org 30 בדצמבר 2012 אתר אינטרנט: http://digmi.org סיכום הרצאות של פרופ גנאדי לוין בשנת לימודים 2013 מייל של המרצב: levin@math.huji.ac.il אפשר לקבוע פגישה. הקורסלאמבוססעלאףספרספציפי,
פונקציות מרוכבות 80519 אור דגמי, or@digmi.org 30 בדצמבר 2012 אתר אינטרנט: http://digmi.org סיכום הרצאות של פרופ גנאדי לוין בשנת לימודים 2013 מייל של המרצב: levin@math.huji.ac.il אפשר לקבוע פגישה. הקורסלאמבוססעלאףספרספציפי,
gra לא שימושי -rad רדיינים. רדיין = רק ברדיינים. נניח שיש לנו משולש ישר זוית. היחס בין שתי הצלעות שמול הזוית הישרה, נקבע ע"י הזוית.
 A-PDF MERGER DEMO 56 פונקציות טריגונומטריות במחשבון בד"כ יש אופציות: deg מעלות מניח חלוקת המעגל ל 6 חלקים, כל אחד מעלה למה עשו 6? זה מספר עם הרבה מחלקים וזה גם קרוב ל 65 6 π π 6 π π α α α 6 8 π 6 57 ~
A-PDF MERGER DEMO 56 פונקציות טריגונומטריות במחשבון בד"כ יש אופציות: deg מעלות מניח חלוקת המעגל ל 6 חלקים, כל אחד מעלה למה עשו 6? זה מספר עם הרבה מחלקים וזה גם קרוב ל 65 6 π π 6 π π α α α 6 8 π 6 57 ~
= 2. + sin(240 ) = = 3 ( tan(α) = 5 2 = sin(α) = sin(α) = 5. os(α) = + c ot(α) = π)) sin( 60 ) sin( 60 ) sin(
 א. s in(0 c os(0 s in(60 c os(0 s in(0 c os(0 s in(0 c os(0 s in(0 0 s in(70 מתאים לזהות של cos(θsin(φ : s in(θ φ s in(θcos(φ sin ( π cot ( π cos ( 4πtan ( 4π sin ( π cos ( π sin ( π cos ( 4π sin ( 4π
א. s in(0 c os(0 s in(60 c os(0 s in(0 c os(0 s in(0 c os(0 s in(0 0 s in(70 מתאים לזהות של cos(θsin(φ : s in(θ φ s in(θcos(φ sin ( π cot ( π cos ( 4πtan ( 4π sin ( π cos ( π sin ( π cos ( 4π sin ( 4π
אם לא דברנו בסוף מספיק על שרשראות עם מספר מצבים אינסופי פשוט תתעלמו מהתרגילים המתאימים.
 תרגילים בשרשראות מרקוב. + תרגילים מבחינות עבר אם לא דברנו בסוף מספיק על שרשראות עם מספר מצבים אינסופי פשוט תתעלמו מהתרגילים המתאימים..תהי Xn שרשרת מרקוב סופית עם מטריצת מעבר דו-סטוכסטית )סכום של כל עמודה
תרגילים בשרשראות מרקוב. + תרגילים מבחינות עבר אם לא דברנו בסוף מספיק על שרשראות עם מספר מצבים אינסופי פשוט תתעלמו מהתרגילים המתאימים..תהי Xn שרשרת מרקוב סופית עם מטריצת מעבר דו-סטוכסטית )סכום של כל עמודה
חשבון אינפיניטסימלי (2)
 חשבון אינפיניטסימלי (2) איתי שפירא 30 ביוני 2017 מתוך הרצאות מהאונברסיטה העברית 2017. i.j.shpir@gmil.com תוכן עניינים 1 מבוא והשלמות 5 1.1 כלל לופיטל................................. 5 1.2 חקירת פונקציות..............................
חשבון אינפיניטסימלי (2) איתי שפירא 30 ביוני 2017 מתוך הרצאות מהאונברסיטה העברית 2017. i.j.shpir@gmil.com תוכן עניינים 1 מבוא והשלמות 5 1.1 כלל לופיטל................................. 5 1.2 חקירת פונקציות..............................
סדרות - תרגילים הכנה לבגרות 5 יח"ל
 סדרות - הכנה לבגרות 5 יח"ל 5 יח"ל סדרות - הכנה לבגרות איברים ראשונים בסדרה) ) S מסמן סכום תרגיל S0 S 5, S6 בסדרה הנדסית נתון: 89 מצא את האיבר הראשון של הסדרה תרגיל גוף ראשון, בשנייה הראשונה לתנועתו עבר
סדרות - הכנה לבגרות 5 יח"ל 5 יח"ל סדרות - הכנה לבגרות איברים ראשונים בסדרה) ) S מסמן סכום תרגיל S0 S 5, S6 בסדרה הנדסית נתון: 89 מצא את האיבר הראשון של הסדרה תרגיל גוף ראשון, בשנייה הראשונה לתנועתו עבר
מערך תרגיל קורס סמסטר ב תשע ה בחשבון אינפיניטסימלי 2 למדעי המחשב
 מערך תרגיל קורס 89-33 סמסטר ב תשע ה בחשבון אינפיניטסימלי למדעי המחשב יוני 05, גרסה 0.9 מבוא נתחיל עם כמה דגשים: דף הקורס נמצא באתר.www.math-wiki.com שאלות בנוגע לחומר הלימודי מומלץ לשאול בדף השיחה באתר
מערך תרגיל קורס 89-33 סמסטר ב תשע ה בחשבון אינפיניטסימלי למדעי המחשב יוני 05, גרסה 0.9 מבוא נתחיל עם כמה דגשים: דף הקורס נמצא באתר.www.math-wiki.com שאלות בנוגע לחומר הלימודי מומלץ לשאול בדף השיחה באתר
קבוצה היא שם כללי לתיאור אוסף כלשהו של איברים.
 א{ www.sikumuna.co.il מהי קבוצה? קבוצה היא שם כללי לתיאור אוסף כלשהו של איברים. קבוצה היא מושג יסודי במתמטיקה.התיאור האינטואיטיבי של קבוצה הוא אוסף של עצמים כלשהם. העצמים הנמצאים בקבוצה הם איברי הקבוצה.
א{ www.sikumuna.co.il מהי קבוצה? קבוצה היא שם כללי לתיאור אוסף כלשהו של איברים. קבוצה היא מושג יסודי במתמטיקה.התיאור האינטואיטיבי של קבוצה הוא אוסף של עצמים כלשהם. העצמים הנמצאים בקבוצה הם איברי הקבוצה.
co ארזים 3 במרץ 2016
 אלגברה לינארית 2 א co ארזים 3 במרץ 2016 ניזכר שהגדרנו ווקטורים וערכים עצמיים של מטריצות, והראינו כי זהו מקרה פרטי של ההגדרות עבור טרנספורמציות. לכן כל המשפטים והמסקנות שהוכחנו לגבי טרנספורמציות תקפים גם
אלגברה לינארית 2 א co ארזים 3 במרץ 2016 ניזכר שהגדרנו ווקטורים וערכים עצמיים של מטריצות, והראינו כי זהו מקרה פרטי של ההגדרות עבור טרנספורמציות. לכן כל המשפטים והמסקנות שהוכחנו לגבי טרנספורמציות תקפים גם
אלגברה ליניארית 1 א' פתרון 7
 אלגברה ליניארית 1 א' פתרון 7 2 1 1 1 0 1 1 0 1 0 2 1 1 0 1 0 2 1 2 1 1 0 2 1 0 1 1 3 1 2 3 1 2 0 1 5 1 0 1 1 0 1 0 1 1 0 0 1 0 1 1 0 0 1 0 0 4 0 0 0.1 עבור :A לכן = 3.rkA עבור B: נבצע פעולות עמודה אלמנטריות
אלגברה ליניארית 1 א' פתרון 7 2 1 1 1 0 1 1 0 1 0 2 1 1 0 1 0 2 1 2 1 1 0 2 1 0 1 1 3 1 2 3 1 2 0 1 5 1 0 1 1 0 1 0 1 1 0 0 1 0 1 1 0 0 1 0 0 4 0 0 0.1 עבור :A לכן = 3.rkA עבור B: נבצע פעולות עמודה אלמנטריות
הסקה סטטיסטית/תקציר/תלמה לויתן
 הסקה סטטיסטית/תקציר/תלמה לויתן בניסוי אקראי נמדד ערכו של משתנה כמותי משתנה המחקר ואולם התפלגות המשתנה אינה ידועה החוקר מעוניין לענות על שאלות הנוגעות לערכי הנחות: - משפחת ההתפלגות של ידועה (ניווכח שזה
הסקה סטטיסטית/תקציר/תלמה לויתן בניסוי אקראי נמדד ערכו של משתנה כמותי משתנה המחקר ואולם התפלגות המשתנה אינה ידועה החוקר מעוניין לענות על שאלות הנוגעות לערכי הנחות: - משפחת ההתפלגות של ידועה (ניווכח שזה
הרצאה תרגילים סמינר תורת המספרים, סמסטר אביב פרופ' יעקב ורשבסקי
 הרצאה תרגילים סמינר תורת המספרים, סמסטר אביב 2011 2010 פרופ' יעקב ורשבסקי אסף כץ 15//11 1 סמל לזנדר יהי מספר שלם קבוע, ו K שדה גלובלי המכיל את חבורת שורשי היחידה מסדר µ. תהי S קבוצת הראשוניים הארכימדיים
הרצאה תרגילים סמינר תורת המספרים, סמסטר אביב 2011 2010 פרופ' יעקב ורשבסקי אסף כץ 15//11 1 סמל לזנדר יהי מספר שלם קבוע, ו K שדה גלובלי המכיל את חבורת שורשי היחידה מסדר µ. תהי S קבוצת הראשוניים הארכימדיים
פתרונות מלאים אלגברה 1 מ בחן אמצע חורף תשס"ג מטריצה הפיכה ב- הפיכה סקלרית, לכן A = αi
 פתרונות מלאים אלגברה מ - 4 - בחן אמצע חורף תשס"ג -.. משך הבחינה :.5 שעות. שאלה מס' היא שאלת תרגילי בית. אין להשתמש בחומר עזר או מחשבונים. יש לענות על כל שאלה בדף נפרד ולנמק את התשובות. נא לרשום את השם
פתרונות מלאים אלגברה מ - 4 - בחן אמצע חורף תשס"ג -.. משך הבחינה :.5 שעות. שאלה מס' היא שאלת תרגילי בית. אין להשתמש בחומר עזר או מחשבונים. יש לענות על כל שאלה בדף נפרד ולנמק את התשובות. נא לרשום את השם
חשבון אינפיניטסימלי מתקדם II 21 ביוני 2012
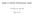 חשבון אינפיניטסימלי מתקדם 836 II אור דגמי, or@digmi.org ביוני אתר אינטרנט: http://digmi.org סיכום הרצאות של פרופ ארז לפיד בשנת לימודים נושאים לקורס. המרחב.C(K). קירוב ע י פולינומים, משפט Stone-Weirstrss
חשבון אינפיניטסימלי מתקדם 836 II אור דגמי, or@digmi.org ביוני אתר אינטרנט: http://digmi.org סיכום הרצאות של פרופ ארז לפיד בשנת לימודים נושאים לקורס. המרחב.C(K). קירוב ע י פולינומים, משפט Stone-Weirstrss
דף סיכום אלגברה לינארית
 דף סיכום אלגברה לינארית מרחבי עמודות, שורות, אפס: = = c + c + + c k k כל פתרון של המערכת : A=b נתונה מטריצה :m = מרחב השורות של המטריצה spa = spa מרחב העמודות של המטריצה { r, r, rm { c, c, c מרחב הפתרונות
דף סיכום אלגברה לינארית מרחבי עמודות, שורות, אפס: = = c + c + + c k k כל פתרון של המערכת : A=b נתונה מטריצה :m = מרחב השורות של המטריצה spa = spa מרחב העמודות של המטריצה { r, r, rm { c, c, c מרחב הפתרונות
אלגברה לינארית 2 יובל קפלן סיכום הרצאות מר שמואל ברגר בקורס "אלגברה לינארית 2" (80135) באוניברסיטה העברית,
 אלגברה לינארית 2 יובל קפלן סיכום הרצאות מר שמואל ברגר בקורס "אלגברה לינארית 2" (80135 באוניברסיטה העברית, 7 2006 תוכן מחברת זו הוקלד ונערך על-ידי יובל קפלן אין המרצה אחראי לכל טעות שנפלה בו סודר באמצעות
אלגברה לינארית 2 יובל קפלן סיכום הרצאות מר שמואל ברגר בקורס "אלגברה לינארית 2" (80135 באוניברסיטה העברית, 7 2006 תוכן מחברת זו הוקלד ונערך על-ידי יובל קפלן אין המרצה אחראי לכל טעות שנפלה בו סודר באמצעות
א הקיטסי ' טטסל אובמ רלדנ הינור בג '
 מבוא לסטטיסטיקה א' נדלר רוניה גב' מדדי פיזור Varablty Measures of עד עתה עסקנו במדדים מרכזיים. אולם, אחת התכונות החשובות של ההתפלגות, מלבד מיקום מרכזי, הוא מידת הפיזור של ההתפלגות. יכולות להיות מספר התפלגויות
מבוא לסטטיסטיקה א' נדלר רוניה גב' מדדי פיזור Varablty Measures of עד עתה עסקנו במדדים מרכזיים. אולם, אחת התכונות החשובות של ההתפלגות, מלבד מיקום מרכזי, הוא מידת הפיזור של ההתפלגות. יכולות להיות מספר התפלגויות
אינפי 1 פרופ י. בנימיני אביב תש ע
 אינפי 1 פרופ י. בנימיני אביב תש ע ברשימות ראשוניות אלה יש בוודאי שגיאות רבות: טעויות דפוס, אי בהירויות ואפילו טעויות מתמטיות. תודתי נתונה מראש לכל מי שיעביר אלי הערות ותיקונים מכל סוג. בכתיבת הרשימות נעזרתי
אינפי 1 פרופ י. בנימיני אביב תש ע ברשימות ראשוניות אלה יש בוודאי שגיאות רבות: טעויות דפוס, אי בהירויות ואפילו טעויות מתמטיות. תודתי נתונה מראש לכל מי שיעביר אלי הערות ותיקונים מכל סוג. בכתיבת הרשימות נעזרתי
פתרון תרגיל בית 6 מבוא לתורת החבורות סמסטר א תשע ז
 פתרון תרגיל בית 6 מבוא לתורת החבורות 88-211 סמסטר א תשע ז הוראות בהגשת הפתרון יש לרשום שם מלא, מספר ת ז ומספר קבוצת תרגול. תאריך הגשת התרגיל הוא בתרגול בשבוע המתחיל בתאריך ג טבת ה תשע ז, 1.1.2017. שאלות
פתרון תרגיל בית 6 מבוא לתורת החבורות 88-211 סמסטר א תשע ז הוראות בהגשת הפתרון יש לרשום שם מלא, מספר ת ז ומספר קבוצת תרגול. תאריך הגשת התרגיל הוא בתרגול בשבוע המתחיל בתאריך ג טבת ה תשע ז, 1.1.2017. שאלות
תרגול 1: מד"ר 1 הפרדת משתנים משוואות,, 0 הומוגניות משוואות מציבים לינאריות כאשר 0 המשוואה הומוגנית של כפונקציה של בלבד. משוואות ברנולי מסמנים או:
 אריאל סטולרמן 1 סיכומי תרגולים: סיכומים במד"ר 1 סמסטר קיץ 2009 (פרופ' ודים אוסטפנקו) תרגול 1: סוגים של מד"ר ודרכי פתרון: חשוב: לשים לב לקבוע c המצורף כתוצאה מאינטגרציה דרך פתרון שיטה צורה הפרדת משתנים
אריאל סטולרמן 1 סיכומי תרגולים: סיכומים במד"ר 1 סמסטר קיץ 2009 (פרופ' ודים אוסטפנקו) תרגול 1: סוגים של מד"ר ודרכי פתרון: חשוב: לשים לב לקבוע c המצורף כתוצאה מאינטגרציה דרך פתרון שיטה צורה הפרדת משתנים
תרגול מס' 1 3 בנובמבר 2012
 תרגול מס' 1 3 בנובמבר 2012 1 מערכת המספרים השלמים בשיעור הקרוב אנו נעסוק בקבוצת המספרים השלמים Z עם הפעולות (+) ו ( ), ויחס סדר (>) או ( ). כל התכונות הרגילות והידועות של השלמים מתקיימות: חוק הקיבוץ (אסוציאטיביות),
תרגול מס' 1 3 בנובמבר 2012 1 מערכת המספרים השלמים בשיעור הקרוב אנו נעסוק בקבוצת המספרים השלמים Z עם הפעולות (+) ו ( ), ויחס סדר (>) או ( ). כל התכונות הרגילות והידועות של השלמים מתקיימות: חוק הקיבוץ (אסוציאטיביות),
אלגברה לינארית (1) - פתרון תרגיל 11
 אלגברה לינארית ( - פתרון תרגיל דרגו את המטריצות הבאות לפי אלגוריתם הדירוג של גאוס (א R R4 R R4 R=R+R R 3=R 3+R R=R+R R 3=R 3+R 9 4 3 7 (ב 9 4 3 7 7 4 3 9 4 3 4 R 3 R R3=R3 R R 4=R 4 R 7 4 3 9 7 4 3 8 6
אלגברה לינארית ( - פתרון תרגיל דרגו את המטריצות הבאות לפי אלגוריתם הדירוג של גאוס (א R R4 R R4 R=R+R R 3=R 3+R R=R+R R 3=R 3+R 9 4 3 7 (ב 9 4 3 7 7 4 3 9 4 3 4 R 3 R R3=R3 R R 4=R 4 R 7 4 3 9 7 4 3 8 6
שדות הגדרת השדה: חשבון מודולו n: הגדרה: שדה F הוא קבוצה שיש בין אבריה שתי פעולות משפט: יהא F שדה. משפט: יהא F שדה ו- (mod )
 שדות הגדרת השדה: הגדרה: שדה F הוא קבוצה שיש בין אבריה שתי פעולות אחת נקראת חיבור ותסומן ב + האחרת נקראת כפל ותסומן ב * כך שתתקיימנה הדרישות הבאות: a, b F a b. סגירות לחיבור: F a F a 0 0 a a a, b, c F a
שדות הגדרת השדה: הגדרה: שדה F הוא קבוצה שיש בין אבריה שתי פעולות אחת נקראת חיבור ותסומן ב + האחרת נקראת כפל ותסומן ב * כך שתתקיימנה הדרישות הבאות: a, b F a b. סגירות לחיבור: F a F a 0 0 a a a, b, c F a
אלגברה ליניארית 1 א' פתרון 2
 אלגברה ליניארית א' פתרון 3 4 3 3 7 9 3. נשתמש בכתיבה בעזרת מטריצה בכל הסעיפים. א. פתרון: 3 3 3 3 3 3 9 אז ישנו פתרון יחיד והוא = 3.x =, x =, x 3 3 הערה: אפשר גם לפתור בדרך קצת יותר ארוכה, אבל מבלי להתעסק
אלגברה ליניארית א' פתרון 3 4 3 3 7 9 3. נשתמש בכתיבה בעזרת מטריצה בכל הסעיפים. א. פתרון: 3 3 3 3 3 3 9 אז ישנו פתרון יחיד והוא = 3.x =, x =, x 3 3 הערה: אפשר גם לפתור בדרך קצת יותר ארוכה, אבל מבלי להתעסק
אוטומטים- תרגול 8 שפות חסרות הקשר
 אוטומטים- תרגול 8 שפות חסרות הקשר דקדוק חסר הקשר דקדוק חסר הקשר הנו רביעיה > S
אוטומטים- תרגול 8 שפות חסרות הקשר דקדוק חסר הקשר דקדוק חסר הקשר הנו רביעיה > S
תרגול משפט הדיברגנץ. D תחום חסום וסגור בעל שפה חלקה למדי D, ותהי F פו' וקטורית :F, R n R n אזי: נוסחת גרין I: הוכחה: F = u v כאשר u פו' סקלרית:
 משפט הדיברגנץ תחום חסום וסגור בעל שפה חלקה למדי, ותהי F פו' וקטורית :F, R n R n אזי: div(f ) dxdy = F, n dr נוסחת גרין I: uδv dxdy = u v n dr u, v dxdy הוכחה: F = (u v v, u x y ) F = u v כאשר u פו' סקלרית:
משפט הדיברגנץ תחום חסום וסגור בעל שפה חלקה למדי, ותהי F פו' וקטורית :F, R n R n אזי: div(f ) dxdy = F, n dr נוסחת גרין I: uδv dxdy = u v n dr u, v dxdy הוכחה: F = (u v v, u x y ) F = u v כאשר u פו' סקלרית:
פרק 5 טורי חזקות 5.5 טור לורן. (z z 0 ) m. c n = 1. 2πi γ (ξ z 0 ) n+1dξ, .a 1 = 1 f(z)dz בפרט,.a 2πi γ m וגם 0 0 < z z 0 < r בעיגול הנקוב z.
 פרק 5 טורי חזקות 5.5 טור לורן הגדרה 5. טורלורןסביבקוטב z מסדרm שלפונקציה( f(z הואמהצורה n m a n(z z m. למשל,טורלורן שלהפונקציה e z /z 2 סביב הוא + 2./z 2 +/z+/2+/3!z+/4!z משפט 5. תהי f פונקציה אנליטית
פרק 5 טורי חזקות 5.5 טור לורן הגדרה 5. טורלורןסביבקוטב z מסדרm שלפונקציה( f(z הואמהצורה n m a n(z z m. למשל,טורלורן שלהפונקציה e z /z 2 סביב הוא + 2./z 2 +/z+/2+/3!z+/4!z משפט 5. תהי f פונקציה אנליטית
מתמטיקה בדידה תרגול מס' 13
 מתמטיקה בדידה תרגול מס' 13 נושאי התרגול: תורת הגרפים. 1 מושגים בסיסיים נדון בגרפים מכוונים. הגדרה 1.1 גרף מכוון הוא זוג סדור E G =,V כך ש V ו E. V הגרף נקרא פשוט אם E יחס אי רפלקסיבי. כלומר, גם ללא לולאות.
מתמטיקה בדידה תרגול מס' 13 נושאי התרגול: תורת הגרפים. 1 מושגים בסיסיים נדון בגרפים מכוונים. הגדרה 1.1 גרף מכוון הוא זוג סדור E G =,V כך ש V ו E. V הגרף נקרא פשוט אם E יחס אי רפלקסיבי. כלומר, גם ללא לולאות.
מודלים חישוביים תרגולמס 5
 מודלים חישוביים תרגולמס 5 30 במרץ 2016 נושאי התרגול: דקדוקים חסרי הקשר. למת הניפוח לשפות חסרות הקשר. פעולות סגור לשפות חסרות הקשר. 1 דקדוקים חסרי הקשר נזכיר כי דקדוק חסר הקשר הוא רביעיה =(V,Σ,R,S) G, כך
מודלים חישוביים תרגולמס 5 30 במרץ 2016 נושאי התרגול: דקדוקים חסרי הקשר. למת הניפוח לשפות חסרות הקשר. פעולות סגור לשפות חסרות הקשר. 1 דקדוקים חסרי הקשר נזכיר כי דקדוק חסר הקשר הוא רביעיה =(V,Σ,R,S) G, כך
[ ] Observability, Controllability תרגול 6. ( t) t t קונטרולבילית H למימדים!!) והאובז' דוגמא: x. נשתמש בעובדה ש ) SS rank( S) = rank( עבור מטריצה m
![[ ] Observability, Controllability תרגול 6. ( t) t t קונטרולבילית H למימדים!!) והאובז' דוגמא: x. נשתמש בעובדה ש ) SS rank( S) = rank( עבור מטריצה m [ ] Observability, Controllability תרגול 6. ( t) t t קונטרולבילית H למימדים!!) והאובז' דוגמא: x. נשתמש בעובדה ש ) SS rank( S) = rank( עבור מטריצה m](/thumbs/72/67672989.jpg) Observabiliy, Conrollabiliy תרגול 6 אובזרווביליות אם בכל רגע ניתן לשחזר את ( (ומכאן גם את המצב לאורך זמן, מתוך ידיעת הכניסה והיציאה עד לרגע, וזה עבור כל צמד כניסה יציאה, אז המערכת אובזרוובילית. קונטרולביליות
Observabiliy, Conrollabiliy תרגול 6 אובזרווביליות אם בכל רגע ניתן לשחזר את ( (ומכאן גם את המצב לאורך זמן, מתוך ידיעת הכניסה והיציאה עד לרגע, וזה עבור כל צמד כניסה יציאה, אז המערכת אובזרוובילית. קונטרולביליות
תורת הקבוצות ניר אדר ניר אדר.
 גירסה 101 2432010 גירסה 100 6122003 תורת הקבוצות מסמך זה הורד מהאתר http://wwwunderwarcoil אין להפיץ מסמך זה במדיה כלשהי, ללא אישור מפורש מאת המחבר מחבר המסמך איננו אחראי לכל נזק, ישיר או עקיף, שיגרם עקב
גירסה 101 2432010 גירסה 100 6122003 תורת הקבוצות מסמך זה הורד מהאתר http://wwwunderwarcoil אין להפיץ מסמך זה במדיה כלשהי, ללא אישור מפורש מאת המחבר מחבר המסמך איננו אחראי לכל נזק, ישיר או עקיף, שיגרם עקב
