ΤΡΟΠΟΠΟΙΗΣΕΙΣ ΤΟΥ ΣΧΗΜΑΤΟΣ ΠΑΡΑΜΕΤΡΟΠΟΙΗΣΗΣ ΚΑΤΑΚΟΡΥΦΩΝ ΚΙΝΗΣΕΩΝ ΜΕΤΑΦΟΡΑΣ KAIN FRITSCH ΚΑΙ ΙΕΡΕΥΝΗΣΗ ΤΗΣ ΠΡΟΓΝΩΣΤΙΚΗΣ ΤΟΥ ΙΚΑΝΟΤΗΤΑΣ
|
|
|
- Παντελεήμων Δελή
- 9 χρόνια πριν
- Προβολές:
Transcript
1 ΤΡΟΠΟΠΟΙΗΣΕΙΣ ΤΟΥ ΣΧΗΜΑΤΟΣ ΠΑΡΑΜΕΤΡΟΠΟΙΗΣΗΣ ΚΑΤΑΚΟΡΥΦΩΝ ΚΙΝΗΣΕΩΝ ΜΕΤΑΦΟΡΑΣ KAIN FRITSCH ΚΑΙ ΙΕΡΕΥΝΗΣΗ ΤΗΣ ΠΡΟΓΝΩΣΤΙΚΗΣ ΤΟΥ ΙΚΑΝΟΤΗΤΑΣ Ν. ΜΑΖΑΡΑΚΗΣ 1,2, Β. ΚΟΤΡΩΝΗ 2, Κ. ΛΑΓΟΥΒΑΡ ΟΣ 2 ΚΑΙ Α. ΑΡΓΥΡΙΟΥ 1 1 Πανεπιστηµιο Πατρών Τµήµα Φυσικής. 2 Εθνικό Αστεροσκοπείο Αθηνών. ΠΕΡΙΛΗΨΗ Στην παρούσα εργασία διερευνάται η προγνωστική ικανότητα βροχής του αριθµητικού µοντέλου ΜΜ5, χρησιµοποιώντας το σχήµα παραµετροποίησης των κατακόρυφων κινήσεων µεταφοράς των Kain Fritch και διαφόρων τροποποιήσεων του. Η µελέτη αφορά 2 ηµέρες της θερµής περιόδου των ετών 25-27, κατά τις οποίες παρατηρήθηκαν έντονες βροχοπτώσεις πάνω από τον Ελλαδικό χώρο. Οι τροποποιήσεις στο σχήµα παραµετροποίησης που εξετάζονται αφορούν: (i) στη µεγιστοποίηση της παραµέτρου αποδοτικότητας βροχόπτωσης, (ii) στην αλλαγή του χρονικού βήµατος εφαρµογής του σχήµατος, (iii) στην εξώθηση του σχήµατος να παράγει περισσότερη/λιγότερη νεφική µάζα εξαιτίας των κατακόρυφων κινήσεων µεταφοράς και (iv) την τροποποίηση της κατακόρυφης κατατοµής των ανοδικών ρευµάτων στο µοντέλο νέφους που χρησιµοποιείται στο σχήµα. THE SENSITIVITY OF NUMERICAL FORECASTS TO VARIOUS MODIFICATIONS OF THE KAIN FRITSCH CONVECTIVE PARAMETERIZATION SCHEME DURING THE WARM PERIOD N. MΑΖΑRAΚIS 1,2, Β. ΚΟΤRONI 2, Κ. LΑGOUVΑRDOS 2 AND Α. ΑRGIRΙΟΥ 1 1 University of Patras Department of Physics. 2 National Observatory of Athens. ABSTRACT The sensitivity of numerical model quantitative precipitation forecasts to the various modifications of the Kain Fritsch (KF) convective parameterization scheme (CPS) is examined for twenty selected cases characterized by intense convective activity and widespread precipitation over Greece, during the warm period of Τhe study is conducted using MM5 model. The modifications include: (i) maximization of the convective scheme precipitation efficiency, (ii) variation of the convective time step, (iii) forcing of the convective scheme to produce more/less cloud material and (iv) alteration of the vertical profile of updraft mass flux detrainment. 1. ΕΙΣΑΓΩΓΗ Μία από τις µεγαλύτερες δυσκολίες αλλά και προκλήσεις της αριθµητικής πρόγνωσης καιρού είναι η ορθή πρόγνωση της βροχόπτωσης. Η δυσκολία αυτή, σε ότι αφορά τον Ελλαδικό χώρο, γίνεται εντονότερη κατά τη θερµή περίοδο του έτους που η µετωπική δραστηριότητα είναι µειωµένη και το κυρίαρχο ρόλο στη διαµόρφωση των γεγονότων βροχής παίζουν πλέον οι κατακόρυφες κινήσεις µεταφοράς (Mazarakis et al., 28). Τα κυριότερα σφάλµατα που κάνουν τα αριθµητικά µοντέλα σε ότι αφορά την πρόγνωση του
2 υετού είναι: (i) η λανθασµένη εκτίµηση της ποσότητας του, (ii) η λανθασµένη χωροθέτηση του, (iii) τα λάθη στη διάρκεια και τη γενικότερη εξέλιξη των φαινοµένων, ενώ σε αρκετές περιπτώσεις το αριθµητικό µοντέλο είτε δίνει υετό σε περιοχές που τελικά δεν βρέχει ή ακόµα συχνότερα αποτυγχάνει να προσοµοιώσει την εκδήλωση υετού σε περιοχές που τελικά αυτός παρατηρείται. Οι αδυναµίες των αριθµητικών µοντέλων µπορούν να αποδοθούν σε διάφορες αιτίες καθώς η λειτουργία τους βασίζεται σε ένα πλήθος παραδοχών, συµβάσεων και απλοποιήσεων, οι οποίες έχουν άµεσο αντίκτυπο στο τελικό αποτέλεσµα της πρόγνωσης. Σηµαντικότατο ρόλο στη διαµόρφωση του προγνωστικού πεδίου του υετού παίζει το σχήµα παραµετροποίησης των κατακόρυφων κινήσεων µεταφοράς (ΠΚΚΜ), καθώς όχι µόνο η επιλογή του, αλλά και η διαφορετική παραµετροποίηση του, όπως θα δούµε παρακάτω, έχουν άµεσο αντίκτυπο στην πρόγνωση. Ανάµεσα στα διάφορα σχήµατα ΠΚΚΜ (Mazarakis et al., 29), τα καλύτερα αποτελέσµατα σε περιπτώσεις που παρατηρείται έντονη καταιγιδοφόρος θερινή δραστηριότητα πάνω από τον ελλαδικό χώρο, δίνει το σχήµα των Kain Fritsch (KF), (Kain and Fritsch, 1993). Ωστόσο η εφαρµογή του συγκεκριµένου σχήµατος παρουσιάζει κάποια µειονεκτήµατα τα οποία τελικά οδηγούν σε συστηµατικά λάθη στην εκτίµηση του προβλεπόµενου υετού. Ένα ίσως από τα σηµαντικότερα, είναι η υποεκτίµηση της ποσότητας του εκτιµώµενου υετού, σφάλµα το οποίο παρουσιάζεται σε όλα τα εύρη τιµών µε εξαίρεση µόνο την ασθενή βροχόπτωση. Η παρούσα εργασία είναι αφιερωµένη στην προσπάθεια βελτίωσης της προγνωστικής ικανότητας του αριθµητικού µοντέλου MM5 κατά τη διάρκεια της θερµής περιόδου. Για το λόγο αυτό, χρησιµοποιώντας το σχήµα KF στην γνήσια έκδοση του, όπως τροποποιήθηκε από τον Kain το 24 (Kain 24), και πλήθος άλλων τροποποιήσεων, γίνεται προσπάθεια να διερευνηθεί κατά πόσο µπορούν οι τροποποιήσεις που εφαρµόζονται να βελτιώσουν την πρόγνωση του υετού. 2. ΠΡΟΓΝΩΣΤΙΚΟ ΜΟΝΤΕΛΟ Ε ΟΜΕΝΑ ΚΑΙ ΜΕΘΟ ΟΛΟΓΙΑ ΕΠΑΛΗΘΕΥΣΗΣ Το αριθµητικό προγνωστικό µοντέλο που χρησιµοποιείται στην παρούσα µελέτη είναι το MM5. Η εφαρµογή του µοντέλου γίνεται σε δύο πλέγµατα: το εξωτερικό, µε ανάλυση 24 km που περιλαµβάνει σχεδόν το σύνολο της Ευρώπης και τη Μεσόγειο και το εσωτερικό, µε ανάλυση 8 km που περιλαµβάνει την ευρύτερη περιοχή του Ελλαδικού χώρου (34 Β 42 Β, 18 Α 3 Α). Ως αρχικές και οριακές συνθήκες για τις προσοµοιώσεις χρησιµοποιήθηκαν οι αναλύσεις για τις : UTC της κάθε µέρας και οι προγνώσεις από t+6 h ως t+48 h αντίστοιχα από το παγκόσµιο µοντέλο NCEP/GFS. Το σχήµα ΠΚΚΜ που χρησιµοποιείται είναι το σχήµα των Kain Fritsch στη γνήσια έκδοση του, ενώ παράλληλα εκτελούνται και οκτώ επιπλέον προσοµοιώσεις για κάθε εξεταζόµενη περίπτωση (συνολικά πραγµατοποιήθηκαν και αναλύθηκαν εννέα προσοµοιώσεις για κάθε µία εκ των είκοσι εξεταζόµενων περιπτώσεων, δηλαδή 18 προσοµοιώσεις στο σύνολο), χρησιµοποιώντας κάθε φορά διαφορετική τροποποίηση του σχήµατος. Επιγραµµατικά, οι τροποποιήσεις που χρησιµοποιούνται είναι η µεγιστοποίηση της αποδοτικότητας της βροχόπτωσης (Spenser and Stensrud, 1998), η αλλαγή του χρονικού βήµατος ανάκλησης του σχήµατος (Yang and Arritt, 21; Gallus and Segal 21), η µεταβολή του ρυθµού παραγωγής υετού από το σχήµα, οι αλλαγές στην συνάρτηση ενεργοποίησης του σχήµατος και η τροποποίηση της κατακόρυφης κατατοµής των ανοδικών ρευµάτων (Anderson et al., 2
3 27). Ο αριθµός των εξεταζόµενων περιπτώσεων είναι 2 και έχουν επιλεγεί στο χρονικό διάστηµα από 15 Μαΐου έως 3 Σεπτεµβρίου των ετών Οι εξάωρες αθροιστικές βροχοπτώσεις που προσοµοιώθηκαν µε το µοντέλο MM5 συγκρίθηκαν µε τις παρατηρήσεις βροχόπτωσης από 116 µετεωρολογικούς σταθµούς, της Εθνικής Μετεωρολογικής Υπηρεσίας και του Εθνικού Αστεροσκοπείου Αθηνών. Η στατιστική ανάλυση περιλαµβάνει τον υπολογισµό των παρακάτω στατιστικών δεικτών: µεροληψία (Bias), µέσο απόλυτο σφάλµα (Mean Absolute Error) και κρίσιµο δείκτη επιτυχίας (Threat) για τα ακόλουθα πέντε διαφορετικά κατώφλια ύψους βροχής:.1, 1, 2.5, 5 και 1 mm. 3. ΠΕΡΙΓΡΑΦΗ ΤΡΟΠΟΠΟΙΗΣΕΩΝ ΤΟΥ ΣΧΗΜΑΤΟΣ KAIN - FRITSCH 3.1 Μεγιστοποίηση της αποδοτικότητας της βροχόπτωσης (PEF9) Στο γνήσιο σχήµα η αποδοτικότητα της βροχόπτωσης (precipitation efficiency) κυµαίνεται από.1 έως.9. Στην παρούσα τροποποίηση έχουµε απλά θέσει την αποδοτικότητα της βροχόπτωσης σταθερή και ίση µε τη µέγιστη τιµή της, δηλαδή.9. Αυτό πρακτικά σηµαίνει ότι το 9% των υδρατµών που συµπυκνώνονται στο νέφος µετατρέπονται σε υετό, αναγκάζοντας έτσι το σχήµα να παράξει τη µέγιστη δυνατή ποσότητα υετού. 3.2 Αλλαγή του χρονικού βήµατος ανάκλησης του σχήµατος (1ΜΙΝ, 15ΜΙΝ) Στην επιχειρησιακή αλυσίδα πρόγνωσης η ρουτίνα του σχήµατος ΠΚΚΜ των Kain Fritsch καλείται από το αριθµητικό µοντέλο µε χρονικό βήµα τα 5 λεπτά (convective time step). Στην παρούσα τροποποίηση ελέγχονται δύο διαφορετικοί χρόνοι: (i) θέτουµε το χρονικό βήµα ίσο µε 1 λεπτό και (ii) θέτουµε το χρονικό βήµα ίσο µε 15 λεπτά. 3.3 Μεταβολή του ρυθµού παραγωγής υετού από το σχήµα (, RATE1) Στο σχήµα των Kain Fritsch ο υπολογισµός του παραγόµενου υετού δq c που οφείλεται στις κατακόρυφες κινήσεις µεταφοράς βασίζεται στην σχέση των Ogura and Cho (1973): δz δqc = qc 1 exp c (1) w όπου q c η αναλογία µίγµατος των υδροσταγόνων του νέφους, w η µέση κατακόρυφη ταχύτητα στο στρώµα δz και c είναι µία σταθερά η οποία αντιστοιχεί στον ρυθµό µε τον οποίο οι υδροσταγόνες του νέφους µετατρέπονται σε υδροσταγόνες υετού. Όσο υψηλότερες τιµές παίρνει η σταθερά c, τόσο πιο γρήγορα παράγονται οι υδροσταγόνες που φτάνουν τελικά στο έδαφος ως υετός. Στο γνήσιο σχήµα η σταθερά c ισούται µε.1. Στην παρούσα εργασία θέλοντας να αντιµετωπίσουµε την έντονη τάση υποεκτίµησης του αριθµητικού µοντέλου στα µέτρια και µεγάλα ποσά βροχόπτωσης, κατά τη διάρκεια των θερινών καταιγίδων επιλέχθηκε η τιµή.1. Επειδή όµως σε περιπτώσεις που η 3
4 καταιγιδοφόρος δραστηριότητα συνεχίζεται για αρκετές ώρες, η τιµή αυτή µπορεί να επιφέρει σηµαντική µείωση του παραγόµενου, από το αριθµητικό µοντέλο, υετού στις µεταγενέστερες ώρες της εξέλιξης του φαινοµένου επιλέξαµε να µελετήσουµε και τη συµπεριφορά του σχήµατος όταν ο ρυθµός c είναι ίσος µε.1. Η µείωση της σταθεράς c µπορεί να επιφέρει θετικά αποτελέσµατα σε περιπτώσεις όπου οι καταιγίδες δεν εντοπίζονται µόνο κατά τις µεσηµεριανές και απογευµατινές ώρες, αλλά συνεχίζονται και κατά τη διάρκεια της νύχτας. 3.4 Αλλαγές στη συνάρτηση ενεργοποίησης (, EAYSTRIG2) Λόγω γενικότερα της µικρής χωρικής κλίµακας που λαµβάνουν χώρα οι καταιγίδες αστάθειας κατά τη διάρκεια της θερµής περιόδου, το σχήµα ΠΚΚΜ σε αρκετές περιπτώσεις δεν ενεργοποιείται καθώς οριακά δεν ικανοποιείται το βασικό κριτήριο της συνάρτησης ενεργοποίησης, το οποίο αναφέρει ότι σε ένα πλεγµατικό στοιχείο το σχήµα KF ενεργοποιείται όταν ικανοποιείται η πρώτη συνθήκη της παρακάτω σχέσης: >, ευνοείται η αστάθεια T LCL +δτ νν - T ENV (2), ευνοείται η ευστάθεια όπου T LCL η θερµοκρασία της αέριας µάζας στη στάθµη συµπύκνωσης λόγω εξαναγκασµένης ανόδου, T ENV η θερµοκρασία περιβάλλοντος και δτ νν η διαταραχή της θερµοκρασίας (Fritsch and Chappell, 198). Στην παρούσα τροποποίηση, επιθυµώντας το σχήµα ΠΚΚΜ να ενεργοποιείται πιο εύκολα στα πλεγµατικά στοιχεία στα οποία οριακά έχουµε ευστάθεια, έχει προστεθεί στο 1 ο µέλος της σχέσης 2 ο συντελεστής.5 και ο συντελεστής 1. ώστε να αυξηθεί η πιθανότητα να ενεργοποιηθεί το σχήµα σε οριακά ευσταθείς καταστάσεις. 3.5 Τροποποίηση της κατακόρυφης κατατοµής των ανοδικών ρευµάτων () Η τελευταία τροποποίηση είναι ίσως η πιο σύνθετη από αυτές που ήδη έχουν παρουσιαστεί. Αρχικά αναπτύχθηκε για το αριθµητικό µοντέλο WRF (Weather Research and Forecasting Model) από τον Anderson (27) και µε τις κατάλληλες τροποποιήσεις προσαρµόστηκε για να λειτουργεί και στο αριθµητικό µοντέλο MM5. Ο πυρήνας της τροποποίησης είναι η αλλαγή του τρόπου εκροής των ανοδικών ρευµάτων, του µονοδιάστατου µοντέλου νέφους που χρησιµοποιείται στο σχήµα KF, στο περιβάλλον. Έτσι το επίπεδο εκροής αλλάζει και αντί του επιπέδου ισορροπίας χρησιµοποιείται το επίπεδο της ελάχιστης ισοδύναµης δυνητικής θερµοκρασίας ή διαφορετικά το στρώµα τήξης (melting layer, ML). 4. ΣΤΑΤΙΣΤΙΚΗ ΑΞΙΟΛΟΓΗΣΗ ΤΩΝ ΙΑΦΟΡΩΝ ΤΡΟΠΟΠΟΙΗΣΕΩΝ ΤΟΥ ΣΧΗΜΑΤΟΣ KAIN - FRITSCH Στην παρούσα ενότητα παρουσιάζονται τα αποτελέσµατα της στατιστικής ανάλυσης που πραγµατοποιήθηκε χρησιµοποιώντας εκτός από το γνήσιο σχήµα KF και τις οκτώ επιµέρους τροποποιήσεις. Αναλυτικά λοιπόν σε ότι αφορά τη συχνότητα µεροληψίας Β 4
5 Συχνότητα Μεροληψίας - Β 2 1,5 1,5,1 1 2,5 5 1 Κατώφλι Βροχόπτωσης (mm) PEF9 RATE1 (α) Κρίσιµος είκτης Επ ιτυχίας - C S I,8,6,4,2,1 1 2,5 5 1 Κατώφλι βροχόπτωσης (mm) PEF9 RATE1 (β) Πιθανότητα ανίχνευσης - P O D 1,8,6,4,2,1 1 2,5 5 1 Κατώφλι Βροχόπτωσης (mm) PEF9 RATE1 (γ) Λόγος Ψευδών Συναγερµών - F A R,6,4,2,1 1 2,5 5 1 Κατώφλι βροχόπτωσης (mm) PEF9 RATE1 (δ) Μέσο Απόλυτο Σφάλµα - ΜΑΕ >2 Εύρος βροχόπτωσης (mm) PEF9 RATE1 (ε) Ποσότητα µεροληψίας - Q B >2 Εύρος βροχόπτωσης (mm) ΣΧΗΜΑ 1. (α) Συχνότητα µεροληψίας (Β), (β) Κρίσιµος δείκτης επιτυχίας (CSI), (γ) Πιθανότητα ανίχνευσης (POD), (δ) Λόγος ψευδών συναγερµών (FAR), (ε) Μέσο απόλυτο σφάλµα (ΜΑΕ), (στ) ποσότητα µεροληψίας (QB). PEF9 RATE1 (στ) (σχ. 1α) βλέπουµε ότι όταν το ύψος του υετού ξεπερνάει τα 5 και τα 1 mm, η γενικότερη τάση του αριθµητικού µοντέλου να υποεκτιµά τη χωρική κατανοµή του υετού διατηρείται ανεξαρτήτως από το αν έχει χρησιµοποιηθεί η γνήσια ή µία τροποποιηµένη εκδοχή του σχήµατος. Παρόλα αυτά, για τα συγκεκριµένα κατώφλια βροχόπτωσης παρατηρούµε µία ξεκάθαρη βελτίωση της πρόγνωσης όταν αυξήσουµε το ρυθµό παραγωγής του υετού από το σχήµα παραµετροποίησης (τροποποίηση RATE1). Η συγκεκριµένη τροποποίηση δίνει εξίσου καλά αποτελέσµατα και για τα µικρότερα κατώφλια βροχόπτωσης, παρά το γεγονός ότι για την ασθενή βροχόπτωση (>.1 mm και >1 mm) υπάρχει µία µικρή υπεροχή της αύξησης του χρονικού βήµατος ανάκλησης του σχήµατος στα 15 λεπτά από τα 5 λεπτά που 5
6 χρησιµοποιούνται σαν χρονικό βήµα στο γνήσιο σχήµα. Ειδικότερα στα µεγάλα ύψη βροχής εκτός από την υπεροχή της τροποποίησης RATE1, καλύτερα αποτελέσµατα σε σύγκριση µε το γνήσιο σχήµα δίνουν επιπλέον οι τροποποιήσεις και στα 5 mm, και, και PEF9 στα 1 mm αντίστοιχα. Σε ότι αφορά τον κρίσιµο δείκτη επιτυχίας CSI (σχ. 1β), όπως ήταν αναµενόµενο οι τιµές του φθίνουν προοδευτικά µε την αύξηση του κατωφλίου βροχόπτωσης, µε τις µικρότερες τιµές (<,3) να παρατηρούνται στα µεγάλα κατώφλια βροχόπτωσης (>1 mm). Οµοίως µε τα αποτελέσµατα για το δείκτη µεροληψίας, η υπεροχή της τροποποίησης RATE1 διατηρείται για τα κατώφλια των 2.5 και των 5. mm ενώ και οι υπόλοιπες τροποποιήσεις δίνουν παρόµοια αποτελέσµατα, µε εξαίρεση την τροποποίηση και που γενικά στις µέτριες και µεγάλες βροχές οι επιδόσεις τους είναι χαµηλές. Αντίθετα στο µικρότερο κατώφλι (>.1 mm) όταν το µοντέλο εξωθηθεί να παράξει περισσότερη νεφική µάζα () είναι ξεκάθαρη η βελτίωση της προγνωστικής ικανότητάς του. Οι διαφορές των αποτελεσµάτων των υπόλοιπων τροποποιήσεων, παρά τη µικρή υπεροχή της τροποποίησης των, είναι κατά κανόνα µικρές για το ίδιο κατώφλι ενώ στο αντίστοιχο του 1. mm η υπεροχή των 15ΜΙΝ, έστω και οριακά διατηρείται. Ειδικότερα στα µεγάλα ύψη βροχής (>1 mm) εκτός από την υπεροχή της τροποποίησης RATE1, καλύτερα αποτελέσµατα σε σύγκριση µε το γνήσιο σχήµα δίνουν επιπλέον οι τροποποιήσεις, και PEF9. Αναφορικά µε την πιθανότητα ανίχνευσης POD (σχ. 1γ) η τροποποίηση δίνει τα καλύτερα αποτελέσµατα σε σχέση µε τις άλλες, αλλά όµως δεν θα πρέπει να παραβλεφθεί το γεγονός ότι οι υψηλές τιµές της POD συνοδεύονται από µεγάλες τιµές του δείκτη µεροληψίας για τη συγκεκριµένη τροποποίηση. Στο κατώφλι του 1. mm η πρόσθεση του συντελεστή.5 στη συνάρτηση ενεργοποίησης φαίνεται να βελτιώνει έστω και οριακά την απόδοση της προγνωστικής ικανότητας του µοντέλου ενώ οι υπόλοιπες τροποποιήσεις, µε εξαίρεση τη που δίνει φτωχά αποτελέσµατα, δεν διαφέρουν σηµαντικά. Στα 2.5 και τα 5 mm η υπεροχή της τροποποίησης RATE1, όπως και στους προαναφερθέντες δείκτες, διατηρείται, χωρίς µάλιστα αυτές να συνδυάζονται από µεγάλες τιµές του λόγου των ψευδών συναγερµών FAR (σχ. 1δ). Για τα ίδια κατώφλια, καλές σχετικά τιµές δίνει και η τροποποίηση των, οι οποίες συνδυάζονται και µε ικανοποιητικές τιµές του λόγου των ψευδών συναγερµών. Στα µεγάλα ύψη βροχής (>1 mm) ανεξαρτήτως επιλογής τροποποίησης, η προγνωστική ικανότητα του µοντέλου είναι µικρή αλλά και πάλι παρατηρείται µία µικρή βελτίωση σε σχέση µε το γνήσιο KF σχήµα όταν χρησιµοποιούνται οι τροποποιήσεις RATE1 και PEF9. Σε ότι αφορά την ικανότητα του µοντέλου να προβλέπει σωστά την ποσότητα της βροχής είναι φανερό από τα σχήµατα 1ε και 1στ, ότι κατά τη διάρκεια της θερµής περιόδου το µοντέλο δεν είναι ικανό να προβλέψει σωστά τις µέτριες και µεγάλες βροχοπτώσεις. Η συµπεριφορά βέβαια αυτή µπορεί να δικαιολογηθεί από το γεγονός ότι οι θερινές καταιγίδες αστάθειας χαρακτηρίζονται από έντονο τοπικό χαρακτήρα αλλά και από µεγάλες τιµές ρυθµού βροχόπτωσης, οι οποίες µπορούν σε σύντοµο χρονικό διάστηµα να δώσουν µεγάλες ποσότητες βροχής. Είναι χαρακτηριστική η αύξηση του µέσου απόλυτου σφάλµατος µε την αύξηση των τιµών του εύρους βροχόπτωσης ενώ χαρακτηριστικές είναι οι µεγάλες τιµές για βροχοπτώσεις > 2 mm. Η τάση υποεκτίµησης της ποσότητας του υετού από το µοντέλο φαίνεται ότι είναι ένα χαρακτηριστικό πρόβληµα της θερµής 6
7 περιόδου καθώς ανάλογη στατιστική επεξεργασία που έχει γίνει για δύο συνεχόµενες χρονιές για το µοντέλο BOLAM πάνω από τον Ελλαδικό χώρο (Lagouvardos et al., 23), έδωσε θετικές τιµές της ποσότητα µεροληψίας έως και το εύρος των 5-1 mm. Στα ίδια ραβδογράµµατα παρατηρούµε επίσης ότι τελικά µόνο στο µικρότερο εύρος των mm το µοντέλο έχει την τάση να υπερεκτιµά ελαφρώς τον υετό. Σε αυτό το εύρος η τροποποίηση χάρη στη µείωση του υετού που προκαλεί, παρουσιάζει τη µικρότερη υπερεκτίµηση, χωρίς όµως τα καλά αποτελέσµατα να συνεχίζονται και στα µεγαλύτερα κατώφλια, αφού η τάση υποεκτίµησης είναι εµφανής. Παρόλα αυτά οι τροποποιήσεις που ωθούν το σχήµα να παράξει περισσότερο υετό φαίνεται να έχουν θετική επίδραση στις τιµές της ποσότητας µεροληψίας. Για παράδειγµα στον πίνακα 1 που ακολουθεί εµφανίζονται τα αποτελέσµατα της προσοµοίωσης µίας πρόσφατης περίπτωσης της 3 ης Αυγούστου του έτους 29, για την παράµετρο της βροχόπτωσης. Η συγκεκριµένη ηµέρα ήταν µία τυπική καλοκαιρινή µέρα η οποία άρχισε µε αίθριο καιρό αλλά κατά τις θερµές ώρες της ηµέρας δηµιουργήθηκαν αναπτύξεις πάνω από τον ηπειρωτικό κορµό της Ελλάδας, οι οποίες έδωσαν αρκετά ισχυρές καταιγίδες κυρίως πάνω από τις ορεινές περιοχές της Ηπείρου, της Πίνδου και της Κεντρικής Πελοποννήσου, ενώ στις παραθαλάσσιες περιοχές, µε εξαίρεση το Βόρειο Ιόνιο, ο καιρός διατηρήθηκε καλός. Στον πίνακα 1 η 2 η στήλη περιέχει τις πραγµατικές µετρήσεις αθροιστικής βροχόπτωσης από το δίκτυο των βροχοµέτρων που έχουν χρησιµοποιηθεί για το χρονικό διάστηµα από 12. έως 18. UTC, ενώ αντίστοιχα η 3 η στήλη το αποτέλεσµα της προσοµοίωσης µε τη χρήση του γνήσιου KF σχήµατος, η 4 η στήλη τα αποτελέσµατα µε τη χρήση της τροποποίησης RATE1 και η 5 η στήλη τα αποτελέσµατα µε τη χρήση του ταυτόχρονου συνδυασµού δύο τροποποιήσεων, της RATE1 και της PEF9. Από τις τιµές του πίνακα παρατηρούµε ότι ο ταυτόχρονος συνδυασµός των δύο τροποποιήσεων βελτιώνει σηµαντικά την προγνωστική ικανότητα του µοντέλου σε σχέση µε τη χρησιµοποίηση του γνήσιου σχήµατος. Παρόλα αυτά, όπως άλλωστε αναµενόταν, οι προγνωστικές τιµές όσο µεγαλώνει το ύψος τηςτης παρατηρούµενης βροχόπτωσης, ΠΙΝΑΚΑΣ 1. Συγκριτικός πίνακας για την αθροιστική βροχόπτωση µεταξύ της πραγµατικής τιµής και της προγνωστικής τιµής από το αριθµητικό µοντέλο ΜΜ5 µε τη χρήση του γνήσιου KF σχήµατος () και του σχήµατος µε τις τροποποιήσεις RATE1 και του συνδυασµού RATE1 και PEF9. Σταθµός Βροχόπτωση από RATE1 RATE1 PEF UTC Αγρίνιο Άρτα ερβίζιανα Ιωαννίνων Φολόη Ηλείας Κέρκυρα Κονισκός Τρικάλων Μεγαλόπολη Βεγορίτιδα Βέροια Μιλιανά Άρτας Πίστιανα Άρτας
8 υπολείπονται σηµαντικά από την πραγµατικότητα. Αξιοσηµείωτη επίσης για τη συγκεκριµένη ηµέρα ήταν και η αποτυχία του µοντέλου να προγνώσει την ισχυρή βροχή που εκδηλώθηκε στην Κέρκυρα. Μορφοποιήθηκε: Εσοχή: Πρώτη γραµµή: εκ. 5. ΣΥΜΠΕΡΑΣΜΑΤΑ Στην παρούσα εργασία παρουσιάστηκαν διάφορες τροποποιήσεις του σχήµατος ΠΚΚΜ των Kain Fritsch και εξετάστηκε το κατά πόσο µπορούν να βελτιώσουν την προγνωστική ικανότητα του µοντέλου ΜΜ5 για τη βροχόπτωση, κατά τη διάρκεια της θερµής περιόδου για 2 επιλεγµένες ηµέρες όπου παρατηρήθηκε έντονη ανάπτυξη καταιγίδων πάνω από τον Ελλαδικό χώρο. Το γενικότερο συµπέρασµα που προκύπτει από την επεξεργασία των αποτελεσµάτων είναι ότι η πρόγνωση της βροχής κατά τη διάρκεια θερινών καταιγίδων αποτελεί µία εξαιρετικά σύνθετη διαδικασία η οποία εξαρτάται από πολλές παραµέτρους. Αδιαµφισβήτητο πάντως είναι το γεγονός ότι τροποποιώντας το σχήµα KF µπορεί να βελτιωθεί η πρόγνωση του πεδίου της βροχής. Έτσι όταν ωθήσαµε το σχήµα ΠΚΚΜ να παράξει περισσότερο υετό µέσω της τροποποίησης RATE1 υπήρξε φανερή βελτίωση των επιµέρους στατιστικών δεικτών κυρίως στα κατώφλια των 2.5 και 5 mm. Θετική επίσης ήταν και η επίδραση της αύξησης του χρόνου ανάκλησης του σχήµατος από τα 5 min, που είναι στο αυθεντικό σχήµα, στα 15 min. Το τελικό συµπέρασµα που εξάγεται από την παρούσα µελέτη είναι ότι κατά τη διάρκεια των θερινών καταιγίδων η προσοµοίωση της βροχόπτωσης γίνεται ορθότερα όταν το σχήµα παραµετροποίησης ωθείται να παράξει µεγαλύτερες ποσότητες υετού από ότι το γνήσιο σχήµα (τροποποίηση RATE1), αλλά και όταν η ρουτίνα του σχήµατος καλείται από το αριθµητικό µοντέλο ανά µεγαλύτερα χρονικά διαστήµατα (τροποποίηση 15 ΜΙΝ). ΒΙΒΛΙΟΓΡΑΦΙΑ Anderson, C.J., R.W. Arritt, and J.S. Kain, 27: An Alternative Mass Flux Profile in the Kain Fritsch Convective Parameterization and Its Effects in Seasonal Precipitation. J. Hydrometeor., 8, Fritsch, J. M., and C. F. Chappell, 198: Numerical prediction of convectively driven mesoscale pressure systems. Part I: Convective parameterization. J. Atmos. Sci., 37, Gallus, W. A., and M. Segal, 21: Impact of improved initialization of mesoscale features on convective system rainfall in 1-km Eta simulations. Wea. Forecasting, 16, Kain, J.S., 24: The Kain Fritsch Convective Parameterization: An Update. J. Appl. Meteor., 43, Lagouvardos K., V. Kotroni, A. Koussis, Η. Feidas, Α. Buzzi and P. Malguzzi (23). The meteorological model BOLAM at the National Observatory of Athens: assessment of two-year operational use. Journal of Applied Meteorology, 42, Mazarakis, N., V. Kotroni, K. Lagouvardos and A. Argiriou, 28: Storms and lightning activity in Greece during the warm period of J. Appl. Meteor., 47, Mazarakis, N., V. Kotroni, K. Lagouvardos, A. Argiriou, 29: The sensitivity of numerical forecasts to convective parameterization during the warm period and the use of lightning data as an indicator for convective occurrence, Atmos. Research, 94, Issue 4, Ogura, Y., and H. R. Cho, 1973: Diagnostic determination of cumulus cloud populations from observed largescale variables. J. Atmos. Sci., 3, Spencer, P.L., and D.J. Stensrud, 1998: Simulating Flash Flood Events: Importance of the Subgrid Representation of Convection. Mon. Wea. Rev., 126, Yang, Z., and R. W. Arritt, 21: Ensemble simulations of regional flood and drought climates. Preprints, Precipitation Extremes: Prediction, Impacts, and Responses, Albuquerque, NM, Amer. Meteor. Soc.,
INVESTIGATION OF THE ROLE OF DIFFERENT CONVECTIVE PARAMETERIZATION SCHEMES ON THE PREDICTION OF SUMMER PRECIPITATION EVENTS OVER GREECE
 ΙΕΡΕΥΝΗΣΗ ΤΗΣ ΠΡΟΓΝΩΣΤΙΚΗΣ ΙΚΑΝΟΤΗΤΑΣ ΤΩΝ ΣΧΗΜΑΤΩΝ ΠΑΡΑΜΕΤΡΟΠΟΙΗΣΗΣ ΤΩΝ ΚΑΤΑΚΟΡΥΦΩΝ ΑΝΟ ΙΚΩΝ ΚΙΝΗΣΕΩΝ ΜΕΤΑΦΟΡΑΣ ΣΕ ΠΕΡΙΠΤΩΣΕΙΣ ΘΕΡΙΝΩΝ ΚΑΤΑΙΓΙ ΩΝ Ν. ΜΑΖΑΡΑΚΗΣ,2, Β. ΚΟΤΡΩΝΗ 2, Κ. ΛΑΓΟΥΒΑΡ ΟΣ 2 ΚΑΙ Α. ΑΡΓΥΡΙΟΥ
ΙΕΡΕΥΝΗΣΗ ΤΗΣ ΠΡΟΓΝΩΣΤΙΚΗΣ ΙΚΑΝΟΤΗΤΑΣ ΤΩΝ ΣΧΗΜΑΤΩΝ ΠΑΡΑΜΕΤΡΟΠΟΙΗΣΗΣ ΤΩΝ ΚΑΤΑΚΟΡΥΦΩΝ ΑΝΟ ΙΚΩΝ ΚΙΝΗΣΕΩΝ ΜΕΤΑΦΟΡΑΣ ΣΕ ΠΕΡΙΠΤΩΣΕΙΣ ΘΕΡΙΝΩΝ ΚΑΤΑΙΓΙ ΩΝ Ν. ΜΑΖΑΡΑΚΗΣ,2, Β. ΚΟΤΡΩΝΗ 2, Κ. ΛΑΓΟΥΒΑΡ ΟΣ 2 ΚΑΙ Α. ΑΡΓΥΡΙΟΥ
ΒΙΟΓΡΑΦΙΚΟ ΣΗΜΕΙΩΜΑ. ΕΠΩΝΥΜΟ : Μαζαράκης ΟΝΟΜΑ. : Νικόλαος ΗΜ/ΝΙΑ ΓΕΝΝΗΣΗΣ : 20.07.1974 ΤΗΛΕΦΩΝΟ : 210 5766859 697 80 52 622 E-MAIL
 1 ΒΙΟΓΡΑΦΙΚΟ ΣΗΜΕΙΩΜΑ ΕΠΩΝΥΜΟ : Μαζαράκης ΟΝΟΜΑ : Νικόλαος ΗΜ/ΝΙΑ ΓΕΝΝΗΣΗΣ : 20.07.1974 ΤΗΛΕΦΩΝΟ : 210 5766859 697 80 52 622 E-MAIL : nikosmazarakis@yahoo.gr, info@meteomarine.gr Επαγγελματική Σελίδα :
1 ΒΙΟΓΡΑΦΙΚΟ ΣΗΜΕΙΩΜΑ ΕΠΩΝΥΜΟ : Μαζαράκης ΟΝΟΜΑ : Νικόλαος ΗΜ/ΝΙΑ ΓΕΝΝΗΣΗΣ : 20.07.1974 ΤΗΛΕΦΩΝΟ : 210 5766859 697 80 52 622 E-MAIL : nikosmazarakis@yahoo.gr, info@meteomarine.gr Επαγγελματική Σελίδα :
Τεχνική έκθεση θεωρητικής τεκµηρίωσης αριθµητικής προσοµοίωσης βροχοπτώσεων (Τµήµα 2 ο ) ΟΜΑ Α ΕΡΓΟΥ:
 ΕΥΚΑΛΙΩΝ Εκτίµηση πληµµυρικών ροών στην Ελλάδα σε συνθήκες υδροκλιµατικής µεταβλητότητας: Ανάπτυξη φυσικά εδραιωµένου εννοιολογικού-πιθανοτικού πλαισίου και υπολογιστικών εργαλείων Τεχνική έκθεση θεωρητικής
ΕΥΚΑΛΙΩΝ Εκτίµηση πληµµυρικών ροών στην Ελλάδα σε συνθήκες υδροκλιµατικής µεταβλητότητας: Ανάπτυξη φυσικά εδραιωµένου εννοιολογικού-πιθανοτικού πλαισίου και υπολογιστικών εργαλείων Τεχνική έκθεση θεωρητικής
H ΠΡΟΓΝΩΣΗ ΤΟΥ ΚΑΙΡΟΥ ΣΤΗΝ ΠΕΡΙΟΧΗ ΤΗΣ ΗΠΕΙΡΟΥ
 H ΠΡΟΓΝΩΣΗ ΤΟΥ ΚΑΙΡΟΥ ΣΤΗΝ ΠΕΡΙΟΧΗ ΤΗΣ ΗΠΕΙΡΟΥ Αριθμητικές προσομοιώσεις των ατμοσφαιρικών συνθηκών σε πλέγμα υψηλής ανάλυσης, στην περιοχή της Ηπείρου. Σύστημα προειδοποίησης εμφάνισης ακραίων καιρικών
H ΠΡΟΓΝΩΣΗ ΤΟΥ ΚΑΙΡΟΥ ΣΤΗΝ ΠΕΡΙΟΧΗ ΤΗΣ ΗΠΕΙΡΟΥ Αριθμητικές προσομοιώσεις των ατμοσφαιρικών συνθηκών σε πλέγμα υψηλής ανάλυσης, στην περιοχή της Ηπείρου. Σύστημα προειδοποίησης εμφάνισης ακραίων καιρικών
Πυθαρούλης Ι.
 Εφαρμογή του Αριθμητικού Μοντέλου Πρόγνωσης Καιρού WRF στο πρόγραμμα DAPHNE Πυθαρούλης Ι. pyth@geo.auth.gr www.daphne-meteo.gr Τομέας Μετεωρολογίας και Κλιματολογίας Τμήμα Γεωλογίας, ΑΠΘ Weather Research
Εφαρμογή του Αριθμητικού Μοντέλου Πρόγνωσης Καιρού WRF στο πρόγραμμα DAPHNE Πυθαρούλης Ι. pyth@geo.auth.gr www.daphne-meteo.gr Τομέας Μετεωρολογίας και Κλιματολογίας Τμήμα Γεωλογίας, ΑΠΘ Weather Research
ΑΝΑΛΥΣΗ ΤΗΣ ΑΠΟΚΛΙΣΗΣ ΑΠΟ ΤΗΝ ΗΜΙΤΟΝΟΕΙΔΗ ΚΑΜΠΥΛΗ ΒΡΟΧΟΠΤΩΣΗΣ ΚΑΙ ΧΡΗΣΗ ΤΗΣ ΩΣ ΔΕΙΚΤΗ ΚΛΙΜΑΤΙΚΗΣ ΑΛΛΑΓΗΣ
 ΑΝΑΛΥΣΗ ΤΗΣ ΑΠΟΚΛΙΣΗΣ ΑΠΟ ΤΗΝ ΗΜΙΤΟΝΟΕΙΔΗ ΚΑΜΠΥΛΗ ΒΡΟΧΟΠΤΩΣΗΣ ΚΑΙ ΧΡΗΣΗ ΤΗΣ ΩΣ ΔΕΙΚΤΗ ΚΛΙΜΑΤΙΚΗΣ ΑΛΛΑΓΗΣ Καλύβας Θ., Ζέρβας Ε.¹ ¹ Σχολή Θετικών Επιστημών και Τεχνολογίας, Ελληνικό Ανοικτό Πανεπιστήμιο,
ΑΝΑΛΥΣΗ ΤΗΣ ΑΠΟΚΛΙΣΗΣ ΑΠΟ ΤΗΝ ΗΜΙΤΟΝΟΕΙΔΗ ΚΑΜΠΥΛΗ ΒΡΟΧΟΠΤΩΣΗΣ ΚΑΙ ΧΡΗΣΗ ΤΗΣ ΩΣ ΔΕΙΚΤΗ ΚΛΙΜΑΤΙΚΗΣ ΑΛΛΑΓΗΣ Καλύβας Θ., Ζέρβας Ε.¹ ¹ Σχολή Θετικών Επιστημών και Τεχνολογίας, Ελληνικό Ανοικτό Πανεπιστήμιο,
Εθνικό Αστεροσκοπείο Αθηνών, Ινστιτούτο Περιβάλλοντος και Βιώσιμης Ανάπτυξης
 ΔΙΚΤΥΟ ΑΥΤΟΜΑΤΩΝ ΜΕΤΕΩΡΟΛΟΓΙΚΩΝ ΣΤΑΘΜΩΝ ΤΟΥ ΕΘΝΙΚΟΥ ΑΣΤΕΡΟΣΚΟΠΕΙΟΥ ΑΘΗΝΩΝ: ΠΑΡΟΥΣΑ ΚΑΤΑΣΤΑΣΗ ΚΑΙ ΠΡΟΟΠΤΙΚΕΣ Κ. ΛΑΓΟΥΒΑΡΔΟΣ, Β. ΚΟΤΡΩΝΗ, Σ. ΒΟΥΓΙΟΥΚΑΣ, Δ. ΚΑΤΣΑΝΟΣ, Ι. ΚΩΛΕΤΣΗΣ, Σ. ΛΥΚΟΥΔΗΣ ΚΑΙ Ν. ΜΑΖΑΡΑΚΗΣ
ΔΙΚΤΥΟ ΑΥΤΟΜΑΤΩΝ ΜΕΤΕΩΡΟΛΟΓΙΚΩΝ ΣΤΑΘΜΩΝ ΤΟΥ ΕΘΝΙΚΟΥ ΑΣΤΕΡΟΣΚΟΠΕΙΟΥ ΑΘΗΝΩΝ: ΠΑΡΟΥΣΑ ΚΑΤΑΣΤΑΣΗ ΚΑΙ ΠΡΟΟΠΤΙΚΕΣ Κ. ΛΑΓΟΥΒΑΡΔΟΣ, Β. ΚΟΤΡΩΝΗ, Σ. ΒΟΥΓΙΟΥΚΑΣ, Δ. ΚΑΤΣΑΝΟΣ, Ι. ΚΩΛΕΤΣΗΣ, Σ. ΛΥΚΟΥΔΗΣ ΚΑΙ Ν. ΜΑΖΑΡΑΚΗΣ
Παραδοτέο Π4.2 Τεχνική έκθεση θεωρητικής τεκµηρίωσης µοντέλων πρόγνωσης καταιγίδων
 ΕΥΡΩΠΑΪΚΗ ΕΝΩΣΗ ΕΥΡΩΠΑΪΚΟ ΤΑΜΕΙΟ ΠΕΡΙΦΕΡΕΙΑΚΗΣ ΑΝΑΠΤΥΞΗΣ ΕΥΚΑΛΙΩΝ Εκτίµηση πληµµυρικών ροών στην Ελλάδα σε συνθήκες υδροκλιµατικής µεταβλητότητας: Ανάπτυξη φυσικά εδραιωµένου εννοιολογικού-πιθανοτικού
ΕΥΡΩΠΑΪΚΗ ΕΝΩΣΗ ΕΥΡΩΠΑΪΚΟ ΤΑΜΕΙΟ ΠΕΡΙΦΕΡΕΙΑΚΗΣ ΑΝΑΠΤΥΞΗΣ ΕΥΚΑΛΙΩΝ Εκτίµηση πληµµυρικών ροών στην Ελλάδα σε συνθήκες υδροκλιµατικής µεταβλητότητας: Ανάπτυξη φυσικά εδραιωµένου εννοιολογικού-πιθανοτικού
ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΕΦΑΡΜΟΣΜΕΝΗΣ ΦΥΣΙΚΗΣ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΕΦΑΡΜΟΣΜΕΝΗ ΦΥΣΙΚΗ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΕΦΑΡΜΟΣΜΕΝΗΣ ΦΥΣΙΚΗΣ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΕΦΑΡΜΟΣΜΕΝΗ ΦΥΣΙΚΗ ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΤΗΣ ΑΤΜΟΣΦΑΙΡΑΣ ΠΑΡΑΤΗΡΗΣΙΑΚΗ ΚΑΙ ΑΡΙΘΜΗΤΙΚΗ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΕΦΑΡΜΟΣΜΕΝΗΣ ΦΥΣΙΚΗΣ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΕΦΑΡΜΟΣΜΕΝΗ ΦΥΣΙΚΗ ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΤΗΣ ΑΤΜΟΣΦΑΙΡΑΣ ΠΑΡΑΤΗΡΗΣΙΑΚΗ ΚΑΙ ΑΡΙΘΜΗΤΙΚΗ
ΑΝΑΠΤΥΞΗ ΣΥΣΤΗΜΑΤΟΣ ΓΕΩΓΡΑΦΙΚΩΝ ΠΛΗΡΟΦΟΡΙΩΝ ΓΙΑ ΤΗΝ ΑΞΙΟΛΟΓΗΣΗ ΤΩΝ ΠΡΟΓΝΩΣΤΙΚΩΝ ΠΕ ΙΩΝ ΒΡΟΧΟΠΤΩΣΗΣ ΤΟΥ ΜΕΤΕΩΡΟΛΟΓΙΚΟΥ ΜΟΝΤΕΛΟΥ BOLAM2000 1
 ΑΝΑΠΤΥΞΗ ΣΥΣΤΗΜΑΤΟΣ ΓΕΩΓΡΑΦΙΚΩΝ ΠΛΗΡΟΦΟΡΙΩΝ ΓΙΑ ΤΗΝ ΑΞΙΟΛΟΓΗΣΗ ΤΩΝ ΠΡΟΓΝΩΣΤΙΚΩΝ ΠΕ ΙΩΝ ΒΡΟΧΟΠΤΩΣΗΣ ΤΟΥ ΜΕΤΕΩΡΟΛΟΓΙΚΟΥ ΜΟΝΤΕΛΟΥ BOLAM2000 1 ΧΑΡΑΛΑΜΠΟΣ ΦΕΙ ΑΣ 2, ΘΕΜΙΣΤΟΚΛΗΣ ΚΟΝΤΟΣ 2, ΣΟΥΛΑΚΕΛΛΗΣ ΝΙΚΟΛΑΟΣ
ΑΝΑΠΤΥΞΗ ΣΥΣΤΗΜΑΤΟΣ ΓΕΩΓΡΑΦΙΚΩΝ ΠΛΗΡΟΦΟΡΙΩΝ ΓΙΑ ΤΗΝ ΑΞΙΟΛΟΓΗΣΗ ΤΩΝ ΠΡΟΓΝΩΣΤΙΚΩΝ ΠΕ ΙΩΝ ΒΡΟΧΟΠΤΩΣΗΣ ΤΟΥ ΜΕΤΕΩΡΟΛΟΓΙΚΟΥ ΜΟΝΤΕΛΟΥ BOLAM2000 1 ΧΑΡΑΛΑΜΠΟΣ ΦΕΙ ΑΣ 2, ΘΕΜΙΣΤΟΚΛΗΣ ΚΟΝΤΟΣ 2, ΣΟΥΛΑΚΕΛΛΗΣ ΝΙΚΟΛΑΟΣ
Προειδοποιήσεις πλημμυρών από μετεωρολογικές παρατηρήσεις και προγνώσεις
 Προειδοποιήσεις πλημμυρών από μετεωρολογικές παρατηρήσεις και προγνώσεις Β. Κοτρώνη Κ. Λαγουβάρδος Ινστιτούτο Ερευνών Περιβάλλοντος Εθνικού Αστεροσκοπείου Αθηνών ΙΕΠΒΑ/ΕΑΑ "Υπηρεσίες και προϊόντα υποστήριξης
Προειδοποιήσεις πλημμυρών από μετεωρολογικές παρατηρήσεις και προγνώσεις Β. Κοτρώνη Κ. Λαγουβάρδος Ινστιτούτο Ερευνών Περιβάλλοντος Εθνικού Αστεροσκοπείου Αθηνών ΙΕΠΒΑ/ΕΑΑ "Υπηρεσίες και προϊόντα υποστήριξης
Αριθμητική πρόγνωση καιρού και η συμβολή της στην πρόγνωση τοπικών πλημμυρών
 Αριθμητική πρόγνωση καιρού και η συμβολή της στην πρόγνωση τοπικών πλημμυρών Αναστάσιος Παπαδόπουλος Ινστιτούτο Θαλάσσιων Βιολογικών Πόρων και Εσωτερικών Υδάτων Πρόγνωση Καιρού Οι πρώτες επιστημονικές
Αριθμητική πρόγνωση καιρού και η συμβολή της στην πρόγνωση τοπικών πλημμυρών Αναστάσιος Παπαδόπουλος Ινστιτούτο Θαλάσσιων Βιολογικών Πόρων και Εσωτερικών Υδάτων Πρόγνωση Καιρού Οι πρώτες επιστημονικές
 Π ρόγνωση καιρού λέγεται η διαδικασία πρόβλεψης των ατµοσφαιρικών συνθηκών που πρόκειται να επικρατήσουν σε µια συγκεκριµένη περιοχή, για κάποια ορισµένη µελλοντική χρονική στιγµή ή περίοδο. Στην ουσία
Π ρόγνωση καιρού λέγεται η διαδικασία πρόβλεψης των ατµοσφαιρικών συνθηκών που πρόκειται να επικρατήσουν σε µια συγκεκριµένη περιοχή, για κάποια ορισµένη µελλοντική χρονική στιγµή ή περίοδο. Στην ουσία
Μη μετρούμενες λεκάνες απορροής: Διερεύνηση στη λεκάνη του Πηνειού Θεσσαλίας, στη θέση Σαρακίνα
 Μη μετρούμενες λεκάνες απορροής: Διερεύνηση στη λεκάνη του Πηνειού Θεσσαλίας, στη θέση Σαρακίνα Βασίλειος Γουργουλιός και Ιωάννης Ναλμπάντης ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΚΑΙ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ
Μη μετρούμενες λεκάνες απορροής: Διερεύνηση στη λεκάνη του Πηνειού Θεσσαλίας, στη θέση Σαρακίνα Βασίλειος Γουργουλιός και Ιωάννης Ναλμπάντης ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΚΑΙ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ
Παρατήρηση και πρόγνωση έντονων καιρικών φαινομένων: σχεδιάζοντας την επόμενη ημέρα
 Παρατήρηση και πρόγνωση έντονων καιρικών φαινομένων: σχεδιάζοντας την επόμενη ημέρα Observing and forecasting severe weather events: planning for the future Κ. Λαγουβάρδος, Εθνικό Αστεροσκοπείο Αθηνών
Παρατήρηση και πρόγνωση έντονων καιρικών φαινομένων: σχεδιάζοντας την επόμενη ημέρα Observing and forecasting severe weather events: planning for the future Κ. Λαγουβάρδος, Εθνικό Αστεροσκοπείο Αθηνών
1. Εισαγωγή Βάση δεδομένων Μεθοδολογία Νευρωνικών Δικτύων Αποτελέσματα Βιβλιογραφια Παραρτήμα Ι...
 ΣΥΣΤΗΜΑ ΠΑΡΑΚΟΛΟΥΘΗΣΗΣ ΑΕΡΟΣΩΜΑΤΙ ΙΑΚΗΣ ΡΥΠΑΝΣΗΣ ΣΕ ΣΧΕ ΟΝ ΠΡΑΓΜΑΤΙΚΟ ΧΡΟΝΟ ΠΑΡΑ ΟΤΕΟ 7 ΜΕΘΟ ΟΛΟΓΙΑ ΓΙΑ ΚΑΤΗΓΟΡΙΟΠΟΙΗΣΗ ΣΥΝΟΠΤΙΚΩΝ ΚΑΤΑΣΤΑΣΕΩΝ ΚΑΙ ΗΜΙΟΥΡΓΙΑ ΣΥΝΟΠΤΙΚΩΝ ΠΡΟΤΥΠΩΝ Συγγραφείς: Φίλιππος Τύµβιος
ΣΥΣΤΗΜΑ ΠΑΡΑΚΟΛΟΥΘΗΣΗΣ ΑΕΡΟΣΩΜΑΤΙ ΙΑΚΗΣ ΡΥΠΑΝΣΗΣ ΣΕ ΣΧΕ ΟΝ ΠΡΑΓΜΑΤΙΚΟ ΧΡΟΝΟ ΠΑΡΑ ΟΤΕΟ 7 ΜΕΘΟ ΟΛΟΓΙΑ ΓΙΑ ΚΑΤΗΓΟΡΙΟΠΟΙΗΣΗ ΣΥΝΟΠΤΙΚΩΝ ΚΑΤΑΣΤΑΣΕΩΝ ΚΑΙ ΗΜΙΟΥΡΓΙΑ ΣΥΝΟΠΤΙΚΩΝ ΠΡΟΤΥΠΩΝ Συγγραφείς: Φίλιππος Τύµβιος
Ανάπτυξη προγνωστικού συστήματος ταχείας απόκρισης για την πρόγνωση της εξάπλωσης δασικών πυρκαγιών στα πλαίσια του προγράμματος DISARM
 Ανάπτυξη προγνωστικού συστήματος ταχείας απόκρισης για την πρόγνωση της εξάπλωσης δασικών πυρκαγιών στα πλαίσια του προγράμματος DISARM Θοδωρής Μ. Γιάνναρος (Επιστημονικός συνεργάτης) Βασιλική Κοτρώνη
Ανάπτυξη προγνωστικού συστήματος ταχείας απόκρισης για την πρόγνωση της εξάπλωσης δασικών πυρκαγιών στα πλαίσια του προγράμματος DISARM Θοδωρής Μ. Γιάνναρος (Επιστημονικός συνεργάτης) Βασιλική Κοτρώνη
Κλιματική Αλλαγή. Χρήστος Σπύρου ΧΑΡΟΚΟΠΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΓΕΩΓΡΑΦΙΑΣ ΕΛ. ΒΕΝΙΖΕΛΟΥ 70, ΑΘΗΝΑ.
 ΧΑΡΟΚΟΠΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΓΕΩΓΡΑΦΙΑΣ ΕΛ. ΒΕΝΙΖΕΛΟΥ 70, 176 71 ΑΘΗΝΑ Κλιματική Αλλαγή Χρήστος Σπύρου scspir@gmail.com Βασικό σύγγραμμα: Κατσαφάδος Π. και Μαυροματίδης Η., 2015: Εισαγωγή στη Φυσική της
ΧΑΡΟΚΟΠΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΓΕΩΓΡΑΦΙΑΣ ΕΛ. ΒΕΝΙΖΕΛΟΥ 70, 176 71 ΑΘΗΝΑ Κλιματική Αλλαγή Χρήστος Σπύρου scspir@gmail.com Βασικό σύγγραμμα: Κατσαφάδος Π. και Μαυροματίδης Η., 2015: Εισαγωγή στη Φυσική της
 Ν έφη ονοµάζονται οι αιωρούµενοι ατµοσφαιρικοί σχηµατισµοί οι οποίοι αποτελούνται από υδροσταγόνες, παγοκρυστάλλους ή και από συνδυασµό υδροσταγόνων και παγοκρυστάλλων. Ουσιαστικά πρόκειται για το αποτέλεσµα
Ν έφη ονοµάζονται οι αιωρούµενοι ατµοσφαιρικοί σχηµατισµοί οι οποίοι αποτελούνται από υδροσταγόνες, παγοκρυστάλλους ή και από συνδυασµό υδροσταγόνων και παγοκρυστάλλων. Ουσιαστικά πρόκειται για το αποτέλεσµα
ΣΥΣΧΕΤΙΣΗ ΗΛΕΚΤΡΙΚΩΝ ΕΚΚΕΝΩΣΕΩΝ ΚΑΙ ΦΑΣΜΑΤΙΚΩΝ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΤΩΝ ΝΕΦΩΝ ΣΕ ΔΟΡΥΦΟΡΙΚΕΣ ΕΙΚΟΝΕΣ METEOSAT-8 ΣΤΗΝ ΠΕΡΙΟΧΗ ΤΗΣ ΜΕΣΟΓΕΙΟΥ
 ΣΥΣΧΕΤΙΣΗ ΗΛΕΚΤΡΙΚΩΝ ΕΚΚΕΝΩΣΕΩΝ ΚΑΙ ΦΑΣΜΑΤΙΚΩΝ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΤΩΝ ΝΕΦΩΝ ΣΕ ΔΟΡΥΦΟΡΙΚΕΣ ΕΙΚΟΝΕΣ METEOSAT-8 ΣΤΗΝ ΠΕΡΙΟΧΗ ΤΗΣ ΜΕΣΟΓΕΙΟΥ Σταύρος Κολιός 1 και Χαράλαμπος Φείδας 1 1 Πανεπιστήμιο Αιγαίου, Τμήμα
ΣΥΣΧΕΤΙΣΗ ΗΛΕΚΤΡΙΚΩΝ ΕΚΚΕΝΩΣΕΩΝ ΚΑΙ ΦΑΣΜΑΤΙΚΩΝ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΤΩΝ ΝΕΦΩΝ ΣΕ ΔΟΡΥΦΟΡΙΚΕΣ ΕΙΚΟΝΕΣ METEOSAT-8 ΣΤΗΝ ΠΕΡΙΟΧΗ ΤΗΣ ΜΕΣΟΓΕΙΟΥ Σταύρος Κολιός 1 και Χαράλαμπος Φείδας 1 1 Πανεπιστήμιο Αιγαίου, Τμήμα
ΕΘΝΙΚΗ ΜΕΤΕΩΡΟΛΟΓΙΚΗ ΥΠΗΡΕΣΙΑ - ΕΜΥ
 ΕΘΝΙΚΗ ΜΕΤΕΩΡΟΛΟΓΙΚΗ ΥΠΗΡΕΣΙΑ - ΕΜΥ ΔΕΥΤΕΡΟ ΔΕΚΑΗΜΕΡΟ ΝΟΕΜΒΡΙΟΥ 2017, ΚΑΤΑ ΠΕΡΙΟΔΟΥΣ ΚΑΙ ΚΑΤΑ ΤΟΠΟΥΣ ΕΝΤΟΝΕΣ ΒΡΟΧΟΠΤΩΣΕΙΣ - ΠΛΗΜΜΥΡΙΚΑ ΦΑΙΝΟΜΕΝΑ ΕΙΣΑΓΩΓΗ Ο φετινός Νοέμβριος, ο τελευταίος φθινοπωρινός
ΕΘΝΙΚΗ ΜΕΤΕΩΡΟΛΟΓΙΚΗ ΥΠΗΡΕΣΙΑ - ΕΜΥ ΔΕΥΤΕΡΟ ΔΕΚΑΗΜΕΡΟ ΝΟΕΜΒΡΙΟΥ 2017, ΚΑΤΑ ΠΕΡΙΟΔΟΥΣ ΚΑΙ ΚΑΤΑ ΤΟΠΟΥΣ ΕΝΤΟΝΕΣ ΒΡΟΧΟΠΤΩΣΕΙΣ - ΠΛΗΜΜΥΡΙΚΑ ΦΑΙΝΟΜΕΝΑ ΕΙΣΑΓΩΓΗ Ο φετινός Νοέμβριος, ο τελευταίος φθινοπωρινός
Αρχές Μετεωρολογίας και Κλιματολογίας (Διάλεξη 10)
 ΧΑΡΟΚΟΠΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΓΕΩΓΡΑΦΙΑΣ ΕΛ. ΒΕΝΙΖΕΛΟΥ 70, 176 71 ΑΘΗΝΑ Αρχές Μετεωρολογίας και Κλιματολογίας (Διάλεξη 10) Πέτρος Κατσαφάδος pkatsaf@hua.gr Τμήμα Γεωγραφίας Χαροκόπειο Πανεπιστήμιο Αθηνών
ΧΑΡΟΚΟΠΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΓΕΩΓΡΑΦΙΑΣ ΕΛ. ΒΕΝΙΖΕΛΟΥ 70, 176 71 ΑΘΗΝΑ Αρχές Μετεωρολογίας και Κλιματολογίας (Διάλεξη 10) Πέτρος Κατσαφάδος pkatsaf@hua.gr Τμήμα Γεωγραφίας Χαροκόπειο Πανεπιστήμιο Αθηνών
ΠΕΡΙΟΧΙΚΕΣ ΚΛΙΜΑΤΙΚΕΣ ΠΡΟΓΝΩΣΕΙΣ ΣΤΗΝ ΠΕΡΙΟΧΗ ΤΗΣ ΑΝΑΤΟΛΙΚΗΣ ΜΕΣΟΓΕΙΟΥ: ΑΠΟΤΕΛΕΣΜΑΤΑ ΓΙΑ ΤΗ ΧΡΟΝΙΚΗ ΠΕΡΙΟ Ο
 ΠΕΡΙΟΧΙΚΕΣ ΚΛΙΜΑΤΙΚΕΣ ΠΡΟΓΝΩΣΕΙΣ ΣΤΗΝ ΠΕΡΙΟΧΗ ΤΗΣ ΑΝΑΤΟΛΙΚΗΣ ΜΕΣΟΓΕΙΟΥ: ΑΠΟΤΕΛΕΣΜΑΤΑ ΓΙΑ ΤΗ ΧΡΟΝΙΚΗ ΠΕΡΙΟ Ο 71-20 1 Εισαγωγή Είναι πλέον αδιαµφισβήτητο ότι το κλίµα έχει αλλάξει και θα συνεχίζει να αλλάζει
ΠΕΡΙΟΧΙΚΕΣ ΚΛΙΜΑΤΙΚΕΣ ΠΡΟΓΝΩΣΕΙΣ ΣΤΗΝ ΠΕΡΙΟΧΗ ΤΗΣ ΑΝΑΤΟΛΙΚΗΣ ΜΕΣΟΓΕΙΟΥ: ΑΠΟΤΕΛΕΣΜΑΤΑ ΓΙΑ ΤΗ ΧΡΟΝΙΚΗ ΠΕΡΙΟ Ο 71-20 1 Εισαγωγή Είναι πλέον αδιαµφισβήτητο ότι το κλίµα έχει αλλάξει και θα συνεχίζει να αλλάζει
Υγρασία Θερμοκρασία Άνεμος Ηλιακή Ακτινοβολία. Κατακρημνίσματα
 Ζαΐμης Γεώργιος Υγρασία Θερμοκρασία Άνεμος Ηλιακή Ακτινοβολία Κατακρημνίσματα ΝΕΡΟ - Τρεις μορφές Υγρασία στην Ατμόσφαιρα Εξάτμιση και Διαπνοή Ελλάδα που περισσότερες βροχοπτώσεις και γιατί; Υγρασία
Ζαΐμης Γεώργιος Υγρασία Θερμοκρασία Άνεμος Ηλιακή Ακτινοβολία Κατακρημνίσματα ΝΕΡΟ - Τρεις μορφές Υγρασία στην Ατμόσφαιρα Εξάτμιση και Διαπνοή Ελλάδα που περισσότερες βροχοπτώσεις και γιατί; Υγρασία
ΑΣΚΗΣΗ 6 ΒΡΟΧΗ. 1. Βροχομετρικές παράμετροι. 2. Ημερήσια πορεία της βροχής
 ΑΣΚΗΣΗ 6 ΒΡΟΧΗ Η βροχή αποτελεί μία από τις σπουδαιότερες μετεωρολογικές παραμέτρους. Είναι η πιο κοινή μορφή υετού και αποτελείται από σταγόνες που βρίσκονται σε υγρή κατάσταση. 1. Βροχομετρικές παράμετροι
ΑΣΚΗΣΗ 6 ΒΡΟΧΗ Η βροχή αποτελεί μία από τις σπουδαιότερες μετεωρολογικές παραμέτρους. Είναι η πιο κοινή μορφή υετού και αποτελείται από σταγόνες που βρίσκονται σε υγρή κατάσταση. 1. Βροχομετρικές παράμετροι
Νίκος Μαζαράκης Αθήνα 2010
 Νίκος Μαζαράκης Αθήνα 2010 Οι χάρτες των 850 Hpa είναι ένα από τα βασικά προγνωστικά επίπεδα για τη παράµετρο της θερµοκρασίας. Την πίεση των 850 Hpa τη συναντάµε στην ατµόσφαιρα σε ένα µέσο ύψος περί
Νίκος Μαζαράκης Αθήνα 2010 Οι χάρτες των 850 Hpa είναι ένα από τα βασικά προγνωστικά επίπεδα για τη παράµετρο της θερµοκρασίας. Την πίεση των 850 Hpa τη συναντάµε στην ατµόσφαιρα σε ένα µέσο ύψος περί
ΕΡΓΟ: ''Βελτίωση της γνώσης σχετικά με τον καθορισμό της ελάχιστα απαιτούμενης. στάθμης/παροχής υδάτινων σωμάτων''
 Department of Meteorology And Climatology ΕΡΓΟ: ''Βελτίωση της γνώσης σχετικά με τον καθορισμό της ελάχιστα απαιτούμενης στάθμης/παροχής υδάτινων σωμάτων'' Π3.2_Εκτίμηση μελλοντικών τιμών βροχής και θερμοκρασίας
Department of Meteorology And Climatology ΕΡΓΟ: ''Βελτίωση της γνώσης σχετικά με τον καθορισμό της ελάχιστα απαιτούμενης στάθμης/παροχής υδάτινων σωμάτων'' Π3.2_Εκτίμηση μελλοντικών τιμών βροχής και θερμοκρασίας
 ΣΥΣΤΗΜΑ ΠΑΡΑΚΟΛΟΥΘΗΣΗΣ ΑΕΡΟΣΩΜΑΤΙ ΙΑΚΗΣ ΡΥΠΑΝΣΗΣ ΣΕ ΣΧΕ ΟΝ ΠΡΑΓΜΑΤΙΚΟ ΧΡΟΝΟ ΠΑΡΑ ΟΤΕΟ 6 ΑΝΑΠΤΥΞΗ ΜΕΘΟ ΟΛΟΓΙΑΣ ΓΙΑ ΤΗΝ ΑΠΟΤΥΠΩΣΗ ΤΗΣ ΑΕΡΟΣΩΜΑΤΙ ΙΑΚΗΣ ΡΥΠΑΝΣΗΣ ΑΠΟ ΟΡΥΦΟΡΙΚΑ Ε ΟΜΕΝΑ ΚΑΙ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ
ΣΥΣΤΗΜΑ ΠΑΡΑΚΟΛΟΥΘΗΣΗΣ ΑΕΡΟΣΩΜΑΤΙ ΙΑΚΗΣ ΡΥΠΑΝΣΗΣ ΣΕ ΣΧΕ ΟΝ ΠΡΑΓΜΑΤΙΚΟ ΧΡΟΝΟ ΠΑΡΑ ΟΤΕΟ 6 ΑΝΑΠΤΥΞΗ ΜΕΘΟ ΟΛΟΓΙΑΣ ΓΙΑ ΤΗΝ ΑΠΟΤΥΠΩΣΗ ΤΗΣ ΑΕΡΟΣΩΜΑΤΙ ΙΑΚΗΣ ΡΥΠΑΝΣΗΣ ΑΠΟ ΟΡΥΦΟΡΙΚΑ Ε ΟΜΕΝΑ ΚΑΙ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ
Διασπορά ατμοσφαιρικών ρύπων
 Διασπορά ατμοσφαιρικών ρύπων Καθηγητής Δημοσθένης A. Σαρηγιάννης Εργαστήριο Περιβαλλοντικής Μηχανικής Τμήμα Χημικών Μηχανικών Πολυτεχνική Σχολή Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Βασικές ατμοσφαιρικές
Διασπορά ατμοσφαιρικών ρύπων Καθηγητής Δημοσθένης A. Σαρηγιάννης Εργαστήριο Περιβαλλοντικής Μηχανικής Τμήμα Χημικών Μηχανικών Πολυτεχνική Σχολή Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Βασικές ατμοσφαιρικές
Μελέτη Προέγκρισης Χωροθέτησης του Μικρού Υδροηλεκτρικού Σταθμού Βαλορέματος. Υδρολογική μελέτη
 Περιεχόμενα Μελέτη Προέγκρισης Χωροθέτησης του Μικρού Υδροηλεκτρικού Σταθμού Βαλορέματος Υδρολογική μελέτη Εισαγωγή 1 Γενικά χαρακτηριστικά 1 Παραγωγή ημερήσιων παροχών στη θέση Σμίξη 2 Καμπύλες διάρκειας
Περιεχόμενα Μελέτη Προέγκρισης Χωροθέτησης του Μικρού Υδροηλεκτρικού Σταθμού Βαλορέματος Υδρολογική μελέτη Εισαγωγή 1 Γενικά χαρακτηριστικά 1 Παραγωγή ημερήσιων παροχών στη θέση Σμίξη 2 Καμπύλες διάρκειας
Ευστάθεια Συστηµάτων Αυτοµάτου Ελέγχου: Αλγεβρικά κριτήρια
 ΚΕΣ : Αυτόµατος Έλεγχος ΚΕΣ Αυτόµατος Έλεγχος Ευστάθεια Συστηµάτων Αυτοµάτου Ελέγχου: Αλγεβρικά κριτήρια 6 Nicol Tptouli Ευστάθεια και θέση πόλων Σ.Α.Ε ΚΕΣ : Αυτόµατος Έλεγχος Βιβλιογραφία Ενότητας Παρασκευόπουλος
ΚΕΣ : Αυτόµατος Έλεγχος ΚΕΣ Αυτόµατος Έλεγχος Ευστάθεια Συστηµάτων Αυτοµάτου Ελέγχου: Αλγεβρικά κριτήρια 6 Nicol Tptouli Ευστάθεια και θέση πόλων Σ.Α.Ε ΚΕΣ : Αυτόµατος Έλεγχος Βιβλιογραφία Ενότητας Παρασκευόπουλος
Q 12. c 3 Q 23. h 12 + h 23 + h 31 = 0 (6)
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών Τοµέας Υδατικών Πόρων Μάθηµα: Τυπικά Υδραυλικά Έργα Μέρος 2: ίκτυα διανοµής Άσκηση E0: Μαθηµατική διατύπωση µοντέλου επίλυσης απλού δικτύου διανοµής
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών Τοµέας Υδατικών Πόρων Μάθηµα: Τυπικά Υδραυλικά Έργα Μέρος 2: ίκτυα διανοµής Άσκηση E0: Μαθηµατική διατύπωση µοντέλου επίλυσης απλού δικτύου διανοµής
ΕΡΓΟ: ''Βελτίωση της γνώσης σχετικά με τον καθορισμό της ελάχιστα. απαιτούμενης στάθμης/παροχής υδάτινων σωμάτων''
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΓΕΩΛΟΓΙΑΣ ΕΡΓΟ: ''Βελτίωση της γνώσης σχετικά με τον καθορισμό της ελάχιστα απαιτούμενης στάθμης/παροχής υδάτινων σωμάτων'' Π3.1_Ανάλυση
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΓΕΩΛΟΓΙΑΣ ΕΡΓΟ: ''Βελτίωση της γνώσης σχετικά με τον καθορισμό της ελάχιστα απαιτούμενης στάθμης/παροχής υδάτινων σωμάτων'' Π3.1_Ανάλυση
ΚΛΙΜΑΤΟΛΟΓΙΑ CLIMATOLOGY
 10 ο COMECAP 2010, Πρακτικά Συνεδρίου, Πάτρα 10 th COMECAP 2010, Proceedings, Patras, Greece ΚΛΙΜΑΤΟΛΟΓΙΑ CLIMATOLOGY ΥΧΡΟΥΡΟΝΗΚΖ ΓΗΑΚΤΜΑΝΖ ΣΧΝ ΖΛΔΚΣΡΗΚΧΝ ΔΚΚΔΝΧΔΧΝ ΣΖΝ ΔΛΛΑΓΑ ΓΗΑ ΣΖΝ ΥΡΟΝΗΚΖ ΠΔΡΗΟΓΟ 1998-2007
10 ο COMECAP 2010, Πρακτικά Συνεδρίου, Πάτρα 10 th COMECAP 2010, Proceedings, Patras, Greece ΚΛΙΜΑΤΟΛΟΓΙΑ CLIMATOLOGY ΥΧΡΟΥΡΟΝΗΚΖ ΓΗΑΚΤΜΑΝΖ ΣΧΝ ΖΛΔΚΣΡΗΚΧΝ ΔΚΚΔΝΧΔΧΝ ΣΖΝ ΔΛΛΑΓΑ ΓΗΑ ΣΖΝ ΥΡΟΝΗΚΖ ΠΔΡΗΟΓΟ 1998-2007
Ονοματεπώνυμο: Επιμέλεια διαγωνίσματος: Αξιολόγηση :
 Ονοματεπώνυμο: Μάθημα: Υλη: Επιμέλεια διαγωνίσματος: Αξιολόγηση : Φυσική Προσανατολισμου Γ Λυκείου Ταλαντώσεις Σχολικό έτος 2017-2018 Σελίδα 1 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Σύνολο Σελίδων:
Ονοματεπώνυμο: Μάθημα: Υλη: Επιμέλεια διαγωνίσματος: Αξιολόγηση : Φυσική Προσανατολισμου Γ Λυκείου Ταλαντώσεις Σχολικό έτος 2017-2018 Σελίδα 1 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Σύνολο Σελίδων:
ΑΡΙΘΜΗΤΙΚΑ ΜΟΝΤΕΛΑ ΠΡΟΓΝΩΣΗΣ ΚΑΙΡΟΥ. Κ. Λαγουβάρδος
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΘΜΗΤΙΚΑ ΜΟΝΤΕΛΑ ΠΡΟΓΝΩΣΗΣ ΚΑΙΡΟΥ Κ. Λαγουβάρδος Ινστιτούτο Ερευνών Περιβάλλοντος Εθνικό Αστεροσκοπείο Αθηνών ΤΙ ΕΙΝΑΙ ΑΡΙΘΜΗΤΙΚΗ ΠΡΟΓΝΩΣΗ ΚΑΙΡΟΥ Επίλυση των εξισώσεων
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΘΜΗΤΙΚΑ ΜΟΝΤΕΛΑ ΠΡΟΓΝΩΣΗΣ ΚΑΙΡΟΥ Κ. Λαγουβάρδος Ινστιτούτο Ερευνών Περιβάλλοντος Εθνικό Αστεροσκοπείο Αθηνών ΤΙ ΕΙΝΑΙ ΑΡΙΘΜΗΤΙΚΗ ΠΡΟΓΝΩΣΗ ΚΑΙΡΟΥ Επίλυση των εξισώσεων
''Σεπτέμβριος 2015: οι ακραίες μέγιστες θερμοκρασίες στο 1ο δεκαήμερο και κλιματολογικά στοιχεία του μήνα''
 ''Σεπτέμβριος 2015: οι ακραίες μέγιστες θερμοκρασίες στο 1ο δεκαήμερο και κλιματολογικά στοιχεία του μήνα'' Ο Σεπτέμβριος ως μεταβατικός μήνας από το καλοκαίρι στο φθινόπωρο, ιδιαίτερα το πρώτο δεκαήμερο,
''Σεπτέμβριος 2015: οι ακραίες μέγιστες θερμοκρασίες στο 1ο δεκαήμερο και κλιματολογικά στοιχεία του μήνα'' Ο Σεπτέμβριος ως μεταβατικός μήνας από το καλοκαίρι στο φθινόπωρο, ιδιαίτερα το πρώτο δεκαήμερο,
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΑΝΑΛΥΣΗ ΙΣΧΥΡΩΝ ΒΡΟΧΟΠΤΩΣΕΩΝ ΣΤΟΝ ΕΛΛΗΝΙΚΟ ΧΩΡΟ ΚΑΤΑ ΤΥΠΟ ΚΑΙΡΟΥ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΙΕΠΙΣΤΗΜΟΝΙΚΟ - ΙΑΤΜΗΜΑΤIΚΟ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥ ΩΝ «ΕΠΙΣΤΗΜΗ & ΤΕΧΝΟΛΟΓΙΑ Υ ΑΤΙΚΩΝ ΠΟΡΩΝ» ΑΝΑΛΥΣΗ ΙΣΧΥΡΩΝ ΒΡΟΧΟΠΤΩΣΕΩΝ ΣΤΟΝ ΕΛΛΗΝΙΚΟ ΧΩΡΟ ΚΑΤΑ ΤΥΠΟ ΚΑΙΡΟΥ Κωνσταντίνα
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΙΕΠΙΣΤΗΜΟΝΙΚΟ - ΙΑΤΜΗΜΑΤIΚΟ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥ ΩΝ «ΕΠΙΣΤΗΜΗ & ΤΕΧΝΟΛΟΓΙΑ Υ ΑΤΙΚΩΝ ΠΟΡΩΝ» ΑΝΑΛΥΣΗ ΙΣΧΥΡΩΝ ΒΡΟΧΟΠΤΩΣΕΩΝ ΣΤΟΝ ΕΛΛΗΝΙΚΟ ΧΩΡΟ ΚΑΤΑ ΤΥΠΟ ΚΑΙΡΟΥ Κωνσταντίνα
Κεφάλαιο 5 Κριτήρια απόρριψης απόμακρων τιμών
 Κεφάλαιο 5 Κριτήρια απόρριψης απόμακρων τιμών Σύνοψη Στο κεφάλαιο αυτό παρουσιάζονται δύο κριτήρια απόρριψης απομακρυσμένων από τη μέση τιμή πειραματικών μετρήσεων ενός φυσικού μεγέθους και συγκεκριμένα
Κεφάλαιο 5 Κριτήρια απόρριψης απόμακρων τιμών Σύνοψη Στο κεφάλαιο αυτό παρουσιάζονται δύο κριτήρια απόρριψης απομακρυσμένων από τη μέση τιμή πειραματικών μετρήσεων ενός φυσικού μεγέθους και συγκεκριμένα
Στο στάδιο ανάλυσης των αποτελεσµάτων: ανάλυση ευαισθησίας της λύσης, προσδιορισµός της σύγκρουσης των κριτηρίων.
 ΠΕΡΙΛΗΨΗ Η τεχνική αυτή έκθεση περιλαµβάνει αναλυτική περιγραφή των εναλλακτικών µεθόδων πολυκριτηριακής ανάλυσης που εξετάσθηκαν µε στόχο να επιλεγεί η µέθοδος εκείνη η οποία είναι η πιο κατάλληλη για
ΠΕΡΙΛΗΨΗ Η τεχνική αυτή έκθεση περιλαµβάνει αναλυτική περιγραφή των εναλλακτικών µεθόδων πολυκριτηριακής ανάλυσης που εξετάσθηκαν µε στόχο να επιλεγεί η µέθοδος εκείνη η οποία είναι η πιο κατάλληλη για
«Η μεθοδολογία υπολογισμού του Ανέμου για τη δημιουργία βιώσιμων αιολικών πάρκων»
 «Η μεθοδολογία υπολογισμού του Ανέμου για τη δημιουργία βιώσιμων αιολικών πάρκων» Συνέδριο TEE με θέμα: «Ενέργεια: Σημερινή εικόνα Σχεδιασμός Προοπτικές», Ξενοδοχείο DIVANI CARAVEL 8, 9 και 10 Μαρτίου
«Η μεθοδολογία υπολογισμού του Ανέμου για τη δημιουργία βιώσιμων αιολικών πάρκων» Συνέδριο TEE με θέμα: «Ενέργεια: Σημερινή εικόνα Σχεδιασμός Προοπτικές», Ξενοδοχείο DIVANI CARAVEL 8, 9 και 10 Μαρτίου
Εισαγωγή ΕΙΣΑΓΩΓΗ ΣΤΑ ΓΣΠ
 ΕΙΣΑΓΩΓΗ ΣΤΑ ΓΣΠ Τα τελευταία 25 χρόνια, τα προβλήµατα που σχετίζονται µε την διαχείριση της Γεωγραφικής Πληροφορίας αντιµετωπίζονται σε παγκόσµιο αλλά και εθνικό επίπεδο µε την βοήθεια των Γεωγραφικών
ΕΙΣΑΓΩΓΗ ΣΤΑ ΓΣΠ Τα τελευταία 25 χρόνια, τα προβλήµατα που σχετίζονται µε την διαχείριση της Γεωγραφικής Πληροφορίας αντιµετωπίζονται σε παγκόσµιο αλλά και εθνικό επίπεδο µε την βοήθεια των Γεωγραφικών
Μελέτη προβλημάτων ΠΗΙ λόγω λειτουργίας βοηθητικών προωστήριων μηχανισμών
 «ΔιερΕΥνηση Και Aντιμετώπιση προβλημάτων ποιότητας ηλεκτρικής Ισχύος σε Συστήματα Ηλεκτρικής Ενέργειας (ΣΗΕ) πλοίων» (ΔΕΥ.Κ.Α.Λ.Ι.ΩΝ) πράξη ΘΑΛΗΣ-ΕΜΠ, πράξη ένταξης 11012/9.7.2012, MIS: 380164, Κωδ.ΕΔΕΙΛ/ΕΜΠ:
«ΔιερΕΥνηση Και Aντιμετώπιση προβλημάτων ποιότητας ηλεκτρικής Ισχύος σε Συστήματα Ηλεκτρικής Ενέργειας (ΣΗΕ) πλοίων» (ΔΕΥ.Κ.Α.Λ.Ι.ΩΝ) πράξη ΘΑΛΗΣ-ΕΜΠ, πράξη ένταξης 11012/9.7.2012, MIS: 380164, Κωδ.ΕΔΕΙΛ/ΕΜΠ:
ΑΡΙΘΜΗΤΙΚΗ ΠΡΟΓΝΩΣΗ ΚΑΙΡΟΥ - ΜΕΤΕΩΡΟΛΟΓΙΚΑ ΜΟΝΤΕΛΑ
 ΕΙΣΑΓΩΓΗ ΣΤHN ΑΡΙΘΜΗΤΙΚΗ ΠΡΟΓΝΩΣΗ ΚΑΙΡΟΥ - ΜΕΤΕΩΡΟΛΟΓΙΚΑ ΜΟΝΤΕΛΑ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ Επιστήµη και Τεχνολογία Υδάτινων Πόρων ΕΜΠ Ι ΑΣΚΟΥΣΑ: Β. ΚΟΤΡΩΝΗ ΑΚΑ ΗΜΑΙΚΟ ΕΤΟΣ: 2003-2004 ΙΣΤΟΡΙΚΗ ΑΝΑ
ΕΙΣΑΓΩΓΗ ΣΤHN ΑΡΙΘΜΗΤΙΚΗ ΠΡΟΓΝΩΣΗ ΚΑΙΡΟΥ - ΜΕΤΕΩΡΟΛΟΓΙΚΑ ΜΟΝΤΕΛΑ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ Επιστήµη και Τεχνολογία Υδάτινων Πόρων ΕΜΠ Ι ΑΣΚΟΥΣΑ: Β. ΚΟΤΡΩΝΗ ΑΚΑ ΗΜΑΙΚΟ ΕΤΟΣ: 2003-2004 ΙΣΤΟΡΙΚΗ ΑΝΑ
ΚΕΦΑΛΑΙΟ 3 ΜΕΛΕΤΗ ΑΠΟ ΟΣΗΣ ΚΑΙ ΕΠΙΤΥΧΙΑΣ ΗΜΕΡΗΣΙΩΝ ΗΜΟΣΙΩΝ ΚΑΙ Ι ΙΩΤΙΚΩΝ ΛΥΚΕΙΩΝ ΕΙΣΑΓΩΓΗ
 ΚΕΦΑΛΑΙΟ 3 ΜΕΛΕΤΗ ΑΠΟ ΟΣΗΣ ΚΑΙ ΕΠΙΤΥΧΙΑΣ ΗΜΕΡΗΣΙΩΝ ΗΜΟΣΙΩΝ ΚΑΙ Ι ΙΩΤΙΚΩΝ ΛΥΚΕΙΩΝ ΕΙΣΑΓΩΓΗ Στο κεφάλαιο αυτό θα εξετάσουµε την απόδοση και την επιτυχία των υποψηφίων η µερησίων δηµοσίων και ιδιωτικών λυκείων
ΚΕΦΑΛΑΙΟ 3 ΜΕΛΕΤΗ ΑΠΟ ΟΣΗΣ ΚΑΙ ΕΠΙΤΥΧΙΑΣ ΗΜΕΡΗΣΙΩΝ ΗΜΟΣΙΩΝ ΚΑΙ Ι ΙΩΤΙΚΩΝ ΛΥΚΕΙΩΝ ΕΙΣΑΓΩΓΗ Στο κεφάλαιο αυτό θα εξετάσουµε την απόδοση και την επιτυχία των υποψηφίων η µερησίων δηµοσίων και ιδιωτικών λυκείων
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΝΕΥΡΩΝΙΚΑ ΙΚΤΥΑ
 ΘΕΜΑ ο (2.5 µονάδες) ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΝΕΥΡΩΝΙΚΑ ΙΚΤΥΑ Τελικές εξετάσεις 26 Ιανουαρίου 2004 ιάρκεια: 2 ώρες (9:00-:00) Στην παρακάτω
ΘΕΜΑ ο (2.5 µονάδες) ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΝΕΥΡΩΝΙΚΑ ΙΚΤΥΑ Τελικές εξετάσεις 26 Ιανουαρίου 2004 ιάρκεια: 2 ώρες (9:00-:00) Στην παρακάτω
ΦΥΣΙΚΗ ΤΗΣ ΑΤΜΟΣΦΑΙΡΑΣ ΚΑΙ ΤΟΥ ΠΕΡΙΒΑΛΛΟΝΤΟΣ
 ΦΥΣΙΚΗ ΤΗΣ ΑΤΜΟΣΦΑΙΡΑΣ ΚΑΙ ΤΟΥ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Ενότητα: Φυσική Ατμοσφαιρικού Περιβάλλοντος Μέρος 5 ο Η ΕΞΕΛΙΣΣΟΜΕΝΗ ΚΛΙΜΑΤΙΚΗ ΑΛΛΑΓΗ Δημήτρης Μελάς Καθηγητής Το φαινόμενο του θερμοκηπίου είναι ένα φυσικό
ΦΥΣΙΚΗ ΤΗΣ ΑΤΜΟΣΦΑΙΡΑΣ ΚΑΙ ΤΟΥ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Ενότητα: Φυσική Ατμοσφαιρικού Περιβάλλοντος Μέρος 5 ο Η ΕΞΕΛΙΣΣΟΜΕΝΗ ΚΛΙΜΑΤΙΚΗ ΑΛΛΑΓΗ Δημήτρης Μελάς Καθηγητής Το φαινόμενο του θερμοκηπίου είναι ένα φυσικό
Τ Ε Χ Ν Ο Λ Ο Γ Ι Α Κ Λ Ι Μ Α Τ Ι Σ Μ Ο Υ ( Ε ) - Φ Ο Ρ Τ Ι Α 1
 Τ Ε Χ Ν Ο Λ Ο Γ Ι Α Κ Λ Ι Μ Α Τ Ι Σ Μ Ο Υ ( Ε ) - Φ Ο Ρ Τ Ι Α 1 ΦΟΡΤΙΑ Υπό τον όρο φορτίο, ορίζεται ουσιαστικά το πoσό θερµότητας, αισθητό και λανθάνον, που πρέπει να αφαιρεθεί, αντίθετα να προστεθεί κατά
Τ Ε Χ Ν Ο Λ Ο Γ Ι Α Κ Λ Ι Μ Α Τ Ι Σ Μ Ο Υ ( Ε ) - Φ Ο Ρ Τ Ι Α 1 ΦΟΡΤΙΑ Υπό τον όρο φορτίο, ορίζεται ουσιαστικά το πoσό θερµότητας, αισθητό και λανθάνον, που πρέπει να αφαιρεθεί, αντίθετα να προστεθεί κατά
Μεγέθη Κυκλοφοριακής Ροής
 ΚΕΦΑΛΑΙΟ 2 Μεγέθη Κυκλοφοριακής Ροής 2.1 ΕΙΣΑΓΩΓΗ Η κυκλοφορική ροή (traffic flow) αφορά στην κίνηση οχημάτων ή πεζών σε μια οδό και προσδιορίζεται από μεγέθη κυκλοφορικής ροής (traffic flow variables)
ΚΕΦΑΛΑΙΟ 2 Μεγέθη Κυκλοφοριακής Ροής 2.1 ΕΙΣΑΓΩΓΗ Η κυκλοφορική ροή (traffic flow) αφορά στην κίνηση οχημάτων ή πεζών σε μια οδό και προσδιορίζεται από μεγέθη κυκλοφορικής ροής (traffic flow variables)
Τα κύρια σηµεία της παρούσας διδακτορικής διατριβής είναι: Η πειραµατική µελέτη της µεταβατικής συµπεριφοράς συστηµάτων γείωσης
 Κεφάλαιο 5 ΣΥΜΠΕΡΑΣΜΑΤΑ Το σηµαντικό στην επιστήµη δεν είναι να βρίσκεις καινούρια στοιχεία, αλλά να ανακαλύπτεις νέους τρόπους σκέψης γι' αυτά. Sir William Henry Bragg 5.1 Ανακεφαλαίωση της διατριβής
Κεφάλαιο 5 ΣΥΜΠΕΡΑΣΜΑΤΑ Το σηµαντικό στην επιστήµη δεν είναι να βρίσκεις καινούρια στοιχεία, αλλά να ανακαλύπτεις νέους τρόπους σκέψης γι' αυτά. Sir William Henry Bragg 5.1 Ανακεφαλαίωση της διατριβής
ΑΚΡΑΙΕΣ ΒΡΟΧΟΠΤΩΣΕΙΣ ΣΤΟΝ ΕΛΛΑΔΙΚΟ ΧΩΡΟ ΣΤΙΣ ΙΟΥΛΙΟΥ 2017
 ΕΘΝΙΚΗ ΜΕΤΕΩΡΟΛΟΓΙΚΗ ΥΠΗΡΕΣΙΑ ΔΙΕΥΘΥΝΣΗ ΚΛΙΜΑΤΟΛΟΓΙΑΣ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΓΩΝ ΥΔΡΟΜΕΤΕΩΡΟΛΟΓΙΑΣ Άρτεμις Παπαπέτρου ΠΕ Μετεωρολόγος Τμηματάρχης Εφαρμογών Υδρομετεωρολογίας ΑΚΡΑΙΕΣ ΒΡΟΧΟΠΤΩΣΕΙΣ ΣΤΟΝ ΕΛΛΑΔΙΚΟ
ΕΘΝΙΚΗ ΜΕΤΕΩΡΟΛΟΓΙΚΗ ΥΠΗΡΕΣΙΑ ΔΙΕΥΘΥΝΣΗ ΚΛΙΜΑΤΟΛΟΓΙΑΣ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΓΩΝ ΥΔΡΟΜΕΤΕΩΡΟΛΟΓΙΑΣ Άρτεμις Παπαπέτρου ΠΕ Μετεωρολόγος Τμηματάρχης Εφαρμογών Υδρομετεωρολογίας ΑΚΡΑΙΕΣ ΒΡΟΧΟΠΤΩΣΕΙΣ ΣΤΟΝ ΕΛΛΑΔΙΚΟ
Οι καταιγίδες διακρίνονται σε δύο κατηγορίες αναλόγως του αιτίου το οποίο προκαλεί την αστάθεια τις ατμόσφαιρας:
 ΑΝΑΛΥΣΗ ΣΥΧΝΟΤΗΤΑΣ ΡΑΓΔΑΙΩΝ ΒΡΟΧΩΝ Καταιγίδα (storm): Πρόκειται για μια ισχυρή ατμοσφαιρική διαταραχή, η οποία χαρακτηρίζεται από την παρουσία μιας περιοχής χαμηλών ατμοσφαιρικών πιέσεων και από ισχυρούς
ΑΝΑΛΥΣΗ ΣΥΧΝΟΤΗΤΑΣ ΡΑΓΔΑΙΩΝ ΒΡΟΧΩΝ Καταιγίδα (storm): Πρόκειται για μια ισχυρή ατμοσφαιρική διαταραχή, η οποία χαρακτηρίζεται από την παρουσία μιας περιοχής χαμηλών ατμοσφαιρικών πιέσεων και από ισχυρούς
Μέγιστη θερµοκρασία. Ελάχιστη. Μέση. Υετός
 Μέγιστη Ελάχιστη Μέση Υετός Ηλιοφάνεια Ο Σεπτέµβρης µας έδωσε την πραγµατική εικόνα του Φθινοπώρου που είναι αρκετά σπάνια τα τελευταία χρόνια τουλάχιστον για την Κεντρική και Νότια Ελλάδα. Είχε σηµαντικές
Μέγιστη Ελάχιστη Μέση Υετός Ηλιοφάνεια Ο Σεπτέµβρης µας έδωσε την πραγµατική εικόνα του Φθινοπώρου που είναι αρκετά σπάνια τα τελευταία χρόνια τουλάχιστον για την Κεντρική και Νότια Ελλάδα. Είχε σηµαντικές
Όµβριες καµπύλες για το οδικό έργο Καναβάρι- οµβαίνα-πρόδροµος
 Όµβριες καµπύλες για το οδικό έργο Καναβάρι- οµβαίνα-πρόδροµος Περιοχή έργου Η µελέτη αυτή εκπονήθηκε στα πλαίσια της υδραυλικής µελέτης αποστράγγισης της οδού Καναβάρι- οµβαίνα-πρόδροµος που ανατέθηκε
Όµβριες καµπύλες για το οδικό έργο Καναβάρι- οµβαίνα-πρόδροµος Περιοχή έργου Η µελέτη αυτή εκπονήθηκε στα πλαίσια της υδραυλικής µελέτης αποστράγγισης της οδού Καναβάρι- οµβαίνα-πρόδροµος που ανατέθηκε
Η πολυπλοκότητα της Ατµόσφαιρας και οι δυσκολίες στην Πρόγνωση του Καιρού. ΕΘΝΙΚΗ ΜΕΤΕΩΡΟΛΟΓΙΚΗ ΥΠΗΡΕΣΙΑ ρ Γ. Σακελλαρίδης Υποδιοικητής ΕΜΥ
 Η πολυπλοκότητα της Ατµόσφαιρας και οι δυσκολίες στην Πρόγνωση του Καιρού ΕΘΝΙΚΗ ΜΕΤΕΩΡΟΛΟΓΙΚΗ ΥΠΗΡΕΣΙΑ ρ Γ. Σακελλαρίδης Υποδιοικητής ΕΜΥ ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ Περιγραφή της πολυπλοκότητας που εµφανίζεται
Η πολυπλοκότητα της Ατµόσφαιρας και οι δυσκολίες στην Πρόγνωση του Καιρού ΕΘΝΙΚΗ ΜΕΤΕΩΡΟΛΟΓΙΚΗ ΥΠΗΡΕΣΙΑ ρ Γ. Σακελλαρίδης Υποδιοικητής ΕΜΥ ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ Περιγραφή της πολυπλοκότητας που εµφανίζεται
Ονοματεπώνυμο: Επιμέλεια διαγωνίσματος: Αξιολόγηση :
 Ονοματεπώνυμο: Μάθημα: Υλη: Επιμέλεια διαγωνίσματος: Αξιολόγηση : Φυσική Προσανατολισμου Γ Λυκείου Ταλαντώσεις Σχολικό έτος 2017-2018 Σελίδα 1 Διαγώνισμα Ταλαντώσεις Θέμα Α Στις ημιτελείς προτάσεις Α.1
Ονοματεπώνυμο: Μάθημα: Υλη: Επιμέλεια διαγωνίσματος: Αξιολόγηση : Φυσική Προσανατολισμου Γ Λυκείου Ταλαντώσεις Σχολικό έτος 2017-2018 Σελίδα 1 Διαγώνισμα Ταλαντώσεις Θέμα Α Στις ημιτελείς προτάσεις Α.1
Φλόκα Ελενα Αναπληρώτρια Καθηγήτρια Τομέας Φυσικής Περιβάλλοντος-Μετεωρολογίας Τμήμα Φυσικής Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών
 Φλόκα Ελενα Αναπληρώτρια Καθηγήτρια Τομέας Φυσικής Περιβάλλοντος-Μετεωρολογίας Τμήμα Φυσικής Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών ILATIC Project, Ημερίδα 14 Οκτωβρίου 2014, Λεμεσός Σκοπός Να αποτυπωθούν
Φλόκα Ελενα Αναπληρώτρια Καθηγήτρια Τομέας Φυσικής Περιβάλλοντος-Μετεωρολογίας Τμήμα Φυσικής Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών ILATIC Project, Ημερίδα 14 Οκτωβρίου 2014, Λεμεσός Σκοπός Να αποτυπωθούν
ΣΤΟΧΑΣΤΙΚΗ ΠΡΟΣΟΜΟΙΩΣΗ ΤΗΣ ΧΩΡΙΚΗΣ ΔΟΜΗΣ ΤΗΣ ΒΡΟΧΗΣ. Παρουσίαση διπλωματικής εργασίας Αθανάσιος Πασχάλης Επιβλέπων καθηγητής: Δημήτρης Κουτσογιάννης
 ΣΤΟΧΑΣΤΙΚΗ ΠΡΟΣΟΜΟΙΩΣΗ ΤΗΣ ΧΩΡΙΚΗΣ ΔΟΜΗΣ ΤΗΣ ΒΡΟΧΗΣ Παρουσίαση διπλωματικής εργασίας Αθανάσιος Πασχάλης Επιβλέπων καθηγητής: Δημήτρης Κουτσογιάννης Διάρθρωση ρ της παρουσίασης Εισαγωγή Στατιστική επεξεργασία
ΣΤΟΧΑΣΤΙΚΗ ΠΡΟΣΟΜΟΙΩΣΗ ΤΗΣ ΧΩΡΙΚΗΣ ΔΟΜΗΣ ΤΗΣ ΒΡΟΧΗΣ Παρουσίαση διπλωματικής εργασίας Αθανάσιος Πασχάλης Επιβλέπων καθηγητής: Δημήτρης Κουτσογιάννης Διάρθρωση ρ της παρουσίασης Εισαγωγή Στατιστική επεξεργασία
Τεχνική Υδρολογία (Ασκήσεις)
 Τμήμα Δασολογίας & Διαχείρισης Περιβάλλοντος & Φυσικών Πόρων Εργαστήριο Διευθέτησης Ορεινών Υδάτων και Διαχείρισης Κινδύνου Προπτυχιακό Πρόγραμμα Σπουδών Τεχνική Υδρολογία (Ασκήσεις) Κεφάλαιο 2 ο : Κατακρημνίσματα
Τμήμα Δασολογίας & Διαχείρισης Περιβάλλοντος & Φυσικών Πόρων Εργαστήριο Διευθέτησης Ορεινών Υδάτων και Διαχείρισης Κινδύνου Προπτυχιακό Πρόγραμμα Σπουδών Τεχνική Υδρολογία (Ασκήσεις) Κεφάλαιο 2 ο : Κατακρημνίσματα
4.4 Βάσεις Δεδομένων με πολλές Μεταβλητές
 4.4 Βάσεις Δεδομένων με πολλές Μεταβλητές Σε αυτή την ενότητα θα παρουσιάσουμε μερικά παραδείγματα με βάσεις δεδομένων που έχουν μονοδιάστατη έξοδο και πολυδιάστατη είσοδο. Οι βάσεις δεδομένων προέρχονται
4.4 Βάσεις Δεδομένων με πολλές Μεταβλητές Σε αυτή την ενότητα θα παρουσιάσουμε μερικά παραδείγματα με βάσεις δεδομένων που έχουν μονοδιάστατη έξοδο και πολυδιάστατη είσοδο. Οι βάσεις δεδομένων προέρχονται
ΣΤΑΤΙΣΤΙΚΗ ΕΠΙΧΕΙΡΗΣΕΩΝ ΕΙΔΙΚΑ ΘΕΜΑΤΑ. Κεφάλαιο 10. Εισαγωγή στην εκτιμητική
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΣΤΑΤΙΣΤΙΚΗ ΕΠΙΧΕΙΡΗΣΕΩΝ ΕΙΔΙΚΑ ΘΕΜΑΤΑ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΠΑΤΡΑΣ Εργαστήριο Λήψης Αποφάσεων & Επιχειρησιακού Προγραμματισμού Καθηγητής Ι. Μητρόπουλος ΣΤΑΤΙΣΤΙΚΗ ΕΠΙΧΕΙΡΗΣΕΩΝ ΕΙΔΙΚΑ ΘΕΜΑΤΑ
Κεφάλαιο 6. Εισαγωγή στη µέθοδο πεπερασµένων όγκων επίλυση ελλειπτικών και παραβολικών διαφορικών εξισώσεων
 Κεφάλαιο 6 Εισαγωγή στη µέθοδο πεπερασµένων όγκων επίλυση ελλειπτικών παραβολικών διαφορικών εξισώσεων 6.1 Εισαγωγή Η µέθοδος των πεπερασµένων όγκων είναι µία ευρέως διαδεδοµένη υπολογιστική µέθοδος επίλυσης
Κεφάλαιο 6 Εισαγωγή στη µέθοδο πεπερασµένων όγκων επίλυση ελλειπτικών παραβολικών διαφορικών εξισώσεων 6.1 Εισαγωγή Η µέθοδος των πεπερασµένων όγκων είναι µία ευρέως διαδεδοµένη υπολογιστική µέθοδος επίλυσης
ΙΕΡΕΥΝΗΣΗ ΤΗΣ ΑΚΡΙΒΕΙΑΣ ΤΩΝ ΗΜΟΓΡΑΦΙΚΩΝ Ε ΟΜΕΝΩΝ
 ΚΕΦΑΛΑΙΟ 9 ΙΕΡΕΥΝΗΣΗ ΤΗΣ ΑΚΡΙΒΕΙΑΣ ΤΩΝ ΗΜΟΓΡΑΦΙΚΩΝ Ε ΟΜΕΝΩΝ Τα δηµογραφικά δεδοµένα τα οποία προέρχονται από τις απογραφές πληθυσµού, τις καταγραφές της φυσικής και µεταναστευτικής κίνησης του πληθυσµού
ΚΕΦΑΛΑΙΟ 9 ΙΕΡΕΥΝΗΣΗ ΤΗΣ ΑΚΡΙΒΕΙΑΣ ΤΩΝ ΗΜΟΓΡΑΦΙΚΩΝ Ε ΟΜΕΝΩΝ Τα δηµογραφικά δεδοµένα τα οποία προέρχονται από τις απογραφές πληθυσµού, τις καταγραφές της φυσικής και µεταναστευτικής κίνησης του πληθυσµού
Παναγιώτης Γ. Κοσμόπουλος 1, Παναγιώτης Θ. Νάστος 1,
 Μελέτη των επεισοδίων σκόνης στην Αθήνα από δορυφορικά δεδομένα την περίοδο 2000-20052005 Παναγιώτης Γ. Κοσμόπουλος 1, Παναγιώτης Θ. Νάστος 1, Δημήτρης Γ. Κασκαούτης 2,3, Χάρης Δ. Καμπεζίδης 2 1 Τμήμα
Μελέτη των επεισοδίων σκόνης στην Αθήνα από δορυφορικά δεδομένα την περίοδο 2000-20052005 Παναγιώτης Γ. Κοσμόπουλος 1, Παναγιώτης Θ. Νάστος 1, Δημήτρης Γ. Κασκαούτης 2,3, Χάρης Δ. Καμπεζίδης 2 1 Τμήμα
Μια από τις σημαντικότερες δυσκολίες που συναντά ο φυσικός στη διάρκεια ενός πειράματος, είναι τα σφάλματα.
 Εισαγωγή Μετρήσεις-Σφάλματα Πολλές φορές θα έχει τύχει να ακούσουμε τη λέξη πείραμα, είτε στο μάθημα είτε σε κάποια είδηση που αφορά τη Φυσική, τη Χημεία ή τη Βιολογία. Είναι όμως γενικώς παραδεκτό ότι
Εισαγωγή Μετρήσεις-Σφάλματα Πολλές φορές θα έχει τύχει να ακούσουμε τη λέξη πείραμα, είτε στο μάθημα είτε σε κάποια είδηση που αφορά τη Φυσική, τη Χημεία ή τη Βιολογία. Είναι όμως γενικώς παραδεκτό ότι
Κοτρώνη Βασιλική ΙΕΠΒΑ ΕΑΑ
 Κοτρώνη Βασιλική ΙΕΠΒΑ ΕΑΑ Θεματικά αντικείμενα Πρόγνωση κεραυνικής δραστηριότητας / WRF Κλιματολογία κεραυνικής δραστηριότητας Άμεση πρόγνωση κεραυνικής δραστηριότητας Κεραυνική δραστηριότητα & aerosols
Κοτρώνη Βασιλική ΙΕΠΒΑ ΕΑΑ Θεματικά αντικείμενα Πρόγνωση κεραυνικής δραστηριότητας / WRF Κλιματολογία κεραυνικής δραστηριότητας Άμεση πρόγνωση κεραυνικής δραστηριότητας Κεραυνική δραστηριότητα & aerosols
ΒΙΟΓΡΑΦΙΚΟ ΣΗΜΕΙΩΜΑ. Δημήτριος Κατσάνος
 ΒΙΟΓΡΑΦΙΚΟ ΣΗΜΕΙΩΜΑ Δημήτριος Κατσάνος ΑΤΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΟΝΟΜΑ : ΔΗΜΗΤΡΙΟΣ ΕΠΩΝΥΜΟ : ΚΑΤΣΑΝΟΣ ΗΜΕΡΟΜΗΝΙΑ ΓΕΝΝΗΣΗΣ : 04/06/1974 ΣΤΟΙΧΕΙΑ ΕΠΙΚΟΙΝΩΝΙΑΣ ΑΡΙΘ. ΤΗΛΕΦΩΝΟΥ : 210 8109136 / 697 4598389 Ε-MAIL :
ΒΙΟΓΡΑΦΙΚΟ ΣΗΜΕΙΩΜΑ Δημήτριος Κατσάνος ΑΤΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΟΝΟΜΑ : ΔΗΜΗΤΡΙΟΣ ΕΠΩΝΥΜΟ : ΚΑΤΣΑΝΟΣ ΗΜΕΡΟΜΗΝΙΑ ΓΕΝΝΗΣΗΣ : 04/06/1974 ΣΤΟΙΧΕΙΑ ΕΠΙΚΟΙΝΩΝΙΑΣ ΑΡΙΘ. ΤΗΛΕΦΩΝΟΥ : 210 8109136 / 697 4598389 Ε-MAIL :
ΠΑΝΕΠΙΣΤΗΜΙΑΚΑ ΦΡΟΝΤΙΣΤΗΡΙΑ ΚΟΛΛΙΝΤΖΑ. Ερωτήσεις πολλαπλής επιλογής. Συντάκτης: Δημήτριος Κρέτσης
 ΠΑΝΕΠΙΣΤΗΜΙΑΚΑ ΦΡΟΝΤΙΣΤΗΡΙΑ ΚΟΛΛΙΝΤΖΑ Ερωτήσεις πολλαπλής επιλογής Συντάκτης: Δημήτριος Κρέτσης 1. Ο κλάδος της περιγραφικής Στατιστικής: α. Ασχολείται με την επεξεργασία των δεδομένων και την ανάλυση
ΠΑΝΕΠΙΣΤΗΜΙΑΚΑ ΦΡΟΝΤΙΣΤΗΡΙΑ ΚΟΛΛΙΝΤΖΑ Ερωτήσεις πολλαπλής επιλογής Συντάκτης: Δημήτριος Κρέτσης 1. Ο κλάδος της περιγραφικής Στατιστικής: α. Ασχολείται με την επεξεργασία των δεδομένων και την ανάλυση
Εκτενής περίληψη (Extended abstract in Greek)
 Εκτενής περίληψη (Extended abstract in Greek) Την 14 η και 15 η Νοεμβρίου 217, μία βροχόπτωση με σημαντική ένταση εκδηλώθηκε στη Δυτική Αττική, με αποτέλεσμα την εμφάνιση αιφνίδιας πλημμύρας στην περιοχή,
Εκτενής περίληψη (Extended abstract in Greek) Την 14 η και 15 η Νοεμβρίου 217, μία βροχόπτωση με σημαντική ένταση εκδηλώθηκε στη Δυτική Αττική, με αποτέλεσμα την εμφάνιση αιφνίδιας πλημμύρας στην περιοχή,
ΕΝΟΤΗΤΑ III ΒΑΣΙΚΕΣ ΜΕΘΟ ΟΙ ΑΝΑΛΥΣΗΣ
 ΕΝΟΤΗΤΑ III ΒΑΣΙΚΕΣ ΜΕΘΟ ΟΙ ΑΝΑΛΥΣΗΣ Βασικός τελικός στόχος κάθε επιστηµονικής τεχνολογικής εφαρµογής είναι: H γενική βελτίωση της ποιότητας του περιβάλλοντος Η βελτίωση της ποιότητας ζωής Τα µέσα µε τα
ΕΝΟΤΗΤΑ III ΒΑΣΙΚΕΣ ΜΕΘΟ ΟΙ ΑΝΑΛΥΣΗΣ Βασικός τελικός στόχος κάθε επιστηµονικής τεχνολογικής εφαρµογής είναι: H γενική βελτίωση της ποιότητας του περιβάλλοντος Η βελτίωση της ποιότητας ζωής Τα µέσα µε τα
ΚΕΦΑΛΑΙΟ 2 Γ ΙΕΥΘΥΝΣΗ ΑΘΗΝΑΣ - 5 Ο ΓΡΑΦΕΙΟ ΣΧΟΛΙΚΟ ΕΤΟΣ ΠΕΡΙΓΡΑΦΗ ΤΩΝ Ε ΟΜΕΝΩΝ ΜΕ ΑΡΙΘΜΗΤΙΚΕΣ ΚΑΙ ΓΡΑΦΙΚΕΣ ΜΕΘΟ ΟΥΣ
 ΚΕΦΑΛΑΙΟ 2 Γ ΙΕΥΘΥΝΣΗ ΑΘΗΝΑΣ - 5 Ο ΓΡΑΦΕΙΟ ΣΧΟΛΙΚΟ ΕΤΟΣ 2000-2001 ΠΕΡΙΓΡΑΦΗ ΤΩΝ Ε ΟΜΕΝΩΝ ΜΕ ΑΡΙΘΜΗΤΙΚΕΣ ΚΑΙ ΓΡΑΦΙΚΕΣ ΜΕΘΟ ΟΥΣ Το τµήµα αυτό της έρευνας αναφέρεται στην Γ τάξη όλων των Ενιαίων Λυκείων του
ΚΕΦΑΛΑΙΟ 2 Γ ΙΕΥΘΥΝΣΗ ΑΘΗΝΑΣ - 5 Ο ΓΡΑΦΕΙΟ ΣΧΟΛΙΚΟ ΕΤΟΣ 2000-2001 ΠΕΡΙΓΡΑΦΗ ΤΩΝ Ε ΟΜΕΝΩΝ ΜΕ ΑΡΙΘΜΗΤΙΚΕΣ ΚΑΙ ΓΡΑΦΙΚΕΣ ΜΕΘΟ ΟΥΣ Το τµήµα αυτό της έρευνας αναφέρεται στην Γ τάξη όλων των Ενιαίων Λυκείων του
Ranking the importance of real-time traffic and weather variables when examining crash injury severity
 16ο Ειδικό Συνέδριο της Ελληνικής Εταιρείας Επιχειρησιακών Ερευνών και τη 12η Συνάντηση Πολυκριτήριας Ανάλυσης Αποφάσεων. Εμπορικό και Βιομηχανικό Επιμελητήριο Πειραιά 15-17 Φεβρουαρίου 2018 Ranking the
16ο Ειδικό Συνέδριο της Ελληνικής Εταιρείας Επιχειρησιακών Ερευνών και τη 12η Συνάντηση Πολυκριτήριας Ανάλυσης Αποφάσεων. Εμπορικό και Βιομηχανικό Επιμελητήριο Πειραιά 15-17 Φεβρουαρίου 2018 Ranking the
5. ΤΟ ΓΕΝΙΚΟ ΓΡΑΜΜΙΚΟ ΜΟΝΤΕΛΟ (GENERAL LINEAR MODEL) 5.1 Εναλλακτικά μοντέλα του απλού γραμμικού μοντέλου: Το εκθετικό μοντέλο
 5. ΤΟ ΓΕΝΙΚΟ ΓΡΑΜΜΙΚΟ ΜΟΝΤΕΛΟ (GENERAL LINEAR MODEL) 5.1 Εναλλακτικά μοντέλα του απλού γραμμικού μοντέλου: Το εκθετικό μοντέλο Ένα εναλλακτικό μοντέλο της απλής γραμμικής παλινδρόμησης (που χρησιμοποιήθηκε
5. ΤΟ ΓΕΝΙΚΟ ΓΡΑΜΜΙΚΟ ΜΟΝΤΕΛΟ (GENERAL LINEAR MODEL) 5.1 Εναλλακτικά μοντέλα του απλού γραμμικού μοντέλου: Το εκθετικό μοντέλο Ένα εναλλακτικό μοντέλο της απλής γραμμικής παλινδρόμησης (που χρησιμοποιήθηκε
Μετεωρολογικό Ραντάρ και πρόγνωση σφοδρών καταιγίδων και πλημμυρών Μιχαήλ Σιούτας
 Μετεωρολογικό Ραντάρ και πρόγνωση σφοδρών καταιγίδων και πλημμυρών Μιχαήλ Σιούτας Κέντρο Μετεωρολογικών Εφαρμογών ΕΛΓΑ Αεροδρόμιο Μακεδονία, Θεσσαλονίκη Μετεωρολογικό Ραντάρ Το Μετεωρολογικό Ραντάρ ή Ραντάρ
Μετεωρολογικό Ραντάρ και πρόγνωση σφοδρών καταιγίδων και πλημμυρών Μιχαήλ Σιούτας Κέντρο Μετεωρολογικών Εφαρμογών ΕΛΓΑ Αεροδρόμιο Μακεδονία, Θεσσαλονίκη Μετεωρολογικό Ραντάρ Το Μετεωρολογικό Ραντάρ ή Ραντάρ
ΤΕΚΜΗΡΙΩΣΗ ΕΙΚΤΩΝ ΒΑΣΕΩΝ (ΑΝΑΘΕΩΡΗΜΕΝΗ)
 ΤΕΚΜΗΡΙΩΣΗ ΕΙΚΤΩΝ ΒΑΣΕΩΝ (ΑΝΑΘΕΩΡΗΜΕΝΗ) Η πρόβλεψη των βάσεων είναι ένα δύσκολο και παρακινδυνευµένο εγχείρηµα, κάθε χρόνο, διότι αν και υπάρχουν τα βασικά βαθµολογικά και άλλα στοιχεία δεν είναι γνωστές
ΤΕΚΜΗΡΙΩΣΗ ΕΙΚΤΩΝ ΒΑΣΕΩΝ (ΑΝΑΘΕΩΡΗΜΕΝΗ) Η πρόβλεψη των βάσεων είναι ένα δύσκολο και παρακινδυνευµένο εγχείρηµα, κάθε χρόνο, διότι αν και υπάρχουν τα βασικά βαθµολογικά και άλλα στοιχεία δεν είναι γνωστές
Εποχιακή (μεσοπρόθεσμη) πρόβλεψη κινδύνου πυρκαγιών. Αθανάσιος ΣΦΕΤΣΟΣ
 Εποχιακή (μεσοπρόθεσμη) πρόβλεψη κινδύνου πυρκαγιών προγνωστική χαρτογράφηση κινδύνου πυρκαγιάς, με βάση το Καναδικό Σύστημα Μετεωρολογικού Δείκτη Κινδύνου FWI Αθανάσιος ΣΦΕΤΣΟΣ Εργαστήριο Περιβαλλοντικών
Εποχιακή (μεσοπρόθεσμη) πρόβλεψη κινδύνου πυρκαγιών προγνωστική χαρτογράφηση κινδύνου πυρκαγιάς, με βάση το Καναδικό Σύστημα Μετεωρολογικού Δείκτη Κινδύνου FWI Αθανάσιος ΣΦΕΤΣΟΣ Εργαστήριο Περιβαλλοντικών
ΑΡΙΘΜΗΤΙΚΗ ΠΡΟΓΝΩΣΗ ΚΑΙΡΟΥ - ΜΕΤΕΩΡΟΛΟΓΙΚΑ ΜΟΝΤΕΛΑ
 ΕΙΣΑΓΩΓΗ ΣΤHN ΑΡΙΘΜΗΤΙΚΗ ΠΡΟΓΝΩΣΗ ΚΑΙΡΟΥ - ΜΕΤΕΩΡΟΛΟΓΙΚΑ ΜΟΝΤΕΛΑ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ Επιστήµη και Τεχνολογία Υδάτινων Πόρων ΕΜΠ ΔΙΔΑΣΚΟΥΣΑ: Β. ΚΟΤΡΩΝΗ ΑΚΑΔΗΜΑΙΚΟ ΕΤΟΣ: 2010-2011 ΙΣΤΟΡΙΚΗ ΑΝΑ
ΕΙΣΑΓΩΓΗ ΣΤHN ΑΡΙΘΜΗΤΙΚΗ ΠΡΟΓΝΩΣΗ ΚΑΙΡΟΥ - ΜΕΤΕΩΡΟΛΟΓΙΚΑ ΜΟΝΤΕΛΑ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ Επιστήµη και Τεχνολογία Υδάτινων Πόρων ΕΜΠ ΔΙΔΑΣΚΟΥΣΑ: Β. ΚΟΤΡΩΝΗ ΑΚΑΔΗΜΑΙΚΟ ΕΤΟΣ: 2010-2011 ΙΣΤΟΡΙΚΗ ΑΝΑ
ΒΑΘΜΟΝΟΜΗΣΗ ΚΑΙ ΕΦΑΡΜΟΓΗ ΜΙΑΣ ΥΠΕΡΥΘΡΗΣ ΟΡΥΦΟΡΙΚΗΣ ΤΕΧΝΙΚΗΣ ΕΚΤΙΜΗΣΗΣ ΤΗΣ ΒΡΟΧΟΠΤΩΣΗΣ ΓΙΑ ΤΗΝ ΠΕΡΙΟΧΗ ΤΗΣ ΜΕΣΟΓΕΙΟΥ
 ΒΑΘΜΟΝΟΜΗΣΗ ΚΑΙ ΕΦΑΡΜΟΓΗ ΜΙΑΣ ΥΠΕΡΥΘΡΗΣ ΟΡΥΦΟΡΙΚΗΣ ΤΕΧΝΙΚΗΣ ΕΚΤΙΜΗΣΗΣ ΤΗΣ ΒΡΟΧΟΠΤΩΣΗΣ ΓΙΑ ΤΗΝ ΠΕΡΙΟΧΗ ΤΗΣ ΜΕΣΟΓΕΙΟΥ Χ. Φείδας 1, Γ. Κοκολάτος 1, Α.J. Negri 2, Μ. Manyin 2, Ν. Χρυσουλάκης 3 1 Πανεπιστήµιο
ΒΑΘΜΟΝΟΜΗΣΗ ΚΑΙ ΕΦΑΡΜΟΓΗ ΜΙΑΣ ΥΠΕΡΥΘΡΗΣ ΟΡΥΦΟΡΙΚΗΣ ΤΕΧΝΙΚΗΣ ΕΚΤΙΜΗΣΗΣ ΤΗΣ ΒΡΟΧΟΠΤΩΣΗΣ ΓΙΑ ΤΗΝ ΠΕΡΙΟΧΗ ΤΗΣ ΜΕΣΟΓΕΙΟΥ Χ. Φείδας 1, Γ. Κοκολάτος 1, Α.J. Negri 2, Μ. Manyin 2, Ν. Χρυσουλάκης 3 1 Πανεπιστήµιο
4.1 Εισαγωγή. Μετεωρολογικός κλωβός
 4 Θερμοκρασία 4.1 Εισαγωγή Η θερμοκρασία αποτελεί ένα μέτρο της θερμικής κατάστασης ενός σώματος, δηλ. η θερμοκρασία εκφράζει το πόσο ψυχρό ή θερμό είναι το σώμα. Η θερμοκρασία του αέρα μετράται διεθνώς
4 Θερμοκρασία 4.1 Εισαγωγή Η θερμοκρασία αποτελεί ένα μέτρο της θερμικής κατάστασης ενός σώματος, δηλ. η θερμοκρασία εκφράζει το πόσο ψυχρό ή θερμό είναι το σώμα. Η θερμοκρασία του αέρα μετράται διεθνώς
0.3m. 12m N = N = 84 N = 8 N = 168 N = 32. v =0.2 N = 15. tot
 ΚΕΦΑΛΑΙΟ : Αριθµητικές Εφαρµογές... Παράδειγµα γ: Ελαστική ευστάθεια πασσαλοθεµελίωσης Το παράδειγµα αυτό αφορά την µελέτη της ελαστικής ευστάθειας φορέως θεµελίωσης, ο οποίος αποτελείται από µια πεδιλοδοκό
ΚΕΦΑΛΑΙΟ : Αριθµητικές Εφαρµογές... Παράδειγµα γ: Ελαστική ευστάθεια πασσαλοθεµελίωσης Το παράδειγµα αυτό αφορά την µελέτη της ελαστικής ευστάθειας φορέως θεµελίωσης, ο οποίος αποτελείται από µια πεδιλοδοκό
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΣΗΣΗ 5
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥ ΩΝ ΦΥΣΙΚΗ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΣΗΣΗ 5 Προσδιορισµός του ύψους του οραικού στρώµατος µε τη διάταξη lidar. Μπαλής
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥ ΩΝ ΦΥΣΙΚΗ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΣΗΣΗ 5 Προσδιορισµός του ύψους του οραικού στρώµατος µε τη διάταξη lidar. Μπαλής
Δορυφορικός Σταθμός της ΕΜΥ
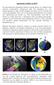 Δορυφορικός Σταθμός της ΕΜΥ Οι μετεωρολογικοί δορυφόροι πολικής τροχιάς πετούν σε σταθερό ύψος μερικών εκατοντάδων χιλιομέτρων από την επιφάνεια της γης, καταγράφοντας με πολύ μεγάλη ακρίβεια την δομή
Δορυφορικός Σταθμός της ΕΜΥ Οι μετεωρολογικοί δορυφόροι πολικής τροχιάς πετούν σε σταθερό ύψος μερικών εκατοντάδων χιλιομέτρων από την επιφάνεια της γης, καταγράφοντας με πολύ μεγάλη ακρίβεια την δομή
Συνεργαζόμενοι φορείς: ΕΤΜΕ: Πέππας & Συνεργάτες Ε.Ε. Γραφείο Μαχαίρα Α.Ε. Εθνικό Μετσόβιο Πολυτεχνείο Τομέας Υδατικών Πόρων και Περιβάλλοντος
 ΕΥΡΩΠΑΪΚΗ ΕΝΩΣΗ ΕΥΡΩΠΑΪΚΟ ΤΑΜΕΙΟ ΠΕΡΙΦΕΡΕΙΑΚΗΣ ΑΝΑΠΤΥΞΗΣ ΔΕΥΚΑΛΙΩΝ Εκτίμηση πλημμυρικών ροών στην Ελλάδα σε συνθήκες υδροκλιματικής μεταβλητότητας: Ανάπτυξη φυσικά εδραιωμένου εννοιολογικού πιθανοτικού
ΕΥΡΩΠΑΪΚΗ ΕΝΩΣΗ ΕΥΡΩΠΑΪΚΟ ΤΑΜΕΙΟ ΠΕΡΙΦΕΡΕΙΑΚΗΣ ΑΝΑΠΤΥΞΗΣ ΔΕΥΚΑΛΙΩΝ Εκτίμηση πλημμυρικών ροών στην Ελλάδα σε συνθήκες υδροκλιματικής μεταβλητότητας: Ανάπτυξη φυσικά εδραιωμένου εννοιολογικού πιθανοτικού
Η ΙΣΧΥΣ ΕΝΟΣ ΕΛΕΓΧΟΥ. (Power of a Test) ΚΕΦΑΛΑΙΟ 21
 ΚΕΦΑΛΑΙΟ 21 Η ΙΣΧΥΣ ΕΝΟΣ ΕΛΕΓΧΟΥ (Power of a Test) Όπως είδαμε προηγουμένως, στον Στατιστικό Έλεγχο Υποθέσεων, ορίζουμε δύο είδη πιθανών λαθών (κινδύνων) που μπορεί να συμβούν όταν παίρνουμε αποφάσεις
ΚΕΦΑΛΑΙΟ 21 Η ΙΣΧΥΣ ΕΝΟΣ ΕΛΕΓΧΟΥ (Power of a Test) Όπως είδαμε προηγουμένως, στον Στατιστικό Έλεγχο Υποθέσεων, ορίζουμε δύο είδη πιθανών λαθών (κινδύνων) που μπορεί να συμβούν όταν παίρνουμε αποφάσεις
ΑΝΑΖΗΤΗΣΗ ΣΥΣΧΕΤΙΣΗΣ ΜΕΤΑΞΥ ΚΛΙΜΑΤΙΚΩΝ ΔΕΙΚΤΩΝ ΜΑΚΡΑΣ ΚΛΙΜΑΚΑΣ ΚΑΙ ΜΕΤΕΩΡΟΛΟΓΙΚΗΣ ΞΗΡΑΣΙΑΣ ΣΤΗΝ ΕΛΛΑΔΑ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΟΜΕΑΣ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΑΝΑΖΗΤΗΣΗ ΣΥΣΧΕΤΙΣΗΣ ΜΕΤΑΞΥ ΚΛΙΜΑΤΙΚΩΝ ΔΕΙΚΤΩΝ ΜΑΚΡΑΣ ΚΛΙΜΑΚΑΣ ΚΑΙ ΜΕΤΕΩΡΟΛΟΓΙΚΗΣ ΞΗΡΑΣΙΑΣ ΣΤΗΝ ΕΛΛΑΔΑ Εμμανουέλα Ιακωβίδου Επιβλέπων
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΟΜΕΑΣ ΥΔΑΤΙΚΩΝ ΠΟΡΩΝ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΑΝΑΖΗΤΗΣΗ ΣΥΣΧΕΤΙΣΗΣ ΜΕΤΑΞΥ ΚΛΙΜΑΤΙΚΩΝ ΔΕΙΚΤΩΝ ΜΑΚΡΑΣ ΚΛΙΜΑΚΑΣ ΚΑΙ ΜΕΤΕΩΡΟΛΟΓΙΚΗΣ ΞΗΡΑΣΙΑΣ ΣΤΗΝ ΕΛΛΑΔΑ Εμμανουέλα Ιακωβίδου Επιβλέπων
Σ ΤΑΤ Ι Σ Τ Ι Κ Η. Statisticum collegium Iii
 Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium Iii Η Κανονική Κατανομή Λέμε ότι μία τυχαία μεταβλητή X, ακολουθεί την Κανονική Κατανομή με παραμέτρους και και συμβολίζουμε X N, αν έχει συνάρτηση πυκνότητας
Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium Iii Η Κανονική Κατανομή Λέμε ότι μία τυχαία μεταβλητή X, ακολουθεί την Κανονική Κατανομή με παραμέτρους και και συμβολίζουμε X N, αν έχει συνάρτηση πυκνότητας
Τρίκαλα, 27/12/2011. Συνεντεύξεις. «Μεγαλύτερες σε διάρκεια ξηρασίες»
 Τρίκαλα, 27/12/2011 Συνεντεύξεις «Μεγαλύτερες σε διάρκεια ξηρασίες» Τι επισημαίνει στην ΕΡΕΥΝΑ για την περιοχή μας ο κ. Σοφοκλής Ε. Δρίτσας, ερευνητής στο Εργαστήριο Δημογραφικών και Κοινωνικών Αναλύσεων
Τρίκαλα, 27/12/2011 Συνεντεύξεις «Μεγαλύτερες σε διάρκεια ξηρασίες» Τι επισημαίνει στην ΕΡΕΥΝΑ για την περιοχή μας ο κ. Σοφοκλής Ε. Δρίτσας, ερευνητής στο Εργαστήριο Δημογραφικών και Κοινωνικών Αναλύσεων
1. Σκοπός της έρευνας
 Στατιστική ανάλυση και ερμηνεία των αποτελεσμάτων των εξετάσεων πιστοποίησης ελληνομάθειας 1. Σκοπός της έρευνας Ο σκοπός αυτής της έρευνας είναι κυριότατα πρακτικός. Η εξέταση των δεκτικών/αντιληπτικών
Στατιστική ανάλυση και ερμηνεία των αποτελεσμάτων των εξετάσεων πιστοποίησης ελληνομάθειας 1. Σκοπός της έρευνας Ο σκοπός αυτής της έρευνας είναι κυριότατα πρακτικός. Η εξέταση των δεκτικών/αντιληπτικών
Μελέτη της Τροπόσφαιρας στο Νομό Ιωαννίνων με χρήση του MetricaNet
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ - ΤΜΗΜΑ ΑΓΡΟΝΟΜΩΝ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΔΑΙΣΙΑΣ ΚΑΙ ΤΟΠΟΓΡΑΦΙΑΣ Μελέτη της Τροπόσφαιρας στο Νομό Ιωαννίνων με χρήση του MetricaNet ΣΥΜΕΩΝ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ - ΤΜΗΜΑ ΑΓΡΟΝΟΜΩΝ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΔΑΙΣΙΑΣ ΚΑΙ ΤΟΠΟΓΡΑΦΙΑΣ Μελέτη της Τροπόσφαιρας στο Νομό Ιωαννίνων με χρήση του MetricaNet ΣΥΜΕΩΝ
Όταν τα υδροσταγονίδια ή παγοκρύσταλλοι ενός νέφους, ενώνονται μεταξύ τους ή μεγαλώνουν, τότε σχηματίζουν μεγαλύτερες υδροσταγόνες με βάρος που
 5 Νέφη - Υετός 6.3 Βροχή Όταν τα υδροσταγονίδια ή παγοκρύσταλλοι ενός νέφους, ενώνονται μεταξύ τους ή μεγαλώνουν, τότε σχηματίζουν μεγαλύτερες υδροσταγόνες με βάρος που ξεπερνά την άνωση, με αποτέλεσμα
5 Νέφη - Υετός 6.3 Βροχή Όταν τα υδροσταγονίδια ή παγοκρύσταλλοι ενός νέφους, ενώνονται μεταξύ τους ή μεγαλώνουν, τότε σχηματίζουν μεγαλύτερες υδροσταγόνες με βάρος που ξεπερνά την άνωση, με αποτέλεσμα
ΠΑΡΑΔΟΤΕΟ ΠΕ3 Υπολογισμός του υδρολογικού ισοζυγίου του ταμιευτήρα Μόρνου και πρόγνωση ακραίων επεισοδίων βροχής
 ΠΑΡΑΔΟΤΕΟ ΠΕ3 Υπολογισμός του υδρολογικού ισοζυγίου του ταμιευτήρα Μόρνου και πρόγνωση ακραίων επεισοδίων βροχής ΕΡΓΟ: «Λεπτομερής αποτύπωση κατακρημνισμάτων, εκτίμηση του υδρολογικού ισοζυγίου στον ταμιευτήρα
ΠΑΡΑΔΟΤΕΟ ΠΕ3 Υπολογισμός του υδρολογικού ισοζυγίου του ταμιευτήρα Μόρνου και πρόγνωση ακραίων επεισοδίων βροχής ΕΡΓΟ: «Λεπτομερής αποτύπωση κατακρημνισμάτων, εκτίμηση του υδρολογικού ισοζυγίου στον ταμιευτήρα
ΙΕΡΕΥΝΗΣΗ ΚΑΙ ΑΝΑΛΥΤΙΚΗ ΠΑΡΟΥΣΙΑΣΗ ΥΠΟΛΟΓΙΣΜΩΝ ΚΛΩΘΟΕΙ ΟΥΣ, Ι ΙΑΙΤΕΡΑ ΣΕ ΜΗ ΤΥΠΙΚΕΣ ΕΦΑΡΜΟΓΕΣ.
 ΙΕΡΕΥΝΗΣΗ ΚΑΙ ΑΝΑΛΥΤΙΚΗ ΠΑΡΟΥΣΙΑΣΗ ΥΠΟΛΟΓΙΣΜΩΝ ΚΛΩΘΟΕΙ ΟΥΣ, Ι ΙΑΙΤΕΡΑ ΣΕ ΜΗ ΤΥΠΙΚΕΣ ΕΦΑΡΜΟΓΕΣ. Ν. Ε. Ηλιού Επίκουρος Καθηγητής Τµήµατος Πολιτικών Μηχανικών Πανεπιστηµίου Θεσσαλίας Γ.. Καλιαµπέτσος Επιστηµονικός
ΙΕΡΕΥΝΗΣΗ ΚΑΙ ΑΝΑΛΥΤΙΚΗ ΠΑΡΟΥΣΙΑΣΗ ΥΠΟΛΟΓΙΣΜΩΝ ΚΛΩΘΟΕΙ ΟΥΣ, Ι ΙΑΙΤΕΡΑ ΣΕ ΜΗ ΤΥΠΙΚΕΣ ΕΦΑΡΜΟΓΕΣ. Ν. Ε. Ηλιού Επίκουρος Καθηγητής Τµήµατος Πολιτικών Μηχανικών Πανεπιστηµίου Θεσσαλίας Γ.. Καλιαµπέτσος Επιστηµονικός
ΚΕΦΑΛΑΙΟ 5 ΜΕΛΕΤΗ ΑΠΟ ΟΣΗΣ ΚΑΙ ΕΠΙΤΥΧΙΑΣ ΙΑΦΟΡΩΝ ΚΑΤΗΓΟΡΙΩΝ ΜΕΓΕΘΩΝ ΗΜΕΡΗΣΙΩΝ ΛΥΚΕΙΩΝ ΕΙΣΑΓΩΓΗ
 ΚΕΦΑΛΑΙΟ 5 ΜΕΛΕΤΗ ΑΠΟ ΟΣΗΣ ΚΑΙ ΕΠΙΤΥΧΙΑΣ ΙΑΦΟΡΩΝ ΚΑΤΗΓΟΡΙΩΝ ΜΕΓΕΘΩΝ ΗΜΕΡΗΣΙΩΝ ΛΥΚΕΙΩΝ ΕΙΣΑΓΩΓΗ Μια διαφορετική κατανοµή των λυκείων µπορούµε να πάρουµε αν µελετήσουµε την κατηγορία του λυκείου ανάλογα
ΚΕΦΑΛΑΙΟ 5 ΜΕΛΕΤΗ ΑΠΟ ΟΣΗΣ ΚΑΙ ΕΠΙΤΥΧΙΑΣ ΙΑΦΟΡΩΝ ΚΑΤΗΓΟΡΙΩΝ ΜΕΓΕΘΩΝ ΗΜΕΡΗΣΙΩΝ ΛΥΚΕΙΩΝ ΕΙΣΑΓΩΓΗ Μια διαφορετική κατανοµή των λυκείων µπορούµε να πάρουµε αν µελετήσουµε την κατηγορία του λυκείου ανάλογα
2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
Κεφάλαιο 3ο: ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ 2ο ΜΕΡΟΣ
 Κεφάλαιο 3ο: ΙΑΦΟΡΙΚΟ ΟΓΙΜΟ ο ΜΕΡΟ Ερωτήσεις του τύπου «ωστό - άθος». * Αν µια συνάρτηση f είναι συνεχής στο διάστηµα [α, β], παραγωγίσιµη στο διάστηµα (α, β) και f (α) = f (β), τότε υπάρχει τουλάχιστον
Κεφάλαιο 3ο: ΙΑΦΟΡΙΚΟ ΟΓΙΜΟ ο ΜΕΡΟ Ερωτήσεις του τύπου «ωστό - άθος». * Αν µια συνάρτηση f είναι συνεχής στο διάστηµα [α, β], παραγωγίσιµη στο διάστηµα (α, β) και f (α) = f (β), τότε υπάρχει τουλάχιστον
Ρυθµιστές PID. Βρόχος Ανατροφοδότησης Αναλογικός Ρυθµιστής (Ρ) Ολοκληρωτικός Ρυθµιστής (Ι) ιαφορικός Ρυθµιστής (D) Ρύθµιση PID
 Ρυθµιστές PID Βρόχος Ανατροφοδότησης Αναλογικός Ρυθµιστής (Ρ) Ολοκληρωτικός Ρυθµιστής (Ι) ιαφορικός Ρυθµιστής (D) Ρύθµιση PID 1 Βρόχος Ανατροφοδότησης! Θεωρούµε το βρόχο ανατροφοδότησης SP ιεργασία D G
Ρυθµιστές PID Βρόχος Ανατροφοδότησης Αναλογικός Ρυθµιστής (Ρ) Ολοκληρωτικός Ρυθµιστής (Ι) ιαφορικός Ρυθµιστής (D) Ρύθµιση PID 1 Βρόχος Ανατροφοδότησης! Θεωρούµε το βρόχο ανατροφοδότησης SP ιεργασία D G
Επιλογή και επανάληψη. Λογική έκφραση ή συνθήκη
 Επιλογή και επανάληψη Η ύλη που αναπτύσσεται σε αυτό το κεφάλαιο είναι συναφής µε την ύλη που αναπτύσσεται στο 2 ο κεφάλαιο. Όπου υπάρχουν διαφορές αναφέρονται ρητά. Προσέξτε ιδιαίτερα, πάντως, ότι στο
Επιλογή και επανάληψη Η ύλη που αναπτύσσεται σε αυτό το κεφάλαιο είναι συναφής µε την ύλη που αναπτύσσεται στο 2 ο κεφάλαιο. Όπου υπάρχουν διαφορές αναφέρονται ρητά. Προσέξτε ιδιαίτερα, πάντως, ότι στο
ΑΝΑΛΥΣΗ ΚΙΝ ΥΝΩΝ ΓΙΑ ΤΟΥΣ ΦΟΡΕΙΣ ΥΛΟΠΟΙΗΣΗΣ ΕΡΓΩΝ ΤΟΥ ΚΠΣ
 ΑΝΑΛΥΣΗ ΚΙΝ ΥΝΩΝ ΓΙΑ ΤΟΥΣ ΦΟΡΕΙΣ ΥΛΟΠΟΙΗΣΗΣ ΕΡΓΩΝ ΤΟΥ ΚΠΣ 2000 2006 I. ΕΙΣΑΓΩΓΗ Η Αρχή Πληρωµής του ΚΠΣ ανέθεσε την εκπόνηση σχετικής µελέτης που αποσκοπεί στη χαρτογράφηση και γενικότερη παρουσίαση των
ΑΝΑΛΥΣΗ ΚΙΝ ΥΝΩΝ ΓΙΑ ΤΟΥΣ ΦΟΡΕΙΣ ΥΛΟΠΟΙΗΣΗΣ ΕΡΓΩΝ ΤΟΥ ΚΠΣ 2000 2006 I. ΕΙΣΑΓΩΓΗ Η Αρχή Πληρωµής του ΚΠΣ ανέθεσε την εκπόνηση σχετικής µελέτης που αποσκοπεί στη χαρτογράφηση και γενικότερη παρουσίαση των
ΠΕΙΡΑΜΑΤΙΚΕΣ ΠΡΟΣΟΜΟΙΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 4. είναι η πραγματική απόκριση του j δεδομένου (εκπαίδευσης ή ελέγχου) και y ˆ j
 Πειραματικές Προσομοιώσεις ΚΕΦΑΛΑΙΟ 4 Όλες οι προσομοιώσεις έγιναν σε περιβάλλον Matlab. Για την υλοποίηση της μεθόδου ε-svm χρησιμοποιήθηκε το λογισμικό SVM-KM που αναπτύχθηκε στο Ecole d Ingenieur(e)s
Πειραματικές Προσομοιώσεις ΚΕΦΑΛΑΙΟ 4 Όλες οι προσομοιώσεις έγιναν σε περιβάλλον Matlab. Για την υλοποίηση της μεθόδου ε-svm χρησιμοποιήθηκε το λογισμικό SVM-KM που αναπτύχθηκε στο Ecole d Ingenieur(e)s
ΑΝΑΛΥΣΗ ΕΥΑΙΣΘΗΣΙΑΣ Εισαγωγή
 1 ΑΝΑΛΥΣΗ ΕΥΑΙΣΘΗΣΙΑΣ Εισαγωγή Η ανάλυση ευαισθησίας μιάς οικονομικής πρότασης είναι η μελέτη της επιρροής των μεταβολών των τιμών των παραμέτρων της πρότασης στη διαμόρφωση της τελικής απόφασης. Η ανάλυση
1 ΑΝΑΛΥΣΗ ΕΥΑΙΣΘΗΣΙΑΣ Εισαγωγή Η ανάλυση ευαισθησίας μιάς οικονομικής πρότασης είναι η μελέτη της επιρροής των μεταβολών των τιμών των παραμέτρων της πρότασης στη διαμόρφωση της τελικής απόφασης. Η ανάλυση
