Tests and model choice : asymptotics
|
|
|
- Φοίβη Αποστολίδης
- 6 χρόνια πριν
- Προβολές:
Transcript
1 1/ 50 Tests and model choice : asymptotics J. Rousseau CEREMADE, Université Paris-Dauphine & Oxford University (soon) Greek Stochastics, Milos
2 Outline 2/ 50 1 Bayesian testing : the Bayes factor Bayes factor Consistency of the Bayes factor or of the model selection : 2 Non parametric tests Parametric vs Nonparametric Construction of nonparametric priors A special case : Point null hypothesis Parametric null hypothesis 3 General conditions for consistency of B 1/2 in non iid case for GOF types 4 Nonparametric/Nonparametric case 5 Conclusion
3 Outline 3/ 50 1 Bayesian testing : the Bayes factor Bayes factor Consistency of the Bayes factor or of the model selection : 2 Non parametric tests Parametric vs Nonparametric Construction of nonparametric priors A special case : Point null hypothesis Parametric null hypothesis 3 General conditions for consistency of B 1/2 in non iid case for GOF types 4 Nonparametric/Nonparametric case 5 Conclusion
4 Bayes factor if BF 0/1 large H 0 else H 1 4/ 50 Model X : f ( θ), θ Θ ; θ Π Testing problem H 0 : θ Θ 0, H 1 : θ Θ 1, Θ 0 Θ 1 = ( or Π[Θ 0 Θ 1 ] = 0) 0-1 loss function Bayes estimate : δ π = 1 iff Π[Θ 1 X] > Π[Θ 0 X] Posterior odds ratio Π[Θ 0 X] Π[Θ 1 X] = Θ 0 f (X θ)dπ 0 (θ) π[θ 0] Θ 1 f (X θ)dπ 1 (θ) π[θ 1 ] }{{} m 0 (X) m 1 (X) BF 0/1 := m 0(X) m 1 (X), dπ j(θ) = 1I Θj dπ(θ) Π(Θ j )
5 Model choice 5/ 50 Multiple models M j : f j,θj, θ j Θ j Hierarchical Prior dπ(j, θ j ) = Π(j)dΠ j (θ j ) Posterior dπ(j, θ j X) Π(j)dΠ j (θ j )f j,θj (X), dπ(j X) Π(j) f j,θj (X)dΠ j (θ j ) Θ } j {{} m j (X) 0-1 loss function Bayes estimate δ π (X) = argmax{π(m j X) m j (X) Π(M j ), j J}
6 Outline 6/ 50 1 Bayesian testing : the Bayes factor Bayes factor Consistency of the Bayes factor or of the model selection : 2 Non parametric tests Parametric vs Nonparametric Construction of nonparametric priors A special case : Point null hypothesis Parametric null hypothesis 3 General conditions for consistency of B 1/2 in non iid case for GOF types 4 Nonparametric/Nonparametric case 5 Conclusion
7 Consistency of the Bayes factor BF 0/1 = m 0(X) m 1 (X) 7/ 50 Definition 1 The Bayes factor is said consistent IFF BF 0/1 +, in proba when X f θ H 0 BF 0/1 0, in proba when X f θ H 1 Interpretation : As n goes to infinity you are bound to make the correct decision
8 Consistency of the model selection 8/ 50 true model True parameter θ j Θ j M = min{θ j ; θ Θ j }, Θ j Θ j Θ j Θ j e.g. Mixtures, Variable selections, graph selection etc... Consistency δ π is consistent iff P θ (δ π M ) 0 Whether BF or model selection procedure : based on the asymptotic behaviour of the marginal likelihoods m j (X)
9 BIC approximation of the marginal likelihood 9/ 50 Bayes factor : marginal likelihood ratio : acts like a penalized likelihood ratio BIC approximation in finite dim & regular models X = X n = (X 1,..., X n ) log m j (X n ) = log f (X n ^θ j ) d j 2 log n + O p(1) d j = dim(θ j ), ^θ j = MLE under Θ j. Different penalization if non regular or infinite dim
10 How does BIC work? 10/ 50 l n (θ; M) = log f (X n θ; M). m j (X n ) = e l n(^θ j,m j ) Θ j e l n(θ;m j ) l n (^θ j ;M j ) π j (θ)dθ, ^θ j = mle in Θ j Local asymptotic normality+ consistency l n (θ) l n (^θ j ) = n(θ ^θ j ) t I(^θ j )(θ ^θ j ) (1 + o p (1)) 2 Π j ( θ ^θ j > ɛ X n ) = o p (1) positive, continuous and finite prior density 0 < inf π j (θ) sup π j (θ) < + θ ^θ j <ɛ θ ^θ j <ɛ
11 Extension to irregular models : a more general approach 11/ 50 True parameter θ, Θ j R d j, m j (X n ) = e l n(θ j ) e l n(θ) l n (θ j ) π j (θ)dθ, θ j =KL - projtn onto Θ j Θ j Deterministic approximation l n (θ) l n (θ j ) nh(θ j, θ), H(θ j, θ) = E θ ( ) l n (θ j ) l n(θ) log m j (X n ) = l n (θ j }{{} ) + log Π j (H(θ j, θ) 1/n) +o p (log n) }{{} model bias prior penalty n
12 Understanding the prior penalty Π j (H(θ j, θ) 1/n) 12/ 50 Regular models H(θ j, θ) = (θ θ j )t I(θ j )(θ θ j ) (1 + o(1)) 2 Π j (H(θ j, θ) 1/n) π j(θ j )(C/n)d j /2 Irregular models d j 2 log n + O p(1) H(θ j, θ) (θ θ j )t I(θ j )(θ θ j ) (1 + o(1)) 2 [We need to understand the geometry associated to H(θ j, θ).]
13 Example of mixture models : overspecified case k k f θ (x) = p j g γj (x), γ j Γ, p j = 1 j=1 j=1 If true distribution k f θ (x) = pj g γ j (x), k < k j=1 k = 2 and k = 1 [Then the model is non identifyable] f θ (x) = p 1 g γ1 + (1 p 1 )g γ2, f (x) = g γ Then f θ = f θ IFF p 1 = 1, γ 1 = γ or γ 1 = γ 2 = γ Θ = {θ : f θ = f θ } {θ } even up to a permutation 13/ 50
14 14/ 50 Understanding H(θ j, θ) in mixtures f θ (x) = k j=1 p j g γ j (x), M k = {f θ (x) = k j=1 p jg γj (x), γ j Γ} k < k & θ k = θ H(θ, θ)? varies with the configuration t = (t 1,, t k, t k +1) t = (t j, j k + 1) is the partition of {1,, k} t j = {l; γ l γ j ɛ}, j k ; t k +1 = {l; min j k θ l θ j > ɛ} On t ; p(j) = l t j p l, q l = p l /p(j) if l t j k H(θ, θ) q l γ l γ j + p(j) p j + j=1 l tj l t j + l t k +1 p l p l p(j) γ l γ j 2
15 Π k (H(θ, θ) 1/n) 15/ 50 prior If α < d/2 (p 1,, p k ) D(α,, α), γ j iid πγ Π k (H(θ, θ) 1/n) n (k d+k 1+(k k )α)/2 [ (prior) sparsest configuration : emptying the extra states] If α > d/2 Π k (H(θ, θ) 1/n) n (k d+k 1+(k k )d/2)/2 [ (prior) sparsest configuration : merging the extra states] Prior penalty D < dim(θ k )
16 Impact on consistency 16/ 50 Θ BF k/k+1 = k f θ (X n )π k (θ)dθ Θ k+1 f θ (X n )π k+1 (θ)dθ If θ Θ k+1 \ Θ k (Regular models) log m k (X n ) = l n (θ k ) l n(θ ) + O p (log n) nkl(θ, θ k ) If θ Θ k Θ k+1 irregular model D = dim(θ k )+α, if α < d/2 & D = dim(θ k )+d/2if α > d/2 Then log BF k/k+1 = dim(θ k) D log n + o p (log n) + 2
17 Nonparametric cases : At least one of the models is NP Case 1 : Parametric vs Non parametric : M 0 : θ 0 Θ R d, M 1 : θ 1 Θ 1, dim(θ 1 ) = + e.g. Goodness of fit tests ; testing for linearity in regression etc... Case 2 : Nonparametric vs Nonparametric M 0 : θ 0 Θ 0, M 1 : θ 1 Θ 1, dim(θ 1 ), dim(θ 0 ) = + e.g. Testing for monotonicity, independence, two sample tests etc... Case 3 : High dimensional model selection M k : θ Θ k R d k, k K, card(k)large e.g. regression models (variable selection) 17/ 50
18 Outline 18/ 50 1 Bayesian testing : the Bayes factor Bayes factor Consistency of the Bayes factor or of the model selection : 2 Non parametric tests Parametric vs Nonparametric Construction of nonparametric priors A special case : Point null hypothesis Parametric null hypothesis 3 General conditions for consistency of B 1/2 in non iid case for GOF types 4 Nonparametric/Nonparametric case 5 Conclusion
19 Parametric vs NP 19/ 50 X n = (X 1,..., X n ) fθ n, Test problem : Θ 0 R d, dim(θ 1 ) = + H 0 : fθ n F 0 = {fθ n, θ Θ 0}, H 1 : fθ n F 1 = {fθ n, θ Θ 1} Examples : iid Goodness of fit in iid cases : X i f, F 0 = {f θ, θ Θ 0 }, F 1 = F0 c. Linear/partially linear y i = α + β t w i + f (x i ) + ɛ i, ɛ i N(0, σ 2 ) H 0 : f = 0, H 1 : f 0
20 Parametric vs NP 19/ 50 X n = (X 1,..., X n ) fθ n, Test problem : Θ 0 R d, dim(θ 1 ) = + H 0 : fθ n F 0 = {fθ n, θ Θ 0}, H 1 : fθ n F 1 = {fθ n, θ Θ 1} Examples : iid Goodness of fit in iid cases : X i f, F 0 = {f θ, θ Θ 0 }, F 1 = F0 c. Linear/partially linear y i = α + β t w i + f (x i ) + ɛ i, ɛ i N(0, σ 2 ) H 0 : f = 0, H 1 : f 0
21 Outline 20/ 50 1 Bayesian testing : the Bayes factor Bayes factor Consistency of the Bayes factor or of the model selection : 2 Non parametric tests Parametric vs Nonparametric Construction of nonparametric priors A special case : Point null hypothesis Parametric null hypothesis 3 General conditions for consistency of B 1/2 in non iid case for GOF types 4 Nonparametric/Nonparametric case 5 Conclusion
22 21/ 50 Non parametric priors on F 1 H 0 : f F 0 = {f θ, θ Θ}, H 1 : f F 1 Θ R d Parameter space F = F 0 F 1 Non parametric prior π 1 on F 1 Prior on H 1 Your favourite nonparametric prior e.g. Gaussian processes, Levy processes, Mixtures Check that Π 1 [F 0 ] = 0, e.g. F 0 = {N(µ, σ 2 ), (µ, σ) R R + }, Π 1 : k p j N(µ j, σ 2 j ), k > 1 j=1 Should we care for more? Yes : consistency
23 21/ 50 Non parametric priors on F 1 H 0 : f F 0 = {f θ, θ Θ}, H 1 : f F 1 Θ R d Parameter space F = F 0 F 1 Non parametric prior π 1 on F 1 Prior on H 1 Your favourite nonparametric prior e.g. Gaussian processes, Levy processes, Mixtures Check that Π 1 [F 0 ] = 0, e.g. F 0 = {N(µ, σ 2 ), (µ, σ) R R + }, Π 1 : k p j N(µ j, σ 2 j ), k > 1 j=1 Should we care for more? Yes : consistency
24 21/ 50 Non parametric priors on F 1 H 0 : f F 0 = {f θ, θ Θ}, H 1 : f F 1 Θ R d Parameter space F = F 0 F 1 Non parametric prior π 1 on F 1 Prior on H 1 Your favourite nonparametric prior e.g. Gaussian processes, Levy processes, Mixtures Check that Π 1 [F 0 ] = 0, e.g. F 0 = {N(µ, σ 2 ), (µ, σ) R R + }, Π 1 : k p j N(µ j, σ 2 j ), k > 1 j=1 Should we care for more? Yes : consistency
25 Outline 22/ 50 1 Bayesian testing : the Bayes factor Bayes factor Consistency of the Bayes factor or of the model selection : 2 Non parametric tests Parametric vs Nonparametric Construction of nonparametric priors A special case : Point null hypothesis Parametric null hypothesis 3 General conditions for consistency of B 1/2 in non iid case for GOF types 4 Nonparametric/Nonparametric case 5 Conclusion
26 23/ 50 Case of point null hypothesis (case of iid observations) Prior on F 1 = F {f 0 } H 0 : f = f 0, H 1 : f f 0 Corresponds to a prior on F Π(f ) = p 0 δ (f0 )+(1 p 0 )Π 1 (f ), Π 1 = proba on F Π 1 ({f 0 }) = 0 Dass & Lee : BF 0/1 always consistent under f 0. if dπ 1 (. X n ) is consistent at f F {f 0 }, then the BF 0,1 is consistent under f.
27 23/ 50 Case of point null hypothesis (case of iid observations) Prior on F 1 = F {f 0 } H 0 : f = f 0, H 1 : f f 0 Corresponds to a prior on F Π(f ) = p 0 δ (f0 )+(1 p 0 )Π 1 (f ), Π 1 = proba on F Π 1 ({f 0 }) = 0 Dass & Lee : BF 0/1 always consistent under f 0. if dπ 1 (. X n ) is consistent at f F {f 0 }, then the BF 0,1 is consistent under f.
28 Remark on Dass & Lee 24/ 50 Convergence under f 0 Comes from Doob theorem because Π[{f 0 }] = p 0 > 0 Π(f ) = p 0 δ (f0 ) + (1 p 0 )Π 1 (f ) Harder to detect H 0 than H 1 : f 0 F, can be approximated under F 1 typically H 1 : BF 0/1 e nc(f ) H 0 : BF 0/1 n q 0
29 On posterior concentration 25/ 50 Posterior concentration ɛ n = o(1) Prove that E θ [Π (d(θ, θ ) > Mɛ n Y n )] = o(1), l n (θ) = log f θ (Y n ) Conditions 1 KL condition [ ] π KL n (θ, θ) nɛ 2 n, V n (θ, θ) κnɛ 2 n e ncɛ2 n KL n (θ, θ) = E θ (l n (θ ) l n (θ)), V n (θ, θ) = V θ (l n (θ ) l n (θ)) 2 Testing condition Θ n Θ : π(θ c n) e n(c+2)ɛ2 n and φ n [0, 1] E θ (φ n ) = o(1), sup E θ (1 φ n ) e n(c+2)ɛ2 n d(θ,θ)>mɛ n,θ Θ n
30 On posterior concentration 25/ 50 Posterior concentration ɛ n = o(1) Prove that E θ [Π (d(θ, θ ) > Mɛ n Y n )] = o(1), l n (θ) = log f θ (Y n ) Conditions 1 KL condition [ ] π KL n (θ, θ) nɛ 2 n, V n (θ, θ) κnɛ 2 n e ncɛ2 n KL n (θ, θ) = E θ (l n (θ ) l n (θ)), V n (θ, θ) = V θ (l n (θ ) l n (θ)) 2 Testing condition Θ n Θ : π(θ c n) e n(c+2)ɛ2 n and φ n [0, 1] E θ (φ n ) = o(1), sup E θ (1 φ n ) e n(c+2)ɛ2 n d(θ,θ)>mɛ n,θ Θ n
31 Proof 26/ 50 Π (d(θ, θ ) > ɛ n Y n B ) = n e l n(θ) l n (θ ) dπ(θ) Θ el n(θ) l n (θ ) dπ(θ) := N n D n [ E θ [Π (d(θ, θ ) > ɛ n Y n )] = E θ φ n N ] [ n + E θ (1 φ n ) N ] n D n D n [ ] E θ [φ n ] + P θ D n < e n(c+3/2)ɛ2 n + e n(c+3/2)ɛ2 ne θ (N n (1 φ n )) [ ] = E θ [φ n ] + P θ D n < e n(c+3/2)ɛ2 n + e n(c+3/2)ɛ2 n E θ (1 φ n )dπ(θ B [ ] ( n ) = o(1) + P θ D n < e n(c+2)ɛ2 n + e n(c+3/2)ɛ2 n e n(c+2)ɛ2 n + Π(Θ c n) [ ] = o(1) + P θ D n < e n(c+2)ɛ2 n
32 27/ 50 Control of P θ [ ] D n < e n(c+2)ɛ2 n : KL condition D n = e l n(θ) l n (θ ) dπ(θ) e l n(θ) l n (θ ) dπ(θ) Θ S n 1I ln (θ) l n (θ )> 3/2nɛ 2el n(θ) l n (θ ) dπ(θ) n S n e 3/2nɛ2 nπ(s n {l n (θ) l n (θ ) > 3/2nɛ 2 n}) ( ) = e 3/2nɛ2 n π(s n ) π(s n {l n (θ) l n (θ ) 3/2nɛ 2 n}) and ( ) P θ π(s n {l n (θ) l n (θ ) 3/2nɛ 2 n}) > π(s n )/2 2 ( ) P θ l n (θ) l n (θ ) 3/2nɛ 2 n dπ(θ) 1 π(s n ) S n }{{} nɛ 2 n KL condition: 1 nɛ 2 n
33 28/ 50 What are these tests? The tests φ n depend on the metric d(θ, θ ) Case of iid data with weak topology U = {f ; ϕ j f (x)dx ϕ j f 0 (x)dx ɛ, j = 1,, J} : Tests always exist L 1 metric : d(f, f ) = f (x) f (x) dx φ n = max φ n,fl, φ n,fl = 1I n i=1 [1I yi A(f l,f 0 ) P f0 (A(f l,f 0 ))]>nδ f l f 0 1 with A(f l, f 0 ) = {y; f l (y) > f 0 (y)} [existence of tests Bound on the L 1 covering number N(.) e ncɛ2 n ]
34 28/ 50 What are these tests? The tests φ n depend on the metric d(θ, θ ) Case of iid data with weak topology U = {f ; ϕ j f (x)dx ϕ j f 0 (x)dx ɛ, j = 1,, J} : Tests always exist L 1 metric : d(f, f ) = f (x) f (x) dx φ n = max φ n,fl, φ n,fl = 1I n i=1 [1I yi A(f l,f 0 ) P f0 (A(f l,f 0 ))]>nδ f l f 0 1 with A(f l, f 0 ) = {y; f l (y) > f 0 (y)} [existence of tests Bound on the L 1 covering number N(.) e ncɛ2 n ]
35 29/ 50 Summary of the first day : BF 0/1 = m 0(Y n ) m 1 (Y n ) Parametric log m j (Y n ) = l n (θ j ) D j 2 log n +o p (log n) }{{} log π j (d(θ j,θ) 1/n) Regular model D j = dim(θ j ) Irregular model D j = D j (θ ) dim(θ j ) Important for convergence : if θ Θ j Θ j+1 D j (θ ) < D j+1 (θ )
36 29/ 50 Summary of the first day : BF 0/1 = m 0(Y n ) m 1 (Y n ) Parametric log m j (Y n ) = l n (θ j ) D j 2 log n +o p (log n) }{{} log π j (d(θ j,θ) 1/n) Regular model D j = dim(θ j ) Irregular model D j = D j (θ ) dim(θ j ) Important for convergence : if θ Θ j Θ j+1 D j (θ ) < D j+1 (θ )
37 29/ 50 Summary of the first day : BF 0/1 = m 0(Y n ) m 1 (Y n ) Parametric log m j (Y n ) = l n (θ j ) D j 2 log n +o p (log n) }{{} log π j (d(θ j,θ) 1/n) Regular model D j = dim(θ j ) Irregular model D j = D j (θ ) dim(θ j ) Important for convergence : if θ Θ j Θ j+1 D j (θ ) < D j+1 (θ )
38 Summary 2 : towards nonparametric 30/ 50 Posterior concentration rates π(b n Y n B ) = n e l n(θ) l n (θ ) dπ(θ) Θ el n(θ) l n (θ ) dπ(θ) := N n D n Lower bound on D n : P θ [D n > e nɛ2n(c+3/2) ] = 1 + o(1) If ( ) π {θ; KL n (θ, θ) nɛ 2 n, V n (θ, θ) nɛ 2 n} e ncɛ2 n Upper bound of N n = B n e l n(θ) l n (θ ) dπ(θ) P θ [N n = o(e nɛ2 n(c+3/2) ] = 1 + o(1) Either Existence of tests φ n : H 0 : θ = θ vs H 1 : θ B n Or π(b n ) = o(e n(c+3/2)ɛ2 n )
39 Summary 2 : towards nonparametric 30/ 50 Posterior concentration rates π(b n Y n B ) = n e l n(θ) l n (θ ) dπ(θ) Θ el n(θ) l n (θ ) dπ(θ) := N n D n Lower bound on D n : P θ [D n > e nɛ2n(c+3/2) ] = 1 + o(1) If ( ) π {θ; KL n (θ, θ) nɛ 2 n, V n (θ, θ) nɛ 2 n} e ncɛ2 n Upper bound of N n = B n e l n(θ) l n (θ ) dπ(θ) P θ [N n = o(e nɛ2 n(c+3/2) ] = 1 + o(1) Either Existence of tests φ n : H 0 : θ = θ vs H 1 : θ B n Or π(b n ) = o(e n(c+3/2)ɛ2 n )
40 Summary 2 : towards nonparametric 30/ 50 Posterior concentration rates π(b n Y n B ) = n e l n(θ) l n (θ ) dπ(θ) Θ el n(θ) l n (θ ) dπ(θ) := N n D n Lower bound on D n : P θ [D n > e nɛ2n(c+3/2) ] = 1 + o(1) If ( ) π {θ; KL n (θ, θ) nɛ 2 n, V n (θ, θ) nɛ 2 n} e ncɛ2 n Upper bound of N n = B n e l n(θ) l n (θ ) dπ(θ) P θ [N n = o(e nɛ2 n(c+3/2) ] = 1 + o(1) Either Existence of tests φ n : H 0 : θ = θ vs H 1 : θ B n Or π(b n ) = o(e n(c+3/2)ɛ2 n )
41 Summary 2 : towards nonparametric 30/ 50 Posterior concentration rates π(b n Y n B ) = n e l n(θ) l n (θ ) dπ(θ) Θ el n(θ) l n (θ ) dπ(θ) := N n D n Lower bound on D n : P θ [D n > e nɛ2n(c+3/2) ] = 1 + o(1) If ( ) π {θ; KL n (θ, θ) nɛ 2 n, V n (θ, θ) nɛ 2 n} e ncɛ2 n Upper bound of N n = B n e l n(θ) l n (θ ) dπ(θ) P θ [N n = o(e nɛ2 n(c+3/2) ] = 1 + o(1) Either Existence of tests φ n : H 0 : θ = θ vs H 1 : θ B n Or π(b n ) = o(e n(c+3/2)ɛ2 n )
42 Outline 31/ 50 1 Bayesian testing : the Bayes factor Bayes factor Consistency of the Bayes factor or of the model selection : 2 Non parametric tests Parametric vs Nonparametric Construction of nonparametric priors A special case : Point null hypothesis Parametric null hypothesis 3 General conditions for consistency of B 1/2 in non iid case for GOF types 4 Nonparametric/Nonparametric case 5 Conclusion
43 General result under non i.i.d observations : sufficient conditions 32/ 50 Context Under M 0 : Y f n 0,θ 0, θ 0 Θ 0 R d Under M 1 : Y f n 1,θ 1, θ 1 Θ 1 (infinite dim) d n (.,.) (semi) metric on the distributions (e.g. total variation, KL, etc. ) lim inf n lim inf n inf d n (f 1,θ1, f 0,θ0 ) := d(θ 1, M 0 ) θ 0 Θ 0 inf d n (f 0,θ0, f 1,θ1 ) := d(θ 0, M 1 ) θ 1 Θ 1 [ Typically M 0 M 1 ]
44 Conditions under M 1 (bigger model) : θ = θ 1 - often easier 33/ 50 bound from above m 0 (Y n ) and from below m 1 (Y n ) m j (Y n ) = e l n(j,θ) l n (θ ) dπ j (θ) Θ j d(θ, M 0 ) > 0 (separated case) If [ ɛ > 0, P θ m 1 (Y n ) < e nɛ2] = o(1) [Consistency under M 1 ] If, ɛ > 0, a > 0 and tests φ n and Θ 0,n Θ 0 s.t. E θ [φ n ] = o(1), sup θ 0 Θ 0,n E θ0 [1 φ n ] e an, π 0 (Θ c 0,n ) < e nɛ [Statistical separation between θ and M 0 ] Then B 0/1 < e an/2, with proba going to 1 under P θ
45 34/ 50 Conditions under M 0 (smaller model) ; θ M 0 M 1 Case : d(θ, M 1 ) = 0, & Θ 0 R d (parametric) If k 0 > 0 n k0/2 [ π 0 {θ Θ0 : KL(f0,θ n, f 0,θ n ) 1, V (f n 0,θ, f n 0,θ ) 1)}] C for some positive constants C. (NP) f θ = f 0,θ If ɛ n 0 with A ɛn (θ ) = {θ Θ 1 : d n (fθ n, f 1,θ n ) < ɛ n} such that 1. Pθ n [ [ π1 A c ɛn (θ ) Y ]] = o(1) 2. n k0/2 π 1 [A ɛn (θ )] = o(1). Then B 0/1 + under P θ
46 34/ 50 Conditions under M 0 (smaller model) ; θ M 0 M 1 Case : d(θ, M 1 ) = 0, & Θ 0 R d (parametric) If k 0 > 0 n k0/2 [ π 0 {θ Θ0 : KL(f0,θ n, f 0,θ n ) 1, V (f n 0,θ, f n 0,θ ) 1)}] C for some positive constants C. (NP) f θ = f 0,θ If ɛ n 0 with A ɛn (θ ) = {θ Θ 1 : d n (fθ n, f 1,θ n ) < ɛ n} such that 1. Pθ n [ [ π1 A c ɛn (θ ) Y ]] = o(1) 2. n k0/2 π 1 [A ɛn (θ )] = o(1). Then B 0/1 + under P θ
47 Application to Partial linear regressions 35/ 50 y i = α + β t w i + f (x i ) + ɛ i, ɛ i N(0, σ 2 ) (w i, x i ) G i.i.d, E[w] = 0, E[ww t ] > 0 M 0 : (α, β, f, σ) s.t. [ (α H(f ) := inf E + (β ) t w f (x) ) ] 2 = 0 (α,β ) R d+1 M 1 : (α, β, f, σ) s.t. y i = α 1 + β t 1 w i + ɛ i H(f ) := [ (α inf E + (β ) t w f (x) ) ] 2 > 0 (α,β ) R d+1
48 36/ 50 prior hierarchical (adaptive) Gaussian process prior on f K f = τ k Z k ξ k, k=1 (ξ k ) = BON K P, Z k N(0, 1) (α, β, σ) π 0 h j (x) = E[w j X = x], w = (w 1,, w d ) If j s.t. < h j, ξ 1 > 0 then B 0/1 is consistent under M 0 like n ρ
49 Nonparametric/Nonparametric testing problem B 0/1 = m 0 (Y )/m 1 (Y ) 37/ 50 Both M 0 and M 1 are non parametric & M 0 M 1 Lower bound Not too hard but sharp? m j (Y ) e (c j +2)nɛ 2 n,j, π j (B KL (θ, nɛ 2 n,j )) e nc j ɛ 2 n upper bound Harder Tests control : ok tools for it e l n(θ) l n (θ ) dπ j (θ) e c j nɛ2 n,j d(θ,θ)>ɛ n,j Control on d(θ,θ) ɛ n,j e l n(θ) l n (θ ) dπ j (θ) : damn it [ ] E θ [N n,j ] := E θ Ifd(θ d(θ e l n(θ) l n (θ ) dπ, M j ) = 0,θ) ɛn,j j (θ) Fubini = π j (d(θ, θ) ɛ n,j )? e c j nɛ2 n,j
50 Nonparametric/Nonparametric testing problem B 0/1 = m 0 (Y )/m 1 (Y ) 37/ 50 Both M 0 and M 1 are non parametric & M 0 M 1 Lower bound Not too hard but sharp? m j (Y ) e (c j +2)nɛ 2 n,j, π j (B KL (θ, nɛ 2 n,j )) e nc j ɛ 2 n upper bound Harder Tests control : ok tools for it e l n(θ) l n (θ ) dπ j (θ) e c j nɛ2 n,j d(θ,θ)>ɛ n,j Control on d(θ,θ) ɛ n,j e l n(θ) l n (θ ) dπ j (θ) : damn it [ ] E θ [N n,j ] := E θ Ifd(θ d(θ e l n(θ) l n (θ ) dπ, M j ) = 0,θ) ɛn,j j (θ) Fubini = π j (d(θ, θ) ɛ n,j )? e c j nɛ2 n,j
51 38/ 50 Setups where this approach works Ghosal, Lembert, VdV & Rousseau, Szabo Multiple models Θ λ, λ Λ (possibly continuous) Aim ^λ = argmax{π(λ Y n ), λ Λ} π(λ Y n ) π(λ)m λ (Y n ) What is λ? Two contexts Almost finite case : Λ N, Θ λ Θ λ+1 and λ 0 s.t. θ Θ λ0, λ = min{λ; θ Θ λ } Boundary case θ Cl( λ Θ λ ) but λ, θ / Θ λ Claim : λ = Oracle where λ = min λ {ɛ n,λ, λ Λ} ɛ n,λ : π λ (d(θ, θ) ɛ n,λ ) e cnɛ2 n,λ, [Sharp tools like BIC ]
52 38/ 50 Setups where this approach works Ghosal, Lembert, VdV & Rousseau, Szabo Multiple models Θ λ, λ Λ (possibly continuous) Aim ^λ = argmax{π(λ Y n ), λ Λ} π(λ Y n ) π(λ)m λ (Y n ) What is λ? Two contexts Almost finite case : Λ N, Θ λ Θ λ+1 and λ 0 s.t. θ Θ λ0, λ = min{λ; θ Θ λ } Boundary case θ Cl( λ Θ λ ) but λ, θ / Θ λ Claim : λ = Oracle where λ = min λ {ɛ n,λ, λ Λ} ɛ n,λ : π λ (d(θ, θ) ɛ n,λ ) e cnɛ2 n,λ, [Sharp tools like BIC ]
53 Where does the oracle come from? 39/ 50 m λ (Y n f θ,λ (Y n ) ) = Θ λ f θ (Y n ) dπ λ(θ) e l n(θ) l n (θ ) dπ λ (θ) d(θ,θ ) ɛ n,λ e c 1nɛ 2 nπ λ (d(θ, θ) ɛ n, ) e c 2nɛ 2 nπ λ (d(θ, θ) ɛ n ) + e nc 2ɛ 2 n Under stringent conditions π(λ : ɛ n,λ Mɛ n,λ Y n ) 1 ^λ {λ : ɛ n,λ Mɛ n,λ } [Only useful if λ λ ɛ n,λ >> ɛ n,λ ]
54 40/ 50 NP priors M 0 and M 1 Testing for monotonicity Y = (y 1,, y n ) iid f, or y i = f (x i ) + ɛ i, Model M 0 : f = decreasing Model M 1 : f has no shape constraints. 1 rst idea Prior on M 0 : Mixtures of U(0, θ) f P (y) = 0 1I y θ dp(θ), P DP(AG) θ Prior on smooth densities : e.g. Mixtures of Betas f P (y) = 0 g z,z/ɛ (y)dp(ɛ), (z, P) π z DP(AG) [Bad idea ]
55 40/ 50 NP priors M 0 and M 1 Testing for monotonicity Y = (y 1,, y n ) iid f, or y i = f (x i ) + ɛ i, Model M 0 : f = decreasing Model M 1 : f has no shape constraints. 1 rst idea Prior on M 0 : Mixtures of U(0, θ) f P (y) = 0 1I y θ dp(θ), P DP(AG) θ Prior on smooth densities : e.g. Mixtures of Betas f P (y) = 0 g z,z/ɛ (y)dp(ɛ), (z, P) π z DP(AG) [Bad idea ]
56 1rst solution 41/ 50 y i [0, 1] k f (x) = f ω,k := kω j 1 [(j 1)/k,j/k[ (x), j=1 k ω j = 1 j=1 Prior k P; (ω 1,, ω k ) π k, e.g. D(α 1,, α k ) Posterior probabilities [ ] π[m 0 Y ] = π max(ω j ω j 1 ) 0 j Y Problem : if f M 0 but has flat parts
57 Result 42/ 50 Question :?? π[m 0 Y ] = 1 + o pf (1) if f M 0. Answers : Not always ({ }) f (x) f (y) g(δ) := Leb x; inf δ y>x y x For all f 0 s.t. g(δ) = 0, if P π [ k (n/ log n) 1/5 Y ] = 1 + o p (1) P π [M 0 Y ] = 1 + o p (1) Consistent test e.g. if k 3 P(λ). For all f 0 s.t. g(δ) = δ, idem with k 7 P(λ).
58 Inconsistencies 43/ 50 If f 0 is constant on [a, b] (0, 1) and if π(3/(b a) < k < n/ log nly n ) 1 then with probability greater than 1/2 (asymptotically) π(m 0 Y n ) < 1/2 [Inconsistency of the testing procedure]
59 Comments 44/ 50 Not satisfying : Cannot be consistent over whole set of decreasing functions. Increasing the set of functions by lowering k leads to poor power. Change of loss function new test based on Choice of ɛ? P π [d(f, M 1 ) ɛ Y ]
60 Moving away (slightly) from the 0-1 loss function for unseparated hypotheses [JB Salomond] 45/ 50 New loss function L τ (θ, δ) = Equivalent to testing { 0 if d(θ, M0 ) τ 1 if d(θ, M 0 ) > τ H 0 : d(θ, M 0 ) τ, H 1 : d(θ, M 0 ) > τ Bayes estimator { δ π 0 if π (d(θ, M0 ) τ Y = n ) > 1/2 1 if otherwise
61 46/ 50 Choice of τ If prior information on tolerance level τ chosen a priori Calibration by τ n smallest s.t. Type I error sup P θ [π (d(θ, M 0 ) τ n Y n ) 1/2] = o(1) θ M 0 Study of ρ n s.t. (separation rate) sup P θ [π (d(θ, M 0 ) τ n Y n ) < 1/2] = o(1) θ:d(θ,m 0 )>ρ n [Control of type II error over ρ n separated hypotheses] In quite a few examples : ρ n minimax separation rate
62 46/ 50 Choice of τ If prior information on tolerance level τ chosen a priori Calibration by τ n smallest s.t. Type I error sup P θ [π (d(θ, M 0 ) τ n Y n ) 1/2] = o(1) θ M 0 Study of ρ n s.t. (separation rate) sup P θ [π (d(θ, M 0 ) τ n Y n ) < 1/2] = o(1) θ:d(θ,m 0 )>ρ n [Control of type II error over ρ n separated hypotheses] In quite a few examples : ρ n minimax separation rate
63 46/ 50 Choice of τ If prior information on tolerance level τ chosen a priori Calibration by τ n smallest s.t. Type I error sup P θ [π (d(θ, M 0 ) τ n Y n ) 1/2] = o(1) θ M 0 Study of ρ n s.t. (separation rate) sup P θ [π (d(θ, M 0 ) τ n Y n ) < 1/2] = o(1) θ:d(θ,m 0 )>ρ n [Control of type II error over ρ n separated hypotheses] In quite a few examples : ρ n minimax separation rate
64 46/ 50 Choice of τ If prior information on tolerance level τ chosen a priori Calibration by τ n smallest s.t. Type I error sup P θ [π (d(θ, M 0 ) τ n Y n ) 1/2] = o(1) θ M 0 Study of ρ n s.t. (separation rate) sup P θ [π (d(θ, M 0 ) τ n Y n ) < 1/2] = o(1) θ:d(θ,m 0 )>ρ n [Control of type II error over ρ n separated hypotheses] In quite a few examples : ρ n minimax separation rate
65 47/ 50 Difficulties : τ n chosen asymptotically Difficult analysis in some cases : Not necessarily to determine τ n. e.g. in the case of testing for monotonicity only for simple families of priors optimal τ n = τ 0 v n where v n known τ 0 arbitrary. Calibration of τ 0 for finite n? Can we trust purely asymptotic results to calibrate a procedure?
66 47/ 50 Difficulties : τ n chosen asymptotically Difficult analysis in some cases : Not necessarily to determine τ n. e.g. in the case of testing for monotonicity only for simple families of priors optimal τ n = τ 0 v n where v n known τ 0 arbitrary. Calibration of τ 0 for finite n? Can we trust purely asymptotic results to calibrate a procedure?
67 47/ 50 Difficulties : τ n chosen asymptotically Difficult analysis in some cases : Not necessarily to determine τ n. e.g. in the case of testing for monotonicity only for simple families of priors optimal τ n = τ 0 v n where v n known τ 0 arbitrary. Calibration of τ 0 for finite n? Can we trust purely asymptotic results to calibrate a procedure?
68 Semi-parametric : θ = (ψ, η) 48/ 50 M 1 : ψ = ψ 0, M 2 : ψ ψ 0 Cox hazard : h θ (x z) = e ψt z η(x), M 1 : ψ = 0 Long memory parameter : M 1 : h = 0 Y N(0, T n (f θ )), f θ (x) = (1 cos x) h η(x), η > 0 C b Saved by BvM π(v n (ψ ^ψ) A Y ) Pr(N d (0, 1) A) B 1/2 v d/2 n +
69 Semi-parametric : θ = (ψ, η) 48/ 50 M 1 : ψ = ψ 0, M 2 : ψ ψ 0 Cox hazard : h θ (x z) = e ψt z η(x), M 1 : ψ = 0 Long memory parameter : M 1 : h = 0 Y N(0, T n (f θ )), f θ (x) = (1 cos x) h η(x), η > 0 C b Saved by BvM π(v n (ψ ^ψ) A Y ) Pr(N d (0, 1) A) B 1/2 v d/2 n +
70 The 2 - samples test 49/ 50 X n = (X 1,, X n ) iid F X, Y n = (Y 1,, Y n ) iid F Y H 0 : F X = F Y = F H 1 : F X F Y Prior H 0 : F π and H 1 : F X, F Y π ind. B 1/2 = m 2n(X n, Y n ) m n (X n )m n (Y n ), consistency? Hardly any literature (Bayesian) on 2 - sample test Holmes et al. [PolyaT] Dunson & Lock [ parametric] Chen & Hansen [censored-polyat]
71 Other ways of getting away from 0-1 loss functions 50/ 50 distance penalized losses Robert & Rousseau, Rousseau Goodness of fit test : Y n = (y 1,, y n ), y i iid f H 0 : f F 0 = {f θ, θ Θ R d }, H 1 : f / F 0 L(θ, δ) = Bayes test { (d(θ, M0 ) ɛ)1i d(θ,m0 )>ɛ when δ = 0 (ɛ d(θ, M 0 ))1I d(θ,m0 ) ɛ when δ = 1 δ π = 1 E π [d(θ, M 0 ) Y n ] > ɛ Calibration of ɛ using a conditional predictive p-value p(y n ) = P θ (T (Y n ) > T (y n ) ^θ, y n )π 0 (θ)dθ Θ
72 Other ways 51/ 50 There are many other ways...
73 52/ 50 Point null hypothesis : Consistency of BF consistency of the posterior under H 1 Parametric null : more involved. Π 1 can be more favorable to f θ0 than Π 0. Nonparametric Null. e.g. F 0 = {f } need to be even more carefull Are BIC or BIC type formula better than BF?
74 52/ 50 Point null hypothesis : Consistency of BF consistency of the posterior under H 1 Parametric null : more involved. Π 1 can be more favorable to f θ0 than Π 0. Nonparametric Null. e.g. F 0 = {f } need to be even more carefull Are BIC or BIC type formula better than BF?
75 52/ 50 Point null hypothesis : Consistency of BF consistency of the posterior under H 1 Parametric null : more involved. Π 1 can be more favorable to f θ0 than Π 0. Nonparametric Null. e.g. F 0 = {f } need to be even more carefull Are BIC or BIC type formula better than BF?
76 52/ 50 Point null hypothesis : Consistency of BF consistency of the posterior under H 1 Parametric null : more involved. Π 1 can be more favorable to f θ0 than Π 0. Nonparametric Null. e.g. F 0 = {f } need to be even more carefull Are BIC or BIC type formula better than BF?
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
Theorem 8 Let φ be the most powerful size α test of H
 Testing composite hypotheses Θ = Θ 0 Θ c 0 H 0 : θ Θ 0 H 1 : θ Θ c 0 Definition 16 A test φ is a uniformly most powerful (UMP) level α test for H 0 vs. H 1 if φ has level α and for any other level α test
Testing composite hypotheses Θ = Θ 0 Θ c 0 H 0 : θ Θ 0 H 1 : θ Θ c 0 Definition 16 A test φ is a uniformly most powerful (UMP) level α test for H 0 vs. H 1 if φ has level α and for any other level α test
Bayesian statistics. DS GA 1002 Probability and Statistics for Data Science.
 Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Solution Series 9. i=1 x i and i=1 x i.
 Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecture 34 Bootstrap confidence intervals
 Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Biostatistics for Health Sciences Review Sheet
 Biostatistics for Health Sciences Review Sheet http://mathvault.ca June 1, 2017 Contents 1 Descriptive Statistics 2 1.1 Variables.............................................. 2 1.1.1 Qualitative........................................
Biostatistics for Health Sciences Review Sheet http://mathvault.ca June 1, 2017 Contents 1 Descriptive Statistics 2 1.1 Variables.............................................. 2 1.1.1 Qualitative........................................
An Introduction to Signal Detection and Estimation - Second Edition Chapter II: Selected Solutions
 An Introduction to Signal Detection Estimation - Second Edition Chapter II: Selected Solutions H V Poor Princeton University March 16, 5 Exercise : The likelihood ratio is given by L(y) (y +1), y 1 a With
An Introduction to Signal Detection Estimation - Second Edition Chapter II: Selected Solutions H V Poor Princeton University March 16, 5 Exercise : The likelihood ratio is given by L(y) (y +1), y 1 a With
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Lecture 12: Pseudo likelihood approach
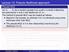 Lecture 12: Pseudo likelihood approach Pseudo MLE Let X 1,...,X n be a random sample from a pdf in a family indexed by two parameters θ and π with likelihood l(θ,π). The method of pseudo MLE may be viewed
Lecture 12: Pseudo likelihood approach Pseudo MLE Let X 1,...,X n be a random sample from a pdf in a family indexed by two parameters θ and π with likelihood l(θ,π). The method of pseudo MLE may be viewed
Statistics 104: Quantitative Methods for Economics Formula and Theorem Review
 Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
Local Approximation with Kernels
 Local Approximation with Kernels Thomas Hangelbroek University of Hawaii at Manoa 5th International Conference Approximation Theory, 26 work supported by: NSF DMS-43726 A cubic spline example Consider
Local Approximation with Kernels Thomas Hangelbroek University of Hawaii at Manoa 5th International Conference Approximation Theory, 26 work supported by: NSF DMS-43726 A cubic spline example Consider
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Fractional Colorings and Zykov Products of graphs
 Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
6. MAXIMUM LIKELIHOOD ESTIMATION
 6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
Models for Probabilistic Programs with an Adversary
 Models for Probabilistic Programs with an Adversary Robert Rand, Steve Zdancewic University of Pennsylvania Probabilistic Programming Semantics 2016 Interactive Proofs 2/47 Interactive Proofs 2/47 Interactive
Models for Probabilistic Programs with an Adversary Robert Rand, Steve Zdancewic University of Pennsylvania Probabilistic Programming Semantics 2016 Interactive Proofs 2/47 Interactive Proofs 2/47 Interactive
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
D Alembert s Solution to the Wave Equation
 D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Durbin-Levinson recursive method
 Durbin-Levinson recursive method A recursive method for computing ϕ n is useful because it avoids inverting large matrices; when new data are acquired, one can update predictions, instead of starting again
Durbin-Levinson recursive method A recursive method for computing ϕ n is useful because it avoids inverting large matrices; when new data are acquired, one can update predictions, instead of starting again
CHAPTER 101 FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD
 CHAPTER FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD EXERCISE 36 Page 66. Determine the Fourier series for the periodic function: f(x), when x +, when x which is periodic outside this rge of period.
CHAPTER FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD EXERCISE 36 Page 66. Determine the Fourier series for the periodic function: f(x), when x +, when x which is periodic outside this rge of period.
STAT200C: Hypothesis Testing
 STAT200C: Hypothesis Testing Zhaoxia Yu Spring 2017 Some Definitions A hypothesis is a statement about a population parameter. The two complementary hypotheses in a hypothesis testing are the null hypothesis
STAT200C: Hypothesis Testing Zhaoxia Yu Spring 2017 Some Definitions A hypothesis is a statement about a population parameter. The two complementary hypotheses in a hypothesis testing are the null hypothesis
Estimation for ARMA Processes with Stable Noise. Matt Calder & Richard A. Davis Colorado State University
 Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Lecture 21: Properties and robustness of LSE
 Lecture 21: Properties and robustness of LSE BLUE: Robustness of LSE against normality We now study properties of l τ β and σ 2 under assumption A2, i.e., without the normality assumption on ε. From Theorem
Lecture 21: Properties and robustness of LSE BLUE: Robustness of LSE against normality We now study properties of l τ β and σ 2 under assumption A2, i.e., without the normality assumption on ε. From Theorem
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in
 Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
5. Choice under Uncertainty
 5. Choice under Uncertainty Daisuke Oyama Microeconomics I May 23, 2018 Formulations von Neumann-Morgenstern (1944/1947) X: Set of prizes Π: Set of probability distributions on X : Preference relation
5. Choice under Uncertainty Daisuke Oyama Microeconomics I May 23, 2018 Formulations von Neumann-Morgenstern (1944/1947) X: Set of prizes Π: Set of probability distributions on X : Preference relation
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
ω ω ω ω ω ω+2 ω ω+2 + ω ω ω ω+2 + ω ω+1 ω ω+2 2 ω ω ω ω ω ω ω ω+1 ω ω2 ω ω2 + ω ω ω2 + ω ω ω ω2 + ω ω+1 ω ω2 + ω ω+1 + ω ω ω ω2 + ω
 0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Abstract Storage Devices
 Abstract Storage Devices Robert König Ueli Maurer Stefano Tessaro SOFSEM 2009 January 27, 2009 Outline 1. Motivation: Storage Devices 2. Abstract Storage Devices (ASD s) 3. Reducibility 4. Factoring ASD
Abstract Storage Devices Robert König Ueli Maurer Stefano Tessaro SOFSEM 2009 January 27, 2009 Outline 1. Motivation: Storage Devices 2. Abstract Storage Devices (ASD s) 3. Reducibility 4. Factoring ASD
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Repeated measures Επαναληπτικές μετρήσεις
 ΠΡΟΒΛΗΜΑ Στο αρχείο δεδομένων diavitis.sav καταγράφεται η ποσότητα γλυκόζης στο αίμα 10 ασθενών στην αρχή της χορήγησης μιας θεραπείας, μετά από ένα μήνα και μετά από δύο μήνες. Μελετήστε την επίδραση
ΠΡΟΒΛΗΜΑ Στο αρχείο δεδομένων diavitis.sav καταγράφεται η ποσότητα γλυκόζης στο αίμα 10 ασθενών στην αρχή της χορήγησης μιας θεραπείας, μετά από ένα μήνα και μετά από δύο μήνες. Μελετήστε την επίδραση
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1
 Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a
On the general understanding of the empirical Bayes method
 On the general understanding of the empirical Bayes method Judith Rousseau 1, Botond Szabó 2 1 Paris Dauphin, Paris, France 2 Budapest University of Technology and Economics, Budapest, Hungary ERCIM 2014,
On the general understanding of the empirical Bayes method Judith Rousseau 1, Botond Szabó 2 1 Paris Dauphin, Paris, France 2 Budapest University of Technology and Economics, Budapest, Hungary ERCIM 2014,
Math 6 SL Probability Distributions Practice Test Mark Scheme
 Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
Arithmetical applications of lagrangian interpolation. Tanguy Rivoal. Institut Fourier CNRS and Université de Grenoble 1
 Arithmetical applications of lagrangian interpolation Tanguy Rivoal Institut Fourier CNRS and Université de Grenoble Conference Diophantine and Analytic Problems in Number Theory, The 00th anniversary
Arithmetical applications of lagrangian interpolation Tanguy Rivoal Institut Fourier CNRS and Université de Grenoble Conference Diophantine and Analytic Problems in Number Theory, The 00th anniversary
Uniform Convergence of Fourier Series Michael Taylor
 Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
General 2 2 PT -Symmetric Matrices and Jordan Blocks 1
 General 2 2 PT -Symmetric Matrices and Jordan Blocks 1 Qing-hai Wang National University of Singapore Quantum Physics with Non-Hermitian Operators Max-Planck-Institut für Physik komplexer Systeme Dresden,
General 2 2 PT -Symmetric Matrices and Jordan Blocks 1 Qing-hai Wang National University of Singapore Quantum Physics with Non-Hermitian Operators Max-Planck-Institut für Physik komplexer Systeme Dresden,
Various types of likelihood
 Various types of likelihood 1. likelihood, marginal likelihood, conditional likelihood, profile likelihood, adjusted profile likelihood, Bayesian asymptotics 2. quasi-likelihood, composite likelihood 3.
Various types of likelihood 1. likelihood, marginal likelihood, conditional likelihood, profile likelihood, adjusted profile likelihood, Bayesian asymptotics 2. quasi-likelihood, composite likelihood 3.
The challenges of non-stable predicates
 The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
FORMULAS FOR STATISTICS 1
 FORMULAS FOR STATISTICS 1 X = 1 n Sample statistics X i or x = 1 n x i (sample mean) S 2 = 1 n 1 s 2 = 1 n 1 (X i X) 2 = 1 n 1 (x i x) 2 = 1 n 1 Xi 2 n n 1 X 2 x 2 i n n 1 x 2 or (sample variance) E(X)
FORMULAS FOR STATISTICS 1 X = 1 n Sample statistics X i or x = 1 n x i (sample mean) S 2 = 1 n 1 s 2 = 1 n 1 (X i X) 2 = 1 n 1 (x i x) 2 = 1 n 1 Xi 2 n n 1 X 2 x 2 i n n 1 x 2 or (sample variance) E(X)
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Problem Set 3: Solutions
 CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
TMA4115 Matematikk 3
 TMA4115 Matematikk 3 Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet Trondheim Spring 2010 Lecture 12: Mathematics Marvellous Matrices Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet
TMA4115 Matematikk 3 Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet Trondheim Spring 2010 Lecture 12: Mathematics Marvellous Matrices Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet
Figure A.2: MPC and MPCP Age Profiles (estimating ρ, ρ = 2, φ = 0.03)..
 Supplemental Material (not for publication) Persistent vs. Permanent Income Shocks in the Buffer-Stock Model Jeppe Druedahl Thomas H. Jørgensen May, A Additional Figures and Tables Figure A.: Wealth and
Supplemental Material (not for publication) Persistent vs. Permanent Income Shocks in the Buffer-Stock Model Jeppe Druedahl Thomas H. Jørgensen May, A Additional Figures and Tables Figure A.: Wealth and
Introduction to the ML Estimation of ARMA processes
 Introduction to the ML Estimation of ARMA processes Eduardo Rossi University of Pavia October 2013 Rossi ARMA Estimation Financial Econometrics - 2013 1 / 1 We consider the AR(p) model: Y t = c + φ 1 Y
Introduction to the ML Estimation of ARMA processes Eduardo Rossi University of Pavia October 2013 Rossi ARMA Estimation Financial Econometrics - 2013 1 / 1 We consider the AR(p) model: Y t = c + φ 1 Y
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
ECE 308 SIGNALS AND SYSTEMS FALL 2017 Answers to selected problems on prior years examinations
 ECE 308 SIGNALS AND SYSTEMS FALL 07 Answers to selected problems on prior years examinations Answers to problems on Midterm Examination #, Spring 009. x(t) = r(t + ) r(t ) u(t ) r(t ) + r(t 3) + u(t +
ECE 308 SIGNALS AND SYSTEMS FALL 07 Answers to selected problems on prior years examinations Answers to problems on Midterm Examination #, Spring 009. x(t) = r(t + ) r(t ) u(t ) r(t ) + r(t 3) + u(t +
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
About these lecture notes. Simply Typed λ-calculus. Types
 About these lecture notes Simply Typed λ-calculus Akim Demaille akim@lrde.epita.fr EPITA École Pour l Informatique et les Techniques Avancées Many of these slides are largely inspired from Andrew D. Ker
About these lecture notes Simply Typed λ-calculus Akim Demaille akim@lrde.epita.fr EPITA École Pour l Informatique et les Techniques Avancées Many of these slides are largely inspired from Andrew D. Ker
SCITECH Volume 13, Issue 2 RESEARCH ORGANISATION Published online: March 29, 2018
 Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Probability and Random Processes (Part II)
 Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
12. Radon-Nikodym Theorem
 Tutorial 12: Radon-Nikodym Theorem 1 12. Radon-Nikodym Theorem In the following, (Ω, F) is an arbitrary measurable space. Definition 96 Let μ and ν be two (possibly complex) measures on (Ω, F). We say
Tutorial 12: Radon-Nikodym Theorem 1 12. Radon-Nikodym Theorem In the following, (Ω, F) is an arbitrary measurable space. Definition 96 Let μ and ν be two (possibly complex) measures on (Ω, F). We say
Overview. Transition Semantics. Configurations and the transition relation. Executions and computation
 Overview Transition Semantics Configurations and the transition relation Executions and computation Inference rules for small-step structural operational semantics for the simple imperative language Transition
Overview Transition Semantics Configurations and the transition relation Executions and computation Inference rules for small-step structural operational semantics for the simple imperative language Transition
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
HW 3 Solutions 1. a) I use the auto.arima R function to search over models using AIC and decide on an ARMA(3,1)
 HW 3 Solutions a) I use the autoarima R function to search over models using AIC and decide on an ARMA3,) b) I compare the ARMA3,) to ARMA,0) ARMA3,) does better in all three criteria c) The plot of the
HW 3 Solutions a) I use the autoarima R function to search over models using AIC and decide on an ARMA3,) b) I compare the ARMA3,) to ARMA,0) ARMA3,) does better in all three criteria c) The plot of the
Exercises to Statistics of Material Fatigue No. 5
 Prof. Dr. Christine Müller Dipl.-Math. Christoph Kustosz Eercises to Statistics of Material Fatigue No. 5 E. 9 (5 a Show, that a Fisher information matri for a two dimensional parameter θ (θ,θ 2 R 2, can
Prof. Dr. Christine Müller Dipl.-Math. Christoph Kustosz Eercises to Statistics of Material Fatigue No. 5 E. 9 (5 a Show, that a Fisher information matri for a two dimensional parameter θ (θ,θ 2 R 2, can
Lecture 2. Soundness and completeness of propositional logic
 Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
Reminders: linear functions
 Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Computable error bounds for asymptotic expansions formulas of distributions related to gamma functions
 Computable error bounds for asymptotic expansions formulas of distributions related to gamma functions Hirofumi Wakaki (Math. of Department, Hiroshima Univ.) 20.7. Hiroshima Statistical Group Meeting at
Computable error bounds for asymptotic expansions formulas of distributions related to gamma functions Hirofumi Wakaki (Math. of Department, Hiroshima Univ.) 20.7. Hiroshima Statistical Group Meeting at
172,,,,. P,. Box (1980)P, Guttman (1967)Rubin (1984)P, Meng (1994), Gelman(1996)De la HorraRodriguez-Bernal (2003). BayarriBerger (2000)P P.. : Casell
 20104 Chinese Journal of Applied Probability and Statistics Vol.26 No.2 Apr. 2010 P (,, 200083) P P. Wang (2006)P, P, P,. : P,,,. : O212.1, O212.8. 1., (). : X 1, X 2,, X n N(θ, σ 2 ), σ 2. H 0 : θ = θ
20104 Chinese Journal of Applied Probability and Statistics Vol.26 No.2 Apr. 2010 P (,, 200083) P P. Wang (2006)P, P, P,. : P,,,. : O212.1, O212.8. 1., (). : X 1, X 2,, X n N(θ, σ 2 ), σ 2. H 0 : θ = θ
Supplementary Materials: Proofs
 Supplementary Materials: Proofs The following lemmas prepare for the proof of concentration properties on prior density π α (β j /σ for j = 1,..., p n on m n -dimensional vector β j /σ. As introduced earlier,
Supplementary Materials: Proofs The following lemmas prepare for the proof of concentration properties on prior density π α (β j /σ for j = 1,..., p n on m n -dimensional vector β j /σ. As introduced earlier,
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
 Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
Instruction Execution Times
 1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
The Pohozaev identity for the fractional Laplacian
 The Pohozaev identity for the fractional Laplacian Xavier Ros-Oton Departament Matemàtica Aplicada I, Universitat Politècnica de Catalunya (joint work with Joaquim Serra) Xavier Ros-Oton (UPC) The Pohozaev
The Pohozaev identity for the fractional Laplacian Xavier Ros-Oton Departament Matemàtica Aplicada I, Universitat Politècnica de Catalunya (joint work with Joaquim Serra) Xavier Ros-Oton (UPC) The Pohozaev
P AND P. P : actual probability. P : risk neutral probability. Realtionship: mutual absolute continuity P P. For example:
 (B t, S (t) t P AND P,..., S (p) t ): securities P : actual probability P : risk neutral probability Realtionship: mutual absolute continuity P P For example: P : ds t = µ t S t dt + σ t S t dw t P : ds
(B t, S (t) t P AND P,..., S (p) t ): securities P : actual probability P : risk neutral probability Realtionship: mutual absolute continuity P P For example: P : ds t = µ t S t dt + σ t S t dw t P : ds
ECE598: Information-theoretic methods in high-dimensional statistics Spring 2016
 ECE598: Information-theoretic methods in high-dimensional statistics Spring 06 Lecture 7: Information bound Lecturer: Yihong Wu Scribe: Shiyu Liang, Feb 6, 06 [Ed. Mar 9] Recall the Chi-squared divergence
ECE598: Information-theoretic methods in high-dimensional statistics Spring 06 Lecture 7: Information bound Lecturer: Yihong Wu Scribe: Shiyu Liang, Feb 6, 06 [Ed. Mar 9] Recall the Chi-squared divergence
Last Lecture. Biostatistics Statistical Inference Lecture 19 Likelihood Ratio Test. Example of Hypothesis Testing.
 Last Lecture Biostatistics 602 - Statistical Iferece Lecture 19 Likelihood Ratio Test Hyu Mi Kag March 26th, 2013 Describe the followig cocepts i your ow words Hypothesis Null Hypothesis Alterative Hypothesis
Last Lecture Biostatistics 602 - Statistical Iferece Lecture 19 Likelihood Ratio Test Hyu Mi Kag March 26th, 2013 Describe the followig cocepts i your ow words Hypothesis Null Hypothesis Alterative Hypothesis
Bounding Nonsplitting Enumeration Degrees
 Bounding Nonsplitting Enumeration Degrees Thomas F. Kent Andrea Sorbi Università degli Studi di Siena Italia July 18, 2007 Goal: Introduce a form of Σ 0 2-permitting for the enumeration degrees. Till now,
Bounding Nonsplitting Enumeration Degrees Thomas F. Kent Andrea Sorbi Università degli Studi di Siena Italia July 18, 2007 Goal: Introduce a form of Σ 0 2-permitting for the enumeration degrees. Till now,
A Bonus-Malus System as a Markov Set-Chain. Małgorzata Niemiec Warsaw School of Economics Institute of Econometrics
 A Bonus-Malus System as a Markov Set-Chain Małgorzata Niemiec Warsaw School of Economics Institute of Econometrics Contents 1. Markov set-chain 2. Model of bonus-malus system 3. Example 4. Conclusions
A Bonus-Malus System as a Markov Set-Chain Małgorzata Niemiec Warsaw School of Economics Institute of Econometrics Contents 1. Markov set-chain 2. Model of bonus-malus system 3. Example 4. Conclusions
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
Section 9.2 Polar Equations and Graphs
 180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
Practice Exam 2. Conceptual Questions. 1. State a Basic identity and then verify it. (a) Identity: Solution: One identity is csc(θ) = 1
 Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
Homework for 1/27 Due 2/5
 Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
From the finite to the transfinite: Λµ-terms and streams
 From the finite to the transfinite: Λµ-terms and streams WIR 2014 Fanny He f.he@bath.ac.uk Alexis Saurin alexis.saurin@pps.univ-paris-diderot.fr 12 July 2014 The Λµ-calculus Syntax of Λµ t ::= x λx.t (t)u
From the finite to the transfinite: Λµ-terms and streams WIR 2014 Fanny He f.he@bath.ac.uk Alexis Saurin alexis.saurin@pps.univ-paris-diderot.fr 12 July 2014 The Λµ-calculus Syntax of Λµ t ::= x λx.t (t)u
Υπολογιστική Φυσική Στοιχειωδών Σωματιδίων
 Υπολογιστική Φυσική Στοιχειωδών Σωματιδίων Όρια Πιστότητας (Confidence Limits) 2/4/2014 Υπολογ.Φυσική ΣΣ 1 Τα όρια πιστότητας -Confidence Limits (CL) Tα όρια πιστότητας μιας μέτρησης Μπορεί να αναφέρονται
Υπολογιστική Φυσική Στοιχειωδών Σωματιδίων Όρια Πιστότητας (Confidence Limits) 2/4/2014 Υπολογ.Φυσική ΣΣ 1 Τα όρια πιστότητας -Confidence Limits (CL) Tα όρια πιστότητας μιας μέτρησης Μπορεί να αναφέρονται
557: MATHEMATICAL STATISTICS II RESULTS FROM CLASSICAL HYPOTHESIS TESTING
 Most Powerful Tests 557: MATHEMATICAL STATISTICS II RESULTS FROM CLASSICAL HYPOTHESIS TESTING To construct and assess the quality of a statistical test, we consider the power function β(θ). Consider a
Most Powerful Tests 557: MATHEMATICAL STATISTICS II RESULTS FROM CLASSICAL HYPOTHESIS TESTING To construct and assess the quality of a statistical test, we consider the power function β(θ). Consider a
