ιαχείριση Ιεραρχικών Σχηµάτων στο Σηµασιολογικό Ιστό
|
|
|
- Ναχώρ Σερπετζόγλου
- 10 χρόνια πριν
- Προβολές:
Transcript
1 Εθνικό Μετσόβιο Πολυτεχνείο ιαχείριση Ιεραρχικών Σχηµάτων στο Σηµασιολογικό Ιστό Υποστήριξη ιδακτορικής ιατριβής Θοδωρής αλαµάγκας
2 Σηµασιολογικός Ιστός Από το Ιστό στον Σηµασιολογικό Ιστό: Έλλειψη ενιαίου και αυστηρού τρόπου οργάνωσης των δεδοµένων στον Ιστό. υσκολίες στην ανταλλαγή και επεξεργασία των δεδοµένων σε πολλές πηγές. Επέκταση του Ιστού στον Σηµασιολογικό Ιστό: οµή, οργάνωση και σηµασιολογία στο περιεχόµενο. Η πληροφορία αποκτά σηµασία. Η πληροφορία γίνεται κατανοητή σε επίπεδο µηχανής. Εργαλεία: τεχνολογίες XML* (W3) 2
3 Τεχνολογίες XML* (W3) Η πληροφορία αποκτά σηµασία: Τα δεδοµένα/µεταδεδοµένα του Ιστού σηµαδεύονται µε ετικέττες. Βασική µορφή κωδικοποίησης είναι η γλώσσα XML. Πλαίσιο XML/F, Γλώσσα Οντολογιών XML/OWL. Σηµασιολογικός Εµπλουτισµός Χαµηλός Μέτριος Υψηλός XML F OWL 3
4 Τεχνολογίες XML* (W3) Η πληροφορία αποκτά σηµασία: Τα δεδοµένα/µεταδεδοµένα του Ιστού σηµαδεύονται µε ετικέττες. Βασική µορφή κωδικοποίησης είναι η γλώσσα XML. Πλαίσιο XML/F, Γλώσσα Οντολογιών XML/OWL. Σηµασιολογικός Εµπλουτισµός Χαµηλός Μέτριος Υψηλός XML F OWL 4
5 Τεχνολογίες XML* (W3) Τα δεδοµένα του Ιστού σηµαδεύονται µε ετικέττες: <photo> <camera code= > <model> anon 30 </model> <color> silver </color> <price> 1000 </price> <focus> auto </focus> code </camera> <lens>. " " </lens> </photo Ιεραρχική αναπαράσταση "anon 30" model color "silver" camera price photo 1000 focus "auto" lens... 5
6 Τεχνολογίες XML* (W3) Τα µεταδεδοµένα για τους πόρους του Ιστού σηµαδεύονται µε ετικέττες: <photo><review><camera> <rdf:description rdf:about=" > <model> anon 30 </model> <color> silver </color> <price> 1000 </price> <focus> auto </focus> <seller> <rdf:description rdf:about= > <name> ANON Ltd. </name> </rdf:description> <seller> </rdf:description> </camera><lens> </lens></review></photo> 6
7 Τεχνολογίες XML* (W3) photo Ιεραρχική αναπαράσταση: review camera rdf:description lens... rdf:about model price focus seller "anon 30" color "silver" "auto" rdf:description 1000 rdf:about name " 'ANON Ltd." 7
8 Ο ρόλος των ιεραρχιών Στις τεχνολογίες XML* (W3) σηµαντικός είναι ο ρόλος των ιεραρχικών σχηµάτων (ιεραρχίες). XML: δέντρο (γράφος αν υπάρχουν αναφορές) F(s): γράφος Μελετούµε ιεραρχίες δεντρική µορφής Κωδικοποιήσεις XML (XML, F, ) 8
9 Το πρόβληµα Οι ιεραρχίες αντιµετωπίζονται ως σύνολα από µεµονωµένα στοιχεία (κόµβους). Ιεραρχίες = απλοί σηµασιολογικοί οδηγοί ιάσχισης (browsing) ιατύπωσης ερωτήσεων έκφρασης µονοπατιού (path expressions): /cameras/manual/item[price<1000] 9
10 Το πρόβληµα Ιστός: πολλές ιεραρχίες που οργανώνουν δεδοµένα για το ίδιο πεδίο γνώσης (knowledge domain). Χρήσιµες ερωτήσεις: βρείτε τις ιεραρχίες που οργανώνουν υλικό φωτογραφικού εξοπλισµού µε τρόπο παρόµοιο µε αυτόν µιας ιεραρχίας-πρότυπο (δοµική/σηµασιολογική οµοιότητα). 10
11 Το πρόβληµα οµική/σηµασιολογική οµοιότητα (H1) Adorama (H2) &H cameras & lenses digital cameras & lenses digital lenses 35mm SL cameras printers lenses 35mm SL cameras memory cards point & shoot 11
12 Το πρόβληµα οµική/σηµασιολογική οµοιότητα (H1) Adorama (H2) &H cameras & lenses digital cameras & lenses digital lenses 35mm SL cameras printers lenses 35mm SL cameras memory cards point & shoot 12
13 Το πρόβληµα Ιστός: πολλές ιεραρχίες που οργανώνουν δεδοµένα για το ίδιο πεδίο γνώσης (knowledge domain). Χρήσιµες ερωτήσεις: βρείτε το κοµµάτι µιας ιεραρχίας που δεν υπάρχει σε µια άλλη (διαχείριση δοµικής πληροφορίας). 13
14 Το πρόβληµα ιαχείριση δοµικής πληροφορίας (H1) Adorama (H2) &H cameras & lenses digital cameras & lenses digital lenses 35mm SL cameras printers lenses 35mm SL cameras memory cards point & shoot Το κοµµάτι του Η1 που δεν υπάρχει στο Η2 point & shoot printers 14
15 Σκοπός της ιατριβής Ανάδειξη των ιεραρχιών σε οντότητες πρώτης τάξης. ιατύπωση πλαισίου διαχείρισης ιεραρχιών τριών κατευθύνσεων: Προσδιορισµός οµόλογων ιεραρχιών. οµικός χειρισµός ιεραρχιών. ιαχείριση ιεραρχιών και δεδοµένων. 15
16 Συνεισφορά της ιατριβής Μεθοδολογία προσδιορισµού οµόλογων ιεραρχιών. Ορισµός µετρικής δοµικής οµοιότητας µεταξύ ιεραρχιών και σχεδιασµός αλγορίθµων υπολογισµού της. Εφαρµογή τεχνικών συσταδοποίησης (clustering) για τον προσδιορισµό οµάδων από ιεραρχίες µε παρόµοια οργάνωση. Υλοποίηση πρότυπου συστήµατος για την αξιολόγηση της µεθοδολογίας. 16
17 Συνεισφορά της ιατριβής οµικός χειρισµός ιεραρχιών. Μελέτη αλγεβρικών ιδιοτήτων των ιεραρχιών ως δεντρικές δοµές. Ορισµός 3 τελεστών διαχείρισης δοµικής πληροφορίας (ένωση, τοµή, διαφορά) µε ιδιότητες παρόµοιες µε αυτές των αντίστοιχων τελεστών της συνολοθεωρίας. ιαχείριση ιεραρχιών και δεδοµένων. Ορισµός τελεστών που συνδυάζουν διαχείριση µονοπατιών στις ιεραρχίες, και κλασσικές σχεσιακές ερωτήσεις στα δεδοµένα. 17
18 ...στη συνέχεια > ΠΡΟΣ ΙΟΡΙΣΜΟΣ ΟΜΟΛΟΓΩΝ ΙΕΡΑΡΧΙΩΝ ΟΜΙΚΗ ΙΑΧΕΙΡΙΣΗ ΙΕΡΑΡΧΙΩΝ ΙΑΧΕΙΡΙΣΗ ΙΕΡΑΡΧΙΩΝ ΚΑΙ Ε ΟΜΕΝΩΝ ΣΥΜΠΕΡΑΣΜΑΤΑ ΜΕΛΛΟΝΤΙΚΗ ΟΥΛΕΙΑ 18
19 Συντακτικά προβλήµατα δέντρων Σειρά συντακτικών πράξεων δέντρων (tree edit script): µια σειρά πράξεων που µετασχηµατίζουν ένα δέντρο Τ1 σε ένα δέντρο Τ2. Συντακτική απόσταση δέντρων (T1,T2) (tree edit distance): το ελάχιστο από τα κόστη σειρών συντακτικών πράξεων που µετασχηµατίζουν ένα δέντρο Τ1 σε ένα δέντρο Τ2. 19
20 Συντακτικά προβλήµατα δέντρων Μετασχηµατισµός του Τ1 σε Τ2: T1 A insert K A K T2 A replace,k insert P A K O A delete delete insert A K insert O P A A P 20
21 Συντακτικά προβλήµατα δέντρων Μετασχηµατισµός του Τ1 σε Τ2: (T1,T2)=5 T1 Ins(,,2) ep(,o) T2 A A K A K A K O P P ep(,k) ep(,) Ins(P,,1) P A K A K 21
22 Συντακτικά προβλήµατα δέντρων οµική απόσταση δέντρων (structural distance): S(T1,T2)=(T1,T2)/max(T1,T2) (T1,T2): συντακτική απόσταση Τ1, Τ2, max(t1,t2): το µέγιστο από τα κόστη σειρών συντακτικών πράξεων που µετασχηµατίζουν το Τ1 στο Τ2 (διαγραφή όλων των κόµβων του Τ1 και εισαγωγή όλων των κόµβων του Τ2). 22
23 Συντακτικά προβλήµατα δέντρων οµική απόσταση δέντρων (structural distance): S(T1,T2)=(T1,T2)/max(T1,T2)=5/12=41% T1 Ins(,,2) ep(,o) T2 A A K A K A K O P P ep(,k) ep(,) Ins(P,,1) P A K A K 23
24 Αλγόριθµοι συντακτικών αποστάσεων δέντρων Αλγόριθµοι Πράξεις Πράξεις στα φύλλα Selkow77 Zhang89 hawathe96 (I) hawathe99 (II) εισαγωγή κόµβου, διαγραφή κόµβου, αντικατάσταση κόµβου εισαγωγή κόµβου, διαγραφή κόµβου, αντικατάσταση κόµβου εισαγωγή κόµβου, διαγραφή κόµβου, αντικατάσταση κόµβου, µετακίνηση υποδέντρου εισαγωγή κόµβου, διαγραφή κόµβου, αντικατάσταση κόµβου εισαγωγή κόµβου, διαγραφή κόµβου εισαγωγή κόµβου, διαγραφή κόµβου εισαγωγή κόµβου, διαγραφή κόµβου 24
25 Βελτίωση υπολογισµού δοµικής απόστασης οµικές περιλήψεις δέντρων (structural summaries). Μείωση επαναλαµβανόµενων και φωλιασµένων κόµβων. Νέος αλγόριθµος υπολογισµού δοµικής απόστασης Βελτιωµένη απόδοση σε σχέση µε τον αλγόριθµο hawathe99 (II). 25
26 οµικές περιλήψεις Επαναλαµβανόµενα φωλιασµένοι κόµβοι (Τ1) Επαναλαµβανόµενοι κόµβοι (Τ2) T1 T2 26
27 Μείωση επαν. φωλιασµένων (ΕΦ) (ΕΦ) Βασικός έλεγχος για τον τρέχοντα κόµβο Ν: Αν υπάρχει απόγονος µε την ίδια ετικέττα, τότε όλα τα υποδέντρα του Ν µετακινούνται στον απόγονο αυτό. T1 T2 T3 A A A A A A P A A P P A A P P 27
28 Μείωση επαναλαµβανόµενων κόµβων (Ε) T1 (Ε) Βασικός έλεγχος για τον τρέχοντα κόµβο Ν: Αν έχει ξανασυναντηθεί σε ίδιο µονοπάτι (έστω path/n), τότε τα υποδέντρα του Ν µετακινούνται στο path/n, και ο κόµβος διαγράφεται. T2 οµική περίληψη του Τ1 A A A A A A P A A P P A A P P 28
29 Νέος αλγόριθµος υπολογισµού δοµικής απόστασης Πράξεις: εισαγωγή (ci=1), διαγραφή (cd=1), αντικατάσταση (cr=1,0) κόµβου. Αναδροµή alculateistance(): καλείται µια φορά για κάθε ζευγάρι κόµβων s και t στο ίδιο βάθος σε δύο δέντρα. Η µεταβλητή [i][j] διατηρεί την συντακτική απόσταση µεταξύ του δέντρου µε ρίζα s, µε τα πρώτα i υποδέντρα του, και του δέντρου µε ρίζα t, µε τα πρώτα j υποδέντρα του. 29
30 Νέος αλγόριθµος υπολογισµού δοµικής απόστασης T1 T2 A A K P [2][3] = 30
31 Νέος αλγόριθµος υπολογισµού δοµικής απόστασης T1 A T2 A K T1 T2 K A A P P [2][3] = min ( [2][3-1] + 3, 31
32 Νέος αλγόριθµος υπολογισµού δοµικής απόστασης T1 A T2 A K T1 T2 K A A P P [2][3] = min ( [2][3-1] + 3, [2-1][3] + 2, T1 T2 A A K P 32
33 Νέος αλγόριθµος υπολογισµού δοµικής απόστασης T1 A T2 A K T1 T2 K t1 t2 K A A P P P [2][3]=min([2][3-1]+3, [2-1][3]+3, [2-1][3-1]+alc(t1,t2) ) A T1 T2 A K T1 A T2 A P 33
34 Νέος αλγόριθµος υπολογισµού δοµικής απόστασης Βελτιωµένη απόδοση σε σχέση µε τον αλγόριθµο hawathe99 (II). Αποφυγή υπολογισµού συντακτικών γράφων (edit graphs). Συντακτικοί γράφοι: πλέγµα από κόµβους. ιαγραφή = οριζόντια γραµµή Εισαγωγή = κάθετη γραµµή Αντικατάσταση = διαγώνια γραµµή Σειρές συντακτ. πράξεων = µονοπάτια στον γράφο. 34
35 Αξιολόγηση Εισαγωγή της δοµική απόστασης σε τεχνικές συσταδοποίησης (clustering). Ανακάλυψη συστάδων δέντρων που αναπαριστούν ιεραρχίες µε παρόµοια δοµή Χρήση αλγορίθµων hawathe και νέου. Αξιολόγηση απόδοσης. Αξιολόγηση ποιότητας. 35
36 Αξιολόγηση απόδοσης Νέος αλγόριθµος: µε/χωρίς δοµ. περιλήψεις 36
37 Αξιολόγηση απόδοσης Νέος αλγόριθµος vs hawathe 37
38 Αξιολόγηση απόδοσης Νέος αλγόριθµος: συνολική απόδοση 38
39 Αξιολόγηση ποιότητας Προβλήµατα αξιολόγησης ποιότητας συσταδοποίησης: Άγνωστα τα σωστά µέλη των συστάδων. Παραγωγή δειγµάτων δέντρων ως XML αρχεία, µε δοθέντα T ως οδηγούς (10 T, σύνολα 1000 δέντρων). Αλγόριθµοι συσταδοποίησης: single link (+LUTO) Μετρικές αξιολόγησης: Ακρίβεια (precicion) P: το ποσοστό των σωστών µελών που έχουν οι συστάδες σε σχέση µε αυτά που θα έπρεπε να έχουν. Ευστοχία (recall) : το ποσοστό των σωστών µελών που έχουν οι συστάδες. 39
40 Αξιολόγηση ποιότητας hawathe (maxrepeat=3) hawathe (maxrepeat=6) Χωρίς οµ. Περιλήψεις Με οµ. Περιλήψεις Χωρίς οµ. Περιλήψεις Με οµ. Περιλήψεις P=0.71, =0.9 P=0.71, =0.9 P=0.58, =0.89 P=0.83, =0.96 Νέος Αλγόρ. (maxrepeat=3) Νέος Αλγορ. (maxrepeat=6) Χωρίς οµ. Περιλήψεις Με οµ. Περιλήψεις Χωρίς οµ. Περιλήψεις Με οµ. Περιλήψεις P=1, =0.98 P=1, =0.98 P=1, =0.97 P=1, =
41 Συµπεράσµατα αξιολόγησης Ηχρήση δοµικών περιλήψεων διατηρεί την ποιότητα της συσταδοποίησης. ηχρήση τους βελτιώνει την απόδοση της συσταδοποίησης. Ο νέος αλγόριθµος υπολογισµού δοµικής απόστασης βελτιώνει περαιτέρω την απόδοση. Επιβεβαίωση αποτελεσµάτων και µε άλλους αλγόριθµους συσταδοποίησης/ταξινόµησης. 41
42 Συγκρίσεις Υπάρχουσες εργασίες: Συσταδοποίηση XML κειµένων (Nierman). Συσταδοποίηση T σχηµάτων (Xlust) οµικές αποστάσεις για εκτιµήσεις elta (Xdiff, Laiff, Xyiff). ιαφορές: Χρήση δοµικών περιλήψεων (γενική η χρήση τους). ιατήρηση των καλών ιδιοτήτων στις αποστάσεις (minimality). 42
43 Σύνοψη συνεισφοράς Μεθοδολογία προσδιορισµού οµόλογων ιεραρχιών. Ορισµός µετρικής δοµικής οµοιότητας µεταξύ ιεραρχιών και σχεδιασµός αλγορίθµων υπολογισµού της. Εφαρµογή τεχνικών συσταδοποίησης (clustering) για τον προσδιορισµό οµάδων από ιεραρχίες µε παρόµοια οργάνωση. Υλοποίηση πρότυπου συστήµατος για την αξιολόγηση της µεθοδολογίας. 43
44 ...στη συνέχεια ΠΡΟΣ ΙΟΡΙΣΜΟΣ ΟΜΟΛΟΓΩΝ ΙΕΡΑΡΧΙΩΝ > ΟΜΙΚΗ ΙΑΧΕΙΡΙΣΗ ΙΕΡΑΡΧΙΩΝ ΙΑΧΕΙΡΙΣΗ ΙΕΡΑΡΧΙΩΝ ΚΑΙ Ε ΟΜΕΝΩΝ ΣΥΜΠΕΡΑΣΜΑΤΑ ΜΕΛΛΟΝΤΙΚΗ ΟΥΛΕΙΑ 44
45 Αλγεβρικές ιδιότητες ιεραρχιών έντρο ιεραρχίας µε κόµβους Ν και ρίζα r: < {r} N, P >: xpy ισχύει αν πατέρας(x,y) (ή p(x,y)) Σχέση υποσύνολο: T1 T2 Για κάθε xpy στο Τ1, τότε xp tr y στο Τ2 Για κάθε xp tr y στο Τ2 (µε x,y στο Τ1), τότε xp tr y στο Τ1 ιαισθητικά: Το Τ1 κατασκευάζεται από το Τ2, διαγράφοντας κόµβους και µετακινώντας τα παιδιά σε υψηλότερα επίπεδα. 45
46 Αλγεβρικές ιδιότητες ιεραρχιών Έστω δέντρο ιεραρχίας Tg (καθολικό δέντρο) και Sg={Ti, Ti Tg} (Θ) Η σχέση < Sg, > είναι σχέση µερικής διάταξης: Ανακλαστική: Ti Ti Αντισυµµετρική: Ti Tj και Tj Ti δίνει Ti=Tj Μεταβατική: Ti Tj και Tj Tk δίνει Ti Tk Ορίζουµε 2 τελεστές για δέντρα Ti: ένωση, τοµή 46
47 Ένωση Έστω δέντρα ιεραρχίας T1 και Τ2 από το σύνολο Sg={Ti, Ti Tg}. Η ένωση Τ3 των T1 και Τ2, T1 Τ2, είναι ένα δέντρο µε: όλους τους κόµβους Ν των T1 και Τ2 όλη την δοµική πληροφορία των T1 και Τ2 ιαισθητικά, το Τ3 κατασκευάζεται από το Τg, διαγράφοντας όλους τους κόµβους εκτός από αυτούς του Ν, και µετακινώντας τα παιδιά σε υψηλότερα επίπεδα. 47
48 Ένωση T1 T2 T3 S N P = N P I E F J M M H G J K F H I E J K F H G 48
49 Ένωση T1 T2 T3 S N P = N P I E F J M M H G J K F H I E J K F H G 49
50 Ένωση T1 T2 T3 S N P = N P I E F J M M H G J K F H I E J K F H G 50
51 Ένωση T1 T2 T3 S N P = N P I E F J M M H G J K F H I E J K F H G 51
52 Ένωση T1 T2 T3 S N P = N P I E F J M M H G J K F H I E J K F H G 52
53 Ένωση T1 T G N P I E F G J T2 N P I E J K H F M G M J K H 53
54 Τοµή Έστω δέντρα ιεραρχίας T1 και Τ2 από το σύνολο Sg={Ti, Ti Tg}. Η τοµή Τ3 των T1 και Τ2, T1 Τ2, είναι ένα δέντρο µε: τους κοινούς κόµβους Ν των T1 και Τ2 την κοινή δοµική πληροφορία των T1 και Τ2 ιαισθητικά, το Τ3 κατασκευάζεται από το Τg, διαγράφοντας όλους τους κόµβους εκτός από αυτούς του Ν, και µετακινώντας τα παιδιά σε υψηλότερα επίπεδα. 54
55 Τοµή T1 T2 T3 S N P = I E F J M F J H G J F H K H 55
56 οµή Πλέγµατος Έστω δέντρο ιεραρχίας Tg και Sg={Ti, Ti Tg} και η σχέση µερικής διάταξης < Sg, >. (Θ) Η πράξη ένωση, Tj Τk, δίνει το ελάχιστο άνω όριο των Tj και Τk: Tj Tj Τk και Tk Tj Τk (Θ) Η πράξη τοµή, Tj Τk, δίνει το µέγιστο κάτω όριο των Tj και Τk: Tj Τk Tj και Tj Τk Tk (Θ) H σχέση µερικής διάταξης < Sg, > είναι πλέγµα (lattice) (και µάλιστα distributive). 56
57 Νόµοι T1 T1 = T1 T1 T2 = T2 T1 T1 (T2 T3) = (T1 T2) T3 T1 (T1 T2) = Τ1 Τ1 (Τ2 Τ3) = (Τ1 Τ2) (Τ1 Τ3) (και αντίστοιχα για την ) 57
58 Συµπλήρωµα Έστω δέντρο ιεραρχίας T1 από το σύνολο Sg={Ti, Ti Tg}. Το συµπλήρωµα Τ 1 του T1 είναι ένα δέντρο µε: όλους τους κόµβους του Tg που δεν υπάρχουν στο Τ1 (η ρίζα συµπεριλαµβάνεται) την δοµική πληροφορία του Tg που δεν υπάρχει στο Τ1 ιαισθητικά, το Τ 1 κατασκευάζεται από το Τg, διαγράφοντας όλους τους κόµβους που ανήκουν στο Τ1, και µετακινώντας τα παιδιά σε υψηλότερα επίπεδα. 58
59 ιαφορά Έστω δέντρα ιεραρχίας T1 και Τ2 από το σύνολο Sg={Ti, Ti Tg}. Η διαφορά του Τ2 από το Τ1, Τ2 - Τ1, ορίζεται ως εξής: Τ2 - Τ1 = Τ2 Τ 1 ιαισθητικά: η δοµική πληροφορία του Τ2 που δεν περιέχεται στο Τ1. 59
60 ιαφορά T2 T1 T3 N P S = N P M I E F J K M J F H G K H 60
61 Νόµοι T1 T1 = T1 T1 T2 = T2 T1 T1 (T2 T3) = (T1 T2) T3 T1 (T1 T2) = Τ1 Τ1 (Τ2 Τ3) = (Τ1 Τ2) (Τ1 Τ3) Τ1 - (Τ2 Τ3) = (Τ1 - Τ2) (Τ1 - Τ3) (και αντίστοιχα για την ) (Θ) H σχέση µερικής διάταξης < Sg, > είναι boolean πλέγµα (boolean lattice). 61
62 H παραδοχή του καθολικού δέντρου Κατασκευή καθολικού δέντρου: Συνεπή (consistent) δέντρα: δεν έχουν δοµικές αναντιστοιχίες Συµβατά (compatible) δέντρα µπορούν καθοριστούν µοναδικά οι δοµικές σχέσεις του καθολικού δέντρου έντρα ιεραρχιών, συνεπή και συµβατά, δίνουν ένα καθολικό δέντρο. 62
63 Συνεπή δέντρα (ανά δύο) Ti, Tj συνεπή δέντρα: Για κάθε xp tr y στο Τi, τότε xp tr y στο Τj Για κάθε xp tr y στο Τj, τότε xp tr y στο Τi Όπου x,y οι κοινοί κόµβοι των Τi και Τj T1 T2 T3 T4 E E F 63
64 Συνεπή δέντρα (ανά δύο) Ti, Tj συνεπή δέντρα: Για κάθε xp tr y στο Τi, τότε xp tr y στο Τj Για κάθε xp tr y στο Τj, τότε xp tr y στο Τi Όπου x,y οι κοινοί κόµβοι των Τi και Τj T1 T2 T3 T4 E E F συνεπή 64
65 Συνεπή δέντρα (ανά δύο) Ti, Tj συνεπή δέντρα: Για κάθε xp tr y στο Τi, τότε xp tr y στο Τj Για κάθε xp tr y στο Τj, τότε xp tr y στο Τi Όπου x,y οι κοινοί κόµβοι των Τi και Τj T1 T2 T3 T4 E E F ασυνεπή 65
66 Συνεπή δέντρα (ανά δύο) Η συνέπεια δέντρων ανά δύο δεν είναι αρκετή για την κατασκευή ενός καθολικού δέντρου: T1 T2 T3 A A A 66
67 Συνεπή δέντρα (ανά δύο) Η συνέπεια δέντρων ανά δύο δεν είναι αρκετή για την κατασκευή ενός καθολικού δέντρου: T1 T2 T3 A A A Β 67
68 Συνεπή δέντρα Συνέπεια δέντρων: συνέπεια ανά δύο σταθερότητα (stability) ζευγαριών κόµβων (x,y) µε xp tr y: Έστω Gx τα δέντρα µε x και όχι y, Gy τα δέντρα µε y και όχι x Αν για κάθε ζευγάρι δέντρων (Τx, Τy), Τx στο Gx και Τy στο Gy, υπάρχει κόµβος z µε xp tr z στο Tx και zp tr y στο Ty, τότε (x,y) σταθερό. Η σταθερότητα εγγυάται ότι ποτέ δεν θα δηµιουργηθούν αναντιστοιχίες κατά την κατασκευή του καθολικού δέντρου. 68
69 Συµβατά δέντρα T1 T2 T3 T4 E E F 69
70 Συµβατά δέντρα T1 T2 T3 T4 E E F 70
71 Συµβατά δέντρα T1 T2 T3 T4 E E F Ε?? F 71
72 Συµβατά δέντρα Ti, Tj συµβατά δέντρα: Για κάθε κοινό κόµβο x των Τi, Τj, ο πατέραςτουy, p(y,x), είναι επίσης κοινός κόµβος T1 T2 T3 T4 E E F F Ε F 72
73 Θεωρήµατα (Θ1) Έστω ένα σύνολο δέντρων συµβατά ανά δύο. Το καθολικό δέντρο Tg που παράγεται από οποιοδήποτε ζευγάρι δέντρων είναι συµβατό µε τα υπόλοιπα. (Θ2) Έστω ένα σύνολο δέντρων συνεπών. Το καθολικό δέντρο Tg που παράγεται από οποιοδήποτε ζευγάρι δέντρων οδηγεί σε συνεπές σύνολο. 73
74 Θεωρήµατα (Θ3) Ο ορισµός για τα συνεπή δέντρα καλύπτει όλα τα σύνολα δέντρων για τα οποία η κατασκευή καθολικού δέντρου οδηγεί σε συνεπή δέντρα. (Θ4) Έστω ένα σύνολο δέντρων συνεπών. Το καθολικό δέντρο Tg που παράγεται είναι µοναδικό. 74
75 Θεωρήµατα (Θ3) Ο ορισµός για τα συνεπή δέντρα καλύπτει όλα τα σύνολα δέντρων για τα οποία η κατασκευή καθολικού δέντρου οδηγεί σε συνεπή δέντρα. (Θ4) Έστω ένα σύνολο δέντρων συνεπών. Το καθολικό δέντρο Tg που παράγεται είναι µοναδικό. Συµπέρασµα: έντρα ιεραρχιών, συνεπή και συµβατά, δίνουν ένα καθολικό δέντρο. 75
76 Πώς φτιάχνεται το καθολικό δέντρο; Έστω δέντρα ιεραρχίας T1 και Τ2, από σύνολο δέντρων συνεπών και συµβατών. Το καθολικό δέντρο Tg των T1 και Τ2, είναι ένα δέντρο µε: όλους τους κόµβους Ν των T1 και Τ2 όλη την δοµική πληροφορία των T1 και Τ2 ιαισθητικά, το Τ3 κατασκευάζεται από τα Τ1, Τ2: κρατώντας όλες τις κοινές σχέσεις p(x,y), κρατώντας από το Τ1 όλες τις σχέσεις πατέρα p(x,y) που δεν υπάρχουν στο Τ2, ούτε καν µε την µορφή απογόνου a(x,y) (αντίστοιχα και για το Τ2). 76
77 Πώς φτιάχνεται το καθολικό δέντρο; T1 T G N P I E F G J T2 N P I E J K H F M G M J K H 77
78 Πώς φτιάχνεται το καθολικό δέντρο; T1 T G N P I E F G J T2 N P I E J K H F M G M J K H 78
79 (H1) Adorama caps hoods lenses point & shoot cameras & lenses 35mm SL APS cameras digital printers lose Up filters UV PL film Παραδείγµατα slide negative b&w (H2) &H SL cameras 35mm systems lenses photo APS other formats medium general filters bags tripods digital photography cameras printers memory cards scanners film scanners flatbed scanners (H3) itzameras digital cameras 35mm SL point & shoot APS camcorders filters Matching categories (nodes) Adorama : &H : itzcameras cameras & lenses : photo : mm SL : SL cameras : 35mm SL digital : digital photography : --- cameras : cameras : digital cameras 79
80 (H2 U s H3) SL cameras 35mm systems lenses photo APS other formats medium general filters bags tripods digital photography cameras Παραδείγµατα printers point & shoot memory cards scanners film scanners camcorders flatbed scanners Exist in &H's catalog but not in itzameras catalog Exist in itzameras but not in &H's catalog Exist in &H's catalog and in itzameras catalog Matching categories (nodes) &H : itzameras cameras : digital cameras SL cameras : 35mm SL H1-(H2 U s H3) caps hoods lose Up UV PL film b&w slide negative 80
81 H1- H2 H1 - H3 Παραδείγµατα caps hoods point & shoot lose Up UV PL film b&w slide negative caps lenses hoods cameras & lenses digital printers UV lose Up PL film negative b&w slide s (H1- H2) (H1- H3) caps hoods UV PL film b&w slide lose Up negative 81
82 Συγκρίσεις Ενοποίηση σχηµάτων (schema integration) Ανίχνευση αναντιστοιχιών Κατασκευή ενοποιηµένου σχήµατος (merge) ιαχείριση σύνθετων αντικειµένων (complex obejcts) Τελεστές επιλογής, ανακατασκευής (ancilhon) Γενική διαχείριση µοντέλων (generic model management) (ONO: ernstein): Υψηλού επιπέδου τελεστές διαχείρισης µοντέλων Έλλειψη αλγεβρικών ιδιοτήτων 82
83 Σύνοψη συνεισφοράς οµικός χειρισµός ιεραρχιών. Μελέτη αλγεβρικών ιδιοτήτων των ιεραρχιών ως δεντρικές δοµές. Ορισµός 3 τελεστών διαχείρισης δοµικής πληροφορίας (ένωση, τοµή, διαφορά) µε ιδιότητες παρόµοιες µε αυτές των αντίστοιχων τελεστών της συνολοθεωρίας. Έλεγχος πλαισίου ορθότητας: η περίπτωση ύπαρξης καθολικού δέντρου η περίπτωση έλλειψης καθολικού δέντρου 83
84 ...στη συνέχεια ΠΡΟΣ ΙΟΡΙΣΜΟΣ ΟΜΟΛΟΓΩΝ ΙΕΡΑΡΧΙΩΝ ΟΜΙΚΗ ΙΑΧΕΙΡΙΣΗ ΙΕΡΑΡΧΙΩΝ > ΙΑΧΕΙΡΙΣΗ ΙΕΡΑΡΧΙΩΝ ΚΑΙ Ε ΟΜΕΝΩΝ ΣΥΜΠΕΡΑΣΜΑΤΑ ΜΕΛΛΟΝΤΙΚΗ ΟΥΛΕΙΑ 84
85 εδοµένα Τα δεδοµένα οργανώνονται σε πόρους (resource items). Πόρος Σχέση (relation): (a1, a2,, an), όπου a1, a2, ιδιότητες (attributes) Οι πόροι αντιστοιχίζονται στα φύλλα των ιεραρχιών. Ιεραρχία + πόροι = σχήµα καταλόγου (catalog schema). 85
86 Σχήµα καταλόγου X Hierarchy cameras & lenses digital filters film atalog schema caps hoods lenses point & shoot 35mm SL APS cameras printers UV PL slide negative SL cameras 5 6 igital printers brand model price brand model ppm esource items anon EOS hp Nikon N hp Pentax ZX-M hp ata 86
87 εντρικές Σχέσεις (TSs) Σχήµατα καταλόγου µε κοινούς πόρους εναλλακτικά µονοπάτια για τους ίδιους πόρους εντρικές Σχέσεις (Tree-stuctured elations) Αφορούν έναν πόρο. Έχουν µορφή AN/O γράφου. Τα µονοπάτια οργανώνονται σε σύνολα από Oσυνιστώσες. O-συνιστώσα: AN-οµάδα από µονοπάτια ή 1 µονοπάτι. Μονοπάτια = πρότυπα (patterns) 87
88 εντρικές Σχέσεις (TSs) X X camera & lenses cameras photo 35mm systems 35mm SL photo photo photo 35mm SL bodies lenses 35mm systems (a) SL cameras brand model price (b) SL systems brand model price lens_id 88
89 εντρικές Σχέσεις (TSs) O-1 camera & lenses cameras X photo O-2 35mm systems 35mm SL photo X photo photo 35mm SL bodies lenses 35mm systems (a) SL cameras brand model price (b) SL systems brand model price lens_id 89
90 εντρικές Σχέσεις (TSs) O-1 camera & lenses cameras X photo O-2 35mm systems O-3 35mm SL photo X photo O-4 photo 35mm SL bodies lenses 35mm systems (a) SL cameras brand model price (b) SL systems brand model price lens_id 90
91 εντρικές Σχέσεις (TSs) O-1 camera & lenses cameras X photo O-2 35mm systems O-3 35mm SL photo X photo O-4 photo 35mm SL bodies lenses 35mm systems (a) SL cameras brand model price (b) SL systems brand model price lens_id 91
92 Επιλογή, Προβολή, Γινόµενο Επιλογή: σ <attribute condition> <path condition> (TS) path condition: {=,, } Σχεσιακή επιλογή + επιλογή σε µονοπάτια/o συνιστώσες 92
93 ΕΠΙΛΟΓΗ: Φωτογρ. µηχανές, όχι Pentax, ακριβότερες των 200ε, έχοντας το /photo/35mm systems στο µονοπάτι τους σ <brand!= Pentax, price>200> < /photo/35mm systems $_> (SL systems) X X photo 35mm SL bodies photo lenses photo 35mm systems photo 35mm systems (a) SL systems (b) SL systems brand model price lens_id brand model price lens_id anon EOS anon EOS Nikon N Nikon N Pentax ZX-M
94 Επιλογή, Προβολή, Γινόµενο Επιλογή: σ <attribute condition> <path condition> (TS) path condition: {=,, } Σχεσιακή επιλογή + επιλογή σε µονοπάτια/o συνιστώσες Προβολή: π <attribute list> <variable list> (TS) variable list: {$i (µεταβλητή µονοπατιού), #i (O µεταβλητή)} Σχεσιακή προβολή + προβολή σε µονοπάτια/o συνιστώσες 94
95 ΠΡΟΒΟΛΗ: Φωτογρ. µηχανές, µε µόνο το µοντέλο και τον αντίστοιχο φακό τους, κρατώντας το δεξιότερο µονοπάτι π <model, lens_id> <#2> (SL systems) X X photo 35mm SL photo photo photo bodies lenses 35mm systems 35mm systems (a) SL systems (b) SL systems brand model price lens_id model lens_id anon EOS EOS-3 1 Nikon N N65 2 Pentax ZX-M ZX-M
96 Επιλογή, Προβολή, Γινόµενο Επιλογή: σ <attribute condition> <path condition> (TS) path condition: {=,, } Σχεσιακή επιλογή + επιλογή σε µονοπάτια/o συνιστώσες Προβολή: π <attribute list> <variable list> (TS) variable list: {$i (µεταβλητή µονοπατιού), #i (O µεταβλητή)} Σχεσιακή προβολή + προβολή σε µονοπάτια/o συνιστώσες Γινόµενο: (ΤS1) Χ (TS2) Σχεσιακό γινόµενο + συνδυασµός µονοπατιών 96
97 ΓΙΝΟΜΕΝΟ: (SL systems) X (Lenses) 35mm SL bodies photo X photo lenses photo 35mm systems X X = camera & lenses lenses 35mm SL bodies photo photo lenses camera & lenses lenses X photo 35mm systems camera & lenses lenses (a) SL systems (b) Lenses cbrand cmodel cprice anon EOS Nikon N Pentax ZX-M clensid lbrand Sigma Tamron... lensid lprice (c) SL systems cbrand cmodel cprice clensid anon EOS anon EOS Nikon N Nikon N Pentax ZX-M lbrand Sigma Tamron Sigma Tamron Sigma lensid lprice Pentax ZX-M Tamron
98 Ένωση, Τοµή, ιαφορά Ένωση: (TS) (TS) Σχεσιακή ένωση + ένωση O συνιστωσών Τοµή: (TS) (TS) Σχεσιακή τοµή + ένωση O συνιστωσών ιαφορά: (ΤS) - (TS) Σχεσιακή διαφορά + O συνιστώσες της πρώτης TS 98
99 ΕΝΩΣΗ: (SL systems) (SL systems) X X X 35mm SL photo photo U = photo 35mm SL photo photo photo bodies lenses 35mm systems bodies lenses 35mm systems (a) SL systems (b) SL systems (c) SL systems cbrand cmodel cprice anon EOS Nikon N Pentax ZX-M clensid cbrand cmodel cprice clensid cbrand cmodel cprice clensid anon EOS anon EOS Nikon FM Nikon N Pentax ZX-M Pentax ZX-M Nikon FM
100 ind, Path Τελεστές ανακατασκευής. ind: (TS) Επιστρέφει ρίζα, πόρους και δεδοµένα. Path: P<path>((TS)) Επιστρέφει πόρους και δεδοµένα κάτω από νέο µονοπάτι. 100
101 ind photo X (SL systems) photo photo 35mm SL lenses 35mm systems X bodies (a) SL systems (b) SL systems brand model price lens_id brand model price lens_id anon EOS anon EOS Nikon N Nikon N Pentax ZX-M
102 Path X P < /photo/package/35mm > (SL systems) photo package X 35mm (a) (b) SL systems SL systems brand model price lens_id brand model price lens_id anon EOS anon EOS Nikon N Nikon N
103 Συγκρίσεις Γλώσσες ερωτήσεων Ιστού (WebSQL, WebOQL). Άλγεβρες ηµιδοµηµένων δεδοµένων. ΥΑΤ ιαφορές: Τα µονοπάτια ως πρότυπα (PANA project). Inductive database framework Εναλλακτικά µονοπάτια. Σύνθετα µονοπάτια. 103
104 Σύνοψη συνεισφοράς ιαχείριση ιεραρχιών και δεδοµένων. Ορισµός τελεστών που συνδυάζουν διαχείριση µονοπατιών στις ιεραρχίες ως πρότυπα, και κλασσικές σχεσιακές ερωτήσεις στα δεδοµένα. Τελεστές επιλογές: Επιλογή, Προβολή, Γινόµενο Ένωση, Τοµή, ιαφορά Τελεστές ανακατασκευής: ind, Path Υλοποίηση πρότυπου συστήµατος. 104
105 ...στη συνέχεια ΠΡΟΣ ΙΟΡΙΣΜΟΣ ΟΜΟΛΟΓΩΝ ΙΕΡΑΡΧΙΩΝ ΟΜΙΚΗ ΙΑΧΕΙΡΙΣΗ ΙΕΡΑΡΧΙΩΝ ΙΑΧΕΙΡΙΣΗ ΙΕΡΑΡΧΙΩΝ ΚΑΙ Ε ΟΜΕΝΩΝ > ΣΥΜΠΕΡΑΣΜΑΤΑ ΜΕΛΛΟΝΤΙΚΗ ΟΥΛΕΙΑ 105
106 Συµπεράσµατα ιατύπωση πλαισίου διαχείρισης ιεραρχιών τριών κατευθύνσεων ως οντότητες πρώτης τάξης: Προσδιορισµός οµόλογων ιεραρχιών. οµικός χειρισµός ιεραρχιών. ιαχείριση ιεραρχιών και δεδοµένων. 106
107 Συµπεράσµατα Προσδιορισµός οµόλογων ιεραρχιών. Μετρική δοµικής απόστασης. Αποδοτικές τεχνικές συσταδοποίησης ιεραρχιών µέσω δοµικών περιλήψεων ιεραρχιών. οµικός χειρισµός ιεραρχιών. Τελεστές χειρισµού δοµής ιεραρχιών µε σηµασιολογία συνολοθεωρίας. ιαχείριση ιεραρχιών και δεδοµένων. Τελεστές διαχείρισης µονοπατιών και δεδοµένων 107
108 Μελλοντική ουλειά Προσδιορισµός οµόλογων ιεραρχιών: Μελέτη ιδιοτήτων αποστάσεων. ιανυσµατική αναπαράσταση ιεραρχιών. οµικός χειρισµός ιεραρχιών. Χαλάρωση συνθηκών κατασκευής καθολικού δέντρου. Παραλλαγές συµβατότητας δέντρων 108
109 Μελλοντική ουλειά Μοντέλο γράφου: Μεταφορά του πλαισίου διαχείρισης ιεραρχιών σε γράφους. Μελέτη αλγεβρικών ιδιοτήτων. Ορισµός τελεστών. Σύνθετα ταιριάσµατα: Χρήση ταιριασµάτων 1:Ν αντί για 1:1. Εφαρµογές πλαισίου διαχείρισης ιεραρχιών. 109
110 ηµοσιεύσεις/αναφορές T. alamagas, T. heng, K. J. Winkel, T. Sellis, lustering XML documents using structural summaries, ET Workshop on lustering Information over the Web (lustwebά04), Heraklion, Greece, 2004 (to appear). P. ouros, T. alamagas, T. Sellis, M. Terrovitis, PatManQL: A language to manipulate patterns and data in hierarchical catalogs, ET Workshop on Pattern epresentation and Management (PaMa 04), Heraklion, Greece, 2004 (to appear). T. alamagas, T. heng, K. J. Winkel, T. Sellis, lustering XML documents by structure, in Proceedings of the 3rd Hellenic onference on Artificial Intelligence, May 5-8, Samos, Greece, 2004 (to appear).. Theodoratos, T. alamagas, Querying and Integrating Ontologies Viewed as onceptual Schemas, in Proceedings of 22nd International onference on onceptual Modeling (E'03), Oct 13-16, hicago, Illinois, USA,
111 ηµοσιεύσεις/αναφορές (Υπό κρίση) T. alamagas, A. Meliou, T. Sellis, Modeling and Manipulating the structure of hierarchical schemas for the Web, submitted to the Journal of Information etrieval, Feb 2004, T. alamagas, T. heng, K. J. Winkel, T. Sellis, lustering XML documents by structure, submitted to the Information Systems Journal, Oct
112 112
113 Νέος αλγόριθµος υπολογισµού δοµικής απόστασης int alculateistance(treenode s, TreeNode t) { int[][] = new int[numofhildren(s)+1][numofhildren(t)+1]; [0][0] = Updateost(LabelOf(s), LabelOf(t)); for (int i = 1; i <= numofhildren(s); i++) [i][0] = [i-1][0] + numofnodes(s_i); αρχικοποιήσεις for (int j = 1; j <= numofhildren(t); j++) [0][j] = [0][j-1] + numofnodes(t_j); for (int i = 1; i <= numofhildren(s); i++) for (int j = 1; j <= numofhildren(t); j++) [i][j] = Min([i][j-1] + numofnodes(t_j), [i-1][j] + numofnodes(s_i), [i-1][j-1] + alculateistance(s_i,t_j)); eturn [numofhildren(s)][numofhildren(t)]; } 113
114 Αξιολόγηση απόδοσης hawathe: µε/χωρίς δοµ. περιλήψεις 114
115 Αξιολόγηση απόδοσης hawathe: υπολογισµός συντακτικού γράφου 115
116 Ένωση T1 T2 T3 S N P = N P I E F J M M H G J K F H I E J K F H G 116
117 Ένωση T1 T2 T3 S N P = N P I E F J M M H G J K F H I E J K F H G 117
118 Ένωση T1 T2 T3 S N P = N P I E F J M M H G J K F H I E J K F H G 118
119 Τοµή Έστω δέντρα ιεραρχίας T1 και Τ2 από το σύνολο Sg={Ti, Ti Tg}. Η τοµή Τ3 των T1 και Τ2, T1 Τ2, είναι ένα δέντρο µε: τους κοινούς κόµβους Ν των T1 και Τ2 την κοινή δοµική πληροφορία των T1 και Τ2 ιαισθητικά, το Τ3 κατασκευάζεται από το Τg, διαγράφοντας όλους τους κόµβους εκτός από αυτούς του Ν, και µετακινώντας τα παιδιά σε υψηλότερα επίπεδα. 119
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ Γλώσσα Ερωτήσεων για εδοµένα ενδρικής οµής ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ του ΜΠΟΥΡΟΥ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ Γλώσσα Ερωτήσεων για εδοµένα ενδρικής οµής ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ του ΜΠΟΥΡΟΥ
Semantic-based Querying of Tree-Structured Data. Οργάνωση εδοµένων µε ενδρικές οµές
 Semantic-based Queying of Tee-Stuctued Data ηµήτρης Θεοδωράτος Θοδωρής αλαµάγκας Αντώνης Κουφόπουλος (New Jesey Institute of Technology, ΗΠΑ) (Εθνικό Μετσόβιο Πολυτεχνείο) (Εθνικό Μετσόβιο Πολυτεχνείο)
Semantic-based Queying of Tee-Stuctued Data ηµήτρης Θεοδωράτος Θοδωρής αλαµάγκας Αντώνης Κουφόπουλος (New Jesey Institute of Technology, ΗΠΑ) (Εθνικό Μετσόβιο Πολυτεχνείο) (Εθνικό Μετσόβιο Πολυτεχνείο)
Ουρά Προτεραιότητας: Heap
 Ουρά Προτεραιότητας: Heap ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ομές εδομένων (Αναπαράσταση,) οργάνωση και διαχείριση συνόλων αντικειμένων για
Ουρά Προτεραιότητας: Heap ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ομές εδομένων (Αναπαράσταση,) οργάνωση και διαχείριση συνόλων αντικειμένων για
Οργάνωση Γεωγραφικών. πληροφοριών
 Οργάνωση Γεωγραφικών Οργάνωση γεωγραφικών 1 Ορισµοί - ορολογία εδοµένα (Data) ένα σύνολο από γεγονότα και στοιχεία, τα οποία έχουν συλλεχθεί για κάποιο συγκεκριµένο σκοπό Πληροφορίες (Information) επεξεργασµένα
Οργάνωση Γεωγραφικών Οργάνωση γεωγραφικών 1 Ορισµοί - ορολογία εδοµένα (Data) ένα σύνολο από γεγονότα και στοιχεία, τα οποία έχουν συλλεχθεί για κάποιο συγκεκριµένο σκοπό Πληροφορίες (Information) επεξεργασµένα
Σημασιολογική Ολοκλήρωση Δεδομένων με τη χρήση Οντολογιών
 Σημασιολογική Ολοκλήρωση Δεδομένων με τη χρήση Οντολογιών Λίνα Μπουντούρη - Μανόλης Γεργατσούλης Ιόνιο Πανεπιστήμιο 15ο Πανελλήνιο Συνέδριο Ακαδημαϊκών Βιβλιοθηκών Διαδίκτυο και Επίπεδα ετερογένειας δεδομένων
Σημασιολογική Ολοκλήρωση Δεδομένων με τη χρήση Οντολογιών Λίνα Μπουντούρη - Μανόλης Γεργατσούλης Ιόνιο Πανεπιστήμιο 15ο Πανελλήνιο Συνέδριο Ακαδημαϊκών Βιβλιοθηκών Διαδίκτυο και Επίπεδα ετερογένειας δεδομένων
Ουρά Προτεραιότητας: Heap
 Ουρά Προτεραιότητας: Heap ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια Χρήσης Το παρόν εκπαιδευτικό
Ουρά Προτεραιότητας: Heap ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια Χρήσης Το παρόν εκπαιδευτικό
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΥΠΟΛΟΓΙΣΤΩΝ Πρότυπο Σύστηµα Αποθήκευσης και ιαχείρισης Σχηµάτων RDFS ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΥΠΟΛΟΓΙΣΤΩΝ Πρότυπο Σύστηµα Αποθήκευσης και ιαχείρισης Σχηµάτων RDFS ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
ιµελής Σχέση ιατεταγµένο ζεύγος (α, β): ύο αντικείµενα (όχι κατ ανάγκη διαφορετικά) σε καθορισµένη σειρά. Γενίκευση: διατεταγµένη τριάδα (α, β, γ), δι
 Σχέσεις ιδάσκοντες: Φ. Αφράτη, Σ. Ζάχος,. Σούλιου Επιµέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ιµελής Σχέση ιατεταγµένο ζεύγος (α, β):
Σχέσεις ιδάσκοντες: Φ. Αφράτη, Σ. Ζάχος,. Σούλιου Επιµέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ιµελής Σχέση ιατεταγµένο ζεύγος (α, β):
ΜΑΘΗΜΑ 6. Σχήµατα ιαλειτουργικότητας Μεταδεδοµένων. Το RDF Το Warwick Framework. Ιόνιο Πανεπιστήµιο - Τµήµα Αρχειονοµίας - Βιβλιοθηκονοµίας
 ΜΑΘΗΜΑ 6 195 Σχήµατα ιαλειτουργικότητας Μεταδεδοµένων Το RDF Το Warwick Framework 196 1 Resource Data Framework RDF Τα πολλαπλά και πολλαπλής προέλευσης σχήµατα παραγωγής δηµιουργούν την ανάγκη δηµιουργίας
ΜΑΘΗΜΑ 6 195 Σχήµατα ιαλειτουργικότητας Μεταδεδοµένων Το RDF Το Warwick Framework 196 1 Resource Data Framework RDF Τα πολλαπλά και πολλαπλής προέλευσης σχήµατα παραγωγής δηµιουργούν την ανάγκη δηµιουργίας
ΚΕΦΑΛΑΙΟ 18. 18 Μηχανική Μάθηση
 ΚΕΦΑΛΑΙΟ 18 18 Μηχανική Μάθηση Ένα φυσικό ή τεχνητό σύστηµα επεξεργασίας πληροφορίας συµπεριλαµβανοµένων εκείνων µε δυνατότητες αντίληψης, µάθησης, συλλογισµού, λήψης απόφασης, επικοινωνίας και δράσης
ΚΕΦΑΛΑΙΟ 18 18 Μηχανική Μάθηση Ένα φυσικό ή τεχνητό σύστηµα επεξεργασίας πληροφορίας συµπεριλαµβανοµένων εκείνων µε δυνατότητες αντίληψης, µάθησης, συλλογισµού, λήψης απόφασης, επικοινωνίας και δράσης
Εισαγωγή στην επιστήμη των υπολογιστών. Οργάνωση εδομένων Κεφάλαιο 11ο ομές εδομένων
 Εισαγωγή στην επιστήμη των υπολογιστών Οργάνωση εδομένων Κεφάλαιο 11ο ομές εδομένων 1 ομή εδομένων Μια δομή δεδομένων (data structure) χρησιμοποιεί μια συλλογή από σχετικές μεταξύ τους μεταβλητές, οι οποίες
Εισαγωγή στην επιστήμη των υπολογιστών Οργάνωση εδομένων Κεφάλαιο 11ο ομές εδομένων 1 ομή εδομένων Μια δομή δεδομένων (data structure) χρησιμοποιεί μια συλλογή από σχετικές μεταξύ τους μεταβλητές, οι οποίες
Επεξεργασία Ερωτήσεων
 Εισαγωγή Επεξεργασία Ερωτήσεων ΜΕΡΟΣ 1 Γενική Εικόνα του Μαθήματος 1. Μοντελοποίηση (Μοντέλο Ο/Σ, Σχεσιακό, Λογικός Σχεδιασμός) 2. Προγραμματισμός (Σχεσιακή Άλγεβρα, SQL) ημιουργία/κατασκευή Εισαγωγή εδομένων
Εισαγωγή Επεξεργασία Ερωτήσεων ΜΕΡΟΣ 1 Γενική Εικόνα του Μαθήματος 1. Μοντελοποίηση (Μοντέλο Ο/Σ, Σχεσιακό, Λογικός Σχεδιασμός) 2. Προγραμματισμός (Σχεσιακή Άλγεβρα, SQL) ημιουργία/κατασκευή Εισαγωγή εδομένων
Επεξεργασία Ερωτήσεων
 Εισαγωγή Επεξεργασία Ερωτήσεων Σ Β Βάση εδομένων Η ομή ενός ΣΒ Βάσεις Δεδομένων 2006-2007 Ευαγγελία Πιτουρά 1 Βάσεις Δεδομένων 2006-2007 Ευαγγελία Πιτουρά 2 Εισαγωγή Εισαγωγή ΜΕΡΟΣ 1 (Χρήση Σ Β ) Γενική
Εισαγωγή Επεξεργασία Ερωτήσεων Σ Β Βάση εδομένων Η ομή ενός ΣΒ Βάσεις Δεδομένων 2006-2007 Ευαγγελία Πιτουρά 1 Βάσεις Δεδομένων 2006-2007 Ευαγγελία Πιτουρά 2 Εισαγωγή Εισαγωγή ΜΕΡΟΣ 1 (Χρήση Σ Β ) Γενική
Database System Concepts and Architecture (Αρχιτεκτονική, οµές, και Μοντέλα)
 Database System Concepts and Architecture (Αρχιτεκτονική, οµές, και Μοντέλα) Μοντέλα, οµές (Σχήµα) και Αντιπρόσωποι (Data Models, Schema, and Instances) DBMS αρχιτεκτονική ιάφοροι τύποι γλωσσών και διεπαφές
Database System Concepts and Architecture (Αρχιτεκτονική, οµές, και Μοντέλα) Μοντέλα, οµές (Σχήµα) και Αντιπρόσωποι (Data Models, Schema, and Instances) DBMS αρχιτεκτονική ιάφοροι τύποι γλωσσών και διεπαφές
ΜΕΡΟΣ Ι: ΓΕΩΓΡΑΦΙΚΑ Ε ΟΜΕΝΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΓΕΩΓΡΑΦΙΚΩΝ ΠΛΗΡΟΦΟΡΙΩΝ Η ΦΥΣΗ ΤΩΝ ΓΕΩΓΡΑΦΙΚΩΝ Ε ΟΜΕΝΩΝ...
 ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ ΜΕΡΟΣ Ι: ΓΕΩΓΡΑΦΙΚΑ Ε ΟΜΕΝΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΓΕΩΓΡΑΦΙΚΩΝ ΠΛΗΡΟΦΟΡΙΩΝ...1 1. Η ΦΥΣΗ ΤΩΝ ΓΕΩΓΡΑΦΙΚΩΝ Ε ΟΜΕΝΩΝ...3 Κατηγορίες των Γεωγραφικών εδοµένων...3 Γεωγραφικές οντότητες...3 ιαστάσεις
ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ ΜΕΡΟΣ Ι: ΓΕΩΓΡΑΦΙΚΑ Ε ΟΜΕΝΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΓΕΩΓΡΑΦΙΚΩΝ ΠΛΗΡΟΦΟΡΙΩΝ...1 1. Η ΦΥΣΗ ΤΩΝ ΓΕΩΓΡΑΦΙΚΩΝ Ε ΟΜΕΝΩΝ...3 Κατηγορίες των Γεωγραφικών εδοµένων...3 Γεωγραφικές οντότητες...3 ιαστάσεις
Αναπαράσταση Γνώσης και Αναζήτηση στον Σηµασιολογικό Ιστό
 Αναπαράσταση Γνώσης και Αναζήτηση στον Σηµασιολογικό Ιστό Αλέξανδρος Βαλαράκος (alexv@iit.demokritos.gr) (alexv@aegean.gr) Υποψήφιος ιδάκτορας Τµήµα Μηχανικών Υπολογιστικών και Πληροφοριακών Συστηµάτων.
Αναπαράσταση Γνώσης και Αναζήτηση στον Σηµασιολογικό Ιστό Αλέξανδρος Βαλαράκος (alexv@iit.demokritos.gr) (alexv@aegean.gr) Υποψήφιος ιδάκτορας Τµήµα Μηχανικών Υπολογιστικών και Πληροφοριακών Συστηµάτων.
ιαχείριση και Ανάκτηση Εικόνας µε χρήση Οµοιότητας Γράφων (WW-test)
 ιαχείριση και Ανάκτηση Εικόνας µε χρήση Οµοιότητας Γράφων (WW-test) Θεοχαράτος Χρήστος Εργαστήριο Ηλεκτρονικής (ELLAB), Τµήµα Φυσικής, Πανεπιστήµιο Πατρών email: htheohar@upatras.gr http://www.ellab.physics.upatras.gr/users/theoharatos/default.htm
ιαχείριση και Ανάκτηση Εικόνας µε χρήση Οµοιότητας Γράφων (WW-test) Θεοχαράτος Χρήστος Εργαστήριο Ηλεκτρονικής (ELLAB), Τµήµα Φυσικής, Πανεπιστήµιο Πατρών email: htheohar@upatras.gr http://www.ellab.physics.upatras.gr/users/theoharatos/default.htm
Δρ. Βασίλειος Γ. Καμπουρλάζος Δρ. Ανέστης Γ. Χατζημιχαηλίδης
 Μάθημα 7 ο Δρ. Βασίλειος Γ. Καμπουρλάζος Τμήμα Μηχανικών Πληροφορικής Τ.Ε. ΤΕΙ Ανατολικής Μακεδονίας και Θράκης 2016-2017 Μια Ενοποιητική Προσέγγιση στην ΥΝ Η Θεωρία Πλεγμάτων στην ΥΝ. Υπολογιστικές Μεθοδολογίες
Μάθημα 7 ο Δρ. Βασίλειος Γ. Καμπουρλάζος Τμήμα Μηχανικών Πληροφορικής Τ.Ε. ΤΕΙ Ανατολικής Μακεδονίας και Θράκης 2016-2017 Μια Ενοποιητική Προσέγγιση στην ΥΝ Η Θεωρία Πλεγμάτων στην ΥΝ. Υπολογιστικές Μεθοδολογίες
Σχέσεις. ιδάσκοντες:. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 Σχέσεις ιδάσκοντες:. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ιμελής Σχέση ιατεταγμένο ζεύγος (α, β): ύο αντικείμενα
Σχέσεις ιδάσκοντες:. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ιμελής Σχέση ιατεταγμένο ζεύγος (α, β): ύο αντικείμενα
έντρα ιδάσκοντες:. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο
 έντρα ιδάσκοντες:. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο έντρα έντρο: πρότυπο ιεραρχικής δομής. Αναπαράσταση
έντρα ιδάσκοντες:. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο έντρα έντρο: πρότυπο ιεραρχικής δομής. Αναπαράσταση
Παραδοτέο Π.2.1. Υπερχώρος και διαχείριση μοντέλων
 Έργο: Τίτλος Υποέργου: «ΘΑΛΗΣ: Ενίσχυση της Διεπιστημονικής ή και Διιδρυματικής έρευνας και καινοτομίας με δυνατότητα προσέλκυσης ερευνητών υψηλού επιπέδου από το εξωτερικό μέσω της διενέργειας βασικής
Έργο: Τίτλος Υποέργου: «ΘΑΛΗΣ: Ενίσχυση της Διεπιστημονικής ή και Διιδρυματικής έρευνας και καινοτομίας με δυνατότητα προσέλκυσης ερευνητών υψηλού επιπέδου από το εξωτερικό μέσω της διενέργειας βασικής
ΣΧΕΣΙΑΚΟ ΜΟΝΤΕΛΟ (Relational Model) Μαθ. #10
 ΣΧΕΣΙΑΚΟ ΜΟΝΤΕΛΟ (Relational Model) Μαθ. #10 Πράξεις Αλλαγής εδοµένων INSERT (εισαγωγή) Αυτός ο τελεστής παρέχει µια λίστα από πεδία τιµών για µια καινούργια πλειάδα η οποία θα εισαχθεί σε µια σχέση R
ΣΧΕΣΙΑΚΟ ΜΟΝΤΕΛΟ (Relational Model) Μαθ. #10 Πράξεις Αλλαγής εδοµένων INSERT (εισαγωγή) Αυτός ο τελεστής παρέχει µια λίστα από πεδία τιµών για µια καινούργια πλειάδα η οποία θα εισαχθεί σε µια σχέση R
Βάσεις εδοµένων. Βασίλειος Βεσκούκης, Εµµ. Στεφανάκης ΜΟΝΤΕΛΟΠΟΙΗΣΗ Ε ΟΜΕΝΩΝ, ΚΛΑΣΙΚΑ ΜΟΝΤΕΛΑ Ε ΟΜΕΝΩΝ
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Αγρονόµων Τοπογράφων Μηχανικών Βάσεις εδοµένων Βασίλειος Βεσκούκης, Εµµ. Στεφανάκης v.vescoukis@cs.ntua.gr ΜΟΝΤΕΛΟΠΟΙΗΣΗ Ε ΟΜΕΝΩΝ, ΚΛΑΣΙΚΑ ΜΟΝΤΕΛΑ Ε ΟΜΕΝΩΝ Μοντέλα εδοµένων
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Αγρονόµων Τοπογράφων Μηχανικών Βάσεις εδοµένων Βασίλειος Βεσκούκης, Εµµ. Στεφανάκης v.vescoukis@cs.ntua.gr ΜΟΝΤΕΛΟΠΟΙΗΣΗ Ε ΟΜΕΝΩΝ, ΚΛΑΣΙΚΑ ΜΟΝΤΕΛΑ Ε ΟΜΕΝΩΝ Μοντέλα εδοµένων
υαδικό έντρο Αναζήτησης (BSTree)
 Εργαστήριο 6 υαδικό έντρο Αναζήτησης (BSTree) Εισαγωγή Οι περισσότερες δοµές δεδοµένων, που εξετάσαµε µέχρι τώρα (λίστες, στοίβες, ουρές) ήταν γραµ- µικές (ή δοµές δεδοµένων µιας διάστασης). Στην παράγραφο
Εργαστήριο 6 υαδικό έντρο Αναζήτησης (BSTree) Εισαγωγή Οι περισσότερες δοµές δεδοµένων, που εξετάσαµε µέχρι τώρα (λίστες, στοίβες, ουρές) ήταν γραµ- µικές (ή δοµές δεδοµένων µιας διάστασης). Στην παράγραφο
ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 έντρα ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο έντρα έντρο: πρότυπο ιεραρχικής δομής.
έντρα ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο έντρα έντρο: πρότυπο ιεραρχικής δομής.
Ουρά Προτεραιότητας: Heap
 Ουρά Προτεραιότητας: Heap Επιμέλεια διαφανειών: Δ. Φωτάκης (λίγες τροποποιήσεις: Α. Παγουρτζής) Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Δομές Δεδομένων (Αναπαράσταση,)
Ουρά Προτεραιότητας: Heap Επιμέλεια διαφανειών: Δ. Φωτάκης (λίγες τροποποιήσεις: Α. Παγουρτζής) Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Δομές Δεδομένων (Αναπαράσταση,)
Επεξεργασία Ερωτήσεων
 Εισαγωγή Σ Β Σύνολο από προγράμματα για τη διαχείριση της Β Επεξεργασία Ερωτήσεων Αρχεία ευρετηρίου Κατάλογος συστήματος Αρχεία δεδομένων ΒΑΣΗ Ε ΟΜΕΝΩΝ Σύστημα Βάσεων εδομένων (ΣΒ ) Βάσεις Δεδομένων 2007-2008
Εισαγωγή Σ Β Σύνολο από προγράμματα για τη διαχείριση της Β Επεξεργασία Ερωτήσεων Αρχεία ευρετηρίου Κατάλογος συστήματος Αρχεία δεδομένων ΒΑΣΗ Ε ΟΜΕΝΩΝ Σύστημα Βάσεων εδομένων (ΣΒ ) Βάσεις Δεδομένων 2007-2008
Το εσωτερικό ενός Σ Β
 Επεξεργασία Ερωτήσεων 1 Εισαγωγή ΜΕΡΟΣ 1 Γενική Εικόνα του Μαθήµατος Μοντελοποίηση (Μοντέλο Ο/Σ, Σχεσιακό, Λογικός Σχεδιασµός) Προγραµµατισµός (Σχεσιακή Άλγεβρα, SQL) ηµιουργία/κατασκευή Εισαγωγή εδοµένων
Επεξεργασία Ερωτήσεων 1 Εισαγωγή ΜΕΡΟΣ 1 Γενική Εικόνα του Μαθήµατος Μοντελοποίηση (Μοντέλο Ο/Σ, Σχεσιακό, Λογικός Σχεδιασµός) Προγραµµατισµός (Σχεσιακή Άλγεβρα, SQL) ηµιουργία/κατασκευή Εισαγωγή εδοµένων
ΗΥ562 Προχωρημένα Θέματα Βάσεων Δεδομένων Efficient Query Evaluation over Temporally Correlated Probabilistic Streams
 ΗΥ562 Προχωρημένα Θέματα Βάσεων Δεδομένων Efficient Query Evaluation over Temporally Correlated Probabilistic Streams Αλέκα Σεληνιωτάκη Ηράκλειο, 26/06/12 aseliniotaki@csd.uoc.gr ΑΜ: 703 1. Περίληψη Συνεισφοράς
ΗΥ562 Προχωρημένα Θέματα Βάσεων Δεδομένων Efficient Query Evaluation over Temporally Correlated Probabilistic Streams Αλέκα Σεληνιωτάκη Ηράκλειο, 26/06/12 aseliniotaki@csd.uoc.gr ΑΜ: 703 1. Περίληψη Συνεισφοράς
Σχέσεις. Διμελής Σχέση. ΣτοΊδιοΣύνολο. Αναπαράσταση
 Διμελής Σχέση Σχέσεις Διδάσκοντες: Φ. Αφράτη, Δ. Επιμέλεια διαφανειών: Δ. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Διατεταγμένο ζεύγος (α, β): Δύο αντικείμενα
Διμελής Σχέση Σχέσεις Διδάσκοντες: Φ. Αφράτη, Δ. Επιμέλεια διαφανειών: Δ. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Διατεταγμένο ζεύγος (α, β): Δύο αντικείμενα
Αντικείµενο: Θεµελιώδες πρόβληµα της επιστήµης µας εδοµένα
 Εισαγωγή 1 Ζήτω οι Βάσεις εδοµένων!! Αντικείµενο: Θεµελιώδες πρόβληµα της επιστήµης µας εδοµένα Μοντελοποίηση Αποθήκευση Επεξεργασία (εύρεση πληροφορίας σχετικής µε µια συγκεκριµένη ερώτηση) Σωστή Λειτουργία
Εισαγωγή 1 Ζήτω οι Βάσεις εδοµένων!! Αντικείµενο: Θεµελιώδες πρόβληµα της επιστήµης µας εδοµένα Μοντελοποίηση Αποθήκευση Επεξεργασία (εύρεση πληροφορίας σχετικής µε µια συγκεκριµένη ερώτηση) Σωστή Λειτουργία
Πίνακας περιεχοµένων
 Πίνακας περιεχοµένων ΠΡΩΤΟ ΜΕΡΟΣ... 1 Κεφάλαιο 1 Εισαγωγή στα συστήµατα ρευµάτων δεδοµένων... 3 1.1 Εισαγωγή... 3 1.2 Η ανεπάρκεια των συµβατικών Σ Β... 4 1.3 Το µοντέλο ρεύµατος δεδοµένων... 7 1.4 Ερωτήµατα
Πίνακας περιεχοµένων ΠΡΩΤΟ ΜΕΡΟΣ... 1 Κεφάλαιο 1 Εισαγωγή στα συστήµατα ρευµάτων δεδοµένων... 3 1.1 Εισαγωγή... 3 1.2 Η ανεπάρκεια των συµβατικών Σ Β... 4 1.3 Το µοντέλο ρεύµατος δεδοµένων... 7 1.4 Ερωτήµατα
 «Υποστήριξη της Ψηφιοποίησης και Τεκµηρίωσης του Αρχείου του Κέντρου Λαογραφίας» Γιώργος Κουταλιέρης, Τεχνικός ιευθυντής, SYSTEMA TECHNOLOGIES Α.Ε. gkout@systema.gr Σύνοψη Αντικείµενο Υλοποίησης Πλαίσιο
«Υποστήριξη της Ψηφιοποίησης και Τεκµηρίωσης του Αρχείου του Κέντρου Λαογραφίας» Γιώργος Κουταλιέρης, Τεχνικός ιευθυντής, SYSTEMA TECHNOLOGIES Α.Ε. gkout@systema.gr Σύνοψη Αντικείµενο Υλοποίησης Πλαίσιο
Εισαγωγή στην. Εισαγωγή Σ Β. Αρχεία ευρετηρίου Κατάλογος. συστήματος. Αρχεία δεδομένων
 Εισαγωγή στην Επεξεργασία Ερωτήσεων 1 Εισαγωγή Σ Β Σύνολο από προγράμματα για τη διαχείριση της Β Αρχεία ευρετηρίου Κατάλογος ΒΑΣΗ Ε ΟΜΕΝΩΝ Αρχεία δεδομένων συστήματος Σύστημα Βάσεων εδομένων (ΣΒ ) 2 :
Εισαγωγή στην Επεξεργασία Ερωτήσεων 1 Εισαγωγή Σ Β Σύνολο από προγράμματα για τη διαχείριση της Β Αρχεία ευρετηρίου Κατάλογος ΒΑΣΗ Ε ΟΜΕΝΩΝ Αρχεία δεδομένων συστήματος Σύστημα Βάσεων εδομένων (ΣΒ ) 2 :
Κεφάλαιο 4 Σημασιολογία μιας Απλής Προστακτικής Γλώσσας
 Κεφάλαιο 4 Σημασιολογία μιας Απλής Προστακτικής Γλώσσας Προπτυχιακό μάθημα Αρχές Γλωσσών Προγραμματισμού Π. Ροντογιάννης 1 Εισαγωγή - 1 Μία κλασσική γλώσσα προγραμματισμού αποτελείται από: Εκφράσεις (των
Κεφάλαιο 4 Σημασιολογία μιας Απλής Προστακτικής Γλώσσας Προπτυχιακό μάθημα Αρχές Γλωσσών Προγραμματισμού Π. Ροντογιάννης 1 Εισαγωγή - 1 Μία κλασσική γλώσσα προγραμματισμού αποτελείται από: Εκφράσεις (των
ΤΙΤΛΟΣ ΙΠΛΩΜΑΤΙΚΗΣ ΕΡΓΑΣΙΑΣ: GoNToggle: ΕΞΥΠΝΗ ΜΗΧΑΝΗ ΑΝΑΖΗΤΗΣΗΣ ΜΕ ΧΡΗΣΗ ΟΝΤΟΛΟΓΙΩΝ ΠΕΡΙΟΧΗ ΕΡΕΥΝΑΣ: ΣΥΓΓΡΑΦΕΑΣ:
 ΤΙΤΛΟΣ ΙΠΛΩΜΑΤΙΚΗΣ ΕΡΓΑΣΙΑΣ: GoNToggle: ΕΞΥΠΝΗ ΜΗΧΑΝΗ ΑΝΑΖΗΤΗΣΗΣ ΜΕ ΧΡΗΣΗ ΟΝΤΟΛΟΓΙΩΝ ΠΕΡΙΟΧΗ ΕΡΕΥΝΑΣ: Υπολογιστικά Συστήµατα & Τεχνολογίες Πληροφορικής ΣΥΓΓΡΑΦΕΑΣ: Γιώργος Γιαννόπουλος, διδακτορικός φοιτητής
ΤΙΤΛΟΣ ΙΠΛΩΜΑΤΙΚΗΣ ΕΡΓΑΣΙΑΣ: GoNToggle: ΕΞΥΠΝΗ ΜΗΧΑΝΗ ΑΝΑΖΗΤΗΣΗΣ ΜΕ ΧΡΗΣΗ ΟΝΤΟΛΟΓΙΩΝ ΠΕΡΙΟΧΗ ΕΡΕΥΝΑΣ: Υπολογιστικά Συστήµατα & Τεχνολογίες Πληροφορικής ΣΥΓΓΡΑΦΕΑΣ: Γιώργος Γιαννόπουλος, διδακτορικός φοιτητής
Βάσεις Δεδομένων ΙΙ. Διάλεξη 5 η XML και ΒΔ στο Διαδίκτυο
 Βάσεις Δεδομένων ΙΙ Διάλεξη 5 η XML και ΒΔ στο Διαδίκτυο Δ. Χριστοδουλάκης - Α. Φωκά Τμήμα Μηχανικών Η/Υ & Πληροφορικής - Εαρινό Εξάμηνο 2007 Εισαγωγή Πολλές εφαρμογές διαδικτύου υποστηρίζουν web διεπαφές
Βάσεις Δεδομένων ΙΙ Διάλεξη 5 η XML και ΒΔ στο Διαδίκτυο Δ. Χριστοδουλάκης - Α. Φωκά Τμήμα Μηχανικών Η/Υ & Πληροφορικής - Εαρινό Εξάμηνο 2007 Εισαγωγή Πολλές εφαρμογές διαδικτύου υποστηρίζουν web διεπαφές
Διδάσκοντες: Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 Σχέσεις Διδάσκοντες: Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Διμελής Σχέση Διατεταγμένο ζεύγος (α, β):
Σχέσεις Διδάσκοντες: Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Διμελής Σχέση Διατεταγμένο ζεύγος (α, β):
5. Επερώτηση XML Εγγράφων: Εισαγωγή στη Γλώσσα XQuery
 Πανεπιστήμιο Πειραιώς Σχολή Τεχνολογιών Πληροφορικής και Επικοινωνιών Τμήμα Ψηφιακών Συστημάτων 5. Επερώτηση XML Εγγράφων: Εισαγωγή στη Γλώσσα XQuery ιαχείριση εδομένων στον Παγκόσμιο Ιστό Χρήστος ουλκερίδης
Πανεπιστήμιο Πειραιώς Σχολή Τεχνολογιών Πληροφορικής και Επικοινωνιών Τμήμα Ψηφιακών Συστημάτων 5. Επερώτηση XML Εγγράφων: Εισαγωγή στη Γλώσσα XQuery ιαχείριση εδομένων στον Παγκόσμιο Ιστό Χρήστος ουλκερίδης
P-Μiner : ιαχείριση Πυλών Καταλόγων (Portals) µε Υποστήριξη ιαδικασιών Εξόρυξης εδοµένων Χρήσης
 P-Μiner : ιαχείριση Πυλών Καταλόγων (Portals) µε Υποστήριξη ιαδικασιών Εξόρυξης εδοµένων Χρήσης ιπλωµατική Εργασία του Θεοδώρου Ι. Γαλάνη ΠΕΡΙΛΗΨΗ Γενικά Με την εξάπλωση του διαδικτύου όλο και περισσότεροι
P-Μiner : ιαχείριση Πυλών Καταλόγων (Portals) µε Υποστήριξη ιαδικασιών Εξόρυξης εδοµένων Χρήσης ιπλωµατική Εργασία του Θεοδώρου Ι. Γαλάνη ΠΕΡΙΛΗΨΗ Γενικά Με την εξάπλωση του διαδικτύου όλο και περισσότεροι
Εισαγωγή στην πληροφορική
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Αγρονόµων Τοπογράφων Μηχανικών Εισαγωγή στην πληροφορική Βασίλειος Βεσκούκης ρ. Ηλεκτρολόγος Μηχανικός & Μηχανικός Υπολογιστών ΕΜΠ v.vescoukis@cs.ntua.gr Αλγόριθµοι, στοιχεία
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Αγρονόµων Τοπογράφων Μηχανικών Εισαγωγή στην πληροφορική Βασίλειος Βεσκούκης ρ. Ηλεκτρολόγος Μηχανικός & Μηχανικός Υπολογιστών ΕΜΠ v.vescoukis@cs.ntua.gr Αλγόριθµοι, στοιχεία
Υποστήριξη στη ιαχείριση Γνώσης
 Υποστήριξη στη ιαχείριση Γνώσης Νίκος Καρακαπιλίδης Industrial Management & Information Systems Lab MEAD, University of Patras, Greece nikos@mech.upatras.gr Βασικές έννοιες ιάρθρωση ενότητας Γνώση και
Υποστήριξη στη ιαχείριση Γνώσης Νίκος Καρακαπιλίδης Industrial Management & Information Systems Lab MEAD, University of Patras, Greece nikos@mech.upatras.gr Βασικές έννοιες ιάρθρωση ενότητας Γνώση και
Κεφάλαιο 20. Ανακάλυψη Γνώσης σε Βάσεις δεδοµένων. Τεχνητή Νοηµοσύνη - Β' Έκδοση Ι. Βλαχάβας, Π. Κεφαλάς, Ν. Βασιλειάδης, Φ. Κόκκορας, Η.
 Κεφάλαιο 20 Ανακάλυψη Γνώσης σε Βάσεις δεδοµένων Τεχνητή Νοηµοσύνη - Β' Έκδοση Ι. Βλαχάβας, Π. Κεφαλάς, Ν. Βασιλειάδης, Φ. Κόκκορας, Η. Σακελλαρίου Τεχνητή Νοηµοσύνη, B' Έκδοση - 1 - Ανακάλυψη Γνώσης σε
Κεφάλαιο 20 Ανακάλυψη Γνώσης σε Βάσεις δεδοµένων Τεχνητή Νοηµοσύνη - Β' Έκδοση Ι. Βλαχάβας, Π. Κεφαλάς, Ν. Βασιλειάδης, Φ. Κόκκορας, Η. Σακελλαρίου Τεχνητή Νοηµοσύνη, B' Έκδοση - 1 - Ανακάλυψη Γνώσης σε
Εισαγωγή Αλγόριθµοι Αποτελέσµατα Επίλογος Ορισµός του Προβλήµατος Ευθυγράµµιση : Εύρεση ενός γεωµετρικού µετασχηµατισµού που ϕέρνει κοντά δύο τρισδιάσ
 Εισαγωγή Αλγόριθµοι Αποτελέσµατα Επίλογος Αλγόριθµοι Ευθυγράµµισης Τρισδιάστατων Αντικειµένων Τµήµα Πληροφορικής και Τηλεπικοινωνιών Εθνικό & Καποδιστριακό Πανεπιστήµιο Αθηνών 20 Οκτωβρίου 2005 Εισαγωγή
Εισαγωγή Αλγόριθµοι Αποτελέσµατα Επίλογος Αλγόριθµοι Ευθυγράµµισης Τρισδιάστατων Αντικειµένων Τµήµα Πληροφορικής και Τηλεπικοινωνιών Εθνικό & Καποδιστριακό Πανεπιστήµιο Αθηνών 20 Οκτωβρίου 2005 Εισαγωγή
Πανεπιστήμιο Πειραιώς Σχολή Τεχνολογιών Πληροφορικής και Επικοινωνιών Τμήμα Ψηφιακών Συστημάτων ομές εδομένων
 Πανεπιστήμιο Πειραιώς Σχολή Τεχνολογιών Πληροφορικής και Επικοινωνιών Τμήμα Ψηφιακών Συστημάτων 6. Δυαδικά Δέντρα 2 ομές εδομένων 4 5 Χρήστος ουλκερίδης Τμήμα Ψηφιακών Συστημάτων 18/11/2016 Εισαγωγή Τα
Πανεπιστήμιο Πειραιώς Σχολή Τεχνολογιών Πληροφορικής και Επικοινωνιών Τμήμα Ψηφιακών Συστημάτων 6. Δυαδικά Δέντρα 2 ομές εδομένων 4 5 Χρήστος ουλκερίδης Τμήμα Ψηφιακών Συστημάτων 18/11/2016 Εισαγωγή Τα
Κεφάλαιο 8. Βασικές Αρχές Αναπαράστασης Γνώσης και Συλλογιστικής. Τεχνητή Νοηµοσύνη - Β' Έκδοση
 Κεφάλαιο 8 Βασικές Αρχές Αναπαράστασης Γνώσης και Συλλογιστικής Τεχνητή Νοηµοσύνη - Β' Έκδοση Ι. Βλαχάβας, Π. Κεφαλάς, Ν. Βασιλειάδης, Φ. Κόκκορας, Η. Σακελλαρίου Αναπαράσταση Γνώσης Σύνολο συντακτικών
Κεφάλαιο 8 Βασικές Αρχές Αναπαράστασης Γνώσης και Συλλογιστικής Τεχνητή Νοηµοσύνη - Β' Έκδοση Ι. Βλαχάβας, Π. Κεφαλάς, Ν. Βασιλειάδης, Φ. Κόκκορας, Η. Σακελλαρίου Αναπαράσταση Γνώσης Σύνολο συντακτικών
MBR Ελάχιστο Περιβάλλον Ορθογώνιο (Minimum Bounding Rectangle) Το µικρότερο ορθογώνιο που περιβάλλει πλήρως το αντικείµενο 7 Παραδείγµατα MBR 8 6.
 Πανεπιστήµιο Πειραιώς - Τµήµα Πληροφορικής Εξόρυξη Γνώσης από εδοµένα (Data Mining) Εξόρυξη Γνώσης από χωρικά δεδοµένα (κεφ. 8) Γιάννης Θεοδωρίδης Νίκος Πελέκης http://isl.cs.unipi.gr/db/courses/dwdm Περιεχόµενα
Πανεπιστήµιο Πειραιώς - Τµήµα Πληροφορικής Εξόρυξη Γνώσης από εδοµένα (Data Mining) Εξόρυξη Γνώσης από χωρικά δεδοµένα (κεφ. 8) Γιάννης Θεοδωρίδης Νίκος Πελέκης http://isl.cs.unipi.gr/db/courses/dwdm Περιεχόµενα
Εξόρυξη Γνώσης µε SQL Server 2005 Analysis Services
 Εξόρυξη Γνώσης µε SQL Server 2005 Analysis Services Γεράσιµος Μαρκέτος Οµάδα ιαχείρισης εδοµένων, Τµήµα Πληροφορικής, Πανεπιστήµιο Πειραιώς (http://isl.cs.unipi.gr/db) οµή παρουσίασης SQL Server 2005 Επιχειρηµατική
Εξόρυξη Γνώσης µε SQL Server 2005 Analysis Services Γεράσιµος Μαρκέτος Οµάδα ιαχείρισης εδοµένων, Τµήµα Πληροφορικής, Πανεπιστήµιο Πειραιώς (http://isl.cs.unipi.gr/db) οµή παρουσίασης SQL Server 2005 Επιχειρηµατική
inding B Binding -Library Cell
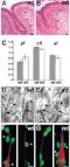 Cell-Library Binding Εισαγωγή Library Binding (technology mapping): η µετατροπή ενός λογικού δικτύου σε διασύνδεση στοιχείων µίας βιβλιοθήκης (τεχνολογίας). Παρέχει ολοκληρωµένη κατασκευαστική αναπαράσταση
Cell-Library Binding Εισαγωγή Library Binding (technology mapping): η µετατροπή ενός λογικού δικτύου σε διασύνδεση στοιχείων µίας βιβλιοθήκης (τεχνολογίας). Παρέχει ολοκληρωµένη κατασκευαστική αναπαράσταση
Δρ. Βασίλειος Γ. Καμπουρλάζος Δρ. Ανέστης Γ. Χατζημιχαηλίδης
 Μάθημα 7β Δρ. Βασίλειος Γ. Καμπουρλάζος Τμήμα Μηχανικών Πληροφορικής Τ.Ε. ΤΕΙ Ανατολικής Μακεδονίας και Θράκης 2017-2018 Μια Ενοποιητική Προσέγγιση στην ΥΝ Η Θεωρία Πλεγμάτων στην ΥΝ. Υπολογιστικές Μεθοδολογίες
Μάθημα 7β Δρ. Βασίλειος Γ. Καμπουρλάζος Τμήμα Μηχανικών Πληροφορικής Τ.Ε. ΤΕΙ Ανατολικής Μακεδονίας και Θράκης 2017-2018 Μια Ενοποιητική Προσέγγιση στην ΥΝ Η Θεωρία Πλεγμάτων στην ΥΝ. Υπολογιστικές Μεθοδολογίες
ΚΑΤΑΝΕΜΗΜΕΝΕΣ ΒΑΣΕΙΣ Ε ΟΜΕΝΩΝ
 ΚΑΤΑΝΕΜΗΜΕΝΕΣ ΒΑΣΕΙΣ Ε ΟΜΕΝΩΝ 1 ΓΕΝΙΚΑ Μια κατανεµηµένη βάση δεδοµένων (distributed database) µπορεί να οριστεί σαν µια οµάδα από λογικά συνδεόµενες βάσεις δεδοµένων που είναι διεσπαρµένες σε ένα δίκτυο
ΚΑΤΑΝΕΜΗΜΕΝΕΣ ΒΑΣΕΙΣ Ε ΟΜΕΝΩΝ 1 ΓΕΝΙΚΑ Μια κατανεµηµένη βάση δεδοµένων (distributed database) µπορεί να οριστεί σαν µια οµάδα από λογικά συνδεόµενες βάσεις δεδοµένων που είναι διεσπαρµένες σε ένα δίκτυο
Ουρά Προτεραιότητας: Heap
 Δομές Δεδομένων Ουρά Προτεραιότητας: Heap Διδάσκοντες: Σ. Ζάχος, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο (Αναπαράσταση,)
Δομές Δεδομένων Ουρά Προτεραιότητας: Heap Διδάσκοντες: Σ. Ζάχος, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο (Αναπαράσταση,)
Ημερίδα διάχυσης αποτελεσμάτων έργου Ιωάννινα, 14/10/2015
 MIS έργου:346983 Τίτλος Έργου: Epirus on Androids: Έμπιστη, με Διαφύλαξη της Ιδιωτικότητας και Αποδοτική Διάχυση Πληροφορίας σε Κοινωνικά Δίκτυα με Γεωγραφικές Εφαρμογές Έργο συγχρηματοδοτούμενο από την
MIS έργου:346983 Τίτλος Έργου: Epirus on Androids: Έμπιστη, με Διαφύλαξη της Ιδιωτικότητας και Αποδοτική Διάχυση Πληροφορίας σε Κοινωνικά Δίκτυα με Γεωγραφικές Εφαρμογές Έργο συγχρηματοδοτούμενο από την
Δομές δεδομένων και ψηφιακή αναπαράσταση χωρικών φαινομένων
 Ενότητα 4 η Δομές δεδομένων και ψηφιακή αναπαράσταση χωρικών φαινομένων Βύρωνας Νάκος Καθηγητής Ε.Μ.Π. - bnakos@central.ntua.gr Bασίλης Κρασανάκης Υποψήφιος διδάκτορας Ε.Μ.Π. - krasvas@mail.ntua.gr Β.
Ενότητα 4 η Δομές δεδομένων και ψηφιακή αναπαράσταση χωρικών φαινομένων Βύρωνας Νάκος Καθηγητής Ε.Μ.Π. - bnakos@central.ntua.gr Bασίλης Κρασανάκης Υποψήφιος διδάκτορας Ε.Μ.Π. - krasvas@mail.ntua.gr Β.
Ανάκτηση Πληροφορίας. Διδάσκων: Φοίβος Μυλωνάς. Διάλεξη #03
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Ανάκτηση Πληροφορίας Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #03 Βασικές έννοιες Ανάκτησης Πληροφορίας Δομή ενός συστήματος IR Αναζήτηση με keywords ευφυής
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Ανάκτηση Πληροφορίας Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #03 Βασικές έννοιες Ανάκτησης Πληροφορίας Δομή ενός συστήματος IR Αναζήτηση με keywords ευφυής
Επεξεργασία Ερωτήσεων
 Εισαγωγή στην Επεξεργασία Ερωτήσεων 1 Εισαγωγή ΣΔΒΔ Σύνολο από προγράµµατα για τη διαχείριση της ΒΔ Αρχεία ευρετηρίου Κατάλογος ΒΑΣΗ ΔΕΔΟΜΕΝΩΝ Αρχεία δεδοµένων συστήµατος Σύστηµα Βάσεων Δεδοµένων (ΣΒΔ)
Εισαγωγή στην Επεξεργασία Ερωτήσεων 1 Εισαγωγή ΣΔΒΔ Σύνολο από προγράµµατα για τη διαχείριση της ΒΔ Αρχεία ευρετηρίου Κατάλογος ΒΑΣΗ ΔΕΔΟΜΕΝΩΝ Αρχεία δεδοµένων συστήµατος Σύστηµα Βάσεων Δεδοµένων (ΣΒΔ)
Department of Computer Science University of Cyprus. EPL342 Databases. Lecture 8: RM II. Relational Model. (Chapter )
 Department of Computer Science University of Cyprus EPL342 Databases Lecture 8: RM II Relational Model (Chapter 5.2-5.3) ιδάσκων: Παναγιώτης Ανδρέου http://www.cs.ucy.ac.cy/courses/epl342 8-1 Περιεχόμενο
Department of Computer Science University of Cyprus EPL342 Databases Lecture 8: RM II Relational Model (Chapter 5.2-5.3) ιδάσκων: Παναγιώτης Ανδρέου http://www.cs.ucy.ac.cy/courses/epl342 8-1 Περιεχόμενο
Γλώσσες Σήµανσης (Markup Languages) Τεχνολογία ιαδικτύου και Ηλεκτρονικό Εµπόριο
 Γλώσσες Σήµανσης (Markup Languages) Τεχνολογία ιαδικτύου και Ηλεκτρονικό Εµπόριο 1 Γλώσσες Σήµανσης Γλώσσες σήµανσης: Αρχικά για τον καθορισµό εµφάνισης σελίδων, γραµµατοσειρών. Στη συνέχεια επεκτάθηκαν
Γλώσσες Σήµανσης (Markup Languages) Τεχνολογία ιαδικτύου και Ηλεκτρονικό Εµπόριο 1 Γλώσσες Σήµανσης Γλώσσες σήµανσης: Αρχικά για τον καθορισµό εµφάνισης σελίδων, γραµµατοσειρών. Στη συνέχεια επεκτάθηκαν
Πανεπιστήµιο Πειραιώς Τµήµα Πληροφορικής. Εξόρυξη Γνώσης από εδοµένα (Data Mining) Συσταδοποίηση. Γιάννης Θεοδωρίδης
 Πανεπιστήµιο Πειραιώς Τµήµα Πληροφορικής Εξόρυξη Γνώσης από εδοµένα (Data Mining) Συσταδοποίηση Γιάννης Θεοδωρίδης Οµάδα ιαχείρισης εδοµένων Εργαστήριο Πληροφοριακών Συστηµάτων http://isl.cs.unipi.gr/db
Πανεπιστήµιο Πειραιώς Τµήµα Πληροφορικής Εξόρυξη Γνώσης από εδοµένα (Data Mining) Συσταδοποίηση Γιάννης Θεοδωρίδης Οµάδα ιαχείρισης εδοµένων Εργαστήριο Πληροφοριακών Συστηµάτων http://isl.cs.unipi.gr/db
ΤΕΤΡΑ ΙΑ ΑΝΑΛΥΣΗΣ Ε ΟΜΕΝΩΝ, ΤΕΥΧΟΣ 15 (σσ ) DATA ANALYSIS BULLETIN, ISSUE 15 (pp ) Ιεραρχική Ανάλυση
 ΤΕΤΡΑ ΙΑ ΑΝΑΛΥΣΗΣ Ε ΟΜΕΝΩΝ, ΤΕΥΧΟΣ 15 (σσ. 81-89) DATA ANALYSIS BULLETIN, ISSUE 15 (pp. 81-89) Ιεραρχική Ανάλυση ηµήτριος Καραπιστόλης Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ίδρυµα Θεσσαλονίκης Περίληψη
ΤΕΤΡΑ ΙΑ ΑΝΑΛΥΣΗΣ Ε ΟΜΕΝΩΝ, ΤΕΥΧΟΣ 15 (σσ. 81-89) DATA ANALYSIS BULLETIN, ISSUE 15 (pp. 81-89) Ιεραρχική Ανάλυση ηµήτριος Καραπιστόλης Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ίδρυµα Θεσσαλονίκης Περίληψη
Δοµές Δεδοµένων. Αλγόριθµοι & Πολυπλοκότητα (Χειµώνας 2011) Ουρές Προτεραιότητας 2
 Δοµές Δεδοµένων Αλγόριθµοι & Πολυπλοκότητα (Χειµώνας 2011) Ουρές Προτεραιότητας 2 Δοµές Δεδοµένων (Αναπαράσταση,) οργάνωση και διαχείριση συνόλων αντικειµένων για αποδοτική ενηµέρωση και ανάκτηση πληροφορίας.
Δοµές Δεδοµένων Αλγόριθµοι & Πολυπλοκότητα (Χειµώνας 2011) Ουρές Προτεραιότητας 2 Δοµές Δεδοµένων (Αναπαράσταση,) οργάνωση και διαχείριση συνόλων αντικειµένων για αποδοτική ενηµέρωση και ανάκτηση πληροφορίας.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ. ΕΠΛ 035: οµές εδοµένων και Αλγόριθµοι για Ηλεκτρολόγους Μηχανικούς και Μηχανικούς Υπολογιστών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 035: οµές εδοµένων και Αλγόριθµοι για Ηλεκτρολόγους Μηχανικούς και Μηχανικούς Υπολογιστών Ακαδηµαϊκό έτος 2010 2011, Χειµερινό εξάµηνο Παρασκευή - 17/12/10 (08:30-11:30)
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 035: οµές εδοµένων και Αλγόριθµοι για Ηλεκτρολόγους Μηχανικούς και Μηχανικούς Υπολογιστών Ακαδηµαϊκό έτος 2010 2011, Χειµερινό εξάµηνο Παρασκευή - 17/12/10 (08:30-11:30)
Query-by-Example (QBE)
 Φροντιστήριο 8 o Χειµερινό Εξάµηνο 2009-10 Τµήµα Μηχανικών Η/Υ και Πληροφορικής Πολυτεχνική Σχολή, Πανεπιστήµιο Πατρών Πέµπτη, 3 εκεµβρίου 2009 Τι είναι η QBE; Γλώσσα επερωτήσεων σε σχεσιακές ϐάσεις δεδοµένων
Φροντιστήριο 8 o Χειµερινό Εξάµηνο 2009-10 Τµήµα Μηχανικών Η/Υ και Πληροφορικής Πολυτεχνική Σχολή, Πανεπιστήµιο Πατρών Πέµπτη, 3 εκεµβρίου 2009 Τι είναι η QBE; Γλώσσα επερωτήσεων σε σχεσιακές ϐάσεις δεδοµένων
Αποθήκες εδοµένων και Εξόρυξη Γνώσης (Data Warehousing & Data Mining)
 Πανεπιστήµιο Πειραιώς Τµήµα Πληροφορικής Αποθήκες εδοµένων και Εξόρυξη Γνώσης (Data Warehousing & Data Mining) Εξόρυξη Γνώσης από Χωρικά εδοµένα (spatial data mining) Γιάννης Θεοδωρίδης, Νίκος Πελέκης
Πανεπιστήµιο Πειραιώς Τµήµα Πληροφορικής Αποθήκες εδοµένων και Εξόρυξη Γνώσης (Data Warehousing & Data Mining) Εξόρυξη Γνώσης από Χωρικά εδοµένα (spatial data mining) Γιάννης Θεοδωρίδης, Νίκος Πελέκης
ΘΕΜΑΤΑ ΔΙΠΛΩΜΑΤΙΚΩΝ ΕΡΓΑΣΙΩΝ Εργ. Συστημάτων Βάσεων Γνώσεων & Δεδομένων CONTEXT AWARE ΣΥΣΤΗΜΑΤΑ ΔΙΑΧΕΙΡΙΣΗΣ ΒΑΣΕΩΝ ΔΕΔΟΜΕΝΩΝ ΕΙΣΑΓΩΓΙΚΟ ΣΗΜΕΙΩΜΑ
 CONTEXT AWARE ΣΥΣΤΗΜΑΤΑ ΔΙΑΧΕΙΡΙΣΗΣ ΒΑΣΕΩΝ ΔΕΔΟΜΕΝΩΝ ΕΙΣΑΓΩΓΙΚΟ ΣΗΜΕΙΩΜΑ Με τις συγκεκριμένες διπλωματικές εργασίες, ο στόχος μας είναι να κατασκευάσουμε το πρώτο ερευνητικό Σχεσιακό Σύστημα Διαχείρισης
CONTEXT AWARE ΣΥΣΤΗΜΑΤΑ ΔΙΑΧΕΙΡΙΣΗΣ ΒΑΣΕΩΝ ΔΕΔΟΜΕΝΩΝ ΕΙΣΑΓΩΓΙΚΟ ΣΗΜΕΙΩΜΑ Με τις συγκεκριμένες διπλωματικές εργασίες, ο στόχος μας είναι να κατασκευάσουμε το πρώτο ερευνητικό Σχεσιακό Σύστημα Διαχείρισης
Βάσεις εδοµένων. Βασίλειος Βεσκούκης, Εµµ. Στεφανάκης ΣΥΣΤΗΜΑΤΑ ΙΑΧΕΙΡΙΣΗΣ ΒΑΣΕΩΝ Ε ΟΜΕΝΩΝ
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Αγρονόµων Τοπογράφων Μηχανικών Βάσεις εδοµένων Βασίλειος Βεσκούκης, Εµµ. Στεφανάκης v.vescoukis@cs.ntua.gr ΣΥΣΤΗΜΑΤΑ ΙΑΧΕΙΡΙΣΗΣ ΒΑΣΕΩΝ Ε ΟΜΕΝΩΝ Συστήµατα ιαχείρισης Βάσεων
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Αγρονόµων Τοπογράφων Μηχανικών Βάσεις εδοµένων Βασίλειος Βεσκούκης, Εµµ. Στεφανάκης v.vescoukis@cs.ntua.gr ΣΥΣΤΗΜΑΤΑ ΙΑΧΕΙΡΙΣΗΣ ΒΑΣΕΩΝ Ε ΟΜΕΝΩΝ Συστήµατα ιαχείρισης Βάσεων
Σχεδιασµός Ανάπτυξη Οντολογίας
 Σχεδιασµός Ανάπτυξη Οντολογίας ΈλεναΜάντζαρη, Γλωσσολόγος, Ms.C. ΙΑΤΡΟΛΕΞΗ: Ανάπτυξη Υποδοµής Γλωσσικής Τεχνολογίας για το Βιοϊατρικό Τοµέα Τι είναι η οντολογία; Μιαοντολογίαείναιέναλεξικόόρωνπου διατυπώνονται
Σχεδιασµός Ανάπτυξη Οντολογίας ΈλεναΜάντζαρη, Γλωσσολόγος, Ms.C. ΙΑΤΡΟΛΕΞΗ: Ανάπτυξη Υποδοµής Γλωσσικής Τεχνολογίας για το Βιοϊατρικό Τοµέα Τι είναι η οντολογία; Μιαοντολογίαείναιέναλεξικόόρωνπου διατυπώνονται
Αναλυτικές λειτουργίες ΣΓΠ
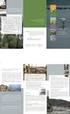 Αναλυτικές λειτουργίες ΣΓΠ Γενικά ερωτήµατα στα οποία απαντά ένα ΣΓΠ Εντοπισµού (locaton) Ιδιότητας (condton) Τάσεων (trend) ιαδροµών (routng) Μορφών ή προτύπων (pattern) Και µοντέλων (modellng) παραδείγµατα
Αναλυτικές λειτουργίες ΣΓΠ Γενικά ερωτήµατα στα οποία απαντά ένα ΣΓΠ Εντοπισµού (locaton) Ιδιότητας (condton) Τάσεων (trend) ιαδροµών (routng) Μορφών ή προτύπων (pattern) Και µοντέλων (modellng) παραδείγµατα
ΘΕΜΑ 1 Τεχνικές Εξαγωγής Συµφράσεων από εδοµένα Κειµένου και Πειραµατική Αξιολόγηση
 ΘΕΜΑ 1 Τεχνικές Εξαγωγής Συµφράσεων από εδοµένα Κειµένου και Πειραµατική Αξιολόγηση Οι συµφράσεις είναι ακολουθίες όρων οι οποίοι συνεµφανίζονται σε κείµενο µε µεγαλύτερη συχνότητα από εκείνη της εµφάνισης
ΘΕΜΑ 1 Τεχνικές Εξαγωγής Συµφράσεων από εδοµένα Κειµένου και Πειραµατική Αξιολόγηση Οι συµφράσεις είναι ακολουθίες όρων οι οποίοι συνεµφανίζονται σε κείµενο µε µεγαλύτερη συχνότητα από εκείνη της εµφάνισης
ΑΛΓΟΡΙΘΜΟΙ. Τι είναι αλγόριθμος
 ΑΛΓΟΡΙΘΜΟΙ Στο σηµείωµα αυτό αρχικά εξηγείται η έννοια αλγόριθµος και παραθέτονται τα σπουδαιότερα κριτήρια που πρέπει να πληρεί κάθε αλγόριθµος. Στη συνέχεια, η σπουδαιότητα των αλγορίθµων συνδυάζεται
ΑΛΓΟΡΙΘΜΟΙ Στο σηµείωµα αυτό αρχικά εξηγείται η έννοια αλγόριθµος και παραθέτονται τα σπουδαιότερα κριτήρια που πρέπει να πληρεί κάθε αλγόριθµος. Στη συνέχεια, η σπουδαιότητα των αλγορίθµων συνδυάζεται
Μεταγλωττιστές. Γιώργος Δημητρίου. Μάθημα 9 ο
 Γιώργος Δημητρίου Μάθημα 9 ο Ενδιάμεσος Κώδικας Απεικόνιση ανάμεσα στον αρχικό και στον τελικό κώδικα Γραμμικές αναπαραστάσεις: Ενδιάμεσος κώδικας πλησιέστερα στον τελικό ευκολότερη παραγωγή τελικού κώδικα
Γιώργος Δημητρίου Μάθημα 9 ο Ενδιάμεσος Κώδικας Απεικόνιση ανάμεσα στον αρχικό και στον τελικό κώδικα Γραμμικές αναπαραστάσεις: Ενδιάμεσος κώδικας πλησιέστερα στον τελικό ευκολότερη παραγωγή τελικού κώδικα
Εργαστήριο Σημασιολογικού Ιστού
 Εργαστήριο Σημασιολογικού Ιστού Ενότητα 1: Σημασιολογία και Μεταδεδομένα Μ.Στεφανιδάκης 10-2-2017 Η αρχή: Το όραμα του Σημασιολογικού Ιστού Tim Berners-Lee, James Hendler and Ora Lassila, The Semantic
Εργαστήριο Σημασιολογικού Ιστού Ενότητα 1: Σημασιολογία και Μεταδεδομένα Μ.Στεφανιδάκης 10-2-2017 Η αρχή: Το όραμα του Σημασιολογικού Ιστού Tim Berners-Lee, James Hendler and Ora Lassila, The Semantic
Μηχανική Μάθηση Μερωνυµιών για Αναγνώριση Γεγονότων
 Μηχανική Μάθηση Μερωνυµιών για Αναγνώριση Γεγονότων Αναστάσιος Σκαρλατίδης 1,2 anskarl@iit.demokritos.gr επιβλέπων: Καθ. Βούρος Γ. 1 1 Τµήµα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστηµάτων Πανεπιστήµιο
Μηχανική Μάθηση Μερωνυµιών για Αναγνώριση Γεγονότων Αναστάσιος Σκαρλατίδης 1,2 anskarl@iit.demokritos.gr επιβλέπων: Καθ. Βούρος Γ. 1 1 Τµήµα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστηµάτων Πανεπιστήµιο
Ανάλυση και Σχεδιασµός Πληροφοριακών Συστηµάτων
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 1/10 2/20 3/15 4/10 5/20 6/20 7/10 /105 Συνολο Ανάλυση και Σχεδιασµός Πληροφοριακών Συστηµάτων ΕΞΕΤΑΣΗ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 1/10 2/20 3/15 4/10 5/20 6/20 7/10 /105 Συνολο Ανάλυση και Σχεδιασµός Πληροφοριακών Συστηµάτων ΕΞΕΤΑΣΗ
Orchid: Integrating Schema Mapping and ETL ICDE 2008
 Orchid: Integrating Schema Mapping and ETL ICDE 2008 Δομουχτσίδης Παναγιώτης Γενικά Data warehouse (DW): Είναι μία αποθήκη πληροφοριών οργανωμένη από ένα ενοποιημένο μοντέλο. Τα δεδομένα συλλέγονται από
Orchid: Integrating Schema Mapping and ETL ICDE 2008 Δομουχτσίδης Παναγιώτης Γενικά Data warehouse (DW): Είναι μία αποθήκη πληροφοριών οργανωμένη από ένα ενοποιημένο μοντέλο. Τα δεδομένα συλλέγονται από
Χωρικές και Πολυμεσικές Βάσεις Δεδομένων (ΠΜΣ) Ενδεικτικές ερωτήσεις-θέματα για την εξέταση της θεωρίας
 Χωρικές και Πολυμεσικές Βάσεις Δεδομένων (ΠΜΣ) Ενδεικτικές ερωτήσεις-θέματα για την εξέταση της θεωρίας 1. Ποια είναι τα βασικά πλεονεκτήματα ενός παραδοσιακού σχεσιακού συστήματος βάσεων δεδομένων και
Χωρικές και Πολυμεσικές Βάσεις Δεδομένων (ΠΜΣ) Ενδεικτικές ερωτήσεις-θέματα για την εξέταση της θεωρίας 1. Ποια είναι τα βασικά πλεονεκτήματα ενός παραδοσιακού σχεσιακού συστήματος βάσεων δεδομένων και
ΕΙΣΑΓΩΓΗ ΣΤΙΣ Β ΣΕ Ε Σ Ι ΟΜΕΝ
 ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΒΑΣΕΙΣ Ε ΟΜΕΝΩΝ Βασικές Έννοιες - εδοµένα { Νίκος, Μιχάλης, Μαρία, Θάλασσα, Αυτοκίνητο }, αριθµοί, π.χ. {1, 2, 3, 5, 78}, συµβολοσειρές (strings) π.χ. { Κώστας, 5621, ΤΡ 882, 6&5 #1, +
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΒΑΣΕΙΣ Ε ΟΜΕΝΩΝ Βασικές Έννοιες - εδοµένα { Νίκος, Μιχάλης, Μαρία, Θάλασσα, Αυτοκίνητο }, αριθµοί, π.χ. {1, 2, 3, 5, 78}, συµβολοσειρές (strings) π.χ. { Κώστας, 5621, ΤΡ 882, 6&5 #1, +
Εισαγωγή. Γενική Εικόνα του Μαθήµατος. Το εσωτερικό ενός Σ Β. Εισαγωγή. Εισαγωγή Σ Β Σ Β. Αρχεία ευρετηρίου Κατάλογος συστήµατος Αρχεία δεδοµένων
 Βάσεις εδοµένων 2003-2004 Ευαγγελία Πιτουρά 1 ΜΕΡΟΣ 1 Γενική Εικόνα του Μαθήµατος Επεξεργασία Ερωτήσεων Μοντελοποίηση (Μοντέλο Ο/Σ, Σχεσιακό, Λογικός Σχεδιασµός) Προγραµµατισµός (Σχεσιακή Άλγεβρα, SQL)
Βάσεις εδοµένων 2003-2004 Ευαγγελία Πιτουρά 1 ΜΕΡΟΣ 1 Γενική Εικόνα του Μαθήµατος Επεξεργασία Ερωτήσεων Μοντελοποίηση (Μοντέλο Ο/Σ, Σχεσιακό, Λογικός Σχεδιασµός) Προγραµµατισµός (Σχεσιακή Άλγεβρα, SQL)
Μοντέλα και Τεχνικές Αξιολόγησης. Ενεργειακών και Περιβαλλοντικών Πολιτικών
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών Και Μηχανικών Υπολογιστών ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΩΝ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΑΤΑΞΕΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΑΠΟΦΑΣΕΩΝ Εργαστήριο Συστημάτων Αποφάσεων και Διοίκησης Μοντέλα
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών Και Μηχανικών Υπολογιστών ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΩΝ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΑΤΑΞΕΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΑΠΟΦΑΣΕΩΝ Εργαστήριο Συστημάτων Αποφάσεων και Διοίκησης Μοντέλα
Δηµοσθένης Σταµάτης Τµήµα Πληροφορικής ΑΤΕΙ ΘΕΣΣΑΛΟΝΙΚΗΣ ΔΕΝΤΡΑ (TREES) B C D E F G H I J K L M
 Δοµές Δεδοµένων & Ανάλυση Αλγορίθµων 3ο Εξάµηνο Δέντρα Δυαδικά Δέντρα Δυαδικά Δέντρα Αναζήτησης (inary Search Trees) http://aetos.it.teithe.gr/~demos/teaching_r.html Δηµοσθένης Σταµάτης Τµήµα Πληροφορικής
Δοµές Δεδοµένων & Ανάλυση Αλγορίθµων 3ο Εξάµηνο Δέντρα Δυαδικά Δέντρα Δυαδικά Δέντρα Αναζήτησης (inary Search Trees) http://aetos.it.teithe.gr/~demos/teaching_r.html Δηµοσθένης Σταµάτης Τµήµα Πληροφορικής
Σχεσιακή Άλγεβρα. Κεφάλαιο 4. Database Management Systems, R. Ramakrishnan and J. Gehrke
 Σχεσιακή Άλγεβρα Κεφάλαιο 4 Database Management Systems, R. Ramakrishnan and J. Gehrke 1 Γλώσσες Σχεσιακών Αιτηµάτων v Γλώσσες Αιτηµάτων: Ε ιτρέ ουν τη ιαχείριση και την Ανάκτηση εδοµένων α ό µια Β. v
Σχεσιακή Άλγεβρα Κεφάλαιο 4 Database Management Systems, R. Ramakrishnan and J. Gehrke 1 Γλώσσες Σχεσιακών Αιτηµάτων v Γλώσσες Αιτηµάτων: Ε ιτρέ ουν τη ιαχείριση και την Ανάκτηση εδοµένων α ό µια Β. v
Δέντρα Απόφασης (Decision(
 Δέντρα Απόφασης (Decision( Trees) Το μοντέλο που δημιουργείται είναι ένα δέντρο Χρήση της τεχνικής «διαίρει και βασίλευε» για διαίρεση του χώρου αναζήτησης σε υποσύνολα (ορθογώνιες περιοχές) Ένα παράδειγμα
Δέντρα Απόφασης (Decision( Trees) Το μοντέλο που δημιουργείται είναι ένα δέντρο Χρήση της τεχνικής «διαίρει και βασίλευε» για διαίρεση του χώρου αναζήτησης σε υποσύνολα (ορθογώνιες περιοχές) Ένα παράδειγμα
Συνόψεις για Δεδομένα XML με Ετερογενές Περιεχόμενο
 are needed to see this picture. Συνόψεις για Δεδομένα XML με Ετερογενές Περιεχόμενο Άλκης Πολυζώτης UC Santa Cruz Μίνως Γαροφαλάκης Intel Research, Berkeley Ανακεφαλαίωση QuickTime and a Ησυνόψιση είναι
are needed to see this picture. Συνόψεις για Δεδομένα XML με Ετερογενές Περιεχόμενο Άλκης Πολυζώτης UC Santa Cruz Μίνως Γαροφαλάκης Intel Research, Berkeley Ανακεφαλαίωση QuickTime and a Ησυνόψιση είναι
Εισαγωγή στο RDF. Το Resource Description Framework (RDF) Σταύρος Πολυβίου
 Εισαγωγή στο RDF Σταύρος Πολυβίου Το Resource Description Framework (RDF) RDF: µία γλώσσα περιγραφής πληροφοριών (metadata) που αφορούν πόρους (resources) στο world wide web. Παραδείγµατα: ο τίτλος, ο
Εισαγωγή στο RDF Σταύρος Πολυβίου Το Resource Description Framework (RDF) RDF: µία γλώσσα περιγραφής πληροφοριών (metadata) που αφορούν πόρους (resources) στο world wide web. Παραδείγµατα: ο τίτλος, ο
Ορισµοί Σχεσιακού Μοντέλου και Τροποποιήσεις Σχέσεων σε SQL
 Ορισµοί Σχεσιακού Μοντέλου και Τροποποιήσεις Σχέσεων σε SQL Βάσεις εδοµένων 2011-2012 Ευαγγελία Πιτουρά 1 Εισαγωγή Μοντελοποίηση Στα προηγούµενα µαθήµατα: Εννοιολογικός Σχεδιασµός Βάσεων Δεδοµένων (µε
Ορισµοί Σχεσιακού Μοντέλου και Τροποποιήσεις Σχέσεων σε SQL Βάσεις εδοµένων 2011-2012 Ευαγγελία Πιτουρά 1 Εισαγωγή Μοντελοποίηση Στα προηγούµενα µαθήµατα: Εννοιολογικός Σχεδιασµός Βάσεων Δεδοµένων (µε
ΠΡΟΧΩΡΗΜΕΝΑ ΘΕΜΑΤΑ ΒΑΣΕΩΝ Ε ΟΜΕΝΩΝ 6-2
 ΠΡΟΧΩΡΗΜΕΝΑ ΘΕΜΑΤΑ ΒΑΣΕΩΝ Ε ΟΜΕΝΩΝ ΚΕΦΑΛΑΙΟ 6 ΧΡΟΝΙΚΕΣ ΒΑΣΕΙΣ Ε ΟΜΕΝΩΝ 6-1 ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΟΜΙΛΙΑΣ Εισαγωγή Φύση του χρόνου TSQL-2 SQL/Temporal 6-2 ΕΙΣΑΓΩΓΗ Ποια η ανάγκη για χρονικές εφαρµογές; εξαγωγή
ΠΡΟΧΩΡΗΜΕΝΑ ΘΕΜΑΤΑ ΒΑΣΕΩΝ Ε ΟΜΕΝΩΝ ΚΕΦΑΛΑΙΟ 6 ΧΡΟΝΙΚΕΣ ΒΑΣΕΙΣ Ε ΟΜΕΝΩΝ 6-1 ΠΕΡΙΓΡΑΦΗ ΤΗΣ ΟΜΙΛΙΑΣ Εισαγωγή Φύση του χρόνου TSQL-2 SQL/Temporal 6-2 ΕΙΣΑΓΩΓΗ Ποια η ανάγκη για χρονικές εφαρµογές; εξαγωγή
Red-black δέντρα (Κεφ. 5)
 Red-black δέντρα (Κεφ. ) Δομές Δεδομένων Παπαγιαννόπουλος Δημήτριος 30 Μαρτίου 07 30 Μαρτίου 07 papagianno@ceid.upatras.gr . Εισαγωγή Περιεχόμενα. Ορισμός red-black δέντρων 3. Αναζήτηση σε red-black δέντρα
Red-black δέντρα (Κεφ. ) Δομές Δεδομένων Παπαγιαννόπουλος Δημήτριος 30 Μαρτίου 07 30 Μαρτίου 07 papagianno@ceid.upatras.gr . Εισαγωγή Περιεχόμενα. Ορισμός red-black δέντρων 3. Αναζήτηση σε red-black δέντρα
Βάσεις Δεδομένων (Databases)
 Βάσεις Δεδομένων (Databases) ΕΠΛ 342 Χειμερινό Εξάμηνο 2011 Διδάσκοντες Καθηγητές Γιώργος Σαμάρας (ΧΩΔ01 109) Περιεχόμενο Διάλεξης Κεφάλαιο 5: Το Σχεσιακό Μοντέλο Δεδομένων Περιορισμοί Σχεσιακού Μοντέλου
Βάσεις Δεδομένων (Databases) ΕΠΛ 342 Χειμερινό Εξάμηνο 2011 Διδάσκοντες Καθηγητές Γιώργος Σαμάρας (ΧΩΔ01 109) Περιεχόμενο Διάλεξης Κεφάλαιο 5: Το Σχεσιακό Μοντέλο Δεδομένων Περιορισμοί Σχεσιακού Μοντέλου
Βασικές δοµές δεδοµένων. Ορολογία λιστών. 8.1 Βασικές έννοιες δοµών δεδοµένων 8.2 Υλοποίηση δοµών δεδοµένων 8.3 Μια σύντοµη υπόθεση εργασίας
 ΚΕΦΑΛΑΙΟ 8: Αφηρηµένοι τύποι δεδοµένων 8.1 οµές δεδοµένων (data structures) 8.1 Βασικές έννοιες δοµών δεδοµένων 8.2 Υλοποίηση δοµών δεδοµένων 8.3 Μια σύντοµη υπόθεση εργασίας Αδόµητα δεδοµένα οδός Ζέας
ΚΕΦΑΛΑΙΟ 8: Αφηρηµένοι τύποι δεδοµένων 8.1 οµές δεδοµένων (data structures) 8.1 Βασικές έννοιες δοµών δεδοµένων 8.2 Υλοποίηση δοµών δεδοµένων 8.3 Μια σύντοµη υπόθεση εργασίας Αδόµητα δεδοµένα οδός Ζέας
Ενότητα 7 Ουρές Προτεραιότητας
 Ενότητα Ουρές Προτεραιότητας ΗΥ4 - Παναγιώτα Φατούρου Ουρές Προτεραιότητας Θεωρούµε ένα χώρο κλειδιών U και έστω ότι µε κάθε κλειδί Κ (τύπου Key) έχει συσχετισθεί κάποια πληροφορία Ι (τύπου Type). Έστω
Ενότητα Ουρές Προτεραιότητας ΗΥ4 - Παναγιώτα Φατούρου Ουρές Προτεραιότητας Θεωρούµε ένα χώρο κλειδιών U και έστω ότι µε κάθε κλειδί Κ (τύπου Key) έχει συσχετισθεί κάποια πληροφορία Ι (τύπου Type). Έστω
ιαµέριση - Partitioning
 ιαµέριση - Partitioning ιαµέριση ιαµέριση είναι η διαµοίραση αντικειµένων σε οµάδες µε στόχο την βελτιστοποίηση κάποιας συνάρτησης. Στην σύνθεση η διαµέριση χρησιµοποιείται ως εξής: Οµαδοποίηση µεταβλητών
ιαµέριση - Partitioning ιαµέριση ιαµέριση είναι η διαµοίραση αντικειµένων σε οµάδες µε στόχο την βελτιστοποίηση κάποιας συνάρτησης. Στην σύνθεση η διαµέριση χρησιµοποιείται ως εξής: Οµαδοποίηση µεταβλητών
Διάλεξη 17: O Αλγόριθμος Ταξινόμησης HeapSort
 Διάλεξη 17: O Αλγόριθμος Ταξινόμησης HeapSort Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Η διαδικασία PercolateDown, Δημιουργία Σωρού O Αλγόριθμος Ταξινόμησης HeapSort Υλοποίηση, Παραδείγματα
Διάλεξη 17: O Αλγόριθμος Ταξινόμησης HeapSort Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Η διαδικασία PercolateDown, Δημιουργία Σωρού O Αλγόριθμος Ταξινόμησης HeapSort Υλοποίηση, Παραδείγματα
Έλεγχος Ταυτοχρονισμού
 Έλεγχος Ταυτοχρονισμού Κεφάλαιο 17 Database Management Systems 3ed, R. Ramakrishnan and J. Gehrke Ελληνική Μετάφραση: Γεώργιος Ευαγγελίδης 1 Συγκρουσιακώς Σειριοποιήσιμα Χρονοπρογράμματα Δυο χρονοπρογράμματα
Έλεγχος Ταυτοχρονισμού Κεφάλαιο 17 Database Management Systems 3ed, R. Ramakrishnan and J. Gehrke Ελληνική Μετάφραση: Γεώργιος Ευαγγελίδης 1 Συγκρουσιακώς Σειριοποιήσιμα Χρονοπρογράμματα Δυο χρονοπρογράμματα
Εισαγωγή στην Επεξεργασία Ερωτήσεων. Βάσεις Δεδομένων Ευαγγελία Πιτουρά 1
 Εισαγωγή στην Επεξεργασία Ερωτήσεων Βάσεις Δεδομένων 2013-2014 Ευαγγελία Πιτουρά 1 Επεξεργασία Ερωτήσεων Θα δούμε την «πορεία» μιας SQL ερώτησης (πως εκτελείται) Ερώτηση SQL Ερώτηση ΣΒΔ Αποτέλεσμα Βάσεις
Εισαγωγή στην Επεξεργασία Ερωτήσεων Βάσεις Δεδομένων 2013-2014 Ευαγγελία Πιτουρά 1 Επεξεργασία Ερωτήσεων Θα δούμε την «πορεία» μιας SQL ερώτησης (πως εκτελείται) Ερώτηση SQL Ερώτηση ΣΒΔ Αποτέλεσμα Βάσεις
Δεδομένα και Πληροφορίες
 Εισαγωγή Δεδομένα και Πληροφορίες, Βάση Δεδομένων, Σύστημα Διαχείρισης Βάσεων Δεδομένων (Ορισμοί, Γλώσσες & Διεπαφές, Κατηγορίες), Σύστημα Βάσης Δεδομένων, Κατάλογος Δεδομένων Μεταδεδομένα, Λειτουργική
Εισαγωγή Δεδομένα και Πληροφορίες, Βάση Δεδομένων, Σύστημα Διαχείρισης Βάσεων Δεδομένων (Ορισμοί, Γλώσσες & Διεπαφές, Κατηγορίες), Σύστημα Βάσης Δεδομένων, Κατάλογος Δεδομένων Μεταδεδομένα, Λειτουργική
Ορισμοί Σχεσιακού Μοντέλου και Τροποποιήσεις Σχέσεων σε SQL
 Εισαγωγή Μοντελοποίηση Στα προηγούμενα μαθήματα: Ορισμοί Σχεσιακού Μοντέλου και Τροποποιήσεις Σχέσεων σε SQL Εννοιολογικός Σχεδιασμός Βάσεων εδομένων (με χρήση του Μοντέλου Οντοτήτων/Συσχετίσεων) Λογικός
Εισαγωγή Μοντελοποίηση Στα προηγούμενα μαθήματα: Ορισμοί Σχεσιακού Μοντέλου και Τροποποιήσεις Σχέσεων σε SQL Εννοιολογικός Σχεδιασμός Βάσεων εδομένων (με χρήση του Μοντέλου Οντοτήτων/Συσχετίσεων) Λογικός
Εισαγωγή στις Βάσεις Δεδομζνων II
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΣΙΑ ΠΑΝΕΠΙΣΗΜΙΟ ΚΡΗΣΗ Εισαγωγή στις Βάσεις Δεδομζνων II Ενότητα: Το Σχεσιακό Μοντζλο Διδάσκων: Πηγουνάκης Κωστής ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΣΧΟΛΗ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ Άδειες Χρήσης Το
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΣΙΑ ΠΑΝΕΠΙΣΗΜΙΟ ΚΡΗΣΗ Εισαγωγή στις Βάσεις Δεδομζνων II Ενότητα: Το Σχεσιακό Μοντζλο Διδάσκων: Πηγουνάκης Κωστής ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΣΧΟΛΗ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ Άδειες Χρήσης Το
Θεωρία Υπολογισμού και Πολυπλοκότητα Μαθηματικό Υπόβαθρο
 Θεωρία Υπολογισμού και Πολυπλοκότητα Μαθηματικό Υπόβαθρο Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Σύνολα Συναρτήσεις και Σχέσεις Γραφήματα Λέξεις και Γλώσσες Αποδείξεις ΕΠΛ 211 Θεωρία
Θεωρία Υπολογισμού και Πολυπλοκότητα Μαθηματικό Υπόβαθρο Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Σύνολα Συναρτήσεις και Σχέσεις Γραφήματα Λέξεις και Γλώσσες Αποδείξεις ΕΠΛ 211 Θεωρία
Εργαστήριο Σημασιολογικού Ιστού
 Εργαστήριο Σημασιολογικού Ιστού Ενότητα 1: Σημασιολογία και Μεταδεδομένα Μ.Στεφανιδάκης 5-2-2016. Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα.
Εργαστήριο Σημασιολογικού Ιστού Ενότητα 1: Σημασιολογία και Μεταδεδομένα Μ.Στεφανιδάκης 5-2-2016. Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα.
Θεωρία Υπολογισμού και Πολυπλοκότητα Ασυμφραστικές Γλώσσες (1)
 Θεωρία Υπολογισμού και Πολυπλοκότητα Ασυμφραστικές Γλώσσες (1) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Ασυμφραστικές Γραμματικές (2.1) Τυπικός Ορισμός Σχεδιασμός Ασυμφραστικών Γραμματικών
Θεωρία Υπολογισμού και Πολυπλοκότητα Ασυμφραστικές Γλώσσες (1) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Ασυμφραστικές Γραμματικές (2.1) Τυπικός Ορισμός Σχεδιασμός Ασυμφραστικών Γραμματικών
