ΠΕΡΙ ΟΙΚΩΝ. Τεταρτημόρια

Transcript

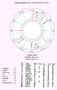
1 ΠΕΡΙ ΟΙΚΩΝ Οι οίκοι είναι ένα από τα κυριότερα ερμηνευτικά μέσα που χρησιμοποιεί η αστρολογία. Μαζί με τους πλανήτες, τα ζώδια και τις όψεις αποτελούν τις βασικές αρχές στις οποίες στηρίζεται η ερμηνεία ενός ωροσκοπίου. Κάθε ωροσκόπιο, αρχίζοντας από το ανατολικό σημείο, διαιρείται σε 12 οίκους, καθένας από τους οποίους πραγματεύεται διαφορετικούς τομείς της ζωής. καταλήγει στην ακμή του 7ου οίκου. Περιλαμβάνει τους 9ο, 8ο και 7ο οίκο. Ονομάζεται Μεσημβρινό, Θερινό, Θηλυκό, Χολερικό και είναι το τεταρτημόριο της νεανικής ηλικίας. Το γ τεταρτημόριο αρχίζει από την ακμή του 7ου και καταλήγει στην ακμή του 4ου. Περιλαμβάνει τους 6ο, 5ο και 4ο οίκο. Ονομάζεται Δυτικό, Τεταρτημόρια Ένας γνωστός τρόπος διαίρεσης του ωροσκοπίου είναι ο χωρισμός του σε τέσσερα τεταρτημόρια, τα οποία οροθετούνται από τις ακμές των τεσσάρων γωνιακών οίκων και καθένα απ αυτά περιλαμβάνει τρεις οίκους. Ένα από τα αρχαιότερα γραπτά που αναφέρονται στα τεταρτημόρια, είναι το ποίημα του Μανίλιου Astronomica, όπου περιγράφεται λεπτομερώς η φύση και οι ιδιότητές τους. Το α τεταρτημόριο αρχίζει από την Ανατολή και καταλήγει στο Μεσουράνημα. Περιλαμβάνει τους 12ο, 11ο και 10ο οίκο. Ονομάζεται Ανατολικό, Εαρινό, Αρσενικό, Αιματώδες και είναι το τεταρτημόριο της παιδικής ηλικίας. Το β τεταρτημόριο αρχίζει από το σημείο του Μεσουρανήματος και Φθινοπωρινό, Αρσενικό, Μελαγχολικό και είναι το τεταρτημόριο της ώριμης ηλικίας. Το δ τεταρτημόριο ξεκινά από την ακμή του 4ου και εκτείνεται έως την ακμή του 1ου. Περιλαμβάνει τους 3ο, 2ο και 1ο οίκο. Ονομάζεται Βόρειο, Θηλυκό, Χειμερινό, Φλεγματικό και είναι το τεταρτημόριο των γηρατειών. 83

2 Αξιολόγηση και δύναμη των οίκων Οι 1ος, 10ος, 7ος και 4ος, ονομάζονται γωνιακοί οίκοι ή γωνίες. Οι 2ος, 11ος, 8ος και 5ος ονομάζονται διάδοχοι οίκοι. Οι 3ος, 12ος, 9ος και 6ος ονομάζονται κατιόντες οίκοι. Οι γωνιακοί θεωρούνται περισσότερο σημαντικοί και ακολουθούν οι διάδοχοι και οι κατιόντες. Η σειρά ταξινόμησης των οίκων, ως προς τη δύναμη και τη σημασία τους, είναι η εξής: 1ος, 10ος, 7ος, 4ος, 11ος, 5ος, 9ος, 3ος, 2ος, 8ος, 6ος, 12ος. Η κατάταξη αυτή των οίκων στην πράξη εξηγείται και εφαρμόζεται με τον ακόλουθο τρόπο: Αν δύο πλανήτες είναι ισοδύναμοι σε θεμελιώδεις αρετές, αυτός που βρίσκεται στον 1ο οίκο έχει μεγαλύτερη δύναμη επιρροής μέσα στο χάρτη από αυτόν που βρίσκεται στο 10ο κ.ο.κ. Αν λάβουμε υπόψη ότι ο Ωροσκόπος αντιπροσωπεύει το φως, τη ζωή και τη ζωτικότητα, οι όψεις που σχηματίζει κάθε ακμή οίκου προς τον Ωροσκόπο επιδρούν καθοριστικά στη δύναμη και τη σημασία του οίκου αυτού. Συμπερασματικά, οι σχέσεις των υπόλοιπων οίκων με τον Ωροσκόπο είναι πολύ σημαντικές. Έτσι έχουμε: - Οι 4ος, 7ος, 10ος έχουν ιδιαίτερη σχέση με τον Ωροσκόπο, αφού σχηματίζουν τετράγωνο και αντίθεση προς αυτόν. - Ο 11ος και ο 5ος θεωρούνται ευνοϊκοί οίκοι, λόγω των ευεργετικών όψεων που σχηματίζουν με τον Ωροσκόπο, αλλά ως διάδοχοι, έχουν μέτρια δύναμη. - Ο 9ος, αν και κατιών, είναι ευμενής επειδή κάνει τρίγωνο με τον Ωροσκόπο, είναι ψηλά στον ορίζοντα και ο Ήλιος έχει χαρά εκεί. - Ο 3ος είναι ο λιγότερο τυχερός, επειδή είναι κατιών οίκος και βρίσκεται κάτω από τον ορίζοντα. - Οι 2ος, 8ος, 6ος, 12ος δεν κάνουν παραδοσιακές όψεις προς τον Ωροσκόπο και έτσι θεωρούνται άτυχοι και εξασθενημένοι. Ιδιαίτερα οι 6ος, 8ος και 12ος θεωρούνταν ανέκαθεν οι πλέον κακότυχοι οίκοι. 84

3 Κανόνας των 5 (Τετράβιβλος, βιβλίο 3ο, κεφ. 10, σελ ) Πριν αναφερθούμε αναλυτικά στην ερμηνεία των οίκων από την παραδοσιακή αστρολογία, πρέπει να λάβουμε υπόψη μας τον κανόνα του Πτολεμαίου, σύμφωνα με τον οποίο οι πλανήτες που πλησιάζουν την ακμή ενός οίκου θεωρούνται ένοικοι του οίκου αυτού, αν απέχουν 5 από την ακμή του. Έτσι, αν για παράδειγμα, η ακμή του 10ου οίκου βρεθεί στις Τοξότη, ο οίκος αυτός θα ξεκινά από τις Τοξότη ( ). Ο κανόνας αυτός του Πτολεμαίου, ο επονομαζόμενος και κανόνας των πέντε μοιρών, τηρείται πάντοτε από τους αστρολόγους οι οποίοι ασκούν την Ωριαία αστρολογία. Οι οίκοι στην παραδοσιακή αστρολογία Οι αρχαίες ελληνικές ονομασίες των 12 οίκων 1ος: Ανατολή ή Ωροσκόπος 2ος: Αναφορά 3ος: Θεά 4ος: Υπόγειον* 5ος: Καλή Τύχη 6ος: Κακή Τύχη 7ος: Δύσις 8ος: Επικαταφορά 9ος: Θεός 10ος: Μεσουράνημα 11ος: Αγαθός Δαίμων 12ος: Κακός Δαίμων * Μια άλλη ελληνική ονομασία για τον 4ο οίκο είναι Δαιμόνιον, η οποία συναντάται μόνο στον Μανίλιο. 85

4 Η ερμηνεία των οίκων στη σύγχρονη Ωριαία αστρολογία Το πιο σημαντικό βήμα στην Ωριαία αστρολογία είναι να βρεθεί ο σωστός οίκος που αφορά στην υπόθεση-ερώτηση. Απαιτείται πολύχρονη πείρα στην Ωριαία για να επιτευχθεί η σωστή επιλογή των οίκων, τόσο σύμφωνα με τον αρχικό χάρτη όσο και με τους παράγωγους οίκους. Στην Ωριαία Αστρολογία - Τα χαμένα κλειδιά (σελ. 97) διαβάζουμε: Ο αστρολόγος που δεν γνωρίζει πώς να επιλέξει τους κατάλληλους σύμφωνα με τη φύση της ερώτησης οίκους, μοιάζει με τον άφρονα άνθρωπο ο οποίος αγοράζει πολλά έπιπλα και δεν ξέρει πού να τα τοποθετήσει. Στο ίδιο βιβλίο (σελ ) οι ιδιότητες των οίκων συνοψίζονται ως εξής: 1ος (Ωροσκόπος): 2ος: 3ος: 4ος: 5ος: 6ος: 7ος: 8ος: 9ος: 10ος (Μεσουράνημα): 11ος: 12ος: Ο ερωτών Η περιουσία του, τα κινητά αγαθά του Τα αδέλφια του Ο πατέρας και τα ακίνητα αγαθά του ερωτώντος Τα παιδιά του Οι υπάλληλοι και η υγεία του Η σύζυγός του Ο τρόπος του θανάτου του Η θρησκεία και τα μακρινά ταξίδια Κοινωνική θέση και καταξίωση Οι φίλοι του ερωτώντος, οι στόχοι και οι επιθυμίες του Οι κρυφοί εχθροί του 90

5 Παράγωγοι οίκοι Πρόκειται για μια μέθοδο εκ νέου υπολογισμού των οίκων, η οποία μετατρέπει το χάρτη έτσι, ώστε ο οίκος που αντιπροσωπεύει το ζητούμενο, να μετατραπεί σε έναν καινούργιο 1ο οίκο και οι υπόλοιποι οίκοι να αριθμούνται με τη σειρά τους πάνω στο ζωδιακό κύκλο, ξεκινώντας από το νέο αυτό οίκο. Με τη μέθοδο αυτή, στην Ωριαία αστρολογία καθένας από τους δώδεκα οίκους του αρχικού χάρτη μπορεί να εκληφθεί ως 1ος παράγωγος οίκος. Για παράδειγμα, σε μια ερώτηση σχετική με κάποιο φίλο, ο 11ος οίκος του αρχικού χάρτη μετατρέπεται στον καινούργιο 1ο οίκο του φίλου. Τα κινητά αγαθά του φίλου θα σημειοδοτούνται από το 12o οίκο του αρχικού χάρτη, που είναι ο 2ος παράγωγος του 1ου. Ο αδελφός του φίλου θα αντιπροσωπεύεται από τον 1ο οίκο του αρχικού χάρτη, ο οποίος είναι ο παράγωγος 3ος του 11ου και ούτω καθ εξής. Συμπερασματικά, το σύστημα των παράγωγων οίκων είναι απλώς μια μέθοδος με την οποία ο αστρολόγος γυρίζει το χάρτη και χρησιμοποιεί * Όσον αφορά στο θρησκευτικό αίσθημα των κατοικούντων στα μοναστήρια, αυτό θα φανεί από τον 9ο και όχι από το 12ο οίκο. 97

6 κάποιον άλλο οίκο ως 1ο. Στις περιπτώσεις αυτές συνήθως κάποιος τρίτος άνθρωπος, εκτός από τον ερωτώντα, είναι αναμεμειγμένος στην υπόθεση την οποία αφορά ο χάρτης. Ο ερωτών όμως παραμένει πάντοτε στον αρχικό 1ο οίκο. Τα δύο παραδείγματα που ακολουθούν, θα βοηθήσουν στην καλύτερη κατανόηση της τεχνικής των παράγωγων οίκων: (α) Θα τα πάει καλά ο αδελφός μου με τον καινούργιο συνεταίρο του; Αρχικοί οίκοι 1ος οίκος: Εγώ, ο ερωτών Παράγωγοι οίκοι 1ος παράγωγος οίκος: Ο αρχικός 3ος οίκος μετατρέπεται σε 1ο οίκο του αδελφού. 3ος οίκος: Αδελφός 7ος παράγωγος οίκος: Ο αρχικός 9ος οίκος μετατρέπεται σε 7ο οίκο του αδελφού, αφού αντιπροσωπεύει τον συνεταίρό του. (β) Θα γυρίσει από το εξωτερικό το παιδί του συνεταίρου μου; Αρχικοί οίκοι 1ος οίκος: Εγώ, ο ερωτών 7ος οίκος: Συνεταίρος Παράγωγοι οίκοι 1ος παράγωγος οίκος: Ο αρχικός 7ος οίκος μετατρέπεται σε 1ο οίκο του συνεταίρου. 5ος παράγωγος οίκος: Ο αρχικός 11ος οίκος μετατρέπεται στον 5ο παράγωγο του συνεταίρου, που αντιπροσωπεύει τα παιδιά του. 98

7 Η χρήση των παράγωγων οίκων είναι απαραίτητη στις περιπτώσεις κατά τις οποίες ο ερωτών υποβάλλει μια ερώτηση που αφορά σε άλλο πρόσωπο και όχι τον ίδιο. Με άλλα λόγια, αν κάποιος κάνει μια ερώτηση για κάποιον άλλο, γνωστό του (βλ. χάρτη σελ. 342), αυτός ο άλλος δεν εκπροσωπείται από τον πρώτο οίκο του αρχικού χάρτη. 99