Ένατο µέρος. ... Συνέχεια από το προηγούµενο
|
|
|
- Αντιγόνη Γερμανός
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Ένατο µέρος... Συνέχεια από το προηγούµενο Στη συνέχεια θα ήθελα να αναλύσω ορισµένες ενδιαφέρουσες ελληνιστικές τεχνικές που είναι γενικής σηµασίας, µε την έννοια που περιέγραψα προηγουµένως, δηλαδή τεχνικές που έχουν βαρύτητα στη ζωή ως σύνολο. Με τη µελέτη των τεχνικών αυτών µπορείτε να αποκτήσετε ένα είδος "προφίλ" για το σύνολο της ζωής. Όλες οι ελληνιστικές αναλύσεις, οι οποίες έπονται και αφορούν σε µεµονωµένα θέµατα ή µεµονωµένα χρονικά διαστήµατα, υπόκεινται αυτοµάτως σε αυτές τις τεχνικές και θα πρέπει να συµµορφώνονται µαζί τους. Πριν προχωρήσω πρέπει να αναφερθώ και στο θέµα του τροπικού και αστρικού ζωδιακού στην ελληνιστική αστρολογία. Είναι εξαιρετικά δύσκολο να τεκµηριωθεί ποιες ήταν στην πραγµατικότητα οι προθέσεις των ιδρυτών της ελληνιστικής αστρολογίας, µε βάση τις οποιεσδήποτε ενδείξεις µέσα από κείµενα. Είναι επίσης σχεδόν αδύνατο να πούµε ότι οι ελληνιστικοί αστρολόγοι, πρακτικά, προτιµούσαν ένα ζωδιακό κύκλο έναντι ενός άλλου, για τον απλό λόγο ότι οι ζωδιακοί κύκλοι σχεδόν ταυτίζονταν κατά τη διάρκεια της ελληνιστικής περιόδου, οπότε δεν θα µπορούσαν να τους έχουν "δοκιµάσει", ας πούµε, εµπειρικά. Επιπλέον, δεν είναι καν σαφές ότι το πρόβληµα του τροπικού έναντι του αστρικού ζωδιακού κύκλου περνούσε έστω από το νου των ελληνιστικών αστρολόγων, µε οποιονδήποτε θεµατικό ή γνωστικό τρόπο. Αυτό που θα πω είναι ότι στους πειραµατισµούς και τις δοκιµές µας µε τις ελληνιστικές τεχνικές, βρήκαµε ότι ο τροπικός ζωδιακός κύκλος λειτουργεί πολύ καλύτερα από τον αστρικό ζωδιακό κύκλο, ιδιαίτερα στην περίπτωση της εφαρµογής των Χρονοκρατόρων. Εξακολουθεί να απαιτείται πολλή µελέτη ακόµα σ αυτόν τον τοµέα. Για παράδειγµα, ενδέχεται να υπάρχουν ορισµένα χαρακτηριστικά των ζωδίων, ορισµένα πολύ παράξενα χαρακτηριστικά, που δεν αποτελούν πια µέρος της σύγχρονης αστρολογίας, όπως είναι τα ανθρώπινα ζώδια έναντι των ζωωδών, τα υδάτινα έναντι των γήινων, τα στείρα έναντι των γόνιµων κ.ο.κ. Μερικά από τα χαρακτηριστικά αυτά µπορεί, στην πραγµατικότητα, να είναι βασισµένα στον αστρικό ζωδιακό κύκλο. Όπως είπα, όµως, αυτό είναι ένα θέµα που απαιτεί σηµαντική έρευνα. Η έµφαση στον τροπικό ζωδιακό κύκλο παγιώθηκε 1
2 βέβαια και, κατά κάποιον τρόπο, επιβεβαιώθηκε από τις ιδέες του Πτολεµαίου, ο οποίος προσυπογράφει κατηγορηµατικά έναν τροπικό ζωδιακό κύκλο. Κάνει όµως την ενδιαφέρουσα δήλωση κατά την επιχειρηµατολογία του για τον τροπικό ζωδιακό ότι αυτή µοιάζει να ήταν η πρόθεση των προγενέστερων αστρολόγων ή, τουλάχιστον, ότι ο τροπικός ζωδιακός κύκλος φαίνεται να υποδηλώνεται σε ορισµένες ελληνιστικές ιδέες. εν θα προχωρήσω περισσότερο σ αυτό, αλλά έχετε απλώς υπόψη ότι εξακολουθεί να αποτελεί ένα αναπάντητο ερώτηµα. Για να αρχίσω τώρα να µιλάω για τις γενικές τεχνικές που αφορούν στο σύνολο ενός ωροσκοπίου, πρέπει πρώτα να προσδιορίσω τους πλανήτες "δείκτες" που είναι πρωταρχικής σηµασίας καθώς και τις σηµαντικότερες θέσεις στο χάρτη, γιατί στο µεγαλύτερο µέρος τους όλες οι γενικές τεχνικές βασίζονται σ αυτές τις κύριες θέσεις. Οι θέσεις αυτές είναι: - Ο Ωροσκόπος - Σε σηµαντικά µικρότερο βαθµό το Μεσουράνηµα, µε το οποίο θυµηθείτε ότι εννοώ το δέκατο ζώδιο από το ζώδιο του Ωροσκόπου. - Ο Κλήρος της Τύχης, οποίος ήταν µία απίστευτα σηµαντική θέση στην ελληνιστική αστρολογία και θεωρείται πως είναι, στην ιεραρχία, σχεδόν ισοδύναµος µε τον Ωροσκόπο. - Τα δύο φώτα, δηλαδή ο Ήλιος και η Σελήνη, που έχουν κεντρική σηµασία σε όλες σχεδόν αυτές τις τεχνικές. - Μετά ακολουθεί µία θέση η οποία µπορεί να µην είναι πολύ οικεία στους σύγχρονους αστρολόγους και είναι αυτή που αποκαλούµε Προγενέθλια Συζυγία. Πρόκειται για την κοντινότερη σύνοδο (Νέα Σελήνη) ή αντίθεση (Πανσέληνο) του Ήλιου και της Σελήνης πριν από τη γέννηση κάποιου. Αν είχατε, λοιπόν, Πανσέληνο λίγο πριν τη γέννησή σας, τότε ως σηµείο της Προγενέθλιας Συζυγίας σας ορίζεται η µοίρα ( ) που βρισκόταν η Σελήνη σε αυτήν την αντίθεση Ήλιου-Σελήνης. Η µοίρα ( ) αυτή σηµειώνεται στο χάρτη γέννησης, θα µπορούσατε να πείτε, ως ένα ευαίσθητο σηµείο ή ένα πολύ σηµαντικό σηµείο. Αρκετές τεχνικές είναι λοιπόν δοµηµένες γύρω από την Προγενέθλια Συζυγία και, για το λόγο 2
3 αυτό, η σηµασία της δεν µπορεί να είχε υπερεκτιµηθεί στην πρακτική της ελληνιστικής αστρολογίας. Η πρώτη τεχνική ή µάλλον, µερικές τεχνικές, που πρέπει κατά κάποιον τρόπο να µελετηθούν µαζί, σχετίζονται µε τους πρωτεύοντες κυβερνήτες του ωροσκοπίου. Μερικοί από σας, ως σύγχρονοι αστρολόγοι, µπορεί από συνήθεια να εκλαµβάνετε τον κυβερνήτη του Ωροσκόπου ως κυβερνήτη του ωροσκοπίου. Μερικοί από σας, µέσα από τη µελέτη της παραδοσιακής αστρολογίας, µπορεί να έχετε µάθει να παίρνετε τον επικυρίαρχο του ωροσκοπίου, χρησιµοποιώντας κάποια περίπλοκη µέθοδο «ζυγίσµατος». Το ελληνιστικό αντίστοιχο του κυβερνήτη του ωροσκοπίου προσδιορίζεται ουσιαστικά µε πολύ διαφορετικούς τρόπους. Ο κυβερνήτης του Ωροσκόπου µόνο συµπτωµατικά θα µπορούσε να είναι και κυβερνήτης του ωροσκοπίου. Στην πραγµατικότητα, οι ελληνιστικοί αστρολόγοι δεν έχουν µόνο έναν κυβερνήτη του ωροσκοπίου. Έχουν ουσιαστικά δύο πλανήτες που εξυπηρετούν µία λειτουργία µαζί: ένας πλανήτης που κυβερνά το ωροσκόπιο ως σύνολο και ένας άλλος που έχει διαφορετική λειτουργία. Επιτρέψτε µου λοιπόν να αρχίσω µε τον ορισµό του "κυρίου της κατοικίας" του ωροσκοπίου (domicile master of the nativity). Αυτή είναι µια κατά γράµµα µετάφραση της ελληνικής λέξης "οικοδεσπότης", την οποία θα σας µεταφέρω στα αγγλικά: "oikodespotes". Ο κυβερνήτης ενός µεµονωµένου ζωδίου στην ελληνιστική αστρολογία ονοµάζεται οικοδεσπότης αυτού του ζωδίου. Έτσι, για παράδειγµα, ο οικοδεσπότης του Κριού είναι ο Άρης και ο οικοδεσπότης του Ταύρου είναι η Αφροδίτη κ.ο.κ. Ο Οικοδεσπότης του ωροσκοπίου είναι ένα είδος γενίκευσης αυτής της έννοιας, όπου βρίσκουµε έναν πλανήτη που, ας πούµε, αξιώνει το σύνολο του ωροσκοπίου ως οικητήριόν του και συνεπώς κατέχει κύριο ρόλο στο χάρτη. Ο προσδιορισµός τώρα αυτού του Οικοδεσπότη του ωροσκοπίου γίνεται µε τρόπο σχετικά µηχανικό, αν και υπάρχουν ορισµένες περιπτώσεις και ορισµένοι χάρτες, όπου µπορεί να είναι λίγο "επικίνδυνο" να προβεί κανείς σ αυτόν τον προσδιορισµό. Γενικά µιλώντας όµως, αυτό το οποίο αναζητά κανείς στον προσδιορισµό του συγκεκριµένου 3
4 πλανήτη είναι πρώτα απ όλα το φως που κυριαρχεί. Με την απλούστερη έννοια, αυτό σηµαίνει ότι αναζητούµε: - τον Ήλιο σε ένα ωροσκόπιο µέρας και - τη Σελήνη σε ένα ωροσκόπιο νύχτας. Αν όµως ο Ήλιος, για παράδειγµα σε ένα ωροσκόπιο µέρας, βρίσκεται σε κατιόν ζώδιο, ενώ η Σελήνη είναι, ας πούµε σε γωνιακό ζώδιο, η Σελήνη είναι αυτή που θα επικρατεί έναντι του Ήλιου για τον προσδιορισµό του Οικοδεσπότη του ωροσκοπίου. Και παρόµοια, αν σε ένα ωροσκόπιο νύχτας η Σελήνη δεν βρίσκεται σε καλή θέση, και αυτό ισχύει όταν η Σελήνη βρίσκεται σε κατιόν ζώδιο (απόκλιµα), ενώ ο Ήλιος βρίσκεται σε γωνιακό ή ακόµα και σε διάδοχο ζώδιο (επαναφορά), τότε θα επικρατεί κανονικά ο Ήλιος. Μ άλλα λόγια αυτό που γίνεται είναι ότι έχουµε ένα είδος συναγωνισµού µεταξύ των δύο σηµειοδοτών, του Ήλιου και της Σελήνης, και πρέπει να προσδιορίσουµε ποιος από τους δύο είναι καταλληλότερος για να αναθέτει ή να µεταβιβάζει ευθύνες σε έναν συγκεκριµένο πλανήτη στο χάρτη, ο οποίος θα ονοµάζεται Οικοδεσπότης του ωροσκοπίου. Αν τύχει να είναι και οι δύο πλανήτες, και ο Ήλιος και η Σελήνη, σε κατιόντα ζώδια στο χάρτη, τότε αυτό που πρέπει κανονικά να κάνετε είναι να περάσετε εξ ορισµού στον Ωροσκόπο. Έτσι λοιπόν: -Αν δεν υπάρχει σαφής επικράτηση ανάµεσα στον Ήλιο και τη Σελήνη, τότε πρέπει να περνάει κανείς στον Ωροσκόπο ή -αν και τα δύο φώτα βρίσκονται σε κατιόντα ζώδια, τότε πρέπει κανείς να περνάει στον Ωροσκόπο. Αφού θα έχετε προσδιορίσει τον Επικρατέστερο, στην ιδανική περίπτωση τον Ήλιο σε έναν ηµερήσιο χάρτη και τη Σελήνη σε ένα νυχτερινό χάρτη, κοιτάζετε τους δύο κυβερνήτες: του ζωδίου και της θέσης στην οποία βρίσκεται αυτός ο Επικρατέστερος στο χάρτη. Πιο συγκεκριµένα: - κοιτάζετε πρώτα για τον κυβερνήτη του ζωδίου του Επικρατέστερου, ας πούµε του Ήλιου σε έναν ηµερήσιο χάρτη, και µετά 4
5 - κοιτάζετε τον κυβερνήτη του ορίου του Ήλιου. Οι δύο αυτοί πλανήτες µαζί έχουν την ευθύνη να συνεργάζονται, έχουν αυτόν τον πολύ ειδικό ρόλο, τον οποίο θα ορίσω σε λίγο. Ας ρίξουµε µια µατιά στο χάρτη του Αϊνστάιν, έτσι ώστε να δούµε απλώς ένα παράδειγµα για το πώς θα προσδιορίζουµε αυτόν το συγκεκριµένο σηµαντικό πλανήτη ή, µάλλον, το ζεύγος πλανητών. Ο Αϊνστάιν έχει τον Ήλιο του στον ένατο οίκο ολόκληρου ζωδίου, είναι δηλαδή σε κατιόντα οίκο. Και έχει τη Σελήνη του στον έκτο οίκο ολόκληρου ζωδίου, που επίσης είναι κατιών οίκος. Σύµφωνα µε τον αλγόριθµο για τον προσδιορισµό του Οικοδεσπότη του ωροσκοπίου, πρέπει να περάσουµε στον Ωροσκόπο. Ο κυβερνήτης του Ωροσκόπου στο χάρτη του Αϊνστάιν είναι η Σελήνη και ο κυβερνήτης του ορίου της ανατέλλουσας µοίρας είναι η Αφροδίτη. Αυτό σηµαίνει ότι το συγκεκριµένο ζεύγος πλανητών θα παίζει το ρόλο που ανέφερα προηγουµένως. Θα µπορούσατε να κατανοήσετε τον Οικοδεσπότη του ωροσκοπίου (τον πλανήτη που κυβερνά το ζώδιο του Ήλιου ή της Σελήνης ή του Ωροσκόπου), θα µπορούσατε να κατανοήσετε τον πλανήτη αυτόν ως τον πλανήτη που ορίζει την πολιτική στο χάρτη ορίζει επίσης την ηµερήσια διάταξη για τη ζωή του ατόµου ανάλογα µε τη φύση του, ως πλανήτης. Κυβερνήτης του ορίου είναι ο πλανήτης που έχει αυτό που θα µπορούσατε να θεωρήσετε ένα είδος περιοριστικού ρόλου ή ένας είδος εποπτείας πάνω στον πλανήτη που ορίζει την πολιτική ή ορίζει την ηµερήσια διάταξη για τη ζωή κάποιου. Έτσι, ο Οικοδεσπότης του ωροσκοπίου που είναι ο κυβερνήτης του Επικρατέστερου (Ήλιος, Σελήνη, Ωροσκόπος) δεν είναι τελείως ελεύθερος να κάνει αυτό ακριβώς που θέλει, αλλά το κάνει υποκείµενος στους περιορισµούς του κυβερνήτη του ορίου. Έτσι, στην περίπτωση του Αϊνστάιν, έχουµε: - τη Σελήνη ως πλανήτη που θέτει την ηµερήσια διάταξη για τη ζωή του και - την Αφροδίτη ως πλανήτη που παρέχει εποπτεία. Το κείµενό µας, τώρα, µας λέει ότι είναι σηµαντικό να προσδιορίσουµε σε τι σχηµατισµό βρίσκονται στην πραγµατικότητα αυτοί οι δύο πλανήτες στο χάρτη αν δηλαδή σχετίζονται µεταξύ τους µε όψη, ευρισκόµενοι σε ζώδια που έχουν κάποια σχέση µεταξύ τους. Ο 5
6 λόγος γι αυτό είναι ότι θέλετε τον πλανήτη που εποπτεύει (τον κυβερνήτη του ορίου του Επικρατέστερου) να είναι σε θέση να παρέχει αυτήν την εποπτεία στον Οικοδεσπότη του ωροσκοπίου. Στην περίπτωση του Αϊνστάιν, έχουµε τη Σελήνη και την Αφροδίτη ουσιαστικά σε ένα πολύ κλειστό τρίγωνο, µε διαφορά τριών µοιρών, το οποίο αποτελεί ουσιαστικά την ανοχή που θα όριζαν οι ελληνιστικοί αστρολόγοι στην επεξεργασία τους για τις όψεις. Αν όµως οι δύο αυτοί πλανήτες δεν βρίσκονταν σε απευθείας όψη, αλλά βρίσκονταν στα ίδια ζώδια, θα µπορούσαν και πάλι να βρίσκονται σε σχηµατισµό τέτοιο, ώστε ο πλανήτης της εποπτείας να µπορεί να επιτελέσει το ρόλο του σε σχέση µε τον Οικοδεσπότη του ωροσκοπίου. Όπως είπα, λοιπόν, στην περίπτωση του Αϊνστάιν, έχουµε τη Σελήνη και την Αφροδίτη να επιτελούν αυτήν τη διπλή λειτουργία. Σε ό,τι αφορά στην εκτίµηση της κατάστασης των δύο αυτών πλανητών, αυτό που µας ενδιαφέρει κυρίως είναι κατά πόσον είναι αγαθοποιοί ή κακοποιοί στο ωροσκόπιο. Επανέρχοµαι λοιπόν στο σχήµα που περιέγραψα προηγουµένως στην οµιλία µου, για τις τρεις κύριες συνθήκες που προσδιορίζουν το βαθµό στον οποίο οι πλανήτες είναι αγαθοποιοί ή κακοποιοί σε ένα δεδοµένο χάρτη. Έτσι, στο χάρτη του Αϊνστάιν: - τόσο η Σελήνη όσο και η Αφροδίτη είναι εκτός οµάδας, πράγµα που τις καθιστά κάπως λιγότερο σε θέση να επιτελέσουν τις δικές τους αντίστοιχες αγαθοποιούς "ηµερήσιες διατάξεις" σ αυτό το συγκεκριµένο χάρτη. - Η Αφροδίτη βρίσκεται σε γωνιακό ζώδιο και σε καλή θέση. Είναι σε θέση σχηµατισµού µε το ανατέλλον ζώδιο, µε αποτέλεσµα να καθίσταται πιο αγαθοποιός µε αυτήν την σχέση. - Η Σελήνη, όµως, βρίσκεται σε κατιόν ζώδιο και δεν συνδέεται µε το ανατέλλον ζώδιο. - Κανένας από τους δύο αυτούς πλανήτες δεν είναι στις δικές του θέσεις. Η Αφροδίτη δεν έχει θεµελιώδη δύναµη στη θέση στην οποία βρίσκεται στον Κριό, όπως δεν έχει θεµελιώδη δύναµη ούτε η Σελήνη στον Τοξότη. - Ουσιαστικά, η Αφροδίτη βρίσκεται σε αντίθεση µε την ίδια της την κατοικία. Και ένας πλανήτης σε αντίθεση µε την ίδια του την κατοικία, δηλαδή αυτό που θα αποκαλούσαµε έναν πλανήτη σε αδυναµία (εναντίωµα) στην παραδοσιακή αστρολογία ή, σε κάποιο βαθµό, και στη σύγχρονη. εν καθίσταται ασθενέστερος από αυτήν τη θέση, αλλά τα κείµενα µάς λένε ότι µετατρέπεται κάπως σε κακό δεν µπορώ να βρω καλύτερη λέξη 6
7 είναι κάπως στην άγρια πλευρά και τείνει να γίνεται υπεραντιδραστικός σε ό,τι αφορά σε αυτόν τον συγκεκριµένο χάρτη, είναι στην αντι-κατοικία του, όσο πιο µακριά από το σπίτι του µπορεί να βρίσκεται. εν είναι πολύ καλά σ αυτήν τη θέση, αλλά του δίνει παράλληλα ελευθερία να δρα µε κάποια υπερβολή. εν πρόκειται να το περιγράψω αυτό πλήρως στη ζωή του Αϊνστάιν. Αυτό που θα πω είναι ότι µερικοί µπορεί να το βρουν κάπως περίεργο για τους συγκεκριµένους πλανήτες (Σελήνη, Αφροδίτη), το να είναι αυτοί οι δύο οι πλανήτες που ορίζουν την "ηµερήσια διάταξη" και παρέχουν την εποπτεία στη ζωή του Αϊνστάιν ως σύνολο. Αλλά αυτό που θα πρέπει να έχετε στο νου σας είναι πως όταν µελετάµε τη ζωή του Αϊνστάιν κάτω από το ελληνιστικό πρίσµα, δεν κοιτάζουµε απλώς την επιστηµονική του σταδιοδροµία, η οποία όπως όλοι γνωρίζουµε ήταν εξαιρετικά επιτυχηµένη, ούτε µελετάµε την ψυχολογία του. Ουσιαστικά, µελετάµε τη ζωή του στο σύνολό της, η οποία περιλαµβάνει θέµατα, ξέρετε, όπως ο γάµος και τα παιδιά και όλα αυτά τα µάλλον ταπεινά θέµατα που απαντώνται στη ζωή του καθενός. Και η ερµηνεία αυτών των θεµάτων, λίγο έως πολύ, συµβαδίζει µε το γεγονός ότι έχει ως πλανήτη που ορίζει την «ηµερήσια διάταξη» τη Σελήνη, η οποία είναι εκτός οµάδας και όχι τόσο καλά τοποθετηµένη στο χάρτη και έναν πλανήτη εποπτείας που είναι κάπως άγριος. Πρέπει να επαναλάβω και πάλι ότι δεν είναι σκοπός µου στην οµιλία αυτή να προβώ σε λεπτοµερείς περιγραφές και να τις συσχετίσω µε τη ζωή του Αϊνστάιν, αλλά αυτό που προσπαθώ στην πραγµατικότητα κυρίως να κάνω είναι να περιγράψω αυτήν την τεχνική. Υπάρχει τώρα ένας δεύτερος πλανήτης, ο οποίος είναι εξίσου σηµαντικός στη γενική διακυβέρνηση του ωροσκοπίου και αυτός ονοµάζεται Κύριος του ωροσκοπίου. Παρεµπιπτόντως, θα έπρεπε να έχω ήδη πει ότι και οι δύο αυτοί ορισµοί για τον Οικοδεσπότη και τον Κύριο του ωροσκοπίου αποδίδονται στον Νετσέψω και τον Πετοσίρη, δύο από τους ιδρυτές της ελληνιστικής αστρολογίας. Άρα, οι διακρίσεις αυτές και οι αλγόριθµοι που σας παρουσιάζω φτάνουν πίσω στα πρώτα επίπεδα της ελληνιστικής παράδοσης και, συνεπώς, πρέπει να λαµβάνονται αρκετά σοβαρά υπόψη. Συνεχίζεται... 7
έκατο µέρος Συνέχεια από το προηγούµενο Τρόπος εύρεσης του Κυρίου του ωροσκοπίου
 έκατο µέρος Συνέχεια από το προηγούµενο Ο προσδιορισµός τώρα του Κυρίου του ωροσκοπίου είναι πολύ περίπλοκος. Στην πραγµατικότητα, είναι πολύ πιο δύσκολος από τον προσδιορισµό του Οικοδεσπότη του ωροσκοπίου,
έκατο µέρος Συνέχεια από το προηγούµενο Ο προσδιορισµός τώρα του Κυρίου του ωροσκοπίου είναι πολύ περίπλοκος. Στην πραγµατικότητα, είναι πολύ πιο δύσκολος από τον προσδιορισµό του Οικοδεσπότη του ωροσκοπίου,
Έκτο µέρος. ... Συνέχεια από το προηγούµενο
 Έκτο µέρος 1... Συνέχεια από το προηγούµενο Προηγουµένως µίλησα για τις πολλαπλές απτές σηµασίες των ελληνιστικών πλανητών µε τις οποίες θα πρέπει να επανεξοικειωθούµε για να αποκοµίσουµε πλήρες όφελος
Έκτο µέρος 1... Συνέχεια από το προηγούµενο Προηγουµένως µίλησα για τις πολλαπλές απτές σηµασίες των ελληνιστικών πλανητών µε τις οποίες θα πρέπει να επανεξοικειωθούµε για να αποκοµίσουµε πλήρες όφελος
Ενδέκατο µέρος. ... Συνέχεια από το προηγούµενο
 Ενδέκατο µέρος... Συνέχεια από το προηγούµενο Έτσι, ο κυβερνήτης του Kλήρου της Τύχης παίζει κι αυτός κάποιο ρόλο σ αυτήν τη ναυτική µεταφορά. Αυτή η τρίτη τεχνική, που συνδυάζεται µε τη µελέτη του Ωροσκόπου
Ενδέκατο µέρος... Συνέχεια από το προηγούµενο Έτσι, ο κυβερνήτης του Kλήρου της Τύχης παίζει κι αυτός κάποιο ρόλο σ αυτήν τη ναυτική µεταφορά. Αυτή η τρίτη τεχνική, που συνδυάζεται µε τη µελέτη του Ωροσκόπου
ΠΛΑΝΗΤΕΣ ΕΝΤΟΣ ΚΑΙ ΕΚΤΟΣ ΟΜΑΔΑΣ (Τετράβιβλος, βιβλίο 1ο, κεφ. 7, σελ. 42-43, Περί ημερινών και νυκτερινών ).
 ΠΛΑΝΗΤΕΣ ΕΝΤΟΣ ΚΑΙ ΕΚΤΟΣ ΟΜΑΔΑΣ (Τετράβιβλος, βιβλίο 1ο, κεφ. 7, σελ. 42-43, Περί ημερινών και νυκτερινών ). Οι ομάδες των πλανητών (Sects) και η σπουδαιότητά τους σε ένα χάρτη Η πρωταρχική ενέργεια που
ΠΛΑΝΗΤΕΣ ΕΝΤΟΣ ΚΑΙ ΕΚΤΟΣ ΟΜΑΔΑΣ (Τετράβιβλος, βιβλίο 1ο, κεφ. 7, σελ. 42-43, Περί ημερινών και νυκτερινών ). Οι ομάδες των πλανητών (Sects) και η σπουδαιότητά τους σε ένα χάρτη Η πρωταρχική ενέργεια που
Αποφθέγματα για χαμένα αντικείμενα και αγνοούμενα πρόσωπα
 Αποφθέγματα για χαμένα αντικείμενα και αγνοούμενα πρόσωπα Ανεύρεση χαμένων ή παραπεταμένων αντικειμένων Σε ωριαίους χάρτες που αναφέρονται στην ανεύρεση χαμένων ή παραπεταμένων αντικειμένων πρέπει να ελεγχθούν
Αποφθέγματα για χαμένα αντικείμενα και αγνοούμενα πρόσωπα Ανεύρεση χαμένων ή παραπεταμένων αντικειμένων Σε ωριαίους χάρτες που αναφέρονται στην ανεύρεση χαμένων ή παραπεταμένων αντικειμένων πρέπει να ελεγχθούν
Άλλος ένας χάρτης- µάθηµα, που χειρίζεται δύο βασικά θέµατα: - Το θέµα των υποδοχών, αµοιβαίων ή µεικτών, και - Το θέµα του χρονικού προσδιορισµού.
 Άλλος ένας χάρτης- µάθηµα, που χειρίζεται δύο βασικά θέµατα: - Το θέµα των υποδοχών, αµοιβαίων ή µεικτών, και - Το θέµα του χρονικού προσδιορισµού. Με αυτόν τον ωριαίο χάρτη επιβεβαιώνεται, ακόµα µια φορά,
Άλλος ένας χάρτης- µάθηµα, που χειρίζεται δύο βασικά θέµατα: - Το θέµα των υποδοχών, αµοιβαίων ή µεικτών, και - Το θέµα του χρονικού προσδιορισµού. Με αυτόν τον ωριαίο χάρτη επιβεβαιώνεται, ακόµα µια φορά,
ΠΕΡΙ ΟΙΚΩΝ. Τεταρτημόρια
 ΠΕΡΙ ΟΙΚΩΝ Οι οίκοι είναι ένα από τα κυριότερα ερμηνευτικά μέσα που χρησιμοποιεί η αστρολογία. Μαζί με τους πλανήτες, τα ζώδια και τις όψεις αποτελούν τις βασικές αρχές στις οποίες στηρίζεται η ερμηνεία
ΠΕΡΙ ΟΙΚΩΝ Οι οίκοι είναι ένα από τα κυριότερα ερμηνευτικά μέσα που χρησιμοποιεί η αστρολογία. Μαζί με τους πλανήτες, τα ζώδια και τις όψεις αποτελούν τις βασικές αρχές στις οποίες στηρίζεται η ερμηνεία
Οι πιο ακανθώδεις ερωτήσεις, για όσους ασκούν την ωριαία αστρολογία, είναι αυτές που
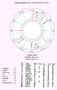 Οι πιο ακανθώδεις ερωτήσεις, για όσους ασκούν την ωριαία αστρολογία, είναι αυτές που αφορούν στην εύρεση αντικειµένων και τον χρόνο στον οποίο το αντικείµενο θα ευρεθεί. Είναι το είδος της ερώτησης που
Οι πιο ακανθώδεις ερωτήσεις, για όσους ασκούν την ωριαία αστρολογία, είναι αυτές που αφορούν στην εύρεση αντικειµένων και τον χρόνο στον οποίο το αντικείµενο θα ευρεθεί. Είναι το είδος της ερώτησης που
Πέµπτο µέρος. Η συνέχεια από το προηγούµενο
 1 Πέµπτο µέρος Η συνέχεια από το προηγούµενο Στην αρχική αραβική περίοδο, τώρα, οι αστρολόγοι έµοιαζαν όντως να προσκολλώνται σ αυτήν τη διάκριση, αλλά σε κάποιο σηµείο στην πορεία, κατά το τέλος της αραβικής
1 Πέµπτο µέρος Η συνέχεια από το προηγούµενο Στην αρχική αραβική περίοδο, τώρα, οι αστρολόγοι έµοιαζαν όντως να προσκολλώνται σ αυτήν τη διάκριση, αλλά σε κάποιο σηµείο στην πορεία, κατά το τέλος της αραβικής
ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΙΟΥΝΙΟΣ 2019
 Σελ:1 ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΙΟΥΝΙΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη Κριός Ήλιος Ταύρος Ερμής Δίδυμοι Αφροδίτη Καρκίνος
Σελ:1 ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΙΟΥΝΙΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη Κριός Ήλιος Ταύρος Ερμής Δίδυμοι Αφροδίτη Καρκίνος
ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΙΟΥΛΙΟΣ 2019
 Σελ:1 ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΙΟΥΛΙΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη Κριός Ήλιος Ταύρος Ερμής Δίδυμοι Αφροδίτη Καρκίνος
Σελ:1 ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΙΟΥΛΙΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη Κριός Ήλιος Ταύρος Ερμής Δίδυμοι Αφροδίτη Καρκίνος
ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΜΑΪΟΣ 2019
 Σελ:1 ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΜΑΪΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη Κριός Ήλιος Ταύρος Ερμής Δίδυμοι Αφροδίτη Καρκίνος Άρης
Σελ:1 ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΜΑΪΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη Κριός Ήλιος Ταύρος Ερμής Δίδυμοι Αφροδίτη Καρκίνος Άρης
ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΣΕΠΤΕΜΒΡΙΟΣ
 Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΣΕΠΤΕΜΒΡΙΟΣ 2018 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη
Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΣΕΠΤΕΜΒΡΙΟΣ 2018 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη
ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ
 Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΔΕΚΕΜΒΡΙΟΣ 2018 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη
Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΔΕΚΕΜΒΡΙΟΣ 2018 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη
ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ
 Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΝΟΕΜΒΡΙΟΣ 2018 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη
Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΝΟΕΜΒΡΙΟΣ 2018 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη
Γ Λ Ω Σ Σ Α Ρ Ι. Άγονα ζώδια: Δίδυμοι, Λέων, Παρθένος.
 Γ Λ Ω Σ Σ Α Ρ Ι Άγονα ζώδια: Δίδυμοι, Λέων, Παρθένος. Αδυναμία: Ένας πλανήτης βρίσκεται σε αδυναμία όταν είναι τοποθετημένος στο απέναντι ζώδιο από αυτό που κυβερνά, π.χ. η αδυναμία της Σελήνης είναι στον
Γ Λ Ω Σ Σ Α Ρ Ι Άγονα ζώδια: Δίδυμοι, Λέων, Παρθένος. Αδυναμία: Ένας πλανήτης βρίσκεται σε αδυναμία όταν είναι τοποθετημένος στο απέναντι ζώδιο από αυτό που κυβερνά, π.χ. η αδυναμία της Σελήνης είναι στον
ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΦΕΒΡΟΥΑΡΙΟΣ
 Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΕΙΣΟΔΟΣ ΠΛΑΝΗΤΗ ΣΕ ΖΩΔΙΟ ΑΣΤΡΟΛΟΓΙΚΑ
Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΕΙΣΟΔΟΣ ΠΛΑΝΗΤΗ ΣΕ ΖΩΔΙΟ ΑΣΤΡΟΛΟΓΙΚΑ
ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ
 Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΙΑΝΟΥΑΡΙΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη
Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΙΑΝΟΥΑΡΙΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη
ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ
 Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΜΑΡΤΙΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη
Σελ:1 ΠΑ.ΣΥ.Φ.Α. ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΦΙΛΩΝ ΑΣΤΡΟΛΟΓΙΑΣ ΜΑΡΤΙΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη
Ωριαία ερώτηση: ΘΑ ΞΑΝΑΒΡΩ ΤΟ ΧΑΜΕΝΟ ΧΑΡΤΟΦΥΛΑΚΑ;
 Ωριαία ερώτηση: ΘΑ ΞΑΝΑΒΡΩ ΤΟ ΧΑΜΕΝΟ ΧΑΡΤΟΦΥΛΑΚΑ; HORARY CHART 31/7/2007 03:09:11 μ.μ. 23Ε43, 37Ν58 (ΕΕD -3) Κυριαρχία +5 Έξαρση +4 Τριπλότητα +3 Όρια +2 εκανός +1 Αδυναμία -5 Πτώση -4 Περιπλανώμενος -5
Ωριαία ερώτηση: ΘΑ ΞΑΝΑΒΡΩ ΤΟ ΧΑΜΕΝΟ ΧΑΡΤΟΦΥΛΑΚΑ; HORARY CHART 31/7/2007 03:09:11 μ.μ. 23Ε43, 37Ν58 (ΕΕD -3) Κυριαρχία +5 Έξαρση +4 Τριπλότητα +3 Όρια +2 εκανός +1 Αδυναμία -5 Πτώση -4 Περιπλανώμενος -5
ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΑΠΡΙΛΙΟΣ 2019
 Σελ:1 ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΑΠΡΙΛΙΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη Κριός Ήλιος Ταύρος Ερμής Δίδυμοι Αφροδίτη Καρκίνος
Σελ:1 ΜΗΝΙΑΙΟ ΑΣΤΡΟΛΟΓΙΚΟ ΗΜΕΡΟΛΟΓΙΟ ΑΠΡΙΛΙΟΣ 2019 Σελ:2 ΕΠΕΞΗΓΗΣΗ ΑΣΤΡΟΛΟΓΙΚΩΝ ΣΥΜΒΟΛΩΝ ΠΟΥ ΧΡΗΣΙΜΟΠΟΙΟΥΝΤΑΙ ΣΤΟ ΗΜΕΡΟΛΟΓΙΟ ΑΣΤΡΟΛΟΓΙΚΑ ΣΥΜΒΟΛΑ Σελήνη Κριός Ήλιος Ταύρος Ερμής Δίδυμοι Αφροδίτη Καρκίνος
ΑΠΟΦΘΕΓΜΑΤΑ Αστρολογικές συμβουλές για την ερμηνεία ενός ωριαίου χάρτη
 ΑΠΟΦΘΕΓΜΑΤΑ Αστρολογικές συμβουλές για την ερμηνεία ενός ωριαίου χάρτη Κατά τη διάρκεια των αιώνων, πολλοί αξιόλογοι μελετητές της αστρολογίας παρατήρησαν ότι ορισμένα αποτελέσματα επαναλαμβάνονταν κάτω
ΑΠΟΦΘΕΓΜΑΤΑ Αστρολογικές συμβουλές για την ερμηνεία ενός ωριαίου χάρτη Κατά τη διάρκεια των αιώνων, πολλοί αξιόλογοι μελετητές της αστρολογίας παρατήρησαν ότι ορισμένα αποτελέσματα επαναλαμβάνονταν κάτω
Τρίτο µέρος. ... Συνέχεια από το προηγούµενο
 Τρίτο µέρος 1... Συνέχεια από το προηγούµενο Οι ελληνιστικοί αστρολόγοι ευθύνονταν για την εισαγωγή αυτού του περίπλοκου δόγµατος των κλήρων, που µπορεί να γνωρίζετε µε το όνοµα Αραβικοί κλήροι. εν είναι
Τρίτο µέρος 1... Συνέχεια από το προηγούµενο Οι ελληνιστικοί αστρολόγοι ευθύνονταν για την εισαγωγή αυτού του περίπλοκου δόγµατος των κλήρων, που µπορεί να γνωρίζετε µε το όνοµα Αραβικοί κλήροι. εν είναι
ΧΡΗΜΑΤΙΣΤΗΡΙΑΚΗ ΑΣΤΡΟΛΟΓΙΑ
 22 ΧΡΗΜΑΤΙΣΤΗΡΙΑΚΗ ΑΣΤΡΟΛΟΓΙΑ H έρευνα του πρώτου μέρους αυτού του βιβλίου αναφέρεται αποκλειστικά στο αμερικανικό χρηματιστήριο. Κατά συνέπεια, η μελέτη των ωροσκοπίων των μετοχών που παρατίθενται στα
22 ΧΡΗΜΑΤΙΣΤΗΡΙΑΚΗ ΑΣΤΡΟΛΟΓΙΑ H έρευνα του πρώτου μέρους αυτού του βιβλίου αναφέρεται αποκλειστικά στο αμερικανικό χρηματιστήριο. Κατά συνέπεια, η μελέτη των ωροσκοπίων των μετοχών που παρατίθενται στα
Γλωσσάρι ελληνικής αστρολογίας. Γλωσσάρι ελληνικών αστρολογικών όρων
 285 Γλωσσάρι ελληνικών αστρολογικών όρων 287 ΓΛΩΣΣΑΡΙ Ἀγαθοδαιμονῶ: Η παρουσία ενός πλανήτη ή άλλου αστρολογικού σημείου στον 11o τόπο-οίκο, που ήταν γνωστός και ως Ἀγαθὸς Δαίμων. Ἀγαθοποιός: Η λέξη αναφέρεται
285 Γλωσσάρι ελληνικών αστρολογικών όρων 287 ΓΛΩΣΣΑΡΙ Ἀγαθοδαιμονῶ: Η παρουσία ενός πλανήτη ή άλλου αστρολογικού σημείου στον 11o τόπο-οίκο, που ήταν γνωστός και ως Ἀγαθὸς Δαίμων. Ἀγαθοποιός: Η λέξη αναφέρεται
ΕΙΝΑΙ Η ΑΣΤΡΟΛΟΓΙΑ ΜΙΑ ΜΕΘΟΔΟΣ ΑΥΤΟΓΝΩΣΙΑΣ; 1
 ΕΙΝΑΙ Η ΑΣΤΡΟΛΟΓΙΑ ΜΙΑ ΜΕΘΟΔΟΣ ΑΥΤΟΓΝΩΣΙΑΣ; 1 Στο σημείο αυτό του οδοιπορικού γνωριμίας με τις διάφορες μεθόδους αυτογνωσίας θα συναντήσουμε την Αστρολογία και θα μιλήσουμε για αυτή. Θα ερευνήσουμε δηλαδή
ΕΙΝΑΙ Η ΑΣΤΡΟΛΟΓΙΑ ΜΙΑ ΜΕΘΟΔΟΣ ΑΥΤΟΓΝΩΣΙΑΣ; 1 Στο σημείο αυτό του οδοιπορικού γνωριμίας με τις διάφορες μεθόδους αυτογνωσίας θα συναντήσουμε την Αστρολογία και θα μιλήσουμε για αυτή. Θα ερευνήσουμε δηλαδή
Η ιστορία της αστρολογίας ανάγεται στη 2η χιλιετία π.χ.
 Η ιστορία της αστρολογίας ανάγεται στη 2η χιλιετία π.χ. Η Βαβυλωνιακή αστρολογία λέγεται ότι είχε επηρεάσει τους Έλληνες ήδη από τα μέσα του 4ου π.χ. αιώνα. Ακόμη και αν η προέλευση της αστρολογίας των
Η ιστορία της αστρολογίας ανάγεται στη 2η χιλιετία π.χ. Η Βαβυλωνιακή αστρολογία λέγεται ότι είχε επηρεάσει τους Έλληνες ήδη από τα μέσα του 4ου π.χ. αιώνα. Ακόμη και αν η προέλευση της αστρολογίας των
ΕΚΛΕΙΨΕΙΣ. Οι εκλείψεις στην Ωριαία αστρολογία
 ΕΚΛΕΙΨΕΙΣ Οι εκλείψεις στην Ωριαία αστρολογία Οι εκλείψεις παίζουν σημαντικό ρόλο στην Ωριαία αστρολογία. Από τα βάθη των αιώνων μέχρι σήμερα πολλοί αστρονόμοι και αστρολόγοι έχουν μελετήσει το φαινόμενο
ΕΚΛΕΙΨΕΙΣ Οι εκλείψεις στην Ωριαία αστρολογία Οι εκλείψεις παίζουν σημαντικό ρόλο στην Ωριαία αστρολογία. Από τα βάθη των αιώνων μέχρι σήμερα πολλοί αστρονόμοι και αστρολόγοι έχουν μελετήσει το φαινόμενο
μάθημα πρώτο: συναστρία 6 μάθημα δεύτερο: Ήλιοσ 8 μάθημα τρίτο: σελήνη 32 μάθημα τέταρτο: ερμησ 50 μάθημα πεμπτο: αφροδίτη 64 μάθημα εκτο: αρης 76
 περιεχόμενα μάθημα πρώτο: συναστρία 6 μάθημα δεύτερο: Ήλιοσ 8 μάθημα τρίτο: σελήνη 32 μάθημα τέταρτο: ερμησ 50 μάθημα πεμπτο: αφροδίτη 64 μάθημα εκτο: αρης 76 μάθημα έβδομο: δίας 82 μάθημα ογδοο: κρονοσ
περιεχόμενα μάθημα πρώτο: συναστρία 6 μάθημα δεύτερο: Ήλιοσ 8 μάθημα τρίτο: σελήνη 32 μάθημα τέταρτο: ερμησ 50 μάθημα πεμπτο: αφροδίτη 64 μάθημα εκτο: αρης 76 μάθημα έβδομο: δίας 82 μάθημα ογδοο: κρονοσ
Η ΜΟΝΑΧΙΚΗ ΑΥΤΟΚΡΑΤΟΡΙΑ ΤΟΥ BILL GATES
 Η ΜΟΝΑΧΙΚΗ ΑΥΤΟΚΡΑΤΟΡΙΑ ΤΟΥ BILL GATES Σεμνός δημιουργός ή ευφυής κροίσος; Θα ήταν μεγάλη παράλειψη για ένα βιβλίο που εξετάζει τη σχέση χρήματος και αστρολογίας να μην αναφερθεί στους παράγοντες εκείνους
Η ΜΟΝΑΧΙΚΗ ΑΥΤΟΚΡΑΤΟΡΙΑ ΤΟΥ BILL GATES Σεμνός δημιουργός ή ευφυής κροίσος; Θα ήταν μεγάλη παράλειψη για ένα βιβλίο που εξετάζει τη σχέση χρήματος και αστρολογίας να μην αναφερθεί στους παράγοντες εκείνους
Είμαι ο Kaypacha με μια άλλη έκθεση Πέλε. Είναι για την 10η Ιουνίου του 2015.
 Η Έκθεση Πέλε για τις 10 Ιουνίου του 2015 Καλημέρα! Είμαι ο Kaypacha με μια άλλη έκθεση Πέλε. Είναι για την 10η Ιουνίου του 2015. Η Σελήνη είναι τώρα στον Κριό και ο Ήλιος στους Διδύμους, ζώντας για την
Η Έκθεση Πέλε για τις 10 Ιουνίου του 2015 Καλημέρα! Είμαι ο Kaypacha με μια άλλη έκθεση Πέλε. Είναι για την 10η Ιουνίου του 2015. Η Σελήνη είναι τώρα στον Κριό και ο Ήλιος στους Διδύμους, ζώντας για την
Η ερώτηση είχε ως εξής: «Θα αγοράσω το σπίτι που είδα σήµερα στη εξοχή; Θα είναι προς όφελός
 Η κυρία που διατύπωσε την ερώτηση είναι προσωπική φίλη και έψαχνε πολύ καιρό για ένα σπίτι µεγαλύτερο και µε περισσότερες ανέσεις, δίχως να µένει ικανοποιηµένη µε τις διάφορες προτάσεις που της έκαναν.
Η κυρία που διατύπωσε την ερώτηση είναι προσωπική φίλη και έψαχνε πολύ καιρό για ένα σπίτι µεγαλύτερο και µε περισσότερες ανέσεις, δίχως να µένει ικανοποιηµένη µε τις διάφορες προτάσεις που της έκαναν.
Λίγα για το Πριν, το Τώρα και το Μετά.
 1 Λίγα για το Πριν, το Τώρα και το Μετά. Ψάχνοντας από το εσωτερικό κάποιων εφημερίδων μέχρι σε πιο εξειδικευμένα περιοδικά και βιβλία σίγουρα θα έχουμε διαβάσει ή θα έχουμε τέλος πάντων πληροφορηθεί,
1 Λίγα για το Πριν, το Τώρα και το Μετά. Ψάχνοντας από το εσωτερικό κάποιων εφημερίδων μέχρι σε πιο εξειδικευμένα περιοδικά και βιβλία σίγουρα θα έχουμε διαβάσει ή θα έχουμε τέλος πάντων πληροφορηθεί,
Κεφαλαιο Δεκατο πεμπτο ΠΟΥ ΚΑΙ ΠΟΤΕ;
 Κεφαλαιο Δεκατο πεμπτο ΠΟΥ ΚΑΙ ΠΟΤΕ; Μέχρι στιγμής έχουν αναφερθεί όλοι οι παράγοντες που πρέπει να εξεταστούν για να μπορέσει κανείς να εκτιμήσει σωστά το όποιο αποτέλεσμα σε ένα χάρτη ωριαίας ερώτησης,
Κεφαλαιο Δεκατο πεμπτο ΠΟΥ ΚΑΙ ΠΟΤΕ; Μέχρι στιγμής έχουν αναφερθεί όλοι οι παράγοντες που πρέπει να εξεταστούν για να μπορέσει κανείς να εκτιμήσει σωστά το όποιο αποτέλεσμα σε ένα χάρτη ωριαίας ερώτησης,
Μαθήματα Feng Shui - Η Φύση και τα Στοιχεία των Άστρων. Συντάχθηκε απο τον/την Τάκης Καραγιαννόπουλος
 Τα Άστρα μπορεί να είναι εκ φύσεως καλά ή κακά. Η φύση τους όμως εξαρτάται από τον παράγοντα Χρόνο. Έτσι ένα καλό άστρο μπορεί να γίνει δυσμενές και να προκαλεί κακοτυχία σε κάποια συγκεκριμένη περίοδο
Τα Άστρα μπορεί να είναι εκ φύσεως καλά ή κακά. Η φύση τους όμως εξαρτάται από τον παράγοντα Χρόνο. Έτσι ένα καλό άστρο μπορεί να γίνει δυσμενές και να προκαλεί κακοτυχία σε κάποια συγκεκριμένη περίοδο
Το ταξίδι στην 11η διάσταση
 Το ταξίδι στην 11η διάσταση Το κείμενο αυτό δεν αντιπροσωπεύει το πώς παρουσιάζονται οι 11 διστάσεις βάση της θεωρίας των υπερχορδών! Είναι περισσότερο «τροφή για σκέψη» παρά επιστημονική άποψη. Οι σκέψεις
Το ταξίδι στην 11η διάσταση Το κείμενο αυτό δεν αντιπροσωπεύει το πώς παρουσιάζονται οι 11 διστάσεις βάση της θεωρίας των υπερχορδών! Είναι περισσότερο «τροφή για σκέψη» παρά επιστημονική άποψη. Οι σκέψεις
ΣΧΕΔΙΑΓΡΑΜΜΑ ΑΡΙΣΤΟΤΕΛΗΣ ΠΟΛΙΤΙΚΑ
 ΣΧΕΔΙΑΓΡΑΜΜΑ ΑΡΙΣΤΟΤΕΛΗΣ ΠΟΛΙΤΙΚΑ Ο λόγος που ο Αριστοτέλης μελέτησε την έννοια της αρετής στα Ηθικά Νικομάχεια είναι γιατί αυτή αποτελεί προϋπόθεση όχι μόνο για την ευδαιμονία του ατόμου αλλά και ολόκληρης
ΣΧΕΔΙΑΓΡΑΜΜΑ ΑΡΙΣΤΟΤΕΛΗΣ ΠΟΛΙΤΙΚΑ Ο λόγος που ο Αριστοτέλης μελέτησε την έννοια της αρετής στα Ηθικά Νικομάχεια είναι γιατί αυτή αποτελεί προϋπόθεση όχι μόνο για την ευδαιμονία του ατόμου αλλά και ολόκληρης
ΑΝΑΛΥΣΗ 1 ΕΝΑΤΟ ΜΑΘΗΜΑ, Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 1 ΕΝΑΤΟ ΜΑΘΗΜΑ, 5-10-13 Μ. Παπαδημητράκης. 1 Τώρα θα μιλήσουμε για την έννοια της περιοχής, η οποία έχει κεντρικό ρόλο στη μελέτη της έννοιας του ορίου (ακολουθίας και συνάρτησης). Αν > 0, ονομάζουμε
ΑΝΑΛΥΣΗ 1 ΕΝΑΤΟ ΜΑΘΗΜΑ, 5-10-13 Μ. Παπαδημητράκης. 1 Τώρα θα μιλήσουμε για την έννοια της περιοχής, η οποία έχει κεντρικό ρόλο στη μελέτη της έννοιας του ορίου (ακολουθίας και συνάρτησης). Αν > 0, ονομάζουμε
Πανεπιστήμιο Πατρών Μεταπτυχιακό Τμήμα Διοίκησης Επιχειρήσεων
 Πανεπιστήμιο Πατρών Μεταπτυχιακό Τμήμα Διοίκησης Επιχειρήσεων Μελέτη με θέμα: Διερεύνηση του βαθμού ανάπτυξης εμπιστοσύνης και ασφάλειας στην καθημερινή χρήση του διαδικτύου Ερωτηματολόγιο 1. Πόσο καιρό
Πανεπιστήμιο Πατρών Μεταπτυχιακό Τμήμα Διοίκησης Επιχειρήσεων Μελέτη με θέμα: Διερεύνηση του βαθμού ανάπτυξης εμπιστοσύνης και ασφάλειας στην καθημερινή χρήση του διαδικτύου Ερωτηματολόγιο 1. Πόσο καιρό
Η Έκθεση Πέλε 17 Φεβρουαρίου, Γεια σας ~ Καλημέρα ~
 Η Έκθεση Πέλε 17 Φεβρουαρίου, 2016 Γεια σας ~ Καλημέρα ~ Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε, έναν αστρολογικό στοχασμό. Είναι για την εβδομάδα της 17ης Φεβρουαρίου του 2016, και αυτή είναι
Η Έκθεση Πέλε 17 Φεβρουαρίου, 2016 Γεια σας ~ Καλημέρα ~ Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε, έναν αστρολογικό στοχασμό. Είναι για την εβδομάδα της 17ης Φεβρουαρίου του 2016, και αυτή είναι
ΓΙΑΤΙ ΚΟΥΡΑΖΟΜΑΣΤΕ ΌΤΑΝ ΚΛΑΙΜΕ ΕΡΓΑΣΙΑ ΤΟΥ ΜΑΘΗΤΑΡΑ ΣΤΕΦΑΝΟΥ ΧΑΤΖΗΝΙΚΗΤΑ Γ3
 ΓΙΑΤΙ ΚΟΥΡΑΖΟΜΑΣΤΕ ΌΤΑΝ ΚΛΑΙΜΕ ΕΡΓΑΣΙΑ ΤΟΥ ΜΑΘΗΤΑΡΑ ΣΤΕΦΑΝΟΥ ΧΑΤΖΗΝΙΚΗΤΑ Γ3 Έχω παρατηρήσει ότι συχνά κουράζομαι πολύ μετά το κλάμα. Γιατί συμβαίνει αυτό; Σε αντίθεση με μια σειρά άλλων εκφράσεων συναισθημάτων,
ΓΙΑΤΙ ΚΟΥΡΑΖΟΜΑΣΤΕ ΌΤΑΝ ΚΛΑΙΜΕ ΕΡΓΑΣΙΑ ΤΟΥ ΜΑΘΗΤΑΡΑ ΣΤΕΦΑΝΟΥ ΧΑΤΖΗΝΙΚΗΤΑ Γ3 Έχω παρατηρήσει ότι συχνά κουράζομαι πολύ μετά το κλάμα. Γιατί συμβαίνει αυτό; Σε αντίθεση με μια σειρά άλλων εκφράσεων συναισθημάτων,
Η Έκθεση Πέλε 15 Φεβρουαρίου 2017
 Η Έκθεση Πέλε 15 Φεβρουαρίου 2017 Γεια σας! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε. Είναι μια από εκείνες τις ημέρες όπου θέλω απλώς να καθίσω στην στέγη και να βλέπω τα σύννεφα... έτσι αυτό κάνω!
Η Έκθεση Πέλε 15 Φεβρουαρίου 2017 Γεια σας! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε. Είναι μια από εκείνες τις ημέρες όπου θέλω απλώς να καθίσω στην στέγη και να βλέπω τα σύννεφα... έτσι αυτό κάνω!
Η καμπύλωση του χώρου-θεωρία της σχετικότητας
 Η καμπύλωση του χώρου-θεωρία της σχετικότητας Σύμφωνα με τη Γενική Θεωρία της Σχετικότητας που διατύπωσε ο Αϊνστάιν, το βαρυτικό πεδίο κάθε μάζας δημιουργεί μια καμπύλωση στον χώρο (μάλιστα στον χωροχρόνο),
Η καμπύλωση του χώρου-θεωρία της σχετικότητας Σύμφωνα με τη Γενική Θεωρία της Σχετικότητας που διατύπωσε ο Αϊνστάιν, το βαρυτικό πεδίο κάθε μάζας δημιουργεί μια καμπύλωση στον χώρο (μάλιστα στον χωροχρόνο),
Η Έκθεση Πέλε - 29 Σεπτεμβρίου, Γεια σας!
 Η Έκθεση Πέλε - 29 Σεπτεμβρίου, 2016 Γεια σας! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε για τις 29 Σεπτεμβρίου 2016. Ξέρω ότι είναι με μια μέρα καθυστέρηση και συνήθως κάνω αυτά τα πράγματα την
Η Έκθεση Πέλε - 29 Σεπτεμβρίου, 2016 Γεια σας! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε για τις 29 Σεπτεμβρίου 2016. Ξέρω ότι είναι με μια μέρα καθυστέρηση και συνήθως κάνω αυτά τα πράγματα την
ΛΟΓΙΣΜΟΣ ΜΙΑΣ ΜΕΤΑΒΛΗΤΗΣ, ΕΣΠΙ 1
 ΛΟΓΙΣΜΟΣ ΜΙΑΣ ΜΕΤΑΒΛΗΤΗΣ, ΕΣΠΙ 1 ΣΥΝΑΡΤΗΣΕΙΣ Η έννοια της συνάρτησης είναι θεμελιώδης στο λογισμό και διαπερνά όλους τους μαθηματικούς κλάδους. Για το φοιτητή είναι σημαντικό να κατανοήσει πλήρως αυτή
ΛΟΓΙΣΜΟΣ ΜΙΑΣ ΜΕΤΑΒΛΗΤΗΣ, ΕΣΠΙ 1 ΣΥΝΑΡΤΗΣΕΙΣ Η έννοια της συνάρτησης είναι θεμελιώδης στο λογισμό και διαπερνά όλους τους μαθηματικούς κλάδους. Για το φοιτητή είναι σημαντικό να κατανοήσει πλήρως αυτή
GEORGE BERKELEY ( )
 42 GEORGE BERKELEY (1685-1753) «Ο βασικός σκοπός του Berkeley δεν ήταν να αμφισβητήσει την ύπαρξη των εξωτερικών αντικειμένων, αλλά να υποστηρίξει την άποψη ότι τα πνεύματα ήταν τα μόνα ανεξάρτητα όντα,
42 GEORGE BERKELEY (1685-1753) «Ο βασικός σκοπός του Berkeley δεν ήταν να αμφισβητήσει την ύπαρξη των εξωτερικών αντικειμένων, αλλά να υποστηρίξει την άποψη ότι τα πνεύματα ήταν τα μόνα ανεξάρτητα όντα,
Το Ηµερολόγιο των Μάγιας και τα Χρήµατα από τον ρ. Καρλ Τζοχάν Κάλλεµαν
 Το Ηµερολόγιο των Μάγιας και τα Χρήµατα Από τον ρ. Καρλ Τζοχάν Κάλλεµαν Λοιπόν, ήθελα να µιλήσω για δυο πράγµατα που νοµίζω δεν συνδέονται πάντα αλλά, πραγµατικά θα τους άξιζε µια σύνδεση. Το ένα είναι
Το Ηµερολόγιο των Μάγιας και τα Χρήµατα Από τον ρ. Καρλ Τζοχάν Κάλλεµαν Λοιπόν, ήθελα να µιλήσω για δυο πράγµατα που νοµίζω δεν συνδέονται πάντα αλλά, πραγµατικά θα τους άξιζε µια σύνδεση. Το ένα είναι
Αστρολογία για την Ψυχή Η Έκθεση Πέλε 21 Ιουνΐου, 2017
 Αστρολογία για την Ψυχή Η Έκθεση Πέλε 21 Ιουνΐου, 2017 Hola! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε για τις 21 Ιουνίου 2017. Το Ηλιοστάσιο, μόλις χτες τη νύχτα ο Ήλιος πήγε στον Καρκίνο, και σήμερα
Αστρολογία για την Ψυχή Η Έκθεση Πέλε 21 Ιουνΐου, 2017 Hola! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε για τις 21 Ιουνίου 2017. Το Ηλιοστάσιο, μόλις χτες τη νύχτα ο Ήλιος πήγε στον Καρκίνο, και σήμερα
Προειδοποιητικοί κανόνες (Considerations before judgment)
 Προειδοποιητικοί κανόνες (Considerations before judgment) της έσποινας Γιαννακοπούλου Ένα ευαίσθητο κεφάλαιο, που φαίνεται ότι δεν έχει κατανοηθεί πλήρως από τους ασκούντες την Ωριαία, είναι οι προειδοποιητικοί
Προειδοποιητικοί κανόνες (Considerations before judgment) της έσποινας Γιαννακοπούλου Ένα ευαίσθητο κεφάλαιο, που φαίνεται ότι δεν έχει κατανοηθεί πλήρως από τους ασκούντες την Ωριαία, είναι οι προειδοποιητικοί
Η Έκθεση Πέλε για τις 4 Νοεμβρίου, Γεια σας! Καλημέρα!
 Η Έκθεση Πέλε για τις 4 Νοεμβρίου, 2015 Γεια σας! Καλημέρα! Είμαι ο Kaypacha με την εβδομαδιαία έκθεση Πέλε για τις 4 Νοεμβρίου του 2015. Αστρολογία για την Ψυχή. Είναι μια άποψη για το τι συμβαίνει με
Η Έκθεση Πέλε για τις 4 Νοεμβρίου, 2015 Γεια σας! Καλημέρα! Είμαι ο Kaypacha με την εβδομαδιαία έκθεση Πέλε για τις 4 Νοεμβρίου του 2015. Αστρολογία για την Ψυχή. Είναι μια άποψη για το τι συμβαίνει με
Άρθρο :Ευδοκία Πεπονούλα
 Άρθρο :Ευδοκία Πεπονούλα Ο γενέθλιος χάρτης της Ιαπωνίας έχει Ήλιο στις 22 ο 37 του Υδροχόου. Ενεργοποιεί δηλαδή την κλείδα Ουρανού Σελήνης στις 23 ο του Σκορπιού. Μας μιλά λοιπόν για ένα κράτος με παλιές
Άρθρο :Ευδοκία Πεπονούλα Ο γενέθλιος χάρτης της Ιαπωνίας έχει Ήλιο στις 22 ο 37 του Υδροχόου. Ενεργοποιεί δηλαδή την κλείδα Ουρανού Σελήνης στις 23 ο του Σκορπιού. Μας μιλά λοιπόν για ένα κράτος με παλιές
ΕΡΩΤΙΚΑ ΠΟΙΗΜΑΤΑ ΜΑΘΗΤΏΝ ΚΑΙ ΜΑΘΗΤΡΙΩΝ
 ΕΡΩΤΙΚΑ ΠΟΙΗΜΑΤΑ ΜΑΘΗΤΏΝ ΚΑΙ ΜΑΘΗΤΡΙΩΝ Στο πλαίσιο του μαθήματος της Νεοελληνικής Λογοτεχνίας της Γ Γυμνασίου οι μαθητές ήρθαν σε επαφή με ένα δείγμα ερωτικής ποίησης. Συγκεκριμένα διδάχτηκαν το ποίημα
ΕΡΩΤΙΚΑ ΠΟΙΗΜΑΤΑ ΜΑΘΗΤΏΝ ΚΑΙ ΜΑΘΗΤΡΙΩΝ Στο πλαίσιο του μαθήματος της Νεοελληνικής Λογοτεχνίας της Γ Γυμνασίου οι μαθητές ήρθαν σε επαφή με ένα δείγμα ερωτικής ποίησης. Συγκεκριμένα διδάχτηκαν το ποίημα
Η Έκθεση Πέλε 8 Μαρτίου 2017
 Η Έκθεση Πέλε 8 Μαρτίου 2017 Γεια σας~ Καλημέρα~ Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε. Κάνει λίγο κρύο και φυσάει έξω, οπότε θα απογειωθώ από τον πλανήτη Γη και θα πάω στις μακρινές σφαίρες
Η Έκθεση Πέλε 8 Μαρτίου 2017 Γεια σας~ Καλημέρα~ Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε. Κάνει λίγο κρύο και φυσάει έξω, οπότε θα απογειωθώ από τον πλανήτη Γη και θα πάω στις μακρινές σφαίρες
Η ΕΠΙΣΤΗΜΗ ΚΑΙ ΤΑ ΜΥΣΤΙΚΑ ΤΗΣ ΜΕΛΕΤΗΣ ΤΩΝ ΑΣΤΡΩΝ. Αστρολογία. Julia και Derek parker
 Η ΕΠΙΣΤΗΜΗ ΚΑΙ ΤΑ ΜΥΣΤΙΚΑ ΤΗΣ ΜΕΛΕΤΗΣ ΤΩΝ ΑΣΤΡΩΝ Αστρολογία Julia και Derek parker ΙΔΙΟΚΤΗΣΙΑ ΕΙΔΗΣΕΙΣ ΝΤΟΤ ΚΟΜ Α.Ε. ΕΚΔOΣΕΙΣ ΣΚΑΪ Διεύθυνση New Business, ΣΚΑΪ Συντονισµός παραγωγής BIBΛIOΣYNEPΓATIKH
Η ΕΠΙΣΤΗΜΗ ΚΑΙ ΤΑ ΜΥΣΤΙΚΑ ΤΗΣ ΜΕΛΕΤΗΣ ΤΩΝ ΑΣΤΡΩΝ Αστρολογία Julia και Derek parker ΙΔΙΟΚΤΗΣΙΑ ΕΙΔΗΣΕΙΣ ΝΤΟΤ ΚΟΜ Α.Ε. ΕΚΔOΣΕΙΣ ΣΚΑΪ Διεύθυνση New Business, ΣΚΑΪ Συντονισµός παραγωγής BIBΛIOΣYNEPΓATIKH
Αστρολογία για την Ψυχή Η Έκθεση Πέλε 21 Σεπτεμβρίου, 2017
 Αστρολογία για την Ψυχή Η Έκθεση Πέλε 21 Σεπτεμβρίου, 2017 Γεια σας! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε για τις 21 Σεπτεμβρίου του 2017. Δείτε, είμαι στη μέση του Machu Picchu στο Περού. Δείτε
Αστρολογία για την Ψυχή Η Έκθεση Πέλε 21 Σεπτεμβρίου, 2017 Γεια σας! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε για τις 21 Σεπτεμβρίου του 2017. Δείτε, είμαι στη μέση του Machu Picchu στο Περού. Δείτε
μαθημα δεύτερο: Βασικοί ορισμοί και κανόνεσ 9 MAΘΗΜΑ ΤΡΙΤΟ: Το συναισθηματικό μας υπόβαθρο 16
 περιεχόμενα μάθημα πρώτο: αστρολογία & σχέσεις 6 μαθημα δεύτερο: Βασικοί ορισμοί και κανόνεσ 9 MAΘΗΜΑ ΤΡΙΤΟ: Το συναισθηματικό μας υπόβαθρο 16 ΜΑΘΗΜΑ ΤΕΤΑΡΤΟ: με ποιον τρόπο αγαπάμε 42 ΜΑΘΗΜΑ ΠΕΜΠΤΟ: με
περιεχόμενα μάθημα πρώτο: αστρολογία & σχέσεις 6 μαθημα δεύτερο: Βασικοί ορισμοί και κανόνεσ 9 MAΘΗΜΑ ΤΡΙΤΟ: Το συναισθηματικό μας υπόβαθρο 16 ΜΑΘΗΜΑ ΤΕΤΑΡΤΟ: με ποιον τρόπο αγαπάμε 42 ΜΑΘΗΜΑ ΠΕΜΠΤΟ: με
Μεθοδολογία Έρευνας Κοινωνικών Επιστημών
 Μεθοδολογία Έρευνας Κοινωνικών Επιστημών Dr. Anthony Montgomery Επίκουρος Καθηγητής Εκπαιδευτικής & Κοινωνικής Πολιτικής antmont@uom.gr Ποιός είναι ο σκοπός του μαθήματος μας? Στο τέλος του σημερινού μαθήματος,
Μεθοδολογία Έρευνας Κοινωνικών Επιστημών Dr. Anthony Montgomery Επίκουρος Καθηγητής Εκπαιδευτικής & Κοινωνικής Πολιτικής antmont@uom.gr Ποιός είναι ο σκοπός του μαθήματος μας? Στο τέλος του σημερινού μαθήματος,
όπου D(f ) = (, 0) (0, + ) = R {0}. Είναι Σχήµα 10: Η γραφική παράσταση της συνάρτησης f (x) = 1/x.
 3 Ορια συναρτήσεων 3. Εισαγωγικές έννοιες. Ας ϑεωρήσουµε την συνάρτηση f () = όπου D(f ) = (, 0) (0, + ) = R {0}. Είναι Σχήµα 0: Η γραφική παράσταση της συνάρτησης f () = /. ϕυσικό να αναζητήσουµε την
3 Ορια συναρτήσεων 3. Εισαγωγικές έννοιες. Ας ϑεωρήσουµε την συνάρτηση f () = όπου D(f ) = (, 0) (0, + ) = R {0}. Είναι Σχήµα 0: Η γραφική παράσταση της συνάρτησης f () = /. ϕυσικό να αναζητήσουµε την
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 8
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 8 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2014/nt2014.html https://sites.google.com/site/maths4edu/home/14
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 8 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2014/nt2014.html https://sites.google.com/site/maths4edu/home/14
Οδηγός διαφοροποίησης για την πρωτοβάθµια
 Οδηγός διαφοροποίησης για την πρωτοβάθµια Γιατί χρειάζεται να κάνουµε τόσο ειδική διαφοροποίηση; Τα παιδιά που βρίσκονται στο φάσµα του αυτισµού έχουν διαφορετικό τρόπο σκέψης και αντίληψης για τον κόσµο,
Οδηγός διαφοροποίησης για την πρωτοβάθµια Γιατί χρειάζεται να κάνουµε τόσο ειδική διαφοροποίηση; Τα παιδιά που βρίσκονται στο φάσµα του αυτισµού έχουν διαφορετικό τρόπο σκέψης και αντίληψης για τον κόσµο,
Σύνοψη Θεωρίας ΟΡΙΣΜΟΣ ΚΑΙ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΑΛΓΟΡΙΘΜΩΝ
 1 ο ΓΥΜΝΑΣΙΟ ΘΕΡΜΗΣ Τάξη: Γ Μάθημα: Πληροφορική Εξεταστέα ύλη: Παρ11.1 & 11.2 Σύνοψη Θεωρίας ΟΡΙΣΜΟΣ ΚΑΙ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΑΛΓΟΡΙΘΜΩΝ Αλγόριθμος είναι μια πεπερασμένη σειρά ενεργειών που περιγράφει τη διαδικασία
1 ο ΓΥΜΝΑΣΙΟ ΘΕΡΜΗΣ Τάξη: Γ Μάθημα: Πληροφορική Εξεταστέα ύλη: Παρ11.1 & 11.2 Σύνοψη Θεωρίας ΟΡΙΣΜΟΣ ΚΑΙ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΑΛΓΟΡΙΘΜΩΝ Αλγόριθμος είναι μια πεπερασμένη σειρά ενεργειών που περιγράφει τη διαδικασία
Modern Greek Beginners
 2016 HIGHER SCHOOL CERTIFICATE EXAMINATION Modern Greek Beginners ( Section I Listening) Transcript Familiarisation Text Καλημέρα. Καλημέρα σας. Μπορώ να σας βοηθήσω; Ήρθα να πάρω αυτό το δέμα. Σήμερα
2016 HIGHER SCHOOL CERTIFICATE EXAMINATION Modern Greek Beginners ( Section I Listening) Transcript Familiarisation Text Καλημέρα. Καλημέρα σας. Μπορώ να σας βοηθήσω; Ήρθα να πάρω αυτό το δέμα. Σήμερα
ΑΠΟΔΡΑΣΗ ΑΠΟ ΤΗ ΒΙΒΛΙΟΘΗΚΗ ΤΟΥ ΤΡΟΜΟΥ
 ΑΠΟΔΡΑΣΗ ΑΠΟ ΤΗ ΒΙΒΛΙΟΘΗΚΗ ΤΟΥ ΤΡΟΜΟΥ - Α,α,α,α,α,α,α! ούρλιαξε η Νεφέλη - Τρομερό! συμπλήρωσε η Καλλιόπη - Ω, Θεέ μου! αναφώνησα εγώ - Απίστευτα τέλειο! είπε η Ειρήνη και όλες την κοιτάξαμε λες και είπε
ΑΠΟΔΡΑΣΗ ΑΠΟ ΤΗ ΒΙΒΛΙΟΘΗΚΗ ΤΟΥ ΤΡΟΜΟΥ - Α,α,α,α,α,α,α! ούρλιαξε η Νεφέλη - Τρομερό! συμπλήρωσε η Καλλιόπη - Ω, Θεέ μου! αναφώνησα εγώ - Απίστευτα τέλειο! είπε η Ειρήνη και όλες την κοιτάξαμε λες και είπε
Περί της «Αρχής ανεξαρτησίας των κινήσεων»
 Περί της «Αρχής ανεξαρτησίας των κινήσεων» Παρακολουθώ στο δίκτυο τις τελευταίες µέρες να γίνεται συζήτηση για την «Αρχή ανεξαρτησίας των κινήσεων» ή την «επαλληλία εξισώσεων κίνησης». Προσπαθώ στο µέτρο
Περί της «Αρχής ανεξαρτησίας των κινήσεων» Παρακολουθώ στο δίκτυο τις τελευταίες µέρες να γίνεται συζήτηση για την «Αρχή ανεξαρτησίας των κινήσεων» ή την «επαλληλία εξισώσεων κίνησης». Προσπαθώ στο µέτρο
Αστρολογία για την Ψυχή Η Έκθεση Πέλε 10 Μαϊου 2017
 Αστρολογία για την Ψυχή Η Έκθεση Πέλε 10 Μαϊου 2017 Γεια σας ~ Καλημέρα ~ Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε, εδώ στο Flamingo Beach, (Κόστα Ρίκα) στις 10 Μαΐου 2017! Το νιώθετε; Νιώθετε ότι
Αστρολογία για την Ψυχή Η Έκθεση Πέλε 10 Μαϊου 2017 Γεια σας ~ Καλημέρα ~ Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε, εδώ στο Flamingo Beach, (Κόστα Ρίκα) στις 10 Μαΐου 2017! Το νιώθετε; Νιώθετε ότι
Η Έκθεση Πέλε 28, Δεκεμβρίου, Γεια σας! Αγνή Ζωή!
 Η Έκθεση Πέλε 28, Δεκεμβρίου, 2016 Γεια σας! Αγνή Ζωή! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε. Είμαι πολύ ενθουσιασμένος σήμερα, επειδή για τα Χριστούγεννα πήρα ένα Stabylcam. Αυτό υποτίθεται
Η Έκθεση Πέλε 28, Δεκεμβρίου, 2016 Γεια σας! Αγνή Ζωή! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε. Είμαι πολύ ενθουσιασμένος σήμερα, επειδή για τα Χριστούγεννα πήρα ένα Stabylcam. Αυτό υποτίθεται
Αστρολογία για την Ψυχή Η Έκθεση Πέλε 17 Ιανουαρίου, 2018
 Αστρολογία για την Ψυχή Η Έκθεση Πέλε 17 Ιανουαρίου, 2018 Γεια σας, κάτοικοι της Γης! Είμαι ο Kaypacha με άλλη μια εβδομαδιαία Έκθεση Πέλε, για την 17η Ιανουαρίου 2018. Και φυσικά, -είμαι κάτω δίπλα στο
Αστρολογία για την Ψυχή Η Έκθεση Πέλε 17 Ιανουαρίου, 2018 Γεια σας, κάτοικοι της Γης! Είμαι ο Kaypacha με άλλη μια εβδομαδιαία Έκθεση Πέλε, για την 17η Ιανουαρίου 2018. Και φυσικά, -είμαι κάτω δίπλα στο
Αστρολογία για την Ψυχή Η Έκθεση Πέλε 28 Ιουνΐου, 2017
 Αστρολογία για την Ψυχή Η Έκθεση Πέλε 28 Ιουνΐου, 2017 Hola! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε. Αυτή είναι η τελευταία Έκθεση Πέλε για το μήνα Ιούνιο, 28 Ιουνίου για να είμαι ακριβής, του
Αστρολογία για την Ψυχή Η Έκθεση Πέλε 28 Ιουνΐου, 2017 Hola! Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε. Αυτή είναι η τελευταία Έκθεση Πέλε για το μήνα Ιούνιο, 28 Ιουνίου για να είμαι ακριβής, του
Κεφάλαιο 9 ο Κ 5, 4 4, 5 0, 0 0,0 5, 4 4, 5. Όπως βλέπουµε το παίγνιο δεν έχει καµιά ισορροπία κατά Nash σε αµιγείς στρατηγικές διότι: (ΙΙ) Α Κ
 Κεφάλαιο ο Μεικτές Στρατηγικές Τώρα θα δούµε ένα παράδειγµα στο οποίο κάθε παίχτης έχει τρεις στρατηγικές. Αυτό θα µπορούσε να είναι η µορφή που παίρνει κάποιος µετά που έχει απαλείψει όλες τις αυστηρά
Κεφάλαιο ο Μεικτές Στρατηγικές Τώρα θα δούµε ένα παράδειγµα στο οποίο κάθε παίχτης έχει τρεις στρατηγικές. Αυτό θα µπορούσε να είναι η µορφή που παίρνει κάποιος µετά που έχει απαλείψει όλες τις αυστηρά
Είμαι ο Kaypacha με την εβδομαδιαία έκθεση Πέλε, και αυτή είναι η 15η Σεπτεμβρίου του 2015.
 Η Έκθεση Πέλε 15 Σεπτεμβρίου, 2015 Γεια σας! Namaste! * Το έκανα στη Λίμνη των Θαυμάτων στο Boulder του Κολοράντο! Είμαι ο Kaypacha με την εβδομαδιαία έκθεση Πέλε, και αυτή είναι η 15η Σεπτεμβρίου του
Η Έκθεση Πέλε 15 Σεπτεμβρίου, 2015 Γεια σας! Namaste! * Το έκανα στη Λίμνη των Θαυμάτων στο Boulder του Κολοράντο! Είμαι ο Kaypacha με την εβδομαδιαία έκθεση Πέλε, και αυτή είναι η 15η Σεπτεμβρίου του
Πλειστηριασμός Για να πλειοδοτήσει κάποιος άξονας θα πρέπει να αναλάβει την υποχρέωση
 Πλειστηριασμός Προκειμένου να περιγράψουμε το χέρι μας στο συμπαίκτη, χρησιμοποιούμε μια ειδική διεθνή γλώσσα τα Μπριτζικά ή Μπριτζιακά. Τα καλά νέα είναι ότι αυτή η γλώσσα έχει μόνο λίγες λεξούλες. Πλειστηριασμός
Πλειστηριασμός Προκειμένου να περιγράψουμε το χέρι μας στο συμπαίκτη, χρησιμοποιούμε μια ειδική διεθνή γλώσσα τα Μπριτζικά ή Μπριτζιακά. Τα καλά νέα είναι ότι αυτή η γλώσσα έχει μόνο λίγες λεξούλες. Πλειστηριασμός
1 / 15 «ΟΙ ΓΛΩΣΣΕΣ ΚΑΙ ΕΓΩ» Ερωτηµατολόγιο για τους µαθητές της 3 ης Γυµνασίου. Μάρτιος 2007
 1 / 15 ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Έρευνα υποστηριζόµενη από τη Γενική ιεύθυνση Εκπαίδευσης και Πολιτισµού της Ε.Ε., στο πλαίσιο του προγράµµατος Σωκράτης «ΟΙ ΓΛΩΣΣΕΣ ΚΑΙ ΕΓΩ» Ερωτηµατολόγιο
1 / 15 ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Έρευνα υποστηριζόµενη από τη Γενική ιεύθυνση Εκπαίδευσης και Πολιτισµού της Ε.Ε., στο πλαίσιο του προγράµµατος Σωκράτης «ΟΙ ΓΛΩΣΣΕΣ ΚΑΙ ΕΓΩ» Ερωτηµατολόγιο
THE ECONOMIST ΟΜΙΛΙΑ ALVARO PEREIRA DIRECTOR OF COUNTRY STUDIES, ECONOMICS DEPARTMENT, OECD
 THE ECONOMIST ΟΜΙΛΙΑ ALVARO PEREIRA DIRECTOR OF COUNTRY STUDIES, ECONOMICS DEPARTMENT, OECD TO THE 20 th ROUNDTABLE WITH THE GOVERNMENT OF GREECE EUROPE: SHAKEN AND STIRRED? GREECE: A SKILFUL ACORBAT?
THE ECONOMIST ΟΜΙΛΙΑ ALVARO PEREIRA DIRECTOR OF COUNTRY STUDIES, ECONOMICS DEPARTMENT, OECD TO THE 20 th ROUNDTABLE WITH THE GOVERNMENT OF GREECE EUROPE: SHAKEN AND STIRRED? GREECE: A SKILFUL ACORBAT?
KEΦΑΛΑΙΟ 1 AN HMΟΥΝ ΜΕΓΑΛΟΣ. Όταν είσαι μικρός ένα πράγμα είναι σίγουρο. Ότι θέλεις να μεγαλώσεις όσο πιο γρήγορα γίνεται.
 KEΦΑΛΑΙΟ 1 AN HMΟΥΝ ΜΕΓΑΛΟΣ Όταν είσαι μικρός ένα πράγμα είναι σίγουρο. Ότι θέλεις να μεγαλώσεις όσο πιο γρήγορα γίνεται. Ο μπαμπάς μου λέει ότι αυτά είναι χαζομάρες και ότι όταν μεγαλώσω θα θέλω να ήμουν
KEΦΑΛΑΙΟ 1 AN HMΟΥΝ ΜΕΓΑΛΟΣ Όταν είσαι μικρός ένα πράγμα είναι σίγουρο. Ότι θέλεις να μεγαλώσεις όσο πιο γρήγορα γίνεται. Ο μπαμπάς μου λέει ότι αυτά είναι χαζομάρες και ότι όταν μεγαλώσω θα θέλω να ήμουν
Η Έκθεση Πέλε για τις 24 Ιουνίου του 2015. Γειά σας!
 Η Έκθεση Πέλε για τις 24 Ιουνίου του 2015 Γειά σας! Είμαι ο Kaypacha με την εβδομαδιαία έκθεση Πέλε. Η έκθεση αυτή είναι για τις 24 Ιουνίου, 2015. Ναι, πράγματι, αυτή είναι η στιγμή. Ακριβώς σήμερα, έχουμε
Η Έκθεση Πέλε για τις 24 Ιουνίου του 2015 Γειά σας! Είμαι ο Kaypacha με την εβδομαδιαία έκθεση Πέλε. Η έκθεση αυτή είναι για τις 24 Ιουνίου, 2015. Ναι, πράγματι, αυτή είναι η στιγμή. Ακριβώς σήμερα, έχουμε
Η Έκθεση Πέλε 16 Νοεμβρίου, Γειά σας!
 Η Έκθεση Πέλε 16 Νοεμβρίου, 2016 Γειά σας! Είμαι ο Kaypacha, με την εβδομαδιαία Έκθεση Πέλε, μια αστρολογική άποψη του τι συμβαίνει εδώ στον πλανήτη Γη, για την 16η Νοεμβρίου του 2016. Είμαι εδώ στην ανατολική
Η Έκθεση Πέλε 16 Νοεμβρίου, 2016 Γειά σας! Είμαι ο Kaypacha, με την εβδομαδιαία Έκθεση Πέλε, μια αστρολογική άποψη του τι συμβαίνει εδώ στον πλανήτη Γη, για την 16η Νοεμβρίου του 2016. Είμαι εδώ στην ανατολική
«Πούλα τα όσο θες... πούλα ας πούµε το καλάµι από 200 ευρώ, 100. Κατάλαβες;»
 «Πούλα τα όσο θες... πούλα ας πούµε το καλάµι από 200 ευρώ, 100. Κατάλαβες;» Οπου (Α) ο καλούµενος - χρήστης της υπ' αριθ. 698... (µέλος της Χ.Α.) Οπου (Β) ο καλών Ηµεροµηνία: 20/09/2013 Εναρξη: 22:12':00''
«Πούλα τα όσο θες... πούλα ας πούµε το καλάµι από 200 ευρώ, 100. Κατάλαβες;» Οπου (Α) ο καλούµενος - χρήστης της υπ' αριθ. 698... (µέλος της Χ.Α.) Οπου (Β) ο καλών Ηµεροµηνία: 20/09/2013 Εναρξη: 22:12':00''
, όπου οι σταθερές προσδιορίζονται από τις αρχικές συνθήκες.
 Στην περίπτωση της ταλάντωσης µε κρίσιµη απόσβεση οι δύο γραµµικώς ανεξάρτητες λύσεις εκφυλίζονται (καταλήγουν να ταυτίζονται) Στην περιοχή ασθενούς απόσβεσης ( ) δύο γραµµικώς ανεξάρτητες λύσεις είναι
Στην περίπτωση της ταλάντωσης µε κρίσιµη απόσβεση οι δύο γραµµικώς ανεξάρτητες λύσεις εκφυλίζονται (καταλήγουν να ταυτίζονται) Στην περιοχή ασθενούς απόσβεσης ( ) δύο γραµµικώς ανεξάρτητες λύσεις είναι
Η έκθεση Πέλε - 28η Απριλίου 2015. Hola ~ Μπουένος Dias ~
 Η έκθεση Πέλε - 28η Απριλίου 2015 Hola ~ Μπουένος Dias ~ Είμαι ο Kaypacha με την εβδομαδιαία έκθεση Πέλε για τις 28 Απριλίου του 2015. Έρχομαι στη φύση για να ανανεώσω την ψυχή μου. Θεέ μου, μετά από μια
Η έκθεση Πέλε - 28η Απριλίου 2015 Hola ~ Μπουένος Dias ~ Είμαι ο Kaypacha με την εβδομαδιαία έκθεση Πέλε για τις 28 Απριλίου του 2015. Έρχομαι στη φύση για να ανανεώσω την ψυχή μου. Θεέ μου, μετά από μια
Η Έκθεση Πέλε 1 Δεκεμβρίου του Γεια σας!
 Η Έκθεση Πέλε 1 Δεκεμβρίου του 2016 Γεια σας! Εδώ είμαι στους καταρράκτες Kuang Si έξω από το Luang Prabang, στο Λάος. Και έχει δυνατό θόρυβο δίπλα στους καταρράκτες, οπότε πάω να βρω ένα ποιο κατάλληλο
Η Έκθεση Πέλε 1 Δεκεμβρίου του 2016 Γεια σας! Εδώ είμαι στους καταρράκτες Kuang Si έξω από το Luang Prabang, στο Λάος. Και έχει δυνατό θόρυβο δίπλα στους καταρράκτες, οπότε πάω να βρω ένα ποιο κατάλληλο
Απορρόφηση Αερίων (2)
 Απορρόφηση Αερίων (2) Λεπτομερής Ανάλυση Θεωρούμε έναν πύργο απορρόφησης που μπορεί να περιέχει δίσκους ή να είναι τύπου πληρωτικού υλικού ή άλλου τύπου. Τελικός σκοπός είναι να βρούμε το μέγεθος του πύργου.
Απορρόφηση Αερίων (2) Λεπτομερής Ανάλυση Θεωρούμε έναν πύργο απορρόφησης που μπορεί να περιέχει δίσκους ή να είναι τύπου πληρωτικού υλικού ή άλλου τύπου. Τελικός σκοπός είναι να βρούμε το μέγεθος του πύργου.
Πώς να μελετάμε τη Βίβλο
 Πώς να μελετάμε τη Βίβλο του David Batty Οδηγός Μελέτης Έκδοση 5 Πώς να μελετάμε τη Βίβλο Οδηγός Μελέτης 5η έκδοση του David Batty Σημείωση: Τα εδάφια της Βίβλου όπου αυτά αναφέρονται, είναι από τη νεοελληνική
Πώς να μελετάμε τη Βίβλο του David Batty Οδηγός Μελέτης Έκδοση 5 Πώς να μελετάμε τη Βίβλο Οδηγός Μελέτης 5η έκδοση του David Batty Σημείωση: Τα εδάφια της Βίβλου όπου αυτά αναφέρονται, είναι από τη νεοελληνική
x ν+1 =ax ν (1-x ν ) ή αλλιώς η απλούστερη περίπτωση ακολουθίας αριθμών με χαοτική συμπεριφορά.
 1 x ν+1 =ax ν (1-x ν ) ή αλλιώς η απλούστερη περίπτωση ακολουθίας αριθμών με χαοτική συμπεριφορά. Πριν λίγα χρόνια, όταν είχε έρθει στην Ελλάδα ο νομπελίστας χημικός Ilya Prigogine (πέθανε πρόσφατα), είχε
1 x ν+1 =ax ν (1-x ν ) ή αλλιώς η απλούστερη περίπτωση ακολουθίας αριθμών με χαοτική συμπεριφορά. Πριν λίγα χρόνια, όταν είχε έρθει στην Ελλάδα ο νομπελίστας χημικός Ilya Prigogine (πέθανε πρόσφατα), είχε
ΔΕΟ 24 Δημόσια διοίκηση και πολιτική. Τόμος 2 ος : Η διάρθρωση του Ελληνικού κράτους. Η Ελληνική Δημόσια Διοίκηση
 Τόμος 2 ος : Η διάρθρωση του Ελληνικού κράτους Η Ελληνική Δημόσια Διοίκηση Kυβέρνηση και Διακυβέρνηση Στην ακαδημαϊκή βιβλιογραφία, υπάρχει σαφής διάκριση ανάμεσα στην κρατική κυβερνητική και την κρατική
Τόμος 2 ος : Η διάρθρωση του Ελληνικού κράτους Η Ελληνική Δημόσια Διοίκηση Kυβέρνηση και Διακυβέρνηση Στην ακαδημαϊκή βιβλιογραφία, υπάρχει σαφής διάκριση ανάμεσα στην κρατική κυβερνητική και την κρατική
ΘΕΑΤΡΙΚΟ 2 ΠΟΛΙΤΙΚΗ ΚΟΥΖΙΝΑ
 ΘΕΑΤΡΙΚΟ 2 ΠΟΛΙΤΙΚΗ ΚΟΥΖΙΝΑ ΠΟΛΙΤΙΚΗ ΚΟΥΖΙΝΑ ΕΓΓΟΝΟΣ: Παππού, γιατί προτιμάς να βάζεις κανέλα και όχι κύμινο στα σουτζουκάκια; ΠΑΠΠΟΥΣ: Το κύμινο είναι κομματάκι δυνατό. Κάνει τους ανθρώπους να κλείνονται
ΘΕΑΤΡΙΚΟ 2 ΠΟΛΙΤΙΚΗ ΚΟΥΖΙΝΑ ΠΟΛΙΤΙΚΗ ΚΟΥΖΙΝΑ ΕΓΓΟΝΟΣ: Παππού, γιατί προτιμάς να βάζεις κανέλα και όχι κύμινο στα σουτζουκάκια; ΠΑΠΠΟΥΣ: Το κύμινο είναι κομματάκι δυνατό. Κάνει τους ανθρώπους να κλείνονται
Λήστευαν το δημόσιο χρήμα - Το B' Μέρος με τους αποκαλυπτικούς διαλόγους Άκη - Σμπώκου
 Λήστευαν το δημόσιο χρήμα - Το B' Μέρος με τους αποκαλυπτικούς διαλόγους Άκη - Σμπώκου - από τον Φουάτ σε τρεις εταιρίες χρήματα... μπλου μπρουμέλ, άλλη μια P.A κάπως έτσι και άλλη μία που μου είχες πει
Λήστευαν το δημόσιο χρήμα - Το B' Μέρος με τους αποκαλυπτικούς διαλόγους Άκη - Σμπώκου - από τον Φουάτ σε τρεις εταιρίες χρήματα... μπλου μπρουμέλ, άλλη μια P.A κάπως έτσι και άλλη μία που μου είχες πει
Η Έκθεση Πέλε - 13 Απριλίου, Γειά σε όλους ~ * Ο Kaypacha μοιράζεται την οθόνη του που τρέχει το Solar Fire Software.
 Η Έκθεση Πέλε - 13 Απριλίου, 2016 Γειά σε όλους ~ * Ο Kaypacha μοιράζεται την οθόνη του που τρέχει το Solar Fire Software. * Είμαι o Kaypacha με την εβδομαδιαία Έκθεση Πέλε. Είναι στην πραγματικότητα για
Η Έκθεση Πέλε - 13 Απριλίου, 2016 Γειά σε όλους ~ * Ο Kaypacha μοιράζεται την οθόνη του που τρέχει το Solar Fire Software. * Είμαι o Kaypacha με την εβδομαδιαία Έκθεση Πέλε. Είναι στην πραγματικότητα για
Ανάλυση κατά Συστάδες. Cluster analysis
 Ανάλυση κατά Συστάδες Cluster analysis 1 H ανάλυση κατά συστάδες είναι µια µέθοδος που σκοπό έχει να κατατάξει σε οµάδες τις υπάρχουσες παρατηρήσεις χρησιµοποιώντας την πληροφορία που υπάρχει σε κάποιες
Ανάλυση κατά Συστάδες Cluster analysis 1 H ανάλυση κατά συστάδες είναι µια µέθοδος που σκοπό έχει να κατατάξει σε οµάδες τις υπάρχουσες παρατηρήσεις χρησιµοποιώντας την πληροφορία που υπάρχει σε κάποιες
Η Έκθεση Πέλε 29 Ιουλίου, 2015
 Η Έκθεση Πέλε 29 Ιουλίου, 2015 Γεια σας! Είμαι ο Kaypacha με την εβδομαδιαία έκθεση Πέλε για τις 29 Ιουλίου 2015. Πρόκειται για κάτι σαν «Δελτίο Αστρολογίας». Σήμερα, ο Ήλιος είναι σε σύνοδο με τον Ερμή
Η Έκθεση Πέλε 29 Ιουλίου, 2015 Γεια σας! Είμαι ο Kaypacha με την εβδομαδιαία έκθεση Πέλε για τις 29 Ιουλίου 2015. Πρόκειται για κάτι σαν «Δελτίο Αστρολογίας». Σήμερα, ο Ήλιος είναι σε σύνοδο με τον Ερμή
* Ο Kaypacha μοιράζεται την οθόνη του που τρέχει το πρόγραμμα.
 Η Έκθεση Πέλε - 4 Μαΐου,2016 Γεια σας ~ Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε, και είναι 4 Μαΐου του 2016. Ήρθε η ώρα για ένα μικρό αστρονομικό και αστρολογικό μάθημα για όλους! Έχει περάσει
Η Έκθεση Πέλε - 4 Μαΐου,2016 Γεια σας ~ Είμαι ο Kaypacha με την εβδομαδιαία Έκθεση Πέλε, και είναι 4 Μαΐου του 2016. Ήρθε η ώρα για ένα μικρό αστρονομικό και αστρολογικό μάθημα για όλους! Έχει περάσει
Η Έκθεση Πέλε 6 Ιανουαρίου, 2016
 Η Έκθεση Πέλε 6 Ιανουαρίου, 2016 Γεια σας! Καλημέρα! Είμαι ο Kaypacha με την εβδομαδιαία έκθεση Πέλε. Είναι για την 6η Ιανουαρίου του 2016. Είμαι εδώ επάνω στο πλοίο MS Dixie Queen. Αυτό είναι το «Σπίτι
Η Έκθεση Πέλε 6 Ιανουαρίου, 2016 Γεια σας! Καλημέρα! Είμαι ο Kaypacha με την εβδομαδιαία έκθεση Πέλε. Είναι για την 6η Ιανουαρίου του 2016. Είμαι εδώ επάνω στο πλοίο MS Dixie Queen. Αυτό είναι το «Σπίτι
Οι 7 Γέφυρες του Königsberg
 Οι 7 Γέφυρες του Königsberg o Ένας γρίφος που έχει ανάγκη επίλυσης 1 Το πρόβληµα (1/3) Οι 7 Γέφυρες του Königsberg είναι ένα διάσηµο µαθηµατικό πρόβληµα εµπνευσµένο από µια πραγµατική πόλη στη Γερµανία.
Οι 7 Γέφυρες του Königsberg o Ένας γρίφος που έχει ανάγκη επίλυσης 1 Το πρόβληµα (1/3) Οι 7 Γέφυρες του Königsberg είναι ένα διάσηµο µαθηµατικό πρόβληµα εµπνευσµένο από µια πραγµατική πόλη στη Γερµανία.
Θέμα: Συνέντευξη της Υπουργού Εργασίας και Κοινωνικής Ασφάλισης, Λούκας Τ. Κατσέλη, στο ραδιοφωνικό σταθμό ΣΚΑΪ και το δημοσιογράφο Μπ.
 ΥΠΟΥΡΓΕΙΟ ΕΡΓΑΣΙΑΣ ΚΑΙ ΚΟΙΝΩΝΙΚΗΣ ΑΣΦΑΛΙΣΗΣ ΓΡΑΦΕΙΟ ΤΥΠΟΥ ΔΕΛΤΙΟ ΤΥΠΟΥ Ημερομηνία: Τετάρτη, 20 Οκτωβρίου 2010 Θέμα: Συνέντευξη της Υπουργού Εργασίας και Κοινωνικής Ασφάλισης, Λούκας Τ. Κατσέλη, στο ραδιοφωνικό
ΥΠΟΥΡΓΕΙΟ ΕΡΓΑΣΙΑΣ ΚΑΙ ΚΟΙΝΩΝΙΚΗΣ ΑΣΦΑΛΙΣΗΣ ΓΡΑΦΕΙΟ ΤΥΠΟΥ ΔΕΛΤΙΟ ΤΥΠΟΥ Ημερομηνία: Τετάρτη, 20 Οκτωβρίου 2010 Θέμα: Συνέντευξη της Υπουργού Εργασίας και Κοινωνικής Ασφάλισης, Λούκας Τ. Κατσέλη, στο ραδιοφωνικό
Αστρολογία. Εναλλακτική επιστήμη ή ψευδοεπιστήμη;
 4 ο Γενικό Λύκειο Κοζάνης Αστρολογία Εναλλακτική επιστήμη ή ψευδοεπιστήμη; Παρουσίαση της Ερευνητικής Εργασίας της Α Λυκείου, για το Α τετράμηνο 2012-2013 Επιβλέπων καθηγητής: Θεοχάρης Ταντανάσης Χωρισμός
4 ο Γενικό Λύκειο Κοζάνης Αστρολογία Εναλλακτική επιστήμη ή ψευδοεπιστήμη; Παρουσίαση της Ερευνητικής Εργασίας της Α Λυκείου, για το Α τετράμηνο 2012-2013 Επιβλέπων καθηγητής: Θεοχάρης Ταντανάσης Χωρισμός
Modern Greek Beginners
 2017 HIGHER SCHOOL CERTIFICATE EXAMINATION Modern Greek Beginners ( Section I Listening) Transcript Familiarisation Text Τι θέλεις να σπουδάσεις του χρόνου; Θέλω να γίνω φαρμακοποιός. Σε ποιο πανεπιστήμιο;
2017 HIGHER SCHOOL CERTIFICATE EXAMINATION Modern Greek Beginners ( Section I Listening) Transcript Familiarisation Text Τι θέλεις να σπουδάσεις του χρόνου; Θέλω να γίνω φαρμακοποιός. Σε ποιο πανεπιστήμιο;
Η διατήρηση της μηχανικής ενέργειας στην ελεύθερη πτώση.
 Η διατήρηση της μηχανικής ενέργειας στην ελεύθερη πτώση. (µε τη βοήθεια χρονοφωτογράφισης) Αφήνουµε µια µικρή σφαίρα, µάζας 0,2kg, να πέσει ελεύθερα, δίπλα σε ένα χάρακα, βαθµολογηµένο σε cm και τραβήξαµε
Η διατήρηση της μηχανικής ενέργειας στην ελεύθερη πτώση. (µε τη βοήθεια χρονοφωτογράφισης) Αφήνουµε µια µικρή σφαίρα, µάζας 0,2kg, να πέσει ελεύθερα, δίπλα σε ένα χάρακα, βαθµολογηµένο σε cm και τραβήξαµε
Αστρολογία για την Ψυχή Η Έκθεση Πέλε 31 Μαΐου, 2017
 Αστρολογία για την Ψυχή Η Έκθεση Πέλε 31 Μαΐου, 2017 Aloha! Είμαι ο Kaypacha με την Έκθεση Πέλε για τις 31 Μαΐου του 2017. Αυτό είναι το North Fork του American River εδώ (Καλιφόρνια) που ξεχειλίζει με
Αστρολογία για την Ψυχή Η Έκθεση Πέλε 31 Μαΐου, 2017 Aloha! Είμαι ο Kaypacha με την Έκθεση Πέλε για τις 31 Μαΐου του 2017. Αυτό είναι το North Fork του American River εδώ (Καλιφόρνια) που ξεχειλίζει με
ο ΣΤΑΤΙΚΟΣ ΗΛΕΚΤΡΙΣΜΟΣ
 ο ΣΤΑΤΙΚΟΣ ΗΛΕΚΤΡΙΣΜΟΣ η ΕΜΠΕΙΡΙΑ ΓΕΓΟΝΟΤΑ και ΑΝΤΙΚΕΙΜΕΝΑ οι ΙΔΕΕΣ και οι ΕΝΝΟΙΕΣ ηλεκτρικό φορτίο και ηλεκτρικό φορτίο στο µεταξύ κάποιος τον αναγκάζει να µε πλησιάζει κι όσο µε πλησιάζει τόσο περισσότερο
ο ΣΤΑΤΙΚΟΣ ΗΛΕΚΤΡΙΣΜΟΣ η ΕΜΠΕΙΡΙΑ ΓΕΓΟΝΟΤΑ και ΑΝΤΙΚΕΙΜΕΝΑ οι ΙΔΕΕΣ και οι ΕΝΝΟΙΕΣ ηλεκτρικό φορτίο και ηλεκτρικό φορτίο στο µεταξύ κάποιος τον αναγκάζει να µε πλησιάζει κι όσο µε πλησιάζει τόσο περισσότερο
Ι. Πανάρετος.: Καλησπέρα κυρία Γουδέλη, καλησπέρα κύριε Ρουμπάνη.
 (Συνέντευξη του Ι. Πανάρετου στην Νίνα Γουδέλη και τον Γρηγόρη Ρουμπάνη για τα θέματα της Παιδείας (Μήπως ζούμε σ άλλη χώρα;, ραδιοφωνικός σταθμός Αθήνα, 9.84) Ν. Γουδέλη: Καλησπέρα κύριε Πανάρετε. Γ.
(Συνέντευξη του Ι. Πανάρετου στην Νίνα Γουδέλη και τον Γρηγόρη Ρουμπάνη για τα θέματα της Παιδείας (Μήπως ζούμε σ άλλη χώρα;, ραδιοφωνικός σταθμός Αθήνα, 9.84) Ν. Γουδέλη: Καλησπέρα κύριε Πανάρετε. Γ.
ΣΧΕΔΙΑΓΡΑΜΜΑ ΑΡΙΣΤΟΤΕΛΗΣ ΗΘΙΚΑ ΝΙΚΟΜΑΧΕΙΑ
 ΣΧΕΔΙΑΓΡΑΜΜΑ ΑΡΙΣΤΟΤΕΛΗΣ ΗΘΙΚΑ ΝΙΚΟΜΑΧΕΙΑ Για τον Αριστοτέλη, όλες οι ενέργειες των ανθρώπων γίνονται για κάποιο τέλος, δηλαδή για κάποιο σκοπό που είναι ο ανώτερος όλων των αγαθών, την ευδαιμονία. Σύμφωνα
ΣΧΕΔΙΑΓΡΑΜΜΑ ΑΡΙΣΤΟΤΕΛΗΣ ΗΘΙΚΑ ΝΙΚΟΜΑΧΕΙΑ Για τον Αριστοτέλη, όλες οι ενέργειες των ανθρώπων γίνονται για κάποιο τέλος, δηλαδή για κάποιο σκοπό που είναι ο ανώτερος όλων των αγαθών, την ευδαιμονία. Σύμφωνα
