|
|
|
- ἸωσαΦάτ Φιλιππίδης
- 9 χρόνια πριν
- Προβολές:
Transcript
1 Επιμέλεια: xr.tsif Σελίδα 1
2 ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΓΙΑ ΜΑΘΗΤΙΚΟΥΣ ΔΙΑΓΩΝΙΣΜΟΥΣ ΕΚΦΩΝΗΣΕΙΣ ΤΕΥΧΟΣ 5ο ΑΣΚΗΣΕΙΣ Αφιερωμένο σε κάθε μαθητή που ασχολείται ή πρόκειται να ασχοληθεί με Μαθηματικούς διαγωνισμούς Τσιφάκης Χρήστος : xr.tsif Επιμέλεια: xr.tsif Σελίδα
3 ΘΕΜΑ 401 Δίνεται τρίγωνο ABC με AB AC. Πάνω στην βάση BC παίρνουμε σημείο D και πάνω στην πλευρά AC παίρνουμε το σημείο E έτσι ώστε η γωνία DAB να είναι ίση με το διπλάσιο της γωνίας CDE. Να αποδειχθεί ότι AD AE. ΘΕΜΑ 40 Δύο κύκλοι (O,R ),(O,R ) βρίσκονται ο ένας εκτός του άλλου. Να βρεθεί 1 1 α) Το μικρότερο ευθύγραμμο τμήμα που συνδέει σημεία των κύκλων. β) Το μεγαλύτερο ευθύγραμμο τμήμα που συνδέει σημεία των κύκλων. (Να γίνουν οι αποδείξεις). ΘΕΜΑ 403 Να δείξετε ότι δεν υπάρχουν φυσικοί αριθμοί m,n τέτοιοι ώστε οι αριθμοί m n και n m να είναι τετράγωνα φυσικών αριθμών. ΘΕΜΑ 404 Δίνονται οι πραγματικοί αριθμοί x,y για τους οποίους ισχύει ότι: x y a 4 και Να βρεθεί η ελάχιστη τιμή του x y a 3a 5, όπου και ο a είναι πραγματικός αριθμός. x y. ΘΕΜΑ 405 (Karanus) Εάν οι x,ψ,z πραγματικοί θετικοί αριθμοί τέτοιοι ώστε x ψ z 3, να 3 1 ψ 1 z 1 x αποδείξετε ότι 3. (Αρχιμήδης 008) x ψ z Επιμέλεια: xr.tsif Σελίδα 3
4 ΘΕΜΑ 406 (Karanus) Να βρεθεί ο μέγιστος θετικός ακέραιος x για τον οποίο ο αριθμός 18 x A είναι τετράγωνο ακεραίου αριθμού. ΘΕΜΑ 407 (Karanus) Αν x,ψ,z είναι θετικοί πραγματικοί αριθμοί τέτοιοι ώστε x ψ z 5 να y yz z προσδιορίσετε την ελάχιστη δυνατή τιμή της παράστασης A x x. z x y ΘΕΜΑ 408 Να βρείτε όλους τους ακεραίους n, για τους οποίους ο αριθμός είναι τετράγωνο ακεραίου. viewtopic.php?f=111&t= USAJMO: &t=404350& n n n ΘΕΜΑ 409 Να βρείτε όλους τους ακέραιους n για τους οποίους ο αριθμός είναι τέλειο τετράγωνο ακεραίου. n n n ΘΕΜΑ 410 Αν a,b,c θετικοί πραγματικοί αριθμοί για τους οποίους c a b να δείξετε ότι a b c 3abc (a b) c. ΘΕΜΑ 411 Αν a,b είναι πραγματικοί αριθμοί τέτοιοι ώστε 3a b και 3b a, να δείξετε ότι a b ( 3a b 3b a) 4 ab. Επιμέλεια: xr.tsif Σελίδα 4
5 ΘΕΜΑ 41 Να βρείτε τον μικρότερο τετραψήφιο αριθμό n για τον οποίο το σύστημα 3 3 x y x y y x n x y x y n 1 ΘΕΜΑ 413 έχει ακέραια ρίζα. Να βρείτε όλα τα ζεύγη φυσικών αριθμών (m,n)τέτοια ώστε τ (m) τ (n 15) 1 3τ (n 3n), όπου με τ(n) συμβολίζουμε το πλήθος των (θετικών) διαιρετών του φυσικού αριθμού n. ΘΕΜΑ 414 Τρείς μαθητές, οι A, B, συμμετέχουν σε ένα μαθηματικό διαγωνισμό. Στο διαγωνισμό δόθηκαν για λύση 5 προβλήματα. Η μέγιστη βαθμολογία για κάθε πρόβλημα είναι θετικός ακέραιος αριθμός, διαφορετικός για κάθε πρόβλημα. Ο μαθητής A έλυσε πλήρως 4 από τα προβλήματα και συγκέντρωσε 1 βαθμούς, ενώ ο μαθητής B έλυσε πλήρως 3 προβλήματα και η συνολική του βαθμολογία ήταν βαθμοί. Αν ο μαθητής έλυσε πλήρως όλα τα προβλήματα, να βρείτε τη μέγιστη και την ελάχιστη τιμή της βαθμολογίας του. ΘΕΜΑ 415 Δίνεται ισόπλευρο τρίγωνο πλευράς n, όπου n ένας θετικός ακέραιος. Σε κάθε πλευρά θεωρούμε σημεία που τη διαιρούν σε n ίσα τμήματα. Χρησιμοποιώντας αυτά τα σημεία φέρουμε παράλληλες στις πλευρές του τριγώνου. Έστω c το n πλήθος των ρόμβων πλευράς 1, που σχηματίζονται. Να δείξετε ότι η μεγαλύτερη λύση της ανίσωσης c 009 είναι πρώτος αριθμός. n Επιμέλεια: xr.tsif Σελίδα 5
6 ΘΕΜΑ 416 Μπορούμε να χωρίσουμε ένα ισόπλευρο τρίγωνο σε 011 μικρότερα τρίγωνα χρησιμοποιώντας 1 ευθείες; ΘΕΜΑ 417 x y z Να δείξετε ότι 1, για όλους τους y yz z x xz z x xy y πραγματικούς αριθμούς x,ψ,z για τους οποίους ορίζονται τα κλάσματα. ΘΕΜΑ 418 Έστω m,n *. Αν ακεραίου, να δείξετε ότι m / 3n και ο αριθμός m 3n. n m είναι τέλειο τετράγωνο ΘΕΜΑ 419 Ένα σύνολο ακεραίων λέγεται καλό αν κανένα στοιχείο του δε διαιρεί το άθροισμα των υπολοίπων. Πόσα το πολύ στοιχεία έχει ένα καλό υποσύνολο του συνόλου {1,,3,...,63}; ΘΕΜΑ 40 Να εξετάσετε αν υπάρχουν ρητοί a,b,c,d τέτοιοι ώστε 1 3 (a b 3) (c d 3). ΘΕΜΑ 41 Να προσδιορίσετε τους ακεραίους x,ψ έτσι ώστε x y Επιμέλεια: xr.tsif Σελίδα 6
7 ΘΕΜΑ 4 Μπορούμε να τοποθετήσουμε 011 σημεία στο επίπεδο έτσι ώστε: η απόσταση μεταξύ δύο οποιονδήποτε σημείων να είναι διαφορετική από 1 και κάθε μοναδιαίος κύκλος με κέντρο ένα από αυτά τα σημεία να αφήνει ακριβώς 1005 από αυτά τα σημεία στο εξωτερικό του; ΘΕΜΑ 43 Πόσα στοιχεία έχει το σύνολο ΘΕΜΑ 44 n 7 n n 6 {x x, n 1,,...,01} ; Να βρείτε τις θετικές ακέραιες ρίζες της εξίσωσης 3 (x y) (x y 6). ΘΕΜΑ 45 (Karanus) Να αποδειχθεί ότι υπάρχουν θετικοί πραγματικοί αριθμοί α και β για τους οποίους, αν ισχύει α β α β,τότε θα ισχύει α β. (ΑΡΧΙΜΗΔΗΣ 1999) ΘΕΜΑ 46 (Karanus) 4 3 Να βρεθούν όλοι οι φυσικοί αριθμοί n ώστε η A n 4n 5n 6n να είναι τετράγωνο φυσικού αριθμού. (ΑΡΧΙΜΗΔΗΣ 1997) ΘΕΜΑ 47 (Karanus) Να εξετάσετε εάν μπορούμε να ξαναγράψουμε τους αριθμούς 1,,3,4,5,6,7,8,9,10 σε μία σειρά ώστε: Επιμέλεια: xr.tsif Σελίδα 7
8 α) το άθροισμα οποιωνδήποτε τριών διαδοχικών αριθμών στη νέα σειρά,να μην υπερβαίνει το 16. β) το άθροισμα οποιωνδήποτε τριών διαδοχικών αριθμών στη νέα σειρά,να μην υπερβαίνει το 15. ΘΕΜΑ 48 Να λυθεί στο Ν το σύστημα: ΘΕΜΑ 49 x 7y 4z 10w 109. z y x 7 Έστω M ένα σύνολο θετικών ακεραίων τέτοιο ώστε: i) 1 M ii) Αν x M τότε x 3 M iii) Αν 4x 5 M τότε x M Να δείξετε ότι το M περιέχει 8 τουλάχιστον πρώτους και 8 τουλάχιστον σύνθετους αριθμούς. ΘΕΜΑ 430 Να βρείτε το n αν ισχύει 5 6 n n 4 n 5 ΘΕΜΑ 431 (freyia) Υποθέτουμε ότι υπάρχουν τρεις πραγματικές συναρτήσεις f,g,h ορισμένες στο A για τις οποίες ισχύουν f(x)g(x) h (x),g(x)h(x) f (x),h(x)f(x) g (x), για κάθε x A. Να αποδείξετε ότι f(x) g(x) h(x). Επιμέλεια: xr.tsif Σελίδα 8
9 ΘΕΜΑ 43 (gauss1988) Να εξετάσετε αν ο αριθμός είναι πρώτος. ΘΕΜΑ 43β (Παύλος Μαραγκουδάκης) Έστω A Να βρεθεί το υπόλοιπο της διαίρεσης του A με το 7. Ενισχύοντας την προσπάθεια του Θάνου να γίνουν κατανοητές οι λύσεις τέτοιου είδους ασκήσεων από μαθητές Γυμνασίου, να δώσω ένα είδος μεθοδολογίας για αυτές. Θα γράψω όλα όσα είναι απαραίτητα να γνωρίζουμε για τις ισοτιμίες: (α) Γράφουμε a b(modn) αν και μόνο αν ο φυσικός αριθμός n διαιρεί την διαφορά a b των ακεραίων a,b. (β) Αν a τότε a b(modn) και το υπόλοιπο της διαίρεσης του b με τον n είναι u, u(modn). (γ), m N. m m a b(modn) a b (modn) (δ) a b(modn) aq bq(modn),q N. (ε) a b(modn),c d(modn) a c b d(modn) a c b d(modn) ac bd(modn) (στ) a b(modn) a k b k(modn) για κάθε k Z. Επιμέλεια: xr.tsif Σελίδα 9
10 (ζ) Σε ασκήσεις τέτοιου είδους, όπου θέλουμε να βρούμε το υπόλοιπο της m διαίρεσης του a με το n, προσπαθούμε (αν αυτό είναι εφικτό), να καταλήξουμε σε ισοτιμία της μορφής: k a 0(modn) ή k a 1(modn) ή k a 1(modn). ΘΕΜΑ 433 (Παύλος Μαραγκουδάκης) α) Να βρεθεί η μεγαλύτερη δύναμη (100! ). k 7 που διαιρεί το 100! 100! β) Αν P, να βρεθεί το υπόλοιπο της διαίρεσης του P με το 7. k 7 ΘΕΜΑ 434 Να προσδιορίσετε όλες τις τριάδες (p,m,n) όπου p πρώτος και m,n μη αρνητικοί ακέραιοι, που είναι λύσεις της εξίσωσης m 3 p n 8. Ένα συγγενές θέμα (άσκηση 16) είδαμε εδώ: viewtopic.php?p=69084#p69084 ΘΕΜΑ 435 Να βρεθούν οι ακέραιες ρίζες της εξίσωσης x y 4z 8t 16xyzt. ΘΕΜΑ 436 Οι ρητοί αριθμοί x και y και ο περιττός θετικός ακέραιος n είναι τέτοιοι ώστε. Να δείξετε ότι x y. n n x x y y Επιμέλεια: xr.tsif Σελίδα 10
11 ΘΕΜΑ 437 Οι θετικοί πραγματικοί αριθμοί p,q είναι τέτοιοι ώστε Να δείξετε p q ότι p(p 1) q(q 1). Ποια η ελάχιστη τιμή της παράστασης 1 1 ; p(p 1) q(q 1) ΘΕΜΑ 438 Διαθέτουμε 100 βαρίδια βάρους 1,,3,...,100 κιλών αντίστοιχα. Τοποθετούμε όλα τα παραπάνω βαρίδια σε ζυγαριά ώστε αυτή να ισορροπεί. Να δείξετε ότι μπορούμε να αφαιρέσουμε δύο βαρίδια από κάθε πλευρά της ζυγαριάς και αυτή να εξακολουθεί να ισορροπεί! ΘΕΜΑ 439 Να προσδιορίσετε όλα τα ζεύγη θετικών ακεραίων (m,n) τέτοια ώστε οι m n n m αριθμοί και να είναι ακέραιοι. n m m n ΘΕΜΑ 440 Δίνεται ισοσκελές τρίγωνο ABC με βάση BC. Έστω D σημείο της πλευράς AB, Mτο μέσον της BC και E σημείο της πλευράς AC έτσι ώστε να είναι MB DB EC. Να αποδείξετε ότι τα τρίγωνα BDM, DEM, CEM είναι όμοια. ΘΕΜΑ 441 Θεωρούμε τραπέζιο ABCD με AD / /BC και AD BC. Έστω E το μέσο της διαγωνίου BD και F το ίχνος της καθέτου από το B στην AD. Να δείξετε ότι το τραπέζιο είναι ισοσκελές αν και μόνο αν το συμμετρικό του A ως προς το F και το συμμετρικό του C ως προς το E συμπίπτουν. Επιμέλεια: xr.tsif Σελίδα 11
12 ΘΕΜΑ 44 Στις κάθετες πλευρές AB και AC ορθογωνίου τριγώνου ABC κατασκευάζουμε εξωτερικά τα τετράγωνα ABDE και ACFG. Αν DC AB {U}, BF AC {V}, UV BD {P}, UV CF {Q}, να δείξετε ότι DF PQ UV. ΘΕΜΑ 443 Το σημείο D είναι το μέσο της πλευράς AC τριγώνου ABC και οι DE, DF διχοτόμοι των γωνιών A DB, CDB ότι EF DM. αντίστοιχα. Αν EF DB {M} να δείξετε ΘΕΜΑ 444 α) Να αποδείξετε ότι ο αριθμός (Παύλος Μαραγκουδάκης) A είναι ακέραιος. 3 β) Να βρείτε τα τελευταία ψηφία του αριθμού A. γ) Να βρείτε τα 7 τελευταία ψηφία του αριθμού ΘΕΜΑ 445 Να βρεθούν οι τιμές των ακεραίων αριθμών x,y, που επαληθεύουν την εξίσωση: x y x y. ΘΕΜΑ 446 (vzf) Αν για τους πραγματικούς αριθμούς a,b ισχύει ότι βρεθούν οι λύσεις της εξίσωσης (x a) (x b) x 0. a b a b ab 4 να Επιμέλεια: xr.tsif Σελίδα 1
13 ΘΕΜΑ 447 (vzf) Αν οι αριθμοί x,y,z είναι τέτοιοι ώστε x 0,y 1 0,z 0 και x y z 3, να αποδείξετε ότι x(y 1) (y 1)(z ) x(z ) 3. x y 1 y z 3 x z Για ποιές τιμές των x,y,z ισχύει η ισότητα; ΘΕΜΑ 448 Να λυθεί στους ακεραίους η εξίσωση 3 3 x y 4x 5y z 01. είναι η 405 viewtopic.php?f=109&t=15584&start=860 ΘΕΜΑ 449 Αν a,b,c 0 με a b c 3 να δείξετε ότι a b c 3. b c a Πριν δώσω την αναλυτική απόδειξη, θα γράψω μια πολύ χρήσιμη ανισότητα (που αναφέρεται ως "Γενικευμένη ανισότητα του Andreescu" ) Αν a,a,...,a,b,b,...,b 0,m 1,0 r m 1, τότε: 1 n 1 n a a a (a a... a ) b b b n (b b... b ) m m m m 1 n 1 n... r r r mr1 r 1 n 1 n. a a 1 n H ισότητα ισχύει, όταν.... b b 1 n ΘΕΜΑ 450 Αν a,b,c 0 με 1 ab bc ca να δείξετε ότι 3 Επιμέλεια: xr.tsif Σελίδα 13
14 a b c 1. a bc 1 b ca 1 c ab 1 a b c Θα χρησιμοποιήσουμε την ανισότητα Andreescu και την ταυτότητα του Euler H ανισότητα Andreescu έχει αναφερθεί προηγουμένως. Η ταυτότητα του Euler είναι η εξής: a b c 3abc (a b c)(a b c ab ac bc) 1 (a b c)[(a b) (b c) (c a) ]. ΘΕΜΑ Στον πίνακα είναι γραμμένος ο αριθμός 13. Σβήνουμε το τελευταίο του ψηφίο και στον αριθμό που προκύπτει προσθέτουμε το τετραπλάσιο αυτού του ψηφίου. Μπορούμε επαναλαμβάνοντας τη διαδικασία να πάρουμε τον αριθμό ; ΘΕΜΑ 45 * Ένα μη κενό σύνολο A είναι τέτοιο ώστε για κάθε x Aνα υπάρχουν y,z A με y z έτσι ώστε x y z. α) Βρείτε ένα τέτοιο σύνολο με 01 στοιχεία. β) Ποιος είναι ο ελάχιστος αριθμός στοιχείων ενός τέτοιου συνόλου; ΘΕΜΑ 453 Αν n 1 ακέραιος και pπρώτος, τέτοιοι ώστε n / p 1 και ότι ο αριθμός 4p 3 είναι τέλειο τετράγωνο ακεραίου. 3 p / n 1 να δείξετε Επιμέλεια: xr.tsif Σελίδα 14
15 ΘΕΜΑ 454 Αν a,b,c 0 με a b c, να δείξετε ότι a b c b c a a b c 3. bc(b c) ca(c a) ab(a b) ΘΕΜΑ 455 Βρείτε το ελάχιστο της παράστασης a b 1. ΘΕΜΑ a 1 b όπου a,b 0 με Να βρείτε τις ακέραιες ρίζες της εξίσωσης x 006 4y 4y 007y. ΘΕΜΑ 457 (vzf) Βρείτε τους x,y,u,v που ικανοποιούν το σύστημα των εξισώσεων: x 7y 3v 5u 16 8x 4y 6v u 16. x 6y 4v 8u 16 5x 3y 7v u 16 ΘΕΜΑ 458 (vzf) Να βρείτε τις ακέραιες ρίζες της εξίσωσης 5x 5xy 5y 7x 14y. ΘΕΜΑ 459 (vzf) Να αποδείξετε ότι αν p είναι ο n οστός πρώτος αριθμός, τότε ισχύει n (η ισότητα ισχύει μόνο για n 1). pn n 1 Επιμέλεια: xr.tsif Σελίδα 15
16 ΘΕΜΑ 460 (vzf) ax by (x y) Να βρεθούν οι πραγματικές λύσεις (x,y,z) του συστήματος: by cz (y z) cz ax (z x) με a,b,c δεδομένους θετικούς πραγματικούς αριθμούς. ΘΕΜΑ 461 (vzf) Έστω S ένα σύνολο με n στοιχεία ( n ) και έστω A,A,...,A υποσύνολα 1 m του S (m ). Αν για κάθε δύο διαφορετικά στοιχεία x,y S υπάρχει ένα υποσύνολο m n. A τέτοιο ώστε i x A και y A i i ή x A και y A, αποδείξτε ότι i i Είναι από βαλκανιάδες: f#p f#p8805. ΘΕΜΑ 46 (vzf) Έστω n θετικός ακέραιος. Δείξτε ότι ο n [( 3) ] είναι περιττός αριθμός. (Όπου με [x] συμβολίζουμε το ακέραιο μέρος του αριθμού x ). ΘΕΜΑ 463 (freyia) Να αποδείξετε ότι ο αριθμός ακέραιο. 13 n n, διαιρείται με τον αριθμό 730, με n Mε αφορμή την ΑΣΚΗΣΗ 463 και την λύση που έδωσε ο Θάνος, θα γράψω το θεώρημα του Fermat, ώστε να μπορούμε πλέον να το χρησιμοποιούμε. *********************************************************** Επιμέλεια: xr.tsif Σελίδα 16
17 ΜΙΚΡΟ ΘΕΩΡΗΜΑ ΤΟΥ FERMAT Αν pπρώτος, a Z και (a,p) 1 τότε: a 1(modp). p 1 *********************************************************** Άμεση συνέπεια αυτού του θεωρήματος είναι το εξής: Αν pπρώτος και a Z τότε p a a(modp). *********************************************************** Για παράδειγμα: a a(mod13) a a πολ13. Για εξοικείωση με το θεώρημα του Fermat, δίνονται οι παρακάτω ασκήσεις: ΘΕΜΑ 464 Δείξτε ότι: διαιρείται με το 17. Λύση: Νομίζω ότι η συγκεκριμένη άσκηση λύνεται απλούστερα χωρίς το θεώρημα n n Fermat, παρά μόνο με χρήση της ιδιότητας (a b) / (a b ) όταν n είναι περιττός φυσικός. Πράγματι, το 17 διαιρεί όλα τα αθροίσματα , 15, 3 14, 4 13, 5 1, 6 11, 7 10, 8 9 και φυσικά διαιρεί και το Β τρόπος Με Fermat, γράφω την λύση για εξοικείωση με το θεώρημα αυτό: Επιμέλεια: xr.tsif Σελίδα 17
18 17 1 1(mod17) 17 (mod17) (mod17) Mε πρόσθεση, έχουμε: (mod17) 917(mod17) πολ17. ΘΕΜΑ 465 Δείξτε ότι το υπόλοιπο της διαίρεσης του Από το μικρό θεώρημα του Fermat : Λύση: 7 1 με το 73 είναι (mod73) 1 1(mod73). Επομένως το υπόλοιπο είναι 1. ΘΕΜΑ 466 Δείξτε ότι ο αριθμός 5 3 9a 10a 4a διαιρείται με το 15 για κάθε Λύση: a * N. Θα αποδείξουμε ότι η παράσταση διαιρείται από τους 3 και 5, οπότε, επειδή είναι πρώτοι μεταξύ τους, θα διαιρείται και από το γινόμενό τους, που είναι το 15. Από το θεώρημα του Fermat είναι 5 a a(mod5) και 3 a a(mod 3). Επιμέλεια: xr.tsif Σελίδα 18
19 Δουλεύοντας mod3 έχουμε : a 10a 4a 9a 10a 4a 9a 6a 3(3a a) 0(mod 3). Δουλεύοντας mod5 έχουμε a 10a 4a 9a 10a 4a 5a 10a 5(a a ) 0(mod5). Τελειώσαμε. Β τρόπος a 10a 4a 3(3a 3a a) a a 5 3 3(3a 3a a) (a 1)a(a 1) πoλ3. (*) το γινόμενο 3 διαδοχικών ακεραίων (a 1)a(a 1) πoλ a 10a 4a 10a 10a 5a [(a 5a 4a) (5a 5a)] (a a a) (a )(a 1)a(a 1)(a ) 5(a a) πoλ5. (**) το γινόμενο 5 διαδοχικών ακεραίων (a )(a 1)a(a 1)(a ) πoλ5. και 3, 5 πρώτοι μεταξύ τους οπότε προκύπτει το ζητούμενο. ΘΕΜΑ 467 Να βρεθεί το υπόλοιπο της διαίρεσης του αριθμού Λύση: 4n 5 10 με το 13. Επειδή οι αριθμοί 10,13 είναι πρώτοι μεταξύ τους, από το θεώρημα Fermat 1 4n 4n5 5 ισχύει 10 1(mod13) 10 1(mod13) ( mod13). Εκτελώντας τη διαίρεση 10000:13 βρίσκουμε υπόλοιπο 3, το οποίο είναι και το ζητούμενο. Επιμέλεια: xr.tsif Σελίδα 19
20 ΘΕΜΑ 468 Αν p,q είναι δύο διαφορετικοί πρώτοι αριθμοί, να αποδείξετε ότι: q1 p1 p q 1(modpq). Λύση: Επειδή οι p,q είναι διαφορετικοί πρώτοι, είναι πρώτοι μεταξύ τους. Άρα, από το θεώρημα Fermat έχουμε p 1(modq) και ισχύει προφανώς q 1 q 0(modq), p 1 άρα q1 p1 p q 1(modq) (1). Με τον ίδιο ακριβώς τρόπο προκύπτει και q1 p1 p q 1(modp) (). Επειδή οι p,q είναι διαφορετικοί πρώτοι, είναι πρώτοι μεταξύ τους, οπότε q1 p1 p q 1(modpq). ΘΕΜΑ 469 Να εξετάσετε αν υπάρχει πρώτος αριθμός pτέτοιος ώστε να είναι: Λύση: Ο μοναδικός πρώτος με αυτή την ιδιότητα είναι ο 5. Πράγματι, από το θεώρημα Fermat είναι p 3(modp) 3(modp) p 5 p 5. p (modp) οπότε ισχύει p p 3. ΘΕΜΑ 470 Να αποδείξετε ότι το κλάσμα n 3 n 4 n 3n 1 είναι ανάγωγο, για κάθε ακέραιο n. Επιμέλεια: xr.tsif Σελίδα 0
21 ΘΕΜΑ 471 Να βρεθούν όλοι οι ακέραιοι n, για τους οποίους ο αριθμός 3 A n (n 4) n(7n 10) 10, να είναι τέλειο τετράγωνο ακεραίου. ΘΕΜΑ 47 Βρείτε τις μη αρνητικές ακέραιες λύσεις της εξίσωσης 3 3 x 7x 35x 7 y. ΘΕΜΑ 473 Αν x,y,z διαδοχικοί ακέραιοι τέτοιοι ώστε να βρείτε το βρείτε x y z 45 το μέγιστο του x y z. ΘΕΜΑ 474 Αν x,y θετικοί αριθμοί τέτοιοι ώστε (1 x)(1 y) να δείξετε ότι 1 xy 6. xy ΘΕΜΑ 475 Έστω x,y,z μη αρνητικοί αριθμοί τέτοιοι ώστε xy yz zx 0. Να δείξετε ότι x y y z y z z x z x x y x y z 5. y z x y z x y z x y z x xy yz zx Πότε ισχύει η ισότητα; ΘΕΜΑ 476 Αν a,b,c θετικοί αριθμοί, να δείξετε ότι 5a 5c 8b 8(a b) (b c) (c a) 4ac (abc) 3 9. cyc Επιμέλεια: xr.tsif Σελίδα 1
22 Μια λύση: b#p5051. ΘΕΜΑ 477 Αν οι ακέραιοι x,y,z είναι τέτοιοι ώστε x y z 0 να δείξετε ότι 3 / xyz. ΘΕΜΑ 478 Να λυθεί το σύστημα x y y y x x 3 3. ΘΕΜΑ 479 Βρείτε όλους τους θετικούς ακεραίους a,b για τους οποίους a(a b) 1 / (a b)(b 1) 1. ΘΕΜΑ 480 (α) Αν οι αριθμοί x y και οι x,y ρητοί; x y όπου x,y είναι ρητοί είναι υποχρεωτικά (β) Αν οι αριθμοί x y, x y και υποχρεωτικά οι x,y ρητοί; ΘΕΜΑ 481 x 3 y όπου x,y είναι ρητοί είναι Αν 1 x1 n και n n 1 1 y1 n να συγκρίνετε τους αριθμούς y x x,y. ΘΕΜΑ 48 Να δείξετε ότι (a a b b ) 3(a b ab ), a,b. Επιμέλεια: xr.tsif Σελίδα
23 ΘΕΜΑ 483 Έστω S υποσύνολο του A {1,, 3,...,9} τέτοιο ώστε να μην υπάρχουν δύο ίσα αθροίσματα a b, a,bs, a b. Πόσα το πολύ στοιχεία έχει το S ; 6b#p ΘΕΜΑ 484 Έστω a b θετικοί ακέραιοι ίδιας αρτιότητας. Δείξτε ότι η εξίσωση x (a a 1)(x b 1) (b 1) 0 έχει θετικές ακέραιες ρίζες καμία από τις οποίες δεν είναι τέλειο τετράγωνο ακεραίου. ΘΕΜΑ 485 Οι θετικοί αριθμοί x,y,z είναι τέτοιοι ώστε x yz y zx z xy (x y z). Να δείξετε ότι x y z 6. ΘΕΜΑ 486 Θεωρούμε τραπέζιο ABCD με AD / /BC τέτοιο ώστε AB AD BC. Να δείξετε ότι η διχοτόμος της A διχοτομεί την πλευρά CD. ΘΕΜΑ 487 a a b b c c Να δείξετε ότι 3( a b c), για όλους τους bc ca ab θετικούς αριθμούς a,b,c με ab bc ca 1. ΘΕΜΑ 488 Να δείξετε ότι αριθμούς a,b,c με a b c 3 b c c a a b 1 3 a b c 1., για όλους τους θετικούς Επιμέλεια: xr.tsif Σελίδα 3
24 ΘΕΜΑ 489 Να δείξετε ότι 1 cyc a 3. cyc a 1 6 για όλους τους θετικούς αριθμούς a,b,c με a a 1 Λύση: Είναι από την x y xy. a 1 a a 1 a a ( ) a a 1 a. a a 1 a a 1 a a 1 Αρκεί τώρα, να αποδειχθεί ότι a b c 3. Όμως, από την ανισότητα ΑΜ ΓΜ είναι 6 a b c 3 abc 3, αφού abc 1. Αυτό συμβαίνει επειδή πάλι από την ΑΜ ΓΜ έχουμε abc 1. 3 a b c abc ΘΕΜΑ 490 Να δείξετε ότι x y z a b c xy yz zx για όλους τους θετικούς αριθμούς a,b,c,x,y,z με a b c 3. Πάλι Cauchy-Schwarz: Είναι Λύση: Επιμέλεια: xr.tsif Σελίδα 4
25 x y z ( x y z ) ( x y z ) xy yz zx, a b c a b c 3 όπου έγινε χρήση της a b c 3(a b c ) και της (a b c) 3(ab bc ca) για a x κ.τ.λ. ΘΕΜΑ 491 Να δείξετε ότι για όλους τους θετικούς αριθμούς a,b,c ab bc ac a c a b b c (a b ) c (b c ) a (c a ) b 0. Καταρχήν λόγω της ab(a b ) a b Οι τριάδες ab(a b) Λύση: (a b ) (a b) παίρνουμε ότι (1). (a,b,c), (a b,a c,b c ), (ab,ac,bc) έχουν την ίδια διάταξη συνεπώς το ίδιο συμβαίνει και με τις τριάδες (a,b,c), (ab(a b ), ac(a c ),bc(b c )), άρα τελικά οι τριάδες (ab(a b ),ac(a c ),bc(b c )) και αντίθετη διάταξη. Συνεπώς από την ανισότητα της αναδιάταξης παίρνουμε: 1 1 1,, a b a c b c έχουν ab(a b ) ac(a c ) bc(b c ) ab(a b ) a c b c a b a b Επιμέλεια: xr.tsif Σελίδα 5
26 (1) ac(a c ) bc(b c ) ab(a b) ac(a c) bc(b c) a c b c c(a b ) b(a c ) a(b c ), που είναι η ζητούμενη.. ΘΕΜΑ 49 Έστω x,y με x y 1. Βρείτε το ελάχιστο του * 1 1 x y x y. ΘΕΜΑ 493 (a) Βρείτε μια λύση της εξίσωσης (b) Δείξτε ότι η εξίσωση x y 1010 στο σύνολο των ακεραίων. x y z έχει άπειρες ακέραιες λύσεις. Είναι από εδώ: ΣΗΜΕΙΩΣΕΙΣ Θα προσπαθήσω να εξηγήσω εδώ ποιοί θετικοί ακέραιοι γράφονται σαν άθροισμα δύο ακέραιων τετραγώνων και με πόσους τρόπους μπορεί να γίνει αυτό. Το πρώτο λήμμα είναι αρκετά απλό και η απόδειξή του αφήνεται στον αναγνώστη. Λήμμα 1: Αν n 3(mod4) τότε ο n δεν μπορεί να γραφτεί σαν άθροισμα δύο τετραγώνων. Το επόμενο λήμμα μάλλον είναι γνωστό σε αρκετούς. Μια απόδειξή του βασίζεται σε τετραγωνικά ισοϋπόλοιπα για τα οποία ίσως να μιλήσουμε άλλη φορά. Λήμμα : Αν p 3(mod4) πρώτος και p / m n, τότε p / m και p / n. Επιμέλεια: xr.tsif Σελίδα 6
27 (Άρα p / m n.) Πόρισμα 3: Αν ο αριθμός n γράφεται σαν άθροισμα δύο τετραγώνων, και k p 3(mod4) πρώτος που διαιρεί τον n τότε υπάρχει k ώστε ο p διαιρεί τον n αλλά ο k 1 p δεν τον διαιρεί. Η απόδειξη είναι σχετικά εύκολη και αφήνεται στον αναγνώστη. Θα δούμε σε λίγο ότι ισχύει και το αντίστροφο. Για αρχή Θεώρημα 4 (Fermat): Κάθε πρώτος της μορφής p γραφτεί σαν άθροισμα δύο τετραγώνων Μπορείτε να βρείτε αρκετές αποδείξεις εδώ. 1(mod4) μπορεί να Παρατήρηση 5: Αν ο n και ο m μπορούν να γραφούν σαν αθροίσματα δύο τετραγώνων (επιτρέπουμε την χρησιμοποίηση του 0), τότε το ίδιο ισχύει και για τον n m. Η απόδειξη υπάρχει και στο παραπάνω link, αλλά την βάζω διότι είναι σύντομη, εξαιρετικά όμορφη και θα χρησιμεύσει αργότερα. Απόδειξη: Αν n b και m c d τότε nm ( c bd) (ad bc). Επειδή ο γράφεται σαν άθροισμα δύο τετραγώνων, και κάθε τετράγωνο γράφεται σαν άθροισμα δύο τετραγώνων έχουμε : Θεώρημα 6: Ο αριθμός n γράφεται σαν άθροισμα δύο τετραγώνων αν και μόνο αν όλοι οι διαιρέτες του της μορφής p 3(mod4) βρίσκονται σε άρτια δύναμη στην παραγοντοποίηση του n. Τώρα ξέρουμε ποιοί αριθμοί γράφονται σαν άθροισμα δύο τετραγώνων αλλά με Επιμέλεια: xr.tsif Σελίδα 7
28 πόσους τρόπους μπορεί να γίνει αυτό; Θεώρημα 4β: Κάθε πρώτος της μορφής p μοναδικό τρόπο σαν άθροισμα δύο τετραγώνων. 1(mod4) μπορεί να γραφτεί με Για παράδειγμα, ο μόνος τρόπος να γράψουμε το 1997 ως άθροισμα δύο τετραγώνων είναι Το 1997 που μας απασχόλησε σε άλλη άσκηση μπορεί να γραφτεί σαν 1997 (1 1 ) (9 34 ) (9 34 ) και χρησιμοποιώντας τον τύπο στην απόδειξη της παρατήρησης 5 βρίσκουμε 1997 (1 1 ) (9 34 ) (9 34 ) (1 1 ) ( ) (1 1 ) (9 34 ) (9 34 ) (1 1 ) ( ) Το θεώρημα λέει πως αν δουλέψουμε όπως πιο πάνω τότε μπορούμε να βρούμε όλους τους τρόπους που γράφεται ένας αριθμός σαν άθροισμα δύο τετραγώνων. (Δεν είμαι σίγουρος αν αυτό το θεώρημα είναι του Gauss ή όχι. Μπορεί όμως να αποδειχθεί χρησιμοποιώντας Gaussian integers.) Μπορεί κάποιος να μετρήσει με πόσους τρόπους μπορεί να γίνει αυτό αλλά είναι λίγο πολύπλοκο και θέλει αρκετή προσοχή. (Για παράδειγμα, στην άσκηση που μας ενδιέφερε είχα πει πως γίνεται με τρεις τρόπους επειδή μετρούσα το μία φορά και το δύο φορές.) ΘΕΜΑ 494 Έστω a,b,c,d με a b 1. Δείξτε ότι (1 bd) (a b 1)(c d 1). Επιμέλεια: xr.tsif Σελίδα 8
29 ΘΕΜΑ 495 (sokratis lyras) Έστω η ακολουθία a με n δείξετε ότι a c n a a,a b,c 0,a και 1 n1 ab 0. Nα a a b c n1 a Z a,b, Z για κάθε i N. i ab Πρόκειται για το Πρόβλημα 3 της Βαλκανικής Μαθηματικής Ολυμπιάδας του ΘΕΜΑ 496 Λύστε στους πρώτους την εξίσωση p q r s t. ΘΕΜΑ 497 Να βρείτε όλους τους θετικούς ακεραίους που είναι ίσοι με 300 φορές το άθροισμα των ψηφίων τους. ΘΕΜΑ 498 Υπάρχουν ακέραιοι 0 a b c, τέτοιοι ώστε b a c b a c ; ΘΕΜΑ 499 Να λυθεί η εξίσωση a b [a,b] (a,b) ΘΕΜΑ 500 Αν οι διαφορετικοί ανά δύο και μη μηδενικοί αριθμοί a,b,c,d είναι τέτοιοι ώστε ac bd και a b c d 4, να βρείτε το μέγιστο του a c b d. b c d a c a d b Επιμέλεια: xr.tsif Σελίδα 9
ΤΡΟΠΟΠΟΙΗΣΗ ΕΤΑΙΡΙΚΟΥ ΣΥΜΦΩΝΗΤΙΚΟΥ Στην Πάτρα σήμερα την 4 ΜΑΡΤΙΟΥ 2013 οι παρακάτω συμβαλλόμενοι: ΑΓΓΕΛΕΤΟΠΟΥΛΟΥ ΑΦΡΟΔΙΤΗ ΑΛΕΞΟΠΟΥΛΟΥ
 ΤΡΟΠΟΠΟΙΗΣΗ ΕΤΑΙΡΙΚΟΥ ΣΥΜΦΩΝΗΤΙΚΟΥ Στην Πάτρα σήμερα την 4 ΜΑΡΤΙΟΥ 2013 οι παρακάτω συμβαλλόμενοι: ΑΓΓΕΛΕΤΟΠΟΥΛΟΥ ΑΦΡΟΔΙΤΗ ΑΛΕΞΟΠΟΥΛΟΥ ΗΡΩ ΑΝΑΓΝΩΣΤΟΥ ΓΕΩΡΓΙΟΣ ΑΝΔΡΙΟΠΟΥΛΟΣ ΙΩΑΝΝΗΣ ΑΤΤΕΪΑ ΔΗΜΟΣΘΕΝΗΣ ΒΑΣΙΛΕΙΟΥ
ΤΡΟΠΟΠΟΙΗΣΗ ΕΤΑΙΡΙΚΟΥ ΣΥΜΦΩΝΗΤΙΚΟΥ Στην Πάτρα σήμερα την 4 ΜΑΡΤΙΟΥ 2013 οι παρακάτω συμβαλλόμενοι: ΑΓΓΕΛΕΤΟΠΟΥΛΟΥ ΑΦΡΟΔΙΤΗ ΑΛΕΞΟΠΟΥΛΟΥ ΗΡΩ ΑΝΑΓΝΩΣΤΟΥ ΓΕΩΡΓΙΟΣ ΑΝΔΡΙΟΠΟΥΛΟΣ ΙΩΑΝΝΗΣ ΑΤΤΕΪΑ ΔΗΜΟΣΘΕΝΗΣ ΒΑΣΙΛΕΙΟΥ
http://www.mathematica.gr/forum/viewtopic.php?f=109&t=15584
 Επιμέλεια : xr.tsif Σελίδα 1 ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΓΙΑ ΜΑΘΗΤΙΚΟΥΣ ΔΙΑΓΩΝΙΣΜΟΥΣ ΕΚΦΩΝΗΣΕΙΣ ΤΕΥΧΟΣ ΑΣΚΗΣΕΙΣ 101-00 Αφιερωμέν σε κάθε μαθητή πυ ασχλείται ή πρόκειται να ασχληθεί με Μαθηματικύς διαγωνισμύς
Επιμέλεια : xr.tsif Σελίδα 1 ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΓΙΑ ΜΑΘΗΤΙΚΟΥΣ ΔΙΑΓΩΝΙΣΜΟΥΣ ΕΚΦΩΝΗΣΕΙΣ ΤΕΥΧΟΣ ΑΣΚΗΣΕΙΣ 101-00 Αφιερωμέν σε κάθε μαθητή πυ ασχλείται ή πρόκειται να ασχληθεί με Μαθηματικύς διαγωνισμύς
Κατερίνα Ροζάκου. Διδακτορική Διατριβή. Οι πολιτικές του δώρου: Κοινωνικές και πολιτισμικές διαστάσεις της εθελοντικής εργασίας.
 Πανεπιστήμιο Αιγαίου Σχολή Κοινωνικών Επιστημών Τμήμα Κοινωνικής Ανθρωπολογίας και Ιστορίας Κατερίνα Ροζάκου Διδακτορική Διατριβή Οι πολιτικές του δώρου: Κοινωνικές και πολιτισμικές διαστάσεις της εθελοντικής
Πανεπιστήμιο Αιγαίου Σχολή Κοινωνικών Επιστημών Τμήμα Κοινωνικής Ανθρωπολογίας και Ιστορίας Κατερίνα Ροζάκου Διδακτορική Διατριβή Οι πολιτικές του δώρου: Κοινωνικές και πολιτισμικές διαστάσεις της εθελοντικής
Π.Δ. 396/94 (ΦΕΚ 220 Α
 Π.Δ. 396/94 (ΦΕΚ 220 Α - Διόρθ. Σφάλμ. στο ΦΕΚ 6 Α): Ελάχιστες προδιαγραφές ασφάλειας και υγείας για τη χρήση από τους εργαζόμενους εξοπλισμών ατομικής προστασίας κατά την εργασία σε συμμόρφωση προς την
Π.Δ. 396/94 (ΦΕΚ 220 Α - Διόρθ. Σφάλμ. στο ΦΕΚ 6 Α): Ελάχιστες προδιαγραφές ασφάλειας και υγείας για τη χρήση από τους εργαζόμενους εξοπλισμών ατομικής προστασίας κατά την εργασία σε συμμόρφωση προς την
ΑΝΩΤΑΤΗ ΣΧΟΛΗ ΠΑΙΔΑΓΩΓΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΑΝΑΡΤΗΤΕΑ ΣΤΗ ΔΙΑΥΓΕΙΑ Α.Σ.ΠΑΙ.Τ.Ε. ΑΝΩΤΑΤΗ ΣΧΟΛΗ ΠΑΙΔΑΓΩΓΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΕΔΡΑ: ΑΜΑΡΟΥΣΙΟ (ΣΤΑΘΜΟΣ «ΕΙΡΗΝΗ» ΗΣΑΠ) Αριθμ. Πρωτ.:Δ/2450 ΤΑΧ.Δ/ΝΣΗ : ΗΡΑΚΛΕΙΟ ΑΤΤΙΚΗΣ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΑΝΑΡΤΗΤΕΑ ΣΤΗ ΔΙΑΥΓΕΙΑ Α.Σ.ΠΑΙ.Τ.Ε. ΑΝΩΤΑΤΗ ΣΧΟΛΗ ΠΑΙΔΑΓΩΓΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΕΔΡΑ: ΑΜΑΡΟΥΣΙΟ (ΣΤΑΘΜΟΣ «ΕΙΡΗΝΗ» ΗΣΑΠ) Αριθμ. Πρωτ.:Δ/2450 ΤΑΧ.Δ/ΝΣΗ : ΗΡΑΚΛΕΙΟ ΑΤΤΙΚΗΣ
ΚΑΤΑΣΤΑΤΙΚΟ ΤΗΣ ΑΝΩΝΥΜΗΣ ΕΤΑΙΡΕΙΑΣ «ΓΑΛΑΞΙΔΙ ΘΑΛΑΣΣΙΕΣ ΚΑΛΛΙΕΡΓΕΙΕΣ ΑΝΩΝΥΜΗ ΕΤΑΙΡΙΑ» ΚΕΦΑΛΑΙΟ Α Σύσταση, επωνυμία, έδρα, σκοπός και διάρκεια
 ΚΑΤΑΣΤΑΤΙΚΟ ΤΗΣ ΑΝΩΝΥΜΗΣ ΕΤΑΙΡΕΙΑΣ «ΓΑΛΑΞΙΔΙ ΘΑΛΑΣΣΙΕΣ ΚΑΛΛΙΕΡΓΕΙΕΣ ΑΝΩΝΥΜΗ ΕΤΑΙΡΙΑ» ΚΕΦΑΛΑΙΟ Α Σύσταση, επωνυμία, έδρα, σκοπός και διάρκεια Άρθρο 1 Συστήνεται με το παρόν καταστατικό Ανώνυμη Εταιρία με
ΚΑΤΑΣΤΑΤΙΚΟ ΤΗΣ ΑΝΩΝΥΜΗΣ ΕΤΑΙΡΕΙΑΣ «ΓΑΛΑΞΙΔΙ ΘΑΛΑΣΣΙΕΣ ΚΑΛΛΙΕΡΓΕΙΕΣ ΑΝΩΝΥΜΗ ΕΤΑΙΡΙΑ» ΚΕΦΑΛΑΙΟ Α Σύσταση, επωνυμία, έδρα, σκοπός και διάρκεια Άρθρο 1 Συστήνεται με το παρόν καταστατικό Ανώνυμη Εταιρία με
ΘΕΜΑΤΟΛΟΓΙΟ ΚΑΙ ΟΔΗΓΙΕΣ ΟΡΓΑΝΩΣΗΣ & ΛΕΙΤΟΥΡΓΙΑΣ ΕΙΔΙΚΩΝ ΕΚΠΑΙΔΕΥΣΕΩΝ ΣΚΑΠΑΝΙΚΗΣ
 ΘΕΜΑΤΟΛΟΓΙΟ ΚΑΙ ΟΔΗΓΙΕΣ ΟΡΓΑΝΩΣΗΣ & ΛΕΙΤΟΥΡΓΙΑΣ ΕΙΔΙΚΩΝ ΕΚΠΑΙΔΕΥΣΕΩΝ ΣΚΑΠΑΝΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗ ΣΚΑΠΑΝΙΚΗΣ Α. ΣΚΟΠΟΣ Η Εκπαίδευση έχει σκοπό την παροχή κατάλληλων και εξειδικευμένων γνώσεων σχετικά με την κατασκευαστική
ΘΕΜΑΤΟΛΟΓΙΟ ΚΑΙ ΟΔΗΓΙΕΣ ΟΡΓΑΝΩΣΗΣ & ΛΕΙΤΟΥΡΓΙΑΣ ΕΙΔΙΚΩΝ ΕΚΠΑΙΔΕΥΣΕΩΝ ΣΚΑΠΑΝΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗ ΣΚΑΠΑΝΙΚΗΣ Α. ΣΚΟΠΟΣ Η Εκπαίδευση έχει σκοπό την παροχή κατάλληλων και εξειδικευμένων γνώσεων σχετικά με την κατασκευαστική
ΑΠΟΦΑΣΗ 34750/2006 (Αριθμός καταθέσεως πράξεως 43170/2006) ΤΟ ΠΟΛΥΜΕΛΕΣ ΠΡΩΤΟΔΙΚΕΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΔΙΑΔΙΚΑΣΙΑ ΕΚΟΥΣΙΑΣ ΔΙΚΑΙΟΔΟΣΙΑΣ ΣΥΓΚΡΟΤΗΘΗΚΕ από
 ΑΠΟΦΑΣΗ 34750/2006 (Αριθμός καταθέσεως πράξεως 43170/2006) ΤΟ ΠΟΛΥΜΕΛΕΣ ΠΡΩΤΟΔΙΚΕΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΔΙΑΔΙΚΑΣΙΑ ΕΚΟΥΣΙΑΣ ΔΙΚΑΙΟΔΟΣΙΑΣ ΣΥΓΚΡΟΤΗΘΗΚΕ από τους Δικαστές Κυριάκο Μπαμπαλίδη, Πρόεδρο Πρωτοδικών,
ΑΠΟΦΑΣΗ 34750/2006 (Αριθμός καταθέσεως πράξεως 43170/2006) ΤΟ ΠΟΛΥΜΕΛΕΣ ΠΡΩΤΟΔΙΚΕΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΔΙΑΔΙΚΑΣΙΑ ΕΚΟΥΣΙΑΣ ΔΙΚΑΙΟΔΟΣΙΑΣ ΣΥΓΚΡΟΤΗΘΗΚΕ από τους Δικαστές Κυριάκο Μπαμπαλίδη, Πρόεδρο Πρωτοδικών,
ΕΝΩΠΙΟΝ ΠΑΝΤΟΣ ΑΡΜΟΔΙΟΥ ΔΙΚΑΣΤΗΡΙΟΥ ΚΑΙ ΠΑΣΗΣ ΔΗΜΟΣΙΑΣ ΑΡΧΗΣ ΕΞΩΔΙΚΗ ΔΙΑΜΑΡΤΥΡΙΑ ΠΡΟΣΚΛΗΣΗ ΔΗΛΩΣΗ
 ΕΝΩΠΙΟΝ ΠΑΝΤΟΣ ΑΡΜΟΔΙΟΥ ΔΙΚΑΣΤΗΡΙΟΥ ΚΑΙ ΠΑΣΗΣ ΔΗΜΟΣΙΑΣ ΑΡΧΗΣ ΕΞΩΔΙΚΗ ΔΙΑΜΑΡΤΥΡΙΑ ΠΡΟΣΚΛΗΣΗ ΔΗΛΩΣΗ 1. ΑΓΟΡΑΝΟΥ Νικολάου, Ιατρού Ε.Σ.Υ., Επιμελητή Α Γενικής Ιατρικής στο Κέντρο Υγείας Ν. Μάκρης, δικαιοδοσίας
ΕΝΩΠΙΟΝ ΠΑΝΤΟΣ ΑΡΜΟΔΙΟΥ ΔΙΚΑΣΤΗΡΙΟΥ ΚΑΙ ΠΑΣΗΣ ΔΗΜΟΣΙΑΣ ΑΡΧΗΣ ΕΞΩΔΙΚΗ ΔΙΑΜΑΡΤΥΡΙΑ ΠΡΟΣΚΛΗΣΗ ΔΗΛΩΣΗ 1. ΑΓΟΡΑΝΟΥ Νικολάου, Ιατρού Ε.Σ.Υ., Επιμελητή Α Γενικής Ιατρικής στο Κέντρο Υγείας Ν. Μάκρης, δικαιοδοσίας
ΤΜΗΜΑ ΦΙΛΟΣΟΦΙΑΣ ΚΑΙ ΠΑΙΔΑΓΩΓΙΚΗΣ Πρόγραμμα Μεταπτυχιακών Σπουδών Φιλοσοφίας ΕΣΩΤΕΡΙΚΟΣ ΚΑΝΟΝΙΣΜΟΣ ΛΕΙΤΟΥΡΓΙΑΣ
 ΤΜΗΜΑ ΦΙΛΟΣΟΦΙΑΣ ΚΑΙ ΠΑΙΔΑΓΩΓΙΚΗΣ Πρόγραμμα Μεταπτυχιακών Σπουδών Φιλοσοφίας ΕΣΩΤΕΡΙΚΟΣ ΚΑΝΟΝΙΣΜΟΣ ΛΕΙΤΟΥΡΓΙΑΣ Υπουργικές αποφάσεις λειτουργίας: Υ.Α. Ζ1/9760/23.12.14 (ΦΕΚ 3591/31.12.14, τ. Β ), Υ.Α. Β7/29073/6.7.06
ΤΜΗΜΑ ΦΙΛΟΣΟΦΙΑΣ ΚΑΙ ΠΑΙΔΑΓΩΓΙΚΗΣ Πρόγραμμα Μεταπτυχιακών Σπουδών Φιλοσοφίας ΕΣΩΤΕΡΙΚΟΣ ΚΑΝΟΝΙΣΜΟΣ ΛΕΙΤΟΥΡΓΙΑΣ Υπουργικές αποφάσεις λειτουργίας: Υ.Α. Ζ1/9760/23.12.14 (ΦΕΚ 3591/31.12.14, τ. Β ), Υ.Α. Β7/29073/6.7.06
ΚΑΤΑΣΤΑΤΙΚΟ Του Συλλόγου με την επωνυμία ΠΑΝΕΛΛΗΝΙΑ ΕΝΩΣΗ ΦΙΛΩΝ ΤΟΙΧΟΣΦΑΙΡΙΣΗΣ
 ΚΑΤΑΣΤΑΤΙΚΟ Του Συλλόγου με την επωνυμία ΠΑΝΕΛΛΗΝΙΑ ΕΝΩΣΗ ΦΙΛΩΝ ΤΟΙΧΟΣΦΑΙΡΙΣΗΣ ΚΕΦΑΛΑΙΟ Α Επωνυμία- Έδρα- Σκοπός-Πόροι ΑΡΘΡΟ 1 Ιδρύεται Σωματείο με την επωνυμία «Πανελλήνια Ένωση Φίλων Τοιχοσφαίρισης»
ΚΑΤΑΣΤΑΤΙΚΟ Του Συλλόγου με την επωνυμία ΠΑΝΕΛΛΗΝΙΑ ΕΝΩΣΗ ΦΙΛΩΝ ΤΟΙΧΟΣΦΑΙΡΙΣΗΣ ΚΕΦΑΛΑΙΟ Α Επωνυμία- Έδρα- Σκοπός-Πόροι ΑΡΘΡΟ 1 Ιδρύεται Σωματείο με την επωνυμία «Πανελλήνια Ένωση Φίλων Τοιχοσφαίρισης»
ΚΩΔΙΚΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΗΣ ΔΕΟΝΤΟΛΟΓΙΑΣ ΕΠΙΣΚΕΠΤΩΝ ΥΓΕΙΑΣ
 ΠΑΝΕΛΛΗΝΙΟΣ ΣΥΛΛΟΓΟΣ ΕΠΙΣΚΕΠΤΩΝ ΥΓΕΙΑΣ Π.Σ.Ε.Υ. - Ν.Π.Δ.Δ. ΥΠΟΜΝΗΜΑ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΕΠΙΣΚΕΠΤΩΝ ΥΓΕΙΑΣ Π.Σ.Ε.Υ.-Ν.Π.Δ.Δ. ΚΩΔΙΚΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΗΣ ΔΕΟΝΤΟΛΟΓΙΑΣ ΕΠΙΣΚΕΠΤΩΝ ΥΓΕΙΑΣ ΑΘΗΝΑ 2015 1 Πίνακας περιεχομένων
ΠΑΝΕΛΛΗΝΙΟΣ ΣΥΛΛΟΓΟΣ ΕΠΙΣΚΕΠΤΩΝ ΥΓΕΙΑΣ Π.Σ.Ε.Υ. - Ν.Π.Δ.Δ. ΥΠΟΜΝΗΜΑ ΠΑΝΕΛΛΗΝΙΟΥ ΣΥΛΛΟΓΟΥ ΕΠΙΣΚΕΠΤΩΝ ΥΓΕΙΑΣ Π.Σ.Ε.Υ.-Ν.Π.Δ.Δ. ΚΩΔΙΚΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΗΣ ΔΕΟΝΤΟΛΟΓΙΑΣ ΕΠΙΣΚΕΠΤΩΝ ΥΓΕΙΑΣ ΑΘΗΝΑ 2015 1 Πίνακας περιεχομένων
Σύμβαση για την πρόσληψη, τοποθέτηση και τις συνθήκες εργασίας των εργαζόμενων μεταναστών, 1939, Νο. 66 1
 Σύμβαση για την πρόσληψη, τοποθέτηση και τις συνθήκες εργασίας των εργαζόμενων μεταναστών, 1939, Νο. 66 1 Υιοθετήθηκε την 28η Ιουνίου 1939 από τη Γενική Συνδιάσκεψη της Διεθνούς Οργάνωσης Εργασίας κατά
Σύμβαση για την πρόσληψη, τοποθέτηση και τις συνθήκες εργασίας των εργαζόμενων μεταναστών, 1939, Νο. 66 1 Υιοθετήθηκε την 28η Ιουνίου 1939 από τη Γενική Συνδιάσκεψη της Διεθνούς Οργάνωσης Εργασίας κατά
ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΣΤΗΝ ΕΦΑΡΜΟΣΜΕΝΗ ΛΟΓΙΣΤΙΚΗ ΚΑΙ ΕΛΕΓΚΤΙΚΗ
 ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΣΤΗΝ ΕΦΑΡΜΟΣΜΕΝΗ ΛΟΓΙΣΤΙΚΗ ΚΑΙ ΕΛΕΓΚΤΙΚΗ Διπλωματική Εργασία ΑΠΟ ΤΟΝ ΚΩΔΙΚΑ ΒΙΒΛΙΩΝ ΚΑΙ ΣΤΟΙΧΕΙΩΝ ΣΤΟΝ ΚΩΔΙΚΑ ΦΟΡΟΛΟΓΙΚΗΣ ΑΠΕΙΚΟΝΙΣΗΣ
ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΣΤΗΝ ΕΦΑΡΜΟΣΜΕΝΗ ΛΟΓΙΣΤΙΚΗ ΚΑΙ ΕΛΕΓΚΤΙΚΗ Διπλωματική Εργασία ΑΠΟ ΤΟΝ ΚΩΔΙΚΑ ΒΙΒΛΙΩΝ ΚΑΙ ΣΤΟΙΧΕΙΩΝ ΣΤΟΝ ΚΩΔΙΚΑ ΦΟΡΟΛΟΓΙΚΗΣ ΑΠΕΙΚΟΝΙΣΗΣ
Ν.1676/1986 ΜΕΡΟΣ ΤΡΙΤΟ ΕΠΙΒΟΛΗ ΦΟΡΟΥ ΣΤΗ ΣΥΓΚΕΝΤΡΩΣΗ ΚΕΦΑΛΑΙΩΝ
 Αρθρο 17. Επιβολή φόρου Ν.1676/1986 ΜΕΡΟΣ ΤΡΙΤΟ ΕΠΙΒΟΛΗ ΦΟΡΟΥ ΣΤΗ ΣΥΓΚΕΝΤΡΩΣΗ ΚΕΦΑΛΑΙΩΝ Επιβάλλεται, σύμφωνα με τις διατάξεις του παρόντος νόμου, φόρος με την ονομασία «φόρος στη συγκέντρωση κεφαλαίων»,
Αρθρο 17. Επιβολή φόρου Ν.1676/1986 ΜΕΡΟΣ ΤΡΙΤΟ ΕΠΙΒΟΛΗ ΦΟΡΟΥ ΣΤΗ ΣΥΓΚΕΝΤΡΩΣΗ ΚΕΦΑΛΑΙΩΝ Επιβάλλεται, σύμφωνα με τις διατάξεις του παρόντος νόμου, φόρος με την ονομασία «φόρος στη συγκέντρωση κεφαλαίων»,
ΠΡΑΚΤΙΚΟΥ 10 / 14-06 - 2011
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΕΡΙΦΕΡΕΙΑ ΙΟΝΙΩΝ ΝΗΣΩΝ ΟΙΚΟΝΟΜΙΚΗ ΕΠΙΤΡΟΠΗ Κέρκυρα, 14-06 /2011 ΠΡΑΚΤΙΚΟΥ 10 / 14-06 - 2011 Στην Κέρκυρα σήμερα 14-06 - 2011 ημέρα Tρίτη και ώρα 18:30, συνεδρίασε, η Οικονομική Επιτροπή,
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΕΡΙΦΕΡΕΙΑ ΙΟΝΙΩΝ ΝΗΣΩΝ ΟΙΚΟΝΟΜΙΚΗ ΕΠΙΤΡΟΠΗ Κέρκυρα, 14-06 /2011 ΠΡΑΚΤΙΚΟΥ 10 / 14-06 - 2011 Στην Κέρκυρα σήμερα 14-06 - 2011 ημέρα Tρίτη και ώρα 18:30, συνεδρίασε, η Οικονομική Επιτροπή,
ΕΠΙΤΡΟΠΗ ΕΘΝΙΚΗΣ ΑΜΥΝΑΣ ΚΑΙ ΕΞΩΤΕΡΙΚΩΝ ΥΠΟΘΕΣΕΩΝ ΝΟΜΟΣΧΕ ΙΟ. «Στρατολογία των Ελλήνων» Άρθρο 1 Υπόχρεοι σε στράτευση
 ΕΠΙΤΡΟΠΗ ΕΘΝΙΚΗΣ ΑΜΥΝΑΣ ΚΑΙ ΕΞΩΤΕΡΙΚΩΝ ΥΠΟΘΕΣΕΩΝ ΝΟΜΟΣΧΕ ΙΟ «Στρατολογία των Ελλήνων» Άρθρο 1 Υπόχρεοι σε στράτευση 1. Όλοι οι Έλληνες πολίτες, από την 1η Ιανουαρίου του έτους κατά το οποίο διανύουν το
ΕΠΙΤΡΟΠΗ ΕΘΝΙΚΗΣ ΑΜΥΝΑΣ ΚΑΙ ΕΞΩΤΕΡΙΚΩΝ ΥΠΟΘΕΣΕΩΝ ΝΟΜΟΣΧΕ ΙΟ «Στρατολογία των Ελλήνων» Άρθρο 1 Υπόχρεοι σε στράτευση 1. Όλοι οι Έλληνες πολίτες, από την 1η Ιανουαρίου του έτους κατά το οποίο διανύουν το
ΑΡΧΙΤΕΚΤΟΝΙΚΟΣ ΙΑΓΩΝΙΣΜΟΣ ΓΙΑ ΤΟ ΠΑΡΚΟ ΠΑΛΛΟΥΡΟΚΑΜΠΟΥ ΣΤΟΝ ΗΜΟ ΛΑΤΣΙΩΝ ΠΡΟΓΡΑΜΜΑ ΑΡΧΙΤΕΚΤΟΝΙΚΟΥ ΙΑΓΩΝΙΣΜΟΥ
 ΠΑΡΑΡΤΗΜΑ 1 ΑΡΧΙΤΕΚΤΟΝΙΚΟΣ ΙΑΓΩΝΙΣΜΟΣ ΓΙΑ ΤΟ ΠΑΡΚΟ ΠΑΛΛΟΥΡΟΚΑΜΠΟΥ ΣΤΟΝ ΗΜΟ ΛΑΤΣΙΩΝ ΠΡΟΓΡΑΜΜΑ ΑΡΧΙΤΕΚΤΟΝΙΚΟΥ ΙΑΓΩΝΙΣΜΟΥ ΣΕΛ. - 1 - Πρόγραμμα ιαγωνισμού Γενικό Πλαίσιο: Η περιοχή Παλλουρόκαμπος στο ήμο Λατσιών
ΠΑΡΑΡΤΗΜΑ 1 ΑΡΧΙΤΕΚΤΟΝΙΚΟΣ ΙΑΓΩΝΙΣΜΟΣ ΓΙΑ ΤΟ ΠΑΡΚΟ ΠΑΛΛΟΥΡΟΚΑΜΠΟΥ ΣΤΟΝ ΗΜΟ ΛΑΤΣΙΩΝ ΠΡΟΓΡΑΜΜΑ ΑΡΧΙΤΕΚΤΟΝΙΚΟΥ ΙΑΓΩΝΙΣΜΟΥ ΣΕΛ. - 1 - Πρόγραμμα ιαγωνισμού Γενικό Πλαίσιο: Η περιοχή Παλλουρόκαμπος στο ήμο Λατσιών
Κεφάλαιο Πέμπτο Εθνοπολιτισμική Ζωή και Εμπειρίες Ελληνικότητας των Ελληνοαυστραλών Εφήβων
 Κεφάλαιο Πέμπτο Εθνοπολιτισμική Ζωή και Εμπειρίες Ελληνικότητας των Ελληνοαυστραλών Εφήβων Στο πλαίσιο του παρόντος κεφαλαίου εξετάζονται οι κοινές ενδοοικογενειακές δραστηριότητες και η γλωσσική αλληλεπίδραση
Κεφάλαιο Πέμπτο Εθνοπολιτισμική Ζωή και Εμπειρίες Ελληνικότητας των Ελληνοαυστραλών Εφήβων Στο πλαίσιο του παρόντος κεφαλαίου εξετάζονται οι κοινές ενδοοικογενειακές δραστηριότητες και η γλωσσική αλληλεπίδραση
ΣΧΕΔΙΟ ΝΟΜΟΥ Δασικά οικοσυστήματα: Ορισμοί, μέτρα προστασίας, ανάπτυξης και διαχείρισης ΚΕΦΑΛΑΙΟ Α ΤΡΟΠΟΠΟΙΗΣΕΙΣ ΤΟΥ Ν. 998/1979 (ΦΕΚ Α 289)
 ΣΧΕΔΙΟ ΝΟΜΟΥ Δασικά οικοσυστήματα: Ορισμοί, μέτρα προστασίας, ανάπτυξης και διαχείρισης ΚΕΦΑΛΑΙΟ Α ΤΡΟΠΟΠΟΙΗΣΕΙΣ ΤΟΥ Ν. 998/1979 (ΦΕΚ Α 289) Άρθρο 1 - Γενικές διατάξεις 1. Το άρθρο 1 του ν. 998/1979 αντικαθίσταται
ΣΧΕΔΙΟ ΝΟΜΟΥ Δασικά οικοσυστήματα: Ορισμοί, μέτρα προστασίας, ανάπτυξης και διαχείρισης ΚΕΦΑΛΑΙΟ Α ΤΡΟΠΟΠΟΙΗΣΕΙΣ ΤΟΥ Ν. 998/1979 (ΦΕΚ Α 289) Άρθρο 1 - Γενικές διατάξεις 1. Το άρθρο 1 του ν. 998/1979 αντικαθίσταται
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΔΗΜΟΤΙΚΟ ΣΧΟΛΕΙΟ ΦΛΩΡΙΝΑΣ ΠΡΟΓΡΑΜΜΑ ΑΓΩΓΗΣ ΥΓΕΙΑΣ
 ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΔΗΜΟΤΙΚΟ ΣΧΟΛΕΙΟ ΦΛΩΡΙΝΑΣ ΠΡΟΓΡΑΜΜΑ ΑΓΩΓΗΣ ΥΓΕΙΑΣ Τίτλος προγράμματος: «Ανάπτυξη της αυτοεκτίμησης» Τάξη: Α Εκπαιδευτικός: Βασιλική Αντωνογιάννη Σχολικό έτος: 2013-14 Σύνολο μαθητών
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΔΗΜΟΤΙΚΟ ΣΧΟΛΕΙΟ ΦΛΩΡΙΝΑΣ ΠΡΟΓΡΑΜΜΑ ΑΓΩΓΗΣ ΥΓΕΙΑΣ Τίτλος προγράμματος: «Ανάπτυξη της αυτοεκτίμησης» Τάξη: Α Εκπαιδευτικός: Βασιλική Αντωνογιάννη Σχολικό έτος: 2013-14 Σύνολο μαθητών
Α. ΚΥΡΟΣ ΚΑΙ ΑΠΟΔΕΙΚΤΙΚΗ ΔΥΝΑΜΗ ΒΙΒΛΙΩΝ ΚΑΙ ΣΤΟΙΧΕΙΩΝ ΧΡOΝΟΣ ΔΙΑΤHΡΗΣΗΣ ΒΙΒΛIΩΝ, ΣΤΟΙΧΕIΩΝ ΔΙΑΦYΛΑΞΗ
 ΚΥΡΟΣ ΚΑΙ ΑΠΟΔΕΙΚΤΙΚΗ ΔΥΝΑΜΗ ΒΙΒΛΙΩΝ ΚΑΙ ΣΤΟΙΧΕΙΩΝ ΧΡOΝΟΣ ΔΙΑΤHΡΗΣΗΣ ΒΙΒΛIΩΝ, ΣΤΟΙΧΕIΩΝ ΔΙΑΦYΛΑΞΗ Εφαρμόζεται από 1.1.2007 αλλά και για προηγούμενα χρόνια εφόσον οι διατάξεις αυτές είναι επιεικέστερες
ΚΥΡΟΣ ΚΑΙ ΑΠΟΔΕΙΚΤΙΚΗ ΔΥΝΑΜΗ ΒΙΒΛΙΩΝ ΚΑΙ ΣΤΟΙΧΕΙΩΝ ΧΡOΝΟΣ ΔΙΑΤHΡΗΣΗΣ ΒΙΒΛIΩΝ, ΣΤΟΙΧΕIΩΝ ΔΙΑΦYΛΑΞΗ Εφαρμόζεται από 1.1.2007 αλλά και για προηγούμενα χρόνια εφόσον οι διατάξεις αυτές είναι επιεικέστερες
Ενότητα 1. Στο τέλος κάθε κειμένου υπάρχουν ερωτήσεις και εργασίες, που μας βοηθούν να καταλάβουμε καλύτερα τα κείμενα αυτά.
 Ενότητα 1 Ταξίδια, τόποι, μεταφορικά μέσα Π ώς θα μελετούμε κάθε ενότητα Κάθε ενότητα αποτελείται από τέσσερα (4) κείμενα. Στο τέλος κάθε κειμένου υπάρχουν ερωτήσεις και εργασίες, που μας βοηθούν να καταλάβουμε
Ενότητα 1 Ταξίδια, τόποι, μεταφορικά μέσα Π ώς θα μελετούμε κάθε ενότητα Κάθε ενότητα αποτελείται από τέσσερα (4) κείμενα. Στο τέλος κάθε κειμένου υπάρχουν ερωτήσεις και εργασίες, που μας βοηθούν να καταλάβουμε
ΤΑ ΥΔΡΟΓΡΑΦΗΜΑΤΑ Παροχή υδατορεύματος σε μια συγκεκριμένη θέση, Q
 ΑΠΟΡΡΟΗ Επιφανειακή απορροή: το μέρος του νερού που κινείται πάνω στην επιφάνεια του εδάφους. Ενδιάμεση απορροή: Άμεση απορροή: Βασική απορροή: το μέρος του νερού που κινείται αμέσως κάτω από την επιφάνεια
ΑΠΟΡΡΟΗ Επιφανειακή απορροή: το μέρος του νερού που κινείται πάνω στην επιφάνεια του εδάφους. Ενδιάμεση απορροή: Άμεση απορροή: Βασική απορροή: το μέρος του νερού που κινείται αμέσως κάτω από την επιφάνεια
Διακήρυξη πλειοδοτικού Διαγωνισμού Εκμίσθωσης Κυλικείου των συστεγαζόμενων μονάδων Γυμνασίου και Λυκείου Αρεόπολης
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Δήμος Ανατολικής Μάνης Σχολική Επιτροπή Β'/θμιας Εκπ/σης Ελευθερολακώνων 23200 - Γύθειο Πληρ.: Δρακουλάκου Ελένη Τηλ.: 2733360349, 6946558500 Φαξ: 2733360348 Γύθειο 06-03-2013 Αριμ.
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Δήμος Ανατολικής Μάνης Σχολική Επιτροπή Β'/θμιας Εκπ/σης Ελευθερολακώνων 23200 - Γύθειο Πληρ.: Δρακουλάκου Ελένη Τηλ.: 2733360349, 6946558500 Φαξ: 2733360348 Γύθειο 06-03-2013 Αριμ.
ΤΡΟΠΟΠΟΙΗΣΗ ΕΤΑΙΡΙΚΟΥ ΣΥΜΦΩΝΗΤΙΚΟΥ
 ΤΡΟΠΟΠΟΙΗΣΗ ΕΤΑΙΡΙΚΟΥ ΣΥΜΦΩΝΗΤΙΚΟΥ Στην Πάτρα σήμερα την 3 ΟΚΤΩΒΡΊΟΥ 2011 οι παρακάτω συμβαλλόμενοι: 1.ΑΝΑΣΤΑΣΟΠΟΥΛΟΣ 2.ΑΝΔΡΙΟΠΟΥΛΟΣ 3.ΒΟΥΛΔΗΣ 4.ΚΟΣΜΑΣ 5.ΛΑΜΠΡΟΠΟΥΛΟΣ 6.ΛΑΜΠΡΟΠΟΥΛΟΣ 7.ΜΑΝΙΑΤΗΣ 8.ΜΙΣΑΗΛΙΔΗΣ
ΤΡΟΠΟΠΟΙΗΣΗ ΕΤΑΙΡΙΚΟΥ ΣΥΜΦΩΝΗΤΙΚΟΥ Στην Πάτρα σήμερα την 3 ΟΚΤΩΒΡΊΟΥ 2011 οι παρακάτω συμβαλλόμενοι: 1.ΑΝΑΣΤΑΣΟΠΟΥΛΟΣ 2.ΑΝΔΡΙΟΠΟΥΛΟΣ 3.ΒΟΥΛΔΗΣ 4.ΚΟΣΜΑΣ 5.ΛΑΜΠΡΟΠΟΥΛΟΣ 6.ΛΑΜΠΡΟΠΟΥΛΟΣ 7.ΜΑΝΙΑΤΗΣ 8.ΜΙΣΑΗΛΙΔΗΣ
Σύμφωνα με ανακοίνωση του αρμόδιου φορέα Ε.Ο.Π.Π.Ε.Π. στην ιστοσελίδα του: ΑΝΑΓΓΕΛΙΑ ΔΙΔΑΣΚΑΛΙΑΣ
 Σύμφωνα με ανακοίνωση του αρμόδιου φορέα Ε.Ο.Π.Π.Ε.Π. στην ιστοσελίδα του: ΑΝΑΓΓΕΛΙΑ ΔΙΔΑΣΚΑΛΙΑΣ ΔΙΚΑΙΟΛΟΓΗΤΙΚΑ ΑΝΑΓΓΕΛΙΑΣ ΕΝΑΡΞΗΣ ΑΣΚΗΣΕΩΣ ΕΠΑΓΓΕΛΜΑΤΟΣ ΤΗΣ ΔΙΔΑΣΚΑΛΙΑΣ ΣΕ ΦΡΟΝΤΙΣΤΗΡΙΑ ΚΑΙ ΚΕΝΤΡΑ ΞΕΝΩΝ
Σύμφωνα με ανακοίνωση του αρμόδιου φορέα Ε.Ο.Π.Π.Ε.Π. στην ιστοσελίδα του: ΑΝΑΓΓΕΛΙΑ ΔΙΔΑΣΚΑΛΙΑΣ ΔΙΚΑΙΟΛΟΓΗΤΙΚΑ ΑΝΑΓΓΕΛΙΑΣ ΕΝΑΡΞΗΣ ΑΣΚΗΣΕΩΣ ΕΠΑΓΓΕΛΜΑΤΟΣ ΤΗΣ ΔΙΔΑΣΚΑΛΙΑΣ ΣΕ ΦΡΟΝΤΙΣΤΗΡΙΑ ΚΑΙ ΚΕΝΤΡΑ ΞΕΝΩΝ
Η παρακμή του εργατικού κινήματος είναι μια διαδικασία που έχει ήδη διαρκέσει. πολλά χρόνια, τώρα ζούμε τα επεισόδια του τέλους της.
 Η παρακμή του εργατικού κινήματος είναι μια διαδικασία που έχει ήδη διαρκέσει πολλά χρόνια, τώρα ζούμε τα επεισόδια του τέλους της. 1 / 7 Αυτή η διαδικασία, φυσικά, δεν ήταν μια ευθεία πορεία από την ακμή
Η παρακμή του εργατικού κινήματος είναι μια διαδικασία που έχει ήδη διαρκέσει πολλά χρόνια, τώρα ζούμε τα επεισόδια του τέλους της. 1 / 7 Αυτή η διαδικασία, φυσικά, δεν ήταν μια ευθεία πορεία από την ακμή
ΚΕΦΑΛΑΙΟ Α ΓΕΝΙΚΕΣ ΔΙΑΤΑΞΕΙΣ. Άρθρο 1 Πεδίο εφαρμογής
 Υπουργική Απόφαση 1726/2003 «Διαδικασία προκαταρκτικής περιβαλλοντικής εκτίμησης και αξιολόγησης, έγκρισης περιβαλλοντικών όρων, καθώς και έγκρισης επέμβασης ή παραχώρησης δάσους ή δασικής έκτασης στα
Υπουργική Απόφαση 1726/2003 «Διαδικασία προκαταρκτικής περιβαλλοντικής εκτίμησης και αξιολόγησης, έγκρισης περιβαλλοντικών όρων, καθώς και έγκρισης επέμβασης ή παραχώρησης δάσους ή δασικής έκτασης στα
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ (Τ.Ε.Ι.) ΚΑΒΑΛΑΣ ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ. Θέμα πτυχιακής εργασίας:
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ (Τ.Ε.Ι.) ΚΑΒΑΛΑΣ ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ Θέμα πτυχιακής εργασίας: Προμελέτη σκοπιμότητας επενδυτικού σχεδίου που αφορά τον εκσυγχρονισμό υφιστάμενης
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ (Τ.Ε.Ι.) ΚΑΒΑΛΑΣ ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ Θέμα πτυχιακής εργασίας: Προμελέτη σκοπιμότητας επενδυτικού σχεδίου που αφορά τον εκσυγχρονισμό υφιστάμενης
ΕΣΩΤΕΡΙΚΟΙ ΚΑΝΟΝΙΣΜΟΙ ΛΕΙΤΟΥΡΓΙΑΣ ΤΗΣ ΣΧΟΛΗΣ
 ΕΣΩΤΕΡΙΚΟΙ ΚΑΝΟΝΙΣΜΟΙ ΛΕΙΤΟΥΡΓΙΑΣ ΤΗΣ ΣΧΟΛΗΣ ΚΑΝΟΝΙΣΜΟΣ Ο κανονισμός 14 των Κανονισμών Λειτουργίας Δημοσίων Σχολείων Μέσης Εκπαίδευσης 311/2005 αναφέρεται επί λέξει: Κάθε σχολική μονάδα διαμορφώνει με
ΕΣΩΤΕΡΙΚΟΙ ΚΑΝΟΝΙΣΜΟΙ ΛΕΙΤΟΥΡΓΙΑΣ ΤΗΣ ΣΧΟΛΗΣ ΚΑΝΟΝΙΣΜΟΣ Ο κανονισμός 14 των Κανονισμών Λειτουργίας Δημοσίων Σχολείων Μέσης Εκπαίδευσης 311/2005 αναφέρεται επί λέξει: Κάθε σχολική μονάδα διαμορφώνει με
ΣΧΕΔΙΟ ΝΟΜΟΥ ΔΑΣΙΚΕΣ ΣΥΝΕΤΑΙΡΙΣΤΙΚΕΣ ΟΡΓΑΝΩΣΕΙΣ
 ΣΧΕΔΙΟ ΝΟΜΟΥ ΔΑΣΙΚΕΣ ΣΥΝΕΤΑΙΡΙΣΤΙΚΕΣ ΟΡΓΑΝΩΣΕΙΣ ΚΕΦΑΛΑΙΟ Α ΓΕΝΙΚΕΣ ΔΙΑΤΑΞΕΙΣ Άρθρο 1 Ορισμός σκοπός διαβάθμιση δραστηριότητες 1. Η Δασική Συνεταιριστική Οργάνωση (ΔΑ.Σ.Ο.) είναι αυτόνομη ένωση προσώπων,
ΣΧΕΔΙΟ ΝΟΜΟΥ ΔΑΣΙΚΕΣ ΣΥΝΕΤΑΙΡΙΣΤΙΚΕΣ ΟΡΓΑΝΩΣΕΙΣ ΚΕΦΑΛΑΙΟ Α ΓΕΝΙΚΕΣ ΔΙΑΤΑΞΕΙΣ Άρθρο 1 Ορισμός σκοπός διαβάθμιση δραστηριότητες 1. Η Δασική Συνεταιριστική Οργάνωση (ΔΑ.Σ.Ο.) είναι αυτόνομη ένωση προσώπων,
ΝΟΜΟΣ ΥΠ' ΑΡΙΘ. 4194 Κώδικας Δικηγόρων
 ΝΟΜΟΣ ΥΠ' ΑΡΙΘ. 4194 Κώδικας Δικηγόρων ΝΟΜΟΣ ΥΠ' ΑΡΙΘ. 4194 Κώδικας Δικηγόρων. (ΦΕΚ Α' 208/27-09-2013) Ο ΠΡΟΕΔΡΟΣ ΤΗΣ ΕΛΛΗΝΙΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ Εκδίδομε τον ακόλουθο νόμο που ψήφισε η Βουλή: Αρθρο 1. Η φύση
ΝΟΜΟΣ ΥΠ' ΑΡΙΘ. 4194 Κώδικας Δικηγόρων ΝΟΜΟΣ ΥΠ' ΑΡΙΘ. 4194 Κώδικας Δικηγόρων. (ΦΕΚ Α' 208/27-09-2013) Ο ΠΡΟΕΔΡΟΣ ΤΗΣ ΕΛΛΗΝΙΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ Εκδίδομε τον ακόλουθο νόμο που ψήφισε η Βουλή: Αρθρο 1. Η φύση
Του Σταύρου Ν. PhD Ψυχολόγου Αθλητικού Ψυχολόγου
 Του Σταύρου Ν. PhD Ψυχολόγου Αθλητικού Ψυχολόγου Η σχέση και η αλληλεπίδραση των αθλητών, των προπονητών και των γονιών αποτελεί μια αναπόσπαστη διαδικασία στην αθλητική ανάπτυξη του παιδιού. Η αλληλεπίδραση
Του Σταύρου Ν. PhD Ψυχολόγου Αθλητικού Ψυχολόγου Η σχέση και η αλληλεπίδραση των αθλητών, των προπονητών και των γονιών αποτελεί μια αναπόσπαστη διαδικασία στην αθλητική ανάπτυξη του παιδιού. Η αλληλεπίδραση
Προς συμπλήρωση των ανωτέρω σχετικών εγκυκλίων σας γνωρίζουμε τα ακόλουθα:
 Ελληνική ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΕΣΩΤΕΡΙΚΩΝ ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΠΛΗΘΥΣΜΟΥ & ΚΟΙΝΩΝΙΚΗΣ ΣΥΝΟΧΗΣ ΓΕΝ. Δ/ΝΣΗ ΔΙΟΙΚ. ΥΠΟΣΤΗΡΙΞΗΣ Δ/ΝΣΗ ΙΘΑΓΕΝΕΙΑΣ ΤΜΗΜΑ ΚΑΘΟΡΙΣΜΟΥ ΙΘΑΓΕΝΕΙΑΣ Ταχ. Δ/νση : Σταδίου 31 Ταχ.
Ελληνική ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΕΣΩΤΕΡΙΚΩΝ ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΠΛΗΘΥΣΜΟΥ & ΚΟΙΝΩΝΙΚΗΣ ΣΥΝΟΧΗΣ ΓΕΝ. Δ/ΝΣΗ ΔΙΟΙΚ. ΥΠΟΣΤΗΡΙΞΗΣ Δ/ΝΣΗ ΙΘΑΓΕΝΕΙΑΣ ΤΜΗΜΑ ΚΑΘΟΡΙΣΜΟΥ ΙΘΑΓΕΝΕΙΑΣ Ταχ. Δ/νση : Σταδίου 31 Ταχ.
Η Φυσική με Πειράματα
 Α Γυμνασίου Η Φυσική με Πειράματα Πρόγραμμα Σπουδών Περιγραφή Το μάθημα της Φυσικής, η "Φυσική με Πειράματα", στην πρώτη τάξη του Γυμνασίου προβλέπεται να διδάσκεται μία ώρα την εβδομάδα, στην τάξη ή στο
Α Γυμνασίου Η Φυσική με Πειράματα Πρόγραμμα Σπουδών Περιγραφή Το μάθημα της Φυσικής, η "Φυσική με Πειράματα", στην πρώτη τάξη του Γυμνασίου προβλέπεται να διδάσκεται μία ώρα την εβδομάδα, στην τάξη ή στο
Ετήσια Οικονομική Έκθεση της χρήσης από 1η Ιανουαρίου έως 31η Δεκεμβρίου 2012. Βάσει του άρθρου 4 του Ν. 3556/2007
 Ετήσια Οικονομική Έκθεση της χρήσης από 1η Ιανουαρίου έως 31η Δεκεμβρίου 2012 Βάσει του άρθρου 4 του Ν. 3556/2007 ΠΕΡΙΕΧΟΜΕΝΑ Α. Δηλώσεις των Μελών του Διοικητικού Συμβουλίου... 5 Β. Έκθεση Ελέγχου Ανεξάρτητου
Ετήσια Οικονομική Έκθεση της χρήσης από 1η Ιανουαρίου έως 31η Δεκεμβρίου 2012 Βάσει του άρθρου 4 του Ν. 3556/2007 ΠΕΡΙΕΧΟΜΕΝΑ Α. Δηλώσεις των Μελών του Διοικητικού Συμβουλίου... 5 Β. Έκθεση Ελέγχου Ανεξάρτητου
ΠΡΑΞΗ ΝΟΜΟΘΕΤΙΚΟΥ ΠΕΡΙΕΧΟΜΕΝΟΥ
 ΠΡΑΞΗ ΝΟΜΟΘΕΤΙΚΟΥ ΠΕΡΙΕΧΟΜΕΝΟΥ Δημοσιονομικοί κανόνες και άλλες διατάξεις Ο ΠΡΟΕΔΡΟΣ ΤΗΣ ΕΛΛΗΝΙΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ Έχοντας υπόψη: 1. Την παράγραφο 1 του άρθρου 44 του Συντάγματος. 2. Την έκτακτη περίπτωση
ΠΡΑΞΗ ΝΟΜΟΘΕΤΙΚΟΥ ΠΕΡΙΕΧΟΜΕΝΟΥ Δημοσιονομικοί κανόνες και άλλες διατάξεις Ο ΠΡΟΕΔΡΟΣ ΤΗΣ ΕΛΛΗΝΙΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ Έχοντας υπόψη: 1. Την παράγραφο 1 του άρθρου 44 του Συντάγματος. 2. Την έκτακτη περίπτωση
Η διαπολιτισμική εκπαίδευση στη μουσουλμανική μειονότητα της Δ. Θράκης- Εμπειρία στον Ελληνικό χώρο (Α0011) ΨΑΡΡΙΑΝΟΥ ΙΑΚΩΒΗ ΕΙΡΗΝΗ ΕΙΣΑΓΩΓΗ
 Η διαπολιτισμική εκπαίδευση στη μουσουλμανική μειονότητα της Δ. Θράκης- Εμπειρία στον Ελληνικό χώρο (Α0011) ΨΑΡΡΙΑΝΟΥ ΙΑΚΩΒΗ ΕΙΡΗΝΗ ΕΙΣΑΓΩΓΗ Τα εκπαιδευτικά και γλωσσικά προβλήματα των αλλοδαπών μαθητών
Η διαπολιτισμική εκπαίδευση στη μουσουλμανική μειονότητα της Δ. Θράκης- Εμπειρία στον Ελληνικό χώρο (Α0011) ΨΑΡΡΙΑΝΟΥ ΙΑΚΩΒΗ ΕΙΡΗΝΗ ΕΙΣΑΓΩΓΗ Τα εκπαιδευτικά και γλωσσικά προβλήματα των αλλοδαπών μαθητών
2. Λόγοι που οδηγούν στην κατάρτιση σύμβασης μερικής απασχόλησης.
 LEGAL INSIGHTS ΣΥΜΒΑΣΗ ΜΕΡΙΚΗΣ ΑΠΑΣΧΟΛΗΣΗΣ Παναγιώτης Ζαχαράκης Στο παρόν κείμενο γίνεται ανάλυση της έννοιας και των μορφών της σύμβασης μερικής απασχόλησης, των λόγων που οδηγούν στην κατάρτιση αυτής,
LEGAL INSIGHTS ΣΥΜΒΑΣΗ ΜΕΡΙΚΗΣ ΑΠΑΣΧΟΛΗΣΗΣ Παναγιώτης Ζαχαράκης Στο παρόν κείμενο γίνεται ανάλυση της έννοιας και των μορφών της σύμβασης μερικής απασχόλησης, των λόγων που οδηγούν στην κατάρτιση αυτής,
ΚΑΤΑΣΤΑΤΙΚΟ ΕΠΩΝΥΜΙΑ. Άρθρο 1 Συνιστάται Σωµατείο µε την επωνυµία Όµιλος Φιλίππων Ιωαννίνων. ΣΚΟΠΟΣ
 ΚΑΤΑΣΤΑΤΙΚΟ ΕΠΩΝΥΜΙΑ Άρθρο 1 Συνιστάται Σωµατείο µε την επωνυµία Όµιλος Φιλίππων Ιωαννίνων. ΣΚΟΠΟΣ Άρθρο 2 Σκοπός του Σωµατείου είναι η διάδοση της Ιππασίας και του φιλίππου πνεύµατος γενικά µε όλα τα
ΚΑΤΑΣΤΑΤΙΚΟ ΕΠΩΝΥΜΙΑ Άρθρο 1 Συνιστάται Σωµατείο µε την επωνυµία Όµιλος Φιλίππων Ιωαννίνων. ΣΚΟΠΟΣ Άρθρο 2 Σκοπός του Σωµατείου είναι η διάδοση της Ιππασίας και του φιλίππου πνεύµατος γενικά µε όλα τα
Ο ΠΡΟΕΔΡΟΣ ΤΗΣ ΒΟΥΛΗΣ ΤΩΝ ΕΛΛΗΝΩΝ. Άρθρο πρώτο.
 ΝΟΜΟΣ: 1634/86 Κύρωση των πρωτοκόλλων 1980 «Για την προστασία της Μεσογείου θαλάσσης από τη ρύπανση από χερσαίες πηγές» και 1982 «περί των ειδικά προστατευομένων περιοχών της Μεσογείου» (ΦΕΚ 104/Α/18-07-86)
ΝΟΜΟΣ: 1634/86 Κύρωση των πρωτοκόλλων 1980 «Για την προστασία της Μεσογείου θαλάσσης από τη ρύπανση από χερσαίες πηγές» και 1982 «περί των ειδικά προστατευομένων περιοχών της Μεσογείου» (ΦΕΚ 104/Α/18-07-86)
ΣΩΜΑ ΠΡΟΣΚΟΠΩΝ ΚΥΠΡΟΥ. Εσωτερικός Κανονισμός. Προσκοπικού Πρατηρίου
 ΣΩΜΑ ΠΡΟΣΚΟΠΩΝ ΚΥΠΡΟΥ Εσωτερικός Κανονισμός Προσκοπικού Πρατηρίου Λευκωσία Μάιος 2010 Περιεχόμενα: 1. Υπόσταση.... 2 2. Σκοπός... 2 3. Λειτουργία... 2 4. Διαχειριστική Επιτροπή..... 2 5. Πελάτες.... 4
ΣΩΜΑ ΠΡΟΣΚΟΠΩΝ ΚΥΠΡΟΥ Εσωτερικός Κανονισμός Προσκοπικού Πρατηρίου Λευκωσία Μάιος 2010 Περιεχόμενα: 1. Υπόσταση.... 2 2. Σκοπός... 2 3. Λειτουργία... 2 4. Διαχειριστική Επιτροπή..... 2 5. Πελάτες.... 4
ΘΕΜΑ : : Εισηγητική έκθεση Δ τριμήνου του έτους 2013 προς την οικονομική επιτροπή, για την εκτέλεση του προϋπολογισμού.
 Από το πρακτικό της 18/3/2014 ΔΗΜΟΣ ΑΜΠΕΛΟΚΗΠΩΝ ΜΕΝΕΜΕΝΗΣ ΟΙΚΟΝΟΜΙΚΗ ΕΠΙΤΡΟΠΗ Πληρ: Koυκουλιώτης Ε. Τηλ. 2313313689 Αριθ. Απόφασης 047/2014 ΘΕΜΑ : : Εισηγητική έκθεση Δ τριμήνου του έτους 2013 προς την
Από το πρακτικό της 18/3/2014 ΔΗΜΟΣ ΑΜΠΕΛΟΚΗΠΩΝ ΜΕΝΕΜΕΝΗΣ ΟΙΚΟΝΟΜΙΚΗ ΕΠΙΤΡΟΠΗ Πληρ: Koυκουλιώτης Ε. Τηλ. 2313313689 Αριθ. Απόφασης 047/2014 ΘΕΜΑ : : Εισηγητική έκθεση Δ τριμήνου του έτους 2013 προς την
6o ΕΝΗΜΕΡΩΤΙΚΟ. των αιρετών του ΚΥΣΔΕ Γρηγόρη Καλομοίρη και Χρήστου Φιρτινίδη, εκπροσώπων των Συνεργαζόμενων Εκπαιδευτικών Κινήσεων
 6o ΕΝΗΜΕΡΩΤΙΚΟ των αιρετών του ΚΥΣΔΕ Γρηγόρη Καλομοίρη και Χρήστου Φιρτινίδη, εκπροσώπων των Συνεργαζόμενων Εκπαιδευτικών Κινήσεων Θέμα: Άσκηση ιδιωτικού έργου ή εργασίας από εκπαιδευτικούς Συνάδελφοι,
6o ΕΝΗΜΕΡΩΤΙΚΟ των αιρετών του ΚΥΣΔΕ Γρηγόρη Καλομοίρη και Χρήστου Φιρτινίδη, εκπροσώπων των Συνεργαζόμενων Εκπαιδευτικών Κινήσεων Θέμα: Άσκηση ιδιωτικού έργου ή εργασίας από εκπαιδευτικούς Συνάδελφοι,
Ορεστιάδα 16/01/2015. Αρ.πρωτ.369
 1 ΑΝΑΡΤΗΤΕΑ ΣΤΟ ΔΙΑΔΙΚΤΥΟ ΥΠΟΥΡΓΕΙΟ ΟΙΚΟΝΟΜΙΚΩΝ ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΔΗΜΟΣΙΩΝ ΕΣΟΔΩΝ ΓΕΝΙΚΗ Δ/ΝΣΗ ΦΟΡΟΛΟΓΙΚΗΣ ΔΙΟΙΚΗΣΗΣ Δ.Ο.Υ ΟΡΕΣΤΙΑΔΑΣ Ταχ. Δ/νση: Ιπποκράτους 30 Τ.Κ. : 68200 Πληροφ. : Κος Πάλλας Δ. Τηλέφωνο
1 ΑΝΑΡΤΗΤΕΑ ΣΤΟ ΔΙΑΔΙΚΤΥΟ ΥΠΟΥΡΓΕΙΟ ΟΙΚΟΝΟΜΙΚΩΝ ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΔΗΜΟΣΙΩΝ ΕΣΟΔΩΝ ΓΕΝΙΚΗ Δ/ΝΣΗ ΦΟΡΟΛΟΓΙΚΗΣ ΔΙΟΙΚΗΣΗΣ Δ.Ο.Υ ΟΡΕΣΤΙΑΔΑΣ Ταχ. Δ/νση: Ιπποκράτους 30 Τ.Κ. : 68200 Πληροφ. : Κος Πάλλας Δ. Τηλέφωνο
Συνήγορος του Καταναλωτή Νομολογία ΕφΑθ 5253/2003
 ΕφΑθ 5253/2003 Τράπεζες. Στεγαστικά δάνεια. Γενικοί Όροι Συναλλαγών. Καταχρηστικοί όροι. Έξοδα χρηματοδότησης. Προμήθεια φακέλου Παράνομες επιβαρύνσεις. Υπέρμετρες εγγυήσεις. Καταγγελία σύμβασης δανείου.
ΕφΑθ 5253/2003 Τράπεζες. Στεγαστικά δάνεια. Γενικοί Όροι Συναλλαγών. Καταχρηστικοί όροι. Έξοδα χρηματοδότησης. Προμήθεια φακέλου Παράνομες επιβαρύνσεις. Υπέρμετρες εγγυήσεις. Καταγγελία σύμβασης δανείου.
Υπό Παναγιώτη Δαλκαφούκη, μέλους Ένωσης Ελλήνων Ποινικολόγων
 2008 Υπό Παναγιώτη Δαλκαφούκη, μέλους Ένωσης Ελλήνων Ποινικολόγων 1. Λόγω διάλυσης της Βουλής δεν αποτελεί: α) Αν έχουν παραιτηθεί ή καταψηφιστεί από αυτή, δύο Κυβερνήσεις και η σύνθεσή της δεν εξασφαλίζει
2008 Υπό Παναγιώτη Δαλκαφούκη, μέλους Ένωσης Ελλήνων Ποινικολόγων 1. Λόγω διάλυσης της Βουλής δεν αποτελεί: α) Αν έχουν παραιτηθεί ή καταψηφιστεί από αυτή, δύο Κυβερνήσεις και η σύνθεσή της δεν εξασφαλίζει
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΕΣΩΤΕΡΙΚΩΝ ΑΝΑΠΛΗΡΩΤΗΣ ΥΠΟΥΡΓΟΣ Προς: Δημάρχους της Χώρας Αθήνα, 16 Δεκεμβρίου 2013 Α.Π.:2271. Αγαπητέ κ.
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΕΣΩΤΕΡΙΚΩΝ ΑΝΑΠΛΗΡΩΤΗΣ ΥΠΟΥΡΓΟΣ Προς: Δημάρχους της Χώρας Αθήνα, 16 Δεκεμβρίου 2013 Α.Π.:2271 Αγαπητέ κ. Δήμαρχε Σας στέλνω συνημμένη την μελέτη στελέχωσης του δήμου σας,
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΕΣΩΤΕΡΙΚΩΝ ΑΝΑΠΛΗΡΩΤΗΣ ΥΠΟΥΡΓΟΣ Προς: Δημάρχους της Χώρας Αθήνα, 16 Δεκεμβρίου 2013 Α.Π.:2271 Αγαπητέ κ. Δήμαρχε Σας στέλνω συνημμένη την μελέτη στελέχωσης του δήμου σας,
ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗ ΛΟΓΙΣΤΙΚΗ
 ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗ ΛΟΓΙΣΤΙΚΗ ΑΘΗΝΑ 2015 1 Το επιστημονικό περιεχόμενο του παρόντος βιβλίου έχει υποβληθεί σε κριτική ανάγνωση και εγκριθεί με το σύστημα των κριτών. Η κριτική ανάγνωση πραγματοποιήθηκε από
ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗ ΛΟΓΙΣΤΙΚΗ ΑΘΗΝΑ 2015 1 Το επιστημονικό περιεχόμενο του παρόντος βιβλίου έχει υποβληθεί σε κριτική ανάγνωση και εγκριθεί με το σύστημα των κριτών. Η κριτική ανάγνωση πραγματοποιήθηκε από
O ΑΓΩΝΑΣ ΤΟΥ ΕΦΗΒΟΥ ΓΙΑ ΑΝΕΞΑΡΤΗΣΙΑ
 Διαγώνισμα Έκφρασης Έκθεσης Α Λυκείου Όνομα: Επώνυμο: Τμήμα: Ημερομηνία: 13.04.2014 Κείμενο Α O ΑΓΩΝΑΣ ΤΟΥ ΕΦΗΒΟΥ ΓΙΑ ΑΝΕΞΑΡΤΗΣΙΑ Ανησυχώντας για την απειρία των παιδιών τους, που μπαίνουν στον κόσμο των
Διαγώνισμα Έκφρασης Έκθεσης Α Λυκείου Όνομα: Επώνυμο: Τμήμα: Ημερομηνία: 13.04.2014 Κείμενο Α O ΑΓΩΝΑΣ ΤΟΥ ΕΦΗΒΟΥ ΓΙΑ ΑΝΕΞΑΡΤΗΣΙΑ Ανησυχώντας για την απειρία των παιδιών τους, που μπαίνουν στον κόσμο των
ΕΙΔΙΚΗ ΣΥΓΓΡΑΦΗ ΥΠΟΧΡΕΩΣΕΩΝ ΤΕΥΧΟΣ 2 ΑΠΟ 2 ΠΑΡΑΡΤΗΜΑΤΑ Α.Δ. 737
 ΠΕΠ ΑΤΤΙΚΗΣ 2007 2013 ΕΥΡΩΠΑΪΚΗ EΝΩΣΗ ΕΥΡΩΠΑΪΚΟ ΤΑΜΕΙΟ ΠΕΡΙΦΕΡΕΙΑΚΗΣ ΑΝΑΠΤΥΞΗΣ ΕΡΓΑ Ο.Σ.Ε. Α.Ε. ΔΙΕΥΘΥΝΣΗ ΣΥΜΒΑΣΕΩΝ ΚΑΙ ΠΡΟΜΗΘΕΙΩΝ ΕΡΓΟ : ΦΥΤΟΤΕΧΝΙΚΕΣ ΕΡΓΑΣΙΕΣ ΓΙΑ ΤΗΝ ΣΤΑΘΕΡΟΠΟΙΗΣΗ ΚΑΙ ΤΗΝ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ
ΠΕΠ ΑΤΤΙΚΗΣ 2007 2013 ΕΥΡΩΠΑΪΚΗ EΝΩΣΗ ΕΥΡΩΠΑΪΚΟ ΤΑΜΕΙΟ ΠΕΡΙΦΕΡΕΙΑΚΗΣ ΑΝΑΠΤΥΞΗΣ ΕΡΓΑ Ο.Σ.Ε. Α.Ε. ΔΙΕΥΘΥΝΣΗ ΣΥΜΒΑΣΕΩΝ ΚΑΙ ΠΡΟΜΗΘΕΙΩΝ ΕΡΓΟ : ΦΥΤΟΤΕΧΝΙΚΕΣ ΕΡΓΑΣΙΕΣ ΓΙΑ ΤΗΝ ΣΤΑΘΕΡΟΠΟΙΗΣΗ ΚΑΙ ΤΗΝ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ
Αριθμός Απόφασης 48/2014 ΤΟ ΠΟΛΥΜΕΛΕΣ ΠΡΩΤΟΔΙΚΕΙΟ ΧΑΝΙΩΝ
 ΠΡΩΤΟΔΙΚΕΙΟ ΧΑΝΙΩΝ Αριθμός Απόφασης 48/2014 ΤΟ ΠΟΛΥΜΕΛΕΣ ΠΡΩΤΟΔΙΚΕΙΟ ΧΑΝΙΩΝ (Διαδικασία Εκουσίας Δικαιοδοσίας) ΣΥΓΚΡΟΤΗΘΗΚΕ από τους Δικαστές Χρυσή Φυντριλάκη, Πρόεδρο Πρωτοδικών, Ιωάννη Ευαγγελάτο, Πρωτοδίκη-Εισηγητή,
ΠΡΩΤΟΔΙΚΕΙΟ ΧΑΝΙΩΝ Αριθμός Απόφασης 48/2014 ΤΟ ΠΟΛΥΜΕΛΕΣ ΠΡΩΤΟΔΙΚΕΙΟ ΧΑΝΙΩΝ (Διαδικασία Εκουσίας Δικαιοδοσίας) ΣΥΓΚΡΟΤΗΘΗΚΕ από τους Δικαστές Χρυσή Φυντριλάκη, Πρόεδρο Πρωτοδικών, Ιωάννη Ευαγγελάτο, Πρωτοδίκη-Εισηγητή,
Διαδικασίες υποβολής προτάσεων Προϋποθέσεις για την ένταξη έργων στο ΕΠ Κρήτη 2014-2020
 ΠΕΡΙΦΕΡΕΙΑ ΚΡΗΤΗΣ Διαδικασίες υποβολής προτάσεων Προϋποθέσεις για την ένταξη έργων στο ΕΠ Κρήτη 2014-2020 Ηράκλειο 23 Δεκεμβρίου 2015 Α. Γενικά Στοιχεία Καν 1303/2013 ΕΕ Ν. 4314/2014 (ΦΕΚ 265/τ. Α/23.12.2014)
ΠΕΡΙΦΕΡΕΙΑ ΚΡΗΤΗΣ Διαδικασίες υποβολής προτάσεων Προϋποθέσεις για την ένταξη έργων στο ΕΠ Κρήτη 2014-2020 Ηράκλειο 23 Δεκεμβρίου 2015 Α. Γενικά Στοιχεία Καν 1303/2013 ΕΕ Ν. 4314/2014 (ΦΕΚ 265/τ. Α/23.12.2014)
Προς: Πίνακας Αποδεκτών Ταχ. Δ/νση: Καρ. Σερβίας 8. 1. Δ.Ε.Κ.Ο. και Ν.Π.Ι.Δ. Ταχ. Κώδικας: 101 84 Αθήνα
 ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΟΙΚΟΝΟΜΙΚΩΝ Αθήνα, 13/8/2012 ΓΕΝΙΚΗ Δ/ΝΣΗ ΟΙΚΟΝΟΜΙΚΗΣ ΠΟΛΙΤΙΚΗΣ Αρ. Πρωτ: 36035 /ΔΕΚΟ 1350 Δ/ΝΣΗ ΔΕΚΟ Προς: Πίνακας Αποδεκτών Ταχ. Δ/νση: Καρ. Σερβίας 8 1. Δ.Ε.Κ.Ο. και Ν.Π.Ι.Δ. Ταχ.
ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΟΙΚΟΝΟΜΙΚΩΝ Αθήνα, 13/8/2012 ΓΕΝΙΚΗ Δ/ΝΣΗ ΟΙΚΟΝΟΜΙΚΗΣ ΠΟΛΙΤΙΚΗΣ Αρ. Πρωτ: 36035 /ΔΕΚΟ 1350 Δ/ΝΣΗ ΔΕΚΟ Προς: Πίνακας Αποδεκτών Ταχ. Δ/νση: Καρ. Σερβίας 8 1. Δ.Ε.Κ.Ο. και Ν.Π.Ι.Δ. Ταχ.
Μάριος Χάκκας. Το Ψαράκι της γυάλας
 Μάριος Χάκκας Το Ψαράκι της γυάλας 1. Γραμματολογικά: Το διήγημα Το ψαράκι της γυάλας πρωτοδημοσιεύτηκε το 1971 μαζί με άλλα δύο διηγήματα, Ένα κορίτσι και ο Γιάννης το θεριό μυρμήγκι, στο συλλογικό τόμο
Μάριος Χάκκας Το Ψαράκι της γυάλας 1. Γραμματολογικά: Το διήγημα Το ψαράκι της γυάλας πρωτοδημοσιεύτηκε το 1971 μαζί με άλλα δύο διηγήματα, Ένα κορίτσι και ο Γιάννης το θεριό μυρμήγκι, στο συλλογικό τόμο
Η ΑΥΤΕΠΑΓΓΕΛΤΗ ΑΝΑΖΗΤΗΣΗ ΔΙΚΑΙΟΛΟΓΗΤΙΚΩΝ ΜΙΑ ΚΡΙΤΙΚΗ ΑΠΟΤΙΜΗΣΗ. ( Διοικητική Ενημέρωση, τ.51, Οκτώβριος Νοέμβριος Δεκέμβριος 2009)
 Η ΑΥΤΕΠΑΓΓΕΛΤΗ ΑΝΑΖΗΤΗΣΗ ΔΙΚΑΙΟΛΟΓΗΤΙΚΩΝ ΜΙΑ ΚΡΙΤΙΚΗ ΑΠΟΤΙΜΗΣΗ ( Διοικητική Ενημέρωση, τ.5, Οκτώβριος Νοέμβριος Δεκέμβριος 009). Η θέσπιση του νέου μέτρου Η σημαντικότερη απόπειρα καινοτομικής δράσης της
Η ΑΥΤΕΠΑΓΓΕΛΤΗ ΑΝΑΖΗΤΗΣΗ ΔΙΚΑΙΟΛΟΓΗΤΙΚΩΝ ΜΙΑ ΚΡΙΤΙΚΗ ΑΠΟΤΙΜΗΣΗ ( Διοικητική Ενημέρωση, τ.5, Οκτώβριος Νοέμβριος Δεκέμβριος 009). Η θέσπιση του νέου μέτρου Η σημαντικότερη απόπειρα καινοτομικής δράσης της
ΕΑΣ ΙΕΡΑΠΕΤΡΑΣ ΠΑΠΑ ΛΑΚΚΟΙ Τηλ. 2842024282, 22248 Fax: 2842026263 Enosi1@otenet.gr ΙΕΡΑΠΕΤΡΑ, 24/01/2014 ΤΚ 72200 Αρ.Πρωτ. 1939
 1 ΕΑΣ ΙΕΡΑΠΕΤΡΑΣ ΠΑΠΑ ΛΑΚΚΟΙ Τηλ. 2842024282, 22248 Fax: 2842026263 Enosi1@otenet.gr ΙΕΡΑΠΕΤΡΑ, 24/01/2014 ΤΚ 72200 Αρ.Πρωτ. 1939 Προς: Μ.Μ.Ε. ΕΝΙΑΙΟ ΑΓΡΟΤΙΚΟ ΣΥΛΛΟΓΟ ΙΕΡΑΠΕΤΡΑΣ ΑΓΡΟΤΙΚΗ ΕΠΙΤΡΟΠΗ ΔΗΜΟΥ
1 ΕΑΣ ΙΕΡΑΠΕΤΡΑΣ ΠΑΠΑ ΛΑΚΚΟΙ Τηλ. 2842024282, 22248 Fax: 2842026263 Enosi1@otenet.gr ΙΕΡΑΠΕΤΡΑ, 24/01/2014 ΤΚ 72200 Αρ.Πρωτ. 1939 Προς: Μ.Μ.Ε. ΕΝΙΑΙΟ ΑΓΡΟΤΙΚΟ ΣΥΛΛΟΓΟ ΙΕΡΑΠΕΤΡΑΣ ΑΓΡΟΤΙΚΗ ΕΠΙΤΡΟΠΗ ΔΗΜΟΥ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ 12/3/2015 ΝΟΜΟΣ ΑΡΓΟΛΙΔΑΣ 5157 ΔΗΜΟΣ ΝΑΥΠΛΙΕΩΝ : 34 Τ. Κ.
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ναύπλιο 12/3/2015 ΝΟΜΟΣ ΑΡΓΟΛΙΔΑΣ Αριθμ. Πρωτ. 5157 ΔΗΜΟΣ ΝΑΥΠΛΙΕΩΝ Ταχ. Δ/νση : Βασ. Κων/νου 34 Τ. Κ. : 21100 Τηλ : 2752360941/942 Πληρ. : Καλογήρου Ελένη ΔΙΑΚΗΡΥΞΗ ΔΗΜΟΠΡΑΣΙΑΣ ΓΙΑ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ναύπλιο 12/3/2015 ΝΟΜΟΣ ΑΡΓΟΛΙΔΑΣ Αριθμ. Πρωτ. 5157 ΔΗΜΟΣ ΝΑΥΠΛΙΕΩΝ Ταχ. Δ/νση : Βασ. Κων/νου 34 Τ. Κ. : 21100 Τηλ : 2752360941/942 Πληρ. : Καλογήρου Ελένη ΔΙΑΚΗΡΥΞΗ ΔΗΜΟΠΡΑΣΙΑΣ ΓΙΑ
Ετήσια οικονομική έκθεση της χρήσης από 1 η Ιανουαρίου έως 31 η Δεκεμβρίου 2009 2
 ΠΕΡΙΕΧΟΜΕΝΑ Α. Δηλώσεις των Μελών του Διοικητικού Συμβουλίου... 4 Β. Έκθεση Ελέγχου Ανεξάρτητου Ορκωτού Ελεγκτή Λογιστή... 5 Γ. Ετήσια Έκθεση του Διοικητικού Συμβουλίου... 7 Δ. Ετήσιες Οικονομικές Καταστάσεις...
ΠΕΡΙΕΧΟΜΕΝΑ Α. Δηλώσεις των Μελών του Διοικητικού Συμβουλίου... 4 Β. Έκθεση Ελέγχου Ανεξάρτητου Ορκωτού Ελεγκτή Λογιστή... 5 Γ. Ετήσια Έκθεση του Διοικητικού Συμβουλίου... 7 Δ. Ετήσιες Οικονομικές Καταστάσεις...
Β. 'Εκπτωση 50% στα οίκοθεν πρόσθετα τέλη για βεβαιωμένες οφειλές χρονικής περιόδου
 -- 355 -- * ΑΣΦΑΛΙΣΤΙΚΑ * Νο. 5 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Αθήνα 26/1/1999 ΙΔΡΥΜΑ ΚΟΙΝΩΝΙΚΩΝ ΑΣΦΑΛΙΣΕΩΝ ΔΙΟΙΚΗΣΗ Αριθ. Πρωτ: Ε33/3 ΓΕΝ. Δ/ΝΣΗ ΑΣΦ/ΚΩΝ ΥΠΗΡΕΣΙΩΝ ΤΜΗΜΑΤΑ ΚΟΙΝΩΝ - ΟΙΚΟΔ/ΚΩΝ ΕΠΙΧ/ΣΕΩΝ ΚΑΙ ΑΝΑΓΚΑΣΤΙΚΩΝ
-- 355 -- * ΑΣΦΑΛΙΣΤΙΚΑ * Νο. 5 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Αθήνα 26/1/1999 ΙΔΡΥΜΑ ΚΟΙΝΩΝΙΚΩΝ ΑΣΦΑΛΙΣΕΩΝ ΔΙΟΙΚΗΣΗ Αριθ. Πρωτ: Ε33/3 ΓΕΝ. Δ/ΝΣΗ ΑΣΦ/ΚΩΝ ΥΠΗΡΕΣΙΩΝ ΤΜΗΜΑΤΑ ΚΟΙΝΩΝ - ΟΙΚΟΔ/ΚΩΝ ΕΠΙΧ/ΣΕΩΝ ΚΑΙ ΑΝΑΓΚΑΣΤΙΚΩΝ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΑΛΑΜΑΤΑΣ (Τ.Ε.Ι.Κ.) ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΑΣ ΓΕΩΠΟΝΙΑΣ (ΣΤΕΓ) ΤΜΗΜΑ ΦΥΤΙΚΗΣ ΠΑΡΑΓΩΓΗΣ (Φ.Π.) ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΜΕ ΘΕΜΑ:
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΑΛΑΜΑΤΑΣ (Τ.Ε.Ι.Κ.) ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΑΣ ΓΕΩΠΟΝΙΑΣ (ΣΤΕΓ) ΤΜΗΜΑ ΦΥΤΙΚΗΣ ΠΑΡΑΓΩΓΗΣ (Φ.Π.) ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΜΕ ΘΕΜΑ: «Συγκριτική αξιολόγηση μεθόδων συλλογής ελαιοκάρπου και
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΑΛΑΜΑΤΑΣ (Τ.Ε.Ι.Κ.) ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΑΣ ΓΕΩΠΟΝΙΑΣ (ΣΤΕΓ) ΤΜΗΜΑ ΦΥΤΙΚΗΣ ΠΑΡΑΓΩΓΗΣ (Φ.Π.) ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΜΕ ΘΕΜΑ: «Συγκριτική αξιολόγηση μεθόδων συλλογής ελαιοκάρπου και
ΑΔΑ: 4ΙΦΝΚ-ΔΘ. Αθήνα, 14 Δεκεμβρίου 2010 Αριθ. Πρωτ.: 71351. Ταχυδρομική. Σταδίου 27 Διεύθυνση: Ταχυδρομικός Κώδικας: 101 83 ΑΘΗΝΑ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΕΣΩΤΕΡΙΚΩΝ ΑΠΟΚΕΝΤΡΩΣΗΣ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΗΣ ΔΙΑΚΥΒΕΡΝΗΣΗΣ ΓΕΝΙΚΗ ΔΙΕΥΘΥΝΣΗ ΤΟΠΙΚΗΣ ΑΥTΟΔΙΟΙΚΗΣΗΣ ΔΙΕΥΘΥΝΣΗ ΟΡΓΑΝΩΣΗΣ & ΛΕΙΤΟΥΡΓΙΑΣ ΟΡΓΑΝΙΣΜΩΝ ΤΟΠΙΚΗΣ ΑΥΤΟΔΙΟΙΚΗΣΗΣ ΑΔΑ: Ταχυδρομική
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΕΣΩΤΕΡΙΚΩΝ ΑΠΟΚΕΝΤΡΩΣΗΣ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΗΣ ΔΙΑΚΥΒΕΡΝΗΣΗΣ ΓΕΝΙΚΗ ΔΙΕΥΘΥΝΣΗ ΤΟΠΙΚΗΣ ΑΥTΟΔΙΟΙΚΗΣΗΣ ΔΙΕΥΘΥΝΣΗ ΟΡΓΑΝΩΣΗΣ & ΛΕΙΤΟΥΡΓΙΑΣ ΟΡΓΑΝΙΣΜΩΝ ΤΟΠΙΚΗΣ ΑΥΤΟΔΙΟΙΚΗΣΗΣ ΑΔΑ: Ταχυδρομική
ΙΔ.Ε.Η. Α.Ε. ΕΤΗΣΙΑ ΟΙΚΟΝΟΜΙΚΗ ΕΚΘΕΣΗ
 ΙΔ.Ε.Η. Α.Ε. ΕΤΗΣΙΑ ΟΙΚΟΝΟΜΙΚΗ ΕΚΘΕΣΗ ΧΡΗΣΗΣ 1η ΙΑΝΟΥΑΡΙΟΥ ΕΩΣ 31η ΔΕΚΕΜΒΡΙΟΥ 2014 Σύμφωνα με τα Διεθνή Πρότυπα Χρηματοοικονομικής Αναφοράς (ΔΠΧΑ) ως έχουν υιοθετηθεί από την Ευρωπαϊκή Ένωση Οικονομικές
ΙΔ.Ε.Η. Α.Ε. ΕΤΗΣΙΑ ΟΙΚΟΝΟΜΙΚΗ ΕΚΘΕΣΗ ΧΡΗΣΗΣ 1η ΙΑΝΟΥΑΡΙΟΥ ΕΩΣ 31η ΔΕΚΕΜΒΡΙΟΥ 2014 Σύμφωνα με τα Διεθνή Πρότυπα Χρηματοοικονομικής Αναφοράς (ΔΠΧΑ) ως έχουν υιοθετηθεί από την Ευρωπαϊκή Ένωση Οικονομικές
ΕΠΙΜΕΛΕΙΑ: ΞΗΡΟΣ ΑΝΤΩΝΙΟΣ: ΔΙΚΗΓΟΡΟΣ-ΝΟΜΙΚΟΣ ΣΥΜΒΟΥΛΟΣ ΔΕΥΑΜΒ ΠΑΝΑΓΙΩΤΙΔΗΣ ΠΑΝΑΓΙΩΤΗΣ: Δ/ΚΟΣ ΥΠΑΛΛΗΛΟΣ ΔΕΥΑΜΒ
 ΕΠΙΜΕΛΕΙΑ: ΞΗΡΟΣ ΑΝΤΩΝΙΟΣ: ΔΙΚΗΓΟΡΟΣ-ΝΟΜΙΚΟΣ ΣΥΜΒΟΥΛΟΣ ΔΕΥΑΜΒ ΠΑΝΑΓΙΩΤΙΔΗΣ ΠΑΝΑΓΙΩΤΗΣ: Δ/ΚΟΣ ΥΠΑΛΛΗΛΟΣ ΔΕΥΑΜΒ 2 ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ - ΑΡΘΡΟ Σελίδα Κεφάλαιο Α' Αντικείμενο Γενικοί Όροι 1. Αντικείμενο του
ΕΠΙΜΕΛΕΙΑ: ΞΗΡΟΣ ΑΝΤΩΝΙΟΣ: ΔΙΚΗΓΟΡΟΣ-ΝΟΜΙΚΟΣ ΣΥΜΒΟΥΛΟΣ ΔΕΥΑΜΒ ΠΑΝΑΓΙΩΤΙΔΗΣ ΠΑΝΑΓΙΩΤΗΣ: Δ/ΚΟΣ ΥΠΑΛΛΗΛΟΣ ΔΕΥΑΜΒ 2 ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ - ΑΡΘΡΟ Σελίδα Κεφάλαιο Α' Αντικείμενο Γενικοί Όροι 1. Αντικείμενο του
ΤΑ ΕΠΙΠΕΔΑ ΟΡΓΑΝΩΣΗΣ ΤΩΝ ΠΟΛΥΚΥΤΤΑΡΩΝ ΟΡΓΑΝΣΙΜΩΝ ΟΙ ΖΩΙΚΟΙ ΙΣΤΟΙ 2 ο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ
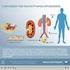 ΤΑ ΕΠΙΠΕΔΑ ΟΡΓΑΝΩΣΗΣ ΤΩΝ ΠΟΛΥΚΥΤΤΑΡΩΝ ΟΡΓΑΝΣΙΜΩΝ ΟΙ ΖΩΙΚΟΙ ΙΣΤΟΙ 2 ο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΤΑ ΟΝΟΜΑΤΑ ΤΩΝ ΜΑΘΗΤΩΝ ΤΗΣ ΟΜΑΔΑΣ ΣΑΣ:.. ΔΡΑΣΤΗΡΙΟΤΗΤΑ 1 η Οι ιστοί των οργάνων του πεπτικού συστήματος Α) Ένα σημαντικό
ΤΑ ΕΠΙΠΕΔΑ ΟΡΓΑΝΩΣΗΣ ΤΩΝ ΠΟΛΥΚΥΤΤΑΡΩΝ ΟΡΓΑΝΣΙΜΩΝ ΟΙ ΖΩΙΚΟΙ ΙΣΤΟΙ 2 ο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΤΑ ΟΝΟΜΑΤΑ ΤΩΝ ΜΑΘΗΤΩΝ ΤΗΣ ΟΜΑΔΑΣ ΣΑΣ:.. ΔΡΑΣΤΗΡΙΟΤΗΤΑ 1 η Οι ιστοί των οργάνων του πεπτικού συστήματος Α) Ένα σημαντικό
ΣΥΧΝΕΣ ΕΡΩΤΗΣΕΙΣ-ΑΠΑΝΤΗΣΕΙΣ. 1. Ποιες υπηρεσίες και φορείς υποχρεούνται να εφαρμόσουν τη ρύθμιση;
 ΚΑΤΑΡΓΗΣΗ ΤΗΣ ΥΠΟΒΟΛΗΣ ΕΠΙΚΥΡΩΜΕΝΩΝ ΑΝΤΙΓΡΑΦΩΝ ΕΓΓΡΑΦΩΝ (άρθρο 1 ν. 4250/2014 ΦΕΚ 74/τ.Α /26-3-2014) ΣΥΧΝΕΣ ΕΡΩΤΗΣΕΙΣ-ΑΠΑΝΤΗΣΕΙΣ 1. Ποιες υπηρεσίες και φορείς υποχρεούνται να εφαρμόσουν τη ρύθμιση; Η ρύθμιση
ΚΑΤΑΡΓΗΣΗ ΤΗΣ ΥΠΟΒΟΛΗΣ ΕΠΙΚΥΡΩΜΕΝΩΝ ΑΝΤΙΓΡΑΦΩΝ ΕΓΓΡΑΦΩΝ (άρθρο 1 ν. 4250/2014 ΦΕΚ 74/τ.Α /26-3-2014) ΣΥΧΝΕΣ ΕΡΩΤΗΣΕΙΣ-ΑΠΑΝΤΗΣΕΙΣ 1. Ποιες υπηρεσίες και φορείς υποχρεούνται να εφαρμόσουν τη ρύθμιση; Η ρύθμιση
ΔΙΚΤΥΟΥ ΑΠΟΧΕΤΕΥΣΗΣ» Η ΠΡΟΕΔΡΟΣ
 18ης Οκτωβρίου 18, 582 00 Έδεσσα τηλ. 2381025555, fax. 2381051255 Εργασία: Αποφράξεις δικτύου αποχέτευσης Προϋπολογισμός: 30.100,00 (με Φ.Π.Α.) Αριθμός Μελέτης: 35/2013 Έδεσσα, 27-12-2013 ΔΙΑΚΗΡΥΞΗ ΠΡΟΧΕΙΡΟΥ
18ης Οκτωβρίου 18, 582 00 Έδεσσα τηλ. 2381025555, fax. 2381051255 Εργασία: Αποφράξεις δικτύου αποχέτευσης Προϋπολογισμός: 30.100,00 (με Φ.Π.Α.) Αριθμός Μελέτης: 35/2013 Έδεσσα, 27-12-2013 ΔΙΑΚΗΡΥΞΗ ΠΡΟΧΕΙΡΟΥ
Αιτιολογική έκθεση Προς τη Βουλή των Ελλήνων
 Αιτιολογική έκθεση Προς τη Βουλή των Ελλήνων Οι οργανισμοί τοπικής αυτοδιοίκησης (ΟΤΑ) της χώρας, ως έκφραση της λαϊκής κυριαρχίας, αποτελούν θεμελιώδη θεσµό του δηµόσιου βίου των Ελλήνων, όπως αυτός κατοχυρώνεται
Αιτιολογική έκθεση Προς τη Βουλή των Ελλήνων Οι οργανισμοί τοπικής αυτοδιοίκησης (ΟΤΑ) της χώρας, ως έκφραση της λαϊκής κυριαρχίας, αποτελούν θεμελιώδη θεσµό του δηµόσιου βίου των Ελλήνων, όπως αυτός κατοχυρώνεται
Αριθμός 3121/2014 ΤΟ ΠΟΛΥΜΕΛΕΣ ΠΡΩΤΟ ΙΚΕΙΟ ΠΕΙΡΑΙΩΣ ( ιαδικασία Εκουσίας ικαιοδοσίας)
 ΠΡΩΤΟ ΙΚΕΙΟ ΠΕΙΡΑΙΩΣ Αριθμός 3121/2014 ΤΟ ΠΟΛΥΜΕΛΕΣ ΠΡΩΤΟ ΙΚΕΙΟ ΠΕΙΡΑΙΩΣ ( ιαδικασία Εκουσίας ικαιοδοσίας) Συγκροτήθηκε από τους ικαστές Σοφία Καλούδη Πρόεδρο Πρωτοδικών-εισηγήτρια, Γεώργιο Ξυνόπουλο και
ΠΡΩΤΟ ΙΚΕΙΟ ΠΕΙΡΑΙΩΣ Αριθμός 3121/2014 ΤΟ ΠΟΛΥΜΕΛΕΣ ΠΡΩΤΟ ΙΚΕΙΟ ΠΕΙΡΑΙΩΣ ( ιαδικασία Εκουσίας ικαιοδοσίας) Συγκροτήθηκε από τους ικαστές Σοφία Καλούδη Πρόεδρο Πρωτοδικών-εισηγήτρια, Γεώργιο Ξυνόπουλο και
Πρακτικό 6/2012 της συνεδρίασης της Επιτροπής Ποιότητας Ζωής, του Δήμου Λήμνου, της 4ης Μαΐου 2012.
 Πρακτικό 6/2012 της συνεδρίασης της Επιτροπής Ποιότητας Ζωής, του Δήμου Λήμνου, της 4ης Μαΐου 2012. Στη Μύρινα, σήμερα στις 4 του μήνα Μαΐου του έτους 2012, ημέρα Παρασκευή και ώρα 12:00 στο Δημοτικό Κατάστημα
Πρακτικό 6/2012 της συνεδρίασης της Επιτροπής Ποιότητας Ζωής, του Δήμου Λήμνου, της 4ης Μαΐου 2012. Στη Μύρινα, σήμερα στις 4 του μήνα Μαΐου του έτους 2012, ημέρα Παρασκευή και ώρα 12:00 στο Δημοτικό Κατάστημα
ΤΙΜΟΛΟΓΙΟ ΜΕΛΕΤΗΣ ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΕΡ. ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ Π.Ε. ΧΑΛΚΙΔΙΚΗΣ ΔΗΜΟΣ ΠΟΛΥΓΥΡΟΥ ΔΙΕΥΘΥΝΣΗ ΤΕΧΝΙΚΩΝ ΥΠΗΡΕΣΙΩΝ ΕΡΓΟ:
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΕΡ. ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ Π.Ε. ΧΑΛΚΙΔΙΚΗΣ ΔΗΜΟΣ ΠΟΛΥΓΥΡΟΥ ΔΙΕΥΘΥΝΣΗ ΤΕΧΝΙΚΩΝ ΥΠΗΡΕΣΙΩΝ ΕΡΓΟ: ΑΠΟΚΑΤΑΣΤΑΣΗ ΧΩΡΟΥ ΑΝΕΞΕΛΕΓΚΤΗΣ ΔΙΑΘΕΣΗΣ ΑΠΟΒΛΗΤΩΝ ΠΟΛΥΓΥΡΟΥ Αρ. Μελ. 7/2013 ΧΡΗΜΑΤΟΔΟΤΗΣΗ:
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΕΡ. ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ Π.Ε. ΧΑΛΚΙΔΙΚΗΣ ΔΗΜΟΣ ΠΟΛΥΓΥΡΟΥ ΔΙΕΥΘΥΝΣΗ ΤΕΧΝΙΚΩΝ ΥΠΗΡΕΣΙΩΝ ΕΡΓΟ: ΑΠΟΚΑΤΑΣΤΑΣΗ ΧΩΡΟΥ ΑΝΕΞΕΛΕΓΚΤΗΣ ΔΙΑΘΕΣΗΣ ΑΠΟΒΛΗΤΩΝ ΠΟΛΥΓΥΡΟΥ Αρ. Μελ. 7/2013 ΧΡΗΜΑΤΟΔΟΤΗΣΗ:
Η ΦΟΡΟΛΟΓΗΣΗ ΤΩΝ ΦΥΣΙΚΩΝ ΠΡΟΣΩΠΩΝ ΣΤΗΝ ΕΥΡΩΠΑΙΚΗ ΕΝΩΣΗ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΚΡΗΤΗΣ ΣΧΟΛΗ ΙΟΙΚΗΣΕΙΣ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ Η ΦΟΡΟΛΟΓΗΣΗ ΤΩΝ ΦΥΣΙΚΩΝ ΠΡΟΣΩΠΩΝ ΣΤΗΝ ΕΥΡΩΠΑΙΚΗ ΕΝΩΣΗ ΣΠΟΥ ΑΣΤΕΣ: ΘΕΜΙΣΤΟΚΛΗΣ ΤΡΙΑΝΤΑΦΥΛΛΟΥ ΒΑΣΙΛΕΙΟΣ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΚΡΗΤΗΣ ΣΧΟΛΗ ΙΟΙΚΗΣΕΙΣ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ Η ΦΟΡΟΛΟΓΗΣΗ ΤΩΝ ΦΥΣΙΚΩΝ ΠΡΟΣΩΠΩΝ ΣΤΗΝ ΕΥΡΩΠΑΙΚΗ ΕΝΩΣΗ ΣΠΟΥ ΑΣΤΕΣ: ΘΕΜΙΣΤΟΚΛΗΣ ΤΡΙΑΝΤΑΦΥΛΛΟΥ ΒΑΣΙΛΕΙΟΣ
www.kapalearn.gr e-mail: info@kapalearn.gr ΚΟΡΙΝΘΟΥ 255, ΚΑΝΑΚΑΡΗ 101 ΤΗΛ. 2610 625.360, 2610 624.009, FAX 2610 625.366
 Α. Ο άνθρωπος, όπως υπογραμμίζει ο συγγραφέας, δεν είναι ρυθμιστής του κόσμου, παρά διαχειριστής του. Αυτή την παρεξήγηση, που ίσχυε για αιώνες, θέλησε να διαλύσει ο πανεπιστήμων άνθρωπος της Αναγέννησης,
Α. Ο άνθρωπος, όπως υπογραμμίζει ο συγγραφέας, δεν είναι ρυθμιστής του κόσμου, παρά διαχειριστής του. Αυτή την παρεξήγηση, που ίσχυε για αιώνες, θέλησε να διαλύσει ο πανεπιστήμων άνθρωπος της Αναγέννησης,
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΣΧΕΔΙΟ ΠΡΟΤΑΣΕΩΝ ΓΙΑ ΤΗ ΛΕΙΤΟΥΡΓΙΑ ΤΩΝ ΑΕΙ. (Θεσμική Επιτροπή Συγκλήτου Πανεπιστημίου Πατρών) ΑΠΟΦΑΣΗ ΣΥΓΚΛΗΤΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΣΧΕΔΙΟ ΠΡΟΤΑΣΕΩΝ ΓΙΑ ΤΗ ΛΕΙΤΟΥΡΓΙΑ ΤΩΝ ΑΕΙ (Θεσμική Επιτροπή Συγκλήτου Πανεπιστημίου Πατρών) ΑΠΟΦΑΣΗ ΣΥΓΚΛΗΤΟΥ (Συνεδρία 455/8.12.2010) 1 1. ΓΕΝΙΚΟ ΠΛΑΙΣΙΟ Η αναγνώριση της Παιδείας
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΣΧΕΔΙΟ ΠΡΟΤΑΣΕΩΝ ΓΙΑ ΤΗ ΛΕΙΤΟΥΡΓΙΑ ΤΩΝ ΑΕΙ (Θεσμική Επιτροπή Συγκλήτου Πανεπιστημίου Πατρών) ΑΠΟΦΑΣΗ ΣΥΓΚΛΗΤΟΥ (Συνεδρία 455/8.12.2010) 1 1. ΓΕΝΙΚΟ ΠΛΑΙΣΙΟ Η αναγνώριση της Παιδείας
Κώδικας Μετανάστευσης Κοινωνικής Ένταξης και λοιπές διατάξεις ΝΟΜΟΣ 4251/2014
 Κώδικας Μετανάστευσης Κοινωνικής Ένταξης και λοιπές διατάξεις ΝΟΜΟΣ 4251/2014 ΤΜΗΜΑ ΔΙΑΡΚΟΥΣ ΚΩΔΙΚΑ ΝΟΜΟΘΕΣΙΑΣ «ΡΑΠΤΑΡΧΗΣ» ΥΠΟΥΡΓΕΙΟ ΕΣΩΤΕΡΙΚΩΝ ΚΑΙ ΔΙΟΙΚΗΤΙΚΗΣ ΑΝΑΣΥΓΚΡΟΤΗΣΗΣ ΔΙΟΙΚΗΤΙΚΗ ΜΕΤΑΡΡΥΘΜΙΣΗ ΚΑΙ
Κώδικας Μετανάστευσης Κοινωνικής Ένταξης και λοιπές διατάξεις ΝΟΜΟΣ 4251/2014 ΤΜΗΜΑ ΔΙΑΡΚΟΥΣ ΚΩΔΙΚΑ ΝΟΜΟΘΕΣΙΑΣ «ΡΑΠΤΑΡΧΗΣ» ΥΠΟΥΡΓΕΙΟ ΕΣΩΤΕΡΙΚΩΝ ΚΑΙ ΔΙΟΙΚΗΤΙΚΗΣ ΑΝΑΣΥΓΚΡΟΤΗΣΗΣ ΔΙΟΙΚΗΤΙΚΗ ΜΕΤΑΡΡΥΘΜΙΣΗ ΚΑΙ
ΣΥΝΘΗΚΗ SCHENGEN (ΣΕΝΓΚΕΝ)
 ΣΥΝΘΗΚΗ SCHENGEN (ΣΕΝΓΚΕΝ) ΣΥΜΒΑΣΗ ΕΦΑΡΜΟΓΗΣ ΤΗΣ ΣΥΜΦΩΝΙΑΣ ΤΟΥ ΣΕΝΓΚΕΝ της 14ης Ιουνίου 1985 μεταξύ των κυβερνήσεων των κρατών της Οικονομικής Ένωσης Μπενελούξ, της Ομοσπονδιακής Δημοκρατίας της Γερμανίας
ΣΥΝΘΗΚΗ SCHENGEN (ΣΕΝΓΚΕΝ) ΣΥΜΒΑΣΗ ΕΦΑΡΜΟΓΗΣ ΤΗΣ ΣΥΜΦΩΝΙΑΣ ΤΟΥ ΣΕΝΓΚΕΝ της 14ης Ιουνίου 1985 μεταξύ των κυβερνήσεων των κρατών της Οικονομικής Ένωσης Μπενελούξ, της Ομοσπονδιακής Δημοκρατίας της Γερμανίας
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Αθήνα, 04-05-2015
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Αθήνα, 04-05-2015 ΥΠΟΥΡΓΕΙΟ ΥΓΕΙΑΣ & Αρ.Πρωτ.Γ4β/ΓΠ/οικ. ΚΟΙΝΩΝΙΚΩΝ ΑΣΦΑΛΙΣΕΩΝ ΓΕΝΙΚΗ Δ/ΝΣΗ ΔΗΜΟΣΙΑΣ ΥΓΕΙΑΣ & ΥΠΗΡΕΣΙΩΝ ΥΓΕΙΑΣ ΔΙΕΥΘΥΝΣΗ ΕΠΑΓΓΕΛΜΑΤΙΩΝ ΥΓΕΙΑΣ Ταχ Δ/νση: Αριστοτέλους
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Αθήνα, 04-05-2015 ΥΠΟΥΡΓΕΙΟ ΥΓΕΙΑΣ & Αρ.Πρωτ.Γ4β/ΓΠ/οικ. ΚΟΙΝΩΝΙΚΩΝ ΑΣΦΑΛΙΣΕΩΝ ΓΕΝΙΚΗ Δ/ΝΣΗ ΔΗΜΟΣΙΑΣ ΥΓΕΙΑΣ & ΥΠΗΡΕΣΙΩΝ ΥΓΕΙΑΣ ΔΙΕΥΘΥΝΣΗ ΕΠΑΓΓΕΛΜΑΤΙΩΝ ΥΓΕΙΑΣ Ταχ Δ/νση: Αριστοτέλους
Πρώτη Έκθεση της Ελλάδας
 Φ092.22/739 Προαιρετικό Πρωτόκολλο στη Σύμβαση για τα Δικαιώματα του Παιδιού σχετικά με την εμπλοκή των παιδιών σε ένοπλες συρράξεις ΕΙΣΑΓΩΓΗ Πρώτη Έκθεση της Ελλάδας 1. Η Ελλάδα υπέγραψε το Προαιρετικό
Φ092.22/739 Προαιρετικό Πρωτόκολλο στη Σύμβαση για τα Δικαιώματα του Παιδιού σχετικά με την εμπλοκή των παιδιών σε ένοπλες συρράξεις ΕΙΣΑΓΩΓΗ Πρώτη Έκθεση της Ελλάδας 1. Η Ελλάδα υπέγραψε το Προαιρετικό
ΚΥΑ Φ.80000/οικ.16011/1709
 ΚΥΑ Φ.80000/οικ.16011/1709 Θέμα: «Όροι, προϋποθέσεις συμμετοχής, ύψος της χρηματοδότησης ανά ωφελούμενο, σύναψη σύμβασης και διαδικασία παρακολούθησης και πληρωμής παρόχων, για τη λειτουργία του προγράμματος
ΚΥΑ Φ.80000/οικ.16011/1709 Θέμα: «Όροι, προϋποθέσεις συμμετοχής, ύψος της χρηματοδότησης ανά ωφελούμενο, σύναψη σύμβασης και διαδικασία παρακολούθησης και πληρωμής παρόχων, για τη λειτουργία του προγράμματος
ΜΕΡΟΣ Ι ΤΙΤΛΟΣ Ι. Άρθρο Ι-1. Ίδρυση της Ένωσης. Άρθρο Ι-2. Οι αξίες της Ένωσης
 16.12.2004 EL Επίσημη Εφημερίδα της Ευρωπαϊκής Ένωσης C 310/11 ΜΕΡΟΣ Ι ΤΙΤΛΟΣ Ι ΟΡΙΣΜΟΣ ΚΑΙ ΣΤΟΧΟΙ ΤΗΣ ΕΝΩΣΗΣ Άρθρο Ι-1 Ίδρυση της Ένωσης 1. Εκφράζοντας τη βούληση των πολιτών και των κρατών της Ευρώπης
16.12.2004 EL Επίσημη Εφημερίδα της Ευρωπαϊκής Ένωσης C 310/11 ΜΕΡΟΣ Ι ΤΙΤΛΟΣ Ι ΟΡΙΣΜΟΣ ΚΑΙ ΣΤΟΧΟΙ ΤΗΣ ΕΝΩΣΗΣ Άρθρο Ι-1 Ίδρυση της Ένωσης 1. Εκφράζοντας τη βούληση των πολιτών και των κρατών της Ευρώπης
Σκόπελος 2015. Ο Αντιπρόεδρος του Δ.Σ. της ΔΕΥΑΣ. Ευάγγελος Γ. Τσουκαλάς
 ΠΕΡΙΛΗΨΗ ΔΙΑΚΗΡΥΞΗΣ Η Δημοτική Επιχείρηση Ύδρευσης και Αποχέτευσης Σκοπέλου (ΔΕΥΑΣ) που έχει την έδρα της στη Σκόπελο (37003 Σκόπελος) προκηρύσσει Πρόχειρο Διαγωνισμό με σφραγισμένες προσφορές με το σύστημα
ΠΕΡΙΛΗΨΗ ΔΙΑΚΗΡΥΞΗΣ Η Δημοτική Επιχείρηση Ύδρευσης και Αποχέτευσης Σκοπέλου (ΔΕΥΑΣ) που έχει την έδρα της στη Σκόπελο (37003 Σκόπελος) προκηρύσσει Πρόχειρο Διαγωνισμό με σφραγισμένες προσφορές με το σύστημα
ΕΠΙΔΟΤΗΣΕΙΣ ΕΩΣ 20.000 ΣΤΟΥΣ ΝΕΟΥΣ ΑΓΡΟΤΕΣ
 ΕΝΗΜΕΡΩΤΙΚΟ ΣΗΜΕΙΩΜΑ ΕΠΙΔΟΤΗΣΕΙΣ ΕΩΣ 20.000 ΣΤΟΥΣ ΝΕΟΥΣ ΑΓΡΟΤΕΣ ΜΕΤΡΟ 112 Εγκατάσταση Νέων Γεωργών ΣΥΜΒΟΥΛΟΙ ΠΟΙΟΤΗΤΑΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ Λεωφ. Βουλιαγμένης & Δωδεκανήσου 3 174 56 Άλιμος Αθήνα ΤΗΛ: 210 9933888
ΕΝΗΜΕΡΩΤΙΚΟ ΣΗΜΕΙΩΜΑ ΕΠΙΔΟΤΗΣΕΙΣ ΕΩΣ 20.000 ΣΤΟΥΣ ΝΕΟΥΣ ΑΓΡΟΤΕΣ ΜΕΤΡΟ 112 Εγκατάσταση Νέων Γεωργών ΣΥΜΒΟΥΛΟΙ ΠΟΙΟΤΗΤΑΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ Λεωφ. Βουλιαγμένης & Δωδεκανήσου 3 174 56 Άλιμος Αθήνα ΤΗΛ: 210 9933888
ΑΠΟΦΑΣΗ. Η Εθνική Επιτροπή Τηλεπικοινωνιών και Ταχυδρομείων (ΕΕΤΤ),
 Μαρούσι, 23-6-2009 ΑΡΙΘ. ΑΠ.: 528/075 ΑΠΟΦΑΣΗ Κανονισμός Καθορισμού των Τελών Διέλευσης, των Τελών Χρήσης Δικαιωμάτων Διέλευσης και του Ύψους των Εγγυήσεων Καλής Εκτέλεσης των Εργασιών Διέλευσης για όλη
Μαρούσι, 23-6-2009 ΑΡΙΘ. ΑΠ.: 528/075 ΑΠΟΦΑΣΗ Κανονισμός Καθορισμού των Τελών Διέλευσης, των Τελών Χρήσης Δικαιωμάτων Διέλευσης και του Ύψους των Εγγυήσεων Καλής Εκτέλεσης των Εργασιών Διέλευσης για όλη
ΚΑΤΑΣΤΑΤΙΚΟ ΚΕΝΤΡΟΥ ΝΕΟΤΗΤΑΣ. ΙΔΡΥΣΗ Ιδρύεται Κέντρο Νεότητας µε την επωνυµία «Κέντρο Νεότητας... µε έδρα...
 ΚΑΤΑΣΤΑΤΙΚΟ ΚΕΝΤΡΟΥ ΝΕΟΤΗΤΑΣ ΑΡΘΡΟ 1 ΙΔΡΥΣΗ Ιδρύεται Κέντρο Νεότητας µε την επωνυµία «Κέντρο Νεότητας... µε έδρα... ΑΡΘΡΟ 2 Στο Καταστατικό αυτό «Κέντρο Νεότητας» σηµαίνει: «εθελοντική-κοινοτική οργάνωση
ΚΑΤΑΣΤΑΤΙΚΟ ΚΕΝΤΡΟΥ ΝΕΟΤΗΤΑΣ ΑΡΘΡΟ 1 ΙΔΡΥΣΗ Ιδρύεται Κέντρο Νεότητας µε την επωνυµία «Κέντρο Νεότητας... µε έδρα... ΑΡΘΡΟ 2 Στο Καταστατικό αυτό «Κέντρο Νεότητας» σηµαίνει: «εθελοντική-κοινοτική οργάνωση
ΑΓΡΟΤΙΚΑ ΑΔΙΚΗΜΑΤΑ. Ν. 3585/2007, Προστασία του περιβάλλοντος, αγροτική ασφάλεια και άλλες διατάξεις
 ΑΓΡΟΤΙΚΑ ΑΔΙΚΗΜΑΤΑ Ν. 3585/2007, Προστασία του περιβάλλοντος, αγροτική ασφάλεια και άλλες διατάξεις Αρ. 1 Ίδρυση Αποστολή 1. Στο Υπουργείο Δημόσιας Τάξης ιδρύεται αυτοτελής Υπηρεσία με τον τίτλο «Ελληνική
ΑΓΡΟΤΙΚΑ ΑΔΙΚΗΜΑΤΑ Ν. 3585/2007, Προστασία του περιβάλλοντος, αγροτική ασφάλεια και άλλες διατάξεις Αρ. 1 Ίδρυση Αποστολή 1. Στο Υπουργείο Δημόσιας Τάξης ιδρύεται αυτοτελής Υπηρεσία με τον τίτλο «Ελληνική
ΘΕΜΑ; "Το συν/γιια ως μέσον διεθνούς πληρωμής" ΣΠΟΥΔΑΣΤΡΙΑ: ΚΟΝΣΤΑΝΤΙΝΙΑΟΥ ΑΓΑΠΗ ΕΠΙΒΛΕΠΟΝ ΚΑΘΗΓΗΤΗΣ: ΠΙΠΙΑΙΑΓΚΟΠΟΥΛΟΣ ΜΙΧΑΑΗΣ
 T.E.l. ΚΑΒΑΛΑΣ ΣΧΟΛΗ ΛΙΟίΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟ ΜΙΑΣ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΘΕΜΑ; "Το συν/γιια ως μέσον διεθνούς πληρωμής" ΣΠΟΥΔΑΣΤΡΙΑ: ΚΟΝΣΤΑΝΤΙΝΙΑΟΥ ΑΓΑΠΗ ΕΠΙΒΛΕΠΟΝ ΚΑΘΗΓΗΤΗΣ: ΠΙΠΙΑΙΑΓΚΟΠΟΥΛΟΣ ΜΙΧΑΑΗΣ
T.E.l. ΚΑΒΑΛΑΣ ΣΧΟΛΗ ΛΙΟίΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟ ΜΙΑΣ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΘΕΜΑ; "Το συν/γιια ως μέσον διεθνούς πληρωμής" ΣΠΟΥΔΑΣΤΡΙΑ: ΚΟΝΣΤΑΝΤΙΝΙΑΟΥ ΑΓΑΠΗ ΕΠΙΒΛΕΠΟΝ ΚΑΘΗΓΗΤΗΣ: ΠΙΠΙΑΙΑΓΚΟΠΟΥΛΟΣ ΜΙΧΑΑΗΣ
ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ
 1195 ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ ΤΗΣ ΕΛΛΗΝΙΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ Με την υπ αριθ. 14509/Δ1/3 2 2014 απόφαση του Υπουργού Παιδείας και Θρησκευμάτων, που εκδόθηκε σύμφωνα με τις
1195 ΕΦΗΜΕΡΙΣ ΤΗΣ ΚΥΒΕΡΝΗΣΕΩΣ ΤΗΣ ΕΛΛΗΝΙΚΗΣ ΔΗΜΟΚΡΑΤΙΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ Με την υπ αριθ. 14509/Δ1/3 2 2014 απόφαση του Υπουργού Παιδείας και Θρησκευμάτων, που εκδόθηκε σύμφωνα με τις
Θέµα: ιακήρυξη πρόχειρου διαγωνισµού για την εργασία ιαχείριση ογκωδών και
 ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΘΕΣΣΑΛΟΝΙΚΗΣ ΗΜΟΣ ΘΕΡΜΑΪΚΟΥ /ΝΣΗ ΙΟΙΚΗΤΙΚΩΝ & ΟΙΚΟΝΟΜΙΚΩΝ ΥΠΗΡΕΣΙΩΝ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΗΣ ΥΠΗΡΕΣΙΑΣ ΓΡΑΦΕΙΟ ΠΡΟΜΗΘΕΙΩΝ /νση:μεγ.αλεξάνδρου 2, Περαία Πληροφορίες: Γκατζογιάννης Σπύρος
ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΘΕΣΣΑΛΟΝΙΚΗΣ ΗΜΟΣ ΘΕΡΜΑΪΚΟΥ /ΝΣΗ ΙΟΙΚΗΤΙΚΩΝ & ΟΙΚΟΝΟΜΙΚΩΝ ΥΠΗΡΕΣΙΩΝ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΗΣ ΥΠΗΡΕΣΙΑΣ ΓΡΑΦΕΙΟ ΠΡΟΜΗΘΕΙΩΝ /νση:μεγ.αλεξάνδρου 2, Περαία Πληροφορίες: Γκατζογιάννης Σπύρος
ΠΕΡΙΓΡΑΦΙΚΟ ΤΙΜΟΛΟΓΙΟ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΕΡΓΟ: ΑΣΦΑΛΤΟΣΤΡΩΣΗ ΟΔΩΝ Δ.Ε. ΔΟΒΡΑ ΝΟΜΟΣ ΗΜΑΘΙΑΣ ΔΗΜΟΣ ΒΕΡΟΙΑΣ ΔΙΕΥΘΥΝΣΗ ΥΠΗΡΕΣΙΩΝ ΤΜΗΜΑ ΤΕΧΝΙΚΟ ΣΥΝΤ. ΕΡΓΩΝ ΠΡ/ΣΜΟΣ: 40.000,00 ΑΡ. ΜΕΛ.: 25/2015 ΑΡ. ΕΡΓΟΥ: 10/2015 ΠΕΡΙΓΡΑΦΙΚΟ ΤΙΜΟΛΟΓΙΟ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΕΡΓΟ: ΑΣΦΑΛΤΟΣΤΡΩΣΗ ΟΔΩΝ Δ.Ε. ΔΟΒΡΑ ΝΟΜΟΣ ΗΜΑΘΙΑΣ ΔΗΜΟΣ ΒΕΡΟΙΑΣ ΔΙΕΥΘΥΝΣΗ ΥΠΗΡΕΣΙΩΝ ΤΜΗΜΑ ΤΕΧΝΙΚΟ ΣΥΝΤ. ΕΡΓΩΝ ΠΡ/ΣΜΟΣ: 40.000,00 ΑΡ. ΜΕΛ.: 25/2015 ΑΡ. ΕΡΓΟΥ: 10/2015 ΠΕΡΙΓΡΑΦΙΚΟ ΤΙΜΟΛΟΓΙΟ
Το σχέδιο έχει ως βάση ένα ενιαίο σύστημα κλειστών αγωγών το οποίο εκτείνεται
 Να θυμόμαστε ότι ο νόμος Ν 3199/2003 για την προστασία και διαχείριση υδάτων ψ ηφίστηκε από την Ελλάδα ώστε να εναρμονισθεί με την οδηγία πλαίσιο 2000/60/ΕΚ του Ευρωπαϊκού Κοινοβουλίου «Διαχείριση και
Να θυμόμαστε ότι ο νόμος Ν 3199/2003 για την προστασία και διαχείριση υδάτων ψ ηφίστηκε από την Ελλάδα ώστε να εναρμονισθεί με την οδηγία πλαίσιο 2000/60/ΕΚ του Ευρωπαϊκού Κοινοβουλίου «Διαχείριση και
Σχετ: Το από 21.07.2008 έγγραφό σας (αρ. πρωτ. εισερχ. 932/28.7.2008). Σε απάντηση του ως άνω σχετικού, θα θέλαμε να παρατηρήσουμε τα εξής:
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΡΟΣ: Ελληνικά Ταχυδρομεία Κεντρική Υπηρεσία Δνση Στρατηγικής και Ανάπτυξης Τομέας Ρυθμιστικού Πλαισίου και Ανταγωνισμού Σταδίου 60 101 88 Αθήνα Αθήνα, 13 Οκτωβρίου 2008 Αρ. Πρωτ.:1263
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΡΟΣ: Ελληνικά Ταχυδρομεία Κεντρική Υπηρεσία Δνση Στρατηγικής και Ανάπτυξης Τομέας Ρυθμιστικού Πλαισίου και Ανταγωνισμού Σταδίου 60 101 88 Αθήνα Αθήνα, 13 Οκτωβρίου 2008 Αρ. Πρωτ.:1263
Νεοελληνική Λογοτεχνία Θεωρητικής Κατεύθυνσης 4-6-2014 Α1. Β1. Ορόσημο www.orosimo.gr Τηλ. 2810 222 724
 Νεοελληνική Λογοτεχνία Θεωρητικής Κατεύθυνσης 4-6-2014 Α1. Ο Γ. Βιζυηνός χαρακτηρίζεται εκτός των άλλων, ως δραματικός πεζογράφος. Η περίτεχνη πλοκή της αφήγησης, με τις εναλλαγές των σκηνών ή των συγκρούσεων,
Νεοελληνική Λογοτεχνία Θεωρητικής Κατεύθυνσης 4-6-2014 Α1. Ο Γ. Βιζυηνός χαρακτηρίζεται εκτός των άλλων, ως δραματικός πεζογράφος. Η περίτεχνη πλοκή της αφήγησης, με τις εναλλαγές των σκηνών ή των συγκρούσεων,
Αριθμός 9769/2014 TO ΠΟΛΥΜΕΛΕΣ ΠΡΩΤΟΔΙΚΕΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΔΙΑΔΙΚΑΣΙΑ ΕΚΟΥΣΙΑΣ ΔΙΚΑΙΟΔΟΣΙΑΣ ΣΥΓΚΡΟΤΗΘΗΚΕ από τους Δικαστές Μυρσίνη Κοντογιάννη, Πρόεδρο
 Αριθμός 9769/2014 TO ΠΟΛΥΜΕΛΕΣ ΠΡΩΤΟΔΙΚΕΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΔΙΑΔΙΚΑΣΙΑ ΕΚΟΥΣΙΑΣ ΔΙΚΑΙΟΔΟΣΙΑΣ ΣΥΓΚΡΟΤΗΘΗΚΕ από τους Δικαστές Μυρσίνη Κοντογιάννη, Πρόεδρο Πρωτοδικών, η οποία ορίστηκε Αναπληρωματική Πρόεδρος
Αριθμός 9769/2014 TO ΠΟΛΥΜΕΛΕΣ ΠΡΩΤΟΔΙΚΕΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΔΙΑΔΙΚΑΣΙΑ ΕΚΟΥΣΙΑΣ ΔΙΚΑΙΟΔΟΣΙΑΣ ΣΥΓΚΡΟΤΗΘΗΚΕ από τους Δικαστές Μυρσίνη Κοντογιάννη, Πρόεδρο Πρωτοδικών, η οποία ορίστηκε Αναπληρωματική Πρόεδρος
Δικαιολογητικά αναγνώρισης και εκκαθάρισης για την κάλυψη των δαπανών μετακινουμένων υπαλλήλων εντός και εκτός της Επικράτειας και άλλες διατάξεις.
 Αριθμ. 2/54866/0022/20-7-1999 (ΦΕΚ Β 1583/Β/6-8-1999) Δικαιολογητικά αναγνώρισης και εκκαθάρισης για την κάλυψη των δαπανών μετακινουμένων υπαλλήλων εντός και εκτός της Επικράτειας και άλλες διατάξεις.
Αριθμ. 2/54866/0022/20-7-1999 (ΦΕΚ Β 1583/Β/6-8-1999) Δικαιολογητικά αναγνώρισης και εκκαθάρισης για την κάλυψη των δαπανών μετακινουμένων υπαλλήλων εντός και εκτός της Επικράτειας και άλλες διατάξεις.
ΕΡΓΟ: ΕΙ ΙΚΗ ΣΥΓΓΡΑΦΗ ΥΠΟΧΡΕΩΣΕΩΝ
 ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΣΕΡΡΩΝ ΗΜΟΣ ΑΜΦΙΠΟΛΗΣ ΤΜΗΜΑ ΤΕΧΝΙΚΩΝ ΥΠΗΡΕΣΙΩΝ ΕΡΓΟ: Α.Μ: ΚΑΤΑΣΚΕΥΗ ΠΡΟΣΤΑΤΕΥΤΙΚΟΥ ΤΟΙΧΙΟΥ ΝΕΚΡΟΤΑΦΕΙΩΝ ΤΚ ΚΟΡΜΙΣΤΑΣ 16 / 2013 ΕΙ ΙΚΗ ΣΥΓΓΡΑΦΗ ΥΠΟΧΡΕΩΣΕΩΝ ΑΡΘΡΟ 1ο : ΑΝΤΙΚΕΙΜΕΝΟ
ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΣΕΡΡΩΝ ΗΜΟΣ ΑΜΦΙΠΟΛΗΣ ΤΜΗΜΑ ΤΕΧΝΙΚΩΝ ΥΠΗΡΕΣΙΩΝ ΕΡΓΟ: Α.Μ: ΚΑΤΑΣΚΕΥΗ ΠΡΟΣΤΑΤΕΥΤΙΚΟΥ ΤΟΙΧΙΟΥ ΝΕΚΡΟΤΑΦΕΙΩΝ ΤΚ ΚΟΡΜΙΣΤΑΣ 16 / 2013 ΕΙ ΙΚΗ ΣΥΓΓΡΑΦΗ ΥΠΟΧΡΕΩΣΕΩΝ ΑΡΘΡΟ 1ο : ΑΝΤΙΚΕΙΜΕΝΟ
ΠΕΡΙΓΡΑΦΙΚΟ ΤΙΜΟΛΟΓΙΟ ΕΡΓΟΥ
 ΠΕΡΙΓΡΑΦΙΚΟ ΤΙΜΟΛΟΓΙΟ ΕΡΓΟΥ ΓΕΝΙΚΟΙ ΟΡΟΙ Aντικείμενο του παρόντος τιμολογίου είναι ο καθορισμός τιμών μονάδος των εργασιών, που είναι απαραίτητες για την έντεχνη ολοκλήρωση του Εργου, όπως προδιαγράφεται
ΠΕΡΙΓΡΑΦΙΚΟ ΤΙΜΟΛΟΓΙΟ ΕΡΓΟΥ ΓΕΝΙΚΟΙ ΟΡΟΙ Aντικείμενο του παρόντος τιμολογίου είναι ο καθορισμός τιμών μονάδος των εργασιών, που είναι απαραίτητες για την έντεχνη ολοκλήρωση του Εργου, όπως προδιαγράφεται
ΕΡΓΟ: ΑΓΡΟΤΙΚΗ ΟΔΟΠΟΙΙΑ Δ.Κ. ΚΟΛΙΝΔΡΟΥ ΔΗΜΟΥ ΠΥΔΝΑΣ-ΚΟΛΙΝΔΡΟΥ ΤΙΜΟΛΟΓΙΟ ΜΕΛΕΤΗΣ
 ΕΡΓΟ: ΑΓΡΟΤΙΚΗ ΟΔΟΠΟΙΙΑ Δ.Κ. ΚΟΛΙΝΔΡΟΥ ΔΗΜΟΥ ΠΥΔΝΑΣ-ΚΟΛΙΝΔΡΟΥ ΦΟΡΕΑΣ: ΔΗΜΟΣ ΠΥΔΝΑΣ ΚΟΛΙΝΔΡΟΥ Αρ.Μελ.: 8/2014 ΠΡΟΫΠΟΛΟΓΙΣΜΟΥ: 499.897,03 ΤΙΜΟΛΟΓΙΟ ΜΕΛΕΤΗΣ 1. ΓΕΝΙΚΟΙ ΟΡΟΙ Aντικείμενο του παρόντος τιμολογίου
ΕΡΓΟ: ΑΓΡΟΤΙΚΗ ΟΔΟΠΟΙΙΑ Δ.Κ. ΚΟΛΙΝΔΡΟΥ ΔΗΜΟΥ ΠΥΔΝΑΣ-ΚΟΛΙΝΔΡΟΥ ΦΟΡΕΑΣ: ΔΗΜΟΣ ΠΥΔΝΑΣ ΚΟΛΙΝΔΡΟΥ Αρ.Μελ.: 8/2014 ΠΡΟΫΠΟΛΟΓΙΣΜΟΥ: 499.897,03 ΤΙΜΟΛΟΓΙΟ ΜΕΛΕΤΗΣ 1. ΓΕΝΙΚΟΙ ΟΡΟΙ Aντικείμενο του παρόντος τιμολογίου
ΚΕΦΑΛΑΙΟ Α Τροποποίηση διατάξεων του ν. 3316/2005
 ΣΧΕΔΙΟ ΝΟΜΟΥ Μεταρρύθμιση Συστήματος Ανάθεσης και Εκτέλεσης συμβάσεων Μελετών και Δημοσίων Έργων Ίδρυση Αρχής Ελέγχου Μελετών και Έργων και λοιπές διατάξεις ΚΕΦΑΛΑΙΟ Α Τροποποίηση διατάξεων του ν. 3316/2005
ΣΧΕΔΙΟ ΝΟΜΟΥ Μεταρρύθμιση Συστήματος Ανάθεσης και Εκτέλεσης συμβάσεων Μελετών και Δημοσίων Έργων Ίδρυση Αρχής Ελέγχου Μελετών και Έργων και λοιπές διατάξεις ΚΕΦΑΛΑΙΟ Α Τροποποίηση διατάξεων του ν. 3316/2005
ΘΕΜΑ: «Κινητικότητα υπαλλήλων σε διαθεσιμότητα»
 ΑΝΑΡΤΗΤΕΑ ΣΤΟ ΔΙΑΔΙΚΤΥΟ ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΔΙΟΙΚΗΤΙΚΗΣ ΜΕΤΑΡΡΥΘΜΙΣΗΣ & ΗΛΕΚΤΡΟΝΙΚΗΣ ΔΙΑΚΥΒΕΡΝΗΣΗΣ ΓΕΝΙΚΗ ΔΙΕΥΘΥΝΣΗ ΚΑΤΑΣΤΑΣΗΣ ΠΡΟΣΩΠΙΚΟΥ Ταχυδρομική Διεύθυνση: Βασ. Σοφίας 15 106 74, Αθήνα τηλ.213
ΑΝΑΡΤΗΤΕΑ ΣΤΟ ΔΙΑΔΙΚΤΥΟ ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΔΙΟΙΚΗΤΙΚΗΣ ΜΕΤΑΡΡΥΘΜΙΣΗΣ & ΗΛΕΚΤΡΟΝΙΚΗΣ ΔΙΑΚΥΒΕΡΝΗΣΗΣ ΓΕΝΙΚΗ ΔΙΕΥΘΥΝΣΗ ΚΑΤΑΣΤΑΣΗΣ ΠΡΟΣΩΠΙΚΟΥ Ταχυδρομική Διεύθυνση: Βασ. Σοφίας 15 106 74, Αθήνα τηλ.213
