ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Τ. ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ

Transcript

1 ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Τ. ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΘΕΩΡΗΤΙΚΗ ΔΙΕΡΕΥΝΗΣΗ ΑΝΑΚΤΗΣΗΣ ΘΕΡΜΟΤΗΤΑΣ ΑΠΟ ΗΛΕΚΤΡΟΠΑΡΑΓΩΓΑ ΖΕΥΓΗ ΚΑΙ ΕΚΜΕΤΑΛΛΕΥΣΗΣ ΤΗΣ ΜΕΣΩ ΚΥΚΛΟΥ RANKINE ΟΡΓΑΝΙΚΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΚΥΚΛΟΥ ΨΥΞΗΣ ΜΕ ΕΓΧΥΤΗΡΕΣ ΣΙΑΜΠΑΝΟΣ ΠΑΝΑΓΙΩΤΗΣ (Α.Μ.: ) ΕΠΙΒΛΕΠΩΝ ΚΑΘΗΓΗΤΗΣ : ΑΛΕΞΗΣ ΓΕΩΡΓΙΟΣ

2 Ευχαριστίες Ευχαριστώ τον επιβλέποντα καθηγητή μου κ. Αλέξη για όλη την καθοδήγηση που μου έδωσε για την πτυχιακή εργασία και συγκεκριμένα για τον κώδικα στο Mathcad σχετικά με τον υπολογισμό του Οργανικού κύκλου Rankine, τον κύκλο ψύξης για τους εγχυτήρες και για την υπόλοιπη βοήθεια που ήταν σχετική με την εργασία. Ευχαριστώ τον κ Νίκα για την βοήθεια του, για τον υπολογισμό του συντελεστή μετάδοσης θερμότητας. Ευχαριστώ και την εταιρία caterpillar για τις πληροφορίες που μου έδωσε σχετικά με το ηλεκτροπαραγωγό ζεύγος με το οποίο έγιναν οι υπολογισμοί.

3 ΠΕΡΙΛΗΨΗ Σε μια μηχανή ντίζελ κατά την καύση του καυσίμου δεν μπορεί να γίνει πλήρης εκμετάλλευση όλης της θερμότητας που εκλύεται από το καύσιμο και όπως όλες οι θερμικές μηχανές έχουν κάποιο βαθμό απόδοσης. Αυτό το ποσό της θερμότητας συνήθως μένει ανεκμετάλλευτο και απορρίπτεται στο περιβάλλον. Σε μηχανές μεγάλης ισχύος είναι αναγκαίο να εκμεταλλευόμαστε αυτά τα ποσά της θερμότητας. Στην συγκεκριμένη εργασία μελετάται η εκμετάλλευση αυτών των ποσών θερμότητας για την παραγωγή ισχύος, την παραγωγή ψύξης και τη θέρμανση. Η παραγωγή ισχύος επιτυγχάνεται με οργανικό κύκλο Rankine, η παραγωγή ψύξης επιτυγχάνεται με κύκλο ψύξης με εγχυτήρες και η θέρμανση επιτυγχάνεται με την εκμετάλλευση του νερού ψύξης, του λιπαντικού λαδιού και των καυσαερίων της μηχανής Ντίζελ. Πιο συγκεκριμένα γίνονται οι θερμοδυναμικοί υπολογισμοί του οργανικού κύκλου Rankine και του κύκλου ψύξης με εγχυτήρες. Οι δύο πιο πάνω κύκλοι εργάζονται με το οργανικό ρευστό Ra. Η συγκεκριμένη μηχανή Ντίζελ έχει στην έξοδο της μια γεννήτρια δηλαδή δουλεύει σαν ένα ηλεκτροπαραγωγό ζεύγος. ΑBSTRACT A Diesel machine can t take advantage of all the heat that is been released from the combustible and as all heat engines it has a performance level. This amount of heat that is usually been untapped and been rejected to the environment. In diesel engines of high rate of power it is necessary to exploit this amount of heat. In this particular project it is been examined the exploitation of this amount of heat for the power generation, cooling production and heat production. Power generation can be accomplished by an organic Rankine cycle, cooling production can be realized by an ejector refrigeration cycle and heat production can be realized by circulating cooling water of diesel engine. Specifically in that thermodynamic calculations have been done for organic Rankine cycle and for ejector refrigeration cycle. The working fluid for these two cycles is Ra.The diesel engine in its output has a generator and working as generating set.

4 ΠΕΡΙΕΧΟΜΕΝΑ ΣΥΜΒΟΛΙΣΜΟΙ... ΚΕΦΑΛΑΙΟ : ΕΙΣΑΓΩΓΗ....ΗΛΕΚΤΡΟΠΑΡΑΓΩΓΟ ΖΕΓΟΣ ΟΡΓΑΝΙΚΟΣ ΚΥΚΛΟΣ RANKINE.... ΚΥΚΛΟΣ ΨΥΞΗΣ ΜΕ ΕΓΧΥΤΗΡΕΣ... ΚΕΦΑΛΑΙΟ : ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΑΝΑΛΥΣΗ....ΗΛΕΚΤΡΟΠΑΡΑΓΩΓΟ ΖΕΥΓΟΣ....ΟΡΓΑΝΙΚΟΣ ΚΥΚΛΟΣ RANKINE....ΨΥΞΗ ΜΕ ΕΓΧΥΤΗΡΕΣ....ΕΝΑΛΛΑΚΤΗΣ ΘΕΡΜΟΤΗΤΑΣ....ΕΞΙΣΩΣΗ SOAVE... ΚΕΦΑΛΙΑΟ. ΕΡΓΑΖΟΜΕΝΟ ΜΕΣΟ Ra....ΕΠΙΛΟΓΗ ΡΕΥΣΤΟΥ ΣΤΟΝ ΟΡΓΑΝΙΚΟ ΚΥΚΛΟ RANKINE....ΨΥΚΤΙΚΟ ΡΕΥΣΤΟ Ra... 9 ΚΕΦΑΛΑΙΟ : ΠΑΡΑΜΕΤΡΙΚΗ ΜΕΛΕΤΗ ΕΝΔΕΙΚΤΙΚΟΣ ΥΠΟΛΟΓΙΣΜΟΣ Για τον οργανικό κύκλο RANKINE Για τον κύκλο ψύξης με εγχυτήρες..... Για τον εναλλάκτη θερμότητας....παρουσιαση ΑΠΟΤΕΛΕΣΜΑΤΩΝ..... ΟΡΓΑΝΙΚΟΣ ΚΥΚΛΟ RANKINE..... ΚΥΚΛΟΣ ΨΥΞΗΣ ΜΕ ΕΓΧΥΤΗΡΕΣ....ΔΙΑΓΡΑΜΜΑΤΑ... 9 ΟΡΓΑΝΙΚΟΣ ΚΥΚΛΟΣ RANKINE... 9 ΚΥΚΛΟΣ ΨΥΞΗΣ ΜΕ ΕΓΧΥΤΗΡΕΣ... 9.ΣΥΜΠΕΡΑΣΜΑΤΑ ΠΑΡΑΡΤΗΜΑ... 0 ΣΧΕΣΕΙΣ P-V-T KAI ΚΑΘΑΡΗ ΟΥΣΙΑ... 0 ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΟΓΚΟΜΕΤΡΙΚΕΣ ΙΔΙΟΤΗΤΕΣ... 0 ΠΙΝΑΚΑΣ ΘΕΡΜΟΡΕΥΣΤΟΔΥΝΑΜΙΚΩΝ ΙΔΙΟΤΗΤΩΝ ΤΟΥ ΝΕΡΟ... 0 ΠΗΓΕΣ... 0

5 ΣΥΜΒΟΛΙΣΜΟΙ Σύμβολο Επεξήγηση Μόναδες A επιφάνεια συναλλαγής θερμότητας του m εναλλάκτη d διάμετρος του αγωγού m d in αντίστοιχη διάμετρος από την εσωτερική m πλευρά του εναλλάκτη d out αντίστοιχη διάμετρος από την εξωτερική m πλευρά του εναλλάκτη h ειδική ενθαλπία kg h hot συντελεστής θερμικής συναγωγιμότητας του θερμού ρευστού W m K h cold συντελεστής θερμικής συναγωγιμότητας του ψυχρού ρευστού W m K k Συντελεστής θερμικής αγωγιμότητας W m ν παροχή μάζας του νερού mk kg ΜΒ μοριακό βάρος s kg kmol Νu αριθμός Nusselt P πίεση bar P s πίεση των ατμών Pr αριθμός Prandtl Q θερμική ισχύς που απορρίπτεται από την kw μηχανή Diesel Q θερμική ισχύς που παραλαμβάνει το νερό kw και την οδηγεί στην τετράοδη βαλβίδα Re D αριθμός Reynolts S ειδική εντροπία kgk Τ θερμοκρασία αναφοράς Τ in θερμοκρασία εισόδου του ρευστού στο εναλλάκτη Τ out θερμοκρασία εξόδου του ρευστού από τον εναλλάκτη U συνολικός συντελεστής μετάδοσης θερμότητας W m K v f ειδικός όγκος του υγρού m kg V ογκομετρική παροχή του ρευστού m s W T μηχανική ισχύς του στροβίλου kw Ζ συντελεστής συμπιεστότητας

6 u ταχύτητα του ρευστού m/s μέση λογαριθμική θερμοκρασιακή διαφορά η s ισεντροπικός βαθμός απόδοσης - μ δυναμικό ιξώδες Nsec m ν κινηματικό ιξώδες m sec ρ πυκνότητα kg m ΔΤ lm Συμβολισμοί οργανικού κύκλου Rankine h ειδική ενθαλπία στην έξοδο του συμπυκνωτή kg h ειδική ενθαλπία στην έξοδο της αντλίας kg h ειδική ενθαλπία στην έξοδο του λέβητα kg h ειδική ενθαλπία στην έξοδο του στροβίλου kg m R παροχή μάζας του ψυκτικού ρευστού kg s P g πίεση του λέβητα bar P c πίεση του συμπυκνωτή bar Q G θερμική ισχύς του λέβητα kw Q c θερμική ισχύς του συμπυκνωτή kw t c θερμοκρασία του συμπυκνωτή t g θερμοκρασία της ατμογεννήτριας V ρ συντελεστής της εξίσωσης για τον υπολογισμό της πίεσης W p μηχανική ισχύς της αντλίας kw η Β βαθμός απόδοσης του λέβητα η R car θεωρητικός βαθμός απόδοσης Carnot του κύκλου η R θεωρητικός βαθμός απόδοσης του κύκλου Συμβολισμοί Κύκλου Ψύξης με Εγχυτήρες COP c βαθμός συμπεριφοράς του κύκλου Carnot COP th βαθμός συμπεριφοράς της εγκατάστασης h ειδική ενθαλπία στην έξοδο της ατμογεννήτριας kg h ειδική ενθαλπία στην έξοδο του ατμοποιητή kg

7 h ειδική ενθαλπία στην έξοδο του εγχυτήρα kg h ειδική ενθαλπία στην έξοδο του συμπυκνωτή kg h ενθαλπία στην έξοδο της εκτονωτικής βαλβίδας kg m e παροχή μάζας στον ατμοποιητή kg m g παροχή μάζας στην ατμογεννήτρια s kg s Q c θερμική ισχύς του συμπυκνωτή kw Q e θερμική ισχύς του ατμοποιητή kw Q G θερμική ισχύς της ατμογεννήτριας kw P c πίεση στον συμπυκνωτή bar P e πίεση στον ατμοποιητή bar P g πίεση στην ατμογεννήτρια bar w λόγος των παροχών μαζών του κύκλου W p μηχανική ισχύς της αντλίας kw

8 ΚΕΦΑΛΑΙΟ : ΕΙΣΑΓΩΓΗ Η μηχανή Diesel αποβάλλει ποσά θερμότητας: Από τα καυσαέρια Από το νερό ψύξης Από το λιπαντικό λάδι Το καθ ένα από αυτά τα ποσά θερμότητας οδηγείται σε ένα εναλλάκτη θερμότητας ξεχωριστά. Εν συνεχεία ο κάθε εναλλάκτης από αυτούς είναι συνδεδεμένος με ένα ενιαίο κύκλωμα νερού. Υπάρχουν τρεις πιθανές περιπτώσεις να οδηγηθεί το νερό το οποίο έχει περάσει από τους εναλλάκτες. Κατά την διάρκεια του χειμώνα το ενιαίο κύκλωμα νερού από την μηχανή Ντίζελ θα οδηγείται στο κύκλωμα θέρμανσης μέσω νερού στους χώρους της βιομηχανίας στα fan coil units. Το καλοκαίρι το ενιαίο κύκλωμα νερού από την μηχανή Ντίζελ θα οδηγείται στην ατμογεννήτρια στο κύκλο ψύξης με εγχυτήρες για παραγωγή ψύξης που θα χρησιμεύει για κλιματισμό των χώρων της βιομηχανίας ενός αλλού κυκλώματος νερού που θα οδηγείται στα fan coil units. Σε περιπτώσεις που η ισχύς φτάνει το μέγιστο θα λειτουργεί ο οργανικός κύκλος Rankine που στην έξοδο του θα έχει μια γεννήτρια για την παραγωγή ισχύος που θα καλύπτει τα επιπλέον φορτία. Το νερό ψύξης από την μηχανή Ντίζελ θα οδηγείται στην κατάλληλη κατεύθυνση μέσω μια τετράοδης βάνας.

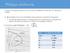
9 . ΗΛΕΚΤΡΟΠΑΡΑΓΩΓΟ ΖΕΓΟΣ Οι μηχανές εσωτερικής καύσης μπορούν φτάσουν μέχρι ένα βαθμό απόδοσης της τάξης του 0%. Δηλαδή το 0% είναι εκμεταλλεύσιμο ενώ το υπόλοιπο 0% απορρίπτεται στο περιβάλλον ανεκμετάλλευτο. Με αφορμή την ενεργειακή κρίση καθίσταται αναγκαίο να μελετηθούν τρόποι με τους οποίους μπορούμε να εκμεταλλευτούμε αυτά τα ποσά θερμότητα τα οποία απορρίπτονται στο περιβάλλον. Η συγκεκριμένη μηχανή Ντίζελ-γεννήτρια που χρησιμοποιείται είναι το μοντέλο: C 00 ΑΝΟΙΧΤΟΥ ΤΥΠΟΥ της εταιρίας caterpillar. Γενικά χαρακτηριστικά μηχανής ΤΕΧΝΙΚΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΜΕΓΕΘΗ Γεννήτρια (συντελεστής ισχύος =0,) 00kVA 00ekW Κατανάλωση καυσίμου 00%φορτίο 0L/hr %φορτίο,9l/hr 0%φορτίο,L/hr Σύστημα ψύξης περιορισμός πίεσης ροή αέρα 0,kPa παροχή όγκου αέρα στο εναλλάκτη m /min ΕΙΣΑΓΩΓΗ ΑΕΡΑ αέρα καύσης, m /min ΣΥΣΤΗΜΑ ΕΞΑΤΜΙΣΗΣ θερμοκρασία καυσαερίων, ογκομετρική παροχή 9, m /min διάμετρος αγωγού εξάτμισης, mm ΑΠΟΡΡΙΨΗ ΘΕΡΜΟΤΗΤΑΣ σύστημα ψύξης 9kW καυσαέρια 0kW από την μηχανή στην ατμόσφαιρα kw από την γεννήτρια στην ατμόσφαιρα,kw ΕΚΠΟΜΠΕΣ ΡΥΠΩΝ NOx,mg/m CO 0,mg/m HC,mg/m PM,9mg/m 9

10 Στοιχεία μηχανής Ντίζελ Η μηχανή έχει κυλίνδρους, είναι Χ, σαν καύσιμο έχει το πετρέλαιο, ο λόγος συμπίεσης είναι,: και ο άξονας περιστρέφεται με 00rpm. Εικόνα. Το ηλεκτροπαραγωγό ζεύγος C 00 ΑΝΟΙΧΤΟΥ ΤΥΠΟΥ της εταιρίας caterpillar 0

11 . ΟΡΓΑΝΙΚΟΣ ΚΥΚΛΟΣ RANKINE Η ενεργειακή κατανάλωση αυξάνεται και η αύξηση της βιομηχανοποίησης οδηγεί στην χειροτέρευση του περιβάλλοντος και αύξηση της θερμοκρασίας. Για να μπορέσουμε να καλύπτουμε μελλοντικά ενεργειακά φορτία και συγχρόνως να μειωθούν οι ρύποι για το φαινόμενο του θερμοκηπίου και η εξάρτηση από τα ορυκτά καύσιμα καθίσταται αναγκαία η ανάπτυξη των ενεργειακών συστημάτων προς την κατεύθυνση της εξοικονόμησης ενέργειας. Μελέτες έχουν δείξει ότι το 0% της συνολικής θερμικής ενέργειας που παράγεται στην βιομηχανία είναι ανεκμετάλλευτη, []. Ανάμεσα από τις διάφορες τεχνολογίες που υπάρχουν o οργανικός κύκλος Rankine θεωρείται μια αποδοτική λύση για την ανάκτηση θερμότητας που χρησιμεύει για την παραγωγή ισχύος και τούτο διότι οι απαιτούμενες θερμοκρασίες δεν είναι υψηλές. Παράλληλα αναπτύσσονται πολλές εφαρμογές όπως η καύση βιομάζας, η γεωθερμία, η ηλιακή ακτινοβολία και σε μηχανές εσωτερικής καύσης, []. Η ιδέα της χρήσης του οργανικού κύκλου Rankine στις μηχανές εσωτερικής καύσης πρωτοεμφανίστηκε στις ενεργειακές κρίσεις του 90. Συγκρινόμενος με άλλες τεχνολογίες ανάκτησης θερμότητας δίνεται βάσει στον οργανικό κύκλο Rankine λόγω της υψηλής θερμικής απόδοσης του, της απλότητας του και της δυνατότητας να λειτουργεί σε ένα εύρος χαμηλής και μεσαίας τάξης θερμότητας μικρότερη από τους 00 περίπου, []. Ένα από τα μειονεκτήματα του οργανικού κύκλου Rankine είναι ότι όταν συνδυάζεται με μια μηχανή εσωτερικής καύσης αυτή δεν δουλεύει συνέχεια σε πλήρη ισχύς. Συγχρόνως απαιτείται μεγάλος χώρος για να λειτουργήσει η εγκατάσταση, []. Μια παράμετρος για την λειτουργία του οργανικού κύκλου Rankine είναι το εργαζόμενο μέσο με το οποίο λειτουργεί. Οι ιδιότητες του εργαζόμενου μέσου έχουν μεγάλη επιρροή στην λειτουργία του συστήματος. Το εργαζόμενο μέσο με καλές ιδιότητες οδηγεί σε υψηλή απόδοση και ικανοποιεί τις περιβαλλοντικές απαιτήσεις. Γίνονται πολλές έρευνες για την επιλογή του εργαζόμενου μέσου. Κανένα εργαζόμενο μέσο δεν είναι το καλύτερο για όλες τις εφαρμογές. Στην συγκεκριμένη μελέτη το σύστημα θα λειτουργεί με Ra, []. Για να επιτευχθεί βέλτιστη λειτουργία στο σύστημα θα πρέπει να επιλεγούν σωστά οι εξής παράμετροι: Η πίεση του λέβητα ανάκτησης Το μέγεθος της υπερθέρμανσης Η θερμοκρασία συμπύκνωσης

12 Στο παρακάτω σχήμα φαίνεται ένα διάγραμμα ροής μιας τυπικής εγκατάστασης οργανικού κύκλου Rankine: Σχήμα. Διάγραμμα ροής oργανικού κύκλου Rankine Στην παρακάτω εικόνα φαίνεται μια εγκατάσταση οργανικού κύκλου Rankine Εικόνα. Εγκατάσταση οργανικού κύκλου Rankine ονομαστικής ισχύς kw

13 . ΚΥΚΛΟΣ ΨΥΞΗΣ ΜΕ ΕΓΧΥΤΗΡΕΣ H ανάγκη για κλιματισμό και για ψύξη σε χώρες με κλίμα θερμό είναι προφανής. Οι ενεργειακές καταναλώσεις σε όλο τον κόσμο αυξάνονται. Ο κύκλος ψύξης με εγχύτηρες δεν καταναλώνει τόση ηλεκτρική ενέργεια όπως ο κύκλος ψύξης με συμπίεση ατμών αλλά στο σύστημα παρέχεται θερμική ενέργεια, []. Οι πηγές θερμότητας του κύκλου ψύξης με εγχυτήρες όπως και στο οργανικό κύκλο Rankine μπορεί να είναι η ηλιακή ακτινοβολία, η γεωθερμία και οι μηχανές εσωτερικής καύσης, []. Στην συγκεκριμένη μελέτη η θερμική ενέργεια παρέχεται από μια μηχανή εσωτερικής καύσης (Ηλεκτροπαραγωγό ζεύγος για την παραγωγή ισχύος) από ποσά θερμότητας που αποβάλλονται από τα καυσαέρια και από τα δίκτυα ψύξης της μηχανής. Αυτά τα ποσά θερμότητας δεν έχουν κάποια χρήση τις περισσότερες φορές στα ηλεκτροπαραγωγά ζεύγη και έτσι μένουν ανεκμετάλλευτα. Στην παρακάτω εικόνα φαίνεται μια εγκατάσταση κύκλου ψύξης με εγχυτήρες : Εικόνα. Εγκατάσταση κύκλου ψύξης με εγχυτήρες από μια πειραματική διάταξη στο Πανεπιστήμιο της Ταιβάν

14 ΚΕΦΑΛΑΙΟ : ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΑΝΑΛΥΣΗ. ΗΛΕΚΤΡΟΠΑΡΑΓΩΓΟ ΖΕΥΓΟΣ To προτεινόμενο κύκλωμα της εγκατάστασης είναι το παρακάτω: Σχήμα. Κύκλωμα της εγκατάστασης To παρακάτω σχήμα είναι ένα ενδεικτικό διάγραμμα που δείχνει πως συνδυάζεται η μηχανή Diesel με τον οργανικό κύκλο Rankine και τον κύκλο ψύξης με εγχυτήρες:

15 Σχήμα. Κύκλωμα Η/Ζ με οργανικό κύκλο Rankine Θεωρούμε ότι ο εναλλάκτης θερμότητας που χρησιμοποιεί το νερό ψύξης του ηλεκτροπαραγωγού ζεύγους έχει βαθμό απόδοσης % (η εναλλ = %). Q : η θερμότητα που απορρίπτεται από την μηχανή Diesel Q : η θερμότητα που παραλαμβάνει το νερό και το οδηγεί στην τετράοδη βαλβίδα Ισχύει η εξίσωση Q = η εναλλ Q Θεωρούμε ότι ο λέβητας στον οργανικό κύκλο Rankine είναι 90% (η εναλλ = 90%). Q : η θερμότητα που παραλαμβάνει το οργανικό ρευστό από την πλευρά του οργανικού κύκλου Rankine Q = 09kW Q = η εναλλ Q = % 09kW = kw Q = m ν C ρ ΔΤ => m ν = Q C ρ ΔΤ = kw,90 kg Q G = η B Q = 90% kw = 90kW kg =,9 (90 ) s

16 . ΟΡΓΑΝΙΚΟΣ ΚΥΚΛΟΣ RANKINE Ένα σύστημα οργανικού κύκλου Rankine αποτελείται από ένα ατμοποιητή, ένα στρόβιλο, ένα συμπυκνωτή και μια αντλία. Το εργαζόμενο ψυκτικό μέσο απορροφά θερμότητα από την μηχανή Diesel στον ατμοποιητή και αυξάνει θερμοκρασία και πίεση και συγχρόνως ατμοποιείται και υπερθερμαίνεται στην φάση αυτή. Στη συνέχεια οδηγείται σε ένα στρόβιλο για να εκτονωθεί με σκοπό την παραγωγή ισχύος. Τέλος οδηγείται σε συμπυκνωτή για να συμπυκνωθεί το εργαζόμενο μέσο και συμπιέζεται μέσω της αντλίας ξανά στον ατμοποιητή, []. To παρακάτω διάγραμμα απεικονίζει τον οργανικό κύκλο Rankine σε άξονες θερμοκρασίας (t) εντροπίας (s). Διάγραμμα. Διάγραμμα t-s για τον οργανικό κύκλο Rankine Σε ένα ιδανικό κύκλο RANKINE το εργαζόμενο μέσο εκτονώνεται αδιαβατικά και αντιστρεπτά δηλαδή ισεντροπικά μέσω ενός στροβίλου σε μία χαμηλότερη πίεση και θερμοκρασία στην είσοδο του συμπυκνωτή. Εφαρμόζοντας τον πρώτο θερμοδυναμικό νόμο στο στρόβιλο και αγνοώντας την κινητική και δυναμική ενέργεια μεταξύ εισόδου και εξόδου έχουμε, []: q = h h + w T q = 0 γιατί η διεργασία θεωρείται αδιαβατική, αλλά όχι ισεντροπική

17 Εάν θεωρήσουμε ισεντροπικό βαθμό απόδοσης η s = 0%, τότε η s = h h h h s υπολογίζεται η ενθαλπία h w T = h h γνωρίζοντας ότι η ενθαλπία στο σημείο είναι μεγαλύτερη από το σημείο h < h μπορούμε να αλλάξουμε την εξίσωση έτσι ώστε το αποτέλεσμα να είναι πάντα θετικό w T = h h W T = m R w T = m R (h h ) Όπου m R η παροχή μάζας του οργανικού ρευστού Ra Ο λέβητας ανάκτησης θερμότητας διαφέρει από τον κλασικό λέβητα που είναι στο συμβατικό κύκλο Rankine και είναι ένα εναλλάκτης θερμότητας. Παρομοίως και για τον λέβητα ανάκτησης θερμότητας εφαρμόζεται ο πρώτος θερμοδυναμικός νόμος. Το έργο στο λέβητα είναι μηδενικό γιατί ούτε καταναλώνεται έργο ούτε προσδίδεται έργο στο σύστημα. q G = h h + w w = 0 Q G = m R (h h ) O συμπυκνωτής είναι συνήθως είναι ένας εναλλάκτης θερμότητας τύπου κελύφουςαυλών που είναι τοποθετημένος κοντά στον στρόβιλο και στην έξοδο του μετατρέπει τον ατμό σε υγρό. Για την ψύξη του χρησιμοποιείται ένα ανεμιστήρας που δημιουργεί ένα ρεύμα αέρα προς τον συμπυκνωτή. Από τον πρώτο θερμοδυναμικό νόμο υπολογίζεται η παροχή θερμότητας από τον συμπυκνωτή. Το έργο στο συμπυκνωτή είναι μηδενικό γιατί ούτε καταναλώνεται έργο ούτε προσδίδεται έργο στο σύστημα, []. q c = h h + w w = 0 Q c = m R (h h ) Η αντλία είναι μια συσκευή που κινεί ένα υγρό από μια περιοχή χαμηλής πίεσης σε μια περιοχή υψηλής πίεσης. Στην περίπτωση του κύκλου Rankine η χαμηλή πίεση είναι η πίεση του συμπυκνωτή ενώ η υψηλή πίεση είναι η πίεση του λέβητα ανάκτησης. Εφαρμόζοντας τον πρώτο θερμοδυναμικό νόμο υπολογίζεται η απαιτούμενη ισχύς της αντλίας, []. και q = h h + w p q = 0 γιατί η διεργασία θεωρείται αδιαβατική και ισεντροπική

18 W p = m R w p = m R (h h ) Ο υπολογισμός της απόδοσης του κύκλου υπολογίζεται ως ο λόγος της καθαρής ισχύος W netπρος τη θερμική ισχύ που παρέχεται από εξωτερικές πηγές. Η καθαρή ισχύς είναι η διαφορά της ισχύος που αποδίδει ο στρόβιλος και της ισχύος που καταναλώνει η αντλία. W net = W T W P Η θερμότητα που παρέχεται από εξωτερικές πηγές, είναι η θερμότητα που αποδίδει ο λέβητας ανάκτησης θερμότητας στο οργανικό ρευστό (Q G). Ο θεωρητικός βαθμός απόδοσης του κύκλου είναι: η R = W net Q G = W T W P Q G. ΨΥΞΗ ΜΕ ΕΓΧΥΤΗΡΕΣ O εγχυτήρας είναι μια συσκευή μέσα στην οποία ένα ρευστό υψηλής πίεσης αναρροφά ένα άλλο ρευστό χαμηλής πίεσης, με αποτέλεσμα τα δύο ρευστά να αναμειγνύονται και το αναμειχθέν μείγμα να εξέρχεται σε μια ενδιάμεση πίεση, []. Στο παρακάτω διάγραμμα ροής απεικονίζεται ο κύκλος ψύξης με εγχυτήρες με τα εξαρτήματα με τα οποία αποτελείται. Σχήμα. Διάγραμμα ροής για τον κύκλο ψύξης με εγχυτήρες

19 To παρακάτω διάγραμμα θερμοκρασίας (t) εντροπίας (s) απεικονίζει τον κύκλο ψύξης με εγχυτήρες. Διάγραμμα. Διάγραμμα (t-s) για τον κύκλο ψύξης με εγχυτήρες Με βάσει τον θερμικό ισολογισμό στον εγχυτήρα: h + w h = ( + w)h Σημείο To σημείο ένα είναι η έξοδος από την ατμογεννήτρια και το ψυκτικό ρευστό έχει την πίεση της ατμογεννήτριας (P g ) και την θερμοκρασία της ατμογεννήτριας (Τ g ), []. Τ = Τ g P = P g Σημείο Το σημείο είναι η έξοδος του ατμοποιητή και το ψυκτικό ρευστό έχει την πίεση του ατμοποιητή (P e ) και την θερμοκρασία του ατμοποιητή (Τ e ), []. Τ = Τ e P = P e Σημείο 9

20 Το σημείο είναι η έξοδος του εγχυτήρα και έχει την πίεση του συμπυκνωτή (P c ). Με βάση τον θερμικό ισολογισμό στον εγχυτήρα μπορεί να υπολογιστεί η ενθαλπία στο σημείο. Οπού w = m e. m g h = h +w h +w P = P c Σημείο Το σημείο βρίσκεται μέσα στο συμπυκνωτή και είναι βοηθητικό για τους υπολογισμούς. Καθώς το ψυκτικό ρευστό συμπυκνώνεται μέσα στον εναλλάκτη θερμότητας είναι το σημείο που συναντά την καμπύλη κορεσμού και έχει την πίεση του συμπυκνωτή (P c ) και την θερμοκρασία του συμπυκνωτή (Τ c ), []. Τ = Τ c P = P c Σημείο Η έξοδος του συμπυκνωτή είναι το σημείο και έχει την πίεση του συμπυκνωτή (P c ) και την θερμοκρασία του συμπυκνωτή (Τ c ). Τ = Τ c P = P c Σημείο Η έξοδος της αντλίας είναι το σημείο και έχει την πίεση της ατμογεννήτριας (P g ) P = P g S = S h = h + v f (P P ) T = T + h h C ρl Η παροχή μάζας στην ατμογεννήτρια (m g) υπολογίζεται από το πρώτο θερμοδυναμικό νόμο: Q G = m g (h h ) => m g = Q G h h Η παροχή μάζας στον ατμοποιητή (m g) υπολογίζεται ως εξής: 0

21 w = m e => m m e = w m g g Η θερμική ισχύς του ατμοποιητή: Q e = m e (h h ) Η θερμική ισχύς του συμπυκνωτή: Q c = (m e + m g) (h h ) Η μηχανική ισχύς της αντλίας: W p = m g (h h ) Ο βαθμός συμπεριφοράς της εγκατάστασης : COP th = Q e Q G+W p Ο αντίστοιχος βαθμός του κύκλου Carnot, []: COP c = T g T c T g T c T c T e. ΕΝΑΛΛΑΚΤΗΣ ΘΕΡΜΟΤΗΤΑΣ Ο εναλλάκτης θερμότητας είναι μια συσκευή που χρησιμοποιείται για την μεταφορά της θερμικής ενέργειας μεταξύ δύο ρευστών μέσω μια σταθερής επιφάνειας. Τα ρευστά μπορεί να είναι χημικές ενώσεις ή μείγματα. Οι τυπικές εφαρμογές ενός εναλλάκτη θερμότητας που περιλαμβάνει την ψύξη ή την θέρμανση του ρεύματος του ρευστού είναι η ατμοποίηση ή η συμπύκνωση του ρευστού και η ανάκτηση ενέργειας ή η αποβολή θερμότητας, []. Υπάρχουν δυο ειδών εναλλάκτες θερμότητας με βάσει την διεύθυνση ροής των δυο ρευστών: Αντιρροής Ομορροής Στην συγκεκριμένη εργασία θα μελετήσουμε ένα εναλλάκτη αντιρροής. Για το υπολογισμό ενός εναλλάκτη υπάρχουν δυο μέθοδοι που βασίζονται στη: Μέση λογαριθμική θερμοκρασιακή διαφορά Αριθμό μονάδων μεταφοράς

22 Στην συγκεκριμένη εργασία θα μελετήσουμε θα υπολογίσουμε τον εναλλάκτη με τη μέθοδο της μέσης λογαριθμικής θερμοκρασιακής διαφοράς, []. Η ροή θερμότητας μεταξύ ενός θερμού ρεύματος και ενός ψυχρού ρεύματος με αυτή την μέθοδο υπολογίζεται από την εξίσωση: Q = U A ΔΤ lm Q : ροή θερμότητας σε Watt U: ο συνολικός συντελεστής μετάδοσης θερμότητας σε W m K A: η επιφάνειας συναλλαγής θερμότητας του εναλλάκτη σε m ΔΤ lm : η μέση λογαριθμική θερμοκρασίακη διαφορά σε Κ Η μέση λογαριθμική διαφορά θερμοκρασίας προσδιορίζεται από την εξίσωση: ΔΤ lm = ΔΤ in ΔΤ out ln ΔΤ in ΔΤ out ΔΤ in = T h,in T c,out για εναλλάκτη θερμότητας αντιρροής ΔΤ out = T h,out T c,in για εναλλάκτη θερμότητας αντιρροής Ο συνολικός συντελεστής θερμότητας (U) υπολογίζεται από την εξίσωση: = + U h hot h cold h hot : ο συντελεστής θερμικής συναγωγιμότητας του θερμού ρευστού σε h cold : ο συντελεστής θερμικής συναγωγιμότητας του ψυχρού ρευστού σε W m K W m K Ο συντελεστής θερμικής συναγωγιμότητας (h) μπορεί να υπολογιστεί από την εξίσωση που εκφράζει τον αριθμό Nusselt: Νu = h d k Νu: o αριθμός Nusselt d: η διάμετρος του αγωγού σε m k: ο συντελεστής θερμικής αγωγιμότητας σε W m K Η εξίσωση για να υπολογίσουμε τον συντελεστή θερμικής συναγωγιμότητας μπορεί να πάρει την μορφή Νu = h d k k Νu => h = d,[]

23 Για την περίπτωση του θερμού ρεύματος υπολογίζουμε τον αντίστοιχο συντελεστή θερμικής συναγωγιμότητας. Το θερμό ρεύμα που για την συγκεκριμένη περίπτωση είναι το νερό θα κυκλοφορεί από την εσωτερική πλευρά του εναλλάκτη για τον οργανικό κύκλο Rankine. h hot = k Νu d in d in : η αντίστοιχη διάμετρος από την εσωτερική πλευρά του εναλλάκτη Για την περίπτωση του ψυχρού ρεύματος υπολογίζουμε τον αντίστοιχο συντελεστή θερμικής συναγωγιμότητας. Το ψυχρό ρεύμα που για την συγκεκριμένη περίπτωση είναι το ψυκτικό ρευστό Ra θα κυκλοφορεί από την εξωτερική πλευρά του εναλλάκτη. h cold = k Νu d out d out : η αντίστοιχη διάμετρος από την εξωτερική πλευρά του εναλλάκτη Ως θερμοκρασία αναφοράς λαμβάνεται υπόψη η μέση θερμοκρασία εισόδου και εξόδου: Τ = Τ in+τ out Τ : η θερμοκρασία αναφοράς Τ in : Η θερμοκρασία εισόδου του ρευστού στο εναλλάκτη Τ out : Η θερμοκρασία εξόδου του ρευστού από τον εναλλάκτη Με βάσει την θερμοκρασία αναφοράς για το κάθε ρευστό, βρίσκονται από πίνακες οι εξής θερμο-φυσικές ιδιότητες, []: Ο αριθμός Prandtl (Pr) Το δυναμικό ιξώδες (μ) σε N sec m Η πυκνότητα (ρ) σε kg m Ο συντελεστής θερμικής αγωγιμότητας (k) σε W m K Το κινηματικό ιξώδες (ν) σε m sec Έπειτα υπολογίζεται ο αριθμός Reynolts: Re D = u d ν Re D : ο αριθμός Reynolts

24 u: η ταχύτητα του ρευστού σε m/s H ταχύτητα του ρευστού υπολογίζεται ως εξής: Έχουμε την εξίσωση V = u Α => u = V V : η ογκομετρική παροχή του ρευστού σε m Α: το εμβαδόν της διατομής σε m A s Για κυκλική διατομή Α = π d την μορφή: η εξίσωση για τον υπολογισμό της ταχύτητας παίρνει u = V π d Στην συγκεκριμένη περίπτωση η παροχή μάζας έχει υπολογιστεί, άρα βάσει της πυκνότητας καθορίζεται η ογκομετρική παροχή: V = m ρ Αφού υπολογιστεί ο αριθμός Reynolts επιλέγεται κάποια συσχέτιση αριθμού Nusselt ανάλογα την περίπτωση του κάθε προβλήματος. Η συσχέτιση Nusselt επιλέγεται με το είδος της ροής που επικρατεί, δηλαδή αν είναι στρωτή ροή ή τυρβώδης ροή, την τιμή που έχει ο αριθμός Reynolts, ο αριθμός Prandtl και διαφορές άλλες παραμέτρους. Η συσχέτιση Nusselt στην απλή της μορφή είναι μια συνάρτηση του αριθμού Reynolts και του αριθμού Prandtl. Nu = f(re, Pr) Αφού γίνουν αυτοί οι υπολογισμοί μπορούν να καθοριστούν, ο συντελεστής θερμικής συναγωγιμότητας, ο συνολικός συντελεστής θερμότητας και να η επιφάνεια του εναλλάκτη, []. Στο παρακάτω σχήμα απεικονίζεται ένας εναλλάκτης αντιρροής Σχήμα. Ροές σε εναλλάκτη θερμότητας

25 . Διάγραμμα (Τ-L) σε εναλλάκτη θερμότητας αντιρροής T c,in : Η θερμοκρασία εισόδου στον εναλλάκτη για το ψυχρό ρεύμα T c,out : Η θερμοκρασία εξόδου στον εναλλάκτη για το ψυχρό ρεύμα T h,in : Η θερμοκρασία εισόδου στον εναλλάκτη για το θερμό ρεύμα T h,out : Η θερμοκρασία εξόδου στον εναλλάκτη για το θερμό ρεύμα

26 . ΕΞΙΣΩΣΗ SOAVE Για τον υπολογισμό της θερμοκρασίας, της πίεσης, της ενθαλπίας και της εντροπίας σε κάθε σημείο χρησιμoποιούνται οι παρακάτω εξισώσεις οι οποίες λαμβάνουν παραμέτρους σύμφωνα με τον Soave. Περισσότερες πληροφορίες υπάρχουν στο παράρτημα. Χρησιμοποιώντας τη γενική μορφή της κυβικής καταστατικής εξίσωσης P = R T V b Θ (V η) (V b) (V +δ V+ε) Και την κυβική μορφή της εξίσωσης Ζ Z + (δ Β )Z + [Θ + ε δ (Β + )] Ζ [ε (Β + ) + Θ η ] = 0 Η εξίσωση Soave λαμβάνει τις εξής παραμέτρους: η = b, δ = b, ε = 0, Θ = α(τ r ) α(τ r ) = [( + 0, +, ω + 0, ω ) ( Τ r )] Τ r : αναγόμενη θερμοκρασία Τ r = T Τ cr ω = log( P r ) για Τ r = 0, b P cr R T cr = 0,0 a P cr (R T cr ) = 0, Β = b P R T δ = b P R T Θ = Θ P (R T) ε = ε ( P R T ) η = η P R T Ισχύει και η εξίσωση για τον υπολογισμό της πίεσης: R T P = a R T Z P b [ + m ( T T )] cr R T Z P R T Z ( P + b) Η εξίσωση της τάσης ατμών για τις διάφορες θερμοκρασίες ατμοποίησης του ψυκτικού μέσου Ra υπολογίζεται από την εξίσωση: P s (T) = 0,0 e J(T) e J(T) = V ρ0 + V ρ T + V ρ T + V ρ T + V ρ (V ρ T) ln (V ρ T) T

27 V ρ0 =,09, V ρ = ,, V ρ = 0.0 0, V ρ = 0, 0, V ρ = 0,99, V ρ = 0, 0 Η ενθαλπία σε κάθε σημείο υπολογίζεται από την εξίσωση: h(t, P, Z) =,9 + T T0 C ρ (T)dT MB DH(T,P,Z) 0MB DH(T, P, Z) = a b ln ( Z Ζ + B(T, P) ) 0, T cr R P cr b B(T, P) = 0.0 T cr T [ + m ( T T cr )] P P cr H εντροπία σε κάθε σημείο υπολογίζεται από την εξίσωση: S(T, P, Z) =,0 + T Cρ(T) T0 T dt MB DS(T,P,Z) 0MB m Z T ln ( ) R T(Z ) Z + B(T, P) T cr DS(T, P, Z) = R ln ( Z B(T,P) ) R ln ( Z ) 0, Z P R T cr [ + P cr b m ( T T cr )] m T Tcr ln ( Ζ ) Ζ +B(T,P) Η δε ειδική θερμοχωρητικότητα υπό σταθερή πίεση εκτιμάται από την εξίσωση: C ρ (T) = C ρ0 + C ρ T + C ρ T C ρ0 = 9,00 C ρ =, 0 C ρ =,9 0

28 ΚΕΦΑΛΙΑΟ. ΕΡΓΑΖΟΜΕΝΟ ΜΕΣΟ Ra. ΕΠΙΛΟΓΗ ΡΕΥΣΤΟΥ ΣΤΟΝ ΟΡΓΑΝΙΚΟ ΚΥΚΛΟ RANKINE H αποδοτική λειτουργία ενός οργανικού κύκλου Rankine εξαρτάται σημαντικά από την επιλογή του εργαζόμενου ρευστού. Η μεταφορά θερμότητας εξαρτάται από το ρευστό και από τις συνθήκες λειτουργίας, [9]. Ιδανικά χαρακτηριστικά ενός εργαζόμενου μέσου: Μεγάλη λανθάνουσα θερμότητα Ένα ρευστό με μεγάλη λανθάνουσα θερμότητα και μεγάλη πυκνότητα απορροφά μεγαλύτερο ποσό θερμότητας από τον ατμοποιητή, έτσι μπορεί να μειωθεί η παροχή μάζας, το μέγεθος της εγκατάστασης και η κατανάλωση της αντλίας, [9]. Χαμηλή περιβαλλοντική επιβάρυνση Δύο βασικοί παράμετροι για την προστασία του περιβάλλοντος που πρέπει να ληφθούν υπόψη είναι η καταστροφή της τρύπας του όζοντος και η υπερθέρμανση του πλανήτη Ασφάλεια Το ρευστό πρέπει να είναι μη τοξικό, μη εύφλεκτο και μη διαβρωτικό, [9]. Εύκολη διαθεσιμότητα και χαμηλό κόστος

29 . ΨΥΚΤΙΚΟ ΡΕΥΣΤΟ Ra To Ra είναι ένα αλογονοαλκάνιο ψυκτικό μέσο με θερμοδυναμικές ιδιότητες παρόμοιες με αυτές του R και με αμελητέα καταστροφή στην τρύπα του όζοντος. Ο χημικός δεσμός του είναι CH FCF και σημείο βρασμού στους -, για ατμοσφαιρική πίεση. Οι φιάλες αποθήκευσης του είναι χρώματος μπλε. Άλλα ονόματα για το Ra είναι τετραφθοροαιθάνιο, Forane a, Genetron a, Florason a, Suvaa και HFC-a, [0]. Το Ra χρησιμοποιείται σαν ψυκτικό μέσο σε ψύξη οικιακής χρήσης και για κλιματισμό αυτοκινήτων. Άλλες χρήσεις του ψυκτικού είναι ψυκτικό για υπολογιστές, προωθητικό για αεροβόλα και συστατικό για σιλικόνη. Παράλληλα το Ra μπορεί να χρησιμοποιηθεί σαν οργανικό διαλυτικό μέσο για την εξαγωγή αρωματικών ενώσεων. Μπορεί να χρησιμοποιηθεί και σαν διαλυτικό στην οργανική χημεία, [0]. Το Ra πρωτοεμφανίστηκε στις αρχές του 990 σαν αντικαταστατής του R- το οποίο είχε καταστρέψει τις ιδιότητες του όζοντος. Το Ra είναι φιλικό προς το περιβάλλον και δεν επιφέρει καταστροφή στην τρύπα του όζοντος. Η επαφή του Ra με φωτιά ή με κάποια ζεστή επιφάνεια όταν αυτή υπερβεί τους 0 μπορεί να οδηγήσει σε αποσύνθεση και στην εκπομπή των τοξικών αερίων του υδροφθόριο και των καρβολυνικών ενώσεων. Το Ra σύμφωνα με μετρήσεις έχει χαρακτηριστεί ως μη τοξικό. Υπάρχει όμως κίνδυνός κατά την εισπνοή του. Το Ra είναι πυκνότερο από τον αέρα και εκτοπίζει τον αέρα στους πνεύμονες. Αν εισπνευσθεί μεγάλη ποσότητα μπορεί να προκαλέσει ασφυξία. Αυτό το φαινόμενο συμβάλει στους περισσότερους θανάτους από ότι σε αναπνευστικά προβλήματα. Τα σπρέι που περιέχουν σαν συστατικό το Ra μπορεί να προκαλέσουν τύφλωση όταν έρθουν σε επαφή με το μάτι, [0]. 9

30 ΚΕΦΑΛΑΙΟ : ΠΑΡΑΜΕΤΡΙΚΗ ΜΕΛΕΤΗ Στην συνέχεια θα γίνει παραμετρική μελέτη για τον οργανικό κύκλο Rankine και για τον κύκλο ψύξης με εγχυτήρες. Για τον οργανικό κύκλο Rankine θα γίνει παραμετρική μελέτη για διαφορετικές θερμοκρασίες συμπύκνωσης από τους έως τους 0,θερμοκρασία ατμοποίησης και θερμοκρασίας υπέρθερμου ατμού τους 90. Για το κύκλο ψύξης με εγχυτήρες για διαφορετικές θερμοκρασίες συμπύκνωσης από τους έως τους 0, για διαφορετικές θερμοκρασίες ατμοποίησης από τους 0 έως τους και για διαφορετικούς λόγους παροχής μάζας από 0, έως 0.. Οι υπολογισμοί γίνανε με το πρόγραμμα Mathcad.. ΕΝΔΕΙΚΤΙΚΟΣ ΥΠΟΛΟΓΙΣΜΟΣ.. Για τον οργανικό κύκλο RANKINE Για t g = T g = +, =,K Για t c = 0 T c = 0 +, =,K H υψηλή πίεση P g υπολογίζεται με βάσει την εξίσωση P s (T) σε συνάρτηση με τη θερμοκρασία T g P g = P s (T g ) = 0,0 e J(T g) e J(T g) = V ρ0 + V ρ T g + V ρ T g + V ρ T g + V ρ (V ρ T g ) T g ln (V ρ T g ) Η υψηλή πίεση είναι P g = 9,09bar H χαμηλή πίεση P c υπολογίζεται με βάσει την εξίσωση P s (T) σε συνάρτηση με τη θερμοκρασία T c P c = P s (T c ) = 0,0 e J(T c ) e J(T c ) = V ρ0 + V ρ T c + V ρ T c + V ρ T c + V ρ (V ρ T c ) T c ln (V ρ T c ) Η χαμηλή πίεση είναι P c = 0,0bar Σημείο (επάνω στην καμπύλη κορεσμού) T = T c =,K P = P c = 0,0bar 0

31 Έχουμε την κυβική εξίσωση Ζ Z + (δ Β )Z + [Θ + ε δ (Β + )] Ζ [ε (Β + ) + Θ η ] = 0 Με τους συντελεστές της: Β = b P R T δ = b P R T Θ = Θ P (R T) ε = ε ( P R T ) η = η P R T η = b, δ = b, ε = 0, Θ = α(τ r ) α(τ r ) = [( + 0, +, ω + 0, ω ) ( Τ r )] Με την βοήθεια του Mathcad λύνεται η εξίσωση και οι λύσεις της κυβικής εξίσωσης είναι οι εξής: Ζ = η 0,009 Ζ = η 0,9 Ζ = η 0,9 Η σωστή λύση είναι η = η ρίζα άρα Ζ = Ζ = η = 0,9 Η ενθαλπία στο σημείο υπολογίζεται από την εξίσωση h (T, P, Ζ ) =,9 + T T0 C ρ (T )dt MB DH(T,P,Ζ ) 0MB DH(T, P, Ζ ) = a b ln ( Ζ Ζ + B(T, P ) ) 0, T cr R P cr b [ + m ( T T cr )] Μετά από υπολογισμούς προκύπτει ότι h =,09 Η εντροπία στο σημείο υπολογίζεται από την εξίσωση S (T, P, Ζ ) =,0 + T Cρ(T) T0 T dt MB m Ζ T ln ( Z + B(T, P ) ) R T (Ζ ) T cr DS(T,P,Ζ ) 0MB kg

32 DS(T, P, Ζ ) = R ln ( Z B(T, P ) ) R ln ( Ζ ) 0, R T cr Ζ P P cr b [ + m ( T T cr )] m Ζ T ln ( Ζ + B(T, P ) ) T cr Μετά από υπολογισμούς προκύπτει ότι S =,9 Σημείο T = T c =,K P = P c = 0,0bar Η διαφορά μεταξύ του σημείο και του σημείο είναι η λανθάνουσα θερμότητα για την θερμοκρασία T h = h L(T ) kg K L(T ) = r T cr MB [,0 ( T T cr ) 0, + 0,9 a ( T T cr ) c ] h = h L(T ) =, kg Με παρόμοιο τρόπο υπολογίζεται και η εντροπία στο σημείο S = S L(T ) T Σημείο =,0 kg K Από το διάγραμμα προκύπτει ότι P = P g = 9,09bar Λαμβάνεται υπόψη ότι η αντλία έχει ισεντροπικό βαθμό απόδοσης 00% (η s,p = 00%) άρα S = S =,0 kg K Η ενθαλπία στο σημείο υπολογίζεται από την εξίσωση h = h + v f (P P ) 0 v f = 0,0009 m ειδικός όγκος για το Ra kg h =, m + 0,0009 (9,09bar 0,0bar) 0 kg kg h =, +, =,0 kg kg kg

33 Η θερμοκρασία στο σημείο υπολογίζεται ως εξής: Από το ορισμό της ειδικής θερμοχωρητικότητας υπό σταθερή πίεση C ρ = ΔΗ ΔΤ ΔΤ = ΔΗ C ρ ΔΤ = Τ Τ και ΔΗ = h h ΔΤ = ΔΗ C ρ => Τ Τ = h h C ρ => Τ = Τ + h h C ρ Τ =,K +,0 kg, kg =.9K. kg K Σημείο Από το διάγραμμα προκύπτει ότι P = P g = 9,09bar Από το διάγραμμα προκύπτει ότι Τ = Τ g =,K Το σημείο υπολογίζεται όπως το σημείο Επιλύουμε την κυβική εξίσωση Ζ όπως στο σημείο και οι τρεις ρίζες είναι : Ζ = η 0, Ζ = η 0, Ζ = η 0,9 Η σωστή λύση είναι η = η ρίζα άρα Ζ = Ζ = η = 0,9 Η ενθαλπία στο σημείο υπολογίζεται από την εξίσωση h (T, P, Ζ ) =,9 + T T0 C ρ (T )dt MB DH(T,P,Ζ ) 0MB DH(T, P, Ζ ) = a b ln ( Ζ Ζ + B(T, P ) ) 0, T cr R P cr b [ + m ( T T cr )] m Ζ T ln ( Z + B(T, P ) ) R T (Ζ ) T cr

34 Μετά από υπολογισμούς προκύπτει ότι h = 09,9 Η εντροπία στο σημείο υπολογίζεται από την εξίσωση S (T, P, Ζ ) =,0 + T Cρ(T) T0 T dt MB DS(T,P,Ζ ) 0MB DS(T, P, Ζ ) = R ln ( Z B(T, P ) ) R ln ( Ζ ) 0, R T cr Ζ P P cr b [ + m ( T T cr )] kg m Z T ln ( Ζ + B(T, P ) ) T cr Μετά από υπολογισμούς προκύπτει ότι S =,9 Σημείο kg K Από το διάγραμμα προκύπτει ότι P = P g = 9,09bar Ο κύκλος έχει σχεδιασθεί έτσι ώστε η θερμοκρασία του ψυκτικού να είναι βαθμούς πάνω από την t g t = t g + = 90 Επιλύουμε την κυβική εξίσωση Ζ όπως στο σημείο και οι τρεις ρίζες είναι : Ζ = η 0,9 Ζ = η 0,9 Ζ = η 0, Η σωστή λύση είναι η = η ρίζα άρα Ζ = Ζ = η = 0, Η ενθαλπία στο σημείο υπολογίζεται από την εξίσωση: h (T, P, Ζ ) =,9 + T T0 C ρ (T )dt MB DH(T,P,Ζ ) 0MB DH(T, P, Ζ ) = a b ln ( Ζ Ζ + B(T, P ) ) 0, T cr R P cr b [ + m ( T T cr )] m Ζ T ln ( Z + B(T, P ) ) R T (Ζ ) T cr

35 Μετά από υπολογισμούς προκύπτει ότι h =,0 Η εντροπία στο σημείο υπολογίζεται από την εξίσωση S (T, P, Ζ ) =,0 + T Cρ(T) dt T0 T MB DS(T,P,Ζ ) 0MB DS(T, P, Ζ ) = R ln ( Z B(T, P ) ) R ln ( Ζ ) 0, R T cr Ζ P P cr b [ + m ( T T cr )] kg m Z T ln ( Ζ + B(T, P ) ) T cr Μετά από υπολογισμούς προκύπτει ότι S =, Σημείο s kg K Το σημείο s είναι εντός καμπύλης κορεσμού διότι s=ss<s Από το διάγραμμα προκύπτει ότι T s = T c =,K Από το διάγραμμα προκύπτει ότι P s = P c = 0,0bar Το σημείο s είναι ένα θεωρητικό σημείο αν ο στρόβιλος είχε ισεντροπικό βαθμό απόδοσης 00%. S s = S =, kg K Υπολογίζεται η ενθαλπία στο σημείο s, αφού πρώτα εκτιμάται η ποιότητα στο εν λόγω σημείο S s = S x s + ( x s )S =>x s = S s S =,,0 kg K kg K S S,9,0 kg K kg K = 0,9 h s = x s h + ( x s ) h = 0,9,09 + ( 0,9), =,9 kg kg Σημείο Την ενθαλπία στο σημείο μπορούμε να την υπολογίσουμε με βάσει τον ισεντροπικό βαθμό απόδοσης και τις ενθαλπίες στα σημεία s και. Θεωρούμε ισεντροπικό βαθμό απόδοσης του στροβίλου (η s,τ = 0%). η s = h h h h s => kg

36 h = h η s (h h s ) =,0,9 = h = 9,0 kg kg 0, (,0 kg Από το διάγραμμα προκύπτει ότι P = P c = 0,0bar Τα ζητούμενα για το σημείο είναι η θερμοκρασία και εντροπία. Η εύρεση της πίεσης και της ενθαλπίας μπορεί να γίνει βάσει των παρακάτω εξισώσεων: P = R T a [+m ( V b V = R T Ζ P V (V+b) T Tcr )] h (T, P, Ζ ) =,9 + T T0 C ρ (T )dt MB DH(T,P,Ζ ) 0MB DH(T, P, Ζ ) = a b ln ( Ζ Ζ + B(T, P ) ) 0, T cr R P cr b [ + m ( T T cr )] m Ζ T ln ( Z + B(T, P ) ) T (Ζ ) T cr Μετά από κατάλληλους μετασχηματισμούς προκύπτουν δύο εξισώσεις με δύο αγνώστους. P = R T a [+m ( R T b Z R T Z P T Tcr )] ( R T Z +b) P P h (T, P, Ζ ) =,9 + T T0 C ρ (T )dt MB a b ln( Ζ Ζ +B(T,P ) ) 0, R T cr Pcr b [+m ( T Tcr )] m 0MB T Tcr Ζ ln( Z+B(T,P ) ) R T (Ζ ) Έχουμε δύο εξισώσεις και δύο άγνωστους οπότε λύνεται ένα σύστημα και P = 0,0bar T =.K

37 Η εντροπία στο σημείο υπολογίζεται από την εξίσωση S (T, P, Ζ ) =,0 + T Cρ(T) dt T0 T MB DS(T,P,Ζ ) 0MB DS(T, P, Ζ ) = R ln ( Z B(T, P ) ) R ln ( Ζ ) 0, R T cr Ζ P P cr b [ + m ( T T cr )] m Z T ln ( Ζ + B(T, P ) ) T cr Μετά από υπολογισμούς προκύπτει ότι S =,9 Η παροχή μάζας του ψυκτικού ρευστού υπολογίζεται με την εξίσωση του ρυθμού μεταφοράς θερμότητας στο λέβητα ανάκτηση θερμότητας: Q G = m (h h ) => m = kg K Q G = 90kW (h h ) (,0 kg,0 kg H ισχύς του στροβίλου στην έξοδο του είναι: kg =, ) s W T = m (h h ) =, kg s (,0 9,0 ) =,kw kg kg H ισχύς της αντλίας είναι: W P = m (h h ) =, kg s (,0, ) =,9kW kg kg H ισχύς του συμπυκνωτή είναι: Q c = m (h h )=, kg s (9,0, ) =,kw kg kg Ο θεωρητικός βαθμός απόδοσης του κύκλου είναι: η R = W T W P Q g =,κw,9κw, kg s = 0,9 =,9% Ο θεωρητικός βαθμός απόδοσης Carnot του κύκλου είναι: η R car = T c T h =,K,K =,%

38 .. Για τον κύκλο ψύξης με εγχυτήρες Για t g = 90 T g = 90 +,K =,K Για t c = 0 T c = 0 +,K =,K Για t e = 0 T e = 0 +,K =,K H υψηλή πίεση στην ατμογεννήτρια P g υπολογίζεται με βάσει την εξίσωση P s (T) συναρτήσει της θερμοκρασίας T g P g = P s (T g ) = 0,0 e J(T g) e J(T g) = V ρ0 + V ρ T g + V ρ T g + V ρ T g + V ρ (V ρ T g ) T g ln (V ρ T g ) Η υψηλή πίεση είναι P g =,bar H ενδιάμεση πίεση στον συμπυκνωτή P c υπολογίζεται με βάσει την εξίσωση P s (T) συναρτήσει της θερμοκρασίας T c P c = P s (T c ) = 0,0 e J(T c ) e J(T c ) = V ρ0 + V ρ T c + V ρ T c + V ρ T c + V ρ (V ρ T c ) T c ln (V ρ T c ) Η υψηλή πίεση είναι P c = 0,0bar H χαμηλή πίεση στον ατμοποιητή P e υπολογίζεται με βάσει την εξίσωση P s (T) συναρτήσει της θερμοκρασίας T e P e = P s (T e ) = 0,0 e J(T e ) e J(T e ) = V ρ0 + V ρ T e + V ρ T e + V ρ T e + V ρ (V ρ T e ) T e ln (V ρ T e ) Η υψηλή πίεση είναι P e =,bar Σημείο Από το διάγραμμα προκύπτει ότι T = T g =,K Από το διάγραμμα προκύπτει ότι P = P g =,bar Επιλύουμε την κυβική εξίσωση Ζ όπως στο Οργανικό κύκλο Rankine και οι τρεις ρίζες είναι:

39 Ζ = η 0, Ζ = η 0,0 Ζ = η 0, Η σωστή λύση είναι η = η ρίζα άρα Ζ = Ζ = η =0, Η ενθαλπία στο σημείο υπολογίζεται από την εξίσωση h (T, P, Ζ ) =,9 + T T0 C ρ (T )dt MB DH(T,P,Ζ ) 0MB DH(T, P, Ζ ) = a b ln ( Ζ Ζ + B(T, P ) ) 0, T cr R P cr b [ + m ( T T cr )] Μετά από υπολογισμούς προκύπτει ότι h = 0, Η εντροπία στο σημείο υπολογίζεται από την εξίσωση S (T, P, Ζ ) =,0 + T Cρ(T) T0 T dt MB m Ζ T ln ( Z + B(T, P ) ) R T (Ζ ) T cr DS(T,P,Ζ ) 0MB DS(T, P, Ζ ) = R ln ( Z B(T, P ) ) R ln ( Ζ ) 0, R T cr Ζ P P cr b [ + m ( T T cr )] kg m Ζ T ln ( Ζ + B(T, P ) ) T cr Μετά από υπολογισμούς προκύπτει ότι S =, Σημείο Από το διάγραμμα προκύπτει ότι T = T e =,K Από το διάγραμμα προκύπτει ότι P = P e =,bar Επιλύουμε την κυβική εξίσωση Ζ όπως στο Οργανικό κύκλο Rankine και οι τρεις ρίζες είναι: kg K 9

40 Ζ = η 0,0 Ζ = η 0,09 Ζ = η 0,909 Η σωστή λύση είναι η = η ρίζα άρα Ζ = Ζ = η = 0,909 Η ενθαλπία στο σημείο υπολογίζεται από την εξίσωση h (T, P, Ζ ) =,9 + T T0 C ρ (T )dt MB DH(T,P,Ζ ) 0MB DH(T, P, Ζ ) = a ln ( Ζ ) 0, b Ζ +B(T,P ) R T cr [ + m ( P cr b T )] T cr m T Tcr Ζ ln ( ) R T Z+B(T,P ) (Ζ ) Μετά από υπολογισμούς προκύπτει ότι h =,9 Η εντροπία στο σημείο υπολογίζεται από την εξίσωση S (T, P, Ζ ) =,0 + T Cρ(T) T0 T dt MB DS(T,P,Ζ ) 0MB DS(T, P, Ζ ) = R ln ( Z B(T,P ) Ζ ) R ln ( Ζ P ) 0, R [ + m ( T T cr )] m T Tcr ln ( Ζ ) Ζ +B(T,P ) Μετά από υπολογισμούς προκύπτει ότι S =, Σημείο kg kg K T cr P cr b Από θερμικό ισολογισμό στο σημείο μπορεί να υπολογιστεί η ενθαλπία στο σημείο : h m e + h m g = h (m e + m g) =>h = h +w h +w h = 9, kg Από το διάγραμμα προκύπτει ότι P = P c = 0,0bar Η εύρεση της θερμοκρασίας και του συντελεστή Ζ μπορεί να γίνει βάσει των παρακάτω εξισώσεων: 0

41 P = R T a [+m ( V b V = R T Ζ P V (V+b) T Tcr )] h (T, P, Ζ ) =,9 + T T0 C ρ (T )dt MB DH(T,P,Ζ ) 0MB DH(T, P, Ζ ) = a ln ( Ζ ) 0, b Ζ +B(T,P ) R T cr [ + m ( P cr b T )] T cr m T Tcr Ζ ln ( ) R T Z+B(T,P ) (Ζ ) Μετά από κατάλληλους μετασχηματισμούς προκύπτουν δύο εξισώσεις με δύο αγνώστους. P = R T a [+m ( b R T Z R T Z P P h (T, P, Ζ ) =,9 + T Tcr )] ( R T Z+b) P T T0 C ρ (T )dt MB a b ln( Ζ Ζ+B(T,P )) 0, R T cr Pcr b [+m ( T Tcr )] m T ln( Ζ Z+B(T,P )) R T (Ζ ) Tcr 0MB Έχουμε δύο εξισώσεις και δύο άγνωστους οπότε λύνεται ένα σύστημα και Τ =,0Κ Ζ = 0,99 Η εντροπία στο σημείο υπολογίζεται από την εξίσωση: S (T, P, Ζ ) =,0 + T Cρ(T) T0 T dt MB DS(T,P,Ζ ) 0MB DS(T, P, Ζ ) = R ln ( Z B(T,P ) Ζ ) R ln ( Ζ P ) 0, R [ + m ( T T cr )] m T Tcr ln ( Ζ ) Ζ +B(T,P ) Μετά από υπολογισμούς προκύπτει ότι S =, Σημείο kg K T cr P cr b

42 Από το διάγραμμα προκύπτει ότι T = T c =,K Από το διάγραμμα προκύπτει ότι P = P c = 0,0bar Επιλύουμε την κυβική εξίσωση Ζ όπως στο Οργανικό κύκλο Rankine και οι τρεις ρίζες είναι: Ζ = η 0,009 Ζ = η 0,9 Ζ = η 0,9 Η σωστή λύση είναι η = η ρίζα άρα Ζ = Ζ = η = 0,9 Η ενθαλπία στο σημείο υπολογίζεται από την εξίσωση: h (T, P, Ζ ) =,9 + T T0 C ρ (T )dt MB DH(T,P,Ζ ) 0MB DH(T, P, Ζ ) = a ln ( Ζ ) 0, b Ζ +B(T,P ) R T cr [ + m ( P cr b T )] T cr m T Tcr Ζ ln ( ) R T Z+B(T,P ) (Ζ ) Μετά από υπολογισμούς προκύπτει ότι h =,09 Η εντροπία στο σημείο υπολογίζεται από την εξίσωση S (T, P, Ζ ) =,0 + T Cρ(T) T0 T dt MB DS(T,P,Ζ ) 0MB DS(T, P, Ζ ) = R ln ( Z B(T,P ) Ζ ) R ln ( Ζ P ) 0, R [ + m ( T T cr )] m T Tcr ln ( Ζ ) Ζ +B(T,P ) Μετά από υπολογισμούς προκύπτει ότι S =,9 Σημείο Από το διάγραμμα προκύπτει ότι T = T c =,K kg K Από το διάγραμμα προκύπτει ότι P = P c = 0,0bar kg T cr P cr b

43 Η διαφορά μεταξύ του σημείο και του σημείο είναι η λανθάνουσα θερμότητα για την θερμοκρασία T h = h L(T ) L(T ) = r T cr MB [,0 ( T T cr ) 0, + 0,9 a ( T T cr ) c ] h = h L(T ) =, kg Με παρόμοιο τρόπο υπολογίζεται και η εντροπία στο σημείο S = S L(T ) T Σημείο =,0 kg K Από το διάγραμμα προκύπτει ότι T = T e =,K Από το διάγραμμα προκύπτει ότι P = P e =,bar Η διαφορά μεταξύ του σημείο και του σημείο είναι η λανθάνουσα θερμότητα για την θερμοκρασία T h = h L(T ) L(T ) = r T cr MB [,0 ( T T cr ) 0, + 0,9 a ( T T cr ) c ] h = h L(T ) =,9 kg Με παρόμοιο τρόπο υπολογίζεται και η εντροπία στο σημείο S = S L(T ) T Σημείο =,99 kg K Από το διάγραμμα προκύπτει ότι T = T e =,K Από το διάγραμμα προκύπτει ότι P = P e =,bar Αφού η διεργασία - είναι ισενθαλπική h = h =, Για το σημείο υπολογίζεται η ξηρότητα για υπολογιστεί μετά η εντροπία. h = x h + ( x ) h => =,,9 kg K kg K h h,9 kg K kg K x = h h = 0,9 kg

44 S = x S + ( x ) S =, kg K Σημείο Από το διάγραμμα προκύπτει ότι P = P g =,bar Λαμβάνεται υπόψη ότι η αντλία έχει ισεντροπικό βαθμό απόδοσης 00%(η s,p = 00%) άρα S = S =,0 kg K Η ενθαλπία στο σημείο υπολογίζεται από την εξίσωση h = h + v f (P P ) 0 v f = 0,0009 m ειδικός όγκος για το Ra kg h =, m + 0,0009 (,bar 0,0bar) 0 kg kg h =, +,00 =, kg kg kg Η θερμοκρασία στο σημείο υπολογίζεται ως εξής: C ρ = ΔΗ Από το ορισμό της ειδικής θερμοχωρητικότητας υπό σταθερή πίεση ΔΤ ΔΤ = ΔΗ C ρ ΔΤ = Τ Τ και ΔΗ = h h ΔΤ = ΔΗ C ρ => Τ Τ = h h C ρ => Τ = Τ + h h C ρ Τ =,K +, kg, kg =,9K, kg K Υπολογισμός της παροχής μάζας από την πλευρά της ατμογεννήτριας m g = Q G h h = 90kW =,9 kg 0, kg, s kg Υπολογισμός της παροχής μάζας από την πλευρά του ατμοποιητή m e = w m g = 0,,9 kg H ισχύς του ατμοποιητή είναι: s kg =,9 s

45 Q e = m e (h h ) =,9 kg,009kw H ισχύς του συμπυκνωτή είναι: Q c = (m e + m g) (h h ) = (,9 kg, =,kw H ισχύς της αντλίας είναι: W p = m g (h h ) =,9 kg s s (,9, ) = kg kg s kg +,9 ) (9, s kg (,, ) =,kw kg kg O θεωρητικός συντελεστής συμπεριφοράς υπολογίζεται ως εξής: COP th = Q e Q G+W p =,009kW 90kW+,kW = 0, O συντελεστής συμπεριφοράς Carnot υπολογίζεται ως εξής: COP c = T g T c T g T c =,K,K T c T e,k,k,k,k =,9.. Για τον εναλλάκτη θερμότητας Αρχικά για την περίπτωση του οργανικού κύκλου Rankine στο λέβητας ανάκτησης θερμότητας θα έχουμε: T c,in =, T c,out = 90 T h,out = T h,in = 90 ΔΤ in = T h,in T c,out = = 0 ΔΤ out = T h,out T c,in =, =, ΔΤ lm = ΔΤ in ΔΤ out ln ΔΤ in ΔΤ out = 0, ln 0, =, ln 0 ο αριθμός ln 0 δεν ορίζεται Για να οριστεί η μέση λογαριθμική διαφορά θερμοκρασίας θεωρούμε ότι η θερμοκρασία εξόδου του ψυχρού ρεύματος είναι λίγο μικρότερη: Αν T c,out = 9, τότε

46 ΔΤ in = T h,in T c,out = 90 9, = 0, ΔΤ lm = ΔΤ in ΔΤ out ln ΔΤ in ΔΤ out = 0,, ln 0,, =, Υπολογισμός ολικού συντελεστής μετάδοσης θερμότητας U: = + U h hot h cold Για το νερό (θερμό ρεύμα) h hot = k Νu d in Για μέση θερμοκρασία Τ νερ = 90 + Για Τ νερ =Κ => Pr f =, αριθμός Prandtl μ f = 0 N sec m =, =, + =,Κ δυναμικό ιξώδες k f = 0 W m K συντελεστής θερμικής αγωγιμότητας ν = μ = 0 N sec m ρ 990 kg m V = m =,9 kg s ρ 990 kg ρ = 990 kg m πυκνότητα m =,9 0 m =, 0 κινηματικό ιξώδες sec m s ογκομετρική παροχή u = V A = V π (d in ) = V =,9 0 m s π (d in ) π (0 0 m) =, m s ταχύτητα ρευστού Re D = u d in ν =,m s 0 0 m, 0 m sec = αριθμός Reynolts Nu = 0,0 Re D (/) Pr 0, = 0,0 (/), 0, = 99 αριθμός Nusselt h hot = k Νu = 0 W m K 99 = 0 d in 0 0 m συναγωγιμότητας Για το Ra (ψυχρό ρεύμα) h cold = k Νu d out W m K συντελεστής θερμικής

47 Τ Ra = 90 +, =, Για Τ=, και P=,bar έχουμε: Pr =,0 αριθμός Prandtl μ = 0,9 0 N sec m δυναμικό ιξώδες k =, 0 W m K συντελεστής θερμικής αγωγιμότητας m ν = 0, 0 κινηματικό ιξώδες sec ρ = μ = 0,9 0 N sec m ν 0, 0 m sec V = m =,0 kg s ρ 90,9 kg m =, 0 = 90,9 kg m πυκνότητα m s ογκομετρική παροχή u = V A = V π (d out ) = V =, 0 m s π (d out ) π ( 0 m) =, m s ταχύτητα ρευστού Re D = u d out ν =,m s 0 m 0, 0 m sec = 09 αριθμός Reynolts Nu = 0,0 Re D (/) Pr 0, = 0,0 09 (/),0 0, = 0 αριθμός Nusselt h cold = k Νu =, 0 W m K 0 d out 0 m συναγωγιμότητας = + = U h hot h cold W 0 m K =99 W m K ολικός συντελεστής μετάδοσης θερμότητας Q = U A ΔΤ lm => A = συναλλαγής του εναλλάκτη + Q = U ΔΤ lm συντελεστής θερμικής =,0 0 => U = W 99 W m m K K 90 0 W W m K,K => A =,m επιφάνεια Για την περίπτωση της ψύξης με εγχυτήρες η ατμογεννήτρια θα έχει εμβαδόν: T c,in =, T c,out = 9, T h,out =

48 T h,in = 90 ΔΤ in = T h,in T c,out = 90 9, = 0, ΔΤ out = T h,out T c,in =, =, ΔΤ lm = ΔΤ in ΔΤ out ln ΔΤ in ΔΤ out = 0,, ln 0,, =, A = Q U ΔΤ lm = 90 0 W => A = W,m m,k K. ΠΑΡΟΥΣΙΑΣΗ ΑΠΟΤΕΛΕΣΜΑΤΩΝ.. ΟΡΓΑΝΙΚΟΣ ΚΥΚΛΟ RANKINE Στον παρακάτω πίνακα παρουσιάζονται για τις διάφορες θερμοκρασίες συμπύκνωσης (t c ), η παροχή μάζας του δικτύου (m ), η ισχύς του στροβίλου (W T), της αντλίας (W P), του συμπυκνωτή (Q c), ο θεωρητικός βαθμός απόδοσης (η R ) και ο θεωρητικός βαθμός απόδοσης του Carnot (η R carn ): t c ( ) m ( s W T(kW) W P(kW) Q c(kw) η R η R carn,,, 0,9,9%,% 0, 9,,,0,0%,%,,,9,,9%,9% 0,,,9,,9%,% Στους παρακάτω πίνακες παρουσιάζεται για κάθε σημείο η θερμοκρασία (t), η πίεση (P), η ενθαλπία (h) και η εντροπία (s), ανάλογα με τη θερμοκρασία συμπύκνωσης (t c ):

49 Για t c = s t( ) P(bar) h( ) kg K,9 0,9,09, 9,09 0,9,09 9,09 09,9,9 90 9,09,0,,00,9,0,,9,9,,9,0, Για t c = 0 s t( ) P(bar) h( ) kg K 0,00 09,,00, 9,09,,00 9,09 09,9,9 90 9,09,0,,,00,9,9 0,00 9,, 0,00,, 9

50 Για t c = s t( ) P(bar) h( ) kg K,,9,00,9 9,09 9,0,00 9,09 09,9,9 90 9,09,0, 9,999, 9,00,0,,0,,,900, Για t c = 0 s t( ) P(bar) h( ) kg K 0 0,0,,0,9 9,09,0,0 9,09 09,9,9 90 9,09,0,,9 0,0 9,0,9 0 0,0,9, 0 0,0,09,9 0

51 .. ΚΥΚΛΟΣ ΨΥΞΗΣ ΜΕ ΕΓΧΥΤΗΡΕΣ Στους παρακάτω πίνακες εμφανίζονται για κάθε σημείο η θερμοκρασία (t), η πίεση (P), η ενθαλπία (h) και η εντροπία (s), ανάλογα με τη θερμοκρασία συμπύκνωσης (t c ), με τη θερμοκρασία ατμοποίησης (t e ) και το λόγο της παροχής των μαζών (w): t c = t e = 0 w=0, σημεία t ( ) P(bar) h( ) ) kg kg K 90, 0,, 0,,9,,0,9 9,,9,9 0,9,09 0, 0,9,009,, 0,0,09,9,0, 0,,9,99 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9 9,,0,,9 9,,,9 0,9,09,9 0,9,09,, 0,0,09,9,0,,9,9,99

52 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9,,00,9,9 9,,9,9 0,9,09,9 0,9,0,, 0,0,09,9,0,,9,9,99 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,0,9,9,,9 9,,9,9 0,9,09,0 0,9,0,, 0,0,09,9,0,,0,9,99

53 t c = 0 t e = 0 w=0, σημεία t ( ) P(bar) h( 90, 0,, 0,,9,,0,00 9,, 0,00 09,,00 0, 09,,09,,,,00 0,00,, 0,,9,99 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9 9,,0,9,00 9,, 0,00 09,,00,9 09,,0,,,,00 0,00,,,9,9,99

54 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9,,00,,00 9,, 0,00 09,,00,9 09,,0,,,,00 0,00,,,9,9,99 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,0,9,9,,00 9,,9 0,00 09,,00,0 09,,0,,,,00 0,00,,,0,9,99

55 t c = t e = 0 w=0, σημεία t ( ) P(bar) h( 90, 0,, 0,,9,,09, 9,,,,9,00 0,,9,09,, 9,,00,,900, 0,,9,99 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9 9,,0,99, 9,,,,9,00,9,9,099,, 9,,00,,900,,9,9,99

56 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9,,00,, 9,,,,9,00,9,9,09,, 9,,00,,900,,9,9,99 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,0,9,9,9, 9,,,,9,00,0,9,09,, 9,,00,,900,,0,9,99

57 t c = 0 t e = 0 w=0, σημεία t ( ) P(bar) h( 90, 0,, 0,,9,,9 0,0 9,, 0 0,0,,0 0,,,,99,,,0 0 0,0,09,9 0,,9,99 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9 9,,0 9,99 0,0 9,,9 0 0,0,,0,9,,,99,,,0 0 0,0,09,9,9,9,99

58 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9,,00 9, 0,0 9,,0 0 0,0,,0,9,,0,99,,,0 0 0,0,09,9,9,9,99 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,0,9,9 0, 0,0 9,, 0 0,0,,0,0,,,99,,,0 0 0,0,09,9,0,9,99

59 t c = t e = 0 w=0, σημεία t ( ) P(bar) h( t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9 9,,0,9,9 0,,09,9 0,9,09,9 0,9,09,, 0,0,09,9,0,,9,9,99 9

60 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9,,00,,9 0,00,09,9 0,9,09,9 0,9,0,, 0,0,09,9,0,,9,9,99 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,0,9,9,,9 0,0,9,9 0,9,09,0 0,9,0,, 0,0,09,9,0,,0,9,99 0

61 t c = 0 t e = 0 w=0, σημεία t ( ) P(bar) h( 90, 0,, 0,,9,,99,00 0,,9 0,00 09,,00 0, 09,,09,,,,00 0,00,, 0,,9,99 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9 9,,0,,00 0,,9 0,00 09,,00,9 09,,0,,,,00 0,00,,,9,9,99

62 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9,,00,,00 0,00,9 0,00 09,,00,9 09,,0,,,,00 0,00,,,9,9,99 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,0,9,9,,00 0,0,99 0,00 09,,00,0 09,,0,,,,00 0,00,,,0,9,99

63 t c = t e = 0 w=0, σημεία t ( ) P(bar) h( 90, 0,, 0,,9,,00, 0,,9,,9,00 0,,9,09,, 9,,00,,900, 0,,9,99 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9 9,,0,, 0,,9,,9,00,9,9,099,, 9,,00,,900,,9,9,99

64 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9,,00,, 0,00,9,,9,00,9,9,09,, 9,,00,,900,,9,9,99 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,0,9,9,0, 0,0,,,9,00,0,9,09,, 9,,00,,900,,0,9,99

65 t c = 0 t e = 0 w=0, σημεία t ( ) P(bar) h( 90, 0,, 0,,9,,99 0,0 0,, 0 0,0,,0 0,,,,99,,,0 0 0,0,09,9 0,,9,99 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9 9,,0,00 0,0 0,, 0 0,0,,0,9,,,99,,,0 0 0,0,09,9,9,9,99

66 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9,,00, 0,0 0,00, 0 0,0,,0,9,,0,99,,,0 0 0,0,09,9,9,9,99 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,0,9,9,0 0,0 0,0, 0 0,0,,0,0,,,99,,,0 0 0,0,09,9,0,9,99

67 t c = t e = 0 w=0, σημεία t ( ) P(bar) h( 90, 0,, 0,,9,,,9 9,9,9,9 0,9,09 0, 0,9,009,, 0,0,09,9,0, 0,,9,99 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9 9,,0,9,9 9,,9,9 0,9,09,9 0,9,09,, 0,0,09,9,0,,9,9,99

68 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9,,00,,9 99,,9,9 0,9,09,9 0,9,0,, 0,0,09,9,0,,9,9,99 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,0,9,9,,9 99,9,999,9 0,9,09,0 0,9,0,, 0,0,09,9,0,,0,9,99

69 t c = 0 t e = 0 w=0, σημεία t ( ) P(bar) h( 90, 0,, 0,,9,,,00 9,9,0 0,00 09,,00 0, 09,,09,,,,00 0,00,, 0,,9,99 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9 9,,0,90,00 9,,9 0,00 09,,00,9 09,,0,,,,00 0,00,,,9,9,99 9

70 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9,,00 9,09,00 99,, 0,00 09,,00,9 09,,0,,,,00 0,00,,,9,9,99 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,0,9,9 9,09,00 99,9, 0,00 09,,00,0 09,,0,,,,00 0,00,,,0,9,99 0

71 t c = t e = 0 w=0, σημεία t ( ) P(bar) h( 90, 0,, 0,,9, 9,, 9,9,9,,9,00 0,,9,09,, 9,,00,,900, 0,,9,99 t c = t e = w=0, σημεία t ( ) P(bar) h( s ( 90, 0,,,9 9,,0 0,09, 9,,0,,9,00,9,9,099,, 9,,00,,900,,9,9,99

72 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9,,00 0,09, 99,,,,9,00,9,9,09,, 9,,00,,900,,9,9,99 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,0,9,9 0,90, 99,9,,,9,00,0,9,09,, 9,,00,,900,,0,9,99

73 t c = 0 t e = 0 w=0, σημεία t ( ) P(bar) h( 90, 0,, 0,,9,,0 0,0 9,9, 0 0,0,,0 0,,,,99,,,0 0 0,0,09,9 0,,9,99 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9 9,,0, 0,0 9,, 0 0,0,,0,9,,,99,,,0 0 0,0,09,9,9,9,99

74 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9,,00, 0,0 99,,00 0 0,0,,0,9,,0,99,,,0 0 0,0,09,9,9,9,99 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,0,9,9, 0,0 99,9, 0 0,0,,0,0,,,99,,,0 0 0,0,09,9,0,9,99

75 t c = t e = 0 w=0, σημεία t ( ) P(bar) h( 90, 0,, 0,,9,,,9 9,,,9 0,9,09 0, 0,9,009,, 0,0,09,9,0, 0,,9,99 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9 9,,0,9,9 9,,9,9 0,9,09,9 0,9,09,, 0,0,09,9,0,,9,9,99

76 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9,,00,9,9 9,,,9 0,9,09,9 0,9,0,, 0,0,09,9,0,,9,9,99 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,0,9,9,99,9 9,0,9,9 0,9,09,0 0,9,0,, 0,0,09,9,0,,0,9,99

77 t c = 0 t e = 0 w=0, σημεία t ( ) P(bar) h( 90, 0,, 0,,9,,9,00 9,,90 0,00 09,,00 0, 09,,09,,,,00 0,00,, 0,,9,99 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9 9,,0,9,00 9,,0 0,00 09,,00,9 09,,0,,,,00 0,00,,,9,9,99

78 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9,,00,,00 9,, 0,00 09,,00,9 09,,0,,,,00 0,00,,,9,9,99 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,0,9,9,0,00 9,0,9 0,00 09,,00,0 09,,0,,,,00 0,00,,,0,9,99

79 t c = t e = 0 w=0, σημεία t ( ) P(bar) h( 90, 0,, 0,,9,,99, 9,,09,,9,00 0,,9,09,, 9,,00,,900, 0,,9,99 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9 9,,0,99, 9,,,,9,00,9,9,099,, 9,,00,,900,,9,9,99 9

80 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9,,00,0, 9,,09,,9,00,9,9,09,, 9,,00,,900,,9,9,99 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,0,9,9,9, 9,0,0,,9,00,0,9,09,, 9,,00,,900,,0,9,99 0

81 t c = 0 t e = 0 w=0, σημεία t ( ) P(bar) h( 90, 0,, 0,,9,,09 0,0 9,, 0 0,0,,0 0,,,,99,,,0 0 0,0,09,9 0,,9,99 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9 9,,0,9 0,0 9,, 0 0,0,,0,9,,,99,,,0 0 0,0,09,9,9,9,99

82 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90 0,9,,00, 0,0 9,, 0 0,0,,0,9,,0,99,,,0 0 0,0,09,9,9,9,99 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,0,9,9, 0,0 9,0,0 0 0,0,,0,0,,,99,,,0 0 0,0,09,9,0,9,99

83 t c = t e = 0 w=0, σημεία t ( ) P(bar) h( 90, 0,, 0,,9, 0,00,9 9,0,,9 0,9,09 0, 0,9,009,, 0,0,09,9,0, 0,,9,99 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9 9,,0 0,0,9 9,0,,9 0,9,09,9 0,9,09,, 0,0,09,9,0,,9,9,99

84 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9,,00,,9 9,9,,9 0,9,09,9 0,9,0,, 0,0,09,9,0,,9,9,99 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,0,9,9,0,9 9,9,,9 0,9,09,0 0,9,0,, 0,0,09,9,0,,0,9,99

85 t c = 0 t e = 0 w=0, σημεία t ( ) P(bar) h( 90, 0,, 0,,9,,0,00 9,0,9 0,00 09,,00 0, 09,,09,,,,00 0,00,, 0,,9,99 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9 9,,0,00,00 9,0, 0,00 09,,00,9 09,,0,,,,00 0,00,,,9,9,99

86 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9,,00,,00 9,9, 0,00 09,,00,9 09,,0,,,,00 0,00,,,9,9,99 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,0,9,9,09,00 9,9, 0,00 09,,00,0 09,,0,,,,00 0,00,,,0,9,99

87 t c = t e = 0 w=0, σημεία t ( ) P(bar) h( 90, 0,, 0,,9,,9, 9,0,,,9,00 0,,9,09,, 9,,00,,900, 0,,9,99 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9 9,,0,0, 9,0,9,,9,00,9,9,099,, 9,,00,,900,,9,9,99

88 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9,,00,, 9,9,,,9,00,9,9,09,, 9,,00,,900,,9,9,99 t c = t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,0,9,9,99, 9,9,9,,9,00,0,9,09,, 9,,00,,900,,0,9,99

89 t c = 0 t e = 0 w=0, σημεία t ( ) P(bar) h( 90, 0,, 0,,9,, 0,0 9,0,9 0 0,0,,0 0,,,,99,,,0 0 0,0,09,9 0,,9,99 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9 9,,0, 0,0 9,0,9 0 0,0,,0,9,,,99,,,0 0 0,0,09,9,9,9,99 9

90 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,9,,00, 0,0 9,9,99 0 0,0,,0,9,,0,99,,,0 0 0,0,09,9,9,9,99 t c = 0 t e = w=0, σημεία t ( ) P(bar) h( 90, 0,,,0,9,9,09 0,0 9,9, 0 0,0,,0,0,,,99,,,0 0 0,0,09,9,0,9,99 90

91 Στον παρακάτω πίνακα για τις διάφορες θερμοκρασίες ατμοποιήσης (t e ) και για τους διάφορους λόγους παροχής μαζών (w) παρουσιάζεται η παροχή μάζας του ατμοποιητή (m e), η παροχή μάζας της ατμογεννήτριας (m g), η ισχύς του ατμοποιητή (Q e), της αντλίας (W P), του συμπυκνωτή (Q c), ο θεωρητικός συντελεστής συμπεριφοράς (COP th ) και ο συντελεστής συμπεριφοράς του κύκλου Carnot (COP carnot ): t e = 0 w = 0, t c ( ) m e( s m g( s Q e(kw) Q c(kw) W p(kw) COP th COP carnot,09, 9,0 9,9, 0,99,,09,9 9,,0, 0,9,0 0,,9 9,9,0, 0,9,,9,9,009,, 0,,9 0 t e = w = 0, t c ( ) m e( s m g( s Q e(kw) Q c(kw) W p(kw) COP th COP carnot,09, 9,,00, 0,00,00,09,9 9,9 9,, 0,999, 0,,9 9,90,00, 0,99,09,9,9 9,9,, 0,909,9 0 t e = w = 0, t c ( ) m e( m s g( s Q e(kw) Q c(kw) W p(kw) COP th COP carnot,09, 9,9,, 0,0,,09,9 9, 0,99, 0,0,0 0,,9 9,999,, 0,9,9,9,9 9,0,, 0,99, 0 9

92 t e = w = 0, t c ( ) m e( s m g( s Q e(kw) Q c(kw) W p(kw) COP th COP carnot,09, 9,,, 0,09,99,09,9 9,09,, 0,09, 0,,9 9,0 0,99, 0,09,,9,9 9,9,09, 0,9,99 0 t e = 0 w = 0, t c ( ) m e( m s g( s Q e(kw) Q c(kw) W p(kw) COP th COP carnot 0,,,,00, 0,99, 0,,9,,, 0,,0 0 0,0,9,99,9, 0,, 0,,9,0 0,0, 0,,9 0 t e = w = 0, t c ( ) m e( m s g( s Q e(kw) Q c(kw) W p(kw) COP th COP carnot 0,,,,, 0,,00 0,,9,0,09, 0,9, 0 0,0,9,,00, 0,99,09 0,,9,,09, 0,,9 0 t e = w = 0, t c ( ) m e( s m g( s Q e(kw) Q c(kw) W p(kw) COP th COP carnot 0,,,,, 0,, 0,,9,0,9, 0,0,0 0 0,0,9,9,9, 0,99,9 0,,9,,0, 0,, 0 9

93 t e = w = 0, t c ( ) m e( s m g( s Q e(kw) Q c(kw) W p(kw) COP th COP carnot 0,, 9,09,9, 0,9,99 0,,9,09,, 0,, 0 0,0,9,09,, 0,09, 0,,9,9,, 0,90,99 0 t e = 0 w = 0, t c ( ) m e( m s g( s Q e(kw) Q c(kw) W p(kw) COP th COP carnot 0,9,,0 0,0, 0,9, 0,9,9,9 9,09, 0,,0 0,00,9,9,9, 0,,,00,9 0,0,9, 0,099,9 0 t e = w = 0, t c ( ) m e( m s g( s Q e(kw) Q c(kw) W p(kw) COP th COP carnot 0,9,,9,, 0,,00 0,9,9,00 0,, 0,9, 0,00,9,,9, 0,9,09,00,9,,0, 0,,9 0 t e = w = 0, t c ( ) m e( s m g( s Q e(kw) Q c(kw) W p(kw) COP th COP carnot 0,9,,,9, 0,, 0,9,9,00,, 0,0,0 0,00,9,9 0,0, 0,,9,00,9,9,9, 0,, 0 9

94 t e = w = 0, t c ( ) m e( s m g( s Q e(kw) Q c(kw) W p(kw) COP th COP carnot 0,9, 9,00,9, 0,,99 0,9,9,9,9, 0,, 0,00,9,09,0, 0,,,00,9,099 9,, 0,0,99 0 t e = 0 w = 0, t c ( ) m e( m s g( s Q e(kw) Q c(kw) W p(kw) COP th COP carnot,9,,9,, 0,9,,0,9 0,,9, 0,9,0 0,0,9,90,, 0,9,,,9,9 0,99, 0,9,9 0 t e = w = 0, t c ( ) m e( m s g( s Q e(kw) Q c(kw) W p(kw) COP th COP carnot,9,, 0,9, 0,,00,0,9,0,, 0,90, 0,0,9 0,0,, 0,9,09,,9,9,, 0,,9 0 t e = w = 0, t c ( ) m e( s m g( s Q e(kw) Q c(kw) W p(kw) COP th COP carnot,9,,9,0, 0,,,0,9,0 9,, 0,0,0 0,0,9,00,09, 0,,9,,9 9,0,9, 0,, 0 9

95 t e = w = 0, t c ( ) m e( s m g( s Q e(kw) Q c(kw) W p(kw) COP th COP carnot,9,,0,9, 0,9,99,0,9,9,90, 0,09, 0,0,9,0 9,, 0,,,,9,,9, 0,,99 0 t e = 0 w = 0, t c ( ) m e( kg s ) m g( kg s ) Q e(kw) Q c(kw) W p(kw) COP th COP carnot,, 0, 9,, 0,9, 0,90,9 0,0 9,, 0,,0,0,9 0,9 9,00, 0,, 0,00,9 00,9,9, 0,,9 t e = w = 0, t c ( ) m e( m s g( s Q e(kw) Q c(kw) W p(kw) COP th COP carnot,,,9 9,, 0,,00 0,90,9 0,00 9,9, 0,,,0,9 0,0 9,09, 0,9,09 0,00,9 0,0,, 0,,9 t e = w = 0, t c ( ) m e( s m g( s Q e(kw) Q c(kw) W p(kw) COP th COP carnot,,,09 00,909, 0,,,90,9,00 9,99, 0,0,0 0,0,9 09, 9,9, 0,,9,00,9 0,9 9,, 0,0, 0 9

96 t e = w = 0, t c ( ) m e( s m g( s Q e(kw) Q c(kw) W p(kw) COP th COP carnot,,,00 0,9, 0,,99,90,9, 00,9, 0,9, 0,0,9,9 9,9, 0,,,00,9 0,09 9,9, 0,,99 0 9

97 COP/COPc η/ηc. ΔΙΑΓΡΑΜΜΑΤΑ ΟΡΓΑΝΙΚΟΣ ΚΥΚΛΟΣ RANKINE η/ηc tc( ο C) η/ηc ΚΥΚΛΟΣ ΨΥΞΗΣ ΜΕ ΕΓΧΥΤΗΡΕΣ w=0, tc( ο C) te=0 te= te= te= 9

98 COP/COPc COP/COPc w=0, tc( ο C) te=0 te= te= te= w=0, tc( ο C) te=0 te= te= te= 9

99 COP/COPc COP/COPc w=0, tc( ο C) te=0 te= te= te= w=0, te=0 te= te= te= tc( ο C) 99

100 . ΣΥΜΠΕΡΑΣΜΑΤΑ Στον οργανικό κύκλο Rankine παρατηρούμε ότι όσο μειώνεται η θερμοκρασία συμπύκνωσης τόσο αυξάνεται ο βαθμός απόδοσης, με εύρος από,9% ως,9%. Για τον κύκλο ψύξης με εγχυτήρες παρατηρούμε ότι ο συντελεστής συμπεριφοράς COP και η θερμοκρασία συμπύκνωσης είναι αντιστρόφως ανάλογα. Ο συντελεστής COP και η θερμοκρασία ατμοποίησης είναι ανάλογα όπως επίσης είναι ανάλογα ο συντελεστής COP και η αναλογία της παροχής μαζών. Παρατηρούμε ότι ο θεωρητικός συντελεστής συμπεριφοράς έχει ένα εύρος από 0, ως 0,. Στα διαγράμματα n/n c και COP/COP c παρουσιάζεται ο εξεργειακός βαθμός απόδοσης. Για τον οργανικό κύκλο Rankine όσο αυξάνεται η θερμοκρασία συμπύκνωσης τόσο αυξάνεται ο εξεργειακός βαθμός απόδοσης. Το ίδιο ισχύει και για τον κύκλο ψύξης με εγχυτήρες για τη θερμοκρασία συμπύκνωσης. Η θερμοκρασία ατμοποίησης είναι αντιστρόφως ανάλογη με τον εξεργειακό βαθμό απόδοσης. Παρατηρούμε ότι ο οργανικός κύκλος Rankine έχει μέγιστο βαθμό απόδοσης έως και,9% στην συγκεκριμένη μελέτη και μπορεί να θεωρηθεί μια αποδοτική λύση για ανάκτηση θερμότητας για την παραγωγή ισχύος. Παρομοίως και ο κύκλος ψύξης με εγχυτήρες που έχει εφαρμογή στην παραγωγή ψύξης και έχει μέγιστο συντελεστή συμπεριφοράς έως και 0, για την συγκεκριμένη μελέτη, μπορεί να είναι μια αποδοτική λύση αφού δεν καταναλώνει σημαντική ηλεκτρική ενέργεια όπως άλλα συστήματα ψύξης. 00

101 ΠΑΡΑΡΤΗΜΑ ΣΧΕΣΕΙΣ P-V-T KAI ΚΑΘΑΡΗ ΟΥΣΙΑ ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΟΓΚΟΜΕΤΡΙΚΕΣ ΙΔΙΟΤΗΤΕΣ Οι ογκομετρικές ιδιότητες μιας καθαρής ουσίας σε μια δεδομένη κατάσταση εκφράζονται με τον συντελεστή συμπιεστότητας Ζ ο οποίος μπορεί να εκφραστεί συναρτήσει της θερμοκρασίας και της πίεσης είτε συναρτήσει της θερμοκρασίας και του όγκου, []. Z = P V = f R T P (T, P) = f V (T, V) V: ο μοριακός όγκος P: η απόλυτη πίεση Τ: η απόλυτη θερμοκρασία R: η παγκόσμια σταθερά των αερίων Η τιμή της παγκόσμιας σταθεράς των αερίων εξαρτάται από τις μονάδες μέτρησης που χρησιμοποιούνται. H επιλογή των ανεξαρτήτων μεταβλητών (θερμοκρασίας πίεσης) ή (θερμοκρασίας - όγκου) εξαρτάται από την εφαρμογή. Για τα ιδανικά αέρια ο συντελεστής συμπιεστότητας είναι. Για τα πραγματικά αέρια ο συντελεστής συμπιεστότητας μεταβάλλεται. Για πραγματικά ρευστά ο συντελεστής συμπιεστότητας είναι μικρότερος και κυμαίνεται μεταξύ του 0, και του 0, ανάλογα με την θερμοκρασία και την πίεση. Ο συντελεστής συμπιεστότητας είναι αδιάστατος αριθμός και συχνά υπολογίζεται από τη συνάρτηση της αναγόμενης θερμοκρασίας Τ r και της αδιάστατης πίεσης P r, []. Τ r = T Τ cr P r = P P cr Τ cr, P cr : Κρίσιμες θερμοκρασίες και πιέσεις της εξεταζόμενης ουσίας Ο συντελεστής συμπιεστότητας μπορεί να υπολογιστεί και από την συνάρτηση της αδιάστατης θερμοκρασίας Τ r και του αδιάστατου όγκου V r. 0

102 V r = V V cr V cr : χαρακτηριστική ιδιότητα για την ουσία που χρησιμοποιείται Ο συντελεστής συμπιεστότητας υπολογισμένος από την συνάρτηση με αδιάστατες μεταβλητές: Z = f Pr (T r, P r ) = f Vr (T r, V r ) Η συνάρτηση του συντελεστή συμπιεστότητας με αδιάστατες μεταβλητές βοηθάει να παρουσιαστούν πολλές ουσίες γραφικά σε γενικευμένη μορφή. Για παράδειγμα οι Obert και Nelson έχουν βρει πειραματικά δεδομένα θερμοκρασίας, πίεσης και όγκου και πως με αυτά μεταβάλλεται ο συντελεστής συμπιεστότητας, []. Σχήμα. Συντελεστής συμπιεστότητας και αδιάστατης πίεσης, [] 0

103 Σχήμα. Συντελεστής συμπιεστότητας με μειωμένη πίεση, [] Σχήμα.συντελεστής συμπιεστότητας και μειωμένης πίεσης [] Η καταστατική εξίσωση είναι μια αλγεβρική σχέση μεταξύ της πίεσης, όγκου και θερμοκρασίας. Υπάρχουν τρεις τύποι καταστατικής εξίσωσης: Η πρώτη σχετίζεται με την μοριακή θεωρία Η δεύτερη είναι με αναλυτικό τρόπο υπολογισμού με βάση την θερμοκρασία και την πίεση 0

104 Η Τρίτη είναι με εμπειρική μέθοδο Αναλυτική καταστατική εξίσωση Η καταστατική εξίσωση χρησιμοποιείται για να περιγράψει και αέρια και υγρά. Αυτή χρησιμοποιείται με την εξίσωση Z = f V (T, V) και πρέπει να είναι το ελάχιστο = ου βαθμού ο όγκος. Ο όρος αναλυτική καταστατική εξίσωση υποδηλώνει ότι στη συνάρτηση f V (T, V) ο όγκος δεν είναι μεγαλύτερος του = ου βαθμού. Όταν η θερμοκρασία και η πίεση είναι προσδιορισμένα ο όγκος μπορεί να βρεθεί αναλυτικά. Διατύπωση κυβικής εξίσωσης Είναι δυνατόν να διατυπώσουμε όλες τις πιθανές κυβικές εξισώσεις σε μια γενική μορφή με συνολικά πέντε παραμέτρους. Αν μια παράμετρο δεν ενσωματώνει την μη συμπιεστότητα των υγρών λαμβάνω ότι η πίεση πλησιάζει το άπειρο καθώς ο όγκος πλησιάζει την παράμετρο b. Η γενική κυβική μορφή της πίεσης είναι P = R T V b Θ (V η) (V b) (V +δ V+ε) Οι παράμετροι Θ,b,η,δ,ε μπορεί να είναι είτε μια σταθερά, είτε 0 είτε μια συνάρτηση της πίεσης και της θερμοκρασίας. Σχήμα. Οι τιμές που παίρνει οι παράμετροι για την κάθε εξίσωση [] Στον πίνακα φαίνονται οι σχέσεις και οι τιμές που λαμβάνονται οι παράμετροι Ισχύει η=b 0

105 Σχήμα. Οι τιμές που παίρνει οι τιμές που παίρνουν οι παράμετροι για την κάθε εξίσωση [] Στον πίνακα φαίνεται η συνάρτηση α(τ) για την κάθε καταστατική εξίσωση. Η εξίσωση P = R T f V (T, V) Θ (V η) V b (V b) (V +δ V+ε) μπορεί να μετασχηματιστεί στην μορφή Z = Z = V ( Θ RT ) V (V η) V b (V b) (V +δ V+ε) Η εξίσωση μπορεί να γραφτεί στην εξής μορφή όταν η θερμοκρασία και η πίεση είναι καθορισμένα. Z + (δ Β )Z + [Θ + ε δ (Β + )] Ζ [ε (Β + ) + Θ η ] = 0 Όταν η τιμή του συντελεστή Ζ υπολογίζεται από αυτήν την εξίσωση, και είναι γνωστή η πίεση και η θερμοκρασία ο όγκος υπολογίζεται από την σχέση V = Z R T P Οι αδιάστατοι παράμετροι υπολογίζονται ως εξής. Β = b P R T δ = b P R T Θ = Θ P (R T) ε = ε ( P R T ) η = η P R T 0

106 ΠΙΝΑΚΑΣ ΘΕΡΜΟΡΕΥΣΤΟΔΥΝΑΜΙΚΩΝ ΙΔΙΟΤΗΤΩΝ ΤΟΥ ΝΕΡΟ 0