ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ. Μελέτη Ακουστικής Κλειστών Χώρων Και Ηλεκτρακουστικής Εγκατάστασης Με Έμφαση Στην Ηχώ
|
|
|
- Μαρία Παχής
- 9 χρόνια πριν
- Προβολές:
Transcript
1 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ: Τηλεπικοινωνιών και Τεχνολογίας Πληροφορίας (Τ. & Τ.Π.) ΕΡΓΑΣΤΗΡΙΟ ΕΝΣΥΡΜΑΤΗΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΣ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ του φοιτητή του Τμήματος Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών της Πολυτεχνικής Σχολής του Πανεπιστημίου Πατρών Γαβριήλ Καμάρη του Περικλή Α.Μ Θέμα Μελέτη Ακουστικής Κλειστών Χώρων Και Ηλεκτρακουστικής Εγκατάστασης Με Έμφαση Στην Ηχώ Επιβλέπων: Καθηγητής Ιωάννης Μουρτζόπουλος N o : Πάτρα, Ιούλιος 2012 ΠΑΝΕΠΙΣΤΗΜΙΟΥΠΟΛΗ ΠΑΤΡΑΣ Τηλ: ΡΙΟ - ΠΑΤΡΑ Τηλ:
2 ii
3 iii ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ: Τηλεπικοινωνιών και Τεχνολογίας Πληροφορίας (Τ. & Τ.Π.) ΕΡΓΑΣΤΗΡΙΟ ΕΝΣΥΡΜΑΤΗΣ ΤΗΛΕΠΙΚΟΙΝΩ- ΝΙΑΣ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ του φοιτητή του Τμήματος Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών της Πολυτεχνικής Σχολής του Πανεπιστημίου Πατρών Γαβριήλ Καμάρη του Περικλή Α.Μ Θέμα Μελέτη Ακουστικής Κλειστών Χώρων Και Ηλεκτρακουστικής Εγκατάστασης Με Έμφαση Στην Ηχώ Επιβλέπων: Καθηγητής Ιωάννης Μουρτζόπουλος Αριθμός Διπλωματικής Εργασίας: Πάτρα, Ιούλιος 2012
4 iv
5 v ΠΙΣΤΟΠΟΙΗΣΗ Πιστοποιείται ότι η Διπλωματική Εργασία με θέμα: Μελέτη Ακουστικής Κλειστών Χώρων Και Ηλεκτρακουστικής Εγκατάστασης Με Έμφαση Στην Ηχώ του φοιτητή του Τμήματος Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών της Πολυτεχνικής Σχολής του Πανεπιστημίου Πατρών: Γαβριήλ Καμάρη Αριθμός Μητρώου: 5338 Παρουσιάστηκε δημόσια και εξετάστηκε στο Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών στις 25/7/2012 Ο επιβλέπων Ο Διευθυντής του Τομέα Ιωάννης Μουρτζόπουλος Καθηγητής Νικόλαος Φακωτάκης Καθηγητής
6 vi
7 vii Αριθμός Διπλωματικής Εργασίας: Τίτλος: Μελέτη Ακουστικής Κλειστών Χώρων Και Ηλεκτρακουστικής Εγκατάστασης Με Έμφαση Στην Ηχώ Φοιτητής: Γαβριήλ Καμάρης του Περικλή Επιβλέπων: Ιωάννης Μουρτζόπουλος, Καθηγητής Περίληψη Στην παρούσα Διπλωματική Εργασία εξετάζεται η ακουστική ποιότητα της κεντρικής αίθουσας (Ι1) του Συνεδριακού και Πολιτιστικού Κέντρου του Πανεπιστημίου Πατρών 1. Η ακουστική παράμετρος που ερευνάται είναι η Ενόχληση από ηχώ. Για τον σκοπό αυτό αναπτύχθηκε αλγόριθμος στο περιβάλλον MATLAB που υλοποιεί το Κριτήριο Ενόχλησης από Ηχώ που διατύπωσαν οι Dietsch and Kraak[1] γνωστό και ως Echo Disturbance Criterion ή δείκτης EK. Για τις ανάγκες της διπλωματικής εργασίας πραγματοποιήθηκαν μετρήσεις κρουστικών αποκρίσεων σε διάφορες θέσεις στην πλατεία της αίθουσας με παντοκατευθυντικό μικρόφωνο και με την αμφιωτική διάταξη της κούκλας KEMAR. Επίσης χρησιμοποιήθηκαν κρουστικές αποκρίσεις από προσομοίωση στο πρόγραμμα ακουστικής προσομοίωσης CATT-Acoustic, για τις διάφορες θέσεις. Στη συνέχεια οι κρουστικές αναλύονται από τον αλγόριθμο και εξάγονται τα διαγράμματα με τα κρίσιμα όρια εφαρμογής του κριτηρίου. Τέλος γίνεται η σύγκριση ανάμεσα στις κρουστικές που λάβαμε από το μοντέλο και από τις μετρήσεις. Όπως φαίνεται υπάρχουν σχετικές διαφορές ανάμεσά τους. Οι μετρήσεις τονίζουν κάποια προβλήματα που στην πράξη δεν υφίστανται. Λέξεις-κλειδιά: Ακουστική κλειστών χώρων, κριτήριο ενόχλησης από ηχώ, Dietsch & Kraak, EK, Ανάκλαση, CATT-Acoustic. 1
8
9 Περιεχόμενα 1 Εισαγωγή 1 2 Θεωρία Ηχητική διάδοση σε μη ελεύθερα πεδία Ανάκλαση του ήχου Διέλευση Απορρόφηση Διάχυση Ακουστικές Παράμετροι χώρου Χρόνος Αντήχησης RT Ηχοστάθμη σε κάποια απόσταση Lp Στάθμη λόγου απευθείας προς ανακλώμενο ήχοl d r Ποσοστιαία μείωση αντιληπτότητας φωνημάτων (%AL cons ) Το μοντέλο των ειδώλων Μοντέλα διάδοσης του ήχου Περιγραφή της θεωρίας των ειδώλων Σύνοψη Κρουστική απόκριση Sweep σήματα διέγερσης και η χρήση τους στις μετρήσεις ακουστικής απόκρισης Το κριτήριο των Dietsch & Kraak Ανάγκη για ένα αντικειμενικό κριτήριο Θεωρητικό υπόβαθρο Υλοποίηση Μετρήσεις στην κεντρική αίθουσα του ΣΠΚ Θέσεις μετρήσεων Μετρητική διάταξη
10 ΠΕΡΙΕΧΟΜΕΝΑ iii Διαδικασία μέτρησης Υλοποίηση του κριτηρίου Dietsch & Kraak Περιγραφή του αλγορίθμου Διαγράμματα Αποτελέσματα Σύγκριση Μετρήσεων - Προσομοιώσεων Σύνοψη αποτελεσμάτων Συμπεράσματα Σύνοψη Προτάσεις, Βελτιώσεις ΑΚώδικας υλοποίησης σε περιβάλλον MATLAB 57 ΒΚώδικας εξωτερικών συναρτήσεων 60
11 Κεφάλαιο 1 Εισαγωγή Η ακουστική των χώρων είναι ένα θέμα που απασχόλησε τον άνθρωπο από τα αρχαία χρόνια. Θέατρα εξαιρετικής ακουστικής σώζονται μέχρι σήμερα. Τα μόνα, όμως κείμενα που περιγράφουν κάποιους κανόνες κατασκευής και καλής ακουστικής των θεάτρων, είναι αυτά του Ρωμαίου Βιτρούβιου 1 του 25π.Χ.. Κατά την αναγέννηση γίνεται η μετάβαση από ανοιχτά θέατρα σε κλειστούς χώρους. Μέχρι τον 19ο αιώνα, ωστόσο, δεν δινόταν ιδιαίτερη προσοχή στην ακουστική των κλειστών χώρων. Η πρώτη προσπάθεια βελτίωσης της ακουστικής έγινε από τον Joseph Henry στην αίθουσα διαλέξεων του Smithsonian Institution (Washington), το Ο Henry ήταν ο πρώτος που επισήμανε την κακή ακουστική συμπεριφορά των χώρων εξαιτίας της ηχούς και του εστιασμού του ήχου σε συγκεκριμένα σημεία. Με παρατηρήσεις ο Henry διαπίστωσε ότι καθυστέρηση μικρότερη των 53ms δεν προκαλεί την αίσθηση της ηχούς. Η παρατήρηση αυτή οδήγησε αργότερα τον Haas στην διατύπωση του φαινομένου γνωστού ως φαινόμενο Haas (Haas effect). Εκείνος, όμως, που έφερε επανάσταση στην ακουστική κλειστών χώρων ήταν ο Wallace Sabine, καθηγητής στο Harvard University. Ο Sabine αντιλήφθηκε τη σημασία της αντήχησης για την ακουστική ποιότητα των χώρων και την επίδραση της απορρόφησης των υλικών στην αντήχηση των χώρων (1915). Η μελέτη της ακουστικής κλειστών χώρων παρουσιάζει ιδιαίτερο ενδιαφέρον για τον μηχανικό, καθώς σχετίζεται τόσο με την ποιότητα του ήχου που φτάνει στη θέση του δέκτη όσο και με την παρατηρούμενη στάθμη η οποία επηρεάζεται από τις διαδοχικές ανακλάσεις. 1 De Architectura:Ch VII De locis consonatibus ad theatra eligendis
12 2 Ένας κλειστός χώρος λέμε ότι έχει καλή ακουστική όταν πληροί ορισμένες προϋποθέσεις. Ο ήχος θα πρέπει να φτάνει σε όλα τα σημεία με μικρή σχετική μείωση της στάθμης. Το φαινόμενο της επικάλυψης θα πρέπει είτε να μην εμφανίζεται καθόλου, είτε να είναι περιορισμένο. Ο ρυθμός μείωσης του ήχου να είναι βέλτιστος, με αποτέλεσμα τη βέλτιστη μετάδοση της ομιλίας και ακρόαση της μουσικής. Μετρήσεις από τους Beranek, Hidaka και Masuda έδειξαν ότι στις καλύτερες αίθουσες μουσικής η τιμή RT για τη μεσαία περιοχή συχνοτήτων είναι 1.3s και 1.6s. Για τον EDT η τιμή είναι στα 1.7s. Σε έναν χώρο δεν πρέπει να υπάρχουν δυσάρεστα φαινόμενα όπως ηχώ, ηχητικές σκιές, ηχητικές παραμορφώσεις και ηχητικές συγκεντρώσεις. Τέλος ο χώρος θα πρέπει να διαθέτει επαρκή ηχομόνωση για να περιορίσει τον εισερχόμενο θόρυβο από το περιβάλλον 2. Στην παρούσα διπλωματική θα επικεντρωθούμε στο φαινόμενο της ηχούς. Ηχώ θεωρείτε κάθε ήχος που φτάνει στον δέκτη μετά τον απευθείας ήχο και γίνεται αντιληπτός ως ξεχωριστό ηχητικό γεγονός. Η ηχώ δεν πρέπει να συγχέεται με την αντήχηση. Η ηχώ, σε αντίθεση με την αντήχηση, η οποία πολλές φορές θεωρείται επιθυμητή, καταστρέφει την καλή ακουστική των χώρων διότι η επικοινωνία γίνεται δύσκολη και αλλοιώνεται ο ρυθμός της μουσικής. Η εμφάνιση της ηχούς δεν εξαρτάται μόνο από την χρονική καθυστέρηση των ανακλώμενων ηχητικών ακτίνων αλλά και από την γωνία πρόσπτωσης και την στάθμη της ανακλώμενης ηχητικής ακτίνας κ.λ.π. Το φαινόμενο της ηχούς παρουσιάζεται όταν η ανάκλαση σε σχέση με τον απευθείας ήχο έχουν διαφορά τουλάχιστον 100ms. Αν θεωρήσουμε την ταχύτητα του ήχου σε κανονικές συνθήκες 340m/sec, αυτό σημαίνει ότι για να εμφανιστεί ηχώ χρειάζεται μία διαδρομή τουλάχιστον 34m μέσα στον χώρο (δηλαδή κάποια ανακλαστική επιφάνεια που απέχει τουλάχιστον 17m). Πειράματα του Haas (1950)[2] έδειξαν ότι το φαινόμενο της ηχούς μπορεί να παρατηρηθεί και για μικρότερες καθυστερήσεις. Στην περίπτωση αυτή οι καθυστερημένοι ήχοι πρέπει να έχουν μεγαλύτερη στάθμη από τον αρχικό. Αυτό το φαινόμενο είναι πολύ έντονο όταν ο δευτερεύων ήχος προέρχεται από αναπαραγωγή. Ο Haas έδειξε ότι αν η ανάκλαση καθυστερεί από 5 εώς 35ms, για να είναι διακριτή η ηχώ πρέπει να έχει στάθμη περίπου 18dB 2 Κατά τον Beranek η τιμή των κριτηρίων NCB πρέπει να είναι μικρότερη από
13 3 10dB μεγαλύτερη από τον αρχικό ήχο. Όταν η καθυστέρηση είναι μεγαλύτερη των 100ms, το φαινόμενο εμφανίζεται ανεξάρτητα από την στάθμη. Αν η στάθμη δεν είναι τόσο δυνατή, απλά ενισχύεται ο αρχικός ήχος. Το φαινόμενο αυτό ονομάζεται φαινόμενο Haas. Ένας αντικειμενικός δείκτης ενόχλησης από ηχώ ήταν απαραίτητο να διατυπωθεί. Το 1950 οι Bolt & Doak [3] εξέτασαν το φαινόμενο του Haas για ομιλία. Καθόρισαν πειραματικά τα όρια και 90% ενόχλησης από ηχώ. Το λάθος ήταν ότι το όριο προέκυψε εξετάζοντας ένα δωμάτιο με αντήχηση 0.8s. Αυτό σημαίνει ότι όλα τα δωμάτια εξετάζονται με το όριο το οποίο προέκυψε από αυτό το συγκεκριμένο δωμάτιο. Επίσης κατά τον προσδιορισμό του ορίου δεν λήφθηκε υπόψη ότι μία ομάδα λίγο πιο αδύναμων ανακλάσεων μπορεί να επιφέρει το ίδιο αποτέλεσμα. Ο δείκτης Echograd (αλλιώς συντελεστής ηχούς ) του Niese [4] διατυπώθηκε περισσότερο για την καταληπτότητα τις ομιλίας, παρά για την ενόχληση από δυνατές, διακριτές ανακλάσεις. Σημαντικό είναι ότι ο δείκτης Echograd προκύπτει από σύγκριση με την ιδανική κρουστική. Επίσης δεν έχει διατυπωθεί για σήμα μουσικής. Το 1977, ο Schmidt πρότεινε ένα κριτήριο για ομιλία και μουσική [5]. Ένας δείκτης ονομάστηκε απόλυτη ονομαστική αδράνεια του αυτιού E τm (t). Ο Schmidt ολοκλήρωσε για τ = 5ms με το τετράγωνο της κρουστικής και σύγκρινε με αυτό όπως φαίνεται στον τύπο 1.1. L = 10 log 10E τ5 E τm db (1.1) Προτάθηκαν διαφορετικές σταθερές χρόνου τ M για μουσική και ομιλία. Μία ηχώ αναγνωρίζεται αν το L 3dB και η ανάκλαση φτάνει 50ms μετά τον απευθείας ήχο. Όλα τα αποτελέσματα επαληθεύθηκαν με υποκειμενικά τεστ σε συνθετικό ακουστικό χώρο. Το κριτήριο που πρότεινε ο Yamamoto[6] είναι παρόμοιο με αυτό του Schmidt. Ο Yamamoto δούλεψε με σήματα 10ms σε τρεις οκτάβες (f M = 0.5, 1και2kHz) και έκανε υποκειμενικά τεστ. Συμπέρανε λοιπόν ότι το χρονικό όριο στο οποίο γίνεται αντιληπτή η ηχώ εξαρτάται από τη συχνότητα. Υπολόγισε 45ms για f M = 0.5kHz, 35ms για f M = 1kHz και 25ms για f M = 2kHz. Έτσι, πρότεινε να συγκρίνεται η κρουστική απόκριση του δωματίου με μία νέα ειδική καμπύλη. Αυτή φαίνεται στο σχήμα 1.1. Η περιβάλλουσα παραμένει σταθερή μέχρι το τέλος του απευθείας σήματος και έπειτα
14 4 κατεβαίνει μέχρι να συναντήσει κάποια ανάκλαση. Σε εκείνο το σημείο υπολογίζεται η διαφορά L και προκύπτει η τιμή του κριτηρίου. Σχήμα 1.1: Παράδειγμα εφαρμογής του κριτηρίου που ανέπτυξε ο Yamamoto Για 0.5kHz είναι dB, για 1kHz είναι dB και για 2kHz είναι dB, στη συνέχεια η καμπύλη παραμένει σταθερή κατά την διάρκεια της ανάκλασης και μετά πέφτει κ.ο.κ. Εδώ πρέπει να τονίσουμε ότι αυτά ισχύουν για ήχους διάρκειας 10ms (τόση είναι η διάρκεια που θεωρεί ο Yamamoto για τον συντομότερο αντιληπτό ήχο). Ακόμα δεν έχει εξεταστεί αν η διαδικασία αυτή μπορεί να εφαρμοστεί σε πραγματικά σήματα ομιλίας και μουσικής. Τέλος, το 1985 οι Dietsch & Kraak διατύπωσαν το δικό τους κριτήριο το οποίο και εξετάζεται στην παρούσα διπλωματική εργασία. Τα κεφάλαια της διπλωματικής έχουν ως εξής: Κεφάλαιο 2 :Στο δεύτερο κεφάλαιο παρουσιάζεται εισαγωγική θεωρία για την ακουστική κλειστών χώρων, τις ακουστικές παραμέτρους και τις ακουστικές μετρήσεις στους χώρους. Τέλος παρουσιάζεται το θεωρητικό υπόβαθρο του ίδιου του κριτηρίου. Κεφάλαιο 3 : Στο τρίτο κεφάλαιο παρουσιάζεται η διαδικασία των
15 μετρήσεων που πάρθηκαν για την ανάγκη της παρούσας διπλωματικής εργασίας στην κεντρική αίθουσα του Πολιτιστικού και Συνεδριακού Κέντρου του Πανεπιστημίου Πατρών. Κεφάλαιο 4 : Στο τέταρτο κεφάλαιο παρουσιάζεται ο αλγόριθμος που αναπτύχθηκε για την υλοποίηση του Κριτηρίου στο περιβάλλον Μatlab. Κεφάλαιο 5 : Τα αποτελέσματα του κριτηρίου για τις μετρήσεις και τις προσομοιώσεις παρουσιάζονται και συγκρίνονται. Κεφάλαιο 6 : Αναφέρονται τα συμπεράσματα και προτείνονται περαιτέρω βελτιώσεις. 5
16 6
17 Κεφάλαιο 2 Θεωρία Η μελέτη και ο σχεδιασμός των ακουστικών ιδιοτήτων ενός κλειστού χώρου (π.χ. κινηματογραφική αίθουσα, αίθουσα διαλέξεων, δωμάτιο γραφείου/ κατοικίας) ξεκινά πάντα με υπολογισμό και εκτίμηση των παραμέτρων του ακουστικού περιβάλλοντος, όπως αυτό ορίζεται από τη γεωμετρία και τα χαρακτηριστικά απορρόφησης του χώρου. Ο τελικός στόχος σε κάθε περίπτωση είναι η βέλτιστη μετάδοση του ήχου και η ελαχιστοποίηση των παραμορφώσεων που εισάγονται από το χώρο και επηρεάζουν αρνητικά την ποιότητα του αναπαραγόμενου ήχου (π.χ. ασάφεια της ακουστικής εικόνας του αρχικού σήματος, μείωση της αντιληπτότητας της ομιλίας κ.λ.π.). Οι παραμορφώσεις αυτές εξαρτώνται άμεσα από τα γεωμετρικά χαρακτηριστικά του χώρου και τις διαδρομές που διαγράφει το ηχητικό σήμα έως ότου φτάσει στον δέκτη-ακροατή. 2.1 Ηχητική διάδοση σε μη ελεύθερα πεδία Από την ίδια του τη φύση, ο ήχος είναι ένα φαινόμενο που δεν υφίσταται στατικά. Η γέννηση και η υπόστασή του είναι ρητά συνυφασμένες με τη διάδοσή του μέσα σε ένα υλικό, ελαστικό, και αδρανές μέσο. Κατά την πορεία του, το ηχητικό κύμα αφενός καταναλώνει την αρχική ενέργεια που του έχει δοθεί και αφετέρου συναντά πολλών ειδών εμπόδια, τα οποία μεταβάλλουν τα χαρακτηριστικά του. Τα ηχητικά κύματα σπανίως διαδίδονται σε εντελώς ελεύθερα πεδία. Το πιθανότερο είναι ότι στη διαδρομή τους θα συναντή-
18 2.1 Ηχητική διάδοση σε μη ελεύθερα πεδία 8 σουν πολλών ειδών εμπόδια: φυσικά ή τεχνητά, ορατά ή αόρατα. Για ένα ηχητικό κύμα, εμπόδιο θεωρείται οποιαδήποτε μεταβολή της φύσης του μέσου διάδοσης, αν και για την ακουστική εσωτερικών χώρων μεγαλύτερο ενδιαφέρον παρουσιάζουν τα τεχνητά και ορατά εμπόδια, όπως οι επιφάνειες και τα έπιπλα ενός δωματίου. Τα μεγάλα προβλήματα που αντιμετωπίζει η ακουστική είναι: πρώτον, ότι τα ηχητικά κύματα είναι αόρατα δεύτερον, ότι συμπεριφέρονται εντελώς διαφορετικά ανάλογα με τη συχνότητα τους και, τρίτον, ότι τα αποτελέσματα της συμβολής τους με τα διάφορα εμπόδια που συναντούν στην πορεία τους, δεν μετριούνται εύκολα και άμεσα. Όταν ένα κύμα προσκρούσει σε μια επιφάνεια όπως, για παράδειγμα, σε έναν τοίχο του δωματίου μας, θα λάβουν ταυτόχρονα χώρα τα τρία γνωστά φαινόμενα: ανάκλαση, απορρόφηση και διάθλαση Ανάκλαση του ήχου Η ανάκλαση (reflection) είναι άμεσο αποτέλεσμα της κρούσης του κύματος πάνω σε μια επιφάνεια. Αυτό σημαίνει ότι, αν το εμπόδιο είναι συμπαγές, ακλόνητα στερεωμένο και 100% ανελαστικό, το κύμα θα προσκρούσει ελαστικά και θα έχουμε την ολική ανάκλαση του. Στην ακραία αυτή περίπτωση δεν θα παρουσιαστεί καθόλου απορρόφηση, και όλος ο ήχος θα επιστρέψει πάλι πίσω, μειωμένος φυσικά σε ένταση λόγω της κρούσης. Μάλιστα, η γωνία ανάκλασης είναι προβλέψιμη, αφού είναι ίδια με τη γωνία πρόσπτωσης, και η διεύθυνση του ανακλώμενου κύματος είναι συμμετρική ως προς το νοητό άξονα που περνά από το σημείο κρούσης και είναι κάθετος στην επιφάνεια. Στο σχήμα 2.1, μπορεί κανείς να δει τι συμβαίνει όταν παρεμβληθεί κάποιο εμπόδιο στην πορεία ενός ηχητικού κύματος. Ένα μέρος της ενέργειας του ανακλάται και το υπόλοιπο μεταβιβάζεται στο εμπόδιο, όπου και καταναλώνεται με δύο τρόπους: κάποιο ποσοστό της απορροφάται από το ίδιο το εμπόδιο, και κάποιο θέτει σε κίνηση την επιφάνεια του, δημιουργώντας ένα νέο κύμα που εκπέμπεται από την άλλη του πλευρά (σχήμα 2.1). Έτσι, είναι πολύ εύκολο να σχεδιαστούν οι ανακλάσεις που θα πραγματοποιηθούν σε ένα χώρο με δεδομένες επιφάνειες, ή αντίθετα να διαμορφωθούν οι κλίσεις των επιφανειών του χώρου, έτσι ώστε να οδηγούνται οι ανακλάσεις στα επιθυμητά σημεία. Αυτό, φυσικά, ισχύει κυρίως για τις μεσαίες και υψηλές συχνότητες που συμπεριφέρονται όπως ακρι-
19 2.1 Ηχητική διάδοση σε μη ελεύθερα πεδία 9 βώς και οι ακτίνες φωτός, ενώ αντίθετα οι χαμηλές λειτουργούν σαν κύματα που διαχέονται σε όλο το χώρο και δεν έχουν σαφή διεύθυνση. Σχήμα 2.1: Πρόσπτωση ηχητικού κύματος σε επίπεδη ανακλαστική επιφάνεια. Η γωνία πρόσπτωσης (π) ισούται με τη γωνία ανάκλασης (α) Διέλευση Αν δεν ισχύουν οι ιδανικές συνθήκες, ένα ποσοστό της ενέργειας του ηχητικού κύματος εισχωρεί στο εμπόδιο. Δεχόμενο αυτή την ενέργεια, το εμπόδιο τίθεται σε ταλάντωση δημιουργώντας ένα νέο ηχητικό κύμα που εκπέμπεται από την άλλη του πλευρά. Η αποτροπή της διέλευσης του ήχου από το εμπόδιο αποτελεί το κυριότερο ζητούμενο στην ηχομόνωση χώρων. Αυτή επιτυγχάνεται μόνο αν επιτευχθεί να μη δονηθεί το εμπόδιο. Αυτό εξαρτάται από την ελαστικότητα του, άρα την πυκνότητα του, έτσι μια λύση στο πρόβλημα αυτό, θα αποτελούσε η αύξηση της μάζας του υλικού.
20 2.2 Ακουστικές Παράμετροι χώρου Απορρόφηση Για τη δημιουργία όμως του νέου κύματος δεν χρησιμοποιείται όλο το ποσό της ενέργειας που εισχωρεί στο εμπόδιο. Ένα μέρος της θα καταναλωθεί από το ίδιο το εμπόδιο, λόγω των εσωτερικών τριβών και των συντονισμών, που προκαλούνται μέσα στους πόρους του υλικού του. Το φαινόμενο αυτό ονομάζεται απορρόφηση και έχει μεγαλύτερη ισχύ στις υψηλές συχνότητες, οι οποίες απορροφώνται εύκολα (λόγω του μικρού τους μήκους κύματος) από πορώδη υλικά μικρού πλάτους, όπως οι κουρτίνες και τα χαλιά. Η απορροφητικότητα ενός υλικού δίνεται μέσω του συντελεστή απορροφητικότητας α, που παίρνει τιμές από 0 (100% ανάκλαση) έως 1 (100% απορρόφηση) Διάχυση Η διάχυση επιτυγχάνεται μέσω ειδικά διαμορφωμένων και πολύπλοκων κατασκευών, που καταφέρνουν να διασπάσουν το ηχητικό κύμα στις επιμέρους συχνότητες, από τις οποίες αποτελείται, και να δημιουργήσουν ένα πεδίο ανάκλασης που απλώνεται ομοιόμορφα σε όλη την έκταση του χώρου. Οι διαχυτές, είναι οι πιο διαδεδομένες διατάξεις για την ακουστική βελτίωση των χώρων ακρόασης και οι πλέον ιδανικές για μικρούς χώρους και κυρίως για χώρους, όπου έχουμε την αναπαραγωγή πολυκάναλης μουσικής. 2.2 Ακουστικές Παράμετροι χώρου Οι ακουστικές παράμετροι του χώρου μπορούν να υπολογιστούν (διαδικασία που γίνεται κατά το σχεδιασμό και τη μελέτη του χώρου) ή να μετρηθούν (διαδικασία που γίνεται αφού ο χώρος έχει κατασκευαστεί). Η βασικότερη από αυτές είναι ίσως ο Χρόνος αντήχησης (RT 60 ). Άλλες παράμετροι είναι η καταλυπτότητα φωνής, η κατανομή της ακουστικής πίεσης και η στάθμη λόγου κατ ευθείαν προς ανακλώμενου ήχου. Η μέτρηση της κρουστικής απόκρισης του χώρου, θεωρείται πλέον ότι περιέχει όλη την χρήσιμη πληροφορία για τον προσδιορισμό της ακουστικής συμπεριφοράς του χώρου, δηλαδή όλων των χρήσιμων παραμέτρων. Αυτή είτε υπολογίζεται, με την βοή-
21 2.2 Ακουστικές Παράμετροι χώρου 11 θεια του υπολογιστή, είτε μετριέται με τη χρήση του κατάλληλου εξοπλισμού επί τόπου στον χώρο [7] Χρόνος Αντήχησης RT 60 Ο χρόνος αντήχησης ορίζεται ως εκείνος ο χρόνος μέσα στον οποίο η ηχοστάθμη θα πέσει κατά 60dB μετά από την διακοπή του σήματος διέγερσης [8]. Ο Sabine καθόρισε πειραματικά τη μεταβλητή αυτή ως: RT 60 = 0.161V A (2.1) όπου RT ο χρόνος αντήχησης σε δευτερόλεπτα, V ο όγκος του δωματίου σε m 3 και A = S 1 a S n a n η απόσβεση του δωματίου Ηχοστάθμη σε κάποια απόσταση Lp Κατά Hopkins-Stryker, η συνολική ηχοστάθμη (λόγω κατ ευθείαν και ανακλώμενου ήχου) που παράγεται από κάποια πηγή σε κλειστό χώρο δίνεται από τη σχέση: L p = P W L + 10log( D 4πr + 4 ) (2.2) 2 R όπου, R = Sa,P W L(dB) η στάθμη ισχύος της πηγής, D ο λόγος 1 a κατεθυντικότητάς της και r(m) η απόσταση πηγής - δέκτη Στάθμη λόγου απευθείας προς ανακλώμενο ήχοl d r Ο λόγος αυτός δίνεται από τη σχέση: L d r = 10log( DR )(db) (2.3) 16πr2
22 2.3 Το μοντέλο των ειδώλων Ποσοστιαία μείωση αντιληπτότητας φωνημάτων (%AL cons ) Κατά Peutz, η μείωση αντιληπτοτητας των φωνηέντων της ομιλίας που θα φθάσει στον δέκτη, δίνεται από την σχέση: %AL cons = 200r2 RT 2 60 V D (2.4) 2.3 Το μοντέλο των ειδώλων Μοντέλα διάδοσης του ήχου Αν και ο ήχος διαδίδεται με κύματα, η βασική κυματική θεωρία αδυνατεί να περιγράψει τη διάδοσή του σε κλειστούς χώρους, ειδικά για σχετικά υψηλές συχνότητες. Αυτό, σε συνδυασμό με το γεγονός ότι η λύση των κυματικών εξισώσεων είναι εξαιρετικά πολύπλοκη, οδήγησε στην ανάπτυξη άλλων θεωριών, οι οποίες βασίζονται σε φυσικά μοντέλα διάδοσης του ήχου στηριγμένα σε γεωμετρικές αρχές. Τα μοντέλα αυτά θεωρούν ότι ο ήχος συμπεριφέρεται σαν ακτίνα φωτός ( κάτι που συμβαίνει και στην πράξη για συχνότητες > 2000Hz) και αντανακλάται με γωνία σταθερή και ίση ως προς την γωνία πρόσπτωσης, ενώ τα φαινόμενα διάθλασης ή εξάρτησης από την συχνότητα αγνοούνται. Τέτοια μοντέλα, γενικευμένα και για πολύπλοκα σχήματα, υλοποιούνται πλέον με προγράμματα Η/Υ και επιτρέπουν την μελέτη της πορείας των ακτίνων και, κατ επέκταση, την ακριβή πρόβλεψη του ακουστικού πεδίου, που δημιουργεί μια ακουστική πηγή, σε οποιοδήποτε σημείο, σε κάποιον συγκεκριμένο γεωμετρικό χώρο. Τα προγράμματα αυτά αποτελούν και την ακριβέστερη μέθοδο μελέτης και σχεδίασης της ακουστικής διάφορων χώρων, και είναι η βάση των μεθόδων της εικονικής ακρόασης. Μια τέτοια ανάλυση μπορεί να αποτρέψει τη συγκέντρωση πολλών ανακλάσεων, στο ίδιο σημείο ή την δημιουργία άλλων ακουστικών προβλημάτων, κατά την ακουστική λειτουργία του χώρου. Παρακάτω, θα γίνει μια ανάλυση του μοντέλου σε απλούς, παραλληλεπίπεδους γεωμετρικούς χώρους.
23 2.3 Το μοντέλο των ειδώλων 13 Σχήμα 2.2: Χωρική και χρονική κατανομή των φαινομένων της (α) απορρόφησης, (β) ανάκλασης και (γ) διάχυσης Περιγραφή της θεωρίας των ειδώλων Θεωρείται πως σε έναν ακουστικό χώρο μια πηγή εκπέμπει σφαιρικό κύμα μιας συχνότητας. Στο Σχήμα 2.3 φαίνεται η πηγή, που βρίσκεται στην θέση X(x, y, z) και ο δέκτης, που βρίσκεται στο σημείο X (x, y, z ). Το αποτέλεσμα της ανάκλασης εκφράζεται από μια νέα πηγή-είδωλο, που σχηματίζεται σε συμμετρική θέση, ως προς την αρχική πηγή και την ανακλώσα επιφάνεια. Η συνολική πίεση που φτάνει στον δέκτη υπολογίζεται από τον τύπο 2.5. p(ω, X, X, ) = { ej( ω c Rs ) 4π R s + ej( ω c R i ) 4π R i }e jωt (2.5)
24 2.3 Το μοντέλο των ειδώλων 14 Όπου τα R s και R i είναι τα μέτρα της διανυσματικής απόστασης, μεταξύ της θέσης του δέκτη και της θέσης της ακουστικής πηγής και του ακουστικού ειδώλου αντίστοιχα. Σχήμα 2.3: Έκφραση της ανάκλασης με την εισαγωγή ενός ακουστικού ειδώλου της πηγής Για έναν παραλληλεπίπεδο χώρο και θεωρώντας ότι μετά από κάθε ανάκλαση στην αντίστοιχη επιφάνεια (που έχει συντελεστή ανάκλασης β) η πίεση του ήχου θα ελαττώνεται στο πλάτος της κατά β, η συνολική πίεση από όλες τις ανακλάσεις, στην θέση του δέκτη θα δίνεται από τον τύπο 2.6. p(t, X, X, ω) = 8 ϱ=1 r= β x β x2 β y1 β y2 β zz1 β y2 e j ω c t r r+r p 4π r p + r r (2.6) Το r p δίνει το διανυσματικό μέτρο της απόστασης κάθε ειδώλου από τον δέκτη (Σχήμα 2.5) και το r r δίνει την (άπειρη) πρόσθεση
25 2.3 Το μοντέλο των ειδώλων 15 Σχήμα 2.4: Ο ήχος ανακλάται με γωνία σταθερή και ίση ως προς την γωνία πρόσπτωσης νέων δωματίων διάστασης r r. Οι συντελεστές β είναι οι συντελεστές ανάκλασης κάθε επιφάνειας του αρχικού δωματίου. Με την μέθοδο αυτή δημιουργούνται δηλαδή είδωλα από χώρους διατεταγμένους συμμετρικά προς τις πλευρές του αρχικού δωματίου. Προφανώς, αν το σήμα έχει περισσότερες από μία συχνότητες, ισχύει και πάλι η ίδια σχέση και η πίεση υπολογίζεται εύκολα με κατάλληλο αλγόριθμο Σύνοψη Η θεωρία ειδώλων παράγει τη συνάρτηση μεταφοράς μεταξύ δύο σημείων (πηγής και δέκτη) που βρίσκονται στο εσωτερικό του υπό μελέτη χώρου, θεωρώντας ότι κάθε ανάκλαση του αρχικού ηχητικού σήματος, που παράγεται από την ηχητική πηγή, μπορεί να μοντελοποιηθεί ως μια εικονική πηγή γεωμετρικό είδωλο της αρχικής. Έτσι, η τελικά υπολογιζόμενη κρουστική απόκριση αποτελεί το άθροισμα κρουστικών με πλάτος και χρονική καθυστέρηση που εξαρτώνται από την απορρόφηση των τοιχωμάτων του χώρου που εμπλέκονται σε κάθε διαδοχή ανακλάσεων και τη συνολική απόσταση ειδώλου δέκτη αντίστοιχα. Βασική προϋπόθεση για τον παραπάνω υπολογισμό είναι ότι όλα τα είδωλα ενεργο-
26 2.4 Κρουστική απόκριση 16 Σχήμα 2.5: Το σύνολο των ειδώλων που προκύπτουν από την ανάκλαση του ήχου στις επιφάνειες που περικλείουν το χώρο. ποιούνται συγχρόνως με τη διέγερση της πηγής, δημιουργώντας το καθένα ένα σφαιρικό κύμα. Για λόγους απλοποίησης, φαινόμενα διάθλασης των ηχητικών ακτίνων αγνοούνται. 2.4 Κρουστική απόκριση Στην θεωρία επεξεργασίας σημάτων, η κρουστική απόκριση (Impulse Response - IR) ενός δεδομένου συστήματος, είναι η έξοδος του συστήματος όταν η διέγερση είναι μία κρουστική. Η κρουστική διέγερση μοντελοποιείται θεωρητικά με συνάρτηση δ(t) του Dirac στο πεδίο του συνεχούς χρόνου, ή με τη δ[n] του Kronecker στο πεδίο του διακριτού χρόνου. Η δ(t) του Dirac ορίζεται όπως στον τύπο 2.7: { + t = 0, δ(t) = (2.7) 0 t 0 και δ(t) dt = 1 (2.8)
27 2.4 Κρουστική απόκριση 17 όπου το t δηλώνει τον δείκτη του συνεχούς χρόνου [9]. Πρέπει να σημειωθεί ότι από μαθηματικής πλευράς η συνάρτηση δ(t) είναι μία κατανομή, παρά το ότι συνήθως θεωρείται συνάρτηση. Αντίστοιχα, στο πεδίο του διακριτού χρόνου το δ[n] του Kronecker ορίζεται ως 2.9: { 1, n = 0 δ[n] = (2.9) 0, όπου το n είναι ο δείκτης του διακριτού χρόνου (συνήθως n = kt όπου T η περίοδος δειγματοληψίας). Αν ένα σύστημα είναι γραμμικό χρονικά αμετάβλητο (LTI) μπορεί να προσδιοριστεί πλήρως από την κρουστική του απόκριση και η έξοδος του συστήματος στο πεδίο του χρόνου θα είναι η συνέληξη της εισόδου με την κρουστική απόκριση[10]. Στην ακουστική, τα ηχητικά κύματα που εκπέμπει μία πηγή ανακλώνται και διαθλώνται από της επιφάνειες του χώρου. Αυτές οι ανακλάσεις έχουν σαν αποτέλεσμα την εναπόθεση καθυστερημένων και φιλτραρισμένων αντιγράφων της πηγής στη θέση του δέκτη και ο χώρος θεωρείται γραμμικό χρονικά αμετάβλητο σύστημα. Έτσι, η κρουστική απόκριση του δωματίου έχει καίρια σημασία αφού περιέχει όλες τις πληροφορίες για την ακουστική για συγκεκριμένη θέση πηγής-δέκτη. Όταν ένα ηχητικό σήμα s(t) παράγεται σε ένα κλειστό δωμάτιο με κρουστική απόκριση h r (t), το σήμα με την αντήχηση y(t) λαμβάνεται από τη σχέση 2.10: y(t) = t 0 s(τ)h r (t τ) dτ, 0 t < L (2.10) όπου L είναι το μήκος της κρουστικής. Ωστόσο, στις πρακτικές εφαρμογές όπου η πηγή κινείται η κρουστική του δωματίου είναι χρονικά μεταβαλλόμενη και η προηγούμενη σχέση 2.10 παίρνει τη μορφή που φαίνεται στη σχέση y(t, θ) = t 0 s(τ)h r (t τ, θ) dτ, 0 t < L (2.11) όπου το θ δηλώνει την εξάρτηση από την θέση στο δωμάτιο. Η κρουστική μιας αίθουσας συναυλιών φαίνεται στο σχήμα 2.6 (a) στο πεδίο του χρόνου (b) στο πεδίο της συχνότητας. Το φάσμα του δωματίου συνήθως καλείται συνάρτηση μεταφοράς(room
28 2.4 Κρουστική απόκριση Amplitude (a) Time (s) Magnitude (db) Frequency Response Smoothed Frequency Response (1/3 oct) (b) 4 Frequency (Hz) Σχήμα 2.6: Πεδίο του χρόνου (a) και πεδίο της συχνότητας (b) αναπαράσταση μέτρησης κρουστικής απόκρισης δωματίου που πάρθηκε στην κεντρική αίθουσα του συνεδριακού κέντρου του Πανεπιστημίου Πατρών
29 2.4 Κρουστική απόκριση 19 Transfer Function - RTF). Η αλλοίωση του φάσματος που προκαλείται από τις ανακλάσεις(και κυρίως από τις πρώιμες ανακλάσεις) παρουσιάζεται στην συνάρτηση μεταφοράς που φαίνεται στο σχημα 2.6 (b). Ας συμειωθει ότι η αντίληψη της συχνότητας για το ανθρώπινο αυτι ειναι περιορισμένη και οι μικρές φασματικές λεπτομέριες δεν είναι ουσιαστικές. Γι αυτο το λόγο, οι μηχανικοί πολλές φορές αρκει να εξετάσουν την εξομαλυμένη συνάρτηση μεταφοράς (βλέπε 2.6 (b)) [11]. Μέτρηση της κρουστικής απόκρισης χώρου Η ιδανική συνάρτηση δ(t) είναι ένα μαθηματικό εργαλείο και προφανώς δεν μπορεί να αναπαρασταθεί στην πραγματικότητα. Για να μετρήσουμε τις κρουστικές αποκρίσεις, σε κλειστούς ακουστικούς χώρους έχουν χρησιμοποιηθεί πυροβολισμοί, μπαλόνια, παλαμάκια ή άλλοι κρουστικοί ήχοι. Ωστόσο, για μία ακριβή μέτρηση κρουστικής απόκρισης ένα καλώς ορισμένο σήμα διέγερσης πρέπει να χρησιμοποιηθεί. Η ISO [12] προτείνει την χρήση της ψευδοτυχαίας ακολουθίας μεγίστου μήκους (MLS) και δίνει τις παρακάτω οδηγίες: Η πηγή θα πρέπει να είναι όσο το δυνατόν παντοκατευθηντική και το μικρόφωνο θα πρέπει να είναι και αυτό παντοκατευθυντικό. Πολλαπλές μετρήσεις πρέπει να παίρνονται κ ένας μέσος όρος να υπολογίζεται ώστε να μειώνεται το σφάλμα που προέρχεται από περιβαλλοντικό θόρυβο. Το μικρόφωνο πρέπει να τοποθετείται τουλάχιστον στο 1/4 του μικρότερου μήκους κύματος από την κοντινότερη επιφάνεια ανάκλασης. Η ελάχιστη απόσταση πομπού-δέκτη d θα πρέπει να είναι τουλάχιστον: V d = 2 σε m (2.12) c RT όπου V είναι ο όγκος του δωματίου, c η ταχύτητα του ήχου και RT ο αναμενόμενος χρόνος αντήχησης. Ένα ακόμα χρησιμοποιούμενο σημα διέγερσης ειναι το sinesweep; πολλές φορές έχει αποδειχθεί καταλληλότερο από το σήμα MLS [13, 14].
30 2.5 Sweep σήματα διέγερσης και η χρήση τους στις μετρήσεις ακουστικής απόκρισης 20 Πρώιμες ανακλάσεις και καθυστερημένη αντήχηση Στην ακουστική χώρων η κρουστική συχνά διαχωρίζεται σε τρεις περιοχές, που φαίνονται στο σχήμα 2.7: (i) ο απευθείας ήχος, (ii) οι πρώιμες ανακλάσεις (iii) οι τελικές ανακλάσεις και στο σχήμα 2.8 φαίνεται η Log square αναπαράσταση της κρουστικής. Ο απευθείας ήχος είναι το σήμα στο ελεύθερο πεδίο, π.χ. ήχος που φτάνει χωρίς παραμορφώσεις. Η αρχική καθυστέρηση πριν την εμφάνιση της πρώτης κορυφής στην κρουστική, αναπαριστά την απόσταση πηγής-δέκτη. Μετά τον απευθείας ήχο, φτάνουν οι πρώιμες ανακλάσεις. Οι πρώιμες ανακλάσεις θεωρούνται σχετικά αραιές και καλύπτουν μία μικρή χρονική περίοδο. Στην αντίληψη μας για τον ήχο, οι πρώιμες ανακλάσεις επηρεάζουν κυρίως την χροιά του ήχου και εκλαμβάνονται σαν χρωματισμός [15, 16]. Το τελευταίο κομμάτι της κρουστικής ονομάζεται καθυστερημένη αντήχηση και δημιουργεί την αντηχούσα ουρά του σήματος [17, 16]. Η καθυστερημένη αντήχηση παρουσιάζεται στο πεδίο της διάχυσης όπου η κρουστική του δωματίου εμφανίζει στοχαστικά χαρακτηριστικά και παράγει μία αλλοίωση που θεωρείται θόρυβος[18]. Συνήθως, η καθυστερημένη αντήχηση είναι ανεπιθύμητη για την μετάδοση ομιλίας αφού ελαττώνει την καταληπτότητα και μειώνει την αποδοτικότητα των συστημάτων αυτόματης αναγνώρισης ομιλίας. Επιπροσθέτως, οι καθυστερημένη αντήχηση συμβάλει στην αντίληψη του χώρου και δημιουργεί μία αίσθηση συνέχειας του ήχου[19]. Στην ακουστική των μικρών δωματίων όπου ο δέκτης είναι κοντά στις ανακλώσες επιφάνειες οι πρώιμες ανακλάσεις είναι οι κυρίαρχες, ενώ η καθυστερημένη αντήχηση κυριαρχεί στα μεγάλα δωμάτια. 2.5 Sweep σήματα διέγερσης και η χρήση τους στις μετρήσεις ακουστικής απόκρισης Μια από τις νεότερες και πιο ακριβείς μεθόδους μέτρησης είναι αυτή με την χρήση sweep ημιτονοειδών σημάτων ως σήματα διέγερσης. Τα sweep σήματα παρουσιάζουν μια διττή υπόσταση, εμφανίζοντας μοναδικές ιδιότητες τόσο στο πεδίο του χρόνου, όσο και στο πεδίο της συχνότητας. Οι μετρήσεις με χρήση sweep σημάτων διέγερσης ανήκουν σε μια ευρύτερη κατηγορία μετρήσεων.
31 2.5 Sweep σήματα διέγερσης και η χρήση τους στις μετρήσεις ακουστικής απόκρισης 21 Direct Sound Late reverberation Early Reflections Σχήμα 2.7: Τα διαφορετικά μέρη της κρουστικής απόκρισης δωματίου
32 2.5 Sweep σήματα διέγερσης και η χρήση τους στις μετρήσεις ακουστικής απόκρισης Amplitude (db) Time (s) Σχήμα 2.8: Log square αναπαράσταση της κρουστικής του δωματίου Σύμφωνα με αυτή, οποιοδήποτε ακουστικό σήμα (θόρυβος, μουσική κτλ.) μπορεί να χρησιμοποιηθεί ως σήμα διέγερσης. Παρόλα αυτά, τα sweep σήματα επικράτησαν για πολλούς λόγους με σημαντικότερους, αυτούς της φασματικής κατανομής τους, της εύκολης αντιστροφής, της συμπεριφοράς τους ως προς τις αρμονικές παραμορφώσεις και του χαμηλού λόγου μέγιστης προς RMS τιμής (crest factor) που παρουσιάζουν. Η μέθοδος μέτρησης με χρήση sweep σημάτων διέγερσης παρουσιάζει αρκετά πλεονεκτήματα. Το φάσμα ενός μη περιοδικού sweep σήματος είναι σχεδόν όμοιο με αυτό του μέσου όρου του περιοδικά επαναλαμβανόμενου ίδιου σήματος. Αυτό σημαίνει ότι δεν είναι απαραίτητη η επανάληψη της μέτρησης για την συγκρότηση του επιθυμητού φάσματος της απόκρισης, σε αντίθεση με μεθόδους που στηρίζονται στη χρήση σημάτων διέγερσης λευκού ή τυχαίου φάσματος. Το σήμα διέγερσης μπορεί λοιπόν να αναπαραχθεί μόνο μια φορά και στη συνέχεια να γίνει η επεξεργασία της απόκρισης, μειώνοντας έτσι τον απαιτούμενο χρόνο μέτρησης στο μισό και επιτυγχάνοντας την ίδια σχεδόν φασματική ανάλυση και λόγο σήματος προς θόρυβο.
33 2.6 Το κριτήριο των Dietsch & Kraak Το κριτήριο των Dietsch & Kraak Ανάγκη για ένα αντικειμενικό κριτήριο Πολλοί θα αναρωτιούνται σε τί χρησιμεύει ένα αντικειμενικό κριτήριο για την ηχώ (echo). Από ερευνητικής άποψης η ηχώ ορίζεται ως επανάληψη ενός ηχητικού σήματος η οποία γίνεται αντιληπτή. Το μέτρο της ενόχλησης αλλάζει από άτομο σε άτομο, όπως καθετί που είναι υποκειμενικό. Επιπροσθέτως η ακουστική σχετίζεται και με τη θέση στο χώρο. Έτσι, για τη συστηματική μελέτη των ακουστικών παραμέτρων ενός χώρου χρειαζόμαστε κάποια αντικειμενικά κριτήρια. Αυτό είναι σημαντικό ώστε τα λάθη στην ακουστική του χώρου να μπορούν να προβλεφθούν στη φάση του σχεδιασμού. Χοντρικά, η ηχώ γίνεται αντιληπτή ως διακριτή, από μία ανάκλαση η οποία φτάνει στον δέκτη τουλάχιστον 50ms μετά τον απευθείας ήχο. Για λεπτομερέστερη μελέτη όμως χρειαζόμαστε κι άλλες παραμέτρους. Αυτές είναι: - Καθυστέρηση της ανάκλασης - Διαφορά στάθμης της ηχητικής πίεσης - Η δομή του ηχητικού σήματος - Το συχνοτικό περιεχόμενο του σήματος - Οι ενδιάμεσες κρυμμένες ανακλάσεις ανάμεσα στο απευθείας σήμα μας και την ανάκλαση που εξετάζουμε. Κάτω από ένα ελάχιστο χρονικό όριο, η ηχώ θα γίνεται ενοχλητική. Το όριο είναι 50ms για την ομιλία και 80ms για την μουσική.[20] Θεωρητικό υπόβαθρο Το 1986, οι Dietsch και Kraak[1] πρότειναν ένα αντικειμενικό κριτήριο για τον προσδιορισμό ενοχλητικών ανακλάσεων σε έναν ακουστικό χώρο. Για τον προσδιορισμό των διαφόρων παραμέτρων διεξήγαγαν υποκειμενικά πειράματα. Δημιούργησαν έναν συνθετικό ακουστικό χώρο σε ανηχωικό δωμάτιο και σε αυτόν αναπαρήγαγαν ηχητικά δείγματα μουσικής και ομιλίας. Μουσικά κομμάτια ρυθμικά αργά και ρυθμικά γρήγορα, όπως και ένα απόσπασμα ομιλίας (άνδρας σε 6,5 συλλαβές/ δευτερόλεπτο). Τα βασικά τους συμπεράσματα ήταν ότι κάτω από ένα χρονικό όριο, απευθείας προς ανακλώμενο ήχο, είναι αδύνατον κάποια ανάκλαση να εκληφθεί ως ενοχλητική. Αν ξεπεραστεί αυτό το
34 2.6 Το κριτήριο των Dietsch & Kraak 24 χρονικό όριο, το απαραίτητο πλάτος της ανάκλασης που θα εκληφθεί ως ενοχλητική, μειώνεται όσο αυξάνεται ο χρόνος. Αυτό σημαίνει ότι τα δύο φυσικά μεγέθη είναι αντιστρόφως ανάλογα. Το συμπέρασμα αυτό εκφράζεται μαθηματικά με την ισότητα p V n t V = const. (2.13) όπου ο εκθέτης n πρέπει να καθοριστεί. Μέχρι τότε το μόνο γνωστό αντικειμενικό κριτήριο για την ακουστική χώρων, που συνδύαζε τα δύο φυσικά μεγέθη (πλάτος και χρόνος άφιξης) ήταν το χρονικό κέντρο βάρους t s το οποίο πρότειναν οι Kürer και Cremer : t s = 0 0 t f(t) dt f(t) dt (2.14) σαν f(t) προτάθηκε από τον Kürer η p 2 (t). Έτσι, τελικά παίρνουμε τον ορισμό: t s = t p(t) n dt 0 0 p(t) n dt (2.15) Για να εξαχθεί το t s για κάποια συγκεκριμένη ανάκλαση αρκεί να αλλάξει το άνω όριο ολοκλήρωσης και να μπει στη θέση του μία μεταβλητή. Έτσι λαμβάνουμε την Συνάρτηση Δόμησης του Χρονικού Κέντρου Βάρους: t s (τ) = τ t p(t) n dt 0 τ p(t) n dt 0 (2.16) Για την κατανόηση μιας τέτοιας απεικόνισης στην ανάλυση, τα σχήματα 2.9 και 2.10 είναι βασικά.
35 2.6 Το κριτήριο των Dietsch & Kraak 25 Σχήμα 2.9: Συμπεριφορά του t S σε μία ισχυρή ανάκλαση. Σχήμα 2.10: Συμπεριφορά του t S σε πολλαπλές ανακλάσεις μικρού σχετικά πλάτους (ομάδα ανακλάσεων).
36 2.6 Το κριτήριο των Dietsch & Kraak 26 Η απεικόνιση του κριτηρίου για χρονική διάρκεια τ τελικά δίνεται από τον τύπο: EK(τ) = t S(τ) τ E (2.17) Τέλος, θα πρέπει τα μέγιστα της καμπύλης αυτής ( t s ) να συγκριθούν με κάποια κρίσιμα όρια για την ηχώ. τ Με την πειραματική διαδικασία στον συνθετικό ακουστικό χώρο υπολογιστήκαν όλες οι απαραίτητες παράμετροι για την αριθμητική υλοποίηση και εφαρμογή του κριτηρίου. Οι τιμές του συντελεστή n, για μουσική n = 1 και για ομιλία n = 2/3. Οι τιμές τ E, για μουσική τ E = 14ms και για ομιλία τ E = 9ms. Το κριτήριο ισχύει επίσης και για επαναλαμβανόμενες ανακλάσεις (φαινόμενο flutter echo). Τα ελάχιστα χρονικά διαστήματα που πρέπει να απέχουν δύο ανακλάσεις για να είναι αντιληπτές ως ξεχωριστές υπολογίστηκαν, t min = 80ms για τη μουσική και t min = 50ms για την ομιλία. Τέλος, υπολογίστηκαν οι τιμές των ορίων, οι οποίες φαίνονται στον πίνακα 2.1. Τα όρια έχουν τη μορφή EK grn όπου το N% είναι το ποσοστό των ακροατών που θα εκλάβουν την ανάκλαση ως ενοχλητική. Εφαρμογή σε πραγματικό χώρο έγινε στις αίθουσες του Deutsche Theater Berlin και της Kammerspielen Berlin όπου είχαν εκφραστεί παράπονα για ενοχλητική ηχώ κατά την ομιλία. Δείγματα από τις κρουστικές αποκρίσεις σε συγκεκριμένες θέσεις στους δύο χώρους παρουσιάζονται στα σχήματα 2.11 και 2.12 ως παράδειγμα. Στο σχήμα2.11a διακρίνεται μία δυνατή σχετικά ανάκλαση στα 80ms (> t Emin = 50ms). Αυτή όπως φαίνεται στο b προκαλεί μια υπέρβαση του ορίου για EK 10% και για EK 50%. Στο σχήμα 2.12a υπάρχει μία περιοχή στα 50 55ms, με ανακλάσεις οι οποίες μόλις που ενοχλούν το 10% του ακροατηρίου, στην περιοχή γύρω στα 100ms υπάρχουν οι πιο δυνατές ανακλάσεις, οι οποίες απέχουν περίπου 50ms από τις προηγούμενες και θα ακουστούν σαν ξεχωριστές. Μουσική Ομιλία EK 10% 1,5 0,9 EK 50% 1,8 1,0 Πίνακας 2.1: Τα όρια που προκύπτουν για το κριτήριο
37 2.6 Το κριτήριο των Dietsch & Kraak 27 Σχήμα 2.11: Εφαρμογή του κριτηρίου για την ομιλία στο Deutschen Theater Berlin: a) Κρουστική του χώρου, b) Ανάπτυξη του κριτηρίου EK(τ).( )EK 50%, ( - ) EK 10%. Σχήμα 2.12: Εφαρμογή του κριτηρίου για την ομιλία στο Kammerspielen Berlin: a) Κρουστική του χώρου, b) Ανάπτυξη του κριτηρίου EK(τ).( )EK 50%, ( - ) EK 10%.
38 2.6 Το κριτήριο των Dietsch & Kraak 28
39 Κεφάλαιο 3 Υλοποίηση 3.1 Μετρήσεις στην κεντρική αίθουσα του ΣΠΚ Θέσεις μετρήσεων Οι κρουστικές αποκρίσεις μετρήθηκαν στις θέσεις της αίθουσας που έχουν χρησιμοποιηθεί και κατά την προσομοίωση της ακουστικής της αίθουσας με το λογισμικό CATT Acoustic, ώστε να υπάρχει συμβατότητα και να είναι δυνατή η σύγκριση αυτών. Οι θέσεις φαίνονται στο Σχήμα 3.1. Για κάθε θέση πάρθηκαν μετρήσεις για τρεις διαφορετικές γωνίες στο επίπεδο Χ/Υ. Για 0 o (κεφάλι ευθεία μπροστά),για 45 o (κεφάλι στραμμένο αριστερά) και +45 o (κεφάλι στραμμένο δεξιά) όπως και μετρήσεις με παντοκατευθυντικό μικρόφωνο Μετρητική διάταξη Ο χώρος που αποτελεί το προς μελέτη σύστημα, διεγέρθηκε με ένα σήμα στο ηχείο και καταγράφηκε η έξοδος του συστήματος με ένα μικρόφωνο. Η διέγερση είναι ένα λογαριθμικό sine-sweep και η καταγραφή γίνεται με την κούκλα KEMAR και αμφιωτική διάταξη μικροφώνων και ένα παντοκατευθυντικό μικρόφωνο. Ο ηλεκτρονικός υπολογιστής και η κάρτα ήχου είναι ο βοηθητικός εξοπλισμός που χρησιμοποιείται για τη συγχρονισμένη αναπαραγωγή και καταγραφή των παραπάνω σημάτων. Η σχηματική αναπαράσταση της διάταξης φαίνεται στο σχήμα 3.2. Στον Πίνακα 3.1
40 3.1 Μετρήσεις στην κεντρική αίθουσα του ΣΠΚ 30 Σχήμα 3.1: Οι ακριβείς θέσεις των μετρήσεων.
41 3.1 Μετρήσεις στην κεντρική αίθουσα του ΣΠΚ 31 Σήμα εισόδου Logarithmic Sine Sweep Κάρτα ήχου Presonus Firepod Υπολογιστής MacBook Pro Ηχείο ATC SCM20-2 Active Monitor Μικρόφωνα GRASS Kemar Dummy Head Μικρόφωνο DPA 4052 (με προσαρμογή της true OMNI nose) Λογισμικό FuzzMeasure v.3 Πίνακας 3.1: Κατάλογος εξοπλισμού. παρουσιάζεται ο αναλυτικός κατάλογος του εξοπλισμού. Σχήμα 3.2: Η Διάταξη που χρησιμοποιήθηκε για τις μετρήσεις. Το ηχείο, η πηγή του σήματος. Η αίθουσα, αντιπροσωπεύει το προς μελέτη σύστημα και η κούκλα KEMAR, καταγράφει την έξοδο του συστήματος. Ο υπολογιστής με την κάρτα ήχου, είναι βοηθητικός εξοπλισμός για την αναπαραγωγή, την καταγραφή και επεξεργασία των σημάτων.
42 3.1 Μετρήσεις στην κεντρική αίθουσα του ΣΠΚ Διαδικασία μέτρησης Το ηχείο τοποθετείται στο κέντρο της σκηνής σε απόσταση 1.7m από το δάπεδο, στραμμένο προς το κοινό. Αρχικά γίνεται αναπαραγωγή λευκού θορύβου και ρυθμίζεται η στάθμη εξόδου του ηχείου στα 95dB στο 1m, στάθμη αρκετή για να διεγείρει ηχητικά τον χώρο. Η στάθμη μετράται με ηχόμετρο. Η κούκλα KEMAR τοποθετείται στην πρώτη θέση που θα πραγματοποιηθεί η μέτρηση της κρουστικής απόκρισης και ρυθμίζεται η στάθμη των μικροφώνων ώστε το σήμα να είναι αρκετά δυνατό για την ηχογράφηση 1. Η στάθμη εισόδου ορίζεται με τη βοήθεια του λογισμικού Fuzzmeasure (Σχήμα 3.3) και ρυθμίζοντας το Gain στους προενισχυτές των μικροφώνων στην κάρτα ήχου. Πίσω στο λογισμικό πάλι, θέτουμε τα διάφορα χαρακτηριστικά του σήματος διέγερσης που θα στείλουμε στο ηχείο για να πάρουμε την κρουστική απόκριση. Στην περίπτωση μας, όπως ήδη έχει αναφερθεί, έχουμε ένα logarithmic sine-sweep διάρκειας 5sec. Τέλος η συχνότητα δειγματοληψίας για το σήμα εισόδου ρυθμίζεται στα 44.1kHz. Σε κάθε θέση παίρνουμε συνολικά τέσσερις μετρήσεις, όπως προαναφέρθηκε, για τρεις διαφορετικές γωνίες και μία παντοκατευθυντική, απλά πατώντας το κουμπάκι measure στην διεπαφή χρήστη του προγράμματος. Το Fuzzmeasure επίσης μας παρέχει τη δυνατότητα για μία γρήγορη επίβλεψη της μέτρησης, δίνοντάς μας την κρουστική και το διάγραμμα απόκρισης συχνότητας του χώρου. 2 1 γνωρίζουμε ότι όσο πιο δυνατό είναι το σήμα τόσο καλύτερος είναι ο SNR, παράλληλα προσέχουμε το σήμα μας να μην είναι υπερβολικά δυνατό γιατί θα έχουμε ψαλιδισμό (clipping) και παραμόρφωση του σήματος. 2 Ας σημειωθεί ότι το λογισμικό Fuzzmasure δεν είναι το μοναδικό που μπορεί να χρησιμοποιηθεί για τέτοιου είδους μετρήσεις. Ένα πιο επαγγελματικό λογισμικό που παρέχει εκτός των άλλων αρκετά διαφορετικά σήματα διέγερσης (όπως πχ MLS ακολουθίες) και τρέχει σε πλατφόρμα Windows είναι το WinMLS. Τέλος το REW είναι ένα ελεύθερο λογισμικό για τη διεξαγωγή μετρήσεων πάλι για την πλατφόρμα των Windows.
43 3.1 Μετρήσεις στην κεντρική αίθουσα του ΣΠΚ 33 Σχήμα 3.3: Το πολύ απλό περιβάλλον του λογισμικού Fuzzmeasure, που χρησιμοποιήθηκε για τη διεξαγωγή των μετρήσεων. Οι ρυθμίσεις του σήματος εξόδου, οι ρυθμίσεις εισόδου και τέλος οι μετρητές στάθμης. Σχήμα 3.4: Το περιβάλλον του λογισμικού Fuzzmeasure μετά τη διεξαγωγή των μετρήσεων.
44 3.1 Μετρήσεις στην κεντρική αίθουσα του ΣΠΚ 34
45 Κεφάλαιο 4 Υλοποίηση του κριτηρίου Dietsch & Kraak 4.1 Περιγραφή του αλγορίθμου Στο πλαίσιο της διπλωματικής εργασίας υλοποιήθηκε στο περιβάλλον Matlab αλγόριθμος, ο οποίος υπολογίζει την καμπύλη του κριτηρίου των Dietsch & Kraak. Είσοδος του αλγορίθμου είναι η κρουστική απόκριση του χώρου σε μορφή.wav. Έξοδος είναι τα διαγράμματα με τις απεικονίσεις των καμπυλών για μουσική και ομιλία. Ο πλήρης κώδικας παρουσιάζεται στο Παράρτημα Α. Αρχικά στον αλγόριθμο καθορίζονται διάφορες παράμετροι και σταθερές που θα χρειαστούν για την επεξεργασία των δεδομένων. Η διάρκεια της κρουστικής περιορίζεται στα 250ms (11025 δείγματα με συχνότητα δειγματοληψίας 44100Hz). Τα αρχεία με τις κρουστικές, κανονικοποιημένες στα 0dB, πρέπει να είναι στον ίδιο φάκελο με τον κώδικα. Όλα τα αρχεία διαβάζονται και υφίστανται επεξεργασία με επαναληπτική διαδικασία. Τα διάφορα μέρη του μαθηματικού τύπου 2.17 υπολογίζονται σταδιακά. Ο αριθμητής απαιτεί τον υπολογισμό της σχέσης Δύο διανύσματα κρατάνε τις τιμές p(t) n t και p(t) n για κάθε t, αντίστοιχα για τον αριθμητή και τον παρονομαστή. Οι επόμενοι πίνακες ολοκληρώνουν τ τ από 0 μέχρι τ ώστε να δημιουργηθούν τα p(t) n t dt και p(t) n dt. Έχουμε πλέον το t S (τ) διαιρώντας ένα προς ένα τα στοιχεία των δύο τελευταίων διανυσμάτων. Όμοια λειτουργεί και ο κώδικας που υπολογίζει τις τιμές του κριτηρίου για την ομιλία. Ο κώδικας απεικόνισης των αποτελεσμάτων και αποθήκευσης παρουσιά- 0 0
46 4.1 Περιγραφή του αλγορίθμου 36 ζεται παρακάτω. Το διάγραμμα ροής του κώδικα παρουσιάζεται στο σχήμα Διαγράμματα Τα διαγράμματα απεικόνισης εξάγονται με κώδικα υλοποιημένο στο περιβάλλον Matlab. Σε κάθε διάγραμμα παρουσιάζεται η κρουστική απόκριση για κάθε διαφορετική θέση δέκτη (η θέση της πηγής είναι σταθερή). Από την κρουστική έχει αφαιρεθεί η αρχική καθυστέρηση της μέτρησης. Πάνω από την κρουστική παρουσιάζονται τα διαγράμματα του κριτηρίου για μουσική και ομιλία και τα όρια EK 10% και EK 50% για μουσική και ομιλία όπως παρουσιάστηκαν στον πίνακα 2.1. Ο συνολικός κώδικας φαίνεται στο Παράρτημα Α.
47 4.1 Περιγραφή του αλγορίθμου 37 Σχήμα 4.1: Το Flowchart του υλοποιημένου αλγορίθμου
48 4.1 Περιγραφή του αλγορίθμου 38
49 Κεφάλαιο 5 Αποτελέσματα Για τις θέσεις στις οποίες εξετάζουμε την ακουστική συμπεριφορά του χώρου, εξετάζουμε τις κρουστικές που μετρήσαμε σε σχέση με αυτές που υπολογίζει το λογισμικό CATT. Τα αποτελέσματα του κριτηρίου για τις θέσεις αντιπαραβάλλονται παρακάτω. Σχήμα 5.1: Οι θέσεις των δεκτών στο μοντέλο μας
50 5.1 Σύγκριση Μετρήσεων - Προσομοιώσεων Σύγκριση Μετρήσεων - Προσομοιώσεων Σχήμα 5.2: Το διάγραμμα του CATT για το κριτήριο στη θέση FOH Plot for position FOH CATT 1.4 EK 10% Music D & K OMNI IR EK 50% Speech EK 10% Speech D&K for Music D&K for Speech IR time (s) Σχήμα 5.3: Εξομοίωση FOH
51 5.1 Σύγκριση Μετρήσεων - Προσομοιώσεων 41 Plot for position FOH Measurement 1.4 EK 10% Music D & K OMNI IR EK 50% Speech EK 10% Speech D&K for Music D&K for Speech IR time (s) Σχήμα 5.4: Μέτρηση FOH Θέση Κονσόλας (FOH) Στη θέση της κονσόλας, στο κέντρο της πλατείας, παρατηρείται οριακή προσέγγιση στο όριο EK 10% speech από την κρουστική που προέκυψε από την εξομοίωση στο λογισμικό CATT - Acoustic. Η αντίστοιχη μέτρηση δεν δείχνει κάποιο πρόβλημα. Στα 50ms μετά την άφιξη του απευθείας ήχου, συμβαίνει υπέρβαση του κατώτατου ορίου του κριτηρίου. Επειδή ο χρόνος άφιξης της ανάκλασης είναι πολύ μικρός (μικρότερος από το όριο 80ms), η ανάκλαση δεν θα είναι ενοχλητική. Παρατηρείται επίσης ότι η εξομοίωση έχει συγκεντρωμένη περισσότερη ενέργεια στις διακριτές ανακλάσεις σε σχέση με την μέτρηση. Θέση Δ16 Για τη θέση Δ16, μπροστά από τη σκηνή, παρατηρείται ότι η ισχυρή ανάκλαση στα 40ms προκαλεί έντονη αύξηση στην καμπύλη πρόβλεψης του κριτηρίου. Στην πραγματικότητα δεν υπάρχει πρόβλημα σε αυτή τη θέση, όπως δείχνει και η μέτρηση, αφού η ανάκλαση αυτή έρχεται πολύ νωρίς. Στο λογισμικό προσομοίωσης δίνεται η δυνατότητα να εντοπιστεί η επιφάνεια από όπου προέρχεται η ανάκλαση. Αυτή φαίνεται να είναι η μετόπη
52 5.1 Σύγκριση Μετρήσεων - Προσομοιώσεων 42 Σχήμα 5.5: Το διάγραμμα του CATT για το κριτήριο στη θέση D16 Plot for position D16 CATT 1.4 EK 10% Music D & K OMNI IR EK 50% Speech EK 10% Speech D&K for Music D&K for Speech IR time (s) Σχήμα 5.6: Εξομοίωση D16 πάνω από τη σκηνή. Θέση Ζ7 Στη Θέση Ζ7 υπάρχουν ισχυρές ανακλάσεις από τις πλευρικές επιφάνειες των τοίχων. Ωστόσο αυτές δεν δημιουργούν πρόβλημα
53 5.1 Σύγκριση Μετρήσεων - Προσομοιώσεων 43 Plot for position D16 Measurenet 1.4 EK 10% Music D & K OMNI IR EK 50% Speech EK 10% Speech D&K for Music D&K for Speech IR time (s) Σχήμα 5.7: Μέτρηση D16 Σχήμα 5.8: Το διάγραμμα του CATT για το κριτήριο στη θέση Z7 αφού έρχονται κατά ομάδες και έτσι εξομαλύνεται η εντύπωση της ισχυρής διακριτής ανάκλασης που θα προκαλέσει ενόχληση. Θέση Ι16 Η θέση Ι16 κοντά στο κέντρο της αίθουσας δεν παρουσιάζει
54 5.1 Σύγκριση Μετρήσεων - Προσομοιώσεων 44 Plot for position Z7 CATT 1.4 EK 10% Music D & K OMNI IR EK 50% Speech EK 10% Speech D&K for Music D&K for Speech IR time (s) Σχήμα 5.9: Εξομοίωση Z7 Plot for position Z7 Measurement 1.4 EK 10% Music D & K OMNI IR EK 50% Speech EK 10% Speech D&K for Music D&K for Speech IR time (s) Σχήμα 5.10: Μέτρηση Z7
55 5.1 Σύγκριση Μετρήσεων - Προσομοιώσεων 45 Σχήμα 5.11: Το διάγραμμα του CATT για το κριτήριο στη θέση I16 Plot for position I16 CATT 1.4 EK 10% Music D & K OMNI IR EK 50% Speech EK 10% Speech D&K for Music D&K for Speech IR time (s) Σχήμα 5.12: Εξομοίωση I16 κάποιο ιδιαίτερο πρόβλημα. Η προσομοίωση είναι πολύ κοντά στη μέτρηση. Θέση Ν17 Η θέση Ν17 βρίσκεται πάνω από το μεσαίο διάζωμα στο κέντρο
56 5.1 Σύγκριση Μετρήσεων - Προσομοιώσεων 46 Plot for position I16 Measurement 1.4 EK 10% Music D & K OMNI IR EK 50% Speech EK 10% Speech D&K for Music D&K for Speech IR time (s) Σχήμα 5.13: Μέτρηση I16 Σχήμα 5.14: Το διάγραμμα του CATT για το κριτήριο στη θέση N17 και οι ισχυρές ανακλάσεις προέρχονται από τα επίπεδα του εξώστη που βρίσκονται σχετικά κοντά σε αυτή. Παρά το ότι η προσομοίωση δείχνει κάποια υπέρβαση του ορίου για την ομιλία, η μέτρηση δεν παρουσιάζει κάποιο πρόβλημα.
57 5.1 Σύγκριση Μετρήσεων - Προσομοιώσεων 47 Plot for position N17 CATT 1.4 EK 10% Music D & K OMNI IR EK 50% Speech EK 10% Speech D&K for Music D&K for Speech IR time (s) Σχήμα 5.15: Εξομοίωση N17 Plot for position N17 Measurement 1.4 EK 10% Music D & K OMNI IR EK 50% Speech EK 10% Speech D&K for Music D&K for Speech IR time (s) Σχήμα 5.16: Μέτρηση N17
58 5.1 Σύγκριση Μετρήσεων - Προσομοιώσεων 48 Σχήμα 5.17: Το διάγραμμα του CATT για το κριτήριο στη θέση P6 Plot for position P6 CATT 1.4 EK 10% Music D & K OMNI IR EK 50% Speech EK 10% Speech D&K for Music D&K for Speech IR time (s) Σχήμα 5.18: Εξομοίωση P6 Θέση Ρ6 Η θέση Ρ6 βρίσκεται κάτω από τον εξώστη και κοντά στους πλαϊνούς τοίχους. Παρά τις πολλαπλές και αρκετά ισχυρές ανακλάσεις που φτάνουν στη θέση, παρατηρείται ότι το κριτήριο δεν αναδεικνύει κάποιο πρόβλημα. Αυτό δικαιολογείται επειδή
59 5.1 Σύγκριση Μετρήσεων - Προσομοιώσεων 49 Plot for position P6 Measurement 1.4 EK 10% Music D & K OMNI IR EK 50% Speech EK 10% Speech D&K for Music D&K for Speech IR time (s) Σχήμα 5.19: Μέτρηση P6 οι πολλές κοντινές χρονικά ανακλάσεις παρόμοιου πλάτους δεν δημιουργούν ενοχλητική εντύπωση στον ακροατή. Σχήμα 5.20: Το διάγραμμα του CATT για το κριτήριο στη θέση Φ10 Θέση Φ10 Η θέση Φ10 βρίσκεται στην τελευταία σειρά κάτω από τον
Ακουστική Κλειστών Χώρων
 Ακουστική Κλειστών Χώρων Παναγιώτης Χατζηαντωνίου Καθηγητής Δ.Ε. Πληροφορικός PhD Ψηφιακής Τεχνολογίας Ήχου Τοπικό Θεµατικό Δίκτυο Περιβαλλοντικής Εκπαίδευσης Ν. Αχαΐας «Ακουστική και Ιστορική Ξενάγηση
Ακουστική Κλειστών Χώρων Παναγιώτης Χατζηαντωνίου Καθηγητής Δ.Ε. Πληροφορικός PhD Ψηφιακής Τεχνολογίας Ήχου Τοπικό Θεµατικό Δίκτυο Περιβαλλοντικής Εκπαίδευσης Ν. Αχαΐας «Ακουστική και Ιστορική Ξενάγηση
ΚΥΜΑ ΗΧΟΣ ΙΑΘΛΑΣΗ ΠΕΡΙΘΛΑΣΗ ΑΝΑΚΛΑΣΗ ΣΥΜΒΟΛΗ
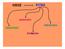 ΗΧΟΣ ΚΥΜΑ ΙΑΘΛΑΣΗ ΑΝΑΚΛΑΣΗ ΠΕΡΙΘΛΑΣΗ ΣΥΜΒΟΛΗ Έχουμε ανάκλαση κάθε φορά που ένα κύμα το οποίο διαδίδεται σε υλικό μέσο συναντά άλλο μέσο που έχει διαφορετική πυκνότητα απότοπρώτο. Εισερχόμενος παλμός ιερχόμενος
ΗΧΟΣ ΚΥΜΑ ΙΑΘΛΑΣΗ ΑΝΑΚΛΑΣΗ ΠΕΡΙΘΛΑΣΗ ΣΥΜΒΟΛΗ Έχουμε ανάκλαση κάθε φορά που ένα κύμα το οποίο διαδίδεται σε υλικό μέσο συναντά άλλο μέσο που έχει διαφορετική πυκνότητα απότοπρώτο. Εισερχόμενος παλμός ιερχόμενος
ΚΥΜΑ ΗΧΟΣ ΔΙΑΘΛΑΣΗ ΠΕΡΙΘΛΑΣΗ ΑΝΑΚΛΑΣΗ ΣΥΜΒΟΛΗ
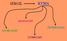 ΗΧΟΣ ΚΥΜΑ ΔΙΑΘΛΑΣΗ ΑΝΑΚΛΑΣΗ ΠΕΡΙΘΛΑΣΗ ΣΥΜΒΟΛΗ Ανάκλαση Απορρόφηση Διάθλαση Θ εξ Θ εισ Διέλευση Λεία επιφάνεια ; Ανωμαλίες επιφάνειας < λ Όταν ακούμε μια συναυλία σε ένα ανοιχτό χώρο το ηχητικό πεδίο που
ΗΧΟΣ ΚΥΜΑ ΔΙΑΘΛΑΣΗ ΑΝΑΚΛΑΣΗ ΠΕΡΙΘΛΑΣΗ ΣΥΜΒΟΛΗ Ανάκλαση Απορρόφηση Διάθλαση Θ εξ Θ εισ Διέλευση Λεία επιφάνεια ; Ανωμαλίες επιφάνειας < λ Όταν ακούμε μια συναυλία σε ένα ανοιχτό χώρο το ηχητικό πεδίο που
ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΗΧΗΤΙΚΕΣ ΕΓΚΑΤΑΣΤΑΣΕΙΣ
 ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΗΧΗΤΙΚΕΣ ΕΓΚΑΤΑΣΤΑΣΕΙΣ ΑΚΟΥΣΤΙΚΗ ΚΑΛΥΨΗ ΓΙΑΝΝΗΣ ΜΟΥΡΤΖΟΠΟΥΛΟΣ ΚΑΘΗΓΗΤΗΣ ΟΜΑΔΑ ΤΕΧΝΟΛΟΓΙΑΣ ΗΧΟΥ & ΑΚΟΥΣΤΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΕΝΣΥΡΜΑΤΗΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ
ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΗΧΗΤΙΚΕΣ ΕΓΚΑΤΑΣΤΑΣΕΙΣ ΑΚΟΥΣΤΙΚΗ ΚΑΛΥΨΗ ΓΙΑΝΝΗΣ ΜΟΥΡΤΖΟΠΟΥΛΟΣ ΚΑΘΗΓΗΤΗΣ ΟΜΑΔΑ ΤΕΧΝΟΛΟΓΙΑΣ ΗΧΟΥ & ΑΚΟΥΣΤΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΕΝΣΥΡΜΑΤΗΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ
ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ 9. ΗΧΗΤΙΚΕΣ ΕΓΚΑΤΑΣΤΑΣΕΙΣ ΑΚΟΥΣΤΙΚΗ ΚΑΛΥΨΗ ΓΙΑΝΝΗΣ ΜΟΥΡΤΖΟΠΟΥΛΟΣ ΚΑΘΗΓΗΤΗΣ
 ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ 9. ΗΧΗΤΙΚΕΣ ΕΓΚΑΤΑΣΤΑΣΕΙΣ ΑΚΟΥΣΤΙΚΗ ΚΑΛΥΨΗ ΓΙΑΝΝΗΣ ΜΟΥΡΤΖΟΠΟΥΛΟΣ ΚΑΘΗΓΗΤΗΣ ΟΜΑΔΑ ΤΕΧΝΟΛΟΓΙΑΣ ΗΧΟΥ & ΑΚΟΥΣΤΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΕΝΣΥΡΜΑΤΗΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ
ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ 9. ΗΧΗΤΙΚΕΣ ΕΓΚΑΤΑΣΤΑΣΕΙΣ ΑΚΟΥΣΤΙΚΗ ΚΑΛΥΨΗ ΓΙΑΝΝΗΣ ΜΟΥΡΤΖΟΠΟΥΛΟΣ ΚΑΘΗΓΗΤΗΣ ΟΜΑΔΑ ΤΕΧΝΟΛΟΓΙΑΣ ΗΧΟΥ & ΑΚΟΥΣΤΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΕΝΣΥΡΜΑΤΗΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ
28/4/2015. Papadakis Nikos 1. Ακουστική Μεγάλων Χώρων. Ακουστική Μικρών Κλειστών Χώρων. Ακουστική Συναυλιακών Χώρων και Επίδραση στην Ακοή
 Βασικές έννοιες Ακουστική Η ακουστική (acoustics) είναι ο κλάδος της φυσικής που μελετά τις ιδιότητες και τη συμπεριφορά του ήχου. Κλάδοι Ακουστικής: Ακουστική Συναυλιακών Χώρων και Επίδραση στην Ακοή
Βασικές έννοιες Ακουστική Η ακουστική (acoustics) είναι ο κλάδος της φυσικής που μελετά τις ιδιότητες και τη συμπεριφορά του ήχου. Κλάδοι Ακουστικής: Ακουστική Συναυλιακών Χώρων και Επίδραση στην Ακοή
Μέτρηση του χρόνου αντήχησης
 Μέτρηση του χρόνου αντήχησης Ουσιαστικά, αν μετρήσω την κρουστική απόκριση του χώρου, μπορώ να υπολογίσω το χρόνο αντήχησης White noise, sweep, MLS sequence Μέθοδος του μηδενισμού της πηγής Μέθοδος της
Μέτρηση του χρόνου αντήχησης Ουσιαστικά, αν μετρήσω την κρουστική απόκριση του χώρου, μπορώ να υπολογίσω το χρόνο αντήχησης White noise, sweep, MLS sequence Μέθοδος του μηδενισμού της πηγής Μέθοδος της
Δομικά Υλικά Μάθημα ΙΙΙ. Ηχος & Ηχητικά Φαινόμενα
 Δομικά Υλικά Μάθημα ΙΙΙ Ηχος & Ηχητικά Φαινόμενα Ηχος: Μια μηχανική διαταραχή η οποία προκαλείται από μια πηγή και διαδίδεται με ορισμένη ταχύτητα σε ένα ελαστικό μέσο. Μια περιοδική ταλάντωση των μορίων
Δομικά Υλικά Μάθημα ΙΙΙ Ηχος & Ηχητικά Φαινόμενα Ηχος: Μια μηχανική διαταραχή η οποία προκαλείται από μια πηγή και διαδίδεται με ορισμένη ταχύτητα σε ένα ελαστικό μέσο. Μια περιοδική ταλάντωση των μορίων
Εργαστήριο Ηλεκτρoακουστικής Άσκηση 5 - Σελίδα 1 ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΣΚΗΣΗ 5 ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΟΜΟΙΩΣΗ ΤΗΣ ΑΚΟΥΣΤΙΚΗΣ ΣΥΜΠΕΡΙΦΟΡΑΣ ΚΛΕΙΣΤΩΝ ΧΩΡΩΝ
 Εργαστήριο Ηλεκτρoακουστικής Άσκηση 5 - Σελίδα 1 ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΣΚΗΣΗ 5 1. ΕΙΣΑΓΩΓΗ ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΟΜΟΙΩΣΗ ΤΗΣ ΑΚΟΥΣΤΙΚΗΣ ΣΥΜΠΕΡΙΦΟΡΑΣ ΚΛΕΙΣΤΩΝ ΧΩΡΩΝ Όπως είναι γνωστό, η ακριβής προσομοίωση των ακουστικών
Εργαστήριο Ηλεκτρoακουστικής Άσκηση 5 - Σελίδα 1 ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΣΚΗΣΗ 5 1. ΕΙΣΑΓΩΓΗ ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΟΜΟΙΩΣΗ ΤΗΣ ΑΚΟΥΣΤΙΚΗΣ ΣΥΜΠΕΡΙΦΟΡΑΣ ΚΛΕΙΣΤΩΝ ΧΩΡΩΝ Όπως είναι γνωστό, η ακριβής προσομοίωση των ακουστικών
Φλώρος Ανδρέας. Επίκ. Καθηγητής
 Μάθημα: «Ηλεκτροακουστική & Ακουστική Χώρων» Διάλεξη 7 η : «Ακουστική Χώρων» Φλώρος Ανδρέας Επίκ. Καθηγητής Αλυσίδα ηχητικής αναπαραγωγής Ψ/Α Ακροατής Προενισχυτής Ενισχυτής Χώρος Ο χώρος είναι σημαντικό
Μάθημα: «Ηλεκτροακουστική & Ακουστική Χώρων» Διάλεξη 7 η : «Ακουστική Χώρων» Φλώρος Ανδρέας Επίκ. Καθηγητής Αλυσίδα ηχητικής αναπαραγωγής Ψ/Α Ακροατής Προενισχυτής Ενισχυτής Χώρος Ο χώρος είναι σημαντικό
ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΚΟΥΣΤΙΚΕΣ ΣΤΑΘΜΕΣ, ΜΕΤΡΗΣΕΙΣ, ΘΟΡΥΒΟΣ, ΗΧΟΜΟΝΩΣΗ ΓΙΑΝΝΗΣ ΜΟΥΡΤΖΟΠΟΥΛΟΣ ΚΑΘΗΓΗΤΗΣ
 ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΚΟΥΣΤΙΚΕΣ ΣΤΑΘΜΕΣ, ΜΕΤΡΗΣΕΙΣ, ΘΟΡΥΒΟΣ, ΗΧΟΜΟΝΩΣΗ ΓΙΑΝΝΗΣ ΜΟΥΡΤΖΟΠΟΥΛΟΣ ΚΑΘΗΓΗΤΗΣ ΟΜΑΔΑ ΤΕΧΝΟΛΟΓΙΑΣ ΗΧΟΥ & ΑΚΟΥΣΤΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΕΝΣΥΡΜΑΤΗΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ
ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΚΟΥΣΤΙΚΕΣ ΣΤΑΘΜΕΣ, ΜΕΤΡΗΣΕΙΣ, ΘΟΡΥΒΟΣ, ΗΧΟΜΟΝΩΣΗ ΓΙΑΝΝΗΣ ΜΟΥΡΤΖΟΠΟΥΛΟΣ ΚΑΘΗΓΗΤΗΣ ΟΜΑΔΑ ΤΕΧΝΟΛΟΓΙΑΣ ΗΧΟΥ & ΑΚΟΥΣΤΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΕΝΣΥΡΜΑΤΗΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ
Διακριτές ανακλάσεις = συμβολή κυμάτων
 Ανάκλαση Διακριτές ανακλάσεις = συμβολή κυμάτων Διαφορετικές διαδρομές = Χρονική διαφορά άφιξης του ήχου Οι συντεταγμένες (x,y) μιας σημειακής πηγής και ενός σημειακού δέκτη είναι (5,2) m και (3,1) m αντίστοιχα.
Ανάκλαση Διακριτές ανακλάσεις = συμβολή κυμάτων Διαφορετικές διαδρομές = Χρονική διαφορά άφιξης του ήχου Οι συντεταγμένες (x,y) μιας σημειακής πηγής και ενός σημειακού δέκτη είναι (5,2) m και (3,1) m αντίστοιχα.
Στάσιμα κύματα - Μέτρηση της ταχύτητας του ήχου με το σωλήνα Kundt
 Στάσιμα κύματα - Μέτρηση της ταχύτητας του ήχου με το σωλήνα Kundt Η χρησιμοποιούμενη διάταξη φαίνεται στο ακόλουθο σχήμα: Το μεγάφωνο του σωλήνα Kundt συνδέεται στην έξοδο SIGNAL OUT της γεννήτριας συχνοτήτων.
Στάσιμα κύματα - Μέτρηση της ταχύτητας του ήχου με το σωλήνα Kundt Η χρησιμοποιούμενη διάταξη φαίνεται στο ακόλουθο σχήμα: Το μεγάφωνο του σωλήνα Kundt συνδέεται στην έξοδο SIGNAL OUT της γεννήτριας συχνοτήτων.
papost/
 Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
Ακουστική αιθουσών. LESSON_07_2009.doc
 Ακουστική αιθουσών Ορισμός Θεωρούμε ηχητική πηγή που βρίσκεται μέσα σε μια αίθουσα. Τα ηχητικά κύματα διαδίδονται απομακρυνόμενα από την πηγή μέχρις ότου συναντήσουν τα τοιχώματα της αίθουσας, εκεί όπου
Ακουστική αιθουσών Ορισμός Θεωρούμε ηχητική πηγή που βρίσκεται μέσα σε μια αίθουσα. Τα ηχητικά κύματα διαδίδονται απομακρυνόμενα από την πηγή μέχρις ότου συναντήσουν τα τοιχώματα της αίθουσας, εκεί όπου
ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ
 ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ 1. ΕΓΚΑΡΣΙΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ Κύματα κατά μήκος τεντωμένου νήματος Στο τεντωμένο με δύναμη νήμα του Σχήματος 1.1α δημιουργούμε μια εγκάρσια διαταραχή (παράλληλη με τη διεύθυνση
ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ 1. ΕΓΚΑΡΣΙΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ Κύματα κατά μήκος τεντωμένου νήματος Στο τεντωμένο με δύναμη νήμα του Σχήματος 1.1α δημιουργούμε μια εγκάρσια διαταραχή (παράλληλη με τη διεύθυνση
Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα. Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ
 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ Πουλιάσης Αντώνης Φυσικός M.Sc. 2 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Γεωμετρική
Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ Πουλιάσης Αντώνης Φυσικός M.Sc. 2 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Γεωμετρική
κριτήρια αξιολόγησης ΚΕΦΑΛΑΙΟ 5 1o Κριτήριο αξιολόγησης
 1o Κριτήριο αξιολόγησης Θέμα 1ο α Δύο σφαίρες Α και Β συγκρούονται κεντρικά ελαστικά Ποια ή ποιες από τις παρακάτω προτάσεις είναι σωστές και γιατί; Α Η σφαίρα Α θα γυρίσει προς τα πίσω αν είναι m A
1o Κριτήριο αξιολόγησης Θέμα 1ο α Δύο σφαίρες Α και Β συγκρούονται κεντρικά ελαστικά Ποια ή ποιες από τις παρακάτω προτάσεις είναι σωστές και γιατί; Α Η σφαίρα Α θα γυρίσει προς τα πίσω αν είναι m A
1 Ο ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ - ΕΚΦΩΝΗΣΕΙΣ
 Ο ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ - ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις - 4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη συμπληρώνει σωστά
Ο ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ - ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις - 4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη συμπληρώνει σωστά
Ακουστική κλειστών χώρων
 Ακουστική κλειστών χώρων ακουστικά χαρακτηριστικά μιας αίθουσας Πρέπει να ληφθούν υπόψη: Ήσυχο περιβάλλον Επαρκής ένταση ήχου σε κάθε σημείο της αίθουσας Σωστή κατανομή των ήχων Κατάλληλη μίξη-διαχωρισμός
Ακουστική κλειστών χώρων ακουστικά χαρακτηριστικά μιας αίθουσας Πρέπει να ληφθούν υπόψη: Ήσυχο περιβάλλον Επαρκής ένταση ήχου σε κάθε σημείο της αίθουσας Σωστή κατανομή των ήχων Κατάλληλη μίξη-διαχωρισμός
Διάλεξη 4. Η Φυσική της Μουσικής Τ.Ε.Ι. Ιονίων Νήσων. Διάθλαση και Περίθλαση Κυμάτων Κύματα σε Δύο Διαστάσεις Doppler Effect και Shock Waves
 Η Φυσική της Μουσικής Τ.Ε.Ι. Ιονίων Νήσων Διάλεξη 4 Διάθλαση και Περίθλαση Κυμάτων Κύματα σε Δύο Διαστάσεις Doppler Effect και Shock Waves Ανασκόπηση Διάλεξης 3 Αναφερθήκαμε στην Απλή Αρμονική Κίνηση (ΑΑΚ)
Η Φυσική της Μουσικής Τ.Ε.Ι. Ιονίων Νήσων Διάλεξη 4 Διάθλαση και Περίθλαση Κυμάτων Κύματα σε Δύο Διαστάσεις Doppler Effect και Shock Waves Ανασκόπηση Διάλεξης 3 Αναφερθήκαμε στην Απλή Αρμονική Κίνηση (ΑΑΚ)
Φυσική για Μηχανικούς
 Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων. Φυσική για Μηχανικούς Κύματα
Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων. Φυσική για Μηχανικούς Κύματα
ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΑ ΗΧΟΥ εισαγωγή
 ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΑ ΗΧΟΥ εισαγωγή ΓΙΑΝΝΗΣ ΜΟΥΡΤΖΟΠΟΥΛΟΣ ΚΑΘΗΓΗΤΗΣ ΟΜΑΔΑ ΤΕΧΝΟΛΟΓΙΑΣ ΗΧΟΥ & ΑΚΟΥΣΤΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΕΝΣΥΡΜΑΤΗΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ
ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΑ ΗΧΟΥ εισαγωγή ΓΙΑΝΝΗΣ ΜΟΥΡΤΖΟΠΟΥΛΟΣ ΚΑΘΗΓΗΤΗΣ ΟΜΑΔΑ ΤΕΧΝΟΛΟΓΙΑΣ ΗΧΟΥ & ΑΚΟΥΣΤΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΕΝΣΥΡΜΑΤΗΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
ΠΡΟΤΕΙΝΟΜΕΝΟ ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ. ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ και ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΠΡΟΤΕΙΝΟΜΕΝΟ ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ ΜΑΘΗΜΑ: ΤΑΞΗ: ΕΝΟΤΗΤΕΣ: ΕΙΣΗΓΗΤΗΣ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ και ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ (ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ) ΜΙΧΕΛΑΚΑΚΗΣ ΗΛΙΑΣ 1.Διδακτικός στόχοι: Να ορίζουν το στάσιμο
ΠΡΟΤΕΙΝΟΜΕΝΟ ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ ΜΑΘΗΜΑ: ΤΑΞΗ: ΕΝΟΤΗΤΕΣ: ΕΙΣΗΓΗΤΗΣ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ και ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ (ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ) ΜΙΧΕΛΑΚΑΚΗΣ ΗΛΙΑΣ 1.Διδακτικός στόχοι: Να ορίζουν το στάσιμο
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER
 4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
Φυσική για Μηχανικούς
 Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων. Φυσική για Μηχανικούς Κύματα
Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων. Φυσική για Μηχανικούς Κύματα
Άσκηση 36 Μελέτη ακουστικών κυμάτων σε ηχητικό σωλήνα
 Μιχάλης Καλογεράκης 9 ο Εξάμηνο ΣΕΜΦΕ ΑΜ:911187 Υπεύθυνος Άσκησης: Κος Πέογλος Ημερομηνία Διεξαγωγής:3/11/25 Άσκηση 36 Μελέτη ακουστικών κυμάτων σε ηχητικό σωλήνα 1) Εισαγωγή: Σκοπός και στοιχεία Θεωρίας
Μιχάλης Καλογεράκης 9 ο Εξάμηνο ΣΕΜΦΕ ΑΜ:911187 Υπεύθυνος Άσκησης: Κος Πέογλος Ημερομηνία Διεξαγωγής:3/11/25 Άσκηση 36 Μελέτη ακουστικών κυμάτων σε ηχητικό σωλήνα 1) Εισαγωγή: Σκοπός και στοιχεία Θεωρίας
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ. Εργαστήριο 8 ο. Αποδιαμόρφωση PAM-PPM με προσαρμοσμένα φίλτρα
 Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Εργαστήριο 8 ο Αποδιαμόρφωση PAM-PPM με προσαρμοσμένα φίλτρα Βασική Θεωρία Σε ένα σύστημα μετάδοσης
Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Εργαστήριο 8 ο Αποδιαμόρφωση PAM-PPM με προσαρμοσμένα φίλτρα Βασική Θεωρία Σε ένα σύστημα μετάδοσης
ΔΙΑΓΩΝΙΣΜΑ 05 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3 ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) U β A
 Σελίδα 1 από 5 ΔΙΑΓΩΝΙΣΜΑ 05 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3 ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α και
Σελίδα 1 από 5 ΔΙΑΓΩΝΙΣΜΑ 05 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3 ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α και
Πολιτικός Μηχανικός Ph.D.
 Βασίλειος Μαχαιράς Πολιτικός Μηχανικός Ph.D. Ηχομονωτική προστασία κτιρίου Πανεπιστήμιο Θεσσαλίας Πολυτεχνική Σχολή ΤμήμαΠολιτικών Μηχανικών Διάλεξη 11 η /2016 Ακουστική Ακουστική είναι η επιστήμη που
Βασίλειος Μαχαιράς Πολιτικός Μηχανικός Ph.D. Ηχομονωτική προστασία κτιρίου Πανεπιστήμιο Θεσσαλίας Πολυτεχνική Σχολή ΤμήμαΠολιτικών Μηχανικών Διάλεξη 11 η /2016 Ακουστική Ακουστική είναι η επιστήμη που
Φύση του φωτός. Θεωρούμε ότι το φως έχει διττή φύση: διαταραχή που διαδίδεται στο χώρο. μήκος κύματος φωτός. συχνότητα φωτός
 Γεωμετρική Οπτική Φύση του φωτός Θεωρούμε ότι το φως έχει διττή φύση: ΚΥΜΑΤΙΚΗ Βασική ιδέα Το φως είναι μια Η/Μ διαταραχή που διαδίδεται στο χώρο Βασική Εξίσωση Φαινόμενα που εξηγεί καλύτερα (κύμα) μήκος
Γεωμετρική Οπτική Φύση του φωτός Θεωρούμε ότι το φως έχει διττή φύση: ΚΥΜΑΤΙΚΗ Βασική ιδέα Το φως είναι μια Η/Μ διαταραχή που διαδίδεται στο χώρο Βασική Εξίσωση Φαινόμενα που εξηγεί καλύτερα (κύμα) μήκος
Εργαστήριο Ηλεκτρoακουστικής Άσκηση 2 - Σελίδα 1 ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΣΚΗΣΗ 2
 Εργαστήριο Ηλεκτρoακουστικής Άσκηση 2 - Σελίδα 1 ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΣΚΗΣΗ 2 MEΤΡΗΣΗ ΠΕΡΙΒΑΛΛΟΝΤΙΚΟΥ ΘΟΡΥΒΟΥ ΚΑΙ ΗΧΟΜΟΝΩΣΗΣ 1. ΕΙΣΑΓΩΓΗ Σαν θόρυβος ορίζεται συνήθως η κατηγορία των ανεπιθύμητων ήχων, που
Εργαστήριο Ηλεκτρoακουστικής Άσκηση 2 - Σελίδα 1 ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΣΚΗΣΗ 2 MEΤΡΗΣΗ ΠΕΡΙΒΑΛΛΟΝΤΙΚΟΥ ΘΟΡΥΒΟΥ ΚΑΙ ΗΧΟΜΟΝΩΣΗΣ 1. ΕΙΣΑΓΩΓΗ Σαν θόρυβος ορίζεται συνήθως η κατηγορία των ανεπιθύμητων ήχων, που
Σήματα και Συστήματα. Διάλεξη 2: Στοιχειώδη Σήματα Συνεχούς Χρόνου. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 2: Στοιχειώδη Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Στοιχειώδη Σήματα Συνεχούς Χρόνου 1. Μοναδιαία Βηματική Συνάρτηση 2. Κρουστική Συνάρτηση ή
Σήματα και Συστήματα Διάλεξη 2: Στοιχειώδη Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Στοιχειώδη Σήματα Συνεχούς Χρόνου 1. Μοναδιαία Βηματική Συνάρτηση 2. Κρουστική Συνάρτηση ή
Άσκηση 3 Υπολογισμός του μέτρου της ταχύτητας και της επιτάχυνσης
 Άσκηση 3 Υπολογισμός του μέτρου της ταχύτητας και της επιτάχυνσης Σύνοψη Σκοπός της συγκεκριμένης άσκησης είναι ο υπολογισμός του μέτρου της στιγμιαίας ταχύτητας και της επιτάχυνσης ενός υλικού σημείου
Άσκηση 3 Υπολογισμός του μέτρου της ταχύτητας και της επιτάχυνσης Σύνοψη Σκοπός της συγκεκριμένης άσκησης είναι ο υπολογισμός του μέτρου της στιγμιαίας ταχύτητας και της επιτάχυνσης ενός υλικού σημείου
Δυναμική Ανάλυση Κατασκευών - Πειράματα Μονοβαθμίων Συστημάτων (ΜΒΣ) σε Σεισμική Τράπεζα
 ΠΠΜ 5: Ανάλυση Κατασκευών με Η/Υ, Πειράματα ΜΒΣ σε Σεισμική Τράπεζα Πανεπιστήμιο Κύπρου Πολυτεχνική Σχολή Τμήμα Πολιτικών Μηχανικών και Μηχανικών Περιβάλλοντος ΠΠΜ 5: Ανάλυση Κατασκευών με Η/Υ Δυναμική
ΠΠΜ 5: Ανάλυση Κατασκευών με Η/Υ, Πειράματα ΜΒΣ σε Σεισμική Τράπεζα Πανεπιστήμιο Κύπρου Πολυτεχνική Σχολή Τμήμα Πολιτικών Μηχανικών και Μηχανικών Περιβάλλοντος ΠΠΜ 5: Ανάλυση Κατασκευών με Η/Υ Δυναμική
Σήματα και Συστήματα. Διάλεξη 1: Σήματα Συνεχούς Χρόνου. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 1: Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Εισαγωγή στα Σήματα 1. Σκοποί της Θεωρίας Σημάτων 2. Κατηγορίες Σημάτων 3. Χαρακτηριστικές Παράμετροι
Σήματα και Συστήματα Διάλεξη 1: Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Εισαγωγή στα Σήματα 1. Σκοποί της Θεωρίας Σημάτων 2. Κατηγορίες Σημάτων 3. Χαρακτηριστικές Παράμετροι
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Κύματα Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων.
Φυσική για Μηχανικούς Κύματα Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων.
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΦΥΣΙΚΗΣ ΙΙ
 ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΦΥΣΙΚΗΣ ΙΙ ΘΕΜΑ 1 ο (βαθµοί 2) Σώµα µε µάζα m=5,00 kg είναι προσαρµοσµένο στο ελεύθερο άκρο ενός κατακόρυφου ελατηρίου και ταλαντώνεται εκτελώντας πέντε (5) πλήρης ταλαντώσεις σε χρονικό
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΦΥΣΙΚΗΣ ΙΙ ΘΕΜΑ 1 ο (βαθµοί 2) Σώµα µε µάζα m=5,00 kg είναι προσαρµοσµένο στο ελεύθερο άκρο ενός κατακόρυφου ελατηρίου και ταλαντώνεται εκτελώντας πέντε (5) πλήρης ταλαντώσεις σε χρονικό
Φυσική Ο.Π. Γ Λυκείου
 Φυσική Ο.Π. Γ Λυκείου ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις (Α-Α) και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α) Δύο σώματα συγκρούονται κεντρικά
Φυσική Ο.Π. Γ Λυκείου ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις (Α-Α) και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α) Δύο σώματα συγκρούονται κεντρικά
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 8 ο : Προσαρμοσμένα Φίλτρα Βασική
Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 8 ο : Προσαρμοσμένα Φίλτρα Βασική
ΠΟΥ ΔΙΑΔΙΔΕΤΑΙ ΤΟ ΦΩΣ
 1 ΦΩΣ Στο μικρόκοσμο θεωρούμε ότι το φως έχει δυο μορφές. Άλλοτε το αντιμετωπίζουμε με τη μορφή σωματιδίων που ονομάζουμε φωτόνια. Τα φωτόνια δεν έχουν μάζα αλλά μόνον ενέργεια. Άλλοτε πάλι αντιμετωπίζουμε
1 ΦΩΣ Στο μικρόκοσμο θεωρούμε ότι το φως έχει δυο μορφές. Άλλοτε το αντιμετωπίζουμε με τη μορφή σωματιδίων που ονομάζουμε φωτόνια. Τα φωτόνια δεν έχουν μάζα αλλά μόνον ενέργεια. Άλλοτε πάλι αντιμετωπίζουμε
3. Εγκάρσιο γραμμικό κύμα που διαδίδεται σε ένα ομογενές ελαστικό μέσον και κατά την
 ΚΥΜΑΤΑ 1. Μια πηγή Ο που βρίσκεται στην αρχή του άξονα, αρχίζει να εκτελεί τη χρονική στιγμή 0, απλή αρμονική ταλάντωση με εξίσωση 6 10 ημ S. I.. Το παραγόμενο γραμμικό αρμονικό κύμα διαδίδεται κατά τη
ΚΥΜΑΤΑ 1. Μια πηγή Ο που βρίσκεται στην αρχή του άξονα, αρχίζει να εκτελεί τη χρονική στιγμή 0, απλή αρμονική ταλάντωση με εξίσωση 6 10 ημ S. I.. Το παραγόμενο γραμμικό αρμονικό κύμα διαδίδεται κατά τη
ΑΠΟΚΡΙΣΗ ΣΥΣΤΗΜΑΤΩΝ ΣΤΟ ΠΕΔΙΟ ΤΟΥ ΧΡΟΝΟΥ ΚΑΙ ΤΩΝ ΣΥΧΝΟΤΗΤΩΝ
 ΑΠΟΚΡΙΣΗ ΣΥΣΤΗΜΑΤΩΝ ΣΤΟ ΠΕΔΙΟ ΤΟΥ ΧΡΟΝΟΥ ΚΑΙ ΤΩΝ ΣΥΧΝΟΤΗΤΩΝ ΣΚΟΠΟΣ ΤΗΣ ΑΣΚΗΣΗΣ Σημαντική πληροφορία για τη συμπεριφορά και την ευστάθεια ενός γραμμικού συστήματος, παίρνεται, μελετώντας την απόκρισή του
ΑΠΟΚΡΙΣΗ ΣΥΣΤΗΜΑΤΩΝ ΣΤΟ ΠΕΔΙΟ ΤΟΥ ΧΡΟΝΟΥ ΚΑΙ ΤΩΝ ΣΥΧΝΟΤΗΤΩΝ ΣΚΟΠΟΣ ΤΗΣ ΑΣΚΗΣΗΣ Σημαντική πληροφορία για τη συμπεριφορά και την ευστάθεια ενός γραμμικού συστήματος, παίρνεται, μελετώντας την απόκρισή του
ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗΣ
 Εργαστήριο Ηλεκτρακουστικής Ι Άσκηση 1 - Σελίδα 1 ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ 1. ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ/ΣΥΣΤΗΜΑΤΩΝ ΚΑΙ ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ Αρχικά, για την καλύτερη κατανόηση
Εργαστήριο Ηλεκτρακουστικής Ι Άσκηση 1 - Σελίδα 1 ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ 1. ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ/ΣΥΣΤΗΜΑΤΩΝ ΚΑΙ ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ Αρχικά, για την καλύτερη κατανόηση
25/3/2009. Η επεξεργασία του ψηφιακού σήματος υλοποιείται μέσω κατάλληλου αλγορίθμου. Φλώρος Ανδρέας Επίκ. Καθηγητής Παράμετροι ελέγχου
 Από το προηγούμενο μάθημα... Μάθημα: «Ψηφιακή Επεξεργασία Ήχου» Δάλ Διάλεξη 4 η : «Επεξεργαστές Ε ξ έ Δυναμικής Περιοχής (Mέρος έ ΙΙ)» Η επεξεργασία του ψηφιακού σήματος υλοποιείται μέσω κατάλληλου αλγορίθμου
Από το προηγούμενο μάθημα... Μάθημα: «Ψηφιακή Επεξεργασία Ήχου» Δάλ Διάλεξη 4 η : «Επεξεργαστές Ε ξ έ Δυναμικής Περιοχής (Mέρος έ ΙΙ)» Η επεξεργασία του ψηφιακού σήματος υλοποιείται μέσω κατάλληλου αλγορίθμου
Σύστημα ενίσχυσης ήχου εξωτερικού χώρου (Outdoor Sound Reinforcement System)
 Σύστημα ενίσχυσης ήχου εξωτερικού χώρου (Outdoor Sound Reinforcement System) Εισαγωγή Η μελέτη των συστημάτων ενίσχυσης ήχου αρχίζει με μια ανάλυση ενός απλού συστήματος εξωτερικού χώρου (outdoor system).
Σύστημα ενίσχυσης ήχου εξωτερικού χώρου (Outdoor Sound Reinforcement System) Εισαγωγή Η μελέτη των συστημάτων ενίσχυσης ήχου αρχίζει με μια ανάλυση ενός απλού συστήματος εξωτερικού χώρου (outdoor system).
Ψηφιακή Επεξεργασία Σηµμάτων
 Ψηφιακή Επεξεργασία Σηµμάτων Διάλεξη 3: DSP for Audio Δρ. Θωµμάς Ζαρούχας Επιστηµμονικός Συνεργάτης Μεταπτυχιακό Πρόγραµμµμα: Τεχνολογίες και Συστήµματα Ευρυζωνικών Εφαρµμογών και Υπηρεσιών 1 Προεπισκόπηση
Ψηφιακή Επεξεργασία Σηµμάτων Διάλεξη 3: DSP for Audio Δρ. Θωµμάς Ζαρούχας Επιστηµμονικός Συνεργάτης Μεταπτυχιακό Πρόγραµμµμα: Τεχνολογίες και Συστήµματα Ευρυζωνικών Εφαρµμογών και Υπηρεσιών 1 Προεπισκόπηση
1. Η συχνότητα αρμονικού κύματος είναι f = 0,5 Hz ενώ η ταχύτητα διάδοσης του υ = 2 m / s.
 1. Η συχνότητα αρμονικού κύματος είναι f = 0,5 Hz ενώ η ταχύτητα διάδοσης του υ = 2 m / s. Να βρεθεί το μήκος κύματος. 2. Σε ένα σημείο του Ειρηνικού ωκεανού σχηματίζονται κύματα με μήκος κύματος 1 m και
1. Η συχνότητα αρμονικού κύματος είναι f = 0,5 Hz ενώ η ταχύτητα διάδοσης του υ = 2 m / s. Να βρεθεί το μήκος κύματος. 2. Σε ένα σημείο του Ειρηνικού ωκεανού σχηματίζονται κύματα με μήκος κύματος 1 m και
ΦΥΣΙΚΗ Γ ΓΥΜΝΑΣΙΟΥ - ΘΕΩΡΙΑ - ΤΥΠΟΛΟΓΙΟ
 ΦΥΣΙΚΗ Γ ΓΥΜΝΑΣΙΟΥ - ΘΕΩΡΙΑ - ΤΥΠΟΛΟΓΙΟ 1 2 Ισχύς που «καταναλώνει» μια ηλεκτρική_συσκευή Pηλ = V. I Ισχύς που Προσφέρεται σε αντιστάτη Χαρακτηριστικά κανονικής λειτουργίας ηλεκτρικής συσκευής Περιοδική
ΦΥΣΙΚΗ Γ ΓΥΜΝΑΣΙΟΥ - ΘΕΩΡΙΑ - ΤΥΠΟΛΟΓΙΟ 1 2 Ισχύς που «καταναλώνει» μια ηλεκτρική_συσκευή Pηλ = V. I Ισχύς που Προσφέρεται σε αντιστάτη Χαρακτηριστικά κανονικής λειτουργίας ηλεκτρικής συσκευής Περιοδική
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 5 ο : Προσαρμοσμένα Φίλτρα Βασική
Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 5 ο : Προσαρμοσμένα Φίλτρα Βασική
max 0 Eκφράστε την διαφορά των δύο θετικών λύσεων ώς πολλαπλάσιο του ω 0, B . Αναλύοντας το Β σε σειρά άπειρων όρων ώς προς γ/ω 0 ( σειρά
 . Να αποδείξετε ότι σε ένα ταλαντούμενο σύστημα ενός βαθμού ελευθερίας, μάζας και σταθεράς ελατηρίου s με πολύ ασθενή απόσβεση (γω, όπου γ r/, r η σταθερά αντίστασης και s/ ) το πλήρες εύρος στο μισό του
. Να αποδείξετε ότι σε ένα ταλαντούμενο σύστημα ενός βαθμού ελευθερίας, μάζας και σταθεράς ελατηρίου s με πολύ ασθενή απόσβεση (γω, όπου γ r/, r η σταθερά αντίστασης και s/ ) το πλήρες εύρος στο μισό του
Συστήματα συντεταγμένων
 Κεφάλαιο. Για να δημιουργήσουμε τρισδιάστατα αντικείμενα, που μπορούν να παρασταθούν στην οθόνη του υπολογιστή ως ένα σύνολο από γραμμές, επίπεδες πολυγωνικές επιφάνειες ή ακόμη και από ένα συνδυασμό από
Κεφάλαιο. Για να δημιουργήσουμε τρισδιάστατα αντικείμενα, που μπορούν να παρασταθούν στην οθόνη του υπολογιστή ως ένα σύνολο από γραμμές, επίπεδες πολυγωνικές επιφάνειες ή ακόμη και από ένα συνδυασμό από
ΙΑΤΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ ΥΠΕΡΗΧΟΓΡΑΦΙΑ
 ΙΑΤΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ ΥΠΕΡΗΧΟΓΡΑΦΙΑ Γενικές Αρχές Φυσικής Κ. Χατζημιχαήλ ΙΑΤΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ ΥΠΕΡΗΧΟΓΡΑΦΙΑ Καλώς ήλθατε Καλή αρχή Υπερηχογραφία Ανήκει στις τομογραφικές μεθόδους απεικόνισης Δεν έχει ιονίζουσα
ΙΑΤΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ ΥΠΕΡΗΧΟΓΡΑΦΙΑ Γενικές Αρχές Φυσικής Κ. Χατζημιχαήλ ΙΑΤΡΙΚΗ ΑΠΕΙΚΟΝΙΣΗ ΥΠΕΡΗΧΟΓΡΑΦΙΑ Καλώς ήλθατε Καλή αρχή Υπερηχογραφία Ανήκει στις τομογραφικές μεθόδους απεικόνισης Δεν έχει ιονίζουσα
Περιεχόμενα. Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14
 Περιεχόμενα Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14 Κεφάλαιο 2 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΕΝΑ ΕΠΙΠΕΔΟ 20 2.1 Οι συντεταγμένες
Περιεχόμενα Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14 Κεφάλαιο 2 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΕΝΑ ΕΠΙΠΕΔΟ 20 2.1 Οι συντεταγμένες
1. Ποια μεγέθη ονομάζονται μονόμετρα και ποια διανυσματικά;
 ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Ποια μεγέθη ονομάζονται μονόμετρα και ποια διανυσματικά; Μονόμετρα ονομάζονται τα μεγέθη τα οποία, για να τα προσδιορίσουμε πλήρως, αρκεί να γνωρίζουμε
ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Ποια μεγέθη ονομάζονται μονόμετρα και ποια διανυσματικά; Μονόμετρα ονομάζονται τα μεγέθη τα οποία, για να τα προσδιορίσουμε πλήρως, αρκεί να γνωρίζουμε
Μελέτη και Ανάπτυξη Λογισµικού για την Εξοµοίωση Κλειστού Χώρου
 Ακουστική 2002 AcP030 Μελέτη και Ανάπτυξη Λογισµικού για την Εξοµοίωση Κλειστού Χώρου Φλώρος Ανδρέας Τάτλας Νικ.-Αλέξ. αµαλού Κέλλυ ρ. Ηλ. Μηχανικός 1 ιπλ. Ηλ. Μηχανικός 1 ιπλ. Ηλ. Μηχανικός 2 floros@wcl.ee.upatras.gr
Ακουστική 2002 AcP030 Μελέτη και Ανάπτυξη Λογισµικού για την Εξοµοίωση Κλειστού Χώρου Φλώρος Ανδρέας Τάτλας Νικ.-Αλέξ. αµαλού Κέλλυ ρ. Ηλ. Μηχανικός 1 ιπλ. Ηλ. Μηχανικός 1 ιπλ. Ηλ. Μηχανικός 2 floros@wcl.ee.upatras.gr
Διαγώνισμα Φυσική Κατεύθυνσης Γ Λυκείου
 Διαγώνισμα Φυσική Κατεύθυνσης Γ Λυκείου Επιμέλεια Θεμάτων Σ.Π.Μαμαλάκης Ζήτημα 1 ον 1.. Μια ακτίνα φωτός προσπίπτει στην επίπεδη διαχωριστική επιφάνεια δύο μέσων. Όταν η διαθλώμενη ακτίνα κινείται παράλληλα
Διαγώνισμα Φυσική Κατεύθυνσης Γ Λυκείου Επιμέλεια Θεμάτων Σ.Π.Μαμαλάκης Ζήτημα 1 ον 1.. Μια ακτίνα φωτός προσπίπτει στην επίπεδη διαχωριστική επιφάνεια δύο μέσων. Όταν η διαθλώμενη ακτίνα κινείται παράλληλα
4.2. Ασκήσεις στο φαινόμενο Doppler
 4.2. Ασκήσεις στο φαινόμενο Doppler 1) Συχνότητα και διάρκεια ενός ήχου Μια ηχητική πηγή κινείται με ταχύτητα υ s =40m/s πλησιάζοντας έναν ακίνητο παρατηρητή Α. Σε μια στιγμή εκπέμπει έναν ήχο διάρκειας
4.2. Ασκήσεις στο φαινόμενο Doppler 1) Συχνότητα και διάρκεια ενός ήχου Μια ηχητική πηγή κινείται με ταχύτητα υ s =40m/s πλησιάζοντας έναν ακίνητο παρατηρητή Α. Σε μια στιγμή εκπέμπει έναν ήχο διάρκειας
1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη;
 ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης. Στην Κινηματική
ΚΕΦΑΛΑΙΟ 2 ο ΚΙΝΗΣΗ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης. Στην Κινηματική
Ακουστική)και)Ψυχοακουστική
 Τι είναι ήχος; Ορισμός ΕΛΟΤ 263.1 (1.184): Ακουστική)και)Ψυχοακουστική Διάλεξη'2:' Η'φυσική'του'ήχου ' «Ως ήχος ορίζεται η μηχανική διαταραχή που διαδίδεται με ορισμένη ταχύτητα μέσα σε ένα μέσο που μπορεί
Τι είναι ήχος; Ορισμός ΕΛΟΤ 263.1 (1.184): Ακουστική)και)Ψυχοακουστική Διάλεξη'2:' Η'φυσική'του'ήχου ' «Ως ήχος ορίζεται η μηχανική διαταραχή που διαδίδεται με ορισμένη ταχύτητα μέσα σε ένα μέσο που μπορεί
Δίκτυα Κινητών και Προσωπικών Επικοινωνιών
 Δίκτυα Κινητών και Προσωπικών Επικοινωνιών Ασύρματο Περιβάλλον στις Κινητές Επικοινωνίες Άγγελος Ρούσκας Τμήμα Ψηφιακών Συστημάτων Πανεπιστήμιο Πειραιώς Ραδιοδίαυλοι Απαραίτητη η γνώση των χαρακτηριστικών
Δίκτυα Κινητών και Προσωπικών Επικοινωνιών Ασύρματο Περιβάλλον στις Κινητές Επικοινωνίες Άγγελος Ρούσκας Τμήμα Ψηφιακών Συστημάτων Πανεπιστήμιο Πειραιώς Ραδιοδίαυλοι Απαραίτητη η γνώση των χαρακτηριστικών
ΕΡΓΑΣΙΑ ΣΤΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ
 ΕΡΓΑΣΙΑ ΣΤΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Τι ονομάζεται μηχανικό κύμα; Να περιγράψετε το μηχανισμό διάδοσής του. 2. Τι χρειάζεται για να δημιουργηθεί και να διαδοθεί ένα μηχανικό κύμα; Διαδίδονται
ΕΡΓΑΣΙΑ ΣΤΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Τι ονομάζεται μηχανικό κύμα; Να περιγράψετε το μηχανισμό διάδοσής του. 2. Τι χρειάζεται για να δημιουργηθεί και να διαδοθεί ένα μηχανικό κύμα; Διαδίδονται
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
Κίνηση ΚΕΦΑΛΑΙΟ 2 Β ΓΥΜΝΑΣΙΟΥ
 Κίνηση ΚΕΦΑΛΑΙΟ 2 Β ΓΥΜΝΑΣΙΟΥ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης.
Κίνηση ΚΕΦΑΛΑΙΟ 2 Β ΓΥΜΝΑΣΙΟΥ 2.1 Περιγραφή της Κίνησης 1. Τι είναι η Κινηματική; Ποια κίνηση ονομάζεται ευθύγραμμη; Κινηματική είναι ο κλάδος της Φυσικής που έχει ως αντικείμενο τη μελέτη της κίνησης.
Public Address (PA) Ενίσχυση Συναυλιών. Κύκλος Διαλέξεων Ηλεκτρακουστικής 20/2/2012. Δευτέρα, 20 Φεβρουαρίου 12
 Public Address (PA) Ενίσχυση Συναυλιών Κύκλος Διαλέξεων Ηλεκτρακουστικής Ι.Ε.Μ.Α. 20/2/2012 Public Address = Απευθύνω δημόσια λόγο Εφόσον προσδιορίσουμε τους στόχους και τις ανάγκες μας......σχεδιάζουμε
Public Address (PA) Ενίσχυση Συναυλιών Κύκλος Διαλέξεων Ηλεκτρακουστικής Ι.Ε.Μ.Α. 20/2/2012 Public Address = Απευθύνω δημόσια λόγο Εφόσον προσδιορίσουμε τους στόχους και τις ανάγκες μας......σχεδιάζουμε
Ήχος. Τεχνολογία Πολυμέσων και Πολυμεσικές Επικοινωνίες 04-1
 Ήχος Χαρακτηριστικά του ήχου Ψηφιοποίηση με μετασχηματισμό Ψηφιοποίηση με δειγματοληψία Κβαντοποίηση δειγμάτων Παλμοκωδική διαμόρφωση Συμβολική αναπαράσταση μουσικής Τεχνολογία Πολυμέσων και Πολυμεσικές
Ήχος Χαρακτηριστικά του ήχου Ψηφιοποίηση με μετασχηματισμό Ψηφιοποίηση με δειγματοληψία Κβαντοποίηση δειγμάτων Παλμοκωδική διαμόρφωση Συμβολική αναπαράσταση μουσικής Τεχνολογία Πολυμέσων και Πολυμεσικές
Γ.Κονδύλη 1 & Όθωνος-Μ αρούσι Τ ηλ. Κέντρο: , /
 Γ.Κονδύλη & Όθωνος-Μ αρούσι Τ ηλ. Κέντρο:20-6.24.000, http:/ / www.akadimos.gr ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ 204 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Επιμέλεια Θεμάτων: Παπαδόπουλος Πασχάλης ΘΕΜΑ
Γ.Κονδύλη & Όθωνος-Μ αρούσι Τ ηλ. Κέντρο:20-6.24.000, http:/ / www.akadimos.gr ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ 204 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Επιμέλεια Θεμάτων: Παπαδόπουλος Πασχάλης ΘΕΜΑ
Μελέτη και εικονική διαμόρφωση ακουστικής σε αίθουσα διδασκαλίας
 Μελέτη και εικονική διαμόρφωση ακουστικής σε αίθουσα διδασκαλίας Ιωάννης Γ. Μαλαφής, Π.Δ. 407/82 Εργαστήριο Μουσικής Ακουστικής Τεχνολογίας, Τμήμα Μουσικών Σπουδών, Πανεπιστήμιο Αθηνών. Παναγιώτης Ε. Χατζημανολάκης
Μελέτη και εικονική διαμόρφωση ακουστικής σε αίθουσα διδασκαλίας Ιωάννης Γ. Μαλαφής, Π.Δ. 407/82 Εργαστήριο Μουσικής Ακουστικής Τεχνολογίας, Τμήμα Μουσικών Σπουδών, Πανεπιστήμιο Αθηνών. Παναγιώτης Ε. Χατζημανολάκης
HMY 333 Φωτονική Διάλεξη 12 Οπτικοί κυματοδηγοί
 4 Hsiu. Ha Ανάκλαση και μετάδοση του φωτός σε μια διηλεκτρική επαφή HMY 333 Φωτονική Διάλεξη Οπτικοί κυματοδηγοί i i i r i si c si v c hp://www.e.readig.ac.u/clouds/awell/ c 3 Γωνία πρόσπτωσης < κρίσιμη
4 Hsiu. Ha Ανάκλαση και μετάδοση του φωτός σε μια διηλεκτρική επαφή HMY 333 Φωτονική Διάλεξη Οπτικοί κυματοδηγοί i i i r i si c si v c hp://www.e.readig.ac.u/clouds/awell/ c 3 Γωνία πρόσπτωσης < κρίσιμη
Εργαστήριο Ηλεκτρoακουστικής Άσκηση 4 - Σελίδα 1 ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΣΚΗΣΗ 4 ΜΕΤΡΗΣΗ, ΑΝΑΛΥΣΗ ΚΑΙ ΠΡΟΒΛΕΨΗ ΤΗΣ ΑΚΟΥΣΤΙΚΗΣ ΣΥΜΠΕΡΙΦΟΡΑΣ ΚΛΕΙΣΤΩΝ ΧΩΡΩΝ
 Εργαστήριο Ηλεκτρoακουστικής Άσκηση 4 - Σελίδα 1 ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΣΚΗΣΗ 4 ΜΕΤΡΗΣΗ, ΑΝΑΛΥΣΗ ΚΑΙ ΠΡΟΒΛΕΨΗ ΤΗΣ ΑΚΟΥΣΤΙΚΗΣ 1. ΕΙΣΑΓΩΓΗ ΣΥΜΠΕΡΙΦΟΡΑΣ ΚΛΕΙΣΤΩΝ ΧΩΡΩΝ Κάθε κλειστός χώρος παρουσιάζει ειδικά ακουστικά
Εργαστήριο Ηλεκτρoακουστικής Άσκηση 4 - Σελίδα 1 ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΣΚΗΣΗ 4 ΜΕΤΡΗΣΗ, ΑΝΑΛΥΣΗ ΚΑΙ ΠΡΟΒΛΕΨΗ ΤΗΣ ΑΚΟΥΣΤΙΚΗΣ 1. ΕΙΣΑΓΩΓΗ ΣΥΜΠΕΡΙΦΟΡΑΣ ΚΛΕΙΣΤΩΝ ΧΩΡΩΝ Κάθε κλειστός χώρος παρουσιάζει ειδικά ακουστικά
Δομικά Υλικά Μάθημα ΙV. Ηχος & Ηχητικά Φαινόμενα II
 Δομικά Υλικά Μάθημα ΙV Ηχος & Ηχητικά Φαινόμενα II Συντελεστής Ανάκλασης r Συντελεστής Ανάκλασης r Ο λόγος της ανακλώμενης (W r ) ηχητικής ενέργειας από την επιφάνεια προς την προσπίπτουσα (W i ) Συντελεστής
Δομικά Υλικά Μάθημα ΙV Ηχος & Ηχητικά Φαινόμενα II Συντελεστής Ανάκλασης r Συντελεστής Ανάκλασης r Ο λόγος της ανακλώμενης (W r ) ηχητικής ενέργειας από την επιφάνεια προς την προσπίπτουσα (W i ) Συντελεστής
ΦΥΣ. 131 Τελική εξέταση: 10-Δεκεμβρίου-2005
 ΦΥΣ. 131 Τελική εξέταση: 10-Δεκεμβρίου-2005 Πριν αρχίσετε συμπληρώστε τα στοιχεία σας (ονοματεπώνυμο και αριθμό ταυτότητας). Ονοματεπώνυμο Αριθμός ταυτότητας Σας δίνονται 20 ισότιμα προβλήματα (10 βαθμοί
ΦΥΣ. 131 Τελική εξέταση: 10-Δεκεμβρίου-2005 Πριν αρχίσετε συμπληρώστε τα στοιχεία σας (ονοματεπώνυμο και αριθμό ταυτότητας). Ονοματεπώνυμο Αριθμός ταυτότητας Σας δίνονται 20 ισότιμα προβλήματα (10 βαθμοί
Φαινόμενο Doppler (Γ. Μ.) Φαινόμενο Doppler. Φαινόμενο Doppler είναι η διαφορά των συχνοτήτων που μετρούν οι παρατηρητές
 Φαινόμενο Doppler Για την κατανόηση του φαινομένου αυτού εισάγουμε τα παρακάτω σύμβολα και πρέπει να εξηγήσουμε τη σημασία τους. : πηγή ηχητικών κυμάτων : ανιχνευτής ηχητικών κυμάτων : συχνότητα ηχητικών
Φαινόμενο Doppler Για την κατανόηση του φαινομένου αυτού εισάγουμε τα παρακάτω σύμβολα και πρέπει να εξηγήσουμε τη σημασία τους. : πηγή ηχητικών κυμάτων : ανιχνευτής ηχητικών κυμάτων : συχνότητα ηχητικών
ΚΕΦΑΛΑΙΟ 2ο: ΜΗΧΑΝΙΚΑ- ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ.
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
2.2. Συμβολή και στάσιμα κύματα. Ομάδα Δ.
 2.2. Συμβολή και στάσιμα κύματα. Ομάδα Δ. 2.2.41. Μια χορδή σε ταλάντωση ή δυο στάσιμα κύματα. Μια χορδή μήκους 5m είναι στερεωμένη στα άκρα της Κ και Λ.. Όταν θέσουμε σε ταλάντωση το μέσον της Μ, απαιτείται
2.2. Συμβολή και στάσιμα κύματα. Ομάδα Δ. 2.2.41. Μια χορδή σε ταλάντωση ή δυο στάσιμα κύματα. Μια χορδή μήκους 5m είναι στερεωμένη στα άκρα της Κ και Λ.. Όταν θέσουμε σε ταλάντωση το μέσον της Μ, απαιτείται
ΚΥΜΑΤΑ 1. Νίκος Κανδεράκης
 ΚΥΜΑΤΑ 1 Νίκος Κανδεράκης Ταλάντωση Πλάτος x o Περίοδος T χρόνος για μία ταλάντωση Α Β Α Συχνότητα f αριθμός ταλαντώσεων σε 1s συχνότητα = αριθμός ταλαντώσεων/χρόνο ή f = N/t Αν Ν = 1 τότε t = T f = N/t
ΚΥΜΑΤΑ 1 Νίκος Κανδεράκης Ταλάντωση Πλάτος x o Περίοδος T χρόνος για μία ταλάντωση Α Β Α Συχνότητα f αριθμός ταλαντώσεων σε 1s συχνότητα = αριθμός ταλαντώσεων/χρόνο ή f = N/t Αν Ν = 1 τότε t = T f = N/t
Τεχνολογία Πολυμέσων. Ενότητα # 4: Ήχος Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Τεχνολογία Πολυμέσων Ενότητα # 4: Ήχος Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το
Τεχνολογία Πολυμέσων Ενότητα # 4: Ήχος Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το
ΗΧΗΤΙΚΕΣ ΕΓΚΑΤΑΣΤΑΣΕΙΣ
 ΗΧΗΤΙΚΕΣ ΕΓΚΑΤΑΣΤΑΣΕΙΣ ΤΥΠΙΚΑ ΠΑΡΑΔΕΙΓΜΑΤΑ ΓΙΑΝΝΗΣ ΜΟΥΡΤΖΟΠΟΥΛΟΣ ΚΑΘΗΓΗΤΗΣ ΟΜΑΔΑ ΤΕΧΝΟΛΟΓΙΑΣ ΗΧΟΥ & ΑΚΟΥΣΤΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΕΝΣΥΡΜΑΤΗΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ
ΗΧΗΤΙΚΕΣ ΕΓΚΑΤΑΣΤΑΣΕΙΣ ΤΥΠΙΚΑ ΠΑΡΑΔΕΙΓΜΑΤΑ ΓΙΑΝΝΗΣ ΜΟΥΡΤΖΟΠΟΥΛΟΣ ΚΑΘΗΓΗΤΗΣ ΟΜΑΔΑ ΤΕΧΝΟΛΟΓΙΑΣ ΗΧΟΥ & ΑΚΟΥΣΤΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΕΝΣΥΡΜΑΤΗΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ- ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 4 ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΜΥΤΙΛΗΝΗΣ ΤΕΛΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ- ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΠΩΝΥΜΟ. ΗΜΕΡ/ΝΙΑ : 15/05/2015 ΘΕΜΑ A Να γράψετε στο τετράδιό σας τον αριθμό καθεμίας από τις παρακάτω
4 ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΜΥΤΙΛΗΝΗΣ ΤΕΛΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ- ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΠΩΝΥΜΟ. ΗΜΕΡ/ΝΙΑ : 15/05/2015 ΘΕΜΑ A Να γράψετε στο τετράδιό σας τον αριθμό καθεμίας από τις παρακάτω
Εργαστήριο Ηλεκτρoακουστικής Άσκηση 6 - Σελίδα 1 ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΣΚΗΣΗ 6 ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΟΜΟΙΩΣΗ ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗΣ ΕΓΚΑΤΑΣΤΑΣΗΣ
 Εργαστήριο Ηλεκτρoακουστικής Άσκηση 6 - Σελίδα 1 ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΣΚΗΣΗ 6 1. ΕΙΣΑΓΩΓΗ ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΟΜΟΙΩΣΗ ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗΣ ΕΓΚΑΤΑΣΤΑΣΗΣ Στην άσκηση αυτή θα πρέπει να υλοποιήσετε ηλεκτροακουστική
Εργαστήριο Ηλεκτρoακουστικής Άσκηση 6 - Σελίδα 1 ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΣΚΗΣΗ 6 1. ΕΙΣΑΓΩΓΗ ΥΠΟΛΟΓΙΣΤΙΚΗ ΠΡΟΣΟΜΟΙΩΣΗ ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗΣ ΕΓΚΑΤΑΣΤΑΣΗΣ Στην άσκηση αυτή θα πρέπει να υλοποιήσετε ηλεκτροακουστική
Εξίσωση γραμμικού αρμονικού κύματος
 Εξίσωση γραμμικού αρμονικού κύματος Το γραμμικό αρμονικό κύμα έχει εξ ορισμού τα εξής γνωρίσματα: Κύμα = Διάδοση ενέργειας χωρίς μεταφορά ύλης. Επιτρεπτή η συμμετοχή της ύλης στον κυματικό μηχανισμό. Απαραίτητη
Εξίσωση γραμμικού αρμονικού κύματος Το γραμμικό αρμονικό κύμα έχει εξ ορισμού τα εξής γνωρίσματα: Κύμα = Διάδοση ενέργειας χωρίς μεταφορά ύλης. Επιτρεπτή η συμμετοχή της ύλης στον κυματικό μηχανισμό. Απαραίτητη
Για τις παρακάτω ερωτήσεις 2-4 να γράψετε στο τετράδιο σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
 46 Χρόνια ΦΡΟΝΤΙΣΤΗΡΙΑ ΜΕΣΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΣΑΒΒΑΪ Η-ΜΑΝΩΛΑΡΑΚΗ ΠΑΓΚΡΑΤΙ : Χρυσ Σµύρνης 3 : Τηλ.: 0760470 ΙΑΓΩΝΙΣΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 007 ΘΕΜΑ. Ποιες από τις παρακάτω προτάσεις είναι σωστές (Σ)
46 Χρόνια ΦΡΟΝΤΙΣΤΗΡΙΑ ΜΕΣΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΣΑΒΒΑΪ Η-ΜΑΝΩΛΑΡΑΚΗ ΠΑΓΚΡΑΤΙ : Χρυσ Σµύρνης 3 : Τηλ.: 0760470 ΙΑΓΩΝΙΣΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 007 ΘΕΜΑ. Ποιες από τις παρακάτω προτάσεις είναι σωστές (Σ)
Κύκλος διαλέξεων ακουστικής. Εισαγωγή στα θέματα
 Κύκλος διαλέξεων ακουστικής Εισαγωγή στα θέματα In memoriam Χρήστου Κουτσοδημάκη Τι είναι ήχος? Ότι ακούω. (?) ΕΛΟΤ 263.1 Ήχος ορίζεται ως η μηχανική διαταραχή που διαδίδεται με ορισμένη ταχύτητα
Κύκλος διαλέξεων ακουστικής Εισαγωγή στα θέματα In memoriam Χρήστου Κουτσοδημάκη Τι είναι ήχος? Ότι ακούω. (?) ΕΛΟΤ 263.1 Ήχος ορίζεται ως η μηχανική διαταραχή που διαδίδεται με ορισμένη ταχύτητα
Δ Ι Α Γ Ω Ν Ι Σ Μ Α Φ Υ Σ Ι Κ Η Σ Θ Ε Τ Ι Κ Ω Ν Σ Π Ο Υ Δ Ω Ν Γ Λ Υ Κ Ε Ι Ο Υ 05/1 / Ε Π Ω Ν Υ Μ Ο :...
 Δ Ι Α Γ Ω Ν Ι Σ Μ Α Φ Υ Σ Ι Κ Η Σ Θ Ε Τ Ι Κ Ω Ν Σ Π Ο Υ Δ Ω Ν Γ Λ Υ Κ Ε Ι Ο Υ 05/1 / 2 0 1 8 Ε Π Ω Ν Υ Μ Ο :... Ο Ν Ο Μ Α : Τ Μ Η Μ Α : Ε Π Ι Μ Ε Λ Ε Ι Α Θ Ε Μ Α Τ Ω Ν : ΦΑΡΜΑΚΗΣ Π. ΜΠΑΡΛΙΚΑΣ Σ. ΘΕΜΑ A
Δ Ι Α Γ Ω Ν Ι Σ Μ Α Φ Υ Σ Ι Κ Η Σ Θ Ε Τ Ι Κ Ω Ν Σ Π Ο Υ Δ Ω Ν Γ Λ Υ Κ Ε Ι Ο Υ 05/1 / 2 0 1 8 Ε Π Ω Ν Υ Μ Ο :... Ο Ν Ο Μ Α : Τ Μ Η Μ Α : Ε Π Ι Μ Ε Λ Ε Ι Α Θ Ε Μ Α Τ Ω Ν : ΦΑΡΜΑΚΗΣ Π. ΜΠΑΡΛΙΚΑΣ Σ. ΘΕΜΑ A
Κεφάλαιο 15 Κίνηση Κυµάτων. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 15 Κίνηση Κυµάτων Περιεχόµενα Κεφαλαίου 15 Χαρακτηριστικά των Κυµάτων Είδη κυµάτων: Διαµήκη και Εγκάρσια Μεταφορά ενέργειας µε κύµατα Μαθηµατική Περιγραφή της Διάδοσης κυµάτων Η Εξίσωση του Κύµατος
Κεφάλαιο 15 Κίνηση Κυµάτων Περιεχόµενα Κεφαλαίου 15 Χαρακτηριστικά των Κυµάτων Είδη κυµάτων: Διαµήκη και Εγκάρσια Μεταφορά ενέργειας µε κύµατα Μαθηµατική Περιγραφή της Διάδοσης κυµάτων Η Εξίσωση του Κύµατος
Συλλογή & Επεξεργασία Δεδομένων Εργαστήριο 7 Ακούγοντας Πρώτη Ματιά στην Ανάλυση Fourier. Σύστημα Συλλογής & Επεξεργασίας Μετρήσεων
 Συλλογή & Επεξεργασία Δεδομένων Εργαστήριο 7 Ακούγοντας Πρώτη Ματιά στην Ανάλυση Fourier. Σύστημα Συλλογής & Επεξεργασίας Μετρήσεων Σκοπός Βασική δομή ενός προγράμματος στο LabVIEW. Εμπρόσθιο Πλαίσιο (front
Συλλογή & Επεξεργασία Δεδομένων Εργαστήριο 7 Ακούγοντας Πρώτη Ματιά στην Ανάλυση Fourier. Σύστημα Συλλογής & Επεξεργασίας Μετρήσεων Σκοπός Βασική δομή ενός προγράμματος στο LabVIEW. Εμπρόσθιο Πλαίσιο (front
Εργαστήριο Μηχανικής Ρευστών. Εργασία 1 η : Πτώση πίεσης σε αγωγό κυκλικής διατομής
 Εργαστήριο Μηχανικής Ρευστών Εργασία 1 η : Πτώση πίεσης σε αγωγό κυκλικής διατομής Ονοματεπώνυμο:Κυρκιμτζής Γιώργος Σ.Τ.Ε.Φ. Οχημάτων - Εξάμηνο Γ Ημερομηνία εκτέλεσης Πειράματος : 12/4/2000 Ημερομηνία
Εργαστήριο Μηχανικής Ρευστών Εργασία 1 η : Πτώση πίεσης σε αγωγό κυκλικής διατομής Ονοματεπώνυμο:Κυρκιμτζής Γιώργος Σ.Τ.Ε.Φ. Οχημάτων - Εξάμηνο Γ Ημερομηνία εκτέλεσης Πειράματος : 12/4/2000 Ημερομηνία
ΘΟΡΥΒΟΣ ΗΧΟΔΟΣΙΜΕΤΡΙΑ Σιδερής Ευστάθιος
 ΘΟΡΥΒΟΣ ΗΧΟΔΟΣΙΜΕΤΡΙΑ Σιδερής Ευστάθιος 1. Θόρυβος Θόρυβος είναι κάθε υπερβολικός ή ανεπιθύμητος ήχος ο οποίος προκαλεί στον αποδέκτη άνθρωπο δυσφορία ή ακόμα και απώλεια ακοής. Δεκάδες εκατομμύρια εργαζόμενοι
ΘΟΡΥΒΟΣ ΗΧΟΔΟΣΙΜΕΤΡΙΑ Σιδερής Ευστάθιος 1. Θόρυβος Θόρυβος είναι κάθε υπερβολικός ή ανεπιθύμητος ήχος ο οποίος προκαλεί στον αποδέκτη άνθρωπο δυσφορία ή ακόμα και απώλεια ακοής. Δεκάδες εκατομμύρια εργαζόμενοι
Διαγώνισμα Φυσικής Κατεύθυνσης Γ Λυκείου
 Διαγώνισμα Φυσικής Κατεύθυνσης Γ Λυκείου Ζήτημα 1 ον 1.. Ένα σημειακό αντικείμενο εκτελεί απλή αρμονική ταλάντωση. Τις χρονικές στιγμές που το μέτρο της ταχύτητας του αντικειμένου είναι μέγιστο, το μέτρο
Διαγώνισμα Φυσικής Κατεύθυνσης Γ Λυκείου Ζήτημα 1 ον 1.. Ένα σημειακό αντικείμενο εκτελεί απλή αρμονική ταλάντωση. Τις χρονικές στιγμές που το μέτρο της ταχύτητας του αντικειμένου είναι μέγιστο, το μέτρο
Εισαγωγή στα χαρακτηριστικά των μικροφώνων
 ΕΙΔΗ ΜΙΚΡΟΦΩΝΩΝ Επιμέλεια: Νίκος Σκιαδάς ΠΕ 17.13 Μουσικής Τεχνολογίας Το μικρόφωνο πήρε την ονομασία του από τον Ντέιβιντ Χιουζ, ο οποίος επινόησε μια διάταξη μεταφοράς ήχου που ήταν τόσο ευαίσθητη, που
ΕΙΔΗ ΜΙΚΡΟΦΩΝΩΝ Επιμέλεια: Νίκος Σκιαδάς ΠΕ 17.13 Μουσικής Τεχνολογίας Το μικρόφωνο πήρε την ονομασία του από τον Ντέιβιντ Χιουζ, ο οποίος επινόησε μια διάταξη μεταφοράς ήχου που ήταν τόσο ευαίσθητη, που
ENOTHTA 1: ΚΡΟΥΣΕΙΣ ΣΗΜΕΙΩΣΕΙΣ
 ΚΕΦΑΛΑΙΟ 5 Ο : ΚΡΟΥΣΕΙΣ ΦΑΙΝΟΜΕΝΟ DOPPLER ENOTHT 1: ΚΡΟΥΣΕΙΣ ΣΗΜΕΙΩΣΕΙΣ Κρούση: Κρούση ονομάζουμε το φαινόμενο κατά το οποίο δύο ή περισσότερα σώματα έρχονται σε επαφή για πολύ μικρό χρονικό διάστημα κατά
ΚΕΦΑΛΑΙΟ 5 Ο : ΚΡΟΥΣΕΙΣ ΦΑΙΝΟΜΕΝΟ DOPPLER ENOTHT 1: ΚΡΟΥΣΕΙΣ ΣΗΜΕΙΩΣΕΙΣ Κρούση: Κρούση ονομάζουμε το φαινόμενο κατά το οποίο δύο ή περισσότερα σώματα έρχονται σε επαφή για πολύ μικρό χρονικό διάστημα κατά
2.2. Συμβολή και στάσιμα κύματα. Ομάδα Δ.
 2.2. Συμβολή και στάσιμα κύματα. Ομάδα Δ. 2.2.41. Μια χορδή σε ταλάντωση ή δυο στάσιμα κύματα. Μια χορδή μήκους 5m είναι στερεωμένη στα άκρα της Κ και Λ.. Όταν θέσουμε σε ταλάντωση το μέσον της Μ, απαιτείται
2.2. Συμβολή και στάσιμα κύματα. Ομάδα Δ. 2.2.41. Μια χορδή σε ταλάντωση ή δυο στάσιμα κύματα. Μια χορδή μήκους 5m είναι στερεωμένη στα άκρα της Κ και Λ.. Όταν θέσουμε σε ταλάντωση το μέσον της Μ, απαιτείται
Παραρτήματα. Παράρτημα 1 ο : Μιγαδικοί Αριθμοί
 Παράρτημα ο : Μιγαδικοί Αριθμοί Παράρτημα ο : Μετασχηματισμός Lplce Παράρτημα 3 ο : Αντίστροφος μετασχηματισμός Lplce Παράρτημα 4 ο : Μετασχηματισμοί δομικών διαγραμμάτων Παράρτημα 5 ο : Τυποποιημένα σήματα
Παράρτημα ο : Μιγαδικοί Αριθμοί Παράρτημα ο : Μετασχηματισμός Lplce Παράρτημα 3 ο : Αντίστροφος μετασχηματισμός Lplce Παράρτημα 4 ο : Μετασχηματισμοί δομικών διαγραμμάτων Παράρτημα 5 ο : Τυποποιημένα σήματα
ÁÎÉÁ ÅÊÐÁÉÄÅÕÔÉÊÏÓ ÏÌÉËÏÓ
 Θέµα Α ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ (ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ) 3 ΜΑΪOY 016 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και, δίπλα, το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει
Θέµα Α ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ (ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ) 3 ΜΑΪOY 016 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και, δίπλα, το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει
Δυναμική Μηχανών I. Επίλυση Προβλημάτων Αρχικών Συνθηκών σε Συνήθεις. Διαφορικές Εξισώσεις με Σταθερούς Συντελεστές
 Δυναμική Μηχανών I Επίλυση Προβλημάτων Αρχικών Συνθηκών σε Συνήθεις 5 3 Διαφορικές Εξισώσεις με Σταθερούς Συντελεστές 2015 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com
Δυναμική Μηχανών I Επίλυση Προβλημάτων Αρχικών Συνθηκών σε Συνήθεις 5 3 Διαφορικές Εξισώσεις με Σταθερούς Συντελεστές 2015 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com
Ψηφιακός ήχος και κινούμενα γραφικά
 ΕΣΔ200 Δημιουργία Περιεχομένου ΙI Ψηφιακός ήχος και κινούμενα γραφικά Εισαγωγή Το παρακάτω σχήμα περιγράφει τους δυνατούς τρόπους δημιουργίας αποθήκευσης και. αναπαραγωγής ψηφιακού ήχου Ο Ήχος από φυσική
ΕΣΔ200 Δημιουργία Περιεχομένου ΙI Ψηφιακός ήχος και κινούμενα γραφικά Εισαγωγή Το παρακάτω σχήμα περιγράφει τους δυνατούς τρόπους δημιουργίας αποθήκευσης και. αναπαραγωγής ψηφιακού ήχου Ο Ήχος από φυσική
ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΚΟΥΣΤΙΚΗ ΚΛΕΙΣΤΩΝ ΧΩΡΩΝ
 ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΚΟΥΣΤΙΚΗ ΚΛΕΙΣΤΩΝ ΧΩΡΩΝ ΓΙΑΝΝΗΣ ΜΟΥΡΤΖΟΠΟΥΛΟΣ ΚΑΘΗΓΗΤΗΣ ΟΜΑΔΑ ΤΕΧΝΟΛΟΓΙΑΣ ΗΧΟΥ & ΑΚΟΥΣΤΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΕΝΣΥΡΜΑΤΗΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ
ΗΛΕΚΤΡΟΑΚΟΥΣΤΙΚΗ ΑΚΟΥΣΤΙΚΗ ΚΛΕΙΣΤΩΝ ΧΩΡΩΝ ΓΙΑΝΝΗΣ ΜΟΥΡΤΖΟΠΟΥΛΟΣ ΚΑΘΗΓΗΤΗΣ ΟΜΑΔΑ ΤΕΧΝΟΛΟΓΙΑΣ ΗΧΟΥ & ΑΚΟΥΣΤΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΕΝΣΥΡΜΑΤΗΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΥΠΟΛΟΓΙΣΤΩΝ
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Σχολή Θετικών Επιστημών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ Ι Μπατιστάτος Μιχάλης Εργαστήριο ο : Διαμόρφωση ΑΜ Βασική Θεωρία Εισαγωγή
Σχολή Θετικών Επιστημών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ Ι Μπατιστάτος Μιχάλης Εργαστήριο ο : Διαμόρφωση ΑΜ Βασική Θεωρία Εισαγωγή
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
