Σειρά Προβλημάτων 4 Λύσεις
|
|
|
- Καλλιόπη Παναγιώτα Παπακώστας
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις Να αποφασίσετε κατά πόσο οι πιο κάτω προδιαγραφές είναι ορθές σύμφωνα με την έννοια της μερικής ορθότητας και την έννοια της ολικής ορθότητας. Να αιτιολογήσετε σύντομα τις απαντήσεις σας (δεν είναι απαραίτητο να κατασκευάσετε αποδείξεις με τους κανόνες). Η εντολή skip είναι μια εντολή η οποία δεν εκτελεί τίποτα και ικανοποιεί τον κανόνα {φ skip {φ. (α) {x = 12 y = 7 skip {z = 12 (β) {x > 6 y > 3 if x > y x := y; y := x {3 < x < 6 (γ) {x 28 y > 1 while (x!= y) x := x+1 {x = y (α) Η προδιαγραφή δεν είναι ορθή ούτε με την έννοια της μερικής ούτε με την έννοια της ολικής ορθότητας: Η προσυνθήκη δεν προσδιορίζει την αρχική τιμή της μεταβλητής z και επομένως είναι αδύνατο να εγγυηθούμε ότι μετά την εκτέλεση του προγράμματος η τιμή της z θα είναι ίση με 12. (β) Η προδιαγραφή δεν είναι ορθή ούτε με την έννοια της μερικής ούτε με την έννοια της ολικής ορθότητας. Για παράδειγμα, θεωρήστε το στιγμιότυπο όπου x = 7 και y = 8. Το στιγμιότυπο αυτό είναι συμβατό με την προσυνθήκη της προδιαγραφής. Εντούτοις, εκτέλεση της εντολής if δεν θα αλλάξει την τιμή της μεταβλητής x η οποία θα παραμείνει ίση με 7 που δεν ικανοποιεί τη μετασυνθήκη του προγράμματος. (γ) Παρατηρούμε ότι το πρόγραμμα δεν τερματίζει. Επομένως η πρόταση είναι αληθής με την έννοια της μερικής ορθότητας αλλά όχι με την έννοια της ολικής ορθότητας. Άσκηση 2 (30 μονάδες) Να αποδείξετε την ορθότητα των πιο κάτω προδιαγραφών (ολική ορθότητα). (α) = tot {x 0 P {y = x! όπου ο κώδικας του Ρ δίνεται πιο κάτω. a := x; y := 1; while (a > 0){ y := y * a; a := a - 1; (β) = tot { n 1 C { m=p q, p = max { A[i] 0 i < n, q = min { A[i] 0 i < n όπου ο κώδικας του C δίνεται πιο κάτω. p := A[0]; q := A[0]; i := 0; while (i < n){ if (A[i] > p) p := A[i]; if (A[i] < q) q := A[i]; skip; i++; m := p*q; Σειρά Προβλημάτων 4 Λύσεις Χειμερινό Εξάμηνο 2018 Σελίδα 1
2 (α) Η αμετάβλητη συνθήκη είναι η y = x! / a! 0 a και η μεταβλητή έκφραση είναι η a. {x 0 {1 = x!/x! 0 x Ενδυνάμωση συνθήκης a := x; {1 = x!/a! 0 a Κανόνας ανάθεσης y := 1; {y = x!/a! 0 a Κανόνας ανάθεσης while (a>0) { {y = x!/a! 0 a a>0 0 a = E 0 Αμετ. συνθήκη και φρουρός {y*a = x!/(a 1)! 0 a 1 0 a 1 < E 0 Κανόνας συνεπαγωγής y := y*a; {y = x!/(a 1)! 0 a 1 0 a 1 < E 0 Κανόνας ανάθεσης a := a 1; {y = x!/a! 0 a 0 a < E 0 Κανόνας ανάθεσης {y = x!/a! 0 a a 0 Κανόνας while {y=x! (β) Για σκοπούς απλούστευσης της λύσης η τρίτη εντολή του προγράμματος έχει γραφτεί ως i:= 1. Σε αυτή την περίπτωση η αμετάβλητη συνθήκη και η μεταβλητή έκφραση είναι: η = p = max { A[k] 0 k < i q = min { A[m] 0 k <i i n E = n i' Στην περίπτωση του ψευδοκώδικα όπως δίνεται στην εκφώνηση, η μόνη διαφορά θα ήταν ότι η αμετάβλητη συνθήκη θα ήταν: η = p = max [ {A[0] { A[k] 0 k < i ] q = min [ {A[0] { A[m] 0 k <i] i n Ακολουθεί η απόδειξη της προδιαγραφής. { n 1 { A[0] = max { A[k] 0 k <1, A[0] = min { A[m] 0 k < 1 1 n 0 n 1 Συνεπαγωγή p := A[0]; { p = max { A[k] 0 k < 1, A[0] = min { A[m] 0 k < 1 1 n 0 n 1 q := A[0]; { p = max { A[k] 0 k 1, q = min { A[m] 0 k 1 1 n 1 n i := 1; { p = max { A[k] 0 k i, q = min { A[k] 0 k < i i n 0 n i while (i < n){ { p = max { A[m] 0 k < i, q = min { A[m] 0 k < i i n i <n 0 n i=e 0 Αμ. Συνθ.+ Φρ. + Μετ. Εκφρ. {A[i]>p A[i]=max{ A[k] 0 k<i+1,q=min{a[k] 0 k<i+1 i+1 n 0 n i 1<E 0 A[i] p [p=max{a[k] 0 k<i+1 i+1 n 0 n i 1<E 0 A[i]<q A[i]=min{A[k] 0 k<i+1 A[i] q q=min{a[k] 0 k<i+1] Συνεπαγωγή if (A[i] > p) { A[i]=max{ A[k] 0 k<i+1, q = min{a[k] 0 m<i+1 i+1 n 0 n i 1<E 0 p := A[i]; { p = max{ A[k] 0 k<i+1, q = min{a[k] 0 m<i+1 i+1 n 0 n i 1<E 0 Σειρά Προβλημάτων 4 Λύσεις Χειμερινό Εξάμηνο 2018 Σελίδα 2
3 {p=max{a[k] 0 k<i+1 i+1 n 0 n i 1<E 0 A[i]<q A[i]=min{A[k] 0 k<i+1 A[i] q q=min{a[k] 0 k<i+1 {A[i]<q p=max{a[k] 0 k<i+1,a[i]=min{a[k] 0 k<i+1 i+1 n 0 n i 1<E 0 A[i] q p=max{a[k] 0 k<i+1,q=min{a[k] 0 k<i+1 i+1 n 0 n i 1<E 0 if (A[i] < q) { p=max{ A[k] 0 k<i+1, A[i]=min{A[k] 0 k<i+1 i+1 n 0 n i 1<E 0 q := A[i]; { p = max{ A[k] 0 k<i+1, q = min{a[k] 0 k<i+1 i+1 n 0 n i 1<E 0 { p = max{ A[k] 0 k<i+1, q = min{a[k] 0 k<i+1 i+1 n 0 n i 1<E 0 skip; { p = max{ A[k] 0 k<i+1, q = min{a[k] 0 k<i+1 i+1 n 0 n i 1<E 0 Συνεπαγωγή Καν. if { p = max{ A[k] 0 k<i+1, q = min{a[k] 0 k<i+1 i+1 n 0 n i 1<E 0 Καν. if i++; { p = max { A[k] 0 k < i, q = min { A[k] 0 k < i i n 0 n i < E 0 { p = max { A[k] 0 k < i, q = min { A[k] 0 k < i i n i n Καν. total while { p q =p q, p = max { A[i] 0 i < n, q = min { A[i] 0 i < n Συνεπαγωγή m := p*q; { m=p q, p = max { A[i] 0 i < n, q = min { A[i] 0 i < n Άσκηση 3 (11 μονάδες) Θέλουμε να προσθέσουμε στη γλώσσα WHILE (διαφάνεια 9 5), εντολές της μορφής: case B of {1:C 1; 2:C 2; ; n: C n Οι εντολές αυτές εκτελούνται ως εξής: (1) Πρώτα υπολογίζεται η έκφραση Β για να δώσει μια τιμή x. (2) Αν το x = i, 1 i n, τότε εκτελείται η εντολή C i. (3) Διαφορετικά, η εντολή δεν εκτελεί καμιά ενέργεια και η ροή του προγράμματος προχωρεί στην επόμενη εντολή (αν υπάρχει). (α) Θεωρήστε τον πιο κάτω κανόνα για την εντολή. : ; ; : Να εξηγήσετε γιατί ο κανόνας αυτός είναι λανθασμένος. (β) Να προτείνετε διορθωμένη εκδοχή του πιο κανόνα από το μέρος (α) και να την χρησιμοποιήσετε για να αποδείξετε την ορθότητα της πιο κάτω προδιαγραφής. {1 x x 3 case x of {1: y:= x 1; 2: y:= x 2; 3: y:= x 3 {y = 0 (α) Ο κανόνας αυτός είναι λανθασμένος γιατί αγνοεί την περίπτωση που η τιμή του Β δεν ανήκει στο πεδίο {1,,n. Για να ικανοποιείται η προδιαγραφή από τον συγκεκριμένο τύπο Σειρά Προβλημάτων 4 Λύσεις Χειμερινό Εξάμηνο 2018 Σελίδα 3
4 εντολής ο κανόνας θα πρέπει να λαμβάνει υπόψη και αυτή την επιπρόσθετη περίπτωση, όπως διατυπώνεται στην πιο κάτω διορθωμένη μορφή του κανόνα. 1,,, 1,, 1: ; ; : (β) Για να αποδείξουμε την προδιαγραφή {1 x x 3 case x of {1: y:= x 1; 2: y:= x 2; 3: y:= x 3 {y = 0 Πρέπει να αποδείξουμε τις επιμέρους προδιαγραφές 1. {1 x x 3 x = 1 y:= x 1 {y = 0 2. {1 x x 3 x = 2 y:= x 2 {y = 0 3. {1 x x 3 x = 3 y:= x 3 {y = 0 4. (1 x x 3 x {1,2,3) y = 0 Οι τρεις πρώτες επιβεβαιώνονται εύκολα μέσω του κανόνα της ανάθεσης και το κανόνα της ενδυνάμωσης προσυνθήκης. Όσον αφορά το τέταρτο σκέλος της προδιαγραφής, είναι εύκολο να δούμε ότι 1 x x 3 x {1,2,3 False και επομένως False y = 0. Άσκηση 4 (14 μονάδες) Θεωρήστε το μοντέλο Kriple Μ=(W, R, L), όπου W = {a,b,c,d,e R = {(a,c), (a,e),(b,a),(b,c),(d,e),(e,a), και L(a) = {p, L(b)={p,q, L(c)={p,q, L(d) = {q και L(e) = {. (α) Να παρουσιάσετε το μοντέλο Μ γραφικά. (β) Για κάθε μια από τις πιο κάτω ιδιότητες να αποφασίσετε κατά πόσο υπάρχει κόσμος του μοντέλου Μ που να τις ικανοποιεί. i. p p iv. (p q) ii. q q v. p p iii. p q vi. (p p) (α) Ακολουθεί το δοσμένο μοντέλο σε γραφική αναπαράσταση. e d {q c {p,q {p a b {p,q Σειρά Προβλημάτων 4 Λύσεις Χειμερινό Εξάμηνο 2018 Σελίδα 4
5 (β) p q q p q (p q) p p (p p) p a False True True True False True b False True True True True True c True False False False True True d False False False False True True e False False True True True True Άσκηση 5 Να δείξετε ότι οι πιο κάτω προτάσεις του βασικού τροπικού λογισμού είναι έγκυρες. (α) (φ ψ) ( φ ψ) (β) Τ ( φ φ) (α) Η πρόταση είναι αληθής. Η απόδειξη έχει ως εξής: Έστω κόσμος w σε κάποιο μοντέλο Kripke M. Τότε w (φ ψ) αν και μόνο αν x φ ψ για κάποιο x τέτοιο ώστε (w,x) R αν και μόνο αν x φ ή x ψ για κάποιο x τέτοιο ώστε (w,x) R αν και μόνο αν x φ για κάποιο x τέτοιο ώστε (w,x) R ή x ψ για κάποιο x τέτοιο ώστε (w,x) R αν και μόνο αν w φ ή w ψ αν και μόνο αν w φ ψ Αυτό ολοκληρώνει την απόδειξη. (β) Η πρόταση είναι αληθής. Η απόδειξη έχει ως εξής: Έστω κόσμος w σε κάποιο μοντέλο Kripke M. Έχουμε τα εξής: Έστω w T και w φ τότε x Τ για κάποιο x τέτοιο ώστε (w,x) R και y φ για κάθε y τέτοιο ώστε (w,y) R τότε True για κάποιο x τέτοιο ώστε (w,x) R και y φ για κάθε y τέτοιο ώστε (w,y) R τότε υπάρχει κάποιο x τέτοιο ώστε (w,x) R και y φ για κάθε y τέτοιο ώστε (w,y) R τότε x φ για κάποιο x τέτοιο ώστε (w,y) R τότε w φ Αυτό ολοκληρώνει την απόδειξη. Σειρά Προβλημάτων 4 Λύσεις Χειμερινό Εξάμηνο 2018 Σελίδα 5
6 Άσκηση 6 (20 μονάδες) Να αποδείξετε τα πιο κάτω λογικά επακόλουθα του Τροπικού Λογισμού ΚΤ45. (α) ( p q) ( q p) (β) ( p q) (p q) (α) 1. p p LEM 2. p πρ. υπ. p πρ. υπ. 3. q πρ. υπ p Καν. 5, γραμμή 2 4. p copy 2 p πρ. υπ 5. q p 3 4 p e 3 6. ( q p) i 3 5 e 3,5 7. ( p q) ( q p) i 6 q e 6 8. p q ( p q) i ( p q) ( q p) i ( p q) ( q p) e 1, 2 10 (β) Θα αποδείξουμε τις δύο κατευθύνσεις ξεχωριστά αφού αντικαταστήσουμε τον όρο p με τον ισοδύναμο p. 1. ( p q) πρ. υπόθεση 2. p πρ. υπόθεση 3. p q e 1 4. q πρ. υπόθεση 5. p ΜΤ 3, 4 6. p e 5 7. p T 6 8. e 7, 2 9. q RAA q i p q i (p q) i ( p q) (p q) i 1 12 Σειρά Προβλημάτων 4 Λύσεις Χειμερινό Εξάμηνο 2018 Σελίδα 6
7 1. (p q) πρ. υπόθεση 2. p πρ. υπόθεση 3. q πρ. υπόθεση 4. q πρ. υπόθεση 5. q Τ 4 6. e 3, 5 7. q i p q e 1 9. p MT 8, p i e 2, q RAA p q i ( p q) i (p q) ( p q) i 1 14 Σειρά Προβλημάτων 4 Λύσεις Χειμερινό Εξάμηνο 2018 Σελίδα 7
Λύσεις Σειράς Ασκήσεων 5
 Άσκηση 1 Λύσεις Σειράς Ασκήσεων 5 Να υπολογίσετε τις ασθενέστερες προσυνθήκες έτσι ώστε οι πιο κάτω προδιαγραφές να είναι ορθές σύμφωνα (i) με την έννοια της μερικής ορθότητας και (ii) με την έννοια της
Άσκηση 1 Λύσεις Σειράς Ασκήσεων 5 Να υπολογίσετε τις ασθενέστερες προσυνθήκες έτσι ώστε οι πιο κάτω προδιαγραφές να είναι ορθές σύμφωνα (i) με την έννοια της μερικής ορθότητας και (ii) με την έννοια της
Λύσεις Σειράς Ασκήσεων 5
 Άσκηση 1 (α) {x = 12 y = 7} skip {y = 7} Λύσεις Σειράς Ασκήσεων 5 Η προδιαγραφή αυτή είναι ορθή τόσο με την έννοια της μερικής ορθότητας όσο και με την έννοια της ολικής ορθότητας. Αυτό οφείλεται στο γεγονός
Άσκηση 1 (α) {x = 12 y = 7} skip {y = 7} Λύσεις Σειράς Ασκήσεων 5 Η προδιαγραφή αυτή είναι ορθή τόσο με την έννοια της μερικής ορθότητας όσο και με την έννοια της ολικής ορθότητας. Αυτό οφείλεται στο γεγονός
Λύσεις Σειράς Ασκήσεων 5
 Λύσεις Σειράς Ασκήσεων 5 Άσκηση 1 (α) Ακολουθεί η απόδειξη της προδιαγραφής (0) { A[X] = x A[Y] = y X Y (1) { A[Y] = y A[X] + Α[Υ] A[Y] = x X Y (2) A[X] := A[X] + A[Y]; (3) { A[Y] = y A[X] A[Y] = x X Y
Λύσεις Σειράς Ασκήσεων 5 Άσκηση 1 (α) Ακολουθεί η απόδειξη της προδιαγραφής (0) { A[X] = x A[Y] = y X Y (1) { A[Y] = y A[X] + Α[Υ] A[Y] = x X Y (2) A[X] := A[X] + A[Y]; (3) { A[Y] = y A[X] A[Y] = x X Y
Λύσεις Σειράς Ασκήσεων 5
 Άσκηση Λύσεις Σειράς Ασκήσεων 5 Έστω P και Q συνθήκες και S ένα πρόγραμμα. Να εξηγήσετε με λόγια τις πιο κάτω προδιαγραφές (i) με την έννοια της μερικής ορθότητας και (ii) με την έννοια της ολικής ορθότητας.
Άσκηση Λύσεις Σειράς Ασκήσεων 5 Έστω P και Q συνθήκες και S ένα πρόγραμμα. Να εξηγήσετε με λόγια τις πιο κάτω προδιαγραφές (i) με την έννοια της μερικής ορθότητας και (ii) με την έννοια της ολικής ορθότητας.
Λύσεις Σειράς Ασκήσεων 5
 Άσκηση 1 Λύσεις Σειράς Ασκήσεων 5 Να υπολογίσετε τις ασθενέστερες προσυνθήκες έτσι ώστε οι πιο κάτω προδιαγραφές να είναι ορθές σύμφωνα (i) με την έννοια της μερικής ορθότητας και (ii) με την έννοια της
Άσκηση 1 Λύσεις Σειράς Ασκήσεων 5 Να υπολογίσετε τις ασθενέστερες προσυνθήκες έτσι ώστε οι πιο κάτω προδιαγραφές να είναι ορθές σύμφωνα (i) με την έννοια της μερικής ορθότητας και (ii) με την έννοια της
Σειρά Προβλημάτων 5 Λύσεις
 Άσκηση 1 (15 μονάδες) Σειρά Προβλημάτων 5 Λύσεις Να δώσετε προδιαγραφές (τριάδες Hoare) για τα πιο κάτω προγράμματα: (α) Ένα πρόγραμμα το οποίο παίρνει ως δεδομένο εισόδου δύο πίνακες Α και Β και ελέγχει
Άσκηση 1 (15 μονάδες) Σειρά Προβλημάτων 5 Λύσεις Να δώσετε προδιαγραφές (τριάδες Hoare) για τα πιο κάτω προγράμματα: (α) Ένα πρόγραμμα το οποίο παίρνει ως δεδομένο εισόδου δύο πίνακες Α και Β και ελέγχει
Σειρά Προβλημάτων 1 Λύσεις
 Σειρά Προβλημάτων 1 Λύσεις Άσκηση 1 Να διατυπώσετε τον πιο κάτω συλλογισμό στον Προτασιακό Λογισμό και να τον αποδείξετε χρησιμοποιώντας τη Μέθοδο της Επίλυσης. Δηλαδή, να δείξετε ότι αν ισχύουν οι πέντε
Σειρά Προβλημάτων 1 Λύσεις Άσκηση 1 Να διατυπώσετε τον πιο κάτω συλλογισμό στον Προτασιακό Λογισμό και να τον αποδείξετε χρησιμοποιώντας τη Μέθοδο της Επίλυσης. Δηλαδή, να δείξετε ότι αν ισχύουν οι πέντε
Σειρά Προβλημάτων 4 Ημερομηνία Παράδοσης: 13/11/13
 Σειρά Προβλημάτων 4 Ημερομηνία Παράδοσης: 13/11/13 Άσκηση 1 (20 μονάδες) Οι ιδιότητες διατυπώνοντας στην PLTL ως εξής: (α) Αν ο καταχωρητής Κ 1 κάποια στιγμή πάρει την τιμή 1 θα διατηρήσει την τιμή αυτή
Σειρά Προβλημάτων 4 Ημερομηνία Παράδοσης: 13/11/13 Άσκηση 1 (20 μονάδες) Οι ιδιότητες διατυπώνοντας στην PLTL ως εξής: (α) Αν ο καταχωρητής Κ 1 κάποια στιγμή πάρει την τιμή 1 θα διατηρήσει την τιμή αυτή
Ανάλυση της Ορθότητας Προγραμμάτων
 Ανάλυση της Ορθότητας Προγραμμάτων Στην ενότητα αυτή θα μελετηθούν τα εξής θέματα: Η διαδικαστική γλώσσα προγραμματισμού WHILE Τριάδες Hoare Μερική και Ολική Ορθότητα Προγραμμάτων Κανόνες Απόδειξης Μερικής
Ανάλυση της Ορθότητας Προγραμμάτων Στην ενότητα αυτή θα μελετηθούν τα εξής θέματα: Η διαδικαστική γλώσσα προγραμματισμού WHILE Τριάδες Hoare Μερική και Ολική Ορθότητα Προγραμμάτων Κανόνες Απόδειξης Μερικής
Ανάλυση της Ορθότητας Προγραμμάτων
 Ανάλυση της Ορθότητας Προγραμμάτων Στην ενότητα αυτή θα μελετηθούν τα εξής θέματα: Η διαδικαστική γλώσσα προγραμματισμού WHILE Τριάδες Hoare Μερική και Ολική Ορθότητα Προγραμμάτων ΚανόνεςΑπόδειξηςΜερικήςΟρθότητας
Ανάλυση της Ορθότητας Προγραμμάτων Στην ενότητα αυτή θα μελετηθούν τα εξής θέματα: Η διαδικαστική γλώσσα προγραμματισμού WHILE Τριάδες Hoare Μερική και Ολική Ορθότητα Προγραμμάτων ΚανόνεςΑπόδειξηςΜερικήςΟρθότητας
Ανάλυση της Ορθότητας Προγραμμάτων (HR Κεφάλαιο 4)
 Ανάλυση της Ορθότητας Προγραμμάτων (HR Κεφάλαιο 4) Στην ενότητα αυτή θα μελετηθούν τα εξής θέματα: Η διαδικαστική γλώσσα προγραμματισμού WHILE Τριάδες Hoare Μερική και Ολική Ορθότητα Προγραμμάτων Κανόνες
Ανάλυση της Ορθότητας Προγραμμάτων (HR Κεφάλαιο 4) Στην ενότητα αυτή θα μελετηθούν τα εξής θέματα: Η διαδικαστική γλώσσα προγραμματισμού WHILE Τριάδες Hoare Μερική και Ολική Ορθότητα Προγραμμάτων Κανόνες
Σειρά Προβλημάτων 1 Λύσεις
 Σειρά Προβλημάτων 1 Λύσεις Άσκηση 1 O πιο κάτω συλλογισμός (αποτελεί μικρή παραλλαγή συλλογισμού που) αποδίδεται στον Samuel Clarke και προέρχεται από την εργασία του Demonstration of the Being and Attributes
Σειρά Προβλημάτων 1 Λύσεις Άσκηση 1 O πιο κάτω συλλογισμός (αποτελεί μικρή παραλλαγή συλλογισμού που) αποδίδεται στον Samuel Clarke και προέρχεται από την εργασία του Demonstration of the Being and Attributes
Σειρά Προβλημάτων 1 Λύσεις
 Σειρά Προβλημάτων 1 Λύσεις Άσκηση 1 Σκοπεύετε να διοργανώσετε ένα πάρτι για τους συμφοιτητές σας κάτω από τους πιο κάτω περιορισμούς. Π1. Η Μαίρη δεν μπορεί να έρθει. Π2. Ο Ηλίας και η Αντιγόνη είτε θα
Σειρά Προβλημάτων 1 Λύσεις Άσκηση 1 Σκοπεύετε να διοργανώσετε ένα πάρτι για τους συμφοιτητές σας κάτω από τους πιο κάτω περιορισμούς. Π1. Η Μαίρη δεν μπορεί να έρθει. Π2. Ο Ηλίας και η Αντιγόνη είτε θα
Λύσεις Σειράς Ασκήσεων 4
 Άσκηση 1 Λύσεις Σειράς Ασκήσεων 4 Θεωρήστε το σύνολο των ατομικών προτάσεων ΑΡ = {α, π, ε} που αντιστοιχούν στις ενέργειες αποστολής μηνύματος, παραλαβής μηνύματος και επιστροφής αποτελέσματος που εκτελούνται
Άσκηση 1 Λύσεις Σειράς Ασκήσεων 4 Θεωρήστε το σύνολο των ατομικών προτάσεων ΑΡ = {α, π, ε} που αντιστοιχούν στις ενέργειες αποστολής μηνύματος, παραλαβής μηνύματος και επιστροφής αποτελέσματος που εκτελούνται
Κεφάλαιο 5 Αξιωματική Σημασιολογία και Απόδειξη Ορθότητας Προγραμμάτων
 Κεφάλαιο 5 Αξιωματική Σημασιολογία και Απόδειξη Ορθότητας Προγραμμάτων Προπτυχιακό μάθημα Αρχές Γλωσσών Προγραμματισμού Π. Ροντογιάννης 1 Εισαγωγή Τα προγράμματα μιας (κλασικής) γλώσσας προγραμματισμού
Κεφάλαιο 5 Αξιωματική Σημασιολογία και Απόδειξη Ορθότητας Προγραμμάτων Προπτυχιακό μάθημα Αρχές Γλωσσών Προγραμματισμού Π. Ροντογιάννης 1 Εισαγωγή Τα προγράμματα μιας (κλασικής) γλώσσας προγραμματισμού
Ασκήσεις Επανάληψης Λύσεις
 Άσκηση 1 Ασκήσεις Επανάληψης Λύσεις (α) Το επακόλουθο (A (B C)) ((A C) (A B)) είναι ψευδές. Αυτό φαίνεται στην ανάθεση τιμών [Α] = Τ, [Β] = F, [C] = T. (β) Ακολουθεί η απόδειξη του επακόλουθου. 1. x(p(x)
Άσκηση 1 Ασκήσεις Επανάληψης Λύσεις (α) Το επακόλουθο (A (B C)) ((A C) (A B)) είναι ψευδές. Αυτό φαίνεται στην ανάθεση τιμών [Α] = Τ, [Β] = F, [C] = T. (β) Ακολουθεί η απόδειξη του επακόλουθου. 1. x(p(x)
Λύσεις Σειράς Ασκήσεων 1
 Λύσεις Σειράς Ασκήσεων 1 Άσκηση 1 p q r p (q r) (p q) p q r ( r p q) T T T T F T T T T F F F F T T F T T T T T T F F T T T T F T T T F T T F T F T F T T F F T T F T F F F F T F T T Ο πιο πάνω πίνακας παρουσιάζει
Λύσεις Σειράς Ασκήσεων 1 Άσκηση 1 p q r p (q r) (p q) p q r ( r p q) T T T T F T T T T F F F F T T F T T T T T T F F T T T T F T T T F T T F T F T F T T F F T T F T F F F F T F T T Ο πιο πάνω πίνακας παρουσιάζει
Ασκήσεις Επανάληψης Λύσεις
 Άσκηση 1 Ασκήσεις Επανάληψης Λύσεις (α) Το επακόλουθο (A (B C)) ((A C) (A B)) είναι ψευδές. Αυτό φαίνεται στην ανάθεση τιμών [Α] = Τ, [Β] = F, [C] = T. (β) Ακολουθεί η απόδειξη του επακόλουθου. 1. x(p(x)
Άσκηση 1 Ασκήσεις Επανάληψης Λύσεις (α) Το επακόλουθο (A (B C)) ((A C) (A B)) είναι ψευδές. Αυτό φαίνεται στην ανάθεση τιμών [Α] = Τ, [Β] = F, [C] = T. (β) Ακολουθεί η απόδειξη του επακόλουθου. 1. x(p(x)
Λύσεις Σειράς Ασκήσεων 1
 Λύσεις Σειράς Ασκήσεων 1 Άσκηση 1 Έστω οι προτάσεις / προϋπόθεσεις: Π1. Σε όσους αρέσει η τέχνη αρέσουν και τα λουλούδια. Π2. Σε όσους αρέσει το τρέξιμο αρέσει και η μουσική. Π3. Σε όσους δεν αρέσει η
Λύσεις Σειράς Ασκήσεων 1 Άσκηση 1 Έστω οι προτάσεις / προϋπόθεσεις: Π1. Σε όσους αρέσει η τέχνη αρέσουν και τα λουλούδια. Π2. Σε όσους αρέσει το τρέξιμο αρέσει και η μουσική. Π3. Σε όσους δεν αρέσει η
Λύσεις 1 ης Σειράς Ασκήσεων
 Λύσεις 1 ης Σειράς Ασκήσεων Άσκηση 1 Έστω οι ατομικές προτάσεις A 1 = H Αντιγόνη κέρδισε τον αγώνα, A 3 = H Αντιγόνη πήρε την τρίτη θέση, Β 2 = Ο Βίκτορας πήρε την δεύτερη θέση, Γ 3 = Ο Γιάννης πήρε την
Λύσεις 1 ης Σειράς Ασκήσεων Άσκηση 1 Έστω οι ατομικές προτάσεις A 1 = H Αντιγόνη κέρδισε τον αγώνα, A 3 = H Αντιγόνη πήρε την τρίτη θέση, Β 2 = Ο Βίκτορας πήρε την δεύτερη θέση, Γ 3 = Ο Γιάννης πήρε την
Σειρά Προβλημάτων 5 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { R η R είναι μια κανονική έκφραση η οποία παράγει μια μη πεπερασμένη γλώσσα} (β) { G η G είναι μια CFG η οποία
Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { R η R είναι μια κανονική έκφραση η οποία παράγει μια μη πεπερασμένη γλώσσα} (β) { G η G είναι μια CFG η οποία
Λύσεις Σειράς Ασκήσεων 4
 Άσκηση 1 Λύσεις Σειράς Ασκήσεων 4 Έστω το σύνολο ατομικών προτάσεων ΑΡ = {red, yellow, green}. Με βάση τις ατομικές προτάσεις ΑΡ διατυπώστε τις πιο κάτω προτάσεις που αφορούν την κατάσταση των φώτων της
Άσκηση 1 Λύσεις Σειράς Ασκήσεων 4 Έστω το σύνολο ατομικών προτάσεων ΑΡ = {red, yellow, green}. Με βάση τις ατομικές προτάσεις ΑΡ διατυπώστε τις πιο κάτω προτάσεις που αφορούν την κατάσταση των φώτων της
Σειρά Προβλημάτων 1 Λύσεις
 ΕΠΛ664: Ανάλυση και Επαλθευση Συστημάτων Τμμα Πληροφορικς Άσκηση 1 Σειρά Προβλημάτων 1 Λύσεις (α) Χρησιμοποιούμε τις επιπλέον μεταβλητές PC0, PC1, (program counters) οι οποίες παίρνουν ως τιμές ονόματα
ΕΠΛ664: Ανάλυση και Επαλθευση Συστημάτων Τμμα Πληροφορικς Άσκηση 1 Σειρά Προβλημάτων 1 Λύσεις (α) Χρησιμοποιούμε τις επιπλέον μεταβλητές PC0, PC1, (program counters) οι οποίες παίρνουν ως τιμές ονόματα
Σειρά Προβλημάτων 1 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 1 Λύσεις (α) Χρησιμοποιούμε τις επιπλέον μεταβλητές PC i, (program counters) οι οποίες παίρνουν ως τιμές ονόματα των γραμμών του κώδικα όπως φαίνεται πιο κάτω. Process P i :
Άσκηση 1 Σειρά Προβλημάτων 1 Λύσεις (α) Χρησιμοποιούμε τις επιπλέον μεταβλητές PC i, (program counters) οι οποίες παίρνουν ως τιμές ονόματα των γραμμών του κώδικα όπως φαίνεται πιο κάτω. Process P i :
ΕΠΑΛΗΘΕΥΣΗ ΠΡΟΓΡΑΜΜΑΤΩΝ Ι
 ΕΠΑΛΗΘΕΥΣΗ ΠΡΟΓΡΑΜΜΑΤΩΝ Ι Η τυπική επαλήθευση βάση μοντέλου είναι κατάλληλη για συστήματα επικοινωνούντων διεργασιών (π.χ. κατανεμημένα συστήματα) όπου το βασικό πρόβλημα είναι ο έλεγχος αλλά γενικά δεν
ΕΠΑΛΗΘΕΥΣΗ ΠΡΟΓΡΑΜΜΑΤΩΝ Ι Η τυπική επαλήθευση βάση μοντέλου είναι κατάλληλη για συστήματα επικοινωνούντων διεργασιών (π.χ. κατανεμημένα συστήματα) όπου το βασικό πρόβλημα είναι ο έλεγχος αλλά γενικά δεν
Λύσεις Σειράς Ασκήσεων 2
 Άσκηση 1 Λύσεις Σειράς Ασκήσεων 2 Ακολουθεί η διατύπωση των προτάσεων στον Κατηγορηματικό Λογισμό. (α) Δεν υπάρχουν δύο διαφορετικές πτήσεις με τον ίδιο αριθμό. x 1, d 1, a 1, s 1, t 1, x 2, d 2, a 2,
Άσκηση 1 Λύσεις Σειράς Ασκήσεων 2 Ακολουθεί η διατύπωση των προτάσεων στον Κατηγορηματικό Λογισμό. (α) Δεν υπάρχουν δύο διαφορετικές πτήσεις με τον ίδιο αριθμό. x 1, d 1, a 1, s 1, t 1, x 2, d 2, a 2,
Λύσεις 1 ης Σειράς Ασκήσεων
 Λύσεις 1 ης Σειράς Ασκήσεων Άσκηση 1 α) p q r (p s) ((s t) t) 1. p q r προϋπόθεση 2. p s προσωρινή υπόθεση 3. s t προσωρινή υπόθεση 4. p e 1 5. s ΜP 2,4 6. t ΜP 3,5 7. (s t) t i 3, 6 8. (p s) ((s t) t)
Λύσεις 1 ης Σειράς Ασκήσεων Άσκηση 1 α) p q r (p s) ((s t) t) 1. p q r προϋπόθεση 2. p s προσωρινή υπόθεση 3. s t προσωρινή υπόθεση 4. p e 1 5. s ΜP 2,4 6. t ΜP 3,5 7. (s t) t i 3, 6 8. (p s) ((s t) t)
Λύσεις 2 ης Σειράς Ασκήσεων
 Λύσεις 2 ης Σειράς Ασκήσεων Άσκηση 1 Στην άσκηση αυτή σας ζητείται να διατυπώσετε στον Κατηγορηματικό Λογισμό ένα σύνολο από απαιτήσεις/προτάσεις που σχετίζονται με ένα κοινωνικό δίκτυο χρησιμοποιώντας
Λύσεις 2 ης Σειράς Ασκήσεων Άσκηση 1 Στην άσκηση αυτή σας ζητείται να διατυπώσετε στον Κατηγορηματικό Λογισμό ένα σύνολο από απαιτήσεις/προτάσεις που σχετίζονται με ένα κοινωνικό δίκτυο χρησιμοποιώντας
Σειρά Προβλημάτων 1 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 1 Λύσεις (α) Χρησιμοποιούμε τις επιπλέον μεταβλητές PC 1, PC 2, (program counters) οι οποίες παίρνουν ως τιμές ονόματα των γραμμών του κώδικα όπως φαίνεται πιο κάτω. bool y 1
Άσκηση 1 Σειρά Προβλημάτων 1 Λύσεις (α) Χρησιμοποιούμε τις επιπλέον μεταβλητές PC 1, PC 2, (program counters) οι οποίες παίρνουν ως τιμές ονόματα των γραμμών του κώδικα όπως φαίνεται πιο κάτω. bool y 1
Η γλώσσα προγραμματισμού C
 Η γλώσσα προγραμματισμού C Εντολές ελέγχου ροής προγράμματος (if-else & switch) Η εντολή if-else Η εντολή if-else υπάρχει σχεδόν σε όλες τις γλώσσες προγραμματισμού. Χρησιμοποιείται για τον έλεγχο της
Η γλώσσα προγραμματισμού C Εντολές ελέγχου ροής προγράμματος (if-else & switch) Η εντολή if-else Η εντολή if-else υπάρχει σχεδόν σε όλες τις γλώσσες προγραμματισμού. Χρησιμοποιείται για τον έλεγχο της
Βρόχοι. Εντολή επανάληψης. Το άθροισμα των αριθμών 1 5 υπολογίζεται με την εντολή. Πρόβλημα. Πώς θα υπολογίσουμε το άθροισμα των ακέραιων ;
 Εντολή επανάληψης Το άθροισμα των αριθμών 1 5 υπολογίζεται με την εντολή Πρόβλημα Πώς θα υπολογίσουμε το άθροισμα των ακέραιων 1 5000; Ισοδύναμοι υπολογισμοί του Ισοδύναμοι υπολογισμοί του Ισοδύναμοι υπολογισμοί
Εντολή επανάληψης Το άθροισμα των αριθμών 1 5 υπολογίζεται με την εντολή Πρόβλημα Πώς θα υπολογίσουμε το άθροισμα των ακέραιων 1 5000; Ισοδύναμοι υπολογισμοί του Ισοδύναμοι υπολογισμοί του Ισοδύναμοι υπολογισμοί
Σειρά Προβλημάτων 3 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 3 Λύσεις Να δώσετε ασυμφραστικές γραμματικές που να παράγουν τις πιο κάτω γλώσσες: (α) { w {(, )} * οι παρενθέσεις στην w είναι ισοζυγισμένες } (β) { a k b m c 2m a k k > 0,
Άσκηση 1 Σειρά Προβλημάτων 3 Λύσεις Να δώσετε ασυμφραστικές γραμματικές που να παράγουν τις πιο κάτω γλώσσες: (α) { w {(, )} * οι παρενθέσεις στην w είναι ισοζυγισμένες } (β) { a k b m c 2m a k k > 0,
Λύσεις Σειράς Ασκήσεων 2
 Λύσεις Σειράς Ασκήσεων 2 Άσκηση 1 N φιλόσοφοι κάθονται γύρω από ένα τραπέζι με N καρέκλες, N πιάτα και N πιρούνια. Όταν κάποιος φιλόσοφος πεινάσει παίρνει τα δύο πιρούνια που βρίσκονται δίπλα από το πιάτο
Λύσεις Σειράς Ασκήσεων 2 Άσκηση 1 N φιλόσοφοι κάθονται γύρω από ένα τραπέζι με N καρέκλες, N πιάτα και N πιρούνια. Όταν κάποιος φιλόσοφος πεινάσει παίρνει τα δύο πιρούνια που βρίσκονται δίπλα από το πιάτο
Σειρά Προβλημάτων 5 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) ({ G η G είναι μια ασυμφραστική γραμματική που δεν παράγει καμιά λέξη με μήκος μικρότερο του 2 } (β) { Μ,w
Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) ({ G η G είναι μια ασυμφραστική γραμματική που δεν παράγει καμιά λέξη με μήκος μικρότερο του 2 } (β) { Μ,w
Προγραμματισμός ΗΥ και Υπολογιστική Φυσική. Χρήστος Γκουμόπουλος
 Προγραμματισμός ΗΥ και Υπολογιστική Φυσική Χρήστος Γκουμόπουλος Προγραμματισμός ΗΥ και Υπολογιστική Φυσική Χρήστος Γκουμόπουλος Προγραμματισμός ΗΥ και Υπολογιστική Φυσική Χρήστος Γκουμόπουλος Προγραμματισμός
Προγραμματισμός ΗΥ και Υπολογιστική Φυσική Χρήστος Γκουμόπουλος Προγραμματισμός ΗΥ και Υπολογιστική Φυσική Χρήστος Γκουμόπουλος Προγραμματισμός ΗΥ και Υπολογιστική Φυσική Χρήστος Γκουμόπουλος Προγραμματισμός
if(συνθήκη) {... // οµάδα εντολών } C: Από τη Θεωρία στην Εφαρµογή 5 ο Κεφάλαιο
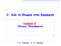 C: Από τη Θεωρία στην Εφαρµογή Κεφάλαιο 5 ο Έλεγχος Προγράµµατος Γ. Σ. Τσελίκης Ν. Δ. Τσελίκας Η εντολή if (Ι) Η εντολή if είναι µία από τις βασικότερες δοµές ελέγχου ροής στη C, αλλά και στις περισσότερες
C: Από τη Θεωρία στην Εφαρµογή Κεφάλαιο 5 ο Έλεγχος Προγράµµατος Γ. Σ. Τσελίκης Ν. Δ. Τσελίκας Η εντολή if (Ι) Η εντολή if είναι µία από τις βασικότερες δοµές ελέγχου ροής στη C, αλλά και στις περισσότερες
ιαφάνειες παρουσίασης #3
 ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟ http://www.corelab.ece.ntua.gr/courses/programming/ ιδάσκοντες: Στάθης Ζάχος (zachos@cs.ntua.gr) Νίκος Παπασπύρου (nickie@softlab.ntua.gr) ιαφάνειες παρουσίασης #3!Λογικά διαγράµµατα
ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟ http://www.corelab.ece.ntua.gr/courses/programming/ ιδάσκοντες: Στάθης Ζάχος (zachos@cs.ntua.gr) Νίκος Παπασπύρου (nickie@softlab.ntua.gr) ιαφάνειες παρουσίασης #3!Λογικά διαγράµµατα
ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΥΠΟΛΟΓΙΣΜΟΣ Εντολές επιλογής και αποφάσεων 1 ο Φύλλο Εργασιών Εισαγωγικές ασκήσεις για την εντολή if ΑΠΑΝΤΗΣΕΙΣ
 ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΥΠΟΛΟΓΙΣΜΟΣ Κεφάλαιο 10 : Εντολές επιλογής και αποφάσεων 1 ο Φύλλο Εργασιών Εισαγωγικές ασκήσεις για την εντολή if ΑΠΑΝΤΗΣΕΙΣ 1. Ποιες από τις παρακάτω εντολές είναι σωστές; α) if A + B
ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΥΠΟΛΟΓΙΣΜΟΣ Κεφάλαιο 10 : Εντολές επιλογής και αποφάσεων 1 ο Φύλλο Εργασιών Εισαγωγικές ασκήσεις για την εντολή if ΑΠΑΝΤΗΣΕΙΣ 1. Ποιες από τις παρακάτω εντολές είναι σωστές; α) if A + B
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 664: Ανάλυση και Επαλήθευση Συστημάτων ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ ΗΜΕΡΟΜΗΝΙΑ : Πέμπτη, 21 Μαρτίου 2013 ΔΙΑΡΚΕΙΑ : 14:00 16:00 ΔΙΔΑΣΚΟΥΣΑ : Άννα Φιλίππου Ονοματεπώνυμο:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 664: Ανάλυση και Επαλήθευση Συστημάτων ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ ΗΜΕΡΟΜΗΝΙΑ : Πέμπτη, 21 Μαρτίου 2013 ΔΙΑΡΚΕΙΑ : 14:00 16:00 ΔΙΔΑΣΚΟΥΣΑ : Άννα Φιλίππου Ονοματεπώνυμο:
Σειρά Προβλημάτων 4 Λύσεις
 Σειρά Προβλημάτων 4 Λύσεις Άσκηση 1 Θεωρήστε την ακόλουθη δομή Kripke. {entry} 0 1 {active} 2 {active, request} 3 {active, response} Να διατυπώσετε τις πιο κάτω προτάσεις στην LTL (αν αυτό είναι εφικτό)
Σειρά Προβλημάτων 4 Λύσεις Άσκηση 1 Θεωρήστε την ακόλουθη δομή Kripke. {entry} 0 1 {active} 2 {active, request} 3 {active, response} Να διατυπώσετε τις πιο κάτω προτάσεις στην LTL (αν αυτό είναι εφικτό)
Σειρά Προβλημάτων 3 Ημερομηνία Παράδοσης: 04/04/16
 ΜΕΡΟΣ Α Άσκηση 1 Σειρά Προβλημάτων 3 Ημερομηνία Παράδοσης: 04/04/16 Δύο ιδιότητες φ και ψ είναι ισοδύναμες μεταξύ τους, φ ψ, αν, για κάθε δομή Kripke M, M φ αν και μόνο αν M ψ. Να αποφασίσετε ποια από
ΜΕΡΟΣ Α Άσκηση 1 Σειρά Προβλημάτων 3 Ημερομηνία Παράδοσης: 04/04/16 Δύο ιδιότητες φ και ψ είναι ισοδύναμες μεταξύ τους, φ ψ, αν, για κάθε δομή Kripke M, M φ αν και μόνο αν M ψ. Να αποφασίσετε ποια από
Στην εντολή while η επανάληψη συνεχίζεται όσο η λογική έκφραση έχει τιμή false.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΕΠΑΛ (ΟΜΑΔΑ Α ) & ΜΑΘΗΜΑΤΩΝ ΕΙΔΙΚΟΤΗΤΑΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 08/04/2015 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΔΟΜΗΜΕΝΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ Α Α1. Να χαρακτηρίσετε τις
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΤΑΞΗ ΕΠΑΛ (ΟΜΑΔΑ Α ) & ΜΑΘΗΜΑΤΩΝ ΕΙΔΙΚΟΤΗΤΑΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 08/04/2015 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΔΟΜΗΜΕΝΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ Α Α1. Να χαρακτηρίσετε τις
Διαδικασιακός Προγραμματισμός
 Τμήμα ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ ΤΕΙ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ Διαδικασιακός Προγραμματισμός Διάλεξη 5 η Έλεγχος Προγράμματος Οι διαλέξεις βασίζονται στο βιβλίο των Τσελίκη και Τσελίκα C: Από τη Θεωρία στην Εφαρμογή
Τμήμα ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ ΤΕΙ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ Διαδικασιακός Προγραμματισμός Διάλεξη 5 η Έλεγχος Προγράμματος Οι διαλέξεις βασίζονται στο βιβλίο των Τσελίκη και Τσελίκα C: Από τη Θεωρία στην Εφαρμογή
ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΥΠΟΛΟΓΙΣΤΩΝ & ΥΠΟΛΟΓΙΣΤΙΚΗ ΦΥΣΙΚΗ
 ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΥΠΟΛΟΓΙΣΤΩΝ & ΥΠΟΛΟΓΙΣΤΙΚΗ ΦΥΣΙΚΗ Μέρος 5ο ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ 1 Η ΕΝΤΟΛΗ for Με την εντολή for δημιουργούμε βρόχους επανάληψης σε
ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΥΠΟΛΟΓΙΣΤΩΝ & ΥΠΟΛΟΓΙΣΤΙΚΗ ΦΥΣΙΚΗ Μέρος 5ο ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ 1 Η ΕΝΤΟΛΗ for Με την εντολή for δημιουργούμε βρόχους επανάληψης σε
Υπολογιστικά & Διακριτά Μαθηματικά
 Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 2:Στοιχεία Μαθηματικής Λογικής Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 2:Στοιχεία Μαθηματικής Λογικής Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
3 ο Εργαστήριο Μεταβλητές, Τελεστές
 3 ο Εργαστήριο Μεταβλητές, Τελεστές Μια μεταβλητή έχει ένα όνομα και ουσιαστικά είναι ένας δείκτης σε μια συγκεκριμένη θέση στη μνήμη του υπολογιστή. Στη θέση μνήμης στην οποία δείχνει μια μεταβλητή αποθηκεύονται
3 ο Εργαστήριο Μεταβλητές, Τελεστές Μια μεταβλητή έχει ένα όνομα και ουσιαστικά είναι ένας δείκτης σε μια συγκεκριμένη θέση στη μνήμη του υπολογιστή. Στη θέση μνήμης στην οποία δείχνει μια μεταβλητή αποθηκεύονται
Προτασιακός Λογισμός (HR Κεφάλαιο 1)
 Προτασιακός Λογισμός (HR Κεφάλαιο 1) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Σύνταξη Λογικός Συμπερασμός Σημασιολογία Ορθότητα και Πληρότητα Κανονικές Μορφές Προτάσεις Horn ΕΠΛ 412 Λογική
Προτασιακός Λογισμός (HR Κεφάλαιο 1) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Σύνταξη Λογικός Συμπερασμός Σημασιολογία Ορθότητα και Πληρότητα Κανονικές Μορφές Προτάσεις Horn ΕΠΛ 412 Λογική
Δομές ελέγχου ροής προγράμματος
 Δομές ελέγχου ροής προγράμματος Υπάρχουν δύο είδη δομών ελέγχου ροής (control flow): Οι δομές επιλογής και Οι δομές επανάληψης Δομές ελέγχου ροής προγράμματος Είδος δομής Δομές επιλογής Δομή ελέγχου ροής
Δομές ελέγχου ροής προγράμματος Υπάρχουν δύο είδη δομών ελέγχου ροής (control flow): Οι δομές επιλογής και Οι δομές επανάληψης Δομές ελέγχου ροής προγράμματος Είδος δομής Δομές επιλογής Δομή ελέγχου ροής
A2. Να γράψετε για κάθε περίπτωση τον αριθμό της πρότασης και δίπλα το γράμμα που δίνει τη σωστή επιλογή.
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΥΠΟΛΟΓΙΣΤΩΝ/Γ' ΕΠΑ.Λ. ΗΜΕΡΟΜΗΝΙΑ: 17-1-2016 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: Ι.ΜΙΧΑΛΕΑΚΟΣ-Χ.ΠΑΠΠΑ-Α.ΚΑΤΡΑΚΗ ΘΕΜΑ Α Α1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας δίπλα
ΜΑΘΗΜΑ / ΤΑΞΗ : ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΥΠΟΛΟΓΙΣΤΩΝ/Γ' ΕΠΑ.Λ. ΗΜΕΡΟΜΗΝΙΑ: 17-1-2016 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: Ι.ΜΙΧΑΛΕΑΚΟΣ-Χ.ΠΑΠΠΑ-Α.ΚΑΤΡΑΚΗ ΘΕΜΑ Α Α1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας δίπλα
ΘΕΜΑ Α. Α1. Να γράψετε στο. 2. Τα του. τις. αριθμητικές. πρώτες. β. Να. Σελίδα 1 από 5. 2) χ 2. χ Τ_Ρ(α) ΓΡΑΨΕ. ΓΡΑΨΕ χ χ χ+2
 ΜΑΘΗΜΑΑ / ΤΑΞΗ : ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 25/11/2017 ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς απόό τις παρακάτω προτάσεις 1-10 και δίπλα
ΜΑΘΗΜΑΑ / ΤΑΞΗ : ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 25/11/2017 ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς απόό τις παρακάτω προτάσεις 1-10 και δίπλα
Σειρά Προβλημάτων 3 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 3 Λύσεις Να δώσετε ασυμφραστικές γραμματικές που να παράγουν τις πιο κάτω γλώσσες: (α) { x x η τιμή της αριθμητικής έκφρασης 10 2n + 10 n + 1, n 1} (β) { a i b j c k d m i, j,
Άσκηση 1 Σειρά Προβλημάτων 3 Λύσεις Να δώσετε ασυμφραστικές γραμματικές που να παράγουν τις πιο κάτω γλώσσες: (α) { x x η τιμή της αριθμητικής έκφρασης 10 2n + 10 n + 1, n 1} (β) { a i b j c k d m i, j,
Ο βρόχος for Η εντολή for χρησιμοποιείται για τη δημιουργία επαναληπτικών βρόχων στη C
 Ο βρόχος for Η εντολή for χρησιμοποιείται για τη δημιουργία επαναληπτικών βρόχων στη C Επαναληπτικός βρόχος καλείται το τμήμα του κώδικα μέσα σε ένα πρόγραμμα, το οποίο εκτελείται από την αρχή και επαναλαμβάνεται
Ο βρόχος for Η εντολή for χρησιμοποιείται για τη δημιουργία επαναληπτικών βρόχων στη C Επαναληπτικός βρόχος καλείται το τμήμα του κώδικα μέσα σε ένα πρόγραμμα, το οποίο εκτελείται από την αρχή και επαναλαμβάνεται
Σειρά Προβλημάτων 4 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing (αυθεντικός ορισμός) η οποία να διαγιγνώσκει τη γλώσσα { ww w {a,b}* }. (β) Να διατυπώσετε την τυπική περιγραφή
Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing (αυθεντικός ορισμός) η οποία να διαγιγνώσκει τη γλώσσα { ww w {a,b}* }. (β) Να διατυπώσετε την τυπική περιγραφή
Σειρά Προβλημάτων 5 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { Μ η Μ είναι μια ΤΜ η οποία διαγιγνώσκει το πρόβλημα ΙΣΟΔΥΝΑΜΙΑ ΤΜ (διαφάνεια 9 25)} (α) Γνωρίζουμε ότι το
Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { Μ η Μ είναι μια ΤΜ η οποία διαγιγνώσκει το πρόβλημα ΙΣΟΔΥΝΑΜΙΑ ΤΜ (διαφάνεια 9 25)} (α) Γνωρίζουμε ότι το
Φροντιστήριο 2 Λύσεις
 Φροντιστήριο 2 Λύσεις Άσκηση 1 1. p ( p r) προϋπόθεση 2. r προϋπόθεση 3. q προσωρινή υπόθεση 4. p προσωρινή υπόθεση 5. p r ΜP 6. p προσωρινή υπόθεση r προσωρινή υπόθεση 7. i 4, 6 8. r e 9. r e 5, 8, 6
Φροντιστήριο 2 Λύσεις Άσκηση 1 1. p ( p r) προϋπόθεση 2. r προϋπόθεση 3. q προσωρινή υπόθεση 4. p προσωρινή υπόθεση 5. p r ΜP 6. p προσωρινή υπόθεση r προσωρινή υπόθεση 7. i 4, 6 8. r e 9. r e 5, 8, 6
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ : Λογική στην Πληροφορική Δείγμα Ενδιάμεσης Εξέτασης Σκελετοί Λύσεων Άσκηση [0 μονάδες] α Να αναφέρετε τρεις μεθόδους μέσω των οποίων μπορούμε να αποφασίσουμε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ : Λογική στην Πληροφορική Δείγμα Ενδιάμεσης Εξέτασης Σκελετοί Λύσεων Άσκηση [0 μονάδες] α Να αναφέρετε τρεις μεθόδους μέσω των οποίων μπορούμε να αποφασίσουμε
Κατηγορηματικός Λογισμός (ΗR Κεφάλαιο 2.1-2.5)
 Κατηγορηματικός Λογισμός (ΗR Κεφάλαιο 2.1-2.5) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Εισαγωγή στον Κατηγορηματικό Λογισμό Σύνταξη Κανόνες Συμπερασμού Σημασιολογία ΕΠΛ 412 Λογική στην
Κατηγορηματικός Λογισμός (ΗR Κεφάλαιο 2.1-2.5) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Εισαγωγή στον Κατηγορηματικό Λογισμό Σύνταξη Κανόνες Συμπερασμού Σημασιολογία ΕΠΛ 412 Λογική στην
Προγραµµατισµός Η/Υ. Μέρος2
 Προγραµµατισµός Η/Υ Μέρος2 Περιεχόμενα Επανάληψη Βασικών Σύμβολων Διαγραμμάτων Ροής Αλγόριθμος Ψευδοκώδικας Παραδείγματα Αλγορίθμων Γλώσσες προγραμματισμού 2 Επανάληψη Βασικών Σύμβολων Διαγραμμάτων Ροής
Προγραµµατισµός Η/Υ Μέρος2 Περιεχόμενα Επανάληψη Βασικών Σύμβολων Διαγραμμάτων Ροής Αλγόριθμος Ψευδοκώδικας Παραδείγματα Αλγορίθμων Γλώσσες προγραμματισμού 2 Επανάληψη Βασικών Σύμβολων Διαγραμμάτων Ροής
Σειρά Προβλημάτων 5 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { D το D είναι ένα DFA το οποίο αποδέχεται όλες τις λέξεις στο Σ * } (α) Για να διαγνώσουμε το πρόβλημα μπορούμε
Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { D το D είναι ένα DFA το οποίο αποδέχεται όλες τις λέξεις στο Σ * } (α) Για να διαγνώσουμε το πρόβλημα μπορούμε
for for for for( . */
 Εισαγωγή Στον Προγραµµατισµό «C» Βρόχοι Επανάληψης Πανεπιστήµιο Πελοποννήσου Τµήµα Πληροφορικής & Τηλεπικοινωνιών Νικόλαος Δ. Τσελίκας Νικόλαος Προγραµµατισµός Δ. Τσελίκας Ι Ο βρόχος for Η εντολή for χρησιµοποιείται
Εισαγωγή Στον Προγραµµατισµό «C» Βρόχοι Επανάληψης Πανεπιστήµιο Πελοποννήσου Τµήµα Πληροφορικής & Τηλεπικοινωνιών Νικόλαος Δ. Τσελίκας Νικόλαος Προγραµµατισµός Δ. Τσελίκας Ι Ο βρόχος for Η εντολή for χρησιµοποιείται
Όταν το πρόγραμμα φτάσει σε αυτή την εντολή και ο καταχωρητής PINA έχει την τιμή
 5. Εντολή while() Η εντολή while() είναι ίσως η πιο πολυχρησιμοποιούμενη εντολή κατά τη σύνταξη κώδικα σε γλώσσα προγραμματισμού C για μικροελεγκτές. Το κυρίως μέρος του προγράμματος κλείνεται σχεδόν πάντα
5. Εντολή while() Η εντολή while() είναι ίσως η πιο πολυχρησιμοποιούμενη εντολή κατά τη σύνταξη κώδικα σε γλώσσα προγραμματισμού C για μικροελεγκτές. Το κυρίως μέρος του προγράμματος κλείνεται σχεδόν πάντα
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Η/Υ. Δομή Επιλογής. Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Η/Υ Δομή Επιλογής Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Δομή Επιλογής (Απόφασης) Εκτέλεση υπό συνθήκη IF THEN IF THEN ELSE IF THEN
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Η/Υ Δομή Επιλογής Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Δομή Επιλογής (Απόφασης) Εκτέλεση υπό συνθήκη IF THEN IF THEN ELSE IF THEN
Γ ΤΑΞΗ ΗΜΕΡΗΣΙΟΥ ΕΠΑ.Λ ΜΑΘΗΜΑ ΕΙ ΙΚΟΤΗΤΑΣ ΟΜΗΜΕΝΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΕΚΦΩΝΗΣΕΙΣ
 1 ΘΕΜΑ 1 Γ ΤΑΞΗ ΗΜΕΡΗΣΙΟΥ ΕΠΑ.Λ ΜΑΘΗΜΑ ΕΙ ΙΚΟΤΗΤΑΣ ΟΜΗΜΕΝΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΕΚΦΩΝΗΣΕΙΣ Α) Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω προτάσεις και δίπλα τη λέξη Σωστό, αν είναι σωστή,
1 ΘΕΜΑ 1 Γ ΤΑΞΗ ΗΜΕΡΗΣΙΟΥ ΕΠΑ.Λ ΜΑΘΗΜΑ ΕΙ ΙΚΟΤΗΤΑΣ ΟΜΗΜΕΝΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΕΚΦΩΝΗΣΕΙΣ Α) Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω προτάσεις και δίπλα τη λέξη Σωστό, αν είναι σωστή,
Ελεγχος, Αξιοπιστία και Διασφάλιση Ποιότητας Λογισµικού Πολυπλοκότητα
 Ελεγχος, Αξιοπιστία και Διασφάλιση Ποιότητας Λογισµικού Πολυπλοκότητα Τµήµα Διοίκησης Επιχειρήσεων Τει Δυτικής Ελλάδας Μεσολόγγι Δρ. Α. Στεφανή Διάλεξη 5 2 Εγκυροποίηση Λογισµικού Εγκυροποίηση Λογισµικού
Ελεγχος, Αξιοπιστία και Διασφάλιση Ποιότητας Λογισµικού Πολυπλοκότητα Τµήµα Διοίκησης Επιχειρήσεων Τει Δυτικής Ελλάδας Μεσολόγγι Δρ. Α. Στεφανή Διάλεξη 5 2 Εγκυροποίηση Λογισµικού Εγκυροποίηση Λογισµικού
ιαφάνειες παρουσίασης #3
 ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ http://www.corelab.ece.ntua.gr/courses/programming/ ιδάσκοντες: Στάθης Ζάχος (zachos@cs.ntua.gr) Νίκος Παπασπύρου (nickie@softlab.ntua.gr) ιαφάνειες παρουσίασης
ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ http://www.corelab.ece.ntua.gr/courses/programming/ ιδάσκοντες: Στάθης Ζάχος (zachos@cs.ntua.gr) Νίκος Παπασπύρου (nickie@softlab.ntua.gr) ιαφάνειες παρουσίασης
Διαδικασιακός Προγραμματισμός
 Τμήμα ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ ΤΕΙ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ Διαδικασιακός Προγραμματισμός Διάλεξη 6 η Βρόχοι Επανάληψης Οι διαλέξεις βασίζονται στο βιβλίο των Τσελίκη και Τσελίκα C: Από τη Θεωρία στην Εφαρμογή
Τμήμα ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ ΤΕΙ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ Διαδικασιακός Προγραμματισμός Διάλεξη 6 η Βρόχοι Επανάληψης Οι διαλέξεις βασίζονται στο βιβλίο των Τσελίκη και Τσελίκα C: Από τη Θεωρία στην Εφαρμογή
ιαδικαστικός Προγραμματισμός
 ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ιαδικαστικός Προγραμματισμός Α Εξάμηνο Μάθημα 2 ο : Εντολές ελέγχου > εντολές υπό συνθήκη Στόχοι μαθήματος Να κατανοήσετε τη σχέση μεταξύ εντολών και παραστάσεων. Να αναγνωρίζετε
ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ιαδικαστικός Προγραμματισμός Α Εξάμηνο Μάθημα 2 ο : Εντολές ελέγχου > εντολές υπό συνθήκη Στόχοι μαθήματος Να κατανοήσετε τη σχέση μεταξύ εντολών και παραστάσεων. Να αναγνωρίζετε
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Δομημένος Προγραμματισμός. Τμήμα Επιχειρηματικού Σχεδιασμού και Πληροφοριακών Συστημάτων
 Δομημένος Προγραμματισμός Τμήμα Επιχειρηματικού Σχεδιασμού και Πληροφοριακών Συστημάτων www.bpis.teicrete.gr Τμήμα Επιχειρηματικού Σχεδιασμού και Πληροφοριακών Συστημάτων www.bpis.teicrete.gr 2 Νέο Πρόγραμμα
Δομημένος Προγραμματισμός Τμήμα Επιχειρηματικού Σχεδιασμού και Πληροφοριακών Συστημάτων www.bpis.teicrete.gr Τμήμα Επιχειρηματικού Σχεδιασμού και Πληροφοριακών Συστημάτων www.bpis.teicrete.gr 2 Νέο Πρόγραμμα
Σημειώσεις του εργαστηριακού μαθήματος Πληροφορική ΙΙ. Εισαγωγή στην γλώσσα προγραμματισμού
 Σημειώσεις του εργαστηριακού μαθήματος Πληροφορική ΙΙ Εισαγωγή στην γλώσσα προγραμματισμού Ακαδημαϊκό έτος 2016-2017, Εαρινό εξάμηνο Οι σημειώσεις βασίζονται στα συγγράμματα: A byte of Python (ελληνική
Σημειώσεις του εργαστηριακού μαθήματος Πληροφορική ΙΙ Εισαγωγή στην γλώσσα προγραμματισμού Ακαδημαϊκό έτος 2016-2017, Εαρινό εξάμηνο Οι σημειώσεις βασίζονται στα συγγράμματα: A byte of Python (ελληνική
d k 10 k + d k 1 10 k d d = k i=0 d i 10 i.
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΥΠΟΛΟΓΙΣΤΩΝ & ΥΠΟΛΟΓΙΣΤΙΚΗ ΦΥΣΙΚΗ
 ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΥΠΟΛΟΓΙΣΤΩΝ & ΥΠΟΛΟΓΙΣΤΙΚΗ ΦΥΣΙΚΗ Μέρος 4ο ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ 1 ΟΙ ΤΕΛΕΣΤΕΣ ΣΥΓΚΡΙΣΗΣ Με τους τελεστές σύγκρισης, συγκρίνουμε τις
ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΥΠΟΛΟΓΙΣΤΩΝ & ΥΠΟΛΟΓΙΣΤΙΚΗ ΦΥΣΙΚΗ Μέρος 4ο ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ 1 ΟΙ ΤΕΛΕΣΤΕΣ ΣΥΓΚΡΙΣΗΣ Με τους τελεστές σύγκρισης, συγκρίνουμε τις
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 412: Λογική στην Πληροφορική Ενδιάμεση Εξέταση Ημερομηνία : Τετάρτη 24 Οκτωβρίου, 2018 Διάρκεια : 12:00 13:30 Διδάσκουσα : Άννα Φιλίππου Ονοματεπώνυμο: ΠΡΟΧΕΙΡΕΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 412: Λογική στην Πληροφορική Ενδιάμεση Εξέταση Ημερομηνία : Τετάρτη 24 Οκτωβρίου, 2018 Διάρκεια : 12:00 13:30 Διδάσκουσα : Άννα Φιλίππου Ονοματεπώνυμο: ΠΡΟΧΕΙΡΕΣ
ΠΛΗΡΟΦΟΡΙΚΗ ΙΙ (JAVA) 11/3/2008
 ΠΛΗΡΟΦΟΡΙΚΗ ΙΙ (JAVA) 11/3/2008 Κατασκευαστές (Constructors) Ειδικός τύπος μεθόδων, οι οποίες: - είναι public και έχουν το ίδιο όνομα με αυτό της κλάσης - χρησιμοποιούνται για να αρχικοποιήσουν κάποιες
ΠΛΗΡΟΦΟΡΙΚΗ ΙΙ (JAVA) 11/3/2008 Κατασκευαστές (Constructors) Ειδικός τύπος μεθόδων, οι οποίες: - είναι public και έχουν το ίδιο όνομα με αυτό της κλάσης - χρησιμοποιούνται για να αρχικοποιήσουν κάποιες
Εντολές επιλογής Επαναλήψεις (if, switch, while)
 Εντολές επιλογής Επαναλήψεις (if, switch, while) Οι σημειώσεις αυτές έχουν σαν στόχο την μάθηση εντολών επιλογής (if, switch, while) που ελέγχουν τη ροή εκτέλεσης ενός προγράμματος. Πρώτα όμως, είναι αναγκαίο
Εντολές επιλογής Επαναλήψεις (if, switch, while) Οι σημειώσεις αυτές έχουν σαν στόχο την μάθηση εντολών επιλογής (if, switch, while) που ελέγχουν τη ροή εκτέλεσης ενός προγράμματος. Πρώτα όμως, είναι αναγκαίο
Η γλώσσα προγραμματισμού C
 Η γλώσσα προγραμματισμού C Εντολές ελέγχου ροής προγράμματος (if-else & switch) Η εντολή if-else Η εντολή if-else υπάρχει σχεδόν σε όλες τις γλώσσες προγραμματισμού. Χρησιμοποιείται για τον έλεγχο της
Η γλώσσα προγραμματισμού C Εντολές ελέγχου ροής προγράμματος (if-else & switch) Η εντολή if-else Η εντολή if-else υπάρχει σχεδόν σε όλες τις γλώσσες προγραμματισμού. Χρησιμοποιείται για τον έλεγχο της
Σειρά Προβλημάτων 3 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 3 Λύσεις Να δώσετε ασυμφραστικές γραμματικές που να παράγουν τις πιο κάτω γλώσσες: (α) { a m b n c p m,n,p 0 και είτε m + n = p είτε m = n + p } (β) { xx rev yy rev x, y {a,b}
Άσκηση 1 Σειρά Προβλημάτων 3 Λύσεις Να δώσετε ασυμφραστικές γραμματικές που να παράγουν τις πιο κάτω γλώσσες: (α) { a m b n c p m,n,p 0 και είτε m + n = p είτε m = n + p } (β) { xx rev yy rev x, y {a,b}
Σειρά Προβλημάτων 1 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 1 Λύσεις (α) Χρησιμοποιούμε τις επιπλέον μεταβλητές PC 0, PC 1, (program counters) οι οποίες παίρνουν ως τιμές ονόματα των γραμμών του κώδικα όπως φαίνεται πιο κάτω. P[0] P[1]
Άσκηση 1 Σειρά Προβλημάτων 1 Λύσεις (α) Χρησιμοποιούμε τις επιπλέον μεταβλητές PC 0, PC 1, (program counters) οι οποίες παίρνουν ως τιμές ονόματα των γραμμών του κώδικα όπως φαίνεται πιο κάτω. P[0] P[1]
1. Πότε χρησιμοποιούμε την δομή επανάληψης; Ποιες είναι οι διάφορες εντολές (μορφές) της;
 1. Πότε χρησιμοποιούμε την δομή επανάληψης; Ποιες είναι οι διάφορες (μορφές) της; Η δομή επανάληψης χρησιμοποιείται όταν μια σειρά εντολών πρέπει να εκτελεστεί σε ένα σύνολο περιπτώσεων, που έχουν κάτι
1. Πότε χρησιμοποιούμε την δομή επανάληψης; Ποιες είναι οι διάφορες (μορφές) της; Η δομή επανάληψης χρησιμοποιείται όταν μια σειρά εντολών πρέπει να εκτελεστεί σε ένα σύνολο περιπτώσεων, που έχουν κάτι
ΠΛΗΡΟΦΟΡΙΚΗ Ι (MATLAB) Ενότητα 2
 ΠΛΗΡΟΦΟΡΙΚΗ Ι (MATLAB) Ενότητα 2 Σημειώσεις βασισμένες στο βιβλίο Το MATLAB στην Υπολογιστική Επιστήμη και Τεχνολογία Μια Εισαγωγή Έλεγχος συνθηκών - if Ας μελετήσουμε το πρόβλημα του υπολογισμού του ελάχιστου
ΠΛΗΡΟΦΟΡΙΚΗ Ι (MATLAB) Ενότητα 2 Σημειώσεις βασισμένες στο βιβλίο Το MATLAB στην Υπολογιστική Επιστήμη και Τεχνολογία Μια Εισαγωγή Έλεγχος συνθηκών - if Ας μελετήσουμε το πρόβλημα του υπολογισμού του ελάχιστου
Εισαγωγή στον Προγραµµατισµό. Διάλεξη 3 η : Επίλυση Προβληµάτων Χειµερινό Εξάµηνο 2011
 Εισαγωγή στον Προγραµµατισµό Διάλεξη 3 η : Επίλυση Προβληµάτων Χειµερινό Εξάµηνο 2011 Τελεστής σύντοµης ανάθεσης Τελεστής σύντοµης ανάθεσης (shorthand assignment operator) µεταβλητή = µεταβλητή τελεστής
Εισαγωγή στον Προγραµµατισµό Διάλεξη 3 η : Επίλυση Προβληµάτων Χειµερινό Εξάµηνο 2011 Τελεστής σύντοµης ανάθεσης Τελεστής σύντοµης ανάθεσης (shorthand assignment operator) µεταβλητή = µεταβλητή τελεστής
Στοιχεία προτασιακής λογικής
 Σ. Κοσμαδάκης Στοιχεία προτασιακής λογικής Λογικές πράξεις and, or, not Για οποιεσδήποτε τιμές αλήθειας s, t στο σύνολο {true, false}, οι γνωστές πράξεις s and t, s or t, not s δίνουν αποτελέσματα στο
Σ. Κοσμαδάκης Στοιχεία προτασιακής λογικής Λογικές πράξεις and, or, not Για οποιεσδήποτε τιμές αλήθειας s, t στο σύνολο {true, false}, οι γνωστές πράξεις s and t, s or t, not s δίνουν αποτελέσματα στο
Σειρά Προβλημάτων 4 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing (αυθεντικός ορισμός) η οποία να διαγιγνώσκει τη γλώσσα { w#z w, z {a,b}* και η z είναι υπολέξη της w}. Συγκεκριμένα,
Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing (αυθεντικός ορισμός) η οποία να διαγιγνώσκει τη γλώσσα { w#z w, z {a,b}* και η z είναι υπολέξη της w}. Συγκεκριμένα,
Σελίδα 1 από 7 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ ΜΑΘΗΜΑ / ΤΑΞΗ : ΑΕΠΠ / ΘΕΡΙΝΑ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ:
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΑΕΠΠ / ΘΕΡΙΝΑ ΣΕΙΡΑ: 1 η ΗΜΕΡΟΜΗΝΙΑ: 08-09-2013 ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω προτάσεις 1-8 και δίπλα τη λέξη Σωστό, αν είναι σωστή, ή τη λέξη
ΜΑΘΗΜΑ / ΤΑΞΗ : ΑΕΠΠ / ΘΕΡΙΝΑ ΣΕΙΡΑ: 1 η ΗΜΕΡΟΜΗΝΙΑ: 08-09-2013 ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω προτάσεις 1-8 και δίπλα τη λέξη Σωστό, αν είναι σωστή, ή τη λέξη
Είδη εντολών. Απλές εντολές. Εντολές ελέγχου. Εκτελούν κάποια ενέργεια. Ορίζουν τον τρόπο με τον οποίο εκτελούνται άλλες εντολές
 Μορφές Εντολών Είδη εντολών Απλές εντολές Εκτελούν κάποια ενέργεια Εντολές ελέγχου Ορίζουν τον τρόπο με τον οποίο εκτελούνται άλλες εντολές Εντολές και παραστάσεις Μιαεντολήείναιμιαπαράστασηπου ακολουθείται
Μορφές Εντολών Είδη εντολών Απλές εντολές Εκτελούν κάποια ενέργεια Εντολές ελέγχου Ορίζουν τον τρόπο με τον οποίο εκτελούνται άλλες εντολές Εντολές και παραστάσεις Μιαεντολήείναιμιαπαράστασηπου ακολουθείται
1 ο Διαγώνισμα Ύλη: Συναρτήσεις μέχρι και τα ακρότατα
 Θέμα Α Α1. Θεωρήστε τον παρακάτω ισχυρισμό: 1 ο Διαγώνισμα Ύλη: Συναρτήσεις μέχρι και τα ακρότατα 018-19 «Για κάθε ζεύγος πραγματικών συναρτήσεων,g :, 0 ή g 0» ισχύει ότι g 0 αν και μόνο αν α) Να χαρακτηρίσετε
Θέμα Α Α1. Θεωρήστε τον παρακάτω ισχυρισμό: 1 ο Διαγώνισμα Ύλη: Συναρτήσεις μέχρι και τα ακρότατα 018-19 «Για κάθε ζεύγος πραγματικών συναρτήσεων,g :, 0 ή g 0» ισχύει ότι g 0 αν και μόνο αν α) Να χαρακτηρίσετε
Προτασιακός Λογισμός (HR Κεφάλαιο 1)
 Προτασιακός Λογισμός (HR Κεφάλαιο 1) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Σύνταξη Λογικός Συμπερασμός Σημασιολογία Ορθότητα και Πληρότητα Κανονικές Μορφές Προτάσεις Horn ΕΠΛ 412 Λογική
Προτασιακός Λογισμός (HR Κεφάλαιο 1) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Σύνταξη Λογικός Συμπερασμός Σημασιολογία Ορθότητα και Πληρότητα Κανονικές Μορφές Προτάσεις Horn ΕΠΛ 412 Λογική
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΟΝΟΜΑΤΕΠΩΝΥΜΟ:
 ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΟΝΟΜΑΤΕΠΩΝΥΜΟ: Θέμα 1ο I. Δίνεται το παρακάτω τμήμα αλγορίθμου. Να εξετάσετε αν ικανοποιεί τα αλγοριθμικά κριτήρια. Γράψε 'Δώσε
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΟΝΟΜΑΤΕΠΩΝΥΜΟ: Θέμα 1ο I. Δίνεται το παρακάτω τμήμα αλγορίθμου. Να εξετάσετε αν ικανοποιεί τα αλγοριθμικά κριτήρια. Γράψε 'Δώσε
Κατ οίκον Εργασία 2 Λύσεις
 Κατ οίκον Εργασία 2 Λύσεις Άσκηση 1 Ακολουθεί η διατύπωση των προτάσεων στον προτασιακό λογισμό. (α) Κάθε ενεργός χρήστης είναι είτε διαχειριστής είτε κανονικός χρήστης του συστήματος. x [Ενεργός (x) Διαχειριστής(x)
Κατ οίκον Εργασία 2 Λύσεις Άσκηση 1 Ακολουθεί η διατύπωση των προτάσεων στον προτασιακό λογισμό. (α) Κάθε ενεργός χρήστης είναι είτε διαχειριστής είτε κανονικός χρήστης του συστήματος. x [Ενεργός (x) Διαχειριστής(x)
ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΔΟΜΗΜΕΝΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Γ ΕΠΑΛ
 ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΔΟΜΗΜΕΝΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Γ ΕΠΑΛ ΘΕΜΑ Α Α.1 Να χαρακτηρίσετε σωστή (Σ) ή λανθασμένη (Λ) καθεμία από τις παρακάτω προτάσεις (Μονάδες 10) 1. Ένας αλγόριθμος μπορεί να έχει άπειρα βήματα
ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΔΟΜΗΜΕΝΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Γ ΕΠΑΛ ΘΕΜΑ Α Α.1 Να χαρακτηρίσετε σωστή (Σ) ή λανθασμένη (Λ) καθεμία από τις παρακάτω προτάσεις (Μονάδες 10) 1. Ένας αλγόριθμος μπορεί να έχει άπειρα βήματα
Σειρά Προβλημάτων 5 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { G,k η G είναι μια ασυμφραστική γραμματική η οποία παράγει κάποια λέξη 1 n όπου n k } (β) { Μ,k η Μ είναι
Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) { G,k η G είναι μια ασυμφραστική γραμματική η οποία παράγει κάποια λέξη 1 n όπου n k } (β) { Μ,k η Μ είναι
Λειτουργικά. Συστήματα Ι. Φ ρ ο ν τ ι σ τ ή ρ ι ο. Αριστείδης Ηλίας. Εργαστήριο Ηλεκτρονικών Υπολογιστών
 Λειτουργικά Αριστείδης Ηλίας Συστήματα Ι Φ ρ ο ν τ ι σ τ ή ρ ι ο Shell Scripting Εισαγωγή Ένα shell script είναι μια λίστα εντολών που εκτελούνται ακολουθιακά Εκτελούνται ανάλογα με το κέλυφος και για
Λειτουργικά Αριστείδης Ηλίας Συστήματα Ι Φ ρ ο ν τ ι σ τ ή ρ ι ο Shell Scripting Εισαγωγή Ένα shell script είναι μια λίστα εντολών που εκτελούνται ακολουθιακά Εκτελούνται ανάλογα με το κέλυφος και για
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Λογική. Δημήτρης Πλεξουσάκης
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Λογική Δημήτρης Πλεξουσάκης 2ο μέρος σημειώσεων: Συστήματα Αποδείξεων για τον ΠΛ, Μορφολογική Παραγωγή, Κατασκευή Μοντέλων Τμήμα Επιστήμης Υπολογιστών Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Λογική Δημήτρης Πλεξουσάκης 2ο μέρος σημειώσεων: Συστήματα Αποδείξεων για τον ΠΛ, Μορφολογική Παραγωγή, Κατασκευή Μοντέλων Τμήμα Επιστήμης Υπολογιστών Άδειες Χρήσης
Θέματα Προγραμματισμού Η/Υ
 Πρόγραμμα Μεταπτυχιακών Σπουδών Πληροφορική και Υπολογιστική Βιοϊατρική Θέματα Προγραμματισμού Η/Υ Ενότητα 7: Θεματική Ενότητα: Δομές επανάληψης ΘΕΜΑΤΑ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Η/Υ Θεματική Ενότητα 7 Δομές επανάληψης
Πρόγραμμα Μεταπτυχιακών Σπουδών Πληροφορική και Υπολογιστική Βιοϊατρική Θέματα Προγραμματισμού Η/Υ Ενότητα 7: Θεματική Ενότητα: Δομές επανάληψης ΘΕΜΑΤΑ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Η/Υ Θεματική Ενότητα 7 Δομές επανάληψης
Α3. Ποια είναι τα πλεονεκτήματα του Δομημένου προγραμματισμού; (Μονάδες 10)
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΔΟΜΗΜΕΝΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ / Γ ΕΠΑΛ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 08 / 02 / 2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: Ι. ΜΙΧΑΛΕΑΚΟΣ Γ.ΝΙΤΟΔΑΣ ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις
ΜΑΘΗΜΑ / ΤΑΞΗ : ΔΟΜΗΜΕΝΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ / Γ ΕΠΑΛ ΣΕΙΡΑ: ΗΜΕΡΟΜΗΝΙΑ: 08 / 02 / 2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: Ι. ΜΙΧΑΛΕΑΚΟΣ Γ.ΝΙΤΟΔΑΣ ΘΕΜΑ Α Α1. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις
ΜΑΘΗΜΑ / ΤΑΞΗ : ΑΕΠΠ / Γ ΓΕ.Λ. ΟΙΚ & ΠΛΗΡ (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΓΙΑΝΝΗΣ ΜΙΧΑΛΕΑΚΟΣ ΘΕΜΑ Α
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΑΕΠΠ / Γ ΓΕ.Λ. ΟΙΚ & ΠΛΗΡ (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 25-9-2016 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΓΙΑΝΝΗΣ ΜΙΧΑΛΕΑΚΟΣ ΘΕΜΑ Α Α1. Να γράψετε τον αριθμό για καθεμία από τις παρακάτω προτάσεις 1-5 και, δίπλα,
ΜΑΘΗΜΑ / ΤΑΞΗ : ΑΕΠΠ / Γ ΓΕ.Λ. ΟΙΚ & ΠΛΗΡ (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 25-9-2016 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΓΙΑΝΝΗΣ ΜΙΧΑΛΕΑΚΟΣ ΘΕΜΑ Α Α1. Να γράψετε τον αριθμό για καθεμία από τις παρακάτω προτάσεις 1-5 και, δίπλα,
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 412: Λογική στην Πληροφορική Ενδιάμεση Εξέταση Σκελετοί Λύσεων Ημερομηνία : Σάββατο, 27 Οκτωβρίου 2012 Διάρκεια : 11:00 13:00 Διδάσκουσα : Άννα Φιλίππου Άσκηση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 412: Λογική στην Πληροφορική Ενδιάμεση Εξέταση Σκελετοί Λύσεων Ημερομηνία : Σάββατο, 27 Οκτωβρίου 2012 Διάρκεια : 11:00 13:00 Διδάσκουσα : Άννα Φιλίππου Άσκηση
ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ
 Σάββατο, 4 Ιουνίου 2005 ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ Γ ΛΥΚΕΙΟΥ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΘΕΜΑ 1o Α. 1. Να αναφέρετε ονοµαστικά τα κριτήρια που πρέπει απαραίτητα να ικανοποιεί ένας αλγόριθµος.
Σάββατο, 4 Ιουνίου 2005 ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ Γ ΛΥΚΕΙΟΥ ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ ΘΕΜΑ 1o Α. 1. Να αναφέρετε ονοµαστικά τα κριτήρια που πρέπει απαραίτητα να ικανοποιεί ένας αλγόριθµος.
Κεφάλαιο 4 Σημασιολογία μιας Απλής Προστακτικής Γλώσσας
 Κεφάλαιο 4 Σημασιολογία μιας Απλής Προστακτικής Γλώσσας Προπτυχιακό μάθημα Αρχές Γλωσσών Προγραμματισμού Π. Ροντογιάννης 1 Εισαγωγή - 1 Μία κλασσική γλώσσα προγραμματισμού αποτελείται από: Εκφράσεις (των
Κεφάλαιο 4 Σημασιολογία μιας Απλής Προστακτικής Γλώσσας Προπτυχιακό μάθημα Αρχές Γλωσσών Προγραμματισμού Π. Ροντογιάννης 1 Εισαγωγή - 1 Μία κλασσική γλώσσα προγραμματισμού αποτελείται από: Εκφράσεις (των
Αλγοριθμική & Δομές Δεδομένων- Γλώσσα Προγραμματισμού Ι (PASCAL) (PASCAL ) Εντολές Ελέγχου & Επανάληψης
 Αλγοριθμική & Δομές Δεδομένων- Γλώσσα Προγραμματισμού Ι (PASCAL) (PASCAL ) Εντολές Ελέγχου & Επανάληψης Εντολές Ελέγχου 2 Γενικά Εντολές λήψης αποφάσεων Επιτρέπουν στο πρόγραμμα να εκτελεί διαφορετικές
Αλγοριθμική & Δομές Δεδομένων- Γλώσσα Προγραμματισμού Ι (PASCAL) (PASCAL ) Εντολές Ελέγχου & Επανάληψης Εντολές Ελέγχου 2 Γενικά Εντολές λήψης αποφάσεων Επιτρέπουν στο πρόγραμμα να εκτελεί διαφορετικές
