Εργαστήριο Ψηφιακών Κυκλωμάτων
|
|
|
- Διογένης Σκλαβούνος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Μηχανές Πεπερασμένων Καταστάσεων Χειμερινό Εξάμηνο ΗΥ220 University of Crete 1
2 Τι είναι οι FSMs? 10 FSM Κερματοδέκτης open Μηχανισμός Αυτόματου 20 Απελευθέρωσης Πωλητή 30 cents each can ΗΥ220 University of Crete 2
3 Τι είναι οι FSMs? cents each can OPEN OPEN Give 10 ΗΥ220 University of Crete 3
4 FSMs Οι μηχανές πεπερασμένων καταστάσεων Finite State Machines (FSMs) πιο αφηρημένος τρόπος να εξετάζουμε ακολουθιακά κυκλώματα Είσοδοι, έξοδοι, τρέχουσα κατάσταση, επόμενη κατάσταση Σε κάθε ακμή του ρολογιού συνδυαστική λογική παράγει τις εξόδους και την επόμενη κατάσταση σαν συνάρτησεις των εισόδων και της τρέχουσας κατάστασης. ΗΥ220 University of Crete 4
5 Χαρακτηριστικά των FSM Η επόμενη κατάσταση είναι συνάρτηση της τρέχουσας κατάστασης και των εισόδων Moore Machine: Οι έξοδοι είναι συνάρτηση της inputa κατάστασης State / output Mealy Machine: Οι έξοδοι είναι συνάρτηση της κατάστασης και των εισόδων inputa/outputa inputb State inputb/outputb ΗΥ220 University of Crete 5
6 Βήματα Σχεδίασης 1. Περιγραφή φήλειτουργία του κυκλώματος (functional specification) 2. Διάγραμμα μετάβασης καταστάσεων (state transition diagram) 3. Πίνακας καταστάσεων και μεταβάσεων με συβολικά ονόματα (symbolic state transition table) 4. Κωδικοποίηση η καταστάσεων (state encoding) 5. Εξαγωγή λογικών συναρτήσεων 6. Διάγραμμα κυκλώματος FFs για την κατάσταση ΣΛ για την επόμενη κατάσταση και τις εξόδους ΗΥ220 University of Crete 6
7 Αναπαράσταση FSM Καταστάσεις: όλες οι πιθανές τιμές στα ακολουθιακά στοιχεία μνήμης (FFs) Μεταβάσεις: αλλαγή κατάστασης Αλλαγή τις κατάστασης με το ρολόι αφού ελέγχει την φόρτωση τιμής στα στοιχεία μνήμης (FFs) 001 In = 0 In = 1 Ακολουθιακή λογική In = In = 1 Ακολουθία μέσω μιας σειράς καταστάσεων Βασίζεται στην ακολουθία των τιμών στις εισόδους ΗΥ220 University of Crete 7
8 Παράδειγμα FSM Count couples Η έξοδος γίνεται 1 για κάθε ζευγάρι από 1 Moore FSM zero [0] one1 [0] two1s [1] ΗΥ220 University of Crete 8
9 Moore FSM: general & state module moore(out, Clock, Reset, In); output Out; input Clock, Reset, In; zero [0] reg Out; 1 0 reg [1:0] CurrentState; // state reg 0 reg [1:0] NextState; // State assignment parameter STATE_Zero = 2 h0, STATE_One1 = 2 h1 h1, STATE_Two1s = 2 h2, STATE_X = 2 hx; // Implement the state register posedge Clock) begin if (Reset) CurrentState <= STATE_Zero; else CurrentState t <= NextState; t one1 [0] two1s [1] ΗΥ220 University of Crete 9
10 Moore FSM : combinatorial or CurrentState) begin NextState = CurrentState; Out = 1 b0; case (CurrentState) STATE_Zero: begin // last input was a zero if (In) NextState t = STATE_One1; STATE_One1: begin // we've seen one 1 if (In) NextState = STATE_ Two1s; 0 else NextState = STATE_Zero; STATE_Two1s: begin // we've seen at 2 ones Out = 1; if (In) NextState = STATE_One1; else NextState = STATE_Zero default: begin // in case we reach a bad state Out = 1 bx; NextState = STATE_Zero; case 0 zero [0] one1 [0] two1s [1] ΗΥ220 University of Crete 10
11 Παράδειγμα FSM Count couples Η έξοδος γίνεται 1 για κάθε ζευγάρι από 1 Mealy FSM Είσοδος 0/0 Έξοδος zero 0/0 1/0 1/1 one1 ΗΥ220 University of Crete 11
12 Mealy FSM module mealy(clock, Reset, In, Out); input Clock, Reset, In; output Out; reg Out; reg CurrentState;// state register reg NextState; parameter STATE_Zero = STATE_One1 = 1 b0, 1 b1; Clock) begin if (Reset) CurrentState <= STATE_Zero; else CurrentState <= NextState; 0/0 zero one1 1/0 0/0 1/1 (In or CurrentState) t begin NextState = CurrentState; Out = 1 b0; case (CurrentState) STATE_Zero: if (In) NextState = STATE_One1; STATE_One1: begin // we've seen one 1 NextState = STATE_Zero; if (In) Out = 1; module case ΗΥ220 University of Crete 12
13 Moore vs Mealy CLK Input Moore Out State Zero Zero One 1 Two 1s Mealy Out State Zero Zero One 1 Zero ΗΥ220 University of Crete 13
14 Moore vs Mealy Συμπεριφορά Moore απλοποιούν τη σχεδίαση αδυναμία αντίδρασης στις εισόδους στον ίδιο κύκλο έξοδοι ένα κύκλο μετά διαφορετικές καταστάσεις για κάθε αντίδραση Mealy συνήθως λιγότερες καταστάσεις άμεση αντίδραση στις εισόδους έξοδοι στον ίδιο κύκλο δυσκολότερη σχεδίαση αφού καθυστερημένη είσοδος παράγει καθυστερημένη έξοδο (μεγάλα μονοπάτια) H Mealy γίνεται Moore αν βάλουμε καταχωρητές στις εξόδους ΗΥ220 University of Crete 14
15 Moore Machine σε 1 always block (Bad Idea) module reduce (clk, reset, in, out); input clk, reset, in; output out; reg out; reg [1:0] state; // state register parameter zero = 0, one1 = 1, two1s = 2; 0 0 zero [0] 1 one1 [0] 1 two1s [1] 0 1 ΗΥ220 University of Crete 15
16 Moore Machine σε 1 always block (Bad Idea) clk) case (state) zero: begin out <= 0; if (in) state <= one1; else state <= zero; one1: if (in) begin state <= two1s; out <= 1; else begin state <= zero; out <= 0; two1s: if (in) begin state <= two1s; out <= 1; else begin state <= zero; out <= 0; default: begin state <= zero; out <= 0; case module Οι έξοδοι είναι καταχωρητές Μπερδεμένο!!! Η έξοδος αλλάζει στον επόμενο κύκλο ΗΥ220 University of Crete 16
17 Υλοποίηση FSMs Mealy outputs inputs combinational logic next state combinational logic Moore outputs current state Προτεινόμενο στυλ υλοποίησης FSM Η συνδυαστική λογική καταστάσεων σε always block (πάντα default) Ο καταχωρητής κατάστασης σε ένα ξεχωριστό always block (clocked πάντα reset) Έξοδοι είτε από το always της CL είτε από wires ΗΥ220 University of Crete 17
18 Moore Mealy Dataflow CLK INPUTS Next Statet Registers Outputs CLK INPUTS Next State Registers Outputs ΗΥ220 University of Crete 18
19 Απλή FSM ΗΥ220 University of Crete 19
20 Απλή FSM (1/3) module fsm( Receive, Start, Stop, Error, Clk, Reset_); // input Start, Stop, Error, Clk, Reset_; output Receive; // parameter [1:0] IdleState = 0, ReceiveState = 1, ErrorState = 2; // reg [1:0] FSMstate, nxtfsmstate; // Clk) begin if (~Reset_) FSMstate <= #`dh IdleState; else FSMstate <= #`dh nxtfsmstate; // or Start or Stop or Error) begin // case(fsmstate) ΗΥ220 University of Crete 20
21 Απλή FSM (2/3) IdleState: begin if(error) nxtfsmstate <= ErrorState; else begin if(start) nxtfsmstate <= ReceiveState; else nxtfsmstate <= IdleState; ReceiveState: begin if(error) nxtfsmstate <= ErrorState; else begin if(stop) ( nxtfsmstate <= IdleState; else nxtfsmstate <= ReceiveState; ErrorState : nxtfsmstate <= IdleState; default case : nxtfsmstate <= IdleState; ΗΥ220 University of Crete 21
22 Απλή FSM (3/3) Οι έξοδοι The Moore Output wire Receive = FSMstate[0]; The Mealy Output wire Receive = ((FSMstate == IdleState ) & Start) ((FSMstate == ReceiveState) & ~Error & ~Stop ); module d ΗΥ220 University of Crete 22
23 Παράδειγμα: «Αυτόματος Πωλητής» (1/5) Βγάζει αναψυκτικό όταν βάλουμε 15 λεπτά του Κερματοδέκτης για νομίσματα των 5 και 10 λεπτών του Δεν δίνει ρέστα! Rst Κερματοδέκτης in5 in10 FSM Αυτόματου Πωλητή open Μηχανισμός Απελευθέρωσης Clk ΗΥ220 University of Crete 23
24 Παράδειγμα: «Αυτόματος Πωλητής» (2/5) Αφηρημένη Αναπαράσταση Τυπικές είσοδοι: 3 των 5 5, 10 10, 5 2 των 10 Δά Διάγραμμα Καταστάσεων: Είσοδοι: in5, in10, reset, clock Έξοδοι: open Assumptions: in5 και in10 θέτονται για 1 κύκλο Μένουμε στην ίδια κατάσταση αν δεν έρθει είσοδος Όταν έρθει reset πάμε στην αρχική κατάσταση S3 in5 S7 [open] in5 S1 in5 in10 S4 [open] S0 Reset in10 in5 S2 S5 [open] in10 S6 [open] ΗΥ220 University of Crete 24
25 Παράδειγμα: «Αυτόματος Πωλητής» (3/5) Ελαχιστοποίηση καταστάσεων επαναχρησιμοποίηση in10 Reset 0 in5 5 in10 in5 10 in5 in10 15 [open] present inputs next output state In10 in5 state open symbolic state table ΗΥ220 University of Crete 25
26 Παράδειγμα: «Αυτόματος Πωλητής» (4/5) Κωδικοποίηση Καταστάσεων Τυπική pres. state inputs next state output Q1 Q0 in10 in5 D1 D0 open ΗΥ220 University of Crete 26
27 Παράδειγμα: «Αυτόματος Πωλητής» (5/5) Κωδικοποίηση Καταστάσεων One hot present state inputs next state output Q3 Q2 Q1 Q0 in10 in5 D3 D2 D1 D0 open ΗΥ220 University of Crete 27
28 Διαγράμματα καταστάσεων Moore and Mealy Moore machine Έξοδοι από κατάσταση Reset Mealy machine Έξοδοι στις μεταβάσεις Reset in10 in10 0 [0] in5 5 [0] in5 10 [0] in5 in10 in5 in10 in5 in10 in10/0 0 in5/0 in10/1 5 in5/0 10 in5 in10 /0 in5 in10 /0 in5 in10 /0 in5 in10 15 [1] in5 in10 /1 ΗΥ220 University of Crete 28
29 Moore Verilog FSM module ving (open, clk, Rst, in5, in10); input clk, Rst, in5, in10; output open; Reset reg open; reg [1:0] state; // state register reg [1:0] next_state; parameter zero = 0, five = 1, ten = 2, fifteen = 3; or in10 or state) 0 case (state) in5 in10 [0] zero: begin if (in5) next_state = five; in5 else if (in10) next_state = ten; else next_state = zero; in10 5 open = 0; in5 in10 [0] in5 fifteen: begin next_state = zero; 10 open = 1; in10 in5 in10 [0] default: begin in5 in10 case next_ state = zero; open = 0; g clk) if (Rst) state <= zero; else state <= next_state; module ΗΥ220 University of Crete [1]
30 Mealy Verilog FSM module ving (open, Clk, Rst, in5, in10); input Clk, Rst, in5, in10; output open; reg open; reg [1:0] state; // state register reg [1:0] next_state; parameter zero = 0, five = 1, ten = 2, fifteen = 3; or in10 or state) case (state) zero: begin open = 0; if (in10) next_state = ten; else if (in5) next_state = five; else next_state = zero; five: begin if (in5) begin next_state = ten; open = 0; else if (in10 ) begin next_state = zero; open = 1; else begin case next_ state = five; open = 0; in10/1 in10/0 in5/0 in5/0 in5 in10 / Reset in5 in10 /0 clk) if (Rst) state <= zero; else state <= next_state; module ΗΥ220 University of Crete 30 in5 in10 /0 in5 in10 /0
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων
 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2017-2018 Μηχανές Πεπερασμένων Καταστάσεων ΗΥ220 - Βασίλης Παπαευσταθίου & Γιώργος Καλοκαιρινός 1 FSMs Οι μηχανές πεπερασμένων καταστάσεων Finite
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2017-2018 Μηχανές Πεπερασμένων Καταστάσεων ΗΥ220 - Βασίλης Παπαευσταθίου & Γιώργος Καλοκαιρινός 1 FSMs Οι μηχανές πεπερασμένων καταστάσεων Finite
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωµάτων
 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωµάτων Χειµερινό Εξάµηνο 2007-2008 Μηχανές Πεπερασµένων Καταστάσεων ΗΥ220 - Βασίλης Παπαευσταθίου 1 FSMs Οι µηχανές πεπερασµένων καταστάσεων Finite State Machines (FSMs) πιο
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωµάτων Χειµερινό Εξάµηνο 2007-2008 Μηχανές Πεπερασµένων Καταστάσεων ΗΥ220 - Βασίλης Παπαευσταθίου 1 FSMs Οι µηχανές πεπερασµένων καταστάσεων Finite State Machines (FSMs) πιο
Εργαστήριο Οργάνωσης Η/Υ. Δαδαλιάρης Αντώνιος
 Εργαστήριο Οργάνωσης Η/Υ Δαδαλιάρης Αντώνιος dadaliaris@uth.gr Χρησιμοποιούμε τις μηχανές πεπερασμένων καταστάσεων (finite state machines FSMs) για την μοντελοποίηση της συμπεριφοράς ενός κυκλώματος, η
Εργαστήριο Οργάνωσης Η/Υ Δαδαλιάρης Αντώνιος dadaliaris@uth.gr Χρησιμοποιούμε τις μηχανές πεπερασμένων καταστάσεων (finite state machines FSMs) για την μοντελοποίηση της συμπεριφοράς ενός κυκλώματος, η
«Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων» Χειμερινό εξάμηνο Μηχανές Πεπερασμένων Καταστάσεων
 «Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων» Χειμερινό εξάμηνο 2016-2017 Μηχανές Πεπερασμένων Καταστάσεων Παρασκευάς Κίτσος http://diceslab.cied.teiwest.gr Επίκουρος Καθηγητής Tμήμα Μηχανικών Πληροφορικής ΤΕ
«Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων» Χειμερινό εξάμηνο 2016-2017 Μηχανές Πεπερασμένων Καταστάσεων Παρασκευάς Κίτσος http://diceslab.cied.teiwest.gr Επίκουρος Καθηγητής Tμήμα Μηχανικών Πληροφορικής ΤΕ
ΗΥ225 Οργάνωση Υπολογιστών. Εισαγωγή στη Verilog
 ΗΥ225 Οργάνωση Υπολογιστών Εισαγωγή στη Verilog Processors are everywhere ARM based products CS225: How to build your own processor University of Crete ΗΥ225 2 Intel 8086 Processor 1978 29.000 transistors
ΗΥ225 Οργάνωση Υπολογιστών Εισαγωγή στη Verilog Processors are everywhere ARM based products CS225: How to build your own processor University of Crete ΗΥ225 2 Intel 8086 Processor 1978 29.000 transistors
ΗΥ220: Εργαστήριο σχεδίασης ψηφιακών κυκλωμάτων Χριστόφορος Κάχρης
 Πανεπιστήμιο Κρήτης Τμήμα Επιστήμης Υπολογιστών ΗΥ220: Εργαστήριο σχεδίασης ψηφιακών κυκλωμάτων Χριστόφορος Κάχρης 4-11-2009 Πρόοδος Θέμα 1 ο (25%): 1. Βρείτε την μεγίστη συχνότητα λειτουργίας του παρακάτω
Πανεπιστήμιο Κρήτης Τμήμα Επιστήμης Υπολογιστών ΗΥ220: Εργαστήριο σχεδίασης ψηφιακών κυκλωμάτων Χριστόφορος Κάχρης 4-11-2009 Πρόοδος Θέμα 1 ο (25%): 1. Βρείτε την μεγίστη συχνότητα λειτουργίας του παρακάτω
HY220 Pipelines and FSMs Χειμεριν Χειμερι ό Εξ άμη Εξ ν άμη ο
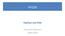 HY220 Pipelines and FSMs Χειμερινό Εξάμηνο 2009 2010 Latency Throughput Tc a[n] b[n] x[n] a[0] a[1] a[2] a[3] a[4] a[5] a[6] a[7] c[n] Input Regs +1 + Output Reg Input Regs Output Reg b[0] b[1] b[2] b[3]
HY220 Pipelines and FSMs Χειμερινό Εξάμηνο 2009 2010 Latency Throughput Tc a[n] b[n] x[n] a[0] a[1] a[2] a[3] a[4] a[5] a[6] a[7] c[n] Input Regs +1 + Output Reg Input Regs Output Reg b[0] b[1] b[2] b[3]
Σχεδίαση Ψηφιακών Συστημάτων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Σχεδίαση Ψηφιακών Συστημάτων Ενότητα 6: Σύγχρονα Ακολουθιακά Κυκλώματα Κυριάκης Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Σχεδίαση Ψηφιακών Συστημάτων Ενότητα 6: Σύγχρονα Ακολουθιακά Κυκλώματα Κυριάκης Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών
HY430 Εργαςτήριο Ψηφιακών Κυκλωμάτων. 1 ΗΥ430 - Διάλεξθ 10θ - Μθχανζσ Ρεπεραςμζνων Κατάςταςεων
 HY430 Εργαςτήριο Ψηφιακών Κυκλωμάτων Διδάςκων: Χ. ωτηρίου, Βοηθόσ: (θα ανακοινωθεί) http://inf-server.inf.uth.gr/courses/ce430/ 1 Περιεχόμενα Τι είναι ΜΡΚ; Ταξινόμθςθ Ακολουκιακϊν Μοντζλων Υπολογιςμοφ
HY430 Εργαςτήριο Ψηφιακών Κυκλωμάτων Διδάςκων: Χ. ωτηρίου, Βοηθόσ: (θα ανακοινωθεί) http://inf-server.inf.uth.gr/courses/ce430/ 1 Περιεχόμενα Τι είναι ΜΡΚ; Ταξινόμθςθ Ακολουκιακϊν Μοντζλων Υπολογιςμοφ
Περιγραφή Κυκλωμάτων με χρήση της VHDL. Δομική περιγραφή και περιγραφή Μηχανών Πεπερασμένων Καταστάσεων
 Περιγραφή Κυκλωμάτων με χρήση της VHDL Δομική περιγραφή και περιγραφή Μηχανών Πεπερασμένων Καταστάσεων Οργάνωση Παρουσίασης Περιγραφή Δομής σε VHDL (Structural Description) Μηχανές Πεπερασμένων Καταστάσεων
Περιγραφή Κυκλωμάτων με χρήση της VHDL Δομική περιγραφή και περιγραφή Μηχανών Πεπερασμένων Καταστάσεων Οργάνωση Παρουσίασης Περιγραφή Δομής σε VHDL (Structural Description) Μηχανές Πεπερασμένων Καταστάσεων
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ. Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 18: Διαδικασία Σχεδίασης Ψηφιακών Συστηµάτων - Επανάληψη
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 18: Διαδικασία Σχεδίασης Ψηφιακών Συστηµάτων - Επανάληψη ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 18: Διαδικασία Σχεδίασης Ψηφιακών Συστηµάτων - Επανάληψη ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ. Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 13: Διαδικασία Σχεδιασµού Ακολουθιακών Κυκλωµάτων (Κεφάλαιο 6.
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 13: Διαδικασία Σχεδιασµού Ακολουθιακών Κυκλωµάτων (Κεφάλαιο 6.3) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy)
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 13: Διαδικασία Σχεδιασµού Ακολουθιακών Κυκλωµάτων (Κεφάλαιο 6.3) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy)
«Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο Διάλεξη 8 η : Μηχανές Πεπερασμένων Κaταστάσεων σε FPGAs
 ΤΕΙ Δυτικής Ελλάδας Τμήμα Μηχανικών Πληροφορικής ΤΕ Εργαστήριο Σχεδίασης Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων «Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο 2016-2017 Διάλεξη 8 η :
ΤΕΙ Δυτικής Ελλάδας Τμήμα Μηχανικών Πληροφορικής ΤΕ Εργαστήριο Σχεδίασης Ψηφιακών Ολοκληρωμένων Κυκλωμάτων και Συστημάτων «Σχεδιασμός Ψηφιακών Συστημάτων σε FPGA» Εαρινό εξάμηνο 2016-2017 Διάλεξη 8 η :
Πρόγραμμα Μεταπτυχιακών Σπουδών «Πληροφορική και Εφαρμογές»
 Πρόγραμμα Μεταπτυχιακών Σπουδών «Πληροφορική και Εφαρμογές» Αρχές Ψηφιακής Τεχνολογίας Σχεδιασμός σύνθετων συστημάτων Γιάννης Βογιατζής 28-29 Βασικές λογικές πύλες = Driver = AND = + OR = XOR = Inverter
Πρόγραμμα Μεταπτυχιακών Σπουδών «Πληροφορική και Εφαρμογές» Αρχές Ψηφιακής Τεχνολογίας Σχεδιασμός σύνθετων συστημάτων Γιάννης Βογιατζής 28-29 Βασικές λογικές πύλες = Driver = AND = + OR = XOR = Inverter
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 12: Ανάλυση Ακολουθιακών Κυκλωµάτων (Κεφάλαιο 6.2) Μηχανές Καταστάσεων ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy)
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 12: Ανάλυση Ακολουθιακών Κυκλωµάτων (Κεφάλαιο 6.2) Μηχανές Καταστάσεων ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy)
Σχεδιασμός Ψηφιακών Συστημάτων
 ΗΜΥ 2: Σχεδιασμό Ψηφιακών Συστημάτων, Χειμερινό Εξάμηνο 28 Νοε-8 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 28 Ανάλυση Ακολουθιακών Κυκλωμάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου
ΗΜΥ 2: Σχεδιασμό Ψηφιακών Συστημάτων, Χειμερινό Εξάμηνο 28 Νοε-8 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 28 Ανάλυση Ακολουθιακών Κυκλωμάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου
«Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων» Χειμερινό εξάμηνο Ακολουθιακός Κώδικας
 «Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων» Χειμερινό εξάμηνο 2016-2017 Ακολουθιακός Κώδικας Παρασκευάς Κίτσος http://diceslab.cied.teiwest.gr Επίκουρος Καθηγητής Tμήμα Μηχανικών Πληροφορικής ΤΕ E-mail: pkitsos@teimes.gr
«Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων» Χειμερινό εξάμηνο 2016-2017 Ακολουθιακός Κώδικας Παρασκευάς Κίτσος http://diceslab.cied.teiwest.gr Επίκουρος Καθηγητής Tμήμα Μηχανικών Πληροφορικής ΤΕ E-mail: pkitsos@teimes.gr
Ψηφιακή Λογική Σχεδίαση
 Ψηφιακή Λογική Σχεδίαση Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα Αδειοδότησης Το παρόν
Ψηφιακή Λογική Σχεδίαση Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα Αδειοδότησης Το παρόν
ΗΜΥ 210: Σχεδιασμός Ψηφιακών Συστημάτων. Ανάλυση Ακολουθιακών Κυκλωμάτων 1
 ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Ανάλυση Ακολουθιακών Κυκλωμάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Ανάλυση Ακολουθιακών Κυκλωμάτων Ανάλυση: Ο καθορισμός μιας κατάλληλης περιγραφής η οποία επιδεικνύει
ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Ανάλυση Ακολουθιακών Κυκλωμάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Ανάλυση Ακολουθιακών Κυκλωμάτων Ανάλυση: Ο καθορισμός μιας κατάλληλης περιγραφής η οποία επιδεικνύει
Μετρητής Ριπής ΛΟΓΙΚΗ ΣΧΕΔΙΑΣΗ. Αναφορά 9 ης. εργαστηριακής άσκησης: ΑΦΡΟΔΙΤΗ ΤΟΥΦΑ Α.Μ.:2024201100032
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΣΧΟΛΗ ΟΙΚΟΝΟΜΙΑΣ, ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΛΟΓΙΚΗ ΣΧΕΔΙΑΣΗ Αναφορά 9 ης εργαστηριακής άσκησης: Μετρητής Ριπής ΑΦΡΟΔΙΤΗ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΣΧΟΛΗ ΟΙΚΟΝΟΜΙΑΣ, ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΛΟΓΙΚΗ ΣΧΕΔΙΑΣΗ Αναφορά 9 ης εργαστηριακής άσκησης: Μετρητής Ριπής ΑΦΡΟΔΙΤΗ
Behavioral & Mixed VHDL Architectures Finite State Machines in VHDL
 ΗΜΥ211 Εργαστήριο Ψηφιακών Συστημάτων Behavioral & Mixed VHDL Architectures Finite State Machines in VHDL Διδάσκoντες: Δρ. Γιώργος Ζάγγουλοςκαι Δρ. Παναγιώτα Δημοσθένους Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων
ΗΜΥ211 Εργαστήριο Ψηφιακών Συστημάτων Behavioral & Mixed VHDL Architectures Finite State Machines in VHDL Διδάσκoντες: Δρ. Γιώργος Ζάγγουλοςκαι Δρ. Παναγιώτα Δημοσθένους Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων
ΗΜΥ211 Εργαστήριο Ψηφιακών Συστημάτων
 ΗΜΥ211 Εργαστήριο Ψηφιακών Συστημάτων Behavioral & Mixed VHDL Architectures Finite State Machines in VHDL Διδάσκων: Γιώργος Ζάγγουλος Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
ΗΜΥ211 Εργαστήριο Ψηφιακών Συστημάτων Behavioral & Mixed VHDL Architectures Finite State Machines in VHDL Διδάσκων: Γιώργος Ζάγγουλος Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
Ψηφιακή Λογική Σχεδίαση
 Ψηφιακή Λογική Σχεδίαση Γ. Θεοδωρίδης Ψηφιακή Λογική Σχεδίαση Γ. Θεοδωρίδης 1 Κεφάλαιο 8 Σχεδίαση στο Επίπεδο Μεταφοράς Περιεχομένων Καταχωρητών Ψηφιακή Λογική Σχεδίαση Γ. Θεοδωρίδης 2 Περίγραμμα Κεφαλαίου
Ψηφιακή Λογική Σχεδίαση Γ. Θεοδωρίδης Ψηφιακή Λογική Σχεδίαση Γ. Θεοδωρίδης 1 Κεφάλαιο 8 Σχεδίαση στο Επίπεδο Μεταφοράς Περιεχομένων Καταχωρητών Ψηφιακή Λογική Σχεδίαση Γ. Θεοδωρίδης 2 Περίγραμμα Κεφαλαίου
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων
 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2013-2014 ΗΥ220 - Γιώργος Καλοκαιρινός & Bασίλης Παπαευσταθίου 1 Verilog: Τα βασικά ΗΥ220 - Γιώργος Καλοκαιρινός & Bασίλης Παπαευσταθίου 2 Η εξέλιξη
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2013-2014 ΗΥ220 - Γιώργος Καλοκαιρινός & Bασίλης Παπαευσταθίου 1 Verilog: Τα βασικά ΗΥ220 - Γιώργος Καλοκαιρινός & Bασίλης Παπαευσταθίου 2 Η εξέλιξη
Behavioral & Mixed VHDL Architectures Finite State Machines in VHDL
 ΗΜΥ211 Εργαστήριο Ψηφιακών Συστημάτων Behavioral & Mixed VHDL Architectures Finite State Machines in VHDL Διδάσκoντες: Δρ. Αγαθοκλής Παπαδόπουλος και Δρ. Γιώργος Ζάγγουλος Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων
ΗΜΥ211 Εργαστήριο Ψηφιακών Συστημάτων Behavioral & Mixed VHDL Architectures Finite State Machines in VHDL Διδάσκoντες: Δρ. Αγαθοκλής Παπαδόπουλος και Δρ. Γιώργος Ζάγγουλος Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ. Χειµερινό Εξάµηνο 2016 Συµπληρωµατική ΔΙΑΛΕΞΗ 14: Περιγραφή Ακολουθιακών Κυκλωµάτων στη VHDL
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 Συµπληρωµατική ΔΙΑΛΕΞΗ 14: Περιγραφή Ακολουθιακών Κυκλωµάτων στη VHDL ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy)
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 Συµπληρωµατική ΔΙΑΛΕΞΗ 14: Περιγραφή Ακολουθιακών Κυκλωµάτων στη VHDL ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy)
Ψηφιακά Κυκλώματα (2 ο μέρος) ΜΥΥ-106 Εισαγωγή στους Η/Υ και στην Πληροφορική
 Ψηφιακά Κυκλώματα (2 ο μέρος) ΜΥΥ-6 Εισαγωγή στους Η/Υ και στην Πληροφορική Ακολουθιακά κυκλώματα είσοδοι.. ακολουθιακή λογική.. έξοδοι. ανάδραση Η λειτουργία μνήμης στηρίζεται στη ανάδραση (feedback):
Ψηφιακά Κυκλώματα (2 ο μέρος) ΜΥΥ-6 Εισαγωγή στους Η/Υ και στην Πληροφορική Ακολουθιακά κυκλώματα είσοδοι.. ακολουθιακή λογική.. έξοδοι. ανάδραση Η λειτουργία μνήμης στηρίζεται στη ανάδραση (feedback):
Ελίνα Μακρή
 Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
Χ. Σωτηρίου. Σχήμα 1: Προτεινόμενο Πρόγραμμα Επαλήθευσης του ολοκληρωμένου Επεξεργαστή
 È Ò Ô Ø Ñ Ó ÃÖ Ø ¹ ÌÑ Ñ Ô Ø Ñ ÍÔÓÐÓ ØôÒ À;¾ ¹ ÇÖ ÒÛ ÍÔÓÐÓ ØôÒ Ö Ò Ü Ñ ÒÓ ¹ Ñ ³ ØÓ ¾¼½½¹¾¼½¾ ³ ¹ ÍÐÓÔÓ ÌÑ Ñ ØÓ Ð ÕÓÙ ÇÐÓ Ð ÖÛ ØÓÙ Ô Ü Ö Ø ¾»»¾¼½ Û ½¾»»¾¼½ Χ. Σωτηρίου ½ ËØ ÕÓ Ø ³ Οι στόχοι της ένατης άσκησης
È Ò Ô Ø Ñ Ó ÃÖ Ø ¹ ÌÑ Ñ Ô Ø Ñ ÍÔÓÐÓ ØôÒ À;¾ ¹ ÇÖ ÒÛ ÍÔÓÐÓ ØôÒ Ö Ò Ü Ñ ÒÓ ¹ Ñ ³ ØÓ ¾¼½½¹¾¼½¾ ³ ¹ ÍÐÓÔÓ ÌÑ Ñ ØÓ Ð ÕÓÙ ÇÐÓ Ð ÖÛ ØÓÙ Ô Ü Ö Ø ¾»»¾¼½ Û ½¾»»¾¼½ Χ. Σωτηρίου ½ ËØ ÕÓ Ø ³ Οι στόχοι της ένατης άσκησης
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων
 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2017-2018 Verilog: Τα βασικά ΗΥ220 - Βασίλης Παπαευσταθίου & Γιώργος Καλοκαιρινός 1 Η εξέλιξη στη σχεδίαση ψηφιακών κυκλωμάτων Μεγάλη εξέλιξη τα τελευταία
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2017-2018 Verilog: Τα βασικά ΗΥ220 - Βασίλης Παπαευσταθίου & Γιώργος Καλοκαιρινός 1 Η εξέλιξη στη σχεδίαση ψηφιακών κυκλωμάτων Μεγάλη εξέλιξη τα τελευταία
Ψηφιακή Σχεδίαση. Δρ. Μηνάς Δασυγένης Εργαστήριο Ψηφιακών Συστημάτων και Αρχιτεκτονικής Υπολογιστών
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 8: Μανδαλωτές SR, S R D Flip-Flops Αφέντη Σκλάβου, Σχεδιασμός Ακολουθιακών κυκλωμάτων, Πίνακας Καταστάσεων, Διάγραμμα Καταστάσεων
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 8: Μανδαλωτές SR, S R D Flip-Flops Αφέντη Σκλάβου, Σχεδιασμός Ακολουθιακών κυκλωμάτων, Πίνακας Καταστάσεων, Διάγραμμα Καταστάσεων
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ. Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 15: Καταχωρητές (Registers)
 ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 15: Καταχωρητές (Registers) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη q Καταχωρητές Παράλληλης
ΗΜΥ 210 ΣΧΕΔΙΑΣΜΟΣ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Χειµερινό Εξάµηνο 2016 ΔΙΑΛΕΞΗ 15: Καταχωρητές (Registers) ΧΑΡΗΣ ΘΕΟΧΑΡΙΔΗΣ Επίκουρος Καθηγητής, ΗΜΜΥ (ttheocharides@ucy.ac.cy) Περίληψη q Καταχωρητές Παράλληλης
HY225 Οργάνωςη Τπολογιςτών
 HY225 Οργάνωςη Τπολογιςτών Διδάςκοντεσ: Δ. Νικολόπουλοσ, Χ. ωτηρίου. http://www.csd.uoc.gr/~hy225 1 Περιεχόμενα Τυπικι οι Σχεδίαςθσ Ιεραρχία ςτθν Σχεδίαςθ Μθχανζσ Ρεπεραςμζνων Καταςτάςεων Η Γλϊςςα Τι είναι
HY225 Οργάνωςη Τπολογιςτών Διδάςκοντεσ: Δ. Νικολόπουλοσ, Χ. ωτηρίου. http://www.csd.uoc.gr/~hy225 1 Περιεχόμενα Τυπικι οι Σχεδίαςθσ Ιεραρχία ςτθν Σχεδίαςθ Μθχανζσ Ρεπεραςμζνων Καταςτάςεων Η Γλϊςςα Τι είναι
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωµάτων Τµήµα Επιστήµης Υπολογιστών Χειµερινό Εξάµηνο
 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωµάτων Τµήµα Επιστήµης Υπολογιστών Χειµερινό Εξάµηνο 2006-2007 Εκφώνηση Εργαστηρίου Στο εργαστήριο του µαθήµατος σας ζητείται να σχεδιάσετε, να υλοποιήσετε και να επαληθεύσετε
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωµάτων Τµήµα Επιστήµης Υπολογιστών Χειµερινό Εξάµηνο 2006-2007 Εκφώνηση Εργαστηρίου Στο εργαστήριο του µαθήµατος σας ζητείται να σχεδιάσετε, να υλοποιήσετε και να επαληθεύσετε
26-Nov-09. ΗΜΥ 210: Λογικός Σχεδιασμός, Χειμερινό Εξάμηνο Καταχωρητές 1. Διδάσκουσα: Μαρία Κ. Μιχαήλ
 ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 2009 Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης
ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 2009 Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης
HY430 Εργαστήριο Ψηφιακών Κυκλωμάτων. Πολυπλέκτες Καμπύλη Παρέτο. Κωδικοποιητές/Από-κωδικοποιητές D FF
 HY430 Εργαστήριο Ψηφιακών Κυκλωμάτων Διδάσκων: Χ. Σωτηρίου, Βοηθός: (θα ανακοινωθεί) http://inf-server.inf.uth.gr/courses/ce430/ Περιεχόμενα Περιγραφές και Συνθέσιμες Δομές Πολυπλέκτες Καμπύλη Παρέτο Κωδικοποιητές/Από-κωδικοποιητές
HY430 Εργαστήριο Ψηφιακών Κυκλωμάτων Διδάσκων: Χ. Σωτηρίου, Βοηθός: (θα ανακοινωθεί) http://inf-server.inf.uth.gr/courses/ce430/ Περιεχόμενα Περιγραφές και Συνθέσιμες Δομές Πολυπλέκτες Καμπύλη Παρέτο Κωδικοποιητές/Από-κωδικοποιητές
Επιβεβαίωση ορθής λειτουργίας απλών ψηφιακών κυκλωμάτων
 Επιβεβαίωση ορθής λειτουργίας απλών ψηφιακών κυκλωμάτων Δημήτρης Κωνσταντίνου, Γιώργος Δημητρακόπουλος Εφόσον έχουμε περιγράψει το κύκλωμά μας σε System Verilog θα πρέπει να βεβαιωθούμε πως λειτουργεί
Επιβεβαίωση ορθής λειτουργίας απλών ψηφιακών κυκλωμάτων Δημήτρης Κωνσταντίνου, Γιώργος Δημητρακόπουλος Εφόσον έχουμε περιγράψει το κύκλωμά μας σε System Verilog θα πρέπει να βεβαιωθούμε πως λειτουργεί
6 η Θεµατική Ενότητα : Σχεδίαση Συστηµάτων σε Επίπεδο Καταχωρητή
 6 η Θεµατική Ενότητα : Σχεδίαση Συστηµάτων σε Επίπεδο Καταχωρητή Εισαγωγή Η σχεδίαση ενός ψηφιακού συστήµατος ως ακολουθιακή µηχανή είναι εξαιρετικά δύσκολη Τµηµατοποίηση σε υποσυστήµατα µε δοµικές µονάδες:
6 η Θεµατική Ενότητα : Σχεδίαση Συστηµάτων σε Επίπεδο Καταχωρητή Εισαγωγή Η σχεδίαση ενός ψηφιακού συστήµατος ως ακολουθιακή µηχανή είναι εξαιρετικά δύσκολη Τµηµατοποίηση σε υποσυστήµατα µε δοµικές µονάδες:
VERILOG. Γενικά περί γλώσσας
 VERILOG Γενικά περί γλώσσας Χρησιµότητα της Verilog Υψηλού επιπέδου περιγραφή της συµπεριφοράς του συστήµατος µε σκοπό την εξοµοίωση. RTL περιγραφή της λειτουργίας του συστήµατος µε σκοπό τη σύνθεσή του
VERILOG Γενικά περί γλώσσας Χρησιµότητα της Verilog Υψηλού επιπέδου περιγραφή της συµπεριφοράς του συστήµατος µε σκοπό την εξοµοίωση. RTL περιγραφή της λειτουργίας του συστήµατος µε σκοπό τη σύνθεσή του
ΗΜΥ 210: Σχεδιασμός Ψηφιακών Συστημάτων. Καταχωρητές 1
 ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές
ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων Καταχωρητές Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές
ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων
 ΗΜΥ 2: Λογικός Σχεδιασμός, Χειμερινό Εξάμηνο 28 8//28 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 28 Σχεδιασμός Ακολουθιακών Κυκλωμάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα
ΗΜΥ 2: Λογικός Σχεδιασμός, Χειμερινό Εξάμηνο 28 8//28 ΗΜΥ-2: Σχεδιασμός Ψηφιακών Συστημάτων Χειμερινό Εξάμηνο 28 Σχεδιασμός Ακολουθιακών Κυκλωμάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήμιο Κύπρου Τμήμα
VHDL για Σχεδιασµό Ακολουθιακών Κυκλωµάτων
 VHDL για Σχεδιασµό Ακολουθιακών Κυκλωµάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήµιο Κύπρου Τµήµα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών n VHDL Processes Περίληψη n Εντολές If-Then-Else και CASE
VHDL για Σχεδιασµό Ακολουθιακών Κυκλωµάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Πανεπιστήµιο Κύπρου Τµήµα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών n VHDL Processes Περίληψη n Εντολές If-Then-Else και CASE
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων
 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2017-2018 Λογικές Πύλες, Στοιχεία Μνήμης, Συνδυαστική Λογική και Κυματομορφές ΗΥ220 - Βασίλης Παπαευσταθίου & Γιώργος Καλοκαιρινός 1 Τα βασικά της
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2017-2018 Λογικές Πύλες, Στοιχεία Μνήμης, Συνδυαστική Λογική και Κυματομορφές ΗΥ220 - Βασίλης Παπαευσταθίου & Γιώργος Καλοκαιρινός 1 Τα βασικά της
Δημοκρίτειο Πανεπιστήμιο Θράκης Τμήμα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών. Συστήματα VLSI. Πρόοδος Άνοιξη 2018
 Δημοκρίτειο Πανεπιστήμιο Θράκης Τμήμα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Γ. Δημητρακόπουλος Συστήματα VLSI Πρόοδος Άνοιξη 2018 Άσκηση 1 Όλο το κύκλωμα τροφοδοτείται με το ίδιο ρολόι και το
Δημοκρίτειο Πανεπιστήμιο Θράκης Τμήμα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Γ. Δημητρακόπουλος Συστήματα VLSI Πρόοδος Άνοιξη 2018 Άσκηση 1 Όλο το κύκλωμα τροφοδοτείται με το ίδιο ρολόι και το
ΗΥ-225. Verilog HDL. Τα βασικά...
 ΗΥ-225 Verilog HDL. Τα βασικά... Βασική Ροή Σχεδίασης Requirements RTL Model Simulate Synthesize Gate-level Model Simulate Test Bench ASIC or FPGA Place & Route Timing Model Simulate ΗΥ-225 Ιάκωβος Μαυροειδής
ΗΥ-225 Verilog HDL. Τα βασικά... Βασική Ροή Σχεδίασης Requirements RTL Model Simulate Synthesize Gate-level Model Simulate Test Bench ASIC or FPGA Place & Route Timing Model Simulate ΗΥ-225 Ιάκωβος Μαυροειδής
ΗΜΥ 210: Σχεδιασμός Ψηφιακών Συστημάτων. VHDL για Ακολουθιακά Κυκλώματα 1
 ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων VHDL για Σχεδιασμό Ακολουθιακών Κυκλωμάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Περίληψη VHDL Processes Εντολές If-Then Then-Else και CASE Περιγραφή Flip-Flop Flop με VHDL
ΗΜΥ-210: Σχεδιασμός Ψηφιακών Συστημάτων VHDL για Σχεδιασμό Ακολουθιακών Κυκλωμάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Περίληψη VHDL Processes Εντολές If-Then Then-Else και CASE Περιγραφή Flip-Flop Flop με VHDL
Περίληψη. ΗΜΥ-210: Λογικός Σχεδιασµός Εαρινό Εξάµηνο Καθιερωµένα Γραφικά Σύµβολα. ΗΜΥ 210: Λογικός Σχεδιασµός, Εαρινό Εξάµηνο 2005
 ΗΜΥ 2: Λογικός Σχεδιασµός, Εαρινό Εξάµηνο 25 Απρ-5 ΗΜΥ-2: Λογικός Σχεδιασµός Εαρινό Εξάµηνο 25 Κεφάλαιο 6 ii: Ανάλυση Ακολουθιακών Κυκλωµάτων Περίληψη Καθιερωµένα Γραφικά Σύµβολα Χαρακτηριστικοί Πίνακες
ΗΜΥ 2: Λογικός Σχεδιασµός, Εαρινό Εξάµηνο 25 Απρ-5 ΗΜΥ-2: Λογικός Σχεδιασµός Εαρινό Εξάµηνο 25 Κεφάλαιο 6 ii: Ανάλυση Ακολουθιακών Κυκλωµάτων Περίληψη Καθιερωµένα Γραφικά Σύµβολα Χαρακτηριστικοί Πίνακες
Τεχνικές σχεδιασμού μονοπατιών ολίσθησης
 Τεχνικές σχεδιασμού μονοπατιών ολίσθησης (Scan Path Design Techniques) Περίγραμμα παρουσίασης Προβλήματα ελέγχου ορθής λειτουργίας ακολουθιακών κυκλωμάτων Μονοπάτι ολίσθησης (scan path) Στοιχεία μνήμης
Τεχνικές σχεδιασμού μονοπατιών ολίσθησης (Scan Path Design Techniques) Περίγραμμα παρουσίασης Προβλήματα ελέγχου ορθής λειτουργίας ακολουθιακών κυκλωμάτων Μονοπάτι ολίσθησης (scan path) Στοιχεία μνήμης
ΜΥΥ- 402 Αρχιτεκτονική Υπολογιστών Γλώσσα περιγραφής υλικού: Verilog
 ΜΥΥ- 402 Αρχιτεκτονική Υπολογιστών Γλώσσα περιγραφής υλικού: Verilog Αρης Ευθυμίου Το σημερινό μάθημα! Η γλώσσα περιγραφής υλικού Verilog Περίληψη των αντίστοιχων μαθημάτων Ψηφιακής σχεδίασης έμφαση σε
ΜΥΥ- 402 Αρχιτεκτονική Υπολογιστών Γλώσσα περιγραφής υλικού: Verilog Αρης Ευθυμίου Το σημερινό μάθημα! Η γλώσσα περιγραφής υλικού Verilog Περίληψη των αντίστοιχων μαθημάτων Ψηφιακής σχεδίασης έμφαση σε
Εισαγωγή στη Verilog με το ISE
 Εισαγωγή στη Verilog με το ISE Πατάμε new project Δίνουμε όνομα και κατάλογο όπου θα αποθηκευτεί το project. Next όπου επιλέγουμε chip και preferred language βάζουμε Verilog Next και στο Create new source
Εισαγωγή στη Verilog με το ISE Πατάμε new project Δίνουμε όνομα και κατάλογο όπου θα αποθηκευτεί το project. Next όπου επιλέγουμε chip και preferred language βάζουμε Verilog Next και στο Create new source
HY330 Ψηφιακά Κυκλώματα - Εισαγωγή στα Συστήματα VLSI. 1 ΗΥ330 - Διάλεξη 7η - Ακολουθιακά Κυκλώματα
 HY330 Ψηφιακά - Εισαγωγή στα Συστήματα VLSI Διδάσκων: Χ. Σωτηρίου, Βοηθοί: θα ανακοινωθούν http://inf-server.inf.uth.gr/courses/ce330 1 Μανταλωτές θετικής, αρνητικής πολικότητας Σχεδίαση με Μανταλωτές
HY330 Ψηφιακά - Εισαγωγή στα Συστήματα VLSI Διδάσκων: Χ. Σωτηρίου, Βοηθοί: θα ανακοινωθούν http://inf-server.inf.uth.gr/courses/ce330 1 Μανταλωτές θετικής, αρνητικής πολικότητας Σχεδίαση με Μανταλωτές
«Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων» Χειμερινό εξάμηνο Συντρέχων Κώδικας
 «Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων» Χειμερινό εξάμηνο 216-217 Συντρέχων Κώδικας Παρασκευάς Κίτσος http://diceslab.cied.teiwest.gr Επίκουρος Καθηγητής Tμήμα Μηχανικών Πληροφορικής ΤΕ E-mail: pkitsos@teimes.gr
«Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων» Χειμερινό εξάμηνο 216-217 Συντρέχων Κώδικας Παρασκευάς Κίτσος http://diceslab.cied.teiwest.gr Επίκουρος Καθηγητής Tμήμα Μηχανικών Πληροφορικής ΤΕ E-mail: pkitsos@teimes.gr
Χρονισμός και Απόδοση Υπολογιστικών Συστημάτων
 ΗΥ 232 Οργάνωση και στον Σχεδίαση Η/Y Διάλεξη 7 Χρονισμός και Απόδοση Υπολογιστικών Συστημάτων Νίκος Μπέλλας Τμήμα Μηχανικών Η/Υ, Τηλεπικοινωνιών και Δικτύων 1 Τι σημαίνει απόδοση; Αεροσκάφος NYC to Paris
ΗΥ 232 Οργάνωση και στον Σχεδίαση Η/Y Διάλεξη 7 Χρονισμός και Απόδοση Υπολογιστικών Συστημάτων Νίκος Μπέλλας Τμήμα Μηχανικών Η/Υ, Τηλεπικοινωνιών και Δικτύων 1 Τι σημαίνει απόδοση; Αεροσκάφος NYC to Paris
Πανεπιστήμιο Δυτικής Μακεδονίας. Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών. Ψηφιακή Σχεδίαση
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 9: Ελαχιστοποίηση και Κωδικοποίηση Καταστάσεων, Σχεδίαση με D flip-flop, Σχεδίαση με JK flip-flop, Σχεδίαση με T flip-flop Δρ. Μηνάς
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 9: Ελαχιστοποίηση και Κωδικοποίηση Καταστάσεων, Σχεδίαση με D flip-flop, Σχεδίαση με JK flip-flop, Σχεδίαση με T flip-flop Δρ. Μηνάς
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωµάτων
 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωµάτων Χειµερινό Εξάµηνο 2007-2008 Verilog: Τα βασικά ΗΥ220 - Βασίλης Παπαευσταθίου 1 Η εξέλιξη στη σχεδίαση ψηφιακών κυκλωµάτων Μεγάλη εξέλιξη τα τελευταία 30 χρόνια Στις
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωµάτων Χειµερινό Εξάµηνο 2007-2008 Verilog: Τα βασικά ΗΥ220 - Βασίλης Παπαευσταθίου 1 Η εξέλιξη στη σχεδίαση ψηφιακών κυκλωµάτων Μεγάλη εξέλιξη τα τελευταία 30 χρόνια Στις
Ολοκληρωμένα Κυκλώματα
 Δημοκρίτειο Πανεπιστήμιο Θράκης Τμήμα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Γ. Δημητρακόπουλος Ολοκληρωμένα Κυκλώματα Πρόοδος - Φθινόπωρο 2017 Θέμα 1 ο Σχεδιάστε το datapath για τον υπολογισμό
Δημοκρίτειο Πανεπιστήμιο Θράκης Τμήμα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Γ. Δημητρακόπουλος Ολοκληρωμένα Κυκλώματα Πρόοδος - Φθινόπωρο 2017 Θέμα 1 ο Σχεδιάστε το datapath για τον υπολογισμό
Περίληψη. ΗΜΥ-210: Λογικός Σχεδιασµός Εαρινό Εξάµηνο Παράδειγµα: Καταχωρητής 2-bit. Καταχωρητής 4-bit. Μνήµη Καταχωρητών
 ΗΜΥ-210: Λογικός Σχεδιασµός Εαρινό Κεφάλαιο 7 i: Καταχωρητές Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές Ολίσθησης Σειριακή Φόρτωση Σειριακή Ολίσθηση Καταχωρητές Ολίσθησης Παράλληλης Φόρτωσης
ΗΜΥ-210: Λογικός Σχεδιασµός Εαρινό Κεφάλαιο 7 i: Καταχωρητές Περίληψη Καταχωρητές Παράλληλης Φόρτωσης Καταχωρητές Ολίσθησης Σειριακή Φόρτωση Σειριακή Ολίσθηση Καταχωρητές Ολίσθησης Παράλληλης Φόρτωσης
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ (Τ.Ε.Ι.) ΚΡΗΤΗΣ Τµήµα Εφαρµοσµένης Πληροφορικής & Πολυµέσων. Ψηφιακή Σχεδίαση. Κεφάλαιο 5: Σύγχρονη Ακολουθιακή
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ (Τ.Ε.Ι.) ΚΡΗΤΗΣ Τµήµα Εφαρµοσµένης Πληροφορικής & Πολυµέσων Ψηφιακή Σχεδίαση Κεφάλαιο 5: Σύγχρονη Ακολουθιακή Λογική Σύγχρονα Ακολουθιακά Κυκλώµατα Είσοδοι Συνδυαστικό κύκλωµα
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ (Τ.Ε.Ι.) ΚΡΗΤΗΣ Τµήµα Εφαρµοσµένης Πληροφορικής & Πολυµέσων Ψηφιακή Σχεδίαση Κεφάλαιο 5: Σύγχρονη Ακολουθιακή Λογική Σύγχρονα Ακολουθιακά Κυκλώµατα Είσοδοι Συνδυαστικό κύκλωµα
Σχεδίαση κυκλωμάτων με SystemVerilog: 2o μέρος
 Σχεδίαση κυκλωμάτων με SystemVerilog: 2o μέρος Γιώργος Δημητρακόπουλος Περιγραφή κυκλωμάτων με προγραμματιστικές δομές υψηλού επιπέδου Κύριος στόχος των γλωσσών περιγραφής υλικού είναι να απαλλάξουν το
Σχεδίαση κυκλωμάτων με SystemVerilog: 2o μέρος Γιώργος Δημητρακόπουλος Περιγραφή κυκλωμάτων με προγραμματιστικές δομές υψηλού επιπέδου Κύριος στόχος των γλωσσών περιγραφής υλικού είναι να απαλλάξουν το
Σχεδίαση της Μονάδας Ελέγχου
 ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΣΧΕΔΙΑΣΗ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ - VHDL ΥΛΙΚΟ ΚΑΙ ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ Ενότητα 5 Σχεδίαση της Μονάδας Ελέγχου Καθηγητής Αντώνης Πασχάλης 2017 Γενικές Γραμμές Σχεδίαση
ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΣΧΕΔΙΑΣΗ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ - VHDL ΥΛΙΚΟ ΚΑΙ ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ Ενότητα 5 Σχεδίαση της Μονάδας Ελέγχου Καθηγητής Αντώνης Πασχάλης 2017 Γενικές Γραμμές Σχεδίαση
Σειρά Ασκήσεων 11: Βασική FSM Ελέγχου του Επεξεργαστή
 1 of 6 ΗΥ-225: Οργάνωση Υπολογιστών Άνοιξη 2009 Τµ. Επ. Υπολογιστών Πανεπιστήµιο Κρήτης Σειρά Ασκήσεων 11: Βασική FSM Ελέγχου του Επεξεργαστή Προθεσµία έως Κυριακή 12 Απριλίου 2009, ώρα 23:59 (βδοµάδα
1 of 6 ΗΥ-225: Οργάνωση Υπολογιστών Άνοιξη 2009 Τµ. Επ. Υπολογιστών Πανεπιστήµιο Κρήτης Σειρά Ασκήσεων 11: Βασική FSM Ελέγχου του Επεξεργαστή Προθεσµία έως Κυριακή 12 Απριλίου 2009, ώρα 23:59 (βδοµάδα
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων
 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2017-2018 Verilog: Στυλ Κώδικα και Synthesizable Verilog ΗΥ220 - Βασίλης Παπαευσταθίου & Γιώργος Καλοκαιρινός 1 Τα στυλ του κώδικα Τρεις βασικές κατηγορίες
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2017-2018 Verilog: Στυλ Κώδικα και Synthesizable Verilog ΗΥ220 - Βασίλης Παπαευσταθίου & Γιώργος Καλοκαιρινός 1 Τα στυλ του κώδικα Τρεις βασικές κατηγορίες
ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΥΛΙΚΟ ΚΑΙ ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ. Ενότητα 1. Λογικής Σχεδίασης. Καθηγητής Αντώνης Πασχάλης
 ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΣΧΕΔΙΑΣΗ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ - VHL ΥΛΙΚΟ ΚΑΙ ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ Ενότητα 1 Αρχές και Πρακτικές Ακολουθιακής Λογικής Σχεδίασης Καθηγητής Αντώνης Πασχάλης 217 Γενικές
ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΣΧΕΔΙΑΣΗ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ - VHL ΥΛΙΚΟ ΚΑΙ ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ Ενότητα 1 Αρχές και Πρακτικές Ακολουθιακής Λογικής Σχεδίασης Καθηγητής Αντώνης Πασχάλης 217 Γενικές
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Εργαστήριο Ηλεκτρονικής. Ψηφιακά Ηλεκτρονικά. Ακολουθιακή Λογική. Επιμέλεια Διαφανειών: Δ.
 Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Ακολουθιακή Λογική Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Εισαγωγή Είσοδοι Συνδυαστικό Κύκλωμα Έξοδοι Στοιχεία Μνήμης Κατάσταση
Πανεπιστήμιο Πατρών Τμήμα Φυσικής Ψηφιακά Ηλεκτρονικά Ακολουθιακή Λογική Επιμέλεια Διαφανειών: Δ. Μπακάλης Πάτρα, Φεβρουάριος 2009 Εισαγωγή Είσοδοι Συνδυαστικό Κύκλωμα Έξοδοι Στοιχεία Μνήμης Κατάσταση
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωµάτων
 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωµάτων Χειµερινό Εξάµηνο 2006-2007 Verilog: Στυλ Κώδικα και Synthesizable Verilog ΗΥ220 - Βασίλης Παπαευσταθίου 1 Τα στυλ του κώδικα Τρεις βασικές κατηγορίες Συµπεριφοράς
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωµάτων Χειµερινό Εξάµηνο 2006-2007 Verilog: Στυλ Κώδικα και Synthesizable Verilog ΗΥ220 - Βασίλης Παπαευσταθίου 1 Τα στυλ του κώδικα Τρεις βασικές κατηγορίες Συµπεριφοράς
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων
 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2018-2019 Verilog: Μια πιο κοντινή ματιά ΗΥ220 - Βασίλης Παπαευσταθίου 1 Δομή της γλώσσας Μοιάζει αρκετά με τη C Preprocessor Keywords Τελεστές =
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2018-2019 Verilog: Μια πιο κοντινή ματιά ΗΥ220 - Βασίλης Παπαευσταθίου 1 Δομή της γλώσσας Μοιάζει αρκετά με τη C Preprocessor Keywords Τελεστές =
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων
 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2017-2018 Verilog: Μια πιο κοντινή ματιά ΗΥ220 - Βασίλης Παπαευσταθίου & Γιώργος Καλοκαιρινός 1 Δομή της γλώσσας Μοιάζει αρκετά με τη C Preprocessor
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2017-2018 Verilog: Μια πιο κοντινή ματιά ΗΥ220 - Βασίλης Παπαευσταθίου & Γιώργος Καλοκαιρινός 1 Δομή της γλώσσας Μοιάζει αρκετά με τη C Preprocessor
Μικροηλεκτρονική - VLSI
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 7: Ακολουθιακή Λογική Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μικροηλεκτρονική - VLSI Ενότητα 7: Ακολουθιακή Λογική Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες
Ασύγχρονοι Απαριθμητές. Διάλεξη 7
 Ασύγχρονοι Απαριθμητές Διάλεξη 7 Δομή της διάλεξης Εισαγωγή στους Απαριθμητές Ασύγχρονος Δυαδικός Απαριθμητής Ασύγχρονος Δεκαδικός Απαριθμητής Ασύγχρονος Δεκαδικός Απαριθμητής με Latch Ασκήσεις 2 Ασύγχρονοι
Ασύγχρονοι Απαριθμητές Διάλεξη 7 Δομή της διάλεξης Εισαγωγή στους Απαριθμητές Ασύγχρονος Δυαδικός Απαριθμητής Ασύγχρονος Δεκαδικός Απαριθμητής Ασύγχρονος Δεκαδικός Απαριθμητής με Latch Ασκήσεις 2 Ασύγχρονοι
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΣΧΟΛΗ ΟΙΚΟΝΟΜΙΑΣ, ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΛΟΓΙΚΗ ΣΧΕΔΙΑΣΗ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΣΧΟΛΗ ΟΙΚΟΝΟΜΙΑΣ, ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΛΟΓΙΚΗ ΣΧΕΔΙΑΣΗ Αναφορά 8 ης εργαστηριακής άσκησης: Αποκωδικοποιητής ΔΗΜΗΤΡΙΟΣ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΣΧΟΛΗ ΟΙΚΟΝΟΜΙΑΣ, ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΛΟΓΙΚΗ ΣΧΕΔΙΑΣΗ Αναφορά 8 ης εργαστηριακής άσκησης: Αποκωδικοποιητής ΔΗΜΗΤΡΙΟΣ
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων
 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2015-2016 ΗΥ220 -Γιώργος Καιλοκαιρινός & Βασίλης Παπαευσταθίου 1 Λογικές Πύλες, Στοιχεία Μνήμης, Συνδυαστική Λογική και Κυματομορφές ΗΥ220 -Γιώργος
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Χειμερινό Εξάμηνο 2015-2016 ΗΥ220 -Γιώργος Καιλοκαιρινός & Βασίλης Παπαευσταθίου 1 Λογικές Πύλες, Στοιχεία Μνήμης, Συνδυαστική Λογική και Κυματομορφές ΗΥ220 -Γιώργος
HY130 Ψηφιακή Σχεδίαση
 HY130 Ψηφιακή Σχεδίαση Διδάσκων Εργαστηρίου: Χ. Σωτηρίου http://inf-server.inf.uth.gr/courses/ce130/ 1 2 1 3 Μοιάζει αρκετά με την C Προ-επεξεργαστή (Preprocessor) Λέξεις Κλειδιά (Keywords) Τελεστές =
HY130 Ψηφιακή Σχεδίαση Διδάσκων Εργαστηρίου: Χ. Σωτηρίου http://inf-server.inf.uth.gr/courses/ce130/ 1 2 1 3 Μοιάζει αρκετά με την C Προ-επεξεργαστή (Preprocessor) Λέξεις Κλειδιά (Keywords) Τελεστές =
100 ΕΡΩΤΗΣΕΙΣ ΜΕ ΤΙΣ ΑΝΤΙΣΤΟΙΧΕΣ ΑΠΑΝΤΗΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ
 100 ΕΡΩΤΗΣΕΙΣ ΜΕ ΤΙΣ ΑΝΤΙΣΤΟΙΧΕΣ ΑΠΑΝΤΗΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ 1) Να μετατρέψετε τον δεκαδικό αριθμό (60,25) 10, στον αντίστοιχο δυαδικό 11111,11 111001,01 111100,01 100111,1 111100,01 2)
100 ΕΡΩΤΗΣΕΙΣ ΜΕ ΤΙΣ ΑΝΤΙΣΤΟΙΧΕΣ ΑΠΑΝΤΗΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΑ 1) Να μετατρέψετε τον δεκαδικό αριθμό (60,25) 10, στον αντίστοιχο δυαδικό 11111,11 111001,01 111100,01 100111,1 111100,01 2)
K24 Ψηφιακά Ηλεκτρονικά 9: Flip-Flops
 K24 Ψηφιακά Ηλεκτρονικά 9: TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ ΤΕΧΝΟΛΟΓΙΚΟ Περιεχόμενα 1 2 3 Γενικά Ύστερα από τη μελέτη συνδυαστικών ψηφιακών κυκλωμάτων, θα μελετήσουμε
K24 Ψηφιακά Ηλεκτρονικά 9: TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ ΤΕΧΝΟΛΟΓΙΚΟ Περιεχόμενα 1 2 3 Γενικά Ύστερα από τη μελέτη συνδυαστικών ψηφιακών κυκλωμάτων, θα μελετήσουμε
Εργαστήριο Ψηφιακών Κυκλωμάτων. Χειμερινό Εξάμηνο
 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Verilog: Μια πιο κοντινή ματιά Χειμερινό Εξάμηνο 2009 2010 Δομή της γλώσσας Μοιάζει αρκετά με τη C Preprocessor Keywords Τελεστές = ==,!= , = &&? : & and or
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Verilog: Μια πιο κοντινή ματιά Χειμερινό Εξάμηνο 2009 2010 Δομή της γλώσσας Μοιάζει αρκετά με τη C Preprocessor Keywords Τελεστές = ==,!= , = &&? : & and or
Σχεδίαση Ψηφιακών Συστημάτων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Σχεδίαση Ψηφιακών Συστημάτων Ενότητα 2: Βασικές Μονάδες Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Σχεδίαση Ψηφιακών Συστημάτων Ενότητα 2: Βασικές Μονάδες Κυριάκης - Μπιτζάρος Ευστάθιος Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες
Κεφάλαιο 7 ο. Γ. Τσιατούχας. VLSI Technology and Computer Architecture Lab. Ακολουθιακή Λογική 2
 ΚΥΚΛΩΜΑΤΑ VLSI Ακολουθιακή Λογική Κεφάλαιο 7 ο Γ. Τσιατούχας ΚΥΚΛΩΜΑΤΑ VLSI Διάρθρωση 1. Δισταθή κυκλώματα Μεταστάθεια 2. Μανδαλωτές 3. Flip Flops Flops 4. Δομές διοχέτευσης 5. Διανομή ρολογιού 6. Συγχρονισμός
ΚΥΚΛΩΜΑΤΑ VLSI Ακολουθιακή Λογική Κεφάλαιο 7 ο Γ. Τσιατούχας ΚΥΚΛΩΜΑΤΑ VLSI Διάρθρωση 1. Δισταθή κυκλώματα Μεταστάθεια 2. Μανδαλωτές 3. Flip Flops Flops 4. Δομές διοχέτευσης 5. Διανομή ρολογιού 6. Συγχρονισμός
Κεφάλαιο 10 ο. Γ. Τσιατούχας. VLSI Systems and Computer Architecture Lab. Ακολουθιακή Λογική 2
 ΚΥΚΛΩΜΑΤΑ VLSI Πανεπιστήμιο Ιωαννίνων Ακολουθιακή Λογική Κεφάλαιο 10 ο Τμήμα Μηχανικών Η/Υ και Πληροφορικής Γ. Τσιατούχας ΚΥΚΛΩΜΑΤΑ VLSI Διάρθρωση 1. Δισταθή κυκλώματα Μεταευστάθεια 2. Μανδαλωτές 3. Flip
ΚΥΚΛΩΜΑΤΑ VLSI Πανεπιστήμιο Ιωαννίνων Ακολουθιακή Λογική Κεφάλαιο 10 ο Τμήμα Μηχανικών Η/Υ και Πληροφορικής Γ. Τσιατούχας ΚΥΚΛΩΜΑΤΑ VLSI Διάρθρωση 1. Δισταθή κυκλώματα Μεταευστάθεια 2. Μανδαλωτές 3. Flip
Ψηφιακή Σχεδίαση Ενότητα 10:
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 10: Καταχωρητές & Μετρητές Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Εργαστήριο Ψηφιακών Συστημάτων και Αρχιτεκτονικής Υπολογιστών http://arch.icte.uowm.gr/mdasyg
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ψηφιακή Σχεδίαση Ενότητα 10: Καταχωρητές & Μετρητές Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Εργαστήριο Ψηφιακών Συστημάτων και Αρχιτεκτονικής Υπολογιστών http://arch.icte.uowm.gr/mdasyg
Εργαστήριο Ψηφιακών Κυκλωμάτων
 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Verilog: Στυλ Κώδικα και Synthesizable Verilog Χειμερινό Εξάμηνο 2009 2010 Τα στυλ του κώδικα Τρεις βασικές κατηγορίες Behavioral (procedural) Dataflow Structural Synthesizable
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωμάτων Verilog: Στυλ Κώδικα και Synthesizable Verilog Χειμερινό Εξάμηνο 2009 2010 Τα στυλ του κώδικα Τρεις βασικές κατηγορίες Behavioral (procedural) Dataflow Structural Synthesizable
Εργαστήριο Οργάνωσης Η/Υ. Δαδαλιάρης Αντώνιος
 Εργαστήριο Οργάνωσης Η/Υ Δαδαλιάρης Αντώνιος dadaliaris@uth.gr Συνδυαστικό Κυκλωμα: Το κύκλωμα του οποίου οι έξοδοι εξαρτώνται αποκλειστικά από τις τρέχουσες εισόδους του. Ακολουθιακό Κύκλωμα: Το κύκλωμα
Εργαστήριο Οργάνωσης Η/Υ Δαδαλιάρης Αντώνιος dadaliaris@uth.gr Συνδυαστικό Κυκλωμα: Το κύκλωμα του οποίου οι έξοδοι εξαρτώνται αποκλειστικά από τις τρέχουσες εισόδους του. Ακολουθιακό Κύκλωμα: Το κύκλωμα
Καταχωρητές, Μετρητές και Ακολουθιακά Κυκλώματα
 ΗΜΥ211 Εργαστήριο Ψηφιακών Συστημάτων Καταχωρητές, Μετρητές και Ακολουθιακά Κυκλώματα Διδάσκoντες: Γιώργος Ζάγγουλος και Λάζαρος Ζαχαρία Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
ΗΜΥ211 Εργαστήριο Ψηφιακών Συστημάτων Καταχωρητές, Μετρητές και Ακολουθιακά Κυκλώματα Διδάσκoντες: Γιώργος Ζάγγουλος και Λάζαρος Ζαχαρία Πανεπιστήμιο Κύπρου Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
ΗΜΥ 210: Σχεδιασμός Ψηφιακών Συστημάτων 15/11/2010. Σχεδιασμός Ακολουθιακών Κυκλωμάτων 1
 ΗΜΥ 20: Σχεδιασμός Ψηφιακών Συστημάτων 5//200 ΗΜΥ-20: Σχεδιασμός Ψηφιακών Συστημάτων Σχεδιασμός Ακολουθιακών Κυκλωμάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Σχεδιασμός Ακολουθιακών Κυκλωμάτων Αρχή: Μια λίστα/περιγραφή
ΗΜΥ 20: Σχεδιασμός Ψηφιακών Συστημάτων 5//200 ΗΜΥ-20: Σχεδιασμός Ψηφιακών Συστημάτων Σχεδιασμός Ακολουθιακών Κυκλωμάτων Διδάσκουσα: Μαρία Κ. Μιχαήλ Σχεδιασμός Ακολουθιακών Κυκλωμάτων Αρχή: Μια λίστα/περιγραφή
Απόδειξη Ισοδυναμίας Συναρτήσεων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΣΧΟΛΗ ΟΙΚΟΝΟΜΙΑΣ, ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΛΟΓΙΚΗ ΣΧΕΔΙΑΣΗ Αναφορά 2ης εργαστηριακής άσκησης: Απόδειξη Ισοδυναμίας
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΣΧΟΛΗ ΟΙΚΟΝΟΜΙΑΣ, ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΛΟΓΙΚΗ ΣΧΕΔΙΑΣΗ Αναφορά 2ης εργαστηριακής άσκησης: Απόδειξη Ισοδυναμίας
Οδηγίες εγκατάστασης και χρήσης του Quartus
 Εγκατάσταση του Quartus Οδηγίες εγκατάστασης και χρήσης του Quartus Δημήτρης Μαγγίρας, Γιώργος Δημητρακόπουλος 1. Κατεβάζουμε την έκδοση 13.0SP1 από εδώ ακολουθώντας τις οδηγίες που φαίνονται στην εικόνα.
Εγκατάσταση του Quartus Οδηγίες εγκατάστασης και χρήσης του Quartus Δημήτρης Μαγγίρας, Γιώργος Δημητρακόπουλος 1. Κατεβάζουμε την έκδοση 13.0SP1 από εδώ ακολουθώντας τις οδηγίες που φαίνονται στην εικόνα.
ΠΕΡΙΕΧΟΜΕΝΑ. Πρόλογος...9 ΚΕΦ. 1. ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ - ΚΩΔΙΚΕΣ
 ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος...9 ΚΕΦ. 1. ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ - ΚΩΔΙΚΕΣ 1.1 Εισαγωγή...11 1.2 Τα κύρια αριθμητικά Συστήματα...12 1.3 Μετατροπή αριθμών μεταξύ των αριθμητικών συστημάτων...13 1.3.1 Μετατροπή ακέραιων
ΠΕΡΙΕΧΟΜΕΝΑ Πρόλογος...9 ΚΕΦ. 1. ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ - ΚΩΔΙΚΕΣ 1.1 Εισαγωγή...11 1.2 Τα κύρια αριθμητικά Συστήματα...12 1.3 Μετατροπή αριθμών μεταξύ των αριθμητικών συστημάτων...13 1.3.1 Μετατροπή ακέραιων
Ελίνα Μακρή
 Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
Χρονισμός Σύγχρονων Κυκλωμάτων, Καταχωρητές και Μανταλωτές. Χειμερινό Εξάμηνο
 HY220 Χρονισμός Σύγχρονων Κυκλωμάτων, Καταχωρητές και Μανταλωτές Χειμερινό Εξάμηνο 2009 20102010 Γενικό Μοντέλο Σύγχρονων Κυκλωμάτων clock input input CL reg CL reg output option feedback Τα καλώδια, εκτός
HY220 Χρονισμός Σύγχρονων Κυκλωμάτων, Καταχωρητές και Μανταλωτές Χειμερινό Εξάμηνο 2009 20102010 Γενικό Μοντέλο Σύγχρονων Κυκλωμάτων clock input input CL reg CL reg output option feedback Τα καλώδια, εκτός
Λογική Σχεδίαση Ι - Εξεταστική Φεβρουαρίου 2013 Διάρκεια εξέτασης : 160 Ονοματεπώνυμο : Α. Μ. Έτος σπουδών:
 Λογική Σχεδίαση Ι - Εξεταστική Φεβρουαρίου 23 Διάρκεια εξέτασης : 6 Ονοματεπώνυμο : Α. Μ. Έτος σπουδών: Θέμα (,5 μονάδες) Στις εισόδους του ακόλουθου κυκλώματος c b a εφαρμόζονται οι κάτωθι κυματομορφές.
Λογική Σχεδίαση Ι - Εξεταστική Φεβρουαρίου 23 Διάρκεια εξέτασης : 6 Ονοματεπώνυμο : Α. Μ. Έτος σπουδών: Θέμα (,5 μονάδες) Στις εισόδους του ακόλουθου κυκλώματος c b a εφαρμόζονται οι κάτωθι κυματομορφές.
Πανεπιστήμιο Πατρών. Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών
 Πανεπιστήμιο Πατρών Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Εργαστήριο Σχεδίασης Ολοκληρωμένων Κυκλωμάτων Σχεδιασμός Ολοκληρωμένων Συστημάτων με τεχνικές VLSI Χειμερινό Εξάμηνο 2015 FSM
Πανεπιστήμιο Πατρών Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Εργαστήριο Σχεδίασης Ολοκληρωμένων Κυκλωμάτων Σχεδιασμός Ολοκληρωμένων Συστημάτων με τεχνικές VLSI Χειμερινό Εξάμηνο 2015 FSM
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωµάτων
 ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωµάτων Χειµερινό Εξάµηνο 2007-2008 Verilog: Μια πιο κοντινή µατιά ΗΥ220 - Βασίλης Παπαευσταθίου 1 οµή της γλώσσας Μοιάζει αρκετά µε τηc Preprocessor Keywords Τελεστές = &
ΗΥ220 Εργαστήριο Ψηφιακών Κυκλωµάτων Χειµερινό Εξάµηνο 2007-2008 Verilog: Μια πιο κοντινή µατιά ΗΥ220 - Βασίλης Παπαευσταθίου 1 οµή της γλώσσας Μοιάζει αρκετά µε τηc Preprocessor Keywords Τελεστές = &
K24 Ψηφιακά Ηλεκτρονικά 10: Ακολουθιακά Κυκλώματα
 K24 Ψηφιακά Ηλεκτρονικά : TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ ΤΕΧΝΟΛΟΓΙΚΟ Περιεχόμενα 2 3 Γενικά Όπως είδαμε και σε προηγούμενα μαθήματα, ένα ψηφιακό κύκλωμα ονομάζεται
K24 Ψηφιακά Ηλεκτρονικά : TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ ΤΕΧΝΟΛΟΓΙΚΟ Περιεχόμενα 2 3 Γενικά Όπως είδαμε και σε προηγούμενα μαθήματα, ένα ψηφιακό κύκλωμα ονομάζεται
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI II
 Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI II 4 η Εργαστηριακή Άσκηση Περιγραφή Κυκλωμάτων με Ακολουθιακές Εντολές Άδειες Χρήσης Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης Creative Commons
Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων VLSI II 4 η Εργαστηριακή Άσκηση Περιγραφή Κυκλωμάτων με Ακολουθιακές Εντολές Άδειες Χρήσης Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης Creative Commons
Παράρτηµα Γ. Τα Βασικά της Λογικής Σχεδίασης. Οργάνωση και Σχεδίαση Υπολογιστών Η ιασύνδεση Υλικού και Λογισµικού, 4 η έκδοση
 Οργάνωση και Σχεδίαση Υπολογιστών Η ιασύνδεση Υλικού και Λογισµικού, 4 η έκδοση Παράρτηµα Γ Τα Βασικά της Λογικής Σχεδίασης ιαφάνειες διδασκαλίας του πρωτότυπου βιβλίου µεταφρασµένες στα ελληνικά και εµπλουτισµένες
Οργάνωση και Σχεδίαση Υπολογιστών Η ιασύνδεση Υλικού και Λογισµικού, 4 η έκδοση Παράρτηµα Γ Τα Βασικά της Λογικής Σχεδίασης ιαφάνειες διδασκαλίας του πρωτότυπου βιβλίου µεταφρασµένες στα ελληνικά και εµπλουτισµένες
Ακολουθιακές εντολές. (Peter Ashenden, The Students Guide to VHDL)
 Ακολουθιακές εντολές (Peter Ashenden, The Students Guide to VHDL) Εντολή If Τα βασικά χαρακτηριστικά της είναι τα εξής: Μπορεί να χρησιµοποιηθεί για τον έλεγχο µίας ή περισσοτέρων συνθηκών. Η πρώτη συνθήκη
Ακολουθιακές εντολές (Peter Ashenden, The Students Guide to VHDL) Εντολή If Τα βασικά χαρακτηριστικά της είναι τα εξής: Μπορεί να χρησιµοποιηθεί για τον έλεγχο µίας ή περισσοτέρων συνθηκών. Η πρώτη συνθήκη
Καταχωρητές,Σύγχρονοι Μετρητές και ΑκολουθιακάΚυκλώματα
 ΗΜΥ211 Εργαστήριο Ψηφιακών Συστηµάτων Καταχωρητές,Σύγχρονοι Μετρητές και ΑκολουθιακάΚυκλώματα ιδάσκων: ρ. Γιώργος Ζάγγουλος Πανεπιστήµιο Κύπρου Τµήµα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Ατζέντα
ΗΜΥ211 Εργαστήριο Ψηφιακών Συστηµάτων Καταχωρητές,Σύγχρονοι Μετρητές και ΑκολουθιακάΚυκλώματα ιδάσκων: ρ. Γιώργος Ζάγγουλος Πανεπιστήµιο Κύπρου Τµήµα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Ατζέντα
Εισαγωγή στην πληροφορική
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Εισαγωγή στην πληροφορική Ενότητα 4: Ψηφιακή Λογική, Άλγεβρα Boole, Πίνακες Αλήθειας (Μέρος B) Αγγελίδης Παντελής Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Εισαγωγή στην πληροφορική Ενότητα 4: Ψηφιακή Λογική, Άλγεβρα Boole, Πίνακες Αλήθειας (Μέρος B) Αγγελίδης Παντελής Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών
UNIVERSITY OF CALIFORNIA. EECS 150 Fall ) You are implementing an 4:1 Multiplexer that has the following specifications:
 UNIVERSITY OF CALIFORNIA Department of Electrical Engineering and Computer Sciences EECS 150 Fall 2001 Prof. Subramanian Midterm II 1) You are implementing an 4:1 Multiplexer that has the following specifications:
UNIVERSITY OF CALIFORNIA Department of Electrical Engineering and Computer Sciences EECS 150 Fall 2001 Prof. Subramanian Midterm II 1) You are implementing an 4:1 Multiplexer that has the following specifications:
Άσκηση 3 Ένα νέο είδος flip flop έχει τον ακόλουθο πίνακα αληθείας : I 1 I 0 Q (t+1) Q (t) 1 0 ~Q (t) Κατασκευάστε τον πίνακα
 Άσκηση Δίδονται οι ακόλουθες κυματομορφές ρολογιού και εισόδου D που είναι κοινή σε ένα D latch και ένα D flip flop. Το latch είναι θετικά ενεργό, ενώ το ff θετικά ακμοπυροδοτούμενο. Σχεδιάστε τις κυματομορφές
Άσκηση Δίδονται οι ακόλουθες κυματομορφές ρολογιού και εισόδου D που είναι κοινή σε ένα D latch και ένα D flip flop. Το latch είναι θετικά ενεργό, ενώ το ff θετικά ακμοπυροδοτούμενο. Σχεδιάστε τις κυματομορφές
Ψηφιακή Λογική Σχεδίαση
 Ψηφιακή Λογική Σχεδίαση Επιμέλεια: Νίκος Φακωτάκης, Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα Αδειοδότησης Το παρόν υλικό διατίθεται
Ψηφιακή Λογική Σχεδίαση Επιμέλεια: Νίκος Φακωτάκης, Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σημείωμα Αδειοδότησης Το παρόν υλικό διατίθεται
