ÊåöÜëáéï 4. ÅëåãêôÝò. Åðéäéùêüìåíïé óôü ïé:
|
|
|
- Σωτηρία Βικελίδης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ÊåöÜëáéï 4 ÅëåãêôÝò Åðéäéùêüìåíïé óôü ïé: Óêïðüò áõôïý ôïõ êåöáëáßïõ åßíáé íá âïçèþóåé ôïõò ìáèçôýò: Ö Íá ãíùñßæïõí ôéò êáôçãïñßåò ôùí åëåãêôþí êáé ôçí ñçóéìüôçôü ôïõò. Ö Íá ãíùñßæïõí ôï ðþò óõìðåñéöýñïíôáé, ðïéá åßíáé ôá óýìâïëü ôïõò êáé ðïéá ôá ôå íéêü ôïõò áñáêôçñéóôéêü. Ö Íá áíáãíùñßæïõí ôá âáóéêü êõêëþìáôá ôùí åëåãêôþí.
2 êåöüëáéï 4 4. ÅëåãêôÝò Óêïðüò ôïõ åëåãêôþ åßíáé ç óýãêñéóç ôçò åëåã üìåíçò ìåôáâëçôþò [y(t)] ìå ôçí åðéèõìçôþ ôéìþ [r(t)]. ÅÜí ôï áðïôýëåóìá ôçò óýãêñéóçò åßíáé äéüöïñï ôïõ ìçäåíüò, ôüôå ï åëåãêôþò ìåôáâüëåé ôï óþìá åîüäïõ Ýôóé, þóôå ç äéáöïñü e(t)=r(t)-y(t) íá ìçäåíéóôåß. Ó Þìá 4.: Óýìâïëá åëåãêôþ (r = åðéèõìçôþ ôéìþ, y = åëåã üìåíç ìåôáâëçôþ, e = óöüëìá). Ï åëåãêôþò ìáæß ìå ôï ìåôáôñïðýá êáé ôï ìç áíéóìü ñýèìéóçò ôïõ ôåëéêïý óôïé åßïõ åëýã ïõ, áðïôåëïýí ôç ñõèìéóôéêþ äéüôáîç. Ïé åñãáóßåò ðïõ åêôåëåß ç ñõèìéóôéêþ äéüôáîç óôá ðëáßóéá åíüò ÓõóôÞìáôïò ÁõôïìÜôïõ ÅëÝã ïõ åßíáé ïé åîþò: 4 ÌÝôñçóç ôçò åëåã üìåíçò ìåôáâëçôþò y(t). 4 Óýãêñéóç ôçò åëåã üìåíçò ìåôáâëçôþò ìå ôçí åðéèõìçôþ ôéìþ r(t). Ôï áðïôýëåóìá áõôþò ôçò óýãêñéóçò ëýãåôáé óöüëìá e(t). e( t) = r( t) y( t) 4 Åíßó õóç ôïõ óöüëìáôïò êáé äçìéïõñãßá óþìáôïò åîüäïõ (t) ñïíéêü ìåôáâëçôïý. 4 Ñýèìéóç ôçò ñïþò ôçò åíýñãåéáò Þ ôçò ìüæáò ôïõ åëåã üìåíïõ óõóôþìáôïò. 4. Ôáîéíüìçóç åëåãêôþí Ïé êáíïíéóìïß (DIN 9225) äéáêñßíïõí ôïõò åëåãêôýò Á) áíüëïãá ìå ôï åßäïò ôçò åëåã üìåíçò ìåôáâëçôþò óå: 4 ÅëåãêôÝò èåñìïêñáóßáò 4 ÅëåãêôÝò ñïþò 4 ÅëåãêôÝò óôñïöþí 4 ÅëåãêôÝò èýóçò ê.ëð. Â) áíüëïãá ìå ôïí ôñüðï ìåôáâïëþò ôçò åðéèõìçôþò ôéìþò óå: 4 ÅëåãêôÝò óôáèåñþò åðéèõìçôþò ôéìþò. Óôïõò åëåãêôýò áõôïýò ç åðéèõìçôþ ôéìþ åßíáé óôáèåñþ. 4 ÅëåãêôÝò áêïëïõèßáò, óôïõò ïðïßïõò ç åðéèõìçôþ ôéìþ áëëüæåé ìå ôï ñüíï. 4 ÅëåãêôÝò ìå ñïíéêü ìåôáâáëëüìåíç åðéèõìçôþ ôéìþ. Óôïõò åëåãêôýò áõôïýò ç åðéèõìçôþ ôéìþ ìåôáâüëëåôáé ìå âüóç Ýíá ðñïêáèïñéóìýíï ðñüãñáììá. 96
3 ÅëåãêôÝò Ã) áíüëïãá ìå ôç ìåôáâïëþ ôïõ óþìáôïò åîüäïõ óå: 4 Óõíå åßò åëåãêôýò 4 Ðåñéïäéêïýò åëåãêôýò: åëåãêôýò äýï èýóåùí êáé ôñéþí èýóåùí. 4 Äåéãìáôïëåéðôéêïýò åëåãêôýò. Ä) áíüëïãá ìå ôç âçìáôéêþ ñïíéêþ ôïõò áðüêñéóç óå: 4 Áíáëïãéêïýò åëåãêôýò (åëåãêôþò-ñ) 4 Ïëïêëçñùôéêïýò åëåãêôýò (åëåãêôþò-i) 4 Äéáöïñéêïýò åëåãêôýò (åëåãêôþò-d) 4 Áíáëïãéêïýò / ïëïêëçñùôéêïýò åëåãêôýò (åëåãêôþò-i) 4 Áíáëïãéêïýò / äéáöïñéêïýò åëåãêôýò (åëåãêôþò-d) 4 Áíáëïãéêïýò / ïëïêëçñùôéêïýò / äéáöïñéêïýò åëåãêôýò (åëåãêôþò-id) E) áíüëïãá ìå ôç ìïñöþ ôïõ óþìáôïò åîüäïõ óå: 4 Áíáëïãéêïýò êáé 4 Øçöéáêïýò åëåãêôýò Óô) áíüëïãá ìå ôï åßäïò ôçò åíýñãåéáò ôñïöïäïóßáò (âïçèçôéêþ ôñïöïäïóßá) óå: 4 ÅëåãêôÝò ùñßò âïçèçôéêþ åíýñãåéá 4 ÅëåãêôÝò ìå âïçèçôéêþ åíýñãåéá. ÐáñáêÜôù èá ìåëåôþóïõìå ôïõò åëåãêôýò áíüëïãá ìå ôç âçìáôéêþ ôïõò ñïíéêþ áðüêñéóç. 4.2 Áíáëïãéêüò åëåãêôþò ÅëåãêôÞò- (roportional) O åëåãêôþò- Ý åé áðëþ êáôáóêåõþ êáé åðïìýíùò ìéêñü êüóôïò. ¼ôáí óå Ýíá óýóôçìá áõôïìüôïõ åëýã ïõ äñá îáöíéêü ìéá äéáôáñá Þ, ôüôå ï åëåãêôþò áðïêñßíåôáé áìýóùò, ùñßò ñïíéêþ êáèõóôýñçóç, êáé áíáëïãéêü. Áðü ôçí ðáñáôþñçóç ôçò ñïíéêþò áðüêñéóçò (ó. 4.2) ðñïêýðôåé üôé ôï óþìá åîüäïõ ôïõ åëåãêôþ (t) åßíáé áíüëïãï ôïõ óþìáôïò åéóüäïõ e(t). ÅðïìÝíùò, éó ýåé ç ó Ýóç: üðïõ ç åíßó õóç ôïõ åëåãêôþ. u = e (4.) 97
4 êåöüëáéï 4 Ó Þìá 4.2: ÂçìáôéêÞ ñïíéêþ áðüêñéóç ôïõ åëåãêôþ-ñ. u = 2 e u = e Áðü ôçí ðáñáðüíù ñïíéêþ áðüêñéóç ôïõ åëåãêôþ äéáðéóôþíåé êáíåßò åýêïëá, üôé ï åëåãêôþò-: 4 Åßíáé Ýíáò ãñþãïñïò åëåãêôþò êáé áíôéäñü óôéò äéáôáñá Ýò ùñßò ñïíéêþ êáèõóôýñçóç. 4 ñåéüæåôáé ðüíôá Ýíá óþìá (óöüëìá) óôçí åßóïäü ôïõ, ãéá íá ëåéôïõñãþóåé êáé ãé áõôü ñçóéìïðïéåßôáé åêåß üðïõ äåí áðáéôåßôáé áêñéâþò Ýëåã ïò. 2 Ó Þìá 4.3: Óýìâïëï ôïõ åëåãêôþ-ñ. ¼ôáí ôï óþìá åéóüäïõ ìåôáâüëëåôáé êáôü Äe(t), ôüôå Ý ïõìå ìéá áíôßóôïé ç ìåôáâïëþ ôïõ óþìáôïò åîüäïõ Ä (t), üðïôå éó ýåé: 98
5 ÅëåãêôÝò Äu () t Äe() t = (4.2) Ó Þìá 4.3.: Ãñáöéêüò ïñéóìüò ôçò åíßó õóçò Êñ. Ìå âüóç ôçí åîßóùóç (4.) ôïõ åëåãêôþ, óõìðëçñþíïõìå ôïí ðáñáêüôù ðßíáêá êáé áðü ôéò ôéìýò áõôýò ðñïêýðôåé ç óôáôéêþ áñáêôçñéóôéêþ ôïõ åëåãêôþ- (ó Þìá 4.4). e(t) p= p=2 0V 0V 0V 9V 9V 0V 8V 8V 0V 7V 7V 0V 6V 6V 0V 5V 5V 0V 4V 4V 8V 3V 3V 6V 2V 2V 4V V V 2V e(t) p= p= V -V -V -2V -2V -2V -4V -3V -3V -6V -4V -4V -8V -5V -5V -0V -6V -6V -0V -7V -7V -0V -8V -8V -0V 99
6 êåöüëáéï 4 êüñïò U max e min =2 X 2 X = e max U h e U min êüñïò Ó Þìá 4.4: ÓôáôéêÝò áñáêôçñéóôéêýò ôïõ åëåãêôþ-ñ ãéá Ê Ñ = êáé ãéá Ê Ñ =2 Ðáñáôçñþíôáò ôéò ðáñáðüíù áñáêôçñéóôéêýò, äéáðéóôþíïõìå üôé óå êüèå áñáêôçñéóôéêþ âñßóêåôáé ìéá ðåñéï Þ ìýóá óôçí ïðïßá õðüñ åé áíáëïãéêþ (ãñáììéêþ) ó Ýóç ìåôáîý óþìáôïò åîüäïõ êáé óþìáôïò åéóüäïõ ôïõ åëåãêôþ. Ç ðåñéï Þ áõôþ ïíïìüæåôáé áíáëïãéêþ ðåñéï Þ Ñ. Åðßóçò äéáðéóôþíïõìå üôé áõîüíïíôáò ôçí åíßó õóç Ê Ñ ìåéþíåôáé ç áíáëïãéêþ ðåñéï Þ Ñ êáé áíôéóôñüöùò, äçëáäþ: X = (4.3) Óýìöùíá ìå ôá DIN 9226, ùò áíáëïãéêþ ðåñéï Þ ïñßæåôáé ç ðåñéï Þ ìýóá óôçí ïðïßá ðñýðåé íá ìåôáâëçèåß ç åëåã üìåíç ìåôáâëçôþ y(t), ãéá íá ìåôáêéíçèåß ôï ôåëéêü óôïé åßïõ åëýã ïõ áðü ôï êüôù Ýùò ôï Üíù üñéï ôçò ðåñéï Þò ñýèìéóçò (U min Ýùò U max ). ÅîÜëëïõ áðü ôï ó Þìá 4.4 ëáìâüíïõìå: max =. e max min =. e min max - min =. (e max - e min ) áëëü max - min = u h êáé e max - e min = X Üñá U h h = X X (4.4) U = X = u h Y X h max = u h Y h max X % = Y u h h max 00 X U h = áðüëõôç áíáëïãéêþ ðåñéï Þ (4.5) 00
7 ÅëåãêôÝò ÓõíÞèùò ïé êáôáóêåõáóôýò äßíïõí ôç ó åôéêþ áíáëïãéêþ ðåñéï Þ åðß ôïéò åêáôü, äçëáäþ: X X % = 00% Yhmax üðïõ X max = ç ìýãéóôç ðåñéï Þ åëýã ïõ êáé Y max = ç ðåñéï Þ ìýóá óôçí ïðïßá ï åëåãêôþò åßíáé óå èýóç íá ñõèìßóåé ôçí åëåã üìåíç ìåôáâëçôþ [y(t)]. Ïðüôå ç ðñïçãïýìåíç ó Ýóç ãßíåôáé: U h X % = 00% Ymax Ìåôáîý ôçò åíßó õóçò êáé ôçò áíáëïãéêþò ðåñéï Þò ôïõ åëåãêôþ, åöüóïí Y h = u h, éó ýåé ç ó Ýóç: 00 = X% (4.6) ÐáñÜäåéãìá: Ôï ýøïò ôçò óôüèìçò ôïõ õãñïý ìéáò äåîáìåíþò öèüíåé ôá 2 m. Ç ðåñéï Þ ñýèìéóçò åßíáé 00% êáé ç åíßó õóç ôïõ åëåãêôþ åßíáé = 20%. Íá õðïëïãßóåôå ôçí áíáëïãéêþ ðåñéï Þ X %. X U Y 20% m 00% 00% 2m h % = 00% = = max 25% X =20% U =00% H X =00% 2m y m =2m y Ó Þìá 4.4.: ÓôáôéêÞ áñáêôçñéóôéêþ ôïõ åëåãêôþ-ñ óå Üîïíåò åëåã üìåíçò ìåôáâëçôþò y/ñõèìéóôéêïý óþìáôïò ( ). 0
8 êåöüëáéï 4 ÐáñÜäåéãìá ëåéôïõñãßáò åëåãêôþ-. Óôï ðáñáêüôù ó Þìá 4.5 öáßíåôáé Ýíá ìç áíéêü óýóôçìá áõôïìüôïõ åëýã ïõ óôüèìçò õãñïý. Ç åëåã üìåíç ìåôáâëçôþ y(t) åßíáé ôï ýøïò ôçò óôüèìçò ôïõ õãñïý ìýóá óôï äï åßï. Ñõèìéóôéêü óþìá åßíáé ôï Üíïéãìá (Ç) ôçò âáëâßäáò. Ç åêñïþ ôïõ íåñïý Q á äñá óáí äéáôáñá Þ (z). Ôï ýøïò ôïõ íåñïý (h) ôçò äåîáìåíþò ìåôñåßôáé ìå ôç âïþèåéá ôïõ ðëùôþñá. ¼ôáí ç óôüèìç ôïõ íåñïý áíåâáßíåé, ôüôå áíôßóôïé á ç âüíá ìå ôç âïþèåéá ôïõ ìï ëïâñá ßoíá êëåßíåé ôï Üíïéãìá ôçò ñïþò ôïõ íåñïý. Áíôßèåôá, üôáí Ý ïõìå åêñïþ ôïõ íåñïý ôçò äåîáìåíþò, ç âáëâßäá ìå ôç âïþèåéá ôïõ ìï ëïý áíïßãåé ôçí ïðþ êáé Ýôóé Ý ïõìå ìåãáëýôåñç åéóñïþ ôïõ õãñïý. Ç åðéèõìçôþ óôüèìç ñõèìßæåôáé ìå áýîçóç Þ ìåßùóç ôïõ ìþêïõò ôïõ ðëùôþñá. á â ìï ëïâñá ßïíáò Q e u H ñýèìéóç åðéèõìçôþò ôéìþò r 0 > y(t)=h Q a =z Ó Þìá 4.5: Ìç áíéêü óýóôçìá áõôïìüôïõ åëýã ïõ óôüèìçò ÂáóéêÝò ãíþóåéò ôåëåóôéêþí åíéó õôþí Óôçí ðáñïýóá ðáñüãñáöï èá ìåëåôþóïõìå Ýíá âáóéêü óôïé åßï ôùí áíáëïãéêþí çëåêôñïíéêþí êáé ôùí êõêëùìüôùí ôùí óõóôçìüôùí áõôïìüôïõ åëýã ïõ, ôïí ôåëåóôéêü åíéó õôþ, (ÔÅ). Ïé óýã ñïíïé ÔÅ êáôáóêåõüæïíôáé õðü ìïñöþ ïëïêëçñùìýíùí êõêëùìüôùí êáé åðïìýíùò ï ñþóôçò äåí Ý åé ïõäåìßá äõíáôüôçôá ðñüóâáóçò óôï åóùôåñéêü ôïõ. Ôï åóùôåñéêü êýêëùìá Üëëùóôå åßíáé áñêåôü ðïëýðëïêï êáé äåí Ý åé óçìáóßá óôéò ðñáêôéêýò åöáñìïãýò. ÅðïìÝíùò, åêåßíï ðïõ åíäéáöýñåé ôï ñþóôç åßíáé ï óêïðüò ôïõ êüèå áêñïäýêôç êáé ïé éäéüôçôýò ôïõ. ÊÜèå ÔÅ, áíåîüñôçôá ôçò ôå íïëïãßáò êáôáóêåõþò ôïõ, áðïôåëåßôáé áðü Ýíáí åíéó õôþ äéáöïñüò (ó Þìá 4.6á). 02
9 ÅëåãêôÝò Ó Þìá 4.6: Êýêëùìá åéóüäïõ ÔÅ (á) êáé óýìâïëï ÔÅ (â). Ï ÔÅ ôñïöïäïôåßôáé ìå ìéá óõììåôñéêþ ôüóç ±5V. ÄéáèÝôåé äýï åéóüäïõò, ôç ìç áíáóôñýöïõóá (u e2 ) êáé ôçí áíáóôñýöïõóá (u e ) êáé ìéá Ýîïäï (u á ). ëëåò ôüóåéò ôñïöïäïóßáò åßíáé ±8V, ±2V, ±8V, ±24V. Éäéüôçôåò ôïõ ôåëåóôéêïý åíéó õôþ ÌåñéêÝò áðü ôéò ðéï âáóéêýò éäéüôçôåò ôùí ÔÅ åßíáé: Á) ÌåãÜëç áíôßóôáóç åéóüäïõ ( i ) Ç áíôßóôáóç åéóüäïõ ìåôñåßôáé ìåôáîý ôùí äýï åéóüäùí êáé åßíáé ôçò ôüîçò 0 2 Ù. ( i =0 2 Ù). i Ù 0 Ù i 2 Ó Þìá 4.6.: Êýêëùìá ìýôñçóçò ôçò áíôßóôáóçò åéóüäïõ ôïõ ÔÅ. 03
10 êåöüëáéï 4 Â) ÌéêñÞ áíôßóôáóç åîüäïõ ( ï ) Ôï êýêëùìá åîüäïõ ôïõ ÔÅ éóïäõíáìåß ìå ìéá ðçãþ ôüóçò óå óåéñü ìå ôçí áíôßóôáóç ï. 0 u 0 Ó Þìá 4.6.2: Êýêëùìá åîüäïõ ôïõ ÔÅ. Ç áíôßóôáóç åîüäïõ ( ï ) óôïõò éäáíéêïýò ÔÅ èåùñåßôáé ìçäåíéêþ. Óôçí ðñüîç üìùò åßíáé ôçò ôüîçò ôùí 50 00Ù. Ã) ÌåãÜëç åíßó õóç (V ï ) Ìå ôïí üñï «åíßó õóç» åííïïýìå ôçí áýîçóç Þ ôç ìåßùóç ðïõ õößóôáôáé Ýíá óþìá ðïõ åöáñìüæåôáé ìåôáîý ôùí äýï åéóüäùí åíüò ÔÅ. Ó Þìá 4.6.3: Óýìâïëï ôåëåóôéêïý åíéó õôþ: Ç åíßó õóç ôùí ÔÅ åßíáé ôçò ôüîçò Ýùò (V ï = Ýùò ). Ä) Ñåýìáôá åéóüäïõ ðïëý ìéêñü i = i 2»0 i i 2 Ó Þìá 4.6.4: Ñåýìáôá åéóüäïõ ôïõ ÔÅ. 04
11 ÅëåãêôÝò Óôïí éäáíéêü ÔÅ ôá ñåýìáôá åéóüäïõ èåùñïýíôáé ìçäåíéêü ëïãù ôçò ìåãüëçò áíôßóôáóçò åéóüäïõ. Óôçí ðñüîç åßíáé ôçò ôüîçò ôùí 20nA. Áðëü êýêëùìá ÔÅ ) ÁíáóôñÝöùí ÔÅ ìå áíôßóôáóç åéóüäïõ êáé êëüäï áíüäñáóçò. Ó Þìá 4.6.5: Êõêëþìáôá ÔÅ ìå áíüäñáóç. ÅðåéäÞ ôï ñåýìá i Ýðåôáé üôé ç áíáóôñýöïõóá åßóïäïò Ý åé ìçäýí äõíáìéêü. Óôçí ðñüîç ëýìå üôé ç åßóïäïò Í åßíáé åéêïíéêþ ãç. Áõôü åßíáé óùóôü, äéüôé ç ôüóç u d, ôüóç ìåôáîý Í êáé Ñ ðñýðåé íá åßíáé ìçäýí, ãéá íá ìðïñåß íá ëåéôïõñãþóåé ï ÔÅ. ÅÜí u d ¹0, ôüôå ç Ýîïäïò ôïõ ÔÅ, ëüãù ôçò ìåãüëçò åíßó õóçò, âñßóêåôáé óôïí êüñï (ìýãéóôï óþìá åîüäïõ). Óôï ðáñáðüíù êýêëùìá éó ýåé: I = I 2 V V I = êáé I = i 0 2 z z2 Þ V V V z = = z z V z o i o 2 2 i Çëåêôñïíéêüò áíáëïãéêüò åëåãêôþò-ñ ¼ðùò ãíùñßæïõìå, óôçí åßóïäï êüèå åëåãêôþ õðüñ åé ï óõãêñéôþò. Ï óõãêñéôþò Ý åé äýï åéóüäïõò êáé ìéá Ýîïäï. Óôç ìç áíáóôñýöïõóá åßóïäï óõíäýïõìå ôï äüôç åðéèõìçôþò ôéìþò, åíþ óôçí áíáóôñýöïõóá åßóïäï óõíäýïõìå ôï óþìá ôçò åëåã üìåíçò ìåôáâëçôþò. ÅðåéäÞ ôï óþìá áõôü óõíþèùò óõíïäåýåôáé áðü ìéêñýò äéáôáñá Ýò (èüñõâïé), ïé ïðïßåò äåí ïöåßëïíôáé óôéò äéáôáñá Ýò ðïõ äñïõí ðüíù óôï ñõèìéæüìåíï óýóôçìá, áëëü óôç äïìþ êáé óôï åßäïò ôïõ óõóôþìáôïò áõôïìüôïõ åëýã ïõ, óõíäýïõìå óôçí áíáóôñýöïõóá åßóïäï Ýíá çëåêôñïíéêü ößëôñï ãéá ôçí åîïìüëõíóç ôïõ óþìáôïò áðü ôï èüñõâï. 05
12 êåöüëáéï r 7 TE y 2 3 TE2 C U Ó Þìá 4.7: Çëåêôñïíéêü êýêëùìá åëåãêôþ Ñ. Ôï äéêôýùìá () 2 C áðïôåëåß ôï ößëôñï ôïõ óþìáôïò ôçò åëåã üìåíçò ìåôáâëçôþò (y). Êáôüðéí ìå ôï êýêëùìá ôïõ áíáóôñýöïíôïò ôåëåóôéêïý åíéó õôþ TE 2 êáé 3, 4 áíáóôñýöåôáé ç ðïëéêüôçôá ôïõ óþìáôïò y y C TE2 (-) -y è Ó Þìá 4.7.: Êýêëùìá áíáóôñïöþò ôçò åëåã üìåíçò ìåôáâëçôþò. Ôï áíåóôñáììýíï ó Þìá ìýóù ôçò 5 ïäçãåßôáé óôï óõãêñéôþ. 06
13 ÅëåãêôÝò 8 r 7 TE2 (r-y) 6 5 -y è2-5v 7 Ó Þìá 4.7.2: Êýêëùìá óõãêñéôþ. Óôï óõãêñéôþ ðñïóôßèåíôáé ôá óþìáôá (r) êáé y êáé ôï áðïôýëåóìá ôçò óýãêñéóçò áíáóôñýöåôáé, äçëáäþ: ( ) ( ) r y = r y ÅðåéäÞ ç äéáöïñü (r-y) ëüãù ôçò óõíäåóìïëïãßáò ôïõ TE 2 Ý åé áíáóôñáöåß, ïäçãïýìå ôï óþìá áõôü óôïí TE 3 êáé ëáìâüíïõìå ôç äéáöïñü ôùí äýï óçìüôùí ùñßò áíáóôñïöþ. Óôç óõíý åéá ôï óþìá ïäçãåßôáé óå Ýíá ðïôåíóéüìåôñï êáé áðü ôç ìåóáßá ëþøç óå Ýíá ôåëåóôéêü åíéó õôþ óå ìç áíáóôñýöïõóá óõíäåóìïëïãßá. (r-y) I u d TE2 2 u e 0 Ó Þìá 4.7.3: Âáèìßäá åíßó õóçò. i = 0 u Ud = 0 e = u 0 ( ) u = i = u = ue = ip0 u 0 e 0 p 0 0 u = u = u 0 e e 0 0 u Üñá p = = = åíßó õóç e 0 07
14 êåöüëáéï ÅëåãêôÞò-É ÅëåãêôÞò ïëïêëþñùóçò (É = Integral) O åëåãêôþò-é áèñïßæåé ôï óöüëìá (e) óå óõíüñôçóç ìå ôï ñüíï (t). ÅÜí èåùñþóïõìå Ýíá óôáèåñü óöüëìá e, ôüôå ôï óþìá åîüäïõ ( ) ôïõ åëåãêôþ åßíáé: = I (e.ät e.ät 2 e.ät 3 e.ät 4 ) = I.e.(Ät Ät 2 Ät 3 Ät 4...) = I.e.Ät = I.e.Ät = I.e.(t-t O ) = I.e.t (ãéá t O =0) Ç åîßóùóç ç ïðïßá ðåñéãñüöåé ôç óõìðåñéöïñü ôïõ åëåãêôþ äßíåôáé áðü ôç ó Ýóç: u = e Ät (4.7) I e Ät Ät 2 Ät 3 Ät 4 Ät 5 Ät 6 t t t 2 t 3 t 4 t 5 t 6 t = ñõèìéóôéêü óþìá I = óõíôåëåóôþò ïëïêëþñùóçò e= óöüëìá (e=r-y) Ät= ìéêñü ñïíéêü äéüóôçìá Ó Þìá 4.8: ÂçìáôéêÞ áðüêñéóç åëåãêôþ É. Èåùñþíôáò ôï óõíôåëåóôþ ïëïêëþñùóçò ( I ) êáé ôï óöüëìá (e) óôáèåñü, ôï ñõèìéóôéêü óþìá åîáñôüôáé ìüíï áðü ôï ñüíï (t). Ç ëåéôïõñãßá ôïõ åëåãêôþ ãßíåôáé ðåñéóóüôåñï êáôáíïçôþ áðü ôçí ðáñáêüôù âçìáôéêþ ñïíéêþ áðüêñéóç. 08
15 ÅëåãêôÝò e,5v V t t 2V sec t t Ó Þìá 4.9: ÂçìáôéêÞ ñïíéêþ áðüêñéóç ôïõ åëåãêôþ-é. Ðáñáôçñþíôáò ôï ó Þìá 4.9 äéáðéóôþíïõìå üôé:. Åíþ ôï óþìá óôçí åßóïäï ìåôáâüëëåôáé áðüôïìá, ôï ñõèìéóôéêü óþìá ìåôáâüëëåôáé áñãü. Ï åëåãêôþò- É åßíáé áñãüò. 2. ¼óï ñïíéêü äéüóôçìá õðüñ åé óöüëìá óôçí åßóïäï ôïõ åëåãêôþ, ç Ýîïäïò ôïõ ( ) óõíå þò áíåâáßíåé. ÅðïìÝíùò êáé ôï ôåëéêü óôïé åßï åëýã ïõ áõîüíåé áíôßóôïé á ôç ñïþ ôçò åíýñãåéáò ðñïò ôï åëåã üìåíï óýóôçìá. 3. Ôï óþìá åîüäïõ ôïõ åëåãêôþ äéáôçñåß ôçí ôåëåõôáßá ôïõ ôéìþ, áêüìç êáé üôáí ôï óþìá åéóüäïõ (ôï óöüëìá) Ý åé ìçäåíéóôåß. Áõôü óçìáßíåé üôé ó Ýíá êëåéóôü óýóôçìá áõôïìüôïõ åëýã ïõ ôï ñõèìéóôéêü óþìá èá áõîüíåé óõíå þò, ìý ñéò üôïõ ìçäåíéóôåß ôï óöüëìá. Óôï ñïíéêü óçìåßï t ðáñáôçñïýìå üôé, åíþ ôï óöüëìá ìçäåíßæåôáé, ç Ýîïäïò äéáôçñåß ôçí ôåëåõôáßá ôéìþ ìå ôçí ïðïßá ìçäåíßóôçêå ôï óöüëìá. Åîáéôßáò ôùí éäéïôþôùí ðïõ áíáöýñèçêáí ðáñáðüíù, ï åëåãêôþò É ñçóéìïðïéåßôáé óå óõóôþìáôá áõôïìüôïõ åëýã ïõ üðïõ áðáéôåßôáé áêñéâþò Ýëåã ïò. Ôï óýìâïëï ôïõ åëåãêôþ-é öáßíåôáé óôï ðáñáêüôù ó Þìá 4.0 êáé ðáñéóôüíåé ôç âçìáôéêþ ñïíéêþ áðüêñéóç. I r e y Ó Þìá 4.0: Óýìâïëï ôïõ åëåãêôþ-é. 09
16 êåöüëáéï 4 Ï óõíôåëåóôþò ïëïêëþñùóçò I áðïôåëåß ôå íéêü áñáêôçñéóôéêü ôïõ åëåãêôþ êáé ïñßæåôáé áðü ôç ó Ýóç: I u e Ät = üðïõ [ ] I = sec (4.8) ÅðïìÝíùò, ãéá óôáèåñü óþìá óöüëìáôïò e, ï óõíôåëåóôþò I åßíáé ï ëüãïò ôïõ ñõèìéóôéêïý óþìáôïò ðñïò ôï óþìá åéóüäïõ e, ôç ñïíéêþ óôéãìþ t=sec. Áðü ôï ó Þìá 4.9 õðïëïãßæïõìå ôï óõíôåëåóôþ I : u e 2V = t,5v sec I = = ÐïëëÝò öïñýò ïé êáôáóêåõáóôýò, áíôß ôïõ óõíôåëåóôþ I, äßíïõí ôï ñüíï ïëïêëþñùóçò Ô I. Ï ñüíïò Ô I åßíáé ßóïò ìå ôçí áíôßóôñïöç ôéìþ ôïõ I :,33 sec T I = (4.9) I êáé ïñßæåôáé ãñáöéêü ìå ôç âïþèåéá ôïõ ó Þìáôïò 4.: e e 0 t üñïò e 0 T I t Ó Þìá 4.: Õðïëïãéóìüò ôïõ Ô É áðü ôç ãñáöéêþ ðáñüóôáóç. ÅðïìÝíùò, ï ñüíïò ïëïêëþñùóçò Ô I åßíáé ï ñüíïò ðïõ ñåéüæåôáé ç Ýîïäïò ôïõ åëåãêôþ-é, ãéá íá öèüóåé óôçí ßäéá ôéìþ ôïõ óþìáôïò åéóüäïõ (e). Ï ñüíïò Ô I åßíáé ðéï åý ñçóôïò óôéò ðñáêôéêýò åöáñìïãýò, ãéáôß ìáò êáèïñßæåé ôçí ôá ýôçôá áíüäïõ ôïõ ñõèìéóôéêïý óþìáôïò. 0
17 ÅëåãêôÝò Ïóï ìéêñüôåñïò åßíáé ï ñüíïò Ô I, ôüóï ãñçãïñüôåñïò åßíáé ï åëåãêôþò Þ ãñçãïñüôåñá öèüíåé ôï óþìá óôïí êüñï êáé ôï ôåëéêü óôïé åßï åëýã ïõ ïäçãåßôáé óôçí Üíù ïñéáêþ èýóç. ¼ðùò èá äïýìå êáôü ôç ìåëýôç ôùí êëåéóôþí óõóôçìüôùí, Ýíáò ìéêñüò ñüíïò (Ô I ) ðñïêáëåß ôçí ßäéá óõìðåñéöïñü óôï êëåéóôü óýóôçìá, ôçí ïðïßá èá ðñïêáëïýóå Ýíáò åëåãêôþò-ñ ìå ðïëý ìåãüëç åíßó õóç ( ) Çëåêôñïíéêü êýêëùìá åëåãêôþ-é Á) ÅëåãêôÞò-É óå áíáóôñýöïõóá óõíäåóìïëïãßá Ôï çëåêôñïíéêü êýêëùìá ôïõ åëåãêôþ-é áðïôåëåßôáé áðü Ýíáí TE ìå ðõêíùôþ óôïí êëüäï áíüäñáóçò. Ó Þìá 4.2: Êýêëùìá ïëïêëçñùôþ. Ç óõìðåñéöïñü ôïõ ðáñáðüíù êõêëþìáôïò öáßíåôáé áðü ôéò ðáñáêüôù âçìáôéêýò áðïêñßóåéò: Ó Þìá 4.3: ÂçìáôéêÞ áðüêñéóç ôïõ åëåãêôþ É ôïõ ó Þìáôïò 4.2.
18 êåöüëáéï 4 ÐáñáôçñÞóåéò: Äu Ç ôá ýôçôá ìåôáâïëþò ôïõ óþìáôïò åîüäïõ á, üôáí ôï óþìá åéóüäïõ åßíáé óôáèåñü, åîáñôüôáé áðü ôï ñüíï ïëïêëþñùóçò T I Ät. Ìéêñüò ñüíïò T I óõíåðüãåôáé ìåãüëç áýîçóç ôçò ôüóçò u á êáé áíôéóôñüöùò (ó Þìá 4.3). 4 Ç ôá ýôçôá ìåôáâïëþò åîáñôüôáé åðßóçò êáé áðü ôï ýøïò ôïõ óþìáôïò åéóüäïõ. ÌåãÜëï óþìá åéóüäïõ ðñïêáëåß ôá åßá áýîçóç ôïõ óþìáôïò åîüäïõ u á (ó Þìá 4.3). Ðñüóèåôåò ðëçñïöïñßåò Ìå i e = 0 Þ i O = i u = i á jùc u e = i O. O uá jùc = = = () jù c jùt e O O I T I = O.c = ñüíïò ïëïêëþñùóçò G(jù) = jùt áñìïíéêþ áðüêñéóç ÅÜí èýóïõìå üðïõ j ù= s ç ðáñáðüíù ó Ýóç ïíïìüæåôáé óõíüñôçóç ìåôáöïñüò êáé ãñüöåôáé: I G = st I 4.4 ÅëåãêôÞò-D Äéáöïñéêüò åëåãêôþò (D=Differential) O åëåãêôþò-d Ý åé äéáöïñéêþ óõìðåñéöïñü, äçëáäþ ôï óþìá åîüäïõ ( ) ìåôáâüëëåôáé áíüëïãá ìå ôç ñïíéêþ ìåôáâïëþ ôïõ óþìáôïò åéóüäïõ (e). e t üðïõ D = óõíôåëåóôþò äéáöüñéóçò (=T D ) u Äe = D (4.0) Ät 2
19 ÅëåãêôÝò ÅÜí äéåãåßñïõìå ôïí åëåãêôþ-d ìå Ýíá âçìáôéêü óþìá, ôüôå ëáìâüíïõìå e Äe t t t 2 r e y' D(Þ T D ) åëåãêôþò t t t 2 (á) (â) Ó Þìá 4.4: ÂçìáôéêÞ ñïíéêþ áðüêñéóç ôïõ åëåãêôþ-d (á) êáé óýìâïëï (â). ÄéáâÜæïíôáò ôçí åîßóùóç (4.0) ôïõ åëåãêôþ-d ðáñáôçñïýìå üôé, üôáí ç ìåôáâïëþ ôïõ óþìáôïò åéóüäïõ (Äe) ëáìâüíåé þñá óå ñüíï ðïõ ôåßíåé óôï ìçäýí (óå ìçäåíéêü ñüíï), ôï óþìá óôçí Ýîïäï ôåßíåé óôï Üðåéñï. u Äe = D 0 Áíôßèåôá, üôáí ôï óþìá óôçí åßóïäï åßíáé óôáèåñü, ôüôå Ý ïõìå: A A J J J 4 J Ó Þìá 4.5: ÂçìáôéêÞ ñïíéêþ áðüêñéóç ôïõ åëåãêôþ-d. 3
20 êåöüëáéï 4 ãéá t e(t) = e O Äe e e 0 t 2 e(t) = e O 0 0 = = = = D = 2 Ät t t Ät 0 u 0 0 ÓõìðÝñáóìá: 4 ¼ôáí ôï óþìá åéóüäïõ ôïõ åëåãêôþ-d åßíáé óôáèåñü, ôüôå ç Ýîïäïò åßíáé ìçäýí. 4 ñá, ï åëåãêôþò-d ñçóéìïðïéåßôáé, üôáí ç åëåã üìåíç ìåôáâëçôþ åìöáíßæåé áðüôïìåò ìåôáâïëýò. Ëüãù áõôþò ôçò óõìðåñéöïñüò ôïõ, ï åëåãêôþò D äåí ñçóéìïðïéåßôáé ðïôý ìüíïò ùò åëåãêôþò áëëü ðüíôïôå óå óõíäõáóìü ìå ôïí Ñ Çëåêôñïíéêü êýêëùìá åëåãêôþ-d Ôá âáóéêü êýêëùìá ôïõ åëåãêôþ-d öáßíåôáé óôï ðáñáêüôù ó Þìá. I 2 I C I d3 e Ðñüóèåôåò ðëçñïöïñßåò Ó Þìá 4.6: Çëåêôñoíéêü êýêëùìá åëåãêôþ D. Ìå ôç âïþèåéá ôïõ ðáñáðüíù êõêëþìáôïò ãñüöïõìå ôéò åîéóþóåéò: i i = 0 e u = jùc 2 i = êáé i2 = i d 0 u e e jùc jùc 2 = i = = i u = = = áñìïíéêþ áðüêñéóç e G(jù) jùc jùtd T D =.c = ñüíïò äéáöüñéóçò Þ ñüíïò ðñïðïñåßáò 4
4.5 ÅëåãêôÞò-PI ÅëåãêôÞò ìå áíáëïãéêþ êáé ïëïêëçñùôéêþ óõìðåñéöïñü
 ÅëåãêôÝò Ç åðéêñáôïýóá åîßóùóç ôïõ åëåãêôþ-d åßíáé ôçò ìïñöþò: u = D d dt êáé ç óõíüñôçóç ìåôáöïñüò: G u = s D u = = D s óõíüñôçóç ìåôáöïñüò 4.5 ÅëåãêôÞò-I ÅëåãêôÞò ìå áíáëïãéêþ êáé ïëïêëçñùôéêþ óõìðåñéöïñü
ÅëåãêôÝò Ç åðéêñáôïýóá åîßóùóç ôïõ åëåãêôþ-d åßíáé ôçò ìïñöþò: u = D d dt êáé ç óõíüñôçóç ìåôáöïñüò: G u = s D u = = D s óõíüñôçóç ìåôáöïñüò 4.5 ÅëåãêôÞò-I ÅëåãêôÞò ìå áíáëïãéêþ êáé ïëïêëçñùôéêþ óõìðåñéöïñü
ÌåëÝôç ôçò óõìðåñéöïñüò ôïõ óõóôþìáôïò Áõôüìáôïõ ÅëÝã ïõ (êëåéóôïý âñü ïõ)
 ÊåöÜëáéï 7 ÌåëÝôç ôçò óõìðåñéöïñüò ôïõ óõóôþìáôïò Áõôüìáôïõ ÅëÝã ïõ (êëåéóôïý âñü ïõ) Åðéäéùêüìåíïé óôü ïé: Ï óêïðüò áõôïý ôïõ êåöáëáßïõ åßíáé íá âïçèþóåé ôïõò ìáèçôýò: Ö Íá êáôáíïïýí êáé åîçãïýí ôçí åðßäñáóç
ÊåöÜëáéï 7 ÌåëÝôç ôçò óõìðåñéöïñüò ôïõ óõóôþìáôïò Áõôüìáôïõ ÅëÝã ïõ (êëåéóôïý âñü ïõ) Åðéäéùêüìåíïé óôü ïé: Ï óêïðüò áõôïý ôïõ êåöáëáßïõ åßíáé íá âïçèþóåé ôïõò ìáèçôýò: Ö Íá êáôáíïïýí êáé åîçãïýí ôçí åðßäñáóç
r + u R Óõ íïãåííþôñéá ÅëåãêôÞò CHII u R 4 ON 1 e OFF t 1 t 2 t 3 t 4 e 2 3 e 1
 ÊåöÜëáéï 8 ÓõóôÞìáôá Áõôüìáôïõ ÅëÝã ïõ ìå Äéáêïðôéêïýò ÅëåãêôÝò Åðéäéùêüìåíïé óôü ïé: Ï óêïðüò áõôïý ôïõ êåöáëáßïõ åßíáé íá âïçèþóåé ôïõò ìáèçôýò: Ö Íá ãíùñßæïõí ôç ëåéôïõñãßá ôïõ åëåãêôþ äýï èýóåùí. Ö
ÊåöÜëáéï 8 ÓõóôÞìáôá Áõôüìáôïõ ÅëÝã ïõ ìå Äéáêïðôéêïýò ÅëåãêôÝò Åðéäéùêüìåíïé óôü ïé: Ï óêïðüò áõôïý ôïõ êåöáëáßïõ åßíáé íá âïçèþóåé ôïõò ìáèçôýò: Ö Íá ãíùñßæïõí ôç ëåéôïõñãßá ôïõ åëåãêôþ äýï èýóåùí. Ö
ÊåöÜëáéï 1. ÅéóáãùãÞ. Åðéäéùêüìåíïé óôü ïé:
 ÊåöÜëáéï 1 ÅéóáãùãÞ Åðéäéùêüìåíïé óôü ïé: Óêïðüò áõôïý ôïõ êåöáëáßïõ åßíáé íá âïçèþóåé ôïõò ìáèçôýò: Ö Íá äéáêñßíïõí ôéò âáóéêýò âáèìßäåò åíüò áíïéêôïý êáé åíüò êëåéóôïý óõóôþìáôïò áõôïìüôïõ åëýã ïõ. Ö
ÊåöÜëáéï 1 ÅéóáãùãÞ Åðéäéùêüìåíïé óôü ïé: Óêïðüò áõôïý ôïõ êåöáëáßïõ åßíáé íá âïçèþóåé ôïõò ìáèçôýò: Ö Íá äéáêñßíïõí ôéò âáóéêýò âáèìßäåò åíüò áíïéêôïý êáé åíüò êëåéóôïý óõóôþìáôïò áõôïìüôïõ åëýã ïõ. Ö
ÐåñéãñáöÞ Ãñáììéêþí Óôïé åßùí (Âáèìßäùí) Åëåã üìåíá ÓõóôÞìáôá
 ÊåöÜëáéï 3 ÐåñéãñáöÞ Ãñáììéêþí Åðéäéùêüìåíïé óôü ïé: Óêïðüò áõôïý ôïõ êåöáëáßïõ åßíáé íá âïçèþóåé ôïõò ìáèçôýò: Ö Íá áíáãíùñßæïõí ôéò êáôçãïñßåò ôùí ñõèìéæüìåíùí óõóôçìüôùí. Ö Íá êáôáôüóóïõí ôï óýóôçìá
ÊåöÜëáéï 3 ÐåñéãñáöÞ Ãñáììéêþí Åðéäéùêüìåíïé óôü ïé: Óêïðüò áõôïý ôïõ êåöáëáßïõ åßíáé íá âïçèþóåé ôïõò ìáèçôýò: Ö Íá áíáãíùñßæïõí ôéò êáôçãïñßåò ôùí ñõèìéæüìåíùí óõóôçìüôùí. Ö Íá êáôáôüóóïõí ôï óýóôçìá
ÓÕÍÄÕÁÓÔÉÊÇ É, ÓÅÐÔÅÌÂÑÉÏÓ ÏÌÁÄÁ ÈÅÌÁÔÙÍ B
 ÓÕÍÄÕÁÓÔÉÊÇ É, ÓÅÐÔÅÌÂÑÉÏÓ 2008 - ÏÌÁÄÁ ÈÅÌÁÔÙÍ B ÈÝìá. Èåùñïýìå ôï óýíïëï Ω {; 2; ; 2008}. (á ( âáèìüò Ðüóåò åßíáé ïé ìåôáèýóåéò ôùí óôïé åßùí ôïõ Ω óôéò ïðïßåò ôá Üñôéá óôïé åßá êáôáëáìâüíïõí ôéò ôåëåõôáßåò
ÓÕÍÄÕÁÓÔÉÊÇ É, ÓÅÐÔÅÌÂÑÉÏÓ 2008 - ÏÌÁÄÁ ÈÅÌÁÔÙÍ B ÈÝìá. Èåùñïýìå ôï óýíïëï Ω {; 2; ; 2008}. (á ( âáèìüò Ðüóåò åßíáé ïé ìåôáèýóåéò ôùí óôïé åßùí ôïõ Ω óôéò ïðïßåò ôá Üñôéá óôïé åßá êáôáëáìâüíïõí ôéò ôåëåõôáßåò
Ó ÅÄÉÁÓÌÏÓ - ÊÁÔÁÓÊÅÕÇ ÓÔÏÌÉÙÍ & ÅÉÄÉÊÙÍ ÅÎÁÑÔÇÌÁÔÙÍ ÊËÉÌÁÔÉÓÌÏÕ V X
 V X A B+24 AEROGRAMÌI Ïé äéáóôüóåéò ôùí óôïìßùí ôçò óåéñüò Å öáßíïíôáé óôï ðáñáêüôù ó Þìá. Áíôßóôïé á, ïé äéáóôüóåéò ôùí óôïìßùí ôçò óåéñüò ÂÔ öáßíïíôáé óôï Ó Þìá Å. Ãéá ôïí ðñïóäéïñéóìü ôçò ðáñáããåëßáò
V X A B+24 AEROGRAMÌI Ïé äéáóôüóåéò ôùí óôïìßùí ôçò óåéñüò Å öáßíïíôáé óôï ðáñáêüôù ó Þìá. Áíôßóôïé á, ïé äéáóôüóåéò ôùí óôïìßùí ôçò óåéñüò ÂÔ öáßíïíôáé óôï Ó Þìá Å. Ãéá ôïí ðñïóäéïñéóìü ôçò ðáñáããåëßáò
ÓÕÍÄÕÁÓÔÉÊÇ É, ÓÅÐÔÅÌÂÑÉÏÓ ÏÌÁÄÁ ÈÅÌÁÔÙÍ Á
 ÓÕÍÄÕÁÓÔÉÊÇ É, ÓÅÐÔÅÌÂÑÉÏÓ 2008 - ÏÌÁÄÁ ÈÅÌÁÔÙÍ Á ÈÝìá. Èåùñïýìå ôï óýíïëï Ω {; 2; ; 2008}. (á ( âáèìüò Ðüóåò åßíáé ïé ìåôáèýóåéò ôùí óôïé åßùí ôïõ Ω óôéò ïðïßåò ôï óôïé åßï âñßóêåôáé óå êüðïéá áðü ôéò
ÓÕÍÄÕÁÓÔÉÊÇ É, ÓÅÐÔÅÌÂÑÉÏÓ 2008 - ÏÌÁÄÁ ÈÅÌÁÔÙÍ Á ÈÝìá. Èåùñïýìå ôï óýíïëï Ω {; 2; ; 2008}. (á ( âáèìüò Ðüóåò åßíáé ïé ìåôáèýóåéò ôùí óôïé åßùí ôïõ Ω óôéò ïðïßåò ôï óôïé åßï âñßóêåôáé óå êüðïéá áðü ôéò
ÊåöÜëáéï 3 ÏÑÉÆÏÕÓÅÓ. 3.1 ÅéóáãùãÞ
 28 ÊåöÜëáéï 3 ÏÑÉÆÏÕÓÅÓ 3.1 ÅéóáãùãÞ Ãéá êüèå ôåôñáãùíéêü ðßíáêá A áíôéóôïé åß Ýíáò ðñáãìáôéêüò áñéèìüò ï ïðïßïò êáëåßôáé ïñßæïõóá êáé óõíþèùò óõìâïëßæåôáé ìå A Þ det(a). ÌåôáèÝóåéò: Ìéá áðåéêüíéóç ôïõ
28 ÊåöÜëáéï 3 ÏÑÉÆÏÕÓÅÓ 3.1 ÅéóáãùãÞ Ãéá êüèå ôåôñáãùíéêü ðßíáêá A áíôéóôïé åß Ýíáò ðñáãìáôéêüò áñéèìüò ï ïðïßïò êáëåßôáé ïñßæïõóá êáé óõíþèùò óõìâïëßæåôáé ìå A Þ det(a). ÌåôáèÝóåéò: Ìéá áðåéêüíéóç ôïõ
ÊåöÜëáéï 4 ÄÉÁÍÕÓÌÁÔÁ. 4.1 ÅéóáãùãÞ (ÃåùìåôñéêÞ)
 44 ÊåöÜëáéï 4 ÄÉÁÍÕÓÌÁÔÁ 4.1 ÅéóáãùãÞ (ÃåùìåôñéêÞ) Óå äéüöïñåò öõóéêýò åöáñìïãýò õðüñ ïõí ìåãýèç ôá ïðïßá ìðïñïýí íá áñáêôçñéóèïýí ìüíï ìå Ýíá áñéèìü. ÔÝôïéá ìåãýèç, üðùò ãéá ðáñüäåéãìá, ç èåñìïêñáóßá
44 ÊåöÜëáéï 4 ÄÉÁÍÕÓÌÁÔÁ 4.1 ÅéóáãùãÞ (ÃåùìåôñéêÞ) Óå äéüöïñåò öõóéêýò åöáñìïãýò õðüñ ïõí ìåãýèç ôá ïðïßá ìðïñïýí íá áñáêôçñéóèïýí ìüíï ìå Ýíá áñéèìü. ÔÝôïéá ìåãýèç, üðùò ãéá ðáñüäåéãìá, ç èåñìïêñáóßá
¼ñãáíá Èåñìïêñáóßáò - ÓõóêåõÝò Øõêôéêþí Ìç áíçìüôùí
 ¼ñãáíá Èåñìïêñáóßáò - ÓõóêåõÝò Øõêôéêþí Ìç áíçìüôùí ÈåñìïóôÜôçò ÓõíôÞñçóçò REF-DF-SM ÅëÝã åé Ýíá èåñìïóôïé åßï PTC Êëßìáêá èåñìïêñáóßáò: -19? +99 C ëåã ïò áðüøõîçò - dfrst Ôñßá ñåëý: óõìðéåóôþò (30Á, 2ÇÑ),
¼ñãáíá Èåñìïêñáóßáò - ÓõóêåõÝò Øõêôéêþí Ìç áíçìüôùí ÈåñìïóôÜôçò ÓõíôÞñçóçò REF-DF-SM ÅëÝã åé Ýíá èåñìïóôïé åßï PTC Êëßìáêá èåñìïêñáóßáò: -19? +99 C ëåã ïò áðüøõîçò - dfrst Ôñßá ñåëý: óõìðéåóôþò (30Á, 2ÇÑ),
3.1 Íá âñåèåß ôï ðåäßï ïñéóìïý ôçò óõíüñôçóçò f: 4 x. (iv) f(x, y, z) = sin x 2 + y 2 + 3z Íá âñåèïýí ôá üñéá (áí õðüñ ïõí): lim
 3.1 Íá âñåèåß ôï ðåäßï ïñéóìïý ôçò óõíüñôçóçò f: 4 x (i) f(x, y) = sin 1 2 (x + y) (ii) f(x, y) = y 2 + 3 (iii) f(x, y, z) = 25 x 2 y 2 z 2 (iv) f(x, y, z) = z +ln(1 x 2 y 2 ) 3.2 (i) óôù f(x, y, z) =
3.1 Íá âñåèåß ôï ðåäßï ïñéóìïý ôçò óõíüñôçóçò f: 4 x (i) f(x, y) = sin 1 2 (x + y) (ii) f(x, y) = y 2 + 3 (iii) f(x, y, z) = 25 x 2 y 2 z 2 (iv) f(x, y, z) = z +ln(1 x 2 y 2 ) 3.2 (i) óôù f(x, y, z) =
( ) ξî τέτοιο, + Ý åé ìßá ôïõëü éóôïí ñßæá óôï äéüóôçìá ( ) h x =,να δείξετε ότι υπάρχει ( α,β) x ΕΦΑΡΜΟΓΕΣ ΣΤΙΣ ΠΑΡΑΓΩΓΟΥΣ
 . Äßíåôáé ç óõíüñôçóç : [, + ) R óõíå Þò óôï äéüóôçìá [,+ ) êáé ðáñáãùãßóéìç óôï äéüóôçìá (,+ ), ãéá ôçí ïðïßá éó ýåé ( ) = α. óôù üôé õðüñ åé κî R, þóôå íá éó ýåé ( ) κ ãéá êüèå Î (,+ ). Íá äåßîåôå üôé
. Äßíåôáé ç óõíüñôçóç : [, + ) R óõíå Þò óôï äéüóôçìá [,+ ) êáé ðáñáãùãßóéìç óôï äéüóôçìá (,+ ), ãéá ôçí ïðïßá éó ýåé ( ) = α. óôù üôé õðüñ åé κî R, þóôå íá éó ýåé ( ) κ ãéá êüèå Î (,+ ). Íá äåßîåôå üôé
2.4 ñçóéìïðïéþíôáò ôïí êáíüíá áëõóßäáò íá âñåèåß ç dr
 2.1 i) Íá âñåèïýí ïé óõíôåôáãìýíåò ôïõ óçìåßïõ óôï ïðïßï ç åõèåßá r = 2 + t)i + 1 2t)j + 3tk ôýìíåé ôï åðßðåäï xz. ii) Íá âñåèïýí ïé óõíôåôáãìýíåò ôïõ óçìåßïõ óôï ïðïßï ç åõèåßá r = ti + 1 + 2t)j 3tk ôýìíåé
2.1 i) Íá âñåèïýí ïé óõíôåôáãìýíåò ôïõ óçìåßïõ óôï ïðïßï ç åõèåßá r = 2 + t)i + 1 2t)j + 3tk ôýìíåé ôï åðßðåäï xz. ii) Íá âñåèïýí ïé óõíôåôáãìýíåò ôïõ óçìåßïõ óôï ïðïßï ç åõèåßá r = ti + 1 + 2t)j 3tk ôýìíåé
å) Íá âñåßôå ôï äéüóôçìá ðïõ äéáíýåé ôï êéíçôü êáôü ôï ñïíéêü äéüóôçìá áðü ôï ðñþôï Ýùò ôï Ýâäïìï äåõôåñüëåðôï ôçò êßíçóþò ôïõ.
 ÌÁÈÇÌÁÔÉÊÁ ÃÅÍÉÊÇÓ ÐÁÉÄÅÉÁÓ Ã ËÕÊÅÉÏÕ È Å Ì Á 1 ï 3 ï Ä É Á Ã Ù Í É Ó Ì Á á êéçôü êéåßôáé ðüù óôï Üîïá x~x. Ç èýóç ôïõ êüèå ñïéêþ óôéãìþ t äßåôáé áðü ôç 3 óõüñôçóç x(t) = t 1t + 60t + 1, üðïõ ôï t ìåôñéýôáé
ÌÁÈÇÌÁÔÉÊÁ ÃÅÍÉÊÇÓ ÐÁÉÄÅÉÁÓ Ã ËÕÊÅÉÏÕ È Å Ì Á 1 ï 3 ï Ä É Á Ã Ù Í É Ó Ì Á á êéçôü êéåßôáé ðüù óôï Üîïá x~x. Ç èýóç ôïõ êüèå ñïéêþ óôéãìþ t äßåôáé áðü ôç 3 óõüñôçóç x(t) = t 1t + 60t + 1, üðïõ ôï t ìåôñéýôáé
Äéáôáñá Þ. +2% _ r=åýñïò åëýã ïõ. t áí. t åî. êáé t åî
 ÊåöÜëáéï 9 Áîéïëüãçóç åíüò ÓõóôÞìáôïò Áõôüìáôïõ ÅëÝã ïõ Åðéäéùêüìåíïé óôü ïé: Ï óêïðüò áõôïý ôïõ êåöáëáßïõ åßíáé íá âïçèþóåé ôïõò ìáèçôýò: Ö Íá ãíùñßæïõí êáé íá êáôáíïïýí ôá ðïéïôéêü áñáêôçñéóôéêü åíüò
ÊåöÜëáéï 9 Áîéïëüãçóç åíüò ÓõóôÞìáôïò Áõôüìáôïõ ÅëÝã ïõ Åðéäéùêüìåíïé óôü ïé: Ï óêïðüò áõôïý ôïõ êåöáëáßïõ åßíáé íá âïçèþóåé ôïõò ìáèçôýò: Ö Íá ãíùñßæïõí êáé íá êáôáíïïýí ôá ðïéïôéêü áñáêôçñéóôéêü åíüò
Ðñïêýðôïõí ôá ðáñáêüôù äéáãñüììáôá.
 ÌÅÈÏÄÏËÏÃÉÁ Ãéá Ýíá óþìá ðïõ åêôåëåß åõèýãñáììç ïìáëü ìåôáâáëëüìåíç êßíçóç éó ýïõí ïé ôýðïé: õ=õ ï +á. t x=õ. ï t+ át. ÅÜí ôï óþìá îåêéíüåé áðü ôçí çñåìßá, äçëáäþ ç áñ éêþ ôá ýôçôá åßíáé õ ï =0, ôüôå ïé
ÌÅÈÏÄÏËÏÃÉÁ Ãéá Ýíá óþìá ðïõ åêôåëåß åõèýãñáììç ïìáëü ìåôáâáëëüìåíç êßíçóç éó ýïõí ïé ôýðïé: õ=õ ï +á. t x=õ. ï t+ át. ÅÜí ôï óþìá îåêéíüåé áðü ôçí çñåìßá, äçëáäþ ç áñ éêþ ôá ýôçôá åßíáé õ ï =0, ôüôå ïé
ÊåöÜëáéï 5 ÄÉÁÍÕÓÌÁÔÉÊÏÉ ÙÑÏÉ. 5.1 ÅéóáãùãÞ. 56 ÊåöÜëáéï 5. ÄÉÁÍÕÓÌÁÔÉÊÏÉ ÙÑÏÉ
 55 56 ÊåöÜëáéï 5. ÄÉÁÍÕÓÌÁÔÉÊÏÉ ÙÑÏÉ ÊåöÜëáéï 5 ÄÉÁÍÕÓÌÁÔÉÊÏÉ ÙÑÏÉ 5.1 ÅéóáãùãÞ Ïñéóìüò: íá óýíïëï V êáëåßôáé äéáíõóìáôéêüò þñïò Þ ãñáììéêüò þñïò ðüíù óôïí IR áí (á) ôï V åßíáé êëåéóôü ùò ðñïò ôç ðñüóèåóç,
55 56 ÊåöÜëáéï 5. ÄÉÁÍÕÓÌÁÔÉÊÏÉ ÙÑÏÉ ÊåöÜëáéï 5 ÄÉÁÍÕÓÌÁÔÉÊÏÉ ÙÑÏÉ 5.1 ÅéóáãùãÞ Ïñéóìüò: íá óýíïëï V êáëåßôáé äéáíõóìáôéêüò þñïò Þ ãñáììéêüò þñïò ðüíù óôïí IR áí (á) ôï V åßíáé êëåéóôü ùò ðñïò ôç ðñüóèåóç,
1. Íá ëõèåß ç äéáöïñéêþ åîßóùóç (15 ìïí.) 2. Íá âñåèåß ç ãåíéêþ ëýóç ôçò äéáöïñéêþò åîßóùóçò (15 ìïí.)
 ÔÅÉ ËÜñéóáò, ÔìÞìá Ìç áíïëïãßáò ÌáèçìáôéêÜ ÉI, ÅîÝôáóç Ðåñéüäïõ Éïõíßïõ 24/6/21 ÄéäÜóêùí: Á éëëýáò Óõíåöáêüðïõëïò 1. Íá ëõèåß ç äéáöïñéêþ åîßóùóç (15 ìïí.) (3x 2 + 6xy 2 )dx + (6x 2 y + 4y 3 )dy = 2. Íá
ÔÅÉ ËÜñéóáò, ÔìÞìá Ìç áíïëïãßáò ÌáèçìáôéêÜ ÉI, ÅîÝôáóç Ðåñéüäïõ Éïõíßïõ 24/6/21 ÄéäÜóêùí: Á éëëýáò Óõíåöáêüðïõëïò 1. Íá ëõèåß ç äéáöïñéêþ åîßóùóç (15 ìïí.) (3x 2 + 6xy 2 )dx + (6x 2 y + 4y 3 )dy = 2. Íá
Áóõìðôùôéêïß Óõìâïëéóìïß êáé Éåñáñ ßá ÓõíáñôÞóåùí
 Áóõìðôùôéêïß Óõìâïëéóìïß êáé Éåñáñ ßá ÓõíáñôÞóåùí Çëßáò Ê. Óôáõñüðïõëïò Ïêôþâñéïò 006 1 Áóõìðôùôéêïß Óõìâïëéóìïß ÎåêéíÜìå äéáôõðþíïíôáò ôïõò ïñéóìïýò ôùí ðýíôå ãíùóôþí áóõìðôùôéêþí óõìâïëéóìþí: Ïñéóìüò
Áóõìðôùôéêïß Óõìâïëéóìïß êáé Éåñáñ ßá ÓõíáñôÞóåùí Çëßáò Ê. Óôáõñüðïõëïò Ïêôþâñéïò 006 1 Áóõìðôùôéêïß Óõìâïëéóìïß ÎåêéíÜìå äéáôõðþíïíôáò ôïõò ïñéóìïýò ôùí ðýíôå ãíùóôþí áóõìðôùôéêþí óõìâïëéóìþí: Ïñéóìüò
Ανώτερα Μαθηματικά Ι. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 7: Οριακή Τιμή Συνάρτησης. Αθανάσιος Μπράτσος. Τμήμα Ναυπηγών Μηχανικών ΤΕ
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά Ι Ενότητα 7: Οριακή Τιμή Συνάρτησης Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος διατίθεται
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά Ι Ενότητα 7: Οριακή Τιμή Συνάρτησης Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος διατίθεται
3.1 H Ýííïéá ôçò óõíüñôçóçò ÐÁÑÁÄÅÉÃÌÁÔÁ - ÅÖÁÑÌÏÃÅÓ
 .1 Ç Ýííïéá ôçò óõíüñôçóçò 55.1 H Ýííïéá ôçò óõíüñôçóçò Åñþ ôçóç 1 Ôé ëýãåôáé óõíüñôçóç; ÁðÜíôçóç Ç ó Ýóç åêåßíç ðïõ êüèå ôéìþ ôçò ìåôáâëçôþò x, áíôéóôïé ßæåôáé óå ìéá ìüíï ôéìþ ôçò ìåôáâëçôþò y ëýãåôáé
.1 Ç Ýííïéá ôçò óõíüñôçóçò 55.1 H Ýííïéá ôçò óõíüñôçóçò Åñþ ôçóç 1 Ôé ëýãåôáé óõíüñôçóç; ÁðÜíôçóç Ç ó Ýóç åêåßíç ðïõ êüèå ôéìþ ôçò ìåôáâëçôþò x, áíôéóôïé ßæåôáé óå ìéá ìüíï ôéìþ ôçò ìåôáâëçôþò y ëýãåôáé
9. ÁíÜðôõîç ðñïãñáììüôùí ìå ñïíéêýò ëåéôïõñãßåò.
 9. ÁíÜðôõîç ðñïãñáììüôùí ìå ñïíéêýò ëåéôïõñãßåò. 9.1 ÃåíéêÜ. Ôá ðåñéóóüôåñá PLC äéáèýôïõí óçìáíôéêýò åõêïëßåò üóïí áöïñü óôïí ðñïãñáììáôéóìü ñïíéêþí ëåéôïõñãéþí ìå ñçóéìïðïßçóç ôùí ñïíéêþí ëåéôïõñãéþí
9. ÁíÜðôõîç ðñïãñáììüôùí ìå ñïíéêýò ëåéôïõñãßåò. 9.1 ÃåíéêÜ. Ôá ðåñéóóüôåñá PLC äéáèýôïõí óçìáíôéêýò åõêïëßåò üóïí áöïñü óôïí ðñïãñáììáôéóìü ñïíéêþí ëåéôïõñãéþí ìå ñçóéìïðïßçóç ôùí ñïíéêþí ëåéôïõñãéþí
ÄéáêñéôÝò êáé óõíå åßò ôõ áßåò ìåôáâëçôýò ÁóêÞóåéò
 ÄéáêñéôÝò êáé óõíå åßò ôõ áßåò ìåôáâëçôýò ÁóêÞóåéò Áíôþíçò Ïéêïíüìïõ aeconom@math.uoa.gr ÌáÀïõ óêçóç (Ross, Exer. 4.8) Áí E[X] êáé V ar[x] 5 íá âñåßôå. E[( + X) ],. V ar[4 + X]. óêçóç (Ross, Exer. 4.64)
ÄéáêñéôÝò êáé óõíå åßò ôõ áßåò ìåôáâëçôýò ÁóêÞóåéò Áíôþíçò Ïéêïíüìïõ aeconom@math.uoa.gr ÌáÀïõ óêçóç (Ross, Exer. 4.8) Áí E[X] êáé V ar[x] 5 íá âñåßôå. E[( + X) ],. V ar[4 + X]. óêçóç (Ross, Exer. 4.64)
Üóêçóç 15. ÕëéêÜ - åîáñôþìáôá äéêôýïõ ðåðéåóìýíïõ áýñá êáé ðíåõìáôéêýò óõóêåõýò
 ÕëéêÜ - åîáñôþìáôá äéêôýïõ ðåðéåóìýíïõ áýñá êáé ðíåõìáôéêýò óõóêåõýò Óôü ïé ôçò Üóêçóçò äéüñêåéá Üóêçóçò: 6 äéäáêôéêýò þñåò Óôï ôýëïò ôçò Üóêçóçò ïé ìáèçôýò èá åßíáé éêáíïß: é íá áíáãíùñßæïõí ôá åîáñôþìáôá
ÕëéêÜ - åîáñôþìáôá äéêôýïõ ðåðéåóìýíïõ áýñá êáé ðíåõìáôéêýò óõóêåõýò Óôü ïé ôçò Üóêçóçò äéüñêåéá Üóêçóçò: 6 äéäáêôéêýò þñåò Óôï ôýëïò ôçò Üóêçóçò ïé ìáèçôýò èá åßíáé éêáíïß: é íá áíáãíùñßæïõí ôá åîáñôþìáôá
ÓÕÍÈÇÊÇ ÁÌÅÔÁÈÅÔÏÔÇÔÁÓ ÓÕÓÔÇÌÁÔÏÓ ÔÏÉ ÙÌÁÔÙÍ ÐÁÑÁÑÔÇÌÁ Â
 ÓÕÍÈÇÊÇ ÁÌÅÔÁÈÅÔÏÔÇÔÁÓ ÓÕÓÔÇÌÁÔÏÓ ÔÏÉ ÙÌÁÔÙÍ ÐÁÑÁÑÔÇÌÁ Â ÐÁÑÁÑÔÇÌÁ Â 464 ÅÊÙÓ 000 - Ó ÏËÉÁ ÓÕÍÈÇÊÇ ÁÌÅÔÁÈÅÔÏÔÇÔÁÓ ÓÕÓÔÇÌÁÔÏÓ ÔÏÉ ÙÌÁÔÙÍ Â.1 ÁÓÕÌÌÅÔÑÏ ÓÕÓÔÇÌÁ Η N / ( 0. + 0.1 η) 0.6 ν ν, η 3, η > 3...
ÓÕÍÈÇÊÇ ÁÌÅÔÁÈÅÔÏÔÇÔÁÓ ÓÕÓÔÇÌÁÔÏÓ ÔÏÉ ÙÌÁÔÙÍ ÐÁÑÁÑÔÇÌÁ Â ÐÁÑÁÑÔÇÌÁ Â 464 ÅÊÙÓ 000 - Ó ÏËÉÁ ÓÕÍÈÇÊÇ ÁÌÅÔÁÈÅÔÏÔÇÔÁÓ ÓÕÓÔÇÌÁÔÏÓ ÔÏÉ ÙÌÁÔÙÍ Â.1 ÁÓÕÌÌÅÔÑÏ ÓÕÓÔÇÌÁ Η N / ( 0. + 0.1 η) 0.6 ν ν, η 3, η > 3...
ÏÑÉÁÊÇ ÔÉÌÇ ÓÕÍÁÑÔÇÓÇÓ
 ÌÜèçìá 7 ÏÑÉÁÊÇ ÔÉÌÇ ÓÕÍÁÑÔÇÓÇÓ Óôï ìüèçìá áõôü èá äïèåß ç Ýííïéá ôïõ ïñßïõ ìéáò ðñáãìáôéêþò óõíüñôçóçò ìå ôñüðï ðñïóáñìïóìýíï óôéò áðáéôþóåéò ôùí äéáöüñùí åöáñìïãþí, ðïõ áðáéôïýíôáé óôçí åðéóôþìç ôïõ.
ÌÜèçìá 7 ÏÑÉÁÊÇ ÔÉÌÇ ÓÕÍÁÑÔÇÓÇÓ Óôï ìüèçìá áõôü èá äïèåß ç Ýííïéá ôïõ ïñßïõ ìéáò ðñáãìáôéêþò óõíüñôçóçò ìå ôñüðï ðñïóáñìïóìýíï óôéò áðáéôþóåéò ôùí äéáöüñùí åöáñìïãþí, ðïõ áðáéôïýíôáé óôçí åðéóôþìç ôïõ.
B i o f l o n. Ãéá åöáñìïãýò ìåôáöïñüò çìéêþí
 B i o f l o n Ãéá åöáñìïãýò ìåôáöïñüò çìéêþí Ç åôáéñåßá Aflex, ç ïðïßá éäñýèçêå ôï 1973, Þôáí ç ðñþôç ðïõ ó åäßáóå ôïí åýêáìðôï óùëþíá PTFE ãéá ôç ìåôáöïñü çìéêþí õãñþí ðñßí áðü 35 ñüíéá. Ï åëéêïåéäþò
B i o f l o n Ãéá åöáñìïãýò ìåôáöïñüò çìéêþí Ç åôáéñåßá Aflex, ç ïðïßá éäñýèçêå ôï 1973, Þôáí ç ðñþôç ðïõ ó åäßáóå ôïí åýêáìðôï óùëþíá PTFE ãéá ôç ìåôáöïñü çìéêþí õãñþí ðñßí áðü 35 ñüíéá. Ï åëéêïåéäþò
16. ÌåëÝôç ôùí óõíáñôþóåùí y=çìx, y=óõíx êáé ôùí ìåôáó çìáôéóìþí ôïõò.
 55 16. ÌåëÝôç ôùí óõíáñôþóåùí y=çìx, y=óõíx êáé ôùí ìåôáó çìáôéóìþí ôïõò. A ÌÝñïò 1. Íá êáôáóêåõüóåéò óôï Function Probe ôç ãñáöéêþ ðáñüóôáóç ôçò y=çìx. Óôïí ïñéæüíôéï Üîïíá íá ïñßóåéò êëßìáêá áðü ôï -4ð
55 16. ÌåëÝôç ôùí óõíáñôþóåùí y=çìx, y=óõíx êáé ôùí ìåôáó çìáôéóìþí ôïõò. A ÌÝñïò 1. Íá êáôáóêåõüóåéò óôï Function Probe ôç ãñáöéêþ ðáñüóôáóç ôçò y=çìx. Óôïí ïñéæüíôéï Üîïíá íá ïñßóåéò êëßìáêá áðü ôï -4ð
ÐÑÏÓÅÃÃÉÓÇ ÐÁÑÁÃÙÃÙÍ
 ÌÜèçìá 6 ÐÑÏÓÅÃÃÉÓÇ ÐÁÑÁÃÙÃÙÍ ÅéóáãùãÞ 1Ç ðñïóýããéóç ôçò ôéìþò ôçò ðáñáãþãïõ ìéáò óõíüñôçóçò ñçóéìïðïéåßôáé êõñßùò: i) üôáí ëüãù ôçò ðïëýðëïêçò ìïñöþò ôïõ ôýðïõ ôçò åßíáé áäýíáôïò ï èåùñçôéêüò õðïëïãéóìüò
ÌÜèçìá 6 ÐÑÏÓÅÃÃÉÓÇ ÐÁÑÁÃÙÃÙÍ ÅéóáãùãÞ 1Ç ðñïóýããéóç ôçò ôéìþò ôçò ðáñáãþãïõ ìéáò óõíüñôçóçò ñçóéìïðïéåßôáé êõñßùò: i) üôáí ëüãù ôçò ðïëýðëïêçò ìïñöþò ôïõ ôýðïõ ôçò åßíáé áäýíáôïò ï èåùñçôéêüò õðïëïãéóìüò
ÁÑÉÈÌÇÔÉÊÇ ËÕÓÇ ÓÕÍÇÈÙÍ ÄÉÁÖÏÑÉÊÙÍ ÅÎÉÓÙÓÅÙÍ
 ÌÜèçìá 8 ÁÑÉÈÌÇÔÉÊÇ ËÕÓÇ ÓÕÍÇÈÙÍ ÄÉÁÖÏÑÉÊÙÍ ÅÎÉÓÙÓÅÙÍ 8.1 ÅéóáãùãéêÝò Ýííïéåò Åßíáé Þäç ãíùóôü óôïí áíáãíþóôç üôé ç åðßëõóç ôùí ðåñéóóüôåñùí ðñïâëçìüôùí ôùí èåôéêþí åðéóôçìþí ïäçãåß óôç ëýóç ìéáò äéáöïñéêþò
ÌÜèçìá 8 ÁÑÉÈÌÇÔÉÊÇ ËÕÓÇ ÓÕÍÇÈÙÍ ÄÉÁÖÏÑÉÊÙÍ ÅÎÉÓÙÓÅÙÍ 8.1 ÅéóáãùãéêÝò Ýííïéåò Åßíáé Þäç ãíùóôü óôïí áíáãíþóôç üôé ç åðßëõóç ôùí ðåñéóóüôåñùí ðñïâëçìüôùí ôùí èåôéêþí åðéóôçìþí ïäçãåß óôç ëýóç ìéáò äéáöïñéêþò
Ανώτερα Μαθηματικά Ι. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 8: Συνέχεια Συνάρτησης. Αθανάσιος Μπράτσος. Τμήμα Ναυπηγών Μηχανικών ΤΕ
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά Ι Ενότητα 8: Συνέχεια Συνάρτησης Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος διατίθεται
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά Ι Ενότητα 8: Συνέχεια Συνάρτησης Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος διατίθεται
Ìáèáßíïõìå ôéò áðïäåßîåéò
 50. Βήµα ο Μαθαίνουµε τις αποδείξεις ã) Ùò ðñïò ôçí áñ Þ ôùí áîüíùí, áí êáé ìüíï áí Ý ïõí áíôßèåôåò óõíôåôáãìýíåò. ÄçëáäÞ: á = á êáé â = â ÂÞìá Ìáèáßíïõìå ôéò áðïäåßîåéò ä) Ùò ðñïò ôç äé ïôüìï ôçò çò êáé
50. Βήµα ο Μαθαίνουµε τις αποδείξεις ã) Ùò ðñïò ôçí áñ Þ ôùí áîüíùí, áí êáé ìüíï áí Ý ïõí áíôßèåôåò óõíôåôáãìýíåò. ÄçëáäÞ: á = á êáé â = â ÂÞìá Ìáèáßíïõìå ôéò áðïäåßîåéò ä) Ùò ðñïò ôç äé ïôüìï ôçò çò êáé
ÅÑÃÁÓÔÇÑÉÏ ÇËÅÊÔÑÉÊÙÍ ÅÃÊÁÔÁÓÔÁÓÅÙÍ ÏÑÃÁÍÁ ÅËÅÃ ÏÕ ÇËÅÊÔÑÉÊÙÍ ÊÕÊËÙÌÁÔÙÍ Ç ðñáãìáôïðïßçóç áõôþò ôçò Üóêçóçò Ý åé óáí óêïðü íá åîïéêåéùèïýí ïé ìáèçôýò
 2 ÏÑÃÁÍÁ ÅËÅÃ ÏÕ ÇËÅÊÔÑÉÊÙÍ ÊÕÊËÙÌÁÔÙÍ ÅÑÃÁÓÔÇÑÉÏ ÇËÅÊÔÑÉÊÙÍ ÅÃÊÁÔÁÓÔÁÓÅÙÍ ÏÑÃÁÍÁ ÅËÅÃ ÏÕ ÇËÅÊÔÑÉÊÙÍ ÊÕÊËÙÌÁÔÙÍ Ç ðñáãìáôïðïßçóç áõôþò ôçò Üóêçóçò Ý åé óáí óêïðü íá åîïéêåéùèïýí ïé ìáèçôýò ìå ôá üñãáíá
2 ÏÑÃÁÍÁ ÅËÅÃ ÏÕ ÇËÅÊÔÑÉÊÙÍ ÊÕÊËÙÌÁÔÙÍ ÅÑÃÁÓÔÇÑÉÏ ÇËÅÊÔÑÉÊÙÍ ÅÃÊÁÔÁÓÔÁÓÅÙÍ ÏÑÃÁÍÁ ÅËÅÃ ÏÕ ÇËÅÊÔÑÉÊÙÍ ÊÕÊËÙÌÁÔÙÍ Ç ðñáãìáôïðïßçóç áõôþò ôçò Üóêçóçò Ý åé óáí óêïðü íá åîïéêåéùèïýí ïé ìáèçôýò ìå ôá üñãáíá
ÓÕÍÁÑÔÇÓÅÉÓ ÐÏËËÙÍ ÌÅÔÁÂËÇÔÙÍ
 66 ÊåöÜëáéï 3 ÓÕÍÁÑÔÇÓÅÉÓ ÐÏËËÙÍ ÌÅÔÁÂËÇÔÙÍ 3.1 ÅéóáãùãÞ óôù üôé S åßíáé Ýíá óýíïëï áðü óçìåßá óôïí n äéüóôáôï þñï. Ìéá óõíüñôçóç (ðïõ ïñßæåôáé óôï S) åßíáé ìéá ó Ýóç ç ïðïßá ó åôßæåé êüèå óôïé åßï ôïõ
66 ÊåöÜëáéï 3 ÓÕÍÁÑÔÇÓÅÉÓ ÐÏËËÙÍ ÌÅÔÁÂËÇÔÙÍ 3.1 ÅéóáãùãÞ óôù üôé S åßíáé Ýíá óýíïëï áðü óçìåßá óôïí n äéüóôáôï þñï. Ìéá óõíüñôçóç (ðïõ ïñßæåôáé óôï S) åßíáé ìéá ó Ýóç ç ïðïßá ó åôßæåé êüèå óôïé åßï ôïõ
Προτεινόμενα θέματα Πανελλαδικών εξετάσεων. Χημεία Θετικής Κατεύθυνσης ΕΛΛΗΝΟΕΚΔΟΤΙΚΗ
 Προτεινόμενα θέματα Πανελλαδικών εξετάσεων Χημεία Θετικής Κατεύθυνσης 2o ΕΛΛΗΝΟΕΚΔΟΤΙΚΗ 1.1. ÓùóôÞ áðüíôçóç åßíáé ç Ä. ΘΕΜΑ 1ο 1.2. ñçóéìïðïéïýìå ôçí êáôáíïìþ ôùí çëåêôñïíßùí óå áôïìéêü ôñï éáêü óýìöùíá
Προτεινόμενα θέματα Πανελλαδικών εξετάσεων Χημεία Θετικής Κατεύθυνσης 2o ΕΛΛΗΝΟΕΚΔΟΤΙΚΗ 1.1. ÓùóôÞ áðüíôçóç åßíáé ç Ä. ΘΕΜΑ 1ο 1.2. ñçóéìïðïéïýìå ôçí êáôáíïìþ ôùí çëåêôñïíßùí óå áôïìéêü ôñï éáêü óýìöùíá
ΕΛΕΝΗ ΓΕΡΟΥΛΑΝΟΥ. Εικονογράφηση ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ ΓΙΑ ΠΑΙΔΙΑ ΝΗΠΙΑΓΩΓΕΙΟΥ ΛΗΔΑ ΒΑΡΒΑΡΟΥΣΗ ΕΚΔΟΣΕΙΣ ΠΑΠΑΔΟΠΟΥΛΟΣ
 ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ ΓΙΑ ΠΑΙΔΙΑ ΝΗΠΙΑΓΩΓΕΙΟΥ ΕΛΕΝΗ ΓΕΡΟΥΛΑΝΟΥ Εικονογράφηση ΛΗΔΑ ΒΑΡΒΑΡΟΥΣΗ ΕΚΔΟΣΕΙΣ ΠΑΠΑΔΟΠΟΥΛΟΣ ΕΚΔΟΣΕΙΣ ΠΑΠΑΔΟΠΟΥΛΟΣ Ï ðéï ìåãüëïò êáé ï ðéï óçìáíôéêüò ðáéäáãùãéêüò êáíüíáò äåí åßíáé ôï íá
ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ ΓΙΑ ΠΑΙΔΙΑ ΝΗΠΙΑΓΩΓΕΙΟΥ ΕΛΕΝΗ ΓΕΡΟΥΛΑΝΟΥ Εικονογράφηση ΛΗΔΑ ΒΑΡΒΑΡΟΥΣΗ ΕΚΔΟΣΕΙΣ ΠΑΠΑΔΟΠΟΥΛΟΣ ΕΚΔΟΣΕΙΣ ΠΑΠΑΔΟΠΟΥΛΟΣ Ï ðéï ìåãüëïò êáé ï ðéï óçìáíôéêüò ðáéäáãùãéêüò êáíüíáò äåí åßíáé ôï íá
Ανώτερα Μαθηματικά Ι. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 11: Διανυσματική Συνάρτηση. Αθανάσιος Μπράτσος. Τμήμα Ναυπηγών Μηχανικών ΤΕ
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά Ι Ενότητα 11: Διανυσματική Συνάρτηση Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος διατίθεται
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά Ι Ενότητα 11: Διανυσματική Συνάρτηση Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος διατίθεται
SPLINES. ÌÜèçìá ÓõíÜñôçóç spline Ïñéóìïß êáé ó åôéêü èåùñþìáôá
 ÌÜèçìá 4 SPLINES 4.1 ÓõíÜñôçóç spline 4.1.1 Ïñéóìïß êáé ó åôéêü èåùñþìáôá Óôï ÌÜèçìá ÐïëõùíõìéêÞ ðáñåìâïëþ åîåôüóôçêå ôï ðñüâëçìá ôçò åýñåóçò ôùí ðïëõùíýìùí ðáñåìâïëþò, äçëáäþ ðïëõùíýìùí ðïõ óõíýðéðôáí
ÌÜèçìá 4 SPLINES 4.1 ÓõíÜñôçóç spline 4.1.1 Ïñéóìïß êáé ó åôéêü èåùñþìáôá Óôï ÌÜèçìá ÐïëõùíõìéêÞ ðáñåìâïëþ åîåôüóôçêå ôï ðñüâëçìá ôçò åýñåóçò ôùí ðïëõùíýìùí ðáñåìâïëþò, äçëáäþ ðïëõùíýìùí ðïõ óõíýðéðôáí
ιαδικασία åãêáôüóôáóçò MS SQL Server, SingularLogic Accountant, SingularLogic Accountant Ìéóèïäïóßá
 1.1 ÃåíéêÝò ðëçñïöïñßåò ãéá ôçí Express Ýêäïóç ôïõ SQL Server... 3 1.2 ÃåíéêÝò ðëçñïöïñßåò ãéá ôçí åãêáôüóôáóç... 3 2.1 ÅãêáôÜóôáóç Microsoft SQL Server 2008R2 Express Edition... 4 2.1 Åíåñãïðïßçóç ôïõ
1.1 ÃåíéêÝò ðëçñïöïñßåò ãéá ôçí Express Ýêäïóç ôïõ SQL Server... 3 1.2 ÃåíéêÝò ðëçñïöïñßåò ãéá ôçí åãêáôüóôáóç... 3 2.1 ÅãêáôÜóôáóç Microsoft SQL Server 2008R2 Express Edition... 4 2.1 Åíåñãïðïßçóç ôïõ
Μαθηματικά ΙΙΙ. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 15: Προσέγγιση συνήθων διαφορικών εξισώσεων Μέρος Ι. Αθανάσιος Μπράτσος
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 15: Προσέγγιση συνήθων διαφορικών εξισώσεων Μέρος Ι Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 15: Προσέγγιση συνήθων διαφορικών εξισώσεων Μέρος Ι Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας
1. i) ÊÜèå üñïò ðñïêýðôåé áðü ôçí ðñüóèåóç ôïõ óôáèåñïý áñéèìïý 3 óôïí ðñïçãïýìåíï, ïðüôå Ý ïõìå áñéèìçôéêþ ðñüïäï á í ìå ðñþôï üñï
 5. ÐÑÏÏÄÏÉ 7 5. ÁñéèìçôéêÞ ðñüïäïò Á ÏìÜäá. i) ÊÜèå üñïò ðñïêýðôåé áðü ôçí ðñüóèåóç ôïõ óôáèåñïý áñéèìïý 3 óôïí ðñïçãïýìåíï, ïðüôå Ý ïõìå áñéèìçôéêþ ðñüïäï á í ìå ðñþôï üñï á = 7 êáé äéáöïñü ù = 3. Óõíåðþò
5. ÐÑÏÏÄÏÉ 7 5. ÁñéèìçôéêÞ ðñüïäïò Á ÏìÜäá. i) ÊÜèå üñïò ðñïêýðôåé áðü ôçí ðñüóèåóç ôïõ óôáèåñïý áñéèìïý 3 óôïí ðñïçãïýìåíï, ïðüôå Ý ïõìå áñéèìçôéêþ ðñüïäï á í ìå ðñþôï üñï á = 7 êáé äéáöïñü ù = 3. Óõíåðþò
4.5 ÁóêÞóåéò çìéêþò éóïññïðßáò ìå åðßäñáóç óôç èýóç éóïññïðßáò
 4.5 ÁóêÞóåéò çìéêþò éóïññïðßáò ìå åðßäñáóç óôç èýóç éóïññïðßáò Óôéò áóêþóåéò ìå åðßäñáóç óôç èýóç ìéáò éóïññïðßáò ãßíåôáé áíáöïñü óå ðåñéóóüôåñåò áðü ìßá èýóåéò éóïññïðßáò. Ïé èýóåéò éóïññïðßáò åßíáé äéáäï
4.5 ÁóêÞóåéò çìéêþò éóïññïðßáò ìå åðßäñáóç óôç èýóç éóïññïðßáò Óôéò áóêþóåéò ìå åðßäñáóç óôç èýóç ìéáò éóïññïðßáò ãßíåôáé áíáöïñü óå ðåñéóóüôåñåò áðü ìßá èýóåéò éóïññïðßáò. Ïé èýóåéò éóïññïðßáò åßíáé äéáäï
Ανώτερα Μαθηματικά Ι. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 10: Παράγωγος Συνάρτησης Μέρος ΙI. Αθανάσιος Μπράτσος. Τμήμα Ναυπηγών Μηχανικών ΤΕ
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά Ι Ενότητα 10: Παράγωγος Συνάρτησης Μέρος ΙI Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά Ι Ενότητα 10: Παράγωγος Συνάρτησης Μέρος ΙI Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος
ÕÄÑÏËÇØÉÅÓ ÔÕÐÏÕ Á2 - Á4 ÌÅ ÁÍÔÉÐÁÃÅÔÉÊÇ ÐÑÏÓÔÁÓÉÁ
 ÕÄÑÏËÇØÉÅÓ ÔÕÐÏÕ Á - Á ÌÅ ÁÍÔÉÐÁÃÅÔÉÊÇ ÐÑÏÓÔÁÓÉÁ Ç ÅÕÄÏÓ ÁÂÅÅ êáôáóêåõüæåé õäñïëçøßåò Üñäåõóçò ôýðïõ SCHLUMBERGER ïé ïðïßåò áíôáðïêñßíïíôáé ðëþñùò ðñïò ôéò äéåèíåßò ðñïäéáãñáöýò, êáôáóêåõüæïíôáé ìå Þ ùñßò
ÕÄÑÏËÇØÉÅÓ ÔÕÐÏÕ Á - Á ÌÅ ÁÍÔÉÐÁÃÅÔÉÊÇ ÐÑÏÓÔÁÓÉÁ Ç ÅÕÄÏÓ ÁÂÅÅ êáôáóêåõüæåé õäñïëçøßåò Üñäåõóçò ôýðïõ SCHLUMBERGER ïé ïðïßåò áíôáðïêñßíïíôáé ðëþñùò ðñïò ôéò äéåèíåßò ðñïäéáãñáöýò, êáôáóêåõüæïíôáé ìå Þ ùñßò
ÓÕÍÅ ÅÉÁ ÓÕÍÁÑÔÇÓÇÓ. 8.1 ÃåíéêÝò Ýííïéåò êáé ïñéóìïß
 ÌÜèçìá 8 ÓÕÍÅ ÅÉÁ ÓÕÍÁÑÔÇÓÇÓ ¼ìïéá, üðùò êáé óôï ÌÜèçìá ÏñéáêÞ ôéìþ óõíüñôçóçò, äßíïíôáé ðåñéëçðôéêü ïé âáóéêüôåñïé ïñéóìïß êáé èåùñþìáôá ðïõ áíáöýñïíôáé óôç óõíý åéá ìéáò ðñáãìáôéêþò óõíüñôçóçò, åíþ ï
ÌÜèçìá 8 ÓÕÍÅ ÅÉÁ ÓÕÍÁÑÔÇÓÇÓ ¼ìïéá, üðùò êáé óôï ÌÜèçìá ÏñéáêÞ ôéìþ óõíüñôçóçò, äßíïíôáé ðåñéëçðôéêü ïé âáóéêüôåñïé ïñéóìïß êáé èåùñþìáôá ðïõ áíáöýñïíôáé óôç óõíý åéá ìéáò ðñáãìáôéêþò óõíüñôçóçò, åíþ ï
ÓÔÁÔÉÊÏÓ ÇËÅÊÔÑÉÓÌÏÓ Ðåñéå üìåíá
 ÓÔÁÔÉÊÏÓ ÇËÅÊÔÑÉÓÌÏÓ Ðåñéå üìåíá Íüìïò ôïõ Coulomb Çëåêôñéêü Ðåäßï - íôáóç ÄõíáìéêÝò ÃñáììÝò Äõíáìéêü - ÄéáöïñÜ Äõíáìéêïý ÐõêíùôÝò ÃéÜííçò Ãáúóßäçò - ÅÊÖÅ ßïõ Äéáôýðùóç ôïõ Íüìïõ F F - F r F Ç HëåêôñïóôáôéêÞ
ÓÔÁÔÉÊÏÓ ÇËÅÊÔÑÉÓÌÏÓ Ðåñéå üìåíá Íüìïò ôïõ Coulomb Çëåêôñéêü Ðåäßï - íôáóç ÄõíáìéêÝò ÃñáììÝò Äõíáìéêü - ÄéáöïñÜ Äõíáìéêïý ÐõêíùôÝò ÃéÜííçò Ãáúóßäçò - ÅÊÖÅ ßïõ Äéáôýðùóç ôïõ Íüìïõ F F - F r F Ç HëåêôñïóôáôéêÞ
Íá èõìçèïýìå ôç èåùñßá...
 ÇËÅÊÔÑÉÊÏ ÐÅÄÉÏ Íá èõìçèïýìå ôç èåùñßá....1 Ôé ïíïìüæïõìå çëåêôñéêü ðåäßï; Çëåêôñéêü ðåäßï ïíïìüæïõìå ôïí þñï ìýóá óôïí ïðïßï áí âñåèåß Ýíá çëåêôñéêü öïñôßï èá äå èåß äýíáìç. Ãéá íá åîåôüóïõìå áí óå êüðïéï
ÇËÅÊÔÑÉÊÏ ÐÅÄÉÏ Íá èõìçèïýìå ôç èåùñßá....1 Ôé ïíïìüæïõìå çëåêôñéêü ðåäßï; Çëåêôñéêü ðåäßï ïíïìüæïõìå ôïí þñï ìýóá óôïí ïðïßï áí âñåèåß Ýíá çëåêôñéêü öïñôßï èá äå èåß äýíáìç. Ãéá íá åîåôüóïõìå áí óå êüðïéï
Estimation Theory Exercises*
 Estimation Theory Exercises* Öþôçò ÓéÜííçò ÐáíåðéóôÞìéï Áèçíþí, ÔìÞìá Ìáèçìáôéêü fsiannis@math.uoa.gr December 22, 2009 * Áðü ôéò óçìåéþóåéò "ÓôáôéóôéêÞ Óõìðåñáóìáôïëïãßá" ôïõ Ô. ÐáðáúùÜííïõ, ôéò óçìåéþóåéò
Estimation Theory Exercises* Öþôçò ÓéÜííçò ÐáíåðéóôÞìéï Áèçíþí, ÔìÞìá Ìáèçìáôéêü fsiannis@math.uoa.gr December 22, 2009 * Áðü ôéò óçìåéþóåéò "ÓôáôéóôéêÞ Óõìðåñáóìáôïëïãßá" ôïõ Ô. ÐáðáúùÜííïõ, ôéò óçìåéþóåéò
ÄÉÁÍÕÓÌÁÔÉÊÏÓ ÄÉÁÖÏÑÉÊÏÓ ËÏÃÉÓÌÏÓ
 ÌÜèçìá 18 ÄÉÁÍÕÓÌÁÔÉÊÏÓ ÄÉÁÖÏÑÉÊÏÓ ËÏÃÉÓÌÏÓ 18.1 ÅéóáãùãÞ 1 Óôï ìüèçìá áõôü äßíïíôáé ïé âáóéêýò Ýííïéåò ôïõ Äéáíõóìáôéêïý Äéáöïñéêïý Ëïãéóìïý, ðïõ åßíáé ó åôéêýò ìå ôéò âáèìùôýò Þ ôéò äéáíõóìáôéêýò óõíáñôþóåéò
ÌÜèçìá 18 ÄÉÁÍÕÓÌÁÔÉÊÏÓ ÄÉÁÖÏÑÉÊÏÓ ËÏÃÉÓÌÏÓ 18.1 ÅéóáãùãÞ 1 Óôï ìüèçìá áõôü äßíïíôáé ïé âáóéêýò Ýííïéåò ôïõ Äéáíõóìáôéêïý Äéáöïñéêïý Ëïãéóìïý, ðïõ åßíáé ó åôéêýò ìå ôéò âáèìùôýò Þ ôéò äéáíõóìáôéêýò óõíáñôþóåéò
à ËÕÊÅÉÏÕ ÈÅÌÁÔÁ ÖÕÓÉÊÇÓ ÈÅÔÉÊÇÓ ÊÁÉ ÔÅ ÍÏËÏÃÉÊÇÓ ÊÁÔÅÕÈÕÍÓÇÓ. ÈÅÌÁ 1ï
 1 Ã ËÕÊÅÉÏÕ ÈÅÌÁÔÁ ÖÕÓÉÊÇÓ ÈÅÔÉÊÇÓ ÊÁÉ ÔÅ ÍÏËÏÃÉÊÇÓ ÊÁÔÅÕÈÕÍÓÇÓ ÈÅÌÁ 1ï Óôéò åñùôþóåéò 1 4 íá ãñüøåôå óôï ôåôñüäéü óáò ôïí áñéèìü ôçò åñþôçóçò êáé äßðëá ôï ãñüììá ðïõ áíôéóôïé åß óôç óùóôþ áðüíôçóç. 1.
1 Ã ËÕÊÅÉÏÕ ÈÅÌÁÔÁ ÖÕÓÉÊÇÓ ÈÅÔÉÊÇÓ ÊÁÉ ÔÅ ÍÏËÏÃÉÊÇÓ ÊÁÔÅÕÈÕÍÓÇÓ ÈÅÌÁ 1ï Óôéò åñùôþóåéò 1 4 íá ãñüøåôå óôï ôåôñüäéü óáò ôïí áñéèìü ôçò åñþôçóçò êáé äßðëá ôï ãñüììá ðïõ áíôéóôïé åß óôç óùóôþ áðüíôçóç. 1.
3524 ÅÖÇÌÅÑÉÓ ÔÇÓ ÊÕÂÅÑÍÇÓÅÙÓ (ÔÅÕ ÏÓ ÄÅÕÔÅÑÏ)
 F ÅÖÇÌÅÑÉÓ ÔÇÓ ÊÕÂÅÑÍÇÓÅÙÓ ÔÇÓ ÅËËÇÍÉÊÇÓ ÄÇÌÏÊÑÁÔÉÁÓ 3523 ÔÅÕ ÏÓ ÄÅÕÔÅÑÏ Áñ. Öýëëïõ 252 28 Öåâñïõáñßïõ 2002 ÁÐÏÖÁÓÅÉÓ Áñéè. 19306/Ã2 ÐñïãñÜììáôá Óðïõäþí Ôå íéêþí Åðáããåëìáôéêþí Åêðáéäåõôçñßùí (Ô.Å.Å.).
F ÅÖÇÌÅÑÉÓ ÔÇÓ ÊÕÂÅÑÍÇÓÅÙÓ ÔÇÓ ÅËËÇÍÉÊÇÓ ÄÇÌÏÊÑÁÔÉÁÓ 3523 ÔÅÕ ÏÓ ÄÅÕÔÅÑÏ Áñ. Öýëëïõ 252 28 Öåâñïõáñßïõ 2002 ÁÐÏÖÁÓÅÉÓ Áñéè. 19306/Ã2 ÐñïãñÜììáôá Óðïõäþí Ôå íéêþí Åðáããåëìáôéêþí Åêðáéäåõôçñßùí (Ô.Å.Å.).
Ανώτερα Μαθηματικά Ι. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 15: Ορισμένο Ολοκλήρωμα Μέρος ΙΙΙ - Εφαρμογές. Αθανάσιος Μπράτσος
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά Ι Ενότητα 5: Ορισμένο Ολοκλήρωμα Μέρος ΙΙΙ - Εφαρμογές Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά Ι Ενότητα 5: Ορισμένο Ολοκλήρωμα Μέρος ΙΙΙ - Εφαρμογές Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο
1.1 Ïé öõóéêïß áñéèìïß - ÄéÜôáîç öõóéêþí, Óôñïããõëïðïßçóç
 1.1 Ïé öõóéêïß áñéèìïß - ÄéÜôáîç öõóéêþí, Óôñïããõëïðïßçóç 7 1.1 Ïé öõóéêïß áñéèìïß - ÄéÜôáîç öõóéêþí, Óôñïããõëïðïßçóç Åñþ ôçóç 1 Ðïéïé áñéèìïß ïíïìüæïíôáé öõóéêïß; Ðþò ôïõò óõìâïëßæïõìå êáé ðþò ùñßæïíôáé;
1.1 Ïé öõóéêïß áñéèìïß - ÄéÜôáîç öõóéêþí, Óôñïããõëïðïßçóç 7 1.1 Ïé öõóéêïß áñéèìïß - ÄéÜôáîç öõóéêþí, Óôñïããõëïðïßçóç Åñþ ôçóç 1 Ðïéïé áñéèìïß ïíïìüæïíôáé öõóéêïß; Ðþò ôïõò óõìâïëßæïõìå êáé ðþò ùñßæïíôáé;
1.1 ÊáñôåóéáíÝò óõíôåôáãìýíåò óôï 3-äéÜóôáôï þñï
 ÊåöÜëáéï 1 ÄÉÁÍÕÓÌÁÔÁ 1.1 ÊáñôåóéáíÝò óõíôåôáãìýíåò óôï 3-äéÜóôáôï þñï óôù ç ôñéüäá (a, b, c). Ôï óýíïëï ôùí ôñéüäùí êáëåßôáé 3-äéÜóôáôïò þñïò êáé óõìâïëßæåôáé ìå IR 3. Åéäéêüôåñá ç ôñéüäá (a, b, c) ïñßæåé
ÊåöÜëáéï 1 ÄÉÁÍÕÓÌÁÔÁ 1.1 ÊáñôåóéáíÝò óõíôåôáãìýíåò óôï 3-äéÜóôáôï þñï óôù ç ôñéüäá (a, b, c). Ôï óýíïëï ôùí ôñéüäùí êáëåßôáé 3-äéÜóôáôïò þñïò êáé óõìâïëßæåôáé ìå IR 3. Åéäéêüôåñá ç ôñéüäá (a, b, c) ïñßæåé
Óåë. 1 ÃÕÌÍÁÓÉÏ ÈÅÌÁÔÁ ÃÑÁÐÔÙÍ ÅÎÅÔÁÓÅÙÍ ÐÅÑÉÏÄÏÕ ÌÁÚÏÕ-ÉÏÕÍÉÏÕ Ó ÏËÉÊÏ ÅÔÏÓ ÔÁÎÇ: Ã ÌÁÈÇÌÁ: ÖÕÓÉÊÇ ÅÉÓÇÃÇÔÇÓ:
 ÃÕÌÍÁÓÉÏ ÈÅÌÁÔÁ ÃÑÁÐÔÙÍ ÅÎÅÔÁÓÅÙÍ ÐÅÑÉÏÄÏÕ ÌÁÚÏÕ-ÉÏÕÍÉÏÕ Ó ÏËÉÊÏ ÅÔÏÓ ÔÁÎÇ: Ã ÌÁÈÇÌÁ: ÖÕÓÉÊÇ ÅÉÓÇÃÇÔÇÓ: Çì/íßá: ÈÅÌÁ 1ï Óõìðëçñþóôå ìå ôç óùóôþ Þ ôéò óùóôýò ðñïôüóåéò ôçí ðáñáêüôù öñüóç: Ç çëåêôñéêþ ðçãþ
ÃÕÌÍÁÓÉÏ ÈÅÌÁÔÁ ÃÑÁÐÔÙÍ ÅÎÅÔÁÓÅÙÍ ÐÅÑÉÏÄÏÕ ÌÁÚÏÕ-ÉÏÕÍÉÏÕ Ó ÏËÉÊÏ ÅÔÏÓ ÔÁÎÇ: Ã ÌÁÈÇÌÁ: ÖÕÓÉÊÇ ÅÉÓÇÃÇÔÇÓ: Çì/íßá: ÈÅÌÁ 1ï Óõìðëçñþóôå ìå ôç óùóôþ Þ ôéò óùóôýò ðñïôüóåéò ôçí ðáñáêüôù öñüóç: Ç çëåêôñéêþ ðçãþ
ΠΕΙΡΑΜΑ ΕΦΕΛΚΥΣΜΟΥ. 2. Βασικοί Ορισμοί. P / A o. Ονομαστική ή Μηχανική Τάση P / A. Πραγματική Τάση. Oνομαστική ή Μηχανική Επιμήκυνση L o
 ΠΕΙΡΑΜΑ ΕΦΕΛΚΥΣΜΟΥ 1. Εισαγωγή Σε ένα πείραμα εφελκυσμού, ένα δοκίμιο μήκους L και εγκάρσιας διατομής A υφίσταται συνεχώς αυξανόμενη μονοαξονική επιμήκυνση [συνήθως χρησιμοποιώντας σταθερή ταχύτητα v (crss-head
ΠΕΙΡΑΜΑ ΕΦΕΛΚΥΣΜΟΥ 1. Εισαγωγή Σε ένα πείραμα εφελκυσμού, ένα δοκίμιο μήκους L και εγκάρσιας διατομής A υφίσταται συνεχώς αυξανόμενη μονοαξονική επιμήκυνση [συνήθως χρησιμοποιώντας σταθερή ταχύτητα v (crss-head
ÐïëëÝò åôáéñßåò ðñïóöýñïõí õðçñåóßåò
 Ferral Ferral Της Πηνελόπης Λεονταρά Σήμανση CE: Πως γίνεται ο έλεγχος της παραγωγικής Ï êáèïñéóìüò ôïõ åëýã ïõ ðáñáãùãþò óå Ýíá êáôáóêåõáóôéêü óýìöùíá ìå ôéò ôå íéêýò ðñïäéáãñáöýò ãéá ôá êïõöþìáôá, óôçí
Ferral Ferral Της Πηνελόπης Λεονταρά Σήμανση CE: Πως γίνεται ο έλεγχος της παραγωγικής Ï êáèïñéóìüò ôïõ åëýã ïõ ðáñáãùãþò óå Ýíá êáôáóêåõáóôéêü óýìöùíá ìå ôéò ôå íéêýò ðñïäéáãñáöýò ãéá ôá êïõöþìáôá, óôçí
ÌÅÑÏÓ 3 ΥΠΗΡΕΣΙΕΣ ΥΠΟΣΤΗΡΙΞΗΣ ΤΗΣ ΚΛΙΝΙΚΗΣ ΠΡΑΞΗΣ ÁÐÁÉÔÇÓÅÙÍ ÕÐÇÑÅÓÉÙÍ. Υπηρεσίες Ιατρικής Πληροφορικής και Τηλεϊατρικής 9 ÂÁÓÉÊÅÓ ÊÁÔÅÕÈÕÍÓÅÉÓ
 138 Υπηρεσίες Ιατρικής Πληροφορικής και Τηλεϊατρικής ÌÅÑÏÓ 3 ΥΠΗΡΕΣΙΕΣ ΥΠΟΣΤΗΡΙΞΗΣ ΤΗΣ ΚΛΙΝΙΚΗΣ ΠΡΑΞΗΣ 9 ÂÁÓÉÊÅÓ ÊÁÔÅÕÈÕÍÓÅÉÓ 10 ÌÏÍÔÅËÏ ÁÐÏÔÉÌÇÓÇÓ ÔÙÍ ÁÐÁÉÔÇÓÅÙÍ 11 ÔÏÌÅÉÓ ÅÖÁÑÌÏÃÇÓ ÔÙÍ ÕÐÇÑÅÓÉÙÍ 139
138 Υπηρεσίες Ιατρικής Πληροφορικής και Τηλεϊατρικής ÌÅÑÏÓ 3 ΥΠΗΡΕΣΙΕΣ ΥΠΟΣΤΗΡΙΞΗΣ ΤΗΣ ΚΛΙΝΙΚΗΣ ΠΡΑΞΗΣ 9 ÂÁÓÉÊÅÓ ÊÁÔÅÕÈÕÍÓÅÉÓ 10 ÌÏÍÔÅËÏ ÁÐÏÔÉÌÇÓÇÓ ÔÙÍ ÁÐÁÉÔÇÓÅÙÍ 11 ÔÏÌÅÉÓ ÅÖÁÑÌÏÃÇÓ ÔÙÍ ÕÐÇÑÅÓÉÙÍ 139
BÜíåò êáé êéíçôþñåò ãéá fan-coils ÊéíçôÞñåò êáé ìéêñýò âüíåò ìå 2.5mm äéáäñïìþ åìâüëïõ
 ÊéíçôÞñåò êáé ìéêñýò âüíåò ìå mm äéáäñïìþ åìâüëïõ ( ) fan-coils êáé æùíþí. ñçóéìïðïéïýíôáé óáí âüíåò äéáíïìþò êáé êüôù áðü ïñéóìýíåò ðñïûðïèýóåéò êáé áíüìåéîçò (ïé ôéìýò óôï Kvs óôï bypass åßíáé 7% ìéêñüôåñåò
ÊéíçôÞñåò êáé ìéêñýò âüíåò ìå mm äéáäñïìþ åìâüëïõ ( ) fan-coils êáé æùíþí. ñçóéìïðïéïýíôáé óáí âüíåò äéáíïìþò êáé êüôù áðü ïñéóìýíåò ðñïûðïèýóåéò êáé áíüìåéîçò (ïé ôéìýò óôï Kvs óôï bypass åßíáé 7% ìéêñüôåñåò
[ ] ÐáñÜñôçìá É : Éóüôñïðåò ôáíõóôéêýò óõíáñôþóåéò 1. Ïñéóìüò: Ï óõììåôñéêüò ôáíõóôþò B êáëåßôáé éóüôñïðç óõíüñôçóç ôïõ óõììåôñéêïý ôáíõóôþ A (Á.
![[ ] ÐáñÜñôçìá É : Éóüôñïðåò ôáíõóôéêýò óõíáñôþóåéò 1. Ïñéóìüò: Ï óõììåôñéêüò ôáíõóôþò B êáëåßôáé éóüôñïðç óõíüñôçóç ôïõ óõììåôñéêïý ôáíõóôþ A (Á. [ ] ÐáñÜñôçìá É : Éóüôñïðåò ôáíõóôéêýò óõíáñôþóåéò 1. Ïñéóìüò: Ï óõììåôñéêüò ôáíõóôþò B êáëåßôáé éóüôñïðç óõíüñôçóç ôïõ óõììåôñéêïý ôáíõóôþ A (Á.](/thumbs/61/46104077.jpg) ÐÁÑÁÑÔÇÌÁÔÁ 76 77 ÐáñÜñôçìá É : Éóüôñïðåò ôáíõóôéêýò óõíáñôþóåéò Ïñéóìüò: Ï óõììåôñéêüò ôáíõóôþò êáëåßôáé éóüôñïðç óõíüñôçóç ôïõ óõììåôñéêïý ôáíõóôþ f( (Á. üôáí ãéá êüèå êáíïíéêü ïñèïãþíéï ôáíõóôþ Q éó
ÐÁÑÁÑÔÇÌÁÔÁ 76 77 ÐáñÜñôçìá É : Éóüôñïðåò ôáíõóôéêýò óõíáñôþóåéò Ïñéóìüò: Ï óõììåôñéêüò ôáíõóôþò êáëåßôáé éóüôñïðç óõíüñôçóç ôïõ óõììåôñéêïý ôáíõóôþ f( (Á. üôáí ãéá êüèå êáíïíéêü ïñèïãþíéï ôáíõóôþ Q éó
ÐÉÍÁÊÅÓ ÔÉÌÙÍ ÁÍÔÉÊÅÉÌÅÍÉÊÙÍ ÁÎÉÙÍ
 ÕÐÏÕÑÃÅÉÏ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ÏÉÊÏÍÏÌÉÊÙÍ ÃÅÍÉÊÇ ÄÉÅÕÈÕÍÓÇ ÄÇÌÏÓÉÁÓ ÐÅÑÉÏÕÓÉÁÓ & ÅÈÍÉÊÙÍ ÊËÇÑÏÄÏÔÇÌÁÔÙÍ ÄÉÅÕÈÕÍÓÇ ÔÅ ÍÉÊÙÍ ÕÐÇÑÅÓÉÙÍ & ÓÔÅÃÁÓÇÓ ÔÌÇÌÁ ÁÍÔÉÊÅÉÌÅÍÉÊÏÕ ÐÑÏÓÄÉÏÑÉÓÌÏÕ ÖÏÑÏËÏÃÇÔÅÁÓ ÁÎÉÁÓ ÁÊÉÍÇÔÙÍ
ÕÐÏÕÑÃÅÉÏ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ÏÉÊÏÍÏÌÉÊÙÍ ÃÅÍÉÊÇ ÄÉÅÕÈÕÍÓÇ ÄÇÌÏÓÉÁÓ ÐÅÑÉÏÕÓÉÁÓ & ÅÈÍÉÊÙÍ ÊËÇÑÏÄÏÔÇÌÁÔÙÍ ÄÉÅÕÈÕÍÓÇ ÔÅ ÍÉÊÙÍ ÕÐÇÑÅÓÉÙÍ & ÓÔÅÃÁÓÇÓ ÔÌÇÌÁ ÁÍÔÉÊÅÉÌÅÍÉÊÏÕ ÐÑÏÓÄÉÏÑÉÓÌÏÕ ÖÏÑÏËÏÃÇÔÅÁÓ ÁÎÉÁÓ ÁÊÉÍÇÔÙÍ
Εφαρμοσμένα Μαθηματικά
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Εφαρμοσμένα Μαθηματικά Ενότητα 11: Προσέγγιση μερικών διαφορικών εξισώσεων - Παραβολικές Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Εφαρμοσμένα Μαθηματικά Ενότητα 11: Προσέγγιση μερικών διαφορικών εξισώσεων - Παραβολικές Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ
ÐÏËËÁÐËÁ ÏËÏÊËÇÑÙÌÁÔÁ
 ÌÜèçìá 9 ÐÏËËÁÐËÁ ÏËÏÊËÇÑÙÌÁÔÁ 9. ÄéðëÜ ïëïêëçñþìáôá 9.. ÅéóáãùãÞ Ãéá ôçí êáëýôåñç êáôáíüçóç ôïõ ïñéóìýíïõ ïëïêëçñþìáôïò ìéáò óõíüñôçóçò äýï ìåôáâëçôþí, äçëáäþ ôïõ äéðëïý ïëïêëçñþìáôïò, êñßíåôáé áðáñáßôçôï
ÌÜèçìá 9 ÐÏËËÁÐËÁ ÏËÏÊËÇÑÙÌÁÔÁ 9. ÄéðëÜ ïëïêëçñþìáôá 9.. ÅéóáãùãÞ Ãéá ôçí êáëýôåñç êáôáíüçóç ôïõ ïñéóìýíïõ ïëïêëçñþìáôïò ìéáò óõíüñôçóçò äýï ìåôáâëçôþí, äçëáäþ ôïõ äéðëïý ïëïêëçñþìáôïò, êñßíåôáé áðáñáßôçôï
ÃÕÌÍÁÓÉÏ ÈÅÌÁÔÁ ÃÑÁÐÔÙÍ ÅÎÅÔÁÓÅÙÍ ÐÅÑÉÏÄÏÕ ÉÏÕÍÉÏÕ Ó ÏËÉÊÏ ÅÔÏÓ ÔÁÎÇ: Ã ÌÁÈÇÌÁ: ÖÕÓÉÊÇ ÅÉÓÇÃÇÔÇÓ:
 ÃÕÌÍÁÓÉÏ ÈÅÌÁÔÁ ÃÑÁÐÔÙÍ ÅÎÅÔÁÓÅÙÍ ÐÅÑÉÏÄÏÕ ÉÏÕÍÉÏÕ Ó ÏËÉÊÏ ÅÔÏÓ ÔÁÎÇ: Ã ÌÁÈÇÌÁ: ÖÕÓÉÊÇ ÅÉÓÇÃÇÔÇÓ: Çì/íßá: ÈÅÌÁ 1ï Ðïéåò áðü ôéò ðáñáêüôù ðñïôüóåéò åßíáé óùóôýò êáé ðïéåò ëüèïò; a. Óôçí çëýêôñéóç ìå ôñéâþ
ÃÕÌÍÁÓÉÏ ÈÅÌÁÔÁ ÃÑÁÐÔÙÍ ÅÎÅÔÁÓÅÙÍ ÐÅÑÉÏÄÏÕ ÉÏÕÍÉÏÕ Ó ÏËÉÊÏ ÅÔÏÓ ÔÁÎÇ: Ã ÌÁÈÇÌÁ: ÖÕÓÉÊÇ ÅÉÓÇÃÇÔÇÓ: Çì/íßá: ÈÅÌÁ 1ï Ðïéåò áðü ôéò ðáñáêüôù ðñïôüóåéò åßíáé óùóôýò êáé ðïéåò ëüèïò; a. Óôçí çëýêôñéóç ìå ôñéâþ
ÄÉÁÍÕÓÌÁÔÉÊÅÓ ÓÕÍÁÑÔÇÓÅÉÓ
 ÌÜèçìá 17 ÄÉÁÍÕÓÌÁÔÉÊÅÓ ÓÕÍÁÑÔÇÓÅÉÓ 17.1 ÅéóáãùãéêÝò Ýííïéåò 17.1.1 Ïñéóìüò äéáíõóìáôéêþò óõíüñôçóçò 1 Õðåíèõìßæåôáé ï ïñéóìüò ôçò ðñáãìáôéêþò óõíüñôçóçò ìéáò ðñáãìáôéêþò ìåôáâëçôþò, ðïõ ãéá åõêïëßá óôç
ÌÜèçìá 17 ÄÉÁÍÕÓÌÁÔÉÊÅÓ ÓÕÍÁÑÔÇÓÅÉÓ 17.1 ÅéóáãùãéêÝò Ýííïéåò 17.1.1 Ïñéóìüò äéáíõóìáôéêþò óõíüñôçóçò 1 Õðåíèõìßæåôáé ï ïñéóìüò ôçò ðñáãìáôéêþò óõíüñôçóçò ìéáò ðñáãìáôéêþò ìåôáâëçôþò, ðïõ ãéá åõêïëßá óôç
ATHINA COURT. ÐïëõôåëÞ Äéáìåñßóìáôá
 ATHINA COURT ÐïëõôåëÞ Äéáìåñßóìáôá ΣΥΓΚΡΟΤΗΜΑ ΙΑΜΕΡΙΣΜΑΤΩΝ ΑΘΗΝΑ Το συγκρότημα διαμερισμάτων AΘΗΝΑ βρίσκεται σε μια ήσυχη περιοχή στην Έγκωμη, Γωνία Γρηγόρη Αυξεντίου & Αρχιεπισκόπου Λεοντίου και αποτελείται
ATHINA COURT ÐïëõôåëÞ Äéáìåñßóìáôá ΣΥΓΚΡΟΤΗΜΑ ΙΑΜΕΡΙΣΜΑΤΩΝ ΑΘΗΝΑ Το συγκρότημα διαμερισμάτων AΘΗΝΑ βρίσκεται σε μια ήσυχη περιοχή στην Έγκωμη, Γωνία Γρηγόρη Αυξεντίου & Αρχιεπισκόπου Λεοντίου και αποτελείται
Üóêçóç 23. ëåã ïò Èåñìïêñáóßáò þñïõ ìå ÅëåãêôÞ äýï ÈÝóåùí
 ëåã ïò Èåñìïêñáóßáò þñïõ ìå ÅëåãêôÞ äýï ÈÝóåùí Óôü ïé ôçò Üóêçóçò äéüñêåéá Üóêçóçò: 12 äéäáêôéêýò þñåò Óôï ôýëïò ôçò Üóêçóçò ïé ìáèçôýò èá åßíáé éêáíïß: é íá ãíùñßæïõí êáé åîçãïýí ôç ëåéôïõñãßá ôïõ åëåãêôþ
ëåã ïò Èåñìïêñáóßáò þñïõ ìå ÅëåãêôÞ äýï ÈÝóåùí Óôü ïé ôçò Üóêçóçò äéüñêåéá Üóêçóçò: 12 äéäáêôéêýò þñåò Óôï ôýëïò ôçò Üóêçóçò ïé ìáèçôýò èá åßíáé éêáíïß: é íá ãíùñßæïõí êáé åîçãïýí ôç ëåéôïõñãßá ôïõ åëåãêôþ
Εφαρμοσμένα Μαθηματικά
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Εφαρμοσμένα Μαθηματικά Ενότητα 6: Προσέγγιση παραγώγων Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος διατίθεται
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Εφαρμοσμένα Μαθηματικά Ενότητα 6: Προσέγγιση παραγώγων Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος διατίθεται
Üóêçóç 21. ÌåëÝôç ÅëåãêôÞ ÑI
 ÌåëÝôç ÅëåãêôÞ ÑI Óôü ïé ôçò Üóêçóçò äéüñêåéá Üóêçóçò: 12 äéäáêôéêýò þñåò Óôï ôýëïò ôçò Üóêçóçò ïé ìáèçôýò èá åßíáé éêáíïß: é íá ãíùñßæïõí ôç ëåéôïõñãßá ôïõ êéíçôþñá óõíå ïýò ñåýìáôïò: 1. íá õðïëïãßæïõí
ÌåëÝôç ÅëåãêôÞ ÑI Óôü ïé ôçò Üóêçóçò äéüñêåéá Üóêçóçò: 12 äéäáêôéêýò þñåò Óôï ôýëïò ôçò Üóêçóçò ïé ìáèçôýò èá åßíáé éêáíïß: é íá ãíùñßæïõí ôç ëåéôïõñãßá ôïõ êéíçôþñá óõíå ïýò ñåýìáôïò: 1. íá õðïëïãßæïõí
Ç íýá Ýííïéá ôïõ ýðíïõ!
 ΑΞΕΣΟΥΑΡ Ç íýá Ýííïéá ôïõ ýðíïõ! ÅããõÜôáé ôçí áóöüëåéá êáé õãåßá ôïõ ìùñïý êáôü ôç äéüñêåéá ôïõ ýðíïõ! AP 1270638 Õðüóôñùìá Aerosleep, : 61,00 AP 125060 ÊÜëõììá Aerosleep, : 15,30 ÁóöáëÞò, ðüíôá áñêåôüò
ΑΞΕΣΟΥΑΡ Ç íýá Ýííïéá ôïõ ýðíïõ! ÅããõÜôáé ôçí áóöüëåéá êáé õãåßá ôïõ ìùñïý êáôü ôç äéüñêåéá ôïõ ýðíïõ! AP 1270638 Õðüóôñùìá Aerosleep, : 61,00 AP 125060 ÊÜëõììá Aerosleep, : 15,30 ÁóöáëÞò, ðüíôá áñêåôüò
4. ÁíÜðôõîç ðñïãñüììáôïò óå ðñïãñáììáôéæüìåíï ëïãéêü åëåãêôþ.
 Ðñïãñáììáôéæüìåíïé Ëïãéêïß ÅëåãêôÝò (PLC) 4. ÁíÜðôõîç ðñïãñüììáôïò óå ðñïãñáììáôéæüìåíï ëïãéêü åëåãêôþ. 4. ÃåíéêÜ. Óôéò åíüôçôåò ðïõ áêïëïõèïýí èá äïýìå, ðùò ðñïãñáììáôßæïõìå Ýíá PLC. Ãéá ôéò áðáéôþóåéò
Ðñïãñáììáôéæüìåíïé Ëïãéêïß ÅëåãêôÝò (PLC) 4. ÁíÜðôõîç ðñïãñüììáôïò óå ðñïãñáììáôéæüìåíï ëïãéêü åëåãêôþ. 4. ÃåíéêÜ. Óôéò åíüôçôåò ðïõ áêïëïõèïýí èá äïýìå, ðùò ðñïãñáììáôßæïõìå Ýíá PLC. Ãéá ôéò áðáéôþóåéò
Ανώτερα Μαθηματικά Ι. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 12: Αόριστο Ολοκλήρωμα. Αθανάσιος Μπράτσος. Τμήμα Ναυπηγών Μηχανικών ΤΕ
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά Ι Ενότητα : Αόριστο Ολοκλήρωμα Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος διατίθεται
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά Ι Ενότητα : Αόριστο Ολοκλήρωμα Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος διατίθεται
Μαθηματικά ΙΙΙ. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 16: Προσέγγιση συνήθων διαφορικών εξισώσεων Μέρος ΙΙ. Αθανάσιος Μπράτσος
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 16: Προσέγγιση συνήθων διαφορικών εξισώσεων Μέρος ΙΙ Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 16: Προσέγγιση συνήθων διαφορικών εξισώσεων Μέρος ΙΙ Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας
1ï ÊñéôÞñéï Áîéïëüãçóçò
 1ï ÊñéôÞñéï Áîéïëüãçóçò óå üëç ôçí ýëç ÖõóéêÞò. à ôüîç ÊáèçãçôÞò: ¼íïìá: Âáèìüò: ÈÅÌÁ 1ï Åéê. 1 A. -2ìC ç Á êáé +2ìC ç  -1ìC ç Á êáé -1ìC ç  -9ìC ç Á êáé -9ìC ç  D. +1ìC ç Á êáé +1ìC ç  ÅðéëÝîôå ôç
1ï ÊñéôÞñéï Áîéïëüãçóçò óå üëç ôçí ýëç ÖõóéêÞò. à ôüîç ÊáèçãçôÞò: ¼íïìá: Âáèìüò: ÈÅÌÁ 1ï Åéê. 1 A. -2ìC ç Á êáé +2ìC ç  -1ìC ç Á êáé -1ìC ç  -9ìC ç Á êáé -9ìC ç  D. +1ìC ç Á êáé +1ìC ç  ÅðéëÝîôå ôç
ÏñãÜíùóç ÐñïãñÜììáôïò
 ÊåöÜëáéï 4 ÏñãÜíùóç ÐñïãñÜììáôïò Åðéäéùêüìåíïé óôü ïé: ¼ôáí ïëïêëçñþóåôå ôç ìåëýôç áõôïý ôïõ êåöáëáßïõ, èá åßóôå éêáíïß: é íá ðåñéãñüöåôå ôéò åíôïëýò ðïõ ñçóéìïðïéïýíôáé óôá õðïðñïãñüììáôá êáé óôï êýñéï
ÊåöÜëáéï 4 ÏñãÜíùóç ÐñïãñÜììáôïò Åðéäéùêüìåíïé óôü ïé: ¼ôáí ïëïêëçñþóåôå ôç ìåëýôç áõôïý ôïõ êåöáëáßïõ, èá åßóôå éêáíïß: é íá ðåñéãñüöåôå ôéò åíôïëýò ðïõ ñçóéìïðïéïýíôáé óôá õðïðñïãñüììáôá êáé óôï êýñéï
HVAC Products. Äéáêüðôçò 3 ôá õôþôùí On-off åëåãêôþò ðïéüôçôáò áýñá ÈåñìïóôÜôåò ãéá fan-coils
 2 HVAC Products Äéáêüðôçò 3 ôá õôþôùí On-off åëåãêôþò ðïéüôçôáò áýñá ÈåñìïóôÜôåò ãéá fan-coils Åðßôïé ïò äéáêüðôçò 3 ôá õôþôùí Åðßôïé ïò äéáêüðôçò 3 ôá õôþôùí ìå åðéëïãýá off I-II-III RAB90 1(40) 15,18
2 HVAC Products Äéáêüðôçò 3 ôá õôþôùí On-off åëåãêôþò ðïéüôçôáò áýñá ÈåñìïóôÜôåò ãéá fan-coils Åðßôïé ïò äéáêüðôçò 3 ôá õôþôùí Åðßôïé ïò äéáêüðôçò 3 ôá õôþôùí ìå åðéëïãýá off I-II-III RAB90 1(40) 15,18
ÐÑÏÓÅÃÃÉÓÇ ÐÁÑÁÃÙÃÙÍ
 ÌÜèçìá 6 ÐÑÏÓÅÃÃÉÓÇ ÐÁÑÁÃÙÃÙÍ Ç ðñïóýããéóç ôçò ôéìþò ôçò ðáñáãþãïõ ìéáò óõíüñôçóçò ñçóéìïðïéåßôáé óôéò ðáñáêüôù êõñßùò ðåñéðôþóåéò: i) üôáí ëüãù ôçò ðïëýðëïêçò ìïñöþò ôïõ ôýðïõ ìéáò óõíüñôçóçò åßíáé áäýíáôïò
ÌÜèçìá 6 ÐÑÏÓÅÃÃÉÓÇ ÐÁÑÁÃÙÃÙÍ Ç ðñïóýããéóç ôçò ôéìþò ôçò ðáñáãþãïõ ìéáò óõíüñôçóçò ñçóéìïðïéåßôáé óôéò ðáñáêüôù êõñßùò ðåñéðôþóåéò: i) üôáí ëüãù ôçò ðïëýðëïêçò ìïñöþò ôïõ ôýðïõ ìéáò óõíüñôçóçò åßíáé áäýíáôïò
ÄÉÁÍÕÓÌÁÔÉÊÅÓ ÓÕÍÁÑÔÇÓÅÉÓ
 30 ÊåöÜëáéï 2 ÄÉÁÍÕÓÌÁÔÉÊÅÓ ÓÕÍÁÑÔÇÓÅÉÓ 2.1 ÅéóáãùãÞ ¼ðùò êáé óôïí IR 2, Ýôóé êáé óôïí IR 3 ìðïñïýìå íá ïñßóïõìå ìéá êáìðýëç ðáñáìåôñéêü. ÄçëáäÞ, íá Ý åé ôç ìïñöþ x = x(t), y = y(t), z = z(t), üðïõ t åßíáé
30 ÊåöÜëáéï 2 ÄÉÁÍÕÓÌÁÔÉÊÅÓ ÓÕÍÁÑÔÇÓÅÉÓ 2.1 ÅéóáãùãÞ ¼ðùò êáé óôïí IR 2, Ýôóé êáé óôïí IR 3 ìðïñïýìå íá ïñßóïõìå ìéá êáìðýëç ðáñáìåôñéêü. ÄçëáäÞ, íá Ý åé ôç ìïñöþ x = x(t), y = y(t), z = z(t), üðïõ t åßíáé
ÁðáñéèìçôÝò- ÓõãêñéôÝò
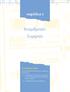 ÊåöÜëáéï 5 ÁðáñéèìçôÝò- ÓõãêñéôÝò Åðéäéùêüìåíïé óôü ïé: ¼ôáí ïëïêëçñþóåôå ôç ìåëýôç áõôïý ôïõ êåöáëáßïõ, èá åßóôå éêáíïß: é íá ðåñéãñüöåôå ôéò åíôïëýò ðïõ ñçóéìïðïéïýíôáé ãéá ôïí ðñïãñáììáôéóìü ôùí áðáñéèìçôþí
ÊåöÜëáéï 5 ÁðáñéèìçôÝò- ÓõãêñéôÝò Åðéäéùêüìåíïé óôü ïé: ¼ôáí ïëïêëçñþóåôå ôç ìåëýôç áõôïý ôïõ êåöáëáßïõ, èá åßóôå éêáíïß: é íá ðåñéãñüöåôå ôéò åíôïëýò ðïõ ñçóéìïðïéïýíôáé ãéá ôïí ðñïãñáììáôéóìü ôùí áðáñéèìçôþí
ÊåöÜëáéï 7. ÁíáëïãéêÝò Ýîïäïé. Åðéäéùêüìåíïé óôü ïé:
 ÊåöÜëáéï 7 ÁíáëïãéêÝò Ýîïäïé Åðéäéùêüìåíïé óôü ïé: ¼ôáí ïëïêëçñþóåôå ôç ìåëýôç áõôïý ôïõ êåöáëáßïõ, èá åßóôå éêáíïß: é íá ðåñéãñüöåôå ôá áñáêôçñéóôéêü ôùí äéáôüîåùí ðïõ ìåôáôñýðïõí ôá øçöéáêü óþìáôá óå
ÊåöÜëáéï 7 ÁíáëïãéêÝò Ýîïäïé Åðéäéùêüìåíïé óôü ïé: ¼ôáí ïëïêëçñþóåôå ôç ìåëýôç áõôïý ôïõ êåöáëáßïõ, èá åßóôå éêáíïß: é íá ðåñéãñüöåôå ôá áñáêôçñéóôéêü ôùí äéáôüîåùí ðïõ ìåôáôñýðïõí ôá øçöéáêü óþìáôá óå
ÐÏËÕÙÍÕÌÉÊÇ ÐÁÑÅÌÂÏËÇ
 ÌÜèçìá 3 ÐÏËÕÙÍÕÌÉÊÇ ÐÁÑÅÌÂÏËÇ 3.1 ÅéóáãùãÞ Åßíáé ãíùóôü üôé óôá äéüöïñá ðñïâëþìáôá ôùí åöáñìïãþí ôéò ðåñéóóüôåñåò öïñýò ðáñïõóéüæïíôáé óõíáñôþóåéò ðïõ ðåñéãñüöïíôáé áðü ðïëýðëïêïõò ôýðïõò, äçëáäþ ôýðïõò
ÌÜèçìá 3 ÐÏËÕÙÍÕÌÉÊÇ ÐÁÑÅÌÂÏËÇ 3.1 ÅéóáãùãÞ Åßíáé ãíùóôü üôé óôá äéüöïñá ðñïâëþìáôá ôùí åöáñìïãþí ôéò ðåñéóóüôåñåò öïñýò ðáñïõóéüæïíôáé óõíáñôþóåéò ðïõ ðåñéãñüöïíôáé áðü ðïëýðëïêïõò ôýðïõò, äçëáäþ ôýðïõò
ÌÁÈÇÌÁÔÉÊÇ ËÏÃÉÊÇ Ë1 5ï ðáêýôï áóêþóåùí
 ÌÁÈÇÌÁÔÉÊÇ ËÏÃÉÊÇ Ë1 5ï ðáêýôï áóêþóåùí ñþóôïò ÊïíáîÞò, A.M. 200416 ìðë 30-06-2005 óêçóç 1. óôù R N n ; n 1. ËÝìå üôé ç R åßíáé "áñéèìçôéêþ" áí õðüñ åé ôýðïò ö(x 1 ; : : : ; x n ) ôçò Ã1 èá ôýôïéïò ðïõ
ÌÁÈÇÌÁÔÉÊÇ ËÏÃÉÊÇ Ë1 5ï ðáêýôï áóêþóåùí ñþóôïò ÊïíáîÞò, A.M. 200416 ìðë 30-06-2005 óêçóç 1. óôù R N n ; n 1. ËÝìå üôé ç R åßíáé "áñéèìçôéêþ" áí õðüñ åé ôýðïò ö(x 1 ; : : : ; x n ) ôçò Ã1 èá ôýôïéïò ðïõ
ÓÅÉÑÅÓ TAYLOR ÊÁÉ LAURENT
 ÊåöÜëáéï 7 ÓÅÉÑÅÓ TAYLOR ÊÁÉ LAURENT 7. Áêïëïõèßåò ¼ðùò êáé ãéá ôïõò ðñáãìáôéêïýò áñéèìïýò, ìéá (Üðåéñç) áêïëïõèßá ìðïñåß íá èåùñçèåß ùò óõíüñôçóç ìå ðåäßï ïñéóìïý ôïõò èåôéêïýò áêýñáéïõò. ÄçëáäÞ, ìéá
ÊåöÜëáéï 7 ÓÅÉÑÅÓ TAYLOR ÊÁÉ LAURENT 7. Áêïëïõèßåò ¼ðùò êáé ãéá ôïõò ðñáãìáôéêïýò áñéèìïýò, ìéá (Üðåéñç) áêïëïõèßá ìðïñåß íá èåùñçèåß ùò óõíüñôçóç ìå ðåäßï ïñéóìïý ôïõò èåôéêïýò áêýñáéïõò. ÄçëáäÞ, ìéá
Cel animation. ÅöáñìïãÝò ðïëõìýóùí
 ÅöáñìïãÝò ðïëõìýóùí Cel animation Ç ôå íéêþ áõôþ óõíßóôáôáé óôçí êáôáóêåõþ ðïëëþí ó åäßùí ðïõ äéáöýñïõí ìåôáîý ôïõò óå óõãêåêñéìýíá óçìåßá. Ôá ó Ýäéá áõôü åíáëëüóóïíôáé ôï Ýíá ìåôü ôï Üëëï äßíïíôáò ôçí
ÅöáñìïãÝò ðïëõìýóùí Cel animation Ç ôå íéêþ áõôþ óõíßóôáôáé óôçí êáôáóêåõþ ðïëëþí ó åäßùí ðïõ äéáöýñïõí ìåôáîý ôïõò óå óõãêåêñéìýíá óçìåßá. Ôá ó Ýäéá áõôü åíáëëüóóïíôáé ôï Ýíá ìåôü ôï Üëëï äßíïíôáò ôçí
ÊÅÖÁËÁÉÏ 11 ÁÍÔÉÓÔÁÈÌÉÓÇ ÔÏÕ ÓÕÍÔÅËÅÓÔÇ ÉÓ ÕÏÓ R S T C C M 3~ C
 ÊÅÖÁËÁÉÏ 11 ÁÍÔÉÓÔÁÈÌÉÓÇ ÔÏÕ ÓÕÍÔÅËÅÓÔÇ ÉÓ ÕÏÓ R S T M 3~ ÁÍÁËÕÓÇ ÇËÅÊÔÑÉÊÙÍ ÊÕÊËÙÌÁÔÙÍ 11.1. ÅÐÉÐÔÙÓÅÉÓ ÁÌÇËÏÕ ÓÕÍÔÅËÅÓÔÇ ÉÓ ÕÏÓ Ï óõíôåëåóôþò éó ýïò óõí ö åßíáé ï ëüãïò ôçò ðñáãìáôéêþò éó ýïò P ðñïò
ÊÅÖÁËÁÉÏ 11 ÁÍÔÉÓÔÁÈÌÉÓÇ ÔÏÕ ÓÕÍÔÅËÅÓÔÇ ÉÓ ÕÏÓ R S T M 3~ ÁÍÁËÕÓÇ ÇËÅÊÔÑÉÊÙÍ ÊÕÊËÙÌÁÔÙÍ 11.1. ÅÐÉÐÔÙÓÅÉÓ ÁÌÇËÏÕ ÓÕÍÔÅËÅÓÔÇ ÉÓ ÕÏÓ Ï óõíôåëåóôþò éó ýïò óõí ö åßíáé ï ëüãïò ôçò ðñáãìáôéêþò éó ýïò P ðñïò
ÁÏÑÉÓÔÏ ÏËÏÊËÇÑÙÌÁ. ÌÜèçìá ÅéóáãùãéêÝò Ýííïéåò ÐáñÜãïõóá óõíüñôçóç
 ÌÜèçìá 0 ÁÏÑÉÓÔÏ ÏËÏÊËÇÑÙÌÁ 0. ÅéóáãùãéêÝò Ýííïéåò Óôï ìüèçìá áõôü èá äïèïýí ïé êõñéüôåñïé êáíüíåò ïëïêëþñùóçò, ðïõ êýñéá åìöáíßæïíôáé óôéò ôå íïëïãéêýò åöáñìïãýò. Äéåõêñéíßæåôáé üôé áêïëïõèþíôáò ìßá áõóôçñü
ÌÜèçìá 0 ÁÏÑÉÓÔÏ ÏËÏÊËÇÑÙÌÁ 0. ÅéóáãùãéêÝò Ýííïéåò Óôï ìüèçìá áõôü èá äïèïýí ïé êõñéüôåñïé êáíüíåò ïëïêëþñùóçò, ðïõ êýñéá åìöáíßæïíôáé óôéò ôå íïëïãéêýò åöáñìïãýò. Äéåõêñéíßæåôáé üôé áêïëïõèþíôáò ìßá áõóôçñü
> ÁíáãåíÝò óôüäéï (ðïëý ìåãüëç äéüñêåéá) Ôï áíáãåíýò åßíáé ôï óôüäéï ôçò áíüðôõîçò. Ç ôñß á áñ ßæåé íá ãåííéýôáé êáé ðïëý ãñþãïñá ðáßñíåé ôçí ïëïêëçñù
 ÊåöÜëáéï 5.2 ÓôÜäéá áíüðôõîçò ôçò ôñß áò Óêïðüò ôïõ êåöáëáßïõ áõôïý åßíáé ïé ìáèçôýò/ ôñéåò íá ãíùñßóïõí ôá óôüäéá áíüðôõîçò ôçò ôñß áò. > ÅéóáãùãÞ Ïé ôñß åò óå üðïéïí ôýðï ôñé þìáôïò êáé áí áíþêïõí (
ÊåöÜëáéï 5.2 ÓôÜäéá áíüðôõîçò ôçò ôñß áò Óêïðüò ôïõ êåöáëáßïõ áõôïý åßíáé ïé ìáèçôýò/ ôñéåò íá ãíùñßóïõí ôá óôüäéá áíüðôõîçò ôçò ôñß áò. > ÅéóáãùãÞ Ïé ôñß åò óå üðïéïí ôýðï ôñé þìáôïò êáé áí áíþêïõí (
J-Y(St)Y Ôçëåöùíéêü êáëþäéï åóùôåñéêïý þñïõ ìå èùñüêéóç êáôü VDE 0815
 J-Y(St)Y Ôçëåöùíéêü êáëþäéï åóùôåñéêïý þñïõ ìå èùñüêéóç êáôü VDE 0815 ÅÖÁÑÌÏÃÇ ñçóéìïðïéïýíôáé óå ìüíéìåò åãêáôáóôüóåéò ãéá ôç ìåôüäïóç áíáëïãéêïý Þ øçöéáêïý óþìáôïò. Ôï ðåäßï åöáñìïãþí ôïõò ðåñéëáìâüíåé
J-Y(St)Y Ôçëåöùíéêü êáëþäéï åóùôåñéêïý þñïõ ìå èùñüêéóç êáôü VDE 0815 ÅÖÁÑÌÏÃÇ ñçóéìïðïéïýíôáé óå ìüíéìåò åãêáôáóôüóåéò ãéá ôç ìåôüäïóç áíáëïãéêïý Þ øçöéáêïý óþìáôïò. Ôï ðåäßï åöáñìïãþí ôïõò ðåñéëáìâüíåé
Åîéóþóåéò 1ïõ âáèìïý
 algevra-a-lykeiou-kef-07-08.qxd 9/8/00 9:00 Page 00 7 Åîéóþóåéò ïõ âáèìïý Ç åîßóùóç áx + â = 0 áx = â (ìå á 0) (ìå á = â = 0) â Ý åé áêñéâþò ìßá ëýóç, ôç x =. á áëçèåýåé ãéá êüèå ðñáãìáôéêü áñéèìü x (ôáõôüôçôá
algevra-a-lykeiou-kef-07-08.qxd 9/8/00 9:00 Page 00 7 Åîéóþóåéò ïõ âáèìïý Ç åîßóùóç áx + â = 0 áx = â (ìå á 0) (ìå á = â = 0) â Ý åé áêñéâþò ìßá ëýóç, ôç x =. á áëçèåýåé ãéá êüèå ðñáãìáôéêü áñéèìü x (ôáõôüôçôá
V 1 V 2 = P 2 , V 2
 55. 4.3 Íüìïé ôùí áåñßùí Áðáñáßôçôåò ãíþóåéò Èåùñßáò ¼ëåò ïé ïõóßåò óôçí áýñéá öõóéêþ êáôüóôáóç óõìðåñéöýñïíô áé ìå ôïí ßäéï ôñüðï êáé éäéáßôåñá üóïí áöïñü ôçí óõìðåñéöïñü ôïõò óôéò ìåôáâïëýò ôçò ðßåóçò,
55. 4.3 Íüìïé ôùí áåñßùí Áðáñáßôçôåò ãíþóåéò Èåùñßáò ¼ëåò ïé ïõóßåò óôçí áýñéá öõóéêþ êáôüóôáóç óõìðåñéöýñïíô áé ìå ôïí ßäéï ôñüðï êáé éäéáßôåñá üóïí áöïñü ôçí óõìðåñéöïñü ôïõò óôéò ìåôáâïëýò ôçò ðßåóçò,
ÌÉÃÁÄÉÊÅÓ ÓÕÍÁÑÔÇÓÅÉÓ
 ÌÜèçìá 5 ÌÉÃÁÄÉÊÅÓ ÓÕÍÁÑÔÇÓÅÉÓ 5.1 ÅéóáãùãÞ Óôï ìüèçìá áõôü èá äïèïýí ïé âáóéêüôåñåò Ýííïéåò ôùí ìéãáäéêþí óõíáñôþóåùí. Ï áíáãíþóôçò, ãéá ìéá åêôåíýóôåñç ìåëýôç, ðáñáðýìðåôáé óôç âéâëéïãñáößá ôïõ ìáèþìáôïò
ÌÜèçìá 5 ÌÉÃÁÄÉÊÅÓ ÓÕÍÁÑÔÇÓÅÉÓ 5.1 ÅéóáãùãÞ Óôï ìüèçìá áõôü èá äïèïýí ïé âáóéêüôåñåò Ýííïéåò ôùí ìéãáäéêþí óõíáñôþóåùí. Ï áíáãíþóôçò, ãéá ìéá åêôåíýóôåñç ìåëýôç, ðáñáðýìðåôáé óôç âéâëéïãñáößá ôïõ ìáèþìáôïò
Ανώτερα Μαθηματικά Ι. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 6: Γραμμική Άλγεβρα. Αθανάσιος Μπράτσος. Τμήμα Ναυπηγών Μηχανικών ΤΕ
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά Ι Ενότητα 6: Γραμμική Άλγεβρα Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος διατίθεται
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά Ι Ενότητα 6: Γραμμική Άλγεβρα Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος διατίθεται
ÊåöÜëáéï 6. ÁíáëïãéêÝò åßóïäïé. Åðéäéùêüìåíïé óôü ïé:
 ÊåöÜëáéï 6 ÁíáëïãéêÝò åßóïäïé Åðéäéùêüìåíïé óôü ïé: ¼ôáí ïëïêëçñþóåôå ôç ìåëýôç áõôïý ôïõ êåöáëáßïõ, èá åßóôå éêáíïß: é íá ðåñéãñüöåôå ôá áñáêôçñéóôéêü ôùí äéáôüîåùí ðïõ ìåôáôñýðïõí áíáëïãéêü ìåãýèç óå
ÊåöÜëáéï 6 ÁíáëïãéêÝò åßóïäïé Åðéäéùêüìåíïé óôü ïé: ¼ôáí ïëïêëçñþóåôå ôç ìåëýôç áõôïý ôïõ êåöáëáßïõ, èá åßóôå éêáíïß: é íá ðåñéãñüöåôå ôá áñáêôçñéóôéêü ôùí äéáôüîåùí ðïõ ìåôáôñýðïõí áíáëïãéêü ìåãýèç óå
ÓÅÉÑÅÓ. ÌÜèçìá Áêïëïõèßåò áñéèìþí Ïñéóìüò áêïëïõèßáò
 ÌÜèçìá 2 ÓÅÉÑÅÓ 2. Áêïëïõèßåò áñéèìþí Êñßíåôáé óêüðéìï íá äïèåß ðåñéëçðôéêü ðñéí áðü ôç ìåëýôç ôùí óåéñþí ç Ýííïéá ôçò áêïëïõèßáò áñéèìþí. Ï áíáãíþóôçò, ãéá ìéá åêôåíýóôåñç ìåëýôç, ðáñáðýìðåôáé óôç âéâëéïãñáößá
ÌÜèçìá 2 ÓÅÉÑÅÓ 2. Áêïëïõèßåò áñéèìþí Êñßíåôáé óêüðéìï íá äïèåß ðåñéëçðôéêü ðñéí áðü ôç ìåëýôç ôùí óåéñþí ç Ýííïéá ôçò áêïëïõèßáò áñéèìþí. Ï áíáãíþóôçò, ãéá ìéá åêôåíýóôåñç ìåëýôç, ðáñáðýìðåôáé óôç âéâëéïãñáößá
Üóêçóç 9. Ðñïãñáììáôéóìüò ìåôñçôþí êáé óõíäõáóìüò ìåôñçôþ-óõãêñéôþí
 Ðñïãñáììáôéóìüò ìåôñçôþí êáé óõíäõáóìüò ìåôñçôþ-óõãêñéôþí Óôü ïé ôçò Üóêçóçò äéüñêåéá Üóêçóçò: 6 äéäáêôéêýò þñåò Óôï ôýëïò ôçò Üóêçóçò ïé ìáèçôýò èá åßíáé éêáíïß: é íá åðéëýãïõí ôá êáôüëëçëá üñãáíá êáé
Ðñïãñáììáôéóìüò ìåôñçôþí êáé óõíäõáóìüò ìåôñçôþ-óõãêñéôþí Óôü ïé ôçò Üóêçóçò äéüñêåéá Üóêçóçò: 6 äéäáêôéêýò þñåò Óôï ôýëïò ôçò Üóêçóçò ïé ìáèçôýò èá åßíáé éêáíïß: é íá åðéëýãïõí ôá êáôüëëçëá üñãáíá êáé
ÅÑÙÔÇÓÅÉÓ. Åõèýãñáììç êßíçóç. ôçò ìåôáôüðéóþò ôïõ êáé íá âñåßôå ôçí ôéìþ ôçò. Ðüóï åßíáé ôï äéüóôçìá ðïõ äéüíõóå ôï êéíçôü óôç äéáäñïìþ áõôþ;
 63 63 ÅÑÙÔÇÓÅÉÓ 1. Íá áíáöýñåôå ðïéá áðü ôá óþìáôá ðïõ öáßíïíôáé óôçí åéêüíá êéíïýíôáé A. Ùò ðñïò ôç Ãç B. Ùò ðñïò ôï áõôïêßíçôï. 5. íá êéíçôü ìåôáôïðßæåôáé áðü ôç èýóç Ì 1 óôç èýóç Ì 2. Íá ó åäéüóåôå
63 63 ÅÑÙÔÇÓÅÉÓ 1. Íá áíáöýñåôå ðïéá áðü ôá óþìáôá ðïõ öáßíïíôáé óôçí åéêüíá êéíïýíôáé A. Ùò ðñïò ôç Ãç B. Ùò ðñïò ôï áõôïêßíçôï. 5. íá êéíçôü ìåôáôïðßæåôáé áðü ôç èýóç Ì 1 óôç èýóç Ì 2. Íá ó åäéüóåôå
ÈÅÌÁ 1ï. ÈÅÌÁ 2ï. ÈÅÌÁ 3ï. Óåë. 1 ÃÕÌÍÁÓÉÏ ÈÅÌÁÔÁ ÃÑÁÐÔÙÍ ÅÎÅÔÁÓÅÙÍ ÐÅÑÉÏÄÏÕ ÌÁÚÏÕ-ÉÏÕÍÉÏÕ Ó ÏËÉÊÏ ÅÔÏÓ ÔÁÎÇ: Â ÌÁÈÇÌÁ: ÖÕÓÉÊÇ ÅÉÓÇÃÇÔÇÓ:
 ÃÕÌÍÁÓÉÏ ÈÅÌÁÔÁ ÃÑÁÐÔÙÍ ÅÎÅÔÁÓÅÙÍ ÐÅÑÉÏÄÏÕ ÌÁÚÏÕ-ÉÏÕÍÉÏÕ Ó ÏËÉÊÏ ÅÔÏÓ ÔÁÎÇ: Â ÌÁÈÇÌÁ: ÖÕÓÉÊÇ ÅÉÓÇÃÇÔÇÓ: Çì/íßá: ÈÅÌÁ 1ï Äýï áõôïêßíçôá Á êáé Â êéíïýíôáé ìå ìýóåò ôá ýôçôåò 60km/h êáé 90km/h êáé äéáíýïõí
ÃÕÌÍÁÓÉÏ ÈÅÌÁÔÁ ÃÑÁÐÔÙÍ ÅÎÅÔÁÓÅÙÍ ÐÅÑÉÏÄÏÕ ÌÁÚÏÕ-ÉÏÕÍÉÏÕ Ó ÏËÉÊÏ ÅÔÏÓ ÔÁÎÇ: Â ÌÁÈÇÌÁ: ÖÕÓÉÊÇ ÅÉÓÇÃÇÔÇÓ: Çì/íßá: ÈÅÌÁ 1ï Äýï áõôïêßíçôá Á êáé Â êéíïýíôáé ìå ìýóåò ôá ýôçôåò 60km/h êáé 90km/h êáé äéáíýïõí
2. Ôé åßíáé ï ðñïãñáììáôéæüìåíïò ëïãéêüò åëåãêôþò.
 Ðñïãñáììáôéæüìåíïé Ëïãéêïß ÅëåãêôÝò (PLC) PLC. Áí èýëïõìå íá áíáæçôþóïõìå ôçí áéôßá ãé áõôü, èá ëýãáìå üôé ìüëëïí äåí ðñïëüâáìå! Ïé åîåëßîåéò óôçí çëåêôñïíéêþ Þôáí ñáãäáßåò, åíþ áíôßèåôá ç âéïìç áíéêþ
Ðñïãñáììáôéæüìåíïé Ëïãéêïß ÅëåãêôÝò (PLC) PLC. Áí èýëïõìå íá áíáæçôþóïõìå ôçí áéôßá ãé áõôü, èá ëýãáìå üôé ìüëëïí äåí ðñïëüâáìå! Ïé åîåëßîåéò óôçí çëåêôñïíéêþ Þôáí ñáãäáßåò, åíþ áíôßèåôá ç âéïìç áíéêþ
Συντακτική ανάλυση. Μεταγλωττιστές. (μέρος 3ον) Νίκος Παπασπύου, Κωστής Σαγώνας
 Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Μεταγλωττιστές Νίκος Παπασπύου, Κωστής Σαγώνας Συντακτική ανάλυση (μέρος 3ον) Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό
Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Μεταγλωττιστές Νίκος Παπασπύου, Κωστής Σαγώνας Συντακτική ανάλυση (μέρος 3ον) Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό
