dc(x) kc(x) = 0 d 2 c(x) dx d 4 v(x) + kv(x) = p(x) dx 4 p(t) du(t) + ω 0 u(t) = dt d 4 X(x) d 2 q(t) dq(t) d q(t) = p θ(x) = v (x) κ(x) = θ (x)
|
|
|
- Δημοσθένης Κακριδής
- 8 χρόνια πριν
- Προβολές:
Transcript
1 T/5: : Εφαρμοσμένα Μαθηματικά. Να γίνει κατανοητό σε πολύ μεγαλύτερο αθμό απ τα γνωστά διδακτικά συγγράμματα Συνήθων Διαφορικών Εξισώσεων ότι οι εξισώσεις αυτές έχουν ευρεία χρησιμότητα σε ποικίλα προλήματα της Επιστήμης του Δηλαδή αποτελούν «εργαλείο» και του Προς το σκοπό αυτό όλα τα ασικά είδη των ταλαντώσεων και συντονισμός), τη Μηχανική των Υλικών (δοκοί, δοκοί επί ελαστικής άσεως, λυγισμός στύλου, ιξοελαστικότητα και ερπυσμός), τις Πλάκες (κυκλική πλάκα), τη Δυναμική των από το άκρο σωλήνα, γραμμές ροής), την Περιαλλοντική Υδραυλική (μεταφορά και αποδόμηση ρύπου σε ένα υδατόρρευμα) και την Περιαλλοντική Μηχανική γενικότερα (αποδόμηση ρύπου). Το παρόν είναι μόνο το ένα (το πρώτο: Εφαρμοσμένες Συνήθεις Διαφορικές Εξισώσεις για Πολιτικούς Μηχανικούς) από τα τρία τεύχη του συγγράμματος Εφαρμοσμένα Μαθηματικά. Τα τεύχη αυτά είναι τα εξής: Tεύχος : Εφαρμοσμένες Συνήθεις Διαφορικές Εξισώσεις : Εφαρμοσμένες Ασκήσεις και Nobook II Tεύχος 3: Χρήσιμες Εντολές της Mhic ΜΑΘΗΜΑΤΙΚΑ ΜΗΧΑΝΙΚΟΥΣ. Nα οηθηθούν ο φοιτητής και η φοιτήτρια Πολιτικός Μηχανικός που για οποιοδήποτε λόγο δε διαθέτουν σ επαρκή αθμό τις απαιτούμενες μαθηματικές γνώσεις να κατανοήσουν ευκολότερα την ύλη των Συνήθων Τμημάτων Πολιτικών Μηχανικών ή ακόμη και από κάθε Πολιτικό Μηχανικό που θα ήθελε να ξαναθυμηθεί τις Συνήθεις Διαφορικές Εξισώσεις. d c(x) kc(x) V d v(x) ΜΑΘΗΜΑΤΙΚΑ kv(x) du() p() d u() ΜΗΧΑΝΙΚΟΥΣ ξω ω u() d d q() dq() Εφαρμοσμένες Εξισώσεις Cd Συνήθεις KΔιαφορικές d q() p d () θ(x) v (x) κ(x) θ (x) M(x) κ (x) Q(x) M (x) Q (x) v (x) p(τ) ξω ( τ) in[ω ( τ)] dτ u() Νικόλαοςω Ι. rfc v() v nh ( /τ)
2 T/5: :5 Εφαρμοσμένα Μαθηματικά. Να γίνει κατανοητό σε πολύ μεγαλύτερο αθμό απ τα γνωστά διδακτικά συγγράμματα Συνήθων Διαφορικών Εξισώσεων ότι οι εξισώσεις αυτές έχουν ευρεία χρησιμότητα σε ποικίλα προλήματα της Επιστήμης του Δηλαδή αποτελούν «εργαλείο» και του Προς το σκοπό αυτό όλα τα ασικά είδη των ταλαντώσεων και συντονισμός), τη Μηχανική των Υλικών (δοκοί, δοκοί επί ελαστικής άσεως, λυγισμός στύλου, ιξοελαστικότητα και ερπυσμός), τις Πλάκες (κυκλική πλάκα), τη Δυναμική των από το άκρο σωλήνα, γραμμές ροής), την Περιαλλοντική Υδραυλική (μεταφορά και αποδόμηση ρύπου σε ένα υδατόρρευμα) και την Περιαλλοντική Μηχανική γενικότερα (αποδόμηση ρύπου). Το παρόν είναι μόνο το ένα (το δεύτερο: Εφαρμοσμένες Ασκήσεις και Nobook II για Πολιτικούς Μηχανικούς) από τα τρία τεύχη του συγγράμματος Εφαρμοσμένα Μαθηματικά. Τα τεύχη αυτά είναι τα εξής: Tεύχος : Εφαρμοσμένες Συνήθεις Διαφορικές Εξισώσεις : Εφαρμοσμένες Ασκήσεις και Nobook II Tεύχος 3: Χρήσιμες Eντολές της Mhic ΜΑΘΗΜΑΤΙΚΑ ΜΗΧΑΝΙΚΟΥΣ. Nα οηθηθούν ο φοιτητής και η φοιτήτρια Πολιτικός Μηχανικός που για οποιοδήποτε λόγο δε διαθέτουν σ επαρκή αθμό τις απαιτούμενες μαθηματικές γνώσεις να κατανοήσουν ευκολότερα την ύλη των Συνήθων Τμημάτων Πολιτικών Μηχανικών ή ακόμη και από κάθε Πολιτικό Μηχανικό που θα ήθελε να ξαναθυμηθεί τις Συνήθεις Διαφορικές Εξισώσεις. d c(x) kc(x) V d v(x) kv(x) ΜΑΘΗΜΑΤΙΚΑ du() p() d u() ΜΗΧΑΝΙΚΟΥΣ ξω ω u() d d q() Εφαρμοσμένες dq() Ασκήσεις και Nobook II Cd Kd q() p d () θ(x) v (x) κ(x) θ (x) M(x) κ (x) Q(x) M (x) Q (x) v (x) p(τ) ξω ( τ) in[ω ( τ)] dτ u() Νικόλαοςω Ι. rfc v() v nh ( /τ)
3 T3/5: :53 Εφαρμοσμένα Μαθηματικά. Να γίνει κατανοητό σε πολύ μεγαλύτερο αθμό απ τα γνωστά διδακτικά συγγράμματα Συνήθων Διαφορικών Εξισώσεων ότι οι εξισώσεις αυτές έχουν ευρεία χρησιμότητα σε ποικίλα προλήματα της Επιστήμης του Δηλαδή αποτελούν «εργαλείο» και του Προς το σκοπό αυτό όλα τα ασικά είδη των ταλαντώσεων και συντονισμός), τη Μηχανική των Υλικών (δοκοί, δοκοί επί ελαστικής άσεως, λυγισμός στύλου, ιξοελαστικότητα και ερπυσμός), τις Πλάκες (κυκλική πλάκα), τη Δυναμική των από το άκρο σωλήνα, γραμμές ροής), την Περιαλλοντική Υδραυλική (μεταφορά και αποδόμηση ρύπου σε ένα υδατόρρευμα) και την Περιαλλοντική Μηχανική γενικότερα (αποδόμηση ρύπου). Το παρόν 3 είναι μόνο το ένα (το τρίτο: Χρήσιμες Εντολές της Mhic ) από τα τρία τεύχη του συγγράμματος Εφαρμοσμένα Μαθηματικά. Τα τεύχη αυτά είναι τα εξής: Tεύχος : Εφαρμοσμένες Συνήθεις Διαφορικές Εξισώσεις : Εφαρμοσμένες Ασκήσεις και Nobook II Tεύχος 3: Χρήσιμες Εντολές της Mhic ΜΑΘΗΜΑΤΙΚΑ ΜΗΧΑΝΙΚΟΥΣ. Nα οηθηθούν ο φοιτητής και η φοιτήτρια Πολιτικός Μηχανικός που για οποιοδήποτε λόγο δε διαθέτουν σ επαρκή αθμό τις απαιτούμενες μαθηματικές γνώσεις να κατανοήσουν ευκολότερα την ύλη των Συνήθων 3 Τμημάτων Πολιτικών Μηχανικών ή ακόμη και από κάθε Πολιτικό Μηχανικόπου που θα ήθελε να ξαναθυμηθεί τις Συνήθεις Διαφορικές Εξισώσεις. d c(x) kc(x) V d v(x) kv(x) ΜΑΘΗΜΑΤΙΚΑ du() p() d u() ΜΗΧΑΝΙΚΟΥΣ ξω ω u() d 3 d q() dq() Εντολές της Mhic Χρήσιμες Cd Kd q() p d () θ(x) v (x) κ(x) θ (x) M(x) κ (x) Q(x) M (x) Q (x) v (x) p(τ) ξω ( τ) in[ω ( τ)] dτ u() Νικόλαοςω Ι. rfc v() v nh ( /τ)
4 -9-8 6:58 Εφαρμοσμένα Μαθηματικά Ι. Να γίνει κατανοητό σε πολύ μεγαλύτερο αθμό απ τα γνωστά διδακτικά συγγράμματα για τα πιο πάνω κεφάλαια των Εφαρμοσμένων Μαθηματικών ότι τα κεφάλαια αυτά έχουν ευρεία χρησιμότητα σε ποικίλα προλήματα της Επιστήμης του Δηλαδή αποτελούν «εργαλείο» και του Πολιτικού Μηχανικού. Προς το σκοπό αυτό έχουν συμπεριληφθεί στο σύγγραμμα αυτό και πολλές εφαρμογές που αφορούν άμεσα στην Επιστήμη του Συγκεκριμένα έχουν συμπεριληφθεί εφαρμογές από τη Δυναμική και τις Ταλαντώσεις, τη Μηχανική των Υλικών, την Επίπεδη Ελαστικότητα και την Ιξοελαστικότητα, τις Δοκούς και τις Πλάκες, τη Δυναμική των Κατασκευών, τη Θραυστομηχανική (Μηχανική της Θραύσεως), την Εδαφομηχανική, τη Ρευστομηχανική, την Περιαλλοντική Υδραυλική και την Περιαλλοντική Μηχανική γενικότερα και τέλος την Κυκλοφοριακή Ροή. Οι εφαρμογές αυτές δείχνουν την ιδιαίτερη χρησιμότητα των Εφαρμοσμένων Μαθηματικών III στην Επιστήμη του να κατανοούν άμεσα την πρακτική χρησιμότητα των μεθόδων επιλύσεως που έχουν μελετήσει αμέσως πριν στα πιο πάνω κεφάλαια των Εφαρμοσμένων Μαθηματικών. Το παρόν είναι μόνο ένα (το πρώτο: Εφαρμοσμένες Διαφορικές Εξισώσεις με Μερικές Παραγώγους, Ολοκληρωτικές Εξισώσεις, Μιγαδικές Συναρτήσεις ) από τα δύο τεύχη του παρόντος συγγράμματος Εφαρμοσμένα Μαθηματικά Ι. Τα τεύχη αυτά είναι τα εξής: Tεύχος : Εφαρμοσμένες Διαφορικές Εξισώσεις με Μερικές Παραγώγους, Ολοκληρωτικές Εξισώσεις, Μιγαδικές Συναρτήσεις : Εφαρμοσμένες Ασκήσεις και Nobook IΙI ΜΑΘΗΜΑΤΙΚΑ I ΜΗΧΑΝΙΚΟΥΣ. Nα οηθηθούν ο φοιτητής και η φοιτήτρια Πολιτικός Μηχανικός που για οποιοδήποτε λόγο δε διαθέτουν σ επαρκή αθμό τις απαιτούμενες μαθηματικές γνώσεις να κατανοήσουν ευκολότερα την ύλη των πιο πάνω κεφαλαίων των Εφαρμοσμένων Μαθηματικών. Προς το σκοπό αυτό το μαθηματικό επίπεδο είναι εδώ κάπως χαμηλότερο από το συνηθισμένο. Επίσης υπάρχουν και πάρα πολλές επεξηγήσεις και διασαφηνίσεις στοιχειώδους χαρακτήρα που συνήθως παραλείπονται. Με τον τρόπο αυτόν η μελέτη του συγγράμματος αυτού δεν παρουσιάζει ιδιαίτερη δυσκολία. Το διδακτικό αυτό σύγγραμμα (σε δύο τεύχη) αναφέρεται στις Διαφορικές Εξισώσεις με Μερικές Παραγώγους, στις Ολοκληρωτικές Εξισώσεις καθώς και στις Μιγαδικές Συναρτήσεις. Σκοπός του είναι να αποτελέσει ένα διδακτικό σύγγραμμα κατάλληλο για το μάθημα Εφαρμοσμένα Μαθηματικά I στο τρίτο εξάμηνο σπουδών του Τμήματος Πολιτικών Μηχανικών της Πολυτεχνικής Σχολής του Πανεπιστημίου Πατρών. Μπορεί όμως θαυμάσια να χρησιμοποιηθεί και από φοιτητές και φοιτήτριες και άλλων Σχολών και Τμημάτων Πολιτικών Μηχανικών ή ακόμη και από κάθε Πολιτικό Μηχανικό που θα ήθελε να ξαναθυμηθεί τις Διαφορικές Εξισώσεις με Μερικές Παραγώγους, τις Ολοκληρωτικές Εξισώσεις και τις Μιγαδικές Συναρτήσεις. c c (x, ) x V kc, rfc c p(x, y, ) ΜΑΘΗΜΑΤΙΚΑ ρh I ΜΗΧΑΝΙΚΟΥΣ (xv ξ ) dξ c(x, ) f (ξ) xp π u u Εφαρμοσμένες Διαφορικές v Εξισώσεις v EA ρa f (x, ), με Μερικές ρaπαραγώγους, p(x,) h Εξισώσεις, h Μιγαδικές Συναρτήσεις u uολοκληρωτικές, k x k z για Πολιτικούς, V k grd h Μηχανικούς cv Vx Vy Vx Vy T/5: Φ ε() J()σ () J ( τ)σ (τ) dτ, {J()} {Y()} Νικόλαος Ι. σx σy RΦ(z), σ y σ xiτ xy [z Φ (z) Ψ(z)] Ω (z) dz Γ iq C
5 -9-8 7:6 Εφαρμοσμένα Μαθηματικά Ι. Να γίνει κατανοητό σε πολύ μεγαλύτερο αθμό απ τα γνωστά διδακτικά συγγράμματα για τα πιο πάνω κεφάλαια των Εφαρμοσμένων Μαθηματικών ότι τα κεφάλαια αυτά έχουν ευρεία χρησιμότητα σε ποικίλα προλήματα της Επιστήμης του Δηλαδή αποτελούν «εργαλείο» και του Πολιτικού Μηχανικού. Προς το σκοπό αυτό έχουν συμπεριληφθεί στο σύγγραμμα αυτό και πολλές εφαρμογές που αφορούν άμεσα στην Επιστήμη του Συγκεκριμένα έχουν συμπεριληφθεί εφαρμογές από τη Δυναμική και τις Ταλαντώσεις, τη Μηχανική των Υλικών, την Επίπεδη Ελαστικότητα και την Ιξοελαστικότητα, τις Δοκούς και τις Πλάκες, τη Δυναμική των Κατασκευών, τη Θραυστομηχανική (Μηχανική της Θραύσεως), την Εδαφομηχανική, τη Ρευστομηχανική, την Περιαλλοντική Υδραυλική και την Περιαλλοντική Μηχανική γενικότερα και τέλος την Κυκλοφοριακή Ροή. Οι εφαρμογές αυτές δείχνουν την ιδιαίτερη χρησιμότητα των Εφαρμοσμένων Μαθηματικών III στην Επιστήμη του να κατανοούν άμεσα την πρακτική χρησιμότητα των μεθόδων επιλύσεως που έχουν μελετήσει αμέσως πριν στα πιο πάνω κεφάλαια των Εφαρμοσμένων Μαθηματικών. Το παρόν είναι μόνο ένα (το δεύτερο: Εφαρμοσμένες Ασκήσεις και Nobook III για Πολιτικούς Μηχανικούς) από τα δύο τεύχη του παρόντος συγγράμματος Εφαρμοσμένα Μαθηματικά Ι για Πολιτικούς Μηχανικούς. Τα τεύχη αυτά είναι τα εξής: Tεύχος : Εφαρμοσμένες Διαφορικές Εξισώσεις με Μερικές Παραγώγους, Ολοκληρωτικές Εξισώσεις, Μιγαδικές Συναρτήσεις : Εφαρμοσμένες Ασκήσεις και Nobook IΙI ΜΑΘΗΜΑΤΙΚΑ I ΜΗΧΑΝΙΚΟΥΣ. Nα οηθηθούν ο φοιτητής και η φοιτήτρια Πολιτικός Μηχανικός που για οποιοδήποτε λόγο δε διαθέτουν σ επαρκή αθμό τις απαιτούμενες μαθηματικές γνώσεις να κατανοήσουν ευκολότερα την ύλη των πιο πάνω κεφαλαίων των Εφαρμοσμένων Μαθηματικών. Προς το σκοπό αυτό το μαθηματικό επίπεδο είναι εδώ κάπως χαμηλότερο από το συνηθισμένο. Επίσης υπάρχουν και πάρα πολλές επεξηγήσεις και διασαφηνίσεις στοιχειώδους χαρακτήρα που συνήθως παραλείπονται. Με τον τρόπο αυτόν η μελέτη του συγγράμματος αυτού δεν παρουσιάζει ιδιαίτερη δυσκολία. Το διδακτικό αυτό σύγγραμμα (σε δύο τεύχη) αναφέρεται στις Διαφορικές Εξισώσεις με Μερικές Παραγώγους, στις Ολοκληρωτικές Εξισώσεις καθώς και στις Μιγαδικές Συναρτήσεις. Σκοπός του είναι να αποτελέσει ένα διδακτικό σύγγραμμα κατάλληλο για το μάθημα Εφαρμοσμένα Μαθηματικά I στο τρίτο εξάμηνο σπουδών του Τμήματος Πολιτικών Μηχανικών της Πολυτεχνικής Σχολής του Πανεπιστημίου Πατρών. Μπορεί όμως θαυμάσια να χρησιμοποιηθεί και από φοιτητές και φοιτήτριες και άλλων Σχολών και Τμημάτων Πολιτικών Μηχανικών ή ακόμη και από κάθε Πολιτικό Μηχανικό που θα ήθελε να ξαναθυμηθεί τις Διαφορικές Εξισώσεις με Μερικές Παραγώγους, τις Ολοκληρωτικές Εξισώσεις και τις Μιγαδικές Συναρτήσεις. c c (x, ) x V kc, rfc c p(x, y, ) ΜΑΘΗΜΑΤΙΚΑ ρh I ΜΗΧΑΝΙΚΟΥΣ ΓΙΑ ΠΟΛΙΤΙΚΟΥΣ (xv ξ ) c(x, ) f (ξ) xp dξ π u u v v EA ρa Εφαρμοσμένες f (x, ), και ρaνobook p(x,) Ασκήσεις III h h u u, k x k z, V k grd h cv Vx Vy Vx Vy T5/5: Φ ε() J()σ () J ( τ)σ (τ) dτ, {J()} {Y()} Νικόλαος Ι. σx σy RΦ(z), σ y σ xiτ xy [z Φ (z) Ψ(z)] Ω (z) dz Γ iq C
ΓΕΝΙΚΕΣ ΑΡΧΕΣ ΓΙΑ ΤΟ ΝΕΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ
 ΓΕΝΙΚΕΣ ΑΡΧΕΣ ΓΙΑ ΤΟ ΝΕΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ 1. Τα μαθήματα που έχουν προβιβάσιμο βαθμό δεν μεταφέρονται. (Θα αναγράφονται στην αναλυτική βαθμολογία στο εξάμηνο που έχουν περαστεί). 2. Όσοι οφείλουν υποχρεωτικό
ΓΕΝΙΚΕΣ ΑΡΧΕΣ ΓΙΑ ΤΟ ΝΕΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ 1. Τα μαθήματα που έχουν προβιβάσιμο βαθμό δεν μεταφέρονται. (Θα αναγράφονται στην αναλυτική βαθμολογία στο εξάμηνο που έχουν περαστεί). 2. Όσοι οφείλουν υποχρεωτικό
γλωσσάρι - συντομεύσεις
 γλωσσάρι - συντομεύσεις ΠΠΣ ΠΜΣ ΔΠΜΣ ΣΘΕ ΚΜ Θ Φ Ε ΔΜ ECTS Κ Υ Β ΕΑ ΘΜ ΠΙΦΜ ΣΠΕΕ ΥΠ δξγλ τμφυσ ΓΝΜ ΘΡΜ ΕΦΜ ΠΛΗ ΣΠΕ Πρόγραμμα Προπτυχιακών Σπουδών Πρόγραμμα Μεταπτυχιακών Σπουδών Διατμηματικό Πρόγραμμα Μεταπτυχιακών
γλωσσάρι - συντομεύσεις ΠΠΣ ΠΜΣ ΔΠΜΣ ΣΘΕ ΚΜ Θ Φ Ε ΔΜ ECTS Κ Υ Β ΕΑ ΘΜ ΠΙΦΜ ΣΠΕΕ ΥΠ δξγλ τμφυσ ΓΝΜ ΘΡΜ ΕΦΜ ΠΛΗ ΣΠΕ Πρόγραμμα Προπτυχιακών Σπουδών Πρόγραμμα Μεταπτυχιακών Σπουδών Διατμηματικό Πρόγραμμα Μεταπτυχιακών
ΠΡΟΓΡΑΜΜΑ ΧΕΙΜΕΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ ΕΠΙ ΠΤΥΧΙΩ ΕΑΡΙΝΗ ΕΞΕΤΑΣΤΙΚΗ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΔΕΥΤΕΡΑ 23/1/2017 ΤΡΙΤΗ 24/1/2017 1η 1ο ΑΝΑΛΥΤΙΚΗ ΓΕΩΜΕΤΡΙΑ ΚΑΙ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ, 4 3ο ΘΕΡΜΟΔΥΝΑΜΙΚΗ, 4 Γαλλικά (9.00 11.00)
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΔΕΥΤΕΡΑ 23/1/2017 ΤΡΙΤΗ 24/1/2017 1η 1ο ΑΝΑΛΥΤΙΚΗ ΓΕΩΜΕΤΡΙΑ ΚΑΙ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ, 4 3ο ΘΕΡΜΟΔΥΝΑΜΙΚΗ, 4 Γαλλικά (9.00 11.00)
12.00 ΓΕΩΔΑΙΣΙΑ Ζ. 01AB, 02AB, 02B, 03AB, 04B, 04A, Αμφ. 1,2. Ζ. 01ΑΒ, 02Α, 02Β, 03ΑΒ, 3,5, Αμφ. 1,2 ΑΝΑΛΥΣΗ Ζ. 01ΑΒ, 02Α ΑΝΑΛΥΣΗ
 18/1/2016 12.00 ΓΕΩΔΑΙΣΙΑ Ζ. 01AB, 02AB, 02B, 03AB, 04B, 04A, Αμφ. 1,2 15.00 ΘΕΜΕΛΙΩΣΕΙΣ, 3,5, Αμφ. 1,2 18.00 ΣΥΝΔΥΑΣΜΕΝΕΣ ΜΕΤΑΦΟΡΕΣ - ΕΙΔΙΚΑ ΣΥΣΤΗΜΑΤΑ Ζ. 18.00 ΤΕΧΝΙΚΗ ΣΕΙΣΜΟΛΟΓΙΑ Ζ.04Β, 04Α, 2Α, 2Β 19/1/2016
18/1/2016 12.00 ΓΕΩΔΑΙΣΙΑ Ζ. 01AB, 02AB, 02B, 03AB, 04B, 04A, Αμφ. 1,2 15.00 ΘΕΜΕΛΙΩΣΕΙΣ, 3,5, Αμφ. 1,2 18.00 ΣΥΝΔΥΑΣΜΕΝΕΣ ΜΕΤΑΦΟΡΕΣ - ΕΙΔΙΚΑ ΣΥΣΤΗΜΑΤΑ Ζ. 18.00 ΤΕΧΝΙΚΗ ΣΕΙΣΜΟΛΟΓΙΑ Ζ.04Β, 04Α, 2Α, 2Β 19/1/2016
Ζ. 01ΑΒ, 02Α, 02Β, 03ΑΒ, 04Β, 04Α, 2Α, 2Β, 3,5 Αμφ. 1,2. Σελίδα 1
 18/1/2016 12.00 ΓΕΩΔΑΙΣΙΑ Ζ. 01AB, 02AB, 02B, 03AB, 04B, 04A, Αμφ. 1,2 15.00 ΘΕΜΕΛΙΩΣΕΙΣ, 3,5, 18.00 ΣΥΝΔΥΑΣΜΕΝΕΣ ΜΕΤΑΦΟΡΕΣ - ΕΙΔΙΚΑ ΣΥΣΤΗΜΑΤΑ Ζ.01ΑΒ, 02Α, 02Β, 18.00 ΤΕΧΝΙΚΗ ΣΕΙΣΜΟΛΟΓΙΑ Ζ.04Β, 04Α, 2Α,
18/1/2016 12.00 ΓΕΩΔΑΙΣΙΑ Ζ. 01AB, 02AB, 02B, 03AB, 04B, 04A, Αμφ. 1,2 15.00 ΘΕΜΕΛΙΩΣΕΙΣ, 3,5, 18.00 ΣΥΝΔΥΑΣΜΕΝΕΣ ΜΕΤΑΦΟΡΕΣ - ΕΙΔΙΚΑ ΣΥΣΤΗΜΑΤΑ Ζ.01ΑΒ, 02Α, 02Β, 18.00 ΤΕΧΝΙΚΗ ΣΕΙΣΜΟΛΟΓΙΑ Ζ.04Β, 04Α, 2Α,
ΤΕΧΝΙΚΗ ΕΚΘΕΣΗ ΣΤΑΤΙΚΟΥ ΚΑΙ ΑΝΤΙΣΕΙΣΜΙΚΟΥ ΥΠΟΛΟΓΙΣΜΟΥ ME TO ΠΡΟΓΡΑΜΜΑ S T A T I C S 2010 ΠΑΡΑΔΟΧΕΣ Ι ΦΟΡΤΙΑ
 ΤΕΧΝΙΚΗ ΕΚΘΕΣΗ ΣΤΑΤΙΚΟΥ ΚΑΙ ΑΝΤΙΣΕΙΣΜΙΚΟΥ ΥΠΟΛΟΓΙΣΜΟΥ ME TO ΠΡΟΓΡΑΜΜΑ S T A T I C S 2010 Ι ΦΟΡΤΙΑ ΠΑΡΑΔΟΧΕΣ α. Μόνιμα Ειδικό βάρος Ο. Σ.... 2.4 t/m3 Επικάλυψη δαπέδων... 100 kg/m2 Επικάλυψη δώματος...
ΤΕΧΝΙΚΗ ΕΚΘΕΣΗ ΣΤΑΤΙΚΟΥ ΚΑΙ ΑΝΤΙΣΕΙΣΜΙΚΟΥ ΥΠΟΛΟΓΙΣΜΟΥ ME TO ΠΡΟΓΡΑΜΜΑ S T A T I C S 2010 Ι ΦΟΡΤΙΑ ΠΑΡΑΔΟΧΕΣ α. Μόνιμα Ειδικό βάρος Ο. Σ.... 2.4 t/m3 Επικάλυψη δαπέδων... 100 kg/m2 Επικάλυψη δώματος...
ΕΞΑΜΗΝΟ ΕΞΑΜΗΝΟ. (κατ. Φυσικού. Εφαρμογών) Μαθηματικού Εφαρμογών) και Σχεδιασμοί Αμφ. 1, Εμβιομηχανική του μυοσκελετικού αμφ.
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2010-2011 ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ 1 ΤΕΛΙΚΟ ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2010-2011 ΗΜ/ΝΙΑ ΩΡΑ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2010-2011 ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ 1 ΤΕΛΙΚΟ ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2010-2011 ΗΜ/ΝΙΑ ΩΡΑ
ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔ. ΕΤΟΥΣ (ΜΕΤΑ ΤΗ ΔΙΑΚΟΠΗ ΑΠΟ 4/9) ΣΧΟΛΗ ΝΑΥΠΗΓΩΝ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ
 Τετάρτη 13.11.2013 10:00 Ναυπηγικό Σχέδιο PC_LAB (Ομάδες) Υδροστατική & Ευστάθεια Πλοίου Ι Αμφιθέατρo Δ Κτ. Δ Αιθ. 105, 106, 201, 202 Ανάλυση & Σχεδίαση Σκαφών από Σύνθετα Υλικά Κτ. Δ Αιθ. 105 Συστήματα
Τετάρτη 13.11.2013 10:00 Ναυπηγικό Σχέδιο PC_LAB (Ομάδες) Υδροστατική & Ευστάθεια Πλοίου Ι Αμφιθέατρo Δ Κτ. Δ Αιθ. 105, 106, 201, 202 Ανάλυση & Σχεδίαση Σκαφών από Σύνθετα Υλικά Κτ. Δ Αιθ. 105 Συστήματα
ΚΕΦΑΛΑΙΟ 2 ο ΜΑΘΗΜΑΤΙΚΗ ΠΕΡΙΓΡΑΦΗ ΣΥΣΤΗΜΑΤΩΝ
 ΚΕΦΑΛΑΙΟ ο ΜΑΘΗΜΑΤΙΚΗ ΠΕΡΙΓΡΑΦΗ ΣΥΣΤΗΜΑΤΩΝ Ανάλυση συστήματος Εισαγωγή Μαθηματική Περιγραφή Διαφορικές Εξισώσεις Μετασχηματισμός LLCE Συνάρτηση Μεταφοράς Βήματα για την μελέτη του συστήματος Ορισμός του
ΚΕΦΑΛΑΙΟ ο ΜΑΘΗΜΑΤΙΚΗ ΠΕΡΙΓΡΑΦΗ ΣΥΣΤΗΜΑΤΩΝ Ανάλυση συστήματος Εισαγωγή Μαθηματική Περιγραφή Διαφορικές Εξισώσεις Μετασχηματισμός LLCE Συνάρτηση Μεταφοράς Βήματα για την μελέτη του συστήματος Ορισμός του
Σε ότι αφορά τα επί μέρους μαθήματα ισχύουν τα εξής: ΜΕΤΑΒΑΤΙΚΕΣ ΔΙΑΤΑΞΕΙΣ για τα ΥΠΟΧΡΕΩΤΙΚΑ ΜΑΘΗΜΑΤΑ
 ΜΕΤΑΒΑΤΙΚΕΣ ΔΙΑΤΑΞΕΙΣ Παλαιού Προγράμματος Σπουδών (Οι διατάξεις αυτές αφορούν τους φοιτητές του Τμήματος Φυσικής, οι οποίοι παρακολουθούν το παλαιό πρόγραμμα σπουδών, δηλ. γράφτηκαν στο Α εξάμηνο το Ακαδ.
ΜΕΤΑΒΑΤΙΚΕΣ ΔΙΑΤΑΞΕΙΣ Παλαιού Προγράμματος Σπουδών (Οι διατάξεις αυτές αφορούν τους φοιτητές του Τμήματος Φυσικής, οι οποίοι παρακολουθούν το παλαιό πρόγραμμα σπουδών, δηλ. γράφτηκαν στο Α εξάμηνο το Ακαδ.
ΤΕΛΙΚΟ ΠΡΟΓΡΑΜΜΑ ΧΕΙΜΕΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ & ΕΠΙ ΠΤΥΧΙΩ ΕΑΡΙΝΗ ΕΞΕΤΑΣΤΙΚΗ
 ΠΑΡΑΣΚΕΥΗ 19/1/20 ΠΕΜΠΤΗ 18/1/2 ΤΕΤΑΡΤΗ 17/1/2018 ΤΡΙΤΗ 16/1/2018 ΔΕΥΤΕΡΑ 15/1/2 ΣΗΜΕΙΩΣΗ 1: Ο ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΤΗΣ ΕΠΙ ΠΤΥΧΙΩ ΕΞΕΤΑΣΗΣ ΤΩΝ ΜΑΘΗΜΑΤΩΝ ΕΑΡΙΝΩΝ ΕΞΑΜΗΝΩΝ, ΣΗΜΕΙΩΝΕΤΑΙ ΜΕ ΚΟΚΚΙΝΟ ΚΑΙ ΜΠΛΕ ΧΡΩΜΑ.
ΠΑΡΑΣΚΕΥΗ 19/1/20 ΠΕΜΠΤΗ 18/1/2 ΤΕΤΑΡΤΗ 17/1/2018 ΤΡΙΤΗ 16/1/2018 ΔΕΥΤΕΡΑ 15/1/2 ΣΗΜΕΙΩΣΗ 1: Ο ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΤΗΣ ΕΠΙ ΠΤΥΧΙΩ ΕΞΕΤΑΣΗΣ ΤΩΝ ΜΑΘΗΜΑΤΩΝ ΕΑΡΙΝΩΝ ΕΞΑΜΗΝΩΝ, ΣΗΜΕΙΩΝΕΤΑΙ ΜΕ ΚΟΚΚΙΝΟ ΚΑΙ ΜΠΛΕ ΧΡΩΜΑ.
Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών
 Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών Οι παρούσες σημειώσεις αποτελούν βοήθημα στο μάθημα Αριθμητικές Μέθοδοι του 5 ου εξαμήνου του ΤΜΜ ημήτρης Βαλουγεώργης Καθηγητής Εργαστήριο Φυσικών
Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών Οι παρούσες σημειώσεις αποτελούν βοήθημα στο μάθημα Αριθμητικές Μέθοδοι του 5 ου εξαμήνου του ΤΜΜ ημήτρης Βαλουγεώργης Καθηγητής Εργαστήριο Φυσικών
Κεφάλαιο 1: Προβλήµατα τύπου Sturm-Liouville
 Κεφάλαιο : Προβλήµατα τύπου Stur-Liouvie. Ορισµός προβλήµατος Stur-Liouvie Πολλές τεχνικές επίλυσης µερικών διαφορικών εξισώσεων βασίζονται στην αναγωγή της µερικής διαφορικής εξίσωσης σε συνήθεις διαφορικές
Κεφάλαιο : Προβλήµατα τύπου Stur-Liouvie. Ορισµός προβλήµατος Stur-Liouvie Πολλές τεχνικές επίλυσης µερικών διαφορικών εξισώσεων βασίζονται στην αναγωγή της µερικής διαφορικής εξίσωσης σε συνήθεις διαφορικές
ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΤΙΚΗΣ ΕΑΡΙΝΩΝ ΕΞΑΜΗΝΩΝ & ΕΠΙ ΠΤΥΧΙΩ ΕΞΕΤΑΣΤΙΚΗΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ ( )
 ΠΑΡΑΣΚΕΥΗ 19/6/2015 ΠΕΜΠΤΗ 18/6/2015 ΤΕΤΑΡΤΗ 17/6/2015 ΤΡΙΤΗ 16/6/2015 ΔΕΥΤΕΡΑ 15/6/2015 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΤΙΚΗΣ ΕΑΡΙΝΩΝ ΕΞΑΜΗΝΩΝ
ΠΑΡΑΣΚΕΥΗ 19/6/2015 ΠΕΜΠΤΗ 18/6/2015 ΤΕΤΑΡΤΗ 17/6/2015 ΤΡΙΤΗ 16/6/2015 ΔΕΥΤΕΡΑ 15/6/2015 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΤΙΚΗΣ ΕΑΡΙΝΩΝ ΕΞΑΜΗΝΩΝ
ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΤΙΚΗΣ ΕΑΡΙΝΩΝ ΕΞΑΜΗΝΩΝ & ΕΠΙ ΠΤΥΧΙΩ ΕΞΕΤΑΣΤΙΚΗΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2014-15 (ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ 1 )
 ΠΑΡΑΣΚΕΥΗ 19/6/2015 ΠΕΜΠΤΗ 18/6/2015 ΤΕΤΑΡΤΗ 17/6/2015 ΤΡΙΤΗ 16/6/2015 ΔΕΥΤΕΡΑ 15/6/2015 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΤΙΚΗΣ ΕΑΡΙΝΩΝ ΕΞΑΜΗΝΩΝ
ΠΑΡΑΣΚΕΥΗ 19/6/2015 ΠΕΜΠΤΗ 18/6/2015 ΤΕΤΑΡΤΗ 17/6/2015 ΤΡΙΤΗ 16/6/2015 ΔΕΥΤΕΡΑ 15/6/2015 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΤΙΚΗΣ ΕΑΡΙΝΩΝ ΕΞΑΜΗΝΩΝ
ΗΜ/ΝΙΑ ΩΡΑ 1ο ΕΞΑΜΗΝΟ ΩΡΑ 3ο ΕΞΑΜΗΝΟ ΩΡΑ 5ο ΕΞΑΜΗΝΟ ΩΡΑ 7ο ΕΞΑΜΗΝΟ ΩΡΑ 9ο ΕΞΑΜΗΝΟ Δευτέρα 23/1/ ΓΕΩΔΑΙΣΙΑ ΜΕΤΑΦΟΡΕΣ - ΕΙΔΙΚΑ ΣΥΣΤΗΜΑΤΑ
 23/1/2017 12.00 ΓΕΩΔΑΙΣΙΑ 15.00 ΘΕΜΕΛΙΩΣΕΙΣ 18.00 ΣΥΝΔΥΑΣΜΕΝΕΣ ΜΕΤΑΦΟΡΕΣ - ΕΙΔΙΚΑ ΣΥΣΤΗΜΑΤΑ 24/1/2017 12.00 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ 8.30 ΕΦΑΡΜΟΣΜΕΝΗ ΥΔΡΑΥΛΙΚΗ 18.00 ΤΕΧΝΙΚΗ ΣΕΙΣΜΟΛΟΓΙΑ 25/1/2017 26/1/2017 27/1/2017
23/1/2017 12.00 ΓΕΩΔΑΙΣΙΑ 15.00 ΘΕΜΕΛΙΩΣΕΙΣ 18.00 ΣΥΝΔΥΑΣΜΕΝΕΣ ΜΕΤΑΦΟΡΕΣ - ΕΙΔΙΚΑ ΣΥΣΤΗΜΑΤΑ 24/1/2017 12.00 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ 8.30 ΕΦΑΡΜΟΣΜΕΝΗ ΥΔΡΑΥΛΙΚΗ 18.00 ΤΕΧΝΙΚΗ ΣΕΙΣΜΟΛΟΓΙΑ 25/1/2017 26/1/2017 27/1/2017
ΠΡΟΓΡΑΜΜΑ ΕΑΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ & ΕΠΙ ΠΤΥΧΙΩ ΧΕΙΜΕΡΙΝΑ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΕΑΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ & ΕΠΙ ΠΤΥΧΙΩ ΧΕΙΜΕΡΙΝΑ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-17 1η ΚΟΡΜΟΥ ΜΑΘΗΜΑΤΙΚΟΥ ΦΥΣΙΚΟΥ ΜΑΘΗΜΑΤΙΚΟΥ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΕΑΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ & ΕΠΙ ΠΤΥΧΙΩ ΧΕΙΜΕΡΙΝΑ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-17 1η ΚΟΡΜΟΥ ΜΑΘΗΜΑΤΙΚΟΥ ΦΥΣΙΚΟΥ ΜΑΘΗΜΑΤΙΚΟΥ
ΘΕΜΑ 1: ίδεται η περιγραφή µίας κίνησης ενός µονοδιάστατου Συνεχούς κατά Lagrange
 ΜΗΧΑΝΙΚΗ ΤΟΥ ΣΥΝΕΧΟΥΣ ΜΕΣΟΥ Σχολή Πολιτικών Μηχανικών, Εξ. ιδ. 04 Καθηγητής Ι. Βαρδουλάκης, Σ.Ε.Μ.Φ.Ε. 8:30 π.µ., Πέµπτη 8 Ιουλίου 004 ΘΕΜΑ : ίδεται η περιγραφή µίας κίνησης ενός µονοδιάστατου Συνεχούς
ΜΗΧΑΝΙΚΗ ΤΟΥ ΣΥΝΕΧΟΥΣ ΜΕΣΟΥ Σχολή Πολιτικών Μηχανικών, Εξ. ιδ. 04 Καθηγητής Ι. Βαρδουλάκης, Σ.Ε.Μ.Φ.Ε. 8:30 π.µ., Πέµπτη 8 Ιουλίου 004 ΘΕΜΑ : ίδεται η περιγραφή µίας κίνησης ενός µονοδιάστατου Συνεχούς
Δυναμική Μηχανών I. Διάλεξη 8. Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ
 Δυναμική Μηχανών I Διάλεξη 8 Χειμερινό Εξάμηνο 23 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ Ανακοινώσεις To μάθημα MATLAB/simulink για όσους δήλωσαν συμμετοχή έως χθες θα γίνει στις 6//24: Office Hours: Δευτέρα -3 μμ,
Δυναμική Μηχανών I Διάλεξη 8 Χειμερινό Εξάμηνο 23 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ Ανακοινώσεις To μάθημα MATLAB/simulink για όσους δήλωσαν συμμετοχή έως χθες θα γίνει στις 6//24: Office Hours: Δευτέρα -3 μμ,
ΠΑΡΑΡΤΗΜΑ 2 Μεταβατικές Διατάξεις
 Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών ΠΑΡΑΡΤΗΜΑ 2 Μεταβατικές Διατάξεις 1. Μαθήματα του Τμήματος Μαθηματικών και Εφαρμοσμένων Μαθηματικών στα οποία έχεις επιτύχει μέχρι το Σεπτέμβριο 2017 αναγνωρίζονται
Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών ΠΑΡΑΡΤΗΜΑ 2 Μεταβατικές Διατάξεις 1. Μαθήματα του Τμήματος Μαθηματικών και Εφαρμοσμένων Μαθηματικών στα οποία έχεις επιτύχει μέχρι το Σεπτέμβριο 2017 αναγνωρίζονται
Δυναμική Μηχανών I. Διάλεξη 7. Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ
 Δυναμική Μηχανών I Διάλεξη 7 Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ 1 Περιεχόμενα Επανάληψη 1 ου μέρους μαθήματος: Μοντελοποίηση & Κατάστρωση Δυναμικών Εξισώσεων Εισαγωγή 2 ου μέρους μαθήματος:
Δυναμική Μηχανών I Διάλεξη 7 Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ 1 Περιεχόμενα Επανάληψη 1 ου μέρους μαθήματος: Μοντελοποίηση & Κατάστρωση Δυναμικών Εξισώσεων Εισαγωγή 2 ου μέρους μαθήματος:
ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦ ΑΡΜ ΟΣΜ ΕΝΩΝ Μ ΑΘΗΜ ΑΤΙΚΩΝ ΚΑΙ Φ ΥΣΙΚΩΝ ΕΠΙΣΤΗΜ ΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 3-4 ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 3-4 ΗΜ/ΝΙΑ 1ο-2ο 3ο-4ο 5ο-6ο 5ο-6ο Μαθηματικού 7ο-8ο Φυσικού
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦ ΑΡΜ ΟΣΜ ΕΝΩΝ Μ ΑΘΗΜ ΑΤΙΚΩΝ ΚΑΙ Φ ΥΣΙΚΩΝ ΕΠΙΣΤΗΜ ΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 3-4 ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 3-4 ΗΜ/ΝΙΑ 1ο-2ο 3ο-4ο 5ο-6ο 5ο-6ο Μαθηματικού 7ο-8ο Φυσικού
ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΕΩΝ ΣΕΠΤΕΜΒΡΙΟΥ ο ΕΤΟΣ 2ο ΕΤΟΣ 3ο ΕΤΟΣ 4ο ΕΤΟΣ 5ο ΕΤΟΣ ΠΛΗΡΟΦΟΡΙΚΗ Εισηγητής: ΜυστακίδηςΕ. Επιτηρητές:
 Πέμπτη 27/8/15 ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΕΩΝ ΣΕΠΤΕΜΒΡΙΟΥ 2015 1ο ΕΤΟΣ 2ο ΕΤΟΣ 3ο ΕΤΟΣ 4ο ΕΤΟΣ 5ο ΕΤΟΣ ΠΛΗΡΟΦΟΡΙΚΗ ΕΔΑΦΟΜΗΧΑΝΙΚΗ ΙΙ ΣΙΔ. ΣΚΥΡΟΔΕΜΑ ΙΙ Εισηγητής: ΜυστακίδηςΕ. Εισηγ.: Καλλιόγλου Π. Εισηγητής: Περδικάρης
Πέμπτη 27/8/15 ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΕΩΝ ΣΕΠΤΕΜΒΡΙΟΥ 2015 1ο ΕΤΟΣ 2ο ΕΤΟΣ 3ο ΕΤΟΣ 4ο ΕΤΟΣ 5ο ΕΤΟΣ ΠΛΗΡΟΦΟΡΙΚΗ ΕΔΑΦΟΜΗΧΑΝΙΚΗ ΙΙ ΣΙΔ. ΣΚΥΡΟΔΕΜΑ ΙΙ Εισηγητής: ΜυστακίδηςΕ. Εισηγ.: Καλλιόγλου Π. Εισηγητής: Περδικάρης
ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΣΕΠΤΕΜΒΡΙΟΥ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ
 ΠΑΡΑΣΚΕΥΗ 30/8/2019 ΠΕΜΠΤΗ 29/8/2019 ΤΕΤΑΡΤΗ 28/8/2019 ΤΡΙΤΗ 27/8/2019 ΔΕΥΤΕΡΑ 26/8/2019 1ο-2ο 3ο-4ο ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ 5ο-6ο 7ο-8ο ΠΡΟΓΡΑΜΜΑ
ΠΑΡΑΣΚΕΥΗ 30/8/2019 ΠΕΜΠΤΗ 29/8/2019 ΤΕΤΑΡΤΗ 28/8/2019 ΤΡΙΤΗ 27/8/2019 ΔΕΥΤΕΡΑ 26/8/2019 1ο-2ο 3ο-4ο ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ 5ο-6ο 7ο-8ο ΠΡΟΓΡΑΜΜΑ
Ελληνική Δημοκρατία ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ Σχολή ΜΗΧΑΝΙΚΩΝ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πολυτεχνειούπολη - ΧΑΝΙΑ
 Ελληνική Δημοκρατία ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ Σχολή ΜΗΧΑΝΙΚΩΝ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πολυτεχνειούπολη - ΧΑΝΙΑ ------------------------------------------------------------------------------------------------------- Προπτυχιακό
Ελληνική Δημοκρατία ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ Σχολή ΜΗΧΑΝΙΚΩΝ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πολυτεχνειούπολη - ΧΑΝΙΑ ------------------------------------------------------------------------------------------------------- Προπτυχιακό
ΠΡΟΓΡΑΜΜΑ ΠΡΟΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ Υ 4 6
 ΠΡΟΓΡΑΜΜΑ ΠΡΟΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ 2017-2018 1 ο εξάμηνο 1) Γραμμική Άλγεβρα και Αναλυτική Γεωμετρία Υ 4 6 2) Φυσική Ι Υ 4 6 3) Χημεία για μηχανικούς Υ 4 5 4) Τεχνικές Σχεδιάσεις και CAD Υ 4 3 5) Απειροστικός
ΠΡΟΓΡΑΜΜΑ ΠΡΟΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ 2017-2018 1 ο εξάμηνο 1) Γραμμική Άλγεβρα και Αναλυτική Γεωμετρία Υ 4 6 2) Φυσική Ι Υ 4 6 3) Χημεία για μηχανικούς Υ 4 5 4) Τεχνικές Σχεδιάσεις και CAD Υ 4 3 5) Απειροστικός
ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΕΩΝ ΧΕΙΜΕΡΙΝΩΝ ΕΞΑΜΗΝΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ ΓΙΑ ΤΟΥΣ ΕΠΙ ΠΤΥΧΙΩ ΦΟΙΤΗΤΕΣ ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ 1
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 20-201 ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΕΩΝ ΧΕΙΜΕΡΙΝΩΝ ΕΞΑΜΗΝΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 20-201 ΓΙΑ ΤΟΥΣ ΕΠΙ ΠΤΥΧΙΩ ΦΟΙΤΗΤΕΣ ΟΡΘΗ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 20-201 ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΕΩΝ ΧΕΙΜΕΡΙΝΩΝ ΕΞΑΜΗΝΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 20-201 ΓΙΑ ΤΟΥΣ ΕΠΙ ΠΤΥΧΙΩ ΦΟΙΤΗΤΕΣ ΟΡΘΗ
ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ Από 28/8/2017 έως 29/9/2017. ΗΜ/ΝΙΑ ΩΡΑ 1ο/2ο ΩΡΑ 3ο/4ο ΩΡΑ 5ο/6ο ΩΡΑ 7ο/8ο ΩΡΑ 9ο ΔΕΥΤΕΡΑ 28/8/2017 ΤΡΙΤΗ 29/8/2017
 28/8/2017 29/8/2017 12:00 Δομικές Μηχανές 15:00 Σιδηροδρομική Τεχνική Εφαρμοσμένη Οικονομική Στοιχεία Φιλοσοφίας & Θεωρία Γνώσεων 12.00 Τεχνική Μηχανική ΙΙΙ 15:00 Στοιχεία Δικαίου και (Δυναμική του Στερεού
28/8/2017 29/8/2017 12:00 Δομικές Μηχανές 15:00 Σιδηροδρομική Τεχνική Εφαρμοσμένη Οικονομική Στοιχεία Φιλοσοφίας & Θεωρία Γνώσεων 12.00 Τεχνική Μηχανική ΙΙΙ 15:00 Στοιχεία Δικαίου και (Δυναμική του Στερεού
ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΤΙΚΗΣ ΕΑΡΙΝΩΝ ΕΞΑΜΗΝΩΝ & ΕΠΙ ΠΤΥΧΙΩ ΕΞΕΤΑΣΤΙΚΗΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ (ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ 4 )
 ΠΑΡΑΣΚΕΥΗ 19/6/2015 ΠΕΜΠΤΗ 18/6/2015 ΤΕΤΑΡΤΗ 17/6/2015 ΤΡΙΤΗ 16/6/2015 ΔΕΥΤΕΡΑ 15/6/2015 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΤΙΚΗΣ ΕΑΡΙΝΩΝ ΕΞΑΜΗΝΩΝ
ΠΑΡΑΣΚΕΥΗ 19/6/2015 ΠΕΜΠΤΗ 18/6/2015 ΤΕΤΑΡΤΗ 17/6/2015 ΤΡΙΤΗ 16/6/2015 ΔΕΥΤΕΡΑ 15/6/2015 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΤΙΚΗΣ ΕΑΡΙΝΩΝ ΕΞΑΜΗΝΩΝ
ΚΟΡΜΟΥ. ΜΑΘΗΜΑΤΙΚΟΥ ΦΥΣΙΚΟΥ ΜΑΘΗΜΑΤΙΚΟΥ ΦΥΣΙΚΟΥ ΜΑΘΗΜΑΤΙΚΟΥ ΦΥΣΙΚΟΥ 5ο 7ο 9ο
 ΡΑΣΚΕΥΗ 25/1/2019 ΠΕΜΠΤΗ 24/1/2019 ΤΕΤΑΡΤΗ 23/1/2019 ΤΡΙΤΗ 22/1/2019 ΔΕΥΤΕΡΑ 21/1/2019 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΧΕΙΜΕΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ
ΡΑΣΚΕΥΗ 25/1/2019 ΠΕΜΠΤΗ 24/1/2019 ΤΕΤΑΡΤΗ 23/1/2019 ΤΡΙΤΗ 22/1/2019 ΔΕΥΤΕΡΑ 21/1/2019 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΧΕΙΜΕΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ
ΚΟΡΜΟΥ. ΜΑΘΗΜΑΤΙΚΟΥ ΦΥΣΙΚΟΥ ΜΑΘΗΜΑΤΙΚΟΥ ΦΥΣΙΚΟΥ ΜΑΘΗΜΑΤΙΚΟΥ ΦΥΣΙΚΟΥ 5ο 7ο 9ο
 ΠΑΡΑΣΚΕΥΗ 18/1/201 ΠΕΜΠΤΗ 17/1/2019 ΤΕΤΑΡΤΗ 16/1/2019 ΤΡΙΤΗ 15/1/2019 ΔΕΥΤΕΡΑ 14/1/2019 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΧΕΙΜΕΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ
ΠΑΡΑΣΚΕΥΗ 18/1/201 ΠΕΜΠΤΗ 17/1/2019 ΤΕΤΑΡΤΗ 16/1/2019 ΤΡΙΤΗ 15/1/2019 ΔΕΥΤΕΡΑ 14/1/2019 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΧΕΙΜΕΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ
Δυναμική Μηχανών I. Δυναμικά Μοντέλα Συνεχούς Μέσου
 Δυναμική Μηχανών I 8 1 Δυναμικά Μοντέλα Συνεχούς Μέσου 2015 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com Απαγορεύεται οποιαδήποτε αναπαραγωγή χωρίς άδεια Μοντελοποίηση
Δυναμική Μηχανών I 8 1 Δυναμικά Μοντέλα Συνεχούς Μέσου 2015 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com Απαγορεύεται οποιαδήποτε αναπαραγωγή χωρίς άδεια Μοντελοποίηση
ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΤΙΚΗΣ ΕΑΡΙΝΩΝ ΕΞΑΜΗΝΩΝ & ΕΠΙ ΠΤΥΧΙΩ ΕΞΕΤΑΣΤΙΚΗΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ (ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ 5 )
 ΠΑΡΑΣΚΕΥΗ 19/6/2015 ΠΕΜΠΤΗ 18/6/2015 ΤΕΤΑΡΤΗ 17/6/2015 ΤΡΙΤΗ 16/6/2015 ΔΕΥΤΕΡΑ 15/6/2015 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΤΙΚΗΣ ΕΑΡΙΝΩΝ ΕΞΑΜΗΝΩΝ
ΠΑΡΑΣΚΕΥΗ 19/6/2015 ΠΕΜΠΤΗ 18/6/2015 ΤΕΤΑΡΤΗ 17/6/2015 ΤΡΙΤΗ 16/6/2015 ΔΕΥΤΕΡΑ 15/6/2015 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΤΙΚΗΣ ΕΑΡΙΝΩΝ ΕΞΑΜΗΝΩΝ
ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΣΕΠΤΕΜΒΡΙΟΥ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ
 1ο-2ο 3ο-4ο ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ 5ο-6ο 7ο-8ο 9ο ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΣΕΠΤΕΜΒΡΙΟΥ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2017-18 1η 1o - 2ο 3o - 4ο
1ο-2ο 3ο-4ο ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ 5ο-6ο 7ο-8ο 9ο ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΣΕΠΤΕΜΒΡΙΟΥ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2017-18 1η 1o - 2ο 3o - 4ο
ΚΟΡΜΟΥ. ΜΑΘΗΜΑΤΙΚΟΥ ΦΥΣΙΚΟΥ ΜΑΘΗΜΑΤΙΚΟΥ ΦΥΣΙΚΟΥ ΜΑΘΗΜΑΤΙΚΟΥ ΦΥΣΙΚΟΥ 5ο 7ο 9ο
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΧΕΙΜΕΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-17 1η 5ο 7ο 9ο ΔΕΥΤΕΡΑ 23/1/2017 ΘΕΡΜΟΔΥΝΑΜΙΚΗ, 4 --------- Γαλλικά
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΧΕΙΜΕΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-17 1η 5ο 7ο 9ο ΔΕΥΤΕΡΑ 23/1/2017 ΘΕΡΜΟΔΥΝΑΜΙΚΗ, 4 --------- Γαλλικά
β. Το πλάτος της σύνθετης ταλάντωσης είναι : Α = (Α 1 ² + Α 2 ² + 2 Α 1 Α 2 συν φ) (φ = π rad) Α = (Α 1 ² + Α 2 ² + 2 Α 1 Α 2 συν π) Α = [Α 1 ² + Α 2
 1) Ένα κινητό εκτελεί συγχρόνως δύο απλές αρμονικές ταλαντώσεις που γίνονται στην ίδια διεύθυνση και γύρω από την θέση ισορροπίας με εξισώσεις : x 1 = 3 ημ [(2 π) t] και x 2 = 4 ημ [(2 π) t + φ], (S.I.).
1) Ένα κινητό εκτελεί συγχρόνως δύο απλές αρμονικές ταλαντώσεις που γίνονται στην ίδια διεύθυνση και γύρω από την θέση ισορροπίας με εξισώσεις : x 1 = 3 ημ [(2 π) t] και x 2 = 4 ημ [(2 π) t + φ], (S.I.).
ΠΡΟΓΡΑΜΜΑ ΧΕΙΜΕΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ 1
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΧΕΙΜΕΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-17 ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ 1 1η 5ο 7ο 9ο ΠΑΡΑΣΚΕΥΗ 27/1/201 ΠΕΜΠΤΗ 26/1/2017
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΧΕΙΜΕΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-17 ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ 1 1η 5ο 7ο 9ο ΠΑΡΑΣΚΕΥΗ 27/1/201 ΠΕΜΠΤΗ 26/1/2017
ΥΠΟΛΟΓΙΣΤΙΚΕΣ ΜΕΘΟ ΟΙ
 ΥΠΟΛΟΓΙΣΤΙΚΕΣ ΜΕΘΟ ΟΙ Σηµειώσεις µαθήµατος ηµήτρης Βαλουγεώργης Αναπληρωτής Καθηγητής Τµήµα Μηχανολόγων Μηχανικών Βιοµηχανίας Εργαστήριο Φυσικών και Χηµικών ιεργασιών Πολυτεχνική Σχολή Πανεπιστήµιο Θεσσαλίας
ΥΠΟΛΟΓΙΣΤΙΚΕΣ ΜΕΘΟ ΟΙ Σηµειώσεις µαθήµατος ηµήτρης Βαλουγεώργης Αναπληρωτής Καθηγητής Τµήµα Μηχανολόγων Μηχανικών Βιοµηχανίας Εργαστήριο Φυσικών και Χηµικών ιεργασιών Πολυτεχνική Σχολή Πανεπιστήµιο Θεσσαλίας
Το νέο Πρόγραμμα Προπτυχιακών Σπουδών μετά τις αλλαγές διαμορφώνεται ως εξής: Υ 4 6
 Το νέο Πρόγραμμα Προπτυχιακών Σπουδών μετά τις αλλαγές διαμορφώνεται ως εξής: 1 ο εξάμηνο 1) Γραμμική Άλγεβρα και Αναλυτική Γεωμετρία Υ 4 6 2) Φυσική Ι Υ 4 6 3) Χημεία για μηχανικούς Υ 4 5 4) Τεχνικές
Το νέο Πρόγραμμα Προπτυχιακών Σπουδών μετά τις αλλαγές διαμορφώνεται ως εξής: 1 ο εξάμηνο 1) Γραμμική Άλγεβρα και Αναλυτική Γεωμετρία Υ 4 6 2) Φυσική Ι Υ 4 6 3) Χημεία για μηχανικούς Υ 4 5 4) Τεχνικές
p = p n, (2) website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Ιδανικά ρευστά Μαάιτα Τζαμάλ-Οδυσσέας 7 Απριλίου 2019 1 Καταστατικές εξισώσεις ιδανικού ρευστού Ιδανικό ρευστό είναι ένα υποθετικό
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Ιδανικά ρευστά Μαάιτα Τζαμάλ-Οδυσσέας 7 Απριλίου 2019 1 Καταστατικές εξισώσεις ιδανικού ρευστού Ιδανικό ρευστό είναι ένα υποθετικό
ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ 1
 ΕΘΝΚΟ ΜΕΤΣΟΒΟ ΠΟΛΥΤΕΧΝΕΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΚΩΝ ΚΑ ΦΥΣΚΩΝ ΕΠΣΤΗΜΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2011-2012 ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2011-2012 ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ 1 ΗΜ/ΝΑ 1ο-2ο 3ο-4ο 5ο-6ο
ΕΘΝΚΟ ΜΕΤΣΟΒΟ ΠΟΛΥΤΕΧΝΕΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΚΩΝ ΚΑ ΦΥΣΚΩΝ ΕΠΣΤΗΜΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2011-2012 ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2011-2012 ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ 1 ΗΜ/ΝΑ 1ο-2ο 3ο-4ο 5ο-6ο
Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α
 Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2017
 ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2017 Εισαγωγή στο Μάθημα Μηχανική των Υλικών Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr Εισαγωγή/ Μηχανική Υλικών 1 Χρονοδιάγραμμα 2017 Φεβρουάριος
ΜΗΧΑΝΙΚΗ ΤΩΝ ΥΛΙΚΩΝ 2017 Εισαγωγή στο Μάθημα Μηχανική των Υλικών Κώστας Γαλιώτης, καθηγητής Τμήμα Χημικών Μηχανικών galiotis@chemeng.upatras.gr Εισαγωγή/ Μηχανική Υλικών 1 Χρονοδιάγραμμα 2017 Φεβρουάριος
Εργαστηριακή Άσκηση 4 Προσδιορισμός του μέτρου στρέψης υλικού με τη μέθοδο του στροφικού εκκρεμούς.
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Όνομα : Κάραλης Νικόλας Α/Μ: 09104042 Εργαστηριακή Άσκηση 4 Προσδιορισμός του μέτρου στρέψης υλικού με τη μέθοδο του στροφικού
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Όνομα : Κάραλης Νικόλας Α/Μ: 09104042 Εργαστηριακή Άσκηση 4 Προσδιορισμός του μέτρου στρέψης υλικού με τη μέθοδο του στροφικού
ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΣΕΠΤΕΜΒΡΙΟΥ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ
 ΠΑΡΑΣΚΕΥΗ 2/9/2016 ΠΕΜΠΤΗ 1/9/2016 ΤΕΤΑΡΤΗ 31/8/2016 ΤΡΙΤΗ 30/8/2016 ΔΕΥΤΕΡΑ 29/8/2016 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΗΣ ΕΞΕΤΑΣΤΙΚΗΣ
ΠΑΡΑΣΚΕΥΗ 2/9/2016 ΠΕΜΠΤΗ 1/9/2016 ΤΕΤΑΡΤΗ 31/8/2016 ΤΡΙΤΗ 30/8/2016 ΔΕΥΤΕΡΑ 29/8/2016 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΗΣ ΕΞΕΤΑΣΤΙΚΗΣ
Όταν το ελατήριο έχει μάζα
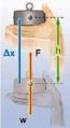 Όταν το ελατήριο έχει μάζα Εισαγωγή Αφορμή για την παρούσα ανάρτηση ήταν η θέση που διατύπωσε ο Γιάννης ο Κυριακόπουλος όσον αφορά στην συχνότητα ταλάντωσης ενός σώματος, το οποίο είναι δεμένο σε ελατήριο
Όταν το ελατήριο έχει μάζα Εισαγωγή Αφορμή για την παρούσα ανάρτηση ήταν η θέση που διατύπωσε ο Γιάννης ο Κυριακόπουλος όσον αφορά στην συχνότητα ταλάντωσης ενός σώματος, το οποίο είναι δεμένο σε ελατήριο
ΠΡΟΓΡΑΜΜΑ ΕΑΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ & ΕΠΙ ΠΤΥΧΙΩ ΧΕΙΜΕΡΙΝΑ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΕΑΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ & ΕΠΙ ΠΤΥΧΙΩ ΧΕΙΜΕΡΙΝΑ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2017-18 1η ΚΟΡΜΟΥ ΜΑΘΗΜΑΤΙΚΟΥ ΦΥΣΙΚΟΥ ΜΑΘΗΜΑΤΙΚΟΥ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΕΑΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ & ΕΠΙ ΠΤΥΧΙΩ ΧΕΙΜΕΡΙΝΑ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2017-18 1η ΚΟΡΜΟΥ ΜΑΘΗΜΑΤΙΚΟΥ ΦΥΣΙΚΟΥ ΜΑΘΗΜΑΤΙΚΟΥ
ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔ. ΕΤΟΥΣ ΗΜ/ΝΙΑ ΩΡΑ 1ο/2ο ΩΡΑ 3ο/4ο ΩΡΑ 5ο/6ο ΩΡΑ 7ο/8ο ΩΡΑ 9ο ΔΕΥΤΕΡΑ 27/8/
 27/8/2018 Μηχανική του Στερεού Σώματος Γκ. ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔ. ΕΤΟΥΣ 2017-18 15.00 Κατασκευή Οδών 18.00 Προεντεταμένο Σκυρόδεμα 18.00 Πειραματική Υδραυλική 28/8/2018 29/8/2018 Λογισμός
27/8/2018 Μηχανική του Στερεού Σώματος Γκ. ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔ. ΕΤΟΥΣ 2017-18 15.00 Κατασκευή Οδών 18.00 Προεντεταμένο Σκυρόδεμα 18.00 Πειραματική Υδραυλική 28/8/2018 29/8/2018 Λογισμός
ΔΗΛΩΣΗ ΥΠΟΧΡΕΩΤΙΚΩΝ ΚΑΙ ΚΑΤ ΕΠΙΛΟΓΗΝ ΜΑΘΗΜΑΤΩΝ ΤΟΥ ΑΚΑΔΗΜΑΪΚΟΥ ΈΤΟΥΣ (για τους φοιτητές με έτος εισαγωγής 1999 και παλαιότερα)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΔΗΛΩΣΗ ΥΠΟΧΡΕΩΤΙΚΩΝ ΚΑΙ ΚΑΤ ΕΠΙΛΟΓΗΝ ΜΑΘΗΜΑΤΩΝ ΤΟΥ ΑΚΑΔΗΜΑΪΚΟΥ ΈΤΟΥΣ 2015-2016 (για τους φοιτητές με έτος εισαγωγής 1999 και παλαιότερα) ΕΠΩΝΥΜΟ: ΑΡΙΘΜ. ΜΗΤΡΩΟΥ:....
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΔΗΛΩΣΗ ΥΠΟΧΡΕΩΤΙΚΩΝ ΚΑΙ ΚΑΤ ΕΠΙΛΟΓΗΝ ΜΑΘΗΜΑΤΩΝ ΤΟΥ ΑΚΑΔΗΜΑΪΚΟΥ ΈΤΟΥΣ 2015-2016 (για τους φοιτητές με έτος εισαγωγής 1999 και παλαιότερα) ΕΠΩΝΥΜΟ: ΑΡΙΘΜ. ΜΗΤΡΩΟΥ:....
Ασκήσεις στη συνέχεια συναρτήσεων. τέτοια ώστε. lim. και
 Ασκήσεις στη συνέχεια συναρτήσεων Άσκηση η Να βρεθούν τα ολικά ακρότατα των συναρτήσεων ) x, 0, ) x x a x x x, x x x x Άσκηση η Αν : a, συνεχής στο, τέτοια ώστε x x και x x Να αποδείξετε ότι η συνάρτηση
Ασκήσεις στη συνέχεια συναρτήσεων Άσκηση η Να βρεθούν τα ολικά ακρότατα των συναρτήσεων ) x, 0, ) x x a x x x, x x x x Άσκηση η Αν : a, συνεχής στο, τέτοια ώστε x x και x x Να αποδείξετε ότι η συνάρτηση
ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΣΕΠΤΕΜΒΡΙΟΥ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ
 1ο-2ο 3ο-4ο ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ 5ο-6ο 7ο-8ο 9ο ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΣΕΠΤΕΜΒΡΙΟΥ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-17 1η 1o - 2ο 3o - 4ο
1ο-2ο 3ο-4ο ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ 5ο-6ο 7ο-8ο 9ο ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΣΕΠΤΕΜΒΡΙΟΥ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-17 1η 1o - 2ο 3o - 4ο
ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΣΕΠΤΕΜΒΡΙΟΥ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2014-15 (ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ 2)
 ΠΑΡΑΣΚΕΥΗ 4/9/2015 ΠΕΜΠΤΗ 3/9/2015 ΤΕΤΑΡΤΗ 2/9/2015 ΤΡΙΤΗ 1/9/2015 ΔΕΥΤΕΡΑ 31/8/2015 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΗΣ ΕΞΕΤΑΣΤΙΚΗΣ
ΠΑΡΑΣΚΕΥΗ 4/9/2015 ΠΕΜΠΤΗ 3/9/2015 ΤΕΤΑΡΤΗ 2/9/2015 ΤΡΙΤΗ 1/9/2015 ΔΕΥΤΕΡΑ 31/8/2015 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΗΣ ΕΞΕΤΑΣΤΙΚΗΣ
( s ) Παραγώγιση στο χρόνο. Ολοκλήρωση στο χρόνο. Θεώρηµα αρχικής και τελικής τιµής Ο ΜΟΝΟΠΛΕΥΡΟΣ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE. Σεραφείµ Καραµπογιάς
 Ο ΜΟΝΟΠΛΕΥΡΟΣ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ APACE Παραγώγιση στο χρόνο d x( ) sx ( s ) x ( ) [ x ) ] X X x( ) e ( s Μετασχηµατισµός aplace παραγώγου dx ( ) sx Ολοκλήρωση στο χρόνο Μετασχηµατισµός aplace ολοκληρώµατος
Ο ΜΟΝΟΠΛΕΥΡΟΣ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ APACE Παραγώγιση στο χρόνο d x( ) sx ( s ) x ( ) [ x ) ] X X x( ) e ( s Μετασχηµατισµός aplace παραγώγου dx ( ) sx Ολοκλήρωση στο χρόνο Μετασχηµατισµός aplace ολοκληρώµατος
Περιεχόµενα. 0.1 Υλη του Μαθήµατος : Συγγράµµατα, Βιβλιογραϕία... 4
 Περιεχόµενα 0.1 Υλη του Μαθήµατος :.................................... 1 0.2 Συγγράµµατα, Βιβλιογραϕία................................ 4 1 Βασικές Εννοιες 6 1.1 Εισαγωγικές-Θεµελιώδεις Εννοιες.............................
Περιεχόµενα 0.1 Υλη του Μαθήµατος :.................................... 1 0.2 Συγγράµµατα, Βιβλιογραϕία................................ 4 1 Βασικές Εννοιες 6 1.1 Εισαγωγικές-Θεµελιώδεις Εννοιες.............................
Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΧΑΡΑΛΑΜΠΟΠΟΥΛΟΣ ΑΝΤΩΝΙΟΣ, ΓΡΗΓΟΡΙΟΣ. Ακ. έτος Χειμερινό εξάμηνο
 Ακ. έτος 214-215 Χειμερινό εξάμηνο Page 1 of 17 Ακ. έτος 214-215 Χειμερινό εξάμηνο ΕΝΟΤΗΤΑ: Μάθημα Ερώτηση Πλήθος απαντήσεων Διάμεσος Μέσος Όρος Τυπική απόκλιση Ελάχιστη Μέγιστη Οι στόχοι του μαθήματος
Ακ. έτος 214-215 Χειμερινό εξάμηνο Page 1 of 17 Ακ. έτος 214-215 Χειμερινό εξάμηνο ΕΝΟΤΗΤΑ: Μάθημα Ερώτηση Πλήθος απαντήσεων Διάμεσος Μέσος Όρος Τυπική απόκλιση Ελάχιστη Μέγιστη Οι στόχοι του μαθήματος
Δυναμική Μηχανών I. Διάλεξη 20. Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ
 Δυναμική Μηχανών I Διάλεξη 2 Χειμερινό Εξάμηνο 213 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ 1 Ανακοινώσεις Εξέταση Μαθήματος: 1/4/214, 12. Απαιτείται αποδεικτικό ταυτότητας Απαγορεύεται η παρουσία & χρήση κινητού!
Δυναμική Μηχανών I Διάλεξη 2 Χειμερινό Εξάμηνο 213 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ 1 Ανακοινώσεις Εξέταση Μαθήματος: 1/4/214, 12. Απαιτείται αποδεικτικό ταυτότητας Απαγορεύεται η παρουσία & χρήση κινητού!
ΠΡΟΓΡΑΜΜΑ ΤΜΗΜΑΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟΔΟΥ ΙΑΝΟΥΑΡΙΟΥ - ΦΕΒΡΟΥΑΡΙΟΥ ου ΕΞΑΜΗΝΟΥ ΣΠΟΥΔΩΝ ( Μόνο για φοιτητές 6 ου έτους και ανωτέρω)
 ΣΧΟΛΗ ΠΟΛΥΤΕΧΝΙΚΗ 2ου ΕΞΑΜΗΝΟΥ ΣΠΟΥΔΩΝ 11-1-2010 ΔΕΥΤΕΡΑ 12-15 ΑΠΜ2,ΑΠΜ3 Γεωλογία για Πολιτικούς Μηχανικούς Παπαντωνόπουλος - Χρυσικός 14-1-2010 ΠΕΜΠΤΗ 15-18 ΑΠΜ2,ΑΠΜ3 Προγραμματισμός και Εφαρμογές Η/Υ
ΣΧΟΛΗ ΠΟΛΥΤΕΧΝΙΚΗ 2ου ΕΞΑΜΗΝΟΥ ΣΠΟΥΔΩΝ 11-1-2010 ΔΕΥΤΕΡΑ 12-15 ΑΠΜ2,ΑΠΜ3 Γεωλογία για Πολιτικούς Μηχανικούς Παπαντωνόπουλος - Χρυσικός 14-1-2010 ΠΕΜΠΤΗ 15-18 ΑΠΜ2,ΑΠΜ3 Προγραμματισμός και Εφαρμογές Η/Υ
ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΕΩΝ ΕΑΡΙΝΩΝ-ΧΕΙΜΕΡΙΝΩΝ ΕΞΑΜΗΝΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ
 ΕΘΝΚΟ ΜΕΤΣΟΒΟ ΠΟΛΥΤΕΧΝΕΟ ΣΧΟΛΗ ΕΦ ΑΡΜ ΟΣΜ ΕΝΩΝ Μ ΑΘΗΜ ΑΤΚΩΝ ΚΑ Φ ΥΣΚΩΝ ΕΠΣΤΗΜ ΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 3-4 ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΕΩΝ ΕΑΡΝΩΝ-ΧΕΜΕΡΝΩΝ ΕΞΑΜΗΝΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 3-4 ΗΜ/ΝΑ 1ο-2ο 3ο-4ο 5ο-6ο 5ο-6ο Μαθηματικού
ΕΘΝΚΟ ΜΕΤΣΟΒΟ ΠΟΛΥΤΕΧΝΕΟ ΣΧΟΛΗ ΕΦ ΑΡΜ ΟΣΜ ΕΝΩΝ Μ ΑΘΗΜ ΑΤΚΩΝ ΚΑ Φ ΥΣΚΩΝ ΕΠΣΤΗΜ ΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 3-4 ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΕΩΝ ΕΑΡΝΩΝ-ΧΕΜΕΡΝΩΝ ΕΞΑΜΗΝΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 3-4 ΗΜ/ΝΑ 1ο-2ο 3ο-4ο 5ο-6ο 5ο-6ο Μαθηματικού
2ο ΕΞΑΜΗΝΟ ΩΡΕΣ ΔΕΥΤΕΡΑ ΤΡΙΤΗ ΤΕΤΑΡΤΗ ΠΕΜΠΤΗ ΠΑΡΑΣΚΕΥΗ ΩΡΕΣ. Τεχνική Μηχανική Ι ΓιαννακόπουλοςΑ (A)
 2ο ΕΞΑΜΗΝΟ 9-10 Τεχνική Μηχανική Ι 9-10 Γιαννακόπουλος Α (A) Τεχνική Μηχανική Ι ΓιαννακόπουλοςΑ (A) 12-13 Αγγλικά 12-13 Πιθανότητες Στατιστική Σπηλιωτόπουλος Μ. (A2) Τσουτσουλοπούλου Μ. Φυσική ΙΙ Καρακασίδης
2ο ΕΞΑΜΗΝΟ 9-10 Τεχνική Μηχανική Ι 9-10 Γιαννακόπουλος Α (A) Τεχνική Μηχανική Ι ΓιαννακόπουλοςΑ (A) 12-13 Αγγλικά 12-13 Πιθανότητες Στατιστική Σπηλιωτόπουλος Μ. (A2) Τσουτσουλοπούλου Μ. Φυσική ΙΙ Καρακασίδης
10 ΣΥΝΗΘΕΙΣ ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ
 SECTION 0 ΣΥΝΗΘΕΙΣ ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ 0. Ορισµοί Συνήθης διαφορική εξίσωση (Σ Ε) καλείται µια εξίσωση της µορφής f [y (n), y (n ),..., y'', y', y, x] 0 όπου y', y'',..., y (n ), y (n) είναι οι παράγωγοι
SECTION 0 ΣΥΝΗΘΕΙΣ ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ 0. Ορισµοί Συνήθης διαφορική εξίσωση (Σ Ε) καλείται µια εξίσωση της µορφής f [y (n), y (n ),..., y'', y', y, x] 0 όπου y', y'',..., y (n ), y (n) είναι οι παράγωγοι
Δυναμική και Έλεγχος E-L Ηλεκτρομηχανικών Συστημάτων
 Δυναμική και Έλεγχος E-L Ηλεκτρομηχανικών Συστημάτων Ενότητα 3: Παραδείγματα Περιγραφής Δυναμικών Συστημάτων I Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας
Δυναμική και Έλεγχος E-L Ηλεκτρομηχανικών Συστημάτων Ενότητα 3: Παραδείγματα Περιγραφής Δυναμικών Συστημάτων I Καθηγητής Αντώνιος Αλεξανδρίδης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας
ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΣΕΠΤΕΜΒΡΙΟΥ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ ( )
 ΠΑΡΑΣΚΕΥΗ 4/9/2015 ΠΕΜΠΤΗ 3/9/2015 ΤΕΤΑΡΤΗ 2/9/2015 ΤΡΙΤΗ 1/9/2015 ΔΕΥΤΕΡΑ 31/8/2015 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΗΣ ΕΞΕΤΑΣΤΙΚΗΣ
ΠΑΡΑΣΚΕΥΗ 4/9/2015 ΠΕΜΠΤΗ 3/9/2015 ΤΕΤΑΡΤΗ 2/9/2015 ΤΡΙΤΗ 1/9/2015 ΔΕΥΤΕΡΑ 31/8/2015 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΗΣ ΕΞΕΤΑΣΤΙΚΗΣ
ΠΡΟΓΡΑΜΜΑ ΧΕΙΜΕΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ - ΕΠΙ ΠΤΥΧΙΩ ΕΞΕΤΑΣΤΙΚΗ ΕΑΡΙΝΩΝ ΜΑΘΗΜΑΤΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ 1
 ΠΑΡΑΣΚΕΥΗ 22/1/2016 ΠΕΜΠΤΗ 21/1/201 ΤΕΤΑΡΤΗ 20/1/2016 ΤΡΙΤΗ 19/1/2016 ΔΕΥΤΕΡΑ 18/1/201 ΠΡΟΓΡΑΜΜΑ ΧΕΙΜΕΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ - ΕΠΙ ΠΤΥΧΙΩ ΕΞΕΤΑΣΤΙΚΗ ΕΑΡΙΝΩΝ ΜΑΘΗΜΑΤΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2015-16 ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ
ΠΑΡΑΣΚΕΥΗ 22/1/2016 ΠΕΜΠΤΗ 21/1/201 ΤΕΤΑΡΤΗ 20/1/2016 ΤΡΙΤΗ 19/1/2016 ΔΕΥΤΕΡΑ 18/1/201 ΠΡΟΓΡΑΜΜΑ ΧΕΙΜΕΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ - ΕΠΙ ΠΤΥΧΙΩ ΕΞΕΤΑΣΤΙΚΗ ΕΑΡΙΝΩΝ ΜΑΘΗΜΑΤΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2015-16 ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ
ΠΠΜ 220: Στατική Ανάλυση Κατασκευών Ι
 Πανεπιστήµιο Κύπρου Πολυτεχνική Σχολή Τµήµα Πολιτικών Μηχανικών και Μηχανικών Περιβάλλοντος Γενικές οδηγίες: Ακαδηµαϊκό Έτος 2004 Χειµερινό Εξάµηνο ΠΠΜ 220: Στατική Ανάλυση Κατασκευών Ι 3 η Σειρά Ασκήσεων
Πανεπιστήµιο Κύπρου Πολυτεχνική Σχολή Τµήµα Πολιτικών Μηχανικών και Μηχανικών Περιβάλλοντος Γενικές οδηγίες: Ακαδηµαϊκό Έτος 2004 Χειµερινό Εξάµηνο ΠΠΜ 220: Στατική Ανάλυση Κατασκευών Ι 3 η Σειρά Ασκήσεων
Δυναμική Μηχανών I. Σύνοψη Εξεταστέας Ύλης
 Δυναμική Μηχανών I 9 1 Σύνοψη Εξεταστέας Ύλης 2015 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com Απαγορεύεται οποιαδήποτε αναπαραγωγή χωρίς άδεια Ύλη Δυναμικής Μηχανών
Δυναμική Μηχανών I 9 1 Σύνοψη Εξεταστέας Ύλης 2015 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com Απαγορεύεται οποιαδήποτε αναπαραγωγή χωρίς άδεια Ύλη Δυναμικής Μηχανών
ΠΡΟΤΑΣΗ ΝΕΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΣΠΟΥ ΩΝ
 ΕΠΙΤΡΟΠΗ ΠΡΟΓΡΑΜΜΑΤΟΣ ΣΠΟΥ ΩΝ ΤΜΗΜΑΤΟΣ ΦΥΣΙΚΗΣ Α.Π.Θ. 2010-2011 ΠΡΟΤΑΣΗ ΝΕΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΣΠΟΥ ΩΝ Εισαγωγικά: Το σχέδιο περιλαµβάνει τον προτεινόµενο κατάλογο υποχρεωτικών µαθηµάτων µε τις αντίστοιχες
ΕΠΙΤΡΟΠΗ ΠΡΟΓΡΑΜΜΑΤΟΣ ΣΠΟΥ ΩΝ ΤΜΗΜΑΤΟΣ ΦΥΣΙΚΗΣ Α.Π.Θ. 2010-2011 ΠΡΟΤΑΣΗ ΝΕΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΣΠΟΥ ΩΝ Εισαγωγικά: Το σχέδιο περιλαµβάνει τον προτεινόµενο κατάλογο υποχρεωτικών µαθηµάτων µε τις αντίστοιχες
2ο ΕΞΑΜΗΝΟ ΩΡΕΣ ΔΕΥΤΕΡΑ ΤΡΙΤΗ ΤΕΤΑΡΤΗ ΠΕΜΠΤΗ ΠΑΡΑΣΚΕΥΗ ΩΡΕΣ. Τεχνική Μηχανική Ι ΓιαννακόπουλοςΑ (A)
 2ο ΕΞΑΜΗΝΟ 9-10 Τεχνική Μηχανική Ι 9-10 Αγγλικά Πιθανότητες Στατιστική Σπηλιωτόπουλος Μ. (A2) Γιαννακόπουλος Α Τσουτσουλοπούλου Μ. Φυσική ΙΙ Καρακασίδης Θ. 16-17 16-17 Απειροστικός Λογισμός ΙΙ Γραμμένος
2ο ΕΞΑΜΗΝΟ 9-10 Τεχνική Μηχανική Ι 9-10 Αγγλικά Πιθανότητες Στατιστική Σπηλιωτόπουλος Μ. (A2) Γιαννακόπουλος Α Τσουτσουλοπούλου Μ. Φυσική ΙΙ Καρακασίδης Θ. 16-17 16-17 Απειροστικός Λογισμός ΙΙ Γραμμένος
H διδασκαλία της Ανάλυσηs ΙΙ
 H διδασκαλία της Ανάλυσηs ΙΙ Λουκάς Βλάχος 0.75 0.25-0.25-0.75 11/2/2003-0.75 1 0.25-0.25-0.25 0.25 0.75 Θέµατα Τα εδοµένα Ποιος είναι ο σκοπός του µαθήµατος; Ερωτήσεις Μια πολύ συνηθισµένη διδακτική πρακτική
H διδασκαλία της Ανάλυσηs ΙΙ Λουκάς Βλάχος 0.75 0.25-0.25-0.75 11/2/2003-0.75 1 0.25-0.25-0.25 0.25 0.75 Θέµατα Τα εδοµένα Ποιος είναι ο σκοπός του µαθήµατος; Ερωτήσεις Μια πολύ συνηθισµένη διδακτική πρακτική
2ου ΕΞΑΜΗΝΟΥ ΣΠΟΥΔΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ 2ου ΕΞΑΜΗΝΟΥ ΣΠΟΥΔΩΝ 12-6-2017 ΔΕΥΤΕΡΑ 9-12 * Εφαρμοσμένα Μαθηματικά ΙΙ Περδίου 12-6-2017 ΔΕΥΤΕΡΑ 15-18 ΑΠΜ2,ΑΠΜ3 Αγγλικά & Τεχνική Ορολογία Ι ** Ατματζίδη 12-6-2017 ΔΕΥΤΕΡΑ 15-18 ΑΠΜ2,ΑΠΜ3
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ 2ου ΕΞΑΜΗΝΟΥ ΣΠΟΥΔΩΝ 12-6-2017 ΔΕΥΤΕΡΑ 9-12 * Εφαρμοσμένα Μαθηματικά ΙΙ Περδίου 12-6-2017 ΔΕΥΤΕΡΑ 15-18 ΑΠΜ2,ΑΠΜ3 Αγγλικά & Τεχνική Ορολογία Ι ** Ατματζίδη 12-6-2017 ΔΕΥΤΕΡΑ 15-18 ΑΠΜ2,ΑΠΜ3
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2013-2014
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 3-4 ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 3-4 ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ 3 ΗΜ/ΝΙΑ 1ο-2ο Φυσική Φυσικού
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 3-4 ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 3-4 ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ 3 ΗΜ/ΝΙΑ 1ο-2ο Φυσική Φυσικού
Δυναμική Μηχανών I. Προσέγγιση Galerkin
 Δυναμική Μηχανών I 8 2 Προσέγγιση Galerkin Χειμερινό Εξάμηνο 214 Τμήμα Μηχανολόγων Μηχανικών, ΕΜΠ Δημήτριος Τζεράνης, Ph.D. 215 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com
Δυναμική Μηχανών I 8 2 Προσέγγιση Galerkin Χειμερινό Εξάμηνο 214 Τμήμα Μηχανολόγων Μηχανικών, ΕΜΠ Δημήτριος Τζεράνης, Ph.D. 215 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com
ΔΥΝΑΜΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ- ΕΞΙΣΩΣΕΙΣ NAVIER STOKES
 ΔΥΝΑΜΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ- ΕΞΙΣΩΣΕΙΣ NAVIER STOKES ΙΣΟΡΡΟΠΙΑ ΔΥΝΑΜΕΩΝ ΣΕ ΕΝΑΝ ΑΠΕΙΡΟΣΤΟ ΟΓΚΟ ΡΕΥΣΤΟΥ Στο κεφάλαιο αυτό θα εξετάσουμε την ισορροπία των δυνάμεων οι οποίες ασκούνται σε ένα τυχόν σωματίδιο ρευστού.
ΔΥΝΑΜΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ- ΕΞΙΣΩΣΕΙΣ NAVIER STOKES ΙΣΟΡΡΟΠΙΑ ΔΥΝΑΜΕΩΝ ΣΕ ΕΝΑΝ ΑΠΕΙΡΟΣΤΟ ΟΓΚΟ ΡΕΥΣΤΟΥ Στο κεφάλαιο αυτό θα εξετάσουμε την ισορροπία των δυνάμεων οι οποίες ασκούνται σε ένα τυχόν σωματίδιο ρευστού.
ΠΡΟΓΡΑΜΜΑ ΕΑΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ & ΕΠΙ ΠΤΥΧΙΩ ΧΕΙΜΕΡΙΝΑ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ
 ΠΑΡΑΣΚΕΥΗ 24/5/2019 ΠΕΜΠΤΗ 23/5/2019 ΤΕΤΑΡΤΗ 22/5/2 ΤΡΙΤΗ 21/5/2019 ΔΕΥΤΕΡΑ 20/5/201 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΕΑΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ & ΕΠΙ
ΠΑΡΑΣΚΕΥΗ 24/5/2019 ΠΕΜΠΤΗ 23/5/2019 ΤΕΤΑΡΤΗ 22/5/2 ΤΡΙΤΗ 21/5/2019 ΔΕΥΤΕΡΑ 20/5/201 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ ΕΑΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ & ΕΠΙ
ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔ. ΕΤΟΥΣ ΗΜ/ΝΙΑ ΩΡΑ 1ο/2ο ΩΡΑ 3ο/4ο ΩΡΑ 5ο/6ο ΩΡΑ 7ο/8ο ΩΡΑ 9ο ΔΕΥΤΕΡΑ 26/8/2019
 ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔ. ΕΤΟΥΣ 2018-19 26/8/2019 Μηχανική του Στερεού Σώματος 12.00 Τεχνική Σεισμολογία 18.00 Προεντεταμένο Σκυρόδεμα 27/8/2019 28/8/2019 Αντοχή των Υλικών 12.00 Αντισεισμικός
ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔ. ΕΤΟΥΣ 2018-19 26/8/2019 Μηχανική του Στερεού Σώματος 12.00 Τεχνική Σεισμολογία 18.00 Προεντεταμένο Σκυρόδεμα 27/8/2019 28/8/2019 Αντοχή των Υλικών 12.00 Αντισεισμικός
ΠΡΟΓΡΑΜΜΑ ΧΕΙΜΕΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ - ΕΠΙ ΠΤΥΧΙΩ ΕΞΕΤΑΣΤΙΚΗ ΕΑΡΙΝΩΝ ΜΑΘΗΜΑΤΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ 2
 ΠΡΟΓΡΑΜΜΑ ΧΕΙΜΕΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ - ΕΠΙ ΠΤΥΧΙΩ ΕΞΕΤΑΣΤΙΚΗ ΕΑΡΙΝΩΝ ΜΑΘΗΜΑΤΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2015-16 ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ 2 1η 5ο-6ο 7ο-8ο 9ο ΔΕΥΤΕΡΑ 18/1/201 ΜΗΧΑΝΙΚΗ Ι (ΣΤΑΤΙΚΗ) ΑΜΦ.1,2,3,4 ΣΤΑΤΙΣΤΙΚΗ ΦΥΣΙΚΗ,
ΠΡΟΓΡΑΜΜΑ ΧΕΙΜΕΡΙΝΗΣ ΕΞΕΤΑΣΤΙΚΗΣ - ΕΠΙ ΠΤΥΧΙΩ ΕΞΕΤΑΣΤΙΚΗ ΕΑΡΙΝΩΝ ΜΑΘΗΜΑΤΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2015-16 ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ 2 1η 5ο-6ο 7ο-8ο 9ο ΔΕΥΤΕΡΑ 18/1/201 ΜΗΧΑΝΙΚΗ Ι (ΣΤΑΤΙΚΗ) ΑΜΦ.1,2,3,4 ΣΤΑΤΙΣΤΙΚΗ ΦΥΣΙΚΗ,
= R {x συν x = 0} ισχύει: 1 ( εφ x)' = συν
 ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Α Α. Έστω μια συνάρτηση f ορισμένη σε ένα διάστημα Δ και ένα εσωτερικό σημείο
ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Α Α. Έστω μια συνάρτηση f ορισμένη σε ένα διάστημα Δ και ένα εσωτερικό σημείο
( ) ( ) ( ) Ασκήσεις στην ελαστική γραµµή. Γενικές Εξισώσεις. Εφαρµογές. 1. Η γέφυρα. ΤΜ ΙΙΙ Ασκήσεις : Ι. Βαρδουλάκης & Ι. Στεφάνου, Οκτώβριος
 ΤΜ ΙΙΙ Ασκήσεις : Ι. Βαρδουλάκης & Ι. Στεφάνου, Οκτώβριος 005 Ασκήσεις στην ελαστική γραµµή Γενικές Εξισώσεις () p w ( x) = x+ M ( x) = w ( x) p w ( ) ( ) ( ) ( ) ( x) = x + x+ onst x p x onst x dm x =
ΤΜ ΙΙΙ Ασκήσεις : Ι. Βαρδουλάκης & Ι. Στεφάνου, Οκτώβριος 005 Ασκήσεις στην ελαστική γραµµή Γενικές Εξισώσεις () p w ( x) = x+ M ( x) = w ( x) p w ( ) ( ) ( ) ( ) ( x) = x + x+ onst x p x onst x dm x =
ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔ. ΕΤΟΥΣ ΗΜ/ΝΙΑ ΩΡΑ 1ο/2ο ΩΡΑ 3ο/4ο ΩΡΑ 5ο/6ο ΩΡΑ 7ο/8ο ΩΡΑ 9ο ΔΕΥΤΕΡΑ 27/8/2018
 27/8/2018 8.30 Μηχανική του Στερεού Σώματος ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔ. ΕΤΟΥΣ 2017-18 12.00 Τεχνική Σεισμολογία 18.00 Προεντεταμένο Σκυρόδεμα 18.00 Πειραματική Υδραυλική 28/8/2018 29/8/2018
27/8/2018 8.30 Μηχανική του Στερεού Σώματος ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔ. ΕΤΟΥΣ 2017-18 12.00 Τεχνική Σεισμολογία 18.00 Προεντεταμένο Σκυρόδεμα 18.00 Πειραματική Υδραυλική 28/8/2018 29/8/2018
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ A N A K O I N Ω Σ Η
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ Θεσσαλονίκη 10/2/2016 A N A K O I N Ω Σ Η Τα μαθήματα του Προπτυχιακού Προγράμματος Σπουδών στο Τμήμα Μαθηματικών για το
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ Θεσσαλονίκη 10/2/2016 A N A K O I N Ω Σ Η Τα μαθήματα του Προπτυχιακού Προγράμματος Σπουδών στο Τμήμα Μαθηματικών για το
S dt T V. Επιμέλεια - Υπολογισμοί: Κ. Παπαμιχάλης Δρ. Φυσικής
 Μελέτη της κίνησης μηχανικού ταλαντωτή που προκαλεί διάδοση ελαστικού κύματος σε μονοδιάστατο ελαστικό μέσο Επιμέλεια - Υπολογισμοί: Κ. Παπαμιχάλης Δρ. Φυσικής Κεντρική ιδέα Στην εργασία αυτή, γίνεται
Μελέτη της κίνησης μηχανικού ταλαντωτή που προκαλεί διάδοση ελαστικού κύματος σε μονοδιάστατο ελαστικό μέσο Επιμέλεια - Υπολογισμοί: Κ. Παπαμιχάλης Δρ. Φυσικής Κεντρική ιδέα Στην εργασία αυτή, γίνεται
Ερωτήσεις αντιστοίχισης
 Ερωτήσεις αντιστοίχισης. * Να συµπληρώσετε τον πίνακα ΙΙ, έτσι ώστε σε κάθε γραφική παράσταση συνάρτησης f της στήλης Α του πίνακα Ι να αντιστοιχεί η γραφική παράσταση της παράγουσάς της από τη στήλη Β.
Ερωτήσεις αντιστοίχισης. * Να συµπληρώσετε τον πίνακα ΙΙ, έτσι ώστε σε κάθε γραφική παράσταση συνάρτησης f της στήλης Α του πίνακα Ι να αντιστοιχεί η γραφική παράσταση της παράγουσάς της από τη στήλη Β.
5 ου & 6 ου ΕΞΑΜΗΝΟΥ. 8:30 Δυναμική Ναυπηγικών Κατασκευών Κτ. Δ. Αιθ. 105, 106, 201, 202, 209
 ΣΧΟΛΗ ΝΑΥΠΗΓΩΝ ΠΕΡΙΟΔΟΣ Μεταφορικές & Ανυψωτικές Μηχανές Α, Δ, Ζ. 1 27.08.2012 Τεχνολογική Α, Δ, Ζ. Δυναμική Ναυπηγικών μ.μ. Φιλοσοφία της Επιστήμης 106 μ.μ. Θεωρία της Γνώσης στη Νεότερη & Σύγχρονη Φιλοσοφία
ΣΧΟΛΗ ΝΑΥΠΗΓΩΝ ΠΕΡΙΟΔΟΣ Μεταφορικές & Ανυψωτικές Μηχανές Α, Δ, Ζ. 1 27.08.2012 Τεχνολογική Α, Δ, Ζ. Δυναμική Ναυπηγικών μ.μ. Φιλοσοφία της Επιστήμης 106 μ.μ. Θεωρία της Γνώσης στη Νεότερη & Σύγχρονη Φιλοσοφία
ΚΑΤΑΝΟΜΕΣ Ι ΙΑΣΤΑΤΩΝ ΤΥΧΑΙΩΝ ΜΕΤΑΒΛΗΤΩΝ (Συνέχεια)
 ΚΑΤΑΝΟΜΕΣ Ι ΙΑΣΤΑΤΩΝ ΤΥΧΑΙΩΝ ΜΕΤΑΒΛΗΤΩΝ (Συνέχεια) Χαράλαµπος Α. Χαραλαµπίδης 11 Ιανουαρίου 21 Η δεσµευµένη µέση τιµή µιας τυχαίας µεταβλητής Y σε δεδοµένο σηµείο µιας άλλης τυχαίας µεταϐλητής X = x, συµϐολιϲόµενη
ΚΑΤΑΝΟΜΕΣ Ι ΙΑΣΤΑΤΩΝ ΤΥΧΑΙΩΝ ΜΕΤΑΒΛΗΤΩΝ (Συνέχεια) Χαράλαµπος Α. Χαραλαµπίδης 11 Ιανουαρίου 21 Η δεσµευµένη µέση τιµή µιας τυχαίας µεταβλητής Y σε δεδοµένο σηµείο µιας άλλης τυχαίας µεταϐλητής X = x, συµϐολιϲόµενη
ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔ. ΕΤΟΥΣ ΗΜ/ΝΙΑ ΩΡΑ 1ο/2ο ΩΡΑ 3ο/4ο ΩΡΑ 5ο/6ο ΩΡΑ 7ο/8ο ΩΡΑ 9ο
 27/8/2018 28/8/2018 29/8/2018 8.30 Μηχανική του Στερεού Σώματος Ζ. 8.30 Τεχνικά Υλικά Ι Ζ. ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔ. ΕΤΟΥΣ 2017-18 8.30 Αντοχή των Υλικών Ζ. 12, 15.00 Κατασκευή Οδών Ζ. 1,3,7,4,2
27/8/2018 28/8/2018 29/8/2018 8.30 Μηχανική του Στερεού Σώματος Ζ. 8.30 Τεχνικά Υλικά Ι Ζ. ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔ. ΕΤΟΥΣ 2017-18 8.30 Αντοχή των Υλικών Ζ. 12, 15.00 Κατασκευή Οδών Ζ. 1,3,7,4,2
ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔ. ΕΤΟΥΣ ΗΜ/ΝΙΑ ΩΡΑ 1ο ΩΡΑ 2o ΩΡΑ 3o ΩΡΑ 4ο ΩΡΑ 5o ΩΡΑ 6ο ΩΡΑ 7o ΩΡΑ 8o ΩΡΑ 9ο ΔΕΥΤΕΡΑ 26/8/2019
 ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔ. ΕΤΟΥΣ 2018-19 26/8/2019 Μηχανική του Στερεού Σώματος Θαλάσσια Υδραυλική και Λιμενικά Έργα 27/8/2019 Γεωδαισία Ειδικά Θέματα Λιμενικών Έργων (Ζ) 28/8/2019 Γενική
ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔ. ΕΤΟΥΣ 2018-19 26/8/2019 Μηχανική του Στερεού Σώματος Θαλάσσια Υδραυλική και Λιμενικά Έργα 27/8/2019 Γεωδαισία Ειδικά Θέματα Λιμενικών Έργων (Ζ) 28/8/2019 Γενική
ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔ. ΕΤΟΥΣ ΗΜ/ΝΙΑ ΩΡΑ 1ο ΩΡΑ 2o ΩΡΑ 3o ΩΡΑ 4ο ΩΡΑ 5o ΩΡΑ 6ο ΩΡΑ 7o ΩΡΑ 8o ΩΡΑ 9ο ΔΕΥΤΕΡΑ 26/8/2019
 ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔ. ΕΤΟΥΣ 2018-19 26/8/2019 Μηχανική του Στερεού Σώματος 15.00 Εδαφομηχανική ΙΙ Θαλάσσια Υδραυλική και Λιμενικά Έργα Προεντεταμένο Σκυρόδεμα 27/8/2019 Αντοχή των Υλικών
ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔ. ΕΤΟΥΣ 2018-19 26/8/2019 Μηχανική του Στερεού Σώματος 15.00 Εδαφομηχανική ΙΙ Θαλάσσια Υδραυλική και Λιμενικά Έργα Προεντεταμένο Σκυρόδεμα 27/8/2019 Αντοχή των Υλικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΑΚΑΔ. ΕΤΟΣ ΑΝΩΤΑΤΗ ΣΧΟΛΗ ΠΑΙΔΑΓΩΓΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ. Ακριβές Απόσπασμα Πρακτικού Σ.
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΑΚΑΔ. ΕΤΟΣ 2017-18 ΑΝΩΤΑΤΗ ΣΧΟΛΗ ΠΑΙΔΑΓΩΓΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Α.Σ.ΠΑΙ.Τ.Ε. ΕΔΡΑ: ΑΜΑΡΟΥΣΙΟ (ΣΤΑΘΜΟΣ «ΕΙΡΗΝΗ» ΗΣΑΠ) ΤΑΧ. Δ/ΝΣΗ: ΗΡΑΚΛΕΙΟ ΑΤΤΙΚΗΣ Τ.Κ. 141 21 ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΑΚΑΔ. ΕΤΟΣ 2017-18 ΑΝΩΤΑΤΗ ΣΧΟΛΗ ΠΑΙΔΑΓΩΓΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Α.Σ.ΠΑΙ.Τ.Ε. ΕΔΡΑ: ΑΜΑΡΟΥΣΙΟ (ΣΤΑΘΜΟΣ «ΕΙΡΗΝΗ» ΗΣΑΠ) ΤΑΧ. Δ/ΝΣΗ: ΗΡΑΚΛΕΙΟ ΑΤΤΙΚΗΣ Τ.Κ. 141 21 ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ
Γράφημα της συνάρτησης = (δηλ. της περιττής περιοδικής επέκτασης της f = f( x), 0 x p στο R )
 Γράφημα της συνάρτησης f( x), αν p x< 0 F( x) = f( x), αν 0 x p και F( x+ 2 p) = F( x), x R (δηλ. της περιττής περιοδικής επέκτασης της f = f( x), 0 x p στο R ) ΠΡΟΛΟΓΟΣ Το Βιβλίο αυτό απευθύνεται στους
Γράφημα της συνάρτησης f( x), αν p x< 0 F( x) = f( x), αν 0 x p και F( x+ 2 p) = F( x), x R (δηλ. της περιττής περιοδικής επέκτασης της f = f( x), 0 x p στο R ) ΠΡΟΛΟΓΟΣ Το Βιβλίο αυτό απευθύνεται στους
Αποτίµηση εκπαιδευτικού έργου
 Τ Μ Η Μ Α Φ Υ Σ Ι Κ Η Σ ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ Αποτίµηση εκπαιδευτικού έργου Εαρινό εξάµηνο 27-2 Ι ΑΣΚΩΝ: ΠΕΡΙΒΟΛΑΡΟΠΟΥΛΟΣ Λ. ΜΑΘΗΜΑ: ΗΛΕΚΤΡΟ ΥΝΑΜΙΚΗ ΙΙ ΠΕΡΙΕΧΟΜΕΝΑ Α. Αξιολόγηση διδασκαλίας Α1 Β. Αξιολόγηση
Τ Μ Η Μ Α Φ Υ Σ Ι Κ Η Σ ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ Αποτίµηση εκπαιδευτικού έργου Εαρινό εξάµηνο 27-2 Ι ΑΣΚΩΝ: ΠΕΡΙΒΟΛΑΡΟΠΟΥΛΟΣ Λ. ΜΑΘΗΜΑ: ΗΛΕΚΤΡΟ ΥΝΑΜΙΚΗ ΙΙ ΠΕΡΙΕΧΟΜΕΝΑ Α. Αξιολόγηση διδασκαλίας Α1 Β. Αξιολόγηση
ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔ. ΕΤΟΥΣ ΗΜ/ΝΙΑ ΩΡΑ 1ο ΩΡΑ 2o ΩΡΑ 3o ΩΡΑ 4ο ΩΡΑ 5o ΩΡΑ 6ο ΩΡΑ 7o ΩΡΑ 8o ΩΡΑ 9ο ΔΕΥΤΕΡΑ 26/8/2019
 ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔ. ΕΤΟΥΣ 2018-19 26/8/2019 Μηχανική του Στερεού Σώματος 2, 11, 13, 15, 17, 12, Αμφ. 1/2 (557) Θαλάσσια Υδραυλική και Λιμενικά Έργα Ζ. Αιθ. 1, 7, 17, 12, Αμφ. 1/2 (382)
ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔ. ΕΤΟΥΣ 2018-19 26/8/2019 Μηχανική του Στερεού Σώματος 2, 11, 13, 15, 17, 12, Αμφ. 1/2 (557) Θαλάσσια Υδραυλική και Λιμενικά Έργα Ζ. Αιθ. 1, 7, 17, 12, Αμφ. 1/2 (382)
ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΕΩΝ ΧΕΙΜΕΡΙΝΩΝ ΕΞΑΜΗΝΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦ ΑΡΜ ΟΣΜ ΕΝΩΝ Μ ΑΘΗΜ ΑΤΙΚΩΝ ΚΑΙ Φ ΥΣΙΚΩΝ ΕΠΙΣΤΗΜ ΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2012-201 ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΕΩΝ ΧΕΙΜΕΡΙΝΩΝ ΕΞΑΜΗΝΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2012-201 ΗΜ/ΝΙΑ 1ο ο 5ο (κατ.
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦ ΑΡΜ ΟΣΜ ΕΝΩΝ Μ ΑΘΗΜ ΑΤΙΚΩΝ ΚΑΙ Φ ΥΣΙΚΩΝ ΕΠΙΣΤΗΜ ΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2012-201 ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΕΩΝ ΧΕΙΜΕΡΙΝΩΝ ΕΞΑΜΗΝΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2012-201 ΗΜ/ΝΙΑ 1ο ο 5ο (κατ.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ A N A K O I N Ω Σ Η
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ Θεσσαλονίκη 1-2013 A N A K O I N Ω Σ Η Τα μαθήματα του Προπτυχιακού Προγράμματος Σπουδών στο Τμήμα Μαθηματικών για το εαρινό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ Θεσσαλονίκη 1-2013 A N A K O I N Ω Σ Η Τα μαθήματα του Προπτυχιακού Προγράμματος Σπουδών στο Τμήμα Μαθηματικών για το εαρινό
4. Δίνεται το πολυώνυμο P(x) = x 3 2x 2 + x 12 α) Να αιτιολογήσετε γιατί το διώνυμο x 3 είναι παράγοντας του P(x) β) Να λύσετε την εξίσωση P(x) = 0
 1. α) Να βρείτε το υπόλοιπο και το πηλίκο της διαίρεσης (x 3 6x 2 +11x 2) : (x 3) β) Αν P(x) = x 3 6x 2 +11x + λ να βρείτε το λ R ώστε η διαίρεση P(x) : (x 3) να έχει υπόλοιπο 0. 2. Δίνονται τα πολυώνυμα:
1. α) Να βρείτε το υπόλοιπο και το πηλίκο της διαίρεσης (x 3 6x 2 +11x 2) : (x 3) β) Αν P(x) = x 3 6x 2 +11x + λ να βρείτε το λ R ώστε η διαίρεση P(x) : (x 3) να έχει υπόλοιπο 0. 2. Δίνονται τα πολυώνυμα:
Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί Η ΠΑΡΑΓΩΓΟΣ. Η ΕΝΝΟΙΑ ΤΗΣ ΑΝΑΛΥΤΙΚΗΣ ΣΥΝΑΡΗΣΗΣ Διδάσκων : Επίκ. Καθ. Κολάσης Χαράλαμπος Άδειες Χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί Η ΠΑΡΑΓΩΓΟΣ. Η ΕΝΝΟΙΑ ΤΗΣ ΑΝΑΛΥΤΙΚΗΣ ΣΥΝΑΡΗΣΗΣ Διδάσκων : Επίκ. Καθ. Κολάσης Χαράλαμπος Άδειες Χρήσης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ A N A K O I N Ω Σ Η
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ Θεσσαλονίκη 13-2-2015 A N A K O I N Ω Σ Η Τα μαθήματα του Προπτυχιακού Προγράμματος Σπουδών στο Τμήμα Μαθηματικών για το
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ Θεσσαλονίκη 13-2-2015 A N A K O I N Ω Σ Η Τα μαθήματα του Προπτυχιακού Προγράμματος Σπουδών στο Τμήμα Μαθηματικών για το
Σεµινάριο Αυτοµάτου Ελέγχου
 ΤΕΙ ΠΕΙΡΑΙΑ Τµήµα Αυτοµατισµού Σεµινάριο Αυτοµάτου Ελέγχου Ειδικά θέµατα Ανάλυσης συστηµάτων Σύνθεσης συστηµάτων ελέγχου Μελέτης στοχαστικών συστηµάτων. Καλλιγερόπουλος Σεµινάριο Αυτοµάτου Ελέγχου Ανάλυση
ΤΕΙ ΠΕΙΡΑΙΑ Τµήµα Αυτοµατισµού Σεµινάριο Αυτοµάτου Ελέγχου Ειδικά θέµατα Ανάλυσης συστηµάτων Σύνθεσης συστηµάτων ελέγχου Μελέτης στοχαστικών συστηµάτων. Καλλιγερόπουλος Σεµινάριο Αυτοµάτου Ελέγχου Ανάλυση
ΠΡΟΓΡΑΜΜΑ (ΔΙΠΛΗΣ) ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟΔΟΥ ΦΕΒΡΟΥΑΡΙΟΥ 2015, ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ (ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ 3)
 ΠΑΡΑΣΚΕΥΗ 6/2/2015 ΠΕΜΠΤΗ 5/2/2015 ΤΕΤΑΡΤΗ 4/2/2015 ΤΡΙΤΗ 3/2/2015 ΔΕΥΤΕΡΑ 2/2/2015 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ (ΔΙΠΛΗΣ) ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟΔΟΥ
ΠΑΡΑΣΚΕΥΗ 6/2/2015 ΠΕΜΠΤΗ 5/2/2015 ΤΕΤΑΡΤΗ 4/2/2015 ΤΡΙΤΗ 3/2/2015 ΔΕΥΤΕΡΑ 2/2/2015 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΡΟΓΡΑΜΜΑ (ΔΙΠΛΗΣ) ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟΔΟΥ
Δυναμική Μηχανών I. Διάλεξη 13. Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ
 Δυναμική Μηχανών I Διάλεξη 13 Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ 1 Περιεχόμενα Iδιότητες Ιδιοανυσμάτων Συστήματα χωρίς απόσβεση Ιδιοανυσματικός Μετασχηματισμός Συστήματα χωρίς απόσβεση
Δυναμική Μηχανών I Διάλεξη 13 Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ 1 Περιεχόμενα Iδιότητες Ιδιοανυσμάτων Συστήματα χωρίς απόσβεση Ιδιοανυσματικός Μετασχηματισμός Συστήματα χωρίς απόσβεση
Μερικές Διαφορικές Εξισώσεις
 Πανεπιστήμιο Πατρών, Τμήμα Μαθηματικών Μερικές Διαφορικές Εξισώσεις Χειμερινό εξάμηνο ακαδημαϊκού έτους 24-25, Διδάσκων: Α.Τόγκας ο φύλλο προβλημάτων Ονοματεπώνυμο - ΑΜ: ΜΔΕ ο φύλλο προβλημάτων Α. Τόγκας
Πανεπιστήμιο Πατρών, Τμήμα Μαθηματικών Μερικές Διαφορικές Εξισώσεις Χειμερινό εξάμηνο ακαδημαϊκού έτους 24-25, Διδάσκων: Α.Τόγκας ο φύλλο προβλημάτων Ονοματεπώνυμο - ΑΜ: ΜΔΕ ο φύλλο προβλημάτων Α. Τόγκας
ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΣΕΠΤΕΜΒΡΙΟΥ 2016
 ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΣΕΠΤΕΜΒΡΙΟΥ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΑΚΑΔ. ΕΤΟΥΣ 2015-29 Αυγούστου Γραμμική Άλγεβρα & Αναλυτική Γεωμετρία Αντίσταση & Πρόωση Μελέτη & Εξοπλισμός Ι Προγραμματισμός &
ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΣΕΠΤΕΜΒΡΙΟΥ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΑΚΑΔ. ΕΤΟΥΣ 2015-29 Αυγούστου Γραμμική Άλγεβρα & Αναλυτική Γεωμετρία Αντίσταση & Πρόωση Μελέτη & Εξοπλισμός Ι Προγραμματισμός &
