|
|
|
- Κλήμεντος Αλεξιάδης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Σχεσιακή Άλγεβρα Αθανάσιος Σταυρακούδης Άνοιξη / 23
2 Επισκόπηση 1 Συνολοθεωρητικές πράξεις Η σχεσιακή πράξη της ένωσης Η σχεσιακή πράξη της διαφοράς Η σχεσιακή πράξη της τομής Επιπλέον παραδείγματα συνολοθεωρητικών πράξεων 2 / 23
3 Η σχεσιακή πράξη της ένωσης Ορισμός της ένωσης: r s = {t t r or t s} Ενωση δύο σχέσεων r(r) και s(s), που έχουν συμβατότητα τύπου, είναι μια νέα σχέση που έχει σχήμα (επικεφαλίδα) ίδιο με αυτό της r και s, και κορμό το σύνολο των κορμών των r και s, δηλαδή όλες τις πλειάδες που ανήκουν στην r, ή στην s, η και στις δύο πλειάδες. Η ένωση συμβολίζεται με r s ή r UNION s. 3 / 23
4 Παράδειγμα ένωσης σχέσεων r s r = {1, 2} s = {2, 3} r s = {1, 2, 3} 4 / 23
5 Παράδειγμα ένωσης σχέσεων r s r = {1, 2} s = {2, 3} r s = {1, 2, 3} 1 b 10 2 b 10 1 b 10 2 b 10 r s r s 5 / 23
6 Ενωση και αντιμεταθετική ιδιότητα Ισχύει η αντιμεταθετική ιδιότητα Παράδειγμα 1 b 10 r (s t) = (r s) t 2 b 10 1 b 10 2 b 10 2 b 10 1 b 10 r s r s s r 6 / 23
7 Ενωση και προσεταιριστική ιδιότητα Ισχύει η προσεταιριστική ιδιότητα r (s t) = (r s) t Λόγω αυτής της της ιδιότητας, είναι δυνατό να γραφεί η παρακάτω παράσταση χωρίς παρενθέσεις: r s t για να δηλώσει την ένωση τριών ή περισσότερων σχέσεων. 7 / 23
8 Η σχεσιακή πράξη της διαφοράς Ορισμός της διαφοράς: r s = {t t r and t / s} Διαφορά δύο σχέσεων r(r) και s(s), που έχουν συμβατότητα τύπου, είναι μια νέα σχέση που έχει σχήμα (επικεφαλίδα) ίδιο με αυτό της r και s, και κορμό τις πλειάδες που ανήκουν στην r αλλά όχι στην s. Η διαφορά συμβολίζεται με r s ή r MINUS s. 8 / 23
9 Παράδειγμα διαφοράς δύο σχέσεων r s r = {1, 2} s = {2, 3} r s = {1} s r = {3} 9 / 23
10 Παράδειγμα διαφοράς δύο σχέσεων r s r = {1, 2} s = {2, 3} r s = {1} s r = {3} 1 b 10 2 b 10 1 b 10 2 b 10 r s r s s r 10 / 23
11 Αντιμεταθετική και προσεταιριστική ιδιότητα Στη σχεσιακή πράξη της διαφοράς: Δεν ισχύει η αντιμεταθετική ιδιότητα r s s r Δεν ισχύει η προσεταιριστική ιδιότητα Υπενθύμιση r (s t) (r s) t (3 2) (8 3) 2 11 / 23
12 Η σχεσιακή πράξη της τομής Ορισμός της τομής: r s = {t t r and t s} Τομή δύο σχέσεων r(r) και s(s), που έχουν συμβατότητα τύπου, είναι μια νέα σχέση που έχει σχήμα (επικεφαλίδα) ίδιο με αυτό της r και s, και κορμό τις πλειάδες που ανήκουν στην r και στην s, δηλαδή τις κοινές πλειάδες. Η τομή συμβολίζεται με r s ή r INTERSECT s. 12 / 23
13 Παράδειγμα τομής δύο σχέσεων r s r = {1, 2} s = {2, 3} r s = {2} 13 / 23
14 Παράδειγμα τομής δύο σχέσεων r s r = {1, 2} s = {2, 3} r s = {2} 1 b 10 2 b 10 r s r s 14 / 23
15 Τομή και αντιμεταθετική ιδιότητα Ισχύει η αντιμεταθετική ιδιότητα Παράδειγμα r s = s r 1 b 10 2 b 10 r s r s s r 15 / 23
16 Τομή και προσεταιριστική ιδιότητα Ισχύει η προσεταιριστική ιδιότητα r (s t) = (r s) t Λόγω αυτής της της ιδιότητας, είναι δυνατό να γραφεί η παρακάτω παράσταση χωρίς παρενθέσεις: r s t για να δηλώσει την τομή τριών ή περισσότερων σχέσεων. 16 / 23
17 Η τομή είναι παράγωγη πράξη Εναλλακτικός ορισμός της τομής r s = r (r s) Δηλαδή το αποτέλεσμα της τομής r s ισούται με το α- ποτέλεσμα της διαφοράς της r από τη διαφορά r s. Παράδειγμα Δώστε εσείς ένα παράδειγμα που να επιβεβαιώνει (ή να αναιρεί) τον παραπάνω ορισμό. 17 / 23
18 Pane Amore 1 Pane, amore e fantasia, (1953) 2 Pane, amore e gelosia, (1954) 3 Pane, amore e..., (1955) 18 / 23
19 Pane amore actorid f name Vittorio De Sica Gina Lollobrigida Marisa Merlini Memmo Carotenuto Roberto Risso Tina Pica Vittoria Crispo actorid g name Vittorio De Sica Gina Lollobrigida Marisa Merlini Memmo Carotenuto Tina Pica Saro Urzì Vittoria Crispo 19 / 23
20 Pane amore (Ερωτήματα συμμετοχής) Επαιξαν σε τουλάχιστον μία ταινία f g Επαιξαν και στις δύο πρώτες ταινίες f g Επαιξαν μόνο στην πρώτη ταινία f g Επαιξαν μόνο στη δεύτερη ταινία g f 20 / 23
21 Τομή fantasia gelosia actorid f name Vittorio De Sica Gina Lollobrigida Marisa Merlini Memmo Carotenuto Roberto Risso Tina Pica Vittoria Crispo actorid name Vittorio De Sica Gina Lollobrigida Marisa Merlini Memmo Carotenuto Tina Pica Vittoria Crispo actorid g name Vittorio De Sica Gina Lollobrigida Marisa Merlini Memmo Carotenuto Tina Pica Saro Urzì Vittoria Crispo 21 / 23
22 Διαφορά fantasia gelosia actorid f name Vittorio De Sica Gina Lollobrigida Marisa Merlini Memmo Carotenuto Roberto Risso Tina Pica Vittoria Crispo actorid name Roberto Risso actorid g name Vittorio De Sica Gina Lollobrigida Marisa Merlini Memmo Carotenuto Tina Pica Saro Urzì Vittoria Crispo 22 / 23
23 Σχόλια και ερωτήσεις Σας ευχαριστώ για την προσοχή σας Είμαι στη διάθεσή σας για σχόλια, απορίες και ερωτήσεις 23 / 23
1 / 106
 Σχεσιακή Άλγεβρα Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=154 Άνοιξη 2016 1 / 106 Σχεσιακή άλγεβρα Η σχεσιακή άλγεβρα είναι μια διαδικαστική (procedural) γλώσσα. Διαθέτει
Σχεσιακή Άλγεβρα Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=154 Άνοιξη 2016 1 / 106 Σχεσιακή άλγεβρα Η σχεσιακή άλγεβρα είναι μια διαδικαστική (procedural) γλώσσα. Διαθέτει
 Σχεσιακή Άλγεβρα Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=154 Άνοιξη 2014 1 / 88 Σχεσιακή άλγεβρα Η σχεσιακή άλγεβρα είναι μια διαδικαστική (procedural) γλώσσα. Διαθέτει
Σχεσιακή Άλγεβρα Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=154 Άνοιξη 2014 1 / 88 Σχεσιακή άλγεβρα Η σχεσιακή άλγεβρα είναι μια διαδικαστική (procedural) γλώσσα. Διαθέτει
Ηλεκτρονικοί Υπολογιστές II
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρονικοί Υπολογιστές II Σχεσιακή άλγεβρα Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρονικοί Υπολογιστές II Σχεσιακή άλγεβρα Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Ηλεκτρονικοί Υπολογιστές II
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρονικοί Υπολογιστές II Σχεσιακή άλγεβρα Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρονικοί Υπολογιστές II Σχεσιακή άλγεβρα Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
 Σχεσιακή Άλγεβρα Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr Άνοιξη 2014 1 / 15 Επισκόπηση 1 Οι βασικές πράξεις προβολής και επιλογής Η σχεσιακή πράξη της προβολής Η σχεσιακή πράξη της επιλογής
Σχεσιακή Άλγεβρα Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr Άνοιξη 2014 1 / 15 Επισκόπηση 1 Οι βασικές πράξεις προβολής και επιλογής Η σχεσιακή πράξη της προβολής Η σχεσιακή πράξη της επιλογής
Kεφ.2: Σχεσιακό Μοντέλο (επανάληψη) Κεφ.6.1: Σχεσιακή Άλγεβρα
 Kεφ.2: Σχεσιακό Μοντέλο (επανάληψη) Κεφ.6.1: Σχεσιακή Άλγεβρα Database System Concepts, 6 th Ed. Silberschatz, Korth and Sudarshan See www.db-book.com for conditions on re-use Παράδειγμα Σχέσης attributes
Kεφ.2: Σχεσιακό Μοντέλο (επανάληψη) Κεφ.6.1: Σχεσιακή Άλγεβρα Database System Concepts, 6 th Ed. Silberschatz, Korth and Sudarshan See www.db-book.com for conditions on re-use Παράδειγμα Σχέσης attributes
DISTINCT, LIKE, NULL, AND, OR, BETWEEN
 Περισσότερα για τα απλά ερωτήματα SQL DISTINCT, LIKE, NULL, AND, OR, BETWEEN Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr Άνοιξη 2014 1 / 66 Σκοπός του μαθήματος Αποκλείσετε διπλοεγγραφές από
Περισσότερα για τα απλά ερωτήματα SQL DISTINCT, LIKE, NULL, AND, OR, BETWEEN Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr Άνοιξη 2014 1 / 66 Σκοπός του μαθήματος Αποκλείσετε διπλοεγγραφές από
Σχεσιακή Άλγεβρα και Σχεσιακός Λογισμός. Σχεσιακή Άλγεβρα Σχεσιακός Λογισμός
 7 Σχεσιακή Άλγεβρα και Σχεσιακός Λογισμός Σχεσιακή Άλγεβρα Σχεσιακός Λογισμός Σχεσιακή Άλγεβρα H Σχεσιακή Άλγεβρα (relational algebra) ορίζει ένα σύνολο πράξεων που εφαρμόζονται σε μία ή περισσότερες σχέσεις
7 Σχεσιακή Άλγεβρα και Σχεσιακός Λογισμός Σχεσιακή Άλγεβρα Σχεσιακός Λογισμός Σχεσιακή Άλγεβρα H Σχεσιακή Άλγεβρα (relational algebra) ορίζει ένα σύνολο πράξεων που εφαρμόζονται σε μία ή περισσότερες σχέσεις
Η SQL ως γλώσσα ερωτημάτων. Υπενθυμίζουμε: Σχέση = Πίνακας Πλειάδα = Εγγραφή = Γραμμή (Πίνακα) Πεδίο = Γνώρισμα (Σχέσης) = Στήλη (Πίνακα)
 Η SQL ως γλώσσα ερωτημάτων Υπενθυμίζουμε: Σχέση = Πίνακας Πλειάδα = Εγγραφή = Γραμμή (Πίνακα) Πεδίο = Γνώρισμα (Σχέσης) = Στήλη (Πίνακα) Η γλώσσα SQL Η SQL αποτελείται από: DDL (Data Definition Language)
Η SQL ως γλώσσα ερωτημάτων Υπενθυμίζουμε: Σχέση = Πίνακας Πλειάδα = Εγγραφή = Γραμμή (Πίνακα) Πεδίο = Γνώρισμα (Σχέσης) = Στήλη (Πίνακα) Η γλώσσα SQL Η SQL αποτελείται από: DDL (Data Definition Language)
Αλγεβρικές Παραστάσεις
 Αλγεβρικές Παραστάσεις 1.1 Πράξεις με πραγματικούς αριθμούς (Επαναλήψεις-συμπληρώσεις) 1 1.1 Πράξεις με πραγματικούς αριθμούς (Επαναλήψεις-συμπληρώσεις) Α Οι πραγματικοί αριθμοί και οι πράξεις τους Πραγματικοί
Αλγεβρικές Παραστάσεις 1.1 Πράξεις με πραγματικούς αριθμούς (Επαναλήψεις-συμπληρώσεις) 1 1.1 Πράξεις με πραγματικούς αριθμούς (Επαναλήψεις-συμπληρώσεις) Α Οι πραγματικοί αριθμοί και οι πράξεις τους Πραγματικοί
Πρόσθεση, αφαίρεση και πολλαπλασιασμός φυσικών αριθμών
 Πρόσθεση, αφαίρεση και πολλαπλασιασμός φυσικών αριθμών TINΑ ΒΡΕΝΤΖΟΥ www.ma8eno.gr www.ma8eno.gr Σελίδα 1 Πρόσθεση, αφαίρεση και πολλαπλασιασμός φυσικών αριθμών Στους πραγματικούς αριθμούς ορίστηκαν οι
Πρόσθεση, αφαίρεση και πολλαπλασιασμός φυσικών αριθμών TINΑ ΒΡΕΝΤΖΟΥ www.ma8eno.gr www.ma8eno.gr Σελίδα 1 Πρόσθεση, αφαίρεση και πολλαπλασιασμός φυσικών αριθμών Στους πραγματικούς αριθμούς ορίστηκαν οι
#1.1 Τι είναι η Βάση Δεδομένων
 1 2 #1.1 Τι είναι η Βάση Δεδομένων Βάση δεδομένων είναι ένα πλήθος στοιχείων συναφών μεταξύ τους, τοποθετημένα και ταξινομημένα με συγκεκριμένο τρόπο. Με τη χρήση μιας Βάσης Δεδομένων μπορούμε: να καταχωρούμε
1 2 #1.1 Τι είναι η Βάση Δεδομένων Βάση δεδομένων είναι ένα πλήθος στοιχείων συναφών μεταξύ τους, τοποθετημένα και ταξινομημένα με συγκεκριμένο τρόπο. Με τη χρήση μιας Βάσης Δεδομένων μπορούμε: να καταχωρούμε
Το Σχεσιακό Μοντέλο. Βάσεις Δεδομένων Ευαγγελία Πιτουρά 1
 Το Σχεσιακό Μοντέλο Βάσεις Δεδομένων 2013-2014 Ευαγγελία Πιτουρά 1 Μοντελοποίηση Σχήμα (database schema): η περιγραφή της δομής της πληροφορίας που είναι αποθηκευμένη στη βδ με τη χρήση ενός μοντέλου δεδομένων
Το Σχεσιακό Μοντέλο Βάσεις Δεδομένων 2013-2014 Ευαγγελία Πιτουρά 1 Μοντελοποίηση Σχήμα (database schema): η περιγραφή της δομής της πληροφορίας που είναι αποθηκευμένη στη βδ με τη χρήση ενός μοντέλου δεδομένων
Βάσεις δεδομένων. (4 ο μάθημα) Ηρακλής Βαρλάμης
 Βάσεις δεδομένων (4 ο μάθημα) Ηρακλής Βαρλάμης varlamis@hua.gr Περιεχόμενα Επέκταση του μοντέλου ΟΣ Κληρονομικότητα Εξειδίκευση/Γενίκευση Περιορισμοί Ιεραρχίες και πλέγματα Συνάθροιση Συνέχεια στο σχεσιακό
Βάσεις δεδομένων (4 ο μάθημα) Ηρακλής Βαρλάμης varlamis@hua.gr Περιεχόμενα Επέκταση του μοντέλου ΟΣ Κληρονομικότητα Εξειδίκευση/Γενίκευση Περιορισμοί Ιεραρχίες και πλέγματα Συνάθροιση Συνέχεια στο σχεσιακό
Σχεσιακή Άλγεβρα Σχεδιασμός Βάσεων Δεδομένων
 Σχεσιακή Άλγεβρα Σχεδιασμός Βάσεων Δεδομένων Μαρία Χαλκίδη Εισαγωγή Εννοιολογικός Σχεδιασμός Βάσεων Δεδομένων (με χρήση του Μοντέλου Οντοτήτων/Συσχετίσεων) Λογικός Σχεδιασμός Βάσεων Δεδομένων (με χρήση
Σχεσιακή Άλγεβρα Σχεδιασμός Βάσεων Δεδομένων Μαρία Χαλκίδη Εισαγωγή Εννοιολογικός Σχεδιασμός Βάσεων Δεδομένων (με χρήση του Μοντέλου Οντοτήτων/Συσχετίσεων) Λογικός Σχεδιασμός Βάσεων Δεδομένων (με χρήση
Ηλεκτρονικοί Υπολογιστές II
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρονικοί Υπολογιστές II Ερωτήματα επιλογής SQL, σύζευξη, διάζευξη, NULL, ταίριασμα κειμένου Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Άδειες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρονικοί Υπολογιστές II Ερωτήματα επιλογής SQL, σύζευξη, διάζευξη, NULL, ταίριασμα κειμένου Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Άδειες
Σχεσιακή Άλγεβρα. Παύλος Εφραιμίδης. Βάσεις Δεδομένων Σχεσιακή Άλγεβρα 1
 Σχεσιακή Άλγεβρα Παύλος Εφραιμίδης Βάσεις Δεδομένων Σχεσιακή Άλγεβρα 1 Θεμελίωση της Σχεσιακού Μοντέλου Δεδομένων Σχεσιακή Άλγεβρα Σχεσιακός Λογισμός Στο μάθημα θα πούμε για Σχεσιακή Άλγεβρα Βάσεις Δεδομένων
Σχεσιακή Άλγεβρα Παύλος Εφραιμίδης Βάσεις Δεδομένων Σχεσιακή Άλγεβρα 1 Θεμελίωση της Σχεσιακού Μοντέλου Δεδομένων Σχεσιακή Άλγεβρα Σχεσιακός Λογισμός Στο μάθημα θα πούμε για Σχεσιακή Άλγεβρα Βάσεις Δεδομένων
Βάσεις Δεδομένων (Databases)
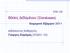 Βάσεις Δεδομένων (Databases) ΕΠΛ 342 Χειμερινό Εξάμηνο 2011 Διδάσκοντες Καθηγητές Γιώργος Σαμάρας (ΧΩΔ01 109) Σύνδεση Ισότητας (Equi-Join) Θ στην σύνδεση είναι = (=-Join) r r.ai = s.aj s =-σύνδεση του
Βάσεις Δεδομένων (Databases) ΕΠΛ 342 Χειμερινό Εξάμηνο 2011 Διδάσκοντες Καθηγητές Γιώργος Σαμάρας (ΧΩΔ01 109) Σύνδεση Ισότητας (Equi-Join) Θ στην σύνδεση είναι = (=-Join) r r.ai = s.aj s =-σύνδεση του
ΜΑΘΗΜΑΤΙΚΑ Α ΓΥΜΝΑΣΙΟΥ ΑΝΔΡΕΣΑΚΗΣ ΔΗΜΗΤΡΗΣ ΦΥΛΛΑ ΕΡΓΑΣΙΑΣ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΕΝΟΤΗΤΑ Α.7.2. ΑΠΟΛΥΤΗ ΤΙΜΗ ΑΝΤΙΘΕΤΟΙ - ΣΥΓΚΡΙΣΗ ΟΝΟΜΑΤΕΠΩΝΥΜΟ
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΕΝΟΤΗΤΑ Α.7.2. ΑΠΟΛΥΤΗ ΤΙΜΗ ΑΝΤΙΘΕΤΟΙ - ΣΥΓΚΡΙΣΗ ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΗΜΕΡΟΜΗΝΙΑ / / Πόσες μονάδες απέχει από την αρχή Ο το σημείο Α; Πόσες μονάδες απέχει από την αρχή Ο το σημείο Β; Πόσες μονάδες
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΕΝΟΤΗΤΑ Α.7.2. ΑΠΟΛΥΤΗ ΤΙΜΗ ΑΝΤΙΘΕΤΟΙ - ΣΥΓΚΡΙΣΗ ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΗΜΕΡΟΜΗΝΙΑ / / Πόσες μονάδες απέχει από την αρχή Ο το σημείο Α; Πόσες μονάδες απέχει από την αρχή Ο το σημείο Β; Πόσες μονάδες
Το Σχεσιακό Μοντέλο. Βάσεις Δεδομένων 2014-2015. Ευαγγελία Πιτουρά 1
 Το Σχεσιακό Μοντέλο Ευαγγελία Πιτουρά 1 Μοντελοποίηση Σχήμα (database schema): η περιγραφή της δομής της πληροφορίας που είναι αποθηκευμένη στη βδ με τη χρήση ενός μοντέλου δεδομένων Μοντέλο Δεδομένων:
Το Σχεσιακό Μοντέλο Ευαγγελία Πιτουρά 1 Μοντελοποίηση Σχήμα (database schema): η περιγραφή της δομής της πληροφορίας που είναι αποθηκευμένη στη βδ με τη χρήση ενός μοντέλου δεδομένων Μοντέλο Δεδομένων:
καλών σχεσιακών σχημάτων
 Εισαγωγή Θα εξετάσουμε πότε ένα σχεσιακό σχήμα για μια βάση δεδομένων είναι «καλό» Λογικός Σχεδιασμός Σχεσιακών Σχημάτων Γενικές Οδηγίες Η Μέθοδος της Αποσύνθεσης (γενική μεθοδολογία) Επιθυμητές Ιδιότητες
Εισαγωγή Θα εξετάσουμε πότε ένα σχεσιακό σχήμα για μια βάση δεδομένων είναι «καλό» Λογικός Σχεδιασμός Σχεσιακών Σχημάτων Γενικές Οδηγίες Η Μέθοδος της Αποσύνθεσης (γενική μεθοδολογία) Επιθυμητές Ιδιότητες
Βάσεις Δεδομένων Ευαγγελία Πιτουρά 2. Εννοιολογικός Σχεδιασμός Βάσεων εδομένων (με χρήση του Μοντέλου Οντοτήτων/Συσχετίσεων)
 Σχεσιακή Άλγεβρα Βάσεις Δεδομένων 2009-2010 Ευαγγελία Πιτουρά 1 Εισαγωγή Στα προηγούμενα μαθήματα: Εννοιολογικός Σχεδιασμός Βάσεων εδομένων (με χρήση του Μοντέλου Οντοτήτων/Συσχετίσεων) Λογικός Σχεδιασμός
Σχεσιακή Άλγεβρα Βάσεις Δεδομένων 2009-2010 Ευαγγελία Πιτουρά 1 Εισαγωγή Στα προηγούμενα μαθήματα: Εννοιολογικός Σχεδιασμός Βάσεων εδομένων (με χρήση του Μοντέλου Οντοτήτων/Συσχετίσεων) Λογικός Σχεδιασμός
 Υποερωτήματα στην SQL Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr 1 / 31 Η ανάγκη για υποερώτημα Ποιος υπάλληλος παίρνει το μεγαλύτερο μισθό; Αν ξέραμε το μεγαλύτερο μισθό, πχ 2000, θα γράφαμε:
Υποερωτήματα στην SQL Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr 1 / 31 Η ανάγκη για υποερώτημα Ποιος υπάλληλος παίρνει το μεγαλύτερο μισθό; Αν ξέραμε το μεγαλύτερο μισθό, πχ 2000, θα γράφαμε:
Βάσεις Δεδομένων 2010-2011 Ευαγγελία Πιτουρά 2. Εννοιολογικός Σχεδιασμός Βάσεων εδομένων (με χρήση του Μοντέλου Οντοτήτων/Συσχετίσεων)
 Σχεσιακή Άλγεβρα Βάσεις Δεδομένων 2010-2011 Ευαγγελία Πιτουρά 1 Εισαγωγή Στα προηγούμενα μαθήματα: Εννοιολογικός Σχεδιασμός Βάσεων εδομένων (με χρήση του Μοντέλου Οντοτήτων/Συσχετίσεων) Λογικός Σχεδιασμός
Σχεσιακή Άλγεβρα Βάσεις Δεδομένων 2010-2011 Ευαγγελία Πιτουρά 1 Εισαγωγή Στα προηγούμενα μαθήματα: Εννοιολογικός Σχεδιασμός Βάσεων εδομένων (με χρήση του Μοντέλου Οντοτήτων/Συσχετίσεων) Λογικός Σχεδιασμός
Λογικός Σχεδιασμός Σχεσιακών Σχημάτων: Αποσύνθεση
 Λογικός Σχεδιασμός Σχεσιακών Σχημάτων: Αποσύνθεση Βάσεις Δεδομένων 2010-2011 Ευαγγελία Πιτουρά 1 Εισαγωγή Θα εξετάσουμε πότε ένα σχεσιακό σχήμα για μια βάση δεδομένων είναι «καλό» Γενικές Οδηγίες Η Μέθοδος
Λογικός Σχεδιασμός Σχεσιακών Σχημάτων: Αποσύνθεση Βάσεις Δεδομένων 2010-2011 Ευαγγελία Πιτουρά 1 Εισαγωγή Θα εξετάσουμε πότε ένα σχεσιακό σχήμα για μια βάση δεδομένων είναι «καλό» Γενικές Οδηγίες Η Μέθοδος
Ένας απλός τρόπος αναπαράστασης δεδομένων: ένας διδιάστατος πίνακας που λέγεται σχέση Γνωρίσματα
 Εισαγωγή Σχεσιακό Μοντέλο Σχεδιασμός μιας Β : Βήματα Ανάλυση Απαιτήσεων Τι δεδομένα θα αποθηκευτούν, ποιες εφαρμογές θα κτιστούν πάνω στα δεδομένα, ποιες λειτουργίες είναι συχνές Εννοιολογικός Σχεδιασμός
Εισαγωγή Σχεσιακό Μοντέλο Σχεδιασμός μιας Β : Βήματα Ανάλυση Απαιτήσεων Τι δεδομένα θα αποθηκευτούν, ποιες εφαρμογές θα κτιστούν πάνω στα δεδομένα, ποιες λειτουργίες είναι συχνές Εννοιολογικός Σχεδιασμός
ΙΣΧΥΡΙΣΜΟΙ & ΑΝΤΙΠΑΡΑΔΕΙΓΜΑΤΑ ΒΑΣΙΜΕΝΑ ΣΤΟ ΣΧΟΛΙΚΟ ΒΙΒΛΙΟ ΓΙΑ ΤΟ ΘΕΜΑ Α
 ΙΣΧΥΡΙΣΜΟΙ & ΑΝΤΙΠΑΡΑΔΕΙΓΜΑΤΑ ΒΑΣΙΜΕΝΑ ΣΤΟ ΣΧΟΛΙΚΟ ΒΙΒΛΙΟ ΓΙΑ ΤΟ ΘΕΜΑ Α 1. Θεωρήστε τον παρακάτω ισχυρισμό : «Αν δυο συναρτήσεις με πεδίο ορισμού Α, Β αντιστοίχως και ορίζονται οι g o, g τότε υποχρεωτικά
ΙΣΧΥΡΙΣΜΟΙ & ΑΝΤΙΠΑΡΑΔΕΙΓΜΑΤΑ ΒΑΣΙΜΕΝΑ ΣΤΟ ΣΧΟΛΙΚΟ ΒΙΒΛΙΟ ΓΙΑ ΤΟ ΘΕΜΑ Α 1. Θεωρήστε τον παρακάτω ισχυρισμό : «Αν δυο συναρτήσεις με πεδίο ορισμού Α, Β αντιστοίχως και ορίζονται οι g o, g τότε υποχρεωτικά
Σχεσιακή Άλγεβρα. Συνολοθεωρητικές Πράξεις. Εκφράσεις. Ειδικές Πράξεις. Θεμελίωση της Σχεσιακού Μοντέλου Δεδομένων. Σχεσιακός Λογισμός
 Σχεσιακή Άλγεβρα Παύλος Εφραιμίδης Θεμελίωση της Σχεσιακού Μοντέλου Δεδομένων Σχεσιακή Άλγεβρα Σχεσιακός Λογισμός ΣτομάθημαθαπούμεγιαΣχεσιακή Άλγεβρα Βάσεις Δεδομένων Σχεσιακή Άλγεβρα 1 Βάσεις Δεδομένων
Σχεσιακή Άλγεβρα Παύλος Εφραιμίδης Θεμελίωση της Σχεσιακού Μοντέλου Δεδομένων Σχεσιακή Άλγεβρα Σχεσιακός Λογισμός ΣτομάθημαθαπούμεγιαΣχεσιακή Άλγεβρα Βάσεις Δεδομένων Σχεσιακή Άλγεβρα 1 Βάσεις Δεδομένων
ΗΥ360: Αρχεία και Βάσεις Δεδομένων Διδάσκων: Πλεξουσάκης Δημήτρης. Φροντιστήριο Σχεσιακή Άλγεβρα Δημητράκη Κατερίνα
 ΗΥ360: Αρχεία και Βάσεις Δεδομένων Διδάσκων: Πλεξουσάκης Δημήτρης Φροντιστήριο Σχεσιακή Άλγεβρα Δημητράκη Κατερίνα Αντιστοίχιση Μοντέλο Οντοτήτων Σχέσεων Σχεσιακό μοντέλο ID Customer ID Name 1928 Γιώργος
ΗΥ360: Αρχεία και Βάσεις Δεδομένων Διδάσκων: Πλεξουσάκης Δημήτρης Φροντιστήριο Σχεσιακή Άλγεβρα Δημητράκη Κατερίνα Αντιστοίχιση Μοντέλο Οντοτήτων Σχέσεων Σχεσιακό μοντέλο ID Customer ID Name 1928 Γιώργος
Σχεσιακή Άλγεβρα. Βάσεις Δεδομένων : Σχεσιακή Άλγεβρα 1
 Εισαγωγή Στα προηγούμενα μαθήματα: Εννοιολογικός Σχεδιασμός Βάσεων εδομένων (με χρήση του Μοντέλου Οντοτήτων/Συσχετίσεων) Λογικός Σχεδιασμός Βάσεων εδομένων (με χρήση του Σχεσιακού Μοντέλου) Αντιστοιχία
Εισαγωγή Στα προηγούμενα μαθήματα: Εννοιολογικός Σχεδιασμός Βάσεων εδομένων (με χρήση του Μοντέλου Οντοτήτων/Συσχετίσεων) Λογικός Σχεδιασμός Βάσεων εδομένων (με χρήση του Σχεσιακού Μοντέλου) Αντιστοιχία
Ένας απλός τρόπος αναπαράστασης δεδομένων: ένας διδιάστατος πίνακας που λέγεται σχέση Γνωρίσματα
 Εισαγωγή Σχεσιακό Μοντέλο Σχεδιασμός μιας Β : Βήματα Ανάλυση Απαιτήσεων Τι δεδομένα θα αποθηκευτούν, ποιες εφαρμογές θα κτιστούν πάνω στα δεδομένα, ποιες λειτουργίες είναι συχνές Εννοιολογικός Σχεδιασμός
Εισαγωγή Σχεσιακό Μοντέλο Σχεδιασμός μιας Β : Βήματα Ανάλυση Απαιτήσεων Τι δεδομένα θα αποθηκευτούν, ποιες εφαρμογές θα κτιστούν πάνω στα δεδομένα, ποιες λειτουργίες είναι συχνές Εννοιολογικός Σχεδιασμός
Βάσεις Δεδομένων : Λογικός Σχεδιασμός 1. καλών σχεσιακών σχημάτων. Λογικός Σχεδιασμός Σχεσιακών Σχημάτων. Γενικές Κατευθύνσεις.
 Εισαγωγή Θα εξετάσουμε πότε ένα σχεσιακό σχήμα για μια βάση δεδομένων είναι «καλό» Λογικός Σχεδιασμός Σχεσιακών Σχημάτων Γενικές Οδηγίες Η Μέθοδος της Αποσύνθεσης (γενική μεθοδολογία) Επιθυμητές Ιδιότητες
Εισαγωγή Θα εξετάσουμε πότε ένα σχεσιακό σχήμα για μια βάση δεδομένων είναι «καλό» Λογικός Σχεδιασμός Σχεσιακών Σχημάτων Γενικές Οδηγίες Η Μέθοδος της Αποσύνθεσης (γενική μεθοδολογία) Επιθυμητές Ιδιότητες
αριθμούς Βασικές ασκήσεις Βασική θεωρία iii) φυσικοί; ii) ακέραιοι; iii) ρητοί;
 Πράξεις με πραγματικούς αριθμούς Βασικές ασκήσεις Βασική θεωρία Ρητοί και άρρητοι αριθμοί. α) Ποιοι αριθμοί ονομάζονται: iii) φυσικοί; ii) ακέραιοι; iii) ρητοί; iv) άρρητοι; v) πραγματικοί; β) Να βρείτε
Πράξεις με πραγματικούς αριθμούς Βασικές ασκήσεις Βασική θεωρία Ρητοί και άρρητοι αριθμοί. α) Ποιοι αριθμοί ονομάζονται: iii) φυσικοί; ii) ακέραιοι; iii) ρητοί; iv) άρρητοι; v) πραγματικοί; β) Να βρείτε
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Θεωρία Υπολογισμού Ενότητα 2: Σύνολα και σχέσεις Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Θεωρία Υπολογισμού Ενότητα 2: Σύνολα και σχέσεις Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
ΑΛΓΕΒΡΑ Α ΓΥΜΝΑΣΙΟΥ ΘΕΤΙΚΟΙ ΚΑΙ ΑΡΝΗΤΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ
 ΘΕΤΙΚΟΙ ΚΑΙ ΑΡΝΗΤΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ ΚΕΦΑΛΑΙΟ 7 Ο ΘΕΤΙΚΟΙ ΚΑΙ ΑΡΝΗΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ 1. Όταν μπροστα" (αριστερα") απο" ε"ναν αριθμο" γραφει" το συ"μβολο + το"τε ο αριθμο"ς
ΘΕΤΙΚΟΙ ΚΑΙ ΑΡΝΗΤΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ ΚΕΦΑΛΑΙΟ 7 Ο ΘΕΤΙΚΟΙ ΚΑΙ ΑΡΝΗΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ 1. Όταν μπροστα" (αριστερα") απο" ε"ναν αριθμο" γραφει" το συ"μβολο + το"τε ο αριθμο"ς
1.1 A. ΟΙ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΟΙ
 . A. ΟΙ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΟΙ ΠΡΑΞΕΙΣ ΤΟΥΣ ΘΕΩΡΙΑ. Τα σύνολα των αριθµών Το σύνολο των φυσικών αριθµών. Το σύνολο των ακεραίων αριθµών. N {0,,, 3 } Z { 3,,, 0,,, 3 } Το σύνολο των ρητών αριθµών. Q
. A. ΟΙ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΟΙ ΠΡΑΞΕΙΣ ΤΟΥΣ ΘΕΩΡΙΑ. Τα σύνολα των αριθµών Το σύνολο των φυσικών αριθµών. Το σύνολο των ακεραίων αριθµών. N {0,,, 3 } Z { 3,,, 0,,, 3 } Το σύνολο των ρητών αριθµών. Q
ΗΥ360 Αρχεία και Βάσεις Δεδομένων. Φροντιστήριο στην Σχεσιακή Άλγεβρα.
 ΗΥ360 Αρχεία και Βάσεις Δεδομένων Φροντιστήριο στην Σχεσιακή Άλγεβρα. Σχεσιακή Άλγεβρα Εισαγωγή Σύνολο τελεστών που εφαρμόζονται σε μία ή περισσότερες σχέσεις Όλες οι πράξεις της σχεσιακής άλγεβρας επιστρέφουν
ΗΥ360 Αρχεία και Βάσεις Δεδομένων Φροντιστήριο στην Σχεσιακή Άλγεβρα. Σχεσιακή Άλγεβρα Εισαγωγή Σύνολο τελεστών που εφαρμόζονται σε μία ή περισσότερες σχέσεις Όλες οι πράξεις της σχεσιακής άλγεβρας επιστρέφουν
Οργάνωση Βάσεων Βιοϊατρικών Δεδομένων Εξόρυξη Γνώσης Βιοϊατρικών Δεδομένων. Σεμινάριο 3: Σχεσιακή Άλγεβρα
 Οργάνωση Βάσεων Βιοϊατρικών Δεδομένων Εξόρυξη Γνώσης Βιοϊατρικών Δεδομένων Σεμινάριο 3: Σχεσιακή Άλγεβρα Ευάγγελος Καρκαλέτσης, Αναστασία Κριθαρά, Γεώργιος Πετάσης Εργαστήριο Τεχνολογίας Γνώσεων & Λογισμικού,
Οργάνωση Βάσεων Βιοϊατρικών Δεδομένων Εξόρυξη Γνώσης Βιοϊατρικών Δεδομένων Σεμινάριο 3: Σχεσιακή Άλγεβρα Ευάγγελος Καρκαλέτσης, Αναστασία Κριθαρά, Γεώργιος Πετάσης Εργαστήριο Τεχνολογίας Γνώσεων & Λογισμικού,
 Υποερωτήματα SQL Παραδείγματα και εφαρμογές από τη βάση δεδομένων company Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr astavrak@uoi.gr @AStavrakoudis Άνοιξη 2016 1 / 55 Περιεχόμενα 1 Απλά υποερωτήματα
Υποερωτήματα SQL Παραδείγματα και εφαρμογές από τη βάση δεδομένων company Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr astavrak@uoi.gr @AStavrakoudis Άνοιξη 2016 1 / 55 Περιεχόμενα 1 Απλά υποερωτήματα
Σχεσιακή Άλγεβρα. Βάσεις Δεδομένων Ευαγγελία Πιτουρά 1
 Σχεσιακή Άλγεβρα Βάσεις Δεδομένων 2017-2018 1 Τι έχουμε δει έως σήμερα Σχεδιασμό βάσεων δεδομένων μοντέλο Οντοτήτων/Συσχετίσεων σχεσιακό μοντέλο (ορισμός σχήματος) Μια γλώσσα ορισμού δεδομένων ΓΟΔ (για
Σχεσιακή Άλγεβρα Βάσεις Δεδομένων 2017-2018 1 Τι έχουμε δει έως σήμερα Σχεδιασμό βάσεων δεδομένων μοντέλο Οντοτήτων/Συσχετίσεων σχεσιακό μοντέλο (ορισμός σχήματος) Μια γλώσσα ορισμού δεδομένων ΓΟΔ (για
Βάσεις Δεδομένων (Databases)
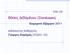 Βάσεις Δεδομένων (Databases) ΕΠΛ 342 Χειμερινό Εξάμηνο 2011 Διδάσκοντες Καθηγητές Γιώργος Σαμάρας (ΧΩΔ01 109) Έλεγχος Μέλους Συνόλου (Set Membership) Οι IN και NOT IN τελεστές ελέγχουν για μονό membership
Βάσεις Δεδομένων (Databases) ΕΠΛ 342 Χειμερινό Εξάμηνο 2011 Διδάσκοντες Καθηγητές Γιώργος Σαμάρας (ΧΩΔ01 109) Έλεγχος Μέλους Συνόλου (Set Membership) Οι IN και NOT IN τελεστές ελέγχουν για μονό membership
Σχεσιακή Άλγεβρα. Βάσεις Δεδομένων Ευαγγελία Πιτουρά 1
 Σχεσιακή Άλγεβρα Βάσεις Δεδομένων 2018-2019 1 Τι έχουμε δει έως σήμερα Σχεδιασμό βάσεων δεδομένων μοντέλο Οντοτήτων/Συσχετίσεων σχεσιακό μοντέλο (ορισμός σχήματος) Μια γλώσσα ορισμού δεδομένων ΓΟΔ (για
Σχεσιακή Άλγεβρα Βάσεις Δεδομένων 2018-2019 1 Τι έχουμε δει έως σήμερα Σχεδιασμό βάσεων δεδομένων μοντέλο Οντοτήτων/Συσχετίσεων σχεσιακό μοντέλο (ορισμός σχήματος) Μια γλώσσα ορισμού δεδομένων ΓΟΔ (για
Σχεσιακή Άλγεβρα. Βάσεις Δεδομένων Ευαγγελία Πιτουρά 1
 Σχεσιακή Άλγεβρα 1 Ανακοινώθηκε το 1 ο Σύνολο Ασκήσεων στη σελίδα του μαθήματος Ημερομηνία Παράδοσης 3/11/2016 2 Τι έχουμε δει έως σήμερα Σχεδιασμό και Υλοποίηση Σχεσιακών Βάσεων δεδομένων Μια γλώσσα ορισμού
Σχεσιακή Άλγεβρα 1 Ανακοινώθηκε το 1 ο Σύνολο Ασκήσεων στη σελίδα του μαθήματος Ημερομηνία Παράδοσης 3/11/2016 2 Τι έχουμε δει έως σήμερα Σχεδιασμό και Υλοποίηση Σχεσιακών Βάσεων δεδομένων Μια γλώσσα ορισμού
Σχεσιακή Άλγεβρα. Βάσεις Δεδομένων Ευαγγελία Πιτουρά 1
 Σχεσιακή Άλγεβρα Ευαγγελία Πιτουρά 1 Τι έχουμε δει έως σήμερα Σχεδιασμό και Υλοποίηση Σχεσιακών Βάσεων δεδομένων Μια γλώσσα ορισμού δεδομένων ΓΟΔ (για τον ορισμό των σχημάτων) ένας μεταφραστής της ΓΟΔ
Σχεσιακή Άλγεβρα Ευαγγελία Πιτουρά 1 Τι έχουμε δει έως σήμερα Σχεδιασμό και Υλοποίηση Σχεσιακών Βάσεων δεδομένων Μια γλώσσα ορισμού δεδομένων ΓΟΔ (για τον ορισμό των σχημάτων) ένας μεταφραστής της ΓΟΔ
ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ - ΣΧΕΣΙΑΚΗ ΑΛΓΕΒΡΑ
 ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ - ΣΧΕΣΙΑΚΗ ΑΛΓΕΒΡΑ Διδάσκων του μαθήματος 2 Δρ. Λεωνίδας Φραγγίδης Τμήμα Διοίκησης Επιχειρήσεων ΤΕΙ ΑΜΘ Email: fragidis@teiemt.gr Ώρες Γραφείου: Τρίτη (10:00 12:00) Προτεινόμενα Βιβλία
ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ - ΣΧΕΣΙΑΚΗ ΑΛΓΕΒΡΑ Διδάσκων του μαθήματος 2 Δρ. Λεωνίδας Φραγγίδης Τμήμα Διοίκησης Επιχειρήσεων ΤΕΙ ΑΜΘ Email: fragidis@teiemt.gr Ώρες Γραφείου: Τρίτη (10:00 12:00) Προτεινόμενα Βιβλία
Σχεδιασµός Σχεσιακών Σχηµάτων
 Σχεδιασµός Σχεσιακών Σχηµάτων 1 Σχεδιασµός Σχεσιακών Σχηµάτων Σχεδιασµός καλών σχεσιακών σχηµάτων Μη τυπικές - γενικές κατευθύνσεις Θεωρία κανονικών µορφών που θα βασίζεται στις συναρτησιακές εξαρτήσεις
Σχεδιασµός Σχεσιακών Σχηµάτων 1 Σχεδιασµός Σχεσιακών Σχηµάτων Σχεδιασµός καλών σχεσιακών σχηµάτων Μη τυπικές - γενικές κατευθύνσεις Θεωρία κανονικών µορφών που θα βασίζεται στις συναρτησιακές εξαρτήσεις
Σχεσιακός Λογισμός. Σχεσιακός Λογισμός Πλειάδων. σχεσιακά πλήρης γλώσσα
 Εισαγωγή Σχεσιακό Μοντέλο Τυπικές Γλώσσες Ερωτήσεων Σχεσιακή Άλγεβρα Πλειάδων Πεδίου Βάσεις Δεδομένων 2005-2006 Ευαγγελία Πιτουρά 1 Βάσεις Δεδομένων 2005-2006 Ευαγγελία Πιτουρά 2 Γιατί σχεσιακό λογισμό;
Εισαγωγή Σχεσιακό Μοντέλο Τυπικές Γλώσσες Ερωτήσεων Σχεσιακή Άλγεβρα Πλειάδων Πεδίου Βάσεις Δεδομένων 2005-2006 Ευαγγελία Πιτουρά 1 Βάσεις Δεδομένων 2005-2006 Ευαγγελία Πιτουρά 2 Γιατί σχεσιακό λογισμό;
Βάσεις εδοµένων Ευαγγελία Πιτουρά 2. Εννοιολογικός Σχεδιασµός Βάσεων Δεδοµένων (µε χρήση του Μοντέλου Οντοτήτων/Συσχετίσεων)
 Σχεσιακή Άλγεβρα Βάσεις εδοµένων 2011-2012 Ευαγγελία Πιτουρά 1 Εισαγωγή Στα προηγούµενα µαθήµατα: Εννοιολογικός Σχεδιασµός Βάσεων Δεδοµένων (µε χρήση του Μοντέλου Οντοτήτων/Συσχετίσεων) Λογικός Σχεδιασµός
Σχεσιακή Άλγεβρα Βάσεις εδοµένων 2011-2012 Ευαγγελία Πιτουρά 1 Εισαγωγή Στα προηγούµενα µαθήµατα: Εννοιολογικός Σχεδιασµός Βάσεων Δεδοµένων (µε χρήση του Μοντέλου Οντοτήτων/Συσχετίσεων) Λογικός Σχεδιασµός
Απαντήσεις θεωρίας Κεφάλαιο 1ο. (α μέρος)
 Μαθηματικά Γ Γυμνασίου Απαντήσεις θεωρίας Κεφάλαιο 1ο. (α μέρος) 1. Πως προσθέτουμε δυο πραγματικούς αριθμούς; Για να προσθέσουμε δύο ομόσημους αριθμούς, προσθέτουμε τις απόλυτες τιμές τους και στο άθροισμά
Μαθηματικά Γ Γυμνασίου Απαντήσεις θεωρίας Κεφάλαιο 1ο. (α μέρος) 1. Πως προσθέτουμε δυο πραγματικούς αριθμούς; Για να προσθέσουμε δύο ομόσημους αριθμούς, προσθέτουμε τις απόλυτες τιμές τους και στο άθροισμά
Σχεσιακός Λογισµός. Σχεσιακός Λογισµός Πλειάδων. σχεσιακά πλήρης γλώσσα
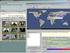 Σχεσιακό Μοντέλο Τυπικές Γλώσσες Ερωτήσεων Σχεσιακή Άλγεβρα Πλειάδων Πεδίου Βάσεις εδοµένων 2004-2005 Ευαγγελία Πιτουρά 1 Βάσεις εδοµένων 2004-2005 Ευαγγελία Πιτουρά 2 Γιατί σχεσιακό λογισµό; αδυναµία
Σχεσιακό Μοντέλο Τυπικές Γλώσσες Ερωτήσεων Σχεσιακή Άλγεβρα Πλειάδων Πεδίου Βάσεις εδοµένων 2004-2005 Ευαγγελία Πιτουρά 1 Βάσεις εδοµένων 2004-2005 Ευαγγελία Πιτουρά 2 Γιατί σχεσιακό λογισµό; αδυναµία
Σχεδιασµός Σχεσιακών Σχηµάτων
 Βάσεις εδοµένων 2003-2004 Ευαγγελία Πιτουρά 1 Σχεδιασµός Σχεσιακών Σχηµάτων Σχεδιασµός καλών σχεσιακών σχηµάτων Μη τυπικές - γενικές κατευθύνσεις Θεωρία κανονικών µορφών που θα βασίζεται στις συναρτησιακές
Βάσεις εδοµένων 2003-2004 Ευαγγελία Πιτουρά 1 Σχεδιασµός Σχεσιακών Σχηµάτων Σχεδιασµός καλών σχεσιακών σχηµάτων Μη τυπικές - γενικές κατευθύνσεις Θεωρία κανονικών µορφών που θα βασίζεται στις συναρτησιακές
Κεφάλαιο 10 Άλλες Πράξεις Θεωρίας Συνόλων
 Κεφάλαιο 10 Άλλες Πράξεις Θεωρίας Συνόλων Σύνοψη Στο παρόν κεφάλαιο θα παρουσιαστεί η πράξη της διαίρεσης. Στο κομμάτι των ασκήσεων θα γίνει συνολική επισκόπηση ερωτημάτων που εμπλέκουν πράξεις συνόλων.
Κεφάλαιο 10 Άλλες Πράξεις Θεωρίας Συνόλων Σύνοψη Στο παρόν κεφάλαιο θα παρουσιαστεί η πράξη της διαίρεσης. Στο κομμάτι των ασκήσεων θα γίνει συνολική επισκόπηση ερωτημάτων που εμπλέκουν πράξεις συνόλων.
Σχεδιασμός μιας Β : Βήματα
 Σχεσιακό Μοντέλο 1 Εισαγωγή Ανάλυση Απαιτήσεων Σχεδιασμός μιας Β : Βήματα Τι δεδομένα θα αποθηκευτούν, ποιες εφαρμογές θα κτιστούν πάνω στα δεδομένα, ποιες λειτουργίες είναι συχνές Εννοιολογικός Σχεδιασμός
Σχεσιακό Μοντέλο 1 Εισαγωγή Ανάλυση Απαιτήσεων Σχεδιασμός μιας Β : Βήματα Τι δεδομένα θα αποθηκευτούν, ποιες εφαρμογές θα κτιστούν πάνω στα δεδομένα, ποιες λειτουργίες είναι συχνές Εννοιολογικός Σχεδιασμός
Τμήμα Πληροφορικής ΑΠΘ
 Βάσεις Δεδομένων Εργαστήριο ΙΙI Τμήμα Πληροφορικής ΑΠΘ 2013-2014 2 Σκοπός του 3 ου εργαστηρίου Σκοπός αυτού του εργαστηρίου είναι: η μελέτη ερωτημάτων επιλογής, προβολής και απλών συνδέσεων σε δύο ή περισσότερες
Βάσεις Δεδομένων Εργαστήριο ΙΙI Τμήμα Πληροφορικής ΑΠΘ 2013-2014 2 Σκοπός του 3 ου εργαστηρίου Σκοπός αυτού του εργαστηρίου είναι: η μελέτη ερωτημάτων επιλογής, προβολής και απλών συνδέσεων σε δύο ή περισσότερες
Σχεσιακό Μοντέλο. Εισαγωγή. Βάσεις εδοµένων : Σχεσιακό Μοντέλο 1
 Σχεσιακό Μοντέλο Βάσεις εδοµένων 2011-2012 Ευαγγελία Πιτουρά 1 Εισαγωγή O σχεδιασμός μιας βάση δεδομένων κωδικοποιεί κάποιο μέρος του φυσικού κόσμου Ένα μοντέλο δεδομένων είναι ένα σύνολο από έννοιες για
Σχεσιακό Μοντέλο Βάσεις εδοµένων 2011-2012 Ευαγγελία Πιτουρά 1 Εισαγωγή O σχεδιασμός μιας βάση δεδομένων κωδικοποιεί κάποιο μέρος του φυσικού κόσμου Ένα μοντέλο δεδομένων είναι ένα σύνολο από έννοιες για
ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ Α ΓΥΜΝΑΣΙΟΥΣΤΗΝ ΑΛΓΕΒΡΑ. Άρτιοι αριθμοί ονομάζονται οι αριθμοί που διαιρούνται με το 2 και περιττοί εκείνοι
 ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ Α ΓΥΜΝΑΣΙΟΥΣΤΗΝ ΑΛΓΕΒΡΑ 1)Ποιοι αριθμοί ονομάζονται άρτιοι και ποιοι περιττοί ; Άρτιοι αριθμοί ονομάζονται οι αριθμοί που διαιρούνται με το 2 και περιττοί εκείνοι που δεν διαιρούνται
ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ Α ΓΥΜΝΑΣΙΟΥΣΤΗΝ ΑΛΓΕΒΡΑ 1)Ποιοι αριθμοί ονομάζονται άρτιοι και ποιοι περιττοί ; Άρτιοι αριθμοί ονομάζονται οι αριθμοί που διαιρούνται με το 2 και περιττοί εκείνοι που δεν διαιρούνται
Διάλεξη 13: Γλώσσα Επεξεργασίας Δεδομένων/ Data Manipulation Language (SQL DML) I. Διδάσκων: Παναγιώτης Ανδρέου
 Διάλεξη 13: Γλώσσα Επεξεργασίας Δεδομένων/ Data Manipulation Language (SQL DML) I Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Εισαγωγή στις έννοιες: Εισαγωγή στην SQL DML SELECT, FROM, WHERE,
Διάλεξη 13: Γλώσσα Επεξεργασίας Δεδομένων/ Data Manipulation Language (SQL DML) I Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Εισαγωγή στις έννοιες: Εισαγωγή στην SQL DML SELECT, FROM, WHERE,
Σχεσιακός Λογισµός. Σχεσιακό Μοντέλο. Έννοιες Τυπικές Γλώσσες Ερωτήσεων Σχεσιακή Άλγεβρα Σχεσιακός Λογισµός Πλειάδων Σχεσιακός Λογισµός Πεδίου
 Σχεσιακός Λογισµός Βάσεις εδοµένων 2002-2003 Ευαγγελία Πιτουρά 1 Σχεσιακός Λογισµός Σχεσιακό Μοντέλο Έννοιες Τυπικές Γλώσσες Ερωτήσεων Σχεσιακή Άλγεβρα Σχεσιακός Λογισµός Πλειάδων Σχεσιακός Λογισµός Πεδίου
Σχεσιακός Λογισµός Βάσεις εδοµένων 2002-2003 Ευαγγελία Πιτουρά 1 Σχεσιακός Λογισµός Σχεσιακό Μοντέλο Έννοιες Τυπικές Γλώσσες Ερωτήσεων Σχεσιακή Άλγεβρα Σχεσιακός Λογισµός Πλειάδων Σχεσιακός Λογισµός Πεδίου
Οργάνωση Βάσεων Βιοϊατρικών Δεδομένων Εξόρυξη Γνώσης Βιοϊατρικών Δεδομένων
 Οργάνωση Βάσεων Βιοϊατρικών Δεδομένων Εξόρυξη Γνώσης Βιοϊατρικών Δεδομένων Σεμινάριο 7, μέρος 2 ο : Αλγόριθμοι για επεξεργασία ερωτήσεων και βελτιστοποίηση Ευάγγελος Καρκαλέτσης, Αναστασία Κριθαρά, Γεώργιος
Οργάνωση Βάσεων Βιοϊατρικών Δεδομένων Εξόρυξη Γνώσης Βιοϊατρικών Δεδομένων Σεμινάριο 7, μέρος 2 ο : Αλγόριθμοι για επεξεργασία ερωτήσεων και βελτιστοποίηση Ευάγγελος Καρκαλέτσης, Αναστασία Κριθαρά, Γεώργιος
Δοκιμασίες πολλαπλών επιλογών
 Δοκιμασίες πολλαπλών επιλογών ) Η απόλυτη τιμή θετικού αριθμού είναι: Α. Ο αντίθετός του Β. Ο ίδιος ο αριθμός Γ. Ο αντίστροφός του 2) Αν x =3, τότε Α. x=3 Β. x 0 Γ. x=-3 Δ. x=3 ή x=-3 3) Με το -x συμβολίζουμε
Δοκιμασίες πολλαπλών επιλογών ) Η απόλυτη τιμή θετικού αριθμού είναι: Α. Ο αντίθετός του Β. Ο ίδιος ο αριθμός Γ. Ο αντίστροφός του 2) Αν x =3, τότε Α. x=3 Β. x 0 Γ. x=-3 Δ. x=3 ή x=-3 3) Με το -x συμβολίζουμε
f(x) = 2x+ 3 / Α f Α.
 ΣΥΝΑΡΤΗΣΕΙΣ 8 ο ΜΑΘΗΜΑ.7. Σύνολο τιμών f(a) της f / A B Ορισμός: Το σύνολο τιμών της συνάρτησης f / Α Β περιλαμβάνει εκείνα τα y Β για τα οποία υπάρχει x Α : «Η εξίσωση y= f ( x) να έχει λύση ως προς x»
ΣΥΝΑΡΤΗΣΕΙΣ 8 ο ΜΑΘΗΜΑ.7. Σύνολο τιμών f(a) της f / A B Ορισμός: Το σύνολο τιμών της συνάρτησης f / Α Β περιλαμβάνει εκείνα τα y Β για τα οποία υπάρχει x Α : «Η εξίσωση y= f ( x) να έχει λύση ως προς x»
ΡΗΤΟΙ ΑΡΙΘΜΟΙ - ΘΕΩΡΙΑ
 ΡΗΤΟΙ ΑΡΙΘΜΟΙ - ΘΕΩΡΙΑ Α. ΟΡΙΣΜΟΙ Θετικοί αριθµοί είναι οι αριθµοί που έχουν πρόσηµο το + (πολλές φορές το + παραλείπεται) π.χ. +3, +105, +, + 0,7, 326. Αρνητικοί αριθµοί είναι οι αριθµοί που έχουν πρόσηµο
ΡΗΤΟΙ ΑΡΙΘΜΟΙ - ΘΕΩΡΙΑ Α. ΟΡΙΣΜΟΙ Θετικοί αριθµοί είναι οι αριθµοί που έχουν πρόσηµο το + (πολλές φορές το + παραλείπεται) π.χ. +3, +105, +, + 0,7, 326. Αρνητικοί αριθµοί είναι οι αριθµοί που έχουν πρόσηµο
Σχεσιακή Άλγεβρα. Προγράμματα που απαντούν σε επερωτήσεις για τον τρέχον στιγμιότυπο της βάσης δεδομένων (querying)
 Εισαγωγή Στα προηγούμενα μαθήματα: Εννοιολογικός Σχεδιασμός Βάσεων εδομένων (με χρήση του Μοντέλου Οντοτήτων/Συσχετίσεων) Λογικός Σχεδιασμός Βάσεων εδομένων (με χρήση του Σχεσιακού Μοντέλου) Μετατροπή
Εισαγωγή Στα προηγούμενα μαθήματα: Εννοιολογικός Σχεδιασμός Βάσεων εδομένων (με χρήση του Μοντέλου Οντοτήτων/Συσχετίσεων) Λογικός Σχεδιασμός Βάσεων εδομένων (με χρήση του Σχεσιακού Μοντέλου) Μετατροπή
ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ. Πράξεις στο Σχεσιακό Μοντέλο
 ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ Χειμερινό Εξάμηνο 2013 Πράξεις Διαχείρισης Δεδομένων Σχεσιακή Άλγεβρα Δρ. Βαγγελιώ Καβακλή ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ, ΤΜΗΜΑ ΠΟΛΙΤΙΣΜΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΑΣ 1 Πράξεις στο Σχεσιακό
ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ Χειμερινό Εξάμηνο 2013 Πράξεις Διαχείρισης Δεδομένων Σχεσιακή Άλγεβρα Δρ. Βαγγελιώ Καβακλή ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ, ΤΜΗΜΑ ΠΟΛΙΤΙΣΜΙΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΑΣ 1 Πράξεις στο Σχεσιακό
Βάσεις Δεδομένων Σύνθετα SQL queries
 Βάσεις Δεδομένων Σύνθετα SQL queries Παύλος Εφραιμίδης Βάσεις Δεδομένων SQL - Μέρος Δεύτερο 1 Ασάφεια και Πλήρη Ονόματα Ονόματα Πεδίων: Στην SQL, τα ονόματα των πεδίων (γνωρισμάτων) σε κάθε σχέση είναι
Βάσεις Δεδομένων Σύνθετα SQL queries Παύλος Εφραιμίδης Βάσεις Δεδομένων SQL - Μέρος Δεύτερο 1 Ασάφεια και Πλήρη Ονόματα Ονόματα Πεδίων: Στην SQL, τα ονόματα των πεδίων (γνωρισμάτων) σε κάθε σχέση είναι
Μ Α Θ Η Μ Α Τ Ι Κ Α Α Γ Υ Μ Ν Α Σ Ι Ο Υ
 Μ Α Θ Η Μ Α Τ Ι Κ Α Α Γ Υ Μ Ν Α Σ Ι Ο Υ 1 Συνοπτική θεωρία Ερωτήσεις αντικειμενικού τύπου Ασκήσεις Διαγωνίσματα 2 ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ ΕΡΩΤΗΣΕΙΣ-ΑΠΑΝΤΗΣΕΙΣ 1. Πότε ένας φυσικός αριθμός λέγεται άρτιος; Άρτιος
Μ Α Θ Η Μ Α Τ Ι Κ Α Α Γ Υ Μ Ν Α Σ Ι Ο Υ 1 Συνοπτική θεωρία Ερωτήσεις αντικειμενικού τύπου Ασκήσεις Διαγωνίσματα 2 ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ ΕΡΩΤΗΣΕΙΣ-ΑΠΑΝΤΗΣΕΙΣ 1. Πότε ένας φυσικός αριθμός λέγεται άρτιος; Άρτιος
Σχεσιακή Άλγεβρα. Εισαγωγή. Εισαγωγή. Εισαγωγή. Παράδειγμα. Εισαγωγή. Ταινία Τίτλος Έτος Διάρκεια Είδος. Παίζει Όνομα-Ηθοποιού Τίτλος Έτος.
 Εισαγωγή Στα προηγούμενα μαθήματα: Εννοιολογικός Σχεδιασμός Βάσεων εδομένων (με χρήση του Μοντέλου Οντοτήτων/Συσχετίσεων) Λογικός Σχεδιασμός Βάσεων εδομένων (με χρήση του Σχεσιακού Μοντέλου) Αντιστοιχία
Εισαγωγή Στα προηγούμενα μαθήματα: Εννοιολογικός Σχεδιασμός Βάσεων εδομένων (με χρήση του Μοντέλου Οντοτήτων/Συσχετίσεων) Λογικός Σχεδιασμός Βάσεων εδομένων (με χρήση του Σχεσιακού Μοντέλου) Αντιστοιχία
Σχεσιακή Άλγεβρα. Βάσεις Δεδομένων Ευαγγελία Πιτουρά 1
 Σχεσιακή Άλγεβρα Βάσεις Δεδομένων 2013-2014 Ευαγγελία Πιτουρά 1 Τι έχουμε δει έως σήμερα Σχεδιασμό και Υλοποίηση Σχεσιακών Βάσεων δεδομένων Μια γλώσσα ορισμού δεδομένων ΓΟΔ (για τον ορισμό των σχημάτων)
Σχεσιακή Άλγεβρα Βάσεις Δεδομένων 2013-2014 Ευαγγελία Πιτουρά 1 Τι έχουμε δει έως σήμερα Σχεδιασμό και Υλοποίηση Σχεσιακών Βάσεων δεδομένων Μια γλώσσα ορισμού δεδομένων ΓΟΔ (για τον ορισμό των σχημάτων)
Βάσεις Δεδομένων Σύνθετα SQL queries. Ψευδώνυμα (Aliases) (2) Ψευδώνυμα (Aliases) (1) Ασάφεια και Πλήρη Ονόματα. Ερώτημα χωρίς τον όρο WHERE (1)
 Ασάφεια και Πλήρη Ονόματα Βάσεις Δεδομένων Σύνθετα SQL queries Παύλος Εφραιμίδης Βάσεις Δεδομένων SQL - Μέρος Δεύτερο 1 Ονόματα Πεδίων: Στην SQL, τα ονόματα των πεδίων (γνωρισμάτων) σε κάθε σχέση είναι
Ασάφεια και Πλήρη Ονόματα Βάσεις Δεδομένων Σύνθετα SQL queries Παύλος Εφραιμίδης Βάσεις Δεδομένων SQL - Μέρος Δεύτερο 1 Ονόματα Πεδίων: Στην SQL, τα ονόματα των πεδίων (γνωρισμάτων) σε κάθε σχέση είναι
Βάσεις Δεδομένων : Σχεσιακό Μοντέλο 1. Ένας απλός τρόπος αναπαράστασης δεδομένων: ένας διδιάστατος πίνακας που λέγεται σχέση.
 Εισαγωγή Σχεσιακό Μοντέλο Ανάλυση Απαιτήσεων Σχεδιασμός μιας Β : Βήματα Τι δεδομένα θα αποθηκευτούν, ποιες εφαρμογές θα κτιστούν πάνω στα δεδομένα, ποιες λειτουργίες είναι συχνές Εννοιολογικός Σχεδιασμός
Εισαγωγή Σχεσιακό Μοντέλο Ανάλυση Απαιτήσεων Σχεδιασμός μιας Β : Βήματα Τι δεδομένα θα αποθηκευτούν, ποιες εφαρμογές θα κτιστούν πάνω στα δεδομένα, ποιες λειτουργίες είναι συχνές Εννοιολογικός Σχεδιασμός
ΚΕΦΑΛΑΙΟ 3 ο Αλγεβρα BOOLE και Λογικές Πύλες
 ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΑΕΡΟΣΚΑΦΩΝ ΤΕΙ ΣΤΕΡΕΑΣ ΕΛΛΑΔΑΣ ΕΙΣΑΓΩΓΗ στους Η/Υ Διδάσκουσα Δρ. Β. Σγαρδώνη 2013-14 ΚΕΦΑΛΑΙΟ 3 ο Αλγεβρα BOOLE και Λογικές Πύλες Α. ΑΛΓΕΒΡΑ Boole Η Άλγεβρα Boole (Boolean algebra) πήρε
ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΑΕΡΟΣΚΑΦΩΝ ΤΕΙ ΣΤΕΡΕΑΣ ΕΛΛΑΔΑΣ ΕΙΣΑΓΩΓΗ στους Η/Υ Διδάσκουσα Δρ. Β. Σγαρδώνη 2013-14 ΚΕΦΑΛΑΙΟ 3 ο Αλγεβρα BOOLE και Λογικές Πύλες Α. ΑΛΓΕΒΡΑ Boole Η Άλγεβρα Boole (Boolean algebra) πήρε
1 / 97
 Τα πρώτα ερωτήματα SQL Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr Άνοιξη 2014 1 / 97 Περιεχόμενα 1 Εισαγωγικά σχόλια και παρατηρήσεις 2 Απλά ερωτήματα προβολής, επιλέγοντας στήλες από ένα πίνακα
Τα πρώτα ερωτήματα SQL Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr Άνοιξη 2014 1 / 97 Περιεχόμενα 1 Εισαγωγικά σχόλια και παρατηρήσεις 2 Απλά ερωτήματα προβολής, επιλέγοντας στήλες από ένα πίνακα
Σχεδιασµός µιας Β. Ένας απλός τρόπος αναπαράστασης δεδοµένων: ένας διδιάστατος πίνακας που λέγεται σχέση Γνωρίσµατα
 Εισαγωγή Σχεσιακό Μοντέλο Σχεδιασµός µιας Β : Βήµατα Ανάλυση Απαιτήσεων Τι δεδοµένα θα αποθηκευτούν, ποιες εφαρµογές θα κτιστούν πάνω στα δεδοµένα, ποιες λειτουργίες είναι συχνές Εννοιολογικός Σχεδιασµός
Εισαγωγή Σχεσιακό Μοντέλο Σχεδιασµός µιας Β : Βήµατα Ανάλυση Απαιτήσεων Τι δεδοµένα θα αποθηκευτούν, ποιες εφαρµογές θα κτιστούν πάνω στα δεδοµένα, ποιες λειτουργίες είναι συχνές Εννοιολογικός Σχεδιασµός
DELETE, UPDATE, INSERT.
 Ενημέρωση βάσης δεδομένων με SQL DELETE, UPDATE, INSERT Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr Άνοιξη 2014 1 / 88 Περιεχόμενα 1 Γενικά για την αποθήκευση δεδομένων και την ενημέρωση της
Ενημέρωση βάσης δεδομένων με SQL DELETE, UPDATE, INSERT Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr Άνοιξη 2014 1 / 88 Περιεχόμενα 1 Γενικά για την αποθήκευση δεδομένων και την ενημέρωση της
ΜΑΘΗΜΑ 13 1.2 ΣΥΝΑΡΤΗΣΕΙΣ Σύνθεση συναρτήσεων
 ΜΑΘΗΜΑ 3. ΣΥΝΑΡΤΗΣΕΙΣ Σύνθεση συναρτήσεων Θεωρία Σχόλια Ασκήσεις ΘΕΩΡΙΑ. Ορισµός Έστω οι συναρτήσεις : A R, :Β R Το τυχαίο A, µε την A. αντιστοιχίζεται στην τιµή Αν η τιµή αυτή ( ) B θα αντιστοιχίζεται
ΜΑΘΗΜΑ 3. ΣΥΝΑΡΤΗΣΕΙΣ Σύνθεση συναρτήσεων Θεωρία Σχόλια Ασκήσεις ΘΕΩΡΙΑ. Ορισµός Έστω οι συναρτήσεις : A R, :Β R Το τυχαίο A, µε την A. αντιστοιχίζεται στην τιµή Αν η τιµή αυτή ( ) B θα αντιστοιχίζεται
Φροντιστήριο Σχεσιακή Άλγεβρα (μέρος 2 ο ) - Σχεσιακός Λογισμός Δημητράκη Κατερίνα
 ΗΥ360: Αρχεία και Βάσεις Δεδομένων Διδάσκων : Πλεξουσάκης Δημήτρης Φροντιστήριο Σχεσιακή Άλγεβρα (μέρος 2 ο ) - Σχεσιακός Λογισμός Δημητράκη Κατερίνα Σχεσιακή Άλγεβρα Εισαγωγή Σύνολο τελεστών που εφαρμόζονται
ΗΥ360: Αρχεία και Βάσεις Δεδομένων Διδάσκων : Πλεξουσάκης Δημήτρης Φροντιστήριο Σχεσιακή Άλγεβρα (μέρος 2 ο ) - Σχεσιακός Λογισμός Δημητράκη Κατερίνα Σχεσιακή Άλγεβρα Εισαγωγή Σύνολο τελεστών που εφαρμόζονται
Τμήμα Πληροφορικής ΑΠΘ
 Βάσεις Δεδομένων Εργαστήριο ΙΙ Τμήμα Πληροφορικής ΑΠΘ 2013-2014 2 Σκοπός του 2 ου εργαστηρίου Σκοπός αυτού του εργαστηρίου είναι: Η μελέτη ερωτημάτων σε μία μόνο σχέση. Εξετάζουμε τους τελεστές επιλογής
Βάσεις Δεδομένων Εργαστήριο ΙΙ Τμήμα Πληροφορικής ΑΠΘ 2013-2014 2 Σκοπός του 2 ου εργαστηρίου Σκοπός αυτού του εργαστηρίου είναι: Η μελέτη ερωτημάτων σε μία μόνο σχέση. Εξετάζουμε τους τελεστές επιλογής
DELETE, UPDATE, INSERT
 Ενημέρωση βάσης δεδομένων με SQL DELETE, UPDATE, INSERT Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr astavrak@uoi.gr @AStavrakoudis Άνοιξη 2016 1 / 103 Περιεχόμενα 1 Γενικά για την αποθήκευση
Ενημέρωση βάσης δεδομένων με SQL DELETE, UPDATE, INSERT Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr astavrak@uoi.gr @AStavrakoudis Άνοιξη 2016 1 / 103 Περιεχόμενα 1 Γενικά για την αποθήκευση
Τελεστής Προβολής - Παράδειγμα. Π Πόλη, Εξάμηνο (Φοιτητές)
 Σχεσιακή Άλγεβρα Προβολή, Επιλογή, Καρτεσιανό Γινόμενο, Ένωση, Διαφορά, Σύνθεση Τελεστών, Μετονομασία, Παραδείγματα Ερωτήσεων, Τομή Συνόλων, Φυσική Σύζευξη 1 Σχεσιακή Άλγεβρα Η σχεσιακή άλγεβρα (relational
Σχεσιακή Άλγεβρα Προβολή, Επιλογή, Καρτεσιανό Γινόμενο, Ένωση, Διαφορά, Σύνθεση Τελεστών, Μετονομασία, Παραδείγματα Ερωτήσεων, Τομή Συνόλων, Φυσική Σύζευξη 1 Σχεσιακή Άλγεβρα Η σχεσιακή άλγεβρα (relational
1 / 87
 Τα πρώτα ερωτήματα SQL Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr Άνοιξη 2016 1 / 87 Δυο λόγια για την SQL Υλοποίηση του σχεσιακού μοντέλου δεδομένων του E.F. Codd, αρχικά ως DSl/Alpha, αργότερα
Τα πρώτα ερωτήματα SQL Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr Άνοιξη 2016 1 / 87 Δυο λόγια για την SQL Υλοποίηση του σχεσιακού μοντέλου δεδομένων του E.F. Codd, αρχικά ως DSl/Alpha, αργότερα
Πράξεις με πραγματικούς αριθμούς (επαναλήψεις - συμπληρώσεις )
 ΜΑΘΗΜΑΤΙΚΑ α x +β
ΜΑΘΗΜΑΤΙΚΑ α x +β
Ηλεκτρονικοί Υπολογιστές II
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρονικοί Υπολογιστές II Ενημέρωση βάσης δεδομένων με τις εντολές INSERT, DELETE, UPDATE Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Άδειες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρονικοί Υπολογιστές II Ενημέρωση βάσης δεδομένων με τις εντολές INSERT, DELETE, UPDATE Διδάσκων: Επίκουρος Καθηγητής Αθανάσιος Σταυρακούδης Άδειες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ - ΤΜΗΥΠ ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ - ΤΜΗΥΠ ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ Ι Β. Μεγαλοοικονόμου, Δ. Χριστοδουλάκης Σχεσιακό Μοντέλο SQLΜέρος Α Ακ.Έτος 2008-09 (μεβάσητιςσημειώσειςτωνsilberchatz, Korth και Sudarshan και του C. Faloutsos
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ - ΤΜΗΥΠ ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ Ι Β. Μεγαλοοικονόμου, Δ. Χριστοδουλάκης Σχεσιακό Μοντέλο SQLΜέρος Α Ακ.Έτος 2008-09 (μεβάσητιςσημειώσειςτωνsilberchatz, Korth και Sudarshan και του C. Faloutsos
7.5 ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΡΗΤΩΝ
 1 7.5 ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΡΗΤΩΝ ΘΕΩΡΙΑ 1. Κανόνας πολλαπλασιασµού : Το γινόµενο δύο οµοσήµων αριθµών είναι θετικός ενώ το γινόµενο δύο ετεροσήµων είναι αρνητικός ηλαδή (+) (+) = + και ( ) ( ) = + Ενώ (+) (
1 7.5 ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΡΗΤΩΝ ΘΕΩΡΙΑ 1. Κανόνας πολλαπλασιασµού : Το γινόµενο δύο οµοσήµων αριθµών είναι θετικός ενώ το γινόµενο δύο ετεροσήµων είναι αρνητικός ηλαδή (+) (+) = + και ( ) ( ) = + Ενώ (+) (
SQL: Αιτήματα. Κεφάλαιο 5. Database Management Systems, R. Ramakrishnan and J. Gehrke
 SQL: Αιτήματα Κεφάλαιο 5 Database Management Systems, R. Ramakrishnan and J. Gehrke Στιγμιότυπα Στιγμιότυπα των σχέσεων Sailors Reserves και Boats. Αν στο κλειδί της σχέσης Reserved δε συμμετείχε το γνώρισμα
SQL: Αιτήματα Κεφάλαιο 5 Database Management Systems, R. Ramakrishnan and J. Gehrke Στιγμιότυπα Στιγμιότυπα των σχέσεων Sailors Reserves και Boats. Αν στο κλειδί της σχέσης Reserved δε συμμετείχε το γνώρισμα
Συνοπτική Θεωρία Μαθηματικών Α Γυμνασίου
 Web page: www.ma8eno.gr e-mail: vrentzou@ma8eno.gr Η αποτελεσματική μάθηση δεν θέλει κόπο αλλά τρόπο, δηλαδή ma8eno.gr Συνοπτική Θεωρία Μαθηματικών Α Γυμνασίου Αριθμητική - Άλγεβρα Γεωμετρία Άρτιος λέγεται
Web page: www.ma8eno.gr e-mail: vrentzou@ma8eno.gr Η αποτελεσματική μάθηση δεν θέλει κόπο αλλά τρόπο, δηλαδή ma8eno.gr Συνοπτική Θεωρία Μαθηματικών Α Γυμνασίου Αριθμητική - Άλγεβρα Γεωμετρία Άρτιος λέγεται
Εισαγωγή στις Βάσεις Δεδομζνων II
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΣΙΑ ΠΑΝΕΠΙΣΗΜΙΟ ΚΡΗΣΗ Εισαγωγή στις Βάσεις Δεδομζνων II Ενότητα: Σχεσιακή Άλγεβρα Διδάσκων: Πηγουνάκης Κωστής ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΣΧΟΛΗ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ Άδειες Χρήσης Το παρόν
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΣΙΑ ΠΑΝΕΠΙΣΗΜΙΟ ΚΡΗΣΗ Εισαγωγή στις Βάσεις Δεδομζνων II Ενότητα: Σχεσιακή Άλγεβρα Διδάσκων: Πηγουνάκης Κωστής ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΣΧΟΛΗ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ Άδειες Χρήσης Το παρόν
 Λογικές Συναρτήσεις με το Excel/OpenCalc Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr Αλήθεια ή ψέμα Μια οποιαδήποτε παράσταση μπορεί να χαρακτηριστεί ως αληθής ή ψευδής. Αληθής: TRUE ή 1 Ψευδής:
Λογικές Συναρτήσεις με το Excel/OpenCalc Αθανάσιος Σταυρακούδης http://stavrakoudis.econ.uoi.gr Αλήθεια ή ψέμα Μια οποιαδήποτε παράσταση μπορεί να χαρακτηριστεί ως αληθής ή ψευδής. Αληθής: TRUE ή 1 Ψευδής:
ΘΕΩΡΙΑ Α ΓΥΜΝΑΣΙΟΥ. Η διαίρεση καλείται Ευκλείδεια και είναι τέλεια όταν το υπόλοιπο είναι μηδέν.
 ΑΛΓΕΒΡΑ 1 ο ΚΕΦΑΛΑΙΟ ΘΕΩΡΙΑ Α ΓΥΜΝΑΣΙΟΥ 1. Τι είναι αριθμητική παράσταση; Με ποια σειρά εκτελούμε τις πράξεις σε μια αριθμητική παράσταση ώστε να βρούμε την τιμή της; Αριθμητική παράσταση λέγεται κάθε
ΑΛΓΕΒΡΑ 1 ο ΚΕΦΑΛΑΙΟ ΘΕΩΡΙΑ Α ΓΥΜΝΑΣΙΟΥ 1. Τι είναι αριθμητική παράσταση; Με ποια σειρά εκτελούμε τις πράξεις σε μια αριθμητική παράσταση ώστε να βρούμε την τιμή της; Αριθμητική παράσταση λέγεται κάθε
Σχεδιασμός μιας εφαρμογής ΒΔ: Βήματα. 1. Συλλογή και Ανάλυση Απαιτήσεων(requirement analysis)
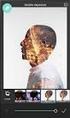 Σχεσιακό Μοντέλο Βάσεις εδοµένων 2012-2013 Ευαγγελία Πιτουρά 1 Σχεδιασμός μιας εφαρμογής ΒΔ: Βήματα 1. Συλλογή και Ανάλυση Απαιτήσεων(requirement analysis) Εισαγωγή Τι δεδομένα θα αποθηκευτούν, ποιες εφαρμογές
Σχεσιακό Μοντέλο Βάσεις εδοµένων 2012-2013 Ευαγγελία Πιτουρά 1 Σχεδιασμός μιας εφαρμογής ΒΔ: Βήματα 1. Συλλογή και Ανάλυση Απαιτήσεων(requirement analysis) Εισαγωγή Τι δεδομένα θα αποθηκευτούν, ποιες εφαρμογές
Το Σχεσιακό Μοντέλο. Βάσεις Δεδομένων Ευαγγελία Πιτουρά 1
 Το Σχεσιακό Μοντέλο Βάσεις Δεδομένων 2018-2019 Ευαγγελία Πιτουρά 1 Μοντελοποίηση Σχήμα (database schema): η περιγραφή της δομής της πληροφορίας που είναι αποθηκευμένη στη βδ καθώς και των περιορισμών ακεραιότητας
Το Σχεσιακό Μοντέλο Βάσεις Δεδομένων 2018-2019 Ευαγγελία Πιτουρά 1 Μοντελοποίηση Σχήμα (database schema): η περιγραφή της δομής της πληροφορίας που είναι αποθηκευμένη στη βδ καθώς και των περιορισμών ακεραιότητας
2 ο Σύνολο Ασκήσεων. Βάσεις Δεδομένων 2013-2014 Ευαγγελία Πιτουρά 1
 2 ο Σύνολο Ασκήσεων Οι βαθμοί θα ανακοινωθούν αύριο μαζί με τους βαθμούς της προγραμματιστικής άσκησης Τα αστεράκια δείχνουν τον εκτιμώμενο βαθμό δυσκολίας (*) εύκολο (**) μέτριο (***) δύσκολο Βάσεις Δεδομένων
2 ο Σύνολο Ασκήσεων Οι βαθμοί θα ανακοινωθούν αύριο μαζί με τους βαθμούς της προγραμματιστικής άσκησης Τα αστεράκια δείχνουν τον εκτιμώμενο βαθμό δυσκολίας (*) εύκολο (**) μέτριο (***) δύσκολο Βάσεις Δεδομένων
Περιεχόμενα. Μέρος Ι Εισαγωγή στα συστήματα βάσεων δεδομένων Πρόλογος... 33
 Περιεχόμενα Πρόλογος... 33 Μέρος Ι Εισαγωγή στα συστήματα βάσεων δεδομένων... 39 1 Μια βόλτα στις βάσεις δεδομένων... 41 1.1 Η πρώτη βάση δεδομένων... 42 1.1.1 Άλλοι τρόποι... 42 1.1.2 Απαιτήσεις της εφαρμογής...
Περιεχόμενα Πρόλογος... 33 Μέρος Ι Εισαγωγή στα συστήματα βάσεων δεδομένων... 39 1 Μια βόλτα στις βάσεις δεδομένων... 41 1.1 Η πρώτη βάση δεδομένων... 42 1.1.1 Άλλοι τρόποι... 42 1.1.2 Απαιτήσεις της εφαρμογής...
Ψηφιακή Σχεδίαση Εργαστήριο Τ.Ε.Ι. ΚΡΗΤΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜ. ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ
 Ψηφιακή Σχεδίαση Εργαστήριο Τ.Ε.Ι. ΚΡΗΤΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜ. ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ 2015-2016 Άλγεβρα Boole (Boolean Algebra) Βασικοί ορισμοί Η άλγεβρα Boole μπορεί να οριστεί
Ψηφιακή Σχεδίαση Εργαστήριο Τ.Ε.Ι. ΚΡΗΤΗΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜ. ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ 2015-2016 Άλγεβρα Boole (Boolean Algebra) Βασικοί ορισμοί Η άλγεβρα Boole μπορεί να οριστεί
Βάσεις εδοµένων. Συνολοθεωρητικές Πράξεις. Ειδικές Πράξεις. Εκφράσεις. Θεµελίωση της Σχεσιακού Μοντέλου εδοµένων. Σχεσιακή Άλγεβρα Σχεσιακός Λογισµός
 Θεµελίωση της Σχεσιακού Μοντέλου εδοµένων Βάσεις εδοµένων Σχεσιακή Άλγεβρα Σχεσιακός Λογισµός Παύλος Εφραιµίδης pefraimi at ee.duth.gr Στο µάθηµα θα πούµε για Σχεσιακή Άλγεβρα Βάσεις εδοµένων Σχεσιακή
Θεµελίωση της Σχεσιακού Μοντέλου εδοµένων Βάσεις εδοµένων Σχεσιακή Άλγεβρα Σχεσιακός Λογισµός Παύλος Εφραιµίδης pefraimi at ee.duth.gr Στο µάθηµα θα πούµε για Σχεσιακή Άλγεβρα Βάσεις εδοµένων Σχεσιακή
Λογικός Σχεδιασµός Σχεσιακών Σχηµάτων: Αποσύνθεση. Βάσεις εδοµένων Ευαγγελία Πιτουρά 1
 Λογικός Σχεδιασµός Σχεσιακών Σχηµάτων: Αποσύνθεση Βάσεις εδοµένων 2011-2012 Ευαγγελία Πιτουρά 1 Εισαγωγή Θα εξετάσουµε πότε ένα σχεσιακό σχήµα για µια βάση δεδοµένων είναι «καλό» Γενικές Οδηγίες Η Μέθοδος
Λογικός Σχεδιασµός Σχεσιακών Σχηµάτων: Αποσύνθεση Βάσεις εδοµένων 2011-2012 Ευαγγελία Πιτουρά 1 Εισαγωγή Θα εξετάσουµε πότε ένα σχεσιακό σχήµα για µια βάση δεδοµένων είναι «καλό» Γενικές Οδηγίες Η Μέθοδος
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ - ΤΜΗΥΠ ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ - ΤΜΗΥΠ ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ Ι Β. Μεγαλοοικονόμου, Δ. Χριστοδουλάκης Σχεσιακό Μοντέλο ΙΙΙ Ακ.Έτος 2008-09 (μεβάσητιςσημειώσειςτωνsilberchatz, Korth και Sudarshan και του C. Faloutsos CMU)
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ - ΤΜΗΥΠ ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ Ι Β. Μεγαλοοικονόμου, Δ. Χριστοδουλάκης Σχεσιακό Μοντέλο ΙΙΙ Ακ.Έτος 2008-09 (μεβάσητιςσημειώσειςτωνsilberchatz, Korth και Sudarshan και του C. Faloutsos CMU)
Λογικός Σχεδιασµός Σχεσιακών Σχηµάτων: Αποσύνθεση
 Λογικός Σχεδιασµός Σχεσιακών Σχηµάτων: Αποσύνθεση Βάσεις εδοµένων 2012-2013 Ευαγγελία Πιτουρά 1 Εισαγωγή Θα εξετάσουμε πότε ένα σχεσιακό σχήμα για μια βάση δεδομένων είναι «καλό» Γενικές Οδηγίες Η Μέθοδος
Λογικός Σχεδιασµός Σχεσιακών Σχηµάτων: Αποσύνθεση Βάσεις εδοµένων 2012-2013 Ευαγγελία Πιτουρά 1 Εισαγωγή Θα εξετάσουμε πότε ένα σχεσιακό σχήμα για μια βάση δεδομένων είναι «καλό» Γενικές Οδηγίες Η Μέθοδος
Σχεσιακός Λογισμός. Εισαγωγή. Σχεσιακό Μοντέλο. Τυπικές Γλώσσες Ερωτήσεων Σχεσιακή Άλγεβρα Σχεσιακός Λογισμός Πλειάδων Σχεσιακός Λογισμός Πεδίου
 Σχεσιακός Λογισμός Βάσεις Δεδομένων 2009-2010 Ευαγγελία Πιτουρά 1 Εισαγωγή Σχεσιακό Μοντέλο Τυπικές Γλώσσες Ερωτήσεων Σχεσιακή Άλγεβρα Σχεσιακός Λογισμός Πλειάδων Σχεσιακός Λογισμός Πεδίου Βάσεις Δεδομένων
Σχεσιακός Λογισμός Βάσεις Δεδομένων 2009-2010 Ευαγγελία Πιτουρά 1 Εισαγωγή Σχεσιακό Μοντέλο Τυπικές Γλώσσες Ερωτήσεων Σχεσιακή Άλγεβρα Σχεσιακός Λογισμός Πλειάδων Σχεσιακός Λογισμός Πεδίου Βάσεις Δεδομένων
Σχεσιακή Άλγεβρα Relational Algebra
 Σχεσιακή Άλγεβρα Relational Algebra Ορίζει ένα σύνολο τελεστών που εφαρμόζονται σε μια ή σε περισσότερες σχέσεις. Οι τελεστές ορίζουν πράξεις οι οποίες διακρίνονται σε Πράξεις μεταξύ συνόλων (σχέση είναι
Σχεσιακή Άλγεβρα Relational Algebra Ορίζει ένα σύνολο τελεστών που εφαρμόζονται σε μια ή σε περισσότερες σχέσεις. Οι τελεστές ορίζουν πράξεις οι οποίες διακρίνονται σε Πράξεις μεταξύ συνόλων (σχέση είναι
