Maria Bazini Diploma Thesis
|
|
|
- Άφροδίτη Ὑπατια Ευταξίας
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΣΤΕΡΕΑΣ ΚΑΤΑΣΤΑΣΗΣ Ηλεκτρονική δομή της 1,,5-τριαζίνης με γραμμικό συνδυασμό ατομικών και υβριδικών τροχιακών Μαρία Μπαζίνη Διπλωματική Εργασία Επιβλέπων: Κωνσταντίνος Σιμσερίδης ΑΘΗΝΑ 017
2
3 NATIONAL AND KAPODISTRIAN UNIVERSITY OF ATHENS DEPARTMENT OF PHYSICS SECTION OF SOLID STATE PHYSICS Electronc structure of 1,,5-trazne wth lnear combnaton of atomc and hybrd orbtals Mara Bazn Dploma Thess Supervsor: Constantnos Smserdes ATHENS 017
4
5 Περίληψη Μελετάμε την ηλεκτρονική δομή της 1,,5-τριαζίνης ή s-τριαζίνης (C H N ) με γραμμικό συνδυασμό ατομικών και υβριδικών τροχιακών. Δηλαδή, η μοριακή κυματοσυνάρτηση εκϕράζεται ως γραμμικός συνδυασμός των ατομικών και υβριδικών τροχιακών των στοιχείων που συνιστούν το μόριο. Λαμβάνουμε υπ όψιν τα p z ατομικά τροχιακά των ατόμων άνθρακα και αζώτου, τα 1s ατομικά τροχιακά των ατόμων υ- δρογόνου και τα sp υβριδικά τροχιακά, τα οποία προκύπτουν από την ανάμιξη των p x, p y και s ατομικών τροχιακών των ατόμων άνθρακα και αζώτου. Δηλαδή, μας απασχολεί μόνο ο ϕλοιός σθένους των ατόμων. Επιλύοντας την χρονοανεξάρτητη εξίσωση Schrödnger, καταλήγουμε σε ένα σύστημα εξισώσεων, από το οποίο βρίσκουμε τις ιδιοενέργειες και τα ιδιοανύσματα του μελετούμενου μορίου. Ετσι, βρίσκουμε το χαρακτήρα κάθε ενεργειακής στάθμης του μορίου. Δηλαδή, εξετάζουμε το κατά πόσο η κυματοσυνάρτηση, η οποία αντιστοιχεί στην κάθε ενεργειακή στάθμη οϕείλεται σε κάθε είδος ατομικού ή υβριδικού τροχιακού. Υπάρχουν ενεργειακές στάθμες οι οποίες οϕείλονται αποκλειστικά στα p z ατομικά τροχιακά των ατόμων άνθρακα και αζώτου. Αντίθετα, οι άλλες οϕείλονται λιγότερο ή περισσότερο είτε στα υβριδικά τροχιακά του δακτυλίου είτε σε αυτά που αντιπροσωπεύουν το δεσμό άνθρακα - υδρογόνου είτε στα υβριδικά τροχιακά του αζώτου που αντιστοιχούν στο ασύζευκτο ζεύγος των ηλεκτρονίων σθένους του. Επίσης, βρίσκουμε το HOMO, το LUMO και το μεταξύ τους ενεργειακό χάσμα E g και προσπαθούμε να ελαχιστοποιήσουμε την απόκλιση των θεωρητικών αποτελεσμάτων από τα αντίστοιχα πειραματικά, μεταβάλλοντας τις παραμετρούς ισχυρής δεσμεύσεως, οι οποίες εμπλέκονται στους υ- πολογισμούς. Η γεωμετρία προέρχεται από το NIST [1]. Χρησιμοποιούμε πρόγραμμα σε γλώσσα προγραμματισμού fortran.
6
7 Abstract We study the electronc structure of 1,,5-trazne or s-trazne (C H N ) wth lnear combnaton of atomc and hybrd orbtals. Specfcally, the molecular wave functon s expressed as a lnear combnaton of the atomc and hybrd orbtals of the elements that consttute the molecule. We take nto account the p z atomc orbtals of the atoms of carbon and ntrogen, the 1s atomc orbtals of the atoms of hydrogen and the sp hybrd orbtals made by the mxng the p x, p y and s atomc orbtals of carbon and ntrogen. Ths means that we take nto account only the valence shell. By solvng the Schrödnger equaton, we arrve at a system of equatons, by whch we calculate the egenenerges and the egenvectors of the molecule. In that way, we determne the character of every energy level of the molecule. In other words, we calculate the degree to whch every wave functon correspondng to a certan energy level s a result of any of the types of atomc or hybrd orbtals taken nto account. Some energy levels are made up exclusvely from the p z atomc orbtals of the atoms of carbon and ntrogen. Other energy levels correspond more or less to ether the hybrd orbtals of the man rng, the orbtals that represent the bond between carbon and hydrogen or the hybrd orbtals that represent the ntrogen s lone par of valence electrons. Moreover, we calculate the HOMO, the LUMO and the energy gap between them, E g and we try to mnmze the devaton between the theoretcal results and the correspondng expermental results, by changng the tght bndng parameters whch are nvolved n the calculatons. The geometry of the molecule orgnates from NIST [1]. We use a program wrtten n fortran language.
8
9 ΕΥΧΑΡΙΣΤΙΕΣ Θα ήθελα να ευχαριστήσω θερμά τον Επιβλέποντα καθηγητή, Κωνσταντίνο Σιμσερίδη, για την πολύτιμη βοήθεια και καθοδήγησή του καθ όλη τη διάρκεια της εκπόνησης αυτής της Διπλωματικής εργασίας. Επίσης, θα ήθελα να ευχαριστήσω την οικογένειά μου, ειδικά τη μητέρα μου, για τη στήριξή τους καθ όλη τη διάρκεια των σπουδών μου.
10
11 Περιεχόμενα Πρόλογος 0.1 Γλωσσάριο Συμβολοθήκη v 1 Γραμμικός Συνδυασμός Ατομικών Τροχιακών Γενικά για την LCAO Η LCAO στο μοριακό ιόν του υδρογόνου Ετεροπολικός Δεσμός: NaCl ,,5-τριαζίνη: sp υβριδισμός του άνθρακα και του αζώτου Ανάλυση των sp υβριδικών τροχιακών στην 1,,5-τριαζίνη σε s, p x και p y ατομικά τροχιακά Τύποι ομοιοπολικών δεσμών μεταξύ ατομικών τροχιακών Γραμμικός συνδυασμός τροχιακών στην 1,,5-τριαζίνη με sp υβριδικά τροχιακά αζώτων και ανθράκων, p z ατομικά τροχιακά αζώτων και ανθράκων και 1s ατομικά τροχιακά υδρογόνων Η μέθοδος LCAO με p z ατομικά τροχιακά σε επίπεδα οργανικά μόρια 70.1 Μέθοδος Hückel: Συζευγμένα Συστήματα LCAO στο βενζόλιο με p z τροχιακά Βενζόλιο (Benzene, C 6 H 6 ) ,,5-τριαζίνη (1,,5-trazne, C H N ) Ηλεκτρονική δομή της 1,,5-τριαζίνης με εϕαρμογή της μεθόδου LCAO με συνδυασμό sp υβριδικών τροχιακών ανθράκων
12 και αζώτων, p z ατομικών τροχιακών ανθράκων και αζώτων και 1s ατομικών τροχιακών υδρογόνων 8.1 Μεταβάλλοντας μία μόνο παράμετρο Μεταβάλλοντας δύο παραμέτρους μαζί Μεταβάλλοντας όλες τις παραμέτρους Μεταβάλλοντας τις παραμέτρους για b = Μεταβάλλοντας τις παραμέτρους για b = Αʹ Εξίσωση Schrödnger και στοιχεία πίνακα σε αναπαράσταση θέσεως 146 Βʹ Προγράμματα 148 ΒΙΒΛΙΟΓΡΑΦΙΑ 161
13 Προλογος 0.1 Γλωσσάριο Ακολουθεί πίνακας με τις κυριότερες συντομογραϕίες και τη σημαντικότερη ορολογία. Πίνακας 1: Γλωσσάριο σύντμηση όνομα abbrevaton name LCAO Γραμμικός Συνδυασμός LCAO Lnear Combnaton Ατομικών Τροχιακών of Atomc Orbtals HOMO Υψηλότερο Κατειλημμένο HOMO Hghest Occuped Μοριακό Τροχιακό Molecular Orbtal LUMO Χαμηλότερο μη Κατειλημμένο LUMO Lowest Unoccuped Μοριακό Τροχιακό Molecular Orbtal επιτόπια ενέργεια on-ste energy συζευγμένο conjugated ασύζευκτα ζεύγη ηλεκτρονίων lone pars ρίζα radcal ιόν καρβενίου carbenum on κυκλική cyclc άκυκλη acyclc ετεροάτομα heteroatoms
14 v 0. Συμβολοθήκη Πίνακας : Συμβολοθήκη. Περιέχονται μερικά γενικά σύμβολα. σύμβολο ονομασία στην ελληνική ονομασία στην αγγλική b Παράγοντας αλληλεπιδράσεως σε δεσμό Interacton factor n a bond που εμπλέκει ένα άτομο Υδρογόνου nvolvng one Hydrogen atom c = b Παράγοντας αλληλεπιδράσεως σε δεσμό Interacton factor n a bond μεταξύ δύο ατόμων Υδρογόνου between two Hydrogen atoms σ σ δεσμός σ bond π π δεσμός π bond h Σταθερά του Planck Planck constant h Ανηγμένη σταθερά του Planck Reduced Planck constant m μάζα ηλεκτρονίου electron mass E p C Επιτόπια Ενέργεια του p On-ste energy of Carbon s Τροχιακού του Άνθρακα p orbtal E s C Επιτόπια Ενέργεια του s On-ste energy of Carbon s Τροχιακού του Άνθρακα s orbtal Θα συμβολίζουμε τις μονάδες μετρήσεως ενός ϕυσικού μεγέθους M με [M].
15 Κεϕάλαιο 1 Γραμμικός Συνδυασμός Ατομικών Τροχιακών Εδώ θα αναλύσουμε τη μέθοδο του Γραμμικού Συνδυασμού Ατομικών Τροχιακών (Lnear Combnaton of Atomc Orbtals, LCAO) []. 1.1 Γενικά για την LCAO Η μέθοδος του γραμμικού συνδυασμού των ατομικών τροχιακών προέκυψε α- πό την προσπάθεια των ϕυσικών και χημικών να εξηγήσουν τη ϕύση του χημικού δεσμού. Αυτό το μοντέλο, εκτός του ότι μας εξηγεί το χημικό δεσμό, μας δίνει ποσοτικές και ποιοτικές πληροϕορίες για τη στερεοχημεία, τις διαστάσεις και για αρκετές ϕασματοσκοπικές ποσότητες των διαϕόρων μορίων. Η κύρια ιδέα της μεθόδου είναι να εκϕράσουμε την μοριακή κυματοσυνάρτηση ψ( r) μέσω γραμμικού συνδυασμού των ατομικών κυματοσυναρτήσεων. Γύρω από τον πυρήνα κάθε ατόμου που συμμετέχει σε ένα δεσμό, η λύση της εξίσωσης Schrödnger προσεγγίζει την ατομική κυματοσυνάρτηση. Ετσι, σε ένα χημικό δεσμό η αντίστοιχη μοριακή κυματοσυνάρτηση στη μέθοδο LCAO θεωρείται ως μια υπέρθεση - γραμμικός συνδυασμός - των αντίστοιχων ατομικών τροχιακών. Γενικά, το μοριακό τροχιακό ψ( r) γράϕεται ως γραμμικός συνδυασμός ατομικών τροχιακών ϕ ν ( r), δηλαδή ψ( r) = N I c ν ϕ ν ( r), (1.1) ν=1 =1 όπου ο δείκτης ν αναϕέρεται στο ν άτομο του μορίου και ο δείκτης στο τροχιακό. Υπάρχουν, ας υποθέσουμε, N άτομα και I τροχιακά. Στην περίπτωση που στο 1
16 χημικό δεσμό συνεισϕέρει ένα μόνο τροχιακό από κάθε άτομο, τότε δεν υπάρχει το δεύτερο άθροισμα. Εϕαρμόζουμε την Εξ. (1.1) στην χρονοανεξάρτητη εξίσωση Schrödnger Ĥψ( r) = Eψ( r), (1.) όπου Ĥ είναι ο τελεστής της Χαμιλτονιανής και E οι ιδιοτιμές της ενέργειας. Πολλαπλασιάζουμε με ϕ jµ ( r) και ολοκληρώνουμε στο χώρο c ν d rϕ jµ ( r) Ĥϕ ν ( r) = E c ν d rϕ jµ ( r) ϕ ν ( r). (1.) ν ν Δηλαδή, καταλήγουμε στο ομογενές γραμμικό σύστημα c ν H jµν = E c ν S jµν. (1.4) ν ν Τα στοιχεία πίνακα της Χαμιλτονιανής (δηλαδή τα στοιχεία πίνακα της επικαλύψεως των κυματοσυναρτήσεων μέσω της Χαμιλτονιανής) είναι H jµν = ϕ jµ Ĥ ϕ ν = d rϕ jµ ( r) Ĥϕ ν ( r). (1.5) και τα στοιχεία πίνακα της επικαλύψεως των κυματοσυναρτήσεων είναι S jµν = ϕ jµ ϕ ν = d rϕ jµ ( r) ϕ ν ( r), (1.6) όπως ϕαίνεται και στο παράρτημα Αʹ. Στη διπλωματική αυτή εργασία, αϕού συζητήσουμε μερικές χαρακτηριστικές περιπτώσεις εϕαρμογής της LCAO, θα την εϕαρμόσουμε στην περίπτωση του μορίου της 1,,5-τριαζίνης. Στην εϕαρμογή της μεθόδου LCAO, είναι δυνατό να χρησιμοποιηθούν μόνο τα p z ατομικά τροχιακά, τα οποία είναι κάθετα στο επίπεδο του οργανικού μορίου. Στην περίπτωση αυτή, η Εξ. (1.1) γίνεται ψ( r) = N c ν p z ν( r), (1.7) ν=1 όπου ο δείκτης ν αναϕέρεται στο ν άτομο, από τα συνολικά N άτομα του μορίου. Οπότε, χρησιμοποιώντας την Εξ. (1.7), πολλαπλασιάζοντας με p z µ( r) και ολοκληρώνοντας στο χώρο, η Εξ. (1.) γίνεται c ν d rp z µ( r) Ĥp z ν( r) = E c ν d rp z µ( r) p z ν( r). (1.8) ν ν
17 Δηλαδή, καταλήγουμε στο ομογενές γραμμικό σύστημα c ν H µν = E c ν S µν. (1.9) ν ν Εδώ και H µν = p z µ Ĥ p zν = S µν = p z µ p z ν = d rp z µ( r) Ĥp z ν( r). (1.10) d rp z µ( r) p z ν( r). (1.11) Θεωρώντας τώρα ότι τα στοιχεία πίνακα της επικαλύψεως της Εξ. (1.11) είναι ίσα με δ µν (δ του Kronecker), δηλαδή ότι τα p z ατομικά τροχιακά είναι ορθοκανονικά, η Εξ. (1.9) γίνεται N (H µν Eδ µν ) c ν = 0. (1.1) ν=1 Συνεπώς, πρέπει να διαγωνοποιήσουμε τη Χαμιλτονιανή. Τότε, θα προκύψουν l = 1,..., N ιδιοτιμές (E l ) και ιδιοανύσματα με συνιστώσες c lν. Υποθέσαμε ορθοκανονικότητα των τροχιακών p z που εντοπίζονται σε διαϕορετικά άτομα (το οποίο μπορεί να επιτευχθεί με κατάλληλη εκλογή ατομικοειδών τροχιακών). Γενικότερα, εκτός από τα μόρια, η LCAO χρησιμοποιείται ευρέως και στη ϕυσική στερεάς κατάστασης εξηγώντας διάϕορες ιδιότητες των στερεών. Συγκεκριμένα, μπορεί να εξηγήσει την κατάταξη των στερεών σε μέταλλα, ημιμέταλλα, ημιαγωγούς και μονωτές. Ομως, παρά τις δυνατότητες που προσϕέρει, η εϕαρμογή της μεθόδου γίνεται πολυπλοκότερη όσο αυξάνεται ο αριθμός των παραμέτρων. Μειονέκτημα της μεθόδου θεωρείται η ύπαρξη παραμέτρων οι οποίες είτε θεωρούνται δεδομένες μέσω συγκρίσεως με άλλους υπολογισμούς και το πείραμα, είτε εκϕράζονται συναρτήσει ατομικών μεγεθών, όπως το μήκος των δεσμών μεταξύ γειτονικών ατόμων. Ο καλύτερος τρόπος κατανόησης της μεθόδου είναι η εϕαρμογή σε ένα απλό σύστημα, όπως π.χ. εις το μοριακό ιόν του υδρογόνου (δείτε 1.), το χλωριούχο νάτριο (δείτε 1.) και την 1,,5-τριαζίνη (δείτε 1.4, 1.5, 1.7,.). Η εϕαρμογή της LCAO στο μόριο του βενζολίου και της 1,,5-τριαζίνης πραγματοποιείται για εξοικείωση με ένα σχετικά πολυπλοκότερο σύστημα, του οποίου η δομή ομοιάζει με αυτή των αζωτούχων βάσεων του γενετικού υλικού, εξαιτίας της ύπαρξης αρωματικών επίπεδων κυκλικών δακτυλίων. Κατόπιν, θα μελετήσουμε τέτοια επίπεδα οργανικά μόρια αποτελούμενα από ατομα C, N, O, H.
18 4 1. Η LCAO στο μοριακό ιόν του υδρογόνου Στο μοριακό ιόν του υδρογόνου, το μοναδικό ηλεκτρόνιο μοιράζεται την ταυτόχρονη έλξη των δύο πυρήνων A και B. Η μοριακή κυματοσυνάρτηση που περιγράϕει την κίνηση του ηλεκτρονίου θεωρείται γραμμικός συνδυασμός των ατομικών τροχιακών 1s που περιγράϕουν την κίνηση του ηλεκτρονίου γύρω από κάθε πυρήνα ξεχωριστά αν αυτός ήταν μοναδικός του συστήματος. Θεωρούμε ότι γνωρίζουμε τις ατομικές ιδιοενέργειες ϵ και ιδιοσυναρτήσεις ϕ ( r) που αναϕέρονται στις γνωστές ιδιοκαταστάσεις του ατόμου του υδρογόνου []. Η μοριακή Χαμιλτονιανή είναι Ĥ = ˆp m + U( r R A ) + U( r R B ). (1.1) Ο πρώτος και ο δεύτερος όρος συναποτελούν την ατομική ( atomc ) Χαμιλτονιανή του ατόμου A, ενώ ο πρώτος και ο τρίτος όρος συναποτελούν την ατομική Χαμιλτονιανή του ατόμου B. Ετσι όταν το ηλεκτρόνιο βρίσκεται στην περιοχή του πυρήνα A [δηλαδή όταν r R A α Bohr και r R B α Bohr, όπου α Bohr είναι η ακτίνα Bohr του ατόμου του υδρογόνου, RA ( R B ) είναι το διάνυσμα θέσεως του πυρήνα A (B) και r το διάνυσμα θέσεως του ηλεκτρονίου], η δυναμική ενέργεια που αντιλαμβάνεται το ηλεκτρόνιο είναι παρόμοια με αυτή του απομονωμένου ατόμου και η κυματοσυνάρτηση είναι παρόμοια με την ατομική δηλαδή ψ( r) ϕ 1s ( r R A ). Αντίστοιχα κοντά στην περιοχή του πυρήνα B έχουμε ψ( r) ϕ 1s ( r R B ). Οπότε η μοριακή κυματοσυνάρτηση θεωρείται ο γραμμικός συνδυασμός των δύο ατομικών ψ( r) = c A ϕ 1s ( r R A ) + c B ϕ 1s ( r R B ) (1.14) όπου c A, c B μιγαδικοί αριθμοί που εκϕράζουν τον βαθμό συμμετοχής των επιμέρους ατομικών τροχιακών. Τα μέτρα στο τετράγωνο των δύο αυτών συντελεστών εκϕράζουν την πιθανότητα να βρεθεί το ηλεκτρόνιο στην περιοχή γύρω από τον α- ντίστοιχο πυρήνα. Περαιτέρω, για απλότητα θα γράϕουμε ϕ A = ϕ 1s ( r R A ) και ϕ B = ϕ 1s ( r R B ). Η Εξ. (1.) γίνεται Ĥ(c A ϕ A + c B ϕ B ) = E(c A ϕ A + c B ϕ B ) (1.15) Πολλαπλασιάζουμε με το συζυγές του ϕ A και ολοκληρώνουμε στο χώρο. Εναλλακτικά γράϕουμε dv = d r. c A dv ϕ AĤϕ A + c B dv ϕ AĤϕ B = Ec A dv ϕ Aϕ A + Ec B dv ϕ Aϕ B. (1.16)
19 5 Ορίζουμε ϵ A H AA = V H AB = S S AB = dv ϕ AĤϕ A, (1.17) dv ϕ AĤϕ B, (1.18) dv ϕ Aϕ B, (1.19) ενώ dv ϕ Aϕ A = 1. (1.0) Άρα c A ϵ A + c B V = Ec A + Ec B S. (1.1) Είναι γνωστές οι ιδιοσυναρτήσεις του ατόμου του υδρογόνου [], η ϕ A είναι η 1s δηλαδή η ϕ 100 που μπορεί να θεωρηθεί πραγματική και θετική. Πράγματι [], σε σϕαιρικές συντεταγμένες r, θ, φ, ϕ 100 (r, θ, φ) = (πa 0) 1/ e r a 0, (1.) όπου a 0 είναι η ακτίνα Bohr. Άρα S > 0. Επίσης V < 0 διότι κλασικά είναι ένας όρος που οδηγεί στην έλξη των ατόμων δηλαδή χαμηλώνει την ενέργεια. Επίσης, να σημειωθεί ότι ϵ A H AA = dv ϕ AĤϕ A dv ϕ AĤatomc ϕ A = HAA atomc ϵ A. (1.) Το atomc δηλώνει ατομική Χαμιλτονιανή δηλαδή τους (1ο και ο) όρους της Εξ.( 1.1). Τελικά η Εξ. 1.1 γράϕεται (ϵ A E)c A + (V ES)c B = 0. (1.4) Πολλαπλασιάζουμε τώρα με το συζυγές του ϕ B και ολοκληρώνουμε στο χώρο. c A dv ϕ BĤϕ A + c B dv ϕ BĤϕ B = Ec A dv ϕ Bϕ A + Ec B dv ϕ Bϕ B. (1.5) Αλλά ϵ B H BB = dv ϕ BĤϕ B, (1.6)
20 6 κι ακόμα V H BA = dv ϕ BĤϕ A, (1.7) S BA = dv ϕ Bϕ A = S. (1.8) Ακόμα dv ϕ Bϕ B = 1, (1.9) λόγω ορθοκανονικότητας. Εν τέλει βγάζουμε την εξίσωση c A V + c B ϵ B = Ec A S + Ec B. (1.0) Επειδή στο άτομο του υδρογόνου οι ϕ A και ϕ B είναι πραγματικές V = V και S = S οπότε c A V + c B ϵ B = Ec A S + Ec B. Τελικά η Εξ. 1.0 γράϕεται Επίσης ισχύει (V ES)c A + (ϵ B E)c B = 0. (1.1) ϵ A = ϕ A Ĥ ϕ A = ϕ B Ĥ ϕ B = ϵ B ϵ (1.) Άρα από τις Εξ.(1.4, 1.1, 1.) έχουμε σε μορϕή πινάκων: ( ) ( ) ( ϵ E V ES ca 0 = V ES ϵ E 0 c B ). (1.) Για να έχει μη τετριμμένη λύση το παραπάνω σύστημα της Εξ. (1.) θα πρέπει η ορίζουσα να μηδενίζεται. det = 0 (ϵ E) (V ES) = 0 (ϵ E) = (V ES). (1.4) Λύνοντας ως προς E παίρνουμε δύο ιδιοτιμές της ενέργειας E a = ϵ V 1 S (1.5) και E b = ϵ + V (1.6) 1 + S Η ιδιοενέργεια E a αντιστοιχεί στη λεγόμενη αντιδεσμική (antbondng) κατάσταση, ενώ η ιδιοενέργεια E b αντιστοιχεί στη λεγόμενη δεσμική (bondng) κατάσταση. Οι ονομασίες αυτές θα εξηγηθούν παρακάτω.
21 Αντικαθιστούμε πρώτα την E a που δίνεται από την Εξ. (1.5) στην (1.) για να βρούμε τους συντελεστές c A και c B. Κάνοντας τις πράξεις βγάζουμε ότι c A = c B. Αυτό σημαίνει ότι δεδομένης της μορϕής των ϕ A και ϕ B που δεν είναι παρά οι 1s ιδιοσυναρτήσεις του ατόμου του υδρογόνου που δεν μηδενίζονται πουθενά στο χώρο δηλαδή δεν έχουν κόμβο (δεσμό, node), οι αντίθετοι συντελεστές συνεπάγονται ότι θα υπάρχει στην μοριακή ιδιοσυνάρτηση ψ( r) που δίνεται από την Εξ ένα σημείο μηδενισμού, δηλαδή ένας κόμβος. Αυτό σημαίνει ότι πρόκειται για την 1η διεγερμένη κατάσταση του κβαντικού ϕρέατος του μοριακού ιόντος του υδρογόνου. Άρα αυτός ο συνδυασμός δεν αντιστοιχεί στην θεμελιώδη κατάσταση του κβαντικού ϕρέατος εξ ου και το όνομα αντιδεσμική. Κανονικοποιούμε την αντιδεσμική ιδιοσυνάρτηση και έχουμε: ψ ψdv = 1 (c Aϕ A c Aϕ B)(c A ϕ A c A ϕ B )dv = 1. (1.7) 7 Άρα Δηλαδή συνολικά c A = c A = c B = 1 (1 S). (1.8) 1 (1 S) e θ. (1.9) όπου θ αυθαίρετη ϕάση. Αντικαθιστούμε τώρα την E b που δίνεται από την Εξ. (1.6) στην (1.) για να βρούμε τους συντελεστές c A και c B. Κάνοντας τις πράξεις έχουμε c A = c B. Αυτό σημαίνει ότι δεδομένης της μορϕής των ϕ A και ϕ B που δεν είναι παρά οι 1s ιδιοσυναρτήσεις του ατόμου του υδρογόνου που δεν μηδενίζονται πουθενά στο χώρο δηλαδή δεν έχουν κόμβο (δεσμό, node), οι ίσοι συντελεστές συνεπάγονται ότι ΔΕΝ θα υπάρχει στην μοριακή ιδιοσυνάρτηση ψ( r) που δίνεται από την Εξ σημείο μηδενισμού, δηλαδή ΔΕΝ θα υπάρχει κόμβος. Αυτό σημαίνει ότι πρόκειται για τη θεμελιώδη κατάσταση του κβαντικού ϕρέατος του μοριακού ιόντος του υδρογόνου εξ ου και το όνομα δεσμική. Από την κανονικοποίηση της δεσμικής έχουμε c A = 1 (1 + S). (1.40) Δηλαδή συνολικά c A = c B = 1 (1 + S) e φ. (1.41) όπου φ αυθαίρετη ϕάση.
22 8 Σημειωτέον ότι αϕού συμϕώνως με τα παραπάνω, η δεσμική E b αντιστοιχεί στη θεμελιώδη κατάσταση και η αντιδεσμική E a αντιστοιχεί στην 1η διεγερμένη κατάσταση θα πρέπει E a > E b. Δεδομένου ότι 1 > S > 0, και λόγω των Εξ. ( ) θα πρέπει V < ϵs. Εξάλλου, η επικάλυψη S είναι αρκετά μικρότερη από 1. Από τις Εξ. ( ) προκύπτει E a ϵ = ϵs V 1 S lm S 0 E a ϵ = V > 0 (1.4) και ϵ E b = ϵs V 1 + S lm ϵ E b = V > 0. (1.4) S 0 Δηλαδή για αρκετά μικρό S, E a > ϵ > E b. Η περίπτωση S = 0 παρουσιάζεται στην παρακάτω Εικόνα 1.1. Σχήμα 1.1: Μοριακό ιόν Η +. Παρουσιάζεται η περίπτωση S = 0.
23 9 1. Ετεροπολικός Δεσμός: NaCl Η μέθοδος του γραμμικού συνδυασμού ατομικών τροχιακών (LCAO) εϕαρμόζεται παρομοίως στα διατομικά ιοντικά μόρια. Ενα τέτοιο μόριο είναι το NaCl. Τα μοριακά τροχιακά θα γραϕούν και πάλι ως γραμμικός συνδυασμός ατομικών τροχιακών. Η δομή των απομονωμένων ατόμων είναι: για το νάτριο (Na): [Ne]s 1 = [1s s p 6 ]s 1 και για το χλώριο (Cl): [Ne]s p 5. Θα χρησιμοποιήσουμε την ϕ s ( r R A ) για το Na και την ϕ p ( r R B ) για το Cl. Η μοριακή κυματοσυνάρτηση θα είναι ο γραμμικός συνδυασμός των δύο ατομικών ψ( r) = c A ϕ s ( r R A ) + c B ϕ p ( r R B ). (1.44) Από τη χρονοανεξάρτητη εξίσωση Schrödnger και αντικαθιστώντας την ψ( r) έχουμε Ĥ(c A ϕ sa + c B ϕ pb ) = E(c A ϕ sa + c B ϕ pb ). (1.45) Για απλότητα γράψαμε παραπάνω και θα γράϕουμε από εδώ και πέρα ϕ sa = ϕ s ( r R A ) και ϕ pb = ϕ p ( r R B ). Πολλαπλασιάζουμε και τα δύο μέλη της παραπάνω εξίσωσης με την ϕ sa και ολοκληρώνουμε σε όλο τον χώρο. Οπότε: ϕ saĥc Aϕ sa dv + ϕ saĥc Bϕ pb dv = ϕ saec A ϕ sa dv + ϕ saec B ϕ pb dv Ορίζουμε (1.46) ϵ A = ϕ saĥϕ sadv (1.47) V = ϕ saĥϕ pbdv (1.48) S = ϕ saϕ pb dv (1.49) και λόγω ορθοκανονικότητας ισχύει ϕ saϕ sa dv = 1. (1.50) Τα αντικαθιστούμε στην Εξ. (1.46) και παίρνουμε c A ϵ A + c B V = Ec A + Ec B S (1.51) (ϵ A E)c A + (V ES)c B = 0. (1.5)
24 10 Στη συνέχεια πολλαπλασιάζουμε την Εξ. (1.45) με ϕ pb και ολοκληρώνουμε σε όλο τον χώρο, άρα έχουμε ϕ pbĥc Aϕ sa dv + ϕ pbĥc Bϕ pb dv = ϕ pbec A ϕ sa dv + ϕ pbec B ϕ pb dv Ορίζουμε όπως πριν ϵ B = (1.5) ϕ pbĥϕ pbdv, (1.54) ενώ και V = S = ϕ pbĥϕ sadv (1.55) ϕ pbϕ sa dv. (1.56) Ακόμα, λόγω ορθοκανονικότητας ϕ pbϕ pb dv = 1. (1.57) Άρα έχουμε την παρακάτω εξίσωση c A V + c B ϵ B = Ec A S + Ec B (1.58) (V ES )c A + (ϵ B E)c B = 0. (1.59) Ομως ισχύει V = V και S = S, διότι οι ϕ sa και ϕ pb είναι πραγματικές, οπότε έχουμε το παρακάτω σύστημα δύο εξισώσεων σε μορϕή πινάκων ( ) ( ) ϵa E V ES ca = V ES ϵ B E c B ( 0 0 Μη τετριμμένη λύση έχουμε όταν η ορίζουσα είναι μηδενική, δηλαδή ). (1.60) (ϵ A E)(ϵ B E) (V ES)(V ES) = 0 (1.61) Λύνοντας την εξίσωση καταλήγουμε στο τριώνυμο (1 S )E + (SV ϵ A ϵ B )E + ϵ A ϵ B V = 0. (1.6) Επιπλέον ορίζουμε V = ϵ A ϵ B (1.6)
25 και ϵ = ϵ A + ϵ B. (1.64) όπου το V είναι θετικό. Αυτό προκύπτει από τις ενέργειες ιονισμού του νατρίου και του χλωρίου. Κατ αρχήν υποθέτουμε ότι ϵ A H AA = ϕ saĥϕ sadv αλλά ϕ saĥatomc ϕ sa dv = HAA atomc ϵ A, (1.65) δηλαδή ότι κοντά στο Νάτριο η μοριακή Χαμιλτονιανή μπορεί να προσεγγιστεί χονδροειδώς από την ατομική Χαμιλτονιανή. Γνωρίζουμε ότι η ενέργεια ιονισμού του Νατρίου I(Na) = 5.14 ev = ϵ A και του Χλωρίου I(Cl) = 1.97 ev = ϵ B, οπότε ϵ A > ϵ B και άρα V > 0. Ακόμα, 11 ϵ A = ϵ + V, (1.66) ϵ B = ϵ V. (1.67) Οπότε, μετά από αντικατάσταση των Εξ. (1.6)-(1.64), το τριώνυμο της Εξ. (1.6) γίνεται (1 S )E + (SV ϵ)e + ϵ V V = 0 (1.68) με διακρίνουσα η οποία έχει λύσεις και = β 4αγ = 4(V ϵs) + 4V (1 S ) (1.69) E b = ϵ SV (V ϵs) + V (1 S ) 1 S (1.70) E a = ϵ SV + (V ϵs) + V (1 S ). (1.71) 1 S Εάν για απλότητα θεωρήσουμε S = 0, έχουμε: E b = ϵ V + V (1.7) και E a = ϵ + V + V. (1.7) Στο Σχήμα (1.) παρουσιάζεται το διάγραμμα των ενεργειακών σταθμών του NaCl για την περίπτωση S = 0.
26 1 Σχήμα 1.: Διάγραμμα ενεργειακών σταθμών του NaCl για S = 0.
27 1.4 1,,5-τριαζίνη: sp υβριδισμός του άνθρακα και του αζώτου Στην ενότητα αυτή, θα συζητήσουμε το λεγόμενο sp υβριδισμό που περιγράϕεται στο Σχήμα 1.. Ας υποθέσουμε ότι αναμιγνύουμε, δηλαδή υβριδίζουμε ένα s και δύο p ατομικά τροχιακά του ιδίου ϕλοιού ενώ αϕήνουμε ανεπηρέαστο το τρίτο p ατομικό τροχιακό. Τότε σχηματίζονται τρία ισοδύναμα sp υβριδικά τροχιακά. Επί παραδείγματι, ανακατεύουμε τα s, p x, p y, ενώ αϕήνουμε ανεπηρέαστο το p z. Επειδή τα s, p x, p y είναι συμμετρικά ως προς το επίπεδο xy, το ίδιο θα ισχύει για τα τρία sp υβριδικά τροχιακά. Μάλιστα, αϕού οι υβριδισμοί γίνονται ώστε τα τρία sp να είναι ισοδύναμα, θα πρέπει να σχηματίζουν μεταξύ τους γωνία 10 o. Τα υβριδισμένα τροχιακά έχουν ίσες ενεργειακές στάθμες, μεταξύ αυτών της μίας s και των δύο p που υβριδίζονται, ενώ η στάθμη p που δεν συμμετέχει παραμένει ανεπηρέαστη. Ο υβριδισμός sp συμβαίνει όταν το άτομο προσδένεται σε τρία άτομα ή ομάδες ατόμων και έχει κατά 1/ χαρακτήρα s και κατά / χαρακτήρα p. Τα τρία sp υβρίδια δείχνουν προς τις κορυϕές ισοπλεύρου τριγώνου, το κέντρο του οποίου καταλαμβάνει το άτομο με τον sp υβριδισμό και τις κορυϕές τα άτομα ή οι ομάδες των ατόμων με τις οποίες αυτό συνδέεται. Οπότε, τα τρία sp υβρίδια σχηματίζουν μεταξύ τους γωνία 10 o. Το ϕαινόμενο αυτό συμβαίνει σε μόρια όπως το αιθένιο, το βενζόλιο και την 1,,5-τριαζίνη, την οποία θα μελετήσουμε αναλυτικά παρακάτω. Στο βενζόλιο (C 6 H 6 ), οι άνθρακες έχουν sp υβριδισμό (υβριδίζονται το s και π.χ. τα p x, p y ατομικά τροχιακά), οπότε προκύπτει η κυκλική δομή που παρουσιάζεται στο Σχήμα 1.. Κάθε άνθρακας χρησιμοποιεί δύο sp τροχιακά για να δεθεί με τους δύο γειτονικούς του άνθρακες, σχηματίζοντας δύο sp sp σ δεσμούς. Ε- πίσης, κάθε άνθρακας χρησιμοποιεί το τρίτο sp τροχιακό του για να δεθεί με το γειτονικό του άτομο υδρογόνου με sp s σ δεσμό. Επιπλέον, οι άνθρακες δένονται με ppπ δεσμό μέσω των p z ατομικών τροχιακών τους. Συνεπώς, ο δεσμός μεταξύ των ανθράκων είναι τύπου σ αλλά και τύπου π. Τα τρία sp υβριδικά τροχιακά του άνθρακα σχηματίζουν μεταξύ τους γωνία 10 o. Στην 1,,5-τριαζίνη (C H N ), οι άνθρακες και τα άζωτα εναλλάσσονται στον δακτύλιο, όπως ϕαίνεται στο Σχήμα 1.. Οπως και στο βενζόλιο, οι άνθρακες έχουν sp υβριδισμό. Κάθε άνθρακας χρησιμοποιεί δύο sp τροχιακά για να δεθεί με τα δύο γειτονικά του άζωτα με sp sp σ δεσμούς, ενώ χρησιμοποιεί το τρίτο sp τροχιακό του για να δεθεί με το γειτονικό του άτομο υδρογόνου με sp s σ δεσμό. Ομοίως, τα άζωτα εμϕανίζουν sp υβριδισμό, στον οποίο υβριδίζονται το s και π.χ. τα p x, p y ατομικά τροχιακά. Ετσι, σχηματίζουν τρία sp υβριδικά τροχιακά. Κάθε άζωτο χρησιμοποιεί τα δύο sp τροχιακά για να συνδεθεί με τα γειτονικά του άτομα 1
28 14 άνθρακα. Ομως, σε αντίθεση με τον άνθρακα, το τρίτο sp τροχιακό κάθε αζώτου δε χρησιμοποιείται σε δεσμούς μέσα στο μόριο, διότι είναι κατειλημμένο από το ζεύγος ασύζευκτων ηλεκτρονίων του (Σχήμα 1.). Συνεπώς, σχηματίζει δύο sp sp σ δεσμούς με τους δύο γειτονικούς του άνθρακες, ενώ δε συνδέεται με άλλα άτομα, διότι το ζεύγος ασύζευκτων ηλεκτρονίων του καταλαμβάνει το τρίτο sp υβριδικό τροχιακό του [4]. Τα τρία sp υβριδικά τροχιακά του αζώτου σχηματίζουν μεταξύ τους γωνία 10 o. Επιπλέον, οι άνθρακες και τα άζωτα συνδέονται με ppπ δεσμό μέσω των p z ατομικών τροχιακών τους. Ετσι, ο δεσμός μεταξύ των ανθράκων και των αζώτων είναι τύπου σ, αλλά και τύπου π. Σχήμα 1.: Σχηματικά, ο sp υβριδισμός στο βενζόλιο και στην 1,,5-τριαζίνη.
29 1.5 Ανάλυση των sp υβριδικών τροχιακών στην 1,,5-τριαζίνη σε s, p x και p y ατομικά τροχιακά Στην 1,,5-τριαζίνη, θα αναλύσουμε τα sp υβριδικά τροχιακά γύρω από κάθε άτομο άνθρακα και αζώτου στα s, p x και p y αντίστοιχα ατομικά τροχιακά. Στο Σχήμα 1.4 ϕαίνονται τα sp γύρω από κάθε άτομο άνθρακα και αζώτου, αλλά και τα 1s ατομικά τροχιακά των ατόμων υδρογόνου. Στο μόριο της 1,,5-τριαζίνης, τα άτομα αζώτου βρίσκονται στις θέσεις 1, και 5, ενώ εναλλάσσονται με άτομα άνθρακα στις θέσεις,4 και 6. Στην ανάλυση που ακολουθεί, επιλέγουμε την ίδια αρίθμηση, τοποθετώντας άτομα αζώτου στις θέσεις 1,,5 και άτομα άνθρακα στις θέσεις,4,6, όπως ϕαίνεται στο Σχήμα Σχήμα 1.4: Τα sp υβριδικά τροχιακά γύρω από κάθε άτομο άνθρακα και αζώτου και τα 1s ατομικά τροχιακά των ατόμων υδρογόνου. Εξετάζοντας το μόριο της τριαζίνης π.χ. από πάνω, για κάθε άτομο άνθρακα και αζώτου, ονομάζουμε δ το sp τροχιακό που το συνδέει με το γειτονικό του άτομο δεξιά, α το sp τροχιακό που το συνδέει με το γειτονικό του άτομο αριστερά και ε το sp τροχιακό που το συνδέει με το άτομο που βρίσκεται προς τα έξω. Χρησιμοποιούμε τους δείκτες N και C για τα τροχιακά των ατόμων αζώτου και άνθρακα αντίστοιχα. Στην παρακάτω ανάλυση λαμβάνουμε υπ όψη τρεις παράγοντες ήτοι την κανονικοποίηση, τα σχετικά βάρη των s και p ατομικών τροχιακών στο sp μοριακό τροχιακό και τη γεωμετρία, δηλαδή το Σχήμα 1.4. Επίσης, για απλότητα, για τα s, p x, p y ατομικά τροχιακά των ατόμων άνθρακα και αζώτου γράϕουμε s, p x, p y, με
30 16 τους αντίστοιχους δείκτες. Για το άτομο αζώτου στην πρώτη θέση: Το δ N αναλύεται συναρτήσει των s N, p x N και p y N ως δ N = c 1 s N + c p xn + c p yn (1.74) Με κανονικοποίηση παίρνουμε δ N d r = 1 (c 1s N +c p xn +c p yn)(c 1 s N +c p xn +c p yn )d r = 1. (1.75) Κάνοντας τις πράξεις καταλήγουμε στην εξίσωση c 1 s N d r + c p xn d r + c p yn d r + + c c 1 p xns N d r + c 1c s Np yn d r + c c p xnp yn d r + c c 1 p yns N d r + c c p ynp xn d r = 1, η οποία λόγω ορθοκανονικότητας γίνεται c 1c s Np xn d r (1.76) c 1 + c + c = 1. (1.77) Επειδή κάθε sp τροχιακό έχει κατά 1/ s χαρακτήρα και κατά / p χαρακτήρα c + c = c 1. (1.78) Λύνοντας το σύστημα των Εξ. (1.77)-(1.78), βρίσκουμε c 1 = 1 c + c =. (1.79) Επιπλέον, από τη γεωμετρία έχουμε c c = cos (0 o ) cos (60 o ) = ( ) ( 1 = c = c. (1.80) ) Λύνοντας το σύστημα των Εξ. (1.79)-(1.80), θεωρώντας π.χ. πραγματικές λύσεις για τις τιμές των c 1, c, c, βρίσκουμε c 1 = ±, c = ± 6, c = ±. (1.81)
31 Επιλέγουμε το + για το c 1, το + για το c και το για το c αϕού θέλουμε να ικανοποιείται το Σχήμα 1.4. Άρα, δ N = 1 (s N + 1 p xn p yn). (1.8) Το α N αναλύεται συναρτήσει των s N, και p xn ως 17 α N = c 1 s N + c p xn. (1.8) αϕού κείται πάνω στον άξονα x. Με κανονικοποίηση παίρνουμε α N d r = 1 (c 1s N + c p xn)(c 1 s N + c p xn )d r = 1. (1.84) Λαμβάνοντας πάλι υπ όψιν την ορθοκανονικότητα των ατομικών τροχιακών, c 1 + c = 1. (1.85) Επειδή κάθε sp τροχιακό έχει κατά 1/ s χαρακτήρα και κατά / p χαρακτήρα c = c 1. (1.86) Λύνοντας το σύστημα των Εξ. (1.85)-(1.86), θεωρώντας π.χ. πραγματικές λύσεις για τις τιμές των c 1, c, βρίσκουμε 1 c 1 = ±, c = ±. (1.87) 1 Συνεπώς, έχουμε c 1 = και σύμϕωνα με το σχήμα, διαλέγουμε το c έτσι ώστε c =. Τελικά, βρίσκουμε Το ε N αναλύεται συναρτήσει των s, p xn και p yn ως α N = 1 (s N p xn). (1.88) ε N = c 1 s N + c p xn + c p yn. (1.89) Η κανονικοποίηση του ε N, λαμβάνοντας υπ όψιν την ορθοκανονικότητα των ατομικών τροχιακών, καταλήγει στην c 1 + c + c = 1. (1.90)
32 18 Επειδή κάθε sp τροχιακό έχει κατά 1/ s χαρακτήρα και κατά / p χαρακτήρα, Λύνοντας το σύστημα των Εξ. (1.90)-(1.91), βρίσκουμε Επιπλέον, από τη γεωμετρία έχουμε c + c = c 1. (1.91) c 1 = 1, c + c =. (1.9) c c = cos (0 o ) cos (60 o ) = ( ) ( 1 = c = c. (1.9) ) Λύνοντας το σύστημα των Εξ. (1.9)-(1.9), θεωρώντας π.χ. πραγματικές λύσεις για τις τιμές των c 1, c, c, βρίσκουμε Οπότε π.χ. c 1 = c = και c 6 = c 1 = ±, c = ± 6, c = ±. (1.94) και σύμϕωνα με το σχήμα διαλέγουμε τα c και c έτσι ώστε 1. Τελικά, ε N = 1 (s N + 1 p xn + p yn). (1.95) Για το άτομο άνθρακα στη δεύτερη θέση: Στη συνέχεια, έτσι όπως εργαστήκαμε για το πρώτο άτομο του άνθρακα, θα εργαστούμε και για το δεύτερο. Οι εξισώσεις που θα βρούμε θα πρέπει και αυτές να ικανοποιούν το σχήμα που παραθέσαμε προηγουμένως, έτσι ώστε να σχηματισθεί τελικώς ο δακτύλιος του βενζολίου, τον οποίο θέλουμε να διαμορϕώσουμε. Το ε C θα είναι συναρτήσει του s C και του p xc, άρα της μορϕής ε C = c 1 s C + c p xc (1.96) και λαμβάνοντας και πάλι υπ όψιν την κανονικοποίηση, το σχετικό βάρος των s και p ατομικών τροχιακών και το σχήμα, καταλήγουμε στην έκϕραση ε C = 1 (s C + p xc ) (1.97)
33 δηλαδή 1 c 1 = +, c = +. (1.98) Το δ C θα είναι συναρτήσει των s C, p xc, p yc, δηλαδή της μορϕής δ C = c 1 s C + c p xc + c p yc. (1.99) Ακολουθώντας την ίδια διαδικασία, καταλήγουμε στην έκϕραση δ C = 1 (s C 1 p xc 19 p yc) (1.100) δηλαδή c 1 = +, c = 6, c =. (1.101) Το α C θα είναι συναρτήσει των s C, p xc, p yc, δηλαδή της μορϕής α C = c 1 s C + c p xc + c p yc. (1.10) Ακολουθώντας την ίδια διαδικασία, καταλήγουμε στην έκϕραση α C = 1 (s C 1 p xc + p yc) (1.10) δηλαδή c 1 = +, c = 6, c = +. (1.104) Για το άτομο αζώτου στην τρίτη θέση: Με όμοιο τρόπο, το δ N θα είναι συναρτήσει του s N και του p xn, άρα της μορϕής και καταλήγουμε στην έκϕραση δ N = c 1 s N + c p xn (1.105) δηλαδή δ N = 1 (s N p xn ) (1.106) 1 c 1 = +, c =. (1.107)
34 0 Τελικά Το α N θα είναι συναρτήσει των s N, p xn, p yn, δηλαδή της μορϕής α N = c 1 s N + c p xn + c p yn. (1.108) α N = 1 (s N + 1 p xn + p yn) (1.109) όπου c 1 = +, c = + 6, c = +. (1.110) Το ε N θα είναι συναρτήσει των s N, p xn, p yn, δηλαδή της μορϕής ε N = c 1 s N + c p xn + c p yn. (1.111) Ακολουθώντας την ίδια διαδικασία, καταλήγουμε στην έκϕραση ε N = 1 (s N + 1 p xn p yn) (1.11) δηλαδή c 1 = +, c = + 6, c =. (1.11) Επαναλαμβάνουμε την ίδια διαδικασία και για τα υπόλοιπα άτομα, μέχρι να ϕτάσουμε στο άτομο άνθρακα στην έκτη θέση, το οποίο συνδέεται με το άτομο αζώτου στην πρώτη θέση, όπως ϕαίνεται και στο Σχήμα 1.4. Για το άτομο άνθρακα στην έκτη θέση: Το δ C θα είναι συναρτήσει των s C, p xc δηλαδή της μορϕής δ C = c 1 s C + c p xc. (1.114) Ομοίως με τα προηγούμενα, καταλήγουμε στην έκϕραση 1 δ C = (s + p x ) (1.115) δηλαδή 1 c 1 = +, c = +. (1.116) Το α C, θα είναι συναρτήσει των s C, p xc, p yc δηλαδή της μορϕής α C = c 1 s C + c p xc + c p yc. (1.117)
35 1 Ακολουθώντας την ίδια διαδικασία, καταλήγουμε στην έκϕραση α C = 1 (s C 1 p xc p yc) (1.118) όπου c 1 = +, c = 6, c =. (1.119) Το ε C, θα είναι συναρτήσει των s C, p xc, p yc δηλαδή της μορϕής ε C = c 1 s C + c p xc + c p yc. (1.10) Ακολουθώντας την ίδια διαδικασία, καταλήγουμε στην έκϕραση ε C = 1 (s C 1 p xc + p yc) (1.11) όπου c 1 = +, c = 6, c = +. (1.1) 1.6 Τύποι ομοιοπολικών δεσμών μεταξύ ατομικών τροχιακών. Ας εξετάσουμε λίγο τους τύπους των ομοιοπολικών δεσμών μεταξύ ατομικών τροχιακών που απεικονίζονται στο Σχήμα 1.5. Για το χαρακτηρισμό ενός δεσμού ως σ ή π, σκεϕτόμαστε πού τοποθετείται η επικάλυψη των τροχιακών που συμμετέχουν στο δεσμό σε σχέση με τους πυρήνες των αντιστοίχων ατόμων. Η επικάλυψη είναι S = dv ψ A ψ B, όπου ψ A και ψ B οι κυματοσυναρτήσεις των τροχιακών που συμμετέχουν στο δεσμό, τις οποίες μπορούμε να θεωρήσουμε εδώ πραγματικές. Εάν το μέγιστο της επικαλύψεως βρίσκεται πάνω στο ευθύγραμμο τμήμα που συνδέει τους δύο πυρήνες, ο δεσμός χαρακτηρίζεται ως σ. Εάν η επικάλυψη είναι μέγιστη άνωθεν και κάτωθεν του ευθυγράμμου τμήματος που συνδέει τους δύο πυρήνες, ο δεσμός χαρακτηρίζεται ως π. Ο δεσμός π είναι ασθενέστερος του δεσμού σ. Οι χαρακτηρισμοί σ και π χρησιμοποιούνται ακόμα και όταν ενώνονται υβριδικά τροχιακά. Συνήθως, ισχύει το εξής: ο απλός δεσμός είναι (σ), ο διπλός δεσμός (σ, π) και ο τριπλός δεσμός (σ, π, π). Ετσι, ο διπλός δεσμός (σ, π) είναι μεν ισχυρότερος του απλού (σ), αλλά όχι δύο ϕορές ισχυρότερος, ενώ ο τριπλός δεσμός (σ, π, π) είναι ισχυρότερος του διπλού (σ, π). Στο Σχήμα 1.5, απεικονίζονται μόνο οι περιπτώσεις στις
36 οποίες η επικάλυψη των ατομικών τροχιακών είναι θετική (S > 0) και αυξάνεται η πυκνότητα πιθανότητας στο χώρο μεταξύ των πυρήνων, δηλαδή απεικονίζονται μόνο τα δεσμικά μοριακά τροχιακά. Για τα αντιδεσμικά μοριακά τροχιακά, η επικάλυψη των ατομικών τροχιακών είναι αρνητική (S < 0), άρα μειώνεται η πυκνότητα πιθανότητας στο χώρο μεταξύ των πυρήνων, οπότε εμϕανίζεται μια επιπλέον κομβική επιϕάνεια. Η δε συνθήκη S = 0 χαρακτηρίζεται ως μη δεσμική και αντιστοιχεί στην περίπτωση κατά την οποία δεν υπάρχει αλληλεπίδραση μεταξύ των ατομικών τροχιακών. Μπορεί ακόμη να γίνει η γενίκευση ότι η ισχύς ενός δεσμού είναι περίπου ανάλογη προς την έκταση της επικαλύψεως των ατομικών τροχιακών, δηλαδή οι δεσμοί σχηματίζονται κατά τέτοιο τρόπο ώστε να μεγιστοποιείται η επικάλυψη. Στην περίπτωση S > 0, η ηλεκτρονιακή πυκνότητα στο χώρο μεταξύ των πυρήνων αυξάνεται, οπότε οι πυρήνες θωρακίζονται μεταξύ τους και έτσι η άπωσή τους μειώνεται. Αυτό σημαίνει ελάττωση της ενέργειας του μορίου και επομένως δεσμική κατάσταση. Στην περίπτωση S < 0, ο χώρος μεταξύ των πυρήνων απογυμνώνεται από ηλεκτρονιακό νέϕος, το οποίο συγκεντρώνεται περισσότερο στην εξωτερικό χώρο, με αποτέλεσμα την ενίσχυση των απωθητικών δυνάμεων μεταξύ των πυρήνων, οπότε έχουμε μια αντιδεσμική κατάσταση. Στη αντιδεσμική κατάσταση, υπάρχει μια επιπλέον κομβική επιϕάνεια μεταξύ των πυρήνων (όπου η πυκνότητα πιθανότητας μηδενίζεται). Η ισχύς των δεσμών μεταξύ s ή p ατομικών τροχιακών μπορεί να αποδοθεί με εμπειρικές εκϕράσεις της μορϕής W.A. Harrson [5] V spσ = 1.4 h md (1.1) V ppπ = 0.6 h md (1.14) V ppσ =. h md (1.15) V ssσ = 1. h md (1.16) όπου m είναι η μάζα του ηλεκτρονίου ( kg) και d η απόσταση των πυρήνων των ατόμων. Οταν ο προσανατολισμός των ατομικών τροχιακών είναι α- ντίθετος από αυτόν που δείχνει το Σχήμα 1.5, αλλάζει το πρόσημο από σε +. Οταν στο δεσμό ή γενικότερα στην αλληλεπίδραση συμμετέχει ένα άτομο υδρογόνου, η V spσ πολλαπλασιάζεται με μια παράμετρο b, ενώ όταν συμμετέχουν δύο άτομα υδρογόνου, η V ssσ πολλαπλασιάζεται με μια παράμετρο c. Οι παράμετροι b και c είναι εμπειρικές και χρησιμοποιούνται διότι οι εκϕράσεις που έχουν δοθεί προηγουμένως στις Εξ. 1.1 και 1.16 δεν ισχύουν για τα ατομικά τροχιακά s του υδρογόνου, λόγω μετατοπίσεως του ηλεκτρονικού νέϕους των υδρογόνων. Θεωρούμε c = b [6].
37 Σχήμα 1.5: Δεσμοί μεταξύ s ή p ατομικών τροχιακών. Η ισχύς τους δίνεται από τους τύπους (1.1), (1.14), (1.15), (1.16). Οταν ο προσανατολισμός των ατομικών τροχιακών είναι αντίθετος από αυτόν που δείχνει το σχήμα, αλλάζει το πρόσημο από σε +.
38 4 1.7 Γραμμικός συνδυασμός τροχιακών στην 1,,5-τριαζίνη με sp υβριδικά τροχιακά αζώτων και ανθράκων, p z ατομικά τροχιακά αζώτων και ανθράκων και 1s ατομικά τροχιακά υδρογόνων Εδώ ακολουθούμε την πορεία που περιγράϕεται αναλυτικά αλλού [6]. Το πρώτο βήμα για την εϕαρμογή της μεθόδου του γραμμικού συνδυασμού των τροχιακών είναι η προσέγγιση της μοριακής κυματοσυνάρτησης ως άθροισμα των sp υβριδικών τροχιακών των ατόμων αζώτου και άνθρακα (που συμβολίζουμε δ N, α N, ε N και δ C, α C, ε C αντιστοίχως), των p z ατομικών τροχιακών των ατόμων αζώτου και άνθρακα (που συμβολίζουμε απλώς p zn και p zc αντιστοίχως) και των 1s ατομικών τροχιακών των υδρογόνων (που συμβολίζουμε s H ). Γενικά, όπως αναϕέραμε στην αρχή του κεϕαλαίου (Εξ. 1.1), το μοριακό τροχιακό ψ( r) γράϕεται ως γραμμικός συνδυασμός ατομικών τροχιακών ϕ ν ( r) δηλαδή ψ( r) = N ν=1 I c ν ϕ ν ( r), (1.17) =1 όπου ο δείκτης ν προσδιορίζει το άτομο του μορίου και ο δείκτης το είδος του τροχιακού (δ, α, p z, ε, s H ), ενώ υποθέσαμε ότι υπάρχουν N άτομα και I τροχιακά. Στην περίπτωση της 1,,5-τριαζίνης, στα πλαίσια της παρούσης προσεγγίσεως, θεωρούμε ότι έχουμε πλεγματικά σημεία, καθένα από τα οποία αποτελείται από το σύστημα ενός ατόμου αζώτου και του γειτονικού του ατόμου άνθρακα. Δηλαδή N =. Σε κάθε πλεγματικό σημείο, υπάρχει ένα άτομο αζώτου με 4 τροχιακά και ένα άτομο άνθρακα με 5 τροχιακά, συγκεκριμένα: τρία sp υβριδικά τροχιακά του αζώτου, το p z ατομικό τροχιακό του αζώτου, τρία sp υβριδικά τροχιακά του άνθρακα, το p z ατομικό τροχιακό του άνθρακα και το 1s ατομικό τροχιακό του υδρογόνου. Στην συγκεκριμένη περίπτωση, η Εξ γίνεται ψ( r) = ν=1 9 c ν ϕ ν ( r). (1.18) =1 Ο συντελεστής c ν είναι διαϕορετικός για το κάθε είδος ατόμου και των τροχιακών που περιλαμβάνει, ενώ εξαιτίας της συμμετρίας του μορίου, οι συντελεστές κάθε πλεγματικού σημείου ως προς το ίδιο τροχιακό διαϕέρουν μεταξύ τους κατά μία ϕάση e kϕ, όπου k = 0, 1,.
39 5 Ετσι η μορϕή της κυματοσυνάρτησης είναι: ψ = c 1 δ N1 + c 1 e ϕ δ N + c 1 e ϕ δ N5 + (1.19) c α N1 + c e ϕ α N + c e ϕ α N5 + c p zn1 + c e ϕ p zn + c e ϕ p zn5 + c 4 ε N1 + c 4 e ϕ ε N + c 4 e ϕ ε N5 + c 5 δ C + c 5 e ϕ δ C4 + c 5 e ϕ δ C6 + c 6 α C + c 6 e ϕ α C4 + c 6 e ϕ α C6 + c 7 p zc + c 7 e ϕ p zc4 + c 7 e ϕ p zc6 + c 8 ε C + c 8 e ϕ ε C4 + c 8 e ϕ ε C6 + c 9 s H + c 9 e ϕ s H4 + c 9 e ϕ s H6 Λόγω συμμετρίας, e ϕ = 1. Θεωρούμε τη χρονοανεξάρτητη εξίσωση Schrödnger Hψ = Eψ. (1.10) Στη συνέχεια, θα συνδυάσουμε τις 1.19 και 1.10 και θα πολλαπλασιάσουμε κάθε ϕορά με τη συζυγή κυματοσυνάρτηση κάθε τροχιακού δ N1, α N1, p zn1, ε N1, δ C, α C, p zc, ε C και s H του πρώτου πλεγματικού σημείου, δηλαδή με δn1, α N1, p zn1, ε N1, δ C, α C, p zc, ε C και s H. Θα προκύψει ένα σύστημα εννέα εξισώσεων (Εξ παρακάτω) για τον υπολογισμό των εννέα αγνώστων c 1, c, c, c 4, c 5, c 6, c 7, c 8, c 9 του αναπτύγματος της μοριακής κυματοσυνάρτησης Να σημειωθεί ότι παραλείπονται οι επικαλύψεις των κυματοσυναρτήσεων δια- ϕορετικών ατόμων, δηλαδή στο δεύτερο μέλος της εξίσωσης Schrödnger κρατώνται μόνο εσωτερικά γινόμενα των ιδίων κυματασυναρτήσεων που είναι ίσα με τη μονάδα. Τα υβριδικά τροχιακά δ, α, ε, όπως και τα ατομικά τροχιακά s H, p z είναι πραγματικές κυματοσυναρτήσεις, άρα είναι ίσες με τις συζυγείς τους. Λόγω συμμετρίας, υπάρχει ισότητα ορισμένων στοιχείων του πίνακα της Χαμιλτονιανής, ενώ κάποια άλλα στοιχεία πίνακα θεωρούνται για απλότητα προσεγγιστικά ίσα.
40 6 Πίνακας 1.1: Συνοψίζονται τα στοιχεία πίνακα της Χαμιλτονιανής, τα οποία αναϕέρονται σε αλληλεπίδραση μεταξύ sp υβριδικών τροχιακών ανθράκων και αζώτων ή και 1s ατομικών τροχιακών υδρογόνων. δ N1 H δ N1 = α N1 H α N1 ε N1 H ε N1 α N1 H ε N1 = ε N1 H δ N1 α N1 H δ N1 δ C H δ C = α C H α C ε C H ε C α C H ε C = ε C H δ C α C H δ C δ N1 H δ C6 = δ C H δ N = α N1 H α C6 = α C H α N = α N1 H α C = δ C H δ N1 α N1 H ε C6 = ε C H α N = α C H ε N1 δ N1 H ε C = ε N1 H δ C6 = δ C H ε N δ N1 H α C6 = α C H δ N = α N1 H δ C ε N1 H ε C6 = ε C H ε N = ε N1 H ε C δ N1 H ε C6 = ε C H δ N = ε N1 H α C6 α C H ε N = α N1 H ε C = ε N1 H δ C α N1 H δ C6 = δ C H α N = δ N1 H α C s H6 H δ N1 = s H H δ N = s H H α N1 s H6 H α N1 = s H H α N = s H H δ N1 s H H α C = s H H δ C s H6 H ε N1 = s H H ε N = s H H ε N1
41 7 Σχήμα 1.6: Ανω αριστερά: Θέσεις ατόμων [1]. Η πειραματική απόσταση C-N και C-H συμπίπτουν με αυτές που παρατίθενται στην αναϕορά [7]. Στα υπόλοιπα: Αναπαράσταση αλληλεπιδράσεων μεταξύ υβριδικών ή/και ατομικών τροχιακών.
42 8 Σχήμα 1.7: (Συνέχεια Σχήματος 1.6) Αναπαράσταση αλληλεπιδράσεων μεταξύ υβριδικών ή/και ατομικών τροχιακών.
43 Παρακάτω, ακολουθεί ο υπολογισμός όλων των στοιχείων πίνακα της Χαμιλτονιανής. Στους υπολογισμούς αυτούς, τα ατομικά τροχιακά τύπου p αναλύονται σε δύο συνιστώσες, μία παράλληλη στον άξονα που συνδέει τα δύο άτομα και μία κάθετη σε αυτόν. Κάνουμε τις εξής προσεγγίσεις: Για να υπολογίσουμε τα στοιχεία πίνακα της Χαμιλτονιανής μεταξύ ατομικών τροχιακών υδρογόνων s H, υβριδικών τροχιακών αζώτων α N, δ N, ε N και υβριδικών τροχιακών ανθράκων α C, δ C, ε C, εκϕράζουμε τα υβριδικά τροχιακά σε s, p x και p y συνιστώσες χρησιμοποιώντας την ανάλυση που έγινε στην 1.5, για να μπορέσουμε να χρησιμοποιήσουμε τους τύπους του Harrson, δηλαδή τις Εξ. 1.1, 1.14, 1.15, Τότε, γενικώς, τα ατομικά τροχιακά τύπου p αναλύονται σε δύο συνιστώσες, μία παράλληλη στον άξονα που συνδέει τα δύο άτομα και μία κάθετη σε αυτόν. Για παράδειγμα, στη σύνδεση μεταξύ των τροχιακών δ N1 και s H, ο άξονας x σχηματίζει γωνία 60 o με τον άξονα που συνδέει τα δύο άτομα, ας τον πούμε ξ. Ετσι, το ατομικό τροχιακό p x αναλύεται στην παράλληλη στον άξονα ξ συνιστώσα p x// και στην κάθετη σε αυτόν p x συνιστώσα. Η ίδια τακτική ακολουθείται και για το p y, καθώς και στα υπόλοιπα στοιχεία πίνακα, στα οποία παρουσιάζεται το ίδιο ϕαινόμενο. Θεωρούμε ότι τα στοιχεία πίνακα της Χαμιλτονιανής μεταξύ γειτονικών ατομικών τροχιακών p x και p y μηδενίζονται, όταν ο σχετικός προσανατολισμός τους δίνει μηδενική επικάλυψη χωρίς τη Χαμιλτονιανή, οπότε και με τη Χαμιλτονιανή αναμένεται τα στοιχεία πίνακα αυτά να είναι πολύ μικρά. Για παράδειγμα, τα τροχιακά p xn1 και p yc6 είναι κάθετα μεταξύ τους, μην επιτρέποντας πλευρική επικάλυψη. Ομοίως, τα τροχιακά p yn1 και s C6 προσανατολίζονται με τέτοιο τρόπο ώστε η επικάλυψη κατά μήκος του άξονα x να είναι μηδενική. Θεωρούμε ότι τα στοιχεία πίνακα της Χαμιλτονιανής μεταξύ διαϕορετικών ατομικών τροχιακών του ίδιου ατόμου (s, p x, p y, p z ) μηδενίζονται, αϕού τα ατομικά τροχιακά είναι ορθογώνιες κυματοσυναρτήσεις και γύρω από κάθε άτομο η Χαμιλτονιανή του μορίου Ĥ είναι προσεγγιστικά ίση με τη Χαμιλτονιανή του ατόμου Ĥατόμου. Θεωρούμε ότι τα στοιχεία πίνακα της Χαμιλτονιανής μεταξύ γειτονικών ατομικών τροχιακών s και p z μηδενίζονται, επειδή ο σχετικός προσανατολισμός τους δίνει μηδενική επικάλυψη χωρίς τη Χαμιλτονιανή, οπότε και με τη Χαμιλτονιανή αναμένεται τα στοιχεία πίνακα αυτά να είναι πολύ μικρά. Η εμπειρική παράμετρος b υπεισέρχεται στους τύπους του Harrson, δηλαδή στις Εξ. 1.1, 1.14, 1.15, 1.16, όταν οι δεσμοί εμπλέκουν άτομα υδρο- 9
44 0 γόνου, διότι οι δεσμοί που εμπλέκουν άτομα υδρογόνου εμϕανίζουν μεγάλη μετατόπιση του ηλεκτρονιακού νέϕους και επιπλέον θα πρέπει να είναι ασθενέστεροι, αϕού τα υδρογόνα αντικαθίστανται εύκολα στις οργανικές ενώσεις. Σε πρώτη προσέγγιση, θεωρούμε τα στοιχεία πίνακα της Χαμιλτονιανής μεταξύ ιδίων ατομικών τροχιακών του ιδίου ατόμου άνθρακα και ιδίων ατομικών τροχιακών του ιδίου αζώτου (π.χ. s με s, p με p) ίσα με τα αντίστοιχα στοιχεία πίνακα της ατομικής Χαμιλτονιανής, δηλαδή με τις λεγόμενες οι επιτόπιες ατομικές ενέργειες, οι οποίες προσδιορίζονται από τις ενέργειες ιονισμού του απομονωμένου ατόμου του άνθρακα και του αζώτου των p και s ατομικών τροχιακών αντιστοίχως. Αυτές είναι ίσες με E sn C = 5.54 ev, E pn C = 1.14 ev, E pc C = ev και E sc C = ev [8]. Αργότερα, θα αϕήσουμε αυτή την προσέγγιση, διότι το περιβάλλον ενός ατόμου άνθρακα εντός ενός επιπέδου οργανικού μορίου, όπως η 1,,5-τριαζίνη, δεν είναι ταυτόσημο με το περιβάλλον ενός απομονωμένου ατόμου άνθρακα ή ενός απομονωμένου ατόμου αζώτου. Θεωρούμε το στοιχείο πίνακα της Χαμιλτονιανής μεταξύ των 1s ατομικών τροχιακών του υδρογόνου ίσο με το αντίστοιχο στοιχείο πίνακα της ατομικής Χαμιλονιανής, δηλαδή με τη λεγόμενη επιτόπια ατομική ενέργεια, η οποία προσδιορίζεται από την ενέργεια ιονισμού του απομονωμένου ατόμου του υδρογόνου του 1s ατομικού τροχιακού. Ισούται με E 1s H = 1.6 ev [8]. Εχει χρησιμοποιηθεί η προσέγγιση ανεξάρτητων ηλεκτρονίων, δηλαδή αγνοούμε τις απωστικές δυνάμεις μεταξύ ηλεκτρονίων. Ως Χαμιλτονιανή του συστήματος, χρησιμοποιούμε το άθροισμα των τελεστών της κινητικής και δυναμικής ενέργειας που περιγράϕουν την κίνηση του ηλεκτρονίου. Στις παρακάτω πράξεις, χρησιμοποιούμε τις πειραματικές αποστάσεις δύο γειτονικών ατόμων άνθρακα και αζώτου και ενός ατόμου άνθρακα με το συνδεδεμένο σε αυτόν άτομο υδρογόνου, οι οποίες είναι 1.7 Α και Α, αντιστοίχως [7], όπως ϕαίνεται στο Σχήμα 1.6. Στους παρακάτω υπολογισμούς, θα χρειαστεί η ποσότητα ε 1 = h 4.6 ev (1.11) m(ab) όπου m είναι η μάζα του ηλεκτρονίου και (AB) είναι η απόσταση μεταξύ ενός ατόμου αζώτου στη θέση A και ενός ατόμου άνθρακα στη θέση B. Επίσης,
45 1 θα χρειαστούν τα πηλίκα ( ) AB , AΓ ( ) AB (1.1) BΓ όπου Γ είναι η θέση του υδρογόνου που συνδέεται με το αντίστοιχο άτομο άνθρακα. Στη συνέχεια, παρουσιάζονται αναλυτικά οι υπολογισμοί των στοιχείων πίνακα της Χαμιλτονιανής με όλα τα τροχιακά που εμπλέκουν το πρώτο πλεγματικό σημείο, δηλαδή το σύστημα του αζώτου που βρίσκεται στην πρώτη θέση της αλυσίδας και του άνθρακα που βρίσκεται στη δεύτερη θέση της αλυσίδας του μορίου. Λόγω της συμμετρίας που παρουσιάζει το μόριο, ορισμένα στοιχεία πίνακα ισούνται με κάποια από τα υπόλοιπα. Επίσης, λόγω ερμιτιανότητας, όλα τα στοιχεία πίνακα είναι ίσα με τα συζυγή τους, για παράδειγμα s H H δ C = δ C H s H και δ N1 H α C = α C H δ N1. Για απλότητα, με s, p x, p y συμβολίζονται τα s, p x, p y ατομικά τροχιακά του αζώτου και του άνθρακα, με τους αντίστοιχους δείκτες για το κάθε άτομο. s H H δ N1 = s H H 1 (s N1 + 1 p xn1 p yn1) = 1 s H H s N s H H p xn1 1 s H H p yn1 = 1 s H H s N s H1 H p xn s H H p xn1// 1 0 s H1 H p yn1 1 s H H p yn1// = 1 V ssσ (d = (BΓ)) b V spσ (d = (BΓ)) cos 4 o b 1 ( 1)V spσ (d = (BΓ)) cos 56 o b = b ( AB BΓ ( h 1. m(ab) h m(ab) 1.4 h ) m(ab) = b ( ) ( AB ε ) BΓ b ev ) (1.1)
46 s H6 H α N1 = s H6 H 1 (s N1 p xn1 ) >= 1 (< s H6 H s N1 > < s H6 H p xn1 ) = 1 ( V ssσ b 0 s H6 H p xn1 ) s H6 H p xn1// = 1 (V ssσ (d = (BΓ)) b ) ( 1) V spσ (d = (BΓ)) cos 6 o b = 1 h ( ) ( AB 1. b 1.4 ) b m(ab) BΓ = b ( ) ( AB ε ) b ev BΓ (1.14) s H H α N = s H H 1 (s N + 1 p xn + = 1 ( s H H s N + 1 s H H p xn + p yn) s H H p yn = 1 ( V ssσ (d = (BΓ)) b s H H p xn + 1 s H H p xn// ) + 0 s H H p yn + s H H p yn// = 1 ( V ssσ (d = (BΓ)) b + 1 V spσ (d = (BΓ)) cos 4 o b + ) ( = b ( AB ε 1 AΓ.1006 b ev 1. ) ) ) V spσ(d = (BΓ)) cos 56 o b (1.15)
47 s H H α N1 = s H H 1 (s N1 p xn1 ) = 1 s H H s N1 = 1 s H H s N1 = 1 V ssσ (d = (BΓ)) b = b ( AB ε 1 BΓ 0 s H H p xn1 s H H p xn1// V spσ(d = (BΓ)) cos 4 o b ) ( ) b ev s H H p xn1 (1.16) s H6 H δ N1 = s H6 H 1 (s N1 + 1 p xn1 = 1 ( s H6 H s N1 + 1 s H6 H p xn1 p yn1) s H6 H p yn1 ) = 1 (V ssσ b s H6 H p xn1 + 1 s H6 H p xn1// 0 s H6 H p yn1 s H6 H p yn1// ) = 1 ( V ssσ (d = (BΓ)) b + 1 ( 1) V spσ (d = (BΓ)) cos 6 o b = 1 [ h 1. m(ab) h ( 1. + ( ) AB b + BΓ m(ab) h ( ) AB b] = b BΓ m(ab) ( AB ε 1 BΓ ) ( AB BΓ ) b ev ) V spσ(d = (BΓ)) cos 64 o b ) b (1.17)
48 4 s H H δ N = s H H 1 (s N p xn1 ) = 1 ( s H H s N s H H p xn ) = 1 (V ssσ (d = (BΓ)) b 0 s H H p xn s H H p xn// ) = 1 (V ssσ (d = (BΓ)) b ) V spσ (d = (BΓ)) cos 4 o b = 1 ( h 1. m(ab) = b ( AB ε 1 BΓ ( ) AB b BΓ ) ) ( h m(ab) b ev s H H δ C = s H H 1 (s C 1 6 p xc 1 p yc ) = 1 s H H s C 1 6 s H H p xc 1 s H H p yc ( ) AB b) BΓ (1.18) = 1 s H H s C 1 6 s H H p xc// 1 0 s H H p yc = b V ssσ (d = (AΓ)) 1 6 V spσ (d = (AΓ)) = b ( ) ( AB ε ) b ev AΓ (1.19) s H H α C = s H H 1 (s C 1 6 p xc + 1 p yc ) = 1 s H H s C 1 6 s H H p xc + 1 s H H p yc = 1 s H H s C 1 6 s H H p xc// s H H p yc = b V ssσ (d = (AΓ)) 1 6 V spσ (d = (AΓ)) = b ( ) ( AB ε ) b ev AΓ (1.140)
49 5 s H H ε C = s H H 1 (s C + p xc ) = 1 s H H s C + = 1 V ssσ b + 0 s H H p xc + s H H p xc// = 1 V ssσ (d = (AΓ)) b + V spσ(d = (AΓ)) b = 1. h ( ) AB 1.4 h b m(ab) AΓ m(ab) = b ( ) AB ( ε ) 1.85 b ev BΓ ( ) AB b AΓ s H H p xc (1.141) s H H ε N1 = s H H 1 (s N1 + 1 p xn1 + p yn1) = 1 s H H s N s H H p xn1 + 1 s H H p yn1 = 1 s H H s N s H H p xn s H H p xn1// s H1 H p yn1 + 1 s H H p yn1// (1.14) = 1 V ssσ (d = (BΓ)) b V spσ (d = (BΓ)) cos 4 o b + 1 ( 1) V spσ (d = (BΓ)) cos 56 o b = ( 1. b ( AB ε 1 BΓ ) 1.49 b ev )
50 6 s H6 H ε N1 = s H6 H 1 (s N1 + 1 p xn1 + = 1 ( s H6 H s N1 + 1 s H6 H p xn1 + p yn1) s H6 H p yn1 ) = 1 (V ssσ b s H6 H p xn1 + 1 s H6 H p xn1 // + 0 s H6 H p yn1 + s H6 H p yn1// ) = 1 [ V ssσ (d = (BΓ)) b + 1 ( 1) V spσ (d = (BΓ)) cos 6 o b + = b ( h ( ) AB h ( AB 1. + m(ab) BΓ m(ab) BΓ h ( ) ) AB = b ( ) AB ε m(ab) 1 BΓ BΓ [ ] b ev ] V spσ(d = (BΓ)) cos 64 o b ) (1.14) s H H ε N = s H H 1 (s N + 1 p xn p yn) = 1 s H H s N s H H p xn 1 s H H p yn = 1 s H H s N s H1 H p xn s H H p xn// 1 0 s H H p yn 1 s H H p yn// = 1 V ssσ (d = (BΓ)) b V spσ (d = (BΓ)) cos 4 o b 1 V spσ (d = (BΓ)) cos 56 o b = b ( ) ( AB ε 1 1. BΓ 1.49 b ev ) (1.144)
51 7 δ C H α N = 1 (s C 1 p xc = 1 ( s C H s N + 1 s C H p xn + p xc H p yn p yc H s N [ V ssσ (d = (AB)) + 1 V spσ (d = (AB)) cos 60 o + p yn) p yc) H 1 (s N + 1 p xn + s C H p yn 1 p xc H s N 1 p xc H p xn ) p yc H p xn p yc H p yn V spσ(d = (AB)) cos 0 o = 1 1 ( 1) V spσ (d = (AB)) cos 60 o 1 [( 1) V ppσ(d = (AB)) cos 60 o + V ppπ (d = (AB)) cos 0 o ] [( 1) V ppσ(d = (AB)) cos 0 o cos 60 o + ( 1) V ppπ (d = (AB)) cos 60 o cos 0 o ] ( 1) V spσ(d = (AB)) cos 0 o [( 1) V ppσ(d = (AB)) cos 0 o cos 60 o + ( 1) V ppπ (d = (AB)) cos 60 o cos 0 o ] [( 1) V ppσ(d = (AB)) cos 0 o + ] V ppπ (d = (AB)) cos 60 o ] = 1 [ V ssσ (d = (AB)) + 1 V spσ(d = (AB)) + V spσ(d = (AB)) + 1 V spσ(d = (AB)) V ppσ(d = (AB)) 0 8 V ppπ(d = (AB)) + 8 V 0 ppσ(d = (AB)) + 8 V ppπ(d = (AB)) + V spσ(d = (AB)) + 8 V ppσ(d = (AB)) V ppπ(d = (AB)) V ppσ(d = (AB)) 0 ] 8 V ppπ(d = (AB)) = 1 [ V ssσ (d = (AB)) + ] V spσ (d = (AB)) + V ppσ (d = (AB)) = 1 ( ε ) ev (1.145)
Ηλεκτρονική δομή του βενζολίου με γραμμικό συνδυασμό ατομικών και υβριδικών τροχιακών
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΣΤΕΡΕΑΣ ΚΑΤΑΣΤΑΣΗΣ Ηλεκτρονική δομή του βενζολίου με γραμμικό συνδυασμό ατομικών και υβριδικών τροχιακών Στέϕανος Μπάσιμ Ατάτα
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΣΤΕΡΕΑΣ ΚΑΤΑΣΤΑΣΗΣ Ηλεκτρονική δομή του βενζολίου με γραμμικό συνδυασμό ατομικών και υβριδικών τροχιακών Στέϕανος Μπάσιμ Ατάτα
Νικόλαος Καμηλάρης Διπλωματική Εργασία
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΣΤΕΡΕΑΣ ΚΑΤΑΣΤΑΣΗΣ Γραμμικός συνδυασμός τροχιακών για τη μελέτη επιπέδων οργανικών μορίων με έμϕαση στο βενζόλιο και το καρβαζόλιο
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΣΤΕΡΕΑΣ ΚΑΤΑΣΤΑΣΗΣ Γραμμικός συνδυασμός τροχιακών για τη μελέτη επιπέδων οργανικών μορίων με έμϕαση στο βενζόλιο και το καρβαζόλιο
Ηλεκτρονική δομή επιπέδων οργανικών μορίων με γραμμικό συνδυασμό ατομικών τροχιακών: έμϕαση σε μόρια με οξυγόνο εντός - εκτός μοριακού δακτυλίου
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΣΤΕΡΕΑΣ ΚΑΤΑΣΤΑΣΗΣ Ηλεκτρονική δομή επιπέδων οργανικών μορίων με γραμμικό συνδυασμό ατομικών τροχιακών: έμϕαση σε μόρια με οξυγόνο
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΣΤΕΡΕΑΣ ΚΑΤΑΣΤΑΣΗΣ Ηλεκτρονική δομή επιπέδων οργανικών μορίων με γραμμικό συνδυασμό ατομικών τροχιακών: έμϕαση σε μόρια με οξυγόνο
Ανόργανη Χημεία. Τμήμα Τεχνολογίας Τροφίμων. Ενότητα 5 η : Ομοιοπολικοί δεσμοί & μοριακή δομή. Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής
 Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 5 η : Ομοιοπολικοί δεσμοί & μοριακή δομή Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Ο Ομοιοπολικός Δεσμός 2 Ο δεσμός Η Η στο μόριο Η
Τμήμα Τεχνολογίας Τροφίμων Ανόργανη Χημεία Ενότητα 5 η : Ομοιοπολικοί δεσμοί & μοριακή δομή Οκτώβριος 2018 Δρ. Δημήτρης Π. Μακρής Αναπληρωτής Καθηγητής Ο Ομοιοπολικός Δεσμός 2 Ο δεσμός Η Η στο μόριο Η
ΘΕΩΡΙΑ ΔΕΣΜΟΥ ΣΘΕΝΟΥΣ ΘΕΩΡΙΑ ΜΟΡΙΑΚΩΝ ΤΡΟΧΙΑΚΩΝ
 ΕΡΜΗΝΕΙΑ ΣΧΗΜΑΤΙΣΜΟΥ ΧΗΜΙΚΩΝ ΕΣΜΩΝ ΘΕΩΡΙΑ ΔΕΣΜΟΥ ΣΘΕΝΟΥΣ ΘΕΩΡΙΑ ΜΟΡΙΑΚΩΝ ΤΡΟΧΙΑΚΩΝ ΘΕΩΡΙΑ ΕΣΜΟΥ ΣΘΕΝΟΥΣ 1. Κατά την ανάπτυξη ομοιοπολικού δεσμού ανάμεσα σε δύο άτομα, τροχιακά της στιβάδας σθένους του
ΕΡΜΗΝΕΙΑ ΣΧΗΜΑΤΙΣΜΟΥ ΧΗΜΙΚΩΝ ΕΣΜΩΝ ΘΕΩΡΙΑ ΔΕΣΜΟΥ ΣΘΕΝΟΥΣ ΘΕΩΡΙΑ ΜΟΡΙΑΚΩΝ ΤΡΟΧΙΑΚΩΝ ΘΕΩΡΙΑ ΕΣΜΟΥ ΣΘΕΝΟΥΣ 1. Κατά την ανάπτυξη ομοιοπολικού δεσμού ανάμεσα σε δύο άτομα, τροχιακά της στιβάδας σθένους του
1.12 Ηλεκτρονιακά κύματα και χημικοί δεσμοί
 1.12 Ηλεκτρονιακά κύματα και χημικοί δεσμοί Ο Lewis πρότεινε το μοντέλο του κοινού ηλεκτρονιακού ζεύγους των δεσμών το 1916, σχεδόνμιαδεκαετίαπριναπότηθεωρίατουde Broglie τηςδυαδικότηταςκύματος-σωματιδίου.
1.12 Ηλεκτρονιακά κύματα και χημικοί δεσμοί Ο Lewis πρότεινε το μοντέλο του κοινού ηλεκτρονιακού ζεύγους των δεσμών το 1916, σχεδόνμιαδεκαετίαπριναπότηθεωρίατουde Broglie τηςδυαδικότηταςκύματος-σωματιδίου.
Μοριακή δομή. Απλοϊκή εικόνα του μορίου του νερού. Ηλεκτρονιακοί τύποι κατά Lewis. Δημόκριτος π.χ.
 Μοριακή δομή Και καθώς τα άτομα κινούνται στο κενό, συγκρούονται και αλληλοσυμπλέκονται και μερικά αναπηδούν και άλλα ενώνονται και παραμένουν μαζί σύμφωνα με το σχήμα και το μέγεθος και την τάξη τους.
Μοριακή δομή Και καθώς τα άτομα κινούνται στο κενό, συγκρούονται και αλληλοσυμπλέκονται και μερικά αναπηδούν και άλλα ενώνονται και παραμένουν μαζί σύμφωνα με το σχήμα και το μέγεθος και την τάξη τους.
7 ο Κεφάλαιο Οργανική Χημεία. Δ. Παπαδόπουλος, χημικός
 7 ο Κεφάλαιο Οργανική Χημεία Δ. Παπαδόπουλος, χημικός Βύρωνας, 2015 Θεωρίες ερμηνείας του ομοιοπολικού δεσμού με βάση την κβαντική θεωρία. Θεωρία δεσμού σθένους. Θεωρία των μοριακών τροχιακών. Κάθε θεωρία
7 ο Κεφάλαιο Οργανική Χημεία Δ. Παπαδόπουλος, χημικός Βύρωνας, 2015 Θεωρίες ερμηνείας του ομοιοπολικού δεσμού με βάση την κβαντική θεωρία. Θεωρία δεσμού σθένους. Θεωρία των μοριακών τροχιακών. Κάθε θεωρία
Κεφάλαιο 1 Χημικός δεσμός
 Κεφάλαιο 1 Χημικός δεσμός 1.1 Άτομα, Ηλεκτρόνια, και Τροχιακά Τα άτομα αποτελούνται από + Πρωτόνια φορτισμένα θετικά μάζα = 1.6726 X 10-27 kg Νετρόνια ουδέτερα μάζα = 1.6750 X 10-27 kg Ηλεκτρόνια φορτισμένα
Κεφάλαιο 1 Χημικός δεσμός 1.1 Άτομα, Ηλεκτρόνια, και Τροχιακά Τα άτομα αποτελούνται από + Πρωτόνια φορτισμένα θετικά μάζα = 1.6726 X 10-27 kg Νετρόνια ουδέτερα μάζα = 1.6750 X 10-27 kg Ηλεκτρόνια φορτισμένα
I. ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. math-gr
 I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
Ασκήσεις. Γράψτε μια δομή Lewis για καθένα από τα παρακάτω μόρια και βρείτε τα τυπικά φορτία των ατόμων. (α) CΟ (β) ΗΝO 3 (γ) ClΟ 3 (δ) ΡΟCl 3
 Ασκήσεις Γράψτε μια δομή Lewis για καθένα από τα παρακάτω μόρια και βρείτε τα τυπικά φορτία των ατόμων. (α) CΟ (β) ΗΝO 3 (γ) ClΟ 3 (δ) ΡΟCl 3 Γεωμετρία Μορίων Θεωρία VSEPR Μοριακή γεωμετρία: είναι η διάταξη
Ασκήσεις Γράψτε μια δομή Lewis για καθένα από τα παρακάτω μόρια και βρείτε τα τυπικά φορτία των ατόμων. (α) CΟ (β) ΗΝO 3 (γ) ClΟ 3 (δ) ΡΟCl 3 Γεωμετρία Μορίων Θεωρία VSEPR Μοριακή γεωμετρία: είναι η διάταξη
1.15 Ο δεσμός στο μεθάνιο και ο υβριδισμός τροχιακού
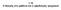 1.15 Ο δεσμός στο μεθάνιο και ο υβριδισμός τροχιακού Η δομή του Μεθανίου τετραεδρική γωνίες δεσμού = 109.5 Μήκη δεσμού = 110 pm αλλά η δομή εμφανίζεται ασυνεπής με την ηλεκτρονική διάταξη του άνθρακα Η
1.15 Ο δεσμός στο μεθάνιο και ο υβριδισμός τροχιακού Η δομή του Μεθανίου τετραεδρική γωνίες δεσμού = 109.5 Μήκη δεσμού = 110 pm αλλά η δομή εμφανίζεται ασυνεπής με την ηλεκτρονική διάταξη του άνθρακα Η
14 ο VIDEO 21/11/2013 Από 1ω,5λ έως το τέλος
 ΚΕΦΑΛΑΙΟ 0: ΜΟΡΙΑ Η ΕΝΟΤΗΤΑ: ΕΝΕΡΓΕΙΑ ΔΥΟ ΑΤΟΜΩΝ, Σελ. 4-46 του βιβλίου ΚΣ 4 ο VIDEO //0 Από ω,5λ έως το τέλος Η η ενότητα αναφέρεται στο γράφημα που παριστά την αλληλεπίδραση δύο ουδέτερων ατόμων καθώς
ΚΕΦΑΛΑΙΟ 0: ΜΟΡΙΑ Η ΕΝΟΤΗΤΑ: ΕΝΕΡΓΕΙΑ ΔΥΟ ΑΤΟΜΩΝ, Σελ. 4-46 του βιβλίου ΚΣ 4 ο VIDEO //0 Από ω,5λ έως το τέλος Η η ενότητα αναφέρεται στο γράφημα που παριστά την αλληλεπίδραση δύο ουδέτερων ατόμων καθώς
1.12 Ηλεκτρονιακά κύματα και χημικοί δεσμοί
 1.12 Ηλεκτρονιακά κύματα και χημικοί δεσμοί Ο Lewis πρότεινε το μοντέλο του κοινού ηλεκτρονιακού ζεύγους των δεσμών το 1916, σχεδόνμιαδεκαετίαπριναπότηθεωρίατουde Broglie τηςδυαδικότηταςκύματος-σωματιδίου.
1.12 Ηλεκτρονιακά κύματα και χημικοί δεσμοί Ο Lewis πρότεινε το μοντέλο του κοινού ηλεκτρονιακού ζεύγους των δεσμών το 1916, σχεδόνμιαδεκαετίαπριναπότηθεωρίατουde Broglie τηςδυαδικότηταςκύματος-σωματιδίου.
Διάλεξη 7: Μοριακή Δομή
 Μεμονωμένα άτομα: Μόνο τα ευγενή αέρια Μόρια: Τα υπόλοιπα άτομα σχηματίζουν μόρια Γιατί; Διότι η ολική ενέργεια ενός ευσταθούς μορίου είναι μικρότερη από την ολική ενέργεια των μεμονωμένων ατόμων που αποτελούν
Μεμονωμένα άτομα: Μόνο τα ευγενή αέρια Μόρια: Τα υπόλοιπα άτομα σχηματίζουν μόρια Γιατί; Διότι η ολική ενέργεια ενός ευσταθούς μορίου είναι μικρότερη από την ολική ενέργεια των μεμονωμένων ατόμων που αποτελούν
21/11/2013 ETY-202 ETY-202 ΎΛΗ & ΦΩΣ 06. Ο ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ. 1396; office Δ013 ΙΤΕ. Στέλιος Τζωρτζάκης
 stzortz@iesl.forth.gr 1396; office Δ013 ΙΤΕ 2 ΎΛΗ & ΦΩΣ 06. Ο ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ Στέλιος Τζωρτζάκης Ο ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ 1 3 4 Το δυναμικό του αρμονικού ταλαντωτή Η παραβολική προσέγγιση βρίσκει άμεση
stzortz@iesl.forth.gr 1396; office Δ013 ΙΤΕ 2 ΎΛΗ & ΦΩΣ 06. Ο ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ Στέλιος Τζωρτζάκης Ο ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ 1 3 4 Το δυναμικό του αρμονικού ταλαντωτή Η παραβολική προσέγγιση βρίσκει άμεση
Περίληψη 1 ου Κεφαλαίου
 Περίληψη 1 ου Κεφαλαίου Άτοµο: θετικά φορτισµένος πυρήνας περικυκλωµένος από αρνητικά φορτισµένα ηλεκτρόνια Ηλεκτρονική δοµή ατόµου περιγράφεται από κυµατοσυνάρτηση Ηλεκτρόνια καταλαµβάνουν τροχιακά γύρω
Περίληψη 1 ου Κεφαλαίου Άτοµο: θετικά φορτισµένος πυρήνας περικυκλωµένος από αρνητικά φορτισµένα ηλεκτρόνια Ηλεκτρονική δοµή ατόµου περιγράφεται από κυµατοσυνάρτηση Ηλεκτρόνια καταλαµβάνουν τροχιακά γύρω
Κβαντομηχανική σε. τρεις διαστάσεις. Εξίσωση Schrödinger σε 3D. Τελεστές 2 )
 vs of Io vs of Io D of Ms Scc & gg Couo Ms Scc ική Θεωλης ική Θεωλης ιδάσκων: Λευτέρης Λοιδωρίκης Π 746 dok@cc.uo.g cs.s.uo.g/dok ομηχ ομηχ δ ά τρεις διαστ Εξίσωση Schödg σε D Σε μία διάσταση Σε τρείς
vs of Io vs of Io D of Ms Scc & gg Couo Ms Scc ική Θεωλης ική Θεωλης ιδάσκων: Λευτέρης Λοιδωρίκης Π 746 dok@cc.uo.g cs.s.uo.g/dok ομηχ ομηχ δ ά τρεις διαστ Εξίσωση Schödg σε D Σε μία διάσταση Σε τρείς
Γεωμετρία Μορίων Θεωρία VSEPR
 Γεωμετρία Μορίων Θεωρία VSEPR Γεωμετρία Μορίων Θεωρία VSEPR Γεωμετρία Μορίων Θεωρία VSEPR Μεθοδολογία για την πρόβλεψη της μοριακής γεωμετρία: Γράφουμε τον ηλεκτρονιακό τύπο κατά Lewis. Μετρούμε το συνολικό
Γεωμετρία Μορίων Θεωρία VSEPR Γεωμετρία Μορίων Θεωρία VSEPR Γεωμετρία Μορίων Θεωρία VSEPR Μεθοδολογία για την πρόβλεψη της μοριακής γεωμετρία: Γράφουμε τον ηλεκτρονιακό τύπο κατά Lewis. Μετρούμε το συνολικό
7 ο Κεφάλαιο Οργανική Χημεία. Δ. Παπαδόπουλος, χημικός
 7 ο Κεφάλαιο Οργανική Χημεία Δ. Παπαδόπουλος, χημικός ΓΕΛ Καρέα, 2018 Θεωρίες ερμηνείας του ομοιοπολικού δεσμού με βάση την κβαντική θεωρία. Θεωρία δεσμού σθένους. Θεωρία των μοριακών τροχιακών. Κάθε θεωρία
7 ο Κεφάλαιο Οργανική Χημεία Δ. Παπαδόπουλος, χημικός ΓΕΛ Καρέα, 2018 Θεωρίες ερμηνείας του ομοιοπολικού δεσμού με βάση την κβαντική θεωρία. Θεωρία δεσμού σθένους. Θεωρία των μοριακών τροχιακών. Κάθε θεωρία
. Να βρεθεί η Ψ(x,t).
 ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ Ασκήσεις Κεφαλαίου II Άσκηση 1: Εάν η κυματοσυνάρτηση Ψ(,0) παριστάνει ένα ελεύθερο σωματίδιο, με μάζα m, στη μία διάσταση την χρονική στιγμή t=0: (,0) N ep( ), όπου N 1/ 4. Να βρεθεί η
ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ Ασκήσεις Κεφαλαίου II Άσκηση 1: Εάν η κυματοσυνάρτηση Ψ(,0) παριστάνει ένα ελεύθερο σωματίδιο, με μάζα m, στη μία διάσταση την χρονική στιγμή t=0: (,0) N ep( ), όπου N 1/ 4. Να βρεθεί η
Γιατί ο σχηματισμός του CΗ 4 δεν μπορεί να ερμηνευθεί βάσει της διεγερμένης κατάστασης του ατόμου C;
 Γιατί ο σχηματισμός του CΗ 4 δεν μπορεί να ερμηνευθεί βάσει της διεγερμένης κατάστασης του ατόμου C; 1. Οι 4 ομοιοπολικοί δεσμοί στο μεθάνιο θα ήταν δύο τύπων: ένας δεσμός από την επικάλυψη του τροχιακού
Γιατί ο σχηματισμός του CΗ 4 δεν μπορεί να ερμηνευθεί βάσει της διεγερμένης κατάστασης του ατόμου C; 1. Οι 4 ομοιοπολικοί δεσμοί στο μεθάνιο θα ήταν δύο τύπων: ένας δεσμός από την επικάλυψη του τροχιακού
ΘΕΜΑ 1 ο 1. Πόσα ηλεκτρόνια στη θεµελιώδη κατάσταση του στοιχείου 18 Ar έχουν. 2. Ο µέγιστος αριθµός των ηλεκτρονίων που είναι δυνατόν να υπάρχουν
 ΚΕΦΑΛΑΙΟ 1 ο Απαντήσεις των ερωτήσεων από πανελλήνιες 2001 2014 ΘΕΜΑ 1 ο 1. Πόσα ηλεκτρόνια στη θεµελιώδη κατάσταση του στοιχείου 18 Ar έχουν µαγνητικό κβαντικό αριθµό m l = 1 ; α. 6. β. 8. γ. 4. δ. 2.
ΚΕΦΑΛΑΙΟ 1 ο Απαντήσεις των ερωτήσεων από πανελλήνιες 2001 2014 ΘΕΜΑ 1 ο 1. Πόσα ηλεκτρόνια στη θεµελιώδη κατάσταση του στοιχείου 18 Ar έχουν µαγνητικό κβαντικό αριθµό m l = 1 ; α. 6. β. 8. γ. 4. δ. 2.
ΚΒΑΝΤΙΚΗ ΜΗΧΑΝΙΚΗ ΙΙ - Ενότητα 5
 Κβαντική Μηχανική ΙΙ Ακ. Ετος 2013-14, Α. Λαχανάς 1/ 53 ΚΒΑΝΤΙΚΗ ΜΗΧΑΝΙΚΗ ΙΙ - Ενότητα 5 Α. Λαχανάς ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ, Τµήµα Φυσικής Τοµέας Πυρηνικής Φυσικής & Στοιχειωδών Σωµατιδίων Ακαδηµαικό έτος
Κβαντική Μηχανική ΙΙ Ακ. Ετος 2013-14, Α. Λαχανάς 1/ 53 ΚΒΑΝΤΙΚΗ ΜΗΧΑΝΙΚΗ ΙΙ - Ενότητα 5 Α. Λαχανάς ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ, Τµήµα Φυσικής Τοµέας Πυρηνικής Φυσικής & Στοιχειωδών Σωµατιδίων Ακαδηµαικό έτος
ΕΙΣΑΓΩΓΗ ΗΛΕΚΤΡΟΝΙΑΚΗ ΔΟΜΗ ΤΩΝ ΑΤΟΜΩΝ Η ΔΟΜΗ ΤΟΥ ΑΤΟΜΟΥ IV. ΟΙ ΚΒΑΝΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΤΑ ΤΡΟΧΙΑΚΑ
 ΗΛΕΚΤΡΟΝΙΑΚΗ ΔΟΜΗ ΤΩΝ ΑΤΟΜΩΝ Η ΔΟΜΗ ΤΟΥ ΑΤΟΜΟΥ IV. ΟΙ ΚΒΑΝΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΤΑ ΤΡΟΧΙΑΚΑ Ν. ΜΠΕΚΙΑΡΗΣ ΕΙΣΑΓΩΓΗ Στο ατομικό πρότυπο του Bohr ο κύριος κβαντικός αριθμός (n) εισάγεται αυθαίρετα, για τον καθορισμό
ΗΛΕΚΤΡΟΝΙΑΚΗ ΔΟΜΗ ΤΩΝ ΑΤΟΜΩΝ Η ΔΟΜΗ ΤΟΥ ΑΤΟΜΟΥ IV. ΟΙ ΚΒΑΝΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΤΑ ΤΡΟΧΙΑΚΑ Ν. ΜΠΕΚΙΑΡΗΣ ΕΙΣΑΓΩΓΗ Στο ατομικό πρότυπο του Bohr ο κύριος κβαντικός αριθμός (n) εισάγεται αυθαίρετα, για τον καθορισμό
Θεωρία δεσµού σθένους - Υβριδισµός. Αντιδράσεις προσθήκης Αντιδράσεις απόσπασης. Αντιδράσεις υποκατάστασης Πολυµερισµός
 11 ο Μάθηµα: Θεωρία δεσµού σθένους - Υβριδισµός 12 ο Μάθηµα: Αντιδράσεις προσθήκης Αντιδράσεις απόσπασης 13 ο Μάθηµα: Αντιδράσεις υποκατάστασης Πολυµερισµός 14 ο Μάθηµα: Αντιδράσεις οξείδωσης - αναγωγής
11 ο Μάθηµα: Θεωρία δεσµού σθένους - Υβριδισµός 12 ο Μάθηµα: Αντιδράσεις προσθήκης Αντιδράσεις απόσπασης 13 ο Μάθηµα: Αντιδράσεις υποκατάστασης Πολυµερισµός 14 ο Μάθηµα: Αντιδράσεις οξείδωσης - αναγωγής
ΑΤΟΜΙΚΑ ΤΟΜΙΚΑ ΠΡΟΤΥΠΑ
 ΑΤΟΜΙΚΑ ΠΡΟΤΥΠΑ Thomson (σταφιδόψωμο) Rutherford (πλανητικό μοντέλο) Bohr (επιτρεπόμενες τροχιές ενεργειακές στάθμες) Κβαντομηχανική β ή (τροχιακό) ρχ 24/9/2008 1 ΑΤΟΜΙΚΟ ΠΡΟΤΥΠΟ Bohr 1η Συνθήκη (Μηχανική
ΑΤΟΜΙΚΑ ΠΡΟΤΥΠΑ Thomson (σταφιδόψωμο) Rutherford (πλανητικό μοντέλο) Bohr (επιτρεπόμενες τροχιές ενεργειακές στάθμες) Κβαντομηχανική β ή (τροχιακό) ρχ 24/9/2008 1 ΑΤΟΜΙΚΟ ΠΡΟΤΥΠΟ Bohr 1η Συνθήκη (Μηχανική
Μάθημα 21 ο. Το σχήμα των μορίων. Θεωρία VSEPR. Θεωρία Δεσμού Σθένους- Υβριδισμός
 Μάθημα 21 ο Το σχήμα των μορίων Θεωρία VSEPR Θεωρία Δεσμού Σθένους- Υβριδισμός Συμβολισμός A = Κεντρικό άτομο X = Συναρμοτής E = Μονήρες ζεύγος SN: Στερεοχημικός αριθμός Γενική και Ανόργανη Χημεία 2016-17
Μάθημα 21 ο Το σχήμα των μορίων Θεωρία VSEPR Θεωρία Δεσμού Σθένους- Υβριδισμός Συμβολισμός A = Κεντρικό άτομο X = Συναρμοτής E = Μονήρες ζεύγος SN: Στερεοχημικός αριθμός Γενική και Ανόργανη Χημεία 2016-17
1 p p a y. , όπου H 1,2. u l, όπου l r p και u τυχαίο μοναδιαίο διάνυσμα. Δείξτε ότι μπορούν να γραφούν σε διανυσματική μορφή ως εξής.
 ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ Ασκήσεις Κεφαλαίου V Άσκηση : Οι θεμελιώδεις σχέσεις μετάθεσης της στροφορμής επιτρέπουν την ύπαρξη ακέραιων και ημιπεριττών ιδιοτιμών Αλλά για την τροχιακή στροφορμή L r p γνωρίζουμε ότι
ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ Ασκήσεις Κεφαλαίου V Άσκηση : Οι θεμελιώδεις σχέσεις μετάθεσης της στροφορμής επιτρέπουν την ύπαρξη ακέραιων και ημιπεριττών ιδιοτιμών Αλλά για την τροχιακή στροφορμή L r p γνωρίζουμε ότι
Ομοιοπολικός εσμός Θεωρία Lewis
 Ομοιοπολικός εσμός Θεωρία Lewis Oμοιοπολικός δεσμός: αμοιβαία συνεισφορά ηλεκτρονίων σθένους κοινά ζεύγη ηλεκτρονίων δομή ευγενούς αερίου (κανόνας της οκτάδας) Πλεονεκτήματα: η πληρέστερη προ-κβαντική
Ομοιοπολικός εσμός Θεωρία Lewis Oμοιοπολικός δεσμός: αμοιβαία συνεισφορά ηλεκτρονίων σθένους κοινά ζεύγη ηλεκτρονίων δομή ευγενούς αερίου (κανόνας της οκτάδας) Πλεονεκτήματα: η πληρέστερη προ-κβαντική
ΧΗΜΙΚΟΣ ΕΣΜΟΣ ΙΙ : ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ ΘΕΩΡΗΣΗ ΤΟΥ ΕΣΜΟΥ
 ΧΗΜΙΚΟΣ ΕΣΜΟΣ ΙΙ : ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ ΘΕΩΡΗΣΗ ΤΟΥ ΟΜΟΙΟΠΟΛΙΚΟΥ Ή ΟΜΟΣΘΕΝΟΥΣ ΕΣΜΟΥ Παππάς Χρήστος Επίκουρος Καθηγητής Το μόριο του Η 2 Σύμφωνα με τη θεωρία του Lewis στο μόριο του Η 2 τα άτομα συγκρατούνται
ΧΗΜΙΚΟΣ ΕΣΜΟΣ ΙΙ : ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ ΘΕΩΡΗΣΗ ΤΟΥ ΟΜΟΙΟΠΟΛΙΚΟΥ Ή ΟΜΟΣΘΕΝΟΥΣ ΕΣΜΟΥ Παππάς Χρήστος Επίκουρος Καθηγητής Το μόριο του Η 2 Σύμφωνα με τη θεωρία του Lewis στο μόριο του Η 2 τα άτομα συγκρατούνται
Μάθημα 22 ο. Θεωρία Δεσμού Σθένους- Υβριδισμός
 Μάθημα 22 ο Θεωρία Δεσμού Σθένους- Υβριδισμός Linus Pauling Έγραψε τη μονογραφία : Nature of the chemical bond Τιμήθηκε για το έργο του με το βραβείο Nobel το 1954 Εισήγαγε την ιδέα του υβριδισμού Υβριδισμένα
Μάθημα 22 ο Θεωρία Δεσμού Σθένους- Υβριδισμός Linus Pauling Έγραψε τη μονογραφία : Nature of the chemical bond Τιμήθηκε για το έργο του με το βραβείο Nobel το 1954 Εισήγαγε την ιδέα του υβριδισμού Υβριδισμένα
ΤΕΧΝΟΛΟΓΙΑ & ΕΠΙΣΤΗΜΗ ΤΩΝ ΥΛΙΚΩΝ
 Τμήμα Τεχνολόγων Περιβάλλοντος Κατεύθυνσης Συντήρησης Πολιτισμικής Κληρονομιάς ΤΕΧΝΟΛΟΓΙΑ & ΕΠΙΣΤΗΜΗ ΤΩΝ ΥΛΙΚΩΝ 3 η Ενότητα ΔΕΣΜΟΙ Δημήτριος Λαμπάκης ΜΟΡΙΑΚΗ ΔΟΜΗ Μεμονωμένα άτομα: Μόνο τα ευγενή αέρια
Τμήμα Τεχνολόγων Περιβάλλοντος Κατεύθυνσης Συντήρησης Πολιτισμικής Κληρονομιάς ΤΕΧΝΟΛΟΓΙΑ & ΕΠΙΣΤΗΜΗ ΤΩΝ ΥΛΙΚΩΝ 3 η Ενότητα ΔΕΣΜΟΙ Δημήτριος Λαμπάκης ΜΟΡΙΑΚΗ ΔΟΜΗ Μεμονωμένα άτομα: Μόνο τα ευγενή αέρια
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ. Σύγxρονη Φυσική II. Μοριακή Δομή Ι Διδάσκων : Επίκ. Καθ. Μ. Μπενής
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Σύγxρονη Φυσική II Μοριακή Δομή Ι Διδάσκων : Επίκ. Καθ. Μ. Μπενής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Σύγxρονη Φυσική II Μοριακή Δομή Ι Διδάσκων : Επίκ. Καθ. Μ. Μπενής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ. Ασκήσεις Κεφαλαίου Ι
 ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ Ασκήσεις Κεφαλαίου Ι Άσκηση 1: Θεωρήστε δύο ορθοκανονικά διανύσματα ψ 1 και ψ και υποθέστε ότι αποτελούν βάση σε ένα χώρο δύο διαστάσεων. Θεωρήστε επίσης ένα τελαστή T που ορίζεται στο χώρο
ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ Ασκήσεις Κεφαλαίου Ι Άσκηση 1: Θεωρήστε δύο ορθοκανονικά διανύσματα ψ 1 και ψ και υποθέστε ότι αποτελούν βάση σε ένα χώρο δύο διαστάσεων. Θεωρήστε επίσης ένα τελαστή T που ορίζεται στο χώρο
Spin του πυρήνα Μαγνητική διπολική ροπή Ηλεκτρική τετραπολική ροπή. Τάσος Λιόλιος Μάθημα Πυρηνικής Φυσικής
 Spin του πυρήνα Μαγνητική διπολική ροπή Ηλεκτρική τετραπολική ροπή Τάσος Λιόλιος Μάθημα Πυρηνικής Φυσικής Εξάρτηση του πυρηνικού δυναμικού από άλλους παράγοντες (πλην της απόστασης) Η συνάρτηση του δυναμικού
Spin του πυρήνα Μαγνητική διπολική ροπή Ηλεκτρική τετραπολική ροπή Τάσος Λιόλιος Μάθημα Πυρηνικής Φυσικής Εξάρτηση του πυρηνικού δυναμικού από άλλους παράγοντες (πλην της απόστασης) Η συνάρτηση του δυναμικού
) σχηματίζονται : α. Ένας σ και δύο π δεσμοί β. Τρεις σ δεσμοί γ. Ένας π και δύο σ δεσμοί δ. Τρεις π δεσμοί.
 ΘΕΜΑΤΑ Θγ 1 0 ΚΕΦΑΛΑΙΟ 1.1. Σε ένα πολυηλεκτρονιακό άτομο ο μέγιστος αριθμός ηλεκτρονίων με κβαντικούς αριθμούς n= και m s = -½ είναι : α. οκτώ β. τέσσερα γ. δύο δ. ένα 1.. Από τα επόμενα χημικά στοιχεία
ΘΕΜΑΤΑ Θγ 1 0 ΚΕΦΑΛΑΙΟ 1.1. Σε ένα πολυηλεκτρονιακό άτομο ο μέγιστος αριθμός ηλεκτρονίων με κβαντικούς αριθμούς n= και m s = -½ είναι : α. οκτώ β. τέσσερα γ. δύο δ. ένα 1.. Από τα επόμενα χημικά στοιχεία
Εισαγωγή σε προχωρημένες μεθόδους υπολογισμού στην Επιστήμη των Υλικών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εισαγωγή σε προχωρημένες μεθόδους υπολογισμού στην Επιστήμη των Υλικών Χτίζοντας τους κρυστάλλους από άτομα Είδη δεσμών Διδάσκων : Επίκουρη Καθηγήτρια
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εισαγωγή σε προχωρημένες μεθόδους υπολογισμού στην Επιστήμη των Υλικών Χτίζοντας τους κρυστάλλους από άτομα Είδη δεσμών Διδάσκων : Επίκουρη Καθηγήτρια
Η Ψ = Ε Ψ. Ψ = f(x, y, z, t, λ)
 Κυματική εξίσωση του Schrödinger (196) Η Ψ = Ε Ψ Η: τελεστής Hamilton (Hamiltonian operator) εκτέλεση μαθηματικών πράξεων επί της κυματοσυνάρτησης Ψ. Ε: ολική ενέργεια των ηλεκτρονίων δυναμική ενέργεια
Κυματική εξίσωση του Schrödinger (196) Η Ψ = Ε Ψ Η: τελεστής Hamilton (Hamiltonian operator) εκτέλεση μαθηματικών πράξεων επί της κυματοσυνάρτησης Ψ. Ε: ολική ενέργεια των ηλεκτρονίων δυναμική ενέργεια
Κεφάλαιο 1. Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς
 Κεφάλαιο 1 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 2 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 1.1 Κίνηση σε κεντρικά δυναµικά 1.1.1 Κλασική περιγραφή Η Χαµιλτωνιανή κλασικού συστήµατος που κινείται
Κεφάλαιο 1 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 2 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 1.1 Κίνηση σε κεντρικά δυναµικά 1.1.1 Κλασική περιγραφή Η Χαµιλτωνιανή κλασικού συστήµατος που κινείται
ΦΟΡΤΙΣΜΕΝΟΣ ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ ΜΕΣΑ ΣΕ ΟΜΟΓΕΝΕΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ: ΤΕΛΕΣΤΕΣ ΔΗΜΙΟΥΡΓΙΑΣ ΚΑΙ ΚΑΤΑΣΤΡΟΦΗΣ, ΒΑΣΙΚΗ ΚΑΤΑΣΤΑΣΗ, ΕΛΑΧΙΣΤΗ ΕΝΕΡΓΕΙΑ ΣΥΖΗΤΗΣΗ
 ΦΟΡΤΙΣΜΕΝΟΣ ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ ΜΕΣΑ ΣΕ ΟΜΟΓΕΝΕΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ: ΤΕΛΕΣΤΕΣ ΔΗΜΙΟΥΡΓΙΑΣ ΚΑΙ ΚΑΤΑΣΤΡΟΦΗΣ, ΒΑΣΙΚΗ ΚΑΤΑΣΤΑΣΗ, ΕΛΑΧΙΣΤΗ ΕΝΕΡΓΕΙΑ ΣΥΖΗΤΗΣΗ Ξεκινώντας από τους τελεστές δημιουργίας και καταστροφής
ΦΟΡΤΙΣΜΕΝΟΣ ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ ΜΕΣΑ ΣΕ ΟΜΟΓΕΝΕΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ: ΤΕΛΕΣΤΕΣ ΔΗΜΙΟΥΡΓΙΑΣ ΚΑΙ ΚΑΤΑΣΤΡΟΦΗΣ, ΒΑΣΙΚΗ ΚΑΤΑΣΤΑΣΗ, ΕΛΑΧΙΣΤΗ ΕΝΕΡΓΕΙΑ ΣΥΖΗΤΗΣΗ Ξεκινώντας από τους τελεστές δημιουργίας και καταστροφής
ˆ ˆ. (τελεστής καταστροφής) (τελεστής δημιουργίας) Το δυναμικό του συστήματός μας (αρμονικός ταλαντωτής μέσα σε ομογενές ηλεκτρικό πεδίο) είναι
 ΜΟΝΟΔΙΑΣΤΑΤΟΣ ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ ΜΕΣΕ ΣΕ ΟΜΟΓΕΝΕΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ: ΤΕΛΕΣΤΕΣ ΔΗΜΙΟΥΡΓΙΑΣ ΚΑΙ ΚΑΤΑΣΤΡΟΦΗΣ, ΒΑΣΙΚΗ ΚΑΤΑΣΤΑΣΗ, ΕΛΑΧΙΣΤΗ ΕΝΕΡΓΕΙΑ ΣΥΖΗΤΗΣΗ Ξεκινώντας από τους τελεστές δημιουργίας και καταστροφής
ΜΟΝΟΔΙΑΣΤΑΤΟΣ ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ ΜΕΣΕ ΣΕ ΟΜΟΓΕΝΕΣ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ: ΤΕΛΕΣΤΕΣ ΔΗΜΙΟΥΡΓΙΑΣ ΚΑΙ ΚΑΤΑΣΤΡΟΦΗΣ, ΒΑΣΙΚΗ ΚΑΤΑΣΤΑΣΗ, ΕΛΑΧΙΣΤΗ ΕΝΕΡΓΕΙΑ ΣΥΖΗΤΗΣΗ Ξεκινώντας από τους τελεστές δημιουργίας και καταστροφής
Διάλεξη 3: Το άτομο του Υδρογόνου. Αναζητούμε λύσεις της χρονοανεξάρτητης εξίσωσης Schrödinger για το κεντρικό δυναμικό
 Αναζητούμε λύσεις της χρονοανεξάρτητης εξίσωσης Schöding για το κεντρικό δυναμικό Μ. Μπενής. Διαλέξεις Μαθήματος Σύγχρονης Φυσικής ΙΙ. Ιωάννινα 3 k V ) Αποδεικνύεται ότι οι λύσεις της ακτινικής εξίσωσης
Αναζητούμε λύσεις της χρονοανεξάρτητης εξίσωσης Schöding για το κεντρικό δυναμικό Μ. Μπενής. Διαλέξεις Μαθήματος Σύγχρονης Φυσικής ΙΙ. Ιωάννινα 3 k V ) Αποδεικνύεται ότι οι λύσεις της ακτινικής εξίσωσης
ETY-202 ΎΛΗ & ΦΩΣ 07. ΣΤΡΟΦΟΡΜΗ ΚΑΙ ΤΟ ΑΤΟΜΟ ΤΟΥ ΥΔΡΟΓΟΝΟΥ
 stzortz@iesl.forth.gr 1396; office Δ013 ΙΤΕ 2 ΎΛΗ & ΦΩΣ 07. ΣΤΡΟΦΟΡΜΗ ΚΑΙ ΤΟ ΑΤΟΜΟ ΤΟΥ ΥΔΡΟΓΟΝΟΥ Θεωρία της στροφορμής Στέλιος Τζωρτζάκης 1 3 4 Υπενθύμιση βασικών εννοιών της στροφορμής κυματοσυνάρτηση
stzortz@iesl.forth.gr 1396; office Δ013 ΙΤΕ 2 ΎΛΗ & ΦΩΣ 07. ΣΤΡΟΦΟΡΜΗ ΚΑΙ ΤΟ ΑΤΟΜΟ ΤΟΥ ΥΔΡΟΓΟΝΟΥ Θεωρία της στροφορμής Στέλιος Τζωρτζάκης 1 3 4 Υπενθύμιση βασικών εννοιών της στροφορμής κυματοσυνάρτηση
Υλικά Ηλεκτρονικής & Διατάξεις
 Τμήμα Ηλεκτρονικών Μηχανικών Υλικά Ηλεκτρονικής & Διατάξεις 2 η σειρά διαφανειών Δημήτριος Λαμπάκης ΜΟΡΙΑΚΗ ΔΟΜΗ Μεμονωμένα άτομα: Μόνο τα ευγενή αέρια Μόρια: Τα υπόλοιπα άτομα σχηματίζουν μόρια, γιατί
Τμήμα Ηλεκτρονικών Μηχανικών Υλικά Ηλεκτρονικής & Διατάξεις 2 η σειρά διαφανειών Δημήτριος Λαμπάκης ΜΟΡΙΑΚΗ ΔΟΜΗ Μεμονωμένα άτομα: Μόνο τα ευγενή αέρια Μόρια: Τα υπόλοιπα άτομα σχηματίζουν μόρια, γιατί
Οι δομές, οι οποίες δεν περιέχουν τυπικά φορτία υψηλά (δηλαδή είναι 2) είναι:
 Answers to Homework Set 3 12162016 1. Πριν από μερικά χρόνια δημοσιεύθηκε η σύνθεση του ιόντος 5 +. Ποια είναι η πλέον πιθανή α) γεωμετρία ηλεκτρονικών ζευγών, και β) μοριακή γεωμετρική δομή του ιόντος
Answers to Homework Set 3 12162016 1. Πριν από μερικά χρόνια δημοσιεύθηκε η σύνθεση του ιόντος 5 +. Ποια είναι η πλέον πιθανή α) γεωμετρία ηλεκτρονικών ζευγών, και β) μοριακή γεωμετρική δομή του ιόντος
Χρονοανεξάρτητη Μη-Εκφυλισμένη Θεωρία Διαταραχών
 Χρονοανεξάρτητη Μη-Εκφυλισμένη Θεωρία Διαταραχών Δομή Διάλεξης Ανασκόπηση συμβολισμού Dirac Διαταραχές σε σύστημα δύο καταστάσεων Η γενική μέθοδος μη-εκφυλισμένης θεωρίας διαταραχών Εφαρμογή: Διαταραχή
Χρονοανεξάρτητη Μη-Εκφυλισμένη Θεωρία Διαταραχών Δομή Διάλεξης Ανασκόπηση συμβολισμού Dirac Διαταραχές σε σύστημα δύο καταστάσεων Η γενική μέθοδος μη-εκφυλισμένης θεωρίας διαταραχών Εφαρμογή: Διαταραχή
Μοριακή δομή Ο2 σύμφωνα με VB διαμαγνητικό
 Μοριακή δομή Ο 2 σύμφωνα με VB? διαμαγνητικό Θεωρία Μοριακών Τροχιακών Μolecular Orbital Theory (MO) Τα μοριακά τροχιακά (molecular orbital) είναι κυματοσυναρτήσεις οι οποίες προκύτπουναπότογραμμικόσυνδυασμότωνκυματοσυναρτήσεωντωναο.
Μοριακή δομή Ο 2 σύμφωνα με VB? διαμαγνητικό Θεωρία Μοριακών Τροχιακών Μolecular Orbital Theory (MO) Τα μοριακά τροχιακά (molecular orbital) είναι κυματοσυναρτήσεις οι οποίες προκύτπουναπότογραμμικόσυνδυασμότωνκυματοσυναρτήσεωντωναο.
κυματικής συνάρτησης (Ψ) κυματική συνάρτηση
 Στην κβαντομηχανική ο χώρος μέσα στον οποίο κινείται το ηλεκτρόνιο γύρω από τον πυρήνα παύει να περιγράφεται από μια απλή τροχιά, χαρακτηριστικό του μοντέλου του Bohr, αλλά περιγράφεται ο χώρος μέσα στον
Στην κβαντομηχανική ο χώρος μέσα στον οποίο κινείται το ηλεκτρόνιο γύρω από τον πυρήνα παύει να περιγράφεται από μια απλή τροχιά, χαρακτηριστικό του μοντέλου του Bohr, αλλά περιγράφεται ο χώρος μέσα στον
Απαντησεις στις ερωτησεις της εξετασης της 24 ης Ιουνιου 2005
 ΑΤΜΟΦ Απαντησεις στις ερωτησεις της εξετασης της 4 ης Ιουνιου 005. Ερωτηση που αφορα στις ασκησεις του εργαστηριου. Α) Με βάση τη σχέση που συνδέει τις αποστάσεις α και b με την εστιακή απόσταση του σφαιρικού
ΑΤΜΟΦ Απαντησεις στις ερωτησεις της εξετασης της 4 ης Ιουνιου 005. Ερωτηση που αφορα στις ασκησεις του εργαστηριου. Α) Με βάση τη σχέση που συνδέει τις αποστάσεις α και b με την εστιακή απόσταση του σφαιρικού
Ομοιοπολικός Δεσμός. Ασκήσεις
 Ασκήσεις Ομοιοπολικός Δεσμός 1. Δίνεται η οργανική ένωση CH 3 -CH 2 -C CH της οποίας τα άτομα αριθμούνται από 1 έως 4, όπως φαίνεται παραπάνω. Πόσοι και τι είδους σ δεσμοί και π δεσμοί υπάρχουν στην ένωση;
Ασκήσεις Ομοιοπολικός Δεσμός 1. Δίνεται η οργανική ένωση CH 3 -CH 2 -C CH της οποίας τα άτομα αριθμούνται από 1 έως 4, όπως φαίνεται παραπάνω. Πόσοι και τι είδους σ δεσμοί και π δεσμοί υπάρχουν στην ένωση;
ΦΥΣΙΚΟΧΗΜΕΙΑ I Ενότητα 10 Μοριακή Δομή Δημήτρης Κονταρίδης Αναπληρωτής Καθηγητής Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών
 ΦΥΣΙΚΟΧΗΜΕΙΑ I Ενότητα 10 Μοριακή Δομή Δημήτρης Κονταρίδης Αναπληρωτής Καθηγητής Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Ενδεικτική βιβλιογραφία 1. ATKINS, ΦΥΣΙΚΟΧΗΜΕΙΑ P.W. Atkins, J. De Paula (Atkins
ΦΥΣΙΚΟΧΗΜΕΙΑ I Ενότητα 10 Μοριακή Δομή Δημήτρης Κονταρίδης Αναπληρωτής Καθηγητής Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Ενδεικτική βιβλιογραφία 1. ATKINS, ΦΥΣΙΚΟΧΗΜΕΙΑ P.W. Atkins, J. De Paula (Atkins
ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 73
 ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 73 ΚΕΦΑΛΑΙΟ 4 ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 4.. Εισαγωγή Στο παρόν κεφάλαιο θα μελετηθούν οι ελεύθερες ταλαντώσεις συστημάτων που περιγράφονται
ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 73 ΚΕΦΑΛΑΙΟ 4 ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 4.. Εισαγωγή Στο παρόν κεφάλαιο θα μελετηθούν οι ελεύθερες ταλαντώσεις συστημάτων που περιγράφονται
ΦΥΣΙΚΟΧΗΜΕΙΑ I Ενότητα 11 Διατομικά Μόρια Δημήτρης Κονταρίδης Αναπληρωτής Καθηγητής Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών
 ΦΥΣΙΚΟΧΗΜΕΙΑ I Ενότητα 11 Διατομικά Μόρια Δημήτρης Κονταρίδης Αναπληρωτής Καθηγητής Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Ενδεικτική βιβλιογραφία 1. ATKINS, ΦΥΣΙΚΟΧΗΜΕΙΑ P.W. Atkins, J. De Paula (Atkins
ΦΥΣΙΚΟΧΗΜΕΙΑ I Ενότητα 11 Διατομικά Μόρια Δημήτρης Κονταρίδης Αναπληρωτής Καθηγητής Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Ενδεικτική βιβλιογραφία 1. ATKINS, ΦΥΣΙΚΟΧΗΜΕΙΑ P.W. Atkins, J. De Paula (Atkins
Nobel Φυσικής για Κβαντική Ηλεκτροδυναμική
 Spin Nobel Φυσικής για Κβαντική Ηλεκτροδυναμική Δομή Διάλεξης Το πείραμα Stern-Gerlach: Πειραματική απόδειξη spin Ο δισδιάστατος χώρος καταστάσεων spin του ηλεκτρονίου: οι πίνακες Pauli Χρονική εξέλιξη
Spin Nobel Φυσικής για Κβαντική Ηλεκτροδυναμική Δομή Διάλεξης Το πείραμα Stern-Gerlach: Πειραματική απόδειξη spin Ο δισδιάστατος χώρος καταστάσεων spin του ηλεκτρονίου: οι πίνακες Pauli Χρονική εξέλιξη
Κομβικές επιφάνειες. Από τη γνωστή σχέση: Ψ(r, θ, φ) = R(r).Θ(θ).Φ(φ) για Ψ = 0 θα πρέπει είτε R(r) = 0 ή Θ(θ).Φ(φ) = 0
 Κομβικές επιφάνειες Από τα σχήματα των ατομικών τροχιακών αλλά και από τις μαθηματικές εκφράσεις είναι φανερό ότι υπάρχουν επιφάνειες όπου το Ψ 2 μηδενίζεται, πάνω στις οποίες δηλαδή είναι αδύνατο να βρεθεί
Κομβικές επιφάνειες Από τα σχήματα των ατομικών τροχιακών αλλά και από τις μαθηματικές εκφράσεις είναι φανερό ότι υπάρχουν επιφάνειες όπου το Ψ 2 μηδενίζεται, πάνω στις οποίες δηλαδή είναι αδύνατο να βρεθεί
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
Λυμένες ασκήσεις στροφορμής
 Λυμένες ασκήσεις στροφορμής Θα υπολογίσουμε τη δράση των τελεστών κλίμακας J ± σε μια τυχαία ιδιοκατάσταση j, m των τελεστών J και Jˆ. Λύση Δείξαμε ότι η κατάσταση Jˆ± j, m είναι επίσης ιδιοκατάσταση των
Λυμένες ασκήσεις στροφορμής Θα υπολογίσουμε τη δράση των τελεστών κλίμακας J ± σε μια τυχαία ιδιοκατάσταση j, m των τελεστών J και Jˆ. Λύση Δείξαμε ότι η κατάσταση Jˆ± j, m είναι επίσης ιδιοκατάσταση των
1.4 ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕΔΟ
 34 4 ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕΔΟ Άξονας Πάνω σε μια ευθεία επιλέγουμε δύο σημεία Ο και Ι, έτσι ώστε το διάνυσμα OI να έχει μέτρο και να βρίσκεται στην ημιευθεία O Λέμε τότε ότι έχουμε έναν άξονα με αρχή
34 4 ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕΔΟ Άξονας Πάνω σε μια ευθεία επιλέγουμε δύο σημεία Ο και Ι, έτσι ώστε το διάνυσμα OI να έχει μέτρο και να βρίσκεται στην ημιευθεία O Λέμε τότε ότι έχουμε έναν άξονα με αρχή
και χρησιμοποιώντας τον τελεστή A r P αποδείξτε ότι για
 ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ Ασκήσεις Κεφαλαίου IV Άσκηση 1: Σωματίδιο μάζας Μ κινείται στην περιφέρεια κύκλου ακτίνας R. Υπολογίστε τις επιτρεπόμενες τιμές της ενέργειας, τις αντίστοιχες κυματοσυναρτήσεις και τον εκφυλισμό.
ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ Ασκήσεις Κεφαλαίου IV Άσκηση 1: Σωματίδιο μάζας Μ κινείται στην περιφέρεια κύκλου ακτίνας R. Υπολογίστε τις επιτρεπόμενες τιμές της ενέργειας, τις αντίστοιχες κυματοσυναρτήσεις και τον εκφυλισμό.
Δομή Διάλεξης. Εύρεση ακτινικού μέρους εξίσωσης Schrödinger. Εφαρμογή σε σφαιρικό πηγάδι δυναμικού απείρου βάθους. Εφαρμογή σε άτομο υδρογόνου
 Κεντρικά Δυναμικά Δομή Διάλεξης Εύρεση ακτινικού μέρους εξίσωσης Schrödinger Εφαρμογή σε σφαιρικό πηγάδι δυναμικού απείρου βάθους Εφαρμογή σε άτομο υδρογόνου Ακτινική Συνιστώσα Ορμής Έστω Χαμιλτονιανή
Κεντρικά Δυναμικά Δομή Διάλεξης Εύρεση ακτινικού μέρους εξίσωσης Schrödinger Εφαρμογή σε σφαιρικό πηγάδι δυναμικού απείρου βάθους Εφαρμογή σε άτομο υδρογόνου Ακτινική Συνιστώσα Ορμής Έστω Χαμιλτονιανή
Ατομική και ηλεκτρονιακή δομή των στερεών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ατομική και ηλεκτρονιακή δομή των στερεών Εισαγωγή Διδάσκων : Επίκουρη Καθηγήτρια Χριστίνα Λέκκα Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ατομική και ηλεκτρονιακή δομή των στερεών Εισαγωγή Διδάσκων : Επίκουρη Καθηγήτρια Χριστίνα Λέκκα Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
1. Μετάπτωση Larmor (γενικά)
 . Μετάπτωση Larmor (γενικά) Τι είναι η μετάπτωση; Μετάπτωση είναι η αλλαγή της διεύθυνσης του άξονα περιστροφής ενός περιστρεφόμενου αντικειμένου. Αν ο άξονας περιστροφής ενός αντικειμένου περιστρέφεται
. Μετάπτωση Larmor (γενικά) Τι είναι η μετάπτωση; Μετάπτωση είναι η αλλαγή της διεύθυνσης του άξονα περιστροφής ενός περιστρεφόμενου αντικειμένου. Αν ο άξονας περιστροφής ενός αντικειμένου περιστρέφεται
Επίλυση Συστήματος Γραμμικών Διαφορικών Εξισώσεων
 Επίλυση Συστήματος Γραμμικών Διαφορικών Εξισώσεων. Γραμμικοί Μετασχηματισμοί Ανυσμάτων Θεωρούμε χώρο δύο διαστάσεων και συμβατικά ένα ορθογώνιο σύστημα αξόνων για την περιγραφή κάθε ανύσματος του χώρου
Επίλυση Συστήματος Γραμμικών Διαφορικών Εξισώσεων. Γραμμικοί Μετασχηματισμοί Ανυσμάτων Θεωρούμε χώρο δύο διαστάσεων και συμβατικά ένα ορθογώνιο σύστημα αξόνων για την περιγραφή κάθε ανύσματος του χώρου
Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Κβαντομηχανική ΙΙ
 Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Κβαντομηχανική ΙΙ Χρονικά Ανεξάρτητη Θεωρία Διαταραχών. Τα περισσότερα φυσικά συστήματα που έχομε προσεγγίσει μέχρι τώρα περιγράφονται από μία κύρια Χαμιλτονιανή η οποία
Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Κβαντομηχανική ΙΙ Χρονικά Ανεξάρτητη Θεωρία Διαταραχών. Τα περισσότερα φυσικά συστήματα που έχομε προσεγγίσει μέχρι τώρα περιγράφονται από μία κύρια Χαμιλτονιανή η οποία
Τι είναι βαθμωτό μέγεθος? Ένα μέγεθος που περιγράφεται μόνο με έναν αριθμό (π.χ. πίεση)
 TETY Εφαρμοσμένα Μαθηματικά Ενότητα ΙΙ: Γραμμική Άλγεβρα Ύλη: Διανυσματικοί χώροι και διανύσματα, μετασχηματισμοί διανυσμάτων, τελεστές και πίνακες, ιδιοδιανύσματα και ιδιοτιμές πινάκων, επίλυση γραμμικών
TETY Εφαρμοσμένα Μαθηματικά Ενότητα ΙΙ: Γραμμική Άλγεβρα Ύλη: Διανυσματικοί χώροι και διανύσματα, μετασχηματισμοί διανυσμάτων, τελεστές και πίνακες, ιδιοδιανύσματα και ιδιοτιμές πινάκων, επίλυση γραμμικών
Δρ. Ιωάννης Καλαμαράς, Διδάκτωρ Χημικός. 100 Ερωτήσεις τύπου Σωστού Λάθους Στο τέλος οι απαντήσεις
 1 ο Κεφάλαιο Χημείας Θετικής Κατεύθυνσης Γ Λυκείου 100 Ερωτήσεις τύπου Σωστού Λάθους Στο τέλος οι απαντήσεις 1. Η εξίσωση E = h v μας δίνει την ενέργεια μιας ηλεκτρομαγνητικής ακτινοβολίας 2. H κβαντική
1 ο Κεφάλαιο Χημείας Θετικής Κατεύθυνσης Γ Λυκείου 100 Ερωτήσεις τύπου Σωστού Λάθους Στο τέλος οι απαντήσεις 1. Η εξίσωση E = h v μας δίνει την ενέργεια μιας ηλεκτρομαγνητικής ακτινοβολίας 2. H κβαντική
Διάλεξη 2: Κεντρικά Δυναμικά. Αναζητούμε λύσεις της χρονοανεξάρτητης εξίσωσης Schrödinger για κεντρικά δυναμικά
 Διάλεξη : Κεντρικά Δυναμικά Αναζητούμε λύσεις της χρονοανεξάρτητης εξίσωσης Schöing για κεντρικά δυναμικά Μ. Μπενής. Διαλέξεις Μαθήματος Σύγχρονης Φυσικής ΙΙ. Ιωάννινα 03 Κεντρικά δυναμικά Εξάρτηση δυναμικού
Διάλεξη : Κεντρικά Δυναμικά Αναζητούμε λύσεις της χρονοανεξάρτητης εξίσωσης Schöing για κεντρικά δυναμικά Μ. Μπενής. Διαλέξεις Μαθήματος Σύγχρονης Φυσικής ΙΙ. Ιωάννινα 03 Κεντρικά δυναμικά Εξάρτηση δυναμικού
ΘΕΜΑ 1. Δίνονται. h = 6,63 10 ΑΠΑΝΤΗΣΗΗ Ε 1. σχέση. οπότε έχουμε: ii) Με βάση ΘΕΜΑ 2. η: [Αr] 3d s ατομική ακτίνα. τις απαντήσεις σας.
![ΘΕΜΑ 1. Δίνονται. h = 6,63 10 ΑΠΑΝΤΗΣΗΗ Ε 1. σχέση. οπότε έχουμε: ii) Με βάση ΘΕΜΑ 2. η: [Αr] 3d s ατομική ακτίνα. τις απαντήσεις σας. ΘΕΜΑ 1. Δίνονται. h = 6,63 10 ΑΠΑΝΤΗΣΗΗ Ε 1. σχέση. οπότε έχουμε: ii) Με βάση ΘΕΜΑ 2. η: [Αr] 3d s ατομική ακτίνα. τις απαντήσεις σας.](/thumbs/102/153828250.jpg) ΑΝΟΡΓΑΝΗ ΧΗΜΕΙΑ 1 ο Εξάμηνο Χημικων Μηχανικών Εξεταστική Περίοδος Σεπτέμβριος 2019 Διδάσκοντες: Γ. Κακάλη, Κ. Κορδάτος 5/9/20199 ΘΕΜΑ 1 i) Να υπολογιστεί η ενέργεια ιοντισμού 1 mol υδρογόνου με βάση τη
ΑΝΟΡΓΑΝΗ ΧΗΜΕΙΑ 1 ο Εξάμηνο Χημικων Μηχανικών Εξεταστική Περίοδος Σεπτέμβριος 2019 Διδάσκοντες: Γ. Κακάλη, Κ. Κορδάτος 5/9/20199 ΘΕΜΑ 1 i) Να υπολογιστεί η ενέργεια ιοντισμού 1 mol υδρογόνου με βάση τη
Λύσεις Θεµάτων - Κβαντοµηχανική ΙΙ (Τµήµα Α. Λαχανά) Ειδική Εξεταστική Περίοδος - 11ης Μαρτίου 2013
 ΘΕΜΑ 1: ( 3 µονάδες ) Λύσεις Θεµάτων - Κβαντοµηχανική ΙΙ (Τµήµα Α. Λαχανά) Ειδική Εξεταστική Περίοδος - 11ης Μαρτίου 2013 Ηλεκτρόνιο κινείται επάνω από µία αδιαπέραστη και αγώγιµη γειωµένη επιφάνεια που
ΘΕΜΑ 1: ( 3 µονάδες ) Λύσεις Θεµάτων - Κβαντοµηχανική ΙΙ (Τµήµα Α. Λαχανά) Ειδική Εξεταστική Περίοδος - 11ης Μαρτίου 2013 Ηλεκτρόνιο κινείται επάνω από µία αδιαπέραστη και αγώγιµη γειωµένη επιφάνεια που
Κύριος κβαντικός αριθμός (n)
 Κύριος κβαντικός αριθμός (n) Επιτρεπτές τιμές: n = 1, 2, 3, Καθορίζει: το μέγεθος του ηλεκτρονιακού νέφους κατά μεγάλο μέρος, την ενέργεια του τροχιακού τη στιβάδα στην οποία κινείται το ηλεκτρόνιο Όσομεγαλύτερηείναιητιμήτουn
Κύριος κβαντικός αριθμός (n) Επιτρεπτές τιμές: n = 1, 2, 3, Καθορίζει: το μέγεθος του ηλεκτρονιακού νέφους κατά μεγάλο μέρος, την ενέργεια του τροχιακού τη στιβάδα στην οποία κινείται το ηλεκτρόνιο Όσομεγαλύτερηείναιητιμήτουn
1o Kριτήριο Αξιολόγησης
 1o Kριτήριο Αξιολόγησης 11 ΚΒΑΝΤΙΚΟΙ ΑΡΙΘΜΟΙ - ΑΡΧΕΣ ΟΜΗΣΗΣ ΠΟΛΥΗΛΕΚΤΡΟΝΙΑΚΩΝ ΑΤΟΜΩΝ ΖΗΤΗΜΑ 1ο Στις ερωτήσεις 1-4 βάλτε σε κύκλο το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Κατά τις µεταπτώσεις: L
1o Kριτήριο Αξιολόγησης 11 ΚΒΑΝΤΙΚΟΙ ΑΡΙΘΜΟΙ - ΑΡΧΕΣ ΟΜΗΣΗΣ ΠΟΛΥΗΛΕΚΤΡΟΝΙΑΚΩΝ ΑΤΟΜΩΝ ΖΗΤΗΜΑ 1ο Στις ερωτήσεις 1-4 βάλτε σε κύκλο το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Κατά τις µεταπτώσεις: L
Κεφάλαιο 1. Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς
 Κεφάλαιο 1 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 2 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 1.1 Ατοµο του Υδρογόνου 1.1.1 Κατάστρωση του προβλήµατος Ας ϑεωρήσουµε πυρήνα ατοµικού αριθµού Z
Κεφάλαιο 1 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 2 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 1.1 Ατοµο του Υδρογόνου 1.1.1 Κατάστρωση του προβλήµατος Ας ϑεωρήσουµε πυρήνα ατοµικού αριθµού Z
Εξετάσεις 1ης Ιουλίου Για την ϐασική κατάσταση του ατόµου του Υδρογόνου της οποίας η κανονικοποιηµένη στην µονάδα
 ΘΕΜΑ 1: Λύσεις Θεµάτων - Κβαντοµηχανική ΙΙ Εξετάσεις 1ης Ιουλίου 13 Τµήµα Α. Λαχανά) Α ) Για την πρώτη διεγερµένη κατάσταση του ατόµου του Υδρογόνου µε τροχιακή στροφορµή l = 1 να προσδιορισθουν οι αποστάσεις
ΘΕΜΑ 1: Λύσεις Θεµάτων - Κβαντοµηχανική ΙΙ Εξετάσεις 1ης Ιουλίου 13 Τµήµα Α. Λαχανά) Α ) Για την πρώτη διεγερµένη κατάσταση του ατόµου του Υδρογόνου µε τροχιακή στροφορµή l = 1 να προσδιορισθουν οι αποστάσεις
ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ
 ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ Α. Υπολογισμός της θέσης του κέντρου μάζας συστημάτων που αποτελούνται από απλά διακριτά μέρη. Τα απλά διακριτά
ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ Α. Υπολογισμός της θέσης του κέντρου μάζας συστημάτων που αποτελούνται από απλά διακριτά μέρη. Τα απλά διακριτά
το ένα με ηλεκτρικό φορτίο Ζe και το άλλο με e. Η χαμιλτονιανή του συστήματος (στο πλαίσιο της προσέγγισης Coulomb) μπορεί να έλθει στη μορφή
 ΚΕΦΑΛΑΙΟ 9: ΑΤΟΜΑ, Σελ. 19 έως 14 του βιβλίου ΚΣ ENOTHTA 1 Η, 13 ο VIDEO, 15/11/013, Από 55λ έως 1ω,5λ (τέλος), Σελ. 19 έως 13 του βιβλίου ΚΣ: ΙΔΙΟΤΗΤΕΣ Της ΒΑΣΙΚΉΣ ΚΑΤΑΣΤΑΣΗΣ ΥΔΡΟΓΟΝΟΕΙΔΟΥΣ ΔΥΝΑΜΙΚΟΥ
ΚΕΦΑΛΑΙΟ 9: ΑΤΟΜΑ, Σελ. 19 έως 14 του βιβλίου ΚΣ ENOTHTA 1 Η, 13 ο VIDEO, 15/11/013, Από 55λ έως 1ω,5λ (τέλος), Σελ. 19 έως 13 του βιβλίου ΚΣ: ΙΔΙΟΤΗΤΕΣ Της ΒΑΣΙΚΉΣ ΚΑΤΑΣΤΑΣΗΣ ΥΔΡΟΓΟΝΟΕΙΔΟΥΣ ΔΥΝΑΜΙΚΟΥ
Σπιν 1 2. Γενικά. Ŝ και S ˆz γράφονται. ιδιοκαταστάσεις αποτελούν ορθοκανονική βάση στον χώρο των καταστάσεων του σπιν 1 2.
 Σπιν Γενικά Θα χρησιμοποιήσουμε τις γενικές σχέσεις που αποδείξαμε στην ανάρτηση «Εύρεση των ιδιοτιμών της στροφορμής», που, όπως είδαμε, ισχύουν για κάθε γενική στροφορμή ˆ J με συνιστώσες Jˆ, Jˆ, J ˆ,
Σπιν Γενικά Θα χρησιμοποιήσουμε τις γενικές σχέσεις που αποδείξαμε στην ανάρτηση «Εύρεση των ιδιοτιμών της στροφορμής», που, όπως είδαμε, ισχύουν για κάθε γενική στροφορμή ˆ J με συνιστώσες Jˆ, Jˆ, J ˆ,
Σφαίρα σε ράγες: Η συνάρτηση Lagrange. Ν. Παναγιωτίδης
 Η Εξίσωση Euler-Lagrange Σφαίρα σε ράγες: Η συνάρτηση Lagrange Ν. Παναγιωτίδης Έστω σύστημα δυο συγκλινόντων ραγών σε σχήμα Χ που πάνω τους κυλίεται σφαίρα ακτίνας. Θεωρούμε σύστημα συντεταγμένων με οριζόντιους
Η Εξίσωση Euler-Lagrange Σφαίρα σε ράγες: Η συνάρτηση Lagrange Ν. Παναγιωτίδης Έστω σύστημα δυο συγκλινόντων ραγών σε σχήμα Χ που πάνω τους κυλίεται σφαίρα ακτίνας. Θεωρούμε σύστημα συντεταγμένων με οριζόντιους
ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΣΑΝΑΤΛΙΣΜΥ Β ΛΥΚΕΙΥ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΥ Να δώσετε τους ορισμούς: διάνυσμα, μηδενικό διάνυσμα, μέτρο διανύσματος, μοναδιαίο διάνυσμα Διάνυσμα AB ονομάζεται ένα ευθύγραμμο
ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΣΑΝΑΤΛΙΣΜΥ Β ΛΥΚΕΙΥ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΥ Να δώσετε τους ορισμούς: διάνυσμα, μηδενικό διάνυσμα, μέτρο διανύσματος, μοναδιαίο διάνυσμα Διάνυσμα AB ονομάζεται ένα ευθύγραμμο
Σχ. 1: Τυπική μορφή μοριακού δυναμικού.
 ΤΕΤΥ - Σύγχρονη Φυσική Κεφ. 6-1 Κεφάλαιο 6. Μόρια Εδάφια: 6.a. Μόρια και μοριακοί δεσμοί 6.b. Κβαντομηχανική περιγραφή του χημικού δεσμού 6.c. Περιστροφή και ταλάντωση μορίων 6.d. Μοριακά φάσματα 6.a.
ΤΕΤΥ - Σύγχρονη Φυσική Κεφ. 6-1 Κεφάλαιο 6. Μόρια Εδάφια: 6.a. Μόρια και μοριακοί δεσμοί 6.b. Κβαντομηχανική περιγραφή του χημικού δεσμού 6.c. Περιστροφή και ταλάντωση μορίων 6.d. Μοριακά φάσματα 6.a.
Â. Θέλουμε να βρούμε τη μέση τιμή
 ΜΕΣΗ ΤΙΜΗ ΕΝΟΣ ΕΡΜΙΤΙΑΝΟΥ ΤΕΛΕΣΤΗ Έστω ο ερμιτιανός τελεστής Â. Θέλουμε να βρούμε τη μέση τιμή Â μια χρονική στιγμή, που αυθαίρετα, αλλά χωρίς βλάβη της γενικότητας, θεωρούμε χρονική στιγμή μηδέν, όπου
ΜΕΣΗ ΤΙΜΗ ΕΝΟΣ ΕΡΜΙΤΙΑΝΟΥ ΤΕΛΕΣΤΗ Έστω ο ερμιτιανός τελεστής Â. Θέλουμε να βρούμε τη μέση τιμή Â μια χρονική στιγμή, που αυθαίρετα, αλλά χωρίς βλάβη της γενικότητας, θεωρούμε χρονική στιγμή μηδέν, όπου
ΜΙΓΑΔΙΚΟ ΔΥΝΑΜΙΚΟ ΓΕΝΙΚΑ. Έστω σωμάτιο, στις τρεις διαστάσεις, που βρίσκεται υπό την επίδραση μιγαδικού δυναμικού της μορφής
 ΜΙΓΑΔΙΚΟ ΔΥΝΑΜΙΚΟ ΓΕΝΙΚΑ Έστω σωμάτιο, στις τρεις διαστάσεις, που βρίσκεται υπό την επίδραση μιγαδικού δυναμικού της μορφής Re Im V r V r i V r, όπου οι συναρτήσεις Re,Im V r V r είναι πραγματικές συναρτήσεις
ΜΙΓΑΔΙΚΟ ΔΥΝΑΜΙΚΟ ΓΕΝΙΚΑ Έστω σωμάτιο, στις τρεις διαστάσεις, που βρίσκεται υπό την επίδραση μιγαδικού δυναμικού της μορφής Re Im V r V r i V r, όπου οι συναρτήσεις Re,Im V r V r είναι πραγματικές συναρτήσεις
ΥΛΙΚΑ ΠΑΡΟΝ ΚΑΙ ΜΕΛΛΟΝ
 ΥΛΙΚΑ ΠΑΡΟΝ ΚΑΙ ΜΕΛΛΟΝ Ι 4 Δεσμοί ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ μεταξύ ατόμων γίνονται με τα ηλεκτρόνια σθένους κατά τέτοιο τρόπο ώστε να ελαττώνεται η συνολική ενέργεια του
ΥΛΙΚΑ ΠΑΡΟΝ ΚΑΙ ΜΕΛΛΟΝ Ι 4 Δεσμοί ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ μεταξύ ατόμων γίνονται με τα ηλεκτρόνια σθένους κατά τέτοιο τρόπο ώστε να ελαττώνεται η συνολική ενέργεια του
Πρόβλημα 4.9.
 Πρόβλημα 4.9. Να βρεθεί το δυναμικό V() παντού στο χώρο ενός θετικά φορτισμένου φύλλου απείρων διαστάσεων με επιφανειακή πυκνότητα φορτίου σ. Πάρτε τον άξονα κάθετα στο φύλλο και θεωρήστε ότι το φύλλο
Πρόβλημα 4.9. Να βρεθεί το δυναμικό V() παντού στο χώρο ενός θετικά φορτισμένου φύλλου απείρων διαστάσεων με επιφανειακή πυκνότητα φορτίου σ. Πάρτε τον άξονα κάθετα στο φύλλο και θεωρήστε ότι το φύλλο
1.2 Συντεταγμένες στο Επίπεδο
 1 Συντεταγμένες στο Επίπεδο Τι εννοούμε με την έννοια άξονας; ΑΠΑΝΤΗΣΗ Πάνω σε μια ευθεία επιλέγουμε δύο σημεία και Ι έτσι ώστε το διάνυσμα OI να έχει μέτρο 1 και να βρίσκεται στην ημιευθεία O Λέμε τότε
1 Συντεταγμένες στο Επίπεδο Τι εννοούμε με την έννοια άξονας; ΑΠΑΝΤΗΣΗ Πάνω σε μια ευθεία επιλέγουμε δύο σημεία και Ι έτσι ώστε το διάνυσμα OI να έχει μέτρο 1 και να βρίσκεται στην ημιευθεία O Λέμε τότε
ΚΕΦΑΛΑΙΟ 3 Ο 3.2 Η ΕΝΝΟΙΑ ΤΟΥ ΓΡΑΜΜΙΚΟΥ ΣΥΣΤΗΜΑΤΟΣ ΚΑΙ Η. (Σ) όπου α, β, α, β, είναι οι
 ΚΕΦΑΛΑΙΟ 3 Ο ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ 3. Η ΕΝΝΟΙΑ ΤΟΥ ΓΡΑΜΜΙΚΟΥ ΣΥΣΤΗΜΑΤΟΣ ΚΑΙ Η ΓΡΑΦΙΚΗ ΕΠΙΛΥΣΗ ΤΟΥ. Ποια είναι η μορφή ενός συστήματος δύο γραμμικών εξισώσεων, δύο αγνώστων; Να δοθεί παράδειγμα.
ΚΕΦΑΛΑΙΟ 3 Ο ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ 3. Η ΕΝΝΟΙΑ ΤΟΥ ΓΡΑΜΜΙΚΟΥ ΣΥΣΤΗΜΑΤΟΣ ΚΑΙ Η ΓΡΑΦΙΚΗ ΕΠΙΛΥΣΗ ΤΟΥ. Ποια είναι η μορφή ενός συστήματος δύο γραμμικών εξισώσεων, δύο αγνώστων; Να δοθεί παράδειγμα.
Κίνηση σε Μονοδιάστατα Τετραγωνικά Δυναμικά
 Κίνηση σε Μονοδιάστατα Τετραγωνικά Δυναμικά Δομή Διάλεξης Τετραγωνικό Πηγάδι Δυναμικού: Δέσμιες καταστάσεις - ιδιοτιμές Οριακές Περιπτώσεις: δ δυναμικό, άπειρο βάθος Σκέδαση σε μια διάσταση: Σκαλοπάτι
Κίνηση σε Μονοδιάστατα Τετραγωνικά Δυναμικά Δομή Διάλεξης Τετραγωνικό Πηγάδι Δυναμικού: Δέσμιες καταστάσεις - ιδιοτιμές Οριακές Περιπτώσεις: δ δυναμικό, άπειρο βάθος Σκέδαση σε μια διάσταση: Σκαλοπάτι
Δομή Διάλεξης. Οι τελεστές της τροχιακής στροφορμής στην αναπαράσταση της θέσης. Τελεστές δημιουργίας και καταστροφής για ιδιοκαταστάσεις στροφορμής
 Τροχιακή Στροφορμή Δομή Διάλεξης Οι τελεστές της τροχιακής στροφορμής στην αναπαράσταση της θέσης Τελεστές δημιουργίας και καταστροφής για ιδιοκαταστάσεις στροφορμής Ιδιοτιμές και ιδιοκαταστάσεις της L
Τροχιακή Στροφορμή Δομή Διάλεξης Οι τελεστές της τροχιακής στροφορμής στην αναπαράσταση της θέσης Τελεστές δημιουργίας και καταστροφής για ιδιοκαταστάσεις στροφορμής Ιδιοτιμές και ιδιοκαταστάσεις της L
ΘΕΜΑ 1 ο 1. Πόσα ηλεκτρόνια στη θεµελιώδη κατάσταση του στοιχείου 18 Ar έχουν. 2. Ο µέγιστος αριθµός των ηλεκτρονίων που είναι δυνατόν να υπάρχουν
 ΚΕΦΑΛΑΙΟ 1 ο Ερωτήσεις από πανελλήνιες εξετάσεις από το 2001 ως το 2014 ΘΕΜΑ 1 ο 1. Πόσα ηλεκτρόνια στη θεµελιώδη κατάσταση του στοιχείου 18 Ar έχουν µαγνητικό κβαντικό αριθµό m l = 1 ; α. 6. β. 8. γ.
ΚΕΦΑΛΑΙΟ 1 ο Ερωτήσεις από πανελλήνιες εξετάσεις από το 2001 ως το 2014 ΘΕΜΑ 1 ο 1. Πόσα ηλεκτρόνια στη θεµελιώδη κατάσταση του στοιχείου 18 Ar έχουν µαγνητικό κβαντικό αριθµό m l = 1 ; α. 6. β. 8. γ.
ΜΑΘΗΜΑ / ΤΑΞΗ : ΧΗΜΕΙΑ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1 ΗΜΕΡΟΜΗΝΙΑ: ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: Μαρίνος Ιωάννου, Γιώργος Καντώνης
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΧΗΜΕΙΑ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1 ΗΜΕΡΟΜΗΝΙΑ: 02 11-2014 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: Μαρίνος Ιωάννου, Γιώργος Καντώνης ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α A1. Tα τροχιακά 2p και 2p y ενός ατόμου διαφέρουν:
ΜΑΘΗΜΑ / ΤΑΞΗ : ΧΗΜΕΙΑ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1 ΗΜΕΡΟΜΗΝΙΑ: 02 11-2014 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: Μαρίνος Ιωάννου, Γιώργος Καντώνης ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α A1. Tα τροχιακά 2p και 2p y ενός ατόμου διαφέρουν:
μαγνητικό πεδίο τυχαίας κατεύθυνσης
 Σπιν 1 μέσα σε ομογενές, χρονικά ανεξάρτητο μαγνητικό πεδίο τυχαίας κατεύθυνσης 1) Ηλεκτρόνιο βρίσκεται μέσα σε ομογενές, χρονικά ανεξάρτητο μαγνητικό πεδίο B B ˆ ˆ ˆ 0xex B0 yey B0 zez, όπου B0 x, B0
Σπιν 1 μέσα σε ομογενές, χρονικά ανεξάρτητο μαγνητικό πεδίο τυχαίας κατεύθυνσης 1) Ηλεκτρόνιο βρίσκεται μέσα σε ομογενές, χρονικά ανεξάρτητο μαγνητικό πεδίο B B ˆ ˆ ˆ 0xex B0 yey B0 zez, όπου B0 x, B0
Λύση Α. Σωστή η επιλογή α. Β.
 1) Αρνητικά φορτισμένο σωμάτιο κινείται σε ομογενές ηλεκτρικό πεδίο μεγάλης έκτασης. Να επιλέξετε τη σωστή πρόταση. Αν η κατεύθυνση της κίνησης του σωματίου παραμένει σταθερή, τότε: α. Συμπίπτει με την
1) Αρνητικά φορτισμένο σωμάτιο κινείται σε ομογενές ηλεκτρικό πεδίο μεγάλης έκτασης. Να επιλέξετε τη σωστή πρόταση. Αν η κατεύθυνση της κίνησης του σωματίου παραμένει σταθερή, τότε: α. Συμπίπτει με την
ΙΟΝΤΙΚΟΣ ΔΕΣΜΟΣ ΠΑΡΑΔΕΙΓΜΑ
 ΧΗΜΙΚΟΣ ΔΕΣΜΟΣ Είδη Δεσµών Ιοντικός Δεσµός (Ionic bond): σχηµατίζεται πάντα µεταξύ ηλεκτροθετικών και ηλεκτραρνητικών στοιχείων και περιλαµβάνει την πλήρη µεταφορά ενός ή περισσοτέρων ηλεκτρονίων από το
ΧΗΜΙΚΟΣ ΔΕΣΜΟΣ Είδη Δεσµών Ιοντικός Δεσµός (Ionic bond): σχηµατίζεται πάντα µεταξύ ηλεκτροθετικών και ηλεκτραρνητικών στοιχείων και περιλαµβάνει την πλήρη µεταφορά ενός ή περισσοτέρων ηλεκτρονίων από το
ΣΗΜΕΙΩΣΕΙΣ ΑΤΟΜΙΚΗΣ (FineStructureA) Ακαδ. Ετος: Ε. Βιτωράτος
 ΣΗΜΕΙΩΣΕΙΣ ΑΤΟΜΙΚΗΣ (FineStructureA) Ακαδ. Ετος: 016-017 Ε. Βιτωράτος Υπολογισμός της ενέργειας αλληλεπίδρασης σπιν-τροχιάς στην περίπτωση του υδρογόνου Η τιμή της ενέργειας αλληλεπίδρασης σπιν-τροχιάς
ΣΗΜΕΙΩΣΕΙΣ ΑΤΟΜΙΚΗΣ (FineStructureA) Ακαδ. Ετος: 016-017 Ε. Βιτωράτος Υπολογισμός της ενέργειας αλληλεπίδρασης σπιν-τροχιάς στην περίπτωση του υδρογόνου Η τιμή της ενέργειας αλληλεπίδρασης σπιν-τροχιάς
2
 1 2 3 4 5 6 7 8 9 Η μικρότερη σταθερότητα της βινυλικής ρίζας (για παράδειγμα σε σχέση με τη μεθυλική) θα μπορούσε να εξηγηθεί στη βάση του πόσο ισχυρά έλκονται τα ηλεκτρόνια από το κάθε άτομο άνθρακα.
1 2 3 4 5 6 7 8 9 Η μικρότερη σταθερότητα της βινυλικής ρίζας (για παράδειγμα σε σχέση με τη μεθυλική) θα μπορούσε να εξηγηθεί στη βάση του πόσο ισχυρά έλκονται τα ηλεκτρόνια από το κάθε άτομο άνθρακα.
Ατομική και Μοριακή Φυσική
 Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μετσόβιο Πολυτεχνείο Ατομική και Μοριακή Φυσική Θεωρία Προσεγγίσεων Λιαροκάπης Ευθύμιος Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μετσόβιο Πολυτεχνείο Ατομική και Μοριακή Φυσική Θεωρία Προσεγγίσεων Λιαροκάπης Ευθύμιος Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Ατομική και Μοριακή Φυσική
 Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μετσόβιο Πολυτεχνείο Ατομική και Μοριακή Φυσική Σύστημα με δύο ηλεκτρόνια Λιαροκάπης Ευθύμιος Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μετσόβιο Πολυτεχνείο Ατομική και Μοριακή Φυσική Σύστημα με δύο ηλεκτρόνια Λιαροκάπης Ευθύμιος Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ. Κβαντική Θεωρία ΙΙ. Θεωρία Διαταραχών Διδάσκων: Καθ. Λέανδρος Περιβολαρόπουλος
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κβαντική Θεωρία ΙΙ Θεωρία Διαταραχών Διδάσκων: Καθ. Λέανδρος Περιβολαρόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κβαντική Θεωρία ΙΙ Θεωρία Διαταραχών Διδάσκων: Καθ. Λέανδρος Περιβολαρόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Ατομική Ακτίνα ατομική ακτίνα δραστικού μείωση δραστικό πυρηνικό φορτίο και ο κύριος κβαντικός αριθμός των εξωτ. ηλεκτρονίων
 ATOMIKH AKTINA Ατομική Ακτίνα ορίζεται ως το μισό της απόστασης μεταξύ δύο γειτονικών ατόμων, όπως αυτά διατάσσονται στο κρυσταλλικό πλέγμα του στοιχείου. Η ατομική ακτίνα ενός στοιχείου: Κατά μήκος μιας
ATOMIKH AKTINA Ατομική Ακτίνα ορίζεται ως το μισό της απόστασης μεταξύ δύο γειτονικών ατόμων, όπως αυτά διατάσσονται στο κρυσταλλικό πλέγμα του στοιχείου. Η ατομική ακτίνα ενός στοιχείου: Κατά μήκος μιας
ΓΕΝΙΚΗ ΚΑΙ ΑΝΟΡΓΑΝΗ ΧΗΜΕΙΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΓΕΝΙΚΗ ΚΑΙ ΑΝΟΡΓΑΝΗ ΧΗΜΕΙΑ Ενότητα # (6): Τροχιακά και υβριδισμός Ακρίβος Περικλής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΓΕΝΙΚΗ ΚΑΙ ΑΝΟΡΓΑΝΗ ΧΗΜΕΙΑ Ενότητα # (6): Τροχιακά και υβριδισμός Ακρίβος Περικλής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
