Σηµειώσεις. Μικροοικονοµικής Θεωρίας ΙΙΙ (ΜΙΚΟ 201)
|
|
|
- Καλλιόπη Σπηλιωτόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Σηµειώσεις Μικροοικονοµικής Θεωρίας ΙΙΙ (ΜΙΚΟ 201) «Γενική Ισορροπία του Πλήρους Ανταγωνισµού» Βαγγέλης Τζουβελέκας Ρέθυµνο, 2003
2 ΚΕΦΑΛΑΙΟ 2 ΓΕΝΙΚΗ ΙΣΟΡΡΟΠΙΑ ΤΟΥ ΠΛΗΡΟΥΣ ΑΝΤΑΓΩΝΙΣΜΟΥ 2.1 Γενική Ισορροπία και Πλήρης Ανταγωνισµός Ας δούµε τώρα πως ένα οικονοµικό σύστηµα το οποίο χαρακτηρίζεται από πλήρη ανταγωνισµό οδηγείται µέσα από τον µηχανισµό των τιµών στην επίτευξη γενικής ισορροπίας. Όπως γνωρίζουµε ήδη κάθε καταναλωτής ατοµικά µεγιστοποιεί την ωφέλεια του στο σηµείο όπου ο οριακός του λόγος υποκατάστασης µεταξύ των αγαθών Χ και Υ ισούται µε τον λόγο των τιµών των αγαθών. Ας υποθέσουµε ότι υπάρχουν δύο άτοµα ο Α και Β ο καθένας εκ των οποίων επιθυµεί την µεγιστοποίηση της ωφέλειας του. Ας υποθέσουµε επίσης ότι ο λόγος των τιµών των αγαθών είναι δεδοµένος και δίνεται από την ευθεία x / Y, ενώ οι παραγωγικές δυνατότητες της οικονοµία δίνονται από την συνάρτηση µετασχηµατισµού ΤΤ. ΙΑΓΡΑΜΜΑ 2.1 ΓΕΝΙΚΗ ΙΣΟΡΡΟΠΙΑ ΚΑΙ ΠΛΗΡΗΣ ΑΝΤΑΓΩΝΙΣΜΟΣ Υ Υ Υ / Χ Υ Α Τ Υ Α Γ U Τ Υ Β Υ Β Ζ U B Ε Υ / Χ O Α X Α X Α Τ X O Β X Β Τ X Β X Με βάση τα παραπάνω δεδοµένα ο Α θα επιλέξει να προσφέρει εργασία και κεφάλαιο έτσι ώστε να παραχθεί ποσότητα O X από το Χ και OY από το Υ. Με βάση όµως τις καµπύλες αδιαφορίας του µεγιστοποιεί την χρησιµότητα του στο σηµείο Γ όπου επιθυµεί να καταναλώσει O X από το Χ και O Y από το Υ. Εποµένως δηµιουργείται στην οικονοµία υπερβάλλουσα προσφορά από το αγαθό Χ ίση µε O X O X = X X = E > 0 και υπερβάλλουσα ζήτηση για το αγαθό Υ ίση S µε O Y O Y = Y Y = E < 0. D Σε συνθήκες όµως πλήρους ανταγωνισµού οι τιµές των αγαθών είναι κοινές για όλους τους καταναλωτές. Εποµένως και ο καταναλωτής Β αντιµετωπίζει τον ίδιο - 1 -
3 λόγο τιµών. Με βάση όµως τις δικές του προτιµήσεις επιλέγει το σηµείο Ζ ως προς την παραγωγή των δύο αγαθών και το σηµείο Ε ως προς την κατανάλωση τους. ηλαδή επιθυµεί να παραχθεί OY B B OX B B από το αγαθό Χ. Αντίστοιχα επιθυµεί να καταναλώσει OY και OX ποσότητες µε OY OY = YY = E >0 και υπερβάλλουσα ζήτηση για το αγαθό Χ ίση µε B B B B B B S OX OX = XX = E < 0. B B B B B B D ποσότητα από το αγαθό Υ και B B B B ποσότητα από τα δύο αγαθά. ηλαδή υπάρχει υπερβάλλουσα προσφορά από το αγαθό Υ ίση Εάν τώρα η υπερβάλλουσα προσφορά του Υ από τον Β είναι ίση µε την υπερβάλλουσα ζήτηση για το ίδιο αγαθό από τον Α και εάν η υπερβάλλουσα προσφορά του Χ από τον Α είναι ίση µε την υπερβάλλουσα ζήτηση για το Χ από τον Β τότε το σύστηµα θα ισορροπήσει σε αυτό το σηµείο όπου ο οριακός λόγος υποκατάστασης στην κατανάλωση των δύο αγαθών είναι κοινός και για τους δύο καταναλωτές και ίσος µε τον λόγο των τιµών των δύο αγαθών. Εάν όµως δεν συµβαίνει αυτό τότε οι πιέσεις στην αγοραία ζήτηση και προσφορά των δύο αγαθών θα διαµορφώσουν νέες τιµές για τα αγαθά µέχρι να βρεθούν σε ισορροπία. 2.2 Η Ύπαρξη Τιµών Γενικής Ισορροπίας Στην προηγούµενη ενότητα αποδείχθηκε ότι η ύπαρξη πλήρους ανταγωνισµού µπορεί να οδηγήσει σε ισορροπία τις αγορές των αγαθών και των παραγωγικών συντελεστών σε όλες τις αγορές συγχρόνως. Με βάση τις υποθέσεις που έχουµε κάνει στην αρχή της ανάλυσης κάτι τέτοιο όµως δεν διασφαλίζεται πάντοτε. Ο πρώτος που ασχολήθηκε µε το πρόβληµα αυτό ήταν ο Γάλλος οικονοµολόγος Leon Walras. Ας υποθέσουµε προς το παρών ότι στην οικονοµία υπάρχουν n αγαθά σε απόλυτα σταθερή προσφορά. Ας υποθέσουµε ότι ( = 1, 2,..., n) S είναι η συνολικά προσφερόµενη ποσότητα από το αγαθό στην οικονοµία και είναι η τιµή του αγαθού. Η συνολική ζήτηση για το αγαθό εξαρτάται από τις τιµές όλων των αγαθών και αποτελεί το άθροισµα των ατοµικών συναρτήσεων ζήτησης για όλους τους καταναλωτές. ηλαδή ισχύει: D( 1, 2,..., n) ή D ( P ) (2.2.1) όπου P είναι το σύνολο των τιµών των επιµέρους αγαθών στην οικονοµία. Το ερώτηµα που υφίσταται είναι κατά πόσο υπάρχει ένα σύνολο τιµών για όλα τα αγαθά στην οικονοµία έτσι ώστε να ισχύει - 2 -
4 ή ( ) = D P S (2.2.2α) ( ) ( ) ED P = D P S = 0 (2.2.2β) όπου ED είναι η υπερβάλλουσα ζήτηση για το αγαθό. Σύµφωνα µε τον Walras οι συναρτήσεις ζήτησης και εποµένως οι συναρτήσεις υπερβάλλουσας ζήτησης είναι οµογενείς µηδενικού βαθµού, δηλαδή εάν διπλασιαστούν όλες οι τιµές των αγαθών στην οικονοµία, η ζήτηση του κάθε αγαθού θα παραµείνει αµετάβλητη. Αυτό σηµαίνει ότι µπορεί να υπάρξει ισορροπία των σχετικών τιµών των αγαθών. Πλέον της οµογένειας, οι συναρτήσεις ζήτησης είναι συνεχείς, δηλαδή εάν οι τιµές των αγαθών µεταβληθούν κατά ένα µικρό ποσό, οι ζητούµενες ποσότητες των αγαθών επίσης θα µεταβληθούν κατά ένα µικρό ποσό. Ας υποθέσουµε στο σηµείο αυτό ότι στην οικονοµία υπάρχουν δύο αγαθά (Χ και Υ) και δύο καταναλωτές (Α και Β). Ο εισοδηµατικός περιορισµός του καταναλωτή Α δίνεται D + D = S + S X X Y Y X X Y Y (2.2.3) όπου και είναι αντίστοιχα η συνολική ζήτηση και προσφορά του αγαθού από D S τον καταναλωτή Α και η τιµή του αγαθού (ι=χ, Υ). Σε ισορροπία θα ισχύει: ή ( ) ( ) D S + D S = 0 X X X Y Y Y ED + ED = 0 X X Y Y (2.2.4α) (2.2.4β) όπου ED είναι η υπερβάλλουσα ζήτηση για το αγαθό από τον Α. Αντίστοιχα µπορεί να προκύψει και ο ανάλογος εισοδηµατικός περιορισµός για τον Β. δηλαδή: B B ED + ED = 0 X X Y Y (2.2.5) Από την (2.2.4β) και την (2.2.5) προκύπτει: ( ) ( ) B B ED + ED + ED + ED = 0 X X X Y Y Y ED + ED = 0 X X Y Y (2.2.6) - 3 -
5 Η παραπάνω σχέση, στην γενική της µορφή, αποτελεί τον νόµο του Walras: ( ) ED P = 0 (2.2.7) ο οποίος υποδηλώνει ότι η συνολική υπερβάλλουσα ζήτηση στην οικονοµία είναι µηδέν για οποιοδήποτε σύνολο τιµών. Θα πρέπει να τονιστεί στο σηµείο αυτό ότι ο νόµος του Walras ισχύει για οποιοδήποτε σύνολο τιµών και όχι µόνο για τις τιµές ισορροπίας. είχνει δε ότι οι συνθήκες ισορροπίας σε n αγορές δεν είναι ανεξάρτητες. Κατά τον νόµο του Walras µία εξίσωση έστω η n-οστή είναι περιττή και έτσι ο αριθµός των εξισώσεων µειώνεται σε (n-1). Οι (n-1) άγνωστοι του συστήµατος στην (2.2.7), δηλαδή οι τιµές ισορροπίας, εκφράζονται σε όρους του n-οστού αγνώστου (τιµής). Εποµένως το σύστηµα στην (2.2.7) έχει λύση ως προς τους λόγους των τιµών των αγαθών και όχι ως προς τις απόλυτες τιµές τους. υστυχώς όµως όπως αναγνώρισε και ο ίδιος ο Walras η λύση του συστήµατος δεν είναι τόσο απλή. Πρώτον, οι εξισώσεις δεν είναι απαραίτητα γραµµικές και εποµένως το σύστηµα δεν έχει λύση. εύτερον, θα πρέπει οι τιµές ισορροπίας να είναι µη-αρνητικές κάτι όµως που δεν διασφαλίζετε κατά την λύση του συστήµατος. Για να αποδειχθεί έµµεσα λοιπόν η ύπαρξη τιµών ισορροπίας είναι πρώτα απαραίτητο να αποδειχθεί ότι η ισορροπία αυτή πράγµατι υπάρχει. Ένας απλός τρόπος για αυτή την απόδειξη είναι η χρήση του θεωρήµατος του Brouwer σύµφωνα µε το οποίο: Οποιαδήποτε συνεχής συνάρτηση f( x) ενός κλειστού, περιορισµένου και κυρτού συνόλου µέσα στον ίδιο τον εαυτό του έχει τουλάχιστον ένα x ορισµένο σηµείο τέτοιο ώστε να ισχύει f( x ) = x Υποθέστε ότι η f( x) είναι µία συνεχής συνάρτηση που ορίζεται στο διάστηµα [0,1] και ότι λαµβάνει τιµές επίσης στο διάστηµα [0,1]. Η συνάρτηση αυτή αφορά ένα κλειστό σύνολο δεδοµένου ότι αυτό περιλαµβάνει τα όρια του, περιορισµένο καθώς καµία από τις διαστάσεις του δεν είναι απείρως µεγάλη και κυρτό υπό την έννοια ότι δεν έχει ασυνέχειες. Η συνάρτηση αυτή υπακούει στο θεώρηµα του Brouwer και εποµένως υπάρχει κάποιο παρακάτω διάγραµµα 2.2. x f( x ) = για το οποίο ισχύει x. Αυτό φαίνεται στο - 4 -
6 ΙΑΓΡΑΜΜΑ 1.10 ΘΕΩΡΗΜΑ ΤΟΥ ΟΡΙΣΜΕΝΟΥ ΣΗΜΕΙΟΥ ΤΟΥ BROUWER f(x) 1 f(x ) O 45 0 x 1 x Η γεωµετρική απεικόνιση της παραπάνω συνάρτησης είναι µία συνεχής καµπύλη που αρχίζει από το x=0 και τελειώνει στο x=1 πάνω στον άξονα των πραγµατικών αριθµών. Η καµπύλη αυτή είναι περιορισµένη στο τετράγωνο 1x1 όπως φαίνεται από το παραπάνω διάγραµµα. Η µεταβλητή x λαµβάνει όλες τις τιµές µεταξύ 0 και 1, όπου και αυτές οι τελευταίες συµπεριλαµβάνονται. Σύµφωνα µε το θεώρηµα του Brouwer υπάρχει τουλάχιστον ένα σηµείο (µία τιµή της µεταβλητής x) όπου η καµπύλη f(x) τέµνει την διαγώνιο που διέρχεται από την αρχή των αξόνων. Στο σηµείο αυτό (Α) ισχύει f( x )= x καθώς παντού στην διαγώνιο ισχύει g(x)=x. Προκειµένου να χρησιµοποιήσουµε το θεώρηµα του Brouwer για να αποδείξουµε την ύπαρξη τιµών ισορροπίας θα πρέπει πρώτα να ορίσουµε το σύνολο των τιµών των αγαθών µε τέτοιο τρόπο ώστε αυτό να κατέχει τις επιθυµητές ιδιότητες (κλειστό, περιορισµένο και κυρτό). Επειδή µόνο οι σχετικές τιµές των αγαθών έχουν σηµασία στο υπόδειγµα της ανταλλαγής, µπορούµε να ορίσουµε τις τιµές των αγαθών µε τέτοιο τρόπο έτσι ώστε το άθροισµα τους να είναι ίσο µε την µονάδα. Αυτό µπορεί να συµβεί οµαλοποιώντας τις τιµές ως εξής: = = 1 (2.2.8) - 5 -
7 υποθέτοντας παράλληλα ότι τουλάχιστον µία τιµή είναι µη-µηδενική δηλαδή τουλάχιστον ένα από τα n αγαθά είναι σπάνιο. εδοµένης της οµογένειας µηδενικού βαθµού των συναρτήσεων υπερβάλλουσας ζήτησης, οι νέες αυτές οµαλοποιηµένες τιµές θα διατηρούν σταθερό τον σχετικό τους λόγο, δηλαδή θα ισχύει: j = j (2.2.9) Στο σύνολο έστω Φ όλων των πιθανών συνδυασµών των n µη-αρνητικών τιµών που έχουν άθροισµα ίσο µε την µονάδα όπως ορίστηκε παραπάνω είναι περιορισµένο, κλειστό και κυρτό και εποµένως έχει εφαρµογή το θεώρηµα του Brouwer. Πριν παρουσιάσουµε την απόδειξη είναι απαραίτητο στο σηµείο αυτό να γενικεύσουµε το υπόδειγµα λαµβάνοντας υπόψη µας την ύπαρξη ελεύθερων αγαθών τα οποία δεν έχουν αγοραία τιµή (π.χ. περιβάλλον). Για τα αγαθά αυτά υπάρχει αρνητική υπερβάλλουσα ζήτηση γεγονός όµως που δεν επηρεάζει την ύπαρξη ισορροπίας στην οικονοµία. Εποµένως οι συνθήκες ισορροπίας στην (2.2.2β) µπορούν να οριστούν ως εξής: ( ) ( ) ( ) ( ) = = ED P D P S 0 P > 0 = ED P D P S 0 P = 0 (2.2.10) Το παραπάνω σύστηµα εξακολουθεί να υπακούει στον νόµο του Walras. Χρησιµοποιώντας τον παραπάνω ορισµό της γενικής ισορροπίας και έχοντας υπόψη µας ότι οι τιµές έχουν οµαλοποιηθεί έτσι ώστε το άθροισµα τους είναι ίσο µε την µονάδα µπορούµε να κατασκευάσουµε µία συνεχή συνάρτηση που µετασχηµατίζει ένα σύνολο τιµών σε ένα άλλο. Η συνάρτηση αυτή βασίζεται στην υπόθεση ότι οι τιµές των αγαθών που βρίσκονται σε υπερβάλλουσα ζήτηση θα πρέπει να αυξηθούν, ενώ οι τιµές των αγαθών που βρίσκονται σε υπερβάλλουσα προσφορά θα πρέπει να µειωθούν. Έτσι ορίζουµε τη µαθηµατική απεικόνιση για οποιοδήποτε σύνολο τιµών ως εξής: ( ) ( ) F P = + ED P (2.2.11) - 6 -
8 Εάν για τιµές P το αγαθό βρίσκεται σε υπερβάλλουσα ζήτηση ED ( P ) > 0 η τιµή του αυξάνεται, ενώ εάν είναι αρνητική η υπερβάλλουσα ζήτηση ED ( P)< 0 τότε η τιµή του µειώνεται. Επειδή οι συναρτήσεις υπερβάλλουσας ζήτησης είναι συνεχείς, η παραπάνω σχέση επίσης είναι συνεχής. Παραµένουν ωστόσο δύο προβλήµατα σχετικά µε την απεικόνιση της σχέσης (2.2.11). Πρώτα από όλα τίποτε δεν εξασφαλίζει ότι οι νέες τιµές θα είναι µη-αρνητικές. Εποµένως θα πρέπει να η παραπάνω σχέση να οριστεί ως εξής: ( ) = + ( ) F P max ED P,0 (2.2.12) ηλαδή οι νέες τιµές θα πρέπει να είναι είτε θετικές είτε µηδέν. Η παραπάνω συνάρτηση είναι επίσης συνεχής. Το δεύτερο πρόβληµα σχετίζεται µε την οµαλοποίηση των νέων τιµών έτσι ώστε αυτές να αθροίζουν στην µονάδα. Αυτό µπορεί να γίνει κατά ανάλογο τρόπο µε την (2.2.8). Έτσι η παραπάνω σχέση αποτελεί µία συνεχή περιορισµένη απεικόνιση ενός πραγµατικού συνόλου στον εαυτό του. Υποθέτοντας ότι οι νέες τιµές αθροίζουν στην µονάδα η συνάρτηση στην (2.2.12) ικανοποιεί όλες τις συνθήκες του θεωρήµατος του Brouwer και εποµένως έχει κάποιο σταθερό σηµείο. Εάν αυτό το σηµείο το συµβολίσουµε µε τότε θα ισχύει: ( ) = + max ED P,0 (2.2.13) Αλλά αυτό σηµαίνει ότι P είναι το σύνολο των τιµών ισορροπίας καθώς για > 0 ισχύει: ( ) ( ) = + ED P ED P = 0 (2.2.14α) και για = 0 ( ) ( ) = + ED P 0 ED P 0 (2.2.14β) 2.3 Προσαρµογή των Τιµών Ισορροπίας Η επίτευξη των τιµών ισορροπίας στην αγορά µπορεί να επηρεαστεί σηµαντικά από το επίπεδο πληροφόρησης που έχουν τόσο οι παραγωγοί όσο και οι καταναλωτές. Μέχρι τώρα έχουµε υποθέσει ότι οι ανταγωνιστικές τιµές προσδιορίζονται γρήγορα - 7 -
9 και είναι γνωστές µε βεβαιότητα σε όλους τους συµµετέχοντες στην αγορά. Γνωρίζουµε από την προηγούµενη ενότητα ότι κάτω από ορισµένες προϋποθέσεις υπάρχει µία τιµή ισορροπίας για την οποία ισχύει ότι ( ) = ( ) D S (2.3.1) όπου D και S είναι οι συναρτήσεις ζήτησης και προσφοράς αντίστοιχα για το αγαθό. Πώς όµως προσαρµόζεται η τιµή ισορροπίας στην τιµή. Σύµφωνα µε τον Walras η προσαρµογή της αγοράς προς την τιµή ισορροπίας υποκινείται από τις µεταβολές στην συνάρτηση υπερβάλλουσας ζήτησης για διαφορετικές τιµές, δηλαδή ακολουθείται µία διαδικασία αναζήτησης (tatonnement rocess) όπου οι παραγωγοί και οι καταναλωτές αντιδρούν στις αλλαγές των τιµών κινούµενοι κατά µήκος των καµπυλών ζήτησης και προσφοράς µέχρι να φθάσουν στο συνδυασµό ισορροπίας. = k D ( ) s ( ) = k ED ( ), k > 0 t (2.3.2) όπου ΕD ( ) είναι η υπερβάλλουσα ζήτηση του αγαθού για κάθε τιµή. Με βάση την παραπάνω σχέση η τιµή του αγαθού θα αυξηθεί εάν υπάρχει θετική υπερβάλλουσα ζήτηση, ενώ θα µειωθεί εάν υπάρχει αρνητική υπερβάλλουσα ζήτηση. Η διαδικασία αυτή παρουσιάζεται διαγραµµατικά στο παρακάτω διάγραµµα 1.11 για διαφορετικές κλίσεις της καµπύλης προσφοράς του αγαθού. Στο δεξιό διάγραµµα όπου η κλίση της καµπύλης προσφοράς είναι θετική, για τιµές µεγαλύτερες από την τιµή ισορροπίας ( 0 ) η αγορά παρουσιάζει υπερβάλλουσα προσφορά (ή αρνητική υπερβάλλουσα ζήτηση). Εποµένως σύµφωνα µε την (2.3.2) η τιµή του αγαθού θα µειωθεί έτσι ώστε να προσεγγίζει την τιµή ισορροπίας 0. Αντίστοιχα για τιµές µικρότερες της τιµής ισορροπίας η υπερβάλλουσα ζήτηση είναι θετική και εποµένως η τιµή του αγαθού τείνει να αυξηθεί έως ότου γίνει ίση µε 0. Εάν όµως η καµπύλη προσφοράς του αγαθού έχει αρνητική κλίση, όπως στο δεξιό διάγραµµα, τότε για τιµές µεγαλύτερες από την τιµή ισορροπίας η υπερβάλλουσα ζήτηση είναι θετική και εποµένως η τιµή του αγαθού τείνει να αυξηθεί αποµακρυνόµενη από την τιµή 0. Εάν η τιµή είναι µικρότερη από 0, τότε στην αγορά διαµορφώνεται υπερβάλλουσα προσφορά (ή αρνητική υπερβάλλουσα ζήτηση) και η τιµή τείνει να µειωθεί αποµακρυνόµενη και πάλι από την τιµή ισορροπίας. Στην περίπτωση αυτή ο µηχανισµός προσαρµογής του Walras δεν θα οδηγήσει την αγορά στην µακροχρόνια τιµή ισορροπίας
10 ΙΑΓΡΑΜΜΑ 1.11 ΠΡΟΣΑΡΜΟΓΗ ΣΤΙΣ ΤΙΜΕΣ ΙΣΟΡΡΟΠΙΑΣ ΚΑΤΑ WLRS ED<0 S ED>0 0 0 S ED>0 D ED<0 D O Ευσταθής Ισορροπία Q O Ασταθής Ισορροπία Q Τα παραπάνω αποτελέσµατα µπορούµε να τα δούµε διαγραµµατικά εξετά ζοντας την συνάρτηση υπερβάλλουσας ζήτησης. Τρεις διαφορετικές µορφές της συνάρτησης αυτής παρουσιάζονται στο παρακάτω διάγραµµα Πρώτα στο σχήµα (α) η αγοραία ισορροπία στην τιµή 0 είναι ευσταθής, καθώς για οποιαδήποτε τιµή > 0 η διαδικασία προσαρµογής του Walras θα οδηγήσει την αγορά στην τιµή 0. Η συνάρτηση υπερβάλλουσας ζήτησης έχει αρνητική κλίση γεγονός που σηµαίνει ότι κινείται αντίθετα σε οποιαδήποτε µεταβολή της τιµής του αγαθού. Η συνάρτηση αυτή της υπερβάλλουσας ζήτησης αντιστοιχεί στην αριστερή απεικόνιση της αγοραίας ισορροπίας του διαγράµµατος Αντίθετα στο σχήµα (β) η ισορροπία δεν είναι ευσταθής καθώς η κλίση της συνάρτησης υπερβάλλουσας ζήτησης είναι θετική και εποµένως κινείται προς την ίδια κατεύθυνση µε τις αντίστοιχες µεταβολές στην τιµή του αγαθού. Τέλος, στο σχήµα (γ) παρουσιάζεται µία πολλαπλή ισορροπία η οποία είναι ευσταθής για τις τιµές 1 και 3 και ασταθής για την τιµή 2. Γενικά µόνο στην περίπτωση που η συνάρτηση υπερβάλλουσας ζήτησης έχει αρνητική κλίση δηλαδή ισχύει ( ) ED < 0 η ισορροπία είναι ευσταθής και ο µηχανισµός προσαρµογής του Walras θα οδηγήσει την αγορά προς τα εκεί. Η διαδικασία προσαρµογής του Walras αποτελεί µία διαφορική εξίσωση η οποία µπορεί να αναλυθεί µε την βοήθεια των σειρών Taylor γύρω από οποιαδήποτε τιµή ισορροπίας. Με άλλα λόγια η (2.3.2) µπορεί να εκφρασθεί ως: t ( ) ED k ( ) (2.3.3) - 9 -
11 η οποία είν αι µία διαφορική εξίσωση πρώτης τάξης η οποία έχει τις ίδιες ιδιότητες ευστάθειας όπως και η (2.3.2). Η γενική λύση της (2.3.3) έχει την µορφή: 0 ked ( ) t = e + (2.3.4) () ( ) όπου 0 αντιπροσωπεύει την αρχική τιµή κατά την χρονική περίοδο t=0. Για να είναι ευσταθές το σύστηµα, δηλαδή για να προσεγγίζει το καθώς το t αυξάνει θα πρέπει να ισχύει ( ) ( t ) την τιµή ισορροπίας ED < 0. ηλαδή µία αύξηση της τιµής θα πρέπει να µειώσει την υπερβάλλουσα ζήτηση για το αγαθό και αντίστοιχ α µία µείωση της τιµής θα πρέπει να αυξήσει την υπερβάλλουσα ζήτηση. ΙΑΓΡΑΜΜΑ 1.12 ΠΡΟΣΑΡΜΟΓΗ ΣΤΙΣ ΤΙΜΕΣ ΙΣΟΡΡΟΠΙΑΣ ΚΑΤΑ WLRS ΜΕΣΩ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΥΠΕΡΒΑΛΛΟΥΣΑΣ ΖΗΤΗΣΗΣ ED( ) ED( ) ED( ) (α) Ευσταθής Ισορροπία (β) Ασταθής Ισορροπία (γ) Πολλαπλή Ισορροπία Σε αντίθεση µε τον Walras, ο οποίος θεώρησε τον µηχανισµό των τιµών ως την κινητήρια δύναµη προσαρµογής της αγοράς, ο Marshall θεώρησε ότι οι προσαρµογή στις ζητούµενες και προσφερόµενες ποσότητες από την πλευρά των καταναλωτών και παραγωγών αντίστοιχα οδηγούν την αγορά σε ισορροπία µεταβάλλοντας τις τιµές. Σύµφωνα µε τον Marshall ο µηχανισµός προσαρµογής της αγοράς στην ισορροπία µπορεί να αναπαρασταθεί ως εξής: q t = k D ( ) ( ) = q S q k ED ( ) q, > k 0 (2.3.5)
12 1 1 όπου, D ( q ) και ( ) S q είναι οι αντίστροφες συναρτήσεις ζήτησης και προσφοράς και αντιπροσωπεύουν την τιµή που οι καταναλωτές είναι διατεθειµένοι να πληρώσουν (δηλαδή η οριακή τους χρησ ιµότητα) και οι παραγωγοί απαιτούν (δηλαδή το οριακό κόστος παραγωγής) για δεδοµένη ποσότητα του αγαθού. Με άλλα λόγια οι µεταβολές στην ποσότητα προκαλούνται από διαφορές µεταξύ των τιµών που είναι διατεθειµένοι οι καταναλωτές να καταβάλουν και οι παραγωγοί να λάβουν για κάθε ποσότητα του αγαθού. Παρά το γεγονός ότι ο Marshall προσπάθησε να εµπλουτίσει την γνώση µας αναφορικά µε τον µηχανισµό που οι αγορές φθάνουν σε ισορροπία, και οι δύο θεωρητικές προσεγγίσεις παρουσιάζουν κάποια σηµαντικά µειονεκτήµατα. Πρώτα από όλα οι διαδικασίες αυτές προσαρµογής των τιµών και των ποσοτήτων στην αγορά δεν αντιπροσωπεύουν κάποια αριστοποιητική συµπεριφορά των οικονοµικών µονάδων. Μία συνεπής θεωρητική προσέγγιση προσαρµογής της αγοράς στην ισορροπία θα έπρεπε να λάβει υπόψη της και το κόστος που συνεπάγεται η επίτευξη αυτής της ισορροπίας στην αγορά και πως οι οικονοµικές µονάδες δρουν αριστοποιητι κά προκειµένου να το ελαχιστοποιήσουν. Εάν για παράδειγµα οι τιµές των αγαθών µπορούν εύκολα να αλλάξουν χωρίς σηµαντικό κόστος για τους παραγωγούς και η πληροφόρηση για τις νέες τιµές διαδίδεται γρήγορα µεταξύ των καταναλωτών, η αγορά θα προσεγγίζει την αγοραία τιµή ισορροπίας µέσω του µηχανισµού των τιµών του Walras. Αντίθετα σε άλλες αγορές που οι τιµές δεν µπορούν εύκολα να µεταβληθούν χωρίς σηµαντικό κόστος (π.χ. ύπαρξη µακροχρόνιου συµβολαίου) και η ανταλλασσόµενη ποσότητα µπορεί να µεταβληθεί εύκολα, προσεγγίζουν το σηµείο µακροχρόνιας ισορροπίας µέσω του µηχανισµού του Marshall. Κλασσικό παράδειγµα τέτοιων διαδικασιών προσαρµογής είναι η αγορά εργασίας όπου η απασχόληση τείνει να προσαρµόζεται στις κυκλικές διακυµάνσεις της ζήτησης και όχι το επίπεδο των µισθών. Βέβαια σε κάθε περίπτωση και οι δύο µηχανισµοί προσαρµογής της αγοράς στην µακροχρόνια ισορροπία απαιτεί ότι οι αποφάσεις τόσο των παραγωγών όσο και των καταναλωτών γίνονται ταυτόχρονα γεγονός που καθιστά δύσκολη την εξεύρεση λύσης. Κατά καιρούς έχουν αναπτυχθεί διάφορα υποδείγµατα συµπεριφοράς των οικονοµικών παραγόντων, όπου η ανάλυση της τιµολόγησης και προσαρµογής της αγοράς γίνεται στην βραχυχρόνια περίοδο. Για παράδειγµα εάν οι παραγωγοί βασιζόταν στις προσδοκώµενες τιµές της αγοράς για τις αποφάσεις τους στην τρέχουσα περίοδο, τότε η παραγωγή θα µπορούσε να θεωρηθεί σταθερή καθώς δεν θα υπήρχε αντίδραση της προσφοράς στις οποιεσδήποτε µεταβολές των τιµών την
13 τρέχουσα περίοδο. Ας υποθέσουµε ότι οι καταναλωτές αντιδρούν στην τρέχουσα τιµή της αγοράς την οποία γνωρίζουν µε βεβαιότητα, ενώ αντίθετα οι παραγωγοί αντιδρούν µόνο στην προσδοκώµενη τιµή της αγοράς. ηλαδή θα ισχύει: D Q = γ δ (2.3.6α) t t και ( ) Q = α+ β E t (2.3.6β) S t όπου D Q t και Q είναι οι συναρτήσεις ζήτησης και προσφοράς αντίστοιχα και E ( ) S t είναι οι προσδοκώµενη τιµή της αγοράς για τους παραγωγούς κατά την περίο δο t η οποία εξαρτάται σε µεγάλο βαθµό από το επίπεδο πληροφόρησης που έχουν οι παραγωγοί. Η λύση του παραπάνω υποδείγµατος προσαρµοζόµενων προσδοκιών (adatve exectatons) εξαρτάται προφανώς από τον τρόπο που οι παραγωγοί διαµορφώνουν τις προσδοκίες τους για τις τιµές την τρέχουσα περίοδο. Εάν οι παραγωγοί είναι µυωπικοί και προσδοκούν ότι η τιµή την περίοδο t θα είναι αυτή που επικρατούσε στην αγορά την περίοδο t-1 τότε προκύπτει το γνωστό υπόδειγµα του E =. ιστού της αράχνης (cobweb model) όπου ( ) t t 1 Το υπόδειγµα αυτό παρουσιάζεται στο παρακάτω διάγραµµα 1.13 για ευσταθή και ασταθή ισορροπία. Αρχικά η τιµή την περίοδο t-3 καθορίζεται σε t-3 στην οποία οι παραγωγοί είναι διατεθειµένοι να προφέρουν Q t-3 ποσότητα στην αγορά. Για την ποσότητα όµως αυτή οι καταναλωτές είναι διατεθειµένοι να πληρώσουν t-2. ηµιουργείται έτσι υπερβάλλουσα ζήτηση στην αγορά η οποία θα ωθήσει την τιµή προς τα πάνω. Για τη νέα αυτή τιµή οι παραγωγοί είναι διατεθειµένοι την επόµενη περίοδο να προσφέρουν Q t-2 ποσότητα στην αγορά για την οποία οι καταναλωτές είναι διατεθειµένοι να πληρώσουν t-1. Η διαδικασία αυτή συνεχίζεται και για τις επόµενες περιόδους ώσπου η αγορά να καταλήξει µακροχρόνια στην τιµή και ποσότητα ισορροπίας που ορίζεται στο σηµείο Α. Αντίθετα στο διάγραµµα (β) η ισορροπία δεν είναι ευσταθής καθώς η προσ δοκίες των παραγωγών και η προθυµία των καταναλωτών να πληρώσουν οδηγούν την αγορά µακριά από την µακροχρόνια ισορροπία. Αυτό συµβαίνει όταν η κλίση της καµπύλης προσφοράς είναι µικρότερη από την κλίση της καµπύλης ζήτησης. Το υπόδειγµα του ιστού της αράχνης µπορεί να παρουσιαστεί µαθηµατικά από µία εξίσωση διαφορών: t
14 = ( ) β t 0 + δ (2.3.7) Εάν ισχύει βδ> 1 τότε η ισορροπία της αγοράς είναι ευσταθής, ενώ εάν ισχύει βδ< 1 η ισορροπία είναι ασταθής. ΙΑΓΡΑΜΜΑ 1.13 ΤΟ ΥΠΟ ΕΙΓΜΑ ΤΟΥ ΙΣΤΟΥ ΤΗΣ ΑΡΑΧΝΗΣ ΣΕ ΕΥΣΤΑΘΗ ΚΑΙ ΑΣΤΑΘΗ ΙΣΟΡΡΟΠΙΑ S S t-3 t-1 t-1 t-3 t-2 D t-2 t D O Q t-2 Q t-1 Q t-3 (α) Ευσταθής Ισορροπία Q O Q t Q t-2 Q t-3 Q t-1 (β) Ασταθής Ισορροπία Q Σε αντίθεση µε το υπόδειγµα των προσαρµοζόµενων προσδοκιών, ο Muth το 1961, πρότεινε ότι η διαµόρφωση των προσδοκιών των οικονοµικών µονάδων στην αγορά για να είναι συνεπείς µε την αριστοποιητική τους συµπεριφορά θα πρέπει να είναι ορθολογικές µε την ενσωµάτωση σε αυτές όλων των διαθέσιµων πληροφοριών που υπάρχουν στην αγορά. Ειδικότερα εάν ο παραγωγός γνωρίζει την ακριβή µορφή της καµπύλης προσφοράς και της ζήτησης θα µπορούσε να υπολογίσει την τιµή ισορροπίας από την παρακάτω σχέση: γ δ = β + α (2.3.8) η οποία αποτελεί την προσδοκώµενη σε αυτόν τιµή για την περίοδο t. Χρησιµοποιώντας αυτή την προσδοκώµενη τιµή η αγορά θα βρεθεί άµεσα σε ισορροπία υποθέτοντας ότι το κόστος πληροφόρησης και συναλλαγών είναι µηδέν
Η ΘΕΩΡΙΑ ΤΗΣ ΕΠΙΧΕΙΡΗΣΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΘΗΓΗΤΗΣ ΚΩΣΤΑΣ ΒΕΛΕΝΤΖΑΣ Η ΘΕΩΡΙΑ ΤΗΣ ΕΠΙΧΕΙΡΗΣΗΣ. Μερικές έννοιες Η συνάρτηση παραγωγής (, ), όπου είναι το συνολικό προϊόν και και οι συντελεστές
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΘΗΓΗΤΗΣ ΚΩΣΤΑΣ ΒΕΛΕΝΤΖΑΣ Η ΘΕΩΡΙΑ ΤΗΣ ΕΠΙΧΕΙΡΗΣΗΣ. Μερικές έννοιες Η συνάρτηση παραγωγής (, ), όπου είναι το συνολικό προϊόν και και οι συντελεστές
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΑΘΟΥΣ 1. Σε ένα κανονικό αγαθό, όταν αυξάνεται το εισόδηµα των καταναλωτών, τότε αυξάνεται και η συνολική δαπάνη των καταναλωτών 2.
 ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΑΘΟΥΣ 1. Σε ένα κανονικό αγαθό, όταν αυξάνεται το εισόδηµα των καταναλωτών, τότε αυξάνεται και η συνολική δαπάνη των καταναλωτών 2. Το µαγνητόφωνο ενός παιδιού είναι καταναλωτό αγαθό
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΑΘΟΥΣ 1. Σε ένα κανονικό αγαθό, όταν αυξάνεται το εισόδηµα των καταναλωτών, τότε αυξάνεται και η συνολική δαπάνη των καταναλωτών 2. Το µαγνητόφωνο ενός παιδιού είναι καταναλωτό αγαθό
ΤΟΥΡΙΣΤΙΚΗ ΟΙΚΟΝΟΜΙΚΗ ΚΕΦΑΛΑΙΟ 6 ΘΕΩΡΙΑ ΠΡΟΤΙΜΗΣΕΩΝ ΚΑΙ ΕΠΙΛΟΓΩΝ ΤΟΥ ΤΟΥΡΙΣΤΑ-ΚΑΤΑΝΑΛΩΤΗ
 ΤΟΥΡΙΣΤΙΚΗ ΟΙΚΟΝΟΜΙΚΗ ΚΕΦΑΛΑΙΟ 6 ΘΕΩΡΙΑ ΠΡΟΤΙΜΗΣΕΩΝ ΚΑΙ ΕΠΙΛΟΓΩΝ ΤΟΥ ΤΟΥΡΙΣΤΑ-ΚΑΤΑΝΑΛΩΤΗ ΘΕΩΡΙΑ ΠΡΟΤΙΜΗΣΕΩΝ ΚΑΙ ΕΠΙΛΟΓΩΝ ΤΟΥ ΤΟΥΡΙΣΤΑ- ΚΑΤΑΝΑΛΩΤΗ ΔΙΑΡΘΡΩΣΗ ΘΕΜΑΤΙΚΩΝ ΕΝΟΤΗΤΩΝ ΚΕΦΑΛΑΙΟΥ Η θεωρία της οριακής
ΤΟΥΡΙΣΤΙΚΗ ΟΙΚΟΝΟΜΙΚΗ ΚΕΦΑΛΑΙΟ 6 ΘΕΩΡΙΑ ΠΡΟΤΙΜΗΣΕΩΝ ΚΑΙ ΕΠΙΛΟΓΩΝ ΤΟΥ ΤΟΥΡΙΣΤΑ-ΚΑΤΑΝΑΛΩΤΗ ΘΕΩΡΙΑ ΠΡΟΤΙΜΗΣΕΩΝ ΚΑΙ ΕΠΙΛΟΓΩΝ ΤΟΥ ΤΟΥΡΙΣΤΑ- ΚΑΤΑΝΑΛΩΤΗ ΔΙΑΡΘΡΩΣΗ ΘΕΜΑΤΙΚΩΝ ΕΝΟΤΗΤΩΝ ΚΕΦΑΛΑΙΟΥ Η θεωρία της οριακής
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΘΕΩΡΙΑ ΓΕΝΙΚΗΣ ΙΣΟΡΡΟΠΙΑΣ ΧΡΗΣΕΩΝ ΓΗΣ
 ΚΕΦΑΛΑΙΟ 8 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΘΕΩΡΙΑ ΓΕΝΙΚΗΣ ΙΣΟΡΡΟΠΙΑΣ ΧΡΗΣΕΩΝ ΓΗΣ Όταν εξετάζουµε µία συγκεκριµένη αγορά, πχ. την αστική αγορά εργασίας, η ανάλυση αυτή ονοµάζεται µερικής ισορροπίας. Όταν η ανάλυση µας περιλαµβάνει
ΚΕΦΑΛΑΙΟ 8 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΘΕΩΡΙΑ ΓΕΝΙΚΗΣ ΙΣΟΡΡΟΠΙΑΣ ΧΡΗΣΕΩΝ ΓΗΣ Όταν εξετάζουµε µία συγκεκριµένη αγορά, πχ. την αστική αγορά εργασίας, η ανάλυση αυτή ονοµάζεται µερικής ισορροπίας. Όταν η ανάλυση µας περιλαµβάνει
ΑΝΑ ΚΕΦΑΛΑΙΟ. geeconomy@yahoo.com. Γ Ι Ω Ρ Γ Ο Σ Κ Α Μ Α Ρ Ι Ν Ο Σ Ο Ι Κ Ο Ν Ο Μ Ο Λ Ο Γ Ο Σ ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2012
 ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2012 1 ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2012 ΑΝΑ ΚΕΦΑΛΑΙΟ Στο παρόν είναι συγκεντρωµένες όλες σχεδόν οι ερωτήσεις κλειστού τύπου που
ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2012 1 ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2012 ΑΝΑ ΚΕΦΑΛΑΙΟ Στο παρόν είναι συγκεντρωµένες όλες σχεδόν οι ερωτήσεις κλειστού τύπου που
Επαναληπτικές ερωτήσεις πολλαπλής επιλογής: Κεφάλαιο 1 ο
 Επαναληπτικές ερωτήσεις πολλαπλής επιλογής: Κεφάλαιο 1 ο 1. Σε γραµµική ΚΠ της µορφής Y = a+ β X : α. Η µέγιστη ποσότητα για το αγαθό Υ παράγεται όταν Y = β β. Η µέγιστη ποσότητα για το αγαθό Χ παράγεται
Επαναληπτικές ερωτήσεις πολλαπλής επιλογής: Κεφάλαιο 1 ο 1. Σε γραµµική ΚΠ της µορφής Y = a+ β X : α. Η µέγιστη ποσότητα για το αγαθό Υ παράγεται όταν Y = β β. Η µέγιστη ποσότητα για το αγαθό Χ παράγεται
Α5. Όταν η ζήτηση για ένα αγαθό είναι ελαστική, τότε πιθανή αύξηση της τιµής του, θα οδηγήσει σε µείωση της καταναλωτικής δαπάνης για αυτό το αγαθό
 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑ ΕΠΙΛΟΓΗΣ ΟΛΩΝ ΤΩΝ ΚΑΤΕΥΘΥΝΣΕΩΝ ΙΑΓΩΝΙΣΜΑ 1 (για άριστα διαβασµένους) ΟΜΑ Α Α Να απαντήσετε στις επόµενες ερωτήσεις πολλαπλής επιλογής A1. Σε γραµµική ΚΠ της µορφής Y =
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑ ΕΠΙΛΟΓΗΣ ΟΛΩΝ ΤΩΝ ΚΑΤΕΥΘΥΝΣΕΩΝ ΙΑΓΩΝΙΣΜΑ 1 (για άριστα διαβασµένους) ΟΜΑ Α Α Να απαντήσετε στις επόµενες ερωτήσεις πολλαπλής επιλογής A1. Σε γραµµική ΚΠ της µορφής Y =
ΕΦΑΡΜΟΣΜΕΝΗ ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΣΚΗΣΕΙΣ ΕΙΣΑΓΩΓΗ Ο ΜΗΧΑΝΙΣΜΟΣ ΤΗΣ ΑΓΟΡΑΣ
 ΕΦΑΡΜΟΣΜΕΝΗ ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΣΚΗΣΕΙΣ ΕΙΣΑΓΩΓΗ Ο ΜΗΧΑΝΙΣΜΟΣ ΤΗΣ ΑΓΟΡΑΣ Άσκηση 1 Αν το επιτόκιο είναι 10%, ποια είναι η παρούσα αξία των κερδών της Monroe orporation στα επόμενα 5 χρόνια; Χρόνια στο μέλλον
ΕΦΑΡΜΟΣΜΕΝΗ ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΣΚΗΣΕΙΣ ΕΙΣΑΓΩΓΗ Ο ΜΗΧΑΝΙΣΜΟΣ ΤΗΣ ΑΓΟΡΑΣ Άσκηση 1 Αν το επιτόκιο είναι 10%, ποια είναι η παρούσα αξία των κερδών της Monroe orporation στα επόμενα 5 χρόνια; Χρόνια στο μέλλον
Ασκήσεις 1. Με τα δεδομένα του παρακάτω πίνακα: Τιμή (Ρ) Ποσότητα (Q D )
 2 ο ΚΕΦΑΛΑΙΟ ΕΡΩΤΗΣΕΙΣ 1. Ποια είναι η επιδίωξη του καταναλωτή και ποιοι παράγοντες την περιορίζουν; 2. Ποιος καταναλωτής ονομάζεται ορθολογικός και πότε λέμε ότι βρίσκεται σε ισορροπία; 3. Να διατυπώσετε
2 ο ΚΕΦΑΛΑΙΟ ΕΡΩΤΗΣΕΙΣ 1. Ποια είναι η επιδίωξη του καταναλωτή και ποιοι παράγοντες την περιορίζουν; 2. Ποιος καταναλωτής ονομάζεται ορθολογικός και πότε λέμε ότι βρίσκεται σε ισορροπία; 3. Να διατυπώσετε
 ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΘΕΩΡΙΑ-ΜΑΘΗΜΑ ΠΕΜΠΤΟ-ΕΚΤΟ ΕΚΤΟ ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ-ΙΣΟΡΡΟΠΙΑ ΙΣΟΡΡΟΠΙΑ ΤΟΥ ΚΑΤΑΝΑΛΩΤΗ ΤΜΗΜΑ ΕΠΙΧΕΙΡΗΜΑΤΙΚΟΥ ΣΧΕ ΙΑΣΜΟΥ & ΠΛΗΡΟΦΟΡΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Ακαδηµαϊκό Έτος 2011-2012 ΕΠΙΧ Μικροοικονοµική
ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΘΕΩΡΙΑ-ΜΑΘΗΜΑ ΠΕΜΠΤΟ-ΕΚΤΟ ΕΚΤΟ ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ-ΙΣΟΡΡΟΠΙΑ ΙΣΟΡΡΟΠΙΑ ΤΟΥ ΚΑΤΑΝΑΛΩΤΗ ΤΜΗΜΑ ΕΠΙΧΕΙΡΗΜΑΤΙΚΟΥ ΣΧΕ ΙΑΣΜΟΥ & ΠΛΗΡΟΦΟΡΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Ακαδηµαϊκό Έτος 2011-2012 ΕΠΙΧ Μικροοικονοµική
Γενική Ισορροπία- Υπαρξη και µοναδικότητα. Υπαρξη ϐαλρασιανής ισορροπίας. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς.
 Γενική Ισορροπία- Υπαρξη και µοναδικότητα Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 2013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία- Υπαρξη και µοναδικότητα 19 Απριλίου 2013 1 / 44 ύο Ϲητήµατα
Γενική Ισορροπία- Υπαρξη και µοναδικότητα Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 2013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία- Υπαρξη και µοναδικότητα 19 Απριλίου 2013 1 / 44 ύο Ϲητήµατα
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ
 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Κεφάλαιο 2 ο : Η Ζήτηση των Αγαθών ΕΠΙΜΕΛΕΙΑ: ΝΙΚΟΣ Χ. ΤΖΟΥΜΑΚΑΣ ΟΙΚΟΝΟΜΟΛΟΓΟΣ Οι τιμές των αγαθών προσδιορίζονται στην αγορά από την αλληλεπίδραση της ζήτησης και της προσφοράς.
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Κεφάλαιο 2 ο : Η Ζήτηση των Αγαθών ΕΠΙΜΕΛΕΙΑ: ΝΙΚΟΣ Χ. ΤΖΟΥΜΑΚΑΣ ΟΙΚΟΝΟΜΟΛΟΓΟΣ Οι τιμές των αγαθών προσδιορίζονται στην αγορά από την αλληλεπίδραση της ζήτησης και της προσφοράς.
ΑΣΚΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΓΙΑ ΔΥΝΑΤΟΥΣ ΛΥΤΕΣ
 ΑΣΚΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΓΙΑ ΔΥΝΑΤΟΥΣ ΛΥΤΕΣ 1. Σε γραμμική ΚΠΔ της μορφής Y a X : α. Η μέγιστη ποσότητα για το αγαθό Υ παράγεται όταν Y β. Η μέγιστη ποσότητα για το αγαθό Χ παράγεται όταν Y a γ. Η μέγιστη
ΑΣΚΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΓΙΑ ΔΥΝΑΤΟΥΣ ΛΥΤΕΣ 1. Σε γραμμική ΚΠΔ της μορφής Y a X : α. Η μέγιστη ποσότητα για το αγαθό Υ παράγεται όταν Y β. Η μέγιστη ποσότητα για το αγαθό Χ παράγεται όταν Y a γ. Η μέγιστη
Α.Ο.Θ ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΑΝΑ ΚΕΦΑΛΑΙΟ
 Α.Ο.Θ ΕΡΩΣΗΕΙ ΚΛΕΙΣΟΤ ΣΤΠΟΤ ΑΝΑ ΚΕΥΑΛΑΙΟ Γ τάξης Γενικοφ Λυκείου ΝΙΚΟ ΠΕΡΟΤΛΑΚΗ Οικονομολόγος, ΙΕΡΑΠΕΣΡΑ Σηλ. 6977246129 ΑΟΘ ΝΙΚΟ ΠΕΡΟΥΛΑΚΗ Οικονομολόγος ελίδα 1 Γ τάξης Γενικοφ Λυκείου ΕΡΩΣΗΕΙ ΚΛΕΙΣΟΤ
Α.Ο.Θ ΕΡΩΣΗΕΙ ΚΛΕΙΣΟΤ ΣΤΠΟΤ ΑΝΑ ΚΕΥΑΛΑΙΟ Γ τάξης Γενικοφ Λυκείου ΝΙΚΟ ΠΕΡΟΤΛΑΚΗ Οικονομολόγος, ΙΕΡΑΠΕΣΡΑ Σηλ. 6977246129 ΑΟΘ ΝΙΚΟ ΠΕΡΟΥΛΑΚΗ Οικονομολόγος ελίδα 1 Γ τάξης Γενικοφ Λυκείου ΕΡΩΣΗΕΙ ΚΛΕΙΣΟΤ
 25. Μία τυπική επιχείρηση που λειτουργεί σε καθεστώς τέλειου ανταγωνισμού, στη μακροχρόνια θέση ισορροπίας της: α. πραγματοποιεί θετικά οικονομικά κέρδη. β. πραγματοποιεί μηδενικά οικονομικά κέρδη. γ.
25. Μία τυπική επιχείρηση που λειτουργεί σε καθεστώς τέλειου ανταγωνισμού, στη μακροχρόνια θέση ισορροπίας της: α. πραγματοποιεί θετικά οικονομικά κέρδη. β. πραγματοποιεί μηδενικά οικονομικά κέρδη. γ.
3. ΠΟΡΟΙ ΚΑΙ ΔΙΕΘΝΕΣ ΕΜΠΟΡΙΟ: ΥΠΟΔΕΙΓΜΑ HECKSCHER-OHLIN
 3. ΠΟΡΟΙ ΚΑΙ ΔΙΕΘΝΕΣ ΕΜΠΟΡΙΟ: ΥΠΟΔΕΙΓΜΑ HESHER-OHIN Υπάρχουν δύο συντελεστές παραγωγής, το κεφάλαιο και η εργασία τους οποίους χρησιμοποιεί η επιχείρηση για να παράγει προϊόν Y μέσω μιας συνάρτησης παραγωγής
3. ΠΟΡΟΙ ΚΑΙ ΔΙΕΘΝΕΣ ΕΜΠΟΡΙΟ: ΥΠΟΔΕΙΓΜΑ HESHER-OHIN Υπάρχουν δύο συντελεστές παραγωγής, το κεφάλαιο και η εργασία τους οποίους χρησιμοποιεί η επιχείρηση για να παράγει προϊόν Y μέσω μιας συνάρτησης παραγωγής
ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ. Θεωρία Χρησιµότητας και Συµπεριφοράς του Καταναλωτή
 ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ Θεωρία Χρησιµότητας και Συµπεριφοράς του Καταναλωτή Εισαγωγή: Όπως γνωρίζουµε, το οικονοµικό πρόβληµα εστιάζεται στην αποτελεσµατική κατανοµή των ανεπαρκών οικονοµικών πόρων στις εναλλακτικές
ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ Θεωρία Χρησιµότητας και Συµπεριφοράς του Καταναλωτή Εισαγωγή: Όπως γνωρίζουµε, το οικονοµικό πρόβληµα εστιάζεται στην αποτελεσµατική κατανοµή των ανεπαρκών οικονοµικών πόρων στις εναλλακτικές
3. Η παρακάτω συνάρτηση παραγωγής παρουσιάζει φθίνουσες, σταθερές, ή αύξουσες οικονοµίες κλίµακας; παραγωγής παρουσιάζει σταθερές αποδόσεις κλίµακας.
 1. Μια επιχείρηση έχει συνάρτηση παραγωγής την f(k,l), όπου Κ είναι οι µονάδες κεφαλαίου και L είναι οι µονάδες εργασίας που χρησιµοποιεί. Αν ξέρουµε ότι το οριακό προϊόν της εργασίας είναι θετικό, αλλά
1. Μια επιχείρηση έχει συνάρτηση παραγωγής την f(k,l), όπου Κ είναι οι µονάδες κεφαλαίου και L είναι οι µονάδες εργασίας που χρησιµοποιεί. Αν ξέρουµε ότι το οριακό προϊόν της εργασίας είναι θετικό, αλλά
Διάλεξη 3. Οικονομικά της ευημερίας. Οικονομικά της ευημερίας 3/9/2017. Περίγραμμα. Εργαλεία δεοντολογικής ανάλυσης
 Περίγραμμα Διάλεξη Εργαλεία δεοντολογικής ανάλυσης Συνθήκες για αποτελεσματικότητα κατά areto Συνθήκες για ισορροπία σε ανταγωνιστικές αγορές Το πρώτο θεώρημα των οικονομικών της ευημερίας Το δεύτερο θεώρημα
Περίγραμμα Διάλεξη Εργαλεία δεοντολογικής ανάλυσης Συνθήκες για αποτελεσματικότητα κατά areto Συνθήκες για ισορροπία σε ανταγωνιστικές αγορές Το πρώτο θεώρημα των οικονομικών της ευημερίας Το δεύτερο θεώρημα
ΑΝΑ ΚΕΦΑΛΑΙΟ. geeconomy@yahoo.com. Γ Ι Ω Ρ Γ Ο Σ Κ Α Μ Α Ρ Ι Ν Ο Σ Ο Ι Κ Ο Ν Ο Μ Ο Λ Ο Γ Ο Σ ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2015
 ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2015 1 ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2015 ΑΝΑ ΚΕΦΑΛΑΙΟ Στο παρόν είναι συγκεντρωµένες όλες σχεδόν οι ερωτήσεις κλειστού τύπου που
ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2015 1 ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ 2000 2015 ΑΝΑ ΚΕΦΑΛΑΙΟ Στο παρόν είναι συγκεντρωµένες όλες σχεδόν οι ερωτήσεις κλειστού τύπου που
Οι τιμές των αγαθών προσδιορίζονται στην αγορά από την αλληλεπίδραση των δυνάμεων της ζήτησης και της προσφοράς.
 ΤΙΜΗ ΚΕΦΑΛΑΙΟ ΔΕΥΤΕΡΟ: Η ΖΗΤΗΣΗ Οι τιμές των αγαθών προσδιορίζονται στην αγορά από την αλληλεπίδραση των δυνάμεων της ζήτησης και της προσφοράς. Χρησιμότητα ενός αγαθού, για τον καταναλωτή, είναι η ικανοποίηση
ΤΙΜΗ ΚΕΦΑΛΑΙΟ ΔΕΥΤΕΡΟ: Η ΖΗΤΗΣΗ Οι τιμές των αγαθών προσδιορίζονται στην αγορά από την αλληλεπίδραση των δυνάμεων της ζήτησης και της προσφοράς. Χρησιμότητα ενός αγαθού, για τον καταναλωτή, είναι η ικανοποίηση
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ. και το Κόστος
 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Κεφάλαιο 3 ο : Η Παραγωγή της Επιχείρησης και το Κόστος ΕΠΙΜΕΛΕΙΑ: ΝΙΚΟΣ Χ. ΤΖΟΥΜΑΚΑΣ ΟΙΚΟΝΟΜΟΛΟΓΟΣ Ερωτήσεις πολλαπλής επιλογής 1. Το συνολικό προϊόν παίρνει την μέγιστη τιμή
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Κεφάλαιο 3 ο : Η Παραγωγή της Επιχείρησης και το Κόστος ΕΠΙΜΕΛΕΙΑ: ΝΙΚΟΣ Χ. ΤΖΟΥΜΑΚΑΣ ΟΙΚΟΝΟΜΟΛΟΓΟΣ Ερωτήσεις πολλαπλής επιλογής 1. Το συνολικό προϊόν παίρνει την μέγιστη τιμή
Γενική Ανταγωνιστική Ισορροπία και Αποτελεσματικές κατά Pareto Κατανομές σε Ανταλλακτική Οικονομία
 Γενική Ανταγωνιστική Ισορροπία και Αποτελεσματικές κατά Pareto Κατανομές σε Ανταλλακτική Οικονομία Βασικές Υποθέσεις (i) Οι αγορές όλων των αγαθών είναι τέλεια ανταγωνιστικές. Οι καταναλωτές και οι επιχειρήσεις
Γενική Ανταγωνιστική Ισορροπία και Αποτελεσματικές κατά Pareto Κατανομές σε Ανταλλακτική Οικονομία Βασικές Υποθέσεις (i) Οι αγορές όλων των αγαθών είναι τέλεια ανταγωνιστικές. Οι καταναλωτές και οι επιχειρήσεις
Ερωτήσεις και Ασκήσεις κεφ. 5, Ο προσδιορισμός των τιμών Ερωτήσεις πολλαπλής επιλογής : Ερωτήσεις σωστού λάθους.
 Ερωτήσεις και Ασκήσεις κεφ. 5, Ο προσδιορισμός των τιμών. Η τιμή ισορροπίας ενός κανονικού αγαθού αυξάνεται όταν: 0 α. η προσφορά μειώνεται και η ζήτηση παραμένει σταθερή β. η ζήτηση παραμένει σταθερή
Ερωτήσεις και Ασκήσεις κεφ. 5, Ο προσδιορισμός των τιμών. Η τιμή ισορροπίας ενός κανονικού αγαθού αυξάνεται όταν: 0 α. η προσφορά μειώνεται και η ζήτηση παραμένει σταθερή β. η ζήτηση παραμένει σταθερή
Διάλεξη 3. Οικονομικά της ευημερίας 2/26/2016. Περίγραμμα. Εργαλεία δεοντολογικής ανάλυσης. Αποτελεσματικότητα κατά Pareto: ορισμός. ορισμός.
 Περίγραμμα Διάλεξη Εργαλεία δεοντολογικής ανάλυσης υνθήκες για αποτελεσματικότητα κατά areto υνθήκες για ισορροπία σε ανταγωνιστικές αγορές Το πρώτο θεώρημα των οικονομικών της ευημερίας Το δεύτερο θεώρημα
Περίγραμμα Διάλεξη Εργαλεία δεοντολογικής ανάλυσης υνθήκες για αποτελεσματικότητα κατά areto υνθήκες για ισορροπία σε ανταγωνιστικές αγορές Το πρώτο θεώρημα των οικονομικών της ευημερίας Το δεύτερο θεώρημα
Διάλεξη 10. Γενική Ισορροπία VA 30
 Διάλεξη 10 Γενική Ισορροπία V 30 1 Μερική & Γενική Ισορροπία Μέχρι τώρα εξετάζαμε γενικά την αγορά ενός αγαθού μεμονωμένα. Το πώς δηλαδή η προσφορά και η ζήτηση επηρεάζονται από την τιμή του συγκεκριμένου
Διάλεξη 10 Γενική Ισορροπία V 30 1 Μερική & Γενική Ισορροπία Μέχρι τώρα εξετάζαμε γενικά την αγορά ενός αγαθού μεμονωμένα. Το πώς δηλαδή η προσφορά και η ζήτηση επηρεάζονται από την τιμή του συγκεκριμένου
Q D1 = P και Q S = P.
 ΚΕΦΑΛΑΙΟ 5: Ο ΠΡΟΣ ΙΟΡΙΣΜΟΣ ΤΩΝ ΤΙΜΩΝ Να σηµειώσετε µε Σ (σωστό) ή Λ (λάθος) στο τέλος των προτάσεων: 1. Τιµή ισορροπίας είναι η τιµή στην οποία η ζητούµενη ποσότητα είναι ίση µε την προσφερόµενη ποσότητα.
ΚΕΦΑΛΑΙΟ 5: Ο ΠΡΟΣ ΙΟΡΙΣΜΟΣ ΤΩΝ ΤΙΜΩΝ Να σηµειώσετε µε Σ (σωστό) ή Λ (λάθος) στο τέλος των προτάσεων: 1. Τιµή ισορροπίας είναι η τιµή στην οποία η ζητούµενη ποσότητα είναι ίση µε την προσφερόµενη ποσότητα.
ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΑΠΟ ΟΛΑ ΤΑ ΚΕΦΑΛΑΙΑ
 ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΑΠΟ ΟΛΑ ΤΑ ΚΕΦΑΛΑΙΑ (Πρόκειται, κυρίως, για θέματα κλειστού τύπου από τις εξετάσεις των προηγούμενων ετών). Α. ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΑΘΟΣ 1. Σε ένα κανονικό αγαθό, όταν αυξάνεται το
ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΑΠΟ ΟΛΑ ΤΑ ΚΕΦΑΛΑΙΑ (Πρόκειται, κυρίως, για θέματα κλειστού τύπου από τις εξετάσεις των προηγούμενων ετών). Α. ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΑΘΟΣ 1. Σε ένα κανονικό αγαθό, όταν αυξάνεται το
Η ΠΡΟΣΦΟΡΑ ΤΩΝ ΑΓΑΘΩΝ
 ΚΕΦΑΛΑΙΟ ΤΕΤΑΡΤΟ Η ΠΡΟΣΦΟΡΑ ΤΩΝ ΑΓΑΘΩΝ 1. Εισαγωγή Όπως έχουμε τονίσει, η κατανόηση του τρόπου με τον οποίο προσδιορίζεται η τιμή ενός αγαθού απαιτεί κατανόηση των δύο δυνάμεων της αγοράς, δηλαδή της ζήτησης
ΚΕΦΑΛΑΙΟ ΤΕΤΑΡΤΟ Η ΠΡΟΣΦΟΡΑ ΤΩΝ ΑΓΑΘΩΝ 1. Εισαγωγή Όπως έχουμε τονίσει, η κατανόηση του τρόπου με τον οποίο προσδιορίζεται η τιμή ενός αγαθού απαιτεί κατανόηση των δύο δυνάμεων της αγοράς, δηλαδή της ζήτησης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τµήµα Οικονοµικών Επιστηµών Ακαδηµαϊκό έτος (διαβάζουμε κεφ. 4 από Μ. Χλέτσο και σημειώσεις στο eclass)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τµήµα Οικονοµικών Επιστηµών Ακαδηµαϊκό έτος 2016-17 ΠΟΛΙΤΙΚΗ ΟΙΚΟΝΟΜΙΑ ΤΗΣ ΚΟΙΝΩΝΙΚΗΣ ΠΟΛΙΤΙΚΗΣ (διαβάζουμε κεφ. 4 από Μ. Χλέτσο και σημειώσεις στο eclass) 1 ιάλεξη2 Ανταγωνισμός, οικονομική
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τµήµα Οικονοµικών Επιστηµών Ακαδηµαϊκό έτος 2016-17 ΠΟΛΙΤΙΚΗ ΟΙΚΟΝΟΜΙΑ ΤΗΣ ΚΟΙΝΩΝΙΚΗΣ ΠΟΛΙΤΙΚΗΣ (διαβάζουμε κεφ. 4 από Μ. Χλέτσο και σημειώσεις στο eclass) 1 ιάλεξη2 Ανταγωνισμός, οικονομική
4.1 Ζήτηση για Ασφάλιση. Πλήρη κάλυψη.
 4. Ζήτηση για Ασφάλιση. Πλήρη κάλυψη. Η αγορά ασφαλιστικών συµφωνιών είναι µία ιδιαίτερη περίπτωση αγοράς δικαιωµάτων. Αντικείµενο της αγοράς αυτής είναι να δώσει την ευκαιρία µεταβίβασης εισοδήµατος από
4. Ζήτηση για Ασφάλιση. Πλήρη κάλυψη. Η αγορά ασφαλιστικών συµφωνιών είναι µία ιδιαίτερη περίπτωση αγοράς δικαιωµάτων. Αντικείµενο της αγοράς αυτής είναι να δώσει την ευκαιρία µεταβίβασης εισοδήµατος από
ΑΣΚΗΣΕΙΣ ΣΤΟ ΥΠΟ ΕΙΓΜΑ ΖΗΤΗΣΗΣ ΚΑΙ ΠΡΟΣΦΟΡΑΣ
 ΑΣΚΗΣΕΙΣ ΣΤΟ ΥΠΟ ΕΙΓΜΑ ΖΗΤΗΣΗΣ ΚΑΙ ΠΡΟΣΦΟΡΑΣ Άσκηση 1: ίνεται ο πίνακας ζήτησης και προσφοράς ενός αγαθού Χ: Τιµή Ζητούµενη Προσφερόµενη ποσότητα ποσότητα 54 10 3 50 1 19 46 14 15 44 15 13 40 17 9 Ζητείται
ΑΣΚΗΣΕΙΣ ΣΤΟ ΥΠΟ ΕΙΓΜΑ ΖΗΤΗΣΗΣ ΚΑΙ ΠΡΟΣΦΟΡΑΣ Άσκηση 1: ίνεται ο πίνακας ζήτησης και προσφοράς ενός αγαθού Χ: Τιµή Ζητούµενη Προσφερόµενη ποσότητα ποσότητα 54 10 3 50 1 19 46 14 15 44 15 13 40 17 9 Ζητείται
8. Η ζήτηση ενός αγαθού µεταβάλλεται προς την αντίθετη κατεύθυνση µε τη µεταβολή της τιµής του υποκατάστατου αγαθού.
 ΚΕΦΑΛΑΙΟ 2 : Η ΖΗΤΗΣΗ Να σηµειώσετε το σωστό ή το λάθος στο τέλος των προτάσεων: 1. Η επιδίωξη της µέγιστης χρησιµότητας αποτελεί βασικό χαρακτηριστικό της συµπεριφοράς του καταναλωτή στη ζήτηση αγαθών.
ΚΕΦΑΛΑΙΟ 2 : Η ΖΗΤΗΣΗ Να σηµειώσετε το σωστό ή το λάθος στο τέλος των προτάσεων: 1. Η επιδίωξη της µέγιστης χρησιµότητας αποτελεί βασικό χαρακτηριστικό της συµπεριφοράς του καταναλωτή στη ζήτηση αγαθών.
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) ΕΠΙΛΟΓΗΣ (ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ) 25 ΜΑΪΟΥ 2016 ΕΚΦΩΝΗΣΕΙΣ ΟΜΑ Α ΠΡΩΤΗ
 ΘΕΜΑ Α ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) ΕΠΙΛΟΓΗΣ (ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ) 25 ΜΑΪΟΥ 2016 ΕΚΦΩΝΗΣΕΙΣ ΟΜΑ Α ΠΡΩΤΗ Α1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας,
ΘΕΜΑ Α ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) ΕΠΙΛΟΓΗΣ (ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ) 25 ΜΑΪΟΥ 2016 ΕΚΦΩΝΗΣΕΙΣ ΟΜΑ Α ΠΡΩΤΗ Α1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας,
Εξετάσεις Η επιβολή από το κράτος κατώτατης τιμής στα αγροτικά προϊόντα έχει ως σκοπό την προστασία του εισοδήματος των αγροτών.
 ΚΕΦΑΛΑΙΟ 5: Ο ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΩΝ ΤΙΜΩΝ Να σημειώσετε με Σ (σωστό) ή Λ (λάθος) στο τέλος των προτάσεων: 1. Η επιβολή από το κράτος ανώτατης τιμής σε ένα προϊόν δημιουργεί συνήθως «μαύρη αγορά». Εξετάσεις
ΚΕΦΑΛΑΙΟ 5: Ο ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΩΝ ΤΙΜΩΝ Να σημειώσετε με Σ (σωστό) ή Λ (λάθος) στο τέλος των προτάσεων: 1. Η επιβολή από το κράτος ανώτατης τιμής σε ένα προϊόν δημιουργεί συνήθως «μαύρη αγορά». Εξετάσεις
0 χ1 χ2 Ι2 χ3 Ι5 Ι3 χ
 ΠΝΕΠΙΣΤΗΜΙΟ ΜΚΕ ΟΝΙΣ - ΤΜΗΜ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΘΗΓΗΤΗΣ ΚΩΣΤΣ ΕΛΕΝΤΖΣ ΠΟΤΕΛΕΣΜΤ ΥΠΟΚΤΣΤΣΗΣ ΚΙ ΕΙΣΟ ΗΜΤΟΣ Ι1 χ/ Ρ=0 χ/ Ρ>0 χ/ Ρ
ΠΝΕΠΙΣΤΗΜΙΟ ΜΚΕ ΟΝΙΣ - ΤΜΗΜ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΘΗΓΗΤΗΣ ΚΩΣΤΣ ΕΛΕΝΤΖΣ ΠΟΤΕΛΕΣΜΤ ΥΠΟΚΤΣΤΣΗΣ ΚΙ ΕΙΣΟ ΗΜΤΟΣ Ι1 χ/ Ρ=0 χ/ Ρ>0 χ/ Ρ
ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑ ΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 2016 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΠΙΛΟΓΗΣ (ΝΕΟ ΚΑΙ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ)
 ΑΡΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΠΙΛΟΓΗΣ (ΝΕΟ ΚΑΙ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ) ΟΜΑ Α ΠΡΩΤΗ ΘΕΜΑ Α Α1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας, δίπλα στο γράµµα που αντιστοιχεί
ΑΡΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΠΙΛΟΓΗΣ (ΝΕΟ ΚΑΙ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ) ΟΜΑ Α ΠΡΩΤΗ ΘΕΜΑ Α Α1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας, δίπλα στο γράµµα που αντιστοιχεί
2 ο ΚΕΦΑΛΑΙΟ (Προκαταρκτικές ασκήσεις για εξάσκησης)
 2 ο ΚΕΦΑΛΑΙΟ (Προκαταρκτικές ασκήσεις για εξάσκησης) 1. Χρησιμοποιώντας τα στοιχεία του παρακάτω πίνακα που δείχνουν τις ζητούμενες ποσότητες του αγαθού Χ από τρεις διαφορετικούς καταναλωτές, οι οποίες
2 ο ΚΕΦΑΛΑΙΟ (Προκαταρκτικές ασκήσεις για εξάσκησης) 1. Χρησιμοποιώντας τα στοιχεία του παρακάτω πίνακα που δείχνουν τις ζητούμενες ποσότητες του αγαθού Χ από τρεις διαφορετικούς καταναλωτές, οι οποίες
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ
 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑ ΕΠΙΛΟΓΗΣ 2012 ΕΚΦΩΝΗΣΕΙΣ ΟΜΑ Α ΠΡΩΤΗ ΘΕΜΑ Α Α1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας δίπλα στο γράµµα που αντιστοιχεί σε κάθε πρόταση
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑ ΕΠΙΛΟΓΗΣ 2012 ΕΚΦΩΝΗΣΕΙΣ ΟΜΑ Α ΠΡΩΤΗ ΘΕΜΑ Α Α1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας δίπλα στο γράµµα που αντιστοιχεί σε κάθε πρόταση
ΑΣΚΗΣΕΙΣ. 1η οµάδα. 2. Έστω ο επόµενος πίνακας παραγωγικών δυνατοτήτων: Χ Υ Κόστος. Κόστος ευκαιρίας Ψ Α /3
 ΑΣΚΗΣΕΙΣ 1η οµάδα 1. Έστω επιχείρηση που διαθέτει 5 εργάτες. Κάθε εργάτης µπορεί να παράγει 12 µονάδες από το αγαθό Υ. Επιπλέον γνωρίζουµε ότι η ΚΠ είναι γραµµική µε το συνδυασµό X = 45, Y = 24 να είναι
ΑΣΚΗΣΕΙΣ 1η οµάδα 1. Έστω επιχείρηση που διαθέτει 5 εργάτες. Κάθε εργάτης µπορεί να παράγει 12 µονάδες από το αγαθό Υ. Επιπλέον γνωρίζουµε ότι η ΚΠ είναι γραµµική µε το συνδυασµό X = 45, Y = 24 να είναι
ΑΟΘ : ΘΕΜΑΤΑ ΑΣΚΗΣΕΙΣ ΠΑΝΕΛΛΑΔΙΚΩΝ
 ΘΕΜΑΤΑ ΑΣΚΗΣΕΙΣ ΠΑΝΕΛΛΑΔΙΚΩΝ 2000 2017 : ΚΕΦΑΛΑΙΟ 5 Ο 1 ΑΟΘ : ΘΕΜΑΤΑ ΑΣΚΗΣΕΙΣ ΠΑΝΕΛΛΑΔΙΚΩΝ 2000 2017 ΚΕΦΑΛΑΙΟ 5ο 1. Οι συναρτήσεις αγοραίας ζήτησης και προσφοράς ενός αγαθού είναι αντίστοιχα: Q D1 = 600
ΘΕΜΑΤΑ ΑΣΚΗΣΕΙΣ ΠΑΝΕΛΛΑΔΙΚΩΝ 2000 2017 : ΚΕΦΑΛΑΙΟ 5 Ο 1 ΑΟΘ : ΘΕΜΑΤΑ ΑΣΚΗΣΕΙΣ ΠΑΝΕΛΛΑΔΙΚΩΝ 2000 2017 ΚΕΦΑΛΑΙΟ 5ο 1. Οι συναρτήσεις αγοραίας ζήτησης και προσφοράς ενός αγαθού είναι αντίστοιχα: Q D1 = 600
ΕΡΓΑΣΙΕΣ 5 ου ΚΕΦΑΛΑΙΟΥ 1 η Ομάδα: Ερωτήσεις πολλαπλής επιλογής
 ΕΡΓΑΣΙΕΣ 5 ου ΚΕΦΑΛΑΙΟΥ 1 η Ομάδα: Ερωτήσεις πολλαπλής επιλογής 1. Η επιβολή στην αγορά ενός αγαθού μιας τιμής που είναι μικρότερη της τιμής ισορροπίας θα προκαλέσει: α) Πλεόνασμα β) Έλλειμμα γ) Νέα ισορροπία
ΕΡΓΑΣΙΕΣ 5 ου ΚΕΦΑΛΑΙΟΥ 1 η Ομάδα: Ερωτήσεις πολλαπλής επιλογής 1. Η επιβολή στην αγορά ενός αγαθού μιας τιμής που είναι μικρότερη της τιμής ισορροπίας θα προκαλέσει: α) Πλεόνασμα β) Έλλειμμα γ) Νέα ισορροπία
ΑΟΘ : ΘΕΜΑΤΑ ΑΣΚΗΣΕΙΣ ΕΞΕΤΑΣΕΩΝ 2000 2013
 12 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΑΟΘ : ΘΕΜΑΤΑ ΑΣΚΗΣΕΙΣ ΕΞΕΤΑΣΕΩΝ 2000 2013 ΚΕΦΑΛΑΙΟ 5ο (µε 2ο, 3ο και 4ο) ΗΜΕΡΗΣΙΑ 9/2000 ΗΜΕΡΗΣΙΑ 6/2000 ΕΣΜΕΣ 2000 ΕΣΜΕΣ 1998 28. ίνονται οι συναρτήσεις ζήτησης και προσφοράς
12 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΑΟΘ : ΘΕΜΑΤΑ ΑΣΚΗΣΕΙΣ ΕΞΕΤΑΣΕΩΝ 2000 2013 ΚΕΦΑΛΑΙΟ 5ο (µε 2ο, 3ο και 4ο) ΗΜΕΡΗΣΙΑ 9/2000 ΗΜΕΡΗΣΙΑ 6/2000 ΕΣΜΕΣ 2000 ΕΣΜΕΣ 1998 28. ίνονται οι συναρτήσεις ζήτησης και προσφοράς
ΙΑΓΩΝΙΣΜΟΣ ΓΙΑ ΤΗΝ ΠΛΗΡΩΣΗ ΘΕΣΕΩΝ ΗΜΟΣΙΩΝ ΥΠΗΡΕΣΙΩΝ ΚΑΙ ΝΟΜΙΚΩΝ ΠΡΟΣΩΠΩΝ ΤΟΥ ΗΜΟΣΙΟΥ TOMEΑ ΚΑΤΗΓΟΡΙΑ ΠΕ ΕΞΕΤΑΣΗ ΣΤΟ ΜΑΘΗΜΑ: «OIKONOMIKH»
 ΑΝΩΤΑΤΟ ΣΥΜΒΟΥΛΙΟ ΕΠΙΛΟΓΗΣ ΠΡΟΣΩΠΙΚΟΥ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΙΑΓΩΝΙΣΜΟΥ ΙΑΓΩΝΙΣΜΟΣ ΓΙΑ ΤΗΝ ΠΛΗΡΩΣΗ ΘΕΣΕΩΝ ΗΜΟΣΙΩΝ ΥΠΗΡΕΣΙΩΝ ΚΑΙ ΝΟΜΙΚΩΝ ΠΡΟΣΩΠΩΝ ΤΟΥ ΗΜΟΣΙΟΥ TOMEΑ ΚΑΤΗΓΟΡΙΑ ΠΕ ΕΞΕΤΑΣΗ ΣΤΟ ΜΑΘΗΜΑ: «OIKONOMIKH»
ΑΝΩΤΑΤΟ ΣΥΜΒΟΥΛΙΟ ΕΠΙΛΟΓΗΣ ΠΡΟΣΩΠΙΚΟΥ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΙΑΓΩΝΙΣΜΟΥ ΙΑΓΩΝΙΣΜΟΣ ΓΙΑ ΤΗΝ ΠΛΗΡΩΣΗ ΘΕΣΕΩΝ ΗΜΟΣΙΩΝ ΥΠΗΡΕΣΙΩΝ ΚΑΙ ΝΟΜΙΚΩΝ ΠΡΟΣΩΠΩΝ ΤΟΥ ΗΜΟΣΙΟΥ TOMEΑ ΚΑΤΗΓΟΡΙΑ ΠΕ ΕΞΕΤΑΣΗ ΣΤΟ ΜΑΘΗΜΑ: «OIKONOMIKH»
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ
 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Κεφάλαιο 5 ο : Ο Προσδιορισμός των Τιμών ΕΠΙΜΕΛΕΙΑ: ΝΙΚΟΣ Χ. ΤΖΟΥΜΑΚΑΣ ΟΙΚΟΝΟΜΟΛΟΓΟΣ Ασκήσεις 1. Οι συναρτήσεις ζήτησης και προσφοράς ενός αγαθού είναι: =20-2P και S =5+3P αντίστοιχα.
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Κεφάλαιο 5 ο : Ο Προσδιορισμός των Τιμών ΕΠΙΜΕΛΕΙΑ: ΝΙΚΟΣ Χ. ΤΖΟΥΜΑΚΑΣ ΟΙΚΟΝΟΜΟΛΟΓΟΣ Ασκήσεις 1. Οι συναρτήσεις ζήτησης και προσφοράς ενός αγαθού είναι: =20-2P και S =5+3P αντίστοιχα.
από την ποσοστιαία μεταβολή της ζητούμενης ποσότητας προς την ποσοστιαία Σχέση ελαστικότητας ζήτησης και κλίση της καμπύλης ζήτησης.
 ΕΛΑΣΤΙΚΟΤΗΤΑ ΖΗΤΗΣΗΣ Ορισμός: Η ελαστικότητα ζήτησης, ενός αγαθού ως προς την τιμή του δίνεται από την ποσοστιαία μεταβολή της ζητούμενης ποσότητας προς την ποσοστιαία μεταβολή της τιμής του. Δηλαδή %
ΕΛΑΣΤΙΚΟΤΗΤΑ ΖΗΤΗΣΗΣ Ορισμός: Η ελαστικότητα ζήτησης, ενός αγαθού ως προς την τιμή του δίνεται από την ποσοστιαία μεταβολή της ζητούμενης ποσότητας προς την ποσοστιαία μεταβολή της τιμής του. Δηλαδή %
Μικροοικονομική. Ζήτηση και προσφορά
 Μικροοικονομική Ζήτηση και προσφορά Ο νόμος της ζήτησης Σύμφωνα με το Νόμο της Ζήτησης, όταν μειώνεται η τιμή ενός αγαθού, αυξάνεται η ζητούμενη ποσότητά του και το αντίστροφο με τους προσδιοριστικούς
Μικροοικονομική Ζήτηση και προσφορά Ο νόμος της ζήτησης Σύμφωνα με το Νόμο της Ζήτησης, όταν μειώνεται η τιμή ενός αγαθού, αυξάνεται η ζητούμενη ποσότητά του και το αντίστροφο με τους προσδιοριστικούς
(i) Νόμος Ζήτησης. Μικροοικονομία Εξετάζει τη συμπεριφορά του οικονομούντος ατόμου (καταναλωτή, παραγωγού επιχείρησης)
 ΕΙΣΑΩΗ Μικροοικονομία Εξετάζει τη συμπεριφορά του οικονομούντος ατόμου (καταναλωτή, παραγωγού επιχείρησης) Μικροοικονομία ή Θεωρία Τιμών Σημείο αναφοράς είναι ο προσδιορισμός της τιμής ενός αγαθού. Ν Ο
ΕΙΣΑΩΗ Μικροοικονομία Εξετάζει τη συμπεριφορά του οικονομούντος ατόμου (καταναλωτή, παραγωγού επιχείρησης) Μικροοικονομία ή Θεωρία Τιμών Σημείο αναφοράς είναι ο προσδιορισμός της τιμής ενός αγαθού. Ν Ο
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ
 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑ ΕΠΙΛΟΓΗΣ 011 ΕΚΦΩΝΗΣΕΙΣ ΟΜΑ Α ΠΡΩΤΗ Α1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας δίπλα στο γράµµα που αντιστοιχεί σε κάθε πρόταση τη λέξη
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑ ΕΠΙΛΟΓΗΣ 011 ΕΚΦΩΝΗΣΕΙΣ ΟΜΑ Α ΠΡΩΤΗ Α1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας δίπλα στο γράµµα που αντιστοιχεί σε κάθε πρόταση τη λέξη
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2014
 Ε_3.Αλ3Ε(ε) ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑ: ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ / ΕΠΙΛΟΓΗΣ Ηµεροµηνία: Κυριακή 4 Μαΐου 2014 ιάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΟΜΑ Α ΠΡΩΤΗ Α1. Να χαρακτηρίσετε τις προτάσεις που
Ε_3.Αλ3Ε(ε) ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑ: ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ / ΕΠΙΛΟΓΗΣ Ηµεροµηνία: Κυριακή 4 Μαΐου 2014 ιάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΟΜΑ Α ΠΡΩΤΗ Α1. Να χαρακτηρίσετε τις προτάσεις που
2.10. Τιμή και ποσότητα ισορροπίας
 .. Τιμή και ποσότητα ισορροπίας ίδαμε ότι η βασική επιδίωξη των επιχειρήσεων είναι η επίτευξη του μέγιστου κέρδους με την πώληση όσο το δυνατόν μεγαλύτερων ποσοτήτων ενός αγαθού στη μεγαλύτερη δυνατή τιμή
.. Τιμή και ποσότητα ισορροπίας ίδαμε ότι η βασική επιδίωξη των επιχειρήσεων είναι η επίτευξη του μέγιστου κέρδους με την πώληση όσο το δυνατόν μεγαλύτερων ποσοτήτων ενός αγαθού στη μεγαλύτερη δυνατή τιμή
Μικροοικονομική. Ελαστικότητες
 Μικροοικονομική Ελαστικότητες Σημασία ελαστικοτήτων Είδαμε πως οι δυνάμεις της προσφοράς και της ζήτησης αλληλεπιδρούν και σχηματίζουν σημεία ισορροπίας στα οποία σε μία δεδομένη τιμή ισορροπίας η προσφερόμενη
Μικροοικονομική Ελαστικότητες Σημασία ελαστικοτήτων Είδαμε πως οι δυνάμεις της προσφοράς και της ζήτησης αλληλεπιδρούν και σχηματίζουν σημεία ισορροπίας στα οποία σε μία δεδομένη τιμή ισορροπίας η προσφερόμενη
Η προσδοκώµενη χρησιµότητα του κέρδους όταν η πιθανότητα η τιµή του προϊόντος Ρ1 είναι ψ, χ το επίπεδο παραγωγής και c(x) η συνάρτηση κόστους, είναι
 3. Θεωρία της Επιχείρησης 3. Η Ανταγωνιστική Επιχείρηση. Το τµήµα αυτό έχει δύο στόχους. Πρώτα να δείξει ότι αν υπάρχει ουδετερότητα απέναντι στον κίνδυνο, τότε η µέση αξία ενός αβέβαιου γεγονότος είναι
3. Θεωρία της Επιχείρησης 3. Η Ανταγωνιστική Επιχείρηση. Το τµήµα αυτό έχει δύο στόχους. Πρώτα να δείξει ότι αν υπάρχει ουδετερότητα απέναντι στον κίνδυνο, τότε η µέση αξία ενός αβέβαιου γεγονότος είναι
Α1. ΘΕΜΑ Α. 1. Λ 2. Σ 3. Λ 4. Σ 5. Λ Α2.1. Β Α2.2. Δ
 ΛΥΣΗ Α1. 1. Λ 2. Σ 3. Λ 4. Σ 5. Λ Α2.1. Β Α2.2. Δ ΘΕΜΑ Α. ΘΕΜΑ Β. Β1. Ο νόμος της φθίνουσας ή μη ανάλογης απόδοσης δηλώνει ότι στη βραχυχρόνια περίοδο παραγωγής, δηλαδή στην περίοδο που υπάρχει ίνας τουλάχιστον
ΛΥΣΗ Α1. 1. Λ 2. Σ 3. Λ 4. Σ 5. Λ Α2.1. Β Α2.2. Δ ΘΕΜΑ Α. ΘΕΜΑ Β. Β1. Ο νόμος της φθίνουσας ή μη ανάλογης απόδοσης δηλώνει ότι στη βραχυχρόνια περίοδο παραγωγής, δηλαδή στην περίοδο που υπάρχει ίνας τουλάχιστον
ΔΕΟ43. Απάντηση 2ης ΓΕ Επιμέλεια: Γιάννης Σαραντής. ΘΕΡΜΟΠΥΛΩΝ 17 Περιστέρι ,
 ΔΕΟ43 Απάντηση 2ης ΓΕ 2016-2017 Επιμέλεια: Γιάννης Σαραντής 1 ΑΣΚΗΣΗ Νο 1 (20%) ΟΔΗΓΙΑ: Σε κάθε ερώτηση πολλαπλής επιλογής επιλέγετε μία απάντηση, και η επιλογή σας σημειώνεται με 1 στο αντίστοιχο πεδίο
ΔΕΟ43 Απάντηση 2ης ΓΕ 2016-2017 Επιμέλεια: Γιάννης Σαραντής 1 ΑΣΚΗΣΗ Νο 1 (20%) ΟΔΗΓΙΑ: Σε κάθε ερώτηση πολλαπλής επιλογής επιλέγετε μία απάντηση, και η επιλογή σας σημειώνεται με 1 στο αντίστοιχο πεδίο
Κεφάλαιο 32 Ανταλλαγή
 HL R. VRIN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Εκδόσεις Κριτική Κεφάλαιο 32 Ανταλλαγή Ύλη για τη Μίκρο ΙΙ: όλο το κεφάλαιο Ανάλυση μερικής ισορροπίας/ανάλυση γενικής ισορροπίας Τέλειος ανταγωνισμός/ατελής
HL R. VRIN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Εκδόσεις Κριτική Κεφάλαιο 32 Ανταλλαγή Ύλη για τη Μίκρο ΙΙ: όλο το κεφάλαιο Ανάλυση μερικής ισορροπίας/ανάλυση γενικής ισορροπίας Τέλειος ανταγωνισμός/ατελής
ΔΗΜΟΣΙΑ ΟΙΚΟΝΟΜΙΚΗ Ι
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΔΗΜΟΣΙΑ ΟΙΚΟΝΟΜΙΚΗ Ι Ενότητα 3: Εργαλεία Κανονιστικής Ανάλυσης Κουτεντάκης Φραγκίσκος Γαληνού Αργυρώ Τμήμα Οικονομικών Επιστημών Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΔΗΜΟΣΙΑ ΟΙΚΟΝΟΜΙΚΗ Ι Ενότητα 3: Εργαλεία Κανονιστικής Ανάλυσης Κουτεντάκης Φραγκίσκος Γαληνού Αργυρώ Τμήμα Οικονομικών Επιστημών Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΤΟΥΡΙΣΤΙΚΗ ΟΙΚΟΝΟΜΙΚΗ ΚΕΦΑΛΑΙΟ 12 ΘΕΩΡΙΑ ΤΟΥΡΙΣΤΙΚΗΣ ΠΑΡΑΓΩΓΗΣ
 ΤΟΥΡΙΣΤΙΚΗ ΟΙΚΟΝΟΜΙΚΗ ΚΕΦΑΛΑΙΟ 12 ΘΕΩΡΙΑ ΤΟΥΡΙΣΤΙΚΗΣ ΠΑΡΑΓΩΓΗΣ ΘΕΩΡΙΑ ΤΟΥΡΙΣΤΙΚΗΣ ΠΑΡΑΓΩΓΗΣ ΔΙΑΡΘΡΩΣΗ ΘΕΜΑΤΙΚΩΝ ΕΝΟΤΗΤΩΝ ΚΕΦΑΛΑΙΟΥ Η τουριστική παραγωγή στο βραχυχρόνιο διάστημα. Η τουριστική παραγωγή
ΤΟΥΡΙΣΤΙΚΗ ΟΙΚΟΝΟΜΙΚΗ ΚΕΦΑΛΑΙΟ 12 ΘΕΩΡΙΑ ΤΟΥΡΙΣΤΙΚΗΣ ΠΑΡΑΓΩΓΗΣ ΘΕΩΡΙΑ ΤΟΥΡΙΣΤΙΚΗΣ ΠΑΡΑΓΩΓΗΣ ΔΙΑΡΘΡΩΣΗ ΘΕΜΑΤΙΚΩΝ ΕΝΟΤΗΤΩΝ ΚΕΦΑΛΑΙΟΥ Η τουριστική παραγωγή στο βραχυχρόνιο διάστημα. Η τουριστική παραγωγή
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΕΠΙΛΟΓΗΣ ΓΙΑ ΟΛΕΣ ΤΙΣ ΚΑΤΕΥΘΥΝΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 2002
 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΕΠΙΛΟΓΗΣ ΓΙΑ ΟΛΕΣ ΤΙΣ ΚΑΤΕΥΘΥΝΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΕΙΣ Μονάδες ΟΜΑ Α Α Στις προτάσεις από Α µέχρι και Α, να γράψετε στο τετράδιό σας τον αριθµό της καθεµιάς και
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΕΠΙΛΟΓΗΣ ΓΙΑ ΟΛΕΣ ΤΙΣ ΚΑΤΕΥΘΥΝΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΕΙΣ Μονάδες ΟΜΑ Α Α Στις προτάσεις από Α µέχρι και Α, να γράψετε στο τετράδιό σας τον αριθµό της καθεµιάς και
ΕΡΓΑΣΙΕΣ 4 ου ΚΕΦΑΛΑΙΟΥ. 1 η Ομάδα: Ερωτήσεις πολλαπλής επιλογής
 ΕΡΓΑΣΙΕΣ 4 ου ΚΕΦΑΛΑΙΟΥ 1 η Ομάδα: Ερωτήσεις πολλαπλής επιλογής 1. Σύμφωνα με το νόμο της προσφοράς: α) Η προσφερόμενη ποσότητα ενός αγαθού αυξάνεται όταν μειώνεται η τιμή του στην αγορά β) Η προσφερόμενη
ΕΡΓΑΣΙΕΣ 4 ου ΚΕΦΑΛΑΙΟΥ 1 η Ομάδα: Ερωτήσεις πολλαπλής επιλογής 1. Σύμφωνα με το νόμο της προσφοράς: α) Η προσφερόμενη ποσότητα ενός αγαθού αυξάνεται όταν μειώνεται η τιμή του στην αγορά β) Η προσφερόμενη
ΚΕΦΑΛΑΙΟ 2 ο : Η ζήτηση των αγαθών
 ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΑΔΙΚΩΝ 2000 2017 : ΚΕΦΑΛΑΙΟ 2 Ο 1 Στο συγκεκριμένο αρχείο υπάρχουν οι ερωτήσεις κλειστού τύπου της ύλης του 2 ου κεφαλαίου και τέθηκαν στις πανελλαδικές: - Ημερησίων και
ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΠΑΝΕΛΛΑΔΙΚΩΝ 2000 2017 : ΚΕΦΑΛΑΙΟ 2 Ο 1 Στο συγκεκριμένο αρχείο υπάρχουν οι ερωτήσεις κλειστού τύπου της ύλης του 2 ου κεφαλαίου και τέθηκαν στις πανελλαδικές: - Ημερησίων και
ΕΠΙΧΕΙΡΗΣΕΙΣ ΚΑΙ ΑΝΤΑΓΩΝΙΣΤΙΚΕΣ ΑΓΟΡΕΣ
 ΕΠΙΧΕΙΡΗΣΕΙΣ ΚΑΙ ΑΝΤΑΓΩΝΙΣΤΙΚΕΣ ΑΓΟΡΕΣ Κεφάλαιο 11 Τα χαρακτηριστικά των ανταγωνιστικών αγορών! Τα κύρια χαρακτηριστικά των ανταγωνιστικών αγορών είναι: " Στην αγορά συµµετέχουν πολλοί αγοραστές και πωλητές
ΕΠΙΧΕΙΡΗΣΕΙΣ ΚΑΙ ΑΝΤΑΓΩΝΙΣΤΙΚΕΣ ΑΓΟΡΕΣ Κεφάλαιο 11 Τα χαρακτηριστικά των ανταγωνιστικών αγορών! Τα κύρια χαρακτηριστικά των ανταγωνιστικών αγορών είναι: " Στην αγορά συµµετέχουν πολλοί αγοραστές και πωλητές
Ο ΠΡΟΣΔΙΟΡΙΣΜΟΣ TΩN ΤΙΜΩΝ
 ΚΕΦΑΛΑΙΟ ΠΕΜ Ο ΠΡΟΣΔΙΟΡΙΣΜΟΣ TΩN ΤΙΜΩΝ 1. Έννοια και λειτουργία της αγοράς Σε μια πρωτόγονη οικονομία, όπως του Ροβινσώνα Κρούσου, όπου δεν υπάρχει καταμερισμός της εργασίας ο άνθρωπος παράγει μόνος του
ΚΕΦΑΛΑΙΟ ΠΕΜ Ο ΠΡΟΣΔΙΟΡΙΣΜΟΣ TΩN ΤΙΜΩΝ 1. Έννοια και λειτουργία της αγοράς Σε μια πρωτόγονη οικονομία, όπως του Ροβινσώνα Κρούσου, όπου δεν υπάρχει καταμερισμός της εργασίας ο άνθρωπος παράγει μόνος του
10. Η επιδίωξη της μέγιστης χρησιμότητας αποτελεί βασικό χαρακτηριστικό της συμπεριφοράς του καταναλωτή στη ζήτηση αγαθών.
 ΚΕΦΑΛΑΙΟ 2 : Η ΖΗΤΗΣΗ Να σημειώσετε το σωστό ή το λάθος στο τέλος των προτάσεων: 1. Όταν η ζήτηση ενός αγαθού είναι ελαστική, η συνολική δαπάνη των καταναλωτών για το αγαθό αυτό μειώνεται καθώς αυξάνεται
ΚΕΦΑΛΑΙΟ 2 : Η ΖΗΤΗΣΗ Να σημειώσετε το σωστό ή το λάθος στο τέλος των προτάσεων: 1. Όταν η ζήτηση ενός αγαθού είναι ελαστική, η συνολική δαπάνη των καταναλωτών για το αγαθό αυτό μειώνεται καθώς αυξάνεται
ΚΑΜΠΥΛΗ ENGEL ΚΑΙ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΖΗΤΗΣΗΣ ΚΑΤΑ MARSHALL ΚΑΙ HICKS. 1. Η καµπύλη Engel
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΘΗΓΗΤΗΣ ΚΩΣΤΑΣ ΒΕΛΕΝΤΖΑΣ ΚΑΜΠΥΛΗ ENGEL ΚΑΙ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΖΗΤΗΣΗΣ ΚΑΤΑ ARSALL ΚΑΙ ICKS. Η καµπύλη Egel Η καµπύλη Egel παράγεται από την
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΘΗΓΗΤΗΣ ΚΩΣΤΑΣ ΒΕΛΕΝΤΖΑΣ ΚΑΜΠΥΛΗ ENGEL ΚΑΙ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΖΗΤΗΣΗΣ ΚΑΤΑ ARSALL ΚΑΙ ICKS. Η καµπύλη Egel Η καµπύλη Egel παράγεται από την
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΝΑΛΥΣΗ ΤΗΣ ΚΑΤΑΝΑΛΩΣΗΣ ΚΑΙ ΤΗΣ ΠΑΡΑΓΩΓΗΣ
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΝΑΛΥΣΗ ΤΗΣ ΚΑΤΑΝΑΛΩΣΗΣ ΚΑΙ ΤΗΣ ΠΑΡΑΓΩΓΗΣ Εξέταση Φεβρουαρίου 2012 / ιάρκεια: 2 ώρες ιδάσκοντες: Μ. Αθανασίου, Γ.
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΝΑΛΥΣΗ ΤΗΣ ΚΑΤΑΝΑΛΩΣΗΣ ΚΑΙ ΤΗΣ ΠΑΡΑΓΩΓΗΣ Εξέταση Φεβρουαρίου 2012 / ιάρκεια: 2 ώρες ιδάσκοντες: Μ. Αθανασίου, Γ.
ΠΕΡΙΕΧΟΜΕΝΑ. ΜΕΡΟΣ Α Θεωρία Ζήτησης Ενός Αγαθού - Ανάλυση Συμπεριφοράς Καταναλωτή
 ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ Α Θεωρία Ζήτησης Ενός Αγαθού - Ανάλυση Συμπεριφοράς Καταναλωτή ΕΙΣΑΓΩΓΗ Έννοια και Στόχοι της Μικροοικονομικής Θεωρίας 1. Γενικά...27 2. Το Πρόβλημα της Επιλογής...29 ΚΕΦΑΛΑΙΟ 1 Θεωρία
ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ Α Θεωρία Ζήτησης Ενός Αγαθού - Ανάλυση Συμπεριφοράς Καταναλωτή ΕΙΣΑΓΩΓΗ Έννοια και Στόχοι της Μικροοικονομικής Θεωρίας 1. Γενικά...27 2. Το Πρόβλημα της Επιλογής...29 ΚΕΦΑΛΑΙΟ 1 Θεωρία
ΚΕΦΑΛΑΙΟ ΤΕΤΑΡΤΟ Η ΠΡΟΣΦΟΡΑ ΤΩΝ ΑΓΑΘΩΝ
 ΚΕΦΑΛΑΙΟ ΤΕΤΑΡΤΟ Η ΠΡΟΣΦΟΡΑ ΤΩΝ ΑΓΑΘΩΝ 1. Τι πρέπει να κατανοήσει ο μαθητής Το κεφάλαιο εξετάζει την προσφορά των αγαθών, η οποία βασίζεται στη θεωρία παραγωγής και στη συμπεριφορά της επιχείρησης. Στο
ΚΕΦΑΛΑΙΟ ΤΕΤΑΡΤΟ Η ΠΡΟΣΦΟΡΑ ΤΩΝ ΑΓΑΘΩΝ 1. Τι πρέπει να κατανοήσει ο μαθητής Το κεφάλαιο εξετάζει την προσφορά των αγαθών, η οποία βασίζεται στη θεωρία παραγωγής και στη συμπεριφορά της επιχείρησης. Στο
ΔΕΟ34. Ενδεικτική Απάντηση 1ης γραπτής εργασίας Επιμέλεια: Γιάννης Σαραντής
 ΔΕΟ34 Ενδεικτική Απάντηση 1ης γραπτής εργασίας 2016-17 Επιμέλεια: Γιάννης Σαραντής 16/11/2016 2 Ερώτηση 1 α1) Αρχικό σημείο ισορροπίας της αγοράς είναι το σημείο Δ και η τιμή ισορροπίας του κλάδου είναι
ΔΕΟ34 Ενδεικτική Απάντηση 1ης γραπτής εργασίας 2016-17 Επιμέλεια: Γιάννης Σαραντής 16/11/2016 2 Ερώτηση 1 α1) Αρχικό σημείο ισορροπίας της αγοράς είναι το σημείο Δ και η τιμή ισορροπίας του κλάδου είναι
Άσκηση 1. Μικροοικονοµική 5. ΖΗΤΗΣΗ ΚΑΙ ΠΡΟΣΦΟΡΑ. 5η Εισήγηση. Αξία ραδιοφώνων. Αριθµός ραδιοφώνων που χάνονται κάθε εβδοµάδα
 Αριθµός φυλάκων Αριθµός ραδιοφώνων που χάνονται κάθε Άσκηση 1 Αξία ραδιοφώνων που χάνονται κάθε Πρόσθετο όφελος από κάθε φρουρό 0 100 1000 1 70 700 300 2 50 500 200 3 40 400 100 4 32 320 80 5 25 250 70
Αριθµός φυλάκων Αριθµός ραδιοφώνων που χάνονται κάθε Άσκηση 1 Αξία ραδιοφώνων που χάνονται κάθε Πρόσθετο όφελος από κάθε φρουρό 0 100 1000 1 70 700 300 2 50 500 200 3 40 400 100 4 32 320 80 5 25 250 70
ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ ΚΑΤΑΝΑΛΩΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ
 Ένθετο Κεφάλαιο ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ ΚΑΤΑΝΑΛΩΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ Μικροοικονομική Ε. Σαρτζετάκης 1 Καταναλωτική συμπεριφορά Σκοπός αυτής της διάλεξης είναι να εξετάσουμε τον τρόπο με τον οποίο οι καταναλωτές
Ένθετο Κεφάλαιο ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ ΚΑΤΑΝΑΛΩΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ Μικροοικονομική Ε. Σαρτζετάκης 1 Καταναλωτική συμπεριφορά Σκοπός αυτής της διάλεξης είναι να εξετάσουμε τον τρόπο με τον οποίο οι καταναλωτές
ΕΡΓΑΣΙΕΣ 4 ου ΚΕΦΑΛΑΙΟΥ. 1 η Ομάδα: Ερωτήσεις πολλαπλής επιλογής
 ΕΡΓΑΣΙΕΣ 4 ου ΚΕΦΑΛΑΙΟΥ 1 η Ομάδα: Ερωτήσεις πολλαπλής επιλογής 1. Σύμφωνα με το νόμο της προσφοράς: α) Η προσφερόμενη ποσότητα ενός αγαθού αυξάνεται όταν μειώνεται η τιμή του στην αγορά β) Η προσφερόμενη
ΕΡΓΑΣΙΕΣ 4 ου ΚΕΦΑΛΑΙΟΥ 1 η Ομάδα: Ερωτήσεις πολλαπλής επιλογής 1. Σύμφωνα με το νόμο της προσφοράς: α) Η προσφερόμενη ποσότητα ενός αγαθού αυξάνεται όταν μειώνεται η τιμή του στην αγορά β) Η προσφερόμενη
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΕΠΙΛΟΓΗΣ 2008
 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΕΠΙΛΟΓΗΣ 2008 ΕΚΦΩΝΗΣΕΙΣ ΟΜΑ Α Α Για τις προτάσεις από Α.1 µέχρι και Α.5 να γράψετε στο τετράδιό σας τον αριθµό της καθεµιάς και δίπλα σε κάθε αριθµό τη λέξη Σωστό, αν η πρόταση
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΕΠΙΛΟΓΗΣ 2008 ΕΚΦΩΝΗΣΕΙΣ ΟΜΑ Α Α Για τις προτάσεις από Α.1 µέχρι και Α.5 να γράψετε στο τετράδιό σας τον αριθµό της καθεµιάς και δίπλα σε κάθε αριθµό τη λέξη Σωστό, αν η πρόταση
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Α.Ο.Θ. ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ Θέματα και Απαντήσεις
 Α.Ο.Θ. ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ Θέματα και Απαντήσεις Επιμέλεια: Ομάδα Οικονομολόγων http://www.othisi.gr 2 Παρασκευή, 14 Ιουνίου 2019 ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡ/ΚΗΣ ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΟΜΑΔΑ ΠΡΩΤΗ
Α.Ο.Θ. ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ Θέματα και Απαντήσεις Επιμέλεια: Ομάδα Οικονομολόγων http://www.othisi.gr 2 Παρασκευή, 14 Ιουνίου 2019 ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡ/ΚΗΣ ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΟΜΑΔΑ ΠΡΩΤΗ
Γενική Ανταγωνιστική Ισορροπία σε Οικονομία με Έναν Καταναλωτή και Έναν Παραγωγό
 Γενική Ανταγωνιστική Ισορροπία σε Οικονομία με Έναν Καταναλωτή και Έναν Παραγωγό - Ορισμός. Μια ανταγωνιστική οικονομία που διέπεται από το θεσμό της ατομικής ιδιοκτησίας είναι μια οικονομία όπου: (i)
Γενική Ανταγωνιστική Ισορροπία σε Οικονομία με Έναν Καταναλωτή και Έναν Παραγωγό - Ορισμός. Μια ανταγωνιστική οικονομία που διέπεται από το θεσμό της ατομικής ιδιοκτησίας είναι μια οικονομία όπου: (i)
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 14 ΙΟΥΝΙΟΥ 2019 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΑΠΑΝΤΗΣΕΙΣ
 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 14 ΙΟΥΝΙΟΥ 2019 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΑΠΑΝΤΗΣΕΙΣ ΟΜΑΔΑ ΠΡΩΤΗ ΘΕΜΑ Α Α.1 α. Λάθος β. Σωστό γ. Λάθος δ. Σωστό ε. Σωστό Α.2 β Α.3 γ ΟΜΑΔΑ
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 14 ΙΟΥΝΙΟΥ 2019 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΑΠΑΝΤΗΣΕΙΣ ΟΜΑΔΑ ΠΡΩΤΗ ΘΕΜΑ Α Α.1 α. Λάθος β. Σωστό γ. Λάθος δ. Σωστό ε. Σωστό Α.2 β Α.3 γ ΟΜΑΔΑ
Ημερομηνία: Τετάρτη 4 Απριλίου 2018 Διάρκεια Εξέτασης: 3 ώρες
 ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Ημερομηνία: Τετάρτη 4 Απριλίου 2018 Διάρκεια Εξέτασης: 3 ώρες ΟΜΑΔΑ Α Να γράψετε στο τετράδιό σας το γράμμα κάθε πρότασης και δίπλα σε κάθε γράμμα
ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Ημερομηνία: Τετάρτη 4 Απριλίου 2018 Διάρκεια Εξέτασης: 3 ώρες ΟΜΑΔΑ Α Να γράψετε στο τετράδιό σας το γράμμα κάθε πρότασης και δίπλα σε κάθε γράμμα
ΟΙΚΟΝΟΜΙΚΗ ΤΩΝ ΔΙΚΤΥΩΝ ΚΑΙ ΤΗΣ ΠΛΗΡΟΦΟΡΗΣΗΣ (ECΟ465) ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ ΜΕΡΟΣ Α
 ΟΙΚΟΝΟΜΙΚΗ ΤΩΝ ΔΙΚΤΥΩΝ ΚΑΙ ΤΗΣ ΠΛΗΡΟΦΟΡΗΣΗΣ (ECΟ465) ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ ΜΕΡΟΣ Α 1 o Ο κλάδος των τηλεπικοινωνιών (τηλέφωνο, fax, e-mail, υπηρεσίες μηνυμάτων, κ.τ.λ) αποτελεί το πιο απλό και φυσικό παράδειγμα
ΟΙΚΟΝΟΜΙΚΗ ΤΩΝ ΔΙΚΤΥΩΝ ΚΑΙ ΤΗΣ ΠΛΗΡΟΦΟΡΗΣΗΣ (ECΟ465) ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ ΜΕΡΟΣ Α 1 o Ο κλάδος των τηλεπικοινωνιών (τηλέφωνο, fax, e-mail, υπηρεσίες μηνυμάτων, κ.τ.λ) αποτελεί το πιο απλό και φυσικό παράδειγμα
 4 Προσφοράκαι Ζήτηση Προσφορά και Ζήτηση Ηπροσφοράκαιηζήτησηείναιοιδύολέξεις που χρησιµοποιούν πιο συχνά οι οικονοµολόγοι. Ηπροσφοράκαιηζήτησηείναιοιδυνάµεις που κάνουν τις αγορές των οικονοµιών να δουλεύουν.
4 Προσφοράκαι Ζήτηση Προσφορά και Ζήτηση Ηπροσφοράκαιηζήτησηείναιοιδύολέξεις που χρησιµοποιούν πιο συχνά οι οικονοµολόγοι. Ηπροσφοράκαιηζήτησηείναιοιδυνάµεις που κάνουν τις αγορές των οικονοµιών να δουλεύουν.
Ζήτηση, Προσφορά και Ισορροπία στην Ανταγωνιστική Αγορά
 Ζήτηση, Προσφορά και Ισορροπία στην Ανταγωνιστική Αγορά - Ορισμός: Η αγορά ενός αγαθού είναι η διαδικασία (θεσμικό πλαίσιο) μέσω της οποίας έρχονται σε επικοινωνία οι αγοραστές και οι πωλητές του συγκεκριμένου
Ζήτηση, Προσφορά και Ισορροπία στην Ανταγωνιστική Αγορά - Ορισμός: Η αγορά ενός αγαθού είναι η διαδικασία (θεσμικό πλαίσιο) μέσω της οποίας έρχονται σε επικοινωνία οι αγοραστές και οι πωλητές του συγκεκριμένου
ε = 5 / 4. Αν η τιµή του αγαθού αυξηθεί κατά 10% ποια ποσοστιαία µεταβολή της
 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑ ΕΠΙΛΟΓΗΣ ΟΛΩΝ ΤΩΝ ΚΑΤΕΥΘΥΝΣΕΩΝ ΙΑΓΩΝΙΣΜΑ 3 (για άριστα διαβασµένους) ΟΜΑ Α Α Να απαντήσετε στις επόµενες ερωτήσεις πολλαπλής επιλογής Α1. Σε δύο σηµεία της ίδιας ζήτησης
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑ ΕΠΙΛΟΓΗΣ ΟΛΩΝ ΤΩΝ ΚΑΤΕΥΘΥΝΣΕΩΝ ΙΑΓΩΝΙΣΜΑ 3 (για άριστα διαβασµένους) ΟΜΑ Α Α Να απαντήσετε στις επόµενες ερωτήσεις πολλαπλής επιλογής Α1. Σε δύο σηµεία της ίδιας ζήτησης
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΕΠΙΛΟΓΗΣ ΓΙΑ ΟΛΕΣ ΤΙΣ ΚΑΤΕΥΘΥΝΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 2002 ΟΜΑ Α Α
 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΕΠΙΛΟΓΗΣ ΓΙΑ ΟΛΕΣ ΤΙΣ ΚΑΤΕΥΘΥΝΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΟΜΑ Α Α Στις προτάσεις από Α1 µέχρι και Α5, να γράψετε στο τετράδιό σας τον αριθµό της καθεµιάς και δίπλα σε κάθε αριθµό
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΕΠΙΛΟΓΗΣ ΓΙΑ ΟΛΕΣ ΤΙΣ ΚΑΤΕΥΘΥΝΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΟΜΑ Α Α Στις προτάσεις από Α1 µέχρι και Α5, να γράψετε στο τετράδιό σας τον αριθµό της καθεµιάς και δίπλα σε κάθε αριθµό
Για τις παρακάτω προτάσεις Α2 και Α3 να γράψετε στο τετράδιό σας τον αριθµό της πρότασης και, δίπλα, το γράµµα που αντιστοιχεί στη σωστή απάντηση.
 ΑΡΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΠΙΛΟΓΗΣ (ΝΕΟ ΚΑΙ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ) ΘΕΜΑ Α ΟΜΑ Α ΠΡΩΤΗ Α1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας, δίπλα στο γράµµα που αντιστοιχεί
ΑΡΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΠΙΛΟΓΗΣ (ΝΕΟ ΚΑΙ ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ) ΘΕΜΑ Α ΟΜΑ Α ΠΡΩΤΗ Α1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας, δίπλα στο γράµµα που αντιστοιχεί
10. Η επιδίωξη της μέγιστης χρησιμότητας αποτελεί βασικό χαρακτηριστικό της συμπεριφοράς του καταναλωτή στη ζήτηση αγαθών.
 ΚΕΦΑΛΑΙΟ 2 : Η ΖΗΤΗΣΗ Να σημειώσετε το σωστό ή το λάθος στο τέλος των προτάσεων: 1. Όταν η ζήτηση ενός αγαθού είναι ελαστική, η συνολική δαπάνη των καταναλωτών για το αγαθό αυτό μειώνεται καθώς αυξάνεται
ΚΕΦΑΛΑΙΟ 2 : Η ΖΗΤΗΣΗ Να σημειώσετε το σωστό ή το λάθος στο τέλος των προτάσεων: 1. Όταν η ζήτηση ενός αγαθού είναι ελαστική, η συνολική δαπάνη των καταναλωτών για το αγαθό αυτό μειώνεται καθώς αυξάνεται
Δεύτερο πακέτο ασκήσεων και λύσεων
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 04-05 Τμήμα Οικονομικών Επιστημών Μάθημα: Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής Δεύτερο πακέτο ασκήσεων και λύσεων Αντιστοιχούν τέσσερις μονάδες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 04-05 Τμήμα Οικονομικών Επιστημών Μάθημα: Μικροοικονομική Ανάλυση της Κατανάλωσης και της Παραγωγής Δεύτερο πακέτο ασκήσεων και λύσεων Αντιστοιχούν τέσσερις μονάδες
2o Μάθηµα. Χαράλαµπος Χρήστου 1/7 Σηµειώσεις: ηµόσια Οικονοµική Ι/2 ο Μάθηµα
 2o Μάθηµα Αναφέραµε στο πρώτο µάθηµα τρόπους µε τους οποίους το κράτος επηρεάζει την οικονοµική συµπεριφορά µας. (νοµικό πλαίσιο, το κράτος αγοράζει και παράγει αγαθά και υπηρεσίες, ρυθµίζει τις πολιτικές
2o Μάθηµα Αναφέραµε στο πρώτο µάθηµα τρόπους µε τους οποίους το κράτος επηρεάζει την οικονοµική συµπεριφορά µας. (νοµικό πλαίσιο, το κράτος αγοράζει και παράγει αγαθά και υπηρεσίες, ρυθµίζει τις πολιτικές
3.1 Ανεξάρτητες αποφάσεις - Κατανομή χρόνου μεταξύ εργασίας και σχόλης
 3. ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΝΑΛΥΣΗ ΤΗΣ ΑΓΟΡΑΣ ΕΡΓΑΣΙΑΣ (ΝΕΟΚΛΑΣΙΚΟ ΥΠΟΔΕΙΓΜΑ). ΠΡΟΣΦΟΡΑ ΕΡΓΑΣΙΑΣ Ως προσφορά εργασίας ορίζεται το σύνολο των ωρών εργασίας που προσφέρονται προς εκμίσθωση μία δεδομένη χρονική στιγμή.
3. ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΝΑΛΥΣΗ ΤΗΣ ΑΓΟΡΑΣ ΕΡΓΑΣΙΑΣ (ΝΕΟΚΛΑΣΙΚΟ ΥΠΟΔΕΙΓΜΑ). ΠΡΟΣΦΟΡΑ ΕΡΓΑΣΙΑΣ Ως προσφορά εργασίας ορίζεται το σύνολο των ωρών εργασίας που προσφέρονται προς εκμίσθωση μία δεδομένη χρονική στιγμή.
Ελαστικότητες Ζήτησης
 Ελαστικότητες Ζήτησης - Η ευαισθησία της ζητούμενης ποσότητας x σε μεταβολές της τιμής μπορεί να μετρηθεί άμεσα από το λόγο Δx / Δ (ήαπότην παράγωγο x / ). - Αυτό το μέτρο ευαισθησίας έχει το μειονέκτημα
Ελαστικότητες Ζήτησης - Η ευαισθησία της ζητούμενης ποσότητας x σε μεταβολές της τιμής μπορεί να μετρηθεί άμεσα από το λόγο Δx / Δ (ήαπότην παράγωγο x / ). - Αυτό το μέτρο ευαισθησίας έχει το μειονέκτημα
Ημερομηνία: Τετάρτη 12 Απριλίου 2017 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Ημερομηνία: Τετάρτη 12 Απριλίου 2017 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις παρακάτω προτάσεις να γράψετε στο τετράδιό σας τον αριθμό
ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Ημερομηνία: Τετάρτη 12 Απριλίου 2017 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις παρακάτω προτάσεις να γράψετε στο τετράδιό σας τον αριθμό
ΣΥΝΘΕΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ
 ΣΥΝΘΕΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Α. Με ολοκληρωμένη λύση ΘΕΜΑ 1 ο Επιχείρηση χρησιμοποιεί την εργασία ως μοναδικό μεταβλητό παραγωγικό συντελεστή. Τα στοιχεία κόστους της επιχείρησης δίνονται στον επόμενο πίνακα:
ΣΥΝΘΕΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Α. Με ολοκληρωμένη λύση ΘΕΜΑ 1 ο Επιχείρηση χρησιμοποιεί την εργασία ως μοναδικό μεταβλητό παραγωγικό συντελεστή. Τα στοιχεία κόστους της επιχείρησης δίνονται στον επόμενο πίνακα:
Διάλεξη 7. Εξίσωση Slutsky. Οι επιδράσεις µιας µεταβολής της
 Οι επιδράσεις µιας µεταβολής της τιµής Διάλεξη 7 Εξίσωση Slutsk Τι θα συµβεί όταν µειωθεί η τιµή ενός αγαθού; Αποτέλεσµα υποκατάστασης : το αγαθό γίνεται σχετικά πιο φτηνό και γι αυτό ο καταναλωτής υποκαθιστά
Οι επιδράσεις µιας µεταβολής της τιµής Διάλεξη 7 Εξίσωση Slutsk Τι θα συµβεί όταν µειωθεί η τιµή ενός αγαθού; Αποτέλεσµα υποκατάστασης : το αγαθό γίνεται σχετικά πιο φτηνό και γι αυτό ο καταναλωτής υποκαθιστά
Μικροοικονοµική Θεωρία. Γενική ισορροπία και παραγωγή. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς. 24 Σεπτεµβρίου 2014
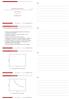 Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 4 Σεπτεµβρίου 014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 4 Σεπτεµβρίου 014 1 / 60. Η παραγωγή στη γενική ισορροπία έχει πάλι µεγάλη
Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 4 Σεπτεµβρίου 014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 4 Σεπτεµβρίου 014 1 / 60. Η παραγωγή στη γενική ισορροπία έχει πάλι µεγάλη
Ερωτήσεις πολλαπλών επιλογών
 Ερωτήσεις πολλαπλών επιλογών 1. Έστω ότι μία οικονομία, που βρίσκεται πάνω στην καμπύλη των παραγωγικών της δυνατοτήτων, παράγει σε μία συγκεκριμένη χρονική στιγμή 10 τόνους υφάσματος και 00 τόνους τροφίμων.
Ερωτήσεις πολλαπλών επιλογών 1. Έστω ότι μία οικονομία, που βρίσκεται πάνω στην καμπύλη των παραγωγικών της δυνατοτήτων, παράγει σε μία συγκεκριμένη χρονική στιγμή 10 τόνους υφάσματος και 00 τόνους τροφίμων.
Πολιτική Οικονομία Ενότητα
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 03: Ζήτηση και προσφορά αγαθών Πολυξένη Ράγκου Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 03: Ζήτηση και προσφορά αγαθών Πολυξένη Ράγκου Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Ερωτήσεις πολλαπλών επιλογών
 Ερωτήσεις πολλαπλών επιλογών Β1) Υποθέστε ότι στη θέση ισορροπίας της αγοράς ενός αγαθού η ζήτησή του ως προς την τιμή του είναι ελαστική. Μία μείωση της προσφοράς του αγαθού, με όλους τους άλλους παράγοντες
Ερωτήσεις πολλαπλών επιλογών Β1) Υποθέστε ότι στη θέση ισορροπίας της αγοράς ενός αγαθού η ζήτησή του ως προς την τιμή του είναι ελαστική. Μία μείωση της προσφοράς του αγαθού, με όλους τους άλλους παράγοντες
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2014
 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑ: ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ / ΕΠΙΛΟΓΗΣ Α1. α. Λάθος β. Σωστό γ. Σωστό δ. Λάθος ε. Σωστό Α2. δ Α3. β Ηµεροµηνία: Κυριακή 4 Μαΐου 2014 ιάρκεια Εξέτασης: 3 ώρες ΑΠΑΝΤΗΣΕΙΣ ΟΜΑ
ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑ: ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ / ΕΠΙΛΟΓΗΣ Α1. α. Λάθος β. Σωστό γ. Σωστό δ. Λάθος ε. Σωστό Α2. δ Α3. β Ηµεροµηνία: Κυριακή 4 Μαΐου 2014 ιάρκεια Εξέτασης: 3 ώρες ΑΠΑΝΤΗΣΕΙΣ ΟΜΑ
Να χαρακτηρίσετε ως σωστές ή λανθασµένες τις επόµενες προτάσεις: Α3. Τα ελεύθερα αγαθά αποτελούν αντικείµενο µελέτης της Οικονοµικής Επιστήµης.
 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑ ΕΠΙΛΟΓΗΣ ΟΛΩΝ ΤΩΝ ΚΑΤΕΥΘΥΝΣΕΩΝ ΙΑΓΩΝΙΣΜΑ 8 (για καλά διαβασµένους) ΟΜΑ Α Α Να απαντήσετε στις επόµενες ερωτήσεις πολλαπλής επιλογής Α1. Όταν η ζήτηση αποδίδεται γραφικά
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑ ΕΠΙΛΟΓΗΣ ΟΛΩΝ ΤΩΝ ΚΑΤΕΥΘΥΝΣΕΩΝ ΙΑΓΩΝΙΣΜΑ 8 (για καλά διαβασµένους) ΟΜΑ Α Α Να απαντήσετε στις επόµενες ερωτήσεις πολλαπλής επιλογής Α1. Όταν η ζήτηση αποδίδεται γραφικά
ΑΠΑΝΤΗΣΕΙΣ ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ)/ ΟΜΑΔΑ ΠΡΩΤΗ
 ΑΠΑΝΤΗΣΕΙΣ ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ)/29.12.2015 ΘΕΜΑ Α ΟΜΑΔΑ ΠΡΩΤΗ Α1. α) Λάθος β) Σωστό γ) Λάθος δ)σωστό ε) Λάθος Α2. δ Α3. δ ΟΜΑΔΑ ΔΕΥΤΕΡΗ ΘΕΜΑ Β Β1.α) Το εισόδημα των καταναλωτών.
ΑΠΑΝΤΗΣΕΙΣ ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ)/29.12.2015 ΘΕΜΑ Α ΟΜΑΔΑ ΠΡΩΤΗ Α1. α) Λάθος β) Σωστό γ) Λάθος δ)σωστό ε) Λάθος Α2. δ Α3. δ ΟΜΑΔΑ ΔΕΥΤΕΡΗ ΘΕΜΑ Β Β1.α) Το εισόδημα των καταναλωτών.
Προσφορά Εργασίας Προτιμήσεις και Συνάρτηση Χρησιμότητας ( Χ,Α συνάρτηση χρησιμότητας U(X,A)
 Προσφορά Εργασίας - Έστω ότι υπάρχουν δύο αγαθά Α και Χ στην οικονομία. Το αγαθό Α παριστάνει τα διάφορα καταναλωτικά αγαθά. Το αγαθό Χ παριστάνει τον ελεύθερο χρόνο. Προτιμήσεις και Συνάρτηση Χρησιμότητας
Προσφορά Εργασίας - Έστω ότι υπάρχουν δύο αγαθά Α και Χ στην οικονομία. Το αγαθό Α παριστάνει τα διάφορα καταναλωτικά αγαθά. Το αγαθό Χ παριστάνει τον ελεύθερο χρόνο. Προτιμήσεις και Συνάρτηση Χρησιμότητας
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2017 Β ΦΑΣΗ
 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΣΠΟΥ ΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Ηµεροµηνία: Μ. Τετάρτη 12 Απριλίου 2017 ιάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΟΜΑ Α ΠΡΩΤΗ Α1.
ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΣΠΟΥ ΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ Ηµεροµηνία: Μ. Τετάρτη 12 Απριλίου 2017 ιάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΟΜΑ Α ΠΡΩΤΗ Α1.
