1. Ένα σώμα m=1kg εκτελεί απλή αρμονική ταλάντωση και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο, φαίνεται στο σχήμα.
|
|
|
- Αοιδή Αποστολίδης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Γενικές ασκήσεις Θέματα εξετάσεων από το 1ο κεφάλαιο ΚΕΦΑΛΑΙΟ 1 1 Ένα σώμα m=1kg εκτελεί απλή αρμονική ταλάντωση και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο, φαίνεται στο σχήμα α Να βρείτε τη σταθερά D και την ολική ενέργεια του ταλαντωτή β Να γράψετε τις εξισώσεις x=f(t) και υ=f(t) γ Ποιες χρονικές στιγμές το σώμα έχει στιγμιαία υ = 0 ; δ Ποια χρονικά διαστήματα είναι τα διανύσματα υ και F ομόρροπα; (π 2 =10) 2 Σώμα μάζας m =2 kg ισορροπεί στερεωμένο στο κάτω άκρο ιδανικού κατακόρυφου ελατηρίου σταθεράς k=200 N/m, το άλλο άκρο του οποίου είναι ακλόνητο στερεωμένο Το σώμα εκτρέπεται κατακόρυφα από τη ΘΙ του ώστε το ελατήριο να είναι στο φυσικό του μήκος Δίνουμε στο σώμα αρχική ταχύτητα υ0 3 m/s, προς τα κάτω θεωρώντας τη χρονική στιγμή αυτή t=0 και y>0 α Να γράψετε την εξίσωση της επιτάχυνσης α=f(t) β Να υπολογήσετε το μέτρο της μέγιστης δύναμης που δέχεται το σώμα από το ελατήριο γ Ποια χρονική στιγμή το σώμα αποκτά τη μέγιστη ταχύτητά του για πρώτη φορά μετά τη στιγμή t=0; δ Να βρείτε μέχρι τότε το έργο της συνισταμένης δύναμης που ενεργεί στον ταλαντωτή Δίνεται g=10 m/s 2 3 Ένα σώμα μάζας m=10 kg συνδέεται στο άκρο οριζόντιου ελατηρίου σταθεράς k Το σύστημα κάνει αατ πλάτους 0,2 m και στο σχήμα φαίνεται το διάγραμμα φάσης - χρόνου α Να υπολογίσετε τη σταθερά k του ελατηρίου β Να γράψετε τις εξισώσεις x=f(t) και υ=f(t) γ Να βρείτε τον ελάχιστο χρόνο για να γίνει μέγιστη η ταχύτητα του σώματος δ Το έργο της δύναμης επαναφοράς στο χρονικό διάστημα του ερωτήματος γ 4 Το σώμα μάζας m=1 kg του σχήματος αρχικά ηρεμεί στερεωμένο στο άκρο του ελατηρίου σταθεράς k=100 Ν/m Ασκούμε κατακόρυφη δύναμη σταθερού μέτρου F=10 Ν όπως φαίνεται στο σχήμα α Να δείξετε ότι το σύστημα κάνει αρμονική ταλάντωση και να βρείτε το πλάτος της β Όταν το σώμα αποκτήσει μέγιστη ταχύτητα καταργείται η δύναμη F Να υπολογίσετε: i Την ταχύτητα του σώματος τη στιγμή που καταργείται η δύναμη 147
2 ΚΕΦΑΛΑΙΟ 1 Γενικές ασκήσεις Θέματα εξετάσεων από το 1ο κεφάλαιο ii Το νέο πλάτος ταλάντωσης 5 Ένα σώμα m=1 kg κάνει ευθύγραμμη κίνηση και η εξίσωση κίνησής του είναι: x=0,1+0,05 ημ(10t) SI α Να δείξετε ότι το σώμα κάνει αατ και να βρείτε το πλάτος ταλάντωσης β Να υπολογίσετε την μέγιστη ταχύτητα του σώματος γ Να βρείτε το μέτρο της δύναμης επαναφοράς F επαν τη στιγμή 3π s 20 δ Να βρείτε τον ρυθμό μεταβολής της κινητικής ενέργειας τη στιγμή 2π s 5 6 Tο σώμα του σχήματος ισορροπεί με τη βοήθεια της δύναμης F μέτρου 20 N Tη χρονική στιγμή t=0 η δύναμη F καταργείται Δίνονται: k=200 N/m, m=2 kg, g=10 m/s 2 α Να γράψετε την χρονική εξίσωση της δυναμικής ενέργειας της ταλάντωσης Θεωρείστε ότι για t=0 είναι x>0 β Ποιο είναι το έργο της δύναμης επαναφοράς από τη στιγμή t=0 μέχρι τη στιγμή που το σώμα αποκτά μέγιστη ταχύτητα; γ Ποια είναι η σχέση της δύναμης του ελατηρίου σε συνάρτηση με τον χρόνο F ελ =f(t); δ Σε ποιες θέσεις το σώμα αποκτά ταχύτητα μέτρου υ max /2; ε Ποιος είναι ο μέγιστος ρυθμός μεταβολής της ορμής του σώματος; 7 Σύστημα ελατήριο k=200 N/m και σώμα μάζας m=2 kg κάνει αατ και η μέγιστη κινητική του ενέργεια είναι: K max = 4J α Να υπολογιστούν το πλάτος και η περίοδος της ταλάντωσης β Φέρνουμε το σύστημα σ ένα μέσο που ασκεί δύναμη τριβής της μορφής F 4 υ (SI) Να βρείτε το πλάτος της ταλάντωσης μετά από χρόνο π 5Τ n2 και την ενέργεια που έχει χάσει το σύστημα μέχρι τότε b Δίνονται ότι Λ και η περίοδος της φθίνουσας ταλάντωσης είναι περίπου ίση με την 2m ιδιοπερίοδο 8 Ένα σώμα μάζας m=1 kg συνδέεται στα άκρα συστήματος ελατηρίων ίδιου φυσικού μήκους όπως στο σχήμα, τα οποία έχουν σταθερές k 1 =100 N/m και k 2 =300 N/m Το σώμα εκτρέπεται από τη θέση ισορροπίας του κατά 0,05 m και αφήνεται ελεύθερο α Να δειχθεί ότι εκτελεί αρμονική κίνηση και να βρεθεί η περίοδος της κίνησης β Τη στιγμή που το σώμα έχει μέγιστη ταχύτητα, κόβεται το 2ο ελατήριο Να βρείτε το νέο πλάτος ταλάντωσης του σώματος γ Όταν το σώμα είναι σε ακραία θέση ασκείται δύναμη τριβής της μορφής F = b υ (SI) Αν σε χρόνο t=3τ το πλάτος ελαττώνεται κατά 50%, να βρείτε την σταθερά Λ και το έργο της δύναμης απόσβεσης μέχρι τότε Η περίοδος της φθίνουσας ταλάντωσης είναι περίπου ίση με την ιδιοπερίοδο 9 Σώμα μάζας m=1 kg ισορροπεί στο κάτω άκρο κατακόρυφου ελατηρίου σταθεράς k=100 N/m Εκτρέπουμε το σώμα από τη ΘΙ του μέχρι το φυσικό μήκος του ελατηρίου και το αφήνουμε ελεύθερο τη στιγμή t=0 θεωρώντας x>0 α Να κάνετε το διάγραμμα κινητικής ενέργειας με το χρόνο και να βρείτε την κινητική ενέργεια του ταλαντωτή τη στιγμή t 1 =0,4π s 148
3 Γενικές ασκήσεις Θέματα εξετάσεων από το 1ο κεφάλαιο ΚΕΦΑΛΑΙΟ 1 β Τη στιγμή t 1 =0,4π s αρχίζει να επενεργεί δύναμη απόσβεσης F= 0,2 υ (SI) Nα βρείτε το πλατος του ταλαντωτή μετά από 20 n2 s Δίνονται: Λ=b/2m, g=10m/s 2 10 Το ένα άκρο κατακόρυφου ιδανικού ελατηρίου είναι στερεωμένο σε οριζόντιο δάπεδο Στο άλλο άκρο του είναι σταθερά συνδεμένο σώμα Α μάζας Μ=3 kg, πάνω στον οποίο είναι τοποθετημένο σώμα Β μάζας m=1 kg To σύστημα ισορροπεί και το ελατήριο είναι συσπειρωμένο από το φυσικό του μήκος κατά 0,4 m Πιέζουμε το σύστημα προς τα κάτω κατά d=0,8 m και το αφήνουμε ελεύθερο τη στιγμή t=0 α Nα υπολογίσετε την γωνιακή συχνότητα ω του συστήματος και τη σταθερά D κάθε μάζας χωριστά β Nα αποδείξετε ότι το σώμα Β θα χάσει την επαφή του με το σώμα Α γ Ποιο θα είναι τότε το μέτρο της ταχύτητας και το μέτρο της επιτάχυνσης του κάθε σώματος; Δίνεται: g=10m/s 2 11 Δίνεται η διάταξη του σχήματος Τη χρονική στιγμή t=0 κόβουμε το νήμα και όταν το σώμα μάζας m 2 =3 kg φτάνει στο έδαφος, το σώμα μάζας m 1 =1 kg έχει εκτελέσει δύο πλήρεις ταλαντώσεις α Να γραφεί η εξίσωση της απομάκρυνσης σε συνάρτηση με το χρόνο, της απλής αρμονικής ταλάντωσης που κάνει το σώμα μάζας m 1 β Να υπολογίσετε το ύψος h Δίνονται η σταθερά του ελατηρίου k=100n/m, η επιτάχυνση βαρύτητας g=10 m/s 2, να θεωρήσετε θετική τη φορά προς τα κάτω και π 2 =20 12 Οριζόντιος δίσκος κάνει απλή αρμονική ταλάντωση σε κατακόρυφη διεύθυνση, με πλάτος A=0,25 m και περίοδος T=2 s Όταν ο δίσκος βρίσκεται στην κατώτατη θέση της τροχιάς, τοποθετούμε πάνω του μικρό σώμα μάζας 2kg α Αν θεωρήσουμε ότι το σύστημα διατηρεί σταθερό πλάτος και περίοδο, να βρεθεί η σχέση της δύναμης που δέχεται το σώμα από το δίσκο σε σχέση με την απομάκρυνση y και να γίνει η αντίστοιχη γραφική παράσταση β Αν η περίοδος παραμείνει σταθερή, για ποια μέγιστη τιμή του πλάτους, το σώμα οριακά τείνει να εγκαταλείψει το δίσκο; γ Αν μεταβάλλουμε τη συχνότητα της ταλάντωσης, για ποια μέγιστη γωνιακή συχνότητα μόλις που χάνεται η επαφή σώματος - δίσκου, αν το πλάτος είναι Α=0,25m; Δίνονται: π 2 = 10 και g = 10 m/s 2 13 Σώμα μάζας m=4 kg εκτελεί εξαναγκασμένη ταλάντωση πλάτους Α=0,4 m, στερεωμένο στο άκρο ελατηρίου σταθεράς k=400 N/m, υπό την επίδραση εξωτερικής περιοδικής 3 δύναμης με συχνότητα f Δ = Hz Το σώμα τη χρονική στιγμή π t=0 βρισκόταν στην θέση ισορροπίας του, ξεκινώντας κατά τη θετική φορά α Να γραφεί η εξίσωση της ταλάντωσης που πραγματοποιεί το σύστημα και να υπολο-γιστεί η ολική ενέργεια 4 β Αυξάνουμε τη συχνότητα του διεγέρτη σε f Δ = Hz Τι θα π συμβεί με το πλάτος της ταλάντωσης και γιατί; γ Πόση θα έπρεπε να ήταν η μάζα m 1 του σώματος στο αρχικό πείραμα, για να παρουσίαζε το σύστημα μέγιστη ικανότητα απορρόφησης ενέργειας από το διεγέρτη; Θεωρείστε ότι η σταθερά απόσβεσης b του συστήματος είναι πολύ μικρή 149
4 ΚΕΦΑΛΑΙΟ 1 Γενικές ασκήσεις Θέματα εξετάσεων από το 1ο κεφάλαιο 14 Σώμα m=1 kg κάνει φθίνουσα μηχανική ταλάντωση και η απομάκρυνση με - n8 t το χρόνο είναι: x = 0,4 e συν ωt SI Αν σε χρόνο t=3τ το πλάτος ελαττώνεται κατά 50%, να βρείτε: α την σταθερά Λ και την περίοδο Τ της φθίνουσας ταλάντωσης, β τον χρόνο υποδιπλασιασμού του πλάτους, γ τον χρόνο υποδιπλασιασμού της ενέργειας δ το έργο της δύναμης απόσβεσης μέχρι τη στιγμή 3Τ (π 2 =10) 15 Σώμα μάζας m=2 kg κάνει αατ και η κινητική ενέργειά του μεταβάλλεται σε συνάρτηση με την απομάκρυνση y, από τη θέση ισορροπίας του, σύμφωνα 2 με τη σχέση: K = y SI α Να υπολογιστούν το πλάτος και η γωνιακή συχνότητα ω της ταλάντωσης β Να βρείτε τις θέσεις που είναι U=3K γ Στις θέσεις του ερωτήματος β να βρείτε το μέτρο του ρυθμού μεταβολής της δυναμικής ενέργειας της ταλάντωσης 8 kg δ Φέρουμε το σύστημα σ ένα μέσο που έχει b π s τριβής της μορφής F και ασκεί δύναμη bυ Αν δίνεται ότι σε μία φθίνουσα ταλάντωση είναι Λ=b/2m, να βρείτε το πλάτος της ταλάντωσης μετά από 5T n2 και την ενέργεια που έχει χαθεί μέχρι τότε Θεωρείστε ότι το αρχικό πλάτος Α 0 είναι η τιμή που βρήκατε στο ερώτημα (α) και ότι η περίοδος της φθίνουσας ταλάντωσης είναι περίπου ίση με αυτήν της απλής αρμονικής ταλάντωσης 16 Ένα υλικό σημείο εκτελεί αατ Η απομάκρυνσή του από τη θέση ισορροπίας του δίνεται από το διάγραμμα του σχήματος k φ Σ1 Να υπολογιστούν: α τα μεγέθη Α, ω, φ 0 της κίνησης β Ο χρόνος στον οποίο η απομάκρυνση από τη θέση ισορροπίας είναι x 0,2m στα πρώτα 22s γ Η χρονική στιγμή που το σώμα περνάει για πρώτη φορά από τη θέση ισορροπίας του 17 Σώμα Σ 1 μάζας m 1 = 1kg ισορροπεί πάνω σε λείο κεκλιμένο επίπεδο που σχηματίζει με τον ορίζοντα γωνία φ = 30 ο Το σώμα Σ 1 είναι δεμένο στην άκρη ιδανικού ελατηρίου σταθεράς k=100ν/m το άλλο άκρο του οποίου στερεώνεται στη βάση του κεκλιμένου επιπέδου, όπως φαίνεται στο σχήμα Εκτρέπουμε το σώμα Σ 1 κατά d 1 =0,1m από τη θέση ισορροπίας του κατά μήκος του κεκλιμένου επιπέδου και το αφήνουμε ελεύθερο 1 Να αποδείξετε ότι το σώμα Σ 1 εκτελεί απλή αρμονική ταλάντωση 2 Να υπολογίσετε τη μέγιστη τιμή του μέτρου του ρυθμού μεταβολής της ορμής του σώματος Σ 1 150
5 Γενικές ασκήσεις Θέματα εξετάσεων από το 1ο κεφάλαιο ΚΕΦΑΛΑΙΟ 1 Μετακινούμε το σώμα Σ 1 προς τα κάτω κατά μήκος του κεκλιμένου επιπέδου μέχρι το ελατήριο να συμπιεστεί από το φυσικό του μήκος κατά ΔL=0,3m Τοποθετούμε ένα δεύτερο σώμα Σ μάζας m 2 =1kg στο κεκλιμένο επίπεδο, ώστε να είναι σε επαφή με το σώμα Σ 1, και ύστερα αφήνουμε τα σώματα ελεύθερα 3 Να υπολογίσετε τη σταθερά επαναφοράς του σώματος Σ 2 κατά τη διάρκεια της ταλάντωσής του 4 Να υπολογίσετε σε πόση απόσταση από τη θέση που αφήσαμε ελεύθερα τα σώματα, χάνεται η επαφή μεταξύ τους k φ Σ1 Σ2 Δίνονται: ημ30 o = 1/2, g = 10m/s 2 18 Ένα σώμα, μάζας m=0,5 kg, εκτελεί απλή αρμονική ταλάντωση με συχνότητα f=(5/π) Ηz, ενώ διανύει σε κάθε περίοδο της ταλάντωσής του διάστημα d=2 m Το σώμα δέχεται κατά τη διάρκεια της ταλάντωσής του, και στη διεύθυνση της κίνησής του, δύο δυνάμεις F και 1 F, εκ των οποίων η 2 F είναι σταθερή 2 με μέτρο F 2 =10 Ν και φορά αρνητική Τη χρονική στιγμή t=0 το σημείο διέρχεται επιταχυνόμενο από τη θέση x 1 = 3 / 4 m α Να υπολογίσετε το πλάτος και τη σταθερά επαναφοράς D της ταλάντωσης β Να υπολογίσετε την αρχική φάση φ 0 της ταλάντωσης γ Να υπολογίσετε το ποσοστό % της κινητικής ενέργειας του σώματος ως προς την ολική ενέργεια ταλάντωσης, τη χρονική στιγμή t=0 δ Να γράψετε την εξίσωση της δύναμης F 1 σε συνάρτηση με το χρόνο 19 Ένα κατακόρυφο ελατήριο σταθεράς k=100 N/m έχει το άνω άκρο του στερεωμένο σε οροφή Στο κάτω άκρο του ελατηρίου έχει προσδεθεί σώμα Σ 1 μάζας m 1 =3 kg που ισορροπεί Τη χρονική στιγμή t 0 =0, ένα βλήμα Σ 2 μάζας m 2 =1 kg, που κινείται στον άξονα του ελατηρίου με ταχύτητα μέτρου υ και φορά προς τα πάνω, προσκρούει στο σώμα Σ 1 και σφηνώνεται σ αυτό Το συσσωμάτωμα ξεκινά να εκτελεί απλή αρμονική ταλάντωση με αρχική ταχύτητα μέτρου υ συσ = 3 /2 m/s Θεωρώντας θετική την κατακόρυφη προς τα κάτω φορά, να βρείτε: α την επιμήκυνση d 1 του ελατηρίου ως προς το φυσικό του μήκος, στη θέση ισορροπίας ΘΙ του σώματος Σ 1, β το μέτρο της ταχύτητας του βλήματος υ, γ το πλάτος Α της ταλάντωσης του συσσωματώματος, δ την εξίσωση υ=f(t) της ταχύτητας ταλάντωσης του συσσωματώματος Δίνεται η επιτάχυνση της βαρύτητας g=10 m/s 2 20 Στα δύο άκρα λείου επιπέδου στερεώνουμε τα άκρα δύο ιδανικών ελατηρίων με σταθερές k 1 =60 Ν/m και k 2 =140 Ν/m αντίστοιχα Στα ελεύθερα άκρα των ελατηρίων, δένουμε ένα σώμα Σ μάζας m=2 kg ώστε τα ελατήρια να έχουν το φυσικό τους μήκος (όπως φαίνεται στο σχήμα) Εκτρέπουμε το σώμα Σ κατά Α=0,2 m προς τα δεξιά και τη χρονική στιγμή t 0 =0 αφήνουμε το σώμα ελεύθερο α Να αποδείξετε ότι το σώμα Σ εκτελεί απλή αρμονική ταλάντωση 151
6 ΚΕΦΑΛΑΙΟ 1 Γενικές ασκήσεις Θέματα εξετάσεων από το 1ο κεφάλαιο β Να γράψετε τη σχέση που δίνει την απομάκρυνση του σώματος Σ από τη θέση ισορροπίας σε συνάρτηση με το χρόνο Να θεωρήσετε θετική την φορά προς τα δεξιά γ Να εκφράσετε το λόγο της δυναμικής ενέργειας της ταλάντωσης προς τη μέγιστη κινητική ενέργεια σε συνάρτηση με την απομάκρυνση x δ Τη στιγμή που το ελατήριο βρίσκεται στη θέση x=+α/2 αφαιρείται ακαριαία το ελατήριο k 2 Να υπολογίσετε το πλάτος της νέας ταλάντωσης 21 Το αριστερό άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k = 400 Ν/m στερεώνεται ακλόνητα και στο δεξιό άκρο του προσδένεται σώμα Σ 1 μάζας m 1 =3 kg, το οποίο μπορεί να κινείται σε λείο οριζόντιο δάπεδο Πάνω στο Σ 1 τοποθετείται δεύτερο σώμα Σ 2 μάζας m 2 =1 kg Εκτοξεύουμε προς τα δεξιά το σύστημα από τη θέση ισορροπίας του, με ταχύτητα μέτρου υ και παράλληλη με το οριζόντιο επίπεδο, όπως στο σχήμα, οπότε το σύστημα εκτελεί γραμμική αρμονική ταλάντωση Τα δύο σώματα διατηρούν την επαφή στη διάρκεια της ταλάντωσης α Να υπολογίσετε τη γωνιακή συχνότητα της ταλάντωσης καθώς και τις σταθερές ταλάντωσης D ολ, D 1 και D 2 του συστήματος και των σωμάτων Σ 1 και Σ 2 αντίστοιχα β Να τοποθετήσετε το σύστημα σε μια τυχαία θέση της ταλάντωσής του, να σχεδιάσετε και να περιγράψετε σε τρία κατάλληλα σχήματα τις δυνάμεις, που δέχονται: το σύστημα Σ 1 Σ 2, το Σ 1 και το Σ 2 γ Να παραστήσετε γραφικά την αλγεβρική τιμή της στατικής τριβής από το Σ 1 στο Σ 2 σε συνάρτηση με την απομάκρυνση x από τη ΘΙ του, για πλάτος ταλάντωσης Α=3 cm δ Να υπολογίσετε τη μέγιστη τιμή της αρχικής ταχύτητας εκτόξευσης υ max, του συστήματος των Σ 1, Σ 2 ώστε το σώμα Σ 2 να μην ολισθήσει πάνω στο σώμα Σ 1 Δίνεται η επιτάχυνση της βαρύτητας g=10 m/s 2 και ο συντελεστής στατικής τριβής μεταξύ των δύο σωμάτων Σ 1 και Σ 2 είναι μ=0,5 22 Σώμα μάζας m=1 kg αφήνεται από ύψος h=1,2 m πάνω από το ελεύθερο άκρο κατακόρυφου ελατηρίου, το άλλο άκρο του οποίου είναι στερεωμένο στο έδαφος Όταν το σώμα συναντά το ελεύθερο άκρο του ελατηρίου, προσκολλάται και παραμένει σε συνεχή επαφή μ αυτό Αν η μέγιστη συσπείρωση του ελατηρίου είναι Δx max = 0,6 m α Να υπολογιστεί η σταθερά k του ελατηρίου β Να υπολογιστεί το πλάτος Α και η γωνιακή συχνότητα ω της αατ που εκτελεί το σώμα γ Όταν το σώμα είναι σε ακραία θέση ασκείται δύναμη τριβής της μορφής F = b υ (SI) Αν σε χρόνο t=2τ το πλάτος ελαττώνεται κατά 50%, να βρείτε την σταθερά Λ και το έργο της δύναμης απόσβεσης μέχρι τότε Η περίοδος της φθίνουσας ταλάντωσης είναι περίπου ίση με την ιδιοπερίοδο Δίνεται g=10m/s 2 23 Σώμα εκτελεί φθίνουσα ταλάντωση δεχόμενο δύναμη τριβής F bυ, με το b να παίρνει μικρές τιμές Το σώμα αρχικά έχει ενέργεια Εο 50J και 152
7 Γενικές ασκήσεις Θέματα εξετάσεων από το 1ο κεφάλαιο ΚΕΦΑΛΑΙΟ 1 μετά από 10 πλήρεις αιωρήσεις έχει Ε =12,5J α Αν οι 10 αιωρήσεις χρειάζονται 5 s για να πραγματοποιηθούν, να υπολογίσετε την τιμή του Λ β Πόση ενέργεια είχε το σύστημα μετά από 5 πλήρεις αιωρήσεις; 24 Tο σύστημα του σχήματος κάνει φθίνουσα ταλάντωση ( F bυ ) Δίνονται τα μεγέθη k= 10 N/m και m=0,1 kg Τη στιγμή t=0 που αρχίζει το φαινόμενο το πλάτος είναι Α 0 =0,4 m α Ποια από τις επόμενες τιμές της περιόδου είναι πιθανότερη για τη φθίνουσα μηχανική ταλάντωση; i 0,2 π s, ii 0,3 π s, iii 0,45 π s β Να βρείτε την τιμή της σταθεράς b, αν γνωρίζετε ότι σε χρόνο n2 10 s, το πλάτος είναι Α 0 /4 Δίνεται: Λ= b/2m 25 Σώμα μάζας m=2 kg ισορροπεί δεμένο στο κάτω άκρο κατακόρυφου ελατηρίου σταθεράς k=200 N/m, το πάνω άκρο του οποίου είναι στερεωμένο σε ακλόνητο σημείο Το σώμα εκτελεί φθίνουσα ταλάντωση και η δύναμη απόσβεσης που επενεργεί πάνω του είναι της μορφής F=-0,5υ (SI) Εφαρμόζουμε στο σύστημα περιοδική δύναμη διέγερσης με συχνότητα 5/π Ηz, οπότε αποκαθίσταται ταλάντωση σταθερού πλάτους που είναι ίσο με 0,2m Αν η αρχική φάση της ταλάντωσης σταθερού πλάτους είναι φ 0 =0, τότε: α Να γράψετε τις εξισώσεις της απομάκρυνσης και της ταχύτητας της εξαναγκασμένης ταλάντωσης β Να υπολογίσετε το μέγιστο ρυθμό απορρόφησης ενέργειας του ταλαντωτή από τον διεγέρτη, κατά τη διάρκεια μιας περιόδου γ Να δικαιολογήσετε αν θα αυξηθεί ή θα ελαττωθεί το πλάτος της ταλάντωσης αν αυξήσουμε τη συχνότητα του διεγέρτη 26 Σώμα εκτελεί ταυτόχρονα δύο αατ πάνω στην ίδια ευθεία και γύρω από την ίδια θέση ισορροπίας Οι γραφικές παραστάσεις των απομακρύνσεων σε συνάρτηση με το χρόνο για τις δύο ταλαντώσεις φαίνονται στο σχήμα α Να γραφεί η εξίσωση της απομάκρυνσης με το χρόνο για κάθε μία αρμονική ταλάντωση β Να γραφεί η εξίσωση της απομάκρυνσης για τη σύνθετη κίνηση που προκύπτει γ Να βρείτε ποια χρονική στιγμή οι απομακρύνσεις των δύο αρχικών ταλαντώσεων είναι αντίθετες για πρώτη φορά 27 Σώμα μάζας m=0,1 Kg εκτελεί ταυτόχρονα δύο αατ της ίδιας διεύθυνσης και γύρω από την ίδια θέση ισορροπίας με εξισώσεις x 1 =Α 1 ημ(ωt+π/2) και x 2 =Α 2 ημ(ωt+π) με Α 1 =Α 2 Αν η κινητική ενέργεια της συνισταμένης ταλάντωσης μηδενίζεται 10 φορές το δευτερόλεπτο και η μέγιστη δύναμη επαναφοράς που ασκείται στο σώμα κατά τη διάρκεια της ταλάντωσης είναι F max =60 Ν, να υπολογίσετε: α τη σταθερά επαναφοράς της ταλάντωσης, β τα πλάτη των συνιστωσών ταλαντώσεων γ Να γράψετε τη χρονική εξίσωση απομάκρυνσης της συνισταμένης ταλάντωσης δ Να υπολογίσετε την ολική ενέργεια της συνισταμένης ταλάντωσης 153
8 ΚΕΦΑΛΑΙΟ 1 Γενικές ασκήσεις Θέματα εξετάσεων από το 1ο κεφάλαιο ε Να υπολογίσετε το μέτρο της ταχύτητας του σώματος τη στιγμή που ο ρυθμός μεταβολής της ορμής έχει μέτρο 30 Ν Να θεωρήσετε ότι π 2 =10 28 Σώμα μάζας m=1 kg εκτελεί δύο απλές αρμονικές ταλαντώσεις ίδιας συχνότητας, ίδιας διεύθυνσης, γύρω από την ίδια θέση ισορροπίας με εξισώσεις: x 1 = π 3 ημ 10t 3 και x 2 = π 1 ημ 10t 6 (x 1, x 2 σε cm, t σε s) α Να γράψετε την εξίσωση ταχύτητας - χρόνου της σύνθετης ταλάντωσης β Να βρείτε την ενέργεια του υλικού σημείου που εκτελεί τη σύνθετη ταλάντωση γ Να βρείτε το μέτρο της ταχύτητας του σώματος όταν x=1cm 29 Η κίνηση ενός σωματιδίου περιγράφεται από την εξίσωση: y 8 συν 2t ημ 202t ( y σε cm, t σε s) α Αναγνωρείστε το είδος της κίνησης και αναφέρετε τις προϋποθέσεις που πρέπει να ισχύουν για τις δύο συνιστώσες κινήσεις β Γράψτε τις εξισώσεις των δύο κινήσεων που είναι οι συνιστώσες της κίνησης που δίνεται γ Πόσες φορές σε χρόνο Δt=2π s μεγιστοποιείται το πλάτος της συνισταμένης κίνησης; δ Πόσες φορές γίνεται η κίνηση στο χρονικό διάστημα που μηδενίζεται δύο διαδοχικές φορές το πλάτος; 154
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24 Εκφώνηση άσκησης 6. Ένα σώμα, μάζας m, εκτελεί απλή αρμονική ταλάντωση έχοντας ολική ενέργεια Ε. Χωρίς να αλλάξουμε τα φυσικά χαρακτηριστικά του συστήματος, προσφέρουμε στο σώμα
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24 Εκφώνηση άσκησης 6. Ένα σώμα, μάζας m, εκτελεί απλή αρμονική ταλάντωση έχοντας ολική ενέργεια Ε. Χωρίς να αλλάξουμε τα φυσικά χαρακτηριστικά του συστήματος, προσφέρουμε στο σώμα
7. Ένα σώμα εκτελεί Α.Α.Τ. Η σταθερά επαναφοράς συστήματος είναι.
 ΚΕΦΑΛΑΙΟ 1 ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 6α. Σφαίρα μάζας ισορροπεί δεμένη στο πάνω άκρο κατακόρυφου
ΚΕΦΑΛΑΙΟ 1 ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 6α. Σφαίρα μάζας ισορροπεί δεμένη στο πάνω άκρο κατακόρυφου
γ. Πόση επιτάχυνση θα έχει το σώμα τη στιγμή που έχει απομάκρυνση 0,3 m;
 ΘΕΜΑ Γ 1. Ένα σώμα εκτελεί αρμονική ταλάντωση με εξίσωση 0,6 ημ 8 S.I.. α. Να βρείτε την περίοδο και τον αριθμό των ταλαντώσεων που εκτελεί το σώμα σε ένα λεπτό της ώρας. β. Να γράψετε τις εξισώσεις της
ΘΕΜΑ Γ 1. Ένα σώμα εκτελεί αρμονική ταλάντωση με εξίσωση 0,6 ημ 8 S.I.. α. Να βρείτε την περίοδο και τον αριθμό των ταλαντώσεων που εκτελεί το σώμα σε ένα λεπτό της ώρας. β. Να γράψετε τις εξισώσεις της
ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ ΠΡΟΣΠΑΘΕΙΑ ΣΑΣ ΚΙ 2014
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΘΕΜΑ Α A1. Στις ερωτήσεις 1 9 να επιλέξετε το γράμμα που αντιστοιχεί στη σωστή απάντηση, χωρίς να αιτιολογήσετε την επιλογή σας.
 ΜΑΘΗΜΑ / Προσανατολισμός / ΤΑΞΗ ΑΡΙΘΜΟΣ ΦΥΛΛΟΥ ΕΡΓΑΣΙΑΣ: ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ : ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ: ΦΥΣΙΚΗ/ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ / Γ ΛΥΚΕΙΟΥ 1 Ο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ( ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ) ΘΕΜΑ Α A1. Στις ερωτήσεις
ΜΑΘΗΜΑ / Προσανατολισμός / ΤΑΞΗ ΑΡΙΘΜΟΣ ΦΥΛΛΟΥ ΕΡΓΑΣΙΑΣ: ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ : ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ: ΦΥΣΙΚΗ/ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ / Γ ΛΥΚΕΙΟΥ 1 Ο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ( ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ) ΘΕΜΑ Α A1. Στις ερωτήσεις
1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI).
 1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI). Να βρείτε: α. το πλάτος της απομάκρυνσης, της ταχύτητας και της επιτάχυνσης. β.
1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI). Να βρείτε: α. το πλάτος της απομάκρυνσης, της ταχύτητας και της επιτάχυνσης. β.
ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ
 ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ 1. Κατακόρυφο ελατήριο σταθεράς k=1000 N /m έχει το κάτω άκρο του στερεωμένο σε ακίνητο σημείο. Στο πάνω άκρο του ελατηρίου έχει προσδεθεί σώμα Σ 1 μάζας m 1 =8 kg, ενώ ένα δεύτερο
ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ 1. Κατακόρυφο ελατήριο σταθεράς k=1000 N /m έχει το κάτω άκρο του στερεωμένο σε ακίνητο σημείο. Στο πάνω άκρο του ελατηρίου έχει προσδεθεί σώμα Σ 1 μάζας m 1 =8 kg, ενώ ένα δεύτερο
4. Σώμα Σ 1 μάζας m 1 =1kg ισορροπεί πάνω σε λείο κεκλιμένο επίπεδο που σχηματίζει με τον ορίζοντα γωνία φ=30 ο. Το σώμα Σ 1 είναι δεμένο στην άκρη
 1. Δίσκος μάζας Μ=1 Kg είναι στερεωμένος στο πάνω άκρο κατακόρυφου ελατηρίου, σταθεράς k=200 N/m. Το άλλο άκρο του ελατηρίου είναι στερεωμένο σε οριζόντιο δάπεδο. Πάνω στο δίσκο κάθεται ένα πουλί με μάζα
1. Δίσκος μάζας Μ=1 Kg είναι στερεωμένος στο πάνω άκρο κατακόρυφου ελατηρίου, σταθεράς k=200 N/m. Το άλλο άκρο του ελατηρίου είναι στερεωμένο σε οριζόντιο δάπεδο. Πάνω στο δίσκο κάθεται ένα πουλί με μάζα
ΟΡΟΣΗΜΟ Ένα υλικό σημείο που κάνει α.α.τ πλάτους Α=10cm τη χρονική στιγμή t=0s έχει απομάκρυνση x 5 3 cm. Να βρείτε την αρχική φάση φ 0
 Απλή Αρμονική Ταλάντωση ΚΕΦΑΛΑΙΟ 1 Σώμα που εκτελεί απλή αρμονική ταλάντωση και χρησιμοποιούμε τις εξισώσεις. 1.56 Ένα υλικό σημείο που κάνει α.α.τ πλάτους Α=10cm τη χρονική στιγμή t=0s έχει απομάκρυνση
Απλή Αρμονική Ταλάντωση ΚΕΦΑΛΑΙΟ 1 Σώμα που εκτελεί απλή αρμονική ταλάντωση και χρησιμοποιούμε τις εξισώσεις. 1.56 Ένα υλικό σημείο που κάνει α.α.τ πλάτους Α=10cm τη χρονική στιγμή t=0s έχει απομάκρυνση
2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
1.1 Κινηματική προσέγγιση
 1.1 Κινηματική προσέγγιση ΣΑ 1.8: Η απομάκρυνση από τη θέση ισορροπίας ενός σώματος που κάνει αατ δίνεται σε συνάρτηση με το χρόνο από τη σχέση x=10 ημ(π/4t) (x σε cm και t σε s). Να βρείτε: Α) το πλάτος
1.1 Κινηματική προσέγγιση ΣΑ 1.8: Η απομάκρυνση από τη θέση ισορροπίας ενός σώματος που κάνει αατ δίνεται σε συνάρτηση με το χρόνο από τη σχέση x=10 ημ(π/4t) (x σε cm και t σε s). Να βρείτε: Α) το πλάτος
2. Σώμα εκτελεί Α.Α.Τ. και η εξίσωση της απομάκρυνσης σε σχέση με το χρόνο είναι:
 1. Σώμα εκτελεί Α.Α.Τ. με περίοδο 2 s και πλάτος ταλάντωσης 0,1 m. Τη χρονική στιγμή 0 το σώμα διέρχεται από τη θέση ισορροπίας του με θετική ταχύτητα. Να υ πολογιστούν: α) η συχνότητα και η γωνιακή συχνότητα
1. Σώμα εκτελεί Α.Α.Τ. με περίοδο 2 s και πλάτος ταλάντωσης 0,1 m. Τη χρονική στιγμή 0 το σώμα διέρχεται από τη θέση ισορροπίας του με θετική ταχύτητα. Να υ πολογιστούν: α) η συχνότητα και η γωνιακή συχνότητα
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΕΛΑΤΗΡΙΟ-ΚΡΟΥΣΗ. Σε όσες ασκήσεις απαιτείται δίνεται επιτάχυνση βαρύτητας g=10 m/s 2.
 ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΕΛΑΤΗΡΙΟ-ΚΡΟΥΣΗ Σε όσες ασκήσεις απαιτείται δίνεται επιτάχυνση βαρύτητας g=10 m/s 2. ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Η δύναμη επαναφοράς που ασκείται σε ένα σώμα μάζας m που εκτελεί απλή αρμονική
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΕΛΑΤΗΡΙΟ-ΚΡΟΥΣΗ Σε όσες ασκήσεις απαιτείται δίνεται επιτάχυνση βαρύτητας g=10 m/s 2. ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Η δύναμη επαναφοράς που ασκείται σε ένα σώμα μάζας m που εκτελεί απλή αρμονική
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος 1. Τρία διαπασών Δ 1, Δ 2 παράγουν ήχους με συχνότητες 214 Hz, 220 Hz και f 3 αντίστοιχα. Όταν πάλλονται ταυτόχρονα τα διαπασών Δ
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος 1. Τρία διαπασών Δ 1, Δ 2 παράγουν ήχους με συχνότητες 214 Hz, 220 Hz και f 3 αντίστοιχα. Όταν πάλλονται ταυτόχρονα τα διαπασών Δ
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Στ.
 1.1. Μηχανικές Ταλαντώσεις. Ομάδα Στ. 101) Δυο σώματα αφήνονται να κινηθούν. Δυο σώματα Σ 1 και Σ 2, ίδιας μάζας m=2kg, συγκρατιόνται σε λείο κεκλιμένο επίπεδο απέχοντας κατά D=1,5m από την κορυφή του
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Στ. 101) Δυο σώματα αφήνονται να κινηθούν. Δυο σώματα Σ 1 και Σ 2, ίδιας μάζας m=2kg, συγκρατιόνται σε λείο κεκλιμένο επίπεδο απέχοντας κατά D=1,5m από την κορυφή του
ΤΑΛΑΝΤΩΣΕΙΣ. . Ερωτήσεις αντιστοίχισης. Σχήμα 2 από τη θέση ισορροπίας του δίνεται από την εξίσωση x = Aημωt.
 ΤΑΛΑΝΤΩΣΕΙΣ. Ερωτήσεις αντιστοίχισης Οδηγία: Για να απαντήσετε στις παρακάτω ερωτήσεις αρκεί να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και τα κατάλληλα ζεύγη γραμμάτων - αριθμών.. Σημειακό
ΤΑΛΑΝΤΩΣΕΙΣ. Ερωτήσεις αντιστοίχισης Οδηγία: Για να απαντήσετε στις παρακάτω ερωτήσεις αρκεί να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και τα κατάλληλα ζεύγη γραμμάτων - αριθμών.. Σημειακό
Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της ερώτησης και δίπλα σε κάθε αριθμό το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 Μάθημα/Τάξη: Φυσική Γ Λυκείου Κεφάλαιο: Ταλαντώσεις Ονοματεπώνυμο Μαθητή: Ημερομηνία: 7-11-2016 Επιδιωκόμενος Στόχος: 80/100 Θέμα A Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της ερώτησης και δίπλα
Μάθημα/Τάξη: Φυσική Γ Λυκείου Κεφάλαιο: Ταλαντώσεις Ονοματεπώνυμο Μαθητή: Ημερομηνία: 7-11-2016 Επιδιωκόμενος Στόχος: 80/100 Θέμα A Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της ερώτησης και δίπλα
Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη
ΟΡΟΣΗΜΟ. 1ο Κριτήριο αξιολόγησης στα κεφ Θέμα 1. Κριτήρια αξιολόγησης Ταλαντώσεις - Κύματα.
 1ο Κριτήριο αξιολόγησης στα κεφ. 1-2 Θέμα 1 Ποια από τις παρακάτω προτάσεις είναι σωστή; 1. Ένα σώμα μάζας m είναι δεμένο στην ελεύθερη άκρη κατακόρυφου ιδανικού ελατηρίου σταθεράς k και ηρεμεί στη θέση
1ο Κριτήριο αξιολόγησης στα κεφ. 1-2 Θέμα 1 Ποια από τις παρακάτω προτάσεις είναι σωστή; 1. Ένα σώμα μάζας m είναι δεμένο στην ελεύθερη άκρη κατακόρυφου ιδανικού ελατηρίου σταθεράς k και ηρεμεί στη θέση
1. Ένα σώμα μάζας είναι στερεωμένο στην άκρη οριζοντίου ιδανικού ελατηρίου, του οποίου το άλλο άκρο είναι ακλόνητα στερεωμένο.
 1. Ένα σώμα μάζας είναι στερεωμένο στην άκρη οριζοντίου ιδανικού ελατηρίου σταθεράς, του οποίου το άλλο άκρο είναι ακλόνητα στερεωμένο. Το σώμα εκτελεί απλή αρμονική ταλάντωση, κατά τη διεύθυνση του άξονα
1. Ένα σώμα μάζας είναι στερεωμένο στην άκρη οριζοντίου ιδανικού ελατηρίου σταθεράς, του οποίου το άλλο άκρο είναι ακλόνητα στερεωμένο. Το σώμα εκτελεί απλή αρμονική ταλάντωση, κατά τη διεύθυνση του άξονα
Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 Μάθημα/Τάξη: ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Κεφάλαιο: ΤΑΛΑΝΤΩΣΕΙΣ - ΚΡΟΥΣΕΙΣ Ονοματεπώνυμο Μαθητή: Ημερομηνία: Επιδιωκόμενος Στόχος: 70/100 Θέμα A Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης
Μάθημα/Τάξη: ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Κεφάλαιο: ΤΑΛΑΝΤΩΣΕΙΣ - ΚΡΟΥΣΕΙΣ Ονοματεπώνυμο Μαθητή: Ημερομηνία: Επιδιωκόμενος Στόχος: 70/100 Θέμα A Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης
ΑΣΚΗΣΕΙΣ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΚΡΟΥΣΕΙΣ
 ΑΣΚΗΣΕΙΣ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΚΡΟΥΣΕΙΣ ΟΡΙΖΟΝΤΙΟ ΕΠΙΠΕΔΟ 1.Ένα σώμα μάζας m=4kg είναι δεμένο στο άκρο οριζόντιου ελατηρίου σταθεράςk=400n/m, το άλλο άκρο του οποίου είναι είναι ακλόνητα στερεωμένη. To
ΑΣΚΗΣΕΙΣ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΚΡΟΥΣΕΙΣ ΟΡΙΖΟΝΤΙΟ ΕΠΙΠΕΔΟ 1.Ένα σώμα μάζας m=4kg είναι δεμένο στο άκρο οριζόντιου ελατηρίου σταθεράςk=400n/m, το άλλο άκρο του οποίου είναι είναι ακλόνητα στερεωμένη. To
Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της ερώτησης και δίπλα σε κάθε αριθμό το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 Μάθημα/Τάξη: Φυσική Γ Λυκείου Κεφάλαιο: Ταλαντώσεις Ονοματεπώνυμο Μαθητή: Ημερομηνία: 13-11-2017 Επιδιωκόμενος Στόχος: 80/100 Θέμα A Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της ερώτησης και δίπλα
Μάθημα/Τάξη: Φυσική Γ Λυκείου Κεφάλαιο: Ταλαντώσεις Ονοματεπώνυμο Μαθητή: Ημερομηνία: 13-11-2017 Επιδιωκόμενος Στόχος: 80/100 Θέμα A Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της ερώτησης και δίπλα
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1η ΗΜΕΡΟΜΗΝΙΑ: 24/07/2014
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1η ΗΜΕΡΟΜΗΝΙΑ: 4/07/014 ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1η ΗΜΕΡΟΜΗΝΙΑ: 4/07/014 ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί
Διαγώνισμα Φυσικής Προσανατολισμού Γ Λυκείου. Ταλαντώσεις. Θέμα Α
 Διαγώνισμα Φυσικής Προσανατολισμού Γ Λυκείου Θέμα Α 1. Ένα σώμα εκτελεί απλή αρμονική ταλάντωση περιόδου Τ και τη χρονική στιγμή t=0 βρίσκεται στην ακραία αρνητική του απομάκρυνση. Μετά από χρόνο t 1 =
Διαγώνισμα Φυσικής Προσανατολισμού Γ Λυκείου Θέμα Α 1. Ένα σώμα εκτελεί απλή αρμονική ταλάντωση περιόδου Τ και τη χρονική στιγμή t=0 βρίσκεται στην ακραία αρνητική του απομάκρυνση. Μετά από χρόνο t 1 =
Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς
 Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς 1. Δύο σώματα ίδιας μάζας εκτελούν Α.Α.Τ. Στο διάγραμμα του σχήματος παριστάνεται η συνισταμένη δύναμη που ασκείται σε κάθε σώμα σε συνάρτηση
Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς 1. Δύο σώματα ίδιας μάζας εκτελούν Α.Α.Τ. Στο διάγραμμα του σχήματος παριστάνεται η συνισταμένη δύναμη που ασκείται σε κάθε σώμα σε συνάρτηση
ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ - ΑΣΚΗΣΕΙΣ
 ΚΙΝΗΜΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 1. Στο παρακάτω διάγραμμα απομάκρυνσης-χρόνου φαίνονται οι γραφικές παραστάσεις για δύο σώματα 1 και 2 τα οποία εκτελούν Α.Α.Τ. Να βρείτε τη σχέση που συνδέει τις μέγιστες επιταχύνσεις
ΚΙΝΗΜΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 1. Στο παρακάτω διάγραμμα απομάκρυνσης-χρόνου φαίνονται οι γραφικές παραστάσεις για δύο σώματα 1 και 2 τα οποία εκτελούν Α.Α.Τ. Να βρείτε τη σχέση που συνδέει τις μέγιστες επιταχύνσεις
Εκφώνηση 1. α). β). γ). Επιλέξτε τη σωστή πρόταση και αιτιολογείστε.
 Εκφώνηση 1 Στο σχήμα το σώμα μάζας ισορροπεί χαμηλότερα κατά h από τη θέση φυσικού μήκους του ελατηρίου. Από τη θέση φυσικού μήκους του ελατηρίου αφήνουμε σώμα ίσης μάζας ( ) να κάνει ελεύθερη πτώση στην
Εκφώνηση 1 Στο σχήμα το σώμα μάζας ισορροπεί χαμηλότερα κατά h από τη θέση φυσικού μήκους του ελατηρίου. Από τη θέση φυσικού μήκους του ελατηρίου αφήνουμε σώμα ίσης μάζας ( ) να κάνει ελεύθερη πτώση στην
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ
 ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ 1. Ένα σώμα μάζας m= 2 kg εκτελεί απλή αρμονική ταλάντωση σε οριζόντια διεύθυνση. Στη θέση με απομάκρυνση x 1 =+2m το μέτρο της ταχύτητας του είναι u 1 =4m /s, ενώ στη θέση με απομάκρυνση
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ 1. Ένα σώμα μάζας m= 2 kg εκτελεί απλή αρμονική ταλάντωση σε οριζόντια διεύθυνση. Στη θέση με απομάκρυνση x 1 =+2m το μέτρο της ταχύτητας του είναι u 1 =4m /s, ενώ στη θέση με απομάκρυνση
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΚΡΟΥΣΕΙΣ ΚΑΙ ΤΑΛΑΝΤΩΣΕΙΣ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
 ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΚΡΟΥΣΕΙΣ ΚΑΙ ΤΑΛΑΝΤΩΣΕΙΣ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΘΕΜΑ Α (μονάδες 25) Α1. Σε μια Α.Α.Τ. η εξίσωση της απομάκρυνσης είναι x=a.συνωt. Τη χρονική στιγμή
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΚΡΟΥΣΕΙΣ ΚΑΙ ΤΑΛΑΝΤΩΣΕΙΣ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΘΕΜΑ Α (μονάδες 25) Α1. Σε μια Α.Α.Τ. η εξίσωση της απομάκρυνσης είναι x=a.συνωt. Τη χρονική στιγμή
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : OKTΩΒΡΙΟΣ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : OKTΩΒΡΙΟΣ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : OKTΩΒΡΙΟΣ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας
2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
ΠΡΟΣΟΜΟΙΩΣΗ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ Γʹ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΥΡΙΑΚΗ 13 ΟΚΤΩΒΡΙΟΥ 2016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5)
 ΠΡΟΣΟΜΟΙΩΣΗ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ Γʹ ΤΑΞΗΣ Θέμα A ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΥΡΙΑΚΗ 13 ΟΚΤΩΒΡΙΟΥ 2016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) Οδηγία: Να γράψετε στο τετράδιό σας, δίπλα στον
ΠΡΟΣΟΜΟΙΩΣΗ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ Γʹ ΤΑΞΗΣ Θέμα A ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΥΡΙΑΚΗ 13 ΟΚΤΩΒΡΙΟΥ 2016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) Οδηγία: Να γράψετε στο τετράδιό σας, δίπλα στον
ΔΙΑΓΩΝΙΣΜΑ Αου ΤΕΤΡΑΜΗΝΟΥ ΣΤΑ ΚΕΦΑΛΑΙΑ ΤΑΛΑΝΤΩΣΕΙΣ ΚΡΟΥΣΕΙΣ 4 ο ΛΥΚΕΙΟ ΜΥΤΙΛΗΝΗΣ 11/1/16
 ΔΙΑΓΩΝΙΣΜΑ Αου ΤΕΤΡΑΜΗΝΟΥ ΣΤΑ ΚΕΦΑΛΑΙΑ ΤΑΛΑΝΤΩΣΕΙΣ ΚΡΟΥΣΕΙΣ 4 ο ΛΥΚΕΙΟ ΜΥΤΙΛΗΝΗΣ 11/1/16 Θέμα Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιο σας τον αριθμό της πρότασης και δίπλα το γράμμα που
ΔΙΑΓΩΝΙΣΜΑ Αου ΤΕΤΡΑΜΗΝΟΥ ΣΤΑ ΚΕΦΑΛΑΙΑ ΤΑΛΑΝΤΩΣΕΙΣ ΚΡΟΥΣΕΙΣ 4 ο ΛΥΚΕΙΟ ΜΥΤΙΛΗΝΗΣ 11/1/16 Θέμα Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιο σας τον αριθμό της πρότασης και δίπλα το γράμμα που
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Ε.
 .. Μηχανικές. Ομάδα Ε...8. Δυο ΑΑΤ και μία Ταλάντωση. Ένα σώμα μάζας kg ηρεμεί σε λείο κεκλιμένο επίπεδο κλίσεως θ=30, δεμένο στο άκρο ελατηρίου σταθεράς k =40Ν/m, ενώ εφάπτεται στο ε- λεύθερο άκρο ενός
.. Μηχανικές. Ομάδα Ε...8. Δυο ΑΑΤ και μία Ταλάντωση. Ένα σώμα μάζας kg ηρεμεί σε λείο κεκλιμένο επίπεδο κλίσεως θ=30, δεμένο στο άκρο ελατηρίου σταθεράς k =40Ν/m, ενώ εφάπτεται στο ε- λεύθερο άκρο ενός
ΔΙΑΓΩΝΙΣΜΑ 01 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α
 Σελίδα από ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ () ΘΕΜΑ Α Α. Με την πάροδο του χρόνου και καθώς τα αμορτισέρ ενός αυτοκινήτου παλιώνουν και φθείρονται:
Σελίδα από ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ () ΘΕΜΑ Α Α. Με την πάροδο του χρόνου και καθώς τα αμορτισέρ ενός αυτοκινήτου παλιώνουν και φθείρονται:
ΚΕΦΑΛΑΙΟ 1ο: ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ.
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΘΕΜΑΤΑ ΠΡΟΣ ΕΠΙΛΥΣΗ ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΘΕΜΑΤΑ ΠΡΟΣ ΕΠΙΛΥΣΗ ΘΕΜΑ Β Ερώτηση. Ένα σώμα, μάζας,
ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΘΕΜΑΤΑ ΠΡΟΣ ΕΠΙΛΥΣΗ ΘΕΜΑ Β Ερώτηση. Ένα σώμα, μάζας,
Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση
 Ταλαντώσεις Θέμα Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση Α1. Αν μεταβληθεί η ολική ενέργεια της ταλάντωσης
Ταλαντώσεις Θέμα Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση Α1. Αν μεταβληθεί η ολική ενέργεια της ταλάντωσης
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Ε.
 1.1. Μηχανικές. Ομάδα Ε. 1.1.81. Δυο ΑΑΤ και μία Ταλάντωση. Ένα σώμα μάζας 1kg ηρεμεί σε λείο κεκλιμένο επίπεδο κλίσεως θ=30, δεμένο στο άκρο ελατηρίου σταθεράς k 1 =40Ν/m, ενώ εφάπτεται στο ε- λεύθερο
1.1. Μηχανικές. Ομάδα Ε. 1.1.81. Δυο ΑΑΤ και μία Ταλάντωση. Ένα σώμα μάζας 1kg ηρεμεί σε λείο κεκλιμένο επίπεδο κλίσεως θ=30, δεμένο στο άκρο ελατηρίου σταθεράς k 1 =40Ν/m, ενώ εφάπτεται στο ε- λεύθερο
ΘΕΜΑ Α Να γράψετε στο τετράδιο σας τον αριθμό καθεμιάς από τις παρακάτω προτάσεις Α1 Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 05-06 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 08//05 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Να γράψετε στο τετράδιο σας τον αριθμό καθεμιάς από
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 05-06 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 08//05 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Να γράψετε στο τετράδιο σας τον αριθμό καθεμιάς από
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ
 ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ 30/9/08 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ 30/9/08 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
Όλα τα θέματα των πανελληνίων στις μηχανικές ταλαντώσεις έως και το 2014 ΣΑΛΑΝΣΩΕΙ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΣΑΛΑΝΣΩΗ ΒΑΙΚΕ ΕΝΝΟΙΕ. Ερωτήσεις Πολλαπλής Επιλογής
 έως και το 04 ΣΑΛΑΝΣΩΕΙ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΣΑΛΑΝΣΩΗ ΒΑΙΚΕ ΕΝΝΟΙΕ Ερωτήσεις Πολλαπλής Επιλογής. Να μεταφέρετε στο τετράδιό σας τον παρακάτω πίνακα που αναφέρεται στην απλή αρμονική ταλάντωση και να συμπληρώσετε
έως και το 04 ΣΑΛΑΝΣΩΕΙ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΣΑΛΑΝΣΩΗ ΒΑΙΚΕ ΕΝΝΟΙΕ Ερωτήσεις Πολλαπλής Επιλογής. Να μεταφέρετε στο τετράδιό σας τον παρακάτω πίνακα που αναφέρεται στην απλή αρμονική ταλάντωση και να συμπληρώσετε
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ στις αμείωτες μηχανικές ΤΑΛΑΝΤΩΣΕΙΣ- ΚΡΟΥΣΕΙΣ (1) ΟΝΟΜΑΤΕΠΩΝΥΜΟ
 ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ στις αμείωτες μηχανικές ΤΑΛΑΝΤΩΣΕΙΣ- ΚΡΟΥΣΕΙΣ (1) ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΘΕΜΑ Α Α1.Ένα σώμα μάζας m είναι δεμένο και ισορροπεί στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k 1 του
ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ στις αμείωτες μηχανικές ΤΑΛΑΝΤΩΣΕΙΣ- ΚΡΟΥΣΕΙΣ (1) ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΘΕΜΑ Α Α1.Ένα σώμα μάζας m είναι δεμένο και ισορροπεί στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k 1 του
Φροντιστήρια Εν-τάξη Σελίδα 1 από 6
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 11/09/2016 ΘΕΜΑ Α Να γράψετε στο τετραδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Ένα
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 11/09/2016 ΘΕΜΑ Α Να γράψετε στο τετραδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Ένα
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ ΘΕΜΑ 1 Α. Ερωτήσεις πολλαπλής επιλογής 1. Σώμα εκτελεί Α.Α.Τ με περίοδο Τ και πλάτος Α. Αν διπλασιάσουμε το πλάτος της ταλάντωσης τότε η περίοδος της θα : α. παραμείνει
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ ΘΕΜΑ 1 Α. Ερωτήσεις πολλαπλής επιλογής 1. Σώμα εκτελεί Α.Α.Τ με περίοδο Τ και πλάτος Α. Αν διπλασιάσουμε το πλάτος της ταλάντωσης τότε η περίοδος της θα : α. παραμείνει
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΥΓΟΥΣΤΟΥ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 5
 ΑΡΧΗ ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Ο : ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΥΓΟΥΣΤΟΥ 08 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 5 Στις παρακάτω ερωτήσεις έως 4 να γράψετε στο τετράδιό σας τον
ΑΡΧΗ ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Ο : ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΥΓΟΥΣΤΟΥ 08 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 5 Στις παρακάτω ερωτήσεις έως 4 να γράψετε στο τετράδιό σας τον
α. Από τη μάζα του σώματος που ταλαντώνεται. β. Μόνο από τα πλάτη των επιμέρους απλών αρμονικών ταλαντώσεων.
 ιαγώνισμα στη φυσική θετικού προσανατολισμού Ύλη: μηχανικές ταλαντώσεις ιάρκεια 3 ώρες ΘΕΜΑ Α Στις προτάσεις Α1 έως Α8 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
ιαγώνισμα στη φυσική θετικού προσανατολισμού Ύλη: μηχανικές ταλαντώσεις ιάρκεια 3 ώρες ΘΕΜΑ Α Στις προτάσεις Α1 έως Α8 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
ΕΝΕΡΓΕΙΑ ΚΑΙ ΤΑΛΑΝΤΩΣΗ
 ΕΝΕΡΓΕΙΑ ΚΑΙ ΤΑΛΑΝΤΩΣΗ 1. Ελατήριο σταθεράς K τοποθετείται κατακόρυφα με το πάνω άκρο του στερεωμένο σε ακλόνητο σημείο. Ένα σώμα μάζας M=1 kg δένεται στο κάτω άκρο του ελατηρίου και η επιμήκυνση που προκαλεί
ΕΝΕΡΓΕΙΑ ΚΑΙ ΤΑΛΑΝΤΩΣΗ 1. Ελατήριο σταθεράς K τοποθετείται κατακόρυφα με το πάνω άκρο του στερεωμένο σε ακλόνητο σημείο. Ένα σώμα μάζας M=1 kg δένεται στο κάτω άκρο του ελατηρίου και η επιμήκυνση που προκαλεί
Α. Για ποιο από τα δυο σώματα καταναλώσαμε περισσότερη ενέργεια;
 1. Στην κάτω άκρη ενός ιδανικού ελατήριου είναι δεμένο ένα σώμα που έχει μάζα m 1 = m και ισορροπεί. Στην κάτω άκρη ενός άλλου ομοίου ελατήριου είναι δεμένο ένα άλλο σώμα που έχει μάζα m 2 = 4m και ισορροπεί.
1. Στην κάτω άκρη ενός ιδανικού ελατήριου είναι δεμένο ένα σώμα που έχει μάζα m 1 = m και ισορροπεί. Στην κάτω άκρη ενός άλλου ομοίου ελατήριου είναι δεμένο ένα άλλο σώμα που έχει μάζα m 2 = 4m και ισορροπεί.
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 24/09/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 017-018 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΟΠ / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 4/09/017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 017-018 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΟΠ / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 4/09/017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
Φθίνουσες Εξαναγκασμένες Ταλαντώσεις. Ομάδα Γ.
 Φθίνουσες Εξαναγκασμένες. Ομάδα Γ. 1.3.21. Υπολογίσατε το πλάτος στην εξαναγκασμένη ταλάντωση. k = 40 N m m= 5kg Το σώμα του σχήματος βρίσκεται πάνω σε λεία σανίδα συνδεδεμένο με ιδανικό ελατήριο. Κινούμενο
Φθίνουσες Εξαναγκασμένες. Ομάδα Γ. 1.3.21. Υπολογίσατε το πλάτος στην εξαναγκασμένη ταλάντωση. k = 40 N m m= 5kg Το σώμα του σχήματος βρίσκεται πάνω σε λεία σανίδα συνδεδεμένο με ιδανικό ελατήριο. Κινούμενο
Κρούσεις. 5. Σε μια ελαστική κρούση δεν διατηρείται α. η ολική κινητική ενέργεια του συστήματος. β. η ορμή του συστήματος.
 ο ΘΕΜΑ Κρούσεις Α Ερωτήσεις πολλαπλής επιλογής Στην παρακάτω ερώτηση να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση Σε κάθε κρούση ισχύει α η
ο ΘΕΜΑ Κρούσεις Α Ερωτήσεις πολλαπλής επιλογής Στην παρακάτω ερώτηση να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση Σε κάθε κρούση ισχύει α η
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 17-10-11 ΑΠΟΦΟΙΤΟΙ ΣΕΙΡΑ Α Θέµα 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 δίπλα το γράµµα που αντιστοιχεί στη
17-10-11 ΑΠΟΦΟΙΤΟΙ ΣΕΙΡΑ Α Θέµα 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 δίπλα το γράµµα που αντιστοιχεί στη
ΘΕΜΑ Β Β1. Ένας ταλαντωτής εκτελεί φθίνουσα ταλάντωση με πλάτος που μειώνεται εκθετικά με το
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 2015-2016 ΜΑΘΗΜΑ / ΤΑΞΗ : ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 08/11/2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Α1 δ Α2 γ Α3 δ Α4 α Α5 β ΘΕΜΑ Β Β1 Ένας ταλαντωτής
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 2015-2016 ΜΑΘΗΜΑ / ΤΑΞΗ : ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 08/11/2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Α1 δ Α2 γ Α3 δ Α4 α Α5 β ΘΕΜΑ Β Β1 Ένας ταλαντωτής
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 2 o ΔΙΑΓΩΝΙΣΜΑ ΝΟΕΜΒΡΙΟΣ 2018: ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 2 ο ΔΙΑΓΩΝΙΣΜΑ ΤΑΛΑΝΤΩΣΕΙΣ - ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 2 ο ΔΙΑΓΩΝΙΣΜΑ ΤΑΛΑΝΤΩΣΕΙΣ - ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
Γενικό κριτήριο αξιολόγησης στις ταλαντώσεις
 Ταλαντώσεις ΚΕΦΑΛΑΙΟ 1 Θέμα 1 Γενικό κριτήριο αξιολόγησης στις ταλαντώσεις 1. Σε απλή αρμονική ταλάντωση ποια από τις επόμενες προτάσεις είναι σωστή; α. Η επιτάχυνση έχει φορά προς τη θέση ισορροπίας.
Ταλαντώσεις ΚΕΦΑΛΑΙΟ 1 Θέμα 1 Γενικό κριτήριο αξιολόγησης στις ταλαντώσεις 1. Σε απλή αρμονική ταλάντωση ποια από τις επόμενες προτάσεις είναι σωστή; α. Η επιτάχυνση έχει φορά προς τη θέση ισορροπίας.
ΕΡΓΑΣΙΑ ΣΤΟ ΠΡΩΤΟ ΚΕΦΑΛΑΙΟ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ.
 ΕΡΓΑΣΙΑ ΣΤΟ ΠΡΩΤΟ ΚΕΦΑΛΑΙΟ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ. ΕΡΩΤΗΣΗ 1 Στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 400 N/m είναι κρεμασμένο σώμα μάζας m = 1 kg. Το σύστημα ελατήριο-σώμα εξαναγκάζεται
ΕΡΓΑΣΙΑ ΣΤΟ ΠΡΩΤΟ ΚΕΦΑΛΑΙΟ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ. ΕΡΩΤΗΣΗ 1 Στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 400 N/m είναι κρεμασμένο σώμα μάζας m = 1 kg. Το σύστημα ελατήριο-σώμα εξαναγκάζεται
Ενδεικτικές Λύσεις. Θέµα Α
 3ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Στη σύνθεση δύο απλών αρµονικών ταλαντώσεων της ίδιας συχνότητας που γίνονται γύρω από το ίδιο σηµείο και στην ίδια διεύθυνση,
3ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Στη σύνθεση δύο απλών αρµονικών ταλαντώσεων της ίδιας συχνότητας που γίνονται γύρω από το ίδιο σηµείο και στην ίδια διεύθυνση,
Κρούσεις. 1 ο ΘΕΜΑ. Φυσική Γ Θετ. και Τεχν/κης Κατ/σης. Θέματα εξετάσεων
 ο ΘΕΜΑ Κρούσεις Α. Ερωτήσεις πολλαπλής επιλογής Στην παρακάτω ερώτηση να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Σε κάθε κρούση ισχύει
ο ΘΕΜΑ Κρούσεις Α. Ερωτήσεις πολλαπλής επιλογής Στην παρακάτω ερώτηση να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Σε κάθε κρούση ισχύει
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ 1
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Δύο εγκάρσια κύματα
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Δύο εγκάρσια κύματα
προς ένα ακίνητο σωμάτιο α (πυρήνας Ηe), το οποίο είναι ελεύθερο να κινηθεί,
 ΚΡΟΥΣΕΙΣ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ 1. Σφαίρα Α μάζας 3m κινείται πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική φορά και συγκρούεται κεντρικά και ελαστικά με άλλη σφαίρα Β μάζας m που κινείται κατά την
ΚΡΟΥΣΕΙΣ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ 1. Σφαίρα Α μάζας 3m κινείται πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική φορά και συγκρούεται κεντρικά και ελαστικά με άλλη σφαίρα Β μάζας m που κινείται κατά την
Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ
 1 Ονοματεπώνυμο.. Υπεύθυνος Καθηγητής: Γκαραγκουνούλης Ιωάννης Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ > Τρίτη 3-1-2012 2 ΘΕΜΑ 1ο Να γράψετε
1 Ονοματεπώνυμο.. Υπεύθυνος Καθηγητής: Γκαραγκουνούλης Ιωάννης Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ > Τρίτη 3-1-2012 2 ΘΕΜΑ 1ο Να γράψετε
Επανάληψη: Κρούσεις και φαινόμενο Doppler (Φ24) 4. α. β. ii. iii. 6. α.
 Επανάληψη: Κρούσεις και φαινόμενο Doppler (Φ24) 1. Μια σφαίρα με μάζα m 1 συγκρούεται μετωπικά και ελαστικά με μια ακίνητη σφαίρα μάζας m 2. Ποια πρέπει να είναι η σχέση της μάζας m 1 με τη μάζα m 2 ώστε:
Επανάληψη: Κρούσεις και φαινόμενο Doppler (Φ24) 1. Μια σφαίρα με μάζα m 1 συγκρούεται μετωπικά και ελαστικά με μια ακίνητη σφαίρα μάζας m 2. Ποια πρέπει να είναι η σχέση της μάζας m 1 με τη μάζα m 2 ώστε:
Μάθημα: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ. Ονοματεπώνυμο: Τμήμα: Β ΘΕΜΑΤΑ: Θέμα 1. (5Χ5=25 μον)
 Μάθημα: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Καθηγητής/τρια: Χρόνος: Ονοματεπώνυμο: Τμήμα: Β ΘΕΜΑΤΑ: Θέμα 1. (5Χ5=25 μον) 1. Σε μια φθίνουσα ταλάντωση ποιο από τα παρακάτω μεγέθη παραμένει σταθερό: α) το πλάτος
Μάθημα: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Καθηγητής/τρια: Χρόνος: Ονοματεπώνυμο: Τμήμα: Β ΘΕΜΑΤΑ: Θέμα 1. (5Χ5=25 μον) 1. Σε μια φθίνουσα ταλάντωση ποιο από τα παρακάτω μεγέθη παραμένει σταθερό: α) το πλάτος
Επαναληπτικό διαγώνισµα Ταλαντώσεις Στερεό σώµα
 Επαναληπτικό διαγώνισµα Ταλαντώσεις Στερεό σώµα Θέµα ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Ένα σηµειακό
Επαναληπτικό διαγώνισµα Ταλαντώσεις Στερεό σώµα Θέµα ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Ένα σηµειακό
Επαναληπτικό Διαγώνισμα Φυσικής Γ Λυκείου Κρούσεις-Ταλαντώσεις-Κύματα
 Επαναληπτικό Διαγώνισμα Φυσικής Γ Λυκείου Κρούσεις-Ταλαντώσεις-Κύματα Θέμα Α 1) Η ιδιοσυχνότητα ενός συστήματος που εκτελεί εξαναγκασμένη ταλάντωση χωρίς τριβή είναι 20 Hz. Το πλάτος της ταλάντωσης γίνεται
Επαναληπτικό Διαγώνισμα Φυσικής Γ Λυκείου Κρούσεις-Ταλαντώσεις-Κύματα Θέμα Α 1) Η ιδιοσυχνότητα ενός συστήματος που εκτελεί εξαναγκασμένη ταλάντωση χωρίς τριβή είναι 20 Hz. Το πλάτος της ταλάντωσης γίνεται
Ημερομηνία: Παρασκευή 27 Οκτωβρίου 2017 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΑΠΟ /0/07 ΕΩΣ //07 η ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Παρασκευή 7 Οκτωβρίου 07 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις
ΑΠΟ /0/07 ΕΩΣ //07 η ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Παρασκευή 7 Οκτωβρίου 07 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις
ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ : ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση Ένα σώμα εκτελεί απλή
ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ : ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση Ένα σώμα εκτελεί απλή
T 4 T 4 T 2 Τ Τ Τ 3Τ Τ Τ 4
 ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ 29 ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Σηµειακό αντικείµενο εκτελεί απλή αρµονική ταλάντωση. Η αποµάκρυνση χ από τη θέση ισορροπίας του είναι: α. ανάλογη του χρόνου. β. αρµονική συνάρτηση
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ 29 ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Σηµειακό αντικείµενο εκτελεί απλή αρµονική ταλάντωση. Η αποµάκρυνση χ από τη θέση ισορροπίας του είναι: α. ανάλογη του χρόνου. β. αρµονική συνάρτηση
5. Ένα σώµα ταλαντώνεται µεταξύ των σηµείων Α και Ε. Στο σχήµα φαίνονται πέντε θέσεις Α,Β,Γ, και Ε, οι οποίες ισαπέχουν µεταξύ 1
 1. Σώµα 10g εκτελεί α.α.τ. γύρω από σηµείο Ο και η αποµάκρυνση δίνεται από τη σχέση: x=10ηµπt (cm), ζητούνται: i) Πόσο χρόνο χρειάζεται για να πάει από το Ο σε σηµείο Μ όπου x=5cm ii) Ποια η ταχύτητά του
1. Σώµα 10g εκτελεί α.α.τ. γύρω από σηµείο Ο και η αποµάκρυνση δίνεται από τη σχέση: x=10ηµπt (cm), ζητούνται: i) Πόσο χρόνο χρειάζεται για να πάει από το Ο σε σηµείο Μ όπου x=5cm ii) Ποια η ταχύτητά του
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Γ Λ ΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 27/11/2016. Θέμα A Στις ερωτήσεις Α1-Α4 επιλέξτε την σωστή απάντηση
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Γ Λ ΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 27/11/2016 Θέμα A Στις ερωτήσεις Α1-Α4 επιλέξτε την σωστή απάντηση Α1. Ένα σύστημα ελατηρίου μάζας εκτελεί απλή αρμονική ταλάντωση πλάτους Α. Αν τετραπλασιάσουμε
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Γ Λ ΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 27/11/2016 Θέμα A Στις ερωτήσεις Α1-Α4 επιλέξτε την σωστή απάντηση Α1. Ένα σύστημα ελατηρίου μάζας εκτελεί απλή αρμονική ταλάντωση πλάτους Α. Αν τετραπλασιάσουμε
ΘΕΜΑ Α. Α.1. Ένα σύστηµα ελατηρίου-µάζας εκτελεί απλή αρµονική ταλάντωση πλάτους Α.
 ΘΕΜΑ Α Στις ημιτελείς προτάσεις Α 1 Α 6 να γράψετε στο τετράδιο σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη συμπληρώνει σωστά. Α.1. Ένα σύστηµα ελατηρίου-µάζας
ΘΕΜΑ Α Στις ημιτελείς προτάσεις Α 1 Α 6 να γράψετε στο τετράδιο σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη συμπληρώνει σωστά. Α.1. Ένα σύστηµα ελατηρίου-µάζας
Θέμα 1 ο (Μονάδες 25)
 ΙΙΑΑΓΓΩΝΝΙΙΣΣΜΑΑ ΦΦΥΥΣΣΙΙΚΚΗΗΣΣ ΚΚΑΑΤΤΕΕΥΥΘΘΥΥΝΝΣΣΗΗΣΣ ΑΑΠΟΟΦΦΟΟΙΙΤΤΩΝΝ 0055 -- -- 00 Θέμα ο. Ένα σημειακό αντικείμενο που εκτελεί ΑΑΤ μεταβαίνει από τη θέση ισορροπίας του σε ακραία θέση σε χρόνο s. Η
ΙΙΑΑΓΓΩΝΝΙΙΣΣΜΑΑ ΦΦΥΥΣΣΙΙΚΚΗΗΣΣ ΚΚΑΑΤΤΕΕΥΥΘΘΥΥΝΝΣΣΗΗΣΣ ΑΑΠΟΟΦΦΟΟΙΙΤΤΩΝΝ 0055 -- -- 00 Θέμα ο. Ένα σημειακό αντικείμενο που εκτελεί ΑΑΤ μεταβαίνει από τη θέση ισορροπίας του σε ακραία θέση σε χρόνο s. Η
[ Απ. α) , β) µατος. Εκτρέπουµε το σύστηµα προς τα κάτω κατά x=0,5 m και το αφήνουµε ελεύθερο.
 47. Σώµα (Σ 1 ) είναι τοποθετηµένο πάνω σε σώµα (Σ ) και το σύστηµα εκτελεί Α.Α.Τ. κατακόρυφα µε περίοδο Τ. α) Να εκφράσετε τη δύναµη αντίδρασης F του σώµατος (Σ ) στο σώµα (Σ 1 ), σε συνάρτηση µε την
47. Σώµα (Σ 1 ) είναι τοποθετηµένο πάνω σε σώµα (Σ ) και το σύστηµα εκτελεί Α.Α.Τ. κατακόρυφα µε περίοδο Τ. α) Να εκφράσετε τη δύναµη αντίδρασης F του σώµατος (Σ ) στο σώµα (Σ 1 ), σε συνάρτηση µε την
ΘΕΜΑ Α. (Μονάδες 5) (Μονάδες 5)
 ΘΕΜΑ Α 1) Σύστημα ελατηρίου-σώματος με μάζα m εκτελεί απλή αρμονική ταλάντωση με σταθερά επαναφοράς k. Αν η μάζα του σώματος τετραπλασιαστεί τότε: α/ το πλάτος της ταλάντωσης θα τετραπλασιαστεί β/ η περίοδος
ΘΕΜΑ Α 1) Σύστημα ελατηρίου-σώματος με μάζα m εκτελεί απλή αρμονική ταλάντωση με σταθερά επαναφοράς k. Αν η μάζα του σώματος τετραπλασιαστεί τότε: α/ το πλάτος της ταλάντωσης θα τετραπλασιαστεί β/ η περίοδος
α. β. γ. δ. Μονάδες 5 α. β. γ. δ. Μονάδες 5 α. ελαστική β. ανελαστική γ. πλαστική δ. έκκεντρη
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 27/09/2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 27/09/2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΚΑΙ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΜΕ ΑΙΤΙΟΛΟΓΗΣΗ ΜΕΡΟΣ 2. έχει το φυσικό του μήκος και η πάνω άκρη του είναι δεμένη σε σταθερό σημείο.
 ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΚΑΙ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΜΕ ΑΙΤΙΟΛΟΓΗΣΗ ΜΕΡΟΣ. Ένα ιδανικό ελατήριο σταθεράς = 00 N/ που έχει τον άξονα του κατακόρυφο έχει το φυσικό του μήκος και η πάνω άκρη του είναι δεμένη σε
ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΚΑΙ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΜΕ ΑΙΤΙΟΛΟΓΗΣΗ ΜΕΡΟΣ. Ένα ιδανικό ελατήριο σταθεράς = 00 N/ που έχει τον άξονα του κατακόρυφο έχει το φυσικό του μήκος και η πάνω άκρη του είναι δεμένη σε
Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις
 Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις ~ Διάρκεια: 3 ώρες ~ Θέμα Α Α1. Η ορμή συστήματος δύο σωμάτων που συγκρούονται διατηρείται: α. Μόνο στην πλάγια κρούση. β. Μόνο στην έκκεντρη
Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις ~ Διάρκεια: 3 ώρες ~ Θέμα Α Α1. Η ορμή συστήματος δύο σωμάτων που συγκρούονται διατηρείται: α. Μόνο στην πλάγια κρούση. β. Μόνο στην έκκεντρη
4 ο Γενικό Λύκειο Κοζάνης Φυσική κατεύθυνσης Γ τάξης
 4 ο Γενικό Λύκειο Κοζάνης Φυσική κατεύθυνσης Γ τάξης 1 ΠΑΡΑΤΗΡΗΣΕΙΣ 1. Στην ελαστική κρούση όπου το ένα σώμα είναι ακίνητο αρχικά εφαρμόζω τις γνωστές σχέσεις : Για το σώμα m 1 που αρχικά κινείται με ταχύτητα
4 ο Γενικό Λύκειο Κοζάνης Φυσική κατεύθυνσης Γ τάξης 1 ΠΑΡΑΤΗΡΗΣΕΙΣ 1. Στην ελαστική κρούση όπου το ένα σώμα είναι ακίνητο αρχικά εφαρμόζω τις γνωστές σχέσεις : Για το σώμα m 1 που αρχικά κινείται με ταχύτητα
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 17-10-11 ΑΠΟΦΟΙΤΟΙ ΣΕΙΡΑ Α Θέµα 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 δίπλα το γράµµα που αντιστοιχεί
17-10-11 ΑΠΟΦΟΙΤΟΙ ΣΕΙΡΑ Α Θέµα 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 δίπλα το γράµµα που αντιστοιχεί
Ενδεικτικές Λύσεις. Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Σε µία ϕθίνουσα ταλάντωση στην οποία το πλάτος µειώνεται εκθετικά µε το χρόνο : (ϐ) όταν η σταθερά απόσβεσης b µεγαλώνει, το
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Σε µία ϕθίνουσα ταλάντωση στην οποία το πλάτος µειώνεται εκθετικά µε το χρόνο : (ϐ) όταν η σταθερά απόσβεσης b µεγαλώνει, το
1.1. Μηχανικές Ταλαντώσεις.
 1.1. Μηχανικές. 1) Εξισώσεις ΑΑΤ Ένα υλικό σηµείο κάνει α.α.τ. µε πλάτος 0,1m και στην αρχή των χρόνων, βρίσκεται σε σηµείο Μ µε απο- µάκρυνση 5cm, αποµακρυνόµενο από τη θέση ισορροπίας. Μετά από 1s περνά
1.1. Μηχανικές. 1) Εξισώσεις ΑΑΤ Ένα υλικό σηµείο κάνει α.α.τ. µε πλάτος 0,1m και στην αρχή των χρόνων, βρίσκεται σε σηµείο Μ µε απο- µάκρυνση 5cm, αποµακρυνόµενο από τη θέση ισορροπίας. Μετά από 1s περνά
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 2019
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 019 Κινηματική ΑΣΚΗΣΗ Κ.1 Η επιτάχυνση ενός σώματος που κινείται ευθύγραμμα δίνεται από τη σχέση a = (4 t ) m s. Υπολογίστε την ταχύτητα και το διάστημα που διανύει το σώμα
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 019 Κινηματική ΑΣΚΗΣΗ Κ.1 Η επιτάχυνση ενός σώματος που κινείται ευθύγραμμα δίνεται από τη σχέση a = (4 t ) m s. Υπολογίστε την ταχύτητα και το διάστημα που διανύει το σώμα
ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 2ο set - μέρος Α - Απαντήσεις ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ο set - μέρος Α - Απαντήσεις ΘΕΜΑ Β Ερώτηση. Ένα σώμα εκτελεί
ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ο set - μέρος Α - Απαντήσεις ΘΕΜΑ Β Ερώτηση. Ένα σώμα εκτελεί
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΘΕΜΑTA Β
 1 ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΘΕΜΑTA Β 1) Tο σώμα Β του σχήματος είναι ακίνητο πάνω σε λείο οριζόντιο δάπεδο και δεμένο στην άκρη ιδανικού ελατηρίου. Το σώμα Α, μάζας ma, κινούμενο με ταχύτητα υα=3 m/s κατά
1 ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΘΕΜΑTA Β 1) Tο σώμα Β του σχήματος είναι ακίνητο πάνω σε λείο οριζόντιο δάπεδο και δεμένο στην άκρη ιδανικού ελατηρίου. Το σώμα Α, μάζας ma, κινούμενο με ταχύτητα υα=3 m/s κατά
Κριτήριο αξιολόγησης: Κρούσεις Αμείωτες Μηχανικές Ταλαντώσεις
 Κριτήριο αξιολόγησης: Κρούσεις Αμείωτες Μηχανικές Ταλαντώσεις Θέμα Α. (Για τις ερωτήσεις Α. έως και Α.4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη σωστή
Κριτήριο αξιολόγησης: Κρούσεις Αμείωτες Μηχανικές Ταλαντώσεις Θέμα Α. (Για τις ερωτήσεις Α. έως και Α.4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΕΝΩΣΗ ΦΥΣΙΚΩΝ ΚΥΠΡΟΥ
 33 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Α Φάση) Κυριακή, 16 Δεκεμβρίου 2018 Ώρα: 10:00-13:00 Οδηγίες: 1) Το δοκίμιο αποτελείται από επτά (7) σελίδες και πέντε (5) θέματα. 2) Να απαντήσετε σε όλα τα
33 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Α Φάση) Κυριακή, 16 Δεκεμβρίου 2018 Ώρα: 10:00-13:00 Οδηγίες: 1) Το δοκίμιο αποτελείται από επτά (7) σελίδες και πέντε (5) θέματα. 2) Να απαντήσετε σε όλα τα
1. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου.
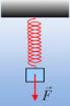 ΤΑΛΑΝΤΩΣΗ ΜΕΤΑ ΑΠΟ ΚΡΟΥΣΗ.. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου. Σώμα μάζας = g κινείται σε λείο οριζόντιο επίπεδο με ταχύτητα υ μέτρου υ = 5 /s συγκρούεται
ΤΑΛΑΝΤΩΣΗ ΜΕΤΑ ΑΠΟ ΚΡΟΥΣΗ.. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου. Σώμα μάζας = g κινείται σε λείο οριζόντιο επίπεδο με ταχύτητα υ μέτρου υ = 5 /s συγκρούεται
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ)
 ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) 30/9/208 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) 30/9/208 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΚΕΜΒΡΙΟΣ 2018 ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΤΑΛΑΝΤΩΣΕΙΣ ΚΑΙ ΣΤΙΣ ΚΡΟΥΣΕΙΣ
 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΚΕΜΒΡΙΟΣ 2018 ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΤΑΛΑΝΤΩΣΕΙΣ ΚΑΙ ΣΤΙΣ ΚΡΟΥΣΕΙΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Α. Α1. Κατά τη διάρκεια μιας
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΚΕΜΒΡΙΟΣ 2018 ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΤΑΛΑΝΤΩΣΕΙΣ ΚΑΙ ΣΤΙΣ ΚΡΟΥΣΕΙΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Α. Α1. Κατά τη διάρκεια μιας
Φάσμα. Group προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι.
 σύγχρονο Φάσμα Group προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι. μαθητικό φροντιστήριο Γραβιάς 85 ΚΗΠΟΥΠΟΛΗ 50.51.557 50.56.296 25ης Μαρτίου 111 ΠΕΤΡΟΥΠΟΛΗ 50.27.990 50.20.990 25ης Μαρτίου 74 Πλ.ΠΕΤΡΟΥΠΟΛΗΣ 50.50.658
σύγχρονο Φάσμα Group προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι. μαθητικό φροντιστήριο Γραβιάς 85 ΚΗΠΟΥΠΟΛΗ 50.51.557 50.56.296 25ης Μαρτίου 111 ΠΕΤΡΟΥΠΟΛΗ 50.27.990 50.20.990 25ης Μαρτίου 74 Πλ.ΠΕΤΡΟΥΠΟΛΗΣ 50.50.658
ΘΕΜΑΤΑ. Θέμα Α (5X5=25μον) Α1. Σώμα μάζας m που είναι προσδεμένο σε οριζόντιο ελατήριο σταθεράς k, όταν. Α2. Όταν δυο σώματα συγκρούονται πλαστικά:
 ΔΙΑΓΩΝΙΣΜΑ Μάθημα : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Καθηγητής/τρια: Ονοματεπώνυμο: Τμήμα: ΘΕΜΑΤΑ Θέμα Α (5X5=25μον) Α1. Σώμα μάζας m που είναι προσδεμένο σε οριζόντιο ελατήριο σταθεράς k, όταν απομακρύνεται
ΔΙΑΓΩΝΙΣΜΑ Μάθημα : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Καθηγητής/τρια: Ονοματεπώνυμο: Τμήμα: ΘΕΜΑΤΑ Θέμα Α (5X5=25μον) Α1. Σώμα μάζας m που είναι προσδεμένο σε οριζόντιο ελατήριο σταθεράς k, όταν απομακρύνεται
Ασκήσεις Εμπέδωσης Μηχανικ ές ταλαντώέ σέις
 Ασκήσεις Εμπέδωσης Μηχανικ ές ταλαντώέ σέις Όπου χρειάζεται, θεωρείστε ότι g = 10m/s 2 1. Σε μία απλή αρμονική ταλάντωση η μέγιστη απομάκρυνση από την θέση ισορροπίας είναι Α = 30cm. Ο χρόνος που χρειάζεται
Ασκήσεις Εμπέδωσης Μηχανικ ές ταλαντώέ σέις Όπου χρειάζεται, θεωρείστε ότι g = 10m/s 2 1. Σε μία απλή αρμονική ταλάντωση η μέγιστη απομάκρυνση από την θέση ισορροπίας είναι Α = 30cm. Ο χρόνος που χρειάζεται
12ο ΓΕΛ ΠΕΙΡΑΙΑ 12/10/2010 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗΝ ΑΑΤ
 1ο ΓΕΛ ΠΕΙΡΑΙΑ 1/10/010 Ονοµατεπώνυµο: Τµήµα: Γθετ ΟΜΑΔΑ Α Διάρκεια: 45 min ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗΝ ΑΑΤ Ένα ιδανικό κατακόρυφο ελατήριο, έχει σταθερά k=400ν/m και στηρίζεται µε
1ο ΓΕΛ ΠΕΙΡΑΙΑ 1/10/010 Ονοµατεπώνυµο: Τµήµα: Γθετ ΟΜΑΔΑ Α Διάρκεια: 45 min ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗΝ ΑΑΤ Ένα ιδανικό κατακόρυφο ελατήριο, έχει σταθερά k=400ν/m και στηρίζεται µε
Μηχανικές ταλαντώσεις
 ο ΘΕΜΑ Μηχανικές ταλαντώσεις Α Ερωτήσεις Πολλαπλής Επιλογής Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση Η εξίσωση της
ο ΘΕΜΑ Μηχανικές ταλαντώσεις Α Ερωτήσεις Πολλαπλής Επιλογής Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση Η εξίσωση της
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : OKΤΩΒΡΙΟΣ 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7
 ΑΡΧΗ ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : OKΤΩΒΡΙΟΣ 205 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 ΘΕΜΑ Ο : Στις παρακάτω ερωτήσεις έως 4 να γράψετε στο τετράδιό σας τον αριθμό
ΑΡΧΗ ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : OKΤΩΒΡΙΟΣ 205 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 ΘΕΜΑ Ο : Στις παρακάτω ερωτήσεις έως 4 να γράψετε στο τετράδιό σας τον αριθμό
