2) Ορμή και ρυθμός μεταβολής της στην κυκλική κίνηση. 3) Ένα σύστημα σωμάτων σε πτώση. 4) Ένα σύστημα επιταχύνεται. Γ) Ορμή και διατήρηση ορμής
|
|
|
- Λαμία Ρόκας
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Γ) Ορμή και διατήρηση ορμής 1) Στο ταβάνι, στον τοίχο ή στο πάτωμα; Βρισκόμαστε σε ένα δωμάτιο όπου ταβάνι τοίχος και δάπεδο έχουν φτιαχτεί από το ίδιο υλικό και κάνουμε το εξής πείραμα. Εκτοξεύουμε μπαλάκι του τένις μάζας m με κάποια ταχύτητα μέτρου υ ο, προς το ταβάνι, τον τοίχο, και το δάπεδο, (προς μία κατεύθυνση κάθε φορά). Σε κάθε περίπτωση το μέτρο της ταχύτητας από το μπαλάκι λίγο πριν αυτό χτυπήσει σε κάποια επιφάνεια υ 1 και το διάνυσμα της ταχύτητας ακριβώς κάθετο (στην επιφάνεια), την στιγμή ακριβώς πριν την κρούση και αμέσως μετά. Η ανακλώμενη ταχύτητα έχει μέτρο υ 2. Η δε χρονική διάρκεια Δt είναι ίδια και στις τρεις κρούσεις. Αν F 1, F 2, F 3, τα μέτρα των δυνάμεων που δέχεται το μπαλάκι από το ταβάνι, τον τοίχο, και το δάπεδο αντίστοιχα, η σχέση που περιγράφει σωστά τα μέτρα των δυνάμεων είναι: α. F 1 > F 2 > F 3 β. F 1 > F 3 > F 2 γ. F 3 > F 1 > F 2 δ. F 3 > F 2 > F 1 Απ: δ 2) Ορμή και ρυθμός μεταβολής της στην κυκλική κίνηση. Ένα σώμα μάζας 2kg ηρεμεί στο άκρο νήματος μήκους 45cm, όπως στο σχήμα (θέση Α). Εκτρέπουμε το σώμα φέρνοντάς το στη θέση Β, ώστε το νήμα να είναι τεντωμένο και οριζόντιο και το αφήνουμε να κινηθεί. Να βρεθούν η ορμή και ο ρυθμός μεταβολής της ορμής του σώματος: i) Μόλις αφεθεί να κινηθεί στη θέση Β. ii) Τη στιγμή που το νήμα θα γίνει κατακόρυφο (θέση Β). Απ: 0, 20kgm/s 2, 6kgm/s, 40kgm/s 2. 3) Ένα σύστημα σωμάτων σε πτώση. Δύο σώματα Α και Β με μάζες m 1 =0,3kg και m 2 =0,5kg αντίστοιχα, είναι δεμένα στα άκρα ενός ιδανικού ελατηρίου, σταθεράς k=40ν/m και φυσικού μήκους l 0 =0,4m. Συγκρατούμε με το χέρι μας το Α σώμα, ενώ το Β ταλαντώνεται σε κατακόρυφη διεύθυνση. Κάποια στιγμή αφήνουμε ελεύθερο και το σώμα Α, οπότε το σύστημα των σωμάτων πέφτει. i) Σε μια στιγμή t 1 που το μήκος του ελατηρίου είναι l 1 =0,6m να βρεθούν: α) Ο ρυθμός μεταβολής της ορμής του σώματος Α β) Ο ρυθμός μεταβολής της ορμής του Β σώματος. ii) Διατηρείται η συνολική ορμή του συστήματος των σωμάτων; Να δικαιολογήστε την απάντησή σας. Απ: 11kgm/s 2, -3kgm/s 2, Όχι 4) Ένα σύστημα επιταχύνεται. Σε λείο οριζόντιο επίπεδο σύρεται ένα αμαξίδιο μάζας 1kg, με την
2 επίδραση μιας σταθερής οριζόντιας δύναμης F=12Ν. Πάνω στο αμαξίδιο, έχει προσδεθεί με νήμα ένα σώμα Σ, μάζας 0,2kg. Ο συντελεστής τριβής μεταξύ των δύο σωμάτων είναι μ=0,5. Κάποια στιγμή t 0 =0, το καροτσάκι έχει ταχύτητα 2m/s. i) Να βρεθεί η ορμή και ο ρυθμός μεταβολής της ορμής του συστήματος τη στιγμή αυτή. ii) Αν την παραπάνω χρονική στιγμή, κοπεί το νήμα και το σώμα Σ ολισθαίνει πάνω στο αμαξίδιο: α) Να σχεδιάστε τις δυνάμεις που ασκούνται σε κάθε σώμα και να τις διακρίνετε σε εσωτερικές και εξωτερικές για το σύστημα αμαξίδιο-σώμα Σ. β) Να υπολογιστεί η ορμή και ο ρυθμός μεταβολής της ορμής του αμαξιδίου 1s, μετά το κόψιμο του νήματος. Ποιες οι αντίστοιχες απαντήσεις για το σώμα Σ; γ) Να βρεθεί η ορμή και ο ρυθμός μεταβολής της ορμής του συστήματος τη στιγμή αυτή. Απ: 2,4kgm/s, 12kgm/s 2, 13kgm/s, 11kgm/s 2, 1.4kgm/s, 1kgm/s 2, 14.4kgm/s, 12kgm/s 2 5) Το περπάτημα πάνω σε μια σανίδα. Σε λείο οριζόντιο επίπεδο, ηρεμεί μια σανίδα μάζας m, ενώ πάνω της είναι ακίνητο ένα παιδί μάζας Μ=4m. Σε μια στιγμή το παιδί αρχίζει να περπατά προς τα δεξιά με ταχύτητα (ως προς το έδαφος) υ 1. i) Να σχεδιάστε τις δυνάμεις που ασκούνται στο παιδί και στη σανίδα. ii) Να επιλέξτε την σωστή πρόταση για τη σανίδα: α) Θα παραμείνει ακίνητη. β) Θα κινηθεί προς τα δεξιά. γ) Θα κινηθεί προς τα αριστερά. iii) Αν φτάνοντας στο άκρο Α της σανίδας, το παιδί σταματήσει, τότε τελικά η σανίδα: α) Θα σταματήσει. β) Θα κινείται με ταχύτητα υ 1 προς τα αριστερά. γ) Θα κινείται με ταχύτητα 4υ 1. Να δικαιολογήστε τις απαντήσεις σας. Απ: αριστερά, σταματάει 6) Τι κρούση έγινε; Σε λείο οριζόντιο επίπεδο, κινούνται δύο σώματα Α και Β, με μάζες 2kg και 3kg αντίστοιχα, το ένα προς το άλλο, με ταχύτητες που έχουν το ίδιο μέτρο υ =5m/s. i) Να βρείτε την ορμή του συστήματος των δύο σωμάτων. ii) Αν το Α σώμα μετά την κρούση, κινηθεί προς τα αριστερά με ταχύτητα μέτρου 7m/s, με ποια ταχύτητα θα κινηθεί το σώμα Β; iii) Να βρεθεί η μεταβολή της ορμής κάθε σώματος που οφείλεται στην κρούση. iv) Στην παραπάνω κρούση η μηχανική ενέργεια παραμένει σταθερή; Να δικαιολογήσετε την απάντησή σας. 7) Μια ακόμη πλαστική κρούση. Ένα σώμα Α μάζας 2kg κινείται με ταχύτητα 5m/s, προς τα δεξιά και συγκρούεται μετωπικά και πλαστικά με σώμα Β. Μετά την κρούση το συσσωμάτωμα κινείται προς τ αριστερά με ταχύτητα 2m/s. i) Ποιες προτάσεις είναι σωστές και ποιες λάθος: α) Το σώμα Β ήταν αρχικά ακίνητο.
3 β) Η μεταβολή της ορμής του Α σώματος έχει φορά προς τ αριστερά και μέτρο 14 kg m/s. γ) Το σώμα Β δεν άλλαξε κατεύθυνση κίνησης κατά την κρούση. ii) Ποια ήταν η αρχική ταχύτητα του σώματος Β, αν η μάζα του είναι 5kg; Απ: Λ, Σ, Σ, -4,8m/s 8) Η ορμή και ένα σύστημα σωμάτων. Δυο σώματα Α και Β με μάζες m 1 =2kg και m 2 =1kg αντίστοιχα, ηρεμούν σε λείο οριζόντιο επίπεδο, έχοντας συμπιέσει ένα ιδανικό ελατήριο κατά Δl=0,2m, με τη βοήθεια νήματος. Σε μια στιγμή τραβάμε το Α σώμα ασκώντας του μια σταθερή οριζόντια δύναμη F=6Ν, όπως στο σχήμα, για χρονικό διάστημα Δt=2s. i) Να βρεθεί η ορμή που αποκτά το σύστημα των σωμάτων. Μετά από την κατάργηση της δύναμης, κάποια στιγμή κόβουμε το νήμα που συνδέει τα δυο σώματα. Παρατηρούμε ότι το σώμα Β επιβραδύνεται και τελικά ακινητοποιείται μετά την απελευθέρωση του ελατηρίου. Να βρεθούν: ii) Η τελική ταχύτητα του Α σώματος. iii) Η σταθερά του ελατηρίου. iv) Ο ρυθμός μεταβολής της ορμής του σώματος Β αμέσως μετά το κόψιμο του νήματος. Απ: 12kgm/s, 6m/s, 600N/m, -120kgm/s 2 9) Οι αρχές διατήρησης της ορμής και της ενέργειας. Σε λείο οριζόντιο επίπεδο ηρεμούν δυο σώματα Α και Β, με μάζες Μ=2kg και m=1kg, δεμένα στα άκρα ιδανικού ελατηρίου με φυσικό μήκος l 0 =0,5m. Πιάνοντας τα δυο σώματα συμπιέζουμε το ελατήριο, μέχρι το ελατήριο να αποκτήσει μήκος l 1 =0,2m και τα αφήνουμε ελεύθερα να κινηθούν. Τη στιγμή t 1 που το ελατήριο αποκτά μήκος l 2 =0,6m για πρώτη φορά, το σώμα Α έχει ταχύτητα μέτρου υ 1 =1m/s. Τη στιγμή αυτή πιάνουμε και ακινητοποιούμε ακαριαία το σώμα Α. i) Να βρεθεί η ταχύτητα του σώματος Β τη στιγμή t 1. ii) Να υπολογιστεί η σταθερά του ελατηρίου. iii) Ποιο είναι το μέγιστο μήκος που θα αποκτήσει το ελατήριο; iv) Πόση είναι η μέγιστη ταχύτητα που θα αποκτήσει το σώμα Β; Απ: 2m/s, 75N/m, 0,75m, 1,25 5 m/s 10) Ένα σώμα πάνω σε αμαξίδιο. Ένα σώμα μάζας m=1kg ηρεμεί πάνω σε αμαξίδιο μάζας Μ=3kg, συμπιέζοντας ένα ελατήριο κατά Δl=0,2m, με τη βοήθεια νήματος, όπως στο σχήμα. Το σώμα Σ δεν είναι δεμένο στο ελατήριο, ενώ δεν αναπτύσσονται τριβές μεταξύ αμαξιδίου και εδάφους, αλλά ούτε και
4 μεταξύ σώματος Σ και αμαξιδίου. Σε μια στιγμή κόβουμε το νήμα και το σώμα Σ εγκαταλείπει το ελατήριο έχοντας αποκτήσει ταχύτητα υ 1 =1,8m/s προς τα δεξιά. i) Να εξηγείστε γιατί θα κινηθεί και το αμαξίδιο, βρίσκοντας και την ταχύτητα που αποκτά. ii) Μόλις το σώμα Σ φτάσει στην απέναντι πλευρά του αμαξιδίου, προσκολλάται σε αυτήν. Να βρεθεί η απώλεια της μηχανικής ενέργειας κατά την πρόσκρουση αυτή. iii) Να υπολογιστεί η αρχική συσπείρωση του ελατηρίου. Απ: -0,6m/s, 2,16J, 108N/m 11) Ένας κύβος πάνω σε σανίδα. Σε λείο οριζόντιο επίπεδο ηρεμεί μια μακριά σανίδα, πάνω στην οποία βρίσκεται ένας ξύλινος κύβος. Ένα βλήμα κινούμενο οριζόντια σφηνώνεται στον κύβο. i) Αν δεν υπάρχουν τριβές μεταξύ κύβου και σανίδας, ποιες προτάσεις είναι σωστές και ποιες λάθος. α) Κατά την κρούση μεταξύ βλήματος και κύβου, η ορμή του βλήματος διατηρείται. β) Μετά την κρούση το συσσωμάτωμα θα κινηθεί με σταθερή ταχύτητα πάνω στη σανίδα. γ) Μετά την κρούση, η σανίδα θα κινηθεί προς τα δεξιά. δ) Η μηχανική ενέργεια του συστήματος παραμένει σταθερή. ii) Αν εμφανίζεται τριβή μεταξύ κύβου και σανίδας, παρατηρούμε ότι η σανίδα κινείται προς τα δεξιά, ενώ μετά από λίγο σταματά να γλιστρά πάνω της ο κύβος. Η διάρκεια της κρούσης βλήματος-κύβου είναι αμελητέα, τότε: α) Κατά την κρούση μεταξύ βλήματος και κύβου, η ορμή του συστήματος βλήμακύβος διατηρείται. β) Μετά την κρούση το συσσωμάτωμα θα κινηθεί με σταθερή ταχύτητα πάνω στη σανίδα. γ) Μετά την κρούση, η σανίδα θα κινηθεί προς τα δεξιά λόγω της ορμής του κύβου. δ) Η ορμή του συστήματος βλήμα-κύβος-σανίδα διατηρείται σταθερή. ε) Ο ρυθμός μεταβολής της ορμής της σανίδας παραμένει σταθερός, μέχρι να σταματήσει πάνω της ο κύβος. στ) Τελικά κάποια στιγμή θα σταματήσει η κίνηση του κύβου πάνω στη σανίδα και από εκεί και πέρα, το σύστημα θα κινηθεί με σταθερή ταχύτητα. Να δικαιολογήσετε τις απαντήσεις σας. i) Λ, Σ, Λ, Λ ii) Σ, Λ, Λ, Σ, Σ, Σ 12) Πυροβόλο και τριβή Πυροβόλο μάζας Μ = 1000 kg μαζί με το βλήμα, εκπυρσοκροτεί και εκτοξεύει οριζόντια το βλήμα μάζας m =5 kg, με ταχύτητα υ 0 =200 m/s. Το πυροβόλο μετά την ανάκρουση διανύει στο οριζόντιο δάπεδο διάστημα 0,5 m και σταματά. Να βρείτε: α) Την ταχύτητα ανάκρουσης του πυροβόλου. β) Το συντελεστή τριβής με το οριζόντιο επίπεδο. 13) Κιβώτιο και βλήμα Ξύλινο κιβώτιο μάζας M = 19 kg ηρεμεί σε οριζόντιο επίπεδο με το οποίο παρουσιάζει συντελεστή τριβής μ = 0,25. Βλήμα μάζας m = 1 kg κινούμενο οριζόντια, σφηνώνεται με ταχύτητα υ = 100 m/s στο κέντρο μάζας του κιβωτίου. Η διάρκεια της κρούσης είναι Δt 1 = 0,1 s. Στη συνέχεια δημιουργείται συσσωμάτωμα, το οποίο κινείται στο οριζόντιο επίπεδο για χρόνο Δt 2 διανύοντας διάστημα s μέχρι να σταματήσει. Να βρείτε:
5 α) Την ταχύτητα του συσσωματώματος αμέσως μετά την κρούση. β) Τη μέση δύναμη που δέχτηκε το βλήμα από το ξύλινο κιβώτιο κατά τη διάρκεια της κρούσης. γ) Τη χρονική διάρκεια Δt 2 και το διάστημα s. 14) Μια πλαστική κρούση Δυο σώματα με μάζες m 1 = 0,4 kg και m 2 = 0,6 kg, κινούνται πάνω σε οριζόντιο επίπεδο με το οποίο έχουν συντελεστή τριβής μ = 0,2. Τα σώματα κινούνται σε αντίθετες κατευθύνσεις και συγκρούονται πλαστικά έχοντας κατά τη στιγμή της κρούσης ταχύτητες υ 1 = 20 m/s και υ 2 = 5 m/s αντίστοιχα. Να υπολογίσετε: α) Την ταχύτητα του συσσωματώματος αμέσως μετά την κρούση. β) Την απώλεια της κινητικής ενέργειας του συστήματος λόγω της κρούσης. γ) Το διάστημα που θα διανύσει το συσσωμάτωμα μετά την κρούση. 15) Βλήμα - κιβώτιο Βλήμα μάζας m = 50 g κινούμενο οριζόντια με ταχύτητα υ 0 = 200 m/s, χτυπάει σε ξύλινο σώμα μάζας Μ = 95 g που είναι ακίνητο πάνω σε οριζόντιο επίπεδο και ενσωματώνεται σε αυτό. Αν ο συντελεστής τριβής μεταξύ σώματος και επιπέδου είναι μ = 0,4 να βρείτε: α) Την ταχύτητα του συσσωματώματος αμέσως μετά την πλαστική κρούση. β) Το διάστημα που θα διανύσει το συσσωμάτωμα μέχρι να σταματήσει. γ) Το ποσοστό της κινητικής ενέργειας του συστήματος που έγινε θερμότητα. 16) Βλήμα - κιβώτιο - ελατήριο Σώμα μάζας m = 50 g κινούμενο οριζόντια με ταχύτητα υ 0 = 200 m/s, χτυπάει σε ξύλινο σώμα μάζας Μ = 0,095 kg που είναι ακίνητο πάνω σε λείο οριζόντιο επίπεδο και εξέρχεται από αυτό με ταχύτητα υ. Το συσσωμάτωμα στη συνέχεια συμπιέζει οριζόντιο ελατήριο που έχει τη μια άκρη του στον κατακόρυφο τοίχο. Η σταθερά του ελατηρίου είναι k = 200 N/m. Αν η μέγιστη συμπίεση του ελατηρίου είναι χ = 0,2 m να βρείτε: α) Την ταχύτητα υ του βλήματος. β) Την απώλεια ενέργειας και το ποσοστό απώλειας ενέργειας του συστήματος. 17) Βαλλιστικό εκκρεμές Ένα βλήμα μάζας m = 10 g κινείται οριζόντια με ταχύτητα υ 0 = 400 m/s. Το βλήμα συγκρούεται με ένα κομμάτι ξύλο που έχει μάζα Μ = 1000 g και είναι κρεμασμένο από νήμα μήκους L = 1 m. Το βλήμα διαπερνάει το ξύλο και βγαίνει από αυτό με ταχύτητα υ = 20 m/s. Βρείτε: α) Την απώλεια ενέργειας του συστήματος κατά την κρούση. β) Το μέγιστο ύψος που θα φτάσει το ξύλο μετά την κρούση. γ) Τη μέγιστη γωνία κλίσης του νήματος μετά την κρούση. 18) Βλήμα και αβαρής ράβδος Ένα κομμάτι ξύλου μάζας Μ = 1 kg, είναι στερεωμένο στην άκρη μιας ράβδου που θεωρείται χωρίς βάρος και έχει μήκος L = 80 cm, η άλλη άκρη της οποίας είναι στερεωμένη σε δακτύλιο που περιβάλλει κατακόρυφο άξονα γύρω από τον οποίο μπορεί να περιστρέφεται χωρίς τριβές. Το ξύλινο σώμα είναι τοποθετημένο πάνω σε οριζόντιο επίπεδο. Βλήμα μάζας m = 20 g κινείται οριζόντια και κάθετα με τη ράβδο με ταχύτητα υ 0 = 400 m/s χτυπάει το ξύλο και βγαίνει από αυτό με ταχύτητα υ 0 = 20 m/s. Αν το ξύλινο σώμα κάνει 4 στροφές μέχρι να σταματήσει βρείτε:
6 α) Την ταχύτητα του ξύλου αμέσως μετά την κρούση. β) Ποιος είναι ο συντελεστής τριβής μεταξύ σώματος και επιπέδου; 19) Μια μπάλα εκτοξεύεται οριζόντια. Ένα παιδί μάζας 50kg είναι ακίνητο σε λείο οριζόντιο επίπεδο, κρατώντας στο χέρι του μια σφαίρα μάζας 1kg. Σε μια στιγμή εκτοξεύει τη σφαίρα οριζόντια με αρχική ταχύτητα υ 0 =10m/s, από ύψος h=1,8m. i) Να υπολογιστεί η κινητική ενέργεια της σφαίρας τη στιγμή που φτάνει στο έδαφος. ii) Πόσο απέχει η σφαίρα από το παιδί, τη στιγμή που αγγίζει το έδαφος; iii) Να υπολογιστεί το έργο της δύναμης F 1 που άσκησε το παιδί στην μπάλα κατά την εκτόξευσή της και το έργο της αντίδρασής της F 2. Απ: 68J, 6,12m, 50J, 1J 20) Ορμή - δύναμη - έργο Ένα σώμα μάζας 1Kg κινείται ευθύγραμμα σε οριζόντιο επίπεδο και η ταχύτητά του δίνεται από τη σχέση: υ = 4 t, (S.I.). Το σώμα και το οριζόντιο επίπεδο παρουσιάζουν τριβή με συντελεστή μ=0,2. Δίνεται ακόμη ότι στο σώμα δρα σταθερή οριζόντια δύναμη κατά την κατεύθυνση της κίνησης με μέτρο F, ενώ g=10m/s 2. α) Να υπολογίσετε την τιμή της συνισταμένης δύναμης που δέχεται το σώμα. β) Να υπολογίσετε την ορμή του σώματος 5s μετά την έναρξη της κίνησης. γ) Να σχεδιάσετε και να υπολογίσετε όλες τις δυνάμεις που δρουν στο σώμα. δ) Να υπολογίσετε το συνολικό έργο που παράγουν οι παραπάνω δυνάμεις στα 5 πρώτα δευτερόλεπτα της κίνησης. Απ: Α. ΣF=4Ν, Β. p=20kg m/s, Γ. Τ=2Ν, w=10n, N=10N, F=6N, Δ. Wολ=200J. 21) Κεκλιμένο επίπεδο και κρούση Ένα σώμα Σ 1 μάζας m 1 =2Kg αφήνεται ελεύθερο πάνω σε λείο κεκλιμένο επίπεδο, από ύψος h=0,8m. Α. Να υπολογίσετε: α) τη δυναμική ενέργεια του σώματος Σ 1 στη θέση εκκίνησης. β) το μέτρο της ταχύτητας του σώματος Σ 1 στη βάση του κεκλιμένου επιπέδου. Β. Το σώμα Σ 1 μετά την κίνηση στο κεκλιμένο επίπεδο μπαίνει ομαλά σε οριζόντιο επίπεδο με το οποίο έχει συντελεστή τριβής ολίσθησης μ=0,2 και αφού διανύσει απόσταση S=3m κάνει μετωπική πλαστική κρούση με ένα ακίνητο σώμα Σ 2 ίσης μάζας. Να υπολογίσετε: α) το μέτρο της ταχύτητας του σώματος Σ 1 ακριβώς πριν απ την κρούση. β) το μέτρο της ταχύτητας του συσσωματώματος αμέσως μετά την κρούση. Δίνεται: g=10m/s 2. Απ: Α. α. u g =16J, β. u=4m/s, B. α. u 1 =2m/s, β. u σ =1m/s. 22) Μια πλαστική κρούση και η μέση δύναμη Δύο σώματα Α και Β με μάζες m Α =15kg και m B =5kg και ταχύτητες της ίδιας διεύθυνσης και αντίθετης φοράς συγκρούονται μετωπικά και πλαστικά πάνω σε οριζόντιο επίπεδο. Οι ταχύτητες των σωμάτων αμέσως πριν την κρούση είναι υ A =5m/s και υ B =3m/s. Το συσσωμάτωμα παρουσιάζει με το οριζόντιο επίπεδο συντελεστή τριβής μ=0,3. Να βρείτε:
7 Α. την ταχύτητα του συσσωματώματος αμέσως μετά τη σύγκρουση. Β. σε πόση απόσταση από τη θέση κρούσης θα σταματήσει το συσσωμάτωμα. Γ. το μέτρο της μέσης δύναμης που δέχτηκε το σώμα Β κατά την κρούση, αν η διάρκεια της κρούσης ήταν Δt=0,12s. Δίνεται: g = 10 m/s 2. Δεχτείτε ότι η κρούση αρχίζει και τελειώνει στην ίδια θέση. Απ: Α. u=3m/s, Β. Δx=1,5m, Γ. F=250N.
3.1. Διατήρηση της Ορμής.
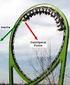
 3.1. Διατήρηση της Ορμής. 3.1.Ορμή και ρυθμός μεταβολής της ορμής. Ένα σώμα μάζας m=2kg εκτελεί ομαλή κυκλική κίνηση με ταχύτητα υ=5m/s σε κύκλο κέντρου Ο και ακτίνας R=10m. i) Υπολογίστε την ορμή του
3.1. Διατήρηση της Ορμής. 3.1.Ορμή και ρυθμός μεταβολής της ορμής. Ένα σώμα μάζας m=2kg εκτελεί ομαλή κυκλική κίνηση με ταχύτητα υ=5m/s σε κύκλο κέντρου Ο και ακτίνας R=10m. i) Υπολογίστε την ορμή του
3.1. Διατήρηση της Ορμής.
 3.1. Διατήρηση της Ορμής. 3.1.Ορμή και ρυθμός μεταβολής της ορμής. Ένα σώμα μάζας m=2kg εκτελεί ομαλή κυκλική κίνηση με ταχύτητα υ=5m/s σε κύκλο κέντρου Ο και ακτίνας R=10m. υ Γ Ο Α i) Υπολογίστε την ορμή
3.1. Διατήρηση της Ορμής. 3.1.Ορμή και ρυθμός μεταβολής της ορμής. Ένα σώμα μάζας m=2kg εκτελεί ομαλή κυκλική κίνηση με ταχύτητα υ=5m/s σε κύκλο κέντρου Ο και ακτίνας R=10m. υ Γ Ο Α i) Υπολογίστε την ορμή
3.2. Διατήρηση της Ορμής. Ομάδα Γ.
 3.2. Διατήρηση της Ορμής. Ομάδα Γ. 3.21. Η ορμή και ένα σύστημα σωμάτων. Δυο σώματα Α και Β με μάζες m 1 =2kg και m 2 =1kg αντίστοιχα, ηρεμούν σε λείο οριζόντιο επίπεδο, έχοντας συμπιέσει ένα ιδανικό ελατήριο
3.2. Διατήρηση της Ορμής. Ομάδα Γ. 3.21. Η ορμή και ένα σύστημα σωμάτων. Δυο σώματα Α και Β με μάζες m 1 =2kg και m 2 =1kg αντίστοιχα, ηρεμούν σε λείο οριζόντιο επίπεδο, έχοντας συμπιέσει ένα ιδανικό ελατήριο
4.1. Κρούσεις. Κρούσεις. 4.1.Ταχύτητες κατά την ελαστική κρούση Η Ορμή είναι διάνυσμα. 4.3.Κρούση και Ενέργεια.
 4.1.. 4.1.Ταχύτητες κατά την ελαστική κρούση. Σε λείο οριζόντιο επίπεδο κινείται ένα σώμα Α μάζας m 1 =0,2kg με ταχύτητα υ 1 =6m/s και συγκρούεται κεντρικά και ελαστικά με δεύτερο σώμα Β μάζας m 2 =0,4kg.
4.1.. 4.1.Ταχύτητες κατά την ελαστική κρούση. Σε λείο οριζόντιο επίπεδο κινείται ένα σώμα Α μάζας m 1 =0,2kg με ταχύτητα υ 1 =6m/s και συγκρούεται κεντρικά και ελαστικά με δεύτερο σώμα Β μάζας m 2 =0,4kg.
[50m/s, 2m/s, 1%, -10kgm/s, 1000N]
![[50m/s, 2m/s, 1%, -10kgm/s, 1000N] [50m/s, 2m/s, 1%, -10kgm/s, 1000N]](/thumbs/64/51024975.jpg) ΚΕΦΑΛΑΙΟ 5 ο - ΜΕΡΟΣ Α : ΚΡΟΥΣΕΙΣ ΕΝΟΤΗΤΑ 1: ΚΡΟΥΣΕΙΣ 1. Σώμα ηρεμεί σε οριζόντιο επίπεδο. Βλήμα κινούμενο οριζόντια με ταχύτητα μέτρου και το με ταχύτητα, διαπερνά το σώμα χάνοντας % της κινητικής του
ΚΕΦΑΛΑΙΟ 5 ο - ΜΕΡΟΣ Α : ΚΡΟΥΣΕΙΣ ΕΝΟΤΗΤΑ 1: ΚΡΟΥΣΕΙΣ 1. Σώμα ηρεμεί σε οριζόντιο επίπεδο. Βλήμα κινούμενο οριζόντια με ταχύτητα μέτρου και το με ταχύτητα, διαπερνά το σώμα χάνοντας % της κινητικής του
Κρούσεις. Ομάδα Γ. Κρούσεις Ενέργεια Ταλάντωσης και Ελαστική κρούση Κρούση και τριβές Κεντρική ανελαστική κρούση
 . Ομάδα Γ. 4.1.21. Ενέργεια Ταλάντωσης και Ελαστική κρούση. Μια πλάκα μάζας Μ=4kg ηρεμεί στο πάνω άκρο ενός κατακόρυφου ελατηρίου, σταθεράς k=250ν/m, το άλλο άκρο του οποίου στηρίζεται στο έδαφος. Εκτρέπουμε
. Ομάδα Γ. 4.1.21. Ενέργεια Ταλάντωσης και Ελαστική κρούση. Μια πλάκα μάζας Μ=4kg ηρεμεί στο πάνω άκρο ενός κατακόρυφου ελατηρίου, σταθεράς k=250ν/m, το άλλο άκρο του οποίου στηρίζεται στο έδαφος. Εκτρέπουμε
ΚΡΟΥΣΕΙΣ. γ) Δ 64 J δ) 64%]
![ΚΡΟΥΣΕΙΣ. γ) Δ 64 J δ) 64%] ΚΡΟΥΣΕΙΣ. γ) Δ 64 J δ) 64%]](/thumbs/65/53613594.jpg) 1. Μικρή σφαίρα Σ1, μάζας 2 kg που κινείται πάνω σε λείο επίπεδο με ταχύτητα 10 m/s συγκρούεται κεντρικά και ελαστικά με ακίνητη σφαίρα Σ2 μάζας 8 kg. Να υπολογίσετε: α) τις ταχύτητες των σωμάτων μετά
1. Μικρή σφαίρα Σ1, μάζας 2 kg που κινείται πάνω σε λείο επίπεδο με ταχύτητα 10 m/s συγκρούεται κεντρικά και ελαστικά με ακίνητη σφαίρα Σ2 μάζας 8 kg. Να υπολογίσετε: α) τις ταχύτητες των σωμάτων μετά
[απ. α) =2 m/s, β) h=1,25 m, γ) =9 J, =8 J]
![[απ. α) =2 m/s, β) h=1,25 m, γ) =9 J, =8 J] [απ. α) =2 m/s, β) h=1,25 m, γ) =9 J, =8 J]](/thumbs/52/30027619.jpg) Ορµή 1. Ένα αυτοκίνητο μάζας 1000 kg κινείται με ταχύτητα 72 km/h. Κάποια στιγμή προσκρούει σε τοίχο και σταματάει. Αν η διάρκεια της σύγκρουσης είναι 0,2 s να βρείτε α) Την μεταβολή της ορμής του β) Τη
Ορµή 1. Ένα αυτοκίνητο μάζας 1000 kg κινείται με ταχύτητα 72 km/h. Κάποια στιγμή προσκρούει σε τοίχο και σταματάει. Αν η διάρκεια της σύγκρουσης είναι 0,2 s να βρείτε α) Την μεταβολή της ορμής του β) Τη
προς ένα ακίνητο σωμάτιο α (πυρήνας Ηe), το οποίο είναι ελεύθερο να κινηθεί,
 ΚΡΟΥΣΕΙΣ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ 1. Σφαίρα Α μάζας 3m κινείται πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική φορά και συγκρούεται κεντρικά και ελαστικά με άλλη σφαίρα Β μάζας m που κινείται κατά την
ΚΡΟΥΣΕΙΣ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ 1. Σφαίρα Α μάζας 3m κινείται πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική φορά και συγκρούεται κεντρικά και ελαστικά με άλλη σφαίρα Β μάζας m που κινείται κατά την
ΑΣΚΗΣΕΙΣ ΚΡΟΥΣΗΣ. Ελαστική κρούση
 Ελαστική κρούση 1. Σώμα μάζας m 1 = 2 kg που κινείται προς τα δεξιά με ταχύτητα μέτρου υ 1 = 4 m / s συγκρούεται κεντρικά και ελαστικά με άλλη σφαίρα μάζας m 2 = 4 kg που κινείται και αυτή προς τα δεξιά
Ελαστική κρούση 1. Σώμα μάζας m 1 = 2 kg που κινείται προς τα δεξιά με ταχύτητα μέτρου υ 1 = 4 m / s συγκρούεται κεντρικά και ελαστικά με άλλη σφαίρα μάζας m 2 = 4 kg που κινείται και αυτή προς τα δεξιά
4.1.α. Κρούσεις. Κρούσεις. 4.1.21. Ενέργεια Ταλάντωσης και Ελαστική κρούση. 4.1.22. Κρούση και τριβές. 4.1.23. Κεντρική ανελαστική κρούση
 4.1.α.. 4.1.21. Ενέργεια Ταλάντωσης και Ελαστική κρούση. Μια πλάκα µάζας Μ=4kg ηρεµεί στο πάνω άκρο ενός κατακόρυφου ελατηρίου, σταθεράς k=250ν/m, το άλλο άκρο του οποίου στηρίζεται στο έδαφος. Εκτρέπουµε
4.1.α.. 4.1.21. Ενέργεια Ταλάντωσης και Ελαστική κρούση. Μια πλάκα µάζας Μ=4kg ηρεµεί στο πάνω άκρο ενός κατακόρυφου ελατηρίου, σταθεράς k=250ν/m, το άλλο άκρο του οποίου στηρίζεται στο έδαφος. Εκτρέπουµε
ΕΡΓΑΣΙΑ ΧΡΙΣΤΟΥΓΕΝΝΩΝ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ 25/12/2016 ΘΕΜΑ
 ΕΡΓΑΣΙΑ ΧΡΙΣΤΟΥΓΕΝΝΩΝ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ 5//06 ΘΕΜΑ Στις παρακάτω ερωτήσεις - 7 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα σε κάθε αριθμό το γράµμα που αντιστοιχεί στη
ΕΡΓΑΣΙΑ ΧΡΙΣΤΟΥΓΕΝΝΩΝ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ 5//06 ΘΕΜΑ Στις παρακάτω ερωτήσεις - 7 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα σε κάθε αριθμό το γράµμα που αντιστοιχεί στη
των δύο σφαιρών είναι. γ.
 ΘΕΜΑ B Σφαίρα µάζας κινούµενη µε ταχύτητα µέτρου υ συγκρούεται κεντρικά και ελαστικά µε ακίνητη σφαίρα ίσης µάζας Να βρείτε τις σχέσεις που δίνουν τις ταχύτητες των δύο σφαιρών, µετά την κρούση, µε εφαρµογή
ΘΕΜΑ B Σφαίρα µάζας κινούµενη µε ταχύτητα µέτρου υ συγκρούεται κεντρικά και ελαστικά µε ακίνητη σφαίρα ίσης µάζας Να βρείτε τις σχέσεις που δίνουν τις ταχύτητες των δύο σφαιρών, µετά την κρούση, µε εφαρµογή
Επανάληψη: Κρούσεις και φαινόμενο Doppler (Φ24) 4. α. β. ii. iii. 6. α.
 Επανάληψη: Κρούσεις και φαινόμενο Doppler (Φ24) 1. Μια σφαίρα με μάζα m 1 συγκρούεται μετωπικά και ελαστικά με μια ακίνητη σφαίρα μάζας m 2. Ποια πρέπει να είναι η σχέση της μάζας m 1 με τη μάζα m 2 ώστε:
Επανάληψη: Κρούσεις και φαινόμενο Doppler (Φ24) 1. Μια σφαίρα με μάζα m 1 συγκρούεται μετωπικά και ελαστικά με μια ακίνητη σφαίρα μάζας m 2. Ποια πρέπει να είναι η σχέση της μάζας m 1 με τη μάζα m 2 ώστε:
ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ ΠΡΟΣΠΑΘΕΙΑ ΣΑΣ ΚΙ 2014
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΕΠΑΝΑΛΗΠΤΙΚΗ ΕΡΓΑΣΙΑ ΦΥΣΙΚΗΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 2015 ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ
 ΕΠΑΝΑΛΗΠΤΙΚΗ ΕΡΓΑΣΙΑ ΦΥΣΙΚΗΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 2015 ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ Οριζόντια βολή: Είναι η κίνηση (παραβολική τροχιά) που κάνει ένα σώμα το οποίο βάλλεται με οριζόντια ταχύτητα U 0 μέσα στο πεδίο βαρύτητας
ΕΠΑΝΑΛΗΠΤΙΚΗ ΕΡΓΑΣΙΑ ΦΥΣΙΚΗΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 2015 ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ Οριζόντια βολή: Είναι η κίνηση (παραβολική τροχιά) που κάνει ένα σώμα το οποίο βάλλεται με οριζόντια ταχύτητα U 0 μέσα στο πεδίο βαρύτητας
Ερωτήσεις του τύπου Σωστό /Λάθος
 Ερωτήσεις του τύπου Σωστό /Λάθος Οδηγία: Για να απαντήσετε στις παρακάτω ερωτήσεις, αρκεί να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και δεξιά απ αυτόν το γράμμα Σ αν την κρίνετε σωστή ή το
Ερωτήσεις του τύπου Σωστό /Λάθος Οδηγία: Για να απαντήσετε στις παρακάτω ερωτήσεις, αρκεί να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και δεξιά απ αυτόν το γράμμα Σ αν την κρίνετε σωστή ή το
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΕΛΑΤΗΡΙΟ-ΚΡΟΥΣΗ. Σε όσες ασκήσεις απαιτείται δίνεται επιτάχυνση βαρύτητας g=10 m/s 2.
 ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΕΛΑΤΗΡΙΟ-ΚΡΟΥΣΗ Σε όσες ασκήσεις απαιτείται δίνεται επιτάχυνση βαρύτητας g=10 m/s 2. ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Η δύναμη επαναφοράς που ασκείται σε ένα σώμα μάζας m που εκτελεί απλή αρμονική
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΕΛΑΤΗΡΙΟ-ΚΡΟΥΣΗ Σε όσες ασκήσεις απαιτείται δίνεται επιτάχυνση βαρύτητας g=10 m/s 2. ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Η δύναμη επαναφοράς που ασκείται σε ένα σώμα μάζας m που εκτελεί απλή αρμονική
ΕΡΓΟ ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ - ΙΣΧΥΣ
 ΕΡΓΟ ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ - ΙΣΧΥΣ 1. Στο σώμα του σχήματος έχει βάρος Β = 20Ν είναι ακίνητο και του ασκούνται οι δυνάμεις F 1 = 5Ν, F 2 = 10Ν, F 3 = 15Ν και F 4 = 10Ν. Αν το σώμα μετακινηθεί οριζόντια προς
ΕΡΓΟ ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ - ΙΣΧΥΣ 1. Στο σώμα του σχήματος έχει βάρος Β = 20Ν είναι ακίνητο και του ασκούνται οι δυνάμεις F 1 = 5Ν, F 2 = 10Ν, F 3 = 15Ν και F 4 = 10Ν. Αν το σώμα μετακινηθεί οριζόντια προς
Κρούσεις. Ομάδα Δ. Κρούσεις Μια κρούση και οι τριβές Κρούση σφαίρας με άλλη ακίνητη.
 . Ομάδα Δ. 4.1.41. Μια κρούση και οι τριβές. Σε οριζόντιο επίπεδο ηρεμούν δυο σώματα Α και Β με μάζες m=1kg και Μ=3kg αντίστοιχα, τα οποία απέχουν απόσταση d=4,75m. Το Β είναι δεμένο στο άκρο ιδανικού
. Ομάδα Δ. 4.1.41. Μια κρούση και οι τριβές. Σε οριζόντιο επίπεδο ηρεμούν δυο σώματα Α και Β με μάζες m=1kg και Μ=3kg αντίστοιχα, τα οποία απέχουν απόσταση d=4,75m. Το Β είναι δεμένο στο άκρο ιδανικού
ΕΡΓΟ - ΕΝΕΡΓΕΙΑ F 2 F 3 F 1 F 4
 1. F 2 F 3 F 1 F 4 Στο σώμα του παραπάνω σχήματος βάρους Β = 20Ν ασκούνται οι δυνάμεις F 1 = 5Ν, F 2 = 10Ν, F 3 = 15Ν και F 4 = 10Ν. Αν το σώμα μετακινηθεί οριζόντια προς τα δεξιά κατά 2m να υπολογισθεί
1. F 2 F 3 F 1 F 4 Στο σώμα του παραπάνω σχήματος βάρους Β = 20Ν ασκούνται οι δυνάμεις F 1 = 5Ν, F 2 = 10Ν, F 3 = 15Ν και F 4 = 10Ν. Αν το σώμα μετακινηθεί οριζόντια προς τα δεξιά κατά 2m να υπολογισθεί
Λύση Ισχύει : ΔΡ 1 = Ρ 1 Ρ 1 ΔΡ 1 = m 1 υ 1 m 1 υ 1 m 1 υ 1 = ΔΡ 1 + m 1 υ 1 υ 1 = (ΔΡ 1 + m 1 υ 1 ) / m 1 υ 1 = [ (6)] / 1 υ 1 = 2 m / s. Η αρ
![Λύση Ισχύει : ΔΡ 1 = Ρ 1 Ρ 1 ΔΡ 1 = m 1 υ 1 m 1 υ 1 m 1 υ 1 = ΔΡ 1 + m 1 υ 1 υ 1 = (ΔΡ 1 + m 1 υ 1 ) / m 1 υ 1 = [ (6)] / 1 υ 1 = 2 m / s. Η αρ Λύση Ισχύει : ΔΡ 1 = Ρ 1 Ρ 1 ΔΡ 1 = m 1 υ 1 m 1 υ 1 m 1 υ 1 = ΔΡ 1 + m 1 υ 1 υ 1 = (ΔΡ 1 + m 1 υ 1 ) / m 1 υ 1 = [ (6)] / 1 υ 1 = 2 m / s. Η αρ](/thumbs/93/112718435.jpg) 1)Σώμα μάζας m 1 = 0,3 kg που κινείται με οριζόντια ταχύτητα υ 1 = 100 m / s συγκρούεται πλαστικά με σώμα μάζας m 2 = 1,7 kg που βρίσκεται αρχικά ακίνητο πάνω σε λείο οριζόντιο επίπεδο. Να υπολογίσετε
1)Σώμα μάζας m 1 = 0,3 kg που κινείται με οριζόντια ταχύτητα υ 1 = 100 m / s συγκρούεται πλαστικά με σώμα μάζας m 2 = 1,7 kg που βρίσκεται αρχικά ακίνητο πάνω σε λείο οριζόντιο επίπεδο. Να υπολογίσετε
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Ε.
 1.1. Μηχανικές. Ομάδα Ε. 1.1.81. Δυο ΑΑΤ και μία Ταλάντωση. Ένα σώμα μάζας 1kg ηρεμεί σε λείο κεκλιμένο επίπεδο κλίσεως θ=30, δεμένο στο άκρο ελατηρίου σταθεράς k 1 =40Ν/m, ενώ εφάπτεται στο ε- λεύθερο
1.1. Μηχανικές. Ομάδα Ε. 1.1.81. Δυο ΑΑΤ και μία Ταλάντωση. Ένα σώμα μάζας 1kg ηρεμεί σε λείο κεκλιμένο επίπεδο κλίσεως θ=30, δεμένο στο άκρο ελατηρίου σταθεράς k 1 =40Ν/m, ενώ εφάπτεται στο ε- λεύθερο
ΕΡΓΑΣΙΑ 3 ΟΡΜΗ-ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΟΡΜΗΣ
 ΕΡΓΑΣΙΑ 3 ΟΡΜΗ-ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΟΡΜΗΣ Παρατηρήσεις-Υποδείξεις Μετωπική λέγεται η κρούση κατά την οποία τα διανύσματα των ταχυτήτων πριν την κρούση των σωμάτων που συγκρούονται βρίσκονται στην ίδια ευθεία.
ΕΡΓΑΣΙΑ 3 ΟΡΜΗ-ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΟΡΜΗΣ Παρατηρήσεις-Υποδείξεις Μετωπική λέγεται η κρούση κατά την οποία τα διανύσματα των ταχυτήτων πριν την κρούση των σωμάτων που συγκρούονται βρίσκονται στην ίδια ευθεία.
ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΣΤΗΝ ΕΝΟΤΗΤΑ ΟΡΜΗ ΡΥΘΜΟΣ ΜΕΤΑΒΟΛΗΣ ΤΗΣ ΟΡΜΗΣ ΑΡΧΗ ΔΙΑΤΗΡΗΣΗΣ ΤΗΣ ΟΡΜΗΣ Τάξη Β : Προσανατολισμού Θετικών Σπουδών
 ΘΕΜΑ Α Στις ερωτήσεις Α1 Α3 μία από τις απαντήσεις είναι σωστή Α1.Η μονάδα μέτρησης της ορμής στο Διεθνές Σύστημα (S.I.) είναι: α) β) 1Ν.s γ) δ) Α2.Ένα παιδί εκτοξεύει κατακόρυφα προς τα πάνω μια μικρή
ΘΕΜΑ Α Στις ερωτήσεις Α1 Α3 μία από τις απαντήσεις είναι σωστή Α1.Η μονάδα μέτρησης της ορμής στο Διεθνές Σύστημα (S.I.) είναι: α) β) 1Ν.s γ) δ) Α2.Ένα παιδί εκτοξεύει κατακόρυφα προς τα πάνω μια μικρή
ΘΕΜΑΤΑ. Θέμα Α (5X5=25μον) Α1. Σώμα μάζας m που είναι προσδεμένο σε οριζόντιο ελατήριο σταθεράς k, όταν. Α2. Όταν δυο σώματα συγκρούονται πλαστικά:
 ΔΙΑΓΩΝΙΣΜΑ Μάθημα : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Καθηγητής/τρια: Ονοματεπώνυμο: Τμήμα: ΘΕΜΑΤΑ Θέμα Α (5X5=25μον) Α1. Σώμα μάζας m που είναι προσδεμένο σε οριζόντιο ελατήριο σταθεράς k, όταν απομακρύνεται
ΔΙΑΓΩΝΙΣΜΑ Μάθημα : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Καθηγητής/τρια: Ονοματεπώνυμο: Τμήμα: ΘΕΜΑΤΑ Θέμα Α (5X5=25μον) Α1. Σώμα μάζας m που είναι προσδεμένο σε οριζόντιο ελατήριο σταθεράς k, όταν απομακρύνεται
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΓΕ.Λ. [Ημερομηνία] ΟΡΜΗ-ΚΡΟΥΣΕΙΣ ΣΤΕΦΑΝΟΥ Μ. ΦΥΣΙΚΟΣ
![ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΓΕ.Λ. [Ημερομηνία] ΟΡΜΗ-ΚΡΟΥΣΕΙΣ ΣΤΕΦΑΝΟΥ Μ. ΦΥΣΙΚΟΣ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΓΕ.Λ. [Ημερομηνία] ΟΡΜΗ-ΚΡΟΥΣΕΙΣ ΣΤΕΦΑΝΟΥ Μ. ΦΥΣΙΚΟΣ](/thumbs/52/30414008.jpg) ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΓΕ.Λ [Ημερομηνία] ΟΡΜΗ-ΚΡΟΥΣΕΙΣ ΣΤΕΦΑΝΟΥ Μ. ΦΥΣΙΚΟΣ ΠΑΡΑΤΗΡΗΣΕΙΣ 1. Στην ελαστική κρούση όπου το ένα σώμα είναι ακίνητο αρχικά εφαρμόζω τις γνωστές σχέσεις : Για το σώμα m 1 που αρχικά
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΓΕ.Λ [Ημερομηνία] ΟΡΜΗ-ΚΡΟΥΣΕΙΣ ΣΤΕΦΑΝΟΥ Μ. ΦΥΣΙΚΟΣ ΠΑΡΑΤΗΡΗΣΕΙΣ 1. Στην ελαστική κρούση όπου το ένα σώμα είναι ακίνητο αρχικά εφαρμόζω τις γνωστές σχέσεις : Για το σώμα m 1 που αρχικά
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Ε.
 .. Μηχανικές. Ομάδα Ε...8. Δυο ΑΑΤ και μία Ταλάντωση. Ένα σώμα μάζας kg ηρεμεί σε λείο κεκλιμένο επίπεδο κλίσεως θ=30, δεμένο στο άκρο ελατηρίου σταθεράς k =40Ν/m, ενώ εφάπτεται στο ε- λεύθερο άκρο ενός
.. Μηχανικές. Ομάδα Ε...8. Δυο ΑΑΤ και μία Ταλάντωση. Ένα σώμα μάζας kg ηρεμεί σε λείο κεκλιμένο επίπεδο κλίσεως θ=30, δεμένο στο άκρο ελατηρίου σταθεράς k =40Ν/m, ενώ εφάπτεται στο ε- λεύθερο άκρο ενός
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Στ.
 1.1. Μηχανικές Ταλαντώσεις. Ομάδα Στ. 101) Δυο σώματα αφήνονται να κινηθούν. Δυο σώματα Σ 1 και Σ 2, ίδιας μάζας m=2kg, συγκρατιόνται σε λείο κεκλιμένο επίπεδο απέχοντας κατά D=1,5m από την κορυφή του
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Στ. 101) Δυο σώματα αφήνονται να κινηθούν. Δυο σώματα Σ 1 και Σ 2, ίδιας μάζας m=2kg, συγκρατιόνται σε λείο κεκλιμένο επίπεδο απέχοντας κατά D=1,5m από την κορυφή του
ΕΡΓΑΣΙΑ 3 ΟΡΜΗ-ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΟΡΜΗΣ
 ΕΡΓΑΣΙΑ 3 ΟΡΜΗ-ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΟΡΜΗΣ Παρατηρήσεις-Υποδείξεις Μετωπική λέγεται η κρούση κατά την οποία τα διανύσματα των ταχυτήτων πριν την κρούση των σωμάτων που συγκρούονται βρίσκονται στην ίδια ευθεία.
ΕΡΓΑΣΙΑ 3 ΟΡΜΗ-ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΟΡΜΗΣ Παρατηρήσεις-Υποδείξεις Μετωπική λέγεται η κρούση κατά την οποία τα διανύσματα των ταχυτήτων πριν την κρούση των σωμάτων που συγκρούονται βρίσκονται στην ίδια ευθεία.
ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ
 ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ 1. Κατακόρυφο ελατήριο σταθεράς k=1000 N /m έχει το κάτω άκρο του στερεωμένο σε ακίνητο σημείο. Στο πάνω άκρο του ελατηρίου έχει προσδεθεί σώμα Σ 1 μάζας m 1 =8 kg, ενώ ένα δεύτερο
ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ 1. Κατακόρυφο ελατήριο σταθεράς k=1000 N /m έχει το κάτω άκρο του στερεωμένο σε ακίνητο σημείο. Στο πάνω άκρο του ελατηρίου έχει προσδεθεί σώμα Σ 1 μάζας m 1 =8 kg, ενώ ένα δεύτερο
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 1 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 5) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 1 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 5) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
0. Ασκήσεις επανάληψης.
 0. Ασκήσεις επανάληψης. 1. Κίνηση με μεταβλητή κατακόρυφη δύναμη Ένα σώμα μάζας 2kg βρίσκεται ακίνητο στο έδαφος. Σε μια στιγμή δέχεται την επίδραση μιας μεταβλητής κατακόρυφης δύναμης F, το μέτρο της
0. Ασκήσεις επανάληψης. 1. Κίνηση με μεταβλητή κατακόρυφη δύναμη Ένα σώμα μάζας 2kg βρίσκεται ακίνητο στο έδαφος. Σε μια στιγμή δέχεται την επίδραση μιας μεταβλητής κατακόρυφης δύναμης F, το μέτρο της
ΔΥΝΑΜΙΚΗ ΣΕ ΔΥΟ ΔΙΑΣΤΑΣΕΙΣ
 ΔΥΝΑΜΙΚΗ ΣΕ ΔΥΟ ΔΙΑΣΤΑΣΕΙΣ 1. Ένα σώμα μάζας 2kg ηρεμεί σε λείο οριζόντιο επίπεδο. Σε μια στιγμή ασκούνται πάνω του οι οριζόντιες δυνάμεις που εμφανίζονται στο σχήμα. Δίνονται F 1 =8 3N, F 2 =14N, F 3
ΔΥΝΑΜΙΚΗ ΣΕ ΔΥΟ ΔΙΑΣΤΑΣΕΙΣ 1. Ένα σώμα μάζας 2kg ηρεμεί σε λείο οριζόντιο επίπεδο. Σε μια στιγμή ασκούνται πάνω του οι οριζόντιες δυνάμεις που εμφανίζονται στο σχήμα. Δίνονται F 1 =8 3N, F 2 =14N, F 3
ΕΡΓΑΣΙΑ 2 ΕΡΓΟ-ΕΝΕΡΓΕΙΑ
 ΕΡΓΑΣΙΑ 2 ΕΡΓΟ-ΕΝΕΡΓΕΙΑ 1. Σώμα μάζας m=10κg κινείται πάνω σε οριζόντιο επίπεδο με την επίδραση δύναμης με μέτρο F=100Ν που σχηματίζει με το οριζόντιο επίπεδο γωνία φ=30 ο. Αν ο συντελεστής τριβής ολίσθησης
ΕΡΓΑΣΙΑ 2 ΕΡΓΟ-ΕΝΕΡΓΕΙΑ 1. Σώμα μάζας m=10κg κινείται πάνω σε οριζόντιο επίπεδο με την επίδραση δύναμης με μέτρο F=100Ν που σχηματίζει με το οριζόντιο επίπεδο γωνία φ=30 ο. Αν ο συντελεστής τριβής ολίσθησης
ΕΛΑΣΤΙΚΗ ΚΡΟΥΣΗ. =1 kg που κινείται προς τα δεξιά με ταχύτητα μέτρου u 1. =8m /s συγκρούεται κεντρικά
 ΕΛΑΣΤΙΚΗ ΚΡΟΥΣΗ 1. Σφαίρα μάζας m 1 =1 kg που κινείται προς τα δεξιά με ταχύτητα μέτρου u 1 =8m /s συγκρούεται κεντρικά και ελαστικά με άλλη σφαίρα μάζας =3 kg που κινείται προς τα αριστερά με ταχύτητα
ΕΛΑΣΤΙΚΗ ΚΡΟΥΣΗ 1. Σφαίρα μάζας m 1 =1 kg που κινείται προς τα δεξιά με ταχύτητα μέτρου u 1 =8m /s συγκρούεται κεντρικά και ελαστικά με άλλη σφαίρα μάζας =3 kg που κινείται προς τα αριστερά με ταχύτητα
των δύο σφαιρών είναι
 ΘΕΜΑ B. Μια μικρή σφαίρα μάζας συγκρούεται μετωπικά και ελαστικά με ακίνητη μικρή σφαίρα μάζας. Μετά την κρούση οι σφαίρες κινούνται με αντίθετες ταχύτητες ίσων μέτρων. Ο λόγος των μαζών των δύο σφαιρών
ΘΕΜΑ B. Μια μικρή σφαίρα μάζας συγκρούεται μετωπικά και ελαστικά με ακίνητη μικρή σφαίρα μάζας. Μετά την κρούση οι σφαίρες κινούνται με αντίθετες ταχύτητες ίσων μέτρων. Ο λόγος των μαζών των δύο σφαιρών
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24 Εκφώνηση άσκησης 6. Ένα σώμα, μάζας m, εκτελεί απλή αρμονική ταλάντωση έχοντας ολική ενέργεια Ε. Χωρίς να αλλάξουμε τα φυσικά χαρακτηριστικά του συστήματος, προσφέρουμε στο σώμα
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24 Εκφώνηση άσκησης 6. Ένα σώμα, μάζας m, εκτελεί απλή αρμονική ταλάντωση έχοντας ολική ενέργεια Ε. Χωρίς να αλλάξουμε τα φυσικά χαρακτηριστικά του συστήματος, προσφέρουμε στο σώμα
ΚΕΦΑΛΑΙΟ 1: ΜΗΧΑΝΙΚΗ ΣΥΣΤΗΜΑΤΟΣ ΣΩΜΑΤΩΝ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ
 ΚΕΦΑΛΑΙΟ : ΜΗΧΑΝΙΚΗ ΣΥΣΤΗΜΑΤΟΣ ΣΩΜΑΤΩΝ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ Κατηγορία Α (7 ΠΕΡΙΟΔΟΙ). α. Μπορείτε να τρέξετε αρκετά γρήγορα ώστε να αποκτήσετε την ίδια ορμή με ένα αυτοκίνητο που κινείται με ταχύτητα μέτρου
ΚΕΦΑΛΑΙΟ : ΜΗΧΑΝΙΚΗ ΣΥΣΤΗΜΑΤΟΣ ΣΩΜΑΤΩΝ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ Κατηγορία Α (7 ΠΕΡΙΟΔΟΙ). α. Μπορείτε να τρέξετε αρκετά γρήγορα ώστε να αποκτήσετε την ίδια ορμή με ένα αυτοκίνητο που κινείται με ταχύτητα μέτρου
ΔΥΝΑΜΙΚΗ ΣΕ ΔΥΟ ΔΙΑΣΤΑΣΕΙΣ
 1. Από σημείο Α κεκλιμένου επιπέδου γωνίας κλίσης ρίχνεται προς τα πάνω, στη διεύθυνση του επιπέδου σώμα μάζας m = 2kgr με αρχική ταχύτητα u o = 20 m/sec. Αν δεν υπάρχουν τριβές να βρείτε: α)την αντίδραση
1. Από σημείο Α κεκλιμένου επιπέδου γωνίας κλίσης ρίχνεται προς τα πάνω, στη διεύθυνση του επιπέδου σώμα μάζας m = 2kgr με αρχική ταχύτητα u o = 20 m/sec. Αν δεν υπάρχουν τριβές να βρείτε: α)την αντίδραση
Δυναμική στο επίπεδο. Ομάδα Γ.
 .3.2. Η τριβή και η κίνηση. στο επίπεδο. Ομάδα Γ. Ένα σώμα μάζας 2kg ηρεμεί σε οριζόντιο επίπεδο με το οποίο παρουσιάζει συντελεστές τριβής μ=μ s =0,2. Σε μια στιγμή t 0 =0 στο σώμα ασκείται μεταβλητή
.3.2. Η τριβή και η κίνηση. στο επίπεδο. Ομάδα Γ. Ένα σώμα μάζας 2kg ηρεμεί σε οριζόντιο επίπεδο με το οποίο παρουσιάζει συντελεστές τριβής μ=μ s =0,2. Σε μια στιγμή t 0 =0 στο σώμα ασκείται μεταβλητή
ΚΡΟΥΣΗ. α. η ολική κινητική ενέργεια του συστήματος. β. η ορμή του συστήματος. 1. Σε κάθε κρούση ισχύει
 ΚΡΟΥΣΗ 1 ο ΘΕΜΑ Α. Ερωτήσεις πολλαπλής επιλογής Στην παρακάτω ερώτηση να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Σε κάθε κρούση ισχύει
ΚΡΟΥΣΗ 1 ο ΘΕΜΑ Α. Ερωτήσεις πολλαπλής επιλογής Στην παρακάτω ερώτηση να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Σε κάθε κρούση ισχύει
Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΚΡΟΥΣΕΙΣ DOPPLER 2012 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α1. Μια
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΙΣ ΚΡΟΥΣΕΙΣ DOPPLER 2012 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α1. Μια
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΟΡΜΗ ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΟΡΜΗΣ ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ
 ΟΡΜΗ ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΟΡΜΗΣ ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Ένας βαρκάρης βρίσκεται πάνω σε μια βάρκα και προσπαθεί να τη μετακινήσει σπρώχνοντας την από μέσα, αλλά αυτό δεν γίνεται. Πώς το εξηγείτε; α) η
ΟΡΜΗ ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΟΡΜΗΣ ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Ένας βαρκάρης βρίσκεται πάνω σε μια βάρκα και προσπαθεί να τη μετακινήσει σπρώχνοντας την από μέσα, αλλά αυτό δεν γίνεται. Πώς το εξηγείτε; α) η
Ισορροπία - Γ Νόμος Newton. 1) Να συμπληρώσετε τον πίνακα για κάθε αλληλεπίδραση. Τριβές αμελητέες. Σ1 Σ2 N S Ν S
 Ισορροπία - Γ Νόμος Newton 1) Να συμπληρώσετε τον πίνακα για κάθε αλληλεπίδραση. Τριβές αμελητέες. Σ1 Σ2 N S Ν S Ζεύγος σωμάτων που αλληλεπιδρούν Δράση - Αντίδραση 2) Να βρεθούν οι δυνάμεις που εξασκούνται
Ισορροπία - Γ Νόμος Newton 1) Να συμπληρώσετε τον πίνακα για κάθε αλληλεπίδραση. Τριβές αμελητέες. Σ1 Σ2 N S Ν S Ζεύγος σωμάτων που αλληλεπιδρούν Δράση - Αντίδραση 2) Να βρεθούν οι δυνάμεις που εξασκούνται
ομαλή κυκλική κίνηση-κρούσεις
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΦΥΣΙΚΗ Ον/μο:.. Β Λυκείου Ύλη:Οριζόντια βολή- Γεν. Παιδεία ομαλή κυκλική κίνηση-κρούσεις 8 -- Θέμα ο : ) Ένα σώμα εκτελεί ομαλή κυκλική κίνηση και η επιβατική του ακτίνα διαγράφει γωνία
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΦΥΣΙΚΗ Ον/μο:.. Β Λυκείου Ύλη:Οριζόντια βολή- Γεν. Παιδεία ομαλή κυκλική κίνηση-κρούσεις 8 -- Θέμα ο : ) Ένα σώμα εκτελεί ομαλή κυκλική κίνηση και η επιβατική του ακτίνα διαγράφει γωνία
Φυσική Γ' Λυκείου Θετικής και Τεχνολογικής Κατεύθυνσης. Κρούσεις
 Κρούσεις 1. Μια μπάλα του τένις ολισθαίνει σε λείο οριζόντιο επίπεδο χωρίς να περιστρέφεται, όπως φαίνεται στο σχήμα 1. Η μπάλα συγκρούεται με κατακόρυφο ακλόνητο τοίχο και γυρίζει πίσω, όπως φαίνεται
Κρούσεις 1. Μια μπάλα του τένις ολισθαίνει σε λείο οριζόντιο επίπεδο χωρίς να περιστρέφεται, όπως φαίνεται στο σχήμα 1. Η μπάλα συγκρούεται με κατακόρυφο ακλόνητο τοίχο και γυρίζει πίσω, όπως φαίνεται
5o ΚΕΦΑΛΑΙΟ : «ΚΡΟΥΣΕΙΣ»
 5o ΚΕΦΑΛΑΙΟ : «ΚΡΟΥΣΕΙΣ» 2 ο ΛΥΚΕΙΟ ΧΑΪΔΑΡΙΟΥ 1 5 ο ΚΕΦΑΛΑΙΟ: «ΚΡΟΥΣΕΙΣ» ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ 5.Ε.1. 5.Ε.2. 5.Ε.3. 5.Ε.4. 5.Ε.5. 5.Ε.6. Ποιες από τις παρακάτω προτάσεις είναι η σωστή; Σκέδαση ονομάζουμε
5o ΚΕΦΑΛΑΙΟ : «ΚΡΟΥΣΕΙΣ» 2 ο ΛΥΚΕΙΟ ΧΑΪΔΑΡΙΟΥ 1 5 ο ΚΕΦΑΛΑΙΟ: «ΚΡΟΥΣΕΙΣ» ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ 5.Ε.1. 5.Ε.2. 5.Ε.3. 5.Ε.4. 5.Ε.5. 5.Ε.6. Ποιες από τις παρακάτω προτάσεις είναι η σωστή; Σκέδαση ονομάζουμε
Δυναμική. Ομάδα Γ. Δυναμική Κατακόρυφη βολή και γραφικές παραστάσεις Κατακόρυφη βολή και κάποια συμπεράσματα.
 . Ομάδα Γ. 1.2.21. Κατακόρυφη βολή και γραφικές παραστάσεις Από ένα σημείο Ο σε ύψος Η=25m από το έδαφος εκτοξεύεται κατακόρυφα προς τα πάνω ένα σώμα με αρχική ταχύτητα υ 0 =20m/s. Αν g=10m/s 2, ενώ η
. Ομάδα Γ. 1.2.21. Κατακόρυφη βολή και γραφικές παραστάσεις Από ένα σημείο Ο σε ύψος Η=25m από το έδαφος εκτοξεύεται κατακόρυφα προς τα πάνω ένα σώμα με αρχική ταχύτητα υ 0 =20m/s. Αν g=10m/s 2, ενώ η
ΚΕΦΑΛΑΙΟ 2 ο ΔΙΑΤΗΡΗΣΗ ΟΡΜΗΣ - ΚΡΟΥΣΕΙΣ
 Σχολικό Έτος 08-09 3 ΚΕΦΑΛΑΙΟ ο ΔΙΑΤΗΡΗΣΗ ΟΡΜΗΣ - ΚΡΟΥΣΕΙΣ. ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΙΑΣ Α. ΕΣΩΤΕΡΙΚΕΣ ΚΑΙ ΕΞΩΤΕΡΙΚΕΣ ΔΥΝΑΜΕΙΣ Όταν ένα σύνολο από σώματα οριστεί ότι αποτελεί σύστημα σωμάτων, τότε οι δυνάμεις που
Σχολικό Έτος 08-09 3 ΚΕΦΑΛΑΙΟ ο ΔΙΑΤΗΡΗΣΗ ΟΡΜΗΣ - ΚΡΟΥΣΕΙΣ. ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΙΑΣ Α. ΕΣΩΤΕΡΙΚΕΣ ΚΑΙ ΕΞΩΤΕΡΙΚΕΣ ΔΥΝΑΜΕΙΣ Όταν ένα σύνολο από σώματα οριστεί ότι αποτελεί σύστημα σωμάτων, τότε οι δυνάμεις που
Διαγώνισμα Φυσικής Β Λυκείου. ~ Ορμή Διατήρηση ορμής ~
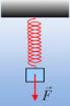
 Διαγώνισμα Φυσικής Β Λυκείου ~ Ορμή Διατήρηση ορμής ~ Θέμα Α Στις παρακάτω ερωτήσεις να επιλέξετε τη σωστή απάντηση. 1) Σε μία πλαστική κρούση δύο σωμάτων: i) Κάθε σώμα υφίσταται μόνιμη παραμόρφωση και
Διαγώνισμα Φυσικής Β Λυκείου ~ Ορμή Διατήρηση ορμής ~ Θέμα Α Στις παρακάτω ερωτήσεις να επιλέξετε τη σωστή απάντηση. 1) Σε μία πλαστική κρούση δύο σωμάτων: i) Κάθε σώμα υφίσταται μόνιμη παραμόρφωση και
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ
 ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ 30/9/08 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ 30/9/08 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ)
 ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) 30/9/208 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) 30/9/208 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
7. Ένα σώμα εκτελεί Α.Α.Τ. Η σταθερά επαναφοράς συστήματος είναι.
 ΚΕΦΑΛΑΙΟ 1 ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 6α. Σφαίρα μάζας ισορροπεί δεμένη στο πάνω άκρο κατακόρυφου
ΚΕΦΑΛΑΙΟ 1 ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 6α. Σφαίρα μάζας ισορροπεί δεμένη στο πάνω άκρο κατακόρυφου
Τα Θέματα που είναι με σκούρο φόντο φέτος (2014) είναι εκτός ύλης
 Τα Θέματα που είναι με σκούρο φόντο φέτος (2014) είναι εκτός ύλης 2013 ΘΕΜΑ Α Για τις ερωτήσεις 1 έως 4 γράψτε τον αριθμό τις ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Για ένα
Τα Θέματα που είναι με σκούρο φόντο φέτος (2014) είναι εκτός ύλης 2013 ΘΕΜΑ Α Για τις ερωτήσεις 1 έως 4 γράψτε τον αριθμό τις ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Για ένα
ΑΣΚΗΣΕΙΣ ΣΤΗΝ Α. Δ. Ο. (Αρχή Διατήρησης Ορμής)
 ΑΣΚΗΣΕΙΣ ΣΤΗΝ Α. Δ. Ο. (Αρχή Διατήρησης Ορμής) 1. Δύο παγοδρόμοι, Α και Β, με μάζες 60 kg και 80 kg αντίστοιχα, βρίσκονται σε απόσταση L, σε οριζόντιο παγοδρόμιο. Στα χέρια τους κρατάνε ένα τεντωμένο σχοινί.
ΑΣΚΗΣΕΙΣ ΣΤΗΝ Α. Δ. Ο. (Αρχή Διατήρησης Ορμής) 1. Δύο παγοδρόμοι, Α και Β, με μάζες 60 kg και 80 kg αντίστοιχα, βρίσκονται σε απόσταση L, σε οριζόντιο παγοδρόμιο. Στα χέρια τους κρατάνε ένα τεντωμένο σχοινί.
ΘΕΜΑ Α: ΔΙΑΡΚΕΙΑ: 180min ΤΜΗΜΑ:. ONOMA/ΕΠΩΝΥΜΟ: ΗΜΕΡΟΜΗΝΙΑ: ΘΕΜΑ 1 ο ΘΕΜΑ 2 ο ΘΕΜΑ 3 ο ΘΕΜΑ 4 ο ΣΥΝΟΛΟ ΜΟΝΑΔΕΣ
 Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΔΙΑΡΚΕΙΑ: 8min ONOM/ΕΠΩΝΥΜΟ: ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ:. ΘΕΜΑ ο ΘΕΜΑ ο ΘΕΜΑ 3 ο ΘΕΜΑ 4 ο ΣΥΝΟΛΟ ΜΟΝΑΔΕΣ ΘΕΜΑ Α:. Σφαίρα μάζας m = m κινείται με ταχύτητα αλγεβρικής τιμής +υ και συγκρούεται
Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΔΙΑΡΚΕΙΑ: 8min ONOM/ΕΠΩΝΥΜΟ: ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ:. ΘΕΜΑ ο ΘΕΜΑ ο ΘΕΜΑ 3 ο ΘΕΜΑ 4 ο ΣΥΝΟΛΟ ΜΟΝΑΔΕΣ ΘΕΜΑ Α:. Σφαίρα μάζας m = m κινείται με ταχύτητα αλγεβρικής τιμής +υ και συγκρούεται
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Δ.
 1.1. Μηχανικές. Ομάδα Δ. 1.1.51. Συνάντηση σωμάτων που ταλαντώνονται. Τα σώματα Α και Β του σχήματος έχουν ίσες μάζες m 1 =m 2 =m=1kg. Τα δύο σώματα ισορροπούν πάνω στο λείο οριζόντιο δάπεδο, με τα ελατήρια
1.1. Μηχανικές. Ομάδα Δ. 1.1.51. Συνάντηση σωμάτων που ταλαντώνονται. Τα σώματα Α και Β του σχήματος έχουν ίσες μάζες m 1 =m 2 =m=1kg. Τα δύο σώματα ισορροπούν πάνω στο λείο οριζόντιο δάπεδο, με τα ελατήρια
1. Ένα σώμα A μάζας, κινούμενο με ταχύτητα πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική κατεύθυνση του άξονα x Ox, συγκρούεται με ακίνητο σώμα Β.
 ΚΡΟΥΣΕΙΣ ΕΠΑΝΑΛΗΨΗ 1. Ένα σώμα A μάζας, κινούμενο με ταχύτητα πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική κατεύθυνση του άξονα x Ox, συγκρούεται με ακίνητο σώμα Β. Α) Αν η κρούση είναι μετωπική και ελαστική
ΚΡΟΥΣΕΙΣ ΕΠΑΝΑΛΗΨΗ 1. Ένα σώμα A μάζας, κινούμενο με ταχύτητα πάνω σε λείο οριζόντιο επίπεδο κατά τη θετική κατεύθυνση του άξονα x Ox, συγκρούεται με ακίνητο σώμα Β. Α) Αν η κρούση είναι μετωπική και ελαστική
ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ - ΑΣΚΗΣΕΙΣ
 ΚΙΝΗΜΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 1. Στο παρακάτω διάγραμμα απομάκρυνσης-χρόνου φαίνονται οι γραφικές παραστάσεις για δύο σώματα 1 και 2 τα οποία εκτελούν Α.Α.Τ. Να βρείτε τη σχέση που συνδέει τις μέγιστες επιταχύνσεις
ΚΙΝΗΜΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ 1. Στο παρακάτω διάγραμμα απομάκρυνσης-χρόνου φαίνονται οι γραφικές παραστάσεις για δύο σώματα 1 και 2 τα οποία εκτελούν Α.Α.Τ. Να βρείτε τη σχέση που συνδέει τις μέγιστες επιταχύνσεις
Διαγώνισμα Φυσικής Προσανατολισμού Β Λυκείου Οριζόντια Βολή Ορμή Κρούσεις
 Διαγώνισμα Φυσικής Προσανατολισμού Β Λυκείου Οριζόντια Βολή Ορμή Κρούσεις Θέμα Α 1) Δύο σώματα ρίχνονται την ίδια χρονική στιγμή από το ίδιο σημείο με οριζόντιες ταχύτητες υ 1 και υ 2, με υ 1 > υ 2. Τα
Διαγώνισμα Φυσικής Προσανατολισμού Β Λυκείου Οριζόντια Βολή Ορμή Κρούσεις Θέμα Α 1) Δύο σώματα ρίχνονται την ίδια χρονική στιγμή από το ίδιο σημείο με οριζόντιες ταχύτητες υ 1 και υ 2, με υ 1 > υ 2. Τα
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 02/10/2016 ΔΙΑΡΚΕΙΑ: 3 ΩΡΕΣ ΘΕΜΑ Α
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 0/0/06 ΔΙΑΡΚΕΙΑ: 3 ΩΡΕΣ ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις -5 να γράψετε στο φύλλο απαντήσεών σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 0/0/06 ΔΙΑΡΚΕΙΑ: 3 ΩΡΕΣ ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις -5 να γράψετε στο φύλλο απαντήσεών σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
Έργο Δύναμης Έργο σταθερής δύναμης
 Παρατήρηση: Σε όλες τις ασκήσεις του φυλλαδίου τα αντικείμενα θεωρούμε ότι οι δυνάμεις ασκούνται στο κέντρο μάζας των αντικειμένων έτσι ώστε αυτά κινούνται μόνο μεταφορικά, χωρίς να μπορούν να περιστραφούν.
Παρατήρηση: Σε όλες τις ασκήσεις του φυλλαδίου τα αντικείμενα θεωρούμε ότι οι δυνάμεις ασκούνται στο κέντρο μάζας των αντικειμένων έτσι ώστε αυτά κινούνται μόνο μεταφορικά, χωρίς να μπορούν να περιστραφούν.
Έργο-Ενέργεια Ασκήσεις Έργου-Ενέργειας Θεώρηµα Μεταβολής της Κινητικής Ενέργειας. ΘΜΚΕ Μεταβλητή δύναµη και κίνηση
 2.2. Ασκήσεις Έργου-Ενέργειας. 2.2.1. Θεώρηµα Μεταβολής της Κινητικής Ενέργειας. ΘΜΚΕ. Ένα σώµα µάζας m=2kg ηρεµεί σε οριζόντιο επίπεδο. Σε µια στιγµή δέχεται την επίδραση οριζόντιας δύνα- µης, το µέτρο
2.2. Ασκήσεις Έργου-Ενέργειας. 2.2.1. Θεώρηµα Μεταβολής της Κινητικής Ενέργειας. ΘΜΚΕ. Ένα σώµα µάζας m=2kg ηρεµεί σε οριζόντιο επίπεδο. Σε µια στιγµή δέχεται την επίδραση οριζόντιας δύνα- µης, το µέτρο
1.1. Μηχανικές Ταλαντώσεις.
 1.1. Μηχανικές. 1) Εξισώσεις ΑΑΤ Ένα υλικό σηµείο κάνει α.α.τ. µε πλάτος 0,1m και στην αρχή των χρόνων, βρίσκεται σε σηµείο Μ µε απο- µάκρυνση 5cm, αποµακρυνόµενο από τη θέση ισορροπίας. Μετά από 1s περνά
1.1. Μηχανικές. 1) Εξισώσεις ΑΑΤ Ένα υλικό σηµείο κάνει α.α.τ. µε πλάτος 0,1m και στην αρχή των χρόνων, βρίσκεται σε σηµείο Μ µε απο- µάκρυνση 5cm, αποµακρυνόµενο από τη θέση ισορροπίας. Μετά από 1s περνά
Κρούσεις. 5. Σε μια ελαστική κρούση δεν διατηρείται α. η ολική κινητική ενέργεια του συστήματος. β. η ορμή του συστήματος.
 ο ΘΕΜΑ Κρούσεις Α Ερωτήσεις πολλαπλής επιλογής Στην παρακάτω ερώτηση να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση Σε κάθε κρούση ισχύει α η
ο ΘΕΜΑ Κρούσεις Α Ερωτήσεις πολλαπλής επιλογής Στην παρακάτω ερώτηση να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση Σε κάθε κρούση ισχύει α η
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Β ΛΥΚΕΙΟΥ
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Β ΛΥΚΕΙΟΥ ΕΠΙΜΕΛΕΙΑ ΘΕΜΑΤΩΝ ΒΑΡΕΛΑΣ ΔΗΜΗΤΡΗΣ ΟΜΑΔΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΘΕΜΑ 1 Στις ερωτήσεις 1-5 να γράψετε στη κολλά σας τον αριθμό της ερώτησης και δίπλα το γράμμα που
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Β ΛΥΚΕΙΟΥ ΕΠΙΜΕΛΕΙΑ ΘΕΜΑΤΩΝ ΒΑΡΕΛΑΣ ΔΗΜΗΤΡΗΣ ΟΜΑΔΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΘΕΜΑ 1 Στις ερωτήσεις 1-5 να γράψετε στη κολλά σας τον αριθμό της ερώτησης και δίπλα το γράμμα που
Α. Για ποιο από τα δυο σώματα καταναλώσαμε περισσότερη ενέργεια;
 1. Στην κάτω άκρη ενός ιδανικού ελατήριου είναι δεμένο ένα σώμα που έχει μάζα m 1 = m και ισορροπεί. Στην κάτω άκρη ενός άλλου ομοίου ελατήριου είναι δεμένο ένα άλλο σώμα που έχει μάζα m 2 = 4m και ισορροπεί.
1. Στην κάτω άκρη ενός ιδανικού ελατήριου είναι δεμένο ένα σώμα που έχει μάζα m 1 = m και ισορροπεί. Στην κάτω άκρη ενός άλλου ομοίου ελατήριου είναι δεμένο ένα άλλο σώμα που έχει μάζα m 2 = 4m και ισορροπεί.
2) Βάρος και κυκλική κίνηση. Β) Κυκλική κίνηση
 Β) Κυκλική κίνηση 1) Υπολογισμοί στην ομαλή κυκλική κίνηση. Μια μικρή σφαίρα, μάζας 2kg, εκτελεί ομαλή κυκλική κίνηση, σε κύκλο κέντρου Ο και ακτίνας 0,5m, όπως στο σχήμα. Τη χρονική στιγμή t=0 η σφαίρα
Β) Κυκλική κίνηση 1) Υπολογισμοί στην ομαλή κυκλική κίνηση. Μια μικρή σφαίρα, μάζας 2kg, εκτελεί ομαλή κυκλική κίνηση, σε κύκλο κέντρου Ο και ακτίνας 0,5m, όπως στο σχήμα. Τη χρονική στιγμή t=0 η σφαίρα
Σελίδα 1 από 6 ΣΧΟΛΙΚΟ ΕΤΟΣ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΙΣ ΚΡΟΥΣΕΙΣ ΔΙΑΡΚΕΙΑ ΕΞΕΤΑΣΗΣ: 3 ΩΡΕΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ:...
 Σελίδα 1 από 6 ΣΧΟΛΙΚΟ ΕΤΟΣ 2012-2013 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΙΣ ΚΡΟΥΣΕΙΣ ΔΙΑΡΚΕΙΑ ΕΞΕΤΑΣΗΣ: 3 ΩΡΕΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ:... TMHMA: ΘΕΜΑ Α Στις Ερωτήσεις πολλαπλής επιλογής 1 εώς 4 να γράψετε
Σελίδα 1 από 6 ΣΧΟΛΙΚΟ ΕΤΟΣ 2012-2013 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΙΣ ΚΡΟΥΣΕΙΣ ΔΙΑΡΚΕΙΑ ΕΞΕΤΑΣΗΣ: 3 ΩΡΕΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ:... TMHMA: ΘΕΜΑ Α Στις Ερωτήσεις πολλαπλής επιλογής 1 εώς 4 να γράψετε
Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 Μάθημα/Τάξη: ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Κεφάλαιο: ΤΑΛΑΝΤΩΣΕΙΣ - ΚΡΟΥΣΕΙΣ Ονοματεπώνυμο Μαθητή: Ημερομηνία: Επιδιωκόμενος Στόχος: 70/100 Θέμα A Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης
Μάθημα/Τάξη: ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Κεφάλαιο: ΤΑΛΑΝΤΩΣΕΙΣ - ΚΡΟΥΣΕΙΣ Ονοματεπώνυμο Μαθητή: Ημερομηνία: Επιδιωκόμενος Στόχος: 70/100 Θέμα A Στις ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης
υ r 1 F r 60 F r A 1
 2.2. Ασκήσεις Έργου-Ενέργειας. 4.2.1. Θεώρηµα Μεταβολής της Κινητικής Ενέργειας. ΘΜΚΕ. Ένα σώµα µάζας m=2kg ηρεµεί σε οριζόντιο επίπεδο. Σε µια στιγµή δέχεται την επίδραση οριζόντιας δύνα- µης, το µέτρο
2.2. Ασκήσεις Έργου-Ενέργειας. 4.2.1. Θεώρηµα Μεταβολής της Κινητικής Ενέργειας. ΘΜΚΕ. Ένα σώµα µάζας m=2kg ηρεµεί σε οριζόντιο επίπεδο. Σε µια στιγµή δέχεται την επίδραση οριζόντιας δύνα- µης, το µέτρο
Κρούσεις. 1 ο ΘΕΜΑ. Φυσική Γ Θετ. και Τεχν/κης Κατ/σης. Θέματα εξετάσεων
 ο ΘΕΜΑ Κρούσεις Α. Ερωτήσεις πολλαπλής επιλογής Στην παρακάτω ερώτηση να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Σε κάθε κρούση ισχύει
ο ΘΕΜΑ Κρούσεις Α. Ερωτήσεις πολλαπλής επιλογής Στην παρακάτω ερώτηση να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Σε κάθε κρούση ισχύει
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 ΦΥΛΛΟ ΑΞΙΟΛΟΓΗΣΗΣ ΘΕΜΑ Α Α.1. δυο σφαίρες με διαφορετικές μάζες συγκρούονται κεντρικά και πλαστικά Αν αμέσως μετά την κρούση η κινητική ενέργεια του συστήματος μηδενίζεται τότε οι σφαίρες πριν την κρούση
ΦΥΛΛΟ ΑΞΙΟΛΟΓΗΣΗΣ ΘΕΜΑ Α Α.1. δυο σφαίρες με διαφορετικές μάζες συγκρούονται κεντρικά και πλαστικά Αν αμέσως μετά την κρούση η κινητική ενέργεια του συστήματος μηδενίζεται τότε οι σφαίρες πριν την κρούση
ΘΕΜΑΤΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΚΕΦΑΛΑΙΑ 1-2 7/12/2014
 ΘΕΜΑΤΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΚΕΦΑΛΑΙΑ 1-2 7/12/2014 ΘΕΜΑ 1 Από τις ερωτήσεις 1-4 να επιλέξετε την σωστή πρόταση: Α1. Σώμα εκτελεί ομαλή κυκλική κίνηση. α) η κεντρομόλος επιτάχυνση
ΘΕΜΑΤΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΚΕΦΑΛΑΙΑ 1-2 7/12/2014 ΘΕΜΑ 1 Από τις ερωτήσεις 1-4 να επιλέξετε την σωστή πρόταση: Α1. Σώμα εκτελεί ομαλή κυκλική κίνηση. α) η κεντρομόλος επιτάχυνση
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Β ΛΥΚΕΙΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΕΦΑΛΑΙΟ 1.1 (ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ - ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ - ΟΡΜΗ) ΚΥΡΙΑΚΗ 18 ΙΑΝΟΥΑΡΙΟΥ 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ 4
 ΑΡΧΗ 1 ΗΣ ΣΕΛΙΔΑΣ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Β ΛΥΚΕΙΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΕΦΑΛΑΙΟ 1.1 (ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ - ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ - ΟΡΜΗ) ΚΥΡΙΑΚΗ 18 ΙΑΝΟΥΑΡΙΟΥ 015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ 4 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό
ΑΡΧΗ 1 ΗΣ ΣΕΛΙΔΑΣ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Β ΛΥΚΕΙΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΕΦΑΛΑΙΟ 1.1 (ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ - ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ - ΟΡΜΗ) ΚΥΡΙΑΚΗ 18 ΙΑΝΟΥΑΡΙΟΥ 015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ 4 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό
Ορμή 2ος Νόμος Νεύτωνα
 2ος Νόμος Νεύτωνα - Ορμή Ορμή 2ος Νόμος Νεύτωνα 1. Ένα αντικείμενο μάζας m = 2kg κινείται σε ευθεία τροχιά. Αρχικά η ταχύτητα του έχει μέτρο υ 1 = 4m/s, ενώ στην συνέχεια αλλάζει και αποκτάει μέτρο υ 2
2ος Νόμος Νεύτωνα - Ορμή Ορμή 2ος Νόμος Νεύτωνα 1. Ένα αντικείμενο μάζας m = 2kg κινείται σε ευθεία τροχιά. Αρχικά η ταχύτητα του έχει μέτρο υ 1 = 4m/s, ενώ στην συνέχεια αλλάζει και αποκτάει μέτρο υ 2
p1 p1 p1 p1 p1 p1 p1 mv m p1 m m p1
 ΚΕΦΑΛΑΙΟ 5 Ο, ΕΝΟΤΗΤΑ : ΚΡΟΥΣΕΙΣ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση. Σώμα Σ μάζας που κινείται προς τα δεξιά στη θετική κατεύθυνση με ταχύτητα μέτρου υ συγκρούεται κεντρικά και πλαστικά με ακίνητο σώμα Σ διπλάσιας
ΚΕΦΑΛΑΙΟ 5 Ο, ΕΝΟΤΗΤΑ : ΚΡΟΥΣΕΙΣ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση. Σώμα Σ μάζας που κινείται προς τα δεξιά στη θετική κατεύθυνση με ταχύτητα μέτρου υ συγκρούεται κεντρικά και πλαστικά με ακίνητο σώμα Σ διπλάσιας
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ. Δίνεται ότι η ροπή αδράνειας του δίσκου ως προς τον άξονα Κ είναι Ι= M R
 ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ 1 Η ράβδος ΟΑ του σχήματος μπορεί να στρέφεται γύρω από τον άξονα z z χωρίς τριβές Tη στιγμή t=0 δέχεται την εφαπτομενική δύναμη F σταθερού μέτρου 0 Ν, με φορά όπως φαίνεται στο σχήμα
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ 1 Η ράβδος ΟΑ του σχήματος μπορεί να στρέφεται γύρω από τον άξονα z z χωρίς τριβές Tη στιγμή t=0 δέχεται την εφαπτομενική δύναμη F σταθερού μέτρου 0 Ν, με φορά όπως φαίνεται στο σχήμα
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΚΡΟΥΣΕΙΣ-ΤΑΛΑΝΤΩΣΕΙΣ
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΚΡΟΥΣΕΙΣ-ΤΑΛΑΝΤΩΣΕΙΣ 5/11/2017 ΘΕΜΑ A Στις ερωτήσεις 1-4 να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ: ΚΡΟΥΣΕΙΣ-ΤΑΛΑΝΤΩΣΕΙΣ 5/11/2017 ΘΕΜΑ A Στις ερωτήσεις 1-4 να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
ΑΣΚΗΣΕΙΣ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΚΡΟΥΣΕΙΣ
 ΑΣΚΗΣΕΙΣ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΚΡΟΥΣΕΙΣ ΟΡΙΖΟΝΤΙΟ ΕΠΙΠΕΔΟ 1.Ένα σώμα μάζας m=4kg είναι δεμένο στο άκρο οριζόντιου ελατηρίου σταθεράςk=400n/m, το άλλο άκρο του οποίου είναι είναι ακλόνητα στερεωμένη. To
ΑΣΚΗΣΕΙΣ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ-ΚΡΟΥΣΕΙΣ ΟΡΙΖΟΝΤΙΟ ΕΠΙΠΕΔΟ 1.Ένα σώμα μάζας m=4kg είναι δεμένο στο άκρο οριζόντιου ελατηρίου σταθεράςk=400n/m, το άλλο άκρο του οποίου είναι είναι ακλόνητα στερεωμένη. To
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ. Ύλη: Ορμή
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Ον/μο:.. B Λυκείου Ύλη: Ορμή 13-11-2016 Θέμα 1 ο : 1) Κατά την πλαστική κρούση δύο σωμάτων: α) η κινητική ενέργεια και η ορμή του συστήματος των σωμάτων παραμένουν σταθερές β) η κινητική
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Ον/μο:.. B Λυκείου Ύλη: Ορμή 13-11-2016 Θέμα 1 ο : 1) Κατά την πλαστική κρούση δύο σωμάτων: α) η κινητική ενέργεια και η ορμή του συστήματος των σωμάτων παραμένουν σταθερές β) η κινητική
1. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου.
 ΤΑΛΑΝΤΩΣΗ ΜΕΤΑ ΑΠΟ ΚΡΟΥΣΗ.. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου. Σώμα μάζας = g κινείται σε λείο οριζόντιο επίπεδο με ταχύτητα υ μέτρου υ = 5 /s συγκρούεται
ΤΑΛΑΝΤΩΣΗ ΜΕΤΑ ΑΠΟ ΚΡΟΥΣΗ.. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου. Σώμα μάζας = g κινείται σε λείο οριζόντιο επίπεδο με ταχύτητα υ μέτρου υ = 5 /s συγκρούεται
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΕΠΑΝΑΛΗΨΗ B ΛΥΚΕΙΟΥ στη Φυσική γενικής παιδείας
 ΕΠΑΝΑΛΗΨΗ B ΛΥΚΕΙΟΥ στη Φυσική γενικής παιδείας ΤΥΠΟΛΟΓΙΟ 1 Άξονας xx Άξονας yy α x =0 α y =g υ x =υ 0 υ y =gt x=υ 0 t y= 1 gt OΡΙΖΟΝΤΙΑ ΒΟΛΗ x y και x x1 x : Αρχή Επαλληλίας (Ανεξαρτησίας) Κινήσεων Μέτρο
ΕΠΑΝΑΛΗΨΗ B ΛΥΚΕΙΟΥ στη Φυσική γενικής παιδείας ΤΥΠΟΛΟΓΙΟ 1 Άξονας xx Άξονας yy α x =0 α y =g υ x =υ 0 υ y =gt x=υ 0 t y= 1 gt OΡΙΖΟΝΤΙΑ ΒΟΛΗ x y και x x1 x : Αρχή Επαλληλίας (Ανεξαρτησίας) Κινήσεων Μέτρο
ΕΝΔΕΙΚΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ
 ΕΝΔΕΙΚΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ 1. Ο άνθρωπος ξεκινά τη στιγμή t=0 από τη θέση x=50 m και όπως φαίνεται στο παρακάτω διάγραμμα κινείται προς τα αριστερά. Στη συνέχεια σε κάθε σημειωμένη θέση στο
ΕΝΔΕΙΚΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ 1. Ο άνθρωπος ξεκινά τη στιγμή t=0 από τη θέση x=50 m και όπως φαίνεται στο παρακάτω διάγραμμα κινείται προς τα αριστερά. Στη συνέχεια σε κάθε σημειωμένη θέση στο
ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 2
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ 50. Σε ένα σώμα μάζας m=2kg που ηρεμεί σε λείο επίπεδο ενεργεί οριζόντια δύναμη F=10Ν για χρόνο t=20s. Να βρεθεί πόσο διάστημα διανύει το σώμα σε χρόνο 25s και να γίνει γραφική παράσταση
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ 50. Σε ένα σώμα μάζας m=2kg που ηρεμεί σε λείο επίπεδο ενεργεί οριζόντια δύναμη F=10Ν για χρόνο t=20s. Να βρεθεί πόσο διάστημα διανύει το σώμα σε χρόνο 25s και να γίνει γραφική παράσταση
Α. Η επιτάχυνση ενός σωματιδίου ως συνάρτηση της θέσης x δίνεται από τη σχέση ax ( ) = bx, όπου b σταθερά ( b= 1 s ). Αν η ταχύτητα στη θέση x
 Εισαγωγή στις Φυσικές Επιστήμες (4 7 09) Μηχανική ΘΕΜΑ Α. Η επιτάχυνση ενός σωματιδίου ως συνάρτηση της θέσης x δίνεται από τη σχέση ax ( ) = bx, όπου b σταθερά ( b= s ). Αν η ταχύτητα στη θέση x 0 = 0
Εισαγωγή στις Φυσικές Επιστήμες (4 7 09) Μηχανική ΘΕΜΑ Α. Η επιτάχυνση ενός σωματιδίου ως συνάρτηση της θέσης x δίνεται από τη σχέση ax ( ) = bx, όπου b σταθερά ( b= s ). Αν η ταχύτητα στη θέση x 0 = 0
ΠEΡΙΕΧΟΜΕΝΑ. Ενότητα 4: Φαινόμενο Doppler Θεωρία Μεθοδολογία Ερωτήσεις Πολλαπλής Επιλογής Πρόλογος... 5
 ΠEΡΙΕΧΟΜΕΝΑ Πρόλογος......................................................... 5 Ενότητα : Κρούσεις Θεωρία Μεθοδολογία.............................................. 9 Ερωτήσεις Πολλαπλής Επιλογής.......................................
ΠEΡΙΕΧΟΜΕΝΑ Πρόλογος......................................................... 5 Ενότητα : Κρούσεις Θεωρία Μεθοδολογία.............................................. 9 Ερωτήσεις Πολλαπλής Επιλογής.......................................
Σάββατο 12 Νοεμβρίου Απλή Αρμονική Ταλάντωση - Κρούσεις. Σύνολο Σελίδων: Επτά (7) - Διάρκεια Εξέτασης: 3 ώρες. Θέμα Α.
 Γ Τάξης Γενικού Λυκείου Σάββατο 1 Νοεμβρίου 016 Απλή Αρμονική Ταλάντωση - Κρούσεις Σύνολο Σελίδων: Επτά (7) - Διάρκεια Εξέτασης: 3 ώρες Ονοματεπώνυμο: Θέμα Α. Στις ημιτελείς προτάσεις Α.1 Α.4 να γράψετε
Γ Τάξης Γενικού Λυκείου Σάββατο 1 Νοεμβρίου 016 Απλή Αρμονική Ταλάντωση - Κρούσεις Σύνολο Σελίδων: Επτά (7) - Διάρκεια Εξέτασης: 3 ώρες Ονοματεπώνυμο: Θέμα Α. Στις ημιτελείς προτάσεις Α.1 Α.4 να γράψετε
Προτεινόμενα ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ
 ΘΕΜΑΤΑ Β. Β1. Από ύψος h (σημείο Α) αφήνουμε να κυλίσει δακτύλιος μάζας m 1 =m χωρίς ολίσθηση σε οδηγό που καταλήγει σε τεταρτοκύκλιο. Στο σημείο Β και όταν η u cm είναι κατακόρυφη ο δακτύλιος εγκαταλείπει
ΘΕΜΑΤΑ Β. Β1. Από ύψος h (σημείο Α) αφήνουμε να κυλίσει δακτύλιος μάζας m 1 =m χωρίς ολίσθηση σε οδηγό που καταλήγει σε τεταρτοκύκλιο. Στο σημείο Β και όταν η u cm είναι κατακόρυφη ο δακτύλιος εγκαταλείπει
ΚΕΦΑΛΑΙΟ 2.1 ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ
 ΚΕΦΑΛΑΙΟ 2.1 91 ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ Α. ΈΡΓΟ ΣΤΑΘΕΡΗΣ ΔΥΝΑΜΗΣ 1. Το σώμα του σχήματος μετακινείται πάνω στο οριζόντιο επίπεδο κατά x=2m. Στο σώμα εκτός του βάρους του και της αντίδρασης του
ΚΕΦΑΛΑΙΟ 2.1 91 ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ Α. ΈΡΓΟ ΣΤΑΘΕΡΗΣ ΔΥΝΑΜΗΣ 1. Το σώμα του σχήματος μετακινείται πάνω στο οριζόντιο επίπεδο κατά x=2m. Στο σώμα εκτός του βάρους του και της αντίδρασης του
Θέμα 1 ο (Μονάδες 25)
 ΙΙΑΑΓΓΩΝΝΙΙΣΣΜΑΑ ΦΦΥΥΣΣΙΙΚΚΗΗΣΣ ΚΚΑΑΤΤΕΕΥΥΘΘΥΥΝΝΣΣΗΗΣΣ ΑΑΠΟΟΦΦΟΟΙΙΤΤΩΝΝ 0055 -- -- 00 Θέμα ο. Ένα σημειακό αντικείμενο που εκτελεί ΑΑΤ μεταβαίνει από τη θέση ισορροπίας του σε ακραία θέση σε χρόνο s. Η
ΙΙΑΑΓΓΩΝΝΙΙΣΣΜΑΑ ΦΦΥΥΣΣΙΙΚΚΗΗΣΣ ΚΚΑΑΤΤΕΕΥΥΘΘΥΥΝΝΣΣΗΗΣΣ ΑΑΠΟΟΦΦΟΟΙΙΤΤΩΝΝ 0055 -- -- 00 Θέμα ο. Ένα σημειακό αντικείμενο που εκτελεί ΑΑΤ μεταβαίνει από τη θέση ισορροπίας του σε ακραία θέση σε χρόνο s. Η
Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις
 Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις ~ Διάρκεια: 3 ώρες ~ Θέμα Α Α1. Η ορμή συστήματος δύο σωμάτων που συγκρούονται διατηρείται: α. Μόνο στην πλάγια κρούση. β. Μόνο στην έκκεντρη
Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις ~ Διάρκεια: 3 ώρες ~ Θέμα Α Α1. Η ορμή συστήματος δύο σωμάτων που συγκρούονται διατηρείται: α. Μόνο στην πλάγια κρούση. β. Μόνο στην έκκεντρη
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ» ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 4o ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 4o ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η
Συλλογή θεμάτων 3 & 4
 Συλλογή θεμάτων 3 & 4 1)Η ταχύτητα ενός κινητού μεταβάλλεται με το χρόνο όπως φαίνεται στο διπλανό διάγραμμα. 20 u(m/s) α. Αφού περιγράψετε την κίνηση του κινητού, να υπολογίσετε τη συνολική του μετατόπιση.
Συλλογή θεμάτων 3 & 4 1)Η ταχύτητα ενός κινητού μεταβάλλεται με το χρόνο όπως φαίνεται στο διπλανό διάγραμμα. 20 u(m/s) α. Αφού περιγράψετε την κίνηση του κινητού, να υπολογίσετε τη συνολική του μετατόπιση.
ΚΕΦΑΛΑΙΟ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ
 55 ΚΕΦΑΛΑΙΟ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ Α. ΠΡΟΣΘΕΣΗ ΔΥΝΑΜΕΩΝ ΝΟΜΟΣ ΤΟΥ HOOKE 1. Να σχεδιάσετε δύο αντίρροπες δυνάμεις F 1=5N και F 2=15N με κλίμακα 1cm/2,5N και να βρείτε την συνισταμένη τους. (Απ.: 10
55 ΚΕΦΑΛΑΙΟ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ Α. ΠΡΟΣΘΕΣΗ ΔΥΝΑΜΕΩΝ ΝΟΜΟΣ ΤΟΥ HOOKE 1. Να σχεδιάσετε δύο αντίρροπες δυνάμεις F 1=5N και F 2=15N με κλίμακα 1cm/2,5N και να βρείτε την συνισταμένη τους. (Απ.: 10
υναµική στο επίπεδο.
 στο επίπεδο. 1.3.1. Η τάση του νήµατος, πού και γιατί; Έστω ότι σε ένα λείο οριζόντιο επίπεδο ηρεµούν δύο σώµατα Α και Β µε µάζες Μ=3kg και m=2kg αντίστοιχα, τα οποία συνδέονται µε ένα νήµα. Σε µια στιγµή
στο επίπεδο. 1.3.1. Η τάση του νήµατος, πού και γιατί; Έστω ότι σε ένα λείο οριζόντιο επίπεδο ηρεµούν δύο σώµατα Α και Β µε µάζες Μ=3kg και m=2kg αντίστοιχα, τα οποία συνδέονται µε ένα νήµα. Σε µια στιγµή
κριτήρια αξιολόγησης ΚΕΦΑΛΑΙΟ 5 1o Κριτήριο αξιολόγησης
 1o Κριτήριο αξιολόγησης Θέμα 1ο α Δύο σφαίρες Α και Β συγκρούονται κεντρικά ελαστικά Ποια ή ποιες από τις παρακάτω προτάσεις είναι σωστές και γιατί; Α Η σφαίρα Α θα γυρίσει προς τα πίσω αν είναι m A
1o Κριτήριο αξιολόγησης Θέμα 1ο α Δύο σφαίρες Α και Β συγκρούονται κεντρικά ελαστικά Ποια ή ποιες από τις παρακάτω προτάσεις είναι σωστές και γιατί; Α Η σφαίρα Α θα γυρίσει προς τα πίσω αν είναι m A
ΚΡΟΥΣΕΙΣ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΜΠΕΝΑΚΗΣ ΜΑΝΩΛΗΣ ΦΥΣΙΚΟΣ
 ΚΡΟΥΣΕΙΣ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΜΠΕΝΑΚΗΣ ΜΑΝΩΛΗΣ ΦΥΣΙΚΟΣ Κρούσεις 1 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΚΡΟΥΣΕΙΣ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ ΚΡΟΥΣΗ : Σύγκρουση δύο σωμάτων
ΚΡΟΥΣΕΙΣ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΜΠΕΝΑΚΗΣ ΜΑΝΩΛΗΣ ΦΥΣΙΚΟΣ Κρούσεις 1 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΚΡΟΥΣΕΙΣ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ ΚΡΟΥΣΗ : Σύγκρουση δύο σωμάτων
