Lecture 8: Quantitative Option Strategies
|
|
|
- Ἕκτωρ Κακριδής
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Lecture 8: Quanttatve Opton trateges Marco Avellaneda G prng emester 009
2 Equty Optons Markets ngle-name optons Electronc tradng n 6 exchanges, cross-lstng of many stocks, penny-wde bd ask spreads for many contracts Index Optons &P 500, NDX, Mns. Traded on the hcago Mercantle Exchange. VIX optons & futures trade n ME as well. ETF Optons Most of the large ETFs are optonable. Traded lke stocks n multple exchanges. PY, QQQQ, XLF are among the most traded optons n the U.
3 Optons Markets Hallburton (HAL) Aprl 09 ALL PUT ymbol Last hange Bd Ask Volume Open Int trke ymbol Last hange Bd Ask Volume Open Int HALDA.X HALPA.X N/A HALDU.X HALPU.X ,37 HALDB.X HALPB.X ,775 HALDZ.X HALPZ.X ,48 HALD.X ,94 15 HALP.X ,59 HALDP.X , HALPP.X ,48 HALDD.X ,693 0 HALPD.X ,440 HALDQ.X ,646.5 HALPQ.X ,770 HALDE.X ,060 5 HALPE.X ,111 HALDR.X , HALPR.X HALDF.X N/A , HALPF.X ,77 HALD.X N/A , HALP.X HALDG.X N/A , HALPG.X HALDT.X N/A HALPT.X HALDH.X N/A , HALPH.X HALDV.X N/A 0.0 4, HALPV.X HALDI.X N/A HALPI.X HALDW.X N/A HALPW.X HALDJ.X N/A HALPJ.X HALDX.X N/A HALPX.X HALDK.X N/A HALPK.X HAL $16.36 Avalable expratons: Mar09, Apr09, Jul09, Oct09, Jan10, Jan11 front months, LEAP, quarterly cycle (Jan cycle for HAL).
4 Put-all Party P e dt Ke rt Put-call party holds for Amercan optons whch are ATM, to wthn reasonable approxmaton. ALL PUT (-P+K*(1-r*40/5))/ d_mp HALD.X H ALP.X % HALDP.X H ALPP.X % Hal pays dvdend of 9 cents at the end of Feb, May, Aug, Nov There are no ex-dvdend dates between now and Aprl 0, 009. Opton markets gve an mpled cost of carry for the stock (mpled forward prce), whch may be dfferent from the nomnal cost of carry. Ths s due to stock-loan consderatons.
5 DIA Optons Apr 18, 009 ymbol Last hange Bd Ask Volume OpenInt TRIKE ymbol Last hange Bd Ask Volume Open Int DIHDX.X N/A DIHPX.X DIHDY.X DIHPY.X DIHDZ.X DIHPZ.X DIHDA.X N/A DIHPA.X DIHDB.X N/A DIHPB.X DIHD. X DIHP.X DIHDD. X DIHPD.X DIHDE.X DIHPE.X DIHDF.X DIHPF.X DIHDG.X DIHPG.X DIHDH. X DIHPH.X , 734 DIJDI.X DIJPI.X DIJDJ.X DIJPJ.X DIJDK.X DIJPK.X , 347 DIJDL.X DIJPL.X , 138 DIJDM.X DIJPM.X , 735 DIJDN.X ,14 66 DIJPN.X , 919 DIJDO.X DIJPO.X , 115 DIJDP.X , DIJPP.X , 505 DIJDQ.X , DIJPQ.X , 688 DIJDR.X , DIJPR.X , 89 DIJD.X , DIJP.X , 035 DIJDT.X ,998 7 DIJPT.X , 58 DIJDU.X ,94 73 DIJPU.X , 580 DIJDV.X , DIJPV.X , 53 DIJDW.X ,41 75 DIJPW.X , 9 DIJDX.X ,65 76 DIJPX.X , 008 DIJDY.X , DIJPY.X DIJDZ.X , DIJPZ.X , 90 DIJDA.X , DIJPA.X , 006 DIJDB.X , DIJPB.X , 35 DIJD.X , DIJP.X , 989 DAVDD.X ,455 8 DAVPD.X , 184 DAVDE.X ,18 83 DAVPE.X , 016 DAVDF.X , DAVPF.X DAVDG.X ,03 85 DAVPG.X DAVDH.X DAVPH.X DAVDI.X N/A DAVPI.X DAVDJ.X N/A DAVPJ.X DAVDK.X N/A DAVPK.X DAVDL. X N/A DAVPL.X DAVDM.X N/A DAVPM. X
6 Impled Dvdend Yeld for DIA Aprl 18, 009 Optons ALL PUT (-P+K*(1-r*40/5))/ d_mp DIJDP.X DIJPP.X % DIJDQ.X DIJPQ.X % Dvdend Yeld from Yahoo.com 3.30% Actual payments are approx 15 cents / month ~ $1.80 ~.60% tep1 n understandng optons markets: fnd the mpled dvdend from the market. If the mpled dvdend s dfferent from the nomnal dvdend then -- check for HTB f d mp > d nom -- check for dvdend reductons f d mp < d nom
7 alculaton of d_{nom}, d_{mp} d nom T ln n 1 1 D e rt Dvdend payment dates d mp 1 atm Patm + ln T K atm e rt
8 Impled Volatlty HAL Aprl 09 ALL PUT ymbol Last B d Ask IVOL Delta trke ymbol Last Bd Ask IVOL Del ta HALDU.X na HALPU.X HALDB.X HALPB.X HALDZ.X HALPZ.X HALD.X HALP.X HALDP.X HALPP.X HALDD.X HALPD.X HALDQ.X HALPQ.X Impled Volatlty ALL PUT trke
9 DIA Volatlty urface, March , 1:00 noon DIA, Mar09 DIA, Jun 30, call put call put DIA, Apr09 DIA, ep 30, call put call put These curves move and provde tradng opportuntes.
10 Many dfferent trades possble -- arry trades usng optons (mpled dvdend vs. actual dvdend, HTB) -- Volatlty surface trades (non-drectonal): tradng dfferent strkes on the same underlyng asset -- hstorcal vol vs mpled vol -- Relatve-value trades across names (non-drectonal) -- sngle-name opton versus far-value -- dsperson tradng (ndex opton versus components) -- Drectonal volatlty trades (long vol/ short vol, etc)
11 kewness -- For equtes, the mpled volatlty curve s decreasng n the strke prce around ATM -- The effect s more pronounced for ndces and etfs than for sngle names
12 Mechancs of opton tradng -- Open poston (long or short) and trade the stock so as to be delta-neutral. -- Adjust the Delta of the opton as the stock/opton prces move ( ) dt d d dt r d r t dt d r dt d d d rdt ddt rdt d d L P d d d dt t d ) ( &... 1
13 Book-keepng: proft/loss from a delta-hedged opton poston P/L θ ( n 1) + V d or P/L 1 Γ ( di ) I dt + V d
14 1-day P/L for Long all/hort tock (onstant volatlty16%) P/L θ ( n 1) θ daly tme - decay, n percent ndex change expected daly volatlty
15 Assumng an mpled volatlty drop of 1% Vol15% loss f stock does not move and volatlty drops 1%
16 A closer look at the proft-loss due to a change n volatlty % move n vol > 8% move n premum for a 6m ATM opton
17 Measurng the Rsk of a Portfolo (assumng delta neutralty) Portfolo of optons on N stocks n j contracts of opton wth underlyng stock, expraton T j, volatlty j Π j j n n j j ( +, T, K, + ) (, T, K, ) ( ( ) ( ) j + + (1 R, Tj, Kj, j 1 R, Tj, Kj, j R j j j j j j j j j Need to defne a jont dstrbuton of stock returns and volatlty returns to calculate statstcs of PNL
18 Factor Model onsder only parallel vol shfts and use 30-day ATM volatltes k m k k k m k k F R F R ς γ ε β N N j j j R R R E R R D R R j j j ',, M E D D M Extract factors from PA of augmented matrx
19 Alternatve Approach usng ETFs d d d ETF ( ) β + γ + ς, ETF ( ) ETF( ) ETF assocated wth stock Model the ATM volatlty returns as a functon of the stock return and changes n the volatlty of the sector. onjecture: there are fewer systematc factors that explan volatlty returns than n the case of stock returns. (m<0) Possble project: do the PA on the Nasdaq 100 optonable stocks analyzng the matrx M for ths case.
20 Modelng the Volatlty kew x ln( K / ) mp ( x, t) mp (0, t) ( 1+ γx + δx +...) Proposton: Under reasonable assumptons on prce process (stoch. vol), If d atm atm d β + ε Then γ β
21 Evoluton of the slope of the 30-day mpled volatlty curve, Avellaneda & Lee, 005
22 Evoluton of rato [slope/leverage coeffcent] The ``roarng 90 s! Far value lne (V) γ β / Avellaneda & Lee, 005
23
24
25
26
27
28
29
Variance of Trait in an Inbred Population. Variance of Trait in an Inbred Population
Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Revew of Mean Trat Value n Inbred Populatons We showed n the last lecture that for a populaton
One and two particle density matrices for single determinant HF wavefunctions. (1) = φ 2. )β(1) ( ) ) + β(1)β * β. (1)ρ RHF
One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
Pricing of Options on two Currencies Libor Rates
Prcng o Optons on two Currences Lbor Rates Fabo Mercuro Fnancal Models, Banca IMI Abstract In ths document we show how to prce optons on two Lbor rates belongng to two derent currences the ormer s domestc,
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα,
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα Βασίλειος Σύρης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Εαρινό εξάμηνο 2008 Economcs Contents The contet The basc model user utlty, rces and
Multi-dimensional Central Limit Theorem
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
Multi-dimensional Central Limit Theorem
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
8.1 The Nature of Heteroskedasticity 8.2 Using the Least Squares Estimator 8.3 The Generalized Least Squares Estimator 8.
8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
α & β spatial orbitals in
The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών. ΗΥ-570: Στατιστική Επεξεργασία Σήµατος. ιδάσκων : Α. Μουχτάρης. εύτερη Σειρά Ασκήσεων.
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
Phasor Diagram of an RC Circuit V R
ESE Lecture 3 Phasor Dagram of an rcut VtV m snt V t V o t urrent s a reference n seres crcut KVL: V m V + V V ϕ I m V V m ESE Lecture 3 Phasor Dagram of an L rcut VtV m snt V t V t L V o t KVL: V m V
ΠΩΣ ΕΠΗΡΕΑΖΕΙ Η ΜΕΡΑ ΤΗΣ ΕΒΔΟΜΑΔΑΣ ΤΙΣ ΑΠΟΔΟΣΕΙΣ ΤΩΝ ΜΕΤΟΧΩΝ ΠΡΙΝ ΚΑΙ ΜΕΤΑ ΤΗΝ ΟΙΚΟΝΟΜΙΚΗ ΚΡΙΣΗ
Σχολή Διοίκησης και Οικονομίας Κρίστια Κυριάκου ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ ΤΜΗΜΑ ΕΜΠΟΡΙΟΥ,ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΝΑΥΤΙΛΙΑΣ Της Κρίστιας Κυριάκου ii Έντυπο έγκρισης Παρουσιάστηκε
Mean-Variance Analysis
Mean-Variance Analysis Jan Schneider McCombs School of Business University of Texas at Austin Jan Schneider Mean-Variance Analysis Beta Representation of the Risk Premium risk premium E t [Rt t+τ ] R1
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
Math 6 SL Probability Distributions Practice Test Mark Scheme
Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
The Simply Typed Lambda Calculus
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
- S P E C I A L R E P O R T - EMPLOYMENT. -January 2012- Source: Cyprus Statistical Service
- S P E C I A L R E P O R T - UN EMPLOYMENT -January 2012- Source: Cyprus Statistical Service This Special Report is brought to you by the Student Career Advisory department of Executive Connections. www.executiveconnections.eu
The challenges of non-stable predicates
The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗ ΔΙΟΙΚΗΣΗ
ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗ ΔΙΟΙΚΗΣΗ ΑΘΙΑΝΟΣ ΣΤΕΡΓΙΟΣ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΤΕ 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Quick Installation Guide
A Installation 1 F H B E C D G 2 www.trust.com/17528/faq Quick Installation Guide C C D Freewave Wireless Audio Set 17528/ 17529 D Installation Configuration Windows XP 4 5 8 Windows 7/ Vista 6 7 9 10
IF(Ingerchange Format) [7] IF C-STAR(Consortium for speech translation advanced research ) [8] IF 2 IF
![IF(Ingerchange Format) [7] IF C-STAR(Consortium for speech translation advanced research ) [8] IF 2 IF](/thumbs/91/106522878.jpg "IF(Ingerchange Format) [7] IF C-STAR(Consortium for speech translation advanced research ) [8] IF 2 IF")
100080 e-mal:{gdxe, cqzong, xubo}@nlpr.a.ac.cn tel:(010)82614468 IF 1 1 1 IF(Ingerchange Format) [7] IF C-STAR(Consortum for speech translaton advanced research ) [8] IF 2 IF 2 IF 69835003 60175012 [6][12]
Κόστος Κεφαλαίου. Estimating Inputs: Discount Rates
Αρτίκης Γ. Παναγιώτης Κόστος Κεφαλαίου Estimating Inputs: Discount Rates Critical ingredient in discounted cashflow valuation. Errors in estimating the discount rate or mismatching cashflows and discount
ΕΓΓΡΑΦΟ ΕΡΓΑΣΙΑΣ ΤΩΝ ΥΠΗΡΕΣΙΩΝ ΤΗΣ ΕΠΙΤΡΟΠΗΣ. Εκθεση χώρας - Κύπρος 2015. {COM(2015) 85 final}
ΕΥΡΩΠΑΪΚΗ ΕΠΙΤΡΟΠΗ Βρυξέλλες, 26.2.2015 SWD(2015) 32 final ΕΓΓΡΑΦΟ ΕΡΓΑΣΙΑΣ ΤΩΝ ΥΠΗΡΕΣΙΩΝ ΤΗΣ ΕΠΙΤΡΟΠΗΣ Εκθεση χώρας - Κύπρος 2015 {COM(2015) 85 final} Το παρόν έγγραφο δεν συνιστά επίσημη θέση της Ευρωπαϊκής
1 Complete Set of Grassmann States
Physcs 610 Homework 8 Solutons 1 Complete Set of Grassmann States For Θ, Θ, Θ, Θ each ndependent n-member sets of Grassmann varables, and usng the summaton conventon ΘΘ Θ Θ Θ Θ, prove the dentty e ΘΘ dθ
Advanced Subsidiary Unit 1: Understanding and Written Response
Write your name here Surname Other names Edexcel GE entre Number andidate Number Greek dvanced Subsidiary Unit 1: Understanding and Written Response Thursday 16 May 2013 Morning Time: 2 hours 45 minutes
Προγραμματισμός Ι. Εγγραφές. Δημήτρης Μιχαήλ. Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο
Προγραμματισμός Ι Εγγραφές Δημήτρης Μιχαήλ Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Η Ανάγκη Ομαδοποίησης Πολλές φορές έχουμε πληροφορίες διαφορετικού τύπου οι οποίες όμως έχουν μεγάλη
8.324 Relativistic Quantum Field Theory II
Lecture 8.3 Relatvstc Quantum Feld Theory II Fall 00 8.3 Relatvstc Quantum Feld Theory II MIT OpenCourseWare Lecture Notes Hon Lu, Fall 00 Lecture 5.: RENORMALIZATION GROUP FLOW Consder the bare acton
Neutralino contributions to Dark Matter, LHC and future Linear Collider searches
Neutralno contrbutons to Dark Matter, LHC and future Lnear Collder searches G.J. Gounars Unversty of Thessalonk, Collaboraton wth J. Layssac, P.I. Porfyrads, F.M. Renard and wth Th. Dakonds for the γz
Section 8.3 Trigonometric Equations
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
Περιεχόµενα. 1. Γενικό πλαίσιο. 2. Η ΚΑΠ σήµερα. 3. Γιατί χρειαζόµαστε τη µεταρρύθµιση; 4. Νέοι στόχοι, µελλοντικά εργαλεία και πολιτικές επιλογές
Ανακοίνωση για το µέλλον της ΚAΠ «Η ΚΑΠπροςτο2020: αντιµετωπίζοντας τις προκλήσεις στον τοµέα των τροφίµων, στους φυσικούς πόρους και στις περιφέρειες» Γ Γεωργίας και Αγροτικής Ανάπτυξης Ευρωπαϊκή Επιτροπή
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Molecular evolutionary dynamics of respiratory syncytial virus group A in
Molecular evolutionary dynamics of respiratory syncytial virus group A in recurrent epidemics in coastal Kenya James R. Otieno 1#, Charles N. Agoti 1, 2, Caroline W. Gitahi 1, Ann Bett 1, Mwanajuma Ngama
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Homework 3 Solutions
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Constant Elasticity of Substitution in Applied General Equilibrium
Constant Elastct of Substtuton n Appled General Equlbru The choce of nput levels that nze the cost of producton for an set of nput prces and a fed level of producton can be epressed as n sty.. f Ltng for
5.4 The Poisson Distribution.
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ/ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ «ΚΛΑ ΕΜΑ ΟΜΑ ΑΣ ΚΑΤΑ ΠΕΡΙΠΤΩΣΗ ΜΕΣΩ ΤΑΞΙΝΟΜΗΣΗΣ ΠΟΛΛΑΠΛΩΝ ΕΤΙΚΕΤΩΝ» (Instance-Based Ensemble
Section 9.2 Polar Equations and Graphs
180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
8. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ. ICA: συναρτήσεις κόστους & εφαρμογές
8. ΕΠΕΞΕΡΓΑΣΊΑ ΣΗΜΆΤΩΝ ICA: συναρτήσεις κόστους & εφαρμογές ΚΎΡΤΩΣΗ (KUROSIS) Αθροιστικό (cumulant) 4 ης τάξεως μίας τ.μ. x με μέσο όρο 0: kurt 4 [ x] = E[ x ] 3( E[ y ]) Υποθέτουμε διασπορά=: kurt[ x]
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
C.S. 430 Assignment 6, Sample Solutions
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
IR Futures Effective Asset Class ก Efficient Frontier
Interest Futures* ก * ก ก ก. ก ก 11 ก ก ก ก ก ( ) ก ก * Interest Futures ก ก ก ก ก ก ก ก ก ก (Synthetic Portfolio) ก * ก ก ก 2 กก IR Futures ก ก (Asset Class) IR Futures Supposedly Most Efficient and Effective
ΠΙΝΑΚΑΣ 1 Μηνιαίο Πλαίσιο για την Παρακολούθηση των εισπράξεων εισφορών των ΦΚΑ στη "Νέα Αρχή" Σύνολο 07/ /2014. Σύνολο
ΠΙΝΑΚΑΣ 1 Μηνιαίο Πλαίσιο για την Παρακολούθηση των εισπράξεων εισφορών των ΦΚΑ στη "Νέα Αρχή" Οφειλή (EUR εκατ.) Δείκτες Απρ 14 Μαι 14 Ιουν 14 Ιουλ 14 Αυγ 14 Σεπ 14 Οκτ 14 Νοε 14 Δεκ 14 Ιαν 15 Φεβ 15
4.6 Autoregressive Moving Average Model ARMA(1,1)
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
Srednicki Chapter 55
Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
ΓΕΩΜΕΣΡΙΚΗ ΣΕΚΜΗΡΙΩΗ ΣΟΤ ΙΕΡΟΤ ΝΑΟΤ ΣΟΤ ΣΙΜΙΟΤ ΣΑΤΡΟΤ ΣΟ ΠΕΛΕΝΔΡΙ ΣΗ ΚΤΠΡΟΤ ΜΕ ΕΦΑΡΜΟΓΗ ΑΤΣΟΜΑΣΟΠΟΙΗΜΕΝΟΤ ΤΣΗΜΑΣΟ ΨΗΦΙΑΚΗ ΦΩΣΟΓΡΑΜΜΕΣΡΙΑ
ΕΘΝΙΚΟ ΜΕΣΟΒΙΟ ΠΟΛΤΣΕΧΝΕΙΟ ΣΜΗΜΑ ΑΓΡΟΝΟΜΩΝ-ΣΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΣΟΜΕΑ ΣΟΠΟΓΡΑΦΙΑ ΕΡΓΑΣΗΡΙΟ ΦΩΣΟΓΡΑΜΜΕΣΡΙΑ ΓΕΩΜΕΣΡΙΚΗ ΣΕΚΜΗΡΙΩΗ ΣΟΤ ΙΕΡΟΤ ΝΑΟΤ ΣΟΤ ΣΙΜΙΟΤ ΣΑΤΡΟΤ ΣΟ ΠΕΛΕΝΔΡΙ ΣΗ ΚΤΠΡΟΤ ΜΕ ΕΦΑΡΜΟΓΗ ΑΤΣΟΜΑΣΟΠΟΙΗΜΕΝΟΤ
Second Order Partial Differential Equations
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Homework 8 Model Solution Section
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Οικονομία. Διάλεξη 8η: Producer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 8η: Producer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Firm Behavior GOAL: Firms choose the maximum possible output (technological
Κόστος Κεφαλαίου. Estimating Inputs: Discount Rates
Αρτίκης Γ. Παναγιώτης Κόστος Κεφαλαίου Estimating Inputs: Discount Rates Critical ingredient in discounted cashflow valuation. Errors in estimating the discount rate or mismatching cashflows and discount
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Οικονομία. Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Τέλος Ενότητας Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί
Νεοκλασική Χρηματοοικονομική. Συμπεριφορική Χρηματοοικονομική
Νεοκλασική Χρηματοοικονομική Συμπεριφορική Χρηματοοικονομική Νεοκλασική Χρηματοοικονομική (Neoclassical Finance) Στη Νεοκλασική Χρηματοοικονομική η έρευνα βασίστηκε αποκλειστικά στο λεγόμενο «ορθολογικό
Statistical Inference I Locally most powerful tests
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Οδηγίες Αγοράς Ηλεκτρονικού Βιβλίου Instructions for Buying an ebook
Οδηγίες Αγοράς Ηλεκτρονικού Βιβλίου Instructions for Buying an ebook Βήμα 1: Step 1: Βρείτε το βιβλίο που θα θέλατε να αγοράσετε και πατήστε Add to Cart, για να το προσθέσετε στο καλάθι σας. Αυτόματα θα
Συστήματα Διαχείρισης Βάσεων Δεδομένων
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Συστήματα Διαχείρισης Βάσεων Δεδομένων Φροντιστήριο 9: Transactions - part 1 Δημήτρης Πλεξουσάκης Τμήμα Επιστήμης Υπολογιστών Tutorial on Undo, Redo and Undo/Redo
Paper Reference. Paper Reference(s) 1776/04 Edexcel GCSE Modern Greek Paper 4 Writing. Thursday 21 May 2009 Afternoon Time: 1 hour 15 minutes
Centre No. Candidate No. Paper Reference(s) 1776/04 Edexcel GCSE Modern Greek Paper 4 Writing Thursday 21 May 2009 Afternoon Time: 1 hour 15 minutes Materials required for examination Nil Paper Reference
2.153 Adaptive Control Lecture 7 Adaptive PID Control
2.153 Adaptive Control Lecture 7 Adaptive PID Control Anuradha Annaswamy aanna@mit.edu ( aanna@mit.edu 1 / 17 Pset #1 out: Thu 19-Feb, due: Fri 27-Feb Pset #2 out: Wed 25-Feb, due: Fri 6-Mar Pset #3 out:
Αποθήκες εδοµένων και Εξόρυξη Γνώσης (Data Warehousing & Data Mining)
Πανεπιστήµιο Πειραιώς Τµήµα Πληροφορικής Αποθήκες εδοµένων και Εξόρυξη Γνώσης (Data Warehousing & Data Mining) Εξόρυξη Χρονικής Γνώσης (temporal data mining) Γιάννης Θεοδωρίδης, Νίκος Πελέκης Οµάδα ιαχείρισης
Right Rear Door. Let's now finish the door hinge saga with the right rear door
Right Rear Door Let's now finish the door hinge saga with the right rear door You may have been already guessed my steps, so there is not much to describe in detail. Old upper one file:///c /Documents
Παραμύθια τησ Χαλιμϊσ, τομ. A Σελύδα 1
Παραμύθια τησ Χαλιμϊσ, τομ. A Σελύδα 1 Παραμύθια τησ Χαλιμϊσ, τομ. A Σελύδα 2 Dervish Abu Bekr, «Παραμύθια τησ Χαλιμϊσ, τομ. Α» Ιούνιοσ 2013 Φωτo εξωφύλλου: Βαςιλεύα Αςπαςύα Μαςούρα Επιμϋλεια ϋκδοςησ:
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Single Stock Analysis Stock Pair Analysis Portfolio Dates Portfolio Dates Correl Maturity VolRatio Ref Stock Correl Ref Stock
Single Stock Analysis Stock Pair Analysis Portfolio Dates Portfolio Dates orrel Maturity Date Monday, December 21, 2009 Date Monday, December 21, 2009 30 Percentile Date Friday, December 19, 2008 Percentile
ΠΙΝΑΚΑΣ 1 Μηνιαίο Πλαίσιο για την Παρακολούθηση των εισπράξεων εισφορών των ΦΚΑ στη "Νέα Αρχή" Σύνολο 07/ /2014. Σύνολο
ΠΙΝΑΚΑΣ 1 Μηνιαίο Πλαίσιο για την Παρακολούθηση των εισπράξεων εισφορών των ΦΚΑ στη "Νέα Αρχή" Οφειλή (EUR εκατ.) Δείκτες Απρ 14 Μαι 14 Ιουν 14 Ιουλ 14 Αυγ 14 Σεπ 14 Οκτ 14 Νοε 14 (1) οφειλών στη ρύθμιση
LECTURE 4 : ARMA PROCESSES
LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
ΠΙΝΑΚΑΣ 1 Μηνιαίο Πλαίσιο για την Παρακολούθηση των εισπράξεων εισφορών των ΦΚΑ στη "Νέα Αρχή" Σύνολο 07/ /2014. Σύνολο
ΠΙΝΑΚΑΣ 1 Μηνιαίο Πλαίσιο για την Παρακολούθηση των εισπράξεων εισφορών των ΦΚΑ στη "Νέα Αρχή" Οφειλή (EUR εκατ.) Δείκτες Απρ 14 Μαι 14 Ιουν 14 Ιουλ 14 Αυγ 14 Σεπ 14 Οκτ 14 Νοε 14 Δεκ 14 Ιαν 15 (1) οφειλών
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ. ΕΠΛ342: Βάσεις Δεδομένων. Χειμερινό Εξάμηνο Φροντιστήριο 10 ΛΥΣΕΙΣ. Επερωτήσεις SQL
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ342: Βάσεις Δεδομένων Χειμερινό Εξάμηνο 2013 Φροντιστήριο 10 ΛΥΣΕΙΣ Επερωτήσεις SQL Άσκηση 1 Για το ακόλουθο σχήμα Suppliers(sid, sname, address) Parts(pid, pname,
A three mutual fund separation theorem
A three mutual fund separaton theorem Fernando Alvarez and Andy Atkeson February 5, 08 Abstract We analyze a one perod economy wth CARA preferences, and normally dstrbuted aggregate rsk. We allow an arbtrary
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
ΠΙΝΑΚΑΣ 1 Μηνιαίο Πλαίσιο για την Παρακολούθηση των εισπράξεων εισφορών των ΦΚΑ στη "Νέα Αρχή" Σύνολο 07/ /2014. Σύνολο
ΠΙΝΑΚΑΣ 1 Μηνιαίο Πλαίσιο για την Παρακολούθηση των εισπράξεων εισφορών των ΦΚΑ στη "Νέα Αρχή" Οφειλή (EUR εκατ.) Δείκτες Απρ 14 Μαι 14 Ιουν 14 Ιουλ 14 Αυγ 14 Σεπ 14 Οκτ 14 Νοε 14 Δεκ 14 Ιαν 15 Φεβ 15
Σύνολο 07/ /2014. Σύνολο
ΠΙΝΑΚΑΣ 1 Μηνιαίο Πλαίσιο για την Παρακολούθηση των εισπράξεων εισφορών των ΦΚΑ στη "Νέα Αρχή" Οκτ 14 Νοε 14 Δεκ 14 Ιαν 15 Φεβ 15 Οφειλή (EUR εκατ.) Δείκτες Απρ 14 Μαι 14 Ιουν 14 Ιουλ 14 Αυγ 14 Σεπ 14
Πανεπιστήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεταπτυχιακών Σπουδών «Πληροφορική»
Πανεπιστήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεταπτυχιακών Σπουδών «Πληροφορική» Μεταπτυχιακή Διατριβή Τίτλος Διατριβής Επίκαιρα Θέματα Ηλεκτρονικής Διακυβέρνησης Ονοματεπώνυμο Φοιτητή Σταμάτιος
M ea sur ing the Fa irness of the W age D istr ibution of Urban W orkers in D ifferen t Industr ies of Ch ina
27 3 20103 Statstcal Research Vol. 27, No13 M ar. 2010 3 :,,, :,;,,,, ;,, ; 1 /3 : ; ; ; : C812: A : 1002-4565 (2010) 03-0003 - 09 M ea sur ng the Fa rness of the W age D str buton of Urban W orkers n
(1) Describe the process by which mercury atoms become excited in a fluorescent tube (3)
Q1. (a) A fluorescent tube is filled with mercury vapour at low pressure. In order to emit electromagnetic radiation the mercury atoms must first be excited. (i) What is meant by an excited atom? (1) (ii)
6.003: Signals and Systems. Modulation
6.003: Signals and Systems Modulation May 6, 200 Communications Systems Signals are not always well matched to the media through which we wish to transmit them. signal audio video internet applications
Generalized Fibonacci-Like Polynomial and its. Determinantal Identities
Int. J. Contemp. Math. Scences, Vol. 7, 01, no. 9, 1415-140 Generalzed Fbonacc-Le Polynomal and ts Determnantal Identtes V. K. Gupta 1, Yashwant K. Panwar and Ompraash Shwal 3 1 Department of Mathematcs,
Example Sheet 3 Solutions
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
RECIPROCATING COMPRESSOR CALCULATION SHEET
Gas properties, flowrate and conditions 1 Gas name Air RECIPRCATING CMPRESSR CALCULATIN SHEET WITH INTERCLER ( Sheet : 1. f 4.) Item or symbol Quantity Unit Item or symbol Quantity Unit 2 Suction pressure,
ΤΕΧΝΙΚΕΣ ΑΝΤΙΚΕΙΜΕΝΟΣΤΡΑΦΟΥΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ. Δημιουργία Κλάσεων και Αντικειμένων Constructors
ΤΕΧΝΙΚΕΣ ΑΝΤΙΚΕΙΜΕΝΟΣΤΡΑΦΟΥΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Δημιουργία Κλάσεων και Αντικειμένων Constructors Κλάσεις και αντικείμενα Ορισμός κλάσης: class
Solution Set #2
. For the followng two harmon waves: (a) Show on a phasor dagram: 05-55-007 Soluton Set # phasor s the omplex vetor evaluated at t 0: f [t] os[ω 0 t] h f [t] 7os ω 0 t π f [t] exp[ 0] + 0 h f [t] 7exp
2. THEORY OF EQUATIONS. PREVIOUS EAMCET Bits.
EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
Newborn Upfront Payment & Newborn Supplement
GREEK Newborn Upfront Payment & Newborn Supplement Female 1: Το μωρό μου θα ρθει σύντομα, θα πρέπει να κανονίσω τα οικονομικά μου. Άκουσα ότι η κυβέρνηση δεν δίνει πλέον το Baby Bonus. Ξέρεις τίποτα γι
Generalized Linear Model [GLM]
![Generalized Linear Model [GLM]](/thumbs/93/113885699.jpg "Generalized Linear Model [GLM]")
Generalzed Lnear Model [GLM]. ก. ก Emal: nkom@kku.ac.th A Lttle Hstory Multple lnear regresson normal dstrbuton & dentty lnk (Legendre, Guass: early 19th century). ANOVA normal dstrbuton & dentty lnk (Fsher:
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΗΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ. Πτυχιακή εργασία ΑΝΑΠΤΥΞΗ ΔΕΙΚΤΩΝ ΠΟΙΟΤΗΤΑΣ ΕΔΑΦΟΥΣ
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΣΧΟΛΗ ΓΕΩΤΕΧΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΔΙΑΧΕΙΡΗΣΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Πτυχιακή εργασία ΑΝΑΠΤΥΞΗ ΔΕΙΚΤΩΝ ΠΟΙΟΤΗΤΑΣ ΕΔΑΦΟΥΣ [Μαρία Μαρκουλλή] Λεμεσός 2015 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ
9.09. # 1. Area inside the oval limaçon r = cos θ. To graph, start with θ = 0 so r = 6. Compute dr
9.9 #. Area inside the oval limaçon r = + cos. To graph, start with = so r =. Compute d = sin. Interesting points are where d vanishes, or at =,,, etc. For these values of we compute r:,,, and the values
SOL GMM BALANCED FUND
SOL GMM BALANCED FUND ΠΙΝΑΚΑΣ ΕΠΕΝΔΥΣΕΩΝ ΑΜΟΙΒΑΙΟΥ ΚΕΦΑΛΑΙΟΥ 2015 Τρίμηνο: Γ ΣΥΝΘΕΣΗ ΕΝΕΡΓΗΤΙΚΟΥ ΑΜΟΙΒΑΙΟΥ ΚΕΦΑΛΑΙΟΥ ΤΕΜΑΧΙΑ ΤΙΜΗ ΣΥΝΟΛΙΚΗ ΑΞΙΑ ΤΕΛΕΥΤΑΙΑΣ ΗΜΕΡΑΣ ΤΡΙΜΗΝΟΥ ΤΕΛΕΥΤΑΙΑΣ ΗΜΕΡΑΣ ΤΡΙΜΗΝΟΥ I.
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Οικονομία. Διάλεξη 10η: Basics of Game Theory part 2 Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 0η: Basics of Game Theory part 2 Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Best Response Curves Used to solve for equilibria in games
Finite Field Problems: Solutions
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
ΘΕΜΑ: «ΣΤΟΙΧΕΙΑ ΡΥΘΜΙΣΕΩΝ ΤΜΗΜΑΤΙΚΗΣ ΚΑΤΑΒΟΛΗΣ Ν.4152/2013, Ν.4305/2014 & Ν.4321/2015 - ΑΠΡΙΛΙΟΥ 2015»
Αθήνα, 25/5/2015 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΙΔΡΥΜΑ ΚΟΙΝΩΝΙΚΩΝ ΑΣΦΑΛΙΣΕΩΝ ΕΝΙΑΙΟ ΤΑΜΕΙΟ ΑΣΦΑΛΙΣΗΣ ΜΙΣΘΩΤΩΝ Δ Ι Ο Ι Κ Η Σ Η ΓΕΝ. Δ/ΝΣΗ ΑΣΦ/ΚΩΝ ΥΠΗΡΕΣΙΩΝ ΔΙΕΥΘΥΝΣΗ ΑΣΦΑΛΙΣΗΣ - ΕΣΟΔΩΝ ΤΜΗΜΑ : ΑΝΑΓΚΑΣΤΙΚΩΝ ΜΕΤΡΩΝ
ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2010 ΜΑΘΗΜΑ: ΛΟΓΙΣΤΙΚΗ ΗΜΕΡΟΜΗΝΙΑ ΚΑΙ ΩΡΑ ΕΞΕΤΑΣΗΣ: Παρασκευή 4 Ιουνίου 2010 07:30
ΕΘΝΙΚΗ ΥΟΛΗ ΔΗΜΟΙΑ ΔΙΟΙΚΗΗ ΙH ΕΚΠΑΙΔΕΤΣΙΚΗ ΕΙΡΑ ΤΜΗΜΑ ΚΟΙΝΩΝΙΚΗΣ ΔΙΟΙΚΗΣΗΣ ΔΙΟΙΚΗΣΗ ΜΟΝΑΔΩΝ ΥΓΕΙΑΣ ΤΕΛΙΚΗ ΕΡΓΑΣΙΑ
Δ ΕΘΝΙΚΗ ΥΟΛΗ ΔΗΜΟΙΑ ΔΙΟΙΚΗΗ ΙH ΕΚΠΑΙΔΕΤΣΙΚΗ ΕΙΡΑ ΤΜΗΜΑ ΚΟΙΝΩΝΙΚΗΣ ΔΙΟΙΚΗΣΗΣ ΔΙΟΙΚΗΣΗ ΜΟΝΑΔΩΝ ΥΓΕΙΑΣ ΤΕΛΙΚΗ ΕΡΓΑΣΙΑ Θέμα: «Αποκενηρωμένες δομές ζηο ζύζηημα σγείας ηης Ασζηρίας : Μια ζσζηημαηική θεωρηηική
Approximation of distance between locations on earth given by latitude and longitude
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Αγορά Ακινήτων και η ελληνική Κρίση
Αγορά Ακινήτων και η ελληνική Κρίση Γκίκας Α. Χαρδούβελης Οικονομικός Σύμβουλος, Eurobank Group Καθηγητής, Τμήμα Χρηματοοικονομικής και Τραπεζικής Διοικητικής, Πανεπιστήμιο Πειραιά PRODEXPO 213 14ο Συνέδριο
Proforma C. Flood-CBA#2 Training Seminars. Περίπτωση Μελέτης Ποταμός Έ βρος, Κοινότητα Λαβάρων
Proforma C Flood-CBA#2 Training Seminars Περίπτωση Μελέτης Ποταμός Έ βρος, Κοινότητα Λαβάρων Proforma A B C D E F Case Η λογική Study Collecting information regarding the site that is to be assessed. Collecting
Code Breaker. TEACHER s NOTES
TEACHER s NOTES Time: 50 minutes Learning Outcomes: To relate the genetic code to the assembly of proteins To summarize factors that lead to different types of mutations To distinguish among positive,
Appendix. Appendix I. Details used in M-step of Section 4. and expect ultimately it will close to zero. αi =α (r 1) [δq(α i ; α (r 1)
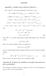Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
Math221: HW# 1 solutions
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
[1] P Q. Fig. 3.1
![[1] P Q. Fig. 3.1](/thumbs/79/80362156.jpg "[1] P Q. Fig. 3.1")
1 (a) Define resistance....... [1] (b) The smallest conductor within a computer processing chip can be represented as a rectangular block that is one atom high, four atoms wide and twenty atoms long. One
Dynamic types, Lambda calculus machines Section and Practice Problems Apr 21 22, 2016
Harvard School of Engineering and Applied Sciences CS 152: Programming Languages Dynamic types, Lambda calculus machines Apr 21 22, 2016 1 Dynamic types and contracts (a) To make sure you understand the
A Sequential Experimental Design based on Bayesian Statistics for Online Automatic Tuning. Reiji SUDA,
Bayes, Bayes mult-armed bandt problem Bayes A Sequental Expermental Desgn based on Bayesan Statstcs for Onlne Automatc Tunng Re SUDA, Ths paper proposes to use Bayesan statstcs for software automatc tunng