ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΙΤΛΟΣ ΔΙΠΛΩΜΑΤΙΚΗΣ ΔΥΝΑΜΙΚΗ ΣΟΛΙΤΟΝΙΩΝ ΣΕ ΣΥΖΕΥΓΜΕΝΑ ΜΗ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ SCHRODINGER ( NLS )
|
|
|
- Αθος Ἀλφαῖος Ζέρβας
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΜΠΕΡΙΔΟΥ ΜΑΡΙΑ ΤΙΤΛΟΣ ΔΙΠΛΩΜΑΤΙΚΗΣ ΕΡΓΑΣΙΑΣ ΔΥΝΑΜΙΚΗ ΣΟΛΙΤΟΝΙΩΝ ΣΕ ΣΥΖΕΥΓΜΕΝΑ ΜΗ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ SCHRODINGER ( NLS ) ΕΠΙΒΛΕΠΩΝ ΚΑΘΗΓΗΤΗΣ : ΒΑΣΙΛΕΙΟΣ ΡΟΘΟΣ ΘΕΣΣΑΛΟΝΙΚΗ ΝΟΕΜΒΡΙΟΣ
2 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΜΠΕΡΙΔΟΥ ΜΑΡΙΑ ΤΙΤΛΟΣ ΔΙΠΛΩΜΑΤΙΚΗΣ ΕΡΓΑΣΙΑΣ ΔΥΝΑΜΙΚΗ ΣΟΛΙΤΟΝΙΩΝ ΣΕ ΣΥΖΕΥΓΜΕΝΑ ΜΗ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ SCHRODINGER ( NLS ) Επιβλέπων καθηγητής: Βασίλειος Ρόθος Εγκρίθηκε από την τριμελή εξεταστική επιτροπή την Δασκαλογιάννης Κωνσταντίνος Συσκάκης Αριστομένης Βασίλειος Ρόθος Καθηγητής ΑΠΘ Καθηγητής ΑΠΘ Καθηγητής ΑΠΘ Θεσσαλονίκη, Νοέμβριος
3 Περιεχόμενα ΠΡΟΛΟΓΟΣ... 6 ΕΥΧΑΡΙΣΤΙΕΣ... 7 ΚΕΦΑΛΑΙΟ ΕΙΣΑΓΩΓΗ ΣΤΑ ΣΟΛΙΤΟΝΙΑ ΓΡΑΜΜΙΚΕΣ ΚΥΜΑΤΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΤΙ ΕΙΝΑΙ ΚΥΜΑ ΚΥΜΑΤΟΣΥΝΑΡΤΗΣΗ ΟΔΕΥΟΝΤΟΣ ΚΥΜΑΤΟΣ ΗΜΙΤΟΝΟΕΙΔΗ ΚΥΜΑΤΑ ΦΑΣΗ ΤΑΧΥΤΗΤΑ ΦΑΣΕΩΣ ΚΑΙ ΤΑΧΥΤΗΤΑ ΟΜΑΔΟΣ ΜΕΤΩΠΑ ΚΥΜΑΤΟΣ ΜΗ ΓΡΑΜΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΠΟΥ ΔΕΧΟΝΤΑΙ ΣΟΛΙΤΟΝΙΚΕΣ ΛΥΣΕΙΣ ΜΕΘΟΔΟΙ ΜΕΛΕΤΗΣ ΣΟΛΙΤΟΝΙΚΩΝ ΛΥΣΕΩΝ ΚΕΦΑΛΑΙΟ ΜΕΛΕΤΗ ΟΠΤΙΚΩΝ ΣΟΛΙΤΟΝΙΩΝ ΕΙΣΑΓΩΓΗ ΔΙΑΚΡΙΣΗ ΟΠΤΙΚΩΝ ΣΟΛΙΤΟΝΙΩΝ ΕΠΕΞΗΓΗΣΗ ΣΥΜΒΟΛΩΝ ΣΤΗΝ ΠΕΡΙΠΤΩΣΗ ΧΡΟΝΙΚΩΝ ΣΟΛΙΤΟΝΙΩΝ ΕΠΕΞΗΓΗΣΗ ΣΥΜΒΟΛΩΝ ΣΤΗΝ ΠΕΡΙΠΤΩΣΗ ΧΩΡΙΚΩΝ ΣΟΛΙΤΟΝΙΩΝ ΟΤΑΝ σ=-1 ΣΤΙΣ ΟΠΤΙΚΕΣ ΙΝΕΣ Η s=+1 ΣΤΑ ΣΥΜΠΑΓΗ ΜΕΣΑ ΟΤΑΝ σ=+1 ΣΤΙΣ ΟΠΤΙΚΕΣ ΙΝΕΣ Η s=-1 ΣΤΑ ΣΥΜΠΑΓΗ ΜΕΣΑ Η ΜΗ ΓΡΑΜΜΙΚΗ ΕΞΙΣΩΣΗ ΤΟΥ SCHRODINGER (ΕΞΙΣΩΣΗ NLS) ΟΠΤΙΚΕΣ ΙΝΕΣ ΣΥΜΠΑΓΗ ΟΠΤΙΚΑ ΜΕΣΑ ΚΑΙ ΕΠΙΠΕΔΟΙ ΔΙΗΛΕΚΤΡΙΚΟΙ ΚΥΜΑΤΟΔΗΓΟΙ ΑΣΤΑΘΕΙΑ ΔΙΑΜΟΡΦΩΣΗΣ ΚΑΙ ΣΟΛΙΤΟΝΙΑ ΦΩΤΕΙΝΑ ΚΑΙ ΣΚΟΤΕΙΝΑ ΣΟΛΙΤΟΝΙΑ ΤΗΣ ΕΞΙΣΩΣΗΣ NLS ΦΩΤΕΙΝΑ ΣΟΛΙΤΟΝΙΑ ΣΚΟΤΕΙΝΑ ΣΟΛΙΤΟΝΙΑ ΚΕΦΑΛΑΙΟ ΣΥΖΕΥΓΜΕΝΕΣ NLS ΚΑΙ ΕΤΕΡΟΔΙΑΜΟΡΦΩΣΗ ΦΑΣΗΣ ΣΥΜΠΑΓΗ ΟΠΤΙΚΑ ΜΕΣΑ ΚΑΙ ΕΠΙΠΕΔΟΙ ΔΙΗΛΕΚΤΡΙΚΟΙ ΚΥΜΑΤΟΔΗΓΟΙ ΓΙΑ ΣΥΖΕΥΓΜΕΝΕΣ NLS ΑΣΤΑΘΕΙΑ ΔΙΑΜΟΡΦΩΣΗΣ ΚΑΙ ΣΟΛΙΤΟΝΙΑ ΓΙΑ ΣΥΖΕΥΓΜΕΝΕΣ NLS ΦΩΤΕΙΝΑ ΣΟΛΙΤΟΝΙΑ (
4 3.5 ΣΚΟΤΕΙΝΑ ΣΟΛΙΤΟΝΙΑ ΚΕΦΑΛΑΙΟ ΑΛΛΗΛΕΠΙΔΡΑΣΗ ΣΚΟΤΕΙΝΩΝ ΣΟΛΙΤΟΝΙΩΝ ΜΕ ΕΠΙΤΟΠΙΣΜΕΝΕΣ ΑΣΑΦΕΙΕΣ ΣΤΙΣ BOSE-EINSTEIN ΣΥΠΥΚΝΩΣΕΙΣ ΕΙΣΑΓΩΓΗ ΜΟΝΤΕΛΟ ΚΑΙ ΑΝΑΛΥΤΙΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ Α. Η ΔΡΑΣΤΙΚΗ ΕΞΙΣΩΣΗ ΚΥΜΑΤΟΣ ΤΩΝ THOMAS-FERMI Β. ΔΥΝΑΜΙΚΑ ΤΩΝ ΣΚΟΤΕΙΝΩΝ ΣΟΛΙΤΟΝΙΩΝ ΚΕΦΑΛΑΙΟ ΣΤΑΤΙΚΑ ΚΑΙ ΔΥΝΑΜΙΚΑ ΤΩΝ ΑΤΟΜΙΚΩΝ ΦΩΤΕΙΝΩΝ ΣΚΟΤΕΙΝΩΝ- ΣΟΛΙΤΟΝΙΩΝ ΠΑΡΟΥΣΙΑ ΑΣΑΦΕΙΩΝ ΤΥΠΟΥ ΣΥΝΑΡΤΗΣΗΣ ΔΕΛΤΑ ΤΟΥ DIRAC I. ΕΙΣΑΓΩΓΗ II. ΜΟΝΤΕΛΑ ΚΑΙ ΑΝΑΛΥΤΙΚΕΣ ΘΕΩΡΙΕΣ Α. ΟΡΓΑΝΩΣΗ-ΔΟΜΗ Β. ΘΕΩΡΙΑ ΔΙΑΤΑΡΑΧΩΝ ΠΑΡΑΡΤΗΜΑ Α ΤΙ ΕΙΝΑΙ ΠΕΡΙΘΛΑΣΗ ΚΑΙ ΤΙ ΔΙΑΣΠΟΡΑ ΤΙ ΕΙΝΑΙ ΑΝΑΚΛΑΣΗ ΚΑΙ ΤΙ ΔΙΑΘΛΑΣΗ ΔΕΙΚΤΗΣ ΔΙΑΘΛΑΣΗΣ ΣΚΕΔΑΣΗ ΚΑΙ ΑΝΤΙΣΤΡΟΦΑ ΠΡΟΒΛΗΜΑΤΑ ΔΙΠΛΘΛΑΣΤΙΚΟΤΗΤΑ ΟΠΤΙΚΗ ΙΝΑ ΠΑΡΑΡΤΗΜΑ Β ( ΟΙ ΕΞΙΣΩΣΕΙΣ ΤΟΥ LAGRANGE H ΘΕΩΡΙΑ ΤΟΥ HAMILTON)81 ΓΕΝΙΚΕΣ ΜΕΘΟΔΟΙ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΓΕΝΙΚΕΥΜΕΝΕΣ ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΣΥΜΒΟΛΙΣΜΟΣ ΕΞΙΣΩΣΕΙΣ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ ΤΑΞΙΝΟΜΗΣΗ ΜΗΧΑΝΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΣΚΛΗΡΟΝΟΜΑ ΚΑΙ ΡΕΟΝΟΜΑ ΣΥΣΤΗΜΑΤΑ ΟΛΟΝΟΜΑ ΚΑΙ ΜΗ ΟΛΟΝΟΜΑ ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΗΡΗΤΙΚΑ ΚΑΙ ΜΗ ΣΥΝΤΗΡΗΤΙΚΑ ΚΙΝΗΤΙΚΚΗ ΕΝΕΡΓΕΙΑ-ΓΕΝΙΚΕΥΜΕΝΕΣ ΤΑΧΥΤΗΤΕΣ ΟΙ ΕΞΙΣΩΣΕΙΣ ΤΟΥ LAGRANGE ΕΞΙΣΩΣΕΙΣ ΤΟΥ LAGRANGE ΓΙΑ ΜΗ ΟΛΟΝΟΜΑ ΣΥΣΤΗΜΑΤΑ
5 ΔΥΝΑΜΙΚΗ ΤΩΝ ΧΑΜΙΛΤΟΝΙΑΝΩΝ ΣΥΣΤΗΜΑΤΩΝ ΟΙ ΕΞΙΣΩΣΕΙΣ ΤΟΥ HAMILTON Η ΣΥΝΑΡΤΗΣΗ ΤΟΥ HAMILTON ΓΙΑ ΣΥΝΤΗΡΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ ΑΓΝΟΗΣΙΜΕΣ Η ΚΥΚΛΙΚΕΣ ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΛΟΓΙΣΜΟΣ ΤΩΝ ΜΕΤΑΒΟΛΩΝ Η ΑΡΧΗ ΤΟΥ HAMILTON ΜΕΓΙΣΤΑ ΚΑΙ ΕΛΑΧΙΣΤΑ ΠΑΡΑΡΤΗΜΑ Γ (ΘΕΩΡΙΑ ΔΙΑΤΑΡΑΧΩΝ) ΚΑΝΟΝΙΚΗ ΔΙΑΤΑΡΑΧΗ ΠΑΡΑΡΤΗΜΑ Δ ΑΡΤΙΚΟΛΕΞΑ Βιβλιογραφία και Παραπομπές
6 ΠΡΟΛΟΓΟΣ Η διπλωματική εργασία που έχετε στα χέρια σας πραγματεύεται ένα πολύ ιδιαίτερο θέμα. Δυναμική σολιτονίων σε συζευγμένα μη γραμμικά συστήματα Schrodinger (NLS). Υπάρχουν σχήματα και βιβλιογραφία που μπορεί να συμβουλευτεί ο μελετητής για την καλύτερη κατανόηση της εργασίας. Στο πρώτο κεφάλαιο γίνεται μια εισαγωγή στα σολιτόνια και υπάρχουν ιστορικά στοιχεία. Στη συνέχεια δίνονται πληροφορίες για το που εφαρμόζονται και σε τι εξυπηρετούν. Επίσης αναφέρονται οι μη-γραμμικές εξισώσεις που δίνουν σολιτονικές λύσεις και αναπτύσσονται οι μέθοδοι μελέτης της εξίσωσης NLS. Στο δεύτερο κεφάλαιο γίνεται εισαγωγή στην οπτική σολιτονίων, διαχωρισμός αυτών σε περιπτώσεις και υπάρχουν πιο αναλυτικά στοιχεία για την NLS. Στο τρίτο κεφάλαιο γίνεται λόγος για τη συζευγμένη NLS και την ετεροδιαμόρφωση φάσης. Στο τέταρτο κεφάλαιο μελετώνται αναλυτικά οι αλληλεπιδράσεις σκοτεινών σολιτονίων με επιτοπισμένες ασάφειες στις Bose-Einstein συμπυκνώσεις. Στο πέμπτο κεφάλαιο αναφέρονται τα στατικά και δυναμικά των ατομικών φωτεινών σκοτεινών σολιτονίων παρουσία ασαφειών έχοντας τη μορφή της συνάρτησης δέλτα του Dirac. Στο τέλος υπάρχουν παραρτήματα τα οποία λειτουργούν ως συμπληρωματικά στοιχεία της κύριας εργασίας και βοηθούν στην καλύτερη κατανόηση του θέματος από τον αναγνώστη. 6
7 ΕΥΧΑΡΙΣΤΙΕΣ Σε αυτό το σημείο θα ήθελα να ευχαριστήσω όλους όσους συνέβαλαν στην διεκπεραίωση αυτής της διπλωματικής εργασίας που σηματοδοτεί το πέρας των Μεταπτυχιακών μου Σπουδών. Θερμές ευχές οφείλω στον επιβλέποντα καθηγητή μου, κ. Βασίλειο Ρόθο, για το ενδιαφέρον του, για την εύρεση ενός θέματος με ιδιαίτερο ενδιαφέρον, για την πρόθυμη και για την έμπρακτη επιστημονική και ηθική υποστήριξη του στη συνέχεια. Η βοήθεια του ήταν πολύτιμη για την ολοκλήρωση αυτής της εργασίας. Ευχαριστώ επίσης το Τμήμα Μαθηματικών, και ειδικότερα τον Τομέα Θεωρητικών Μαθηματικών, για τη γενικότερη στήριξη που μου παρείχαν. Τέλος, θα ήθελα να ευχαριστήσω τους γονείς μου για την αγάπη τους, τη στήριξή τους και την εμπιστοσύνη που μου έδειξαν καθ όλη τη διάρκεια των σπουδών μου. 7
8 ΚΕΦΑΛΑΙΟ ΕΙΣΑΓΩΓΗ ΣΤΑ ΣΟΛΙΤΟΝΙΑ Μελετώντας τα φυσικά φαινόμενα είναι φανερό ότι τα περισσότερα από αυτά είναι μη γραμμικά. Αυτό για πολλά χρόνια περιόριζε τις ερευνητικές δραστηριότητες των ερευνητών και δυσκόλευε την μελέτη τέτοιου είδους φαινομένων. Στην αρχή χρησιμοποιούσαν την αρμονική τους προσέγγιση η οποία αν και ήταν κάπως περιορισμένη έδινε αρκετά καλά αποτελέσματα. Αργότερα, οι ερευνητές εισήγαγαν τις θεωρίες διαταραχών, έτσι ώστε να προσθέσουν και κάποιες μικρές αναρμονικές διορθώσεις στη γραμμική περιγραφή όπου ήταν εφικτό. Σκέφτηκαν πως όταν η μη γραμμικότητα σε ένα φαινόμενο είναι έντονη, η συμπεριφορά του γίνεται ιδιαιτέρως περίπλοκη και οι σχέσεις που το περιγράφουν είναι δύσκολο και καμιά φορά και ακατόρθωτο να υπολογιστούν. Ωστόσο, η πολυπλοκότητα και η αταξία δεν είναι ο κανόνας για ένα μη γραμμικό δυναμικό σύστημα. Υπάρχει μια κατηγορία από μη γραμμικά και ολοκληρώσιμα φυσικά συστήματα, των οποίων οι λύσεις είναι ασυνήθιστα ευσταθείς. Μια από τις πιο αξιοσημείωτες και σημαντικές αυτές λύσεις είναι το σολιτόνιο. Το σολιτόνιο είναι ο σπουδαιότερος κυματικός αντιπρόσωπος της μη γραμμικής δυναμικής και η θεωρία των σολιτονίων είναι ο τρόπος με τον οποίο αντιμετωπίζονται φαινόμενα οργάνωσης και κυματικής διάδοσης σε μη γραμμικά μέσα, με πολλές εφαρμογές όπως στην Οπτική, στην Υδροδυναμική, στη Φυσική Στοιχειωδών Σωματιδίων, στη Φυσική Στερεάς Κατάστασης, στη Φυσική του πλάσματος, στη Βιολογία καθώς και στη Μετεωρολογία. Σολιτόνιο ονομάζεται κάθε εντοπισμένο κύμα (περιορισμένης χωρικής έκτασης) που διαδίδεται μέσα σε ένα μέσο, χωρίς να μεταβάλει τις χαρακτηριστικές του παραμέτρους (την ταχύτητα και τη μορφή του) διατηρώντας την ταυτότητά του ακόμη και μετά από αλληλεπιδράσεις με άλλα σολιτόνια (π.χ. μετωπικές συγκρούσεις). Πρώτη φορά [1] το φαινόμενο του μοναχικού οδεύοντος παλμού παρατηρήθηκε από τον σκωτσέζο μηχανικό John Scott Russell ο οποίος επεσήμανε το 1834 την εντυπωσιακά ευσταθή διάδοση μοναχικών παλμικών κυμάτων κατά μήκος καναλιών και κατέγραψε τις παρατηρήσεις του σχετικά με τις ιδιότητες αυτού που ονόμαζε μοναχικό κύμα μεταφοράς επισημαίνοντας τα εξής: 1. Πρόκειται για κύματα που είναι ανεξάρτητες εντοπισμένες δυναμικές δομές που διαδίδονται χωρίς να μεταβάλλουν μορφή και ταχύτητα. 2. Ένα κύμα που διαδίδεται πάνω στην επιφάνεια του νερού ενός στενού και ρηχού καναλιού βάθους με ταχύτητα, που αυξάνει όταν το πλάτος του κύματος αυξάνει, ακολουθώντας τον τύπο, όπου είναι η επιτάχυνση της βαρύτητας. 3. Μια αρχική μάζα νερού δημιουργεί ανάλογα με το μέγεθος της ένα, δύο, ή περισσότερα μοναχικά κύματα. 8
9 4. Κύματα συμπίεσης (αρνητικού πλάτους) δεν παρατηρήθηκαν. 5. Τα μοναχικά κύματα διασταυρώνονται (αλληλεπιδρούν χωρίς να υφίστανται καμιά αλλοίωση. Οι παρατηρήσεις του Russell παρέμειναν ξεχασμένες για πολλά χρόνια διότι η τότε θεωρία περιέγραφε τη διάδοση γραμμικών μόνο κυμάτων και δε μπορούσε να εξηγήσει το παραπάνω φαινόμενο. Η ουσιαστική έρευνα για μη γραμμικά φαινόμενα ξεκίνησε πολύ αργότερα, ίσως και 50 χρόνια πριν από σήμερα. Η κυμάτωση που παρατήρησε ο Russell, η οποία έδειξε φαινομενική επιμονή να διατηρεί το σχήμα της κατά τη διάδοση είναι σήμερα γνωστή ως σολιτόνιο ή σολιτονικό κύμα και αποτελεί μια από τις σημαντικότερες ανακαλύψεις της μη γραμμικής επιστήμης. Το σολιτόνιο μπορεί να οριστεί σαν ένα χωρικά εντοπισμένο κύμα, ιδιαίτερα ευσταθές, που ελλείψει απωλειών διατηρεί την ενέργεια του και ιδανικά το πλάτος και το εύρος του, ενώ σε άλλη περίπτωση τα μεγέθη αυτά αποτελούν αντικείμενο περιοδικής μόνο διακύμανσης, πάντα χωρίς αυτό να διασπείρεται. Το 1895 οι Korteweg και de Vries ανέπτυξαν τη θεωρία που μπορούσε να ερμηνεύσει την ύπαρξη του σολιτονικού κύματος του Russell της οποίας η έκφραση είναι μια μη γραμμική διαφορική εξίσωση που φέρει το όνομά τους [20,21,22]. Αργότερα, το 1953, οι Fermi, Pasta και Ulam, εκτελώντας μια αριθμητική προσομοίωση διέγερσης ενός μονοδιάστατου σωματιδιακού πλέγματος, παρατήρησαν ότι η μετάδοση ενέργειας σε ένα ρυθμό ακολουθείτο από τη μετάδοση τους σε άλλους ρυθμούς, αλλά τελικά ξαναγύριζε αναλλοίωτη στο αρχικό. Πέρασαν αρκετά χρόνια μέχρι που το 1965 οι Zabusky και Kruskal εξήγησαν θεωρητικά το παραπάνω φαινόμενο ορίζοντας συγχρόνως και το σολιτόνιο [23]. Οι Zabusky και Kruskal ονόμασαν αυτά τα μοναχικά κύματα σολιτόνια (μοναχόνια) για να τονίσουν από τη μια τον εντοπισμένο χαρακτήρα τους και από την άλλη τις σωματιδιακές τους ιδιότητες. Τα σολιτόνια είναι αναλλοίωτα στη διασπορά καθώς επίσης και μετά από τις μεταξύ τους συγκρούσεις. Ένα παράδειγμα στο σχήμα 1.1.α. Το σολιτόνιο είναι μια μαθηματική οντότητα. Αναφέρεται στις ευσταθείς και αναλλοίωτες λύσεις συγκεκριμένων μερικών διαφορικών εξισώσεων, ενώ στην πραγματικότητα τα δευτερογενή φαινόμενα που επιδρούν μακροπρόθεσμα και ασφαλώς οι απώλειες πιστοποιούν ότι δεν υπάρχει τίποτα αναλλοίωτο στη φύση. Χωρίς να γίνει ιδιαίτερη επέκταση στην καθαρά μαθηματική διάσταση τους, οι εξισώσεις που έχουν σολιτονικές λύσεις περιγράφουν συστήματα με άπειρους βαθμούς ελευθερίας, τα οποία είναι πλήρως ολοκληρώσιμα. Τα σολιτονικά κύματα παρουσιάζουν επίσης μεγάλο ενδιαφέρον για φυσικούς και μηχανικούς. Μετά την εργασία των Zabusky και Kruskal, τα σολιτόνια άρχισαν να «εμφανίζονται» παντού. Χρησιμοποιούνται για να περιγράψουν κάποια υδροδυναμικά κύματα (συμπεριλαμβανομένων των τσουνάμις και των rogue waves (κύματα απρόβλεπτης συμπεριφοράς), εντοπισμένα κύματα σε αστροφυσικό πλάσμα, εντοπισμένους ρυθμούς σε μαγνητικούς κρυστάλλους, τη δυναμική βιολογικών συστημάτων, όπως το DNA, τη διάδοση αναλλοίωτων φωτεινών παλμών σε οπτική ίνα και αλλού. Αυτές οι περιπτώσεις των μηγραμμικών κυμάτων περιγράφονται προσεγγιστικά από τις μαθηματικές εξισώσεις που δίνουν σολιτόνια. Τα σολιτονικά αυτά κύματα έχουν τις ιδιότητες των μαθηματικών σολιτονίων. Επίσης είναι δυνατό να σχηματιστούν μέσω της διέγερσης ενός φυσικού συστήματος, το οποίο έχει τις κατάλληλες 9
10 προϋποθέσεις για τη διατήρηση σολιτονίων. Ακόμα και αν η διέγερση δεν έχει ακριβώς τα χαρακτηριστικά της σολιτονικής λύσης, εάν είναι αρκετά ισχυρή, μπορεί να προκαλέσει τη δημιουργία σολιτονικού κύματος. Σχήμα1.1.α: Σύγκρουση σολιτονικών κυμάτων χαμηλής έντασης σε ρηχό νερό. 1.2 ΓΡΑΜΜΙΚΕΣ ΚΥΜΑΤΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΤΙ ΕΙΝΑΙ ΚΥΜΑ Έστω μια [11] χορδή της οποίας η μια άκρη είναι στερεωμένη και η άλλη συγκρατιέται με το χέρι, εάν κινήσουμε δυο, τρεις φορές το χέρι κάθετα προς τη διεύθυνση της χορδής, τότε θα διαπιστώσουμε ότι θα εμφανιστεί μια παραμόρφωση πάνω σ αυτή. Η παραμόρφωση αυτή διαδίδεται πάνω στη χορδή έτσι ώστε να μετακινούνται τα υλικά της σημεία γύρω από μια μέση θέση ισορροπίας αλλά κατά τέτοιο τρόπο ώστε η μορφή της να διατηρείται. Αυτή η διάδοση της διαταραχής μέσα σε ισότροπο και ομογενές μέσο, χωρίς ν αλλοιώνεται η μορφή της, αποτελεί τη χαρακτηριστική ιδιότητα του κύματος. Δηλαδή με τη λέξη κύμα εννοούμε [55] ένα αναγνωρίσιμο σήμα ή διαταραχή, που διαδίδεται με την πάροδο του χρόνου σε ένα μέσο, μεταφέροντας ενέργεια. 10
11 ΚΥΜΑΤΟΣΥΝΑΡΤΗΣΗ ΟΔΕΥΟΝΤΟΣ ΚΥΜΑΤΟΣ Η κυματική διαταραχή [10] που διαδίδεται από ένα σημείο του χώρου σε κάποιο άλλο, χρησιμοποιώντας ως φορέα το μέσο στο οποίο παρατηρείται, χωρίς όμως να μετακινείται το ίδιο το μέσο ονομάζεται κυματική κίνηση. Έστω μια χορδή η οποία διεγείρεται στο ένα άκρο της από μια αρμονική εξωτερική δύναμη. Αν η χορδή έχει άπειρο μήκος τότε τα κύματα που διαδίδονται στο αυτό χωρίς να ανακλώνται πουθενά ονομάζονται οδεύοντα κύματα. Αντίθετα αν η χορδή έχει σταθερά και τα δύο άκρα, τότε τα οδεύοντα κύματα που διαδίδονται πάνω στη χορδή θα ανακλώνται και στα δύο άκρα και επομένως η ταλάντωση της χορδής προκύπτει από το συνδυασμό τέτοιων κυμάτων, που κινούνται εκατέρωθεν κατά μήκος της χορδής και θα σχηματίζονται στάσιμα κύματα. Κύματα σε χορδές είναι εγκάρσια κύματα διότι οι μετατοπίσεις ή ταλαντώσεις του μέσου είναι κάθετες στη διεύθυνση διάδοσης του κύματος (π.χ. το φως). Ενώ οι ταλαντώσεις του μέσου που είναι παράλληλες με τη διεύθυνση διάδοσης του κύματος τα κύματα αυτά ονομάζονται διαμήκη (π.χ. ηχητικά κύματα). Η διαφορική [12] εξίσωση του κύματος ή απλά κυματική εξίσωση είναι: περιγράφει τέτοια κύματα (με μία μόνο μεταβλητή χώρου). Το μέγεθος γνωστό ως κυματική συνάρτηση, παριστάνει τη διαταραχή στο χώρο ) και το χρόνο ( ), είτε πρόκειται για τη μετατόπιση μιας χορδής είτε για τη μεταβολή ενός πεδίου. Σ αυτή τη σχέση είναι η ταχύτητα διαδόσεως του κύματος. Μια λύση της κυματικής εξίσωσης έχει τη μορφή: όπου είναι μια τυχαία διπλά παραγωγίσιμη συνάρτηση της μεταβλητής της Δηλαδή η μπορεί να υψωθεί στο τετράγωνο ή στον κύβο ή να εμφανιστεί σε οποιαδήποτε άλλη έκφραση. Τη μορφή [12] της διαταραχής, δηλ. τη χωρική μεταβολή του κύματος, μπορούμε να τη δούμε αν φωτογραφήσουμε το κύμα σε ορισμένη χρονική στιγμή. Μαθηματικά αυτό ισοδυναμεί με το να αντικαταστήσουμε το χρόνο με μια σταθερά. Π.χ. για είναι χωρική μεταβολή του κύματος. Αν η έχει ένα ορισμένο σχήμα πάνω στη χορδή, τότε η περιγράφει τη διάδοση αυτού του σχήματος με ταχύτητα κατά τη θετική διεύθυνση Η είναι και αυτή μία λύση της κυματικής εξισώσεως και αντιστοιχεί σε μια χωρική μεταβολή του κύματος που διαδίδεται όμως κατά την αρνητική διεύθυνση 11
12 ΗΜΙΤΟΝΟΕΙΔΗ ΚΥΜΑΤΑ Ένα κύμα που έχει ημιτονοειδή μορφή ονομάζεται αρμονικό κύμα. Τα κύματα αυτά παρουσιάζουν ιδιαίτερο ενδιαφέρον, επειδή μπορούμε να τα συνθέσουμε με μεθόδους Fourier και να πάρουμε πολύπλοκές μορφές διαταραχών. Αν Σχήμα 1.2.α: Μορφή ημιτονοειδών κυμάτων. Είναι ένα διαδιδόμενο αρμονικό κύμα. Το όρισμα της ημιτονοειδούς συναρτήσεως θα πρέπει να είναι αδιάστατο μέγεθος και γι αυτό το λόγο έχουμε εισάγει τη θετική σταθερά που ονομάζεται κυματικός αριθμός. Η μέγιστη τιμή της είναι και ονομάζεται πλάτος. Η κυματική συνάρτηση παίρνει την ίδια τιμή έπειτα από μια χωρική περίοδο ή ένα μήκος κύματος, δηλ. Για να ισχύει η ιδιότητα αυτή, ο κυματικός αριθμός θα πρέπει να είναι της μορφής Όμοια, εάν η μορφή του κύματος επαναλαμβάνεται έπειτα από μια χρονική περίοδο δηλ. Η περίοδος μετριέται σ μονάδες χρόνου. Το αντίστροφο μέγεθος της περιόδου είναι η συχνότητα ή ο αριθμός των κυμάτων στη μονάδα του χρόνου. Οπότε έχουμε: 12
13 Σχήμα 1.2.β: Σύγκριση του μήκος κύματος και της συχνότητας μεταξύ κυμάτων Α και Β. Σε αναλογία με τη μηχανική μπορούμε να εισάγουμε την κυκλική συχνότητα. Αν και δεν υπάρχει τίποτα το περιστρεφόμενο, η κυκλική συχνότητα είναι ένα χρήσιμο μέγεθος και έχει μονάδα το ακτίνιο ανά δευτερόλεπτο. Σύμφωνα με τα παραπάνω η νέα έκφραση της κυματικής συνάρτησης είναι: Τα αρμονικά κύματα επεκτείνονται τόσο στο χώρο όσο και στο χρόνο από Άρα είναι μαθηματικές αφαιρέσεις. Εφόσον περιέχουν μόνο μία συχνότητα, τα ονομάζουμε μονοχρωματικά κύματα. Καμιά φυσική διαταραχή δεν έχει αυτή τη μορφή του αρμονικού κύματος, αν και υπάρχουν μερικές που μοιάζουν περισσότερο ή λιγότερο με αυτό και λέγονται τότε ψευδομονοχρωματικές. 13
14 ΦΑΣΗ ΤΑΧΥΤΗΤΑ ΦΑΣΕΩΣ ΚΑΙ ΤΑΧΥΤΗΤΑ ΟΜΑΔΟΣ Φάση ενός αρμονικού κύματος, ορίζεται ως το όρισμα της ημιτονοειδούς συναρτήσεως, δηλ. Η κυματική συνάρτηση (όπως έχει γραφεί) είναι μια ειδική περίπτωση, εφόσον για και είναι Δεν υπάρχει λόγος γιατί να μην μπορεί το πλάτος ενός κύματος να έχει μια οποιαδήποτε τιμή για, Αυτό μπορεί να πραγματοποιηθεί, αν στην ημιτονοειδή συνάρτηση εισάγουμε μια αρχική φάση τέτοια ώστε:. Αν φανταστούμε ότι ένα αρμονικό κύμα διαδίδεται μπροστά μας, τότε μπορούμε να προσδιορίσουμε την ταχύτητα του παρατηρώντας την κίνηση ενός σημείου του οποίου το μέγεθος της διαταραχής παραμένει σταθερό. Για ένα τέτοιο σημείο η φάση είναι σταθερή. Έτσι, η ταχύτητα του κύματος είναι η ταχύτητα με την οποία διαδίδεται η κατάσταση της σταθερής φάσης, δηλ. ( ) ( ) ( ) Το θετικό μέγεθος που είναι η ταχύτητα διαδόσεως ενός αρμονικού κύματος, το ονομάζουμε ταχύτητα φάσεως. Η ποσότητα ονομάζεται ταχύτητα ομάδος του κύματος και χαρακτηρίζει την ταχύτητα που κινείται συνολικά το κύμα καθώς διαδίδεται. ΜΕΤΩΠΑ ΚΥΜΑΤΟΣ Μια επιφάνεια πάνω στην οποία η φάση ενός κύματος είναι σταθερή ονομάζεται μέτωπο κύματος. 14
15 1.3 ΜΗ ΓΡΑΜΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΠΟΥ ΔΕΧΟΝΤΑΙ ΣΟΛΙΤΟΝΙΚΕΣ ΛΥΣΕΙΣ Είναι πλέον αρκετές οι μερικές διαφορικές εξισώσεις που δίνουν σολιτονικές λύσεις και μοντελοποιούν φυσικά συστήματα που δύνανται να εμφανίσουν τέτοια κύματα. Επειδή τα φαινόμενα ονομάζονται «μη-γραμμικά», είναι αναμενόμενο να περιγράφονται και από μη-γραμμικές εξισώσεις. Οι πιο συνηθισμένες μη γραμμικές διαφορικές εξισώσεις εξέλιξης που περιγράφουν ένα μεγάλο εύρος φυσικών φαινομένων και δέχονται σολιτονικές λύσεις είναι οι εξής: Η εξίσωση των Korteweg-de Vries (kdv) Η εξίσωση αυτή, προτάθηκε το 1895 από τους Korteweg και de Vries, αρχικά για να περιγράψει το υδροδυναμικό σολιτόνιο (μοναχικό κύμα), το οποίο παρατηρήθηκε να διαδίδεται στην επιφάνεια νερού και έχει την ακόλουθη μορφή: Σχήμα 1.3.α:Το σολιτόνιο της Kdv σε διάφορες χρονικές στιγμές. Ένας μοναχικός παλμός διαδίδεται αναλλοίωτος προς μια κατεύθυνση. 15
16 Σχήμα 1.3.β: Απεικόνιση της Kdv με u το πλάτος του κύματος, t ο χρόνος και x η κατεύθυνση που διαδίδεται ο παλμός. όπου u το πλάτος του κύματος, t ο χρόνος και x η κατεύθυνση επί της οποίας διαδίδεται ο παλμός, το μοναχικό κύμα. Βέβαια διαπιστώθηκε ότι περιγράφει και ένα πλήθος άλλων φαινομένων όπως: 1. Διάδοση των ακουστικών κυμάτων ιόντων σε μέσο πλάσματος. Τα ακουστικά κύματα ιόντων είναι διαμήκη κύματα τα οποία μεταδίδονται μεταξύ κατιόντων. 2. Κύματα πίεσης σε μίγματα υγρού-αερίου. 3. Μη αρμονικά πλέγματα. 4. Περιστροφή ροή υγρού μέσα σε σωλήνα. 5. Πακέτα θερμικά διεγερμένων φωτονίων σε χαμηλής θερμοκρασίας μη γραμμικούς κρυστάλλους. Η εξίσωση sine-gordon ( SG ) Η εξίσωση SG, προκύπτει από τη εξίσωση διάδοσης αρμονικού κύματος προσθέτοντας έναν όρο ημιτόνου της άγνωστης συνάρτησης, δηλαδή: 16
17 Σχήμα 1.3.γ: Απεικόνιση της SG με το πλάτος του κύματος, ο χρόνος και η κατεύθυνση που διαδίδεται ο παλμός. Περιγράφει φαινόμενα όπως: 1. Μονοδιάστατα μοντέλα στοιχειωδών σωματιδίων. 2. Διάδοση πλατιών κυμάτων (splay waves) πάνω σε βιολογικές μεμβράνες λιπιδίων. 3. Δημιουργία και διάδοση εξαρμόσεων και άλλων πλεγματικών ανωμαλιών και κρυστάλλων και των διαχωριστικών τοιχωμάτων σε φεροηλεκτρικά και φερομαγνητικά υλικά. 4. Αυτοεπαγόμενη διαφάνεια βραχέων οπτικών παλμών, όπου στενοί και έντονοι παλμοί φωτός με κατάλληλο σχήμα (σολιτόνια) μπορούν να διασχίζουν απορροφητικά μέσα με ταχύτητες αρκετά μικρότερες της ταχύτητας του φωτός σα να ήταν τελείως διαφανή. 5. Διάδοση κβάντων μαγνητικής ροής (fluxons) σε μακρές υπεραγώγιμες επαφές Josephson [2,9]. Η εξίσωση SG προκύπτει από μια απλή τροποποίηση μιας εξίσωσης που είναι πολύ γνωστή στη Φυσική την Klein-Gordon (KG). 17
18 Σχήμα 1.3.δ: Λύση της εξίσωσης KG. που αποτελεί τη σχετικιστική μορφή της εξίσωσης Schrodinger. Το όνομα sine- Gordon οφείλεται στην παρουσία του ημιτόνου. Η μη γραμμική εξίσωση Schrodinger (NLS) Οι προηγούμενες δύο εξισώσεις υπό ορισμένες συνθήκες, προσεγγίζονται μετασχηματιζόμενες από τη μη-γραμμική εξίσωση του Schrοdinger (nonlinear Schrodinger equation-nls). Ίσως πρόκειται για τη σημαντικότερη εξίσωση της μη-γραμμικής δυναμικής και σίγουρα η σημαντικότερη της μη-γραμμικής οπτικής. Περιγράφει πλήθος φυσικών συστημάτων τα οποία έχουν να κάνουν με αργά μεταβαλλόμενη περιβάλλουσα κύματος. Η εξίσωση NLS αποτελεί στη Θεωρητική Φυσική μια μη-γραμμική μορφή της εξίσωσης Schrοdinger με την εξής μορφή: 18
19 Σχήμα 1.3.ε: Η λύση για την εξίσωση της NLS. Στην αρχή έγινε χρήση αυτής προκειμένου να μοντελοποιηθούν υδροδυναμικά μοντέλα έτσι ώστε να διαδοθούν σε βαθιά νερά. Σύντομα όμως εφαρμόστηκε στην οπτική και χρησιμοποιείται για την περιγραφή φαινομένων όπως: 1. Μη γραμμικοί παλμοί μέσα σε οπτικές ίνες. 2. Διάδοση θερμικού παλμού μέσα σε στερεό. 3. Ταλαντώσεις πλάσματος, φαινόμενο γνωστό και ως κύματα Langmuir. 4. Μονοδιάστατη αυτοδιαμόρφωση μονοχρωματικής ακτινοβολίας. 5. Self-focusing of a plane wave. Όπως και η εξίσωση KdV, έτσι και η NLS εμφανίζεται συχνά όταν γίνεται μελέτη κατευθυνόμενης διάδοσης κυματοπακέτων μέσα σε διατηρητικό μέσο διάχυσης, στη χαμηλότερη τάξη της μη γραμμικότητας. Αξίζει να αναφερθεί ότι αντίθετα με την κλασική εξίσωση Schrodinger, η NLS δεν περιγράφει την εξέλιξη στο χρόνο μιας κβαντικής κατάστασης, καθώς και το ότι αποτελεί παράδειγμα ολοκληρώσιμου μη γραμμικού μοντέλου. Οι τρεις εξισώσεις που προαναφέρθηκαν επιδέχονται σολιτονικές λύσεις και μπορούν να προκύψουν και λύσεις N-σολιτονίων, όπου παρατηρείται το φαινόμενο της αλληλεπίδρασης μεταξύ των μοναχικών αυτών παλμών. Ακόμα δέχονται λύσεις μη γραμμικών περιοδικών κυμάτων. Η μη γραμμική εξίσωση Schrodinger εμφανίζεται κυρίως σε μη γραμμικά φαινόμενα της οπτικής και διάδοσης κυμάτων σε οπτικές ίνες, όπως: Η αυτοδιαμόρφωση φάσης (self phase modulation), που είναι η αλληλεπίδραση ενός παλμού με τον εαυτό του, εξαιτίας της εξάρτησης του δείκτη διάθλασης του από τη στιγμιαία ισχύ του. Ένας εξαιρετικά βραχύς παλμός φωτός (ηλεκτρομαγνητικός παλμός) που οδεύει μέσα σε ένα οπτικό μέσο (π.χ. Laser ή οπτικές ίνες), παρουσιάζει εξάρτηση του δείκτη διάθλασης του από τη στιγμιαία του ισχύ, εξαιτίας του φαινομένου 19
20 Kerr. Η αλλαγή του δείκτη διάθλασης επιφέρει μια μετατόπιση (στροφή) φάσης του παλμού, διευρύνοντας συμμετρικά το φασματικό του περιεχόμενο, δημιουργώντας έτσι νέες συχνότητες. Η τετρακυματική μίξη ή μίξη τεσσάρων φωτονίων (four wave mixing) Η γένεση δεύτερης αρμονικής (second harmonic generation, γνωστή και ως διπλασιασμός συχνότητας-frequency doubling). Είναι μια μη γραμμική οπτική διαδικασία, κατά την οποία τα φωτόνια που αλληλεπιδρούν με ένα μη γραμμικό υλικό (μέσο) <<συνδυάζονται>> και δημιουργούν νέα φωτόνια με διπλάσια ενέργεια, και επομένως με διπλάσια συχνότητα και το μισό μήκος κύματος των αρχικών φωτονίων. Δηλαδή ένα κύμα που διαπερνά ένα μη γραμμικό κρύσταλλο, δημιουργεί στην έξοδό του ένα κύμα διπλάσιας συχνότητας. Το φαινόμενο Raman ή εξαναγκασμένη Raman. Όταν ένα οπτικό κύμα ταξιδεύει κατά μήκος μιας ίνας, οι μεταβολές στο πεδίο του προκαλούν δονήσεις στα μόρια της ίνας. Η αλληλεπίδραση του φωτός με τα μόρια της ίνας προκαλεί σκέδαση Raman. Πρόκειται για ανελαστική σκέδαση, σε αντίθεση με τη σκέδαση των περισσότερων από τα φωτόνια που είναι ελαστική (τύπου Rayleigh). Από την μεριά της Κβαντομηχανικής, ένα φωτόνιο διεγείρει το μόριο, ή το άτομο, και αυτό με τη σειρά του επανερχόμενο σε μια κατάσταση που δεν είναι η αρχική του εκπέμπει φωτόνιο που διαφέρει από το αρχικό σε συχνότητα (ενέργεια). Σε αντίθεση με τη σκέδαση Rayleigh, το φαινόμενο είναι μη-γραμμικό και αναφέρεται συχνά σα φαινόμενο Raman [3,4]. Το φαινόμενο αυτό σχετίζεται με τη συχνότητα της προσπίπτουσας ακτινοβολίας, ενώ εντείνεται για ακτινοβολία μεγάλης έντασης. Η προσπίπτουσα ακτινοβολία λειτουργεί σαν αντλία, η οποία μέσω του φαινομένου Raman δημιουργεί ακτινοβολία μικρότερης συχνότητας, τη λεγόμενη Stokes. 1.4 ΜΕΘΟΔΟΙ ΜΕΛΕΤΗΣ ΣΟΛΙΤΟΝΙΚΩΝ ΛΥΣΕΩΝ ΑΝΑΛΥΤΙΚΕΣ ΜΕΘΟΔΟΙ Οι μέθοδοι που θα αναπτύξουμε εφαρμόζονται σε σολιτονικές εξισώσεις. Α) Μέθοδος αντίστροφης σκέδασης (inverse scattering transform method- IST). Σε αυτή τη μέθοδο οφείλεται η εύρεση των σολιτονικών λύσεων της μονοδιάστατης NLS. Η IST χρησιμοποιείται για την εύρεση λύσεων σε μηγραμμικά προβλήματα, όταν περιγράφονται πλήρως ολοκληρώσιμες μερικές διαφορικές. Στα γραμμικά προβλήματα, η συνηθέστερη μέθοδος είναι η χρήση μετασχηματισμού Fourier για να μετατραπεί η λύση της εξίσωσης σε πρόβλημα εύρεσης ιδιοτιμών. Διερευνώντας λοιπόν τη διάδοση κύματος, για παράδειγμα με αρχική μορφή μπορεί κανείς να βρει συνεχές φάσμα ιδιοτιμών, που αντιστοιχεί σε επίπεδα κύματα διαδιδόμενα σε ομογενές μέσο, αλλά και διακριτές ιδιοτιμές που αντιστοιχούν στους χωρικά εντοπισμένους ρυθμούς που εμφανίζονται σε ανομοιογενή μέσα. 20
21 Σε ένα μη-γραμμικό πρόβλημα, η μεθόδευση της IST είναι να το μετατρέψει σε γραμμικό πρόβλημα ιδιοτιμών, όπου το αρχικό πεδίο θα παίζει ρόλο δημιουργίας «ενεργού δυναμικού». Όμως καθώς το πεδίο εξελίσσεται κατά τη διάδοση, θα αλλάζουν παράλληλα και οι ιδιοτιμές. Οπότε προσπαθώντας να βρεθούν ιδιοτιμές που παραμένουν αναλλοίωτες καθώς το ενεργό δυναμικό μεταβάλλεται. Συνοπτικά τα βήματα της IST είναι τα ακόλουθα. Για δεδομένο αρχικό πεδίο, βρίσκεται βοηθητική ιδιοσυνάρτηση όπου οι ιδιοτιμές. Τα δεδομένα του προβλήματος «σκέδασης» περιλαμβάνουν τα πλάτη του εκπεμπόμενου και ανακλώμενου κύματος, και αντίστοιχα, τις διακριτές ιδιοτιμές { } και τους συντελεστές των αντίστοιχων ιδιοσυναρτήσεων, Μέσω του μετασχηματισμού Fourier βρίσκεται η εξέλιξη αυτών με το και τελικά, από αυτά, κατασκευάζεται η μορφή του πεδίου Κάθε μία από τις διακριτές ιδιοτιμές δίνει εντοπισμένη λύση, η οποία αντιστοιχεί σε σολιτόνιο. Καθώς οι ιδιοτιμές που ενδιαφέρουν είναι ανεξάρτητες του, οι σολιτονικές λύσεις διατηρούν το σχήμα τους [7,8]. Για τη λύση της NLS με όρους ανώτερης τάξης έχει αναπτυχθεί η διαταρακτική μέθοδος αντίστροφης σκέδασης που «ρίχνει» τη μερική διαφορική σε σύστημα συνήθων διαφορικών που περιγράφουν τις παραμέτρους του παλμού. B) Μεταβολική μέθοδος. Λέγεται και Λαγκραζιανή μέθοδος, είναι διαταρακτική και χρησιμοποιείται πολύ συχνά σε προβλήματα διάδοσης στη μηγραμμική οπτική, από τη πρώτη της εφαρμογή το 1979 [15]. Είναι αδιαβατική μέθοδος, που σημαίνει ότι μπορεί να χρησιμοποιηθεί όταν θεωρούμε πως η διαταραχή στην NLS είναι αρκετά μικρή ώστε να μην επηρεάζει τη μορφή του πεδίου (παλμού), αλλά μόνο τα χαρακτηριστικά του, έτσι ώστε να ισχύει (πλάτος) (εύρος) σταθερό. Έχει την αρχική μορφή του παλμού, η οποία πρέπει να διατηρείται και υπολογίζοντας τη Λαγκραζιανή του προβλήματος, μέσω των εξισώσεων Euler-Lagrange, καταλήγει σε σύστημα συνήθων διαφορικών για τα χαρακτηριστικά του παλμού. Η αδιατάρακτη εξίσωση θα πρέπει να έχει μία καλά ορισμένη λύση, όπως το σολιτόνιο, αλλά δεν είναι και η λύση της αδιατάρακτης. Υπάρχουν και άλλες παρόμοιες μέθοδοι, όπως η Αδιαβατική, η μέθοδος των ροπών και η εύρεση συνήθων διαφορικών μέσω Χαμιλτονιανής, αντί Λαγκρανζιανής ανάλυσης, αλλά δεν είναι τόσο διαδεδομένες [16,17]. Γ) Άμεση μέθοδος διαταραχών. Η μέθοδος αυτή έχει πιο περίπλοκο φορμαλισμό από τη προηγούμενη και απαιτεί τη γνώση και χρήση κάποιας λύσης της αδιατάρακτης εξίσωσης. Έχει όμως το πλεονέκτημα ότι μπορεί να περιγράψει μη-διατηρητικές διαταραχές ενώ μπορεί να δώσει και διορθώσεις στο αρχικό σχήμα του παλμού, εφόσον υπόκειται στις διαταραχές, όπως φαινόμενα ανώτερης τάξης. Η μέθοδος αυτή γραμμικοποιεί την εξίσωση, γύρω από τη λύση της αδιατάρακτης, σε κλιμακούμενες τάξεις διάδοσης. Έτσι στη μηδενική τάξη έχουμε την αδιατάρακτη εξίσωση με τη γνωστή λύση και σε πρώτη τάξη 21
22 έχουμε την αδιατάρακτη εξίσωση, όπου λύνεται σα πρόβλημα ιδιοτιμών, ώστε να κατασκευαστεί τελικά η από τις ιδιοσυναρτήσεις. Επειδή κάποιοι όροι απειρίζονται, απαιτείται ο μηδενισμός των συντελεστών τους. Από το μηδενισμό τους προκύπτουν συνήθεις διαφορικές που περιγράφουν τη μεταβολή των παραμέτρων του παλμού. Η μέθοδος μπορεί να δώσει και τη διόρθωση και να χρησιμοποιηθεί εκ νέου για τον υπολογισμό της δεύτερης τάξης. Η διαδικασία αυτή μοιάζει με τη διαταρακτική μέθοδο αντίστροφης σκέδασης, με την οποία έχει και τις ίδιες συνήθεις διαφορικές σαν αποτέλεσμα. Οι ODEs περιλαμβάνουν ολοκληρώματα που είναι συνήθως δύσκολο να υπολογιστούν αναλυτικά. ΑΡΙΘΜΗΤΙΚΕΣ ΜΕΘΟΔΟΙ ΚΑΙ ΠΡΟΓΡΑΜΜΑΤΑ Α) Μέθοδος χωριζόμενου βήματος (split step Fourier method). Αυτή η μέθοδος είναι και η πλέον συνήθης στην επίλυση της NLS, μαζί με μεθόδους πεπερασμένων στοιχείων. Η split-step είναι μια ψευδο-φασματική μέθοδος, που επιλύει τη μερική διαφορική μεταφέροντας τη στο χώρο των συχνοτήτων. Εφαρμόζεται σε μεγάλη ποικιλία προβλημάτων της μη-γραμμικής οπτικής, όπως διάδοση στην ατμόσφαιρα, οπτικούς συζεύκτες, ίνες βαθμωτού δείκτη διάθλασης και σε πιο συνηθισμένα προβλήματα όπως η διάδοση παλμών σε μονότροπες ίνες και CW ακτίνων σε επίπεδο κυματοδηγό και ελεύθερο μέσο. Στη τελευταία περίπτωση προβλημάτων, την αναφέρουν και σαν beam propagation method. Η περιγραφή της βρίσκεται σε αρκετά κλασικά βιβλία μηγραμμικής οπτικής [18]. Σε αυτό το σημείο γίνεται απλή αναφορά στο ότι απαιτείται διαχωρισμός σε γραμμικούς και μη-γραμμικούς όρους. Η απόσταση διάδοσης χωρίζεται σε βήματα εύρους. Διαχωρίζουμε τους όρους της εξίσωσης σε γραμμικούς και μη-γραμμικούς που ανήκουν σε αντίστοιχο τελεστή. Αρχικά χρησιμοποιούμε μόνο το γραμμικό τελεστή για να βρούμε την εξέλιξη του παλμού στο χώρο Fourier, μετά από. Έχοντας αυτό το αποτέλεσμα επιβάλουμε το μη-γραμμικό τελεστή για διάδοση κατά ένα ολόκληρο βήμα. Τέλος, χρησιμοποιούμε το προηγούμενο αποτέλεσμα επιβάλλοντας πάλι το γραμμικό τελεστή για διάδοση ξανά κατά. Τα σφάλματα από τη μέθοδο αυτή είναι ανάλογα του. Ο κώδικας έχει καλή ακρίβεια και για βήμα της τάξης κρατά σταθερές όλες τις διατηρήσιμες ποσότητες. Β) Προγράμματα επίλυσης συστήματος ODEs. Οι διαταρακτικές μέθοδοι που εφαρμόζονται ξεκινούν από μερικές διαφορικές εξισώσεις και καταλήγουν σε συστήματα συνήθων. Χρησιμοποιείται η μέθοδος Runge-Kutta καθώς και προγράμματα MATLAB. 22
23 ΚΕΦΑΛΑΙΟ 2 ΜΕΛΕΤΗ ΟΠΤΙΚΩΝ ΣΟΛΙΤΟΝΙΩΝ 2.1 ΕΙΣΑΓΩΓΗ Ένας πολύ σημαντικός κλάδος της μη γραμμικής Φυσικής είναι η Φυσική των Σολιτονίων, η οποία σημείωσε μεγάλες επιτυχίες τις τελευταίες δεκαετίες και διακρίθηκε για αυτές διότι δίνει την δυνατότητα παρατήρησης και ανάλυσης δομών και δυναμικής που μοιάζουν σε πολύ διαφορετικούς κλάδους, όπως για παράδειγμα στα ρευστά, στο πλάσμα, στα στερεά, στα στοιχειώδη σωμάτια, στην αστροφυσική, στην οπτική, κ.τ.λ. [26]. Τα θεωρητικά θέματα της Φυσικής Οπτικών Σολιτονίων που χαρακτηρίζονται ως βασικά, παρουσιάζουν μια συνεχόμενη ανάπτυξη. Αφενός από θεωρητική σκοπιά το ενδιαφέρον έγκειται στη μελέτη της δυναμικής των σολιτονίων στα διάφορα μέσα διάδοσης, δεδομένου ότι τα οπτικά συστήματα έχουν πολλές και διαφορετικές ιδιότητες που συχνά τις συνδυάζουν, όπως είναι η μη γραμμικότητα, η διασπορά, η περίθλαση και μπορούν να είναι ενεργά, παθητικά, κ.τ.λ. Αφετέρου υπάρχει ενδιαφέρον από τη μεριά των εφαρμογών που οφείλεται στο γεγονός ότι τα σολιτόνια επειδή έχουν τη μορφή παλμών ή δεσμών που διαδίδονται δίχως παραμόρφωση από τη μεριά αποτελούν ιδανικούς φορείς πληροφορίας (bits) σε τηλεπικοινωνιακά συστήματα μεγάλων αποστάσεων [16], ενώ από την άλλη μεριά μπορούν να χρησιμοποιηθούν στην οδήγηση ή μεταγωγή (switching) οπτικών δεσμών [27]. 2.2 ΔΙΑΚΡΙΣΗ ΟΠΤΙΚΩΝ ΣΟΛΙΤΟΝΙΩΝ Τα οπτικά σολιτόνια μπορούν να διακριθούν σε χρονικά σολιτόνια (temporal solitons), που είναι χρονικά εντοπισμένοι οπτικοί παλμοί που διατηρούν το σχήμα τους και σε χωρικά σολιτόνια (spatial solitons), που είναι χωρικά εντοπισμένες οπτικές δέσμες (ακτίνες) που διατηρούν σταθερό το εγκάρσιο (προς τη διεύθυνση διάδοσης) εύρος τους. Τα χρονικά σολιτόνια παρατηρούνται σε οπτικές ίνες ενώ τα χωρικά σε συμπαγή (bulk) οπτικά μέσα ή σε επίπεδους διηλεκτρικούς κυματοδηγούς, και τα δυο όμως εξελίσσονται παρουσία μη γραμμικής μεταβολής του δείκτη διάθλασης του μέσου που επιβάλλεται από την ένταση του διαδιδόμενου κύματος. Όταν τα ανταγωνιζόμενα φαινόμενα της μη γραμμικότητας και της διασποράς (για τα χρονικά σολιτόνια) ή της περίθλασης (για τα χωρικά σολιτόνια) αντισταθμίσουν ακριβώς το ένα το άλλο, ο παλμός (ή η δέσμη) διαδίδεται χωρίς να παραμορφώνεται, εξαιτίας της παγίδευσης του από τη μη γραμμικότητα του μέσου. Η μη γραμμικότητα είναι υπεύθυνη για το σχηματισμό σολιτονίων και είναι συνήθως τύπου Kerr, δηλαδή μεταβάλλει το δείκτη διάθλασης των μέσων 23
24 ανάλογα με την ένταση που έχει το κύμα. Η εξάρτηση του δείκτη διάθλασης από την ένταση προκαλεί αυτό-εστίαση (ή και από-εστίαση) κατά μήκος της εγκάρσιας χωρικής διάστασης, ενώ για τους χρονικούς παλμούς προκαλεί χρονικά εξαρτημένη αυτοδιαμόρφωση φάσης (self phase modulation-spm). Οπότε χωρικό σολιτόνιο δημιουργείται όταν η τάση για αυτοεστίαση εξισορροπεί τη φυσική τάση για περίθλαση της ακτίνας. Παρομοίως, χρονικός σολιτονικός παλμός δημιουργείται και όταν η SPM εξισορροπεί τη διασπορά. Και στις δύο περιπτώσεις, το σολιτόνιο διαδίδεται στο οπτικό μέσο χωρίς να αλλάζει το σχήμα του και καθώς είναι το ίδιο που διαμορφώνει τις συνθήκες διάδοσης, λέμε ότι «αυτό-παγιδεύεται». Η πρώτη παρατήρηση χωρικού σολιτονίου έγινε το 1964 όπου οπτικές ακτίνες (κύματα σταθερού πλάτους- CW) επέδειξαν αυτό-παγίδευση κατά τη διάδοσή τους σε μη-γραμμικό μέσο [24]. Το φαινόμενο αυτό έγινε περισσότερο κατανοητό τη δεκαετία του 80, μετά από περισσότερα πειράματα. Τα χρονικά σολιτόνια παρατηρήθηκαν λίγο αργότερα, το 1967, όπου επιδείχθηκε η δυνατότητα παλμών να περνούν απαράλλακτοι μέσα από κάποιο οπτικό μέσο. Ένα σημαντικό πείραμα το 1980 έδειξε ότι παλμοί με ορισμένη ένταση μπορούν να διαδίδονται αναλλοίωτοι από διασπορά κατά μήκος οπτικής ίνας [25]. Αυτό πυροδότησε εκτεταμένη έρευνα γύρω από τη δυνατότητα χρήσης σολιτονικών παλμών σα φορείς πληροφορίας κατά μήκος δικτύου οπτικών ινών. Σχήμα 2.2.α: Δημιουργία χωρικού σολιτονίου σε ημιαγώγιμο κυματοδηγό. Στο πρώτο σχήμα φαίνεται το προφίλ έντασης της ακτίνας στην είσοδο, όπου αν η ένταση δεν είναι αρκετή η ακτίνα περιθλάται (μεσαίο σχήμα), ενώ αν είναι κατάλληλη (κάτω σχήμα) διατηρείται σχεδόν αναλλοίωτη. 24
25 Η μη γραμμική εξίσωση που διέπει την εξέλιξη του παλμού (ή της δέσμης), είναι πασίγνωστη ως η μη γραμμική εξίσωση του Schrοdinger ( εξίσωση NLS), που μπορεί να γραφεί σε κανονικοποιημένη μορφή ως εξής: (2.1) Στην παραπάνω εξίσωση το είναι η περιβάλλουσα του ηλεκτρικού πεδίου, το είναι η απόσταση διάδοσης κατά μήκος του μέσου και η μεταβλητή, καθώς και οι παράμετροι και έχουν την εξής σημασία για τα χρονικά ή χωρικά προβλήματα: 2.3 ΕΠΕΞΗΓΗΣΗ ΣΥΜΒΟΛΩΝ ΣΤΗΝ ΠΕΡΙΠΤΩΣΗ ΧΡΟΝΙΚΩΝ ΣΟΛΙΤΟΝΙΩΝ Στη περίπτωση των χρονικών σολιτονίων στις οπτικές ίνες, είναι ο χρόνος σε ένα σύστημα αναφοράς που κινείται κατά μήκος της ίνας με την ταχύτητα ομάδος και, διότι η μη γραμμικότητα Kerr είναι θετική ή αυτόεστιάζουσα (self-focusing), για το τηγμένο από το οποίο είναι κατασκευασμένες οι οπτικές ίνες. Ακόμα, στην ίδια περίπτωση, ο 2 ος όρος στην (2.1) εκφράζει τη διασπορά, η οποία μπορεί να είναι είτε θετική είτε αρνητική ανάλογα με το μήκος κύματος λειτουργίας, οπότε το σ είναι το πρόσημο της διασποράς δεύτερης τάξης ( για μήκος κύματος μικρότερο ή μεγαλύτερο από 1.3 μm αντίστοιχα). 2.4 ΕΠΕΞΗΓΗΣΗ ΣΥΜΒΟΛΩΝ ΣΤΗΝ ΠΕΡΙΠΤΩΣΗ ΧΩΡΙΚΩΝ ΣΟΛΙΤΟΝΙΩΝ Στην περίπτωση των χωρικών σολιτονίων σε συμπαγή οπτικά μέσα ή σε επίπεδους κυματοδηγούς, ξ είναι η εγκάρσια συντεταγμένη άρα ο 2 ος της (2.2.1) εκφράζει την περίθλαση, που σημαίνει ότι σε αυτήν την περίπτωση το πάντοτε! Βέβαια η παράμετρος s μπορεί να παίρνει είτε θετικές, είτε αρνητικές τιμές, για αυτό-εστιάζοντα (self-focusing), όταν είναι ή για αυτόαποεστιάζοντα (self-defocusing), όταν είναι, μη γραμμικά οπτικά μέσα. 2.5 ΟΤΑΝ σ=-1 ΣΤΙΣ ΟΠΤΙΚΕΣ ΙΝΕΣ Η s=+1 ΣΤΑ ΣΥΜΠΑΓΗ ΜΕΣΑ Στην περίπτωση στις οπτικές ίνες, ή στα συμπαγή μέσα ή στους επίπεδους κυματοδηγούς, η μόνιμη κατάσταση της εξίσωσης NLS, δηλαδή η λύση της οποίας έχει τη μορφή ενός συνεχούς κύματος (continue wave, cw), είναι ασταθής. Η αστάθεια αυτή ονομάζεται αστάθεια 25
26 διαμόρφωσης (γνωστή και σαν αστάθεια Benjamin-Feir [28]), η οποία εκδηλώνεται σαν τη διάλυση του συνεχούς κύματος σε μία σειρά παλμών, που είναι τα λεγόμενα φωτεινά σολιτόνια. Σχήμα 2.5.α: Φωτεινό σολιτόνιο με γενική λύση: [ ]. 2.6 ΟΤΑΝ σ=+1 ΣΤΙΣ ΟΠΤΙΚΕΣ ΙΝΕΣ Η s=-1 ΣΤΑ ΣΥΜΠΑΓΗ ΜΕΣΑ Στην περίπτωση όμως στις οπτικές ίνες, ή στα οπτικά μέσα ή στους επίπεδους κυματοδηγούς, η λύση της cw της εξίσωσης NLS είναι πάντοτε ευσταθής, οπότε δεν υπάρχουν φωτεινά σολιτόνια αλλά είναι δυνατό να υπάρξουν άλλου είδους σολιτόνια, τα λεγόμενα σκοτεινά σολιτόνια, που έχουν τη μορφή βυθισμάτων ( σκοτεινών παλμών) που οδεύουν επάνω στο ευσταθές υπόβαθρο της λύσης cw. 26
27 Σχήμα 2.6.α: Σκοτεινό σολιτόνιο με γενική λύση: [ ( ( ) )] 2.7 Η ΜΗ ΓΡΑΜΜΙΚΗ ΕΞΙΣΩΣΗ ΤΟΥ SCHRODINGER (ΕΞΙΣΩΣΗ NLS) Για την εξαγωγή της βασικής μη γραμμικής κυματικής εξίσωσης, της NLS, πρέπει να γίνει διάκριση δύο διαφορετικών περιπτώσεων: Η διάδοση παλμών σε οπτικές ίνες και η διάδοση δεσμών σε συμπαγή οπτικά μέσα ή σε επίπεδους διηλεκτρικούς κυματοδηγούς. Η διάκριση αυτή γίνεται διότι τα φαινόμενα που ανταγωνίζονται τη μη γραμμικότητα είναι διαφορετικά σε κάθε περίπτωση. Είναι η διασπορά στις οπτικές ίνες και η περίθλαση στα συμπαγή μέσα ή στους επίπεδους κυματοδηγούς. Αυτό οδηγεί σε διαφορετικές φυσικές καταστάσεις οι οποίες θα συζητηθούν ξεχωριστά στις ακόλουθες παραγράφους. 2.8 ΟΠΤΙΚΕΣ ΙΝΕΣ Οι οπτικές ίνες είναι διηλεκτρικοί κυματοδηγοί κυλινδρικού σχήματος, κατασκευασμένοι από τηγμένο, που χαρακτηρίζονται από ένα δείκτη διάθλασης της ακόλουθης μορφής: ( ) (2.2) όπου ω είναι η συχνότητα και η ενεργή τιμή του ηλεκτρικού πεδίου του κύματος. Είναι φανερό ότι η οπτική ίνα παρουσιάζει τόσο διασπορά (λόγω της εξάρτησης του γραμμικού δείκτη διάθλασης από τη συχνότητα), όσο και μη 27
28 γραμμικότητα (λόγω της εξάρτησης του δείκτη διάθλασης από την ένταση, που είναι γνωστή σαν φαινόμενο Kerr). Η διασπορά οφείλεται στο συντονισμό της ιδιοσυχνότητας ταλάντωσης των δεσμίων ηλεκτρονίων με τη συχνότητα του οπτικού κύματος, ενώ η μη γραμμικότητα στην παραμόρφωση των τροχιών των ηλεκτρονίων λόγω του επιβαλλομένου πεδίου [16,29]. Ο χρόνος απόκρισής του φαινομένου Kerr είναι εξαιρετικά μικρός (της τάξης του femtosecond), οπότε το μη γραμμικό τμήμα του δείκτη διάθλασης, που λέγεται συντελεστής Kerr, παίρνει την περίπου σταθερή (ανεξάρτητη της συχνότητας) και θετική τιμή Έστω ότι η διάδοση ενός οπτικού κύματος στην ίνα, του οποίου το ηλεκτρικό πεδίο δίνεται από τη σχέση: (2.3) όπου δηλώνει το πραγματικό μέρος, είναι μια αργά μεταβαλλόμενη περιβάλλουσα σχήματος παλμού (η έννοια της περιβάλλουσας περιγράφεται στο παρακάτω σχήμα), Διαμορφωμένο κύμα Πλάτος περιβάλλουσας Φάσμα Σχήμα:2.7.α 28
29 ενώ και είναι ο κυματάριθμος και η συχνότητα φέροντος (οπτικού) κύματος αντίστοιχα. Στην πραγματικότητα το ηλεκτρικό πεδίο εξαρτάται και από τις εγκάρσιες συντεταγμένες και. Η εξάρτηση όμως αυτή, ορίζεται από το γραμμικό οδηγούμενο ρυθμό (guided mode) της οπτικής ίνας [29], οπότε μπορεί να αποπλεχθεί από το φαινόμενο της διάδοσης στη διαμήκη διεύθυνση, που περιγράφεται από τη συνάρτηση. Αφού τώρα τελευταία θεωρείται αργά μεταβαλλόμενη, το φάσμα συχνότητας του ηλεκτρικού πεδίου θα είναι εντοπισμένο γύρω από τη συχνότητα. Δεδομένου ότι ενδιαφέρει η χωρική εξέλιξη (δηλαδή στη διεύθυνση της, ο κυματάριθμος, που δίνεται από τη σχέση διασποράς, αναπτύσσεται τώρα σε σειρά Taylor γύρω από τη συχνότητα του φέροντος, οπότε θα είναι: (2.4) Επειδή η περιβάλλουσα μεταβάλλεται αργά ως προς και, μπορεί να μετασχηματιστεί κατά Fourier με χρήση των μεταβλητών και Από τις ιδιότητες του μετασχηματισμού Fourier είναι φανερό ότι τα και αντιστοιχούν στα και αντίστοιχα άρα: ( ) Άρα η εξίσωση (2.4) λόγω των παραπάνω μετασχηματισμών εκφράζεται στο πεδίο του χρόνου σαν: Λαμβάνοντας επιπλέον υπόψη και τη μη γραμμικότητα στο δείκτη διάθλασης, ο κυματάριθμος θα εξαρτάται επιπλέον και από το, οπότε στη εξίσωση (2.4) πρέπει να ληφθεί υπόψη και ένας όρος της μορφής ( ). Όμως λόγω των σχέσεων ( ) και η ( ) (διότι από την (2.3) προκύπτει ότι ) Οπότε εάν στην προαναφερθείσα τελεστική εξίσωση εφαρμοστεί η κρατώντας έως και τον όρο της παραγώγου 2 ης τάξης, θα οδηγήσει στη ακόλουθη μη γραμμική κυματική εξίσωση: 29
30 ( ) Στην εξίσωση (2.5) που είναι το αντίστροφο της ταχύτητας ομάδος, ενώ που είναι η διασπορά δεύτερης τάξης (η οποία θα μηδενιζόταν εάν ο δείκτης διάθλασης ήταν ανεξάρτητος της συχνότητας). Η τελευταία παίρνει τιμές που εξαρτώνται από το μήκος κύματος λ του φέροντος οπτικού κύματος. Στις συνήθεις οπτικές ίνες η συνάρτηση είναι φθίνουσα, μηδενίζεται περίπου (το σημείο αυτό λέγεται σημείο μηδενικής διασποράς) και είναι θετική (αρνητική) για μήκη κύματος μικρότερα (μεγαλύτερα) από. Η περιοχή μηκών κύματος που αντιστοιχούν σε λέγεται περιοχή της θετικής ή ομαλής διασποράς, ενώ εκείνη στην οποία είναι λέγεται περιοχή της αρνητικής ή ανώμαλης διασποράς. Από τη άλλη πλευρά, όσον αφορά το συντελεστή του μη γραμμικού όρου, αυτός πρέπει να διορθωθεί κατά ένα αδιάστατο παράγοντα (να γίνει δηλαδή ), ο οποίος εξαρτάται από την εγκάρσια κατανομή του ηλεκτρικού πεδίου. Πρέπει σε αυτό το σημείο να τονιστεί ότι αν δεν υπήρχε ο μη γραμμικός όρος στην εξίσωση (2.5), και θεωρείτο η διάδοση ενός λεπτού παλμού στην ίνα, ο 2 ος όρος (όρος της διασποράς) της εξίσωσης (2.5) θα γινόταν μεγαλύτερος αντιστρόφως ανάλογα με το τετράγωνο του εύρους του παλμού. Αυτό δείχνει ότι ο παλμός θα παραμορφωνόταν (θα διευρυνόταν) λόγω της διασποράς κατά τη διάρκεια της διάδοσής του. Κάνοντας χρήση του μετασχηματισμού, ( είναι το αρχικό εύρος του παλμού) και τη συνάρτηση ( ) η εξίσωση (2.5) γράφεται στην ακόλουθη αδιάστατη μορφή, που είναι γνωστή σαν εξίσωση NLS: όπου (2.6) 30
31 Βέβαια για να καταλήξουμε στην (2.6) πρέπει να γίνουν οι απαραίτητες παραγωγίσεις και κανονικοποιήσεις δηλαδή η (2.5) ξαναγράφεται: ( ) και σύμφωνα με τους παραπάνω μετασχηματισμούς παίρνουμε:, ( ), οπότε: ( ) [ ] ( ) [ ] Τώρα αντικαθιστούμε τις παραπάνω πράξεις στην (*): [(( ) ) ( ) ] ( ) ( ) ( ) Σε αυτό το σημείο γίνονται κάποιες απλοποιήσεις και κανονικοποιήσεις προκειμένου να σχηματιστεί η ζητούμενη σχέση. Πολλαπλασιάζουμε με και στο τέλος θέτουμε και ( ) Δηλαδή σχηματίστηκε η (2.6). 31
32 2.9 ΣΥΜΠΑΓΗ ΟΠΤΙΚΑ ΜΕΣΑ ΚΑΙ ΕΠΙΠΕΔΟΙ ΔΙΗΛΕΚΤΡΙΚΟΙ ΚΥΜΑΤΟΔΗΓΟΙ Σε αντίθεση με τις οπτικές ίνες, που είναι ουσιαστικά μονοδιάστατοι κυματοδηγοί, η διάδοση δεσμών σε επίπεδους κυματοδηγούς ή σε συμπαγή οπτικά μέσα είναι ένα φαινόμενο στο οποίο πρέπει να ληφθεί υπόψη η κατανομή του πεδίου στην εγκάρσια διεύθυνση. Προκειμένου να βρεθεί η κυματική εξίσωση στην περίπτωση αυτή, θα θεωρηθεί η διάδοση ενός βαθμωτού μονοχρωματικού ηλεκτρικού πεδίου σε ένα συμπαγές οπτικό μέσο με δείκτη διάθλασης παρόμοιο με αυτόν στην εξίσωση (2.2). Οπότε θεωρείτε ότι όπου είναι ο γραμμικός δείκτης διάθλασης, ενώ είναι μία συνάρτηση που περιγράφει τη μεταβολή του δείκτη διάθλασης σαν συνάρτηση της έντασης του επιβαλλομένου πεδίου. Η συνάρτηση αυτή, θεωρείται ότι εξαρτάται μόνο από την ένταση και είναι φανερό ότι η απλούστερη περίπτωση είναι που αντιστοιχεί στην κυβική μη γραμμικότητα (Kerr) που έγινε αναφορά στην προηγούμενη παράγραφο. Στην γενικότερη περίπτωση ο συντελεστής Kerr δεν είναι υποχρεωτικά θετικός. Υπάρχουν πολλά υλικά, τόσο στερεά (όπως άμορφο όσο και αέρια (όπως ατμοί ρουβιδίου, νατρίου, κλπ.), που έχουν Έτσι γίνεται διάκριση των μη γραμμικών οπτικών μέσων σε αυτό-εστιάζοντα (self-focusing), όταν έχουν ή σε αυτό-αποεστιάζοντα (self-defocusing), όταν έχουν (οι οπτικές ίνες, π.χ., είναι αυτό-εστιάζοντα μέσα). Έστω τώρα η διάδοση μίας μονοχρωματικής οπτικής δέσμης, της οποίας το ηλεκτρικό πεδίο δίνεται ως (2.7) όπου είναι η στάσιμη (δηλ. ανεξάρτητη του χρόνου ) αργά μεταβαλλόμενη (ως προς και ) περιβάλλουσα, ενώ και είναι αντίστοιχα ο κυματάριθμος και η συχνότητα του φέροντος κύματος (λ είναι το μήκος κύματος της πηγής). Θεωρείτε ακόμα ότι η διάδοση λαμβάνει χώρα στη διεύθυνση οπότε οι διευθύνσεις και είναι οι δύο εγκάρσιες διευθύνσεις. Αντικαθιστώντας τώρα την εξίσωση (2.7) στη διδιάστατη βαθμωτή κυματική εξίσωση που προκύπτει από τις εξισώσεις Maxwell, και εκμεταλλευόμενοι το γεγονός ότι η συνάρτηση μεταβάλλεται αργά στη διεύθυνση διάδοσης, καταλήγουμε στην ακόλουθη κυματική εξίσωση: ( ) (2.8) Σε αυτή τη γενική μη γραμμική παραβολική εξίσωση, οι όροι μέσα στην παρένθεση εκφράζουν την περίθλαση. Είναι σαφές, όπως και στην εξίσωση 32
33 (2.5), όταν δεν υπάρχει η μη γραμμικότητα, η περίθλαση θα διασπείρει την οπτική δέσμη στις εγκάρσιες διευθύνσεις ( και ). Αυτό όμως που είναι πολύ σημαντικό είναι ότι, στην πραγματικότητα, η εξίσωση (2.8) είναι μία διδιάστατη εκδοχή της εξίσωσης NLS. Αυτό προκύπτει εάν κανονικοποιηθούν όλες οι χωρικές μεταβλητές στο και χρησιμοποιηθεί η συνάρτηση: άρα έχουμε: [ ] [ ] [ ] Πήρα το real λόγω της σχέσης (2.6), το κανονικοποιούμε όλες τις χωρικές μεταβλητές στο και το άρα έχουμε τελικά: ( ) (2.8) όπου τώρα για η (2.8) ξαναγράφεται: (2.9) Στην περίπτωση που έχουμε διάδοση σε επίπεδο διηλεκτρικό κυματοδηγό, η (2.9) μπορεί να απλοποιηθεί περαιτέρω. Αυτό συμβαίνει γιατί η κατανομή του πεδίου σε μία από τις εγκάρσιες διευθύνσεις, π.χ. στη διεύθυνση, ορίζεται (όπως και στην περίπτωση της οπτικής ίνας) από τον γραμμικό οδηγούμενο ρυθμό, οπότε αποκλείεται από τη συνάρτηση (και ). Οπότε μπορεί να δειχτεί ότι σε αυτή την περίπτωση αυτή η εξίσωση διάδοσης είναι η (2.9), αλλά χωρίς την παράγωγο ως προς οπότε το αποτέλεσμα είναι η ακόλουθη μονοδιάστατη εξίσωση NLS: (2.10) Οι σχέσεις (2.6) και (2.10) είναι ταυτόσημες διότι εάν εναλλαχθεί το στην (2.6) με το στην (2.10), οι περιπτώσεις (με την επιπλέον αλλαγή οδηγούν στην ίδια εξίσωση κάθε φορά. 33
34 Έτσι χωρίς βλάβη της γενικότητας, θα συνεχιστεί η ανάλυση θεωρώντας στο εξής μόνο την (2.6). Παρόλο που υπάρχει ομοιότητα στη μαθηματική περιγραφή της διάδοσης παλμών σε οπτικές ίνες και τη διάδοση δεσμών σε συμπαγή μέσα ή σε επίπεδους κυματοδηγούς, η φυσική που διέπει αυτά τα δύο φαινόμενα είναι πολύ διαφορετική. Στις οπτικές ίνες, το μήκος κύματος λειτουργίας επιλέγεται συνήθως κοντά στο σημείο μηδενικής διασποράς, που σημαίνει ότι η πολύ ασθενής μη γραμμικότητα Kerr δεν μπορεί να αντισταθμιστεί τη μικρή απομένουσα διασπορά παρά μόνο σε σχετικά μεγάλες αποστάσεις διάδοσης (της τάξης ). Από την άλλη πλευρά, η περίθλαση στα συμπαγή μέσα και στους επίπεδους κυματοδηγούς δεν είναι καθόλου μικρό φαινόμενο, οπότε η μη γραμμικότητα πρέπει να είναι πολύ ισχυρή για να αντισταθμίσει τη διεύρυνση της δέσμης (εδώ οι αποστάσεις είναι της τάξης Οπότε σε αυτήν τη περίπτωση, η προσέγγιση Kerr για την περιγραφή της μη γραμμικότητας δεν είναι πάντα ικανοποιητική, οπότε πρέπει να χρησιμοποιηθούν άλλα μοντέλα που να λαμβάνουν υπόψη, λ.χ., μη γραμμικούς όρους στη συνάρτηση κορεσμό, κ.λπ. [27,30]. Κλείνοντας την παράγραφο αυτή, πρέπει να τονιστεί ότι οι τιμές που μπορεί να παίρνει η παράμετρος είναι καθοριστικές για την αστάθεια διαμόρφωσης και το είδος των σολιτονίων (φωτεινά ή σκοτεινά) που μπορούν να διαδοθούν στα οπτικά μέσα. Αυτό φαίνεται από την εξίσωση (2.6) η οποία μοιάζει πολύ με την αδιάστατη εξίσωση του Schrodinger, που είναι γνωστή από την Κβαντομηχανική, με τη διαφορά ότι το δυναμικό αναπαρίσταται στη (2.6) από το Στη συμβατική εξίσωση του Schrodinger το δυναμικό παγιδεύει το σωμάτιο που αναπαρίσταται από την κυματοσυνάρτηση οπότε κατ αναλογία, στην περίπτωση της εξίσωσης NLS, και όταν το βάθος του ισοδύναμου δυναμικού αυξάνεται ανάλογα με την ένταση με αποτέλεσμα την τοπική παγίδευση της ενέργειας, θα πρέπει το εύρος του παλμού να γίνεται μικρότερο, αντιστρόφως ανάλογα με το Από την άλλη πλευρά, το φαινόμενο της διασποράς (ή της περίθλασης), που αυξάνεται αντιστρόφως ανάλογα με το τετράγωνο του εύρους του παλμού (ή της δέσμης), γίνεται ολοένα και πιο ισχυρό με αποτέλεσμα η διεύρυνση να ανταγωνίζεται το στένεμα εξαιτίας της μη γραμμικότητας. Στην περίπτωση που συμβαίνει μία ακριβής εξισορρόπηση των φαινομένων της παγίδευσης (λόγω μη γραμμικότητας) και της διεύρυνσης (λόγω διασποράς ή περίθλασης) είναι δυνατός ο σχηματισμός παλμών (ή δεσμών) που παραμένουν στάσιμοι, οι οποίοι στην πραγματικότητα είναι λύσεις φωτεινών σολιτονίων της εξίσωσης NLS. Στην περίπτωση που είναι το δυναμικό, αντί να παγιδεύει, απωθεί το σωμάτιο και η απώθηση αυτή, αντί να ανταγωνίζεται, συνεργάζεται με τη διασπορά (ή την περίθλαση). Έτσι, η ενέργεια του κύματος διαχέεται γρήγορα εξαιτίας της διαδικασίας αυτής, γεγονός που σημαίνει ότι δεν είναι δυνατόν να σχηματιστούν φωτεινά σολιτόνια στην περίπτωση 34
35 Όμως, υπάρχει ένα άλλο είδος σολιτονίων που μπορούν να σχηματιστούν στην περίπτωση αυτή, τα λεγόμενα σκοτεινά σολιτόνια, τα οποία είναι ουσιαστικά οπές, δηλαδή τμήματα απουσίας ισχύος, που διαδίδονται πάνω στο υπόβαθρο ενός ευσταθούς συνεχούς κύματος 2.10 ΑΣΤΑΘΕΙΑ ΔΙΑΜΟΡΦΩΣΗΣ ΚΑΙ ΣΟΛΙΤΟΝΙΑ Πολλά μη γραμμικά συστήματα χαρακτηρίζονται από μία αστάθεια που οδηγεί στη διαμόρφωση της μόνιμης κατάστασης, λόγω του ανταγωνισμού μεταξύ των φαινομένων της μη γραμμικότητας και της διασποράς. Το φαινόμενο αυτό αναφέρεται σαν αστάθεια διαμόρφωσης, ή αστάθεια Benjamin-Feir (modulation instability-mi) (οι οποίοι βρήκαν ότι δεν είναι δυνατόν να δημιουργηθεί ένας κυματοσυρμός σταθερού πλάτους σε βαθύ νερό [28]. Σε αυτή την παράγραφο θα δειχθεί ότι η αστάθεια διαμόρφωσης λαμβάνει χώρα στην περίπτωση στην (2.6) (ή στην (2.10)). Η ίδια συνθήκη ( ή απαιτείται και για τη δημιουργία των φωτεινών σολιτονίων, οπότε γίνεται αμέσως αντιληπτή η στενή σχέση που έχουν τα δύο φαινόμενα. Το αρχικό σημείο της ανάλυσης είναι η εξίσωση NLS (2.6). H πιο απλή μη τετριμμένη λύση της εξίσωσης αυτής, είναι αυτή που έχει τη μορφή ενός συνεχούς κύματος (2.11) όπου είναι το πλάτος του κύματος (και η ισχύς του) στη θέση Η λύση αυτή είναι ουσιαστικά η μόνιμη κατάσταση (αφού είναι ανεξάρτητη του χρόνου) του συστήματος και το ερώτημα που πρέπει να απαντηθεί είναι αν αυτή είναι ευσταθής σε μικρές διαταραχές. Για να απαντηθεί το ερώτημα αυτό διαταράσσεται η λύση της (2.11) θεωρώντας ότι: (2.12) Σε αυτό το σημείο γίνονται κάποιες πράξεις που είναι απαραίτητες για να καταλήξουμε σε αυτό που θέλουμε. όπου το συζυγές οπότε: ( ) ( ) 35
36 ( ) ( ) ( ) ( ) Αντικαθιστώντας την (2.12) στην NLS (2.6) εξαιτίας των παραπάνω πράξεων έχουμε: [ ] ( ) ( ) Τώρα γραμμικοποιώντας ως προς τη μικρή διαταραχή και θεωρώντας τα εκθετικά περίπου ίσα με τη μονάδα καταλήγουμε στην ακόλουθη γραμμική εξίσωση: (2.13) Έπειτα χρησιμοποιώντας τον μετασχηματισμό και στη συνέχεια εκφράζοντας τη μιγαδική συνάρτηση στην καρτεσιανή της μορφή, δηλ. Με αυτόν τον τρόπο, η (2.13) καταλήγει σε ένα σύστημα γραμμικών διαφορικών εξισώσεων, για τις οποίες μπορούν να αναζητηθούν λύσεις της μορφής: (2.14) όπου και είναι τα σταθερά πλάτη, ο (γενικά μιγαδικός) κυματάριθμος και (η πραγματική) συχνότητα των αγνώστων συναρτήσεων και Με αυτή τη διαδικασία προκύπτει ένα ομογενές αλγεβρικό σύστημα με αγνώστους τα πλάτη και Είναι εύκολο να δειχθεί ότι το σύστημα αυτό έχει μία τετριμμένη λύση όταν τα και ικανοποιούν την ακόλουθη σχέση διασποράς: (2.15) 36
37 όπου Η ευστάθεια της λύσης (2.11) μπορεί να μελετηθεί πολύ εύκολα με τη βοήθεια της (2.15) σύμφωνα με το κριτήριο που ακολουθεί. Αν ο (μιγαδικός) κυματάριθμος έχει ένα φανταστικό μέρος αρνητικό, τότε η λύση (2.11) θα είναι ασταθής, αφού θα αυξάνεται εκθετικά με το δηλ. Είναι φανερό από την (2.15) ότι η ευστάθεια της μόνιμης κατάστασης (δηλ. του ) εξαρτάται ισχυρά από την τιμή του Στην περίπτωση ο κυματάριθμος είναι πραγματικός για κάθε και το είναι ευσταθές σε μικρές διαταραχές. Αν όμως και στην περίπτωση που είναι ο κυματάριθμος γίνεται φανταστικός με αποτέλεσμα την αστάθεια του Η εγγενής αυτή αστάθεια που εμφανίζεται για λέγεται αστάθεια διαμόρφωσης, αφού οδηγεί σε αυθόρμητη διαμόρφωση της μόνιμης κατάστασης. Έχοντας δείξει ότι όταν η λύση είναι ασταθής, είναι λογικό να περιμένει κανείς ότι μόνο στην περίπτωση αυτή είναι δυνατόν να υπάρχουν χρονικά (χωρικά) εντοπισμένες λύσεις με μηδενιζόμενες ασυμπτωτικές. Πράγματι, στην περίπτωση αυτή, οι κατάλληλες οριακές συνθήκες για την (2.6) είναι στο ενώ για την (2.10) είναι στο Για τις συνθήκες αυτές, οι Sakharov και Shabat έδειξαν ότι η εξίσωση NLS είναι πλήρως ολοκληρώσιμη με το Μετασχηματισμό Αντίστροφης Σκέδασης (ΜΑΣ) και δέχεται τις εντοπισμένες λύσεις των φωτεινών σολιτονίων. Έτσι, όταν η αστάθεια διαμόρφωσης εκδηλώνεται σαν τη διάλυση της λύσης σε μία ακολουθία παλμών, τα οποία είναι τα φωτεινά σολιτόνια. Αντίθετα, όταν, η λύση είναι πάντοτε ευσταθής σε μικρές διαταραχές, οπότε στην περίπτωση αυτή, η εξίσωση NLS δέχεται λύσεις σκοτεινών παλμών που δημιουργούνται επάνω στο υπόβαθρο της λύσης Οι κατάλληλες οριακές συνθήκες τώρα είναι και η εξίσωση NLS είναι επίσης πλήρως ολοκληρώσιμη με το ΜΑΣ και δέχεται τις εντοπισμένες λύσεις των σκοτεινών σολιτονίων ΦΩΤΕΙΝΑ ΚΑΙ ΣΚΟΤΕΙΝΑ ΣΟΛΙΤΟΝΙΑ ΤΗΣ ΕΞΙΣΩΣΗΣ NLS Για να βρεθούν οι λύσεις σολιτονίων της εξίσωσης NLS, θα χρησιμοποιηθεί η μέθοδος ανάλυσης του φασικού επιπέδου [31]. Η μέθοδος αυτή έγκειται στην αναγωγή της μερικής διαφορικής εξίσωσης (PDE) NLS σε μια συνήθη διαφορική εξίσωση (ODE) και κατόπιν στον υπολογισμό των διαχωριστικών καμπυλών (separatrices) στο φασικό επίπεδο του δυναμικού συστήματος που αντιπροσωπεύεται από την ODE, στις οποίες αντιστοιχούν οι λύσεις των μοναχικών κυμάτων. Αυτή η μέθοδος οδηγεί γενικά σε λύσεις μοναχικών κυμάτων, όμως η εξίσωση NLS είναι πλήρως ολοκληρώσιμη, οπότε οι λύσεις μοναχικών κυμάτων είναι πράγματι οι ζητούμενες λύσεις σολιτονίων. 37
38 Θεωρώντας ξανά την (2.6) γίνεται αναζήτηση λύσεων των οποίων η ισχύς είναι στάσιμη στο δηλ. όπου είναι μία πραγματική συνάρτηση που εξαρτάται μόνο από το Υποθέτουμε ότι η άγνωστη συνάρτηση έχει την εξής μορφή: (2.16) όπου είναι μία πραγματική συνάρτηση που εκφράζει τη φάση της λύσης. Έπειτα γίνεται αντικατάσταση της υποτιθέμενης λύσης (2.16) στην (2.6),αφού γίνουν πρώτα όλες οι απαραίτητες παραγωγίσεις. Δηλαδή: [ ] [ ( ) ] ( ) ( ) Τώρα γίνεται αντικατάσταση όλων των παραπάνω αποτελεσμάτων στην (2.6) και προκύπτει το εξής: [ ( ) ] Γίνεται διαγραφή όλων των και μηδενίζονται το πραγματικό και το φανταστικό μέρος οπότε με λίγες πράξεις προκύπτουν τα παρακάτω: ( ) [ ( ) ] 38
39 [ ( ) ] ( ) ( ) Οι παραπάνω εξισώσεις μπορούν να γραφούν ισοδύναμα ως εξής: ή (2.19) Η [ ( ) ] την διαιρείται με το οπότε προκύπτει: [ ( ) ] ( ) ( ) (2.20) όπου ( ) είναι μια συνάρτηση που εξαρτάται μόνο από το ενώ είναι μια συνάρτηση που εξαρτάται μόνο από το Στη συνέχεια μπορεί να γίνει χρήση της συνθήκης συμβιβαστότητας εξισώσεων (2.19), (2.20), και να προκύψει η συνθήκη Οπότε οι (2.19), (2.20) μπορούν να αποπλεχθούν και αρχικά να βρεθεί η φάση που δίνεται σαν: των (2.21) όπου και είναι πραγματικές σταθερές. Από την άλλη πλευρά, προκύπτει η ακόλουθη συνήθη διαφορική εξίσωση για τη συνάρτηση πλάτους : 39
40 (2.22) Είναι φανερό ότι η (2.22) είναι η εξίσωση κίνησης σε ένα μονοδιάστατο δυναμικό σύστημα, που περιγράφεται από την ακόλουθη χαμιλτονιανή συνάρτηση: ( ) ( ) (2.23) όπου ( ) (2.24) και όπου η σταθερά είναι η τιμή της ενέργειας που καθορίζεται από τις αρχικές συνθήκες. Επειδή η μορφή του δυναμικού εξαρτάται από την τιμή της παραμέτρου οι λύσεις που θα υπολογιστούν θα είναι διαφορετικές στις περιπτώσεις και Έτσι θα μελετηθούν ξεχωριστά στη συνέχεια οι περιπτώσεις αυτές, οι οποίες θα οδηγήσουν στις λύσεις φωτεινών και σκοτεινών σολιτονίων αντίστοιχα ΦΩΤΕΙΝΑ ΣΟΛΙΤΟΝΙΑ Στο σχήμα 2.12.α [16] έχουν σχεδιαστεί τα φασικά διαγράμματα της εξίσωσης (2.23), με το φασικό επίπεδο με συντεταγμένες ( ) για διάφορες τιμές των και Ιδιαίτερο ενδιαφέρον παρουσιάζει το Σχ.2.12.α(α), όπου και Αξίζει να σημειωθεί ότι υπάρχουν δύο κέντρα, για και ενέργεια γύρω από τα οποία υπάρχουν περιοδικές τροχιές, που σημαίνει ότι τα αντίστοιχα κύματα είναι περιοδικά. Πολύ κοντά στα κέντρα οι τροχιές είναι ελλειπτικές και τα αντίστοιχα κύματα είναι γραμμικά (συνημιτονοειδή), ενώ πιο μακριά από τα κέντρα, αν και τα κύματα εξακολουθούν να είναι περιοδικά, γίνονται όλο και πιο μη γραμμικά. Ενώ τώρα κάθε φασική τροχιά που αντιστοιχεί σε μη γραμμικό περιοδικό κύμα διαγράφεται συνεχώς (ωρολογιακά) καθώς αυξάνεται το δεν συμβαίνει το ίδιο και για τις δύο διαχωριστικές καμπύλες (separatrices) που αντιστοιχούν σε ενέργεια και σχηματίζουν ένα πλάγιο οκτώ στο Σχ.2.12.α(α): Η δεξιά, για παράδειγμα ομοκλινική τροχιά ξεκινά από το σαγματικό σημείο ( ) και διαγράφεται μόνο μία φορά (ωρολογιακά) στο διάστημα Η τροχιά αυτή αντιστοιχεί σε ένα μοναχικό κύμα, αφού ξεκινά από την αρχή 40
41 τέμνει από επάνω τον άξονα σε μία θέση που αντιστοιχεί στη μέγιστη τιμή του μοναχικού κύματος και επανέρχεται στην αρχή ασυμπτωτικά καθώς Αυτή είναι η αναπαράσταση ενός μοναχικού κύματος στο φασικό επίπεδο. Ακόμα, για τις θετικές τιμές της ενέργειας (δηλ. έξω από τις διαχωριστικές καμπύλες) οι τροχιές είναι πάλι περιοδικές (έχουν άλλη μορφή ασφαλώς) και τα αντίστοιχα κύματα είναι μη γραμμικά περιοδικά κύματα. Το ίδιο συμβαίνει και στα Σχ α(β) και 2.12.α(γ), όπου όλα τα κύματα είναι περιοδικά. Για να γίνει αναλυτικός υπολογισμός της μορφής της ομοκλινικής τροχιάς, δηλ. της λύσης του μοναχικού κύματος, θα γίνει αλλαγή της άγνωστης μεταβλητής σε οπότε η (2.23) ξαναγράφεται: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) Ολοκληρώνοντας στη συνέχεια την (2.25) προκύπτει ότι: (2.26) όπου το αντιπροσωπεύει το κέντρο της εντοπισμένης αυτής λύσης, άρα προκύπτει η ακόλουθη λύση της εξίσωσης NLS, ( ) όπου είναι μια αυθαίρετη σταθερά. Παρατήρηση: η εξίσωση NLS παραμένει αναλλοίωτη σε μετασχηματισμό Γαλιλαίου, οπότε αν η ικανοποιεί την (2.6), τότε την ικανοποιεί και η συνάρτηση [ ( )] 41
42 Αυτό οδηγεί σε μια πιο γενική μορφή μοναχικού κύματος, το οποίο περιλαμβάνει μια πρόσθετη ανεξάρτητη σταθερά την και δίνεται ως [ ] (2.27) Η λύση της (2.27) αντιπροσωπεύει ένα παλμό που είναι το φωτεινό σολιτόνιο, ο οποίος χαρακτηρίζεται από τέσσερις ανεξάρτητες παραμέτρους: το πλάτος (και το αντίστροφο εύρος) την ταχύτητα (και συχνότητα) το κέντρο (και αρχική θέση) και την αρχική φάση 2.13 ΣΚΟΤΕΙΝΑ ΣΟΛΙΤΟΝΙΑ Στο Σχ α [16] έχουν σχεδιαστεί τα φασικά διαγράμματα της (2.23), με για διάφορες τιμές των σταθερών Σύμφωνα με την προηγούμενη ανάλυση, ιδιαίτερο ενδιαφέρον παρουσιάζεται στα σχήματα 2.13.α(α) και 2.13.α(β) στα οποία υπάρχουν διαχωριστικές καμπύλες, που αντιστοιχούν σε διαφορετικού τύπου μοναχικά κύματα. Στο Σχ α(α) ( υπάρχουν δυο ετεροκλινικές τροχιές με την ασυμπτωτική συμπεριφορά που αντιστοιχούν στα λεγόμενα μαύρα σολιτόνια. Από την άλλη πλευρά, στο Σχ α(α) υπάρχουν δύο ομοκλινικές τροχιές με ασυμπτωτική συμπεριφορά που αντιστοιχούν στα λεγόμενα γκρίζα σολιτόνια. Οι τροχιές που είναι εσωτερικές των διαχωριστικών καμπύλων στα Σχ α(α) και 2.13.α(β) είναι όλες περιοδικές και φραγμένες, αντιστοιχώντας σε μη γραμμικά περιοδικά κύματα, ενώ όλες οι άλλες (συμπεριλαμβανομένων και εκείνων που φαίνονται στα Σχ α(γ) και 2.13.α(δ)) αντιπροσωπεύουν επίσης περιοδικές λύσεις, αλλά με τροχιές που δεν είναι φραγμένες. Ακολουθώντας πάλι την μεθοδολογία που παρουσιάστηκε στη περίπτωση της ανώμαλης διασποράς, γίνεται η αλλαγή μεταβλητής: ( ) ( ) ( ) ( ) ( ) 42
43 ( ) { ( ) ( ) ( ) ( ) ( ) ( ) (2.28) Αξίζει να τονιστεί ότι το τελευταίο μέλος της ισότητας στη (2.28), λόγω του ότι τα σαγματικά σημεία στα Σχ. 2(α) και 2(β) αντιστοιχούν στη διπλή ρίζα του κυβικού πολυωνύμου (2 ο μέλος της ισότητας στη (2.28)). Η φυσική σημασία της διπλής ρίζας θα αναλυθεί λίγο πιο κάτω. Η ρίζα είναι η ελάχιστη τιμή της συνάρτησης Εάν ολοκληρωθεί η (2.28) προκύπτει:,, (2.29) [ ] (2.30) Η λύση των (2.29)- (2.30) ονομάζεται γενικά ονομάζεται σκοτεινό σολιτόνιο, αφού αναπαριστά ένα βύθισμα ισχύος σε ένα σταθερό υπόβαθρο. Σε αντίθεση με το φωτεινό σολιτόνιο, το πλάτος του σκοτεινού σολιτονίου (Εξ. (2.29)) έχει μια επιπλέον παράμετρο, την η οποία δηλώνει το βάθος της διαμόρφωσης του υποβάθρου. Επίσης, το σκοτεινό σολιτόνιο χαρακτηρίζεται από μια μη τετριμμένη κατανομή της φάσης (που λαμβάνει χώρα σε μια εντοπισμένη περιοχή) η οποία οδηγεί σε διαφορετικές τιμές στο όριο Οπότε το σκοτεινό σολιτόνιο ονομάζεται τοπολογικό σολιτόνιο, ενώ το φωτεινό, το οποίο δεν παρουσιάζει αλλαγή στη φάση του για ονομάζεται μη τοπολογικό σολιτόνιο. 43
44 Σχήμα 2.12.α: Τα πρώτα τρία σχηματάκια είναι τα φασικά διαγράμματα της εξίσωσης (2.23) για δηλαδή στην περίπτωση των φωτεινών σολιτονίων. (α) 44
45 Σχήμα 2.13.α: Τα επόμενα τέσσερα σχηματάκια είναι τα φασικά διαγράμματα της (2.23) για δηλαδή στην περίπτωση των σκοτεινών σολιτονίων. Στην περίπτωση που το βάθος της διαμόρφωσης πλησιάζει το μηδέν, οπότε οι (2.29)-(2.30) δίνουν [ ( ( ) )] Η λύση αυτή λέγεται μαύρο σολιτόνιο και χαρακτηρίζεται από μια ασυνέχεια στη φάση στο Στην περίπτωση το βάθος της διαμόρφωσης είναι μη μηδενικό και η αντίστοιχη λύση ονομάζεται γκρίζο σολιτόνιο. Είναι εύκολο να διαπιστώσει κανείς ότι και οι δύο αυτές μορφές σκοτεινών σολιτονίων μπορούν να περιγραφούν εναλλακτικά [30] από την ακόλουθη εξίσωση, που είναι ισοδύναμη αλλά πολύ απλούστερη των εξισώσεων (2.29)-(2.30): (2.31) Σχήμα 2.13.β: Τα είδη των οπτικών σολιτονίων της εξίσωσης (2.6) : (a) Φωτεινά σολιτόνια, (b) Μαύρα σολιτόνια, (c) Γκρίζα σολιτόνια. Στην περίπτωση της (2.10) ο οριζόντιος άξονας στα παραπάνω σχήματα είναι ο X. Στην (2.31) είναι ενώ οι παράμετροι και συνδέονται με την απλή σχέση Οπότε αντί για δύο παραμέτρους, χρησιμοποιείται μία, εισάγοντας οπότε η γωνία δείχνει την ολική ολίσθηση της φάσης δια μέσου του σκοτεινού σολιτονίου (που είναι Ακόμα από την (2.31) φαίνεται ότι το σκοτεινό σολιτόνιο είναι ένας σκοτεινός παλμός, μέγιστης ισχύος επάνω στο ευσταθές υπόβαθρο της λύσης (Εξ. (2.11)). Επίσης είναι φανερό ότι η περίπτωση του μαύρου σολιτονίου αντιστοιχεί σε 45
46 ενώ του γκρίζου σε Η ανακεφαλαίωση των μορφών των σκοτεινών αλλά και των φωτεινών σολιτονίων της εξίσωσης NLS παρουσιάζεται στο Σχ β [32]. ΚΕΦΑΛΑΙΟ ΣΥΖΕΥΓΜΕΝΕΣ NLS ΚΑΙ ΕΤΕΡΟΔΙΑΜΟΡΦΩΣΗ ΦΑΣΗΣ Οι συζευγμένες NLS περιγράφουν τη διάδοση και αλληλεπίδραση δύο σολιτονικών παλμών, έχοντας σαν κύριο και συχνά σα μόνο όρο σύζευξης αυτόν που περιγράφει το φαινόμενο της ετεροδιαμόρφωσης φάσης (cross phase modulation-xpm). Η XPM είναι από τα πλέον σημαντικά φαινόμενα και αφορά τη μη-γραμμική αλληλεπίδραση μεταξύ δύο πεδίων, με διαφορετικές κεντρικές συχνότητες, που συμπορεύονται στο μέσο. Όταν τα πεδία συνυπάρξουν στο χώρο ή το χρόνο, έχοντας έστω μερική αλληλοεπικάλυψη, η αμοιβαία επίδραση τους στο δείκτη διάθλασης καταλήγει σε αμοιβαία επίδραση πάνω τους. Η αλληλεπίδραση που περιγράφεται από το XPM είναι ασύμφωνη και ελκτική, ενώ μπορεί να οδηγήσει ακόμα και σε αλληλο-παγίδευση των πεδίων, χωρίς να υπάρξει ανταλλαγή ενέργειας. Το XPM εμφανίζεται πάντα μαζί με το SPM και το όνομά του σημαίνει ετεροδιαμόρφωση φάσης αντιστοίχως. Η ονομασία επίσης προέρχεται από την έρευνα για τα χρονικά σολιτόνια, αλλά ξανά το φαινόμενο έχει αντίστοιχο αποτέλεσμα στα χωρικά καθώς ο δείκτης διάθλασης που γίνεται «αισθητός» από την ακτίνα διαμορφώνεται από την ίδια, αλλά και από τις υπόλοιπες συν-διαδιδόμενες ακτίνες. Το φαινόμενο αυτό μοντελοποιείται σαν όρος μη-γραμμικής σύζευξης μεταξύ NLS εξισώσεων, η κάθε μία εκ των οποίων περιγράφει την εξέλιξη της περιβάλλουσας ενός εκ των πεδίων (παλμών). Οι παλμοί μπορεί να αλληλοπαγιδευτούν ή να περάσουν ο ένας μέσα από τον άλλο, οπότε το XPM να έχει διαρκή ή χρονικά πολύ μικρή επίδραση (σύγκρουση). Τα διανυσματικά σολιτόνια αποτελούνται από δύο ή περισσότερες συνιστώσες (ρυθμούς) οι οποίες αλληλο-παγιδεύονται και διαδίδονται μαζί. Βασική προϋπόθεση για τη δημιουργία ευσταθών μορφών είναι οι δύο ρυθμοί να μη συμβάλουν, ή αλλιώς, η συμβολή τους να μην επηρεάζει το δείκτη διάθλασης, διότι τότε αυτός δε θα έχει μια σταθερή διαμόρφωση με αποτέλεσμα να καταστρέφεται η κυματοδήγηση. Δηλαδή η αλληλεπίδραση μεταξύ των συνιστωσών πρέπει να είναι ασύμφωνη. Η πρώτη πρόταση για διανυσματικό σολιτόνιο έγινε από τον Manakov, ο οποίος θεώρησε ένα πεδίο με δύο συνιστώσες ορθογώνια πολωμένες, έτσι ώστε να μη συμβάλουν [58]. Το σύστημα του αποτελείται από δύο μη-γραμμικά συζευγμένες εξισώσεις, μία για κάθε συνιστώσα. Ο όρος σύζευξης αντιπροσωπεύει την ετεροδιαμόρφωση φάσης (cross phase modulation-xpm), ουσιαστικά την αλλαγή του δείκτη 46
47 διάθλασης που «βλέπει» η μία συνιστώσα λόγω ύπαρξης της άλλης. Το σύστημα του Manakov θέτει τους όρους των SPM και XPM σαν ισοδύναμους και είναι το μόνο ολοκληρώσιμο. Παρόλα αυτά έχουν βρεθεί σολιτονικές λύσεις για συστήματα με διαφορετική σχέση μεταξύ αυτών των όρων. Χαρακτηριστική περίπτωση είναι αυτό που περιγράφει τη διάδοση ορθογώνια πολωμένων ρυθμών σε ίνα με ισχυρή διπλοθλαστικότητα. Ακόμα, κυματομορφές που διατηρούν το σχήμα τους βρίσκονται και στη περίπτωση της ασθενούς διπλοθλαστικότητας, όπου οι ρυθμοί αλληλεπιδρούν σύμφωνα, λόγω του φαινομένου «μίξης τεσσάρων φωτονίων» (four wave mixing-fwm) [57]. Οι συζευγμένοι αυτοί παλμοί αναφέρονται επίσης ως διανυσματικά σολιτόνια. Όλα αυτά τα παραδείγματα αφορούν συζευγμένους θεμελιώδεις (χαμηλούς) ρυθμούς. Ανώτεροι ρυθμοί, χρονικοί και χωρικοί, που συζευγμένοι επιδεικνύουν σημαντική ευστάθεια έχουν παρατηρηθεί σε αριθμητικές εργασίες και πειράματα [59,60]. Οι σολιτονικές αλληλεπιδράσεις συχνά ονομάζονται και «συγκρούσεις», λόγω των σωματιδιακών ιδιοτήτων των σολιτονίων και είναι από τα πιο ενδιαφέροντα ερευνητικά πεδία στη μη-γραμμική Οπτική και όχι μόνο. Χωρίζονται σε δύο κατηγορίες, τις σύμφωνες (coherent), όπου το αποτέλεσμα εξαρτάται από τη σχετική φάση των παλμών και τις ασύμφωνες (incoherent), όπου δεν εξαρτάται. Η αλληλεπίδραση είναι σύμφωνη όταν η χρονική απόκριση του μηγραμμικού μέσου είναι αρκετά σύντομη ώστε να αισθανθεί τα αποτελέσματα της παρεμβολής των σολιτονίων (ή σημάτων) κατά τη μερική ή ολική αλληλοεπικάλυψη τους. Τα υλικά με τους πλέον συνήθεις στην οπτική τύπους μη-γραμμικότητας (Kerr και τετραγωνικής) έχουν τη γρήγορη απόκριση που απαιτείται, αντίθετα τα φωτοδιαθλαστικά υλικά έχουν αργό χρόνο απόκρισης (έστω και επηρεάζονται από τη σχετική φάση μόνο αν παραμένει σταθερή για χρόνο μεγαλύτερο από Για μεγάλη συχνότητα μεταβολής της φάσης οι αλληλεπιδράσεις είναι ουσιαστικά ασύμφωνες. Ένα άλλο σημείο διαφοροποίησης είναι οι διαστάσεις του συστήματος. Αν και τα βασικά χαρακτηριστικά του τρόπου αλληλεπίδρασης των σολιτονικών κυμάτων παρατηρούνται σε διάφορα είδη μη-γραμμικότητας και σε παλμούς και ακτίνες μίας ή περισσοτέρων διαστάσεων, οι αλληλεπιδράσεις παλμών (2+1)D και πάνω γίνονται ιδιαίτερα πολύπλοκες. Αντίθετα, η περίπτωση για Kerr μηγραμμικότητα και (1+1)D σολιτόνια είναι πιο εύκολο να μελετηθεί αναλυτικά, καθώς οι αλληλεπιδράσεις μπορούν να περιγραφούν επακριβώς από τη μέθοδο αντίστροφης σκέδασης [7]. Ακόμα, καθώς το σύστημα που τα περιγράφει είναι ολοκληρώσιμο δεν υπάρχουν απώλειες ενέργειας των παλμών. Για τον ίδιο λόγο, οι συγκρούσεις είναι πλήρως ελαστικές και ο αριθμός των σολιτονίων που συμμετέχουν διατηρείται, τα οποία επίσης διατηρούν τις ταχύτητες τους, (και στις ασύμφωνες αλληλεπιδράσεις διατηρούν και τη προ-σύγκρουσης διεύθυνση διάδοσης). Οπότε, δύο σολιτόνια ίδιας συχνότητας που οδεύουν παράλληλα, με 47
48 μετατόπιση που δε ξεπερνά μερικές φορές το πλάτος τους, και όντας συμφασικά ( ) έλκονται, ενώ αν έχουν αντίθετη φάση ( ) απωθούνται. Για ενδιάμεσες τιμές της φάσης η αλληλεπίδραση τα οδηγεί σε πιο περίπλοκες κινήσεις, συνδυασμούς έλξης-άπωσης, ενώ μπορεί να υπάρξει ανταλλαγή ενέργειας (δείτε το σχήμα 2.8). Η συμφασική παρεμβολή των σολιτονίων αυξάνει την ένταση ανάμεσα τους. Εφόσον το μέσο παρουσιάζει εστιάζουσα μηγραμμικότητα θα αυξηθεί και ο δείκτης διάθλασης στη περιοχή αυτή. Με τον τρόπο αυτό περισσότερο φως στρέφεται προς τη περιοχή ανάμεσα τους και άρα οι παλμοί προσεγγίζουν ο ένας τον άλλο. Το αντίθετο συμβαίνει όταν συμβάλουν καταστροφικά. Η ένταση στο μέσο πέφτει και μαζί της και ο δείκτης διάθλασης σε σχέση με τη γύρω περιοχή. Το φως κινείται μακριά από τις μικρές τιμές του δείκτη και οι παλμοί απωθούνται [18,61]. Σχήμα 3.1.α : Σχηματική αναπαράσταση της ενισχυτικής (άνω σειρά) και καταστροφικής (κάτω) σύμφωνης αλληλεπίδρασης δύο σολιτονικών παλμών. Στη μέση παρίσταται η διαμόρφωση της έντασης και δεξιά του δείκτη διάθλασης. Οι διακεκομμένες παριστούν τους παλμούς μόνους. Στη περίπτωση των συμφασικών σολιτονίων, το αποτέλεσμα της σύγκρουσης τους εξαρτάται από το είδος της μη-γραμμικότητας. Οι πιο συχνές περιπτώσεις είναι του τύπου Kerr και η κορέσιμη. Στα φασικά συστήματα, για μεγάλες τιμές της έντασης του φωτός, η μη-γραμμικότητα είναι ουσιαστικά κορέσιμη. Αυτό σημαίνει ότι για πολύ μεγάλη ένταση ισχυροποιούνται τα φαινόμενα που διακόπτουν την διαρκή αυτοεστίαση κάνοντας τη μη-γραμμική 48
49 απόκριση του υλικού ασθενέστερη από την ιδανική Kerr περίπτωση. Για αυτή τη περίπτωση, τα συμφασικά σολιτόνια έλκονται μέχρι συσσωμάτωσης και μετά εκτελούν περιοδική έλξη-άπωση ταλαντούμενα γύρω από το μέσο της αρχικής τους απόστασης. Τα χωρικά σολιτόνια που ταξιδεύουν συγκλίνοντα με γωνία αρκετά μεγάλη δύνανται να μη παγιδευτούν, αλλά να περάσουν το ένα μέσα από το άλλο, αποκτώντας μια μικρή μετατόπιση. Όταν συγκρούονται σολιτόνια διαφορετικού πλάτους, χρονικά ή χωρικά, υπάρχει πάντα ανταλλαγή ενέργειας. Μετά από τη σύγκρουση τα σολιτόνια μεταβάλλουν το εύρος τους εξισορροπώντας έτσι την αλλαγή του πλάτους. Οι αλληλεπιδράσεις μη-γραμμικών χωροχρονικών παλμών και ακτίνων, διαστάσεων (2+1) και (3+1)D, σε επίπεδο κυματοδηγό ή μαζικό μέσο, είναι φαινόμενα ακόμα πιο πολύπλοκα αλλά και πλουσιότερα σε δυνατά αποτελέσματα. Στη περίπτωση της μη-γραμμικότητας τύπου Kerr, οι αλληλεπιδράσεις είναι σχετικά βραχύβιες, καθώς για ανώμαλη διασπορά οι παλμοί μπορεί να οδηγηθούν σε έντονη αυτοεστίαση και κατάρρευση, ενώ σε μέσο με κανονική διασπορά δύνανται να διαχωριστούν σε δύο ή περισσότερα κυματοπακέτα έκαστος, τα οποία να αλληλεπιδρούν εκ νέου. Παρόλα αυτά, η αλληλεπίδραση μπορεί να οδηγήσει σε φαινόμενα όπως η δημιουργία συσσωματώματος, αμαλγάματος, η χωροχρονική μετάθεση ή σε διάλυση των παλμών [62]. Αξίζει να προσθέσουμε ότι ευσταθέστεροι μη-γραμμικοί παλμοί παρατηρούνται σε μέσα με κορέσιμη μη-γραμμικότητα. Σε κατάλληλες συνθήκες μπορούν να είναι αρκετά ευσταθείς, ώστε να μπορούν να ονομάζονται επίσης «σολιτόνια». Στις αλληλεπιδράσεις τους η διατήρηση του αριθμού των παλμών δεν είναι δεδομένη, όπως στους (1+1)D παλμούς. Έτσι οι παλμοί μπορούν να περάσουν ο ένας μέσα από τον άλλο, να συσσωματωθούν ή να καταστραφούν [57,61]. Ακόμα οι περισσότεροι βαθμοί ελευθερίας στη κίνηση τους επιτρέπουν τη δημιουργία φωτεινών δομών (αν και όχι πάντα ευσταθών) αποτελούμενων από ορισμένο αριθμό αλληλοεπιδρώντων κυματοπακέτων, σε συγκεκριμένες αποστάσεις και με συγκεκριμένη στροφορμή. Για παράδειγμα το ζεύγος σολιτονίων που περιστρέφονται το ένα γύρω από το άλλο, τα δακτυλιοειδή σολιτόνια κ.α. [57,63]. Οι ασύμφωνες αλληλεπιδράσεις είναι ακόμα ένα μεγάλο κεφάλαιο, με έντονο φυσικό και τεχνολογικό ενδιαφέρον. Το τι θεωρούμε όμως ασύμφωνο είναι και θέμα παραδοχών. Ουσιαστικά η πιο ξεκάθαρη περίπτωση είναι τα φωτοδιαθλαστικά υλικά, όπου ο χρόνος απόκρισης τους είναι πολύ μεγαλύτερος από τη μεταβολή της σχετικής φάσης μεταξύ σολιτονίων. Όμως, όταν τα σολιτόνια έχουν μεγάλη συχνοτική διαφορά, η αλληλεπίδραση τους μπορεί να θεωρηθεί ασύμφωνη, και να μοντελοποιηθεί από αντίστοιχες εξισώσεις με καλή προσέγγιση. Ένας έμμεσος τρόπος επίδρασης της φάσης είναι το FWM, αλλά και αυτό υπό περιπτώσεις είναι ασήμαντο και μπορεί να αγνοηθεί στη μοντελοποίηση [64,65,67]. Οι ασύμφωνες αλληλεπιδράσεις είναι πάντα ελκτικές. Οι παλμοί 49
50 υπερτίθενται και αυξάνουν τοπικά το δείκτη διάθλασης, οπότε το φως έχει την τάση να κινηθεί προς τα εκεί. Λόγω της μεγάλης διαφοράς στη συχνότητα όμως, ο ένας κινείται (διαδίδεται) αρκετά πιο γρήγορα από τον άλλο και περνά από μέσα του με μόνο αποτέλεσμα μια μικρή μετατόπιση των παλμών. Σημαντικότερη είναι η επίδραση στους παλμούς στην περίπτωση που αυτοί ξεκινούν αλληλο-επικαλυπτόμενοι. Με αυτό τον τρόπο ο παλμός δε διαπερνά συνολικά τον άλλο και η σύγκρουση τους δεν είναι συμμετρική. Είναι «ατελής» και επιφέρει φασματική μετατόπιση, που μπορεί να οδηγήσει και στη παγίδευση των παλμών [66,67]. Οι ασύμφωνες αλληλεπιδράσεις έχουν ιδιαίτερη σημασία στο πεδίο της οπτικής διότι περιγράφουν τις συγκρούσεις σολιτονικών παλμών διαφορετικών καναλιών σε κάποιο μη-γραμμικό τηλεπικοινωνιακό σύστημα με φασματική πολυπλεξία (wavelength division multiplexing-wdm). 3.2 ΣΥΜΠΑΓΗ ΟΠΤΙΚΑ ΜΕΣΑ ΚΑΙ ΕΠΙΠΕΔΟΙ ΔΙΗΛΕΚΤΡΙΚΟΙ ΚΥΜΑΤΟΔΗΓΟΙ ΓΙΑ ΣΥΖΕΥΓΜΕΝΕΣ NLS Σε αυτή τη παράγραφο εργαζόμαστε όπως ακριβώς και στη παράγραφο 2.9. Μόνο που εδώ έχουμε σύστημα εξισώσεων NLS: (3.1) Οι παραπάνω είναι τα ταυτόσημες με τις: (3.2) (3.3) (3.4) Παρατηρούμε και εδώ ότι όταν εναλλαχθεί το στη (3.1), (3.2) με το στη (3.3), (3.4) οι περιπτώσεις (με την πρόσθετη αλλαγή οδηγούν στις ίδιες εξισώσεις κάθε φορά. Έτσι χωρίς βλάβη της γενικότητας θα συνεχίσουμε την ανάλυση θεωρώντας στο εξής μόνο τις εξισώσεις (3.3) και (3.4). Οι τιμές που που μπορεί να παίρνει η παράμετρος είναι καθοριστικές για την αστάθεια διαμόρφωσης και το είδος των σολιτονίων (φωτεινά ή σκοτεινά) που μπορούν να διαδοθούν στα οπτικά μέσα. 50
51 3.3 ΑΣΤΑΘΕΙΑ ΔΙΑΜΟΡΦΩΣΗΣ ΚΑΙ ΣΟΛΙΤΟΝΙΑ ΓΙΑ ΣΥΖΕΥΓΜΕΝΕΣ NLS Το αρχικό σημείο (α. σ) της ανάλυσης είναι οι εξισώσεις NLS (3.3) και (3.4). Η πιο απλές μη τετριμμένες λύσεις της εξίσωσης αυτής είναι αυτές που έχουν τη μορφή ενός συνεχούς κύματος (cw). όπου είναι το πλάτος των κυμάτων και η ισχύς του στη θέση Σε αυτό το σημείο διαταράσσουμε τις λύσεις (3.5), (3.6) θεωρώντας ότι: (3.5) (3.6) (3.7) (3.8) Αντικαθιστώντας τώρα τις (3.7), (3.8) στις (3.3), (3.4) και γραμμικοποιώντας ως προς τη μικρή διαταραχή και αντίστοιχα έχουμε: ( ) ( ) ( )( ) (διότι Αναλόγως εργαζόμαστε ως προς Δηλαδή έχουμε: Άρα οι (3.3), (3.4) λόγω των (3.7), (3.8) ξαναγράφονται: [ ] 51
52 [( ) ( )] ( ) ( ) [ ] Μετά από γραμμικοποίηση ως προς τις μικρές διαταραχές και επειδή κάποια εκθετικά είναι περίπου ίσα με τη μονάδα καταλήγουμε στην εξής σχέση: ( ) [ ( )] ( ) ( ) Αντίστοιχα προκύπτει μια σχέση και ως προς Θεωρώντας πάλι τις εξισώσεις: (3.3) (3.4) Αναζητούμε λύσεις των οποίων η ισχύς να είναι στο στάσιμες δηλαδή και όπου οι είναι πραγματικές συναρτήσεις που εξαρτώνται μόνο από το Υποθέτουμε λοιπόν ότι οι άγνωστες συναρτήσεις έχουν την μορφή: και τις αντικαθιστώ στις (3.3), (3.4) αντίστοιχα: [ ( ) ] 52
53 (διαγράφουμε όλα τα εκθετικά σε αυτό το σημείο) ( ) [ ( ) ] Χωρίζουμε φανταστικό από πραγματικό μέρος και έχουμε: [ ( ) ] (3.9) ( ) ( ) (3.10) [ ( ) ] Διαιρούμε όλα τα μέλη της παραπάνω σχέσης με το και έχουμε: [ ( ) ] ( ) ( ) όπου ( ), άρα ( ) ( ) (3.12) ( ) ( ) (3.13) [ ( ) ] 53
54 Διαγράφουμε πάλι όλα τα εκθετικά και απλοποιείται η παράστασή μας και χωρίζουμε φανταστικό μέρος από πραγματικό και έχουμε τελικά: [ ( ) ] (3.14) ( ) (3.15) Την (3.14) την διαιρούμε με τη και έχουμε: [ ( ) ] ( ) ( ) (3.16) όπου ( ) άρα διότι ( ) ( ) (3.17) ( ) ( ) (3.18) όπου οι σταθερές είναι οι τιμές της ενέργειας που καθορίζονται από τις αρχικές συνθήκες. Είναι φανερό ότι αφού οι μορφές των δυναμικών εξαρτώνται από τη τιμή της παραμέτρου οι λύσεις που θα υπολογιστούν θα είναι διαφορετικές στις περιπτώσεις και. ( ) ( ) (3.20) 54
55 3.4 ΦΩΤΕΙΝΑ ΣΟΛΙΤΟΝΙΑ ( ( ) Θέτουμε ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) (3.20) 3.5 ΣΚΟΤΕΙΝΑ ΣΟΛΙΤΟΝΙΑ ( ) ( ) ( ) ( ) ( ) ( ) { ( ) 55
56 ( ) ( ) ( ) ( ) (3.21) 56
57 ΚΕΦΑΛΑΙΟ4 4.1 ΑΛΛΗΛΕΠΙΔΡΑΣΗ ΣΚΟΤΕΙΝΩΝ ΣΟΛΙΤΟΝΙΩΝ ΜΕ ΕΠΙΤΟΠΙΣΜΕΝΕΣ ΑΣΑΦΕΙΕΣ ΣΤΙΣ BOSE-EINSTEIN ΣΥΜΠΥΚΝΩΣΕΙΣ Σε αυτή την παράγραφο γίνεται μελέτη στην αλληλεπίδραση των σκοτεινών σολιτονίων με μια επιτοπισμένη ασάφεια στις συμπυκνώσεις Bose- Einstein. Εφαρμόζεται η θεωρία διαταραχών του σολιτονίου για την αναλυτική περιγραφή της αλληλεπίδρασης του δυναμικού του σολιτονίου και την ασάφεια σολιτονίου. Έπειτα από την ανάλυση αυτή προκύπτει ότι ένα σκοτεινό σολιτόνιο μπορεί να ανακλαστεί από μια απωθητική ασάφεια ή να μεταβιβαστεί διαμέσου αυτής με ελεγχόμενο τρόπο, καθώς κοντά στο κρίσιμο σημείο το σολιτόνιο μπορεί σχεδόν να παγιδευτεί από μια ασάφεια. Επιπλέον, αποδεικνύεται ότι ένα ακίνητο σολιτόνιο μπορεί να συλληφθεί και να γίνει οπισθέλκυση από μια αδιαβατική ελκτική ασάφεια. ΕΙΣΑΓΩΓΗ Από τότε που έγινε η πειραματική ανακάλυψη της πύκνωσης Bose- Einstein σε αραιωμένα ατομικά αλκάλια [33] έγινε μια τεράστια ανάπτυξη των ιδιοτήτων της φάσης συμπύκνωσης. Μεταξύ άλλων, πειράματα των συμπυκνώσεων Bose-Einstein (BECs) έχουν αποδείξει υπερρευστότητα της φάσης [34] συμπύκνωσης, την πιθανότητα μίξης τεσσάρων κυμάτων [35], την ενίσχυση φωτός και τη πύκνωση ζωής [36] ατόμων όπως τη δημιουργία τοπολογικών δομών [37] σαν τους στροβίλους, τα πλέγματα στρόβιλου [38] καθώς σκοτεινά [39] και φωτεινά σολιτόνια [40]. Τα παραπάνω δίνουν τη δυνατότητα για πολυάριθμες εφαρμογές των μη-γραμμικών matter-wave physics και κυρίως θυμίζουν την κατάσταση αντιμετώπισης για φωτεινά κύματα και οπτικά πριν πολλές δεκαετίες. Ένα από τα πιο πρόσφατα παραδείγματα μία συνοχική συσκευή matter wave που καλείται atom chip [41] η οποία αποτελείται από μικροκατασκευασμένο ημιαγωγό και στην επιφάνειά του προσαρμοσμένα οπτικά άτομα, στοιχεία όπως κυκλώματα ρεύμα ή charge-carrying wires, συνηχητές κ.τ.λ. Το τελευταίο επιτρέπει την παγίδευση και οδήγηση ή μιλώντας πιο γενικά, ελέγχει την κίνηση των matter waves. Μια πιο μακροπρόθεσμη προοπτική μιας τέτοιας συνοχικής matter wave συσκευής είναι η εξέλιξη αναλογικής πληροφορίας σε νανομετρική κλίμακα. Ένα θέμα που σχετίζεται με τα παραπάνω και παρουσιάζει ενδιαφέρον είναι να μάθουμε πώς να ελέγχουμε την κίνηση των μη-γραμμικών διεγέρσεων της συμπύκνωσης και των διαφορετικών τύπων σολιτονίων. Πειραματικά υπάρχουν αρκετές quantum-phase-engineering τεχνικές για την παραγωγή 57
58 σκοτεινών σολιτονίων σε μια Bose-Einstein πύκνωση [39]. Το ερώτημα που προκύπτει είναι πως μια πύκνωση μπορούσε να επηρεάσει ή ακόμη και να οδηγήσει την κίνησή τους. Αυτή η παράγραφος κάνει ένα βήμα προς αυτή τη κατεύθυνση ερευνώντας την αλληλεπίδραση των σκοτεινών σολιτονίων μέσα σε ένα περιορισμένο δυναμικό με μια εντοπισμένη ανομοιογένεια ή ασάφεια. Η προοπτική δια του παρόντος είναι ότι οι ασάφειες μπορούν να χρησιμοποιηθούν σαν στοιχεία μιας matter wave συσκευής που ελέγχει την κίνηση ενός δικτύου μη-γραμμικών διεγέρσεων. Σκοτεινά σολιτόνια μπορούν να διεγερθούν σε BECs με απωθητικές αλληλεπιδράσεις, ένα τέτοιο σολιτόνιο χαρακτηρίζεται από μια εγκοπή σε μια BEC πυκνότητα και μια φάση άλματος διαμέσου της εντοπισμένης περιοχής. Τα δυναμικά τους σε ένα παγιδευμένο δυναμικό έχουν μελετηθεί θεωρητικά από αρκετούς συγγραφείς [42-45]. Πέρα από την παραπάνω υποκίνηση, τα δυναμικά των BECs παρουσία των ασαφειών έχουν γίνει πρόσφατα θέμα με αυξανόμενο ενδιαφέρον [46]. Μια μέθοδος που έχει μελετηθεί είναι μια αντίδραση της πύκνωσης της διάδοσης με σημαντικά μεγαλύτερες ασάφειες. Η οδεύουσα ασάφεια προκαλεί ένα BEC δυναμικό που οδηγεί οφειλόμενο εις την ενέργεια, στην αποβολή της ασάφειας από την BEC. Σε αυτή την παράγραφο, η έρευνα της αλληλεπίδρασης ενός σολιτονίου με μια μοναδική ασάφεια είναι πολύ σημαντική. Είναι ένα θεμελιώδες ενδιαφέρον στην μη-γραμμική θεωρία κυμάτων και έχει μελετηθεί στη δομή σχεδόν όλων των μη-γραμμικών εξισώσεων εξέλιξης στις σολιτονικές λύσεις [47]. Ωστόσο, στο κείμενο των BECs όπου η σχετική εξίσωση εξέλιξης είναι η Gross-Pitaevskii (GP) εξίσωση με ένα φυλακισμένο δυναμικό [48], η αλληλεπίδραση των σκοτεινών σολιτονίων με ασάφειες δεν έχει μελετηθεί ακόμα λεπτομερώς. Ο σκοπός αυτής της παραγράφου είναι διπλός. Πρώτον, να γίνει εφαρμογή της θεωρίας διαταραχών σολιτονίου [49], χρησιμοποιώντας μια δραστική εξίσωση για την κίνηση ενός σκοτεινού σολιτονίου σε ένα παγιδευμένο δυναμικό παρουσία απωστικών ή ελκτικών ασαφειών. Δεύτερον, να γίνει μελέτη αναλυτική και συγχρόνως αριθμητική στα δυναμικά πύκνωσης και σε ένα σκοτεινό σολιτόνιο παρουσία μιας στατικής (μη διαδιδόμενης) ασάφειας. Αυτή η ανάλυση είναι κάπως γενική, και ίσως χρησιμοποιηθεί για να περιγράψει την αλληλεπίδραση ενός σκοτεινού σολιτονίου με τεχνητές ασάφειες που έχουν προκληθεί από απότομες δέσμες ακτίνων (laser) που χρησιμοποιούνται για να κατασκευάσουν την πυκνότητα των BEC σε πειράματα [39]. Ποικίλες δράσεις αλληλεπίδρασης όπως ανάκλαση, μετάδοση και ημιπαγίδευση του σκοτεινού σολιτονίου από μια απωθητική ασάφεια περιγράφονται και επαληθεύονται από άμεσες προσομοιώσεις. Η επίδραση της ημιπαγίδευσης που βρέθηκε χαρακτηρίζεται από ένα σχετικά μεγάλο χρόνο για την αλληλεπίδραση σολιτονίου-ασάφειας, και ακολουθείται από μια ταλάντωση σολιτονίου σε μια οριοθετημένη χωρική περιοχή. Επιπλέον, η πιθανότητα οπισθέλκυσης ενός 58
59 σκοτεινού σολιτονίου με μια αδιαβατική κίνηση ελκτικής ασάφειας είναι αποδεδειγμένη. Η εργασία αυτή συνεχίζει ως εξής: Στην παράγραφο Α & Β περιγράφονται αναλυτικά αποτελέσματα βασισμένα στην θεωρία διαταραχών που εφευρέθηκε για οπτικά σκοτεινά σολιτόνια. Στην Γ γίνεται λεπτομερή σύγκριση ανάμεσα στις αναλυτικές προβλέψεις και στα αριθμητικά αποτελέσματα που λαμβάνονται από άμεση ολοκλήρωση της GP εξίσωσης. Τέλος εξασφαλίζεται μια περίληψη και προκύπτουν κάποια συμπεράσματα. ΜΟΝΤΕΛΟ ΚΑΙ ΑΝΑΛΥΤΙΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ Α. Η ΔΡΑΣΤΙΚΗ ΕΞΙΣΩΣΗ ΚΥΜΑΤΟΣ ΤΩΝ THOMAS-FERMI Ένα βολικό μοντέλο για να μελετηθεί το μέσο δυναμικό πεδίο των BECs είναι η GP εξίσωση η οποία έχει τον τύπο της (3+1)-διάστασης μη-γραμμικής Schrodinger (NLS) εξίσωσης με ένα εξωτερικό παγιδευμένο δυναμικό [48]. Στην περίπτωση που ο περιορισμός για δύο από τις τρεις χωρικές διαστάσεις είναι πολύ δυνατότερος από την τρίτη διάσταση, η GP εξίσωση [50] μπορεί να αναχθεί σε μια δραστική ημι-(1+1) διάσταση GP εξίσωση [39,51]. Για απωθητικές interatomic αλληλεπιδράσεις, η τελευταία εξίσωση μπορεί να εκφραστεί με τον ακόλουθο αδιάστατο τύπο: (4.1) όπου η χωρική συντεταγμένη και ο χρόνος είναι κανονικοποιημένα στον αρμονικό ταλαντωτή μήκους και περίοδο ταλάντωσης Η συχνότητα ανήκει στις 2-διαστάσεις με ισχυρό περιορισμό. Το κανονικοποιημένο πεδίο περιγράφει την ακόλουθη σχέση κλιμάκωσης: ( ) όπου είναι το μήκος σκέδασης. Για να μελετηθεί η αλληλεπίδραση μιας BEC σκοτεινού σολιτονίου με μια τοπική ασάφεια στη δομή της εξίσωσης (4.1), είναι βολικό να αποσυνθέσουμε το δυναμικό όπως ακολουθεί: (4.2) όπου είναι (συμβατικό παραβολικό) το ανεξάρτητο του χρόνου παγιδευμένο δυναμικό, το οποίο υποτίθεται ότι είναι ομαλό και αργά μεταβαλλόμενο στην σολιτονική κλίμακα, και επιπλέον το απότομο δυναμικό μετράει για μια τοπική ασάφεια στο χώρο στο σημείο και 59
60 περιγράφεται από μια συνάρτηση του Dirac. Η παράμετρος στην εξίσωση (4.2) που μετράει τη δύναμη ασάφειας προϋποθέτει ότι είναι μικρή και ίσως παίρνει θετικές ή αρνητικές τιμές για απωθητικές ή ελκτικές ασάφειες αντιστοίχως. Η ασάφεια δυναμικού προκαλεί παραμόρφωση της συνάρτησης πύκνωσης κύματος [46]. Για να γίνει αναλυτική επεξεργασία της εξίσωσης (4.1), πρώτα πρέπει να κοιτάξουμε το υπόβαθρο του προφίλ του πεδίο ταλαντώσεων, όπου είναι η κανονικοποιημένη πυκνότητα του νέφους της BEC, παρουσία δυναμικού. Κάνοντας παρακάτω παραγωγίσεις προκύπτουν: ( ) ( ) Τα παραπάνω αποτελέσματα τα αντικαθιστούμε στην (4.1) οπότε παίρνουμε το εξής: ( ) ( ) Διαγράφουμε τον κοινό όρο οπότε τελικά προκύπτει: (4.3) Όταν το πλάτος είναι μικρό, ο μη-γραμμικός όρος της εξίσωσης (4.3) μπορεί να παραληφθεί και υποθέτοντας ότι απουσία του δυναμικού το υπόβαθρο πλάτους είναι, ψάχνουμε για μια λύση της εξίσωσης (4.3) με τον τύπο: (4.4) Αντικαθιστώντας την εξίσωση (4.4) μέσα στην εξίσωση (4.3) έχουμε: κρατώντας μόνο την κύρια σειρά όρων σε σχέση με τις παραμέτρους και έχουμε: ή 60
61 ή παραλείποντας όλους τους μη-γραμμικούς όρους σε σχέση με το κρατώντας μόνο την κύρια σειρά όρων σε σχέση με τις παραμέτρους (δείτε παρακάτω) έχουμε: και και οπότε τελικά προκύπτει (4.5) Μια φυσικά σχετική λύση της (4.5) ίσως να ληφθεί ακολούθως. Πρώτα, απουσία της ασάφειας (στην περίπτωση ), υποθέτουμε ένα ανισότροπο cigarshaped harmonic trap, που περιγράφεται από ένα δραστικό μονοδιάστατο δυναμικό, όπου ( ) είναι η συχνότητα της παγίδας στην κατεύθυνση του άξονα. Στην περίπτωση αυτή, η χωρική παράγωγος είναι μικρή και μπορεί να παραληφθεί και σαν αποτέλεσμα μια προσεγγιστική λύση της (4.5) είναι η εξής: που μοιάζει με τη γνωστή Thomas-Fermi (TM) προσέγγιση για την συνάρτηση κύματος, όπου η πυκνότητα είναι δευτεροβάθμια στον όρο. Δεύτερον, για μια ομογενή BEC (στην περίπτωση =0), η (4.5) γίνεται: Επίσης η χωρική λύση της (4.5) είναι η λύσεις η (4.5) εκφράζεται ως εξής: και συνδυάζοντας τις (4.6) Το υπόβαθρο του πεδίου πυκνότητας δίνεται από την εξίσωση (4.4) και (4.6) και περιγράφει κυρίως μια δραστική TF-like πύκνωση συνάρτηση κύματος, τροποποιημένη από μια εντοπισμένη ασάφεια. Αυτή η πύκνωση είναι εικονογραφημένη στο πρώτο σχήμα που ακολουθεί (συμπαγής γραμμή) για και για την αρμονική παγίδευση δυναμικού (διακεκομμένη γραμμή) με, αυτή η τιμή είναι περίπου διπλή τόσο μεγάλη όσο αυτή που χρησιμοποιήθηκε στην πειραματική μελέτη της BEC σκοτεινού σολιτονίου [39]. Παρατηρούμε ότι τόσο για τις εικονογραφημένες όσο και για τους 61
62 αριθμητικούς υπολογισμούς της συνάρτησης, για την εντοπισμένη ασάφεια στο έχει αντικατασταθεί από τη συνάρτηση βήματος ( ) με για απωθητικές ή ελκτικές ασάφειες αντιστοίχως. Έχει ενδιαφέρον να παρατηρήσουμε ότι αυτή η απωστική ασάφεια δημιουργεί μια τρύπα στη πύκνωση της συνάρτησης κύματος, σύμφωνα με τις προβλέψεις που έγιναν νωρίτερα [46], καθώς η ελκτική ασάφεια δημιουργεί κύρτωμα (εξόγκωμα). Σε κάθε περίπτωση, είναι ξεκάθαρο ότι η πύκνωση είναι σχεδιασμένη σαν ένα αντεστραμμένο αρμονικό παγιδευμένο δυναμικό με ένα βάθος ή ένα κύρτωμα, έχοντας το μέγεθος του healing length (το οποίο είναι, περίπου ίσο με τιμές των παραμέτρων που χρησιμοποιήθηκαν) γύρω από την ασάφεια. για τις Β. ΔΥΝΑΜΙΚΑ ΤΩΝ ΣΚΟΤΕΙΝΩΝ ΣΟΛΙΤΟΝΙΩΝ Για να γίνει περιγραφή των δυναμικών ενός σκοτεινού σολιτονίου στην κορυφή του μη ομογενούς υπόβαθρου που περιγράφεται από το δραστικό νέφος TF, αναζητούμε λύσεις για την εξίσωση (4.1) της μορφής: Οπότε γίνονται οι απαιτούμενες παραγωγίσεις δηλαδή: ( ) (4.7) ( ) + ( ) + Λόγω των παραπάνω πράξεων η εξίσωση (4.1) ξαναγράφεται: ( ) 62
63 [ ] Διώχνουμε όλα τα οπότε τελικά έχουμε: Η ικανοποιεί την (4.3) και αντικαθιστά το με το αριστερό μέλος της δηλαδή: ( ) Διαιρούμε με όλα τα μέλη, όπου το όπως είπαμε και νωρίτερα ικανοποιεί την (4.3) και το άγνωστο μιγαδικό πεδίο αναπαριστά ένα σκοτεινό σολιτόνιο, το οποίο ρυθμίζεται από την ακόλουθη δραστική εξίσωση: (4.8) Προφανώς, το δεξιό μέλος και οι μη-γραμμικοί όροι της (4.8) μπορούν να αντιμετωπιστούν ως μια διαταραχή. Για να αποκτήσουμε τη συνεισφορά των μη-γραμμικών όρων εντός της θεωρίας διαταραχών, ίσως χρησιμοποιήσουμε τις εξισώσεις (4.4) και (4.6) και προσεγγίσουμε το σαν, που βασίζεται στο πόσο μικρή είναι η συνάρτηση (που οφείλεται στις αργά μεταβαλλόμενες ιδιότητες της παγίδευσης του δυναμικού και στο πόσο μικρή είναι η παράμετρος που χαρακτηρίζεται από ασάφεια). Με αυτό τον τρόπο και σύμφωνα με το μετασχηματισμό αποκτούμε την ακόλουθη διαταραγμένη NLS για το σκοτεινό σολιτόνιο: Διαιρούμε με το και έχουμε: 63
64 Σε αυτό το σημείο χρειάζεται να γίνουν κάποιες πράξεις. Θα φανούν χρήσιμες σχέσεις που συναντήσαμε προηγουμένως όπως η και η οπότε τώρα κάνουμε τα εξής: επειδή ξέρουμε ότι: έχουμε: Επίσης σύμφωνα με τα παραπάνω από την (4.4) έχουμε ότι και αυτό δικαιολογείται από το γεγονός ότι σύμφωνα με την (4.4) και (4.6) προκύπτει: και επειδή έχουμε ότι. Οπότε: ( ) Λόγω των παραπάνω η ξαναγράφεται: ( ) ( ) ( ) (4.9) 64
65 Όπου η ολοκληρωτική (πλήρης) διαταραχή έχει τον τύπο: ( ) [ ] αυτή ήταν η σχέση (4.10) όπου Απουσία της διαταραχής η (4.9) αναπαριστά μια συμβατική NLS εξίσωση η οποία έχει μια σκοτεινή σολιτονική λύση με τύπο [54]: (4.11) όπου είναι η γωνία φάσης ( ) και περιγράφεται η σκοτεινότητα του σολιτονίου μέσω της σχέσης (για είναι τα ονομαζόμενα μαύρα και γκρι σολιτόνια αντίστοιχα [49]). Για την αναλυτική επίδραση της διαταραχής (4.10) πάνω στο σκοτεινό σολιτόνιο χρησιμοποιούμε την αδιαβατική θεωρία διαταραχών [49,52]. Με αυτή τη προσέγγιση οι παράμετροι του σκοτεινού σολιτονίου (4.11) γίνονται αργά μεταβαλλόμενες συναρτήσεις του αλλά ο συναρτησιακός τύπος παραμένει αμετάβλητος. Έτσι, η φασική γωνία του σολιτονίου γίνεται και σαν αποτέλεσμα, η συντεταγμένη του σολιτονίου γίνεται όπου: (4.12) είναι το κέντρο του σολιτονίου. Όπως έχει δειχθεί στην αναφορά [52], η εξέλιξη της παραμέτρου ορίζεται από την εξίσωση, { } (4.13) Αντικαθιστώντας την εξίσωση (4.10) στην εξίσωση (4.13) παίρνοντας ότι για χωρικά αργά μεταβαλλόμενα παγιδευμένα δυναμικά οι παράγωγοι υψηλότερης τάξης μπορούν να απαλειφθούν έχουμε το ακόλουθο αποτέλεσμα (για ) (4.14) όπου υποθέτουμε επιπλέον ότι το σκοτεινό σολιτόνιο είναι κοντά σε ένα μαύρο, με το να είναι αρκούντος μικρό, προσδιορίζοντας τα ολοκληρώματα στην (4.14) και χρησιμοποιώντας τον ορισμό της (4.12) έχουμε την ακόλουθη δραστική εξίσωση για το σολιτονικό κέντρο: 65
66 (4.15) Η (4.15) αναπαριστά μια εξίσωση κίνησης για ένα κλασικό σωμάτιο με την συντεταγμένη κινούμενο στο δραστικό δυναμικό: { } (4.16) Είναι σημαντικό να σημειώσουμε ότι, απουσία της ασάφειας ( η εξίσωση (.415) περιγράφει την κίνηση ενός σκοτεινού σολιτονίου παρουσία ενός παγιδευμένου δυναμικού και προβλέπει ότι το σολιτόνιο ταλαντώνεται σε μια αρμονική παγίδα. Μια εξίσωση όμοια με τις (4.15), (4.16) μπορεί πρώτα να καθοριστεί χωρίς παραγώγιση [42,43] σκεπτόμενοι τον διπολικό τρόπο μιας πύκνωσης που κουβαλά ένα σκοτεινό σολιτόνιο, και έτσι δεν σχετίζεται άμεσα με την (4.15). Για να διορθώσουμε το αποτέλεσμα που έχει αποκτηθεί από μια πολλαπλή χρονική κλίμακα με την θεωρία του οριακού στρώματος που αναπτύχθηκε πρόσφατα από τον Busch και Anglin [44] οι οποίοι υπέθεσαν ότι το δυναμικό, το υπόβαθρο της πυκνότητας, και η ταχύτητα μεταβάλλονται αργά στην σολιτονική κλίμακα. Στην γενική περίπτωση δεν υποθέτουμε ότι η ασάφεια δυναμικού μεταβάλλεται αργά στην σολιτονική κλίμακα, ωστόσο επικυρώνεται η τροποποίηση της εδαφικής κατάστασης της πύκνωσης παρουσία της ασάφειας. Είναι σημαντικό να αναφέρουμε ότι ο όρος αναλογικά με το στο δυναμικό (4.16) δεν έχει τη θέση που ίσως περιμέναμε βλέποντας τις (4.5) και (4.6). Αυτό αντανακλά το σημειακό χαρακτήρα της ασάφειας: το healing length είναι το μικρότερο δυνατό μήκος που είναι διαθέσιμο στην πυκνότητα αντίστοιχο με τις μεταβολές της πυκνότητας και με τις δραστικές σημειακές ασάφειες που δημιουργεί μια διαταραχή στο υπόβαθρο του σύννεφου στο ίδιο μήκος κλίμακας με του σκοτεινού σολιτονίου. Το αποτέλεσμα της εξίσωσης (4.16) δείχνει ότι ο χαρακτήρας του δραστικού δυναμικού αλλάζει στην περιοχή (σε μια εντοπισμένη περιοχή γύρω από το Συγκεκριμένα, γίνεται απωστική (ελκτική) για για το σκοτεινό σολιτόνιο εξαιτίας της παρουσίας της εντοπισμένης ασάφειας στο κέντρο του παγιδευμένου δυναμικού. 66
67 Σχήμα 1: Το ground state της ασάφειας πύκνωσης (συμπαγής γραμμή), περιγράφει ένα δραστικό Thomas-Fermi νέφος, για ένα αρμονικό παγιδευμένο δυναμικό (διακεκομμένη γραμμή) με Το δυναμικό εξαιτίας της εντοπισμένης ασάφειας στο προσεγγίζεται από μια συνάρτηση βήματος 67
68 ( ) με Στο σχήμα απεικονίζονται και οι δύο περιπτώσεις (a) οι απωστικές και (b) οι ελκτικές ασάφειες. Σχήμα 2: (a) Το δραστικό δυναμικό ( ) ( ) για μια απωστική ασάφεια, με (συμπαγής γραμμή), και για μια ελκτική ασάφεια, με (διακεκομμένη γραμμή). (b) Για το φασικό σχέδιο με έχουν σχεδιαστεί αρκετές τροχιές. Τελείες, μικροί κύκλοι, διαμάντια και αστέρια αντιστοιχούν στα αριθμητικά αποτελέσματα που βγήκαν από άμεση ολοκλήρωση της GP εξίσωσης για διαφορετικές αρχικές θέσεις του σολιτονίου μέσα, έξω ή στην αριστερόστροφη υποδιαστολή αντίστοιχα. (c) Για το φασικό σχέδιο με, έχουν σχεδιαστεί αρκετές τροχιές. Αστέρια που αντιστοιχούν σε αριθμητικά αποτελέσματα έχουν προκύψει από την εξίσωση GP για για ένα μαύρο σολιτόνιο με αρχική θέση στο 68
69 ΚΕΦΑΛΑΙΟ ΣΤΑΤΙΚΑ ΚΑΙ ΔΥΝΑΜΙΚΑ ΤΩΝ ΑΤΟΜΙΚΩΝ ΦΩΤΕΙΝΩΝ ΣΚΟΤΕΙΝΩΝ-ΣΟΛΙΤΟΝΙΩΝ ΠΑΡΟΥΣΙΑ ΑΣΑΦΕΙΩΝ ΤΥΠΟΥ ΣΥΝΑΡΤΗΣΗΣ ΔΕΛΤΑ ΤΟΥ DIRAC I. ΕΙΣΑΓΩΓΗ Οι φυσικές των ατομικών συμπυκνώσεων Bose-Einstein (BECs) [68,69] έχουν δώσει την πιθανότητα μελέτης των καθαρά μη-γραμμικών φαινομένων στην μεσοσκοπική κλίμακα. Συγκεκριμένα, έχει γίνει μια τεράστια, σε σύνολο προσπάθεια ερευνών αφιερωμένη στη μελέτη μακροσκοπικών μη-γραμμικών διεγέρσεων των BECs (δείτε στις [70-74]). Μεγάλο ενδιαφέρον έχουν και τα επονομαζόμενα matter-wave σολιτόνια, των φωτεινών σολιτονίων [73] και σκοτεινών σολιτονίων [74], που μπορούν να «υποστηριχθούν» από τις BECs με απωστικές ή ελκτικές αλληλεπιδράσεις αντίστοιχα. Ωστόσο, αυτοί οι τύποι των σολιτονίων ίσως συνυπάρχουν σε πολλές συνιστώσες των συμπυκνώσεων με απωστικές αλληλεπιδράσεις ([75] και[76]). Έτσι, τα επονομαζόμενα σκοτεινάφωτεινά (DB) σολιτόνια υπάρχουν εξαιτίας του γεγονότος ότι η συνιστώσα του σκοτεινού σολιτονίου δημιουργεί, μέσω των εσωτερικών ομοειδών αλληλεπιδράσεων ένα παγιδευμένο μηχανισμό που επιτρέπει τη συνιστώσα του φωτεινού σολιτονίου να είναι διαμορφωμένη. Τα σκοτεινά-φωτεινά σολιτόνια έχουν μελετηθεί στα μη-γραμμικά οπτικά [77] και στη θεωρία των μη-γραμμικών κυμάτων [78]. Επιπλέον, έχουν αναλυθεί πρόσφατα σε διακριτά σύνολα [79], καθώς οι γενικεύσεις ανωτέρας-διάστασης όπως ονομάζεται στρόβιλος φωτεινών-σκοτεινών δομών μελετήθηκαν στο [80]. Τα DB σολιτόνια έχουν παρατηρηθεί σε πειράματα που διεξήγαγαν σε οπτικά [81,82] και πιο πρόσφατα σε BECs [83-86]. Από την άλλη μεριά, η αλληλεπίδραση σολιτονίων με εντοπισμένες ασάφειες είναι ένα αρκετά γενικό και θεμελιώδες πρόβλημα που έχει τραβήξει πολύ την προσοχή στη θεωρία των μη-γραμμικών κυμάτων [87] και τη φυσική στερεάς κατάστασης [88,89]. Σε αυτό το γενικό πλαίσιο, η αλληλεπίδραση είτε των φωτεινών είτε των σκοτεινών σολιτονίων με ασάφειες τύπου (δέλτα του Dirac) έχουν ερευνηθεί στη δομή των μη-γραμμικών Schr dinger (NLS) [90-93], καθώς σχετικές μελέτες έχουν εμφανιστεί στη φυσική των ατόμων BECs [94-96]. Οι εντοπισμένες ασάφειες ίσως εύκολα μπορούν να δημιουργηθούν σαν άκρως εστιασμένες φωτοδέσμες και μπορούν να χειρίζονται δυναμικά των matter-wave [70], καθώς αυτά έχουν ήδη χρησιμοποιηθεί σε πειράματα για τη δημιουργία σολιτονίων [97,98]. Ωστόσο, για καλύτερη γνώση, το πρόβλημα της αλληλεπίδρασης των matter-wave DB-σολιτονίων με τις εντοπισμένες ασάφειες δεν έχει προχωρήσει πολύ. 69
70 Σκοπός μας είναι να μελετήσουμε αυτό το πρόβλημα στη δομή της θεωρίας ενδιάμεσου πεδίου. Πιο συγκεκριμένα, σκεφτόμαστε μια quasi 1D δύο συνιστωσών απωστικής BECs, που η σύνθεσή της είναι από δύο hyperfine states του ίδιου είδους αλκαλικών [84-86] ένα τέτοιο σύστημα μπορεί να προσεγγιστεί από δύο συζευγμένα 1D Gross-Pitaevskii (GPEs) [70,71,74]. Υποθέτουμε ότι και οι δύο οι συνιστώσες είναι περιορισμένες από τη συνηθισμένη αρμονική παγίδα (παγίδευση), καθώς ένα επιπρόσθετο μικρό πλάτος εντοπισμένης ασάφειας (σαν τη δέλτα) δυναμικού είναι επίσης αναγνωρισμένη και στις δύο συνιστώσες. Χρησιμοποιούμε την Χαμιλτονιανή προσέγγιση της θεωρίας διαταραχών των matter-wave σολιτονίων ([74] για την αναλυτική μελέτη των αδιαβατικών δυναμικών DB σολιτονίων που υποστηρίζονται στο σύστημα. Αυτός ο τρόπος παράγει μια δραστική εξίσωση κίνησης για το κέντρο του DB σολιτονίου. Βρίσκουμε ότι εάν η ασάφεια δυναμικού δρα μόνο στη συνιστώσα του φωτεινού σολιτονίου τότε η αλληλεπίδραση σολιτονίου-ασάφειας είναι δραστικά απωστική (ελκτική) για μια πραγματικά ελκτική (απωστική) ασάφεια. Αυτή η συμπεριφορά είναι άκρως αντίθετη με την αντίστοιχη αλληλεπίδραση σκοτεινού σολιτονίου-ασάφειας, η οποία είναι καθορισμένη από ένα τύπο της ασάφειας (απωστική / ελκτική) [94]. Μελετάμε τη στατικότητα και το δυναμικό των σολιτονίων κοντά σε σταθερά σημεία των δραστικών δυναμικών που σχετίζονται με την προαναφερθείσα εξίσωση κίνησης χρησιμοποιώντας μαζί αναλυτική προσέγγιση και αριθμητικές προσομοιώσεις. Επίσης παρουσιάζουμε μια Bogoliubov-de Gennes (BdG) ανάλυση για να ερευνήσουμε τη φασματική διέγερση των γνήσιων DB-σολιτονίων και να μελετήσουμε την ευστάθειά τους. Όπου βρίσκουμε μια πολύ καλή συμφωνία ανάμεσα στις αναλυτικές προβλέψεις και στα αριθμητικά αποτελέσματα π.χ. οι χαρακτηριστικές συχνότητες που προκύπτουν από την εξίσωση κίνησης και οι ιδιοσυχνότητες των αρχικών καταστάσεων (επίσης γνωστό σαν «ανώμαλες καταστάσεις» [69,72]) που είναι συναφή με τα DB-σολιτόνια. Η ενότητα αυτή είναι δομημένη ως εξής. Στην παράγραφο γίνεται η παρουσίαση του μοντέλου, χρησιμοποιούμε τη θεωρία διαταραχών και παράγουμε την εξίσωση κίνησης για το κέντρο του σολιτονίου. Στη συνέχεια, αναλύουμε το δραστικό δυναμικό και την δράση πάνω στα DB-σολιτόνια και δίνουμε έμφαση στις πιο ενδιαφέρουσες περιπτώσεις, π.χ. όταν η ασάφεια δρα μόνο στη συνιστώσα του φωτεινού σολιτονίου. Έπειτα δίνουμε λίγο προσοχή σε μια συστηματική σύγκριση των αναλυτικών αποτελεσμάτων με τις προσομοιώσεις όπου περιέχει αποτελέσματα των BdG αναλύσεων. Τέλος, διατυπώνουμε τα συμπεράσματά μας. 70
71 II. ΜΟΝΤΕΛΑ ΚΑΙ ΑΝΑΛΥΤΙΚΕΣ ΘΕΩΡΙΕΣ Α. ΟΡΓΑΝΩΣΗ-ΔΟΜΗ Θεωρούμε μια απωστική BEC με δύο συνιστώσες (κατά μήκος της διεύθυνσης ) της οποίας η σύνθεση γίνεται από δύο διαφορετικές υπερβολικά καλές καταστάσεις του ίδιου αλκαλικού ισότοπου. Δεχόμαστε ότι η παγίδα είναι πολύ ανισότροπη με τις διαμήκη και εγκάρσιες παγιδευμένες συχνότητες να είναι περιγράφουμε αυτό το σύστημα με τις ακόλουθες δύο συζευγμένες GPEs [70,71]. όπου το ( ) (5.1) εκφράζει το μέσο πεδίο των κυματικών συναρτήσεων δύο συνιστωσών (κανονικοποιημένο στα νούμερα των ατόμων το είναι η ατομική μάζα, τα είναι τα χημικά δυναμικά, τα είναι οι δραστικές 1D συζευγμένες σταθερές, τα εκφράζουν τα τρία s-wave scattering lengths ( που μετράνε τη σύγκρουση ανάμεσα στα άτομα που ανήκουν στα ίδια ( ή σε διαφορετικά ( είδη, και το αναπαριστά τα εξωτερικά παγιδευμένα δυναμικά. Δεχόμαστε ότι και οι δύο συνιστώσες είναι περιορισμένες από τη συνήθη αρμονική παγίδα, την ονομαζόμενη καθώς μια επιπρόσθετη εντοπισμένη «ασάφεια» δυναμικού, η οποία μπορεί να δημιουργηθεί από μια φωτοδέσμη, είναι επίσης παρούσα. Εάν μια τέτοια ασάφεια είναι ισχυρά εντοπισμένη, τότε μια θεωρητική προσέγγιση είναι το χωρικό προφίλ του σαν μια συνάρτηση που τα παγιδευμένα δυναμικά για δυο συνιστώσες μπορούν να περιγραφούν ως: όπου είναι το φράγμα του πλάτους (εύρους) σε κάθε συνιστώσα. Σημειώνουμε ότι για μια μπλε ή για μια κόκκινη φωτεινή δέσμη, η ασάφεια δυναμικού μπορεί να είναι είτε απωστική ( ή ελκτική ( στα άτομα των αντίστοιχων συνιστωσών της συμπύκνωσης. Ας σκεφτούμε τώρα ότι οι δύο συνιστώσες BEC έπειτα από σκέψη αποτελούνται από δύο διαφορετικές καταστάσεις της Rb, όπως οι καταστάσεις και που χρησιμοποιήθηκαν στα πειράματα [84-86]. Στην πρώτη περίπτωση τα μήκη σκέδασης παίρνουν τις τιμές καθώς στην δεύτερη περίπτωση οι αντίστοιχες τιμές είναι (όπου είναι η ακτίνα του Bohr). Σε κάθε περίπτωση, τα μήκη σκέδασης παίρνουν προσεγγιστικά τις ίδιες τιμές δηλαδή. Έτσι, μετρώντας τις πυκνότητες το μήκος, το χρόνο 71
72 και την ενέργεια σε μονάδες του αντίστοιχα. Αυτά τα βάζουμε στην εξίσωση (5.1) μέσα στον ακόλουθο αδιάστατο τύπο, (5.2) (5.3) Στις παραπάνω εξισώσεις, θέσαμε και όπου οι δείκτες 1 (2) θα αναφέρονται αντίστοιχα σε ένα σκοτεινό (φωτεινό) σολιτόνιο. Σημειώνουμε ότι το αντίστοιχα κανονικοποιημένα χημικά δυναμικά είναι τα και παρακάτω θα υποθέσουμε ότι Τελικά, τα εξωτερικά δυναμικά στις εξισώσεις (5.2)-(5.3) παίρνουν τη μορφή (5.4) (5.5) όπου και είναι η κανονικοποιημένη παγιδευμένη δύναμη και το φράγμα δύναμης, αντίστοιχα. Παρακάτω και οι δύο αυτές παράμετροι θα θεωρηθούν μικρές δηλαδή Πριν προχωρήσουμε είναι απαραίτητο να σκεφτούμε πρώτα την επίδραση της ασάφειας νέφους του Thomas-Fermi (TF) στο σκοτεινό σολιτόνιο. Σύμφωνα με την ανάλυση της αναφοράς [94], η TF πυκνότητα κοντά στο κέντρο της παγίδας, (όπου η ασάφεια είναι εντοπισμένη) μπορεί να προσεγγιστεί σαν: (5.6) (5.7) όπου την την θεωρούμε μικρή σε αντιστοιχία με το χημικό δυναμικό Ο πρώτος όρος του δεξιού μέλους της εξίσωσης (5.7) μετράει την up perturbed TF πυκνότητα (απουσία της ασάφειας), από την άλλη μεριά ο δεύτερος όρος προσεγγίζει την ασάφεια σαν μια συνάρτηση η οποία δημιουργεί στην TF πυκνότητα ένα εντοπισμένο βάθος (εξόγκωμα) για το τελευταίο έχει μια φανερή διακοπτόμενη παράγωγο στο εξαιτίας της συνθήκης στο (δείτε αναφορά [94]). Είναι σημαντικό να σημειώσουμε ότι η εντοπισμένη παραμόρφωση της TF πυκνότητας περιγράφεται από τον δεύτερο όρο στο δεξιό μέλος της εξίσωσης (5.7) η οποία χαρακτηρίζεται από μια χωρική κλίμακα της σειράς healing length δηλαδή της σειράς του σκοτεινού σολιτονίου (το οποίο έχει το υπόβαθρο της TF). Έτσι, η ανάλυσή μας παρακάτω αναφέρεται σε αυτή τη συγκεκριμένη περίπτωση όπου η χωρική κλίμακα της ασάφειας είναι ίδια με αυτή του σολιτονίου. 72
73 Β. ΘΕΩΡΙΑ ΔΙΑΤΑΡΑΧΩΝ Υποθέτουμε ότι το σκοτεινό σολιτόνιο είναι στην κορυφή ενός τροποποιημένου νέφους TF, όπως περιγράφουν οι εξισώσεις (5.6)-(5.7). Ανάλογα η πυκνότητα στις εξισώσεις (5.2)-(5.3) αντικαθίστανται από Επιπλέον, εισάγοντας τους μετασχηματισμούς οι σχέσεις (5.2)-(5.3) γίνονται αντίστοιχα: (5.8) (5.9) όπου, και [ ] (5.10) [ ] (5.11) με. Τις εξισώσεις (5.8)-(5.9) μπορούμε να τις δούμε σαν ένα συζευγμένο σύστημα εξισώσεων NLS, με διαταραχές που δίνονται από τις εξισώσεις (5.10)-(5.11). Απουσία των διαταραχών (, και λαμβάνοντας υπόψη τις συνοριακές συνθήκες οι NLS εξισώσεις (5.8)-(5.9) κατέχουν μια ακριβή αναλυτική DB σολιτονική λύση του ακόλουθου τύπου (δείτε την αναφορά [75]). (5.12) (5.13) όπου το είναι η φασική γωνία του σκοτεινού σολιτονίου, τα αναπαριστούν το εύρος των σκοτεινών και φωτεινών σολιτονίων, τα ορίζουν το πλάτος και το κέντρο του DB σολιτονίου αντίστοιχα. Επίσης το και είναι ο κυματάριθμος και η φάση του φωτεινού σολιτονίου αντίστοιχα. Οι παραπάνω παράμετροι DB-σολιτονίου συνδέονται μέσω των ακόλουθων εξισώσεων: (5.14) (5.15) ( ) (5.16) όπου είναι η ταχύτητα του DB σολιτονίου. Σημειώνουμε ότι το εύρος του φωτεινού σολιτονίου, η συνιστώσα του χημικού δυναμικού του σκοτεινού 73
74 σολιτονίου καθώς επίσης και το πλάτος του DB σολιτονίου συνδέονται με τον ατομικό αριθμό του φωτεινού σολιτονίου που δίνεται από την ακόλουθη εξίσωση (για τις μεταβλητές που εμφανίζονται στις (5.2)-(5.3): (5.17) Ας υποθέσουμε ότι το DB σολιτόνιο αναπτύσσεται αδιαβατικά παρουσία μιας μικρής διαταραχής, και χρησιμοποιώντας την Χαμιλτονιανή προσέγγιση της θεωρίας διαταραχής για τα matter-wave σολιτόνια (δείτε αναφορές [71,74]) μελετάμε τα δυναμικά του DB σολιτονίου. Ξεκινάμε θεωρώντας την Χαμιλτονιανή (ολική ενέργεια) του συστήματος των εξισώσεων (5.8)-(5.9), όταν οι διαταραχές απουσιάζουν ( δηλαδή, (5.18) Η ενέργεια του συστήματος όταν υπολογίστηκε για τη λύση του DB σολιτονίου των εξισώσεων (5.12)-(5.13), παίρνει τη μορφή: ( ) (5.19) Από τη στιγμή που σκεφτήκαμε μια αδιαβατική κίνηση του DB σολιτονίου μπορούμε να υποθέσουμε ότι παρουσία των διαταραχών στις εξισώσεις (5.10)- (5.11), οι παράμετροι του DB σολιτονίου γίνονται αργά μεταβαλλόμενες άγνωστες συναρτήσεις του χρόνου (δείτε [74]). Έτσι, οι παράμετροι του γίνονται:, και σύμφωνα με αυτά οι εξισώσεις (5.14)-(5.15) γίνονται: (5.20) (5.21) όπου χρησιμοποιούμε την εξίσωση (5.17). Η εξέλιξη των παραμέτρων και μπορούν να βρεθούν από τη μέση κίνηση της ενέργειας του DB σολιτονίου. Συγκεκριμένα χρησιμοποιώντας την εξίσωση (5.19), βρίσκουμε ότι: ( ) (5.22) Από την άλλη μεριά, χρησιμοποιώντας τις εξισώσεις (5.18)-(5.19) και τα συζυγή μιγαδικά τους, μπορεί να βρεθεί ότι η εξέλιξη της ενέργειας του DB, εξαιτίας της παρουσίας των διαταραχών δίνεται από τον τύπο: { } (5.23) 74
75 όπου το αστεράκι ορίζει το μιγαδικό συζυγή. Αντικαθιστώντας τα ( από τις εξισώσεις (5.10)-(5.11) μέσα στη (5.23)) και υπολογίζοντας τα ολοκληρώματα, αποκτάμε από τις εξισώσεις (5.20), (5.21), (5.22) και (5.23) ένα σύστημα τριών εξισώσεων για την κίνηση των παραμέτρων του σολιτονίου και Αυτό το σύστημα είναι γραμμικοποιημένο γύρω από τα σταθερά σημεία και φυσικά στη περίπτωση αρκετά μικρού οδηγούμαστε στην ακόλουθη κίνηση της εξίσωσης στην οποία αντικαθιστούμε το μικρό εύρος της θέσης του σολιτονίου με το κέντρο της παγίδας: (5.24) όπου έχουμε χρησιμοποιήσει τις μεταβλητές που χρησιμοποιήθηκαν στις εξισώσεις (5.2)-(5.3).Το δραστικό δυναμικό στη (5.24) δίνεται από όπου η συχνότητα ταλάντωσης και η παράμετρος αντίστοιχα είναι: (5.25) ( ( ) ) (5.26) (5.27) όπου είναι σταθερές της τάξης Ο(1). Η εξίσωση (5.24) έχει τον τύπο της εξίσωσης κίνησης για ένα κλασικό σωμάτιο, με συντεταγμένη κινούμενο στο δραστικό δυναμικό Σημειώνουμε ότι απουσία των ασαφειών ( στη (5.25), η (5.24) δίνει τα αποτελέσματα της αναφοράς [75]). Σύμφωνα με αυτή την εργασία, ένα DB σολιτόνιο ταλαντώνεται σε μια αρμονική παγίδα δύναμης με συχνότητα που δίνεται από την (5.26) η συχνότητα αυτή εξαρτάται από την παράμετρο τον ατομικό αριθμό του φωτεινού σολιτονίου (δείτε το ορισμό του στην (5.19)). 75
76 ΠΑΡΑΡΤΗΜΑ Α ΤΙ ΕΙΝΑΙ ΠΕΡΙΘΛΑΣΗ ΚΑΙ ΤΙ ΔΙΑΣΠΟΡΑ Περίθλαση ή παράθλαση είναι [56] μια διαταραχή της ευθύγραμμης διάδοσης κυμάτων, όταν αυτά διέλθουν μέσα από κάποιο άνοιγμα ή γύρω από τα άκρα κάποιου εμποδίου πολύ μικρών διαστάσεων. Εφόσον υπάρχει κάποιο κύμα ή ειδικότερα κάποια ακτίνα ή χωροχρονικός παλμός που οδεύει σε οπτικό μέσο, υφίσταται περίθλαση. Το φαινόμενο αυτό δεν ενδιαφέρει όταν ο παλμός κυματοδηγείται σε οπτική ίνα περιορισμένης ακτίνας, αλλά σε ελεύθερο μέσο ή και επίπεδο κυματοδηγό είναι αναπόφευκτο. Οφείλεται στη σκέδαση του φωτός από τα μόρια του μέσου και από ατέλειες στη κρυσταλλική δομή που υπάρχουν πάντα. Υπάρχουν διάφορα είδη σκέδασης, ανάλογα με το μήκος κύματος και τη φύση του μέσου (στερεό, υγρό ή αέριο). Επίσης, η σκέδαση μπορεί να προκαλέσει μετατόπιση συχνότητας, όπως η σκέδαση Raman. Η πλέον συνηθισμένη είναι η σκέδαση Rayleigh και η σκέδαση Bragg για υλικά με κρυσταλλική δομή, όπου δεν προκαλούν τέτοια μετατόπιση. Το αποτέλεσμα είναι η διαπλάτυνση της ακτίνας, στην εγκάρσια πλέον διάσταση. Ουσιαστικά το φαινόμενο είναι ανάλογο της ανώμαλης διασποράς στην οποία υφίστανται οι χρονικοί παλμοί, με τη διαφορά ότι δεν υπάρχουν υλικά με μηδενική περίθλαση και ότι είναι φαινόμενο πολύ ισχυρότερο, με εξαίρεση τη διασπορά πολύ στενών παλμών. Τα παραθλώμενα κύματα στη συνέχεια εμφανίζουν φαινόμενα συμβολής με περιοχές ενισχύσεως και εξασθένησης. Πρώτος το παρατήρησε να συμβαίνει στη διάδοση του φωτός ο Francesco Grimaldi ( ) και η περίθλαση ως φαινόμενο στήριξε σημαντικά την κυματική θεωρία του φωτός. Παράθλαση συμβαίνει επίσης και με δέσμες σωματιδίων. Διασπορά είναι φυσικά γραμμικό φαινόμενο και προκαλεί τη χρονική διαπλάτυνση του παλμού. Ο συνδυασμός της με τη μη-γραμμικότητα του μέσου μπορεί να ευνοήσει τη δημιουργία και διάδοση σολιτονίων. Σημαντική επίπτωση της διασποράς είναι ότι οι παλμοί με διαφορετικές κεντρικές συχνότητες διαδίδονται με διαφορετικές ταχύτητες ομάδος. Μια σχέση διασποράς έχει τη γενική μορφή Στην περίπτωση που μπορούμε να λύσουμε τη σχέση αυτή ως προς μπορούμε να γράψουμε ΤΙ ΕΙΝΑΙ ΑΝΑΚΛΑΣΗ ΚΑΙ ΤΙ ΔΙΑΘΛΑΣΗ Ανάκλαση λέγεται η επιστροφή [56] τμήματος ή όλων των σωματιδίων ή των κυμάτων μιας δέσμης, όταν συναντήσουν τη διαχωριστική επιφάνεια δύο μέσων. Οι «νόμοι της ανάκλασης» ορίζουν τα εξής: (1) Η προσπίπτουσα ακτίνα, η ανακλώμενη ακτίνα και η κάθετη προς την επιφάνεια στο σημείο πρόσπτωσης 76
77 βρίσκονται όλες στο ίδιο επίπεδο. (2) Η γωνία προσπτώσεως ισούται προς τη γωνία ανάκλασης. Διάθλαση λέγεται η μεταβολή κατεύθυνσης, που παθαίνει κάποιο μέτωπο κύματος, καθώς περνάει πλάγια από κάποιο μέσο προς ένα άλλο, όπου τροποποιείται η ταχύτητα διάδοσης του. Το φαινόμενο συμβαίνει με όλους τους τύπους κυμάτων, αλλά είναι περισσότερο συχνό στα κύματα φωτός. Στην οπτική η κατεύθυνση μεταβάλλεται σύμφωνα με το «νόμο του Shell», δηλαδή όπου και είναι οι γωνίες που σχηματίζονται από την προσπίπτουσα δέσμη ακτινοβολίας και από τη διαθλώμενη δέσμη προς την κάθετο στο σημείο πρόσπτωσης. Ο νόμος αυτός είναι επίσης γνωστός και ως ένας από τους «νόμους της διάθλασης». Ο άλλος νόμος της ορίζει ότι η προσπίπτουσα ακτίνα, η διαθλώμενη ακτίνα και η κάθετη στο σημείο προσπτώσεως βρίσκονται στο ίδιο επίπεδο. Η μεταβολή της κατεύθυνσης οφείλεται στη μεταβολή της ταχύτητας διάδοσης και στη συνεπαγόμενη μεταβολή του μήκους κύματος. Σχήμα 1.4 ΔΕΙΚΤΗΣ ΔΙΑΘΛΑΣΗΣ Από τη θεωρία του Maxwell βρέθηκε ότι τα ηλεκτρομαγνητικά κύματα διαδίδονται στο κενό με ταχύτητα μέσα σ ένα υλικό μέσο έχει ταχύτητα Αντίθετα, ένα κύμα που διαδίδεται To είναι η ηλεκτρική και η μαγνητική διαπερατότητα του μέσου. Ο απόλυτος δείκτης διάθλασης ορίζεται από τη σχέση:. 77
78 Γενικά οι μαγνητικές ιδιότητες του μέσου επηρεάζουν πολύ λίγο το υλικά που μας ενδιαφέρουν. αφού σε Σχήμα 1.5 ΣΚΕΔΑΣΗ ΚΑΙ ΑΝΤΙΣΤΡΟΦΑ ΠΡΟΒΛΗΜΑΤΑ Με τον όρο πρόβλημα σκέδασης [55] εννοούμε το εξής: Ας θεωρήσουμε ένα μέσο στο οποίο υπάρχει ένα αντικείμενο, ο σκεδαστής. Προς την κατεύθυνση του σκεδαστή στέλνουμε ένα προσπίπτον κύμα, το οποίο αλληλεπιδρά με τον σκεδαστή και παράγει ένα ανακλώμενο κύμα και ένα διερχόμενο (ή «διαθλώμενο») κύμα (σχήμα). Το ευθύ πρόβλημα της σκέδασης είναι το πρόβλημα προσδιορισμού των ιδιοτήτων του ανακλώμενου και του διερχόμενου κύματος (π.χ., πλάτους, κυματαριθμού, συχνότητας κ.λπ.), υπό την προϋπόθεση ότι είναι γνωστές οι ιδιότητες του προσπίπτοντος κύματος και του σκεδαστή. Το αντίστροφο πρόβλημα σκέδασης είναι το πρόβλημα του προσδιορισμού των ιδιοτήτων του σκεδαστή, αν είναι γνωστές οι ιδιότητες των τριών τύπων κύματος. Αντίστροφα προβλήματα εμφανίζονται πολύ συχνά σε διάφορες εφαρμογές της Φυσικής. Για παράδειγμα στη θεωρία του ραντάρ ή του σόναρ γνωρίζουμε τις ιδιότητες του προσπίπτοντος κύματος και χρησιμοποιούμε μετρήσεις των ιδιοτήτων του ανακλώμενου κύματος για να ανιχνεύσουμε την ύπαρξη ή τα χαρακτηριστικά ενός αεροπλάνου ή ενός υποβρύχιου αντικειμένου. Στην τομογραφία χρησιμοποιούμε ακτίνες Χ ή ηχητικά κύματα για να προσδιορίσουμε την ύπαρξη ή τη σύσταση ενός όγκου, ανιχνεύοντας, π.χ., μεταβολές της πυκνότητας. Στην περίπτωση αυτής είναι γνωστά και τα τρία είδη κυμάτων, το προσπίπτον, το ανακλώμενο και το διερχόμενο. Σε γεωφυσικές διερευνήσεις του υπεδάφους προκαλούμε μια έκρηξη στην επιφάνεια της Γης, παράγοντας ελαστικά κύματα. Η μελέτη των κυμάτων που ανακλώνται από διάφορα στρώματα του υπεδάφους μπορεί να μας υποδείξει την ύπαρξη κοιτασμάτων πετρελαίου ή κάποιου άλλου σχηματισμού που παρουσιάζει ενδιαφέρον από γεωλογικής πλευράς. Λόγω 78
79 όλων αυτών των εφαρμογών, η θεωρία της αντίστροφης σκέδασης είναι περιοχή μεγάλου ερευνητικού ενδιαφέροντος στα Εφαρμοσμένα Μαθηματικά. ΔΙΠΛΘΛΑΣΤΙΚΟΤΗΤΑ Ακόμα και οι μονότροπες ίνες δεν είναι στην πραγματικότητα τέτοιες καθώς μπορούν να υποστηρίξουν την συν-διάδοση δύο ρυθμών πολωμένων σε διευθύνσεις κάθετες μεταξύ τους. Έτσι λοιπόν σε μία ιδανικά κατασκευασμένη ίνα, με τέλεια κυλινδρική συμμετρία, ένας ρυθμός που ξεκινά στην χ-διεύθυνση δεν θα «συζευχθεί» με τον αντίστοιχο του στην y-διεύθυνση, ενώ στην πραγματικότητα ακόμα και μικρές αποκλείσεις από τη συμμετρία (λόγω μηχανικών τάσεων για παράδειγμα ή και ατελειών στην κατασκευή) καταλήγουν σε πιο περίπλοκη διάδοση δύο ρυθμών. Η σταθερά διάδοσης ακριβώς λόγω της απουσίας συμμετρίας είναι (έστω και λίγο) διαφορετική για τους δύο αυτούς ρυθμούς, οπότε εμφανίζεται το φαινόμενο της ρυθμικής διπλοθλαστικότητας (modal birefringence). Η ισχύς της ορίζεται ως (1) όπου οι δείκτες διάθλασης για τους κάθετους ρυθμούς [18]. Ο άξονας με τον μικρότερο δείκτη καλείται γρήγορος, ενώ αντίστοιχα ο άλλος, καλείται αργός. Κατά τη διάδοση οι δύο ρυθμοί ανταλλάσσουν ενέργεια με περίοδο (2) ενώ το ονομάζεται και μήκος επανάληψης. Επιπρόσθετα, στις πραγματικές ίνες το δεν είναι σταθερό, και η τιμή του μεταβάλλεται, συνήθως κατά λίγο, με τυχαίο τρόπο. Αυτό έχει σαν αποτέλεσμα να αλλάζει με παρόμοια τυχαίο τρόπο η πόλωση του φωτός μέσα στην ίδια ίνα. Κάτι τέτοιο δεν επηρεάζει την απόδοση της κυματοδήγησης όταν είναι ένα συνεχές κύμα (CW) αυτό που στέλνουμε (οι φωτοανιχνευτές είναι αναίσθητοι σε αλλαγές της πόλωσης). Όταν όμως επιθυμούμε να σταλούν στενοί παλμοί κατά μήκος ίνας πολλών χιλιομέτρων, όπως σε ένα οπτικό τηλεπικοινωνιακό δίκτυο, τότε γεννάται ένα ακόμη πρόβλημα. Καθώς η διπλοθλαστικότητα της ίνας μεταβάλλεται με τυχαίο τρόπο, παρομοίως μεταβάλλονται και οι ταχύτητες ομάδας των ίδιων ρυθμών, με τελικό αποτέλεσμα την διαπλάτυνση του παλμού. Το φαινόμενο αυτό ονομάζεται «Διασπορά Πολωμένων Ρυθμών» (Polarization Mode Dispersion-PDM) [18]. 79
80 Ένας τρόπος που χρησιμοποιείται για τον έλεγχο της τυχαιότητας της διασποράς είναι η επιβολή ισχυρής διπλοθλαστικότητας από κατασκευής της ίνας, έτσι ώστε οι μικρές διακυμάνσεις που μπορεί να παρουσιαστούν να «πνίγονται» και να μην επηρεάζουν σημαντικά την πόλωση. Υπάρχουν διάφορες τεχνικές δημιουργίας τέτοιων ινών με συνηθισμένες πια την επιβολή ελλειπτικότητας στον πυρήνα και την επιβολή μηχανικής τάσης. Οι ίνες αυτές ονομάζονται εν γένει, «οπτικές ίνες διατηρούμενης πόλωσης» και η χρησιμότητά τους έγκειται, πρώτον στο ότι όταν πολωμένο φως (παλμός λέιζερ) μπει στην ίνα «κατά μήκος» ενός εκ των δύο αξόνων πόλωσης, τείνει να διατηρήσει την πόλωσή του. Όταν όμως το φως εισέλθει στην ίνα υπό γωνία, οπότε θα δημιουργηθούν δύο κάθετα πολωμένοι ρυθμοί, αυτοί θα έχουν σημαντική διαφορά στις ταχύτητες τους (φασικές αλλά κυρίως στις ταχύτητες ομάδος) με αποτέλεσμα να τείνουν να διαχωριστούν αρκετά σύντομα και να οδεύσουν πια σα χωριστοί παλμοί σημαντικά μικρότερης ενέργειας. Οι ίνες με ισχυρή διπλοθλαστικότητα μπορεί να έχουν ΟΠΤΙΚΗ ΙΝΑ Μια οπτική ίνα κατασκευάζεται από γυαλί ή πλαστικό. Οι οπτικές ίνες χρησιμοποιούνται στις οπτικές διαδικασίες για τη μεταφορά πληροφορίας με πολύ μεγάλο εύρος ζώνης ( G bit/sec). Μια οπτική ίνα αποτελείται από τον πυρήνα, την επένδυση και το περίβλημα. Η βασική αρχή λειτουργίας βασίζεται στην ολική εσωτερική ανάκλαση του φωτός ανάμεσα στον πυρήνα και το περίβλημα. Για το λόγο αυτό απαιτείται ο δείκτης διάθλασης του πυρήνα να είναι μεγαλύτερος από το δείκτη διάθλασης του περιβλήματος. Σχήμα
ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ ΙΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΝΟΜΙΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΣΠΟΥΔ ΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΔΥΝΑΜΙΚΗΣ Μεθοδολογία Κλεομένης Γ. Τσιγάνης Λέκτορας ΑΠΘ Πρόχειρες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΝΟΜΙΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΣΠΟΥΔ ΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΔΥΝΑΜΙΚΗΣ Μεθοδολογία Κλεομένης Γ. Τσιγάνης Λέκτορας ΑΠΘ Πρόχειρες
2-1 ΕΙΣΑΓΩΓΗ 2-2 ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ
 ΕΞΩΦΥΛΛΟ 43 Εικ. 2.1 Κύμα στην επιφάνεια της θάλασσας. 2-1 ΕΙΣΑΓΩΓΗ Η έννοια «κύμα», από τις πιο βασικές έννοιες της φυσικής, χρησιμοποιήθηκε για την περιγραφή φαινομένων που καλύπτουν ένα ευρύ φάσμα.
ΕΞΩΦΥΛΛΟ 43 Εικ. 2.1 Κύμα στην επιφάνεια της θάλασσας. 2-1 ΕΙΣΑΓΩΓΗ Η έννοια «κύμα», από τις πιο βασικές έννοιες της φυσικής, χρησιμοποιήθηκε για την περιγραφή φαινομένων που καλύπτουν ένα ευρύ φάσμα.
ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ ΙΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΝΟΜΙΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΣΠΟΥΔΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΔΥΝΑΜΙΚΗΣ ( Μεθοδολογία- Παραδείγματα ) Κλεομένης Γ. Τσιγάνης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΝΟΜΙΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΣΠΟΥΔΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΔΥΝΑΜΙΚΗΣ ( Μεθοδολογία- Παραδείγματα ) Κλεομένης Γ. Τσιγάνης
Μοριακή Φασματοσκοπία I. Παραδόσεις μαθήματος Θ. Λαζαρίδης
 Μοριακή Φασματοσκοπία I Παραδόσεις μαθήματος Θ. Λαζαρίδης 2 Τι μελετά η μοριακή φασματοσκοπία; Η μοριακή φασματοσκοπία μελετά την αλληλεπίδραση των μορίων με την ηλεκτρομαγνητική ακτινοβολία Από τη μελέτη
Μοριακή Φασματοσκοπία I Παραδόσεις μαθήματος Θ. Λαζαρίδης 2 Τι μελετά η μοριακή φασματοσκοπία; Η μοριακή φασματοσκοπία μελετά την αλληλεπίδραση των μορίων με την ηλεκτρομαγνητική ακτινοβολία Από τη μελέτη
Επαναληπτικό διαγώνισµα στα Κύµατα
 ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΤΑΙΧΜΙΟ 1 Επαναληπτικό διαγώνισµα στα Κύµατα Θέµα 1 0 Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΤΑΙΧΜΙΟ 1 Επαναληπτικό διαγώνισµα στα Κύµατα Θέµα 1 0 Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
11 ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΑ ΠΕΔΙΑ
 xx ΤΟΜΟΣ ΙI 11 ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΑ ΠΕΔΙΑ 741 11.1 Διαφορική και ολοκληρωτική μορφή των εξισώσεων Maxwell Ρεύμα μετατόπισης...................................... 741 11.2 Οι εξισώσεις Maxwell σε μιγαδική
xx ΤΟΜΟΣ ΙI 11 ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΑ ΠΕΔΙΑ 741 11.1 Διαφορική και ολοκληρωτική μορφή των εξισώσεων Maxwell Ρεύμα μετατόπισης...................................... 741 11.2 Οι εξισώσεις Maxwell σε μιγαδική
1. Η συχνότητα αρμονικού κύματος είναι f = 0,5 Hz ενώ η ταχύτητα διάδοσης του υ = 2 m / s.
 1. Η συχνότητα αρμονικού κύματος είναι f = 0,5 Hz ενώ η ταχύτητα διάδοσης του υ = 2 m / s. Να βρεθεί το μήκος κύματος. 2. Σε ένα σημείο του Ειρηνικού ωκεανού σχηματίζονται κύματα με μήκος κύματος 1 m και
1. Η συχνότητα αρμονικού κύματος είναι f = 0,5 Hz ενώ η ταχύτητα διάδοσης του υ = 2 m / s. Να βρεθεί το μήκος κύματος. 2. Σε ένα σημείο του Ειρηνικού ωκεανού σχηματίζονται κύματα με μήκος κύματος 1 m και
ΚΕΦΑΛΑΙΟ 9 «Κυμάνσεις» Μαρία Κατσικίνη users.auth.gr/~katsiki
 ΚΕΦΑΛΑΙΟ 9 «Κυμάνσεις» Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Σχέση δύναμης - κίνησης Δύναμη σταθερή εφαρμόζεται σε σώμα Δύναμη ανάλογη της απομάκρυνσης (F-kx) εφαρμόζεται σε σώμα Το σώμα
ΚΕΦΑΛΑΙΟ 9 «Κυμάνσεις» Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Σχέση δύναμης - κίνησης Δύναμη σταθερή εφαρμόζεται σε σώμα Δύναμη ανάλογη της απομάκρυνσης (F-kx) εφαρμόζεται σε σώμα Το σώμα
Κεφάλαιο 15 Κίνηση Κυµάτων. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 15 Κίνηση Κυµάτων Περιεχόµενα Κεφαλαίου 15 Χαρακτηριστικά των Κυµάτων Είδη κυµάτων: Διαµήκη και Εγκάρσια Μεταφορά ενέργειας µε κύµατα Μαθηµατική Περιγραφή της Διάδοσης κυµάτων Η Εξίσωση του Κύµατος
Κεφάλαιο 15 Κίνηση Κυµάτων Περιεχόµενα Κεφαλαίου 15 Χαρακτηριστικά των Κυµάτων Είδη κυµάτων: Διαµήκη και Εγκάρσια Μεταφορά ενέργειας µε κύµατα Μαθηµατική Περιγραφή της Διάδοσης κυµάτων Η Εξίσωση του Κύµατος
ΚΕΦΑΛΑΙΟ 2ο: ΜΗΧΑΝΙΚΑ- ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ.
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Διάδοση οπτικών παλμών εντός οπτικών ινών στο πλαίσιο της μη-γραμμικής
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Διάδοση οπτικών παλμών εντός οπτικών ινών στο πλαίσιο της μη-γραμμικής
Κυματική οπτική. Συμβολή Περίθλαση Πόλωση
 Κυματική οπτική Η κυματική οπτική ασχολείται με τη μελέτη φαινομένων τα οποία δεν μπορούμε να εξηγήσουμε επαρκώς με τις αρχές της γεωμετρικής οπτικής. Στα φαινόμενα αυτά περιλαμβάνονται τα εξής: Συμβολή
Κυματική οπτική Η κυματική οπτική ασχολείται με τη μελέτη φαινομένων τα οποία δεν μπορούμε να εξηγήσουμε επαρκώς με τις αρχές της γεωμετρικής οπτικής. Στα φαινόμενα αυτά περιλαμβάνονται τα εξής: Συμβολή
Ελεύθερα ηλεκτρόνια στα μέταλλα-σχέση διασποράς
 Ελεύθερα ηλεκτρόνια στα μέταλλα-σχέση διασποράς Στόχος : Να εξηγήσουμε την επίδραση του δυναμικού του κρυστάλλου στις Ε- Ειδικώτερα: Το δυναμικό του κρυστάλλου 1. εισάγονται χάσματα στα σημεία όπου τέμνονται
Ελεύθερα ηλεκτρόνια στα μέταλλα-σχέση διασποράς Στόχος : Να εξηγήσουμε την επίδραση του δυναμικού του κρυστάλλου στις Ε- Ειδικώτερα: Το δυναμικό του κρυστάλλου 1. εισάγονται χάσματα στα σημεία όπου τέμνονται
. Να βρεθεί η Ψ(x,t).
 ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ Ασκήσεις Κεφαλαίου II Άσκηση 1: Εάν η κυματοσυνάρτηση Ψ(,0) παριστάνει ένα ελεύθερο σωματίδιο, με μάζα m, στη μία διάσταση την χρονική στιγμή t=0: (,0) N ep( ), όπου N 1/ 4. Να βρεθεί η
ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ Ασκήσεις Κεφαλαίου II Άσκηση 1: Εάν η κυματοσυνάρτηση Ψ(,0) παριστάνει ένα ελεύθερο σωματίδιο, με μάζα m, στη μία διάσταση την χρονική στιγμή t=0: (,0) N ep( ), όπου N 1/ 4. Να βρεθεί η
4. Εισαγωγή στην Κυματική
 4. Εισαγωγή στην Κυματική Σύνοψη Στο κεφάλαιο αυτό εισάγεται η έννοια του κύματος, και τα βασικά μεγέθη των κυματικών διαταραχών, όπως η περίοδος, η συχνότητα, το μήκος κύματος και ο κυματάριθμος. Παρουσιάζονται
4. Εισαγωγή στην Κυματική Σύνοψη Στο κεφάλαιο αυτό εισάγεται η έννοια του κύματος, και τα βασικά μεγέθη των κυματικών διαταραχών, όπως η περίοδος, η συχνότητα, το μήκος κύματος και ο κυματάριθμος. Παρουσιάζονται
5 Σχετικιστική μάζα. Στο Σ Πριν Μετά. Στο Σ
 Α Τόγκας - ΑΜ333: Ειδική Θεωρία Σχετικότητας Σχετικιστική μάζα 5 Σχετικιστική μάζα Όπως έχουμε διαπιστώσει στην ειδική θεωρία της Σχετικότητας οι μετρήσεις των χωρικών και χρονικών αποστάσεων εξαρτώνται
Α Τόγκας - ΑΜ333: Ειδική Θεωρία Σχετικότητας Σχετικιστική μάζα 5 Σχετικιστική μάζα Όπως έχουμε διαπιστώσει στην ειδική θεωρία της Σχετικότητας οι μετρήσεις των χωρικών και χρονικών αποστάσεων εξαρτώνται
γ) Να σχεδιάσετε τις γραφικές παραστάσεις απομάκρυνσης - χρόνου, για τα σημεία Α, Β και Γ, τα οποία απέχουν από το ελεύθερο άκρο αντίστοιχα,,
 1. Κατά μήκος μιας ελαστικής χορδής μεγάλου μήκους που το ένα άκρο της είναι ακλόνητα στερεωμένο, διαδίδονται δύο κύματα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι μετρημένα σε και
1. Κατά μήκος μιας ελαστικής χορδής μεγάλου μήκους που το ένα άκρο της είναι ακλόνητα στερεωμένο, διαδίδονται δύο κύματα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι μετρημένα σε και
3. Εγκάρσιο γραμμικό κύμα που διαδίδεται σε ένα ομογενές ελαστικό μέσον και κατά την
 ΚΥΜΑΤΑ 1. Μια πηγή Ο που βρίσκεται στην αρχή του άξονα, αρχίζει να εκτελεί τη χρονική στιγμή 0, απλή αρμονική ταλάντωση με εξίσωση 6 10 ημ S. I.. Το παραγόμενο γραμμικό αρμονικό κύμα διαδίδεται κατά τη
ΚΥΜΑΤΑ 1. Μια πηγή Ο που βρίσκεται στην αρχή του άξονα, αρχίζει να εκτελεί τη χρονική στιγμή 0, απλή αρμονική ταλάντωση με εξίσωση 6 10 ημ S. I.. Το παραγόμενο γραμμικό αρμονικό κύμα διαδίδεται κατά τη
ΕΡΓΑΣΙΑ ΣΤΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ
 ΕΡΓΑΣΙΑ ΣΤΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Τι ονομάζεται μηχανικό κύμα; Να περιγράψετε το μηχανισμό διάδοσής του. 2. Τι χρειάζεται για να δημιουργηθεί και να διαδοθεί ένα μηχανικό κύμα; Διαδίδονται
ΕΡΓΑΣΙΑ ΣΤΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Τι ονομάζεται μηχανικό κύμα; Να περιγράψετε το μηχανισμό διάδοσής του. 2. Τι χρειάζεται για να δημιουργηθεί και να διαδοθεί ένα μηχανικό κύμα; Διαδίδονται
Μηχανική ΙI Ταλαντωτής µε µεταβλητή συχνότητα
 Τµήµα Π Ιωάννου & Θ Αποστολάτου 22/5/2000 Μηχανική ΙI Ταλαντωτής µε µεταβλητή συχνότητα Τι θα συµβεί στην περίοδο ενός εκκρεµούς εάν το µήκος του νήµατος µεταβάλλεται µε αργό ρυθµό; Το πρόβληµα προτάθηκε
Τµήµα Π Ιωάννου & Θ Αποστολάτου 22/5/2000 Μηχανική ΙI Ταλαντωτής µε µεταβλητή συχνότητα Τι θα συµβεί στην περίοδο ενός εκκρεµούς εάν το µήκος του νήµατος µεταβάλλεται µε αργό ρυθµό; Το πρόβληµα προτάθηκε
NTÙÍÉÏÓ ÃÊÏÕÔÓÉÁÓ - ÖÕÓÉÊÏÓ www.geocities.com/gutsi1 -- www.gutsias.gr
 Έστω µάζα m. Στη µάζα κάποια στιγµή ασκούνται δυο δυνάµεις. ( Βλ. σχήµα:) Ποιά η διεύθυνση και ποιά η φορά κίνησης της µάζας; F 1 F γ m F 2 ιατυπώστε αρχή επαλληλίας. M την της Ποιό φαινόµενο ονοµάζουµε
Έστω µάζα m. Στη µάζα κάποια στιγµή ασκούνται δυο δυνάµεις. ( Βλ. σχήµα:) Ποιά η διεύθυνση και ποιά η φορά κίνησης της µάζας; F 1 F γ m F 2 ιατυπώστε αρχή επαλληλίας. M την της Ποιό φαινόµενο ονοµάζουµε
1ο ΘΕΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΕΙΣ
 1ο ΘΕΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΕΙΣ Θέμα 1: Α. Στις ερωτήσεις 1-3 να σημειώσετε το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Ένα σώμα μάζας m
1ο ΘΕΜΑ ΠΡΟΣΟΜΟΙΩΣΗΣ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΕΚΦΩΝΗΣΕΙΣ Θέμα 1: Α. Στις ερωτήσεις 1-3 να σημειώσετε το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Ένα σώμα μάζας m
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ. ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ ΙI Ιούνιος 2004
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ ΙI Ιούνιος 2004 Τμήμα Π. Ιωάννου & Θ. Αποστολάτου Απαντήστε στα 4 θέματα με σαφήνεια συντομία. Η πλήρης απάντηση θέματος εκτιμάται ιδιαίτερα. Καλή
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ ΙI Ιούνιος 2004 Τμήμα Π. Ιωάννου & Θ. Αποστολάτου Απαντήστε στα 4 θέματα με σαφήνεια συντομία. Η πλήρης απάντηση θέματος εκτιμάται ιδιαίτερα. Καλή
ιαγώνισμα στη Φυσική Γ Λυκείου Κατεύθυνσης Επαναληπτικό Ι
 Θέμα 1 ο ιαγώνισμα στη Φυσική Γ Λυκείου Κατεύθυνσης Επαναληπτικό Ι Στα ερωτήματα 1 5 του πρώτου θέματος, να μεταφέρετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα της απάντησης που θεωρείτε
Θέμα 1 ο ιαγώνισμα στη Φυσική Γ Λυκείου Κατεύθυνσης Επαναληπτικό Ι Στα ερωτήματα 1 5 του πρώτου θέματος, να μεταφέρετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα της απάντησης που θεωρείτε
papost/
 Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
Δρ. Παντελής Σ. Αποστολόπουλος Επίκουρος Καθηγητής http://users.uoa.gr/ papost/ papost@phys.uoa.gr ΤΕΙ Ιονίων Νήσων, Τμήμα Τεχνολόγων Περιβάλλοντος ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2016-2017 Οπως είδαμε
Φυσική Γ Θετ. και Τεχν/κης Κατ/σης ΚΥΜΑΤΑ ( )
 ΚΥΜΑΤΑ ( 2.1-2.2) Για τη δημιουργία ενός κύματος χρειάζονται η πηγή της διαταραχής ή πηγή του κύματος, δηλαδή η αιτία που θα προκαλέσει τη διαταραχή και ένα υλικό (μέσο) στο οποίο κάθε μόριο αλληλεπιδρά
ΚΥΜΑΤΑ ( 2.1-2.2) Για τη δημιουργία ενός κύματος χρειάζονται η πηγή της διαταραχής ή πηγή του κύματος, δηλαδή η αιτία που θα προκαλέσει τη διαταραχή και ένα υλικό (μέσο) στο οποίο κάθε μόριο αλληλεπιδρά
1 Ο ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ - ΕΚΦΩΝΗΣΕΙΣ
 Ο ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ - ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις - 4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη συμπληρώνει σωστά
Ο ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ - ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις - 4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη συμπληρώνει σωστά
PLANCK 1900 Προκειμένου να εξηγήσει την ακτινοβολία του μέλανος σώματος αναγκάστηκε να υποθέσει ότι η ακτινοβολία εκπέμπεται σε κβάντα ενέργειας που
 ΑΤΟΜΙΚΗ ΦΥΣΙΚΗ PLANCK 1900 Προκειμένου να εξηγήσει την ακτινοβολία του μέλανος σώματος αναγκάστηκε να υποθέσει ότι η ακτινοβολία εκπέμπεται σε κβάντα ενέργειας που είναι ανάλογα με τη συχνότητα (f). PLANCK
ΑΤΟΜΙΚΗ ΦΥΣΙΚΗ PLANCK 1900 Προκειμένου να εξηγήσει την ακτινοβολία του μέλανος σώματος αναγκάστηκε να υποθέσει ότι η ακτινοβολία εκπέμπεται σε κβάντα ενέργειας που είναι ανάλογα με τη συχνότητα (f). PLANCK
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0
 Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Κεφάλαιο 2 ο Ενότητα 1 η : Μηχανικά Κύματα Θεωρία Γ Λυκείου
 Κεφάλαιο 2 ο Ενότητα 1 η : Μηχανικά Κύματα Θεωρία Γ Λυκείου Τρέχοντα Κύματα Κύμα ονομάζεται η διάδοση μιας διαταραχής σε όλα τα σημεία του ελαστικού μέσου με ορισμένη ταχύτητα. Κατά τη διάδοση ενός κύματος
Κεφάλαιο 2 ο Ενότητα 1 η : Μηχανικά Κύματα Θεωρία Γ Λυκείου Τρέχοντα Κύματα Κύμα ονομάζεται η διάδοση μιας διαταραχής σε όλα τα σημεία του ελαστικού μέσου με ορισμένη ταχύτητα. Κατά τη διάδοση ενός κύματος
Κεφάλαιο 38 Κβαντική Μηχανική
 Κεφάλαιο 38 Κβαντική Μηχανική Περιεχόμενα Κεφαλαίου 38 Κβαντική Μηχανική Μια καινούργια Θεωρία Η κυματοσυνάρτηση και η εξήγησή της. Το πείραμα της διπλής σχισμής. Η αρχή της αβεβαιότητας του Heisenberg.
Κεφάλαιο 38 Κβαντική Μηχανική Περιεχόμενα Κεφαλαίου 38 Κβαντική Μηχανική Μια καινούργια Θεωρία Η κυματοσυνάρτηση και η εξήγησή της. Το πείραμα της διπλής σχισμής. Η αρχή της αβεβαιότητας του Heisenberg.
PLANCK 1900 Προκειμένου να εξηγήσει την ακτινοβολία του μέλανος σώματος αναγκάστηκε να υποθέσει ότι η ακτινοβολία εκπέμπεται σε κβάντα ενέργειας που
 ΑΤΟΜΙΚΗ ΦΥΣΙΚΗ PLANCK 1900 Προκειμένου να εξηγήσει την ακτινοβολία του μέλανος σώματος αναγκάστηκε να υποθέσει ότι η ακτινοβολία εκπέμπεται σε κβάντα ενέργειας που είναι ανάλογα με τη συχνότητα (f). PLANCK
ΑΤΟΜΙΚΗ ΦΥΣΙΚΗ PLANCK 1900 Προκειμένου να εξηγήσει την ακτινοβολία του μέλανος σώματος αναγκάστηκε να υποθέσει ότι η ακτινοβολία εκπέμπεται σε κβάντα ενέργειας που είναι ανάλογα με τη συχνότητα (f). PLANCK
ΚΕΦΑΛΑΙΟ 2 Ο : ΚΥΜΑΤΑ ΕΝΟΤΗΤΑ 2: ΕΠΑΛΛΗΛΙΑ ΚΥΜΑΤΩΝ ΣΥΜΒΟΛΗ ΚΥΜΑΤΩΝ ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΙΑΣ
 ΚΕΦΑΛΑΙΟ Ο : ΚΥΜΑΤΑ ΕΝΟΤΗΤΑ : ΕΠΑΛΛΗΛΙΑ ΚΥΜΑΤΩΝ ΣΥΜΒΟΛΗ ΚΥΜΑΤΩΝ ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΙΑΣ Μελέτη της συμβολής κυμάτων στην επιφάνεια υγρού Τι ονομάζουμε συμβολή κυμάτων; Συμβολή ονομάζουμε την
ΚΕΦΑΛΑΙΟ Ο : ΚΥΜΑΤΑ ΕΝΟΤΗΤΑ : ΕΠΑΛΛΗΛΙΑ ΚΥΜΑΤΩΝ ΣΥΜΒΟΛΗ ΚΥΜΑΤΩΝ ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΙΑΣ Μελέτη της συμβολής κυμάτων στην επιφάνεια υγρού Τι ονομάζουμε συμβολή κυμάτων; Συμβολή ονομάζουμε την
3. Το πρότυπο του Bohr εξήγησε το ότι το φάσμα της ακτινοβολίας που εκπέμπει το αέριο υδρογόνο, είναι γραμμικό.
 ΧΗΜΕΙΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΡΓΑΣΙΑ 16 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΚΒΑΝΤΙΚΗ ΜΗΧΑΝΙΚΗ-ΠΡΟΤΥΠΟ BOHR ΟΜΑΔΑ Α Να χαρακτηρίσετε τις παρακάτω προτάσεις ως Σωστές ή Λάθος και να αιτιολογήσετε αυτές που είναι λάθος : 1.
ΧΗΜΕΙΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΡΓΑΣΙΑ 16 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΚΒΑΝΤΙΚΗ ΜΗΧΑΝΙΚΗ-ΠΡΟΤΥΠΟ BOHR ΟΜΑΔΑ Α Να χαρακτηρίσετε τις παρακάτω προτάσεις ως Σωστές ή Λάθος και να αιτιολογήσετε αυτές που είναι λάθος : 1.
ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ
 ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ 1. ΕΓΚΑΡΣΙΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ Κύματα κατά μήκος τεντωμένου νήματος Στο τεντωμένο με δύναμη νήμα του Σχήματος 1.1α δημιουργούμε μια εγκάρσια διαταραχή (παράλληλη με τη διεύθυνση
ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ 1. ΕΓΚΑΡΣΙΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ Κύματα κατά μήκος τεντωμένου νήματος Στο τεντωμένο με δύναμη νήμα του Σχήματος 1.1α δημιουργούμε μια εγκάρσια διαταραχή (παράλληλη με τη διεύθυνση
ΘΕΜΑ Α ΕΡΩΤΗΣΕΙΣ ΘΕΜΑ Α
 ΘΕΜΑ Α 1. Να επιλέξετε τη σωστή απάντηση. Μηχανικό ονομάζεται το κύμα στο οποίο: α. Μεταφέρεται ύλη στον χώρο κατά την κατεύθυνση διάδοσης του κύματος. β. Μεταφέρεται ορμή και ενέργεια στον χώρο κατά την
ΘΕΜΑ Α 1. Να επιλέξετε τη σωστή απάντηση. Μηχανικό ονομάζεται το κύμα στο οποίο: α. Μεταφέρεται ύλη στον χώρο κατά την κατεύθυνση διάδοσης του κύματος. β. Μεταφέρεται ορμή και ενέργεια στον χώρο κατά την
max 0 Eκφράστε την διαφορά των δύο θετικών λύσεων ώς πολλαπλάσιο του ω 0, B . Αναλύοντας το Β σε σειρά άπειρων όρων ώς προς γ/ω 0 ( σειρά
 . Να αποδείξετε ότι σε ένα ταλαντούμενο σύστημα ενός βαθμού ελευθερίας, μάζας και σταθεράς ελατηρίου s με πολύ ασθενή απόσβεση (γω, όπου γ r/, r η σταθερά αντίστασης και s/ ) το πλήρες εύρος στο μισό του
. Να αποδείξετε ότι σε ένα ταλαντούμενο σύστημα ενός βαθμού ελευθερίας, μάζας και σταθεράς ελατηρίου s με πολύ ασθενή απόσβεση (γω, όπου γ r/, r η σταθερά αντίστασης και s/ ) το πλήρες εύρος στο μισό του
Κεφάλαιο 15 ΚίνησηΚυµάτων. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 15 ΚίνησηΚυµάτων ΠεριεχόµεναΚεφαλαίου 15 Χαρακτηριστικά Κυµατικής Είδη κυµάτων: ιαµήκη και Εγκάρσια Μεταφορά ενέργειας µε κύµατα Μαθηµατική Περιγραφή της ιάδοσης κυµάτων ΗΕξίσωσητουΚύµατος Κανόνας
Κεφάλαιο 15 ΚίνησηΚυµάτων ΠεριεχόµεναΚεφαλαίου 15 Χαρακτηριστικά Κυµατικής Είδη κυµάτων: ιαµήκη και Εγκάρσια Μεταφορά ενέργειας µε κύµατα Μαθηµατική Περιγραφή της ιάδοσης κυµάτων ΗΕξίσωσητουΚύµατος Κανόνας
Γ Λυκείου. 6 Μαρτίου Θεωρητικό Μέρος Θέµα 1 ο
 Θεωρητικό Μέρος Θέµα 1 ο Γ Λυκείου 6 Μαρτίου 2010 A. Μια χορδή βιολιού µε τα δύο άκρα της στερεωµένα, ταλαντώνεται µε συχνότητα 12 Ηz. Στο παρακάτω σχήµα φαίνονται δύο στιγµιότυπα του στάσιµου κύµατος.
Θεωρητικό Μέρος Θέµα 1 ο Γ Λυκείου 6 Μαρτίου 2010 A. Μια χορδή βιολιού µε τα δύο άκρα της στερεωµένα, ταλαντώνεται µε συχνότητα 12 Ηz. Στο παρακάτω σχήµα φαίνονται δύο στιγµιότυπα του στάσιµου κύµατος.
ΔΙΑΓΩΝΙΣΜΑ ΤΕΛΙΚΗΣ ΠΡΟΣΟΜΟΙΩΣΗΣ 2014 ΦΥΣΙΚΗΣ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΕΠΙΜΕΛΕΙΑ ΘΕΜΑΤΩΝ: ΚΟΛΟΣΙΩΝΗΣ ΔΗΜΗΤΡΗΣ
 1 ΔΙΑΓΩΝΙΣΜΑ ΤΕΛΙΚΗΣ ΠΡΟΣΟΜΟΙΩΣΗΣ 2014 ΦΥΣΙΚΗΣ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΕΠΙΜΕΛΕΙΑ ΘΕΜΑΤΩΝ: ΚΟΛΟΣΙΩΝΗΣ ΔΗΜΗΤΡΗΣ ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό κάθε μιας από τις παρακάτω
1 ΔΙΑΓΩΝΙΣΜΑ ΤΕΛΙΚΗΣ ΠΡΟΣΟΜΟΙΩΣΗΣ 2014 ΦΥΣΙΚΗΣ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΕΠΙΜΕΛΕΙΑ ΘΕΜΑΤΩΝ: ΚΟΛΟΣΙΩΝΗΣ ΔΗΜΗΤΡΗΣ ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό κάθε μιας από τις παρακάτω
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα. ΔΙΑΛΕΞΗ 21 Κυματική ΦΥΣ102 1
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 21 Κυματική ΦΥΣ102 1 Χαρακτηριστικά Διάδοσης Κύματος Όλα τα κύματα μεταφέρουν ενέργεια.
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 21 Κυματική ΦΥΣ102 1 Χαρακτηριστικά Διάδοσης Κύματος Όλα τα κύματα μεταφέρουν ενέργεια.
Μέρος 1 ο : Εισαγωγή στο φως
 Μέρος 1 ο : Εισαγωγή στο φως Το φως είναι η ευλογία του Θεού. Είναι γνωστό ότι κατά τη δημιουργία του κόσμου είπε: «καὶ εἶπεν ὁ Θεός γενηθήτω φῶς καὶ ἐγένετο φῶς. καὶ εἶδεν ὁ Θεὸς τὸ φῶς, ὅτι καλόν καὶ
Μέρος 1 ο : Εισαγωγή στο φως Το φως είναι η ευλογία του Θεού. Είναι γνωστό ότι κατά τη δημιουργία του κόσμου είπε: «καὶ εἶπεν ὁ Θεός γενηθήτω φῶς καὶ ἐγένετο φῶς. καὶ εἶδεν ὁ Θεὸς τὸ φῶς, ὅτι καλόν καὶ
Μέθοδοι έρευνας ορυκτών και πετρωμάτων
 Μέθοδοι έρευνας ορυκτών και πετρωμάτων Μάθημα 9 ο Φασματοσκοπία Raman Διδάσκων Δρ. Αδαμαντία Χατζηαποστόλου Τμήμα Γεωλογίας Πανεπιστημίου Πατρών Ακαδημαϊκό Έτος 2017-2018 Ύλη 9 ου μαθήματος Αρχές λειτουργίας
Μέθοδοι έρευνας ορυκτών και πετρωμάτων Μάθημα 9 ο Φασματοσκοπία Raman Διδάσκων Δρ. Αδαμαντία Χατζηαποστόλου Τμήμα Γεωλογίας Πανεπιστημίου Πατρών Ακαδημαϊκό Έτος 2017-2018 Ύλη 9 ου μαθήματος Αρχές λειτουργίας
Διαγώνισμα Φυσικής Κατεύθυνσης Γ Λυκείου
 Διαγώνισμα Φυσικής Κατεύθυνσης Γ Λυκείου Ζήτημα 1 ον 1.. Ένα σημειακό αντικείμενο εκτελεί απλή αρμονική ταλάντωση. Τις χρονικές στιγμές που το μέτρο της ταχύτητας του αντικειμένου είναι μέγιστο, το μέτρο
Διαγώνισμα Φυσικής Κατεύθυνσης Γ Λυκείου Ζήτημα 1 ον 1.. Ένα σημειακό αντικείμενο εκτελεί απλή αρμονική ταλάντωση. Τις χρονικές στιγμές που το μέτρο της ταχύτητας του αντικειμένου είναι μέγιστο, το μέτρο
Γ ΛΥΚΕΙΟΥ ΚΥΜΑΤΑ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ. Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός.
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΚΥΜΑΤΑ Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός / Βασικές Έννοιες Η επιστήμη της Φυσικής συχνά μελετάει διάφορες διαταραχές που προκαλούνται και διαδίδονται στο χώρο.
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΚΥΜΑΤΑ Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός / Βασικές Έννοιες Η επιστήμη της Φυσικής συχνά μελετάει διάφορες διαταραχές που προκαλούνται και διαδίδονται στο χώρο.
7. Ταλαντώσεις σε συστήµατα µε πολλούς βαθµούς ελευθερίας
 7 Ταλαντώσεις σε συστήµατα µε πολλούς βαθµούς ελευθερίας Συζευγµένες ταλαντώσεις Βιβλιογραφία F S Crawford Jr Κυµατική (Σειρά Μαθηµάτων Φυσικής Berkeley, Τόµος 3 Αθήνα 979) Κεφ H J Pai Φυσική των ταλαντώσεων
7 Ταλαντώσεις σε συστήµατα µε πολλούς βαθµούς ελευθερίας Συζευγµένες ταλαντώσεις Βιβλιογραφία F S Crawford Jr Κυµατική (Σειρά Μαθηµάτων Φυσικής Berkeley, Τόµος 3 Αθήνα 979) Κεφ H J Pai Φυσική των ταλαντώσεων
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ο.Ε.Φ.Ε ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ο.Ε.Φ.Ε. 2003 ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Θ Ε Μ Α 1 ο Οδηγία: Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ο.Ε.Φ.Ε. 2003 ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Θ Ε Μ Α 1 ο Οδηγία: Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα
HMY 333 Φωτονική Διάλεξη 12 Οπτικοί κυματοδηγοί
 4 Hsiu. Ha Ανάκλαση και μετάδοση του φωτός σε μια διηλεκτρική επαφή HMY 333 Φωτονική Διάλεξη Οπτικοί κυματοδηγοί i i i r i si c si v c hp://www.e.readig.ac.u/clouds/awell/ c 3 Γωνία πρόσπτωσης < κρίσιμη
4 Hsiu. Ha Ανάκλαση και μετάδοση του φωτός σε μια διηλεκτρική επαφή HMY 333 Φωτονική Διάλεξη Οπτικοί κυματοδηγοί i i i r i si c si v c hp://www.e.readig.ac.u/clouds/awell/ c 3 Γωνία πρόσπτωσης < κρίσιμη
ΘΕΜΑ 1 ο. Φροντιστήριο «ΕΠΙΛΟΓΗ» Ιατροπούλου 12 & σιδ. Σταθμού - Καλαμάτα τηλ.: & 96390
 ΘΕΜΑ 1 ο ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 1 ΙΟΥΝΙΟΥ 006 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ) Να γράψετε στο τετράδιό σας τον
ΘΕΜΑ 1 ο ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 1 ΙΟΥΝΙΟΥ 006 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ) Να γράψετε στο τετράδιό σας τον
ΚΕΦΑΛΑΙΟ 1 - ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ
 ΚΕΦΑΛΑΙΟ 1 - ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ Σύμφωνα με την ηλεκτρομαγνητική θεωρία του Maxwell, το φως είναι εγκάρσιο ηλεκτρομαγνητικό κύμα. Η θεωρία αυτή α. δέχεται ότι κάθε φωτεινή πηγή εκπέμπει φωτόνια.
ΚΕΦΑΛΑΙΟ 1 - ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ Σύμφωνα με την ηλεκτρομαγνητική θεωρία του Maxwell, το φως είναι εγκάρσιο ηλεκτρομαγνητικό κύμα. Η θεωρία αυτή α. δέχεται ότι κάθε φωτεινή πηγή εκπέμπει φωτόνια.
Νέα Οπτικά Μικροσκόπια
 Νέα Οπτικά Μικροσκόπια Αντίθεση εικόνας (contrast) Αντίθεση πλάτους Αντίθεση φάσης Αντίθεση εικόνας =100 x (Ι υποβ -Ι δειγμα )/ Ι υποβ Μικροσκοπία φθορισμού (Χρησιμοποιεί φθορίζουσες χρωστικές για το
Νέα Οπτικά Μικροσκόπια Αντίθεση εικόνας (contrast) Αντίθεση πλάτους Αντίθεση φάσης Αντίθεση εικόνας =100 x (Ι υποβ -Ι δειγμα )/ Ι υποβ Μικροσκοπία φθορισμού (Χρησιμοποιεί φθορίζουσες χρωστικές για το
ΟΡΟΣΗΜΟ ΓΛΥΦΑΔΑΣ. 5.4 Η ταχύτητα υ διάδοσης του κύματος, η περίοδός του Τ και το μήκος κύματος λ, συνδέονται με τη σχέση:
 Αρμονικό κύμα ΚΕΦΑΛΑΙΟ 2 51 Κατά τη διάδοση ενός κύματος σε ένα ελαστικό μέσο: α μεταφέρεται ύλη, β μεταφέρεται ενέργεια και ύλη, γ όλα τα σημεία του ελαστικού μέσου έχουν την ίδια φάση την ίδια χρονική
Αρμονικό κύμα ΚΕΦΑΛΑΙΟ 2 51 Κατά τη διάδοση ενός κύματος σε ένα ελαστικό μέσο: α μεταφέρεται ύλη, β μεταφέρεται ενέργεια και ύλη, γ όλα τα σημεία του ελαστικού μέσου έχουν την ίδια φάση την ίδια χρονική
Το πλάτος της ταλάντωσης του σημείου Σ, μετά τη συμβολή των δυο. α. 0 β. Α γ. 2Α δ. Μονάδες 5
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 04-01-2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ Μ-ΑΓΙΑΝΝΙΩΤΑΚΗ ΑΝ-ΠΟΥΛΗ Κ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 04-01-2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ Μ-ΑΓΙΑΝΝΙΩΤΑΚΗ ΑΝ-ΠΟΥΛΗ Κ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Κύματα Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων.
Φυσική για Μηχανικούς Κύματα Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων.
ΔΙΑΓΩΝΙΣΜΑ 05 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3 ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) U β A
 Σελίδα 1 από 5 ΔΙΑΓΩΝΙΣΜΑ 05 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3 ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α και
Σελίδα 1 από 5 ΔΙΑΓΩΝΙΣΜΑ 05 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3 ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α και
Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: 04/0/204 ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α4 και δίπλα το γράμμα που αντιστοιχεί
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: 04/0/204 ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α4 και δίπλα το γράμμα που αντιστοιχεί
Φυσική Ο.Π. Γ Λυκείου
 Φυσική Ο.Π. Γ Λυκείου ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις (Α-Α) και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α) Δύο σώματα συγκρούονται κεντρικά
Φυσική Ο.Π. Γ Λυκείου ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις (Α-Α) και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α) Δύο σώματα συγκρούονται κεντρικά
Να αιτιολογήσετε την απάντησή σας. Μονάδες 5
 2002 5. Να γράψετε στο τετράδιό σας τη λέξη που συµπληρώνει σωστά καθεµία από τις παρακάτω προτάσεις. γ. Η αιτία δηµιουργίας του ηλεκτροµαγνητικού κύµατος είναι η... κίνηση ηλεκτρικών φορτίων. 1. Ακτίνα
2002 5. Να γράψετε στο τετράδιό σας τη λέξη που συµπληρώνει σωστά καθεµία από τις παρακάτω προτάσεις. γ. Η αιτία δηµιουργίας του ηλεκτροµαγνητικού κύµατος είναι η... κίνηση ηλεκτρικών φορτίων. 1. Ακτίνα
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ- ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 4 ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΜΥΤΙΛΗΝΗΣ ΤΕΛΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ- ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΠΩΝΥΜΟ. ΗΜΕΡ/ΝΙΑ : 15/05/2015 ΘΕΜΑ A Να γράψετε στο τετράδιό σας τον αριθμό καθεμίας από τις παρακάτω
4 ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΜΥΤΙΛΗΝΗΣ ΤΕΛΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ- ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΠΩΝΥΜΟ. ΗΜΕΡ/ΝΙΑ : 15/05/2015 ΘΕΜΑ A Να γράψετε στο τετράδιό σας τον αριθμό καθεμίας από τις παρακάτω
HMY 333 Φωτονική Διάλεξη 07. Ταχύτητα φάσης, ταχύτητα ομάδας και διασπορά. n 2 n O
 Uiersiy of Cyrus Πανεπιστήμιο Κύπρου Uiersiy of Cyrus Πανεπιστήμιο Κύπρου HMY 333 Φωτονική Διάλεξη 7 Ταχύτητα φάσης, ταχύτητα ομάδας και διασπορά Σε ένα μέσο διασποράς, όπως οι οπτικές ίνες, η μορφή του
Uiersiy of Cyrus Πανεπιστήμιο Κύπρου Uiersiy of Cyrus Πανεπιστήμιο Κύπρου HMY 333 Φωτονική Διάλεξη 7 Ταχύτητα φάσης, ταχύτητα ομάδας και διασπορά Σε ένα μέσο διασποράς, όπως οι οπτικές ίνες, η μορφή του
ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 24/04/2016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ (ΑΠΟΦΟΙΤΟΙ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας τον αριθμό
Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 24/04/2016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ (ΑΠΟΦΟΙΤΟΙ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας τον αριθμό
Ηλεκτρομαγνητικά Διαδίδονται στο κενό
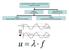 Κύμα: διαταραχή που διαδίδεται στο χώρο και στο χρόνο μεταφέροντας ενέργεια. Μηχανικά Μέσο διάδοσης Ηλεκτρομαγνητικά Διαδίδονται στο κενό Διαμήκη Διεύθυνση διάδοσης παράλληλη στη διαταραχή Εγκάρσια Διεύθυνση
Κύμα: διαταραχή που διαδίδεται στο χώρο και στο χρόνο μεταφέροντας ενέργεια. Μηχανικά Μέσο διάδοσης Ηλεκτρομαγνητικά Διαδίδονται στο κενό Διαμήκη Διεύθυνση διάδοσης παράλληλη στη διαταραχή Εγκάρσια Διεύθυνση
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ» ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 2 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση,
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 2 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση,
ΤΥΠΟΛΟΓΙΟ ΚΕΦΑΛΑΙΟΥ 1 ΗΛΕΚΤΡΙΚΕΣ - ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ
 ΤΥΠΟΛΟΓΙΟ ΚΕΦΑΛΑΙΟΥ ΗΛΕΚΤΡΙΚΕΣ - ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ( t ) Χρονική εξίσωση απομάκρυνσης a ( t ) με a Χρονική εξίσωση ταχύτητας a aa ( t ) με a a Χρονική εξίσωση επιτάχυνσης a Σχέση
ΤΥΠΟΛΟΓΙΟ ΚΕΦΑΛΑΙΟΥ ΗΛΕΚΤΡΙΚΕΣ - ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ( t ) Χρονική εξίσωση απομάκρυνσης a ( t ) με a Χρονική εξίσωση ταχύτητας a aa ( t ) με a a Χρονική εξίσωση επιτάχυνσης a Σχέση
ΤΕΧΝΟΛΟΓΙΑ ΜΗ ΚΑΤΑΣΤΡΟΦΙΚΟΥ ΕΛΕΓΧΟΥ ΘΕΩΡΙΑ ο ΜΑΘΗΜΑ
 ΤΕΧΝΟΛΟΓΙΑ ΜΗ ΚΑΤΑΣΤΡΟΦΙΚΟΥ ΕΛΕΓΧΟΥ ΘΕΩΡΙΑ 2017 7 ο ΜΑΘΗΜΑ Εισαγωγή Κύμα είναι η διάδοση των περιοδικών κινήσεων (ταλαντώσεων) που κάνουν τα στοιχειώδη σωματίδια ενός υλικού γύρω από τη θέση ισορροπίας
ΤΕΧΝΟΛΟΓΙΑ ΜΗ ΚΑΤΑΣΤΡΟΦΙΚΟΥ ΕΛΕΓΧΟΥ ΘΕΩΡΙΑ 2017 7 ο ΜΑΘΗΜΑ Εισαγωγή Κύμα είναι η διάδοση των περιοδικών κινήσεων (ταλαντώσεων) που κάνουν τα στοιχειώδη σωματίδια ενός υλικού γύρω από τη θέση ισορροπίας
Ονοματεπώνυμο. Α) Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λανθασμένες:
 ΔΙΑΓΩΝΙΣΜΑ ΚΥΜΑΤΩΝ (1) ΘΕΜΑ 1 ο Ονοματεπώνυμο. Α) Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λανθασμένες: 1) Κατά τη διάδοση ενός κύματος μεταφέρεται ενέργεια και ορμή, αλλά όχι ύλη. 2) Σε
ΔΙΑΓΩΝΙΣΜΑ ΚΥΜΑΤΩΝ (1) ΘΕΜΑ 1 ο Ονοματεπώνυμο. Α) Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λανθασμένες: 1) Κατά τη διάδοση ενός κύματος μεταφέρεται ενέργεια και ορμή, αλλά όχι ύλη. 2) Σε
Βασικές διαδικασίες παραγωγής πολωμένου φωτός
 Πόλωση του φωτός Βασικές διαδικασίες παραγωγής πολωμένου φωτός πόλωση λόγω επιλεκτικής απορρόφησης - διχρωισμός πόλωση λόγω ανάκλασης από μια διηλεκτρική επιφάνεια πόλωση λόγω ύπαρξης δύο δεικτών διάθλασης
Πόλωση του φωτός Βασικές διαδικασίες παραγωγής πολωμένου φωτός πόλωση λόγω επιλεκτικής απορρόφησης - διχρωισμός πόλωση λόγω ανάκλασης από μια διηλεκτρική επιφάνεια πόλωση λόγω ύπαρξης δύο δεικτών διάθλασης
Γενικές αρχές ακτινοφυσικής Π. ΓΚΡΙΤΖΑΛΗΣ
 Γενικές αρχές ακτινοφυσικής Π. ΓΚΡΙΤΖΑΛΗΣ Μέρος πρώτο ΣΚΟΠΟΣ ΜΑΘΗΜΑΤΟΣ Να εξηγηθούν βασικές έννοιες της φυσικής, που θα βοηθήσουν τον φοιτητή να μάθει: Τι είναι οι ακτίνες Χ Πως παράγονται Ποιες είναι
Γενικές αρχές ακτινοφυσικής Π. ΓΚΡΙΤΖΑΛΗΣ Μέρος πρώτο ΣΚΟΠΟΣ ΜΑΘΗΜΑΤΟΣ Να εξηγηθούν βασικές έννοιες της φυσικής, που θα βοηθήσουν τον φοιτητή να μάθει: Τι είναι οι ακτίνες Χ Πως παράγονται Ποιες είναι
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ
 ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση
ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση
ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 55
 ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 55 ΚΕΦΑΛΑΙΟ 3 ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 3.. Εισαγωγή Αναφέρθηκε ήδη στο ο κεφάλαιο ότι η αναπαράσταση της ταλαντωτικής
ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 55 ΚΕΦΑΛΑΙΟ 3 ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 3.. Εισαγωγή Αναφέρθηκε ήδη στο ο κεφάλαιο ότι η αναπαράσταση της ταλαντωτικής
ΣΕΜΦΕ ΕΜΠ Φυσική ΙΙΙ (Κυματική) Διαγώνισμα επί πτυχίω εξέτασης 02/06/2017 1
 ΣΕΜΦΕ ΕΜΠ Φυσική ΙΙΙ (Κυματική) Διαγώνισμα επί πτυχίω εξέτασης /6/7 Διάρκεια ώρες. Θέμα. Θεωρηστε ενα συστημα δυο σωματων ισων μαζων (μαζας Μ το καθενα) και δυο ελατηριων (χωρις μαζα) με σταθερες ελατηριων
ΣΕΜΦΕ ΕΜΠ Φυσική ΙΙΙ (Κυματική) Διαγώνισμα επί πτυχίω εξέτασης /6/7 Διάρκεια ώρες. Θέμα. Θεωρηστε ενα συστημα δυο σωματων ισων μαζων (μαζας Μ το καθενα) και δυο ελατηριων (χωρις μαζα) με σταθερες ελατηριων
3.1 Η Αρχή της υπέρθεσης (ή της επαλληλίας)
 ΚΕΦ. 3 Γενικές αρχές της κυματικής 3.1-1 3.1 Η Αρχή της υπέρθεσης (ή της επαλληλίας) 3.1.1 Γενική διατύπωση 3.1. Εύρος ισχύος της αρχής της υπέρθεσης 3.1.3 Μαθηματικές συνέπειες της αρχής της υπέρθεσης
ΚΕΦ. 3 Γενικές αρχές της κυματικής 3.1-1 3.1 Η Αρχή της υπέρθεσης (ή της επαλληλίας) 3.1.1 Γενική διατύπωση 3.1. Εύρος ισχύος της αρχής της υπέρθεσης 3.1.3 Μαθηματικές συνέπειες της αρχής της υπέρθεσης
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
Γραµµικά και Μη Γραµµικά Συστήµατα Μετάδοσης
 Γραµµικά και Μη Γραµµικά Συστήµατα Μετάδοσης Τα περισσότερα δίκτυα σήµερα είναι γραµµικά µε κωδικοποίηση γραµµής NRZ Τα µη γραµµικά συστήµατα στηρίζονται στα σολιτόνια µε κωδικοποίηση RZ. Οπτικό σύστηµα
Γραµµικά και Μη Γραµµικά Συστήµατα Μετάδοσης Τα περισσότερα δίκτυα σήµερα είναι γραµµικά µε κωδικοποίηση γραµµής NRZ Τα µη γραµµικά συστήµατα στηρίζονται στα σολιτόνια µε κωδικοποίηση RZ. Οπτικό σύστηµα
ΚΕΦΑΛΑΙΟ 4ο : Θεωρητική προσέγγιση της FDTD
 ΚΦΑΛΑΙΟ 4ο : Θεωρητική προσέγγιση της DTD 4.. ισαγωγή Από τις τρεις µεθόδους πρόβλεψης των επενεργειών της ηλεκτροµαγνητικής ακτινοβολίας πειραµατική αναλυτική υπολογιστική- η υπολογιστική είναι η νεότερη
ΚΦΑΛΑΙΟ 4ο : Θεωρητική προσέγγιση της DTD 4.. ισαγωγή Από τις τρεις µεθόδους πρόβλεψης των επενεργειών της ηλεκτροµαγνητικής ακτινοβολίας πειραµατική αναλυτική υπολογιστική- η υπολογιστική είναι η νεότερη
Η εξίσωση Dirac (Ι) Σπύρος Ευστ. Τζαμαρίας Στοιχειώδη Σωμάτια 1
 Η εξίσωση Dirac (Ι) Σπύρος Ευστ. Τζαμαρίας Στοιχειώδη Σωμάτια 1 Μη- Σχετικιστική Κβαντομηχανική Η μη- σχετικιστική έκφραση για την ενέργεια: Στην QM αντιστοιχούμε την ενέργεια και την ορμή με Τελεστές:
Η εξίσωση Dirac (Ι) Σπύρος Ευστ. Τζαμαρίας Στοιχειώδη Σωμάτια 1 Μη- Σχετικιστική Κβαντομηχανική Η μη- σχετικιστική έκφραση για την ενέργεια: Στην QM αντιστοιχούμε την ενέργεια και την ορμή με Τελεστές:
Ηλεκτρονική δομή ημιαγωγών-περίληψη. Σχέση διασποράς για ελεύθερα ηλεκτρόνια στα μέταλλα-
 E. K. Παλούρα Οπτοηλεκτρονική_semis_summary.doc Ηλεκτρονική δομή ημιαγωγών-περίληψη Σχέση διασποράς για ελεύθερα ηλεκτρόνια στα μέταλλα- Η κυματοσυνάρτηση ψ(r) του ελεύθερου e είναι λύση της Schrödinger:
E. K. Παλούρα Οπτοηλεκτρονική_semis_summary.doc Ηλεκτρονική δομή ημιαγωγών-περίληψη Σχέση διασποράς για ελεύθερα ηλεκτρόνια στα μέταλλα- Η κυματοσυνάρτηση ψ(r) του ελεύθερου e είναι λύση της Schrödinger:
Από τι αποτελείται το Φως (1873)
 Από τι αποτελείται το Φως (1873) Ο James Maxwell έδειξε θεωρητικά ότι το ορατό φως αποτελείται από ηλεκτρομαγνητικά κύματα. Ηλεκτρομαγνητικό κύμα είναι η ταυτόχρονη διάδοση, μέσω της ταχύτητας του φωτός
Από τι αποτελείται το Φως (1873) Ο James Maxwell έδειξε θεωρητικά ότι το ορατό φως αποτελείται από ηλεκτρομαγνητικά κύματα. Ηλεκτρομαγνητικό κύμα είναι η ταυτόχρονη διάδοση, μέσω της ταχύτητας του φωτός
ΕΛΛΗΝΙΚΟ ΑΝΟΙΧΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ η ΕΡΓΑΣΙΑ
 6/11/004 ΕΛΛΗΝΙΚΟ ΑΝΟΙΧΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 34 004-05 η ΕΡΓΑΣΙΑ ΑΣΚΗΣΕΙΣ Προθεσμία παράδοσης 0/1/004 1) Εκκρεμές μήκους L και μάζας m 1 εκτελεί μικρές ταλαντώσεις γύρω από τη θέση ισορροπίας, έχοντας συνδεθεί
6/11/004 ΕΛΛΗΝΙΚΟ ΑΝΟΙΧΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 34 004-05 η ΕΡΓΑΣΙΑ ΑΣΚΗΣΕΙΣ Προθεσμία παράδοσης 0/1/004 1) Εκκρεμές μήκους L και μάζας m 1 εκτελεί μικρές ταλαντώσεις γύρω από τη θέση ισορροπίας, έχοντας συνδεθεί
ΦΥΣΙΚΗ Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 2006 ΕΚΦΩΝΗΣΕΙΣ
 ΦΥΣΙΚΗ Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 006 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις - 4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 006 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις - 4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή
Ανακεφαλαίωση. q Εισήγαμε την έννοια των δεσμών. Ø Ολόνομους και μή ολόνομους δεσμούς. Ø Γενικευμένες συντεταγμένες
 ΦΥΣ 211 - Διαλ.06 1 Ανακεφαλαίωση Τι είδαμε μέχρι τώρα: q Συζητήσαμε συστήματα πολλών σωμάτων Ø Εσωτερικές και εξωτερικές δυνάμεις Ø Νόμους δράσης-αντίδρασης Ø Ορμές, νόμους διατήρησης (γραμμική ορμή,
ΦΥΣ 211 - Διαλ.06 1 Ανακεφαλαίωση Τι είδαμε μέχρι τώρα: q Συζητήσαμε συστήματα πολλών σωμάτων Ø Εσωτερικές και εξωτερικές δυνάμεις Ø Νόμους δράσης-αντίδρασης Ø Ορμές, νόμους διατήρησης (γραμμική ορμή,
Γκύζη 14-Αθήνα Τηλ :
 Γκύζη 14-Αθήνα Τηλ : 10.64.5.777 ΘΕΜΑ Α ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΡΙΤΗ 10 ΙΟΥΝΙΟΥ 014 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ)
Γκύζη 14-Αθήνα Τηλ : 10.64.5.777 ΘΕΜΑ Α ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΡΙΤΗ 10 ΙΟΥΝΙΟΥ 014 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ)
ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης Γ Λυκείου ΓΡΑΠΤΕΣ ΔΟΚΙΜΑΣΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ 2008
 ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης Γ Λυκείου ΓΡΑΠΤΕΣ ΔΟΚΙΜΑΣΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ 2008 Θέμα 1ο Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από
ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης Γ Λυκείου ΓΡΑΠΤΕΣ ΔΟΚΙΜΑΣΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ 2008 Θέμα 1ο Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
Χημεία Γ Λυκείου Θετικής Κατεύθυνσης
 Χημεία Γ Λυκείου Θετικής Κατεύθυνσης Κεφάλαιο 1 Ηλεκτρονιακή δομή των ατόμων 1 Εισαγωγή Δομή του ατόμου Δημόκριτος Αριστοτέλης Dalton Thomson 400 π.χ. 350π.χ. 1808 1897 Απειροελάχιστα τεμάχια ύλης (τα
Χημεία Γ Λυκείου Θετικής Κατεύθυνσης Κεφάλαιο 1 Ηλεκτρονιακή δομή των ατόμων 1 Εισαγωγή Δομή του ατόμου Δημόκριτος Αριστοτέλης Dalton Thomson 400 π.χ. 350π.χ. 1808 1897 Απειροελάχιστα τεμάχια ύλης (τα
Μέτρηση της ταχύτητας του ήχου στον αέρα.
 Α2 Μέτρηση της ταχύτητας του ήχου στον αέρα. 1 Σκοπός Στο πείραμα αυτό θα μελετηθεί η συμπεριφορά των στάσιμων ηχητικών κυμάτων σε σωλήνα με αισθητοποίηση του φαινομένου του ηχητικού συντονισμού. Επίσης
Α2 Μέτρηση της ταχύτητας του ήχου στον αέρα. 1 Σκοπός Στο πείραμα αυτό θα μελετηθεί η συμπεριφορά των στάσιμων ηχητικών κυμάτων σε σωλήνα με αισθητοποίηση του φαινομένου του ηχητικού συντονισμού. Επίσης
ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΕΤΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΕΤΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ Η Επιστήμη της Θερμοδυναμικής ασχολείται με την ποσότητα της θερμότητας που μεταφέρεται σε ένα κλειστό και απομονωμένο σύστημα από μια κατάσταση ισορροπίας σε μια άλλη
ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΕΤΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ Η Επιστήμη της Θερμοδυναμικής ασχολείται με την ποσότητα της θερμότητας που μεταφέρεται σε ένα κλειστό και απομονωμένο σύστημα από μια κατάσταση ισορροπίας σε μια άλλη
Το σύστημα των μη αλληλεπιδραστικών ροών και η σημασία του στην ερμηνεία των ιδιοτήτων των ιδανικών αερίων.
 Το σύστημα των μη αλληλεπιδραστικών ροών και η σημασία του στην ερμηνεία των ιδιοτήτων των ιδανικών αερίων. Θεωρώντας τα αέρια σαν ουσίες αποτελούμενες από έναν καταπληκτικά μεγάλο αριθμό μικροσκοπικών
Το σύστημα των μη αλληλεπιδραστικών ροών και η σημασία του στην ερμηνεία των ιδιοτήτων των ιδανικών αερίων. Θεωρώντας τα αέρια σαν ουσίες αποτελούμενες από έναν καταπληκτικά μεγάλο αριθμό μικροσκοπικών
ΔΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι
 Δυναμική Μηχανών Ι Ακαδημαϊκό έτος: 015-016 ΔΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι - 1.1- Δυναμική Μηχανών Ι Ακαδημαϊκό έτος: 015-016 Copyright ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο Δυναμικής και Κατασκευών - 015.
Δυναμική Μηχανών Ι Ακαδημαϊκό έτος: 015-016 ΔΥΝΑΜΙΚΗ ΜΗΧΑΝΩΝ Ι - 1.1- Δυναμική Μηχανών Ι Ακαδημαϊκό έτος: 015-016 Copyright ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο Δυναμικής και Κατασκευών - 015.
Γιατί δεν πιάνεται; (δεν το αισθανόμαστε- δεν το πιάνουμε)
 Γιατί δεν πιάνεται; (δεν το αισθανόμαστε- δεν το πιάνουμε) Αραχωβίτη Ελένη- Βαλεντίνη Δέγλερη Βασιλική Καντάνη Χριστίνα Κουμψάκη Ελένη Μάλλη Ευγενία Σαϊτάνη Μαρία Σούκουλη Ελευθερία Τριανταφύλλου Βασιλική-
Γιατί δεν πιάνεται; (δεν το αισθανόμαστε- δεν το πιάνουμε) Αραχωβίτη Ελένη- Βαλεντίνη Δέγλερη Βασιλική Καντάνη Χριστίνα Κουμψάκη Ελένη Μάλλη Ευγενία Σαϊτάνη Μαρία Σούκουλη Ελευθερία Τριανταφύλλου Βασιλική-
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 4 ΣΕΛΙ ΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΤΟΥ ΕΞΩΤΕΡΙΚΟΥ ΚΑΙ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΥΠΑΛΛΗΛΩΝ ΣΤΟ ΕΞΩΤΕΡΙΚΟ ΠΕΜΠΤΗ 12 ΣΕΠΤΕΜΒΡΙΟΥ 2013 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ:
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΤΟΥ ΕΞΩΤΕΡΙΚΟΥ ΚΑΙ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΥΠΑΛΛΗΛΩΝ ΣΤΟ ΕΞΩΤΕΡΙΚΟ ΠΕΜΠΤΗ 12 ΣΕΠΤΕΜΒΡΙΟΥ 2013 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΦΥΣΙΚΗ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ:
Spin του πυρήνα Μαγνητική διπολική ροπή Ηλεκτρική τετραπολική ροπή. Τάσος Λιόλιος Μάθημα Πυρηνικής Φυσικής
 Spin του πυρήνα Μαγνητική διπολική ροπή Ηλεκτρική τετραπολική ροπή Τάσος Λιόλιος Μάθημα Πυρηνικής Φυσικής Εξάρτηση του πυρηνικού δυναμικού από άλλους παράγοντες (πλην της απόστασης) Η συνάρτηση του δυναμικού
Spin του πυρήνα Μαγνητική διπολική ροπή Ηλεκτρική τετραπολική ροπή Τάσος Λιόλιος Μάθημα Πυρηνικής Φυσικής Εξάρτηση του πυρηνικού δυναμικού από άλλους παράγοντες (πλην της απόστασης) Η συνάρτηση του δυναμικού
ΤΕΛΟΣ 2ΗΣ ΑΠΟ 4 ΣΕΛΙΔΕΣ
 ΑΡΧΗ 2ΗΣ ΣΕΛΙΔΑΣ ΘΕΜΑ 1 ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 20 ΔΕΚΕΜΒΡΙΟΥ 2014 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΤΕΣΣΕΡΙΣ (4) Α) Για κάθε μία
ΑΡΧΗ 2ΗΣ ΣΕΛΙΔΑΣ ΘΕΜΑ 1 ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 20 ΔΕΚΕΜΒΡΙΟΥ 2014 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΤΕΣΣΕΡΙΣ (4) Α) Για κάθε μία
21/11/2013 ETY-202 ETY-202 ΎΛΗ & ΦΩΣ 06. Ο ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ. 1396; office Δ013 ΙΤΕ. Στέλιος Τζωρτζάκης
 stzortz@iesl.forth.gr 1396; office Δ013 ΙΤΕ 2 ΎΛΗ & ΦΩΣ 06. Ο ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ Στέλιος Τζωρτζάκης Ο ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ 1 3 4 Το δυναμικό του αρμονικού ταλαντωτή Η παραβολική προσέγγιση βρίσκει άμεση
stzortz@iesl.forth.gr 1396; office Δ013 ΙΤΕ 2 ΎΛΗ & ΦΩΣ 06. Ο ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ Στέλιος Τζωρτζάκης Ο ΑΡΜΟΝΙΚΟΣ ΤΑΛΑΝΤΩΤΗΣ 1 3 4 Το δυναμικό του αρμονικού ταλαντωτή Η παραβολική προσέγγιση βρίσκει άμεση
Περιεχόμενα διάλεξης
 4η Διάλεξη Οπτικές ίνες Γ. Έλληνας, Διάλεξη 4, σελ. 1 Περιεχόμενα διάλεξης Ηλεκτρομαγνητικά κύματα Κυματική Εξίσωση Ακριβής Λύση Οπτικών Ινών Ταξινόμηση Τρόπων Αριθμός Τρόπων Γ. Έλληνας, Διάλεξη 4, σελ.
4η Διάλεξη Οπτικές ίνες Γ. Έλληνας, Διάλεξη 4, σελ. 1 Περιεχόμενα διάλεξης Ηλεκτρομαγνητικά κύματα Κυματική Εξίσωση Ακριβής Λύση Οπτικών Ινών Ταξινόμηση Τρόπων Αριθμός Τρόπων Γ. Έλληνας, Διάλεξη 4, σελ.
ÁÎÉÁ ÅÊÐÁÉÄÅÕÔÉÊÏÓ ÏÌÉËÏÓ
 Θέµα Α ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ (ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ) 3 ΜΑΪOY 016 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και, δίπλα, το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει
Θέµα Α ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ (ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ) 3 ΜΑΪOY 016 ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και, δίπλα, το γράµµα που αντιστοιχεί στη φράση η οποία συµπληρώνει
L = T V = 1 2 (ṙ2 + r 2 φ2 + ż 2 ) U (3)
 ΥΠΟΛΟΓΙΣΤΙΚΗ ΑΣΤΡΟΔΥΝΑΜΙΚΗ 3): Κινήσεις αστέρων σε αστρικά συστήματα Βασικές έννοιες Θεωρούμε αστρικό σύστημα π.χ. γαλαξία ή αστρικό σμήνος) αποτελούμενο από μεγάλο αριθμό αστέρων της τάξης των 10 8 10
ΥΠΟΛΟΓΙΣΤΙΚΗ ΑΣΤΡΟΔΥΝΑΜΙΚΗ 3): Κινήσεις αστέρων σε αστρικά συστήματα Βασικές έννοιες Θεωρούμε αστρικό σύστημα π.χ. γαλαξία ή αστρικό σμήνος) αποτελούμενο από μεγάλο αριθμό αστέρων της τάξης των 10 8 10
ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ
 ΦΥΣΙΚΗ Γ.Π. Γ Λυκείου / Το Φως 1. Η υπεριώδης ακτινοβολία : a) δεν προκαλεί αμαύρωση της φωτογραφικής πλάκας. b) είναι ορατή. c) χρησιμοποιείται για την αποστείρωση ιατρικών εργαλείων. d) έχει μήκος κύματος
ΦΥΣΙΚΗ Γ.Π. Γ Λυκείου / Το Φως 1. Η υπεριώδης ακτινοβολία : a) δεν προκαλεί αμαύρωση της φωτογραφικής πλάκας. b) είναι ορατή. c) χρησιμοποιείται για την αποστείρωση ιατρικών εργαλείων. d) έχει μήκος κύματος
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ε π α ν α λ η π τ ι κ ά θ έ µ α τ α 0 0 5 Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 1 ΘΕΜΑ 1 o Για τις ερωτήσεις 1 4, να γράψετε στο τετράδιο σας τον αριθµό της ερώτησης και δίπλα το γράµµα που
ε π α ν α λ η π τ ι κ ά θ έ µ α τ α 0 0 5 Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 1 ΘΕΜΑ 1 o Για τις ερωτήσεις 1 4, να γράψετε στο τετράδιο σας τον αριθµό της ερώτησης και δίπλα το γράµµα που
