ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ

Transcript

1 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΣΥΜΒΟΛΗ ΣΤΗ ΒΕΛΤΙΩΣΗ ΤΗΣ ΑΠΟ ΟΣΗΣ ΑΣΥΡΜΑΤΗΣ ΕΚΠΟΜΠΗΣ Ε ΟΜΕΝΩΝ ΣΕ ΥΠΟΒΡΥΧΙΑ ΑΣΥΡΜΑΤΑ ΙΚΤΥΑ ( Performance Evaluaton of an Underwater Acoustc Data Broadcastng System ) ΚΥΑΝΙ ΗΣ ΓΕΩΡΓΙΟΣ ΕΠΙΒΛΕΠΩΝ ΚΑΘΗΓΗΤΗΣ: ΝΙΚΟΠΟΛΙΤΙ ΗΣ ΠΕΤΡΟΣ ΕΠΙΚΟΥΡΟΣ ΚΑΘΗΓΗΤΗΣ ΤΜΗΜΑΤΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ Α.Π.Θ. ΘΕΣΣΑΛΟΝΙΚΗ ΣΕΠΤΕΜΒΡΙΟΣ 2011

2 Περίληψη H παρούσα εργασία αναφέρεται σε συστήµατα εκποµπής δεδοµένων σε υποβρύχια ακουστικά ασύρµατα δίκτυα. Για τη βελτίωση της απόδοσής τους κάνουν χρήση ενός Μανθάνοντος Αυτοµάτου στο σταθµό βάσης µε σκοπό τη βελτίωση της απόδοσής τους. Εξετάζονται εκτενώς συγκεκριµένοι αλγόριθµοι εκποµπής από το σταθµό βάσης. Με τη βοήθεια προσοµοίωσης εξάγονται αποτελέσµατα, τα οποία αξιολογούνται ως προς την απόδοσή τους προτείνοντας κάποιο από τα παραπάνω συστήµατα. Από τα αποτελέσµατα καλύτερη απόδοση επιδεικνύει το προτεινόµενο σύστηµα το οποίο καταπολεµά αποτελεσµατικά το πρόβληµα της µεγάλης καθυστέρησης υποβρύχιων ακουστικών ασύρµατων δικτύων. 2

3 Abstract Ths paper addresses data dssemnaton systems n underwater acoustc wreless networks. For better performance they employ a Learnng Automaton at the base staton n order to mprove performance. Specfc broadcastng algorthms are examned extensvely. Wth the help of smulaton, results are exported that show better performance of the proposed system that combats the problem of long delays n underwater acoustc wreless networks. 3

4 Ευχαριστίες Θα ήθελα να ευχαριστήσω θερµά τον επιβλέποντα της διπλωµατικής εργασίας κ. Νικοπολιτίδη Πέτρο για την πολύτιµη βοήθεια, καθοδήγηση και υποµονή του σε όλη την πορεία ανάπτυξης και συγγραφής της συγκεκριµένης διπλωµατικής. Τέλος θα ήθελα να ευχαριστήσω την οικογένειά µου για την υποστήριξη που µου προσέφερε όλο αυτό το χρονικό διάστηµα µέχρι το τέλος των σπουδών µου. Σεπτέµβριος 2011 Κυανίδης Γεώργιος 4

5 Περιεχόµενα Περίληψη..2 Abstract... 3 Ευχαριστίες..4 Περιεχόµενα Λίστα Σχηµάτων.6 Κεφάλαιο 1: Εισαγωγή Γενικά....7 Κεφάλαιο 2: Μη Προσαρµοστικά-Προσαρµοστικά Push Συστήµατα Εκποµπής Μη Προσαρµοστικά Push Συστήµατα Εκποµπής Βασικά θέµατα µη προσαρµοστικών Push Συστηµάτων Εκποµπής Επισκόπηση Βιβλιογραφιών Συστήµατα Εκποµπής εδοµένων Υποβρύχια Συστήµατα Εκποµπής Η µέθοδος του Vadya [9] Αλγόριθµος Σχεδιασµού Εκποµπής Επίδραση των σφαλµάτων εκποµπής στην στρατηγική σχεδιασµού Προσαρµοστικό Push Σύστηµα για Υποβρύχια Εκποµπή Τα Αυτόµατα Μάθησης Βασικές Λειτουργίες του Αλγορίθµου Εκποµπής των Προσαρµοστικών Push Συστηµάτων Ο τρόπος Ανανέωσης των Πιθανοτήτων 18 Κεφάλαιο 3: Αποτελέσµατα- Αξιολόγηση Προσοµοίωση Το Προτεινόµενο Σύστηµα Το Μοντέλο του Σταθµού Βάσης Το Μοντέλο των Χρηστών Περιβάλλον Προσοµοίωσης Αποτελέσµατα Προσοµοίωσης Συµπεράσµατα Αποτελεσµάτων..29 Κεφάλαιο 4: Κώδικας Προσοµοίωση...30 Συµπεράσµατα 40 Αναφορές. 41 5

6 Λίστα Σχηµάτων Σχήµα 1: Υποβρύχιο push σύστηµα µε έναν σταθµό βάσης και κινητούς χρήστες. Σχήµα 2: Παράδειγµα 1. Σχήµα 3: Σύγκλιση της εκτίµησης αυτόµατου της πιθανότητας ζήτησης πακέτου. Σχήµα 4: Μέσος χρόνος απόκρισης σε σχέση µε το συντελεστή access skew για τα τρία συστήµατα στο δίκτυο Ν1 για περιοχή κάλυψης 2 km. Σχήµα 5: Μέσος χρόνος απόκρισης σε σχέση µε το συντελεστή access skew για τα τρία συστήµατα στο δίκτυο Ν1 για περιοχή κάλυψης 5 km. Σχήµα 6: Μέσος χρόνος απόκρισης σε σχέση µε το συντελεστή access skew για τα τρία συστήµατα στο δίκτυο Ν1 για περιοχή κάλυψης 10 km. Σχήµα 7: Μέσος χρόνος απόκρισης σε σχέση µε το συντελεστή access skew για τα συστήµατα Contnuous Adaptve Push και Non Adaptve Push στο δίκτυο Ν1. Σχήµα 8: Μέσος χρόνος απόκρισης σε σχέση µε το συντελεστή access skew για τα συστήµατα Contnuous Adaptve Push και Push System wth Colsons στο δίκτυο Ν1. Σχήµα 9: Μέσος χρόνος απόκρισης σε σχέση µε το συντελεστή access skew για τα τρία συστήµατα στο δίκτυο Ν2 για περιοχή κάλυψης 2 km Σχήµα 10: Μέσος χρόνος απόκρισης σε σχέση µε το συντελεστή access skew για τα τρία συστήµατα στο δίκτυο Ν2 για περιοχή κάλυψης 5 km. Σχήµα 11: Μέσος χρόνος απόκρισης σε σχέση µε το συντελεστή access skew για τα τρία συστήµατα στο δίκτυο Ν2 για περιοχή κάλυψης 10 km. Σχήµα 12: Μέσος χρόνος απόκρισης σε σχέση µε τoν συντελεστή access skew για τα συστήµατα Contnuous Adaptve Push [10] και Non Adaptve Push [9] στο δίκτυο Ν2. Σχήµα 13: Μέσος χρόνος απόκρισης σε σχέση µε τoν συντελεστή access skew για τα συστήµατα Contnuous Adaptve Push [10] και Push System wth Colsons στο δίκτυο Ν2. 6

7 Κεφάλαιο 1 : Εισαγωγή 1.1 Γενικά Σε ένα υποβρύχιο περιβάλλον, η εκποµπή αποτελεί µια σηµαντική πρόκληση για την ανάπτυξη των ασύρµατων δικτύων [1-4]. Αυτό οφείλεται στο γεγονός ότι τα ραδιοκύµατα παρουσιάζουν χαµηλές δυνατότητες διάδοσης στο νερό και τα οπτικά κύµατα επηρεάζονται πολύ από το φαινόµενο της σκέδασης και απαιτούν υψηλή ακρίβεια στην κατευθυντικότητα των ακτίνων λέιζερ. Έτσι, η τεχνολογία που παρέχει το φυσικό στρώµα στα υποβρύχια δίκτυα είναι συνήθως υλοποιήσιµη µέσω ακουστικών κυµάτων. Τα υποβρύχια ασύρµατα ακουστικά κανάλια διαθέτουν µοναδικά χαρακτηριστικά, που επηρεάζουν το σχεδιασµό των πρωτοκόλλων των δικτύων. Τα πιο σηµαντικά από αυτά τα χαρακτηριστικά είναι τα ακόλουθα: ιάδοση καθυστέρησης η οποία είναι πέντε τάξεις µεγέθους µεγαλύτερη από εκείνη που βασίζεται σε ραδιοεπικοινωνίες στην ίδια απόσταση, λόγω χαµηλής ταχύτητας του ήχου (1.5km/sec). Το διαθέσιµο εύρος ζώνης των ηχητικών επικοινωνιών είναι χαµηλό και εξαρτάται από την απόσταση µεταξύ των κόµβων επικοινωνίας. Το Ο ρυθµός σφαλµάτων δυαδικών ψηφίων (Bt Error Rate) των υποβρύχιων ακουστικών συνδέσεων είναι υψηλότερο από εκείνο των επίγειων βασισµένων σε ραδιοκύµατα. Τα τελευταία χρόνια υπάρχει µεγάλο ερευνητικό ενδιαφέρον στο σχεδιασµό των πρωτοκόλλων για τα ακουστικά υποθαλάσσια δίκτυα. Πολλά από αυτά τα πρωτόκολλα επικεντρώνονται στην προσαρµογή των ήδη διαθέσιµων MAC πρωτοκόλλων για επίγεια ασύρµατα δίκτυα µε χρήση ραδιοκυµάτων. Τέτοια παραδείγµατα είναι οι υποβρύχιες εκδόσεις των ALOHA, MACA και FAMA MAC πρωτοκόλλων που προτείνονται στα [5-7]. Εκτός από αυτές τις προσαρµογές τα περισσότερα νέα πρωτόκολλα για το ακουστικό περιβάλλον αφορούν δίκτυα µε πολύ-κατευθυντικές ζεύξεις. Ωστόσο, όλοι οι στόχοι των δικτύων που έχουν αµφίδροµες συνδέσεις µε κόµβους, κατά κύριο λόγο προσανατολίζονται σε uncast µετάδοση. Από την άλλη πλευρά, σε καταστάσεις όπου πολλοί χρήστες απαιτούν ένα σύνολο κοινών πληροφοριών από έναν κεντρικό σταθµό βάσης, η εκποµπή δεδοµένων µπορεί να εφαρµοστεί αποτελεσµατικά για αύξηση των επιδόσεων. Τέτοιες εφαρµογές µπορεί να χρησιµοποιηθούν για την παρακολούθηση του περιβάλλοντος (π.χ. ανίχνευση τσουνάµι) όπου τα δεδοµένα µπορούν να µεταδίδονται για την επίτευξη ορισµένων σηµαντικών προορισµών (π.χ. σταθµοί παρακολούθησης) και στο δίκτυο επαναπρογραµµατισµού των υποβρύχιων αισθητήρων των κόµβων του δικτύου. 7

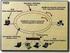
8 Σχήµα 1: Υποβρύχιο push σύστηµα µε έναν σταθµό βάσης και κινητούς χρήστες Τα συστήµατα που παρουσιάζονται παρακάτω, αποτελούνται από ένα σταθµό βάσης (βλ. Σχήµα 1) µε ικανότητες ακουστικής µετάδοσης και έναν αριθµό χρηστών που ακούνε στο σταθµό βάσης. Ο κεντρικός σταθµός βάσης αναλαµβάνει την επικοινωνία µε κάποια επίγεια πηγή πληροφοριών είτε µε ασύρµατη είτε µε ενσύρµατη σύνδεση. Τα συστήµατα αυτά χρησιµοποιούν ένα Αυτόµατο Μάθησης στο σταθµό βάσης, το οποίο περιέχει ένα διάνυσµα που αποθηκεύει την εκτίµηση του σταθµού βάσης στη τρέχουσα πιθανότητα ζήτησης µεταξύ του πλήθους των χρηστών για κάθε πακέτο δεδοµένων. Η προσαρµογή επιτυγχάνεται µε τη χρήση ανάδρασης από τους χρήστες η οποία χρησιµοποιείται από το σταθµό βάσης για την ενηµέρωση του διανύσµατος πιθανότητας εκτίµησης του πακέτου. Παραδείγµατα εφαρµογών όπου υποβρύχια δεδοµένα ραδιοκυµατικής εκποµπής θα ήταν χρήσιµα σε περιβαλλοντική παρακολούθηση (π.χ. ανίχνευση τσουνάµι), σε στήριξη υποβρύχιων επανδρωµένων αποστολών, όπου τα δεδοµένα µπορούν να µεταδίδονται για την επίτευξη ενός αριθµού σχετικών στόχων (π.χ. σταθµοί παρακολούθησης ή παρακολούθησης δυτών, αντίστοιχα). Στη συγκεκριµένη εργασία παρουσιάζονται βασικά προσαρµοστικά συστήµατα µετάδοσης σε υποβρύχια ακουστικά δίκτυα. Με προσοµοιώσεις των συστηµάτων αυτών προκύπτουν αποτελέσµατα, εξάγονται συµπεράσµατα και γίνεται σύγκριση αυτών ως προς την απόδοσή τους. Προτείνεται τελικά ένα σύστηµα το οποίο εµφανίζει την καλύτερη απόδοση σε σχέση µε τα υπόλοιπα συστήµατα που παρουσιάζονται στην συγκεκριµένη εργασία. Η δοµή της εργασίας είναι η ακόλουθη: Κεφάλαιο 1 ο : Εκτενής εισαγωγή στα υποβρύχια ακουστικά ασύρµατα δίκτυα. Κεφάλαιο 2 ο : Παρουσίαση συστηµάτων Μη προσαρµοστικών - προσαρµοστικών Push Συστηµάτων Κεφάλαιο 3 ο : Παρουσίαση Αξιολόγησης Προσοµοίωσης Αποτελεσµάτων Κεφάλαιο 4 ο : Παρουσίαση προσοµοίωσης Συστηµάτων Συµπεράσµατα Αναφορές 8

9 Κεφάλαιο 2 : Μη Προσαρµοστικά- Προσαρµοστικά Push Συστήµατα Εκποµπής 2.1 Μη Προσαρµοστικά Push Συστήµατα Εκποµπής Βασικά θέµατα µη προσαρµοστικών Push συστηµάτων Εκποµπής Η βάση δεδοµένων στο σταθµό βάσης θεωρείται ότι περιέχει πολλά πακέτα πληροφοριών. Τα πακέτα δεν έχουν απαραίτητα το ίδιο µέγεθος. Ο χρόνος που απαιτείται για τη µετάδοση ενός πακέτου µήκους µίας µονάδας αναφέρεται ως µονάδα χρόνου. Έτσι, ο χρόνος που απαιτείται για να µεταδοθεί ένα πακέτο µήκους l είναι l µονάδες χρόνου. Με M υποδηλώνεται ο συνολικός αριθµός των πακέτων πληροφοριών στη βάση δεδοµένων του σταθµoύ βάσης. Τα πακέτα είναι αριθµηµένα από 1 έως Μ. Το l αντιπροσωπεύει το µήκος του πακέτου. Η άφιξη των αιτήσεων από χρήστες θεωρείται ότι θα διέπεται από µια διαδικασία Posson. Η παρουσία ενός πακέτου στην µετάδοση θα αναφέρεται ως η εµφάνιση του πακέτου. Η απόσταση µεταξύ δύο διαδοχικών εµφανίσεων για ένα πακέτο είναι ο χρόνος που χρειάζεται για τη µετάδοση πληροφοριών από την αρχή της πρώτης εµφάνισης µέχρι την έναρξη της δεύτερης. Αν όλες οι συνεχόµενες εµφανίσεις του πακέτου έχουν την ίδια απόσταση µεταξύ τους, τότε η τιµή s υποδηλώνει την απόσταση για το πακέτο. Ο Μέσος Χρόνος Προσπέλασης Πακέτου, συµβολίζεται ως t και ορίζεται ως ο µέσος χρόνος αναµονής ενός χρήστη που χρειάζεται το πακέτο µέχρι την έναρξη της λήψης του πακέτου από το σταθµό βάσης. Εάν όλες οι διαδοχικές εµφανίσεις του πακέτου είναι ίσης απόστασης s µεταξύ τους, τότε, από την υπόθεση της διαδικασίας Posson για τις αφίξεις των αιτήσεων, συνεπάγεται ότι [3] t= s / 2 Η πιθανότητα ζήτησης p υποδηλώνει την πιθανότητα του πακέτου να ζητείται σε κάθε αίτηση. Η πιθανότητα ζήτησης ορίζεται ως ο µέσος όρος για όλους τους χρήστες που εξυπηρετούνται από το σταθµό βάσης. Εδώ, υποθέτουµε ότι όλα τα πακέτα έχουν την ίδια προτεραιότητα. Όταν διάφορα πακέτα έχουν διαφορετικές προτεραιότητες, µπορεί να είναι πιο σηµαντικό να κρατηθούν λιγότερο οι χρόνοι προσπέλασης για ορισµένα πακέτα από κάποια άλλα (ανεξάρτητα της πιθανότητας ζήτησης τους). Μια πιθανή προσέγγιση που να λαµβάνει υπόψη τις προτεραιότητες είναι να αποδίδεται βαρύτητα w στους χρόνους προσπέλασης του πακέτου, σύµφωνα µε την προτεραιότητά του. Όταν προστίθενται οι τιµές της βαρύτητας, η παρακάτω ανάλυση πρέπει να τροποποιηθεί για να αντικατασταθεί κάθε εµφάνιση του p µε ( pw ). Για λόγους απλότητας, θα υποθέσουµε ότι όλα τα πακέτα έχουν την ίδια προτεραιότητα - συνεπώς, w υποτίθεται ότι είναι 1 για όλα τα. Ο Συνολικός Μέσος Χρόνος Προσπέλασης, συµβολίζεται ως t, και ορίζεται ως ο µέσος όρος αναµονής ενός αιτήµατος. Ως εκ τούτου [3], t= p t (1) M = 1 9

10 Όταν οι συνεχόµενες εµφανίσεις του πακέτου απέχουν s µεταξύ τους, τότε t= s / 2, οπότε ο συνολικός µέσος χρόνος προσπέλασης δίνεται από 1 t= p s (2) 2 M = Επισκόπηση Βιβλιογραφίας Συστήµατα Εκποµπής εδοµένων Μια δηµοφιλής προσέγγιση στον τοµέα των συστηµάτων push είναι οι δίσκοι εκποµπής [11]. Τα δεδοµένα µε τη µεγαλύτερη ζήτηση είναι τοποθετηµένα στον ταχύτερο δίσκο, µε αποτέλεσµα τη δηµιουργία ενός περιοδικού σχεδιασµού ώστε να µεταδίδονται πιο συχνά. Επίσης, προτείνονται ορισµένες τεχνικές διαχείρισης µνήµης µε στόχο τη βελτίωση της απόδοσης των χρηστών του συστήµατος σε σχέση µε τις απαιτήσεις του σταθµού βάσης. Το σύστηµα αυτό ασχολείται µε ζητήµατα όπως οι επιπτώσεις των αλλαγών στις τιµές των δεδοµένων του σταθµού βάσης µεταξύ διαδοχικών εκποµπών [15] και της προσθήκης ενός καναλιού ανάδρασης που επιτρέπει στους χρήστες να στέλνουν σαφή αιτήµατα προς τον σταθµό βάσης [16]. Η τελευταία προσέγγιση µπορεί να θεωρηθεί ως ένα υβριδικό σύστηµα. Η προσέγγιση των δίσκων εκποµπής δεν προσαρµόζεται σε µεταβαλλόµενα περιβάλλοντα, καθώς βασίζεται στη γνώση του σταθµού βάσης µε βάση µια στατική ζήτηση των χρηστών για πακέτα πληροφορίας, µε αποτέλεσµα την προκαθορισµένη προγραµµατισµένη εκποµπή. Επιπλέον, τα πακέτα των δεδοµένων περιορίζονται σε σταθερού µεγέθους και δεν παρουσιάζουν έναν τρόπο που καθορίζει έναν βέλτιστο ιδανικό αριθµό δίσκων ή τις αντίστοιχες συχνότητές τους. Αυτοί οι αριθµοί επιλέγονται εµπειρικά, έχοντας ως αποτέλεσµα, ο σταθµός βάσης να αδυνατεί να εκπέµπει τα πακέτα δεδοµένων µε µεγαλύτερη ζήτηση ακόµα και σε περιπτώσεις των στατικών µοντέλων ζήτησης. Υποθέτοντας ότι τα στιγµιότυπα του κάθε πακέτου ισαπέχουν στο πρόγραµµα εκποµπής, συµπεραίνουµε ότι ο µέσος χρόνος απόκρισης ελαχιστοποιείται όταν ο σταθµός βάσης εκπέµπει ένα πακέτο µε συχνότητα ανάλογη της τετραγωνικής ρίζας του παράγοντα d / l, όπου d είναι η συνολική πιθανότητα ζήτησης χρήστη για το πακέτο και l είναι το µήκος του [9]. Στο ίδιο σύστηµα υποστηρίζεται ότι εκτός από το µέσο χρόνο προσπέλασης χρήστη, θα πρέπει να ληφθεί υπόψη και η διακύµανση του χρόνου απόκρισης του σχεδιασµού εκποµπής. Οι αλγόριθµοι αυτοί παρέχουν µια ισορροπία µεταξύ της ελαχιστοποίησης του µέσου χρόνου προσπέλασης χρήστη και των διακυµάνσεων. Οι παραπάνω προσεγγίσεις είναι πρακτικές µόνο για σταθερά περιβάλλοντα, αφού κανένα µέσο ενηµέρωσης των πιθανοτήτων των δεδοµένων δεν προτείνεται. Η εκποµπή δίσκων βασίζεται σε ένα στατικό πρότυπο ζήτησης του σταθµού βάσης, το οποίο έχει ως αποτέλεσµα τα µη προκαθορισµένα προγράµµατα εκποµπής. Επίσης, οι προαναφερθείσες προσεγγίσεις υποθέτουν ότι οι πιθανότητες πρόσβασης των πακέτων δεδοµένων είναι διαθέσιµες και συνεπώς, περιορισµένες σε σχέση µε τη µεταβαλλόµενη ζήτηση. Η µέθοδος που προτείνεται στο [8] και [10] προτείνει ένα σύστηµα ώθησης που είναι προσαρµοσµένο σε δυναµικές απαιτήσεις χρηστών. Χρησιµοποιείται ένα µανθάνον αυτόµατο στο σταθµό βάσης διατηρώντας παράλληλα την υπολογιστική πολυπλοκότητά του συστήµατος στο [9]. 10

11 Χρησιµοποιώντας πληροφορία ανάδρασης από τους χρήστες, το αυτόµατο συνεχώς προσαρµόζεται στη ζήτηση πληροφορίας από τους χρήστες Υποβρύχια Συστήµατα Εκποµπής Παρά το γεγονός ότι µέχρι στιγµής δεν έχουν µελετηθεί εκτενώς τα υποβρύχια δίκτυα, προτείνονται τρία πρωτόκολλα εκποµπής [12-13] βασισµένα σε διόρθωση λαθών (FEC) όπου οι χρήστες µπορούν να ενεργούν ως πράκτορες κατά την εκποµπή του σταθµού βάσης εκποµπής προς τους αποµακρυσµένους χρήστες. Αυτή η λειτουργία βασίζεται στη σχέση εύρους ζώνης-απόστασης του υποθαλάσσιου ακουστικού περιβάλλοντος µε αποτέλεσµα, χρησιµοποιώντας συγκεκριµένες ζώνες συχνοτήτων, τα σήµατα να διανύουν µεγάλες αποστάσεις. Αυτό οδηγεί σε µια µείωση του αριθµού των εκποµπών που απαιτούνται για την ολοκλήρωση της µετάδοσης, η οποία µε τη σειρά της µειώνει και τη συνολική κατανάλωση ενέργειας και το συνολικό χρόνο που χρειάζεται Η Μέθοδος του Vadya [9] Το Λήµµα 1 παρακάτω δηλώνει µια παρατήρηση που προκύπτει από το αποτέλεσµα που παρουσιάζεται στο [15]. Λήµµα 1. Ο αλγόριθµος µετάδοσης µε ελάχιστο συνολικό µέσο χρόνο προσπέλασης προκύπτει όταν οι εµφανίσεις κάθε πακέτου έχουν ίσες αποστάσεις µεταξύ τους. Θεώρηµα 1 (κανόνας τετραγωνικής ρίζας). Υποθέτοντας ότι οι εµφανίσεις κάθε πακέτου έχουν ίσες αποστάσεις µεταξύ τους, ο ελάχιστος συνολικός µέσος χρόνος πρόσβασης επιτυγχάνεται όταν η απόσταση s του κάθε l πακέτου είναι ανάλογη µε l και αντιστρόφως ανάλογη µε p. Οπότε s. p Ο βέλτιστος συνολικός µέσος χρόνος πρόσβασης, που ονοµάζεται t optmal, λαµβάνεται ως: M 1 2 optmal= ( ) 2 p l (3) = 1 t Η t optmal υπολογίζεται υποθέτοντας ότι οι εµφανίσεις του κάθε πακέτου έχουν ίσες αποστάσεις µεταξύ τους. εδοµένου ότι η υπόθεση αυτή δεν µπορεί πάντα να πραγµατοποιηθεί, η t optmal αντιπροσωπεύει ένα κατώτερο όριο για τον συνολικό µέσο χρόνο πρόσβασης που µπορεί να επιτευχθεί. Το κατώτερο όριο, σε γενικές γραµµές, δεν είναι εφικτό. Ωστόσο, όπως φαίνεται στη συνέχεια, είναι δυνατόν να επιτευχθεί συνολικός µέσος χρόνος προσπέλασης σχεδόν ίσος µε αυτόν στο κατώτερο όριο. Στη συνέχεια παρουσιάζεται ο αλγόριθµος εκποµπής του [9]. 11

12 Αλγόριθµος Σχεδιασµού Εκποµπής Κάθε φορά που ο σταθµός βάσης είναι έτοιµος να εκπέµψει ένα νέο πακέτο, καλεί τον αλγόριθµο που παρουσιάζεται εδώ. Ο αλγόριθµος ορίζει το επόµενο πακέτο που πρέπει να µεταδοθεί χρησιµοποιώντας έναν κανόνα απόφασης - αυτός ο κανόνας βασίζεται στο θεώρηµα 1. Από το θεώρηµα 1 συνεπάγεται ότι, για την βέλτιστη απόδοση, οι εµφανίσεις του πακέτου θα πρέπει να έχουν την ίδια απόσταση s µεταξύ τους, έτσι ώστε: 2 s p l = cons tan t,,1 M (4) Η παραπάνω παρατήρηση χρησιµοποιείται στον αλγόριθµό όπως παρουσιάζεται παρακάτω. Με Q υποδηλώνεται η τρέχουσα χρονική στιγµή. Ο αλγόριθµος παρακάτω αποφασίζει για το ποιο πακέτο θα µεταδώσει σε χρόνο Q. Με R( j ) χαρακτηρίζεται η χρονική στιγµή κατά την οποία έγινε η πιο πρόσφατη εκποµπή της εµφάνισης του πακέτου j. Αν το πακέτο j δεν έχει µεταδοθεί ποτέ, το R( j ) ξεκινά µε τιµή -1. Σηµειώνεται ότι το R( j ) ενηµερώνεται όποτε µεταδίδεται το πακέτο j. Η συνάρτηση G( j ) µπορεί να οριστεί ως G j = Q R j p l j M. Ο πρώτος αλγόριθµος προγραµµατισµού εκποµπής 2 ( ) ( ( )) j / j,1 ονοµάζεται αλγόριθµος Α. Αλγόριθµος µετάδοσης Α Βήµα 1. Ορίζεται η µέγιστη τιµή της G( j ) για όλα τα πακέτα j,1 j M. Η G( ) υποδηλώνει τη µέγιστη τιµή του G( j ). Βήµα 2. Επιλέγεται το πακέτο τέτοιο ώστε G( ) = Gmax. Εάν αυτή η ισότητα ισχύει για περισσότερα από ένα πακέτα, επιλέγεται ένα από αυτά αυθαίρετα. Βήµα 3. Μεταδίδεται το πακέτο κατά το χρόνο Q. Βήµα 4. R () = Q. Q - R () είναι το διάστηµα µεταξύ της τρέχουσας χρονικής στιγµής, και του χρόνου κατά 2 τον οποίο µεταδόθηκε το πακέτο. Σηµειώνεται ότι η συνάρτηση G( ) = ( Q R( )) p / l 2 είναι παρόµοια µε τον όρο s p / l στην εξίσωση (4). Το κίνητρο για αυτόν τον αλγόριθµο είναι η προσπάθεια να επιτευχθεί η ισότητα στην εξίσωση (4), στο µέτρο του δυνατού. Παράδειγµα 1. Θεωρούµε µια βάση δεδοµένων που περιέχει 3 πακέτα έτσι ώστε p= 1 1/ 2, p 2= 3 / 8 και p= 3 1/ 8. Ας υποθέσουµε ότι τα πακέτα έχουν µήκη l 1 = 1, l 2 = 2, l 3 = 4 µονάδες χρόνου. Το σχήµα 1 εµφανίζει τα πακέτα που µεταδόθηκαν πρόσφατα από τον σταθµό βάσης (χρόνο<100). Ο παραπάνω αλγόριθµος καλείται να ορίσει το πακέτο που πρέπει να 12

13 µεταδοθεί κατά την χρονική στιγµή 100. Έτσι, Q = 100. Επίσης, στο Σχήµα 2 παρατηρούµε ότι R1= 95, R2= 93, R3= 96. Ο αλγόριθµος υπολογίζει τις τιµές της 2 συνάρτηση G( j) = ( Q R( j)) p / l για j =1,2,3 ως 12.5, 147/16(=9.1875) και 0.5, j j αντίστοιχα. Αφού η G( j ) παίρνει την µεγαλύτερη τιµή για j = 1, το πακέτο 1 µεταδίδεται κατά το χρόνο 100. Σχήµα 2: Παράδειγµα Επίδραση των σφαλµάτων εκποµπής στην στρατηγική σχεδιασµού Οι αλγόριθµοι που παρουσιάζονται παραπάνω δεν λαµβάνουν υπόψη τους σφάλµατα κατά την εκποµπή. Σε αυτήν την ενότητα τροποποιούµε την βασική προσέγγισή µας στο σχεδιασµό αλγορίθµων εκποµπής σχετικά µε την παρουσία σφαλµάτων στην µετάδοση. Μέχρι στιγµής, υποθέτουµε ότι κάθε πακέτο που µεταδίδεται από το σταθµό βάσης λαµβάνεται πάντα σωστά από κάθε χρήστη. εδοµένου ότι το ασύρµατο µέσο υπόκειται σε παρεµβολές και αστοχίες η υπόθεση αυτή δεν ισχύει απαραίτητα. Παραδοσιακά, σε ένα περιβάλλον που υπόκειται σε αστοχίες, τα δεδοµένα είναι κωδικοποιηµένα µε κώδικες ελέγχου σφαλµάτων (error control codes - ECC). Αυτοί οι κωδικοί δίνουν τη δυνατότητα στο χρήστη να "διορθώσει" κάποια σφάλµατα, δηλαδή να ανακτήσει τα δεδοµένα, παρά τα σφάλµατα αυτά. Ωστόσο, οι ECC δεν µπορούν διορθώσουν µεγάλο αριθµό σφαλµάτων στα δεδοµένα. Όταν αυτά τα σφάλµατα ανιχνεύονται (αλλά δεν µπορούν να διορθωθούν από το χρήστη), ο σταθµός βάσης συνήθως καλείται να αναµεταδώσει τα δεδοµένα. Στο ασύµµετρο περιβάλλον που εξετάζεται εδώ, δεν είναι δυνατόν για το χρήστη να ζητήσει από το σταθµό βάσης την αναµετάδοση των δεδοµένων. Αν ένας χρήστης που αναµένει το πακέτο λάβει µια εµφάνιση του πακέτου µε σφάλµατα, το πακέτο απορρίπτεται από το χρήστη, ο οποίος θα πρέπει να περιµένει για την επόµενη εµφάνιση του πακέτου. Στην ενότητα αυτή, θα αξιολογήσουµε τον αντίκτυπο των σφαλµάτων όσον αφορά στη στρατηγική σχεδιασµού εκποµπής. Ας υποθέσουµε ότι υπάρχουν ανεπανόρθωτα σφάλµατα σε ένα πακέτο µε µήκος l µε πιθανότητα E( l ). Ως l δηλώνει το µήκος του πακέτου µετά την κωδικοποίηση µε έναν κωδικό ελέγχου σφάλµατος. Ο συνολικός µέσος χρόνος πρόσβασης, t, υποθέτοντας ότι οι εµφανίσεις του πακέτου έχουν ίσες αποστάσεις µεταξύ του s, δίνεται από τον τύπο: t= 1 2 M = E( l ) s p 1 E( l ) 13

14 Ο κανόνας της τετραγωνικής ρίζας στο θεώρηµα 1, για να λάβει υπ όψη του τα σφάλµατα, πρέπει να τροποποιηθεί µε βάση το Θεώρηµα 2 που ακολουθεί. Θεώρηµα 2. εδοµένου ότι η πιθανότητα εµφάνισης σφαλµάτων σε ένα πακέτο µήκους l είναι E( l ), ο συνολικός µέσος χρόνος προσπέλασης ελαχιστοποιείται όταν: s l p 1 + E( l ) 1 E( l ) Σηµειώνεται ότι όταν όλα τα πακέτα έχουν το ίδιο µήκος, ο όρος 1 E( l ) /1 + E( l ) γίνεται µια σταθερά (ανεξάρτητη του ). Ως εκ τούτου, στην περίπτωση αυτή, το θεώρηµα 2 εκφυλίζεται στο θεώρηµα 1. Το κατώτερο όριο του συνολικού µέσου χρόνου πρόσβασης γίνεται τώρα [20] t M 1 opt _ error= 2 pl = E( l ) ( ) 1 E( l ) 2 Από το θεώρηµα 2 συνεπάγεται ότι σε έναν βέλτιστο αλγόριθµο έχουµε: 2 s p 1 + E( l ) = cons tan t,1 M l 1 E( l ) Οι αλγόριθµοι που παρουσιάστηκαν προηγουµένως µπορεί να τροποποιηθούν λίγο για να ληφθεί υπ όψη και το παραπάνω αποτέλεσµα. Για παράδειγµα, ο αλγόριθµος Α µπορεί να χρησιµοποιηθεί έτσι, µε εξαίρεση ότι η συνάρτηση G( j) θα πρέπει να 2 επαναπροσδιοριστεί ως: 1 + E ( l ) G( j) = ( Q R( I j )) p j / l j,1 j M (5) 1 E ( l ) 14

15 2.2 Προσαρµοστικό Push Σύστηµα για Υποβρύχια Εκποµπή Τα Μανθάνοντα Αυτόµατα Τα Μανθάνοντα Αυτόµατα είναι µηχανισµοί που µπορούν να εφαρµοστούν για την εκµάθηση των χαρακτηριστικών του περιβάλλοντος ενός συστήµατος. Ένα Μανθάνον Αυτόµατο είναι ένα αυτόµατο που βελτιώνει την απόδοσή του µε την αλληλεπίδραση µέσω ενός τυχαίου περιβάλλοντος στο οποίο λειτουργεί. Σκοπός του είναι να βρούµε τη βέλτιστη δυνατή ενέργεια ανάµεσα σε µια σειρά ενεργειών, έτσι ώστε η ποινή που θα δώσει το περιβάλλον να είναι η ελάχιστη. Αυτό σηµαίνει ότι υπάρχει ένας µηχανισµός ανάδρασης που ειδοποιεί και ενηµερώνει το αυτόµατο ανάλογα µε την ποινή του περιβάλλοντος κατά την εκτέλεση µιας συγκεκριµένη ενέργειας. Η λειτουργία ενός Μανθάνοντος Αυτοµάτου αποτελείται από µια ακολουθία κύκλων χρόνου που τελικά οδηγούν σε ελαχιστοποίηση του µέσου κόστους. Το Μανθάνον Αυτόµατο χρησιµοποιεί έναν πίνακα p( n) = p1( n), p2 ( n),..., pa( n) που αντιπροσωπεύει την κατανοµή πιθανοτήτων για την επιλογή µιας από τις ενέργειες a1, a2,..., a κατά τον χρονικό κύκλο n. A Προφανώς A = 1. p ( n) = 1 Ο βασικός πυρήνας της λειτουργίας του Αυτοµάτου [19] είναι ο αλγόριθµος ανανέωσης πιθανότητας, ο οποίος χρησιµοποιεί την απόκριση περιβάλλοντος β(n) που προκαλείται από την επιλεγµένη ενέργεια a κατά την εκτέλεση του χρονικού κύκλου n έτσι ώστε να ενηµερωθεί ο πίνακας κατανοµής πιθανοτήτων p. Αφού ολοκληρωθεί η ενηµέρωση, το αυτόµατο επιλέγει την ενέργεια που εκτελείται στον χρονικό κύκλο p(n+1). Παρακάτω παρουσιάζεται ένα σχήµα ανανέωσης πιθανοτήτων όπου a( n ) µια µεταβλητή που κρατά την ενέργεια που επιλέχθηκε από το σύνολο a1, a2,..., a κατά τον κύκλο του χρόνου n: A p ( n + 1) = p ( n) (1 β( n)) g ( p( n)) + β( n) h ( p( n)), f _ a( n) a p ( n + 1) = p ( n) (1 + β( n)) g ( p( n)) β( n) h ( p( n)), f _ a( n = a ) j j j j (6) Ο κύκλος n ορίζεται ως η χρονική περίοδος κατά την οποία το Μανθάνον Αυτόµατο επιλέγει µία από τις ενέργειες, a1, a2,..., a, την εκτελεί, λαµβάνει την απόκριση A περιβάλλοντος β(n) η οποία ενεργοποιείται από την ενέργεια a και ενηµερώνει τον πίνακα κατανοµής πιθανοτήτων. Οι συναρτήσεις gκαι h συνδέονται µε το κέρδος και τη ποινή της ενέργειας, αντίστοιχα, και το β(n) είναι µια κανονικοποιηµένη µετρική της απόκρισης περιβάλλοντος. Όσο χαµηλότερη είναι η τιµή β(n), τόσο καλύτερη η απόκριση. Όταν η β(n) παίρνει συνεχόµενες τιµές µετά την κανονικοποίηση στο διάστηµα [0,1], τότε το Αυτόµατο είναι γνωστό ως S-model. Στον τοµέα της δικτύωσης, τα µανθάνοντα αυτόµατα έχουν εφαρµοστεί σε διάφορα προβλήµατα 15

16 Βασικές Λειτουργίες του Αλγορίθµου Εκποµπής των Προσαρµοστικών Push Συστηµάτων Ο κεντρικός σταθµός εκποµπής είναι εξοπλισµένος µε ένα S γραµµικό Αυτόµατα Ανταµοιβής-Αδράνειας (S-model Lnear Reward-Inacton Learnng Automaton) που περιέχει τις πιθανότητες p του κεντρικού σταθµού για τις πραγµατικές πιθανότητες ζήτησης d για κάθε ένα πακέτο δεδοµένων από ένα σύνολο πακέτων προς µετάδοση. N N Προφανώς, ισχύει p ( ) ( ) 1 1 n = d 1 n = = όπου Ν είναι ο αριθµός των πακέτων που = εκπέµπει ο κεντρικός σταθµός. Όπως και στην προτεινόµενη προσέγγιση [8] - [10], [17] - [20], σε κάθε κύκλο, ο σταθµό βάσης επιλέγει να µεταδώσει το πακέτο που µεγιστοποιεί την συνάρτηση κόστους: G = T R p l + E l E l (7) 2 ( ) ( ( )) ( / )((1 ( )) / (1 ( ))) όπου Τ είναι η τρέχουσα ώρα, R( ) είναι η χρονική στιγµή του τελευταίου πακέτου εκποµπής, l είναι το µήκος του πακέτου και E( l ) είναι η πιθανότητα του πακέτου µε µήκος l να ληφθεί λανθασµένα. Για τα πακέτα που δεν έχουν προηγουµένως εκπεµφθεί, έχει οριστεί το R σε -1. Αν η µέγιστη τιµή της G( ) είναι κοινή για περισσότερα από ένα πακέτα, ο αλγόριθµος επιλέγει ένα από αυτά αυθαίρετα. Μετά την εκποµπή του πακέτου τη χρονική στιγµή T, η τιµή του R( ) αλλάζει έτσι ώστε R( ) = T. Ο σταθµός βάσης θα εξετάσει τα πακέτα δεδοµένων ώστε να λάβουν ανάδραση από τους χρήστες, έτσι ώστε να υπολογιστεί η πιθανότητα ζήτησης για κάθε πακέτο δεδοµένων. Σηµειώνουµε εδώ ότι η ανάδραση θα αφορά µεµονωµένα πακέτα, έτσι δεν είναι υπεύθυνη να αναγνωρίσει ολόκληρες οµάδες των δεδοµένων. Η εκποµπή ανάδρασης πραγµατοποιείται µε την Code Dvson Multple Access (CDMA), η οποία έχει επίσης χρησιµοποιηθεί στα υποβρύχια ακουστικά περιβάλλοντα Από την άλλη πλευρά, τα πακέτα δεδοµένων εκποµπής κάνουν χρήση ολόκληρου του διαθέσιµου εύρους ζώνης της στενής ζώνης για µετάδοση δεδοµένων. Κάθε χρήστης που ήταν σε αναµονή για το πακέτο που µεταδόθηκε στέλνει την ανατροφοδότησή του στο σταθµό βάσης, χρησιµοποιώντας το CDMA του. Τελικά ο σταθµός βάσης διαχωρίζει τα σήµατα µε τη χρήση ενός συσχετιστή. Ο αριθµός των κινητών χρηστών που µπορούν να υποστηριχθούν στο σύστηµα µε τη βοήθεια του CDMΑ δίνεται από τον τύπο: W ClNum= E FB b / / U N FB 0 (8) όπου ClNum είναι ο αριθµός των υποστηριζόµενων κινητών χρηστών, WFB αντιπροσωπεύει το εύρος ζώνης µετάδοσης για την ανάδραση, U FB αντιπροσωπεύει τη µετάδοση της ανάδρασης δεδοµένων bt rate, και Eb / N 0 είναι η ενέργεια προς το θόρυβο της φασµατικής πυκνότητας ισχύος σε γραµµική κλίµακα. Μπορεί να γίνει εύκολα κατανοητό ότι η αυξηµένη καθυστέρηση (latency) που εισάγει η 16

17 Σχήµα 3: Σύγκλιση της εκτίµησης αυτόµατου της πιθανότητας ζήτησης πακέτου. διάδοση των πακέτων ανάδρασης στη διαδικασία της µετάδοσης δεδοµένων επηρεάζουν όπως είναι αναµενόµενο αρνητικά την απόδοση του συστήµατος και έχουν σαν συνέπεια µια σηµαντική καθυστέρηση στο µέσο χρόνο απόκρισης του συστήµατος του [8]. Το παραπάνω πρόβληµα µπορεί να διασαφηνιστεί µε το παρακάτω παράδειγµα που έχει ως εξής: Ένας κεντρικός σταθµός θεωρείται ότι έχει δυνατότητες ακουστικής µετάδοσης πακέτων δεδοµένων σε ένα περιβάλλον που συντελείται από υποβρύχιους πελάτες, τοποθετηµένους εντός της ακτίνας εµβέλειάς του της τάξης των 10 km. Αυτό δίνει ένα µέγιστο συνολικό χρόνο Round Trp Tme (MAX_RTT) περίπου 13 sec. Τυπικές παράµετροι επικοινωνίας για αποστάσεις µέχρι 10 km αναφέρονται στο [2], και χρησιµοποιούνται επίσης στο κοµµάτι που εξετάζεται η απόδοση του προτεινόµενου συστήµατος. Σύµφωνα λοιπόν, µε τα παραπάνω, θεωρείται διαθέσιµο ένα συνολικό εύρος ζώνης για µετάδοση 10 khz µε ρυθµό µετάδοσης 2.4 kbps data rate. Επιπρόσθετα, το µέγεθος των πακέτων δεδοµένων είναι 1000 bts. Αν χρησιµοποιηθεί ένα εύρος της τάξης 200 Hz του διαθέσιµου εύρους ζώνης για τη µετάδοση των πακέτων ανάδρασης του συστήµατος, τότε το υπόλοιπο είναι διαθέσιµο εξ ολοκλήρου για µετάδοση των πακέτων δεδοµένων προς εξυπηρέτηση των πελατών. Συνεπώς, µε 9.8 khz διαθέσιµο εύρος ζώνης µπορούν να επιτευχθούν ταχύτητες µετάδοσης 2.35 kbps που σηµαίνει χρόνο µετάδοσης πακέτου (tem transmsson tme) 0.42 sec. Επιπλέον, για να µπορούν να χρησιµοποιηθούν όσο το δυνατόν περισσότεροι πελάτες, η σχέση (7) σηµαίνει ότι πρέπει να χρησιµοποιηθεί ένας µικρός ρυθµός µετάδοσης πακέτων ανάδρασης. Για το λόγο αυτό ο ρυθµός µετάδοσης των ανατροφοδοτήσεων µεγέθους 1 bt είναι 0.5 bps για τους πελάτες του [8] και ο απαιτούµενος χρόνος µετάδοσης πακέτων ανάδρασης (feedback transmsson tme) είναι 2 sec. Όσον αφορά την ανταλλαγή του ποσού του εύρους ζώνης µεταξύ των δεδοµένων και της ανάδρασης, µπορεί κανείς να δει ότι για την ίδια τιµή των υποστηριζόµενων χρηστών, αν αφιερώνουµε περισσότερο εύρος ζώνης στην ανάδραση, το ποσοστό ανάδρασης αυξάνεται και το ποσοστό των δεδοµένων µειώνεται. Έτσι, το σύστηµα θα µεταδίδει σε χαµηλότερη ταχύτητα, αλλά θα έχει αυξηµένο ρυθµό µάθησης των απαιτήσεων του χρήστη λόγω του αυξηµένου ποσοστού ανάδρασης. Ωστόσο, σε ένα αργά µεταβαλλόµενο περιβάλλον, που συνήθως βρίσκεται στα πλαίσια δεδοµένων µιας ραδιοκυµατικής εκποµπής, ο ταχύτερος ρυθµός εκµάθησης της πιθανότητας ζήτησης δεν θα παρείχε πρόσθετη απόδοση (όπως φαίνεται στο [16]), έτσι το 17

18 αποτέλεσµα θα ήταν η αύξηση του χρόνου απόκρισης (µειώνοντας έτσι την απόδοση). Η καθυστέρηση διάδοσης δε θα επηρεάσει το υποβρύχιο σύστηµα καθώς µεταδίδει συνεχώς πακέτα δεδοµένων και δεν επιβαρύνεται από την καθυστέρηση διάδοσης. Έτσι λοιπόν από το παραπάνω σενάριο προκύπτει ότι για το σύστηµα του [8] η συλλογή πακέτων ανάδρασης µετά από κάθε εκποµπή πακέτων δεδοµένων θα οδηγήσει σε χρησιµοποίηση των ακουστικών συνδέσεων καθώς η χρησιµοποίηση θα ισούται µε Item _ tme / (MAX _ RTT + Item _ tme + Fdb _ tme) = 0.42/( ) =2.7% όπου Item _ tme + Fdb _ tme είναι οι διάρκειες εκποµπής των πακέτων δεδοµένων και ανάδρασης αντίστοιχα. Για να επιλυθεί το παραπάνω πρόβληµα το σύστηµα µπορεί να αλλάξει, υιοθετώντας ένα συνεχόµενο τρόπο µετάδοσης, κάνοντας τον κεντρικό σταθµό να προχωρά αµέσως στη µετάδοση του επόµενου πακέτου αφού ολοκληρώσει τη µετάδοση του προηγούµενου. Σε αυτήν την περίπτωση ο κεντρικός σταθµός θα ζητά πακέτα ανάδρασης µια φορά κάθε 2 / 0.42 = 5 µεταδόσεις πακέτων, έτσι ώστε να υπάρχει αρκετός χρόνος για τους χρήστες να ολοκληρώσουν προηγούµενες εκποµπές ανατροφοδοτήσης. Ωστόσο ένα νέο πρόβληµα εµφανίζεται σε αυτήν την προσέγγιση. Η αυξηµένη καθυστέρηση στις ακουστικές συνδέσεις οδηγεί σε πρόβληµα συλλογής των πακέτων ανάδρασης καθώς πλέον λαµβάνονται ασύγχρονα σε σχέση µε τις αντίστοιχες µεταδόσεις πακέτων. Αυτό σηµαίνει ότι θα υπάρχουν περιπτώσεις που ο κεντρικός σταθµός θα θέλει επιβεβαίωση σχετικά µε το πακέτο στο οποίο αντιστοιχεί το λαµβανόµενο πακέτο ανάδρασης που λαµβάνει. Στα πλαίσια του προηγούµενου παραδείγµατος, µε τη διαφορά ότι τώρα µεταδίδονται πακέτα δεδοµένων µε συνεχόµενο τρόπο, ένα νέο πακέτο ανάδρασης θα απαιτείται κάθε fdb _ tme sec. Για τη µετάδοση ενός συγκεκριµένου πακέτου Ρ, το πακέτο ανάδρασης µπορεί να φτάσει στον κεντρικό σταθµό σε µέγιστο χρόνο ίσο µε: MAX _ RTT + Item _ tme + Fdb _ tme = 15.4 sec,µετά το ξεκίνηµα της µετάδοσης του πακέτου Ρ. Αυτός ο χρόνος φυσικά αντιστοιχεί στις απαιτήσεις ενός χρήστη τοποθετηµένου στα 10 km από τον κεντρικό σταθµό. Ωστόσο, σε αυτό το χρονικό διάστηµα ο εξυπηρετητής θα έχει εκπέµψει 15.4 / 2 = 8 ακόµη πακέτα δεδοµένων. Για αυτά τα πακέτα ο κεντρικός σταθµός µπορεί κάλλιστα να έχει ήδη λάβει τις ανατροφοδοτήσεις τους αν αυτά αφορούσαν χρήστες τοποθετηµένους κοντύτερα στο σταθµό µετάδοσης από αυτά που στάλθηκαν για το πακέτο P. Από τα παραπάνω προκύπτει ότι µια συνεχόµενη µετάδοση ενός bt πακέτων ανάδρασης οδηγεί σε αβεβαιότητα όσον αφορά στα πακέτα δεδοµένων τα οποία προκάλεσαν την αποστολή των εισερχόµενων πακέτων ανάδρασης. Το πρόβληµα αυτό λύνεται αυξάνοντας το µέγεθος των ανατροφοδοτήσεων ώστε να περιέχουν το d από τα πακέτα τα οποία απαντούν. Συνεπώς κάθε χρήστης στέλνει απαντήσεις µεγέθους 1 + [log 2 N] bts, όπου Ν ο αριθµός των πακέτων προς εκποµπή στη βάση δεδοµένων του κεντρικού σταθµού Ο τρόπος Ανανέωσης των Πιθανοτήτων Για τη συλλογή των πακέτων ανάδρασης από τους χρήστες ο σταθµός εκποµπής χρησιµοποιεί ένα n band κανάλι µέσα σε αυτό των µεταδιδόµενων δεδοµένων. Στο κανάλι αυτό µεταδίδονται (pggybackng) δύο δυαδικοί αριθµοί Α και Β. Το Α είναι ένας αριθµός µεγέθους ενός bt (flag) ενώ το Β αποτελείται από log 2 N αριθµό bts. Όταν ο κεντρικός σταθµός δεν απαιτεί απαντήσεις ανάδρασης από τον πληθυσµό των χρηστών µετά τη µετάδοση ενός πακέτου δεδοµένων ειδοποιεί όλους τους πελάτες θέτοντας στην κεφαλίδα του µεταδιδόµενου πακέτου Α=0. Όταν ο κεντρικός σταθµός απαιτεί αποστολή πακέτων ανάδρασης από τους πελάτες που περιµένουν το πακέτο j, θέτει στην κεφαλίδα του µεταδιδόµενου πακέτου Α=1 και Β= j. Έτσι το πακέτο ανάδρασης που στέλνει κάθε χρήστης όταν έλαβε το πακέτο που ζητούσε 18

19 θα αποτελείται από 1 + [log 2 N] bts, όπου Ν είναι ο αριθµός των πακέτων που µεταδίδει ο σταθµός βάσης. Μετά τη µετάδοση ενός πακέτου που απαιτεί απάντηση µε αποστολή ανάδρασης ο κεντρικός σταθµός θα συνεχίσει κανονικά τη µετάδοση πακέτων για ένα χρονικό διάστηµα ίσο µε τη διάρκεια εκποµπής πακέτου ανάδρασης (feedback transmsson tme). Εντωµεταξύ, οι πελάτες που λαµβάνουν επιτυχώς πακέτα δεδοµένων στο διάστηµα αυτό αναγνωρίζουν τη δυαδική σηµαία Α=0 στην κεφαλίδα των πακέτων και δεν απαντούν µε πακέτο ανάδρασης. Αξίζει να αναφερθεί ότι η διάρκεια εκποµπής ενός πακέτου ανάδρασης είναι µία γνωστή πληροφορία για το σταθµό µετάδοσης καθώς κάθε ανάδραση είναι µεγέθους 1 + [log 2 N] bts και ο ρυθµός µετάδοσης W FB µαζί µε την ταχύτητα µετάδοσης U FB των ανατροφοδοτήσεων είναι γνωστές τιµές. Μετά από κάθε τέτοιο χρονικό διάστηµα ο κεντρικός σταθµός µεταδίδει το επόµενο προγραµµατισµένο πακέτο που απαιτεί απάντηση ενός άλλου πακέτου ανάδρασης. Προφανώς, αν Itm _ tme Fdb _ tme τότε ο κεντρικός σταθµός θα στέλνει πακέτα δεδοµένων που πάντα θα απαιτούν ανάδραση από τους χρήστες. Για να επιλεγεί ένα πακέτο δεδοµένων j προς εκποµπή το οποίο ζητά ανάδραση από τους πελάτες, η συνάρτηση κόστους G εφαρµόζεται ξεχωριστά για να παραχθεί µια ακολουθία πακέτων προς εκποµπή, µε την υπόθεση ότι ο χρόνος περνάει µόνο όταν γίνονται µεταδόσεις πακέτων που αιτούνται απάντηση µέσω ανατροφοδοτήσεων από τους χρήστες. Αυτό σηµαίνει ότι ο κεντρικός σταθµός χρειάζεται να αποθηκεύει σε έναν ξεχωριστό πίνακα R ο οποίος αφορά στο χρόνο που κάθε ένα πακέτο δεδοµένων µεταδόθηκε τελευταία φορά από τον κεντρικό σταθµό. Ο εξυπηρετητής διαβάζει το ID του πακέτου δεδοµένων στο εισερχόµενο πακέτο ανάδραση και χρησιµοποιεί αυτήν την πληροφορία για να ανανεώσει την πιθανότητα του αντίστοιχου πακέτου. Το Μανθάνον Αυτόµατο, το οποίο διατηρεί τον πίνακα πιθανοτήτων ζήτησης p, προσεγγίζει την πραγµατική πιθανότητα εκποµπής d κάθε ενός πακέτου. Αυτός ο ανανεωµένος πλέον πίνακας p χρησιµοποιείται από τον κεντρικό σταθµό για να υπολογισθεί το κόστος G κάθε ενός πακέτου στη διαδικασία επιλογής πακέτου προς εκποµπή, µέχρι να λάβει µέρος η επόµενη ανανέωση. Οι πιθανότητες των πακέτων δεν αλλάζουν όταν η µετάδοση ενός πακέτου j δεν ικανοποιεί κανέναν πελάτη. Ωστόσο, µετά από µία επιτυχή µετάδοση, η πιθανότητα του πακέτου j αλλάζει και συγκεκριµένα αυξάνεται. Μία Lnear Inacton (L R-1 ) εξίσωση ανανέωσης πιθανοτήτων εφαρµόζεται µετά τη µετάδοση κάθε πακέτου. Έτσι λοιπόν, υποθέτοντας ότι πρόκειται για την k th µετάδοση του κεντρικού σταθµού, χρησιµοποιείται η παρακάτω σχέση ανανέωσης πιθανοτήτων: pm( k) a pm ( k + 1) = pm( k) L, m ClNum (9) L p j ( k + 1) = p j ( k) + ( pm( k) a) ClNum m j όπου L, a λαµβάνουν τιµές στο (0,1) και p(k) παίρνει τιµές στο (α,1). Για να αναγνωρίσει ο κεντρικός σταθµός το συνολικό αριθµό χρηστών ClNum, εκπέµπει ένα πακέτο ελέγχου που αναγκάζει όλους τους πελάτες να απαντήσουν µε ένα πακέτο ανάδρασης και έπειτα περιµένει για MAX _ RTT + Item _ tme + Fdb _ tme µέχρι να λάβει όλα αυτά τα πακέτα. Η διαδικασία επιλογής της παραµέτρου L αντικατοπτρίζει το πρόβληµα της ταχύτητας έναντι της ακρίβειας. Όσο πιο χαµηλή η τιµή της L, τόσο 19

20 περισσότερο ακριβείς οι εκτιµήσεις που κάνει το Μανθάνον Αυτόµατο του κεντρικού σταθµού, ένα γεγονός που έρχεται σε βάρος της ταχύτητας σύγκλισης. Αν η πιθανότητα p j που υπολογίσθηκε για ένα πακέτο δεδοµένων j λάβει τιµές πολύ κοντά στο µηδέν, τότε η τιµή G( j ) θα είναι επίσης πολύ κοντά στο µηδέν. Ωστόσο το j, αν και είναι ελάχιστα δηµοφιλές, χρειάζεται µερικές φορές να µεταδίδεται καθώς κάποιοι πελάτες µπορεί να το επιθυµούν. Επιπροσθέτως, η δυναµική φύση των αιτήσεων των πελατών µπορεί να έχει ως συνέπεια το πακέτο αυτό να γίνει περισσότερο δηµοφιλές στο µέλλον. Για αυτό χρησιµοποιείται η παράµετρος α που αποτρέπει την ανάθεση τιµών πολύ κοντινών στο µηδέν στις πιθανότητες p του Μανθάνοντος Αυτοµάτου αυξάνοντας έτσι την προσαρµοστικότητά του. Το γεγονός αυτό καθιστά αυτή την προσέγγιση ελκυστική για εφαρµογές µε δυναµικές απαιτήσεις των χρηστών. Αυτή η σύγκλιση φαίνεται σχηµατικά στο Σχήµα 8, η οποία δείχνει την πιθανότητα εκτίµησης του πακέτου σε σχέση µε τη συνολική πραγµατική πιθανότητα ζήτησης, σε µια προσοµοίωση µιας βάσης δεδοµένων που αποτελείται από τέσσερα πακέτα. Το πρότυπο ζήτησης του χρήστη είναι άγνωστο στο σταθµό βάσης, άρα αρχικά, τα τέσσερα πακέτα έχουν ίσες πιθανότητας εκτίµησης. Έτσι φαίνεται καθαρά ότι επιτυγχάνεται η σύγκλιση της πιθανότητας εκτίµησης του πακέτου που υπολογίζεται από το αυτόµατο µε τη πραγµατική πιθανότητα ζήτησης του πλήθους των χρηστών. 20

21 Κεφάλαιο 3: Αποτελέσµατα - Αξιολόγηση Προσοµοίωσης Για να γίνει η εκτίµηση της απόδοσης των παραπάνω συστηµάτων, προσοµοιώσαµε και συγκρίναµε τα παραπάνω συστήµατα µε στατική round-robn εκποµπή. 3.1 Το Προτεινόµενο Σύστηµα Το προτεινόµενο σύστηµα είναι βασισµένο σε προσαρµοστικά Push Συστήµατα εκποµπής. Το συγκεκριµένο σύστηµα αποτελείται από ένα σταθµό βάσης και από έναν συγκεκριµένο αριθµό χρηστών ClNum. Ο σταθµός βάσης έχει µια βάση δεδοµένων µε Ν πακέτα προς µετάδοση. Κάθε πακέτο έχει πιθανότητα ίση 1/Ν. Ο σταθµός βάσης στην αρχή θεωρεί όλα τα πακέτα ότι έχουν την ίδια πιθανότητα. Το προτεινόµενο σύστηµα όµως όπως προαναφέραµε βασίζεται σε Προσαρµοστικά Συστήµατα, έτσι οι πιθανότητες µετά την πρώτη φορά θα ανανεώνονται συνεχώς. Κάνοντας χρήση της συνάρτησης G επιλέγει τα πακέτα από την βάση δεδοµένων για εκποµπή προς τους χρήστες. Τα πακέτα δεδοµένων εκποµπής κάνουν χρήση όλου του διαθέσιµου εύρους ζώνης για µετάδοση. Για τον λόγο όµως του ότι το προτεινόµενο σύστηµα δεν χρησιµοποιείτο CDMA τα εκπεµπόµενα πακέτα θα έχουν περισσότερο εύρος ζώνης σε σχέση µε τα συστήµατα τα οποία αναλύθηκαν στο προηγούµενο κεφάλαιο Η ανανέωση των πιθανοτήτων γίνεται µε τη βοήθεια ενός Μανθάντος Αυτοµάτου όπως περιγράφει το [10]. Οι χρήστες του προτεινόµενου συστήµατος είναι τυχαία κατανεµηµένοι σε ένα υποβρύχιο περιβάλλον. Οι χρήστες λαµβάνουν τα πακέτα που έχει εκπέµψει ο σταθµός βάσης και στη συνέχεια στέλνουν ως απάντηση ένα πακέτο ανάδρασης. Στο σύστηµα που µελετάµε η µετάδοση των πακέτων ανάδρασης γίνεται χωρίς τη χρήση CDMA σε αντίθεση µε τα προσαρµοστικά συστήµατα που αναλύθηκαν παραπάνω. Αυτό έχει ως αποτέλεσµα τη δηµιουργία συγκρούσεων των πακέτων ανάδρασης που στέλνουν οι χρήστες στον σταθµό βάσης για επιβεβαίωση. 3.2 Το Μοντέλο του Σταθµού Βάσης Στην προσοµοίωση θεωρούµε έναν κεντρικό σταθµό ο οποίος έχει µια βάση δεδοµένων µε Ν ίσου µεγέθους πακέτα. Υποθέτουµε ότι τα πακέτα περιέχουν πληροφορίες σχετικά µε τον συγκεκριµένο χρόνο, έτσι µεταξύ των διαδοχικών εκποµπών στην περίπτωση του ίδιου πακέτου, η πραγµατική πληροφορία περιέχει κάποιες αλλαγές. Ο 21

22 σταθµός βάσης αρχικά δε γνωρίζει την πιθανότητα ζήτησης κάθε πακέτου, άρα αρχικά κάθε πακέτο έχει µια πιθανότητα εκποµπής p ίση µε 1 / Ν. 3.3 Το Μοντέλο των Χρηστών Στην προσοµοίωσή µας εκτός από τον Κεντρικό Σταθµό Βάσης έχουµε και έναν αριθµό χρηστών ClNum. Οι χρήστες αυτοί λόγω του µεταβαλλόµενου χρόνου του κάθε πακέτου δεν έχουν την δυνατότητα προσωρινής αποθήκευσης. Οι χρήστες έχουν πρόσβαση στα πακέτα στο διάστηµα [1,Range]. Αυτή η σειρά συνιστάται από ενέργειες R µεγέθους RSze το καθένα, οι οποίες περιέχουν ισοπίθανα πακέτα ζήτησης. Η πιθανότητα ζήτησης d() ενός πακέτου στην περιοχή, είναι: 1 d( ) = c, όπου θ 1 c = 1/ Rsze, k [1.. R] k k και θ είναι µια παράµετρος που ονοµάζεται access skew. Αυτή είναι η κατανοµή Zpf που χρησιµοποιείται στη µοντελοποίηση των απαιτήσεων των χρηστών [8-11]. Καθώς η τιµή του θ αυξάνεται, η Zpf δηµιουργεί ολοένα και περισσότερα πρότυπα skewed ζήτησης. Κάθε χρήστης βρίσκεται σε απόσταση Χ Km από το σταθµό βάσης, µε το x να είναι οµοιόµορφα κατανεµηµένο στο διάστηµα [1..MAX_DISTANCE]. Για να κωδικοποιήσουµε τον αριθµό των πακέτων που αναγνωρίζονται από τα πακέτα ανάδρασης των 10 bts χρησιµοποιείται αριθµό των πακέτων που αναγνωρίζουν οι ανατροφοδοτήσεις. Η ταχύτητα του ήχου στο νερό έχει οριστεί σε 1,5 Km / sec. Τέλος, δεν λαµβάνουµε υπόψη τα σφάλµατα λήψης καθώς ο στόχος µας είναι να αξιολογήσουµε τη σχετική αύξηση των επιδόσεων των προτεινόµενων προσεγγίσεων σε σχέση µε τις εφαρµογές της [8] και την επίπεδη εκποµπή στο υποβρύχιο περιβάλλον. θ 3.4 Περιβάλλον Προσοµοίωσης Η προσοµοίωση πραγµατοποιείται µέχρι να εκπληρωθούν οι απαιτήσεις NumReq σε κάθε χρήστη, που σηµαίνει ότι γενικά οι απαιτήσεις NumReq * ClNum θα πρέπει να έχουν εξυπηρετηθεί. Για την προσοµοίωση χρησιµοποιήθηκαν οι παρακάτω σταθερές τιµές: Μέγιστος Αριθµός Χρηστών ClNum: 81 Μέγεθος πακέτου: 1000 bts Συνολικός Αριθµός πακέτων: Ν1: 300 Συνολικός Αριθµός πακέτων: Ν2: 60 Παράµετρος ακρίβειας: L=0,15 Παράµετρος: 4 a= 10 Λόγος Eb / N 0= 5 Ταχύτητα ήχου στο νερό: 1,5 km/sec 22

23 Για το [10] σύστηµα χρησιµοποιήσαµε το σύνολο των 10 KHz του διαθέσιµου εύρους ζώνης για τη µετάδοση των πακέτων, συνεπώς, για αυτό το σύστηµα U DATA= 2400bps [2]. Για τα προσαρµοσµένα συστήµατα χρησιµοποιήσαµε το 20% του διαθέσιµου εύρους ζώνης για την υλοποίηση της ανάδρασης του συστήµατος, έτσι για αυτό το σύστηµα W = 8 bps, W = 2bps και κατά συνέπεια U = 1900bps. DATA FEEDACK Επιπλέον, όσον αφορά την ανάδραση του συστήµατος, θέσαµε U FEEDACK= 0.5bps. Για τo σύστηµα που κάνει χρήση 1-bt ανάδραση, για την ίδια διάρκεια ανάδρασης µπορούµε να υποστηρίξουµε 81 χρήστες µε WFEEDACK= 200bps και U FEEDACK= 0.5bps. Έτσι, γι 'αυτό το σύστηµα W = 9.8bps και κατά συνέπεια U = 2352bps. DATA DATA DATA 3.5 Αποτελέσµατα Προσοµοίωσης Οι παρακάτω εικόνες δείχνουν τα αποτελέσµατα που λάβαµε από την προσοµοίωση των Συστηµάτων που προαναφέραµε στα προηγούµενα κεφάλαια. Στη συγκεκριµένη προσοµοίωση έγινε σύγκριση των συστηµάτων σε σχέση µε τον µέσο χρόνο αναµονής µε βάση τον τρόπο αποστολής των πακέτων από το σταθµό βάσης προς και από τους κινητούς χρήστες, σε αποστάσεις 2, 5 και 10 χιλιοµέτρων. Στα Σχήµατα 4-8 απεικονίζονται τα αποτελέσµατα για Ν1 (Range = 300). Συγκεκριµένα, τα σχήµατα 4-6 δείχνουν για µια µέγιστη περιοχή κάλυψης του σταθµού βάσης (MAX_DISTANCE) των 2, 5 και 10 χιλιoµέτρων αντίστοιχα, τις σχετικές παραστάσεις των τεσσάρων συστηµάτων µε µια λογαριθµική κλίµακα (µε βάση το 10) που χρησιµοποιείται για τον άξονα Y. Τα Σχήµατα 7 και 8 δείχνουν τη σχετική απόδοση των Συστηµάτων Contnuous Adaptve Push [10] Non Adaptve Push [9] και Contnuous Adaptve Push [10] Push System wth Colsons. Αυτά το σχεδιαγράµµατα εµφανίζονται µία φορά, καθώς οι επιδόσεις των συστηµάτων είναι ίδιες ανεξάρτητα από την περιοχή κάλυψης του σταθµού βάσης. 23

24 Σχήµα 4: Μέσος χρόνος απόκρισης σε σχέση µε τoν συντελεστή access skew για τα τρία συστήµατα στο δίκτυο Ν1 για περιοχή κάλυψης 2 km. Σχήµα 5: Μέσος χρόνος απόκρισης σε σχέση µε τoν συντελεστή access skew για τα τρία συστήµατα στο δίκτυο Ν1 για περιοχή κάλυψης 5 km. 24

25 Σχήµα 6: Μέσος χρόνος απόκρισης σε σχέση µε τoν συντελεστή access skew για τα τρία συστήµατα στο δίκτυο Ν1 για περιοχή κάλυψης 10 km. Σχήµα 7: Μέσος χρόνος απόκρισης σε σχέση µε τoν συντελεστή access skew για τα συστήµατα Contnuous Adaptve Push [10] και Non Adaptve Push [9]στο δίκτυο Ν1. 25

26 Σχήµα 8: Μέσος χρόνος απόκρισης σε σχέση µε τoν συντελεστή access skew για τα συστήµατα Contnuous Adaptve Push [10] και Push System wth Colsons στο δίκτυο Ν1. Τα Σχήµατα 9-13 απεικονίζουν τα αποτελέσµατα για Ν2 (Range = 60). Συγκεκριµένα, Τα Σχήµατα 9-11 δείχνουν, την µέγιστη περιοχή κάλυψης του σταθµού βάσης (που ορίζεται ως MAX_DISTANCE Στα Σχήµατα) των 2, 5 και 10 χιλιοµέτρων αντίστοιχα, των σχετικών επιδόσεων από τα τέσσερα συστήµατα µε µια λογαριθµική (βάση το 10) κλίµακα που χρησιµοποιείται για τον άξονα Υ. Τα Σχήµατα 12 και 13 δείχνουν τη σχετική απόδοση των Συστηµάτων Contnuous Adaptve Push [10] Non Adaptve Push [9] και Contnuous Adaptve Push [10] Push System wth Colsons. Αυτά τα σχεδιαγράµµατα εµφανίζονται µία φορά, καθώς οι επιδόσεις των συστηµάτων είναι ίδιες ανεξάρτητα από την περιοχή κάλυψης του σταθµού βάσης. Σχήµα 9: Μέσος χρόνος απόκρισης σε σχέση µε τoν συντελεστή access skew για τα τρία συστήµατα στο δίκτυο Ν2 για περιοχή κάλυψης 2 km. 26

27 Σχήµα 10: Μέσος χρόνος απόκρισης σε σχέση µε τoν συντελεστή access skew για τα τρία συστήµατα στο δίκτυο Ν2 για περιοχή κάλυψης 5 km. Σχήµα 11: Μέσος χρόνος απόκρισης σε σχέση µε τoν συντελεστή access skew για τα τρία συστήµατα στο δίκτυο Ν2 για περιοχή κάλυψης 10 km. 27

28 Σχήµα 12: Μέσος χρόνος απόκρισης σε σχέση µε τoν συντελεστή access skew για τα συστήµατα Contnuous Adaptve Push [10] και Non Adaptve Push [9] στο δίκτυο Ν2. Σχήµα 13: Μέσος χρόνος απόκρισης σε σχέση µε τoν συντελεστή access skew για τα συστήµατα Contnuous Adaptve Push [10] και Push System wth Colsons στο δίκτυο Ν2. 28

29 3.6 Συµπεράσµατα Αποτελεσµάτων Τα συµπεράσµατα που προκύπτουν από τις παραπάνω εικόνες είναι τα εξής: Τα συστήµατα Push System wth collsons και Contnuous Adaptve Push [10] υπερτερούν σηµαντικά σε σχέση µε τα υπόλοιπα συστήµατα στα οποία ο µέσος χρόνος απόκρισης είναι χειρότερος κατά την αύξηση της απόστασης κάλυψης του σταθµού βάσης. H απόδοση του προτεινόµενου συστήµατος και του υπάρχοντος υποβρυχίου συστήµατος εκποµπής παραµένει η ίδια ανεξάρτητα από την περιοχή κάλυψης του σταθµού βάσης. Αυτό οφείλεται στο γεγονός ότι και τα δύο συστήµατα έχουν ένα κοινό χαρακτηριστικό: επιτρέπουν τη συνεχή µετάδοση, η οποία «κρύβει» την αυξηµένη καθυστέρηση. Σε αντίθεση, η µέθοδος του Non adaptve [9] περιµένει µετά από την εκποµπή κάθε πακέτου για το σύνολο της διπλάσιας µέγιστης καθυστέρησης διάδοσης συν τη διάρκεια ανάδρασης συν το χρόνο µετάδοσης του πακέτου, προκειµένου να διασφαλίζεται η ανάδραση, κάτι το οποίο φυσικά αποτελεί τεράστια χρονικύ επιβάρυνση Για µικρές τιµές του θ η απόδοση του συστήµατος Contnuous Adaptve [10] όταν Range = 300, είναι λίγο χειρότερη από εκείνη του Non-adaptve. Αυτό οφείλεται στο γεγονός ότι: α) στo Non-adaptve [9] δεν εφαρµόζεται η ανάδραση και συνεπώς δεν επιδεινώνεται η απόδοση σύµφωνα µε τα προαναφερθέντα, β) στο Contnuous [10] για µικρές τιµές του θ το µοντέλο ζήτησης οδηγεί σε επίπεδη εκποµπή των πακέτων του σταθµού βάσης, Με την αύξηση του θ η απόδοση του Contnuous Adaptve [10] και του Push System wth Colsons βελτιώνεται σηµαντικά σε σύγκριση µε την απόδοση του non-adaptve [9]. Όταν Range = 60 <Ν η Non-Adaptve [9] έχει πολύ χειρότερες επιδόσεις από τα συστήµατα Contnuous Adaptve [10] και του προτεινόµενου ακόµα και στην περίπτωση µικρών τιµών θ δεδοµένου ότι ειδοποιεί το σταθµό βάσης να εκπέµπει συχνά µόνο τα απαιτούµενα πακέτα. Έτσι, θα ήταν χρήσιµο ακόµα και σε περιπτώσεις των εφαρµογών που έχουν πρόσβαση σε σηµεία της βάσης δεδοµένων του σταθµού βάσης µε οµοιόµορφες δοµές δεδοµένων. Τέλος βλέπουµε στα Σχήµατα 9 και 14 ότι το προτεινόµενο σύστηµα έχει καλύτερη απόδοση από το Contnuous Adaptve Push [10] και στο περιβάλλον Ν1 και στο περιβάλλον Ν2. Η βασική διαφορά των δύο συστηµάτων είναι ότι το Contnuous Adaptve Push [10] λειτουργεί µε CDMA, ενώ το προτεινόµενο σύστηµα όχι και συνεπώς εκπέµπει µε µεγαλύτερη ταχύτητα τα δεδοµένα του σε σχέση µε το Contnuous Adaptve Push [10]. Αυτό συµβαίνει γιατί η απουσία χρήσης CDMA στο προτεινόµενο σύστηµα δίνει τη δυνατότητα να χρησιµοποιηθεί περισσότερο εύρος ζώνης για την εκποµπή των δεδοµένων. 29

30 Κεφάλαιο 4 : Κώδικας Προσοµοίωσης Για την εξαγωγή των αποτελεσµάτων του συστήµατος χρησιµοποιήθηκε ένα µοντέλο προσοµοίωσης γραµµένο σε γλώσσα προγραµµατισµού C++. Στη συνέχεια παρατίθενται τα κυριότερα σηµεία του πηγαίου κώδικα για κάθε σύστηµα που µελετήθηκε παραπάνω. Non Adaptve Push [9] Αναπαριστούµε τον σταθµό βάσης µε την κλάση controller. Mέσα στην κλάση controller έχουµε δυο ponters που θα υποδεχθούν τις διευθύνσεις ενός πίνακα κλάσεων clents και ενός πίνακα κλάσεων πακέτων (tems ) που δηµιουργούνται µε την κλήση του constractor controller (controller (nt number_of_clents,nt number_of_tems class controller publc: nt number_of_clents; clent *clents; tem *tems; double tme; controller(nt number_of_clents,nt number_of_tems); Παρακάτω παρουσιάζονται οι κλάσεις των πακέτων (tems) και των πελατών (clents). Στα πακέτα έχουµε την µεταβλητή tme_last_transmt_of_tem που κρατάει τη χρονική στιγµή της τελευταίας εκποµπής κάθε πακέτου και την µεταβλητή G η οποία µας βοηθάει να επιλέξουµε ανάµεσα στα πακέτα, ποιο θα σταλεί ανάλογα µε το ποιο έχει τη µεγαλύτερη τιµή G. Στην κλάση clent έχουµε την µεταβλητή selected_packet η οποία κρατάει το πακέτο που περιµένει κάθε χρήστης, τον πίνακα probablty_sum ο οποίος µας βοηθάει να επιλέξουµε µε µια random το πακέτο που περιµένει κάθε χρήστης (selected_packet),και την µεταβλητή number_packets_transmtted η οποία κρατάει τον αριθµό των πακέτων που έχει λάβει επιτυχώς κάθε clent 30

31 class tem publc: tem(); double tme_last_transmt_of_tem; double G; ; class clent publc: clent(); double *probablty; double *probablty_sum; nt selected_packet; double random_number_0_1; nt number_packets_transmtted; ; Η βασική δοµή του προγράµµατος βρίσκεται στη συνάρτηση man. Στην αρχή δηµιουργούµε δύο πίνακες mean_wat_tme_clent και mean_response_tme όπου ο πρώτος θα περιέχει τον µέσο χρόνο αναµονής σε κάθε πελάτη και ο δεύτερος τον µέσο χρόνο αναµονής συνολικά όλων των πελατών για κάθε θ. Για κάθε θ δηµιουργείται ένα αντικείµενο σταθµού βάσης controller contr(number_of_clents, number_of_tems_server) και µέχρι να σταλούν επιτυχώς πακέτα το πρόγραµµα στέλνει πακέτα µέσω της συνάρτησης receve_packet(select_g, contr,number_of_packets_transmtted).τα πακέτα επιλέγονται µε βάση το ποιο πακέτο έχει την µέγιστη πιθανότητα G. Αυτή η επιλογή γίνεται στη συνάρτηση select_greater_g. Μέχρι να σταλθούν πακέτα για κάθε θ βρίσκουµε το mean_response_tme[j]=response_tme/number_of_clent. nt man() mean_wat_tme_clent=new double [number_of_clents]; mean_response_tme=new double[11]; for(nt j=0;j<11;j++) theta=j*0.2; cout<<theta<<"\n"; controller contr(number_of_clents,number_of_tems_server); //for(nt =0;<number_of_clents;++) cout<<contr.clents[].selected_packet<<" "; //f(systema=="n1") controller contr(number_of_clents,300); //else controller contr(number_of_clents,60); for(nt_number_of_packets_transmtted=0;number_of_packets_transmtted<10000;) //cout<<number_of_packets_transmtted<<" "; 31