Στοιχεία Φυσικής Κοσµολογίας
|
|
|
- Ιολανθη Χρηστόπουλος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Στοιχεία Φυσικής Κοσµολογίας Μανώλης Πλειώνης & Σπύρος Βασιλάκος ὺπoτίθɛται γάρ τά µ ɛν άπλαν ɛα τ ων άστρων καί τóν ὰλιoν µ ɛνɛιν άκίνητoν, τάν δ ɛ γ αν πɛριφ ɛρɛσθαι πɛρί τóν ὰλιoν κατά κύκλoυ πɛριφ ɛρɛιαν, òς ɛστιν ɛν µ ɛσω τ ω δρóµω κɛίµɛνoς Αρίσταρχος ο Σάµιος περί το 288 πχ. 1
2 Contents 1 Εισαγωγική Περίληψη 5 2 Βασικές Εννοιες Η Κοσµολογική Αρχή Η Θεωρία της Μεγάλης Εκρηξης Η ιαστολή του Σύµπαντος Συνµετακινούµενες συντεταγµένες Η Μετρική του Χωροχρόνου Κοσµολογική Ερυθροµετατόπιση Βασικά Στοιχεία υναµικής Κοσµολογίας Εξισώσεις Friedmann Καταστατικές Εξισώσεις Κοσµολογικές Παράµετροι Κρίσιµη Πυκνότητα ή Ολική Πυκνότητα Υλοενέργειας Κοσµολογικές Παράµετροι Πυκνότητας Παράµετρος Επιβράδυνσης Σταθερά του Hubble Εποχές Κυριαρχίας των διαφορετικών συνιστωσών στη δυναµική του Σύµπαντος Εποχή Ισοδυναµίας Ακτινοβολίας- Υλης Εποχή Ισοδυναµίας Υλης-Κοσµολογικής Σταθεράς Εποχή Ισοδυναµίας Υλης-Καµπυλότητας Η ηλικία του Σύµπαντος Τα Κλασσικά Μοντέλα του Friedmann Παλλόµενο Σύµπαν k = +1 - (κλειστή γεωµετρία) Συνεχώς διαστελλόµενο Σύµπαν (k = 1 - ανοικτή γεωµετρία) Μοντέλο Einstein-deSitter (k = 0 - επίπεδη γεωµετρία) Κοσµολογική Σταθερά Το Σύµπαν του Αϊνστάϊν Μοντέλο desitter Το Σύµπαν µε Υλη και Κοσµολογική Σταθερά- ΛCDM
3 3.7.4 Φυσική Ερµηνεία της Κοσµολογικής Σταθεράς Σκοτεινή ενέργεια Η ϕυσική ερµηνεία της σκοτεινής ενέργειας Τυπική Απόσταση & Ορίζοντας στο διαστελλόµενο Σύµπαν Τυπική Απόσταση - Ιδιοαπόσταση Κοσµολογικός Ορίζοντας Θερµική Αρχή του Σύµπαντος Εποχή της Ακτινοβολίας Εποχή του Planck Εποχή των ενοποιηµένων ϑεωριών Εποχή του αρχικού πληθωρισµού Το πρόβληµα της επιπεδότητας Το πρόβληµα των µαγνητικών µονοπόλων Το πρόβληµα του ορίζοντα Η ϕυσική του πληθωρισµού Πληθωρισµός και διαταραχές Το Υπόβαθρο της Κοσµικής Ακτινοβολίας Μικροκυµάτων ΠΑΡΑΤΗΡΗΣΙΑΚΗ ΚΟΣΜΟΛΟΓΙΑ Φαινόµενο Μέγεθος και Μέτρο Απόστασης Μετρήσιµες απόστασης στο διαστελλόµενο Σύµπαν Απόσταση Φωτεινότητας Απόσταση Γωνιακής ιαµέτρου Σχέσεις µεταξύ των κοσµικών απόστασεων Συστηµατικά σφάλµατα που επιρεάζουν ϕαινόµενα µεγέθη ιόρθωση Κ Γαλαξιακή Απορρόφηση Εξέλιξη Φωτεινότητας γαλαξιών Τελικό Μέτρο Απόστασης Κοσµική στατιστική Σκοτεινή Υλη
4 7 ΑΣΚΗΣΕΙΣ ΜΕΡΟΥΣ Α 110 4
5 1 Εισαγωγική Περίληψη Η Κοσµολογία είναι η επιστήµη που µελετά την αρχή, την εξέλιξη και την δοµή του Σύµπαντος συνολικά αλλά και των επιµέρους κοσµικών δοµών που το αποτελούν. Η ενασχόληση του ανθρώπου µε τα ερωτήµατα της γέννησης και δοµής του Σύµπαντος είναι όσο παλιά όσο και ο ανθρώπινος πολιτισµός, στην όποια του µορφή. Η Κοσµολογία παρόλο που προσπαθεί να δώσει απάντηση σε ϑεµελιώδη ερωτήµατα που έθεσε ο άνθρωπος από την αυγή ακόµα του πολιτισµού, είναι µια σχετικά νέα επιστήµη. Η ιστορική διαδροµή που διάνυσε η ανθρώπινη νόηση για να ϕτάσει στο σηµείο να µελετά µε αυστηρά επιστηµονικές µεθόδους την ίδια τη γένεση και εξέλιξη του Σύµπαντος είναι πολύ µακρά και έχει περάσει µέσα από δαιδαλώδεις λαβύρινθους αναζήτησης. Οι νόµοι της κίνησης των πλανητών του Κέπλερ, που τεκµηριώθηκαν ουσιαστικά µε την Νευτώνια ϑεωρία της ϐαρύτητας, σηµατοδοτούν την εκκίνηση της σύγχρονης εποχής επιστηµονικής σκέψης. Η δε σύγχρονη Κοσµολογία ξεκινά ουσιαστικά µε την ϑεµελίωση της Γενικής Θεωρίας της Σχετικότητας (ΓΘΣ) το 1915 από τον Αϊνστάϊν. Μια από τις σηµαντικότερες προβλέψεις της ΓΘΣ είναι ότι η ύπαρξη του Σύµπαντος είναι αναγκαστικά συνυφασµένη µε την δυναµική του εξέλιξη, κάτι που ήρθε σε αντίθεση µε την «στατικότητα» που πίστευε ακόµα και ο ίδιος ο ϑεµελιωτής της ΓΘΣ, ο Αϊνστάιν. Πρώτος ο Alexander Friedmann, ένας νεαρός Ρώσος µαθηµατικός το 1922 απέδειξε ότι οι κοσµολογικές λύσεις των εξισώσεων πεδίου προβλέπουν ένα δυναµικά εξελισσόµενο Σύµπαν. Αυτό αποδείχτηκε πειραµατικά το 1929 από τον Αµερικανό αστρονόµο Edwin Hubble που ανακάλυψε την διαστολή του Σύµπαντος, ότι δηλαδή οι γαλαξίες αποµακρύνονται ο ένας από τον άλλο και µε ταχύτητες ανάλογες της απόστασης τους (νόµος του Hubble). Η σύγχρονη κοσµολογία ϑεωρεί ότι το µοντέλο που πιο ορθά ανταποκρίνεται στην ϕυσική πραγµατικότητα που ϐασίζεται στην ΓΘΣ του Αϊνστάιν, είναι αυτό της Μεγάλης Εκρηξης, το οποίο προτάθηκε από τον καθολικό ιερέα George Lemaitre, ϕυσικό και αστρονόµο του Καθολικού Παν/µιου του Λουβέν, το 1927 (2 χρόνια πριν παρατηρηθεί η διαστολή του Σύµπαντος από τον Hubble) αν και µε αρχικά διαφορετικό όνοµα (η υπόθεση του πρωταρχικού ατόµου). Θεµελιώθηκε σε ϑεωρητικό επίπεδο στα µέσα του 20ου αιώνα από τους Gamow, Herman & Alpher οι οποίοι έκαναν συγκεκριµένες προβλέψεις που µπορούσαν να επιβεβαιώσουν ή να απορρίψουν το µοντέλο αυτό. Οι προβλέψεις αυτές επιβεβαιώθηκαν περίτρανα µετά από δεκαετίες, µε την ανακάλυψη από τους Αµερικανούς αστρονόµους Πενσίας και Ουίλσον της λεγόµενης Κοσµικής Ακτινοβολίας Μικροκυµάτων, δηλαδή του ενεργειακού απολιθώµατος της αρχικής ϑερµικής ακτινοβολίας που 5
6 γέµισε το Σύµπαν µετά την Μεγάλη Εκρηξη, της οποίας η ϑερµοκρασία σήµερα είναι 2.73 K περίπου, όπως περίπου προέβλεψε ο Gamow δεκαετίες πριν. Η άλλη σηµαντική πρόβλεψη αυτής την ϑεωρίας ήταν τα ποσά των ελαφρών στοιχείων του περιοδικού πίνακα (υδρογόνου, δευτέριου, ηλίου και λιθίου) που δηµιουργούνται µέσα στα πρώτα 3 λεπτά της Μεγάλης Εκρηξης και που οι παρατηρήσεις επιβεβαίωσαν µε ακρίβεια. Αποσαφηνίζουµε ότι για την σύγχρονη Κοσµολογία ως Μεγάλη Εκρηξη ϑεωρείται η εκρηκτική εκτόνωση µια αρχικά υπέρπυκνης και υπέρθερµης κατάστασης η οποία ϑα µπορούσε να προέλθει από διάφορες εκφάνσεις των ϑεωριών κβαντικής ϐαρύτητας. Τα δε κύρια στοιχεία που υποστηρίζουν την ορθότητα αυτού του γενικού πλαισίου της ϑεωρίας και που δεν ερµηνεύονται στο σύνολο τους από καµία άλλη ϑεωρία είναι : (1) η διαστολή του Σύµπαντος, (2) το υπόβαθρο ακτινοβολίας µικροκυµάτων και (3) η γένεση και τα ποσοστά των ελαφρών χηµικών στοιχείων. Τι υποστηρίζει λοιπόν αυτό το µοντέλο, οι λύσεις των εξισώσεων πεδίου της ΓΘΣ, υποθέτοντας ότι το Σύµπαν είναι οµογενές και ισότροπο σε µεγάλες κλίµακας (µια υπόθεση που έχει επιβε- ϐαιωθεί παρατηρησιακά και που ϑα συζητήσουµε στο επόµενο κεφάλαιο), υποστηρίζουν ότι το Σύµπαν ξεκίνησε να διαστέλλεται πριν από 13.8 περίπου δισεκατοµµύρια χρόνια από µία αρχική κατάσταση υψηλότατης πυκνότητας και ϑερµοκρασίας. Εξαιτίας του απειροστού µεγέθους του Σύµπαντος αυτό αρχικά συµπεριφέρεται ως ένα κβαντικό σύστηµα. Παρά το γεγονός ότι µέχρι σήµερα δεν έχουµε µια πλήρη ϑεωρία κβαντικής ϐαρύτητας, ο χρόνος στον οποίο τα κβάντικά ϕαινόµενα της ϐαρύτητας κυριαρχούν λαµβάνει χώρα µόλις δευτερόλεπτα µετά τη µεγάλη έκρηξη. Στη συνέχεια η σηµερινή εκδοχή της ϑεωρίας υποστηρίζει ότι µόλις δευτερόλεπτα µετά τη µεγάλη έκρηξη το Σύµπαν περνά µια ϕάση επιταχυνόµενης εκθετικής διαστολής (πληθωρισµός) που διαρκεί µέχρι τα δευτερόλεπτα περίπου και η οποία αυξάνει δραστικά το µέγεθος του Σύµπαντος. Το ϐασικό αποτέλεσµα αυτής της πληθωριστικής εποχής είναι ότι αυξάνει σε µακροσκοπικό επίπεδο τις κβαντικές διαταραχές, παρέχοντας τους αρχικούς σπόρους για την δηµιουργία των κοσµικών δοµών αλλά επίσης επιβάλλει και την Ευκλείδια γεωµετρία στο χωρικό µέρος του τετραδιάστατου χωρόχρονου. Στη συνέχεια, δεν είµαστε σίγουροι για το πότε ή γιατί - η περίοδος αυτή της επιταχυνόµενης διαστολής τελειώνει, και η ενέργεια που την οδηγούσε µετατρέπεται σε συνηθισµένη ύλη και ακτινοβολία, και µε αυτό τον τρόπο αρχίζει η συµβατική κοσµική ιστορία του Σύµπαντος. Μετά τον πληθωρισµό το Σύµπαν εισέρχεται στην κλασσική εποχή της ακτινοβολίας και καθώς το Σύµπαν διαστέλλεται και ψύχεται µε την πάροδο του χρόνου, συντίθενται τα δοµικά συστατικά της ύλης, τα πρωτόνια, τα νετρόνια, τα ηλεκτρόνια αλλά και τα νετρίνα. Στις αρχικές υψηλές ϑερµοκρασίες και έως ότου το Σύµπαν να ψυχθεί στους 6
7 4000 K, η αρχική ϑερµική ακτινοβολία είναι συζευγµένη µε την ύλη λόγω των ελεύθερων ηλεκτρονίων που δρουν ουσιαστικά σαν ανακλαστήρες της ακτινοβολίας. Κατόπιν το Σύµπαν εισέρχεται στην εποχή της κυριαρχίας της ύλης (σκοτεινής και ϐαρυονικής), η οποία κυριαρχεί για τα επόµενα 7 δισεκατοµµύρια χρόνια της ιστορίας του Σύµπαντος. Μόλις η ϑερµοκρασία πέσει αρκετά και τα ηλεκτρόνια χάσουν την κινητική τους ενέργεια συζεύγνονται µε τους ατοµικούς πυρήνες για να δηµιουργήσουν άτοµα οπότε και η ακτινοβολία απελευθερώνεται και ξεκινά το αέναο ταξίδι της στο Σύµπαν. Αυτή ακριβώς η ακτινοβολία που παρατήρησαν πρώτοι οι ϱαδιοαστρονόµοι Penzias και Wilson το Σε αυτή την ϕάση αρχίζουν να δηµιουργούνται, µέσω ϐαρυτικών αλληλεπιδράσεων, οι κοσµικές δοµές αρχικά τυπικού µεγέθους αστρικών σµηνών, και ίσως λίγο µικρότερες, και σταδιακά µεγέθους γαλαξιών και σµηνών γαλαξιών. Είναι η παραπάνω εξιστόριση της εξέλιξης του Σύµπαντος µονοσήµαντα καθορισµένη Η α- πάντηση είναι όχι, διότι εξαρτάται από το συνολικό ποσό της υλο-ενέργειας που περιέχει αλλά και από το είδος του κοσµικού ϱευστού που γεµίζει το Σύµπαν. Εάν περιέχει µικρό ποσό υλοενέργειας τότε το Σύµπαν ϑα διαστέλλεται επ άπειρον ( ανοικτό Σύµπαν). Εάν περιέχει µεγάλο ποσό υλο-ενέργειας τότε το Σύµπαν ϑα αρχίσει να συστέλλεται µετά από κάποιο χρονικό διάστη- µα έως ότου συνθλιβεί κάτω από την επίδραση της ιδιο-ϐαρύτητας του ( κλειστό Σύµπαν). Αν όµως περιέχει το κρίσιµο ποσό υλο-ενέργειας, που είναι το σύνορο µεταξύ των δύο παραπάνω περιπτώσεων, τότε το πως ϑα διασταλλεί το Σύµπαν εξαρτάται και από το είδος της υλο-ενέργειας που περιέχει. Πχ, µπορεί το συνολικό ποσό της ύλης στο Σύµπαν, που αποτελείται από την κοινή (ϐαρυονική) ύλη αλλά και από την σκοτεινή ύλη (ύλη που δεν εκπέµπει ηλεκτοµαγνητική ακτινοβολία και αλληλεπιδρά µόνο µέσω της ϐαρυτικής αλληλεπίδρασης) να έχει την κρίσιµη τιµή, οπότε το Σύµπαν ϑα συνεχίσει να διαστέλλεται µε επιβραδυνόµενο σταθερό ϱυθµό. Μπο- ϱεί όµως στην δυναµική του Σύµπαντος να συνεισφέρει και η λεγόµενη σκοτεινή ενέργεια (µια άγνωστης µορφής ενέργεια που τα αποτελέσµατα της προσοµοιάζουν αυτό που οι Κοσµολόγοι ονοµάζουν αντι-ϐαρύτητα ), στην οποία περίπτωση το συνολικό ποσό της ύλης είναι µικρότερο από την κρίσιµη τιµή αλλά συµπληρώνεται από την σκοτεινή ενέργεια οπότε µετά από κάποιο χρόνο, τις ελκτικές δυνάµεις της κοσµικής ιδιο-ϐαρύτητας τις υπερνικά η σκοτεινή ενέργεια. Η διατάραξη της σχέσης ύλης σκοτεινής ενέργειας υπέρ της τελευταίας επιδρά δραµατικά στη µετέπειτα εξέλιξη του Σύµπαντος αλλάζοντας τον ϱυθµό διαστολής του από επιβραδυνόµενο σε επιταχυνόµενο. Τα τελευταία 15 χρόνια µε τις εκπληκτικής σηµασίας παρατηρήσεις των διαταραχών ϑερµοκρασίας του υπόβαθρου µικροκυµάτων (κυρίως µε τα πειράµατα Boomerang και τα δεδοµένα 7
8 των δορυφόρων WMAP και Planck, εικόνα 1), ϐρέθηκε ότι το Σύµπαν έχει το κρίσιµο ποσό υλο-ενέργειας και εποµένως η γεωµετρία του χώρου είναι Ευκλείδια. Επιπλέον, µε την ανάλυση µακρινών υπερκαινοφανών αστέρων, που παρατηρήθηκαν µε τα µεγαλύτερα τηλεσκόπια της Γης, ϐρέθηκε ότι το Σύµπαν διαστέλλεται µε επιταχυνόµενο ϱυθµό. Αυτό συνεπάγεται την συµ- µετοχή στο συνολικό ποσό της συµπαντικής υλο-ενέργειας και της σκοτεινής ενέργειας, όπως αναφέραµε προηγούµενα. Αν και πολλά µοντέλα σκοτεινής ενέργειας έχουν προταθεί, εξαι- ϱετικά ενδιαφέρον µοντέλο, το οποίο αναπαράγει µεν µε ακρίβεια τις παρατηρήσεις δεν είναι απαλλαγµένο δε και αυτό από ϑεωρητικά προβλήµατα, είναι αυτό της λεγόµενη κοσµολογικής σταθεράς (που την πρωτοεισήγαγε ο Αϊνστάιν αυθαίρετα στις εξισώσεις πεδίου της ΓΘΣ για να επιβάλει στατικές λύσεις), που είναι µία ενέργεια σταθερή στον χρόνο. Σχηµατικά µπορούµε να δούµε πως διαστέλλεται το Σύµπαν στην περίπτωση αυτή στην εικόνα 2. Εικόνα 1:: Η εξέλιξη του παράγοντα της διαστολής του Σύµπαντος ως συνάρτηση του κοσµικού χρόνου για την περίπτωση ύπαρξης σκοτεινής ενέργειας µε την µορφή Κοσµολογικής σταθεράς. Μετά την αρχική έκρηξη η διαστολή αρχίζει να επιβραδύνεται λόγω της ιδιοβαρύτητας του Σύµπαντος αλλά µετά από 7 περίπου δισεκατοµµύρια χρόνια την ελκτική δυνάµη της ιδιοβαρύτητας του Σύµπαντος την υπερνικά η ὰντι-ϐαρυτική δράση της σκοτεινής ενέργειας. ύο µοντέλα πα- ϱουσιάζονται : Η περίπτωση Ευκλείδιου Σύµπαντος (δηλαδή Σύµπαν το οποίο περιέχει την κρίσιµη 8
9 τιµή συνολικής υλο-ενέργειας) ϕαίνεται µε την ϱοζ καµπύλη ενώ η περίπτωση κλειστού Σύµπαντος (δηλαδή Σύµπαν το οποίο περιέχει παραπάνω από την κρίσιµη τιµή συνολικής υλο-ενέργειας αλλά και Κοσµολογική σταθερά) ϕαίνεται µε την λευκή καµπύλη. Η Κοσµολογικής σταθερά ϑα µπορούσε να ερµηνευτεί ως η ενέργεια του κενού όπως υποστηρίζει η κβαντοµηχανική (από το γεγονός ότι Ϲεύγη σωµατίων & αντισωµατίων δηµιουργούνται από το κενό και παρόλο που Ϲουν ελάχιστα δίνουν στο κενό µη-µηδενική δυναµική ενέργεια). Στην ΓΘΣ όλες οι µορφές ενέργειας δηµιουργούν ϐαρυτικό πεδίο, άρα και η ενέργεια του κενού. Οµως έχουµε το παράδοξο ότι η κβαντική ϑεωρία πεδίου, που προβλέπει την ύπαρξη κοσµολογικής σταθεράς, προβλέπει επίσης ότι πρέπει να έχει τιµή ϕορές µεγαλύτερη από αυτή που µετράµε µε την µελέτη των µακρινών υπερκαινοφανών αστέρων. Είναι αξιοπερίεργο επίσης ότι η σκοτεινή ενέργεια συµµετέχει στο συνολικό ποσό συµπαντικής υλο-ενέργειας µε ποσοστό που είναι περίπου ίσο µε αυτό της ύλης (σκοτεινής και ϐαρυονικής), γεγονός που αποτελεί το λεγόµενο πρόβληµα σύµπτωσης, µιας και δεν υπάρχει κανείς a priori ϕυσικός λόγος για αυτή την σύµπτωση. Επιπλέον, υπάρχει και το πρόβληµα γιατί το ποσό της συµπαντικής υλο-ενέργειας έχει ακριβώς την κρίσιµη τιµή και όχι οποιανδήποτε από την απειρία των τιµών που ϑα µπορούσε να έχει. Μια πιθανή λύση στα προβλήµατα αυτά µπορεί να αναζητηθεί στο γεγονός ότι εάν το Σύµπαν διαστελλόταν µε ϱυθµό σηµαντικά µεγαλύτερο της κρίσιµης τιµής τότε η ϐαρυτική έλξη δεν ϑα µπορούσε να δράσει καταλυτικά ώστε να καταρρεύσουν ϐαρυτικά οι κοσµικές δοµές και να δηµιουργηθούν αστέρες, στον πυρήνα των οποίων συντίθενται τα απαραίτητα συστατικά στοιχεία για την ύπαρξη Ϲωής (οξυγόνο, άνθρακας κλπ). Αντίστοιχα, εάν το Σύµπαν διαστελλόταν µε ϱυθµό σηµαντικά ϐραδύτερο της κρίσιµης τιµής, εάν δηλαδή περιείχε πολύ µεγαλύτερο συνολικά ποσό υλο-ενέργειας, τότε πάλι πριν προλάβουν να δηµιουργηθούν οι κοσµικές δοµές και οι αστέρες, το Σύµπαν ϑα είχε ξανά-συσταλεί σε µία υπέρθερµη ϑάλασσα ακτινοβολίας. Ε- ποµένως, το ίδιο το γεγονός της ύπαρξης µας προϋποθέτει ότι το Σύµπαν διαστέλλεται περίπου µε τον ϱυθµό που µετράµε. Αυτή η κοσµική συνοµωσία µπορεί να ερµηνευτεί εάν υπάρχουν άπειρα Σύµπαντα, όπου πραγµατώνονται όλοι οι δυνατοί συνδυασµοί παραµέτρων και εκδοχών, και εποµένως σε αυτά όπου οι συνθήκες είναι ευνοϊκές αναπτύσσεται η Ϲωή. Άλλες ερµηνείες ϐασίζονται στη λεγόµενη Ανθρωπική Αρχή (η ασθενής εκδοχή της), δηλαδή ότι η ίδια η ύπαρξη τη ανθρώπινης Ϲωής προϋποθέτει ότι το Σύµπαν περιέχει το συγκεκριµένο ποσό υλο-ενέργειας (όπως επίσης ότι τις συγκεκριµένες τιµές που µετράµε των σταθερών τη ϕύσης). Πολλές ϕορές αυτή η αρχή χρησιµοποιείται σαν πανάκεια για να δώσει λογικοφανή ερµηνεία σε ϕαινόµενα που δυσκολευόµαστε να ερµηνεύσουµε αλλά αυτή της η χρήση είναι αντι-επιστηµονική. Αυτά ϐέβαια 9
10 τα ερωτήµατα ϐρίσκονται στην διεπαφή µεταξύ επιστήµης και ϕιλοσοφίας και ϑα αποτελούν λόγο έντονων συζητήσεων και διανέξεων πιθανώς στο διεινεκές. 2 Βασικές Εννοιες Θα παρουσιάσούµε µερικές ϐασικές έννοιες που είναι προαπαιτούµενες για την κατανόηση της σύγχρονης Κοσµολογίας. 2.1 Η Κοσµολογική Αρχή Η Κοσµολογική αρχή λέει ότι το Σύµπαν είναι οµογενές και ισότροπο σε µεγάλες κλίµακες. Η αρχή αυτή προτάθηκε πρώτα από τον ίδιο τον Αϊνστάϊν χωρίς αρχικά καµία παρατηρησιακή ένδειξη, αλλά για αισθητικούς λόγους και που είχαν να κάνουν µε την αρχή του Μάχ, που έλεγε µε απλά λόγια ότι οι νόµοι της ϕύσης καθορίζονται από την κατανοµή της ύλης σε µεγάλες κλίµακες. Για να µπορέσει ο Αϊνστάϊν να ϑέσει σε στέρεες ϐάσεις την ϑεωρητική κοσµολογία υπέθεσε ότι µια τέτοια απλότητα κυριαρχεί στο Σύµπαν, γεγονός που τον διευκόλυνε να λύσει τις εξισώσεις πεδίου σε κοσµολογικό υπόβαθρο 1. Είναι ενδιαφέρον ότι οι παρατηρήσεις της εποχής ακριβώς το αντίθετο έδειχναν, µιας και οι αστρονόµοι ϑεωρούσαν ότι όλο το Σύµπαν περιορίζονταν σε αυτό που σήµερα ονοµάζουµε Γαλαξία µας του οποίου η κατανοµή των αστέρων και αερίων είναι εντελώς ανισοτροπική. Τι σηµαίνει Οµοιογένεια ; Σηµαίνει ότι το Σύµπαν παραµένει το ίδιο όπου και να ϐρίσκεται ο παρατηρητής. Τι σηµαίνει Ισοτροπία ; Σηµαίνει ότι το Σύµπαν ϕαίνεται το ίδιο σε όποια διεύθυνση και αν κοιτάξει ο παρατηρητής. Είναι εξαιρετικά ενδιαφέρον το γεγονός ότι ενώ οι αιτίες για τις οποίες προτάθηκε η Κοσµολογική αρχή από τον Αϊνστάϊν ήταν µαθηµατικού/φιλοσοφικού περιεχοµένου, σύγχρονες πα- ϱατηρήσεις της κοσµικής ακτινοβολίας µικροκυµάτων στηρίζουν την Κοσµολογική αρχή (ϐλέπε κεφάλαιο 5). Παρόλο που σε µικρές κλίµακες το Σύµπαν είναι εντελώς ανοµοιογενές και ανισότροπο, σε µεγάλες κλίµακες πλησιάζει σταδικά την οµοιογένεια όπως πιστοποιείται από την 1 Η απλούστερη µετρική που είναι συµβατή µε ισοτροπία και οµοιογένια είναι η περίφηµη µετρική Friedmann, Robertson & Walker (FRW). 10
11 στατιστική µελέτη της χωρικής κατανοµής των γαλαξιών, των σµηνών γαλαξιών αλλά και των µακρυνών, σε κοσµολογικές αποστάσεις, ϱαδιογαλαξιών. Αυτές οι µελέτες έχουν αποδείξει ότι όλες οι κοσµικές δοµές είναι σµηνοποιηµένες, δηλαδή υπάρχουν συγκεντρώσεις γαλαξιών, οργανω- µένες σε οµάδες, σµήνη και υπερσµήνη γαλαξιών και ταυτόχρονα υπάρχουν µεγάλες περιοχές κενές (ή σχεδόν κενές) γαλαξιών. Πάνω όµως από κάποια κλίµακα σταµατά αυτή η ιεραρχική κατανοµή και ϕτάνουµε στην οµοιογένεια ( Mpc) 2. Η πιο ισχυρή απόδειξη ότι το Σύµπαν είναι ισότροπο έρχεται από την παρατήρηση της κοσµικής ακτινοβολίας µικροκυµάτων που είναι το ενεργειακό απολιθωµα της αρχέγονης ϑερµικής ακτινοβολίας, από την εποχή που το Σύµπαν ήταν σε υπέρπυκνη και υπέρθερµη κατάσταση. Η κοσµική ακτινοβολία είναι ισοτροπική, σε ένα επίπεδο 1/100, σε όποια κατεύθυνση και αν κοιτάξει ο παρατηρητής αν δε αφαιρέσουµε την εκποµπή του γαλαξία µας και την διπολική ανισοτροπία λόγω της κίνησης του γαλαξία µας µέσα στη διάχυτη αυτή ακτινοβολία, τότε η ισοτροπία είναι σε επίπεδο Η Θεωρία της Μεγάλης Εκρηξης Η σηµαντικότερη σύγχρονη ϑεωρία που ερµηνεύει τη δηµιουργία του Σύµπαντος είναι η ϑεω- ϱία της αρχικής µεγάλης έκρηξης (Bing-Bang ). Στην ϑεωρία αυτή δεχόµαστε ότι το Σύµπαν ξεκίνησε από µια υπέρθερµη και υπέρπυκνη κατάσταση. Μαθηµατικά η αρχή του Σύµπαντος ονοµάζεται ανωµαλία (singularity ) διότι η πυκνότητα και ο όγκος του Σύµπαντος έχουν άπειρη τιµή. Πράγµατι, οι οριακές συνθήκες των εξισώσεων κίνησης για το Σύµπαν (ϐλέπε επόµενο κεφάλαιο) υποθέτουν ότι ο παράγοντας µε τον οποίο διαστέλλεται το σύµπαν [ϐλέπε εξ. (6)] a(t) είναι µηδέν κατά την χρονική στιγµή t = 0. Επίσης η χρονική παράγωγος του α(t) για t = 0 είναι άπειρη, συνεπώς και η αρχική ταχύτητα της διαστολής είναι άπειρη. Άρα είναι αδύνατο στο πλαίσιο της ΓΘΣ να κατανοήσουµε την Φυσική µέσα σε µαθηµατικές ανωµαλίες (Hawking 1969 ). Εποµένως, στο πολύ νεαρό Σύµπαν (τάξης χρόνου Planck) χρειαζόµαστε µια κβαντική ϑεωρία ϐαρύτητας η οποία ϑα ερµηνεύσει τις αρχικές συνθήκες δηµιουργίας του Σύµπαντος. Αφού η ΓΘΣ µας οδηγεί σε µια αρχική ανωµαλία αναπτύχθηκαν κατά καιρούς διάφορες εναλλακτικές ϑεωρίες ώστε να ξεπεράσουν το πρόβληµα αυτό. Πάντως µέχρι σήµερα καµία από αυτές δεν µπόρεσε να αντικαταστήσει την ΓΘΣ διότι η τελευταία επιβεβαιώνεται συνεχώς από τις παρατηρήσεις. Το ερώτηµα που έπρεπε να εξεταστεί από τους Κοσµολόγους ήταν µήπως ένα Σύµπαν οµογενές και ισότροπο δεν πέρασε ποτέ από µια αρχική ανωµαλία. Το ερώτηµα αυτό απαντήθηκε από τους Hawking & Penrose το 1969, οι οποίοι έδειξαν ότι κάθε µοντέλο 2 1 Mpc = έτη ϕωτός 11
12 του Σύµπαντος που έχει τα χαρακτηριστικά της Κοσµολογικής αρχής ξεκινάει πάντα από µια µαθηµατική ανωµαλία. Οι πρώτοι που διατύπωσαν την ϑεωρία της µεγάλης έκρηξης, ως προς την δυναµική της, ήταν ο Lemaitre το 1927 και ως προς την ϕυσική της οι Gamow, Herman & Alpher. Ο Friedmann (1948, 1953, 1967) λύνοντας τις εξισώσεις πεδίου είδε αµέσως ότι αυτές προέβλεπαν ένα εξελισσόµενο µε τον χρόνο Σύµπαν. Επίσης χρησιµοποιώντας το αποτέλεσµα αυτό έδειξε ότι η εντροπία του Σύµπαντος αυξάνει µε την πάροδο του χρόνου, άρα ϑα πρέπει να υπήρξε µια κατάσταση ε- λάχιστης εντροπίας, όπου η ύλη ϑα είχε την µέγιστη δυνατή οργάνωση (η αντίστροφη πορεία ακολουθείται για την κατάρρευση ενός πολύ µεγάλου αστέρα σε µελανή οπή). Παραθέτουµε τους ϐασικούς πυλώνες πάνω στους οποίους στηρίζεται η αρχική µεγάλη έκρηξη. 1. ιαστολή του Σύµπαντος. Ο Hubble το 1929 µελετώντας τους γαλαξίες παρατήρησε µετατόπιση του ϕασµατός τους προς το ερυθρό. Αυτό ερµηνεύτηκε ως ϕαινόµενο ανάλογο του Doppler δηλαδή ότι οι γαλαξίες αποµακρύνονται ο ένας από τον άλλο µε ταχύτητα η οποία ϐρέθηκε να είναι ανάλογη της αποστασής τους. 2. Πυρηνογέννεση. Η ϑεωρία της µεγάλης έκρηξης εξηγεί µε µεγάλη ακρίβεια την δη- µιουργία των σηµαντικότερων στοιχείων του περιοδικού πίνακα από πυρηνικές αντιδράσεις στοιχειωδών σωµατιδίων (πρωτονίων, νετρονίων, κ.α). Στα 4 πρώτα περίπου λεπτά της ε- ξέλιξης του Σύµπαντος δηµιουργήθηκε το ήλιο ( 26%) και τα άλλα ελαφρύτερα στοιχεία (δευτέριο, λίθιο, κ.α). Στην συνέχεια µε την δηµιουργία και την εξέλιξη των αστέρων, το Σύµπαν εµπλουτίζεται διαρκώς µε χηµικά στοιχεία. 3. Η Κοσµική Ακτινοβολία Μικροκυµάτων (C.M.B). Μια σηµαντική απόδειξη για την ορ- ϑότητα της ϑεωρίας της µεγάλης έκρηξης δόθηκε από την ανακάλυψη της Κοσµικής Ακτινοβολίας Μικροκυµάτων C.M.B (ϐλέπε παράγραφο 5.6) η οποία είχε προβλεφθεί ϑεωρητικά από τον Gamow ως αναπόδραστο στοιχείο της ϑερµής µεγάλης έκρηξης. Η ακτινοβολία αυτή είναι ισοτροπική, γεµίζει όλο το Σύµπαν και αντιστοιχεί σε ϕάσµα µελανού σώµατος, µε ϑερµοκρασία 2.73 K. Η µόνη πειστική εξήγηση για την ϕύση της ακτινοβολίας αυτής είναι ότι προέρχεται από ϕωτόνια που γέµισαν το Σύµπαν στα πρώτα στάδια της διαστολής του. ηλαδή η C.M.B είναι ενεργειακό απολίθωµα της µεγάλης έκρηξης. Είναι χαρακτηριστικό ότι καµία άλλη ϑεωρία δεν έχει εξηγήσει και ακόµα περισσότερο δεν είχε προβλέψει την Κοσµική Ακτινοβολία Μικροκυµάτων. 12
13 2.3 Η ιαστολή του Σύµπαντος Μία από τις σηµαντικότερες αστρονοµικές παρατηρήσεις στην ιστορία της σύγχρονης Κοσµολογίας υπήρξε η παρατήρηση ότι οι γαλαξίες αποµακρύνονται από τον παρατηρητή, µε ταχύτητες ανάλογες µε την απόσταση τους. Την σηµαντική αυτή ανακάλυψη έκανε ο αστρονόµος Hubble ϐασιζόµενος και σε προγενέστερες παρατηρήσεις του Slipher χρησιµοποιώντας ϕασµατοσκοπεία γαλαξιών. Παρατήρησε ότι οι γραµµές εκποµπής κάποιων χαρακτηριστικών στοιχείων (όπως η γραµµή Ηα της σειράς Balmer του υδρογόνου) ήταν µετατοπισµένες προς το ερυθρό µέρος του ϕάσµατος των γαλαξιών, σε σχέση µε την αναµενόµενη εκποµπή τους σε ηρεµία. Αυτό σηµαίνει ότι οι γαλαξίες αποµακρύνονται από τον παρατηρητή και αυτή η µετατόπιση του ϕάσµατος ονοµάζεται ερυθροµετατόπιση. Αντίθετα έαν παρατηρηθεί µια µετατόπιση στις υψηλότερες συχνότητες, αυτή ονοµάζεται κυανοµετατόπιση και ενδεικνύει ότι ο γαλαξίας αυτός πλησιάζει τον παρατηρητή. Το ϕαινόµενο αυτό ϑυµίζει το ϕαινόµενο Doppler, αν και στην πραγµατικότητα, όπως ϑα δούµε παρακάτω, οι χωρικές συντεταγµένες των γαλαξιών δεν µεταβάλλονται αλλά ο χώρος ο ίδιος διαστέλλεται και συµπαρασέρνει και τους γαλαξίες. Η µετάθεση των ϕασµατικών γραµµών ενός κινούµενου, ως προς τον παρατηρητή, γαλαξία ορίζεται ως : z = λ 0 λ r λ r (1) όπου λ 0 είναι το µήκος κύµατος της ϕασµατικής γραµµής του γαλαξία που παρατηρούµε και λ r είναι το µήκος κύµατος σε ηρεµία. Εάν έχουµε z > 0 τότε µιλάµε για ερυθροµετατόπιση, ενώ εάν έχουµε z < 0 µιλάµε για κυανοµετατόπιση. Κυανοµετατόπιση παρατηρείται µόνο για ορισµένους κοντινούς γαλαξίες της τοπικής οµάδας γαλαξιών, για τους οποίους η ϐαρυτική έλξη στο κοινό δυναµικό της οµάδας υπερνικά την αρχική ταχύτητα διαστολής, που λόγω εγγύτητας έχει µικρό µέτρο, όπως ϑα δούµε αµέσως παρακάτω. Η ταχύτητα µε την οποία αποµακρύνεται ένας γαλαξίας από τον παρατηρητή δίδεται από την σχέση Doppler: 1 + z = 1 + v/c 1 + v/c for v c, (2) 1 v/c δηλαδή v = cz, µε c την ταχύτητα του ϕωτός. Πρώτος ο Hubble παρατήρησε ότι η ταχύτητα αποµάκρυνσης των γαλαξιών από τον παρατηρητή είναι ανάλογη της απόστασης τους, δηλαδή v = H 0 r (3) 13
14 όπου η σταθερά αναλογίας ονοµάζεται σταθερά του Hubble, παρόλο που µια πιο δόκιµη ονο- µασία είναι παράµετρος Hubble µιας και είναι συνάρτηση του κοσµικού χρόνου. Η σχέση (3) ονοµάζεται νόµος του Hubble. Βρέθηκε δε ότι ο νόµος αυτός είναι ανεξάρτητος της διεύθυνσης παρατήρησης. Αυτό αποτελεί άλλη µια απόδειξη της ισχύως της Κοσµολογικής Αρχής. Το σύµπαν διαστέλλεται ισοτροπικά γύρω από τον παρατηρητή στη Γη και από οποιονδήποτε άλλο παρατηρητή στο Σύµπαν. Αλλά µήπως αυτό σηµαίνει ότι είµαστε στο κέντρο του Σύµπαντος ; Οχι γιατί σύµφωνα µε την Κοσµολογική Αρχή το Σύµπαν είναι οµογενές και ισότροπο, που σηµαίνει ότι είναι ισότροπο γύρω από κάθε σηµείο. Επιπλέον, ο νόµος του Hubble, µε τον παράγοντα H 0 να είναι µια σταθερά ανεξάρτητη διεύθυνσης, συνεπάγεται ότι κάθε παρατηρητής ϐλέπει κάθε άλλο να αποµακρύνεται µε παρόµοιο τρόπο, πιστοποιείται γεγονός που ενισχύει την Κοσµολογική Αρχή της οµογένειας και ισοτροπίας. Εστω λοιπόν σύστηµα αναφοράς µε αρχή το σηµείο Π 0 και δύο γαλαξίες σε σηµεία Π 1 και Π 2 ϐρισκόµενα σε απόσταση r 1 και r 2 από το Π 0. Η ταχύτητα των γαλαξιών στο Π 1 και Π 2 σε σχέση µε το Π 0 είναι v(r 1 ) και v(r 2 ) αντίστοιχα (δες εικόνα 2). Η ταχύτητα του γαλαξία στο Π 2 σε σχέση µε τον γαλαξία στο Π 1, σε απόσταση r 3, είναι εποµένως : v (r 3 ) = v(r 2 ) v(r 1 ) (4) Εικόνα 2: ιανυσµατική απόδοση της ισοτροπικής διαστολής του κοσµικού χώρου. 14
15 Λόγω όµως του νόµου του Hubble στο σύστηµα αναφοράς του Π 0, έχουµε : v(r 1 ) = H 0 r 1 και v(r 2 ) = H 0 r 2 οπότε : v (r 3 ) = H 0 r 2 H 0 r 1 = H 0 (r 2 r 1 ) = H 0 r 3 (5) Άρα ο ίδιος νόµος διαστολής που ισχύει για ένα παρατηρητή στο Π 0 ισχύει και για τον παρατηρητή στο Π 1 και ούτο κάθε εξής. Εποµένως δεν υπάρχει κάποιο κέντρο της διαστολής στο 3-διάστατο χώρο, όπως εσφαλµένα ϑα µπορούσε να ϑεωρήσει κανείς για τον παρατηρητή στη Γη. Το κέντρο διαστολλής ϐρίσκεται στον χωρόχρονο ο οποίος είναι ένας χώρος τεσσάρων διαστάσεων µέσα στον οποίο εµβαπτίζεται ο 3-διάστατος χώρος. Μια ακριβής αναγωγή στις 2 διαστάσεις µπορεί να κατανοηθεί µε την διαστολή της 2-διάστατης επιφάνειας ενός µπαλονιού που το ϕουσκώνουµε. Και σε αυτή την περίπτωση το κέντρο της διαστολής δεν ϐρίσκεται στην διαστελλόµενη επιφάνεια του αλλά στην µη διαστελλόµενη 3η διάσταση. 2.4 Συνµετακινούµενες συντεταγµένες Ενα ϐολικό σύστηµα συντεταγµένων σε ένα χώρο που διαστέλλεται ισοτροπικά είναι το λεγόµενο συνµετακινούµενο σύστηµα συντεταγµένων, που όπως λέει και τό όνοµα του, παρασύρετε από την ίδια την διαστολή. Η σχέση µεταξύ µιας ϕυσικής απόστασης, r, και της συνµετακινούµενης απόστασης, x, είναι γραµµική : r = a(t)x (6) µε την παράµετρο αναλογίας, a(t), να είναι συνάρτηση µόνο του χρόνου (και όχι της διεύθυνσης). Αυτή η παράµετρος ονοµάζεται παράγοντας διαστολής ή αλλιώς παράγοντας κλίµακας. διαστελλόµενο Σύµπαν οι γαλαξίες παραµένουν ακίνητοι (πέρα από µικρές διαταραχές λόγω του τοπικού ϐαρυτικού πεδίου) στο συνµετακινούµενο σύστηµα συντεταγµένων. Στο Εποµένως η συνάρτηση a(t) προσδιορίζει σε ένα διαστελλόµενο Σύµπαν κάθε µήκος r 0, σε κάποια χρονική στιγµή t 0, αν σε κάποιο προγενέστερο χρόνο, t 1, είχε µέγεθος r 1, σύµφωνα µε : r 0 = a(t 0) a(t 1 ) r 1 (7) όπου t 0 > t 1. Εάν ταυτίσουµε το t 0 µε τη σηµερινή ηλικία του Σύµπαντος τότε πολλές ϕορές στη ϐιβλιογραφία ο παράγοντας κλίµακας κανονικοποιείται µε τέτοιο τρόπο ώστε να είναι µονάδα στη σηµερινή εποχή a(t 0 ) 1. Εποµένως, µπορούµε να ϑεωρήσουµε χρησιµοποιώντας την 15
16 παραπάνω σχέση πως µεταβάλλεται και το µήκος κύµατος της ακτινοβολίας, λ, που εκπέµπεται από κάποιο γαλαξία σε χρόνο t 1 και καταλαµβάνεται από τον Γήινο παρατηρητή ως λ 0 στο χρόνο t 0, έχουµε λοιπόν : λ 0 = a(t 0) a(t 1 ) λ 1 = 1 a(t 1 ) λ 1 (8) Εποµένως, χρησιµοποιώντας και τον ορισµό της ϕασµατικής µετατόπισης εξ.(1), παράγουµε την σχέση µεταξύ της ερευθροµετατόπισης και του παράγοντα κλίµακας : 1 + z = λ 0 λ 1 = 1 a(z). (9) Η εξίσωση αυτή είναι πολύ σηµαντική διότι συνδέει την παρατηρησιακή ποσότητα της ερυθροµετάθεσης µε τον παράγοντα διαστολής του Σύµπαντος. Για παράδειγµα εάν υποθέσουµε ότι ένας γαλαξίας παρατηρείται σε ερυθροµετάθεση z = 1 αυτό συνεπάγεται, µέσω της εξίσωσης (9), ότι ο παράγοντας κλίµακας εκείνη την εποχή είναι ο µισός της σηµερινής του τιµής a(z 1) = 0.5. Επανερχόµαστε στο νόµο του Hubble για να δείξουµε ότι είναι ϕυσική απόρροια της οµογενούς διαστολής του Σύµπαντος. Παραγωγίζοντας την εξ.(6) ως προς τον χρόνο, ϐρίσκουµε r = ȧx + aẋ = ȧ a r + u p. Οπου στην παραπάνω σχέση αναγνωρίζουµε ως u p = aẋ τη σχετική ταχύτητα που έχουν οι γαλαξίες εξαιτίας των τοπικών ϐαρυτικών αλληλεπιδράσεων οι οποίες όµως είναι αµελητέες σε κοσµολογικές κλίµακες. Τελικά χρησιµοποιώντας την τελευταία διαπίστωση το µέτρο της διαστολής Hubble δίνεται v = ȧ(t) r = H(t)r, (10) a(t) δηλαδή αναπαράγαµε τον νόµο του Hubble µε την παράµετρο Hubble να δίδεται από τον λόγο H(t) = ȧ(t) a(t). (11) Είναι σηµαντικό να τονίσουµε ότι µε τη ϐοήθεια των εξ.(9) και (11) εξάγουµε τις σχέσεις µεταξύ των διαφορικών dt, da και dz οι οποίες χρησιµοποιούνται όταν ϑέλουµε να µεταφερθούµε από µία κοσµική µεταβλητή σε µία άλλη : dt = da ah(a) = dz (1 + z)h(z) (12) 16
17 ή H 0 dt = da ae(a) = dz (1 + z)e(z) (13) όπου η ποσότητα E(z) = H(z)/H 0 ονοµάζεται κανονικοποιηµένη παράµετρος του Hubble. 2.5 Η Μετρική του Χωροχρόνου Για να µπορέσουµε να µετρήσουµε αποστάσεις στό Σύµπαν πρέπει να ορίσουµε µια µετρική, δηλαδή ένα σύστηµα συνεταγµένων µέσω του οποίου να ορίζεται η απόσταση µεταξύ δύο σηµείων στο 4-διάστατο χωρόχρονο. Λόγω του γεγονότος ότι δεν γνωρίζουµε a priori πια είναι η γεωµετρία που διέπει στο Σύµπαν, η µετρική αυτή ϑα πρέπει να είναι γενική και εύχρηστη κάτω από οποιανδήποτε πιθανή γεωµετρία. Θυµίζουµε ότι η γνωστή Ευκλείδια (ή επίπεδη) γεωµετρία δεν ισχύει σε καµπυλωµένους χώρους. Στην επιφάνεια της σφαίρας (ϑετικά καµπυλωµένος χώρος) ισχύει η γεωµετρία Riemann, ενώ στην επιφάνεια αρνητικής καµπυλότητας ισχύει η γεωµετρία Lobachevsky. Φυσικά τα ίδια ισχύουν και σε επιφάνειες περισσοτέρων διαστάσεων (πχ. σε σφαιρική επιφάνεια N 1 διαστάσεων, εµβαπτισµένης σε χώρο N διαστάσεων, ισχύει η γεωµετρία Riemann, κλπ). Από την Ειδική ϑεωρία της Σχετικότητας γνωρίζουµε ότι η αναλλοίωτη, κάτω από µετασχη- µατισµό του συστήµατος συντεταγµένων, απόσταση µεταξύ δύο γεγονότων µε 4-διάστατες χωροχρονικές συντεταγµένες (t, x, y, z) και (t + dt, x + dx, y + dy, z + dz), δίδεται από την µετρική Minkowski, που περιγράφει µια επίπεδη γεωµετρία για το χωρόχρονο, και δίδεται σε Καρτεσιανές και σφαιρικές συντεταγµένες αντίστοιχα από : ds 2 = c 2 dt 2 + (dx 2 + dy 2 + dz 2 ) = c 2 dt 2 + [ dr 2 + r 2 (dθ 2 + sin 2 θdφ 2 ) ] (14) Θυµίζουµε ότι αυτή η µετρική συµβολίζεται και µε τον τανυστή η ij ο οποίος σε Καρτεσιανές συντεταγµένες γράφεται c η = Τα ϕωτόνια πάντα κινούνται κατά µήκος γεωδεσιακών ds 2 = 0, και εποµένως σε αυτή την πε- ϱίπτωση παραµένουν σταθερές οι σφαιρικές συνετεταγµένες dθ = dφ = 0 (όπως αντίστοιχα στη 17
18 περίπτωση της επιφάνειας µιας σφαίρας όπου οι γεωδεσιακές είναι µέγιστοι κύκλοι οι οποίοι διατηρούν το γεωγραφικό τους µήκος αναλλοίωτο). Στη Γενική ϑεωρία της Σχετικότητας η γεωµετρία του χωρόχρονου συνυπάρχει και συνδέεται µε τα ϐαρυτικά ϕαινόµενα και εποµένως η αντίστοιχη µετρική γίνεται πιο περίπλοκη και έχει την γενική µορφή 3 : ds 2 = g ij dx i dx j (µ, ν = 0, 1, 2, 3) (15) όπου ds 2 είναι η χωροχρονική απόσταση µεταξύ 2 σηµείων x k και x k + dx k, g ij είναι ο µετρικός τανυστής που ορίζει την γεωµετρία του χωρόχρονου, µε x 0 την χρονική συντεταγµένη και x µ (µ = 1, 2, 3) τις χωρικές συντεταγµένες. Η παραπάνω γενική µορφή απλοποιείται εάν υποθέσουµε την Κοσµολογική Αρχή, δηλαδή ότι η κατανοµή της ύλης σε µεγάλες κλίµακες είναι οµογενής και ισότροπη, συνεπακόλουθα και ο χώρος είναι ισοτροπικός ήτοι g ij = 0 για i j. Σε αυτή την περίπτωση έχουµε τον διαχωρισµό του 4-διάστατου χωρόχρονου σε µια χρονική και 3 χωρικές διαστάσεις : ds 2 = g 00 (dx 0 ) 2 + dl 2 = g 00 (dx 0 ) 2 + g µν dx µ dx ν (µ, ν = 1, 2, 3) (16) όπου g 00 (dx 0 ) 2 = c 2 dt 2 και g µν ο χωρικός µετρικός τανυστής, του οποίου σε σφαιρικές συντεταγµένες η πιο γενική µορφή σε ένα διαστελλόµενο χώρο στον οποίο ισχύει η Κοσµολογική Αρχή, είναι : [ ] dr dl 2 = g µν dx µ dx ν = a 2 2 (t) 1 kr 2 + r2 (dθ 2 + sin 2 θdφ 2 ), (17) όπου a(t) παράγοντας κλίµακας, k η σταθερά που καθορίζει την καµπυλότητα του χώρου, και (r, θ, φ) είναι οι σφαιρικές-πολικές συνµετακινούµενες συντεταγµένες. Η παραπάνω µερική ονο- µάζεται µετρική Friedmann-Robertson-Walker (στη συνέχεια ϑα χρησιµοποιούµε τη συντοµογραφία FRW ). 3 Επειδή στην ΓΘΣ όλες οι εξισώσεις δίνονται µε την µορφή τανυστών, χρησιµοποιούµε την σύµβαση της άθροισης του Αϊνστάιν, σύµφωνα µε την οποία, η εµφάνιση σε έναν όρο του ίδιου δείκτη σε άνω και κάτω ϑέση υποδηλώνει άθροιση ως προς όλες τις τιµές που µπορεί να πάρει ο αυτός ο δείκτης (ds 2 = g ijdx i dx j = g ijdx i dx j ). 18
19 Εικόνα 3: ισ-διάστατες επιφάνειες που αντιστοιχούν στις 3 διαφορετικές τιµές της παραµέτρου καµπυλότητας, k. Η σταθερά καµπυλότητας µπορεί να πάρει τιµές +1, 0, 1, που αντιστοιχούν σε τρισδιάστατη σφαίρα, τρισδιάστατο Ευκλείδιο χώρο και τρισδιάστατο υπερβολωειδές (οι αντίστοιχες δισδιάστατες επιφάνειες παρουσιάζονται στην εικόνα 3). Κλειστή γεωµετρία k = +1 είναι η πιο απλή µη-ευκλείδια γεωµετρία στην οποία δύο πα- ϱάλληλες ευθείες τέµνονται, µιας και η ελάχιστη απόσταση µεταξύ δύο σηµείων είναι ο µέγιστος κύκλος που τα ενώνει, το άθροισµα των γωνιών ενός τριγώνου είναι > 180. Ενα σύµπαν µε ϑετική καµπυλότητα είναι πεπερασµένο σε µέγεθος αλλά δεν έχει πέρατα, όπως και η επιφάνεια της σφαίρας είναι πεπερασµένη αλλά χωρίς πέρατα µιας και αν συνεχίζεις να κινείσαι επί µέγιστου κύκλου τελικά ϑα ξαναεπισκευτείς την αφετηρία σου. Κάνοντας τον µετασχηµατισµό r = sin χ, η χωρικά διαστελλόµενη µετρική (17) γίνεται : dl 2 = a 2 (t) [ dχ 2 + sin 2 χ(dθ 2 + sin 2 θdφ 2 ) ]. Στην συνέχεια υπολογίζονται τα ϐασικά γεωµετρικά χαρακτηριστικά της υπερσφαίρας ακολουθώντας την ίδια τακτική µε την δισδιάστατη σφαίρα. Ετσι το εµβαδό µια στοιχειώδους περιοχής από θ εώς θ + dθ και φ εώς φ + dφ της επιφάνειας ακτίνας r c = a(t)r = a(t) sin χ 19
20 δίνεται από την σχέση ds k=1 = r 2 c sin θdθdφ = a 2 (t) sin 2 χ sin θdθdφ. Με ολοκλήρωση του στοιχείου επιφάνειας ds k=1 όταν το το θ µεταβάλλεται από 0 εώς π και το φ από 0 εώς 2π υπολογίζουµε το εµβαδό της επιφάνειας S k=1 (χ) = 4πα 2 sin 2 χ το οποίο παρουσιάζει µέγιστη τιµή 4πα 2 στον ισηµερινό (χ = π/2) ενώ µηδενίζεται στους αντίποδες (χ = π). Ο στοιχειώδης όγκος αντίστοιχα δίνεται dv k=1 = a(t)dχds k=1 = a 3 sin 2 χ sin θdχdθdφ και ολοκληρώνοντας τόσο ως προς στη στερεά γωνία όσο και ως προς χ ϐρίσκουµε τον όγκο της επιφάνειας V k=1 (χ) = a 3 χ 0 π 2π sin 2 χ dχ sin θdθdφ = 2πα 3 (χ 1 sin 2χ) Είναι προφανές ότι στο χ = π ο όγκος παρουσιάζει µέγιστο V (max) k=1 (π) = 2π 2 α 3. Ανοικτή γεωµετρία k = 1 αντιστοιχεί σε αρνητικά καµπυλοµένη επιφάνεια όπου δύο πα- ϱάλληλες ευθείες ποτέ δεν τέµνονται, αποκλίνουν δηλαδή, και εποµένως το Σύµπαν που διέπεται από αυτή την γεωµετρία είναι άπειρο. Επίσης, αντίθετα από την περίπτωση ϑετικής καµπυλότητας, ισχύει ότι το άθροισµα των γωνιών ενός τριγώνου είναι < 180. Ο χώρος ονοµάζεται υπερβολικός και είναι ανοικτός, χωρίς να έχει πεπερασµένο όγκο µε χωρική µετρική : dl 2 = a 2 (t) [ dχ 2 + sinh 2 χ(dθ 2 + sin 2 θdφ 2 ) ] όπου στην (17) έχουµε κάνει τον µετασχηµατισµό r = sinhχ µε 0 χ < +. Τα ϐασικά χαρακτηριστικά του χώρου αυτού µπορούν να προκύψουν, εάν τις τριγωνοµετρικές συναρτήσεις τις αντικαταστήσουµε µε υπερβολικές συναρτήσεις S k= 1 (χ) = 4πα 2 sinh 2 χ 20
21 και V k= 1 (χ) = 2πα 3 ( χ + 1 sin 2χ). 2 Επίπεδη (Ευκλείδια) γεωµετρία k = 0 είναι η γνωστή µας γεωµετρία στην οποία δύο πα- ϱάλληλες ευθείες ποτέ δεν τέµνονται, που το άθροισµα των γωνιών ενός τριγώνου είναι 180. Σε αυτή την περίπτωση ακολουθώντας τα ϐήµµατα που περιγράψαµε παραπάνω έχουµε r = χ, S k=0 = 4πa 2 χ 2 και V k=0 = 4πa 3 χ 3 /3. Συνήθως ϑεωρείται ότι είναι άπειρη η χωρική διάσταση ενός σύµπαντος που διέπεται από αυτή τη γεωµετρία, µιας και εάν είχε πεπερασµένο µέγεθος τότε δυό παράλληλες ευθείες ϑα τέµνονταν. Παρόλα αυτά όµως, αποδείχθηκε, σχετικά πρόσφατα (Nash 1954), ότι όλες οι Ρηµάνιες πολλαπλότητες µπο- ϱούν να εµβαπτιστούν σε Ευκλείδιο χώρο ισοµετρικά (διατηρώντας δηλαδή το µήκος κάθε απόστασης) και εποµένως και ο τόρος, ο οποίος είναι επιφάνεια µε µηδενική καµπυλότητα που όµως έχει πέρατα. Μάλιστα πριν από λίγα χρόνια ϐρέθηκε και η απεικόνηση του 2-διάστατου τόρου εµβαπτισµένου σε 3 διαστάσεις (Borrelli, et al. 2012, Εποµένως, η ένα προς ένα αντιστοιχία µεταξύ µηδενικής καµπυλότητας και άπειρου χώρου αµφισβητείται. 2.6 Κοσµολογική Ερυθροµετατόπιση Στη παράγραφο 2.2 παρουσιάσαµε την µετατόπιση του ϕάσµατος των γαλαξιών σε σχέση µε τον Γήινο παρατηρητή σαν αποτέλεσµα του γνωστού ϕαινοµένου Doppler, λόγω δηλαδή της κίνησης (αποµάκρυνσης) των γαλαξιών σε σχέση µε τον παρατηρητή. Οπως είδαµε όµως παραπάνω, στο συνµετακινούµενο σύστηµα αναφοράς, οι γαλαξίες διατηρούν αναλλοίωτες τις χωρικές συντεταγµένες τους. Εποµένως χρήζει άλλης ερµηνείας η παρατηρούµενη ερυθροµετάθεση. Στην πραγµατικότητα η ερυθροµετάθεση είναι ιδιότητα του µη-ευκλείδιου χωρόχρονου. Για να το κατανοήσουµε, υποθέστε έναν γαλαξία, ϐρισκόµενο στις χωρικές συντεταγµένες (r 1, θ 1, φ 1 ), να εκπέµπει ακτινοβολία την χρονική στιγµή t = t 1, η οποία ϕτάνει σε µας, ϐρισκόµενοι σε συντεταγµένες (r 2, θ 2, φ 2 ), την χρονική στιγµή t = t 0 > t 1 (όπου t 0 σηµερινή ηλικία του Σύµπαντος). Λόγω της Κοσµολογικής αρχής µπορούµε να πάρουµε οποιοδήποτε σηµείο, και τον παρατηρητή, ως αρχή της ακτινικής συντεταγµένης, δηλαδή r 2 = 0. Επίσης, η ακτινοβολία κινείται κατά µήκος γεωδεσιακών και εποµένως ds 2 = 0, και όπως γνωρίζουµε κατά µήκος γεωδεσιακής (µετακινούµενη η ακτινοβολία από r = r 1 στο r = 0 διατηρούν σταθερά τις χωρικές συντεταγµένες (όπως στην επιφάνεια σφαίρας οι γεωδεσιακές, που είναι µέγιστοι κύκλοι που περνούν από τους 21
22 πόλους, διατηρούν σταθερό το γεωγραφικό µήκος). Εποµένως έχουµε θ 1 = θ 2 και φ 1 = φ 2 = dθ = dφ = 0. Άρα από την µετρική Friedmann-Robertson-Walker [ϐλέπε εξ.(16) και (17)] έχουµε ότι : cdt a(t) = dr 1 kr 2. (18) Λόγω του ότι το r µειώνεται κατά µήκος της γεωδεσιακής όσο ο χρόνος t αυξάνει, έχουµε ότι : t0 t 1 cdt 0 a(t) = r 1 dr 1 kr 2 = r1 0 dr 1 kr 2 (19) Το επόµενο κύµα ακτινοβολίας που ϑα ϕύγει από τον γαλαξία την χρονική στιγµή t 1 + δt 1, ϑα ϕτάσει στον παρατηρητή (r = 0) την χρονική στιγµή t 0 + δt 0, και εποµένως : t0 +δt 0 t 1 +δt 1 cdt r1 a(t) = 0 Αλλάζοντας τα όρια ολοκλήρωσης : dr 1 kr 2 = t0 +δt 0 t 1 +δt 1 cdt t0 a(t) = t 1 cdt a(t). (20) t0 t 1 +δt 1 cdt t0 +δt 0 a(t) + t 0 cdt t1 +δt 1 a(t) = t 1 cdt t0 a(t) + t 1 +δt 1 cdt a(t) έχουµε τελικά t0 +δt 0 t 0 cdt t1 +δt 1 a(t) = t 1 cdt a(t) Τώρα εάν δt t µπορούµε να ϑεωρήσουµε ότι η τιµή της a(t) παραµένει σταθερή κατά την διάρκεια ολοκλήρωσης, και εποµένως δt 1 /a(t 1 ) = δt 0 /a(t 0 ), αλλά λόγω του ότι ο χρόνος µεταξύ δύο διαδοχικών κυµάτων ϕωτός, δt 1,0 (όπου το 1 αντιστοιχεί στην εκποµπή και το 0 στο λήψη του κύµατος), αντιστοιχεί και στο µήκος κύµατος τους (δηλαδή δt j λ j ): λ 1 = a(t 1) λ 0 a(t 0 ) και εποµένως αναπαράγουµε την ήδη γνωστή σχέση µεταξύ του παράγοντα κλίµακας και της ερυθροµετατόπισης (εξ. 9), η οποία ονοµάζεται και Κοσµολογική Ερυθροµετατόπιση : 1 + z = λ 0 λ 1 = a(t 0) a(t 1 ) = 1 a(t) (21) 22
23 όπου στην τελευταία ισότητα έχουµε χρησιµοποιήσει την κανονικοποίηση a(t 0 ) = 1. Τι άλλες ϕυσικές διεργασίες µπορούν να δηµιουργήσουν ερυθροµετατόπιση Οταν ένα ϕωτόνιο διαφεύγει µέσα από ένα ισχυρό ϐαρυτικό πεδίο µάζας M και ακτίνας r παράγει έργο για να υπερνικήσει την ϐαρυτική επίδραση και έτσι χάνει ενέργεια. Για να υπολογιστεί αυτή πρέπει να ϑεωρήσουµε την µετρική Schwarzschild που περιγράφει, σύµφωνα µε την Γ.Θ.Σ., το ισχυρό ϐαρυτικό πεδίο γύρω από µια σφαιρική, µη ϕορτισµένη και µη περιστρεφόµενη, κατανοµή µάζας και που η χαρακτηριστική της ακτίνα δίδεται από την : r s = 2GM/c 2. Σύµφωνα µε την παραπάνω µετρική, η ϐαρυτική ερυθροµετατόπιση σε µεγάλη απόσταση από την ϐαρυτική µάζα δίδεται από την : και αναπτύσσοντας σε σειρά Taylor έχουµε : ( 1 + z = 1 r ) s 1/2 (22) r z r s 2r = GM rc 2. (23) Οι τυπική τιµή αυτής της βαρυτικής ερυθρµετατόπισης είναι 10 7, πολύ µικρότερη από αυτές που παρατηρούµε στους γαλαξίες και εποµένως δεν µπορεί να αποτελέσει εναλλακτική ερµηνεία των παρατηρούµενων ερυθροµετατοπίσεων. 23
24 3 Βασικά Στοιχεία υναµικής Κοσµολογίας Στο πλαίσιο της Κοσµολογικής Αρχής µπρούµε να παράγουµε τις εξισώσεις κοσµολογικής εξέλιξης είτε απευθείας και µε την αυστηρότητα που χρειάζεται από τις εξισώσεις πεδίου της Γ.Θ.Σ. είτε χρησιµοποιώντας Νευτώνεια προσέγγιση. Το τελευταίο είναι δυνατόν λόγω του ότι η Κοσµολογική Αρχή µας επιτρέπει να ϑεωρήσουµε στοιχειώδες όγκο µεγέθους τέτοιου ώστε να ισχύει η Νευτώνεια ϐαρύτητα, ως τυπικό κοσµικό όγκο. 3.1 Εξισώσεις Friedmann Η ϐασικότερη διαφορική εξίσωση που περιγράφει την δυναµική εξέλιξη του Σύµπαντος, είναι η εξίσωση Friedmann, την οποία ϑα παράξουµε αµέσως τώρα. Ξεκινάµε από την εξίσωση διατήρησης της ενέργειας, που µας λέει ότι το άθροισµα της κινητικής και δυναµικής ενέργειας ενός στοιχειώδους υλικού σηµείου µάζας m (π.χ ένας γαλαξίας) σε απόσταση r από ένα κέντρο (µπορεί να είναι οπουδήποτε σε ένα οµογενές και ισότροπο Σύµπαν) και µε µάζα εµπεριεχόµενη εντός της απόστασης αυτής να ισούται µε M = (4π/3)ρr 3, παραµένει σταθερό και ισούται µε : E = 1 2 mṙ2 4πGρmr2 3 (24) όπου ρ είναι η πυκνότητα ύλης του Σύµπαντος. Συνήθως ως πυκνότητα ύλης ϑεωρούµε το άθροισµα της πυκνότητας ύλης (ρ m ) και ακτινοβολίας (ρ r ) αντίστοιχα, ρ ρ m + ρ r. Χρησιµοποιώντας τις εξισώσεις (10) και (6) και διαιρώντας µε mx 2 [όπου x η συνµετακινούµενη απόσταση ϐλέπε εξ.(6)], παίρνουµε : ȧ 2 2 4πGρa2 3 = E mx 2 (25) όπου (χρησιµοποιώντας γνώση από την ολοκληρωµένη προσέγγιση της ΓΘΣ) ορίζουµε : E mx 2 = kc2 2 (26) µε k την καµπυλότητα του χώρου, όπως διαφαίνεται από το ότι έχει µονάδες µήκους 2. Η καµπυλότητα πρέπει ϕυσικά να είναι σταθερή εάν ισχύει η Κοσµολογική Αρχή και εποµένως η ποσότητα E είναι ανάλογη του x 2. ηλαδή, ενώ για κάθε ξεχωριστό σωµατίδιο η συνολική ενέργεια του E παραµένει σταθερή, σε ένα διαστελλόµενο Σύµπαν η ποσότητα E αλλάζει σε διαφορετικές απόστασεις. 24
25 Η τελική µορφή της εξίσωσης Friedmann είναι : ȧ 2 a 2 = 8πGρ kc2 3 a 2 + Λc2 3 (27) όπου έχουµε ϐάλει και την συµµετοχή του όρου της Κοσµολογικής Σταθεράς, Λ, που εισήχθει αυθαίρετα από τον Αϊνστάϊν για να πάρει στατικές λύσεις για την εξέλιξη του Σύµπαντος (ϑα δούµε λεπτοµέρειες σε επόµενο κεφάλαιο). Μια δεύτερη σηµαντική εξίσωση, απαραίτητη για την λύση της εξίσωσης Friedmann είναι η λεγόµενη εξίσωση ϱευστού (fluid equation), η οποία περιγράφει πως εξελίσσεται η πυκνότητα σε ένα διαστελλόµενο Σύµπαν. Αυτή προκύπτει από το 1 o νόµο της ϑερµοδυναµικής, εφαρµοζόµενο σε ένα διαστελλόµενο όγκο, V : dq = de + P dv (28) όπου dq είναι η ποσότητα ενέργειας που προστίθεται ή αφαιρείται από το σύστηµα λόγω ϑερµικής ακτινοβολίας ή ϑερµικής αγωγιµότητας, P dv είναι η ενέργεια που παράγεται η καταναλώνεται σαν αποτέλεσµα του έργου που κάνει το σύστηµα και de είναι η συνολική µεταβολή στην εσωτε- ϱική ενέργεια του συστήµατος. Λόγω του ότι η διαστολή του οµογενούς και ισοτροπικού Σύµπαντος είναι αδιαβατική, έχουµε dq = 0. Παραγωγίζοντας ως προς χρόνο τις σχέσεις E(t) = ρ(t)v (t)c 2 και V (t) = (4π/3)a 3 (t)x 3 και ϐάζοντας το αποτέλεσµα στην εξ.(28) ϐρίσκουµε : ( ) V c 2 ρ + 3ρȧ = P V 3ȧ a a και εποµένως καταλήγουµε στη λεγόµενη εξίσωση της συνέχειας : ρ + 3ȧ (ρ + Pc ) a 2 = 0 = ρ + 3H (ρ + Pc ) 2 = 0. (29) Αυτή η οµογενής διαφορική εξίσωση πρώτου ϐαθµού περιγράφει πως µεταβάλεται η πυκνότητα της υλοενέργειας στο διαστελλόµενο Σύµπαν σαν συνάρτηση και της πίεσης του. Χρειαζόµαστε λοιπόν και µια καταστατική εξίσωση που να συνδέει την πυκνότητα µε την πίεση της υλοενέργειας του Σύµπαντος, P = P (ρ), για να µπορέσουµε να λύσουµε το παραπάνω σύστηµα δύο διαφο- ϱικών εξισώσεων και να πάρουµε την δυναµική εξέλιξη του Συµπαντος, δηλαδή την συνάρτηση a = f(t, ρ, k, Λ). 25
26 Μία ακόµα εξίσωση είναι σηµαντική για την µελέτη της δυναµικής του Σύµπαντος, η οποία προκύπτει από τον συνδυασµό των εξίσώσεων Friedmann και ϱευστού. Παραγωγίζοντας την εξ.(27) και χρησιµοποιώντας την εξ.(29) µπορούµε εύκολα να δείξουµε ότι : ( ä a = 4πG ρ + 3P ) 3 c 2 + Λc2 3 (30) και ϐλέπουµε ότι έαν κάποια συνιστώσα της ύλης στο σύµπαν έχει πίεση, αυτή ϑα συνεισφέρει στην αύξηση της ϐαρυτικής δύναµης (έχει ϑετική συνεισφορά µαζί µε την πυκνότητα στο αριστερό µέρος της εξίσωσης) και άρα στην επιβράδυνση της διαστολής. Επιπλέον ϐλέπουµε ότι σε απουσία κοσµολογικής σταθεράς (Λ = 0) το σύµπαν πάντα ϑα επιβραδύνεται (ä < 0). Εάν όµως η κοσµολογική σταθερά είναι µη µηδενική τότε παρατηρώντας την εξ.(30) αναγνωρίζουµε την ύπαρξη µιας δεύτερης δύναµης εκτός της ϐαρυτικής F Λ = 1 3 Λa. Εάν η κοσµολογική σταθερά είναι ϑετική τότε η δύναµη F Λ λειτουργεί ως απωστική δύναµη µεταξύ των σωµατιδίων ( αντιβαρύτητα ) και στην περίπτωση που επιπρόσθετα ισχύει η ανισότητα Λ 4π(G/c 2 )(ρ + 3P/c 2 ), τότε έχουµε επιταχυνόµενη διαστολή (ϐλέπε παράγραφο 3.7.3). Λόγω του ότι τα αριστερά µέρη των εξισώσεων Friedmann περιέχουν τις συνιστώσες που καθο- ϱίζουν την δυναµική συµπεριφορά του παράγοντα κλίµακας, δηλαδή της συνάρτησης που περιγράφει πως ακριβώς διαστέλλεται το σύµπαν συναρτήσει του χρόνου, µπορούµε να ϑεωρήσουµε κάθε συνιστώσα (και όχι µόνο αυτή της ύλης) ως εν δυνάµει (effective) ή καλύτερα εικονικό ϱευστό. Θα µας είναι πολύ χρήσιµη παρακάτω αυτή η µορφή των εξισώσεων. Μπορούµε λοιπόν να ξαναγράψουµε τις εξ.(27), (29) και (30) ως εξής : H 2 = ȧ2 a 2 = 8πG 3 ρ tot kc2 a 2 = 8πG 3 n i=1 ρ i kc2 a 2 (31) ρ tot + 3H ( ρ tot + P ) tot c 2 = 0 = n ( ä a = 4πG ρ tot + 3 ) 3 c 2 P tot = 4πG 3 i [ ( ρ i + 3H ρ i + P )] i c 2 = 0 (32) ( n ρ i + 3 c 2 i=1 ) n P i. (33) όπου το άθροισµα είναι ως προς το πλήθος n των ϱευστών (πραγµατικών ή εικονικών) που συ- i=1 26
27 νεισφέρουν στην συνολικό κοσµικό ϱευστό το οποίο έχει πυκνότητα ρ tot = i ρ i και πίεση P tot = i P i. Από την εξ.(27) και (31) παίρνουµε εποµένως τις σχέσεις ανάµεσα στη σταθερά Λ και την αντίστοιχη πυκνότητα του εικονικού ϱευστού της Κοσµολογικής σταθεράς : 8πG 3 ρ Λ = Λc2 3 = ρ Λ = Λc2 8πG. (34) Με τον ίδιο τρόπο µπορούµε να εξάγουµε σχέσεις µεταξύ των πυκνοτήτων και της πίεσης των όποιων ϱευστών χρησιµοποιώντας την εξ.(30) και εξ.(33). Τέλος υποθέτωντας ότι οι επιµέρους συνιστώσες (πχ. ύλη, ακτινοβολία, κοσµολογική σταθερα κτλ) που αποτελούν το συνολικό κοσµικό ϱευστό δεν αλληλεπιδρούν µεταξύ τους, τότε η εξίσωση συνέχειας (32) ισχύει για το κάθε ένα ϱευστό ξεχωριστά, ήτοι ρ i + 3H ( ρ i + P ) i c 2 = 0 (35) όπου ο δείκτης i εκφράζει τις συνιστώσες του κοσµικού ϱευστού ύλη (i = m), ακτινοβολία (i = r) ή κοσµολογική σταθερά (i = Λ) και συνεπώς έχουµε ρ m είναι η πυκνότητα ύλης, ρ r η πυκνότητα ακτινοβολίας και ρ Λ η πυκνότητα του ϱευστού της Κοσµολογικής σταθεράς, ενώ P i είναι οι αντίστοιχες πιέσεις. 3.2 Καταστατικές Εξισώσεις Οπως έχουµε ήδη πει το σύµπαν διαστέλλεται οµογενώς και ισοτροπικά και εποµένως και αδια- ϐατικά, δηλαδή δεν υπάρχει διαφορική ϱοή ϑερµότητας από µια περιοχή σε άλλη. Αυτό σηµαίνει ότι όπως το Σύµπαν διαστέλλεται αυτό ψύχεται οµογενώς. Άρα εφόσον το Σύµπαν ξεκίνησε από µια υπέρθερµη κατάσταση είναι ϕανερό ότι σε διαφορετικές εποχές της ϑερµικής του εξέλιξης, διαφορετικά είδη σωµατιδίων, κάθε ένα µε την δική του καταστατική εξίσωση, κυριαρχούν στην δυναµική εξέλιξη του σύµπαντος. Πχ. τα σχετικιστικά σωµατίδια ϑα κυριαρχούν στην πρώιµη υπέρθερµη κατάσταση, ενώ η ϐαρυονική ή ψυχρή σκοτεινή ύλη στην ύστερη ψυχρότερη περίοδο. Γενικά για οποιδήποτε ϱευστό µπορούµε να ορίσουµε µια γενική ϐαροτροπική καταστατική εξίσωση, P = P (ρ), που να ισχύει για όλες τις εποχές, παραµετροποιώντας την µε µια παράµετρο w (που ονοµάζεται και παράµετρος της καταστατικής εξίσωσης) ως εξής : P = wρc 2 (36) όπου ρc 2 είναι η πυκνότητα ενέργειας του ϱευστού, που προκύπτει για ένα οποιοδήποτε ϱευ- 27
28 στό/αέριο από την µάζα του, m σε έναν όγκο V, ως εξής : E = mc 2 = ρv c 2 = E/V = ρc 2. Η γνωστή καταστατική εξίσωση των µη-σχετικιστικών ϱευστών (ιδανικών αερίων) δίδεται από την P = ρk BT µ (37) µε µ την µέση µάζα των σωµατιδίων που αποτελούν το ϱευστό. Επίσης ισχύει για αυτά τα ϱευστά ότι : 3k B T = µ v 2 (38) όπου v 2 είναι η διασπορά ταχυτήτων των στοιχείων του ϱευστού. Συνδυάζοντας τις εξισώσεις (37) και (38) παίρνουµε : P = ρ v2 3 (39) και αντικαθιστώντας στην εξ.(36) παίρνουµε την παράµετρο της γενικευµένης καταστατικής ε- ξίσωσης ως : w = v2 3c 2 (40) Στη δική µας περίπτωση είναι ϕανερό ότι οι παραπάνω σχέσεις ϑα ισχύουν ξεχωριστά για τις επιµέρους συνιστώσες P i = w i c 2 ρ i του κοσµικόυ ϱευστού. Οταν τα σωµατίδια είναι µησχετικιστικά (δηλαδή όταν k b T m v 2 µε v 2 c 2 ) τότε η πίεση τους είναι αµελητέα και ισχύει η προσέγγιση της σκόνης, δηλαδή w 1 = w m = 0. Οταν κάποια σωµατίδια είναι σχετικιστικά, δηλαδή η ϑερµοκρασία του σύµπαντος είναι πολύ µεγαλύτερη της µάζας ηρεµίας τους (όταν δηλαδή k b T m v 2, έχουµε v 2 c 2 ), οπότε από την εξ.(40) έχουµε w 2 = w r = 1/3. Για την Κοσµολογική σταθερά από την εξ.(34) παρατηρούµε ότι η αντίστοιχη πυκνότητα δε µεταβάλλεται µε τον χρόνο ήτοι ρ Λ = 0. Συνεπώς από την εξ.(35) εύκολα υπολογίζουµε την παράµετρο της καταστατικής εξίσωσης w 3 = w Λ = 1 δηλαδή έχει αρνητική πίεση! Στις παράγραφους 3.7 και 3.8 ϑα αναπτύξουµε διεξοδικά τα κοσµολογικά µοντέλα µε αρνητική πίεση. Εάν τώρα ολοκληρώσουµε την εξ. (35) παίρνουµε την εξέλιξη των πυκνοτήτων των ϱευστών που απαρτίζουν το κοσµικό ϱευστό. Πράγµατι εάν χρησιµοποιήσουµε τις εξ.(11), (12) και P i = w i ρ i c 2 τότε η εξ. (35) γράφεται dρ i da + 3 a (1 + w i)ρ i = 0 (41) 28
1 Βασικά Στοιχεία υναµικής Κοσµολογίας
 1 Βασικά Στοιχεία υναµικής Κοσµολογίας Στα πλαίσια της Κοσµολογικής Αρχής µπορούµε να παράγουµε τις διαφορικές εξισώσεις της κοσµολογικής εξέλιξης είτε απέυθείας και µε αυστηρότητα από τις εξισώσεις πεδίου
1 Βασικά Στοιχεία υναµικής Κοσµολογίας Στα πλαίσια της Κοσµολογικής Αρχής µπορούµε να παράγουµε τις διαφορικές εξισώσεις της κοσµολογικής εξέλιξης είτε απέυθείας και µε αυστηρότητα από τις εξισώσεις πεδίου
ΚΟΣΜΟΛΟΓΙΑ ΚΟΣΜΟΛΟΓΙΑ είναι ο τομέας τις ϕυσικής που προσπαθεί να εξηγήσει την γένεση και την εξέλιξη του σύμπαντος χρησιμοποιώντας παρατηρήσεις και τ
 ΗΡΑΚΛΕΙΟ, 10 Οκτωβρίου, 2017 ΚΟΣΜΟΛΟΓΙΑ ΓΙΑ ΑΡΧΑΡΙΟΥΣ Πανεπιστήμιο Κρήτης 1- ΚΟΣΜΟΛΟΓΙΑ ΚΟΣΜΟΛΟΓΙΑ είναι ο τομέας τις ϕυσικής που προσπαθεί να εξηγήσει την γένεση και την εξέλιξη του σύμπαντος χρησιμοποιώντας
ΗΡΑΚΛΕΙΟ, 10 Οκτωβρίου, 2017 ΚΟΣΜΟΛΟΓΙΑ ΓΙΑ ΑΡΧΑΡΙΟΥΣ Πανεπιστήμιο Κρήτης 1- ΚΟΣΜΟΛΟΓΙΑ ΚΟΣΜΟΛΟΓΙΑ είναι ο τομέας τις ϕυσικής που προσπαθεί να εξηγήσει την γένεση και την εξέλιξη του σύμπαντος χρησιμοποιώντας
H ΚΟΣΜΟΛΟΓΙΑ ΜΕΤΑ ΑΠΟ 100 ΧΡΟΝΙΑ ΓΕΝΙΚΗΣ ΘΕΩΡΙΑΣ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΟΣ
 H ΚΟΣΜΟΛΟΓΙΑ ΜΕΤΑ ΑΠΟ 100 ΧΡΟΝΙΑ ΓΕΝΙΚΗΣ ΘΕΩΡΙΑΣ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΟΣ ΔΡ. ΣΠΥΡΟΣ ΒΑΣΙΛΑΚΟΣ ΚΕΝΤΡΟ ΕΡΕΥΝΩΝ ΑΣΤΡΟΝΟΜΙΑΣ ΑΚΑΔΗΜΙΑ ΑΘΗΝΩΝ ΑΚΑΔΗΜΙΑ ΑΘΗΝΩΝ 25/11/2015 Η ΧΡΥΣΗ ΠΕΡΙΟΔΟΣ ΤΗΣ ΚΟΣΜΟΛΟΓΙΑΣ 96% του Σύμπαντος
H ΚΟΣΜΟΛΟΓΙΑ ΜΕΤΑ ΑΠΟ 100 ΧΡΟΝΙΑ ΓΕΝΙΚΗΣ ΘΕΩΡΙΑΣ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΟΣ ΔΡ. ΣΠΥΡΟΣ ΒΑΣΙΛΑΚΟΣ ΚΕΝΤΡΟ ΕΡΕΥΝΩΝ ΑΣΤΡΟΝΟΜΙΑΣ ΑΚΑΔΗΜΙΑ ΑΘΗΝΩΝ ΑΚΑΔΗΜΙΑ ΑΘΗΝΩΝ 25/11/2015 Η ΧΡΥΣΗ ΠΕΡΙΟΔΟΣ ΤΗΣ ΚΟΣΜΟΛΟΓΙΑΣ 96% του Σύμπαντος
c 4 (1) Robertson Walker (x 0 = ct) , R 2 (t) = R0a 2 2 (t) (2) p(t) g = (3) p(t) g 22 p(t) g 33
 ΤΟ ΚΑΘΙΕΡΩΜΕΝΟ ΠΡΟΤΥΠΟ ΤΗΣ ΚΟΣΜΟΛΟΓΙΑΣ Α. Η ΕΞΙΣΩΣΗ EINSTEIN Διδάσκων: Θεόδωρος Ν. Τομαράς G µν R µν 1 g µν R = κ T µν, κ 8πG N c 4 (1) Β. Η ΕΞΙΣΩΣΗ FRIEDMANN. Για ομογενή και ισότροπο χωρόχρονο έχουμε
ΤΟ ΚΑΘΙΕΡΩΜΕΝΟ ΠΡΟΤΥΠΟ ΤΗΣ ΚΟΣΜΟΛΟΓΙΑΣ Α. Η ΕΞΙΣΩΣΗ EINSTEIN Διδάσκων: Θεόδωρος Ν. Τομαράς G µν R µν 1 g µν R = κ T µν, κ 8πG N c 4 (1) Β. Η ΕΞΙΣΩΣΗ FRIEDMANN. Για ομογενή και ισότροπο χωρόχρονο έχουμε
Λέανδρος Περιβολαρόπουλος Καθηγητής Παν/μίου Ιωαννίνων
 Open page Λέανδρος Περιβολαρόπουλος http://leandros.physics.uoi.gr Καθηγητής Παν/μίου Ιωαννίνων Αρχείο παρουσίασης διαθέσιμο μέσω του συνδέσμου: https://dl.dropbox.com/u/20653799/talks/eie.ppt Κλίμακες
Open page Λέανδρος Περιβολαρόπουλος http://leandros.physics.uoi.gr Καθηγητής Παν/μίου Ιωαννίνων Αρχείο παρουσίασης διαθέσιμο μέσω του συνδέσμου: https://dl.dropbox.com/u/20653799/talks/eie.ppt Κλίμακες
 Κοσμολογική ερυθρομετατόπιση Ιδιότητα του διαστελλόμενου χώρου. Όπως το Σύμπαν διαστέλλεται το μήκος κύματος του φωτονίου διαστέλλεται ανάλογα με τον παράγοντα διαστολής [συντελεστής Κοσμικής κλίμακας,
Κοσμολογική ερυθρομετατόπιση Ιδιότητα του διαστελλόμενου χώρου. Όπως το Σύμπαν διαστέλλεται το μήκος κύματος του φωτονίου διαστέλλεται ανάλογα με τον παράγοντα διαστολής [συντελεστής Κοσμικής κλίμακας,
1 Ο παράγοντας κλίμακας και ο Νόμος του Hubble
 ΤΟ ΚΑΘΙΕΡΩΜΕΝΟ ΠΡΟΤΥΠΟ ΤΗΣ ΚΟΣΜΟΛΟΓΙΑΣ Διδάσκων: Θεόδωρος Ν. Τομαράς Ο παράγοντας κλίμακας και ο Νόμος του Hubble Σύμφωνα με την Κοσμολογική Αρχή το Σύμπαν είναι σε μεγάλες κλίμακες ομογενές και ισότροπο.
ΤΟ ΚΑΘΙΕΡΩΜΕΝΟ ΠΡΟΤΥΠΟ ΤΗΣ ΚΟΣΜΟΛΟΓΙΑΣ Διδάσκων: Θεόδωρος Ν. Τομαράς Ο παράγοντας κλίμακας και ο Νόμος του Hubble Σύμφωνα με την Κοσμολογική Αρχή το Σύμπαν είναι σε μεγάλες κλίμακες ομογενές και ισότροπο.
Κοσμολογία. Η δημιουργία και η εξέλιξη του Σύμπαντος. Κοσμάς Γαζέας. Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών
 Κοσμολογία Η δημιουργία και η εξέλιξη του Σύμπαντος Κοσμάς Γαζέας Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Οι σχετικές αποστάσεις στο Σύμπαν Hubble Deep Field Hubble Ultra Deep Field Το φαινόμενο
Κοσμολογία Η δημιουργία και η εξέλιξη του Σύμπαντος Κοσμάς Γαζέας Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Οι σχετικές αποστάσεις στο Σύμπαν Hubble Deep Field Hubble Ultra Deep Field Το φαινόμενο
ds 2 = 1 y 2 (dx2 + dy 2 ), y 0, < x < + (1) dx/(1 x 2 ) = 1 ln((1 + x)/(1 x)) για 1 < x < 1. l AB = dx/1 = 2 (2) (5) w 1/2 = ±κx + C (7)
 ΒΑΡΥΤΗΤΑ ΚΑΙ ΚΟΣΜΟΛΟΓΙΑ Θ. Τομαράς 1. ΤΟ ΥΠΕΡΒΟΛΙΚΟ ΕΠΙΠΕΔΟ. Το υπερβολικό επίπεδο ορίζεται με τη μετρική ds = 1 y dx + dy ), y 0, < x < + 1) α) Να υπολογίσετε το μήκος της γραμμής της παράλληλης στον
ΒΑΡΥΤΗΤΑ ΚΑΙ ΚΟΣΜΟΛΟΓΙΑ Θ. Τομαράς 1. ΤΟ ΥΠΕΡΒΟΛΙΚΟ ΕΠΙΠΕΔΟ. Το υπερβολικό επίπεδο ορίζεται με τη μετρική ds = 1 y dx + dy ), y 0, < x < + 1) α) Να υπολογίσετε το μήκος της γραμμής της παράλληλης στον
Κοσμολογία & Αστροσωματιδική Φυσική Μάγδα Λώλα CERN, 28/9/2010
 Κοσμολογία & Αστροσωματιδική Φυσική Μάγδα Λώλα CERN, 28/9/2010 Η φυσική υψηλών ενεργειών µελετά το µικρόκοσµο, αλλά συνδέεται άµεσα µε το µακρόκοσµο Κοσµολογία - Μελέτη της δηµιουργίας και εξέλιξης του
Κοσμολογία & Αστροσωματιδική Φυσική Μάγδα Λώλα CERN, 28/9/2010 Η φυσική υψηλών ενεργειών µελετά το µικρόκοσµο, αλλά συνδέεται άµεσα µε το µακρόκοσµο Κοσµολογία - Μελέτη της δηµιουργίας και εξέλιξης του
Εργαλειοθήκη I: Μετρήσεις σε κοσµολογικές αποστάσεις (µέρος 2 ο )
 Αστροφυσική Υψηλών Ενεργειών Διδάσκ.: Β. Παυλίδου Μετρήσεις σε κοσμολογικές αποστάσεις, μέρος ο 1 Βιβλιογραφία Εργαλειοθήκη I: Μετρήσεις σε κοσµολογικές αποστάσεις (µέρος ο ) Θ. Τοµαρά, σηµειώσεις για
Αστροφυσική Υψηλών Ενεργειών Διδάσκ.: Β. Παυλίδου Μετρήσεις σε κοσμολογικές αποστάσεις, μέρος ο 1 Βιβλιογραφία Εργαλειοθήκη I: Μετρήσεις σε κοσµολογικές αποστάσεις (µέρος ο ) Θ. Τοµαρά, σηµειώσεις για
Η κλασσική, η σχετικιστική και η κβαντική προσέγγιση. Θωµάς Μελίστας Α 3
 Η κλασσική, η σχετικιστική και η κβαντική προσέγγιση Θωµάς Μελίστας Α 3 Σύµφωνα µε την κλασσική µηχανική και την γενική αντίληψη η µάζα είναι µία εγγενής ιδιότητα των φυσικών σωµάτων. Μάζα είναι η ποσότητα
Η κλασσική, η σχετικιστική και η κβαντική προσέγγιση Θωµάς Μελίστας Α 3 Σύµφωνα µε την κλασσική µηχανική και την γενική αντίληψη η µάζα είναι µία εγγενής ιδιότητα των φυσικών σωµάτων. Μάζα είναι η ποσότητα
ΠΑΡΑΤΗΡΗΣΙΑΚΗ ΚΟΣΜΟΛΟΓΙΑ
 Ελένη Πετράκου - National Taiwan University ΠΑΡΑΤΗΡΗΣΙΑΚΗ ΚΟΣΜΟΛΟΓΙΑ Πρόγραμμα επιμόρφωσης ελλήνων εκπαιδευτικών CERN, 7 Νοεμβρίου 2014 You are here! 1929: απομάκρυνση γαλαξιών θεωρία της μεγάλης έκρηξης
Ελένη Πετράκου - National Taiwan University ΠΑΡΑΤΗΡΗΣΙΑΚΗ ΚΟΣΜΟΛΟΓΙΑ Πρόγραμμα επιμόρφωσης ελλήνων εκπαιδευτικών CERN, 7 Νοεμβρίου 2014 You are here! 1929: απομάκρυνση γαλαξιών θεωρία της μεγάλης έκρηξης
1 Μονάδες - Τυπικά μεγέθη. 2 Η Διαστολή και η Ηλικία του Σύμπαντος ΚΟΣΜΟΓΡΑΦΙΑ. 2.1 Ο νόμος του Hubble. Διδάσκων: Θεόδωρος Ν.
 ΚΟΣΜΟΓΡΑΦΙΑ Διδάσκων: Θεόδωρος Ν. Τομαράς Α. ΤΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΤΟΥ ΣΥΜΠΑΝΤΟΣ 1 Μονάδες - Τυπικά μεγέθη 1 light year = 0.951 10 16 m 1 AU = 1.50 10 11 m 1 = 4.85 10 6 rad 1pc 1 parsec 1AU/(1 in rad) = 3.1
ΚΟΣΜΟΓΡΑΦΙΑ Διδάσκων: Θεόδωρος Ν. Τομαράς Α. ΤΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΤΟΥ ΣΥΜΠΑΝΤΟΣ 1 Μονάδες - Τυπικά μεγέθη 1 light year = 0.951 10 16 m 1 AU = 1.50 10 11 m 1 = 4.85 10 6 rad 1pc 1 parsec 1AU/(1 in rad) = 3.1
ΑΣΚΗΣΗ 10. Η σταθερά του Hubble: µέτρηση αποστάσεων γαλαξιών
 ΑΣΚΗΣΗ 10 Η σταθερά του Hubble: µέτρηση αποστάσεων γαλαξιών Περιεχόµενα Κηφείδες Ερυθρά µετατόπιση Φάσµατα γαλαξιών Σκοπός της άσκησης Η µέτρηση της ερυθρής µετατόπισης των γαλαξιών είναι η βασική µέθοδος
ΑΣΚΗΣΗ 10 Η σταθερά του Hubble: µέτρηση αποστάσεων γαλαξιών Περιεχόµενα Κηφείδες Ερυθρά µετατόπιση Φάσµατα γαλαξιών Σκοπός της άσκησης Η µέτρηση της ερυθρής µετατόπισης των γαλαξιών είναι η βασική µέθοδος
Η πρόβλεψη της ύπαρξης και η έµµεση παρατήρηση των µελανών οπών θεωρείται ότι είναι ένα από τα πιο σύγχρονα επιτεύγµατα της Κοσµολογίας.
 Η πρόβλεψη της ύπαρξης και η έµµεση παρατήρηση των µελανών οπών θεωρείται ότι είναι ένα από τα πιο σύγχρονα επιτεύγµατα της Κοσµολογίας. Παρ' όλα αυτά, πρώτος ο γάλλος µαθηµατικός Λαπλάςτο 1796 ανέφερε
Η πρόβλεψη της ύπαρξης και η έµµεση παρατήρηση των µελανών οπών θεωρείται ότι είναι ένα από τα πιο σύγχρονα επιτεύγµατα της Κοσµολογίας. Παρ' όλα αυτά, πρώτος ο γάλλος µαθηµατικός Λαπλάςτο 1796 ανέφερε
Ό,τι θα θέλατε να μάθετε για το Σύμπαν αλλά δεν τολμούσατε να ρωτήσετε! Γιώργος Καρανάνας. École Polytechnique Fédérale de Lausanne
 Ό,τι θα θέλατε να μάθετε για το Σύμπαν αλλά δεν τολμούσατε να ρωτήσετε! Γιώργος Καρανάνας École Polytechnique Fédérale de Lausanne Η κοσμολογία είναι ο κλάδος της Φυσικής που μελετάει την εξέλιξη του Σύμπαντος.
Ό,τι θα θέλατε να μάθετε για το Σύμπαν αλλά δεν τολμούσατε να ρωτήσετε! Γιώργος Καρανάνας École Polytechnique Fédérale de Lausanne Η κοσμολογία είναι ο κλάδος της Φυσικής που μελετάει την εξέλιξη του Σύμπαντος.
Κοσµολογία. Το παρελθόν, το παρόν, και το µέλλον του Σύµπαντος.
 Κοσµολογία Το παρελθόν, το παρόν, και το µέλλον του Σύµπαντος. Τι είναι όµως η Κοσµολογία; Ηκοσµολογία είναι ο κλάδος της φυσικής που µελετά την δηµιουργία και την εξέλιξη του Σύµπαντος. Με τον όρο Σύµπαν
Κοσµολογία Το παρελθόν, το παρόν, και το µέλλον του Σύµπαντος. Τι είναι όµως η Κοσµολογία; Ηκοσµολογία είναι ο κλάδος της φυσικής που µελετά την δηµιουργία και την εξέλιξη του Σύµπαντος. Με τον όρο Σύµπαν
Ο ΝΟΜΟΣ TOY HUBBLE ΚΑΙ Η ΔΙΑΣΤΟΛΗ ΥΠΟΒΑΘΡΟΥ
 Ο ΝΟΜΟΣ TOY HUBBLE ΚΑΙ Η ΔΙΑΣΤΟΛΗ ΤΟΥ ΣΥΜΠΑΝΤΟΣ. Η ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ Κατά την διάρκεια των δεκαετιών του 1920 και 1930 ο αμερικανός αστρονόμος Slipher με τη βοήθεια του φαινομένου Doppler είχε μετρήσει
Ο ΝΟΜΟΣ TOY HUBBLE ΚΑΙ Η ΔΙΑΣΤΟΛΗ ΤΟΥ ΣΥΜΠΑΝΤΟΣ. Η ΑΚΤΙΝΟΒΟΛΙΑ ΥΠΟΒΑΘΡΟΥ Κατά την διάρκεια των δεκαετιών του 1920 και 1930 ο αμερικανός αστρονόμος Slipher με τη βοήθεια του φαινομένου Doppler είχε μετρήσει
7.2. ΠΑΡΑΤΗΡΗΣΕΙΣ (ΚΑΤΑ ΣΕΙΡΑ ΠΡΟΤΕΡΑΙΟΤΗΤΑΣ)
 7. Κοσμολογία 7.1 ΓΕΝΙΚΑ Έχει υποστηριχθεί ότι η πιο σπουδαία επιστημονική ανακάλυψη που έγινε ποτέ είναι ότι το Σύμπαν ολόκληρο, δηλαδή ο,τιδήποτε υπάρχει και είναι δυνατό να υποπέσει στην αντίληψη μας,
7. Κοσμολογία 7.1 ΓΕΝΙΚΑ Έχει υποστηριχθεί ότι η πιο σπουδαία επιστημονική ανακάλυψη που έγινε ποτέ είναι ότι το Σύμπαν ολόκληρο, δηλαδή ο,τιδήποτε υπάρχει και είναι δυνατό να υποπέσει στην αντίληψη μας,
ΕΞΕΡΕΥΝΩΝΤΑΣ ΤΟ ΣΥΜΠΑΝ ΜΕ ΤΑ ΚΥΜΑΤΑ ΤΗΣ ΒΑΡΥΤΗΤΑΣ
 ΕΞΕΡΕΥΝΩΝΤΑΣ ΤΟ ΣΥΜΠΑΝ ΜΕ ΤΑ ΚΥΜΑΤΑ ΤΗΣ ΒΑΡΥΤΗΤΑΣ ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Κατερίνη, 7/5/2016 14 Σεπτεµβρίου 2015 14 Σεπτεµβρίου 2015 14 Σεπτεµβρίου 2015
ΕΞΕΡΕΥΝΩΝΤΑΣ ΤΟ ΣΥΜΠΑΝ ΜΕ ΤΑ ΚΥΜΑΤΑ ΤΗΣ ΒΑΡΥΤΗΤΑΣ ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Κατερίνη, 7/5/2016 14 Σεπτεµβρίου 2015 14 Σεπτεµβρίου 2015 14 Σεπτεµβρίου 2015
0λ έως. Εξάρτηση. ω και ο. του ω: mx x (1) με λύση. όπου το. ), Im. m ( 0 ( ) (2) Re x / ) ) ( / 0 και Im 20.
 ΚΕΦ. 14.1 : ΚΟΣΜΟΛΟΓΙΑ Ι ΣΕΛ. 37 έως 5 ΤΟΥ ΒΙΒΛΙΟΥ ΚΣ. 4 Ο VIDEO, 9/1/14 λ έως 19:4λ Εξάρτηση ρόλος των συντονισμών της διηλεκτρικής συνάρτησης από τη συχνότητα ω και ο Παρουσιάζεται το γράφημα e(ε) και
ΚΕΦ. 14.1 : ΚΟΣΜΟΛΟΓΙΑ Ι ΣΕΛ. 37 έως 5 ΤΟΥ ΒΙΒΛΙΟΥ ΚΣ. 4 Ο VIDEO, 9/1/14 λ έως 19:4λ Εξάρτηση ρόλος των συντονισμών της διηλεκτρικής συνάρτησης από τη συχνότητα ω και ο Παρουσιάζεται το γράφημα e(ε) και
ΕΙΣΑΓΩΓΙΚΟ ΜΑΘΗΜΑ ΑΣΤΡΟΝΟΜΙΑ-ΑΣΤΡΟΦΥΣΙΚΗ. Μανώλης Πλειώνης
 ΕΙΣΑΓΩΓΙΚΟ ΜΑΘΗΜΑ ΑΣΤΡΟΝΟΜΙΑ-ΑΣΤΡΟΦΥΣΙΚΗ Μανώλης Πλειώνης Η κατανοµή της ύλης στο Σύµπαν Γαλαξίες... Οι δομικοί λίθοι του Σύμπαντος (περιέχουν άστρα, σκόνη, αέρια, πλανήτες...) Σμήνη Γαλαξιών Ομάδες Γαλαξιών
ΕΙΣΑΓΩΓΙΚΟ ΜΑΘΗΜΑ ΑΣΤΡΟΝΟΜΙΑ-ΑΣΤΡΟΦΥΣΙΚΗ Μανώλης Πλειώνης Η κατανοµή της ύλης στο Σύµπαν Γαλαξίες... Οι δομικοί λίθοι του Σύμπαντος (περιέχουν άστρα, σκόνη, αέρια, πλανήτες...) Σμήνη Γαλαξιών Ομάδες Γαλαξιών
Λουκάς Βλάχος Τµήµα Φυσικής, ΑΠΘ Εισαγωγή στην αστρονοµία Κεφάλαιο 11: Ο Θάνατος των αστέρων
 Εισαγωγή στην αστρονοµία Κεφάλαιο 11: Ο Θάνατος των αστέρων Λουκάς Βλάχος Τµήµα Φυσικής, ΑΠΘ 28 Νοεµβρίου 2009 Εισαγωγή στην αστρονοµία Κεφάλαιο 11: Ο Θάνατος των αστέρων Λουκάς Βλάχος Τµήµα Φυσικής, ΑΠΘ
Εισαγωγή στην αστρονοµία Κεφάλαιο 11: Ο Θάνατος των αστέρων Λουκάς Βλάχος Τµήµα Φυσικής, ΑΠΘ 28 Νοεµβρίου 2009 Εισαγωγή στην αστρονοµία Κεφάλαιο 11: Ο Θάνατος των αστέρων Λουκάς Βλάχος Τµήµα Φυσικής, ΑΠΘ
Ερευνητική Εργασία με θέμα: «Ερευνώντας τα χρονικά μυστικά του Σύμπαντος»
 Ερευνητική Εργασία με θέμα: «Ερευνώντας τα χρονικά μυστικά του Σύμπαντος» Σωτήρης Τσαντίλας (PhD, MSc), Μαθηματικός Αστροφυσικός Σύντομη περιγραφή: Χρησιμοποιώντας δεδομένα από το διαστημικό τηλεσκόπιο
Ερευνητική Εργασία με θέμα: «Ερευνώντας τα χρονικά μυστικά του Σύμπαντος» Σωτήρης Τσαντίλας (PhD, MSc), Μαθηματικός Αστροφυσικός Σύντομη περιγραφή: Χρησιμοποιώντας δεδομένα από το διαστημικό τηλεσκόπιο
19 ος Πανελλήνιος Μαθητικός Διαγωνισμός Αστρονομίας και Διαστημικής 2014
 Θέµα ο (Ανάπτυξης) 9 ος Πανελλνιος Μαθητικός Διαγωνισμός Αστρονομίας και Διαστημικς 04 Φάση η : «ΙΠΠΑΡΧΟΣ» Ενδεικτικές Λύσεις στα Θέματα Λυκείου Σε διάφορες εποχές ανάπτυξης της Αστρονοµίας διατυπώθηκαν
Θέµα ο (Ανάπτυξης) 9 ος Πανελλνιος Μαθητικός Διαγωνισμός Αστρονομίας και Διαστημικς 04 Φάση η : «ΙΠΠΑΡΧΟΣ» Ενδεικτικές Λύσεις στα Θέματα Λυκείου Σε διάφορες εποχές ανάπτυξης της Αστρονοµίας διατυπώθηκαν
θεμελιακά Ερωτήματα Κοσμολογίας & Αστροφυσικής
 θεμελιακά Ερωτήματα Απόστολος Δ. Παναγιώτου Ομότιμος Καθηγητής Πανεπιστημίου Αθηνών Επιστημονικός Συνεργάτης στο CERN Σχολή Αστρονομίας και Διαστήματος Βόλος, 5 Απριλίου, 2014 1 BIG BANG 10 24 μ 10-19
θεμελιακά Ερωτήματα Απόστολος Δ. Παναγιώτου Ομότιμος Καθηγητής Πανεπιστημίου Αθηνών Επιστημονικός Συνεργάτης στο CERN Σχολή Αστρονομίας και Διαστήματος Βόλος, 5 Απριλίου, 2014 1 BIG BANG 10 24 μ 10-19
Κοσμολογία. Η δομή, η εξέλιξη του Σύμπαντος και τα πειράματα στο CERN. Γιάννης Νταλιάνης (PhD)
 Κοσμολογία Η δομή, η εξέλιξη του Σύμπαντος και τα πειράματα στο CERN Γιάννης Νταλιάνης (PhD) Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Ε. Μ. Πολυτεχνείο Ελληνική Ομάδα Εκλαΐκευσης Γη Τοπική
Κοσμολογία Η δομή, η εξέλιξη του Σύμπαντος και τα πειράματα στο CERN Γιάννης Νταλιάνης (PhD) Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Ε. Μ. Πολυτεχνείο Ελληνική Ομάδα Εκλαΐκευσης Γη Τοπική
ΕΜΕΙΣ ΚΙ Ο ΚΟΣΜΟΣ. Λεονάρδος Γκουβέλης. Διημερίδα Αστροφυσικής 4-5 Απριλίου
 ΕΜΕΙΣ ΚΙ Ο ΚΟΣΜΟΣ Λεονάρδος Γκουβέλης Διημερίδα Αστροφυσικής 4-5 Απριλίου Συνοπτικά: Κοσμολογικές θεωρίες ανά τους αιώνες Σύγχρονη κοσμολογική άποψη Αστρονομικές αποδείξεις της θεωρίας του Big Bang Μεγάλα
ΕΜΕΙΣ ΚΙ Ο ΚΟΣΜΟΣ Λεονάρδος Γκουβέλης Διημερίδα Αστροφυσικής 4-5 Απριλίου Συνοπτικά: Κοσμολογικές θεωρίες ανά τους αιώνες Σύγχρονη κοσμολογική άποψη Αστρονομικές αποδείξεις της θεωρίας του Big Bang Μεγάλα
ΩΡΙΩΝ ΑΣΤΡΟΝΟΜΙΚΗ ΕΤΑΙΡΕΙΑ ΠΑΤΡΑΣ
 ΩΡΙΩΝ ΑΣΤΡΟΝΟΜΙΚΗ ΕΤΑΙΡΕΙΑ ΠΑΤΡΑΣ Κ. Ν. Γουργουλιάτος ΜΑΥΡΕΣ ΤΡΥΠΕΣ Η ΒΑΣΙΚΗ ΙΔΕΑ Αντικείμενα που εμποδίζουν την διάδοση φωτός από αυτά Πρωτοπροτάθηκε γύρω στα 1783 (John( John Michell) ως αντικείμενο
ΩΡΙΩΝ ΑΣΤΡΟΝΟΜΙΚΗ ΕΤΑΙΡΕΙΑ ΠΑΤΡΑΣ Κ. Ν. Γουργουλιάτος ΜΑΥΡΕΣ ΤΡΥΠΕΣ Η ΒΑΣΙΚΗ ΙΔΕΑ Αντικείμενα που εμποδίζουν την διάδοση φωτός από αυτά Πρωτοπροτάθηκε γύρω στα 1783 (John( John Michell) ως αντικείμενο
Η διαστολή του σύμπαντος
 Η διαστολή του σύμπαντος Δρ Μάνος Δανέζης Επίκουρος Καθηγητής Αστροφυσικής Οι γαλαξίες, από την εποχή της ανακάλυψης τους μέχρι σήμερα, αποτέλεσαν και αποτελούν ένα θελκτικό όσο και σημαντικό πεδίο έρευνας,
Η διαστολή του σύμπαντος Δρ Μάνος Δανέζης Επίκουρος Καθηγητής Αστροφυσικής Οι γαλαξίες, από την εποχή της ανακάλυψης τους μέχρι σήμερα, αποτέλεσαν και αποτελούν ένα θελκτικό όσο και σημαντικό πεδίο έρευνας,
Το Σύμπαν. (Δημιουργία, δομή και εξέλιξη) Λουκάς Βλάχος Τμήμα Φυσικής Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης
 Το Σύμπαν (Δημιουργία, δομή και εξέλιξη) Λουκάς Βλάχος Τμήμα Φυσικής Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Μια σημαντική παρατήρηση Η επιστήμη αναζητά την αλήθεια μέσα από το πείραμα και την παρατήρηση.
Το Σύμπαν (Δημιουργία, δομή και εξέλιξη) Λουκάς Βλάχος Τμήμα Φυσικής Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Μια σημαντική παρατήρηση Η επιστήμη αναζητά την αλήθεια μέσα από το πείραμα και την παρατήρηση.
Κίνηση πλανητών Νόµοι του Kepler
 ΦΥΣ 111 - Διαλ.29 1 Κίνηση πλανητών Νόµοι του Keple! Θα υποθέσουµε ότι ο ήλιος είναι ακίνητος (σχεδόν σωστό αφού έχει τόσο µεγάλη µάζα και η γη δεν τον κινεί).! Οι τροχιές των πλανητών µοιάζουν κάπως σα
ΦΥΣ 111 - Διαλ.29 1 Κίνηση πλανητών Νόµοι του Keple! Θα υποθέσουµε ότι ο ήλιος είναι ακίνητος (σχεδόν σωστό αφού έχει τόσο µεγάλη µάζα και η γη δεν τον κινεί).! Οι τροχιές των πλανητών µοιάζουν κάπως σα
Αριστοτέλης (384-322 π.χ) : «Για να ξεκινήσει και να διατηρηθεί μια κίνηση είναι απαραίτητη η ύπαρξη μιας συγκεκριμένης αιτίας»
 Εισαγωγή Επιστημονική μέθοδος Αριστοτέλης (384-322 π.χ) : «Για να ξεκινήσει και να διατηρηθεί μια κίνηση είναι απαραίτητη η ύπαρξη μιας συγκεκριμένης αιτίας» Διατύπωση αξιωματική της αιτίας μια κίνησης
Εισαγωγή Επιστημονική μέθοδος Αριστοτέλης (384-322 π.χ) : «Για να ξεκινήσει και να διατηρηθεί μια κίνηση είναι απαραίτητη η ύπαρξη μιας συγκεκριμένης αιτίας» Διατύπωση αξιωματική της αιτίας μια κίνησης
ΚΟΣΜΟΛΟΓΙΚΑ ΠΡΟΒΛΗΜΑΤΑ ΩΡΙΩΝ ΑΣΤΡΟΝΟΜΙΚΗ ΕΤΑΙΡΕΙΑ ΠΑΤΡΑΣ ΧΕΙΜΩΝΑΣ 2004 Κ.Ν. ΓΟΥΡΓΟΥΛΙΑΤΟΣ
 ΚΟΣΜΟΛΟΓΙΚΑ ΠΡΟΒΛΗΜΑΤΑ ΩΡΙΩΝ ΑΣΤΡΟΝΟΜΙΚΗ ΕΤΑΙΡΕΙΑ ΠΑΤΡΑΣ ΧΕΙΜΩΝΑΣ 2004 Κ.Ν. ΓΟΥΡΓΟΥΛΙΑΤΟΣ Η Μεγάλη Έκρηξη Πριν από 10-15 δις χρόνια γεννήθηκε το Σύμπαν με μια εξαιρετικά θερμή και βίαια διαδικασία Το σύμπαν
ΚΟΣΜΟΛΟΓΙΚΑ ΠΡΟΒΛΗΜΑΤΑ ΩΡΙΩΝ ΑΣΤΡΟΝΟΜΙΚΗ ΕΤΑΙΡΕΙΑ ΠΑΤΡΑΣ ΧΕΙΜΩΝΑΣ 2004 Κ.Ν. ΓΟΥΡΓΟΥΛΙΑΤΟΣ Η Μεγάλη Έκρηξη Πριν από 10-15 δις χρόνια γεννήθηκε το Σύμπαν με μια εξαιρετικά θερμή και βίαια διαδικασία Το σύμπαν
Εισαγωγή στην αστρονοµία Αστρικά πτώµατα (Λευκοί Νάνοι, αστέρες νε. µαύρες τρύπες) Η ϕυσική σε ακρέες καταστάσεις
 τρονίων, µαύρες τρύπες) Η φυσική σε ακρέες καταστάσεις Εισαγωγή στην αστρονοµία Αστρικά πτώµατα (Λευκοί Νάνοι, αστέρες νετρονίων, µαύρες τρύπες) Η ϕυσική σε ακρέες καταστάσεις Λουκάς Βλάχος Τµήµα Φυσικής,
τρονίων, µαύρες τρύπες) Η φυσική σε ακρέες καταστάσεις Εισαγωγή στην αστρονοµία Αστρικά πτώµατα (Λευκοί Νάνοι, αστέρες νετρονίων, µαύρες τρύπες) Η ϕυσική σε ακρέες καταστάσεις Λουκάς Βλάχος Τµήµα Φυσικής,
ΤΟ ΠΛΗΘΩΡΙΣΤΙΚΟ ΜΟΝΤΕΛΟ ΔΥΝΑΤΟΤΗΤΑ ΕΠΙΛΥΣΗΣ ΚΟΣΜΟΛΟΓΙΚΩΝ ΠΡΟΒΛΗΜΑΤΩΝ ΩΡΙΩΝ ΑΣΤΡΟΝΟΜΙΚΗ ΕΤΑΙΡΕΙΑ ΠΑΤΡΑΣ Κ. Ν. ΓΟΥΡΓΟΥΛΙΑΤΟΣ ΧΕΙΜΩΝΑΣ 2004
 ΤΟ ΠΛΗΘΩΡΙΣΤΙΚΟ ΜΟΝΤΕΛΟ ΔΥΝΑΤΟΤΗΤΑ ΕΠΙΛΥΣΗΣ ΚΟΣΜΟΛΟΓΙΚΩΝ ΠΡΟΒΛΗΜΑΤΩΝ ΩΡΙΩΝ ΑΣΤΡΟΝΟΜΙΚΗ ΕΤΑΙΡΕΙΑ ΠΑΤΡΑΣ Κ. Ν. ΓΟΥΡΓΟΥΛΙΑΤΟΣ ΧΕΙΜΩΝΑΣ 2004 ΣΥΝΟΨΗ ΔΕΔΟΜΕΝΩΝ Το μοντέλο της Μεγάλης έκρηξης εξηγεί με ακρίβεια
ΤΟ ΠΛΗΘΩΡΙΣΤΙΚΟ ΜΟΝΤΕΛΟ ΔΥΝΑΤΟΤΗΤΑ ΕΠΙΛΥΣΗΣ ΚΟΣΜΟΛΟΓΙΚΩΝ ΠΡΟΒΛΗΜΑΤΩΝ ΩΡΙΩΝ ΑΣΤΡΟΝΟΜΙΚΗ ΕΤΑΙΡΕΙΑ ΠΑΤΡΑΣ Κ. Ν. ΓΟΥΡΓΟΥΛΙΑΤΟΣ ΧΕΙΜΩΝΑΣ 2004 ΣΥΝΟΨΗ ΔΕΔΟΜΕΝΩΝ Το μοντέλο της Μεγάλης έκρηξης εξηγεί με ακρίβεια
Υπάρχουν οι Μελανές Οπές;
 Υπάρχουν οι Μελανές Οπές; ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Θεσσαλονίκη, 10/2/2014 Σκοτεινοί αστέρες 1783: Ο John Michell ανακαλύπτει την έννοια ενός σκοτεινού αστέρα,
Υπάρχουν οι Μελανές Οπές; ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ Θεσσαλονίκη, 10/2/2014 Σκοτεινοί αστέρες 1783: Ο John Michell ανακαλύπτει την έννοια ενός σκοτεινού αστέρα,
Hamiltonian φορμαλισμός
 ΦΥΣ - Διαλ.0 Hamltonan φορμαλισμός q = H H Οι εξισώσεις Hamlton είναι:, p = p q Ø (p,q) ονομάζονται κανονικές μεταβλητές Ø Η είναι συνάρτηση που ονομάζεται Hamltonan Ø Κανονικές μεταβλητές ~ θέση και ορμή
ΦΥΣ - Διαλ.0 Hamltonan φορμαλισμός q = H H Οι εξισώσεις Hamlton είναι:, p = p q Ø (p,q) ονομάζονται κανονικές μεταβλητές Ø Η είναι συνάρτηση που ονομάζεται Hamltonan Ø Κανονικές μεταβλητές ~ θέση και ορμή
RT = σταθ. (1) de de de
 ΚΕΦ. 14.2 : ΚΟΣΜΟΛΟΓΙΑ ΙΙ ΣΕΛ. 2 έως 2 ΤΟΥ ΒΙΒΛΙΟΥ ΚΣ. 2 Ο VIDEO, 1/14 λ έως 1λ Επαναληψη E o E K E B H Εντροπία των φωτονίων που είναι ανάλογη τουvt διατηρείται. Επομένως και το γινόμενο Επιπλέον, λόγω
ΚΕΦ. 14.2 : ΚΟΣΜΟΛΟΓΙΑ ΙΙ ΣΕΛ. 2 έως 2 ΤΟΥ ΒΙΒΛΙΟΥ ΚΣ. 2 Ο VIDEO, 1/14 λ έως 1λ Επαναληψη E o E K E B H Εντροπία των φωτονίων που είναι ανάλογη τουvt διατηρείται. Επομένως και το γινόμενο Επιπλέον, λόγω
Θεωρητική Εξέταση. 24 ος Πανελλήνιος Διαγωνισμός Αστρονομίας και Διαστημικής η φάση: «ΠΤΟΛΕΜΑΙΟΣ»
 24 ος Πανελλήνιος Διαγωνισμός Αστρονομίας και Διαστημικής 2019 3 η φάση: «ΠΤΟΛΕΜΑΙΟΣ» Θεωρητική Εξέταση 24 ος Πανελλήνιος Διαγωνισμός Αστρονομίας 2019 3 η φάση Θεωρητική Εξέταση 1 Παρακαλούμε, διαβάστε
24 ος Πανελλήνιος Διαγωνισμός Αστρονομίας και Διαστημικής 2019 3 η φάση: «ΠΤΟΛΕΜΑΙΟΣ» Θεωρητική Εξέταση 24 ος Πανελλήνιος Διαγωνισμός Αστρονομίας 2019 3 η φάση Θεωρητική Εξέταση 1 Παρακαλούμε, διαβάστε
Γενική Θεωρία της Σχετικότητας
 Γενική Θεωρία της Σχετικότητας Αδρανειακή Βαρυτική Μάζα Σύμφωνα με τον Νεύτωνα η μάζα ενός σώματος ορίζεται με δύο τρόπους: Μέσω του δευτέρου νόμου F=ma. (Αδρανειακή Μάζα). Ζυγίζοντας το σώμα και εφαρμόζοντας
Γενική Θεωρία της Σχετικότητας Αδρανειακή Βαρυτική Μάζα Σύμφωνα με τον Νεύτωνα η μάζα ενός σώματος ορίζεται με δύο τρόπους: Μέσω του δευτέρου νόμου F=ma. (Αδρανειακή Μάζα). Ζυγίζοντας το σώμα και εφαρμόζοντας
ΑΝΑΚΟΙΝΩΣΗ. Διευκρινίσεις για την ύλη του μαθήματος ΚΟΣΜΟΛΟΓΙΑ
 ΑΝΑΚΟΙΝΩΣΗ Διευκρινίσεις για την ύλη του μαθήματος ΚΟΣΜΟΛΟΓΙΑ Η ύλη του μαθήματος «Κοσμολογία» περιέχεται στις νέες σημειώσεις του μαθήματος (ανάρτηση 2016) και στο βιβλίο γενικής σχετικότητας που έχετε
ΑΝΑΚΟΙΝΩΣΗ Διευκρινίσεις για την ύλη του μαθήματος ΚΟΣΜΟΛΟΓΙΑ Η ύλη του μαθήματος «Κοσμολογία» περιέχεται στις νέες σημειώσεις του μαθήματος (ανάρτηση 2016) και στο βιβλίο γενικής σχετικότητας που έχετε
ΚΕΦΑΛΑΙΟ 5: ΣΥΣΤΗΜΑΤΑ ΠΟΛΛΩΝ ΣΩΜΑΤΩΝ
 ΚΕΦΑΛΑΙΟ 5: ΣΥΣΤΗΜΑΤΑ ΠΟΛΛΩΝ ΣΩΜΑΤΩΝ Στο κεφάλαιο αυτό θα ασχοληθούµε αρχικά µε ένα µεµονωµένο σύστηµα δύο σωµάτων στα οποία ασκούνται µόνο οι µεταξύ τους κεντρικές δυνάµεις, επιτρέποντας ωστόσο και την
ΚΕΦΑΛΑΙΟ 5: ΣΥΣΤΗΜΑΤΑ ΠΟΛΛΩΝ ΣΩΜΑΤΩΝ Στο κεφάλαιο αυτό θα ασχοληθούµε αρχικά µε ένα µεµονωµένο σύστηµα δύο σωµάτων στα οποία ασκούνται µόνο οι µεταξύ τους κεντρικές δυνάµεις, επιτρέποντας ωστόσο και την
Ακουστικό Ανάλογο Μελανών Οπών
 Ακουστικό Ανάλογο Μελανών Οπών ιάδοση ηχητικών κυµάτων σε ρευστά. Ηχητικά κύµατα σε ακίνητο ρευστό. Εξίσωση συνέχειας: ρ t + ~ (ρ~v) =0 Εξίσωση Euler: ~v t +(~v ~ )~v = 1 ρ ~ p ( ~ Φ +...) Μικρές διαταραχές:
Ακουστικό Ανάλογο Μελανών Οπών ιάδοση ηχητικών κυµάτων σε ρευστά. Ηχητικά κύµατα σε ακίνητο ρευστό. Εξίσωση συνέχειας: ρ t + ~ (ρ~v) =0 Εξίσωση Euler: ~v t +(~v ~ )~v = 1 ρ ~ p ( ~ Φ +...) Μικρές διαταραχές:
1 + Φ r /c 2 = 1 (1) (2) c 2 k y 1 + (V/c) 1 + tan 2 α = sin α (3) tan α = k y k x
 ΛΥΣΕΙΣ ΣΕΙΡΑΣ ΑΣΚΗΣΕΩΝ 6 Θ. Τομαράς 1. Πρωτόνια στις κοσμικές ακτίνες φτάνουν ακόμα και ενέργειες της τάξης των 10 20 ev. Να συγκρίνετε την ενέργεια αυτή με την ενέργεια που έχει μια πέτρα που πετάτε με
ΛΥΣΕΙΣ ΣΕΙΡΑΣ ΑΣΚΗΣΕΩΝ 6 Θ. Τομαράς 1. Πρωτόνια στις κοσμικές ακτίνες φτάνουν ακόμα και ενέργειες της τάξης των 10 20 ev. Να συγκρίνετε την ενέργεια αυτή με την ενέργεια που έχει μια πέτρα που πετάτε με
ΚΟΣΜΟΓΡΑΦΙΑ. 1 Τα χαρακτηριστικά του Σύμπαντος. 1.1 Μονάδες - Τυπικά μεγέθη. 1.2 Η Διαστολή και η Ηλικία του Σύμπαντος. Διδάσκων: Θεόδωρος Ν.
 ΚΟΣΜΟΓΡΑΦΙΑ Διδάσκων: Θεόδωρος Ν. Τομαράς Τα χαρακτηριστικά του Σύμπαντος. Μονάδες - Τυπικά μεγέθη light year =.95 6 m AU =.5 m = 4.85 6 rad pc parsec AU/( in rad) = 3. 6 m = 3.26 light years Διαστάσεις
ΚΟΣΜΟΓΡΑΦΙΑ Διδάσκων: Θεόδωρος Ν. Τομαράς Τα χαρακτηριστικά του Σύμπαντος. Μονάδες - Τυπικά μεγέθη light year =.95 6 m AU =.5 m = 4.85 6 rad pc parsec AU/( in rad) = 3. 6 m = 3.26 light years Διαστάσεις
Κεφάλαιο 6. Εισαγωγή στη µέθοδο πεπερασµένων όγκων επίλυση ελλειπτικών και παραβολικών διαφορικών εξισώσεων
 Κεφάλαιο 6 Εισαγωγή στη µέθοδο πεπερασµένων όγκων επίλυση ελλειπτικών παραβολικών διαφορικών εξισώσεων 6.1 Εισαγωγή Η µέθοδος των πεπερασµένων όγκων είναι µία ευρέως διαδεδοµένη υπολογιστική µέθοδος επίλυσης
Κεφάλαιο 6 Εισαγωγή στη µέθοδο πεπερασµένων όγκων επίλυση ελλειπτικών παραβολικών διαφορικών εξισώσεων 6.1 Εισαγωγή Η µέθοδος των πεπερασµένων όγκων είναι µία ευρέως διαδεδοµένη υπολογιστική µέθοδος επίλυσης
Η μουσική των (Υπερ)Χορδών. Αναστάσιος Χρ. Πέτκου Παν. Κρήτης
 Η μουσική των (Υπερ)Χορδών Αναστάσιος Χρ. Πέτκου Παν. Κρήτης H σύγχρονη (αγοραία) αντίληψη για την δηµιουργία του Σύµπαντος (πιθανά εσφαλµένη..) E t Ενέργεια Χρόνος String Theory/M-Theory H Ιστορία της
Η μουσική των (Υπερ)Χορδών Αναστάσιος Χρ. Πέτκου Παν. Κρήτης H σύγχρονη (αγοραία) αντίληψη για την δηµιουργία του Σύµπαντος (πιθανά εσφαλµένη..) E t Ενέργεια Χρόνος String Theory/M-Theory H Ιστορία της
5 Σχετικιστική μάζα. Στο Σ Πριν Μετά. Στο Σ
 Α Τόγκας - ΑΜ333: Ειδική Θεωρία Σχετικότητας Σχετικιστική μάζα 5 Σχετικιστική μάζα Όπως έχουμε διαπιστώσει στην ειδική θεωρία της Σχετικότητας οι μετρήσεις των χωρικών και χρονικών αποστάσεων εξαρτώνται
Α Τόγκας - ΑΜ333: Ειδική Θεωρία Σχετικότητας Σχετικιστική μάζα 5 Σχετικιστική μάζα Όπως έχουμε διαπιστώσει στην ειδική θεωρία της Σχετικότητας οι μετρήσεις των χωρικών και χρονικών αποστάσεων εξαρτώνται
Θέµατα Φυσικής Γενικής Παιδείας Γ Λυκείου 2000
 Θέµατα Φυσικής Γενικής Παιδείας Γ Λυκείου 2 ΕΚΦΩΝΗΣΕΙΣ Ζήτηµα 1ο Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Σύµφωνα
Θέµατα Φυσικής Γενικής Παιδείας Γ Λυκείου 2 ΕΚΦΩΝΗΣΕΙΣ Ζήτηµα 1ο Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Σύµφωνα
Κεφάλαιο 1. Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς
 Κεφάλαιο 1 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 2 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 1.1 Ατοµο του Υδρογόνου 1.1.1 Κατάστρωση του προβλήµατος Ας ϑεωρήσουµε πυρήνα ατοµικού αριθµού Z
Κεφάλαιο 1 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 2 Κβαντική Μηχανική ΙΙ - Περιλήψεις, Α. Λαχανάς 1.1 Ατοµο του Υδρογόνου 1.1.1 Κατάστρωση του προβλήµατος Ας ϑεωρήσουµε πυρήνα ατοµικού αριθµού Z
ΣΥΝΕΧΕΙΣ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΚΑΙ ΣΥΝΕΧΕΙΣ ΣΥΜΜΕΤΡΙΕΣ
 ΣΥΝΕΧΕΙΣ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΚΑΙ ΣΥΝΕΧΕΙΣ ΣΥΜΜΕΤΡΙΕΣ Για ένα φυσικό σύστηµα που περιγράφεται από τις συντεταγµένες όπου συνεχής συµµετρία είναι ένας συνεχής µετασχηµατισµός των συντεταγµένων που αφήνει αναλλοίωτη
ΣΥΝΕΧΕΙΣ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΚΑΙ ΣΥΝΕΧΕΙΣ ΣΥΜΜΕΤΡΙΕΣ Για ένα φυσικό σύστηµα που περιγράφεται από τις συντεταγµένες όπου συνεχής συµµετρία είναι ένας συνεχής µετασχηµατισµός των συντεταγµένων που αφήνει αναλλοίωτη
Εισαγωγή Οι µαύρες τρύπες είναι ουράνια σώµατα σαν όλα τα άλλα, όπως οι πλανήτες και ο ήλιος, τα οποία όµως διαφέρουν από αυτά σε µία µικρή αλλά θεµελ
 ιαθεµατική Εργασία µε Θέµα: Οι Φυσικές Επιστήµες στην Καθηµερινή µας Ζωή Τµήµα: Β 2 Γυµνασίου Υπεύθυνος Καθηγητής: Παζούλης Παναγιώτης Συντακτική Οµάδα: Πάνου Μαρία, Πάνου Γεωργία 1 Εισαγωγή Οι µαύρες
ιαθεµατική Εργασία µε Θέµα: Οι Φυσικές Επιστήµες στην Καθηµερινή µας Ζωή Τµήµα: Β 2 Γυµνασίου Υπεύθυνος Καθηγητής: Παζούλης Παναγιώτης Συντακτική Οµάδα: Πάνου Μαρία, Πάνου Γεωργία 1 Εισαγωγή Οι µαύρες
Εισαγωγή στη Σχετικότητα και την Κοσμολογία ΠΕΡΙΕΧΟΜΕΝΑ ΜΑΘΗΜΑΤΟΣ
 Εισαγωγή στη Σχετικότητα και την Κοσμολογία Διδάσκων: Θεόδωρος Τομαράς, Πανεπιστήμιο Κρήτης ΠΕΡΙΕΧΟΜΕΝΑ ΜΑΘΗΜΑΤΟΣ Εβδομάδα 1 Σχετικότητα 1.1 Η ανεπάρκεια της μηχανικής του Νεύτωνα V1.1.1 Σύντομη εισαγωγή
Εισαγωγή στη Σχετικότητα και την Κοσμολογία Διδάσκων: Θεόδωρος Τομαράς, Πανεπιστήμιο Κρήτης ΠΕΡΙΕΧΟΜΕΝΑ ΜΑΘΗΜΑΤΟΣ Εβδομάδα 1 Σχετικότητα 1.1 Η ανεπάρκεια της μηχανικής του Νεύτωνα V1.1.1 Σύντομη εισαγωγή
Το σύστημα των μη αλληλεπιδραστικών ροών και η σημασία του στην ερμηνεία των ιδιοτήτων των ιδανικών αερίων.
 Το σύστημα των μη αλληλεπιδραστικών ροών και η σημασία του στην ερμηνεία των ιδιοτήτων των ιδανικών αερίων. Θεωρώντας τα αέρια σαν ουσίες αποτελούμενες από έναν καταπληκτικά μεγάλο αριθμό μικροσκοπικών
Το σύστημα των μη αλληλεπιδραστικών ροών και η σημασία του στην ερμηνεία των ιδιοτήτων των ιδανικών αερίων. Θεωρώντας τα αέρια σαν ουσίες αποτελούμενες από έναν καταπληκτικά μεγάλο αριθμό μικροσκοπικών
Σύγχρονη Φυσική 1, Διάλεξη 4, Τμήμα Φυσικής, Παν/μιο Ιωαννίνων Η Αρχές της Ειδικής Θεωρίας της Σχετικότητας και οι μετασχηματισμοί του Lorentz
 1 Η Αρχές της Ειδικής Θεωρίας της Σχετικότητας και οι μετασχηματισμοί του Lorentz Σκοποί της τέταρτης διάλεξης: 25.10.2011 Να κατανοηθούν οι αρχές με τις οποίες ο Albert Einstein θεμελίωσε την ειδική θεωρία
1 Η Αρχές της Ειδικής Θεωρίας της Σχετικότητας και οι μετασχηματισμοί του Lorentz Σκοποί της τέταρτης διάλεξης: 25.10.2011 Να κατανοηθούν οι αρχές με τις οποίες ο Albert Einstein θεμελίωσε την ειδική θεωρία
Τα Κύματα της Βαρύτητας
 Τα Κύματα της Βαρύτητας ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΟΦΑ, 24/1/2015 Πως διαδίδεται η βαρυτική έλξη; 1900: ο Lorentz προτείνει ότι η δύναμη της βαρύτητας δε
Τα Κύματα της Βαρύτητας ΝΙΚΟΛΑΟΣ ΣΤΕΡΓΙΟΥΛΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΟΦΑ, 24/1/2015 Πως διαδίδεται η βαρυτική έλξη; 1900: ο Lorentz προτείνει ότι η δύναμη της βαρύτητας δε
Εργαστήριο 2008. Yπολογισμός της ταχύτητα διαστολής του Σύμπαντος, της ηλικίας του καθώς και της απόστασης μερικών κοντινών γαλαξιών.
 Υπολογισμός σταθεράς Hubble Εργαστήριο 2008 Yπολογισμός της ταχύτητα διαστολής του Σύμπαντος, της ηλικίας του καθώς και της απόστασης μερικών κοντινών γαλαξιών. Εισαγωγή Το 1929, ο Edwin Hubble (με βάση
Υπολογισμός σταθεράς Hubble Εργαστήριο 2008 Yπολογισμός της ταχύτητα διαστολής του Σύμπαντος, της ηλικίας του καθώς και της απόστασης μερικών κοντινών γαλαξιών. Εισαγωγή Το 1929, ο Edwin Hubble (με βάση
Β. ΘΕΜΑΤΑ ΑΣΤΡΟΝΟΜΙΑΣ
 Α. Μια σύντοµη περιγραφή της εργασίας που εκπονήσατε στο πλαίσιο του µαθήµατος της Αστρονοµίας. Β. ΘΕΜΑΤΑ ΑΣΤΡΟΝΟΜΙΑΣ Για να απαντήσεις στις ερωτήσεις που ακολουθούν αρκεί να επιλέξεις την ή τις σωστές
Α. Μια σύντοµη περιγραφή της εργασίας που εκπονήσατε στο πλαίσιο του µαθήµατος της Αστρονοµίας. Β. ΘΕΜΑΤΑ ΑΣΤΡΟΝΟΜΙΑΣ Για να απαντήσεις στις ερωτήσεις που ακολουθούν αρκεί να επιλέξεις την ή τις σωστές
Εισαγωγή στην αστρονοµία (Πως να προετοιµαστώ για τις εξετάσεις;)
 Εισαγωγή στην αστρονοµία (Πως να προετοιµαστώ για τις εξετάσεις;) Λ. Βλάχος 1 Ιανουαρίου 2010 1 Εισαγωγικές Σκέψεις Ενα πολύ σοβαρό ϑέµα, για το οποίο σπάνια συζητάµε στα µαθήµατα, είναι το πως περιµένουν
Εισαγωγή στην αστρονοµία (Πως να προετοιµαστώ για τις εξετάσεις;) Λ. Βλάχος 1 Ιανουαρίου 2010 1 Εισαγωγικές Σκέψεις Ενα πολύ σοβαρό ϑέµα, για το οποίο σπάνια συζητάµε στα µαθήµατα, είναι το πως περιµένουν
ΔΟΜΗ ΚΑΙ ΕΞΕΛΙΞΗ ΤΟΥ ΣΥΜΠΑΝΤΟΣ
 ΚΕΦΑΛΑΙΟ ΕΒΔΟΜΟ ΔΟΜΗ ΚΑΙ ΕΞΕΛΙΞΗ ΤΟΥ ΣΥΜΠΑΝΤΟΣ 7 ΚΕΦΑΛΑΙΟ ΕΒΔΟΜΟ Δ Ο Μ Η Κ Α Ι ΕΞΕΛΙΞΗ ΤΟΥ ΣΥΜΠΑΝΤΟΣ «Μπορεί και μακριά πολύ μέσα στων ουρανών τ' αποκαΐδια την Ανδρομέδα, την Άρκτο ή την Παρθένο... Άραγες
ΚΕΦΑΛΑΙΟ ΕΒΔΟΜΟ ΔΟΜΗ ΚΑΙ ΕΞΕΛΙΞΗ ΤΟΥ ΣΥΜΠΑΝΤΟΣ 7 ΚΕΦΑΛΑΙΟ ΕΒΔΟΜΟ Δ Ο Μ Η Κ Α Ι ΕΞΕΛΙΞΗ ΤΟΥ ΣΥΜΠΑΝΤΟΣ «Μπορεί και μακριά πολύ μέσα στων ουρανών τ' αποκαΐδια την Ανδρομέδα, την Άρκτο ή την Παρθένο... Άραγες
2. Στο ηλιακό στέµµα η ϑερµότητα διαδίδεται µε αγωγιµότητα και η ϱοή ϑερµικής ενέργειας (heat flux)είναι
 4.6 Ασκήσεις 51 4.6 Ασκήσεις 1. Μελετήστε τον στάσιµο ( t = 0) ισόθερµο άνεµο σε επίπεδο, χρησιµοποιώντας πολικές συντεταγµένες και (α) Βρείτε τη χαρακτηριστική απόσταση από τον αστέρα r στην οποία γίνεται
4.6 Ασκήσεις 51 4.6 Ασκήσεις 1. Μελετήστε τον στάσιµο ( t = 0) ισόθερµο άνεµο σε επίπεδο, χρησιµοποιώντας πολικές συντεταγµένες και (α) Βρείτε τη χαρακτηριστική απόσταση από τον αστέρα r στην οποία γίνεται
ΕΙΔΙΚΗ ΘΕΩΡΙΑ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ
 ΕΙΔΙΚΗ ΘΕΩΡΙΑ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ Διδάσκων: Θεόδωρος Ν. Τομαράς 1. Μετασχηματισμοί συντεταγμένων και συμμετρίες. 1α. Στροφές στο επίπεδο. Θεωρείστε δύο καρτεσιανά συστήματα συντεταγμένων στο επίπεδο, στραμμένα
ΕΙΔΙΚΗ ΘΕΩΡΙΑ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ Διδάσκων: Θεόδωρος Ν. Τομαράς 1. Μετασχηματισμοί συντεταγμένων και συμμετρίες. 1α. Στροφές στο επίπεδο. Θεωρείστε δύο καρτεσιανά συστήματα συντεταγμένων στο επίπεδο, στραμμένα
5 Σχετικιστική μάζα. Στο Σ Πριν Μετά. Στο Σ
 Α Τόγκας - ΑΜ333: Ειδική Θεωρία Σχετικότητας Σχετικιστική μάζα 5 Σχετικιστική μάζα Όπως έχουμε διαπιστώσει στην ειδική θεωρία της Σχετικότητας οι μετρήσεις των χωρικών και χρονικών αποστάσεων εξαρτώνται
Α Τόγκας - ΑΜ333: Ειδική Θεωρία Σχετικότητας Σχετικιστική μάζα 5 Σχετικιστική μάζα Όπως έχουμε διαπιστώσει στην ειδική θεωρία της Σχετικότητας οι μετρήσεις των χωρικών και χρονικών αποστάσεων εξαρτώνται
 Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Σχολή Θετικών Επιστημών, Τμήμα Φυσικής Τομέας Αστροφυσικής-Αστρονομίας-Μηχανικής Η μελέτη της φύσης της σκοτεινής ενέργειας χρησιμοποιώντας εξωγαλαξιακές πηγές
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Σχολή Θετικών Επιστημών, Τμήμα Φυσικής Τομέας Αστροφυσικής-Αστρονομίας-Μηχανικής Η μελέτη της φύσης της σκοτεινής ενέργειας χρησιμοποιώντας εξωγαλαξιακές πηγές
Τα φωτόνια από την μεγάλη έκρηξη Τι είναι η Ακτινοβολία υποβάθρου.
 Τα φωτόνια από την μεγάλη έκρηξη Τι είναι η Ακτινοβολία υποβάθρου. Σύμφωνα με την θεωρία της «μεγάλης έκρηξης» (big bang), το Σύμπαν, ξεκινώντας από μηδενικές σχεδόν διαστάσεις (υλικό σημείο), συνεχώς
Τα φωτόνια από την μεγάλη έκρηξη Τι είναι η Ακτινοβολία υποβάθρου. Σύμφωνα με την θεωρία της «μεγάλης έκρηξης» (big bang), το Σύμπαν, ξεκινώντας από μηδενικές σχεδόν διαστάσεις (υλικό σημείο), συνεχώς
Τα είδη της κρούσης, ανάλογα µε την διεύθυνση κίνησης των σωµάτων πριν συγκρουστούν. (α ) Κεντρική (ϐ ) Εκκεντρη (γ ) Πλάγια
 8 Κρούσεις Στην µηχανική µε τον όρο κρούση εννοούµε τη σύγκρουση δύο σωµάτων που κινούνται το ένα σχετικά µε το άλλο.το ϕαινόµενο της κρούσης έχει δύο χαρακτηριστικά : ˆ Εχει πολύ µικρή χρονική διάρκεια.
8 Κρούσεις Στην µηχανική µε τον όρο κρούση εννοούµε τη σύγκρουση δύο σωµάτων που κινούνται το ένα σχετικά µε το άλλο.το ϕαινόµενο της κρούσης έχει δύο χαρακτηριστικά : ˆ Εχει πολύ µικρή χρονική διάρκεια.
Αστρική Εξέλιξη. Η ζωή και ο θάνατος των αστέρων. Κοσμάς Γαζέας. Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών
 Αστρική Εξέλιξη Η ζωή και ο θάνατος των αστέρων Κοσμάς Γαζέας Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Αστρική εξέλιξη Η εξέλιξη ενός αστέρα καθορίζεται από την κατανάλωση διαδοχικών «κύκλων» πυρηνικών
Αστρική Εξέλιξη Η ζωή και ο θάνατος των αστέρων Κοσμάς Γαζέας Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Αστρική εξέλιξη Η εξέλιξη ενός αστέρα καθορίζεται από την κατανάλωση διαδοχικών «κύκλων» πυρηνικών
L = T V = 1 2 (ṙ2 + r 2 φ2 + ż 2 ) U (3)
 ΥΠΟΛΟΓΙΣΤΙΚΗ ΑΣΤΡΟΔΥΝΑΜΙΚΗ 3): Κινήσεις αστέρων σε αστρικά συστήματα Βασικές έννοιες Θεωρούμε αστρικό σύστημα π.χ. γαλαξία ή αστρικό σμήνος) αποτελούμενο από μεγάλο αριθμό αστέρων της τάξης των 10 8 10
ΥΠΟΛΟΓΙΣΤΙΚΗ ΑΣΤΡΟΔΥΝΑΜΙΚΗ 3): Κινήσεις αστέρων σε αστρικά συστήματα Βασικές έννοιες Θεωρούμε αστρικό σύστημα π.χ. γαλαξία ή αστρικό σμήνος) αποτελούμενο από μεγάλο αριθμό αστέρων της τάξης των 10 8 10
ΦΡΟΝΟ «ΚΑΣΑΡΡΕΤΗ» ΣΟΤ «ΚΛΑΙΚΟΤ» ΑΣΟΜΟΤ
 ΦΡΟΝΟ «ΚΑΣΑΡΡΕΤΗ» ΣΟΤ «ΚΛΑΙΚΟΤ» ΑΣΟΜΟΤ ΥΙΟΡΕΝΣΙΝΟ ΓΙΑΝΝΗ Αθήνα, Νοέμβρης 2011 James Clerk Maxwell (1831-1879) 2 Από την ηλεκτρομαγνητική θεωρία του Maxwell γνωρίζουμε ότι : α) Ένα ακίνητο ηλεκτρικό φορτίο
ΦΡΟΝΟ «ΚΑΣΑΡΡΕΤΗ» ΣΟΤ «ΚΛΑΙΚΟΤ» ΑΣΟΜΟΤ ΥΙΟΡΕΝΣΙΝΟ ΓΙΑΝΝΗ Αθήνα, Νοέμβρης 2011 James Clerk Maxwell (1831-1879) 2 Από την ηλεκτρομαγνητική θεωρία του Maxwell γνωρίζουμε ότι : α) Ένα ακίνητο ηλεκτρικό φορτίο
1.1.3 t. t = t2 - t1 1.1.4 x2 - x1. x = x2 x1 . . 1
 1 1 o Κεφάλαιο: Ευθύγραµµη Κίνηση Πώς θα µπορούσε να περιγραφεί η κίνηση ενός αγωνιστικού αυτοκινήτου; Πόσο γρήγορα κινείται η µπάλα που κλώτσησε ένας ποδοσφαιριστής; Απαντήσεις σε τέτοια ερωτήµατα δίνει
1 1 o Κεφάλαιο: Ευθύγραµµη Κίνηση Πώς θα µπορούσε να περιγραφεί η κίνηση ενός αγωνιστικού αυτοκινήτου; Πόσο γρήγορα κινείται η µπάλα που κλώτσησε ένας ποδοσφαιριστής; Απαντήσεις σε τέτοια ερωτήµατα δίνει
Θέµατα Φυσικής Γενικής Παιδείας Γ Λυκείου 2000
 Ζήτηµα 1ο Θέµατα Φυσικής Γενικής Παιδείας Γ Λυκείου 2 Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Σύµφωνα µε το πρότυπο
Ζήτηµα 1ο Θέµατα Φυσικής Γενικής Παιδείας Γ Λυκείου 2 Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Σύµφωνα µε το πρότυπο
Σφαιρικά σώµατα και βαρύτητα
 ΦΥΣ 131 - Διαλ.28 1 Σφαιρικά σώµατα και βαρύτητα q Χρησιµοποιήσαµε τις εκφράσεις F() =! GMm που ισχύουν για σηµειακές µάζες Μ και m. 2 και V () =! GMm q Ένα χαρακτηριστικό γεγονός, που κάνει τους υπολογισµούς
ΦΥΣ 131 - Διαλ.28 1 Σφαιρικά σώµατα και βαρύτητα q Χρησιµοποιήσαµε τις εκφράσεις F() =! GMm που ισχύουν για σηµειακές µάζες Μ και m. 2 και V () =! GMm q Ένα χαρακτηριστικό γεγονός, που κάνει τους υπολογισµούς
1 Ω(t) = k c2 (1) 1 Ω(t 0 ) = ) z RM = O(10 4 ) (2) = a RM. 1 Ω(t bbn ) 1 Ω(t RM ) = = = O(10 10 ) (3)
 ΤΟ ΠΛΗΘΩΡΙΣΤΙΚΟ ΣΥΜΠΑΝ ΠΡΟΣΟΧΗ: ΟΧΙ ΑΡΚΕΤΑ ΕΠΕΞΕΡΓΑΣΜΕΝΕΣ ΣΗΜΕΙΩΣΕΙΣ ΚΥΡΙΑ ΓΙΑ ΝΑ ΕΧΕΤΕ ΤΟ ΤΙ ΘΕΜΑΤΑ ΣΥΖΗΤΗΣΑΜΕ ΣΤΗ ΤΑΞΗ Διδάσκων: Θεόδωρος Ν. Τομαράς 1 Το πρόβλημα των αρχικών συνθηκών της Κοσμολογίας
ΤΟ ΠΛΗΘΩΡΙΣΤΙΚΟ ΣΥΜΠΑΝ ΠΡΟΣΟΧΗ: ΟΧΙ ΑΡΚΕΤΑ ΕΠΕΞΕΡΓΑΣΜΕΝΕΣ ΣΗΜΕΙΩΣΕΙΣ ΚΥΡΙΑ ΓΙΑ ΝΑ ΕΧΕΤΕ ΤΟ ΤΙ ΘΕΜΑΤΑ ΣΥΖΗΤΗΣΑΜΕ ΣΤΗ ΤΑΞΗ Διδάσκων: Θεόδωρος Ν. Τομαράς 1 Το πρόβλημα των αρχικών συνθηκών της Κοσμολογίας
Το Σύμπαν. (Δημιουργία, δομή και εξέλιξη) Λουκάς Βλάχος Τμήμα Φυσικής Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης
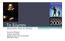 Το Σύμπαν (Δημιουργία, δομή και εξέλιξη) Λουκάς Βλάχος Τμήμα Φυσικής Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Αφιέρωση Θα ήθελα να αφιερώσω αυτή την διάλεξη στο Νίκο Λαμπρόπουλο σαν ένα δείγμα ευγνωμοσύνης
Το Σύμπαν (Δημιουργία, δομή και εξέλιξη) Λουκάς Βλάχος Τμήμα Φυσικής Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Αφιέρωση Θα ήθελα να αφιερώσω αυτή την διάλεξη στο Νίκο Λαμπρόπουλο σαν ένα δείγμα ευγνωμοσύνης
Μετεωρολογία. Ενότητα 7. Δρ. Πρόδρομος Ζάνης Αναπληρωτής Καθηγητής, Τομέας Μετεωρολογίας-Κλιματολογίας, Α.Π.Θ.
 Μετεωρολογία Ενότητα 7 Δρ. Πρόδρομος Ζάνης Αναπληρωτής Καθηγητής, Τομέας Μετεωρολογίας-Κλιματολογίας, Α.Π.Θ. Ενότητα 7: Η κίνηση των αέριων μαζών Οι δυνάμεις που ρυθμίζουν την κίνηση των αέριων μαζών (δύναμη
Μετεωρολογία Ενότητα 7 Δρ. Πρόδρομος Ζάνης Αναπληρωτής Καθηγητής, Τομέας Μετεωρολογίας-Κλιματολογίας, Α.Π.Θ. Ενότητα 7: Η κίνηση των αέριων μαζών Οι δυνάμεις που ρυθμίζουν την κίνηση των αέριων μαζών (δύναμη
Aναλαµπές ακτίνων -γ
 Aναλαµπές ακτίνων -γ Gamma Ray Bursts (GRB) Λουκάς Βλάχος 18/5/2004 1 Γενική παρατήρηση Η αστροφυσική διανύει αυτήν την εποχή τη δηµιουργικότερη περίοδο της ιστορίας της. Η πληθώρα των επίγειων αλλά και
Aναλαµπές ακτίνων -γ Gamma Ray Bursts (GRB) Λουκάς Βλάχος 18/5/2004 1 Γενική παρατήρηση Η αστροφυσική διανύει αυτήν την εποχή τη δηµιουργικότερη περίοδο της ιστορίας της. Η πληθώρα των επίγειων αλλά και
ΣΩΜΑΤΙ ΙΑΚΗ ΦΥΣΗ ΦΩΤΟΣ
 Μάθηµα 1 ο, 30 Σεπτεµβρίου 2008 (9:00-11:00). ΣΩΜΑΤΙ ΙΑΚΗ ΦΥΣΗ ΦΩΤΟΣ Ακτινοβολία µέλανος σώµατος (1900) Plank: έδωσε εξήγηση του φάσµατος (κβαντική ερµηνεία*) ΠΑΡΑ ΟΧΗ Το φως δεν είναι µόνο κύµα. Είναι
Μάθηµα 1 ο, 30 Σεπτεµβρίου 2008 (9:00-11:00). ΣΩΜΑΤΙ ΙΑΚΗ ΦΥΣΗ ΦΩΤΟΣ Ακτινοβολία µέλανος σώµατος (1900) Plank: έδωσε εξήγηση του φάσµατος (κβαντική ερµηνεία*) ΠΑΡΑ ΟΧΗ Το φως δεν είναι µόνο κύµα. Είναι
Η «ΦΥΣΗ» ΤΟΥ ΚΕΝΟΥ ΚΑΙ ΤΗΣ ΒΑΡΥΤΗΤΑΣ
 1 Η «ΦΥΣΗ» ΤΟΥ ΚΕΝΟΥ ΚΑΙ ΤΗΣ ΒΑΡΥΤΗΤΑΣ ΠΡΟΛΟΓΟΣ Θα αποδεχτούµε ότι το παν αποτελείται από το κενό και τα άτοµα, όπως υποστήριξε ο ηµόκριτος; Αν δεχτούµε σαν αξίωµα αυτή την υπόθεση, τι είναι το κενό και
1 Η «ΦΥΣΗ» ΤΟΥ ΚΕΝΟΥ ΚΑΙ ΤΗΣ ΒΑΡΥΤΗΤΑΣ ΠΡΟΛΟΓΟΣ Θα αποδεχτούµε ότι το παν αποτελείται από το κενό και τα άτοµα, όπως υποστήριξε ο ηµόκριτος; Αν δεχτούµε σαν αξίωµα αυτή την υπόθεση, τι είναι το κενό και
Φυσική Β Λυκειου, Γενικής Παιδείας 3ο Φυλλάδιο - Ορµή / Κρούση
 Φυσική Β Λυκειου, Γενικής Παιδείας - Ορµή / Κρούση Επιµέλεια: Μιχάλης Ε. Καραδηµητρίου, MSc Φυσικός http://perifysikhs.wordpress.com 1 Σύστηµα Σωµάτων - Εσωτερικές & Εξωτερικές υνάµεις ύο ή περισσότερα
Φυσική Β Λυκειου, Γενικής Παιδείας - Ορµή / Κρούση Επιµέλεια: Μιχάλης Ε. Καραδηµητρίου, MSc Φυσικός http://perifysikhs.wordpress.com 1 Σύστηµα Σωµάτων - Εσωτερικές & Εξωτερικές υνάµεις ύο ή περισσότερα
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης. Πτυχιακή Εργασία. Σχολή Θετικών Επιστημών. Τμήμα Φυσικής
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Πτυχιακή Εργασία Επιταχυνόμενη διαστολή του σύμπαντος - Πειραματικά δεδομένα Διδασκάλου Στυλιανός AEM: 13269 Επιβλέπων καθηγητής
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Σχολή Θετικών Επιστημών Τμήμα Φυσικής Πτυχιακή Εργασία Επιταχυνόμενη διαστολή του σύμπαντος - Πειραματικά δεδομένα Διδασκάλου Στυλιανός AEM: 13269 Επιβλέπων καθηγητής
Διαδραστική Έκθεση Επιστήμης και Τεχνολογίας
 Διαδραστική Έκθεση Επιστήμης και Τεχνολογίας «Η επιστήμη και η γνώση προχωρούν ρ μπροστά μόνο αν αμφισβητήσουμε τους μεγάλους» Χρονικά της Φυσικής 1905 (Annalen der Physik) Γενική Θεωρία της Σχετικότητας
Διαδραστική Έκθεση Επιστήμης και Τεχνολογίας «Η επιστήμη και η γνώση προχωρούν ρ μπροστά μόνο αν αμφισβητήσουμε τους μεγάλους» Χρονικά της Φυσικής 1905 (Annalen der Physik) Γενική Θεωρία της Σχετικότητας
Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μετσόβιο Πολυτεχνείο. Σεμινάριο Φυσικής Ενότητα 14
 Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μετσόβιο Πολυτεχνείο Σεμινάριο Φυσικής Ενότητα 14 Γεωργακίλας Αλέξανδρος Ζουμπούλης Ηλίας Μακροπούλου Μυρσίνη Πίσσης Πολύκαρπος Άδεια Χρήσης
Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μετσόβιο Πολυτεχνείο Σεμινάριο Φυσικής Ενότητα 14 Γεωργακίλας Αλέξανδρος Ζουμπούλης Ηλίας Μακροπούλου Μυρσίνη Πίσσης Πολύκαρπος Άδεια Χρήσης
Κεφάλαιο 5 : Το φαινόμενο Doppler. Διαστήματα, χωρόχρονος και κοσμικές γραμμές.
 Κεφάλαιο 5 : Το φαινόμενο Dppler. Διαστήματα, χωρόχρονος και κοσμικές γραμμές. 5.1 Το φαινόμενο Dppler. Η ασική εξίσωση ενός διαδιδόμενου ηλεκτρομαγνητικού κύματος είναι: c λ (5.1) όπου c η ταχύτητα διάδοσης,
Κεφάλαιο 5 : Το φαινόμενο Dppler. Διαστήματα, χωρόχρονος και κοσμικές γραμμές. 5.1 Το φαινόμενο Dppler. Η ασική εξίσωση ενός διαδιδόμενου ηλεκτρομαγνητικού κύματος είναι: c λ (5.1) όπου c η ταχύτητα διάδοσης,
Ένα πείραμα θα δημιουργήσει ένα νέο σύμπαν;
 ΤΟ ΜΟΝΤΕΛΟ ΤΗΣ ΜΕΓΑΛΗΣ ΕΚΡΗΞΗΣ (BIG BANG) Ένα πείραμα θα δημιουργήσει ένα νέο σύμπαν; Η θεωρία της Μεγάλης Έκρηξης με όλες τις σύγχρονες παραλλαγές και βελτιώσεις της είναι η πλέον αποδεκτή εκδοχή της
ΤΟ ΜΟΝΤΕΛΟ ΤΗΣ ΜΕΓΑΛΗΣ ΕΚΡΗΞΗΣ (BIG BANG) Ένα πείραμα θα δημιουργήσει ένα νέο σύμπαν; Η θεωρία της Μεγάλης Έκρηξης με όλες τις σύγχρονες παραλλαγές και βελτιώσεις της είναι η πλέον αποδεκτή εκδοχή της
Ο Πυρήνας του Ατόμου
 1 Σκοποί: Ο Πυρήνας του Ατόμου 15/06/12 I. Να δώσει μία εισαγωγική περιγραφή του πυρήνα του ατόμου, και της ενέργειας που μπορεί να έχει ένα σωματίδιο για να παραμείνει δέσμιο μέσα στον πυρήνα. II. III.
1 Σκοποί: Ο Πυρήνας του Ατόμου 15/06/12 I. Να δώσει μία εισαγωγική περιγραφή του πυρήνα του ατόμου, και της ενέργειας που μπορεί να έχει ένα σωματίδιο για να παραμείνει δέσμιο μέσα στον πυρήνα. II. III.
ΑΣΚΗΣΗ 5. Χρώµα στην Αστρονοµία
 ΑΣΚΗΣΗ 5 Χρώµα στην Αστρονοµία Περιεχόµενα Χρώµα στην Αστρονοµία o Χρώµα άστρων o Χρώµα και θερµοκρασία Ο νόµος του Planck o Ακτινοβολία Μέλανος Σώµατος O νόµος της µετατόπισης του Wien Στόχος της άσκησης
ΑΣΚΗΣΗ 5 Χρώµα στην Αστρονοµία Περιεχόµενα Χρώµα στην Αστρονοµία o Χρώµα άστρων o Χρώµα και θερµοκρασία Ο νόµος του Planck o Ακτινοβολία Μέλανος Σώµατος O νόµος της µετατόπισης του Wien Στόχος της άσκησης
ξ i (t) = v i t + ξ i (0) (9) c (t t 0). (10) t = t, z = z 1 2 gt 2 (12)
 Η ΓΕΝΙΚΗ ΘΕΩΡΙΑ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ Διδάσκων: Θεόδωρος Ν. Τομαράς 1 Κίνηση σώματος σε πεδίο βαρύτητας Εδώ θα εφαρμόσουμε την Ι.Α.Ι. και τις γνώσεις μας από την Ειδική Θεωρία της Σχετικότητας για να παράγουμε
Η ΓΕΝΙΚΗ ΘΕΩΡΙΑ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ Διδάσκων: Θεόδωρος Ν. Τομαράς 1 Κίνηση σώματος σε πεδίο βαρύτητας Εδώ θα εφαρμόσουμε την Ι.Α.Ι. και τις γνώσεις μας από την Ειδική Θεωρία της Σχετικότητας για να παράγουμε
Λύσεις: Τελική Εξέταση 28 Αυγούστου 2015
 Φ230: Αστροφυσική Ι Λύσεις: Τελική Εξέταση 28 Αυγούστου 2015 1. Ο Σείριος Α, έχει φαινόμενο οπτικό μέγεθος mv - 1.47 και ακτίνα R1.7𝑅 και αποτελεί το κύριο αστέρι ενός διπλού συστήματος σε απόσταση 8.6
Φ230: Αστροφυσική Ι Λύσεις: Τελική Εξέταση 28 Αυγούστου 2015 1. Ο Σείριος Α, έχει φαινόμενο οπτικό μέγεθος mv - 1.47 και ακτίνα R1.7𝑅 και αποτελεί το κύριο αστέρι ενός διπλού συστήματος σε απόσταση 8.6
Πριν υπάρξει το Σύμπαν
 Πριν υπάρξει το Σύμπαν Μάνος Δανέζης-Στράτος Θεοδοσίου Τομέας Αστροφυσικής, Αστρονομίας και Μηχανικής Τμήμα Φυσικής-Πανεπιστήμιο Αθηνών Όλοι γνωρίζουμε την κλασική Θεωρία της Μεγάλης Έκρηξης, μέσα από
Πριν υπάρξει το Σύμπαν Μάνος Δανέζης-Στράτος Θεοδοσίου Τομέας Αστροφυσικής, Αστρονομίας και Μηχανικής Τμήμα Φυσικής-Πανεπιστήμιο Αθηνών Όλοι γνωρίζουμε την κλασική Θεωρία της Μεγάλης Έκρηξης, μέσα από
3 + O. 1 + r r 0. 0r 3 cos 2 θ 1. r r0 M 0 R 4
 Μηχανική Ι Εργασία #7 Χειμερινό εξάμηνο 8-9 Ν. Βλαχάκης. (α) Ποια είναι η ένταση και το δυναμικό του βαρυτικού πεδίου που δημιουργεί μια ομογενής σφαίρα πυκνότητας ρ και ακτίνας σε όλο το χώρο; Σχεδιάστε
Μηχανική Ι Εργασία #7 Χειμερινό εξάμηνο 8-9 Ν. Βλαχάκης. (α) Ποια είναι η ένταση και το δυναμικό του βαρυτικού πεδίου που δημιουργεί μια ομογενής σφαίρα πυκνότητας ρ και ακτίνας σε όλο το χώρο; Σχεδιάστε
ΜΑΘΗΜΑΤΙΚΑ ΙΙ ιδάσκων : Ε. Στεφανόπουλος 12 ιουνιου 2017
 Πανεπιστηµιο Πατρων Πολυτεχνικη Σχολη Τµηµα Μηχανικων Η/Υ & Πληροφορικης ΜΑΘΗΜΑΤΙΚΑ ΙΙ ιδάσκων : Ε. Στεφανόπουλος 12 ιουνιου 217 Θ1. Θεωρούµε την συνάρτηση f(x, y, z) = 1 + x 2 + 2y 2 z. (αʹ) Να ϐρεθεί
Πανεπιστηµιο Πατρων Πολυτεχνικη Σχολη Τµηµα Μηχανικων Η/Υ & Πληροφορικης ΜΑΘΗΜΑΤΙΚΑ ΙΙ ιδάσκων : Ε. Στεφανόπουλος 12 ιουνιου 217 Θ1. Θεωρούµε την συνάρτηση f(x, y, z) = 1 + x 2 + 2y 2 z. (αʹ) Να ϐρεθεί
ΚΙΝΗΜΑΤΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ
 ΚΙΝΗΜΑΤΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ ΕΙΣΑΓΩΓΗ Σκοπός της κινηματικής είναι η περιγραφή της κίνησης του ρευστού Τα αίτια που δημιούργησαν την κίνηση και η αναζήτηση των δυνάμεων που την διατηρούν είναι αντικείμενο της
ΚΙΝΗΜΑΤΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ ΕΙΣΑΓΩΓΗ Σκοπός της κινηματικής είναι η περιγραφή της κίνησης του ρευστού Τα αίτια που δημιούργησαν την κίνηση και η αναζήτηση των δυνάμεων που την διατηρούν είναι αντικείμενο της
ds ds ds = τ b k t (3)
 Γενικά Μαθηματικά ΙΙΙ Πρώτο σετ ασκήσεων, Λύσεις Άσκηση 1 Γνωρίζουμε ότι το εφαπτόμενο διάνυσμα ( t), ορίζεται ως: t = r = d r ds (1) και επιπλέον το διάνυσμα της καμπυλότητας ( k), ορίζεται ως: d t k
Γενικά Μαθηματικά ΙΙΙ Πρώτο σετ ασκήσεων, Λύσεις Άσκηση 1 Γνωρίζουμε ότι το εφαπτόμενο διάνυσμα ( t), ορίζεται ως: t = r = d r ds (1) και επιπλέον το διάνυσμα της καμπυλότητας ( k), ορίζεται ως: d t k
Θεωρητική Εξέταση. 23 ος Πανελλήνιος Διαγωνισμός Αστρονομίας και Διαστημικής η φάση: «ΠΤΟΛΕΜΑΙΟΣ»
 23 ος Πανελλήνιος Διαγωνισμός Αστρονομίας και Διαστημικής 2018 4 η φάση: «ΠΤΟΛΕΜΑΙΟΣ» Θεωρητική Εξέταση 23 ος Πανελλήνιος Διαγωνισμός Αστρονομίας 2018 4 η φάση Θεωρητική Εξέταση 1 Παρακαλούμε, διαβάστε
23 ος Πανελλήνιος Διαγωνισμός Αστρονομίας και Διαστημικής 2018 4 η φάση: «ΠΤΟΛΕΜΑΙΟΣ» Θεωρητική Εξέταση 23 ος Πανελλήνιος Διαγωνισμός Αστρονομίας 2018 4 η φάση Θεωρητική Εξέταση 1 Παρακαλούμε, διαβάστε
Γραµµική Αλγεβρα Ι. Ενότητα: Εισαγωγικές Εννοιες. Ευάγγελος Ράπτης. Τµήµα Μαθηµατικών
 Ενότητα: Εισαγωγικές Εννοιες Ευάγγελος Ράπτης Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Ενότητα: Εισαγωγικές Εννοιες Ευάγγελος Ράπτης Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
To CERN (Ευρωπαϊκός Οργανισµός Πυρηνικών Ερευνών) είναι το µεγαλύτερο σε έκταση (πειραµατικό) κέντρο πυρηνικών ερευνών και ειδικότερα επί της σωµατιδι
 To CERN (Ευρωπαϊκός Οργανισµός Πυρηνικών Ερευνών) είναι το µεγαλύτερο σε έκταση (πειραµατικό) κέντρο πυρηνικών ερευνών και ειδικότερα επί της σωµατιδιακής φυσικής στον κόσµο. Η ίδρυσή του το έτος 1954
To CERN (Ευρωπαϊκός Οργανισµός Πυρηνικών Ερευνών) είναι το µεγαλύτερο σε έκταση (πειραµατικό) κέντρο πυρηνικών ερευνών και ειδικότερα επί της σωµατιδιακής φυσικής στον κόσµο. Η ίδρυσή του το έτος 1954
Πριν το μεγάλο Μπαμ. Ε. Δανέζης, Ε. Θεοδοσίου Επίκουροι Καθηγητές Αστροφυσικής Πανεπιστήμιο Αθηνών
 Πριν το μεγάλο Μπαμ Ε. Δανέζης, Ε. Θεοδοσίου Επίκουροι Καθηγητές Αστροφυσικής Πανεπιστήμιο Αθηνών Όπως γνωρίζουμε σήμερα η θεωρία της Μεγάλης Έκρηξης είναι η πιο γνωστή θεωρία η οποία επιχειρεί να ερμηνεύσει
Πριν το μεγάλο Μπαμ Ε. Δανέζης, Ε. Θεοδοσίου Επίκουροι Καθηγητές Αστροφυσικής Πανεπιστήμιο Αθηνών Όπως γνωρίζουμε σήμερα η θεωρία της Μεγάλης Έκρηξης είναι η πιο γνωστή θεωρία η οποία επιχειρεί να ερμηνεύσει
Τροχιές σωμάτων σε πεδίο Βαρύτητας. Γιώργος Νικολιδάκης
 Τροχιές σωμάτων σε πεδίο Βαρύτητας Γιώργος Νικολιδάκης 9/18/2013 1 Κωνικές Τομές Είναι καμπύλες που σχηματίζονται καθώς επίπεδα τέμνουν με διάφορες γωνίες επιφάνειες κώνων. Παραβολή Έλλειψη -κύκλος Υπερβολή
Τροχιές σωμάτων σε πεδίο Βαρύτητας Γιώργος Νικολιδάκης 9/18/2013 1 Κωνικές Τομές Είναι καμπύλες που σχηματίζονται καθώς επίπεδα τέμνουν με διάφορες γωνίες επιφάνειες κώνων. Παραβολή Έλλειψη -κύκλος Υπερβολή
