Πολυτεχνική Σχολή Πανεπιστημίου Πατρών. Τμήμα Μηχανικών Η/Υ και Πληροφορικής
|
|
|
- Δημήτηρ Μανιάκης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Πολυτεχνική Σχολή Πανεπιστημίου Πατρών Τμήμα Μηχανικών Η/Υ και Πληροφορικής Διατμηματικό Μεταπτυχιακό Πρόγραμμα Σπουδών Συστήματα Επεξεργασίας Σημάτων και Επικοινωνιών (Σ.Ε.Σ.Ε.) Μεταπτυχιακή Διπλωματική Εργασία «Τεχνικές Προσανατολισμένης Επικοινωνίας για Συνεργατικά Δίκτυα» Τσίνος Χρήστος Α.Μ. 120 Επιβλέπων Καθηγητής: Μπερμπερίδης Κωνσταντίνος Πάτρα 2008
2 2
3 Εισαγωγή Η παρούσα διπλωματική ασχολείται με την εισαγωγή μιας τεχνικής προσανατολισμένης επικοινωνίας σε συνεργατικά συστήματα και εξετάζει την επίδοση της κάτω από εκτίμηση και μοντελοποίηση των συντελεστών της μήτρας του καναλιού. Τα συνεργατικά συστήματα αποτελούν κατανεμημένες εκδοχές συστημάτων MIMO και μεγάλο μέρος της έρευνας που διεξάγεται τα τελευταία χρόνια στις ασύρματες επικοινωνίες επικεντρώνεται σε αυτά. Η δυνατότητα περιγραφής των συντελεστών της μήτρας του καναλιού με μοντέλα πολλαπλών διαδρομών μας οδηγεί στην χρήση μεθόδων υπο-χώρου για την εκτίμηση των παραμέτρων του μοντέλου, κάτι που βελτιώνει αισθητά την επίδοση του εκτιμητή του καναλιού, ειδικά σε χαμηλές τιμές του SNR. Η τεχνική προσανατολισμένης επικοινωνίας που χρησιμοποιούμε στηρίζεται στη διάσπαση ιδιαζουσών τιμών και αρχικά μελετάμε την επίδοση της σε συστήματα MIMO που χρησιμοποιούν εκτίμηση και μοντελοποίηση της μήτρας των συντελεστών του καναλιού. Η συγκεκριμένη μέθοδος προσανατολισμένης επικοινωνίας απαιτεί την γνώση των ιδιαζόντων διανυσμάτων της μήτρας του καναλιού σε πομπό και δέκτη. Έτσι, θα χρησιμοποιηθούν συμπαγείς αναπαραστάσεις των στοιχείων των ιδιαζόντων διανυσμάτων με προβλεπτές χαμηλής τάξης ώστε να μειωθεί η ανατροφοδότηση δεδομένων που απαιτείται στον πομπό. Η συνολική αυτή διάταξη εκτίμησης - μοντελοποίησης των συντελεστών της μήτρας του καναλιού - μοντελοποίησης των ιδιαζόντων διανυσμάτων εφαρμόζεται σε ένα συνεργατικό σύστημα και εξετάζεται η επίδοσης της για τα δύο δημοφιλή πρωτόκολλα συνεργατικής επικοινωνίας. Κλείνοντας, θα ήθελα να ευχαριστήσω τον καθηγητή κ. Κ. Μπερμπερίδη που είχε την επίβλεψη αυτής της διπλωματικής. Η καθοδήγηση του και οι εύστοχες πάντα παρατηρήσεις του συνέβαλαν καθοριστικά στην εκπόνηση της διπλωματικής αυτής. Επίσης, θέλω να ευχαριστήσω τους καθηγητές κ. Ε. Βαρβαρίγο και κ. Θ. Αντωνακόπουλο που αφιέρωσαν τον χρόνο τους για την αξιολόγηση αυτής της διπλωματικής.
4 Περιεχόμενα Περιεχόμενα Εισαγωγή...3 Κεφάλαιο 1: Εισαγωγή Σκοπός Διπλωματικής Εργασίας Το Μοντέλο της Κρουστικής Απόκρισης του Ασύρματου Καναλιού Πίνακας Συμβολισμών Κεφάλαιο 2: Τεχνικές Μοντελοποίησης και Πρόβλεψης των Συντελεστών της Μήτρας του Καναλιού και των Ιδιαζόντων Διανυσμάτων της Εισαγωγή Υπολογισμός του Μοντέλου της Κρουστικής Απόκρισης του Καναλιού με την Μέθοδο ESPRIT Υπολογισμός Προβλεπτών για τα Ιδιάζοντα Διανύσματα Προβλεπτής με Φίλτρο Wiener Προβλεπτής με Μοντέλο AR Το Πρόβλημα της Εκτίμησης του Αριθμού των Μονοπατιών...36 Κεφάλαιο 3: Τεχνικές Προσανατολισμένης Επικοινωνίας για Συστήματα MIMO Εισαγωγή Περιγραφή Συστήματος ΜΙΜΟ Τεχνική Προσανατολισμένης Επικοινωνίας σε Συστήματα ΜΙΜΟ με Πλήρη Γνώση της Κατάστασης του Καναλιού Τεχνική Προσανατολισμένης Επικοινωνίας με Διάσπαση Ιδιαζουσών Τιμών Πειράματα Τεχνική Προσανατολισμένης Επικοινωνίας σε Συστήματα ΜΙΜΟ με Απουσία Γνώσης της Κατάστασης του Καναλιού Εκτιμητής Μέγιστης Πιθανοφάνειας της Μήτρας του Κσνσλιού Τεχνική Προσανατολισμένης Επικοινωνίας με Εκτίμηση της Μήτρας του Καναλιού Τεχνική Προσανατολισμένης Επικοινωνίας με Εκτίμηση και Μοντελοποίση της Μήτρας του Καναλιού Πειράματα...48 Κεφάλαιο 4: Τεχνικές Προσανατολισμένης Επικοινωνίας για Συνεργατικά Συστήματα Εισαγωγή Βασικά Χαρακτηριστικά Συνεργατικών Συστημάτων Περιγραφή Συστήματος To Πρωτόκολλο Επικοινωνίας Ενίσχυσης και Προώθησης To Πρωτόκολλο Επικοινωνίας Αποκωδικοποίησης και Προώθησης Πειράματα Εφαρμογή Τεχνικών Προσανατολισμένης Επικοινωνίας σε Συνεργατικά Συστήματα με Πλήρη Γνώση της Κατάστασης του Καναλιού σε Πομπούς και Δέκτη...62
5 Περιεχόμενα Προσανατολισμένη επικοινωνία με διάσπαση SVD Πειράματα Εφαρμογή Τεχνικών Προσανατολισμένης Επικοινωνίας σε Συνεργατικά Συστήματα με Εκτίμηση και Μοντελοποίηση της Μήτρας των Συντελεστών του Καναλιού Πειράματα...68 Κεφάλαιο 5: Σύνοψη Πιθανές Επεκτάσεις Σύνοψη Πιθανές Επεκτάσεις...74 Βιβλιογραφία
6 Κεφάλαιο 1
7 Κεφάλαιο 1 Κεφάλαιο 1: Εισαγωγή 1.1 Σκοπός Διπλωματικής Εργασίας Οι ασύρματες επικοινωνίες αποτελούν τον πιο διαδεδομένο τρόπο μετάδοσης δεδομένων στην σημερινή εποχή. Η μελέτη των ασύρματων συστημάτων έχει ξεκινήσει από την δεκαετία του 1960, και ως σήμερα έχει σημειωθεί μεγάλη ερευνητική πρόοδος στον τομέα αυτό εξαιτίας της αυξημένης ζήτησης για ασύρματες επικοινωνίες υψηλού ρυθμού και αξιόπιστης μετάδοσης. Όπως είναι γνωστό τα τηλεπικοινωνιακά συστήματα μοντελοποιούνται από ένα πομπό, ένα δέκτη και το κανάλι μέσω του οποίου γίνεται η μετάδοση των δεδομένων. Σε ένα ιδανικό ενσύρματο κανάλι η μοναδική πηγή που είναι δυνατό να υποβαθμίσει την ποιότητα της μετάδοσης είναι ο λευκός προσθετικός Γκαουσιανός θόρυβος. Αντίθετα, σε ένα ασύρματο κανάλι η υποβάθμιση της μετάδόσης των δεδομένων οφείλεται κυρίως στο φαινόμενο της εξασθένησης. Η μεταδιδόμενη ακτινοβολία από την κεραία του πομπού στην κεραία του δέκτη είναι δυνατό να υποστεί ανάκλαση (reflection) ή διασκορπισμό (scattering) λόγω κάποιων εμποδίων (ακόμη και από κάποια στρώματα της ατμόσφαιρας) που παρεμβάλλονται μεταξύ τους, και τελικά να «φτάσει» στον δέκτη μέσω κάποιας άλλης κατεύθυνσης μετάδοσης με κάποια χρονική καθυστέρηση. Η μετάδοση μέσω πολλαπλών διαδρομών, έχει λοιπόν, σαν αποτέλεσμα την θετική ή αρνητική συμβολή των μεταδιδόμενων συνιστωσών του σήματος στο δέκτη και ευθύνεται για τη χρονική μεταβολή του καναλιού. Έτσι κάποιες χρονικές στιγμές το κανάλι είναι ισχυρό (και κατάλληλο για μετάδοση) και κάποιες χρονικές στιγμές είναι ασθενές (και ακατάλληλο για μετάδοση). Ένα δεύτερο χαρακτηριστικό των ασύρματων συστημάτων είναι η παρεμβολή που εισάγεται στην μετάδοση ενός συστήματος από την μετάδοση ενός γειτονικού συστήματος υποβαθμίζοντας επίσης, την ποιότητα της μετάδοσης. Μεγάλο μέρος της έρευνας που γίνεται στα ασύρματα συστήματα, ασχολείται με το πως θα αντιμετωπιστούν τα προβλήματα της εξασθένησης και της παρεμβολής. Η παρατήρηση ότι η αύξηση της επίδοσης του συστήματος μπορεί να επιτευχθεί αν μεταδώσουμε την πληροφορία από πολλαπλά ανεξάρτητα μονοπάτια (ποικιλομορφία diversity) οδήγησε στην εισαγωγή πολλαπλών κεραιών στον πομπό και στον δέκτη, δηλαδή στην δημιουργία των συστημάτων Πολλαπλών Εισόδων Πολλαπλών Εξόδων (Multiple Input Multiple Output MIMO). Τα συστήματα MIMO «άνοιξαν» ένα νέο πεδίο στον τομέα των ασύρματων επικοινωνιών, αφού παρουσιάζουν διαφορετικά πλεονεκτήματα και μειονεκτήματα, ανάλογα με τον τρόπο χρήσης των πολλαπλών κεραιών. Έτσι εναλλακτικά, παρουσιάστηκαν τεχνικές που επιτύγχαναν το μέγιστο κέρδος ποικιλομορφίας που είχε ως αποτέλεσμα την ταχύτερη δυνατή απόσβεση της πιθανότητας σφάλματος με την αύξηση του λόγου σήματος προς θόρυβο, ή τον μέγιστο ρυθμό μετάδοσης
8 Κεφάλαιο 1 συμβόλων (κέρδος πολυπλεξίας multiplexing). Τα προηγούμενα δύο κέρδη είναι αντικρουόμενα και η αύξηση του ενός συνεπάγεται συνήθως μείωση του άλλου. Με το προηγούμενο σκεπτικό έχουν αναπτυχθεί μια πληθώρα τεχνικών όπως η «οικογένεια» αρχιτεκτονικών BLAST, οι τεχνικές προσανατολισμένης επικοινωνίας (beamforming), οι ορθογώνιοι κώδικες (orthogonal codes), οι κώδικες γραμμικής διασποράς (linear dispersion codes) κ.α. Οι προηγούμενες τεχνικές άλλοτε χρησιμοποιούν «έξυπνη» κωδικοποίηση των συμβόλων που πρέπει να μεταδοθούν, και άλλοτε πολλαπλασιάζουν με κατάλληλα διανύσματα τα σύμβολα που μεταδίδονται και λαμβάνονται για να βελτιώσουν την επίδοση του συστήματος. Η εφαρμογή των τεχνικών αυτών, απαιτεί την γνώση του καναλιού στον πομπό και στο δέκτη ή μόνο στο δέκτη. Κατά συνέπεια αυτές οι τεχνικές εφαρμόζονται μαζί με κάποια μέθοδο εκτίμησης του καναλιού η οποία «καταναλώνει» τμήμα του διαθέσιμου εύρους ζώνης για την αποστολή συμβόλων εκμάθησης (training symbols). Ο πρώτος στόχος αυτής της διπλωματικής είναι να παρουσιάσει μεθόδους που εκμεταλλεύονται την δυνατότητα αναπαράστασης της κρουστικής απόκρισης του ασύρματου καναλιού από ένα μοντέλο πολλαπλών μονοπατιών, ώστε να εξάγει ένα μοντέλο το οποίο είναι δυνατό να χρησιμοποιηθεί για την πρόβλεψη των τιμών της κρουστικής απόκρισης σε μεταγενέστερες χρονικές στιγμές μειώνοντας έτσι την απώλεια του εύρους ζώνης από την αποστολή των συμβόλων εκμάθησης σε συστήματα MIMO που χρησιμοποιούν τεχνικές προσανατολισμένης επικοινωνίας. Στο δεύτερο κεφάλαιο, λοιπόν, εξετάζουμε τεχνικές που υπολογίζουν ένα μοντέλο για την κρουστική απόκριση του καναλιού και των ιδιαζόντων διανυσμάτων της, αφού είναι απαραίτητη η γνώση αυτών στην τεχνική προσανατολισμένης επικοινωνίας που βασίζεται στην διάσπαση ιδιαζουσών τιμών την οποία και θα χρησιμοποιήσουμε σε επόμενα κεφάλαια. Συγκεκριμένα, αρχικά θα εξετάζουμε την τεχνική ESPRIT που μπορεί να εξάγει το μοντέλο ενός σήματος που έχει προκύψει από το άθροισμα μιγαδικών εκθετικών συναρτήσεων διαφορετικής συχνότητας και πλάτους από ενθόρυβα δείγματα. Έτσι θα μπορέσουμε να εξάγουμε το μοντέλο της κρουστικής απόκρισης του καναλιού, Στην συνέχεια θα μελετηθούν «συμπαγείς» αναπαραστάσεις των ιδιαζόντων διανυσμάτων με μοντέλα AR και προβλεπτές Wiener τάξης 1 ώστε να μειωθεί σημαντικά ο αριθμός της απαιτούμενης πληροφορίας που πρέπει να ανατροφοδοτηθεί στον πομπό. Στο τρίτο κεφάλαιο θα εξετάσουμε την τεχνική προσανατολισμένης επικοινωνίας με διάσπαση ιδιαζουσών τιμών υπό την πλήρη γνώση του καναλιού, και στην συνέχεια θα εξετάσουμε την επίδοση της με τη χρήση τεχνικών εκτίμησης και μοντελοποίησης της μήτρας των συντελεστών του καναλιού. Στο τέταρτο κεφάλαιο θα παρουσιαστούν τα συστήματα συνεργατικής επικοινωνίας (cooperative systems), τα οποία αποτελούν μια εναλλακτική προσέγγιση των συστημάτων MIMO. Τα συνεργατικά συστήματα, με την χρήση πρωτοκόλλων συνεργασίας δημιουργούν κατανεμημένα συστήματα MIMO από συστήματα μιας κεραίας, αποφεύγοντας έτσι το μεγάλο μέγεθος 8
9 Κεφάλαιο 1 της επιφάνειας του συστήματος που αποτελεί περιοριστικό παράγοντα στον σχεδιασμό των κλασικών συστημάτων MIMO. Στην συνέχεια θα παρουσιαστεί η εφαρμογή της τεχνικής προσανατολισμένης επικοινωνίας σε συνεργατικά συστήματα με γνώση του καναλιού και με εισαγωγή τεχνικών εκτίμησης και μοντελοποίησης του καναλιού, όπως έγινε στην περίπτωση των συστημάτων MIMO του τρίτου κεφαλαίου. Στο πέμπτο κεφάλαιο θα γίνει μια σύνοψη των όσων έχουν παρουσιαστεί και θα αναφερθούν πιθανές επεκτάσεις. Στη συνέχεια του παρόντος κεφαλαίου θα παρουσιασθεί το μοντέλο που χρησιμοποιείται για την κρουστική απόκριση του καναλιού, θα αναφερθούν κάποιοι ορισμοί που εμφανίζονται συχνά και θα παρουσιασθεί ένας πίνακας με τους συμβολισμούς που χρησιμοποιούνται σε αυτή την διπλωματική. 1.2 Το Μοντέλο της Κρουστικής Απόκρισης του Ασύρματου Καναλιού Το μοντέλο πολλαπλών μονοπατιών συνεχούς χρόνου που δίνει την κρουστική απόκριση ενός καναλιού δίνεται από τον τύπο [1], [16]: όπου ωd n a n N n ( n ) j D (, ) n t τ = δ τ τ ( 0) h t a e ω n= 1, (1.1) είναι οι μιγαδικοί συντελεστές εξασθένησης του κάθε μονοπατιού, οι συχνότητες Doppler, τ n οι καθυστερήσεις των μονοπατιών, N ο αριθμός των μονοπατιών και δ η συνάρτηση δ του Dirac. Ας σημειωθεί ότι το προηγούμενο μοντέλο είναι ντετερμινιστικό, δηλαδή οι παράμετροι που παρουσιάζονται στην πιο πάνω σχέση υπολογίζονται με βάση κάποιους τύπους που προέκυψαν από ανάλυση των ηλεκτρομαγνητικών χαρακτηριστικών των ασύρματων καναλιών. Τα εν λόγω χαρακτηριστικά εξαρτώνται από διάφορους παράγοντες όπως για παράδειγμα, από το τρόπο κίνησης του ασύρματου χρήστη (ταχύτητα, κατεύθυνση κτλ.) και το περιβάλλον στο οποίο κινείται (είδος και αριθμός αντικειμένων που παίζουν τον ρόλο του εμποδίου). Σημειώνουμε επίσης, ότι το προηγούμενο μοντέλο υποθέτει κίνηση του ασύρματου χρήστη με σταθερή ταχύτητα σε ευθεία γραμμή, αλλιώς θα πρέπει οι συχνότητες Doppler να μεταβάλλονται χρονικά. Η διακριτή εκδοχή της προηγούμενης σχέσης δίνεται από τον τύπο: N N j D cos n D () ω θ t j t n m = nm = nm. (1.2) n= 1 n= 1 h t a e a e ω Συνήθως όταν είναι επιθυμητή η παραγωγή χρονικά «συσχετιζόμενων» συντελεστών χρησιμοποιείται ένα στατιστικό μοντέλο. Το συγκεκριμένο μοντέλο προκύπτει αν υποθέσουμε ότι η ασύρματη συσκευή βρίσκεται σε 9
10 Κεφάλαιο 1 περιβάλλον με υψηλή σκέδαση (scattering), οπότε και ο αριθμός μονοπατιών της (1.2) N είναι αρκετά μεγάλος ώστε να θεωρηθεί άπειρος. Αν ο τρόπος που διασκορπίζεται η ακτινοβολία είναι ομοιόμορφος, τότε μπορεί να αποδειχθεί ότι η συνάρτηση αυτοσυσχέτισης των συντελεστών δίνεται από: όπου J0 () i ( ωτ ) r ( ) h τ = J0, (1.3) η μηδενικής τάξης συνάρτηση Bessel πρώτου τύπου. Στην περίπτωση που η μετάδοση γίνεται σε περιβάλλον με λίγους ισχυρούς ανακλαστήρες (reflectors) και οι καθυστερήσεις των μονοπατιών οφείλονται σε μεταβολές της κίνησης του ασύρματου χρήστη μπορούμε να χρησιμοποιήσουμε το μοντέλο της (1.2) το οποίο έχει αρχίσει να χρησιμοποιείται στην βιβλιογραφία για την μελέτη διαφόρων προβλημάτων, όπως για παράδειγμα στην [2] για τυφλή ισοστάθμιση (blind equalization). Υποθέτουμε, όπως και σε όλες τις εργασίες που χρησιμοποιείται αυτό το μοντέλο, ότι ισχύει η αρχή της αμοιβαιότητας των καναλιών(channel reciprocity). Έχοντας αναφερθεί με συντομία στα βασικά χαρακτηριστικά του μοντέλου, το μόνο που απομένει είναι να περιγραφεί ο τρόπος επιλογής των παραμέτρων του. Ο τρόπος που συνήθως χρησιμοποιείται είναι ο εξής: Οι συντελεστές κέρδους των μονοπατιών επιλέγονται ως ομοιόμορφα κατανεμημένες μιγαδικές Γκαουσιανές μεταβλητές (κυκλικά συμμετρικές) με διασπορά 1: ( ) anm, ~ C N 0, 1. (1.4) Οι φάσεις θ n υπολογίζονται ως ομοιόμορφα κατανεμημένες μεταβλητές στο π, π. Ο υπολογισμός της μέγιστης συχνότητας Doppler μπορεί να γίνει [ ] από τον τύπο: f = f v c (Hz), (1.5). Dmax c max όπου f c είναι η συχνότητα του φέροντος, v max είναι η μέγιστη ταχύτητα με την οποία είναι πιθανό να κινηθεί το όχημα και c είναι η ταχύτητα του φωτός. Κλείνοντας αναφέρω ότι τα περισσότερα πειράματα που παρουσιάζονται στις παρακάτω ενότητες έχουν διεξαχθεί για ένα μοντέλο 11 μονοπατιών, με ένα ασύρματο χρήστη που κινείται με σταθερή ταχύτητα 20 Km / h και με 6 ρυθμό συμβόλων R = 10 σύμβολα / δευτερόλεπτο. Στα ακόλουθα σχήματα εξετάζεται η μορφή της κρουστικής απόκρισης του ασύρματου καναλιού για διάφορες τιμές αυτών των παραμέτρων. 10
11 Κεφάλαιο 1 Σχήμα 1.1: Η χρονική εξέλιξη ενός συντελεστή της κρουστικής απόκρισης για N = 11, 6 R = 10, v = 20 Km / h. 11
12 Κεφάλαιο 1 α β Σχήμα 1.2: Η χρονική εξέλιξη ενός συντελεστή της κρουστικής απόκρισης για α) N = 3, 6 6 R = 10, v = 20 Km / h, β) N = 51, R = 10, v = 20 Km / h. 12
13 Κεφάλαιο 1 α β Σχήμα 1.3: Η χρονική εξέλιξη ενός συντελεστή της κρουστικής απόκρισης για α) N = 11, 3 5 R = 10, v = 20 Km / h, β) N = 11, R = 10, v = 20 Km / h.. 13
14 Κεφάλαιο 1 α β Σχήμα 1.4: Η χρονική εξέλιξη ενός συντελεστή της κρουστικής απόκρισης για α) N = 11, 6 6 R = 10, v = 2 Km / h, β) N = 11, R = 10, v =60 Km / h. Στο σχήμα 1.2 συγκρίνουμε πως μεταβάλλεται ένας συντελεστής της κρουστικής απόκρισης χρονικά, σε συνάρτηση με των αριθμό των μονοπατιών που συμβάλουν στην δημιουργία του. Στο σχήμα 1.3 γίνεται η ίδια σύγκριση για διαφορετικούς ρυθμούς συμβόλων. Τέλος, στο σχήμα 1.4 η 14
15 Κεφάλαιο 1 σύγκριση γίνεται για διαφορετικές τιμές της ταχύτητας του κινητού η οποία έχει άμεση σχέση με την συχνότητα Doppler. Αυτό που παρατηρούμε είναι ότι καθοριστικό ρόλο στον ρυθμό μεταβολής του συντελεστή παίζει ο ρυθμός συμβόλων. Παρατηρούμε πόσο πιο απλά γίνονται τα πράγματα στην 6 περίπτωση που ο ρυθμός είναι ίσος με R =10, αφού το κανάλι μεταβάλλεται με πολύ αργό ρυθμό. Αντίθετα για τις άλλες δύο περιπτώσεις ο ρυθμός μεταβολής είναι αρκετά μεγάλος. Βέβαια, τα σημερινά τηλεπικοινωνιακά συστήματα λειτουργούν σε υψηλούς ρυθμούς συμβόλου, οπότε είναι λογικό στις εξομοιώσεις να χρησιμοποιήσουμε υψηλούς ρυθμούς συμβόλου που μας εξασφαλίζουν αυτή την χρονική σταθερότητα του καναλιού. Για την ακρίβεια, ο ρυθμός μεταβολής εξαρτάται από την συχνότητα Doppler η οποία είναι ανάλογη της ταχύτητας κίνησης του τηλεπικοινωνιακού συστήματος, αλλά επειδή κανονικοποιούμε στο μοντέλο αυτή την συχνότητα με τον ρυθμό συμβόλων, οι μεταβολές της φαίνεται να μην επηρεάζουν σημαντικά την μεταβολή του συντελεστή του καναλιού για υψηλό ρυθμό συμβόλων. Ας σημειωθεί ότι κανονικοποιούμε την κρουστική απόκριση του καναλιού ώστε να ισχύει: { m ()} 2 1 E h t =. (1.6) Το μέσο λαμβανόμενο SNR στο δέκτη είναι ίσο με το SNR του καναλιού, αφού ισχύει: received m () 2 SNR = h t SNR, (1.7) όπου SNRreceived το SNR που «βλέπει» ο δέκτης και SNR το SNR του καναλιού, οριζόμενο ως: P SNR =, (1.8) N 0 με την μέση ισχύ μετάδοσης και N την φασματική πυκνότητα του P 0 θορύβου. Κλείνοντας, ο αστερισμός που χρησιμοποιήθηκε σε όλα τα πειράματα είναι ο κλασικός BPSK, με τιμές -1 και 1 για τα σύμβολα του, αντίστοιχα. 15
16 Κεφάλαιο Πίνακας συμβολισμών T A Ανάστροφος πίνακας του Α T x Ανάστροφο διάνυσμα του x H A Ανάστροφος και συζυγής μιγαδικός πίνακας του Α H x Ανάστροφο και συζυγή μιγαδικό διάνυσμα του x E x Στατιστικός μέσος όρος του x { } Tr ( A ) I m ( 0, 2 σ ) l Ίχνος του πίνακα Α Μοναδιαίος m x m πίνακας C N Κυκλικά συμμετρική Γκαουσιανή τυχαία μεταβλητή R * x x με μέση τιμή 0 και διακύμανση Σύνολο πραγματικών αριθμών Συζυγής μιγαδικός του x Μέτρο του x R {} x Το πραγματικό μέρος του x I {} x Το φανταστικό μέρος του x { ev} 2 σ l P Πιθανότητα να συμβεί το γεγονός ev a 2 Q (a) ( 1 2π ) exp( x 2)dx x A A Νόρμα διανύσματος x Νόρμα πίνακα Α Ορίζουσα του πίνακα Α log 2 ( x ) Λογάριθμος βάσης 2 του x diag ( p 1,..., p m ) Διαγώνιος πίνακας με διαγώνια στοιχεία p,..., pm 1 16
17 Κεφάλαιο 1 17
18 Κεφάλαιο 2 Κεφάλαιο 2: Τεχνικές Μοντελοποίησης και Πρόβλεψης των Συντελεστών της Μήτρας του Καναλιού και των Ιδιαζόντων Διανυσμάτων της 2.1 Εισαγωγή Στο προηγούμενο κεφάλαιο αναφερθήκαμε στο μοντέλο της κρουστικής απόκρισης του ασύρματου καναλιού και υποθέσαμε την δυνατότητα αναπαράστασης του από ένα άθροισμα εκθετικών μιγαδικών αριθμών διαφορετικών συχνοτήτων και πλατών. Σε αυτό το κεφάλαιο θα ασχοληθούμε με την εξαγωγή ενός τέτοιου μοντέλου από ενθόρυβα δείγματα της κρουστικής απόκρισης που προέκυψαν από κάποια τεχνική εκτίμησης (π.χ. Εκτίμηση Μέγιστης Πιθανοφάνειας ML). Για τον σκοπό αυτό, θα παρουσιάσουμε μια μέθοδο υπο-χώρου (sub - space), την ESPRIT η οποία έχει την δυνατότητα να εκτιμάει τέτοιας μορφής δεδομένα. Στην συνέχεια του κεφαλαίου θα ασχοληθούμε με τεχνικές μοντελοποίησης των ιδιαζόντων διανυσμάτων που προκύπτουν από την διάσπαση ιδιαζουσών τιμών της μήτρας των συντελεστών του καναλιού MIMO. Μια τέτοια μοντελοποίηση είναι απαραίτητη αφού, στην τεχνική προσανατολισμένης επικοινωνίας που χρησιμοποιεί την διάσπαση ιδιαζουσών τιμών είναι απαραίτητη η γνώση των ιδιαζόντων διανυσμάτων στον πομπό. Κατά συνέπεια θα πρέπει να εξεταστούν συμπαγείς αναπαραστάσεις των εν λόγω διανυσμάτων οι οποίες θα απαιτούν ανατροφοδότηση σχετικά λίγων παραμέτρων (του μοντέλου) στο δέκτη. Η παρατήρηση ότι τα ιδιάζοντα διανύσματα μιας μήτρας, της οποίας τα στοιχεία έχουν προκύψει από το μοντέλο της (1.2), μπορούν να μοντελοποιηθούν ικανοποιητικά από ένα προβλεπτή ενός βήματος, μας οδηγεί στην μελέτη συστημάτων που υλοποιούν τον προηγούμενο προβλεπτή με φίλτρα Wiener και μοντέλα AR τάξης 1, τα οποία και συγκρίνουμε ως προς την επίδοση. 2.2 Υπολογισμός του Μοντέλου της Κρουστικής Απόκρισης του Καναλιού με την Μέθοδο ESPRIT Αρχικά, θα μελετήσουμε πως μπορούμε να εξάγουμε το μοντέλο της κρουστικής απόκρισης ενός συστήματος με μία κεραία στον πομπό και μία στον δέκτη (Single Input Single Output). Θεωρούμε ότι η κρουστική απόκριση του συστήματος μπορεί κάθε χρονική στιγμή να αναπαρασταθεί 18
19 Κεφάλαιο 2 από ένα μόνο πολλαπλασιαστικό συντελεστή (επίπεδη εξασθένηση flat fading). Στη συνέχεια θα δούμε πως η μέθοδος επεκτείνεται στα συστήματα ΜΙΜΟ και στα επιλεκτικά στην συχνότητα (frequency selective) κανάλια. Από τον τύπο (1.2) του προηγούμενου κεφαλαίου, ο πολλαπλασιαστικός συντελεστής δίνεται κάθε χρονική στιγμή από την σχέση: h m N D = n. (2.1) n= 1 j m anme ω Επομένως το πρόβλημα της πρόβλεψης των συντελεστών του καναλιού μπορεί να ορισθεί ως: Με δεδομένη την ακολουθία των δεδομένων που αποτελείται από τα δείγματα της κρουστικής απόκρισης του καναλιού [ ] 0,..., M h h 1 τις χρονικές στιγμές m= 0,..., M 1, πρέπει να εκτιμήσουμε τις παραμέτρους {, } a ω. Με βάση τις παραμέτρους που εκτιμήθηκαν, mn D n προβλέπουμε τις τιμές της διαδικασίας εξασθένησης τις χρονικές στιγμές m= M + 1,..., N + R. Η ιδέα της χρήσης μεθόδων υπο-χώρου εισήχθη στο [3], όπου γίνεται η χρήση μιας τροποποιημένης εκδοχής της μεθόδου ROOT-MUSIC. Μια εναλλακτική προσέγγιση που χρησιμοποιεί την μέθοδο ESPRIT αντί της ROOT MUSIC παρουσιάζεται στο [4]. Η μέθοδος ESPRIT έχει αποδεδειγμένα καλύτερη επίδοση από την ROOT-MUSIC στην εκτίμηση των παραμέτρων μιγαδικών ημιτονοειδών συναρτήσεων, οπότε και υιοθετήθηκε η ESPRIT για την εκτίμηση / πρόβλεψη των συντελεστών της κρουστικής απόκρισης του καναλιού. Η μέθοδος ESPRIT περιγράφεται στο [5] και μπορεί να εκτιμήσει μια διαδικασία f που αποτελείται από υπέρθεση μιγαδικών ημιτονοειδών συναρτήσεων ως: P m f ( m) = γ nz, για 0,..., 1 n t = N. (2.2) n= 1 Δηλαδή, η ESPRΙΤ υπολογίζει του πόλους zi και τα πλάτη γ i, και με την βοήθεια της (2.2) υπολογίζεται η εκτίμηση των τιμών της f για τις χρονικές στιγμές m= 0,..., M 1. Επιπλέον, η σχέση 2.2 μας παρέχει τη δυνατότητα πρόβλεψης των τιμών της f στις χρονικές στιγμές m= M + 1,..., N + R. Μπορούμε να παρατηρήσουμε εύκολα ότι η ESPRIT δίνει την λύση στο πρόβλημα του υπολογισμού των παραμέτρων του μοντέλου της κρουστικής απόκρισης του καναλιού, αν θέσουμε στην (2.1) z h n j D = n και amn γ n e ω =. Με δεδομένη την ακολουθία των δεδομένων που αποτελείται από τα δείγματα της κρουστικής απόκρισης του καναλιού [ h,..., 0 hm 1 ] τις χρονικές στιγμές m= 0,..., M 1, αρχικά κατασκευάζουμε την μήτρα Hankel H, διαστάσεων L K, όπου K + L= N + 1 και L K : 19
20 Κεφάλαιο 2 H h h h h h h h h h 0 1 K K = L 1 L N 1. (2.3) Στη συνέχεια υπολογίζουμε με την βοήθεια της μεθόδου SVD, την διάσπαση της μήτρας Hankel σε παράγοντες ως: ( ) H H= UΣV, (2.4) L K K K όπου Σ= diag σ1,..., σk, σ1 σ Κ 0, και U, V, είναι μήτρες με ορθοκανονικές στήλες. Επόμενο βήμα είναι η τμηματοποίηση των μητρών που προέκυψαν ως εξής: H Σ1 0 V 1 H = [ U1 U2] H 0 Σ2 V, (2.5) 2 L όπου D D D K D U1, Σ 1 και V 1. Οι στήλες της μήτρας U 1 αποτελούν μια βάση του D διαστάσεων υπο χώρου του σήματος. Στην συνέχεια εκτιμάμε τους πόλους του σήματος z i επιλύνοντας το παρακάτω σύστημα γραμμικών εξισώσεων: U Φ U (2.6) 1 1, όπου U ( U ), ορίζουμε ως την μήτρα U 1 χωρίς την άνω (κάτω) γραμμή της. 1 1 Οι εκτιμήσεις των πόλων του σήματος z i υπολογίζονται ως: z = λ, (2.7) n n όπου λ n, m= 1,, D, είναι οι ιδιοτιμές της μήτρας Φ. Έχει παρατηρηθεί ότι πόλοι με πλάτος μεγαλύτερο του 1.05 δεν ανήκουν στο σήμα, οπότε και τους απορρίπτουμε. Αφού έχουμε εκτιμήσει τους πόλους του σήματος, στην συνέχεια εκτιμάμε τα μιγαδικά πλάτη γ n της (2.2) επιλύνοντας ένα σύστημα γραμμικών εξισώσεων. Το συγκεκριμένο σύστημα προκύπτει αν στην (2.1) αντικαταστήσουμε τους πόλους zn με τις εκτιμήσεις τους z n, και υπολογίσουμε για κάθε ένα από τα M δείγματα τις τιμές f ( m ) από την (2.2). Η προηγούμενη παρατήρηση μπορεί να γραφεί ως: ή πιο αναλυτικά: h= Z γ, (2.8) 20
21 Κεφάλαιο 2 h γ1 h 1 z 1 z 2 z D γ 2 =, (2.9) M 1 M 1 M 1 hn 1 z 1 z 2 z D γd το οποίο είναι ένα σύστημα γραμμικών εξισώσεων με άγνωστο το διάνυσμα T γ = [ γ1 γ2 γ K ]. Οι εκτιμήσεις των προηγούμενων τιμών μπορούν να υπολογιστούν επιλύνοντας την (2.8) υπό την έννοια των ελαχίστων τετραγώνων: H ( ) 1 H. γ = Z Z Z h (2.9) Η επέκταση της προηγούμενης μεθόδου σε επιλεκτικά στη συχνότητα κανάλια είναι πολύ εύκολη και στηρίζεται στη [6]. Έστω ότι η κρουστική απόκριση του καναλιού αποτελείται από P συντελεστές. Τότε για κάθε ένα συντελεστή έχουμε M χρονικά δείγματα hp0,..., h pm 1, p= 0,..., P 1 με την βοήθεια των οποίων κατασκευάζουμε τις ακόλουθες μήτρες Hankel, οι οποίες μπορούν να γραφούν με την βοήθεια της (2.3) ως: hp0 h p1 hpk 1 hp 1 hp2 h pk H p =, p = 1,..., P 1. (2.10) hpl 1 hpl hpm 1 Στη συνέχεια κατασκευάζουμε την μήτρα H ως: H = [ ] H H H. (2.11) 0 1 P 1 Με βάση την μήτρα H υπολογίζουμε τους πόλους του σήματος (σχέσεις (2.4) έως (2.7)) και στη συνέχεια με βάση την σχέση (2.9) υπολογίζουμε τα μιγαδικά πλάτη γ ως: i H ( ) 1 H Z Z Z h, 1,.., 1. (2.12) γ p = p p = P Όπως παρατηρούμε από την ανωτέρω σχέση, πρέπει να υπολογίσουμε P άγνωστα διανύσματα, ένα για κάθε συντελεστή της κρουστικής απόκρισης. Πρέπει να αναφέρουμε ότι η συγκεκριμένη μέθοδος μπορεί να εφαρμοστεί και σε συστήματα MIMO με τον ίδιο τρόπο για την ομαδοποιημένη εκτίμηση των συντελεστών της κρουστικής απόκρισης του κάθε καναλιού. Σύμφωνα με την [6], μια ομαδοποιημένη εκτίμηση προσφέρει καλύτερες επιδόσεις, αφού εκμεταλλεύεται πιθανή ετερο-συσχέτιση μεταξύ των συντελεστών. Ανεξάρτητα από το αν έχουμε έναν ή πολλαπλούς συντελεστές, με τα όσα έχουν περιγραφεί έχουμε καταφέρει να εκφράσουμε κάθε συντελεστή στη μορφή της (2.2) για τις χρονικές στιγμές m= 0,..., M 1. Με βάση το μοντέλο 21
22 Κεφάλαιο 2 που υπολογίστηκε, αν εφαρμόσουμε την (2.2) για τις χρονικές στιγμές m= M, M + 1,... τότε προκύπτει η πρόβλεψη της τιμής των συντελεστών της κρουστικής απόκρισης για τις συγκεκριμένες χρονικές στιγμές. Στο σχήμα 2.1α παρουσιάζεται η επίδοση της ESPRIT στην εκτίμηση του καναλιού από δείγματα χωρίς θόρυβο. Αυτό που παρουσιάζουμε στο σχήμα είναι το πως μεταβάλλονται χρονικά το πλάτος και η φάση του συντελεστή του καναλιού σε σύγκριση με το πλάτος και την φάση του συντελεστή που υπολογίζει το μοντέλο που εκτιμήθηκε για αριθμό μονοπατιών ίσο με 11, 6 R = 10, v = 20 Km / h και πλήθος δειγμάτων ίσο με 20. Στο σχήμα 2.1β ο αριθμός των δειγμάτων που χρησιμοποιήθηκαν για την εκτίμηση είναι 50 και στο 2.1γ είναι 100. Η μαύρη κατακόρυφη γραμμή διαχωρίζει το διάστημα εκτίμησης από το διάστημα πρόβλεψης. Δηλαδή, αριστερά της μαύρης γραμμής είναι το χρονικό διάστημα στο οποίο αντιστοιχούν τα δείγματα του συντελεστή που έχουμε στην διάθεσή μας. Δεξιά της γραμμής είναι το χρονικό διάστημα κατά το οποίο δεν γνωρίζουμε τις τιμές του συντελεστή και χρησιμοποιούμε το μοντέλο που εκτιμήθηκε για να προβλέψουμε τις τιμές του. Παρατηρούμε ότι 20 δείγματα είναι αρκετά για να εκτιμηθούν οι παράμετροι του μοντέλου. Όπως αναφέραμε και πιο πάνω, ο αριθμός των δειγμάτων που χρειάζεται η ESPRIT είναι ανάλογος των μονοπατιών τα οποία συμβάλουν στην δημιουργία του συντελεστή της κρουστικής απόκρισης. Στην περίπτωση που δεν χρησιμοποιείται επαρκής αριθμός δειγμάτων (σχήμα 2.1α), παρατηρούμε κάποια αισθητή απόκλιση από τη πραγματική τιμή από το πεντηκοστό δείγμα και πέρα. Κατά συνέπεια, όταν απαιτείται μεγάλος αριθμός δειγμάτων ή ισοδύναμα το μοντέλο παραγωγής της κρουστικής απόκρισης περιλαμβάνει μεγάλο αριθμό μονοπατιών, μπορούμε να χρησιμοποιήσουμε ένα μικρότερο αριθμό δειγμάτων από τον απαιτούμενο για την εκτίμηση των παραμέτρων του μοντέλου, και ανάλογα με το σφάλμα που μπορεί να ανεχτεί η εφαρμογή μας να ρυθμίσουμε κατάλληλα το διάστημα πρόβλεψης. Στο σχήμα 2.2α παρουσιάζουμε το μέσο τετραγωνικό σφάλμα της πρόβλεψης, δηλαδή το σφάλμα μεταξύ της πραγματικής κρουστικής απόκρισης και της κρουστικής απόκρισης που υπολογίσθηκε από το μοντέλο που εκτιμήθηκε για τις χρονικές στιγμές m= M, M + 1,... M που αντιστοιχούν στα διαθέσιμα δείγματα [ ] h,..., 0 hm 1, όπου M = 20 δείγματα τα οποία έχουν αλλοιωθεί από θόρυβο έντασης -10:2:40 db. 22
23 Κεφάλαιο 2 α (Πλάτος) α (Φάση) 23
24 Κεφάλαιο 2 β (Πλάτος) β (Φάση) 24
25 Κεφάλαιο 2 γ (Πλάτος) γ (Φάση) 25
26 Κεφάλαιο 2 δ (Πλάτος) δ (Φάση) Σχήμα 2.1: Η χρονική εξέλιξη ενός συντελεστή της κρουστικής απόκρισης και οι υπολογιζόμενες τιμές του από το μοντέλο που υπολόγισε η ESPRIT από α), 5 β) 20, γ) 50, δ) 100 δείγματα του. Τα δείγματα είναι χωρίς θόρυβο. 26
27 Κεφάλαιο 2 Σχήμα 2.2: Το μέσο τετραγωνικό σφάλμα πρόβλεψης για αριθμό δειγμάτων M=20 και διάστημα πρόβλεψης το [21,200] συναρτήσει του SNR. 2.3 Υπολογισμός Προβλεπτών για τα Ιδιάζοντα Διανύσματα Όπως θα είναι είδη γνωστό, ένα σύστημα MIMO μεταδίδει τα σύμβολα μέσω M N καναλιών, όπου M και N ο αριθμός των κεραιών στον πομπό και στον δέκτη αντιστοίχως. Τα συστήματα MIMO θα μελετηθούν αναλυτικά στο τρίτο κεφάλαιο. Εδώ αρκεί να γνωρίζουμε ότι αν τα M N κανάλια είναι μη επιλεκτικά στη συχνότητα, τότε κάθε χρονική στιγμή μπορούμε ομαδοποιημένα να αναπαραστήσουμε την κρουστική απόκριση καθενός από αυτά με τα στοιχεία μιας μήτρας διαστάσεων N M ως: H h h h h h h h h h M M = N1 N2 NM. (2.13) Για λόγους που θα εξηγηθούν στα επόμενα κεφάλαια, η χρήση της τεχνικής προσανατολισμένης επικοινωνίας με διάσπαση ιδιαζουσών τιμών (που αποτελεί και τη βασική τεχνική που μελετάμε σε αυτή τη διπλωματική) απαιτεί την γνώση του κύριου ιδιάζοντος διανύσματος στον πομπό. Το διάνυσμα αυτό, είναι η πρώτη στήλη της μήτρας V που προκύπτει από την T παραγοντοποίηση της H ως H= UΣV, με την χρήση της μεθόδου SVD (Singular Value Decomposition Διάσπαση Ιδιαζουσών Τιμών). Τα στοιχεία του ιδιάζοντος διανύσματος χρησιμοποιούνται για τον πολλαπλασιασμό των 27
28 Κεφάλαιο 2 προς μετάδοση συμβόλων στον πομπό, μια διαδικασία που ονομάζεται προκωδικοποίηση (pre-coding). Αν επεκτείνουμε την προηγούμενη τεχνική σε συνεργατικά συστήματα, εύκολα μπορούμε να δούμε ότι ο κάθε κόμβος θα πρέπει να γνωρίζει το στοιχείο του κύριου ιδιάζοντος διανύσματος που του αντιστοιχεί, με το οποίο και θα πολλαπλασιάσει το προς μετάδοση σύμβολο. Από τα προηγούμενα φαίνεται ότι είναι αναγκαίο να υπολογισθεί ένας προβλεπτής που βάση παρελθοντικών τιμών του κύριου ιδιάζοντος διανύσματος προβλέπει τις τιμές του σε μεταγενέστερες χρονικές στιγμές. Από την παρατήρηση των χρονικών μεταβολών των τιμών του εν λόγω διανύσματος καταλήξαμε στο συμπέρασμα ότι μπορεί να μοντελοποιηθεί από ένα προβλεπτή τάξης 1, δηλαδή μπορούμε να υπολογίσουμε κάθε χρονική στιγμή t την τιμή της θέσης i του ιδιάζοντος διανύσματος από ένα προβλεπτή τύπου FIR που έχει την μορφή: ( ) ( ) x t = wx t 1, 0 i N. (2.13) i i i Επομένως, αν το κύριο ιδιάζον διάνυσμα έχει N στοιχεία τα οποία μπορούν T να αναπαρασταθούν την χρονική στιγμή n ως V () t = v1 () t vn () t, τότε αυτά μπορούν να υπολογισθούν από N προβλεπτές ως: ( ) ( ) v t w v t = vn () t w N vn t ( 1), (2.14) όπου ο είναι ο τελεστής πολλαπλασιασμού μητρών και διανυσμάτων στοιχείο προς στοιχείο. Υπάρχουν διάφορα θέματα τα οποία προκύπτουν, κάποιος για παράδειγμα θα μπορούσε να σκεφτεί ότι μπορεί η μορφή της (2.14) να μην είναι βέλτιστη για ένα κλασικό σύστημα MIMO, αφού σε αυτή τη περίπτωση θα ήταν καλύτερη η χρήση ενός δυσδιάστατου μοντέλου πρόβλεψης. Επιπλέον, αν η κρουστική απόκριση του καναλιού αποτελείται από μικρό αριθμό μονοπατιών, ίσως είναι προτιμότερο να μεταδώσει ο δέκτης τις παραμέτρους του μοντέλου και ο πομπός να ανακατασκευάσει την μήτρα του καναλιού υπολογίζοντας στην συνέχεια το κύριο ιδιάζον διάνυσμα από την εφαρμογή διάσπασης ιδιαζουσών τιμών στην μήτρα που ανακατασκεύασε. Αυτή η παρατήρηση στηρίζεται στο ότι ένας προβλεπτής σαν αυτόν της (2.14) μπορεί να παρουσιάσει προβλήματα σύγκλισης (ιδίως σε χαμηλές τιμές SNR ), οπότε θα πρέπει σε τακτές χρονικές στιγμές ο δέκτης να ανατροφοδοτεί την τιμή του ιδιάζοντος διανύσματος. Έχοντας όμως υπόψιν, ότι στόχος μας είναι να μελετήσουμε τεχνικές προσανατολισμένης επικοινωνίας για συνεργατικά συστήματα με περιορισμούς στην υπολογιστική ισχύ, καταλήγουμε στο συμπέρασμα ότι η χρήση μιας επιπλέον διάσπασης ιδιαζουσών τιμών μπορεί να επιβαρύνει αρκετά το σύστημα. Επίσης, καθώς αυξάνεται το SNR, ο 28
29 Κεφάλαιο 2 αριθμός των αναμεταδόσεων που απαιτούνται για να αποφευχθεί η απόκλιση του προβλεπτή είναι αμελητέος και μάλιστα, συνολικά τα στοιχεία που μεταδίδονται πίσω στους δέκτες είναι λιγότερα ακόμη και αν το μοντέλο της κρουστικής απόκρισης αποτελείται από λίγα μονοπάτια. Μπορεί τα προηγούμενα να φαίνονται κάπως αφηρημένα, αλλά σταδιακά στα επόμενα κεφάλαια θα αναφερθούμε αναλυτικά σε κάθε μέθοδο και θα συνδεθούν άμεσα με τα όσα αναφέρουμε σε αυτή την ενότητα. Το μόνο που πρέπει να γνωρίζουμε στην παρούσα ενότητα είναι ότι: Ο πομπός με κάποιον τρόπο (π.χ.εκτίμηση Μέγιστης Πιθανοφάνειας Κεφάλαιο 3) διαθέτει δείγματα της μήτρας του καναλιού H που δίνεται από την σχέση (2.13), εξάγει ένα μοντέλο με την ESPRIT, το χρησιμοποιεί για να υπολογίσει και να προβλέψει τιμές της κρουστικής απόκρισης, και στην συνέχεια εξάγει τους συντελεστές με το V () 1 w 0 i N 1 τους οποίους και ανατροφοδοτεί στον πομπό μαζί i. Παράλληλα, παρακολουθεί την εξέλιξη του προβλεπτή και αν παρατηρήσει απόκλιση την στιγμή t, μεταδίδει στον πομπό την σωστή τιμή V t και αποτρέπει την απόκλιση. Στόχος αυτής της παραγράφου είναι να () εξετάσει δύο τρόπους υπολογισμού των συντελεστών w 0 i N 1, ο ένας χρησιμοποιεί φίλτρο Wiener και ο άλλος μοντέλα AR. Οι δύο μέθοδοι συγκρίνονται ως προς τον αριθμό των μεταδόσεων που απαιτεί ο καθένας ώστε να παραμένει η εκτίμηση αρκετά κοντά στην πραγματική τιμή (αυτό καθορίζεται με κατώφλι, όπως θα δούμε) για διάφορα «σενάρια» θορύβου στο σύστημα. i Προβλεπτής με Φίλτρο Wiener To 1940 o Wiener σχεδίασε ένα φίλτρο που εκτιμάει βέλτιστα ένα σήμα από ενθόρυβα δείγματα. Πιο συγκεκριμένα το πρόβλημα που επίλυσε ήταν: ο σχεδιασμός ενός φίλτρου που θα εκτιμούσε βέλτιστα ένα σήμα d t από ενθόρυβες παρατηρήσεις που δίνονται από: () () x( t) = d( t) + v( t), (2.15) υποθέτοντας ότι οι d t και u( t ) είναι τυχαίες διαδικασίες στάσιμες με την ευρεία έννοια (wide-sense stationary random process). Αν θεωρήσουμε d t = x t+ 1 και το φίλτρο Wiener είναι αιτιατό, τότε το φίλτρο Wiener που () ( ) υπολογίζουμε είναι ένας προβλεπτής. Σε αυτή την περίπτωση το φίλτρο παράγει μια πρόβλεψη (εκτίμηση) του xt+ ( 1) ως γραμμικό συνδυασμό παρελθοντικών τιμών του x() t. Επιστρέφοντας στο πρόβλημα του υπολογισμού των συντελεστών του φίλτρου Wiener που δίνουν την βέλτιστη εκτίμηση του σήματος d t, αν με x() t συμβολίσουμε την είσοδο του φίλτρου και με wl () () τους συντελεστές της 29
30 Κεφάλαιο 2 κρουστικής απόκρισης του φίλτρου, τότε η έξοδος του φίλτρου Wiener (δηλαδή η εκτίμηση ˆd t δίνεται από τη σχέση: () p 1 dˆ () t = w() l x( t l). (2.16) n= 0 Το πρόβλημα σχεδιασμού του φίλτρου Wiener απαιτεί την εύρεση των συντελεστών του wl που ελαχιστοποιούν το μέσο τετραγωνικό σφάλμα: () 2 { } 2 { ()} () ˆ () ξ = E e t = E d t d t. (2.17) Η εύρεση των συντελεστών του φίλτρου συνίσταται στην επίλυση των γνωστών εξισώσεων Wiener-Hopf: Rw= r, (2.18) x dx R x είναι η Ερμιτιανή Toeplitz μήτρα των αυτοσυσχετίσεων, διάνυσμα που περιέχει τους συντελεστές του φίλτρου, και όπου διάνυσμα των ετεροσυσχετίσεων μεταξύ του επιθυμητού σήματος σήματος που παρατηρούμε r dx w d() t είναι το είναι το και του x( t ). Επιστρέφοντας τώρα στο πρόβλημα της γραμμικής πρόβλεψης, αν είχαμε στην διάθεσή μας δείγματα χωρίς θόρυβο, η γραμμική πρόβλεψη με ένα φίλτρο FIR τάξης p 1 έχει την μορφή: p 1 xˆ ( t+ 1 ) = w( k) x( t k), k = 0,1,, p 1, (2.19) k = 0 Όπως έχει είδη αναφερθεί, το προηγούμενο πρόβλημα ανάγεται στο πρόβλημα της εύρεσης των συντελεστών ενός φίλτρου Wiener θέτοντας d n = x n+ 1. Για να υπολογίσουμε τις εξισώσεις Wiener Hopf αυτής της ( ) ( ) περίπτωσης πρέπει να υπολογίσουμε την δούμε εύκολα είναι ίση με: r dx, η οποία όπως μπορούμε να { } { ( ) ( )} x ( * * r ( k) = E d( n) x ( n k) = E x n+ 1 x n k = r k 1) dk Μπορούμε επομένως να γράψουμε τις σχετικές εξισώσεις ως: +. (2.20) 30
31 Κεφάλαιο 2 ( 0) *( 1) *( 2) *( 1) () 1 ( 0) *() 1 *( 2) ( 2) ( 1) ( 0) * ( 3) rx rx rx rx p w 0 r 1 rx rx rx rx p w 1 r 2 rx rx rx rx p w = r. (2.21) rx( p 1) rx( p 2) rx( p 3) rx( 0) w( p 1) r( p) Το μέσο τετραγωνικό σφάλμα σε αυτή την περίπτωση αποδεικνύεται ότι είναι ίσο με [7] : ( ) () ( 2) () ( ) ( 3) ξ min x p 1 x 1 k = 0 * ( 0) ( ) ( ). (2.22) = r w k r k+ Προχωρώντας σε μια πιο ρεαλιστική υπόθεση, υποθέτουμε τώρα ότι τα δείγματα είναι αλλοιωμένα από θόρυβο. Τότε το σήμα το οποίο θα αποτελέσει την είσοδο στον προβλεπτή Wiener είναι το: y ( t) = x( t) + v( t). (2.23) Στόχος μας πλέον είναι να σχεδιάσουμε ένα φίλτρο το οποίο θα εκτιμάει την τιμή x( n+ 1) ως ένα γραμμικό συνδυασμό p προηγούμενων τιμών του y ( n ): p 1 p 1. (2.24) ( + ) = ( ) ( ) = ( ) ( ) + ( k) xˆ t 1 w k y t k w k x t k v t k= 0 k= 0 Οι εξισώσεις Wiener-Hopf σε αυτή την περίπτωση γράφονται ως: Rw= r. (2.25) y dy Αν ο θόρυβος είναι ασυσχέτιστος με το σήμα x( t ), τότε αυτοσυσχέτισης του y αποτελείται από τα στοιχεία: η μήτρα { } ( ) ( ) * ( ) ( ) ( ) ry k = E y t y t k = rx k + rv k, (2.26) και το διάνυσμα των ετεροσυσχετίσεων μεταξύ του d( t ) και του y () t έχει στοιχεία: dy * * { } { ( 1) ( )} x ( 1) ( ) ( ) ( ) r k = E d t y t k = E x t+ y t k = r k+. (2.27) Τελικά, η μόνη διαφορά με την περίπτωση που τα δείγματα δεν είναι αλλοιωμένα από θόρυβο, είναι ότι η μήτρα αυτοσυσχέτισης του σήματος 31
32 Κεφάλαιο 2 εισόδου είναι Ry = Rx + R v αντί για R x που είναι στην περίπτωση της απουσίας θορύβου. Όπως θα δούμε στην συνέχεια, στην περίπτωση μας αρκεί να υπολογίσουμε για κάθε στοιχείο του κύριου ιδιάζοντος διανύσματος ένα φίλτρο Wiener ενός συντελεστή όπως είχε προαναφερθεί και στη σχέση (2.13) Προβλεπτής με Μοντέλο AR Μια διαδικασία AR (διαδικασία αυτο-παλινδρόμησης - autoregressive process) έχει φάσμα συχνοτήτων το οποίο παρουσιάζει μόνο πόλους (all-pole model) και το οποίο δίνεται από τον τύπο: ( ) H z = 1 b p + k = 1 ( 0) a p ( ) k z k. (2.28) Χαμηλής τάξης μοντέλα AR έχουν χρησιμοποιηθεί στην βιβλιογραφία για την μοντελοποίηση και πρόβλεψη της κρουστικής απόκρισης του καναλιού που δίνεται από ένα μοντέλο πολλαπλών μονοπατιών. Από παρατήρηση των ιδιαζόντων διανυσμάτων καταλήξαμε στο συμπέρασμα ότι και τα ιδιάζοντα διανύσματα μπορούν να μοντελοποιηθούν ικανοποιητικά από μοντέλα AR. Μια κλασική μέθοδος υπολογισμού τον συντελεστών του μοντέλου AR είναι η μέθοδος του Prony. Επειδή η ανάλυση της ξεφεύγει από τους σκοπούς αυτής της διπλωματικής(για μια αναλυτική περιγραφή παραπέμπουμε στο [7]) αναφέρουμε μόνο ότι η μέθοδος αυτή υπολογίζει τους συντελεστές ελαχιστοποιώντας το τετραγωνικό σφάλμα: όπου: E () 2 p = et, (2.29) t= 0 p () = () + ( ) ( ) et xt a k xt k k = 1 Αν εκφράσουμε το προηγούμενο σφάλμα ως: όπου: ( ) ( ) ˆ ( ) p. (2.30) et = xt xt, (2.31) p () ( ) ( k) xˆ t = a k x t, (2.32) k = 1 p 32
33 Κεφάλαιο 2 και αν υπολογίσουμε τους συντελεστές του μοντέλου AR ελαχιστοποιώντας το σφάλμα της (2.29), καταλήγουμε σε ένα μοντέλο AR το οποίο υπολογίζει μια προσέγγιση του ˆx () t όσο πιο κοντά γίνεται στο x( t ). Κατά συνέπεια, έχουμε υπολογίσει ένα μοντέλο το οποίο προβλέπει την τιμή x( t ) ως γραμμικό συνδυασμό τιμών προηγούμενων χρονικών στιγμών. Παρατηρώντας πιο προσεκτικά το μοντέλο AR, βλέπουμε ότι περιέχει τους συντελεστές πρόβλεψης στην γενική του έκφραση, και κατά συνέπεια αρκεί από τα δείγματα να εξάγουμε τις παραμέτρους του μοντέλου AR με κάποια γνωστή μέθοδο και στην συνέχεια να αφαιρέσουμε τον πρώτο συντελεστή (μονάδα) για να προκύψει το μοντέλο πρόβλεψης. Για τον υπολογισμό των συντελεστών του μοντέλου επιλέχθηκε η μέθοδος της συνδιασποράς την οποία και θα περιγράψουμε εν συντομία στη συνέχεια της ενότητας. Όπως αναφέρθηκε πιο πάνω, η μέθοδος του Prony υπολογίζει τους συντελεστές του μοντέλου AR ελαχιστοποιώντας το τετραγωνικό σφάλμα et παρέχεται μόνο της (2.29). Προφανώς, η δυνατότητα υπολογισμού του ( ) για το διάστημα που διαθέτουμε επαρκή δείγματα αφού από την (2.30) αν έχουμε δείγματα για τις χρονικές στιγμές t = 0,, T, τότε μπορούμε να υπολογίσουμε το σφάλμα μόνο για το διάστημα [ p, T ]. Η μέθοδος της συνδιασποράς βασίζεται στην ελαχιστοποίηση του τροποποιημένου τετραγωνικού σφάλματος: T C E () 2 p = et. (2.33) t= p Σύμφωνα με την σχέση (2.33) μπορούμε να υπολογίσουμε τους συντελεστές του μοντέλου από την επίλυση των ακόλουθων εξισώσεων: T * rx ( k, l) = x( t l) x ( t k). (2.34) t= p Το σφάλμα της μεθόδου δίνεται από το ακόλουθο τύπο: p { p } = x( ) + p( ) x( C min E r 0, 0 a k r 0, k). (2.35) Όπως και στην περίπτωση του φίλτρου Wiener αρκεί πάλι να υπολογίσουμε ένα μοντέλο με ένα μόνο συντελεστή για την μοντελοποίηση του ιδιάζοντος διανύσματος. k = 1 33
34 Κεφάλαιο Αποτελέσματα Εξομοιώσεων. Στις ακόλουθες γραφικές συγκρίνουμε τις δύο μεθόδους ως προς τον αριθμό των μεταδόσεων των στοιχείων του κύριου ιδιάζοντος διανύσμάτος που χρειάσθηκαν να γίνουν. Για να γίνουμε πιο συγκεκριμένοι, ο δέκτης αφού εξάγει το μοντέλο(δηλαδή τον ένα συντελεστή) για τα στοιχεία του κύριου ιδιάζοντος διανύσματος, το στέλνει στον πομπό μαζί με την αρχική τιμή του διανύσματος. Ο πομπός με βάση το μοντέλο, προβλέπει τις τιμές του διανύσματος (σε ένα συνεργατικό σύστημα κάθε κόμβος προβλέπει μόνο την τιμή που τον αφορά). Παράλληλα ο δέκτης παρακολουθεί την εξέλιξη του διανύσματος καθώς διεξάγει την ίδια διαδικασία. Έτσι, αν η πρόβλεψη που υπολογίζει διαφέρει σημαντικά (το «πόσο» σημαντικά καθορίζεται από ένα κατώφλι που προεπιλέγουμε), τότε στέλνει στον πομπό την πραγματική τιμή που έχει εκείνη την στιγμή το ιδιάζον διάνυσμα. Έτσι στο σχήμα 2.3α παρουσιάζουμε τον αριθμό των μεταδόσεων συναρτήσει της έντασης του θορύβου που απαιτεί κάθε μέθοδος ώστε να μην διαφέρει η πραγματική από την εκτιμηθείσα τιμή περισσότερο από ένα κατώφλι ίσο με 0.01, 0.05 και 0.1 και β) είναι η ίδια γραφική για κατώφλι ίσο με 1, 5 και 10. Παρατηρούμε ότι οι δύο μέθοδοι έχουν πανομοιότυπη συμπεριφορά και στις δύο περιπτώσεις, οπότε και θα υιοθετήσουμε την μέθοδο με τα μοντέλα AR για την συνέχεια. Επίσης, όπως είναι λογικό βλέπουμε ότι όσο πιο αυστηρό είναι το κατώφλι, τόσο περισσότερες μεταδόσεις χρειάζονται για να διατηρηθεί η τιμή του προβλεπτή κάτω από το κατώφλι. Ο αριθμός των μεταδόσεων μειώνεται με την αύξηση του SNR και γενικά για θετικές τιμές του SNR ο αριθμός των μεταδόσεων είναι περίπου το 1/10 των μεταδόσεων που θα απαιτούνταν αν στέλναμε τα στοιχεία και όχι το μοντέλο AR. Στο δεύτερο σχήμα, οι τιμές των κατωφλίων είναι αρκετά πιο ελαστικές και ο αριθμός των μεταδόσεων είναι μικρότερος. Η επίδραση της τιμής του κατωφλίου στην επίδοση ενός συστήματος θα παρουσιαστεί στην περίπτωση των συνεργατικών συστημάτων στο κεφάλαιο 4. 34
35 Κεφάλαιο 2 α Σχήμα 2.3: Σύγκριση του αριθμού των μεταδόσεων που χρειάζεται ένα φίλτρο Wiener με τον αριθμό μεταδόσεων που χρειάζεται ένα μοντέλο AR(1) για κατώφλια α) 0.01,0.05,0.1 και β) 1,5, 10. β 35
36 Κεφάλαιο Το Πρόβλημα της Εκτίμησης του Αριθμού των Μονοπατιών Επιστρέφοντας στην μέθοδο ESPRIT, αναφέρουμε κάτι που σκόπιμα δεν είχαμε αναφέρει έως την συγκεκριμένη ενότητα. Η μέθοδος ESPRIT για να υπολογίσει τα μιγαδικά ημίτονα (πλάτη και φάσεις) θα πρέπει να γνωρίζει τον αριθμό τους ώστε να επιλέξει κατάλληλα την διάσταση του χώρου σημάτων D στην (2.5). Αν επιλέξουμε μικρότερη τιμή του D από την πραγματική, τότε το μοντέλο που θα προκύψει θα παρουσιάζει σφάλμα εκτίμησης και πρόβλεψης (όπως έχει είδη παρουσιασθεί) ακόμη και για δείγματα χωρίς θόρυβο. Μια εύκολη λύση θα ήταν να επιλέγουμε πάντα μια τιμή επαρκώς μεγάλη, ώστε μην παρουσιάζονται τέτοιας μορφής προβλήματα. Βέβαια, μια τέτοια απόφαση μπορεί να αυξήσει άσκοπα τον υπολογιστικό φόρτο του συστήματός μας, αφού μπορεί για παράδειγμα να βρίσκεται για μεγάλο χρονικό διάστημα σε ένα περιβάλλον με λίγα ισχυρά μονοπάτια. Αν και εμείς στη συνέχεια της διπλωματικής δεν θα ασχοληθούμε περισσότερο με το θέμα (θα υποθέσουμε ότι στο δέκτη είναι με κάποιο τρόπο γνωστός ο αριθμός των μονοπατιών), θα αναφέρουμε εδώ μια προσέγγιση που παρουσιάστηκε στην [8]. Στην συγκεκριμένη εργασία χρησιμοποιείται μια μέθοδος τύπου ESPRIT για εκτίμηση και πρόβλέψη της κρουστικής απόκρισης ενός συστήματος OFDM. Σύμφωνα με τα όσα αναφέρονται, η εκτίμηση του αριθμού των μονοπατιών L είναι ένα πρόβλημα επιλογής μοντέλου το οποίο επιλύεται από την μέθοδο Μήκους Ελάχιστης Περιγραφής (Minimum Description Length MDL). Με βάση την συγκεκριμένη μέθοδο αν έχουμε T δείγματα της κρουστικής απόκρισης [ h0 ht 1 ], και από αυτά εκτιμήσουμε την μήτρα αυτοσυσχέτισης ˆR με την μέθοδο της τροποποιημένης συνδιασποράς, τότε το πλήθος των μονοπατιών μπορεί να εκτιμηθεί ως: ( μ ) 1 T K K ˆ K μ ( λ 1 ) ˆ k k = μ + 1 L= arg min log + μ( 2K μ+ 1) logt 1 μ K 1 1, (2.36) Κ ˆ λ 4 k = μ+ 1 k K μ ˆ λ K όπου { k} = 1 k είναι οι μη διατεταγμένες ιδιοτιμές της μήτρας ˆR. 36
37 Κεφάλαιο 2 37
38 Κεφάλαιο 3 Κεφάλαιο 3: Τεχνικές Προσανατολισμένης Επικοινωνίας για Συστήματα MIMO 3.1 Εισαγωγή Η ιδέα της δημιουργίας πολλαπλών μονοπατιών μετάδοσης στο χώρο με την εισαγωγή πολλαπλών κεραιών στα ασύρματα συστήματα οδήγησε στην δημιουργία των συστημάτων Πολλαπλών Εισόδων Πολλαπλών Εξόδων (Multiple Input Multiple Output MIMO). Οι πολλαπλές κεραίες, μπορούν να χρησιμοποιηθούν με διαφορετικούς τρόπους έχοντας διαφορετικά πλεονεκτήματα και μειονεκτήματα σε κάθε περίπτωση. Βασικά, θα επιθυμούσαμε να μεταδίδουμε όσον το δυνατό περισσότερα σύμβολα παράλληλα επιτυγχάνοντας έτσι το μέγιστο κέρδος πολύπλεξης που παρέχει το σύστημα, και επίσης θα επιθυμούσαμε να επιτύχουμε τον μέγιστο δυνατό ρυθμό με τον οποίο φθίνει η πιθανότητα σφάλματος, κάτι που είναι γνωστό ως κέρδος ποικιλομορφίας. Δυστυχώς, οι προηγούμενες «επιθυμίες» μας είναι αντικρουόμενες και η αύξηση του ενός κέρδους γίνεται εις βάρος του άλλου [24]. Παράλληλα θα πρέπει να λάβουμε υπόψιν ότι γενικά, θα ήταν καλό και η πολυπλοκότητα των συστημάτων να παραμένει σε λογικά επίπεδα, μιας και οι τεχνικές που προτείνονται θα πρέπει να είναι εύκολα εφαρμόσιμες σε μικρές ασύρματες συσκευές, όπως για παράδειγμα τα κινητά τηλέφωνα, τα οποία συνήθως στερούνται υπολογιστικής ισχύος. Σε αυτή την κατεύθυνση, έχουν προταθεί διάφορες τεχνικές, όπως οι τεχνικές των αρχιτεκτονικών BLAST [17], [18] η κωδικοποίηση χρόνου χώρου [20], [21], [22], [23] και οι τεχνικές προσανατολισμένης επικοινωνίας [25]. Σκοπός του κεφαλαίου είναι να μελετήσει την επίδοση των τεχνικών προσανατολισμένης επικοινωνίας και την επίδραση της μη πλήρης γνώσης της κατάστασης του καναλιού σε αυτές τις τεχνικές. Η τεχνική προσανατολισμένης επικοινωνίας που μελετάται είναι η κλασική τεχνική που στηρίζεται στην διάσπαση ιδιαζουσών τιμών. Στην συνέχεια θα εξετάσουμε την τεχνική προσανατολισμένης επικοινωνίας με την χρήση μοντελοποίησης και πρόβλεψης της μήτρας των συντελεστών του καναλιού χρησιμοποιώντας την τεχνική που περιγράφηκε στο προηγούμενο κεφάλαιο. 38
39 Κεφάλαιο Περιγραφή Συστήματος ΜΙΜΟ Ένα σύστημα MIMO επικοινωνίας από σημείο-σε-σημείο (point-to-point), με Μ κεραίες εκπομπής και Ν λήψης που λειτουργεί σε στενό εύρος ζώνης απεικονίζεται στο σχήμα 3.1. Το διακριτό μοντέλο που περιγράφει ένα τέτοιο σύστημα δίνεται από τη σχέση: ή πιο απλά: y1 h11 h1m x1 n 1 = +, (3.1) y h h x n N N1 NM M N y = Hx + n. (3.2) Σχήμα 3.1: Ένα σύστημα MIΜO. Το x είναι το διάνυσμα των συμβόλων που μεταδίδεται από τις Μ κεραίες του πομπού, H είναι η μήτρα διαστάσεων N M των συντελεστών του καναλιού, με στοιχεία τα οποία στην περίπτωση του συστήματος στενού εύρους ζώνης h ij αντιστοιχούν στον μοναδικό συντελεστή της κρουστικής απόκρισης του καναλιού μεταξύ της κεραίας του πομπού j και της κεραίας του δέκτη i. Υποθέτουμε ότι το κανάλι έχει εύρος ζώνης B και μιγαδικό Γκαουσιανό 2 προσθετικό θόρυβο μηδενικής μέσης τιμής με πίνακα συνδιασποράς σ I N, με 2 τη διασπορά σ να ορίζεται όπως είναι γνωστό ως: όπου N N0 σ Ε n i = 2, (3.3) η φασματική πυκνότητα ισχύος του θορύβου. Θεωρούμε ότι υπάρχει ένας περιορισμός στην ισχύ μετάδοσης ίσος με P. Τα στοιχεία της μήτρας H, υπολογίζονται από το μοντέλο μετάδοσης πολλαπλών μονοπατιών που παρουσιάστηκε στο πρώτο κεφάλαιο. Στη συνέχεια περιγράφουμε την τεχνική προσανατολισμένης επικοινωνίας με διάσπαση ιδιαζουσών τιμών. 39
40 Κεφάλαιο Τεχνική Προσανατολισμένης Επικοινωνίας σε Συστήματα ΜΙΜΟ με Πλήρη Γνώση της Κατάστασης του Καναλιού Τεχνική Προσανατολισμένης Επικοινωνίας με Διάσπαση Ιδιαζουσών Τιμών. Η κλασσική μέθοδος προσανατολισμένης επικοινωνίας στηρίζεται στη διάσπαση ιδιαζουσών τιμών (Singular Value Decomposition SVD beamforming) της μήτρας του καναλιού. Η συγκεκριμένη τεχνική απαιτεί την γνώση αυτής της μήτρας στον πομπό και στον δέκτη αφού χρησιμοποιεί τα ιδιάζοντα διανύσματα των μητρών V και U για να προ-κωδικοποιήσει (pre-coding) τα προς μετάδοση σύμβολα στον πομπό και να μορφοποιήσει τα ληφθέντα σύμβολα στο δέκτη (receiver shaping). Θεωρώντας λοιπόν, ότι η μήτρα του καναλιού H που παρουσιάζεται στην σχέση (3.1) είναι γνωστή σε πομπό και σε δέκτη τότε εφαρμόζεται η διάσπαση κατά παράγοντες σε αυτή με τη χρήση της μέθοδου SVD: ( NM ) T H = UΣV, (3.4) N N όπου Σ= diag σ σ, σ σ 0, και U, 1,..., min(, ) 1 min( NM, ) V M M, είναι μήτρες με ορθοκανονικές στήλες. Με την χρήση της προηγούμενης μεθόδου επιτύχαμε την διαίρεση του συστήματος ΜΙΜΟ σε ένα σύνολο από min( NM, ) ανεξάρτητα παράλληλα υπο-κανάλια, κάθε ένα από τα οποία έχει ως μοναδικό συντελεστή κρουστικής απόκρισης την αντίστοιχη ιδιάζουσα τιμή. Με βάση τα προηγούμενα, μια πρώτη προσέγγιση για την εφαρμογή μιας τεχνικής προσανατολισμένης επικοινωνίας σε ένα σύστημα MIΜO είναι η εφαρμογή των κατάλληλων μιγαδικών συντελεστών στα κέρδη των κεραιών του πομπού και του δέκτη έτσι ώστε να επιτραπεί η μετάδοση μόνο στο ιδιόκανάλι με το μεγαλύτερο κέρδος ιδιάζουσα τιμή (single beamforming απλή προσανατολισμένη επικοινωνία). Σε αυτή την περίπτωση τα βέλτιστα ιδιάζοντα διανύσματα που περιέχουν τα προηγούμενα βάρη είναι η πρώτη στήλη της U για τον δέκτη και η πρώτη στήλη της V για τον πομπό. Πιο αναλυτικά, σε περίπτωση που δεν χρησιμοποιούσαμε τεχνική προσανατολισμένης μετάδοσης, κάθε κεραία του πομπού θα μετέδιδε ένα σύμβολο x (χρησιμοποιούμε πάλι BPSK) και ο δέκτης θα λάμβανε: y = Hx + n, (3.2) 1 M όπου η Η δίνεται από την (3.1) και n C. Με την εφαρμογή της τεχνικής απλής προσανατολισμένης επικοινωνίας και συμβολίζοντας τη πρώτη στήλη της U ως u1 και την πρώτη στήλη της V ως v1 η σχέση (3.2) γίνεται: y = xu Hv + nv = σ x+ n, (3.5) H
41 Κεφάλαιο 3 όπου σ 1 είναι η μεγαλύτερη ιδιάζουσα τιμή της μήτρας H. Δηλαδή, το ισοδύναμο σύστημα είναι ένα κανάλι προσθετικού θορύβου με ένα πολλαπλασιαστικό συντελεστή κρουστικής απόκρισης και έχει την μορφή της (3.5). Για το σχεδιασμό του δέκτη, γνωρίζουμε [9] ότι μια βαθμωτή μεταβλητή x μπορεί να εκτιμηθεί από μια βαθμωτή μεταβλητή y με την οποία συνδέεται με τη σχέση (3.5) (ή πιο απλά y = hx H + n, όπου h = w h), με τη βοήθεια της επαρκούς στατιστικής: * h r = y = h x+ n. (3.6) h Ο κανόνας απόφασης για την εύρεση του συμβόλου που έχει μεταδοθεί είναι απλώς ο έλεγχος του προσήμου του πραγματικού μέρους της προηγούμενης στατιστικής. Μια εναλλακτική προσέγγιση είναι να μεταδοθούν σύμβολα παράλληλα σε όλα (ή σε μερικά) τα υπο-κανάλια με ίση κατανομή ισχύος (multiple beamforming πολλαπλή προσανατολισμένη επικοινωνία). Αν χρησιμοποιούνται όλα τα υπο-κανάλια (αριθμού L= min( N, M) ) και μεταδίδονται από τον πομπό τα L σύμβολα του x, η (3.5) γίνεται: 1 H 1 y = U HVx+ nv = Σ x+ n, (3.7) L L 1 L όπου n C. Με άλλα λόγια έχουμε L ισοδύναμα συστήματα SISO που έχουν πολλαπλασιαστικό συντελεστή κρουστικής απόκρισης ίσο με την αντίστοιχη ιδιάζουσα τιμή πολλαπλασιασμένη με την τιμή 1 L. Έτσι για κάθε ανεξάρτητο υπο-κανάλι ισχύει η επαρκής στατιστική της (3.6) για την ανίχνευση του συμβόλου που στάλθηκε μέσα από αυτό). Ας σημειωθεί ότι μπορεί να εφαρμοστεί η παραπάνω τεχνική για μερικά μόνο από τα υπόκανάλια, για παράδειγμα να επιλεχθούν τα L καλύτερα και γίνει μετάδοση μόνο σε αυτά (απορρίπτοντας δηλαδή τα κανάλια με «κακή κατάσταση»). Είναι πολύ εύκολο να δούμε πως μπορούμε να προσαρμόσουμε αυτά που μόλις περιγράφηκαν σε αυτή την περίπτωση. Στο σχήμα 3.3 παρουσιάζεται η τεχνική απλής προσανατολισμένης επικοινωνίας. 41
Τμήμα Μηχανικών Η/Υ και Πληροφορικής. Κινητά Δίκτυα Επικοινωνιών
 Τμήμα Μηχανικών Η/Υ και Πληροφορικής Εργαστήριο Επεξεργασίας Σημάτων και Τηλεπικοινωνιών Κινητά Δίκτυα Επικοινωνιών Μέρος Α: Τηλεπικοινωνιακά Θέματα: Πολλαπλές Κεραίες και Επικοινωνίες Χώρου - Χρόνου Μετάδοση
Τμήμα Μηχανικών Η/Υ και Πληροφορικής Εργαστήριο Επεξεργασίας Σημάτων και Τηλεπικοινωνιών Κινητά Δίκτυα Επικοινωνιών Μέρος Α: Τηλεπικοινωνιακά Θέματα: Πολλαπλές Κεραίες και Επικοινωνίες Χώρου - Χρόνου Μετάδοση
Εξομοίωση Τηλεπικοινωνιακού Συστήματος Βασικής Ζώνης
 Πανεπιστήμιο Πατρών Τμήμα Μηχ. Η/Υ & Πληροφορικής Ακαδημαϊκό Έτος 009-010 Ψ Η Φ Ι Α Κ Ε Σ Τ Η Λ Ε Π Ι Κ Ο Ι Ν Ω Ν Ι ΕΣ η Εργαστηριακή Άσκηση: Εξομοίωση Τηλεπικοινωνιακού Συστήματος Βασικής Ζώνης Στην άσκηση
Πανεπιστήμιο Πατρών Τμήμα Μηχ. Η/Υ & Πληροφορικής Ακαδημαϊκό Έτος 009-010 Ψ Η Φ Ι Α Κ Ε Σ Τ Η Λ Ε Π Ι Κ Ο Ι Ν Ω Ν Ι ΕΣ η Εργαστηριακή Άσκηση: Εξομοίωση Τηλεπικοινωνιακού Συστήματος Βασικής Ζώνης Στην άσκηση
Μελέτη Επίδοσης Συστημάτων Πολλαπλών Εισόδων Πολλαπλών Εξόδων
 Μελέτη Επίδοσης Συστημάτων Πολλαπλών Εισόδων Πολλαπλών Εξόδων Γεώργιος Χ. Αλεξανδρόπουλος Διπλ. Μηχανικός Η/Υ & Πληροφορικής MSc Συστήματα Επεξεργασίας Σημάτων & Εικόνων Εργαστήριο Ασυρμάτων Επικοινωνιών
Μελέτη Επίδοσης Συστημάτων Πολλαπλών Εισόδων Πολλαπλών Εξόδων Γεώργιος Χ. Αλεξανδρόπουλος Διπλ. Μηχανικός Η/Υ & Πληροφορικής MSc Συστήματα Επεξεργασίας Σημάτων & Εικόνων Εργαστήριο Ασυρμάτων Επικοινωνιών
Εργαστήριο 3: Διαλείψεις
 Εργαστήριο 3: Διαλείψεις Διάλειψη (fading) είναι η παραμόρφωση ενός διαμορφωμένου σήματος λόγω της μετάδοσης του σε ασύρματο περιβάλλον. Η προσομοίωση μίας τέτοιας μετάδοσης γίνεται με την μοντελοποίηση
Εργαστήριο 3: Διαλείψεις Διάλειψη (fading) είναι η παραμόρφωση ενός διαμορφωμένου σήματος λόγω της μετάδοσης του σε ασύρματο περιβάλλον. Η προσομοίωση μίας τέτοιας μετάδοσης γίνεται με την μοντελοποίηση
ΣΤΟΧΑΣΤΙΚΑ ΣΗΜΑΤΑ ΚΑΙ ΕΦΑΡΜΟΓΕΣ
 ΣΤΟΧΑΣΤΙΚΑ ΣΗΜΑΤΑ ΚΑΙ ΕΦΑΡΜΟΓΕΣ Ακαδηµαϊκό Έτος 007-008 ιδάσκων: Ν. Παπανδρέου (Π.. 407/80) Πανεπιστήµιο Πατρών Τµήµα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής 1η Εργαστηριακή Άσκηση Αναγνώριση
ΣΤΟΧΑΣΤΙΚΑ ΣΗΜΑΤΑ ΚΑΙ ΕΦΑΡΜΟΓΕΣ Ακαδηµαϊκό Έτος 007-008 ιδάσκων: Ν. Παπανδρέου (Π.. 407/80) Πανεπιστήµιο Πατρών Τµήµα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής 1η Εργαστηριακή Άσκηση Αναγνώριση
Τμήμα Μηχανικών Η/Υ και Πληροφορικής
 Τμήμα Μηχανικών Η/Υ και Πληροφορικής Εργαστήριο Επεξεργασίας Σημάτων και Τηλεπικοινωνιών Ασύρματες και Κινητές Επικοινωνίες Συστήματα πολλαπλών χρηστών και πρόσβαση στο ασύρματο κανάλι Τι θα δούμε στο
Τμήμα Μηχανικών Η/Υ και Πληροφορικής Εργαστήριο Επεξεργασίας Σημάτων και Τηλεπικοινωνιών Ασύρματες και Κινητές Επικοινωνίες Συστήματα πολλαπλών χρηστών και πρόσβαση στο ασύρματο κανάλι Τι θα δούμε στο
Ψηφιακές Τηλεπικοινωνίες. Βέλτιστος Δέκτης
 Ψηφιακές Τηλεπικοινωνίες Βέλτιστος Δέκτης Σύνδεση με τα Προηγούμενα Επειδή το πραγματικό κανάλι είναι αναλογικό, κατά τη διαβίβαση ψηφιακής πληροφορίας, αντιστοιχίζουμε τα σύμβολα σε αναλογικές κυματομορφές
Ψηφιακές Τηλεπικοινωνίες Βέλτιστος Δέκτης Σύνδεση με τα Προηγούμενα Επειδή το πραγματικό κανάλι είναι αναλογικό, κατά τη διαβίβαση ψηφιακής πληροφορίας, αντιστοιχίζουμε τα σύμβολα σε αναλογικές κυματομορφές
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER
 4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
Μετάδοση πληροφορίας - Διαμόρφωση
 Μετάδοση πληροφορίας - Διαμόρφωση MYE006: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Διάρθρωση μαθήματος Μετάδοση Βασικές έννοιες Διαμόρφωση ορισμός είδη
Μετάδοση πληροφορίας - Διαμόρφωση MYE006: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Διάρθρωση μαθήματος Μετάδοση Βασικές έννοιες Διαμόρφωση ορισμός είδη
Μετάδοση πληροφορίας - Διαμόρφωση
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Μετάδοση πληροφορίας - Διαμόρφωση MYE006-ΠΛΕ065: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου Διάρθρωση μαθήματος Βασικές έννοιες μετάδοσης Διαμόρφωση ορισμός
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Μετάδοση πληροφορίας - Διαμόρφωση MYE006-ΠΛΕ065: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου Διάρθρωση μαθήματος Βασικές έννοιες μετάδοσης Διαμόρφωση ορισμός
E[ (x- ) ]= trace[(x-x)(x- ) ]
![E[ (x- ) ]= trace[(x-x)(x- ) ] E[ (x- ) ]= trace[(x-x)(x- ) ]](/thumbs/55/36021260.jpg) 1 ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Σε αυτό το μέρος της πτυχιακής θα ασχοληθούμε λεπτομερώς με το φίλτρο kalman και θα δούμε μια καινούρια έκδοση του φίλτρου πάνω στην εφαρμογή της γραμμικής εκτίμησης διακριτού
1 ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Σε αυτό το μέρος της πτυχιακής θα ασχοληθούμε λεπτομερώς με το φίλτρο kalman και θα δούμε μια καινούρια έκδοση του φίλτρου πάνω στην εφαρμογή της γραμμικής εκτίμησης διακριτού
Mελέτη υλοποίησης τεχνικών κατανεμημένου προσανατολισμού σε πραγματικές συνθήκες
 Mελέτη υλοποίησης τεχνικών κατανεμημένου προσανατολισμού σε πραγματικές συνθήκες Ον/μο: Μπότσης Βασίλης ΑΜ:168 ΣΕΣΕ 2013 Κατανεμημένος προσανατολισμός Πραγματικές συνθήκες Σχήμα δικτύου Σχήμα μετάδοσης
Mελέτη υλοποίησης τεχνικών κατανεμημένου προσανατολισμού σε πραγματικές συνθήκες Ον/μο: Μπότσης Βασίλης ΑΜ:168 ΣΕΣΕ 2013 Κατανεμημένος προσανατολισμός Πραγματικές συνθήκες Σχήμα δικτύου Σχήμα μετάδοσης
Στοχαστικά Σήματα και Τηλεπικοινωνιές
 Στοχαστικά Σήματα και Τηλεπικοινωνιές Ενότητα 7: Βέλτιστο Φίλτρο Wiener και Γραμμικά Περιορισμένο Φίλτρο Ελάχιστης Διασποράς Εφαρμογή στις Έξυπνες Κεραίες Καθηγητής Κώστας Μπερμπερίδης Πολυτεχνική Σχολή
Στοχαστικά Σήματα και Τηλεπικοινωνιές Ενότητα 7: Βέλτιστο Φίλτρο Wiener και Γραμμικά Περιορισμένο Φίλτρο Ελάχιστης Διασποράς Εφαρμογή στις Έξυπνες Κεραίες Καθηγητής Κώστας Μπερμπερίδης Πολυτεχνική Σχολή
Εισαγωγή στις Τηλεπικοινωνίες. Δομή της παρουσίασης
 1 Oct 16 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Διάλεξη 4 η Γεωμετρική Αναπαράσταση
1 Oct 16 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Διάλεξη 4 η Γεωμετρική Αναπαράσταση
EE728 (22Α004) - Προχωρημένα Θέματα Θεωρίας Πληροφορίας 3η σειρά ασκήσεων Διακριτά και Συνεχή Κανάλια. Παράδοση: Έως 22/6/2015
 EE728 (22Α004) - Προχωρημένα Θέματα Θεωρίας Πληροφορίας Φυλλάδιο 13 Δ. Τουμπακάρης 30 Μαΐου 2015 EE728 (22Α004) - Προχωρημένα Θέματα Θεωρίας Πληροφορίας 3η σειρά ασκήσεων Διακριτά και Συνεχή Κανάλια Παράδοση:
EE728 (22Α004) - Προχωρημένα Θέματα Θεωρίας Πληροφορίας Φυλλάδιο 13 Δ. Τουμπακάρης 30 Μαΐου 2015 EE728 (22Α004) - Προχωρημένα Θέματα Θεωρίας Πληροφορίας 3η σειρά ασκήσεων Διακριτά και Συνεχή Κανάλια Παράδοση:
Εργαστήριο Επεξεργασίας Σηµάτων και Τηλεπικοινωνιών Κινητά ίκτυα Επικοινωνιών
 Εργαστήριο Επεξεργασίας Σηµάτων και Τηλεπικοινωνιών Κινητά ίκτυα Επικοινωνιών Εργασία Προσοµοίωσης ενός Τηλεπικοινωνιακού Συστήµατος και Εκτίµηση Απόκρισης Αραιού Καναλιού Εισαγωγή Στην παρούσα εργασία
Εργαστήριο Επεξεργασίας Σηµάτων και Τηλεπικοινωνιών Κινητά ίκτυα Επικοινωνιών Εργασία Προσοµοίωσης ενός Τηλεπικοινωνιακού Συστήµατος και Εκτίµηση Απόκρισης Αραιού Καναλιού Εισαγωγή Στην παρούσα εργασία
x[n] = e u[n 1] 4 x[n] = u[n 1] 4 X(z) = z 1 H(z) = (1 0.5z 1 )(1 + 4z 2 ) z 2 (βʹ) H(z) = H min (z)h lin (z) 4 z 1 1 z 1 (z 1 4 )(z 1) (1)
![x[n] = e u[n 1] 4 x[n] = u[n 1] 4 X(z) = z 1 H(z) = (1 0.5z 1 )(1 + 4z 2 ) z 2 (βʹ) H(z) = H min (z)h lin (z) 4 z 1 1 z 1 (z 1 4 )(z 1) (1) x[n] = e u[n 1] 4 x[n] = u[n 1] 4 X(z) = z 1 H(z) = (1 0.5z 1 )(1 + 4z 2 ) z 2 (βʹ) H(z) = H min (z)h lin (z) 4 z 1 1 z 1 (z 1 4 )(z 1) (1)](/thumbs/61/45634776.jpg) Ασκήσεις με Συστήματα στο Χώρο του Ζ Επιμέλεια: Γιώργος Π. Καφεντζης Δρ. Επιστήμης Η/Υ Πανεπιστημίου Κρήτης Δρ. Επεξεργασίας Σήματος Πανεπιστημίου Rennes 1 7 Νοεμβρίου 015 1. Υπολόγισε τον μετ. Ζ και την
Ασκήσεις με Συστήματα στο Χώρο του Ζ Επιμέλεια: Γιώργος Π. Καφεντζης Δρ. Επιστήμης Η/Υ Πανεπιστημίου Κρήτης Δρ. Επεξεργασίας Σήματος Πανεπιστημίου Rennes 1 7 Νοεμβρίου 015 1. Υπολόγισε τον μετ. Ζ και την
Ακαδηµαϊκό Έτος , Εαρινό Εξάµηνο ιδάσκων Καθ.: Νίκος Τσαπατσούλης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΒΕΣ 6: ΠΡΟΣΑΡΜΟΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΤΙΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ Ακαδηµαϊκό Έτος 26 27, Εαρινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΕΡΩΤΗΣΕΙΣ ΓΙΑ ΕΠΑΝΑΛΗΨΗ Το
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΒΕΣ 6: ΠΡΟΣΑΡΜΟΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΤΙΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ Ακαδηµαϊκό Έτος 26 27, Εαρινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΕΡΩΤΗΣΕΙΣ ΓΙΑ ΕΠΑΝΑΛΗΨΗ Το
Στοχαστικά Σήματα και Τηλεπικοινωνιές
 Στοχαστικά Σήματα και Τηλεπικοινωνιές Ενότητα 2: Ανασκόπηση Στοιχείων Γραμμικής Άλγεβρας Καθηγητής Κώστας Μπερμπερίδης Πολυτεχνική Σχολή Τμήμα Μηχανικών Η/Υ και Πληροφορικής Σκοποί ενότητας Παρουσίαση/υπενθύμιση
Στοχαστικά Σήματα και Τηλεπικοινωνιές Ενότητα 2: Ανασκόπηση Στοιχείων Γραμμικής Άλγεβρας Καθηγητής Κώστας Μπερμπερίδης Πολυτεχνική Σχολή Τμήμα Μηχανικών Η/Υ και Πληροφορικής Σκοποί ενότητας Παρουσίαση/υπενθύμιση
Επεξεργασία Στοχαστικών Σημάτων
 Επεξεργασία Στοχαστικών Σημάτων Ψηφιακή Μετάδοση Αναλογικών Σημάτων Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ψηφιακή Μετάδοση Αναλογικών Σημάτων Τα σύγχρονα συστήματα
Επεξεργασία Στοχαστικών Σημάτων Ψηφιακή Μετάδοση Αναλογικών Σημάτων Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ψηφιακή Μετάδοση Αναλογικών Σημάτων Τα σύγχρονα συστήματα
Επισκόπηση των Στατιστικών Πολυκαναλικών Επικοινωνιών
 Επισκόπηση των Στατιστικών Πολυκαναλικών Επικοινωνιών Φυσικός (Bsc), Ραδιοηλεκτρολόγος (Msc, PhD) Εργαστήριο Κινητών Επικοινωνιών, Ινστιτούτο Πληροφορικής & Τηλεπικοινωνιών, Εθνικό Κέντρο Έρευνας Φυσικών
Επισκόπηση των Στατιστικών Πολυκαναλικών Επικοινωνιών Φυσικός (Bsc), Ραδιοηλεκτρολόγος (Msc, PhD) Εργαστήριο Κινητών Επικοινωνιών, Ινστιτούτο Πληροφορικής & Τηλεπικοινωνιών, Εθνικό Κέντρο Έρευνας Φυσικών
Σήματα και Συστήματα. Διάλεξη 1: Σήματα Συνεχούς Χρόνου. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 1: Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Εισαγωγή στα Σήματα 1. Σκοποί της Θεωρίας Σημάτων 2. Κατηγορίες Σημάτων 3. Χαρακτηριστικές Παράμετροι
Σήματα και Συστήματα Διάλεξη 1: Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Εισαγωγή στα Σήματα 1. Σκοποί της Θεωρίας Σημάτων 2. Κατηγορίες Σημάτων 3. Χαρακτηριστικές Παράμετροι
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧ/ΚΩΝ ΚΑΙ ΜΗΧ. ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΕΠΙΚΟΙΝΩΝΙΩΝ, ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧ/ΚΩΝ ΚΑΙ ΜΗΧ. ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΕΠΙΚΟΙΝΩΝΙΩΝ, ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΔΙΚΤΥΑ ΚΙΝΗΤΩΝ ΚΑΙ ΠΡΟΣΩΠΙΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Ασκήσεις για το ασύρματο
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧ/ΚΩΝ ΚΑΙ ΜΗΧ. ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΕΠΙΚΟΙΝΩΝΙΩΝ, ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΔΙΚΤΥΑ ΚΙΝΗΤΩΝ ΚΑΙ ΠΡΟΣΩΠΙΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ Ασκήσεις για το ασύρματο
ΔΕΚΤΕΣ ΔΙΑΦΟΡΙΚΗΣ ΛΗΨΗΣ
 ΔΕΚΤΕΣ ΔΙΑΦΟΡΙΚΗΣ ΛΗΨΗΣ (Diversity Receivers) Alexandros-Apostolos A. Boulogeorgos e-mail: ampoulog@auth.gr WCS GROUP, EE Dept, AUTH ΑΝΑΓΚΑΙΟΤΗΤΑ ΔΙΑΦΟΡΙΣΜΟΥ Η ισχύς σε κάθε όδευση παρουσιάζει διακυμάνσεις
ΔΕΚΤΕΣ ΔΙΑΦΟΡΙΚΗΣ ΛΗΨΗΣ (Diversity Receivers) Alexandros-Apostolos A. Boulogeorgos e-mail: ampoulog@auth.gr WCS GROUP, EE Dept, AUTH ΑΝΑΓΚΑΙΟΤΗΤΑ ΔΙΑΦΟΡΙΣΜΟΥ Η ισχύς σε κάθε όδευση παρουσιάζει διακυμάνσεις
Στοχαστικά Σήματα και Τηλεπικοινωνιές
 Στοχαστικά Σήματα και Τηλεπικοινωνιές Ενότητα 4: Βέλτιστα Φίλτρα Wiener Καθηγητής Κώστας Μπερμπερίδης Πολυτεχνική Σχολή Τμήμα Μηχανικών Η/Υ και Πληροφορικής Σκοποί ενότητας Παρουσίαση βασικών εννοιών των
Στοχαστικά Σήματα και Τηλεπικοινωνιές Ενότητα 4: Βέλτιστα Φίλτρα Wiener Καθηγητής Κώστας Μπερμπερίδης Πολυτεχνική Σχολή Τμήμα Μηχανικών Η/Υ και Πληροφορικής Σκοποί ενότητας Παρουσίαση βασικών εννοιών των
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 9 : Κανάλι-Σύστημα Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Χωρητικότητα Χ ό καναλιού Το Gaussian κανάλι επικοινωνίας Τα διακριτά
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 9 : Κανάλι-Σύστημα Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Χωρητικότητα Χ ό καναλιού Το Gaussian κανάλι επικοινωνίας Τα διακριτά
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 15 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst15
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 15 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst15
Αναλογικές και Ψηφιακές Επικοινωνίες
 Αναλογικές και Ψηφιακές Επικοινωνίες Ενότητα : Βέλτιστος δέκτης για ψηφιακά διαμορφωμένα σήματα Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Επικοινωνιών Η ΕΝΝΟΙΑ ΤΗΣ ΤΥΧΑΙΑΣ ΜΕΤΑΒΛΗΤΗΣ
Αναλογικές και Ψηφιακές Επικοινωνίες Ενότητα : Βέλτιστος δέκτης για ψηφιακά διαμορφωμένα σήματα Σεραφείμ Καραμπογιάς Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Επικοινωνιών Η ΕΝΝΟΙΑ ΤΗΣ ΤΥΧΑΙΑΣ ΜΕΤΑΒΛΗΤΗΣ
ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ
 1 ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Σε αυτό το μέρος της πτυχιακής θα ασχοληθούμε λεπτομερώς με το φίλτρο kalman και θα δούμε μια καινούρια έκδοση του φίλτρου πάνω στην εφαρμογή της γραμμικής εκτίμησης διακριτού
1 ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Σε αυτό το μέρος της πτυχιακής θα ασχοληθούμε λεπτομερώς με το φίλτρο kalman και θα δούμε μια καινούρια έκδοση του φίλτρου πάνω στην εφαρμογή της γραμμικής εκτίμησης διακριτού
Ιδιάζουσες τιμές πίνακα. y έχουμε αντίστοιχα τις σχέσεις : Αυτές οι παρατηρήσεις συμβάλλουν στην παραγοντοποίηση ενός πίνακα
 Ιδιάζουσες τιμές πίνακα Επειδή οι πίνακες που παρουσιάζονται στις εφαρμογές είναι μη τετραγωνικοί, υπάρχει ανάγκη να βρεθεί μία μέθοδος που να «μελετά» τους μη τετραγωνικούς με «μεθόδους και ποσά» που
Ιδιάζουσες τιμές πίνακα Επειδή οι πίνακες που παρουσιάζονται στις εφαρμογές είναι μη τετραγωνικοί, υπάρχει ανάγκη να βρεθεί μία μέθοδος που να «μελετά» τους μη τετραγωνικούς με «μεθόδους και ποσά» που
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ. Εργαστήριο 8 ο. Αποδιαμόρφωση PAM-PPM με προσαρμοσμένα φίλτρα
 Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Εργαστήριο 8 ο Αποδιαμόρφωση PAM-PPM με προσαρμοσμένα φίλτρα Βασική Θεωρία Σε ένα σύστημα μετάδοσης
Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΨΗΦΙΑΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Εργαστήριο 8 ο Αποδιαμόρφωση PAM-PPM με προσαρμοσμένα φίλτρα Βασική Θεωρία Σε ένα σύστημα μετάδοσης
ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧ/ΚΩΝ & ΜΗΧ/ΚΩΝ Η/Υ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΣΥΝΘΕΣΗ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΔΙΑΤΑΞΕΩΝ Φεβρουάριος 2011
 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧ/ΚΩΝ & ΜΗΧ/ΚΩΝ Η/Υ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΣΥΝΘΕΣΗ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΔΙΑΤΑΞΕΩΝ Φεβρουάριος 0 Θέμα (50): Βιομηχανική μονάδα διαθέτει δύο κτίρια (Α και Β) σε απόσταση 5 Km και σε οπτική
ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧ/ΚΩΝ & ΜΗΧ/ΚΩΝ Η/Υ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΣΥΝΘΕΣΗ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΔΙΑΤΑΞΕΩΝ Φεβρουάριος 0 Θέμα (50): Βιομηχανική μονάδα διαθέτει δύο κτίρια (Α και Β) σε απόσταση 5 Km και σε οπτική
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Εισαγωγή στα Συστήματα Τηλεπικοινωνιών Συστήματα Παλμοκωδικής Διαμόρφωσης
 Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Εισαγωγή στα Συστήματα Τηλεπικοινωνιών Συστήματα Παλμοκωδικής Διαμόρφωσης Καθηγητής Ι. Τίγκελης itigelis@phys.uoa.gr ΚΒΑΝΤΙΣΗ Διαδικασία με την
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Εισαγωγή στα Συστήματα Τηλεπικοινωνιών Συστήματα Παλμοκωδικής Διαμόρφωσης Καθηγητής Ι. Τίγκελης itigelis@phys.uoa.gr ΚΒΑΝΤΙΣΗ Διαδικασία με την
Μελέτη και Προσομοίωση n πομπού για ασύρματη πρόσβαση ΦΟΙΤΗΤΗΣ: ΛΑΖΑΡΙΔΗΣ ΚΩΝΣΤΑΝΤΙΝΟΣ ΕΠΙΒΛΕΠΩΝ ΚΑΘΗΓΗΤΗΣ: ΕΥΣΤΑΘΙΟΥ ΔΗΜΗΤΡΙΟΣ
 Μελέτη και Προσομοίωση 802.11n πομπού για ασύρματη πρόσβαση ΦΟΙΤΗΤΗΣ: ΛΑΖΑΡΙΔΗΣ ΚΩΝΣΤΑΝΤΙΝΟΣ ΕΠΙΒΛΕΠΩΝ ΚΑΘΗΓΗΤΗΣ: ΕΥΣΤΑΘΙΟΥ ΔΗΜΗΤΡΙΟΣ A) Προσομοίωση του φάσματος του καναλιού του προτύπου για να φανεί
Μελέτη και Προσομοίωση 802.11n πομπού για ασύρματη πρόσβαση ΦΟΙΤΗΤΗΣ: ΛΑΖΑΡΙΔΗΣ ΚΩΝΣΤΑΝΤΙΝΟΣ ΕΠΙΒΛΕΠΩΝ ΚΑΘΗΓΗΤΗΣ: ΕΥΣΤΑΘΙΟΥ ΔΗΜΗΤΡΙΟΣ A) Προσομοίωση του φάσματος του καναλιού του προτύπου για να φανεί
Κινητά Δίκτυα Επικοινωνιών. Συμπληρωματικό υλικό. Προσαρμοστική Ισοστάθμιση Καναλιού
 Κινητά Δίκτυα Επικοινωνιών Συμπληρωματικό υλικό Προσαρμοστική Ισοστάθμιση Καναλιού Προσαρμοστικοί Ισοσταθμιστές Για να υπολογίσουμε τους συντελεστές του ισοσταθμιστή MMSE, απαιτείται να λύσουμε ένα γραμμικό
Κινητά Δίκτυα Επικοινωνιών Συμπληρωματικό υλικό Προσαρμοστική Ισοστάθμιση Καναλιού Προσαρμοστικοί Ισοσταθμιστές Για να υπολογίσουμε τους συντελεστές του ισοσταθμιστή MMSE, απαιτείται να λύσουμε ένα γραμμικό
Τηλεπικοινωνιακά Συστήματα Ι
 Τηλεπικοινωνιακά Συστήματα Ι Διάλεξη 3: Ο Θόρυβος στα Τηλεπικοινωνιακά Συστήματα Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Εισαγωγή Τύποι Θορύβου Θερμικός θόρυβος Θόρυβος βολής Θόρυβος περιβάλλοντος
Τηλεπικοινωνιακά Συστήματα Ι Διάλεξη 3: Ο Θόρυβος στα Τηλεπικοινωνιακά Συστήματα Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Εισαγωγή Τύποι Θορύβου Θερμικός θόρυβος Θόρυβος βολής Θόρυβος περιβάλλοντος
Δίκτυα Κινητών και Προσωπικών Επικοινωνιών
 Δίκτυα Κινητών και Προσωπικών Επικοινωνιών Ασύρματο Περιβάλλον στις Κινητές Επικοινωνίες Άγγελος Ρούσκας Τμήμα Ψηφιακών Συστημάτων Πανεπιστήμιο Πειραιώς Ραδιοδίαυλοι Απαραίτητη η γνώση των χαρακτηριστικών
Δίκτυα Κινητών και Προσωπικών Επικοινωνιών Ασύρματο Περιβάλλον στις Κινητές Επικοινωνίες Άγγελος Ρούσκας Τμήμα Ψηφιακών Συστημάτων Πανεπιστήμιο Πειραιώς Ραδιοδίαυλοι Απαραίτητη η γνώση των χαρακτηριστικών
Εισαγωγή. Προχωρημένα Θέματα Τηλεπικοινωνιών. Ανάκτηση Χρονισμού. Τρόποι Συγχρονισμού Συμβόλων. Συγχρονισμός Συμβόλων. t mt
 Προχωρημένα Θέματα Τηλεπικοινωνιών Συγχρονισμός Συμβόλων Εισαγωγή Σε ένα ψηφιακό τηλεπικοινωνιακό σύστημα, η έξοδος του φίλτρου λήψης είναι μια κυματομορφή συνεχούς χρόνου y( an x( t n ) n( n x( είναι
Προχωρημένα Θέματα Τηλεπικοινωνιών Συγχρονισμός Συμβόλων Εισαγωγή Σε ένα ψηφιακό τηλεπικοινωνιακό σύστημα, η έξοδος του φίλτρου λήψης είναι μια κυματομορφή συνεχούς χρόνου y( an x( t n ) n( n x( είναι
1 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ. / 2. Οι όροι Eb. και Ec
 Τµήµα Μηχανικών Υπολογιστών, Τηλεπικοινωνιών και ικτύων ΗΥ 44: Ασύρµατες Επικοινωνίες Εαρινό Εξάµηνο -3 ιδάσκων: Λέανδρος Τασιούλας η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ. Θεωρήστε ένα κυψελωτό σύστηµα, στο οποίο ισχύει το
Τµήµα Μηχανικών Υπολογιστών, Τηλεπικοινωνιών και ικτύων ΗΥ 44: Ασύρµατες Επικοινωνίες Εαρινό Εξάµηνο -3 ιδάσκων: Λέανδρος Τασιούλας η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ. Θεωρήστε ένα κυψελωτό σύστηµα, στο οποίο ισχύει το
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ. Ασύρματη Διάδοση ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ. Ευάγγελος Παπαπέτρου
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Ασύρματη Διάδοση ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου Διάρθρωση μαθήματος Ασύρματη διάδοση Εισαγωγή Κεραίες διάγραμμα ακτινοβολίας, κέρδος, κατευθυντικότητα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Ασύρματη Διάδοση ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου Διάρθρωση μαθήματος Ασύρματη διάδοση Εισαγωγή Κεραίες διάγραμμα ακτινοβολίας, κέρδος, κατευθυντικότητα
Εισαγωγή στις Τηλεπικοινωνίες. Δομή της παρουσίασης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Διάλεξη 3 η Τα Συστήματα στις Τηλεπικοινωνίες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Διάλεξη 3 η Τα Συστήματα στις Τηλεπικοινωνίες
Δίκτυα Κινητών και Προσωπικών Επικοινωνιών
 Δίκτυα Κινητών και Προσωπικών Επικοινωνιών Κυψελωτά Συστήματα και Παρεμβολές Άγγελος Ρούσκας Τμήμα Ψηφιακών Συστημάτων Πανεπιστήμιο Πειραιώς Περιβάλλον με θόρυβο και παρεμβολές Περιβάλλον δύο πομποδεκτών
Δίκτυα Κινητών και Προσωπικών Επικοινωνιών Κυψελωτά Συστήματα και Παρεμβολές Άγγελος Ρούσκας Τμήμα Ψηφιακών Συστημάτων Πανεπιστήμιο Πειραιώς Περιβάλλον με θόρυβο και παρεμβολές Περιβάλλον δύο πομποδεκτών
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - 02/07/08) ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ
 Ονοματεπώνυμο:......... Α.Μ....... Ετος... ΑΙΘΟΥΣΑ:....... I. (περί τις 55μ. = ++5++. Σωστό ή Λάθος: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - //8 ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ (αʹ Αν AB = BA όπου A, B τετραγωνικά και
Ονοματεπώνυμο:......... Α.Μ....... Ετος... ΑΙΘΟΥΣΑ:....... I. (περί τις 55μ. = ++5++. Σωστό ή Λάθος: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - //8 ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ (αʹ Αν AB = BA όπου A, B τετραγωνικά και
I. ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. math-gr
 I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
Πανεπιστήμιο Πατρών Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών. Διάλεξη 4
 Πανεπιστήμιο Πατρών Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Τομέας Συστημάτων και Αυτομάτου Ελέγχου ΠΡΟΣΑΡΜΟΣΤΙΚΟΣ ΕΛΕΓΧΟΣ Διάλεξη 4 Πάτρα 2008 Ντετερμινιστικά Moving Average Μοντέλα Ισχύει:
Πανεπιστήμιο Πατρών Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Τομέας Συστημάτων και Αυτομάτου Ελέγχου ΠΡΟΣΑΡΜΟΣΤΙΚΟΣ ΕΛΕΓΧΟΣ Διάλεξη 4 Πάτρα 2008 Ντετερμινιστικά Moving Average Μοντέλα Ισχύει:
ΤΕΤΥ Εφαρμοσμένα Μαθηματικά 1. Τελεστές και πίνακες. 1. Τελεστές και πίνακες Γενικά. Τι είναι συνάρτηση? Απεικόνιση ενός αριθμού σε έναν άλλο.
 ΤΕΤΥ Εφαρμοσμένα Μαθηματικά 1 Τελεστές και πίνακες 1. Τελεστές και πίνακες Γενικά Τι είναι συνάρτηση? Απεικόνιση ενός αριθμού σε έναν άλλο. Ανάλογα, τελεστής είναι η απεικόνιση ενός διανύσματος σε ένα
ΤΕΤΥ Εφαρμοσμένα Μαθηματικά 1 Τελεστές και πίνακες 1. Τελεστές και πίνακες Γενικά Τι είναι συνάρτηση? Απεικόνιση ενός αριθμού σε έναν άλλο. Ανάλογα, τελεστής είναι η απεικόνιση ενός διανύσματος σε ένα
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Παραγώγιση Εισαγωγή Ορισμός 7. Αν y f x είναι μια συνάρτηση ορισμένη σε ένα διάστημα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Παραγώγιση Εισαγωγή Ορισμός 7. Αν y f x είναι μια συνάρτηση ορισμένη σε ένα διάστημα
Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 5 : Θόρυβος Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Είδη θορύβου Περιγραφή θορύβου Θεώρημα Shannon Hartley Απόδοση ισχύος και εύρους
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 5 : Θόρυβος Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα Ομιλίας Είδη θορύβου Περιγραφή θορύβου Θεώρημα Shannon Hartley Απόδοση ισχύος και εύρους
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 5 ο : Προσαρμοσμένα Φίλτρα Βασική
Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 5 ο : Προσαρμοσμένα Φίλτρα Βασική
Αφαίρεση του Φαινομένου του Μικροφωνισμού σε Ακουστικά Βαρηκοΐας
 Αφαίρεση του Φαινομένου του Μικροφωνισμού σε Ακουστικά Βαρηκοΐας Νιαβής Παναγιώτης Επιβλέπων: Καθ. Γ. Μουστακίδης Περιεχόμενα Εισαγωγή Μικροφωνισμός σε ακουστικά βαρηκοΐας Προσαρμοστική αναγνώριση συστήματος
Αφαίρεση του Φαινομένου του Μικροφωνισμού σε Ακουστικά Βαρηκοΐας Νιαβής Παναγιώτης Επιβλέπων: Καθ. Γ. Μουστακίδης Περιεχόμενα Εισαγωγή Μικροφωνισμός σε ακουστικά βαρηκοΐας Προσαρμοστική αναγνώριση συστήματος
Χρονικές σειρές 2 Ο μάθημα: Εισαγωγή στις χρονοσειρές
 Χρονικές σειρές 2 Ο μάθημα: Εισαγωγή στις χρονοσειρές Εαρινό εξάμηνο 2018-2019 μήμα Μαθηματικών ΑΠΘ Διδάσκουσα: Αγγελική Παπάνα Μεταδιδακτορική Ερευνήτρια Πολυτεχνική σχολή, Α.Π.Θ. & Οικονομικό μήμα, Πανεπιστήμιο
Χρονικές σειρές 2 Ο μάθημα: Εισαγωγή στις χρονοσειρές Εαρινό εξάμηνο 2018-2019 μήμα Μαθηματικών ΑΠΘ Διδάσκουσα: Αγγελική Παπάνα Μεταδιδακτορική Ερευνήτρια Πολυτεχνική σχολή, Α.Π.Θ. & Οικονομικό μήμα, Πανεπιστήμιο
Κωδικοποίηση Χώρου-Χρόνου. Χρόνου
 Κωδικοποίηση Χώρου-Χρόνου Χρόνου Μέρος Ι: Σχήμα Alamouti Ομάδα Ασύρματων Τηλεπικοινωνιακών Συστημάτων Τμήμα Ηλεκτρολόγων Μηχανικών & Μ/Υ Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Γιώργος Καραγιαννίδης Βασίλειος
Κωδικοποίηση Χώρου-Χρόνου Χρόνου Μέρος Ι: Σχήμα Alamouti Ομάδα Ασύρματων Τηλεπικοινωνιακών Συστημάτων Τμήμα Ηλεκτρολόγων Μηχανικών & Μ/Υ Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Γιώργος Καραγιαννίδης Βασίλειος
Στοχαστικές Μέθοδοι στους Υδατικούς Πόρους Φασματική ανάλυση χρονοσειρών
 Στοχαστικές Μέθοδοι στους Υδατικούς Πόρους Φασματική ανάλυση χρονοσειρών Δημήτρης Κουτσογιάννης Τομέας Υδατικών Πόρων και Περιβάλλοντος, Σχολή Πολιτικών Μηχανικών, Εθνικό Μετσόβιο Πολυτεχνείο Αθήνα Επανέκδοση
Στοχαστικές Μέθοδοι στους Υδατικούς Πόρους Φασματική ανάλυση χρονοσειρών Δημήτρης Κουτσογιάννης Τομέας Υδατικών Πόρων και Περιβάλλοντος, Σχολή Πολιτικών Μηχανικών, Εθνικό Μετσόβιο Πολυτεχνείο Αθήνα Επανέκδοση
Τηλεπικοινωνιακά Συστήματα ΙΙ
 Τηλεπικοινωνιακά Συστήματα ΙΙ Διάλεξη 1: Χωρητικότητα Καναλιών Το θεώρημα Shannon - Hartley Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Δυαδική σηματοδοσία 2. Μορφές δυαδικής σηματοδοσίας 3.
Τηλεπικοινωνιακά Συστήματα ΙΙ Διάλεξη 1: Χωρητικότητα Καναλιών Το θεώρημα Shannon - Hartley Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα 1. Δυαδική σηματοδοσία 2. Μορφές δυαδικής σηματοδοσίας 3.
Στα πλαίσια αυτής της άσκησης θα υλοποιηθούν στην αναπτυξιακή κάρτα TMS320C6711. Iσοστάθμιση τηλεπικοινωνιακού καναλιού.
 Ε Ρ Γ Α Σ Τ Η Ρ Ι Α Κ Η Α Σ Κ Η Σ Η 1. Εισαγωγή Υλοποίηση Προσαρμοστικών Φίλτρων Στα πλαίσια αυτής της άσκησης θα υλοποιηθούν στην αναπτυξιακή κάρτα TMS30C6711 DSK προσαρμοστικά φίλτρα FIR που βασίζονται
Ε Ρ Γ Α Σ Τ Η Ρ Ι Α Κ Η Α Σ Κ Η Σ Η 1. Εισαγωγή Υλοποίηση Προσαρμοστικών Φίλτρων Στα πλαίσια αυτής της άσκησης θα υλοποιηθούν στην αναπτυξιακή κάρτα TMS30C6711 DSK προσαρμοστικά φίλτρα FIR που βασίζονται
Δέκτες ΑΜ ΘΟΡΥΒΟΣ ΣΕ ΔΙΑΜΟΡΦΩΣΗ CW
 ΘΟΡΥΒΟΣ ΣΕ ΔΙΑΜΟΡΦΩΣΗ Στα συστήματα διαμόρφωσης (otiuou-ve) το κριτήριο της συμπεριφοράς τους ως προς το θόρυβο, είναι ο λόγος σήματος προς θόρυβο στην έξοδο (output igl-tooie rtio). λόγος σήματος προς
ΘΟΡΥΒΟΣ ΣΕ ΔΙΑΜΟΡΦΩΣΗ Στα συστήματα διαμόρφωσης (otiuou-ve) το κριτήριο της συμπεριφοράς τους ως προς το θόρυβο, είναι ο λόγος σήματος προς θόρυβο στην έξοδο (output igl-tooie rtio). λόγος σήματος προς
Μοντέλο συστήματος αποδιαμόρφωσης παρουσία θορύβου
 Μοντέλο συστήματος αποδιαμόρφωσης παρουσία θορύβου Επίδοση παρουσία θορύβου Η ανάλυση της επίδοσης των συστημάτων διαμόρφωσης παρουσία θορύβου είναι εξαιρετικά σημαντική για τη σχεδίαση των διαφόρων επικοινωνιακών
Μοντέλο συστήματος αποδιαμόρφωσης παρουσία θορύβου Επίδοση παρουσία θορύβου Η ανάλυση της επίδοσης των συστημάτων διαμόρφωσης παρουσία θορύβου είναι εξαιρετικά σημαντική για τη σχεδίαση των διαφόρων επικοινωνιακών
Κινητές επικοινωνίες. Κεφάλαιο 6 Τεχνικές πoλυπλεξίας - CDMA
 Κινητές επικοινωνίες Κεφάλαιο 6 Τεχνικές πoλυπλεξίας - CDMA 1 Πολυπλεξία Η πολυπλεξία επιτρέπει την παράλληλη μετάδοση δεδομένων από διαφορετικές πηγές χωρίς αλληλοπαρεμβολές. Τρία βασικά είδη TDM/TDMA
Κινητές επικοινωνίες Κεφάλαιο 6 Τεχνικές πoλυπλεξίας - CDMA 1 Πολυπλεξία Η πολυπλεξία επιτρέπει την παράλληλη μετάδοση δεδομένων από διαφορετικές πηγές χωρίς αλληλοπαρεμβολές. Τρία βασικά είδη TDM/TDMA
Στοχαστικές Ανελίξεις (2) Αγγελική Αλεξίου
 Στοχαστικές Ανελίξεις (2) Αγγελική Αλεξίου alexiou@unipi.gr 1 Στοχαστικές Διαδικασίες 2 Στοχαστική Διαδικασία Στοχαστικές Ανελίξεις Α. Αλεξίου 3 Στοχαστική Διαδικασία ως συλλογή από συναρτήσεις χρόνου
Στοχαστικές Ανελίξεις (2) Αγγελική Αλεξίου alexiou@unipi.gr 1 Στοχαστικές Διαδικασίες 2 Στοχαστική Διαδικασία Στοχαστικές Ανελίξεις Α. Αλεξίου 3 Στοχαστική Διαδικασία ως συλλογή από συναρτήσεις χρόνου
Εισαγωγή στις Τηλεπικοινωνίες. Δομή της παρουσίασης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Εφαρμογές της Ανάλυσης Fourier Αθανάσιος
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Εφαρμογές της Ανάλυσης Fourier Αθανάσιος
Τμήμα Μηχανικών Η/Υ και Πληροφορικής
 Τμήμα Μηχανικών Η/Υ και Πληροφορικής Εργαστήριο Επεξεργασίας Σημάτων και Τηλεπικοινωνιών Κινητά Δίκτυα Επικοινωνιών Μέρος Α: Τηλεπικοινωνιακά Θέματα: Τεχνικές Ισοστάθμισης Διαύλου Βασικές αρχές Ισοστάθμισης
Τμήμα Μηχανικών Η/Υ και Πληροφορικής Εργαστήριο Επεξεργασίας Σημάτων και Τηλεπικοινωνιών Κινητά Δίκτυα Επικοινωνιών Μέρος Α: Τηλεπικοινωνιακά Θέματα: Τεχνικές Ισοστάθμισης Διαύλου Βασικές αρχές Ισοστάθμισης
E [ -x ^2 z] = E[x z]
![E [ -x ^2 z] = E[x z] E [ -x ^2 z] = E[x z]](/thumbs/69/60621176.jpg) 1 1.ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Σε αυτήν την διάλεξη θα πάμε στο φίλτρο με περισσότερες λεπτομέρειες, και θα παράσχουμε μια νέα παραγωγή για το φίλτρο Kalman, αυτή τη φορά βασισμένο στην ιδέα της γραμμικής
1 1.ΦΙΛΤΡΟ KALMAN ΔΙΑΚΡΙΤΟΥ ΧΡΟΝΟΥ Σε αυτήν την διάλεξη θα πάμε στο φίλτρο με περισσότερες λεπτομέρειες, και θα παράσχουμε μια νέα παραγωγή για το φίλτρο Kalman, αυτή τη φορά βασισμένο στην ιδέα της γραμμικής
Η μονάδα db χρησιμοποιείται για να εκφράσει λόγους (κλάσματα) ομοειδών μεγεθών, αντιστοιχεί δηλαδή σε καθαρούς αριθμούς.
 0. ΥΠΟΛΟΓΙΣΜΟΣ ΣΤΑΘΜΗΣ ΣΗΜΑΤΟΣ 0.. Γενικά Στα τηλεπικοινωνιακά συστήματα, η μέτρηση στάθμης σήματος περιλαμβάνει, ουσιαστικά, τη μέτρηση της ισχύος ή της τάσης (ρεύματος) ενός σήματος σε διάφορα «κρίσιμα»
0. ΥΠΟΛΟΓΙΣΜΟΣ ΣΤΑΘΜΗΣ ΣΗΜΑΤΟΣ 0.. Γενικά Στα τηλεπικοινωνιακά συστήματα, η μέτρηση στάθμης σήματος περιλαμβάνει, ουσιαστικά, τη μέτρηση της ισχύος ή της τάσης (ρεύματος) ενός σήματος σε διάφορα «κρίσιμα»
Συμπίεση Δεδομένων
 Συμπίεση Δεδομένων 2014-2015 Κβάντιση Δρ. Ν. Π. Σγούρος 2 Αναλογικά Ψηφιακά Σήματα Αναλογικό Σήμα x t, t [t min, t max ], x [x min, x max ] Δειγματοληψία t n, x t x n, n = 1,, N Κβάντιση x n x(n) 3 Αλφάβητο
Συμπίεση Δεδομένων 2014-2015 Κβάντιση Δρ. Ν. Π. Σγούρος 2 Αναλογικά Ψηφιακά Σήματα Αναλογικό Σήμα x t, t [t min, t max ], x [x min, x max ] Δειγματοληψία t n, x t x n, n = 1,, N Κβάντιση x n x(n) 3 Αλφάβητο
ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 73
 ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 73 ΚΕΦΑΛΑΙΟ 4 ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 4.. Εισαγωγή Στο παρόν κεφάλαιο θα μελετηθούν οι ελεύθερες ταλαντώσεις συστημάτων που περιγράφονται
ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 73 ΚΕΦΑΛΑΙΟ 4 ΕΛΕΥΘΕΡΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 4.. Εισαγωγή Στο παρόν κεφάλαιο θα μελετηθούν οι ελεύθερες ταλαντώσεις συστημάτων που περιγράφονται
Εισαγωγή στα Προσαρµοστικά Συστήµατα
 ΒΕΣ 06 Προσαρµοστικά Συστήµατα στις Τηλεπικοινωνίες Εισαγωγή στα Προσαρµοστικά Συστήµατα Νικόλας Τσαπατσούλης Επίκουρος Καθηγητής Π..407/80 Τµήµα Επιστήµη και Τεχνολογίας Τηλεπικοινωνιών Πανεπιστήµιο Πελοποννήσου
ΒΕΣ 06 Προσαρµοστικά Συστήµατα στις Τηλεπικοινωνίες Εισαγωγή στα Προσαρµοστικά Συστήµατα Νικόλας Τσαπατσούλης Επίκουρος Καθηγητής Π..407/80 Τµήµα Επιστήµη και Τεχνολογίας Τηλεπικοινωνιών Πανεπιστήµιο Πελοποννήσου
ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ
 Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 8 ο : Προσαρμοσμένα Φίλτρα Βασική
Σχολή Θετικών Επιστημών Τεχνολογίας Τηλεπικοινωνιών Τμήμα Επιστήμης και Τεχνολογίας Τηλεπικοινωνιών ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΟΓΙΚΩΝ & ΨΗΦΙΑΚΩΝ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΠΙΚΟΙΝΩΝΙΕΣ ΙI Εργαστήριο 8 ο : Προσαρμοσμένα Φίλτρα Βασική
Σήματα και Συστήματα. Διάλεξη 2: Στοιχειώδη Σήματα Συνεχούς Χρόνου. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 2: Στοιχειώδη Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Στοιχειώδη Σήματα Συνεχούς Χρόνου 1. Μοναδιαία Βηματική Συνάρτηση 2. Κρουστική Συνάρτηση ή
Σήματα και Συστήματα Διάλεξη 2: Στοιχειώδη Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Στοιχειώδη Σήματα Συνεχούς Χρόνου 1. Μοναδιαία Βηματική Συνάρτηση 2. Κρουστική Συνάρτηση ή
Antenna tuners: Πόσο οφελούν;
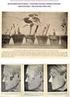 Antenna tuners: Πόσο οφελούν; Σε πείσμα όσων πιστεύουν ότι δεν πρέπει να ασχολούμαστε με «ιδανικά κυκλώματα» αφού δεν είναι δυνατό να πραγματοποιηθούν, η γνώμη μου είναι πως είναι καλό να ξεκινήσουμε με
Antenna tuners: Πόσο οφελούν; Σε πείσμα όσων πιστεύουν ότι δεν πρέπει να ασχολούμαστε με «ιδανικά κυκλώματα» αφού δεν είναι δυνατό να πραγματοποιηθούν, η γνώμη μου είναι πως είναι καλό να ξεκινήσουμε με
ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ. Περιγράψουμε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήματος.
 3. ΚΕΦΑΛΑΙΟ ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ OURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ Περιγράψουμε τον τρόπο ανάπτυξης σε σειρά ourir ενός περιοδικού αναλογικού σήματος. Ορίσουμε το μετασχηματισμό ourir ενός μη περιοδικού
3. ΚΕΦΑΛΑΙΟ ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ OURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ Περιγράψουμε τον τρόπο ανάπτυξης σε σειρά ourir ενός περιοδικού αναλογικού σήματος. Ορίσουμε το μετασχηματισμό ourir ενός μη περιοδικού
Διαμόρφωση μιας Φέρουσας. Προχωρημένα Θέματα Τηλεπικοινωνιών. Διαίρεση εύρους ζώνης καναλιού. Διαμόρφωση Πολλών Φερουσών OFDM
 Διαμόρφωση μιας Φέρουσας Προχωρημένα Θέματα Τηλεπικοινωνιών Διαμόρφωση Πολλαπλών Φερουσών και OFDM (Orthogonal Frquncy Division Multiplxing) Είδαμε ότι τα πραγματικά (μη-ιδανικά) κανάλια εισάγουν διασυμβολική
Διαμόρφωση μιας Φέρουσας Προχωρημένα Θέματα Τηλεπικοινωνιών Διαμόρφωση Πολλαπλών Φερουσών και OFDM (Orthogonal Frquncy Division Multiplxing) Είδαμε ότι τα πραγματικά (μη-ιδανικά) κανάλια εισάγουν διασυμβολική
Εργαστήριο 4: Κυψελωτά Δίκτυα Κινητών Επικοινωνιών
 Εργαστήριο 4: Κυψελωτά Δίκτυα Κινητών Επικοινωνιών Τα κυψελωτά συστήματα εξασφαλίζουν ασύρματη κάλυψη σε μια γεωγραφική περιοχή η οποία διαιρείται σε τμήματα τα οποία είναι γνωστά ως κυψέλες (Εικόνα 1).
Εργαστήριο 4: Κυψελωτά Δίκτυα Κινητών Επικοινωνιών Τα κυψελωτά συστήματα εξασφαλίζουν ασύρματη κάλυψη σε μια γεωγραφική περιοχή η οποία διαιρείται σε τμήματα τα οποία είναι γνωστά ως κυψέλες (Εικόνα 1).
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Συστήματα Επικοινωνιών
 Συστήματα Επικοινωνιών Ενότητα 11: Ψηφιακή Διαμόρφωση Μέρος Α Μιχαήλ Λογοθέτης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Περιγραφή διαμόρφωσης παλμών κατά
Συστήματα Επικοινωνιών Ενότητα 11: Ψηφιακή Διαμόρφωση Μέρος Α Μιχαήλ Λογοθέτης Πολυτεχνική Σχολή Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Σκοποί ενότητας Περιγραφή διαμόρφωσης παλμών κατά
Μάθηµα 12 ο : Πολλαπλή πρόσβαση µε διαίρεση κώδικα (CDMA, code division multiple access)
 Μάθηµα 2 ο : Πολλαπλή πρόσβαση µε διαίρεση κώδικα (CDMA, code division multiple access) Στόχοι: Στο τέλος αυτού του µαθήµατος ο σπουδαστής θα γνωρίζει: Τa λειτουργικά χαρακτηριστικά της τεχνικής πολλαπλής
Μάθηµα 2 ο : Πολλαπλή πρόσβαση µε διαίρεση κώδικα (CDMA, code division multiple access) Στόχοι: Στο τέλος αυτού του µαθήµατος ο σπουδαστής θα γνωρίζει: Τa λειτουργικά χαρακτηριστικά της τεχνικής πολλαπλής
Σπιν 1 2. Γενικά. Ŝ και S ˆz γράφονται. ιδιοκαταστάσεις αποτελούν ορθοκανονική βάση στον χώρο των καταστάσεων του σπιν 1 2.
 Σπιν Γενικά Θα χρησιμοποιήσουμε τις γενικές σχέσεις που αποδείξαμε στην ανάρτηση «Εύρεση των ιδιοτιμών της στροφορμής», που, όπως είδαμε, ισχύουν για κάθε γενική στροφορμή ˆ J με συνιστώσες Jˆ, Jˆ, J ˆ,
Σπιν Γενικά Θα χρησιμοποιήσουμε τις γενικές σχέσεις που αποδείξαμε στην ανάρτηση «Εύρεση των ιδιοτιμών της στροφορμής», που, όπως είδαμε, ισχύουν για κάθε γενική στροφορμή ˆ J με συνιστώσες Jˆ, Jˆ, J ˆ,
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ. Κεφάλαιο 4 : Σήματα Χρήστος Ξενάκης. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 4 : Σήματα Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα ομιλίας Είδη /Κατηγορίες Σημάτων Στοιχειώδη Σήματα Χαρακτηριστικές Τιμές Σημάτων Τεχνικές
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 4 : Σήματα Χρήστος Ξενάκης Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα ομιλίας Είδη /Κατηγορίες Σημάτων Στοιχειώδη Σήματα Χαρακτηριστικές Τιμές Σημάτων Τεχνικές
Συνέλιξη Κρουστική απόκριση
 Συνέλιξη Κρουστική απόκριση Το εργαστήριο αυτό ασχολείται με τα «διασημότερα συστήματα στην επεξεργασία σήματος. Αυτά δεν είναι παρά τα γραμμικά χρονικά αμετάβλητα (ΓΧΑ) συστήματα. Ένα τέτοιο σύστημα μπορεί
Συνέλιξη Κρουστική απόκριση Το εργαστήριο αυτό ασχολείται με τα «διασημότερα συστήματα στην επεξεργασία σήματος. Αυτά δεν είναι παρά τα γραμμικά χρονικά αμετάβλητα (ΓΧΑ) συστήματα. Ένα τέτοιο σύστημα μπορεί
21 a 22 a 2n. a m1 a m2 a mn
 Παράρτημα Α Βασική γραμμική άλγεβρα Στην ενότητα αυτή θα παρουσιαστούν με συνοπτικό τρόπο βασικές έννοιες της γραμμικής άλγεβρας. Ο στόχος της ενότητας είναι να αποτελέσει ένα άμεσο σημείο αναφοράς και
Παράρτημα Α Βασική γραμμική άλγεβρα Στην ενότητα αυτή θα παρουσιαστούν με συνοπτικό τρόπο βασικές έννοιες της γραμμικής άλγεβρας. Ο στόχος της ενότητας είναι να αποτελέσει ένα άμεσο σημείο αναφοράς και
Συστήματα Επικοινωνιών
 Συστήματα Επικοινωνιών Ενότητα 5: Μαθιόπουλος Παναγιώτης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Περιγραφή ενότητας Πλεονεκτήματα-Μειονεκτήματα ψηφιακών επικοινωνιών, Κριτήρια Αξιολόγησης
Συστήματα Επικοινωνιών Ενότητα 5: Μαθιόπουλος Παναγιώτης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Περιγραφή ενότητας Πλεονεκτήματα-Μειονεκτήματα ψηφιακών επικοινωνιών, Κριτήρια Αξιολόγησης
Φίλτρα Kalman. Αναλυτικές μέθοδοι στη Γεωπληροφορική. ιατύπωση του βασικού προβλήματος. προβλήματος. μοντέλο. Πρωτεύων μοντέλο
 Φίλτρα Kalman Εξαγωγή των εξισώσεων τους με βάση το κριτήριο ελαχιστοποίησης της Μεθόδου των Ελαχίστων Τετραγώνων. Αναλυτικές Μέθοδοι στη Γεωπληροφορική Μεταπτυχιακό Πρόγραμμα ΓΕΩΠΛΗΡΟΦΟΡΙΚΗ ιατύπωση του
Φίλτρα Kalman Εξαγωγή των εξισώσεων τους με βάση το κριτήριο ελαχιστοποίησης της Μεθόδου των Ελαχίστων Τετραγώνων. Αναλυτικές Μέθοδοι στη Γεωπληροφορική Μεταπτυχιακό Πρόγραμμα ΓΕΩΠΛΗΡΟΦΟΡΙΚΗ ιατύπωση του
ΕΛΕΓΧΟΣ ΠΑΡΑΓΩΓΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΛΕΓΧΟΣ ΠΑΡΑΓΩΓΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Ενότητα: Αναγνώριση Διεργασίας - Προσαρμοστικός Έλεγχος (Process Identification) Αλαφοδήμος Κωνσταντίνος
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΛΕΓΧΟΣ ΠΑΡΑΓΩΓΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Ενότητα: Αναγνώριση Διεργασίας - Προσαρμοστικός Έλεγχος (Process Identification) Αλαφοδήμος Κωνσταντίνος
Στατιστική είναι το σύνολο των μεθόδων και θεωριών που εφαρμόζονται σε αριθμητικά δεδομένα προκειμένου να ληφθεί κάποια απόφαση σε συνθήκες
 Ορισμός Στατιστική είναι το σύνολο των μεθόδων και θεωριών που εφαρμόζονται σε αριθμητικά δεδομένα προκειμένου να ληφθεί κάποια απόφαση σε συνθήκες αβεβαιότητας. Βασικές έννοιες Η μελέτη ενός πληθυσμού
Ορισμός Στατιστική είναι το σύνολο των μεθόδων και θεωριών που εφαρμόζονται σε αριθμητικά δεδομένα προκειμένου να ληφθεί κάποια απόφαση σε συνθήκες αβεβαιότητας. Βασικές έννοιες Η μελέτη ενός πληθυσμού
Παρεμβολή & πρόγνωση άγνωστης συνάρτησης μέσω σημειακής προσαρμογής
 Ειδικά Θέματα Συνορθώσεων & Εφαρμογές 8 ο εξάμηνο, Ακαδημαϊκό έτος 2018-2019 Παρεμβολή & πρόγνωση άγνωστης συνάρτησης μέσω σημειακής προσαρμογής (Least squares collocation) Χριστόφορος Κωτσάκης Τμήμα Αγρονόμων
Ειδικά Θέματα Συνορθώσεων & Εφαρμογές 8 ο εξάμηνο, Ακαδημαϊκό έτος 2018-2019 Παρεμβολή & πρόγνωση άγνωστης συνάρτησης μέσω σημειακής προσαρμογής (Least squares collocation) Χριστόφορος Κωτσάκης Τμήμα Αγρονόμων
Ψηφιακές Τηλεπικοινωνίες. Πιθανότητα Σφάλματος για Δυαδική Διαμόρφωση
 Ψηφιακές Τηλεπικοινωνίες Πιθανότητα Σφάλματος για Δυαδική Διαμόρφωση Σύνδεση με τα Προηγούμενα Σχεδιάστηκε ο βέλτιστος δέκτης για κανάλι AWGN Επειδή πάντοτε υπάρχει ο θόρυβος, ακόμη κι ο βέλτιστος δέκτης
Ψηφιακές Τηλεπικοινωνίες Πιθανότητα Σφάλματος για Δυαδική Διαμόρφωση Σύνδεση με τα Προηγούμενα Σχεδιάστηκε ο βέλτιστος δέκτης για κανάλι AWGN Επειδή πάντοτε υπάρχει ο θόρυβος, ακόμη κι ο βέλτιστος δέκτης
ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ. Περιγράψουµε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήµατος.
 3. ΚΕΦΑΛΑΙΟ ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ Περιγράψουµε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήµατος. Ορίσουµε το µετασχηµατισµό Fourier ενός µη περιοδικού
3. ΚΕΦΑΛΑΙΟ ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ Περιγράψουµε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήµατος. Ορίσουµε το µετασχηµατισµό Fourier ενός µη περιοδικού
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ. Κεφάλαιο 4 : Σήματα Διάλεξη: Κώστας Μαλιάτσος Χρήστος Ξενάκης, Κώστας Μαλιάτσος. Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων
 ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 4 : Σήματα Διάλεξη: Κώστας Μαλιάτσος Χρήστος Ξενάκης, Κώστας Μαλιάτσος Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα ομιλίας Είδη /Κατηγορίες Σημάτων Στοιχειώδη
ΘΕΩΡΙΑ ΠΛΗΡΟΦΟΡΙΑΣ Κεφάλαιο 4 : Σήματα Διάλεξη: Κώστας Μαλιάτσος Χρήστος Ξενάκης, Κώστας Μαλιάτσος Πανεπιστήμιο Πειραιώς, Τμήμα Ψηφιακών Συστημάτων Περιεχόμενα ομιλίας Είδη /Κατηγορίες Σημάτων Στοιχειώδη
Προχωρημένα Θέματα Ασυρμάτων Επικοινωνιών (2) Αγγελική Αλεξίου
 Προχωρημένα Θέματα Ασυρμάτων Επικοινωνιών (2) Αγγελική Αλεξίου alexiou@unipi.gr 1 Diversity (Ποικιλότητα) 2 Non-Coherent Detection (Ασύμφωνη ανίχνευση) Θεωρούμε το πρόβλημα ασύμφωνης ανίχνευσης (ανίχνευση
Προχωρημένα Θέματα Ασυρμάτων Επικοινωνιών (2) Αγγελική Αλεξίου alexiou@unipi.gr 1 Diversity (Ποικιλότητα) 2 Non-Coherent Detection (Ασύμφωνη ανίχνευση) Θεωρούμε το πρόβλημα ασύμφωνης ανίχνευσης (ανίχνευση
Στοχαστικές Ανελίξεις (1) Αγγελική Αλεξίου
 Στοχαστικές Ανελίξεις (1) Αγγελική Αλεξίου alexiou@unipi.gr 1 Ενότητες Μαθήματος Ενότητα 1 Εισαγωγή Ορισμός Στοχαστικών ανελίξεων Στατιστική Στοχαστικών Διαδικασιών Στασιμότητα Εργοδικότητα Ενότητα 2 Διαδικασίες
Στοχαστικές Ανελίξεις (1) Αγγελική Αλεξίου alexiou@unipi.gr 1 Ενότητες Μαθήματος Ενότητα 1 Εισαγωγή Ορισμός Στοχαστικών ανελίξεων Στατιστική Στοχαστικών Διαδικασιών Στασιμότητα Εργοδικότητα Ενότητα 2 Διαδικασίες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ. Ασύρματη Διάδοση MYE006: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ. Ευάγγελος Παπαπέτρου
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Ασύρματη Διάδοση MYE006: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου Διάρθρωση μαθήματος Εισαγωγή στην ασύρματη διάδοση Κεραίες διάγραμμα ακτινοβολίας, κέρδος,
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Ασύρματη Διάδοση MYE006: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου Διάρθρωση μαθήματος Εισαγωγή στην ασύρματη διάδοση Κεραίες διάγραμμα ακτινοβολίας, κέρδος,
Εργαστήριο 1: Αρχές Κινητών Επικοινωνιών
 1.1 Βασικές μετατροπές Εργαστήριο 1: Αρχές Κινητών Επικοινωνιών Όταν μας ενδιαφέρει ο υπολογισμός μεγεθών σχετικών με στάθμες ισχύος εκπεμπόμενων σημάτων, γίνεται χρήση και της λογαριθμικής κλίμακας με
1.1 Βασικές μετατροπές Εργαστήριο 1: Αρχές Κινητών Επικοινωνιών Όταν μας ενδιαφέρει ο υπολογισμός μεγεθών σχετικών με στάθμες ισχύος εκπεμπόμενων σημάτων, γίνεται χρήση και της λογαριθμικής κλίμακας με
Ασύρματη Διάδοση. Διάρθρωση μαθήματος. Ασύρματη διάδοση (1/2)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Διάρθρωση μαθήματος Ασύρματη Διάδοση MYE006: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου Εισαγωγή στην ασύρματη διάδοση Κεραίες διάγραμμα ακτινοβολίας, κέρδος,
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΤΜΗΜΑ ΜΗΧ. Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Διάρθρωση μαθήματος Ασύρματη Διάδοση MYE006: ΑΣΥΡΜΑΤΑ ΔΙΚΤΥΑ Ευάγγελος Παπαπέτρου Εισαγωγή στην ασύρματη διάδοση Κεραίες διάγραμμα ακτινοβολίας, κέρδος,
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 5 η : Αποκατάσταση Εικόνας
 Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 5 η : Αποκατάσταση Εικόνας Καθ. Κωνσταντίνος Μπερμπερίδης Πολυτεχνική Σχολή Μηχανικών Η/Υ & Πληροφορικής Σκοποί ενότητας Εισαγωγή στις τεχνικές αποκατάστασης
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Ενότητα 5 η : Αποκατάσταση Εικόνας Καθ. Κωνσταντίνος Μπερμπερίδης Πολυτεχνική Σχολή Μηχανικών Η/Υ & Πληροφορικής Σκοποί ενότητας Εισαγωγή στις τεχνικές αποκατάστασης
Ένα αναλογικό σήμα περιέχει άπειρες πιθανές τιμές. Για παράδειγμα ένας απλός ήχος αν τον βλέπαμε σε ένα παλμογράφο θα έμοιαζε με το παρακάτω:
 Σημειώσεις Δικτύων Αναλογικά και ψηφιακά σήματα Ένα αναλογικό σήμα περιέχει άπειρες πιθανές τιμές. Για παράδειγμα ένας απλός ήχος αν τον βλέπαμε σε ένα παλμογράφο θα έμοιαζε με το παρακάτω: Χαρακτηριστικά
Σημειώσεις Δικτύων Αναλογικά και ψηφιακά σήματα Ένα αναλογικό σήμα περιέχει άπειρες πιθανές τιμές. Για παράδειγμα ένας απλός ήχος αν τον βλέπαμε σε ένα παλμογράφο θα έμοιαζε με το παρακάτω: Χαρακτηριστικά
Συστήματα Επικοινωνιών ΙI
 + Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI FSK, MSK Πυκνότητα φάσματος ισχύος βασικής ζώνης + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/
+ Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: cdemestichas@uowm.gr Συστήματα Επικοινωνιών ΙI FSK, MSK Πυκνότητα φάσματος ισχύος βασικής ζώνης + Ιστοσελίδα nιστοσελίδα του μαθήματος: n https://eclass.uowm.gr/courses/icte302/
Σήματα και Συστήματα. Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier 1. Μετασχηματισμός Fourier
Σήματα και Συστήματα Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier 1. Μετασχηματισμός Fourier
Σ ΤΑΤ Ι Σ Τ Ι Κ Η. Statisticum collegium iv
 Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium iv Στατιστική Συμπερασματολογία Ι Σημειακές Εκτιμήσεις Διαστήματα Εμπιστοσύνης Στατιστική Συμπερασματολογία (Statistical Inference) Το πεδίο της Στατιστικής Συμπερασματολογία,
Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium iv Στατιστική Συμπερασματολογία Ι Σημειακές Εκτιμήσεις Διαστήματα Εμπιστοσύνης Στατιστική Συμπερασματολογία (Statistical Inference) Το πεδίο της Στατιστικής Συμπερασματολογία,
ΜΕΛΕΤΗ ΓΝΩΣΤΙΚΩΝΝ ΡΑΔΙΟΣΥΣΤΗΜΑΤΩΝ ΕΠΙΚΟΙΝΩΝΙΑΣ
 ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡOΦΟΡΙΚΗΣ ΤΕ ΜΕΛΕΤΗ ΓΝΩΣΤΙΚΩΝΝ ΡΑΔΙΟΣΥΣΤΗΜΑΤΩΝ ΕΠΙΚΟΙΝΩΝΙΑΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΤΟΥ ΖΗΣΚΑ ΠΑΝΑΓΙΩΤΗ ΕΠΙΒΛΕΠΩΝ ΚΑΘΗΓΗΤΗΣ: Δρ ΕΥΣΤΑΘΙΟΥ ΔΗΜΗΤΡΙΟΣ ΕΠΙΣΚΟΠΗΣΗ ΠΑΡΟΥΣΙΑΣΗΣ Σκοπός Πτυχιακής Εργασίας
ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡOΦΟΡΙΚΗΣ ΤΕ ΜΕΛΕΤΗ ΓΝΩΣΤΙΚΩΝΝ ΡΑΔΙΟΣΥΣΤΗΜΑΤΩΝ ΕΠΙΚΟΙΝΩΝΙΑΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΤΟΥ ΖΗΣΚΑ ΠΑΝΑΓΙΩΤΗ ΕΠΙΒΛΕΠΩΝ ΚΑΘΗΓΗΤΗΣ: Δρ ΕΥΣΤΑΘΙΟΥ ΔΗΜΗΤΡΙΟΣ ΕΠΙΣΚΟΠΗΣΗ ΠΑΡΟΥΣΙΑΣΗΣ Σκοπός Πτυχιακής Εργασίας
10-Μαρτ-2009 ΗΜΥ Παραθύρωση Ψηφιακά φίλτρα
 -Μαρτ-9 ΗΜΥ 49. Παραθύρωση Ψηφιακά φίλτρα . Παραθύρωση / Ψηφιακά Φίλτρα -Μαρτ-9 Είδη παραθύρων Bartlett τριγωνικό: n, n Blacman: πn 4πn.4.5cos +.8cos, n < . Παραθύρωση / Ψηφιακά Φίλτρα -Μαρτ-9 3 Hamming:
-Μαρτ-9 ΗΜΥ 49. Παραθύρωση Ψηφιακά φίλτρα . Παραθύρωση / Ψηφιακά Φίλτρα -Μαρτ-9 Είδη παραθύρων Bartlett τριγωνικό: n, n Blacman: πn 4πn.4.5cos +.8cos, n < . Παραθύρωση / Ψηφιακά Φίλτρα -Μαρτ-9 3 Hamming:
Γιατί Διαμόρφωση; Μια κεραία για να είναι αποτελεσματική πρέπει να είναι περί το 1/10 του μήκους κύματος
 Γιατί Διαμόρφωση; Μετάδοση ενός σήματος χαμηλών συχνοτήτων μέσω ενός ζωνοπερατού καναλιού Παράλληλη μετάδοση πολλαπλών σημάτων πάνω από το ίδιο κανάλι - Διαχωρισμός συχνότητας (Frequency Division Multiplexing)
Γιατί Διαμόρφωση; Μετάδοση ενός σήματος χαμηλών συχνοτήτων μέσω ενός ζωνοπερατού καναλιού Παράλληλη μετάδοση πολλαπλών σημάτων πάνω από το ίδιο κανάλι - Διαχωρισμός συχνότητας (Frequency Division Multiplexing)
