ΑΝΑΛΥΣΗ ΤΩΝ ΕΠΙΦΑΝΕΙΑΚΩΝ ΚΥΜΑΤΩΝ RAYLEIGH ΚΑΙ ΕΦΑΡΜΟΓΗ ΣΕ ΧΩΡΟ ΑΠΟΘΕΣΗΣ ΑΠΟΡΡΙΜΜΑΤΩΝ ΣΤΗ Β. ΙΤΑΛΙΑ ΚΑΙ ΣΤΗ ΒΙΟΜΗΧΑΝΙΚΗ ΠΕΡΙΟΧΗ PORTO PETROLI, GENOA
|
|
|
- Ῥαάβ Ελευθεριάδης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ελτίο της Ελληνικής Γεωλογικής Εταιρίας τοµ. XXXVI, 24 Πρακτικά 1 ου ιεθνούς Συνεδρίου, Θεσ/νίκη Απρίλιος 24 Bulletin of the Geological Society of Greece vol. XXXVI, 24 Proceedings of the 1 th International Congress, Thessaloniki, April 24 ΑΝΑΛΥΣΗ ΤΩΝ ΕΠΙΦΑΝΕΙΑΚΩΝ ΚΥΜΑΤΩΝ RAYLEIGH ΚΑΙ ΕΦΑΡΜΟΓΗ ΣΕ ΧΩΡΟ ΑΠΟΘΕΣΗΣ ΑΠΟΡΡΙΜΜΑΤΩΝ ΣΤΗ Β. ΙΤΑΛΙΑ ΚΑΙ ΣΤΗ ΒΙΟΜΗΧΑΝΙΚΗ ΠΕΡΙΟΧΗ PORTO PETROLI, GENOA Κρητικάκης Σ. Γ. 1, Βαφείδης Α. 1, Gourry J. C. 2 1 Εργαστήριο Εφαρµοσµένης Γεωφυσικής, Τµήµα Μηχανικών Ορυκτών Πόρων, Πολυτεχνείο Κρήτης, 731, Πολυτεχνειούπολη, Χανιά, gkritik@mred.tuc.gr, vafidis@mred.tuc.gr 2 BRGM Development Planning and Natural sks Division, Orléans, France, jc.gourry@brgm.fr ΠΕΡΙΛΗΨΗ To φαινόµενο της διασποράς των επιφανειακών κυµάτων και ειδικότερα των επιφανειακών κυ- µάτων Rayleigh, έχει αποτελέσει τα τελευταία χρόνια εφαλτήριο για την εφαρµογή σύγχρονων τεχνικών της γεωτεχνικής και περιβαλλοντικής γεωφυσικής. Στις µέρες µας, η ανάλυση των επιφανειακών κυµάτων Rayleigh χρησιµοποιείται ευρύτατα για τον προσδιορισµό των ταχυτήτων των εγκαρσίων σεισµικών κυµάτων. Στην εργασία αυτή περιγράφεται κυρίως η µεθοδολογίας ανάλυσης των επιφανειακών κυµάτων Rayleigh, ενώ παράλληλα παρουσιάζονται εφαρµογές της σε σεισµικά δεδοµένα που προέρχονται από διασκοπήσεις, οι οποίες πραγµατοποιήθηκαν στα πλαίσια του Ευρωπαϊκού προγράµµατος HYGEIA, σε δύο περιβαλλοντικά επιβαρηµένες περιοχές: α) στην περιοχή του Monfalcone στη βόρεια Ιταλία και β) στην βιοµηχανική περιοχή Porto Petroli, στη Γένοβα. H µεθοδολογία αυτή αποδεικνύεται πολύ χρήσιµη στην οριοθέτηση του ετερογενούς εδάφους που περιέχει θαµµένα απορρίµµατα στην περιοχή του Monfalcone και στην χαρτογράφηση του α- νάγλυφου του υποβάθρου της βιοµηχανικής περιοχής του Porto Petroli, µέσω του προσδιορισµού των ταχυτήτων των εγκαρσίων σεισµικών κυµάτων. 1 ΕΙΣΑΓΩΓΗ Είναι γνωστό ότι τα επιφανειακά σεισµικά κύµατα παρουσιάζουν έντονο το φαινόµενο της διασποράς (dispersion), δηλαδή της εξάρτησης της ταχύτητας φάσης από τη συχνότητα. Η ταχύτητα φάσης των κυµάτων Rayleigh σε οριζόντια στρωµατωµένο εδαφικό µοντέλο εξαρτάται από τη συχνότητα και τέσσερις εδαφικές παραµέτρους (Schwab and Knopoff, 1972): Ταχύτητα των διαµηκών κυµάτων (P κύµατα) Ταχύτητα των εγκαρσίων κυµάτων (S κύµατα) Πυκνότητα των σχηµατισµών Πάχος κάθε στρώµατος Η ταχύτητα διάδοσης των εγκαρσίων σεισµικών κυµάτων επηρεάζει την καµπύλη διασποράς περισσότερο από όλες τις άλλες εδαφικές παραµέτρους. Για το λόγο αυτό, χρησιµοποιώντας τεχνικές αντιστροφής, είναι δυνατό να προσδιοριστεί η κατανοµή της ταχύτητας των S κυµάτων συναρτήσει του βάθους, από την καµπύλη διασποράς Rayleigh. Η πλευρική µεταβολή της ταχύτητας των εγκαρσίων σεισµικών κυµάτων προσδιορίζεται χρησι- µοποιώντας τεχνικές roll along κατά την απόκτηση των σεισµικών καταγραφών (Miller et al, 1999). Από κάθε καταγραφή κοινής πηγής και µετά την αντιστροφή της θεµελιώδους καµπύλης διασποράς προκύπτει η ταχύτητα των S κυµάτων συναρτήσει του βάθους. Τοποθετώντας τα αποτελέσµατα από κάθε αντιστροφή στο κέντρο του αναπτύγµατος πηγής - γεωφώνων προκύπτει η ψευδοτοµή της ταχύτητας των S κυµάτων. Πολλές εφαρµογές προσδιορισµού της ταχύτητας των εγκαρσίων κυµάτων από σεισµικά δεδο- µένα επιφανειακών κυµάτων (Ραπτάκης, 1995, Stokoe et al., 1994, Misiek, 1996) έχουν αποδείξει την αξιοπιστία της µεθόδου αυτής. Τέλος, οι νέες τάσεις στο συγκεκριµένο αντικείµενο εισάγουν την παράµετρο της πλευρικής ανοµοιογένειας της ταχύτητας στα εδαφικά µοντέλα (Misiek, 1996) για 1234
2 τον χαρακτηρισµό των σχηµατισµών µε άµεσο γεωτεχνικό και περιβαλλοντικό ενδιαφέρον (Miller and Xia, 1999, Miller et al., 1999). 2 ΜΕΘΟ ΟΛΟΓΙΑ ΤΗΣ ΑΝΑΛΥΣΗΣ ΤΩΝ ΕΠΙΦΑΝΕΙΑΚΩΝ ΚΥΜΑΤΩΝ Η ανάλυση των επιφανειακών κυµάτων περιλαµβάνει τη λήψη καταγραφών πλούσιων σε επιφανειακά κύµατα Rayleigh και την αντιστροφή των χαρακτηριστικών καµπύλων διασποράς τους, για τον καθορισµό της ταχύτητας των διατµητικών κυµάτων κατανεµηµένης µε το βάθος. Μια από τις κυριότερες διαδικασίες για την ανάλυση των επιφανειακών κυµάτων είναι ο προσδιορισµός των χαρακτηριστικών καµπύλων διασποράς από τις καταγραφές. Η αντιστροφή των χαρακτηριστικών καµπύλων διασποράς αποτελεί τη δεύτερη σηµαντικότερη φάση της επεξεργασίας. Από τη διαδικασία της αντιστροφής προσδιορίζονται οι παράµετροι του εδαφικού µοντέλου. Η µεθοδολογία της ανάλυσης των επιφανειακών κυµάτων Rayleigh είναι δυνατό να χωριστεί σε δύο διακριτά στάδια (Σχ. 1). Κατά το πρώτο στάδιο, από τις σεισµικές καταγραφές κοινής πηγής, οι ο- ποίες θα πρέπει να περιλαµβάνουν σηµαντική σεισµική ενέργεια κατανεµηµένη στα επιφανειακά κύµατα, προκύπτουν οι πειραµατικές καµπύλες διασποράς. Ενώ στο δεύτερο στάδιο προσδιορίζονται οι θεωρητικές καµπύλες διασποράς για οριζόντια στρωµατωµένο εδαφικό µοντέλο, χρησιµοποιώντας την τεχνική Thomson-Haskell (Haskell, 1953, Schwab and Knopoff, 1972). Τροποποιώντας επαναληπτικά το εδαφικό µοντέλο επιτυγχάνεται η προσαρµογή της θεωρητικής καµπύλης διασποράς στην πειραµατική (διαδικασία που ονοµάζεται αντιστροφή). Έτσι, εφόσον πραγµατοποιηθεί ταύτιση των καµπύλων, προσδιορίζεται το τελικό εδαφικό µοντέλο (κατανοµή της ταχύτητας των εγκαρσίων σεισµικών κυµάτων µε το βάθος). Στις επόµενες παραγράφους περιγράφονται αναλυτικά όλα τα βήµατα που ακολουθούνται κατά τη διαδικασία της ανάλυσης των επιφανειακών κυ- µάτων Rayleigh. Σχήµα 1. ιάγραµµα ροής που περιγράφει τη µεθοδολογία της ανάλυσης των κυµάτων Rayleigh. 1235
3 2.1 Στάδιο Απόκτηση σεισµικών καταγραφών Στα πειράµατα σεισµικής διασκόπησης, τα επιφανειακά κύµατα εµφανίζονται στα σεισµογράµµατα µετά τα κύµατα χώρου και αναγνωρίζονται από το µεγάλο πλάτος και τη σχετικά χαµηλή συχνότητά τους. Η απόκτηση των σεισµικών καταγραφών, στις οποίες θα πρέπει να δεσπόζουν τα επιφανειακά κύµατα, απαιτεί ορισµένες ρυθµίσεις, όπως είναι η επιλογή του κατάλληλου εξοπλισµού (γεώφωνα κατάλληλης ιδιοσυχνότητας και σεισµική πηγή µε ευρύ φασµατικό περιεχόµενο), η ρύθ- µιση της απόστασης πηγής γεωφώνου και της ισαπόστασης των γεωφώνων καθώς και η ρύθµιση του διαστήµατος δειγµατοληψίας και της διάρκειας καταγραφής. Για την συλλογή των σεισµικών δεδοµένων χρησιµοποιείται διάταξη πηγής - γεωφώνων και κύλισή της (roll along) µε σταθερό βήµα προχώρησης, προκειµένου τα αποτελέσµατα της αντιστροφής να ισαπέχουν πάνω στην ψευδοτο- µή. Η σεισµική πηγή παίζει σηµαντικό ρόλο για τη λήψη των δεδοµένων, καθώς όσο πιο πλούσιο συχνοτικό περιεχόµενο παρέχει, τόσο καλύτερη ανάλυση επιτυγχάνεται. Επίσης, για τη διασκόπηση βαθύτερων γεωλογικών σχηµατισµών απαιτείται η καταγραφή σηµαντικής ενέργειας σε χαµηλές συχνότητες. Εκτενέστερες αναφορές σχετικά µε τις βέλτιστες παραµέτρους απόκτησης των σεισµικών καταγραφών έχουν παρουσιαστεί από τους Park et al (1999) Μετασχηµατισµός του κυµατικού πεδίου Οι χαρακτηριστικές καµπύλες διασποράς των επιφανειακών κυµάτων που καταγράφονται από διάταξη κοινής πηγής προκύπτουν µετά την εφαρµογή ενός µετασχηµατισµού του κυµατικού πεδίου από τον χώρο x t στον χώρο p ω (McMechan and Yedlin, 1981). Αρχικά εφαρµόζεται γραµµική χρονική απόκλιση (Linear MoveOut LMO) στα σεισµικά δεδο- µένα: u(x, t) LMO U(x, τ) = U(x, t px) (1) όπου u(x, t) είναι η κατακόρυφη µετατόπιση των υλικών σηµείων στο πεδίο απόστασης χρόνου, τ είναι ο χρόνος καθυστέρησης: τ = t px (2) και p είναι η παράµετρος της σεισµικής ακτίνας (εξ. 3), η οποία για οριζόντια διαδιδόµενα σεισµικά κύµατα ισούται µε το αντίστροφο της σεισµικής ταχύτητας και ονοµάζεται βραδύτητα φάσης (Yilmaz, 1987). p = sin(i) V o i= 9 p = 1 V hor Επίσης, η βραδύτητα φάσης (phase slowness) σχετίζεται µε την ταχύτητας φάσης (c) σύµφωνα µε τη σχέση: 1 p = (4) c Η ταχύτητα φάσης εκφράζει τη ταχύτητα διάδοσης κάθε αρµονικού σεισµικού κύµατος. Εφαρµόζοντας την ιδιότητα της χρονικής µετάθεσης (time shifting) του µετασχηµατισµού Fourier, η γραµµική χρονική απόκλιση πραγµατοποιείται στο χώρο των συχνοτήτων σύµφωνα µε την σχέση: U(x,τ) = U(x,t-px) Ũ(x,f) e -i2πfpx (5) όπου u(x,t) Ũ (x,f) και το σύµβολο υποδηλώνει ζεύγος Fourier. Ακολούθως, αθροίζονται τα ίχνη που έχουν υποστεί γραµµική χρονική απόκλιση στο χώρο τον συχνοτήτων: (3) 1236
4 ~ S(p,f ) = x U ~ (x,f ) e i2πfpx (6) όπου το S ~ εκφράζει το κυµατικό πεδίο στο χώρο (p f). Σχήµα 2. (a) Καµπύλες διασποράς που προέκυψαν από το µετασχηµατισµό του κυµατικού πεδίου της καταγραφής µε κωδικό πεδίου (FFID) 26 (b) στην περιοχή του Monfalcone. ιακρίνεται η θεµελιώδης καµπύλη διασποράς και πιθανόν 2 καµπύλες ανώτερης τάξης. Οι καµπύλες διασποράς αντιστοιχούν σε τοπικά ενεργειακά µέγιστα της κυµατικής ενέργειας που παρατηρούνται στο πεδίο p f και ουσιαστικά απεικονίζουν τη µεταβολή της ταχύτητας φάσης των επιφανειακών κυµάτων Rayleigh συναρτήσει της συχνότητας (σταυροί στο σχ. 2a). Το ενδιαφέρον της ανάλυσης των επιφανειακών κυµάτων στη συγκεκριµένη εργασία επικεντρώνεται στη θεµελιώδη χαρακτηριστική καµπύλη (fundamental dispersion curve), ενώ καµπύλες διασποράς α- νώτερης τάξης (higher modes) εµφανίζουν υψηλότερες ταχύτητες από αυτήν της θεµελιώδους για συγκεκριµένη συχνότητα. 2.2 Στάδιο Προσδιορισµός αρχικού εδαφικού µοντέλου Στις µεθόδους αντιστροφής η µη γραµµική αναλυτική σχέση προσεγγίζεται µε τη χρήση του α- ναπτύγµατος Taylor. Στη συνέχεια εφαρµόζεται επαναληπτική διαδικασία, για την επιτυχή σύγκλισή της οποίας απαιτείται το αρχικό µοντέλο να βρίσκεται «σχετικά» κοντά στη γειτονιά της λύσης. Ε- ποµένως, για την ανάλυση των επιφανειακών κυµάτων Rayleigh είναι πολύ σηµαντική η επιλογή κατάλληλου αρχικού εδαφικού µοντέλου. Έτσι, για τον προσδιορισµό του αρχικού εδαφικού µοντέλου λαµβάνονται υπόψη τα εξής: Από τις καµπύλες διασποράς και για κάθε τιµή ταχύτητας φάσης και συχνότητας είναι δυνατό να προσδιοριστεί το αντίστοιχο µήκος κύµατος των επιφανειακών κυµάτων Rayleigh, σύµφωνα µε τη θεµελιώδη εξίσωση της κυµατικής: c R = λ R f R (7) όπου c R είναι η ταχύτητα φάσης, f R η συχνότητα και λ R το µήκος κύµατος των επιφανειακών κυµάτων Rayleigh. Η κατακόρυφη µετατόπιση των υλικών σηµείων κατά τη διάδοση των επιφανειακών κυµάτων Rayleigh σε βάθος ίσο µε το µήκος κύµατός τους ισούται περίπου µε το 15 % της µετατόπισης στην επιφάνεια (Nazarian, 1984). Άρα, τα επιφανειακά κύµατα Rayleigh διεισδύουν πρακτικά σε µέγιστο βάθος περίπου ίσο µε το µήκος κύµατός τους και εποµένως 1237
5 οι πληροφορίες που εµπεριέχουν για τους εδαφικούς σχηµατισµούς συνοψίζονται µέχρι το βάθος αυτό. Η ταχύτητα των επιφανειακών κυµάτων Rayleigh συνδέεται µε την ταχύτητα των εγκαρσίων σεισµικών κυµάτων (V S) µε τη σχέση: c R (f ) = a V (f ) (8) i S i όπου o αριθµητικός συντελεστής a λαµβάνει τιµές από.874 έως.955 για αντίστοιχες τιµές του λόγου Poisson από. έως.5 (Xia et al, 1999, Stokoe et al, 1994). Εν κατακλείδι, υπολογίζεται το µήκος κύµατος των επιφανειακών κυµάτων Rayleigh από την εξ. 7. Στη συνέχεια καθορίζεται το µέγιστο βάθος (d) διείσδυσης των επιφανειακών κυµάτων και το πάχος των στρωµάτων του εδαφικού µοντέλου, το οποίο αυξάνεται µε το βάθος. Αυτό έχει ως αποτέλεσµα την ικανοποιητική εκτίµηση της κατανοµής της ταχύτητας των εγκαρσίων σεισµικών κυµάτων µε το βάθος. Ακολούθως, θεωρώντας σταθερό λόγο του Poisson (ν) για κάθε εδαφικό στρώµα είναι δυνατό να εκτιµηθεί η ταχύτητα των διαµήκων κυµάτων (Vp). Τέλος, µε τη χρήση εµπειρικών σχέσεων εκτιµάται και η πυκνότητα κάθε εδαφικού στρώµατος. Πληροφορίες από άλλες µεθόδους που αφορούν την ταχύτητα των διαµήκων κυµάτων και την πυκνότητα των γεωλογικών σχηµατισµών είναι δυνατό να χρησιµοποιηθούν απευθείας ως παράµετροι του αρχικού εδαφικού µοντέλου Επίλυση του ευθέως προβλήµατος Η ταχύτητα φάσης των κυµάτων Rayleigh, c, προσδιορίζεται από την συνάρτηση διασποράς F στη µη γραµµική και πεπλεγµένη της µορφή (Schwab and Knopoff, 1972): F(fi, cr i, Vs, Vp, ρ, d) = (i = 1, 2, 3,..., n) (9) όπου f i είναι η συχνότητα σε Hz, c είναι η ταχύτητα φάσης των κυµάτων Rayleigh για τη συχνότητα f i, V S = (Vs 1, Vs 2,., Vs m) T είναι το διάνυσµα των ταχυτήτων των S κυµάτων, µε Vs j την ταχύτητα των S κυµάτων του j στρώµατος (j =1, 2,, m), m είναι ο αριθµός των στρωµάτων, Vp = (Vp 1, Vp 2,., Vp m) T είναι το διάνυσµα των ταχυτήτων των Ρ κυµάτων, µε Vp j την ταχύτητα των Ρ κυµάτων του j στρώµατος, ρ = (ρ 1, ρ 2,, ρ m) T είναι το διάνυσµα των πυκνοτήτων, µε ρ j την πυκνότητα του j στρώµατος και d = (d 1, d 2,, d m-1) Τ είναι το διάνυσµα των παχών, µε d j το πάχος του j στρώµατος. Οι ρίζες της αναλυτικής σχέσης της συνάρτησης διασποράς για συγκεκριµένες παρα- µέτρους του µοντέλου (Vs, Vp, ρ, και d) και για συχνότητα (f i) αντιστοιχούν στις ταχύτητες φάσης των επιφανειακών κυµάτων Rayleigh στη συγκεκριµένη συχνότητα. Σε αυτή την εργασία, εξετάζεται µόνο η θεµελιώδης χαρακτηριστική καµπύλη (fundamental mode) η οποία, σε χαµηλές συχνότητες, αποτελείται από τις µικρότερες θετικές ρίζες της συνάρτησης διασποράς για διάφορες συχνότητες f i = 1, 2,, n. Για να προσδιοριστεί η ταχύτητα φάσης c στις διάφορες συχνότητες f i (i = 1, 2,., n) χρησιµοποιείται η µέθοδος της διχοτόµησης (bisection), η οποία προσδιορίζει τις ρίζες της συνάρτησης διασποράς (εξ. 9, Press et al., 1992). 2.3 Αντιστροφή των καµπύλων διασποράς Εφόσον ο αντικειµενικός στόχος είναι ο µηδενισµός της συνάρτησης διασποράς (εξ. 9), η ταχύτητα φάσης, c, για µια δεδοµένη συχνότητα f i είναι δυνατό να εκφραστεί ως συνάρτηση των ταχυτήτων των S-κυµάτων σύµφωνα µε τη σχέση (Κρητικάκης, 21) : ( Vs Vs,... Vs,{ Vp,, d } f ) c c, = (1) 1, 2 m 1,2,... m ρ1,2,... m 1,2,... m Η συνάρτηση αυτή (εξ. 1) είναι δυνατό να αναπτυχθεί σε σειρά Taylor ως προς Vs διατηρώντας µόνο πρώτης τάξης όρους. Έτσι, προκύπτει η σχέση: i 1238
6 c c = m j= 1 c Vs ( Vs Vs ) j j (11) j V s 1 = V s1 V s 2 = V s 2... V = V sm sm όπου το i = 1, 2,, n είναι ο ο αριθµός των µετρήσεων, ενώ ο εκθέτης συµβολίζει το αρχικό µοντέλο τόσο για τις V s όσο και για τις υπολογισµένες τιµές της ταχύτητας φάσης C Στη διανυσµατική µορφή η ίδια σχέση γράφεται ως εξής: c = J Vs (12) R ij όπου το διάνυσµα: cr = cr cr (13) εκφράζει τη διαφορά ανάµεσα στα διανύσµατα της πειραµατικής και θεωρητικής ταχύτητας φάσης. Το διάνυσµα: Vs = Vs Vs (14) περιέχει τις άγνωστες ταχύτητες Vs αλλά και τις αντίστοιχες Vs του αρχικού εδαφικού µοντέλου. Τέλος, η Ιακωβιανή J ij της συνάρτησης διασποράς, προσδιορίζεται σύµφωνα µε τη σχέση: J F Vs j ij = = (15) F Vs j c c όπου το j = 1, 2,, m, συµβολίζει το πλήθος των εδαφικών στρωµάτων (συµπεριλαµβανοµένου και του ηµιχώρου). Ο προσδιορισµός των µερικών παραγώγων της Ιακωβιανής (εξ. 15) κατά τη διαδικασία της αντιστροφής, επιτυγχάνεται µε τη µέθοδο της πολυωνυµικής παρεµβολής (polynomial extrapolation) του dder (Press et al., 1992). Για το σύστηµα των γραµµικών εξισώσεων (εξ. 12), ορίζεται αντικειµενική συνάρτηση, έτσι ώστε η λύση του να προκύπτει µέσω της ελαχιστοποίησής της: r r r = J Vs c ε (16) χρησιµοποιώντας την µέθοδο Levenberg Marquardt (L-M, Marquardt, 1963) και την τεχνική Singular Value Decomposition (SVD, Press et al., 1992). 3 ΕΦΑΡΜΟΓΗ ΤΗΣ ΜΕΘΟ ΟΛΟΓΙΑΣ ΣΤΗΝ ΠΕΡΙΟΧΗ ΤΟΥ MONFALCONE ΣΤΗ Β. ΙΤΑΛΙΑ H εφαρµογή της µεθοδολογίας της ανάλυσης των επιφανειακών κυµάτων πραγµατοποιήθηκε µε επιτυχία στην περιοχή του Monfalcone στη βόρεια Ιταλία, όπου στόχος της διασκόπησης ήταν να χαρτογραφηθούν πιθανές θέσεις µε θαµµένα απορρίµµατα. Έτσι, για την απόκτηση των σεισµικών δεδοµένων πραγµατοποιήθηκαν 23 καταγραφές κοινής πηγής µε ισαπόσταση πηγών 5 m, χρησι- µοποιώντας την τεχνική roll along. Η ισαπόσταση των γεωφώνων ορίστηκε 2 m και η ελάχιστη α- πόσταση πηγής γεωφώνου 5 m. Για την καταγραφή χρησιµοποιήθηκε 24κάναλος σεισµογράφος και γεώφωνα, τα οποία έχουν την δυνατότητα να καταγράφουν σεισµικές δονήσεις χωρίς να καρφώνονται στο έδαφος (gimbals). O προσδιορισµός της θεµελιώδους καµπύλης διασποράς από τις καταγραφές των επιφανειακών κυµάτων πραγµατοποιήθηκε µε τη χρήση πρότυπων αλγόριθµων που αναπτύχθηκαν στο Ερ- 1239
7 γαστήριο Εφαρµοσµένης Γεωφυσικής του Πολυτεχνείου Κρήτης, χρησιµοποιώντας την τεχνική του µετασχηµατισµού του κυµατικού πεδίου που περιγράφεται στην παράγραφο Οι πειραµατικές καµπύλες διασποράς για την καταγραφή µε κωδικό πεδίου (FFID) 26 απεικονίζονται στο σχή- µα 2a. Για την επίλυση του ευθέως προβλήµατος χρησιµοποιήθηκε µια τροποποιηµένη µέθοδος της Thomson Haskell (Schwab and Knopoff, 1972) ( 2.2.2), ενώ κατά τη διαδικασία της αντιστροφής ακολουθήθηκε η µεθοδολογία που περιγράφεται στην παράγραφο 2.3. Τα αποτελέσµατα της αντιστροφής για την καταγραφή µε FFID 26 απεικονίζονται στο σχήµα 3. ύο στρώµατα χαµηλής ταχύτητας εντοπίζονται σε βάθη περίπου 7.5 m και 21 m και αποδίδονται σε αµµούχο πηλό και άργιλο αντίστοιχα. Το γεγονός αυτό τονίζει την υπεροχή της µεθοδολογίας που περιγράφεται στην εργασία αυτή σε σχέση µε την σεισµική διάθλαση, η οποία αδυνατεί να δώσει ικανοποιητικά αποτελέσµατα σε περιπτώσεις αναστροφής ταχυτήτων, όπως παρατηρήθηκαν στην συγκεκριµένη διασκόπηση. Στο σχήµα 4 παρατίθεται το ερµηνευµένο σεισµικό µοντέλο και η γεωλογική στήλη από παραπλήσια ερευνητική γεώτρηση µε κωδικό S1. Η γεώτρηση αυτή απέχει 18 m από το κέντρο του πρώτου αναπτύγµατος πηγής γεωφώνων. Συνδυάζοντας τα δεδοµένα της γεώτρησης (Πίνακας 1) και της ανάλυσης των επιφανειακών κυµάτων, πραγµατοποιήθηκε γεωλογική ερµηνεία της τοµής της ταχύτητας διάδοσης των S κυµάτων (σχήµα 4). Παρατηρείται ότι το ασβεστολιθικό υπόβαθρο της περιοχής απαντάται σε βάθος που κυµαίνεται από 2 m (στα δυτικά) έως 24 m (στα ανατολικά), ενώ το λεπτό υπερκείµενο στρώµα της αµµούχου αργίλου φαίνεται να πληρώνει τα κοιλώµατα του ασβεστολιθικού ανάγλυφου. Το επιφανειακό στρώµα, όπως έδειξε και η γεώτρηση, αποτελείται από ετερογενές έδαφος σε διάφορες αναλογίες µε στερεά απορρίµµατα. Η περιοχή µε το ερωτηµατικό αντιστοιχεί σε αµφιλεγόµενη ερµηνεία επειδή η πληροφορία για τις ταχύτητες στο σηµείο αυτό προέκυψε από παρεµβολή δεδοµένων γειτονικών περιοχών. Σχήµα 3. Αποτελέσµατα της αντιστροφής για την καταγραφή µε κωδικό πεδίου (FFID) 26. Η θέση της καταγραφής αυτής πάνω στη γραµµή µελέτης υποδεικνύεται στο σχήµα 4. Πίνακας 1. Γεωλογική ερµηνεία της γεώτρησης S1 Άνω επιφάνεια Κάτω επιφάνεια Γεωλογική στρώµατος (m) στρώµατος (m) περιγραφή. 4. Ετερογενές έδαφος µε απορρίµµατα Γκρι αµµούχος πηλός Καφέ πηλός µε ασβεστολιθικές κροκάλες Ιλύς και άργιλος Αµµούχος πηλός Ασβεστολιθικές αµµούχες κροκάλες Αµµούχα άργιλος Κερµατισµένος ασβεστόλιθος (υπόβαθρο) 124
8 Σχήµα 4. Αποτελέσµατα που προέκυψαν από την ανάλυση των επιφανειακών κυµάτων στην περιοχή του Monfalcone στη βόρεια Ιταλία. Η γεωλογική ερµηνεία πραγµατοποιήθηκε µε τη βοήθεια γειτονικής γεώτρησης. 4 ΕΦΑΡΜΟΓΗ ΤΗΣ ΜΕΘΟ ΟΛΟΓΙΑ ΣΤΗΝ ΒΙΟΜΗΧΑΝΙΚΗ ΠΕΡΙΟΧΗ ΤΟΥ PORTO PETROLI, GENOA Η ίδια µεθοδολογία απόκτησης και επεξεργασίας ακολουθήθηκε και στην περιοχή Porto Petroli, στη Γένοβα, όπου διασκοπήθηκαν 4 σεισµικές γραµµές µελέτης, ανάµεσα σε κτήρια της βιοµηχανικής περιοχής. Η χαρτογράφηση του µεταµορφωµένου οφειολιθικού υποβάθρου της περιοχής αποτελεί µια σηµαντική πληροφορία για τον καλύτερο σχεδιασµό άλλων γεωφυσικών µεθόδων και τον εντοπισµό πιθανών θέσεων όπου οι ρύποι είναι δυνατόν να εισχωρήσουν σε βαθύτερους σχηµατισµούς. Οι πειραµατικές καµπύλες διασποράς για την καταγραφή µε FFID 748 της γραµµής µελέτης Profile1 απεικονίζονται στο σχήµα 5a, ενώ τα αντίστοιχα αποτελέσµατα της αντιστροφής παρατίθενται στο σχήµα 5b. Η ψευδοτοµή των ταχυτήτων των S κυµάτων για αυτήν την γραµµή απεικονίζεται στο σχήµα 6. Ο οριζόντιος άξονας αντιστοιχεί στους κωδικούς πεδίου των καταγραφών. Η γεωλογική ερµηνεία της τοµής (προσδιορισµός του ανάγλυφου του υποβάθρου) πραγµατοποιήθηκε µε βάση γεωλογικές πληροφορίες για την περιοχή µελέτης. Σχήµα 5. Πειραµατικές καµπύλες διασποράς για την καταγραφή µε FFID 748 της γραµµής µελέτης Profile1 (a) και τα αντίστοιχα αποτελέσµατα της αντιστροφής (b). 1241
9 Σχήµα 6. Ψευδοτοµή των ταχυτήτων των S κυµάτων για την γραµµή µελέτης Profile 1 στην βιοµηχανική περιοχή του Porto Petroli. 5 ΣΥΜΠΕΡΑΣΜΑΤΑ Για την πραγµατοποίηση της ανάλυσης των επιφανειακών κυµάτων Rayleigh των σεισµικών δεδοµένων στις περιοχές µελέτης που παρουσιάζονται στην εργασία αυτή, η µεθοδολογία που περιγράφεται αναπτύχθηκε σε περιβάλλον MATLAB υποστηριζόµενη από αλγόριθµους σε γλώσσα προγραµµατισµού FORTRAN 77. Συνοπτικά, η µεθοδολογία αυτή για το µετασχηµατισµό του κυµατικού πεδίου στο χώρο p ω χρησιµοποιεί την τεχνική που έχει προταθεί από τους MacMechan and Yedlin (1981) και για τον υπολογισµό της συνάρτησης διασποράς την τροποποιηµένη από τους Schwab and Knopoff (1972) τεχνική Thomson Haskell. Κατά την αντιστροφή χρησιµοποιείται η µέθοδος των ελαχίστων τετραγώνων, η οποία υλοποιείται στην µεθοδολογία της ανάλυσης πινάκων SVD, ενώ η εξασφάλιση της σύγκλισης της αντιστροφής επιτυγχάνεται µε την τεχνική Levenberg Marquardt (L M, Marquardt, 1963). Η µεθοδολογία της ανάλυσης των επιφανειακών κυµάτων Rayleigh αποδείχθηκε πολύ χρήσιµη στην οριοθέτηση του ετερογενούς εδάφους που περιέχει θαµµένα απορρίµµατα στην περιοχή του Monfalcone και στη χαρτογράφηση του αναγλύφου του υποβάθρου της βιοµηχανικής περιοχής του Porto Petroli. Συµπερασµατικά, η µεθοδολογία αυτή αποτελεί ένα χρήσιµο εργαλείο για την αντιµετώπιση περιβαλλοντικών προβληµάτων συνεισφέροντας στην χαρτογράφηση του υπεδάφους µέσω του προσδιορισµού της ταχύτητας των S κυµάτων. ΕΥΧΑΡΙΣΤΙΕΣ Οι συγγραφείς θα ήθελαν να ευχαριστήσουν την Ευρωπαϊκή Ενωση για την οικονοµική υποστήριξη µέσω του προγράµµατος EVKA-CT21-46-HYGEIA (HYbrid Geophysical technology for the Evaluation of Insidious contaminated Areas). 1242
10 ΑΝΑΦΟΡΕΣ Κρητικάκης Σ.Γ. 21. Εκτίµηση της ταχύτητας των εγκαρσίων σεισµικών κυµάτων και των δυναµικών µηχανικών παραµέτρων από καταγραφές επιφανειακών κυµάτων Rayleigh. Μεταπτυχιακή εργασία, Πολυτεχνείο Κρήτης, 177σ. Ραπτάκης Συµβολή στον προσδιορισµό της γεωµετρίας και των δυναµικών ιδιοτήτων των εδαφικών σχηµατισµών και στη σεισµική απόκριση τους. ιδακτορική διατριβή, Πολυτεχνική σχολή Α.Π.Θ. Haskell N.A The dispersion of surface waves in multi-layered media. Bulletin of Seismological Society of America, 43, Marquardt D.W An algorithm for least squares estimation of nonlinear parameters. J. Soc. Indus. Appl. Math., 2, McMechan G.A. & Yedlin M.J Analysis of dispersive waves by wave field transformation. Geophysics, 46, Miller R.D. & Xia J Using MASW to Map Bedrock in Oathle, Kansas, Open file report No Harding Lawson Associates, Lee s Summit, Missouri. Miller R.D., Xia J., Park C.B. & Ivanov J.M Multichannel analysis of surface waves to map bedrock. The Leading Edge, 18(12), Misiek R Surface waves: Application to lithostructural interpretation of near-surface layers in the meter and decameter range, Ph. D. Thesis (unpubl.), University of Ruhr, Bochum. p.19. Nazarian S In situ determination of elastic moduli of soil deposits and pavement system by spectralanalysis-of-surface-waves method. Ph. D. Thesis (unpubl.), University of Texas. Park B.C., Miller D.R. & Xia J Multichannel analysis of surface waves. Geophysics, 64(3), Press W.H., Teukosky S.A., Vetterling W.T. & Flannery B.P Numerical Recipes in Fortran, 2 nd Edition, Cambridge University Press. Schwab F. & Knopoff L Fast surface wave and free mode computations. in Bolt B.A. Edition, Methods in computational physics, Academic Press, Stokoe II K.H., Wright G.W., Bay J.A. & Roesset J.M Characterization of geotechnical sites by SASW method, in Woods R.D. Edition, Geophysical characterization of sites, Oxford Publishers. Xia J., Miller R.D. & Park C.B Estimation of near-surface shear-wave velocity by inversion of Rayleigh waves. Geophysics, 64(3), Yilmaz O Seismic data processing, in Doherty M.S. Edition, Investigations in Geophysics, 2, Society of Exploration Geophysicists. ABSTRACT RAYLEIGH SURFACE WAVE ANALYSIS AND APPLICATION AT THE MONFALCONE LANDFILL, AND AT THE INDUSTRIAL AREA OF PORTO PETROLI, GENOA, NORTHERN ITALY Kritikakis S. G. 1, Vafidis Α. 1, Gourry J. C. 2 1 Applied Geophysics Lab, Department of Mineral Resources Engineering, Technical University of Crete, 731, Polytechnioupolis, Chania, gkritik@mred.tuc.gr, vafidis@mred.tuc.gr 2 BRGM Development Planning and Natural sks Division, Orléans, France, jc.gourry@brgm.fr During the last few years, the dispersion of Rayleigh surface waves has been intensively studied as an alternative to contemporary geotechnical and environmental geophysical techniques. Nowadays, Rayleigh surface wave analysis (SASW, MASW) is widely used for the determination of S-wave velocity distribution with depth. This work aims to the description of the Rayleigh surface wave analysis methodology as well as to the presentation of its application on seismic data from geophysical surveys, carried out for the purposes of the HYGEIA European project, in two polluted areas: a) In the area of Monfalcone, northern Italy and b) in the industrial area of Porto Petroli, Genoa. Rayleigh surface wave analysis proved very useful in locating the lateral and vertical extent of the heterogeneous soil in Monfalcone and in mapping the bedrock relief in Porto Petroli through S- wave velocity determination. 1243
Εκτίμηση Ταχυτήτων Διάδοσης Εγκάρσιου Κύματος από Καταγραφές Επιφανειακών Κυμάτων Rayleigh
 Τεχν. Χρον. Επιστ. Έκδ. ΤΕΕ, Ι, τεύχ. 2-3 24, Tech. Chron. Sci. J. TCG, I, No 2-3 97 Εκτίμηση Ταχυτήτων Διάδοσης Εγκάρσιου Κύματος από Καταγραφές Επιφανειακών Κυμάτων Rayleigh Γ. Σ. ΚΡΗΤΙΚΑΚΗΣ Α. ΒΑΦΕΙΔΗΣ
Τεχν. Χρον. Επιστ. Έκδ. ΤΕΕ, Ι, τεύχ. 2-3 24, Tech. Chron. Sci. J. TCG, I, No 2-3 97 Εκτίμηση Ταχυτήτων Διάδοσης Εγκάρσιου Κύματος από Καταγραφές Επιφανειακών Κυμάτων Rayleigh Γ. Σ. ΚΡΗΤΙΚΑΚΗΣ Α. ΒΑΦΕΙΔΗΣ
Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο Κ Ρ Η Τ Η Σ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΡΥΚΤΩΝ ΠΟΡΩΝ Εργαστήριο Εφαρμοσμένης Γεωφυσικής
 Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο Κ Ρ Η Τ Η Σ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΡΥΚΤΩΝ ΠΟΡΩΝ Εργαστήριο Εφαρμοσμένης Γεωφυσικής ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΓΕΩΦΥΣΙΚΗ ΔΙΑΣΚΟΠΗΣΗ ΜΕ ΤΗ ΜΕΘΟΔΟ ΤΗΣ ΣΕΙΣΜΙΚΗΣ ΤΟΜΟΓΡΑΦΙΑΣ ΓΙΑ ΤΗΝ ΔΗΜΙΟΥΡΓΙΑ ΥΠΟΓΕΙΟΥ
Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο Κ Ρ Η Τ Η Σ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΡΥΚΤΩΝ ΠΟΡΩΝ Εργαστήριο Εφαρμοσμένης Γεωφυσικής ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΓΕΩΦΥΣΙΚΗ ΔΙΑΣΚΟΠΗΣΗ ΜΕ ΤΗ ΜΕΘΟΔΟ ΤΗΣ ΣΕΙΣΜΙΚΗΣ ΤΟΜΟΓΡΑΦΙΑΣ ΓΙΑ ΤΗΝ ΔΗΜΙΟΥΡΓΙΑ ΥΠΟΓΕΙΟΥ
Παραμετρική ανάλυση του συντελεστή ανάκλασης από στρωματοποιημένο πυθμένα δύο στρωμάτων με επικλινή διεπιφάνεια 1
 4 93 Παραμετρική ανάλυση του συντελεστή ανάκλασης από στρωματοποιημένο πυθμένα δύο στρωμάτων με επικλινή διεπιφάνεια Π. Παπαδάκης,a, Γ. Πιπεράκης,b & Μ. Καλογεράκης,,c Ινστιτούτο Υπολογιστικών Μαθηματικών
4 93 Παραμετρική ανάλυση του συντελεστή ανάκλασης από στρωματοποιημένο πυθμένα δύο στρωμάτων με επικλινή διεπιφάνεια Π. Παπαδάκης,a, Γ. Πιπεράκης,b & Μ. Καλογεράκης,,c Ινστιτούτο Υπολογιστικών Μαθηματικών
Η ΣΥΜΒΟΛΗ ΤΗΣ ΣΕΙΣΜΙΚΗΣ ΑΝΑΚΛΑΣΗΣ ΣΤΗΝ ΑΝΑΖΗΤΗΣΗ ΚΟΙΤΑΣΜΑΤΩΝ Υ ΡΟΓΟΝΑΝΘΡΑΚΩΝ
 Η ΣΥΜΒΟΛΗ ΤΗΣ ΣΕΙΣΜΙΚΗΣ ΑΝΑΚΛΑΣΗΣ ΣΤΗΝ ΑΝΑΖΗΤΗΣΗ ΚΟΙΤΑΣΜΑΤΩΝ Υ ΡΟΓΟΝΑΝΘΡΑΚΩΝ Αντώνης Βαφείδης Εργαστήριο Εφαρµοσµένης Γεωφυσικής Τµήµα Μηχανικών Ορυκτών Πόρων, Πολυτεχνείο Κρήτης Χανιά. Μέλος της Εθνικής
Η ΣΥΜΒΟΛΗ ΤΗΣ ΣΕΙΣΜΙΚΗΣ ΑΝΑΚΛΑΣΗΣ ΣΤΗΝ ΑΝΑΖΗΤΗΣΗ ΚΟΙΤΑΣΜΑΤΩΝ Υ ΡΟΓΟΝΑΝΘΡΑΚΩΝ Αντώνης Βαφείδης Εργαστήριο Εφαρµοσµένης Γεωφυσικής Τµήµα Μηχανικών Ορυκτών Πόρων, Πολυτεχνείο Κρήτης Χανιά. Μέλος της Εθνικής
Συμπεράσματα Κεφάλαιο 7.
 7. ΣΥΜΠΕΡΑΣΜΑΤΑ Ο κύριος στόχος της παρούσας διατριβής ήταν η προσομοίωση της σεισμικής κίνησης με τη χρήση τρισδιάστατων προσομοιωμάτων για τους εδαφικούς σχηματισμούς της ευρύτερης περιοχής της Θεσσαλονίκης.
7. ΣΥΜΠΕΡΑΣΜΑΤΑ Ο κύριος στόχος της παρούσας διατριβής ήταν η προσομοίωση της σεισμικής κίνησης με τη χρήση τρισδιάστατων προσομοιωμάτων για τους εδαφικούς σχηματισμούς της ευρύτερης περιοχής της Θεσσαλονίκης.
ΕΦΑΡΜΟΓΗ ΓΕΩΦΥΣΙΚΩΝ ΜΕΘΟ ΩΝ ΜΕ ΤΗΝ ΧΡΗΣΗ ΜΗΧΑΝΗΜΑΤΩΝ ΥΨΗΛΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΓΙΑ ΤΗΝ ΕΞΑΚΡΙΒΩΣΗ ΤΩΝ ΣΥΝΘΗΚΩΝ ΥΠΕ ΑΦΟΥΣ ΣΕ ΤΕΧΝΙΚΑ ΕΡΓΑ
 Page: 1 Αθήνα Απρίλιος 2016 ΕΦΑΡΜΟΓΗ ΓΕΩΦΥΣΙΚΩΝ ΜΕΘΟ ΩΝ ΜΕ ΤΗΝ ΧΡΗΣΗ ΜΗΧΑΝΗΜΑΤΩΝ ΥΨΗΛΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΓΙΑ ΤΗΝ ΕΞΑΚΡΙΒΩΣΗ ΤΩΝ ΣΥΝΘΗΚΩΝ ΥΠΕ ΑΦΟΥΣ ΣΕ ΤΕΧΝΙΚΑ ΕΡΓΑ Κατά την εφαρµογή της µεθοδολογίας αυτής επιτυγχάνεται
Page: 1 Αθήνα Απρίλιος 2016 ΕΦΑΡΜΟΓΗ ΓΕΩΦΥΣΙΚΩΝ ΜΕΘΟ ΩΝ ΜΕ ΤΗΝ ΧΡΗΣΗ ΜΗΧΑΝΗΜΑΤΩΝ ΥΨΗΛΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΓΙΑ ΤΗΝ ΕΞΑΚΡΙΒΩΣΗ ΤΩΝ ΣΥΝΘΗΚΩΝ ΥΠΕ ΑΦΟΥΣ ΣΕ ΤΕΧΝΙΚΑ ΕΡΓΑ Κατά την εφαρµογή της µεθοδολογίας αυτής επιτυγχάνεται
Εσωτερικού της Γης. Κεφάλαιο 2. Αναστασία Α Κυρατζή Τοµέας Γεωφυσικής. Κυρατζή Α.. "Φυσική" της Λιθόσφαιρας" 1
 οµή και Σύσταση του Εσωτερικού της Γης Μάθηµα: Φυσική της Λιθόσφαιρας Κεφάλαιο 2 Αναστασία Α Κυρατζή Τοµέας Γεωφυσικής της Λιθόσφαιρας" 1 Μάθηµα 1 ο Εισαγωγή Ορισµοί Ελαστικά κύµατα Ταχύτητες ιδιότητες
οµή και Σύσταση του Εσωτερικού της Γης Μάθηµα: Φυσική της Λιθόσφαιρας Κεφάλαιο 2 Αναστασία Α Κυρατζή Τοµέας Γεωφυσικής της Λιθόσφαιρας" 1 Μάθηµα 1 ο Εισαγωγή Ορισµοί Ελαστικά κύµατα Ταχύτητες ιδιότητες
ΣΕΙΣΜΙΚΗ ΤΟΜΟΓΡΑΦΙΑ ΣΤΟ ΤΜΗΜΑ ΛΥΓΑΡΙΑ-ΠΕΡΙΒΟΛΙ ΤΟΥ ΟΔΙΚΟΥ ΑΞΟΝΑ Ε65
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΡΥΚΤΩΝ ΠΟΡΩΝ ΤΟΜΕΑΣ ΑΝΙΧΝΕΥΣΗΣ ΚΑΙ ΕΝΤΟΠΙΣΜΟΥ ΟΡΥΚΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΓΕΩΦΥΣΙΚΗΣ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΣΕΙΣΜΙΚΗ ΤΟΜΟΓΡΑΦΙΑ ΣΤΟ ΤΜΗΜΑ ΛΥΓΑΡΙΑ-ΠΕΡΙΒΟΛΙ ΤΟΥ ΟΔΙΚΟΥ
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΡΥΚΤΩΝ ΠΟΡΩΝ ΤΟΜΕΑΣ ΑΝΙΧΝΕΥΣΗΣ ΚΑΙ ΕΝΤΟΠΙΣΜΟΥ ΟΡΥΚΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΓΕΩΦΥΣΙΚΗΣ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΣΕΙΣΜΙΚΗ ΤΟΜΟΓΡΑΦΙΑ ΣΤΟ ΤΜΗΜΑ ΛΥΓΑΡΙΑ-ΠΕΡΙΒΟΛΙ ΤΟΥ ΟΔΙΚΟΥ
ΕΠΙΦΑΝΕΙΑΚΑ ΚΥΜΑΤΑ: ΕΦΑΡΜΟΓΕΣ ΣΕ ΠΕΡΙΒΑΛΛΟΝΤΙΚΑ ΚΑΙ ΓΕΩΤΕΧΝΙΚΑ ΠΡΟΒΛΗΜΑΤΑ
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΡΥΚΤΩΝ ΠΟΡΩΝ ΤΟΜΕΑΣ ΑΝΙΧΝΕΥΣΗΣ ΚΑΙ ΕΝΤΟΠΙΣΜΟΥ ΟΡΥΚΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΓΕΩΦΥΣΙΚΗΣ ΔΙΔΑΚΤΟΡΙΚΗ ΔΙΑΤΡΙΒΗ ΕΠΙΦΑΝΕΙΑΚΑ ΚΥΜΑΤΑ: ΕΦΑΡΜΟΓΕΣ ΣΕ ΠΕΡΙΒΑΛΛΟΝΤΙΚΑ ΚΑΙ ΓΕΩΤΕΧΝΙΚΑ
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΡΥΚΤΩΝ ΠΟΡΩΝ ΤΟΜΕΑΣ ΑΝΙΧΝΕΥΣΗΣ ΚΑΙ ΕΝΤΟΠΙΣΜΟΥ ΟΡΥΚΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΓΕΩΦΥΣΙΚΗΣ ΔΙΔΑΚΤΟΡΙΚΗ ΔΙΑΤΡΙΒΗ ΕΠΙΦΑΝΕΙΑΚΑ ΚΥΜΑΤΑ: ΕΦΑΡΜΟΓΕΣ ΣΕ ΠΕΡΙΒΑΛΛΟΝΤΙΚΑ ΚΑΙ ΓΕΩΤΕΧΝΙΚΑ
ΕΦΑΡΜΟΣΜΕΝΗ ΓΕΩΦΥΣΙΚΗ ΣΕΙΣΜΙΚΗ ΔΙΑΣΚΟΠΗΣΗ
 ΕΦΑΡΜΟΣΜΕΝΗ ΓΕΩΦΥΣΙΚΗ ΣΕΙΣΜΙΚΗ ΔΙΑΣΚΟΠΗΣΗ ΕΙΣΑΓΩΓΗ ΑΝΤΙΚΕΙΜΕΝΟ Μελέτη της δομής των επιφανειακών στρωμάτων του φλοιού της Γης ΣΚΟΠΟΣ Εντοπισμός Γεωλογικών δομών οικονομικής σημασίας και ανίχνευση γεωλογικών
ΕΦΑΡΜΟΣΜΕΝΗ ΓΕΩΦΥΣΙΚΗ ΣΕΙΣΜΙΚΗ ΔΙΑΣΚΟΠΗΣΗ ΕΙΣΑΓΩΓΗ ΑΝΤΙΚΕΙΜΕΝΟ Μελέτη της δομής των επιφανειακών στρωμάτων του φλοιού της Γης ΣΚΟΠΟΣ Εντοπισμός Γεωλογικών δομών οικονομικής σημασίας και ανίχνευση γεωλογικών
Τι είναι η ΓΕΩΦΥΣΙΚΗ
 ΑΣΚΗΣΗ ΠΡΑΞΗ Τι είναι η ΓΕΩΦΥΣΙΚΗ Γεωφυσική Έρευνα Κάθε γεωφυσική έρευνα έχει στόχο τον εντοπισμό και την μελέτη των ιδιοτήτων των υπόγειων στρωμάτων, ή/και τον εντοπισμό και τη μελέτη ανωμαλιών στο υπέδαφος,
ΑΣΚΗΣΗ ΠΡΑΞΗ Τι είναι η ΓΕΩΦΥΣΙΚΗ Γεωφυσική Έρευνα Κάθε γεωφυσική έρευνα έχει στόχο τον εντοπισμό και την μελέτη των ιδιοτήτων των υπόγειων στρωμάτων, ή/και τον εντοπισμό και τη μελέτη ανωμαλιών στο υπέδαφος,
ΕΠΙΦΑΝΕΙΑΚΑ ΚΥΜΑΤΑ (Κύματα στην Επιφάνεια Υγρού Θαλάσσια Κύματα)
 ΕΠΙΦΑΝΕΙΑΚΑ ΚΥΜΑΤΑ (Κύματα στην Επιφάνεια Υγρού Θαλάσσια Κύματα) Εκτός από τα εγκάρσια και τα διαμήκη κύματα υπάρχουν και τα επιφανειακά κύματα τα οποία συνδυάζουν τα χαρακτηριστικά των δυο προαναφερθέντων
ΕΠΙΦΑΝΕΙΑΚΑ ΚΥΜΑΤΑ (Κύματα στην Επιφάνεια Υγρού Θαλάσσια Κύματα) Εκτός από τα εγκάρσια και τα διαμήκη κύματα υπάρχουν και τα επιφανειακά κύματα τα οποία συνδυάζουν τα χαρακτηριστικά των δυο προαναφερθέντων
ΕΛΕΓΧΟΣ ΠΑΡΑΓΩΓΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΛΕΓΧΟΣ ΠΑΡΑΓΩΓΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Ενότητα: Αναγνώριση Διεργασίας - Προσαρμοστικός Έλεγχος (Process Identification) Αλαφοδήμος Κωνσταντίνος
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΛΕΓΧΟΣ ΠΑΡΑΓΩΓΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Ενότητα: Αναγνώριση Διεργασίας - Προσαρμοστικός Έλεγχος (Process Identification) Αλαφοδήμος Κωνσταντίνος
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα. ΔΙΑΛΕΞΗ 21 Κυματική ΦΥΣ102 1
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 21 Κυματική ΦΥΣ102 1 Χαρακτηριστικά Διάδοσης Κύματος Όλα τα κύματα μεταφέρουν ενέργεια.
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 21 Κυματική ΦΥΣ102 1 Χαρακτηριστικά Διάδοσης Κύματος Όλα τα κύματα μεταφέρουν ενέργεια.
Συνδυαστική Εφαρµογή Γεωφυσικών και Εργαστηριακών Μετρήσεων για την Εκτίµηση του Μέτρου Ακαµψίας Μαργαϊκού Σχηµατισµού
 Συνδυαστική Εφαρµογή Γεωφυσικών και Εργαστηριακών Μετρήσεων για την Εκτίµηση του Μέτρου Ακαµψίας Μαργαϊκού Σχηµατισµού Application of Geophysical and Laboratory Methods for the Determination of the Stiffness
Συνδυαστική Εφαρµογή Γεωφυσικών και Εργαστηριακών Μετρήσεων για την Εκτίµηση του Μέτρου Ακαµψίας Μαργαϊκού Σχηµατισµού Application of Geophysical and Laboratory Methods for the Determination of the Stiffness
ΑΣΚΗΣΗ ΠΡΑΞΗ Κεφάλαιο 3 ο
 ΑΣΚΗΣΗ ΠΡΑΞΗ Κεφάλαιο 3 ο Μέθοδος σεισμικής ανάκλασης Παραγωγή ελαστικών κυμάτων τεχνητά στην επιφάνεια της γης Ανάκλαση των κυμάτων πάνω σε ασυνέχειες μέσα στο φλοιό της γης Καταγραφή των απευθείας και
ΑΣΚΗΣΗ ΠΡΑΞΗ Κεφάλαιο 3 ο Μέθοδος σεισμικής ανάκλασης Παραγωγή ελαστικών κυμάτων τεχνητά στην επιφάνεια της γης Ανάκλαση των κυμάτων πάνω σε ασυνέχειες μέσα στο φλοιό της γης Καταγραφή των απευθείας και
Διδακτορική Διατριβή Α : Αριθμητική προσομοίωση της τρισδιάστατης τυρβώδους ροής θραυομένων κυμάτων στην παράκτια ζώνη απόσβεσης
 Διδακτορική Διατριβή Α : Αριθμητική προσομοίωση της τρισδιάστατης τυρβώδους ροής θραυομένων κυμάτων στην παράκτια ζώνη απόσβεσης Στη διδακτορική διατριβή παρουσιάζεται η αριθμητική μέθοδος προσομοίωσης
Διδακτορική Διατριβή Α : Αριθμητική προσομοίωση της τρισδιάστατης τυρβώδους ροής θραυομένων κυμάτων στην παράκτια ζώνη απόσβεσης Στη διδακτορική διατριβή παρουσιάζεται η αριθμητική μέθοδος προσομοίωσης
Αναγνώριση Προτύπων Ι
 Αναγνώριση Προτύπων Ι Ενότητα 1: Μέθοδοι Αναγνώρισης Προτύπων Αν. Καθηγητής Δερματάς Ευάγγελος Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Αναγνώριση Προτύπων Ι Ενότητα 1: Μέθοδοι Αναγνώρισης Προτύπων Αν. Καθηγητής Δερματάς Ευάγγελος Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Τεχνικές Μείωσης Διαστάσεων. Ειδικά θέματα ψηφιακής επεξεργασίας σήματος και εικόνας Σ. Φωτόπουλος- Α. Μακεδόνας
 Τεχνικές Μείωσης Διαστάσεων Ειδικά θέματα ψηφιακής επεξεργασίας σήματος και εικόνας Σ. Φωτόπουλος- Α. Μακεδόνας 1 Εισαγωγή Το μεγαλύτερο μέρος των δεδομένων που καλούμαστε να επεξεργαστούμε είναι πολυδιάστατα.
Τεχνικές Μείωσης Διαστάσεων Ειδικά θέματα ψηφιακής επεξεργασίας σήματος και εικόνας Σ. Φωτόπουλος- Α. Μακεδόνας 1 Εισαγωγή Το μεγαλύτερο μέρος των δεδομένων που καλούμαστε να επεξεργαστούμε είναι πολυδιάστατα.
Ν. Σαμπατακάκης Αν. Καθηγητής Εργαστήριο Τεχνικής Γεωλογίας Παν/μιο Πατρών
 ΚΕΦΑΛΑΙΟ 6 ΥΝΑΜΙΚΗ ΤΩΝ Ε ΑΦΩΝ - ΓΕΩΤΕΧΝΙΚΗ ΣΕΙΣΜΙΚΗ ΜΗΧΑΝΙΚΗ Με τον όρο «δυναμική» εννοείται η συμπεριφορά που παρουσιάζει το έδαφος υπό την επίδραση δυναμικών τάσεων που επιβάλλονται σε αυτό είδη δυναμικών
ΚΕΦΑΛΑΙΟ 6 ΥΝΑΜΙΚΗ ΤΩΝ Ε ΑΦΩΝ - ΓΕΩΤΕΧΝΙΚΗ ΣΕΙΣΜΙΚΗ ΜΗΧΑΝΙΚΗ Με τον όρο «δυναμική» εννοείται η συμπεριφορά που παρουσιάζει το έδαφος υπό την επίδραση δυναμικών τάσεων που επιβάλλονται σε αυτό είδη δυναμικών
ΑΝΩΤΑΤΗ ΣΧΟΛΗ ΠΑΙ ΑΓΩΓΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΕΚΠΑΙ ΕΥΣΗΣ (Α.Σ.ΠΑΙ.Τ.Ε.)
 ΑΝΩΤΑΤΗ ΣΧΟΛΗ ΠΑΙ ΑΓΩΓΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΕΚΠΑΙ ΕΥΣΗΣ (Α.Σ.ΠΑΙ.Τ.Ε.) «Αρχιμήδης ΙΙΙ Ενίσχυση Ερευνητικών ομάδων στην Α.Σ.ΠΑΙ.Τ.Ε.» Υποέργο: 05 Τίτλος: «ΣΥΓΚΡΙΤΙΚΗ ΑΞΙΟΛΟΓΗΣΗ ΑΠΟΤΕΛΕΣΜΑΤΩΝ ΕΠΙΦΑΝΕΙΑΚΩΝ
ΑΝΩΤΑΤΗ ΣΧΟΛΗ ΠΑΙ ΑΓΩΓΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΕΚΠΑΙ ΕΥΣΗΣ (Α.Σ.ΠΑΙ.Τ.Ε.) «Αρχιμήδης ΙΙΙ Ενίσχυση Ερευνητικών ομάδων στην Α.Σ.ΠΑΙ.Τ.Ε.» Υποέργο: 05 Τίτλος: «ΣΥΓΚΡΙΤΙΚΗ ΑΞΙΟΛΟΓΗΣΗ ΑΠΟΤΕΛΕΣΜΑΤΩΝ ΕΠΙΦΑΝΕΙΑΚΩΝ
Α Ρ Ι Σ Τ Ο Τ Ε Λ Ε Ι Ο Π Α Ν Ε Π Ι Σ Τ Η Μ Ι Ο Θ Ε Σ Σ Α Λ Ο Ν Ι Κ Η Σ
 Α Ρ Ι Σ Τ Ο Τ Ε Λ Ε Ι Ο Π Α Ν Ε Π Ι Σ Τ Η Μ Ι Ο Θ Ε Σ Σ Α Λ Ο Ν Ι Κ Η Σ ΤΜΗΜΑ ΓΕΩΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΙΚΗΣ ΓΕΩΛΟΓΙΑΣ ΜΑΘΗΜΑ: ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ ΕΞΑΜΗΝΟ: 7 ο ΔΙΔΑΣΚΟΝΤΕΣ: Β. ΧΡΗΣΤΑΡΑΣ, Καθηγητής Β. ΜΑΡΙΝΟΣ,
Α Ρ Ι Σ Τ Ο Τ Ε Λ Ε Ι Ο Π Α Ν Ε Π Ι Σ Τ Η Μ Ι Ο Θ Ε Σ Σ Α Λ Ο Ν Ι Κ Η Σ ΤΜΗΜΑ ΓΕΩΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΙΚΗΣ ΓΕΩΛΟΓΙΑΣ ΜΑΘΗΜΑ: ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ ΕΞΑΜΗΝΟ: 7 ο ΔΙΔΑΣΚΟΝΤΕΣ: Β. ΧΡΗΣΤΑΡΑΣ, Καθηγητής Β. ΜΑΡΙΝΟΣ,
ΔΙΑΧΕΙΡΙΣΗ ΠΕΡΙΒΑΛΛΟΝΤΟΣ και ΚΛΙΜΑΤΙΚΗ ΑΛΛΑΓΗ. Περιβαλλοντική & Τεχνική Γεωφυσική
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΓΕΩΛΟΓΙΑΣ ΚΑΙ ΓΕΩΠΕΡΙΒΑΛΛΟΝΤΟΣ ΤΟΜΕΑΣ ΓΕΩΦΥΣΙΚΗΣ & ΓΕΩΘΕΡΜΙΑΣ Τ.Ε.Ι. ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Π.Μ.Σ. Σύγχρονες Τεχνολογίες Έργων Διαχ/σης
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΓΕΩΛΟΓΙΑΣ ΚΑΙ ΓΕΩΠΕΡΙΒΑΛΛΟΝΤΟΣ ΤΟΜΕΑΣ ΓΕΩΦΥΣΙΚΗΣ & ΓΕΩΘΕΡΜΙΑΣ Τ.Ε.Ι. ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Π.Μ.Σ. Σύγχρονες Τεχνολογίες Έργων Διαχ/σης
Συνδυαστική Εφαρμογή Γεωφυσικών και Εργαστηριακών Μετρήσεων για τον Προσδιορισμό του Μέτρου Ακαμψίας Μαργαϊκού Σχηματισμού
 Τεχν. Χρον. Επιστ. Έκδ. ΤΕΕ, V, τεύχ. 1-2 2005, Tech. Chron. Sci. J. TCG, V, No 1-2 73 Συνδυαστική Εφαρμογή Γεωφυσικών και Εργαστηριακών Μετρήσεων για τον Προσδιορισμό του Μέτρου Ακαμψίας Μαργαϊκού Σχηματισμού
Τεχν. Χρον. Επιστ. Έκδ. ΤΕΕ, V, τεύχ. 1-2 2005, Tech. Chron. Sci. J. TCG, V, No 1-2 73 Συνδυαστική Εφαρμογή Γεωφυσικών και Εργαστηριακών Μετρήσεων για τον Προσδιορισμό του Μέτρου Ακαμψίας Μαργαϊκού Σχηματισμού
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 η & 2 η : ΟΡΙΑΚΟ ΣΤΡΩΜΑ
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 η & 2 η : ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 η & 2 η : ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού
ΚΩΝΣΤΑΝΤΙΝΟΣ Σ. ΠΟΛΙΤΗΣ Διπλ. Φυσικός Πανεπιστημίου Πατρών Υποψήφιος Διδάκτωρ Ε.Μ.Π. ΒΙΟΓΡΑΦΙΚΟ ΣΗΜΕΙΩΜΑ
 ΚΩΝΣΤΑΝΤΙΝΟΣ Σ. ΠΟΛΙΤΗΣ Διπλ. Φυσικός Πανεπιστημίου Πατρών Υποψήφιος Διδάκτωρ Ε.Μ.Π. ΒΙΟΓΡΑΦΙΚΟ ΣΗΜΕΙΩΜΑ 1. ΒΙΟΓΡΑΦΙΚΑ ΣΤΟΙΧΕΙΑ 1.1 ΠΡΟΣΩΠΙΚΑ ΣΤΟΙΧΕΙΑ Επώνυμο ΠΟΛΙΤΗΣ Όνομα Όνομα πατρός Διεύθυνση Ηλ. διεύθυνση
ΚΩΝΣΤΑΝΤΙΝΟΣ Σ. ΠΟΛΙΤΗΣ Διπλ. Φυσικός Πανεπιστημίου Πατρών Υποψήφιος Διδάκτωρ Ε.Μ.Π. ΒΙΟΓΡΑΦΙΚΟ ΣΗΜΕΙΩΜΑ 1. ΒΙΟΓΡΑΦΙΚΑ ΣΤΟΙΧΕΙΑ 1.1 ΠΡΟΣΩΠΙΚΑ ΣΤΟΙΧΕΙΑ Επώνυμο ΠΟΛΙΤΗΣ Όνομα Όνομα πατρός Διεύθυνση Ηλ. διεύθυνση
ΤΕΧΝΟΛΟΓΙΑ ΜΗ ΚΑΤΑΣΤΡΟΦΙΚΟΥ ΕΛΕΓΧΟΥ ΘΕΩΡΙΑ ο ΜΑΘΗΜΑ
 ΤΕΧΝΟΛΟΓΙΑ ΜΗ ΚΑΤΑΣΤΡΟΦΙΚΟΥ ΕΛΕΓΧΟΥ ΘΕΩΡΙΑ 2017 7 ο ΜΑΘΗΜΑ Εισαγωγή Κύμα είναι η διάδοση των περιοδικών κινήσεων (ταλαντώσεων) που κάνουν τα στοιχειώδη σωματίδια ενός υλικού γύρω από τη θέση ισορροπίας
ΤΕΧΝΟΛΟΓΙΑ ΜΗ ΚΑΤΑΣΤΡΟΦΙΚΟΥ ΕΛΕΓΧΟΥ ΘΕΩΡΙΑ 2017 7 ο ΜΑΘΗΜΑ Εισαγωγή Κύμα είναι η διάδοση των περιοδικών κινήσεων (ταλαντώσεων) που κάνουν τα στοιχειώδη σωματίδια ενός υλικού γύρω από τη θέση ισορροπίας
Μέθοδος των γραμμών πόλωσης των εγκαρσίων κυμάτων
 Μέθοδος των γραμμών πόλωσης των εγκαρσίων κυμάτων Πρώτες αποκλίσεις των SH και SV κυμάτων καθορισμός των ορικών επιφανειών u V =0 και u H =0 Μειονέκτημα : η ανάλυση της πρώτης απόκλισης δεν είναι εύκολη
Μέθοδος των γραμμών πόλωσης των εγκαρσίων κυμάτων Πρώτες αποκλίσεις των SH και SV κυμάτων καθορισμός των ορικών επιφανειών u V =0 και u H =0 Μειονέκτημα : η ανάλυση της πρώτης απόκλισης δεν είναι εύκολη
Κεφάλαιο 15 Κίνηση Κυµάτων. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 15 Κίνηση Κυµάτων Περιεχόµενα Κεφαλαίου 15 Χαρακτηριστικά των Κυµάτων Είδη κυµάτων: Διαµήκη και Εγκάρσια Μεταφορά ενέργειας µε κύµατα Μαθηµατική Περιγραφή της Διάδοσης κυµάτων Η Εξίσωση του Κύµατος
Κεφάλαιο 15 Κίνηση Κυµάτων Περιεχόµενα Κεφαλαίου 15 Χαρακτηριστικά των Κυµάτων Είδη κυµάτων: Διαµήκη και Εγκάρσια Μεταφορά ενέργειας µε κύµατα Μαθηµατική Περιγραφή της Διάδοσης κυµάτων Η Εξίσωση του Κύµατος
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER
 4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
ΑΝΑΛΥΣΗ ΤΗΣ ΑΠΟΚΛΙΣΗΣ ΑΠΟ ΤΗΝ ΗΜΙΤΟΝΟΕΙΔΗ ΚΑΜΠΥΛΗ ΒΡΟΧΟΠΤΩΣΗΣ ΚΑΙ ΧΡΗΣΗ ΤΗΣ ΩΣ ΔΕΙΚΤΗ ΚΛΙΜΑΤΙΚΗΣ ΑΛΛΑΓΗΣ
 ΑΝΑΛΥΣΗ ΤΗΣ ΑΠΟΚΛΙΣΗΣ ΑΠΟ ΤΗΝ ΗΜΙΤΟΝΟΕΙΔΗ ΚΑΜΠΥΛΗ ΒΡΟΧΟΠΤΩΣΗΣ ΚΑΙ ΧΡΗΣΗ ΤΗΣ ΩΣ ΔΕΙΚΤΗ ΚΛΙΜΑΤΙΚΗΣ ΑΛΛΑΓΗΣ Καλύβας Θ., Ζέρβας Ε.¹ ¹ Σχολή Θετικών Επιστημών και Τεχνολογίας, Ελληνικό Ανοικτό Πανεπιστήμιο,
ΑΝΑΛΥΣΗ ΤΗΣ ΑΠΟΚΛΙΣΗΣ ΑΠΟ ΤΗΝ ΗΜΙΤΟΝΟΕΙΔΗ ΚΑΜΠΥΛΗ ΒΡΟΧΟΠΤΩΣΗΣ ΚΑΙ ΧΡΗΣΗ ΤΗΣ ΩΣ ΔΕΙΚΤΗ ΚΛΙΜΑΤΙΚΗΣ ΑΛΛΑΓΗΣ Καλύβας Θ., Ζέρβας Ε.¹ ¹ Σχολή Θετικών Επιστημών και Τεχνολογίας, Ελληνικό Ανοικτό Πανεπιστήμιο,
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΡΥΚΤΩΝ ΠΟΡΩΝ ΤΟΜΕΑΣ ΑΝΙΧΝΕΥΣΗΣ ΚΑΙ ΕΝΤΟΠΙΣΜΟΥ ΟΡΥΚΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΓΕΩΦΥΣΙΚΗΣ
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΡΥΚΤΩΝ ΠΟΡΩΝ ΤΟΜΕΑΣ ΑΝΙΧΝΕΥΣΗΣ ΚΑΙ ΕΝΤΟΠΙΣΜΟΥ ΟΡΥΚΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΓΕΩΦΥΣΙΚΗΣ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΣΕΙΣΜΙΚΗ ΔΙΑΣΚΟΠΗΣΗ ΣΤΟ ΟΙΚΟΠΕΔΟ ΤΟΥ ΠΑΛΑΙΟΥ ΕΡΓΟΣΤΑΣΙΟΥ
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΡΥΚΤΩΝ ΠΟΡΩΝ ΤΟΜΕΑΣ ΑΝΙΧΝΕΥΣΗΣ ΚΑΙ ΕΝΤΟΠΙΣΜΟΥ ΟΡΥΚΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΓΕΩΦΥΣΙΚΗΣ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΣΕΙΣΜΙΚΗ ΔΙΑΣΚΟΠΗΣΗ ΣΤΟ ΟΙΚΟΠΕΔΟ ΤΟΥ ΠΑΛΑΙΟΥ ΕΡΓΟΣΤΑΣΙΟΥ
Φαινόµενα ρευστοποίησης εδαφών στον Ελληνικό χώρο Κεφάλαιο 1
 1 ΚΕΦΑΛΑΙΟ ΕΙΣΑΓΩΓΗ 1.1 Εισαγωγικό σηµείωµα Η προκαλούµενη, κατά τη διάδοση των σεισµικών κυµάτων, εφαρµογή κυκλικών διατµητικών τάσεων οδηγεί τους κορεσµένους χαλαρούς αµµώδεις σχηµατισµούς σε συµπύκνωση.
1 ΚΕΦΑΛΑΙΟ ΕΙΣΑΓΩΓΗ 1.1 Εισαγωγικό σηµείωµα Η προκαλούµενη, κατά τη διάδοση των σεισµικών κυµάτων, εφαρµογή κυκλικών διατµητικών τάσεων οδηγεί τους κορεσµένους χαλαρούς αµµώδεις σχηµατισµούς σε συµπύκνωση.
ΓΕΩΦΥΣΙΚΗ ΙΑΣΚΟΠΗΣΗ ΣΤΟ ΟΡΟΠΕ ΙΟ ΤΟΥ ΟΜΑΛΟΥ, Ν. ΧΑΝΙΩΝ
 ελτίο της Ελληνικής Γεωλογικής Εταιρίας τοµ. XXXVI, 2004 Πρακτικά 10 ου ιεθνούς Συνεδρίου, Θεσ/νίκη Απρίλιος 2004 Bulletin of the Geological Society of Greece vol. XXXVI, 2004 Proceedings of the 10 th
ελτίο της Ελληνικής Γεωλογικής Εταιρίας τοµ. XXXVI, 2004 Πρακτικά 10 ου ιεθνούς Συνεδρίου, Θεσ/νίκη Απρίλιος 2004 Bulletin of the Geological Society of Greece vol. XXXVI, 2004 Proceedings of the 10 th
Κεφάλαιο 3 TΑΣΗ ΚΑΙ ΠΑΡΑΜΟΡΦΩΣΗ
 Κεφάλαιο 3 TΑΣΗ ΚΑΙ ΠΑΡΑΜΟΡΦΩΣΗ ΚΑΤΑ ΤΗΝ ΔΙΑΔΟΣΗ ΤΩΝ ΣΕΙΣΜΙΚΩΝ ΚΥΜΑΤΩΝ ΜΕΣΑ ΣΤΗ ΓΗ ΔΕΧΟΜΑΣΤΕ: ΟΤΙ ΤΟ ΥΛΙΚΟ ΔΙΑΔΟΣΗΣ ΕΧΕΙ ΑΠΟΛΥΤΑ ΕΛΑΣΤΙΚΕΣ ΙΔΙΟΤΗΤΕΣ ΔΕΧΟΜΑΣΤΕ ΜΕ ΑΛΛΑ ΛΟΓΙΑ ΟΤΙ ΤΑ ΣΕΙΣΜΙΚΑ ΚΥΜΑΤΑ ΕΙΝΑΙ
Κεφάλαιο 3 TΑΣΗ ΚΑΙ ΠΑΡΑΜΟΡΦΩΣΗ ΚΑΤΑ ΤΗΝ ΔΙΑΔΟΣΗ ΤΩΝ ΣΕΙΣΜΙΚΩΝ ΚΥΜΑΤΩΝ ΜΕΣΑ ΣΤΗ ΓΗ ΔΕΧΟΜΑΣΤΕ: ΟΤΙ ΤΟ ΥΛΙΚΟ ΔΙΑΔΟΣΗΣ ΕΧΕΙ ΑΠΟΛΥΤΑ ΕΛΑΣΤΙΚΕΣ ΙΔΙΟΤΗΤΕΣ ΔΕΧΟΜΑΣΤΕ ΜΕ ΑΛΛΑ ΛΟΓΙΑ ΟΤΙ ΤΑ ΣΕΙΣΜΙΚΑ ΚΥΜΑΤΑ ΕΙΝΑΙ
2. ΓΕΩΛΟΓΙΑ - ΝΕΟΤΕΚΤΟΝΙΚΗ
 2. 2.1 ΓΕΩΛΟΓΙΑ ΤΗΣ ΕΥΡΥΤΕΡΗΣ ΠΕΡΙΟΧΗΣ Στο κεφάλαιο αυτό παρουσιάζεται συνοπτικά το Γεωλογικό-Σεισμοτεκτονικό περιβάλλον της ευρύτερης περιοχής του Π.Σ. Βόλου - Ν.Ιωνίας. Η ευρύτερη περιοχή της πόλης του
2. 2.1 ΓΕΩΛΟΓΙΑ ΤΗΣ ΕΥΡΥΤΕΡΗΣ ΠΕΡΙΟΧΗΣ Στο κεφάλαιο αυτό παρουσιάζεται συνοπτικά το Γεωλογικό-Σεισμοτεκτονικό περιβάλλον της ευρύτερης περιοχής του Π.Σ. Βόλου - Ν.Ιωνίας. Η ευρύτερη περιοχή της πόλης του
1 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΕΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ
 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΕΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού Οριακού
η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΕΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού Οριακού
Κεφάλαιο 15 ΚίνησηΚυµάτων. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 15 ΚίνησηΚυµάτων ΠεριεχόµεναΚεφαλαίου 15 Χαρακτηριστικά Κυµατικής Είδη κυµάτων: ιαµήκη και Εγκάρσια Μεταφορά ενέργειας µε κύµατα Μαθηµατική Περιγραφή της ιάδοσης κυµάτων ΗΕξίσωσητουΚύµατος Κανόνας
Κεφάλαιο 15 ΚίνησηΚυµάτων ΠεριεχόµεναΚεφαλαίου 15 Χαρακτηριστικά Κυµατικής Είδη κυµάτων: ιαµήκη και Εγκάρσια Μεταφορά ενέργειας µε κύµατα Μαθηµατική Περιγραφή της ιάδοσης κυµάτων ΗΕξίσωσητουΚύµατος Κανόνας
Βασίλειος Μαχαιράς Πολιτικός Μηχανικός Ph.D.
 Βασίλειος Μαχαιράς Πολιτικός Μηχανικός Ph.D. Μη γραμμικός προγραμματισμός: μέθοδοι μονοδιάστατης ελαχιστοποίησης Πανεπιστήμιο Θεσσαλίας Σχολή Θετικών Επιστημών ΤμήμαΠληροφορικής Διάλεξη 6 η /2017 Τι παρουσιάστηκε
Βασίλειος Μαχαιράς Πολιτικός Μηχανικός Ph.D. Μη γραμμικός προγραμματισμός: μέθοδοι μονοδιάστατης ελαχιστοποίησης Πανεπιστήμιο Θεσσαλίας Σχολή Θετικών Επιστημών ΤμήμαΠληροφορικής Διάλεξη 6 η /2017 Τι παρουσιάστηκε
max 0 Eκφράστε την διαφορά των δύο θετικών λύσεων ώς πολλαπλάσιο του ω 0, B . Αναλύοντας το Β σε σειρά άπειρων όρων ώς προς γ/ω 0 ( σειρά
 . Να αποδείξετε ότι σε ένα ταλαντούμενο σύστημα ενός βαθμού ελευθερίας, μάζας και σταθεράς ελατηρίου s με πολύ ασθενή απόσβεση (γω, όπου γ r/, r η σταθερά αντίστασης και s/ ) το πλήρες εύρος στο μισό του
. Να αποδείξετε ότι σε ένα ταλαντούμενο σύστημα ενός βαθμού ελευθερίας, μάζας και σταθεράς ελατηρίου s με πολύ ασθενή απόσβεση (γω, όπου γ r/, r η σταθερά αντίστασης και s/ ) το πλήρες εύρος στο μισό του
2-1 ΕΙΣΑΓΩΓΗ 2-2 ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ
 ΕΞΩΦΥΛΛΟ 43 Εικ. 2.1 Κύμα στην επιφάνεια της θάλασσας. 2-1 ΕΙΣΑΓΩΓΗ Η έννοια «κύμα», από τις πιο βασικές έννοιες της φυσικής, χρησιμοποιήθηκε για την περιγραφή φαινομένων που καλύπτουν ένα ευρύ φάσμα.
ΕΞΩΦΥΛΛΟ 43 Εικ. 2.1 Κύμα στην επιφάνεια της θάλασσας. 2-1 ΕΙΣΑΓΩΓΗ Η έννοια «κύμα», από τις πιο βασικές έννοιες της φυσικής, χρησιμοποιήθηκε για την περιγραφή φαινομένων που καλύπτουν ένα ευρύ φάσμα.
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 03-01-11 ΘΕΡΙΝΑ ΣΕΙΡΑ Β ΘΕΜΑ 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί
03-01-11 ΘΕΡΙΝΑ ΣΕΙΡΑ Β ΘΕΜΑ 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί
21 a 22 a 2n. a m1 a m2 a mn
 Παράρτημα Α Βασική γραμμική άλγεβρα Στην ενότητα αυτή θα παρουσιαστούν με συνοπτικό τρόπο βασικές έννοιες της γραμμικής άλγεβρας. Ο στόχος της ενότητας είναι να αποτελέσει ένα άμεσο σημείο αναφοράς και
Παράρτημα Α Βασική γραμμική άλγεβρα Στην ενότητα αυτή θα παρουσιαστούν με συνοπτικό τρόπο βασικές έννοιες της γραμμικής άλγεβρας. Ο στόχος της ενότητας είναι να αποτελέσει ένα άμεσο σημείο αναφοράς και
Δυναμική Μηχανών I. Ιδιομορφές
 Δυναμική Μηχανών I 6 2 Ιδιομορφές 2015 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com Απαγορεύεται οποιαδήποτε αναπαραγωγή χωρίς άδεια Περιεχόμενα Ιδιομορφές σε Συστήματα
Δυναμική Μηχανών I 6 2 Ιδιομορφές 2015 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com Απαγορεύεται οποιαδήποτε αναπαραγωγή χωρίς άδεια Περιεχόμενα Ιδιομορφές σε Συστήματα
Εφαρµογή της Μεθόδου SASW σε Κεκλιµένο Έδαφος Αριθµητική Προσοµοίωση και Παραµετρική ιερεύνηση Αξιοπιστίας
 Εφαρµογή της Μεθόδου SASW σε Κεκλιµένο Έδαφος Αριθµητική Προσοµοίωση και Παραµετρική ιερεύνηση Αξιοπιστίας Application of Spectral Analysis of Surface Waves (SASW) Method in Sloping Ground Numerical Simulation
Εφαρµογή της Μεθόδου SASW σε Κεκλιµένο Έδαφος Αριθµητική Προσοµοίωση και Παραµετρική ιερεύνηση Αξιοπιστίας Application of Spectral Analysis of Surface Waves (SASW) Method in Sloping Ground Numerical Simulation
Αντιστροφή των εδοµένων Πεδίου της Μεθόδου SASW Αριθµητική Προσοµοίωση και ιερεύνηση της Επίδρασης των Εδαφικών Συνθηκών
 Αντιστροφή των εδοµένων Πεδίου της Μεθόδου SASW Αριθµητική Προσοµοίωση και ιερεύνηση της Επίδρασης των Εδαφικών Συνθηκών Inversion of Field Data of the SASW Method Numerical Simulation and Investigation
Αντιστροφή των εδοµένων Πεδίου της Μεθόδου SASW Αριθµητική Προσοµοίωση και ιερεύνηση της Επίδρασης των Εδαφικών Συνθηκών Inversion of Field Data of the SASW Method Numerical Simulation and Investigation
Μικροζωνικές Μελέτες. Κεφάλαιο 24. Ε.Σώκος Εργαστήριο Σεισμολογίας Παν.Πατρών
 Μικροζωνικές Μελέτες Κεφάλαιο 24 Ε.Σώκος Εργαστήριο Σεισμολογίας Παν.Πατρών Ορισμός Με τον όρο μικροζωνική μελέτη εννοούμε την εκτίμηση των αναμενόμενων εδαφικών κινήσεων σε μία περιοχή λαμβάνοντας υπ
Μικροζωνικές Μελέτες Κεφάλαιο 24 Ε.Σώκος Εργαστήριο Σεισμολογίας Παν.Πατρών Ορισμός Με τον όρο μικροζωνική μελέτη εννοούμε την εκτίμηση των αναμενόμενων εδαφικών κινήσεων σε μία περιοχή λαμβάνοντας υπ
ΔΥΝΑΜΙΚΗ ΘΑΛΑΣΣΙΩΝ ΚΑΤΑΣΚΕΥΩΝ
 ΔΥΝΑΜΙΚΗ ΘΑΛΑΣΣΙΩΝ ΚΑΤΑΣΚΕΥΩΝ ΤΑΛΑΝΤΩΣΕΙΣ ΚΥΛΙΝΔΡΙΚΗΣ ΚΑΤΑΣΚΕΥΗΣ ΛΟΓΩ ΔΙΝΩΝ Γ. Σ. ΤΡΙΑΝΤΑΦYΛΛΟΥ ΚΑΘΗΓΗΤΗΣ ΕΜΠ Διατύπωση των εξισώσεων Θεωρούμε κύλινδρο διαμέτρου D, μήκους l, και μάζας m. Ο κύλινδρος συγκρατειται
ΔΥΝΑΜΙΚΗ ΘΑΛΑΣΣΙΩΝ ΚΑΤΑΣΚΕΥΩΝ ΤΑΛΑΝΤΩΣΕΙΣ ΚΥΛΙΝΔΡΙΚΗΣ ΚΑΤΑΣΚΕΥΗΣ ΛΟΓΩ ΔΙΝΩΝ Γ. Σ. ΤΡΙΑΝΤΑΦYΛΛΟΥ ΚΑΘΗΓΗΤΗΣ ΕΜΠ Διατύπωση των εξισώσεων Θεωρούμε κύλινδρο διαμέτρου D, μήκους l, και μάζας m. Ο κύλινδρος συγκρατειται
Σεισμικές παράμετροι. Κεφάλαιο 12
 Σεισμικές παράμετροι Κεφάλαιο 12 Σεισμικές παράμετροι Σεισμικό μέγεθος Σεισμική ενέργεια Σεισμική ροπή Σεισμική πτώση τάσης Σεισμικό μέγεθος Προέκυψε από την προσπάθεια εκτίμησης της εκλυόμενης ενέργειας.
Σεισμικές παράμετροι Κεφάλαιο 12 Σεισμικές παράμετροι Σεισμικό μέγεθος Σεισμική ενέργεια Σεισμική ροπή Σεισμική πτώση τάσης Σεισμικό μέγεθος Προέκυψε από την προσπάθεια εκτίμησης της εκλυόμενης ενέργειας.
ΘΕΩΡΙΑ ΜΗΧΑΝΙΚΩΝ ΤΑΛΑΝΤΩΣΕΩΝ ΚΑΙ ΕΛΑΣΤΙΚΑ ΚΥΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΘΕΩΡΙΑ ΜΗΧΑΝΙΚΩΝ ΤΑΛΑΝΤΩΣΕΩΝ ΚΑΙ ΕΛΑΣΤΙΚΑ ΚΥΜΑΤΑ Ενότητα 4: Ελαστικά Κύματα Σκορδύλης Εμμανουήλ Καθηγητής Σεισμολογίας, Τομέας Γεωφυσικής,
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΘΕΩΡΙΑ ΜΗΧΑΝΙΚΩΝ ΤΑΛΑΝΤΩΣΕΩΝ ΚΑΙ ΕΛΑΣΤΙΚΑ ΚΥΜΑΤΑ Ενότητα 4: Ελαστικά Κύματα Σκορδύλης Εμμανουήλ Καθηγητής Σεισμολογίας, Τομέας Γεωφυσικής,
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΟΡΥΚΤΩΝ ΠΟΡΩΝ
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΟΡΥΚΤΩΝ ΠΟΡΩΝ Πελαγία Σταμούλη ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Συμβολή της προσομοίωσης δεδομένων γεωραντάρ στην απεικόνιση υπόγειων δεξαμενών αποθήκευσης καυσίμων. ΕΞΕΤΑΣΤΙΚΗ ΕΠΙΤΡΟΠΗ
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΟΡΥΚΤΩΝ ΠΟΡΩΝ Πελαγία Σταμούλη ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Συμβολή της προσομοίωσης δεδομένων γεωραντάρ στην απεικόνιση υπόγειων δεξαμενών αποθήκευσης καυσίμων. ΕΞΕΤΑΣΤΙΚΗ ΕΠΙΤΡΟΠΗ
Q 12. c 3 Q 23. h 12 + h 23 + h 31 = 0 (6)
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών Τοµέας Υδατικών Πόρων Μάθηµα: Τυπικά Υδραυλικά Έργα Μέρος 2: ίκτυα διανοµής Άσκηση E0: Μαθηµατική διατύπωση µοντέλου επίλυσης απλού δικτύου διανοµής
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών Τοµέας Υδατικών Πόρων Μάθηµα: Τυπικά Υδραυλικά Έργα Μέρος 2: ίκτυα διανοµής Άσκηση E0: Μαθηµατική διατύπωση µοντέλου επίλυσης απλού δικτύου διανοµής
Επειδή η χορδή ταλαντώνεται µε την θεµελιώδη συχνότητα θα ισχύει. Όπου L είναι το µήκος της χορδής. Εποµένως, =2 0,635 m 245 Hz =311 m/s
 1. Μία χορδή κιθάρας µήκους 636 cm ρυθµίζεται ώστε να παράγει νότα συχνότητας 245 Hz, όταν ταλαντώνεται µε την θεµελιώδη συχνότητα. (a) Βρείτε την ταχύτητα των εγκαρσίων κυµάτων στην χορδή. (b) Αν η τάση
1. Μία χορδή κιθάρας µήκους 636 cm ρυθµίζεται ώστε να παράγει νότα συχνότητας 245 Hz, όταν ταλαντώνεται µε την θεµελιώδη συχνότητα. (a) Βρείτε την ταχύτητα των εγκαρσίων κυµάτων στην χορδή. (b) Αν η τάση
3.6 Μεικτά ορισμένα προβλήματα. 2. Γράφοµε τις ανωτέρω σχέσεις για q= 1,... Mσε διανυσµατική µορφή : G λ (3.30)
 . Γράφοµε τις ανωτέρω σχέσεις για q=,... Mσε διανυσµατική µορφή : = G λ (3.30) 3. Επειδή ισχύει παράλληλα και d = G, αντικαθιστώντας το από την 3.30 στην αρχική εξίσωση παίρνοµε : d= G G λ / (3.3) 4. Εάν
. Γράφοµε τις ανωτέρω σχέσεις για q=,... Mσε διανυσµατική µορφή : = G λ (3.30) 3. Επειδή ισχύει παράλληλα και d = G, αντικαθιστώντας το από την 3.30 στην αρχική εξίσωση παίρνοµε : d= G G λ / (3.3) 4. Εάν
ΘΕΜΑ Α ΕΡΩΤΗΣΕΙΣ ΘΕΜΑ Α
 ΘΕΜΑ Α 1. Να επιλέξετε τη σωστή απάντηση. Μηχανικό ονομάζεται το κύμα στο οποίο: α. Μεταφέρεται ύλη στον χώρο κατά την κατεύθυνση διάδοσης του κύματος. β. Μεταφέρεται ορμή και ενέργεια στον χώρο κατά την
ΘΕΜΑ Α 1. Να επιλέξετε τη σωστή απάντηση. Μηχανικό ονομάζεται το κύμα στο οποίο: α. Μεταφέρεται ύλη στον χώρο κατά την κατεύθυνση διάδοσης του κύματος. β. Μεταφέρεται ορμή και ενέργεια στον χώρο κατά την
Στο στάδιο ανάλυσης των αποτελεσµάτων: ανάλυση ευαισθησίας της λύσης, προσδιορισµός της σύγκρουσης των κριτηρίων.
 ΠΕΡΙΛΗΨΗ Η τεχνική αυτή έκθεση περιλαµβάνει αναλυτική περιγραφή των εναλλακτικών µεθόδων πολυκριτηριακής ανάλυσης που εξετάσθηκαν µε στόχο να επιλεγεί η µέθοδος εκείνη η οποία είναι η πιο κατάλληλη για
ΠΕΡΙΛΗΨΗ Η τεχνική αυτή έκθεση περιλαµβάνει αναλυτική περιγραφή των εναλλακτικών µεθόδων πολυκριτηριακής ανάλυσης που εξετάσθηκαν µε στόχο να επιλεγεί η µέθοδος εκείνη η οποία είναι η πιο κατάλληλη για
ΕΦΑΡΜΟΓΗ ΓΕΩΦΥΣΙΚΩΝ ΜΕΘΟ ΩΝ ΜΕ ΤΗΝ ΧΡΗΣΗ ΜΗΧΑΝΗΜΑΤΩΝ ΥΨΗΛΗΣ ΤΕΧΝΟΛΟΓΙΑΣ (ΓΕΩΡΑΝΤΑΡ) ΓΙΑ ΤΗΝ ΕΞΑΚΡΙΒΩΣΗ ΙΚΤΥΩΝ ΠΟΛΕΩΣ
 Page: 1 Αθήνα Απρίλιος 2016 ΕΦΑΡΜΟΓΗ ΓΕΩΦΥΣΙΚΩΝ ΜΕΘΟ ΩΝ ΜΕ ΤΗΝ ΧΡΗΣΗ ΜΗΧΑΝΗΜΑΤΩΝ ΥΨΗΛΗΣ ΤΕΧΝΟΛΟΓΙΑΣ (ΓΕΩΡΑΝΤΑΡ) ΓΙΑ ΤΗΝ ΕΞΑΚΡΙΒΩΣΗ ΙΚΤΥΩΝ ΠΟΛΕΩΣ Στόχος της έρευνας Στόχος της έρευνας είναι διερεύνηση των
Page: 1 Αθήνα Απρίλιος 2016 ΕΦΑΡΜΟΓΗ ΓΕΩΦΥΣΙΚΩΝ ΜΕΘΟ ΩΝ ΜΕ ΤΗΝ ΧΡΗΣΗ ΜΗΧΑΝΗΜΑΤΩΝ ΥΨΗΛΗΣ ΤΕΧΝΟΛΟΓΙΑΣ (ΓΕΩΡΑΝΤΑΡ) ΓΙΑ ΤΗΝ ΕΞΑΚΡΙΒΩΣΗ ΙΚΤΥΩΝ ΠΟΛΕΩΣ Στόχος της έρευνας Στόχος της έρευνας είναι διερεύνηση των
Συνθετικές εδαφικές κινήσεις Κεφ.22. Ε.Σώκος Εργαστήριο Σεισμολογίας Παν.Πατρών
 Συνθετικές εδαφικές κινήσεις Κεφ.22 Ε.Σώκος Εργαστήριο Σεισμολογίας Παν.Πατρών Συνθετικές εδαφικές κινήσεις Τι υπολογίζουμε από μια μελέτη σεισμικής επικινδυνότητας..? Μια πιθανολογική εκτίμηση των μέγιστων
Συνθετικές εδαφικές κινήσεις Κεφ.22 Ε.Σώκος Εργαστήριο Σεισμολογίας Παν.Πατρών Συνθετικές εδαφικές κινήσεις Τι υπολογίζουμε από μια μελέτη σεισμικής επικινδυνότητας..? Μια πιθανολογική εκτίμηση των μέγιστων
ΖΩΝΟΠΟΙΗΣΗ ΤΗΣ ΚΑΤΟΛΙΣΘΗΤΙΚΗΣ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑΣ ΣΤΟ ΟΡΟΣ ΠΗΛΙΟ ΜΕ ΤΗ ΣΥΜΒΟΛΗ ΔΕΔΟΜΕΝΩΝ ΣΥΜΒΟΛΟΜΕΤΡΙΑΣ ΜΟΝΙΜΩΝ ΣΚΕΔΑΣΤΩΝ
 EΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΕΙΟ Τμήμα Μηχανικών Μεταλλείων-Μεταλλουργών ΖΩΝΟΠΟΙΗΣΗ ΤΗΣ ΚΑΤΟΛΙΣΘΗΤΙΚΗΣ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑΣ ΜΕ ΤΗ ΣΥΜΒΟΛΗ ΔΕΔΟΜΕΝΩΝ ΣΥΜΒΟΛΟΜΕΤΡΙΑΣ ΜΟΝΙΜΩΝ ΣΚΕΔΑΣΤΩΝ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Κιτσάκη Μαρίνα
EΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΕΙΟ Τμήμα Μηχανικών Μεταλλείων-Μεταλλουργών ΖΩΝΟΠΟΙΗΣΗ ΤΗΣ ΚΑΤΟΛΙΣΘΗΤΙΚΗΣ ΕΠΙΚΙΝΔΥΝΟΤΗΤΑΣ ΜΕ ΤΗ ΣΥΜΒΟΛΗ ΔΕΔΟΜΕΝΩΝ ΣΥΜΒΟΛΟΜΕΤΡΙΑΣ ΜΟΝΙΜΩΝ ΣΚΕΔΑΣΤΩΝ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Κιτσάκη Μαρίνα
Physics by Chris Simopoulos
 ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΘΕΩΡΙΑ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ Να διαβάσετε τις σελίδες 98 έως και 103 του σχολικού βιβλίου. Να προσέξετε ιδιαίτερα τα σχήµατα 5.4, 5.5, 5.9 και 5.13. Να γράψετε τις µαθηµατικές σχέσεις που δίνονται
ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΘΕΩΡΙΑ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ Να διαβάσετε τις σελίδες 98 έως και 103 του σχολικού βιβλίου. Να προσέξετε ιδιαίτερα τα σχήµατα 5.4, 5.5, 5.9 και 5.13. Να γράψετε τις µαθηµατικές σχέσεις που δίνονται
Πιο συγκεκριμένα, η χρήση του MATLAB προσφέρει τα ακόλουθα πλεονεκτήματα.
 i Π Ρ Ο Λ Ο Γ Ο Σ Το βιβλίο αυτό αποτελεί μια εισαγωγή στα βασικά προβλήματα των αριθμητικών μεθόδων της υπολογιστικής γραμμικής άλγεβρας (computational linear algebra) και της αριθμητικής ανάλυσης (numerical
i Π Ρ Ο Λ Ο Γ Ο Σ Το βιβλίο αυτό αποτελεί μια εισαγωγή στα βασικά προβλήματα των αριθμητικών μεθόδων της υπολογιστικής γραμμικής άλγεβρας (computational linear algebra) και της αριθμητικής ανάλυσης (numerical
Διάτρηση, Ανατίναξη και Εισαγωγή στα Υπόγεια Έργα Περιβαλλοντικές επιπτώσεις από τις ανατινάξεις
 Διάτρηση, Ανατίναξη και Εισαγωγή στα Υπόγεια Έργα Περιβαλλοντικές επιπτώσεις από τις ανατινάξεις Δρ Παντελής Λιόλιος Σχολή Μηχανικών Ορυκτών Πόρων Πολυτεχνείο Κρήτης http://minelabmredtucgr Τελευταία ενημέρωση:
Διάτρηση, Ανατίναξη και Εισαγωγή στα Υπόγεια Έργα Περιβαλλοντικές επιπτώσεις από τις ανατινάξεις Δρ Παντελής Λιόλιος Σχολή Μηχανικών Ορυκτών Πόρων Πολυτεχνείο Κρήτης http://minelabmredtucgr Τελευταία ενημέρωση:
Εξάρτηση της σεισμικής κίνησης από τις τοπικές εδαφικές συνθήκες
 Εξάρτηση της σεισμικής κίνησης από τις τοπικές εδαφικές συνθήκες Μηχανικές ιδιότητες του εδάφους θεμελίωσης Πάχος και δυσκαμψία του επιφανειακού ιζηματογενούς στρώματος Κλίση των στρωμάτων και τοπογραφία
Εξάρτηση της σεισμικής κίνησης από τις τοπικές εδαφικές συνθήκες Μηχανικές ιδιότητες του εδάφους θεμελίωσης Πάχος και δυσκαμψία του επιφανειακού ιζηματογενούς στρώματος Κλίση των στρωμάτων και τοπογραφία
1η Εργαστηριακή Άσκηση: Απόκριση κυκλώµατος RC σε βηµατική και αρµονική διέγερση
 Ονοµατεπώνυµο: Αριθµός Μητρώου: Εξάµηνο: Υπογραφή Εργαστήριο Ηλεκτρικών Κυκλωµάτων και Συστηµάτων 1η Εργαστηριακή Άσκηση: Απόκριση κυκλώµατος σε βηµατική και αρµονική διέγερση Μέρος Α : Απόκριση στο πεδίο
Ονοµατεπώνυµο: Αριθµός Μητρώου: Εξάµηνο: Υπογραφή Εργαστήριο Ηλεκτρικών Κυκλωµάτων και Συστηµάτων 1η Εργαστηριακή Άσκηση: Απόκριση κυκλώµατος σε βηµατική και αρµονική διέγερση Μέρος Α : Απόκριση στο πεδίο
Υπολογισμός Κυματικής Δύναμης σε σύστημα πασσάλων Θαλάσσιας Εξέδρας
 Υπολογισμός Κυματικής Δύναμης σε σύστημα πασσάλων Θαλάσσιας Εξέδρας Περιγραφή Προβλήματος Απαιτείται η κατασκευή μιας θαλάσσιας εξέδρας σε θαλάσσια περιοχή με κυματικά χαρακτηριστικά Η = 4.65m, T = 8.5sec.
Υπολογισμός Κυματικής Δύναμης σε σύστημα πασσάλων Θαλάσσιας Εξέδρας Περιγραφή Προβλήματος Απαιτείται η κατασκευή μιας θαλάσσιας εξέδρας σε θαλάσσια περιοχή με κυματικά χαρακτηριστικά Η = 4.65m, T = 8.5sec.
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Ι
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Ι Προσέγγιση και Ομοιότητα Σημάτων Επιμέλεια: Πέτρος Π. Γρουμπός Καθηγητής Γεώργιος Α. Βασκαντήρας Υπ. Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών & Τεχνολογίας Υπολογιστών Άδειες Χρήσης
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ Ι Προσέγγιση και Ομοιότητα Σημάτων Επιμέλεια: Πέτρος Π. Γρουμπός Καθηγητής Γεώργιος Α. Βασκαντήρας Υπ. Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών & Τεχνολογίας Υπολογιστών Άδειες Χρήσης
ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ Γραφικές παραστάσεις, κλίση καµπύλης Μέθοδος των ελαχίστων τετραγώνων
 ΘΕ ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ Γραφικές παραστάσεις, κλίση καµπύλης Μέθοδος των ελαχίστων τετραγώνων 1. Σκοπός Πρόκειται για θεωρητική άσκηση που σκοπό έχει την περιληπτική αναφορά σε θεµατολογίες που αφορούν την
ΘΕ ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ Γραφικές παραστάσεις, κλίση καµπύλης Μέθοδος των ελαχίστων τετραγώνων 1. Σκοπός Πρόκειται για θεωρητική άσκηση που σκοπό έχει την περιληπτική αναφορά σε θεµατολογίες που αφορούν την
Τα φαινόμενα ρευστοποίησης, ο ρόλος τους στα Τεχνικά Έργα και τη σύγχρονη αστικοποίηση
 Τα φαινόμενα ρευστοποίησης, ο ρόλος τους στα Τεχνικά Έργα και τη σύγχρονη αστικοποίηση Γ. Παπαθανασίου Επίκουρος Καθηγητής Εργαστήριο Τεχνικής Γεωλογίας Τομέας Γεωτεχνική Μηχανικής Τμήμα Πολιτικών Μηχανικών
Τα φαινόμενα ρευστοποίησης, ο ρόλος τους στα Τεχνικά Έργα και τη σύγχρονη αστικοποίηση Γ. Παπαθανασίου Επίκουρος Καθηγητής Εργαστήριο Τεχνικής Γεωλογίας Τομέας Γεωτεχνική Μηχανικής Τμήμα Πολιτικών Μηχανικών
2. Ανάλυση του βασικού κινηματικού μηχανισμού των εμβολοφόρων ΜΕΚ
 2. Ανάλυση του βασικού κινηματικού μηχανισμού των εμβολοφόρων ΜΕΚ Προαπαιτούμενες γνώσεις: (α) Γνώσεις των τμημάτων κινηματικού μηχανισμού Μηχανής Εσωτερικής Καύσης (β) Αριθμητικός υπολογισμός παραγώγου
2. Ανάλυση του βασικού κινηματικού μηχανισμού των εμβολοφόρων ΜΕΚ Προαπαιτούμενες γνώσεις: (α) Γνώσεις των τμημάτων κινηματικού μηχανισμού Μηχανής Εσωτερικής Καύσης (β) Αριθμητικός υπολογισμός παραγώγου
ΚΥΜΑΤΑ 1. Νίκος Κανδεράκης
 ΚΥΜΑΤΑ 1 Νίκος Κανδεράκης Ταλάντωση Πλάτος x o Περίοδος T χρόνος για μία ταλάντωση Α Β Α Συχνότητα f αριθμός ταλαντώσεων σε 1s συχνότητα = αριθμός ταλαντώσεων/χρόνο ή f = N/t Αν Ν = 1 τότε t = T f = N/t
ΚΥΜΑΤΑ 1 Νίκος Κανδεράκης Ταλάντωση Πλάτος x o Περίοδος T χρόνος για μία ταλάντωση Α Β Α Συχνότητα f αριθμός ταλαντώσεων σε 1s συχνότητα = αριθμός ταλαντώσεων/χρόνο ή f = N/t Αν Ν = 1 τότε t = T f = N/t
ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΡΥΚΤΩΝ ΠΟΡΩΝ ΤΟΜΕΑΣ ΑΝΙΧΝΕΥΣΗΣ ΚΑΙ ΕΝΤΟΠΙΣΜΟΥ ΟΡΥΚΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΓΕΩΦΥΣΙΚΗΣ
 ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΣΥΜΒΟΛΗ ΤΗΣ ΗΛΕΚΤΡΙΚΗΣ ΤΟΜΟΓΡΑΦΙΑΣ ΣΤΗΝ ΕΚΤΙΜΗΣΗ ΤΟΥ ΠΑΧΟΥΣ ΤΟΥ ΕΔΑΦΙΚΟΥ ΚΑΛΥΜΑΤΟΣ ΣΤΗ ΜΑΥΡΟΠΗΓΗ ΚΟΖΑΝΗΣ ΕΞΕΤΑΣΤΙΚΗ ΕΠΙΤΡΟΠΗ ΒΑΦΕΙΔΗΣ ΑΝΤΩΝΙΟΣ, Καθηγητής(επιβλέπων) ΜΑΝΟΥΤΣΟΓΛΟΥ ΕΜΜΑΝΟΥΗΛ,
ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΣΥΜΒΟΛΗ ΤΗΣ ΗΛΕΚΤΡΙΚΗΣ ΤΟΜΟΓΡΑΦΙΑΣ ΣΤΗΝ ΕΚΤΙΜΗΣΗ ΤΟΥ ΠΑΧΟΥΣ ΤΟΥ ΕΔΑΦΙΚΟΥ ΚΑΛΥΜΑΤΟΣ ΣΤΗ ΜΑΥΡΟΠΗΓΗ ΚΟΖΑΝΗΣ ΕΞΕΤΑΣΤΙΚΗ ΕΠΙΤΡΟΠΗ ΒΑΦΕΙΔΗΣ ΑΝΤΩΝΙΟΣ, Καθηγητής(επιβλέπων) ΜΑΝΟΥΤΣΟΓΛΟΥ ΕΜΜΑΝΟΥΗΛ,
7 ΚΕΦΑΛΑΙΟ ΣΥΝΟΨΗ ΑΠΟΤΕΛΕΣΜΑΤΑ ΠΡΟΟΠΤΙΚΗ
 7 ΚΕΦΑΛΑΙΟ ΣΥΝΟΨΗ ΑΠΟΤΕΛΕΣΜΑΤΑ ΠΡΟΟΠΤΙΚΗ 7.1 Σύνοψη Η παρούσα διατριβή είχε ως στόχο τη µελέτη του φαινοµένου της ρευστοποίησης στην ευρύτερη περιοχή του Αιγαίου και τη δηµιουργία νέων εµπειρικών σχέσεων
7 ΚΕΦΑΛΑΙΟ ΣΥΝΟΨΗ ΑΠΟΤΕΛΕΣΜΑΤΑ ΠΡΟΟΠΤΙΚΗ 7.1 Σύνοψη Η παρούσα διατριβή είχε ως στόχο τη µελέτη του φαινοµένου της ρευστοποίησης στην ευρύτερη περιοχή του Αιγαίου και τη δηµιουργία νέων εµπειρικών σχέσεων
ΣΕΙΣΜΟΣ ΝΔ ΤΗΣ ΖΑΚΥΝΘΟΥ (M=6.8, 26/10/2018)
 ΣΕΙΣΜΟΣ ΝΔ ΤΗΣ ΖΑΚΥΝΘΟΥ (M=6.8, 26/10/2018) 1. ΓΕΝΙΚΑ Στις 01:54 ώρα Ελλάδας (22:54 UTC) της 25 ης Οκτωβρίου 2018 εκδηλώθηκε ισχυρή σεισμική δόνηση μεγέθους 6.8 στη θαλάσσια περιοχή ΝΔ της Ζακύνθου. Τη
ΣΕΙΣΜΟΣ ΝΔ ΤΗΣ ΖΑΚΥΝΘΟΥ (M=6.8, 26/10/2018) 1. ΓΕΝΙΚΑ Στις 01:54 ώρα Ελλάδας (22:54 UTC) της 25 ης Οκτωβρίου 2018 εκδηλώθηκε ισχυρή σεισμική δόνηση μεγέθους 6.8 στη θαλάσσια περιοχή ΝΔ της Ζακύνθου. Τη
Εργαστήριο Επεξεργασίας Σηµάτων και Τηλεπικοινωνιών Κινητά ίκτυα Επικοινωνιών
 Εργαστήριο Επεξεργασίας Σηµάτων και Τηλεπικοινωνιών Κινητά ίκτυα Επικοινωνιών Εργασία Προσοµοίωσης ενός Τηλεπικοινωνιακού Συστήµατος και Εκτίµηση Απόκρισης Αραιού Καναλιού Εισαγωγή Στην παρούσα εργασία
Εργαστήριο Επεξεργασίας Σηµάτων και Τηλεπικοινωνιών Κινητά ίκτυα Επικοινωνιών Εργασία Προσοµοίωσης ενός Τηλεπικοινωνιακού Συστήµατος και Εκτίµηση Απόκρισης Αραιού Καναλιού Εισαγωγή Στην παρούσα εργασία
Κινητά Δίκτυα Επικοινωνιών. Συμπληρωματικό υλικό. Προσαρμοστική Ισοστάθμιση Καναλιού
 Κινητά Δίκτυα Επικοινωνιών Συμπληρωματικό υλικό Προσαρμοστική Ισοστάθμιση Καναλιού Προσαρμοστικοί Ισοσταθμιστές Για να υπολογίσουμε τους συντελεστές του ισοσταθμιστή MMSE, απαιτείται να λύσουμε ένα γραμμικό
Κινητά Δίκτυα Επικοινωνιών Συμπληρωματικό υλικό Προσαρμοστική Ισοστάθμιση Καναλιού Προσαρμοστικοί Ισοσταθμιστές Για να υπολογίσουμε τους συντελεστές του ισοσταθμιστή MMSE, απαιτείται να λύσουμε ένα γραμμικό
ΤΕΤΡΑ ΙΑ ΑΝΑΛΥΣΗΣ Ε ΟΜΕΝΩΝ, ΤΕΥΧΟΣ 15 (σσ ) DATA ANALYSIS BULLETIN, ISSUE 15 (pp ) Ιεραρχική Ανάλυση
 ΤΕΤΡΑ ΙΑ ΑΝΑΛΥΣΗΣ Ε ΟΜΕΝΩΝ, ΤΕΥΧΟΣ 15 (σσ. 81-89) DATA ANALYSIS BULLETIN, ISSUE 15 (pp. 81-89) Ιεραρχική Ανάλυση ηµήτριος Καραπιστόλης Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ίδρυµα Θεσσαλονίκης Περίληψη
ΤΕΤΡΑ ΙΑ ΑΝΑΛΥΣΗΣ Ε ΟΜΕΝΩΝ, ΤΕΥΧΟΣ 15 (σσ. 81-89) DATA ANALYSIS BULLETIN, ISSUE 15 (pp. 81-89) Ιεραρχική Ανάλυση ηµήτριος Καραπιστόλης Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ίδρυµα Θεσσαλονίκης Περίληψη
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ.
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΕΞΙΣΩΣΗ Η/Μ ΚΥΜΑΤΟΣ ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΕΞΙΣΩΣΗ Η/Μ ΚΥΜΑΤΟΣ ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ
Κεφάλαιο M4. Κίνηση σε δύο διαστάσεις
 Κεφάλαιο M4 Κίνηση σε δύο διαστάσεις Κινηµατική σε δύο διαστάσεις Θα περιγράψουµε τη διανυσµατική φύση της θέσης, της ταχύτητας, και της επιτάχυνσης µε περισσότερες λεπτοµέρειες. Θα µελετήσουµε την κίνηση
Κεφάλαιο M4 Κίνηση σε δύο διαστάσεις Κινηµατική σε δύο διαστάσεις Θα περιγράψουµε τη διανυσµατική φύση της θέσης, της ταχύτητας, και της επιτάχυνσης µε περισσότερες λεπτοµέρειες. Θα µελετήσουµε την κίνηση
min f(x) x R n b j - g j (x) = s j - b j = 0 g j (x) + s j = 0 - b j ) min L(x, s, λ) x R n λ, s R m L x i = 1, 2,, n (1) m L(x, s, λ) = f(x) +
 KΕΦΑΛΑΙΟ 4 Κλασσικές Μέθοδοι Βελτιστοποίησης Με Περιορισµούς Ανισότητες 4. ΠΡΟΒΛΗΜΑΤΑ ΜΕ ΠΕΡΙΟΡΙΣΜΟΥΣ ΑΝΙΣΟΤΗΤΕΣ Ζητούνται οι τιµές των µεταβλητών απόφασης που ελαχιστοποιούν την αντικειµενική συνάρτηση
KΕΦΑΛΑΙΟ 4 Κλασσικές Μέθοδοι Βελτιστοποίησης Με Περιορισµούς Ανισότητες 4. ΠΡΟΒΛΗΜΑΤΑ ΜΕ ΠΕΡΙΟΡΙΣΜΟΥΣ ΑΝΙΣΟΤΗΤΕΣ Ζητούνται οι τιµές των µεταβλητών απόφασης που ελαχιστοποιούν την αντικειµενική συνάρτηση
ΟΙ Υ ΡΟΓΕΩΛΟΓΙΚΕΣ ΣΥΝΘΗΚΕΣ ΣΤΗΝ ΛΕΚΑΝΗ ΠΟΤΑΜΙΑΣ ΚΑΙ Η ΑΛΛΗΛΟΕΠΙ ΡΑΣΗ ΤΟΥ Υ ΑΤΙΚΟΥ ΚΑΘΕΣΤΩΤΟΣ ΜΕ ΤΗ ΜΕΛΛΟΝΤΙΚΗ ΛΙΓΝΙΤΙΚΗ ΕΚΜΕΤΑΛΛΕΥΣΗ ΣΤΗΝ ΕΛΑΣΣΟΝΑ
 ελτίο της Ελληνικής εωλογικής Εταιρίας τοµ. XXXVI, 2004 Πρακτικά 10 ου ιεθνούς Συνεδρίου, Θεσ/νίκη Απρίλιος 2004 Bulletin of the Geological Society of Greece vol. XXXVI, 2004 Proceedings of the 10 th International
ελτίο της Ελληνικής εωλογικής Εταιρίας τοµ. XXXVI, 2004 Πρακτικά 10 ου ιεθνούς Συνεδρίου, Θεσ/νίκη Απρίλιος 2004 Bulletin of the Geological Society of Greece vol. XXXVI, 2004 Proceedings of the 10 th International
Τα κύρια σηµεία της παρούσας διδακτορικής διατριβής είναι: Η πειραµατική µελέτη της µεταβατικής συµπεριφοράς συστηµάτων γείωσης
 Κεφάλαιο 5 ΣΥΜΠΕΡΑΣΜΑΤΑ Το σηµαντικό στην επιστήµη δεν είναι να βρίσκεις καινούρια στοιχεία, αλλά να ανακαλύπτεις νέους τρόπους σκέψης γι' αυτά. Sir William Henry Bragg 5.1 Ανακεφαλαίωση της διατριβής
Κεφάλαιο 5 ΣΥΜΠΕΡΑΣΜΑΤΑ Το σηµαντικό στην επιστήµη δεν είναι να βρίσκεις καινούρια στοιχεία, αλλά να ανακαλύπτεις νέους τρόπους σκέψης γι' αυτά. Sir William Henry Bragg 5.1 Ανακεφαλαίωση της διατριβής
ΜΕΤΡΗΣΗ ΔΙΑΦΟΡΑΣ ΦΑΣΗΣ ΔΥΟ ΗΜΙΤΟΝΟΕΙΔΩΝ ΣΗΜΑΤΩΝ
 ΑΣΚΗΣΗ 05 ΜΕΤΡΗΣΗ ΔΙΑΦΟΡΑΣ ΦΑΣΗΣ ΔΥΟ ΗΜΙΤΟΝΟΕΙΔΩΝ ΣΗΜΑΤΩΝ Αντικείμενο της άσκησης αυτής είναι η μέτρηση της διαφοράς φάσης μεταξύ δύο κυματομορφών τάσης σε ένα κύκλωμα εναλλασσομένου ρεύματος με τη βοήθεια
ΑΣΚΗΣΗ 05 ΜΕΤΡΗΣΗ ΔΙΑΦΟΡΑΣ ΦΑΣΗΣ ΔΥΟ ΗΜΙΤΟΝΟΕΙΔΩΝ ΣΗΜΑΤΩΝ Αντικείμενο της άσκησης αυτής είναι η μέτρηση της διαφοράς φάσης μεταξύ δύο κυματομορφών τάσης σε ένα κύκλωμα εναλλασσομένου ρεύματος με τη βοήθεια
ΚΥΜΑΤΟ ΗΓΗΣΗ. «Μικροοπτικές διατάξεις-ολοκληρωµένα οπτικά»
 ΚΥΜΑΤΟ ΗΓΗΣΗ Επίπεδοι κυµατοδηγοί Προσέγγιση γεωµετρικής οπτικής Προσέγγιση κυµατικής οπτικής και συνοριακών συνθηκών Οπτικές ίνες ιασπορά Μέθοδοι ανάπτυξης κυµατοδηγών Ηχρήση των κυµάτων στις επικοινωνίες
ΚΥΜΑΤΟ ΗΓΗΣΗ Επίπεδοι κυµατοδηγοί Προσέγγιση γεωµετρικής οπτικής Προσέγγιση κυµατικής οπτικής και συνοριακών συνθηκών Οπτικές ίνες ιασπορά Μέθοδοι ανάπτυξης κυµατοδηγών Ηχρήση των κυµάτων στις επικοινωνίες
Κεφ. 7: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών
 Κεφ. 7: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών 7. Εισαγωγή (ορισμός προβλήματος, αριθμητική ολοκλήρωση ΣΔΕ, αντικατάσταση ΣΔΕ τάξης n με n εξισώσεις ης τάξης) 7. Μέθοδος Euler 7.3
Κεφ. 7: Συνήθεις διαφορικές εξισώσεις (ΣΔΕ) - προβλήματα αρχικών τιμών 7. Εισαγωγή (ορισμός προβλήματος, αριθμητική ολοκλήρωση ΣΔΕ, αντικατάσταση ΣΔΕ τάξης n με n εξισώσεις ης τάξης) 7. Μέθοδος Euler 7.3
ΣΕΜΦΕ ΕΜΠ Φυσική ΙΙΙ (Κυματική) Διαγώνισμα επί πτυχίω εξέτασης 02/06/2017 1
 ΣΕΜΦΕ ΕΜΠ Φυσική ΙΙΙ (Κυματική) Διαγώνισμα επί πτυχίω εξέτασης /6/7 Διάρκεια ώρες. Θέμα. Θεωρηστε ενα συστημα δυο σωματων ισων μαζων (μαζας Μ το καθενα) και δυο ελατηριων (χωρις μαζα) με σταθερες ελατηριων
ΣΕΜΦΕ ΕΜΠ Φυσική ΙΙΙ (Κυματική) Διαγώνισμα επί πτυχίω εξέτασης /6/7 Διάρκεια ώρες. Θέμα. Θεωρηστε ενα συστημα δυο σωματων ισων μαζων (μαζας Μ το καθενα) και δυο ελατηριων (χωρις μαζα) με σταθερες ελατηριων
Α Ρ Ι Σ Τ Ο Τ Ε Λ Ε Ι Ο Π Α Ν Ε Π Ι Σ Τ Η Μ Ι Ο Θ Ε Σ Σ Α Λ Ο Ν Ι Κ Η Σ
 Α Ρ Ι Σ Τ Ο Τ Ε Λ Ε Ι Ο Π Α Ν Ε Π Ι Σ Τ Η Μ Ι Ο Θ Ε Σ Σ Α Λ Ο Ν Ι Κ Η Σ ΤΜΗΜΑ ΓΕΩΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΙΚΗΣ ΓΕΩΛΟΓΙΑΣ ΜΑΘΗΜΑ: ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ ΕΞΑΜΗΝΟ: 7 ο ΔΙΔΑΣΚΟΝΤΕΣ: Β. ΧΡΗΣΤΑΡΑΣ, Καθηγητής Β. ΜΑΡΙΝΟΣ,
Α Ρ Ι Σ Τ Ο Τ Ε Λ Ε Ι Ο Π Α Ν Ε Π Ι Σ Τ Η Μ Ι Ο Θ Ε Σ Σ Α Λ Ο Ν Ι Κ Η Σ ΤΜΗΜΑ ΓΕΩΛΟΓΙΑΣ ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΙΚΗΣ ΓΕΩΛΟΓΙΑΣ ΜΑΘΗΜΑ: ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ ΕΞΑΜΗΝΟ: 7 ο ΔΙΔΑΣΚΟΝΤΕΣ: Β. ΧΡΗΣΤΑΡΑΣ, Καθηγητής Β. ΜΑΡΙΝΟΣ,
ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ
 ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Θεματική Ενότητα 4 Υπόγεια ροή Νόμος Darcy Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΕΡΙΒΑΛΛΟΝΤΙΚΗ ΓΕΩΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Μ. Πανταζίδου, Αναπληρώτρια Καθηγήτρια ΕΜΠ Θεματική Ενότητα 4 Υπόγεια ροή Νόμος Darcy Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Εισηγητής: Αλέξανδρος Βαλσαμής. Θεμελιώσεις. Φέρουσα Ικανότητα επιφανειακών θεμελιώσεων Γενικά Βασικές εξισώσεις
 Εισηγητής: Αλέξανδρος Βαλσαμής Θεμελιώσεις Φέρουσα Ικανότητα επιφανειακών θεμελιώσεων Γενικά Βασικές εξισώσεις Φέρουσα Ικανότητα Επιφανειακών θεμελιώσεων (πεδίλων) Φέρουσα Ικανότητα Τάσεις κάτω από το
Εισηγητής: Αλέξανδρος Βαλσαμής Θεμελιώσεις Φέρουσα Ικανότητα επιφανειακών θεμελιώσεων Γενικά Βασικές εξισώσεις Φέρουσα Ικανότητα Επιφανειακών θεμελιώσεων (πεδίλων) Φέρουσα Ικανότητα Τάσεις κάτω από το
Παρουσίαση 2 η : Αρχές εκτίμησης παραμέτρων Μέρος 1 ο
 Εφαρμογές Ανάλυσης Σήματος στη Γεωδαισία Παρουσίαση η : Αρχές εκτίμησης παραμέτρων Μέρος ο Βασίλειος Δ. Ανδριτσάνος Αναπληρωτής Καθηγητής Γεώργιος Χλούπης Επίκουρος Καθηγητής Τμήμα Μηχανικών Τοπογραφίας
Εφαρμογές Ανάλυσης Σήματος στη Γεωδαισία Παρουσίαση η : Αρχές εκτίμησης παραμέτρων Μέρος ο Βασίλειος Δ. Ανδριτσάνος Αναπληρωτής Καθηγητής Γεώργιος Χλούπης Επίκουρος Καθηγητής Τμήμα Μηχανικών Τοπογραφίας
ΣΤΟΧΑΣΤΙΚΑ ΣΗΜΑΤΑ ΚΑΙ ΕΦΑΡΜΟΓΕΣ
 ΣΤΟΧΑΣΤΙΚΑ ΣΗΜΑΤΑ ΚΑΙ ΕΦΑΡΜΟΓΕΣ Ακαδηµαϊκό Έτος 007-008 ιδάσκων: Ν. Παπανδρέου (Π.. 407/80) Πανεπιστήµιο Πατρών Τµήµα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής 1η Εργαστηριακή Άσκηση Αναγνώριση
ΣΤΟΧΑΣΤΙΚΑ ΣΗΜΑΤΑ ΚΑΙ ΕΦΑΡΜΟΓΕΣ Ακαδηµαϊκό Έτος 007-008 ιδάσκων: Ν. Παπανδρέου (Π.. 407/80) Πανεπιστήµιο Πατρών Τµήµα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής 1η Εργαστηριακή Άσκηση Αναγνώριση
ΤΟΠΟΓΡΑΦΙΚΑ ΔΙΚΤΥΑ ΚΑΙ ΥΠΟΛΟΓΙΣΜΟΙ ΑΝΑΣΚΟΠΗΣΗ ΘΕΩΡΙΑΣ ΣΥΝΟΡΘΩΣΕΩΝ
 ΤΟΠΟΓΡΑΦΙΚΑ ΔΙΚΤΥΑ ΚΑΙ ΥΠΟΛΟΓΙΣΜΟΙ ΑΝΑΣΚΟΠΗΣΗ ΘΕΩΡΙΑΣ ΣΥΝΟΡΘΩΣΕΩΝ Βασίλης Δ. Ανδριτσάνος Δρ. Αγρονόμος - Τοπογράφος Μηχανικός ΑΠΘ Επίκουρος Καθηγητής ΤΕΙ Αθήνας 3ο εξάμηνο http://eclass.teiath.gr Παρουσιάσεις,
ΤΟΠΟΓΡΑΦΙΚΑ ΔΙΚΤΥΑ ΚΑΙ ΥΠΟΛΟΓΙΣΜΟΙ ΑΝΑΣΚΟΠΗΣΗ ΘΕΩΡΙΑΣ ΣΥΝΟΡΘΩΣΕΩΝ Βασίλης Δ. Ανδριτσάνος Δρ. Αγρονόμος - Τοπογράφος Μηχανικός ΑΠΘ Επίκουρος Καθηγητής ΤΕΙ Αθήνας 3ο εξάμηνο http://eclass.teiath.gr Παρουσιάσεις,
ΜΕΘΟΔΟΣ ΕΛΑΧΙΣΤΩΝ ΤΕΤΡΑΓΩΝΩΝ
 ΜΕΘΟΔΟΣ ΕΛΑΧΙΣΤΩΝ ΤΕΤΡΑΓΩΝΩΝ ΧΑΡΑΞΗ ΓΡΑΦΙΚΗΣ ΠΑΡΑΣΤΑΣΗΣ Δημήτρης Στεφανάκης Η Μέθοδος των Ελαχίστων Τετραγώνων (ΜΕΤ) χρησιμοποιείται για την κατασκευή της γραφικής παράστασης που περιγράφει ένα φαινόμενο,
ΜΕΘΟΔΟΣ ΕΛΑΧΙΣΤΩΝ ΤΕΤΡΑΓΩΝΩΝ ΧΑΡΑΞΗ ΓΡΑΦΙΚΗΣ ΠΑΡΑΣΤΑΣΗΣ Δημήτρης Στεφανάκης Η Μέθοδος των Ελαχίστων Τετραγώνων (ΜΕΤ) χρησιμοποιείται για την κατασκευή της γραφικής παράστασης που περιγράφει ένα φαινόμενο,
ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Α
 ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση θεωρίας 1 ΘΕΜΑ Α Τι ονομάζουμε πραγματική συνάρτηση
ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση θεωρίας 1 ΘΕΜΑ Α Τι ονομάζουμε πραγματική συνάρτηση
ΑΣΚΗΣΗ ΔΙΑΘΛΑΣΗΣ Ασυνέχεια με κλίση
 ΑΣΚΗΣΗ ΔΙΑΘΛΑΣΗΣ Ασυνέχεια με κλίση Για να ναμελετηθεί μία γεωφυσική δομή ασυνέχειας με μεκλίση χρησιμοποιήθηκε η μέθοδος της σεισμικής διάθλασης με μετην εφαρμογή σεισμικού προφίλ 66 66γεωφώνων. Αυτά
ΑΣΚΗΣΗ ΔΙΑΘΛΑΣΗΣ Ασυνέχεια με κλίση Για να ναμελετηθεί μία γεωφυσική δομή ασυνέχειας με μεκλίση χρησιμοποιήθηκε η μέθοδος της σεισμικής διάθλασης με μετην εφαρμογή σεισμικού προφίλ 66 66γεωφώνων. Αυτά
1.8 Χωροθέτηση Θαλάσσιων Κατασκευών
 Επιχειρησιακό Πρόγραμμα Εκπαίδευση και ια Βίου Μάθηση Πρόγραμμα ια Βίου Μάθησης ΑΕΙ για την Επικαιροποίηση Γνώσεων Αποφοίτων ΑΕΙ: Σύγχρονες Εξελίξεις στις Θαλάσσιες Κατασκευές Α.Π.Θ. Πολυτεχνείο Κρήτης
Επιχειρησιακό Πρόγραμμα Εκπαίδευση και ια Βίου Μάθηση Πρόγραμμα ια Βίου Μάθησης ΑΕΙ για την Επικαιροποίηση Γνώσεων Αποφοίτων ΑΕΙ: Σύγχρονες Εξελίξεις στις Θαλάσσιες Κατασκευές Α.Π.Θ. Πολυτεχνείο Κρήτης
Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο Κ Ρ Η Τ Η Σ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΡΥΚΤΩΝ
 Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο Κ Ρ Η Τ Η Σ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΡΥΚΤΩΝ ΠΟΡΩΝ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Συμβολή Των Σεισμικών Μεθόδων Στον Γεωτεχνικό Χαρακτηρισμό Των Γεωλογικών Σχηματισμών Για Την Κατασκευή Της Β Φάσης κτιρίων
Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο Κ Ρ Η Τ Η Σ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΡΥΚΤΩΝ ΠΟΡΩΝ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Συμβολή Των Σεισμικών Μεθόδων Στον Γεωτεχνικό Χαρακτηρισμό Των Γεωλογικών Σχηματισμών Για Την Κατασκευή Της Β Φάσης κτιρίων
Περιεχόμενα. Σειρά VII 2
 Περιεχόμενα 1. Κυματική Θεωρία Stokes ης τάξης. Κυματική Θεωρία Stokes 5 ης τάξης 3. Κυματική Θεωρία Συνάρτησης ροής (Fourier 18 ης τάξης) 4. Cnoial waves 5. Θεωρία μοναχικού κύματος (Solitary wave) 6.
Περιεχόμενα 1. Κυματική Θεωρία Stokes ης τάξης. Κυματική Θεωρία Stokes 5 ης τάξης 3. Κυματική Θεωρία Συνάρτησης ροής (Fourier 18 ης τάξης) 4. Cnoial waves 5. Θεωρία μοναχικού κύματος (Solitary wave) 6.
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ/Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΧΕΙΜΕΡΙΝΑ ΗΜΕΡΟΜΗΝΙΑ: 12/02/12 ΛΥΣΕΙΣ
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 011-01 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ/Γ ΥΚΕΙΟΥ ΣΕΙΡΑ: ΧΕΙΜΕΡΙΝΑ ΗΜΕΡΟΜΗΝΙΑ: 1/0/1 ΥΣΕΙΣ ΘΕΜΑ 1 ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό κάθε µίας από τις παρακάτω ερωτήσεις
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 011-01 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ/Γ ΥΚΕΙΟΥ ΣΕΙΡΑ: ΧΕΙΜΕΡΙΝΑ ΗΜΕΡΟΜΗΝΙΑ: 1/0/1 ΥΣΕΙΣ ΘΕΜΑ 1 ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό κάθε µίας από τις παρακάτω ερωτήσεις
ΕΠΑΝΑΛΗΠΤΙΚΟ ΙΑΓΩΝΙΣΜΑ 2 ΟΥ ΚΕΦΑΛΑΙΟΥ
 ΕΠΑΝΑΛΗΠΤΙΚΟ ΙΑΓΩΝΙΣΜΑ 2 ΟΥ ΚΕΦΑΛΑΙΟΥ Στις ερωτήσεις 1 5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Στο διάγραµµα του σχήµατος παριστάνεται
ΕΠΑΝΑΛΗΠΤΙΚΟ ΙΑΓΩΝΙΣΜΑ 2 ΟΥ ΚΕΦΑΛΑΙΟΥ Στις ερωτήσεις 1 5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1. Στο διάγραµµα του σχήµατος παριστάνεται
Παρεμβολή Ενισχυτών μεταξύ γεωφώνων και καταγραφικού
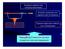 Ενισχυτές σήματος στη σεισμική διασκόπηση Καλώδιο μεταφοράς των σημάτων απο τα γεώφωνα Σεισμικό σήμα πολύ ασθενές για να καταγραφεί Παρεμβολή Ενισχυτών μεταξύ γεωφώνων και καταγραφικού Ενισχυτής Καταγραφικό
Ενισχυτές σήματος στη σεισμική διασκόπηση Καλώδιο μεταφοράς των σημάτων απο τα γεώφωνα Σεισμικό σήμα πολύ ασθενές για να καταγραφεί Παρεμβολή Ενισχυτών μεταξύ γεωφώνων και καταγραφικού Ενισχυτής Καταγραφικό
