5. Κυματικά φαινόμενα
|
|
|
- Φιλοκράτης Καλύβας
- 8 χρόνια πριν
- Προβολές:
Transcript
1 5. Κυματικά φαινόμενα Σύνοψη Στο κεφάλαιο αυτό παρουσιάζονται τα βασικά κυματικά φαινόμενα. Αρχικά παρουσιάζεται η έννοια της επαλληλίας και η σύνθεση των κυμάτων σε μια διάσταση και εξάγεται το φαινόμενο του διακροτήματος. Έπειτα παρουσιάζεται, σε εισαγωγικό επίπεδο, η ανάλυση κυμάτων κατά Forier. Στη συνέχεια παρουσιάζεται η δημιουργία στασίμων κυμάτων με τη σύνθεση ομοίων κυμάτων κινούμενων σε αντίθετες κατευθύνσεις και τα βασικά χαρακτηριστικά τους (κοιλίες και δεσμοί). Αναφέρεται το παράδειγμα των στασίμων κυμάτων σε πακτωμένες χορδές, και εξάγεται η συνθήκη συντονισμού και η εφαρμογή τους στα έγχορδα μουσικά όργανα. Παρουσιάζονται, επίσης, τα φαινόμενα της ανάκλασης και διέλευσης κυμάτων χορδής σε συνοριακή επιφάνεια, και εξάγονται οι συντελεστές ανάκλασης και διέλευσης πλάτους, και οι συντελεστές ανάκλασης και διέλευσης ενέργειας και ισχύος. Παρουσιάζεται, επίσης, το φαινόμενο της διάθλασης και ο νόμος του Snell. Τέλος παρουσιάζονται οι απλές περιπτώσεις του φαινομένου Doppler, και εξάγονται οι εξισώσεις μεταβολής της συχνότητας παρατήρησης. Προαπαιτούμενη γνώση Απαιτείται η γνώση των προηγούμενων κεφαλαίων.. Επαλληλία κυμάτων Η επαλληλία (υπέρθεση) κυμάτων είναι το κυματικό φαινόμενο που μπορεί να απαντήσει στην ερώτηση: τι συμβαίνει, όταν δύο ή περισσότερα κύματα φτάνουν στο ίδιο σημείο του χώρου την ίδια χρονική στιγμή; Σύμφωνα με την αρχή της επαλληλίας (υπέρθεσης), η συνολική μετατόπιση των σωματιδίων μέσα στο υλικό στο συγκεκριμένο σημείο είναι το άθροισμα των μετατοπίσεων που θα προκαλούσε το κάθε κύμα, αν δρούσε μόνο του. Η γενική κυματική εξίσωση: y y (5.) x t μπορεί να δώσει πληροφορίες για το σχήμα του κύματος, καθώς και την ταχύτητα και επιτάχυνση των σωματιδίων του υλικού διαμέσου, του οποίου το κύμα ταξιδεύει. Ο βασικός νόμος της υπέρθεσης είναι ότι, εάν δύο κύματα με κυματοσυναρτήσεις y (x,t) και y (x,t) ικανοποιούν τη γενική κυματική εξίσωση, τότε το ίδιο κάνει και η επαλληλία τους (υπέρθεση) y R = y + y.. Συμβολή κυμάτων Ο όρος συμβολή χρησιμοποιείται, για να εκφράσει το αποτέλεσμα της υπέρθεσης των κυμάτων, και διακρίνεται σε ενισχυτική συμβολή και σε καταστρεπτική συμβολή. Ενισχυτική συμβολή έχουμε, όταν το πλάτος του κύματος, που προέρχεται από την υπέρθεση, είναι μεγαλύτερο από κάθε πλάτος οποιουδήποτε από τα κύματα που υπερθέτονται. Καταστρεπτική συμβολή έχουμε, όταν το πλάτος του κύματος, που προέρχεται από την υπέρθεση, είναι μικρότερο από κάθε πλάτος οποιουδήποτε από τα κύματα που υπερθέτονται. Για παράδειγμα, θεωρήστε δύο κύματα που ταξιδεύουν στην ίδια διεύθυνση και έχουν το ίδιο πλάτος, συχνότητα και μήκος κύματος, αλλά διαφορετικές αρχικές φάσεις: y A sin t x (5.) o o y A sin t x (5.3) Παρακάτω περιγράφονται μερικές χαρακτηριστικές περιπτώσεις σύνθεσης των παραπάνω κυμάτων, ανάλογα με τη διαφορά φάσης τους Δφ (= φ φ ): - Δφ = 0 (ίδια αρχική φάση φ = φ = φ ). Τότε: 66
2 yr y y Ao sin( t x ) Ao sin( t x ) yr Aosin( t x ) (5.4) δηλαδή το συνιστάμενο κύμα y R έχει διπλάσιο πλάτος, αλλά την ίδια συχνότητα και αρχική φάση με τα κύματα που συνθέτονται. - Δφ = π (π.χ. φ = π, φ = 0). Τότε: yr y y Ao sin( t x ) Ao sin( t x) yr 0 (5.5) δηλαδή τα δύο κύματα αλληλοεξουδετερώνονται. - Δφ = π/4 (π.χ. φ = π/4, φ = 0). Τότε: yr y y Ao sin( t x ) Ao sin( t x) 4 yr Aocos sin( t x ) (5.6) 8 8 δηλαδή το συνιστάμενο κύμα y R έχει πλάτος A o cos, την ίδια συχνότητα με τα κύματα που συνθέτονται, και 8 διαφορά φάσης π/8 με το κύμα y. - Δφ = π/3 (π.χ. φ = π/3, φ = 0). Τότε: yr y y Ao sin( t x ) Ao sin( t x) 3 yr Aocos sin( t x ) (5.7) 6 6 δηλαδή το συνιστάμενο κύμα y R έχει πλάτος A o cos, την ίδια συχνότητα με τα κύματα που συνθέτονται, και 6 διαφορά φάσης π/6 με το κύμα y... Διακρότημα Ας θεωρήσουμε δύο κύματα που ταξιδεύουν στην ίδια διεύθυνση με ίδιο πλάτος, αλλά με διαφορετικές συχνότητες: y A sin t x (5.8) o o y A sin t x (5.9) Πώς μοιάζει, όμως, το κύμα που προκύπτει από τη σύνθεση των παραπάνω; Στο σχήμα 5..α φαίνεται η μετατόπιση ως συνάρτηση του χρόνου, κρατώντας το x σταθερό. Το αποτέλεσμα της σύνθεσης είναι: y A sin( t x) A sin( t x) R o o yr Aocos t xsin t x (5.0) Το συνιστάμενο κύμα μπορεί να θεωρηθεί ότι έχει ένα «πλάτος» που από μόνο του αποτελεί μια κυματική διαταραχή με κυματοσυνάρτηση Ao cos t x με συχνότητα. Το ίδιο το κύμα έχει συχνότητα. Σε ένα συγκεκριμένο σημείο του χώρου και, επειδή το πλάτος του κύματος ταλαντώνεται με την ημιδιαφορά των συχνοτήτων, το αυτί (ή ο ηχητικός ανιχνευτής), που βρίσκεται στο σημείο ακρόασης, Σύμφωνα με την τριγωνομετρική ταυτότητα sin sin sin cos 67
3 θα ακούσει ηχητικούς παλμούς συχνότητας, που το πλάτος τους, που αντανακλά στην ηχητική ένταση ακρόασης, θα είναι διαμορφωμένο με τη συχνότητα, όπως ακριβώς φαίνεται στο σχήμα 5..β. Όσο πιο κοντά είναι οι δύο αρχικές συχνότητες τόσο πιο έντονη και αργή είναι η διαμόρφωση του πλάτους. Το στιγμιότυπο σχήμα που παίρνει πλέον το κύμα φαίνεται στο σχήμα 5..β, και ονομάζεται διακρότημα. Τέτοιου είδους υπέρθεση μπορούμε να παρατηρήσουμε, όταν χτυπήσουμε δύο διαπασών που έχουν λίγο διαφορετική συχνότητα, οπότε και θα ακούσουμε μια περιοδική αυξομείωση του ήχου. Οι αυξομειώσεις αυτές λέγονται διακροτήματα. Τα διακροτήματα είναι μια περιοδική αυξομείωση της έντασης, που φτάνει σε ένα σημείο του χώρου, και οφείλονται στην επαλληλία κυμάτων που έχουν παραπλήσιες συχνότητες. Ο αριθμός των διακροτημάτων ανά δευτερόλεπτο, ή η λεγόμενη συχνότητα των διακροτημάτων, ω b, είναι διπλάσια της συχνότητας με την οποία μεταβάλλεται το πλάτος, δηλαδή: b (5.) Σχήμα 5. (α) Μετατόπιση ως συνάρτηση του χρόνου για δύο κύματα με παραπλήσιες συχνότητες, και (β) το αποτέλεσμα της επαλληλίας δύο τέτοιων κυμάτων (διακρότημα). Για παράδειγμα, εάν έχουμε δύο διεγερμένα διαπασών, το ένα με συχνότητα (ω/π) 44Hz και το άλλο με 438Hz, τότε ο συνιστάμενος ήχος έχει συχνότητα ( )/ = 440Hz (που είναι η νότα «Λα») και συχνότητα διακροτημάτων = 4Hz. Συνεπώς, ο ακροατής θα ακούει ήχο συχνότητας 440Hz, του οποίου η ένταση θα αυξομειώνεται τέσσερις φορές το δευτερόλεπτο. Η μέγιστη συχνότητα διακροτημάτων που μπορεί να διακρίνει το ανθρώπινο αυτί είναι 0 διακροτήματα το δευτερόλεπτο. Πολλοί πιανίστες κουρδίζουν το πιάνο τους χρησιμοποιώντας διακροτήματα. Χτυπούν τη χορδή μιας νότας μαζί με μια άλλη γνωστής συχνότητας, και κουρδίζουν τη χορδή, ώσπου να μην ακούγονται διακροτήματα, οπότε οι δύο χορδές παράγουν την ίδια συχνότητα. 3. Ανάλυση κυμάτων κατά Forier Κάθε περιοδική κυματοσυνάρτηση, ανεξαρτήτως πόσο πολύπλοκη είναι, μπορεί να κατασκευαστεί από την υπέρθεση ημιτονοειδών κυμάτων που έχουν κατάλληλες συχνότητες και πλάτη. Οι συνιστώσες συχνότητες μπορούν να βρεθούν από μια μαθηματική τεχνική που ονομάζεται ανάλυση κατά Forier(Φουριέ) ή απλά ανάλυση Forier. Το τετραγωνικό κύμα, που φαίνεται στο σχήμα 5..α, μπορεί να υπολογιστεί, χρησιμοποιώντας τη σειρά Forier: 68
4 y sin t sin3 sin t 5 t (5.) Ο μετασχηματισμός Forier ενός κύματος είναι απλά ένα γράφημα στο «χώρο» των συχνοτήτων, όπου ο x-άξονας προσδιορίζει την συχνότητα ω, ενώ στον y-άξονα δίνεται το πλάτος στην κάθε συχνότητα, το οποίο προσδιορίζει την συνεισφορά της κάθε συχνότητας στο αρχικό κύμα. Στο σχήμα 5..β, φαίνεται ένα κύμα (αριστερά) και ο μετασχηματισμός Forier του (δεξιά). Σχήμα 5. (α) Ανάλυση τετραγωνικού κύματος με σειρές Forier, και (β) κύμα (αριστερά) και ο μετασχηματισμός Forier του (δεξιά). 4. Στάσιμα κύματα Ας θεωρήσουμε δύο κύματα με το ίδιο πλάτος, την ίδια συχνότητα και την ίδια αρχική φάση (φ = φ = 0), τα οποία οδεύουν σε αντίθετες κατευθύνσεις (σχήμα 5.3.α). Πώς θα περιγραφόταν μαθηματικά στην κυματοσυνάρτηση το γεγονός ότι ταξιδεύουν αντίθετα; Η απάντηση είναι ότι το πρόσημο του κυματάριθμου, 69
5 κ, είναι αυτό που καθορίζει αν το κύμα κινείται προς τη «θετική» ( κ) ή την «αρνητική» (+κ) κατεύθυνση (προς τα δεξιά και προς τα αριστερά, αντίστοιχα). Έτσι: Κύμα που οδεύει προς τα δεξιά: y A sin( t x) (5.3) Κύμα που οδεύει προς τα αριστερά: y A sin( t x) (5.4) Σχήμα 5.3 (α) Δύο κύματα που οδεύουν προς αντίθετες κατευθύνσεις, (β) στάσιμο κύμα ως υπέρθεση των δύο προηγούμενων κυμάτων, και (γ) κίνηση σωματιδίων του στάσιμου κύματος. Hυπέρθεση δύο τέτοιων κυμάτων δίνει ένα συνιστάμενο κύμα: ( t x) ( t x) ( t x) ( t x) yr y y Aosin cos x yr A cos sint (5.5) x Το κύμα αυτό έχει πλάτος A cos ( ) και κυκλική συχνότητα ω, ίδια με αυτή των κυμάτων y και y. Καθένα από τα σωματίδια του μέσου διάδοσης αυτού του κύματος πάλλεται εκτελώντας απλή αρμονική κίνηση με την ίδια συχνότητα, ω, αλλά με διαφορετικό πλάτος ανάλογα με τη θέση του σωματιδίου x στο μέσο διάδοσης (το x πλάτος είναι περιοδική συνάρτηση της θέσης x). Αφού το πλάτος του συνιστάμενου κύματος είναι A cos 70
6 , το ελάχιστο πλάτος θα είναι 0 και το μέγιστο πλάτος θα είναι Α ο. Παρατηρούμε, λοιπόν, ότι το συνιστάμενο κύμα έχει πλάτος που ποικίλει από 0 σε Α ο όταν το x αλλάζει κατά ένα μήκος κύματος. Συνεπώς, το πλάτος ταλάντωσης του σωματιδίου που βρίσκεται στη θέση x εξαρτάται από την τιμή του x επίσης περιοδικά. Σύμφωνα με τα παραπάνω, το μέγιστο πλάτος Α ο θα είναι το πλάτος ταλάντωσης μερικών μόνο συγκεκριμένων σωματιδίων, και όχι όλων, και συγκεκριμένα εκείνων των οποίων η θέση x πληροί την x προϋπόθεση cos, όταν δηλαδή: x m x m, m = 0,,, (5.6) Εκείνες οι θέσεις όπου η μετατόπιση είναι πάντα μέγιστη (για όλους τους χρόνους) ονομάζονται κοιλίες. Παρόμοια, υπάρχουν θέσεις, όπου το πλάτος του συνιστάμενου κύματος είναι πάντα μηδενικό, δηλαδή x υπάρχουν μερικά σωματίδια τα οποία είναι πάντα ακίνητα. Αυτό συμβαίνει, όταν cos 0, δηλαδή: x (n ) x (n ), n = 0,,, (5.7) 4 Εκείνες οι θέσεις όπου η μετατόπιση είναι πάντα μηδενική (για όλους τους χρόνους) ονομάζονται δεσμοί. Κύματα που έχουν σημεία τα οποία παραμένουν συνεχώς ακίνητα ονομάζονται στάσιμα κύματα (σχήμα 5.3.β). Σε ένα στάσιμο κύμα, λοιπόν, υπάρχουν σωματίδια που είναι πάντα ακίνητα, ενώ τα υπόλοιπα σωματίδια κινούνται πάνω κάτω, εκτελώντας απλή αρμονική κίνηση με μεγάλη ταχύτητα, με αποτέλεσμα ο παρατηρητής να βλέπει μόνο την περιβάλλουσα της κυματομορφής (σχήμα 5.3.γ). Τα στάσιμα κύματα μπορούν να τα επιβάλουν συνοριακές συνθήκες, όπως θα δούμε στην παράγραφο Στάσιμα κύματα σε χορδές Ένα χαρακτηριστικό παράδειγμα στάσιμων κυμάτων είναι αυτά που δημιουργούνται, όταν διεγείρονται τεντωμένες χορδές, που είναι στερεωμένες και στα δύο άκρα. Αφού τα άκρα της χορδής είναι στερεωμένα, είναι λογικό ότι, σε οποιαδήποτε διέγερση της χορδής, αυτά τα σημεία θα είναι πάντα δεσμοί. Αυτό το γεγονός επιβάλλει ότι για τη δημιουργία στάσιμου κύματος θα πρέπει το μήκος της χορδής L να είναι ακέραιο πολλαπλάσιο του μισού μήκους κύματος, αφού, μόνο τότε, έχουμε δεσμούς στα άκρα της χορδής. Έτσι η συνθήκη για τη δημιουργία στάσιμων κυμάτων σε μια τέτοια χορδή είναι: L n, n =,, 3, (5.8) Η χορδή, λοιπόν, μπορεί να ταλαντωθεί, σχηματίζοντας μόνο συγκεκριμένα χαρακτηριστικά σχήματα ταλάντωσης. Αυτά ονομάζονται κανονικοί τρόποι ταλάντωσης ή ιδιοκαταστάσεις της χορδής, και σε καθέναν από αυτούς αντιστοιχεί μία συχνότητα, η οποία ονομάζεται ιδιοσυχνότητα ή κανονική συχνότητα. Όπως έχει αναφερθεί, η ταχύτητα διάδοσης του κύματος σε μία τεντωμένη χορδή (φασική ταχύτητα) δίνεται από τη σχέση: T (5.9) όπου Τ η τάση της χορδής και ρ η γραμμική πυκνότητά της. Η τάση της χορδής είναι ένα μέτρο του πόσο τεντωμένη είναι η χορδή, και στο σύστημα SI μετριέται σε Ν. Η γραμμική πυκνότητα στο σύστημα SI μετριέται σε kg/m(μάζα ανά μήκος). Από την εξίσωση 5.9 φαίνεται ότι η ταχύτητα διάδοσης του κύματος είναι η ίδια για όλες τις συχνότητες. Συνδυάζοντας τις εξισώσεις 5.8 και 5.9, και επειδή = λν, μπορούμε να υπολογίσουμε τις ιδιοσυχνότητες της χορδής: n T n L, n =,, 3 (5.0) Η χαμηλότερη ιδιοσυχνότητα ν (για n =, όταν δηλαδή λ = L) ονομάζεται θεμελιώδης ή βασική συχνότητα. Οι υπόλοιπες ιδιοσυχνότητες είναι ακέραια πολλαπλάσια της θεμελιώδους, δηλαδή ν = ν, ν 3 = 3ν, κ.ο.κ. Η θεμελιώδης συχνότητα και οι υπόλοιπες ιδιοσυχνότητες αποτελούν αυτό που ονομάζουμε αρμονική σειρά: η θεμελιώδης (ν ) είναι η πρώτη αρμονική, η ιδιοσυχνότητα ν (n = ) είναι η δεύτερη αρμονική κτλ. Τα στάσιμα κύματα που αντιστοιχούν στις 5 πρώτες ιδιοσυχνότητες φαίνονται στο σχήμα
7 Σχήμα 5.4 Τα στάσιμα κύματα που αντιστοιχούν στις 5 πρώτες ιδιοσυχνότητες μιας χορδής μήκους L, στερεωμένης και στα δύο άκρα Έγχορδα μουσικά όργανα Πολλά μουσικά όργανα είναι έγχορδα, από χορδές φτιαγμένες από ατσάλι ή νάιλον, τεντωμένες πάνω στο κυρίως σώμα του μουσικού οργάνου. Παραδείγματα είναι το βιολί, οι κιθάρες, τα πιάνα κ.α. Η εξίσωση που συνδέει τον ήχο, που βγάζουν οι χορδές, με τις μηχανικές ιδιότητες των υλικών, από τα οποία είναι φτιαγμένες, είναι η εξίσωση 5.0, που αποδείξαμε προηγουμένως. Ο ήχος παράγεται, όταν η χορδή διαταραχθεί από τη θέση ισορροπίας της. Τότε στάσιμα κύματα εμφανίζονται στη χορδή, καθώς εγκάρσια κύματα ταξιδεύουν μπρος και πίσω κατά μήκος της χορδής. Τα στάσιμα κύματα έχουν μήκος κύματος που είναι ακέραιο πολλαπλάσιο του λ/. Αυξάνοντας την τάση, ή ελαττώνοντας τη μάζα ανά μονάδα μήκους της χορδής (πρακτικά κάνοντας την χορδή ελαφρύτερη), αυξάνουμε την συχνότητα. Έτσι μπάσες (bass) νότες προκαλούνται από χονδρές και, κατά επέκταση, βαριές χορδές, ενώ πρίμες νότες (treble) από ελαφριές χορδές. Τα όργανα κουρδίζονται (tning) αλλάζοντας την τάση των χορδών. Χαμηλής συχνότητας ήχοι (πολύ μπάσες νότες) παράγονται από μακρύτερες χορδές (L μεγάλο). Για παράδειγμα συγκρίνετε το μήκος των χορδών του διπλού μπάσου με αυτή του βιολιού. 5. Συντονισμός Ας θεωρήσουμε ένα στάσιμο κύμα σε μία τεντωμένη χορδή με σταθερά άκρα. Όλα τα σωματίδια, από τα οποία αποτελείται η χορδή, ταλαντώνονται κάθετα στον άξονα της χορδής με την ίδια συχνότητα, εκτός από τα 7
8 σημεία όπου υπάρχουν δεσμοί, τα οποία παραμένουν ακίνητα. Αφού, όμως, στους δεσμούς τα σωματίδια παραμένουν ακίνητοι, στο στάσιμο κύμα δε διαδίδεται ενέργεια κατά μήκος του κύματος. Η ενέργεια που έχει αποθηκευτεί στο σύστημα (η ενέργεια του αρχικού οδεύοντος κύματος) συνεχώς μεταβάλλεται από ελαστική δυναμική ενέργεια, E Δ, οπότε και το νήμα είναι στιγμιαία ακίνητο, σε κινητική ενέργεια, E Κ, οπότε, όταν η χορδή είναι οριζόντια, τα σωματίδια της έχουν τη μέγιστη ταχύτητά τους. Στις ενδιάμεσες στιγμές τα σωματίδια της χορδής έχουν και κινητική και δυναμική ενέργεια. Το πώς μεταβάλλεται η ενέργεια των σωματιδίων της χορδής σε ένα κύκλο ταλάντωσης, φαίνεται στο σχήμα 5.5.α. Σχήμα 5.5 (α) Η μεταβολή της ενέργειας των σωματιδίων ταλαντευόμενης τεντωμένης χορδής με σταθερά άκρα, και (β) φαινόμενο του συντονισμού: το πλάτος της ταλάντωσης γίνεται μέγιστο, όταν η συχνότητα διέγερσης συμπίπτει ακριβώς με μία από τις συχνότητες συντονισμού. Εάν δεν υπάρχουν απώλειες ενέργειας, π.χ. από τριβές, τα κύματα μπορούν να ταξιδεύουν μπροστά και πίσω ανακλώμενα από τα άκρα για άπειρο χρόνο. Αν συνεχίζουμε να προσθέτουμε ενέργεια στο σύστημα, και δεδομένου ότι δεν υπάρχουν απώλειες, το πλάτος ταλάντωσης των σωματιδίων, άρα και το πλάτος του κύματος, θα αυξάνει συνεχώς. Η συχνότητα του κύματος θα παραμένει σταθερή, αφού εξαρτάται μόνο από το μήκος της 73
9 χορδής. Το πλάτος της ταλάντωσης γίνεται μεγαλύτερο όσο η συχνότητα διέγερσης της χορδής πλησιάζει μία από τις ιδιοσυχνότητες του συστήματος. Το φαινόμενο αυτό ονομάζεται συντονισμός και συμβαίνει όταν: - δεν υπάρχει μηχανισμός απώλειας ενέργειας, και - οι ταλαντώσεις προκαλούνται σε μία συχνότητα που είναι ακριβώς (ή πολύ κοντά) στη συχνότητα του κανονικού ρυθμού ταλάντωσης της χορδής. Οι αντίστοιχες ιδιοσυχνότητες του συστήματος λέγονται συχνότητες συντονισμού. Στο σχήμα 5.5.β φαίνεται η απόκριση ενός τέτοιου συστήματος ως συνάρτηση της συχνότητας διέγερσης. Το πλάτος της ταλάντωσης γίνεται μέγιστο, όταν η συχνότητα διέγερσης συμπίπτει ακριβώς με μία από τις συχνότητες συντονισμού. Εάν οι ταλαντώσεις δεν προκαλούνται κοντά σε μια συχνότητα συντονισμού, η ενέργεια δε μεταδίδεται αποδοτικά από τον τροφοδότη στο σύστημα. 6. Ανάκλαση και μετάδοση κυμάτων χορδής σε συνοριακή επιφάνεια Κάθε μέσον στο οποίο διαδίδονται κύματα εμφανίζει μια αντίσταση στη διάδοσή τους. Στην απλή περίπτωση που το μέσον δεν παρουσιάζει απώλειες και δεν χαρακτηρίζεται από κανένα μηχανισμό κατανάλωσης, η σύνθετη αντίσταση θα καθορίζεται από τους δύο μηχανισμούς αποθήκευσης ενέργειας, την αδράνεια και την ελαστικότητα. Ας περιοριστούμε σε εγκάρσια κύματα που διαδίδονται σε μια χορδή. Η εγκάρσια σύνθετη αντίσταση Ζ στη χορδή ορίζεται ως: Fo Z (5.) o όπου F o είναι το πλάτος της αρμονικής δύναμης που προκαλεί την κυματική διαταραχή και o είναι το πλάτος της εγκάρσιας σωματιδιακής ταχύτητας. Αποδεικνύεται ότι: o Fo (5.) T όπου είναι η ταχύτητα φάσης του προκαλούμενου κύματος και Τ η τάση της χορδής. Αλλά σε μια χορδή έχουμε ήδη αναφέρει ότι: T (5.3) όπου ρ είναι η γραμμική πυκνότητα μάζας της χορδής. Έτσι τελικά έχουμε για την σύνθετη αντίσταση χορδής: Z (5.4) Πως θα συμπεριφερθούν, όμως, τα κύματα σε μια απότομη αλλαγή της σύνθετης αντίστασης; Θεωρήστε μία χορδή που αποτελείται από δύο κομμάτια με διαφορετική σύνθετη αντίσταση, Ζ και Ζ αντίστοιχα, και ένα προσπίπτον κύμα που οδεύει κατά μήκος της χορδής και συναντάει μια ασυνέχεια στη σύνθετη αντίσταση από Ζ σε Ζ στο σημείο x = 0 (σχήμα 5.6.α). Είναι απολύτως λογικό να υποθέσουμε ότι ένα μέρος του κύματος θα ανακλαστεί, και ένα μέρος θα διαδοθεί στο κομμάτι της χορδής με σύνθετη αντίσταση Ζ. Αυτό που μας ενδιαφέρει είναι να υπολογίσουμε το πλάτος του ανακλώμενου και του μεταδιδόμενου κύματος σε σχέση με αυτό του προσπίπτοντος. Για να κάνουμε τον συγκεκριμένο υπολογισμό, χρειαζόμαστε κάποιες συνθήκες που θα συνδέουν με μαθηματικό τρόπο τα τρία κύματα, που λαμβάνουν χώρα στο πρόβλημα. Οι συνθήκες αυτές ονομάζονται συνοριακές συνθήκες: Α. Μια γεωμετρική συνοριακή συνθήκη ότι η απομάκρυνση του σωματιδίου που είναι ακριβώς στο σύνορο (x = 0) είναι ίδια είτε την υπολογίσουμε από δεξιά είτε από αριστερά, έτσι ώστε να μην υπάρχει ασυνέχεια στην απομάκρυνση. Αλλά η παραπάνω συνθήκη δεν είναι αρκετή, διότι η Φυσική υπαγορεύει ομαλή μετάβαση της μιας κυματομορφής μέσω του συνόρου στην άλλη. Στο σχήμα 5.6.β φαίνεται μια απότομη τριγωνική μετάβαση (αριστερά) και μία ομαλή συνημιτονοειδής μετάβαση (δεξιά) του πλάτους του κύματος. Αυτό που θα συμβεί είναι η δεύτερη περίπτωση, και ο λόγος είναι ότι σε διαφορετική περίπτωση μια πεπερασμένη διαφορά στη δύναμη δεξιά και αριστερά του x = 0 θα δρούσε στο σωματίδιο που βρίσκεται στο x = 0, με αποτέλεσμα την κίνησή του παράλληλα με το μήκος της χορδής, πράγμα που προφανώς αντιτίθεται στα εγκάρσια κύματα που μελετάμε. 74
10 Σχήμα 5.6 (α) Κύμα που οδεύει κατά μήκος χορδής η οποία αποτελείται από δύο κομμάτια με διαφορετική σύνθετη αντίσταση, και (β) απότομη τριγωνική μετάβαση (αριστερά) και ομαλή συνημιτονοειδής μετάβαση (δεξιά) του πλάτους του παραπάνω κύματος (συνέχεια της κυματοσυνάρτησης και της παραγώγου στη συνοριακή επιφάνεια). Μετά από την παραπάνω ανάλυση καταλήγουμε στη δεύτερη συνοριακή συνθήκη: y Β. Η παράγωγος της κυματοσυνάρτησης ( ) να είναι συνεχής στο x = 0. x Πριν εφαρμόσουμε τις παραπάνω συνοριακές συνθήκες, γράφουμε τις κυματοσυναρτήσεις για τα τρία κύματα που συμμετέχουν στο πρόβλημα: Προσπίπτον κύμα: yi Aisin( t x) (5.5) Ανακλώμενο κύμα: yr Arsin( t x) (5.6) Μεταδιδόμενο κύμα: yt Atsin( t x) (5.7) Σημειώστε ότι όλα τα κύματα έχουν την ίδια συχνότητα ω. Αυτά που βρίσκονται στο τμήμα της χορδής με ίδια σύνθετη αντίσταση έχουν τον ίδιο κυματάριθμο, όσον αφορά το μέτρο, καθώς ο κυματάριθμος εξαρτάται από την ταχύτητα φάσης του κύματος στο συγκεκριμένο μέσο ( = ω/κ). Η φορά του κύματος καθορίζεται από το πρόσημο του κυματάριθμου, θετικό, όταν το κύμα οδεύει προς τα δεξιά, και αρνητικό, όταν οδεύει προς τα αριστερά. Εφαρμόζουμε τώρα τις συνοριακές συνθήκες, και έχουμε: Συνθήκη Α: ( 0) sin( ) sin( ) sin( ) x yi yr yt Ai t x Ar t x At t x Ai Ar At (5.8) Συνθήκη B: ( i r ) t sin( ) sin( ) sin( ) x y y y Ai t x Ar t x At t x x x ( 0) 75
11 Ai Ar At (5.9) Για όλα τα κύματα ισχύει: Z (5.30) T έτσι οι παραπάνω συνθήκες Α και Β γίνονται: Συνθήκη Α: Ai Ar At (5.3) Συνθήκη Β: Z( Ai Ar ) ZAt (5.3) Λύνοντας το σύστημα των εξισώσεων 5.9 και 5.3 υπολογίζουμε το συντελεστή ανάκλασης πλάτους r, και το συντελεστή μετάδοσης πλάτους t : Ar Z Z Συντελεστής ανάκλασης πλάτους: r (5.33) A Z Z i At Z Συντελεστής μετάδοσης πλάτους: t (5.34) Ai Z Z Βλέπουμε ότι οι παραπάνω συντελεστές: - δεν εξαρτώνται από το ω, και ισχύουν συνεπώς για κύματα όλων των συχνοτήτων, και - είναι πραγματικοί αριθμοί και συνεπώς απαλλαγμένοι από αλλαγές φάσης εκτός από την αλλαγή κατά π που θα αλλάξει το πρόσημο του ανακλώμενου όρου. Οι λόγοι αυτοί εξαρτώνται ολοκληρωτικά από τους λόγους των σύνθετων αντιστάσεων. Αν Z, που σημαίνει π.χ. ότι το σημείο στο x = 0 είναι καρφωμένο, τότε δεν υπάρχει μεταδιδόμενο κύμα. Σ αυτή την Ar περίπτωση, που σημαίνει ότι έχουμε 00% ανάκλαση στο σύνορο (αντιστροφή φάσης κατά π), όπως At ήδη έχουμε επισημάνει για κύματα που διαδίδονται σε καρφωμένες στα άκρα χορδές, και είναι αναγκαία για τη δημιουργία στάσιμων κυμάτων. Μια κυματομάδα που περιέχει πολλές συχνότητες θα διατηρήσει το σχήμα της κατά την ανάκλαση, αλλά θα υποστεί αναστροφή. 7. Ενέργεια κυμάτων χορδής σε συνοριακή επιφάνεια Σε αυτή την παράγραφο θα εξετάσουμε τι συμβαίνει στην ενέργεια ενός κύματος, όταν συναντά ένα σύνορο μεταξύ δύο μέσων με διαφορετική τιμή σύνθετης αντίστασης. Έχουμε δείξει από το προηγούμενο κεφάλαιο ότι η ενέργεια ανά μονάδα μήκους των ταλαντωτών που μεταδίδουν το κύμα είναι E A. Επειδή το κύμα οδεύει με ταχύτητα ίση με, ο ρυθμός με τον οποίο μεταδίδεται η ενέργεια κατά μήκος της χορδής είναι ίση με την ισχύ, P. Επειδή P = E έχουμε: P Ao (5.35) Στο συγκεκριμένο πρόβλημα του συνόρου, ο ρυθμός με τον οποίο φτάνει ενέργεια στο x = 0 είναι ο ρυθμός της ενέργειας του προσπίπτοντος κύματος, δηλαδή: Ai Z Ai (5.36) Ο ρυθμός με τον οποίο απομακρύνεται ενέργεια από το σύνορο, μέσω του ανακλώμενου και του μεταδιδόμενου κύματος είναι: Z Ar Z At (5.37) Χρησιμοποιώντας τις εξισώσεις 5.33 και 5.34 που έχουμε ήδη αποδείξει, η εξίσωση 5.37 γίνεται: Z( Z Z) 4Z Z Ai Z Ai (5.38) ( Z Z) Συγκρίνοντας την εξίσωση 5.36 με την εξίσωση 5.38 καταλήγουμε στο συμπέρασμα ότι όλη η ενέργεια που φτάνει στο σύνορο με το προσπίπτον κύμα απομακρύνεται από το σύνορο με το μεταδιδόμενο κύμα. 76
12 Με βάση τις παραπάνω σχέσεις μπορούμε να υπολογίσουμε τους συντελεστές ανάκλασης και μετάδοσης ενέργειας ή έντασης ως εξής: Συντελεστής ανάκλασης ενέργειας ή έντασης = ανακλώμενη ενέργεια / προσπίπτουσα ενέργεια, δηλαδή: Z Ar Z Z R (5.39) Z Z Z A i Συντελεστής μετάδοσης ενέργειας ή έντασης = μεταδιδόμενη ενέργεια / προσπίπτουσα ενέργεια, δηλαδή: Z At 4ZZ T (5.40) Z ( Z Z) A i 8. Διάθλαση κυμάτων Όπως έχουμε εξηγήσει σε προηγούμενο κεφάλαιο, η φασική ταχύτητα των μηχανικών κυμάτων εξαρτάται από την ελαστική και την αδρανειακή ιδιότητα του μέσου μέσα στο οποίο διαδίδονται. Όταν ένα μηχανικό κύμα διαδοθεί από ένα υλικό σε ένα άλλο υλικό (με διαφορετική φασική ταχύτητα), τότε, και εάν προσπίπτει στη διεπιφάνεια των δύο υλικών υπό γωνία, η πορεία του κύματος στο δεύτερο υλικό εκτρέπεται (βλ. σχήμα 5.7). Η εκτροπή αυτή ονομάζεται διάθλαση του κύματος, και οφείλεται στο γεγονός ότι, όταν το μέτωπο του κύματος (μικρές μαύρες παράλληλες γραμμές στο σχήμα 5.7) βρεθεί ακριβώς στο σύνορο των δύο περιοχών, ένα μέρος κινείται ακόμα στο ένα υλικό και ένα μέρος στο άλλο. Το αποτέλεσμα τελικά θα είναι η εκτροπή του μετώπου του κύματος, όταν αυτό εισέλθει πλήρως στο δεύτερο υλικό. Σχήμα 5.7 Κύμα (την πορεία του κύματος τη δείχνει η κόκκινη γραμμή) που προσπίπτει υπό γωνία θ (σε σχέση με την κάθετο στη συνοριακή επιφάνεια, μπλε διακεκομμένη γραμμή) πάνω σε συνοριακή επιφάνεια μεταξύ δύο υλικών με διαφορετική φασική ταχύτητα και αλλάζει κατεύθυνση, και κινείται πλέον σε νέα γωνία θ. Γενικά, αν θ είναι η γωνία πρόσπτωσης του κύματος στη διεπιφάνεια των δύο υλικών (σε σχέση με την κάθετο) και θ είναι η γωνία εξόδου της πορείας του κύματος στο δεύτερο υλικό, στη διάθλαση ισχύει ο παρακάτω νόμος (γνωστός και ως νόμος του Snell): sin sin (5.4) 77
13 9. Φαινόμενο Doppler Οποτεδήποτε υπάρχει σχετική κίνηση μεταξύ της πηγής των κυμάτων και του δέκτη, η συχνότητα των κυμάτων που ανιχνεύει ο δέκτης είναι διαφορετική από αυτή που θα ανίχνευε ο ίδιος δέκτης, αν δεν υπήρχε σχετική κίνηση. Αυτό το φαινόμενο είναι γνωστό ως φαινόμενο Doppler (Ντόπλερ), προς τιμήν του Αυστριακού φυσικού C.J. Doppler. Το φαινόμενο εξηγείται ποιοτικά, αν παρατηρήσουμε τη σχηματική του αναπαράσταση στο σχήμα 5.8.α. Θεωρήστε ένα αεροπλάνο που κινείται προς το μέρος ενός ακίνητου ακροατή. Έστω ότι τα ηχητικά κύματα, που εκπέμπονται από τις μηχανές του αεροπλάνου, έχουν μια καθορισμένη συχνότητα ν. Ο ακροατής όμως λόγω της κίνησης του αεροπλάνου προς το μέρος του θα λαμβάνει τα μέγιστα των ηχητικών κυμάτων (οι κύκλοι του σχήματος) με συχνότητα ν' μεγαλύτερη από αυτή που πραγματικά έχουν (σχηματικά αυτό δείχνεται με το πύκνωμα των κύκλων). Στην περίπτωση που το αεροπλάνο απομακρυνόταν από τον ακροατή, είναι προφανές ότι οι κύκλοι θα αραίωναν (δες πίσω μέρος του αεροπλάνου στο σχήμα 5.8.α), και ότι η συχνότητα του κύματος, που θα άκουγε ο ακροατής, θα ήταν μικρότερη από την πραγματική. Ας ποσοτικοποιήσουμε το φαινόμενο Doppler για τις εξής τέσσερις περιπτώσεις: - Ο δέκτης πλησιάζει ακίνητο πομπό με ταχύτητα rec (σχήμα 5.8.β). Η συχνότητα ν' που ανιχνεύει ο δέκτης είναι ίση με τον αριθμό των κυμάτων που φτάνουν σε αυτόν ανά μονάδα χρόνου, δηλαδή: t rect rec rec t v rec (5.4) - Ο δέκτης απομακρύνεται από ακίνητο πομπό με ταχύτητα rec (σχήμα 5.8.γ). Παρόμοια, όπως προηγουμένως, έχουμε: t rect rec rec t rec (5.43) - Ο πομπός πλησιάζει ακίνητο δέκτη με ταχύτητα s (σχήμα 5.8.δ). Όταν η πηγή κινείται προς ένα ακίνητο παρατηρητή, το αποτέλεσμα είναι η μείωση του μήκους κύματος, γιατί η πηγή ακολουθεί τα πλησιάζοντα κύματα, και, συνεπώς, τα μέτωπα πλησιάζουν μεταξύ τους. Αν η συχνότητα της πηγής είναι ν και η ταχύτητά της s, τότε στην διάρκεια κάθε ταλαντώσεως καλύπτει απόσταση s/ν και κάθε μήκος κύματος μικραίνει κατά το ποσό αυτό. Άρα το μήκος κύματος που φτάνει στον s παρατηρητή είναι δεν είναι, αλλά. Επομένως η συχνότητα του ήχου που λαμβάνει ο δέκτης είναι: s (5.44) s 78
14 Σχήμα 5.8 (α) Σχηματική αναπαράσταση του φαινομένου Doppler. Χαρακτηριστικές περιπτώσεις σχετικής κίνησης πομπού (s) και δέκτη (r): (β) δέκτης πλησιάζει ακίνητο πομπό με ταχύτητα rec, (γ) δέκτης απομακρύνεται από ακίνητο πομπό με ταχύτητα rec, (δ) πομπός πλησιάζει ακίνητο δέκτη με ταχύτητα s, και (ε) πομπός απομακρύνεται από ακίνητο δέκτη με ταχύτητα s. - Ο πομπός απομακρύνεται από ακίνητο δέκτη με ταχύτητα s (σχήμα 5.8.ε). Αν η πηγή απομακρύνεται από τον παρατηρητή, το εκπεμπόμενο μήκος κύματος είναι κατά s/ν μεγαλύτερο από το λ. Έτσι ο δέκτης λαμβάνει μια μειωμένη συχνότητα: (5.45) s Συνοψίζοντας τις παραπάνω τέσσερις περιπτώσεις, μπορούμε να πούμε ότι, στην περίπτωση που τόσο ο πομπός όσο και ο δέκτης κινούνται μέσα στο μέσο διάδοσης, με ταχύτητες s και rec, αντίστοιχα, ο δέκτης λαμβάνει μια συχνότητα που δίνεται από τη σχέση: 79
15 rec (5.46) s όπου τα πάνω πρόσημα είναι ( στον παρανομαστή, + στον αριθμητή) αντιστοιχούν σε πομπό και δέκτη που πλησιάζουν ο ένας τον άλλο κατά μήκος της γραμμής που τους ενώνει, και τα κάτω πρόσημα (+ στο παρανομαστή, στον αριθμητή), όταν απομακρύνονται ο ένας από τον άλλο. 0. Ασκήσεις Άσκηση 5.: Δύο κύματα, που διαδίδονται στην ίδια διεύθυνση, έχουν κυματοσυναρτήσεις y = 3sin(π440t,6πx+30 ) και y = 3sin(π440t,6πx+60 ). Τα δύο κύματα συμβάλλουν. Να βρεθεί κυματοσυνάρτηση της επαλληλίας τους και η ταχύτητα ομάδας της. Άσκηση 5.: Δύο κύματα με κυματοσυναρτήσεις y = 3sin(00t 6x) και y = 3sin(00t+6x) συμβάλλουν, καθώς κινούνται σε αντίθετες κατευθύνσεις. Βρείτε το στάσιμο κύμα που προκύπτει από την επαλληλία τους. Βρείτε τις μαθηματικές σχέσεις που ορίζουν τις θέσεις των δεσμών και των κοιλιών του στάσιμου κύματος. Άσκηση 5.3: Ένα στάσιμο κύμα δίνεται από τη σχέση y = 3,3sin(9t)cos(4x) (SI). Αν θεωρήσουμε ότι προέρχεται από τη συμβολή δύο ίδιων κυμάτων που κινούνται σε αντίθετες κατευθύνσεις, ποια είναι αυτά τα κύματα; (δώστε κυματοσυναρτήσεις) Άσκηση 5.4: Δυο χορδές ίδιου μήκους, L, και ίδιας γραμμικής πυκνότητας, ρ, κρατούνται ακίνητες στα δυο άκρα τους. Με τι λόγο τάσεων, T /T, πρέπει να τεντωθούν, ώστε η τρίτη (3 η ) αρμονική της πρώτης να είναι ίδια με την έκτη (6 η ) αρμονική της δεύτερης; Άσκηση 5.5: Σε ένα χώρο συνυπάρχουν δυο κύματα με κυματοσυναρτήσεις y = 3sin(680πt+πx) και y = 3sin(680πt πx) (SI), όπου y, y η απομάκρυνση από τη θέση ισορροπίας, t ο χρόνος και x οι θέσεις ισορροπίας των συζευγμένων ταλαντωτών. Βρείτε το σύνθετο κύμα που θα προκύψει από την επαλληλία των παραπάνω (αναλυτική μαθηματική περιγραφή και επεξήγησή του). Πόσο απέχει ο δεύτερος δεσμός και η δεύτερη κοιλία από το x = 0; Άσκηση 5.6: Ένα ασθενοφόρο κινείται στον αυτοκινητόδρομο ισοταχώς με ταχύτητα 33,5m/sec. Η σειρήνα του εκπέμπει ήχο συχνότητας 400Hz. Ποια η συχνότητα που ακούει ο οδηγός ενός αυτοκινήτου που κινείται ισοταχώς, αλλά αντίθετα προς το ασθενοφόρο με ταχύτητα 4,6m/sec (α) όταν πλησιάζει το ασθενοφόρο, και (β) όταν απομακρύνεται από αυτό; Άσκηση 5.7: Σε μια χορδή μήκους L = m με πακτωμένα τα δύο άκρα της, διεγείρουμε τη δεύτερη αρμονική (n = ) στην συχνότητα ν = 400Hz. Αν η τάση της χορδής είναι Τ = 0Ν, ποια η γραμμική πυκνότητα της χορδής; Άσκηση 5.8: Η χορδή ενός βιολιού έχει μήκος 50cm, και χορδίζεται με τέτοιο τρόπο, ώστε να παράγει βασικό τόνο συχνότητας 440Hz (A4). (α) βρείτε την περίοδο της ταλάντωσής της, (β) σε τι απόσταση από το πάνω μέρος (κλειδιά) πρέπει να πατηθεί με το δάκτυλο η χορδή, για να αυξηθεί η συχνότητά της στα 880Hz (A5); (γ) υποθέστε ότι θέλετε να αλλάξετε την τάση της χορδής, για να χαμηλώσετε τον τόνο στα 0Hz (A3). Θα χρειαστεί να αυξήσετε ή να μειώσετε την τάση, και με τι παράγοντα; Άσκηση 5.9: Μια χορδή έχει μήκος L = 0,5m και είναι πακτωμένη στα δύο άκρα της με γραμμική πυκνότητα μάζας ρ = 0,05kg/m, και έχει τεντωθεί με τάση Τ = N. Πόση είναι η συχνότητα που συντονίζει την 5 η αρμονική και πόσο απέχουν δύο διαδοχικοί δεσμοί της; Άσκηση 5.0: Στάσιμο κύμα προέκυψε από τη συμβολή δύο κυμάτων της μορφής y = Αsin(ωt κx) και y = Αsin(ωt+κx). Δίνεται ότι δύο διαδοχικοί δεσμοί απέχουν 0cm και ότι ένα σημείο που βρίσκεται σε 80
16 κοιλία ταλαντώνεται με συχνότητα 5Ηz και πλάτος 8cm. Να γραφεί η κυματοσυνάρτηση του στάσιμου κύματος. Άσκηση 5.: Ηχητικό κύμα πέφτει κάθετα σε τοίχο και μετά την ανάκλασή του σχηματίζεται στάσιμο κύμα μπροστά από τον τοίχο. Στο σημείο Α του τοίχου που ανακλάται το κύμα έχουμε δεσμό. Επίσης δεσμό έχουμε σε ένα σημείο Β που απέχει από το Α απόσταση 40cm. Η ταχύτητα διάδοσης του ήχου είναι 340m/sec και η συχνότητά του 700Ηz. Να προσδιορισθεί ο αριθμός και η θέση των κοιλιών μεταξύ Α και Β. Άσκηση 5.: Τα άκρα χορδής μήκους 80cm είναι στερεωμένα. Πάνω στη χορδή διαδίδεται κύμα συχνότητας 00Ηz και ταχύτητας υ, το οποίο, αφού ανακλαστεί, δημιουργεί στάσιμο κύμα. Αν σχηματίζονται δύο κοιλίες, να βρεθεί η υ. Αν η γραμμική πυκνότητα της χορδής είναι 30g/m, να βρεθεί η τάση που είναι τεντωμένη η παραπάνω χορδή. Άσκηση 5.3: Στάσιμο κύμα περιγράφεται στο SI από την κυματοσυνάρτηση y = 3sin(πt)cos(0πx/3). Ποια η απομάκρυνση σημείου Β με x B=0,4m την στιγμή κατά την οποία ένα άλλο σημείο Γ με x Γ = 0,5m έχει απομάκρυνση y Γ = 0,m; Άσκηση 5.4: Ένα θαλάσσιο κύμα με μήκος κύματος 3,0m ταξιδεύει σε ένα θαλάσσιο χώρο που ο πυθμένα είναι βαθύς με φασική ταχύτητα 6,0m/sec. Ξαφνικά εισέρχεται σε περιοχή που ο πυθμένας είναι αβαθής. Εάν η γωνία εισόδου του κύματος στη διεπιφάνεια του νερού με βαθύ και αβαθή πυθμένα είναι 53, και διαθλάται στην περιοχή του αβαθούς πυθμένα με γωνία 30, να υπολογίσετε ποια είναι η φασική ταχύτητα και το μήκος κύματος του κύματος στην περιοχή του αβαθούς πυθμένα (βλ. σχήμα 5.9). Σχήμα 5.9 Σχηματική αναπαράσταση διάθλασης ακουστικών κυμάτων στη θάλασσα, όταν αυτά εισέρχονται από περιοχές με βαθύ πυθμένα σε περιοχές με αβαθή πυθμένα. 8
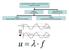
1. Η συχνότητα αρμονικού κύματος είναι f = 0,5 Hz ενώ η ταχύτητα διάδοσης του υ = 2 m / s.
 1. Η συχνότητα αρμονικού κύματος είναι f = 0,5 Hz ενώ η ταχύτητα διάδοσης του υ = 2 m / s. Να βρεθεί το μήκος κύματος. 2. Σε ένα σημείο του Ειρηνικού ωκεανού σχηματίζονται κύματα με μήκος κύματος 1 m και
1. Η συχνότητα αρμονικού κύματος είναι f = 0,5 Hz ενώ η ταχύτητα διάδοσης του υ = 2 m / s. Να βρεθεί το μήκος κύματος. 2. Σε ένα σημείο του Ειρηνικού ωκεανού σχηματίζονται κύματα με μήκος κύματος 1 m και
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
ΚΕΦΑΛΑΙΟ 9 «Κυμάνσεις» Μαρία Κατσικίνη users.auth.gr/~katsiki
 ΚΕΦΑΛΑΙΟ 9 «Κυμάνσεις» Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Σχέση δύναμης - κίνησης Δύναμη σταθερή εφαρμόζεται σε σώμα Δύναμη ανάλογη της απομάκρυνσης (F-kx) εφαρμόζεται σε σώμα Το σώμα
ΚΕΦΑΛΑΙΟ 9 «Κυμάνσεις» Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Σχέση δύναμης - κίνησης Δύναμη σταθερή εφαρμόζεται σε σώμα Δύναμη ανάλογη της απομάκρυνσης (F-kx) εφαρμόζεται σε σώμα Το σώμα
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
Φυσική για Μηχανικούς Εικόνα: O Carlos Santana εκμεταλλεύεται τα στάσιμα κύματα στις χορδές του. Αλλάζει νότα στην κιθάρα του πιέζοντας τις χορδές σε διαφορετικά σημεία, μεγαλώνοντας ή μικραίνοντας το
4. Εισαγωγή στην Κυματική
 4. Εισαγωγή στην Κυματική Σύνοψη Στο κεφάλαιο αυτό εισάγεται η έννοια του κύματος, και τα βασικά μεγέθη των κυματικών διαταραχών, όπως η περίοδος, η συχνότητα, το μήκος κύματος και ο κυματάριθμος. Παρουσιάζονται
4. Εισαγωγή στην Κυματική Σύνοψη Στο κεφάλαιο αυτό εισάγεται η έννοια του κύματος, και τα βασικά μεγέθη των κυματικών διαταραχών, όπως η περίοδος, η συχνότητα, το μήκος κύματος και ο κυματάριθμος. Παρουσιάζονται
3 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 2) ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 3 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 2) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α-Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 3 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 2) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α-Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
ΔΙΑΓΩΝΙΣΜΑ 05 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3 ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) U β A
 Σελίδα 1 από 5 ΔΙΑΓΩΝΙΣΜΑ 05 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3 ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α και
Σελίδα 1 από 5 ΔΙΑΓΩΝΙΣΜΑ 05 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3 ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α και
ΘΕΜΑ Α ΕΡΩΤΗΣΕΙΣ ΘΕΜΑ Α
 ΘΕΜΑ Α 1. Να επιλέξετε τη σωστή απάντηση. Μηχανικό ονομάζεται το κύμα στο οποίο: α. Μεταφέρεται ύλη στον χώρο κατά την κατεύθυνση διάδοσης του κύματος. β. Μεταφέρεται ορμή και ενέργεια στον χώρο κατά την
ΘΕΜΑ Α 1. Να επιλέξετε τη σωστή απάντηση. Μηχανικό ονομάζεται το κύμα στο οποίο: α. Μεταφέρεται ύλη στον χώρο κατά την κατεύθυνση διάδοσης του κύματος. β. Μεταφέρεται ορμή και ενέργεια στον χώρο κατά την
Φυσική Γ Θετ. και Τεχν/κης Κατ/σης ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ
 ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ Στάσιμο κύμα ονομάζεται το αποτέλεσμα της συμβολής δύο κυμάτων της ίδιας συχνότητας και του ίδιου πλάτους που διαδίδονται στο ίδιο μέσο με αντίθετες κατευθύνσεις. Συνήθως προκύπτουν από
ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ Στάσιμο κύμα ονομάζεται το αποτέλεσμα της συμβολής δύο κυμάτων της ίδιας συχνότητας και του ίδιου πλάτους που διαδίδονται στο ίδιο μέσο με αντίθετες κατευθύνσεις. Συνήθως προκύπτουν από
β. δημιουργούνται από πηγή η οποία ταλαντώνεται κάθετα στη διεύθυνση διάδοσης.
 ΜΑΘΗΜΑ /ΤΑΞΗ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΠΩΝΥMΟ: ΗΜΕΡΟΜΗΝΙΑ: 18/11/2017 ΕΞΕΤΑΣΤΕΑ ΥΛΗ: ΤΑΛΑΝΤΩΣΕΙΣ-ΚΥΜΑΤΑ-DOPPLER ΘΕΜΑ Α 1. Τα εγκάρσια μηχανικά κύματα : α. διαδίδονται σε όλα τα μέσα. β.
ΜΑΘΗΜΑ /ΤΑΞΗ: ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΠΩΝΥMΟ: ΗΜΕΡΟΜΗΝΙΑ: 18/11/2017 ΕΞΕΤΑΣΤΕΑ ΥΛΗ: ΤΑΛΑΝΤΩΣΕΙΣ-ΚΥΜΑΤΑ-DOPPLER ΘΕΜΑ Α 1. Τα εγκάρσια μηχανικά κύματα : α. διαδίδονται σε όλα τα μέσα. β.
NTÙÍÉÏÓ ÃÊÏÕÔÓÉÁÓ - ÖÕÓÉÊÏÓ www.geocities.com/gutsi1 -- www.gutsias.gr
 Έστω µάζα m. Στη µάζα κάποια στιγµή ασκούνται δυο δυνάµεις. ( Βλ. σχήµα:) Ποιά η διεύθυνση και ποιά η φορά κίνησης της µάζας; F 1 F γ m F 2 ιατυπώστε αρχή επαλληλίας. M την της Ποιό φαινόµενο ονοµάζουµε
Έστω µάζα m. Στη µάζα κάποια στιγµή ασκούνται δυο δυνάµεις. ( Βλ. σχήµα:) Ποιά η διεύθυνση και ποιά η φορά κίνησης της µάζας; F 1 F γ m F 2 ιατυπώστε αρχή επαλληλίας. M την της Ποιό φαινόµενο ονοµάζουµε
α. 0cm. β. 10cm. γ. 20cm. δ. 40cm.
 ΘΕΜΑ A Α. Ερωτήσεις πολλαπλής επιλογής. Δύο όμοιες πηγές κυμάτων Α και Β στην επιφάνεια μιας ήρεμης λίμνης βρίσκονται σε φάση και παράγουν υδάτινα αρμονικά κύματα. Η καθεμιά παράγει κύμα (πρακτικά) αμείωτου
ΘΕΜΑ A Α. Ερωτήσεις πολλαπλής επιλογής. Δύο όμοιες πηγές κυμάτων Α και Β στην επιφάνεια μιας ήρεμης λίμνης βρίσκονται σε φάση και παράγουν υδάτινα αρμονικά κύματα. Η καθεμιά παράγει κύμα (πρακτικά) αμείωτου
KYMATA Ανάκλαση - Μετάδοση
 ΦΥΣ 131 - Διαλ.34 1 KYMATA Ανάκλαση - Μετάδοση q Παλµός πάνω σε χορδή: Ένα άκρο της σταθερό (δεµένο) Προσπίπτων Ο παλµός ασκεί µια δύναµη προς τα πάνω στον τοίχο ο οποίος ασκεί µια δύναµη προς τα κάτω
ΦΥΣ 131 - Διαλ.34 1 KYMATA Ανάκλαση - Μετάδοση q Παλµός πάνω σε χορδή: Ένα άκρο της σταθερό (δεµένο) Προσπίπτων Ο παλµός ασκεί µια δύναµη προς τα πάνω στον τοίχο ο οποίος ασκεί µια δύναµη προς τα κάτω
ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ. 1 ο ΘΕΜΑ. Α. Ερωτήσεις πολλαπλής επιλογής
 ο ΘΕΜΑ Α. Ερωτήσεις πολλαπλής επιλογής ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ. Το µήκος κύµατος δύο κυµάτων που συµβάλλουν και δηµιουργούν στάσιµο κύµα είναι λ. Η απόσταση µεταξύ δύο διαδοχικών δεσµών του στάσιµου κύµατος θα
ο ΘΕΜΑ Α. Ερωτήσεις πολλαπλής επιλογής ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ. Το µήκος κύµατος δύο κυµάτων που συµβάλλουν και δηµιουργούν στάσιµο κύµα είναι λ. Η απόσταση µεταξύ δύο διαδοχικών δεσµών του στάσιµου κύµατος θα
ΟΡΟΣΗΜΟ Σε δύο σημεία Π Σε δύο σημεία Π Δύο πηγές Π 1
 ΚΕΦΑΛΑΙΟ Συμβολή κυμάτων Στα παρακάτω προβλήματα να θεωρείτε ότι το πλάτος των κυμάτων που συμβάλλουν δεν αλλάζει 5 Σε δύο σημεία Π 1 της ήρεμης επιφάνειας ενός υγρού δημιουργούνται δύο σύγχρονες πηγές,
ΚΕΦΑΛΑΙΟ Συμβολή κυμάτων Στα παρακάτω προβλήματα να θεωρείτε ότι το πλάτος των κυμάτων που συμβάλλουν δεν αλλάζει 5 Σε δύο σημεία Π 1 της ήρεμης επιφάνειας ενός υγρού δημιουργούνται δύο σύγχρονες πηγές,
d = 5 λ / 4 λ = 4 d / 5 λ = 4 0,5 / 5 λ = 0,4 m. H βασική κυματική εξίσωση : υ = λ f υ = 0,4 850 υ = 340 m / s.
 1) Ένα κύμα συχνότητας f = 500 Hz διαδίδεται με ταχύτητα υ = 360 m / s. α. Πόσο απέχουν δύο σημεία κατά μήκος μιας ακτίνας διάδοσης του κύματος, τα οποία παρουσιάζουν διαφορά φάσης Δφ = π / 3 ; β. Αν το
1) Ένα κύμα συχνότητας f = 500 Hz διαδίδεται με ταχύτητα υ = 360 m / s. α. Πόσο απέχουν δύο σημεία κατά μήκος μιας ακτίνας διάδοσης του κύματος, τα οποία παρουσιάζουν διαφορά φάσης Δφ = π / 3 ; β. Αν το
Επαναληπτικό διαγώνισµα στα Κύµατα
 ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΤΑΙΧΜΙΟ 1 Επαναληπτικό διαγώνισµα στα Κύµατα Θέµα 1 0 Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΤΑΙΧΜΙΟ 1 Επαναληπτικό διαγώνισµα στα Κύµατα Θέµα 1 0 Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
ΚΕΦΑΛΑΙΟ 2 Ο : ΚΥΜΑΤΑ ΕΝΟΤΗΤΑ 2: ΕΠΑΛΛΗΛΙΑ ΚΥΜΑΤΩΝ ΣΥΜΒΟΛΗ ΚΥΜΑΤΩΝ ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΙΑΣ
 ΚΕΦΑΛΑΙΟ Ο : ΚΥΜΑΤΑ ΕΝΟΤΗΤΑ : ΕΠΑΛΛΗΛΙΑ ΚΥΜΑΤΩΝ ΣΥΜΒΟΛΗ ΚΥΜΑΤΩΝ ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΙΑΣ Μελέτη της συμβολής κυμάτων στην επιφάνεια υγρού Τι ονομάζουμε συμβολή κυμάτων; Συμβολή ονομάζουμε την
ΚΕΦΑΛΑΙΟ Ο : ΚΥΜΑΤΑ ΕΝΟΤΗΤΑ : ΕΠΑΛΛΗΛΙΑ ΚΥΜΑΤΩΝ ΣΥΜΒΟΛΗ ΚΥΜΑΤΩΝ ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΙΑΣ Μελέτη της συμβολής κυμάτων στην επιφάνεια υγρού Τι ονομάζουμε συμβολή κυμάτων; Συμβολή ονομάζουμε την
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler Ενδεικτικές Λύσεις Θέµα Α Α.1. Η συχνότητα ταλάντωσης µιας πηγής, που παράγει εγκάρσιο αρµονικό κύµα σε ένα ελαστικό µέσο, διπλασιάζεται χωρίς
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler Ενδεικτικές Λύσεις Θέµα Α Α.1. Η συχνότητα ταλάντωσης µιας πηγής, που παράγει εγκάρσιο αρµονικό κύµα σε ένα ελαστικό µέσο, διπλασιάζεται χωρίς
ΚΕΦΑΛΑΙΟ 2ο: ΜΗΧΑΝΙΚΑ- ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ.
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
Ηλεκτρομαγνητικά Διαδίδονται στο κενό
 Κύμα: διαταραχή που διαδίδεται στο χώρο και στο χρόνο μεταφέροντας ενέργεια. Μηχανικά Μέσο διάδοσης Ηλεκτρομαγνητικά Διαδίδονται στο κενό Διαμήκη Διεύθυνση διάδοσης παράλληλη στη διαταραχή Εγκάρσια Διεύθυνση
Κύμα: διαταραχή που διαδίδεται στο χώρο και στο χρόνο μεταφέροντας ενέργεια. Μηχανικά Μέσο διάδοσης Ηλεκτρομαγνητικά Διαδίδονται στο κενό Διαμήκη Διεύθυνση διάδοσης παράλληλη στη διαταραχή Εγκάρσια Διεύθυνση
Δ Ι Α Γ Ω Ν Ι Σ Μ Α Φ Υ Σ Ι Κ Η Σ Θ Ε Τ Ι Κ Ω Ν Σ Π Ο Υ Δ Ω Ν Γ Λ Υ Κ Ε Ι Ο Υ 05/1 / Ε Π Ω Ν Υ Μ Ο :...
 Δ Ι Α Γ Ω Ν Ι Σ Μ Α Φ Υ Σ Ι Κ Η Σ Θ Ε Τ Ι Κ Ω Ν Σ Π Ο Υ Δ Ω Ν Γ Λ Υ Κ Ε Ι Ο Υ 05/1 / 2 0 1 8 Ε Π Ω Ν Υ Μ Ο :... Ο Ν Ο Μ Α : Τ Μ Η Μ Α : Ε Π Ι Μ Ε Λ Ε Ι Α Θ Ε Μ Α Τ Ω Ν : ΦΑΡΜΑΚΗΣ Π. ΜΠΑΡΛΙΚΑΣ Σ. ΘΕΜΑ A
Δ Ι Α Γ Ω Ν Ι Σ Μ Α Φ Υ Σ Ι Κ Η Σ Θ Ε Τ Ι Κ Ω Ν Σ Π Ο Υ Δ Ω Ν Γ Λ Υ Κ Ε Ι Ο Υ 05/1 / 2 0 1 8 Ε Π Ω Ν Υ Μ Ο :... Ο Ν Ο Μ Α : Τ Μ Η Μ Α : Ε Π Ι Μ Ε Λ Ε Ι Α Θ Ε Μ Α Τ Ω Ν : ΦΑΡΜΑΚΗΣ Π. ΜΠΑΡΛΙΚΑΣ Σ. ΘΕΜΑ A
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ : ΚΥΜΑΤΑ (ΤΡΕΧΟΝΤΑ) ΟΝΟΜΑΤΕΠΩΝΥΜΟ:.
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ : ΚΥΜΑΤΑ (ΤΡΕΧΟΝΤΑ) ΟΝΟΜΑΤΕΠΩΝΥΜΟ:.. Αν η εξίσωση ενός αρμονικού κύματος είναι y = 0ημ(6πt - πx) στο S.I., τότε η ταχύτητα διάδοσης του κύματος είναι ίση με: α. 0m/s β. 6m/s γ. m/s δ. 3m/s..
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ : ΚΥΜΑΤΑ (ΤΡΕΧΟΝΤΑ) ΟΝΟΜΑΤΕΠΩΝΥΜΟ:.. Αν η εξίσωση ενός αρμονικού κύματος είναι y = 0ημ(6πt - πx) στο S.I., τότε η ταχύτητα διάδοσης του κύματος είναι ίση με: α. 0m/s β. 6m/s γ. m/s δ. 3m/s..
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος 1. Τρία διαπασών Δ 1, Δ 2 παράγουν ήχους με συχνότητες 214 Hz, 220 Hz και f 3 αντίστοιχα. Όταν πάλλονται ταυτόχρονα τα διαπασών Δ
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών Τζιόλας Χρήστος 1. Τρία διαπασών Δ 1, Δ 2 παράγουν ήχους με συχνότητες 214 Hz, 220 Hz και f 3 αντίστοιχα. Όταν πάλλονται ταυτόχρονα τα διαπασών Δ
ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ
 ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ 1. ΕΓΚΑΡΣΙΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ Κύματα κατά μήκος τεντωμένου νήματος Στο τεντωμένο με δύναμη νήμα του Σχήματος 1.1α δημιουργούμε μια εγκάρσια διαταραχή (παράλληλη με τη διεύθυνση
ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΣΥΜΠΛΗΡΩΜΑ ΘΕΩΡΙΑΣ 1. ΕΓΚΑΡΣΙΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ Κύματα κατά μήκος τεντωμένου νήματος Στο τεντωμένο με δύναμη νήμα του Σχήματος 1.1α δημιουργούμε μια εγκάρσια διαταραχή (παράλληλη με τη διεύθυνση
ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ. 1 ο ΘΕΜΑ. Φυσική Γ' Θετικής και Τεχνολογικής Κατ/σης. Θέματα Εξετάσεων. Α. Ερωτήσεις πολλαπλής επιλογής
 ο ΘΕΜΑ Α. Ερωτήσεις πολλαπλής επιλογής ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ. Το μήκος κύματος δύο κυμάτων που συμβάλλουν και δημιουργούν στάσιμο κύμα είναι λ. Η απόσταση μεταξύ δύο διαδοχικών δεσμών του στάσιμου κύματος θα
ο ΘΕΜΑ Α. Ερωτήσεις πολλαπλής επιλογής ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ. Το μήκος κύματος δύο κυμάτων που συμβάλλουν και δημιουργούν στάσιμο κύμα είναι λ. Η απόσταση μεταξύ δύο διαδοχικών δεσμών του στάσιμου κύματος θα
ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 24/04/2016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ (ΑΠΟΦΟΙΤΟΙ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΔΕΚΑΠΕΝΤΕ (15) ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας
Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 24/04/2016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ (ΑΠΟΦΟΙΤΟΙ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΔΕΚΑΠΕΝΤΕ (15) ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler Ενδεικτικές Λύσεις - Β έκδοση Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler Ενδεικτικές Λύσεις - Β έκδοση Θέµα Α Α.. Σε ένα γραµµικό ελαστικό µέσο διαδίδονται ταυτόχρονα δύο κύµατα µε ίδιο πλάτος, ίδια συχνότητα και
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler Ενδεικτικές Λύσεις - Β έκδοση Θέµα Α Α.. Σε ένα γραµµικό ελαστικό µέσο διαδίδονται ταυτόχρονα δύο κύµατα µε ίδιο πλάτος, ίδια συχνότητα και
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ. ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 4 ΜΑΡΤΙΟΥ 06 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΠΤΑ (7) ΘΕΜΑ ο Στις ερωτήσεις -4 να γράψετε τον
ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 4 ΜΑΡΤΙΟΥ 06 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΠΤΑ (7) ΘΕΜΑ ο Στις ερωτήσεις -4 να γράψετε τον
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler Ενδεικτικές Λύσεις Κυριακή 4 Νοέµβρη 2018 Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler Ενδεικτικές Λύσεις Κυριακή 4 Νοέµβρη 2018 Θέµα Α Α.1. Κατά µήκος µιας ελαστικής χορδής διαδίδεται ένα εγκάρσιο αρµονικό κύµα, χωρίς ενεργειακές
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler Ενδεικτικές Λύσεις Κυριακή 4 Νοέµβρη 2018 Θέµα Α Α.1. Κατά µήκος µιας ελαστικής χορδής διαδίδεται ένα εγκάρσιο αρµονικό κύµα, χωρίς ενεργειακές
Κύματα Εξισώσεις Μεθοδολογία
 Κύματα Εξισώσεις Μεθοδολογία Η εξίσωση του κύματος που εκφράζει την απομάκρυνση y ενός σημείου του μέσου, έστω Μ, που απέχει απόσταση χ από την πηγή τη χρονική στιγμή, είναι: y A ( ) με Η ταχύτητα με την
Κύματα Εξισώσεις Μεθοδολογία Η εξίσωση του κύματος που εκφράζει την απομάκρυνση y ενός σημείου του μέσου, έστω Μ, που απέχει απόσταση χ από την πηγή τη χρονική στιγμή, είναι: y A ( ) με Η ταχύτητα με την
Φυσική προσανατολισμού
 Φυσική προσανατολισμού ΘΕΜΑ Α Στις προτάσεις από - ναβρείτε την σωστή απάντηση. Α. Σε ένα στάσιμο κύμα: Α. όλα τα σημεία του μέσου εκτελούν ταλάντωση του ίδιου πλάτους Β. την μεγαλύτερη ενέργεια ταλάντωσης
Φυσική προσανατολισμού ΘΕΜΑ Α Στις προτάσεις από - ναβρείτε την σωστή απάντηση. Α. Σε ένα στάσιμο κύμα: Α. όλα τα σημεία του μέσου εκτελούν ταλάντωση του ίδιου πλάτους Β. την μεγαλύτερη ενέργεια ταλάντωσης
Μέτρηση της ταχύτητας του ήχου στον αέρα.
 Α2 Μέτρηση της ταχύτητας του ήχου στον αέρα. 1 Σκοπός Στο πείραμα αυτό θα μελετηθεί η συμπεριφορά των στάσιμων ηχητικών κυμάτων σε σωλήνα με αισθητοποίηση του φαινομένου του ηχητικού συντονισμού. Επίσης
Α2 Μέτρηση της ταχύτητας του ήχου στον αέρα. 1 Σκοπός Στο πείραμα αυτό θα μελετηθεί η συμπεριφορά των στάσιμων ηχητικών κυμάτων σε σωλήνα με αισθητοποίηση του φαινομένου του ηχητικού συντονισμού. Επίσης
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler Ενδεικτικές Λύσεις Θέµα Α Α.1. Η ταχύτητα µε την οποία διαδίδεται µια διαταραχή σε ένα οµογενές ελαστικό µέσο : (γ) είναι σταθερή και εξαρτάται
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler Ενδεικτικές Λύσεις Θέµα Α Α.1. Η ταχύτητα µε την οποία διαδίδεται µια διαταραχή σε ένα οµογενές ελαστικό µέσο : (γ) είναι σταθερή και εξαρτάται
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 5o ΔΙΑΓΩΝΙΣΜΑ ΔΙΑΓΩΝΙΣΜΑ - ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 5o ΔΙΑΓΩΝΙΣΜΑ ΔΙΑΓΩΝΙΣΜΑ - ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 5o ΔΙΑΓΩΝΙΣΜΑ ΔΙΑΓΩΝΙΣΜΑ - ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτελείς προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
διαδίδονται δύο αρμονικά εγκάρσια κύματα πλάτους Α 1 , αντίστοιχα. Αν ισχύει ότι Α 2 1 = α 8 max,1 ii. max,2 ) β. λ 2 (υ 1 /υ 2 > 0, v B > 0, v Γ
 ΚΕΦΑΛΑΙΟ 2 Κύματα Γενικά θέματα Α ΕΡΩΤΗΣΕΙΣ 1 Αρμονικό κύμα πλάτους Α διαδίδεται κατά μήκος γραμμικού ελαστικού μέσου με θετική φορά Τη χρονική στιγμή t=0 το υλικό σημείο με x=0 ταλαντώνεται με μέγιστη
ΚΕΦΑΛΑΙΟ 2 Κύματα Γενικά θέματα Α ΕΡΩΤΗΣΕΙΣ 1 Αρμονικό κύμα πλάτους Α διαδίδεται κατά μήκος γραμμικού ελαστικού μέσου με θετική φορά Τη χρονική στιγμή t=0 το υλικό σημείο με x=0 ταλαντώνεται με μέγιστη
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 3 o ΔΙΑΓΩΝΙΣΜΑ ΙΑΝΟΥΑΡΙΟΣ 2019: ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ο ΔΙΑΓΩΝΙΣΜΑ ΚΥΜΑΤΑ ΦΑΙΝΟΜΕΝΟ DOPPLER - ΘΕΜΑΤΑ ΘΕΜΑ Στις προτάσεις Αα έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ο ΔΙΑΓΩΝΙΣΜΑ ΚΥΜΑΤΑ ΦΑΙΝΟΜΕΝΟ DOPPLER - ΘΕΜΑΤΑ ΘΕΜΑ Στις προτάσεις Αα έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
1 Ο ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ - ΕΚΦΩΝΗΣΕΙΣ
 Ο ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ - ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις - 4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη συμπληρώνει σωστά
Ο ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ - ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις - 4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη συμπληρώνει σωστά
Κεφάλαιο T4. Υπέρθεση και στάσιµα κύµατα
 Κεφάλαιο T4 Υπέρθεση και στάσιµα κύµατα Κύµατα και σωµατίδια Τα κύµατα είναι πολύ διαφορετικά από τα σωµατίδια. Τα σωµατίδια έχουν µηδενικό µέγεθος. Τα κύµατα έχουν ένα χαρακτηριστικό µέγεθος το µήκος
Κεφάλαιο T4 Υπέρθεση και στάσιµα κύµατα Κύµατα και σωµατίδια Τα κύµατα είναι πολύ διαφορετικά από τα σωµατίδια. Τα σωµατίδια έχουν µηδενικό µέγεθος. Τα κύµατα έχουν ένα χαρακτηριστικό µέγεθος το µήκος
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
Φυσική Γ Θετ. και Τεχν/κης Κατ/σης ΚΥΜΑΤΑ ( )
 ΚΥΜΑΤΑ ( 2.1-2.2) Για τη δημιουργία ενός κύματος χρειάζονται η πηγή της διαταραχής ή πηγή του κύματος, δηλαδή η αιτία που θα προκαλέσει τη διαταραχή και ένα υλικό (μέσο) στο οποίο κάθε μόριο αλληλεπιδρά
ΚΥΜΑΤΑ ( 2.1-2.2) Για τη δημιουργία ενός κύματος χρειάζονται η πηγή της διαταραχής ή πηγή του κύματος, δηλαδή η αιτία που θα προκαλέσει τη διαταραχή και ένα υλικό (μέσο) στο οποίο κάθε μόριο αλληλεπιδρά
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Γ Λ Υ Κ Ε Ι Ο Υ 08/01/2017 ΘΕΜΑ Α
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Γ Λ Υ Κ Ε Ι Ο Υ 08/01/2017 ΘΕΜΑ Α Στις παρακάτω ερωτήσεις πολλαπλού τύπου 1-7, να επιλέξετε τη σωστή απάντηση και στο απαντητικό σας φύλλο να μεταφέρετε τον αριθμό και το γράμμα της
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Γ Λ Υ Κ Ε Ι Ο Υ 08/01/2017 ΘΕΜΑ Α Στις παρακάτω ερωτήσεις πολλαπλού τύπου 1-7, να επιλέξετε τη σωστή απάντηση και στο απαντητικό σας φύλλο να μεταφέρετε τον αριθμό και το γράμμα της
γ) Να σχεδιάσετε τις γραφικές παραστάσεις απομάκρυνσης - χρόνου, για τα σημεία Α, Β και Γ, τα οποία απέχουν από το ελεύθερο άκρο αντίστοιχα,,
 1. Κατά μήκος μιας ελαστικής χορδής μεγάλου μήκους που το ένα άκρο της είναι ακλόνητα στερεωμένο, διαδίδονται δύο κύματα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι μετρημένα σε και
1. Κατά μήκος μιας ελαστικής χορδής μεγάλου μήκους που το ένα άκρο της είναι ακλόνητα στερεωμένο, διαδίδονται δύο κύματα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι μετρημένα σε και
γ) Να σχεδιάσετε τις γραφικές παραστάσεις απομάκρυνσης - χρόνου, για τα σημεία Α, Β
 ΕΠΑΝΑΛΗΨΗ ΚΥΜΑΤΑ 1. Κατά μήκος μιας ελαστικής χορδής μεγάλου μήκους που το ένα άκρο της είναι ακλόνητα στερεωμένο, διαδίδονται δύο κύματα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι
ΕΠΑΝΑΛΗΨΗ ΚΥΜΑΤΑ 1. Κατά μήκος μιας ελαστικής χορδής μεγάλου μήκους που το ένα άκρο της είναι ακλόνητα στερεωμένο, διαδίδονται δύο κύματα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler Ενδεικτικές Λύσεις Σάββατο 17 εκέµβρη 2016 Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler Ενδεικτικές Λύσεις Σάββατο 17 εκέµβρη 2016 Θέµα Α Α.1 Η συχνότητα ταλάντωσης µιας πηγής, που παράγει εγκάρσιο αρµονικό κύµα σε ένα ελαστικό
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler Ενδεικτικές Λύσεις Σάββατο 17 εκέµβρη 2016 Θέµα Α Α.1 Η συχνότητα ταλάντωσης µιας πηγής, που παράγει εγκάρσιο αρµονικό κύµα σε ένα ελαστικό
ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης Γ Λυκείου ΓΡΑΠΤΕΣ ΔΟΚΙΜΑΣΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ 2009
 ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης Γ Λυκείου ΓΡΑΠΤΕΣ ΔΟΚΙΜΑΣΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ 009 Θέμα 1ο Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από
ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΕΥΑΓΓΕΛΙΚΗΣ ΣΧΟΛΗΣ ΣΜΥΡΝΗΣ Φυσική Θετικής και Τεχνολογικής Κατεύθυνσης Γ Λυκείου ΓΡΑΠΤΕΣ ΔΟΚΙΜΑΣΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ 009 Θέμα 1ο Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από
ιαγώνισµα στη Φυσική Κατεύθυνσης Γ Λυκείου
 ιαγώνισµα στη Φυσική Κατεύθυνσης Γ Λυκείου Ηµεροµηνία: / / 2011 Θ 1 Θ 2 Θ 3 Θ 4 Βαθµός Ονοµατεπώνυµο:. Τµήµα: Γ ΘΕΜΑ 1 ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-10
ιαγώνισµα στη Φυσική Κατεύθυνσης Γ Λυκείου Ηµεροµηνία: / / 2011 Θ 1 Θ 2 Θ 3 Θ 4 Βαθµός Ονοµατεπώνυµο:. Τµήµα: Γ ΘΕΜΑ 1 ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-10
Φυσική Ο.Π. Γ Λυκείου
 Φυσική Ο.Π. Γ Λυκείου ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις (Α-Α) και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α) Δύο σώματα συγκρούονται κεντρικά
Φυσική Ο.Π. Γ Λυκείου ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις (Α-Α) και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α) Δύο σώματα συγκρούονται κεντρικά
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ γ τάξη ενιαίου λυκείου (εξεταστέα ύλη: κρούσεις, ταλαντώσεις, εξίσωση κύματος) διάρκεια εξέτασης: 1.8sec ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ/ΜΑΘΗΤΡΙΑΣ: ΤΜΗΜΑ: ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να επιλέξετε
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ γ τάξη ενιαίου λυκείου (εξεταστέα ύλη: κρούσεις, ταλαντώσεις, εξίσωση κύματος) διάρκεια εξέτασης: 1.8sec ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ/ΜΑΘΗΤΡΙΑΣ: ΤΜΗΜΑ: ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να επιλέξετε
ΦΥΣΙΚΗ Ο.Π Γ ΛΥΚΕΙΟΥ 22 / 04 / 2018
 Γ ΛΥΚΕΙΟΥ 22 / 04 / 2018 ΦΥΣΙΚΗ Ο.Π ΘΕΜΑ Α Α1. Μία ηχητική πηγή που εκπέμπει ήχο συχνότητας κινείται με σταθερή ταχύτητα πλησιάζοντας ακίνητο παρατηρητή, ενώ απομακρύνεται από άλλο ακίνητο παρατηρητή.
Γ ΛΥΚΕΙΟΥ 22 / 04 / 2018 ΦΥΣΙΚΗ Ο.Π ΘΕΜΑ Α Α1. Μία ηχητική πηγή που εκπέμπει ήχο συχνότητας κινείται με σταθερή ταχύτητα πλησιάζοντας ακίνητο παρατηρητή, ενώ απομακρύνεται από άλλο ακίνητο παρατηρητή.
2.2. Συμβολή και στάσιμα κύματα. Ομάδα Δ.
 2.2. Συμβολή και στάσιμα κύματα. Ομάδα Δ. 2.2.41. Μια χορδή σε ταλάντωση ή δυο στάσιμα κύματα. Μια χορδή μήκους 5m είναι στερεωμένη στα άκρα της Κ και Λ.. Όταν θέσουμε σε ταλάντωση το μέσον της Μ, απαιτείται
2.2. Συμβολή και στάσιμα κύματα. Ομάδα Δ. 2.2.41. Μια χορδή σε ταλάντωση ή δυο στάσιμα κύματα. Μια χορδή μήκους 5m είναι στερεωμένη στα άκρα της Κ και Λ.. Όταν θέσουμε σε ταλάντωση το μέσον της Μ, απαιτείται
Θέµατα Πανελληνίων Φυσικής Κατ ο Κεφάλαιο (µέχρι και Στάσιµα)
 Θέµατα Πανελληνίων Φυσικής Κατ. 0 00 0 Α. Η ταχύτητα διάδοσης ενός αρµονικού κύµατος εξαρτάται από α. τη συχνότητα του κύµατος β. τις ιδιότητες του µέσου διάδοσης γ. το πλάτος του κύµατος δ. την ταχύτητα
Θέµατα Πανελληνίων Φυσικής Κατ. 0 00 0 Α. Η ταχύτητα διάδοσης ενός αρµονικού κύµατος εξαρτάται από α. τη συχνότητα του κύµατος β. τις ιδιότητες του µέσου διάδοσης γ. το πλάτος του κύµατος δ. την ταχύτητα
Διαγώνισμα Φυσική Κατεύθυνσης Γ Λυκείου
 Διαγώνισμα Φυσική Κατεύθυνσης Γ Λυκείου Επιμέλεια Θεμάτων Σ.Π.Μαμαλάκης Ζήτημα 1 ον 1.. Μια ακτίνα φωτός προσπίπτει στην επίπεδη διαχωριστική επιφάνεια δύο μέσων. Όταν η διαθλώμενη ακτίνα κινείται παράλληλα
Διαγώνισμα Φυσική Κατεύθυνσης Γ Λυκείου Επιμέλεια Θεμάτων Σ.Π.Μαμαλάκης Ζήτημα 1 ον 1.. Μια ακτίνα φωτός προσπίπτει στην επίπεδη διαχωριστική επιφάνεια δύο μέσων. Όταν η διαθλώμενη ακτίνα κινείται παράλληλα
ΠΕΜΠΤΗ 3 ΙΟΥΝΙΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΠΕΜΠΤΗ ΙΟΥΝΙΟΥ 00 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις - και δίπλα το γράµµα που αντιστοιχεί
ΠΕΜΠΤΗ ΙΟΥΝΙΟΥ 00 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις - και δίπλα το γράµµα που αντιστοιχεί
Κεφάλαιο 15 Κίνηση Κυµάτων. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 15 Κίνηση Κυµάτων Περιεχόµενα Κεφαλαίου 15 Χαρακτηριστικά των Κυµάτων Είδη κυµάτων: Διαµήκη και Εγκάρσια Μεταφορά ενέργειας µε κύµατα Μαθηµατική Περιγραφή της Διάδοσης κυµάτων Η Εξίσωση του Κύµατος
Κεφάλαιο 15 Κίνηση Κυµάτων Περιεχόµενα Κεφαλαίου 15 Χαρακτηριστικά των Κυµάτων Είδη κυµάτων: Διαµήκη και Εγκάρσια Μεταφορά ενέργειας µε κύµατα Μαθηµατική Περιγραφή της Διάδοσης κυµάτων Η Εξίσωση του Κύµατος
β. F = 2ρΑυ 2 γ. F = 1 2 ραυ 2 δ. F = 1 3 ραυ 2
 Στις ερωτήσεις 1-4 να επιλέξετε μια σωστή απάντηση. 1. Ένα σύστημα ελατηρίου - μάζας εκτελεί απλή αρμονική ταλάντωση πλάτους Α. Αν τετραπλασιάσουμε την ολική ενέργεια της ταλάντωσης αυτού του συστήματος
Στις ερωτήσεις 1-4 να επιλέξετε μια σωστή απάντηση. 1. Ένα σύστημα ελατηρίου - μάζας εκτελεί απλή αρμονική ταλάντωση πλάτους Α. Αν τετραπλασιάσουμε την ολική ενέργεια της ταλάντωσης αυτού του συστήματος
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ- ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 4 ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΜΥΤΙΛΗΝΗΣ ΤΕΛΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ- ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΠΩΝΥΜΟ. ΗΜΕΡ/ΝΙΑ : 15/05/2015 ΘΕΜΑ A Να γράψετε στο τετράδιό σας τον αριθμό καθεμίας από τις παρακάτω
4 ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΜΥΤΙΛΗΝΗΣ ΤΕΛΙΚΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ- ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΟΝΟΜΑΤΕΠΩΝΥΜΟ. ΗΜΕΡ/ΝΙΑ : 15/05/2015 ΘΕΜΑ A Να γράψετε στο τετράδιό σας τον αριθμό καθεμίας από τις παρακάτω
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
ΞΗΡΟΔΗΜΑΣ ΠΕΤΡΟΣ ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΩΝ
 1 ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΩΝ 1) Μια πηγή κυμάτων Ο εκτελεί απλή αρμονική ταλάντωση με εξίσωση: y=8 ημπt,(το t σε sec, το y σε cm). H ταχύτητα διάδοσης του παραγόμενου κύματος κατά μήκος του άξονα Οχ είναι υ=20 cm/sec.
1 ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΩΝ 1) Μια πηγή κυμάτων Ο εκτελεί απλή αρμονική ταλάντωση με εξίσωση: y=8 ημπt,(το t σε sec, το y σε cm). H ταχύτητα διάδοσης του παραγόμενου κύματος κατά μήκος του άξονα Οχ είναι υ=20 cm/sec.
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler Σύνολο Σελίδων: έξι (6) - ιάρκεια Εξέτασης: 3 ώρες Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler Σύνολο Σελίδων: έξι (6) - ιάρκεια Εξέτασης: 3 ώρες Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4 να γράψετε στο τετράδιο
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler Σύνολο Σελίδων: έξι (6) - ιάρκεια Εξέτασης: 3 ώρες Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4 να γράψετε στο τετράδιο
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ο.Ε.Φ.Ε ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ο.Ε.Φ.Ε. 2003 ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Θ Ε Μ Α 1 ο Οδηγία: Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ο.Ε.Φ.Ε. 2003 ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Θ Ε Μ Α 1 ο Οδηγία: Στις ερωτήσεις 1-5 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler Σύνολο Σελίδων: επτά (7) - ιάρκεια Εξέτασης: 3 ώρες Κυριακή 4 Νοέµβρη 2018 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κύµατα - Φαινόµενο Doppler Σύνολο Σελίδων: επτά (7) - ιάρκεια Εξέτασης: 3 ώρες Κυριακή 4 Νοέµβρη 2018 Βαθµολογία % Ονοµατεπώνυµο: Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4
Στάσιµο σε χορδή µε ακλόνητα άκρα
 Στάσιµο σε χορδή µε ακλόνητα άκρα Τεντωµένη ελαστική χορδή έχει µήκος L και τα δύο άκρα της Ζ και Η είναι στερεωµένα σε ακλόνητα σηµεία, ενώ η χορδή διατηρείται οριζόντια. Διεγέρτης θέτει το µέσο (Ο) της
Στάσιµο σε χορδή µε ακλόνητα άκρα Τεντωµένη ελαστική χορδή έχει µήκος L και τα δύο άκρα της Ζ και Η είναι στερεωµένα σε ακλόνητα σηµεία, ενώ η χορδή διατηρείται οριζόντια. Διεγέρτης θέτει το µέσο (Ο) της
Γ.Κονδύλη 1 & Όθωνος-Μ αρούσι Τ ηλ. Κέντρο: , /
 Γ.Κονδύλη & Όθωνος-Μ αρούσι Τ ηλ. Κέντρο:20-6.24.000, http:/ / www.akadimos.gr ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ 204 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Επιμέλεια Θεμάτων: Παπαδόπουλος Πασχάλης ΘΕΜΑ
Γ.Κονδύλη & Όθωνος-Μ αρούσι Τ ηλ. Κέντρο:20-6.24.000, http:/ / www.akadimos.gr ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ 204 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Επιμέλεια Θεμάτων: Παπαδόπουλος Πασχάλης ΘΕΜΑ
ΤΥΠΟΛΟΓΙΟ ΚΕΦΑΛΑΙΟΥ 1 ΗΛΕΚΤΡΙΚΕΣ - ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ
 ΤΥΠΟΛΟΓΙΟ ΚΕΦΑΛΑΙΟΥ ΗΛΕΚΤΡΙΚΕΣ - ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ( t ) Χρονική εξίσωση απομάκρυνσης a ( t ) με a Χρονική εξίσωση ταχύτητας a aa ( t ) με a a Χρονική εξίσωση επιτάχυνσης a Σχέση
ΤΥΠΟΛΟΓΙΟ ΚΕΦΑΛΑΙΟΥ ΗΛΕΚΤΡΙΚΕΣ - ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ( t ) Χρονική εξίσωση απομάκρυνσης a ( t ) με a Χρονική εξίσωση ταχύτητας a aa ( t ) με a a Χρονική εξίσωση επιτάχυνσης a Σχέση
3. Εγκάρσιο γραμμικό κύμα που διαδίδεται σε ένα ομογενές ελαστικό μέσον και κατά την
 ΚΥΜΑΤΑ 1. Μια πηγή Ο που βρίσκεται στην αρχή του άξονα, αρχίζει να εκτελεί τη χρονική στιγμή 0, απλή αρμονική ταλάντωση με εξίσωση 6 10 ημ S. I.. Το παραγόμενο γραμμικό αρμονικό κύμα διαδίδεται κατά τη
ΚΥΜΑΤΑ 1. Μια πηγή Ο που βρίσκεται στην αρχή του άξονα, αρχίζει να εκτελεί τη χρονική στιγμή 0, απλή αρμονική ταλάντωση με εξίσωση 6 10 ημ S. I.. Το παραγόμενο γραμμικό αρμονικό κύμα διαδίδεται κατά τη
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ 1 1. Στερεό σώμα περιστρέφεται γύρω από σταθερό άξονα, υπό την επίδραση σταθερής ροπής. Ο ρυθμός παραγωγής έργου: α) ισούται με τη μεταβολή της ενέργειας του σώματος.
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ 1 1. Στερεό σώμα περιστρέφεται γύρω από σταθερό άξονα, υπό την επίδραση σταθερής ροπής. Ο ρυθμός παραγωγής έργου: α) ισούται με τη μεταβολή της ενέργειας του σώματος.
2.2. Συμβολή και στάσιμα κύματα.
 2.2. Συμβολή και στάσιμα κύματα. 2.2.1. Συμβολή και μέγιστο πλάτος Σε δύο σημεία μιας ευθείας ε βρίσκονται δύο σύγχρονες πηγές κυμάτων Ο 1 και Ο 2 οι οποίες παράγουν κύματα με πλάτος Α=2cm και μήκος κύματος
2.2. Συμβολή και στάσιμα κύματα. 2.2.1. Συμβολή και μέγιστο πλάτος Σε δύο σημεία μιας ευθείας ε βρίσκονται δύο σύγχρονες πηγές κυμάτων Ο 1 και Ο 2 οι οποίες παράγουν κύματα με πλάτος Α=2cm και μήκος κύματος
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Στις προτάσεις Α-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Στις προτάσεις Α-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη
Για τις παρακάτω ερωτήσεις 2-4 να γράψετε στο τετράδιο σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
 46 Χρόνια ΦΡΟΝΤΙΣΤΗΡΙΑ ΜΕΣΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΣΑΒΒΑΪ Η-ΜΑΝΩΛΑΡΑΚΗ ΠΑΓΚΡΑΤΙ : Χρυσ Σµύρνης 3 : Τηλ.: 0760470 ΙΑΓΩΝΙΣΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 007 ΘΕΜΑ. Ποιες από τις παρακάτω προτάσεις είναι σωστές (Σ)
46 Χρόνια ΦΡΟΝΤΙΣΤΗΡΙΑ ΜΕΣΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΣΑΒΒΑΪ Η-ΜΑΝΩΛΑΡΑΚΗ ΠΑΓΚΡΑΤΙ : Χρυσ Σµύρνης 3 : Τηλ.: 0760470 ΙΑΓΩΝΙΣΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 007 ΘΕΜΑ. Ποιες από τις παρακάτω προτάσεις είναι σωστές (Σ)
 1. Το σημείο Ο ομογενούς ελαστικής χορδής, τη χρονική στιγμή t= αρχίζει να εκτελεί Α.Α.Τ. με εξίσωση y=,5ημπt ( SI), κάθετα στη διεύθυνση της χορδής. Το κύμα που παράγεται διαδίδεται κατά τη θετική κατεύθυνση
1. Το σημείο Ο ομογενούς ελαστικής χορδής, τη χρονική στιγμή t= αρχίζει να εκτελεί Α.Α.Τ. με εξίσωση y=,5ημπt ( SI), κάθετα στη διεύθυνση της χορδής. Το κύμα που παράγεται διαδίδεται κατά τη θετική κατεύθυνση
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ. ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 11 ΑΠΡΙΛΙΟΥ 2018 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 11 ΑΠΡΙΛΙΟΥ 2018 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε
Φαινόμενο Doppler (Γ. Μ.) Φαινόμενο Doppler. Φαινόμενο Doppler είναι η διαφορά των συχνοτήτων που μετρούν οι παρατηρητές
 Φαινόμενο Doppler Για την κατανόηση του φαινομένου αυτού εισάγουμε τα παρακάτω σύμβολα και πρέπει να εξηγήσουμε τη σημασία τους. : πηγή ηχητικών κυμάτων : ανιχνευτής ηχητικών κυμάτων : συχνότητα ηχητικών
Φαινόμενο Doppler Για την κατανόηση του φαινομένου αυτού εισάγουμε τα παρακάτω σύμβολα και πρέπει να εξηγήσουμε τη σημασία τους. : πηγή ηχητικών κυμάτων : ανιχνευτής ηχητικών κυμάτων : συχνότητα ηχητικών
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΦΥΣΙΚΗΣ ΙΙ
 ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΦΥΣΙΚΗΣ ΙΙ ΘΕΜΑ 1 ο (βαθµοί 2) Σώµα µε µάζα m=5,00 kg είναι προσαρµοσµένο στο ελεύθερο άκρο ενός κατακόρυφου ελατηρίου και ταλαντώνεται εκτελώντας πέντε (5) πλήρης ταλαντώσεις σε χρονικό
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΦΥΣΙΚΗΣ ΙΙ ΘΕΜΑ 1 ο (βαθµοί 2) Σώµα µε µάζα m=5,00 kg είναι προσαρµοσµένο στο ελεύθερο άκρο ενός κατακόρυφου ελατηρίου και ταλαντώνεται εκτελώντας πέντε (5) πλήρης ταλαντώσεις σε χρονικό
ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 24/04/2016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ (ΑΠΟΦΟΙΤΟΙ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας τον αριθμό
Γ ΤΑΞΗ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΚΥΡΙΑΚΗ 24/04/2016 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ (ΑΠΟΦΟΙΤΟΙ) ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ Α Στις ερωτήσεις Α1 Α5 να γράψετε στο τετράδιο σας τον αριθμό
2.2. Συμβολή και στάσιμα κύματα. Ομάδα Δ.
 2.2. Συμβολή και στάσιμα κύματα. Ομάδα Δ. 2.2.41. Μια χορδή σε ταλάντωση ή δυο στάσιμα κύματα. Μια χορδή μήκους 5m είναι στερεωμένη στα άκρα της Κ και Λ.. Όταν θέσουμε σε ταλάντωση το μέσον της Μ, απαιτείται
2.2. Συμβολή και στάσιμα κύματα. Ομάδα Δ. 2.2.41. Μια χορδή σε ταλάντωση ή δυο στάσιμα κύματα. Μια χορδή μήκους 5m είναι στερεωμένη στα άκρα της Κ και Λ.. Όταν θέσουμε σε ταλάντωση το μέσον της Μ, απαιτείται
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Κύματα Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων.
Φυσική για Μηχανικούς Κύματα Εικόνα: Ναυαγοσώστες στην Αυστραλία εκπαιδεύονται στην αντιμετώπιση μεγάλων κυμάτων. Τα κύματα που κινούνται στην επιφάνεια του νερού αποτελούν ένα παράδειγμα μηχανικών κυμάτων.
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ ο Να γράψετε στο τετράδιό σας τον αριθμό καθεμίας από τις παρακάτω ερωτήσεις -4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.. Σε ιδανικό
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ ο Να γράψετε στο τετράδιό σας τον αριθμό καθεμίας από τις παρακάτω ερωτήσεις -4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.. Σε ιδανικό
ΔΙΑΔΟΣΗ ΜΗΧΑΝΙΚΩΝ ΚΥΜΑΤΩΝ. υ=, υ=λ.f, υ= tτ
 1 ΤΥΠΟΛΟΓΙΟ ΚΥΜΑΤΩΝ ΔΙΑΔΟΣΗ ΜΗΧΑΝΙΚΩΝ ΚΥΜΑΤΩΝ Μήκος κύματος Ταχύτητα διάδοσης Συχνότητα Εξίσωση αρμονικού κύματος Φάση αρμονικού κύματος Ταχύτητα ταλάντωσης, Επιτάχυνση Κινητική Δυναμική ενέργεια ταλάντωσης
1 ΤΥΠΟΛΟΓΙΟ ΚΥΜΑΤΩΝ ΔΙΑΔΟΣΗ ΜΗΧΑΝΙΚΩΝ ΚΥΜΑΤΩΝ Μήκος κύματος Ταχύτητα διάδοσης Συχνότητα Εξίσωση αρμονικού κύματος Φάση αρμονικού κύματος Ταχύτητα ταλάντωσης, Επιτάχυνση Κινητική Δυναμική ενέργεια ταλάντωσης
Είδη κυµάτων. Ηλεκτροµαγνητικά κύµατα. Σε κάποιο φυσικό µέσο προκαλείται µια διαταραχή. Το κύµα είναι η διάδοση της διαταραχής µέσα στο µέσο.
 Κεφάλαιο T2 Κύµατα Είδη κυµάτων Παραδείγµατα Ένα βότσαλο πέφτει στην επιφάνεια του νερού. Κυκλικά κύµατα ξεκινούν από το σηµείο που έπεσε το βότσαλο και αποµακρύνονται από αυτό. Ένα σώµα που επιπλέει στην
Κεφάλαιο T2 Κύµατα Είδη κυµάτων Παραδείγµατα Ένα βότσαλο πέφτει στην επιφάνεια του νερού. Κυκλικά κύµατα ξεκινούν από το σηµείο που έπεσε το βότσαλο και αποµακρύνονται από αυτό. Ένα σώµα που επιπλέει στην
Γ ΛΥΚΕΙΟΥ ΚΥΜΑΤΑ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ. Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός.
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΚΥΜΑΤΑ Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός / Βασικές Έννοιες Η επιστήμη της Φυσικής συχνά μελετάει διάφορες διαταραχές που προκαλούνται και διαδίδονται στο χώρο.
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΚΥΜΑΤΑ Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός / Βασικές Έννοιες Η επιστήμη της Φυσικής συχνά μελετάει διάφορες διαταραχές που προκαλούνται και διαδίδονται στο χώρο.
α) Η γενική εξίσωση του αρµονικού κύµατος είναι. Συγκρίνοντάς την µε µία από τις δύο εξισώσεις των τρεχόντων κυµάτων, έστω την εξίσωση
 Λύση ΑΣΚΗΣΗ 1 α) Η γενική εξίσωση του αρµονικού κύµατος είναι. Συγκρίνοντάς την µε µία από τις δύο εξισώσεις των τρεχόντων κυµάτων, έστω την εξίσωση, προκύπτει: και Με αντικατάσταση στη θεµελιώδη εξίσωση
Λύση ΑΣΚΗΣΗ 1 α) Η γενική εξίσωση του αρµονικού κύµατος είναι. Συγκρίνοντάς την µε µία από τις δύο εξισώσεις των τρεχόντων κυµάτων, έστω την εξίσωση, προκύπτει: και Με αντικατάσταση στη θεµελιώδη εξίσωση
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ. 22 Μαΐου 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5)
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Μαΐου 018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Μαΐου 018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί
2.2. Συμβολή και στάσιμα κύματα. Ομάδα Γ.
 2.2. Συμβολή και στάσιμα κύματα. Ομάδα Γ. 2.2.21. σε γραμμικό ελαστικό μέσο. Δύο σύγχρονες πηγές Ο 1 και Ο 2 παράγουν αρμονικά κύματα που διαδίδονται με ταχύτητα υ=2m/s κατά μήκος ενός γραμμικού ελαστικού
2.2. Συμβολή και στάσιμα κύματα. Ομάδα Γ. 2.2.21. σε γραμμικό ελαστικό μέσο. Δύο σύγχρονες πηγές Ο 1 και Ο 2 παράγουν αρμονικά κύματα που διαδίδονται με ταχύτητα υ=2m/s κατά μήκος ενός γραμμικού ελαστικού
ΔΙΑΓΩΝΙΣΜΑ ΘΕΩΡΙΑΣ ΣΤΑ ΚΥΜΑΤΑ(μέχρι ΗΜ) Διάρκεια 90 min
 ΔΙΑΓΩΝΙΣΜΑ ΘΕΩΡΙΑΣ ΣΤΑ ΚΥΜΑΤΑ(μέχρι ΗΜ) Διάρκεια 90 min Θέμα 1 Ερωτήσεις πολαλπλής επιλογής Σε κάθε ερώτηση υπάρχει μόνο μια σωστή απάντηση 1. Η περίοδος (Τ) του κύµατος είναι ίση µε (ποια πρόταση είναι
ΔΙΑΓΩΝΙΣΜΑ ΘΕΩΡΙΑΣ ΣΤΑ ΚΥΜΑΤΑ(μέχρι ΗΜ) Διάρκεια 90 min Θέμα 1 Ερωτήσεις πολαλπλής επιλογής Σε κάθε ερώτηση υπάρχει μόνο μια σωστή απάντηση 1. Η περίοδος (Τ) του κύµατος είναι ίση µε (ποια πρόταση είναι
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ 1 Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Δύο χορδές μιας κιθάρας Χ1, Χ2
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ 1 Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Δύο χορδές μιας κιθάρας Χ1, Χ2
ΘΕΜΑ 1ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
 ΦΥΣΙΚΗ Γ ΤΑΞΗΣ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) ΠΕΜΠΤΗ 3 ΙΟΥΝΙΟΥ 2004 ΘΕΜΑ ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις - 4 και δίπλα το γράµµα που
ΦΥΣΙΚΗ Γ ΤΑΞΗΣ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΥΟ ΚΥΚΛΩΝ) ΠΕΜΠΤΗ 3 ΙΟΥΝΙΟΥ 2004 ΘΕΜΑ ο Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις - 4 και δίπλα το γράµµα που
ΚΕΦΑΛΑΙΟ 2 Ο : ΚΥΜΑΤΑ ΕΝΟΤΗΤΑ 2: ΕΠΑΛΛΗΛΙΑ ΚΥΜΑΤΩΝ ΣΥΜΒΟΛΗ ΚΥΜΑΤΩΝ ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ Ο : ΚΥΜΑΤΑ ΕΝΟΤΗΤΑ : ΕΠΑΛΛΗΛΙΑ ΚΥΜΑΤΩΝ ΣΥΜΒΟΛΗ ΚΥΜΑΤΩΝ ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση. Δύο σύγχρονες κυματικές πηγές, ΘΕΜΑ Β ταλαντώνονται κάθετα στην επιφάνεια ενός υγρού με το ίδιο πλάτος
ΚΕΦΑΛΑΙΟ Ο : ΚΥΜΑΤΑ ΕΝΟΤΗΤΑ : ΕΠΑΛΛΗΛΙΑ ΚΥΜΑΤΩΝ ΣΥΜΒΟΛΗ ΚΥΜΑΤΩΝ ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση. Δύο σύγχρονες κυματικές πηγές, ΘΕΜΑ Β ταλαντώνονται κάθετα στην επιφάνεια ενός υγρού με το ίδιο πλάτος
Επανάληψη: Κρούσεις και φαινόμενο Doppler (Φ24) 4. α. β. ii. iii. 6. α.
 Επανάληψη: Κρούσεις και φαινόμενο Doppler (Φ24) 1. Μια σφαίρα με μάζα m 1 συγκρούεται μετωπικά και ελαστικά με μια ακίνητη σφαίρα μάζας m 2. Ποια πρέπει να είναι η σχέση της μάζας m 1 με τη μάζα m 2 ώστε:
Επανάληψη: Κρούσεις και φαινόμενο Doppler (Φ24) 1. Μια σφαίρα με μάζα m 1 συγκρούεται μετωπικά και ελαστικά με μια ακίνητη σφαίρα μάζας m 2. Ποια πρέπει να είναι η σχέση της μάζας m 1 με τη μάζα m 2 ώστε:
ΔΙΑΓΩΝΙΣΜΑ ΤΕΛΙΚΗΣ ΠΡΟΣΟΜΟΙΩΣΗΣ 2014 ΦΥΣΙΚΗΣ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΕΠΙΜΕΛΕΙΑ ΘΕΜΑΤΩΝ: ΚΟΛΟΣΙΩΝΗΣ ΔΗΜΗΤΡΗΣ
 1 ΔΙΑΓΩΝΙΣΜΑ ΤΕΛΙΚΗΣ ΠΡΟΣΟΜΟΙΩΣΗΣ 2014 ΦΥΣΙΚΗΣ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΕΠΙΜΕΛΕΙΑ ΘΕΜΑΤΩΝ: ΚΟΛΟΣΙΩΝΗΣ ΔΗΜΗΤΡΗΣ ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό κάθε μιας από τις παρακάτω
1 ΔΙΑΓΩΝΙΣΜΑ ΤΕΛΙΚΗΣ ΠΡΟΣΟΜΟΙΩΣΗΣ 2014 ΦΥΣΙΚΗΣ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΕΠΙΜΕΛΕΙΑ ΘΕΜΑΤΩΝ: ΚΟΛΟΣΙΩΝΗΣ ΔΗΜΗΤΡΗΣ ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό κάθε μιας από τις παρακάτω
ΟΜΟΣΠΟΝΔΙΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑΔΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2018 A ΦΑΣΗ ΑΛΓΟΡΙΘΜΟΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 08 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ημερομηνία: Παρασκευή 5 Ιανουαρίου 08 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ημιτελείς προτάσεις
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 08 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ημερομηνία: Παρασκευή 5 Ιανουαρίου 08 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ημιτελείς προτάσεις
max 0 Eκφράστε την διαφορά των δύο θετικών λύσεων ώς πολλαπλάσιο του ω 0, B . Αναλύοντας το Β σε σειρά άπειρων όρων ώς προς γ/ω 0 ( σειρά
 . Να αποδείξετε ότι σε ένα ταλαντούμενο σύστημα ενός βαθμού ελευθερίας, μάζας και σταθεράς ελατηρίου s με πολύ ασθενή απόσβεση (γω, όπου γ r/, r η σταθερά αντίστασης και s/ ) το πλήρες εύρος στο μισό του
. Να αποδείξετε ότι σε ένα ταλαντούμενο σύστημα ενός βαθμού ελευθερίας, μάζας και σταθεράς ελατηρίου s με πολύ ασθενή απόσβεση (γω, όπου γ r/, r η σταθερά αντίστασης και s/ ) το πλήρες εύρος στο μισό του
Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΦΥΣΙΚΗ ΕΚΦΩΝΗΣΕΙΣ
 Επαναληπτικά Θέµατα ΟΕΦΕ 009 Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΦΥΣΙΚΗ ΘΕΜΑ ο ΕΚΦΩΝΗΣΕΙΣ Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράµµα που αντιστοιχεί
Επαναληπτικά Θέµατα ΟΕΦΕ 009 Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΦΥΣΙΚΗ ΘΕΜΑ ο ΕΚΦΩΝΗΣΕΙΣ Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράµµα που αντιστοιχεί
ΕΡΓΑΣΙΑ ΣΤΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ
 ΕΡΓΑΣΙΑ ΣΤΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Τι ονομάζεται μηχανικό κύμα; Να περιγράψετε το μηχανισμό διάδοσής του. 2. Τι χρειάζεται για να δημιουργηθεί και να διαδοθεί ένα μηχανικό κύμα; Διαδίδονται
ΕΡΓΑΣΙΑ ΣΤΑ ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Τι ονομάζεται μηχανικό κύμα; Να περιγράψετε το μηχανισμό διάδοσής του. 2. Τι χρειάζεται για να δημιουργηθεί και να διαδοθεί ένα μηχανικό κύμα; Διαδίδονται
ΣΕΙΡΑ: 3 Κύματα: αρμονικό έως στάσιμο, Στερεό: κινηματική έως διατήρηση στροφορμής
 ΜΑΘΗΜΑ /ΤΑΞΗ: Φυσική Κατεύθυνσης Γ Λυκείου ΟΝΟΜΑΤΕΠΩΝΥMΟ: ΗΜΕΡΟΜΗΝΙΑ: 16/03/014 ΣΕΙΡΑ: 3 ΕΞΕΤΑΣΤΕΑ ΥΛΗ: Κύματα: αρμονικό έως στάσιμο, Στερεό: κινηματική έως διατήρηση στροφορμής ΘΕΜΑ Α Να γράψετε στο τετράδιό
ΜΑΘΗΜΑ /ΤΑΞΗ: Φυσική Κατεύθυνσης Γ Λυκείου ΟΝΟΜΑΤΕΠΩΝΥMΟ: ΗΜΕΡΟΜΗΝΙΑ: 16/03/014 ΣΕΙΡΑ: 3 ΕΞΕΤΑΣΤΕΑ ΥΛΗ: Κύματα: αρμονικό έως στάσιμο, Στερεό: κινηματική έως διατήρηση στροφορμής ΘΕΜΑ Α Να γράψετε στο τετράδιό
2 ο ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 δυαδικό ΦΡΟΝΤΙΣΤΗΡΙΑ ο ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΔΙΑΡΚΕΙΑ: 3 ώρες ΒΑΘΜΟΣ:.. ΗΜΕΡΟΜΗΝΙΑ: 3// ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ: Ατρείδης Γιώργος Θ Ε Μ Α
δυαδικό ΦΡΟΝΤΙΣΤΗΡΙΑ ο ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΔΙΑΡΚΕΙΑ: 3 ώρες ΒΑΘΜΟΣ:.. ΗΜΕΡΟΜΗΝΙΑ: 3// ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ: Ατρείδης Γιώργος Θ Ε Μ Α
ΘΕΜΑ Α Στις ερωτήσεις να επιλέξετε το γράμμα που αντιστοιχεί στη σωστή απάντηση χωρίς να αιτιολογήσετε την επιλογή σας.
 '' Περί Γνώσεως'' Φροντιστήριο Μ.Ε. Φυσική Προσανατολισμού Γ' Λ. ΜΑΘΗΜΑ /Ομάδα Προσανατολισμού Θ.Σπουδών / ΤΑΞΗ : ΑΡΙΘΜΟΣ ΦΥΛΛΟΥ ΕΡΓΑΣΙΑΣ: ΦΥΣΙΚΗ / Προσανατολισμού / Γ ΛΥΚΕΙΟΥ 2 o ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ : ΟΝΟΜΑΤΕΠΩΝΥΜΟ
'' Περί Γνώσεως'' Φροντιστήριο Μ.Ε. Φυσική Προσανατολισμού Γ' Λ. ΜΑΘΗΜΑ /Ομάδα Προσανατολισμού Θ.Σπουδών / ΤΑΞΗ : ΑΡΙΘΜΟΣ ΦΥΛΛΟΥ ΕΡΓΑΣΙΑΣ: ΦΥΣΙΚΗ / Προσανατολισμού / Γ ΛΥΚΕΙΟΥ 2 o ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ : ΟΝΟΜΑΤΕΠΩΝΥΜΟ
ΟΕΦΕ 2009 Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΦΥΣΙΚΗ
 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 1 ΟΕΦΕ 2009 Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΦΥΣΙΚΗ ΘΕΜΑ 1 Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα που
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 1 ΟΕΦΕ 2009 Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΦΥΣΙΚΗ ΘΕΜΑ 1 Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα που
