ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΑΡΑΓΩΓΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ
|
|
|
- Πρίσκα Σερπετζόγλου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΑΡΑΓΩΓΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ: ΠΡΟΣΟΜΟΙΩΣΗ ΣΥΝΘΕΤΗΣ ΔΙΑΤΑΞΗΣ ΠΙΕΖΟΗΛΕΚΤΡΙΚΩΝ ΣΤΟΙΧΕΙΩΝ ΜΕ ΤΗ ΜΕΘΟΔΟ ΤΩΝ ΠΕΠΕΡΑΣΜΕΝΩΝ ΣΤΟΙΧΕΙΩΝ ΕΠΙΜΕΛΕΙΑ: Αγαθοκλέους Θεόφιλος ΕΠΙΒΛΕΠΩΝ ΚΑΘΗΓΗΤΗΣ: Σταυρουλάκης Γεώργιος
2 Χανιά, Σεπτέμβριος 2013 Ευχαριστίες Η παρούσα διπλωματική εργασία δε θα μπορούσε να πραγματοποιηθεί χωρίς τη βοήθεια και υποστήρηξη του κ.γεώργιου Σταυρουλάκη, καθηγητή του τμήματος Μηχανικών Παραγωγής και Διοίκησης του Πολυτεχνείου Κρήτης. Επίσης ένα μεγάλο ευχαριστώ στους γονείς μου Αντρέα και Έρσα για την αμέριστη υποστήριξή τους καθώς και σε όλους τους φίλους μου που με στηρίζουν. 2
3 ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ 1. Εισαγωγή Πιεζοηλεκτρισμός Το φαινόμενο του πιεζοηλεκτρισμού Οι εφαρμογές του πιεζοηλεκτρισμού Πιεζοηλεκτρικά στοιχεία COMSOL Multiphysics Μέθοδος πεπερασμένων στοιχείων Γενικά στοιχεία Ιστορική αναδρομή Στάδια εφαρμογής μεθόδου Βισκοελαστικότητα Επιλογή υλικών διάταξης Επιλογή πιεζοηλεκτρικού υλικού Επιλογή συγκολλητικού υλικού Επιλογή υλικού βάσης Μεθοδολογία ανάλυσης Μέρος Α (PZT-2) Στατική ανάλυση Στατική ανάλυση (πλεγματοποίηση 2 ου επιπέδου) Συγκριτικά αποτελέσματα Ανάλυση εξαρτώμενη από το χρόνο (loss factor 0.3) Ανάλυση εξαρτώμενη από το χρόνο (loss factor 0.8) Συγκεντρωτικά αποτελέσματα Α μέρους Μέρος Β (PVDF) Στατική ανάλυση Ανάλυση εξαρτώμενη από το χρόνο (loss factor 0.3) Ανάλυση εξαρτώμενη από το χρόνο (loss factor 0.8) Συγκεντρωτικά αποτελέσματα Β μέρους Αλλαγή εξωτερικής δύναμης Συγκριτικά αποτελέσματα Συμπεράσματα/Βιβλιογραφία
4 1. ΕΙΣΑΓΩΓΗ Ο σκοπός αυτής της μελέτης είναι η αναλυτική παρουσίαση της μοντελοποίησης μιας σύνθετης διάταξης, που αποτελείται από ένα πιεζοηλεκτρικό στοιχείο τοποθετημένο σε ένα φύλλο αλουμινίου ανάμεσα στα οποία παρεμβάλλεται ένα στρώμα συγκολλητικού υλικού. Η μοντελοποίηση γίνεται ώστε να συσχετιστούν οι πιεζοηλεκτρικές ιδιότητες διαφορετικής προέλευσης πιεζοηλεκτρικών υλικών, με την εφαρμογή εξωτερικής δύναμης στην συγκεκριμένη διάταξη. Η μοντελοποίηση πραγματοποιείται εξ ολοκλήρου στο ειδικό πρόγραμμα COMSOL Multiphysics 3.4, με κάποιες από τις προσομοιώσεις να πραγματοποιούνται μέσω του server του Πολυτεχνείου Κρήτης. Η εργασία χωρίζεται σε δύο κύρια μέρη, το πρώτο αναφέρεται στη μοντελοποίηση της διάταξης με τη χρήση του πιεζοκεραμικού υλικού PZT-2, ενώ το δεύτερο αφορά στην ίδια διαδικασία με την αντικατασταση του PZT-2 απο το πιεζοπολυμερές PVDF. Το μοντέλο που κατασκευάστηκε όπως και η ανάλυση είναι τριών διαστάσεων. 4
5 2. ΠΙΕΖΟΗΛΕΚΤΡΙΣΜΟΣ 2.1 Το φαινόμενο του πιεζοηλεκτρισμού Ο πιεζοηλεκτρισμός είναι η ιδιότητα κάποιων υλικών (κρυσταλλικών, κεραμικών, η υλικών που σχετίζονται με τη βιολογία όπως το DNA και αρκετές πρωτεϊνες), να παράγουν ηλεκτρική τάση όταν δέχονται μηχανική πίεση, τάση ή ταλάντωση. Το αντίστροφο πιεζοηλεκτρικό φαινόμενο συμβαίνει όταν το υλικό υπόκειται σε παραμόρφωση υπό την επίδραση κάποιας ηλεκτρικής τάσης. Ο πιεζοηλεκτρισμός είναι στην ουσία το φαινόμενο της μεταφοράς ελεύθερων φορτίων στα άκρα του κρυσταλλικού πλέγματος. Η έννοια της λέξης πιεζοηλεκτρισμός προέρχεται από τις ελληνικές λέξεις πίεση και ηλεκτρισμός και δηλώνει τον ηλεκτρισμό που παράγεται από ένα υλικό όταν ασκείται εξωτερική πίεση πάνω σε αυτό. Ο πιεζοηλεκτρισμός ανακαλύφθηκε το 1880 απο τους Pierre&Jacques Curie. 2.2 Οι εφαρμογές του πιεζοηλεκτρισμού Το φαινόμενο του πιεζοηλεκτρισμού χρησιμοποιείται σήμερα ευρέως σε πάρα πολλές εφαρμογές. Η εκμεταλευση του φαινομένου σε τεχνολογικό επίπεδο δεν έχει φτάσει σε καμία περιπτωση τα όρια των δυνατοτήτων του. Πολλές πειραματικές μελέτες εξετάζουν την μελοντική εφαρμογή του πιεζοηλεκτρικού φαινομένου σε όλο και περισσότερα πεδία. Αυτή τη στιγμή το φαινόμενο χρησιμοποιείται ευρέως σε εφαρμογές της ακουστικής (ηλεκτροακουστική), στη βιοιατρική, στην κατασκευή μικροζυγαριών, αισθητήρων (επιταχυνσιόμετρα, μετατροπείς δύναμης και πίεσης κ.α.), διεγερτών, αισθητήρων θορύβου κ.α. Μερικές από τις πιλοτικές εφαρμογές του φαινομένου που θα μελετήσουν την λειτουργικότητα του για μια ευρεία μελλοντική εφαρμογη του φαινομένου αφορούν στο πιεζοηλεκτρικό φαινόμενο σαν εναλλακτική μορφή ενέργειας με διατάξεις πιεζοηλεκτρικών στοιχείων που αποθηκεύουν ηλεκτρική ενέργεια μέσω της πίεσης που δέχονται. Τέτοια παραδείγματα αποτελούν η τοποθέτηση πιεζοηλεκτρικών πλακών κάτω από το οδόστρωμα, με σκοπό την αποθήκευση ηλεκτρικού ρεύματος λόγω της πίεσης που ασκεί η κυκλοφορία του δρόμου στις πλάκες, η ακόμα και κάτω από τις πλάκες πεζοδρομίων για τη συλλογή ηλεκτρικού ρεύματος που επαρκεί για το νυχτερινό φωτισμό του δρόμου.όπως μπορεί να διαπιστώσει κανείς από τις πειραματικές και πιλοτικές εφαρμογές του φαινομένου, οι δυνατότητες εφαρμογής και εκμετάλλευσης είναι ακόμα πολύ μεγάλες και η περαιτέρω έρευνα και εξέλιξη θα συμβάλλει ώστε κάποια στιγμή τα οφέλη και οι εφαρμογές του φαινομένου να είναι εύκολα διακριτά ακόμα και στην καθημερινότητά μας αντικαθιστώντας παλιές τεχνολογίες και βελτιώνοντας ίσως την ποιότητα ζωής. 2.3 Πιεζοηλεκτρικά στοιχεία Από τις αρχές της ανακάλυψης του πιεζοηλεκτρικού φαινομένου είχαν βρεθεί διάφορα φυσικά υλικά που κατείχαν τις συγκεκριμένες ιδιότητες. Μερικά από αυτά τα υλικά είναι τα ελαστικά, το μαλλί, το μεταξι, το αλάτι Rochelle, ο χαλαζίας (SiO2) κ.α. Στο εμπόριο σήμερα υπάρχουν πολυάριθμα πιεζοηλεκτρικά υλικά κατασκευασμένα από τον άνθρωπο. Τα σημαντικότερα από αυτά και τα πιο ευρέως 5
6 διαδεομένα είναι το τιτανιούχο βάριο (BaTiO), το τιτανιούχο στρόντιο (SrTiO3), το APD (δισόξινο φωσφορικό αμμώνιο), ο ζιρκονιούχος τιτανιούχος μόλυβδος (PZT), Το συνθετικό πολυμερές PVDF (πολυβινυλιδικό φθώριο) κ.α. 3. COMSOL Multiphysics Το πρόγραμμα COMSOL Multiphysics Το COMSOL Multiphysics είναι ένα ισχυρό πρόγραμμα κατάλληλο για την μοντελοποίηση και την επίλυση όλων των ειδών των επιστημονικών και τεχνικών προβλημάτων που μπορούν να περιγραφούν από μερικές διαφορικές εξισώσεις. Οι μερικές διαφορικές εξισώσεις περιγράφουν πολλούς από τους νόμους της επιστήμης και της φυσικής και παρέχουν τη βάση για τη μοντελοποίηση μεγάλου φάσματος φαινομέων. Το λογισμικό COMSOL Multiphysics προσφέρει στον μηχανικό την δυνατότητα επίλυσης σύνθετων και αλληλεπιδραστικών φυσικών φαινομένων με την μέθοδο των πεπερασμένων στοιχείων. Αποτελεί ιδανική πλατφόρμα μοντελοποίησης και σχεδιασμού σε πληθώρα εφαρμογών όπως αισθητήρες και μικρόηλεκτρομηχανολογικές συσκευές (MEMS), προβλήματα ανάλυσης κατασκευών, σχεδιασμό RF συστημάτων, σχεδιασμό ηχείων, μικροφώνων και ακουστικών συσκευών, μοντελοποίηση και ανάλυση εναλλακτών θερμότητας, συσκευών ανάμειξης, αντιδραστήρων και γενικότερα οποιουδήποτε προβλήματος σχεδιασμού και μοντελοποίησης συζευγμένων φυσικών φαινόμενων. Η πλατφόρμα του COMSOL εμπλουτίζεται συνεχώς με νέα εργαλεία για την μοντελοποίηση όλο και περισσότερων εφαρμογών και προβλημάτων. Πολύ σημαντικό χαρακτηριστικό του προγράμματος είναι η δυνατότητα που παρέχει για αλληλεπίδραση με άλλες πολύ σημαντικές και ευρέως χρησιμοποιούμενες εφαρμογές, όπως η MATLAB, το PROEngineer και το AutoCAD. Η παρούσα εργασία διενεργήθηκε στην πλατφόρμα COMSOL Multiphysics
7 4. ΜΕΘΟΔΟΣ ΠΕΠΕΡΑΣΜΕΝΩΝ ΣΤΟΙΧΕΙΩΝ 4.1 Γενικά στοιχεία Η μέθοδος πεπερασμένων στοιχείων, αποτελεί ένα ισχυρό εργαλείο για την αριθμητική επίλυση ενός μεγάλου φάσματος προβλημάτων του μηχανικού. Οι εφαρμογές της μεθόδου περιλαμβάνουν από την παραμόρφωση και ανάλυση τάσεων σε αυτοκίνητα, αεροπλάνα, κτίρια και γέφυρες, έως την ανάλυση πεδίων ροής και τη ρευστομηχανική. Η αναλυτική λύση των εξισώσεων με τις οποίες περιγράφονται τα διάφορα τεχνικά προβλήματα, είναι δυνατόν να πραγματοποιηθεί σε ελάχιστες περιπτώσεις, μόνο όπου τα προβλήματα είναι πάρα πολύ απλής μορφής. Η ανάγκη επίλυσης προβλημάτων σύνθετης μορφής οδήγησε στην ανάπτυξη διαφόρων προσεγγιστικών μεθόδων επίλυσης. Μία από τις πιο διαδεδομένες μεθόδους τέτοιου είδους είναι και η μέθοδος πεπερασμένων στοιχείων (finite elements method). Η μέθοδος πεπερασμένων στοιχείων, είναι προσεγγιστική, όμως μπορεί να δώσει αξιόπιστα αποτελέσματα και διαθέτει το πλεονέκτημα ότι μπορεί να εφαρμοστεί σε όλων των ειδών τα προβλήματα. Το μειονέκτημα της μεθόδου είναι οι αυξημένες απαιτήσεις σε υπολογιστική ισχύ, ιδίως όταν εφαρμόζεται σε σύνθετα προβλήματα, κάτι όμως που τείνει να εξαληφθεί λόγω της ανάπτυξης και κυκλοφορίας όλο και ισχυρότερων ηλεκτρονικών υπολογιστών. 4.2 Ιστορική αναδρομή Τα πρώτα βήματα για την ανάπτυξη της μεθόδου έγιναν πίσω στο 1941 με αφορμή την επίλυση προβλημάτων στη δομική ανάλυση αεροσκαφών. Το 1941 ο Hrenikoff παρουσίασε τη «μέθοδο των δικτυωμάτων». Το 1943 ο Courant δημοσίευσε μία εργασία, η οποία χρησιμοποιούσε τριγωνική παρεμβολή σε τριγωνικές υποπεριοχές για να μοντελοποιήσει προβλήματαστρέψης. Ο Tourner και άλλοι, δημιούργησαν μητρώα ακαμψίας για δικτυώματα, δοκούς και άλλα στοιχεία και παρουσίασαν τα αποτελέσματά τους το Ο όρος πεπερασμένα στοιχεία πρωτοχρησιμοποιήθηκε το 1960 από τον Clough. Από τις αρχές του 1960, οι μηχανικοί χρησιμοποιούσαν τη μέθοδο για να δώσουν προσεγγιστικές λύσεις σε προβλήματα ανάλυσης τάσεων, ροής ρευστών, μεταφοράς θερμότητας κ.α. Ο Ιωάννης Αργύρης το 1955 σε ένα βιβλίο για θεωρήματα ενέργειας και μητρωικές μεθόδους, έθεσε τα θεμέλια για την μελοντική ανάπτυξη των μελετών στα πεπερασμένα στοιχεία. Το πρώτο βιβλίο για πεπερασμένα στοιχεία από τους Zienkiewicz και Chung κυκλοφοόρησε το Οι μαθηματικές βάσεις της μεθόδου τέθηκαν τη δεκαετία το 70. 7
8 4.3 Στάδια εφαρμογής μεθόδου 1. Εισάγεται η γεωμετρία της κατασκευής σε ένα πρόγραμμα CAD και δημιουργείται το μοντέλο. Το μοντέλο χωρίζεται σε πεπερασμένα στοιχεία και αφού γίνει η πλεγματοποίηση, επιλέγεται το είδος επίλυσης και εισάγονται τα επιπλέον δεδομένα που απατούνται μέσω των ειδικών προγραμμάτων pre processor. Όταν εισαχθούν τα δεδομένα, το μοντέλο εισάγεται στο πρόγραμμα το οποίο θα πραγματοποιήσει την επίλυση του προβλήματος. Τα προγράμματα αυτά καλούνται solvers και χρησιμοποιούν τις αριθμητικές μεθόδους επίλυσης. Μετά το πέρας της επίλυσης καλούνται προγράμματα post processors που αναλαμβάνουν την παρουσίαση και την ανάλυση των αποτελεσμάτων στο μελετητή. 8
9 5. ΒΙΣΚΟΕΛΑΣΤΙΚΟΤΗΤΑ Βισκοελαστικότητα είναι η ιδιότητα κάποιων υλικών να παρουσιάζουν χαρακτηριστικά τόσο ελαστικότητας όσο και ιξώδους, όταν υποβάλλονται σε παραμόρφωση. Παχύρευστα υλικά όπως το μέλι με μεγάλο ιξώδες, αντιστέκονται στη διατμητική ροή, ενώ εντείνονται γραμμικά με το χρόνο όταν τους ασκείται μία τάση. Τα ελαστικά υλικά εντεινονται όταν τους ασκείται μία τάση, ενώ επιστρέφουν άμεσα στην αρχική τους κατάσταση μόλις απομακρυνθεί η τάση αυτή. Τα βισκοελαστικά υλικά συνδυάζουν ιδιότητες και από τις δύο αυτές κατηγορίες υλικών και ως τέτοια εμφανίζουν εξαρτώμενη από το χρόνο παραμόρφωση. Στο 19ο αιώνα φυσικοί όπως οι Maxwell, Boltzmann και Kelvin, ανακαλυψαν τις βισκοελαστικές ιδιότητες καθώς πειραματίστηκαν με τον ερπυσμό, την ανάκτηση σπασμένων γυαλιών, τα μέταλλα και ελαστικά. Η βισκοελαστικότητα εξετάστηκε περαιτέρω στα τέλη του 20 ου αιώνα, όταν είχαν κατασκευαστεί τα συνθετικά πολύμερή υλικά και ήταν ευρεία η εφαρμογή τους. Όλα τα υλικά παρουσιάζουν κάποια βισκοελαστική συμπεριφορά. Στα συνηθισμενα μέταλλα όπως ο σιδηρος η το αλουμίνιο, σε θερμοκρασία δωματίου και με άσκηση μικρής τάσης, η συμπεριφορά τους δε διαφέρει σημαντικά από τη συμπεριφορά από αυτη της γραμμικής ελαστικότητας. Τα συνθετικά πολυμερή, το ξύλο, ακόμα και τα μέταλλα σε υψηλές θερμοκρασίες παρουσιάζουν διακριτές βισκοελαστικές ιδιότητες. Σε κάποιες εφαρμογές ακόμα και μία μικρή βισκοελαστική συμπεριφορά μπορεί να είναι πολύ σημαντική, γι αυτό για να είναι πλήρης και ακριβής μία ανάλυση που αφορά σε τέτοια υλικά θα πρέπει να συμπεριλαμβάνει και την ανάλυση της βισκοελαστικής συμπεριφοράς τους. 9
10 6. ΕΠΙΛΟΓΗ ΥΛΙΚΩΝ ΔΙΑΤΑΞΗΣ 6.1 ΕΠΙΛΟΓΗ ΠΙΕΖΟΗΛΕΚΤΡΙΚΟΥ ΥΛΙΚΟΥ Υπάρχουν δύο κατηγορίες πιεζοηλεκτρικών υλικών που χρησιμοποιούνται ευρέως σαν αισθητήρες η διεγέρτες, τα κεραμικά και τα πολυμερή. Το πιο γνωστό πιεζοκεραμικό υλικό είναι ο ζιρκονιούχος τιτανιούχος μόλυβδος (PZT), με μοριακό τύπο PbZr(X)Ti1(X)O3 όπου το (Χ) λαμβάνει τιμές στο διάστημα (0,1). Απαντάται σε πολλές διαφορετικές συστάσεις, όπως PZT-2, PZT-4, PZT-5A, PZT5H, PZT-G1195, PZT-8. Χρησιμοποιείται ευρέως ως διεγέρτης και αισθητήρας για ένα ευρύ φάσμα συχνοτήτων και είναι κατάλληλος για απαιτήσεις υψηλής ακρίβειας. Αναπτύχθηκε από τους φυσικούς Yutaka Takagi, Gen Shirane, Etsuro Sawaguchi στο Ινστιτούτο Τεχνολογίας του Τόκιο Από τα πιεζοπολυμερή το πιο γνωστό είναι το πολυβινυλικό φθορίδιο (PVDF) και χρησιμοποιούνατι κυρίως σε αισθητήρες. Στην παρούσα εργασία, μελετήθηκε η συμπεριφορά της διάταξης με την παρουσία PZT και πιο συγκεκριμένα PZT-2 και του πολυμερούς PVDF. Μηχανικές ιδιότητες PZT-2: 10
11 6.2 ΕΠΙΛΟΓΗ ΣΥΓΚΟΛΛΗΤΙΚΟΥ ΥΛΙΚΟΥ Για την κατασκευή της μελετούμενης διάταξης είναι αναγκαία η ύπαρξη συγκολλητικού υλικού το οποίο θα παρεμβάλλεται ανάμεσα στο πιεζοηλεκτρικό στοιχείο και τη μεταλική βάση της διάταξης. Ειδικές εποξικές ρητήνες είναι κατάλληλες για τέτοιου είδους συγκολλήσεις και για το σκοπό αυτό μελετήθηκαν ειδικές εποξικές ρητήνες του εμπορίου για την καταλληλότητα τους για χρήση στη διάταξη. Καθώς τα συγκεκριμένα υλικά δεν υπάρχουν αποθηκευμένα στη βιβλιοθήκη υλικών του COMSOL Multiphysics, τα χαρακτηριστικά κάθε στοιχείου θα πρέπει να εισαχθούν στο πρόγραμμα χειροκίνητα. Μελετήθηκαν τρία διαφορετικά συγκολλητικά υλικά: 1.Epotek (Epoxy Technology) 2.Hysol 9361 (Henkel) 3.Tra-BondF113 (Tra-Con) Μηχανικές ιδιότητες εποξικών ρητηνών σε πραγματικές συνθήκες: Young s modulus (E) (psi) Poisson s ratio Maximum stress (psi) Tra-Con F ±12523 Epotek ± 6166 Hysol ± ± ± ± ± ± ± 9 Μετά από μετρήσεις και συγκρίσεις αποτελεσμάτων χρησιμοποιήθηκε στη διάταξη το συγκολλητικο Epotek της εταιρίας Epoxy Technology καθώς διαθέτει τα απαιτούμενα για τη συγκεκριμένη διάταξη χαρακτηριστικά. Οι μηχανικές ιδιότητες του συγκολλητικου Epotek εισηγμένες στο πρόγραμμα: 11
12 6.3 ΕΠΙΛΟΓΗ ΥΛΙΚΟΥ ΒΑΣΗΣ Για τη στήριξη της διάταξης επιλέχθηκε ένα ευρέως χρησιμοποιούμενο μέταλλο, το αλουμίνιο. Μηχανικές ιδιότητες αλουμινίου: 12
13 7. ΜΕΘΟΔΟΛΟΓΙΑ ΑΝΑΛΥΣΗΣ Η ανάλυση αποτελέιται από δύο κύρια μέρη. 1.Όταν το πιεζοηλεκτρικό στοιχείο είναι PZT-2 2.Όταν το πιεζοηλεκτρικό στοιχείο είναι PVDF Επιπροσθέτως σε κάθε μέρος διενεργούνται δύο διαφορετικοί τύποι ανάλυσης. Α) Στατική ανάλυση Β) Εξαρτώμενη απο το χρόνο ανάλυση διαφορετικου ρυθμού απόσβεσης(loss factor) με αποσβενόμενη ταλάντωση, Στην εξαρτώμενη από το χρόνο ανάλυση θα μελετηθεί η συμπεριφορά της διάταξης όταν δημιουργούνται συνθήκες ταλάντωσης στο συγκολλητικό υλικό, λόγω των βισκοελαστικών ιδιοτήτων που παρατηρούνται στα πολυμερή υλικά και πιο συγκεκριμένα στις εποξικές ρητήνες στις οποίες εντάσσεται και το συγκολλητικό υλικό που χρησιμοποιείται στη διάταξη. Τα loss factors που χρησιμοποιούνται είναι 0,3 στη μία περίπτωση και 0,8 στη δεύτερη, ώστε να γίνεται εμφανης η διαφορά αν υφίσταται στη συμπεριφορά της διάταξης. Αναλυτικά στάδια μοντελοποίησης στο COMSOL Multiphysics Καθορισμός περιβάλλοντος Προσδιορισμός τύπου ανάλυσης Σχεδιασμός διάταξης Προσδιορισμός υλικών, των ιδιοτήτων τους και της συμπεριφοράς του μοντέλου 5. Πλεγματοποίηση (Meshing) 6. Επίλυση 7. Συλλογή αποτελεσμάτων 13
14 Τα 3 πρώτα στάδια της διαδικασίας μοντελοποίησης είναι πανομοιότυπα σε όλα τα εξεταζόμενα μοντέλα. Ανοίγοντας το πρόγραμμα COMSOL Multiphysics στο παράθυρο Model Navigator που εμφανίζεται επιλέγουμε η ανάλυση να γίνει σε 3-διάστατο περιβάλλον (1). 14
15 Στη συνέχεια επιλέγουμε ανάλογα με την ανάλυση που θέλουμε να πραγματοποιήσουμε από τα πολυάριθμα είδη που παρέχει το πρόγραμμα. Εδώ πρόκειται για δομική μηχανική ανάλυση που μελετάει το πιεζοηλεκτρικό φαινόμενο, οπότε η διαδρομή είναι Structural Mechanics Module Piezoelectric Effects Piezo Solid (2). Επιλογή τύπου ανάλυσης: 15
16 Τέλος απομένει ο σχεδιασμός της προς μελέτη διάταξης (3). Οι διαστάσεις της διάταξης: Πιεζοηλεκτρικό υλικό (άνω στρώμα) Συγκολλητικο υλικό (ενδιάμεσο στρώμα) Μέταλλο (αλουμίνιο, κατώτερο στρώμα) Μήκος 100mm 100mm 100mm Πλάτος 100mm 100mm 100mm Ύψος 50mm 20mm 50mm Η διάταξη σχεδιασμένη με το σχεδιαστικό εργαλείο του COMSOL Multiphysics: Όπως φαίνεται πρόκειται για μία ορθογωνική διάταξη με τρία «στρώματα». Ξεκινώντας από πάνω, βρίσκουμε το Πιεζοηλεκτρικό υλικό της διάταξης, από κάτω βρίσκεται το συγκολλητικό υλικό και τέλος στο κατώτερο επίπεδο το μέταλλο πάνω στο οποίο εδράζεται η διάταξη. 16
17 8. ΜΕΡΟΣ Α Lead Zirconate Titanate (PZT-2) 8.1 ΣΤΑΤΙΚΗ ΑΝΑΛΥΣΗ 1.Υλικά και ιδιότητες (Subdomain settings) Εφ όσον πρόκειται για απλή στατική ανάλυση, σε αυτό το στάδιο απλά δηλώνουμε τα είδη και τις ιδιότητες των χρησιμοποιούμενων υλικών. Κάποια υλικά βρίσκονται αποθηκευμένα μαζί με τις ιδιότητες του στη Βιβλιοθήκη Υλικών του προγράμματος (Library Material). Όσα δεν βρίσκονται εκεί, ή δεν είναι καθορισμένες όλες οι φυσικές τους ιδιότητες, θα πρέπει ο χρήστης του προγράμματος να τα προσθέσει, βρίσκοντας τις ιδιότητες των υλικών αυτών, μελετώντας την κατάλληλη βιβλιογραφία. Στη συγκεκριμένη περίπτωση, τα υλικά είναι: Άνω στρώμα: PZT-2 Ενδιάμεσο: Epotek301-2 Κατώτερο στρώμα: Αλουμίνιο Καθορισμός του υλικού του άνω στρώματος: 17
18 PZT-2: Epotek301-2: 18
19 Υλικό βάσης (αλουμίνιο): 19
20 2.Καθορισμός οριακών συνθηκών (Boundary settings) Πρώτα καθορίζονται οι μηχανικές συνοριακές συνθήκες. Η διάταξη βρίσκεται πακτωμένη και ακίνητη σε ολόκληρη την αριστερή επιφάνεια της και επίσης δέχεται στην άνω επιφάνεια μία εξωτερική δύναμη μέτρου 500N/m κατά τη z διέυθυνση των αξόνων και με κατεύθυνση προς τα κάτω. Εισαγωγή επιφανειακής δύναμης 500Ν/m: 20
21 Δύναμη 500Ν/m στη z διεύθυνση με κατέυθυνση προς τα κάτω: Η επιφάνεια 10 είναι αυτή που δέχεται τη δύναμη: Οι 3 αριστερές επιφάνειες της διάταξης είναι πακτωμένες και ακίνητες: 21
22 Καθορισμός των συνοριακών συνθηκών της πάκτωσης: Από τη στιγμή που στη διάταξη υπάρχει πιεζοηλεκτρικό υλικό του οποίου τη συμπεριφορά θέλουμε να μελετήσουμε, είναι αναγκαίο ακόμα, να καθοριστούν οι συνοριακές συνθήκες που θα επικρατούν στις επιφάνειες του πιεζοηλεκτρικού υλικού σε σχέση με τη ροή ηλεκτρικού ρεύματος. Έτσι η κατώτερη επιφάνεια του 22
23 πιεζοηλεκτρικού στοιχείου θα συμπεριφέρεται σαν γείωση ενω η ανώτερη θα επιτρέπει τη ροή ρεύματος. Ηλεκτρικές συνοριακές συνθήκες για την άνω επιφάνεια του πιεζοηλεκτρικού στοιχείου: Αντίστοιχα για την κάτω επιφάνεια: 23
24 3.Πλεγματοποίηση (Meshing) Για να εφαρμόσει το COMSOL Multiphysics τη μέθοδο των πεπερασμένων στοιχείων στην υπό μελέτη διάταξη και να επιλύσει το πρόβλημα, είναι απαραίτητη η πλεγματοποίηση της διάταξης με το κατάλληλο εργαλείο που παρέχεται απο το COMSOL. Στο σύνολο της εργασίας, πραγματοποιήθηκε πλεγματοποίηση μόνο σε ένα επίπεδο, καθώς η δεύτερη πλεγματοποίηση θα αύξανε σε σημαντικό βαθμό τον υπολογιστικό φόρτο έτσι ώστε η επίλυση από ένα κοινό ηλεκτρονικό υπολογιστή να γινόταν πολύ χρονοβόρα η ακόμα και αδύνατη. Πλεγματοποίηση σε δεύτερο επίπεδο πραγματοποιήθηκε ενδεικτικά σε μία μόνο περίπτωση για τη σύγκριση των αποτελεσμάτων. Τα αποτελέσματα της πλεγματοποίησης αναλυτικά: Βαθμοί ελευθερίας Σημέια πλέγματος 1721 Στοιχεία πλέγματος 8078 Επιφανειακά στοιχεία Ακμές Η διάταξη μετά το πέρας της πλεγματοποίησης (8078 στοιχεία): 24
25 4.Επίλυση/Παράμετροι επίλυσης Εφ όσον έχουν πραγματοποιηθεί όλες οι απαραίτητες προεργασίες και έχουν καθοριστεί όλες οι παράμετροι ώστε η διάταξη να είναι έτοιμη για την πραγματοποίηση της στατικής ανάλυσης, πρέπει να καθοριστούν οι παράμετροι επίλυσης (solver parameters). Στη συγκεκριμένη περίπτωση η ανάλυση που θα πραγματοποιηθεί είναι στατική, οπότε επιλέγεται Analysis Static και Solver Stationary. Παράμετροι επίλυσης για στατική ανάλυση: 25
26 Στη συγκεκριμένη περίπτωση, η επίλυση πραγματοποιείται άμεσα σε χρόνους κοντά στο 1 λεπτό. Αυτό συμβαίνει επειδή η στατική ανάλυση σε μία απλή σχεδιαστικά διάταξη, αποτελεί ένα σχετικά εύκολο πρόβλημα προς επίλυση από τους σύγχρονους ηλεκτρονικούς υπολογιστές. 26
27 Η παραμόρφωση της διάταξης μετά από την επίλυση: 5.Συλλογή και ανάλυση αποτελεσμάτων Στο στάδιο αυτό, ύστερα από την επίλυση, είναι δυνατή η συλλογή και η αναλυτική κατόπτευση και επεξεργασία των αποτελεσμάτων της στατικής ανάλυσης που πραγματοποιήθηκε μέσω του προγράμματος. Η διάταξη έχει εκτράπεί προς τα κάτω υπό την επίδραση της δύναμης, της οποίας η φορά ήταν z. Η μέγιστη μετατόπιση παρατηρείται στο ελεύθερο άκρο της διάταξης και είναι 0.602μm. 27
28 Συνολική μετατόπιση: Συνολική μετατόπιση κατα μήκος της διάταξης: Όπως είναι αναμενόμενο η μεγαλύτερη ένταση λόγω της εξωτερικής δύναμης εμφανίζεται στο αριστερό πακτωμένο άκρο της διάταξης καθώς και στό συγκολλητικό υλικό και είναι του μεγέθους 1.638*10^-6. Εντάση κατά μήκος της διάταξης: 28
29 Κατανομή της έντασης: Αναμενόμενη είναι και η κατανομή των τάσεων Von Mises, οι οποίες ακολουθούν την κατανομή της έντασης. Η μεγαλύτερη τιμη παρατηρείται και εδώ στο πακτωμένο άκρο της διάταξης και το μέγεθος της είναι 0.122MPa. Τάσεις Von Mises κατά μήκος της διάταξης: 29
30 Κατανομή τάσεων Von Mises: Η σχέση ανάμεσα στην ασκούμενη δύναμη, την ένταση, τις τάσεις που αναπτύσσονται και τις ηλεκτρικές ιδιότητες είναι άμεση. Έτσι είναι αναμενόμενο ότι το ηλεκτρικό δυναμικό διαφοροποιείται ανάλογα με την επηρροή της εξωτερικής δύναμης στη διάταξη. Η διαφορά δυναμικού που παρατηρείται στη διάταξη είναι (0.906,-5.058)V. 30
31 Διάγραμμα ηλεκτρικού δυναμικού: Η κατανομή του ηλεκτρικού δυναμικού: 6.Συγκεντρωτικά αποτελέσματα ΣΥΝΟΛΙΚΗ ΜΕΤΑΤOΠΙΣΗ (μm) ΕΝΤΑΣΗ ΤΑΣΗ (MPa) ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ (V) 31
32 MAXIMUM *10^ (0.906, ) Στατική ανάλυση (πλεγματοποίηση 2ου επιπέδου) Στο στάδιο αυτό, θα πραγματοποιηθέι η ίδια στατική ανάλυση, με τη διάταξη να έχει υποστεί πλεγματοποίηση 2ου επιπέδου. Στο πρόγραμμα COMSOL αυτό επιτυγχάνεται επιλέγοντας Refine Mesh από το μενού του Mesh. Συγκριτικά αποτελέσματα των δύο επιπέδων πλεγματοποίησης: 32
33 Βαθμοί ελευθερίας MESH REFINE MESH Σημέια πλέγματος Στοιχεία πλέγματος Επιφανειακά στοιχεία 3586 Ακμές Όπως φαίνεται από τον πίνακα, η διάταξη έχει χωριστεί σε πολύ περισσότερα τμήματα, επιτρέποντας την ακριβέστερη επίλυση του προβλήματος. Η επίλυση στη συγκεκριμένη περίπτωση πραγματοποιείται περίπου στον τριπλάσιο χρόνο δηλαδή σε 3 λεπτά. Αποτελέσματα επίλυσης: Η συνολική μετατόπιση είναι 0.605μm. Συνολική μετατόπιση: Η μέγιστη ένταση ανέρχεται σε 1.562*10^-6. Ένταση: 33
34 Οι τάσεις Von Mises λαμβάνουν την τιμή 0.129MPa. Τάσεις Von Mises: Το ηλεκτρικό δυναμικό λαμβάνει τις τιμές (1.024,-5.092)V. Το ηλεκτρικό δυναμικό: 34
35 8.1.2 Συγκριτικά αποτελέσματα MESH REFINE MESH ΣΥΝΟΛΙΚΗ ΜΕΤΑΤOΠΙΣ Η (μm) ΕΝΤΑΣΗ ΤΑΣΗ (MPa) ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ (V) *10^ (0.906, ) *10^ (1.024, ) Είναι φανερό ότι η διαφορά των αποτελεσμάτων είναι αρκετά μικρή ώστε να δικαιολογεί τον αυξημένο υπολογιστικό φόρτο που απαιτείται για την πραγματοποίηση της λεπτομερέστερης ανάλυσης στο συγκεκριμένο πρόβλημα. 8.2 ΑΝΑΛΥΣΗ ΜΕ ΑΠΟΣΒΕΝΟΜΕΝΗ ΤΑΛΑΝΤΩΣΗ ΕΞΑΡΤΩΜΕΝΗ ΑΠΟ ΤΟ ΧΡΟΝΟ (συντελεστής απόσβεσης 0.3) 35
36 1.Υλικά και ιδιότητες Τα υλικά της διάταξης παραμένουν ίδια όπως και στην στατική ανάλυση. Θα εισαχθεί στο μεσαίο στρώμα της διάταξης, δηλαδή στο συγκολλητικό υλικό μία αποσβενόμενη ταλάντωση με συντελεστή απόσβεσης (loss factor) 0.3. Loss factor 0,3 στο συγκολλητικό: Η ρύθμιση όπως φαίνεται στο περιβάλλον του COMSOL: 2.Καθορισμός οριακών συνθηκών (Boundary settings) 36
37 Σε αυτό το στάδιο η βασική διαφορά βρίσκεται στην ασκούμενη δύναμη που πλέον είναι ημιτονοειδούς μορφής εξαρτώμενη απο το χρόνο ίση με F= 500*sin(t) με Fmax=500 και φορά όπως η αρχική. Η νέα δύναμη και η επιφάνεια όπου ασκείται: 3.Πλεγματοποίηση (Meshing) Πραγματοποιείται πλεγματοποίηση σε ένα μόνο επίπεδο. Τα στατιστικά στοιχεία της βρίσκονται στο κεφάλαιο Επίλυση/Παράμετροι επίλυσης 37
38 Θα πρέπει να τροποποιηθέι το είδος της ανάλυσης εφ όσον πλέον δεν πρόκειται για απλή στατική ανάλυση. Αυτό επιτυγχάνεται αλλάζοντας τις παραμέτρους επίλυσης από την καταλληλη επιλογή του προγραμματος. Στο είδος ανάλυσης επιλέγεται Time dependent, στο είδος επίλυσης επίσης Time dependent, ενω πρέπει να καθοριστούν και οι ειδικές χρονικές παράμετροι. Η προσομοίωση θα γίνει για δέκα δευτερόλεπτα με το βήμα να έχει καθοριστεί στα 0,3 δευτερόλεπτα. Ο χρόνος αυτός επιλέχθηκε ώστε να έχουν πραγματοποιηθεί τουλάχιστον δύο ταλαντώσεις της ημιτονοειδούς συνάρτησης. Ο χρόνος της προσομοίωσης, σε συνδυασμο με το βήμα των 0.3 δευτερολέπτων δεν αποφέρουν τη μέγιστη ακρίβεια, αλλά ο υπολογιστικός φόρτος μιας μεγαλύτερης σε διαρκεια και ακρίβεια προσομοίωσης μπορεί να γίνει απαγορευτικός, χωρίς ωστόσο να αποφέρει σημαντική βελτίωση των λύσεων. Παρ όλα αυτά, οι επιλεγμένες παράμετροι αρκούν για τη συλλογή ασφαλών αποτελεσμάτων. Η επίλυση αυτου του προβλήματος διαρκεί συνήθως 7 έως 10 λεπτά. Το παράθυρο καθορισμου των Solver Parameters: 5.Συλλογή και ανάλυση αποτελεσμάτων 38
39 Η συνολική μετατόπιση σε συνάρτηση με το χρόνο στις επιφάνειες της διάταξης παρουσιάζεται παρακάτω. Η μέγιστη τιμή της εμφανίζεται στην κατώτερη επιφάνεια και είναι 0.625μm. Συνολική μετατόπιση στην ανώτερη επιφάνεια της διάταξης σε σχέση με το χρόνο: Συνολική μετατόπιση στην κατώτερη επιφάνεια: 39
40 Συνολική μετατόπιση στο σημείο x=0,1, y=0, z=0: 40
41 Συνολικη μετατόπιση κατα τον Χ άξονα: 41
42 Συνολική μετατόπιση κατά τον Υ άξονα: Το διάγραμμα της έντασης κατα μήκος της διάταξης σε συνάρτηση με το χρόνο στην επιφάνεια της διάταξης μας δείχνει ότι η ένταση ακολουθά την ημιτονοειδή συνάρυηση της ασκούμενης δύναμης. Η μέγιστη ένταση έχει μέτρο 1.572*10^-6 και παρατηρείται στο πακτωμένο άκρο. x-axis:μηκος διάταξης y-axis:χρόνος z-axis:ένταση 42
43 Απεικόνηση σε 2 διαστάσεις: 43
44 Όπως και στην στατική ανάλυση η συμπεριφορά των τάσεων Von Mises είναι παρόμοια με τη συμπεριφορά της έντασης. Η μέγιστη τιμή παρατηρείται κοντά στο πακτωμένο άκρο της διάταξης και η αυξομείωση του μέτρου ακολουθά την ημιτονοειδή συνάρτηση του φορτίου που ασκείται. Η μέγιστη τιμή που παρατηρείται είναι MPa. Τάσεις Von Mises: Τάσεις Von Mises: 44
45 Το ηλεκτρικό δυναμικό που παρατηρείται ακολουθεί και αυτό την ημιτονοειδή συνάρτηση της δύναμης. Η διαφορά δυναμικού που παρατηρείται είναι (4.849,-4.874)V. Ηλεκτρικό δυναμικό στην άνω επιφάνεια: Η κατανομή του ηλεκτρικού δυναμικού: 45
46 Το ηλεκτρικό δυναμικό σε διδιάστατη μορφή: 6.Συγκεντρωτικά αποτελέσματα MAXIMUM ΣΥΝΟΛΙΚΗ ΜΕΤΑΤOΠΙΣΗ (μm) ΕΝΤΑΣΗ ΤΑΣΗ (MPa) ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ (V) *10^ (4.849, ) 46
47 8.3 ΑΝΑΛΥΣΗ ΜΕ ΑΠΟΣΒΕΝΟΜΕΝΗ ΤΑΛΑΝΤΩΣΗ ΕΞΑΡΤΩΜΕΝΗ ΑΠΟ ΤΟ ΧΡΟΝΟ (συντελεστής απόσβεσης 0.8) 1.Υλικά και ιδιότητες Το μοναδική αλλαγή που πρέπει να πραγματοποιηθεί σε αυτό το στάδιο είναι η μετατροπή του συντελεστή απόσβεσης loss factor που από 0.3 στην προηγούμενη περίπτωση γίνεται 0.8. Συντελεστης απόσβεσης 0,8: 2.Καθορισμός οριακών συνθηκών (Boundary settings) Οι συνοριακές συνθήκες παραμένουν όπως και στην προηγούμενη περίπτωση, η διάταξη βρίσκεται πακτωμένη στην αριστερή της επιφάνεια, ενώ στην άνω επιφάνεια δέχεται την ίδια εξωτερική δύναμη ημιτονοειδούς μορφής. 3.Πλεγματοποίηση (Meshing) Καμία αλλαγή δεν πραγματοποιείται στην πλεγματοποίηση και στις παραμέτρους της. 47
48 4.Επίλυση/Παράμετροι επίλυσης Οι παράμετροι επίλυσης παραμένουν ίδιες όπως και στην προηγούμενη περίπτωση. Πρόκειται για ανάλυση εξαρτώμενη απο το χρόνο όπως και ο τρόπος επίλυσης. Η επίλυση πραγματοποιείται απο το πρόγραμμα συνήθως σε 7-10 λεπτά. 5.Συλλογή και ανάλυση αποτελεσμάτων Οι μέγιστη τιμή της συνολικής μετατόπισης είναι 0.625μm και εντοπίζεται στην κατώτερη επιφάνεια της διάταξης. Συνολική μετατόπιση στην άνω επιφάνεια: 48
49 Συνολική μετατόπιση στην κατώτερη επιφάνεια: Συνολική μετατόπιση στο σημείο x=0,1, y=0, z=0: 49
50 Συνολική μετατόπιση κατα τον x άξονα: Συνολική μετατόπιση κατά τον y άξονα: 50
51 Η μέγιστη ένταση που παρατηρείται στη διάταξη είναι 1.572*10^-6. x-axis:μηκος διάταξης y-axis:χρόνος z-axis:ένταση Απεικόνηση σε 2 άξονες: 51
52 Η μέγιστη τιμή των τάσεων Von Mises που παρατηρείται είναι MPa. Τάσεις Von Mises: Τάσεις Von Mises: Η διαφορά δυναμικού που παρατηρείται είναι (4.849,-4.874)V. 52
53 Ηλεκτρικό δυναμικό στην άνω επιφάνεια: 53
54 Η κατανομή του ηλεκτρικού δυναμικού: Το ηλεκτρικό δυναμικό σε διδιάστατη μορφή: 6.Συγκεντρωτικά αποτελέσματα MAXIMUM ΣΥΝΟΛΙΚΗ ΜΕΤΑΤOΠΙΣΗ (μm) ΕΝΤΑΣΗ ΤΑΣΗ (MPa) ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ (V) *10^ (4.849, ) 54
55 8.4 ΣΥΓΚΕΝΤΡΩΤΙΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ Α ΜΕΡΟΥΣ PZT-2 ΣΥΝΟΛΙΚΗ ΜΕΤΑΤOΠΙΣ Η (μm) ΕΝΤΑΣΗ ΤΑΣΗ (MPa) ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ (V) STATIC X10^ (0.906, ) TIME DEPENDENT (0.3) TIME DEPENDENT (0.8) *10^ (4.849, ) *10^ (4.849, ) 55
56 9. ΜΕΡΟΣ Β Πολυβινυλικό φθορίδιο (PVDF) 9.1 ΣΤΑΤΙΚΗ ΑΝΑΛΥΣΗ 1.Υλικά και ιδιότητες (Subdomain settings) Σε αυτό το μέρος της εργασίας εξετάζεται η συμπεριφορά της ίδιας διάταξης όταν το πιεζοηλεκτρικό υλικό PZT-2 αντικατασταθεί από το πιεζοπολυμερές PVDF. Έτσι η διάταξη τροποποιείται ακολούθως: Άνω στρώμα: PVDF Ενδιάμεσο: Epotek301-2 Κατώτερο στρώμα: Αλουμίνιο Εισαγωγή του πιεζοπολυμερούς PVDF στη διάταξη: 56
57 2.Καθορισμός οριακών συνθηκών (Boundary settings) Σε αυτό το στάδιο δεν πραγματοποιείται καμία αλλαγή στις παραμέτρους, οι οποίες είναι παρόμοιες με τις παραμέτρους που χρησιμοποιήθηκαν στη στατική ανάλυση του πρώτου μέρους. Η διάταξη παραμένει πακτωμένη από την αριστερή της πλευρά σε ολόκληρη την επιφάνεια, η εξωτερική δύναμη είναι ίδιου μέτρου και φοράς, όπως και οι ηλεκτρικές ιδιότητες του πιεζοηλεκτρικού στοιχείου. 3.Πλεγματοποίηση (Meshing) Η πλεγματοποίηση πραγματοποιήθηκε με την ίδια διαδικασία, παρουσιάζοντας τα ίδια στατιστικά στοιχεία. Τα στατιστικά στοιχεία της πλεγματοποίησης όπως παρουσιάζονται απο το COMSOL Multiphysics: 4.Επίλυση/Παράμετροι επίλυσης Οι παράμετροι επίλυσης είναι οι ίδιες που χρησιμοποιήθηκαν και στην προηγούμενη στατική ανάλυση, ενώ το πρόγραμμα πραγματοποιεί την επίλυση σε χρόνους κάτω του ενός λεπτού, δεδομένου ότι η στατική ανάλυση δεν απαιτεί μεγάλη υπολογιστική ισχυ και δεν δυσκολεύει ένα σύγχρονο Η/Υ. 57
58 5.Συλλογή και ανάλυση αποτελεσμάτων Στο στάδιο αυτό παρουσιάζονται αναλυτικά τα αποτελέσματα της στατικής ανάλυσης. Όπως είναι αναμενόμενο, η διάταξη υπό την επίδραση της δύναμης έχει εκτραπεί προς τα κάτω στο ελέυθερο άκρο της. Η διάταξη υπό την επίδραση της επιφανειακής δύναμης: Η μέγιστη μετατόπιση στο ελέυθερο άκρο της διάταξης ανέρχεται σε 0.423μm. Συνολική μετατόπιση κατα μήκος της διάταξης: 58
59 Η κατανομή της συνολκής μετατόπισης σε μία επιφάνεια της διάταξης: Η μέγιστη ένταση που παρατηρείται στη διάταξη είναι 1.394*10^-6 και παρατηρείται στο μεσαίο στρώμα, αυτό του συγκολλητικού υλικού, ενώ υψηλές είναι και οι τιμές που παρατηρούνται στο πακτωμένο άκρο της διάταξης. Η κατανομή της έντασης στη διάταξη: 59
60 Η ένταση κατα μήκος της διάταξης: Οι τάσεις Von Mises αναπτύσσουν φυσιολογικά τη μέγιστη τιμή τους στο πακτωμένο άκρο της διάταξης. Το μέγιστο μέτρο των τάσεων που αναπτύσσονται είναι 0.16MPa. Η κατανομή των τάσεων Von Mises: 60
61 Οι τάση κατά μήκος της διάταξης: Το ηλεκτρικό δυναμικό που αναπτύσσεται στη διάταξη λόγω των ιδιοτήτων που διέπουν τα πιεζοηλεκτρικά υλικά έχει εύρος (1.384,-4.686)V. Κατανομή του ηλεκτρικού πεδίου στη διάταξη: 61
62 Το ηλεκτρικο πεδίο κατα μήκος της διάταξης: Η κατανομή του ηλεκτρικού πεδίου στην άνω επιφάνεια: 62
63 6.Συγκεντρωτικά αποτελέσματα MAXIMUM ΣΥΝΟΛΙΚΗ ΜΕΤΑΤOΠΙΣΗ (μm) ΕΝΤΑΣΗ ΤΑΣΗ (MPa) ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ (V) *10^ (1.384, ) 63
64 9.2 ΑΝΑΛΥΣΗ ΜΕ ΑΠΟΣΒΕΝΟΜΕΝΗ ΤΑΛΑΝΤΩΣΗ ΕΞΑΡΤΩΜΕΝΗ ΑΠΟ ΤΟ ΧΡΟΝΟ (συντελεστής απόσβεσης 0.3) 1.Υλικά και ιδιότητες Τα υλικά της διάταξης παραμένουν ίδια όπως και στην στατική ανάλυση. Θα εισαχθεί στο στρώμα του συγκολλητικού υλικού η αποσβενόμενη ταλάντωση με συντελεστή απόσβεσης (loss factor) 0.3 όπως στην περίπτωση του PZT-2. 2.Καθορισμός οριακών συνθηκών (Boundary settings) Σε αυτό το στάδιο η βασική διαφορά βρίσκεται στην ασκούμενη δύναμη που πλεον είναι ημιτονοειδούς μορφής εξαρτώμενη απο το χρόνο ίση με F= 500sin(t) με Fmax=500N και φορά όπως η αρχική, ακριβώς όπως στο δεύτερο στάδιο του Α μέρους κατά τη μελέτη της διάταξης με το πιεζοηλεκτρικό PZT-2. 3.Πλεγματοποίηση (Meshing) Ακριβώς όπως και στη στατική ανάλυση. 4.Επίλυση/Παράμετροι επίλυσης Υσχύουν τα ίδια όπως σε κάθε προηγούμενη εξαρτώμενη από το χρόνο ανάλυση. Η επίλυση περατώνεται περίπου σε 7 με 10 λεπτά. 64
65 5.Συλλογή και ανάλυση αποτελεσμάτων Η μέγιστη μετατόπιση που παρατηρείται είναι 0.485μm και εντοπίζεται στην κατώτερη επιφάνεια της διάταξης. Συνολική μετατόπιση στην άνω επιφάνεια: 65
66 Συνολική μετατόπιση στην κατώτερη επιφάνεια: Η μετατοπιση στο σημείο (0.1,0,0) 66
67 Η συνολική μετατόπιση κατά τον x άξονα: Η συνολική μετατόπιση κατά τον y άξονα: 67
68 Η μέγιστη τιμή της έντασης που παρατηρείται στη διάταξη είναι 1.407*10^-6. Η κατανομή της έντασης σε συνάρτηση με το χρόνο: Η κατανομή της έντασης σε 2 διαστάσεις: 68
69 Η μέγιστη τιμή των τάσεων Von Mises που αναπτύσσονται στη διάταξη είναι MPa. Η κατανομή των τάσεων Von Mises: Η κατανομή της μηχανικής τάσης σε 2 διαστάσεις: 69
70 Η διαφορά δυναμικού που παρατηρείται είναι (4.518,-4.534)V. Το ηλεκτρικό πεδίο στην άνω επιφάνεια της διάταξης: Η κατανομή του ηλεκτρικού δυναμικού σε συνάρτηση με το χρόνο: 70
71 Το ηλεκτρικό δυναμικό στο σημείο (0.1,0,0.12): 6.Συγκεντρωτικά αποτελέσματα MAXIMUM ΣΥΝΟΛΙΚΗ ΜΕΤΑΤOΠΙΣΗ (μm) ΕΝΤΑΣΗ ΤΑΣΗ (MPa) ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ (V) *10^ (4.518, ) 71
72 9.3 ΑΝΑΛΥΣΗ ΜΕ ΑΠΟΣΒΕΝΟΜΕΝΗ ΤΑΛΑΝΤΩΣΗ ΕΞΑΡΤΩΜΕΝΗ ΑΠΟ ΤΟ ΧΡΟΝΟ (συντελεστής απόσβεσης 0.8) 1.Υλικά και ιδιότητες Το μοναδικό στοιχείο που αλλάζει στη μοντελοποίηση σε αυτό το στάδιο είναι ο συντελεστής απόσβεσης της ταλάντωσης (loss factor), που απο 0.3 στην προηγούμενη περίπτωση γίνεται Καθορισμός οριακών συνθηκών (Boundary settings) Οι συνοριακές συνθήκες παραμένουν όπως και στην προηγούμενη περίπτωση, η διάταξη βρίσκεται πακτωμένη στην αριστερή της επιφάνεια, ενώ στην άνω επιφάνεια δέχεται μία εξωτερική δύναμη ημιτονοειδούς μορφής. 3.Πλεγματοποίηση (Meshing) Καμία αλλαγή δεν πραγματοποιείται στην πλεγματοποίηση και στις παραμέτρους της. 4.Επίλυση/Παράμετροι επίλυσης Οι παράμετροι επίλυσης παραμένουν ίδιες όπως και στην προηγούμενη περίπτωση. Πρόκειται για ανάλυση εξαρτώμενη απο το χρόνο όπως και ο τρόπος επίλυσης. Η επίλυση πραγματοποιείται απο το πρόγραμμα συνήθως σε 7-10 λεπτά. 5.Συλλογή και ανάλυση αποτελεσμάτων Η μέγιστη τιμή της συνολικής μετατόπισης είναι ξανά 0.485μm. 72
73 Συνολική μετατόπιση στην άνω επιφάνεια: 73
74 Συνολική μετατόπιση στην κατώτερη επιφάνεια: Η μετατοπιση στο σημείο (0.1,0,0) 74
75 Η συνολική μετατόπιση κατά τον x άξονα: Η συνολική μετατόπιση κατά τον y άξονα: 75
76 Η μέγιστη τιμή της έντασης που παρατηρείται στη διάταξη είναι όπως και στο προηγούμενο στάδιο 1.407*10^-6. Η κατανομή της έντασης σε συνάρτηση με το χρόνο: Η κατανομή της έντασης σε 2 διαστάσεις: 76
77 Η μέγιστη τιμή των τάσεων Von Mises που αναπτύσσονται στη διάταξη είναι MPa. Η κατανομή των τάσεων Von Mises: Η κατανομή της μηχανικής τάσης σε 2 διαστάσεις: 77
78 Η διαφορά δυναμικού που παρατηρείται είναι (4.518,-4.534)V. Το ηλεκτρικό πεδίο στην άνω επιφάνεια της διάταξης: Η κατανομή του ηλεκτρικού δυναμικού σε συνάρτηση με το χρόνο: 78
79 Το ηλεκτρικό δυναμικό στο σημείο (0.1,0,0.12): 6.Συγκεντρωτικά αποτελέσματα MAXIMUM ΣΥΝΟΛΙΚΗ ΜΕΤΑΤOΠΙΣΗ (μm) ΕΝΤΑΣΗ ΤΑΣΗ (MPa) ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ (V) *10^ (4.518, ) 9.4 ΣΥΓΚΕΝΤΡΩΤΙΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ Β ΜΕΡΟΥΣ PZT-2 ΣΥΝΟΛΙΚΗ ΜΕΤΑΤOΠΙΣ Η (μm) ΕΝΤΑΣΗ ΤΑΣΗ (MPa) ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ (V) STATIC *10^ (1.384, ) TIME DEPENDENT (0.3) TIME DEPENDENT (0.8) *10^ (4.518, ) *10^ (4.518, ) Είναι φανερό ότι η αλλαγή του συντελεστή απόσβεσης (loss factor) δεν επιφέρει ούτε σε αυτή την περίπτωση κάποια αλλαγή στη συμπεριφορά της διάταξης. Θα εξεταστεί αν υπέυθυνη για αυτά τα αποτελέσματα είναι η μορφή της εξωτερικής δύναμης. 79
80 10. ΑΛΛΑΓΗ ΕΞΩΤΕΡΙΚΗΣ ΔΥΝΑΜΗΣ Στο στάδιο αυτό θα γίνει μία συγκριτική δοκιμή, χρησιμοποιώντας τη διάταξη του Α μέρους, ώστε να διαπιστωθεί αν η μορφή της εξωτερικής δύναμης ευθύνεται για τα όμοια αποτελέσματα στην χρονικά εξαρτώμενη ανάλυση. Η νέα δύναμη που θα χρησιμοποιηθεί, θα είναι η F-500sin(πt) και εξασφαλίζει σημαντικά πιο γρήγορη απόκριση από την μέχρι τώρα χρησιμοποιούμενη δύναμη. 1. ΑΝΑΛΥΣΗ ΜΕ ΑΠΟΣΒΕΝΟΜΕΝΗ ΤΑΛΑΝΤΩΣΗ ΕΞΑΡΤΩΜΕΝΗ ΑΠΟ ΤΟ ΧΡΟΝΟ (συντελεστής απόσβεσης 0.3) Θα παραλειφθούν τα αρχικά στάδια της διαδικασίας και θα γίνει απευθείας παρουσίαση των αποτελεσμάτων. Η διάταξη αποτελείται απο τα εξίς υλικά: Άνω στρώμα: PZT-2 Ενδιάμεσο: Epotek301-2 Κατώτερο στρώμα: Αλουμίνιο Συνολική μετατόπιση: Συνολική μετατόπιση στην άνω επιφάνεια: 80
81 Συνολική μετατόπιση στην κατώτερη επιφάνεια: Ένταση: Κατανομή της έντασης: 81
82 Τάσεις Von Mises: Κατανομή των τάσεων Von Mises: Ηλεκτρικό δυναμικό: Ηλεκτρικό δυναμικό στην άνω επιφάνεια: 82
83 2. ΑΝΑΛΥΣΗ ΜΕ ΑΠΟΣΒΕΝΟΜΕΝΗ ΤΑΛΑΝΤΩΣΗ ΕΞΑΡΤΩΜΕΝΗ ΑΠΟ ΤΟ ΧΡΟΝΟ (συντελεστής απόσβεσης 0.8) Συνολική μετατόπιση: Συνολική μετατόπιση στην άνω επιφάνεια: Συνολική μετατόπιση στην κατώτερη επιφάνεια: 83
84 Ένταση: Κατανομή της έντασης: Τάσεις Von Mises: Κατανομή των τάσεων Von Mises: 84
85 Ηλεκτρικό δυναμικό: Ηλεκτρικό δυναμικό στην άνω επιφάνεια: 3. Συγκριτικά αποτελέσματα TIME DEPENDENT (0.3) TIME DEPENDENT (0.8) ΣΥΝΟΛΙΚΗ ΜΕΤΑΤOΠΙΣ Η (μm) ΕΝΤΑΣΗ ΤΑΣΗ (MPa) ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ (V) *10^ (4.887, ) *10^ (4.887, ) Είναι πλέον φανερό ότι η αλλαγή του συντελεστή απόσβεσης δεν επιφέρει καμία αλλαγή στα αποτελέσματα της επίλυσης. Η νέα δύναμη που χρησιμοποιήθηκε, δίνει καλύτερα αποτελέσματα, λόγω της μεγαλύτερης συχνότητας ταλάντωσης που επιβάλλει, με αποτέλεσμα να πραγματοποιούνται στο ίδιο χρονικό διάστημα πολύ περισσότεροι κύκλοι και να διασφαλίζεται η ακρίβεια των αποτελεσμάτων. Παρ όλα αυτά, η διαφορά στα αποτελέσματα οφείλεται αποκλειστικά και μόνο στην αλλαγή της εξωτερικής δύναμης. 85
86 11. ΣΥΝΟΨΗ/ΣΥΓΚΡΙΤΙΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ Α & Β ΜΕΡΟΥΣ ΣΤΑΤΙΚΗ ΑΝΑΛΥΣΗ ΥΛΙΚΟ ΣΥΝΟΛΙΚΗ ΜΕΤΑΤOΠΙΣΗ (μm) ΕΝΤΑΣΗ ΤΑΣΗ (MPa) ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ (V) PZT-2 PVDF X10^ (0.906, ) *10^ (1.384, ) ΑΝΑΛΥΣΗ ΜΕ ΑΠΟΣΒΕΝΟΜΕΝΗ ΤΑΛΑΝΤΩΣΗ ΕΞΑΡΤΩΜΕΝΗ ΑΠΟ ΤΟ ΧΡΟΝΟ (συντελεστής απόσβεσης 0.3) ΥΛΙΚΟ ΣΥΝΟΛΙΚΗ ΜΕΤΑΤOΠΙΣΗ (μm) ΕΝΤΑΣΗ ΤΑΣΗ (MPa) ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ (V) PZT-2 PVDF *10^ (4.849, ) *10^ (4.518, ) ΑΝΑΛΥΣΗ ΜΕ ΑΠΟΣΒΕΝΟΜΕΝΗ ΤΑΛΑΝΤΩΣΗ ΕΞΑΡΤΩΜΕΝΗ ΑΠΟ ΤΟ ΧΡΟΝΟ (συντελεστής απόσβεσης 0.8) ΥΛΙΚΟ ΣΥΝΟΛΙΚΗ ΜΕΤΑΤOΠΙΣΗ (μm) ΕΝΤΑΣΗ ΤΑΣΗ (MPa) ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ (V) PZT-2 PVDF *10^ (4.849, ) *10^ (4.518, ) 86
87 12. ΣΥΜΠΕΡΑΣΜΑΤΑ Οι δύο τύποι ανάλυσης, η στατική και η εξαρτώμενη από το χρόνο, χρησιμοποιήθηκαν για την ανάλυση του πιεζοηλεκτρικού φαινομένου στη σύνθετη διάταξη. Η εξωτερική δύναμη των 500Ν/m ήταν ίδια για τα διαφορετικά πιεζοηλεκτρικά υλικά που χρησιμοποιήθηκαν. Η ομοιότητα στην ασκούμενη δύναμη, στις συνοριακές συνθήκες και στη γεωμετρία της διάταξης, είχαν ως αποτέλεσμα η σύγκριση των αποτελεσμάτων να είναι αξιόπιστη για κάθε ένα από τα χρησιμοποιούμενα πιεζοηλεκτρικά υλικά. Σύμφωνα με τα αποτελέσματα της στατικής ανάλυσης, το πιεζοπολυμερές PVDF, παρέχει μια ελάχιστα πιο άμεση απόκριση στη σχέση της ασκούμενης δύναμης με την εμφάνιση πιεζοηλεκτρικών ιδιοτήτων. Η εξαρτώμενη από το χρόνο ανάλυση απέδειξε ότι αντικαθιστώντας τη σταθερή εξωτερική δύναμη με ένα δυναμικό φορτίο, οι πιεζοηλεκτρικές ιδιότητες των υλικών ενεργοποιούνται πιο άμεσα και η διαφορά δυναμικού που παρατηρείται είναι πολύ μεγαλύτερη από οτι στην στατική ανάλυση. Μία ανάλυση της ίδιας διάταξης με μικρότερες όμως διαστάσεις, με τέτοιο τρόπο ώστε η διάταξη να έχει πιο άμεση απόκριση στο ασκούμενο φορτίο, θα είχε πολύ μεγάλο ενδιαφέρον όμως αυτό θα αύξανε τον υπολογιστικό φόρτο κατακόρυφα. Άλλη μία αλλαγή που θα μπορούσε να λάβει χώρα, θα ήταν να βελτιωθεί η πλεγματοποίηση του μοντέλου, ώστε να αυξηθούν οι βαθμοί ελευθερίας και να μεγιστοποιηθεί η ακρίβεια των αποτελεσμάτων.τέλος θα είχε μεγάλο ενδιαφέρον η πραγματοποίηση της ίδιας μελέτης, με αλλαγή όμως του τύπου της ταλάντωσης, ώστε να διαπιστωθεί εάν και ποιά είναι η μεταβολή που παρατηρείται τροποποιώντας τα δεδομένα που διέπουν την ταλάντωση του μεσαίου στρώματος του συγκολλητικού υλικού. 87
88 ΒΙΒΛΙΟΓΡΑΦΙΑ [1] Εγχειρίδιο Comsol Multiphysics [2] Finite Element Analysis of Composite Piezoelectric Beam Using Comsol Metwally Emam,Drexel University,2008 [3] Προσομοίωση Σύνθετων Πιεζοηλεκτρικών με τη Μέθοδο Πεπερασμενων Στοιχείων, Διπλωματική Εργασία, Μεταξάς Δρακόπουλος, Πολυτεχνείο Κρήτης 2012 [4] Βισκοελαστική Συμπεριφορά Πολυμερικών Νανοσυνθετών MWCNT-Ρητήνης, Διπλωματική Εργασία, Ξυδού Αναστασία, Πανεπιστήμιο Πατρών [5] Measurement of mechanical properties of three epoxy adhesives at cryogenic temperatures for CCD construction H. Cease, P.F. Derwent, H.T. Diehl, J. Fast, D. Finley Fermi National Accelerator Laboratory Batavia IL November 6, 2006 [6] The Elastic Constants of some Epoxy Resins A.Smith, S.J.Wilkinson, W.N.Reynolds, Nondestructive Testing Centre, UK [7] Πεπερασμένα Στοιχεία, Δρ.Πασχαλίδης Κ.Γκότσης [8] The Young s modulus of silica beads/epoxy composites: Experiments and simulations, Monette, L.Anderson, M. P.Wagner, H.D.Mueller, R.R., Journal of Applied Physics,2/1/94, Vol.75 Issue 3, p1442 [9] Προσομοίωση Σύνθετων Ευφυών Μηχανικών Συστημάτων με Αισθητήρες και Διεγέρτες από Πιεζοηλεκτρικά Υλικά, Σύνδεση με Ευφυείς Μεθόδους Ελέγχου, Γ.Ταϊρίδης, Μεταπτυχιακή Διατριβή, Τμήμα Μηχανικών Παραγωγής και Διοίκησης, 2009 [10] Εντοπισμός και Διόρθωση Βλάβης σε Δομικά Στοιχεία με τη χρήση Ευφυών Υλικών, Μαρία-Στυλιανή Βουτετάκη, Διδακτορική Διατριβή, Πολύτεχνείο Κρήτης, Γενικό Τμήμα, 2009 ΠΑΓΚΟΣΜΙΟΣ ΙΣΤΟΣ
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΑΡΑΓΩΓΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΑΡΑΓΩΓΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΜΕ ΘΕΜΑ: ΠΡΟΣΟΜΟΙΩΣΗ ΣΥΝΘΕΤΩΝ ΠΙΕΖΟΗΛΕΚΤΡΙΚΩΝ ΥΛΙΚΩΝ ΜΕ ΤΗ ΜΕΘΟΔΟ ΤΩΝ ΠΕΠΕΡΑΣΜΕΝΩΝ ΣΤΟΙΧΕΙΩΝ Επιμέλεια: Δρακόπουλος Μεταξάς
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΑΡΑΓΩΓΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΜΕ ΘΕΜΑ: ΠΡΟΣΟΜΟΙΩΣΗ ΣΥΝΘΕΤΩΝ ΠΙΕΖΟΗΛΕΚΤΡΙΚΩΝ ΥΛΙΚΩΝ ΜΕ ΤΗ ΜΕΘΟΔΟ ΤΩΝ ΠΕΠΕΡΑΣΜΕΝΩΝ ΣΤΟΙΧΕΙΩΝ Επιμέλεια: Δρακόπουλος Μεταξάς
Δυναμική διερεύνηση πιεζοηλεκτρικών κατασκευών με χρήση πεπερασμένων στοιχείων
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΑΡΑΓΩΓΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ Εργαστήριο Υπολογιστικής Μηχανικής και Βελτιστοποίησης Δυναμική διερεύνηση πιεζοηλεκτρικών κατασκευών με χρήση πεπερασμένων στοιχείων Σπυρίδων
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΑΡΑΓΩΓΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ Εργαστήριο Υπολογιστικής Μηχανικής και Βελτιστοποίησης Δυναμική διερεύνηση πιεζοηλεκτρικών κατασκευών με χρήση πεπερασμένων στοιχείων Σπυρίδων
Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών
 Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών Οι παρούσες σημειώσεις αποτελούν βοήθημα στο μάθημα Αριθμητικές Μέθοδοι του 5 ου εξαμήνου του ΤΜΜ ημήτρης Βαλουγεώργης Καθηγητής Εργαστήριο Φυσικών
Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών Οι παρούσες σημειώσεις αποτελούν βοήθημα στο μάθημα Αριθμητικές Μέθοδοι του 5 ου εξαμήνου του ΤΜΜ ημήτρης Βαλουγεώργης Καθηγητής Εργαστήριο Φυσικών
ΕΦΑΡΜΟΓΕΣ ΠΕΠΕΡΑΣΜΕΝΩΝ ΣΤΟΙΧΕΙΩΝ ΣΤΗ ΝΑΥΠΗΓΙΚΗ ΚΑΙ ΣΤΗ ΘΑΛΑΣΣΙΑ ΤΕΧΝΟΛΟΓΙΑ
 ΕΦΑΡΜΟΓΕΣ ΠΕΠΕΡΑΣΜΕΝΩΝ ΣΤΟΙΧΕΙΩΝ ΣΤΗ ΝΑΥΠΗΓΙΚΗ ΚΑΙ ΣΤΗ ΘΑΛΑΣΣΙΑ ΤΕΧΝΟΛΟΓΙΑ Εισαγωγή στη μέθοδο των πεπερασμένων στοιχείων Α. Θεοδουλίδης Η Μεθοδος των Πεπερασμένων στοιχείων Η Μέθοδος των ΠΣ είναι μια
ΕΦΑΡΜΟΓΕΣ ΠΕΠΕΡΑΣΜΕΝΩΝ ΣΤΟΙΧΕΙΩΝ ΣΤΗ ΝΑΥΠΗΓΙΚΗ ΚΑΙ ΣΤΗ ΘΑΛΑΣΣΙΑ ΤΕΧΝΟΛΟΓΙΑ Εισαγωγή στη μέθοδο των πεπερασμένων στοιχείων Α. Θεοδουλίδης Η Μεθοδος των Πεπερασμένων στοιχείων Η Μέθοδος των ΠΣ είναι μια
ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Α.Π.Θ.
 Panelco Designer Εγχειρίδιο χρήσης ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Α.Π.Θ. Αναστάσιος Σέξτος, επίκ. καθ. Α.Π.Θ. Ανδρέας Κάππος, καθ. Α.Π.Θ. Panelco Designer Εγχειρίδιο χρήσης Στόχοι λογισμικού Οι βασικοί στόχοι
Panelco Designer Εγχειρίδιο χρήσης ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Α.Π.Θ. Αναστάσιος Σέξτος, επίκ. καθ. Α.Π.Θ. Ανδρέας Κάππος, καθ. Α.Π.Θ. Panelco Designer Εγχειρίδιο χρήσης Στόχοι λογισμικού Οι βασικοί στόχοι
ΠΡΟΣΟΜΟΙΩΣΗ ΟΡΘΟΓΩΝΙΚΗΣ ΚΑΙ ΛΟΞΗΣ ΚΟΠΗΣ ΜΕ ΧΡΗΣΗ ΠΕΠΕΡΑΣΜΕΝΩΝ ΣΤΟΙΧΕΙΩΝ. Ευάγγελος Καστής. Καθ. Αριστομένης Αντωνιάδης ιπλ. Μηχ. (MSc) Χαρά Ευσταθίου
 ΠΡΟΣΟΜΟΙΩΣΗ ΟΡΘΟΓΩΝΙΚΗΣ ΚΑΙ ΛΟΞΗΣ ΚΟΠΗΣ ΜΕ ΧΡΗΣΗ ΠΕΠΕΡΑΣΜΕΝΩΝ ΣΤΟΙΧΕΙΩΝ Καθ. Αριστομένης Αντωνιάδης ιπλ. Μηχ. (MSc) Χαρά Ευσταθίου Ευάγγελος Καστής Πολυτεχνείο Κρήτης-Χανιά 016 Παρουσίαση διπλωματικής
ΠΡΟΣΟΜΟΙΩΣΗ ΟΡΘΟΓΩΝΙΚΗΣ ΚΑΙ ΛΟΞΗΣ ΚΟΠΗΣ ΜΕ ΧΡΗΣΗ ΠΕΠΕΡΑΣΜΕΝΩΝ ΣΤΟΙΧΕΙΩΝ Καθ. Αριστομένης Αντωνιάδης ιπλ. Μηχ. (MSc) Χαρά Ευσταθίου Ευάγγελος Καστής Πολυτεχνείο Κρήτης-Χανιά 016 Παρουσίαση διπλωματικής
10. Εισαγωγή στις Μεθόδους Πεπερασμένων Στοιχείων (ΜΠΣ)
 10. Εισαγωγή στις Μεθόδους Πεπερασμένων Στοιχείων (ΜΠΣ) Χειμερινό εξάμηνο 2018 Πέτρος Κωμοδρόμος komodromos@ucy.ac.cy http://www.eng.ucy.ac.cy/petros 1 Θέματα Εισαγωγή Διατύπωση εξισώσεων ΜΠΣ βάσει μετακινήσεων
10. Εισαγωγή στις Μεθόδους Πεπερασμένων Στοιχείων (ΜΠΣ) Χειμερινό εξάμηνο 2018 Πέτρος Κωμοδρόμος komodromos@ucy.ac.cy http://www.eng.ucy.ac.cy/petros 1 Θέματα Εισαγωγή Διατύπωση εξισώσεων ΜΠΣ βάσει μετακινήσεων
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 η & 2 η : ΟΡΙΑΚΟ ΣΤΡΩΜΑ
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 η & 2 η : ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1 η & 2 η : ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού
website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 6 Ιουνίου 18 1 Οριακό στρώμα και χαρακτηριστικά μεγέθη Στις αρχές του ου αιώνα ο Prandtl θεμελίωσε τη θεωρία
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 6 Ιουνίου 18 1 Οριακό στρώμα και χαρακτηριστικά μεγέθη Στις αρχές του ου αιώνα ο Prandtl θεμελίωσε τη θεωρία
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΜΗΤΡΩΙΚΕΣ ΜΕΘΟΔΟΥΣ ΑΝΑΛΥΣΗΣ ΡΑΒΔΩΤΩΝ ΦΟΡΕΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΣΤΑΤΙΚΗΣ & ΑΝΤΙΣΕΙΣΜΙΚΩΝ ΕΡΕΥΝΩΝ ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΜΗΤΡΩΙΚΕΣ ΜΕΘΟΔΟΥΣ ΑΝΑΛΥΣΗΣ ΡΑΒΔΩΤΩΝ ΦΟΡΕΩΝ Καθηγητής ΕΜΠ ΑΝΑΛΥΣΗ ΡΑΒΔΩΤΩΝ ΦΟΡΕΩΝ ΜΕ ΜΗΤΡΩΙΚΕΣ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΣΤΑΤΙΚΗΣ & ΑΝΤΙΣΕΙΣΜΙΚΩΝ ΕΡΕΥΝΩΝ ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΜΗΤΡΩΙΚΕΣ ΜΕΘΟΔΟΥΣ ΑΝΑΛΥΣΗΣ ΡΑΒΔΩΤΩΝ ΦΟΡΕΩΝ Καθηγητής ΕΜΠ ΑΝΑΛΥΣΗ ΡΑΒΔΩΤΩΝ ΦΟΡΕΩΝ ΜΕ ΜΗΤΡΩΙΚΕΣ
Τμήμα Μηχανικών Παραγωγής και Διοίκησης. Διπλωματική εργασία: Νευροασαφής έλεγχος σε ευφυή ράβδο
 Πολυτεχνείο Κρήτης Τμήμα Μηχανικών Παραγωγής και Διοίκησης Καταγάς Μιχαήλ Α.Μ.:2006010074 Επιβλέπων καθηγητής: Σταυρουλάκης Γεώργιος Διπλωματική εργασία: Νευροασαφής έλεγχος σε ευφυή ράβδο Χανιά, Οκτώβριος
Πολυτεχνείο Κρήτης Τμήμα Μηχανικών Παραγωγής και Διοίκησης Καταγάς Μιχαήλ Α.Μ.:2006010074 Επιβλέπων καθηγητής: Σταυρουλάκης Γεώργιος Διπλωματική εργασία: Νευροασαφής έλεγχος σε ευφυή ράβδο Χανιά, Οκτώβριος
1 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΕΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ
 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΕΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού Οριακού
η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: ΟΡΙΑΚΟ ΣΤΡΩΜΑ ΜΕΛΕΤΗ ΣΤΡΩΤΟΥ ΟΡΙΑΚΟΥ ΣΤΡΩΜΑΤΟΣ ΕΠΑΝΩ ΑΠΟ ΑΚΙΝΗΤΗ ΟΡΙΖΟΝΤΙΑ ΕΠΙΠΕΔΗ ΕΠΙΦΑΝΕΙΑ Σκοπός της άσκησης Στην παρούσα εργαστηριακή άσκηση γίνεται μελέτη του Στρωτού Οριακού
ΜΗ- ΓΡΑΜΜΙΚΗ ΑΝΑΛΥΣΗ ΜΕΤΑΛΛΙΚΩΝ ΠΛΑΙΣΙΩΝ ΓΙΑ ΤΟ ΣΥΝΔΥΑΣΜΕΝΟ ΣΕΝΑΡΙΟ ΤΗΣ ΠΥΡΚΑΓΙΑΣ ΜΕΤΑ ΑΠΟ ΣΕΙΣΜΙΚΑ ΓΕΓΟΝΟΤΑ
 Βόλος 29-3/9 & 1/1 211 ΜΗ- ΓΡΑΜΜΙΚΗ ΑΝΑΛΥΣΗ ΜΕΤΑΛΛΙΚΩΝ ΠΛΑΙΣΙΩΝ ΓΙΑ ΤΟ ΣΥΝΔΥΑΣΜΕΝΟ ΣΕΝΑΡΙΟ ΤΗΣ ΠΥΡΚΑΓΙΑΣ ΜΕΤΑ ΑΠΟ ΣΕΙΣΜΙΚΑ ΓΕΓΟΝΟΤΑ Δάφνη Παντούσα, Msc, Υπ. Διδάκτωρ Ευριπίδης Μυστακίδης, Αναπληρωτής Καθηγητής
Βόλος 29-3/9 & 1/1 211 ΜΗ- ΓΡΑΜΜΙΚΗ ΑΝΑΛΥΣΗ ΜΕΤΑΛΛΙΚΩΝ ΠΛΑΙΣΙΩΝ ΓΙΑ ΤΟ ΣΥΝΔΥΑΣΜΕΝΟ ΣΕΝΑΡΙΟ ΤΗΣ ΠΥΡΚΑΓΙΑΣ ΜΕΤΑ ΑΠΟ ΣΕΙΣΜΙΚΑ ΓΕΓΟΝΟΤΑ Δάφνη Παντούσα, Msc, Υπ. Διδάκτωρ Ευριπίδης Μυστακίδης, Αναπληρωτής Καθηγητής
Προσομοίωση μετωπικού φραιζαρίσματος με πεπερασμένα στοιχεία
 1 Προσομοίωση μετωπικού φραιζαρίσματος με πεπερασμένα στοιχεία 2 Μετωπικό φραιζάρισμα: Χρησιμοποιείται κυρίως στις αρχικές φάσεις της κατεργασίας (φάση εκχόνδρισης) Μεγάλη διάμετρο Μεγάλες προώσεις μείωση
1 Προσομοίωση μετωπικού φραιζαρίσματος με πεπερασμένα στοιχεία 2 Μετωπικό φραιζάρισμα: Χρησιμοποιείται κυρίως στις αρχικές φάσεις της κατεργασίας (φάση εκχόνδρισης) Μεγάλη διάμετρο Μεγάλες προώσεις μείωση
Σχεδιαστικά Προγράμματα Επίπλου
 Σχεδιαστικά Προγράμματα Επίπλου Καθηγήτρια ΦΕΡΦΥΡΗ ΣΩΤΗΡΙΑ Τμήμα ΣΧΕΔΙΑΣΜΟΥ & ΤΕΧΝΟΛΟΓΙΑΣ ΞΥΛΟΥ - ΕΠΙΠΛΟΥ Σχεδιαστικά Προγράμματα Επίπλου Η σχεδίαση με τον παραδοσιακό τρόπο απαιτεί αυξημένο χρόνο, ενώ
Σχεδιαστικά Προγράμματα Επίπλου Καθηγήτρια ΦΕΡΦΥΡΗ ΣΩΤΗΡΙΑ Τμήμα ΣΧΕΔΙΑΣΜΟΥ & ΤΕΧΝΟΛΟΓΙΑΣ ΞΥΛΟΥ - ΕΠΙΠΛΟΥ Σχεδιαστικά Προγράμματα Επίπλου Η σχεδίαση με τον παραδοσιακό τρόπο απαιτεί αυξημένο χρόνο, ενώ
ΕΝΟΤΗΤΑ 8 ΛΟΙΠΟΙ ΑΙΣΘΗΤΗΡΕΣ
 ΕΝΟΤΗΤΑ 8 ΛΟΙΠΟΙ ΑΙΣΘΗΤΗΡΕΣ Στόχος και περίγραμμα της Ενότητας 8 Στόχος της παρουσίασης Η παρουσίαση αδρανειακών αισθητήρων και αισθητήρων που μετράνε υγρασία και θερμοκρασία Σύνοψη Επιταχυνσιόμετρο Τύποι
ΕΝΟΤΗΤΑ 8 ΛΟΙΠΟΙ ΑΙΣΘΗΤΗΡΕΣ Στόχος και περίγραμμα της Ενότητας 8 Στόχος της παρουσίασης Η παρουσίαση αδρανειακών αισθητήρων και αισθητήρων που μετράνε υγρασία και θερμοκρασία Σύνοψη Επιταχυνσιόμετρο Τύποι
Αντισεισμικοί κανονισμοί Κεφ.23. Ε.Σώκος Εργαστήριο Σεισμολογίας Παν.Πατρών
 Κεφ.23 Ε.Σώκος Εργαστήριο Σεισμολογίας Παν.Πατρών Ο αντισεισμικός σχεδιασμός απαιτεί την εκ των προτέρων εκτίμηση των δυνάμεων που αναμένεται να δράσουν επάνω στην κατασκευή κατά τη διάρκεια της ζωής της
Κεφ.23 Ε.Σώκος Εργαστήριο Σεισμολογίας Παν.Πατρών Ο αντισεισμικός σχεδιασμός απαιτεί την εκ των προτέρων εκτίμηση των δυνάμεων που αναμένεται να δράσουν επάνω στην κατασκευή κατά τη διάρκεια της ζωής της
Μελέτη προβλημάτων ΠΗΙ λόγω λειτουργίας βοηθητικών προωστήριων μηχανισμών
 «ΔιερΕΥνηση Και Aντιμετώπιση προβλημάτων ποιότητας ηλεκτρικής Ισχύος σε Συστήματα Ηλεκτρικής Ενέργειας (ΣΗΕ) πλοίων» (ΔΕΥ.Κ.Α.Λ.Ι.ΩΝ) πράξη ΘΑΛΗΣ-ΕΜΠ, πράξη ένταξης 11012/9.7.2012, MIS: 380164, Κωδ.ΕΔΕΙΛ/ΕΜΠ:
«ΔιερΕΥνηση Και Aντιμετώπιση προβλημάτων ποιότητας ηλεκτρικής Ισχύος σε Συστήματα Ηλεκτρικής Ενέργειας (ΣΗΕ) πλοίων» (ΔΕΥ.Κ.Α.Λ.Ι.ΩΝ) πράξη ΘΑΛΗΣ-ΕΜΠ, πράξη ένταξης 11012/9.7.2012, MIS: 380164, Κωδ.ΕΔΕΙΛ/ΕΜΠ:
Η Φυσική των ζωντανών Οργανισμών (10 μονάδες)
 Η Φυσική των ζωντανών Οργανισμών (10 μονάδες) Δεδομένα: Κανονική Ατμοσφαιρική Πίεση, P 0 = 1.013 10 5 Pa = 760 mmhg Μέρος A. Η φυσική του κυκλοφορικού συστήματος. (4.5 μονάδες) Q3-1 Στο Μέρος αυτό θα μελετήσετε
Η Φυσική των ζωντανών Οργανισμών (10 μονάδες) Δεδομένα: Κανονική Ατμοσφαιρική Πίεση, P 0 = 1.013 10 5 Pa = 760 mmhg Μέρος A. Η φυσική του κυκλοφορικού συστήματος. (4.5 μονάδες) Q3-1 Στο Μέρος αυτό θα μελετήσετε
6. ΘΕΡΜΙΚΕΣ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΠΟΛΥΜΕΡΩΝ
 6-1 6. ΘΕΡΜΙΚΕΣ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΠΟΛΥΜΕΡΩΝ 6.1. ΙΑ ΟΣΗ ΤΗΣ ΘΕΡΜΟΤΗΤΑΣ Πολλές βιοµηχανικές εφαρµογές των πολυµερών αφορούν τη διάδοση της θερµότητας µέσα από αυτά ή γύρω από αυτά. Πολλά πολυµερή χρησιµοποιούνται
6-1 6. ΘΕΡΜΙΚΕΣ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΠΟΛΥΜΕΡΩΝ 6.1. ΙΑ ΟΣΗ ΤΗΣ ΘΕΡΜΟΤΗΤΑΣ Πολλές βιοµηχανικές εφαρµογές των πολυµερών αφορούν τη διάδοση της θερµότητας µέσα από αυτά ή γύρω από αυτά. Πολλά πολυµερή χρησιµοποιούνται
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α ΗΜΕΡΟΜΗΝΙΑ: ΑΡΧΩΝ ΜΑΡΚΟΣ-ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ-KΥΡΙΑΚΑΚΗΣ ΓΙΩΡΓΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α ΗΜΕΡΟΜΗΝΙΑ: 19-10-2014 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ-ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ-KΥΡΙΑΚΑΚΗΣ ΓΙΩΡΓΟΣ ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: ΑΠΑΝΤΗΣΕΙΣ Α ΗΜΕΡΟΜΗΝΙΑ: 19-10-2014 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ-ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ-KΥΡΙΑΚΑΚΗΣ ΓΙΩΡΓΟΣ ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4
Εισαγωγή στην Επιστήμη των Υλικών Θερμικές Ιδιότητες Callister Κεφάλαιο 20, Ashby Κεφάλαιο 12
 Εισαγωγή στην Επιστήμη των Υλικών Θερμικές Ιδιότητες Callister Κεφάλαιο 20, Ashby Κεφάλαιο 12 Πως αντιδρά ένα υλικό στην θερμότητα. Πως ορίζουμε και μετράμε τα ακόλουθα μεγέθη: Θερμοχωρητικότητα Συντελεστή
Εισαγωγή στην Επιστήμη των Υλικών Θερμικές Ιδιότητες Callister Κεφάλαιο 20, Ashby Κεφάλαιο 12 Πως αντιδρά ένα υλικό στην θερμότητα. Πως ορίζουμε και μετράμε τα ακόλουθα μεγέθη: Θερμοχωρητικότητα Συντελεστή
ΦΥΛΛΟ ΑΠΑΝΤΗΣΕΩΝ. Όνομα και Επώνυμο: Όνομα Πατέρα:.. Όνομα Μητέρας:.. Σχολείο:.. Τάξη / Τμήμα:... Εξεταστικό Κέντρο:..
 ΦΥΛΛΟ ΑΠΑΝΤΗΣΕΩΝ Όνομα και Επώνυμο: Όνομα Πατέρα:.. Όνομα Μητέρας:.. Σχολείο:.. Τάξη / Τμήμα:... Εξεταστικό Κέντρο:.. ΘΕΜΑ 1 Ο ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ A.1. Παράλληλα συνδεδεμένες είναι οι αντιστάσεις στα κυκλώματα:
ΦΥΛΛΟ ΑΠΑΝΤΗΣΕΩΝ Όνομα και Επώνυμο: Όνομα Πατέρα:.. Όνομα Μητέρας:.. Σχολείο:.. Τάξη / Τμήμα:... Εξεταστικό Κέντρο:.. ΘΕΜΑ 1 Ο ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ A.1. Παράλληλα συνδεδεμένες είναι οι αντιστάσεις στα κυκλώματα:
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ Τμήμα Μηχανικών Παραγωγής και Διοίκησης
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ Τμήμα Μηχανικών Παραγωγής και Διοίκησης ΜΕΛΕΤΗ ΣΥΜΠΕΡΙΦΟΡΑΣ ΣΥΝΘΕΤΗΣ ΠΛΑΚΑΣ ΜΕ ΠΙΕΖΟΗΛΕΚΤΡΙΚΑ ΣΤΟΙΧΕΙΑ ΜΕΤΑΠΤΥΧΙΑΚΗ ΔΙΑΤΡΙΒΗ ΒΟΡΟΣΤΣΟΥΚ ΙΡΙΝΑ ΧΑΝΙΑ 2016 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ Τμήμα Μηχανικών
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ Τμήμα Μηχανικών Παραγωγής και Διοίκησης ΜΕΛΕΤΗ ΣΥΜΠΕΡΙΦΟΡΑΣ ΣΥΝΘΕΤΗΣ ΠΛΑΚΑΣ ΜΕ ΠΙΕΖΟΗΛΕΚΤΡΙΚΑ ΣΤΟΙΧΕΙΑ ΜΕΤΑΠΤΥΧΙΑΚΗ ΔΙΑΤΡΙΒΗ ΒΟΡΟΣΤΣΟΥΚ ΙΡΙΝΑ ΧΑΝΙΑ 2016 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ Τμήμα Μηχανικών
ΜΕΤΡΗΣΕΙΣ ΚΑΙ ΕΦΑΡΜΟΓΕΣ ΥΨΗΛΩΝ ΤΑΣΕΩΝ
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Τομέας Ηλεκτρικής Ισχύος Εργαστήριο Υψηλών Τάσεων ΜΕΤΡΗΣΕΙΣ ΚΑΙ ΕΦΑΡΜΟΓΕΣ ΥΨΗΛΩΝ ΤΑΣΕΩΝ (Αριθμητικές μέθοδοι υπολογισμού
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Τομέας Ηλεκτρικής Ισχύος Εργαστήριο Υψηλών Τάσεων ΜΕΤΡΗΣΕΙΣ ΚΑΙ ΕΦΑΡΜΟΓΕΣ ΥΨΗΛΩΝ ΤΑΣΕΩΝ (Αριθμητικές μέθοδοι υπολογισμού
ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 55
 ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 55 ΚΕΦΑΛΑΙΟ 3 ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 3.. Εισαγωγή Αναφέρθηκε ήδη στο ο κεφάλαιο ότι η αναπαράσταση της ταλαντωτικής
ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 55 ΚΕΦΑΛΑΙΟ 3 ΚΑΤΑΣΤΡΩΣΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΠΟΛΥΒΑΘΜΙΩΝ ΣΥΣΤΗΜΑΤΩΝ 3.. Εισαγωγή Αναφέρθηκε ήδη στο ο κεφάλαιο ότι η αναπαράσταση της ταλαντωτικής
«Αριθμητική και πειραματική μελέτη της διεπιφάνειας χάλυβασκυροδέματος στις σύμμικτες πλάκες με χαλυβδόφυλλο μορφής»
 ΠΕΡΙΛΗΨΗ ΤΗΣ ΔΙΔΑΚΤΟΡΙΚΗΣ ΔΙΑΤΡΙΒΗΣ «Αριθμητική και πειραματική μελέτη της διεπιφάνειας χάλυβασκυροδέματος στις σύμμικτες πλάκες με χαλυβδόφυλλο μορφής» του Θεμιστοκλή Τσαλκατίδη, Δρ. Πολιτικού Μηχανικού
ΠΕΡΙΛΗΨΗ ΤΗΣ ΔΙΔΑΚΤΟΡΙΚΗΣ ΔΙΑΤΡΙΒΗΣ «Αριθμητική και πειραματική μελέτη της διεπιφάνειας χάλυβασκυροδέματος στις σύμμικτες πλάκες με χαλυβδόφυλλο μορφής» του Θεμιστοκλή Τσαλκατίδη, Δρ. Πολιτικού Μηχανικού
3. Τριβή στα ρευστά. Ερωτήσεις Θεωρίας
 3. Τριβή στα ρευστά Ερωτήσεις Θεωρίας Θ3.1 Να συμπληρωθούν τα κενά στις προτάσεις που ακολουθούν: α. Η εσωτερική τριβή σε ένα ρευστό ονομάζεται. β. Η λίπανση των τμημάτων μιας μηχανής οφείλεται στις δυνάμεις
3. Τριβή στα ρευστά Ερωτήσεις Θεωρίας Θ3.1 Να συμπληρωθούν τα κενά στις προτάσεις που ακολουθούν: α. Η εσωτερική τριβή σε ένα ρευστό ονομάζεται. β. Η λίπανση των τμημάτων μιας μηχανής οφείλεται στις δυνάμεις
ΤΑΚΤΙΚΑ ΜΕΛΗ. ΦΕΚ τελευταίου διορισμού. α/α Ονοματεπώνυμο Βαθμίδα Ίδρυμα Σχολή/Τμήμα Γνωστικό Αντικείμενο. Αιτιολόγηση
 Ορισμός Ειδικής Επταμελούς Επιτροπής κρίσης του Αναπληρωτή Καθηγητή Νικολάου Τσούβαλη, στη βαθμίδα του Καθηγητή. Αριθμ. Προκήρυξης: 3908/20.2.2012 Γνωστικό Αντικείμενο: «Μηχανική Συμπεριφορά Υλικών με
Ορισμός Ειδικής Επταμελούς Επιτροπής κρίσης του Αναπληρωτή Καθηγητή Νικολάου Τσούβαλη, στη βαθμίδα του Καθηγητή. Αριθμ. Προκήρυξης: 3908/20.2.2012 Γνωστικό Αντικείμενο: «Μηχανική Συμπεριφορά Υλικών με
Σημειώσεις κεφαλαίου 16 Αρχές επικοινωνίας με ήχο και εικόνα
 Σημειώσεις κεφαλαίου 16 Αρχές επικοινωνίας με ήχο και εικόνα ΠΩΣ ΛΕΙΤΟΥΡΓΟΥΝ ΟΙ ΗΛΕΚΤΡΟΝΙΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Ένα σύστημα ηλεκτρονικής επικοινωνίας αποτελείται από τον πομπό, το δίαυλο (κανάλι) μετάδοσης και
Σημειώσεις κεφαλαίου 16 Αρχές επικοινωνίας με ήχο και εικόνα ΠΩΣ ΛΕΙΤΟΥΡΓΟΥΝ ΟΙ ΗΛΕΚΤΡΟΝΙΚΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Ένα σύστημα ηλεκτρονικής επικοινωνίας αποτελείται από τον πομπό, το δίαυλο (κανάλι) μετάδοσης και
v = 1 ρ. (2) website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Βασικές έννοιες στη μηχανική των ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 17 Φεβρουαρίου 2019 1 Ιδιότητες των ρευστών 1.1 Πυκνότητα Πυκνότητα
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Βασικές έννοιες στη μηχανική των ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 17 Φεβρουαρίου 2019 1 Ιδιότητες των ρευστών 1.1 Πυκνότητα Πυκνότητα
Ενεργειακές Μέθοδοι Υπολογισμού Μετακινήσεων
 Ενεργειακές Μέθοδοι Υπολογισμού Μετακινήσεων Εισαγωγή Ενεργειακές Μέθοδοι Υπολογισμού Μετακινήσεων: Δ03-2 Οι ενεργειακές μέθοδοι αποτελούν τη βάση για υπολογισμό των μετακινήσεων, καθώς η μετακίνηση εισέρχεται
Ενεργειακές Μέθοδοι Υπολογισμού Μετακινήσεων Εισαγωγή Ενεργειακές Μέθοδοι Υπολογισμού Μετακινήσεων: Δ03-2 Οι ενεργειακές μέθοδοι αποτελούν τη βάση για υπολογισμό των μετακινήσεων, καθώς η μετακίνηση εισέρχεται
Theory Greek (Cyprus) Μη γραμμική δυναμική σε Ηλεκτρικά Κυκλώματα (10 μονάδες)
 Q2-1 Μη γραμμική δυναμική σε Ηλεκτρικά Κυκλώματα (10 μονάδες) Παρακαλείστε, να διαβάσετε τις Γενικές Οδηγίες που βρίσκονται σε ξεχωριστό φάκελο πριν ξεκινήσετε την επίλυση αυτού του προβλήματος. Εισαγωγή
Q2-1 Μη γραμμική δυναμική σε Ηλεκτρικά Κυκλώματα (10 μονάδες) Παρακαλείστε, να διαβάσετε τις Γενικές Οδηγίες που βρίσκονται σε ξεχωριστό φάκελο πριν ξεκινήσετε την επίλυση αυτού του προβλήματος. Εισαγωγή
Α3. Σε κύκλωμα LC που εκτελεί αμείωτες ηλεκτρικές ταλαντώσεις η ολική ενέργεια είναι α. ανάλογη του φορτίου του πυκνωτή
 ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΛΑ Β) ΠΑΡΑΣΚΕΥΗ 25 ΜΑΪΟΥ 202 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ) ΘΕΜΑ Α Στις ημιτελείς
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΛΑ Β) ΠΑΡΑΣΚΕΥΗ 25 ΜΑΪΟΥ 202 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ) ΘΕΜΑ Α Στις ημιτελείς
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΠΑΡΑΓΩΓΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΠΑΡΑΓΩΓΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ Εργαστήριο Υπολογιστικής Μηχανικής & Βελτιστοποίησης Διπλωματική Εργασία: «Διερεύνηση δυναμικών ιδιοτήτων σύνθετης δοκού δύο υλικών, με τη μέθοδο
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΠΑΡΑΓΩΓΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ Εργαστήριο Υπολογιστικής Μηχανικής & Βελτιστοποίησης Διπλωματική Εργασία: «Διερεύνηση δυναμικών ιδιοτήτων σύνθετης δοκού δύο υλικών, με τη μέθοδο
Αριθμητική Ολοκλήρωση της Εξίσωσης Κίνησης
 Αριθμητική Ολοκλήρωση της Εξίσωσης Κίνησης Εισαγωγή Αριθμητική Ολοκλήρωση της Εξίσωσης Κίνησης: Δ18- Η δυναμική μετατόπιση u(t) είναι δυνατό να προσδιοριστεί με απ ευθείας αριθμητική ολοκλήρωση της εξίσωσης
Αριθμητική Ολοκλήρωση της Εξίσωσης Κίνησης Εισαγωγή Αριθμητική Ολοκλήρωση της Εξίσωσης Κίνησης: Δ18- Η δυναμική μετατόπιση u(t) είναι δυνατό να προσδιοριστεί με απ ευθείας αριθμητική ολοκλήρωση της εξίσωσης
Καθ. Αριστομένης Αντωνιάδης ρ. Μηχ. Μαρία Παππά. Ευάγγελος ασκαλάκης
 ΥΝΑΜΙΚΗ ΚΑΙ ΘΕΡΜΙΚΗ ΜΕΛΕΤΗ ΤΗΣ ΚΑΤΕΡΓΑΣΙΑΣ ΤΗΣ ΛΕΙΑΝΣΗΣ ΜΕ ΤΗ ΜΕΘΟ Ο ΤΩΝ ΠΕΠΕΡΑΣΜΕΝΩΝ ΣΤΟΙΧΕΙΩΝ Καθ. Αριστομένης Αντωνιάδης ρ. Μηχ. Μαρία Παππά Ευάγγελος ασκαλάκης Πολυτεχνείο Κρήτης Χανιά 2016 Παρουσίαση
ΥΝΑΜΙΚΗ ΚΑΙ ΘΕΡΜΙΚΗ ΜΕΛΕΤΗ ΤΗΣ ΚΑΤΕΡΓΑΣΙΑΣ ΤΗΣ ΛΕΙΑΝΣΗΣ ΜΕ ΤΗ ΜΕΘΟ Ο ΤΩΝ ΠΕΠΕΡΑΣΜΕΝΩΝ ΣΤΟΙΧΕΙΩΝ Καθ. Αριστομένης Αντωνιάδης ρ. Μηχ. Μαρία Παππά Ευάγγελος ασκαλάκης Πολυτεχνείο Κρήτης Χανιά 2016 Παρουσίαση
332 Μηχανολόγων Μηχανικών Βιομηχανίας Θεσσαλίας (Βόλος)
 332 Μηχανολόγων Μηχανικών Βιομηχανίας Θεσσαλίας (Βόλος) Το Τμήμα Μηχανολόγων Μηχανικών Βιομηχανίας ιδρύθηκε το 1985 και δέχτηκε τους πρώτους φοιτητές το 1990. Το Τμήμα εδρεύει στο Βόλο και στεγάζεται σε
332 Μηχανολόγων Μηχανικών Βιομηχανίας Θεσσαλίας (Βόλος) Το Τμήμα Μηχανολόγων Μηχανικών Βιομηχανίας ιδρύθηκε το 1985 και δέχτηκε τους πρώτους φοιτητές το 1990. Το Τμήμα εδρεύει στο Βόλο και στεγάζεται σε
ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Αντικείμενο: Ταλαντώσεις Χρόνος Εξέτασης: 3 ώρες Θέμα 1ο Στις παρακάτω ερωτήσεις 1-5 να γράψετε τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Αντικείμενο: Ταλαντώσεις Χρόνος Εξέτασης: 3 ώρες Θέμα 1ο Στις παρακάτω ερωτήσεις 1-5 να γράψετε τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί
Αγωγιμότητα στα μέταλλα
 Η κίνηση των ατόμων σε κρυσταλλικό στερεό Θερμοκρασία 0 Θερμοκρασία 0 Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo
Η κίνηση των ατόμων σε κρυσταλλικό στερεό Θερμοκρασία 0 Θερμοκρασία 0 Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo
Μικρο μεγεθος που σημαινει γρηγορη αποκριση στις αλλαγες θερμοκρασιας.
 ΘΕΡΜΟΑΝΤΙΣΤΑΣΕΙΣ Ημιαγωγός είναι κάθε υλικό που έχει ειδική αντίσταση με τιμές ανάμεσα σε αυτές των μονωτών (μεγάλη) και των αγωγών (μικρή) και που εμφανίζει ραγδαία μείωση της ειδικής του αντίστασης με
ΘΕΡΜΟΑΝΤΙΣΤΑΣΕΙΣ Ημιαγωγός είναι κάθε υλικό που έχει ειδική αντίσταση με τιμές ανάμεσα σε αυτές των μονωτών (μεγάλη) και των αγωγών (μικρή) και που εμφανίζει ραγδαία μείωση της ειδικής του αντίστασης με
Θέμα: ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΑΓΩΓΟΥ ΜΕΓΑΛΟΥ ΜΗΚΟΥΣ ΜΕ ΕΣΩΤΕΡΙΚΗ ΠΙΕΣΗ ΜΕ ΤΗΝ ΧΡΗΣΗ ΤΩΝ ΠΕΠΕΡΑΣΜΕΝΩΝ ΣΤΟΙΧΕΙΩΝ.
 ΑΝΩΤΑΤΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΕΡΡΩΝ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ Θέμα: ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΑΓΩΓΟΥ ΜΕΓΑΛΟΥ ΜΗΚΟΥΣ ΜΕ ΕΣΩΤΕΡΙΚΗ ΠΙΕΣΗ ΜΕ ΤΗΝ ΧΡΗΣΗ ΤΩΝ ΠΕΠΕΡΑΣΜΕΝΩΝ ΣΤΟΙΧΕΙΩΝ. Φοιτητές
ΑΝΩΤΑΤΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΕΡΡΩΝ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ Θέμα: ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΑΓΩΓΟΥ ΜΕΓΑΛΟΥ ΜΗΚΟΥΣ ΜΕ ΕΣΩΤΕΡΙΚΗ ΠΙΕΣΗ ΜΕ ΤΗΝ ΧΡΗΣΗ ΤΩΝ ΠΕΠΕΡΑΣΜΕΝΩΝ ΣΤΟΙΧΕΙΩΝ. Φοιτητές
Δυναμική ανάλυση μονώροφου πλαισίου
 Κεφάλαιο 1 Δυναμική ανάλυση μονώροφου πλαισίου 1.1 Γεωμετρία φορέα - Δεδομένα Χρησιμοποιείται ο φορέας του Παραδείγματος 3 από το βιβλίο Προσομοίωση κατασκευών σε προγράμματα Η/Υ (Κίρτας & Παναγόπουλος,
Κεφάλαιο 1 Δυναμική ανάλυση μονώροφου πλαισίου 1.1 Γεωμετρία φορέα - Δεδομένα Χρησιμοποιείται ο φορέας του Παραδείγματος 3 από το βιβλίο Προσομοίωση κατασκευών σε προγράμματα Η/Υ (Κίρτας & Παναγόπουλος,
Δυναμική Μηχανών I. Δυναμικά Μοντέλα Συνεχούς Μέσου
 Δυναμική Μηχανών I 8 1 Δυναμικά Μοντέλα Συνεχούς Μέσου 2015 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com Απαγορεύεται οποιαδήποτε αναπαραγωγή χωρίς άδεια Μοντελοποίηση
Δυναμική Μηχανών I 8 1 Δυναμικά Μοντέλα Συνεχούς Μέσου 2015 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com Απαγορεύεται οποιαδήποτε αναπαραγωγή χωρίς άδεια Μοντελοποίηση
Περιεχόμενα Ευχαριστίες...3 Περίληψη Εισαγωγή Γενικά στοιχεία Σκοπός εργασίας Αυξητικά υλικά
 1 Περιεχόμενα Ευχαριστίες...3 Περίληψη...4 1. Εισαγωγή...5 1.1 Γενικά στοιχεία...5 1.2 Σκοπός εργασίας...6 2.Αυξητικά υλικά...7 2.1 Γενική περιγραφή...7 2.2 Αρνητικός λόγος Poisson...8 2.3 Εφαρμογές αυξητικών
1 Περιεχόμενα Ευχαριστίες...3 Περίληψη...4 1. Εισαγωγή...5 1.1 Γενικά στοιχεία...5 1.2 Σκοπός εργασίας...6 2.Αυξητικά υλικά...7 2.1 Γενική περιγραφή...7 2.2 Αρνητικός λόγος Poisson...8 2.3 Εφαρμογές αυξητικών
3 η ΕΝΟΤΗΤΑ ΦΥΣΙΚΕΣ ΚΑΙ ΜΗΧΑΝΙΚΕΣ ΙΔΙΟΤΗΤΕΣ
 ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΜΠ ΤΕΧΝΙΚΑ ΥΛΙΚΑ 3 η ΕΝΟΤΗΤΑ ΦΥΣΙΚΕΣ ΚΑΙ ΜΗΧΑΝΙΚΕΣ ΙΔΙΟΤΗΤΕΣ Ε. Βιντζηλαίου (Συντονιστής), Ε. Βουγιούκας, Ε. Μπαδογιάννης Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΜΠ ΤΕΧΝΙΚΑ ΥΛΙΚΑ 3 η ΕΝΟΤΗΤΑ ΦΥΣΙΚΕΣ ΚΑΙ ΜΗΧΑΝΙΚΕΣ ΙΔΙΟΤΗΤΕΣ Ε. Βιντζηλαίου (Συντονιστής), Ε. Βουγιούκας, Ε. Μπαδογιάννης Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Γενικευμένα Mονοβάθμια Συστήματα
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών Γενικευμένα Mονοβάθμια Συστήματα Ε.Ι. Σαπουντζάκης Καθηγητής ΕΜΠ Δυναμική Ανάλυση Ραβδωτών Φορέων 1 1. Είδη γενικευμένων μονοβαθμίων συστημάτων xu
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών Γενικευμένα Mονοβάθμια Συστήματα Ε.Ι. Σαπουντζάκης Καθηγητής ΕΜΠ Δυναμική Ανάλυση Ραβδωτών Φορέων 1 1. Είδη γενικευμένων μονοβαθμίων συστημάτων xu
'Διερεύνηση αποτελεσματικότητας ασαφούς ελεγκτή για διαφορετικές θέσεις αισθητήρα-διεγέρτη'
 'Διερεύνηση αποτελεσματικότητας ασαφούς ελεγκτή για διαφορετικές θέσεις αισθητήρα-διεγέρτη' ΟΝΟΜΑ ΦΟΙΤΗΤΗ: ΣΕΛΛΗΣ ΗΛΙΑΣ ΑΡΙΘΜΟΣ ΜΗΤΡΩΟΥ: 2004010054 ΤΜΗΜΑ: ΜΗΧΑΝΙΚΩΝ ΠΑΡΑΓΩΓΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΒΛΕΠΩΝ ΚΑΘΗΓΗΤΗΣ
'Διερεύνηση αποτελεσματικότητας ασαφούς ελεγκτή για διαφορετικές θέσεις αισθητήρα-διεγέρτη' ΟΝΟΜΑ ΦΟΙΤΗΤΗ: ΣΕΛΛΗΣ ΗΛΙΑΣ ΑΡΙΘΜΟΣ ΜΗΤΡΩΟΥ: 2004010054 ΤΜΗΜΑ: ΜΗΧΑΝΙΚΩΝ ΠΑΡΑΓΩΓΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΒΛΕΠΩΝ ΚΑΘΗΓΗΤΗΣ
α) = β) Α 1 = γ) δ) Μονάδες 5
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: 19-10-2014 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ-ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ-ΚΥΡΙΑΚΑΚΗΣ ΓΙΩΡΓΟΣ ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4 να γράψετε
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: 19-10-2014 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ-ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ-ΚΥΡΙΑΚΑΚΗΣ ΓΙΩΡΓΟΣ ΘΕΜΑ Α Οδηγία: Στις ερωτήσεις Α1 Α4 να γράψετε
ΠΕΡΙΛΗΨΗ 1. ΕΙΣΑΓΩΓΗ 2. ΚΑΤΑΣΚΕΥΗ
 ΜΕΛΕΤΗ ΕΝΑΛΛΑΚΤΗ ΘΕΡΜΟΤΗΤΑΣ ΕΜΒΑΠΤΙΣΜΕΝΟΥ ΣΕ ΟΧΕΙΟ ΑΠΟΘΗΚΕΥΣΗΣ ΗΛΙΑΚΟΥ ΘΕΡΜΟΣΙΦΩΝΑ. Ν. Χασιώτης, Ι. Γ. Καούρης, Ν. Συρίµπεης. Τµήµα Μηχανολόγων & Αεροναυπηγών Μηχανικών, Πανεπιστήµιο Πατρών 65 (Ρίο) Πάτρα.
ΜΕΛΕΤΗ ΕΝΑΛΛΑΚΤΗ ΘΕΡΜΟΤΗΤΑΣ ΕΜΒΑΠΤΙΣΜΕΝΟΥ ΣΕ ΟΧΕΙΟ ΑΠΟΘΗΚΕΥΣΗΣ ΗΛΙΑΚΟΥ ΘΕΡΜΟΣΙΦΩΝΑ. Ν. Χασιώτης, Ι. Γ. Καούρης, Ν. Συρίµπεης. Τµήµα Μηχανολόγων & Αεροναυπηγών Μηχανικών, Πανεπιστήµιο Πατρών 65 (Ρίο) Πάτρα.
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ-ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ. ΜΕΡΟΣ Α : Άλγεβρα. Κεφάλαιο 2 ο (Προτείνεται να διατεθούν 12 διδακτικές ώρες) Ειδικότερα:
 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ-ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΜΕΡΟΣ Α : Άλγεβρα Κεφάλαιο ο (Προτείνεται να διατεθούν διδακτικές ώρες) Ειδικότερα:. -. (Προτείνεται να διατεθούν 5 διδακτικές ώρες).3 (Προτείνεται να διατεθούν
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ-ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΜΕΡΟΣ Α : Άλγεβρα Κεφάλαιο ο (Προτείνεται να διατεθούν διδακτικές ώρες) Ειδικότερα:. -. (Προτείνεται να διατεθούν 5 διδακτικές ώρες).3 (Προτείνεται να διατεθούν
ηµήτρης Τσίνογλου ρ. Μηχανολόγος Μηχανικός
 ηµήτρης Τσίνογλου ρ. Μηχανολόγος Μηχανικός 1 Αγωγή Χρονικά µεταβαλλόµενη κατάσταση Κεφάλαιο 4 Ορισµός του προβλήµατος Σε πολλές τεχνικές εφαρµογές απαιτείται ο υπολογισµός της θερµικής αγωγής σε χρονικά
ηµήτρης Τσίνογλου ρ. Μηχανολόγος Μηχανικός 1 Αγωγή Χρονικά µεταβαλλόµενη κατάσταση Κεφάλαιο 4 Ορισµός του προβλήµατος Σε πολλές τεχνικές εφαρµογές απαιτείται ο υπολογισµός της θερµικής αγωγής σε χρονικά
ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ A. 1 Εισαγωγή στην Ανάλυση των Κατασκευών 3
 ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ A 1 Εισαγωγή στην Ανάλυση των Κατασκευών 3 1.1 Κατασκευές και δομοστατική 3 1.2 Διαδικασία σχεδίασης κατασκευών 4 1.3 Βασικά δομικά στοιχεία 6 1.4 Είδη κατασκευών 8 1.4.1 Δικτυώματα 8
ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ A 1 Εισαγωγή στην Ανάλυση των Κατασκευών 3 1.1 Κατασκευές και δομοστατική 3 1.2 Διαδικασία σχεδίασης κατασκευών 4 1.3 Βασικά δομικά στοιχεία 6 1.4 Είδη κατασκευών 8 1.4.1 Δικτυώματα 8
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
MATLAB. Εισαγωγή στο SIMULINK. Μονάδα Αυτόματης Ρύθμισης και Πληροφορικής
 MATLAB Εισαγωγή στο SIMULINK Μονάδα Αυτόματης Ρύθμισης και Πληροφορικής Εισαγωγή στο Simulink - Βιβλιοθήκες - Παραδείγματα Εκκίνηση BLOCKS click ή Βιβλιοθήκες Νέο αρχείο click ή Προσθήκη block σε αρχείο
MATLAB Εισαγωγή στο SIMULINK Μονάδα Αυτόματης Ρύθμισης και Πληροφορικής Εισαγωγή στο Simulink - Βιβλιοθήκες - Παραδείγματα Εκκίνηση BLOCKS click ή Βιβλιοθήκες Νέο αρχείο click ή Προσθήκη block σε αρχείο
Πλαστική Κατάρρευση Δοκών
 Πλαστική Κατάρρευση Δοκών ΠΕΡΙΕΧΟΜΕΝΑ Σταδιακή Μελέτη Πλαστικής Κατάρρευσης o Παράδειγμα 1 (ισοστατικός φορέας) o Παράδειγμα 2 (υπερστατικός φορέας) Αμεταβλητότητα Φορτίου Πλαστικής Κατάρρευσης Προσδιορισμός
Πλαστική Κατάρρευση Δοκών ΠΕΡΙΕΧΟΜΕΝΑ Σταδιακή Μελέτη Πλαστικής Κατάρρευσης o Παράδειγμα 1 (ισοστατικός φορέας) o Παράδειγμα 2 (υπερστατικός φορέας) Αμεταβλητότητα Φορτίου Πλαστικής Κατάρρευσης Προσδιορισμός
Δυναμική Μηχανών I. Προσέγγιση Galerkin
 Δυναμική Μηχανών I 8 2 Προσέγγιση Galerkin Χειμερινό Εξάμηνο 214 Τμήμα Μηχανολόγων Μηχανικών, ΕΜΠ Δημήτριος Τζεράνης, Ph.D. 215 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com
Δυναμική Μηχανών I 8 2 Προσέγγιση Galerkin Χειμερινό Εξάμηνο 214 Τμήμα Μηχανολόγων Μηχανικών, ΕΜΠ Δημήτριος Τζεράνης, Ph.D. 215 Δημήτριος Τζεράνης, Ph.D Τμήμα Μηχανολόγων Μηχανικών Ε.Μ.Π. tzeranis@gmail.com
«ΜΕΛΕΤΗ ΙΑΤΑΞΕΩΝ ΦΩΤΟΝΙΚΩΝ ΚΡΥΣΤΑΛΛΩΝ ΓΙΑ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΕΣ ΕΦΑΡΜΟΓΕΣ»
 ΠΡΟΣΚΛΗΣΗ ΕΝ ΙΑΦΕΡΟΝΤΟΣ ΓΙΑ ΕΚΠΟΝΗΣΗ Ι ΑΚΤΟΡΙΚΗΣ ΙΑΤΡΙΒΗΣ «ΜΕΛΕΤΗ ΙΑΤΑΞΕΩΝ ΦΩΤΟΝΙΚΩΝ ΚΡΥΣΤΑΛΛΩΝ ΓΙΑ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΕΣ ΕΦΑΡΜΟΓΕΣ» Υπεύθυνος Καθηγητής: κ. Θωµάς Σφηκόπουλος Υπεύθυνος Επιστηµονικός Συνεργάτες:
ΠΡΟΣΚΛΗΣΗ ΕΝ ΙΑΦΕΡΟΝΤΟΣ ΓΙΑ ΕΚΠΟΝΗΣΗ Ι ΑΚΤΟΡΙΚΗΣ ΙΑΤΡΙΒΗΣ «ΜΕΛΕΤΗ ΙΑΤΑΞΕΩΝ ΦΩΤΟΝΙΚΩΝ ΚΡΥΣΤΑΛΛΩΝ ΓΙΑ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΕΣ ΕΦΑΡΜΟΓΕΣ» Υπεύθυνος Καθηγητής: κ. Θωµάς Σφηκόπουλος Υπεύθυνος Επιστηµονικός Συνεργάτες:
Χαρακτηρισμός και μοντέλα τρανζίστορ λεπτών υμενίων βιομηχανικής παραγωγής: Τεχνολογία μικροκρυσταλλικού πυριτίου χαμηλής θερμοκρασίας
 Χαρακτηρισμός και μοντέλα τρανζίστορ λεπτών υμενίων βιομηχανικής παραγωγής: Τεχνολογία μικροκρυσταλλικού πυριτίου χαμηλής θερμοκρασίας Υποψήφιος Διδάκτορας: Α. Χατζόπουλος Περίληψη Οι τελευταίες εξελίξεις
Χαρακτηρισμός και μοντέλα τρανζίστορ λεπτών υμενίων βιομηχανικής παραγωγής: Τεχνολογία μικροκρυσταλλικού πυριτίου χαμηλής θερμοκρασίας Υποψήφιος Διδάκτορας: Α. Χατζόπουλος Περίληψη Οι τελευταίες εξελίξεις
Εισαγωγή στους Ταλαντωτές Οι ταλαντωτές είναι από τα βασικότερα κυκλώματα στα ηλεκτρονικά. Χρησιμοποιούνται κατά κόρον στα τηλεπικοινωνιακά συστήματα
 Πανεπιστήμιο Θεσσαλίας Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ Υλοποίηση και Εργαστηριακή Αναφορά Ring και Hartley Ταλαντωτών Φοιτητής: Ζωγραφόπουλος Γιάννης Επιβλέπων Καθηγητής: Πλέσσας Φώτιος
Πανεπιστήμιο Θεσσαλίας Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ Υλοποίηση και Εργαστηριακή Αναφορά Ring και Hartley Ταλαντωτών Φοιτητής: Ζωγραφόπουλος Γιάννης Επιβλέπων Καθηγητής: Πλέσσας Φώτιος
Η μηχανική επαφής και η στατική των πέτρινων γεφυριών
 Η μηχανική επαφής και η στατική των πέτρινων γεφυριών Καθηγητής Γεώργιος Σταυρουλάκης Σχολή Μηχανικών Παραγωγής και Διοίκησης, Πολυτεχνείο Κρήτης Επίκουρη Καθηγήτρια Μαρία Σταυρουλάκη Σχολή Αρχιτεκτόνων
Η μηχανική επαφής και η στατική των πέτρινων γεφυριών Καθηγητής Γεώργιος Σταυρουλάκης Σχολή Μηχανικών Παραγωγής και Διοίκησης, Πολυτεχνείο Κρήτης Επίκουρη Καθηγήτρια Μαρία Σταυρουλάκη Σχολή Αρχιτεκτόνων
Στατική Ανάλυση Ναυπηγικών Κατασκευών
 Στατική Ανάλυση Ναυπηγικών Κατασκευών Ενότητα 2: Ελαστικός λυγισμός πρισματικών φορέων Αλέξανδρος Θεοδουλίδης Η χρήση κολονών (υποστυλωμάτων) είναι πολύ διαδεδομένη στα πλοία καθ όσον χρησιμοποιούνται
Στατική Ανάλυση Ναυπηγικών Κατασκευών Ενότητα 2: Ελαστικός λυγισμός πρισματικών φορέων Αλέξανδρος Θεοδουλίδης Η χρήση κολονών (υποστυλωμάτων) είναι πολύ διαδεδομένη στα πλοία καθ όσον χρησιμοποιούνται
Τα κύρια σηµεία της παρούσας διδακτορικής διατριβής είναι: Η πειραµατική µελέτη της µεταβατικής συµπεριφοράς συστηµάτων γείωσης
 Κεφάλαιο 5 ΣΥΜΠΕΡΑΣΜΑΤΑ Το σηµαντικό στην επιστήµη δεν είναι να βρίσκεις καινούρια στοιχεία, αλλά να ανακαλύπτεις νέους τρόπους σκέψης γι' αυτά. Sir William Henry Bragg 5.1 Ανακεφαλαίωση της διατριβής
Κεφάλαιο 5 ΣΥΜΠΕΡΑΣΜΑΤΑ Το σηµαντικό στην επιστήµη δεν είναι να βρίσκεις καινούρια στοιχεία, αλλά να ανακαλύπτεις νέους τρόπους σκέψης γι' αυτά. Sir William Henry Bragg 5.1 Ανακεφαλαίωση της διατριβής
Ανάλυση με πεπερασμένα στοιχεία της κατεργασίας κοπής οδοντώσεων με φραιζάρισμα με κύλιση
 Ανάλυση με πεπερασμένα στοιχεία της κατεργασίας κοπής οδοντώσεων με φραιζάρισμα με κύλιση Χριστοδουλόπουλος Αντώνιος 1 Εισαγωγή Κατηγορίες οδοντωτών τροχών Χαρακτηριστικά μεγέθη Κατασκευαστικές τεχνολογίες
Ανάλυση με πεπερασμένα στοιχεία της κατεργασίας κοπής οδοντώσεων με φραιζάρισμα με κύλιση Χριστοδουλόπουλος Αντώνιος 1 Εισαγωγή Κατηγορίες οδοντωτών τροχών Χαρακτηριστικά μεγέθη Κατασκευαστικές τεχνολογίες
ΑΣΚΗΣΗ ΜΕΤΑ ΟΣΗΣ ΘΕΡΜΟΤΗΤΑΣ ΜΕ ΑΓΩΓΙΜΟΤΗΤΑ ΣΕ ΣΥΝΘΕΤΑ ΤΟΙΧΩΜΑΤΑ
 ΑΣΚΗΣΗ ΜΕΤΑ ΟΣΗΣ ΘΕΡΜΟΤΗΤΑΣ ΜΕ ΑΓΩΓΙΜΟΤΗΤΑ ΣΕ ΣΥΝΘΕΤΑ ΤΟΙΧΩΜΑΤΑ ΣΚΟΠΟΣ Ο προσδιορισμός του συντελεστή θερμικής αγωγιμότητας μεταλλικού υλικού και ο υπολογισμός του συνολικού συντελεστή μεταφοράς θερμότητας
ΑΣΚΗΣΗ ΜΕΤΑ ΟΣΗΣ ΘΕΡΜΟΤΗΤΑΣ ΜΕ ΑΓΩΓΙΜΟΤΗΤΑ ΣΕ ΣΥΝΘΕΤΑ ΤΟΙΧΩΜΑΤΑ ΣΚΟΠΟΣ Ο προσδιορισμός του συντελεστή θερμικής αγωγιμότητας μεταλλικού υλικού και ο υπολογισμός του συνολικού συντελεστή μεταφοράς θερμότητας
ΑΝΑΠΤΥΞΗ ΝΑΝΟΔΟΜΗΜΕΝΩΝ ΥΛΙΚΩΝ ΜΕ ΝΑΝΟΣΩΛΗΝΕΣ ΑΝΘΡΑΚΑ ΓΙΑ ΧΡΗΣΗ ΣΕ ΕΦΑΡΜΟΓΕΣ ΥΨΗΛΗΣ ΑΝΤΟΧΗΣ
 ΑΝΑΠΤΥΞΗ ΝΑΝΟΔΟΜΗΜΕΝΩΝ ΥΛΙΚΩΝ ΜΕ ΝΑΝΟΣΩΛΗΝΕΣ ΑΝΘΡΑΚΑ ΓΙΑ ΧΡΗΣΗ ΣΕ ΕΦΑΡΜΟΓΕΣ ΥΨΗΛΗΣ ΑΝΤΟΧΗΣ Πετούσης Μάρκος, Δρ. Μηχανολόγος Μηχανικός Τμήμα Μηχανολόγων Μηχανικών Τ.Ε. ΤΕΙ Κρήτης Σύνθετα υλικά Σύνθετα υλικά
ΑΝΑΠΤΥΞΗ ΝΑΝΟΔΟΜΗΜΕΝΩΝ ΥΛΙΚΩΝ ΜΕ ΝΑΝΟΣΩΛΗΝΕΣ ΑΝΘΡΑΚΑ ΓΙΑ ΧΡΗΣΗ ΣΕ ΕΦΑΡΜΟΓΕΣ ΥΨΗΛΗΣ ΑΝΤΟΧΗΣ Πετούσης Μάρκος, Δρ. Μηχανολόγος Μηχανικός Τμήμα Μηχανολόγων Μηχανικών Τ.Ε. ΤΕΙ Κρήτης Σύνθετα υλικά Σύνθετα υλικά
«ΕΦΑΡΜΟΓΕΣ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ» 30 Σεπτεμβρίου Αμφιθέατρο Σχολής Θετικών Επιστημών ΑΘΕ12. Ομιλητές
 Τμήμα Μαθηματικών Σπουδαστήριο Διαφορικών Εξισώσεων & Εφαρμογών «ΠΑΝΑΓΙΩΤΗΣ ΣΙΑΦΑΡΙΚΑΣ» 5 η ημερίδα με θέμα: «ΕΦΑΡΜΟΓΕΣ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ» 30 Σεπτεμβρίου 2017 Αμφιθέατρο Σχολής Θετικών Επιστημών ΑΘΕ12
Τμήμα Μαθηματικών Σπουδαστήριο Διαφορικών Εξισώσεων & Εφαρμογών «ΠΑΝΑΓΙΩΤΗΣ ΣΙΑΦΑΡΙΚΑΣ» 5 η ημερίδα με θέμα: «ΕΦΑΡΜΟΓΕΣ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ» 30 Σεπτεμβρίου 2017 Αμφιθέατρο Σχολής Θετικών Επιστημών ΑΘΕ12
ΙΑ ΟΧΙΚΕΣ ΒΕΛΤΙΩΣΕΙΣ
 Tel.: +30 2310998051, Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Σχολή Θετικών Επιστημών Τμήμα Φυσικής 541 24 Θεσσαλονίκη Καθηγητής Γεώργιος Θεοδώρου Ιστοσελίδα: http://users.auth.gr/theodoru ΙΑ ΟΧΙΚΕΣ ΒΕΛΤΙΩΣΕΙΣ
Tel.: +30 2310998051, Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Σχολή Θετικών Επιστημών Τμήμα Φυσικής 541 24 Θεσσαλονίκη Καθηγητής Γεώργιος Θεοδώρου Ιστοσελίδα: http://users.auth.gr/theodoru ΙΑ ΟΧΙΚΕΣ ΒΕΛΤΙΩΣΕΙΣ
Εκτίμηση της στροφικής ικανότητας χαλύβδινων δοκών στις υψηλές θερμοκρασίες θεωρώντας την επιρροή των αρχικών γεωμετρικών ατελειών
 Βόλος 29-3/9 & 1/1 211 Εκτίμηση της στροφικής ικανότητας χαλύβδινων δοκών στις υψηλές θερμοκρασίες θεωρώντας την επιρροή των αρχικών γεωμετρικών ατελειών Δάφνη Παντούσα και Ευριπίδης Μυστακίδης Εργαστήριο
Βόλος 29-3/9 & 1/1 211 Εκτίμηση της στροφικής ικανότητας χαλύβδινων δοκών στις υψηλές θερμοκρασίες θεωρώντας την επιρροή των αρχικών γεωμετρικών ατελειών Δάφνη Παντούσα και Ευριπίδης Μυστακίδης Εργαστήριο
Μεταλλικές Σχάρες Διέλευσης Καλωδίων. Τεχνικές Οδηγίες & Προδιαγραφές
 Μεταλλικές Σχάρες Διέλευσης Καλωδίων Τεχνικές Οδηγίες & Προδιαγραφές Ο κύριος στόχος της εταιρίας είναι η κατασκευή ποιοτικών προ όντων με: πρακτικό σχεδιασμό αυξημένη αντοχή εύκολη και γρήγορη τοποθέτηση
Μεταλλικές Σχάρες Διέλευσης Καλωδίων Τεχνικές Οδηγίες & Προδιαγραφές Ο κύριος στόχος της εταιρίας είναι η κατασκευή ποιοτικών προ όντων με: πρακτικό σχεδιασμό αυξημένη αντοχή εύκολη και γρήγορη τοποθέτηση
Δυναμική Ηλεκτρικών Μηχανών
 Δυναμική Ηλεκτρικών Μηχανών Ενότητα 1: Εισαγωγή Βασικές Αρχές Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Δυναμική Ηλεκτρικών Μηχανών Ενότητα 1: Εισαγωγή Βασικές Αρχές Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΣΧΟ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τομέας Ρευστών Εργαστήριο Θερμικών Στροβιλομηχανών
 ΣΧΟ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τομέας Ρευστών Εργαστήριο Θερμικών Στροβιλομηχανών Αλγόριθμος προσαρμογής διδιάστατων υβριδικών πλεγμάτων στην υπό εξέλιξη λύση ενός πεδίου ροής και πιστοποίηση Διπλωματική Εργασία
ΣΧΟ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τομέας Ρευστών Εργαστήριο Θερμικών Στροβιλομηχανών Αλγόριθμος προσαρμογής διδιάστατων υβριδικών πλεγμάτων στην υπό εξέλιξη λύση ενός πεδίου ροής και πιστοποίηση Διπλωματική Εργασία
Πίνακας 1. Πίνακας προτεινόμενων πτυχιακών εργασιών για το χειμερινό εξάμηνο 2012-13. Αριθμός σπουδαστών
 Πίνακας. Πίνακας προτεινόμενων πτυχιακών εργασιών για το χειμερινό εξάμηνο 0-3 ΤΜΗΜΑ: ΕΝΕΡΓΕΙΑΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ Α/Α Τίτλος θέματος Μέλος Ε.Π Σύντομη περιγραφή Διακόπτες δικτύων ισχύος 3 4 5 Μηχανικά χαρακτηριστικά
Πίνακας. Πίνακας προτεινόμενων πτυχιακών εργασιών για το χειμερινό εξάμηνο 0-3 ΤΜΗΜΑ: ΕΝΕΡΓΕΙΑΚΗΣ ΤΕΧΝΟΛΟΓΙΑΣ Α/Α Τίτλος θέματος Μέλος Ε.Π Σύντομη περιγραφή Διακόπτες δικτύων ισχύος 3 4 5 Μηχανικά χαρακτηριστικά
Συστήματα Αυτομάτου Ελέγχου ΙΙ Γιώργος Σούλτης 167
 Προσομοίωση πραγματικών συστημάτων στο MATLAB Είδαμε μέχρι τώρα πως μπορούμε να υπολογίσουμε την συνάρτηση μεταφοράς σε πραγματικά συστήματα. Ο υπολογισμός της συνάρτησης μεταφοράς στη ουσία είναι η «γραμμικοποίηση»
Προσομοίωση πραγματικών συστημάτων στο MATLAB Είδαμε μέχρι τώρα πως μπορούμε να υπολογίσουμε την συνάρτηση μεταφοράς σε πραγματικά συστήματα. Ο υπολογισμός της συνάρτησης μεταφοράς στη ουσία είναι η «γραμμικοποίηση»
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1η (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 21/10/12
 ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1η (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 21/10/12 ΘΕΜΑ 1 ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα
ΜΑΘΗΜΑ / ΤΑΞΗ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ / Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: 1η (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 21/10/12 ΘΕΜΑ 1 ο Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα
ΣΚΑΛΙΕΡΕΣ Διέλευσης Καλωδίων. Τεχνικές Οδηγίες & Προδιαγραφές
 ΣΚΑΛΙΕΡΕΣ Διέλευσης Καλωδίων Τεχνικές Οδηγίες & Προδιαγραφές Κατάλογος Προϊόντων / Σκοπός και Δομή Ο κύριος στόχος της εταιρίας είναι η κατασκευή ποιοτικών προ όντων με: πρακτικό σχεδιασμό αυξημένη αντοχή
ΣΚΑΛΙΕΡΕΣ Διέλευσης Καλωδίων Τεχνικές Οδηγίες & Προδιαγραφές Κατάλογος Προϊόντων / Σκοπός και Δομή Ο κύριος στόχος της εταιρίας είναι η κατασκευή ποιοτικών προ όντων με: πρακτικό σχεδιασμό αυξημένη αντοχή
ηλεκτρικό ρεύμα ampere
 Ηλεκτρικό ρεύμα Το ηλεκτρικό ρεύμα είναι ο ρυθμός με τον οποίο διέρχεται ηλεκτρικό φορτίο από μια περιοχή του χώρου. Η μονάδα μέτρησης του ηλεκτρικού ρεύματος στο σύστημα SI είναι το ampere (A). 1 A =
Ηλεκτρικό ρεύμα Το ηλεκτρικό ρεύμα είναι ο ρυθμός με τον οποίο διέρχεται ηλεκτρικό φορτίο από μια περιοχή του χώρου. Η μονάδα μέτρησης του ηλεκτρικού ρεύματος στο σύστημα SI είναι το ampere (A). 1 A =
v(t) = Ri(t). (1) website:
 Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση και Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 10 Μαρτίου 2017 1 Βασικά μεγέθη ηλεκτρικών
Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση και Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 10 Μαρτίου 2017 1 Βασικά μεγέθη ηλεκτρικών
Τελεστικοί Ενισχυτές
 Τελεστικοί Ενισχυτές Ενισχυτές-Γενικά: Οι ενισχυτές είναι δίθυρα δίκτυα στα οποία η τάση ή το ρεύμα εξόδου είναι ευθέως ανάλογη της τάσεως ή του ρεύματος εισόδου. Υπάρχουν τέσσερα διαφορετικά είδη ενισχυτών:
Τελεστικοί Ενισχυτές Ενισχυτές-Γενικά: Οι ενισχυτές είναι δίθυρα δίκτυα στα οποία η τάση ή το ρεύμα εξόδου είναι ευθέως ανάλογη της τάσεως ή του ρεύματος εισόδου. Υπάρχουν τέσσερα διαφορετικά είδη ενισχυτών:
Όταν το ελατήριο έχει μάζα
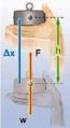 Όταν το ελατήριο έχει μάζα Εισαγωγή Αφορμή για την παρούσα ανάρτηση ήταν η θέση που διατύπωσε ο Γιάννης ο Κυριακόπουλος όσον αφορά στην συχνότητα ταλάντωσης ενός σώματος, το οποίο είναι δεμένο σε ελατήριο
Όταν το ελατήριο έχει μάζα Εισαγωγή Αφορμή για την παρούσα ανάρτηση ήταν η θέση που διατύπωσε ο Γιάννης ο Κυριακόπουλος όσον αφορά στην συχνότητα ταλάντωσης ενός σώματος, το οποίο είναι δεμένο σε ελατήριο
Τμήμα Ηλεκτρολόγων Μηχανικών ΑΥΤΟΝΟΜΗ ΛΕΙΤΟΥΡΓΙΑ ΣΥΓΧΡΟΝΗΣ ΓΕΝΗΤΡΙΑΣ
 ΑΥΤΟΝΟΜΗ ΛΕΙΤΟΥΡΓΙΑ ΣΥΓΧΡΟΝΗΣ ΓΕΝΗΤΡΙΑΣ Οι βασικοί παράγοντες που επηρεάζουν τη συμπεριφορά μιας ΣΓ όταν αυτή λειτουργεί με κάποιο φορτίο είναι αφενός ο συντελεστής ισχύος του φορτίου και αφετέρου το αν
ΑΥΤΟΝΟΜΗ ΛΕΙΤΟΥΡΓΙΑ ΣΥΓΧΡΟΝΗΣ ΓΕΝΗΤΡΙΑΣ Οι βασικοί παράγοντες που επηρεάζουν τη συμπεριφορά μιας ΣΓ όταν αυτή λειτουργεί με κάποιο φορτίο είναι αφενός ο συντελεστής ισχύος του φορτίου και αφετέρου το αν
ΕΞΑΜΗΝΟ ΕΞΑΜΗΝΟ. (κατ. Φυσικού. Εφαρμογών) Μαθηματικού Εφαρμογών) και Σχεδιασμοί Αμφ. 1, Εμβιομηχανική του μυοσκελετικού αμφ.
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2010-2011 ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ 1 ΤΕΛΙΚΟ ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2010-2011 ΗΜ/ΝΙΑ ΩΡΑ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2010-2011 ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ 1 ΤΕΛΙΚΟ ΠΡΟΓΡΑΜΜΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 2010-2011 ΗΜ/ΝΙΑ ΩΡΑ
Μελέτη προβλημάτων ΠΗΙ λόγω του συστήματος γείωσης
 «ΔιερΕΥνηση Και Aντιμετώπιση προβλημάτων ποιότητας ηλεκτρικής Ισχύος σε Συστήματα Ηλεκτρικής Ενέργειας (ΣΗΕ) πλοίων» (ΔΕΥ.Κ.Α.Λ.Ι.ΩΝ) πράξη ΘΑΛΗΣ-ΕΜΠ, πράξη ένταξης 11012/9.7.2012, MIS: 380164, Κωδ.ΕΔΕΙΛ/ΕΜΠ:
«ΔιερΕΥνηση Και Aντιμετώπιση προβλημάτων ποιότητας ηλεκτρικής Ισχύος σε Συστήματα Ηλεκτρικής Ενέργειας (ΣΗΕ) πλοίων» (ΔΕΥ.Κ.Α.Λ.Ι.ΩΝ) πράξη ΘΑΛΗΣ-ΕΜΠ, πράξη ένταξης 11012/9.7.2012, MIS: 380164, Κωδ.ΕΔΕΙΛ/ΕΜΠ:
Ο πυκνωτής είναι μια διάταξη αποθήκευσης ηλεκτρικού φορτίου, επομένως και ηλεκτρικής ενέργειας.
 ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Ο πυκνωτής Ο πυκνωτής είναι μια διάταξη αποθήκευσης ηλεκτρικού φορτίου, επομένως και ηλεκτρικής ενέργειας. Η απλούστερη μορφή πυκνωτή είναι ο επίπεδος πυκνωτής, ο οποίος
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Ο πυκνωτής Ο πυκνωτής είναι μια διάταξη αποθήκευσης ηλεκτρικού φορτίου, επομένως και ηλεκτρικής ενέργειας. Η απλούστερη μορφή πυκνωτή είναι ο επίπεδος πυκνωτής, ο οποίος
Εργαστήριο Τεχνολογίας Υλικών
 Εργαστήριο Τεχνολογίας Υλικών Εργαστηριακή Άσκηση 07 Εφελκυσμός Διδάσκοντες: Δρ Γεώργιος Ι. Γιαννόπουλος Δρ Θεώνη Ασημακοπούλου Δρ Θεόδωρος Λούτας Τμήμα Μηχανολογίας ΑΤΕΙ Πατρών Πάτρα 2011 1 Μηχανικές
Εργαστήριο Τεχνολογίας Υλικών Εργαστηριακή Άσκηση 07 Εφελκυσμός Διδάσκοντες: Δρ Γεώργιος Ι. Γιαννόπουλος Δρ Θεώνη Ασημακοπούλου Δρ Θεόδωρος Λούτας Τμήμα Μηχανολογίας ΑΤΕΙ Πατρών Πάτρα 2011 1 Μηχανικές
μετασχηματιστή. ΤΜΗΜΑ: ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΘΕΜΑ: Περιγράψτε τον τρόπο λειτουργίας ενός μονοφασικού
 ΤΜΗΜΑ: ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΘΕΜΑ: Περιγράψτε τον τρόπο λειτουργίας ενός μονοφασικού μετασχηματιστή. ΕΠΙΒΛΕΠΩΝ ΚΑΘΗΓΗΤΗΣ: κ. Δημήτριος Καλπακτσόγλου ΕΡΓΑΣΙΑ ΤΗΣ: Αικατερίνης-Χρυσοβαλάντης Γιουσμά Α.Ε.Μ:
ΤΜΗΜΑ: ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΘΕΜΑ: Περιγράψτε τον τρόπο λειτουργίας ενός μονοφασικού μετασχηματιστή. ΕΠΙΒΛΕΠΩΝ ΚΑΘΗΓΗΤΗΣ: κ. Δημήτριος Καλπακτσόγλου ΕΡΓΑΣΙΑ ΤΗΣ: Αικατερίνης-Χρυσοβαλάντης Γιουσμά Α.Ε.Μ:
Πίνακας Προτεινόμενων Πτυχιακών Εργασιών
 ΣΧΟΛΗ: ΜΗΧΑΝΙΚΩΝ ΤΜΗΜΑ: ΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ: Α Α/Α Τίτλος Θέματος Μέλος Ε.Π. Σύντομη Περιγραφή Προαπαιτούμενα γνωστικά πεδία Αριθμός Φοιτητών Προμελέτη πλοίου μεταφοράς εμπορευματοκιβωτίων Κ. Γ.
ΣΧΟΛΗ: ΜΗΧΑΝΙΚΩΝ ΤΜΗΜΑ: ΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ: Α Α/Α Τίτλος Θέματος Μέλος Ε.Π. Σύντομη Περιγραφή Προαπαιτούμενα γνωστικά πεδία Αριθμός Φοιτητών Προμελέτη πλοίου μεταφοράς εμπορευματοκιβωτίων Κ. Γ.
Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 03-04 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: 0/0/03 ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α4 και δίπλα
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 03-04 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α ΗΜΕΡΟΜΗΝΙΑ: 0/0/03 ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α4 και δίπλα
Δομή Διάλεξης. Εύρεση επαγόμενων επιφανειακών φορτίων. Εύρεση δύναμης που ασκείται στο πραγματικό φορτίο και αποθηκευμένης ηλεκτροστατικής ενέργειας.
 Μέθοδος Ειδώλων Δομή Διάλεξης 1 ο παράδειγμα εφαρμογής μεθόδου ειδώλων για εύρεση δυναμικού με δεδομένες οριακές συνθήκες και ύπαρξη συμμετρίας: Φορτίο πάνω από άπειρο επίπεδο αγωγό. Εύρεση επαγόμενων
Μέθοδος Ειδώλων Δομή Διάλεξης 1 ο παράδειγμα εφαρμογής μεθόδου ειδώλων για εύρεση δυναμικού με δεδομένες οριακές συνθήκες και ύπαρξη συμμετρίας: Φορτίο πάνω από άπειρο επίπεδο αγωγό. Εύρεση επαγόμενων
Δυναμική Μηχανών I. Διάλεξη 21. Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ
 Δυναμική Μηχανών I Διάλεξη 21 Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ 1 Ανακοινώσεις Εξέταση Μαθήματος: 1/4/2014, 12.00 Απαιτείται αποδεικτικό ταυτότητας (Α.Τ., Διαβατήριο, Διπλ. Οδ.) Απαγορεύεται
Δυναμική Μηχανών I Διάλεξη 21 Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ 1 Ανακοινώσεις Εξέταση Μαθήματος: 1/4/2014, 12.00 Απαιτείται αποδεικτικό ταυτότητας (Α.Τ., Διαβατήριο, Διπλ. Οδ.) Απαγορεύεται
ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦ ΑΡΜ ΟΣΜ ΕΝΩΝ Μ ΑΘΗΜ ΑΤΙΚΩΝ ΚΑΙ Φ ΥΣΙΚΩΝ ΕΠΙΣΤΗΜ ΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 3-4 ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 3-4 ΗΜ/ΝΙΑ 1ο-2ο 3ο-4ο 5ο-6ο 5ο-6ο Μαθηματικού 7ο-8ο Φυσικού
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦ ΑΡΜ ΟΣΜ ΕΝΩΝ Μ ΑΘΗΜ ΑΤΙΚΩΝ ΚΑΙ Φ ΥΣΙΚΩΝ ΕΠΙΣΤΗΜ ΩΝ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 3-4 ΠΡΟΓΡΑΜΜΑ ΕΞΕΤΑΣΕΩΝ ΑΚΑΔΗΜΑΪΚΟΥ ΕΤΟΥΣ 3-4 ΗΜ/ΝΙΑ 1ο-2ο 3ο-4ο 5ο-6ο 5ο-6ο Μαθηματικού 7ο-8ο Φυσικού
Προτεινόμενο Πρόγραμμα Σπουδών. Για το Τμήμα Φυσικής της Σχολής Θετικών Επιστημών (Λαμία) του ΠΘ
 Προτεινόμενο Πρόγραμμα Σπουδών Για το Τμήμα Φυσικής της Σχολής Θετικών Επιστημών (Λαμία) του ΠΘ Εισαγωγή Το πρόγραμμα σπουδών έχει ως στόχο να δώσει τη δυνατότητα στους αποφοίτους του Τμήματος Φυσικής
Προτεινόμενο Πρόγραμμα Σπουδών Για το Τμήμα Φυσικής της Σχολής Θετικών Επιστημών (Λαμία) του ΠΘ Εισαγωγή Το πρόγραμμα σπουδών έχει ως στόχο να δώσει τη δυνατότητα στους αποφοίτους του Τμήματος Φυσικής
Αγωγιμότητα στα μέταλλα
 Η κίνηση των ατόμων σε κρυσταλλικό στερεό Θερμοκρασία 0 Θερμοκρασία 0 Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo
Η κίνηση των ατόμων σε κρυσταλλικό στερεό Θερμοκρασία 0 Θερμοκρασία 0 Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΡΑΥΛΙΚΗΣ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗΣ ΤΕΧΝΙΚΗΣ. Διάλεξη 3: Περιγραφή αριθμητικών μεθόδων (συνέχεια)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΡΑΥΛΙΚΗΣ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗΣ ΤΕΧΝΙΚΗΣ Διάλεξη 3: Περιγραφή αριθμητικών μεθόδων (συνέχεια) Χειμερινό εξάμηνο 2008 Προηγούμενη παρουσίαση... Εξετάσαμε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΡΑΥΛΙΚΗΣ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗΣ ΤΕΧΝΙΚΗΣ Διάλεξη 3: Περιγραφή αριθμητικών μεθόδων (συνέχεια) Χειμερινό εξάμηνο 2008 Προηγούμενη παρουσίαση... Εξετάσαμε
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών. Πολυβάθμια Συστήματα. Ε.Ι. Σαπουντζάκης. Καθηγητής ΕΜΠ. Δυναμική Ανάλυση Ραβδωτών Φορέων
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών Πολυβάθμια Συστήματα Ε.Ι. Σαπουντζάκης Καθηγητής ΕΜΠ Συστήματα με Κατανεμημένη Μάζα και Δυσκαμψία 1. Εξίσωση Κίνησης χωρίς Απόσβεση: Επιβαλλόμενες
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Πολιτικών Μηχανικών Πολυβάθμια Συστήματα Ε.Ι. Σαπουντζάκης Καθηγητής ΕΜΠ Συστήματα με Κατανεμημένη Μάζα και Δυσκαμψία 1. Εξίσωση Κίνησης χωρίς Απόσβεση: Επιβαλλόμενες
ΟΡΙΑΚΟ ΣΤΡΩΜΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΘΕΩΡΗΤΙΚΗ ΑΝΑΛΥΣΗ. Σημειώσεις. Επιμέλεια: Άγγελος Θ. Παπαϊωάννου, Ομοτ. Καθηγητής ΕΜΠ
 ΟΡΙΑΚΟ ΣΤΡΩΜΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΘΕΩΡΗΤΙΚΗ ΑΝΑΛΥΣΗ Σημειώσεις Επιμέλεια: Άγγελος Θ. Παπαϊωάννου, Ομοτ. Καθηγητής ΕΜΠ Αθήνα, Απρίλιος 13 1. Η Έννοια του Οριακού Στρώματος Το οριακό στρώμα επινοήθηκε για
ΟΡΙΑΚΟ ΣΤΡΩΜΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΘΕΩΡΗΤΙΚΗ ΑΝΑΛΥΣΗ Σημειώσεις Επιμέλεια: Άγγελος Θ. Παπαϊωάννου, Ομοτ. Καθηγητής ΕΜΠ Αθήνα, Απρίλιος 13 1. Η Έννοια του Οριακού Στρώματος Το οριακό στρώμα επινοήθηκε για
4.5 Αµφιέρειστες πλάκες
 Τόµος B 4.5 Αµφιέρειστες πλάκες Οι αµφιέρειστες πλάκες στηρίζονται σε δύο απέναντι παρυφές, όπως η s1 στην εικόνα της 4.1. Αν µία αµφιέρειστη πλάκα στηρίζεται επιπρόσθετα σε µία ή δύο ακόµη παρυφές και
Τόµος B 4.5 Αµφιέρειστες πλάκες Οι αµφιέρειστες πλάκες στηρίζονται σε δύο απέναντι παρυφές, όπως η s1 στην εικόνα της 4.1. Αν µία αµφιέρειστη πλάκα στηρίζεται επιπρόσθετα σε µία ή δύο ακόµη παρυφές και
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ. ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 11 ΑΠΡΙΛΙΟΥ 2018 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 11 ΑΠΡΙΛΙΟΥ 2018 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ 1 ο Στις ερωτήσεις 1-4 να γράψετε
6η Εργαστηριακή Άσκηση Μέτρηση διηλεκτρικής σταθεράς σε κύκλωµα RLC
 6η Εργαστηριακή Άσκηση Μέτρηση διηλεκτρικής σταθεράς σε κύκλωµα RLC Θεωρητικό µέρος Αν µεταξύ δύο αρχικά αφόρτιστων αγωγών εφαρµοστεί µία συνεχής διαφορά δυναµικού ή τάση V, τότε στις επιφάνειές τους θα
6η Εργαστηριακή Άσκηση Μέτρηση διηλεκτρικής σταθεράς σε κύκλωµα RLC Θεωρητικό µέρος Αν µεταξύ δύο αρχικά αφόρτιστων αγωγών εφαρµοστεί µία συνεχής διαφορά δυναµικού ή τάση V, τότε στις επιφάνειές τους θα
