Κωδικοποίηση / συμπίεση πολυμεσικών δεδομένων

Transcript

1 ΔΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ Π λ έ Πολυμέσα Κωδικοποίηση / συμπίεση πολυμεσικών δεδομένων Δρ. Γεώργιος Π. Παυλίδης

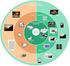
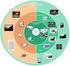
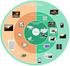
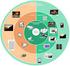
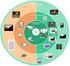
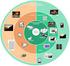
2 Κωδικοποίηση / συμπίεση Χρησιμοποίηση Εφαρμογές Εκμάθηση Σχεδίαση Διασύνδεση χρήστη Υπηρεσίες Ανάλυση περιεχομένου Έγγραφα Ασφάλεια... Συγχρονισμός Επικοινωνία ομάδας Βάσεις δεδομένων Προγραμματισμός Συστήματα Server Μέσων Λειτουργικά Συστήματα Επικοινωνία Οπτική αποθήκευση Ποιότητα υπηρεσιών Δίκτυα Βασικά Αρχιτεκτονική υπολογιστών Κείμενο Ήχος Συμπίεση Γραφικά & Εικόνες Βίντεο Κίνηση 2/41

3 Περιεχόμενα Κωδικοποίηση δεδομένων Εισαγωγικά στοιχεία Μοντελοποίηση πηγής Εντροπία πηγής Αλγόριθμοι κωδικοποίησης Συμπίεση δεδομένων Εισαγωγή Συμπίεση εικόνων JPEG, JPEG2000, Wavelet, Fractals Συμπίεση βίντεο και ήχου H261, H263, H320, MPEG1/2/4 3/41

4 Κωδικοποίηση/Συμπίεση ΚΩ ΙΚΟΠΟΙΗΣΗ Ε ΟΜΕΝΩΝ 4/41

5 Κωδικοποίηση δεδομένων Claude E. Shannon 1948 "A Mathematical Theory of Communication" Θεμελίωση θεωρίας της πληροφορίας Μορφοποίηση θεωρίας συμπίεσης Ορισμός ορίου συμπίεσης χωρίς απώλειες Εισαγωγή της εντροπίας Η (στατιστικά χαρακτηριστικά πηγής) Μαθηματικά αδύνατη υπέρβαση ορίου εντροπίας Ανάπτυξη θεωρίας συμπίεσης με απώλειες Θεωρία συμπίεσης-παραμόρφωσης (rate-distortion) Υπάρχει συνάρτηση R(D) που δίνει το καλύτερο αποτέλεσμα συμπίεσης R για δεδομένη αποδεκτή παραμόρφωση D 5/41

6 Κωδικοποίηση δεδομένων Claude E. Shannon 1948 "A Mathematical Theory of Communication" Ειδική περίπτωση συμπίεσης-παραμόρφωσης R(D)=H (για πηγή πεπερασμένου αλφαβήτου) Η μεγαλύτερη συμπίεση χωρίς απώλειες ισούται με την εντροπία της πηγής Θεωρία κωδικοποίησης πηγής Ενοποιημένη θεωρία συμπίεσης με/χωρίς απώλειες Θέτει τα όρια απόδοσης για όλες τις μεθόδους 6/41

7 Μοντελοποίηση πηγής Έστω βιβλιοθήκη 100x10 6 βιβλίων με 100x10 6 γράμματα α σε έα ένα τυχαίο βιβλίο βλίο Χ Χ = (Χ 1, Χ 2, Χ 3,.) όπου Χ i τα γράμματα Έστω μόνο κεφαλαίοι χαρακτήρες και κενά Α = {Α, Β, C, D, E, F,, Z, SPACE}, το αλφάβητο Για την κωδικοποίηση οι χαρακτήρες του ββλί βιβλίου θεωρούνται τυχαίες μεταβλητές X i με τιμές από το αλφάβητο Α Το βιβλίο αποτελεί έτσι μια άπειρη ακολουθία τυχαίων μεταβλητών είναι μια στοχαστική διεργασία Κωδικοποίηση Μοντελοποίηση 7/41

8 Μοντελοποίηση πηγής Μοντέλο μηδενικής τάξης Κάθε γράμμα είναι στατιστικά ανεξάρτητο από όλα τα άλλα και όλα είναι ισοπίθανα στην εμφάνιση xfoml rxkhrjffjuj zlpwcfwkcyj ffjeyvkcqsghyd qpaamkbzaacibzlhjqd Μοντέλο πρώτης τάξης Κάποια γράμματα εμφανίζονται πιο συχνά από άλλα (π.χ. a, e). Τα γράμματα είναι στατιστικώς ανεξάρτητα αλλά η πιθανότητα εμφάνισής τους ακολουθεί την πιθανότητα αγγλικού κειμένου ocroh hli rgwr nmielwis eu ll nbnesebya th eei alhenhttpa oobttva nah brl Μοντέλο δεύτερης τάξης Η πιθανότητα εμφάνισης γράμματος εξαρτάται από το προηγούμενο και μόνο on ie antsoutinys are t inctore st be s deamy achin d ilonasive tucoowe at teasonare fuso tizin andy tobe seace ctisbe 8/41

9 Μοντελοποίηση πηγής Μοντέλο τρίτης τάξης Η πιθανότητα εμφάνισης γράμματος εξαρτάται από τα δύο προηγούμενα και μόνο γράμματα in no ist lat whey cratict froure birs grocid pondenome of demonstures of the reptagin is regoactiona of cre Γενικό μοντέλο Το βιβλίο συνολικά αντιμετωπίζεται ως στάσιμη στοχαστική διεργασία Τα στατιστικά δε μεταβάλλονται στο χώρο και στο χρόνο Το Γενικό μοντέλο είναι το "υπερσύνολο" των προηγούμενων μοντέλων 9/41

10 Εντροπία πηγής Είναι ένας αριθμός που εξαρτάται από τα στατιστικά χαρακτηριστικά της πηγής. Έστω Χ = (Χ 1, Χ 2, Χ 3, ) και m το μήκος του αλφαβήτου (27) Μοντέλο μηδενικής τάξης (4.75) [bits/character] Μοντέλο πρώτης τάξης (4.07) Μοντέλο δεύτερης τάξης (3.36) 36) P j i πιθανότητα j με δεδομένο i Μοντέλο τρίτης τάξης (2.77) Γενικό μοντέλο (2.3) B n οι πρώτοι n χαρακτήρες 10/41

11 Θεώρημα κωδικοποίησης χωρίς απώλειες Εάν R n* ο ρυθμός δεδομένων βέλτιστου n-τάξης κώδικα συμπίεσης χωρίς απώλειες, τότε * l(b n )=log 2 p(b n ) το μήκος της κωδικο-λέξης του τμήματος B n Το όριο του R n* καθώς το n τείνει στο άπειρο είναι η τιμή της εντροπίας H Η εντροπία αποτελεί το μέτρο εκτίμησης βέλτιστου κώδικα συμπίεσης. Το όριο υπάρχει όσο η πηγή είναι στάσιμη. 11/41

12 Θεώρημα κωδικοποίησης χωρίς απώλειες Έστω πηγή με αλφάβητο δύο γραμμάτων A={a,b} Έστω η ακολουθία 24 γραμμάτων: Μοντέλο πρώτης τάξης 24:24 = 1 bit/char Μοντέλο δεύτερης τάξης 20:24 = bits/char 12/41

13 Θεώρημα κωδικοποίησης χωρίς απώλειες Μοντέλο τρίτης τάξης 17:24 = bits/char Οι υπολογισμοί του R έγιναν με βάση τη σχέση: 13/41

14 Θεωρία συμπίεσης-παραμόρφωσης παραμόρφωσης Στη συμπίεση με απώλειες Τα δεδομένα δεν είναι όμοια με τα πρωτότυπα Πρέπει να εκτιμηθεί η ομοιότητα με τα πρωτότυπα Μέτρο παραμόρφωσης Κοινά μέτρα παραμόρφωσης Μέτρο απόστασης Hamming Μέτρο τετραγωνικού σφάλματος Η θεωρία συμπίεσης-παραμόρφωσης εκφράζει ότι για δεδομένη πηγή και δεδομένο μέτρο παραμόρφωσης, υπάρχει συνάρτηση R(D) η οποία καλείται συνάρτηση ρη ησυμπίεσης-παραμόρφωσης μ ρφ 14/41

15 Θεωρία συμπίεσης-παραμόρφωσης παραμόρφωσης Τυπική συνάρτηση R(D) Όταν τα δείγματα της πηγής είναι ανεξάρτητα, η R(D) μπορεί να εκτιμηθεί από την ελαχιστοποίηση: υπό τις συνθήκες και με Q j i την πυκνότητα πιθανότητας της εξόδου σε σχέση με την είσοδο και d(i,j) την παραμόρφωση μεταξύ των συμβόλων i και j 15/41

16 Κατηγορίες αλγορίθμων κωδικοποίησης Κωδικοποίηση εντροπίας - χωρίς απώλειες - χωρίς σημασιολογική προσέγγιση Κωδικοποίηση πηγής - συχνά με απώλειες - σημασιολογική προσέγγιση Κωδικοποίηση καναλιού - προσαρμογή σε κανάλι επικοινωνίας - Εισαγωγή πλεονασμών Υβριδική κωδικοποίηση συνδυασμός κωδικοποίησης εντροπίας και κωδικοποίησης πηγής 16/41

17 Κατηγορίες αλγορίθμων κωδικοποίησης Κωδικοποίηση εντροπίας Run-length coding Huffman coding Arithmetic coding Κωδικοποίηση πηγής Πρόβλεψη: DPCM Μετασχηματισμός: FFT/DCT Στρωματική κωδικοποίηση: Sub-band ιανυσματικός κβαντισμός (VQ) Κωδικοποίηση καναλιού προσαρμογή σε κανάλι επικοινωνίας παρουσία πλεονασμών Υβριδική κωδικοποίηση JPEG MPEG H.261, H.263 Quicktime... 17/41

18 Run-length coding Κωδικοποίηση εντροπίας Υπόθεση: ύπαρξη μεγάλου μήκους ακολουθιών από ίδια σύμβολα Αντικατάσταση επαναλαμβανόμενων ακολουθιών θώ με έναν αριθμό πλήθους εμφάνισης αυτών σημαντική μείωση των δεδομένων Παράδειγμα 18/41

19 Κωδικοποίηση Huffman Κωδικοποίηση εντροπίας Σύμβολα εισόδου σταθερού πλήθους μετατρέπεται σε ακολουθία ψηφίων εξόδου μεταβλητού μήκους Βέλτιστη κωδικοποίηση για δεδομένα-γνωστά στατιστικά εισόδου 19/41

20 Κωδικοποίηση Huffman Βασική ιδέα: αντιστοίχιση κωδίκων μικρού μήκους σε σύμβολα εισόδου με μεγάλη πιθανότητα (παρόμοια με τον κώδικα Μορς) Από τα γνωστά στατιστικά της πηγής δημιουργείται δέντρο κωδίκων ξεκινώντας από τα φύλλα προς τη ρίζα, ενώνοντας δύο-δύο τα λιγότερο πιθανά σύμβολα 20/41

21 Κωδικοποίηση Huffman Η διαδικασία καταλήγει σε ένα στατικό δέντρο κωδίκων: Εντροπία πηγής: -Σ[p(X)*log(p(X))] = 2.88 bpc Ρυθμός κωδίκων: Σ[p(X)*l(X)] = 2.94 bpc, όπου l(x) το μήκος του δυαδικού κώδικα 21/41

22 Αριθμητική κωδικοποίηση Κωδικοποίηση εντροπίας Τα σύμβολα κατανέμονται στο διάστημα [0,1) ανάλογα με τις πιθανότητες εμφάνισής τους Η διαδοχική δ κωδικοποίηση συμβόλων διασπά το αντίστοιχο υπο-διάστημα σε υπο-υπο-διαστήματα Τελευταίο σύμβολο τιμή από το τελευταίο υπο- διάστημα 22/41

23 Αριθμητική κωδικοποίηση Παράδειγμα αριθμητικής κωδικοποίησης 23/41

24 DPCM (Differential Pulse Code Modulation) ιαφορική Παλμοκωδική ιαμόρφωση Κωδικοποίηση πηγής Κωδικοποίηση με πρόβλεψη Υποθέσεις ιαδοχικά δείγματα ή frames έχουν παρόμοιες τιμές Η πρόβλεψη είναι εφικτή λόγω της υπάρχουσας συσχέτισης Βασικά βήματα Το εισερχόμενο δείγμα ή frame (μπλοκ, pixel) εκτιμάται με χρήση των προηγούμενα επεξεργασμένων δεδομένων Υπολογίζεται η διαφορά ανάμεσα στα εισερχόμενα δεδομένα και τις εκτιμήσεις-προβλέψεις Η διαφορά κβαντίζεται Πρόκληση: η εύρεση του βέλτιστου εκτιμητή Τροποποίηση ιαμόρφωση έλτα: οι τιμές διαφορών κωδικοποιούνται με ακριβώς ένα bit Πληροφορία αν το σήμα αυξάνεται ή μειώνεται 24/41

25 Κωδικοποίηση μετασχηματισμού Κωδικοποίηση πηγής Υποθέσεις Είναι πιο εύκολο να συμπιεστούν δεδομένα στο πεδίο μετασχηματισμού Η επικείμενη επεξεργασία μετασχηματισμού είναι εφικτή Παραδείγματα FFT DCT Κωδικοποίηση κατά ζώνες συχνοτήτων Υπόθεση: μερικές περιοχές συχνοτήτων είναι πιο σημαντικές από άλλες Παράδειγμα Εφαρμογή: MPEG Audio 25/41

26 Κωδικοποίηση Lempel-Ziv Κωδικοποίηση λεξικού Σύμβολα εισόδου μεταβλητού πλήθους μετατρέπεται σε ακολουθία ψηφίων εξόδου σταθερού μήκους Αντιμετωπίζει μεγάλη οικογένεια πηγών Πολύ καλή προσαρμογή σε διαφορετικές πηγές Μεγαλύτερη διάδοση και χρήση 26/41

27 Κωδικοποίηση Lempel-Ziv Ιδέα: έλεγχος εισόδου σε μη-επικαλυπτόμενα τμήματα μεταβλητού μήκους και δημιουργία «λεξικού» λξ ύ με βάση τα δεδομένα που παρουσιάστηκαν 27/41

28 Κωδικοποίηση Lempel-Ziv Θεωρητικά, το λεξικό μπορεί να γίνει απείρως μεγάλο. Στην πράξη τίθεται όριο (Welch 4096 [12 bits per index] LZW) Το μήκος του δείκτη n μπορεί να μεταβάλλεται ανάλογα προς round(log2(n+1)) bits (μεταβλητού-προςμεταβλητού μήκους μορφή του LZ) Για μέγεθος λεξικού 2 m, γίνεται εξοικονόμηση 2 m-1 bits Στην πράξη, ο LZ αποδίδει ικανοποιητικά όταν τα δεδομένα εισόδου είναι μεγάλου πλήθους Η αποσυμπίεση λειτουργεί αντίστροφα Πολλές υλοποιήσεις βασίζονται στον LZ Unix compress, gzip, pkzip, WinZip/Rar 28/41

29 ιανυσματικός κβαντισμός Κωδικοποίηση πηγής Vector quantization (VQ) Μέθοδος συμπίεσης με απώλειες Αλγόριθμος σταθερού-προς-σταθερό μήκος κώδικα Πρόβλημα πολυδιάστατης ολοκλήρωσης 1980, Linde-Buzo-Gray (LBG) πρότειναν αλγόριθμο σχεδίασης διανυσματικού κβαντιστή με βάση ακολουθία εκπαίδευσης Η ακολουθία βοηθά να ξεπεραστεί το πρόβλημα της πολυδιάστατης ολοκλήρωσης Ένας διανυσματικός κβαντιστής σχεδιασμένος με αυτή την αρχή αναφέρεται ως LBG-VQ 29/41

30 ιανυσματικός κβαντισμός Βασική ιδέα παρόμοια με τη στρογγυλοποίηση Μονοδιάστατος VQ: κάθε αριθμός σε καθορισμένο διάστημα τιμών προσεγγίζεται με έναν συγκεκριμένο αριθμό Στο παράδειγμα: Τέσσερις πιθανές τιμές προσέγγισης απαιτούν log 2 4 = 2 bits πληροφορίας 30/41

31 ιανυσματικός κβαντισμός Παράδειγμα δύο διαστάσεων Κάθε ζεύγος τιμών εντός περιοχής ζεύγος τιμών του κόκκινου σημείου της περιοχής 16 περιοχές 4 bits 4 bits VQ ρυθμός δεδομένων 2bits/διάσταση 31/41

32 ιανυσματικός κβαντισμός Οι περιοχές μεταξύ των μπλε διαχωριστικών γραμμών Περιοχές κωδικοποίησης (encoding regions) Το σύνολο των περιοχών Τμηματοποίηση του χώρου (partition of the space) Τα κόκκινα σημεία Κωδικοδιανύσματα (codevectors) Το σύνολο των κωδικοδιανυσμάτων Λεξικό κωδίκων (codebook) 32/41

33 ιανυσματικός κβαντισμός Σχεδίαση VQ εδομένης μιας διανυσματικής πηγής με γνωστά στατιστικά ( δεδομένης ακολουθίας εκπαίδευσης) εδομένου ενός μέτρου παραμόρφωσης εδομένου πλήθους κωδικοδιανυσμάτων ημιουργία λεξικού κωδικοδιανυσμάτων και τμηματοποίησης χώρου που οδηγεί σε ελάχιστη μέση παραμόρφωση Με δεδομένο μέτρο τετραγωνικού σφάλματος η μέση παραμόρφωση ρφ υπολογίζεται γζ από τη σχέση: 33/41

34 ιανυσματικός κβαντισμός Παράδειγμα δημιουργίας VQ δύο διαστάσεων Πηγή Gaussian χωρίς μνήμη, μηδενικής μέσης τιμής και μοναδιαίας διακύμανσης Πράσινα σημεία διανύσματα εκπαίδευσης (4096) LBG αλγόριθμος (D (i-1) ave -D (i) ave )/D (i-1) ave ε=0.001 Πρακτικά: πλήθος διανυσμάτων εκπαίδευσης 1000x πλήθος κωδικοδιανυσμάτων 34/41

35 ιανυσματικός κβαντισμός Εκτίμηση απόδοσης Λόγος σήματος προς παραμόρφωση σε db όπου σ 2 η διακύμανση της πηγής και D ave η μέση τετραγωνική παραμόρφωση ρφ του VQ 35/41

36 Υβριδική κωδικοποίηση Προετοιμασία Παράγει κατάλληλη ψηφιακή αναπαράσταση των πληροφοριών στο μέσο που συμπιέζεται ιαίρεση μιας εικόνας σε μπλοκ (π.χ. των 8x8 pixels) με σταθερό αριθμό bits ανά pixel Επεξεργασία Χρήση αλγορίθμων κωδικοποίησης μετασχηματισμού Κβαντισμός π.χ. μετασχηματισμός από το πεδίο του χρόνου στο πεδίο της συχνότητας με χρήση ιακριτού Μετασχηματισμού Συνημιτόνου (DCT) Κβαντισμός τιμών μετασχηματισμού σε μια συγκεκριμένη ανάλυση (ακρίβεια) π.χ. σε συγκεκριμένο αριθμό bits Κωδικοποίηση εντροπίας Είσοδος: σειριακό ρεύμα δεδομένων μεμονωμένων bits και bytes Έξοδος: σειριακό ρεύμα bits μεγάλες ακολουθίες μηδενικών που εμφανίζονται συχνά μπορούν να συμπιεστούν καθορίζοντας τον αριθμό των εμφανίσεων ακολουθούμενων από 0. 36/41

37 Κωδικοποίηση/Συμπίεση ΣΥΜΠΙΕΣΗ ΣΤΑ ΠΟΛΥΜΕΣΑ 37/41

38 Συμπίεση δεδομένων Συμπίεση στα πολυμέσα Έγχρωμη εικόνα 512x512, 8 bpp, 3 χρωματικών καναλιών απαιτεί 6x10 6 bits (768 KB) Βιβλίο 300 σελίδων Α4 (χωρίς εικόνες) σε ψηφιακή μορφή 2500 χαρακτήρων ανά σελίδα με χαρακτήρες Unicode απαιτεί 12x10 6 bits (1.4 ΜΒ) Ψηφιοποιημένο στα 12μm αρνητικό φωτογραφίας 24x36mm (35mm) 3000x2000 (6 Mpixels) στα 24 bpp απαιτεί 144x10 6 bits (17 MB) Μουσικό κομμάτι διάρκειας 3 λεπτών, ψηφιοποιημένο στα Hz, 16 bps, stereo απαιτεί samples/sec * (3*60) sec * 16 bits/sample * 2 channels 254x10 6 bits (30 MB) Ψηφιοποιημένο στα 70μm ραδιογράφημα 11x17 ιντσών 5000x6000 (30 MPixels) στα 12 bpp απαιτεί 360x106 bits (43 MB) 38/41

39 Συμπίεση δεδομένων Συμπίεση στα πολυμέσα Πολυφασματική φωτογραφία LANDSAT 6000x6000 ανά φασματική περιοχή στα 8 bpp για 6 φασματικές ζώνες απαιτεί 1.7x109 bits (206 MB). Βίντεο διάρκειας 90 λεπτών (χωρίς ήχο) ψηφιοποιημένο ανάλυσης PAL (720x576), 24 bpp απαιτεί (720x576) pixels/frame * 25 frames/sec * 24 bits/pixel * (90x60) sec 1.34x10 12 bits (~168 GB) Βίντεο υψηλής ανάλυσης HD 1920x1080, διάρκειας 90 λεπτών, 24 bpp, 50 fps Απαιτεί (1920x1080) pixels/frame * 50 frames/sec * 24 bits/pixel * (90x60) sec 13.44x10 12 bits (~1.68 TB) 39/41

40 Γενικές απαιτήσεις συμπίεσης ιατήρηση υψηλής ποιότητας συμπιεσμένων δεδομένων Επαρκές ποσοστό συμπίεσης Μικρός αποθηκευτικός χώρος, μικρός χρόνος καθυστέρησης μετάδοσης Χαμηλή πολυπλοκότητα αλγορίθμου κωδικοποίησης (κυρίως αποσυμπίεσης) για γρήγορη ρη αποκωδικοποίηση η [αλλά και κωδικοποίηση] η] Αποτελεσματική υλοποίηση αλγορίθμου, μικρό κόστος υλοποίησης π.χ. μικρές απαιτήσεις μνήμης, υλοποίηση παράλληλης επεξεργασίας, κοκ. 40/41

41 Απαιτήσεις συμπίεσης Εφαρμογές διαλόγου Συμπίεση και αποσυμπίεση σε πραγματικό χρόνο (π.χ. χ 25fps) Καθυστέρηση από άκρο σε άκρο < 150ms Εφαρμογές ανάκτησης Ταχεία προώθηση και απόκριση (forward and backward data retrieval) με ταυτόχρονη προβολή/αναπαραγωγή των δεδομένων Τυχαία προσπέλαση σε stream σε λιγότερο από ½ δευτερόλεπτο Εφαρμογές διαλόγου και ανάκτησης Ανεξαρτησία ως προς το μέγεθος και τον ρυθμό εναλλαγής των frames Συγχρονισμός ήχου, βίντεο και άλλων μέσων ιαλειτουργικότητα και συμβατότητα ανάμεσα σε διαφορετικά συστήματα 41/41