υ = ρω t 1 ε = const ε = ω Основни закони и формули = F v = ωxρ E = const II. ДИНАМИКА I.КИНЕМАТИКА I принцип II принцип dp p III принцип
|
|
|
- Αμάλθεια Κομνηνός
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Основни закони и формули.кинематика. Скорост и ускорение d v dv a v dϕ ω ϕ dω ε ω средна скорост l Δs ( ) t Δ t. тангентно и нормално ускорение a a τ n d 3. Равнопроменливо движение (въртене) aτ const + aτ. t s. t+ aτ. t ε const ω ω + ε. t ϕ ω. t+ ε. t s ϕ ω a ε τ v ωx. ДИНАМИКА. Импулс v v c принцип const, ако F принцип d F F F xt n, F Основно уравнение на Динамиката a F принцип F F. Работа и енергия d Fd F ds Мощност. τ P d/ Fv. Кинетична енергия ot ω Потенциална енергия gh M γ x Dϕ Пълна енергия + xt Δ + n nc В затворена консервативна система const
2 3. Инерчен Момент за цилиндър или диск R за пръстен R ( + R ) за кълбо 5 R за тънък прът l l 3 Теорема на Щайнер c + a спрямо ос M F τ 5. Момент на импулса спрямо полюс L L L спрямо ос L L + L L ω ω L ω особягащ момент ( ± ). d x y z ω x ω ωy ω. ω z.. (. ) (.. ) 6. Основно уравнение при въртене спрямо неподвижен полюс L L d M xt n M M, M L const, ao M спрямо подвижен полюс А L M v v c ( ) L M, ao v v ) c спрямо ос dl L M ε M L L, M M 7. Жироскопи, прецесия и нутация ω ' ωl lg L L x'. Механика на флуидите. Флуидостатика налягане (плътност на енергията) x gh Архимед F g. Флуидодинамика 4. Въртящ момент спрямо полюс M F L dl M масов поток
3 уравнение за непрекъснатост const уравнение на Бернули + gh + const Подемна сила L L π snα L Челно съпротивление D D + πα D. ТО А. ЧТО. Кинематика Трансформации на Лоренц x γ ( x' + t') y y' z z' t γ(' t + x') γ, c c Скъсяване на дължината по направление на движението l l Забавяне на хода на движещи се часовници Δ t Δt / dτ dτ собствено време интервал ds. dτ d 4 мерно време-пространство (, t ) ds d 4 - скорост v u (, ) 4 ускорение a d u/ d τ a u. Динамика u принцип const, ao F принцип d/ dτ F a F маса, енергия и импулс (, ) v v. v v за система M + + U M U - енергия на взаимодействие енергия на свързване + U b Б. ОТО ao F d/ dτ ( ). u - движението е по геодезична линия Вместо гравитация изкривяване на време-пространството G 8πγ G R Rg G тензор на Хилберт-Айнщайн
4 R тензор на Ричи тензор на енергията и импулса метрика g. Термофизика. Идеален газ N ν N μ.. νr μ R 3. n изотермен const, const изохорен const, const изобарен const, const μ адиабатен κ δq const, Основно у-е на МКТ n< ε > ( n) следствия < ε > < ε > U N < ε> ν R Разпределение на Болцман ε n n ε Разпределение на Максуел ε f ( ) 4π 3/ π dn( ) f ( ) d. принцип на ТД δq du + δ Топлоемност δq d c ν c за g топл. на ТДС за ol Приложение на. пр. на ТД към изопроцеси на ид. газ + c R c R c c R c + c за изохорен процес δ d δq du ν Rd δq c R νd за изобарен процес δq du + d δq ν( + ) Rd δq + c R νd
5 за изотермен процес du νc d δq d d d d νr νrln за адиабатен процес δq, δ du κ const. Реален газ ν a ( + )( νb) νr ν a U νc ТД потенциали H U + F U G H H енталпия, FG св. енергия на Хелмхолц и Гибс Ентропия ln Ω δq d. принцип на ТД d за самопроизволен пр. Топлинни машини Цикъл на Карно η Q η η за реална топл. Машина Ефективност на охлаж. Q K 3. Явления на пренос Топлопроводност Закон на Фурие d q λ dx λ λc Вискозитет закон на Максуел du η dy η λ Дифузия закон на Фик dn( x) n D dx D λ λ ηc Dc. Електромагнетизъм Закон на Кулон F q Q, затз.. 4πε Q ϕ, затз.. 4πε 9 9. N 4πε Принцип за суперпозицията ϕ ϕ Връзка ϕ Теореми на електростатиката n q. d. d Поле на равномерно заредена повърн. σ ε ε Поле м/у равномерно заредени повърн. σ ε Поле на равномерно заредена сф. повърн. q, R 4πε, R
6 Поле на равномерно заредено кълбо q, R 4πε, R 3ε Ел. дипол q l Дипол в ел. поле M. F Поляризация P n < > < l > Δ Връзки P χε D ε + P ε + χ D ε ε ε В диелектрик D. d q n P. d q out q n Граница диел. Метал σ D n ε σ σ ε Капацитет q ϕ Капацитет на усп. и посл. св. конд. Енергия на зар. конд. qu U Плътност на тока j v + v nq + + В метал j n v Големина на тока j q Е.Д.Н ε q * Напрежение *. dl U Δ ϕ ± ε q Закон на Ом U R l R локално j за цялата верига ε R + Работа и мощност Q qu Ut P U локално j. / Закон на Ампер F dl B Закон на Био-Савар- Лаплас μ dl db 3 4π Магнитно поле на прав проводник с ток μ B (sn + sn ) 4π a μ B π a Магнитно поле на кръгов проводник μ R B B μ B R 3 Магнитно поле на тор и соленоид B nμ Магнитно поле на движещ се заряд v B c q 4πε
7 Сила на Лоренц F q ( + v B) Теореми на магнитостатиката B. d B. dl μ Магнитен дипол Намагнитеност J n< > n < > Връзки J κh B μ ( H+ J) μ + κ B μ μ H μh Теореме на Ампер в среда H. dl Закон на Фарадей Φ ε d Уравнения на Максуел Допълнителни у-я. Трептения и вълни Хармонично трептене s cos( ωt + ϕ) π ω ν Уравнение на харм. тр. s ω s + Енергия на х.тр. ω v ω sn Φ s ω cos Φ Физическо махало gl ω π gl Математично махало g ω l l π g Пружинно махало ω π Торзионно махало ω D π D Ел. тр. кръг ω L π L Експ. зат. трептения t s cos( ωt+ ϕ) ω ω < ω π ω Уравнение на експ. з. тр. s+ s + ω s Логаритмичен декремент t () λ ln t ( + ) Доброкачественост π ω Q λ Принудени трептения s + s + ω s f cosωt s cos( ωt ϕ) f F Амплитуда и фаза ( ω ω ) + 4 ω ω ϕ actg ω ω Резонанс f ω ω f ω
8 Резонанс на скоростта ω ω ax ω Вълни:. едномерна ξ cos( ωt x) ω. плоска ξ cos( ωt. )., n n 3. сферична ξ cos( ωt ) 4. цилиндрична ξ cos( ωt ) Вълново уравнение ξ Δξ t Δ Скорости:. фазова ω. групова g dω d 3. на трептене ξ ξ t Дисперсия dω d g + d d λ d d λ c g Интерференция + ax n π ao ΔΦ ( + ) π кохерентни вълни. ω ω. Δ ϕ const Стоящи вълни: От възел до възел λ От пик до пик λ От възел до пик λ 4 при отр. от пл. среда се губи λ Скорост на надл. вълни Скорост на напр. вълни ( + μ) Във флуид За опъната струна F Скорост на звука κ R c, κ μ c Енергитични съотн. ε ε ε sn Φ ε ε + ε ε sn Φ ω ε Енерг. поток Φ ε J g Интензитет Φ εg J Ел.магн. вълни J H ε v ε ε + ε ( H ) ε ε + μ g εμ c εμ J ε. Интерференция на светлината δ n n + ±λ / λ ax δ λ ( + ) n
9 Дифракция:. от процеп δ Δ a snθ λ n λ ( + ) ax. от дифр. решетка dsnθ λ Nd snθ λ N Разрешаваща способност на д.р. λ R N Δλ ax n Дифракция на Х-лъчи δ Δ dsnθ λ ax Ефект на Доплер. класически ν ν λ λ ν ν ( ( ) / ) + ao u << ако α sn M. релативен - надлъжен ω ω cosθ ao θ, + ω ω > ω синьо отместване. ao θ π, ω ω < ω + червено отместване. - напречен ако θ π /, ω ω < ω червено отместване.. Кванти Изл. на а.ч.т. изл. способност ν, Pν, ν+ dν, / dν погл. способност погълната a, P / P паднала ν νν, + dν, νν, + dν, аν, Т за ачт... а const < за сиво т. ν, Т Закон на Кирхов за а.ч.т. ν, εν, е aν, универсална функц. Закон на Стефан- Болцман 4 ε ε d ν, ν σ 8 4 σ 5,67. W / K Закон на Вин b λ b 3,9.. Закон на Планк ε πν c K ν, hν / h 34 6, 65.. h /π hc 4. n Фотоефект ε hν + ε γ ε U з заν < ν h / hν J s няма фотоефект (, ) γ Ефект на Комптън Δ λ λ λ f λ ( cos θ) λ h/ c,44
10 Уравнение на Шрьодингер Ψ ΔΨ+ U Ψ t Ψ ΨΨ * dp d. d Основни кв.м.оператори ˆ, ˆ t tˆ t, ˆ Съотн. на неопр. Δx. Δ x / Δt. Δ / Стационарно у-е на Шрьодингер Δ ϕ+ ( U ( )) ϕ t. Ψ (,) t ϕ(). Ψ (, t) ϕ( ) Водороден атом квантуване на момента на импуса J j( j+ ) s( s+ ) L l( l+ ) Lz ± l j ;,5;;,5; ;...; n / s / l ;;;...; n l ± (;;;...; l) n ; ;3;... квантуване на енергията n / n 4 /8εh 3,6 Водородоподобен атом 4 Z /8εh Z 3,6 / n n Спектри Квантуване на магнитния момент Магнетон на Бор μb μ j( j+ ) μ ll ( + ) μs g s( s+ ) μz l μs ± z Атомно ядро 938, 6 M n 939,55M aм.. u 93,5 M масово число Z+N Енергия на свързване Z + ( Z) b H n a Специфична енергия на свързване ε b b / Радиоактивност Видове радиоактивност Естествена радиоактивност λt N N ln λ N λn λt a / a λt
11
Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α
 Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
ttl КОНСТРУИСАЊЕ МОБИЛНИХ МАШИНА манипулатори машина, полужни погонски механизми Конструисање мобилних машина Седмо предавање
 КОНСТРУИСАЊЕ МОБИЛНИХ МАШИНА Седмо предавање манипулатори машина, полужни погонски механизми проф. др Драгослав Јаношевић Кнематички ланци: манипулатори а) L 3 L n L n+1 Ez { L1,L2 a) прости, б) разгранати,
КОНСТРУИСАЊЕ МОБИЛНИХ МАШИНА Седмо предавање манипулатори машина, полужни погонски механизми проф. др Драгослав Јаношевић Кнематички ланци: манипулатори а) L 3 L n L n+1 Ez { L1,L2 a) прости, б) разгранати,
Проф. д-р Ѓорѓи Тромбев ГРАДЕЖНА ФИЗИКА. Влажен воздух 3/22/2014
 Проф. д-р Ѓорѓи Тромбев ГРАДЕЖНА ФИЗИКА Влажен воздух 1 1 Влажен воздух Влажен воздух смеша од сув воздух и водена пареа Водената пареа во влажниот воздух е претежно во прегреана состојба идеален гас.
Проф. д-р Ѓорѓи Тромбев ГРАДЕЖНА ФИЗИКА Влажен воздух 1 1 Влажен воздух Влажен воздух смеша од сув воздух и водена пареа Водената пареа во влажниот воздух е претежно во прегреана состојба идеален гас.
692.66:
 1 69.66:6-83 05.05.05 -,, 015 .. 7... 8 1.... 19 1.1.,.. 19 1.. 8 1.3.. 1.4... 1.4.1.... 33 36 40 1.4.. 44 1.4.3. -... 48.. 53.,.. 56.1., -....... 56..... 6.3.... 71.. 76 3.,.... 77 3 3.1.... 77 3.1.1....
1 69.66:6-83 05.05.05 -,, 015 .. 7... 8 1.... 19 1.1.,.. 19 1.. 8 1.3.. 1.4... 1.4.1.... 33 36 40 1.4.. 44 1.4.3. -... 48.. 53.,.. 56.1., -....... 56..... 6.3.... 71.. 76 3.,.... 77 3 3.1.... 77 3.1.1....
а) Определување кружна фреквенција на слободни пригушени осцилации ωd ωn = ω б) Определување периода на слободни пригушени осцилации
 Динамика и стабилност на конструкции Задача 5.7 За дадената армирано бетонска конструкција од задачата 5. и пресметаните динамички карактеристики: кружна фреквенција и периода на слободните непригушени
Динамика и стабилност на конструкции Задача 5.7 За дадената армирано бетонска конструкција од задачата 5. и пресметаните динамички карактеристики: кружна фреквенција и периода на слободните непригушени
!"#$ % &# &%#'()(! $ * +
 ,!"#$ % &# &%#'()(! $ * + ,!"#$ % &# &%#'()(! $ * + 6 7 57 : - - / :!", # $ % & :'!(), 5 ( -, * + :! ",, # $ %, ) #, '(#,!# $$,',#-, 4 "- /,#-," -$ '# &",,#- "-&)'#45)')6 5! 6 5 4 "- /,#-7 ",',8##! -#9,!"))
,!"#$ % &# &%#'()(! $ * + ,!"#$ % &# &%#'()(! $ * + 6 7 57 : - - / :!", # $ % & :'!(), 5 ( -, * + :! ",, # $ %, ) #, '(#,!# $$,',#-, 4 "- /,#-," -$ '# &",,#- "-&)'#45)')6 5! 6 5 4 "- /,#-7 ",',8##! -#9,!"))
ЈАКОСТ НА МАТЕРИЈАЛИТЕ
 диј е ИКА ски ч. 7 ч. Универзитет Св. Кирил и Методиј Универзитет Машински Св. факултет Кирил и Скопје Методиј во Скопје Машински факултет МОМ ТЕХНИЧКА МЕХАНИКА професор: доц. др Виктор Гаврилоски. ТОРЗИЈА
диј е ИКА ски ч. 7 ч. Универзитет Св. Кирил и Методиј Универзитет Машински Св. факултет Кирил и Скопје Методиј во Скопје Машински факултет МОМ ТЕХНИЧКА МЕХАНИКА професор: доц. др Виктор Гаврилоски. ТОРЗИЈА
 y(t) S x(t) S dy dx E, E E T1 T2 T1 T2 1 T 1 T 2 2 T 2 1 T 2 2 3 T 3 1 T 3 2... V o R R R T V CC P F A P g h V ext V sin 2 S f S t V 1 V 2 V out sin 2 f S t x 1 F k q K x q K k F d F x d V
y(t) S x(t) S dy dx E, E E T1 T2 T1 T2 1 T 1 T 2 2 T 2 1 T 2 2 3 T 3 1 T 3 2... V o R R R T V CC P F A P g h V ext V sin 2 S f S t V 1 V 2 V out sin 2 f S t x 1 F k q K x q K k F d F x d V
И. В. Яковлев Материалы по математике MathUs.ru. Задачник С1
 И В Яковлев Материалы по математике MathUsru Задачник С1 Здесь приведены задачи С1, которые предлагались на ЕГЭ по математике, а также на диагностических, контрольных и тренировочных работах МИОО начиная
И В Яковлев Материалы по математике MathUsru Задачник С1 Здесь приведены задачи С1, которые предлагались на ЕГЭ по математике, а также на диагностических, контрольных и тренировочных работах МИОО начиная
ttl ПОГОНСКИ СИСТЕМИ погони манипулатора са хидроцилиндрима, полужни погонски механизми, Погонски системи Једанаесто предавање
 ПОГОНСКИ СИСТЕМИ Једанаесто предавање погони манипулатора са хидроцилиндрима, полужни погонски механизми, МАНИПУЛАТОРИ прости равански A O 2 Техника конструисања МАНИПУЛАТОРИ прости просторни V X 3 V могући
ПОГОНСКИ СИСТЕМИ Једанаесто предавање погони манипулатора са хидроцилиндрима, полужни погонски механизми, МАНИПУЛАТОРИ прости равански A O 2 Техника конструисања МАНИПУЛАТОРИ прости просторни V X 3 V могући
Ταλαντώσεις 6.1 Απλή Αρµονική Ταλάντωση σε µία ιάσταση Ελατήριο σε οριζόντιο επίπεδο Σχήµα 6.1
 6 Ταλαντώσεις 6.1 Απλή Αρµονική Ταλάντωση σε µία ιάσταση 6.1.1 Ελατήριο σε οριζόντιο επίπεδο Υποθέτουµε ότι το ελατήριο έχει αρχικό µήκος µηδέν, ιδανικό ελατήριο. F=-kx x K M x Σχήµα 6.1 ιαστάσεις µεγεθών
6 Ταλαντώσεις 6.1 Απλή Αρµονική Ταλάντωση σε µία ιάσταση 6.1.1 Ελατήριο σε οριζόντιο επίπεδο Υποθέτουµε ότι το ελατήριο έχει αρχικό µήκος µηδέν, ιδανικό ελατήριο. F=-kx x K M x Σχήµα 6.1 ιαστάσεις µεγεθών
Α Ρ Ι Θ Μ Ο Σ : 6.913
 Α Ρ Ι Θ Μ Ο Σ : 6.913 ΠΡΑΞΗ ΚΑΤΑΘΕΣΗΣ ΟΡΩΝ ΔΙΑΓΩΝΙΣΜΟΥ Σ τ η ν Π ά τ ρ α σ ή μ ε ρ α σ τ ι ς δ ε κ α τ έ σ σ ε ρ ι ς ( 1 4 ) τ ο υ μ ή ν α Ο κ τ ω β ρ ί ο υ, η μ έ ρ α Τ ε τ ά ρ τ η, τ ο υ έ τ ο υ ς δ
Α Ρ Ι Θ Μ Ο Σ : 6.913 ΠΡΑΞΗ ΚΑΤΑΘΕΣΗΣ ΟΡΩΝ ΔΙΑΓΩΝΙΣΜΟΥ Σ τ η ν Π ά τ ρ α σ ή μ ε ρ α σ τ ι ς δ ε κ α τ έ σ σ ε ρ ι ς ( 1 4 ) τ ο υ μ ή ν α Ο κ τ ω β ρ ί ο υ, η μ έ ρ α Τ ε τ ά ρ τ η, τ ο υ έ τ ο υ ς δ
Errata (Includes critical corrections only for the 1 st & 2 nd reprint)
 Wedesday, May 5, 3 Erraa (Icludes criical correcios oly for he s & d repri) Advaced Egieerig Mahemaics, 7e Peer V O eil ISB: 978474 Page # Descripio 38 ie 4: chage "w v a v " "w v a v " 46 ie : chage "y
Wedesday, May 5, 3 Erraa (Icludes criical correcios oly for he s & d repri) Advaced Egieerig Mahemaics, 7e Peer V O eil ISB: 978474 Page # Descripio 38 ie 4: chage "w v a v " "w v a v " 46 ie : chage "y
налазе се у диелектрику, релативне диелектричне константе ε r = 2, на међусобном растојању 2 a ( a =1cm
 1 Два тачкаста наелектрисања 1 400 p и 100p налазе се у диелектрику релативне диелектричне константе ε на међусобном растојању ( 1cm ) као на слици 1 Одредити силу на наелектрисање 3 100p када се оно нађе:
1 Два тачкаста наелектрисања 1 400 p и 100p налазе се у диелектрику релативне диелектричне константе ε на међусобном растојању ( 1cm ) као на слици 1 Одредити силу на наелектрисање 3 100p када се оно нађе:
ТЕХНИЧЕСКИ ПАРАМЕТРИ ПРЕДИ ДА СЕ ОБЪРНЕТЕ КЪМ СЕРВИЗА
 4. Никога не потапяйте уреда във вода или друга течност и не позволявайте вода да проникне до електрическата част на уреда, докато го почиствате! 5. Не използвайте абразивни предмети или разтворители!
4. Никога не потапяйте уреда във вода или друга течност и не позволявайте вода да проникне до електрическата част на уреда, докато го почиствате! 5. Не използвайте абразивни предмети или разтворители!
5. Динамика на конструкции
 Динамика на конструкции. Динамика на конструкции Задача. За дадната армирано бтонска конструкција да с опрдли кружната фрквнција ω приодата на слободнит нпригушни осцилации Т n на основниот тон. Модулот
Динамика на конструкции. Динамика на конструкции Задача. За дадната армирано бтонска конструкција да с опрдли кружната фрквнција ω приодата на слободнит нпригушни осцилации Т n на основниот тон. Модулот
2. Α ν ά λ υ σ η Π ε ρ ι ο χ ή ς. 3. Α π α ι τ ή σ ε ι ς Ε ρ γ ο δ ό τ η. 4. Τ υ π ο λ ο γ ί α κ τ ι ρ ί ω ν. 5. Π ρ ό τ α σ η. 6.
 Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α 1. Ε ι σ α γ ω γ ή 2. Α ν ά λ υ σ η Π ε ρ ι ο χ ή ς 3. Α π α ι τ ή σ ε ι ς Ε ρ γ ο δ ό τ η 4. Τ υ π ο λ ο γ ί α κ τ ι ρ ί ω ν 5. Π ρ ό τ α σ η 6. Τ ο γ ρ α φ ε ί ο 1. Ε ι σ α γ ω
Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α 1. Ε ι σ α γ ω γ ή 2. Α ν ά λ υ σ η Π ε ρ ι ο χ ή ς 3. Α π α ι τ ή σ ε ι ς Ε ρ γ ο δ ό τ η 4. Τ υ π ο λ ο γ ί α κ τ ι ρ ί ω ν 5. Π ρ ό τ α σ η 6. Τ ο γ ρ α φ ε ί ο 1. Ε ι σ α γ ω
L кплп (Калем у кплу прпстпперипдичне струје)
 L кплп (Калем у кплу прпстпперипдичне струје) i L u=? За коло са слике кроз калем ппзнате позната простопериодична струја: индуктивности L претпоставићемо да протиче i=i m sin(ωt + ψ). Услед променљиве
L кплп (Калем у кплу прпстпперипдичне струје) i L u=? За коло са слике кроз калем ппзнате позната простопериодична струја: индуктивности L претпоставићемо да протиче i=i m sin(ωt + ψ). Услед променљиве
НАПРЕГАЊЕ ПРИ ЧИСТО СМОЛКНУВАЊЕ
 Факултет: Градежен Предмет: ЈАКОСТ НА МАТЕРИЈАЛИТЕ НАПРЕГАЊЕ ПРИ ЧИСТО СМОЛКНУВАЊЕ Напрегање на смолкнување е интензитет на сила на единица површина, што дејствува тангенцијално на d. Со други зборови,
Факултет: Градежен Предмет: ЈАКОСТ НА МАТЕРИЈАЛИТЕ НАПРЕГАЊЕ ПРИ ЧИСТО СМОЛКНУВАЊЕ Напрегање на смолкнување е интензитет на сила на единица површина, што дејствува тангенцијално на d. Со други зборови,
Осцилације система са једним степеном слободе кретања
 03-ec-18 Осцилације система са једним степеном слободе кретања Опруга Принудна сила F(t) Вискозни пригушивач ( дампер ) 1 Принудна (пертурбациона) сила опруга Реституциона сила (сила еластичног отпора)
03-ec-18 Осцилације система са једним степеном слободе кретања Опруга Принудна сила F(t) Вискозни пригушивач ( дампер ) 1 Принудна (пертурбациона) сила опруга Реституциона сила (сила еластичног отпора)
σ d γ σ M γ L = ЈАКОСТ 1 x A 4М21ОМ02 АКСИЈАЛНИ НАПРЕГАЊА (дел 2) 2.6. СОПСТВЕНА ТЕЖИНА КАКО АКСИЈАЛНА СИЛА Напонска состојаба
 4МОМ0 ЈАКОСТ АКСИЈАЛНИ НАПРЕГАЊА (дел ) наставник:.6. СОПСТВЕНА ТЕЖИНА КАКО АКСИЈАЛНА СИЛА Напонска состојаба γ 0 ( специфична тежина) 0 ak() G γ G ΣX0 ak() G γ ak ( ) γ Аксијалната сила и напонот, по
4МОМ0 ЈАКОСТ АКСИЈАЛНИ НАПРЕГАЊА (дел ) наставник:.6. СОПСТВЕНА ТЕЖИНА КАКО АКСИЈАЛНА СИЛА Напонска состојаба γ 0 ( специфична тежина) 0 ak() G γ G ΣX0 ak() G γ ak ( ) γ Аксијалната сила и напонот, по
F (x) = kx. F (x )dx. F = kx. U(x) = U(0) kx2
 F (x) = kx x k F = F (x) U(0) U(x) = x F = kx 0 F (x )dx U(x) = U(0) + 1 2 kx2 x U(0) = 0 U(x) = 1 2 kx2 U(x) x 0 = 0 x 1 U(x) U(0) + U (0) x + 1 2 U (0) x 2 U (0) = 0 U(x) U(0) + 1 2 U (0) x 2 U(0) =
F (x) = kx x k F = F (x) U(0) U(x) = x F = kx 0 F (x )dx U(x) = U(0) + 1 2 kx2 x U(0) = 0 U(x) = 1 2 kx2 U(x) x 0 = 0 x 1 U(x) U(0) + U (0) x + 1 2 U (0) x 2 U (0) = 0 U(x) U(0) + 1 2 U (0) x 2 U(0) =
( ) ( 0 ) ( e. ( t) ( ) ( ) λ ( ) λ N λ λ. ln λ / λ. dt = = λ λ. Ιδανική ισορροπία! t, ο λόγος των ενεργοτήτων Β/Α: N b. c b b.
 Αλυσίδες Ραδιενεργών ιασπάσεων A B C ιαδοχικές διασπάσεις: λ λ (σταθερός πυρήνας) dn λnd N 0 η ενεργότητα dn λnd λnd Αρχικές συνθήκες: της πηγης N ( 0) 0 N δεν ειναι λ dn λ N d Nc ( 0) 0 c λ N ( ) N (
Αλυσίδες Ραδιενεργών ιασπάσεων A B C ιαδοχικές διασπάσεις: λ λ (σταθερός πυρήνας) dn λnd N 0 η ενεργότητα dn λnd λnd Αρχικές συνθήκες: της πηγης N ( 0) 0 N δεν ειναι λ dn λ N d Nc ( 0) 0 c λ N ( ) N (
 μ μ dω I ν S da cos θ da λ λ Γ α/β MJ Capítulo 1 % βpic ɛ Eridani V ega β P ic F ormalhaut 10 9 15% 70 Virgem 47 Ursa Maior Debris Disk Debris Disk μ 90% L ac = GM M ac R L ac R M M ac L J T
μ μ dω I ν S da cos θ da λ λ Γ α/β MJ Capítulo 1 % βpic ɛ Eridani V ega β P ic F ormalhaut 10 9 15% 70 Virgem 47 Ursa Maior Debris Disk Debris Disk μ 90% L ac = GM M ac R L ac R M M ac L J T
Ηράκλειο Κρήτης, 22 Ιουνίου 2018 (Παρασκευή)
 Ηράκλειο Κρήτης, 22 Ιουνίου 2018 (Παρασκευή) Επίπεδα А1, А2, В1, В2 (όλες οι ενότητες) Τόπος διεξαγωγής: Πανεπιστήμιο Κρήτης, Πανεπιστημιούπολη Βουτών, ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ, ΑΜΦΙΘΕΑΤΡΟ Β, 2ο όροφο
Ηράκλειο Κρήτης, 22 Ιουνίου 2018 (Παρασκευή) Επίπεδα А1, А2, В1, В2 (όλες οι ενότητες) Τόπος διεξαγωγής: Πανεπιστήμιο Κρήτης, Πανεπιστημιούπολη Βουτών, ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ, ΑΜΦΙΘΕΑΤΡΟ Β, 2ο όροφο
ЛУШПИ МЕМБРАНСКА ТЕОРИЈА
 Вежби ЛУШПИ МЕМБРАНСКА ТЕОРИЈА РОТАЦИОНИ ЛУШПИ ТОВАРЕНИ СО РОТАЦИОНО СИМЕТРИЧЕН ТОВАР ОСНОВНИ ВИДОВИ РОТАЦИОНИ ЛУШПИ ЗАТВОРЕНИ ЛУШПИ ОТВОРЕНИ ЛУШПИ КОМБИНИРАНИ - СФЕРНИ - КОНУСНИ -ЦИЛИНДРИЧНИ - СФЕРНИ
Вежби ЛУШПИ МЕМБРАНСКА ТЕОРИЈА РОТАЦИОНИ ЛУШПИ ТОВАРЕНИ СО РОТАЦИОНО СИМЕТРИЧЕН ТОВАР ОСНОВНИ ВИДОВИ РОТАЦИОНИ ЛУШПИ ЗАТВОРЕНИ ЛУШПИ ОТВОРЕНИ ЛУШПИ КОМБИНИРАНИ - СФЕРНИ - КОНУСНИ -ЦИЛИНДРИЧНИ - СФЕРНИ
Предмет: Задатак 4: Слика 1.0
 Лист/листова: 1/1 Задатак 4: Задатак 4.1.1. Слика 1.0 x 1 = x 0 + x x = v x t v x = v cos θ y 1 = y 0 + y y = v y t v y = v sin θ θ 1 = θ 0 + θ θ = ω t θ 1 = θ 0 + ω t x 1 = x 0 + v cos θ t y 1 = y 0 +
Лист/листова: 1/1 Задатак 4: Задатак 4.1.1. Слика 1.0 x 1 = x 0 + x x = v x t v x = v cos θ y 1 = y 0 + y y = v y t v y = v sin θ θ 1 = θ 0 + θ θ = ω t θ 1 = θ 0 + ω t x 1 = x 0 + v cos θ t y 1 = y 0 +
TeSys contactors a.c. coils for 3-pole contactors LC1-D
 References a.c. coils for 3-pole contactors LC1-D Control circuit voltage Average resistance Inductance of Reference (1) Weight Uc at 0 C ± 10 % closed circuit For 3-pole " contactors LC1-D09...D38 and
References a.c. coils for 3-pole contactors LC1-D Control circuit voltage Average resistance Inductance of Reference (1) Weight Uc at 0 C ± 10 % closed circuit For 3-pole " contactors LC1-D09...D38 and
A 1 A 2 A 3 B 1 B 2 B 3
 16 0 17 0 17 0 18 0 18 0 19 0 20 A A = A 1 î + A 2 ĵ + A 3ˆk A (x, y, z) r = xî + yĵ + zˆk A B A B B A = A 1 B 1 + A 2 B 2 + A 3 B 3 = A B θ θ A B = ˆn A B θ A B î ĵ ˆk = A 1 A 2 A 3 B 1 B 2 B 3 W = F
16 0 17 0 17 0 18 0 18 0 19 0 20 A A = A 1 î + A 2 ĵ + A 3ˆk A (x, y, z) r = xî + yĵ + zˆk A B A B B A = A 1 B 1 + A 2 B 2 + A 3 B 3 = A B θ θ A B = ˆn A B θ A B î ĵ ˆk = A 1 A 2 A 3 B 1 B 2 B 3 W = F
 k k ΚΕΦΑΛΑΙΟ 1 G = (V, E) V E V V V G E G e = {v, u} E v u e v u G G V (G) E(G) n(g) = V (G) m(g) = E(G) G S V (G) S G N G (S) = {u V (G)\S v S : {v, u} E(G)} G v S v V (G) N G (v) = N G ({v}) x V (G)
k k ΚΕΦΑΛΑΙΟ 1 G = (V, E) V E V V V G E G e = {v, u} E v u e v u G G V (G) E(G) n(g) = V (G) m(g) = E(G) G S V (G) S G N G (S) = {u V (G)\S v S : {v, u} E(G)} G v S v V (G) N G (v) = N G ({v}) x V (G)
Κλασσική Θεωρία Ελέγχου
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Ο μετασχηματισμός Laplace Νίκος Καραμπετάκης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Ο μετασχηματισμός Laplace Νίκος Καραμπετάκης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
4. Zapiši Eulerjeve dinamične enačbe za prosto osnosimetrično vrtavko. ω 2
 Mehanikateoretičnavprašanjainodgovori 1/12 Newtonovamehanika 1. Določiravninogibanjatočkevpoljucentralnesile. Ravninagibanjagreskozicentersileinimanormalovsmerivrtilne količine 2. Zapišiperiodogibanjapremočrtnegagibanjapodvplivompotenciala
Mehanikateoretičnavprašanjainodgovori 1/12 Newtonovamehanika 1. Določiravninogibanjatočkevpoljucentralnesile. Ravninagibanjagreskozicentersileinimanormalovsmerivrtilne količine 2. Zapišiperiodogibanjapremočrtnegagibanjapodvplivompotenciala
ΕΡΓΑΣΙΑ 6. Ημερομηνία Παράδοσης: 29/6/09
 ΕΡΓΑΣΙΑ 6 Ημερομηνία Παράδοσης: 9/6/9 1. Ένας ομογενώς φορτισμένος μονωτικός κυκλικός δίσκος ακτίνας με συνολικό φορτίο τοποθετείται στο επίπεδο xy. Να βρείτε το ηλεκτρικό πεδίο σε σημείο P που βρίσκεται
ΕΡΓΑΣΙΑ 6 Ημερομηνία Παράδοσης: 9/6/9 1. Ένας ομογενώς φορτισμένος μονωτικός κυκλικός δίσκος ακτίνας με συνολικό φορτίο τοποθετείται στο επίπεδο xy. Να βρείτε το ηλεκτρικό πεδίο σε σημείο P που βρίσκεται
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής Φυσική Σημασία του Μετασχηματισμού Fourier Ο μετασχηματισμός Fourier
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής Φυσική Σημασία του Μετασχηματισμού Fourier Ο μετασχηματισμός Fourier
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής Μετασχηματισμός Fourier Στο κεφάλαιο αυτό θα εισάγουμε και θα μελετήσουμε
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής Μετασχηματισμός Fourier Στο κεφάλαιο αυτό θα εισάγουμε και θα μελετήσουμε
,, 2015
 621.039.516.4-1000 05.14.14,, 2015 2.... 6..... 7 1. -1000...... 14 1.1. -1000 -... 14 1.2. - 15 1.2.1. 16 1.2.2. 17 1.2.3. -... 18 1.2.4. -. 20 1.3. -1000 -......... 23 1.4. - -1000... 26 1.5. - -1000.....
621.039.516.4-1000 05.14.14,, 2015 2.... 6..... 7 1. -1000...... 14 1.1. -1000 -... 14 1.2. - 15 1.2.1. 16 1.2.2. 17 1.2.3. -... 18 1.2.4. -. 20 1.3. -1000 -......... 23 1.4. - -1000... 26 1.5. - -1000.....
lim Δt Δt 0 da da da dt dt dt dt Αν ο χρόνος αυξηθεί κατά Δt το διάνυσμα θα γίνει Εξετάζουμε την παράσταση
 Έστω διάνυσμα a( t a ( t i a ( t j a ( t k Αν ο χρόνος αυξηθεί κατά Δt το διάνυσμα θα γίνει a( t Δt a ( t Δt i a ( t Δt j a ( t Δt k Εξετάζουμε την παράσταση z z a( t Δt - a( t Δa a ( t Δt - a ( t lim
Έστω διάνυσμα a( t a ( t i a ( t j a ( t k Αν ο χρόνος αυξηθεί κατά Δt το διάνυσμα θα γίνει a( t Δt a ( t Δt i a ( t Δt j a ( t Δt k Εξετάζουμε την παράσταση z z a( t Δt - a( t Δa a ( t Δt - a ( t lim
1.2. Сличност троуглова
 математик за VIII разред основне школе.2. Сличност троуглова Учили смо и дефиницију подударности два троугла, као и четири правила (теореме) о подударности троуглова. На сличан начин наводимо (без доказа)
математик за VIII разред основне школе.2. Сличност троуглова Учили смо и дефиницију подударности два троугла, као и четири правила (теореме) о подударности троуглова. На сличан начин наводимо (без доказа)
Bogoliubov-de Gennes
 Bogoliubov-de Gennes 7 Bogoliubov-de Gennes Bogoliubov H = H 0 + H = Ψ rh 0 rψ r +, Ψ rψ r g r r Ψ r Ψ r Ψ r r g r r r r h 0 h 0 h 0 = h i e m hc A + V r µ 3 Bogoliubov BCS BCS Ψ rψ r, Ψ rψ r 4 Cooper
Bogoliubov-de Gennes 7 Bogoliubov-de Gennes Bogoliubov H = H 0 + H = Ψ rh 0 rψ r +, Ψ rψ r g r r Ψ r Ψ r Ψ r r g r r r r h 0 h 0 h 0 = h i e m hc A + V r µ 3 Bogoliubov BCS BCS Ψ rψ r, Ψ rψ r 4 Cooper
 Molekulare Ebene (biochemische Messungen) Zelluläre Ebene (Elektrophysiologie, Imaging-Verfahren) Netzwerk Ebene (Multielektrodensysteme) Areale (MRT, EEG...) Gene Neuronen Synaptische Kopplung kleine
Molekulare Ebene (biochemische Messungen) Zelluläre Ebene (Elektrophysiologie, Imaging-Verfahren) Netzwerk Ebene (Multielektrodensysteme) Areale (MRT, EEG...) Gene Neuronen Synaptische Kopplung kleine
θβ1.0γθμθ81.β0 (07η.8) - - -, , 2015
 - Ч Ч Ы - 05 θβ.0γθμθ8.β0 (07η.8) μ.. (. 3, 4),.. (. 3, 4),.. (. 4),.. (. 3), Е.. (. 3),.. я (. 3, 4),.. я (. 4), Е.. я (. 4),.. (. 3),.. (. ),.. Ф (. )..:. /......μ -. -, 05. 78., «-»,, «-». μ -,, -,.,
- Ч Ч Ы - 05 θβ.0γθμθ8.β0 (07η.8) μ.. (. 3, 4),.. (. 3, 4),.. (. 4),.. (. 3), Е.. (. 3),.. я (. 3, 4),.. я (. 4), Е.. я (. 4),.. (. 3),.. (. ),.. Ф (. )..:. /......μ -. -, 05. 78., «-»,, «-». μ -,, -,.,
Δυναμική Μηχανών I. Διάλεξη 11. Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ
 Δυναμική Μηχανών I Διάλεξη 11 Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ 1 Περιεχόμενα Γραμμικοποίηση Ευστάθεια Απόκριση Συστημάτων 1 Β.Ε. που περιγράφονται από ΣΔΕ 1 ης τάξης 2 Πρόβλημα/Ερώτημα
Δυναμική Μηχανών I Διάλεξη 11 Χειμερινό Εξάμηνο 2013 Τμήμα Μηχανολόγων Μηχ., ΕΜΠ 1 Περιεχόμενα Γραμμικοποίηση Ευστάθεια Απόκριση Συστημάτων 1 Β.Ε. που περιγράφονται από ΣΔΕ 1 ης τάξης 2 Πρόβλημα/Ερώτημα
? 9 Ξ : Α : 4 < ; : ; 4 ϑ Α Λ Χ< : Χ 9 : Α Α Χ : ;: Ψ 8< ;: 9 : > Α ϑ < > = 8 Α;< 4 <9 Ξ : 9 : > Α 4 Α < >
 # % & ( ) ) +,. / 0, 1 / )., / 2 (& 3 5 % 6 6 7 8 : ; < : / : ; = 5 >
# % & ( ) ) +,. / 0, 1 / )., / 2 (& 3 5 % 6 6 7 8 : ; < : / : ; = 5 >
Vidyamandir Classes. Solutions to Revision Test Series - 2/ ACEG / IITJEE (Mathematics) = 2 centre = r. a
 Per -.(D).() Vdymndr lsses Solutons to evson est Seres - / EG / JEE - (Mthemtcs) Let nd re dmetrcl ends of crcle Let nd D re dmetrcl ends of crcle Hence mnmum dstnce s. y + 4 + 4 6 Let verte (h, k) then
Per -.(D).() Vdymndr lsses Solutons to evson est Seres - / EG / JEE - (Mthemtcs) Let nd re dmetrcl ends of crcle Let nd D re dmetrcl ends of crcle Hence mnmum dstnce s. y + 4 + 4 6 Let verte (h, k) then
8. ΜΑΓΝΗΤΙΣΜΟΣ. Φυσική ΙΙ Δ. Κουζούδης. Πρόβλημα 8.6.
 1 8. ΜΑΓΝΗΤΙΣΜΟΣ Πρόβλημα 8.6. Το σύρμα του παρακάτω σχήματος έχει άπειρο μήκος και διαρρέεται από ρεύμα I. Υπολογίστε με τη βοήθεια του νόμου του Biot-Savart με ολοκλήρωση το μέτρο και την κατεύθυνση
1 8. ΜΑΓΝΗΤΙΣΜΟΣ Πρόβλημα 8.6. Το σύρμα του παρακάτω σχήματος έχει άπειρο μήκος και διαρρέεται από ρεύμα I. Υπολογίστε με τη βοήθεια του νόμου του Biot-Savart με ολοκλήρωση το μέτρο και την κατεύθυνση
Смер: Друмски саобраћај. Висока техничка школа струковних студија у Нишу ЕЛЕКТРОТЕХНИКА СА ЕЛЕКТРОНИКОМ
 Испит из предмета Електротехника са електроником 1. Шест тачкастих наелектрисања Q 1, Q, Q, Q, Q 5 и Q налазе се у теменима правилног шестоугла, као на слици. Познато је: Q1 = Q = Q = Q = Q5 = Q ; Q 1,
Испит из предмета Електротехника са електроником 1. Шест тачкастих наелектрисања Q 1, Q, Q, Q, Q 5 и Q налазе се у теменима правилног шестоугла, као на слици. Познато је: Q1 = Q = Q = Q = Q5 = Q ; Q 1,
ΦΥΕ34 Λύσεις 5 ης Εργασίας
 ΦΥΕ3 Λύσεις 5 ης Εργασίας ) Έστω αρµονικό κύµα της (εκθετικής) µορφής: F( x, t) i( kx ωt+ ϕ ) = Ae. Παραγωγίζοντας βρίσκουµε: = iωf( x, t) t = ikf( x, t) x Παραγωγίζοντας αυτές τις δύο σχέσεις µία ακόµη
ΦΥΕ3 Λύσεις 5 ης Εργασίας ) Έστω αρµονικό κύµα της (εκθετικής) µορφής: F( x, t) i( kx ωt+ ϕ ) = Ae. Παραγωγίζοντας βρίσκουµε: = iωf( x, t) t = ikf( x, t) x Παραγωγίζοντας αυτές τις δύο σχέσεις µία ακόµη
ιανύσµατα A z A y A x 1.1 Αλγεβρικές πράξεις µεταξύ διανυσµάτων 1.2 Εσωτερικό γινόµενο δύο διανυσµάτων ca = ca x ˆx + ca y ŷ + ca z ẑ
 1 ιανύσµατα Ο ϕυσικός χώρος µέσα στον οποίο Ϲούµε και κινούµαστε είναι ένας τρισδιάστατος ευκλείδειος γραµµικός χώ- ϱος. Ισχύουν λοιπόν τα αξιώµατα της Γεωµετρίας του Ευκλείδη, το πυθαγόρειο ϑεώρηµα και
1 ιανύσµατα Ο ϕυσικός χώρος µέσα στον οποίο Ϲούµε και κινούµαστε είναι ένας τρισδιάστατος ευκλείδειος γραµµικός χώ- ϱος. Ισχύουν λοιπόν τα αξιώµατα της Γεωµετρίας του Ευκλείδη, το πυθαγόρειο ϑεώρηµα και
 γ 1 6 M = 0.05 F M = 0.05 F M = 0.2 F M = 0.2 F M = 0.05 F M = 0.05 F M = 0.05 F M = 0.2 F M = 0.05 F 2 2 λ τ M = 6000 M = 10000 M = 15000 M = 6000 M = 10000 M = 15000 1 6 τ = 36 1 6 τ = 102 1 6 M = 5000
γ 1 6 M = 0.05 F M = 0.05 F M = 0.2 F M = 0.2 F M = 0.05 F M = 0.05 F M = 0.05 F M = 0.2 F M = 0.05 F 2 2 λ τ M = 6000 M = 10000 M = 15000 M = 6000 M = 10000 M = 15000 1 6 τ = 36 1 6 τ = 102 1 6 M = 5000
У к у п н о :
 ГОДИШЊИ (ГЛОБАЛНИ) ПЛАН РАДА НАСТАВНИКА Наставни предмет: ФИЗИКА Разред: Седми Ред.број Н А С Т А В Н А Т Е М А / О Б Л А С Т Број часова по теми Број часова за остале обраду типове часова 1. КРЕТАЊЕ И
ГОДИШЊИ (ГЛОБАЛНИ) ПЛАН РАДА НАСТАВНИКА Наставни предмет: ФИЗИКА Разред: Седми Ред.број Н А С Т А В Н А Т Е М А / О Б Л А С Т Број часова по теми Број часова за остале обраду типове часова 1. КРЕТАЊЕ И
Κεφάλαιο 1 ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ. 1.1 Βασικές έννοιες και ορισμοί
 Κεφάλαιο 1 ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ Η έννοια της διαφορικής εξίσωσης εμφανίστηκε για πρώτη φορά στο νόμο του Νεύτωνα. Από τότε διαφορικές εξισώσεις ανακύπτουν σε όλες τις φυσικές επιστήμες, αλλά και
Κεφάλαιο 1 ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ Η έννοια της διαφορικής εξίσωσης εμφανίστηκε για πρώτη φορά στο νόμο του Νεύτωνα. Από τότε διαφορικές εξισώσεις ανακύπτουν σε όλες τις φυσικές επιστήμες, αλλά και
PEGASO WElcOmE to the WOrld Of WEGA
 Welcome to the world of wega PEGASO PEGASO Effective and reliable as any Wega, Wega Pegaso Opaque total black, with its modern color finish, introduces a new approach to coffee station and signifies a
Welcome to the world of wega PEGASO PEGASO Effective and reliable as any Wega, Wega Pegaso Opaque total black, with its modern color finish, introduces a new approach to coffee station and signifies a
Διάνυσμα: έχει μέτρο, διεύθυνση και φορά
 Διάνυσμα: έχει μέτρο, διεύθυνση και φορά Πολλά φυσικά μεγέθη είναι διανυσματικά (π.χ. δύναμη, ταχύτητα, επιτάχυνση, γωνιακή ταχύτητα, ροπή, στροφορμή ) Συμβολισμός του διανύσματος: Συμβολισμός του μέτρου
Διάνυσμα: έχει μέτρο, διεύθυνση και φορά Πολλά φυσικά μεγέθη είναι διανυσματικά (π.χ. δύναμη, ταχύτητα, επιτάχυνση, γωνιακή ταχύτητα, ροπή, στροφορμή ) Συμβολισμός του διανύσματος: Συμβολισμός του μέτρου
ÒÄÆÉÖÌÄ. ÀÒÀßÒ ÉÅÉ ÓÀÌÀÒÈÉ ÖÍØÝÉÏÍÀËÖÒ-ÃÉ ÄÒÄÍÝÉÀËÖÒÉ ÂÀÍÔÏËÄÁÄÁÉÓÈÅÉÓ ÃÀÌÔÊÉ- ÝÄÁÖËÉÀ ÀÌÏÍÀáÓÍÉÓ ÅÀÒÉÀÝÉÉÓ ÏÒÌÖËÄÁÉ, ÒÏÌËÄÁÛÉÝ ÂÀÌÏÅËÄÍÉËÉÀ ÓÀßÚÉÓÉ
 ÒÄÆÉÖÌÄ. ÀÒÀßÒ ÉÅÉ ÓÀÌÀÒÈÉ ÖÍØÝÉÏÍÀËÖÒ-ÃÉ ÄÒÄÍÝÉÀËÖÒÉ ÂÀÍÔÏËÄÁÄÁÉÓÈÅÉÓ ÃÀÌÔÊÉ- ÝÄÁÖËÉÀ ÀÌÏÍÀáÓÍÉÓ ÅÀÒÉÀÝÉÉÓ ÏÒÌÖËÄÁÉ, ÒÏÌËÄÁÛÉÝ ÂÀÌÏÅËÄÍÉËÉÀ ÓÀßÚÉÓÉ ÌÏÌÄÍÔÉÓÀ ÃÀ ÃÀÂÅÉÀÍÄÁÄÁÉÓ ÛÄÛ ÏÈÄÁÉÓ Ä ÄØÔÉ, ÀÂÒÄÈÅÄ
ÒÄÆÉÖÌÄ. ÀÒÀßÒ ÉÅÉ ÓÀÌÀÒÈÉ ÖÍØÝÉÏÍÀËÖÒ-ÃÉ ÄÒÄÍÝÉÀËÖÒÉ ÂÀÍÔÏËÄÁÄÁÉÓÈÅÉÓ ÃÀÌÔÊÉ- ÝÄÁÖËÉÀ ÀÌÏÍÀáÓÍÉÓ ÅÀÒÉÀÝÉÉÓ ÏÒÌÖËÄÁÉ, ÒÏÌËÄÁÛÉÝ ÂÀÌÏÅËÄÍÉËÉÀ ÓÀßÚÉÓÉ ÌÏÌÄÍÔÉÓÀ ÃÀ ÃÀÂÅÉÀÍÄÁÄÁÉÓ ÛÄÛ ÏÈÄÁÉÓ Ä ÄØÔÉ, ÀÂÒÄÈÅÄ
< = ) Τ 1 <Ο 6? <? Ν Α <? 6 ϑ<? ϑ = = Χ? 7 Π Ν Α = Ε = = = ;Χ? Ν !!! ) Τ 1. Ο = 6 Μ 6 < 6 Κ = Δ Χ ; ϑ = 6 = Σ Ν < Α <;< Δ Π 6 Χ6 Ο = ;= Χ Α
 # & ( ) ) +,. /, 1 /. 23 / 4 (& 5 6 7 8 8 9, :;< = 6 > < 6? ;< Β Γ Η. Ι 8 &ϑ Ε ; < 1 Χ6 Β 3 / Κ ;Χ 6 = ; Λ 4 ϑ < 6 Χ ; < = = Χ = Μ < = Φ ; ϑ =
# & ( ) ) +,. /, 1 /. 23 / 4 (& 5 6 7 8 8 9, :;< = 6 > < 6? ;< Β Γ Η. Ι 8 &ϑ Ε ; < 1 Χ6 Β 3 / Κ ;Χ 6 = ; Λ 4 ϑ < 6 Χ ; < = = Χ = Μ < = Φ ; ϑ =
Πανεπιστήμιο Αθηνών Τμήμα Φυσικής. Σημειώσεις I: Κίνηση σε τρεις διαστάσεις, στροφορμή
 Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Κβαντομηχανική ΙI Α. Καρανίκας και Π. Σφήκας Σημειώσεις I: Κίνηση σε τρεις διαστάσεις, στροφορμή 1. Κίνηση σε τρεις διαστάσεις Αποδεικνύεται (με τον ίδιο τρόπο όπως και
Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Κβαντομηχανική ΙI Α. Καρανίκας και Π. Σφήκας Σημειώσεις I: Κίνηση σε τρεις διαστάσεις, στροφορμή 1. Κίνηση σε τρεις διαστάσεις Αποδεικνύεται (με τον ίδιο τρόπο όπως και
46. РЕГИОНАЛЕН НАТПРЕВАР ПО ФИЗИКА април III година. (решенија на задачите)
 46. РЕГИОНАЛЕН НАТПРЕВАР ПО ФИЗИКА 3 април 3 III година (решенија на задачите) Задача. Хеликоптер спасува планинар во опасност, спуштајќи јаже со должина 5, и маса 8, kg до планинарот. Планинарот испраќа
46. РЕГИОНАЛЕН НАТПРЕВАР ПО ФИЗИКА 3 април 3 III година (решенија на задачите) Задача. Хеликоптер спасува планинар во опасност, спуштајќи јаже со должина 5, и маса 8, kg до планинарот. Планинарот испраќа
АКСИЈАЛНО НАПРЕГАЊЕ Катедра за техничка механика и јакост на материјалите
 УНИВЕРЗИТЕТ Св. КИРИЛ иметодиј ГРАДЕЖЕН ФАКУЛТЕТ СКОПЈЕ Катедра за техничка механика и јакост на материјалите http://ktmjm.gf.ukim.edu.mk АКСИЈАЛНО НАПРЕГАЊЕ 17.02.2015 АКСИЈАЛНО НАПРЕГАЊЕ КОГА??? АКСИЈАЛНО
УНИВЕРЗИТЕТ Св. КИРИЛ иметодиј ГРАДЕЖЕН ФАКУЛТЕТ СКОПЈЕ Катедра за техничка механика и јакост на материјалите http://ktmjm.gf.ukim.edu.mk АКСИЈАЛНО НАПРЕГАЊЕ 17.02.2015 АКСИЈАЛНО НАПРЕГАЊЕ КОГА??? АКСИЈАЛНО
МОБИЛНЕ МАШИНЕ I. ttl. хидростатички системи, хидростатичке компоненте: вентили, главни разводници, командни разводници.
 МОБИЛНЕ МАШИНЕ I предавање 8.2 \ хидростатички системи, хидростатичке компоненте: вентили, главни разводници, командни разводници Хидростатички погонски системи N e M e e N h p Q F M m m v m m F o M v
МОБИЛНЕ МАШИНЕ I предавање 8.2 \ хидростатички системи, хидростатичке компоненте: вентили, главни разводници, командни разводници Хидростатички погонски системи N e M e e N h p Q F M m m v m m F o M v
Παρελθόν. (Прошлое) В греческом языке существуют три грамматические
 12 Παρελθόν (Прошлое) В греческом языке существуют три грамматические времена (формы обоих ов) для выражения прошлого: прошедшее время (αόριστος), прошедшее длительное время (παρατατικός) и прошедшее совершенное
12 Παρελθόν (Прошлое) В греческом языке существуют три грамматические времена (формы обоих ов) для выражения прошлого: прошедшее время (αόριστος), прошедшее длительное время (παρατατικός) и прошедшее совершенное
Klausur Strömungslehre
 ...... Name, Matr.-Nr, Unterschrift Klausur Strömungslehre. 3.. Aufgabe a G F A G WV B + V L g G G W + V L g g B V L G g W B L p R T W p a + Wg + h R T W m L L V L m L G pa + Wg + h g W B R T W b G F A
...... Name, Matr.-Nr, Unterschrift Klausur Strömungslehre. 3.. Aufgabe a G F A G WV B + V L g G G W + V L g g B V L G g W B L p R T W p a + Wg + h R T W m L L V L m L G pa + Wg + h g W B R T W b G F A
ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ- ΜΕΘΟΔΟΣ ΕΠΙΛΥΣΗΣ ΠΡΟΒΛΗΜΑΤΩΝ
 Ιόνιο Πανεπιστήμιο - Τμήμα Πληροφορικής Μαθηματικός Λογισμός Ενότητα: ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ- ΜΕΘΟΔΟΣ ΕΠΙΛΥΣΗΣ ΠΡΟΒΛΗΜΑΤΩΝ Παναγιώτης Βλάμος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
Ιόνιο Πανεπιστήμιο - Τμήμα Πληροφορικής Μαθηματικός Λογισμός Ενότητα: ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ- ΜΕΘΟΔΟΣ ΕΠΙΛΥΣΗΣ ΠΡΟΒΛΗΜΑΤΩΝ Παναγιώτης Βλάμος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε
 k k ΚΕΦΑΛΑΙΟ 1 G = (V, E) V E V V V G E G e = {v, u} E v u e v u G G V (G) E(G) n(g) = V (G) m(g) = E(G) G S V (G) S G N G (S) = {u V (G)\S v S : {v, u} E(G)} G v S v V (G) N G (v) = N G ({v}) x V (G)
k k ΚΕΦΑΛΑΙΟ 1 G = (V, E) V E V V V G E G e = {v, u} E v u e v u G G V (G) E(G) n(g) = V (G) m(g) = E(G) G S V (G) S G N G (S) = {u V (G)\S v S : {v, u} E(G)} G v S v V (G) N G (v) = N G ({v}) x V (G)
МАТРИЧНА АНАЛИЗА КОНСТРУКЦИЈА
 Београд, 21.06.2014. За штап приказан на слици одредити најмању вредност критичног оптерећења P cr користећи приближан поступак линеаризоване теорије другог реда и: а) и један елемент, слика 1, б) два
Београд, 21.06.2014. За штап приказан на слици одредити најмању вредност критичног оптерећења P cr користећи приближан поступак линеаризоване теорије другог реда и: а) и један елемент, слика 1, б) два
Βρυξέλλες, 23Οκτωβρίου 2006.
 20.12.2006 Επίσημη Εφημερίδα της Ευρωπαϊκής Ένωσης L 362/67 ΟΔΗΓΙΑ 2006/80/ΕΚ ΤΗΣ ΕΠΙΤΡΟΠΗΣ της 23ης Οκτωβρίου 2006 για την προσαρμογή ορισμένων οδηγιών στον τομέα της ενέργειας, λόγω της προσχώρησης της
20.12.2006 Επίσημη Εφημερίδα της Ευρωπαϊκής Ένωσης L 362/67 ΟΔΗΓΙΑ 2006/80/ΕΚ ΤΗΣ ΕΠΙΤΡΟΠΗΣ της 23ης Οκτωβρίου 2006 για την προσαρμογή ορισμένων οδηγιών στον τομέα της ενέργειας, λόγω της προσχώρησης της
m i N 1 F i = j i F ij + F x
 N m i i = 1,..., N m i Fi x N 1 F ij, j = 1, 2,... i 1, i + 1,..., N m i F i = j i F ij + F x i mi Fi j Fj i mj O P i = F i = j i F ij + F x i, i = 1,..., N P = i F i = N F ij + i j i N i F x i, i = 1,...,
N m i i = 1,..., N m i Fi x N 1 F ij, j = 1, 2,... i 1, i + 1,..., N m i F i = j i F ij + F x i mi Fi j Fj i mj O P i = F i = j i F ij + F x i, i = 1,..., N P = i F i = N F ij + i j i N i F x i, i = 1,...,
T : g r i l l b a r t a s o s Α Γ Ί Α Σ Σ Ο Φ Ί Α Σ 3, Δ Ρ Α Μ Α. Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 0 1 : 0 0 π μ
 Α Γ Ί Α Σ Σ Ο Φ Ί Α Σ 3, Δ Ρ Α Μ Α g r i l l b a r t a s o s Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 1 : 0 π μ Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 0 1 : 0 0 π μ T ortiyas Σ ο υ
Α Γ Ί Α Σ Σ Ο Φ Ί Α Σ 3, Δ Ρ Α Μ Α g r i l l b a r t a s o s Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 1 : 0 π μ Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 0 1 : 0 0 π μ T ortiyas Σ ο υ
ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ & ΠΕΔΙΑ
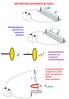 ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ & ΠΕΔΙΑ =0 Αλληλεπιδράσεις μαγνητών με ηλεκτρικά ρεύματα Αλληλεπιδράσεις μαγνητών με κινούμενα ηλεκτρικά φορτία Οι αλληλεπιδράσεις συμβαίνουν μόνον όταν τα ηλεκτρικά φορτία είναι κινούμενα
ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ & ΠΕΔΙΑ =0 Αλληλεπιδράσεις μαγνητών με ηλεκτρικά ρεύματα Αλληλεπιδράσεις μαγνητών με κινούμενα ηλεκτρικά φορτία Οι αλληλεπιδράσεις συμβαίνουν μόνον όταν τα ηλεκτρικά φορτία είναι κινούμενα
Ενότητα 4: Κεντρικές διατηρητικές δυνάμεις
 Ενότητα 4: Κεντρικές διατηρητικές δυνάμεις Έστω F=f κεντρικό πεδίο δυνάμεων. Είναι εύκολο να δείξουμε ότι F=0, δηλ. είναι διατηρητικό: F= V. Σε σφαιρικές συντεταγμένες, γενικά: V ma = F =, V maθ = Fθ =,
Ενότητα 4: Κεντρικές διατηρητικές δυνάμεις Έστω F=f κεντρικό πεδίο δυνάμεων. Είναι εύκολο να δείξουμε ότι F=0, δηλ. είναι διατηρητικό: F= V. Σε σφαιρικές συντεταγμένες, γενικά: V ma = F =, V maθ = Fθ =,
2. Наставни колоквијум Задаци за вежбање ОЈЛЕРОВА МЕТОДА
 . колоквијум. Наставни колоквијум Задаци за вежбање У свим задацима се приликом рачунања добија само по једна вредност. Одступање појединачне вредности од тачне вредности је апсолутна грешка. Вредност
. колоквијум. Наставни колоквијум Задаци за вежбање У свим задацима се приликом рачунања добија само по једна вредност. Одступање појединачне вредности од тачне вредности је апсолутна грешка. Вредност
Κεφάλαιο 3 Κίνηση σε 2 και 3 Διαστάσεις
 Κεφάλαιο 3 Κίνηση σε και 3 Διαστάσεις Κίνηση υλικού σημείου στο επίπεδο ( -D) και στο χώρο (3 -D). Ορισμός διανυσμάτων για την μελέτη της -D 3-D κίνησης: Θέση, Μετατόπιση Μέση και στιγμιαία ταχύτητα Μέση
Κεφάλαιο 3 Κίνηση σε και 3 Διαστάσεις Κίνηση υλικού σημείου στο επίπεδο ( -D) και στο χώρο (3 -D). Ορισμός διανυσμάτων για την μελέτη της -D 3-D κίνησης: Θέση, Μετατόπιση Μέση και στιγμιαία ταχύτητα Μέση
CITY. 7x70. 6x60. arbor ARBOR LTD BULGARIA, ASENOVGRAD BUL. BALGARIA 98V. baby furniture
 ITY M M1 M 7x70 6x60 M M arbor baby furniture www.arbor-bg.com ROR LTD LGRI, NOVGRD L. LGRI 98V ITY N 716-1:008+1:01 G Не използвайте това легло, ако не можете да следвате точно съпътстващите го инструкции.
ITY M M1 M 7x70 6x60 M M arbor baby furniture www.arbor-bg.com ROR LTD LGRI, NOVGRD L. LGRI 98V ITY N 716-1:008+1:01 G Не използвайте това легло, ако не можете да следвате точно съпътстващите го инструкции.
Σήματα και Συστήματα. Διάλεξη 13: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 13: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace 1. Επίλυση Γραμμικών
Σήματα και Συστήματα Διάλεξη 13: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Laplace 1. Επίλυση Γραμμικών
Teor imov r. ta matem. statist. Vip. 94, 2016, stor
 eor imov r. ta matem. statist. Vip. 94, 6, stor. 93 5 Abstract. e article is devoted to models of financial markets wit stocastic volatility, wic is defined by a functional of Ornstein-Ulenbeck process
eor imov r. ta matem. statist. Vip. 94, 6, stor. 93 5 Abstract. e article is devoted to models of financial markets wit stocastic volatility, wic is defined by a functional of Ornstein-Ulenbeck process
( () () ()) () () ()
 ΑΝΑΛΥΣΗ ΙΙ- ΠΟΛΙΤΙΚΟΙ ΜΗΧΑΝΙΚΟΙ ΦΥΛΛΑΔΙΟ /011 1 Έστω r = r( t = ( x( t ( t z( t t I = [ a b] συνάρτηση C τάξης και r = r( t = r ( t = x ( t + ( t z ( t είναι μία διανυσματική + Nα αποδείξετε ότι: d 1 1
ΑΝΑΛΥΣΗ ΙΙ- ΠΟΛΙΤΙΚΟΙ ΜΗΧΑΝΙΚΟΙ ΦΥΛΛΑΔΙΟ /011 1 Έστω r = r( t = ( x( t ( t z( t t I = [ a b] συνάρτηση C τάξης και r = r( t = r ( t = x ( t + ( t z ( t είναι μία διανυσματική + Nα αποδείξετε ότι: d 1 1
ΑΠΑΝΤΗΣΕΙΣ ΓΡΑΠΤΗΣ ΕΞΕΤΑΣΗΣ ΣΤΗ ΦΥΣΙΚΗ
 ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 4// ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΑΠΑΝΤΗΣΕΙΣ ΓΡΑΠΤΗΣ ΕΞΕΤΑΣΗΣ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ α) Για δεδομένη αρχική ταχύτητα υ, με ποια γωνία
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 4// ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΑΠΑΝΤΗΣΕΙΣ ΓΡΑΠΤΗΣ ΕΞΕΤΑΣΗΣ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ α) Για δεδομένη αρχική ταχύτητα υ, με ποια γωνία
m r = F m r = F ( r) m r = F ( v) F = F (x) m dv dt = F (x) vdv = F (x)dx d dt = dx dv dt dx = v dv dx
 m r = F m r = F ( r) m r = F ( v) x F = F (x) m dv dt = F (x) d dt = dx dv dt dx = v dv dx vdv = F (x)dx 2 mv2 x 2 mv2 0 = F (x )dx x 0 K = 2 mv2 W x0 x = x x 0 F (x)dx K K 0 = W x0 x x, x 2 x K 2 K =
m r = F m r = F ( r) m r = F ( v) x F = F (x) m dv dt = F (x) d dt = dx dv dt dx = v dv dx vdv = F (x)dx 2 mv2 x 2 mv2 0 = F (x )dx x 0 K = 2 mv2 W x0 x = x x 0 F (x)dx K K 0 = W x0 x x, x 2 x K 2 K =
1. Τριγωνοµετρικές ταυτότητες.
 . Τριγωνοµετρικές ταυτότητες. co( y co( co( y i( i( y i( y i( co( y co( i( y ± m (. ± ± (. π m (. 3 co ± i( i ± π ± co( (. co( co ( i ( (. 5 i( i( co( (. 6 j j co( + (. 7 j j j i ( (. 8 ( ( y ( y + ( +
. Τριγωνοµετρικές ταυτότητες. co( y co( co( y i( i( y i( y i( co( y co( i( y ± m (. ± ± (. π m (. 3 co ± i( i ± π ± co( (. co( co ( i ( (. 5 i( i( co( (. 6 j j co( + (. 7 j j j i ( (. 8 ( ( y ( y + ( +
Писмени испит из Теорије површинских носача. 1. За континуалну плочу приказану на слици одредити угиб и моменте савијања у означеним тачкама.
 Београд, 24. јануар 2012. 1. За континуалну плочу приказану на слици одредити угиб и моменте савијања у означеним тачкама. dpl = 0.2 m P= 30 kn/m Линијско оптерећење се мења по синусном закону: 2. За плочу
Београд, 24. јануар 2012. 1. За континуалну плочу приказану на слици одредити угиб и моменте савијања у означеним тачкама. dpl = 0.2 m P= 30 kn/m Линијско оптерећење се мења по синусном закону: 2. За плочу
ΑΠΑΝΤΗΣΕΙΣ ΓΡΑΠΤΗΣ ΕΞΕΤΑΣΗΣ ΣΤΗ ΦΥΣΙΚΗ
 ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 4// ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΑΠΑΝΤΗΣΕΙΣ ΓΡΑΠΤΗΣ ΕΞΕΤΑΣΗΣ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ α) Για δεδομένη αρχική ταχύτητα υ, με ποια γωνία
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 4// ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΑΠΑΝΤΗΣΕΙΣ ΓΡΑΠΤΗΣ ΕΞΕΤΑΣΗΣ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ α) Για δεδομένη αρχική ταχύτητα υ, με ποια γωνία
C M. V n: n =, (D): V 0,M : V M P = ρ ρ V V. = ρ
 »»...» -300-0 () -300-03 () -3300 3.. 008 4 54. 4. 5 :.. ;.. «....... :. : 008. 37.. :....... 008.. :. :.... 54. 4. 5 5 6 ... : : 3 V mnu V mn AU 3 m () ; N (); N A 6030 3 ; ( ); V 3. : () 0 () 0 3 ()
»»...» -300-0 () -300-03 () -3300 3.. 008 4 54. 4. 5 :.. ;.. «....... :. : 008. 37.. :....... 008.. :. :.... 54. 4. 5 5 6 ... : : 3 V mnu V mn AU 3 m () ; N (); N A 6030 3 ; ( ); V 3. : () 0 () 0 3 ()
CHAPTER (2) Electric Charges, Electric Charge Densities and Electric Field Intensity
 CHAPTE () Electric Chrges, Electric Chrge Densities nd Electric Field Intensity Chrge Configurtion ) Point Chrge: The concept of the point chrge is used when the dimensions of n electric chrge distriution
CHAPTE () Electric Chrges, Electric Chrge Densities nd Electric Field Intensity Chrge Configurtion ) Point Chrge: The concept of the point chrge is used when the dimensions of n electric chrge distriution
Welcome to the. of wega
 Welcome to the world of wega ATLAS Simple and essential, but with a professional core that can always meet the highest demands. Thanks to its minimalist linear design, Atlas adapts perfectly to any context
Welcome to the world of wega ATLAS Simple and essential, but with a professional core that can always meet the highest demands. Thanks to its minimalist linear design, Atlas adapts perfectly to any context
και A = 1 Το πρόβλημα των μη ομογενών συνοριακών συνθηκών.
 Στις δύο διαστάσεις αφετηρία είναι η σχέση r + r r r A r + q r q Grr (, = ln ln L L (6 από την οποία μπορούμε να προσδιορίσουμε ότι και επομένως R R q = r, L r = L και A = r (7 r + r r r Grr (, = ln rr
Στις δύο διαστάσεις αφετηρία είναι η σχέση r + r r r A r + q r q Grr (, = ln ln L L (6 από την οποία μπορούμε να προσδιορίσουμε ότι και επομένως R R q = r, L r = L και A = r (7 r + r r r Grr (, = ln rr
ВИСОКА ТЕХНИЧКА ШКОЛА СТРУКОВНИХ СТУДИЈА У НИШУ
 ВИСОКА ТЕХНИЧКА ШКОЛА СТРУКОВНИХ СТУДИЈА У НИШУ предмет: МЕХАНИКА 1 студијски програми: ЗАШТИТА ЖИВОТНЕ СРЕДИНЕ И ПРОСТОРНО ПЛАНИРАЊЕ ПРЕДАВАЊЕ БРОЈ 3. 1 Садржај предавања: Статичка одређеност задатака
ВИСОКА ТЕХНИЧКА ШКОЛА СТРУКОВНИХ СТУДИЈА У НИШУ предмет: МЕХАНИКА 1 студијски програми: ЗАШТИТА ЖИВОТНЕ СРЕДИНЕ И ПРОСТОРНО ПЛАНИРАЊЕ ПРЕДАВАЊЕ БРОЈ 3. 1 Садржај предавања: Статичка одређеност задатака
 W τ R W j N H = 2 F obj b q N F aug F obj b q Ψ F aug Ψ ( ) ϱ t + + p = 0 = 0 Ω f = Γ Γ b ϱ = (, t) = (, t) Ω f Γ b ( ) ϱ t + + p = V max 4 3 2 1 0-1 -2-3 -4-4 -3-2 -1 0 1 2 3 4 x 4 x 1 V mn V max
W τ R W j N H = 2 F obj b q N F aug F obj b q Ψ F aug Ψ ( ) ϱ t + + p = 0 = 0 Ω f = Γ Γ b ϱ = (, t) = (, t) Ω f Γ b ( ) ϱ t + + p = V max 4 3 2 1 0-1 -2-3 -4-4 -3-2 -1 0 1 2 3 4 x 4 x 1 V mn V max
Minion Pro Condensed A B C D E F G H I J K L M N O P Q R S T U
 Minion Pro Condensed Latin capitals A B C D E F G H I J K L M N O P Q R S T U V W X Y Z & Æ Ł Ø Œ Þ Ð Á Â Ä À Å Ã Ç É Ê Ë È Í Î Ï Ì İ Ñ Ó Ô Ö Ò Õ Š Ú Û Ü Ù Ý Ÿ Ž Ă Ā Ą Ć Č Ď Đ Ě Ė Ē Ę Ğ Ģ Ī Į Ķ Ĺ Ľ Ļ Ń
Minion Pro Condensed Latin capitals A B C D E F G H I J K L M N O P Q R S T U V W X Y Z & Æ Ł Ø Œ Þ Ð Á Â Ä À Å Ã Ç É Ê Ë È Í Î Ï Ì İ Ñ Ó Ô Ö Ò Õ Š Ú Û Ü Ù Ý Ÿ Ž Ă Ā Ą Ć Č Ď Đ Ě Ė Ē Ę Ğ Ģ Ī Į Ķ Ĺ Ľ Ļ Ń
BX-30T. Box Fan Aνεμιστήρας Box Вентилатор Box INSTRUCTION MANUAL ΒΙΒΛΙΟ ΟΔΗΓΙΩΝ ИНСТРУКЦИИ ЗА ЕКСПЛОАТАЦИЯ
 BX-30T Box Fan Aνεμιστήρας Box Вентилатор Box GB GR BG INSTRUCTION MANUAL ΒΙΒΛΙΟ ΟΔΗΓΙΩΝ ИНСТРУКЦИИ ЗА ЕКСПЛОАТАЦИЯ GB ENGLISH... 3 GR EΛΛΗΝΙΚΑ... 7 BG БЪЛГАРСКИ...11 ENGLISH PLEASE READ THESE INSTRUCTIONS
BX-30T Box Fan Aνεμιστήρας Box Вентилатор Box GB GR BG INSTRUCTION MANUAL ΒΙΒΛΙΟ ΟΔΗΓΙΩΝ ИНСТРУКЦИИ ЗА ЕКСПЛОАТАЦИЯ GB ENGLISH... 3 GR EΛΛΗΝΙΚΑ... 7 BG БЪЛГАРСКИ...11 ENGLISH PLEASE READ THESE INSTRUCTIONS
!!" #7 $39 %" (07) ..,..,.. $ 39. ) :. :, «(», «%», «%», «%» «%». & ,. ). & :..,. '.. ( () #*. );..,..'. + (# ).
 1 00 3 !!" 344#7 $39 %" 6181001 63(07) & : ' ( () #* ); ' + (# ) $ 39 ) : : 00 %" 6181001 63(07)!!" 344#7 «(» «%» «%» «%» «%» & ) 4 )&-%/0 +- «)» * «1» «1» «)» ) «(» «%» «%» + ) 30 «%» «%» )1+ / + : +3
1 00 3 !!" 344#7 $39 %" 6181001 63(07) & : ' ( () #* ); ' + (# ) $ 39 ) : : 00 %" 6181001 63(07)!!" 344#7 «(» «%» «%» «%» «%» & ) 4 )&-%/0 +- «)» * «1» «1» «)» ) «(» «%» «%» + ) 30 «%» «%» )1+ / + : +3
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
 l 0 l 2 l 1 l 1 l 1 l 2 l 2 l 1 l p λ λ µ R N l 2 R N l 2 2 = N x i l p p R N l p N p = ( x i p ) 1 p i=1 l 2 l p p = 2 l p l 1 R N l 1 i=1 x 2 i 1 = N x i i=1 l p p p R N l 0 0 = {i x i 0} R
l 0 l 2 l 1 l 1 l 1 l 2 l 2 l 1 l p λ λ µ R N l 2 R N l 2 2 = N x i l p p R N l p N p = ( x i p ) 1 p i=1 l 2 l p p = 2 l p l 1 R N l 1 i=1 x 2 i 1 = N x i i=1 l p p p R N l 0 0 = {i x i 0} R
Εισαγωγή στην Ανάλυση και Προσοµοίωση Δυναµικών Συστηµάτων
 Εισαγωγή στην Ανάλυση και Προσοµοίωση Δυναµικών Συστηµάτων Control Systems Laboratory Περιγραφή Δυναµικών Συστηµάτων Εξίσωση µεταβολής όγκου Η µεταβολή όγκου ισούται µε τη παροχή υγρού Q που σχετίζεται
Εισαγωγή στην Ανάλυση και Προσοµοίωση Δυναµικών Συστηµάτων Control Systems Laboratory Περιγραφή Δυναµικών Συστηµάτων Εξίσωση µεταβολής όγκου Η µεταβολή όγκου ισούται µε τη παροχή υγρού Q που σχετίζεται
C кплп (Кпндензатпр у кплу прпстпперипдичне струје)
 C кплп (Кпндензатпр у кплу прпстпперипдичне струје) i u За кплп са слике на крајевима кпндензатпра ппзнате капацитивнпсти C претппставићемп да делује ппзнат прпстпперипдичан наппн: u=u m sin(ωt + ϴ). Услед
C кплп (Кпндензатпр у кплу прпстпперипдичне струје) i u За кплп са слике на крајевима кпндензатпра ппзнате капацитивнпсти C претппставићемп да делује ппзнат прпстпперипдичан наппн: u=u m sin(ωt + ϴ). Услед
Εισαγωγή στην Ανάλυση και Προσοµοίωση Δυναµικών Συστηµάτων
 Εισαγωγή στην Ανάλυση και Προσοµοίωση Δυναµικών Συστηµάτων Control Systems Laboratory Περιγραφή Δυναµικών Συστηµάτων Εξίσωση µεταβολής όγκου Η µεταβολή όγκου ισούται µε τη παροχή υγρού Q που σχετίζεται
Εισαγωγή στην Ανάλυση και Προσοµοίωση Δυναµικών Συστηµάτων Control Systems Laboratory Περιγραφή Δυναµικών Συστηµάτων Εξίσωση µεταβολής όγκου Η µεταβολή όγκου ισούται µε τη παροχή υγρού Q που σχετίζεται
6. Αρµονικός ταλαντωτής
 6 Αρµονικός ταλαντωτής Βιβλιογραφία Kittel, W D Knight, A Ruderman, A Helmholz και B J oyer, Μηχανική Πανεπιστηµιακές Εκδόσεις ΕΜΠ, 998 Κεφ 7 F S rawford Jr, Κυµατική Σειρά Μαθηµάτων Φυσικής Berkeley,
6 Αρµονικός ταλαντωτής Βιβλιογραφία Kittel, W D Knight, A Ruderman, A Helmholz και B J oyer, Μηχανική Πανεπιστηµιακές Εκδόσεις ΕΜΠ, 998 Κεφ 7 F S rawford Jr, Κυµατική Σειρά Μαθηµάτων Φυσικής Berkeley,
ΦΥΣ. 211 Τελική Εξέταση 20-Μάη-2016
 ΦΥΣ. Τελική Εξέταση 0-Μάη-06 Πριν ξεκινήσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο, αριθµό ταυτότητας) στο πάνω µέρος της σελίδας αυτής. Για τις λύσεις των ασκήσεων θα πρέπει να χρησιµοποιήσετε µόνο
ΦΥΣ. Τελική Εξέταση 0-Μάη-06 Πριν ξεκινήσετε συµπληρώστε τα στοιχεία σας (ονοµατεπώνυµο, αριθµό ταυτότητας) στο πάνω µέρος της σελίδας αυτής. Για τις λύσεις των ασκήσεων θα πρέπει να χρησιµοποιήσετε µόνο
Универзитет у Крагујевцу Факултет за машинство и грађевинарство у Краљеву Катедра за основне машинске конструкције и технологије материјала
 Теоријски део: Вежба број ТЕРМИЈСКА AНАЛИЗА. Термијска анализа је поступак који је 903.год. увео G. Tamman за добијање криве хлађења(загревања). Овај поступак заснива се на принципу промене топлотног садржаја
Теоријски део: Вежба број ТЕРМИЈСКА AНАЛИЗА. Термијска анализа је поступак који је 903.год. увео G. Tamman за добијање криве хлађења(загревања). Овај поступак заснива се на принципу промене топлотног садржаја
8 η Διάλεξη Ηλεκτρομαγνητική ακτινοβολία, φαινόμενα συμβολής, περίθλαση
 11//17 8 η Διάλεξη Ηλεκτρομαγνητική ακτινοβολία, φαινόμενα συμβολής, περίθλαση Φίλιππος Φαρμάκης Επ. Καθηγητής 1 Ηλεκτρομαγνητισμός Πως συνδέονται ο ηλεκτρισμός με τον μαγνητισμό; Πως παράγονται τα κύματα;
11//17 8 η Διάλεξη Ηλεκτρομαγνητική ακτινοβολία, φαινόμενα συμβολής, περίθλαση Φίλιππος Φαρμάκης Επ. Καθηγητής 1 Ηλεκτρομαγνητισμός Πως συνδέονται ο ηλεκτρισμός με τον μαγνητισμό; Πως παράγονται τα κύματα;
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
Количина топлоте и топлотна равнотежа
 Количина топлоте и топлотна равнотежа Топлота и количина топлоте Топлота је један од видова енергије тела. Енергија коју тело прими или отпушта у топлотним процесима назива се количина топлоте. Количина
Количина топлоте и топлотна равнотежа Топлота и количина топлоте Топлота је један од видова енергије тела. Енергија коју тело прими или отпушта у топлотним процесима назива се количина топлоте. Количина
