Dreptul și condiţiile de muncă în Grecia pentru cetățenii statelor membre U.E.
|
|
|
- Ἀγαπητός Μπλέτσας
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Dreptul și condiţiile de muncă în Grecia pentru cetățenii statelor membre U.E. Cetăţenii români pot munci cu drepturi depline în Grecia. Autorităţile elene au ridicat de la 1 ianuarie 2009 restricţiile pe piaţa muncii greceşti pentru muncitorii români şi bulgari. Permisul de muncă nu mai este deci obligatoriu pe teritoriul Repulicii Elene. Condiţiile de angajare în Grecia Grecia este o republică parlamentară, cu capitala la Atena, a cărei singură limbă oficială este limba greacă. Ca împărțire administrativă, țara este formată din 13 provincii, împărțite la rândul lor în 51 de prefecturi. Pe lângă cele 13 provincii, există și o regiune autonomă, Muntele Athos, un stat monastic sub suveranitate grecească. Moneda oficială a statului este euro. Dacă doriți să lucrați în Grecia, trebuie să știți că aveți exact aceleași drepturi ca un cetățean grec. Puteți intra în Grecia pe baza cărții de identitate sau a pașaportului valabil, iar la accesul pe piața muncii nu aveți nici o restricție. Așadar, aveți aceleași drepturi salariale, condiții de muncă, orar de lucru, liber acces la asigurările sociale și locuințe. De aceleași drepturi se bucură și membrii de familie ai salariatului român (soție, soţ, copii sau persoanele aflate în întreținere). Totuși, dacă doriți să rămâneți mai mult timp, aveți nevoie de carte de rezidență pentru cetățeni europeni. Acest document se eliberează pe o durată de 5 ani sau pe perioadă nedeterminată. În vederea obținerii cărții de rezidență pentru cetățeni europeni sunt necesare următoarele acte: cerere depusă la primăria municipală sau locală sau la poliția locală unde aveți rezidența (după caz) în care trebuie menţionate motivele care stau la baza cererii; copie după paşaport sau carte de identitate; documente de atestare a locului de muncă; extras de cont care dovedește posibilitatea de întreţinere; dovada existenţei unui spaţiu de locuit; certificat de naştere; certificat de căsătorie; după caz, alte documente solicitate de autorități. Programul de lucru săptămânal pentru persoanele salariate nu poate depăşi 48 de ore, incluzând orele suplimentare, şi pentru o perioadă de cel mult 4 luni. În cazul unui orar de lucru de 40 de ore săptămânale, salariatul poate munci 5 ore suplimentare / săptămână, care vor fi plătite la valoarea de 125% din tariful normal / oră. Dacă se depăşeşte limita de 45 de ore săptămânale, numărul de ore suplimentare anuale inferioare sau egale cu 120 va fi calculat la o valoare de 150% din tariful normal / oră, respectiv 175% din tariful normal / oră dacă limita de 120 de ore suplimentare anuale este depăşită. Orarul zilnic de lucru nu poate fi mai mare de 10 ore, iar o pauză de minimum 15 minute este garantată dacă orarul zilnic de muncă depăşeşte 6 ore, timp în care angajatul are dreptul de a părăsi locul de muncă. Nu se lucrează duminica şi în zilele de sărbătoare legală, excepţie făcând anumite domenii de activitate. Codul muncii elen prevede ca orice angajat să aibă dreptul de a beneficia de concediul de odihnă anual. Sunt prevăzute şi garantate prin legislaţie, minimum 24 de zile lucrătoare de concediu / an, respectiv de 20 de zile lucrătoare (pentru salariaţii care lucrează în regim de 5 zile / săptămână). La acestea se adaugă 13 zile libere de sărbători legale, de-a lungul întregului an. 1
2 Legislaţia elenă garantează persoanelor care lucrează dreptul şi la alte forme de repaos profesional, precum concediul de maternitate (de 16 săptămâni, începând cu ultimele 8 săptămâni înainte de naştere) sau concediul parental, care permite tuturor părinţilor angajaţi în sectorul privat dreptul la un maximum de 3 luni şi jumătate de concediu parental fără plată pentru fiecare copil sub 3 ani. Această cerere de concediu este valabilă doar dacă unul dintre părinţi a fost angajat cel puţin un an într-o companie cu cel puţin 50 de angajaţi, iar celălalt părinte este de asemenea angajat. Acest tip de concediu este acordat potrivit unei liste de priorităţi, întocmită în ordinea înscrierilor. Alte 4 zile libere pot fi solicitate de către salariaţii cu copii sub 16 ani, pentru participarea la evenimente şcolare. De reţinut faptul că angajatele cu copii sub 2 ani pot veni cu o oră mai târziu la locul de muncă şi pot pleca cu o oră mai devreme, sau pot beneficia de o pauză de o oră în timpul programului de lucru, pentru a-şi putea alăpta sugarii. În caz de probleme de sănătate, se poate solicita un concediu de boală, a cărui durată depinde de vechimea la locul de muncă la ultimul angajator. Dacă salariatul este înscris la cursuri de dezvoltare profesională, acestuia i se poate acorda şi un concediu de formare profesională. Lucrătorul mai poate solicita concediu şi pentru alte evenimente familiale, precum căsătoria (minimum 5 zile) sau ziua de naştere (1 zi). În plus, orice salariat are dreptul de a cere concediu pentru a-şi căuta un loc de muncă, indiferent de felul în care se sfârşeşte colaborarea cu angajatorul (ajungerea la termen a contractului, concediere, şomaj, demisie). Sistemul de asigurări sociale în Grecia Legislaţia elenă impune ca obligatorie asigurarea medicală. Astfel, orice lucrător salariat trebuie să se asigure la Institutul de Securitate Socială din Grecia (IKA) încă din prima zi de muncă, formalităţile fiind realizate de angajator, în termen de maximum 3 zile de la angajare. Persoana asigurată la IKA are dreptul de a beneficia de îngrijiri de sănătate (medicală, farmaceutică, de spital, dentară, medicamente de prevenire şi de îngrijire medicală adiţională), dar şi de a se bucura de diverse tipuri de ajutoare financiare sub forma alocaţiilor (de maternitate, de graviditate şi de naştere, de boală şi de accidente, de înmormântare şi pensii). De reţinut, însă, este că atât angajatorul cât şi angajatul contribuie separat, lunar, la IKA. Cotizaţiile sociale sunt plătite de către fiecare salariat în parte, angajatorul fiind obligat să anunţe departamentul local IKA dacă observă nereguli în ceea ce priveşte contribuţia salariaţilor săi. Cotizaţiile sociale sunt calculate în funcţie de venitul câştigat şi de zilele de muncă lucrate. Contribuţia constantă la celelalte forme de asigurări sociale obligatorii, prevăzute de sistemul de asigurări din Grecia (asigurarea de boală, asigurarea de maternitate, asigurarea pentru accidente de muncă şi boli profesionale), conferă dreptul de a beneficia de alocaţii specifice precum şi de la alte beneficii (în natură şi/sau în bani). Astfel, asigurarea de boală permite solicitarea unei alocaţii de boală (pentru care numărul de zile, respectiv valoarea ajutorului financiar, variază în funcţie de boala de care suferă asiguratul şi de numărul de ani de vechime). Asigurarea de maternitate acoperă perioada maternităţii şi acordă femeilor asigurate o protecţie financiară, în timpul sarcinii, la naştere, după naştere, sub formă de: alocaţii de naştere (acoperă costul tratamentului la spital sau pentru naşterea acasă), alocaţii de maternitate (suma fiind de 30 de ori salariul zilnic al lucrătorului necalificat şi majorată cu 10% pentru fiecare membru de familie dependent), sau indemnizaţie de graviditate şi lăuzie. În schimb asigurarea pentru accidente de muncă şi boli profesionale prevede forme de alocaţii de boală, acordate: asiguratului, în cazul unei boli profesionale, chiar dacă contribuţia a fost de 2
3 doar 1 zi; familiei asiguratului decedat, în cazul în care moartea acestuia s-a datorat fie unui accident industrial, fie unei boli ocupaţionale, chiar dacă, şi în acest caz, contribuţia a fost de doar 1 zi (alocaţie de deces, pensie de urmaş). Alte beneficii în bani oferite de asigurarea obligatorie la IKA constă în: alocaţie familială; alocaţie de şomaj (200 euro/lună, până la un maxim de 12 luni); pensie; împrumuturi ipotecare; alocaţii de căsătorie, pentru turism social şi pentru divertisment. Decizia de a munci în străinătate necesită o analiză atentă în ceea ce priveşte validitatea ofertei, modalitatea de plecare (printr-o agenţie de recrutare, pe cont propriu), sau normele şi regulile în vigoare din elen. Cu atât mai importantă este însă conştientizarea avantajelor de a munci întotdeauna legal. În cazul unor litigii de muncă, cetățenii români au la dispoziție următoarele coordonate: Formular de inscriere on-line: Telefon asistență inspectorat: & 282 (orar cu publicul 09:00-15:00) Linie telefonică plângeri inspectorat: (orar cu publicul 09:00-17:00) Adrese Inspectoratul Muncii: 1) Probleme sociale (Remunerați, Disponibilizări, Contracte de muncă, Declarații personale, etc) kysepes3@otenet.gr 2) Aplicarea legilor pentru protecția, sănătatea și securitatea angajaților (Accidente de muncă,tehnici pentru ocuparea forței de muncă și Medici specialiști în medicina muncii, etc) kysepetye@ypakp.gr 3) Probleme legate de managmentului personalului, Educație, Buget, Asistență juridică și tehnică kysepes2@otenet.gr Ministerul Muncii, Securității și Protecției Sociale include și Inspecția Muncii (Σ.ΕΠ.Ε), care are ca scop sprijinirea,investigarea și urmărirea penală a încălcări legislații muncii, ocupării forței de muncă ilegale și a muncii nedeclarate atât în sectorul public cât și în sectorul privat. LISTA CU ADRESELE ȘI NUMERELE DE CONTACT ALE ULUI MUNCII DIN GRECIA 3
4 MINISTERUL MUNCII PROTECȚIEI ȘI ASISTENȚEI E din GRECIA Adresa: Str. Pireos nr. 40, Atena Telefon: , Responsabilitățile Ministerului Muncii, Securității și Protecției Sociale cuprind: - Contractele individuale și colective de muncă - Respectarea orelor de muncă stabilite prin lege - Egalitatea între sexe și egalitatea de șanse - Servicii pentru ocuparea forței de muncă - Integrarea socială a lucrătorilor străini în Grecia - Protecția socială și reabilitarea unor categorii speciale - Facilitarea pentru ocuparea forței de muncă a persoanelor cu handicap - Accidente de muncă - Orientare profesională - Prevenirea accidentelor și bolilor profesionale de muncă - Managementul Uniunii Europene și alte resurse legate de dezvoltarea resurselor umane - Reprezentarea Greciei în cadrul Organizației Internaționale a Muncii (OIM) LISTA CU ADRESELE ȘI NUMERELE DE CONTACT ALE ELOR MUNCII DIN GRECIA DEPATAMENTUL Tabel cu adresa, telefon și fax Centrul regional al Inspectoratului Muncii din Grecia (Σ.ΕΠ.Ε) 4
5 Formular de inscriere on-line: Telefon asistență inspectorat: & 282 (orar cu publicul 09:00-15:00) Linie telefonică plângeri inspectorat: (orar cu publicul 09:00-17:00) Adrese Inspectoratul Muncii: 1) Probleme sociale (Remunerați, Disponibilizări, Contracte de muncă, Declarații personale, etc) 2) Aplicarea legilor pentru protecția, sănătatea și securitatea angajaților (Accidente de muncă,tehnici pentru ocuparea forței de muncă și Medici specialiști în medicina muncii, etc) 3) Probleme legate de managmentului personalului, Educație, Buget, Asistență juridică și tehnică ORAR CU PUBLICUL: LUNI VINERI 09:00-13:00 ADRESELE ULUI MUNCII BIROU ADRESA COD TELEFON FAX ADRESA ULUI MUNCII din ATENA PATISION Nr. 37 (etajul 2) POȘTAL & AG. ANARGYRON AG. PARASCHEIVA KORONEU Nr tkeaganarg@yeka.gr MESOGHION Nr tkeagpar@yeka.gr SECȚIA SECTORUL ESTIC ATENA SECȚIA SECTORUL VESTIC ATENA PATISION Nr. 37 (etajul 2) AGHISILAU 10 (etajul 1) tkeanatath@yeka.gr / tkedytath@yeka.gr , 147, & SECȚIA GLYFADA D. GUNARI Nr. 219 & TIRTEU Nr tkegglifadas@yeka.gr & SECȚIA DAFNI SECȚIA KALLITHEA SECȚIA NEA IONIA ALKAMENUS Nr tkedafnis@yeka.gr & ARAPAKI Nr tkealith@yeka.gr BDUL. IRAKLIU tkeperist@yeka.gr & & 28 OCTOBRIU 279 SECȚIA HRISOLORA Nr tkeperist@yeka.gr
6 PERISTERIU PIREU KATHOLIKIS EKKLISIAS Nr tkekenpir@yeka.gr SECȚIUNEA SECTORUL CENTRU-PIREU KATHOLIKIS EKKLISIAS Nr tkekenpir@yeka.gr SECȚIUNEA SECTORUL NORDIC-PIREU BDUL. DIMOKRATIAS Nr. 22 & PAPANASTASIU tkenotpir@yeka.gr SECȚIUNEA NIKEA MADITU Nr tkenikeas@yeka.gr ATTIKI EST TINU Nr. 9, PALLINI dkeanat@yeka.gr SECȚIUNEA PALINI TINU Nr tkepalinis@yeka.gr SECȚIUNEA ANIXIS SECȚIUNEA LAVRIU ELLINIKU STRATU Nr. 7 AGIAS PARASKEVIS Nr tkeanixis@yeka.gr tkelavriou@yeka.gr ATTIKIS VEST KONDULI Nr.1, ELEFSINA dkedytat@yeka.gr SECȚIUNEA KONDULI Nr tkeelefs@yeka.gr
7 ELEFSINA SECȚIUNEA LIOSION NORDUL MACEDONIEI- TRACIA RODOPI DRAMA EVRU KAVALA XANTHI M. ALEXANDRU Nr. 55, ZOFRIA & NORDUL MACEDONIEI și TRACIEI MITROPOLITUL MARONIAS BASILIU Nr. 3A, KOMOTINI MITROPOLITUL MARONIAS BASILIU Nr. 3A, KOMOTINI THEMISTOKLUS Nr. 2 DRAMA 14 MAIU Nr , ALEXANDRUPOLI OMONIAS Nr. 117, KAVALA G. STAVRU Nr , XANTHI dkeanmakth@yeka.gr tkerodopis@yeka.gr tkedramas@yeka.gr & tkeevrou@yeka.gr tkekavalas@yeka.gr tkexathis@yeka.gr & CENTRUL MACEDONIEI CENTRUL MACEDONIEI FRAGKON Nr.14, SALONIC dkekenmak@yeka.gr &
8 SECTORUL NORDIC SALONIC SECTORUL VESTIC SALONIC SECTORUL CENTRAL SALONIC 25 MARTIU Nr AISOPU Nr PROX. KOROMILA Nr & SINDU IMATHIA KILKIS PELLAS PIERIAS SERRON HALKIDIKI VESTUL MACEDONIEI MONASTIRIU Nr. 248, SALONIC MITROPOLEOS Nr. 48, VERIA ARISTIDU Nr. 8, KILKIS FLORINIS Nr. 6, EDESSA KASSANDRU Nr.23, KATERINI M. ALEXANDRU Nr.2 SERRES CONSANTINOPOLE OS Nr. 5, POLIGYROS VEROIAS Nr. 8, KOZANI ARISTOTELUS Nr. 36& VERIAS Nr tkesindou@yeka.gr tkeimath@yeka.gr & tkekilkis@yeka.gr tkepelas@yeka.gr tkepierias@yeka.gr tkeser@yeka.gr tkechalk@yeka.gr & dkedytmak@yeka.gr tkekoz@yeka.gr &
9 KOZANI GREVENON KASTORIA FLORIA PTOLEMAIDA DIOIKITIRIO, GREVENA KHIPRU Nr. 3, KASTORIA IOANNU ARTI Nr.4, FLORINA AGHIAS TRIADOS Nr.17, PTOLEMAIDA & & IPIRU (EPIR) IOANINA ARTA THESPROTIA PREVEZA SALAMANGKA Nr.1, IOANINA REGIUNEA EPIR ,24,26,27 SALAMANGKA Nr ,21,25,28,29 NICOALE ANGHELU Nr.3 & STUDITU, ARTA P.TSALDARI Nr.28 IGUMENITSA A. BAKATSELU Nr. 4, PREVEZA & & & THESSALIA FARSALON Nr.6, LARISA FARSALON Nr
10 LARISA KARDITSA MAGNISIA TRIKALA INSULELE IONICE G.BOTSI Nr.10, KARDITSA ELEFTERIU VENIZELOS Nr.2, VOLOS SOKRATUS Nr.35, TRIKALA CONSTANTIN ZABITSIANU Nr.17, CORFU & INSULELE IONICE &81600 CORFU ZAKHINTOS KEFALONIA & ITHAKI LEFKADA CONSTANTIN ZABITSIANU Nr.17 KUMUTU Nr.6, ZAKHINTOS ANTINOROS Nr.1 & LITHOSTROTU, ARGOSTOLI KEFALONIA 1 PAR. PEFANEROMENIS & AGHIOD PANTELEIMONOS, LEFKADA tkekerk@yeka.gr tkezakin@yeka.gr tkekefith@yeka.gr & tkelefk@yeka.gr GRECIA DE VEST NEA ETHN. ODOS PATRON-ATHINON Nr. 12, PATRA GRECIA DE VEST dkedytel@yeka.gr &
11 ACHAIA ETOLOAKARNANIA ILIA AGRINIU NEA ETHN. ODOS PATRON-ATHINON Nr. 12, PATRA KHIPRU Nr.27, MESOLOGGHI THEMISTOKLEUS Nr.2, PIRGOS ILIA ILIU Nr.10, AGRINIU ,95,96, GRECIA CENTRALĂ FTIOTIDA VIOTIA EVIA EVRITANIA THIVA FOKIDA LIKURGU Nr.6, LAMIA LIKURGU Nr.6, LAMIA SPIRIDONOS Nr.7, LIVADIA ELEFTERIU VENIZELOS & BELUSSARIU Nr.2, HALKIDA Clădirea OAED KARPENISIU EPAMINONDA Nr.17, THIVA K. SATHA Nr.6, AMFISSA GRECIA CENTRALĂ , 76555, & REGIUNEA PELOPONEZ 11
12 PELOPONEZ ARKADIA ARGOLIDA CORINT LAKONIA MESSINIA PLAT. KOLOKOTRONI Nr.20, TRIPOLI PLAT. KOLOKOTRONI Nr.20, TRIPOLI MEGALO ALEXANDRU Nr.12, NAFPLIO PERIANDRU Nr.50, CORINT VRASIDU Nr.78, SPARTA SOLONOS Nr.19, KALAMATA & & & NORDUL EGEEI LESVOS SAMOS CHIOS INSULELE DIN EGEEA DE NORD ELEFTERIU VENIZELOS Nr.2, MITHILINI ELEFTERIU VENIZELOS Nr.2, MITHILINI NIKOLAREIZI & KANARI, SAMOS KOKKALI Nr.2 & KUVELA, CHIOS IU Nr.5 ERMUPOLI SIRU INSULELE CICLADE
13 INSULELE CICLADE SIROS ANDROS THIRAS MILOS NAXOS IU Nr.5 ERMUPOLI SIRU ARISTIDU EMBIRIKU, ANDROS MESARIA TIRAS HORA MILU, PLAKA HORA NAXOS INSULELE DODECANEZE RODOS KOS KALIMNOS KARPATHOS INSULELE DODECANEZE GHEORGHIU MAVRU Nr.2, RODOS GHEORGHIU MAVRU Nr.2 MEROPIDOS Nr.2, KOS ANASTASI KALIMNU T.Θ.149, AVLA PIGADIA, KARPATHOS PLATIA AGHIA EKATERINA Nr.9, IRAKLIO INSULA CRETA &
14 INSULELE DODECANEZE IRAKLIO LASITHI RETHYMNO CHANIA PLATIA AGHIA EKATERINA & SFAKIANAKI, IRAKLIO EPIMENIDU Nr.12A, AGHIOS NIKOLAOS KUNDURIOTI Nr.148, RETHYMNO XANTUDIDU Nr.28, CHANIA & LISTA CU ADRESELE ȘI NUMERELE DE CONTACT ALE ELOR MUNCII DIN GRECIA 14
15 DEPATAMENTUL DE PREVENIRE A RISCURILOR PROFESIONALE TECHNIC-SĂNĂTATE CENTRULUI DE PREVENIRE A RISCURILOR - MACEDONIA- TRACIA DRAMA EVRU IMATHIA KAVALA KASTORIA PIERIAS SERRON HALKIDIKI KOZANI REGIUNEA MACEDONIA - TRACIA FRAGKON Nr.14, SALONIC TEMISTOKLEUS Nr.2, DRAMA 14 MAIU Nr , ALEXANDRUPOLI MITROPOLEOS Nr. 48, VERIA OMONIAS Nr. 117, KAVALA KHIPRU Nr. 3, KASTORIA KASSANDRU Nr.23, KATERINI M. ALEXANDRU Nr.2 SERRES CONSANTINOPOLEOS Nr. 5, POLIGYROS VERIAS Nr. 8, KOZANI kepekmak@otenet.gr & sepedra@otenet.gr & texepeb1@otenet.gr ttyever@otenet.gr sepekav@otenet.gr kepek37@otenet.gr ttyekat@otenet.gr kepek22@otenet.gr & ttyex@otenet.gr & ttekoz@otenet.gr
16 PELLAS FLORINIS Nr. 6, EDESSA CENTRULUI DE PREVENIRE A RISCURILOR- GRECIA CENTRALĂ VIOTIA EVIA MAGNISIA TRIKALA FTIOTIDA EVRITANIA FOKIDA FARSALON Nr.6, LARISA SPIRIDONOS Nr.7, LIVADIA ELEFTERIU VENIZELOS & BELUSSARIU Nr.2, HALKIDA ELEFTERIU VENIZELOS Nr.2, VOLOS SOKRATUS Nr.35, TRIKALA LIKURGU Nr.6, LAMIA Clădirea OAED KARPENISIU K. SATHA Nr.6, AMFISSA kepekkel@otenet.gr & ttyeboio@otenet.gr & tteevia@otenet.gr ttyemag@otenet.gr , & ttyet@otenet.gr & & ttyefth@otenet.gr & ttueeur@otenet.gr ttyefok@otenet.gr CENTRULUI DE PREVENIRE A RISCURILOR ATENA CRETA IRAKLIO AGHISILAU Nr. 10, ATENA PLATIA AGHIA EKATERINA & SFAKIANAKI, IRAKLIO ypou89@otenet.gr ttyeher@otenet.gr XANTUDIDU Nr.28, ypou88@otenet.gr
17 CHANIA CHANIA CENTRULUI DE PREVENIRE A RISCURILOR PIREU INSULELE DIN EGEEA DE SUD ANDROS CICLADE KATHOLIKIS EKKLISIAS Nr.1, PIREU ARISTIDU EMBIRIKU, ANDROS IU Nr.5 ERMUPOLI SIRU kepekpir@otenet.gr gtyeandrou@yeka.gr ttyekykl@otenet.gr & CENTRULUI DE PREVENIRE A RISCURILOR ESTUL ATTIKI INSULELE DIN EGEEA DE NORD SAMOS CHIOS TINU Nr.9, PALLINI NIKOLAREIZI & KANARI, SAMOS KOKKALI Nr.2 & KUVELA, CHIOS kepekan1@otenet.gr ttyesam@otenet.gr ttyexioy@otenet.gr CENTRULUI DE PREVENIRE A RISCURILOR VESTUL ATTIKI PELOPONEZ ARGOLIDA ETHNIKIS ANTISTASEOS & IKARU Nr.20, ELEFSINA MEGALO ALEXANDRU Nr.12, NAFPLIO sepekdat@otenet.gr & & spetear@otenet.gr & CORINT PERIANDRU Nr.50, CORINT sepetkor@otenet.gr
18 MESSINIA ARKADIA SOLONOS Nr.19, KALAMATA PLAT. KOLOKOTRONI Nr.20, TRIPOLI CENTRULUI DE PREVENIRE A RISCURILOR VESTUL GRECIEI EPIR şi INSULELE IONICE ETOLOAKARNANIA ARTA ILIA IOANINA NEA ETHN. ODOS PATRON-ATHINON Nr. 12, PATRA KHIPRU Nr.27, MESOLOGGHI NICOALE ANGHELU Nr.3 & STUDITU, ARTA THEMISTOKLEUS Nr.2, PIRGOS SALAMANGKA Nr.1, IOANINA kepekded@otenet.gr & & ttyeaith@otenet.gr ttyearta@otenet.gr ttyeilia@yeka.gr & ttyeioan@otenet.gr CABINETUL CENTRAL AL ULUI MUNCII DIN 18
19 SECRETARIATUL PRINCIPAL GRECIA BIROU ADRESA COD POSTAL AGHISILAU Nr.10 (etajul 4), ATENA TELEFON FAX INSPECTORI SPECIALI AGHISILAU Nr.10 (etajul 3-4), ATENA (etajul 4) ,200-3, 206-9, 272 TEHNIC (etajul 3) DIRECŢIA DE PLANIFICARE ŞI COORDONARE A INSPECŢIEI E DIRECŢIA DE PLANIFICARE ŞI COORDONARE A INSPECŢIEI TEHNICE şi de SĂNĂTATE DIRECŢIA DE ADMINISTRATIVĂ & ASISTENŢĂ TEHNICĂ AGHISILAU Nr.10 (etajul 5), ATENA AGHISILAU Nr.10 (etajul 3), ATENA AGHISILAU Nr.10 (DEALIGIOGI NEOCLASSIKO), ATENA kysepes3@otenet.gr ,273, 228, kysepetye@ypakp.gr , 273, 228, kysepetye@ypakp.gr LOGISTICĂ ŞI ASISTENŢĂ , 270, ASISTENŢĂ JURIDICĂ , ASISTENŢĂ TEHNICĂ
MINISTÈRE DES AFFAIRES ÉTRANGÈRES DU ROYAUME DES PAYS-BAS LA HAYE
 MINISTÈRE DES AFFAIRES ÉTRANGÈRES DU ROYAUME DES PAYS-BAS LA HAYE CONVENTION SUPPRIMANT L EXIGENCE DE LA LÉGALISATION DES ACTES PUBLICS ÉTRANGERS (La Haye, le 5 octobre 1961) Notification conformément
MINISTÈRE DES AFFAIRES ÉTRANGÈRES DU ROYAUME DES PAYS-BAS LA HAYE CONVENTION SUPPRIMANT L EXIGENCE DE LA LÉGALISATION DES ACTES PUBLICS ÉTRANGERS (La Haye, le 5 octobre 1961) Notification conformément
επενδύστε στην εταιρία που κινεί τις εξελίξεις στην αγορά!
 επενδύστε στην εταιρία που κινεί τις εξελίξεις στην αγορά! Our philosophy Γνωρίστε το μεγαλύτερο όμιλο πλακιδίων και ειδών υγιεινής στην Ελλάδα Η PORCELANA, μέλος του ομίλου επιχειρήσεων XATZHΓΕΩΡΓΙΟΥ
επενδύστε στην εταιρία που κινεί τις εξελίξεις στην αγορά! Our philosophy Γνωρίστε το μεγαλύτερο όμιλο πλακιδίων και ειδών υγιεινής στην Ελλάδα Η PORCELANA, μέλος του ομίλου επιχειρήσεων XATZHΓΕΩΡΓΙΟΥ
GHIDUL LUCRĂTORULUI ROMÂN ÎN REPUBLICA ELENĂ
 GHIDUL LUCRĂTORULUI ROMÂN ÎN REPUBLICA ELENĂ Republica Elenă I Informaţii privind piaţa muncii din Grecia 1. Unde se găsesc posturi vacante? OAED (Agenţia Pentru Ocuparea Forţei de Muncă) în Grecia constituie
GHIDUL LUCRĂTORULUI ROMÂN ÎN REPUBLICA ELENĂ Republica Elenă I Informaţii privind piaţa muncii din Grecia 1. Unde se găsesc posturi vacante? OAED (Agenţia Pentru Ocuparea Forţei de Muncă) în Grecia constituie
Προσθήκες οικοδοµών Extensions of Built - properties. 'Ογκος Volume
 Σύνολο Χώρας 0 72.1 1.10.2.2 Greece, Total ΑΝΑΤΟΛΙΚΗ ΜΑΚΕ ΟΝΙΑ & ΘΡΑΚΗ 7 0.71 10.02 0.0 EASTERN MAKEDONIA AND THRAKI ΝΟΜΟΣ ΡΑΜΑΣ ΝΟΜΟΣ ΚΑΒΑΛΑΣ ΝΟΜΟΣ ΕΒΡΟΥ ΝΟΜΟΣ ΞΑΝΘΗΣ ΝΟΜΟΣ ΡΟ ΟΠΗΣ ΚΕΝΤΡΙΚΗ ΜΑΚΕ ΟΝΙΑ
Σύνολο Χώρας 0 72.1 1.10.2.2 Greece, Total ΑΝΑΤΟΛΙΚΗ ΜΑΚΕ ΟΝΙΑ & ΘΡΑΚΗ 7 0.71 10.02 0.0 EASTERN MAKEDONIA AND THRAKI ΝΟΜΟΣ ΡΑΜΑΣ ΝΟΜΟΣ ΚΑΒΑΛΑΣ ΝΟΜΟΣ ΕΒΡΟΥ ΝΟΜΟΣ ΞΑΝΘΗΣ ΝΟΜΟΣ ΡΟ ΟΠΗΣ ΚΕΝΤΡΙΚΗ ΜΑΚΕ ΟΝΙΑ
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
 Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Προσθήκες οικοδοµών Extensions of Built - properties. 'Ογκος Volume 4.930 3.801.376 968.144 29.792 2.563 957 1.803.342 966.319
 Table 2. Extensions of built-properties, storeys, volume, surface and value thereon, by geographic region. Σύνολο Χώρας 16.778 16.546 12.322.582 3.116.192 81.223 Greece, Total ΑΤΤΙΚΗ ΝΟΜΑΡΧΙΑ ΑΘΗΝΩΝ ΝΟΜΑΡΧΙΑ
Table 2. Extensions of built-properties, storeys, volume, surface and value thereon, by geographic region. Σύνολο Χώρας 16.778 16.546 12.322.582 3.116.192 81.223 Greece, Total ΑΤΤΙΚΗ ΝΟΜΑΡΧΙΑ ΑΘΗΝΩΝ ΝΟΜΑΡΧΙΑ
Διεθνής Οργανισμός Μετανάστευσης
 Ο Διεθνής Οργανισμός Μετανάστευσης είναι ο κυρίαρχος Διεθνής Οργανισμός στον τομέα της μετανάστευσης και δραστηριοποιείται προς αυτήν την κατεύθυνση παρέχοντας υπηρεσίες και συμβουλευτικό ρόλο στις κυβερνήσεις
Ο Διεθνής Οργανισμός Μετανάστευσης είναι ο κυρίαρχος Διεθνής Οργανισμός στον τομέα της μετανάστευσης και δραστηριοποιείται προς αυτήν την κατεύθυνση παρέχοντας υπηρεσίες και συμβουλευτικό ρόλο στις κυβερνήσεις
Νέες οικοδοµές New Built - properties. 'Ογκος Volume
 Table 1. New built-properties, storeys, volume, surface and value thereon, by geographic region. Σύνολο Χώρας 3.637 8.016 5.9.012 1.493.551 54.638.975 Greece, Total ΑΤΤΙΚΗ ΝΟΜΑΡΧΙΑ ΑΘΗΝΩΝ ΝΟΜΑΡΧΙΑ ΑΝΑΤΟΛΙΚΗΣ
Table 1. New built-properties, storeys, volume, surface and value thereon, by geographic region. Σύνολο Χώρας 3.637 8.016 5.9.012 1.493.551 54.638.975 Greece, Total ΑΤΤΙΚΗ ΝΟΜΑΡΧΙΑ ΑΘΗΝΩΝ ΝΟΜΑΡΧΙΑ ΑΝΑΤΟΛΙΚΗΣ
Νέες οικοδοµές New Built - properties. 'Ογκος Volume
 Table 1. New built-properties, storeys, volume, surface and value thereon, by geographic region. Σύνολο Χώρας 2.725 5.499 4.363.712 1.150.6 46.939.888 Greece, Total ΑΤΤΙΚΗ ΝΟΜΑΡΧΙΑ ΑΘΗΝΩΝ ΝΟΜΑΡΧΙΑ ΑΝΑΤΟΛΙΚΗΣ
Table 1. New built-properties, storeys, volume, surface and value thereon, by geographic region. Σύνολο Χώρας 2.725 5.499 4.363.712 1.150.6 46.939.888 Greece, Total ΑΤΤΙΚΗ ΝΟΜΑΡΧΙΑ ΑΘΗΝΩΝ ΝΟΜΑΡΧΙΑ ΑΝΑΤΟΛΙΚΗΣ
Νέες οικοδοµές New Built - properties. 'Ογκος Volume
 Table 1. New built-properties, storeys, volume, surface and value thereon, by geographic region. Σύνολο Χώρας 3.540 7.469 5.7.361 1.450.177 56.494.211 Greece, Total ΑΤΤΙΚΗ ΝΟΜΑΡΧΙΑ ΑΘΗΝΩΝ ΝΟΜΑΡΧΙΑ ΑΝΑΤΟΛΙΚΗΣ
Table 1. New built-properties, storeys, volume, surface and value thereon, by geographic region. Σύνολο Χώρας 3.540 7.469 5.7.361 1.450.177 56.494.211 Greece, Total ΑΤΤΙΚΗ ΝΟΜΑΡΧΙΑ ΑΘΗΝΩΝ ΝΟΜΑΡΧΙΑ ΑΝΑΤΟΛΙΚΗΣ
Προσθήκες οικοδοµών Extensions of Built - properties. 'Ογκος Volume
 Table. Extensions of built-properties, storeys, volume, surface and value thereon, by geographic region. Σύνολο Χώρας 1.44 1. 1..48 8.4.04.68 Greece, Total ΑΤΤΙΚΗ ΝΟΜΑΡΧΙΑ ΑΘΗΝΩΝ ΝΟΜΑΡΧΙΑ ΑΝΑΤΟΛΙΚΗΣ ΑΤΤΙΚΗΣ
Table. Extensions of built-properties, storeys, volume, surface and value thereon, by geographic region. Σύνολο Χώρας 1.44 1. 1..48 8.4.04.68 Greece, Total ΑΤΤΙΚΗ ΝΟΜΑΡΧΙΑ ΑΘΗΝΩΝ ΝΟΜΑΡΧΙΑ ΑΝΑΤΟΛΙΚΗΣ ΑΤΤΙΚΗΣ
'Ογκος Volume. Επιφάνεια Surface 9.384 1.267.272 381.424 4 660.875 196.966 112.399 372.398 1.929 PREFECTURE OF EASTERN ATTIKI ΝΟΜΑΡΧΙΑ ΥΤΙΚΗΣ ΑΤΤΙΚΗΣ
 κατά διοικητική περιφέρεια και νοµό. Μάρτιος 5 Table 4. New dwellings and improvements of dwellings, number of habitable volume and surface thereon, by geographic region. March 5 Όγκος σε µ3, επιφάνεια
κατά διοικητική περιφέρεια και νοµό. Μάρτιος 5 Table 4. New dwellings and improvements of dwellings, number of habitable volume and surface thereon, by geographic region. March 5 Όγκος σε µ3, επιφάνεια
Προσθήκες οικοδοµών Extensions of Built - properties. 'Ογκος Volume
 Ιούλιος 0 Table 2. Extensions of built-properties, storeys, volume, surface and value thereon, by geographic region. July 0 Σύνολο Χώρας 2.002 2. 1.951.92 440..59.53 Greece, Total ΑΤΤΙΚΗ ΝΟΜΑΡΧΙΑ ΑΘΗΝΩΝ
Ιούλιος 0 Table 2. Extensions of built-properties, storeys, volume, surface and value thereon, by geographic region. July 0 Σύνολο Χώρας 2.002 2. 1.951.92 440..59.53 Greece, Total ΑΤΤΙΚΗ ΝΟΜΑΡΧΙΑ ΑΘΗΝΩΝ
Προσθήκες οικοδοµών Extensions of Built - properties. 'Ογκος Volume
 εκέµβριος 06 Table. Extensions of built-properties, storeys, volume, surface and value thereon, by geographic region. December 06 Σύνολο Χώρας..6.63. 0. 6.0. Greece, Total ΑΤΤΙΚΗ ΝΟΜΑΡΧΙΑ ΑΘΗΝΩΝ ΝΟΜΑΡΧΙΑ
εκέµβριος 06 Table. Extensions of built-properties, storeys, volume, surface and value thereon, by geographic region. December 06 Σύνολο Χώρας..6.63. 0. 6.0. Greece, Total ΑΤΤΙΚΗ ΝΟΜΑΡΧΙΑ ΑΘΗΝΩΝ ΝΟΜΑΡΧΙΑ
'Ογκος Volume. Επιφάνεια Surface PREFECTURE OF EASTERN ATTIKI ΝΟΜΑΡΧΙΑ ΥΤΙΚΗΣ ΑΤΤΙΚΗΣ
 κατά διοικητική περιφέρεια και νοµό. Ιούλιος 26 Table 4. New dwellings and improvements of dwellings, number of habitable volume and surface thereon, by geographic region. July 26 in m3, surface in m2
κατά διοικητική περιφέρεια και νοµό. Ιούλιος 26 Table 4. New dwellings and improvements of dwellings, number of habitable volume and surface thereon, by geographic region. July 26 in m3, surface in m2
'Ογκος Volume. Επιφάνεια Surface PREFECTURE OF EASTERN ATTIKI ΝΟΜΑΡΧΙΑ ΥΤΙΚΗΣ ΑΤΤΙΚΗΣ
 κατά διοικητική περιφέρεια και νοµό. εκέµβριος 5 Table 4. New dwellings and improvements of dwellings, number of habitable volume and surface thereon, by geographic region. December 5 in m3, surface in
κατά διοικητική περιφέρεια και νοµό. εκέµβριος 5 Table 4. New dwellings and improvements of dwellings, number of habitable volume and surface thereon, by geographic region. December 5 in m3, surface in
Προσθήκες οικοδοµών Extensions of Built - properties. 'Ογκος Volume
 Πίνακας., όροφοι, όγκος, επιφάνεια και αξία αυτών, κατά διοικητική περιφέρεια και νοµό. Αύγουστος 00 Table. Extensions of built-properties, storeys, volume, surface and value thereon, by geographic region.
Πίνακας., όροφοι, όγκος, επιφάνεια και αξία αυτών, κατά διοικητική περιφέρεια και νοµό. Αύγουστος 00 Table. Extensions of built-properties, storeys, volume, surface and value thereon, by geographic region.
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
 Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
NUTS 2013 Code NUTS 1 NUTS 2 NUTS 3
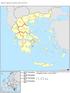 GREECE NUTS 2013 Code NUTS 1 NUTS 2 NUTS 3 EL3 EL30 EL301 EL302 EL303 EL304 EL305 EL306 EL307 EL4 EL41 EL411 EL412 EL413 EL42 EL421 EL422 EL43 EL431 EL432 EL433 EL434 EL5 EL51 EL511 EL512 EL513 EL514 EL515
GREECE NUTS 2013 Code NUTS 1 NUTS 2 NUTS 3 EL3 EL30 EL301 EL302 EL303 EL304 EL305 EL306 EL307 EL4 EL41 EL411 EL412 EL413 EL42 EL421 EL422 EL43 EL431 EL432 EL433 EL434 EL5 EL51 EL511 EL512 EL513 EL514 EL515
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
 1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
riptografie şi Securitate
 riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
GRECIA. Sistemul de securitate socială
 GRECIA Sistemul de securitate socială Asigurările sociale sunt obligatorii şi toţi cetăţenii sunt protejaţi. Există trei sisteme: sistemul asigurărilor sociale pentru protecţia salariaţilor, sistemul de
GRECIA Sistemul de securitate socială Asigurările sociale sunt obligatorii şi toţi cetăţenii sunt protejaţi. Există trei sisteme: sistemul asigurărilor sociale pentru protecţia salariaţilor, sistemul de
COLEGIUL NATIONAL CONSTANTIN CARABELLA TARGOVISTE. CONCURSUL JUDETEAN DE MATEMATICA CEZAR IVANESCU Editia a VI-a 26 februarie 2005.
 SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
Metode iterative pentru probleme neliniare - contractii
 Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Valori limită privind SO2, NOx şi emisiile de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili
 Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
Curs 4 Serii de numere reale
 Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
5.4. MULTIPLEXOARE A 0 A 1 A 2
 5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile
 Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
 Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Curs 1 Şiruri de numere reale
 Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
III. Serii absolut convergente. Serii semiconvergente. ii) semiconvergentă dacă este convergentă iar seria modulelor divergentă.
 III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
5. FUNCŢII IMPLICITE. EXTREME CONDIŢIONATE.
 5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
Integrala nedefinită (primitive)
 nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
Asupra unei inegalităţi date la barajul OBMJ 2006
 Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
 Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
 Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii transversale, scrisă faţă de una dintre axele de inerţie principale:,
 REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
a. 11 % b. 12 % c. 13 % d. 14 %
 1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
Subiecte Clasa a VII-a
 lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
Εμπορική αλληλογραφία Ηλεκτρονική Αλληλογραφία
 - Εισαγωγή Stimate Domnule Preşedinte, Stimate Domnule Preşedinte, Εξαιρετικά επίσημη επιστολή, ο παραλήπτης έχει ένα ειδικό τίτλο ο οποίος πρέπει να χρησιμοποιηθεί αντί του ονόματος του Stimate Domnule,
- Εισαγωγή Stimate Domnule Preşedinte, Stimate Domnule Preşedinte, Εξαιρετικά επίσημη επιστολή, ο παραλήπτης έχει ένα ειδικό τίτλο ο οποίος πρέπει να χρησιμοποιηθεί αντί του ονόματος του Stimate Domnule,
MARCAREA REZISTOARELOR
 1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
 5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
Μπορώ να κάνω ανάληψη στην [χώρα] χωρίς να πληρώσω προμήθεια; Informează dacă există comisioane bancare la retragere numerar într-o anumită țară
![Μπορώ να κάνω ανάληψη στην [χώρα] χωρίς να πληρώσω προμήθεια; Informează dacă există comisioane bancare la retragere numerar într-o anumită țară Μπορώ να κάνω ανάληψη στην [χώρα] χωρίς να πληρώσω προμήθεια; Informează dacă există comisioane bancare la retragere numerar într-o anumită țară](/thumbs/62/47553419.jpg) - General Μπορώ να κάνω ανάληψη στην [χώρα] χωρίς να πληρώσω προμήθεια; Μπορώ να κάνω ανάληψη στην [χώρα] χωρίς να πληρώσω προμήθεια; Informează dacă există comisioane bancare la retragere numerar într-o
- General Μπορώ να κάνω ανάληψη στην [χώρα] χωρίς να πληρώσω προμήθεια; Μπορώ να κάνω ανάληψη στην [χώρα] χωρίς να πληρώσω προμήθεια; Informează dacă există comisioane bancare la retragere numerar într-o
Ecuaţia generală Probleme de tangenţă Sfera prin 4 puncte necoplanare. Elipsoidul Hiperboloizi Paraboloizi Conul Cilindrul. 1 Sfera.
 pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
a n (ζ z 0 ) n. n=1 se numeste partea principala iar seria a n (z z 0 ) n se numeste partea
 Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].
![Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].](/thumbs/72/67648751.jpg) Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
5.5. REZOLVAREA CIRCUITELOR CU TRANZISTOARE BIPOLARE
 5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
 DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
Sisteme diferenţiale liniare de ordinul 1
 1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
V O. = v I v stabilizator
 Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Curs 14 Funcţii implicite. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi"
 Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Conice. Lect. dr. Constantin-Cosmin Todea. U.T. Cluj-Napoca
 Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ - TABLE DES MATIERES
 ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ - TABLE DES MATIERES ΠΡΟΛΟΓΟΣ ΕΙΣΑΓΩΓΗ ΠΑΡΑΡΤΗΜΑ Αναλυτική κατάταξη των κλάδων οικονομικής δραστηριότητας (4-ψήφια ταξινόμηση, ΣΤΑΚΟΔ-92) Κλείδα αντιστοιχίας της Στατιστικής Ταξινόμησης
ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ - TABLE DES MATIERES ΠΡΟΛΟΓΟΣ ΕΙΣΑΓΩΓΗ ΠΑΡΑΡΤΗΜΑ Αναλυτική κατάταξη των κλάδων οικονομικής δραστηριότητας (4-ψήφια ταξινόμηση, ΣΤΑΚΟΔ-92) Κλείδα αντιστοιχίας της Στατιστικής Ταξινόμησης
Aplicaţii ale principiului I al termodinamicii la gazul ideal
 Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Θα ήθελα να ανοίξω ένα τραπεζικό λογαριασμό. Θα ήθελα να κλείσω τον τραπεζικό μου λογαριασμό. ίντερνετ;
 - Γενικά Pot retrage numerar în [țara] fără a plăti comisioane? Μπορώ να κάνω ανάληψη στην [χώρα] χωρίς να πληρώσω προμήθεια; Πληροφόρηση σχετικά με το αν πρέπει να πληρώσετε ποσοστά προμήθειας όταν κάνετε
- Γενικά Pot retrage numerar în [țara] fără a plăti comisioane? Μπορώ να κάνω ανάληψη στην [χώρα] χωρίς να πληρώσω προμήθεια; Πληροφόρηση σχετικά με το αν πρέπει να πληρώσετε ποσοστά προμήθειας όταν κάνετε
Seminariile Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reziduurilor
 Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
5.1. Noţiuni introductive
 ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
Foarte formal, destinatarul ocupă o funcţie care trebuie folosită în locul numelui
 - Introducere Αξιότιμε κύριε Πρόεδρε, Αξιότιμε κύριε Πρόεδρε, Foarte formal, destinatarul ocupă o funcţie care trebuie folosită în locul numelui Αγαπητέ κύριε, Αγαπητέ κύριε, Formal, destinatar de sex
- Introducere Αξιότιμε κύριε Πρόεδρε, Αξιότιμε κύριε Πρόεδρε, Foarte formal, destinatarul ocupă o funcţie care trebuie folosită în locul numelui Αγαπητέ κύριε, Αγαπητέ κύριε, Formal, destinatar de sex
Functii Breviar teoretic 8 ianuarie ianuarie 2011
 Functii Breviar teoretic 8 ianuarie 011 15 ianuarie 011 I Fie I, interval si f : I 1) a) functia f este (strict) crescatoare pe I daca x, y I, x< y ( f( x) < f( y)), f( x) f( y) b) functia f este (strict)
Functii Breviar teoretic 8 ianuarie 011 15 ianuarie 011 I Fie I, interval si f : I 1) a) functia f este (strict) crescatoare pe I daca x, y I, x< y ( f( x) < f( y)), f( x) f( y) b) functia f este (strict)
Seminar 5 Analiza stabilității sistemelor liniare
 Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Anexa nr câmp câmp Lung.
 Anexa nr. 1.4 Modalităţi de transmitere pe cale electronică a Declaraţiilor privind evidenţa nominală a asiguraţilor şi a obligaţiilor de plată către bugetul asigurărilor sociale Condiţii generale Declaraţiile
Anexa nr. 1.4 Modalităţi de transmitere pe cale electronică a Declaraţiilor privind evidenţa nominală a asiguraţilor şi a obligaţiilor de plată către bugetul asigurărilor sociale Condiţii generale Declaraţiile
Anexa nr câmp câmp Lung.
 Anexa nr. 1.4 Modalităţi de transmitere pe cale electronică a Declaraţiilor privind evidenţa nominală a asiguraţilor şi a obligaţiilor de plată către bugetul asigurărilor sociale Condiţii generale Declaraţiile
Anexa nr. 1.4 Modalităţi de transmitere pe cale electronică a Declaraţiilor privind evidenţa nominală a asiguraţilor şi a obligaţiilor de plată către bugetul asigurărilor sociale Condiţii generale Declaraţiile
Definiţia generală Cazul 1. Elipsa şi hiperbola Cercul Cazul 2. Parabola Reprezentari parametrice ale conicelor Tangente la conice
 1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
SERII NUMERICE. Definiţia 3.1. Fie (a n ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0
 SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
ANEXA 1.4. câmp câmp Lung.
 ANEXA 1.4 Modalităţi de transmitere pe cale electronică a Declaraţiilor privind evidenţa nominală a asiguraţilor şi a obligaţiilor de plată către bugetul asigurărilor sociale Condiţii generale Declaraţiile
ANEXA 1.4 Modalităţi de transmitere pe cale electronică a Declaraţiilor privind evidenţa nominală a asiguraţilor şi a obligaţiilor de plată către bugetul asigurărilor sociale Condiţii generale Declaraţiile
1. PROPRIETĂȚILE FLUIDELOR
 1. PROPRIETĂȚILE FLUIDELOR a) Să se exprime densitatea apei ρ = 1000 kg/m 3 în g/cm 3. g/cm 3. b) tiind că densitatea glicerinei la 20 C este 1258 kg/m 3 să se exprime în c) Să se exprime în kg/m 3 densitatea
1. PROPRIETĂȚILE FLUIDELOR a) Să se exprime densitatea apei ρ = 1000 kg/m 3 în g/cm 3. g/cm 3. b) tiind că densitatea glicerinei la 20 C este 1258 kg/m 3 să se exprime în c) Să se exprime în kg/m 3 densitatea
Κλειστό λόγω Canellopoulos Museum 11 Λαυρίου 0 0 Lavrio museum
 ΕΙΣΙΤΗΡΙΑ ΕΠΙΣΚΕΠΤΩΝ ΜΟΥΣΕΙΩΝ, ΚΑΤΑ ΜΗΝΑ, ΕΤΟΥΣ 2009 Admissions to s by month: 2009. Μουσεία ΙΑΝ/JAN ΦΕΒ/FEB ΜΑΡ/MAR ΑΠΡ/APR ΜΑΪ/MAY ΙΟΥΝ/JUN ΙΟΥΛ/JUL ΑΥΓ/AUG ΣΕΠ/SEPT ΟΚΤ/OCT ΝΟΕ/NOV ΕΚ/DEC ΣΥΝ/TOTAL
ΕΙΣΙΤΗΡΙΑ ΕΠΙΣΚΕΠΤΩΝ ΜΟΥΣΕΙΩΝ, ΚΑΤΑ ΜΗΝΑ, ΕΤΟΥΣ 2009 Admissions to s by month: 2009. Μουσεία ΙΑΝ/JAN ΦΕΒ/FEB ΜΑΡ/MAR ΑΠΡ/APR ΜΑΪ/MAY ΙΟΥΝ/JUN ΙΟΥΛ/JUL ΑΥΓ/AUG ΣΕΠ/SEPT ΟΚΤ/OCT ΝΟΕ/NOV ΕΚ/DEC ΣΥΝ/TOTAL
Περίληψη των χαρακτηριστικών του προϊόντος για βιοκτόνο
 Περίληψη των χαρακτηριστικών του προϊόντος για βιοκτόνο Ονομασία προϊόντος: SURE Antibac Foam Hand Wash Free Τύπος(οι) προϊόντος: PT0 - Υγιεινή του ανθρώπου Αριθμός άδειας: Αριθ. αναφ. στοιχείου στο μητρώο
Περίληψη των χαρακτηριστικών του προϊόντος για βιοκτόνο Ονομασία προϊόντος: SURE Antibac Foam Hand Wash Free Τύπος(οι) προϊόντος: PT0 - Υγιεινή του ανθρώπου Αριθμός άδειας: Αριθ. αναφ. στοιχείου στο μητρώο
2.1 Sfera. (EGS) ecuaţie care poartă denumirea de ecuaţia generală asferei. (EGS) reprezintă osferă cu centrul în punctul. 2 + p 2
 .1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
.1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
Ministrul sănătăţii, Florian-Dorel Bodog
 ORDIN Nr. 15/2018/1311/2017 din 5 ianuarie 2018 pentru aprobarea Normelor de aplicare a prevederilor Ordonanţei de urgenţă a Guvernului nr. 158/2005 privind concediile şi indemnizaţiile de asigurări sociale
ORDIN Nr. 15/2018/1311/2017 din 5 ianuarie 2018 pentru aprobarea Normelor de aplicare a prevederilor Ordonanţei de urgenţă a Guvernului nr. 158/2005 privind concediile şi indemnizaţiile de asigurări sociale
Capitolul 14. Asamblari prin pene
 Capitolul 14 Asamblari prin pene T.14.1. Momentul de torsiune este transmis de la arbore la butuc prin intermediul unei pene paralele (figura 14.1). De care din cotele indicate depinde tensiunea superficiala
Capitolul 14 Asamblari prin pene T.14.1. Momentul de torsiune este transmis de la arbore la butuc prin intermediul unei pene paralele (figura 14.1). De care din cotele indicate depinde tensiunea superficiala
Πού μπορώ να βρω τη φόρμα για ; Unde pot găsi un formular pentru? Για να ρωτήσετε που μπορείτε να βρείτε μια φόρμα
 - Γενικά Πού μπορώ να βρω τη φόρμα για ; Unde pot găsi un formular pentru? Για να ρωτήσετε που μπορείτε να βρείτε μια φόρμα Πότε εκδόθηκε το [έγγραφο] σας; Για να ρωτήσετε πότε έχει εκδοθεί ένα έγγραφο
- Γενικά Πού μπορώ να βρω τη φόρμα για ; Unde pot găsi un formular pentru? Για να ρωτήσετε που μπορείτε να βρείτε μια φόρμα Πότε εκδόθηκε το [έγγραφο] σας; Για να ρωτήσετε πότε έχει εκδοθεί ένα έγγραφο
Subiecte Clasa a VIII-a
 Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
BARAJ DE JUNIORI,,Euclid Cipru, 28 mai 2012 (barajul 3)
 BARAJ DE JUNIORI,,Euclid Cipru, 8 mi 0 (brjul ) Problem Arătţi că dcă, b, c sunt numere rele cre verifică + b + c =, tunci re loc ineglitte xy + yz + zx Problem Fie şi b numere nturle nenule Dcă numărul
BARAJ DE JUNIORI,,Euclid Cipru, 8 mi 0 (brjul ) Problem Arătţi că dcă, b, c sunt numere rele cre verifică + b + c =, tunci re loc ineglitte xy + yz + zx Problem Fie şi b numere nturle nenule Dcă numărul
 4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
Esalonul Redus pe Linii (ERL). Subspatii.
 Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
2. Sisteme de forţe concurente...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
 SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
Criptosisteme cu cheie publică III
 Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
city9 city8 city6 city7 city5 28 city3 25 city1 city0 P ijk =
 ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟ (2018-19) Εργασία 3 Εστω ότι μας δίνεται ένα σύνολο από πόλεις και τα μήκη των δρόμων που συνδέουν κάποια ζευγάρια από αυτές, όπως ϕαίνεται στο διπλανό σχήμα. Μιλώντας με μαθηματικούς
ΕΙΣΑΓΩΓΗ ΣΤΟΝ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟ (2018-19) Εργασία 3 Εστω ότι μας δίνεται ένα σύνολο από πόλεις και τα μήκη των δρόμων που συνδέουν κάποια ζευγάρια από αυτές, όπως ϕαίνεται στο διπλανό σχήμα. Μιλώντας με μαθηματικούς
Proiectarea filtrelor prin metoda pierderilor de inserţie
 FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
ministrul muncii, solidarităţii sociale şi familiei şi ministrul sănătăţii publice emit următorul ordin:
 ORDIN nr. 825 din 5 iulie 2006 pentru aprobarea Normelor metodologice de aplicare a Legii nr. 346/2002 privind asigurarea pentru accidente de muncă şi boli profesionale, cu modificările şi completările
ORDIN nr. 825 din 5 iulie 2006 pentru aprobarea Normelor metodologice de aplicare a Legii nr. 346/2002 privind asigurarea pentru accidente de muncă şi boli profesionale, cu modificările şi completările
Metode de interpolare bazate pe diferenţe divizate
 Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
ΟΠΑΠ VLTs ΠΑΡΟΥΣΙΑΣΗ ΔΙΑΔΙΚΑΣΙΑΣ ΕΙΣΑΓΩΓΗΣ ΤΩΝ 16.500 VLTs ΣΤΗΝ ΕΛΛΗΝΙΚΗ ΑΓΟΡΑ
 Παράρτημα 1 ΟΠΑΠ VLTs ΠΑΡΟΥΣΙΑΣΗ ΔΙΑΔΙΚΑΣΙΑΣ ΕΙΣΑΓΩΓΗΣ ΤΩΝ 16.500 VLTs ΣΤΗΝ ΕΛΛΗΝΙΚΗ ΑΓΟΡΑ Σεπτέμβριος 2014 Περιεχόμενα Παρουσίασης Νομικό Ρυθμιστικό Πλαίσιο Ανάπτυξης των VLTs στην Ελλάδα Χρονοδιάγραμμα
Παράρτημα 1 ΟΠΑΠ VLTs ΠΑΡΟΥΣΙΑΣΗ ΔΙΑΔΙΚΑΣΙΑΣ ΕΙΣΑΓΩΓΗΣ ΤΩΝ 16.500 VLTs ΣΤΗΝ ΕΛΛΗΝΙΚΗ ΑΓΟΡΑ Σεπτέμβριος 2014 Περιεχόμενα Παρουσίασης Νομικό Ρυθμιστικό Πλαίσιο Ανάπτυξης των VLTs στην Ελλάδα Χρονοδιάγραμμα
Corectură. Motoare cu curent alternativ cu protecție contra exploziei EDR * _0616*
 Tehnică de acționare \ Automatizări pentru acționări \ Integrare de sisteme \ Servicii *22509356_0616* Corectură Motoare cu curent alternativ cu protecție contra exploziei EDR..71 315 Ediția 06/2016 22509356/RO
Tehnică de acționare \ Automatizări pentru acționări \ Integrare de sisteme \ Servicii *22509356_0616* Corectură Motoare cu curent alternativ cu protecție contra exploziei EDR..71 315 Ediția 06/2016 22509356/RO
«Δεδομένα περιόδου γρίπης »
 «Δεδομένα περιόδου γρίπης 2017-2018» «Ο αντιγριπικός εμβολιασμός από την οπτική του φαρμακοποιού» Κουγιουμτζόγλου Ισίδωρος ΒΙΑΝΕΞ - Market Access Manager Δημογραφικοί Παράγοντες Φυσική μεταβολή πληθυσμού
«Δεδομένα περιόδου γρίπης 2017-2018» «Ο αντιγριπικός εμβολιασμός από την οπτική του φαρμακοποιού» Κουγιουμτζόγλου Ισίδωρος ΒΙΑΝΕΞ - Market Access Manager Δημογραφικοί Παράγοντες Φυσική μεταβολή πληθυσμού
CONCURSUL DE MATEMATICĂ APLICATĂ ADOLF HAIMOVICI, 2017 ETAPA LOCALĂ, HUNEDOARA Clasa a IX-a profil științe ale naturii, tehnologic, servicii
 Clasa a IX-a 1 x 1 a) Demonstrați inegalitatea 1, x (0, 1) x x b) Demonstrați că, dacă a 1, a,, a n (0, 1) astfel încât a 1 +a + +a n = 1, atunci: a +a 3 + +a n a1 +a 3 + +a n a1 +a + +a n 1 + + + < 1
Clasa a IX-a 1 x 1 a) Demonstrați inegalitatea 1, x (0, 1) x x b) Demonstrați că, dacă a 1, a,, a n (0, 1) astfel încât a 1 +a + +a n = 1, atunci: a +a 3 + +a n a1 +a 3 + +a n a1 +a + +a n 1 + + + < 1
Olimpiada Naţională de Matematică Etapa locală Clasa a IX-a M 1
 Calea 13 Septembrie, r 09, Sector 5, 0507, București Tel: +40 (0)1 317 36 50 Fax: +40 (0)1 317 36 54 Olimpiada Naţioală de Matematică Etapa locală -00016 Clasa a IX-a M 1 Fie 1 abc,,, 6 şi ab c 1 Să se
Calea 13 Septembrie, r 09, Sector 5, 0507, București Tel: +40 (0)1 317 36 50 Fax: +40 (0)1 317 36 54 Olimpiada Naţioală de Matematică Etapa locală -00016 Clasa a IX-a M 1 Fie 1 abc,,, 6 şi ab c 1 Să se
HOTARARE nr din 6 septembrie 2006 (*actualizata*)
 HOTARARE nr. 1.218 din 6 septembrie 2006 (*actualizata*) privind stabilirea cerintelor minime de securitate si sanatate in munca pentru asigurarea protectiei lucratorilor impotriva riscurilor legate de
HOTARARE nr. 1.218 din 6 septembrie 2006 (*actualizata*) privind stabilirea cerintelor minime de securitate si sanatate in munca pentru asigurarea protectiei lucratorilor impotriva riscurilor legate de
Laborator 11. Mulţimi Julia. Temă
 Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25
 Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25 LAGĂRELE CU ALUNECARE!" 25.1.Caracteristici.Părţi componente.materiale.!" 25.2.Funcţionarea lagărelor cu alunecare.! 25.1.Caracteristici.Părţi componente.materiale.
Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25 LAGĂRELE CU ALUNECARE!" 25.1.Caracteristici.Părţi componente.materiale.!" 25.2.Funcţionarea lagărelor cu alunecare.! 25.1.Caracteristici.Părţi componente.materiale.
ORDIN nr. 60 din 27 ianuarie 2006 (*actualizat*) pentru aprobarea Normelor de aplicare a prevederilor Ordonanţei de urgenţă
 ORDIN nr. 60 din 27 ianuarie 2006 (*actualizat*) pentru aprobarea Normelor de aplicare a prevederilor Ordonanţei de urgenţă a Guvernului nr. 158/2005 privind concediile şi indemnizaţiile de asigurări sociale
ORDIN nr. 60 din 27 ianuarie 2006 (*actualizat*) pentru aprobarea Normelor de aplicare a prevederilor Ordonanţei de urgenţă a Guvernului nr. 158/2005 privind concediile şi indemnizaţiile de asigurări sociale
T R A I A N ( ) Trigonometrie. \ kπ; k. este periodică (perioada principală T * =π ), impară, nemărginită.
 Trignmetrie Funcţia sinus sin : [, ] este peridică (periada principală T * = ), impară, mărginită. Funcţia arcsinus arcsin : [, ], este impară, mărginită, bijectivă. Funcţia csinus cs : [, ] este peridică
Trignmetrie Funcţia sinus sin : [, ] este peridică (periada principală T * = ), impară, mărginită. Funcţia arcsinus arcsin : [, ], este impară, mărginită, bijectivă. Funcţia csinus cs : [, ] este peridică
Problema a II - a (10 puncte) Diferite circuite electrice
 Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
1.7. AMPLIFICATOARE DE PUTERE ÎN CLASA A ŞI AB
 1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
(JO L 149, , p. 2)
 1971R1408 RO 07.07.2008 008.001 1 Acest document reprezintă un instrument de documentare, iar instituţiile nu îşi asumă responsabilitatea pentru conţinutul său. B REGULAMENTUL (CEE) NR. 1408/71 AL CONSILIULUI
1971R1408 RO 07.07.2008 008.001 1 Acest document reprezintă un instrument de documentare, iar instituţiile nu îşi asumă responsabilitatea pentru conţinutul său. B REGULAMENTUL (CEE) NR. 1408/71 AL CONSILIULUI
Forma actualizata valabila la data de : 6 martie 2017 Prezenta forma actualizata este valabila de la 1 februarie 2014 pana la data selectata
 LEGE nr. 319 din 14 iulie 2006 (*actualizată*) a securităţii şi sănătăţii în muncă EMITENT: PARLAMENTUL PUBLICAT ÎN: MONITORUL OFICIAL nr. 646 din 26 iulie 2006 Data intrarii in vigoare : 1 octombrie 2006
LEGE nr. 319 din 14 iulie 2006 (*actualizată*) a securităţii şi sănătăţii în muncă EMITENT: PARLAMENTUL PUBLICAT ÎN: MONITORUL OFICIAL nr. 646 din 26 iulie 2006 Data intrarii in vigoare : 1 octombrie 2006
ΠΡΟΓΡΑΜΜΑ «PRAXIS» PROIECTUL PRAXIS ΕΝΗΜΕΡΩΣΗ ΚΑΙ ΔΙΑΒΟΥΛΕΥΣΗ ΚΑΙ Η ΚΟΙΝΟΤΙΚΗ ΟΔΗΓΙΑ 2002/14 INFORMARE SI CONSULTARE
 ΠΡΟΓΡΑΜΜΑ «PRAXIS» PROIECTUL PRAXIS ΕΝΗΜΕΡΩΣΗ ΚΑΙ ΔΙΑΒΟΥΛΕΥΣΗ ΚΑΙ Η ΚΟΙΝΟΤΙΚΗ ΟΔΗΓΙΑ 2002/14 INFORMARE SI CONSULTARE Παναγιώτης Κατσαμπάνης Μ- Η ΕΜΠ Επιστημονικός συνεργάτης της ΟΒΕΣ Panagiotis Katsampanis
ΠΡΟΓΡΑΜΜΑ «PRAXIS» PROIECTUL PRAXIS ΕΝΗΜΕΡΩΣΗ ΚΑΙ ΔΙΑΒΟΥΛΕΥΣΗ ΚΑΙ Η ΚΟΙΝΟΤΙΚΗ ΟΔΗΓΙΑ 2002/14 INFORMARE SI CONSULTARE Παναγιώτης Κατσαμπάνης Μ- Η ΕΜΠ Επιστημονικός συνεργάτης της ΟΒΕΣ Panagiotis Katsampanis
Subiecte Clasa a V-a
 (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul numarului intrebarii
(40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul numarului intrebarii
INSTITUTUL NAŢIONAL DE STATISTICĂ
 INSTITUTUL NAŢIONAL DE STATISTICĂ Coordonatorul publicaţiei: Elena Mihaela IAGĂR - Vicepreşedinte Coordonatorii ediţiei: Silvia PISICĂ - Director General Direcţia Generală de Demografie și Statistică Socială
INSTITUTUL NAŢIONAL DE STATISTICĂ Coordonatorul publicaţiei: Elena Mihaela IAGĂR - Vicepreşedinte Coordonatorii ediţiei: Silvia PISICĂ - Director General Direcţia Generală de Demografie și Statistică Socială
Παρουσίαση στο Βουκουρέστι στις 15/04/16 Prezetare în București 15/04/16
 1 ΕΝΗΜΕΡΩΣΗ ΚΑΙ ΔΙΑΒΟΥΛΕΥΣΗ ΣΤΑ ΕΥΡΩΠΑΙΚΑ ΣΥΜΒΟΥΛΙΑ ΕΡΓΑΖΟΜΕΝΩΝ (ΕΣΕ) KAI Η ΚΟΙΝΟΤΙΚΗ ΟΔΗΓΙΑ 2009/38 INFORMAREA ȘI CONSULTAREA ÎN CADRUL COMITETELOR EUROPENE DE ÎNTREPRINDERE (CEI) ȘI DIRECTICA COMUNITARĂ
1 ΕΝΗΜΕΡΩΣΗ ΚΑΙ ΔΙΑΒΟΥΛΕΥΣΗ ΣΤΑ ΕΥΡΩΠΑΙΚΑ ΣΥΜΒΟΥΛΙΑ ΕΡΓΑΖΟΜΕΝΩΝ (ΕΣΕ) KAI Η ΚΟΙΝΟΤΙΚΗ ΟΔΗΓΙΑ 2009/38 INFORMAREA ȘI CONSULTAREA ÎN CADRUL COMITETELOR EUROPENE DE ÎNTREPRINDERE (CEI) ȘI DIRECTICA COMUNITARĂ
