Συστηματικός έλεγχος ορθότητας ταυτόχρονων προγραμμάτων μέσω γράφου καταστάσεων
|
|
|
- Φυλλίς Μακρή
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Συστηματικός έλεγχος ορθότητας ταυτόχρονων προγραμμάτων μέσω γράφου καταστάσεων ΙΙΙ 1 lalis@inf.uth.gr
2 Ιδιότητες προγραμμάτων Ιδιότητα ασφάλειας (safety): ποτέ δεν θα φτάσουμε σε μια κατάσταση που είναι ανεπιθύμητη Ιδιότητα προόδου (progress/liveness): κάποια στιγμή θα φτάσουμε σε μια κατάσταση που είναι επιθυμητή Μια ιδιότητα ασφάλειας μπορεί να εκφραστεί ως άρνηση μιας ιδιότητας προόδου, και το αντίστροφο always {Χ >= 0} not ( eventually {Χ < 0} ) Ένα πρόγραμμα χαρακτηρίζεται ως «ορθό» εφόσον ικανοποιεί τις επιθυμητές ιδιότητες προόδου χωρίς να παραβιάζει τις επιθυμητές ιδιότητες ασφάλειας ΙΙΙ 2 lalis@inf.uth.gr
3 Απόδειξη ιδιοτήτων Ιδανικά, η ορθότητα ενός ταυτόχρονου προγράμματος (συστήματος) πρέπει να επαληθευθεί συστηματικά Θεωρητική προσέγγιση oι επιθυμητές ιδιότητες προσδιορίζονται ρητά η (ουσιαστική) λογική του προγράμματος περιγράφεται με τυπικό τρόπο οι επιθυμητές ιδιότητες αποδεικνύονται με βάση συγκεκριμένους κανόνες/αξιώματα Προσέγγιση διεξοδικού ελέγχου oι επιθυμητές ιδιότητες προσδιορίζονται ρητά ελέγχονται για κάθε δυνατό σενάριο εκτέλεσης (κατάσταση) του συστήματος ΙΙΙ 3 lalis@inf.uth.gr
4 Γράφος καταστάσεων Οι πιθανές εκτελέσεις ενός ταυτόχρονου συστήματος περιγράφονται με την μορφή ενός γράφου G=(V,E) Ο κόμβος v i V αντιστοιχεί σε μια συγκεκριμένη εφικτή/πιθανή κατάσταση (που μπορεί να προκύψει κατά την ταυτόχρονη εκτέλεση) Η κατευθυνόμενη ακμή e=(v i,v j ) E αντιστοιχεί σε μια πιθανή μετάβαση από την κατάσταση v i στην v j Οι μεταβάσεις πραγματοποιούνται μέσα από εντολές που θεωρούμε ότι εκτελούνται ατομικά Μια πιθανή εκτέλεση x={v 0,v 1,v 2, } είναι μια διαδρομή κατά μήκος των ακμών του γράφου ΙΙΙ 4 lalis@inf.uth.gr
5 κατάσταση αρχική κατάσταση μετάβαση σενάριο εκτέλεσης τερματική κατάσταση ΙΙΙ 5 lalis@inf.uth.gr
6 Επαλήθευση ιδιοτήτων Ιδιότητα ασφάλειας (safety property) always Φ Για κάθε κατάσταση v i ισχύει Φ(v i ) Ιδιότητα προόδου (progress property) if Φ1 eventually Φ2 Αν υπάρχει κατάσταση v i που να ισχύει Φ1(v i ), τότε κάθε διαδρομή/εκτέλεση που περνάει από την v i τελικά περνάει (πιθανώς μετά από μεταβάσεις) και από τουλάχιστον μια κατάσταση v j όπου ισχύει Φ2(v j ) ΙΙΙ 6 lalis@inf.uth.gr
7 always Φ 0 Φ 1 Φ 2 Φ 3 Φ 4 Φ 5 Φ 6 Φ 7 Φ 8 Φ 9 Φ 10 Φ ΙΙΙ 7 lalis@inf.uth.gr
8 always Φ 0 Φ 1 Φ 2 Φ Φ 3 Φ 4 5 Φ 6 Φ 7 Φ 8 Φ 9 Φ 10 Φ ΙΙΙ 8 lalis@inf.uth.gr
9 if Φ1 eventually Φ2 0 Φ Φ Φ Φ2 10 ΙΙΙ 9 lalis@inf.uth.gr
10 if Φ1 eventually Φ2 0 Φ1 Φ2 1 2 Φ2 Φ2 3 4 Φ2 5 Φ2 6 Φ2 Φ2 Φ Φ2 10 Φ2 ΙΙΙ 10 lalis@inf.uth.gr
11 Παράδειγμα: ντάμα με βατράχια (α) Μ Μ F F (β) F F M M Οι αρσενικοί βάτραχοι (Μ) μπορούν να κινηθούν μόνο προς τα δεξιά, οι θηλυκοί (F) μόνο προς τα αριστερά Ένας βάτραχος μπορεί να πηδήσει σε μια άδεια πέτρα αν είναι δίπλα του ή αν μεσολαβεί μόνο ένας βάτραχος Αρχικά οι βάτραχοι κάθονται σε μια σειρά από πέτρες όπως στο σχήμα (α) Είναι εφικτό τελικά να φτάσουν στις θέσεις (β); Είναι αυτό εγγυημένο; ΙΙΙ 11 lalis@inf.uth.gr
12 Παράδειγμα: ντάμα με βατράχια MM_FF ΙΙΙ 12
13 Παράδειγμα: ντάμα με βατράχια MM_FF _MMFF M_MFF ΙΙΙ 13
14 Παράδειγμα: ντάμα με βατράχια MM_FF _MMFF M_MFF ΙΙΙ 14
15 Παράδειγμα: ντάμα με βατράχια MM_FF _MMFF M_MFF MFM_F ΙΙΙ 15
16 Παράδειγμα: ντάμα με βατράχια MM_FF _MMFF M_MFF MFM_F MFMF_ MF_MF ΙΙΙ 16
17 Παράδειγμα: ντάμα με βατράχια MM_FF _MMFF M_MFF MFM_F MFMF_ MF_MF MF_FM MFFM FMMF ΙΙΙ 17
18 Παράδειγμα: ντάμα με βατράχια MM_FF _MMFF M_MFF MFM_F MFMF_ MF_MF MF_FM MFFM FMMF _FMFM MFF_M F_MMF ΙΙΙ 18
19 Παράδειγμα: ντάμα με βατράχια MM_FF _MMFF M_MFF MFM_F MFMF_ MF_MF MF_FM MFFM FMMF _FMFM MFF_M F_MMF ΙΙΙ 19
20 Παράδειγμα: ντάμα με βατράχια MM_FF _MMFF M_MFF MFM_F MFMF_ MF_MF MF_FM MFFM FMMF _FMFM MFF_M F_MMF F_MFM ΙΙΙ 20
21 Παράδειγμα: ντάμα με βατράχια MM_FF _MMFF M_MFF MFM_F MFMF_ MF_MF MF_FM MFFM FMMF _FMFM MFF_M F_MMF F_MFM FFM_M ΙΙΙ 21
22 Παράδειγμα: ντάμα με βατράχια MM_FF _MMFF M_MFF MFM_F MFMF_ MF_MF MF_FM MFFM FMMF _FMFM MFF_M F_MMF F_MFM FFM_M FF_MM ΙΙΙ 22
23 Παράδειγμα: ντάμα με βατράχια MM_FF _MMFF M_MFF MMF_F MMFF_ MFM_F M_FMF MFMF_ MF_MF _MFMF MF_FM MFFM FMMF FM_MF _FMFM MFF_M F_MMF FMFM_ F_MFM FMF_M FFM_M F_FMM FF_MM ΙΙΙ 23
24 Γράφοι καταστάσεων με κώδικα int i=0; p1: i=1 p2: i=2 p3: if (i>0) { goto p3 } p1, i is 0 p2, i is 1 p3, i is 2 Σύμβαση: ο μετρητής εντολών (program counter) δείχνει στην επόμενη εντολή προς εκτέλεση Οι εντολές που εμφανίζονται σε μια γραμμή θεωρούμε ότι εκτελούνται ατομικά, οπότε αλλάζει και ο μετρητής εντολών (αναλόγως με την εντολή) Π.χ. η εκτέλεση μιας εντολής αναμονής δεν αλλάζει τον μετρητή εντολών, όσο ισχύει η συνθήκη αναμονής ΙΙΙ 24 lalis@inf.uth.gr
25 Παράδειγμα ασυνέπειας δεδομένων int i=0; : p1: tmp1=i p2: tmp1=tmp1+1; i=tmp1 p3: : q1: tmp2=i q2: tmp2=tmp2+1; i=tmp2 q3: Επιθυμητή ιδιότητα: Όταν οι διεργασίες φτάσουν στις εντολές p3 και q3, τότε η i να έχει την τιμή 2 ΙΙΙ 25 lalis@inf.uth.gr
26 Παράδειγμα ασυνέπειας δεδομένων #εντολής #εντολής i tmp1 tmp2 p1,q1 0,?,? p2,q1 0,0,? p1,q2 0,?,0 p3,q1 1,1,? p2,q2 0,0,0 p1,q3 1,?,1 p3,q2 1,1,1 p3,q2 1,1,0 p2,q3 1,0,1 ρ p2,q3 1,1,1 p3,q3 2,1,2 p3,q3 1,1,1 p3,q3 2,2,1 ΙΙΙ 26 lalis@inf.uth.gr
27 Παράδειγμα ατέρμονης αναμονής int rdy=0; ueue q; : /* prepare data */ p1: rdy=1; p2: WAKEU(q); p3: : q1: if (rdy) goto q4; q2: WAIT(q); q3: /* use data */ Επιθυμητή ιδιότητα: (αν το φτάσει στην εντολή p2) το θα φτάσει στην εντολή q3 ΙΙΙ 27 lalis@inf.uth.gr
28 Παράδειγμα ατέρμονης αναμονής int rdy=0; int w=0; /* εικονική μεταβλητή κατάστασης αναμονής */ : /* prepare data */ p1: rdy=1; p2: if (w) { w=0; } p3: : q1: if (rdy) goto q4; q2: w=1; q3: if (w) { goto q3; } q4: /* use data */ Επιθυμητή ιδιότητα: (αν το φτάσει στην εντολή p2) τελικά η w θα είναι 0 (και το θα φτάσει στην εντολή q4) ΙΙΙ 28 lalis@inf.uth.gr
29 Παράδειγμα ατέρμονης αναμονής #εντολής #εντολής rdy w p1,q1 0,0 p2,q1 1,0 p3,q1 1,0 p2,q4 1,0 p1,q2 0,0 p2,q2 1,0 p1,q3 0,1 p3,q4 1,0 p3,q2 1,0 p2,q3 1,1 ρ p3,q3 1,1 p3,q3 1,0 ΙΙΙ 29 lalis@inf.uth.gr
30 Αλγόριθμος A1 int turn=; : p1: p2: if (turn!=) {goto p2;} p3: CS p4: turn=; goto p1; : q1: q2: if (turn!=) {goto q2;} q3: CS q4: turn=; goto q1; State Description rogram Counter IDL idle no wish to enter CS p1/q1 TRY trying to enter CS p2/q2 CS inside CS p3-p4/q3-q4 ΙΙΙ 30 lalis@inf.uth.gr
31 p1,q1,idl,idl p2,q1,try,idl p1,q2,idl,try p3,q1,cs,idl p2,q2,try,try p4,q1,cs,idl p3,q2,cs,try p1,q1,idl,idl p4,q2,cs,try p2,q1,try,idl p1,q2,idl,try p2,q2,try,try p1,q3,idl,cs p2,q3,try,cs p2,q4,try,cs p1,q4,idl,cs ΙΙΙ 31
32 Παρατήρηση Ο γράφος των καταστάσεων μεγαλώνει πολύ γρήγορα με το μέγεθος του κώδικα Μπορεί να γίνουν απλοποιήσεις, συγχωνεύοντας καταστάσεις και αγνοώντας καταστάσεις που δεν επηρεάζουν την απόδειξη της ιδιότητας που ενδιαφέρει Χρειάζεται προσοχή ώστε να μην απαλειφθούν / αποκρυφθούν ενδιάμεσες καταστάσεις που πιθανώς επηρεάζουν την απόδειξη της ορθότητας ΙΙΙ 32 lalis@inf.uth.gr
33 p1,q1,idl,idl p2,q1,try,idl p1,q2,idl,try p3,q1,cs,idl p2,q2,try,try p4,q1,cs,idl p3,q2,cs,try p1,q1,idl,idl p4,q2,cs,try p2,q1,try,idl p1,q2,idl,try p2,q2,try,try p1,q3,idl,cs p2,q3,try,cs p2,q4,try,cs p1,q4,idl,cs ΙΙΙ 33
34 p1,q1,idl,idl p2,q1,try,idl p1,q2,idl,try p3-p4,q1,cs,idl p2,q2,try,try p3-p4,q2,cs,try p1,q1,idl,idl p2,q1,try,idl p1,q2,idl,try p2,q2,try,try p1,q3-q4,idl,cs p2,q3-q4,try,cs ΙΙΙ 34
35 Αμοιβαίος αποκλεισμός Σε καμία κατάσταση δεν επιτρέπεται το να βρίσκεται στο ΚΤ και το να βρίσκεται στο ΚΤ s : =CS =CS Σε όλες τις καταστάσεις δεν πρέπει να ισχύει ότι το βρίσκεται στο ΚΤ και το βρίσκεται στο ΚΤ s : ( (=CS) (=CS) ) ΙΙΙ 35 lalis@inf.uth.gr
36 p1,q1,idl,idl p2,q1,try,idl p1,q2,idl,try p3-p4,q1,cs,idl p2,q2,try,try p3-p4,q2,cs,try p1,q1,idl,idl p2,q1,try,idl p1,q2,idl,try p2,q2,try,try p1,q3-q4,idl,cs p2,q3-q4,try,cs ΟΚ ΙΙΙ 36
37 Απουσία αδιεξόδου Δεν πρέπει να υπάρχει περίπτωση και να περιμένει το ένα το άλλο ενώ προσπαθούν να μπουν στο ΚΤ, και κανένα να μην καταφέρει τελικά να μπει στο ΚΤ Αν υπάρχει κατάσταση όπου και προσπαθούν να μπουν στο ΚΤ (εφόσον κάθε νήμα λαμβάνει τακτικά τον επεξεργαστή) τότε (για κάθε πιθανή εκτέλεση) υπάρχει μια επόμενη κατάσταση όπου ή είναι στο ΚΤ s : =TRY =TRY next*(s) : =CS =CS ΙΙΙ 37 lalis@inf.uth.gr
38 p1,q1,idl,idl p2,q1,try,idl p1,q2,idl,try p3-p4,q1,cs,idl p2,q2,try,try p3-p4,q2,cs,try p1,q1,idl,idl p2,q1,try,idl p1,q2,idl,try p2,q2,try,try p1,q3-q4,idl,cs p2,q3-q4,try,cs ΟΚ ΙΙΙ 38
39 Απουσία λιμοκτονίας Δεν πρέπει να υπάρχει περίπτωση το να προσπαθεί να μπει στο ΚΤ, και να μην καταφέρει ποτέ να μπει στο ΚΤ Αν υπάρχει κατάσταση όπου προσπαθεί να μπει στο ΚΤ (εφόσον κάθε νήμα λαμβάνει τακτικά τον επεξεργαστή) τότε (για κάθε πιθανή εκτέλεση) υπάρχει μια επόμενη κατάσταση όπου είναι στο ΚΤ s : =TRY next*(s) : =CS ΙΙΙ 39 lalis@inf.uth.gr
40 p1,q1,idl,idl p2,q1,try,idl p1,q2,idl,try p3-p4,q1,cs,idl p2,q2,try,try p3-p4,q2,cs,try p1,q1,idl,idl p2,q1,try,ncs p1,q2,idl,try p2,q2,try,try p1,q3-q4,idl,cs p2,q3-q4,try,cs ΟΚ ΙΙΙ 40
41 Απουσία λιμοκτονίας (συνέχεια) Το μπορεί να μην ενδιαφερθεί να μπει στο ΚΤ ποτέ ή για ένα πολύ μεγάλο χρονικό διάστημα Αν υπάρχει κατάσταση όπου το να προσπαθεί να μπει στο ΚΤ και το δεν προσπαθεί να μπει στο ΚΤ, αν το λάβει τον επεξεργαστή τότε στην αμέσως επόμενη κατάσταση θα καταφέρει να μπει στο ΚΤ s : =TRY =IDL next(s,) : =CS ΙΙΙ 41 lalis@inf.uth.gr
42 p1,q1,idl,idl p2,q1,try,idl p1,q2,idl,try p3-p4,q1,cs,idl p2,q2,try,try p3-p4,q2,cs,try p1,q1,idl,idl p2,q1,try,idl p1,q2,idl,try p2,q2,try,try p1,q3-q4,idl,cs p2,q3-q4,try,cs ΝΟΤ ΟΚ ΙΙΙ 42
43 Αλγόριθμος B2 boolean want=false,want=false; : p1: p2: want=true; p3: if (want) {goto p3;} p4: CS p5: want=false; goto p1; : q1: q2: want=true; q3: if (want) {goto q3;} q4: CS q5: want=false; goto q1; State Description rogram Counter IDL idle no wish to enter CS p1/q1 TRY trying to enter CS p2-p3/q2-q3 CS inside CS p4-p5/q4-q5 ΙΙΙ 43 lalis@inf.uth.gr
44 Απουσία αδιεξόδου Δεν πρέπει να υπάρχει περίπτωση και να περιμένει το ένα το άλλο ενώ προσπαθούν να μπουν στο ΚΤ, και κανένα να μην καταφέρει τελικά να μπει στο ΚΤ Αν υπάρχει κατάσταση όπου και προσπαθούν να μπουν στο ΚΤ (εφόσον κάθε νήμα λαμβάνει τακτικά τον επεξεργαστή) τότε (για κάθε πιθανή εκτέλεση) υπάρχει μια επόμενη κατάσταση όπου ή είναι στο ΚΤ s : =TRY =TRY next*(s) : =CS =CS ΙΙΙ 44 lalis@inf.uth.gr
45 p1,q1 F,F,IDL,IDL p2,q1 F,F,TRY,IDL p1,q2 F,F,IDL,TRY p3,q1 T,F,TRY,IDL p2,q2 F,F,TRY,TRY p1,q3 F,T,IDL,TRY p3,q2 T,F,TRY,TRY p2,q3 F,T,TRY,TRY p3,q3 T,T,TRY,TRY ΝΟΤ ΟΚ ΙΙΙ 45
Συστηματικός έλεγχος ορθότητας ταυτόχρονων προγραμμάτων μέσω γράφου καταστάσεων
 Συστηματικός έλεγχος ορθότητας ταυτόχρονων προγραμμάτων μέσω γράφου καταστάσεων ΙΙΙ 1 lalis@inf.uth.gr Ιδιότητες προγραμμάτων Ιδιότητα ασφάλειας (safety properties): δεν θα φτάσουμε ποτέ σε μια ανεπιθύμητη
Συστηματικός έλεγχος ορθότητας ταυτόχρονων προγραμμάτων μέσω γράφου καταστάσεων ΙΙΙ 1 lalis@inf.uth.gr Ιδιότητες προγραμμάτων Ιδιότητα ασφάλειας (safety properties): δεν θα φτάσουμε ποτέ σε μια ανεπιθύμητη
Προβλήματα ταυτόχρονης εκτέλεσης (για νήματα με κοινή μνήμη)
 Προβλήματα ταυτόχρονης εκτέλεσης (για νήματα με κοινή μνήμη) ΙΙΙ 1 lalis@inf.uth.gr Ταυτόχρονη εκτέλεση Ο προγραμματιστής δεν ελέγχει (άμεσα) την εκτέλεση/εναλλαγή των νημάτων Δεν γνωρίζει πότε θα αρχίσει
Προβλήματα ταυτόχρονης εκτέλεσης (για νήματα με κοινή μνήμη) ΙΙΙ 1 lalis@inf.uth.gr Ταυτόχρονη εκτέλεση Ο προγραμματιστής δεν ελέγχει (άμεσα) την εκτέλεση/εναλλαγή των νημάτων Δεν γνωρίζει πότε θα αρχίσει
Προβλήματα ταυτόχρονης εκτέλεσης (για νήματα με κοινή μνήμη)
 Προβλήματα ταυτόχρονης εκτέλεσης (για νήματα με κοινή μνήμη) ΙΙΙ 1 lalis@inf.uth.gr Υποθέσεις εργασίας Νήματα/διεργασίες με κοινή μνήμη Αυτόματη διακοπή/εναλλαγή νημάτων/διεργασιών (π.χ. πάνω από 1 CPU
Προβλήματα ταυτόχρονης εκτέλεσης (για νήματα με κοινή μνήμη) ΙΙΙ 1 lalis@inf.uth.gr Υποθέσεις εργασίας Νήματα/διεργασίες με κοινή μνήμη Αυτόματη διακοπή/εναλλαγή νημάτων/διεργασιών (π.χ. πάνω από 1 CPU
Προβλήματα ταυτόχρονης εκτέλεσης (για νήματα με κοινή μνήμη)
 Προβλήματα ταυτόχρονης εκτέλεσης (για νήματα με κοινή μνήμη) ΙΙΙ 1 lalis@inf.uth.gr Υποθέσεις εργασίας Νήματα/διεργασίες με κοινή μνήμη Αυτόματη διακοπή/εναλλαγή νημάτων/διεργασιών (π.χ. πάνω από 1 CPU
Προβλήματα ταυτόχρονης εκτέλεσης (για νήματα με κοινή μνήμη) ΙΙΙ 1 lalis@inf.uth.gr Υποθέσεις εργασίας Νήματα/διεργασίες με κοινή μνήμη Αυτόματη διακοπή/εναλλαγή νημάτων/διεργασιών (π.χ. πάνω από 1 CPU
Προβλήματα ταυτόχρονης εκτέλεσης (για νήματα με κοινή μνήμη)
 Προβλήματα ταυτόχρονης εκτέλεσης (για νήματα με κοινή μνήμη) ΙΙΙ 1 lalis@inf.uth.gr Υποθέσεις εργασίας Νήματα/διεργασίες με κοινή μνήμη Αυτόματη διακοπή/εναλλαγή νημάτων/διεργασιών (π.χ. πάνω από 1 CPU
Προβλήματα ταυτόχρονης εκτέλεσης (για νήματα με κοινή μνήμη) ΙΙΙ 1 lalis@inf.uth.gr Υποθέσεις εργασίας Νήματα/διεργασίες με κοινή μνήμη Αυτόματη διακοπή/εναλλαγή νημάτων/διεργασιών (π.χ. πάνω από 1 CPU
Αμοιβαίος αποκλεισμός με κοινή μνήμη. Ταυτόχρονος Προγραμματισμός 1
 Αμοιβαίος αποκλεισμός με κοινή μνήμη 1 lalis@inf.uth.gr Το πρόβλημα Έστω ότι δύο η περισσότερα νήματα επιθυμούν να προσπελάσουν έναν κοινό πόρο, που όμως δεν μπορεί να χρησιμοποιηθεί ταυτόχρονα Η χρήση
Αμοιβαίος αποκλεισμός με κοινή μνήμη 1 lalis@inf.uth.gr Το πρόβλημα Έστω ότι δύο η περισσότερα νήματα επιθυμούν να προσπελάσουν έναν κοινό πόρο, που όμως δεν μπορεί να χρησιμοποιηθεί ταυτόχρονα Η χρήση
Αμοιβαίος αποκλεισμός με κοινή μνήμη. Ταυτόχρονος Προγραμματισμός 1
 Αμοιβαίος αποκλεισμός με κοινή μνήμη 1 lalis@inf.uth.gr Το πρόβλημα Έστω ότι δύο η περισσότερα νήματα επιθυμούν να προσπελάσουν έναν κοινό πόρο, που όμως δεν μπορεί να χρησιμοποιηθεί ταυτόχρονα Η χρήση
Αμοιβαίος αποκλεισμός με κοινή μνήμη 1 lalis@inf.uth.gr Το πρόβλημα Έστω ότι δύο η περισσότερα νήματα επιθυμούν να προσπελάσουν έναν κοινό πόρο, που όμως δεν μπορεί να χρησιμοποιηθεί ταυτόχρονα Η χρήση
Αμοιβαίος αποκλεισμός με κοινή μνήμη. Ταυτόχρονος Προγραμματισμός 1
 Αμοιβαίος αποκλεισμός με κοινή μνήμη 1 lalis@inf.uth.gr Το πρόβλημα Έστω ότι δύο η περισσότερα νήματα επιθυμούν να προσπελάσουν έναν κοινό πόρο, που όμως δεν μπορεί να χρησιμοποιηθεί ταυτόχρονα Η χρήση
Αμοιβαίος αποκλεισμός με κοινή μνήμη 1 lalis@inf.uth.gr Το πρόβλημα Έστω ότι δύο η περισσότερα νήματα επιθυμούν να προσπελάσουν έναν κοινό πόρο, που όμως δεν μπορεί να χρησιμοποιηθεί ταυτόχρονα Η χρήση
Ελεγκτές/Παρακολουθητές (Monitors) Ταυτόχρονος Προγραμματισμός 1
 Ελεγκτές/Παρακολουθητές (Monitors) 1 lalis@inf.uth.gr Ελεγκτές Αμοιβαίος αποκλεισμός στο πλαίσιο ενός τμήματος λογισμικού που προσπελάζεται με δομημένο τρόπο, μέσω προκαθορισμένης διασύνδεσης (API) Ο συγχρονισμός
Ελεγκτές/Παρακολουθητές (Monitors) 1 lalis@inf.uth.gr Ελεγκτές Αμοιβαίος αποκλεισμός στο πλαίσιο ενός τμήματος λογισμικού που προσπελάζεται με δομημένο τρόπο, μέσω προκαθορισμένης διασύνδεσης (API) Ο συγχρονισμός
Κρίσιμη Περιοχή Υπό Συνθήκη (Conditional Critical Regions) Ταυτόχρονος Προγραμματισμός 1
 Κρίσιμη Περιοχή Υπό Συνθήκη (onditional ritical Regions) Ταυτόχρονος Προγραμματισμός 1 lalis@inf.uth.gr Πέρα από ελεγκτές Ο ελεγκτής είναι χρήσιμο εργαλείο συγχρονισμού παρέχει στον προγραμματιστή εγγυημένο
Κρίσιμη Περιοχή Υπό Συνθήκη (onditional ritical Regions) Ταυτόχρονος Προγραμματισμός 1 lalis@inf.uth.gr Πέρα από ελεγκτές Ο ελεγκτής είναι χρήσιμο εργαλείο συγχρονισμού παρέχει στον προγραμματιστή εγγυημένο
Εντοπισμός αδιεξόδου. Κατανεμημένα Συστήματα 1
 Εντοπισμός αδιεξόδου Κατανεμημένα Συστήματα 1 lalis@inf.uth.gr Αδιέξοδο σε κατανεμημένο σύστημα Αδιέξοδο: «κυκλική» και ατέρμονη αναμονή μεταξύ δύο ή περισσοτέρων διεργασιών Το πρόβλημα υφίσταται ήδη σε
Εντοπισμός αδιεξόδου Κατανεμημένα Συστήματα 1 lalis@inf.uth.gr Αδιέξοδο σε κατανεμημένο σύστημα Αδιέξοδο: «κυκλική» και ατέρμονη αναμονή μεταξύ δύο ή περισσοτέρων διεργασιών Το πρόβλημα υφίσταται ήδη σε
Ορθότητα λειτουργίας τμημάτων λογισμικού & δομών δεδομένων υπό ταυτόχρονη εκτέλεση
 Ορθότητα λειτουργίας τμημάτων λογισμικού & δομών δεδομένων υπό ταυτόχρονη εκτέλεση ΙΙΙ 1 lalis@inf.uth.gr Ορθή συμπεριφορά τμήματος λογισμικού Ένα τμήμα λογισμικού (ή ένας ΑΤΔ) προσπελάζεται με δομημένο/ελεγχόμενο
Ορθότητα λειτουργίας τμημάτων λογισμικού & δομών δεδομένων υπό ταυτόχρονη εκτέλεση ΙΙΙ 1 lalis@inf.uth.gr Ορθή συμπεριφορά τμήματος λογισμικού Ένα τμήμα λογισμικού (ή ένας ΑΤΔ) προσπελάζεται με δομημένο/ελεγχόμενο
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 664: Ανάλυση και Επαλήθευση Συστημάτων ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ ΗΜΕΡΟΜΗΝΙΑ : Πέμπτη, 21 Μαρτίου 2013 ΔΙΑΡΚΕΙΑ : 14:00 16:00 ΔΙΔΑΣΚΟΥΣΑ : Άννα Φιλίππου Ονοματεπώνυμο:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 664: Ανάλυση και Επαλήθευση Συστημάτων ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ ΗΜΕΡΟΜΗΝΙΑ : Πέμπτη, 21 Μαρτίου 2013 ΔΙΑΡΚΕΙΑ : 14:00 16:00 ΔΙΔΑΣΚΟΥΣΑ : Άννα Φιλίππου Ονοματεπώνυμο:
Αυτοματοποιημένη Επαλήθευση
 Αυτοματοποιημένη Επαλήθευση Στην ενότητα αυτή θα μελετηθούν τα εξής θέματα: Έλεγχος Μοντέλου Αλγόριθμοι γράφων Αλγόριθμοι αυτομάτων Αυτόματα ως προδιαγραφές ΕΠΛ 664 Ανάλυση και Επαλήθευση Συστημάτων 4-1
Αυτοματοποιημένη Επαλήθευση Στην ενότητα αυτή θα μελετηθούν τα εξής θέματα: Έλεγχος Μοντέλου Αλγόριθμοι γράφων Αλγόριθμοι αυτομάτων Αυτόματα ως προδιαγραφές ΕΠΛ 664 Ανάλυση και Επαλήθευση Συστημάτων 4-1
Υλοποίηση Σηματοφόρων
 Υλοποίηση Σηματοφόρων 1 lalis@inf.uth.gr Υλοποίηση σε επίπεδο συστήματος Εσωτερική κατάσταση: Ένας ακέραιος για την αποθήκευση της τιμής του σηματοφόρου Μια ουρά αναμονής που τοποθετείται ένα νήμα όταν
Υλοποίηση Σηματοφόρων 1 lalis@inf.uth.gr Υλοποίηση σε επίπεδο συστήματος Εσωτερική κατάσταση: Ένας ακέραιος για την αποθήκευση της τιμής του σηματοφόρου Μια ουρά αναμονής που τοποθετείται ένα νήμα όταν
Ψευδοκώδικας. November 7, 2011
 Ψευδοκώδικας November 7, 2011 Οι γλώσσες τύπου ψευδοκώδικα είναι ένας τρόπος περιγραφής αλγορίθμων. Δεν υπάρχει κανένας τυπικός ορισμός της έννοιας του ψευδοκώδικα όμως είναι κοινός τόπος ότι οποιαδήποτε
Ψευδοκώδικας November 7, 2011 Οι γλώσσες τύπου ψευδοκώδικα είναι ένας τρόπος περιγραφής αλγορίθμων. Δεν υπάρχει κανένας τυπικός ορισμός της έννοιας του ψευδοκώδικα όμως είναι κοινός τόπος ότι οποιαδήποτε
Σειρά Προβλημάτων 1 Λύσεις
 ΕΠΛ664: Ανάλυση και Επαλθευση Συστημάτων Τμμα Πληροφορικς Άσκηση 1 Σειρά Προβλημάτων 1 Λύσεις (α) Χρησιμοποιούμε τις επιπλέον μεταβλητές PC0, PC1, (program counters) οι οποίες παίρνουν ως τιμές ονόματα
ΕΠΛ664: Ανάλυση και Επαλθευση Συστημάτων Τμμα Πληροφορικς Άσκηση 1 Σειρά Προβλημάτων 1 Λύσεις (α) Χρησιμοποιούμε τις επιπλέον μεταβλητές PC0, PC1, (program counters) οι οποίες παίρνουν ως τιμές ονόματα
Ελεγκτές/Παρακολουθητές (Monitors) Ταυτόχρονος Προγραμματισμός 1
 Ελεγκτές/Παρακολουθητές (Monitors) 1 lalis@inf.uth.gr Ελεγκτές Αμοιβαίος αποκλεισμός στο πλαίσιο ενός τμήματος λογισμικού που προσπελάζεται με δομημένο τρόπο, μέσω προκαθορισμένης διασύνδεσης (API) Ο συγχρονισμός
Ελεγκτές/Παρακολουθητές (Monitors) 1 lalis@inf.uth.gr Ελεγκτές Αμοιβαίος αποκλεισμός στο πλαίσιο ενός τμήματος λογισμικού που προσπελάζεται με δομημένο τρόπο, μέσω προκαθορισμένης διασύνδεσης (API) Ο συγχρονισμός
Ορθότητα λειτουργίας τμημάτων λογισμικού & δομών δεδομένων υπό ταυτόχρονη εκτέλεση
 Ορθότητα λειτουργίας τμημάτων λογισμικού & δομών δεδομένων υπό ταυτόχρονη εκτέλεση ΙΙΙ 1 lalis@inf.uth.gr Ορθή συμπεριφορά τμήματος λογισμικού Ένα τμήμα λογισμικού (ή ένας ΑΤΔ) προσπελάζεται με δομημένο/ελεγχόμενο
Ορθότητα λειτουργίας τμημάτων λογισμικού & δομών δεδομένων υπό ταυτόχρονη εκτέλεση ΙΙΙ 1 lalis@inf.uth.gr Ορθή συμπεριφορά τμήματος λογισμικού Ένα τμήμα λογισμικού (ή ένας ΑΤΔ) προσπελάζεται με δομημένο/ελεγχόμενο
Διάλεξη 8: Πρόβλημα Αμοιβαίου Αποκλεισμού. ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι
 Διάλεξη 8: Πρόβλημα Αμοιβαίου Αποκλεισμού ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι Τι θα δούμε σήμερα Μοντέλο Κοινόχρηστης Μνήμης Αλγόριθμοι Αμοιβαίου Αποκλεισμού με Ισχυρούς Καταχωρητές ΕΠΛ432: Κατανεµηµένοι
Διάλεξη 8: Πρόβλημα Αμοιβαίου Αποκλεισμού ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι Τι θα δούμε σήμερα Μοντέλο Κοινόχρηστης Μνήμης Αλγόριθμοι Αμοιβαίου Αποκλεισμού με Ισχυρούς Καταχωρητές ΕΠΛ432: Κατανεµηµένοι
Σηματοφόροι (Σηματοφορείς) Ταυτόχρονος Προγραμματισμός 1
 Σηματοφόροι (Σηματοφορείς) 1 lalis@inf.uth.gr Αποφυγή ενεργής αναμονής if () { WAIT(); Μπορεί να γίνει εναλλαγή αφού το νήμα κάνει τον έλεγχο της συνθήκης αναμονής και την βρει αληθή, αλλά προτού αυτό
Σηματοφόροι (Σηματοφορείς) 1 lalis@inf.uth.gr Αποφυγή ενεργής αναμονής if () { WAIT(); Μπορεί να γίνει εναλλαγή αφού το νήμα κάνει τον έλεγχο της συνθήκης αναμονής και την βρει αληθή, αλλά προτού αυτό
Συνεπής παρατήρηση εκτέλεσης & συνεπείς καθολικές καταστάσεις. Κατανεμημένα Συστήματα 1
 Συνεπής παρατήρηση εκτέλεσης & συνεπείς καθολικές καταστάσεις Κατανεμημένα Συστήματα 1 lalis@inf.uth.gr Λογικά συνεπείς τομές Τμήμα τοπικής ιστορίας: h i.k {e i.1,e i.2,e i.k } τμήμα της τοπικής εκτέλεσης
Συνεπής παρατήρηση εκτέλεσης & συνεπείς καθολικές καταστάσεις Κατανεμημένα Συστήματα 1 lalis@inf.uth.gr Λογικά συνεπείς τομές Τμήμα τοπικής ιστορίας: h i.k {e i.1,e i.2,e i.k } τμήμα της τοπικής εκτέλεσης
Τεχνητή Νοημοσύνη. 2η διάλεξη (2015-16) Ίων Ανδρουτσόπουλος. http://www.aueb.gr/users/ion/
 Τεχνητή Νοημοσύνη 2η διάλεξη (2015-16) Ίων Ανδρουτσόπουλος http://www.aueb.gr/users/ion/ 1 Οι διαφάνειες αυτής της διάλεξης βασίζονται στα βιβλία: Τεχνητή Νοημοσύνη των Βλαχάβα κ.ά., 3η έκδοση, Β. Γκιούρδας
Τεχνητή Νοημοσύνη 2η διάλεξη (2015-16) Ίων Ανδρουτσόπουλος http://www.aueb.gr/users/ion/ 1 Οι διαφάνειες αυτής της διάλεξης βασίζονται στα βιβλία: Τεχνητή Νοημοσύνη των Βλαχάβα κ.ά., 3η έκδοση, Β. Γκιούρδας
Σειρά Προβλημάτων 1 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 1 Λύσεις (α) Χρησιμοποιούμε τις επιπλέον μεταβλητές PC 1, PC 2, (program counters) οι οποίες παίρνουν ως τιμές ονόματα των γραμμών του κώδικα όπως φαίνεται πιο κάτω. bool y 1
Άσκηση 1 Σειρά Προβλημάτων 1 Λύσεις (α) Χρησιμοποιούμε τις επιπλέον μεταβλητές PC 1, PC 2, (program counters) οι οποίες παίρνουν ως τιμές ονόματα των γραμμών του κώδικα όπως φαίνεται πιο κάτω. bool y 1
Προβλήματα, αλγόριθμοι, ψευδοκώδικας
 Προβλήματα, αλγόριθμοι, ψευδοκώδικας October 11, 2011 Στο μάθημα Αλγοριθμική και Δομές Δεδομένων θα ασχοληθούμε με ένα μέρος της διαδικασίας επίλυσης υπολογιστικών προβλημάτων. Συγκεκριμένα θα δούμε τι
Προβλήματα, αλγόριθμοι, ψευδοκώδικας October 11, 2011 Στο μάθημα Αλγοριθμική και Δομές Δεδομένων θα ασχοληθούμε με ένα μέρος της διαδικασίας επίλυσης υπολογιστικών προβλημάτων. Συγκεκριμένα θα δούμε τι
Dr. Garmpis Aristogiannis - EPDO TEI Messolonghi
 Προϋποθέσεις για Αµοιβαίο Αποκλεισµό Μόνο µία διεργασία σε κρίσιµο τµήµασεκοινό πόρο Μία διεργασία που σταµατά σε µη κρίσιµο σηµείο δεν πρέπει να επιρεάζει τις υπόλοιπες διεργασίες εν πρέπει να υπάρχει
Προϋποθέσεις για Αµοιβαίο Αποκλεισµό Μόνο µία διεργασία σε κρίσιµο τµήµασεκοινό πόρο Μία διεργασία που σταµατά σε µη κρίσιµο σηµείο δεν πρέπει να επιρεάζει τις υπόλοιπες διεργασίες εν πρέπει να υπάρχει
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ Τ Μ Η Μ Α Π Λ Η Ρ Ο Φ Ο Ρ Ι Κ Η Σ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ Τ Μ Η Μ Α Π Λ Η Ρ Ο Φ Ο Ρ Ι Κ Η Σ ΕΠΛ 035 - ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΑΛΓΟΡΙΘΜΟΙ ΓΙΑ ΗΛΕΚΤΡΟΛΟΓΟΥΣ ΜΗΧΑΝΙΚΟΥΣ ΚΑΙ ΜΗΧΑΝΙΚΟΥΣ ΥΠΟΛΟΓΙΣΤΩΝ Ακαδηµαϊκό έτος 2017-2018 Υπεύθυνος εργαστηρίου: Γεώργιος
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ Τ Μ Η Μ Α Π Λ Η Ρ Ο Φ Ο Ρ Ι Κ Η Σ ΕΠΛ 035 - ΔΟΜΕΣ ΔΕΔΟΜΕΝΩΝ ΚΑΙ ΑΛΓΟΡΙΘΜΟΙ ΓΙΑ ΗΛΕΚΤΡΟΛΟΓΟΥΣ ΜΗΧΑΝΙΚΟΥΣ ΚΑΙ ΜΗΧΑΝΙΚΟΥΣ ΥΠΟΛΟΓΙΣΤΩΝ Ακαδηµαϊκό έτος 2017-2018 Υπεύθυνος εργαστηρίου: Γεώργιος
Εντοπισμός τερματισμού. Κατανεμημένα Συστήματα 1
 Εντοπισμός τερματισμού Κατανεμημένα Συστήματα 1 lalis@inf.uth.gr Μοντέλο συστήματος Μια ομάδα διεργασιών εκτελεί έναν υπολογισμό Κατάσταση διεργασίας: ενεργητική ή παθητική (ανάλογα με το αν εκτελεί μέρος
Εντοπισμός τερματισμού Κατανεμημένα Συστήματα 1 lalis@inf.uth.gr Μοντέλο συστήματος Μια ομάδα διεργασιών εκτελεί έναν υπολογισμό Κατάσταση διεργασίας: ενεργητική ή παθητική (ανάλογα με το αν εκτελεί μέρος
Συνεπείς καθολικές καταστάσεις & επιβεβαίωση ιδιοτήτων. Κατανεμημένα Συστήματα 1
 Συνεπείς καθολικές καταστάσεις & επιβεβαίωση ιδιοτήτων Κατανεμημένα Συστήματα 1 lalis@inf.uth.gr Λογικά συνεπείς τομές Τμήμα τοπικής ιστορίας: h i.k {e i.1,e i.2,e i.k } τμήμα της τοπικής εκτέλεσης στην
Συνεπείς καθολικές καταστάσεις & επιβεβαίωση ιδιοτήτων Κατανεμημένα Συστήματα 1 lalis@inf.uth.gr Λογικά συνεπείς τομές Τμήμα τοπικής ιστορίας: h i.k {e i.1,e i.2,e i.k } τμήμα της τοπικής εκτέλεσης στην
ΛΕΙΤΟΥΡΓΙΚΑ ΣΥΣΤΗΜΑΤΑ
 ΛΕΙΤΟΥΡΓΙΚΑ ΣΥΣΤΗΜΑΤΑ ΛΕΙΤΟΥΡΓΙΚΑ ΣΥΣΤΗΜΑΤΑ Μάθηµα 1 Ο ρόλος του ΛΣ Υλικό Υπολογιστικό σύστηµα Λειτουργικό σύστηµα Λογισµικό Προγράµµατα εφαρµογής Στόχοι του ΛΣ Χρήστες ιευκόλυνση των χρηστών ιευκόλυνση
ΛΕΙΤΟΥΡΓΙΚΑ ΣΥΣΤΗΜΑΤΑ ΛΕΙΤΟΥΡΓΙΚΑ ΣΥΣΤΗΜΑΤΑ Μάθηµα 1 Ο ρόλος του ΛΣ Υλικό Υπολογιστικό σύστηµα Λειτουργικό σύστηµα Λογισµικό Προγράµµατα εφαρµογής Στόχοι του ΛΣ Χρήστες ιευκόλυνση των χρηστών ιευκόλυνση
Αδιέξοδα Ανάθεση Πόρων (Deadlocks Resource Allocation)
 Αδιέξοδα Ανάθεση Πόρων (Deadlocks Resource Allocation) Το Πρόβλημα του Αδιεξόδου Ένα σύνολο από διεργασίες σε αναμονή, όπου η κάθε μια κατέχει έναν αριθμό από πόρους και περιμένει να αποκτήσει και έναν
Αδιέξοδα Ανάθεση Πόρων (Deadlocks Resource Allocation) Το Πρόβλημα του Αδιεξόδου Ένα σύνολο από διεργασίες σε αναμονή, όπου η κάθε μια κατέχει έναν αριθμό από πόρους και περιμένει να αποκτήσει και έναν
Αδιέξοδα Ανάθεση Πόρων (Deadlocks Resource Allocation)
 Αδιέξοδα Ανάθεση Πόρων (Deadlocks Resource Allocation) Εισαγωγή Μοντέλο συστήματος Χαρακτηρισμός και ορισμός κατάστασης αδιεξόδου Μέθοδοι χειρισμού αδιεξόδων Αποτροπή αδιεξόδου (Deadlock Prevention) Αποφυγή
Αδιέξοδα Ανάθεση Πόρων (Deadlocks Resource Allocation) Εισαγωγή Μοντέλο συστήματος Χαρακτηρισμός και ορισμός κατάστασης αδιεξόδου Μέθοδοι χειρισμού αδιεξόδων Αποτροπή αδιεξόδου (Deadlock Prevention) Αποφυγή
Άρα, Τ ser = (A 0 +B 0 +B 0 +A 0 ) επίπεδο 0 + (A 1 +B 1 +A 1 ) επίπεδο 1 + +(B 5 ) επίπεδο 5 = 25[χρονικές µονάδες]
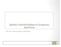
![Άρα, Τ ser = (A 0 +B 0 +B 0 +A 0 ) επίπεδο 0 + (A 1 +B 1 +A 1 ) επίπεδο 1 + +(B 5 ) επίπεδο 5 = 25[χρονικές µονάδες] Άρα, Τ ser = (A 0 +B 0 +B 0 +A 0 ) επίπεδο 0 + (A 1 +B 1 +A 1 ) επίπεδο 1 + +(B 5 ) επίπεδο 5 = 25[χρονικές µονάδες]](/thumbs/27/10818274.jpg) Α. Στο παρακάτω διάγραµµα εµφανίζεται η εκτέλεση ενός παράλληλου αλγόριθµου που λύνει το ίδιο πρόβληµα µε έναν ακολουθιακό αλγόριθµο χωρίς πλεονασµό. Τα Α i και B i αντιστοιχούν σε ακολουθιακά υποέργα
Α. Στο παρακάτω διάγραµµα εµφανίζεται η εκτέλεση ενός παράλληλου αλγόριθµου που λύνει το ίδιο πρόβληµα µε έναν ακολουθιακό αλγόριθµο χωρίς πλεονασµό. Τα Α i και B i αντιστοιχούν σε ακολουθιακά υποέργα
Λειτουργικά Συστήματα Η/Υ
 Λειτουργικά Συστήματα Η/Υ Κεφάλαιο 5 «Αμοιβαίος Αποκλεισμός» Διδάσκων: Δ Λιαροκάπης Διαφάνειες: Π. Χατζηδούκας 1 Αμοιβαίος Αποκλεισμός 1. Εισαγωγή 2. Κρίσιμα τμήματα (Critical Sections) 3. Υλοποίηση του
Λειτουργικά Συστήματα Η/Υ Κεφάλαιο 5 «Αμοιβαίος Αποκλεισμός» Διδάσκων: Δ Λιαροκάπης Διαφάνειες: Π. Χατζηδούκας 1 Αμοιβαίος Αποκλεισμός 1. Εισαγωγή 2. Κρίσιμα τμήματα (Critical Sections) 3. Υλοποίηση του
Σειρά Προβλημάτων 1 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 1 Λύσεις (α) Χρησιμοποιούμε τις επιπλέον μεταβλητές PC 0, PC 1, (program counters) οι οποίες παίρνουν ως τιμές ονόματα των γραμμών του κώδικα όπως φαίνεται πιο κάτω. P[0] P[1]
Άσκηση 1 Σειρά Προβλημάτων 1 Λύσεις (α) Χρησιμοποιούμε τις επιπλέον μεταβλητές PC 0, PC 1, (program counters) οι οποίες παίρνουν ως τιμές ονόματα των γραμμών του κώδικα όπως φαίνεται πιο κάτω. P[0] P[1]
Σηματοφόροι (Σηματοφορείς) Ταυτόχρονος Προγραμματισμός 1
 Σηματοφόροι (Σηματοφορείς) 1 lalis@inf.uth.gr Αποφυγή ενεργής αναμονής εναλλαγή if/while () { WAIT(); Μπορεί να γίνει εναλλαγή αφού το νήμα κάνει τον έλεγχο της συνθήκης αναμονής και την βρει αληθή, αλλά
Σηματοφόροι (Σηματοφορείς) 1 lalis@inf.uth.gr Αποφυγή ενεργής αναμονής εναλλαγή if/while () { WAIT(); Μπορεί να γίνει εναλλαγή αφού το νήμα κάνει τον έλεγχο της συνθήκης αναμονής και την βρει αληθή, αλλά
Όταν το πρόγραμμα φτάσει σε αυτή την εντολή και ο καταχωρητής PINA έχει την τιμή
 5. Εντολή while() Η εντολή while() είναι ίσως η πιο πολυχρησιμοποιούμενη εντολή κατά τη σύνταξη κώδικα σε γλώσσα προγραμματισμού C για μικροελεγκτές. Το κυρίως μέρος του προγράμματος κλείνεται σχεδόν πάντα
5. Εντολή while() Η εντολή while() είναι ίσως η πιο πολυχρησιμοποιούμενη εντολή κατά τη σύνταξη κώδικα σε γλώσσα προγραμματισμού C για μικροελεγκτές. Το κυρίως μέρος του προγράμματος κλείνεται σχεδόν πάντα
Προβλήματα Συγχρονισμού (με ελεγκτή) Ταυτόχρονος Προγραμματισμός 1
 Προβλήματα Συγχρονισμού (με ελεγκτή) Ταυτόχρονος Προγραμματισμός 1 lalis@inf.uth.gr Υλοποίηση σηματοφόρων Οι σηματοφόροι είναι ένας ΑΤΔ με συγκεκριμένες λειτουργίες πρόσβασης Μπορεί να υλοποιηθούν με «φυσικό»
Προβλήματα Συγχρονισμού (με ελεγκτή) Ταυτόχρονος Προγραμματισμός 1 lalis@inf.uth.gr Υλοποίηση σηματοφόρων Οι σηματοφόροι είναι ένας ΑΤΔ με συγκεκριμένες λειτουργίες πρόσβασης Μπορεί να υλοποιηθούν με «φυσικό»
Σειρά Προβλημάτων 5 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) ({ G η G είναι μια ασυμφραστική γραμματική που δεν παράγει καμιά λέξη με μήκος μικρότερο του 2 } (β) { Μ,w
Άσκηση 1 Σειρά Προβλημάτων 5 Λύσεις Να δείξετε ότι οι πιο κάτω γλώσσες είναι διαγνώσιμες. (α) ({ G η G είναι μια ασυμφραστική γραμματική που δεν παράγει καμιά λέξη με μήκος μικρότερο του 2 } (β) { Μ,w
Ανάλυση της Ορθότητας Προγραμμάτων (HR Κεφάλαιο 4)
 Ανάλυση της Ορθότητας Προγραμμάτων (HR Κεφάλαιο 4) Στην ενότητα αυτή θα μελετηθούν τα εξής θέματα: Η διαδικαστική γλώσσα προγραμματισμού WHILE Τριάδες Hoare Μερική και Ολική Ορθότητα Προγραμμάτων Κανόνες
Ανάλυση της Ορθότητας Προγραμμάτων (HR Κεφάλαιο 4) Στην ενότητα αυτή θα μελετηθούν τα εξής θέματα: Η διαδικαστική γλώσσα προγραμματισμού WHILE Τριάδες Hoare Μερική και Ολική Ορθότητα Προγραμμάτων Κανόνες
Διεργασίες (μοντέλο μνήμης & εκτέλεσης) Προγραμματισμός II 1
 Διεργασίες (μοντέλο μνήμης & εκτέλεσης) Προγραμματισμός II 1 lalis@inf.uth.gr Ο κώδικας δεν εκτελείται «μόνος του» Ο εκτελέσιμος κώδικας αποθηκεύεται σε ένα αρχείο Το αρχείο είναι μια «παθητική» οντότητα
Διεργασίες (μοντέλο μνήμης & εκτέλεσης) Προγραμματισμός II 1 lalis@inf.uth.gr Ο κώδικας δεν εκτελείται «μόνος του» Ο εκτελέσιμος κώδικας αποθηκεύεται σε ένα αρχείο Το αρχείο είναι μια «παθητική» οντότητα
Διάλεξη 10: Αλγόριθμοι Αμοιβαίου Αποκλεισμού σε περιβάλλον ανταλλαγής μηνυμάτων. ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι
 Διάλεξη 10: Αλγόριθμοι Αμοιβαίου Αποκλεισμού σε περιβάλλον ανταλλαγής μηνυμάτων ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι Τι θα δούμε σήμερα Αλγόριθμος Χρήση Συντονιστή Αλγόριθμος του Lamport Αλγόριθμος LeLann:
Διάλεξη 10: Αλγόριθμοι Αμοιβαίου Αποκλεισμού σε περιβάλλον ανταλλαγής μηνυμάτων ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι Τι θα δούμε σήμερα Αλγόριθμος Χρήση Συντονιστή Αλγόριθμος του Lamport Αλγόριθμος LeLann:
Διάλεξη 6: Εκλογή Προέδρου σε Σύγχρονους Δακτύλιους. ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι
 Διάλεξη 6: Εκλογή Προέδρου σε Σύγχρονους Δακτύλιους ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι Τι θα δούμε σήμερα Μη Ομοιόμορφος Αλγόριθμος Εκλογής Προέδρου σε Σύγχρονο Δακτύλιο Ομοιόμορφος Αλγόριθμος Εκλογής Προέδρου
Διάλεξη 6: Εκλογή Προέδρου σε Σύγχρονους Δακτύλιους ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι Τι θα δούμε σήμερα Μη Ομοιόμορφος Αλγόριθμος Εκλογής Προέδρου σε Σύγχρονο Δακτύλιο Ομοιόμορφος Αλγόριθμος Εκλογής Προέδρου
Διάλεξη 21: Γράφοι IV - Βραχύτερα Μονοπάτια σε Γράφους
 Διάλεξη 2: Γράφοι IV - Βραχύτερα Μονοπάτια σε Γράφους Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: - Βραχύτερα Μονοπάτια σε γράφους - Ο αλγόριθμος Dijkstra για εύρεση της βραχύτερης απόστασης
Διάλεξη 2: Γράφοι IV - Βραχύτερα Μονοπάτια σε Γράφους Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: - Βραχύτερα Μονοπάτια σε γράφους - Ο αλγόριθμος Dijkstra για εύρεση της βραχύτερης απόστασης
Ανάλυση της Ορθότητας Προγραμμάτων
 Ανάλυση της Ορθότητας Προγραμμάτων Στην ενότητα αυτή θα μελετηθούν τα εξής θέματα: Η διαδικαστική γλώσσα προγραμματισμού WHILE Τριάδες Hoare Μερική και Ολική Ορθότητα Προγραμμάτων ΚανόνεςΑπόδειξηςΜερικήςΟρθότητας
Ανάλυση της Ορθότητας Προγραμμάτων Στην ενότητα αυτή θα μελετηθούν τα εξής θέματα: Η διαδικαστική γλώσσα προγραμματισμού WHILE Τριάδες Hoare Μερική και Ολική Ορθότητα Προγραμμάτων ΚανόνεςΑπόδειξηςΜερικήςΟρθότητας
Εισαγωγή στον Προγραμματισμό
 Εισαγωγή στον Προγραμματισμό Έλεγχος Δημήτρης Μιχαήλ Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ακ. Έτος 2012-2013 Σχεσιακοί Τελεστές και Ισότητας Ένα πρόγραμμα εκτός από αριθμητικές πράξεις
Εισαγωγή στον Προγραμματισμό Έλεγχος Δημήτρης Μιχαήλ Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ακ. Έτος 2012-2013 Σχεσιακοί Τελεστές και Ισότητας Ένα πρόγραμμα εκτός από αριθμητικές πράξεις
Φυσικά και λογικά ρολόγια. Κατανεμημένα Συστήματα 1
 Φυσικά και λογικά ρολόγια Κατανεμημένα Συστήματα 1 lalis@inf.uth.gr Τοπικά γεγονότα/συμβάντα Ορίζουμε ως γεγονός e i.x την x-οστή ενέργεια που έλαβε χώρα τοπικά στην διεργασία P i Το επίπεδο αφαίρεσης
Φυσικά και λογικά ρολόγια Κατανεμημένα Συστήματα 1 lalis@inf.uth.gr Τοπικά γεγονότα/συμβάντα Ορίζουμε ως γεγονός e i.x την x-οστή ενέργεια που έλαβε χώρα τοπικά στην διεργασία P i Το επίπεδο αφαίρεσης
Διάλεξη 9: Αλγόριθμοι Αμοιβαίου Αποκλεισμού με τη χρήση μεταβλητών Ανάγνωσης/Εγγραφής. ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι
 Διάλεξη 9: Αλγόριθμοι Αμοιβαίου Αποκλεισμού με τη χρήση μεταβλητών Ανάγνωσης/Εγγραφής ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι Τι θα δούμε σήμερα Αλγόριθμος Ψησταριάς (Bakery Algorithm) Αλγόριθμος 2- επεξεργαστών
Διάλεξη 9: Αλγόριθμοι Αμοιβαίου Αποκλεισμού με τη χρήση μεταβλητών Ανάγνωσης/Εγγραφής ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι Τι θα δούμε σήμερα Αλγόριθμος Ψησταριάς (Bakery Algorithm) Αλγόριθμος 2- επεξεργαστών
2.4 Κλασσικά Προβλήματα IPC
 2.4 Κλασσικά Προβλήματα IPC 1 Οι φιλόσοφοι που γευματίζουν - Dining Philosophers Μια πρώτη λύση για Ν φιλοσόφους: philosopher (i) while (1) { think; take_fork(i);/* πάρε αριστερό ξυλάκι */ take_fork(i+1
2.4 Κλασσικά Προβλήματα IPC 1 Οι φιλόσοφοι που γευματίζουν - Dining Philosophers Μια πρώτη λύση για Ν φιλοσόφους: philosopher (i) while (1) { think; take_fork(i);/* πάρε αριστερό ξυλάκι */ take_fork(i+1
ΠΛΗΡΟΦΟΡΙΚΗ Ι JAVA Τμήμα θεωρίας με Α.Μ. σε 3, 7, 8 & 9 22/11/07
 Ακαδ έτος 2007-2008 ΠΛΗΡΟΦΟΡΙΚΗ Ι Φερεντίνος 22/11/07 ΠΛΗΡΟΦΟΡΙΚΗ Ι JAVA Τμήμα θεωρίας με ΑΜ σε 3, 7, 8 & 9 22/11/07 Παράδειγμα με if/else if και user input: import javautil*; public class Grades public
Ακαδ έτος 2007-2008 ΠΛΗΡΟΦΟΡΙΚΗ Ι Φερεντίνος 22/11/07 ΠΛΗΡΟΦΟΡΙΚΗ Ι JAVA Τμήμα θεωρίας με ΑΜ σε 3, 7, 8 & 9 22/11/07 Παράδειγμα με if/else if και user input: import javautil*; public class Grades public
Αµοιβαίοςαποκλεισµός. Κατανεµηµένα Συστήµατα 03-1
 Αµοιβαίοςαποκλεισµός Εισαγωγή Συγκεντρωτική προσέγγιση Κατανεµηµένη προσέγγιση Αλγόριθµος Lamport Αλγόριθµος Ricart-Agrawala Προσέγγιση µεταβίβασης σκυτάλης Αλγόριθµος LeLann Αλγόριθµος Raymond Αλγόριθµος
Αµοιβαίοςαποκλεισµός Εισαγωγή Συγκεντρωτική προσέγγιση Κατανεµηµένη προσέγγιση Αλγόριθµος Lamport Αλγόριθµος Ricart-Agrawala Προσέγγιση µεταβίβασης σκυτάλης Αλγόριθµος LeLann Αλγόριθµος Raymond Αλγόριθµος
ΠΡΟΔΙΑΓΡΑΦΗ ΙΔΙΟΤΗΤΩΝ ΜΕ ΧΡΟΝΙΚΗ ΛΟΓΙΚΗ Ι
 ΠΡΟΔΙΑΓΡΑΦΗ ΙΔΙΟΤΗΤΩΝ ΜΕ ΧΡΟΝΙΚΗ ΛΟΓΙΚΗ Ι Ιδιότητες προσεγγισιμότητας (reachability properties): αναφέρονται στο ενδεχόμενο προσέγγισης μιας συγκεκριμένης κατάστασης. Ιδιότητες ασφαλείας (safety properties):
ΠΡΟΔΙΑΓΡΑΦΗ ΙΔΙΟΤΗΤΩΝ ΜΕ ΧΡΟΝΙΚΗ ΛΟΓΙΚΗ Ι Ιδιότητες προσεγγισιμότητας (reachability properties): αναφέρονται στο ενδεχόμενο προσέγγισης μιας συγκεκριμένης κατάστασης. Ιδιότητες ασφαλείας (safety properties):
Αμοιβαίος αποκλεισμός με ασύγχρονη επικοινωνία (ανταλλαγή μηνυμάτων) Ταυτόχρονος Προγραμματισμός 1
 Αμοιβαίος αποκλεισμός με ασύγχρονη επικοινωνία (ανταλλαγή μηνυμάτων) Ταυτόχρονος Προγραμματισμός 1 lalis@inf.uth.gr Μοντέλο δικτύου/επικοινωνίας Αξιοπιστία (δεν χάνονται μηνύματα) Άγνωστη ταχύτητα μετάδοσης
Αμοιβαίος αποκλεισμός με ασύγχρονη επικοινωνία (ανταλλαγή μηνυμάτων) Ταυτόχρονος Προγραμματισμός 1 lalis@inf.uth.gr Μοντέλο δικτύου/επικοινωνίας Αξιοπιστία (δεν χάνονται μηνύματα) Άγνωστη ταχύτητα μετάδοσης
Μεταγλωττιστές Βελτιστοποίηση
 Μεταγλωττιστές Βελτιστοποίηση Νίκος Παπασπύρου nickie@softlab.ntua.gr Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχ. και Μηχ. Υπολογιστών Εργαστήριο Τεχνολογίας Λογισμικού Πολυτεχνειούπολη, 15780
Μεταγλωττιστές Βελτιστοποίηση Νίκος Παπασπύρου nickie@softlab.ntua.gr Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχ. και Μηχ. Υπολογιστών Εργαστήριο Τεχνολογίας Λογισμικού Πολυτεχνειούπολη, 15780
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΗ CTL/LTL
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΗ CTL/LTL ΑΣΚΗΣΗ 1 Θεωρήστε το μοντέλο Μ ενός συστήματος που δίνεται από το αυτόματο του σχήματος p, q s 0 s 1 s 2 q, και το (άπειρο) δέντρο του σχήματος s0 p, q s1 q, s0 p, q
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΗ CTL/LTL ΑΣΚΗΣΗ 1 Θεωρήστε το μοντέλο Μ ενός συστήματος που δίνεται από το αυτόματο του σχήματος p, q s 0 s 1 s 2 q, και το (άπειρο) δέντρο του σχήματος s0 p, q s1 q, s0 p, q
Τεχνολογίες Υλοποίησης Αλγορίθµων
 Τεχνολογίες Υλοποίησης Αλγορίθµων Χρήστος Ζαρολιάγκης Καθηγητής Τµήµα Μηχ/κων Η/Υ & Πληροφορικής Πανεπιστήµιο Πατρών email: zaro@ceid.upatras.gr Ενότητα 3 1 / 25 Ενότητα 3 οκιµή Προγραµµάτων (Program Testing)
Τεχνολογίες Υλοποίησης Αλγορίθµων Χρήστος Ζαρολιάγκης Καθηγητής Τµήµα Μηχ/κων Η/Υ & Πληροφορικής Πανεπιστήµιο Πατρών email: zaro@ceid.upatras.gr Ενότητα 3 1 / 25 Ενότητα 3 οκιµή Προγραµµάτων (Program Testing)
Ανάλυση της Ορθότητας Προγραμμάτων
 Ανάλυση της Ορθότητας Προγραμμάτων Στην ενότητα αυτή θα μελετηθούν τα εξής θέματα: Η διαδικαστική γλώσσα προγραμματισμού WHILE Τριάδες Hoare Μερική και Ολική Ορθότητα Προγραμμάτων Κανόνες Απόδειξης Μερικής
Ανάλυση της Ορθότητας Προγραμμάτων Στην ενότητα αυτή θα μελετηθούν τα εξής θέματα: Η διαδικαστική γλώσσα προγραμματισμού WHILE Τριάδες Hoare Μερική και Ολική Ορθότητα Προγραμμάτων Κανόνες Απόδειξης Μερικής
Κατανεμημένα Συστήματα με Java. Ενότητα # 4: Αμοιβαίος αποκλεισμός Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής
 Κατανεμημένα Συστήματα με Java Ενότητα # 4: Αμοιβαίος αποκλεισμός Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού
Κατανεμημένα Συστήματα με Java Ενότητα # 4: Αμοιβαίος αποκλεισμός Διδάσκων: Γεώργιος Ξυλωμένος Τμήμα: Πληροφορικής Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού
Στόχοι και αντικείμενο ενότητας. Προτάσεις επανάληψης. Έλεγχος ροής προγράμματος. #5.. Εντολές Επανάληψης
 Στόχοι και αντικείμενο ενότητας Έλεγχος ροής προγράμματος (βλ. ενότητα #4) Δομή επανάληψης #5.. Εντολές Επανάληψης Προτάσεις επανάληψης Εντολές while, do while Εντολή for Περί βρόχων (loops) Τελεστές,
Στόχοι και αντικείμενο ενότητας Έλεγχος ροής προγράμματος (βλ. ενότητα #4) Δομή επανάληψης #5.. Εντολές Επανάληψης Προτάσεις επανάληψης Εντολές while, do while Εντολή for Περί βρόχων (loops) Τελεστές,
ΠΛΗΡΟΦΟΡΙΚΗ Ι JAVA Τμήμα θεωρίας με Α.Μ. σε 3, 7, 8 & 9 8/11/07
 Ακαδ έτος 2007-2008 ΠΛΗΡΟΦΟΡΙΚΗ Ι Φερεντίνος 8/11/07 Συμπλήρωμα προηγούμενης εβδομάδας: ΠΛΗΡΟΦΟΡΙΚΗ Ι JAVA Τμήμα θεωρίας με ΑΜ σε 3, 7, 8 & 9 8/11/07 Τι συμβαίνει όταν στην ίδια έκφραση υπάρχει πάνω από
Ακαδ έτος 2007-2008 ΠΛΗΡΟΦΟΡΙΚΗ Ι Φερεντίνος 8/11/07 Συμπλήρωμα προηγούμενης εβδομάδας: ΠΛΗΡΟΦΟΡΙΚΗ Ι JAVA Τμήμα θεωρίας με ΑΜ σε 3, 7, 8 & 9 8/11/07 Τι συμβαίνει όταν στην ίδια έκφραση υπάρχει πάνω από
Προγραμματισμός Ι (HY120)
 Προγραμματισμός Ι (HY20) # μνήμη & μεταβλητές πρόγραμμα & εκτέλεση Ψηφιακά δεδομένα, μνήμη, μεταβλητές 2 Δυαδικός κόσμος Οι υπολογιστές είναι δυαδικές μηχανές Όλη η πληροφορία (δεδομένα και κώδικας) κωδικοποιείται
Προγραμματισμός Ι (HY20) # μνήμη & μεταβλητές πρόγραμμα & εκτέλεση Ψηφιακά δεδομένα, μνήμη, μεταβλητές 2 Δυαδικός κόσμος Οι υπολογιστές είναι δυαδικές μηχανές Όλη η πληροφορία (δεδομένα και κώδικας) κωδικοποιείται
Ενότητα 5: ΜΕΤΑΒΛΗΤΕΣ
 Ενότητα 5: ΜΕΤΑΒΛΗΤΕΣ Οι Μεταβλητές στον Προγραμματισμό Οι μεταβλητές είναι θέσεις μνήμης που έχουν κάποιο όνομα. Όταν δίνω τιμή σε μία μεταβλητή, ουσιαστικά, αποθηκεύουμε στη μνήμη αυτή τον αριθμό που
Ενότητα 5: ΜΕΤΑΒΛΗΤΕΣ Οι Μεταβλητές στον Προγραμματισμό Οι μεταβλητές είναι θέσεις μνήμης που έχουν κάποιο όνομα. Όταν δίνω τιμή σε μία μεταβλητή, ουσιαστικά, αποθηκεύουμε στη μνήμη αυτή τον αριθμό που
ΠΑΝΕΠΙΣΤΗΜΙΟ AΙΓΑIΟΥ & ΑΕΙ ΠΕΙΡΑΙΑ Τ.Τ. Τμήματα Ναυτιλίας και Επιχειρηματικών Υπηρεσιών & Μηχ. Αυτοματισμού ΤΕ. Εισαγωγή στη Python
 ΠΑΝΕΠΙΣΤΗΜΙΟ AΙΓΑIΟΥ & ΑΕΙ ΠΕΙΡΑΙΑ Τ.Τ. Τμήματα Ναυτιλίας και Επιχειρηματικών Υπηρεσιών & Μηχ. Αυτοματισμού ΤΕ ΠΛΗΡΟΦΟΡΙΚΗ ΤΕΧΝΟΛΟΓΙΑ ΚΑΙ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Η/Υ Εισαγωγή στη Python Νικόλαος Ζ. Ζάχαρης Αναπληρωτής
ΠΑΝΕΠΙΣΤΗΜΙΟ AΙΓΑIΟΥ & ΑΕΙ ΠΕΙΡΑΙΑ Τ.Τ. Τμήματα Ναυτιλίας και Επιχειρηματικών Υπηρεσιών & Μηχ. Αυτοματισμού ΤΕ ΠΛΗΡΟΦΟΡΙΚΗ ΤΕΧΝΟΛΟΓΙΑ ΚΑΙ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Η/Υ Εισαγωγή στη Python Νικόλαος Ζ. Ζάχαρης Αναπληρωτής
Προγραμματισμός Ι (ΗΥ120)
 Προγραμματισμός Ι (ΗΥ120) Διάλεξη 17: Λύση Προβλημάτων με Αναδρομή Οι πύργοι του Hanoi Δίνεται ένα χώρος με τρεις θέσεις αποθήκευσης. Δίνεται μια στοίβα από Ν πλάκες σε φθίνον μέγεθος, σε μια από τις τρεις
Προγραμματισμός Ι (ΗΥ120) Διάλεξη 17: Λύση Προβλημάτων με Αναδρομή Οι πύργοι του Hanoi Δίνεται ένα χώρος με τρεις θέσεις αποθήκευσης. Δίνεται μια στοίβα από Ν πλάκες σε φθίνον μέγεθος, σε μια από τις τρεις
Διεργασίες (μοντέλο μνήμης & εκτέλεσης) Προγραμματισμός II 1
 Διεργασίες (μοντέλο μνήμης & εκτέλεσης) Προγραμματισμός II 1 lalis@inf.uth.gr Πρόγραμμα και εκτέλεση προγράμματος Ο εκτελέσιμος κώδικας αποθηκεύεται σε ένα αρχείο Το αρχείο είναι μια «παθητική» οντότητα
Διεργασίες (μοντέλο μνήμης & εκτέλεσης) Προγραμματισμός II 1 lalis@inf.uth.gr Πρόγραμμα και εκτέλεση προγράμματος Ο εκτελέσιμος κώδικας αποθηκεύεται σε ένα αρχείο Το αρχείο είναι μια «παθητική» οντότητα
Αμοιβαίος αποκλεισμός
 Αμοιβαίος αποκλεισμός 1. Εισαγωγή 2. Κρίσιμα τμήματα (Critical Sections) 3. Υλοποίηση του αμοιβαίου αποκλεισμού I. Προσεγγίσεις λογισμικού II. Υποστήριξη εκ μέρους του υλικού III. Σηματοφορείς 4. Κλασσικά
Αμοιβαίος αποκλεισμός 1. Εισαγωγή 2. Κρίσιμα τμήματα (Critical Sections) 3. Υλοποίηση του αμοιβαίου αποκλεισμού I. Προσεγγίσεις λογισμικού II. Υποστήριξη εκ μέρους του υλικού III. Σηματοφορείς 4. Κλασσικά
Κεφάλαια Εντολές επανάληψης. Τρεις εντολές επανάληψης. Επιλογή εντολής επανάληψης ΟΣΟ...ΕΠΑΝΑΛΑΒΕ. Σύνταξη στη ΓΛΩΣΣΑ
 Εντολές επανάληψης Κεφάλαια 02-08 οµές Επανάληψης Επιτρέπουν την εκτέλεση εντολών περισσότερες από µία φορά Οι επαναλήψεις ελέγχονται πάντοτε από κάποια συνθήκη η οποία καθορίζει την έξοδο από το βρόχο
Εντολές επανάληψης Κεφάλαια 02-08 οµές Επανάληψης Επιτρέπουν την εκτέλεση εντολών περισσότερες από µία φορά Οι επαναλήψεις ελέγχονται πάντοτε από κάποια συνθήκη η οποία καθορίζει την έξοδο από το βρόχο
ΠΑΡΑΡΤΗΜΑ IV. ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΑΡΑΡΤΗΜΑ IV Ασκήσεις για το Robolab
 ΠΑΡΑΡΤΗΜΑ IV Παρακάτω παραθέτουμε μία σειρά ασκήσεων για το Robolab ομαδοποιημένων σε κατηγορίες : Επιμέλεια : Κυριακού Γεώργιος 1 Φύλλο Ασκήσεων (πρόκληση με κινητήρες) ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΑΡΑΡΤΗΜΑ
ΠΑΡΑΡΤΗΜΑ IV Παρακάτω παραθέτουμε μία σειρά ασκήσεων για το Robolab ομαδοποιημένων σε κατηγορίες : Επιμέλεια : Κυριακού Γεώργιος 1 Φύλλο Ασκήσεων (πρόκληση με κινητήρες) ΔΙΔΑΚΤΙΚΗ ΤΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΑΡΑΡΤΗΜΑ
Διασυνδεδεμένες Δομές. Λίστες. Προγραμματισμός II 1
 Διασυνδεδεμένες Δομές Λίστες Προγραμματισμός II 1 lalis@inf.uth.gr Διασυνδεδεμένες δομές Η μνήμη ενός πίνακα δεσμεύεται συνεχόμενα η πρόσβαση στο i-οστό στοιχείο είναι άμεση καθώς η διεύθυνση του είναι
Διασυνδεδεμένες Δομές Λίστες Προγραμματισμός II 1 lalis@inf.uth.gr Διασυνδεδεμένες δομές Η μνήμη ενός πίνακα δεσμεύεται συνεχόμενα η πρόσβαση στο i-οστό στοιχείο είναι άμεση καθώς η διεύθυνση του είναι
Λειτουργικά Συστήματα (διαχείριση επεξεργαστή, μνήμης και Ε/Ε)
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 2015-16 Λειτουργικά Συστήματα (διαχείριση επεξεργαστή, και Ε/Ε) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Τι είναι
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 2015-16 Λειτουργικά Συστήματα (διαχείριση επεξεργαστή, και Ε/Ε) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Τι είναι
Σειρά Προβλημάτων 1 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 1 Λύσεις (α) Χρησιμοποιούμε τις επιπλέον μεταβλητές PC i, (program counters) οι οποίες παίρνουν ως τιμές ονόματα των γραμμών του κώδικα όπως φαίνεται πιο κάτω. Process P i :
Άσκηση 1 Σειρά Προβλημάτων 1 Λύσεις (α) Χρησιμοποιούμε τις επιπλέον μεταβλητές PC i, (program counters) οι οποίες παίρνουν ως τιμές ονόματα των γραμμών του κώδικα όπως φαίνεται πιο κάτω. Process P i :
Τι είναι ένα λειτουργικό σύστημα (ΛΣ); Μια άλλη απεικόνιση. Το Λειτουργικό Σύστημα ως μέρος του υπολογιστή
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 2014-15 Λειτουργικά Συστήματα (διαχείριση επεξεργαστή, και Ε/Ε) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Τι είναι
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 2014-15 Λειτουργικά Συστήματα (διαχείριση επεξεργαστή, και Ε/Ε) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Τι είναι
Κεφάλαιο 4 Σημασιολογία μιας Απλής Προστακτικής Γλώσσας
 Κεφάλαιο 4 Σημασιολογία μιας Απλής Προστακτικής Γλώσσας Προπτυχιακό μάθημα Αρχές Γλωσσών Προγραμματισμού Π. Ροντογιάννης 1 Εισαγωγή - 1 Μία κλασσική γλώσσα προγραμματισμού αποτελείται από: Εκφράσεις (των
Κεφάλαιο 4 Σημασιολογία μιας Απλής Προστακτικής Γλώσσας Προπτυχιακό μάθημα Αρχές Γλωσσών Προγραμματισμού Π. Ροντογιάννης 1 Εισαγωγή - 1 Μία κλασσική γλώσσα προγραμματισμού αποτελείται από: Εκφράσεις (των
Σχετική κίνηση αντικειμένων
 Σχετική κίνηση αντικειμένων Πως θα μπορούσε να κινηθεί ένας χαρακτήρας προς την έξοδο ενός λαβύρινθου; Πως θα μπορούσε το αυτοκινητάκι μας να κινείται μέσα στην πίστα; Πως θα μπορούσαμε να αναπαραστήσουμε
Σχετική κίνηση αντικειμένων Πως θα μπορούσε να κινηθεί ένας χαρακτήρας προς την έξοδο ενός λαβύρινθου; Πως θα μπορούσε το αυτοκινητάκι μας να κινείται μέσα στην πίστα; Πως θα μπορούσαμε να αναπαραστήσουμε
ΕΠΛ 664 Ανάλυση και Επαλήθευση Συστημάτων 8-1
 To εργαλείο UPPAAL Στην ενότητα αυτή θα μελετηθούν τα εξής θέματα: Εισαγωγή στo εργαλείο UPPAAL Γλώσσα Μοντελοποίησης Ο προσομοιωτής Ο επαληθευτής ΕΠΛ 664 Ανάλυση και Επαλήθευση Συστημάτων 8-1 Εισαγωγή
To εργαλείο UPPAAL Στην ενότητα αυτή θα μελετηθούν τα εξής θέματα: Εισαγωγή στo εργαλείο UPPAAL Γλώσσα Μοντελοποίησης Ο προσομοιωτής Ο επαληθευτής ΕΠΛ 664 Ανάλυση και Επαλήθευση Συστημάτων 8-1 Εισαγωγή
Νήµαταστην Java. Συγχρονισµός νηµάτων Επικοινωνία νηµάτων Εκτελέσιµα αντικείµενα Νήµατα δαίµονες Οµάδες νηµάτων. Κατανεµηµένα Συστήµατα 11-1
 Νήµαταστην Java Συγχρονισµός νηµάτων Επικοινωνία νηµάτων Εκτελέσιµα αντικείµενα Νήµατα δαίµονες Οµάδες νηµάτων Κατανεµηµένα Συστήµατα 11-1 Νήµαταστην Java γεννηθείσα notify notifyall έτοιµη start εκπνοή
Νήµαταστην Java Συγχρονισµός νηµάτων Επικοινωνία νηµάτων Εκτελέσιµα αντικείµενα Νήµατα δαίµονες Οµάδες νηµάτων Κατανεµηµένα Συστήµατα 11-1 Νήµαταστην Java γεννηθείσα notify notifyall έτοιµη start εκπνοή
Λύσεις 4ης Σειράς Ασκήσεων
 Λύσεις 4ης Σειράς Ασκήσεων Άσκηση 1 Αναγάγουμε τν Κ 0 που γνωρίζουμε ότι είναι μη-αναδρομική (μη-επιλύσιμη) στην γλώσσα: L = {p() η μηχανή Turing Μ τερματίζει με είσοδο κενή ταινία;} Δοσμένης της περιγραφής
Λύσεις 4ης Σειράς Ασκήσεων Άσκηση 1 Αναγάγουμε τν Κ 0 που γνωρίζουμε ότι είναι μη-αναδρομική (μη-επιλύσιμη) στην γλώσσα: L = {p() η μηχανή Turing Μ τερματίζει με είσοδο κενή ταινία;} Δοσμένης της περιγραφής
Διάλεξη 1: Εισαγωγή στον Κατανεμημένο Υπολογισμό. ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι
 Διάλεξη 1: Εισαγωγή στον Κατανεμημένο Υπολογισμό ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι Τι θα δούμε σήμερα Τι είναι ένα Κατανεμημένο Σύστημα; Επικοινωνία, Χρονισμός, Σφάλματα Μοντέλο Ανταλλαγής Μηνυμάτων 1
Διάλεξη 1: Εισαγωγή στον Κατανεμημένο Υπολογισμό ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι Τι θα δούμε σήμερα Τι είναι ένα Κατανεμημένο Σύστημα; Επικοινωνία, Χρονισμός, Σφάλματα Μοντέλο Ανταλλαγής Μηνυμάτων 1
Επίπεδα Γραφήματα : Προβλήματα και Υπολογιστική Πολυπλοκότητα
 Αλγόριθμοι πολυωνυμικού χρόνου Ένας αλγόριθμος πολυωνυμικού χρόνου έχει χρόνο εκτέλεσης όπου είναι μία (θετική) σταθερά Κλάση πολυπλοκότητας : περιλαμβάνει τα προβλήματα που επιδέχονται λύση σε πολυωνυμικό
Αλγόριθμοι πολυωνυμικού χρόνου Ένας αλγόριθμος πολυωνυμικού χρόνου έχει χρόνο εκτέλεσης όπου είναι μία (θετική) σταθερά Κλάση πολυπλοκότητας : περιλαμβάνει τα προβλήματα που επιδέχονται λύση σε πολυωνυμικό
Ιδιοκτησία Αντικειµένου
 Software Transactional Memory H STM υποστηρίζει την εκτέλεση δοσοληψιών από τις διεργασίες, οι οποίες περιέχουν λειτουργίες που ο χρήστης θέλει να εκτελέσει στα διαµοιραζόµενα αντικείµενα. H STM εγγυάται
Software Transactional Memory H STM υποστηρίζει την εκτέλεση δοσοληψιών από τις διεργασίες, οι οποίες περιέχουν λειτουργίες που ο χρήστης θέλει να εκτελέσει στα διαµοιραζόµενα αντικείµενα. H STM εγγυάται
Συνέπεια μνήμης σε πολυπύρηνα/πολυεπεξεργαστικά συστήματα
 Συνέπεια μνήμης σε πολυπύρηνα/πολυεπεξεργαστικά συστήματα ΙΙΙ 1 lalis@inf.uth.gr Απλοποιημένο μοντέλο συστήματος CPU/cores πάνω σε δίαυλο/δίκτυο (bus/interconnect) για απλότητα, εδώ CPU = core Η κυρίως
Συνέπεια μνήμης σε πολυπύρηνα/πολυεπεξεργαστικά συστήματα ΙΙΙ 1 lalis@inf.uth.gr Απλοποιημένο μοντέλο συστήματος CPU/cores πάνω σε δίαυλο/δίκτυο (bus/interconnect) για απλότητα, εδώ CPU = core Η κυρίως
ΤΟ ΠΕΡΙΒΑΛΛΟΝ ΤΗΣ. Εργαλειοθήκη Παρουσιάζετε το έργο σας Εκκινείτε τα σενάριά σας Σταματάτε όλα τα σενάρια. Οι 8 ομάδες της Παλέτας εντολών
 ΤΟ ΠΕΡΙΒΑΛΛΟΝ ΤΗΣ Οι 8 ομάδες της Παλέτας εντολών Εργαλειοθήκη Παρουσιάζετε το έργο σας Εκκινείτε τα σενάριά σας Σταματάτε όλα τα σενάρια Σκηνή Εδώ ζωντανεύει το σενάριό σας Εντολές κάθε ομάδας Αυτή είναι
ΤΟ ΠΕΡΙΒΑΛΛΟΝ ΤΗΣ Οι 8 ομάδες της Παλέτας εντολών Εργαλειοθήκη Παρουσιάζετε το έργο σας Εκκινείτε τα σενάριά σας Σταματάτε όλα τα σενάρια Σκηνή Εδώ ζωντανεύει το σενάριό σας Εντολές κάθε ομάδας Αυτή είναι
Δομή Επανάληψης. Κεφάλαιο 7 Mike Trimos
 Δομή Επανάληψης Κεφάλαιο 7 Mike Trimos Δομή Επανάληψης Η Διαδικασία αυτή ονομάζεται Βρόγχος ή Επανάληψη (Loop) και η εντολή ή το σύνολο των εντολών που επαναλαμβάνονται ονομάζεται Σώμα της Δομής. Η γλώσσα
Δομή Επανάληψης Κεφάλαιο 7 Mike Trimos Δομή Επανάληψης Η Διαδικασία αυτή ονομάζεται Βρόγχος ή Επανάληψη (Loop) και η εντολή ή το σύνολο των εντολών που επαναλαμβάνονται ονομάζεται Σώμα της Δομής. Η γλώσσα
Εισαγωγή στην. Γιάννης Σμαραγδάκης
 Εισαγωγή στην Τεχνολογία Λογισμικού Γιάννης Σμαραγδάκης Γιατί μελετάμε την Τεχνολογία Λογισμικού Λογισμικό υπάρχει παντού σε όλους τους τεχνικούς τομείς (π.χ. αεροδιαστημική) σε όλες τις επιστήμες στον
Εισαγωγή στην Τεχνολογία Λογισμικού Γιάννης Σμαραγδάκης Γιατί μελετάμε την Τεχνολογία Λογισμικού Λογισμικό υπάρχει παντού σε όλους τους τεχνικούς τομείς (π.χ. αεροδιαστημική) σε όλες τις επιστήμες στον
Σειρά Προβλημάτων 3 Ημερομηνία Παράδοσης: 04/04/16
 ΜΕΡΟΣ Α Άσκηση 1 Σειρά Προβλημάτων 3 Ημερομηνία Παράδοσης: 04/04/16 Δύο ιδιότητες φ και ψ είναι ισοδύναμες μεταξύ τους, φ ψ, αν, για κάθε δομή Kripke M, M φ αν και μόνο αν M ψ. Να αποφασίσετε ποια από
ΜΕΡΟΣ Α Άσκηση 1 Σειρά Προβλημάτων 3 Ημερομηνία Παράδοσης: 04/04/16 Δύο ιδιότητες φ και ψ είναι ισοδύναμες μεταξύ τους, φ ψ, αν, για κάθε δομή Kripke M, M φ αν και μόνο αν M ψ. Να αποφασίσετε ποια από
Μεταγλωττιστές Βελτιστοποίηση
 Βελτιστοποίηση (i) Μεταγλωττιστές Βελτιστοποίηση Νίκος Παπασπύρου nickie@softlab.ntua.gr Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχ. και Μηχ. Υπολογιστών Εργαστήριο Τεχνολογίας Λογισμικού Πολυτεχνειούπολη,
Βελτιστοποίηση (i) Μεταγλωττιστές Βελτιστοποίηση Νίκος Παπασπύρου nickie@softlab.ntua.gr Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχ. και Μηχ. Υπολογιστών Εργαστήριο Τεχνολογίας Λογισμικού Πολυτεχνειούπολη,
Red-Black Δέντρα. Red-Black Δέντρα
 Red-Black Δέντρα v 6 3 8 4 z Red-Black Δέντρα Περίληψη Από τα (2,4) δέντρα στα red-black δέντρα Red-black δέντρο Ορισμός Ύψος Εισαγωγή αναδόμηση επαναχρωματισμός Διαγραφή αναδόμηση επαναχρωματισμός προσαρμογή
Red-Black Δέντρα v 6 3 8 4 z Red-Black Δέντρα Περίληψη Από τα (2,4) δέντρα στα red-black δέντρα Red-black δέντρο Ορισμός Ύψος Εισαγωγή αναδόμηση επαναχρωματισμός Διαγραφή αναδόμηση επαναχρωματισμός προσαρμογή
Διάλεξη 4: Εκλογή Προέδρου σε Δακτύλιους. ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι
 Διάλεξη 4: Εκλογή Προέδρου σε Δακτύλιους ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι Τι θα δούμε σήμερα Δακτύλιοι Το πρόβλημα της Εκλογής Προέδρου Εκλογή Προέδρου σε Ανώνυμους Δακτύλιους Ασύγχρονος Αλγόριθμος με
Διάλεξη 4: Εκλογή Προέδρου σε Δακτύλιους ΕΠΛ 432: Κατανεμημένοι Αλγόριθμοι Τι θα δούμε σήμερα Δακτύλιοι Το πρόβλημα της Εκλογής Προέδρου Εκλογή Προέδρου σε Ανώνυμους Δακτύλιους Ασύγχρονος Αλγόριθμος με
Βρόχοι. Εντολή επανάληψης. Το άθροισμα των αριθμών 1 5 υπολογίζεται με την εντολή. Πρόβλημα. Πώς θα υπολογίσουμε το άθροισμα των ακέραιων ;
 Εντολή επανάληψης Το άθροισμα των αριθμών 1 5 υπολογίζεται με την εντολή Πρόβλημα Πώς θα υπολογίσουμε το άθροισμα των ακέραιων 1 5000; Ισοδύναμοι υπολογισμοί του Ισοδύναμοι υπολογισμοί του Ισοδύναμοι υπολογισμοί
Εντολή επανάληψης Το άθροισμα των αριθμών 1 5 υπολογίζεται με την εντολή Πρόβλημα Πώς θα υπολογίσουμε το άθροισμα των ακέραιων 1 5000; Ισοδύναμοι υπολογισμοί του Ισοδύναμοι υπολογισμοί του Ισοδύναμοι υπολογισμοί
HY Λογική Διδάσκων: Δ. Πλεξουσάκης
 HY-180 - Λογική Διδάσκων: Δ. Πλεξουσάκης Πληρότητα της μεθόδου επίλυσης Λήμμα: Αν κάθε μέλος ενός συνόλου όρων περιέχει ένα αρνητικό γράμμα, τότε το σύνολο είναι ικανοποιήσιμο. Άρα για να είναι μη-ικανοποιήσιμο,
HY-180 - Λογική Διδάσκων: Δ. Πλεξουσάκης Πληρότητα της μεθόδου επίλυσης Λήμμα: Αν κάθε μέλος ενός συνόλου όρων περιέχει ένα αρνητικό γράμμα, τότε το σύνολο είναι ικανοποιήσιμο. Άρα για να είναι μη-ικανοποιήσιμο,
«Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων» Χειμερινό εξάμηνο Μηχανές Πεπερασμένων Καταστάσεων
 «Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων» Χειμερινό εξάμηνο 2016-2017 Μηχανές Πεπερασμένων Καταστάσεων Παρασκευάς Κίτσος http://diceslab.cied.teiwest.gr Επίκουρος Καθηγητής Tμήμα Μηχανικών Πληροφορικής ΤΕ
«Σχεδιασμός Ολοκληρωμένων Κυκλωμάτων» Χειμερινό εξάμηνο 2016-2017 Μηχανές Πεπερασμένων Καταστάσεων Παρασκευάς Κίτσος http://diceslab.cied.teiwest.gr Επίκουρος Καθηγητής Tμήμα Μηχανικών Πληροφορικής ΤΕ
Διδάσκων: Κωνσταντίνος Κώστα Διαφάνειες: Δημήτρης Ζεϊναλιπούρ
 ιάλεξη : λάχιστα εννητορικά ένδρα Αλγόριθμος Prim Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: λάχιστα εννητορικά ένδρα () Minimum Spanning Trees Ο αλγόριθμος του Prim για εύρεση σε γράφους
ιάλεξη : λάχιστα εννητορικά ένδρα Αλγόριθμος Prim Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: λάχιστα εννητορικά ένδρα () Minimum Spanning Trees Ο αλγόριθμος του Prim για εύρεση σε γράφους
CTL - Λογική Δένδρου Υπολογισμού (ΗR Κεφάλαιο 3.4)
 CTL - Λογική Δένδρου Υπολογισμού (ΗR Κεφάλαιο 3.4) Στην ενότητα αυτή θα μελετηθούν τα εξής θέματα: Διακλαδωμένες Χρονικές λογικές CTL σύνταξη και ερμηνεία Έλεγχος μοντέλου για τη CTL Σύγκριση των PLTL
CTL - Λογική Δένδρου Υπολογισμού (ΗR Κεφάλαιο 3.4) Στην ενότητα αυτή θα μελετηθούν τα εξής θέματα: Διακλαδωμένες Χρονικές λογικές CTL σύνταξη και ερμηνεία Έλεγχος μοντέλου για τη CTL Σύγκριση των PLTL
Γενικά Στοιχεία Ηλεκτρονικού Υπολογιστή
 Γενικά Στοιχεία Ηλεκτρονικού Υπολογιστή 1. Ηλεκτρονικός Υπολογιστής Ο Ηλεκτρονικός Υπολογιστής είναι μια συσκευή, μεγάλη ή μικρή, που επεξεργάζεται δεδομένα και εκτελεί την εργασία του σύμφωνα με τα παρακάτω
Γενικά Στοιχεία Ηλεκτρονικού Υπολογιστή 1. Ηλεκτρονικός Υπολογιστής Ο Ηλεκτρονικός Υπολογιστής είναι μια συσκευή, μεγάλη ή μικρή, που επεξεργάζεται δεδομένα και εκτελεί την εργασία του σύμφωνα με τα παρακάτω
Μέγιστη ροή. Κατευθυνόμενο γράφημα. Συνάρτηση χωρητικότητας. αφετηρίακός κόμβος. τερματικός κόμβος. Ροή δικτύου. με τις ακόλουθες ιδιότητες
 Κατευθυνόμενο γράφημα Συνάρτηση χωρητικότητας 12 16 2 Ροή δικτύου Συνάρτηση αφετηρίακός κόμβος 13 1 με τις ακόλουθες ιδιότητες 4 14 9 7 4 τερματικός κόμβος Περιορισμός χωρητικότητας: Αντισυμμετρία: Διατήρηση
Κατευθυνόμενο γράφημα Συνάρτηση χωρητικότητας 12 16 2 Ροή δικτύου Συνάρτηση αφετηρίακός κόμβος 13 1 με τις ακόλουθες ιδιότητες 4 14 9 7 4 τερματικός κόμβος Περιορισμός χωρητικότητας: Αντισυμμετρία: Διατήρηση
Εισαγωγικές Έννοιες. ημήτρης Φωτάκης. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών. Εθνικό Μετσόβιο Πολυτεχνείο
 Εισαγωγικές Έννοιες ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Εισαγωγικές Έννοιες ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Λογική. Δημήτρης Πλεξουσάκης
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Λογική Δημήτρης Πλεξουσάκης 2ο μέρος σημειώσεων: Συστήματα Αποδείξεων για τον ΠΛ, Μορφολογική Παραγωγή, Κατασκευή Μοντέλων Τμήμα Επιστήμης Υπολογιστών Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Λογική Δημήτρης Πλεξουσάκης 2ο μέρος σημειώσεων: Συστήματα Αποδείξεων για τον ΠΛ, Μορφολογική Παραγωγή, Κατασκευή Μοντέλων Τμήμα Επιστήμης Υπολογιστών Άδειες Χρήσης
Συγγραφή κώδικα, δοκιμασία, επαλήθευση. Γιάννης Σμαραγδάκης
 Συγγραφή κώδικα, δοκιμασία, επαλήθευση Γιάννης Σμαραγδάκης Προδιαγραφή απαιτήσεων Σχεδιασμός συνεπείς σχέσεις Υψηλό επίπεδο συνεπείς σχέσεις Χαμηλό επίπεδο συνεπείς σχέσεις Πλάνο δοκιμών Κώδικας Συγγραφή
Συγγραφή κώδικα, δοκιμασία, επαλήθευση Γιάννης Σμαραγδάκης Προδιαγραφή απαιτήσεων Σχεδιασμός συνεπείς σχέσεις Υψηλό επίπεδο συνεπείς σχέσεις Χαμηλό επίπεδο συνεπείς σχέσεις Πλάνο δοκιμών Κώδικας Συγγραφή
Πανεπιστήμιο Θεσσαλίας Τμήμα Μηχανικών Η/Υ, Τηλεπικοινωνιών και Δικτύων
 Πανεπιστήμιο Θεσσαλίας Τμήμα Μηχανικών Η/Υ, Τηλεπικοινωνιών και Δικτύων Οργάνωση Η/Υ Ενότητα 1η: Εισαγωγή στην Οργάνωση Η/Υ Άσκηση 1: Αναλύστε τη διαδοχική εκτέλεση των παρακάτω εντολών MIPS με βάση τις
Πανεπιστήμιο Θεσσαλίας Τμήμα Μηχανικών Η/Υ, Τηλεπικοινωνιών και Δικτύων Οργάνωση Η/Υ Ενότητα 1η: Εισαγωγή στην Οργάνωση Η/Υ Άσκηση 1: Αναλύστε τη διαδοχική εκτέλεση των παρακάτω εντολών MIPS με βάση τις
Αριστείδης Παλιούρας Ανακαλύψτε το Scratch 2. Στη δραστηριότητα αυτή θα μάθεις να δημιουργείς τις δικές σου εντολές.
 Διαδικασίες Στη δραστηριότητα αυτή θα μάθεις να δημιουργείς τις δικές σου εντολές. Άνοιξε το προγραμματιστικό περιβάλλον του Scratch 2.0. Κάνε κλικ στην κατηγορία «Άλλες Εντολές». Για να δημιουργήσεις
Διαδικασίες Στη δραστηριότητα αυτή θα μάθεις να δημιουργείς τις δικές σου εντολές. Άνοιξε το προγραμματιστικό περιβάλλον του Scratch 2.0. Κάνε κλικ στην κατηγορία «Άλλες Εντολές». Για να δημιουργήσεις
